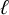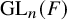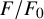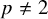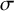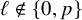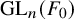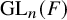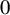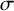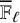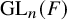1 Introduction
1.1
Let
![]() ${ F}/{ F}_0$
be a quadratic extension of non-Archimedean locally compact fields whose residual characteristic is a prime number p different from
${ F}/{ F}_0$
be a quadratic extension of non-Archimedean locally compact fields whose residual characteristic is a prime number p different from
![]() $2$
. Let
$2$
. Let
![]() $\sigma $
be its nontrivial automorphism, and
$\sigma $
be its nontrivial automorphism, and
![]() ${ G}$
be the general linear group
${ G}$
be the general linear group
![]() $\operatorname {GL}_n({ F})$
for some positive integer n. It is a totally disconnected, locally compact group, on which the involution
$\operatorname {GL}_n({ F})$
for some positive integer n. It is a totally disconnected, locally compact group, on which the involution
![]() $\sigma $
acts componentwise, and the group
$\sigma $
acts componentwise, and the group
![]() ${ G}^\sigma $
of its
${ G}^\sigma $
of its
![]() $\sigma $
-fixed points is equal to
$\sigma $
-fixed points is equal to
![]() $\operatorname {GL}_n(F_0)$
.
$\operatorname {GL}_n(F_0)$
.
Now, fix an algebraically closed field
![]() ${ R}$
of characteristic different from p. A (smooth) representation
${ R}$
of characteristic different from p. A (smooth) representation
![]() $\pi $
of
$\pi $
of
![]() ${ G}$
on an R-vector space V is said to be distinguished (by
${ G}$
on an R-vector space V is said to be distinguished (by
![]() ${ G}^\sigma $
) if V carries a nonzero
${ G}^\sigma $
) if V carries a nonzero
![]() ${ G}^\sigma $
-invariant linear form; more generally, if
${ G}^\sigma $
-invariant linear form; more generally, if
![]() $\chi $
is a smooth character of
$\chi $
is a smooth character of
![]() ${ G}^\sigma $
with values in
${ G}^\sigma $
with values in
![]() ${ R}^\times $
, the representation
${ R}^\times $
, the representation
![]() $\pi $
is said to be
$\pi $
is said to be
![]() $\chi $
-distinguished if V carries a nonzero linear form
$\chi $
-distinguished if V carries a nonzero linear form
![]() $\mathit {\Lambda }$
such that
$\mathit {\Lambda }$
such that
1.2
In the case where R is the field of complex numbers, distinguished irreducible representations of G have been extensively studied:
-
1. They are
 $\sigma $
-self-dual, that is, the contragredient
$\sigma $
-self-dual, that is, the contragredient
 $\pi ^\vee $
of a distinguished irreducible representation
$\pi ^\vee $
of a distinguished irreducible representation
 $\pi $
of G is isomorphic to its
$\pi $
of G is isomorphic to its
 $\sigma $
-conjugate
$\sigma $
-conjugate
 $\pi ^\sigma $
([Reference Flicker16, Reference Prasad32, Reference Prasad33]) and their central character is trivial on
$\pi ^\sigma $
([Reference Flicker16, Reference Prasad32, Reference Prasad33]) and their central character is trivial on
 ${ F}_0^\times $
,
${ F}_0^\times $
, -
2. Any
 $\sigma $
-self-dual discrete series representation of G is either distinguished or
$\sigma $
-self-dual discrete series representation of G is either distinguished or
 $\varkappa $
-distinguished (
$\varkappa $
-distinguished (
 $\varkappa $
denotes the character of
$\varkappa $
denotes the character of
 $F_0^\times $
whose kernel is the subgroup of
$F_0^\times $
whose kernel is the subgroup of
 $F/F_0$
-norms), but not both: This is the dichotomy and disjunction theorem ([Reference Kable23, Reference Anandavardhanan, Kable and Tandon2, Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3]),
$F/F_0$
-norms), but not both: This is the dichotomy and disjunction theorem ([Reference Kable23, Reference Anandavardhanan, Kable and Tandon2, Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3]), -
3. Distinguished generic irreducible representations of G are classified in terms of their cuspidal support ([Reference Anandavardhanan and Rajan4, Reference Matringe26, Reference Matringe27]),
-
4. Distinguished cuspidal representations of G are characterized in terms of their Galois parameter ([Reference Gan and Raghuram17]) and in terms of type theory (see [Reference Sécherre35] and below).
1.3
Distinguished irreducible representations of G with coefficients in a field R of positive characteristic have been less well studied (see [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3, Reference Sécherre35, Reference Kurinczuk and Matringe25, Reference Cui, Lanard and Lu12]). As in the complex case, they are
![]() $\sigma $
-self-dual and their central character is trivial on
$\sigma $
-self-dual and their central character is trivial on
![]() ${ F}_0^\times $
. For
${ F}_0^\times $
. For
![]() $\sigma $
-self-dual supercuspidal representations, that is, irreducible representations which do not occur as subquotients of parabolically induced representations from a proper Levi subgroup, one has a dichotomy and disjunction theorem (see Paragraph 3.2). One also has a distinction criterion in terms of Galois parameters ([Reference Cui, Lanard and Lu12] Proposition 3.15) and in terms of types ([Reference Sécherre35] Theorem 10.9). But there are explicit examples of
$\sigma $
-self-dual supercuspidal representations, that is, irreducible representations which do not occur as subquotients of parabolically induced representations from a proper Levi subgroup, one has a dichotomy and disjunction theorem (see Paragraph 3.2). One also has a distinction criterion in terms of Galois parameters ([Reference Cui, Lanard and Lu12] Proposition 3.15) and in terms of types ([Reference Sécherre35] Theorem 10.9). But there are explicit examples of
![]() $\sigma $
-self-dual nonsupercuspidal cuspidal representations that are neither distinguished nor
$\sigma $
-self-dual nonsupercuspidal cuspidal representations that are neither distinguished nor
![]() $\varkappa $
-distinguished (as in [Reference Sécherre35] Remark 2.18) and of Steinberg representations that are both distinguished and
$\varkappa $
-distinguished (as in [Reference Sécherre35] Remark 2.18) and of Steinberg representations that are both distinguished and
![]() $\varkappa $
-distinguished ([Reference Cui, Lanard and Lu12] Remark 1.9). Also, there is no known classification of distinguished cuspidal representations of
$\varkappa $
-distinguished ([Reference Cui, Lanard and Lu12] Remark 1.9). Also, there is no known classification of distinguished cuspidal representations of
![]() $\operatorname {GL}_n(F)$
for an arbitrary
$\operatorname {GL}_n(F)$
for an arbitrary
![]() $n{\geqslant }3$
(see [Reference Cui, Lanard and Lu12] and Paragraph 4.13 below for
$n{\geqslant }3$
(see [Reference Cui, Lanard and Lu12] and Paragraph 4.13 below for
![]() $n=2$
).
$n=2$
).
In this paper, which can be considered as a sequel to [Reference Sécherre35], where all distinguished supercuspidal R-representations of G have been classified, we investigate the classification of distinguished cuspidal R-representations of G in terms of their supercuspidal support. We:
-
○ reduce this classification to that of distinguished cuspidal representations of level
 $0$
, and from there to finite group theory (see Section 4),
$0$
, and from there to finite group theory (see Section 4), -
○ give a necessary condition of distinction for
 $\sigma $
-self-dual cuspidal representations of G that satisfy a certain parity condition (see Section 5),
$\sigma $
-self-dual cuspidal representations of G that satisfy a certain parity condition (see Section 5), -
○ classify the (distinguished, cuspidal)
 ${\overline {\mathbb {F}}_{\ell }}$
-representations of G having a distinguished cuspidal lift to
${\overline {\mathbb {F}}_{\ell }}$
-representations of G having a distinguished cuspidal lift to
 ${\overline {\mathbb {Q}}_\ell }$
, where
${\overline {\mathbb {Q}}_\ell }$
, where
 ${\overline {\mathbb {Q}}_\ell }$
is an algebraic closure of the field of
${\overline {\mathbb {Q}}_\ell }$
is an algebraic closure of the field of
 $\ell $
-adic numbers with residue field
$\ell $
-adic numbers with residue field
 ${\overline {\mathbb {F}}_{\ell }}$
.
${\overline {\mathbb {F}}_{\ell }}$
.
Let us explain these results in more detail.
1.4
Bushnell and Kutzko [Reference Bushnell and Kutzko9], in work extended to the modular setting by Vignéras [Reference Vignéras41], have given an explicit construction of a collection of pairs
![]() $(\mathbf {J},\boldsymbol {\lambda })$
called extended maximal simple types (which we will abbreviate to types here), consisting of a compact-mod-centre open subgroup
$(\mathbf {J},\boldsymbol {\lambda })$
called extended maximal simple types (which we will abbreviate to types here), consisting of a compact-mod-centre open subgroup
![]() $\mathbf {J}$
of G and an irreducible R-representation
$\mathbf {J}$
of G and an irreducible R-representation
![]() $\boldsymbol {\lambda }$
of
$\boldsymbol {\lambda }$
of
![]() $\mathbf {J}$
such that the representations
$\mathbf {J}$
such that the representations
![]() $\operatorname {ind}_{\mathbf {J}}^{G}(\boldsymbol {\lambda })$
are (irreducible and) cuspidal and such that every cuspidal R-representation of G appears in the collection of
$\operatorname {ind}_{\mathbf {J}}^{G}(\boldsymbol {\lambda })$
are (irreducible and) cuspidal and such that every cuspidal R-representation of G appears in the collection of
![]() $\operatorname {ind}_{\mathbf {J}}^{G}(\boldsymbol {\lambda })$
.
$\operatorname {ind}_{\mathbf {J}}^{G}(\boldsymbol {\lambda })$
.
We need the following invariants associated to a cuspidal R-representation of G following this explicit construction by compact induction (see Paragraphs 4.2 and 4.7):
-
1. the endo-class
 $\boldsymbol {\Theta }$
: a fine refinement of the level introduced by Bushnell–Henniart in [Reference Bushnell and Henniart6] and which applies equally well to the modular setting,
$\boldsymbol {\Theta }$
: a fine refinement of the level introduced by Bushnell–Henniart in [Reference Bushnell and Henniart6] and which applies equally well to the modular setting, -
2. the tame parameter field
 ${ T}$
: a tamely ramified extension of
${ T}$
: a tamely ramified extension of
 ${ F}$
of degree dividing n, uniquely determined up to
${ F}$
of degree dividing n, uniquely determined up to
 ${ F}$
-isomorphism by
${ F}$
-isomorphism by
 $\boldsymbol {\Theta }$
,
$\boldsymbol {\Theta }$
, -
3. the relative degree m: a positive integer such that
 $m[{ T}:{ F}]$
divides n, uniquely determined by
$m[{ T}:{ F}]$
divides n, uniquely determined by
 $\boldsymbol {\Theta }$
and n.
$\boldsymbol {\Theta }$
and n.
Suppose further that
![]() $\boldsymbol {\Theta }$
is
$\boldsymbol {\Theta }$
is
![]() $\sigma $
-self-dual (which follows if for example the cuspidal representation itself is
$\sigma $
-self-dual (which follows if for example the cuspidal representation itself is
![]() $\sigma $
-self-dual), then there is a uniquely determined tamely ramified extension
$\sigma $
-self-dual), then there is a uniquely determined tamely ramified extension
![]() $T_0$
of
$T_0$
of
![]() $F_0$
contained in T such that
$F_0$
contained in T such that
![]() ${ T}$
is isomorphic to
${ T}$
is isomorphic to
![]() ${ T}_0\otimes _{{ F}_0} { F}$
. The Galois group of
${ T}_0\otimes _{{ F}_0} { F}$
. The Galois group of
![]() ${ T}/{ T}_0$
canonically identifies with that of
${ T}/{ T}_0$
canonically identifies with that of
![]() ${ F}/{ F}_0$
, and the unique nontrivial automorphism of
${ F}/{ F}_0$
, and the unique nontrivial automorphism of
![]() ${ T}/{ T}_0$
extending
${ T}/{ T}_0$
extending
![]() $\sigma $
will be denoted by
$\sigma $
will be denoted by
![]() $\sigma $
(see §4.3). Our main theorem on reduction to the level
$\sigma $
(see §4.3). Our main theorem on reduction to the level
![]() $0$
setting is then (see Theorem 4.41):
$0$
setting is then (see Theorem 4.41):
Theorem 1.1.
-
1. There is a natural bijection
(1.1)from the set of isomorphism classes of cuspidal representations of $$ \begin{align} \pi\mapsto \pi_{\mathrm{t}} \end{align} $$
$$ \begin{align} \pi\mapsto \pi_{\mathrm{t}} \end{align} $$
 ${ G}$
with endo-class
${ G}$
with endo-class
 $\boldsymbol {\Theta }$
to the set of isomorphism classes of cuspidal representations of level
$\boldsymbol {\Theta }$
to the set of isomorphism classes of cuspidal representations of level
 $0$
of
$0$
of
 $\operatorname {GL}_m({ T})$
.
$\operatorname {GL}_m({ T})$
.
-
2. The representation
 $\pi $
is
$\pi $
is
 $\sigma $
-self-dual if and only if
$\sigma $
-self-dual if and only if
 $\pi _{\mathrm {t}}$
is
$\pi _{\mathrm {t}}$
is
 $\sigma $
-self-dual.
$\sigma $
-self-dual. -
3. The representation
 $\pi $
is
$\pi $
is
 $\operatorname {GL}_n(F_0)$
-distinguished if and only if
$\operatorname {GL}_n(F_0)$
-distinguished if and only if
 $\pi _{\mathrm {t}}$
is
$\pi _{\mathrm {t}}$
is
 $\operatorname {GL}_m({ T}_0)$
-distinguished.
$\operatorname {GL}_m({ T}_0)$
-distinguished.
The map (1.1) is also compatible with supercuspidal support; see Proposition 4.43 for a precise statement.
1.5
Let us briefly explain how the map (1.1) above is defined. Let
![]() $(\mathbf {J},\boldsymbol {\lambda })$
be a type inducing a cuspidal representation
$(\mathbf {J},\boldsymbol {\lambda })$
be a type inducing a cuspidal representation
![]() $\pi $
of
$\pi $
of
![]() ${ G}$
with
${ G}$
with
![]() $\sigma $
-self-dual endo-class
$\sigma $
-self-dual endo-class
![]() $\boldsymbol {\Theta }$
, tame parameter field T and relative degree m. Then:
$\boldsymbol {\Theta }$
, tame parameter field T and relative degree m. Then:
-
○ the group
 $\mathbf {J}$
has a unique maximal compact subgroup
$\mathbf {J}$
has a unique maximal compact subgroup
 $\mathbf {J}^0$
, and a unique maximal normal pro-p subgroup
$\mathbf {J}^0$
, and a unique maximal normal pro-p subgroup
 $\mathbf {J}^1$
,
$\mathbf {J}^1$
, -
○ there is a group isomorphism
 $\mathbf {J}^0/\mathbf {J}^1\simeq \operatorname {GL}_m(\boldsymbol {l}) $
, where
$\mathbf {J}^0/\mathbf {J}^1\simeq \operatorname {GL}_m(\boldsymbol {l}) $
, where
 $\boldsymbol {l}$
is the residue field of
$\boldsymbol {l}$
is the residue field of
 ${ T}$
,
${ T}$
, -
○ the restriction of
 $\boldsymbol {\lambda }$
to
$\boldsymbol {\lambda }$
to
 $\mathbf {J}^1$
is isotypic for an irreducible representation
$\mathbf {J}^1$
is isotypic for an irreducible representation
 $\eta $
of
$\eta $
of
 $\mathbf {J}^1$
, and this representation
$\mathbf {J}^1$
, and this representation
 $\eta $
extends (noncanonically) to
$\eta $
extends (noncanonically) to
 $\mathbf {J}$
,
$\mathbf {J}$
, -
○ the choice of a representation
 $\boldsymbol {\kappa }$
of
$\boldsymbol {\kappa }$
of
 $\mathbf {J}$
extending
$\mathbf {J}$
extending
 $\eta $
determines a decomposition
$\eta $
determines a decomposition
 $\boldsymbol {\lambda }\simeq \boldsymbol {\kappa }\otimes \boldsymbol {\tau }$
, where
$\boldsymbol {\lambda }\simeq \boldsymbol {\kappa }\otimes \boldsymbol {\tau }$
, where
 $\boldsymbol {\tau }$
is a representation of
$\boldsymbol {\tau }$
is a representation of
 $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
 $\mathbf {J}^1$
, uniquely determined up to isomorphism.
$\mathbf {J}^1$
, uniquely determined up to isomorphism.
The fact that
![]() $\boldsymbol {\Theta }$
is
$\boldsymbol {\Theta }$
is
![]() $\sigma $
-self-dual implies that there is a preferred choice for
$\sigma $
-self-dual implies that there is a preferred choice for
![]() $(\mathbf {J},\boldsymbol {\lambda })$
: The group
$(\mathbf {J},\boldsymbol {\lambda })$
: The group
![]() $\mathbf {J}$
is fixed by
$\mathbf {J}$
is fixed by
![]() $\sigma $
, the representation
$\sigma $
, the representation
![]() $\eta $
is
$\eta $
is
![]() $\sigma $
-self-dual and there exists a natural isomorphism between the space of
$\sigma $
-self-dual and there exists a natural isomorphism between the space of
![]() $G^\sigma $
-invariant linear forms on
$G^\sigma $
-invariant linear forms on
![]() $\pi $
and that of
$\pi $
and that of
![]() $\mathbf {J}\cap { G}^\sigma $
-invariant linear forms on
$\mathbf {J}\cap { G}^\sigma $
-invariant linear forms on
![]() $\boldsymbol {\lambda }$
. Such a type is called generic (see Definition 4.31). We prove (see Proposition 4.16):
$\boldsymbol {\lambda }$
. Such a type is called generic (see Definition 4.31). We prove (see Proposition 4.16):
Proposition 1.2. The representation
![]() $\eta $
has a unique extension
$\eta $
has a unique extension
![]() $\boldsymbol {\kappa }$
to
$\boldsymbol {\kappa }$
to
![]() $\mathbf {J}$
which is both
$\mathbf {J}$
which is both
![]() $\sigma $
-self-dual and
$\sigma $
-self-dual and
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished and whose determinant has order a power of p.
$\mathbf {J}\cap { G}^\sigma $
-distinguished and whose determinant has order a power of p.
The choice of the representation
![]() $\boldsymbol {\kappa }$
given by Proposition 1.2 thus uniquely determines a representation
$\boldsymbol {\kappa }$
given by Proposition 1.2 thus uniquely determines a representation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
.
$\mathbf {J}^1$
.
Now, there is a natural choice, as explained in §4.10, of a
![]() $\sigma $
-fixed maximal compact subgroup
$\sigma $
-fixed maximal compact subgroup
![]() $\mathbf {J}_{\mathrm {t}}^0$
of
$\mathbf {J}_{\mathrm {t}}^0$
of
![]() $\operatorname {GL}_m(T)$
, with normalizer
$\operatorname {GL}_m(T)$
, with normalizer
![]() $\mathbf {J}_{\mathrm {t}}^{\phantom {0}}$
and pro-p-radical
$\mathbf {J}_{\mathrm {t}}^{\phantom {0}}$
and pro-p-radical
![]() $\mathbf {J}_{\mathrm {t}}^1$
, such that there is a
$\mathbf {J}_{\mathrm {t}}^1$
, such that there is a
![]() $\sigma $
-equivariant group isomorphism:
$\sigma $
-equivariant group isomorphism:
The representation
![]() $\boldsymbol {\tau }$
then defines a representation of
$\boldsymbol {\tau }$
then defines a representation of
![]() $\mathbf {J}_{\mathrm {t}}^{\phantom {0}}$
trivial on
$\mathbf {J}_{\mathrm {t}}^{\phantom {0}}$
trivial on
![]() $\mathbf {J}_{\mathrm {t}}^1$
, denoted
$\mathbf {J}_{\mathrm {t}}^1$
, denoted
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
. The cuspidal representation
$\boldsymbol {\tau }_{\mathrm {t}}$
. The cuspidal representation
![]() $\pi _{\mathrm {t}}$
associated with
$\pi _{\mathrm {t}}$
associated with
![]() $\pi $
by the bijection (1.1) is then the compact induction of
$\pi $
by the bijection (1.1) is then the compact induction of
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
to
$\boldsymbol {\tau }_{\mathrm {t}}$
to
![]() $\operatorname {GL}_m(T)$
.
$\operatorname {GL}_m(T)$
.
1.6
Having reduced the classification of distinguished cuspidal
![]() ${ R}$
-representations to level
${ R}$
-representations to level
![]() $0$
, we further reduce this classification to the finite group setting. Let
$0$
, we further reduce this classification to the finite group setting. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${ R}$
-representation of
${ R}$
-representation of
![]() ${ G}$
of level
${ G}$
of level
![]() $0$
with central character
$0$
with central character
![]() $c_{\pi }$
and generic type
$c_{\pi }$
and generic type
![]() $(\mathbf {J},\boldsymbol {\lambda })$
. Restricting
$(\mathbf {J},\boldsymbol {\lambda })$
. Restricting
![]() $\boldsymbol {\lambda }$
to
$\boldsymbol {\lambda }$
to
![]() $\mathbf {J}^0$
defines a cuspidal
$\mathbf {J}^0$
defines a cuspidal
![]() ${ R}$
-representation
${ R}$
-representation
![]() $\mathrm {V}$
of
$\mathrm {V}$
of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
, where
$\operatorname {GL}_n(\boldsymbol {k})$
, where
![]() $\boldsymbol {k}$
is the residue field of
$\boldsymbol {k}$
is the residue field of
![]() ${ F}$
. We prove (see Theorem 4.45):
${ F}$
. We prove (see Theorem 4.45):
Theorem 1.3. Suppose
![]() $n\neq 1$
. The representation
$n\neq 1$
. The representation
![]() $\pi $
is
$\pi $
is
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished if and only if its central character
$\operatorname {GL}_n({ F}_0)$
-distinguished if and only if its central character
![]() $c_\pi $
is trivial on
$c_\pi $
is trivial on
![]() ${ F}_0^\times $
and
${ F}_0^\times $
and
-
1. if
 ${ F}/{ F}_0$
is unramified, then
${ F}/{ F}_0$
is unramified, then
 $\mathrm {V}$
is
$\mathrm {V}$
is
 $\operatorname {GL}_n(\boldsymbol {k}_0)$
-distinguished (
$\operatorname {GL}_n(\boldsymbol {k}_0)$
-distinguished (
 $\boldsymbol {k}_0$
is the residue field of
$\boldsymbol {k}_0$
is the residue field of
 ${ F}_0$
);
${ F}_0$
); -
2. if
 ${ F}/{ F}_0$
is ramified, then n is even,
${ F}/{ F}_0$
is ramified, then n is even,
 $\mathrm {V}$
is
$\mathrm {V}$
is
 $\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-distinguished and acts on the space of its
$\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-distinguished and acts on the space of its $$ \begin{align*} s = \begin{pmatrix} 0 & \mathrm{id} \\ \mathrm{id} & 0 \end{pmatrix} \in \operatorname{GL}_n(\boldsymbol{k}) \end{align*} $$
$$ \begin{align*} s = \begin{pmatrix} 0 & \mathrm{id} \\ \mathrm{id} & 0 \end{pmatrix} \in \operatorname{GL}_n(\boldsymbol{k}) \end{align*} $$
 $\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-invariant linear forms by the sign
$\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-invariant linear forms by the sign
 $c_\pi (\varpi )$
, where
$c_\pi (\varpi )$
, where
 $\varpi $
is any uniformizer of
$\varpi $
is any uniformizer of
 ${ F}$
.
${ F}$
.
As an application, we classify all distinguished cuspidal representations of
![]() $\operatorname {GL}_2(F)$
(see Paragraph 4.13).
$\operatorname {GL}_2(F)$
(see Paragraph 4.13).
1.7
Let
![]() $\pi $
be a cuspidal nonsupercuspidal
$\pi $
be a cuspidal nonsupercuspidal
![]() ${ R}$
-representation of G. Following [Reference Mínguez and Sécherre29], we recall in Paragraph 3.4 that there are a uniquely determined integer
${ R}$
-representation of G. Following [Reference Mínguez and Sécherre29], we recall in Paragraph 3.4 that there are a uniquely determined integer
![]() $r=r(\pi )\geqslant 2$
and a supercuspidal
$r=r(\pi )\geqslant 2$
and a supercuspidal
![]() ${ R}$
-representation
${ R}$
-representation
![]() $\rho $
of
$\rho $
of
![]() $\operatorname {GL}_{n/r}(F)$
such that
$\operatorname {GL}_{n/r}(F)$
such that
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_{r}(\rho )$
, where
$\operatorname {St}_{r}(\rho )$
, where
![]() $\operatorname {St}_r(\rho )$
denotes the unique generic subquotient of the parabolically induced representation
$\operatorname {St}_r(\rho )$
denotes the unique generic subquotient of the parabolically induced representation
(where
![]() $\nu $
denote the unramified character which is the absolute value of
$\nu $
denote the unramified character which is the absolute value of
![]() ${ F}$
composed with the determinant). The representation
${ F}$
composed with the determinant). The representation
![]() $\rho $
is not unique in general, but, if
$\rho $
is not unique in general, but, if
![]() $\pi $
is
$\pi $
is
![]() $\sigma $
-self-dual and r is odd, and if one further demands that
$\sigma $
-self-dual and r is odd, and if one further demands that
![]() $\rho $
be
$\rho $
be
![]() $\sigma $
-self-dual, then
$\sigma $
-self-dual, then
![]() $\rho $
is uniquely determined up to isomorphism (see Proposition 3.8). In this case, we obtain further necessary conditions for distinction (see Theorem 5.1):
$\rho $
is uniquely determined up to isomorphism (see Proposition 3.8). In this case, we obtain further necessary conditions for distinction (see Theorem 5.1):
Theorem 1.4. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal nonsupercuspidal
$\sigma $
-self-dual cuspidal nonsupercuspidal
![]() ${ R}$
-representation of
${ R}$
-representation of
![]() $\operatorname {GL}_n({ F})$
. Assume that the integer
$\operatorname {GL}_n({ F})$
. Assume that the integer
![]() $r=r(\pi )$
is odd, thus
$r=r(\pi )$
is odd, thus
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
for a uniquely determined
$\operatorname {St}_r(\rho )$
for a uniquely determined
![]() $\sigma $
-self-dual supercuspidal representation
$\sigma $
-self-dual supercuspidal representation
![]() $\rho $
of
$\rho $
of
![]() $\operatorname {GL}_{n/r}({ F})$
. If
$\operatorname {GL}_{n/r}({ F})$
. If
![]() $\pi $
is
$\pi $
is
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished, then
$\operatorname {GL}_n({ F}_0)$
-distinguished, then
-
1. the relative degree
 $m=m(\pi )$
and the ramification index of
$m=m(\pi )$
and the ramification index of
 ${ T}/{ T}_0$
have the same parity,
${ T}/{ T}_0$
have the same parity, -
2. the representation
 $\rho $
is
$\rho $
is
 $\operatorname {GL}_{n/r}({ F}_0)$
-distinguished.
$\operatorname {GL}_{n/r}({ F}_0)$
-distinguished.
As a corollary, we extend the disjunction theorem from the supercuspidal setting (that is, the statement that, if
![]() $\ell \neq 2$
, a supercuspidal
$\ell \neq 2$
, a supercuspidal
![]() ${ R}$
-representation is not both distinguished and
${ R}$
-representation is not both distinguished and
![]() $\varkappa $
-distinguished) to include cuspidal
$\varkappa $
-distinguished) to include cuspidal
![]() ${ R}$
-representations
${ R}$
-representations
![]() $\pi $
with
$\pi $
with
![]() $r(\pi )$
odd.
$r(\pi )$
odd.
1.8
Say that an irreducible
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation
${\overline {\mathbb {F}}_{\ell }}$
-representation
![]() $\pi $
of G lifts to
$\pi $
of G lifts to
![]() ${\overline {\mathbb {Q}}_\ell }$
if there exists a free
${\overline {\mathbb {Q}}_\ell }$
if there exists a free
![]() ${\overline {\mathbb {Z}}_\ell }$
-lattice L equipped with a linear action of G such that the
${\overline {\mathbb {Z}}_\ell }$
-lattice L equipped with a linear action of G such that the
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of G on
${\overline {\mathbb {F}}_{\ell }}$
-representation of G on
![]() $L\otimes {\overline {\mathbb {F}}_{\ell }}$
is isomorphic to
$L\otimes {\overline {\mathbb {F}}_{\ell }}$
is isomorphic to
![]() $\pi $
. When this is the case, say that the smooth
$\pi $
. When this is the case, say that the smooth
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation of G on
${\overline {\mathbb {Q}}_\ell }$
-representation of G on
![]() $L\otimes {\overline {\mathbb {Q}}_\ell }$
is a lift of
$L\otimes {\overline {\mathbb {Q}}_\ell }$
is a lift of
![]() $\pi $
to
$\pi $
to
![]() ${\overline {\mathbb {Q}}_\ell }$
. By [Reference Vignéras41], any cuspidal
${\overline {\mathbb {Q}}_\ell }$
. By [Reference Vignéras41], any cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of G lifts to
${\overline {\mathbb {F}}_{\ell }}$
-representation of G lifts to
![]() ${\overline {\mathbb {Q}}_\ell }$
and any of its lifts is cuspidal.
${\overline {\mathbb {Q}}_\ell }$
and any of its lifts is cuspidal.
According to [Reference Kurinczuk and Matringe25] (see Theorem 3.3), any cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of G having a
${\overline {\mathbb {F}}_{\ell }}$
-representation of G having a
![]() $G^\sigma $
-distinguished lift to
$G^\sigma $
-distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
is
${\overline {\mathbb {Q}}_\ell }$
is
![]() $G^\sigma $
-distinguished. The converse holds for supercuspidal
$G^\sigma $
-distinguished. The converse holds for supercuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representations of G (see [Reference Sécherre35] and [Reference Cui, Lanard and Lu12]), but there are examples of
${\overline {\mathbb {F}}_{\ell }}$
-representations of G (see [Reference Sécherre35] and [Reference Cui, Lanard and Lu12]), but there are examples of
![]() $G^\sigma $
-distinguished
$G^\sigma $
-distinguished
![]() ${\overline {\mathbb {F}}_{\ell }}$
-cuspidal representations of
${\overline {\mathbb {F}}_{\ell }}$
-cuspidal representations of
![]() $\operatorname {GL}_2(F)$
with no distinguished lift if
$\operatorname {GL}_2(F)$
with no distinguished lift if
![]() $\ell =2$
(see Paragraph 4.13 and Remark 6.4). In the final section, we classify the
$\ell =2$
(see Paragraph 4.13 and Remark 6.4). In the final section, we classify the
![]() $G^\sigma $
-distinguished cuspidal
$G^\sigma $
-distinguished cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representations of G having a
${\overline {\mathbb {F}}_{\ell }}$
-representations of G having a
![]() $G^\sigma $
-distinguished cuspidal lift to
$G^\sigma $
-distinguished cuspidal lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
(see Propositions 6.1 and 6.2 for a precise statement).
${\overline {\mathbb {Q}}_\ell }$
(see Propositions 6.1 and 6.2 for a precise statement).
1.9
Finally, let us comment on how the main results of this article could be pushed further.
Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal nonsupercuspidal
$\sigma $
-self-dual cuspidal nonsupercuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of G. In the case when
${\overline {\mathbb {F}}_{\ell }}$
-representation of G. In the case when
![]() $r(\pi )$
is even and
$r(\pi )$
is even and
![]() $\ell>2$
, we conjecture that
$\ell>2$
, we conjecture that
![]() $\pi $
is distinguished if and only if it has a distinguished lift to
$\pi $
is distinguished if and only if it has a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
(see Conjecture 6.3). We expect that this conjecture could be approached via the use of the Rankin–Selberg local factors developed in [Reference Kurinczuk and Matringe24].
${\overline {\mathbb {Q}}_\ell }$
(see Conjecture 6.3). We expect that this conjecture could be approached via the use of the Rankin–Selberg local factors developed in [Reference Kurinczuk and Matringe24].
In the case when
![]() $r(\pi )$
is odd, we do not expect the necessary conditions of Theorem 1.4 to be sufficient for distinction. It would be interesting to determine whether any
$r(\pi )$
is odd, we do not expect the necessary conditions of Theorem 1.4 to be sufficient for distinction. It would be interesting to determine whether any
![]() $G^\sigma $
-distinguished cuspidal representation of G has a distinguished lift to
$G^\sigma $
-distinguished cuspidal representation of G has a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
.
${\overline {\mathbb {Q}}_\ell }$
.
Finallly, this work is part of a wider programme aiming at classifying all distinguished generic R-representations of G. Such a classification might be approached by developing a theory of mod
![]() $\ell $
intertwining periods.
$\ell $
intertwining periods.
Structure of the paper
After setting some notation in Section 2, in Section 3 we collect together necessary background from the literature and prove some basic results on
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${ R}$
-representations.
${ R}$
-representations.
Section 4 constitutes the technical heart of the paper. It reduces the problem of classifying distinguished cuspidal
![]() ${ R}$
-representations to level
${ R}$
-representations to level
![]() $0$
.
$0$
.
In Section 5, under a parity condition, we provide necessary conditions for distinction, allowing us to deduce the disjunction theorem and a lifting theorem.
In Section 6, we classify the cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representations having a distinguished cuspidal lift.
${\overline {\mathbb {F}}_{\ell }}$
-representations having a distinguished cuspidal lift.
2 Notation
2.1
Given any non-Archimedean locally compact field
![]() ${ F}$
, we write
${ F}$
, we write ![]() for its ring of integers,
for its ring of integers,
![]() $\mathfrak {p}_{ F}$
for the maximal ideal of
$\mathfrak {p}_{ F}$
for the maximal ideal of ![]() ,
,
![]() $\boldsymbol {k}_{ F}$
for its residue field and
$\boldsymbol {k}_{ F}$
for its residue field and
![]() $q_{ F}$
for the cardinality of
$q_{ F}$
for the cardinality of
![]() $\boldsymbol {k}_{ F}$
.
$\boldsymbol {k}_{ F}$
.
We also write
![]() $\operatorname {val}_{ F}$
for the valuation of
$\operatorname {val}_{ F}$
for the valuation of
![]() ${ F}$
taking any uniformizer to
${ F}$
taking any uniformizer to
![]() $1$
, and
$1$
, and
![]() $|\cdot |_{ F}$
for the absolute value of
$|\cdot |_{ F}$
for the absolute value of
![]() ${ F}$
taking any uniformizer to the inverse of
${ F}$
taking any uniformizer to the inverse of
![]() $q_{ F}$
.
$q_{ F}$
.
Given any finite extension
![]() ${ L}$
of
${ L}$
of
![]() ${ K}$
, we write
${ K}$
, we write
![]() $\mathrm {N}_{{ L}/{ K}}$
and
$\mathrm {N}_{{ L}/{ K}}$
and
![]() $\operatorname {tr}_{{ L}/{ K}}$
for the norm and trace maps.
$\operatorname {tr}_{{ L}/{ K}}$
for the norm and trace maps.
2.2
Given a locally compact, totally disconnected topological group
![]() ${ G}$
and an algebraically closed field
${ G}$
and an algebraically closed field
![]() ${ R}$
of characteristic different from p, we consider smooth representations of
${ R}$
of characteristic different from p, we consider smooth representations of
![]() ${ G}$
on
${ G}$
on
![]() ${ R}$
-vector spaces. We will abbreviate smooth
${ R}$
-vector spaces. We will abbreviate smooth
![]() ${ R}$
-representation to
${ R}$
-representation to
![]() ${ R}$
-representation, or even representation if the coefficient field
${ R}$
-representation, or even representation if the coefficient field
![]() ${ R}$
is clear from the context.
${ R}$
is clear from the context.
An
![]() ${ R}$
-character (or character) of
${ R}$
-character (or character) of
![]() ${ G}$
is a group homomorphism from
${ G}$
is a group homomorphism from
![]() ${ G}$
to
${ G}$
to
![]() ${ R}^\times $
with open kernel.
${ R}^\times $
with open kernel.
Let
![]() $\pi $
be a representation of
$\pi $
be a representation of
![]() ${ G}$
. We write
${ G}$
. We write
![]() $\pi ^\vee $
for its contragredient. Given a character
$\pi ^\vee $
for its contragredient. Given a character
![]() $\chi $
of
$\chi $
of
![]() ${ G}$
, we write
${ G}$
, we write
![]() $\pi \chi $
for the representation
$\pi \chi $
for the representation
![]() $g\mapsto \chi (g)\pi (g)$
of
$g\mapsto \chi (g)\pi (g)$
of
![]() ${ G}$
.
${ G}$
.
Let
![]() $\pi $
be a representation of a closed subgroup
$\pi $
be a representation of a closed subgroup
![]() ${{H}}$
of
${{H}}$
of
![]() ${ G}$
. Given any element
${ G}$
. Given any element
![]() $g\in { G}$
, we write
$g\in { G}$
, we write
![]() $\pi ^g$
for the representation
$\pi ^g$
for the representation
![]() $x\mapsto \pi (gxg^{-1})$
of
$x\mapsto \pi (gxg^{-1})$
of
![]() ${{H}}^g=g^{-1}{{H}} g$
. Given any continuous involution
${{H}}^g=g^{-1}{{H}} g$
. Given any continuous involution
![]() $\sigma $
of
$\sigma $
of
![]() ${ G}$
, we write
${ G}$
, we write
![]() $\pi ^\sigma $
for the representation
$\pi ^\sigma $
for the representation
![]() $\pi \circ \sigma $
of
$\pi \circ \sigma $
of
![]() $\sigma ({{H}})$
. Given any character
$\sigma ({{H}})$
. Given any character
![]() $\mu $
of
$\mu $
of
![]() ${{H}}\cap { G}^\sigma $
, we say that
${{H}}\cap { G}^\sigma $
, we say that
![]() $\pi $
is
$\pi $
is
![]() $\mu $
-distinguished if the space
$\mu $
-distinguished if the space
![]() $\operatorname {Hom}_{{{H}}\cap { G}^\sigma }(\pi ,\chi )$
is nonzero. If
$\operatorname {Hom}_{{{H}}\cap { G}^\sigma }(\pi ,\chi )$
is nonzero. If
![]() $\mu $
is the trivial character, we will abbreviate
$\mu $
is the trivial character, we will abbreviate
![]() $\mu $
-distinguished to
$\mu $
-distinguished to
![]() ${{H}}\cap { G}^\sigma $
-distinguished, or just distinguished.
${{H}}\cap { G}^\sigma $
-distinguished, or just distinguished.
2.3
Let us fix a separable quadratic extension
![]() ${{ F}}/{ F}_0$
of non-Archimedean locally compact fields of residual characteristic p, and let
${{ F}}/{ F}_0$
of non-Archimedean locally compact fields of residual characteristic p, and let
![]() $\sigma $
denote its nontrivial automorphism. Let R be an algebraically closed field of characteristic different from p. Let
$\sigma $
denote its nontrivial automorphism. Let R be an algebraically closed field of characteristic different from p. Let
denote the
![]() $\mathbb {Z}$
-valued character of
$\mathbb {Z}$
-valued character of
![]() ${ F}_0^\times $
with kernel
${ F}_0^\times $
with kernel
![]() $\mathrm {N}_{{{ F}}/{ F}_0}({{ F}}^\times )$
. When needed, we will consider
$\mathrm {N}_{{{ F}}/{ F}_0}({{ F}}^\times )$
. When needed, we will consider
![]() $\varkappa $
as a character with values in
$\varkappa $
as a character with values in
![]() ${ R}$
. We abbreviate
${ R}$
. We abbreviate
![]() $q=q_{{ F}}$
and
$q=q_{{ F}}$
and
![]() $q_0=q_{{ F}_0}$
. We fix a square root
$q_0=q_{{ F}_0}$
. We fix a square root
of
![]() $q_0$
in
$q_0$
in
![]() ${ R}$
and define
${ R}$
and define
 $$ \begin{align} q^{1/2} = \left\{ \begin{array}{ll} q_0^{1/2} & \text{if }{ F}/{ F}_0\text{ is ramified}, \\ q_0 & \text{if }{ F}/{ F}_0\text{ is unramified}, \end{array}\right. \end{align} $$
$$ \begin{align} q^{1/2} = \left\{ \begin{array}{ll} q_0^{1/2} & \text{if }{ F}/{ F}_0\text{ is ramified}, \\ q_0 & \text{if }{ F}/{ F}_0\text{ is unramified}, \end{array}\right. \end{align} $$
which we will use to normalize parabolic induction and restriction functors (see below).
2.4
Given a positive integer
![]() $n{\geqslant }1$
, the automorphism
$n{\geqslant }1$
, the automorphism
![]() $\sigma $
acts on the group
$\sigma $
acts on the group
![]() $\operatorname {GL}_n(F)$
componentwise, thus defines a continuous involution of
$\operatorname {GL}_n(F)$
componentwise, thus defines a continuous involution of
![]() $\operatorname {GL}_n(F)$
, still denoted
$\operatorname {GL}_n(F)$
, still denoted
![]() $\sigma $
. Its fixed points form the subgroup
$\sigma $
. Its fixed points form the subgroup
![]() $\operatorname {GL}_n(F_0)$
.
$\operatorname {GL}_n(F_0)$
.
We denote by
![]() $\nu $
the unramified character ‘absolute value of the determinant’ of
$\nu $
the unramified character ‘absolute value of the determinant’ of
![]() $\operatorname {GL}_n(F)$
and by
$\operatorname {GL}_n(F)$
and by
![]() $\nu ^{1/2}$
the unramified character taking any element whose determinant has valuation
$\nu ^{1/2}$
the unramified character taking any element whose determinant has valuation
![]() $1$
to
$1$
to
![]() $q^{-1/2}$
. We thus have
$q^{-1/2}$
. We thus have
![]() $(\nu ^{1/2})^2=\nu $
. Similarly, we define the characters
$(\nu ^{1/2})^2=\nu $
. Similarly, we define the characters
![]() $\nu ^{\phantom {1}}_0$
and
$\nu ^{\phantom {1}}_0$
and
![]() $\nu _0^{1/2}$
of
$\nu _0^{1/2}$
of
![]() $\operatorname {GL}_n(F_0)$
.
$\operatorname {GL}_n(F_0)$
.
Given positive integers
![]() $n_1,\dots ,n_r$
such that
$n_1,\dots ,n_r$
such that
![]() $n_1+\dots +n_r=n$
and, for each
$n_1+\dots +n_r=n$
and, for each
![]() $i=1,\ldots ,r$
, given an
$i=1,\ldots ,r$
, given an
![]() ${ R}$
-representation
${ R}$
-representation
![]() $\pi _i$
of
$\pi _i$
of
![]() $\operatorname {GL}_{n_i}(F)$
, we write
$\operatorname {GL}_{n_i}(F)$
, we write
for the representation of
![]() $\operatorname {GL}_{n}(F)$
obtained by normalized parabolic induction from
$\operatorname {GL}_{n}(F)$
obtained by normalized parabolic induction from
![]() $\pi _1\otimes \cdots \otimes \pi _r$
along the parabolic subgroup generated by upper triangular matrices and the standard Levi subgroup
$\pi _1\otimes \cdots \otimes \pi _r$
along the parabolic subgroup generated by upper triangular matrices and the standard Levi subgroup
![]() $\operatorname {GL}_{n_1}(F)\times \dots \times \operatorname {GL}_{n_r}(F)$
.
$\operatorname {GL}_{n_1}(F)\times \dots \times \operatorname {GL}_{n_r}(F)$
.
An irreducible R-representation of
![]() $\operatorname {GL}_n(F)$
is said to be cuspidal (respectively, supercuspidal) if it does not occur as a subrepresentation (respectively, a subquotient) of any representation of the form (2.4) with
$\operatorname {GL}_n(F)$
is said to be cuspidal (respectively, supercuspidal) if it does not occur as a subrepresentation (respectively, a subquotient) of any representation of the form (2.4) with
![]() $r{\geqslant }2$
. Any supercuspidal representation of
$r{\geqslant }2$
. Any supercuspidal representation of
![]() $\operatorname {GL}_n(F)$
is cuspidal. When R has characteristic
$\operatorname {GL}_n(F)$
is cuspidal. When R has characteristic
![]() $0$
, any cuspidal representation of
$0$
, any cuspidal representation of
![]() $\operatorname {GL}_n(F)$
is supercuspidal. When R has characteristic
$\operatorname {GL}_n(F)$
is supercuspidal. When R has characteristic
![]() $\ell>0$
, the group
$\ell>0$
, the group
![]() $\operatorname {GL}_n(F)$
may have cuspidal nonsupercuspidal representations (see §3.4).
$\operatorname {GL}_n(F)$
may have cuspidal nonsupercuspidal representations (see §3.4).
Given a representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {GL}_n(F)$
and a character
$\operatorname {GL}_n(F)$
and a character
![]() $\chi $
of
$\chi $
of
![]() $F^\times $
, we will write
$F^\times $
, we will write
![]() $\pi \chi $
for
$\pi \chi $
for
![]() $\pi (\chi \circ \mathrm {det})$
.
$\pi (\chi \circ \mathrm {det})$
.
2.5
Let us fix an algebraic closure
![]() ${\overline {\mathbb {Q}}_\ell }$
of the field of
${\overline {\mathbb {Q}}_\ell }$
of the field of
![]() $\ell $
-adic numbers. Let
$\ell $
-adic numbers. Let
![]() ${\overline {\mathbb {Z}}_\ell }$
denote its ring of integers, and
${\overline {\mathbb {Z}}_\ell }$
denote its ring of integers, and
![]() ${\overline {\mathbb {F}}_{\ell }}$
denote the residue field of
${\overline {\mathbb {F}}_{\ell }}$
denote the residue field of
![]() ${\overline {\mathbb {Z}}_\ell }$
.
${\overline {\mathbb {Z}}_\ell }$
.
We call an irreducible representation
![]() $\pi $
of a locally compact, totally disconnected group
$\pi $
of a locally compact, totally disconnected group
![]() ${ G}$
on a
${ G}$
on a
![]() ${\overline {\mathbb {Q}}_\ell }$
-vector space V integral if it stabilizes a
${\overline {\mathbb {Q}}_\ell }$
-vector space V integral if it stabilizes a
![]() ${\overline {\mathbb {Z}}_\ell }$
-lattice L in V. In this case, we obtain a smooth
${\overline {\mathbb {Z}}_\ell }$
-lattice L in V. In this case, we obtain a smooth
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation
${\overline {\mathbb {F}}_{\ell }}$
-representation
![]() $L\otimes {\overline {\mathbb {F}}_{\ell }}$
of
$L\otimes {\overline {\mathbb {F}}_{\ell }}$
of
![]() ${ G}$
whose isomorphism class may depend on the choice of L.
${ G}$
whose isomorphism class may depend on the choice of L.
If
![]() ${ G}$
is either the group of rational points of a connected reductive linear algebraic F-group or a finite group (see [Reference Vignéras42, Theorem 1] and the Brauer–Nesbitt principle), the smooth
${ G}$
is either the group of rational points of a connected reductive linear algebraic F-group or a finite group (see [Reference Vignéras42, Theorem 1] and the Brauer–Nesbitt principle), the smooth
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation
${\overline {\mathbb {F}}_{\ell }}$
-representation
![]() $L\otimes {\overline {\mathbb {F}}_{\ell }}$
has finite length, and its semisimplification is independent of the choice of L. This semisimplification is called the reduction modulo
$L\otimes {\overline {\mathbb {F}}_{\ell }}$
has finite length, and its semisimplification is independent of the choice of L. This semisimplification is called the reduction modulo
![]() $\ell $
of
$\ell $
of
![]() $\pi $
and is denoted by
$\pi $
and is denoted by
![]() ${{\mathbf {\textsf {r}}}}_\ell (\pi )$
.
${{\mathbf {\textsf {r}}}}_\ell (\pi )$
.
Given an irreducible
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation
${\overline {\mathbb {F}}_{\ell }}$
-representation
![]() $\rho $
of G, we call an irreducible integral
$\rho $
of G, we call an irreducible integral
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation with reduction modulo
${\overline {\mathbb {Q}}_\ell }$
-representation with reduction modulo
![]() $\ell $
equal to
$\ell $
equal to
![]() $\rho $
a
$\rho $
a
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift of
${\overline {\mathbb {Q}}_\ell }$
-lift of
![]() $\rho $
.
$\rho $
.
3 Basic results
In this section, p is an arbitrary prime number,
![]() ${ F}/{ F}_0$
is a separable quadratic extension and
${ F}/{ F}_0$
is a separable quadratic extension and
![]() ${ R}$
has characteristic
${ R}$
has characteristic
![]() $\ell \neq p$
. We fix a positive integer
$\ell \neq p$
. We fix a positive integer
![]() $n{\geqslant }1$
.
$n{\geqslant }1$
.
3.1
Fundamental results of Flicker and Prasad [Reference Flicker16, Reference Prasad32, Reference Prasad33] on irreducible complex representations of
![]() $\operatorname {GL}_n({ F})$
distinguished by
$\operatorname {GL}_n({ F})$
distinguished by
![]() $\operatorname {GL}_n({ F}_0)$
have been extended to irreducible
$\operatorname {GL}_n({ F}_0)$
have been extended to irreducible
![]() ${ R}$
-representations in [Reference Sécherre35] Theorem 4.1.
${ R}$
-representations in [Reference Sécherre35] Theorem 4.1.
Theorem 3.1. Let
![]() $\pi $
be an irreducible representation of
$\pi $
be an irreducible representation of
![]() $\operatorname {GL}_n({ F})$
distinguished by
$\operatorname {GL}_n({ F})$
distinguished by
![]() $\operatorname {GL}_n({ F}_0)$
.
$\operatorname {GL}_n({ F}_0)$
.
-
1. The central character
 $c_\pi $
of
$c_\pi $
of
 $\pi $
is trivial on
$\pi $
is trivial on
 ${ F}_0^\times $
.
${ F}_0^\times $
. -
2. The
 ${ R}$
-vector space
${ R}$
-vector space
 $\operatorname {Hom}_{\operatorname {GL}_n({ F}_0)}(\pi ,{ R})$
has dimension
$\operatorname {Hom}_{\operatorname {GL}_n({ F}_0)}(\pi ,{ R})$
has dimension
 $1$
.
$1$
. -
3. The contragredient
 $\pi ^\vee $
of
$\pi ^\vee $
of
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 $\pi ^\sigma $
.
$\pi ^\sigma $
.
We will say that a representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {GL}_n(F)$
is
$\operatorname {GL}_n(F)$
is
![]() $\sigma $
-self-dual if
$\sigma $
-self-dual if
![]() $\pi ^\vee $
is isomorphic to
$\pi ^\vee $
is isomorphic to
![]() $\pi ^\sigma $
.
$\pi ^\sigma $
.
3.2
For supercuspidal representations, we have the following dichotomy and disjunction theorem ([Reference Kable23] Theorem 4, [Reference Anandavardhanan, Kable and Tandon2] Corollary 1.6 if
![]() $\ell =0$
, [Reference Sécherre35] Theorem 10.8 if
$\ell =0$
, [Reference Sécherre35] Theorem 10.8 if
![]() $p\neq 2$
and [Reference Cui, Lanard and Lu12] Theorem 3.14 if
$p\neq 2$
and [Reference Cui, Lanard and Lu12] Theorem 3.14 if
![]() $\ell \neq 0,2$
).
$\ell \neq 0,2$
).
Theorem 3.2. Let
![]() $\rho $
be a
$\rho $
be a
![]() $\sigma $
-self-dual supercuspidal
$\sigma $
-self-dual supercuspidal
![]() ${ R}$
-representation of
${ R}$
-representation of
![]() $\operatorname {GL}_n({{ F}})$
.
$\operatorname {GL}_n({{ F}})$
.
-
1. If
 $\ell =2$
, then
$\ell =2$
, then
 $\rho $
is distinguished.
$\rho $
is distinguished. -
2. If
 $\ell \neq 2$
, then
$\ell \neq 2$
, then
 $\rho $
is either distinguished or
$\rho $
is either distinguished or
 $\varkappa $
-distinguished, but not both.
$\varkappa $
-distinguished, but not both.
3.3
In this paragraph,
![]() $\ell $
is a prime number different from p and we will consider representations with coefficients in
$\ell $
is a prime number different from p and we will consider representations with coefficients in
![]() ${\overline {\mathbb {Q}}_\ell }$
or
${\overline {\mathbb {Q}}_\ell }$
or
![]() ${\overline {\mathbb {F}}_{\ell }}$
. The following theorem is [Reference Kurinczuk and Matringe25] Theorem 3.4.
${\overline {\mathbb {F}}_{\ell }}$
. The following theorem is [Reference Kurinczuk and Matringe25] Theorem 3.4.
Theorem 3.3. Let
![]() ${\pi }$
be an integral
${\pi }$
be an integral
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation of
${\overline {\mathbb {Q}}_\ell }$
-representation of
![]() $\operatorname {GL}_n({ F})$
. If
$\operatorname {GL}_n({ F})$
. If
![]() ${\pi }$
is distinguished by
${\pi }$
is distinguished by
![]() $\operatorname {GL}_n(F_0)$
, then its reduction mod
$\operatorname {GL}_n(F_0)$
, then its reduction mod
![]() $\ell $
is (irreducible, cuspidal and) distinguished.
$\ell $
is (irreducible, cuspidal and) distinguished.
It follows that any
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_n({ F})$
having a distinguished lift to
$\operatorname {GL}_n({ F})$
having a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
is distinguished. For supercuspidal representations, one has the following converse (see [Reference Sécherre35] Theorem 10.11 if
${\overline {\mathbb {Q}}_\ell }$
is distinguished. For supercuspidal representations, one has the following converse (see [Reference Sécherre35] Theorem 10.11 if
![]() $p\neq 2$
, and [Reference Cui, Lanard and Lu12] Theorem 3.4):
$p\neq 2$
, and [Reference Cui, Lanard and Lu12] Theorem 3.4):
Theorem 3.4. Any
![]() $\operatorname {GL}_n(F_0)$
-distinguished supercuspidal
$\operatorname {GL}_n(F_0)$
-distinguished supercuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_n({{ F}})$
has a
$\operatorname {GL}_n({{ F}})$
has a
![]() $\operatorname {GL}_n(F_0)$
-distinguished lift to
$\operatorname {GL}_n(F_0)$
-distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
.
${\overline {\mathbb {Q}}_\ell }$
.
We also have the following distinguished lift theorem, making Theorem 3.4 more precise.
Theorem 3.5. Let
![]() $\rho $
be a
$\rho $
be a
![]() $\sigma $
-self-dual supercuspidal
$\sigma $
-self-dual supercuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_n({{ F}})$
.
$\operatorname {GL}_n({{ F}})$
.
-
1. The representation
 $\rho $
has a
$\rho $
has a
 $\sigma $
-self-dual lift to
$\sigma $
-self-dual lift to
 ${\overline {\mathbb {Q}}_\ell }$
.
${\overline {\mathbb {Q}}_\ell }$
. -
2. Let
 $\mu $
be a
$\mu $
be a
 $\sigma $
-self-dual lift of
$\sigma $
-self-dual lift of
 $\rho $
to
$\rho $
to
 ${\overline {\mathbb {Q}}_\ell }$
, and suppose that
${\overline {\mathbb {Q}}_\ell }$
, and suppose that
 $\ell \neq 2$
. Then
$\ell \neq 2$
. Then
 $\mu $
is distinguished if and only
$\mu $
is distinguished if and only
 $\rho $
is distinguished.
$\rho $
is distinguished.
Proof. If
![]() $p\neq 2$
, this is [Reference Sécherre35] Theorem 10.11. Assume now that
$p\neq 2$
, this is [Reference Sécherre35] Theorem 10.11. Assume now that
![]() $p=2$
, thus
$p=2$
, thus
![]() $\ell \neq 2$
.
$\ell \neq 2$
.
By Theorem 3.2, the representation
![]() $\rho $
is either distinguished or
$\rho $
is either distinguished or
![]() $\varkappa $
-distinguished. If it is distinguished, it has a
$\varkappa $
-distinguished. If it is distinguished, it has a
![]() $\sigma $
-self-dual lift thanks to Theorem 3.4 and Theorem 3.1(3). If it is
$\sigma $
-self-dual lift thanks to Theorem 3.4 and Theorem 3.1(3). If it is
![]() $\varkappa $
-distinguished, fix a
$\varkappa $
-distinguished, fix a
![]() ${\overline {\mathbb {Q}}_\ell }$
-character
${\overline {\mathbb {Q}}_\ell }$
-character
![]() $\xi $
of
$\xi $
of
![]() $F^\times $
extending the canonical
$F^\times $
extending the canonical
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift of
${\overline {\mathbb {Q}}_\ell }$
-lift of
![]() $\varkappa $
. The reduction mod
$\varkappa $
. The reduction mod
![]() $\ell $
of
$\ell $
of
![]() $\xi $
is an
$\xi $
is an
![]() ${\overline {\mathbb {F}}_{\ell }}$
-character of
${\overline {\mathbb {F}}_{\ell }}$
-character of
![]() $F^\times $
extending
$F^\times $
extending
![]() $\varkappa $
, denoted
$\varkappa $
, denoted
![]() $\chi $
. The representation
$\chi $
. The representation
![]() $\rho \chi $
is distinguished and supercuspidal. It thus has a
$\rho \chi $
is distinguished and supercuspidal. It thus has a
![]() $\sigma $
-self-dual lift
$\sigma $
-self-dual lift
![]() $\pi $
. Then
$\pi $
. Then
![]() $\pi \xi ^{-1}$
is a distinguished lift of
$\pi \xi ^{-1}$
is a distinguished lift of
![]() $\rho $
. This proves (1).
$\rho $
. This proves (1).
Let
![]() $\mu $
be a
$\mu $
be a
![]() $\sigma $
-self-dual lift of
$\sigma $
-self-dual lift of
![]() $\rho $
, and assume that
$\rho $
, and assume that
![]() $\rho $
is distinguished. If
$\rho $
is distinguished. If
![]() $\mu $
is not distinguished, it must then be
$\mu $
is not distinguished, it must then be
![]() $\varkappa $
-distinguished. By Theorem 3.3, this implies that
$\varkappa $
-distinguished. By Theorem 3.3, this implies that
![]() $\rho $
is
$\rho $
is
![]() $\varkappa $
-distinguished, which contradicts the dichotomy and disjunction theorem. Conversely, if
$\varkappa $
-distinguished, which contradicts the dichotomy and disjunction theorem. Conversely, if
![]() $\mu $
is distinguished, then
$\mu $
is distinguished, then
![]() $\rho $
is distinguished thanks to Theorem 3.3.
$\rho $
is distinguished thanks to Theorem 3.3.
3.4
From now on, we consider the case of cuspidal nonsupercuspidal R-representations, thus
![]() $\ell $
is a prime number different from p. Let us recall how they are classified in terms of their supercuspidal support.
$\ell $
is a prime number different from p. Let us recall how they are classified in terms of their supercuspidal support.
Recall that a representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {GL}_n(F)$
on an
$\operatorname {GL}_n(F)$
on an
![]() ${ R}$
-vector space V is generic if V carries a nonzero
${ R}$
-vector space V is generic if V carries a nonzero
![]() ${ R}$
-linear form
${ R}$
-linear form
![]() $\mathit {\Theta }$
such that
$\mathit {\Theta }$
such that
![]() $\mathit {\Theta } (\pi (u)v) = {\theta }(u)v$
for all
$\mathit {\Theta } (\pi (u)v) = {\theta }(u)v$
for all
![]() $v\in V$
and all unipotent upper triangular matrices u, where
$v\in V$
and all unipotent upper triangular matrices u, where
![]() ${\theta }(u) = \psi (u_{1,2}+\dots +u_{n-1,n})$
and
${\theta }(u) = \psi (u_{1,2}+\dots +u_{n-1,n})$
and
![]() $\psi $
is a nontrivial R-character of F.
$\psi $
is a nontrivial R-character of F.
Let
![]() $k{\geqslant }1$
be a positive integer, and
$k{\geqslant }1$
be a positive integer, and
![]() $\rho $
be a supercuspidal
$\rho $
be a supercuspidal
![]() ${ R}$
-representation of
${ R}$
-representation of
![]() $\operatorname {GL}_k({{ F}})$
. According to [Reference Mínguez and Sécherre29] 8.1, for any
$\operatorname {GL}_k({{ F}})$
. According to [Reference Mínguez and Sécherre29] 8.1, for any
![]() $r{\geqslant }1$
, the induced representation
$r{\geqslant }1$
, the induced representation
contains a unique generic irreducible subquotient, denoted
![]() $\operatorname {St}_{r}(\rho )$
.
$\operatorname {St}_{r}(\rho )$
.
Let
![]() $e(\rho )$
be the smallest integer
$e(\rho )$
be the smallest integer
![]() $i{\geqslant }1$
such that
$i{\geqslant }1$
such that
![]() $\rho \nu ^i$
is isomorphic to
$\rho \nu ^i$
is isomorphic to
![]() $\rho $
and
$\rho $
and
![]() $t(\rho )$
be the torsion number of
$t(\rho )$
be the torsion number of
![]() $\rho $
, that is, the number of unramified characters
$\rho $
, that is, the number of unramified characters
![]() $\chi $
of
$\chi $
of
![]() ${{ F}}^\times $
such that
${{ F}}^\times $
such that
![]() $\rho \chi $
is isomorphic to
$\rho \chi $
is isomorphic to
![]() $\rho $
. By [Reference Mínguez and Sécherre31] Lemme 3.6, these integers are related by the identity
$\rho $
. By [Reference Mínguez and Sécherre31] Lemme 3.6, these integers are related by the identity
By [Reference Mínguez and Sécherre29] Théorème 6.14, one has the following classification.
Proposition 3.6. Let
![]() $\pi $
be a cuspidal nonsupercuspidal
$\pi $
be a cuspidal nonsupercuspidal
![]() ${ R}$
-representation of
${ R}$
-representation of
![]() $\operatorname {GL}_n({{ F}})$
.
$\operatorname {GL}_n({{ F}})$
.
-
1. There are a unique positive integer
 $r=r(\pi ){\geqslant }2$
dividing n and a supercuspidal representation
$r=r(\pi ){\geqslant }2$
dividing n and a supercuspidal representation
 $\rho $
of
$\rho $
of
 $\operatorname {GL}_{n/r}({{ F}})$
such that
$\operatorname {GL}_{n/r}({{ F}})$
such that
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 $\operatorname {St}_r(\rho )$
.
$\operatorname {St}_r(\rho )$
. -
2. There is a unique integer
 $v{\geqslant }0$
such that
$v{\geqslant }0$
such that
 $r=e(\rho )\ell ^v$
.
$r=e(\rho )\ell ^v$
. -
3. Let
 $\rho '$
be a supercuspidal representation of
$\rho '$
be a supercuspidal representation of
 $\operatorname {GL}_{n/r}({{ F}})$
. The representation
$\operatorname {GL}_{n/r}({{ F}})$
. The representation
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 $\operatorname {St}_{r}(\rho ')$
if and only if
$\operatorname {St}_{r}(\rho ')$
if and only if
 $\rho '$
is isomorphic to
$\rho '$
is isomorphic to
 $\rho \nu ^i$
for some
$\rho \nu ^i$
for some
 $i\in \mathbb {Z}$
.
$i\in \mathbb {Z}$
.
Note that, conversely, by the same references, if
![]() $\rho $
is a supercuspidal representation of
$\rho $
is a supercuspidal representation of
![]() $\operatorname {GL}_k(F)$
and
$\operatorname {GL}_k(F)$
and
![]() $r=e(\rho )\ell ^v$
for some
$r=e(\rho )\ell ^v$
for some
![]() $v{\geqslant }0$
, the representation
$v{\geqslant }0$
, the representation
![]() $\operatorname {St}_r(\rho )$
is cuspidal.
$\operatorname {St}_r(\rho )$
is cuspidal.
It will be convenient to set
![]() $r(\pi )=1$
for any supercuspidal
$r(\pi )=1$
for any supercuspidal
![]() ${ R}$
-representation
${ R}$
-representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {GL}_n({{ F}})$
.
$\operatorname {GL}_n({{ F}})$
.
3.5
We now classify
![]() $\sigma $
-self-dual cuspidal representations.
$\sigma $
-self-dual cuspidal representations.
Lemma 3.7. Let
![]() $\rho $
be a supercuspidal
$\rho $
be a supercuspidal
![]() ${ R}$
-representation of
${ R}$
-representation of
![]() $\operatorname {GL}_k({{ F}})$
for some
$\operatorname {GL}_k({{ F}})$
for some
![]() $k{\geqslant }1$
. Let
$k{\geqslant }1$
. Let
![]() $r{\geqslant }2$
be such that
$r{\geqslant }2$
be such that
![]() $\operatorname {St}_r(\rho )$
is cuspidal, and suppose that
$\operatorname {St}_r(\rho )$
is cuspidal, and suppose that
![]() $\operatorname {St}_r(\rho )$
is
$\operatorname {St}_r(\rho )$
is
![]() $\sigma $
-self-dual. Then there is an
$\sigma $
-self-dual. Then there is an
![]() $i\in \mathbb {Z}$
, uniquely determined mod
$i\in \mathbb {Z}$
, uniquely determined mod
![]() $e(\rho )$
such that
$e(\rho )$
such that
![]() $\rho ^{\vee \sigma }$
is isomorphic to
$\rho ^{\vee \sigma }$
is isomorphic to
![]() $\rho \nu ^i$
.
$\rho \nu ^i$
.
Proof. The representation
![]() $\operatorname {St}_r(\rho )$
is the unique generic irreducible subquotient of (3.1). The representation
$\operatorname {St}_r(\rho )$
is the unique generic irreducible subquotient of (3.1). The representation
![]() $\operatorname {St}_r(\rho )^{\vee \sigma }$
is thus generic, irreducible and it is a subquotient of
$\operatorname {St}_r(\rho )^{\vee \sigma }$
is thus generic, irreducible and it is a subquotient of
Equivalently (see [Reference Mínguez and Sécherre29] Proposition 2.6), it is a subquotient of
![]() $\rho ^{\vee \sigma }\nu ^{-(r-1)/2}\times \cdots \times \rho ^{\vee \sigma }\nu ^{(r-1)/2}$
. By uniqueness of the generic irreducible subquotient, we thus have
$\rho ^{\vee \sigma }\nu ^{-(r-1)/2}\times \cdots \times \rho ^{\vee \sigma }\nu ^{(r-1)/2}$
. By uniqueness of the generic irreducible subquotient, we thus have
The representation
![]() $\operatorname {St}_r(\rho )$
is thus
$\operatorname {St}_r(\rho )$
is thus
![]() $\sigma $
-self-dual if and only if
$\sigma $
-self-dual if and only if
![]() $\operatorname {St}_r(\rho ^{\vee \sigma })$
is isomorphic to
$\operatorname {St}_r(\rho ^{\vee \sigma })$
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
. The result then follows from Proposition 3.6.
$\operatorname {St}_r(\rho )$
. The result then follows from Proposition 3.6.
Proposition 3.8. Let
![]() $\pi $
be a cuspidal
$\pi $
be a cuspidal
![]() $\sigma $
-self-dual representation of
$\sigma $
-self-dual representation of
![]() $\operatorname {GL}_{n}({{ F}})$
. Set
$\operatorname {GL}_{n}({{ F}})$
. Set
![]() $r=r(\pi )$
and write
$r=r(\pi )$
and write
![]() $k=n/r$
.
$k=n/r$
.
-
1. If r is odd or
 $\ell =2$
, there is a unique
$\ell =2$
, there is a unique
 $\sigma $
-self-dual supercuspidal representation
$\sigma $
-self-dual supercuspidal representation
 $\rho $
of
$\rho $
of
 $\operatorname {GL}_k({{ F}})$
such that
$\operatorname {GL}_k({{ F}})$
such that
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 $\operatorname {St}_r(\rho )$
.
$\operatorname {St}_r(\rho )$
. -
2. Suppose that r is even and
 $\ell \neq 2$
.
$\ell \neq 2$
.-
(a) There are a supercuspidal representation
 $\rho $
of
$\rho $
of
 $\operatorname {GL}_k({{ F}})$
and an
$\operatorname {GL}_k({{ F}})$
and an
 $i\in \{0,1\}$
such that
$i\in \{0,1\}$
such that
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 $\operatorname {St}_r(\rho )$
and
$\operatorname {St}_r(\rho )$
and
 $\rho ^{\vee \sigma }\simeq \rho \nu ^i$
.
$\rho ^{\vee \sigma }\simeq \rho \nu ^i$
. -
(b) Let
 $\rho '$
be a supercuspidal representation of
$\rho '$
be a supercuspidal representation of
 $\operatorname {GL}_k({{ F}})$
and
$\operatorname {GL}_k({{ F}})$
and
 $j\in \{0,1\}$
such that
$j\in \{0,1\}$
such that
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 $\operatorname {St}_r(\rho ')$
and
$\operatorname {St}_r(\rho ')$
and
 $\rho ^{\prime \vee \sigma }\simeq \rho '\nu ^{j}$
. Then
$\rho ^{\prime \vee \sigma }\simeq \rho '\nu ^{j}$
. Then
 $j=i$
, and either
$j=i$
, and either
 $\rho '\simeq \rho $
or
$\rho '\simeq \rho $
or
 $\rho '\simeq \rho \nu ^{r/2}$
.
$\rho '\simeq \rho \nu ^{r/2}$
.
-
Proof. If
![]() $r=1$
, the result is trivial. Let us assume that
$r=1$
, the result is trivial. Let us assume that
![]() $r{\geqslant }2$
. Fix a supercuspidal irreducible representation
$r{\geqslant }2$
. Fix a supercuspidal irreducible representation
![]() $\rho $
of
$\rho $
of
![]() $\operatorname {GL}_k({{ F}})$
such that
$\operatorname {GL}_k({{ F}})$
such that
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
. By Lemma 3.7, there is an
$\operatorname {St}_r(\rho )$
. By Lemma 3.7, there is an
![]() $i\in \mathbb {Z}$
such that
$i\in \mathbb {Z}$
such that
![]() $\rho ^{\vee \sigma }\simeq \rho \nu ^i$
. Changing
$\rho ^{\vee \sigma }\simeq \rho \nu ^i$
. Changing
![]() $\rho $
to
$\rho $
to
![]() $\rho '=\rho \nu ^s$
for some
$\rho '=\rho \nu ^s$
for some
![]() $s\in \mathbb {Z}$
does not change
$s\in \mathbb {Z}$
does not change
![]() $\operatorname {St}_r(\rho )$
, but changes i to
$\operatorname {St}_r(\rho )$
, but changes i to
![]() $i-2s$
. If r is odd or
$i-2s$
. If r is odd or
![]() $\ell =2$
, then
$\ell =2$
, then
![]() $e(\rho )$
is odd, thus
$e(\rho )$
is odd, thus
![]() $2\mathbb {Z}+e(\rho )\mathbb {Z}=\mathbb {Z}$
. This proves (1). Similarly, if r is even and
$2\mathbb {Z}+e(\rho )\mathbb {Z}=\mathbb {Z}$
. This proves (1). Similarly, if r is even and
![]() $\ell \neq 2$
, then
$\ell \neq 2$
, then
![]() $e(\rho )$
is even: we thus may assume that
$e(\rho )$
is even: we thus may assume that
![]() $i\in \{0,1\}$
, proving (2.a). Moreover, if
$i\in \{0,1\}$
, proving (2.a). Moreover, if
![]() $\rho '$
and j are as in (2.b), then
$\rho '$
and j are as in (2.b), then
![]() $j-i$
is even, thus
$j-i$
is even, thus
![]() $j=i$
. Moreover,
$j=i$
. Moreover,
![]() $\rho '$
is isomorphic to
$\rho '$
is isomorphic to
![]() $\rho \nu ^s$
for some
$\rho \nu ^s$
for some
![]() $0{\leqslant }s<e(\rho )$
such that
$0{\leqslant }s<e(\rho )$
such that
![]() $\nu ^{2st(\rho )}=1$
, thus
$\nu ^{2st(\rho )}=1$
, thus
![]() $e(\rho )$
divides
$e(\rho )$
divides
![]() $2s$
.
$2s$
.
3.6
We will need the finite field analogue of 3.4 (see [Reference Vignéras41] III.2.5 or [Reference Cabanes10] Theorem 19.3).
Proposition 3.9. Let
![]() $\boldsymbol {k}$
be a finite field of characteristic p.
$\boldsymbol {k}$
be a finite field of characteristic p.
-
1. Let
 $f{\geqslant }1$
be a positive integer and
$f{\geqslant }1$
be a positive integer and
 $\varrho $
be a supercuspidal representation of
$\varrho $
be a supercuspidal representation of
 $\operatorname {GL}_f(\boldsymbol {k})$
.
$\operatorname {GL}_f(\boldsymbol {k})$
.-
(a) For all
 $u{\geqslant }1$
, the induced representation has a unique generic irreducible subquotient, denoted
$u{\geqslant }1$
, the induced representation has a unique generic irreducible subquotient, denoted $$ \begin{align*} \varrho\times\cdots\times\varrho \quad (u\text{ times}) \end{align*} $$
$$ \begin{align*} \varrho\times\cdots\times\varrho \quad (u\text{ times}) \end{align*} $$
 $\operatorname {st}_{u}(\varrho )$
.
$\operatorname {st}_{u}(\varrho )$
.
-
(b) Let
 $e(\varrho )$
be the order of
$e(\varrho )$
be the order of
 $q^{f}$
mod
$q^{f}$
mod
 $\ell $
. The representation
$\ell $
. The representation
 $\operatorname {st}_{u}(\varrho )$
is cuspidal if and only if
$\operatorname {st}_{u}(\varrho )$
is cuspidal if and only if
 $u=1$
or
$u=1$
or
 $u=e(\varrho )\ell ^v$
for some
$u=e(\varrho )\ell ^v$
for some
 $v{\geqslant }0$
.
$v{\geqslant }0$
.
-
-
2. Let
 $\mathrm {W}$
be a cuspidal representation of
$\mathrm {W}$
be a cuspidal representation of
 $\operatorname {GL}_n(\boldsymbol {k})$
. There exist a unique integer
$\operatorname {GL}_n(\boldsymbol {k})$
. There exist a unique integer
 $u=r(\mathrm {W}){\geqslant }1$
dividing n and a unique supercuspidal representation
$u=r(\mathrm {W}){\geqslant }1$
dividing n and a unique supercuspidal representation
 $\varrho $
of
$\varrho $
of
 $\operatorname {GL}_{n/u}(\boldsymbol {k})$
such that
$\operatorname {GL}_{n/u}(\boldsymbol {k})$
such that
 $\mathrm {W}\simeq \operatorname {st}_u(\varrho )$
.
$\mathrm {W}\simeq \operatorname {st}_u(\varrho )$
.
3.7
As in the previous paragraph,
![]() $\boldsymbol {k}$
is a finite field of characteristic p. Let us recall how to parametrize cuspidal representations of
$\boldsymbol {k}$
is a finite field of characteristic p. Let us recall how to parametrize cuspidal representations of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
by regular characters ([Reference Green19], [Reference Dipper14] Theorem 3.5 and [Reference Dipper and James15, Reference James21]).
$\operatorname {GL}_n(\boldsymbol {k})$
by regular characters ([Reference Green19], [Reference Dipper14] Theorem 3.5 and [Reference Dipper and James15, Reference James21]).
Let
![]() $\overline {\boldsymbol {k}}$
be an algebraic closure of
$\overline {\boldsymbol {k}}$
be an algebraic closure of
![]() $\boldsymbol {k}$
. For any integer
$\boldsymbol {k}$
. For any integer
![]() $s{\geqslant }1$
, let
$s{\geqslant }1$
, let
![]() $\boldsymbol {k}_{s}$
be the extension of
$\boldsymbol {k}_{s}$
be the extension of
![]() $\boldsymbol {k}$
of degree s contained in
$\boldsymbol {k}$
of degree s contained in
![]() $\overline {\boldsymbol {k}}$
. Let
$\overline {\boldsymbol {k}}$
. Let
![]() $\Delta $
denote the group
$\Delta $
denote the group
![]() $\operatorname {Gal}(\boldsymbol {k}_n/\boldsymbol {k})$
. A character of
$\operatorname {Gal}(\boldsymbol {k}_n/\boldsymbol {k})$
. A character of
![]() $\boldsymbol {k}_n^\times $
is
$\boldsymbol {k}_n^\times $
is
![]() $\Delta $
-regular if it is fixed by no nontrivial element of
$\Delta $
-regular if it is fixed by no nontrivial element of
![]() $\Delta $
.
$\Delta $
.
Proposition 3.10.
-
1. Associated with any
 $\Delta $
-regular
$\Delta $
-regular
 ${\overline {\mathbb {Q}}_\ell }$
-character
${\overline {\mathbb {Q}}_\ell }$
-character
 $\xi $
of
$\xi $
of
 $\boldsymbol {k}_n^\times $
, there is a cuspidal
$\boldsymbol {k}_n^\times $
, there is a cuspidal
 ${\overline {\mathbb {Q}}_\ell }$
-representation
${\overline {\mathbb {Q}}_\ell }$
-representation
 $\mathrm {W}_{\xi }$
of
$\mathrm {W}_{\xi }$
of
 $\operatorname {GL}_n(\boldsymbol {k})$
, unique up to isomorphism, such that for all
$\operatorname {GL}_n(\boldsymbol {k})$
, unique up to isomorphism, such that for all $$ \begin{align*} \operatorname{tr} \mathrm{W}_{\xi} (x) = (-1)^{n-1}\cdot \sum\limits_{{\delta}\in\Delta} \xi(x^{\delta}) \end{align*} $$
$$ \begin{align*} \operatorname{tr} \mathrm{W}_{\xi} (x) = (-1)^{n-1}\cdot \sum\limits_{{\delta}\in\Delta} \xi(x^{\delta}) \end{align*} $$
 $x\in \boldsymbol {k}_n^{\times }$
of degree n over
$x\in \boldsymbol {k}_n^{\times }$
of degree n over
 $\boldsymbol {k}$
, where
$\boldsymbol {k}$
, where
 $\boldsymbol {k}_n^{\times }$
is considered as a maximal torus in
$\boldsymbol {k}_n^{\times }$
is considered as a maximal torus in
 $\operatorname {GL}_n(\boldsymbol {k})$
.
$\operatorname {GL}_n(\boldsymbol {k})$
.
-
2. The correspondence
induces a bijection from the set of $$ \begin{align*} \xi\mapsto\mathrm{W}_{\xi} \end{align*} $$
$$ \begin{align*} \xi\mapsto\mathrm{W}_{\xi} \end{align*} $$
 $\Delta $
-conjugacy classes of
$\Delta $
-conjugacy classes of
 $\Delta $
-regular
$\Delta $
-regular
 ${\overline {\mathbb {Q}}_\ell }$
-characters of
${\overline {\mathbb {Q}}_\ell }$
-characters of
 $\boldsymbol {k}_n^\times $
to that of isomorphism classes of cuspidal
$\boldsymbol {k}_n^\times $
to that of isomorphism classes of cuspidal
 ${\overline {\mathbb {Q}}_\ell }$
-representations of
${\overline {\mathbb {Q}}_\ell }$
-representations of
 $\operatorname {GL}_n(\boldsymbol {k})$
.
$\operatorname {GL}_n(\boldsymbol {k})$
.
By reduction mod
![]() $\ell $
, we get the following classification.
$\ell $
, we get the following classification.
Proposition 3.11.
-
1. Given any
 $\Delta $
-regular
$\Delta $
-regular
 ${\overline {\mathbb {Q}}_\ell }$
-character
${\overline {\mathbb {Q}}_\ell }$
-character
 $\xi $
of
$\xi $
of
 $\boldsymbol {k}_n^\times $
, the reduction mod
$\boldsymbol {k}_n^\times $
, the reduction mod
 $\ell $
of
$\ell $
of
 $\mathrm {W}_{\xi }$
, denoted
$\mathrm {W}_{\xi }$
, denoted
 $\overline {\mathrm {W}}_\xi $
, is irreducible and cuspidal, and it only depends on the reduction mod
$\overline {\mathrm {W}}_\xi $
, is irreducible and cuspidal, and it only depends on the reduction mod
 $\ell $
of
$\ell $
of
 $\xi $
.
$\xi $
. -
2. Reduction mod
 $\ell $
induces a bijection from the set of
$\ell $
induces a bijection from the set of
 $\Delta $
-conjugacy classes of
$\Delta $
-conjugacy classes of
 ${\overline {\mathbb {F}}_{\ell }}$
-characters of
${\overline {\mathbb {F}}_{\ell }}$
-characters of
 $\boldsymbol {k}_n^\times $
having a
$\boldsymbol {k}_n^\times $
having a
 $\Delta $
-regular lift to
$\Delta $
-regular lift to
 ${\overline {\mathbb {Q}}_\ell }$
to that of isomorphism classes of cuspidal
${\overline {\mathbb {Q}}_\ell }$
to that of isomorphism classes of cuspidal
 ${\overline {\mathbb {F}}_{\ell }}$
-representations of the group
${\overline {\mathbb {F}}_{\ell }}$
-representations of the group
 $\operatorname {GL}_n(\boldsymbol {k})$
.
$\operatorname {GL}_n(\boldsymbol {k})$
. -
3. The integer
 $r(\overline {\mathrm {W}}_\xi )$
is the greatest divisor r of n such that the reduction of
$r(\overline {\mathrm {W}}_\xi )$
is the greatest divisor r of n such that the reduction of
 $\xi $
mod
$\xi $
mod
 $\ell $
factorizes through a character of
$\ell $
factorizes through a character of
 $\boldsymbol {k}_{n/r}^\times $
.
$\boldsymbol {k}_{n/r}^\times $
.
3.8
Finally, we will need the following distinction criterion for cuspidal
![]() ${\overline {\mathbb {Q}}_\ell }$
-representations (see [Reference Hakim and Murnaghan20] Proposition 6.1 and [Reference Coniglio-Guilloton11] Lemme 3.4.10) of
${\overline {\mathbb {Q}}_\ell }$
-representations (see [Reference Hakim and Murnaghan20] Proposition 6.1 and [Reference Coniglio-Guilloton11] Lemme 3.4.10) of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
when p is odd.
$\operatorname {GL}_n(\boldsymbol {k})$
when p is odd.
Proposition 3.13. Assume that q is odd, n is even and write
![]() $n=2u$
. We consider the group
$n=2u$
. We consider the group
![]() $\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
as a Levi subgroup of
$\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
as a Levi subgroup of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
. Let
$\operatorname {GL}_n(\boldsymbol {k})$
. Let
![]() $\xi $
be a
$\xi $
be a
![]() $\Delta $
-regular
$\Delta $
-regular
![]() ${\overline {\mathbb {Q}}_\ell }$
-character of
${\overline {\mathbb {Q}}_\ell }$
-character of
![]() $\boldsymbol {k}_n^\times $
.
$\boldsymbol {k}_n^\times $
.
-
1. The following assertions are equivalent.
-
(a) The cuspidal
 ${\overline {\mathbb {Q}}_\ell }$
-representation
${\overline {\mathbb {Q}}_\ell }$
-representation
 $\mathrm {W}_\xi $
is
$\mathrm {W}_\xi $
is
 $\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-distinguished.
$\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-distinguished. -
(b) The space of
 $\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-invariant linear forms on
$\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-invariant linear forms on
 $\mathrm {W}_\xi $
has
$\mathrm {W}_\xi $
has
 ${\overline {\mathbb {Q}}_\ell }$
-dimension
${\overline {\mathbb {Q}}_\ell }$
-dimension
 $1$
.
$1$
. -
(c) The cuspidal
 ${\overline {\mathbb {Q}}_\ell }$
-representation
${\overline {\mathbb {Q}}_\ell }$
-representation
 $\mathrm {W}_\xi $
is self-dual.
$\mathrm {W}_\xi $
is self-dual. -
(d) The character
 $\xi $
is trivial on
$\xi $
is trivial on
 $\boldsymbol {k}_u^\times $
.
$\boldsymbol {k}_u^\times $
.
-
-
2. Assume that the conditions of (1) are satisfied, and fix an element
 $\alpha \in \boldsymbol {k}_n^\times $
such that
$\alpha \in \boldsymbol {k}_n^\times $
such that
 $\alpha \notin \boldsymbol {k}_u^\times $
and
$\alpha \notin \boldsymbol {k}_u^\times $
and
 $\alpha ^2\in \boldsymbol {k}_u^\times $
. The element (3.3)where
$\alpha ^2\in \boldsymbol {k}_u^\times $
. The element (3.3)where $$ \begin{align} s = \begin{pmatrix} 0 & \mathrm{id} \\ \mathrm{id} & 0 \end{pmatrix} \in{\operatorname{GL}}_n(\boldsymbol{k}), \end{align} $$
$$ \begin{align} s = \begin{pmatrix} 0 & \mathrm{id} \\ \mathrm{id} & 0 \end{pmatrix} \in{\operatorname{GL}}_n(\boldsymbol{k}), \end{align} $$
 $\mathrm {id }$
is the identity in
$\mathrm {id }$
is the identity in
 $\operatorname {GL}_{u}(\boldsymbol {k})$
, normalizes the group
$\operatorname {GL}_{u}(\boldsymbol {k})$
, normalizes the group
 $\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
and acts on the
$\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
and acts on the
 ${\overline {\mathbb {Q}}_\ell }$
-vector space of
${\overline {\mathbb {Q}}_\ell }$
-vector space of
 $\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-invariant linear forms on
$\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-invariant linear forms on
 $\mathrm {W}_\xi $
by the sign
$\mathrm {W}_\xi $
by the sign
 $-\xi (\alpha )$
.
$-\xi (\alpha )$
.
Remark 3.14. Suppose that
![]() $\mathrm {W}_\xi $
is
$\mathrm {W}_\xi $
is
![]() $\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-distinguished. By [Reference Sécherre35] Lemma 2.6, the cuspidal
$\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-distinguished. By [Reference Sécherre35] Lemma 2.6, the cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation
${\overline {\mathbb {F}}_{\ell }}$
-representation
![]() $\overline {\mathrm {W}}_\xi $
is
$\overline {\mathrm {W}}_\xi $
is
![]() $\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-distinguished as well. More precisely, if we fix a nonzero
$\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-distinguished as well. More precisely, if we fix a nonzero
![]() $\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-invariant
$\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-invariant
![]() ${\overline {\mathbb {Q}}_\ell }$
-linear form
${\overline {\mathbb {Q}}_\ell }$
-linear form
![]() $\mathit {\Lambda }$
on
$\mathit {\Lambda }$
on
![]() $\mathrm {W}_\xi $
together with a
$\mathrm {W}_\xi $
together with a
![]() $\operatorname {GL}_n(\boldsymbol {k})$
-stable
$\operatorname {GL}_n(\boldsymbol {k})$
-stable
![]() ${\overline {\mathbb {Z}}_\ell }$
-lattice
${\overline {\mathbb {Z}}_\ell }$
-lattice
![]() ${L}\subseteq \mathrm {W}_\xi $
, then the associated
${L}\subseteq \mathrm {W}_\xi $
, then the associated
![]() ${\overline {\mathbb {F}}_{\ell }}$
-linear form
${\overline {\mathbb {F}}_{\ell }}$
-linear form
is nonzero and
![]() $\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-invariant. Moreover, if s acts on
$\operatorname {GL}_u(\boldsymbol {k})\times \operatorname {GL}_u(\boldsymbol {k})$
-invariant. Moreover, if s acts on
![]() $\mathit {\Lambda }$
by a sign
$\mathit {\Lambda }$
by a sign
![]() $c\in \{-1,1\}\subseteq \overline {\mathbb {Q}}{}^\times _\ell $
, then s acts on
$c\in \{-1,1\}\subseteq \overline {\mathbb {Q}}{}^\times _\ell $
, then s acts on
![]() $\overline {\mathit {\Lambda }}$
by the image of c in
$\overline {\mathit {\Lambda }}$
by the image of c in
![]() $\overline {\mathbb {F}}{}^\times _\ell $
.
$\overline {\mathbb {F}}{}^\times _\ell $
.
4 Reduction to level zero
In this section, p is odd,
![]() $\ell $
is any prime number different from p and
$\ell $
is any prime number different from p and
![]() ${ R}$
has characteristic
${ R}$
has characteristic
![]() $0$
or
$0$
or
![]() $\ell $
. Let us fix a positive integer
$\ell $
. Let us fix a positive integer
![]() $n{\geqslant }1$
, and set
$n{\geqslant }1$
, and set
![]() ${ G}=\operatorname {GL}_n({{ F}})$
. We fix a character
${ G}=\operatorname {GL}_n({{ F}})$
. We fix a character
which is trivial on
![]() $\mathfrak {p}_{ F}$
but not on
$\mathfrak {p}_{ F}$
but not on ![]() .
.
4.1
Let us recall the definitions and main results of [Reference Bushnell and Kutzko9, Reference Bushnell and Henniart8, Reference Mínguez and Sécherre30, Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] which we will need.
Let
![]() $[\mathfrak {a},{\beta }]$
be a simple stratum in the algebra
$[\mathfrak {a},{\beta }]$
be a simple stratum in the algebra
![]() $\boldsymbol {\mathsf {M}}_{n}({ F})$
of
$\boldsymbol {\mathsf {M}}_{n}({ F})$
of
![]() $n\times n$
matrices with entries in
$n\times n$
matrices with entries in
![]() ${ F}$
. Recall that
${ F}$
. Recall that
![]() $\mathfrak {a}$
is a hereditary
$\mathfrak {a}$
is a hereditary ![]() -order of
-order of
![]() $\boldsymbol {\mathsf {M}}_{n}({ F})$
and
$\boldsymbol {\mathsf {M}}_{n}({ F})$
and
![]() ${\beta }$
is an element of
${\beta }$
is an element of
![]() $\boldsymbol {\mathsf {M}}_{n}({ F})$
such that
$\boldsymbol {\mathsf {M}}_{n}({ F})$
such that
-
○ the
 ${ F}$
-algebra
${ F}$
-algebra
 ${ E}={ F}[{\beta }]$
is a field, and
${ E}={ F}[{\beta }]$
is a field, and -
○ the multiplicative group
 ${ E}^\times $
normalizes
${ E}^\times $
normalizes
 $\mathfrak {a}$
$\mathfrak {a}$
(plus an extra technical condition on
![]() ${\beta }$
which is not necessary to recall here: See [Reference Bushnell and Kutzko9] 1.5.5).
${\beta }$
which is not necessary to recall here: See [Reference Bushnell and Kutzko9] 1.5.5).
Let ![]() be the normalizer of
be the normalizer of
![]() $\mathfrak {a}$
in
$\mathfrak {a}$
in
![]() ${ G}$
and
${ G}$
and
![]() $\mathfrak {p}_{\mathfrak {a}}$
be its Jacobson radical, and set
$\mathfrak {p}_{\mathfrak {a}}$
be its Jacobson radical, and set
![]() $\mathrm {U}^1_{\mathfrak {a}} = 1 + \mathfrak {p}_{\mathfrak {a}}$
. Let
$\mathrm {U}^1_{\mathfrak {a}} = 1 + \mathfrak {p}_{\mathfrak {a}}$
. Let
![]() ${ B}$
be the centralizer of
${ B}$
be the centralizer of
![]() ${ E}$
in
${ E}$
in
![]() $\boldsymbol {\mathsf {M}}_{n}({ F})$
. The intersection
$\boldsymbol {\mathsf {M}}_{n}({ F})$
. The intersection
![]() $\mathfrak {b}=\mathfrak {a}\cap { B}$
is a hereditary order in
$\mathfrak {b}=\mathfrak {a}\cap { B}$
is a hereditary order in
![]() ${ B}$
.
${ B}$
.
Associated with
![]() $[\mathfrak {a},{\beta }]$
in [Reference Bushnell and Kutzko9] Chapter 3, there are compact mod centre open subgroups
$[\mathfrak {a},{\beta }]$
in [Reference Bushnell and Kutzko9] Chapter 3, there are compact mod centre open subgroups
and a nonempty finite set ![]() of characters of
of characters of
![]() ${{H}}^1(\mathfrak {a},{\beta })$
called simple characters, depending on the choice of the character (4.1). We write
${{H}}^1(\mathfrak {a},{\beta })$
called simple characters, depending on the choice of the character (4.1). We write
![]() $\mathbf {J}=\mathbf {J}(\mathfrak {a},{\beta })$
,
$\mathbf {J}=\mathbf {J}(\mathfrak {a},{\beta })$
,
![]() $\mathbf {J}^0=\mathbf {J}^0(\mathfrak {a},{\beta })$
,
$\mathbf {J}^0=\mathbf {J}^0(\mathfrak {a},{\beta })$
,
![]() $\mathbf {J}^1=\mathbf {J}^1(\mathfrak {a},{\beta })$
and
$\mathbf {J}^1=\mathbf {J}^1(\mathfrak {a},{\beta })$
and
![]() ${{H}}^1={{H}}^1(\mathfrak {a},{\beta })$
for simplicity.
${{H}}^1={{H}}^1(\mathfrak {a},{\beta })$
for simplicity.
We will only be interested in the case where
![]() $\mathfrak {b}$
is a maximal order in
$\mathfrak {b}$
is a maximal order in
![]() ${ B}$
, in which case the simple stratum
${ B}$
, in which case the simple stratum
![]() $[\mathfrak {a},{\beta }]$
and the simple characters in
$[\mathfrak {a},{\beta }]$
and the simple characters in ![]() are said to be maximal. For the following result, see [Reference Bushnell and Henniart8] 2.1, 3.2 and [Reference Bushnell and Kutzko9] 5.1.1.
are said to be maximal. For the following result, see [Reference Bushnell and Henniart8] 2.1, 3.2 and [Reference Bushnell and Kutzko9] 5.1.1.
Proposition 4.1. Let
![]() $[\mathfrak {a},{\beta }]$
be a maximal simple stratum.
$[\mathfrak {a},{\beta }]$
be a maximal simple stratum.
-
1. The group
 $\mathbf {J}^0$
is the unique maximal compact subgroup of
$\mathbf {J}^0$
is the unique maximal compact subgroup of
 $\mathbf {J}$
, and
$\mathbf {J}$
, and
 $\mathbf {J}^1$
is its unique maximal normal pro-p-subgroup.
$\mathbf {J}^1$
is its unique maximal normal pro-p-subgroup. -
2. One has
 $\mathbf {J}={ E}^\times \mathbf {J}^0=(\mathbf {J}\cap { B}^\times )\mathbf {J}^1$
and (4.2)
$\mathbf {J}={ E}^\times \mathbf {J}^0=(\mathbf {J}\cap { B}^\times )\mathbf {J}^1$
and (4.2)
-
3. There is an isomorphism of
 ${ E}$
-algebras (4.3)sending
${ E}$
-algebras (4.3)sending $$ \begin{align} { B}\simeq\boldsymbol{\mathsf{M}}_m({ E}), \quad m=n/[{ E}:{ F}], \end{align} $$
$$ \begin{align} { B}\simeq\boldsymbol{\mathsf{M}}_m({ E}), \quad m=n/[{ E}:{ F}], \end{align} $$
 $\mathfrak {b}^\times $
to the maximal compact open subgroup
$\mathfrak {b}^\times $
to the maximal compact open subgroup  , which induces isomorphisms (4.4)where
, which induces isomorphisms (4.4)where $$ \begin{align} \mathbf{J}^0/\mathbf{J}^1 \simeq \mathfrak{b}^\times/\mathrm{U}^1_{\mathfrak{b}} \simeq \operatorname{GL}_{m}(\boldsymbol{l}), \end{align} $$
$$ \begin{align} \mathbf{J}^0/\mathbf{J}^1 \simeq \mathfrak{b}^\times/\mathrm{U}^1_{\mathfrak{b}} \simeq \operatorname{GL}_{m}(\boldsymbol{l}), \end{align} $$
 $\boldsymbol {l}$
is the residue field of
$\boldsymbol {l}$
is the residue field of
 ${ E}$
.
${ E}$
.
-
4. Given any simple character
 , we have
, we have-
(a) the normalizer of
 ${\theta }$
in
${\theta }$
in
 ${ G}$
is equal to
${ G}$
is equal to
 $\mathbf {J}$
, and
$\mathbf {J}$
, and -
(b) there is an irreducible representation
 $\eta $
of
$\eta $
of
 $\mathbf {J}^1$
, unique up to isomorphism, whose restriction to
$\mathbf {J}^1$
, unique up to isomorphism, whose restriction to
 ${{H}}^1$
contains
${{H}}^1$
contains
 ${\theta }$
, and such a representation extends to
${\theta }$
, and such a representation extends to
 $\mathbf {J}$
.
$\mathbf {J}$
.
-
The representation
![]() $\eta $
of (4.b) is called the Heisenberg representation associated with
$\eta $
of (4.b) is called the Heisenberg representation associated with
![]() ${\theta }$
. If
${\theta }$
. If
![]() $\boldsymbol {\kappa }$
is a representation of
$\boldsymbol {\kappa }$
is a representation of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\eta $
, any other extension of
$\eta $
, any other extension of
![]() $\eta $
to
$\eta $
to
![]() $\mathbf {J}$
has the form
$\mathbf {J}$
has the form
![]() $\boldsymbol {\kappa }\boldsymbol {\xi }$
for a unique character
$\boldsymbol {\kappa }\boldsymbol {\xi }$
for a unique character
![]() $\boldsymbol {\xi }$
of
$\boldsymbol {\xi }$
of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
.
$\mathbf {J}^1$
.
Remark 4.2.
-
1. An isomorphism (4.3) as in Proposition 4.1(3) comes from the choice of an
 -basis of an
-basis of an  -lattice
-lattice  in
in
 ${ F}^n$
whose endomorphism algebra is
${ F}^n$
whose endomorphism algebra is
 $\mathfrak {b}$
.
$\mathfrak {b}$
. -
2. Changing the isomorphism (4.3), that is, changing the basis of
 above, has the effect of conjugating the identification (4.4) by an inner automorphism of
above, has the effect of conjugating the identification (4.4) by an inner automorphism of
 $\operatorname {GL}_{m}(\boldsymbol {l})$
.
$\operatorname {GL}_{m}(\boldsymbol {l})$
.
A character
![]() ${\theta }$
of an open pro-p-subgroup
${\theta }$
of an open pro-p-subgroup
![]() ${{H}}$
of
${{H}}$
of
![]() ${ G}$
will be called a maximal simple character if there is a maximal simple stratum
${ G}$
will be called a maximal simple character if there is a maximal simple stratum
![]() $[\mathfrak {a},{\beta }]$
in
$[\mathfrak {a},{\beta }]$
in
![]() $\boldsymbol {\mathsf {M}}_n({ F})$
such that
$\boldsymbol {\mathsf {M}}_n({ F})$
such that
![]() ${{H}}={{H}}^1(\mathfrak {a},{\beta })$
and
${{H}}={{H}}^1(\mathfrak {a},{\beta })$
and ![]() . Given a maximal simple character
. Given a maximal simple character
![]() ${\theta }$
of
${\theta }$
of
![]() ${ G}$
, we will write
${ G}$
, we will write
![]() ${{H}}^1_{\theta }$
for the group on which
${{H}}^1_{\theta }$
for the group on which
![]() ${\theta }$
is defined,
${\theta }$
is defined,
![]() $\mathbf {J}^{}_{\theta }$
for its
$\mathbf {J}^{}_{\theta }$
for its
![]() ${ G}$
-normalizer,
${ G}$
-normalizer,
![]() $\mathbf {J}^0_{\theta }$
for its unique maximal compact subgroup,
$\mathbf {J}^0_{\theta }$
for its unique maximal compact subgroup,
![]() $\mathbf {J}^1_{\theta }$
for its unique maximal normal pro-p-subgroup and
$\mathbf {J}^1_{\theta }$
for its unique maximal normal pro-p-subgroup and
![]() ${ T}$
for the maximal tamely ramified extension of
${ T}$
for the maximal tamely ramified extension of
![]() ${ F}$
in
${ F}$
in
![]() ${ E}={ F}[{\beta }]$
. The following result shows how the latter depends on the choice of
${ E}={ F}[{\beta }]$
. The following result shows how the latter depends on the choice of
![]() $[\mathfrak {a},{\beta }]$
(see [Reference Bushnell and Henniart8] 2.1, 2.5 and 2.6).
$[\mathfrak {a},{\beta }]$
(see [Reference Bushnell and Henniart8] 2.1, 2.5 and 2.6).
Proposition 4.3. Let
![]() $[\mathfrak {a}',{\beta }']$
be a simple stratum such that
$[\mathfrak {a}',{\beta }']$
be a simple stratum such that ![]() , and set
, and set
![]() ${ E}'={ F}[{\beta }']$
.
${ E}'={ F}[{\beta }']$
.
-
1. The orders
 $\mathfrak {a}$
,
$\mathfrak {a}$
,
 $\mathfrak {a}'$
are equal and
$\mathfrak {a}'$
are equal and
 ${ E}$
,
${ E}$
,
 ${ E}'$
have the same degree over
${ E}'$
have the same degree over
 ${ F}$
.
${ F}$
. -
2. The simple stratum
 $[\mathfrak {a},{\beta }']$
is maximal.
$[\mathfrak {a},{\beta }']$
is maximal. -
3. The maximal tamely ramified extension of
 ${ F}$
in
${ F}$
in
 ${ E}'$
is
${ E}'$
is
 $\mathbf {J}_{\theta }^1$
-conjugate to
$\mathbf {J}_{\theta }^1$
-conjugate to
 ${ T}$
.
${ T}$
.
It follows that the
![]() ${ G}$
-conjugacy class of the simple character
${ G}$
-conjugacy class of the simple character
![]() ${\theta }$
uniquely determines the integer m in equation (4.3), as well as the extension
${\theta }$
uniquely determines the integer m in equation (4.3), as well as the extension
![]() ${ T}$
up to
${ T}$
up to
![]() ${ G}$
-conjugacy (or equivalently up to
${ G}$
-conjugacy (or equivalently up to
![]() ${ F}$
-isomorphism). However, the fields
${ F}$
-isomorphism). However, the fields
![]() ${ E}$
,
${ E}$
,
![]() ${ E}'$
need not be isomorphic (see [Reference Bushnell and Henniart8] Example 2.1).
${ E}'$
need not be isomorphic (see [Reference Bushnell and Henniart8] Example 2.1).
4.2
In this paragraph only, we let n vary among all positive integers, and consider the set

where the union is taken over all maximal simple strata of
![]() $\boldsymbol {\mathsf {M}}_n({ F})$
, for any
$\boldsymbol {\mathsf {M}}_n({ F})$
, for any
![]() $n{\geqslant }1$
. It is endowed with an equivalence relation called endo-equivalence ([Reference Bushnell and Henniart6, Reference Bushnell and Henniart7]). An equivalence class for this equivalence relation is called an endo-class (see [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] 3.2).
$n{\geqslant }1$
. It is endowed with an equivalence relation called endo-equivalence ([Reference Bushnell and Henniart6, Reference Bushnell and Henniart7]). An equivalence class for this equivalence relation is called an endo-class (see [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] 3.2).
Given a maximal simple character ![]() with endo-class
with endo-class
![]() $\boldsymbol {\Theta }$
, the degree
$\boldsymbol {\Theta }$
, the degree
![]() $[{ E}:{ F}]$
and the
$[{ E}:{ F}]$
and the
![]() ${ F}$
-isomorphism class of its tame parameter field
${ F}$
-isomorphism class of its tame parameter field
![]() ${ T}$
only depend on
${ T}$
only depend on
![]() $\boldsymbol {\Theta }$
. They are called the degree and tame parameter field of
$\boldsymbol {\Theta }$
. They are called the degree and tame parameter field of
![]() $\boldsymbol {\Theta }$
, respectively.
$\boldsymbol {\Theta }$
, respectively.
For a given n, any two maximal simple characters of
![]() $\operatorname {GL}_n({ F})$
are endo-equivalent if and only if they are
$\operatorname {GL}_n({ F})$
are endo-equivalent if and only if they are
![]() $\operatorname {GL}_n({ F})$
-conjugate.
$\operatorname {GL}_n({ F})$
-conjugate.
Remark 4.4. Note that endo-equivalence is defined in [Reference Bushnell and Henniart6, Reference Bushnell and Henniart7] for arbitrary simple characters, not only for maximal ones, but we will not need this extra generality.
4.3
We go back to the situation of Paragraph 4.1, assuming further that the character
![]() $\psi $
of equation (4.1) is
$\psi $
of equation (4.1) is
![]() $\sigma $
-invariant, which is possible since
$\sigma $
-invariant, which is possible since
![]() $p\neq 2$
. As in [Reference Sécherre35], we will say that:
$p\neq 2$
. As in [Reference Sécherre35], we will say that:
-
○ a simple stratum
 $[\mathfrak {a},{\beta }]$
in
$[\mathfrak {a},{\beta }]$
in
 $\boldsymbol {\mathsf {M}}_n({ F})$
is
$\boldsymbol {\mathsf {M}}_n({ F})$
is
 $\sigma $
-self-dual if
$\sigma $
-self-dual if
 $\mathfrak {a}$
is
$\mathfrak {a}$
is
 $\sigma $
-stable and
$\sigma $
-stable and
 $\sigma ({\beta })=-{\beta }$
,
$\sigma ({\beta })=-{\beta }$
, -
○ a simple character
 ${\theta }$
is
${\theta }$
is
 $\sigma $
-self-dual if the group
$\sigma $
-self-dual if the group
 ${{H}}^1_{\theta }$
is
${{H}}^1_{\theta }$
is
 $\sigma $
-stable and
$\sigma $
-stable and
 ${\theta }^{-1}\circ \sigma ={\theta }$
,
${\theta }^{-1}\circ \sigma ={\theta }$
, -
○ an endo-class
 $\boldsymbol {\Theta }$
of (maximal) simple characters is
$\boldsymbol {\Theta }$
of (maximal) simple characters is
 $\sigma $
-self-dual if for some (or equivalently for any)
$\sigma $
-self-dual if for some (or equivalently for any)
 ${\theta }\in \boldsymbol {\Theta }$
, the character
${\theta }\in \boldsymbol {\Theta }$
, the character
 ${\theta }^{-1}\circ \sigma $
is in
${\theta }^{-1}\circ \sigma $
is in
 $\boldsymbol {\Theta }$
.
$\boldsymbol {\Theta }$
.
Proposition 4.5. Let
![]() ${\theta }$
be a
${\theta }$
be a
![]() $\sigma $
-self-dual maximal simple character.
$\sigma $
-self-dual maximal simple character.
-
1. There is a
 $\sigma $
-stable simple stratum
$\sigma $
-stable simple stratum
 $[\mathfrak {a},{\beta }]$
such that
$[\mathfrak {a},{\beta }]$
such that  .
. -
2. Let
 ${ E}_0$
be the
${ E}_0$
be the
 $\sigma $
-fixed points of
$\sigma $
-fixed points of
 ${ E}$
and
${ E}$
and
 $\boldsymbol {l}_0$
be its residue field. There is an isomorphism (4.3) inducing an isomorphism (4.4) which transports the action of
$\boldsymbol {l}_0$
be its residue field. There is an isomorphism (4.3) inducing an isomorphism (4.4) which transports the action of
 $\sigma $
on
$\sigma $
on
 $\mathbf {J}^0/\mathbf {J}^1$
to
$\mathbf {J}^0/\mathbf {J}^1$
to-
(a) the action of the nontrivial element of
 $\operatorname {Gal}(\boldsymbol {l}/\boldsymbol {l}_0)$
on
$\operatorname {Gal}(\boldsymbol {l}/\boldsymbol {l}_0)$
on
 $\operatorname {GL}_m(\boldsymbol {l})$
if
$\operatorname {GL}_m(\boldsymbol {l})$
if
 ${ E}/{ E}_0$
is unramified,
${ E}/{ E}_0$
is unramified, -
(b) the adjoint action of
(4.5)on $$ \begin{align} \begin{pmatrix} -\mathrm{id}_{i} & 0 \\ 0 & \mathrm{id}_{m-i} \end{pmatrix} \in \operatorname{GL}_m(\boldsymbol{l}) \end{align} $$
$$ \begin{align} \begin{pmatrix} -\mathrm{id}_{i} & 0 \\ 0 & \mathrm{id}_{m-i} \end{pmatrix} \in \operatorname{GL}_m(\boldsymbol{l}) \end{align} $$
 $\operatorname {GL}_m(\boldsymbol {l})$
if
$\operatorname {GL}_m(\boldsymbol {l})$
if
 ${ E}/{ E}_0$
is ramified, for a uniquely determined integer
${ E}/{ E}_0$
is ramified, for a uniquely determined integer
 $i\in \{0,\dots ,\lfloor m/2\rfloor \}$
.
$i\in \{0,\dots ,\lfloor m/2\rfloor \}$
.
-
If
![]() ${\theta }$
is a
${\theta }$
is a
![]() $\sigma $
-self-dual maximal simple character, we will write
$\sigma $
-self-dual maximal simple character, we will write
![]() ${ T}_0$
for the maximal tamely ramified extension of
${ T}_0$
for the maximal tamely ramified extension of
![]() ${ F}_0$
in
${ F}_0$
in
![]() ${ E}_0$
, that is,
${ E}_0$
, that is,
![]() ${ T}_0={ T}\cap { E}_0$
. By [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Lemma 4.10, the canonical homomorphism
${ T}_0={ T}\cap { E}_0$
. By [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Lemma 4.10, the canonical homomorphism
is an isomorphism. Also,
![]() ${ T}/{ T}_0$
and
${ T}/{ T}_0$
and
![]() ${ E}/{ E}_0$
have the same ramification index. By [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Lemma 4.29, the
${ E}/{ E}_0$
have the same ramification index. By [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Lemma 4.29, the
![]() ${ F}_0$
-isomorphism class of
${ F}_0$
-isomorphism class of
![]() ${ T}_0$
is uniquely determined by the endo-class
${ T}_0$
is uniquely determined by the endo-class
![]() $\boldsymbol {\Theta }$
of
$\boldsymbol {\Theta }$
of
![]() ${\theta }$
. And it follows from the isomorphism (4.6) that the
${\theta }$
. And it follows from the isomorphism (4.6) that the
![]() ${ F}_0$
-isomorphism class of
${ F}_0$
-isomorphism class of
![]() ${ T}_0$
determines the
${ T}_0$
determines the
![]() ${ F}$
-isomorphism class of
${ F}$
-isomorphism class of
![]() ${ T}$
.
${ T}$
.
The following result is given by [Reference Sécherre35] Proposition 6.12, Lemma 6.20 and [Reference Sécherre36] Lemme 3.28. (The latter reference in [Reference Sécherre36] is for representations with coefficients in
![]() ${ R}=\mathbb {C}$
, but its proof is still valid in the
${ R}=\mathbb {C}$
, but its proof is still valid in the
![]() $\ell $
-modular case.)
$\ell $
-modular case.)
Proposition 4.6. Let
![]() ${\theta }$
be a
${\theta }$
be a
![]() $\sigma $
-self-dual maximal simple character.
$\sigma $
-self-dual maximal simple character.
-
1. The Heisenberg representation
 $\eta $
of
$\eta $
of
 ${\theta }$
is
${\theta }$
is
 $\sigma $
-self-dual and
$\sigma $
-self-dual and
 $\mathbf {J}^1\cap { G}^\sigma $
-distinguished, and the space
$\mathbf {J}^1\cap { G}^\sigma $
-distinguished, and the space
 $\operatorname {Hom}_{\mathbf {J}^1\cap { G}^\sigma }(\eta , { R})$
has dimension
$\operatorname {Hom}_{\mathbf {J}^1\cap { G}^\sigma }(\eta , { R})$
has dimension
 $1$
.
$1$
. -
2. For any representation
 $\boldsymbol {\kappa }$
of
$\boldsymbol {\kappa }$
of
 $\mathbf {J}$
extending
$\mathbf {J}$
extending
 $\eta $
, there are
$\eta $
, there are-
(a) a unique character
 $\boldsymbol {\xi }$
of
$\boldsymbol {\xi }$
of
 $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
 $\mathbf {J}^1$
such that
$\mathbf {J}^1$
such that
 $\boldsymbol {\kappa }^{\vee \sigma }$
is isomorphic to
$\boldsymbol {\kappa }^{\vee \sigma }$
is isomorphic to
 $\boldsymbol {\kappa }\boldsymbol {\xi }$
,
$\boldsymbol {\kappa }\boldsymbol {\xi }$
, -
(b) a unique character
 $\chi $
of
$\chi $
of
 $\mathbf {J}\cap { G}^\sigma $
trivial on
$\mathbf {J}\cap { G}^\sigma $
trivial on
 $\mathbf {J}^1\cap { G}^\sigma $
such that (4.7)and the restriction of
$\mathbf {J}^1\cap { G}^\sigma $
such that (4.7)and the restriction of $$ \begin{align} \operatorname{Hom}_{\mathbf{J}^1\cap{ G}^\sigma}(\eta,{ R}) = \operatorname{Hom}_{\mathbf{J}\cap{ G}^\sigma}(\boldsymbol{\kappa},\chi^{-1}), \end{align} $$
$$ \begin{align} \operatorname{Hom}_{\mathbf{J}^1\cap{ G}^\sigma}(\eta,{ R}) = \operatorname{Hom}_{\mathbf{J}\cap{ G}^\sigma}(\boldsymbol{\kappa},\chi^{-1}), \end{align} $$
 $\boldsymbol {\xi }$
to
$\boldsymbol {\xi }$
to
 $\mathbf {J}\cap { G}^\sigma $
is equal to
$\mathbf {J}\cap { G}^\sigma $
is equal to
 $\chi ^2$
.
$\chi ^2$
.
-
-
3. Given a representation
 $\boldsymbol {\kappa }$
as in (2) and an irreducible representation
$\boldsymbol {\kappa }$
as in (2) and an irreducible representation
 $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
 $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
 $\mathbf {J}^1$
, the canonical linear map (4.8)is an isomorphism of
$\mathbf {J}^1$
, the canonical linear map (4.8)is an isomorphism of $$ \begin{align} \operatorname{Hom}_{\mathbf{J}^1\cap{ G}^\sigma}(\eta, { R}) \otimes \operatorname{Hom}_{\mathbf{J}\cap{ G}^\sigma}(\boldsymbol{\tau},\chi) \to \operatorname{Hom}_{\mathbf{J}\cap{ G}^\sigma}(\boldsymbol{\kappa}\otimes\boldsymbol{\tau},{ R}) \end{align} $$
$$ \begin{align} \operatorname{Hom}_{\mathbf{J}^1\cap{ G}^\sigma}(\eta, { R}) \otimes \operatorname{Hom}_{\mathbf{J}\cap{ G}^\sigma}(\boldsymbol{\tau},\chi) \to \operatorname{Hom}_{\mathbf{J}\cap{ G}^\sigma}(\boldsymbol{\kappa}\otimes\boldsymbol{\tau},{ R}) \end{align} $$
 ${ R}$
-vector spaces.
${ R}$
-vector spaces.
-
4. There exists a
 $\sigma $
-self-dual representation of
$\sigma $
-self-dual representation of
 $\mathbf {J}$
extending
$\mathbf {J}$
extending
 $\eta $
.
$\eta $
.
Conversely, let
![]() $\boldsymbol {\Theta }$
be a
$\boldsymbol {\Theta }$
be a
![]() $\sigma $
-self-dual endo-class of degree dividing n. By [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Section 4, it contains a
$\sigma $
-self-dual endo-class of degree dividing n. By [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Section 4, it contains a
![]() $\sigma $
-self-dual maximal simple character
$\sigma $
-self-dual maximal simple character
![]() ${\theta }$
in
${\theta }$
in
![]() ${ G}$
, and we have the following classification.
${ G}$
, and we have the following classification.
Proposition 4.7. Let
![]() ${ T}/{ T}_0$
be the quadratic extension associated with
${ T}/{ T}_0$
be the quadratic extension associated with
![]() $\boldsymbol {\Theta }$
as above, and let us write
$\boldsymbol {\Theta }$
as above, and let us write
![]() $m=n/\deg (\boldsymbol {\Theta })$
.
$m=n/\deg (\boldsymbol {\Theta })$
.
-
1. If
 ${ T}/{ T}_0$
is unramified, the
${ T}/{ T}_0$
is unramified, the
 ${ G}$
-conjugacy class of
${ G}$
-conjugacy class of
 ${\theta }$
contains a unique
${\theta }$
contains a unique
 ${ G}^\sigma $
-conjugacy class of
${ G}^\sigma $
-conjugacy class of
 $\sigma $
-self-dual simple characters.
$\sigma $
-self-dual simple characters. -
2. If
 ${ T}/{ T}_0$
is ramified, the number of
${ T}/{ T}_0$
is ramified, the number of
 ${ G}^\sigma $
-conjugacy classes of
${ G}^\sigma $
-conjugacy classes of
 $\sigma $
-self-dual simple characters in the
$\sigma $
-self-dual simple characters in the
 ${ G}$
-conjugacy class of
${ G}$
-conjugacy class of
 ${\theta }$
is equal to
${\theta }$
is equal to
 $\lfloor m/2\rfloor +1$
, each class corresponding bijectively to an integer
$\lfloor m/2\rfloor +1$
, each class corresponding bijectively to an integer
 $i\in \{0,\dots ,\lfloor m/2\rfloor \}$
characterized by Proposition 4.5(2.b).
$i\in \{0,\dots ,\lfloor m/2\rfloor \}$
characterized by Proposition 4.5(2.b).
Remark 4.8. When
![]() ${ T}/{ T}_0$
is ramified, we define (as in [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3, Reference Sécherre35]) the index of a
${ T}/{ T}_0$
is ramified, we define (as in [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3, Reference Sécherre35]) the index of a
![]() $\sigma $
-self-dual maximal simple character
$\sigma $
-self-dual maximal simple character
![]() ${\theta }$
to be the integer
${\theta }$
to be the integer
![]() $i\in \{0,\dots ,\lfloor m/2\rfloor \}$
associated with its
$i\in \{0,\dots ,\lfloor m/2\rfloor \}$
associated with its
![]() ${ G}^\sigma $
-conjugacy class. By [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Remark 4.28 or [Reference Sécherre35] 5.D, if
${ G}^\sigma $
-conjugacy class. By [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Remark 4.28 or [Reference Sécherre35] 5.D, if
![]() ${\theta }$
has index
${\theta }$
has index
![]() $0$
and if
$0$
and if
for some
![]() $i\in \{0,\dots ,\lfloor m/2\rfloor \}$
, then
$i\in \{0,\dots ,\lfloor m/2\rfloor \}$
, then
![]() ${\theta }^{y_i}$
is a
${\theta }^{y_i}$
is a
![]() $\sigma $
-self-dual maximal simple character of index i.
$\sigma $
-self-dual maximal simple character of index i.
4.4
Let
![]() ${\theta }$
be a maximal simple character, and
${\theta }$
be a maximal simple character, and
![]() $[\mathfrak {a},{\beta }]$
be a simple stratum such that
$[\mathfrak {a},{\beta }]$
be a simple stratum such that ![]() . As in 4.1, write
. As in 4.1, write
![]() $\mathbf {J}=\mathbf {J}_{\theta }^{}$
,
$\mathbf {J}=\mathbf {J}_{\theta }^{}$
,
![]() $\mathbf {J}^0=\mathbf {J}^0_{\theta }$
,
$\mathbf {J}^0=\mathbf {J}^0_{\theta }$
,
![]() $\mathbf {J}^1=\mathbf {J}^1_{\theta }$
and
$\mathbf {J}^1=\mathbf {J}^1_{\theta }$
and
![]() ${{H}}^1={{H}}^1_{\theta }$
. Let
${{H}}^1={{H}}^1_{\theta }$
. Let
![]() $\eta $
be the Heisenberg representation of
$\eta $
be the Heisenberg representation of
![]() $\mathbf {J}^1$
associated with
$\mathbf {J}^1$
associated with
![]() ${\theta }$
. In this paragraph, we give a slightly generalized version of [Reference Bushnell and Henniart8] 3.3.
${\theta }$
. In this paragraph, we give a slightly generalized version of [Reference Bushnell and Henniart8] 3.3.
Fix an ![]() -lattice
-lattice ![]() in
in
![]() ${ V}={ F}^n$
whose endomorphism algebra is
${ V}={ F}^n$
whose endomorphism algebra is
![]() $\mathfrak {b}$
. (It is uniquely determined up to homothety as
$\mathfrak {b}$
. (It is uniquely determined up to homothety as
![]() $\mathfrak {b}$
is maximal.) Fix a divisor
$\mathfrak {b}$
is maximal.) Fix a divisor
![]() $u{\geqslant }1$
of m and decompositions
$u{\geqslant }1$
of m and decompositions
in which
![]() ${ V}_*$
is an
${ V}_*$
is an
![]() ${ E}$
-vector space of dimension
${ E}$
-vector space of dimension
![]() $m/u$
and
$m/u$
and ![]() is an
is an ![]() -lattice of rank
-lattice of rank
![]() $m/u$
in
$m/u$
in
![]() ${ V}_*$
. It defines a Levi subgroup
${ V}_*$
. It defines a Levi subgroup
![]() ${ M}$
of
${ M}$
of
![]() ${ G}$
. Fix a pair
${ G}$
. Fix a pair
![]() $({ Q}_-,{ Q}_+)$
of
$({ Q}_-,{ Q}_+)$
of
![]() ${ M}$
-opposite parabolic subgroups of
${ M}$
-opposite parabolic subgroups of
![]() ${ G}$
with Levi component
${ G}$
with Levi component
![]() ${ M}$
, and write
${ M}$
, and write
![]() ${ N}_-$
,
${ N}_-$
,
![]() ${ N}_+$
for their unipotent radicals. Define
${ N}_+$
for their unipotent radicals. Define ![]() . It is a hereditary order, and
. It is a hereditary order, and
![]() $[\mathfrak {a}_*,{\beta }]$
is a maximal simple stratum in
$[\mathfrak {a}_*,{\beta }]$
is a maximal simple stratum in
![]() $\operatorname {End}_{ F}({ V}_*)$
. Write
$\operatorname {End}_{ F}({ V}_*)$
. Write
![]() $\mathbf {J}^{}_*$
,
$\mathbf {J}^{}_*$
,
![]() $\mathbf {J}^{0}_*$
,
$\mathbf {J}^{0}_*$
,
![]() $\mathbf {J}^{1}_*$
and
$\mathbf {J}^{1}_*$
and
![]() ${{H}}^1_*$
for the subgroups associated with it. Compare with [Reference Bushnell and Henniart8] 3.3, which corresponds to the particular case where
${{H}}^1_*$
for the subgroups associated with it. Compare with [Reference Bushnell and Henniart8] 3.3, which corresponds to the particular case where
![]() $u=m$
.
$u=m$
.
The next result follows from [Reference Bushnell and Henniart6] Example 10.9 (compare with Lemma 1 in [Reference Bushnell and Henniart8] 3.3).
Lemma 4.9.
-
1. There are Iwahori decompositions
and $$ \begin{align*} {{H}}^1 &= ({{H}}^1\cap{ N}_-) \cdot ({{H}}^1\cap{ M}) \cdot ({{H}}^1\cap{ N}_+), \\ {{H}}^1\cap{ M} &= {{H}}^1_* \times \dots \times {{H}}^1_* \end{align*} $$
$$ \begin{align*} {{H}}^1 &= ({{H}}^1\cap{ N}_-) \cdot ({{H}}^1\cap{ M}) \cdot ({{H}}^1\cap{ N}_+), \\ {{H}}^1\cap{ M} &= {{H}}^1_* \times \dots \times {{H}}^1_* \end{align*} $$
 $$ \begin{align*} \mathbf{J}^1 &= (\mathbf{J}^1\cap{ N}_-) \cdot (\mathbf{J}^1\cap{ M}) \cdot (\mathbf{J}^1\cap{ N}_+), \\ \mathbf{J}^1\cap{ M} &= \mathbf{J}^1_* \times \dots \times \mathbf{J}^1_*. \end{align*} $$
$$ \begin{align*} \mathbf{J}^1 &= (\mathbf{J}^1\cap{ N}_-) \cdot (\mathbf{J}^1\cap{ M}) \cdot (\mathbf{J}^1\cap{ N}_+), \\ \mathbf{J}^1\cap{ M} &= \mathbf{J}^1_* \times \dots \times \mathbf{J}^1_*. \end{align*} $$
-
2. The character
 ${\theta }$
is trivial on
${\theta }$
is trivial on
 ${{H}}^1\cap { N}_-$
,
${{H}}^1\cap { N}_-$
,
 ${{H}}^1\cap { N}_+$
, and there exists a unique simple character
${{H}}^1\cap { N}_+$
, and there exists a unique simple character  such that
such that
 ${\theta }$
agrees with
${\theta }$
agrees with
 ${\theta }_*\otimes \dots \otimes {\theta }_*$
on
${\theta }_*\otimes \dots \otimes {\theta }_*$
on
 ${{H}}^1\cap { M}$
.
${{H}}^1\cap { M}$
.
Moreover, the map
![]() ${\theta }\mapsto {\theta }_*$
defined by Lemma 4.9(2) is a bijection from
${\theta }\mapsto {\theta }_*$
defined by Lemma 4.9(2) is a bijection from ![]() to
to ![]() : this is an instance of the transfer of [Reference Bushnell and Kutzko9] 3.6.
: this is an instance of the transfer of [Reference Bushnell and Kutzko9] 3.6.
Let
![]() $\eta _*^{}$
denote the Heisenberg representation of
$\eta _*^{}$
denote the Heisenberg representation of
![]() $\mathbf {J}_*^1$
associated with
$\mathbf {J}_*^1$
associated with
![]() ${\theta }_*^{}$
. Compare the next result with Lemma 2 in [Reference Bushnell and Henniart8] 3.3 and the discussion after it.
${\theta }_*^{}$
. Compare the next result with Lemma 2 in [Reference Bushnell and Henniart8] 3.3 and the discussion after it.
Lemma 4.10. Let
![]() $\boldsymbol {\kappa }_*$
be a representation of
$\boldsymbol {\kappa }_*$
be a representation of
![]() $\mathbf {J}_*$
extending
$\mathbf {J}_*$
extending
![]() $\eta _*$
.
$\eta _*$
.
-
1. The set
 $\mathbf {J}_+=({{H}}^1\cap { N}_-)\cdot (\mathbf {J}\cap { Q}_+)$
is a group, and there is a unique representation
$\mathbf {J}_+=({{H}}^1\cap { N}_-)\cdot (\mathbf {J}\cap { Q}_+)$
is a group, and there is a unique representation
 $\boldsymbol {\kappa }_+$
of
$\boldsymbol {\kappa }_+$
of
 $\mathbf {J}_+$
which is trivial on
$\mathbf {J}_+$
which is trivial on
 ${{H}}^1\cap { N}_-$
,
${{H}}^1\cap { N}_-$
,
 $\mathbf {J}^0\cap { N}_+$
and agrees with
$\mathbf {J}^0\cap { N}_+$
and agrees with
 $\boldsymbol {\kappa }_*\otimes \dots \otimes \boldsymbol {\kappa }_*$
on
$\boldsymbol {\kappa }_*\otimes \dots \otimes \boldsymbol {\kappa }_*$
on
 $\mathbf {J}\cap { M}$
.
$\mathbf {J}\cap { M}$
. -
2. The representation
 $\widetilde {\boldsymbol {\kappa }}_+$
of
$\widetilde {\boldsymbol {\kappa }}_+$
of
 $(\mathrm {J}^1\cap { N}_-)\cdot (\mathbf {J}\cap { Q}_+)=\mathbf {J}^1\mathbf {J}_+$
induced by
$(\mathrm {J}^1\cap { N}_-)\cdot (\mathbf {J}\cap { Q}_+)=\mathbf {J}^1\mathbf {J}_+$
induced by
 $\boldsymbol {\kappa }_+$
extends
$\boldsymbol {\kappa }_+$
extends
 $\eta $
.
$\eta $
. -
3. There is a unique irreducible representation
 $\boldsymbol {\kappa }$
of
$\boldsymbol {\kappa }$
of
 $\mathbf {J}$
extending
$\mathbf {J}$
extending
 $\widetilde {\boldsymbol {\kappa }}_+$
.
$\widetilde {\boldsymbol {\kappa }}_+$
.
Proof. That
![]() $\mathbf {J}_+$
is a group follows from the fact that
$\mathbf {J}_+$
is a group follows from the fact that
![]() ${{H}}^1$
is normalized by
${{H}}^1$
is normalized by
![]() $\mathbf {J}$
, thus by
$\mathbf {J}$
, thus by
![]() $\mathbf {J}\cap { Q}_+$
. The existence of
$\mathbf {J}\cap { Q}_+$
. The existence of
![]() $\boldsymbol {\kappa }_+$
follows from the containment
$\boldsymbol {\kappa }_+$
follows from the containment
(see the argument of [Reference Sécherre34] 2.3). Mackey’s formula implies that the restriction of
![]() $\widetilde {\boldsymbol {\kappa }}_+$
to
$\widetilde {\boldsymbol {\kappa }}_+$
to
![]() $\mathbf {J}^1$
is
$\mathbf {J}^1$
is
The restriction of
![]() $\boldsymbol {\kappa }_+$
to
$\boldsymbol {\kappa }_+$
to
![]() $\mathbf {J}^1\cap \mathbf {J}_+=({{H}}^1\cap { N}_-)\cdot (\mathbf {J}^1\cap { Q}_+)$
is the unique representation
$\mathbf {J}^1\cap \mathbf {J}_+=({{H}}^1\cap { N}_-)\cdot (\mathbf {J}^1\cap { Q}_+)$
is the unique representation
![]() $\eta _+$
which is trivial on
$\eta _+$
which is trivial on
![]() ${{H}}^1\cap { N}_-$
,
${{H}}^1\cap { N}_-$
,
![]() $\mathbf {J}^1\cap { N}_+$
and agrees with
$\mathbf {J}^1\cap { N}_+$
and agrees with
![]() $\eta _*\otimes \dots \otimes \eta _*$
on
$\eta _*\otimes \dots \otimes \eta _*$
on
![]() $\mathbf {J}^1\cap { M}$
. The representation it induces to
$\mathbf {J}^1\cap { M}$
. The representation it induces to
![]() $\mathbf {J}^1$
is isomorphic to
$\mathbf {J}^1$
is isomorphic to
![]() $\eta $
: Indeed, this representation contains
$\eta $
: Indeed, this representation contains
![]() ${\theta }$
by Lemma 4.9(2), and it has dimension
${\theta }$
by Lemma 4.9(2), and it has dimension
 $$ \begin{align*} \operatorname{dim} (\eta_*\otimes\dots\otimes\eta_*) \cdot (\mathbf{J}^1\cap{ N}_-:{{H}}^1\cap{ N}_-) &= (\mathbf{J}^1\cap{ M}:{{H}}^1\cap{ M})^{1/2}\cdot (\mathbf{J}^1\cap{ N}_-:{{H}}^1\cap{ N}_-) \\ &= (\mathbf{J}^1:{{H}}^1)^{1/2} \end{align*} $$
$$ \begin{align*} \operatorname{dim} (\eta_*\otimes\dots\otimes\eta_*) \cdot (\mathbf{J}^1\cap{ N}_-:{{H}}^1\cap{ N}_-) &= (\mathbf{J}^1\cap{ M}:{{H}}^1\cap{ M})^{1/2}\cdot (\mathbf{J}^1\cap{ N}_-:{{H}}^1\cap{ N}_-) \\ &= (\mathbf{J}^1:{{H}}^1)^{1/2} \end{align*} $$
which is the dimension of
![]() $\eta $
(see [Reference Mínguez and Sécherre30] 2.3).
$\eta $
(see [Reference Mínguez and Sécherre30] 2.3).
It remains to prove (3). First, uniqueness follows from the fact that any two such extensions differ from a character of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1\mathbf {J}_+$
, and such a character is trivial since
$\mathbf {J}^1\mathbf {J}_+$
, and such a character is trivial since
![]() $p\neq 2$
. Existence follows from [Reference Bushnell and Kutzko9] 5.2.4 (see [Reference Mínguez and Sécherre30] 2.4 in the modular case).
$p\neq 2$
. Existence follows from [Reference Bushnell and Kutzko9] 5.2.4 (see [Reference Mínguez and Sécherre30] 2.4 in the modular case).
The reader will pay attention to the fact that, although
![]() $\mathbf {J}^0\cap { M}$
is equal to
$\mathbf {J}^0\cap { M}$
is equal to
![]() $\mathbf {J}_*^0\times \cdots \times \mathbf {J}_*^0$
, the group
$\mathbf {J}_*^0\times \cdots \times \mathbf {J}_*^0$
, the group
![]() $\mathbf {J}\cap { M}$
is not equal to
$\mathbf {J}\cap { M}$
is not equal to
![]() $\mathbf {J}_*\times \cdots \times \mathbf {J}_*$
in general (unless
$\mathbf {J}_*\times \cdots \times \mathbf {J}_*$
in general (unless
![]() $u=1$
). It is generated by
$u=1$
). It is generated by
![]() $\mathbf {J}^0\cap { M}$
and
$\mathbf {J}^0\cap { M}$
and
![]() ${ E}^\times $
, the latter being diagonal in
${ E}^\times $
, the latter being diagonal in
![]() ${ M}$
.
${ M}$
.
Lemma 4.11.
-
1. The map
(4.10)from isomorphism classes of representations of $$ \begin{align} \boldsymbol{\kappa}_* \mapsto \boldsymbol{\kappa} \end{align} $$
$$ \begin{align} \boldsymbol{\kappa}_* \mapsto \boldsymbol{\kappa} \end{align} $$
 $\mathbf {J}_*$
extending
$\mathbf {J}_*$
extending
 $\eta _*$
to isomorphism classes of representation of
$\eta _*$
to isomorphism classes of representation of
 $\mathbf {J}$
extending
$\mathbf {J}$
extending
 $\eta $
is surjective.
$\eta $
is surjective.
-
2. Any two representations of
 $\mathbf {J}_*$
extending
$\mathbf {J}_*$
extending
 $\eta _*$
have the same image if and only if they are twists of each other by a character of
$\eta _*$
have the same image if and only if they are twists of each other by a character of
 $\mathbf {J}_*^{}$
trivial on
$\mathbf {J}_*^{}$
trivial on
 $\mathbf {J}_*^0$
and of order dividing u.
$\mathbf {J}_*^0$
and of order dividing u.
Proof. The case where
![]() $u=m$
is given by [Reference Bushnell and Henniart8] 3.3, Corollary 1. For the general case, first note that, if
$u=m$
is given by [Reference Bushnell and Henniart8] 3.3, Corollary 1. For the general case, first note that, if
![]() $\boldsymbol {\kappa }$
is the image of
$\boldsymbol {\kappa }$
is the image of
![]() $\boldsymbol {\kappa }_*$
by the map (4.10), and if
$\boldsymbol {\kappa }_*$
by the map (4.10), and if
![]() $\boldsymbol {\xi }_*$
is a character of
$\boldsymbol {\xi }_*$
is a character of
![]() $\mathbf {J}_*$
trivial on
$\mathbf {J}_*$
trivial on
![]() $\mathbf {J}_*^0$
, then the image of
$\mathbf {J}_*^0$
, then the image of
![]() $\boldsymbol {\kappa }_*\boldsymbol {\xi }_*$
by the map (4.10) is equal to
$\boldsymbol {\kappa }_*\boldsymbol {\xi }_*$
by the map (4.10) is equal to
![]() $\boldsymbol {\kappa }\boldsymbol {\xi }^u$
, where
$\boldsymbol {\kappa }\boldsymbol {\xi }^u$
, where
![]() $\boldsymbol {\xi }$
is the character of
$\boldsymbol {\xi }$
is the character of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^0$
coinciding with
$\mathbf {J}^0$
coinciding with
![]() $\boldsymbol {\xi }_*$
on any uniformizer of E. Now, start with a representation
$\boldsymbol {\xi }_*$
on any uniformizer of E. Now, start with a representation
![]() $\boldsymbol {\kappa }$
extending
$\boldsymbol {\kappa }$
extending
![]() $\eta $
. Let
$\eta $
. Let
![]() $\widetilde {\boldsymbol {\kappa }}_+$
denote its restriction to
$\widetilde {\boldsymbol {\kappa }}_+$
denote its restriction to
![]() $\mathbf {J}^1\mathbf {J}_+$
and
$\mathbf {J}^1\mathbf {J}_+$
and
![]() $\boldsymbol {\kappa }_+$
denote the representation of
$\boldsymbol {\kappa }_+$
denote the representation of
![]() $\mathbf {J}_+$
on the space of
$\mathbf {J}_+$
on the space of
![]() $\mathbf {J}^1\cap { N}_-$
-invariants of
$\mathbf {J}^1\cap { N}_-$
-invariants of
![]() $\widetilde {\boldsymbol {\kappa }}_+$
. The restriction of
$\widetilde {\boldsymbol {\kappa }}_+$
. The restriction of
![]() $\boldsymbol {\kappa }_+$
to
$\boldsymbol {\kappa }_+$
to
![]() $\mathbf {J}^0\cap { M}$
has the form
$\mathbf {J}^0\cap { M}$
has the form
for a uniquely determined representation
![]() $\boldsymbol {\kappa }_*^0$
of
$\boldsymbol {\kappa }_*^0$
of
![]() $\mathbf {J}_*^0$
extending
$\mathbf {J}_*^0$
extending
![]() $\eta _*$
. Since any two extensions of
$\eta _*$
. Since any two extensions of
![]() $\boldsymbol {\kappa }_*^0$
to
$\boldsymbol {\kappa }_*^0$
to
![]() $\mathbf {J}_*$
are twists of each other by a character of
$\mathbf {J}_*$
are twists of each other by a character of
![]() $\mathbf {J}_*=E^\times \mathbf {J}_*^0$
trivial on
$\mathbf {J}_*=E^\times \mathbf {J}_*^0$
trivial on
![]() $\mathbf {J}_*^0$
, the result follows.
$\mathbf {J}_*^0$
, the result follows.
Remark 4.12. Suppose that u is equal to m. Let
![]() $y\in { M}\cap { B}^\times $
, and write
$y\in { M}\cap { B}^\times $
, and write ![]() . The groups associated with
. The groups associated with
![]() ${\theta }'$
are
${\theta }'$
are
![]() $\mathbf {J}'=\mathbf {J}^y$
, etc. The group isomorphism
$\mathbf {J}'=\mathbf {J}^y$
, etc. The group isomorphism
![]() ${ B}^\times \simeq \operatorname {GL}_m({ E})$
identifies
${ B}^\times \simeq \operatorname {GL}_m({ E})$
identifies
![]() ${ M}\cap { B}^\times $
with the diagonal torus
${ M}\cap { B}^\times $
with the diagonal torus
![]() ${ E}^\times \times \cdots \times { E}^\times $
, and
${ E}^\times \times \cdots \times { E}^\times $
, and
![]() ${ E}^\times $
normalizes
${ E}^\times $
normalizes
![]() ${\theta }_*$
. The character
${\theta }_*$
. The character
![]() ${\theta }'$
is thus trivial on
${\theta }'$
is thus trivial on
![]() ${{H}}^{1y}\cap { N}_-$
,
${{H}}^{1y}\cap { N}_-$
,
![]() ${{H}}^{1y}\cap { N}_+$
and agrees with
${{H}}^{1y}\cap { N}_+$
and agrees with
![]() ${\theta }_*\otimes \dots \otimes {\theta }_*$
on
${\theta }_*\otimes \dots \otimes {\theta }_*$
on
![]() ${{H}}^{1y}\cap { M}={{H}}^1\cap { M}$
. If
${{H}}^{1y}\cap { M}={{H}}^1\cap { M}$
. If
![]() $\boldsymbol {\kappa }_*$
is a representation of
$\boldsymbol {\kappa }_*$
is a representation of
![]() $\mathbf {J}_*$
extending
$\mathbf {J}_*$
extending
![]() $\eta _*$
, the representation of
$\eta _*$
, the representation of
![]() $\mathbf {J}'$
corresponding to it by the map (4.10) is
$\mathbf {J}'$
corresponding to it by the map (4.10) is
![]() $\boldsymbol {\kappa }^y$
.
$\boldsymbol {\kappa }^y$
.
4.5
Suppose now that the simple character
![]() ${\theta }$
and the simple stratum
${\theta }$
and the simple stratum
![]() $[\mathfrak {a},{\beta }]$
of 4.4 are
$[\mathfrak {a},{\beta }]$
of 4.4 are
![]() $\sigma $
-self-dual. The groups
$\sigma $
-self-dual. The groups
![]() $\mathbf {J}$
,
$\mathbf {J}$
,
![]() $\mathbf {J}^0$
,
$\mathbf {J}^0$
,
![]() $\mathbf {J}^1$
and
$\mathbf {J}^1$
and
![]() ${{H}}^1$
are thus
${{H}}^1$
are thus
![]() $\sigma $
-stable. Suppose also that the decompositions (4.9) are
$\sigma $
-stable. Suppose also that the decompositions (4.9) are
![]() $\sigma $
-stable. (To obtain such decompositions, consider the vertex in the reduced building of
$\sigma $
-stable. (To obtain such decompositions, consider the vertex in the reduced building of
![]() $B^\times $
defined by the
$B^\times $
defined by the ![]() -lattice
-lattice ![]() (see [Reference Bruhat and Tits5]) and choose a
(see [Reference Bruhat and Tits5]) and choose a
![]() $\sigma $
-stable apartment containing this vertex, whose existence is granted by [Reference Delorme and Sécherre13] since
$\sigma $
-stable apartment containing this vertex, whose existence is granted by [Reference Delorme and Sécherre13] since
![]() $p\neq 2$
.)
$p\neq 2$
.)
The Levi subgroup
![]() ${ M}$
is thus
${ M}$
is thus
![]() $\sigma $
-stable, and we may assume that
$\sigma $
-stable, and we may assume that
![]() ${ Q}_-$
,
${ Q}_-$
,
![]() ${ Q}_+$
are
${ Q}_+$
are
![]() $\sigma $
-stable as well. Also, the simple stratum
$\sigma $
-stable as well. Also, the simple stratum
![]() $[\mathfrak {a}_*,{\beta }]$
and the simple character
$[\mathfrak {a}_*,{\beta }]$
and the simple character
![]() ${\theta }_*$
given by Lemma 4.9 are
${\theta }_*$
given by Lemma 4.9 are
![]() $\sigma $
-self-dual. Let
$\sigma $
-self-dual. Let
![]() ${ G}_*$
denote the group
${ G}_*$
denote the group
![]() $\operatorname {Aut}_{ F}({ V}_*)$
. It is isomorphic to
$\operatorname {Aut}_{ F}({ V}_*)$
. It is isomorphic to
![]() $\operatorname {GL}_{n/u}({ F})$
.
$\operatorname {GL}_{n/u}({ F})$
.
We may also assume that our choice of basis induces an isomorphism of groups (4.4) between
![]() $\mathbf {J}^0/\mathbf {J}^1$
and
$\mathbf {J}^0/\mathbf {J}^1$
and
![]() $\operatorname {GL}_m(\boldsymbol {l})$
as in Proposition 4.5(4), transporting the action of
$\operatorname {GL}_m(\boldsymbol {l})$
as in Proposition 4.5(4), transporting the action of
![]() $\sigma $
on
$\sigma $
on
![]() $\mathbf {J}^0/\mathbf {J}^1$
to
$\mathbf {J}^0/\mathbf {J}^1$
to
-
○ the action of the nontrivial element of
 $\operatorname {Gal}(\boldsymbol {l}/\boldsymbol {l}_0)$
on
$\operatorname {Gal}(\boldsymbol {l}/\boldsymbol {l}_0)$
on
 $\operatorname {GL}_m(\boldsymbol {l})$
if
$\operatorname {GL}_m(\boldsymbol {l})$
if
 ${ T}/{ T}_0$
is unramified,
${ T}/{ T}_0$
is unramified, -
○ the adjoint action of (4.5) on
 $\operatorname {GL}_m(\boldsymbol {l})$
for some
$\operatorname {GL}_m(\boldsymbol {l})$
for some
 $i\in \{0,\dots ,\lfloor m/2\rfloor \}$
, if
$i\in \{0,\dots ,\lfloor m/2\rfloor \}$
, if
 ${ T}/{ T}_0$
is ramified.
${ T}/{ T}_0$
is ramified.
Let
![]() $\boldsymbol {\kappa }_*$
be a representation of
$\boldsymbol {\kappa }_*$
be a representation of
![]() $\mathbf {J}_*$
extending
$\mathbf {J}_*$
extending
![]() $\eta _*$
, and let
$\eta _*$
, and let
![]() $\boldsymbol {\kappa }$
correspond to it by the map (4.10).
$\boldsymbol {\kappa }$
correspond to it by the map (4.10).
Lemma 4.13. If
![]() $\boldsymbol {\kappa }_*$
is
$\boldsymbol {\kappa }_*$
is
![]() $\sigma $
-self-dual, then
$\sigma $
-self-dual, then
![]() $\boldsymbol {\kappa }$
is
$\boldsymbol {\kappa }$
is
![]() $\sigma $
-self-dual.
$\sigma $
-self-dual.
Proof. First,
![]() $\boldsymbol {\kappa }_+^{\vee \sigma }$
is trivial on both
$\boldsymbol {\kappa }_+^{\vee \sigma }$
is trivial on both
![]() ${{H}}^1\cap { N}_-$
,
${{H}}^1\cap { N}_-$
,
![]() $\mathbf {J}^1\cap { N}_+$
and agrees with
$\mathbf {J}^1\cap { N}_+$
and agrees with
![]() $\boldsymbol {\kappa }_*^{\vee \sigma }\otimes \dots \otimes \boldsymbol {\kappa }_*^{\vee \sigma }$
on
$\boldsymbol {\kappa }_*^{\vee \sigma }\otimes \dots \otimes \boldsymbol {\kappa }_*^{\vee \sigma }$
on
![]() $\mathbf {J}\cap { M}$
. If
$\mathbf {J}\cap { M}$
. If
![]() $\boldsymbol {\kappa }_*^{}$
is
$\boldsymbol {\kappa }_*^{}$
is
![]() $\sigma $
-self-dual, it follows by uniqueness that
$\sigma $
-self-dual, it follows by uniqueness that
![]() $\boldsymbol {\kappa }_+$
is
$\boldsymbol {\kappa }_+$
is
![]() $\sigma $
-self-dual, thus
$\sigma $
-self-dual, thus
![]() $\widetilde {\boldsymbol {\kappa }}_+$
is
$\widetilde {\boldsymbol {\kappa }}_+$
is
![]() $\sigma $
-self-dual as well. The unique representation of
$\sigma $
-self-dual as well. The unique representation of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\widetilde {\boldsymbol {\kappa }}_+^{\vee \sigma }$
is
$\widetilde {\boldsymbol {\kappa }}_+^{\vee \sigma }$
is
![]() $\boldsymbol {\kappa }^{\vee \sigma }$
, hence
$\boldsymbol {\kappa }^{\vee \sigma }$
, hence
![]() $\boldsymbol {\kappa }$
is
$\boldsymbol {\kappa }$
is
![]() $\sigma $
-self-dual.
$\sigma $
-self-dual.
We will need the following lemma. Let
![]() $\varpi $
be a uniformizer of
$\varpi $
be a uniformizer of
![]() ${ E}$
such that
${ E}$
such that
 $$ \begin{align} \sigma(\varpi)= \left\{ \begin{array}{rl} \varpi & \text{if }{ T}/{ T}_0\text{ is unramified}, \\ -\varpi & \text{if }{ T}/{ T}_0\text{ is ramified}. \end{array}\right. \end{align} $$
$$ \begin{align} \sigma(\varpi)= \left\{ \begin{array}{rl} \varpi & \text{if }{ T}/{ T}_0\text{ is unramified}, \\ -\varpi & \text{if }{ T}/{ T}_0\text{ is ramified}. \end{array}\right. \end{align} $$
Note that the group
![]() $\mathbf {J}$
is generated by
$\mathbf {J}$
is generated by
![]() $\mathbf {J}^0$
and
$\mathbf {J}^0$
and
![]() $\varpi $
.
$\varpi $
.
Lemma 4.14. The group
![]() $\mathbf {J}\cap { G}^\sigma $
is generated by
$\mathbf {J}\cap { G}^\sigma $
is generated by
![]() $\mathbf {J}^0\cap { G}^\sigma $
and an element
$\mathbf {J}^0\cap { G}^\sigma $
and an element
![]() $\varpi '$
such that
$\varpi '$
such that
-
1.
 $\varpi '=\varpi $
if
$\varpi '=\varpi $
if
 ${ T}/{ T}_0$
is unramified,
${ T}/{ T}_0$
is unramified, -
2.
 $\varpi '=\varpi ^2$
if
$\varpi '=\varpi ^2$
if
 ${ T}/{ T}_0$
is ramified and
${ T}/{ T}_0$
is ramified and
 $m\neq 2i$
,
$m\neq 2i$
, -
3.
 $\varpi '\in \varpi \mathbf {J}^0$
if
$\varpi '\in \varpi \mathbf {J}^0$
if
 ${ T}/{ T}_0$
is ramified and
${ T}/{ T}_0$
is ramified and
 $m=2i$
.
$m=2i$
.
Proof. If
![]() ${ T}/{ T}_0$
is unramified: See [Reference Sécherre35] Lemma 9.1. Suppose that
${ T}/{ T}_0$
is unramified: See [Reference Sécherre35] Lemma 9.1. Suppose that
![]() ${ T}/{ T}_0$
is ramified, and assume that there is an
${ T}/{ T}_0$
is ramified, and assume that there is an
![]() $x\in \mathbf {J}\cap { G}^\sigma $
,
$x\in \mathbf {J}\cap { G}^\sigma $
,
![]() $x\notin \langle \varpi ^2,\mathbf {J}^0\cap { G}^\sigma \rangle $
. We have
$x\notin \langle \varpi ^2,\mathbf {J}^0\cap { G}^\sigma \rangle $
. We have
![]() $x=\varpi ^{v}y$
, where
$x=\varpi ^{v}y$
, where
![]() $v\in \mathbb {Z}$
is odd and
$v\in \mathbb {Z}$
is odd and
![]() $y\in \mathbf {J}^0$
satisfies
$y\in \mathbf {J}^0$
satisfies
![]() $\sigma (y)=-y$
. Reducing mod
$\sigma (y)=-y$
. Reducing mod
![]() $\mathbf {J}^1$
, we get an
$\mathbf {J}^1$
, we get an
![]() $\alpha \in \operatorname {GL}_m(\boldsymbol {l})$
such that
$\alpha \in \operatorname {GL}_m(\boldsymbol {l})$
such that
![]() $\sigma (\alpha )=-\alpha $
. Since the involution
$\sigma (\alpha )=-\alpha $
. Since the involution
![]() $\sigma $
acts on
$\sigma $
acts on
![]() $\operatorname {GL}_m(\boldsymbol {l})$
by conjugacy by
$\operatorname {GL}_m(\boldsymbol {l})$
by conjugacy by
(where
![]() $-1$
occurs i times), this implies that
$-1$
occurs i times), this implies that
![]() ${\delta }$
and
${\delta }$
and
![]() $-{\delta }$
are
$-{\delta }$
are
![]() $\operatorname {GL}_m(\boldsymbol {l})$
-conjugate, thus
$\operatorname {GL}_m(\boldsymbol {l})$
-conjugate, thus
![]() $m=2i$
. Conversely, if
$m=2i$
. Conversely, if
![]() $m=2i$
, then
$m=2i$
, then

is
![]() $\sigma $
-anti-invariant, and
$\sigma $
-anti-invariant, and
![]() $\varpi '=\varpi w$
has the required property.
$\varpi '=\varpi w$
has the required property.
We now investigate the behavior of the map (4.10) with respect to distinction. The case where
![]() $u=m$
will be sufficient for our purpose (see Paragraph 4.6).
$u=m$
will be sufficient for our purpose (see Paragraph 4.6).
Lemma 4.15. Suppose that
![]() $u=m$
and
$u=m$
and
![]() $\boldsymbol {\kappa }_*^{}$
is
$\boldsymbol {\kappa }_*^{}$
is
![]() $\mathbf {J}_*^{}\cap { G}_*^\sigma $
-distinguished.
$\mathbf {J}_*^{}\cap { G}_*^\sigma $
-distinguished.
-
1. If
 ${ T}/{ T}_0$
is unramified, or if
${ T}/{ T}_0$
is unramified, or if
 ${ T}/{ T}_0$
is ramified and
${ T}/{ T}_0$
is ramified and
 $m\neq 2i$
, the representation
$m\neq 2i$
, the representation
 $\boldsymbol {\kappa }$
is
$\boldsymbol {\kappa }$
is
 $\mathbf {J}\cap { G}^\sigma $
-distinguished.
$\mathbf {J}\cap { G}^\sigma $
-distinguished. -
2. If
 ${ T}/{ T}_0$
is ramified and
${ T}/{ T}_0$
is ramified and
 $m=2i$
, there exists a quadratic character
$m=2i$
, there exists a quadratic character
 $\boldsymbol {\xi }$
of
$\boldsymbol {\xi }$
of
 $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
 $\mathbf {J}^0$
such that
$\mathbf {J}^0$
such that
 $\boldsymbol {\kappa }\boldsymbol {\xi }$
is
$\boldsymbol {\kappa }\boldsymbol {\xi }$
is
 $\mathbf {J}\cap { G}^\sigma $
-distinguished.
$\mathbf {J}\cap { G}^\sigma $
-distinguished.
Proof. The representation
![]() $\boldsymbol {\kappa }_+$
is
$\boldsymbol {\kappa }_+$
is
![]() $\mathbf {J}_+\cap { G}^\sigma $
-distinguished, thus
$\mathbf {J}_+\cap { G}^\sigma $
-distinguished, thus
![]() $\widetilde {\boldsymbol {\kappa }}_+$
is
$\widetilde {\boldsymbol {\kappa }}_+$
is
![]() $\mathbf {J}^1\mathbf {J}_+\cap { G}^\sigma $
-distinguished. It follows that
$\mathbf {J}^1\mathbf {J}_+\cap { G}^\sigma $
-distinguished. It follows that
![]() $\boldsymbol {\kappa }$
is
$\boldsymbol {\kappa }$
is
![]() $\mathbf {J}^1\mathbf {J}_+\cap { G}^\sigma $
-distinguished. Let
$\mathbf {J}^1\mathbf {J}_+\cap { G}^\sigma $
-distinguished. Let
![]() $\chi $
be the character of
$\chi $
be the character of
![]() $\mathbf {J}\cap { G}^\sigma $
associated with
$\mathbf {J}\cap { G}^\sigma $
associated with
![]() $\boldsymbol {\kappa }$
by Proposition 4.6. It is trivial on
$\boldsymbol {\kappa }$
by Proposition 4.6. It is trivial on
![]() $\mathbf {J}^1\mathbf {J}_+\cap { G}^\sigma $
. Restricting to
$\mathbf {J}^1\mathbf {J}_+\cap { G}^\sigma $
. Restricting to
![]() $\mathbf {J}^0\cap { G}^\sigma $
, it is a character of
$\mathbf {J}^0\cap { G}^\sigma $
, it is a character of
Since
![]() $\mathbf {J}\cap { M}\subseteq \mathbf {J}_+$
, it is trivial on the image of
$\mathbf {J}\cap { M}\subseteq \mathbf {J}_+$
, it is trivial on the image of
![]() $(\mathbf {J}\cap { M})\cap (\mathbf {J}^0\cap { G}^\sigma )$
in
$(\mathbf {J}\cap { M})\cap (\mathbf {J}^0\cap { G}^\sigma )$
in
![]() $\operatorname {GL}_m(\boldsymbol {l})^\sigma $
, which is made of the
$\operatorname {GL}_m(\boldsymbol {l})^\sigma $
, which is made of the
![]() $\sigma $
-fixed points of the diagonal torus
$\sigma $
-fixed points of the diagonal torus
![]() $\textsf {M}=\boldsymbol {l}^\times \times \cdots \times \boldsymbol {l}^\times $
.
$\textsf {M}=\boldsymbol {l}^\times \times \cdots \times \boldsymbol {l}^\times $
.
If
![]() ${ T}/{ T}_0$
is unramified, we have
${ T}/{ T}_0$
is unramified, we have
![]() $\operatorname {GL}_m(\boldsymbol {l})^\sigma =\operatorname {GL}_m(\boldsymbol {l}_0)$
and
$\operatorname {GL}_m(\boldsymbol {l})^\sigma =\operatorname {GL}_m(\boldsymbol {l}_0)$
and
![]() $\textsf {M}^\sigma =\boldsymbol {l}_0^\times \times \cdots \times \boldsymbol {l}_0^\times $
, thus
$\textsf {M}^\sigma =\boldsymbol {l}_0^\times \times \cdots \times \boldsymbol {l}_0^\times $
, thus
![]() $\chi $
is trivial on
$\chi $
is trivial on
![]() $\mathbf {J}^0\cap { G}^\sigma $
. If
$\mathbf {J}^0\cap { G}^\sigma $
. If
![]() ${ T}/{ T}_0$
is ramified, we have
${ T}/{ T}_0$
is ramified, we have
![]() $\operatorname {GL}_m(\boldsymbol {l})^\sigma =\operatorname {GL}_i(\boldsymbol {l})\times \operatorname {GL}_{m-i}(\boldsymbol {l})$
and
$\operatorname {GL}_m(\boldsymbol {l})^\sigma =\operatorname {GL}_i(\boldsymbol {l})\times \operatorname {GL}_{m-i}(\boldsymbol {l})$
and
![]() $\textsf {M}^\sigma =\textsf {M}$
. Again,
$\textsf {M}^\sigma =\textsf {M}$
. Again,
![]() $\chi $
is trivial on
$\chi $
is trivial on
![]() $\mathbf {J}^0\cap { G}^\sigma $
.
$\mathbf {J}^0\cap { G}^\sigma $
.
By Lemma 4.14, it remains to consider the value of
![]() $\chi $
at
$\chi $
at
![]() $\varpi '$
. If
$\varpi '$
. If
![]() ${ T}/{ T}_0$
is unramified, or if
${ T}/{ T}_0$
is unramified, or if
![]() ${ T}/{ T}_0$
is ramified and
${ T}/{ T}_0$
is ramified and
![]() $m\neq 2i$
, we have
$m\neq 2i$
, we have
![]() $\varpi ' \in \mathbf {J}^1\mathbf {J}_+\cap { G}^\sigma $
, thus
$\varpi ' \in \mathbf {J}^1\mathbf {J}_+\cap { G}^\sigma $
, thus
![]() $\chi $
is trivial.
$\chi $
is trivial.
Now, assume that
![]() ${ T}/{ T}_0$
is ramified and
${ T}/{ T}_0$
is ramified and
![]() $m=2i$
. Let
$m=2i$
. Let
![]() $\boldsymbol {\xi }$
be the quadratic character of
$\boldsymbol {\xi }$
be the quadratic character of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^0$
defined by
$\mathbf {J}^0$
defined by
![]() $\xi (\varpi ')=\chi (\varpi ')$
. Then
$\xi (\varpi ')=\chi (\varpi ')$
. Then
![]() $\boldsymbol {\kappa }\boldsymbol {\xi }$
is
$\boldsymbol {\kappa }\boldsymbol {\xi }$
is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished.
$\mathbf {J}\cap { G}^\sigma $
-distinguished.
We will prove in Paragraph 4.6 that the quadratic character
![]() $\boldsymbol {\xi }$
of Lemma 4.15(2) is always trivial: See Corollary 4.19.
$\boldsymbol {\xi }$
of Lemma 4.15(2) is always trivial: See Corollary 4.19.
4.6
As in Paragraph 4.5, the simple character
![]() ${\theta }$
and the simple stratum
${\theta }$
and the simple stratum
![]() $[\mathfrak {a},{\beta }]$
are both maximal
$[\mathfrak {a},{\beta }]$
are both maximal
![]() $\sigma $
-self-dual, and
$\sigma $
-self-dual, and
![]() $\eta $
is the Heisenberg representation of
$\eta $
is the Heisenberg representation of
![]() $\mathbf {J}^1$
associated with
$\mathbf {J}^1$
associated with
![]() ${\theta }$
. The next proposition, which says that
${\theta }$
. The next proposition, which says that
![]() $\eta $
has a canonical extension to
$\eta $
has a canonical extension to
![]() $\mathbf {J}$
, is the core of our proof of Theorem 4.41.
$\mathbf {J}$
, is the core of our proof of Theorem 4.41.
Proposition 4.16. There is, up to isomorphism, a unique representation
![]() $\boldsymbol {\kappa }$
of
$\boldsymbol {\kappa }$
of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\eta $
satisfying the following conditions:
$\eta $
satisfying the following conditions:
-
1. it is both
 $\sigma $
-self-dual and
$\sigma $
-self-dual and
 $\mathbf {J}\cap { G}^\sigma $
-distinguished,
$\mathbf {J}\cap { G}^\sigma $
-distinguished, -
2. its determinant has order a power of p.
This unique representation will be denoted
![]() $\boldsymbol {\kappa }_{{\theta }}$
.
$\boldsymbol {\kappa }_{{\theta }}$
.
Remark 4.17. This extends (and makes more precise) the results of [Reference Sécherre35] (see ibid., Propositions 7.9, 9.4) where
![]() ${\theta }$
is assumed to be generic and either
${\theta }$
is assumed to be generic and either
![]() ${ T}/{ T}_0$
is unramified and m is odd, or
${ T}/{ T}_0$
is unramified and m is odd, or
![]() ${ T}/{ T}_0$
is ramified and
${ T}/{ T}_0$
is ramified and
![]() $m\in \{1,2i\}$
. See also [Reference Sécherre35] Remarks 9.5 and 9.9.
$m\in \{1,2i\}$
. See also [Reference Sécherre35] Remarks 9.5 and 9.9.
Proof. Suppose first that there exists a representation satisfying (1). As in the proof of [Reference Sécherre36] Corollary 6.12, one then easily proves the existence of a representation
![]() $\boldsymbol {\kappa }$
satisfying (1) and (2). Let us prove that such a representation is unique. Any other representation of
$\boldsymbol {\kappa }$
satisfying (1) and (2). Let us prove that such a representation is unique. Any other representation of
![]() $\mathbf {J}$
satisfying the conditions of the proposition is of the form
$\mathbf {J}$
satisfying the conditions of the proposition is of the form
![]() $\boldsymbol {\kappa }\boldsymbol {\phi }$
for some character
$\boldsymbol {\kappa }\boldsymbol {\phi }$
for some character
![]() $\boldsymbol {\phi }$
of
$\boldsymbol {\phi }$
of
![]() $\mathbf {J}$
which is
$\mathbf {J}$
which is
![]() $\sigma $
-self-dual and trivial on
$\sigma $
-self-dual and trivial on
![]() $(\mathbf {J}\cap { G}^\sigma )\mathbf {J}^1$
, and whose order is a power of p. The restriction of
$(\mathbf {J}\cap { G}^\sigma )\mathbf {J}^1$
, and whose order is a power of p. The restriction of
![]() $\boldsymbol {\phi }$
to
$\boldsymbol {\phi }$
to
![]() $\mathbf {J}^0$
can be considered as a character of
$\mathbf {J}^0$
can be considered as a character of
![]() $\operatorname {GL}_m(\boldsymbol {l})$
. Since the latter group is not isomorphic to
$\operatorname {GL}_m(\boldsymbol {l})$
. Since the latter group is not isomorphic to
![]() $\operatorname {GL}_2(\mathbb {F}_2)$
(for
$\operatorname {GL}_2(\mathbb {F}_2)$
(for
![]() $p\neq 2$
), this character factors through the determinant. Its order is thus prime to p, which implies that
$p\neq 2$
), this character factors through the determinant. Its order is thus prime to p, which implies that
![]() $\boldsymbol {\phi }$
is trivial on
$\boldsymbol {\phi }$
is trivial on
![]() $\mathbf {J}^0$
. It is thus a character of
$\mathbf {J}^0$
. It is thus a character of
![]() $\mathbf {J}/(\mathbf {J}\cap { G}^\sigma )\mathbf {J}^0$
which, by Lemma 4.14, has order at most
$\mathbf {J}/(\mathbf {J}\cap { G}^\sigma )\mathbf {J}^0$
which, by Lemma 4.14, has order at most
![]() $2$
. Uniqueness follows from the fact that
$2$
. Uniqueness follows from the fact that
![]() $p\neq 2$
.
$p\neq 2$
.
We are now reduced to proving the existence of a representation
![]() $\boldsymbol {\kappa }$
satisfying (1). If
$\boldsymbol {\kappa }$
satisfying (1). If
![]() $m=1$
, this follows from [Reference Sécherre35] Propositions 7.9, 9.4. (See also Remark 4.17.)
$m=1$
, this follows from [Reference Sécherre35] Propositions 7.9, 9.4. (See also Remark 4.17.)
Now, consider the constructions of 4.4 and 4.5 with
![]() $u=m$
. Thanks to the case where m is equal to
$u=m$
. Thanks to the case where m is equal to
![]() $1$
, there is a representation
$1$
, there is a representation
![]() $\boldsymbol {\kappa }_*$
of
$\boldsymbol {\kappa }_*$
of
![]() $\mathbf {J}_*$
extending
$\mathbf {J}_*$
extending
![]() $\eta _*$
which is both
$\eta _*$
which is both
![]() $\sigma $
-self-dual and
$\sigma $
-self-dual and
![]() $\mathbf {J}^{}_*\cap { G}_*^\sigma $
-distinguished. Let
$\mathbf {J}^{}_*\cap { G}_*^\sigma $
-distinguished. Let
![]() $\boldsymbol {\kappa }$
be the representation of
$\boldsymbol {\kappa }$
be the representation of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\eta $
associated with it by the map (4.10). Lemma 4.13 implies that it is
$\eta $
associated with it by the map (4.10). Lemma 4.13 implies that it is
![]() $\sigma $
-self-dual, and Lemma 4.15 implies that there is a quadratic character
$\sigma $
-self-dual, and Lemma 4.15 implies that there is a quadratic character
![]() $\boldsymbol {\xi }$
of
$\boldsymbol {\xi }$
of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^0$
such that
$\mathbf {J}^0$
such that
![]() $\boldsymbol {\kappa }\boldsymbol {\xi }$
is
$\boldsymbol {\kappa }\boldsymbol {\xi }$
is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished. Since
$\mathbf {J}\cap { G}^\sigma $
-distinguished. Since
![]() $\boldsymbol {\xi }$
is unramified and quadratic,
$\boldsymbol {\xi }$
is unramified and quadratic,
![]() $\boldsymbol {\kappa }\boldsymbol {\xi }$
is also
$\boldsymbol {\kappa }\boldsymbol {\xi }$
is also
![]() $\sigma $
-self-dual and extends
$\sigma $
-self-dual and extends
![]() $\eta $
.
$\eta $
.
Remark 4.18. Notice that this gives another proof of [Reference Sécherre35] Propositions 7.9, 9.4, based on the case
![]() $m=1$
only.
$m=1$
only.
Now, we can improve Lemma 4.15. Suppose we are in the situation of Paragraphs 4.4 and 4.5, with
![]() $u=m$
.
$u=m$
.
Corollary 4.19. Suppose that
![]() $u=m$
. Let
$u=m$
. Let
![]() $\boldsymbol {\kappa }_*$
be a representation of
$\boldsymbol {\kappa }_*$
be a representation of
![]() $\mathbf {J}_*$
extending
$\mathbf {J}_*$
extending
![]() $\eta _*$
and
$\eta _*$
and
![]() $\boldsymbol {\kappa }$
correspond to it by the map (4.10). If
$\boldsymbol {\kappa }$
correspond to it by the map (4.10). If
![]() $\boldsymbol {\kappa }_*^{}$
is
$\boldsymbol {\kappa }_*^{}$
is
![]() $\mathbf {J}_*^{}\cap { G}_*^\sigma $
-distinguished, then
$\mathbf {J}_*^{}\cap { G}_*^\sigma $
-distinguished, then
![]() $\boldsymbol {\kappa }$
is
$\boldsymbol {\kappa }$
is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished.
$\mathbf {J}\cap { G}^\sigma $
-distinguished.
Proof. The result is given by Lemma 4.15, except when
![]() ${ T}/{ T}_0$
is ramified and
${ T}/{ T}_0$
is ramified and
![]() $m=2i$
, which we assume now. Suppose that
$m=2i$
, which we assume now. Suppose that
![]() $\boldsymbol {\kappa }_*^{}$
is
$\boldsymbol {\kappa }_*^{}$
is
![]() $\mathbf {J}_*^{}\cap { G}_*^\sigma $
-distinguished. By Lemma 4.15, there is a quadratic character
$\mathbf {J}_*^{}\cap { G}_*^\sigma $
-distinguished. By Lemma 4.15, there is a quadratic character
![]() $\boldsymbol {\xi }$
of
$\boldsymbol {\xi }$
of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^0$
such that
$\mathbf {J}^0$
such that
![]() $\boldsymbol {\kappa }\boldsymbol {\xi }$
is
$\boldsymbol {\kappa }\boldsymbol {\xi }$
is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished. Let
$\mathbf {J}\cap { G}^\sigma $
-distinguished. Let
![]() $\boldsymbol {\kappa }_{\theta }$
be the representation given by Proposition 4.16, and write
$\boldsymbol {\kappa }_{\theta }$
be the representation given by Proposition 4.16, and write
![]() $\boldsymbol {\kappa }\boldsymbol {\xi }=\boldsymbol {\kappa }_{\theta }\boldsymbol {\phi }$
for some character
$\boldsymbol {\kappa }\boldsymbol {\xi }=\boldsymbol {\kappa }_{\theta }\boldsymbol {\phi }$
for some character
![]() $\boldsymbol {\phi }$
of
$\boldsymbol {\phi }$
of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $(\mathbf {J}\cap { G}^\sigma )\mathbf {J}^1$
. Restricting to
$(\mathbf {J}\cap { G}^\sigma )\mathbf {J}^1$
. Restricting to
![]() $\mathbf {J}^0$
, the character
$\mathbf {J}^0$
, the character
![]() $\boldsymbol {\phi }$
can be seen as a character of
$\boldsymbol {\phi }$
can be seen as a character of
![]() $\operatorname {GL}_m(\boldsymbol {l})$
of the form
$\operatorname {GL}_m(\boldsymbol {l})$
of the form
![]() $\alpha \circ \mathrm {det}$
, for some character
$\alpha \circ \mathrm {det}$
, for some character
![]() $\alpha $
of
$\alpha $
of
![]() $\boldsymbol {l}^\times $
, which is trivial on
$\boldsymbol {l}^\times $
, which is trivial on
![]() $\operatorname {GL}_m(\boldsymbol {l})^\sigma =\operatorname {GL}_i(\boldsymbol {l})\times \operatorname {GL}_i(\boldsymbol {l})$
. This implies that
$\operatorname {GL}_m(\boldsymbol {l})^\sigma =\operatorname {GL}_i(\boldsymbol {l})\times \operatorname {GL}_i(\boldsymbol {l})$
. This implies that
![]() $\alpha $
is trivial, thus
$\alpha $
is trivial, thus
![]() $\boldsymbol {\phi }$
is trivial on
$\boldsymbol {\phi }$
is trivial on
![]() $\mathbf {J}^0$
. Also,
$\mathbf {J}^0$
. Also,
![]() $\boldsymbol {\phi }$
is trivial at
$\boldsymbol {\phi }$
is trivial at
![]() $\varpi '\in \varpi \mathbf {J}^0$
by Lemma 4.14. It is thus trivial. In conclusion, we have
$\varpi '\in \varpi \mathbf {J}^0$
by Lemma 4.14. It is thus trivial. In conclusion, we have
![]() $\boldsymbol {\kappa }=\boldsymbol {\kappa }_{\theta }\boldsymbol {\xi }$
. Taking determinants, we get
$\boldsymbol {\kappa }=\boldsymbol {\kappa }_{\theta }\boldsymbol {\xi }$
. Taking determinants, we get
(The second equality comes from the fact that
![]() $\boldsymbol {\xi }$
is quadratic and
$\boldsymbol {\xi }$
is quadratic and
![]() $p\neq 2$
so
$p\neq 2$
so
![]() $\operatorname {dim} \boldsymbol {\kappa }_{{\theta }}$
is odd.)
$\operatorname {dim} \boldsymbol {\kappa }_{{\theta }}$
is odd.)
There exists a
![]() $y\in { M}\cap { B}^\times $
such that
$y\in { M}\cap { B}^\times $
such that ![]() is a
is a
![]() $\sigma $
-self-dual maximal simple character of index
$\sigma $
-self-dual maximal simple character of index
![]() $0$
(in the sense of Remark 4.8). By Remark 4.12, the simple character of
$0$
(in the sense of Remark 4.8). By Remark 4.12, the simple character of ![]() associated with
associated with
![]() ${\theta }'$
by Lemma 4.9 is still
${\theta }'$
by Lemma 4.9 is still
![]() ${\theta }_*$
, and the representation of
${\theta }_*$
, and the representation of
![]() $\mathbf {J}'=\mathbf {J}^y$
corresponding to
$\mathbf {J}'=\mathbf {J}^y$
corresponding to
![]() $\boldsymbol {\kappa }_*$
by the map (4.10) is
$\boldsymbol {\kappa }_*$
by the map (4.10) is
![]() $\boldsymbol {\kappa }^y$
. Let
$\boldsymbol {\kappa }^y$
. Let
![]() $\boldsymbol {\kappa }_{{\theta }'}$
be the representation associated with
$\boldsymbol {\kappa }_{{\theta }'}$
be the representation associated with
![]() ${\theta }'$
by Proposition 4.16. By Lemma 4.15,
${\theta }'$
by Proposition 4.16. By Lemma 4.15,
![]() $\boldsymbol {\kappa }'$
is distinguished. By the discussion above, it follows that
$\boldsymbol {\kappa }'$
is distinguished. By the discussion above, it follows that
But the characters
![]() $\mathrm {det}\ \boldsymbol {\kappa }$
,
$\mathrm {det}\ \boldsymbol {\kappa }$
,
![]() $\mathrm {det}\ \boldsymbol {\kappa }^y$
have the same order (since they are conjugate to each others), and the latter one has order a power of p thanks to equation (4.14). Now, equation (4.13) implies that
$\mathrm {det}\ \boldsymbol {\kappa }^y$
have the same order (since they are conjugate to each others), and the latter one has order a power of p thanks to equation (4.14). Now, equation (4.13) implies that
![]() $\boldsymbol {\xi }$
has order a power of p. Since
$\boldsymbol {\xi }$
has order a power of p. Since
![]() $\boldsymbol {\xi }$
is quadratic and
$\boldsymbol {\xi }$
is quadratic and
![]() $p\neq 2$
, this character is trivial.
$p\neq 2$
, this character is trivial.
We extract from the proof of Corollary 4.19 the following valuable corollary.
Corollary 4.20. Suppose that
![]() $u=m$
. Let
$u=m$
. Let
![]() $\boldsymbol {\kappa }_{{\theta }_*}$
and
$\boldsymbol {\kappa }_{{\theta }_*}$
and
![]() $\boldsymbol {\kappa }_{{\theta }}$
be the representations associated with
$\boldsymbol {\kappa }_{{\theta }}$
be the representations associated with
![]() ${\theta }_*$
and
${\theta }_*$
and
![]() ${\theta }$
by Proposition 4.16, respectively. Then the map (4.10) takes
${\theta }$
by Proposition 4.16, respectively. Then the map (4.10) takes
![]() $\boldsymbol {\kappa }_{{\theta }_*}$
to
$\boldsymbol {\kappa }_{{\theta }_*}$
to
![]() $\boldsymbol {\kappa }_{{\theta }}$
.
$\boldsymbol {\kappa }_{{\theta }}$
.
We also have the following corollary, which extends [Reference Sécherre35] Lemma 7.10(3), Corollary 9.6(1).
Corollary 4.21. Any
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished representation of
$\mathbf {J}\cap { G}^\sigma $
-distinguished representation of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\eta $
is
$\eta $
is
![]() $\sigma $
-self-dual.
$\sigma $
-self-dual.
Proof. Let
![]() $\boldsymbol {\kappa }$
be a
$\boldsymbol {\kappa }$
be a
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished representation of
$\mathbf {J}\cap { G}^\sigma $
-distinguished representation of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\eta $
, and
$\eta $
, and
![]() $\boldsymbol {\xi }$
be the unique character of
$\boldsymbol {\xi }$
be the unique character of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
such that
$\mathbf {J}^1$
such that
![]() $\boldsymbol {\kappa }=\boldsymbol {\kappa }_{{\theta }}\boldsymbol {\xi }$
. We have to prove that
$\boldsymbol {\kappa }=\boldsymbol {\kappa }_{{\theta }}\boldsymbol {\xi }$
. We have to prove that
![]() $\boldsymbol {\xi }^{-1}\circ \sigma =\boldsymbol {\xi }$
. The fact that
$\boldsymbol {\xi }^{-1}\circ \sigma =\boldsymbol {\xi }$
. The fact that
![]() $\boldsymbol {\kappa }$
is distinguished implies that
$\boldsymbol {\kappa }$
is distinguished implies that
![]() $\boldsymbol {\xi }$
is trivial on
$\boldsymbol {\xi }$
is trivial on
![]() $(\mathbf {J}\cap { G}^\sigma )\mathbf {J}^1$
. Restricting to
$(\mathbf {J}\cap { G}^\sigma )\mathbf {J}^1$
. Restricting to
![]() $\mathbf {J}^0$
, the character
$\mathbf {J}^0$
, the character
![]() $\boldsymbol {\xi }$
can be seen as a character of
$\boldsymbol {\xi }$
can be seen as a character of
![]() $\operatorname {GL}_m(\boldsymbol {l})$
of the form
$\operatorname {GL}_m(\boldsymbol {l})$
of the form
![]() $\alpha \circ \mathrm {det}$
, for some character
$\alpha \circ \mathrm {det}$
, for some character
![]() $\alpha $
of
$\alpha $
of
![]() $\boldsymbol {l}^\times $
.
$\boldsymbol {l}^\times $
.
If
![]() ${ T}/{ T}_0$
is unramified,
${ T}/{ T}_0$
is unramified,
![]() $\alpha $
is trivial on
$\alpha $
is trivial on
![]() $\boldsymbol {l}_0^\times $
, thus
$\boldsymbol {l}_0^\times $
, thus
![]() $\boldsymbol {\xi }^{-1}\circ \sigma $
and
$\boldsymbol {\xi }^{-1}\circ \sigma $
and
![]() $\boldsymbol {\xi }$
coincide on
$\boldsymbol {\xi }$
coincide on
![]() $\mathbf {J}^0$
. They also coincide on
$\mathbf {J}^0$
. They also coincide on
![]() $\varpi \in \mathbf {J}\cap { G}^\sigma $
, thus they are equal.
$\varpi \in \mathbf {J}\cap { G}^\sigma $
, thus they are equal.
If
![]() ${ T}/{ T}_0$
is ramified,
${ T}/{ T}_0$
is ramified,
![]() $\alpha $
is trivial, thus
$\alpha $
is trivial, thus
![]() $\boldsymbol {\xi }^{-1}\circ \sigma $
and
$\boldsymbol {\xi }^{-1}\circ \sigma $
and
![]() $\boldsymbol {\xi }$
are both trivial on
$\boldsymbol {\xi }$
are both trivial on
![]() $\mathbf {J}^0$
. Since
$\mathbf {J}^0$
. Since
![]() $\boldsymbol {\xi }$
is trivial on
$\boldsymbol {\xi }$
is trivial on
![]() $\varpi ^2\in \mathbf {J}\cap { G}^\sigma $
, we get
$\varpi ^2\in \mathbf {J}\cap { G}^\sigma $
, we get
![]() $\boldsymbol {\xi }^{-1}\circ \sigma (\varpi )=\boldsymbol {\xi }^{-1}(-\varpi )=\boldsymbol {\xi }^{-1}(\varpi )=\boldsymbol {\xi }(\varpi )$
, which finishes the proof.
$\boldsymbol {\xi }^{-1}\circ \sigma (\varpi )=\boldsymbol {\xi }^{-1}(-\varpi )=\boldsymbol {\xi }^{-1}(\varpi )=\boldsymbol {\xi }(\varpi )$
, which finishes the proof.
4.7
We now come to the type theoretic description of cuspidal representations of
![]() ${ G}$
. The following proposition follows from [Reference Bushnell and Kutzko9] Theorem 8.4.1, Corollary 6.2.3, Theorem 5.7.1 (see [Reference Mínguez and Sécherre30] Théorèmes 3.4, 3.7 and [Reference Sécherre and Stevens37] Theorem 7.2 in the modular case).
${ G}$
. The following proposition follows from [Reference Bushnell and Kutzko9] Theorem 8.4.1, Corollary 6.2.3, Theorem 5.7.1 (see [Reference Mínguez and Sécherre30] Théorèmes 3.4, 3.7 and [Reference Sécherre and Stevens37] Theorem 7.2 in the modular case).
Proposition 4.22. Let
![]() $\pi $
be a cuspidal representation of
$\pi $
be a cuspidal representation of
![]() ${ G}$
. There is, up to
${ G}$
. There is, up to
![]() ${ G}$
-conjugacy, a unique simple character
${ G}$
-conjugacy, a unique simple character
![]() ${\theta }$
such that the restriction of
${\theta }$
such that the restriction of
![]() $\pi $
to
$\pi $
to
![]() ${{H}}^1_{\theta }$
contains
${{H}}^1_{\theta }$
contains
![]() ${\theta }$
, and it is maximal.
${\theta }$
, and it is maximal.
Let
![]() $\pi $
be a cuspidal representation of
$\pi $
be a cuspidal representation of
![]() ${ G}$
, and let
${ G}$
, and let
![]() ${\theta }$
be a simple character occurring in
${\theta }$
be a simple character occurring in
![]() $\pi $
. Associated with it, there are:
$\pi $
. Associated with it, there are:
-
○ the positive integer
 $m(\pi )=m{\geqslant }1$
defined by equation (4.3), called the relative degree of
$m(\pi )=m{\geqslant }1$
defined by equation (4.3), called the relative degree of
 $\pi $
,
$\pi $
, -
○ the
 ${ G}$
-conjugacy class (or equivalently the
${ G}$
-conjugacy class (or equivalently the
 ${ F}$
-isomorphism class) of the tamely ramified extension
${ F}$
-isomorphism class) of the tamely ramified extension
 ${ T}$
of
${ T}$
of
 ${{ F}}$
associated with
${{ F}}$
associated with
 ${\theta }$
, called the tame parameter field of
${\theta }$
, called the tame parameter field of
 $\pi $
,
$\pi $
, -
○ the endo-class
 $\boldsymbol {\Theta }$
of
$\boldsymbol {\Theta }$
of
 ${\theta }$
, called the endo-class of
${\theta }$
, called the endo-class of
 $\pi $
.
$\pi $
.
(Note that, when
![]() $\pi $
has level
$\pi $
has level
![]() $0$
, one has
$0$
, one has
![]() $m=n$
and
$m=n$
and
![]() ${ T}={ F}$
, and
${ T}={ F}$
, and
![]() $\boldsymbol {\Theta }$
is the null endo-class.)
$\boldsymbol {\Theta }$
is the null endo-class.)
Write
![]() $\mathbf {J}=\mathbf {J}_{\theta }^{}$
,
$\mathbf {J}=\mathbf {J}_{\theta }^{}$
,
![]() $\mathbf {J}^0=\mathbf {J}^0_{\theta }$
,
$\mathbf {J}^0=\mathbf {J}^0_{\theta }$
,
![]() $\mathbf {J}^1=\mathbf {J}^1_{\theta }$
, and let
$\mathbf {J}^1=\mathbf {J}^1_{\theta }$
, and let
![]() $\eta $
be the Heisenberg representation of
$\eta $
be the Heisenberg representation of
![]() ${\theta }$
. The next proposition follows from [Reference Mínguez and Sécherre30] Lemme 5.3, Theorem 3.11.
${\theta }$
. The next proposition follows from [Reference Mínguez and Sécherre30] Lemme 5.3, Theorem 3.11.
Proposition 4.23. Let
![]() $\boldsymbol {\kappa }$
be a representation of
$\boldsymbol {\kappa }$
be a representation of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\eta $
, and define a representation of
$\eta $
, and define a representation of
![]() $\mathbf {J}$
on the space
$\mathbf {J}$
on the space
![]() $\operatorname {Hom}_{\mathbf {J}^1}(\boldsymbol {\kappa },\pi )$
by making
$\operatorname {Hom}_{\mathbf {J}^1}(\boldsymbol {\kappa },\pi )$
by making
![]() $x\in \mathbf {J}$
act on
$x\in \mathbf {J}$
act on
![]() $f\in \operatorname {Hom}_{\mathbf {J}^1}(\boldsymbol {\kappa },\pi )$
by
$f\in \operatorname {Hom}_{\mathbf {J}^1}(\boldsymbol {\kappa },\pi )$
by
This representation, denoted
![]() $\boldsymbol {\tau }$
, has the following properties:
$\boldsymbol {\tau }$
, has the following properties:
-
1. It is irreducible, and trivial on
 $\mathbf {J}^1$
.
$\mathbf {J}^1$
. -
2. If one identifies
 $\mathbf {J}^0/\mathbf {J}^1$
with a finite general linear group as in (4.4), its restriction to
$\mathbf {J}^0/\mathbf {J}^1$
with a finite general linear group as in (4.4), its restriction to
 $\mathbf {J}^0$
is the inflation of a cuspidal representation.
$\mathbf {J}^0$
is the inflation of a cuspidal representation. -
3. The compact induction of
 $\boldsymbol {\kappa }\otimes \boldsymbol {\tau }$
from
$\boldsymbol {\kappa }\otimes \boldsymbol {\tau }$
from
 $\mathbf {J}$
to
$\mathbf {J}$
to
 ${ G}$
is isomorphic to
${ G}$
is isomorphic to
 $\pi $
.
$\pi $
.
Any two representations of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\eta $
differ from a character of
$\eta $
differ from a character of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
. The pair
$\mathbf {J}^1$
. The pair
thus only depends on
![]() $\pi $
and the choice of
$\pi $
and the choice of
![]() ${\theta }$
and not on the choice of
${\theta }$
and not on the choice of
![]() $\boldsymbol {\kappa }$
.
$\boldsymbol {\kappa }$
.
When
![]() $\pi $
varies among all cuspidal representations of
$\pi $
varies among all cuspidal representations of
![]() ${ G}$
and
${ G}$
and
![]() ${\theta }$
varies among all maximal simple characters in
${\theta }$
varies among all maximal simple characters in
![]() $\pi $
, the pairs (4.15) are called extended maximal simple types in [Reference Bushnell and Kutzko9, Reference Mínguez and Sécherre30], which we will abbreviate to types here. A given cuspidal representation of
$\pi $
, the pairs (4.15) are called extended maximal simple types in [Reference Bushnell and Kutzko9, Reference Mínguez and Sécherre30], which we will abbreviate to types here. A given cuspidal representation of
![]() ${ G}$
thus contains, up to
${ G}$
thus contains, up to
![]() ${ G}$
-conjugacy, a unique type
${ G}$
-conjugacy, a unique type
![]() $(\mathbf {J},\boldsymbol {\lambda })$
: There is a unique maximal simple character
$(\mathbf {J},\boldsymbol {\lambda })$
: There is a unique maximal simple character
![]() ${\theta }$
such that
${\theta }$
such that
![]() $\mathbf {J}_{\theta }=\mathbf {J}$
and
$\mathbf {J}_{\theta }=\mathbf {J}$
and
![]() ${\theta }$
occurs in the restriction of
${\theta }$
occurs in the restriction of
![]() $\boldsymbol {\lambda }$
to
$\boldsymbol {\lambda }$
to
![]() ${{H}}^1_{\theta }$
, a representation
${{H}}^1_{\theta }$
, a representation
![]() $\boldsymbol {\kappa }$
of
$\boldsymbol {\kappa }$
of
![]() $\mathbf {J}$
which restricts irreducibly to
$\mathbf {J}$
which restricts irreducibly to
![]() $\mathbf {J}^1$
and a representation
$\mathbf {J}^1$
and a representation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
such that
$\mathbf {J}^1$
such that
![]() $\boldsymbol {\lambda }$
is isomorphic to
$\boldsymbol {\lambda }$
is isomorphic to
![]() $\boldsymbol {\kappa }\otimes \boldsymbol {\tau }$
.
$\boldsymbol {\kappa }\otimes \boldsymbol {\tau }$
.
Remark 4.24. If
![]() $\mathfrak {a}$
is a maximal order in
$\mathfrak {a}$
is a maximal order in
![]() $\boldsymbol {\mathsf {M}}_n({ F})$
, the trivial character of
$\boldsymbol {\mathsf {M}}_n({ F})$
, the trivial character of
![]() $\mathrm {U}^1_{\mathfrak {a}}$
is a maximal simple character, with
$\mathrm {U}^1_{\mathfrak {a}}$
is a maximal simple character, with
![]() ${ E}={ T}={ F}$
and
${ E}={ T}={ F}$
and
![]() $m=n$
. The cuspidal representations of
$m=n$
. The cuspidal representations of
![]() ${ G}$
that contain such a simple character are precisely the cuspidal representations of level
${ G}$
that contain such a simple character are precisely the cuspidal representations of level
![]() $0$
.
$0$
.
Fix a representation
![]() $\boldsymbol {\kappa }$
of
$\boldsymbol {\kappa }$
of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\eta $
, and define
$\eta $
, and define
![]() $\boldsymbol {\tau }$
as in Proposition 4.23, and fix a simple stratum
$\boldsymbol {\tau }$
as in Proposition 4.23, and fix a simple stratum
![]() $[\mathfrak {a},{\beta }]$
such that
$[\mathfrak {a},{\beta }]$
such that ![]() and an isomorphism (4.3). This gives a field
and an isomorphism (4.3). This gives a field
![]() ${ E}$
and an isomorphism
${ E}$
and an isomorphism
![]() $\mathbf {J}^0/\mathbf {J}^1\simeq \operatorname {GL}_m(\boldsymbol {l})$
, where
$\mathbf {J}^0/\mathbf {J}^1\simeq \operatorname {GL}_m(\boldsymbol {l})$
, where
![]() $\boldsymbol {l}$
is the residue field of
$\boldsymbol {l}$
is the residue field of
![]() ${ T}$
.
${ T}$
.
By Proposition 4.23(2), the restriction of
![]() $\boldsymbol {\tau }$
to
$\boldsymbol {\tau }$
to
![]() $\mathbf {J}^0$
is the inflation of a cuspidal irreducible representation, denoted
$\mathbf {J}^0$
is the inflation of a cuspidal irreducible representation, denoted
![]() $\mathrm {V}$
.
$\mathrm {V}$
.
On the other hand, the representation
![]() $\boldsymbol {\tau }$
has a central character: It is a character of the centre
$\boldsymbol {\tau }$
has a central character: It is a character of the centre
![]() ${ E}^\times \mathbf {J}^1/\mathbf {J}^1$
of
${ E}^\times \mathbf {J}^1/\mathbf {J}^1$
of
![]() $\mathbf {J}/\mathbf {J}^1$
or equivalently a tamely ramified character of
$\mathbf {J}/\mathbf {J}^1$
or equivalently a tamely ramified character of
![]() ${ E}^\times $
. Since
${ E}^\times $
. Since
![]() ${ E}$
is totally wildly ramified over its maximal tamely ramified subextension
${ E}$
is totally wildly ramified over its maximal tamely ramified subextension
![]() ${ T}$
, any tamely ramified character of
${ T}$
, any tamely ramified character of
![]() ${ E}^\times $
factors through the norm
${ E}^\times $
factors through the norm
![]() $\mathrm {N}_{{ E}/{ T}}$
. The restriction of
$\mathrm {N}_{{ E}/{ T}}$
. The restriction of
![]() $\boldsymbol {\tau }$
to
$\boldsymbol {\tau }$
to
![]() ${ E}^\times $
is thus a multiple of
${ E}^\times $
is thus a multiple of
![]() $\omega \circ \mathrm {N}_{{ E}/{ T}}$
for a uniquely determined tamely ramified character
$\omega \circ \mathrm {N}_{{ E}/{ T}}$
for a uniquely determined tamely ramified character
![]() $\omega $
of
$\omega $
of
![]() ${ T}^\times $
.
${ T}^\times $
.
The data
![]() $\mathrm {V}$
and
$\mathrm {V}$
and
![]() $\omega $
are subject to the compatibility condition that the restriction of
$\omega $
are subject to the compatibility condition that the restriction of
![]() $\mathrm {V}$
to
$\mathrm {V}$
to
![]() $\boldsymbol {l}^\times $
is a multiple of the character of
$\boldsymbol {l}^\times $
is a multiple of the character of
![]() $\boldsymbol {l}^\times $
whose inflation to
$\boldsymbol {l}^\times $
whose inflation to ![]() is the restriction of
is the restriction of
![]() $\omega ^{p^e}$
, with
$\omega ^{p^e}$
, with
![]() $p^e=[{ E}:{ T}]$
. Associated with
$p^e=[{ E}:{ T}]$
. Associated with
![]() $\mathrm {V}$
by Proposition 3.9, there are a unique integer
$\mathrm {V}$
by Proposition 3.9, there are a unique integer
![]() $u{\geqslant }1$
dividing m and a unique supercuspidal representation
$u{\geqslant }1$
dividing m and a unique supercuspidal representation
![]() $\varrho $
of
$\varrho $
of
![]() $\operatorname {GL}_{m/u}(\boldsymbol {l})$
such that
$\operatorname {GL}_{m/u}(\boldsymbol {l})$
such that
![]() $\mathrm {V}$
is isomorphic to
$\mathrm {V}$
is isomorphic to
![]() $\operatorname {st}_u(\varrho )$
. The next important result is [Reference Mínguez and Sécherre31] Lemma 3.2. The integer
$\operatorname {st}_u(\varrho )$
. The next important result is [Reference Mínguez and Sécherre31] Lemma 3.2. The integer
![]() $r(\pi )$
has been defined in Paragraph 3.4.
$r(\pi )$
has been defined in Paragraph 3.4.
Lemma 4.25. The integer u is equal to
![]() $r(\pi )$
.
$r(\pi )$
.
It follows that
![]() $r(\pi )$
divides m and that
$r(\pi )$
divides m and that
![]() $\pi $
is supercuspidal if and only if
$\pi $
is supercuspidal if and only if
![]() $\mathrm {V}$
is supercuspidal.
$\mathrm {V}$
is supercuspidal.
4.8
Write
![]() $r=r(\pi )$
and
$r=r(\pi )$
and
![]() $k=n/r$
, and let
$k=n/r$
, and let
![]() $\rho $
be a supercuspidal representation of
$\rho $
be a supercuspidal representation of
![]() $\operatorname {GL}_{k}({{ F}})$
such that
$\operatorname {GL}_{k}({{ F}})$
such that
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
given by Proposition 3.6. In this paragraph, we will compare the type theoretic description of
$\operatorname {St}_r(\rho )$
given by Proposition 3.6. In this paragraph, we will compare the type theoretic description of
![]() $\pi $
with that of
$\pi $
with that of
![]() $\rho $
. As in 4.7, we fix a representation
$\rho $
. As in 4.7, we fix a representation
![]() $\boldsymbol {\kappa }$
of
$\boldsymbol {\kappa }$
of
![]() $\mathbf {J}$
extending
$\mathbf {J}$
extending
![]() $\eta $
. It defines an irreducible representation
$\eta $
. It defines an irreducible representation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
, then a cuspidal representation
$\mathbf {J}^1$
, then a cuspidal representation
![]() $\mathrm {V}$
of
$\mathrm {V}$
of
![]() $\operatorname {GL}_m(\boldsymbol {l})$
and a tamely ramified character
$\operatorname {GL}_m(\boldsymbol {l})$
and a tamely ramified character
![]() $\omega $
of
$\omega $
of
![]() ${ T}^\times $
. There is also a (unique) supercuspidal representation
${ T}^\times $
. There is also a (unique) supercuspidal representation
![]() $\varrho $
of
$\varrho $
of
![]() $\operatorname {GL}_{m/r}(\boldsymbol {l})$
such that
$\operatorname {GL}_{m/r}(\boldsymbol {l})$
such that
![]() $\mathrm {V}$
is isomorphic to
$\mathrm {V}$
is isomorphic to
![]() $\operatorname {st}_r(\varrho )$
.
$\operatorname {st}_r(\varrho )$
.
Since r divides m, we may apply the results of 4.4 to the case where
![]() $u=r$
, which we assume now. Let
$u=r$
, which we assume now. Let
![]() ${\theta }_*$
be the simple character associated with
${\theta }_*$
be the simple character associated with
![]() ${\theta }$
by Lemma 4.9.
${\theta }$
by Lemma 4.9.
Lemma 4.26. The representation
![]() $\rho $
contains
$\rho $
contains
![]() ${\theta }_*$
.
${\theta }_*$
.
Proof. This follows from the descriptionFootnote
1
of
![]() $\operatorname {St}_r(\rho )$
in [Reference Mínguez and Sécherre29] Section 6.
$\operatorname {St}_r(\rho )$
in [Reference Mínguez and Sécherre29] Section 6.
Consequently,
![]() $\pi $
and
$\pi $
and
![]() $\rho $
have the same endo-class. We have the following immediate corollary.
$\rho $
have the same endo-class. We have the following immediate corollary.
Corollary 4.27. We have
![]() $m(\pi )=m(\rho )r$
and the representations
$m(\pi )=m(\rho )r$
and the representations
![]() $\pi $
,
$\pi $
,
![]() $\rho $
have the same tame parameter field.
$\rho $
have the same tame parameter field.
Let
![]() $\eta _*$
be the Heisenberg representation associated with
$\eta _*$
be the Heisenberg representation associated with
![]() ${\theta }_*$
, and let
${\theta }_*$
, and let
![]() $\boldsymbol {\kappa }_*$
be a representation of
$\boldsymbol {\kappa }_*$
be a representation of
![]() $\mathbf {J}_*$
extending
$\mathbf {J}_*$
extending
![]() $\eta _*$
such that the representation of
$\eta _*$
such that the representation of
![]() $\mathbf {J}$
associated with it by the map (4.10) is
$\mathbf {J}$
associated with it by the map (4.10) is
![]() $\boldsymbol {\kappa }$
. It defines an irreducible representation
$\boldsymbol {\kappa }$
. It defines an irreducible representation
![]() $\boldsymbol {\tau }_*^{}$
of
$\boldsymbol {\tau }_*^{}$
of
![]() $\mathbf {J}^{}_*$
trivial on
$\mathbf {J}^{}_*$
trivial on
![]() $\mathbf {J}^1_*$
such that the pair
$\mathbf {J}^1_*$
such that the pair
![]() $(\mathbf {J}_*,\boldsymbol {\kappa }_*\otimes \boldsymbol {\tau }_*)$
is a type in
$(\mathbf {J}_*,\boldsymbol {\kappa }_*\otimes \boldsymbol {\tau }_*)$
is a type in
![]() $\rho $
. Associated with this, there are a cuspidal representation
$\rho $
. Associated with this, there are a cuspidal representation
![]() $\varrho _*$
of
$\varrho _*$
of
![]() $\operatorname {GL}_{m/r}(\boldsymbol {l})$
(which is supercuspidal thanks to the comment after Lemma 4.25) and a tamely ramified character
$\operatorname {GL}_{m/r}(\boldsymbol {l})$
(which is supercuspidal thanks to the comment after Lemma 4.25) and a tamely ramified character
![]() $\omega _*$
of
$\omega _*$
of
![]() ${ T}^\times $
. The following proposition compares the pairs
${ T}^\times $
. The following proposition compares the pairs
![]() $(\varrho ,\omega )$
and
$(\varrho ,\omega )$
and
![]() $(\varrho _*,\omega _*)$
associated with
$(\varrho _*,\omega _*)$
associated with
![]() $\boldsymbol {\tau }$
and
$\boldsymbol {\tau }$
and
![]() $\boldsymbol {\tau }_*$
.
$\boldsymbol {\tau }_*$
.
Proposition 4.28. We have
![]() $\varrho \simeq \varrho _*$
and
$\varrho \simeq \varrho _*$
and
![]() $\omega =\omega _*^r$
.
$\omega =\omega _*^r$
.
Proof. Again, the fact that
![]() $\varrho $
is isomorphic to
$\varrho $
is isomorphic to
![]() $\varrho _*$
follows from the description of
$\varrho _*$
follows from the description of
![]() $\operatorname {St}_r(\rho )$
in [Reference Mínguez and Sécherre29] Section 6. It thus remains to prove the second equality. For this, consider the action of
$\operatorname {St}_r(\rho )$
in [Reference Mínguez and Sécherre29] Section 6. It thus remains to prove the second equality. For this, consider the action of
![]() $\mathbf {J}$
on
$\mathbf {J}$
on
where
![]() $\mathscr {I}(\rho ,r)$
is the parabolically induced representation (3.1). By [Reference Sécherre and Stevens38] Proposition 5.6, its restriction to
$\mathscr {I}(\rho ,r)$
is the parabolically induced representation (3.1). By [Reference Sécherre and Stevens38] Proposition 5.6, its restriction to
![]() $\mathbf {J}^0$
is the inflation of the induced representation
$\mathbf {J}^0$
is the inflation of the induced representation
![]() $\varrho _*\times \cdots \times \varrho _*$
of
$\varrho _*\times \cdots \times \varrho _*$
of
![]() $\operatorname {GL}_m(\boldsymbol {l})$
. By tracking the action of
$\operatorname {GL}_m(\boldsymbol {l})$
. By tracking the action of
![]() ${ E}^\times $
in the arguments of [Reference Sécherre and Stevens38] Section 5, we see that it acts on the space (4.16) by the character
${ E}^\times $
in the arguments of [Reference Sécherre and Stevens38] Section 5, we see that it acts on the space (4.16) by the character
In particular,
![]() ${ E}^\times $
acts through this character on the subquotient
${ E}^\times $
acts through this character on the subquotient
![]() $\operatorname {Hom}_{\mathbf {J}^1}(\boldsymbol {\kappa },\pi )$
, which is
$\operatorname {Hom}_{\mathbf {J}^1}(\boldsymbol {\kappa },\pi )$
, which is
![]() $\boldsymbol {\tau }$
.
$\boldsymbol {\tau }$
.
4.9
Suppose that the cuspidal representation
![]() $\pi $
is
$\pi $
is
![]() $\sigma $
-self-dual. We say a type
$\sigma $
-self-dual. We say a type
![]() $(\mathbf {J},\boldsymbol {\lambda })$
is
$(\mathbf {J},\boldsymbol {\lambda })$
is
![]() $\sigma $
-self-dual if
$\sigma $
-self-dual if
![]() $\mathbf {J}$
is
$\mathbf {J}$
is
![]() $\sigma $
-stable and
$\sigma $
-stable and
![]() $\boldsymbol {\lambda }^{\vee \sigma }$
is isomorphic to
$\boldsymbol {\lambda }^{\vee \sigma }$
is isomorphic to
![]() $\boldsymbol {\lambda }$
. The next result is [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Theorem 4.1.
$\boldsymbol {\lambda }$
. The next result is [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Theorem 4.1.
Proposition 4.29. The representation
![]() $\pi $
contains a
$\pi $
contains a
![]() $\sigma $
-self-dual type.
$\sigma $
-self-dual type.
A type
![]() $(\mathbf {J},\boldsymbol {\lambda })$
contains a unique simple character
$(\mathbf {J},\boldsymbol {\lambda })$
contains a unique simple character
![]() ${\theta }$
such that
${\theta }$
such that
![]() $\mathbf {J}_{\theta }=\mathbf {J}$
: It follows that, if
$\mathbf {J}_{\theta }=\mathbf {J}$
: It follows that, if
![]() $(\mathbf {J},\boldsymbol {\lambda })$
is
$(\mathbf {J},\boldsymbol {\lambda })$
is
![]() $\sigma $
-self-dual,
$\sigma $
-self-dual,
![]() ${\theta }$
is
${\theta }$
is
![]() $\sigma $
-self-dual as well. In particular,
$\sigma $
-self-dual as well. In particular,
![]() $\pi $
contains a
$\pi $
contains a
![]() $\sigma $
-self-dual simple character.
$\sigma $
-self-dual simple character.
Let
![]() ${\theta }$
be a
${\theta }$
be a
![]() $\sigma $
-self-dual simple character occurring in
$\sigma $
-self-dual simple character occurring in
![]() $\pi $
, and
$\pi $
, and
![]() $[\mathfrak {a},{\beta }]$
be a
$[\mathfrak {a},{\beta }]$
be a
![]() $\sigma $
-self-dual simple stratum such that
$\sigma $
-self-dual simple stratum such that ![]() (which exists by Proposition 4.5). The
(which exists by Proposition 4.5). The
![]() ${ G}^\sigma $
-conjugacy class (or equivalently the
${ G}^\sigma $
-conjugacy class (or equivalently the
![]() ${ F}_0$
-isomorphism class) of the tamely ramified extension
${ F}_0$
-isomorphism class) of the tamely ramified extension
![]() ${ T}_0$
of
${ T}_0$
of
![]() ${ E}_0$
associated with
${ E}_0$
associated with
![]() ${\theta }$
only depends on
${\theta }$
only depends on
![]() $\pi $
. Associated with
$\pi $
. Associated with
![]() $\pi $
, there is thus a quadratic extension
$\pi $
, there is thus a quadratic extension
![]() ${ T}/{ T}_0$
.
${ T}/{ T}_0$
.
Remark 4.30. When
![]() $\pi $
has level
$\pi $
has level
![]() $0$
, one has
$0$
, one has
![]() ${ T}_0={ F}_0$
.
${ T}_0={ F}_0$
.
If follows from Proposition 4.7 that
![]() $\pi $
contains
$\pi $
contains
-
○ only one
 ${ G}^\sigma $
-conjugacy class of
${ G}^\sigma $
-conjugacy class of
 $\sigma $
-self-dual types if
$\sigma $
-self-dual types if
 ${ T}/{ T}_0$
is unramified,
${ T}/{ T}_0$
is unramified, -
○
 $\lfloor m/2\rfloor +1$
different
$\lfloor m/2\rfloor +1$
different
 ${ G}^\sigma $
-conjugacy classes of
${ G}^\sigma $
-conjugacy classes of
 $\sigma $
-self-dual types if
$\sigma $
-self-dual types if
 ${ T}/{ T}_0$
is ramified.
${ T}/{ T}_0$
is ramified.
Among these
![]() ${ G}^\sigma $
-conjugacy classes of
${ G}^\sigma $
-conjugacy classes of
![]() $\sigma $
-self-dual types, one is of particular importance.
$\sigma $
-self-dual types, one is of particular importance.
Definition 4.31. A
![]() $\sigma $
-self-dual type
$\sigma $
-self-dual type
![]() $(\mathbf {J},\boldsymbol {\lambda })$
is said to be generic if either
$(\mathbf {J},\boldsymbol {\lambda })$
is said to be generic if either
![]() ${ T}/{ T}_0$
is unramified, or
${ T}/{ T}_0$
is unramified, or
![]() ${ T}/{ T}_0$
is ramified and the integer i of Proposition 4.5(2.b) is equal to
${ T}/{ T}_0$
is ramified and the integer i of Proposition 4.5(2.b) is equal to
![]() $\lfloor m/2\rfloor $
.
$\lfloor m/2\rfloor $
.
A
![]() $\sigma $
-self-dual cuspidal representation of
$\sigma $
-self-dual cuspidal representation of
![]() ${ G}$
thus contains, up to
${ G}$
thus contains, up to
![]() ${ G}^\sigma $
-conjugacy, a unique generic
${ G}^\sigma $
-conjugacy, a unique generic
![]() $\sigma $
-self-dual type. The next result is [Reference Sécherre35] Theorem 10.3 (see also [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Section 6).
$\sigma $
-self-dual type. The next result is [Reference Sécherre35] Theorem 10.3 (see also [Reference Anandavardhanan, Kurinczuk, Matringe, Sécherre and Stevens3] Section 6).
Proposition 4.32. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal representation of
$\sigma $
-self-dual cuspidal representation of
![]() ${ G}$
and
${ G}$
and
![]() $(\mathbf {J},\boldsymbol {\lambda })$
be its generic
$(\mathbf {J},\boldsymbol {\lambda })$
be its generic
![]() $\sigma $
-self-dual type. Then
$\sigma $
-self-dual type. Then
![]() $\pi $
is distinguished if and only if
$\pi $
is distinguished if and only if
![]() $\boldsymbol {\lambda }$
is
$\boldsymbol {\lambda }$
is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished.
$\mathbf {J}\cap { G}^\sigma $
-distinguished.
If
![]() $(\mathbf {J},\boldsymbol {\lambda })$
is a
$(\mathbf {J},\boldsymbol {\lambda })$
is a
![]() $\sigma $
-self-dual type, and if
$\sigma $
-self-dual type, and if
![]() ${\theta }$
is the unique simple character contained in
${\theta }$
is the unique simple character contained in
![]() $\boldsymbol {\lambda }$
such that
$\boldsymbol {\lambda }$
such that
![]() $\mathbf {J}_{\theta }=\mathbf {J}$
, we will write
$\mathbf {J}_{\theta }=\mathbf {J}$
, we will write
![]() $\boldsymbol {\lambda }_{\mathrm {w}}$
for the unique representation
$\boldsymbol {\lambda }_{\mathrm {w}}$
for the unique representation
![]() $\boldsymbol {\kappa }_{{\theta }}$
of
$\boldsymbol {\kappa }_{{\theta }}$
of
![]() $\mathbf {J}$
extending the Heisenberg representation of
$\mathbf {J}$
extending the Heisenberg representation of
![]() ${\theta }$
given by Proposition 4.16. The next result extends [Reference Sécherre35] Propositions 7.9, 9.8 to the case of arbitrary
${\theta }$
given by Proposition 4.16. The next result extends [Reference Sécherre35] Propositions 7.9, 9.8 to the case of arbitrary
![]() $\sigma $
-self-dual cuspidal representations.
$\sigma $
-self-dual cuspidal representations.
Proposition 4.33. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal representation of
$\sigma $
-self-dual cuspidal representation of
![]() ${ G}$
. Let
${ G}$
. Let
![]() $(\mathbf {J},\boldsymbol {\lambda })$
be a generic
$(\mathbf {J},\boldsymbol {\lambda })$
be a generic
![]() $\sigma $
-self-dual type in
$\sigma $
-self-dual type in
![]() $\pi $
and
$\pi $
and
![]() $\boldsymbol {\tau }$
be the representation of
$\boldsymbol {\tau }$
be the representation of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
such that
$\mathbf {J}^1$
such that
![]() $\boldsymbol {\lambda }$
is isomorphic to
$\boldsymbol {\lambda }$
is isomorphic to
![]() $\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\tau }$
. Then
$\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\tau }$
. Then
![]() $\pi $
is distinguished if and only if
$\pi $
is distinguished if and only if
![]() $\boldsymbol {\tau }$
is
$\boldsymbol {\tau }$
is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished.
$\mathbf {J}\cap { G}^\sigma $
-distinguished.
Proof. This follows from Proposition 4.32 together with the fact that
and
![]() $\operatorname {Hom}_{\mathbf {J}\cap { G}^\sigma }(\boldsymbol {\lambda }_{\mathrm {w}},{ R})$
has dimension
$\operatorname {Hom}_{\mathbf {J}\cap { G}^\sigma }(\boldsymbol {\lambda }_{\mathrm {w}},{ R})$
has dimension
![]() $1$
(see Proposition 4.6(4)).
$1$
(see Proposition 4.6(4)).
Fix isomorphisms
as in Proposition 4.5(4). The restriction of
![]() $\boldsymbol {\tau }$
to
$\boldsymbol {\tau }$
to
![]() $\mathbf {J}\cap { B}^\times $
is a generic
$\mathbf {J}\cap { B}^\times $
is a generic
![]() $\sigma $
-self-dual type of level
$\sigma $
-self-dual type of level
![]() $0$
in
$0$
in
![]() ${ B}^\times \simeq \operatorname {GL}_m({ E})$
and
${ B}^\times \simeq \operatorname {GL}_m({ E})$
and
![]() $\mathbf {J}/\mathbf {J}^1$
is naturally isomorphic to
$\mathbf {J}/\mathbf {J}^1$
is naturally isomorphic to
![]() $(\mathbf {J}\cap { B}^\times ) / (\mathbf {J}^1\cap { B}^\times )$
. The representation
$(\mathbf {J}\cap { B}^\times ) / (\mathbf {J}^1\cap { B}^\times )$
. The representation
![]() $\boldsymbol {\tau }$
is thus distinguished by
$\boldsymbol {\tau }$
is thus distinguished by
![]() $\mathbf {J}\cap { G}^\sigma $
if and only if its restriction to
$\mathbf {J}\cap { G}^\sigma $
if and only if its restriction to
![]() $\mathbf {J}\cap \operatorname {GL}_m({ E})$
is distinguished by
$\mathbf {J}\cap \operatorname {GL}_m({ E})$
is distinguished by
![]() $\mathbf {J}\cap \operatorname {GL}_m({ E}_0)$
. Proposition 4.33 used twice thus implies that
$\mathbf {J}\cap \operatorname {GL}_m({ E}_0)$
. Proposition 4.33 used twice thus implies that
![]() $\pi $
is distinguished by
$\pi $
is distinguished by
![]() ${ G}^\sigma $
if and only if the cuspidal representation of level
${ G}^\sigma $
if and only if the cuspidal representation of level
![]() $0$
of
$0$
of
![]() $\operatorname {GL}_m({ E})$
compactly induced from the restriction of
$\operatorname {GL}_m({ E})$
compactly induced from the restriction of
![]() $\boldsymbol {\tau }$
to
$\boldsymbol {\tau }$
to
![]() $\mathbf {J}\cap \operatorname {GL}_m({ E})$
is distinguished by
$\mathbf {J}\cap \operatorname {GL}_m({ E})$
is distinguished by
![]() $\operatorname {GL}_m({ E}_0)$
.
$\operatorname {GL}_m({ E}_0)$
.
However, the field extension
![]() ${ E}$
is not canonical. In 4.10, we will canonically associate with
${ E}$
is not canonical. In 4.10, we will canonically associate with
![]() $\pi $
a
$\pi $
a
![]() $\sigma $
-self-dual cuspidal representation
$\sigma $
-self-dual cuspidal representation
![]() $\pi _{\mathrm {t}}$
of level
$\pi _{\mathrm {t}}$
of level
![]() $0$
of
$0$
of
![]() $\operatorname {GL}_m({ T})$
, which is
$\operatorname {GL}_m({ T})$
, which is
![]() $\operatorname {GL}_m({ T}_0)$
-distinguished if and only if
$\operatorname {GL}_m({ T}_0)$
-distinguished if and only if
![]() $\pi $
is
$\pi $
is
![]() ${ G}^\sigma $
-distinguished, where
${ G}^\sigma $
-distinguished, where
![]() ${ T}/{ T}_0$
is the quadratic extension associated with
${ T}/{ T}_0$
is the quadratic extension associated with
![]() $\pi $
. Our strategy is inspired from [Reference Bushnell and Henniart8] Section 3.
$\pi $
. Our strategy is inspired from [Reference Bushnell and Henniart8] Section 3.
The following proposition relates the parity of
![]() $m/r$
to the ramification of
$m/r$
to the ramification of
![]() ${ T}/{ T}_0$
.
${ T}/{ T}_0$
.
Proposition 4.34. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal representation of
$\sigma $
-self-dual cuspidal representation of
![]() $\operatorname {GL}_n({{ F}})$
with quadratic extension
$\operatorname {GL}_n({{ F}})$
with quadratic extension
![]() ${ T}/{ T}_0$
, and write
${ T}/{ T}_0$
, and write
![]() $m=m(\pi )$
,
$m=m(\pi )$
,
![]() $r=r(\pi )$
. Then
$r=r(\pi )$
. Then
 $$ \begin{align*} m/r\text{ is } \left\{ \begin{array}{l} \text{odd if }{ T}/{ T}_0\text{ is unramified}, \\ \text{either even or equal to }1\text{ if }{ T}/{ T}_0\text{ is ramified}. \end{array}\right. \end{align*} $$
$$ \begin{align*} m/r\text{ is } \left\{ \begin{array}{l} \text{odd if }{ T}/{ T}_0\text{ is unramified}, \\ \text{either even or equal to }1\text{ if }{ T}/{ T}_0\text{ is ramified}. \end{array}\right. \end{align*} $$
Proof. Write
![]() $\pi $
as
$\pi $
as
![]() $\operatorname {St}_r(\rho )$
as in Proposition 3.8 with
$\operatorname {St}_r(\rho )$
as in Proposition 3.8 with
![]() $\rho ^{\sigma \vee }\simeq \rho \nu ^i$
for some
$\rho ^{\sigma \vee }\simeq \rho \nu ^i$
for some
![]() $i\in \{0,1\}$
. Then
$i\in \{0,1\}$
. Then
![]() $\rho \nu ^{i/2}$
is a
$\rho \nu ^{i/2}$
is a
![]() $\sigma $
-self-dual supercuspidal representation of
$\sigma $
-self-dual supercuspidal representation of
![]() $\operatorname {GL}_{n/r}({{ F}})$
, and the quadratic extension associated with it is
$\operatorname {GL}_{n/r}({{ F}})$
, and the quadratic extension associated with it is
![]() ${ T}/{ T}_0$
. Applying [Reference Sécherre35] Propositions 8.1, 9.8, we get the expected result.
${ T}/{ T}_0$
. Applying [Reference Sécherre35] Propositions 8.1, 9.8, we get the expected result.
4.10
In order to prove Theorem 4.41, it will be useful to consider the slightly more general situation where
![]() $\pi $
is a cuspidal representation of
$\pi $
is a cuspidal representation of
![]() ${ G}$
with
${ G}$
with
![]() $\sigma $
-self-dual endo-class
$\sigma $
-self-dual endo-class
![]() $\boldsymbol {\Theta }$
. Thus
$\boldsymbol {\Theta }$
. Thus
![]() $\pi $
itself needs not be
$\pi $
itself needs not be
![]() $\sigma $
-self-dual. However, it has a relative degree m and, since
$\sigma $
-self-dual. However, it has a relative degree m and, since
![]() $\boldsymbol {\Theta }$
is
$\boldsymbol {\Theta }$
is
![]() $\sigma $
-self-dual, there is a quadratic extension
$\sigma $
-self-dual, there is a quadratic extension
![]() ${ T}/{ T}_0$
associated with it. Moreover, by Proposition 4.7, it contains, up to
${ T}/{ T}_0$
associated with it. Moreover, by Proposition 4.7, it contains, up to
![]() ${ G}^\sigma $
-conjugacy, a unique generic
${ G}^\sigma $
-conjugacy, a unique generic
![]() $\sigma $
-self-dual maximal simple character
$\sigma $
-self-dual maximal simple character
![]() ${\theta }$
. Let
${\theta }$
. Let
![]() $\mathbf {J}$
be its normalizer in
$\mathbf {J}$
be its normalizer in
![]() ${ G}$
and
${ G}$
and
![]() $\boldsymbol {\kappa }_{{\theta }}$
be the representation of
$\boldsymbol {\kappa }_{{\theta }}$
be the representation of
![]() $\mathbf {J}$
given by Proposition 4.16. Then
$\mathbf {J}$
given by Proposition 4.16. Then
![]() $\pi $
contains a unique type of the form
$\pi $
contains a unique type of the form
for a uniquely determined irreducible representation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
. Fix a
$\mathbf {J}^1$
. Fix a
![]() $\sigma $
-self-dual simple stratum
$\sigma $
-self-dual simple stratum
![]() $[\mathfrak {a},{\beta }]$
and isomorphisms (4.17) as in Proposition 4.5.
$[\mathfrak {a},{\beta }]$
and isomorphisms (4.17) as in Proposition 4.5.
First, we define an open and compact mod centre subgroup
![]() $\mathbf {J}_{\mathrm {t}}$
of
$\mathbf {J}_{\mathrm {t}}$
of
![]() $\operatorname {GL}_m({ T})$
as follows:
$\operatorname {GL}_m({ T})$
as follows:
-
○ if
 ${ T}/{ T}_0$
is unramified,
${ T}/{ T}_0$
is unramified,
 $\mathbf {J}_{\mathrm {t}}$
is the normalizer of
$\mathbf {J}_{\mathrm {t}}$
is the normalizer of  in
in
 $\operatorname {GL}_m({ T})$
,
$\operatorname {GL}_m({ T})$
, -
○ if
 ${ T}/{ T}_0$
is ramified, and if t is a uniformizer of
${ T}/{ T}_0$
is ramified, and if t is a uniformizer of
 ${ T}$
such that
${ T}$
such that
 $\sigma (t)=-t$
, then
$\sigma (t)=-t$
, then
 $\mathbf {J}_{\mathrm {t}}$
is the normalizer in
$\mathbf {J}_{\mathrm {t}}$
is the normalizer in
 $\operatorname {GL}_m({ T})$
of the conjugate of
$\operatorname {GL}_m({ T})$
of the conjugate of  by the diagonal element where t occurs
by the diagonal element where t occurs $$ \begin{align*} \mathrm{diag}(t,\dots,t,1,\dots,1) \in \operatorname{GL}_m({ T}), \end{align*} $$
$$ \begin{align*} \mathrm{diag}(t,\dots,t,1,\dots,1) \in \operatorname{GL}_m({ T}), \end{align*} $$
 $\lfloor m/2\rfloor $
times.
$\lfloor m/2\rfloor $
times.
The group
![]() $\mathbf {J}_{\mathrm {t}}$
(which does not depend on the choice of t in the ramified case) has a unique maximal compact subgroup
$\mathbf {J}_{\mathrm {t}}$
(which does not depend on the choice of t in the ramified case) has a unique maximal compact subgroup
![]() $\mathbf {J}_{\mathrm {t}}^0$
and a unique normal maximal pro-p-subgroup
$\mathbf {J}_{\mathrm {t}}^0$
and a unique normal maximal pro-p-subgroup
![]() $\mathbf {J}_{\mathrm {t}}^1$
. The natural group isomorphism
$\mathbf {J}_{\mathrm {t}}^1$
. The natural group isomorphism
transports the action of
![]() $\sigma \in \operatorname {Gal}({ T}/{ T}_0)$
on
$\sigma \in \operatorname {Gal}({ T}/{ T}_0)$
on
![]() $\mathbf {J}_{\mathrm {t}}^0/\mathbf {J}_{\mathrm {t}}^1$
to
$\mathbf {J}_{\mathrm {t}}^0/\mathbf {J}_{\mathrm {t}}^1$
to
-
○ the action of the nontrivial element of
 $\operatorname {Gal}(\boldsymbol {l}/\boldsymbol {l}_0)$
on
$\operatorname {Gal}(\boldsymbol {l}/\boldsymbol {l}_0)$
on
 $\operatorname {GL}_m(\boldsymbol {l})$
if
$\operatorname {GL}_m(\boldsymbol {l})$
if
 ${ T}/{ T}_0$
is unramified,
${ T}/{ T}_0$
is unramified, -
○ the adjoint action of
(4.20)on $$ \begin{align} \begin{pmatrix} -\mathrm{id}_{\lfloor m/2\rfloor} & 0 \\ 0 & \mathrm{id}_{m-\lfloor m/2\rfloor} \end{pmatrix} \in \operatorname{GL}_m(\boldsymbol{l}), \end{align} $$
$$ \begin{align} \begin{pmatrix} -\mathrm{id}_{\lfloor m/2\rfloor} & 0 \\ 0 & \mathrm{id}_{m-\lfloor m/2\rfloor} \end{pmatrix} \in \operatorname{GL}_m(\boldsymbol{l}), \end{align} $$
 $\operatorname {GL}_m(\boldsymbol {l})$
if
$\operatorname {GL}_m(\boldsymbol {l})$
if
 ${ T}/{ T}_0$
is ramified.
${ T}/{ T}_0$
is ramified.
Remark 4.35. When
![]() ${ T}/{ T}_0$
is ramified, the isomorphism (4.19) depends on the choice of t: changing t to another uniformizer
${ T}/{ T}_0$
is ramified, the isomorphism (4.19) depends on the choice of t: changing t to another uniformizer
![]() $t'$
conjugates the isomorphism by the
$t'$
conjugates the isomorphism by the
![]() $\sigma $
-invariant element
$\sigma $
-invariant element
where
![]() $\alpha $
(which occurs i times) is the image of
$\alpha $
(which occurs i times) is the image of
![]() $t't^{-1}$
in
$t't^{-1}$
in
![]() $\boldsymbol {l}^\times $
. This element is central in
$\boldsymbol {l}^\times $
. This element is central in
![]() $\operatorname {GL}_m(\boldsymbol {l})^\sigma $
.
$\operatorname {GL}_m(\boldsymbol {l})^\sigma $
.
We now associate to
![]() $\boldsymbol {\tau }$
an irreducible representation
$\boldsymbol {\tau }$
an irreducible representation
![]() $\boldsymbol {\tau }_{\mathrm {t}}^{}$
of
$\boldsymbol {\tau }_{\mathrm {t}}^{}$
of
![]() $\mathbf {J}_{\mathrm {t}}^{}$
trivial on
$\mathbf {J}_{\mathrm {t}}^{}$
trivial on
![]() $\mathbf {J}_{\mathrm {t}}^1$
. On the one hand, the restriction of
$\mathbf {J}_{\mathrm {t}}^1$
. On the one hand, the restriction of
![]() $\boldsymbol {\tau }$
to
$\boldsymbol {\tau }$
to
![]() $\mathbf {J}^0$
is the inflation of an irreducible cuspidal representation
$\mathbf {J}^0$
is the inflation of an irreducible cuspidal representation
![]() $\mathrm {V}$
of
$\mathrm {V}$
of
![]() $\operatorname {GL}_m(\boldsymbol {l})$
. On the other hand, the restriction of
$\operatorname {GL}_m(\boldsymbol {l})$
. On the other hand, the restriction of
![]() $\boldsymbol {\tau }$
to
$\boldsymbol {\tau }$
to
![]() ${ E}^\times $
is a multiple of
${ E}^\times $
is a multiple of
![]() $\omega \circ \mathrm {N}_{{ E}/{ T}}$
for a uniquely determined tamely ramified character
$\omega \circ \mathrm {N}_{{ E}/{ T}}$
for a uniquely determined tamely ramified character
![]() $\omega $
of
$\omega $
of
![]() ${ T}^\times $
: See 4.7. Note that
${ T}^\times $
: See 4.7. Note that
![]() $[{ E}:{ T}]=p^e$
for some
$[{ E}:{ T}]=p^e$
for some
![]() $e{\geqslant }1$
.
$e{\geqslant }1$
.
Lemma 4.36. Let
![]() $\mathrm {V}$
and
$\mathrm {V}$
and
![]() $\omega $
be as above.
$\omega $
be as above.
-
1. There is a unique representation
 $\boldsymbol {\tau }_{\mathrm {t}}^{}$
of
$\boldsymbol {\tau }_{\mathrm {t}}^{}$
of
 $\mathbf {J}_{\mathrm {t}}^{}$
trivial on
$\mathbf {J}_{\mathrm {t}}^{}$
trivial on
 $\mathbf {J}_{\mathrm {t}}^1$
such that
$\mathbf {J}_{\mathrm {t}}^1$
such that-
(a) the restriction of
 $\boldsymbol {\tau }_{\mathrm {t}}^{}$
to
$\boldsymbol {\tau }_{\mathrm {t}}^{}$
to
 ${ T}^\times $
is a multiple of the character
${ T}^\times $
is a multiple of the character
 $\omega $
,
$\omega $
, -
(b) the restriction of
 $\boldsymbol {\tau }_{\mathrm {t}}^{}$
to
$\boldsymbol {\tau }_{\mathrm {t}}^{}$
to
 $\mathbf {J}_{\mathrm {t}}^0$
is the inflation of
$\mathbf {J}_{\mathrm {t}}^0$
is the inflation of
 $\mathrm {V}^{(p^{-e})}$
, where
$\mathrm {V}^{(p^{-e})}$
, where
 $\mathrm {V}^{(p^{-e})}$
is the representation of
$\mathrm {V}^{(p^{-e})}$
is the representation of
 $\operatorname {GL}_m(\boldsymbol {l})$
obtained from
$\operatorname {GL}_m(\boldsymbol {l})$
obtained from
 $\mathrm {V}$
by applying the field automorphism
$\mathrm {V}$
by applying the field automorphism
 $x\mapsto x^{p^{-e}}$
.
$x\mapsto x^{p^{-e}}$
.
-
-
2. The pair
 $(\mathbf {J}_{\mathrm {t}},\boldsymbol {\tau }_{\mathrm {t}})$
is a level
$(\mathbf {J}_{\mathrm {t}},\boldsymbol {\tau }_{\mathrm {t}})$
is a level
 $0$
type in
$0$
type in
 $ \operatorname {GL}_m({ T})$
.
$ \operatorname {GL}_m({ T})$
. -
3. Up to isomorphism, the representation
 $\boldsymbol {\tau }_{\mathrm {t}}$
only depends on
$\boldsymbol {\tau }_{\mathrm {t}}$
only depends on
 $\boldsymbol {\tau }$
, and not on the choice of the
$\boldsymbol {\tau }$
, and not on the choice of the
 $\sigma $
-self-dual simple stratum
$\sigma $
-self-dual simple stratum
 $[\mathfrak {a},{\beta }]$
, the uniformizer t and the identification
$[\mathfrak {a},{\beta }]$
, the uniformizer t and the identification
 $\mathbf {J}^0/\mathbf {J}^1\simeq \operatorname {GL}_m(\boldsymbol {l})$
.
$\mathbf {J}^0/\mathbf {J}^1\simeq \operatorname {GL}_m(\boldsymbol {l})$
.
Proof. Uniqueness follows from the fact that
![]() $\mathbf {J}_{\mathrm {t}}^{}$
is generated by
$\mathbf {J}_{\mathrm {t}}^{}$
is generated by
![]() $\mathbf {J}_{\mathrm {t}}^0$
and
$\mathbf {J}_{\mathrm {t}}^0$
and
![]() ${ T}^\times $
, and the existence of
${ T}^\times $
, and the existence of
![]() $\boldsymbol {\tau }_{\mathrm {t}}^{}$
follows from the fact that the restriction of
$\boldsymbol {\tau }_{\mathrm {t}}^{}$
follows from the fact that the restriction of
![]() $\mathrm {V}^{(p^{-e})}$
to
$\mathrm {V}^{(p^{-e})}$
to
![]() $\boldsymbol {l}^\times $
is a multiple of the character of
$\boldsymbol {l}^\times $
is a multiple of the character of
![]() $\boldsymbol {l}^\times $
defined by the restriction of
$\boldsymbol {l}^\times $
defined by the restriction of
![]() $\omega $
to the units of
$\omega $
to the units of
![]() ${ T}^\times $
. Since
${ T}^\times $
. Since
![]() $\mathrm {V}^{(p^{-e})}$
is cuspidal, the pair
$\mathrm {V}^{(p^{-e})}$
is cuspidal, the pair
![]() $(\mathbf {J}_{\mathrm {t}},\boldsymbol {\tau }_{\mathrm {t}})$
is a level
$(\mathbf {J}_{\mathrm {t}},\boldsymbol {\tau }_{\mathrm {t}})$
is a level
![]() $0$
type by construction. It remains to prove (3). Since it will require techniques which are not used anywhere else in the paper, we will prove it apart, in Paragraph 4.14.
$0$
type by construction. It remains to prove (3). Since it will require techniques which are not used anywhere else in the paper, we will prove it apart, in Paragraph 4.14.
It will be convenient to give another description of the representation
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
.
$\boldsymbol {\tau }_{\mathrm {t}}$
.
Lemma 4.37.
-
1. There is a unique group isomorphism
 $\boldsymbol {\pi }:\mathbf {J}/\mathbf {J}^1 \to \mathbf {J}_{\mathrm {t}}^{}/\mathbf {J}_{\mathrm {t}}^1$
such that
$\boldsymbol {\pi }:\mathbf {J}/\mathbf {J}^1 \to \mathbf {J}_{\mathrm {t}}^{}/\mathbf {J}_{\mathrm {t}}^1$
such that-
(a) its restriction to
 $\operatorname {GL}_m(\boldsymbol {l})$
is the automorphism acting entrywise by
$\operatorname {GL}_m(\boldsymbol {l})$
is the automorphism acting entrywise by
 $\phi :x\mapsto x^{p^{e}}$
,
$\phi :x\mapsto x^{p^{e}}$
, -
(b) for all
 $x\in { E}^\times $
, the image of
$x\in { E}^\times $
, the image of
 $x\mathbf {J}^1$
is
$x\mathbf {J}^1$
is
 $\mathrm {N}_{{ E}/{ T}}(x)\mathbf {J}_{\mathrm {t}}^1$
.
$\mathrm {N}_{{ E}/{ T}}(x)\mathbf {J}_{\mathrm {t}}^1$
.
-
-
2. The isomorphism
 $\boldsymbol {\pi }$
is
$\boldsymbol {\pi }$
is
 $\sigma $
-equivariant.
$\sigma $
-equivariant. -
3. The representation
 $\boldsymbol {\tau }_{\mathrm {t}}$
is isomorphic to
$\boldsymbol {\tau }_{\mathrm {t}}$
is isomorphic to
 $\boldsymbol {\tau }\circ \boldsymbol {\pi }^{-1}$
.
$\boldsymbol {\tau }\circ \boldsymbol {\pi }^{-1}$
.
Proof. Again, uniqueness follows from the the fact that
![]() $\mathbf {J}$
is generated by
$\mathbf {J}$
is generated by
![]() $\mathbf {J}^0$
and
$\mathbf {J}^0$
and
![]() ${ E}^\times $
. Existence follows from the fact that
${ E}^\times $
. Existence follows from the fact that
![]() $\mathrm {N}_{{ E}/{ T}}(x)=x^{p^{e}}$
for all
$\mathrm {N}_{{ E}/{ T}}(x)=x^{p^{e}}$
for all ![]() of order prime to p and that
of order prime to p and that
![]() $\mathrm {N}_{{ E}/{ T}}$
induces a group isomorphism from
$\mathrm {N}_{{ E}/{ T}}$
induces a group isomorphism from
![]() ${ E}^\times /(1+\mathfrak {p}_{ E})$
to
${ E}^\times /(1+\mathfrak {p}_{ E})$
to
![]() ${ T}^\times /(1+\mathfrak {p}_{ T})$
.
${ T}^\times /(1+\mathfrak {p}_{ T})$
.
Define
![]() $\boldsymbol {\pi }_1$
to be
$\boldsymbol {\pi }_1$
to be
![]() $\sigma \circ \boldsymbol {\pi }\circ \sigma ^{-1}$
. The restriction of
$\sigma \circ \boldsymbol {\pi }\circ \sigma ^{-1}$
. The restriction of
![]() $\boldsymbol {\pi }_1$
to
$\boldsymbol {\pi }_1$
to
![]() ${ E}^\times $
corresponds to
${ E}^\times $
corresponds to
![]() $\sigma \circ \mathrm {N}_{{ E}/{ T}}\circ \sigma ^{-1}$
, which is equal to
$\sigma \circ \mathrm {N}_{{ E}/{ T}}\circ \sigma ^{-1}$
, which is equal to
![]() $\mathrm {N}_{{ E}/{ T}}$
since
$\mathrm {N}_{{ E}/{ T}}$
since
![]() ${ E}$
and
${ E}$
and
![]() ${ T}$
are stable by
${ T}$
are stable by
![]() $\sigma $
. The restriction of
$\sigma $
. The restriction of
![]() $\boldsymbol {\pi }_1$
to
$\boldsymbol {\pi }_1$
to
![]() $\operatorname {GL}_m(\boldsymbol {l})$
is
$\operatorname {GL}_m(\boldsymbol {l})$
is
-
○ the automorphism defined by making
 $\sigma \circ \phi \circ \sigma ^{-1} = \phi \in \operatorname {Gal}(\boldsymbol {l}/\mathbb {F}_p)$
act entrywise if
$\sigma \circ \phi \circ \sigma ^{-1} = \phi \in \operatorname {Gal}(\boldsymbol {l}/\mathbb {F}_p)$
act entrywise if
 ${ T}/{ T}_0$
is unramified,
${ T}/{ T}_0$
is unramified, -
○ the automorphism
 $\mathrm {Ad}({\delta }^{-1} \phi ({\delta }))\circ \phi =\phi $
if
$\mathrm {Ad}({\delta }^{-1} \phi ({\delta }))\circ \phi =\phi $
if
 ${ T}/{ T}_0$
is ramified, where
${ T}/{ T}_0$
is ramified, where
 ${\delta }$
is the
${\delta }$
is the
 $\phi $
-invariant matrix defined by equation (4.5).
$\phi $
-invariant matrix defined by equation (4.5).
The fact that
![]() $\boldsymbol {\pi }$
is
$\boldsymbol {\pi }$
is
![]() $\sigma $
-equivariant now follows from its uniqueness, and (3) is immediate.
$\sigma $
-equivariant now follows from its uniqueness, and (3) is immediate.
Now, let us describe the behavior of
![]() $\boldsymbol {\tau }\mapsto \boldsymbol {\tau }_{\mathrm {t}}$
with respect to duality and distinction.
$\boldsymbol {\tau }\mapsto \boldsymbol {\tau }_{\mathrm {t}}$
with respect to duality and distinction.
Lemma 4.38.
-
1. The representation
 $\boldsymbol {\tau }_{\mathrm {t}}$
is
$\boldsymbol {\tau }_{\mathrm {t}}$
is
 $\sigma $
-self-dual if and only if
$\sigma $
-self-dual if and only if
 $\boldsymbol {\tau }$
is
$\boldsymbol {\tau }$
is
 $\sigma $
-self-dual.
$\sigma $
-self-dual. -
2. The representation
 $\boldsymbol {\tau }_{\mathrm {t}}$
is
$\boldsymbol {\tau }_{\mathrm {t}}$
is
 $\mathbf {J}_{\mathrm {t}}\cap \operatorname {GL}_m({ T}_0)$
-distinguished if and only if
$\mathbf {J}_{\mathrm {t}}\cap \operatorname {GL}_m({ T}_0)$
-distinguished if and only if
 $\boldsymbol {\tau }$
is
$\boldsymbol {\tau }$
is
 $\mathbf {J}\cap { G}^\sigma $
-distinguished.
$\mathbf {J}\cap { G}^\sigma $
-distinguished.
Proof. Saying that
![]() $\boldsymbol {\tau }$
is
$\boldsymbol {\tau }$
is
![]() $\sigma $
-self-dual is equivalent to saying that the representation
$\sigma $
-self-dual is equivalent to saying that the representation
![]() $\mathrm {V}$
and the character
$\mathrm {V}$
and the character
![]() $\omega \circ \mathrm {N}_{{ E}/{ T}}$
are
$\omega \circ \mathrm {N}_{{ E}/{ T}}$
are
![]() $\sigma $
-self-dual. Assertion (1) follows from the fact that
$\sigma $
-self-dual. Assertion (1) follows from the fact that
![]() $(\mathrm {V}^{(p^{-e})})^{\vee \sigma }$
is isomorphic to
$(\mathrm {V}^{(p^{-e})})^{\vee \sigma }$
is isomorphic to
![]() $(\mathrm {V}^{\vee \sigma })^{(p^{-e})}$
and
$(\mathrm {V}^{\vee \sigma })^{(p^{-e})}$
and
![]() $(\omega \circ \mathrm {N}_{{ E}/{ T}})^{-1}\circ \sigma $
is equal to
$(\omega \circ \mathrm {N}_{{ E}/{ T}})^{-1}\circ \sigma $
is equal to
![]() $(\omega ^{-1}\circ \sigma )\circ \mathrm {N}_{{ E}/{ T}}$
.
$(\omega ^{-1}\circ \sigma )\circ \mathrm {N}_{{ E}/{ T}}$
.
Assertion (2) follows from the fact that
![]() $\boldsymbol {\tau }_{\mathrm {t}}\circ \boldsymbol {\pi }=\boldsymbol {\tau }$
and
$\boldsymbol {\tau }_{\mathrm {t}}\circ \boldsymbol {\pi }=\boldsymbol {\tau }$
and
![]() $\boldsymbol {\pi }$
maps
$\boldsymbol {\pi }$
maps
![]() $(\mathbf {J}/\mathbf {J}^1)^\sigma $
to
$(\mathbf {J}/\mathbf {J}^1)^\sigma $
to
![]() $(\mathbf {J}_{\mathrm {t}}^{}/\mathbf {J}_{\mathrm {t}}^1)^\sigma $
.
$(\mathbf {J}_{\mathrm {t}}^{}/\mathbf {J}_{\mathrm {t}}^1)^\sigma $
.
Corollary 4.39. The pair
![]() $(\mathbf {J}_{\mathrm {t}},\boldsymbol {\tau }_{\mathrm {t}})$
is a generic
$(\mathbf {J}_{\mathrm {t}},\boldsymbol {\tau }_{\mathrm {t}})$
is a generic
![]() $\sigma $
-self-dual type if and only if
$\sigma $
-self-dual type if and only if
![]() $(\mathbf {J},\boldsymbol {\kappa }_{{\theta }}\otimes \boldsymbol {\tau })$
is a generic
$(\mathbf {J},\boldsymbol {\kappa }_{{\theta }}\otimes \boldsymbol {\tau })$
is a generic
![]() $\sigma $
-self-dual type.
$\sigma $
-self-dual type.
4.11
We still are in the situation of Paragraph 4.10. Consider the compactly induced representation
It satisfies the following properties.
Proposition 4.40.
-
1. The representation
 $\pi _{\mathrm {t}}$
is cuspidal, irreducible and has level
$\pi _{\mathrm {t}}$
is cuspidal, irreducible and has level
 $0$
.
$0$
. -
2. One has
 $m(\pi _{\mathrm {t}})=m$
and
$m(\pi _{\mathrm {t}})=m$
and
 $r(\pi _{\mathrm {t}})=r$
.
$r(\pi _{\mathrm {t}})=r$
. -
3. The representation
 $\pi _{\mathrm {t}}$
is
$\pi _{\mathrm {t}}$
is
 $\sigma $
-self-dual if and only if
$\sigma $
-self-dual if and only if
 $\pi $
is
$\pi $
is
 $\sigma $
-self-dual.
$\sigma $
-self-dual. -
4. The representation
 $\pi _{\mathrm {t}}$
is
$\pi _{\mathrm {t}}$
is
 $\operatorname {GL}_m({ T}_0)$
-distinguished if and only
$\operatorname {GL}_m({ T}_0)$
-distinguished if and only
 $\pi $
is
$\pi $
is
 $\operatorname {GL}_n({ F}_0)$
-distinguished.
$\operatorname {GL}_n({ F}_0)$
-distinguished.
Proof. Assertion (1) follows from the fact that
![]() $\pi _{\mathrm {t}}$
is compactly induced from a level
$\pi _{\mathrm {t}}$
is compactly induced from a level
![]() $0$
type in
$0$
type in
![]() $\operatorname {GL}_m({ T})$
(see Lemma 4.36 and Remark 4.24). The first equality of Assertion (2) follows from Remark 4.24, and the second one from Lemma 4.25.
$\operatorname {GL}_m({ T})$
(see Lemma 4.36 and Remark 4.24). The first equality of Assertion (2) follows from Remark 4.24, and the second one from Lemma 4.25.
Suppose that
![]() $\pi $
is
$\pi $
is
![]() $\sigma $
-self-dual. Then
$\sigma $
-self-dual. Then
![]() $\boldsymbol {\tau }$
is
$\boldsymbol {\tau }$
is
![]() $\sigma $
-self-dual (see 4.9). By Lemma 4.38, the representation
$\sigma $
-self-dual (see 4.9). By Lemma 4.38, the representation
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
is
$\boldsymbol {\tau }_{\mathrm {t}}$
is
![]() $\sigma $
-self-dual as well. By compact induction, it follows that
$\sigma $
-self-dual as well. By compact induction, it follows that
![]() $\pi _{\mathrm {t}}$
is
$\pi _{\mathrm {t}}$
is
![]() $\sigma $
-self-dual. The argument also works the other way round, proving (3). Assertion (4) follows from Proposition 4.33 together with Lemma 4.38(2).
$\sigma $
-self-dual. The argument also works the other way round, proving (3). Assertion (4) follows from Proposition 4.33 together with Lemma 4.38(2).
Theorem 4.41.
-
1. The process
(4.22)induces a bijection from the set of isomorphism classes of cuspidal representations of $$ \begin{align} \pi\mapsto\pi_{\mathrm{t}} \end{align} $$
$$ \begin{align} \pi\mapsto\pi_{\mathrm{t}} \end{align} $$
 ${ G}$
with endo-class
${ G}$
with endo-class
 $\boldsymbol {\Theta }$
to that of cuspidal representations of level
$\boldsymbol {\Theta }$
to that of cuspidal representations of level
 $0$
of
$0$
of
 $\operatorname {GL}_m({ T})$
.
$\operatorname {GL}_m({ T})$
.
-
2. The bijection (4.22) maps
 $\sigma $
-self-dual representations onto
$\sigma $
-self-dual representations onto
 $\sigma $
-self-dual representations and
$\sigma $
-self-dual representations and
 ${ G}^\sigma $
-distinguished representations onto
${ G}^\sigma $
-distinguished representations onto
 $\operatorname {GL}_m({ T}_0)$
-distinguished representations.
$\operatorname {GL}_m({ T}_0)$
-distinguished representations. -
3. For any cuspidal representation
 $\pi $
with endo-class
$\pi $
with endo-class
 $\boldsymbol {\Theta }$
and any tamely ramified character
$\boldsymbol {\Theta }$
and any tamely ramified character
 $\chi $
of
$\chi $
of
 ${ F}^\times $
, the representation
${ F}^\times $
, the representation
 $(\pi \chi )_{\mathrm {t}}$
is isomorphic to
$(\pi \chi )_{\mathrm {t}}$
is isomorphic to
 $\pi _{\mathrm {t}}(\chi \circ \mathrm {N}_{{ T}/{ F}})$
.
$\pi _{\mathrm {t}}(\chi \circ \mathrm {N}_{{ T}/{ F}})$
.
Proof. For (1), let
![]() $\pi _0$
be a cuspidal representation of level
$\pi _0$
be a cuspidal representation of level
![]() $0$
of
$0$
of
![]() $\operatorname {GL}_m({ T})$
. It contains a level
$\operatorname {GL}_m({ T})$
. It contains a level
![]() $0$
type
$0$
type
![]() $(\mathbf {J}_{\mathrm {t}},\boldsymbol {\tau }_0)$
for a uniquely determined representation
$(\mathbf {J}_{\mathrm {t}},\boldsymbol {\tau }_0)$
for a uniquely determined representation
![]() $\boldsymbol {\tau }_0$
of
$\boldsymbol {\tau }_0$
of
![]() $\mathbf {J}_{\mathrm {t}}$
trivial on
$\mathbf {J}_{\mathrm {t}}$
trivial on
![]() $\mathbf {J}_{\mathrm {t}}^1$
. It then suffices to check that the process
$\mathbf {J}_{\mathrm {t}}^1$
. It then suffices to check that the process
gives the inverse bijection. For (3), notice that if
![]() $\pi $
contains the type
$\pi $
contains the type
![]() $(\mathbf {J},\boldsymbol {\kappa }_{{\theta }}\otimes \boldsymbol {\tau })$
, then
$(\mathbf {J},\boldsymbol {\kappa }_{{\theta }}\otimes \boldsymbol {\tau })$
, then
![]() $\pi \chi $
contains the type
$\pi \chi $
contains the type
![]() $(\mathbf {J},\boldsymbol {\kappa }_{{\theta }}\otimes \boldsymbol {\tau }\chi ^{\mathbf {J}})$
, where
$(\mathbf {J},\boldsymbol {\kappa }_{{\theta }}\otimes \boldsymbol {\tau }\chi ^{\mathbf {J}})$
, where
![]() $\chi ^{\mathbf {J}}$
is the unique character of
$\chi ^{\mathbf {J}}$
is the unique character of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
whose restriction to
$\mathbf {J}^1$
whose restriction to
![]() $\mathbf {J}\cap { B}^\times \simeq \operatorname {GL}_m({ E})$
is equal to
$\mathbf {J}\cap { B}^\times \simeq \operatorname {GL}_m({ E})$
is equal to
![]() $(\chi \circ \mathrm {N}_{{ E}/{ F}})\circ \mathrm {det}_{ E}$
where
$(\chi \circ \mathrm {N}_{{ E}/{ F}})\circ \mathrm {det}_{ E}$
where
![]() $\mathrm {det}_{ E}$
is the determinant on
$\mathrm {det}_{ E}$
is the determinant on
![]() ${ B}\simeq \boldsymbol {\mathsf {M}}_m({ E})$
. Then
${ B}\simeq \boldsymbol {\mathsf {M}}_m({ E})$
. Then
![]() $(\boldsymbol {\tau }\chi ^{\mathbf {J}})_{\mathrm {t}}$
is isomorphic to the representation
$(\boldsymbol {\tau }\chi ^{\mathbf {J}})_{\mathrm {t}}$
is isomorphic to the representation
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
twisted by the character of
$\boldsymbol {\tau }_{\mathrm {t}}$
twisted by the character of
![]() $\mathbf {J}_{\mathrm {t}}$
trivial on
$\mathbf {J}_{\mathrm {t}}$
trivial on
![]() $\mathbf {J}_{\mathrm {t}}^1$
given by
$\mathbf {J}_{\mathrm {t}}^1$
given by
![]() $(\chi \circ \mathrm {N}_{{ T}/{ F}})\circ \mathrm {det}_{ T}$
, where
$(\chi \circ \mathrm {N}_{{ T}/{ F}})\circ \mathrm {det}_{ T}$
, where
![]() $\mathrm {det}_{ T}$
is the determinant on
$\mathrm {det}_{ T}$
is the determinant on
![]() $\boldsymbol {\mathsf {M}}_m({ T})$
. Assertion (2) is given by Proposition 4.40.
$\boldsymbol {\mathsf {M}}_m({ T})$
. Assertion (2) is given by Proposition 4.40.
Corollary 4.42. Let
![]() $\mu $
be a tamely ramified character of
$\mu $
be a tamely ramified character of
![]() $F_0^\times $
. A cuspidal representation
$F_0^\times $
. A cuspidal representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {GL}_n(F)$
with endo-class
$\operatorname {GL}_n(F)$
with endo-class
![]() $\boldsymbol {\Theta }$
is distinguished by
$\boldsymbol {\Theta }$
is distinguished by
![]() $\mu $
if and only if
$\mu $
if and only if
![]() $\pi _{\mathrm {t}}$
is distinguished by
$\pi _{\mathrm {t}}$
is distinguished by
![]() $\mu \circ \mathrm {N}_{T_0/F_0}$
.
$\mu \circ \mathrm {N}_{T_0/F_0}$
.
Proof. Fix a tamely ramified character
![]() $\xi $
of
$\xi $
of
![]() $F^\times $
extending
$F^\times $
extending
![]() $\mu $
. Then
$\mu $
. Then
![]() $\pi $
is
$\pi $
is
![]() $\mu $
-distinguished if and only if
$\mu $
-distinguished if and only if
![]() $\pi \xi ^{-1}$
is distinguished, and
$\pi \xi ^{-1}$
is distinguished, and
![]() $(\pi \xi ^{-1})_{\mathrm {t}}$
is isomorphic to
$(\pi \xi ^{-1})_{\mathrm {t}}$
is isomorphic to
![]() $\pi _{\mathrm {t}}(\xi ^{-1}\circ \mathrm {N}_{{ T}/{ F}})$
. Thus,
$\pi _{\mathrm {t}}(\xi ^{-1}\circ \mathrm {N}_{{ T}/{ F}})$
. Thus,
![]() $\pi $
is
$\pi $
is
![]() $\mu $
-distinguished if and only if
$\mu $
-distinguished if and only if
![]() $\pi _{\mathrm {t}}$
is distinguished by the character
$\pi _{\mathrm {t}}$
is distinguished by the character
![]() $\xi \circ \mathrm {N}_{{ T}/{ F}}|_{T_0^\times }=\mu \circ \mathrm {N}_{T_0/F_0}$
.
$\xi \circ \mathrm {N}_{{ T}/{ F}}|_{T_0^\times }=\mu \circ \mathrm {N}_{T_0/F_0}$
.
Finally, let us describe the compatibility of the process (4.22) with the description of cuspidal representations in terms of supercuspidal ones of 4.8.
Proposition 4.43. Let
![]() $\pi $
be a cuspidal representation of
$\pi $
be a cuspidal representation of
![]() ${ G}$
with endo-class
${ G}$
with endo-class
![]() $\boldsymbol {\Theta }$
and
$\boldsymbol {\Theta }$
and
![]() $r=r(\pi )$
. Let
$r=r(\pi )$
. Let
![]() $\rho $
be a supercuspidal representation of
$\rho $
be a supercuspidal representation of
![]() $\operatorname {GL}_{n/r}({ F})$
such that
$\operatorname {GL}_{n/r}({ F})$
such that
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
. Then
$\operatorname {St}_r(\rho )$
. Then
![]() $\pi _{\mathrm {t}}$
is isomorphic to
$\pi _{\mathrm {t}}$
is isomorphic to
![]() $\operatorname {St}_r(\rho _{\mathrm {t}})$
.
$\operatorname {St}_r(\rho _{\mathrm {t}})$
.
Remark 4.44. Note that this makes sense since, by Corollary 4.27, the representations
![]() $\pi $
,
$\pi $
,
![]() $\rho $
have the same endo-class
$\rho $
have the same endo-class
![]() $\boldsymbol {\Theta }$
, thus the same quadratic extension
$\boldsymbol {\Theta }$
, thus the same quadratic extension
![]() ${ T}/{ T}_0$
.
${ T}/{ T}_0$
.
Proof. The representation
![]() $\pi $
contains a type of the form
$\pi $
contains a type of the form
![]() $(\mathbf {J},\boldsymbol {\kappa }_{{\theta }}\otimes \boldsymbol {\tau })$
for a unique representation
$(\mathbf {J},\boldsymbol {\kappa }_{{\theta }}\otimes \boldsymbol {\tau })$
for a unique representation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
. Fix a
$\mathbf {J}^1$
. Fix a
![]() $\sigma $
-self-dual simple stratum
$\sigma $
-self-dual simple stratum
![]() $[\mathfrak {a},{\beta }]$
and isomorphisms (4.17) as in Proposition 4.5. Associated with
$[\mathfrak {a},{\beta }]$
and isomorphisms (4.17) as in Proposition 4.5. Associated with
![]() $\boldsymbol {\tau }$
, there are a tamely ramified character
$\boldsymbol {\tau }$
, there are a tamely ramified character
![]() $\omega $
of
$\omega $
of
![]() ${ T}$
, and a cuspidal representation
${ T}$
, and a cuspidal representation
![]() $\mathrm {V}=\operatorname {st}_r(\varrho )$
of
$\mathrm {V}=\operatorname {st}_r(\varrho )$
of
![]() $\operatorname {GL}_{m}(\boldsymbol {l})$
, for some supercuspidal representation
$\operatorname {GL}_{m}(\boldsymbol {l})$
, for some supercuspidal representation
![]() $\varrho $
of
$\varrho $
of
![]() $\operatorname {GL}_{m/r}(\boldsymbol {l})$
. The representation
$\operatorname {GL}_{m/r}(\boldsymbol {l})$
. The representation
![]() $\boldsymbol {\tau }$
is entirely determined by the fact that
$\boldsymbol {\tau }$
is entirely determined by the fact that
-
○ its restriction to
 $\mathbf {J}^0$
is the inflation of
$\mathbf {J}^0$
is the inflation of
 $\mathrm {V}$
,
$\mathrm {V}$
, -
○ its restriction to
 ${ E}^\times $
is a multiple of the character
${ E}^\times $
is a multiple of the character
 $\omega \circ \mathrm {N}_{{ E}/{ T}}$
.
$\omega \circ \mathrm {N}_{{ E}/{ T}}$
.
We now use the results of 4.4 and 4.5 for
![]() $u=r$
. Let
$u=r$
. Let
![]() ${\theta }_*$
be the simple character associated with
${\theta }_*$
be the simple character associated with
![]() ${\theta }$
by Lemma 4.9. Thanks to Corollary 4.20, the representation
${\theta }$
by Lemma 4.9. Thanks to Corollary 4.20, the representation
![]() $\boldsymbol {\kappa }_{{\theta }_*}$
corresponds to
$\boldsymbol {\kappa }_{{\theta }_*}$
corresponds to
![]() $\boldsymbol {\kappa }_{{\theta }}$
via the map (4.10). Paragraph 4.8 says that
$\boldsymbol {\kappa }_{{\theta }}$
via the map (4.10). Paragraph 4.8 says that
![]() $\rho $
contains the type
$\rho $
contains the type
![]() $(\mathbf {J}_*, \boldsymbol {\kappa }_{{\theta }_*}\otimes \boldsymbol {\tau }_*)$
, where
$(\mathbf {J}_*, \boldsymbol {\kappa }_{{\theta }_*}\otimes \boldsymbol {\tau }_*)$
, where
![]() $\boldsymbol {\tau }_*$
is the representation of
$\boldsymbol {\tau }_*$
is the representation of
![]() $\mathbf {J}_*$
trivial on
$\mathbf {J}_*$
trivial on
![]() $\mathbf {J}^1_*$
determined by
$\mathbf {J}^1_*$
determined by
-
○ its restriction to
 $\mathbf {J}_*^0$
is the inflation of
$\mathbf {J}_*^0$
is the inflation of
 $\varrho $
,
$\varrho $
, -
○ its restriction to
 ${ E}^\times $
is a multiple of
${ E}^\times $
is a multiple of
 $\omega _*\circ \mathrm {N}_{{ E}/{ T}}$
, where
$\omega _*\circ \mathrm {N}_{{ E}/{ T}}$
, where
 $\omega _*$
is a tamely ramified character of
$\omega _*$
is a tamely ramified character of
 ${ T}^\times $
such that
${ T}^\times $
such that
 $\omega _*^r=\omega $
.
$\omega _*^r=\omega $
.
Thus,
![]() $\rho _{\mathrm {t}}$
is compactly induced from the level
$\rho _{\mathrm {t}}$
is compactly induced from the level
![]() $0$
type
$0$
type
![]() $(\mathbf {J}_{*,\mathrm {t}},\boldsymbol {\tau }_{*,\mathrm {t}})$
where
$(\mathbf {J}_{*,\mathrm {t}},\boldsymbol {\tau }_{*,\mathrm {t}})$
where
![]() $\boldsymbol {\tau }_{*,\mathrm {t}}$
is determined by
$\boldsymbol {\tau }_{*,\mathrm {t}}$
is determined by
-
○ its restriction to
 $\mathbf {J}_{*,\mathrm {t}}^0$
is the inflation of
$\mathbf {J}_{*,\mathrm {t}}^0$
is the inflation of
 $\varrho ^{(p^{-e})}$
,
$\varrho ^{(p^{-e})}$
, -
○ its restriction to
 ${ T}^\times $
is a multiple of
${ T}^\times $
is a multiple of
 $\omega _*$
.
$\omega _*$
.
Thus,
![]() $\operatorname {St}_r(\rho _{\mathrm {t}})$
is compactly induced from the level
$\operatorname {St}_r(\rho _{\mathrm {t}})$
is compactly induced from the level
![]() $0$
type
$0$
type
![]() $(\mathbf {J}_{\mathrm {t}},\boldsymbol {\delta }),$
where
$(\mathbf {J}_{\mathrm {t}},\boldsymbol {\delta }),$
where
![]() $\boldsymbol {\delta }$
is determined by
$\boldsymbol {\delta }$
is determined by
-
○ its restriction to
 $\mathbf {J}_{\mathrm {t}}^0$
is the inflation of
$\mathbf {J}_{\mathrm {t}}^0$
is the inflation of
 $\operatorname {st}_r(\varrho ^{(p^{-e})})\simeq \mathrm {V}^{(p^{-e})}$
,
$\operatorname {st}_r(\varrho ^{(p^{-e})})\simeq \mathrm {V}^{(p^{-e})}$
, -
○ its restriction to
 ${ T}^\times $
is a multiple of
${ T}^\times $
is a multiple of
 $\omega _*^r=\omega $
.
$\omega _*^r=\omega $
.
It follows that
![]() $\boldsymbol {\delta }$
is isomorphic to
$\boldsymbol {\delta }$
is isomorphic to
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
, whence
$\boldsymbol {\tau }_{\mathrm {t}}$
, whence
![]() $\operatorname {St}_r(\rho _{\mathrm {t}})$
is isomorphic to
$\operatorname {St}_r(\rho _{\mathrm {t}})$
is isomorphic to
![]() $\pi _{\mathrm {t}}$
.
$\pi _{\mathrm {t}}$
.
4.12
Finally, let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal representation of
$\sigma $
-self-dual cuspidal representation of
![]() ${ G}$
, of level
${ G}$
, of level
![]() $0$
. It has a central character
$0$
. It has a central character
![]() $c_\pi $
and its generic type
$c_\pi $
and its generic type
![]() $(\mathbf {J},\boldsymbol {\lambda })$
defines a cuspidal representation
$(\mathbf {J},\boldsymbol {\lambda })$
defines a cuspidal representation
![]() $\mathrm {V}$
of
$\mathrm {V}$
of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
. Assume that
$\operatorname {GL}_n(\boldsymbol {k})$
. Assume that
![]() $n\neq 1$
. In the spirit of Proposition 4.33, we give a necessary and sufficient condition for
$n\neq 1$
. In the spirit of Proposition 4.33, we give a necessary and sufficient condition for
![]() $\pi $
to be distinguished by
$\pi $
to be distinguished by
![]() $\operatorname {GL}_n({ F}_0)$
in terms of
$\operatorname {GL}_n({ F}_0)$
in terms of
![]() $c_\pi $
and
$c_\pi $
and
![]() $\mathrm {V}$
.
$\mathrm {V}$
.
Theorem 4.45. The representation
![]() $\pi $
is
$\pi $
is
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished if and only if its central character
$\operatorname {GL}_n({ F}_0)$
-distinguished if and only if its central character
![]() $c_\pi $
is trivial on
$c_\pi $
is trivial on
![]() ${ F}_0^\times $
and
${ F}_0^\times $
and
-
1. if
 ${ F}/{ F}_0$
is unramified, then
${ F}/{ F}_0$
is unramified, then
 $\mathrm {V}$
is
$\mathrm {V}$
is
 $\operatorname {GL}_n(\boldsymbol {k}_0)$
-distinguished,
$\operatorname {GL}_n(\boldsymbol {k}_0)$
-distinguished, -
2. if
 ${ F}/{ F}_0$
is ramified, then n is even,
${ F}/{ F}_0$
is ramified, then n is even,
 $\mathrm {V}$
is
$\mathrm {V}$
is
 $\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-distinguished and (4.23)acts on the space of its
$\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-distinguished and (4.23)acts on the space of its $$ \begin{align} s = \begin{pmatrix} 0 & \mathrm{id} \\ \mathrm{id} & 0 \end{pmatrix} \in \operatorname{GL}_n(\boldsymbol{k}) \end{align} $$
$$ \begin{align} s = \begin{pmatrix} 0 & \mathrm{id} \\ \mathrm{id} & 0 \end{pmatrix} \in \operatorname{GL}_n(\boldsymbol{k}) \end{align} $$
 $\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-invariant linear forms by the sign
$\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-invariant linear forms by the sign
 $c_\pi (\varpi )$
, where
$c_\pi (\varpi )$
, where
 $\varpi $
is any uniformizer of
$\varpi $
is any uniformizer of
 ${ F}$
.
${ F}$
.
Note that, if
![]() $\pi $
is distinguished and
$\pi $
is distinguished and
![]() $F/F_0$
is ramified, the space of
$F/F_0$
is ramified, the space of
![]() $\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-invariant linear forms on
$\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-invariant linear forms on
![]() $\mathrm {V}$
has dimension
$\mathrm {V}$
has dimension
![]() $1$
by Proposition 3.13.
$1$
by Proposition 3.13.
Proof. By Proposition 4.33, the representation
![]() $\pi $
is
$\pi $
is
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished if and only if
$\operatorname {GL}_n({ F}_0)$
-distinguished if and only if
![]() $\boldsymbol {\lambda }$
is
$\boldsymbol {\lambda }$
is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished. In the unramified case, the result follows from the fact that
$\mathbf {J}\cap { G}^\sigma $
-distinguished. In the unramified case, the result follows from the fact that
![]() $\mathbf {J}\cap { G}^\sigma $
is generated by
$\mathbf {J}\cap { G}^\sigma $
is generated by
![]() ${ F}_0^\times $
and
${ F}_0^\times $
and
![]() $\mathbf {J}^{0}\cap { G}^\sigma $
(see Lemma 4.14) and
$\mathbf {J}^{0}\cap { G}^\sigma $
(see Lemma 4.14) and
![]() $(\mathbf {J}^{0}\cap { G}^\sigma )/(\mathbf {J}^1\cap { G}^\sigma )$
identifies with
$(\mathbf {J}^{0}\cap { G}^\sigma )/(\mathbf {J}^1\cap { G}^\sigma )$
identifies with
![]() $\operatorname {GL}_n(\boldsymbol {k}_0)$
.
$\operatorname {GL}_n(\boldsymbol {k}_0)$
.
Assume now that we are in the ramified case. Since
![]() $c_\pi $
is trivial on
$c_\pi $
is trivial on
![]() ${ F}_0^\times $
and
${ F}_0^\times $
and
![]() $1+\mathfrak {p}_{ F}$
, its value at
$1+\mathfrak {p}_{ F}$
, its value at
![]() $\varpi $
does not depend on the choice of a uniformizer
$\varpi $
does not depend on the choice of a uniformizer
![]() $\varpi $
of
$\varpi $
of
![]() ${ F}$
. We thus may and will assume that
${ F}$
. We thus may and will assume that
![]() $\sigma (\varpi )=-\varpi $
, thus
$\sigma (\varpi )=-\varpi $
, thus
![]() $c_\pi (\varpi )\in \{-1,1\}$
. By Lemma 4.14 again,
$c_\pi (\varpi )\in \{-1,1\}$
. By Lemma 4.14 again,
![]() $\mathbf {J}\cap { G}^\sigma $
is generated by
$\mathbf {J}\cap { G}^\sigma $
is generated by
![]() ${ F}_0^\times $
,
${ F}_0^\times $
,
![]() $\mathbf {J}^{0}\cap { G}^\sigma $
and
$\mathbf {J}^{0}\cap { G}^\sigma $
and
![]() $\varpi w$
, where the element
$\varpi w$
, where the element
![]() $w\in \mathbf {J}^0$
is defined by equation (4.12). The quotient
$w\in \mathbf {J}^0$
is defined by equation (4.12). The quotient
![]() $(\mathbf {J}^{0}\cap { G}^\sigma )/(\mathbf {J}^1\cap { G}^\sigma )$
identifies with
$(\mathbf {J}^{0}\cap { G}^\sigma )/(\mathbf {J}^1\cap { G}^\sigma )$
identifies with
![]() $\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
, the image of w in
$\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
, the image of w in
![]() $\mathbf {J}^0/\mathbf {J}^1\simeq \operatorname {GL}_{n}(\boldsymbol {k})$
is the element s and
$\mathbf {J}^0/\mathbf {J}^1\simeq \operatorname {GL}_{n}(\boldsymbol {k})$
is the element s and
![]() $\varpi s$
acts on the (one-dimensional) space of
$\varpi s$
acts on the (one-dimensional) space of
![]() $\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-invariant linear forms on
$\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-invariant linear forms on
![]() $\mathrm {V}$
as
$\mathrm {V}$
as
![]() $c_\pi (\varpi )s$
.
$c_\pi (\varpi )s$
.
Putting Theorems 4.41 and 4.45 together, we have thus reduced the problem of characterizing distinguished cuspidal representations of
![]() $\operatorname {GL}_n({ F})$
to a problem about distinction of cuspidal representations of finite general linear groups.
$\operatorname {GL}_n({ F})$
to a problem about distinction of cuspidal representations of finite general linear groups.
4.13
As an application of Theorem 4.45, we classify all distinguished cuspidal representations of
![]() $\operatorname {GL}_2(F)$
. The supercuspidal case has been treated in [Reference Sécherre35] and the case where
$\operatorname {GL}_2(F)$
. The supercuspidal case has been treated in [Reference Sécherre35] and the case where
![]() $\ell \neq 2$
has been treated in [Reference Cui, Lanard and Lu12]. It thus remains the case of nonsupercuspidal cuspidal representations for
$\ell \neq 2$
has been treated in [Reference Cui, Lanard and Lu12]. It thus remains the case of nonsupercuspidal cuspidal representations for
![]() $\ell =2$
.
$\ell =2$
.
Proposition 4.46. Suppose that
![]() $\ell =2$
. The
$\ell =2$
. The
![]() $\operatorname {GL}_2(F_0)$
-distinguished cuspidal nonsupercuspidal representations of
$\operatorname {GL}_2(F_0)$
-distinguished cuspidal nonsupercuspidal representations of
![]() $\operatorname {GL}_2(F)$
are the representations
$\operatorname {GL}_2(F)$
are the representations
![]() $\operatorname {St}_2(\chi )$
, where
$\operatorname {St}_2(\chi )$
, where
![]() $\chi $
is a character of
$\chi $
is a character of
![]() $F^\times $
trivial on
$F^\times $
trivial on
![]() ${ F}_0^\times $
.
${ F}_0^\times $
.
Proof. According to Lemma 3.7, and since the character
![]() $\nu $
is trivial when
$\nu $
is trivial when
![]() $\ell =2$
, the
$\ell =2$
, the
![]() $\sigma $
-self-dual nonsupercuspidal cuspidal representations of
$\sigma $
-self-dual nonsupercuspidal cuspidal representations of
![]() $\operatorname {GL}_2(F)$
are the representations of the form
$\operatorname {GL}_2(F)$
are the representations of the form
![]() $\operatorname {St}_2(\chi )$
for a uniquely determined
$\operatorname {St}_2(\chi )$
for a uniquely determined
![]() $\sigma $
-self-dual character
$\sigma $
-self-dual character
![]() $\chi $
of
$\chi $
of
![]() $F^\times $
. Since
$F^\times $
. Since
![]() $\mathrm {N}_{F/F_0}(F^\times )$
has index
$\mathrm {N}_{F/F_0}(F^\times )$
has index
![]() $2$
in
$2$
in
![]() $F_0^\times $
, any
$F_0^\times $
, any
![]() $\sigma $
-self-dual character of
$\sigma $
-self-dual character of
![]() $F^\times $
is trivial on
$F^\times $
is trivial on
![]() $F_0^\times $
. We are thus reduced to proving that the representation
$F_0^\times $
. We are thus reduced to proving that the representation
![]() $\pi = \operatorname {St}_2(1)$
is distinguished.
$\pi = \operatorname {St}_2(1)$
is distinguished.
This representation has level
![]() $0$
and trivial central character. By Theorem 4.45, it is distinguished if and only if the cuspidal representation
$0$
and trivial central character. By Theorem 4.45, it is distinguished if and only if the cuspidal representation
![]() $\mathrm {V}=\operatorname {st}_2(1)$
of
$\mathrm {V}=\operatorname {st}_2(1)$
of
![]() $\operatorname {GL}_2(\boldsymbol {k})$
is
$\operatorname {GL}_2(\boldsymbol {k})$
is
-
○ distinguished by
 $\operatorname {GL}_2(\boldsymbol {k}_0)$
if
$\operatorname {GL}_2(\boldsymbol {k}_0)$
if
 $F/F_0$
is unramified,
$F/F_0$
is unramified, -
○ distinguished by
 $\boldsymbol {k}^\times \times \boldsymbol {k}^\times $
if
$\boldsymbol {k}^\times \times \boldsymbol {k}^\times $
if
 $F/F_0$
is ramified.
$F/F_0$
is ramified.
(The condition on the action of s disappears in the ramified case since
![]() $-1\equiv 1$
mod
$-1\equiv 1$
mod
![]() $\ell =2$
.) We are thus reduced to proving that
$\ell =2$
.) We are thus reduced to proving that
![]() $\mathrm {V}$
is distinguished.
$\mathrm {V}$
is distinguished.
Let W denote the parabolic induction to
![]() $\operatorname {GL}_2(\boldsymbol {k})$
of the trivial character of the Borel subgroup B made of all upper triangular matrices. By [Reference Vignéras40], it is indecomposable of length
$\operatorname {GL}_2(\boldsymbol {k})$
of the trivial character of the Borel subgroup B made of all upper triangular matrices. By [Reference Vignéras40], it is indecomposable of length
![]() $3$
, its socle and cosocle are irreducible and isomorphic to the trivial character and its remaining irreducible subquotient is
$3$
, its socle and cosocle are irreducible and isomorphic to the trivial character and its remaining irreducible subquotient is
![]() $\mathrm {V}$
.
$\mathrm {V}$
.
Let us assume first that
![]() $F/F_0$
is unramified. Then the action of
$F/F_0$
is unramified. Then the action of
![]() $\operatorname {GL}_2(\boldsymbol {k}_0)$
on
$\operatorname {GL}_2(\boldsymbol {k}_0)$
on
![]() $B \backslash \operatorname {GL}_2(\boldsymbol {k})$
has two orbits
$B \backslash \operatorname {GL}_2(\boldsymbol {k})$
has two orbits ![]() and
and ![]() . If one identifies
. If one identifies
![]() $B \backslash \operatorname {GL}_2(\boldsymbol {k})$
with the projective line
$B \backslash \operatorname {GL}_2(\boldsymbol {k})$
with the projective line
![]() $\mathbb {P}^1(\boldsymbol {k})$
, then
$\mathbb {P}^1(\boldsymbol {k})$
, then ![]() and
and ![]() . It follows that W has a two-dimensional space of
. It follows that W has a two-dimensional space of
![]() $\operatorname {GL}_2(\boldsymbol {k}_0)$
-invariant linear forms, generated by
$\operatorname {GL}_2(\boldsymbol {k}_0)$
-invariant linear forms, generated by
![]() $\mathit {\Lambda }_0$
and
$\mathit {\Lambda }_0$
and
![]() $\mathit {\Lambda }_1$
with
$\mathit {\Lambda }_1$
with
These two linear forms vanish on the subspace
![]() ${ R}$
of constant functions. They thus define nonzero linearly independent
${ R}$
of constant functions. They thus define nonzero linearly independent
![]() $\operatorname {GL}_2(\boldsymbol {k}_0)$
-invariant linear forms on
$\operatorname {GL}_2(\boldsymbol {k}_0)$
-invariant linear forms on
![]() $X=W/{ R}$
. If both of them vanish on
$X=W/{ R}$
. If both of them vanish on
![]() $\mathrm {V}$
, then the
$\mathrm {V}$
, then the
![]() $1$
-dimensional quotient
$1$
-dimensional quotient
![]() $X/\mathrm {V}$
has a two-dimensional space of invariant linear forms: contradiction. It thus follows that
$X/\mathrm {V}$
has a two-dimensional space of invariant linear forms: contradiction. It thus follows that
![]() $\mathrm {V}$
is distinguished by
$\mathrm {V}$
is distinguished by
![]() $\operatorname {GL}_2(\boldsymbol {k}_0)$
.
$\operatorname {GL}_2(\boldsymbol {k}_0)$
.
Now, assume that
![]() $F/F_0$
is ramified. Then the action of
$F/F_0$
is ramified. Then the action of
![]() $\boldsymbol {k}^\times \times \boldsymbol {k}^\times $
on
$\boldsymbol {k}^\times \times \boldsymbol {k}^\times $
on
![]() $B \backslash \operatorname {GL}_2(\boldsymbol {k})$
has three orbits
$B \backslash \operatorname {GL}_2(\boldsymbol {k})$
has three orbits ![]() ,
, ![]() and
and ![]() , the first two orbits being single points. They define three linearly independent invariant linear forms
, the first two orbits being single points. They define three linearly independent invariant linear forms
![]() $\mathit {\Lambda }_\infty $
,
$\mathit {\Lambda }_\infty $
,
![]() $\mathit {\Lambda }_0$
and
$\mathit {\Lambda }_0$
and
![]() $\mathit {\Lambda }_1$
. The two linear forms
$\mathit {\Lambda }_1$
. The two linear forms
![]() $\mathit {\Lambda }_\infty - \mathit {\Lambda }_0$
and
$\mathit {\Lambda }_\infty - \mathit {\Lambda }_0$
and
![]() $\mathit {\Lambda }_1$
vanish on the subspace
$\mathit {\Lambda }_1$
vanish on the subspace
![]() ${ R}$
of constant functions. From there, an argument similar to that of the unramified case shows that
${ R}$
of constant functions. From there, an argument similar to that of the unramified case shows that
![]() $\mathrm {V}$
is distinguished by
$\mathrm {V}$
is distinguished by
![]() $\boldsymbol {k}^\times \times \boldsymbol {k}^\times $
.
$\boldsymbol {k}^\times \times \boldsymbol {k}^\times $
.
4.14
In this paragraph, we prove Lemma 4.36(3). First, by Remarks 4.2, 4.35, changing the isomorphism (4.17) and t does not affect the isomorphism class of
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
. Let
$\boldsymbol {\tau }_{\mathrm {t}}$
. Let
![]() $[\mathfrak {a},{\beta }']$
be another
$[\mathfrak {a},{\beta }']$
be another
![]() $\sigma $
-self-dual maximal simple stratum such that
$\sigma $
-self-dual maximal simple stratum such that ![]() . Conjugating by
. Conjugating by
![]() $\mathbf {J}^1$
, we may and will assume that the maximal tamely ramified extension of
$\mathbf {J}^1$
, we may and will assume that the maximal tamely ramified extension of
![]() ${ F}$
in
${ F}$
in
![]() ${ E}'={ F}[{\beta }']$
is
${ E}'={ F}[{\beta }']$
is
![]() ${ T}$
. This gives us another isomorphism
${ T}$
. This gives us another isomorphism
![]() $\boldsymbol {\pi }'$
from
$\boldsymbol {\pi }'$
from
![]() $\mathbf {J}/\mathbf {J}^1$
to
$\mathbf {J}/\mathbf {J}^1$
to
![]() $\mathbf {J}_{\mathrm {t}}^{}/\mathbf {J}_{\mathrm {t}}^1$
. By construction, it coincides with
$\mathbf {J}_{\mathrm {t}}^{}/\mathbf {J}_{\mathrm {t}}^1$
. By construction, it coincides with
![]() $\boldsymbol {\pi }$
on
$\boldsymbol {\pi }$
on
![]() $\mathbf {J}^0/\mathbf {J}^1$
and the image of
$\mathbf {J}^0/\mathbf {J}^1$
and the image of
![]() $x\mathbf {J}^1$
by
$x\mathbf {J}^1$
by
![]() $\boldsymbol {\pi }'$
is equal to
$\boldsymbol {\pi }'$
is equal to
![]() $\mathrm {N}_{{ E}'/{ T}}(x)\mathbf {J}^1$
for all
$\mathrm {N}_{{ E}'/{ T}}(x)\mathbf {J}^1$
for all
![]() $x\in { E}^{\prime \times }$
. We are going to prove that
$x\in { E}^{\prime \times }$
. We are going to prove that
![]() $\boldsymbol {\pi }'$
is equal to
$\boldsymbol {\pi }'$
is equal to
![]() $\boldsymbol {\pi }$
. The result will then follow from the fact that
$\boldsymbol {\pi }$
. The result will then follow from the fact that
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
is equal to
$\boldsymbol {\tau }_{\mathrm {t}}$
is equal to
![]() $\boldsymbol {\tau }\circ \boldsymbol {\pi }$
. For this, it suffices to prove that
$\boldsymbol {\tau }\circ \boldsymbol {\pi }$
. For this, it suffices to prove that
![]() $\boldsymbol {\pi }$
and
$\boldsymbol {\pi }$
and
![]() $\boldsymbol {\pi }'$
take the same value at some given uniformizer of
$\boldsymbol {\pi }'$
take the same value at some given uniformizer of
![]() ${ E}'$
. Let
${ E}'$
. Let
![]() $\varpi $
,
$\varpi $
,
![]() $\varpi '$
be uniformizers of
$\varpi '$
be uniformizers of
![]() ${ E}$
,
${ E}$
,
![]() ${ E}'$
, respectively.
${ E}'$
, respectively.
The centre of
![]() $\mathbf {J}/\mathbf {J}^1$
is
$\mathbf {J}/\mathbf {J}^1$
is
![]() ${ E}^\times \mathbf {J}^1/\mathbf {J}^1={ E}^{\prime \times }\mathbf {J}^1$
, thus
${ E}^\times \mathbf {J}^1/\mathbf {J}^1={ E}^{\prime \times }\mathbf {J}^1$
, thus
![]() ${ E}^{\prime \times }\subseteq { E}^\times \mathbf {J}^1$
. We thus may write
${ E}^{\prime \times }\subseteq { E}^\times \mathbf {J}^1$
. We thus may write
![]() $\varpi '\in \varpi \zeta \mathbf {J}^1$
for some root of unity
$\varpi '\in \varpi \zeta \mathbf {J}^1$
for some root of unity
![]() $\zeta $
of
$\zeta $
of
![]() ${ T}^\times $
of order prime to p. Changing
${ T}^\times $
of order prime to p. Changing
![]() $\varpi '$
to
$\varpi '$
to
![]() $\varpi '\zeta ^{-1}$
, we may and will assume that
$\varpi '\zeta ^{-1}$
, we may and will assume that
![]() $\varpi '\in \varpi \mathbf {J}^1$
. It suffices to prove the following claim.
$\varpi '\in \varpi \mathbf {J}^1$
. It suffices to prove the following claim.
Claim 4.47. We have
![]() $\mathrm {N}_{{ E}'/{ T}}(\varpi ')\equiv \mathrm {N}_{{ E}/{ T}}(\varpi ) \mod 1+\mathfrak {p}_{ T}$
.
$\mathrm {N}_{{ E}'/{ T}}(\varpi ')\equiv \mathrm {N}_{{ E}/{ T}}(\varpi ) \mod 1+\mathfrak {p}_{ T}$
.
First, this is true when
![]() $m=1$
. Indeed, writing
$m=1$
. Indeed, writing
![]() ${ G}_{ T}$
for the centralizer of
${ G}_{ T}$
for the centralizer of
![]() ${ T}$
in
${ T}$
in
![]() ${ G}$
and
${ G}$
and
![]() $\mathrm {det}_{ T}$
for the determinant on
$\mathrm {det}_{ T}$
for the determinant on
![]() ${ G}_{ T}$
, we have
${ G}_{ T}$
, we have
![]() $\mathrm {det}_{ T}(x)=\mathrm {N}_{{ E}/{ T}}(x)$
for all
$\mathrm {det}_{ T}(x)=\mathrm {N}_{{ E}/{ T}}(x)$
for all
![]() $x\in { E}^\times $
, thus
$x\in { E}^\times $
, thus
Now, assume that
![]() $m>1$
. We use the results of 4.4 for
$m>1$
. We use the results of 4.4 for
![]() $u=m$
. Let
$u=m$
. Let ![]() denote the transfer of
denote the transfer of
![]() ${\theta }$
as in Lemma 4.9. Fix a
${\theta }$
as in Lemma 4.9. Fix a
![]() ${ T}$
-embedding
${ T}$
-embedding
such that
![]() $\mathfrak {a}_*$
is normalized by
$\mathfrak {a}_*$
is normalized by
![]() $\iota { E}^{\prime \times }$
, and transfer
$\iota { E}^{\prime \times }$
, and transfer
![]() ${\theta }$
to
${\theta }$
to ![]() in the sense of [Reference Bushnell and Kutzko9] 3.6. The simple character
in the sense of [Reference Bushnell and Kutzko9] 3.6. The simple character
![]() ${\theta }$
is in
${\theta }$
is in ![]() . It follows from [Reference Bushnell and Henniart6] Theorem 8.7 that
. It follows from [Reference Bushnell and Henniart6] Theorem 8.7 that
![]() ${\theta }_*$
,
${\theta }_*$
,
![]() ${\theta }_\bullet $
intertwine in
${\theta }_\bullet $
intertwine in
![]() ${ G}_*$
, and from [Reference Bushnell and Kutzko9] Theorem 3.5.11 that
${ G}_*$
, and from [Reference Bushnell and Kutzko9] Theorem 3.5.11 that
![]() ${\theta }_\bullet ^{}={\theta }_*^x$
for some
${\theta }_\bullet ^{}={\theta }_*^x$
for some ![]() . Changing
. Changing
![]() $\iota $
to
$\iota $
to
![]() $\mathrm {Ad}(x)\circ \iota $
, we thus may assume that
$\mathrm {Ad}(x)\circ \iota $
, we thus may assume that ![]() . By using
. By using
![]() $\iota $
, we get a diagonal embedding
$\iota $
, we get a diagonal embedding
denoted
![]() $\phi $
, which is the identity on
$\phi $
, which is the identity on
![]() ${ T}^\times $
. The Skolem–Noether theorem implies that
${ T}^\times $
. The Skolem–Noether theorem implies that
![]() $\phi =\mathrm {Ad}(g)$
for some
$\phi =\mathrm {Ad}(g)$
for some
![]() $g\in { G}_{ T}$
. Conjugating by g, we thus may assume that
$g\in { G}_{ T}$
. Conjugating by g, we thus may assume that
![]() ${ E}^\times $
and
${ E}^\times $
and
![]() ${ E}^{\prime \times }$
are both diagonal in
${ E}^{\prime \times }$
are both diagonal in
![]() ${ M}$
. The identity
${ M}$
. The identity
![]() $\varpi '\in \varpi \mathbf {J}^1$
thus implies
$\varpi '\in \varpi \mathbf {J}^1$
thus implies
![]() $\varpi '\in \varpi \mathbf {J}_*^1$
. We are thus reduced to the case where
$\varpi '\in \varpi \mathbf {J}_*^1$
. We are thus reduced to the case where
![]() $m=1$
.
$m=1$
.
Remark 4.48. The fact that
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
does not depend on the choice of
$\boldsymbol {\tau }_{\mathrm {t}}$
does not depend on the choice of
![]() ${\beta }$
is claimed in [Reference Bushnell and Henniart8] Lemma 3.6. However, Property (b) of this lemma does not hold: Using the notation of ibid., the restriction of
${\beta }$
is claimed in [Reference Bushnell and Henniart8] Lemma 3.6. However, Property (b) of this lemma does not hold: Using the notation of ibid., the restriction of
![]() $\lambda _{\xi }^{\mathbf {J}}$
to
$\lambda _{\xi }^{\mathbf {J}}$
to
![]() ${ P}^\times $
is a multiple of the character
${ P}^\times $
is a multiple of the character
![]() $\xi \circ \mathrm {N}_{{ P}/{ T}}$
, whereas the restriction of
$\xi \circ \mathrm {N}_{{ P}/{ T}}$
, whereas the restriction of
![]() $(\xi |_{{ T}^\times })^{\mathbf {J}}$
to
$(\xi |_{{ T}^\times })^{\mathbf {J}}$
to
![]() ${ P}^\times $
is
${ P}^\times $
is
![]() $(\xi \circ \mathrm {N}_{{ P}/{ T}})^s$
. (Note that
$(\xi \circ \mathrm {N}_{{ P}/{ T}})^s$
. (Note that
![]() ${ P}$
corresponds to our
${ P}$
corresponds to our
![]() ${ E}$
, and s corresponds to our m.)
${ E}$
, and s corresponds to our m.)
5 The odd case
In this section, p is odd,
![]() $\ell $
is any prime number different from p and the field
$\ell $
is any prime number different from p and the field
![]() ${ R}$
has characteristic
${ R}$
has characteristic
![]() $\ell $
. This section is devoted to the proof of the following theorem.
$\ell $
. This section is devoted to the proof of the following theorem.
Theorem 5.1. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal nonsupercuspidal
$\sigma $
-self-dual cuspidal nonsupercuspidal
![]() ${ R}$
-representation of
${ R}$
-representation of
![]() $\operatorname {GL}_n({ F})$
. Assume that the integer
$\operatorname {GL}_n({ F})$
. Assume that the integer
![]() $r=r(\pi )$
is odd, thus
$r=r(\pi )$
is odd, thus
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
for a uniquely determined
$\operatorname {St}_r(\rho )$
for a uniquely determined
![]() $\sigma $
-self-dual supercuspidal representation
$\sigma $
-self-dual supercuspidal representation
![]() $\rho $
of
$\rho $
of
![]() $\operatorname {GL}_{k}({ F})$
, with
$\operatorname {GL}_{k}({ F})$
, with
![]() $k=n/r$
. If
$k=n/r$
. If
![]() $\pi $
is
$\pi $
is
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished, then
$\operatorname {GL}_n({ F}_0)$
-distinguished, then
-
1. the relative degree
 $m=m(\pi )$
and the ramification index of
$m=m(\pi )$
and the ramification index of
 ${ T}/{ T}_0$
have the same parity,
${ T}/{ T}_0$
have the same parity, -
2. the representation
 $\rho $
is
$\rho $
is
 $\operatorname {GL}_k({ F}_0)$
-distinguished.
$\operatorname {GL}_k({ F}_0)$
-distinguished.
Note that the fact that r is odd and
![]() $r\neq 1$
implies that
$r\neq 1$
implies that
![]() $\ell \neq 2$
.
$\ell \neq 2$
.
5.1
Before we start the proof of Theorem 5.1, let us prove the following disjunction theorem.
Corollary 5.2. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${ R}$
-representation of
${ R}$
-representation of
![]() $\operatorname {GL}_n({ F})$
. Assume that
$\operatorname {GL}_n({ F})$
. Assume that
![]() $r(\pi )$
is odd. Then
$r(\pi )$
is odd. Then
![]() $\pi $
cannot be both distinguished and
$\pi $
cannot be both distinguished and
![]() $\varkappa $
-distinguished.
$\varkappa $
-distinguished.
Proof. Assume that
![]() $\pi $
is both distinguished and
$\pi $
is both distinguished and
![]() $\varkappa $
-distinguished, and let
$\varkappa $
-distinguished, and let
![]() $\chi $
be a tamely ramified character of
$\chi $
be a tamely ramified character of
![]() ${ F}^\times $
extending
${ F}^\times $
extending
![]() $\varkappa $
. Then
$\varkappa $
. Then
![]() $\pi \chi $
is distinguished, it is isomorphic to
$\pi \chi $
is distinguished, it is isomorphic to
![]() $\operatorname {St}_r(\rho \chi )$
and
$\operatorname {St}_r(\rho \chi )$
and
![]() $\rho \chi $
is supercuspidal and
$\rho \chi $
is supercuspidal and
![]() $\sigma $
-self-dual. Theorem 5.1 applied to both
$\sigma $
-self-dual. Theorem 5.1 applied to both
![]() $\pi $
and
$\pi $
and
![]() $\pi \chi $
implies that
$\pi \chi $
implies that
![]() $\rho $
is both distinguished and
$\rho $
is both distinguished and
![]() $\varkappa $
-distinguished. This contradicts Theorem 3.2.
$\varkappa $
-distinguished. This contradicts Theorem 3.2.
We also have the following Distinguished Lift Theorem.
Corollary 5.3. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished cuspidal
$\operatorname {GL}_n({ F}_0)$
-distinguished cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_n({ F})$
with
$\operatorname {GL}_n({ F})$
with
![]() $r(\pi )$
odd. There is a
$r(\pi )$
odd. There is a
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished integral generic
$\operatorname {GL}_n({ F}_0)$
-distinguished integral generic
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation of
${\overline {\mathbb {Q}}_\ell }$
-representation of
![]() $\operatorname {GL}_n({ F})$
whose reduction mod
$\operatorname {GL}_n({ F})$
whose reduction mod
![]() $\ell $
contains
$\ell $
contains
![]() $\pi $
.
$\pi $
.
Proof. Write
![]() $\pi $
as
$\pi $
as
![]() $\operatorname {St}_r(\rho )$
with
$\operatorname {St}_r(\rho )$
with
![]() $\rho $
distinguished. Let
$\rho $
distinguished. Let
![]() $\mu $
be a distinguished integral cuspidal lift of
$\mu $
be a distinguished integral cuspidal lift of
![]() $\rho $
, which exists by Theorem 3.5. Then the generic representation
$\rho $
, which exists by Theorem 3.5. Then the generic representation
![]() $\operatorname {St}_r(\mu )$
satisfies the required property (see [Reference Anandavardhanan1] Theorem 1.3 or [Reference Matringe26] Corollary 4.2 when F has characteristic zero, and observe that the argument in [Reference Matringe26] holds verbatim in positive characteristic thanks to [Reference Jo22, Theorem 4.7]).
$\operatorname {St}_r(\mu )$
satisfies the required property (see [Reference Anandavardhanan1] Theorem 1.3 or [Reference Matringe26] Corollary 4.2 when F has characteristic zero, and observe that the argument in [Reference Matringe26] holds verbatim in positive characteristic thanks to [Reference Jo22, Theorem 4.7]).
Remark 5.4. A
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished integral generic
$\operatorname {GL}_n({ F}_0)$
-distinguished integral generic
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation of
${\overline {\mathbb {Q}}_\ell }$
-representation of
![]() $\operatorname {GL}_n({ F})$
as in Corollary 5.3 may not be cuspidal. See Section 6 for the classification of all distinguished cuspidal
$\operatorname {GL}_n({ F})$
as in Corollary 5.3 may not be cuspidal. See Section 6 for the classification of all distinguished cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representations of
${\overline {\mathbb {F}}_{\ell }}$
-representations of
![]() $\operatorname {GL}_n(F)$
having a cuspidal distinguished lift to
$\operatorname {GL}_n(F)$
having a cuspidal distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
.
${\overline {\mathbb {Q}}_\ell }$
.
Finally, compare Theorem 5.1 with the following finite field analogue.
Proposition 5.5. Let
![]() $\boldsymbol {k}/\boldsymbol {k}_{0}$
be a quadratic extension of finite fields of characteristic p. Let
$\boldsymbol {k}/\boldsymbol {k}_{0}$
be a quadratic extension of finite fields of characteristic p. Let
![]() $\varrho $
be a supercuspidal R-representation of
$\varrho $
be a supercuspidal R-representation of
![]() $\operatorname {GL}_f(\boldsymbol {k})$
for some
$\operatorname {GL}_f(\boldsymbol {k})$
for some
![]() $f{\geqslant }1$
, and r be an odd integer such that
$f{\geqslant }1$
, and r be an odd integer such that
![]() $\operatorname {st}_r(\varrho )$
is cuspidal. If
$\operatorname {st}_r(\varrho )$
is cuspidal. If
![]() $\operatorname {st}_r(\varrho )$
is distinguished by
$\operatorname {st}_r(\varrho )$
is distinguished by
![]() $\operatorname {GL}_{fr}(\boldsymbol {k}_{0})$
, then
$\operatorname {GL}_{fr}(\boldsymbol {k}_{0})$
, then
![]() $\varrho $
is distinguished by
$\varrho $
is distinguished by
![]() $\operatorname {GL}_f(\boldsymbol {k}_{0})$
.
$\operatorname {GL}_f(\boldsymbol {k}_{0})$
.
Proof. First, [Reference Sécherre35] Remark 4.3 tells us that
![]() $\operatorname {st}_r(\varrho )$
is
$\operatorname {st}_r(\varrho )$
is
![]() $\sigma $
-self-dual (where
$\sigma $
-self-dual (where
![]() $\sigma $
is here the nontrivial automorphism of
$\sigma $
is here the nontrivial automorphism of
![]() $\boldsymbol {k}/\boldsymbol {k}_{0}$
). Proposition 3.9 implies that
$\boldsymbol {k}/\boldsymbol {k}_{0}$
). Proposition 3.9 implies that
![]() $\varrho $
is
$\varrho $
is
![]() $\sigma $
-self-dual. By [Reference Sécherre35] Lemma 2.5, it is distinguished by
$\sigma $
-self-dual. By [Reference Sécherre35] Lemma 2.5, it is distinguished by
![]() $\operatorname {GL}_f(\boldsymbol {k}_{0})$
.
$\operatorname {GL}_f(\boldsymbol {k}_{0})$
.
5.2
Let us prove Theorem 5.1(1). Since r is odd, m has the same parity as
![]() $m/r$
, and, since
$m/r$
, and, since
![]() $\pi $
is nonsupercuspidal, we have
$\pi $
is nonsupercuspidal, we have
![]() $r>1$
, thus
$r>1$
, thus
![]() $m>1$
. It follows from [Reference Sécherre35] Proposition 7.1 that, if m is odd,
$m>1$
. It follows from [Reference Sécherre35] Proposition 7.1 that, if m is odd,
![]() ${ T}/{ T}_0$
is unramified, and from Proposition 4.34 that, if m is even,
${ T}/{ T}_0$
is unramified, and from Proposition 4.34 that, if m is even,
![]() ${ T}/{ T}_0$
is ramified.
${ T}/{ T}_0$
is ramified.
5.3
We now start the proof of Theorem 5.1(2). We thus have a distinguished cuspidal representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {GL}_n({ F})$
, which we write
$\operatorname {GL}_n({ F})$
, which we write
![]() $\operatorname {St}_r(\rho )$
with
$\operatorname {St}_r(\rho )$
with
![]() $\rho $
supercuspidal and
$\rho $
supercuspidal and
![]() $\sigma $
-self-dual.
$\sigma $
-self-dual.
Associated with
![]() $\pi $
, there are a positive divisor m of n, a quadratic extension
$\pi $
, there are a positive divisor m of n, a quadratic extension
![]() ${ T}/{ T}_0$
and a cuspidal representation
${ T}/{ T}_0$
and a cuspidal representation
![]() $\pi _{\mathrm {t}}$
of
$\pi _{\mathrm {t}}$
of
![]() $\operatorname {GL}_m({ T})$
. By Proposition 4.40, the representation
$\operatorname {GL}_m({ T})$
. By Proposition 4.40, the representation
![]() $\pi _{\mathrm {t}}$
has level
$\pi _{\mathrm {t}}$
has level
![]() $0$
, it is distinguished by
$0$
, it is distinguished by
![]() $\operatorname {GL}_m({ T}_0)$
and it satisfies
$\operatorname {GL}_m({ T}_0)$
and it satisfies
![]() $r(\pi _{\mathrm {t}})=r$
.
$r(\pi _{\mathrm {t}})=r$
.
Similarly, associated with
![]() $\rho $
, there is a supercuspidal
$\rho $
, there is a supercuspidal
![]() $\sigma $
-self-dual representation
$\sigma $
-self-dual representation
![]() $\rho _{\mathrm {t}}$
of
$\rho _{\mathrm {t}}$
of
![]() $\operatorname {GL}_{m/r}({ T})$
, which has level
$\operatorname {GL}_{m/r}({ T})$
, which has level
![]() $0$
, and is distinguished by
$0$
, and is distinguished by
![]() $\operatorname {GL}_{m/r}({ T}_0)$
if and only if
$\operatorname {GL}_{m/r}({ T}_0)$
if and only if
![]() $\rho $
is distinguished by
$\rho $
is distinguished by
![]() $\operatorname {GL}_k({ F}_0)$
. By Proposition 4.43, the representation
$\operatorname {GL}_k({ F}_0)$
. By Proposition 4.43, the representation
![]() $\pi _{\mathrm {t}}$
is isomorphic to
$\pi _{\mathrm {t}}$
is isomorphic to
![]() $\operatorname {St}_r(\rho _{\mathrm {t}})$
.
$\operatorname {St}_r(\rho _{\mathrm {t}})$
.
It follows that, in order to prove Theorem 5.1(2), we may assume that
![]() $\pi $
has level
$\pi $
has level
![]() $0$
.
$0$
.
5.4
Let
![]() $\pi $
be a distinguished cuspidal representation of level
$\pi $
be a distinguished cuspidal representation of level
![]() $0$
of
$0$
of
![]() $\operatorname {GL}_n({ F})$
. Associated with it, there are its central character
$\operatorname {GL}_n({ F})$
. Associated with it, there are its central character
![]() $c_\pi $
and a cuspidal representation
$c_\pi $
and a cuspidal representation
![]() $\mathrm {V}$
of
$\mathrm {V}$
of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
(see §4.7).
$\operatorname {GL}_n(\boldsymbol {k})$
(see §4.7).
The representation
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
for a unique
$\operatorname {St}_r(\rho )$
for a unique
![]() $\sigma $
-self-dual supercuspidal representation
$\sigma $
-self-dual supercuspidal representation
![]() $\rho $
, and
$\rho $
, and
![]() $\rho $
has level
$\rho $
has level
![]() $0$
. Associated with
$0$
. Associated with
![]() $\rho $
, there are its central character
$\rho $
, there are its central character
![]() $c_\rho $
and a supercuspidal representation
$c_\rho $
and a supercuspidal representation
![]() $\varrho $
of
$\varrho $
of
![]() $\operatorname {GL}_k(\boldsymbol {k})$
. We have the relation
$\operatorname {GL}_k(\boldsymbol {k})$
. We have the relation
and, by Proposition 4.28, the representation
![]() $\mathrm {V}$
is isomorphic to
$\mathrm {V}$
is isomorphic to
![]() $\operatorname {st}_r(\varrho )$
.
$\operatorname {st}_r(\varrho )$
.
Since
![]() $\pi $
is distinguished, its central character is trivial on
$\pi $
is distinguished, its central character is trivial on
![]() ${ F}_0^\times $
. Since
${ F}_0^\times $
. Since
![]() $\rho $
is
$\rho $
is
![]() $\sigma $
-self-dual, the restriction of
$\sigma $
-self-dual, the restriction of
![]() $c_\rho $
to
$c_\rho $
to
![]() ${ F}_0^\times $
has order at most
${ F}_0^\times $
has order at most
![]() $2$
. Restricting the relation (5.1) to
$2$
. Restricting the relation (5.1) to
![]() ${ F}_0^\times $
, and since r is odd, we deduce that
${ F}_0^\times $
, and since r is odd, we deduce that
![]() $c_\rho $
is trivial on
$c_\rho $
is trivial on
![]() ${ F}_0^\times $
.
${ F}_0^\times $
.
5.5
In this paragraph, we will assume that
![]() ${ F}/{ F}_0$
is unramified. By Theorem 4.45, the representation
${ F}/{ F}_0$
is unramified. By Theorem 4.45, the representation
![]() $\mathrm {V}$
is distinguished by
$\mathrm {V}$
is distinguished by
![]() $\operatorname {GL}_n(\boldsymbol {k}_0)$
. By [Reference Sécherre35] Remark 4.3, it is thus
$\operatorname {GL}_n(\boldsymbol {k}_0)$
. By [Reference Sécherre35] Remark 4.3, it is thus
![]() $\sigma $
-self-dual, that is
$\sigma $
-self-dual, that is
It follows from Proposition 3.9 that
![]() $\varrho $
is
$\varrho $
is
![]() $\sigma $
-self-dual. By [Reference Sécherre35] Lemma 2.5, it is thus distinguished by
$\sigma $
-self-dual. By [Reference Sécherre35] Lemma 2.5, it is thus distinguished by
![]() $\operatorname {GL}_k(\boldsymbol {k}_0)$
. Applying Theorem 4.45 again, we deduce that
$\operatorname {GL}_k(\boldsymbol {k}_0)$
. Applying Theorem 4.45 again, we deduce that
![]() $\rho $
is distinguished by
$\rho $
is distinguished by
![]() $\operatorname {GL}_k({ F}_0)$
. This proves Theorem 5.1 in the unramified case.
$\operatorname {GL}_k({ F}_0)$
. This proves Theorem 5.1 in the unramified case.
5.6
From now on, and until the end of this section, we assume that
![]() ${ F}/{ F}_0$
is ramified. By Theorem 4.45, we may write
${ F}/{ F}_0$
is ramified. By Theorem 4.45, we may write
![]() $n=2u$
for some integer
$n=2u$
for some integer
![]() $u{\geqslant }1$
. We write
$u{\geqslant }1$
. We write
![]() ${ G}={ G}_n=\operatorname {GL}_n(\boldsymbol {k})$
,
${ G}={ G}_n=\operatorname {GL}_n(\boldsymbol {k})$
,
![]() ${{H}}={{H}}_n=\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
and
${{H}}={{H}}_n=\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
and
![]() ${ K}={ K}_n$
for the normalizer of
${ K}={ K}_n$
for the normalizer of
![]() ${{H}}$
in
${{H}}$
in
![]() ${ G}$
, which is generated by
${ G}$
, which is generated by
![]() ${{H}}$
and
${{H}}$
and
 $$ \begin{align*} s = s_n = \begin{pmatrix} 0 & \mathrm{id} \\ \mathrm{id} & 0 \end{pmatrix} \in { G}, \end{align*} $$
$$ \begin{align*} s = s_n = \begin{pmatrix} 0 & \mathrm{id} \\ \mathrm{id} & 0 \end{pmatrix} \in { G}, \end{align*} $$
where
![]() $\mathrm {id}$
is the identity in
$\mathrm {id}$
is the identity in
![]() $\operatorname {GL}_{u}(\boldsymbol {k})$
. It will be convenient to introduce the following definition.
$\operatorname {GL}_{u}(\boldsymbol {k})$
. It will be convenient to introduce the following definition.
Definition 5.6. Let
![]() $c\in \{-1,1\}\subseteq { R}^\times $
. An irreducible R-representation V of G is said to be c-distinguished by H if V is H-distinguished and s acts on the space of H-invariant linear forms on V by multiplication by c.
$c\in \{-1,1\}\subseteq { R}^\times $
. An irreducible R-representation V of G is said to be c-distinguished by H if V is H-distinguished and s acts on the space of H-invariant linear forms on V by multiplication by c.
By Theorem 4.45, the representation
![]() $\mathrm {V}$
is
$\mathrm {V}$
is
![]() ${{H}}$
-distinguished and s acts on the one-dimensional vector space
${{H}}$
-distinguished and s acts on the one-dimensional vector space
![]() $\operatorname {Hom}_{{H}}(\mathrm {V},{ R})$
by the sign
$\operatorname {Hom}_{{H}}(\mathrm {V},{ R})$
by the sign
![]() $c=c_\pi (\varpi )$
. In other words,
$c=c_\pi (\varpi )$
. In other words,
![]() $\mathrm {V}$
is c-distinguished by H. We are now reduced to proving the following result. (Note that k is even since n is even and r is odd.)
$\mathrm {V}$
is c-distinguished by H. We are now reduced to proving the following result. (Note that k is even since n is even and r is odd.)
Proposition 5.7. The supercuspidal representation
![]() $\varrho $
is c-distinguished by
$\varrho $
is c-distinguished by
![]() $H_{k}$
.
$H_{k}$
.
Indeed, since r is odd, the identity (5.1) together with Proposition 5.7 will give us
![]() $c=c_\rho (\varpi )$
. It will then follow from Theorem 4.45 that
$c=c_\rho (\varpi )$
. It will then follow from Theorem 4.45 that
![]() $\rho $
is
$\rho $
is
![]() $\operatorname {GL}_k({ F}_0)$
-distinguished.
$\operatorname {GL}_k({ F}_0)$
-distinguished.
5.7
Let
![]() $\pi $
be an irreducible
$\pi $
be an irreducible
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of G. The natural map
${\overline {\mathbb {F}}_{\ell }}$
-representation of G. The natural map
defined by
![]() $f\otimes r\mapsto r(f\otimes \mathrm {id})$
is an isomorphism of R-vector spaces. Moreover, these spaces have dimension at most
$f\otimes r\mapsto r(f\otimes \mathrm {id})$
is an isomorphism of R-vector spaces. Moreover, these spaces have dimension at most
![]() $1$
, and it follows from this isomorphism that
$1$
, and it follows from this isomorphism that
![]() $\pi $
is c-distinguished by H if and only if
$\pi $
is c-distinguished by H if and only if
![]() $\pi \otimes R$
is c-distinguished by H.
$\pi \otimes R$
is c-distinguished by H.
Since G is finite, any irreducible R-representation of G is defined over
![]() ${\overline {\mathbb {F}}_{\ell }}$
, that is, isomorphic to
${\overline {\mathbb {F}}_{\ell }}$
, that is, isomorphic to
![]() $\pi _0\otimes { R}$
for some irreducible
$\pi _0\otimes { R}$
for some irreducible
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation
${\overline {\mathbb {F}}_{\ell }}$
-representation
![]() $\pi _0$
of G. In order to prove Proposition 5.7, we thus may assume that R is equal to
$\pi _0$
of G. In order to prove Proposition 5.7, we thus may assume that R is equal to
![]() ${\overline {\mathbb {F}}_{\ell }}$
.
${\overline {\mathbb {F}}_{\ell }}$
.
5.8
From now on, we assume that R is equal to
![]() ${\overline {\mathbb {F}}_{\ell }}$
. The remaining part of the section will be devoted to the proof of Proposition 5.7.
${\overline {\mathbb {F}}_{\ell }}$
. The remaining part of the section will be devoted to the proof of Proposition 5.7.
Lemma 5.8. There exists a c-distinguished irreducible
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation of
${\overline {\mathbb {Q}}_\ell }$
-representation of
![]() ${ G}$
whose reduction mod
${ G}$
whose reduction mod
![]() $\ell $
contains
$\ell $
contains
![]() $\mathrm {V}$
.
$\mathrm {V}$
.
Proof. Let
![]() $\chi $
denote the unique
$\chi $
denote the unique
![]() ${\overline {\mathbb {F}}_{\ell }}$
-character of
${\overline {\mathbb {F}}_{\ell }}$
-character of
![]() ${ K}$
trivial on
${ K}$
trivial on
![]() ${{H}}$
such that
${{H}}$
such that
![]() $\chi (s)=c$
. Since
$\chi (s)=c$
. Since
![]() $\mathrm {V}$
is c-distinguished, it embeds in
$\mathrm {V}$
is c-distinguished, it embeds in
![]() $\operatorname {Ind}^G_K(\chi )$
. Equivalently, the representation
$\operatorname {Ind}^G_K(\chi )$
. Equivalently, the representation
![]() $\operatorname {Ind}^G_K(\chi )$
, which is self-dual (as
$\operatorname {Ind}^G_K(\chi )$
, which is self-dual (as
![]() $\chi $
is equal to
$\chi $
is equal to
![]() $\chi ^{-1}$
), surjects onto the contragredient
$\chi ^{-1}$
), surjects onto the contragredient
![]() $\mathrm {W}$
of
$\mathrm {W}$
of
![]() $\mathrm {V}$
. Let
$\mathrm {V}$
. Let
![]() $\Pi $
be a projective indecomposable
$\Pi $
be a projective indecomposable
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() ${ G}$
whose unique irreducible quotient is isomorphic to
${ G}$
whose unique irreducible quotient is isomorphic to
![]() $\mathrm {W}$
. Let
$\mathrm {W}$
. Let
![]() $\widetilde {\Pi }$
be the unique projective
$\widetilde {\Pi }$
be the unique projective
![]() ${\overline {\mathbb {Z}}_\ell }$
-representation of
${\overline {\mathbb {Z}}_\ell }$
-representation of
![]() ${ G}$
such that
${ G}$
such that
![]() $\widetilde {\Pi }\otimes {\overline {\mathbb {F}}_{\ell }}$
is isomorphic to
$\widetilde {\Pi }\otimes {\overline {\mathbb {F}}_{\ell }}$
is isomorphic to
![]() $\Pi $
. Let
$\Pi $
. Let
![]() $\Lambda $
be a surjective homomorphism from
$\Lambda $
be a surjective homomorphism from
![]() $\operatorname {Ind}^{ G}_{ K}(\chi )$
to
$\operatorname {Ind}^{ G}_{ K}(\chi )$
to
![]() $\mathrm {W}$
. By projectivity, it defines a nonzero homomorphism
$\mathrm {W}$
. By projectivity, it defines a nonzero homomorphism
![]() $\Lambda '$
from
$\Lambda '$
from
![]() $\Pi $
to
$\Pi $
to
![]() $\operatorname {Ind}^{ G}_{ K}(\chi )$
, then a nonzero homomorphism
$\operatorname {Ind}^{ G}_{ K}(\chi )$
, then a nonzero homomorphism
![]() $\Lambda "$
from
$\Lambda "$
from
![]() $\widetilde {\Pi }$
to
$\widetilde {\Pi }$
to
![]() $\operatorname {Ind}^{ G}_{ K}(\widetilde {\chi })$
, where
$\operatorname {Ind}^{ G}_{ K}(\widetilde {\chi })$
, where
![]() $\widetilde {\chi }$
is the canonical
$\widetilde {\chi }$
is the canonical
![]() ${\overline {\mathbb {Z}}_\ell }$
-lift of
${\overline {\mathbb {Z}}_\ell }$
-lift of
![]() $\chi $
.
$\chi $
.
By inverting
![]() $\ell $
, we deduce that there is an irreducible
$\ell $
, we deduce that there is an irreducible
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation X of G occurring in each of the semi-simple representations
${\overline {\mathbb {Q}}_\ell }$
-representation X of G occurring in each of the semi-simple representations
![]() $J=\operatorname {Ind}^{ G}_{ K}(\widetilde {\chi })\otimes {\overline {\mathbb {Q}}_\ell }$
and
$J=\operatorname {Ind}^{ G}_{ K}(\widetilde {\chi })\otimes {\overline {\mathbb {Q}}_\ell }$
and
![]() $\widetilde {\Pi }\otimes {\overline {\mathbb {Q}}_\ell }$
. It is thus c-distinguished and, by [Reference Serre39] 15.4, its reduction mod
$\widetilde {\Pi }\otimes {\overline {\mathbb {Q}}_\ell }$
. It is thus c-distinguished and, by [Reference Serre39] 15.4, its reduction mod
![]() $\ell $
contains
$\ell $
contains
![]() $\mathrm {W}$
.
$\mathrm {W}$
.
Now, observe that, since
![]() $\widetilde {\chi }$
is quadratic, J is self-dual. The contragredient of X is thus c-distinguished and its reduction mod
$\widetilde {\chi }$
is quadratic, J is self-dual. The contragredient of X is thus c-distinguished and its reduction mod
![]() $\ell $
contains
$\ell $
contains
![]() $\mathrm {V}$
.
$\mathrm {V}$
.
5.9
Let
![]() $\tau $
be a c-distinguished irreducible
$\tau $
be a c-distinguished irreducible
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation as in Lemma 5.8. Consider its cuspidal support: There are positive integers
${\overline {\mathbb {Q}}_\ell }$
-representation as in Lemma 5.8. Consider its cuspidal support: There are positive integers
![]() $n_1,\dots ,n_t$
such that
$n_1,\dots ,n_t$
such that
![]() $n_1+\dots +n_t=n$
and, for each i in
$n_1+\dots +n_t=n$
and, for each i in
![]() $\{1,\dots ,t\}$
, a cuspidal irreducible
$\{1,\dots ,t\}$
, a cuspidal irreducible
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation
${\overline {\mathbb {Q}}_\ell }$
-representation
![]() $\rho _i$
of
$\rho _i$
of
![]() $\operatorname {GL}_{n_i}(\boldsymbol {k})$
such that
$\operatorname {GL}_{n_i}(\boldsymbol {k})$
such that
![]() $\tau $
occurs as a component of the parabolically induced representation
$\tau $
occurs as a component of the parabolically induced representation
![]() $\rho _1\times \dots \times \rho _t$
, denoted
$\rho _1\times \dots \times \rho _t$
, denoted
![]() $\mathrm {W}$
. The representation
$\mathrm {W}$
. The representation
![]() $\mathrm {W}$
is thus c-distinguished. We claim the following.
$\mathrm {W}$
is thus c-distinguished. We claim the following.
Claim 5.9. There is an
![]() $i\in \{1,\dots ,t\}$
such that
$i\in \{1,\dots ,t\}$
such that
![]() $n_i$
is even and
$n_i$
is even and
![]() $\rho _i$
is c-distinguished by
$\rho _i$
is c-distinguished by
![]() $H_{n_i}$
.
$H_{n_i}$
.
Before proving this claim in the next paragraph, let us explain how it implies Proposition 5.7.
Propositions 3.9 and 3.11 imply that, for each
![]() $i\in \{1,\dots ,t\}$
, the reduction mod
$i\in \{1,\dots ,t\}$
, the reduction mod
![]() $\ell $
of
$\ell $
of
![]() $\rho _i$
is irreducible and cuspidal, of the form
$\rho _i$
is irreducible and cuspidal, of the form
![]() $\operatorname {st}_{r_i}(\varrho _i)$
for a unique positive integer
$\operatorname {st}_{r_i}(\varrho _i)$
for a unique positive integer
![]() $r_i$
and a unique supercuspidal representation
$r_i$
and a unique supercuspidal representation
![]() $\varrho _i$
. Since the reduction mod
$\varrho _i$
. Since the reduction mod
![]() $\ell $
of
$\ell $
of
![]() $\tau $
contains
$\tau $
contains
![]() $\mathrm {V}$
, the representation
$\mathrm {V}$
, the representation
![]() $\mathrm {V}$
occurs as an irreducible component of the parabolically induced representation
$\mathrm {V}$
occurs as an irreducible component of the parabolically induced representation
![]() ${{\mathbf {\textsf {r}}}}_\ell (\rho _1)\times \dots \times {{\mathbf {\textsf {r}}}}_\ell (\rho _t)$
. Uniqueness of the supercuspidal support implies that
${{\mathbf {\textsf {r}}}}_\ell (\rho _1)\times \dots \times {{\mathbf {\textsf {r}}}}_\ell (\rho _t)$
. Uniqueness of the supercuspidal support implies that
![]() $\varrho _i\simeq \varrho $
for all i. It follows that either
$\varrho _i\simeq \varrho $
for all i. It follows that either
![]() $r_i=1$
or
$r_i=1$
or
![]() $r_i=e(\varrho )\ell ^{v_i}$
for some
$r_i=e(\varrho )\ell ^{v_i}$
for some
![]() $v_i{\geqslant }0$
. Observe that, as
$v_i{\geqslant }0$
. Observe that, as
![]() $r=e(\varrho )\ell ^{v}$
for some
$r=e(\varrho )\ell ^{v}$
for some
![]() $v{\geqslant }0$
and r is odd, the integer
$v{\geqslant }0$
and r is odd, the integer
![]() $e(\varrho )$
is odd, thus
$e(\varrho )$
is odd, thus
![]() $r_i$
is odd in any case, for all i.
$r_i$
is odd in any case, for all i.
Fix an integer i as in Claim 5.9, and let
![]() $\xi _i$
be a parameter for
$\xi _i$
be a parameter for
![]() $\rho _i$
in the sense of Definition 3.12. It is a
$\rho _i$
in the sense of Definition 3.12. It is a
![]() $\operatorname {Gal}(\boldsymbol {k}_{n_i}/\boldsymbol {k})$
-regular
$\operatorname {Gal}(\boldsymbol {k}_{n_i}/\boldsymbol {k})$
-regular
![]() ${\overline {\mathbb {Z}}_\ell }$
-character of
${\overline {\mathbb {Z}}_\ell }$
-character of
![]() $\boldsymbol {k}_{n_i}^\times $
. By Proposition 3.13, it is trivial on
$\boldsymbol {k}_{n_i}^\times $
. By Proposition 3.13, it is trivial on
![]() $\boldsymbol {k}_{u_i}^\times $
, where
$\boldsymbol {k}_{u_i}^\times $
, where
![]() $u_i$
is defined by
$u_i$
is defined by
![]() $n_i=2u_i$
, and it takes the unique element of
$n_i=2u_i$
, and it takes the unique element of
![]() $\boldsymbol {k}_{n_i}^\times /\boldsymbol {k}_{u_i}^\times $
of order
$\boldsymbol {k}_{n_i}^\times /\boldsymbol {k}_{u_i}^\times $
of order
![]() $2$
to
$2$
to
![]() $-c$
.
$-c$
.
Since the reduction mod
![]() $\ell $
of
$\ell $
of
![]() $\rho _i$
is
$\rho _i$
is
![]() $\operatorname {st}_{r_i}(\varrho )$
, the reduction mod
$\operatorname {st}_{r_i}(\varrho )$
, the reduction mod
![]() $\ell $
of
$\ell $
of
![]() $\xi _i$
takes the form
$\xi _i$
takes the form
![]() $\vartheta \circ \mathrm {N}_{\boldsymbol {k}_{n_i}/\boldsymbol {k}_{k}},$
where
$\vartheta \circ \mathrm {N}_{\boldsymbol {k}_{n_i}/\boldsymbol {k}_{k}},$
where
![]() $\vartheta $
is a parameter for
$\vartheta $
is a parameter for
![]() $\varrho $
.
$\varrho $
.
Since
![]() $n_i=r_ik$
and
$n_i=r_ik$
and
![]() $r_i$
is odd,
$r_i$
is odd,
![]() $\vartheta $
is trivial on
$\vartheta $
is trivial on
![]() $\boldsymbol {k}_{l}^\times $
(where
$\boldsymbol {k}_{l}^\times $
(where
![]() $k=2l$
) and takes the element of
$k=2l$
) and takes the element of
![]() $\boldsymbol {k}_{k}^\times /\boldsymbol {k}_{l}^\times $
of order
$\boldsymbol {k}_{k}^\times /\boldsymbol {k}_{l}^\times $
of order
![]() $2$
to
$2$
to
![]() $-c$
.
$-c$
.
By Proposition 3.13, the canonical
![]() ${\overline {\mathbb {Z}}_\ell }$
-lift of
${\overline {\mathbb {Z}}_\ell }$
-lift of
![]() $\vartheta $
is the parameter of a c-distinguished
$\vartheta $
is the parameter of a c-distinguished
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift of
${\overline {\mathbb {Q}}_\ell }$
-lift of
![]() $\varrho $
, which implies that
$\varrho $
, which implies that
![]() $\varrho $
is c-distinguished (see Remark 3.14). This proves Proposition 5.7.
$\varrho $
is c-distinguished (see Remark 3.14). This proves Proposition 5.7.
5.10
The remaining part of this section will be devoted to the proof of Claim 5.9. We follow the argument of [Reference Matringe28] Section 3, which simplifies in our situation since we deal with finite groups. Let
![]() $\boldsymbol {\mathsf {A}}$
denote the set of t-uples
$\boldsymbol {\mathsf {A}}$
denote the set of t-uples
![]() $\alpha = (\alpha _1,\dots ,\alpha _t)$
where
$\alpha = (\alpha _1,\dots ,\alpha _t)$
where
-
1. for each i, the element
 $\alpha _i$
is a family of
$\alpha _i$
is a family of
 $t+1$
nonnegative integers of the form of sum
$t+1$
nonnegative integers of the form of sum $$ \begin{align*} \alpha_i=(n^{\phantom{+}}_{i,1},\dots,n^{\phantom{+}}_{i,i-1}, n_{i,i}^+,n_{i,i}^-,n^{\phantom{+}}_{i,i+1},\dots,n^{\phantom{+}}_{i,t}) \end{align*} $$
$$ \begin{align*} \alpha_i=(n^{\phantom{+}}_{i,1},\dots,n^{\phantom{+}}_{i,i-1}, n_{i,i}^+,n_{i,i}^-,n^{\phantom{+}}_{i,i+1},\dots,n^{\phantom{+}}_{i,t}) \end{align*} $$
 $n_i$
,
$n_i$
,
-
2. one has
 $n_{1,1}^++\dots +n_{t,t}^+=n_{1,1}^-\dots +n_{t,t}^-$
and
$n_{1,1}^++\dots +n_{t,t}^+=n_{1,1}^-\dots +n_{t,t}^-$
and
 $n_{i,j}=n_{j,i}$
for all
$n_{i,j}=n_{j,i}$
for all
 $i\neq j$
.
$i\neq j$
.
For an
![]() $\alpha \in \boldsymbol {\mathsf {A}}$
, it will be convenient to set
$\alpha \in \boldsymbol {\mathsf {A}}$
, it will be convenient to set
![]() $n^{\phantom {+}}_{i,i}=n_{i,i}^++n_{i,i}^-$
for each integer
$n^{\phantom {+}}_{i,i}=n_{i,i}^++n_{i,i}^-$
for each integer
![]() $i\in \{1,\dots ,t\}$
.
$i\in \{1,\dots ,t\}$
.
As in [Reference Matringe28] 3.1, the set
![]() $\boldsymbol {\mathsf {A}}$
parametrizes the set of
$\boldsymbol {\mathsf {A}}$
parametrizes the set of
![]() $({ P},{{H}})$
-double cosets in
$({ P},{{H}})$
-double cosets in
![]() ${ G}$
, where
${ G}$
, where
![]() ${ P}$
in the parabolic subgroup of
${ P}$
in the parabolic subgroup of
![]() ${ G}$
generated by upper triangular matrices and the standard Levi subgroup
${ G}$
generated by upper triangular matrices and the standard Levi subgroup
![]() ${ M}$
isomorphic to
${ M}$
isomorphic to
![]() ${ G}_{n_1}\times \dots \times { G}_{n_t}$
. Let us explain how this parametrization works. Associated with any
${ G}_{n_1}\times \dots \times { G}_{n_t}$
. Let us explain how this parametrization works. Associated with any
![]() $\alpha \in \boldsymbol {\mathsf {A}}$
, there are
$\alpha \in \boldsymbol {\mathsf {A}}$
, there are
-
○ a standard Levi subgroup
 $$ \begin{align*} { M}_\alpha = (G_{n_{1,1}} \times G_{n_{1,2}} \times\dots\times G_{n_{1,t}}) \times\dots\times (G_{n_{t,1}} \times G_{n_{t,2}} \times\dots\times G_{n_{t,t}}) \subseteq { M}, \end{align*} $$
$$ \begin{align*} { M}_\alpha = (G_{n_{1,1}} \times G_{n_{1,2}} \times\dots\times G_{n_{1,t}}) \times\dots\times (G_{n_{t,1}} \times G_{n_{t,2}} \times\dots\times G_{n_{t,t}}) \subseteq { M}, \end{align*} $$
-
○ a diagonal element
 $$ \begin{align*} d_\alpha = \operatorname{diag}\left( \begin{pmatrix} \mathrm{id}_{n_{1,1}^+} & \\ & -\mathrm{id}_{n_{1,1}^-}\end{pmatrix} , \mathrm{id}_{n_{1,2}},\dots,\mathrm{id}_{n_{1,t}},\dots, \mathrm{id}_{n_{t,1}}, \mathrm{id}_{n_{t,2}}, \dots, \begin{pmatrix} \mathrm{id}_{n_{t,t}^+} & \\ & -\mathrm{id}_{n_{t,t}^-}\end{pmatrix} \right) \in M_\alpha, \end{align*} $$
$$ \begin{align*} d_\alpha = \operatorname{diag}\left( \begin{pmatrix} \mathrm{id}_{n_{1,1}^+} & \\ & -\mathrm{id}_{n_{1,1}^-}\end{pmatrix} , \mathrm{id}_{n_{1,2}},\dots,\mathrm{id}_{n_{1,t}},\dots, \mathrm{id}_{n_{t,1}}, \mathrm{id}_{n_{t,2}}, \dots, \begin{pmatrix} \mathrm{id}_{n_{t,t}^+} & \\ & -\mathrm{id}_{n_{t,t}^-}\end{pmatrix} \right) \in M_\alpha, \end{align*} $$
-
○ a permutation matrix
 $w_\alpha \in G$
defined as follows: Decompose
$w_\alpha \in G$
defined as follows: Decompose
 $\{1,\dots ,n\}$
as the disjoint union of intervals
$\{1,\dots ,n\}$
as the disjoint union of intervals
 $J_{i,j}= \{a_{i,j},a_{i,j}+1,\dots ,b_{i,j}\}$
of length
$J_{i,j}= \{a_{i,j},a_{i,j}+1,\dots ,b_{i,j}\}$
of length
 $n_{i,j}$
, for each
$n_{i,j}$
, for each
 $i,j\in \{1,\dots ,t\}$
, where
$i,j\in \{1,\dots ,t\}$
, where
 $a_{1,1}=1$
,
$a_{1,1}=1$
,
 $a_{i,j+1}=b_{i,j}+1$
if
$a_{i,j+1}=b_{i,j}+1$
if
 $j\neq t$
and
$j\neq t$
and
 $a_{i+1,1}=b_{i,t}+1$
if
$a_{i+1,1}=b_{i,t}+1$
if
 $i\neq t$
; then
$i\neq t$
; then
 $w_\alpha $
is the involution which
$w_\alpha $
is the involution which
-
○ restricts to the identity on
 $J_{i,i}$
for each i,
$J_{i,i}$
for each i, -
○ exchanges the intervals
 $J_{i,j}$
and
$J_{i,j}$
and
 $J_{j,i}$
if
$J_{j,i}$
if
 $i\neq j$
, and sends the kth element of any of these intervals to the kth element of the other one, for all
$i\neq j$
, and sends the kth element of any of these intervals to the kth element of the other one, for all
 $k\in \{1,\dots ,n_{i,j}\}$
.
$k\in \{1,\dots ,n_{i,j}\}$
.
A system of representatives
![]() $(x_{\alpha })_{\alpha \in \boldsymbol {\mathsf {A}}}$
of
$(x_{\alpha })_{\alpha \in \boldsymbol {\mathsf {A}}}$
of
![]() $({ P},{{H}})$
-double cosets in
$({ P},{{H}})$
-double cosets in
![]() ${ G}$
is then obtained by any choice of
${ G}$
is then obtained by any choice of
![]() $x_{\alpha }\in G$
such that
$x_{\alpha }\in G$
such that
 $$ \begin{align} x^{\phantom{1}}_{\alpha} \begin{pmatrix} \mathrm{id}_u & \\ & -\mathrm{id}_u \end{pmatrix} x_{\alpha}^{-1} = e_\alpha, \end{align} $$
$$ \begin{align} x^{\phantom{1}}_{\alpha} \begin{pmatrix} \mathrm{id}_u & \\ & -\mathrm{id}_u \end{pmatrix} x_{\alpha}^{-1} = e_\alpha, \end{align} $$
where
![]() $e_\alpha = d_\alpha w_\alpha $
.
$e_\alpha = d_\alpha w_\alpha $
.
Definition 5.10. An
![]() $\alpha \in \boldsymbol {\mathsf {A}}$
is called admissible if, for any i, there exists a unique j such that
$\alpha \in \boldsymbol {\mathsf {A}}$
is called admissible if, for any i, there exists a unique j such that
![]() $n_{i,j}\neq 0$
. This defines an involution
$n_{i,j}\neq 0$
. This defines an involution
![]() $\sigma _\alpha :i\mapsto j$
on
$\sigma _\alpha :i\mapsto j$
on
![]() $\{1,\dots ,t\}$
.
$\{1,\dots ,t\}$
.
When this is the case, let us write
![]() $H_\alpha $
for the subgroup of
$H_\alpha $
for the subgroup of
![]() ${ M}$
made of the
${ M}$
made of the
![]() $\mathrm {diag}(g_1,\dots ,g_t)\in { M}$
such that
$\mathrm {diag}(g_1,\dots ,g_t)\in { M}$
such that
 $$ \begin{align*} \begin{array}{rcll} g_{\sigma_\alpha(i)} & = & g_i & \text{ for all }i\in\{1,\dots,t\}, \\ g_i &\in & \operatorname{GL}_{n_{i,i}^+}(\boldsymbol{k}) \times \operatorname{GL}_{n_{i,i}^-}(\boldsymbol{k}) & \text{ for all }i\text{ fixed by }\sigma_\alpha. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rcll} g_{\sigma_\alpha(i)} & = & g_i & \text{ for all }i\in\{1,\dots,t\}, \\ g_i &\in & \operatorname{GL}_{n_{i,i}^+}(\boldsymbol{k}) \times \operatorname{GL}_{n_{i,i}^-}(\boldsymbol{k}) & \text{ for all }i\text{ fixed by }\sigma_\alpha. \end{array} \end{align*} $$
Moreover, if
![]() $n_{i,i}^+=n_{i,i}^-$
for all
$n_{i,i}^+=n_{i,i}^-$
for all
![]() $i\in \{1,\dots ,t\}$
, we define a matrix
$i\in \{1,\dots ,t\}$
, we define a matrix
![]() $k_\alpha =\mathrm {diag}(k_1,\dots ,k_t)\in { M}$
by
$k_\alpha =\mathrm {diag}(k_1,\dots ,k_t)\in { M}$
by
This matrix normalizes
![]() $H_\alpha $
, and we write
$H_\alpha $
, and we write
![]() ${ K}_\alpha $
for the group generated by
${ K}_\alpha $
for the group generated by
![]() $H_\alpha $
and
$H_\alpha $
and
![]() $k_\alpha $
.
$k_\alpha $
.
We denote by
![]() ${\theta }_\alpha $
the inner automorphism of the group
${\theta }_\alpha $
the inner automorphism of the group
![]() $\mathrm {PGL}_n(\boldsymbol {k})$
induced by conjugacy by
$\mathrm {PGL}_n(\boldsymbol {k})$
induced by conjugacy by
![]() $e_\alpha $
(which normalizes
$e_\alpha $
(which normalizes
![]() ${ M}_\alpha $
). It is not hard to check that:
${ M}_\alpha $
). It is not hard to check that:
Lemma 5.11. Let Z denote the centre of G.
-
1. An
 $\alpha \in \boldsymbol {\mathsf {A}}$
is admissible if and only if
$\alpha \in \boldsymbol {\mathsf {A}}$
is admissible if and only if
 ${ M}/Z$
is
${ M}/Z$
is
 ${\theta }_\alpha $
-stable in
${\theta }_\alpha $
-stable in
 $G/Z=\mathrm {PGL}_n(\boldsymbol {k})$
.
$G/Z=\mathrm {PGL}_n(\boldsymbol {k})$
. -
2. Suppose that
 $\alpha \in \boldsymbol {\mathsf {A}}$
is admissible. The preimage of
$\alpha \in \boldsymbol {\mathsf {A}}$
is admissible. The preimage of
 $({ M}/Z)^{{\theta }_\alpha }$
in
$({ M}/Z)^{{\theta }_\alpha }$
in
 ${ G}$
, denoted by
${ G}$
, denoted by
 $L_\alpha $
, is
$L_\alpha $
, is  $$ \begin{align*} \left\{ \begin{array}{ll} { K}_\alpha & \text{if }n_{ii}^+=n_{ii}^-\text{ for all }i, \\ H_\alpha & \text{otherwise}. \end{array}\right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{ll} { K}_\alpha & \text{if }n_{ii}^+=n_{ii}^-\text{ for all }i, \\ H_\alpha & \text{otherwise}. \end{array}\right. \end{align*} $$
When
![]() $L_\alpha =K_\alpha $
, we denote by
$L_\alpha =K_\alpha $
, we denote by
![]() $\chi _\alpha $
the character of
$\chi _\alpha $
the character of
![]() $K_\alpha $
trivial on
$K_\alpha $
trivial on
![]() $H_\alpha $
and sending
$H_\alpha $
and sending
![]() $k_\alpha $
to c. Otherwise, we set
$k_\alpha $
to c. Otherwise, we set
![]() $\chi _\alpha $
to be the trivial character of
$\chi _\alpha $
to be the trivial character of
![]() $L_\alpha =H_\alpha $
. We have the following lemma.
$L_\alpha =H_\alpha $
. We have the following lemma.
Lemma 5.12. Suppose that
![]() $\alpha $
is admissible and
$\alpha $
is admissible and
![]() $L_\alpha ={ K}_\alpha $
. Then there is a system of representatives
$L_\alpha ={ K}_\alpha $
. Then there is a system of representatives
![]() $(x_{\alpha })_{\alpha \in \boldsymbol {\mathsf {A}}}$
of
$(x_{\alpha })_{\alpha \in \boldsymbol {\mathsf {A}}}$
of
![]() $({ P},{{H}})$
-double cosets of G satisfying both equation (5.2) and
$({ P},{{H}})$
-double cosets of G satisfying both equation (5.2) and
![]() $x^{\phantom {1}}_{\alpha } s^{\phantom {1}}_n x_{\alpha }^{-1}=k_\alpha $
.
$x^{\phantom {1}}_{\alpha } s^{\phantom {1}}_n x_{\alpha }^{-1}=k_\alpha $
.
Proof. Let us set
![]() $m_i=n_{i,i}^+=n_{i,i}^-=n_{i,i}/2$
for any integer
$m_i=n_{i,i}^+=n_{i,i}^-=n_{i,i}/2$
for any integer
![]() $i\in \{1,\dots ,t\}$
such that
$i\in \{1,\dots ,t\}$
such that
![]() $\sigma _\alpha (i)=i$
. For each
$\sigma _\alpha (i)=i$
. For each
![]() $\alpha \in \boldsymbol {\mathsf {A}}$
, we look for a matrix
$\alpha \in \boldsymbol {\mathsf {A}}$
, we look for a matrix
![]() $x_\alpha \in G$
such that
$x_\alpha \in G$
such that
 $$ \begin{align*} x^{\phantom{1}}_{\alpha} \begin{pmatrix} \mathrm{id}_u & \\ & -\mathrm{id}_u \end{pmatrix} x_{\alpha}^{-1} = e_\alpha \quad \text{and} \quad x^{\phantom{1}}_{\alpha} \begin{pmatrix} & \mathrm{id}_u \\ \mathrm{id}_u & \end{pmatrix} x_{\alpha}^{-1} = k_\alpha. \end{align*} $$
$$ \begin{align*} x^{\phantom{1}}_{\alpha} \begin{pmatrix} \mathrm{id}_u & \\ & -\mathrm{id}_u \end{pmatrix} x_{\alpha}^{-1} = e_\alpha \quad \text{and} \quad x^{\phantom{1}}_{\alpha} \begin{pmatrix} & \mathrm{id}_u \\ \mathrm{id}_u & \end{pmatrix} x_{\alpha}^{-1} = k_\alpha. \end{align*} $$
To make an explicit choice of
![]() $x_\alpha \in G$
, it will be convenient to introduce the matrix
$x_\alpha \in G$
, it will be convenient to introduce the matrix
![]() $v_\alpha \in G$
defined as follows: For all integers
$v_\alpha \in G$
defined as follows: For all integers
![]() $i,j\in \{1,\dots ,t\}$
, the
$i,j\in \{1,\dots ,t\}$
, the
![]() $(i,j)$
-block of
$(i,j)$
-block of
![]() $v_\alpha $
in
$v_\alpha $
in
![]() $\boldsymbol {\mathsf {M}}_{n_i,n_j}(\boldsymbol {k})$
is
$\boldsymbol {\mathsf {M}}_{n_i,n_j}(\boldsymbol {k})$
is
-
○ the identity matrix
 $\mathrm {id}_{n_i}$
if
$\mathrm {id}_{n_i}$
if
 $j=i$
or
$j=i$
or
 $j=\sigma _\alpha (i)<i$
,
$j=\sigma _\alpha (i)<i$
, -
○ its opposite
 $-\mathrm {id}_{n_i}$
if
$-\mathrm {id}_{n_i}$
if
 $j=\sigma _\alpha (i)>i$
,
$j=\sigma _\alpha (i)>i$
, -
○ and
 $0$
otherwise.
$0$
otherwise.
Then we choose
![]() $y_\alpha $
the permutation matrix corresponding to the permutation of minimal length (with the usual generators of the symmetric group) satisfying
$y_\alpha $
the permutation matrix corresponding to the permutation of minimal length (with the usual generators of the symmetric group) satisfying
 $$ \begin{align*} y_\alpha \begin{pmatrix} \mathrm{id}_u & \\ & -\mathrm{id}_u \end{pmatrix} y_{\alpha}^{-1}=l_\alpha, \end{align*} $$
$$ \begin{align*} y_\alpha \begin{pmatrix} \mathrm{id}_u & \\ & -\mathrm{id}_u \end{pmatrix} y_{\alpha}^{-1}=l_\alpha, \end{align*} $$
where
![]() $l_\alpha =\mathrm {diag}(l_1,\dots ,l_t)\in { M}$
is defined by
$l_\alpha =\mathrm {diag}(l_1,\dots ,l_t)\in { M}$
is defined by
 $$ \begin{align*} l_{i}=\mathrm{id}_{n_i}=-l_{\sigma_\alpha(i)} \text{ if } i<\sigma_\alpha(i), \quad l_{i}= \begin{pmatrix} \mathrm{id}_{m_i} & \\ & -\mathrm{id}_{m_i} \end{pmatrix} \text{ if } i=\sigma_\alpha(i). \end{align*} $$
$$ \begin{align*} l_{i}=\mathrm{id}_{n_i}=-l_{\sigma_\alpha(i)} \text{ if } i<\sigma_\alpha(i), \quad l_{i}= \begin{pmatrix} \mathrm{id}_{m_i} & \\ & -\mathrm{id}_{m_i} \end{pmatrix} \text{ if } i=\sigma_\alpha(i). \end{align*} $$
Finally, we put
![]() $x_\alpha =v_\alpha y_\alpha $
, which has the desired property thanks to the equality
$x_\alpha =v_\alpha y_\alpha $
, which has the desired property thanks to the equality
 $$ \begin{align} \begin{pmatrix} \mathrm{id}_k & -\mathrm{id}_k \\ \mathrm{id}_k & \phantom{-} \mathrm{id}_k \end{pmatrix} \begin{pmatrix} \mathrm{id}_k & \\ & -\mathrm{id}_k \end{pmatrix} \begin{pmatrix} \mathrm{id}_k & -\mathrm{id}_k \\ \mathrm{id}_k & \phantom{-} \mathrm{id}_k \end{pmatrix}^{-1}=s_{2k}\end{align} $$
$$ \begin{align} \begin{pmatrix} \mathrm{id}_k & -\mathrm{id}_k \\ \mathrm{id}_k & \phantom{-} \mathrm{id}_k \end{pmatrix} \begin{pmatrix} \mathrm{id}_k & \\ & -\mathrm{id}_k \end{pmatrix} \begin{pmatrix} \mathrm{id}_k & -\mathrm{id}_k \\ \mathrm{id}_k & \phantom{-} \mathrm{id}_k \end{pmatrix}^{-1}=s_{2k}\end{align} $$
valid for any
![]() $k\geq 1$
. With this choice, the careful reader checks by a computation relying again on Equality (5.3), that
$k\geq 1$
. With this choice, the careful reader checks by a computation relying again on Equality (5.3), that
![]() $y^{\phantom {1}}_\alpha s^{\phantom {1}}_n y_\alpha ^{-1} = v_{\alpha }^{-1} k^{\phantom {1}}_\alpha v^{\phantom {1}}_\alpha $
, which is the desired equality.
$y^{\phantom {1}}_\alpha s^{\phantom {1}}_n y_\alpha ^{-1} = v_{\alpha }^{-1} k^{\phantom {1}}_\alpha v^{\phantom {1}}_\alpha $
, which is the desired equality.
Now, we have the following lemma.
Lemma 5.13. There is an admissible
![]() $\alpha \in \boldsymbol {\mathsf {A}}$
such that
$\alpha \in \boldsymbol {\mathsf {A}}$
such that
![]() $\operatorname {Hom}_{L_\alpha }(\rho _1\otimes \dots \otimes \rho _t,\chi _\alpha )$
is nonzero.
$\operatorname {Hom}_{L_\alpha }(\rho _1\otimes \dots \otimes \rho _t,\chi _\alpha )$
is nonzero.
Proof. Given any subgroup X of G, we will write
![]() $\overline {X}$
for its image in
$\overline {X}$
for its image in
![]() $G/Z=\mathrm {PGL}_n(\boldsymbol {k})$
. In particular, we have
$G/Z=\mathrm {PGL}_n(\boldsymbol {k})$
. In particular, we have
![]() $\overline {G}=G/Z$
. Note that
$\overline {G}=G/Z$
. Note that
![]() $\overline {{ K}}={ K}/Z$
is the subgroup of
$\overline {{ K}}={ K}/Z$
is the subgroup of
![]() $\overline {G}$
made of all elements fixed by conjugacy by
$\overline {G}$
made of all elements fixed by conjugacy by
 $$ \begin{align*} \begin{pmatrix}\mathrm{id}_u&0\\ 0 & -\mathrm{id}_u\end{pmatrix} \text{ mod } Z. \end{align*} $$
$$ \begin{align*} \begin{pmatrix}\mathrm{id}_u&0\\ 0 & -\mathrm{id}_u\end{pmatrix} \text{ mod } Z. \end{align*} $$
Let
![]() $\chi $
be the unique character of
$\chi $
be the unique character of
![]() ${ K}$
trivial on
${ K}$
trivial on
![]() ${{H}}$
such that
${{H}}$
such that
![]() $\chi (s)=c$
. The character that it induces on
$\chi (s)=c$
. The character that it induces on
![]() $\overline {{ K}}$
will still be denoted by
$\overline {{ K}}$
will still be denoted by
![]() $\chi $
. Since
$\chi $
. Since
![]() $\mathrm {W}$
is c-distinguished, Mackey’s formula implies that there is an
$\mathrm {W}$
is c-distinguished, Mackey’s formula implies that there is an
![]() $x\in G$
such that
$x\in G$
such that
![]() $\rho $
, the representation of P inflated from
$\rho $
, the representation of P inflated from
![]() $\rho _1\otimes \dots \otimes \rho _t$
, is distinguished by the character
$\rho _1\otimes \dots \otimes \rho _t$
, is distinguished by the character
![]() $\chi ^{x}|_{{{ P}}\cap {{ K}}^{x}}$
. We derive from
$\chi ^{x}|_{{{ P}}\cap {{ K}}^{x}}$
. We derive from
![]() $\rho $
a representation
$\rho $
a representation
![]() $\overline {\rho }$
of
$\overline {\rho }$
of
![]() $\overline {P}$
distinguished by
$\overline {P}$
distinguished by
![]() $\chi ^{x}|_{\overline {{ P}}\cap \overline {{ K}}{}^{x}}$
.
$\chi ^{x}|_{\overline {{ P}}\cap \overline {{ K}}{}^{x}}$
.
In fact, because H is a subgroup of K, we can chose x to be some
![]() ${x_{\alpha }}$
for
${x_{\alpha }}$
for
![]() $\alpha \in \boldsymbol {\mathsf {A}}$
. Now, we claim that for all non admissible
$\alpha \in \boldsymbol {\mathsf {A}}$
. Now, we claim that for all non admissible
![]() $\alpha \in \boldsymbol {\mathsf {A}}$
, the space
$\alpha \in \boldsymbol {\mathsf {A}}$
, the space
is zero, so in particular x can only be of the form
![]() $x_\alpha $
for admissible
$x_\alpha $
for admissible
![]() $\alpha $
. Indeed, it follows from [Reference Matringe28] Proposition 3.5 that, for a nonadmissible
$\alpha $
. Indeed, it follows from [Reference Matringe28] Proposition 3.5 that, for a nonadmissible
![]() $\alpha $
, the group
$\alpha $
, the group
![]() ${ P}\cap H^{x_{\alpha }}$
contains a nontrivial unipotent radical
${ P}\cap H^{x_{\alpha }}$
contains a nontrivial unipotent radical
![]() $U_\alpha $
of some parabolic subgroup of
$U_\alpha $
of some parabolic subgroup of
![]() ${ M}$
, but the character
${ M}$
, but the character
![]() $\chi _\alpha $
is trivial on
$\chi _\alpha $
is trivial on
![]() $U_\alpha $
, so if the space (5.4) were not reduced to zero, we would deduce that
$U_\alpha $
, so if the space (5.4) were not reduced to zero, we would deduce that
![]() $\operatorname {Hom}_{U_\alpha }({\rho },R)$
is nonzero, contradicting the cuspidality of
$\operatorname {Hom}_{U_\alpha }({\rho },R)$
is nonzero, contradicting the cuspidality of
![]() $\rho $
. Hence, we deduce
$\rho $
. Hence, we deduce
![]() $x=x_\alpha $
for an
$x=x_\alpha $
for an
![]() $\alpha $
which is admissible. In this case,
$\alpha $
which is admissible. In this case,
![]() $\overline {{ M}}\cap \overline {{ K}}{}^{{x_{\alpha }}}$
is equal to
$\overline {{ M}}\cap \overline {{ K}}{}^{{x_{\alpha }}}$
is equal to
![]() $\overline {{ M}}{}^{{{\theta }_\alpha }}$
so that the space
$\overline {{ M}}{}^{{{\theta }_\alpha }}$
so that the space
is nonzero. If
![]() $L_\alpha =K_\alpha $
, then
$L_\alpha =K_\alpha $
, then
![]() ${\chi }^{x_{\alpha }}$
is equal to
${\chi }^{x_{\alpha }}$
is equal to
![]() $\chi _\alpha $
thanks to Lemma 5.12. Otherwise,
$\chi _\alpha $
thanks to Lemma 5.12. Otherwise,
![]() ${\chi }^{x_{\alpha }}$
and
${\chi }^{x_{\alpha }}$
and
![]() $\chi _\alpha $
are trivial, thus equal. The statement now follows.
$\chi _\alpha $
are trivial, thus equal. The statement now follows.
Recall that, for any
![]() $i\in \{1,\dots ,t\}$
, either
$i\in \{1,\dots ,t\}$
, either
![]() $r_i=1$
or
$r_i=1$
or
![]() $r_i=e(\varrho )\ell ^{v_i}$
for some
$r_i=e(\varrho )\ell ^{v_i}$
for some
![]() $v_i{\geqslant }0$
.
$v_i{\geqslant }0$
.
Lemma 5.14. Let
![]() $\alpha \in \boldsymbol {\mathsf {A}}$
be as in Lemma 5.13. Then the involution
$\alpha \in \boldsymbol {\mathsf {A}}$
be as in Lemma 5.13. Then the involution
![]() $\sigma _\alpha $
has a fixed point.
$\sigma _\alpha $
has a fixed point.
Proof. Let
![]() ${ I}_1$
be the set of
${ I}_1$
be the set of
![]() $i\in \{1,\dots ,t\}$
such that
$i\in \{1,\dots ,t\}$
such that
![]() $r_i>1$
, let
$r_i>1$
, let
![]() $t_1$
be the cardinality of this set and define
$t_1$
be the cardinality of this set and define
![]() $t_0=t-t_1$
. The identity
$t_0=t-t_1$
. The identity
![]() $r = r_1 + \dots + r_t$
implies
$r = r_1 + \dots + r_t$
implies
Since r,
![]() $e(\varrho )$
and
$e(\varrho )$
and
![]() $\ell $
are odd, it follows that
$\ell $
are odd, it follows that
![]() $t_0+t_1=t$
is odd. Thus,
$t_0+t_1=t$
is odd. Thus,
![]() $\sigma _\alpha $
has a fixed point.
$\sigma _\alpha $
has a fixed point.
Claim 5.9 now follows from Lemmas 5.13, 5.14. Indeed, by Lemma 5.13, there is an admissible
![]() $\alpha \in \boldsymbol {\mathsf {A}}$
such that
$\alpha \in \boldsymbol {\mathsf {A}}$
such that
![]() $\operatorname {Hom}_{L_\alpha }(\rho _1\otimes \dots \otimes \rho _t,\chi _\alpha )$
is nonzero. Since
$\operatorname {Hom}_{L_\alpha }(\rho _1\otimes \dots \otimes \rho _t,\chi _\alpha )$
is nonzero. Since
![]() $L_\alpha $
contains
$L_\alpha $
contains
![]() $H_\alpha $
, the representation
$H_\alpha $
, the representation
![]() $\rho _i$
is, for all i fixed by
$\rho _i$
is, for all i fixed by
![]() $\sigma _\alpha $
, distinguished by the Levi subgroup
$\sigma _\alpha $
, distinguished by the Levi subgroup
By [Reference Sécherre35] Proposition 2.14, this implies that
![]() $n_{i,i}^+=n_{i,i}^-$
for all i fixed by
$n_{i,i}^+=n_{i,i}^-$
for all i fixed by
![]() $\sigma _\alpha $
, thus
$\sigma _\alpha $
, thus
![]() $L_\alpha =K_\alpha $
. By Lemma 5.14, there in an integer
$L_\alpha =K_\alpha $
. By Lemma 5.14, there in an integer
![]() $i\in \{1,\dots ,t\}$
fixed by
$i\in \{1,\dots ,t\}$
fixed by
![]() $\sigma _\alpha $
. The ith block of
$\sigma _\alpha $
. The ith block of
![]() $L_\alpha =K_\alpha $
is
$L_\alpha =K_\alpha $
is
![]() $K_{n_i}$
and
$K_{n_i}$
and
![]() $\chi _\alpha (k_i)=c$
. Thus,
$\chi _\alpha (k_i)=c$
. Thus,
![]() $\rho _i$
is c-distinguished.
$\rho _i$
is c-distinguished.
6 Distinguished lift theorems
In this section, p is odd and
![]() $\ell $
is a prime number different from p. We look for a necessary and sufficient condition for an
$\ell $
is a prime number different from p. We look for a necessary and sufficient condition for an
![]() ${\overline {\mathbb {F}}_{\ell }}$
-cuspidal representation of
${\overline {\mathbb {F}}_{\ell }}$
-cuspidal representation of
![]() $\operatorname {GL}_n({ F})$
to have a
$\operatorname {GL}_n({ F})$
to have a
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished lift to
$\operatorname {GL}_n({ F}_0)$
-distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
. Since the case of supercuspidal representations is treated by Theorems 3.3 and 3.4, we will concentrate on nonsupercuspidal cuspidal representations.
${\overline {\mathbb {Q}}_\ell }$
. Since the case of supercuspidal representations is treated by Theorems 3.3 and 3.4, we will concentrate on nonsupercuspidal cuspidal representations.
6.1
We will prove the following two propositions.
Proposition 6.1. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_n({ F})$
with quadratic extension
$\operatorname {GL}_n({ F})$
with quadratic extension
![]() ${ T}/{ T}_0$
and
${ T}/{ T}_0$
and
![]() $m=m(\pi )$
. Assume that
$m=m(\pi )$
. Assume that
![]() $r=r(\pi )>1$
is odd. Then
$r=r(\pi )>1$
is odd. Then
![]() $\pi $
has a distinguished lift to
$\pi $
has a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
if and only if
${\overline {\mathbb {Q}}_\ell }$
if and only if
-
1. the representation
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 $\operatorname {St}_r(\rho )$
for some
$\operatorname {St}_r(\rho )$
for some
 $\operatorname {GL}_{n/r}({ F}_0)$
-distinguished supercuspidal representation
$\operatorname {GL}_{n/r}({ F}_0)$
-distinguished supercuspidal representation
 $\rho $
of
$\rho $
of
 $\operatorname {GL}_{n/r}({ F})$
,
$\operatorname {GL}_{n/r}({ F})$
, -
2. if e,
 $e_0$
are the orders of the cardinalities of the residue fields
$e_0$
are the orders of the cardinalities of the residue fields
 $\boldsymbol {l}$
,
$\boldsymbol {l}$
,
 $\boldsymbol {l}_0$
of
$\boldsymbol {l}_0$
of
 ${ T}$
,
${ T}$
,
 ${ T}_0$
mod
${ T}_0$
mod
 $\ell $
, then
$\ell $
, then-
(a) either
 ${ T}/{ T}_0$
is unramified and
${ T}/{ T}_0$
is unramified and
 $e_0$
is even,
$e_0$
is even, -
(b) or
 ${ T}/{ T}_0$
is ramified, m is even and
${ T}/{ T}_0$
is ramified, m is even and
 $m/e$
is odd.
$m/e$
is odd.
-
Note that the assumption ‘
![]() $r>1$
is odd’ in Proposition 6.1 implies that
$r>1$
is odd’ in Proposition 6.1 implies that
![]() $\ell \neq 2$
.
$\ell \neq 2$
.
Proposition 6.2. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_n({ F})$
with quadratic extension
$\operatorname {GL}_n({ F})$
with quadratic extension
![]() ${ T}/{ T}_0$
and
${ T}/{ T}_0$
and
![]() $m=m(\pi )$
. Assume that
$m=m(\pi )$
. Assume that
![]() $r=r(\pi )$
is even. Then
$r=r(\pi )$
is even. Then
![]() $\pi $
has a distinguished lift to
$\pi $
has a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
if and only if
${\overline {\mathbb {Q}}_\ell }$
if and only if
-
1. the extension
 ${ T}/{ T}_0$
is ramified,
${ T}/{ T}_0$
is ramified, -
2. one has
 $m=r$
,
$m=r$
, -
3. if we denote by
 $\nu _0$
the normalized absolute value of
$\nu _0$
the normalized absolute value of
 $F_0$
, then
$F_0$
, then-
(a) either
 $\ell \neq 2$
and
$\ell \neq 2$
and
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 $\operatorname {St}_m(\rho )$
for some supercuspidal representation
$\operatorname {St}_m(\rho )$
for some supercuspidal representation
 $\rho $
of
$\rho $
of
 $\operatorname {GL}_{n/m}({ F})$
which is either
$\operatorname {GL}_{n/m}({ F})$
which is either
 $\varkappa $
-distinguished or
$\varkappa $
-distinguished or
 $\nu _{0}^{-1}$
-distinguished,
$\nu _{0}^{-1}$
-distinguished, -
(b) or
 $\ell =m=r=2$
, the cardinality of the residue field of
$\ell =m=r=2$
, the cardinality of the residue field of
 ${ T}$
is congruent to
${ T}$
is congruent to
 $-1$
mod
$-1$
mod
 $4$
and
$4$
and
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 $\operatorname {St}_2(\rho )$
where
$\operatorname {St}_2(\rho )$
where
 $\rho $
is a
$\rho $
is a
 $\operatorname {GL}_{n/2}({ F}_0)$
-distinguished supercuspidal representation of
$\operatorname {GL}_{n/2}({ F}_0)$
-distinguished supercuspidal representation of
 $\operatorname {GL}_{n/2}({ F})$
.
$\operatorname {GL}_{n/2}({ F})$
.
-
We also formulate the following conjecture making Proposition 6.2 more precise when
![]() $\ell>2$
.
$\ell>2$
.
Conjecture 6.3. Assume that
![]() $\ell \neq 2$
. Let
$\ell \neq 2$
. Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of the group
${\overline {\mathbb {F}}_{\ell }}$
-representation of the group
![]() $\operatorname {GL}_n({ F})$
such that
$\operatorname {GL}_n({ F})$
such that
![]() $r(\pi )$
is even. The following assertions are equivalent:
$r(\pi )$
is even. The following assertions are equivalent:
-
1. The representation
 $\pi $
is distinguished,
$\pi $
is distinguished, -
2. The representation
 $\pi $
has a distinguished lift to
$\pi $
has a distinguished lift to
 ${\overline {\mathbb {Q}}_\ell }$
,
${\overline {\mathbb {Q}}_\ell }$
, -
3. The three conditions of Proposition 6.2 hold.
By Proposition 6.2, Theorem 3.3, we know that (2) implies (1) and is equivalent to (3). We thus conjecture that (1) implies (3). See [Reference Cui, Lanard and Lu12] Theorem 4.6 for the case
![]() $n=r=2$
.
$n=r=2$
.
Remark 6.4. When
![]() $\ell =2$
, there are distinguished cuspidal
$\ell =2$
, there are distinguished cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representations of
${\overline {\mathbb {F}}_{\ell }}$
-representations of
![]() $\operatorname {GL}_2({ F})$
with no distinguished lift. This is the case exactly when either
$\operatorname {GL}_2({ F})$
with no distinguished lift. This is the case exactly when either
![]() $F/F_0$
is unramified, or
$F/F_0$
is unramified, or
![]() $F/F_0$
is ramified and q is congruent to
$F/F_0$
is ramified and q is congruent to
![]() $1$
mod
$1$
mod
![]() $4$
. See Paragraph 4.13.
$4$
. See Paragraph 4.13.
6.2
Let
![]() $\pi $
be a
$\pi $
be a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() ${ G}=\operatorname {GL}_n({ F})$
. Let
${ G}=\operatorname {GL}_n({ F})$
. Let
![]() $(\mathbf {J},\boldsymbol {\lambda })$
be a generic
$(\mathbf {J},\boldsymbol {\lambda })$
be a generic
![]() $\sigma $
-self-dual type in
$\sigma $
-self-dual type in
![]() $\pi $
, and let
$\pi $
, and let
![]() $\boldsymbol {\lambda }_{\mathrm {w}}$
be the representation of
$\boldsymbol {\lambda }_{\mathrm {w}}$
be the representation of
![]() $\mathbf {J}$
given by Proposition 4.16 (see Paragraph 4.9) and
$\mathbf {J}$
given by Proposition 4.16 (see Paragraph 4.9) and
![]() $\boldsymbol {\tau }$
be the representation of
$\boldsymbol {\tau }$
be the representation of
![]() $\mathbf {J}$
trivial on
$\mathbf {J}$
trivial on
![]() $\mathbf {J}^1$
such that
$\mathbf {J}^1$
such that
![]() $\boldsymbol {\lambda }$
is isomorphic to
$\boldsymbol {\lambda }$
is isomorphic to
![]() $\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\tau }$
. Associated with
$\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\tau }$
. Associated with
![]() $\pi $
by equation (4.21), there is also a
$\pi $
by equation (4.21), there is also a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation
${\overline {\mathbb {F}}_{\ell }}$
-representation
![]() $\pi _{\mathrm {t}}$
of
$\pi _{\mathrm {t}}$
of
![]() $\operatorname {GL}_m({ T})$
.
$\operatorname {GL}_m({ T})$
.
Lemma 6.5. The following assertions are equivalent.
-
1. The representation
 $\pi $
has a
$\pi $
has a
 $\operatorname {GL}_n({ F}_0)$
-distinguished lift to
$\operatorname {GL}_n({ F}_0)$
-distinguished lift to
 ${\overline {\mathbb {Q}}_\ell }$
.
${\overline {\mathbb {Q}}_\ell }$
. -
2. The representation
 $\boldsymbol {\lambda }$
has a
$\boldsymbol {\lambda }$
has a
 $\mathbf {J}\cap \operatorname {GL}_n({ F}_0)$
-distinguished lift to
$\mathbf {J}\cap \operatorname {GL}_n({ F}_0)$
-distinguished lift to
 ${\overline {\mathbb {Q}}_\ell }$
.
${\overline {\mathbb {Q}}_\ell }$
. -
3. The representation
 $\boldsymbol {\tau }$
has a
$\boldsymbol {\tau }$
has a
 $\mathbf {J}\cap \operatorname {GL}_n({ F}_0)$
-distinguished lift to
$\mathbf {J}\cap \operatorname {GL}_n({ F}_0)$
-distinguished lift to
 ${\overline {\mathbb {Q}}_\ell }$
.
${\overline {\mathbb {Q}}_\ell }$
. -
4. The representation
 $\pi _{\mathrm {t}}$
has a
$\pi _{\mathrm {t}}$
has a
 $\operatorname {GL}_m({ T}_0)$
-distinguished lift to
$\operatorname {GL}_m({ T}_0)$
-distinguished lift to
 ${\overline {\mathbb {Q}}_\ell }$
.
${\overline {\mathbb {Q}}_\ell }$
.
Proof. Fix a
![]() $\sigma $
-self-dual simple stratum
$\sigma $
-self-dual simple stratum
![]() $[\mathfrak {a},{\beta }]$
as well as isomorphisms (4.17) as in Proposition 4.5. Let
$[\mathfrak {a},{\beta }]$
as well as isomorphisms (4.17) as in Proposition 4.5. Let ![]() be the
be the
![]() $\sigma $
-self-dual maximal simple character associated with
$\sigma $
-self-dual maximal simple character associated with
![]() $\boldsymbol {\lambda }$
, and
$\boldsymbol {\lambda }$
, and
![]() $\widetilde {{\theta }}$
be its unique
$\widetilde {{\theta }}$
be its unique
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift: this is a
${\overline {\mathbb {Q}}_\ell }$
-lift: this is a
![]() $\sigma $
-self-dual maximal simple character (with respect to the unique
$\sigma $
-self-dual maximal simple character (with respect to the unique
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift
${\overline {\mathbb {Q}}_\ell }$
-lift
![]() $\widetilde {\psi }$
of the character
$\widetilde {\psi }$
of the character
![]() $\psi $
given by equation (4.1)) having the same
$\psi $
given by equation (4.1)) having the same
![]() ${ G}$
-normalizer
${ G}$
-normalizer
![]() $\mathbf {J}$
as
$\mathbf {J}$
as
![]() ${\theta }$
.
${\theta }$
.
Let
![]() $\widetilde {\boldsymbol {\lambda }}_{\mathrm {w}}$
be the
$\widetilde {\boldsymbol {\lambda }}_{\mathrm {w}}$
be the
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation of
${\overline {\mathbb {Q}}_\ell }$
-representation of
![]() $\mathbf {J}$
associated with
$\mathbf {J}$
associated with
![]() $\widetilde {{\theta }}$
by Proposition 4.16. It is
$\widetilde {{\theta }}$
by Proposition 4.16. It is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished and
$\mathbf {J}\cap { G}^\sigma $
-distinguished and
![]() $\sigma $
-self-dual, and its determinant has order a power of p. It is thus integral. Let us consider its reduction mod
$\sigma $
-self-dual, and its determinant has order a power of p. It is thus integral. Let us consider its reduction mod
![]() $\ell $
. On the one hand, it is
$\ell $
. On the one hand, it is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished,
$\mathbf {J}\cap { G}^\sigma $
-distinguished,
![]() $\sigma $
-self-dual, and its determinant has order a power of p. On the other hand, [Reference Mínguez and Sécherre30] Proposition 2.37 implies that it is an irreducible representation extending the Heisenberg representation associated with
$\sigma $
-self-dual, and its determinant has order a power of p. On the other hand, [Reference Mínguez and Sécherre30] Proposition 2.37 implies that it is an irreducible representation extending the Heisenberg representation associated with
![]() ${\theta }$
. By uniqueness, we deduce that
${\theta }$
. By uniqueness, we deduce that
![]() $\widetilde {\boldsymbol {\lambda }}_{\mathrm {w}}$
is a
$\widetilde {\boldsymbol {\lambda }}_{\mathrm {w}}$
is a
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift of
${\overline {\mathbb {Q}}_\ell }$
-lift of
![]() $\boldsymbol {\lambda }_{\mathrm {w}}$
.
$\boldsymbol {\lambda }_{\mathrm {w}}$
.
Suppose that
![]() $\pi $
has a
$\pi $
has a
![]() ${ G}^\sigma $
-distinguished
${ G}^\sigma $
-distinguished
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift
${\overline {\mathbb {Q}}_\ell }$
-lift
![]() $\widetilde {\pi }$
. Thus,
$\widetilde {\pi }$
. Thus,
![]() $\widetilde {\pi }$
is a
$\widetilde {\pi }$
is a
![]() $\sigma $
-self-dual and cuspidal representation of
$\sigma $
-self-dual and cuspidal representation of
![]() ${ G}$
containing the maximal simple character
${ G}$
containing the maximal simple character
![]() $\widetilde {{\theta }}$
. By Proposition 4.32, this representation
$\widetilde {{\theta }}$
. By Proposition 4.32, this representation
![]() $\widetilde {\pi }$
contains a distinguished generic
$\widetilde {\pi }$
contains a distinguished generic
![]() $\sigma $
-self-dual type, which we may assume to be of the form
$\sigma $
-self-dual type, which we may assume to be of the form
![]() $(\mathbf {J},\widetilde {\boldsymbol {\lambda }})$
with
$(\mathbf {J},\widetilde {\boldsymbol {\lambda }})$
with
![]() $\widetilde {\boldsymbol {\lambda }}=\widetilde {\boldsymbol {\lambda }}_{\mathrm {w}}\otimes \widetilde {\boldsymbol {\tau }}$
and the representation
$\widetilde {\boldsymbol {\lambda }}=\widetilde {\boldsymbol {\lambda }}_{\mathrm {w}}\otimes \widetilde {\boldsymbol {\tau }}$
and the representation
![]() $\widetilde {\boldsymbol {\tau }}$
is
$\widetilde {\boldsymbol {\tau }}$
is
![]() $\mathbf {J}\cap { G}^\sigma $
-distinguished. Reducing mod
$\mathbf {J}\cap { G}^\sigma $
-distinguished. Reducing mod
![]() $\ell $
, we deduce that
$\ell $
, we deduce that
![]() $\pi $
contains the type
$\pi $
contains the type
![]() $\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\delta }$
, where
$\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\delta }$
, where
![]() $\boldsymbol {\delta }$
is the reduction mod
$\boldsymbol {\delta }$
is the reduction mod
![]() $\ell $
of
$\ell $
of
![]() $\widetilde {\boldsymbol {\tau }}$
. But
$\widetilde {\boldsymbol {\tau }}$
. But
![]() $\pi $
also contains the type
$\pi $
also contains the type
![]() $\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\tau }$
, thus
$\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\tau }$
, thus
![]() $\boldsymbol {\delta }$
is isomorphic to
$\boldsymbol {\delta }$
is isomorphic to
![]() $\boldsymbol {\tau }$
, and the reduction mod
$\boldsymbol {\tau }$
, and the reduction mod
![]() $\ell $
of
$\ell $
of
![]() $\widetilde {\boldsymbol {\lambda }}$
is isomorphic to
$\widetilde {\boldsymbol {\lambda }}$
is isomorphic to
![]() $\boldsymbol {\lambda }$
. Thus, (1) implies both (2) and (3).
$\boldsymbol {\lambda }$
. Thus, (1) implies both (2) and (3).
Conversely, suppose that
![]() $\boldsymbol {\tau }$
has a distinguished
$\boldsymbol {\tau }$
has a distinguished
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift
${\overline {\mathbb {Q}}_\ell }$
-lift
![]() $\widetilde {\boldsymbol {\tau }}$
. Then the pair
$\widetilde {\boldsymbol {\tau }}$
. Then the pair
![]() $(\mathbf {J},\widetilde {\boldsymbol {\lambda }}_{\mathrm {w}}\otimes \widetilde {\boldsymbol {\tau }})$
is a distinguished type whose compact induction to
$(\mathbf {J},\widetilde {\boldsymbol {\lambda }}_{\mathrm {w}}\otimes \widetilde {\boldsymbol {\tau }})$
is a distinguished type whose compact induction to
![]() ${ G}$
is a
${ G}$
is a
![]() ${ G}^\sigma $
-distinguished
${ G}^\sigma $
-distinguished
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift of
${\overline {\mathbb {Q}}_\ell }$
-lift of
![]() $\pi $
, and whose reduction mod
$\pi $
, and whose reduction mod
![]() $\ell $
is isomorphic to
$\ell $
is isomorphic to
![]() $\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\tau }\simeq \boldsymbol {\lambda }$
. Thus, (3) implies both (1) and (2).
$\boldsymbol {\lambda }_{\mathrm {w}}\otimes \boldsymbol {\tau }\simeq \boldsymbol {\lambda }$
. Thus, (3) implies both (1) and (2).
Applying these results to the representation
![]() $\pi _{\mathrm {t}}$
, we get that
$\pi _{\mathrm {t}}$
, we get that
![]() $\pi _{\mathrm {t}}$
has a distinguished lift to
$\pi _{\mathrm {t}}$
has a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
if and only if
${\overline {\mathbb {Q}}_\ell }$
if and only if
![]() $\boldsymbol {\tau }_{\mathrm {t}}$
has a distinguished lift to
$\boldsymbol {\tau }_{\mathrm {t}}$
has a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
. The fact that
${\overline {\mathbb {Q}}_\ell }$
. The fact that
![]() $\boldsymbol {\tau }$
is isomorphic to
$\boldsymbol {\tau }$
is isomorphic to
![]() $\boldsymbol {\tau }_{\mathrm {t}}\circ \boldsymbol {\pi }$
(by Lemma 4.37) thus implies that (4) is equivalent to (3).
$\boldsymbol {\tau }_{\mathrm {t}}\circ \boldsymbol {\pi }$
(by Lemma 4.37) thus implies that (4) is equivalent to (3).
It follows from Lemma 6.5, together with Corollary 4.42 and Proposition 4.43, that, in order to prove Propositions 6.1 and 6.2, it suffices to prove them for
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representations of level
${\overline {\mathbb {F}}_{\ell }}$
-representations of level
![]() $0$
. (For Proposition 6.2(3.a), this also follows from the fact that
$0$
. (For Proposition 6.2(3.a), this also follows from the fact that
![]() $\varkappa _{F/F_0}\circ \mathrm {N}_{T_0/F_0}=\varkappa _{T/T_0}$
and
$\varkappa _{F/F_0}\circ \mathrm {N}_{T_0/F_0}=\varkappa _{T/T_0}$
and
![]() $\nu _{F_0}\circ \mathrm {N}_{T_0/F_0}=\nu _{T_0}$
.)
$\nu _{F_0}\circ \mathrm {N}_{T_0/F_0}=\nu _{T_0}$
.)
6.3
We continue with the situation of Paragraph 6.2, assuming further that
![]() $\pi $
has level
$\pi $
has level
![]() $0$
. Thus,
$0$
. Thus,
![]() $\pi $
is a
$\pi $
is a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() ${ G}$
of level
${ G}$
of level
![]() $0$
. We will also assume that
$0$
. We will also assume that
![]() $\pi $
is nonsupercuspidal, that is,
$\pi $
is nonsupercuspidal, that is,
![]() $r=r(\pi )>1$
. Let
$r=r(\pi )>1$
. Let
![]() $(\mathbf {J},\boldsymbol {\lambda })$
be a generic
$(\mathbf {J},\boldsymbol {\lambda })$
be a generic
![]() $\sigma $
-self-dual type in
$\sigma $
-self-dual type in
![]() $\pi $
. Associated with it in Paragraph 4.7, there are
$\pi $
. Associated with it in Paragraph 4.7, there are
-
○ a
 $\sigma $
-self-dual tamely ramified character
$\sigma $
-self-dual tamely ramified character
 $\omega $
of
$\omega $
of
 ${ F}^\times $
, which is the central character
${ F}^\times $
, which is the central character
 $c_\pi $
of
$c_\pi $
of
 $\pi $
,
$\pi $
, -
○ and a
 $\sigma $
-self-dual cuspidal representation
$\sigma $
-self-dual cuspidal representation
 $\mathrm {V}$
of
$\mathrm {V}$
of
 $\operatorname {GL}_n(\boldsymbol {k})$
of the form
$\operatorname {GL}_n(\boldsymbol {k})$
of the form
 $\operatorname {st}_r(\varrho )$
for some supercuspidal representation
$\operatorname {st}_r(\varrho )$
for some supercuspidal representation
 $\varrho $
of
$\varrho $
of
 $\operatorname {GL}_{n/r}(\boldsymbol {k})$
, uniquely determined up to isomorphism (thus
$\operatorname {GL}_{n/r}(\boldsymbol {k})$
, uniquely determined up to isomorphism (thus
 $\mathrm {V}$
is nonsupercuspidal).
$\mathrm {V}$
is nonsupercuspidal).
Recall that the restriction of
![]() $\boldsymbol {\lambda }$
to
$\boldsymbol {\lambda }$
to
![]() $\mathbf {J}^0$
is the inflation of
$\mathbf {J}^0$
is the inflation of
![]() $\mathrm {V}$
, and that its restriction to
$\mathrm {V}$
, and that its restriction to
![]() ${ F}^\times $
is a multiple of
${ F}^\times $
is a multiple of
![]() $\omega $
. Since
$\omega $
. Since
![]() $\mathrm {V}$
is
$\mathrm {V}$
is
![]() $\sigma $
-self-dual, Proposition 3.9 implies that
$\sigma $
-self-dual, Proposition 3.9 implies that
![]() $\varrho $
is
$\varrho $
is
![]() $\sigma $
-self-dual.
$\sigma $
-self-dual.
The action of
![]() $\sigma $
on
$\sigma $
on
![]() $\operatorname {GL}_n(\boldsymbol {k})$
is described in Proposition 4.5: This is the action of the nontrivial automorphism of
$\operatorname {GL}_n(\boldsymbol {k})$
is described in Proposition 4.5: This is the action of the nontrivial automorphism of
![]() $\boldsymbol {k}/\boldsymbol {k}_0$
if
$\boldsymbol {k}/\boldsymbol {k}_0$
if
![]() $F/F_0$
is unramified, and the adjoint action of the element (4.5) with
$F/F_0$
is unramified, and the adjoint action of the element (4.5) with
![]() $i=\lfloor m/2 \rfloor $
otherwise.
$i=\lfloor m/2 \rfloor $
otherwise.
Let us fix a uniformizer
![]() $\varpi $
of F such that
$\varpi $
of F such that
![]() $\varpi \in { F}_0$
if
$\varpi \in { F}_0$
if
![]() $F/F_0$
is unramified, and
$F/F_0$
is unramified, and
![]() $\varpi ^2\in { F}_0$
if
$\varpi ^2\in { F}_0$
if
![]() $F/F_0$
is ramified. (One thus has
$F/F_0$
is ramified. (One thus has
![]() $\sigma (\varpi )=-\varpi $
in the ramified case.)
$\sigma (\varpi )=-\varpi $
in the ramified case.)
Lemma 6.6. The representation
![]() $\pi $
has a
$\pi $
has a
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished lift to
$\operatorname {GL}_n({ F}_0)$
-distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
if and only if
${\overline {\mathbb {Q}}_\ell }$
if and only if
![]() $\mathrm {V}$
has a
$\mathrm {V}$
has a
![]() $\operatorname {GL}_n(\boldsymbol {k})^\sigma $
-distinguished lift
$\operatorname {GL}_n(\boldsymbol {k})^\sigma $
-distinguished lift
![]() $\widetilde {\mathrm {V}}$
to
$\widetilde {\mathrm {V}}$
to
![]() ${\overline {\mathbb {Q}}_\ell }$
such that
${\overline {\mathbb {Q}}_\ell }$
such that
-
1. if
 $F/F_0$
is unramified, then
$F/F_0$
is unramified, then
 $\omega (\varpi )=1$
,
$\omega (\varpi )=1$
, -
2. if
 $F/F_0$
is ramified, then n is even and the element (4.23) acts on the space of
$F/F_0$
is ramified, then n is even and the element (4.23) acts on the space of
 $\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-in- variant linear forms on
$\operatorname {GL}_{n/2}(\boldsymbol {k})\times \operatorname {GL}_{n/2}(\boldsymbol {k})$
-in- variant linear forms on
 $\widetilde {\mathrm {V}}$
by a sign whose reduction mod
$\widetilde {\mathrm {V}}$
by a sign whose reduction mod
 $\ell $
is equal to
$\ell $
is equal to
 $\omega (\varpi )$
.
$\omega (\varpi )$
.
Proof. By Lemma 6.5, the representation
![]() $\pi $
has a
$\pi $
has a
![]() $\operatorname {GL}_n({ F}_0)$
-distinguished lift if and only if the type
$\operatorname {GL}_n({ F}_0)$
-distinguished lift if and only if the type
![]() $\boldsymbol {\lambda }$
has a
$\boldsymbol {\lambda }$
has a
![]() $\mathbf {J}\cap \operatorname {GL}_n(F_0)$
-distinguished lift to
$\mathbf {J}\cap \operatorname {GL}_n(F_0)$
-distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
. Suppose
${\overline {\mathbb {Q}}_\ell }$
. Suppose
![]() $\boldsymbol {\lambda }$
has a distinguished lift
$\boldsymbol {\lambda }$
has a distinguished lift
![]() $\widetilde {\boldsymbol {\lambda }}$
. Then the pair
$\widetilde {\boldsymbol {\lambda }}$
. Then the pair
![]() $(\mathbf {J},\widetilde {\boldsymbol {\lambda }})$
is the generic type of a distinguished cuspidal
$(\mathbf {J},\widetilde {\boldsymbol {\lambda }})$
is the generic type of a distinguished cuspidal
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation
${\overline {\mathbb {Q}}_\ell }$
-representation
![]() $\widetilde {\pi }$
, compactly induced from
$\widetilde {\pi }$
, compactly induced from
![]() $\widetilde {\boldsymbol {\lambda }}$
. Associated with it, there are
$\widetilde {\boldsymbol {\lambda }}$
. Associated with it, there are
-
○ a cuspidal
 ${\overline {\mathbb {Q}}_\ell }$
-representation
${\overline {\mathbb {Q}}_\ell }$
-representation
 $\widetilde {\mathrm {V}}$
of
$\widetilde {\mathrm {V}}$
of
 $\operatorname {GL}_n(\boldsymbol {k})$
lifting
$\operatorname {GL}_n(\boldsymbol {k})$
lifting
 $\mathrm {V}$
,
$\mathrm {V}$
, -
○ a tamely ramified
 ${\overline {\mathbb {Q}}_\ell }$
-character
${\overline {\mathbb {Q}}_\ell }$
-character
 $\widetilde {\omega }$
of
$\widetilde {\omega }$
of
 ${ F}^\times $
lifting
${ F}^\times $
lifting
 $\omega $
.
$\omega $
.
By Theorem 4.45, the character
![]() $\widetilde {\omega }$
is trivial on
$\widetilde {\omega }$
is trivial on
![]() $F_0^\times $
and
$F_0^\times $
and
![]() $\widetilde {\mathrm {V}}$
is distinguished by
$\widetilde {\mathrm {V}}$
is distinguished by
![]() $\operatorname {GL}_n(\boldsymbol {k})^\sigma $
. If
$\operatorname {GL}_n(\boldsymbol {k})^\sigma $
. If
![]() $F/F_0$
is unramified, then
$F/F_0$
is unramified, then
![]() $\widetilde {\omega }(\varpi )=1$
, thus
$\widetilde {\omega }(\varpi )=1$
, thus
![]() $\omega (\varpi )=1$
. If
$\omega (\varpi )=1$
. If
![]() $F/F_0$
is ramified, then
$F/F_0$
is ramified, then
![]() $n=2u$
for some
$n=2u$
for some
![]() $u{\geqslant }1$
and
$u{\geqslant }1$
and
![]() $\widetilde {\mathrm {V}}$
is
$\widetilde {\mathrm {V}}$
is
![]() $\widetilde {\omega }(\varpi )$
-distinguished (in the sense of Definition 5.6), and the reduction mod
$\widetilde {\omega }(\varpi )$
-distinguished (in the sense of Definition 5.6), and the reduction mod
![]() $\ell $
of
$\ell $
of
![]() $\widetilde {\omega }(\varpi )$
is equal to
$\widetilde {\omega }(\varpi )$
is equal to
![]() $\omega (\varpi )$
.
$\omega (\varpi )$
.
Conversely, suppose that
![]() $\mathrm {V}$
has a
$\mathrm {V}$
has a
![]() $\operatorname {GL}_n(\boldsymbol {k})^\sigma $
-distinguished lift
$\operatorname {GL}_n(\boldsymbol {k})^\sigma $
-distinguished lift
![]() $\widetilde {\mathrm {V}}$
satisfying the conditions of the lemma. Let
$\widetilde {\mathrm {V}}$
satisfying the conditions of the lemma. Let
![]() $\widetilde {\omega }$
be a
$\widetilde {\omega }$
be a
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift of
${\overline {\mathbb {Q}}_\ell }$
-lift of
![]() $\omega $
coinciding on the units of
$\omega $
coinciding on the units of
![]() ${ F}$
with the inflation of the central character of
${ F}$
with the inflation of the central character of
![]() $\widetilde {\mathrm {V}}$
, and
$\widetilde {\mathrm {V}}$
, and
-
1. if
 $F/F_0$
is unramified, then
$F/F_0$
is unramified, then
 $\widetilde {\omega }(\varpi )=1$
,
$\widetilde {\omega }(\varpi )=1$
, -
2. if
 $F/F_0$
is ramified, then
$F/F_0$
is ramified, then
 $\widetilde {\omega }(\varpi )\in \{-1,1\}$
and the representation
$\widetilde {\omega }(\varpi )\in \{-1,1\}$
and the representation
 $\widetilde {\mathrm {V}}$
is
$\widetilde {\mathrm {V}}$
is
 $\widetilde {\omega }(\varpi )$
-distinguished.
$\widetilde {\omega }(\varpi )$
-distinguished.
Inflate
![]() $\widetilde {\mathrm {V}}$
to
$\widetilde {\mathrm {V}}$
to
![]() $\mathbf {J}^0$
, and extend it to a representation
$\mathbf {J}^0$
, and extend it to a representation
![]() $\widetilde {\boldsymbol {\lambda }}$
of
$\widetilde {\boldsymbol {\lambda }}$
of
![]() $\mathbf {J}$
by demanding that the restriction of
$\mathbf {J}$
by demanding that the restriction of
![]() $\widetilde {\boldsymbol {\lambda }}$
to
$\widetilde {\boldsymbol {\lambda }}$
to
![]() $F^\times $
is a multiple of
$F^\times $
is a multiple of
![]() $\widetilde {\omega }$
. The representation
$\widetilde {\omega }$
. The representation
![]() $\widetilde {\boldsymbol {\lambda }}$
is then a
$\widetilde {\boldsymbol {\lambda }}$
is then a
![]() $\mathbf {J}\cap \operatorname {GL}_n(F_0)$
-distinguished lift of
$\mathbf {J}\cap \operatorname {GL}_n(F_0)$
-distinguished lift of
![]() $\boldsymbol {\lambda }$
.
$\boldsymbol {\lambda }$
.
6.4
In this paragraph, we assume that
![]() ${ F}/{ F}_0$
is unramified. Remind that q denotes the cardinality of
${ F}/{ F}_0$
is unramified. Remind that q denotes the cardinality of
![]() $\boldsymbol {k}$
and
$\boldsymbol {k}$
and
![]() $q_0$
denotes that of
$q_0$
denotes that of
![]() $\boldsymbol {k}_0$
.
$\boldsymbol {k}_0$
.
Lemma 6.7. Let
![]() $\mathrm {W}$
be a
$\mathrm {W}$
be a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
. It has a
$\operatorname {GL}_n(\boldsymbol {k})$
. It has a
![]() $\operatorname {GL}_n(\boldsymbol {k}_0)$
-distinguished lift to
$\operatorname {GL}_n(\boldsymbol {k}_0)$
-distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
if and only if n is odd and
${\overline {\mathbb {Q}}_\ell }$
if and only if n is odd and
-
1. either
 $\mathrm {W}$
is supercuspidal,
$\mathrm {W}$
is supercuspidal, -
2. or
 $\mathrm {W}$
is nonsupercuspidal and the order of
$\mathrm {W}$
is nonsupercuspidal and the order of
 $q_0$
mod
$q_0$
mod
 $\ell $
is even (thus
$\ell $
is even (thus
 $\ell \neq 2$
).
$\ell \neq 2$
).
Proof. By [Reference Gow18] Theorem 3.6, an irreducible
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation of
${\overline {\mathbb {Q}}_\ell }$
-representation of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
is
$\operatorname {GL}_n(\boldsymbol {k})$
is
![]() $\operatorname {GL}_n(\boldsymbol {k}_0)$
-distinguished if and only if it is
$\operatorname {GL}_n(\boldsymbol {k}_0)$
-distinguished if and only if it is
![]() $\sigma $
-self-dual.
$\sigma $
-self-dual.
First, the condition on the parity of n is necessary: See [Reference Sécherre35] Lemma 2.3 for instance. Now, assume that n is odd. If
![]() $\ell \neq 2$
, the result is given by [Reference Kurinczuk and Matringe25] Proposition 4.6. If
$\ell \neq 2$
, the result is given by [Reference Kurinczuk and Matringe25] Proposition 4.6. If
![]() $\ell =2$
, then
$\ell =2$
, then
![]() $\mathrm {W}$
has the form
$\mathrm {W}$
has the form
![]() $\operatorname {st}_r(\varrho )$
, where
$\operatorname {st}_r(\varrho )$
, where
![]() $\varrho $
is a supercuspidal representation of
$\varrho $
is a supercuspidal representation of
![]() $\operatorname {GL}_{n/r}(\boldsymbol {k})$
and
$\operatorname {GL}_{n/r}(\boldsymbol {k})$
and
![]() $r=2^v$
for some
$r=2^v$
for some
![]() $v{\geqslant }0$
. Since n is odd,
$v{\geqslant }0$
. Since n is odd,
![]() $\mathrm {W}$
must be supercuspidal, and the result is given by [Reference Sécherre35] Remark 2.7.
$\mathrm {W}$
must be supercuspidal, and the result is given by [Reference Sécherre35] Remark 2.7.
Remark 6.8. Let e and
![]() $e_0$
be the orders of q and
$e_0$
be the orders of q and
![]() $q_0$
mod
$q_0$
mod
![]() $\ell $
, respectively. Note that
$\ell $
, respectively. Note that
![]() $r=e(\varrho )\ell ^{v}$
for some
$r=e(\varrho )\ell ^{v}$
for some
![]() $v{\geqslant }0$
, where
$v{\geqslant }0$
, where
![]() $e(\varrho )$
is the order of
$e(\varrho )$
is the order of
![]() $q^{f}$
mod
$q^{f}$
mod
![]() $\ell $
with
$\ell $
with
![]() $f=n/r$
. If n is odd, then f and r are odd, thus
$f=n/r$
. If n is odd, then f and r are odd, thus
![]() $e(\varrho )$
is odd. But
$e(\varrho )$
is odd. But
![]() $e(\varrho )=e/(e,f)$
. It follows that
$e(\varrho )=e/(e,f)$
. It follows that
![]() $e=e_0/(e_0,2)$
is odd. Thus,
$e=e_0/(e_0,2)$
is odd. Thus,
![]() $e_0$
is not divisible by
$e_0$
is not divisible by
![]() $4$
.
$4$
.
Example 6.9. Let
![]() $\mathrm {W}$
be the
$\mathrm {W}$
be the
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation
${\overline {\mathbb {F}}_{\ell }}$
-representation
![]() $\operatorname {st}_e(1)$
of
$\operatorname {st}_e(1)$
of
![]() $\operatorname {GL}_e(\boldsymbol {k})$
. We have
$\operatorname {GL}_e(\boldsymbol {k})$
. We have
![]() $e=e_0/(e_0,2)$
, which is odd if and only if
$e=e_0/(e_0,2)$
, which is odd if and only if
![]() $e_0$
is not divisible by
$e_0$
is not divisible by
![]() $4$
. Thus,
$4$
. Thus,
![]() $\mathrm {W}$
has a
$\mathrm {W}$
has a
![]() $\operatorname {GL}_e(\boldsymbol {k}_0)$
-distinguished lift to
$\operatorname {GL}_e(\boldsymbol {k}_0)$
-distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
if and only if
${\overline {\mathbb {Q}}_\ell }$
if and only if
![]() $e_0$
is divisible by
$e_0$
is divisible by
![]() $2$
but not by
$2$
but not by
![]() $4$
.
$4$
.
Suppose first that
![]() $\pi $
has a distinguished lift to
$\pi $
has a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
. On the one hand, the generic type of such a lift defines a
${\overline {\mathbb {Q}}_\ell }$
. On the one hand, the generic type of such a lift defines a
![]() $\sigma $
-self-dual cuspidal
$\sigma $
-self-dual cuspidal
![]() ${\overline {\mathbb {Q}}_\ell }$
-representation of
${\overline {\mathbb {Q}}_\ell }$
-representation of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
, and [Reference Sécherre35] Lemma 2.3 implies that n is odd, thus r is odd. On the other hand, Theorem 3.3 implies that
$\operatorname {GL}_n(\boldsymbol {k})$
, and [Reference Sécherre35] Lemma 2.3 implies that n is odd, thus r is odd. On the other hand, Theorem 3.3 implies that
![]() $\pi $
is distinguished. It thus follows from Theorem 5.1 that
$\pi $
is distinguished. It thus follows from Theorem 5.1 that
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
for some distinguished supercuspidal representation
$\operatorname {St}_r(\rho )$
for some distinguished supercuspidal representation
![]() $\rho $
of
$\rho $
of
![]() $\operatorname {GL}_{n/r}({ F})$
. Finally, Lemma 6.6 says that
$\operatorname {GL}_{n/r}({ F})$
. Finally, Lemma 6.6 says that
![]() $\mathrm {V}$
has a distinguished lift. It follows from Lemma 6.7 that the order
$\mathrm {V}$
has a distinguished lift. It follows from Lemma 6.7 that the order
![]() $e_0$
of the cardinality of
$e_0$
of the cardinality of
![]() $\boldsymbol {k}_0$
mod
$\boldsymbol {k}_0$
mod
![]() $\ell $
is even.
$\ell $
is even.
We thus proved that, when
![]() ${ F}/{ F}_0$
is unramified, if
${ F}/{ F}_0$
is unramified, if
![]() $\pi $
has a distinguished lift, then r is odd and Conditions (1), (2.a) of Proposition 6.1 are satisfied.
$\pi $
has a distinguished lift, then r is odd and Conditions (1), (2.a) of Proposition 6.1 are satisfied.
Conversely, suppose that the conditions (1), (2.a) of Proposition 6.1 are satisfied. Then
![]() $\mathrm {V}$
has a distinguished lift
$\mathrm {V}$
has a distinguished lift
![]() $\widetilde {\mathrm {V}}$
. By Lemma 6.6, the representation
$\widetilde {\mathrm {V}}$
. By Lemma 6.6, the representation
![]() $\pi $
has a
$\pi $
has a
![]() $\operatorname {GL}_n(F_0)$
-distinguished lift to
$\operatorname {GL}_n(F_0)$
-distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
if and only if
${\overline {\mathbb {Q}}_\ell }$
if and only if
![]() $\omega (\varpi )=1$
. By Paragraph 4.8, the central character
$\omega (\varpi )=1$
. By Paragraph 4.8, the central character
![]() $\omega _*$
of
$\omega _*$
of
![]() $\rho $
satisfies
$\rho $
satisfies
![]() $\omega _*^r=\omega $
. Since
$\omega _*^r=\omega $
. Since
![]() $\rho $
is distinguished, we have
$\rho $
is distinguished, we have
![]() $\omega _*(\varpi )=1$
, thus
$\omega _*(\varpi )=1$
, thus
![]() $\omega (\varpi )=\omega _*(\varpi )^r=1$
.
$\omega (\varpi )=\omega _*(\varpi )^r=1$
.
We proved Proposition 6.1 in the case when
![]() ${ F}/{ F}_0$
is unramified.
${ F}/{ F}_0$
is unramified.
6.5
In this paragraph, we assume that
![]() ${ F}/{ F}_0$
is ramified. Let q denote the cardinality of
${ F}/{ F}_0$
is ramified. Let q denote the cardinality of
![]() $\boldsymbol {k}$
, and let e denote the order of q mod
$\boldsymbol {k}$
, and let e denote the order of q mod
![]() $\ell $
.
$\ell $
.
Lemma 6.10. Let
![]() $\mathrm {W}$
be a self-dual cuspidal
$\mathrm {W}$
be a self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
, isomorphic to
$\operatorname {GL}_n(\boldsymbol {k})$
, isomorphic to
![]() $\operatorname {st}_r(\varrho )$
for some self-dual supercuspidal representation
$\operatorname {st}_r(\varrho )$
for some self-dual supercuspidal representation
![]() $\varrho$
of
$\varrho$
of
![]() $\operatorname {GL}_{n/r}(\boldsymbol {k})$
. Write
$\operatorname {GL}_{n/r}(\boldsymbol {k})$
. Write
![]() $u=\lfloor n/2\rfloor $
. Then
$u=\lfloor n/2\rfloor $
. Then
![]() $\mathrm {W}$
has a lift to
$\mathrm {W}$
has a lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
which is distinguished by
${\overline {\mathbb {Q}}_\ell }$
which is distinguished by
![]() $\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{n-u}(\boldsymbol {k})$
if and only if
$\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{n-u}(\boldsymbol {k})$
if and only if
-
1. either
 $\mathrm {W}$
is supercuspidal,
$\mathrm {W}$
is supercuspidal, -
2. or
 $\mathrm {W}$
is nonsupercuspidal, n is even and
$\mathrm {W}$
is nonsupercuspidal, n is even and-
(a) either
 $\ell \neq 2$
and r,
$\ell \neq 2$
and r,
 $n/e$
are odd,
$n/e$
are odd, -
(b) or
 $\ell \neq 2$
and
$\ell \neq 2$
and
 $r=n$
,
$r=n$
, -
(c) or
 $\ell =n=r=2$
and q is congruent to
$\ell =n=r=2$
and q is congruent to
 $-1$
mod
$-1$
mod
 $4$
, and
$4$
, and
 $\varrho $
is trivial.
$\varrho $
is trivial.
-
Proof. First note that n must be either even or equal to
![]() $1$
: See [Reference Sécherre35] Lemma 2.17 for instance. Also, the supercuspidal case is given by [Reference Sécherre35] Remark 2.21. Let us assume that
$1$
: See [Reference Sécherre35] Lemma 2.17 for instance. Also, the supercuspidal case is given by [Reference Sécherre35] Remark 2.21. Let us assume that
![]() $\mathrm {W}$
is nonsupercuspidal (thus n is even, and we will write
$\mathrm {W}$
is nonsupercuspidal (thus n is even, and we will write
![]() $n=2u$
). We use the notation of Paragraph 3.7.
$n=2u$
). We use the notation of Paragraph 3.7.
Set
![]() $f=n/r$
, and let
$f=n/r$
, and let
![]() $\alpha $
be a
$\alpha $
be a
![]() $\operatorname {Gal}(\boldsymbol {k}_{f}/\boldsymbol {k})$
-regular
$\operatorname {Gal}(\boldsymbol {k}_{f}/\boldsymbol {k})$
-regular
![]() ${\overline {\mathbb {F}}_{\ell }}$
-character of
${\overline {\mathbb {F}}_{\ell }}$
-character of
![]() $\boldsymbol {k}_{f}^\times $
of order
$\boldsymbol {k}_{f}^\times $
of order
![]() $\mathrm {A}$
which is a parameter of
$\mathrm {A}$
which is a parameter of
![]() $\varrho $
in the sense of Definition 3.12. Let
$\varrho $
in the sense of Definition 3.12. Let
![]() $\widetilde {{\upsilon }}$
be the canonical
$\widetilde {{\upsilon }}$
be the canonical
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift of
${\overline {\mathbb {Q}}_\ell }$
-lift of
that is, its unique lift of order
![]() $\mathrm {A}$
. Let
$\mathrm {A}$
. Let
![]() $\widetilde {\mathrm {W}}$
be a cuspidal lift of
$\widetilde {\mathrm {W}}$
be a cuspidal lift of
![]() $\mathrm {W}$
. It is parametrized by a
$\mathrm {W}$
. It is parametrized by a
![]() $\operatorname {Gal}(\boldsymbol {k}_n/\boldsymbol {k})$
-regular character of
$\operatorname {Gal}(\boldsymbol {k}_n/\boldsymbol {k})$
-regular character of
![]() $\boldsymbol {k}_n^\times $
lifting
$\boldsymbol {k}_n^\times $
lifting
![]() ${\upsilon }$
, that is, of the form
${\upsilon }$
, that is, of the form
![]() $\widetilde {{\upsilon }}\phi $
, where
$\widetilde {{\upsilon }}\phi $
, where
![]() $\phi $
is a
$\phi $
is a
![]() ${\overline {\mathbb {Q}}_\ell }$
-character of
${\overline {\mathbb {Q}}_\ell }$
-character of
![]() $\boldsymbol {k}_n^\times $
of order
$\boldsymbol {k}_n^\times $
of order
![]() $\ell ^s$
for some
$\ell ^s$
for some
![]() $s{\geqslant }0$
. Since
$s{\geqslant }0$
. Since
![]() $\mathrm {W}$
is not supercuspidal, one has
$\mathrm {W}$
is not supercuspidal, one has
![]() $s{\geqslant }1$
. The character
$s{\geqslant }1$
. The character
![]() $\widetilde {{\upsilon }}\phi $
has order
$\widetilde {{\upsilon }}\phi $
has order
![]() $\mathrm {A}\ell ^s$
.
$\mathrm {A}\ell ^s$
.
By Proposition 3.13, the representation
![]() $\widetilde {\mathrm {W}}$
is distinguished by
$\widetilde {\mathrm {W}}$
is distinguished by
![]() $\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
if and only if it is self-dual, which is also equivalent (see, for instance, [Reference Sécherre35] (2.7)) to
$\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
if and only if it is self-dual, which is also equivalent (see, for instance, [Reference Sécherre35] (2.7)) to
![]() $\mathrm {A}\ell ^s$
dividing
$\mathrm {A}\ell ^s$
dividing
![]() $q^{u}+1$
. Similarly, the fact that
$q^{u}+1$
. Similarly, the fact that
![]() $\varrho $
is self-dual is equivalent to
$\varrho $
is self-dual is equivalent to
-
○ either
 $f=1$
and
$f=1$
and
 $\varrho $
is a quadratic character (thus,
$\varrho $
is a quadratic character (thus,
 $\mathrm {A}$
is equal to
$\mathrm {A}$
is equal to
 $1$
or
$1$
or
 $2$
),
$2$
), -
○ or f is even and
 $\mathrm {A}$
divides
$\mathrm {A}$
divides
 $q^{f/2}+1$
(thus,
$q^{f/2}+1$
(thus,
 $\mathrm {A}>2$
since q has order
$\mathrm {A}>2$
since q has order
 $f{\geqslant }2$
mod
$f{\geqslant }2$
mod
 $\mathrm {A}$
).
$\mathrm {A}$
).
Suppose that
![]() $\ell \neq 2$
and f is even. If
$\ell \neq 2$
and f is even. If
![]() $\widetilde {\mathrm {W}}$
is distinguished, then
$\widetilde {\mathrm {W}}$
is distinguished, then
![]() $\mathrm {A}$
divides
$\mathrm {A}$
divides
![]() $q^{f/2}+1$
and
$q^{f/2}+1$
and
![]() $q^{u}+1$
. Since
$q^{u}+1$
. Since
![]() $u=rf/2$
, we have
$u=rf/2$
, we have
thus
![]() $\mathrm {A}$
divides
$\mathrm {A}$
divides
![]() $1+(-1)^r$
. Since
$1+(-1)^r$
. Since
![]() $\mathrm {A}>2$
, it follows that r is odd. Also,
$\mathrm {A}>2$
, it follows that r is odd. Also,
![]() $\ell $
divides
$\ell $
divides
![]() $q^u+1$
, that is, the order of
$q^u+1$
, that is, the order of
![]() $q^u$
mod
$q^u$
mod
![]() $\ell $
is
$\ell $
is
![]() $e/(e,u)=2$
, which implies that
$e/(e,u)=2$
, which implies that
![]() $n/e$
is odd. Conversely, suppose that r and
$n/e$
is odd. Conversely, suppose that r and
![]() $n/e$
are odd. The fact that
$n/e$
are odd. The fact that
![]() $\mathrm {A}$
divides
$\mathrm {A}$
divides
![]() $q^{f/2}+1$
and r is odd implies that
$q^{f/2}+1$
and r is odd implies that
![]() $\mathrm {A}$
divides
$\mathrm {A}$
divides
![]() $q^u+1$
. Now,
$q^u+1$
. Now,
![]() $\ell ^s$
divides
$\ell ^s$
divides
![]() $q^n-1=(q^u+1)(q^u-1)$
. If
$q^n-1=(q^u+1)(q^u-1)$
. If
![]() $\ell $
divides
$\ell $
divides
![]() $q^u-1$
, then e divides
$q^u-1$
, then e divides
![]() $u=n/2$
, thus
$u=n/2$
, thus
![]() $n/e$
is even: contradiction. Thus,
$n/e$
is even: contradiction. Thus,
![]() $\ell ^s$
divides
$\ell ^s$
divides
![]() $q^u+1$
, thus
$q^u+1$
, thus
![]() $\widetilde {\mathrm {W}}$
is distinguished.
$\widetilde {\mathrm {W}}$
is distinguished.
Suppose that
![]() $\ell \neq 2$
and
$\ell \neq 2$
and
![]() $f=1$
. Then
$f=1$
. Then
![]() $\varrho $
is a character of
$\varrho $
is a character of
![]() $\boldsymbol {k}^\times $
, thus
$\boldsymbol {k}^\times $
, thus
![]() $r=e\ell ^{v}$
for some
$r=e\ell ^{v}$
for some
![]() $v{\geqslant }0$
. This gives
$v{\geqslant }0$
. This gives
![]() $n/e=\ell ^{v}$
, which is odd. The same argument as above implies that
$n/e=\ell ^{v}$
, which is odd. The same argument as above implies that
![]() $q^u+1$
is a multiple of
$q^u+1$
is a multiple of
![]() $\ell ^s$
. It is also a multiple of
$\ell ^s$
. It is also a multiple of
![]() $\mathrm {A}\in \{1,2\}$
since it is even. Thus,
$\mathrm {A}\in \{1,2\}$
since it is even. Thus,
![]() $\widetilde {\mathrm {W}}$
is distinguished.
$\widetilde {\mathrm {W}}$
is distinguished.
Now, suppose that
![]() $\ell =2$
. If
$\ell =2$
. If
![]() $\widetilde {\mathrm {W}}$
is distinguished and f is even, then, as in the case where
$\widetilde {\mathrm {W}}$
is distinguished and f is even, then, as in the case where
![]() $\ell \neq 2$
, the integer
$\ell \neq 2$
, the integer
![]() $\mathrm {A}>2$
divides
$\mathrm {A}>2$
divides
![]() $q^{f/2}+1$
and
$q^{f/2}+1$
and
![]() $q^{rf/2}+1$
, thus r is odd. But the fact that
$q^{rf/2}+1$
, thus r is odd. But the fact that
![]() $\mathrm {W}$
is cuspidal implies that r is a power of
$\mathrm {W}$
is cuspidal implies that r is a power of
![]() $2$
. It follows that
$2$
. It follows that
![]() $r=1$
: contradiction. Thus,
$r=1$
: contradiction. Thus,
![]() $f=1$
, that is
$f=1$
, that is
![]() $\mathrm {W}$
is the representation
$\mathrm {W}$
is the representation
![]() $\operatorname {st}_n(1)$
with
$\operatorname {st}_n(1)$
with
![]() $n=2^t$
for some
$n=2^t$
for some
![]() $t{\geqslant }1$
. Moreover, q has order m mod
$t{\geqslant }1$
. Moreover, q has order m mod
![]() $2^s$
, that is,
$2^s$
, that is,
![]() $2^s$
divides
$2^s$
divides
![]() $q^{n}-1$
but not
$q^{n}-1$
but not
![]() $q^{u}-1$
. Set
$q^{u}-1$
. Set
We have
![]() $b<s{\leqslant }a+b$
and
$b<s{\leqslant }a+b$
and
![]() $\min (a,b)=1$
. The fact that
$\min (a,b)=1$
. The fact that
![]() $\widetilde {\mathrm {W}}$
is distinguished implies
$\widetilde {\mathrm {W}}$
is distinguished implies
![]() $s{\leqslant }a$
, which gives
$s{\leqslant }a$
, which gives
![]() $b=1<a$
, that is
$b=1<a$
, that is
![]() $4$
divides
$4$
divides
![]() $q^u+1$
. Since u is a power of
$q^u+1$
. Since u is a power of
![]() $2$
, we deduce that
$2$
, we deduce that
![]() $4$
divides
$4$
divides
![]() $q+1$
and
$q+1$
and
![]() $u=1$
.
$u=1$
.
Conversely, suppose that
![]() $\ell =n=r=2$
and
$\ell =n=r=2$
and
![]() $4$
divides
$4$
divides
![]() $q+1$
(hence
$q+1$
(hence
![]() $b=1<a$
). Then any
$b=1<a$
). Then any
![]() $\overline {\mathbb {Q}}_{2}$
-character of
$\overline {\mathbb {Q}}_{2}$
-character of
![]() $\boldsymbol {k}_{2}^\times $
of order
$\boldsymbol {k}_{2}^\times $
of order
![]() $2^a$
parametrizes a distinguished cuspidal
$2^a$
parametrizes a distinguished cuspidal
![]() $\overline {\mathbb {Q}}_{2}$
-representation of
$\overline {\mathbb {Q}}_{2}$
-representation of
![]() $\operatorname {GL}_{2}(\boldsymbol {k})$
lifting
$\operatorname {GL}_{2}(\boldsymbol {k})$
lifting
![]() $\mathrm {W}=\operatorname {st}_2(1)$
.
$\mathrm {W}=\operatorname {st}_2(1)$
.
Example 6.11. The fact that
![]() $\operatorname {GL}_f(\boldsymbol {k})$
has a self-dual supercuspidal
$\operatorname {GL}_f(\boldsymbol {k})$
has a self-dual supercuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation is equivalent to the fact that there is an
${\overline {\mathbb {F}}_{\ell }}$
-representation is equivalent to the fact that there is an
![]() $\boldsymbol {k}$
-regular
$\boldsymbol {k}$
-regular
![]() ${\overline {\mathbb {F}}_{\ell }}$
-character of
${\overline {\mathbb {F}}_{\ell }}$
-character of
![]() $\boldsymbol {k}_{f}^\times $
which is trivial on
$\boldsymbol {k}_{f}^\times $
which is trivial on
![]() $\boldsymbol {k}_{f/2}^\times $
, that is, there exists an integer
$\boldsymbol {k}_{f/2}^\times $
, that is, there exists an integer
![]() $\mathrm {A}$
with the following properties:
$\mathrm {A}$
with the following properties:
-
1.
 $\mathrm {A}$
is prime to
$\mathrm {A}$
is prime to
 $\ell $
and the order of q mod
$\ell $
and the order of q mod
 $\mathrm {A}$
is equal to f,
$\mathrm {A}$
is equal to f, -
2.
 $\mathrm {A}$
divides
$\mathrm {A}$
divides
 $q^{f/2}+1$
.
$q^{f/2}+1$
.
Now, suppose that
![]() $\ell>2$
and
$\ell>2$
and
![]() $f=2$
. Thus,
$f=2$
. Thus,
![]() $\operatorname {GL}_2(\boldsymbol {k})$
has a self-dual supercuspidal
$\operatorname {GL}_2(\boldsymbol {k})$
has a self-dual supercuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation if and only if there exists an integer
${\overline {\mathbb {F}}_{\ell }}$
-representation if and only if there exists an integer
![]() $\mathrm {A}$
prime to
$\mathrm {A}$
prime to
![]() $\ell $
dividing
$\ell $
dividing
![]() $q+1$
but not
$q+1$
but not
![]() $q-1$
, that is, if and only if
$q-1$
, that is, if and only if
![]() $q+1$
has a prime divisor different from
$q+1$
has a prime divisor different from
![]() $2$
and
$2$
and
![]() $\ell $
. Assume this is the case, and let
$\ell $
. Assume this is the case, and let
![]() $\varrho $
be a self-dual supercuspidal
$\varrho $
be a self-dual supercuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_2(\boldsymbol {k})$
. Let
$\operatorname {GL}_2(\boldsymbol {k})$
. Let
![]() $\mathrm {W}$
be the self-dual cuspidal
$\mathrm {W}$
be the self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation
${\overline {\mathbb {F}}_{\ell }}$
-representation
![]() $\operatorname {st}_r(\varrho )$
of
$\operatorname {st}_r(\varrho )$
of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
with
$\operatorname {GL}_n(\boldsymbol {k})$
with
![]() $r=e/(e,2)$
and
$r=e/(e,2)$
and
![]() $m=2r$
. Then r is odd if and only if e is not divisible by
$m=2r$
. Then r is odd if and only if e is not divisible by
![]() $4$
, and
$4$
, and
![]() $n/e=2/(e,2)$
is odd if and only if e is even. If we take
$n/e=2/(e,2)$
is odd if and only if e is even. If we take
![]() $q=9$
and
$q=9$
and
![]() $\ell =7$
, we get
$\ell =7$
, we get
![]() $r=3$
and
$r=3$
and
![]() $n/e=2$
. If we take
$n/e=2$
. If we take
![]() $q=5$
, we get
$q=5$
, we get
![]() $q-1=4$
and
$q-1=4$
and
![]() $q^6-1=1953\times 8$
. Thus, if
$q^6-1=1953\times 8$
. Thus, if
![]() $\ell $
is a prime divisor of
$\ell $
is a prime divisor of
![]() $1953$
, we get
$1953$
, we get
![]() $r=3$
and
$r=3$
and
![]() $n/e=6$
.
$n/e=6$
.
In addition, we have the following result. We assume that
![]() $n=2u$
for some
$n=2u$
for some
![]() $u{\geqslant }1$
.
$u{\geqslant }1$
.
Lemma 6.12. Let
![]() $\mathrm {W}$
be a self-dual cuspidal
$\mathrm {W}$
be a self-dual cuspidal
![]() ${\overline {\mathbb {F}}_{\ell }}$
-representation of
${\overline {\mathbb {F}}_{\ell }}$
-representation of
![]() $\operatorname {GL}_n(\boldsymbol {k})$
of the form
$\operatorname {GL}_n(\boldsymbol {k})$
of the form
![]() $\operatorname {st}_n(\varrho )$
for some quadratic character
$\operatorname {st}_n(\varrho )$
for some quadratic character
![]() $\varrho $
of
$\varrho $
of
![]() $\boldsymbol {k}^\times $
. Assume
$\boldsymbol {k}^\times $
. Assume
![]() $\mathrm {W}$
is distinguished by
$\mathrm {W}$
is distinguished by
![]() $\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
. Then the element (4.23) acts on the space of
$\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
. Then the element (4.23) acts on the space of
![]() $\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
-invariant linear forms on
$\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
-invariant linear forms on
![]() $\mathrm {W}$
by
$\mathrm {W}$
by
 $$ \begin{align*} \left\{ \begin{array}{ll} -1 & \text{if }\varrho\text{ is trivial}, \\ (-1)^{u(q-1)/2} & \text{if }\varrho\text{ is nontrivial}. \end{array}\right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{ll} -1 & \text{if }\varrho\text{ is trivial}, \\ (-1)^{u(q-1)/2} & \text{if }\varrho\text{ is nontrivial}. \end{array}\right. \end{align*} $$
Proof. Let c be the sign such that
![]() $\mathrm {W}$
is c-distinguished. If
$\mathrm {W}$
is c-distinguished. If
![]() $\ell =2$
, the result is immediate since the only sign is
$\ell =2$
, the result is immediate since the only sign is
![]() $1$
. Assume that
$1$
. Assume that
![]() $\ell \neq 2$
. By Lemma 6.10, the representation
$\ell \neq 2$
. By Lemma 6.10, the representation
![]() $\mathrm {W}$
has a distinguished cuspidal
$\mathrm {W}$
has a distinguished cuspidal
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift. Let
${\overline {\mathbb {Q}}_\ell }$
-lift. Let
![]() $\widetilde {\mathrm {W}}$
be such a
$\widetilde {\mathrm {W}}$
be such a
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift and
${\overline {\mathbb {Q}}_\ell }$
-lift and
![]() $\xi $
be a parameter for
$\xi $
be a parameter for
![]() $\widetilde {\mathrm {W}}$
. Let
$\widetilde {\mathrm {W}}$
. Let
![]() $\alpha $
be an element of
$\alpha $
be an element of
![]() $\boldsymbol {k}_{n}$
such that
$\boldsymbol {k}_{n}$
such that
![]() $\alpha \notin \boldsymbol {k}_{u}$
and
$\alpha \notin \boldsymbol {k}_{u}$
and
![]() $\alpha ^2\in \boldsymbol {k}_{u}$
. By Proposition 3.13, the representation
$\alpha ^2\in \boldsymbol {k}_{u}$
. By Proposition 3.13, the representation
![]() $\widetilde {\mathrm {W}}$
is
$\widetilde {\mathrm {W}}$
is
![]() $-\xi (\alpha )$
-distinguished by
$-\xi (\alpha )$
-distinguished by
![]() $\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
. Since
$\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
. Since
![]() $\widetilde {\mathrm {W}}$
lifts
$\widetilde {\mathrm {W}}$
lifts
![]() $\mathrm {W}$
, we have
$\mathrm {W}$
, we have
-
○ the reduction mod
 $\ell $
of the parameter
$\ell $
of the parameter
 $\xi $
is equal to
$\xi $
is equal to
 $(\varrho \circ \mathrm {N}_{\boldsymbol {k}_n/\boldsymbol {k}})\phi $
where
$(\varrho \circ \mathrm {N}_{\boldsymbol {k}_n/\boldsymbol {k}})\phi $
where
 $\phi $
is a character whose order is a power of
$\phi $
is a character whose order is a power of
 $\ell $
(see Proposition 3.11),
$\ell $
(see Proposition 3.11), -
○ the reduction mod
 $\ell $
of
$\ell $
of
 $-\xi (\alpha )$
is equal to c (see Remark 3.14).
$-\xi (\alpha )$
is equal to c (see Remark 3.14).
On the one hand, the character
![]() $\xi $
is trivial on
$\xi $
is trivial on
![]() $\boldsymbol {k}_{u}^\times $
since
$\boldsymbol {k}_{u}^\times $
since
![]() $\widetilde {\mathrm {W}}$
is self-dual (see Proposition 3.13). On the other hand,
$\widetilde {\mathrm {W}}$
is self-dual (see Proposition 3.13). On the other hand,
![]() $\varrho \circ \mathrm {N}_{\boldsymbol {k}_n/\boldsymbol {k}}$
is trivial on
$\varrho \circ \mathrm {N}_{\boldsymbol {k}_n/\boldsymbol {k}}$
is trivial on
![]() $\boldsymbol {k}_{u}^\times $
since
$\boldsymbol {k}_{u}^\times $
since
![]() $\varrho $
is quadratic and the index of
$\varrho $
is quadratic and the index of
![]() $\boldsymbol {k}_{u}^\times $
in
$\boldsymbol {k}_{u}^\times $
in
![]() $\boldsymbol {k}_{n}^\times $
is even. We deduce that
$\boldsymbol {k}_{n}^\times $
is even. We deduce that
![]() $\phi $
is trivial on
$\phi $
is trivial on
![]() $\boldsymbol {k}_{u}^\times $
, thus
$\boldsymbol {k}_{u}^\times $
, thus
![]() $\phi (\alpha )$
is a sign. Since it has order a power of
$\phi (\alpha )$
is a sign. Since it has order a power of
![]() $\ell \neq 2$
, it is trivial. It follows that
$\ell \neq 2$
, it is trivial. It follows that
If
![]() $\varrho $
is trivial, this gives
$\varrho $
is trivial, this gives
![]() $c=-1$
, as expected. Assume now that
$c=-1$
, as expected. Assume now that
![]() $\varrho $
is nontrivial. It thus coincides with
$\varrho $
is nontrivial. It thus coincides with
![]() $\varkappa $
on
$\varkappa $
on
![]() $\boldsymbol {k}^\times $
. Since
$\boldsymbol {k}^\times $
. Since
![]() $\alpha ^2$
is not a square in
$\alpha ^2$
is not a square in
![]() $\boldsymbol {k}_{u}^\times $
, its
$\boldsymbol {k}_{u}^\times $
, its
![]() $\boldsymbol {k}_u/\boldsymbol {k}$
-norm is not a square in
$\boldsymbol {k}_u/\boldsymbol {k}$
-norm is not a square in
![]() $\boldsymbol {k}^\times $
. Thus,
$\boldsymbol {k}^\times $
. Thus,
and one verifies that this is equal to
![]() $\varkappa (-1)^{u}=(-1)^{u(q-1)/2}$
as expected.
$\varkappa (-1)^{u}=(-1)^{u(q-1)/2}$
as expected.
6.6
Let us prove Proposition 6.1 when
![]() ${ F}/{ F}_0$
is ramified. Assume that r is odd, and suppose that
${ F}/{ F}_0$
is ramified. Assume that r is odd, and suppose that
![]() $\pi $
has a distinguished lift to
$\pi $
has a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
. By Theorem 3.3, it is distinguished. Thus, Theorem 5.1 implies that
${\overline {\mathbb {Q}}_\ell }$
. By Theorem 3.3, it is distinguished. Thus, Theorem 5.1 implies that
![]() $n/r$
is even and
$n/r$
is even and
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
for some distinguished supercuspidal representation
$\operatorname {St}_r(\rho )$
for some distinguished supercuspidal representation
![]() $\rho $
of
$\rho $
of
![]() $\operatorname {GL}_{n/r}({ F})$
. Lemma 6.6 says that
$\operatorname {GL}_{n/r}({ F})$
. Lemma 6.6 says that
![]() $\mathrm {V}$
has a distinguished lift. It follows from Lemma 6.10 that
$\mathrm {V}$
has a distinguished lift. It follows from Lemma 6.10 that
![]() $n/e$
is odd.
$n/e$
is odd.
Conversely, assume that r is odd,
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_r(\rho )$
for some distinguished supercuspidal representation
$\operatorname {St}_r(\rho )$
for some distinguished supercuspidal representation
![]() $\rho $
of
$\rho $
of
![]() $\operatorname {GL}_{n/r}({ F})$
of level
$\operatorname {GL}_{n/r}({ F})$
of level
![]() $0$
, n is even and
$0$
, n is even and
![]() $n/e$
is odd. It follows from Lemma 6.10 that
$n/e$
is odd. It follows from Lemma 6.10 that
![]() $\mathrm {V}$
has a distinguished lift
$\mathrm {V}$
has a distinguished lift
![]() $\widetilde {\mathrm {V}}$
. Let
$\widetilde {\mathrm {V}}$
. Let
![]() $\varepsilon \in \{-1,1\}$
be the unique sign such that
$\varepsilon \in \{-1,1\}$
be the unique sign such that
![]() $\widetilde {\mathrm {V}}$
is
$\widetilde {\mathrm {V}}$
is
![]() $\varepsilon $
-distinguished by
$\varepsilon $
-distinguished by
![]() $\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
in the sense of Definition 5.6, with
$\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
in the sense of Definition 5.6, with
![]() $n=2u$
. By Lemma 6.6, the representation
$n=2u$
. By Lemma 6.6, the representation
![]() $\pi $
has a distinguished lift if and only if
$\pi $
has a distinguished lift if and only if
![]() $\omega (\varpi )$
is equal to the image of
$\omega (\varpi )$
is equal to the image of
![]() $\varepsilon $
in
$\varepsilon $
in
![]() $\overline {\mathbb {F}}{}_\ell ^\times $
, denoted c. We are going to prove that this is the case. Let
$\overline {\mathbb {F}}{}_\ell ^\times $
, denoted c. We are going to prove that this is the case. Let
![]() $\omega _*$
be the central character of
$\omega _*$
be the central character of
![]() $\rho $
. By Theorem 4.45, we have
$\rho $
. By Theorem 4.45, we have
-
○ the representation
 $\varrho $
is
$\varrho $
is
 $\omega _*(\varpi )$
-distinguished by
$\omega _*(\varpi )$
-distinguished by
 $\operatorname {GL}_{k/2}(\boldsymbol {k})\times \operatorname {GL}_{k/2}(\boldsymbol {k})$
.
$\operatorname {GL}_{k/2}(\boldsymbol {k})\times \operatorname {GL}_{k/2}(\boldsymbol {k})$
.
(Note that k is even since n is even and r is odd.) By Proposition 4.28, we have
-
○ the sign
 $\omega (\varpi )$
is equal to
$\omega (\varpi )$
is equal to
 $\omega _*(\varpi )^r=\omega _*(\varpi )$
.
$\omega _*(\varpi )^r=\omega _*(\varpi )$
.
Let
![]() $\alpha $
be the unique sign such that
$\alpha $
be the unique sign such that
![]() $\mathrm {V}$
is
$\mathrm {V}$
is
![]() $\alpha $
-distinguished by
$\alpha $
-distinguished by
![]() $\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
. By Remark 3.14, we have
$\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
. By Remark 3.14, we have
![]() $\alpha =c$
. On the other hand, we have
$\alpha =c$
. On the other hand, we have
![]() $\alpha =\omega _*(\varpi )$
by Proposition 5.7. Putting these facts together, we get
$\alpha =\omega _*(\varpi )$
by Proposition 5.7. Putting these facts together, we get
![]() $\omega (\varpi )=\omega _*(\varpi )=\alpha =c$
as expected. This proves Proposition 6.1 if
$\omega (\varpi )=\omega _*(\varpi )=\alpha =c$
as expected. This proves Proposition 6.1 if
![]() ${ F}/{ F}_0$
is ramified. Together with Paragraph 6.4, this finishes the proof of Proposition 6.1.
${ F}/{ F}_0$
is ramified. Together with Paragraph 6.4, this finishes the proof of Proposition 6.1.
6.7
In this paragraph and the next one, we prove Proposition 6.2. Assume that r is even, and let q be the cardinality of
![]() $\boldsymbol {k}$
. Since r divides n, we have
$\boldsymbol {k}$
. Since r divides n, we have
![]() $n=2u$
for some
$n=2u$
for some
![]() $u{\geqslant }1$
.
$u{\geqslant }1$
.
Suppose that
![]() $\pi $
has a distinguished lift. By Paragraph 6.4, this implies that
$\pi $
has a distinguished lift. By Paragraph 6.4, this implies that
![]() $F/F_0$
is ramified. By Lemma 6.6, the representation
$F/F_0$
is ramified. By Lemma 6.6, the representation
![]() $\mathrm {V}$
has a distinguished
$\mathrm {V}$
has a distinguished
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift. By Lemma 6.10, one has
${\overline {\mathbb {Q}}_\ell }$
-lift. By Lemma 6.10, one has
![]() $r=n$
, thus
$r=n$
, thus
![]() $\mathrm {V}$
is isomorphic to
$\mathrm {V}$
is isomorphic to
![]() $\operatorname {st}_n(\varrho )$
for a character
$\operatorname {st}_n(\varrho )$
for a character
![]() $\varrho $
of
$\varrho $
of
![]() $\boldsymbol {k}^\times $
of order at most
$\boldsymbol {k}^\times $
of order at most
![]() $2$
. Besides, if
$2$
. Besides, if
![]() $\ell =2$
, then
$\ell =2$
, then
![]() $n=2$
and q is congruent to
$n=2$
and q is congruent to
![]() $-1$
mod
$-1$
mod
![]() $4$
. Since
$4$
. Since
![]() $r=n$
, the representation
$r=n$
, the representation
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_n(\rho )$
for a tamely ramified character
$\operatorname {St}_n(\rho )$
for a tamely ramified character
![]() $\rho $
of
$\rho $
of
![]() ${ F}^\times $
whose restriction to the units of F is the inflation of
${ F}^\times $
whose restriction to the units of F is the inflation of
![]() $\varrho $
.
$\varrho $
.
Suppose first that
![]() $\ell =2$
. Since
$\ell =2$
. Since
![]() $\pi $
is distinguished (by Theorem 3.3), it is
$\pi $
is distinguished (by Theorem 3.3), it is
![]() $\sigma $
-self-dual (by Theorem 3.1). It follows from Proposition 3.8 that the representation
$\sigma $
-self-dual (by Theorem 3.1). It follows from Proposition 3.8 that the representation
![]() $\rho $
is
$\rho $
is
![]() $\sigma $
-self-dual and from Theorem 3.2 that it is
$\sigma $
-self-dual and from Theorem 3.2 that it is
![]() $F_0^\times $
-distinguished, as expected.
$F_0^\times $
-distinguished, as expected.
Suppose now that
![]() $\ell \neq 2$
. By Proposition 3.8, we may choose
$\ell \neq 2$
. By Proposition 3.8, we may choose
![]() $\rho $
so that
$\rho $
so that
![]() $\rho ^{-1}\circ \sigma =\rho \nu ^i$
for some
$\rho ^{-1}\circ \sigma =\rho \nu ^i$
for some
![]() $i\in \{0,1\}$
, that is,
$i\in \{0,1\}$
, that is,
![]() $\rho \circ \mathrm {N}_{F/F_0}=\nu ^{-i}$
. It remains to prove that the restriction of
$\rho \circ \mathrm {N}_{F/F_0}=\nu ^{-i}$
. It remains to prove that the restriction of
![]() $\rho $
to
$\rho $
to
![]() $F_0^\times $
is either
$F_0^\times $
is either
![]() $\varkappa $
or
$\varkappa $
or
![]() $\nu _0^{-1}$
.
$\nu _0^{-1}$
.
Let c be the sign by which the element (4.23) acts on the space of
![]() $\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
-invariant linear forms on
$\operatorname {GL}_{u}(\boldsymbol {k})\times \operatorname {GL}_{u}(\boldsymbol {k})$
-invariant linear forms on
![]() $\mathrm {V}$
, which is given by Lemma 6.12. Remind that we have fixed a uniformizer
$\mathrm {V}$
, which is given by Lemma 6.12. Remind that we have fixed a uniformizer
![]() $\varpi $
of F such that
$\varpi $
of F such that
![]() $\sigma (\varpi )=-\varpi $
, thus
$\sigma (\varpi )=-\varpi $
, thus
![]() $\varpi _0=\varpi ^2$
is a uniformizer of
$\varpi _0=\varpi ^2$
is a uniformizer of
![]() $F_0$
. The representation
$F_0$
. The representation
![]() $\pi $
is distinguished (by Theorem 3.3) and it follows from Theorem 4.45 that
$\pi $
is distinguished (by Theorem 3.3) and it follows from Theorem 4.45 that
![]() $c=c_\pi (\varpi )$
. We have
$c=c_\pi (\varpi )$
. We have
On the other hand, the identity
![]() $\rho \circ \mathrm {N}_{F/F_0}=\nu ^{-i}$
implies that
$\rho \circ \mathrm {N}_{F/F_0}=\nu ^{-i}$
implies that
![]() $\rho (-\varpi _0)=q^i$
.
$\rho (-\varpi _0)=q^i$
.
Lemma 6.13. We have
![]() $q^{u}\equiv -1$
mod
$q^{u}\equiv -1$
mod
![]() $\ell $
.
$\ell $
.
Proof. Since
![]() $r{\geqslant }2$
and
$r{\geqslant }2$
and
![]() $\pi $
is cuspidal, r has the form
$\pi $
is cuspidal, r has the form
![]() $e(\rho )\ell ^v$
for some
$e(\rho )\ell ^v$
for some
![]() $v{\geqslant }0$
, where
$v{\geqslant }0$
, where
![]() $e(\rho )$
is the order of
$e(\rho )$
is the order of
![]() $q^k$
mod
$q^k$
mod
![]() $\ell $
by equation (3.2). In particular,
$\ell $
by equation (3.2). In particular,
![]() $(q^k)^r=q^n$
is congruent to
$(q^k)^r=q^n$
is congruent to
![]() $1$
mod
$1$
mod
![]() $\ell $
. Moreover, since
$\ell $
. Moreover, since
![]() $\ell $
is odd, one has
$\ell $
is odd, one has
![]() $q^{u}\equiv -1\neq 1$
mod
$q^{u}\equiv -1\neq 1$
mod
![]() $\ell $
.
$\ell $
.
It follows from Lemma 6.13 and equation (6.1) that
 $$ \begin{align*} c = \left\{ \begin{array}{ll} (-1)^i & \text{if }\varrho\text{ is trivial}, \\ (-1)^i \cdot \varkappa(-1)^{u} & \text{otherwise (that is, if }\varrho=\varkappa). \end{array}\right. \end{align*} $$
$$ \begin{align*} c = \left\{ \begin{array}{ll} (-1)^i & \text{if }\varrho\text{ is trivial}, \\ (-1)^i \cdot \varkappa(-1)^{u} & \text{otherwise (that is, if }\varrho=\varkappa). \end{array}\right. \end{align*} $$
Comparing with Lemma 6.12, we get the following corollary.
Corollary 6.14. We have
![]() $i=1$
if
$i=1$
if
![]() $\varrho $
is trivial, and
$\varrho $
is trivial, and
![]() $i=0$
if
$i=0$
if
![]() $\varrho $
is nontrivial.
$\varrho $
is nontrivial.
If
![]() $i=0$
, then
$i=0$
, then
![]() $\rho $
is self-dual. By Theorem 3.2, it is either distinguished or
$\rho $
is self-dual. By Theorem 3.2, it is either distinguished or
![]() $\varkappa $
-distinguished. Since its restriction to the units of F is the inflation of
$\varkappa $
-distinguished. Since its restriction to the units of F is the inflation of
![]() $\varrho =\varkappa $
, we deduce that
$\varrho =\varkappa $
, we deduce that
![]() $\rho $
is
$\rho $
is
![]() $\varkappa $
-distinguished.
$\varkappa $
-distinguished.
If
![]() $i=1$
, then
$i=1$
, then
![]() $\rho \nu ^{1/2}$
is unramified and self-dual. By Theorem 3.2, it is distinguished. Thus, the restriction of
$\rho \nu ^{1/2}$
is unramified and self-dual. By Theorem 3.2, it is distinguished. Thus, the restriction of
![]() $\rho $
to
$\rho $
to
![]() ${ F}_0^\times $
is equal to
${ F}_0^\times $
is equal to
![]() $\nu ^{-1/2}|_{{ F}_0^\times }=\nu _0^{-1}$
.
$\nu ^{-1/2}|_{{ F}_0^\times }=\nu _0^{-1}$
.
6.8
Let us finish the proof of Proposition 6.2. Assume that
![]() $n=r=2u$
for some
$n=r=2u$
for some
![]() $u{\geqslant }1$
, the extension
$u{\geqslant }1$
, the extension
![]() $F/F_0$
is ramified and
$F/F_0$
is ramified and
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\operatorname {St}_n(\rho )$
for some tamely ramified character
$\operatorname {St}_n(\rho )$
for some tamely ramified character
![]() $\rho $
of
$\rho $
of
![]() ${ F}^\times $
. We also assume that
${ F}^\times $
. We also assume that
-
○ either
 $\ell \neq 2$
and the restriction of
$\ell \neq 2$
and the restriction of
 $\rho $
to
$\rho $
to
 ${ F}_0^\times $
is either
${ F}_0^\times $
is either
 $\varkappa $
or
$\varkappa $
or
 $\nu _0^{-1}$
,
$\nu _0^{-1}$
, -
○ or
 $\ell =n=r=2$
, q is congruent to
$\ell =n=r=2$
, q is congruent to
 $-1$
mod
$-1$
mod
 $4$
and
$4$
and
 $\rho $
is trivial on
$\rho $
is trivial on
 $F_0^\times $
.
$F_0^\times $
.
It follows from Lemma 6.10 that
![]() $\mathrm {V}$
has a distinguished
$\mathrm {V}$
has a distinguished
![]() ${\overline {\mathbb {Q}}_\ell }$
-lift
${\overline {\mathbb {Q}}_\ell }$
-lift
![]() $\widetilde {\mathrm {V}}$
, which is
$\widetilde {\mathrm {V}}$
, which is
![]() $\varepsilon $
-distinguished for some sign
$\varepsilon $
-distinguished for some sign
![]() $\varepsilon \in \{-1,1\}$
. By Lemma 6.6, the representation
$\varepsilon \in \{-1,1\}$
. By Lemma 6.6, the representation
![]() $\pi $
has a distinguished lift to
$\pi $
has a distinguished lift to
![]() ${\overline {\mathbb {Q}}_\ell }$
if and only if the reduction of
${\overline {\mathbb {Q}}_\ell }$
if and only if the reduction of
![]() $\varepsilon $
mod
$\varepsilon $
mod
![]() $\ell $
, denoted c, is equal to
$\ell $
, denoted c, is equal to
![]() $\omega (\varpi )$
. Let us prove that this is the case. On the one hand, we have
$\omega (\varpi )$
. Let us prove that this is the case. On the one hand, we have
![]() $\omega (\varpi )=\rho (\varpi )^n=\rho (\varpi _0)^{u}$
. If
$\omega (\varpi )=\rho (\varpi )^n=\rho (\varpi _0)^{u}$
. If
![]() $\ell =2$
, we have
$\ell =2$
, we have
![]() $\omega (\varpi )=1$
. Otherwise, we have
$\omega (\varpi )=1$
. Otherwise, we have
 $$ \begin{align*} \omega(\varpi) = \left\{ \begin{array}{ll} q^{u} & \text{if the restriction of }\rho\text{ to }{ F}_0^\times\text{ is }\nu_0^{-1}, \\ \varkappa(-1)^{u} & \text{if the restriction of }\rho\text{ to }{ F}_0^\times\text{ is }\varkappa. \end{array}\right. \end{align*} $$
$$ \begin{align*} \omega(\varpi) = \left\{ \begin{array}{ll} q^{u} & \text{if the restriction of }\rho\text{ to }{ F}_0^\times\text{ is }\nu_0^{-1}, \\ \varkappa(-1)^{u} & \text{if the restriction of }\rho\text{ to }{ F}_0^\times\text{ is }\varkappa. \end{array}\right. \end{align*} $$
On the other hand,
![]() $\mathrm {V}$
is distinguished, and it is isomorphic to
$\mathrm {V}$
is distinguished, and it is isomorphic to
![]() $\operatorname {st}_n(\varrho ),$
where
$\operatorname {st}_n(\varrho ),$
where
![]() $\varrho $
is the character of
$\varrho $
is the character of
![]() $\boldsymbol {k}^\times $
defined by the restriction of
$\boldsymbol {k}^\times $
defined by the restriction of
![]() $\rho $
to the units of F. One thus may apply Lemma 6.12, which says that
$\rho $
to the units of F. One thus may apply Lemma 6.12, which says that
![]() $\mathrm {V}$
is
$\mathrm {V}$
is
![]() $\alpha $
-distinguished, with
$\alpha $
-distinguished, with
 $$ \begin{align*} \alpha = \left\{ \begin{array}{ll} -1 & \text{if }\varrho\text{ is trivial}, \\ (-1)^{u(q-1)/2} & \text{if }\varrho\text{ is nontrivial}. \end{array}\right. \end{align*} $$
$$ \begin{align*} \alpha = \left\{ \begin{array}{ll} -1 & \text{if }\varrho\text{ is trivial}, \\ (-1)^{u(q-1)/2} & \text{if }\varrho\text{ is nontrivial}. \end{array}\right. \end{align*} $$
Note that
![]() $\alpha =c$
by Remark 3.14, and that
$\alpha =c$
by Remark 3.14, and that
![]() $\varrho $
is trivial if and only if the restriction of
$\varrho $
is trivial if and only if the restriction of
![]() $\rho $
to
$\rho $
to
![]() ${ F}_0^\times $
is equal to
${ F}_0^\times $
is equal to
![]() $\nu _0^{-1}$
. Together with Lemma 6.13, this gives
$\nu _0^{-1}$
. Together with Lemma 6.13, this gives
![]() $\omega (\varpi )=c$
as expected.
$\omega (\varpi )=c$
as expected.
Acknowledgements
We thank Alberto Mínguez and Shaun Stevens for their interest and useful conversations.
Competing interest
The authors have no competing interest to declare.
Financial support
The first author was supported by EPSRC grant EP/V001930/1 and the Heilbronn Institute for Mathematical Research. The third author was partially supported by the Institut Universitaire de France.
This work was partially supported by the Erwin Schrödinger Institute in Vienna, where we benefitted from the Research in Teams grant ‘
![]() $\ell $
-modular Langlands Quotient Theorem and Applications’. We thank the institute for hospitality and for excellent working conditions.
$\ell $
-modular Langlands Quotient Theorem and Applications’. We thank the institute for hospitality and for excellent working conditions.