Introduction

Surface pressure variations in either time or space can cause air flow through soil and snow. It is widely thought that snow acts as an air filter, removing airborne impurities such as trace gases and aerosol particles as they move through the pores of the snow. This process would explain, in part, the incorporation of these materials into both seasonal snow covers and ice cores. The existence of layers in the snow may help explain the uneven distribution of foreign material in ice cores and is an important consideration in determining the effectiveness of snow as a filter.

There was some earlier interest in the idea that air flow in soil could affect heat transfer (Reference Fukuda,Fukuda, 1955). Reference Reimer.Reimer (1980) stated that the effective thermal diffusivity coefficients in snow increase by an order of magnitude during periods of Strong wind but this effect is not alwayys seen in snow. Several mechanisms have been suggested as driving forces for air flow in snow. Reference Clarke,, Fisher and Waddington.Clarke and others (1987) first suggested that turbulence due to wind caused transient pressure perturbations and caused harmonic oscillations in the air column deep in the snow. Reference Clarke, and WaddingtonClarke and Waddington (1991) further developed this mechanism to account for its three-dimensional nature. Reference Colbeck,Colbeck (1989) suggested that a steady surface wind would produce a variation in pressure across a snow surface due to surface relief such as sastrugi. For a homogeneous snow cover, this surface pressure variation causes a pattern of air flow within the snow that decays exponentially with depth while varying with the wavelength of the surface relief along the direction of flow. Reference Cunningham, and WaddingtonCunningham and Waddington (1993) described the mechanics of how air flow due to this mechanism causes filtering in the snow. Reference Albert,, Arons, Davis, Wolff, and BalesAlbert and others (in press) made permeability measurements in layered snow on the Greenland ice sheet, finding an increase with depth which they felt could be an important aspect of air flow in the top meter. Reference Sturm,Sturm (1991) measured large permeabilities in depth hoar in snow in interior Alaska but he did not find that wind pumping had a major effect on the temperature regime within the snow; this does not exclude snow’s role as a filter since the filtering effect can take place with low flow rates over long time periods (Reference Gjessing,Gjessing, 1977). Reference Albert,Albert (1996) showed that layering effects are important in ventilation, that a lower-permeability surface layer (e.g. wind or ice crust) decreases air flow into and through the firn and that channeling can occur in the more permeable layers even if each individual layer is isotropic. Reference Waddington,, Cunningham, Harder, Wolff. and BalesWaddington and others (in press) reviewed this entire field and added some important insights into the nature of the flow fields in heterogeneous snow.

The purpose here is to explore further the effects of snow layering on the flow field in the snow. While the work on homogeneous snow made a good start on understanding snow’s filtering effect, it could not account for the potentially large effects of either crusts with reduced permeability or buried layers of hoar crystals with increased permeability.

Theory

Assuming the pressure perturbation (p’) causing the flux of a gas through porous media is steady, it is usually described by a simplified version of Darcian flow. When permeability (k) varies in the vertical direction (z), this is

(1)

where w is the horizontal coordinate. This equation is separable into horizontal and vertical parts so that, when the surface pressure fluctuation is sinusoidal, the pressure perturbation due to the surface wind can be represented as

(2)

where the surface pressure perturbation is Pcos (2πx/λ) and λ is the wavelength. For the case of homogeneous snow, the solution is a simple analytical expression (Reference Colbeck,Colbeck, 1989)

(3)

For the case of permeability which changes exponentially with depth,

(4)

and f(z) is given by

(5)

where a is a constant and the subscript о represents the background value, in this case the surface Value. While this kind of function could be of interest over the state of the depth of the firn on an ice sheet, the problem of interest here is the near-surface filtering effect of snow that contains distinct layers. Thus the function f(z) in (2) must be obtained by solving

(6)

which comes from substituting (2) into (1). While equations of this type have analytical solutions in some cases (e.g. Reference Villari,Villari, 1982), I solve this equation with a “Matlab” routine which uses a fourth/fifth order Runge-Kutta-Fehlberg method. I make a simple substitution Eor the first derivative, df/dz, and then solve two first-order equations to generate f(z). These solutions tend to be unstable due to round-oil errors (Reference Ames,Ames, 1968, p.210) but the correct solution can be obtained over the range of interest by a precise choice of the first derivative of f at the surface. This is done by trial and error where the initial condition is chosen with increasing precision at each trial until f and its first derivative both go to zero at depth. Once the pressure field is obtained, the air flow in each direction is then calculated from Darcy’s law as the product of the permeability and the pressure gradient in that direction.

Results

In the example cases given here, the permeability of the snow cover is represented by

(7)

where cos is substituted for sin when the first layer at the surface has a low permeability. The value of b controls the difference between the permeability of the layer and the background permeability (k_o), the exponent (n) controls the thickness of the layers and the spacing of the layers is controlled by 2π/a. When the sign is positive, the layers are buried layers of hoar crystals, which have a higher permeability than the background because of the large crystal sizes. When the sign is negative the layers are ice layers or wind crust, which have a reduced permeability because of their higher density or smaller grain-size, respectively. The normalized permeability (k/k_o) of some buried layers is shown in Fig. 1. While this cycle of permeability is repeated indefinitely in the model, the flow decays rapidly with depth since p’ decays with depth.

Fig. 1. Normalized permeability vs depth. Values less than 1.0 indicate an ice layer (b = 1.2) and values greater than 1.0 indicate hour layers (b = 0.1). The solid lines are for n = 100 and the dashed lines are for n = 1000.

Buried Depth Hoar

Reference Sturm,Sturm (1991) found permeability in depth hoar of 5 – 7 times that of unmetamorphosed snow at the same site in Alaska. The normalized pressure field (p’/P) for buried hoar layers is shown in Fig. 2 where the effects of both layers can be seen as small kinks in the isobars. The pressure drop along the layer is greater than it would be in homogeneous snow, but the pressure drop across the layer is reduced. The high permeability in these layers gives rise to large perturbations in the flow fields as shown in figures 3 – 5 for the normalized horizontal, vertical and total fluxes, respectively. For purposes of comparison, each flux is normalized to the largest value of flux on the surface of homogenous snow. The horizontal and total fluxes are high in these layers, although except at the layers solutions for the pressure field differ little. Neither the pressure perturbations nor the vertical flow field penetrate as deeply into snow containing hoar layers. The vertical flow at the surface is only increased 10%, although the average permeability is increased by 25%. This occurs because the layers are buried and therefore they are not as effective as they would be at the surface. The effect on horizontal flow within the hoar layers is dramatic, showing a 9.6-fold increase in total flux in the upper layer and an 8.4-fold increase in the lower layer compared to a homogeneous flow field at those depths.

Fig. 2. Normalized surface pressure vs distance along surface for one-half wavelength shown on top. Normalized pressure field for one-half of the surface-pressure cycle for depth-hoar layers at 10 and 30 cm (b = 0.1 and n = 1000) shown on bottom. There is a large horizontal component to the flow and the vertical pressure drop across a layer is small due to the high permeability of the layer.

Fig. 3. Normalized horizontal flux for the pressure field shown in Fig. 2. Isopleths greater than 1.0 are not shown because of the great concentration of flow in layers. The maximum value in the upper layer is 5.1 and 1.3 in the lower layer.

Because of the small pressure drop across the layers, the vertical flow across the layer is small with the main flow being strongly horizontal. Accordingly, at a depth of 40 cm the vertical flow is only three-quarters of what it would be for homogeneous snow and the strong horizontal flow in the layers reduces the flow just below each layer. The nature of the flow can be clearly seen in Fig. 5 where it is shown that the total flux increases greatly at each layer but that the total flux elsewhere is slightly reduced compared to the flux in homogeneous snow. It is clear that the hoar layers “pipe” the flow horizontally toward the area of low pressure. This may explain the reports of strong air currents produced by boreholes that penetrate into firn (Reference Dubrovin,Dubrovin, 1965).

Fig. 4. Normalized vertical flux for the pressure field shown in Fig. 2. The sudden shift at the layers indicates a sudden reduction in the vertical flow compared to what it would be for homogeneous snow.

Fig. 5. Normalized total flux vs depth at a one-quarter wavelength (x = 25cm) for the pressure field shown in Fig. 2 (solid line) and for homogeneous snow (dashed line). The flux is less everywhere except in the layers where the strong horizontal flow greatly increases the total flux.

When the uppermost layer is lowered to 15 cm and the spacing of the buried layers is increased to 30 cm, the maximum value of flux in the upper layer is still 9.1 times greater than the value in homogeneous snow at that depth and thus the effect of the layering is still strong. When the upper layer is lowered to 20 cm and the spacing of the buried layers is increased to 10 cm, the maximum value of flux in the upper layer drops to 8.6 and so the effect of the layer is only slightly diminished. When the permeability of the hoar layers shown in Fig. 1 is reduced from 11 to 1.8 times the background, the effect on the flow field is also reduced. In the later case, both layers enhance the flow by a factor of 1.7, so the enhancement is nearly proportional to the increase in permeability.

Surface Ice Layer or Crust

If the permeability at the surface is reduced by a finegrained wind crust or surface glazing, the flow into the snow is also reduced. Fig. 6 shows the horizontal flux for three such layers, with the surface layer being one-half the thickness of the buried layers. The pressure field is similar to that shown in Fig. 2, except that the kinks in the isobars are bent in the opposite direction; thus, there is a much larger pressure drop across an ice layer than across a hoar layer and the isobars do not penetrate as deeply because of the ice layers. While the hoar layers showed strong horizontal flows, there is essentially no horizontal flow through the ice layers. The horizontal flow is re-established just below each layer where the permeability increases rapidly. The total flow, shown in Fig. 7, is reduced everywhere due to the ice layers. The vertical flow through the surface is reduced by 6% in this example, although the average permeability is only reduced by 2%. This enhanced effect is Clearly due to the presence of an ice layer on the surface.

Fig. 6. Normalized horizontal flux for snow with ice layers at the surface, 20 and 40 cm depth (b = 1.2 and n = 1000). There is a pocket of horizontal flow at one-quarter wavelength (25 cm ) just below the ice layer but the flow field is reduced everywhere compared to homogeneous snow.

Fig. 7. Normalized total flux vs depth at a one-quarter wavelength (x = 25 cm) for snow described in Fig. 6. The solid line is for snow with ice layers and the dashed line is for homogeneous snow.

Buried Ice Layers or Crusts

Figure 8 shows the total flux for the homogeneous case and for two different buried ice layers that themselves are shown in Fig. 1. The broader response occurs for a thicker layer (n = 100) and the narrower response for a thinner layer (n = 1000). The minimum value of total flux at the layer is independent Of the thickness of the layer but the overall reduction in flow increases with the layer width. Since the reduction in average permeability is small, it is not too important whether the uppermost layer is located on the surface or just below it. When the layers are moved down further, the result is qualitatively similar to that shown in Fig. 8, except the magnitude of the effect is proportionately weaker because the flow is weaker at the greater depths. When the permeability of the layer is increased to one-half of the background (b = 2), the total flow at the upper layer increases significantly. In general, the reduction in total flow at the layer is about proportional to the reduction in the permeability.

Fig. 8. Normalized total flux vs depth at a one-quarter wavelength (x = 25 cm) for snow with buried ice layers (b = 1.2) of different thicknesses. The dashed line is for homogeneous snow (n = ∞), the inner solid line is for the thinnest layer (n = 1000) and the outer solid line is for a thicker layer (n = 100).

The isobars and flow fields are shown in figures 9 and 10 for homogeneous snow and for snow with a buried hoar layer, respectively. For homogeneous snow, the flow field is irrotational since the curl of the velocity field is zero (Reference Sokolnikoff, and RedhefferSokolnikoff and Redheffer, 1958, p.402) and so the flow paths are along the isopleths of horizontal flux which are perpendicular to the isobars. Using the analytical solution for homogeneous snow, the stream function (ψ), which satisfies the requirement that ∇² ψ is zero, is given by

(8)

and thus the horizontal speed of air flow (u) is given by

(9)

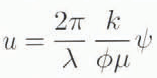
where ϕ is the porosity and µ is the viscosity of air. Then the residence time (τ) for flow along any given streamline is given by

(10)

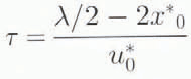
where the x_o* and u_o* are corresponding values at the surface and are related by

(11)

For example, if the air enters at an x_o of λ/8, which is one-half of the distance between the maximum and zero pressure perturbation, the residence time is given by

(12)

which equals

. Thus, the residence time increases rapidly with the spacing of the surface features that cause the sub-surface flow, decreases as the pressure perturbation increases and decreases somewhat as the snow becomes more dense and the permeability decreases.

Fig. 9. Normalized pressure and flow fields for homogeneous snow.

While we do not have a corresponding equation for layered snow, in the examples shown in figures 9 and 10 it is clear that there are two reasons why the residence time is less when hoar layers are present. First, the flow path is shortened since piping through the hoar layer reduces penetration into the deeper snow and, secondly, the flow speeds are higher in the hoar layer than they would be at that depth in homogeneous snow.

Fig. 10. Normalized pressure and flow fields for the layered snow shown in figures 1 – 5.

Discussion and Conclusions

The effect on the flow field is greatest in buried hoar layers where there are large increases in the horizontal and total flows but reduced flows below the layers. This suggests that these layers may preferentially act as atmospheric filters, because of the increased amount and speed of the air that passes through them. However, they have an increased permeability, because of increased grain- and pore-sizes that may reduce their effectiveness. Also, since they are always below the surface, the overlying snow will filter the air somewhat before it enters the hoar layers. Given that these layers capture more of the flow when they are closer to the surface, their proximity to the surface may greatly affect the filtering capability of the entire column of snow.

The main effect of a buried crust or ice layer may be in its ability to concentrate the flow above it and reduce the flow below it.The buried layers shown in figures 6 and 7 reduce the vertical flows by redirecting the air into horizontal flows above the layers. Thus, the total flow just above the layer is the same as what it would be in homogeneous snow. However, the net result of any type of layer appears to be to reduce the flow below the layer. Ice layers do this by reducing the average permeability and the vertical flux through the layer, and hoar layers do it by short-circuiting the flow horizontal through the more permeable horizons. In general, the effect on flow increases as the permeability increases in hoar layers and decreases as the uppermost layer becomes more deeply buried. For the examples given here, the maximum enhancement in horizontal flow is about a factor of 10 and, when coupled with the reduced penetration depth, suggests that the residence times of air flow in the snow could be significantly shortened. Reference Cunningham, and WaddingtonCunningham and Waddington (1993) found that the adsorption coefficient for aerosols is less than 1 when residence times are less than about 28 s, which requires a u_max of no more than 1.3 cm s⁻¹ for a λ of 100 cm. This flow speed is probably smaller than those found in a hoar layer like the upper hoar layer shown in Fig. 3 since, even in homogeneous snow, Reference Colbeck,Colbeck (1989) calculated a flow rate of 3.5 cm s⁻¹ at the 1/e decay depth. If total removal occurs in 3 – 8 s for 0.1 – l/µm particles as Suggested by Reference Harder,, Warren, Charlson and CovertHarder and others (in press). u _max should be no more than 4.4 – 11.8 cms⁻¹. Since this is greater than 3.5 cm s⁻¹, it Suggests that removal of these particles should be complete in this example of homogeneous snow. However, the increased horizontal flow rate through the hoar layer may allow removal of only those aerosols that are captured preferentially at higher air speeds. The capture of those aerosols that are dependent on long residence times will be reduced by both the more rapid flow through the hoar layer and the reduction of flow beneath the hoar layer. The role of such parameters as wavelength and height of surface features, combined with details of the layering, is complicated and difficult to summarize easily. Furthermore, the capture rates of small particles are sensitive to residence time, because diffusion has to have time to operate, while the capture rates for the larger particles are more sensitive to air velocity because of momentum effects.

There are many other important scenarios that could be explored with this model, for example, the interior of Alaska often has a large amount of depth hoar below a less permeable layer on the surface, and the permeability can increase with depth below the surface of the ice sheets. These profiles suggest that there may be strong flows at depth, although preliminary results using the model suggest that the surface layer would reduce the flow at depth, even when there is a large increase in permeability with depth. However. Figure 6 shows that flow can be stronger below a surface layer than in the layer, so strong flows over some distance in buried hoar layers seem possible.