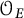1 Introduction
In his seminal paper [Reference Pedersen, Eilers and OlesenPim97], Pimsner introduced a class of
![]() $\mathrm {C}^*$
-algebras, now referred to as Pimsner algebras, that simultaneously generalizes crossed products by
$\mathrm {C}^*$
-algebras, now referred to as Pimsner algebras, that simultaneously generalizes crossed products by
![]() $\mathbb {Z}$
and Cuntz–Krieger algebras, see [Reference Cuntz and KriegerCK80]. The starting point of his construction is, in his terminology, a Hilbert bimodule
$\mathbb {Z}$
and Cuntz–Krieger algebras, see [Reference Cuntz and KriegerCK80]. The starting point of his construction is, in his terminology, a Hilbert bimodule
![]() $(E,\phi )$
over a
$(E,\phi )$
over a
![]() $\mathrm {C}^*$
-algebra A; this means that E is a right Hilbert A-module together with an isometric
$\mathrm {C}^*$
-algebra A; this means that E is a right Hilbert A-module together with an isometric
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\phi : A \rightarrow \mathcal {L}(E)$
from A to the
$\phi : A \rightarrow \mathcal {L}(E)$
from A to the
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathcal {L}(E)$
of adjointable operators on E, that provides the left A-module structure on E. When E is full as a right Hilbert A-module, Pimsner went on to obtain, in analogy with the Toeplitz extension proof of the Bott periodicity and the celebrated Pimsner–Voiculescu sequence, in topological
$\mathcal {L}(E)$
of adjointable operators on E, that provides the left A-module structure on E. When E is full as a right Hilbert A-module, Pimsner went on to obtain, in analogy with the Toeplitz extension proof of the Bott periodicity and the celebrated Pimsner–Voiculescu sequence, in topological
![]() $\operatorname {K}$
-theory, a six-term sequence in
$\operatorname {K}$
-theory, a six-term sequence in
![]() $\operatorname {KK}$
-theory, relating the
$\operatorname {KK}$
-theory, relating the
![]() $\operatorname {KK}$
-groups of the Pimsner algebra to the
$\operatorname {KK}$
-groups of the Pimsner algebra to the
![]() $\operatorname {KK}$
-groups of the
$\operatorname {KK}$
-groups of the
![]() $\mathrm {C}^*$
-algebra A. In fact, an essential ingredient in the proof is the existence of a Toeplitz extension associated with the Pimsner algebra.
$\mathrm {C}^*$
-algebra A. In fact, an essential ingredient in the proof is the existence of a Toeplitz extension associated with the Pimsner algebra.
Since their introduction, Pimsner algebras have been the subject of intense study, from various points of view; even more so, after Katsura [Reference KatsoulisKat04b] generalized the construction, removing the injectivity condition on
![]() $\phi $
. Thus, Pimsner’s construction, as generalized by Katsura, now works for any
$\phi $
. Thus, Pimsner’s construction, as generalized by Katsura, now works for any
![]() $(E,\phi )$
consisting of a right Hilbert A-module E and a
$(E,\phi )$
consisting of a right Hilbert A-module E and a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\phi : A \rightarrow \mathcal {L}(E)$
from A to the
$\phi : A \rightarrow \mathcal {L}(E)$
from A to the
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathcal {L}(E)$
. Such a pair is now referred to as a
$\mathcal {L}(E)$
. Such a pair is now referred to as a
![]() $\mathrm {C}^*$
-correspondence over A. This generalization led Katsura [Reference KasparovKat04a] to further extend the already extensive list of
$\mathrm {C}^*$
-correspondence over A. This generalization led Katsura [Reference KasparovKat04a] to further extend the already extensive list of
![]() $\mathrm {C}^*$
-algebras that fall in this class, by incorporating graph
$\mathrm {C}^*$
-algebras that fall in this class, by incorporating graph
![]() $\mathrm {C}^*$
-algebras; moreover, it was shown in [Reference Kaliszewski, Quigg and RobertsonKat03] that Pimsner algebras also cover what was called crossed product by Hilbert
$\mathrm {C}^*$
-algebras; moreover, it was shown in [Reference Kaliszewski, Quigg and RobertsonKat03] that Pimsner algebras also cover what was called crossed product by Hilbert
![]() $\mathrm {C}^*$
-bimodules in [Reference Adamo, Archey, Georgescu, Forough, Jeong, Strung and ViolaAEE98]. It is to be noted that such a generalization was already considered in the beautiful paper [Reference Muhly and SolelMS98], also providing a plentiful of examples; see also [Reference Abadie and AchigarAA09].
$\mathrm {C}^*$
-bimodules in [Reference Adamo, Archey, Georgescu, Forough, Jeong, Strung and ViolaAEE98]. It is to be noted that such a generalization was already considered in the beautiful paper [Reference Muhly and SolelMS98], also providing a plentiful of examples; see also [Reference Abadie and AchigarAA09].
Leveraging the flexibility of Pimsner’s construction, many structural properties of the Pimsner algebra
![]() $\mathcal {O}_E$
may be studied through a sound grip on the algebra A and the Hilbert A-module E. Adapting such a viewpoint, [Reference KatsuraKat07, Reference KatsuraKPW98] studied the ideal structure of the Pimsner algebras. Various approximation properties are studied, for example, in [Reference Skalski and ZachariasSZ10]. As already mentioned above, [Reference Abadie, Eilers and ExelAA09, Reference Adamo, Archey, Georgescu, Forough, Jeong, Strung and ViolaAEE98] studies Morita equivalence of such algebras. Continuing along the lines initiated by Pimsner and Katsura, [Reference Schmidt and WeberSch15] studies
$\mathcal {O}_E$
may be studied through a sound grip on the algebra A and the Hilbert A-module E. Adapting such a viewpoint, [Reference KatsuraKat07, Reference KatsuraKPW98] studied the ideal structure of the Pimsner algebras. Various approximation properties are studied, for example, in [Reference Skalski and ZachariasSZ10]. As already mentioned above, [Reference Abadie, Eilers and ExelAA09, Reference Adamo, Archey, Georgescu, Forough, Jeong, Strung and ViolaAEE98] studies Morita equivalence of such algebras. Continuing along the lines initiated by Pimsner and Katsura, [Reference Schmidt and WeberSch15] studies
![]() $\operatorname {K}$
-theory of crossed products of Pimsner algebras. Crossed products as well as (co)actions of groups are also the subject of study in [Reference Hossain and GoswamiHN08, Reference KatsuraKQR15], which we shall return to in a moment, as they form the main theme of the present article. [Reference Muhly and SolelMS98] exploits dilation theory and views Pimsner algebras as the
$\operatorname {K}$
-theory of crossed products of Pimsner algebras. Crossed products as well as (co)actions of groups are also the subject of study in [Reference Hossain and GoswamiHN08, Reference KatsuraKQR15], which we shall return to in a moment, as they form the main theme of the present article. [Reference Muhly and SolelMS98] exploits dilation theory and views Pimsner algebras as the
![]() $\mathrm {C}^*$
-envelopes of the tensor algebra of the correspondence
$\mathrm {C}^*$
-envelopes of the tensor algebra of the correspondence
![]() $(E,\phi )$
. [Reference LanceLN04] provides a detailed study of KMS states (and weights) on the Pimsner algebras, a topic which we will again return to in a moment. Providing a connection with the theory of quantum principal bundles, [Reference Arici, Kaad and LandiAKL16] exhibits a class of natural examples arising from q-deformations as Pimsner algebras. Let us mention also the recent [Reference Rennie, Robertson and SimsRRS19] and [Reference Pask and RenniePR06], that makes contact with Connes’ program [Reference ConnesCon94], the former studying Poincaré duality of Pimsner algebras. Finally, the recent preprint [Reference Adamo, Archey, Georgescu, Forough, Jeong, Strung and ViolaAAG+22] studies correspondences over commutative algebras and associated Pimsner algebras from the point of view of Elliott’s program.
$(E,\phi )$
. [Reference LanceLN04] provides a detailed study of KMS states (and weights) on the Pimsner algebras, a topic which we will again return to in a moment. Providing a connection with the theory of quantum principal bundles, [Reference Arici, Kaad and LandiAKL16] exhibits a class of natural examples arising from q-deformations as Pimsner algebras. Let us mention also the recent [Reference Rennie, Robertson and SimsRRS19] and [Reference Pask and RenniePR06], that makes contact with Connes’ program [Reference ConnesCon94], the former studying Poincaré duality of Pimsner algebras. Finally, the recent preprint [Reference Adamo, Archey, Georgescu, Forough, Jeong, Strung and ViolaAAG+22] studies correspondences over commutative algebras and associated Pimsner algebras from the point of view of Elliott’s program.
At the end of his paper, Pimsner remarks [Reference Pedersen, Eilers and OlesenPim97, Remark 4.10], that all his constructions are equivariant, under an action of a locally compact, second countable group. The action of the group on the
![]() $\mathrm {C}^*$
-correspondence is to be taken in the sense of Kasparov [Reference Kajiwara, Pinzari and WatataniKas88]. The details of the remark appear in [Reference Hossain and GoswamiHN08] where the authors consider actions of amenable locally compact groups and show that for such groups, an equivariant
$\mathrm {C}^*$
-correspondence is to be taken in the sense of Kasparov [Reference Kajiwara, Pinzari and WatataniKas88]. The details of the remark appear in [Reference Hossain and GoswamiHN08] where the authors consider actions of amenable locally compact groups and show that for such groups, an equivariant
![]() $\mathrm {C}^*$
-correspondence induces a natural action on the Pimsner algebra. Moreover, the crossed product can be identified as the Pimsner algebra of the crossed product
$\mathrm {C}^*$
-correspondence induces a natural action on the Pimsner algebra. Moreover, the crossed product can be identified as the Pimsner algebra of the crossed product
![]() $\mathrm {C}^*$
-correspondence. Continuing along this line, the authors of [Reference KatsuraKQR15] consider coactions of groups on
$\mathrm {C}^*$
-correspondence. Continuing along this line, the authors of [Reference KatsuraKQR15] consider coactions of groups on
![]() $\mathrm {C}^*$
-correspondences and prove a similar result to that of [Reference Hossain and GoswamiHN08] (see also [Reference Bhattacharjee and GoswamiBKQR15]). The desire to extend these results to the quantum setting, i.e., in the situation where we have a quantum group instead of a group, is one of the major motivations of the present article; and this brings us to the next paragraph.
$\mathrm {C}^*$
-correspondences and prove a similar result to that of [Reference Hossain and GoswamiHN08] (see also [Reference Bhattacharjee and GoswamiBKQR15]). The desire to extend these results to the quantum setting, i.e., in the situation where we have a quantum group instead of a group, is one of the major motivations of the present article; and this brings us to the next paragraph.
Introduced by Woronowicz in his seminal paper [Reference WoronowiczWor87], compact quantum groups are now well established in Connes’ approach to noncommutative geometry. The landmark discovery of
![]() $\text {SU}_q(2)$
by Woronowicz together with the dream of making contact with Connes’ enterprise, resulted, following Wang’s pioneering work on quantum symmetries of finite spaces [Reference WangWan98], in several constructions and insights. Let us mention, albeit incompletely, the work of:
$\text {SU}_q(2)$
by Woronowicz together with the dream of making contact with Connes’ enterprise, resulted, following Wang’s pioneering work on quantum symmetries of finite spaces [Reference WangWan98], in several constructions and insights. Let us mention, albeit incompletely, the work of:
-
• Banica, Bichon, and collaborators on quantum symmetries of discrete structures (see [Reference Baaj and SkandalisBan05a, Reference BanicaBan05b, Reference Bédos, Kaliszewski, Quigg and RobertsonBic03]);
-
• Goswami, Bhowmick, and collaborators on quantum isometries of spectral triples (see [Reference Banica and SkalskiBG09, Reference Banica and VergniouxBG19, Reference Gabriel and WeberGJ18, Reference GoswamiGos20]);
-
• Banica, Skalski, and collaborators on quantum symmetries of
 $\mathrm {C}^*$
-algebras equipped with orthogonal filtrations (see [Reference Bhowmick and GoswamiBMRS19, Reference BichonBS13]); and
$\mathrm {C}^*$
-algebras equipped with orthogonal filtrations (see [Reference Bhowmick and GoswamiBMRS19, Reference BichonBS13]); and -
• more recently, Goswami and collaborators on quantum symmetries of subfactors (see [Reference BanicaBCG22]).
The study of quantum symmetries of
![]() $\mathrm {C}^*$
-algebras have also been rewarding enough. Indeed, for example, it is well-known that there is no ergodic action of a compact group on the Cuntz-algebra
$\mathrm {C}^*$
-algebras have also been rewarding enough. Indeed, for example, it is well-known that there is no ergodic action of a compact group on the Cuntz-algebra
![]() ${\mathcal O}_{n}$
; however,
${\mathcal O}_{n}$
; however,
![]() $\mathcal {O}_n$
admits an ergodic action of a compact quantum group, namely, the (quasi-free action of the) free unitary quantum group, turning
$\mathcal {O}_n$
admits an ergodic action of a compact quantum group, namely, the (quasi-free action of the) free unitary quantum group, turning
![]() ${\mathcal O}_{n}$
into a quantum homogeneous space. Similar richness of quantum symmetries has been observed in other contexts as well. For example, compact quantum groups have been found to preserve fewer KMS states on certain graph
${\mathcal O}_{n}$
into a quantum homogeneous space. Similar richness of quantum symmetries has been observed in other contexts as well. For example, compact quantum groups have been found to preserve fewer KMS states on certain graph
![]() $\mathrm {C}^*$
-algebras as opposed to compact group actions [Reference Joardar and MandalJM21a]. As a necessarily incomplete list of references for the reader interested in this direction, we mention [Reference GabrielGab14, Reference Goswami and JoardarGW16, Reference Kajiwara and WatataniKat17, Reference PaolucciPao97].
$\mathrm {C}^*$
-algebras as opposed to compact group actions [Reference Joardar and MandalJM21a]. As a necessarily incomplete list of references for the reader interested in this direction, we mention [Reference GabrielGab14, Reference Goswami and JoardarGW16, Reference Kajiwara and WatataniKat17, Reference PaolucciPao97].
Keeping in mind, the richness of the two camps – Pimsner algebras at one hand and actions of compact quantum groups on the other, we combine the two in the present article. Thus, we study compact quantum group actions on Pimsner algebras, the underlying philosophy being the same as mentioned above, i.e., studying such actions through actions on the
![]() $\mathrm {C}^*$
-correspondence. To carry out this program, however, we would need a notion of equivariant
$\mathrm {C}^*$
-correspondence. To carry out this program, however, we would need a notion of equivariant
![]() $\mathrm {C}^*$
-correspondences under the action of a compact quantum group. This is based on the fundamental work of Baaj and Skandalis [Reference BichonBS89], where the authors generalize Kasparov’s equivariant
$\mathrm {C}^*$
-correspondences under the action of a compact quantum group. This is based on the fundamental work of Baaj and Skandalis [Reference BichonBS89], where the authors generalize Kasparov’s equivariant
![]() $\operatorname {KK}$
-theory [Reference Kajiwara, Pinzari and WatataniKas88] to the setting where there is no group anymore but a Hopf
$\operatorname {KK}$
-theory [Reference Kajiwara, Pinzari and WatataniKas88] to the setting where there is no group anymore but a Hopf
![]() $\mathrm {C}^*$
-algebra. Having a notion of equivariant
$\mathrm {C}^*$
-algebra. Having a notion of equivariant
![]() $\mathrm {C}^*$
-correspondences at hand, our first theorem reads as follows.
$\mathrm {C}^*$
-correspondences at hand, our first theorem reads as follows.
Theorem 1.1 Let G be a compact quantum group, let
![]() $(A,\alpha )$
be a unital G-
$(A,\alpha )$
be a unital G-
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi ,\lambda )$
be a G-equivariant
$(E,\phi ,\lambda )$
be a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
. Assume further that the Hilbert A-module E is finitely generated and projective. Then there is a unique unital
$(A,\alpha )$
. Assume further that the Hilbert A-module E is finitely generated and projective. Then there is a unique unital
![]() $*$
-homomorphism
$*$
-homomorphism
such that
Moreover, the pair
![]() $(\mathcal {O}_E,\omega )$
is a G-
$(\mathcal {O}_E,\omega )$
is a G-
![]() $\mathrm {C}^*$
-algebra. Here,
$\mathrm {C}^*$
-algebra. Here,
![]() $\mathcal {O}_E$
denotes the Pimsner algebra associated with
$\mathcal {O}_E$
denotes the Pimsner algebra associated with
![]() $(E,\phi )$
;
$(E,\phi )$
;
![]() $(k_E,k_A)$
is the defining universal covariant representation of
$(k_E,k_A)$
is the defining universal covariant representation of
![]() $\mathcal {O}_E$
;
$\mathcal {O}_E$
;
![]() $\alpha $
is the G-action on A and
$\alpha $
is the G-action on A and
![]() $\lambda $
is the G-action on E.
$\lambda $
is the G-action on E.
The above theorem also leads one, naturally, to seek for a possible converse to the theorem. However, to identify the precise formulation of a converse, if at all possible, requires some work. To explain in more detail, let us make the following definition.
Definition 1.2 Let A be a unital
![]() $\mathrm {C}^*$
-algebra, let
$\mathrm {C}^*$
-algebra, let
![]() $(E,\phi )$
be a
$(E,\phi )$
be a
![]() $\mathrm {C}^*$
-correspondence over A (where E is assumed to be finitely generated and projective), and let G be a compact quantum group. An action
$\mathrm {C}^*$
-correspondence over A (where E is assumed to be finitely generated and projective), and let G be a compact quantum group. An action
![]() $\rho : \mathcal {O}_E \rightarrow \mathcal {O}_E \otimes \mathrm {C}(G)$
of G on the Pimsner algebra
$\rho : \mathcal {O}_E \rightarrow \mathcal {O}_E \otimes \mathrm {C}(G)$
of G on the Pimsner algebra
![]() $\mathcal {O}_E$
is said to be a lift if there are G-actions
$\mathcal {O}_E$
is said to be a lift if there are G-actions
![]() $\alpha $
and
$\alpha $
and
![]() $\lambda $
on A and on E, respectively, such that the following are satisfied.
$\lambda $
on A and on E, respectively, such that the following are satisfied.
-
•
 $(A,\alpha )$
is a G-
$(A,\alpha )$
is a G-
 $\mathrm {C}^*$
-algebra;
$\mathrm {C}^*$
-algebra; -
•
 $(E,\phi ,\lambda )$
is a G-equivariant
$(E,\phi ,\lambda )$
is a G-equivariant
 $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
 $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
 $(A,\alpha )$
;
$(A,\alpha )$
; -
•
 $\rho $
coincides with
$\rho $
coincides with
 $\omega $
as in Theorem 1.1.
$\omega $
as in Theorem 1.1.
Now, we can state the question in precise terms.
Question 1.3 Given an action
![]() $\rho $
of a compact quantum group G on the Pimsner algebra
$\rho $
of a compact quantum group G on the Pimsner algebra
![]() $\mathcal {O}_E$
, is
$\mathcal {O}_E$
, is
![]() $\rho $
always a lift?
$\rho $
always a lift?
The answer to the above question is no, however, and counter-examples exist even for group actions. And this leads to our next theorem.
Theorem 1.4 The action
![]() $\rho $
of
$\rho $
of
![]() $\mathbb {T}^n$
on
$\mathbb {T}^n$
on
![]() ${\mathcal O}_{n}$
given by
${\mathcal O}_{n}$
given by
is not a lift. Here,
![]() $\mathcal {O}_n$
is the Cuntz algebra on n-generators, the generators being
$\mathcal {O}_n$
is the Cuntz algebra on n-generators, the generators being
![]() $S_i$
,
$S_i$
,
![]() $i=1,\dots ,n$
and u is the element
$i=1,\dots ,n$
and u is the element
![]() $\sum _{k=1}^{n}S_{k}S_{k}^*\otimes z_{k} \in {\mathcal O}_{n}\otimes \mathrm {C}(\mathbb {T}^{n})$
.
$\sum _{k=1}^{n}S_{k}S_{k}^*\otimes z_{k} \in {\mathcal O}_{n}\otimes \mathrm {C}(\mathbb {T}^{n})$
.
Nevertheless, we are able to answer Question 1.3 positively if we restrict ourselves to the class of Pimsner algebras that are considered in [Reference Arici, Kaad and LandiAKL16], i.e., quantum principal
![]() $\mathbb {T}$
-bundles, as stated in the following theorem.
$\mathbb {T}$
-bundles, as stated in the following theorem.
Theorem 1.5 Let
![]() $(A,\gamma )$
be a unital
$(A,\gamma )$
be a unital
![]() $\mathbb {T}$
-
$\mathbb {T}$
-
![]() $\mathrm {C}^*$
-algebra such that:
$\mathrm {C}^*$
-algebra such that:
-
• the
 $\mathbb {T}$
-action
$\mathbb {T}$
-action
 $\gamma $
is principal;
$\gamma $
is principal; -
• the fixed point algebra
 $A(0)$
is separable;
$A(0)$
is separable; -
• the spectral subspaces
 $A(1)$
and
$A(1)$
and
 $A(-1)$
are full over
$A(-1)$
are full over
 $A(0)$
,
$A(0)$
,
so that there is an isomorphism
![]() $\mathcal {O}_{A(1)} \cong A$
. Let G be a compact quantum group, and let
$\mathcal {O}_{A(1)} \cong A$
. Let G be a compact quantum group, and let
![]() $\rho : A \rightarrow A \otimes \mathrm {C}(G)$
be a gauge-equivariant G-action on A in the sense that for all
$\rho : A \rightarrow A \otimes \mathrm {C}(G)$
be a gauge-equivariant G-action on A in the sense that for all
![]() $z \in \mathbb {T}$
,
$z \in \mathbb {T}$
,
Then
![]() $\rho $
is a lift in the sense of Definition 1.2.
$\rho $
is a lift in the sense of Definition 1.2.
As mentioned previously, compact quantum group actions preserve fewer KMS states on certain graph
![]() $\mathrm {C}^*$
-algebras and it is thus natural to investigate what happens when we have such an action of a compact quantum group on Pimsner algebras as in Theorem 1.1. In [Reference LanceLN04], the authors show that for a quasi-free dynamics on the Pimsner algebra
$\mathrm {C}^*$
-algebras and it is thus natural to investigate what happens when we have such an action of a compact quantum group on Pimsner algebras as in Theorem 1.1. In [Reference LanceLN04], the authors show that for a quasi-free dynamics on the Pimsner algebra
![]() $\mathcal {O}_E$
induced by a continuous one-parameter group of unitary isometries of the
$\mathcal {O}_E$
induced by a continuous one-parameter group of unitary isometries of the
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(E,\phi )$
, KMS states on
$(E,\phi )$
, KMS states on
![]() $\mathcal {O}_E$
are characterized by traces on the
$\mathcal {O}_E$
are characterized by traces on the
![]() $\mathrm {C}^*$
-algebra A. It is thus natural to hope that if the one-parameter group of isometries of the
$\mathrm {C}^*$
-algebra A. It is thus natural to hope that if the one-parameter group of isometries of the
![]() $\mathrm {C}^*$
-correspondence is, in some natural way, compatible with the G-structure on the
$\mathrm {C}^*$
-correspondence is, in some natural way, compatible with the G-structure on the
![]() $\mathrm {C}^*$
-correspondence then G-equivariance of KMS states on the Pimsner algebra may also be characterized by G-equivariance of the corresponding tracial states on A. The necessary compatibility turns out to be the G-equivariance of the generator of the one-parameter group of isometries. Let us now state our next theorem which sums up this paragraph.
$\mathrm {C}^*$
-correspondence then G-equivariance of KMS states on the Pimsner algebra may also be characterized by G-equivariance of the corresponding tracial states on A. The necessary compatibility turns out to be the G-equivariance of the generator of the one-parameter group of isometries. Let us now state our next theorem which sums up this paragraph.
Theorem 1.6 Let G be a compact quantum group of Kac type, let
![]() $(A,\alpha )$
be a unital G-
$(A,\alpha )$
be a unital G-
![]() $\mathrm {C}^*$
-algebra, let
$\mathrm {C}^*$
-algebra, let
![]() $(E,\phi ,\lambda )$
be a G-equivariant
$(E,\phi ,\lambda )$
be a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
, and let
$(A,\alpha )$
, and let
![]() $\omega $
be the G-action on
$\omega $
be the G-action on
![]() $\mathcal {O}_E$
, as obtained in Theorem 1.1 where the Hilbert A-module E is finitely generated and projective. Let
$\mathcal {O}_E$
, as obtained in Theorem 1.1 where the Hilbert A-module E is finitely generated and projective. Let
![]() $\delta $
be the quasi-free dynamics induced by the module dynamics U satisfying the conditions as laid out in [Reference LanceLN04]. Let U be G-equivariant, i.e., for all
$\delta $
be the quasi-free dynamics induced by the module dynamics U satisfying the conditions as laid out in [Reference LanceLN04]. Let U be G-equivariant, i.e., for all
![]() $t \in \mathbb {R}$
,
$t \in \mathbb {R}$
,
Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $(\delta ,\beta )$
-KMS state (where
$(\delta ,\beta )$
-KMS state (where
![]() $\beta \in (0,\infty )$
) on
$\beta \in (0,\infty )$
) on
![]() $\mathcal {O}_E$
, and let
$\mathcal {O}_E$
, and let
![]() $\tau =\varphi \circ k_A$
be the tracial state on A as mentioned above. Then
$\tau =\varphi \circ k_A$
be the tracial state on A as mentioned above. Then
![]() $\varphi $
is G-equivariant if and only if
$\varphi $
is G-equivariant if and only if
![]() $\tau $
is G-equivariant.
$\tau $
is G-equivariant.
We next apply the above general results to the concrete situation where the
![]() $\mathrm {C}^*$
-correspondence arises from a finite, directed graph. In that case, the graph
$\mathrm {C}^*$
-correspondence arises from a finite, directed graph. In that case, the graph
![]() $\mathrm {C}^*$
-algebra coincides with the Pimsner algebra, allowing us to apply the above results. In particular, we recover the results obtained in [Reference Joardar and MandalJM21a, Reference Joardar and MandalJM21b, Reference SchafhauserSW18]. This also enables us to gain a more concrete understanding of most of the results concerning the interaction between quantum symmetries of graphs and its graph
$\mathrm {C}^*$
-algebra coincides with the Pimsner algebra, allowing us to apply the above results. In particular, we recover the results obtained in [Reference Joardar and MandalJM21a, Reference Joardar and MandalJM21b, Reference SchafhauserSW18]. This also enables us to gain a more concrete understanding of most of the results concerning the interaction between quantum symmetries of graphs and its graph
![]() $\mathrm {C}^*$
-algebras. For quite a long time, there have been at least two notions of a quantum automorphism group of a finite, simple, directed graph, namely, one due to Banica [Reference Baaj and SkandalisBan05a] and one due to Bichon [Reference Bédos, Kaliszewski, Quigg and RobertsonBic03]. The relationship between these two notions, however, is not so conspicuous; in particular, it is in general difficult to identify the cases when these two notions coincide. In this direction, we have at our disposal the following theorem to offer.
$\mathrm {C}^*$
-algebras. For quite a long time, there have been at least two notions of a quantum automorphism group of a finite, simple, directed graph, namely, one due to Banica [Reference Baaj and SkandalisBan05a] and one due to Bichon [Reference Bédos, Kaliszewski, Quigg and RobertsonBic03]. The relationship between these two notions, however, is not so conspicuous; in particular, it is in general difficult to identify the cases when these two notions coincide. In this direction, we have at our disposal the following theorem to offer.
Theorem 1.7 Let
![]() ${\mathcal G}$
be a finite, simple graph without any source. If either r or s is injective, then
${\mathcal G}$
be a finite, simple graph without any source. If either r or s is injective, then
![]() $\mathrm {Aut}^{+}_{\mathrm {Bic}}({\mathcal G})$
is isomorphic to
$\mathrm {Aut}^{+}_{\mathrm {Bic}}({\mathcal G})$
is isomorphic to
![]() $\mathrm {Aut}^{+}_{\mathrm {Ban}}({\mathcal G})$
.
$\mathrm {Aut}^{+}_{\mathrm {Ban}}({\mathcal G})$
.
Let us now briefly discuss the organization of the paper. In Section 2, we briefly recall the necessary background on compact quantum groups and their actions on
![]() $\mathrm {C}^*$
-algebras and Hilbert
$\mathrm {C}^*$
-algebras and Hilbert
![]() $\mathrm {C}^*$
-modules. We begin Section 3 with a careful summary of Pimsner’s constructions and prove Theorem 1.1 (Theorem 3.9). It is in this section that we prove Theorem 1.4 (Theorem 3.14) and Theorem 1.5 (Theorem 3.16) as well. Section 4 is devoted to recalling some background on KMS states from [Reference LanceLN04] and to proving Theorem 1.6 (Theorem 4.10). In the remaining three sections, we apply the general results to the question of quantum symmetries of graphs. In Section 5, we discuss the bridge that connects the general results of the previous sections with the situation at hand. We also reprove some results on the quantum symmetries of graphs. Section 6 is devoted to a detailed study and comparison in the case of a simple, directed graph. It is in this section that we prove Theorem 1.7 (Corollary 6.12). The next and the final section, Section 7 is devoted to the case of multigraphs.
$\mathrm {C}^*$
-modules. We begin Section 3 with a careful summary of Pimsner’s constructions and prove Theorem 1.1 (Theorem 3.9). It is in this section that we prove Theorem 1.4 (Theorem 3.14) and Theorem 1.5 (Theorem 3.16) as well. Section 4 is devoted to recalling some background on KMS states from [Reference LanceLN04] and to proving Theorem 1.6 (Theorem 4.10). In the remaining three sections, we apply the general results to the question of quantum symmetries of graphs. In Section 5, we discuss the bridge that connects the general results of the previous sections with the situation at hand. We also reprove some results on the quantum symmetries of graphs. Section 6 is devoted to a detailed study and comparison in the case of a simple, directed graph. It is in this section that we prove Theorem 1.7 (Corollary 6.12). The next and the final section, Section 7 is devoted to the case of multigraphs.
To end this Introduction, let us mention that when a first draft of the present article was being written, the preprint [Reference KatsuraKim14] was brought to our notice. The author proves a similar result to that of ours but goes on to another direction, along the lines of [Reference Hossain and GoswamiHN08, Reference KatsuraKQR15]. In particular, the author considers coactions of not-necessarily-unital Hopf
![]() $\mathrm {C}^*$
-algebras on Pimsner algebras and identifies the crossed product as the Pimsner algebra of the crossed product
$\mathrm {C}^*$
-algebras on Pimsner algebras and identifies the crossed product as the Pimsner algebra of the crossed product
![]() $\mathrm {C}^*$
-correspondence. To our surprise, our proof of Theorem 1.1 is very different to that of [Reference KatsuraKim14]. The author proves Theorem 1.1 for a general
$\mathrm {C}^*$
-correspondence. To our surprise, our proof of Theorem 1.1 is very different to that of [Reference KatsuraKim14]. The author proves Theorem 1.1 for a general
![]() $\mathrm {C}^*$
-correspondence but under an invariance condition of the Katsura ideal. Whereas, we do not require such invariance but restrict ourselves to the case when the Hilbert
$\mathrm {C}^*$
-correspondence but under an invariance condition of the Katsura ideal. Whereas, we do not require such invariance but restrict ourselves to the case when the Hilbert
![]() $\mathrm {C}^*$
-module is finitely generated and projective. There are no other overlaps with the results in [Reference KatsuraKim14].
$\mathrm {C}^*$
-module is finitely generated and projective. There are no other overlaps with the results in [Reference KatsuraKim14].
Notations and conventions
For an object X in some category,
![]() $\mathrm {id}_X$
denotes the identity morphism of X. The norm-closed linear span of a subset S of a Banach space is denoted by
$\mathrm {id}_X$
denotes the identity morphism of X. The norm-closed linear span of a subset S of a Banach space is denoted by
![]() $[S]$
. For a unital
$[S]$
. For a unital
![]() $\mathrm {C}^*$
-algebra A,
$\mathrm {C}^*$
-algebra A,
![]() $1_A$
denotes the unit element in A. For a right Hilbert A-module E,
$1_A$
denotes the unit element in A. For a right Hilbert A-module E,
![]() $\mathcal {L}(E)$
denotes the
$\mathcal {L}(E)$
denotes the
![]() $\mathrm {C}^*$
-algebra of adjointable operators on E, and
$\mathrm {C}^*$
-algebra of adjointable operators on E, and
![]() $\mathcal {K}(E)$
denotes the closed two-sided ideal of compact operators on E. The latter is the norm-closed linear span of
$\mathcal {K}(E)$
denotes the closed two-sided ideal of compact operators on E. The latter is the norm-closed linear span of
![]() $\theta _{\xi ,\eta }$
,
$\theta _{\xi ,\eta }$
,
![]() $\xi , \eta \in E$
- where
$\xi , \eta \in E$
- where
![]() $\theta _{\xi ,\eta }$
is the rank-one operator on E given by
$\theta _{\xi ,\eta }$
is the rank-one operator on E given by
![]() $\theta _{\xi ,\eta }(\zeta )=\xi \langle \eta ,\zeta \rangle $
,
$\theta _{\xi ,\eta }(\zeta )=\xi \langle \eta ,\zeta \rangle $
,
![]() $\zeta \in E$
. We denote the algebraic tensor product by
$\zeta \in E$
. We denote the algebraic tensor product by
![]() $\odot $
. Depending on the context,
$\odot $
. Depending on the context,
![]() $\otimes $
denotes the minimal tensor product of two
$\otimes $
denotes the minimal tensor product of two
![]() $\mathrm {C}^*$
-algebras, or external (also called exterior) tensor product of two Hilbert
$\mathrm {C}^*$
-algebras, or external (also called exterior) tensor product of two Hilbert
![]() $\mathrm {C}^*$
-modules. However, for the internal tensor product of a Hilbert A-module E and a Hilbert B-module F, where F is endowed with a left action of A via the
$\mathrm {C}^*$
-modules. However, for the internal tensor product of a Hilbert A-module E and a Hilbert B-module F, where F is endowed with a left action of A via the
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\phi : A \rightarrow \mathcal {L}(F)$
, is denoted by
$\phi : A \rightarrow \mathcal {L}(F)$
, is denoted by
![]() $E \otimes _{\phi } F$
. A reference for the general theory of Hilbert
$E \otimes _{\phi } F$
. A reference for the general theory of Hilbert
![]() $\mathrm {C}^*$
-modules is [Reference Laca and NeshveyevLan95].
$\mathrm {C}^*$
-modules is [Reference Laca and NeshveyevLan95].
All Hilbert
![]() $\mathrm {C}^*$
-modules considered in this paper are over unital
$\mathrm {C}^*$
-modules considered in this paper are over unital
![]() $\mathrm {C}^*$
-algebras and are assumed to be full, finitely generated, and projective.
$\mathrm {C}^*$
-algebras and are assumed to be full, finitely generated, and projective.
2 Compact quantum groups and their actions
In this section, we recall the basic definitions from the theory of compact quantum groups and their actions on
![]() $\mathrm {C}^*$
-algebras. Our reference is [Reference Neshveyev and TusetNT13] (see also [Reference Maes and Van DaeleMVD98, Reference WangWan98, Reference WoronowiczWor87]).
$\mathrm {C}^*$
-algebras. Our reference is [Reference Neshveyev and TusetNT13] (see also [Reference Maes and Van DaeleMVD98, Reference WangWan98, Reference WoronowiczWor87]).
Definition 2.1 A compact quantum group G is a pair
![]() $(\mathrm {C}(G),\Delta _G)$
consisting of a unital
$(\mathrm {C}(G),\Delta _G)$
consisting of a unital
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}(G)$
and a unital
$\mathrm {C}(G)$
and a unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\Delta _G : \mathrm {C}(G) \rightarrow \mathrm {C}(G) \otimes \mathrm {C}(G)$
satisfying the following conditions:
$\Delta _G : \mathrm {C}(G) \rightarrow \mathrm {C}(G) \otimes \mathrm {C}(G)$
satisfying the following conditions:
-
•
 $(\mathrm {id}_{\mathrm {C}(G)} \otimes \Delta _G) \circ \Delta _G=(\Delta _G \otimes \mathrm {id}_{\mathrm {C}(G)}) \circ \Delta _G$
(coassociativity);
$(\mathrm {id}_{\mathrm {C}(G)} \otimes \Delta _G) \circ \Delta _G=(\Delta _G \otimes \mathrm {id}_{\mathrm {C}(G)}) \circ \Delta _G$
(coassociativity); -
•
 $[\Delta _G(\mathrm {C}(G))(1_{\mathrm {C}(G)} \otimes \mathrm {C}(G))]=[\Delta _G(\mathrm {C}(G))(\mathrm {C}(G) \otimes 1_{\mathrm {C}(G)})]=\mathrm {C}(G) \otimes \mathrm {C}(G)$
(bisimplifiability).
$[\Delta _G(\mathrm {C}(G))(1_{\mathrm {C}(G)} \otimes \mathrm {C}(G))]=[\Delta _G(\mathrm {C}(G))(\mathrm {C}(G) \otimes 1_{\mathrm {C}(G)})]=\mathrm {C}(G) \otimes \mathrm {C}(G)$
(bisimplifiability).
Given a compact quantum group G, there is a canonical dense Hopf-
![]() $*$
-algebra
$*$
-algebra
![]() $\mathbb {C}[G] \subset \mathrm {C}(G)$
on which an antipode
$\mathbb {C}[G] \subset \mathrm {C}(G)$
on which an antipode
![]() $\kappa $
and a counit
$\kappa $
and a counit
![]() $\varepsilon $
are defined. A morphism
$\varepsilon $
are defined. A morphism
![]() $f : G_1 \rightarrow G_2$
between two compact quantum groups
$f : G_1 \rightarrow G_2$
between two compact quantum groups
![]() $G_1$
and
$G_1$
and
![]() $G_2$
is given by a
$G_2$
is given by a
![]() $*$
-homomorphism:
$*$
-homomorphism:
Such a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $f : \mathrm {C}(G_{2}) \rightarrow \mathrm {C}(G_{1})$
is also called a Hopf
$f : \mathrm {C}(G_{2}) \rightarrow \mathrm {C}(G_{1})$
is also called a Hopf
![]() $*$
-homomorphism and we will use these two terms interchangeably.
$*$
-homomorphism and we will use these two terms interchangeably.
Let G be a compact quantum group. Then there is a unique state h, called the Haar state, such that
In general, the Haar state need not be tracial but when it is, the compact quantum group G is said to be of Kac type.
Definition 2.2 Let G be a compact quantum group. A G-
![]() $\mathrm {C}^*$
-algebra is a pair
$\mathrm {C}^*$
-algebra is a pair
![]() $(A,\alpha )$
consisting of a unital
$(A,\alpha )$
consisting of a unital
![]() $\mathrm {C}^*$
-algebra A and a unital
$\mathrm {C}^*$
-algebra A and a unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\alpha : A \rightarrow A \otimes \mathrm {C}(G)$
satisfying the following conditions:
$\alpha : A \rightarrow A \otimes \mathrm {C}(G)$
satisfying the following conditions:
-
•
 $(\alpha \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \alpha =(\mathrm {id}_{A} \otimes \Delta _G)\circ \alpha $
(coassociativity);
$(\alpha \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \alpha =(\mathrm {id}_{A} \otimes \Delta _G)\circ \alpha $
(coassociativity); -
•
 $[\alpha (A)(1_{A} \otimes \mathrm {C}(G))]=A \otimes \mathrm {C}(G)$
(Podleś condition).
$[\alpha (A)(1_{A} \otimes \mathrm {C}(G))]=A \otimes \mathrm {C}(G)$
(Podleś condition).
Let G be a compact quantum group, and let
![]() $(A,\alpha )$
be a G-
$(A,\alpha )$
be a G-
![]() $\mathrm {C}^*$
-algebra. One refers to
$\mathrm {C}^*$
-algebra. One refers to
![]() $\alpha $
as the G-action on A. There is (see [Reference De CommerDC17, pp. 49–Reference Pimsner50]) a norm-dense
$\alpha $
as the G-action on A. There is (see [Reference De CommerDC17, pp. 49–Reference Pimsner50]) a norm-dense
![]() $*$
-subalgebra
$*$
-subalgebra
![]() $\mathcal {S}(A)$
of A, called the spectral subalgebra (or the Podleś subalgebra after [Reference PimsnerPod95, Theorem 1.5]), such that
$\mathcal {S}(A)$
of A, called the spectral subalgebra (or the Podleś subalgebra after [Reference PimsnerPod95, Theorem 1.5]), such that
![]() $\alpha $
restricts to yield a Hopf-
$\alpha $
restricts to yield a Hopf-
![]() $*$
-algebraic coaction
$*$
-algebraic coaction
![]() $\alpha |_{\mathcal {S}(A)} : \mathcal {S}(A) \rightarrow \mathcal {S}(A) \odot \mathbb {C}[G]$
. The G-action
$\alpha |_{\mathcal {S}(A)} : \mathcal {S}(A) \rightarrow \mathcal {S}(A) \odot \mathbb {C}[G]$
. The G-action
![]() $\alpha $
is said to be faithful if the
$\alpha $
is said to be faithful if the
![]() $*$
-algebra generated by the set
$*$
-algebra generated by the set
is norm-dense in
![]() $\mathrm {C}(G)$
. Furthermore, a G-equivariant state on A is a state
$\mathrm {C}(G)$
. Furthermore, a G-equivariant state on A is a state
![]() $\tau $
on A satisfying
$\tau $
on A satisfying
Definition 2.3 [Reference WangWan98, Definition 2.3] Let A be a unital
![]() $\mathrm {C}^*$
-algebra. A quantum automorphism group of A is a pair
$\mathrm {C}^*$
-algebra. A quantum automorphism group of A is a pair
![]() $(G,\alpha ^G)$
consisting of a compact quantum group G and a unital
$(G,\alpha ^G)$
consisting of a compact quantum group G and a unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\alpha ^G : A \rightarrow A \otimes \mathrm {C}(G)$
satisfying the following conditions:
$\alpha ^G : A \rightarrow A \otimes \mathrm {C}(G)$
satisfying the following conditions:
-
• The pair
 $(A,\alpha ^G)$
is a G-
$(A,\alpha ^G)$
is a G-
 $\mathrm {C}^*$
-algebra;
$\mathrm {C}^*$
-algebra; -
• the G-action
 $\alpha ^G$
on A is faithful;
$\alpha ^G$
on A is faithful; -
• if
 $(G',\alpha ^{G'})$
is another pair consisting of a compact quantum group
$(G',\alpha ^{G'})$
is another pair consisting of a compact quantum group
 $G'$
and a unital
$G'$
and a unital
 $*$
-homomorphism
$*$
-homomorphism
 $\alpha ^{G'} : A \rightarrow A \otimes \mathrm {C}(G')$
such that
$\alpha ^{G'} : A \rightarrow A \otimes \mathrm {C}(G')$
such that
 $(A,\alpha ^{G'})$
is a
$(A,\alpha ^{G'})$
is a
 $G'$
-
$G'$
-
 $\mathrm {C}^*$
-algebra and
$\mathrm {C}^*$
-algebra and
 $\alpha ^{G'}$
is faithful then there is a unique morphism
$\alpha ^{G'}$
is faithful then there is a unique morphism
 $f : G' \rightarrow G$
such that
$f : G' \rightarrow G$
such that
 $(\mathrm {id}_A \otimes f)\circ \alpha ^G=\alpha ^{G'}$
.
$(\mathrm {id}_A \otimes f)\circ \alpha ^G=\alpha ^{G'}$
.
Remark 2.4 In general, a quantum automorphism group may fail to exist. To ensure existence, one generally assumes that the considered actions preserve some fixed state on the
![]() $\mathrm {C}^*$
-algebra. We refrain from going into further details, instead refer the interested reader to [Reference WangWan98].
$\mathrm {C}^*$
-algebra. We refrain from going into further details, instead refer the interested reader to [Reference WangWan98].
Example 2.5 [Reference WangWan98, Theorem 3.1] Let
![]() $X_{n}$
be the space consisting of n points. The quantum automorphism group of the
$X_{n}$
be the space consisting of n points. The quantum automorphism group of the
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}(X_{n})$
is the quantum permutation group together with the permutation action, denoted by
$\mathrm {C}(X_{n})$
is the quantum permutation group together with the permutation action, denoted by
![]() $(\text {S}_{n}^{+},\alpha ^{X_n})$
. As a
$(\text {S}_{n}^{+},\alpha ^{X_n})$
. As a
![]() $\mathrm {C}^*$
-algebra,
$\mathrm {C}^*$
-algebra,
![]() $\mathrm {C}(\text {S}_{n}^{+})$
is the universal
$\mathrm {C}(\text {S}_{n}^{+})$
is the universal
![]() $\mathrm {C}^*$
algebra generated by
$\mathrm {C}^*$
algebra generated by
![]() $q_{ij}$
,
$q_{ij}$
,
![]() $i,j=1,\dots ,n$
, satisfying the following relations:
$i,j=1,\dots ,n$
, satisfying the following relations:
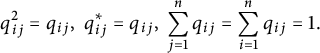 $$\begin{align*}q_{ij}^{2}=q_{ij}, \ q^*_{ij}=q_{ij}, \ \sum_{j=1}^{n}q_{ij}=\sum_{i=1}^{n}q_{ij}=1. \end{align*}$$
$$\begin{align*}q_{ij}^{2}=q_{ij}, \ q^*_{ij}=q_{ij}, \ \sum_{j=1}^{n}q_{ij}=\sum_{i=1}^{n}q_{ij}=1. \end{align*}$$
The comultiplication on the generators is given by
![]() $\Delta _{S^+_n}(q_{ij})=\sum _{k=1}^{n}q_{ik}\otimes q_{kj}$
,
$\Delta _{S^+_n}(q_{ij})=\sum _{k=1}^{n}q_{ik}\otimes q_{kj}$
,
![]() $i,j=1,\dots ,n$
. The action
$i,j=1,\dots ,n$
. The action
![]() $\alpha ^{X_n}$
is given by
$\alpha ^{X_n}$
is given by
![]() $\alpha ^{X_n}(e_j)=\sum _{i=1}^ne_i \otimes q_{ij}$
,
$\alpha ^{X_n}(e_j)=\sum _{i=1}^ne_i \otimes q_{ij}$
,
![]() $j=1,\dots ,n$
, where
$j=1,\dots ,n$
, where
![]() $e_j$
is the indicator function at the point j.
$e_j$
is the indicator function at the point j.
We end this section with one more definition and a remark.
Definition 2.6 [Reference BichonBS89, Definition 2.2] Let G be a compact quantum group, and let
![]() $(B,\beta )$
be a G-
$(B,\beta )$
be a G-
![]() $\mathrm {C}^*$
-algebra. A G-equivariant Hilbert B-module is a pair
$\mathrm {C}^*$
-algebra. A G-equivariant Hilbert B-module is a pair
![]() $(E,\lambda )$
consisting of a right Hilbert B-module E and a linear map
$(E,\lambda )$
consisting of a right Hilbert B-module E and a linear map
![]() $\lambda : E \rightarrow E \otimes \mathrm {C}(G)$
satisfying the following.
$\lambda : E \rightarrow E \otimes \mathrm {C}(G)$
satisfying the following.
-
• For all
 $b \in B$
and
$b \in B$
and
 $\xi ,\eta \in E$
,
$\xi ,\eta \in E$
,
 $\lambda (\xi b)=\lambda (\xi )\beta (b)$
and
$\lambda (\xi b)=\lambda (\xi )\beta (b)$
and
 $\langle \lambda (\xi ),\lambda (\eta ) \rangle =\beta (\langle \xi ,\eta \rangle )$
;
$\langle \lambda (\xi ),\lambda (\eta ) \rangle =\beta (\langle \xi ,\eta \rangle )$
; -
•
 $(\mathrm {id}_E \otimes \Delta _{G})\circ \lambda =(\lambda \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \lambda $
(coassociativity);
$(\mathrm {id}_E \otimes \Delta _{G})\circ \lambda =(\lambda \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \lambda $
(coassociativity); -
•
 $[\lambda (E)(1_B \otimes \mathrm {C}(G))]=E \otimes \mathrm {C}(G)$
(Podleś condition).
$[\lambda (E)(1_B \otimes \mathrm {C}(G))]=E \otimes \mathrm {C}(G)$
(Podleś condition).
Remark 2.7 Let G be a compact quantum group, let
![]() $(B,\beta )$
be a G-
$(B,\beta )$
be a G-
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\lambda )$
be a G-equivariant Hilbert B-module. One refers to
$(E,\lambda )$
be a G-equivariant Hilbert B-module. One refers to
![]() $\lambda $
as the G-action on E. There is (see [Reference VoigtVoi11, p. 1878]) a dense subspace
$\lambda $
as the G-action on E. There is (see [Reference VoigtVoi11, p. 1878]) a dense subspace
![]() $\mathcal {S}(E)$
of E, called the spectral submodule, such that
$\mathcal {S}(E)$
of E, called the spectral submodule, such that
![]() $\lambda $
restricts to yield a coaction
$\lambda $
restricts to yield a coaction
![]() $\lambda |_{\mathcal {S}(E)} : \mathcal {S}(E) \rightarrow \mathcal {S}(E) \odot \mathbb {C}[G]$
. Moreover,
$\lambda |_{\mathcal {S}(E)} : \mathcal {S}(E) \rightarrow \mathcal {S}(E) \odot \mathbb {C}[G]$
. Moreover,
![]() $\mathcal {S}(E)$
is naturally a right
$\mathcal {S}(E)$
is naturally a right
![]() $\mathcal {S}(B)$
-module and the scalar product of E restricts to an
$\mathcal {S}(B)$
-module and the scalar product of E restricts to an
![]() $\mathcal {S}(B)$
-valued scalar product on
$\mathcal {S}(B)$
-valued scalar product on
![]() $\mathcal {S}(E)$
, making
$\mathcal {S}(E)$
, making
![]() $\mathcal {S}(E)$
into a pre-Hilbert
$\mathcal {S}(E)$
into a pre-Hilbert
![]() $\mathcal {S}(B)$
-module. Furthermore, one constructs (see [Reference BichonBS89, Proposition 2.4]) a unitary operator
$\mathcal {S}(B)$
-module. Furthermore, one constructs (see [Reference BichonBS89, Proposition 2.4]) a unitary operator
![]() $V_{\lambda } : E \otimes _{\beta } (B \otimes \mathrm {C}(G)) \rightarrow E \otimes \mathrm {C}(G)$
by
$V_{\lambda } : E \otimes _{\beta } (B \otimes \mathrm {C}(G)) \rightarrow E \otimes \mathrm {C}(G)$
by
for
![]() $\xi \in E$
and
$\xi \in E$
and
![]() $x \in B \otimes \mathrm {C}(G)$
. This unitary in turn determines an action
$x \in B \otimes \mathrm {C}(G)$
. This unitary in turn determines an action
![]() $\mathrm {ad}_{\lambda } : \mathcal {K}(E) \rightarrow \mathcal {K}(E) \otimes \mathrm {C}(G)$
on
$\mathrm {ad}_{\lambda } : \mathcal {K}(E) \rightarrow \mathcal {K}(E) \otimes \mathrm {C}(G)$
on
![]() $\mathcal {K}(E)$
given by
$\mathcal {K}(E)$
given by
for
![]() $T \in \mathcal {K}(E)$
, making
$T \in \mathcal {K}(E)$
, making
![]() $(\mathcal {K}(E),\mathrm {ad}_{\lambda })$
into a G-
$(\mathcal {K}(E),\mathrm {ad}_{\lambda })$
into a G-
![]() $\mathrm {C}^*$
-algebra. Setting
$\mathrm {C}^*$
-algebra. Setting
![]() $T=\theta _{\xi ,\eta }$
for
$T=\theta _{\xi ,\eta }$
for
![]() $\xi ,\eta \in E$
, one obtains
$\xi ,\eta \in E$
, one obtains
![]() $\mathrm {ad}_{\lambda }(\theta _{\xi ,\eta })=\lambda (\xi )\lambda (\eta )^*=\theta _{\lambda (\xi ),\lambda (\eta )}$
.
$\mathrm {ad}_{\lambda }(\theta _{\xi ,\eta })=\lambda (\xi )\lambda (\eta )^*=\theta _{\lambda (\xi ),\lambda (\eta )}$
.
3
 $\mathrm {C}^*$
-correspondences and Pimsner algebras
$\mathrm {C}^*$
-correspondences and Pimsner algebras
In this section, after gathering some preliminaries on
![]() $\mathrm {C}^*$
-correspondences, and on Pimsner algebras, we prove that for a compact quantum group G, a G-equivariant
$\mathrm {C}^*$
-correspondences, and on Pimsner algebras, we prove that for a compact quantum group G, a G-equivariant
![]() $\mathrm {C}^*$
-correspondence naturally gives rise to a G-
$\mathrm {C}^*$
-correspondence naturally gives rise to a G-
![]() $\mathrm {C}^*$
-algebra structure on the Pimsner algebra. We provide necessary and sufficient conditions under which it is guaranteed that a G-
$\mathrm {C}^*$
-algebra structure on the Pimsner algebra. We provide necessary and sufficient conditions under which it is guaranteed that a G-
![]() $\mathrm {C}^*$
-algebra structure on the Pimsner algebra arises in this way. For the basic definitions, our reference is [Reference KatsoulisKat04b] (see also [Reference KatsuraKPW98, Reference Pedersen, Eilers and OlesenPim97]).
$\mathrm {C}^*$
-algebra structure on the Pimsner algebra arises in this way. For the basic definitions, our reference is [Reference KatsoulisKat04b] (see also [Reference KatsuraKPW98, Reference Pedersen, Eilers and OlesenPim97]).
Definition 3.1 Let A be a unital
![]() $\mathrm {C}^*$
-algebra. A
$\mathrm {C}^*$
-algebra. A
![]() $\mathrm {C}^*$
-correspondence over A is a pair
$\mathrm {C}^*$
-correspondence over A is a pair
![]() $(E,\phi )$
, consisting of a right Hilbert A-module E and a unital
$(E,\phi )$
, consisting of a right Hilbert A-module E and a unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\phi :A\rightarrow \mathcal {L}(E)$
from the
$\phi :A\rightarrow \mathcal {L}(E)$
from the
![]() $\mathrm {C}^*$
-algebra A to the
$\mathrm {C}^*$
-algebra A to the
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathcal {L}(E)$
of adjointable operators on E.
$\mathcal {L}(E)$
of adjointable operators on E.
Remark 3.2 We remark that it is not customary to assume
![]() $\phi $
to be unital. But it is easy to see that we lose no generality assuming this. For the justification, we urge the reader to see Remark 3.7.
$\phi $
to be unital. But it is easy to see that we lose no generality assuming this. For the justification, we urge the reader to see Remark 3.7.
Definition 3.3 Let A be a unital
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi )$
be a
$(E,\phi )$
be a
![]() $\mathrm {C}^*$
-correspondence over A. A representation of the
$\mathrm {C}^*$
-correspondence over A. A representation of the
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(E,\phi )$
on a unital
$(E,\phi )$
on a unital
![]() $\mathrm {C}^*$
-algebra B is a pair
$\mathrm {C}^*$
-algebra B is a pair
![]() $(t,\pi )$
, consisting of a linear map
$(t,\pi )$
, consisting of a linear map
![]() $t : E \rightarrow B$
and a unital
$t : E \rightarrow B$
and a unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi : A \rightarrow B$
such that:
$\pi : A \rightarrow B$
such that:
-
•
 $t(\xi )^*t(\eta )=\pi (\langle \xi ,\eta \rangle )$
for all
$t(\xi )^*t(\eta )=\pi (\langle \xi ,\eta \rangle )$
for all
 $\xi ,\eta \in E$
;
$\xi ,\eta \in E$
; -
•
 $t(\phi (a)\xi )=\pi (a)t(\xi )$
for all
$t(\phi (a)\xi )=\pi (a)t(\xi )$
for all
 $a \in A$
and all
$a \in A$
and all
 $\xi \in E$
.
$\xi \in E$
.
It is a fact that for such a representation
![]() $(\pi ,t)$
of the
$(\pi ,t)$
of the
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(E,\phi )$
on the
$(E,\phi )$
on the
![]() $\mathrm {C}^*$
-algebra B,
$\mathrm {C}^*$
-algebra B,
![]() $t(\xi a)=t(\xi )\pi (a)$
for all
$t(\xi a)=t(\xi )\pi (a)$
for all
![]() $\xi \in E$
, and
$\xi \in E$
, and
![]() $a\in A$
. Furthermore, there is a well-defined unital
$a\in A$
. Furthermore, there is a well-defined unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\psi _{t} : {\mathcal K}(E) \rightarrow B$
such that
$\psi _{t} : {\mathcal K}(E) \rightarrow B$
such that
![]() $\psi _{t}(\theta _{\xi ,\eta })=t(\xi )t(\eta )^*$
, for
$\psi _{t}(\theta _{\xi ,\eta })=t(\xi )t(\eta )^*$
, for
![]() $\xi , \eta \in E$
. Moreover, we have
$\xi , \eta \in E$
. Moreover, we have
![]() $\pi (a)\psi _t(k)=\psi _t(\phi (a)k)$
and
$\pi (a)\psi _t(k)=\psi _t(\phi (a)k)$
and
![]() $\psi _{t}(k)t(\xi )=t(k\xi )$
for all
$\psi _{t}(k)t(\xi )=t(k\xi )$
for all
![]() $a \in A$
,
$a \in A$
,
![]() $k \in {\mathcal K}(E)$
, and
$k \in {\mathcal K}(E)$
, and
![]() $\xi \in E$
.
$\xi \in E$
.
Definition 3.4 Let A be a unital
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi )$
be a
$(E,\phi )$
be a
![]() $\mathrm {C}^*$
-correspondence over A. A representation
$\mathrm {C}^*$
-correspondence over A. A representation
![]() $(t,\pi )$
of
$(t,\pi )$
of
![]() $(E,\phi )$
on a unital
$(E,\phi )$
on a unital
![]() $\mathrm {C}^*$
-algebra B is said to be covariant if
$\mathrm {C}^*$
-algebra B is said to be covariant if
![]() $\psi _{t}(\phi (a))=\pi (a)$
for all
$\psi _{t}(\phi (a))=\pi (a)$
for all
![]() $a \in (\ker \phi )^{\perp }$
, where
$a \in (\ker \phi )^{\perp }$
, where
Remark 3.5 We remark that by our standing assumption, E is finitely generated and therefore
![]() $\mathcal {K}(E)=\mathcal {L}(E)$
, which also implies that
$\mathcal {K}(E)=\mathcal {L}(E)$
, which also implies that
![]() $\phi ^{-1}(\mathcal {K}(E))$
coincides with the whole of A. Therefore, the so-called Katsura ideal
$\phi ^{-1}(\mathcal {K}(E))$
coincides with the whole of A. Therefore, the so-called Katsura ideal
![]() $J_E$
, which is defined to be
$J_E$
, which is defined to be
is nothing but
![]() $(\ker \phi )^{\perp }$
. Moreover, it is proved in [Reference KatsuraKPW98] that one can restrict to covariant representations
$(\ker \phi )^{\perp }$
. Moreover, it is proved in [Reference KatsuraKPW98] that one can restrict to covariant representations
![]() $(t,\pi )$
on unital
$(t,\pi )$
on unital
![]() $\mathrm {C}^*$
-algebras B with
$\mathrm {C}^*$
-algebras B with
![]() $\pi $
unital, to define the Pimsner algebra
$\pi $
unital, to define the Pimsner algebra
![]() $\mathcal {O}_E$
, assuming
$\mathcal {O}_E$
, assuming
![]() $\phi $
to be isometric, which is taken care of by the appearance of
$\phi $
to be isometric, which is taken care of by the appearance of
![]() $(\ker \phi )^{\perp }$
in the definition of covariance above.
$(\ker \phi )^{\perp }$
in the definition of covariance above.
Definition 3.6 Let A be a unital
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi )$
be a
$(E,\phi )$
be a
![]() $\mathrm {C}^*$
-correspondence over A. The Pimsner algebra associated with the
$\mathrm {C}^*$
-correspondence over A. The Pimsner algebra associated with the
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(E,\phi )$
is the unital
$(E,\phi )$
is the unital
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathcal {O}_E$
satisfying the following.
$\mathcal {O}_E$
satisfying the following.
-
• There is a covariant representation
 $(k_E,k_A)$
of the
$(k_E,k_A)$
of the
 $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
 $(E,\phi )$
on the
$(E,\phi )$
on the
 $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
 ${\mathcal O}_{E}$
, called the universal covariant representation.
${\mathcal O}_{E}$
, called the universal covariant representation. -
• For any covariant representation
 $(t,\pi )$
of the
$(t,\pi )$
of the
 $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
 $(E,\phi )$
on a unital
$(E,\phi )$
on a unital
 $\mathrm {C}^*$
-algebra B, there is a unique unital
$\mathrm {C}^*$
-algebra B, there is a unique unital
 $*$
-homomorphism
$*$
-homomorphism
 $t \times \pi : {\mathcal O}_{E} \rightarrow B$
, called the integrated form of
$t \times \pi : {\mathcal O}_{E} \rightarrow B$
, called the integrated form of
 $(t,\pi )$
, such that
$(t,\pi )$
, such that  $$\begin{align*}(t \times \pi)\circ k_E=t, \ (t \times \pi)\circ k_A=\pi.\end{align*}$$
$$\begin{align*}(t \times \pi)\circ k_E=t, \ (t \times \pi)\circ k_A=\pi.\end{align*}$$
Remark 3.7 As mentioned above, we lose no generality by assuming
![]() $\phi $
to be unital in our definition of a
$\phi $
to be unital in our definition of a
![]() $\mathrm {C}^*$
-correspondence. Indeed, letting the projection
$\mathrm {C}^*$
-correspondence. Indeed, letting the projection
![]() $\phi (1)$
to be p, for a representation
$\phi (1)$
to be p, for a representation
![]() $(t,\pi )$
, we have
$(t,\pi )$
, we have
implying that t vanishes identically on the submodule
![]() $(1-p)E$
. In particular, for the universal representation
$(1-p)E$
. In particular, for the universal representation
![]() $(k_E,k_A)$
,
$(k_E,k_A)$
,
![]() $k_E$
vanishes identically on
$k_E$
vanishes identically on
![]() $(1-p)E$
and so we may restrict ourselves to the submodule
$(1-p)E$
and so we may restrict ourselves to the submodule
![]() $pE$
. But
$pE$
. But
![]() $\phi (1)$
is the identity operator on this submodule. Therefore, we can and do assume
$\phi (1)$
is the identity operator on this submodule. Therefore, we can and do assume
![]() $\phi $
to be unital.
$\phi $
to be unital.
By the universality, for each
![]() $z\in \mathbb {T}$
, there is a unital
$z\in \mathbb {T}$
, there is a unital
![]() $*$
-automorphism
$*$
-automorphism
![]() $\gamma _{z} : {\mathcal O}_{E} \rightarrow {\mathcal O}_{E}$
such that
$\gamma _{z} : {\mathcal O}_{E} \rightarrow {\mathcal O}_{E}$
such that
![]() $\gamma _{z}(k_A(a))=k_A(a)$
for all
$\gamma _{z}(k_A(a))=k_A(a)$
for all
![]() $a \in A$
and
$a \in A$
and
![]() $\gamma _{z}(k_E(\xi ))=zk_E(\xi )$
for all
$\gamma _{z}(k_E(\xi ))=zk_E(\xi )$
for all
![]() $\xi \in E$
. One observes that
$\xi \in E$
. One observes that
![]() $z \mapsto \gamma _z$
is strongly continuous and the resulting action of
$z \mapsto \gamma _z$
is strongly continuous and the resulting action of
![]() $\mathbb {T}$
,
$\mathbb {T}$
,
![]() $\gamma : \mathcal {O}_E \rightarrow \mathcal {O}_E \otimes \mathrm {C}(\mathbb {T})$
is called the gauge action.
$\gamma : \mathcal {O}_E \rightarrow \mathcal {O}_E \otimes \mathrm {C}(\mathbb {T})$
is called the gauge action.
Definition 3.8 [Reference BichonBS89, Definition 2.9] Let G be a compact quantum group, and let
![]() $(A,\alpha )$
be a G-
$(A,\alpha )$
be a G-
![]() $\mathrm {C}^*$
-algebra. A G-equivariant
$\mathrm {C}^*$
-algebra. A G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
is a triple
$(A,\alpha )$
is a triple
![]() $(E,\phi ,\lambda )$
, consisting of a right Hilbert A-module E, a unital
$(E,\phi ,\lambda )$
, consisting of a right Hilbert A-module E, a unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\phi : A \rightarrow \mathcal {L}(E)$
and a linear map
$\phi : A \rightarrow \mathcal {L}(E)$
and a linear map
![]() $\lambda : E \rightarrow E \otimes \mathrm {C}(G)$
satisfying the following.
$\lambda : E \rightarrow E \otimes \mathrm {C}(G)$
satisfying the following.
-
• The pair
 $(E,\phi )$
is a
$(E,\phi )$
is a
 $\mathrm {C}^*$
-correspondence over A.
$\mathrm {C}^*$
-correspondence over A. -
• The pair
 $(E,\lambda )$
is a G-equivariant Hilbert A-module over the G-
$(E,\lambda )$
is a G-equivariant Hilbert A-module over the G-
 $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
 $(A,\alpha )$
(Definition 2.6).
$(A,\alpha )$
(Definition 2.6). -
• The
 $*$
-homomorphism
$*$
-homomorphism
 $\phi : A \rightarrow \mathcal {L}(E)$
is G-equivariant, i.e.,
$\phi : A \rightarrow \mathcal {L}(E)$
is G-equivariant, i.e.,  $$\begin{align*}(\phi \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(a)=V_{\lambda}(\phi(a) \otimes \mathrm{id})V^*_{\lambda}, \text{ for } a \in A.\end{align*}$$
$$\begin{align*}(\phi \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(a)=V_{\lambda}(\phi(a) \otimes \mathrm{id})V^*_{\lambda}, \text{ for } a \in A.\end{align*}$$
By [Reference BichonBS89, p. 693], the last condition is equivalent to
-
•
 $\lambda (\phi (a)\xi )=(\phi \otimes \mathrm {id}_{\mathrm {C}(G)})(\alpha (a))\lambda (\xi )$
for
$\lambda (\phi (a)\xi )=(\phi \otimes \mathrm {id}_{\mathrm {C}(G)})(\alpha (a))\lambda (\xi )$
for
 $\xi \in E$
and
$\xi \in E$
and
 $a \in A$
.
$a \in A$
.
Theorem 3.9 Let G be a compact quantum group, let
![]() $(A,\alpha )$
be a G-
$(A,\alpha )$
be a G-
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi ,\lambda )$
be a G-equivariant
$(E,\phi ,\lambda )$
be a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
. Then there is a unique unital
$(A,\alpha )$
. Then there is a unique unital
![]() $*$
-homomorphism
$*$
-homomorphism
such that
Furthermore, the pair
![]() $(\mathcal {O}_E,\omega )$
satisfies the conditions in Definition 2.2, making
$(\mathcal {O}_E,\omega )$
satisfies the conditions in Definition 2.2, making
![]() $(\mathcal {O}_E,\omega )$
into a G-
$(\mathcal {O}_E,\omega )$
into a G-
![]() $\mathrm {C}^*$
-algebra.
$\mathrm {C}^*$
-algebra.
Proof We define
![]() $t : E \rightarrow {\mathcal O}_{E} \otimes \mathrm {C}(G)$
and
$t : E \rightarrow {\mathcal O}_{E} \otimes \mathrm {C}(G)$
and
![]() $\pi : A \rightarrow {\mathcal O}_{E}\otimes \mathrm {C}(G)$
by the following:
$\pi : A \rightarrow {\mathcal O}_{E}\otimes \mathrm {C}(G)$
by the following:
We claim that
![]() $(t,\pi )$
is a covariant representation of the
$(t,\pi )$
is a covariant representation of the
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(E,\phi )$
over A. Now, for
$(E,\phi )$
over A. Now, for
![]() $\xi ,\eta \in E$
, we have
$\xi ,\eta \in E$
, we have
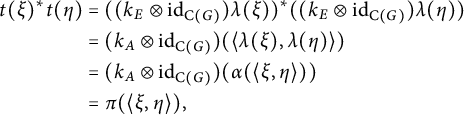 $$ \begin{align*} \begin{aligned} t(\xi)^*t(\eta)={}&((k_E \otimes \mathrm{id}_{\mathrm{C}(G)}) \lambda(\xi))^*((k_E \otimes \mathrm{id}_{\mathrm{C}(G)}) \lambda(\eta))\\ ={}&(k_A \otimes \mathrm{id}_{\mathrm{C}(G)})(\langle \lambda(\xi),\lambda(\eta) \rangle)\\ ={}&(k_A \otimes \mathrm{id}_{\mathrm{C}(G)})(\alpha(\langle \xi,\eta \rangle))\\ ={}&\pi(\langle \xi,\eta \rangle), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} t(\xi)^*t(\eta)={}&((k_E \otimes \mathrm{id}_{\mathrm{C}(G)}) \lambda(\xi))^*((k_E \otimes \mathrm{id}_{\mathrm{C}(G)}) \lambda(\eta))\\ ={}&(k_A \otimes \mathrm{id}_{\mathrm{C}(G)})(\langle \lambda(\xi),\lambda(\eta) \rangle)\\ ={}&(k_A \otimes \mathrm{id}_{\mathrm{C}(G)})(\alpha(\langle \xi,\eta \rangle))\\ ={}&\pi(\langle \xi,\eta \rangle), \end{aligned} \end{align*} $$
where the second equality is by Definition 3.3; and the third equality is by Definition 2.6. Again, for
![]() $a \in A$
and
$a \in A$
and
![]() $\xi \in E$
, we have
$\xi \in E$
, we have
 $$ \begin{align*} \begin{aligned} t(\phi(a)\xi)={}&(k_E \otimes \mathrm{id}_{\mathrm{C}(G)}) \lambda(\phi(a).\xi)\\ ={}&(k_E \otimes \mathrm{id}_{\mathrm{C}(G)})(\phi \otimes \mathrm{id}_{\mathrm{C}(G)})(\alpha(a))\lambda(\xi)\\ ={}&(k_A \otimes \mathrm{id}_{\mathrm{C}(G)})(\alpha(a))(k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi)\\ ={}&\pi(a)t(\xi), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} t(\phi(a)\xi)={}&(k_E \otimes \mathrm{id}_{\mathrm{C}(G)}) \lambda(\phi(a).\xi)\\ ={}&(k_E \otimes \mathrm{id}_{\mathrm{C}(G)})(\phi \otimes \mathrm{id}_{\mathrm{C}(G)})(\alpha(a))\lambda(\xi)\\ ={}&(k_A \otimes \mathrm{id}_{\mathrm{C}(G)})(\alpha(a))(k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi)\\ ={}&\pi(a)t(\xi), \end{aligned} \end{align*} $$
where the second equality is by Definition 2.6; and the third equality is by Definition 3.6. Thus,
![]() $(t,\pi )$
is a representation of the
$(t,\pi )$
is a representation of the
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(E,\phi )$
over A. We recall that there is a unital
$(E,\phi )$
over A. We recall that there is a unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\psi _t : {\mathcal K}(E) \rightarrow {\mathcal O}_{E} \otimes \mathrm {C}(G)$
given by
$\psi _t : {\mathcal K}(E) \rightarrow {\mathcal O}_{E} \otimes \mathrm {C}(G)$
given by
![]() $\psi _t(\theta _{\xi ,\eta })=t(\xi )t(\eta )^{\ast }$
such that
$\psi _t(\theta _{\xi ,\eta })=t(\xi )t(\eta )^{\ast }$
such that
![]() $\psi _t(k)t(\xi )=t(k\xi )$
for all
$\psi _t(k)t(\xi )=t(k\xi )$
for all
![]() $\xi \in E$
and
$\xi \in E$
and
![]() $k \in \mathcal {K}(E)$
; in particular, we have
$k \in \mathcal {K}(E)$
; in particular, we have
![]() $\psi _t(\phi (a))t(\xi )=t(\phi (a)\xi )=\pi (a)t(\xi )$
for all
$\psi _t(\phi (a))t(\xi )=t(\phi (a)\xi )=\pi (a)t(\xi )$
for all
![]() $\xi \in E$
and all
$\xi \in E$
and all
![]() $a \in A$
. Since
$a \in A$
. Since
![]() $[\lambda (E)(1_A \otimes \mathrm {C}(G))]=E \otimes \mathrm {C}(G)$
, using the linearity and the continuity of the maps involved, we get for all
$[\lambda (E)(1_A \otimes \mathrm {C}(G))]=E \otimes \mathrm {C}(G)$
, using the linearity and the continuity of the maps involved, we get for all
![]() $\xi \in E$
and
$\xi \in E$
and
![]() $a \in A$
,
$a \in A$
,
Consequently, for any
![]() $\xi ,\eta \in E$
, and
$\xi ,\eta \in E$
, and
![]() $a \in A$
, we have
$a \in A$
, we have
i.e.,
So again by linearity and continuity of the maps involved, we get
for all
![]() $k \in \mathcal {K}(E)$
. As the
$k \in \mathcal {K}(E)$
. As the
![]() $\mathrm {C}^*$
-algebra A is unital and E is finitely generated,
$\mathrm {C}^*$
-algebra A is unital and E is finitely generated,
![]() ${\mathcal K}(E)={\mathcal L}(E)$
and since
${\mathcal K}(E)={\mathcal L}(E)$
and since
![]() $\psi _{t}$
is a unital
$\psi _{t}$
is a unital
![]() $*$
-homomorphism, we obtain, by plugging
$*$
-homomorphism, we obtain, by plugging
![]() $k=\mathrm {id}_E \in {\mathcal L}(E)$
in the identity above,
$k=\mathrm {id}_E \in {\mathcal L}(E)$
in the identity above,
for all
![]() $a \in A$
, which in particular, shows that
$a \in A$
, which in particular, shows that
![]() $(t,\pi )$
is a covariant representation of the
$(t,\pi )$
is a covariant representation of the
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(E,\phi )$
over A on the unital
$(E,\phi )$
over A on the unital
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() ${\mathcal O}_{E} \otimes \mathrm {C}(G)$
. Therefore, by the universality of
${\mathcal O}_{E} \otimes \mathrm {C}(G)$
. Therefore, by the universality of
![]() ${\mathcal O}_{E}$
, we get a necessarily unique
${\mathcal O}_{E}$
, we get a necessarily unique
![]() $*$
-homomorphism
$*$
-homomorphism
such that
completing the first part of the theorem. To see that
![]() $(\mathcal {O}_E,\omega )$
is indeed a G-
$(\mathcal {O}_E,\omega )$
is indeed a G-
![]() $\mathrm {C}^*$
-algebra, we start with the coassociativity of
$\mathrm {C}^*$
-algebra, we start with the coassociativity of
![]() $\omega $
, i.e.,
$\omega $
, i.e.,
![]() $(\omega \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \omega =(\mathrm {id}_{\mathcal {O}_E} \otimes \Delta _G)\circ \omega $
. Again, by universality (and uniqueness), it suffices to show that the two
$(\omega \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \omega =(\mathrm {id}_{\mathcal {O}_E} \otimes \Delta _G)\circ \omega $
. Again, by universality (and uniqueness), it suffices to show that the two
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $(\omega \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \omega $
and
$(\omega \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \omega $
and
![]() $(\mathrm {id}_{\mathcal {O}_E} \otimes \Delta _G)\circ \omega $
agree on the images
$(\mathrm {id}_{\mathcal {O}_E} \otimes \Delta _G)\circ \omega $
agree on the images
![]() $k_E(E)$
and
$k_E(E)$
and
![]() $k_A(A)$
, i.e.,
$k_A(A)$
, i.e.,
and
However, using
respectively, we see that we are reduced to the coassociativity of
![]() $\lambda $
and
$\lambda $
and
![]() $\alpha $
, respectively. Thus
$\alpha $
, respectively. Thus
![]() $\omega $
is indeed coassociative. For the Podleś condition, we consider the set
$\omega $
is indeed coassociative. For the Podleś condition, we consider the set
Since
![]() $[\lambda (E)(1_A \otimes \mathrm {C}(G))]=E \otimes \mathrm {C}(G)$
and
$[\lambda (E)(1_A \otimes \mathrm {C}(G))]=E \otimes \mathrm {C}(G)$
and
![]() $[\alpha (A)(1_A \otimes \mathrm {C}(G))]=A \otimes \mathrm {C}(G)$
, we see that for each
$[\alpha (A)(1_A \otimes \mathrm {C}(G))]=A \otimes \mathrm {C}(G)$
, we see that for each
![]() $\xi \in E$
,
$\xi \in E$
,
![]() $k_E(\xi ) \in S$
and for each
$k_E(\xi ) \in S$
and for each
![]() $a \in A$
,
$a \in A$
,
![]() $k_A(a) \in S$
. Let x and y be in S. Then we see that
$k_A(a) \in S$
. Let x and y be in S. Then we see that
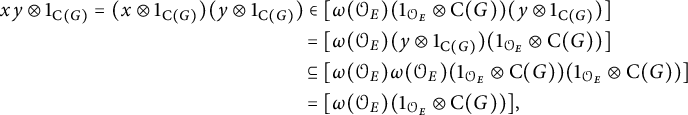 $$ \begin{align*} \begin{aligned} xy \otimes 1_{\mathrm{C}(G)}=(x \otimes 1_{\mathrm{C}(G)})(y \otimes 1_{\mathrm{C}(G)}) \in{}& [\omega(\mathcal{O}_E)(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))(y \otimes 1_{\mathrm{C}(G)})]\\ ={}&[\omega(\mathcal{O}_E)(y \otimes 1_{\mathrm{C}(G)})(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))]\\ \subseteq{}&[\omega(\mathcal{O}_E)\omega(\mathcal{O}_E)(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))]\\ ={}&[\omega(\mathcal{O}_E)(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))], \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} xy \otimes 1_{\mathrm{C}(G)}=(x \otimes 1_{\mathrm{C}(G)})(y \otimes 1_{\mathrm{C}(G)}) \in{}& [\omega(\mathcal{O}_E)(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))(y \otimes 1_{\mathrm{C}(G)})]\\ ={}&[\omega(\mathcal{O}_E)(y \otimes 1_{\mathrm{C}(G)})(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))]\\ \subseteq{}&[\omega(\mathcal{O}_E)\omega(\mathcal{O}_E)(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))]\\ ={}&[\omega(\mathcal{O}_E)(1_{\mathcal{O}_E} \otimes \mathrm{C}(G))], \end{aligned} \end{align*} $$
i.e., S is closed under multiplication. But S contains, as shown above,
![]() $k_E(E)$
and
$k_E(E)$
and
![]() $k_A(A)$
; thus again by universality, S equals
$k_A(A)$
; thus again by universality, S equals
![]() $\mathcal {O}_E.$
Therefore,
$\mathcal {O}_E.$
Therefore,
![]() $(\mathcal {O}_E,\omega )$
is indeed a G-
$(\mathcal {O}_E,\omega )$
is indeed a G-
![]() $\mathrm {C}^*$
-algebra and this completes the proof.
$\mathrm {C}^*$
-algebra and this completes the proof.
Remarks 3.10
-
• We do not need the fact that the Hilbert
 $\mathrm {C}^*$
-module E be full in the above proof.
$\mathrm {C}^*$
-module E be full in the above proof. -
• When the first draft of the present article was being prepared, the preprint [Reference KatsuraKim14] was brought to our notice. In [Reference KatsuraKim14], the author proves Theorem 3.9 in greater generality, under an invariance assumption of the Katsura ideal
 $J_E$
, however. We do not need such an assumption, and as such our proof is an improvement over the proof given in [Reference KatsuraKim14]. On the other hand, we require the Hilbert
$J_E$
, however. We do not need such an assumption, and as such our proof is an improvement over the proof given in [Reference KatsuraKim14]. On the other hand, we require the Hilbert
 $\mathrm {C}^*$
-module E to be finitely generated.
$\mathrm {C}^*$
-module E to be finitely generated. -
• We prove a somewhat stronger statement than the covariance of
 $(t,\pi )$
, in the notations of the above proof, namely, hinging heavily on the unitality of
$(t,\pi )$
, in the notations of the above proof, namely, hinging heavily on the unitality of $$\begin{align*}\psi_t \circ \phi=\pi,\end{align*}$$
$$\begin{align*}\psi_t \circ \phi=\pi,\end{align*}$$
 $\mathrm {C}(G)$
and of
$\mathrm {C}(G)$
and of
 $\mathcal {K}(E)$
.
$\mathcal {K}(E)$
.
Definition 3.11 Let A be a unital
![]() $\mathrm {C}^*$
-algebra, let
$\mathrm {C}^*$
-algebra, let
![]() $(E,\phi )$
be a
$(E,\phi )$
be a
![]() $\mathrm {C}^*$
-correspondence over A, and let G be a compact quantum group. An action
$\mathrm {C}^*$
-correspondence over A, and let G be a compact quantum group. An action
![]() $\rho : \mathcal {O}_E \rightarrow \mathcal {O}_E \otimes \mathrm {C}(G)$
of G on the Pimsner algebra
$\rho : \mathcal {O}_E \rightarrow \mathcal {O}_E \otimes \mathrm {C}(G)$
of G on the Pimsner algebra
![]() $\mathcal {O}_E$
is said to be a lift if there are G-actions
$\mathcal {O}_E$
is said to be a lift if there are G-actions
![]() $\alpha $
and
$\alpha $
and
![]() $\lambda $
on A and on E, respectively, such that the following are satisfied.
$\lambda $
on A and on E, respectively, such that the following are satisfied.
-
•
 $(A,\alpha )$
is a G-
$(A,\alpha )$
is a G-
 $\mathrm {C}^*$
-algebra.
$\mathrm {C}^*$
-algebra. -
•
 $(E,\phi ,\lambda )$
is a G-equivariant
$(E,\phi ,\lambda )$
is a G-equivariant
 $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
 $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
 $(A,\alpha )$
.
$(A,\alpha )$
. -
•
 $\rho $
coincides with
$\rho $
coincides with
 $\omega $
as in Theorem 3.9.
$\omega $
as in Theorem 3.9.
Thanks to the previous theorem, any action of a compact quantum group G on a
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(E,\phi )$
over a
$(E,\phi )$
over a
![]() $\mathrm {C}^*$
-algebra A automatically lifts to an action on the corresponding Pimsner algebra
$\mathrm {C}^*$
-algebra A automatically lifts to an action on the corresponding Pimsner algebra
![]() $\mathcal {O}_E$
. However, we cannot expect all actions on the Pimsner algebra to be lifts of actions on the underlying
$\mathcal {O}_E$
. However, we cannot expect all actions on the Pimsner algebra to be lifts of actions on the underlying
![]() $\mathrm {C}^*$
-correspondence in the sense of Definition 3.11. One may look for a characterization of all the actions on the Pimsner algebra that are lifts of coactions on the underlying
$\mathrm {C}^*$
-correspondence in the sense of Definition 3.11. One may look for a characterization of all the actions on the Pimsner algebra that are lifts of coactions on the underlying
![]() $\mathrm {C}^*$
-correspondence. In general, however, it seems to be a hard problem to obtain such a characterization. We are able to make some progress in this direction. Let us start with a necessary condition.
$\mathrm {C}^*$
-correspondence. In general, however, it seems to be a hard problem to obtain such a characterization. We are able to make some progress in this direction. Let us start with a necessary condition.
Proposition 3.12 Let G be a compact quantum group, let
![]() $(A,\alpha )$
be a G-
$(A,\alpha )$
be a G-
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi ,\lambda )$
be a G-equivariant
$(E,\phi ,\lambda )$
be a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over A. Then for all
$\mathrm {C}^*$
-correspondence over A. Then for all
![]() $z \in \mathbb {T}$
,
$z \in \mathbb {T}$
,
where
![]() $\omega $
as in Theorem 3.9, and
$\omega $
as in Theorem 3.9, and
![]() $\gamma $
is the gauge action on
$\gamma $
is the gauge action on
![]() $\mathcal {O}_E$
.
$\mathcal {O}_E$
.
Proof We begin by observing that it suffices to show, by universality (and uniqueness), that the two
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $(\gamma _z \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \omega $
and
$(\gamma _z \otimes \mathrm {id}_{\mathrm {C}(G)})\circ \omega $
and
![]() $\omega \circ \gamma _z$
agree on
$\omega \circ \gamma _z$
agree on
![]() $k_E(E)$
and
$k_E(E)$
and
![]() $k_A(A)$
, i.e.,
$k_A(A)$
, i.e.,
and
However, using
respectively, and the explicit form of
![]() $\gamma $
provided after Definition 3.6, we see that the above two identities are indeed satisfied. This completes the proof.
$\gamma $
provided after Definition 3.6, we see that the above two identities are indeed satisfied. This completes the proof.
Thus it makes sense to single out the class of actions on the Pimsner algebra that satisfy Proposition 3.12 and allows us to make the following definition.
Definition 3.13 Let A be a unital
![]() $\mathrm {C}^*$
-algebra, let
$\mathrm {C}^*$
-algebra, let
![]() $(E,\phi )$
be a
$(E,\phi )$
be a
![]() $\mathrm {C}^*$
-correspondence over A, and let G be a compact quantum group. An action
$\mathrm {C}^*$
-correspondence over A, and let G be a compact quantum group. An action
![]() $\rho : \mathcal {O}_E \rightarrow \mathcal {O}_E \otimes \mathrm {C}(G)$
of G on the Pimsner algebra
$\rho : \mathcal {O}_E \rightarrow \mathcal {O}_E \otimes \mathrm {C}(G)$
of G on the Pimsner algebra
![]() $\mathcal {O}_E$
is said to be gauge-equivariant if, for all
$\mathcal {O}_E$
is said to be gauge-equivariant if, for all
![]() $z \in \mathbb {T}$
,
$z \in \mathbb {T}$
,
where
![]() $\gamma $
is the gauge action on
$\gamma $
is the gauge action on
![]() $\mathcal {O}_E$
.
$\mathcal {O}_E$
.
The gauge-equivariance is not sufficient though. To produce an example where gauge-equivariance of an action on the Pimsner algebra does not imply that the action is a lift of an action on the
![]() $\mathrm {C}^*$
-correspondence in the sense of Definition 3.11, we recall that the Cuntz algebra
$\mathrm {C}^*$
-correspondence in the sense of Definition 3.11, we recall that the Cuntz algebra
![]() ${\mathcal O}_{n}$
may be seen as the Pimsner algebra arising from the
${\mathcal O}_{n}$
may be seen as the Pimsner algebra arising from the
![]() $\mathrm {C}^*$
-correspondence of its graph. Denoting the generating partial isometries of
$\mathrm {C}^*$
-correspondence of its graph. Denoting the generating partial isometries of
![]() ${\mathcal O}_{n}$
by
${\mathcal O}_{n}$
by
![]() $S_{i}$
, for
$S_{i}$
, for
![]() $i=1,\dots ,n$
, it is clear that for any action
$i=1,\dots ,n$
, it is clear that for any action
![]() $\rho $
of a compact quantum group G to be a lift of an action on the
$\rho $
of a compact quantum group G to be a lift of an action on the
![]() $\mathrm {C}^*$
-correspondence coming from the graph,
$\mathrm {C}^*$
-correspondence coming from the graph,
![]() $\rho $
has to be “linear,” in the sense that
$\rho $
has to be “linear,” in the sense that
![]() $\rho (S_{j})=\sum _{i=1}^n S_{i} \otimes q_{ij}$
for some
$\rho (S_{j})=\sum _{i=1}^n S_{i} \otimes q_{ij}$
for some
![]() $q_{ij} \in \mathrm {C}(G)$
,
$q_{ij} \in \mathrm {C}(G)$
,
![]() $j=1,\dots ,n$
. With this observation in hand, we shall produce a “non-linear,” gauge-equivariant action of the compact (quantum) group
$j=1,\dots ,n$
. With this observation in hand, we shall produce a “non-linear,” gauge-equivariant action of the compact (quantum) group
![]() $\mathbb {T}^n=(\mathrm {C}(\mathbb {T}^{n}),\Delta _{\mathbb {T}^n})$
on
$\mathbb {T}^n=(\mathrm {C}(\mathbb {T}^{n}),\Delta _{\mathbb {T}^n})$
on
![]() ${\mathcal O}_{n}$
. We denote the generating unitaries of
${\mathcal O}_{n}$
. We denote the generating unitaries of
![]() $\mathrm {C}(\mathbb {T}^{n})$
by
$\mathrm {C}(\mathbb {T}^{n})$
by
![]() $z_{1},\dots ,z_{n}$
. We recall that the comultiplication is given on
$z_{1},\dots ,z_{n}$
. We recall that the comultiplication is given on
![]() $z_{i}$
by
$z_{i}$
by
![]() $\Delta (z_{i})=z_{i} \otimes z_{i}$
for all
$\Delta (z_{i})=z_{i} \otimes z_{i}$
for all
![]() $i=1,\dots ,n$
. With these notations, we have the following theorem.
$i=1,\dots ,n$
. With these notations, we have the following theorem.
Theorem 3.14 The action
![]() $\rho $
of
$\rho $
of
![]() $\mathbb {T}^n$
on
$\mathbb {T}^n$
on
![]() ${\mathcal O}_{n}$
given by
${\mathcal O}_{n}$
given by
is “non-linear,” and gauge-equivariant, where u is the element
![]() $\sum _{k=1}^{n}S_{k}S_{k}^*\otimes z_{k} \in {\mathcal O}_{n}\otimes \mathrm {C}(\mathbb {T}^{n})$
.
$\sum _{k=1}^{n}S_{k}S_{k}^*\otimes z_{k} \in {\mathcal O}_{n}\otimes \mathrm {C}(\mathbb {T}^{n})$
.
Proof We begin by observing that
![]() $\rho $
so defined is clearly gauge-equivariant and “non-linear.” We have to show that it indeed defines an action of
$\rho $
so defined is clearly gauge-equivariant and “non-linear.” We have to show that it indeed defines an action of
![]() $\mathbb {T}^n$
. First, let us check that
$\mathbb {T}^n$
. First, let us check that
![]() $\rho $
is a well-defined
$\rho $
is a well-defined
![]() $*$
-homomorphism.
$*$
-homomorphism.
To begin with, using the unitarity of
![]() $z_{i}$
, for
$z_{i}$
, for
![]() $i=1,\dots ,n$
, it is easy to see that u is a unitary element of
$i=1,\dots ,n$
, it is easy to see that u is a unitary element of
![]() ${\mathcal O}_{n}\otimes \mathrm {C}(\mathbb {T}^{n})$
, and so for all
${\mathcal O}_{n}\otimes \mathrm {C}(\mathbb {T}^{n})$
, and so for all
![]() $1 \leq i,j \leq n$
,
$1 \leq i,j \leq n$
,
Moreover,
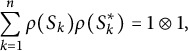 $$\begin{align*}\sum_{k=1}^{n}\rho(S_k)\rho(S^*_k)=1 \otimes 1,\end{align*}$$
$$\begin{align*}\sum_{k=1}^{n}\rho(S_k)\rho(S^*_k)=1 \otimes 1,\end{align*}$$
so that by the universality of
![]() ${\mathcal O}_{n}$
,
${\mathcal O}_{n}$
,
![]() $\rho $
is well-defined. It is also easy to observe that for all
$\rho $
is well-defined. It is also easy to observe that for all
![]() $1 \leq i,j \leq n$
,
$1 \leq i,j \leq n$
,
and coassociativity of
![]() $\rho $
follows. Again using
$\rho $
follows. Again using
for all
![]() $i=1,\dots ,n$
, one can see that
$i=1,\dots ,n$
, one can see that
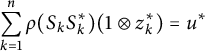 $$\begin{align*}\sum_{k=1}^{n}\rho(S_{k}S_{k}^*)(1 \otimes z_{k}^*)=u^*\end{align*}$$
$$\begin{align*}\sum_{k=1}^{n}\rho(S_{k}S_{k}^*)(1 \otimes z_{k}^*)=u^*\end{align*}$$
and consequently,
 $$\begin{align*}\sum_{k=1}^{n}\rho(S_{i}S_{k}S_{k}^*)(1 \otimes z_{k}^*)=(S_{i} \otimes 1_{\mathrm{C}(\mathbb{T}^n)})uu^*=S_{i} \otimes 1_{\mathrm{C}(\mathbb{T}^n)}\end{align*}$$
$$\begin{align*}\sum_{k=1}^{n}\rho(S_{i}S_{k}S_{k}^*)(1 \otimes z_{k}^*)=(S_{i} \otimes 1_{\mathrm{C}(\mathbb{T}^n)})uu^*=S_{i} \otimes 1_{\mathrm{C}(\mathbb{T}^n)}\end{align*}$$
for all
![]() $i=1,\dots ,n$
. Thus
$i=1,\dots ,n$
. Thus
![]() $S_{i} \otimes 1_{\mathrm {C}(\mathbb {T}^n)}$
, for all
$S_{i} \otimes 1_{\mathrm {C}(\mathbb {T}^n)}$
, for all
![]() $i=1,\dots ,n$
, belongs to
$i=1,\dots ,n$
, belongs to
![]() $[\rho ({\mathcal O}_{n})(1_{\mathcal {O}_n} \otimes \mathrm {C}(\mathbb {T}^{n}))]$
and arguing as in the last part of the proof of Theorem 3.9, the Podleś condition follows. This completes the proof.
$[\rho ({\mathcal O}_{n})(1_{\mathcal {O}_n} \otimes \mathrm {C}(\mathbb {T}^{n}))]$
and arguing as in the last part of the proof of Theorem 3.9, the Podleś condition follows. This completes the proof.
Now, we shall prove that the gauge-equivariance condition as in Definition 3.13 is also sufficient, provided we restrict ourselves to the class of Pimsner algebras arising from principal
![]() $\mathbb {T}$
-bundles, as described below (we provide a detailed description as this example covers a lot of other instances). We remark, however, that the special structure of a
$\mathbb {T}$
-bundles, as described below (we provide a detailed description as this example covers a lot of other instances). We remark, however, that the special structure of a
![]() $\mathbb {T}$
-principal bundle is only used to ensure that the Hilbert
$\mathbb {T}$
-principal bundle is only used to ensure that the Hilbert
![]() $\mathrm {C}^*$
-module for the
$\mathrm {C}^*$
-module for the
![]() $\mathrm {C}^*$
-correspondence is full and finitely generated, so that our Theorem 3.9 applies.
$\mathrm {C}^*$
-correspondence is full and finitely generated, so that our Theorem 3.9 applies.
Example 3.15 [Reference Abadie, Eilers and ExelAA09, Reference Adamo, Archey, Georgescu, Forough, Jeong, Strung and ViolaAEE98, Reference Arici, Kaad and LandiAKL16] We recall that a unital
![]() $\mathbb {T}$
-
$\mathbb {T}$
-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\gamma )$
(without any chance of confusion, we denote the toral action by the same symbol,
$(A,\gamma )$
(without any chance of confusion, we denote the toral action by the same symbol,
![]() $\gamma $
, as was used to denote the gauge action) comes with an associated
$\gamma $
, as was used to denote the gauge action) comes with an associated
![]() $\mathbb {Z}$
-grading defined as follows. We call an element
$\mathbb {Z}$
-grading defined as follows. We call an element
![]() $a \in A$
homogeneous of degree
$a \in A$
homogeneous of degree
![]() $n \in \mathbb {Z}$
if
$n \in \mathbb {Z}$
if
![]() $\gamma _z(a)=z^na$
for all
$\gamma _z(a)=z^na$
for all
![]() $z \in \mathbb {T}$
and write
$z \in \mathbb {T}$
and write
![]() $\mathrm {deg}(a)=n$
. For each
$\mathrm {deg}(a)=n$
. For each
![]() $n \in \mathbb {Z}$
, we let
$n \in \mathbb {Z}$
, we let
![]() $A(n)$
denote the set consisting of homogeneous elements of degree n:
$A(n)$
denote the set consisting of homogeneous elements of degree n:
![]() $A(n)=\{a \in A \mid \mathrm {deg}(a)=n\}$
. The collection
$A(n)=\{a \in A \mid \mathrm {deg}(a)=n\}$
. The collection
![]() $\{A(n)\}_{n \in \mathbb {Z}}$
enjoys the following:
$\{A(n)\}_{n \in \mathbb {Z}}$
enjoys the following:
-
• for each
 $n \in \mathbb {Z}$
,
$n \in \mathbb {Z}$
,
 $A(n)$
is a closed subspace of A;
$A(n)$
is a closed subspace of A; -
• for
 $m,n \in \mathbb {Z}$
,
$m,n \in \mathbb {Z}$
,
 $A(m)A(n) \subseteq A(m+n)$
;
$A(m)A(n) \subseteq A(m+n)$
; -
• for each
 $n \in \mathbb {Z}$
,
$n \in \mathbb {Z}$
,
 $A(n)^*=A(-n)$
;
$A(n)^*=A(-n)$
; -
• the algebraic direct sum
 $\bigoplus _{n \in \mathbb {Z}}A(n)$
is norm-dense in A.
$\bigoplus _{n \in \mathbb {Z}}A(n)$
is norm-dense in A.
In particular, the fixed point subalgebra
![]() $A(0)$
is a
$A(0)$
is a
![]() $\mathrm {C}^*$
-algebra and the first spectral subspace
$\mathrm {C}^*$
-algebra and the first spectral subspace
![]() $A(1)$
is a right Hilbert
$A(1)$
is a right Hilbert
![]() $A(0)$
-module, where the right
$A(0)$
-module, where the right
![]() $A(0)$
-module structure is given by multiplication from the right within the
$A(0)$
-module structure is given by multiplication from the right within the
![]() $\mathrm {C}^*$
-algebra A, and the
$\mathrm {C}^*$
-algebra A, and the
![]() $A(0)$
-valued inner product is given by
$A(0)$
-valued inner product is given by
for
![]() $\xi ,\eta \in A(1)$
. We define the
$\xi ,\eta \in A(1)$
. We define the
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\phi : A(0) \rightarrow {\mathcal L}(A(1))$
by
$\phi : A(0) \rightarrow {\mathcal L}(A(1))$
by
for
![]() $\xi \in A(1)$
and
$\xi \in A(1)$
and
![]() $a \in A(0)$
. Yet, the pair
$a \in A(0)$
. Yet, the pair
![]() $(A(1),\phi )$
is not a
$(A(1),\phi )$
is not a
![]() $\mathrm {C}^*$
-correspondence over
$\mathrm {C}^*$
-correspondence over
![]() $A(0)$
in our sense; we still require that
$A(0)$
in our sense; we still require that
![]() $A(1)$
be full and finitely generated over
$A(1)$
be full and finitely generated over
![]() $A(0)$
. We recall that the
$A(0)$
. We recall that the
![]() $\mathbb {T}$
-action
$\mathbb {T}$
-action
![]() $\gamma $
on the
$\gamma $
on the
![]() $\mathbb {T}$
-
$\mathbb {T}$
-
![]() $\mathrm {C}^*$
-algebra A is said to be principal if the associated
$\mathrm {C}^*$
-algebra A is said to be principal if the associated
![]() $\mathbb {Z}$
-grading is strong, i.e., for
$\mathbb {Z}$
-grading is strong, i.e., for
![]() $m,n \in \mathbb {Z}$
,
$m,n \in \mathbb {Z}$
,
Assume further, that the
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $A(0)$
is separable, that
$A(0)$
is separable, that
![]() $A(1)$
and
$A(1)$
and
![]() $A(-1)$
are full over
$A(-1)$
are full over
![]() $A(0)$
. Then
$A(0)$
. Then
![]() $(A(1),\phi )$
is a
$(A(1),\phi )$
is a
![]() $\mathrm {C}^*$
-correspondence over
$\mathrm {C}^*$
-correspondence over
![]() $A(0)$
. In this case, the Pimsner algebra
$A(0)$
. In this case, the Pimsner algebra
![]() ${\mathcal O}_{A(1)}$
associated with the
${\mathcal O}_{A(1)}$
associated with the
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(A(1),\phi )$
is isomorphic to A and the gauge action coincides with the initial
$(A(1),\phi )$
is isomorphic to A and the gauge action coincides with the initial
![]() $\mathbb {T}$
-action (thus relieving us from any possible confusion with the choice of notation).
$\mathbb {T}$
-action (thus relieving us from any possible confusion with the choice of notation).
Theorem 3.16 Let
![]() $(A,\gamma )$
be a unital
$(A,\gamma )$
be a unital
![]() $\mathbb {T}$
-
$\mathbb {T}$
-
![]() $\mathrm {C}^*$
-algebra such that:
$\mathrm {C}^*$
-algebra such that:
-
• the
 $\mathbb {T}$
-action
$\mathbb {T}$
-action
 $\gamma $
is principal;
$\gamma $
is principal; -
• the fixed point algebra
 $A(0)$
is separable;
$A(0)$
is separable; -
• the spectral subspaces
 $A(1)$
and
$A(1)$
and
 $A(-1)$
are full over
$A(-1)$
are full over
 $A(0)$
,
$A(0)$
,
so that by Example 3.15, there is an isomorphism
![]() $\mathcal {O}_{A(1)} \cong A$
. Let G be a compact quantum group, and let
$\mathcal {O}_{A(1)} \cong A$
. Let G be a compact quantum group, and let
![]() $\rho : A \rightarrow A \otimes \mathrm {C}(G)$
be a gauge-equivariant G-action on A in the sense of Definition 3.13, i.e., for all
$\rho : A \rightarrow A \otimes \mathrm {C}(G)$
be a gauge-equivariant G-action on A in the sense of Definition 3.13, i.e., for all
![]() $z \in \mathbb {T}$
,
$z \in \mathbb {T}$
,
Then
![]() $\rho $
is a lift in the sense of Definition 3.11.
$\rho $
is a lift in the sense of Definition 3.11.
Proof We begin by observing that the gauge-equivariance of
![]() $\rho $
yields
$\rho $
yields
i.e.,
![]() $\rho $
preserves the
$\rho $
preserves the
![]() $\mathrm {C}^*$
-algebra and the module
$\mathrm {C}^*$
-algebra and the module
![]() $A(1)$
. Let us denote the restricted actions
$A(1)$
. Let us denote the restricted actions
![]() $\rho |_{A(0)}$
and
$\rho |_{A(0)}$
and
![]() $\rho |_{A(1)}$
on
$\rho |_{A(1)}$
on
![]() $A(0)$
and
$A(0)$
and
![]() $A(1)$
by
$A(1)$
by
![]() $\alpha $
and
$\alpha $
and
![]() $\lambda $
, respectively. We will show that
$\lambda $
, respectively. We will show that
![]() $(A(0),\alpha )$
is a G-
$(A(0),\alpha )$
is a G-
![]() $\mathrm {C}^*$
-algebra,
$\mathrm {C}^*$
-algebra,
![]() $(A(1),\phi ,\lambda )$
is a G-equivariant
$(A(1),\phi ,\lambda )$
is a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
and that
$(A,\alpha )$
and that
![]() $\rho $
coincides with
$\rho $
coincides with
![]() $\omega $
, where
$\omega $
, where
![]() $\omega $
as in Theorem 3.9.
$\omega $
as in Theorem 3.9.
To that end, we first remark that
![]() $\alpha $
is indeed a unital
$\alpha $
is indeed a unital
![]() $*$
-homomorphism and
$*$
-homomorphism and
![]() $\lambda $
is indeed a linear map; these follow from the corresponding property of
$\lambda $
is indeed a linear map; these follow from the corresponding property of
![]() $\rho $
. Next, we observe that coassociativity of both
$\rho $
. Next, we observe that coassociativity of both
![]() $\alpha $
and
$\alpha $
and
![]() $\lambda $
follow from that of
$\lambda $
follow from that of
![]() $\rho $
. Now, we fix
$\rho $
. Now, we fix
![]() $\xi , \eta \in A(1)$
and
$\xi , \eta \in A(1)$
and
![]() $a \in A(0)$
. Then
$a \in A(0)$
. Then
and
all the equalities being clear from the facts that
![]() $\rho $
is a
$\rho $
is a
![]() $*$
-homomorphism and that
$*$
-homomorphism and that
![]() $\lambda =\rho |_{A(1)}$
and
$\lambda =\rho |_{A(1)}$
and
![]() $\alpha =\rho |_{A(0)}$
. Thus, we see that indeed condition (1) of Definition 2.2, conditions (1) and (2) of Definition 2.6 and conditions (1) and (3
$\alpha =\rho |_{A(0)}$
. Thus, we see that indeed condition (1) of Definition 2.2, conditions (1) and (2) of Definition 2.6 and conditions (1) and (3
![]() $^{\prime }$
) of Definition 3.2 are satisfied by
$^{\prime }$
) of Definition 3.2 are satisfied by
![]() $\alpha $
and
$\alpha $
and
![]() $\lambda $
. The proof will be complete, by uniqueness of
$\lambda $
. The proof will be complete, by uniqueness of
![]() $\omega $
in Theorem 3.9, provided we could show the Podleś conditions for
$\omega $
in Theorem 3.9, provided we could show the Podleś conditions for
![]() $\alpha $
and
$\alpha $
and
![]() $\lambda $
. We now proceed to do so.
$\lambda $
. We now proceed to do so.
We recall that there is a conditional expectation
![]() $\operatorname {E} :A \rightarrow A$
, given by
$\operatorname {E} :A \rightarrow A$
, given by
and that
![]() $A(0)$
coincides with
$A(0)$
coincides with
![]() $\operatorname {E}(A)$
. Since
$\operatorname {E}(A)$
. Since
![]() $\rho $
is gauge-equivariant, we have
$\rho $
is gauge-equivariant, we have
Then
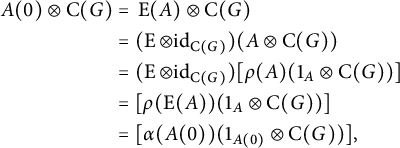 $$ \begin{align*} \begin{aligned} A(0) \otimes \mathrm{C}(G)={}&\operatorname{E}(A) \otimes \mathrm{C}(G)\\ ={}&(\operatorname{E} \otimes \mathrm{id}_{\mathrm{C}(G)})(A \otimes \mathrm{C}(G))\\ ={}&(\operatorname{E} \otimes \mathrm{id}_{\mathrm{C}(G)})[\rho(A)(1_A \otimes \mathrm{C}(G))]\\ ={}&[\rho(\operatorname{E}(A))(1_A \otimes \mathrm{C}(G))]\\ ={}&[\alpha(A(0))(1_{A(0)} \otimes \mathrm{C}(G))], \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} A(0) \otimes \mathrm{C}(G)={}&\operatorname{E}(A) \otimes \mathrm{C}(G)\\ ={}&(\operatorname{E} \otimes \mathrm{id}_{\mathrm{C}(G)})(A \otimes \mathrm{C}(G))\\ ={}&(\operatorname{E} \otimes \mathrm{id}_{\mathrm{C}(G)})[\rho(A)(1_A \otimes \mathrm{C}(G))]\\ ={}&[\rho(\operatorname{E}(A))(1_A \otimes \mathrm{C}(G))]\\ ={}&[\alpha(A(0))(1_{A(0)} \otimes \mathrm{C}(G))], \end{aligned} \end{align*} $$
where the first and fifth equalities use the fact that
![]() $A(0)=\operatorname {E}(A)$
; the third equality uses the Podleś condition for
$A(0)=\operatorname {E}(A)$
; the third equality uses the Podleś condition for
![]() $\rho $
; the fourth equality uses the identity just above this computation; and finally, the fifth equality uses the fact that
$\rho $
; the fourth equality uses the identity just above this computation; and finally, the fifth equality uses the fact that
![]() $\alpha =\rho |_{A(0)}$
. Therefore,
$\alpha =\rho |_{A(0)}$
. Therefore,
![]() $(A(0),\alpha )$
is a G-
$(A(0),\alpha )$
is a G-
![]() $\mathrm {C}^*$
-algebra.
$\mathrm {C}^*$
-algebra.
Now, let
![]() $\operatorname {P} : A \rightarrow A$
denote the projection onto
$\operatorname {P} : A \rightarrow A$
denote the projection onto
![]() $A(1)$
, obtained from the Banach space decomposition of A,
$A(1)$
, obtained from the Banach space decomposition of A,
Again, since
![]() $\rho $
is gauge-equivariant, we have
$\rho $
is gauge-equivariant, we have
Then
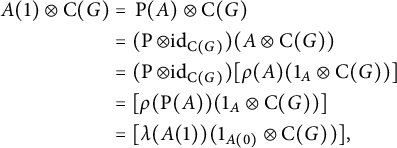 $$ \begin{align*} \begin{aligned} A(1) \otimes \mathrm{C}(G)={}&\operatorname{P}(A) \otimes \mathrm{C}(G)\\ ={}&(\operatorname{P} \otimes \mathrm{id}_{\mathrm{C}(G)})(A \otimes \mathrm{C}(G))\\ ={}&(\operatorname{P} \otimes \mathrm{id}_{\mathrm{C}(G)})[\rho(A)(1_A \otimes \mathrm{C}(G))]\\ ={}&[\rho(\operatorname{P}(A))(1_A \otimes \mathrm{C}(G))]\\ ={}&[\lambda(A(1))(1_{A(0)} \otimes \mathrm{C}(G))], \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} A(1) \otimes \mathrm{C}(G)={}&\operatorname{P}(A) \otimes \mathrm{C}(G)\\ ={}&(\operatorname{P} \otimes \mathrm{id}_{\mathrm{C}(G)})(A \otimes \mathrm{C}(G))\\ ={}&(\operatorname{P} \otimes \mathrm{id}_{\mathrm{C}(G)})[\rho(A)(1_A \otimes \mathrm{C}(G))]\\ ={}&[\rho(\operatorname{P}(A))(1_A \otimes \mathrm{C}(G))]\\ ={}&[\lambda(A(1))(1_{A(0)} \otimes \mathrm{C}(G))], \end{aligned} \end{align*} $$
where the first and fifth equalities use the fact that
![]() $A(1)=\operatorname {P}(A)$
; the third equality uses the Podleś condition for
$A(1)=\operatorname {P}(A)$
; the third equality uses the Podleś condition for
![]() $\rho $
; the fourth equality uses the identity just above this computation; and finally, the fifth equality uses the fact that
$\rho $
; the fourth equality uses the identity just above this computation; and finally, the fifth equality uses the fact that
![]() $\lambda =\rho |_{A(1)}$
. Therefore,
$\lambda =\rho |_{A(1)}$
. Therefore,
![]() $(A(1),\phi ,\lambda )$
is a G-equivariant
$(A(1),\phi ,\lambda )$
is a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A(0),\alpha )$
. Thus as observed above, by the uniqueness of
$(A(0),\alpha )$
. Thus as observed above, by the uniqueness of
![]() $\omega $
in Theorem 3.9, the proof is now complete.
$\omega $
in Theorem 3.9, the proof is now complete.
4 KMS states on the Pimsner algebras
In this section, after briefly recalling how a KMS state with respect to a quasi-free dynamics on a Pimsner algebra induced by a module dynamics in the sense of [Reference LanceLN04] looks like, we provide a necessary and sufficient condition for it to be a G-equivariant state, for the action
![]() $\omega $
from Theorem 3.9, where G is a compact quantum group of Kac type. A general reference for KMS states on a
$\omega $
from Theorem 3.9, where G is a compact quantum group of Kac type. A general reference for KMS states on a
![]() $\mathrm {C}^*$
-algebra is [Reference Bhowmick, Mandal, Roy and SkalskiBR97].
$\mathrm {C}^*$
-algebra is [Reference Bhowmick, Mandal, Roy and SkalskiBR97].
Definition 4.1 Let A be a unital
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi )$
be a
$(E,\phi )$
be a
![]() $\mathrm {C}^*$
-correspondence over A. For
$\mathrm {C}^*$
-correspondence over A. For
![]() $n \in \mathbb {N}$
, we define a
$n \in \mathbb {N}$
, we define a
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(E^{(n)},\phi _{(n)})$
over A as follows. We set
$(E^{(n)},\phi _{(n)})$
over A as follows. We set
![]() $E^{(0)}=A$
,
$E^{(0)}=A$
,
![]() $E^{(1)}=E$
and
$E^{(1)}=E$
and
![]() $E^{(n+1)}=E \otimes _{\phi _{(n)}} E^{(n)}$
for
$E^{(n+1)}=E \otimes _{\phi _{(n)}} E^{(n)}$
for
![]() $n \geq 1$
. We also define
$n \geq 1$
. We also define
![]() $\phi _{(0)}$
to be the identity of A,
$\phi _{(0)}$
to be the identity of A,
![]() $\phi _{(1)}=\phi $
and for
$\phi _{(1)}=\phi $
and for
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $\phi _{(n+1)}(a)=\phi (a) \otimes \mathrm {id}_{E^{(n)}}$
.
$\phi _{(n+1)}(a)=\phi (a) \otimes \mathrm {id}_{E^{(n)}}$
.
We recall that
and
![]() $(\xi a) \otimes \eta =\xi \otimes (\phi (a)\eta )$
for
$(\xi a) \otimes \eta =\xi \otimes (\phi (a)\eta )$
for
![]() $\xi , \eta \in E$
and
$\xi , \eta \in E$
and
![]() $a \in A$
. More generally,
$a \in A$
. More generally,
We refer the reader to [Reference Laca and NeshveyevLan95, Chapter 4] for a detailed discussion on interior tensor product of Hilbert
![]() $\mathrm {C}^*$
-modules.
$\mathrm {C}^*$
-modules.
Remark 4.2 We remark that we have omitted
![]() $\phi $
in the expression
$\phi $
in the expression
![]() $\xi \otimes \eta $
, for the sake of notational convenience and will do so without further comment.
$\xi \otimes \eta $
, for the sake of notational convenience and will do so without further comment.
Proposition 4.3 [Reference BichonBS89, Proposition 2.10] Let G be a compact quantum group, let
![]() $(A,\alpha )$
be a G-
$(A,\alpha )$
be a G-
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi ,\lambda )$
be a G-equivariant
$(E,\phi ,\lambda )$
be a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
. Then there is a linear map
$(A,\alpha )$
. Then there is a linear map
such that the triple
![]() $(E^{(2)},\phi _{(2)},\lambda _{(2)})$
satisfies the conditions of Definition 3.2, making
$(E^{(2)},\phi _{(2)},\lambda _{(2)})$
satisfies the conditions of Definition 3.2, making
![]() $(E^{(2)},\phi _{(2)},\lambda _{(2)})$
into a G-equivariant
$(E^{(2)},\phi _{(2)},\lambda _{(2)})$
into a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
. In Sweedler notation, for
$(A,\alpha )$
. In Sweedler notation, for
![]() $\xi ,\eta \in \mathcal {S}(E)$
(the spectral submodule),
$\xi ,\eta \in \mathcal {S}(E)$
(the spectral submodule),
![]() $\lambda _{(2)}$
is given by
$\lambda _{(2)}$
is given by
Remark 4.4 We remark that the above proposition uses, together with (and in the notations from) [Reference BichonBS89, Proposition 2.10], the following isomorphisms.
-
• Since both A and
 $\mathrm {C}(G)$
are unital, we have (see [Reference BichonBS89, p. 686]),
$\mathrm {C}(G)$
are unital, we have (see [Reference BichonBS89, p. 686]),  $$\begin{align*}\widetilde{M}(A \otimes \mathrm{C}(G)) \cong A \otimes \mathrm{C}(G);\end{align*}$$
$$\begin{align*}\widetilde{M}(A \otimes \mathrm{C}(G)) \cong A \otimes \mathrm{C}(G);\end{align*}$$
-
• since
 $\phi $
is unital, we have (see [Reference BichonBS89, p. 693]),
$\phi $
is unital, we have (see [Reference BichonBS89, p. 693]),  $$\begin{align*}(A \otimes \mathrm{C}(G)) \otimes_{\phi \otimes \mathrm{id}_{\mathrm{C}(G)}} (E \otimes \mathrm{C}(G)) \cong E \otimes \mathrm{C}(G);\end{align*}$$
$$\begin{align*}(A \otimes \mathrm{C}(G)) \otimes_{\phi \otimes \mathrm{id}_{\mathrm{C}(G)}} (E \otimes \mathrm{C}(G)) \cong E \otimes \mathrm{C}(G);\end{align*}$$
-
• and finally, we have (see [Reference BichonBS89, p. 693, proof of Proposition 2.10]),
 $$\begin{align*}(E \otimes_{\phi} E) \otimes \mathrm{C}(G) \cong (E \otimes \mathrm{C}(G)) \otimes_{\phi \otimes \mathrm{id}_{\mathrm{C}(G)}} (E \otimes \mathrm{C}(G)).\end{align*}$$
$$\begin{align*}(E \otimes_{\phi} E) \otimes \mathrm{C}(G) \cong (E \otimes \mathrm{C}(G)) \otimes_{\phi \otimes \mathrm{id}_{\mathrm{C}(G)}} (E \otimes \mathrm{C}(G)).\end{align*}$$
Corollary 4.5 Let G be a compact quantum group, let
![]() $(A,\alpha )$
be a G-
$(A,\alpha )$
be a G-
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi ,\lambda )$
be a G-equivariant
$(E,\phi ,\lambda )$
be a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
. Then, for each
$(A,\alpha )$
. Then, for each
![]() $n \geq 1$
, there is a linear map
$n \geq 1$
, there is a linear map
such that the triple
![]() $(E^{(n)},\phi _{(n)},\lambda _{(n)})$
satisfies the conditions of Definition 3.2, making
$(E^{(n)},\phi _{(n)},\lambda _{(n)})$
satisfies the conditions of Definition 3.2, making
![]() $(E^{(n)},\phi _{(n)},\lambda _{(n)})$
into a G-equivariant
$(E^{(n)},\phi _{(n)},\lambda _{(n)})$
into a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
. In Sweedler notation, for
$(A,\alpha )$
. In Sweedler notation, for
![]() $\xi _1,\dots ,\xi _n \in \mathcal {S}(E)$
,
$\xi _1,\dots ,\xi _n \in \mathcal {S}(E)$
,
![]() $\lambda _{(n)}$
is given by
$\lambda _{(n)}$
is given by
Let A be a unital
![]() $\mathrm {C}^*$
-algebra, and let E be a right Hilbert A-module. The algebra
$\mathrm {C}^*$
-algebra, and let E be a right Hilbert A-module. The algebra
![]() $\mathcal {L}(E)$
is isomorphic to
$\mathcal {L}(E)$
is isomorphic to
![]() $E \otimes _A \mathrm {Hom}_A(E,A)$
, yielding a unique linear map
$E \otimes _A \mathrm {Hom}_A(E,A)$
, yielding a unique linear map
![]() $\mathrm {Tr} : \mathcal {L}(E) \rightarrow A/[A,A]$
such that
$\mathrm {Tr} : \mathcal {L}(E) \rightarrow A/[A,A]$
such that
![]() $\mathrm {Tr}(x \otimes f)=f(x)$
mod
$\mathrm {Tr}(x \otimes f)=f(x)$
mod
![]() $[A,A]$
. Let
$[A,A]$
. Let
![]() $\tau $
be any tracial linear functional on A. Then
$\tau $
be any tracial linear functional on A. Then
![]() $\mathrm {Tr}_{\tau }=\tau \circ \mathrm {Tr}$
is a tracial linear functional on
$\mathrm {Tr}_{\tau }=\tau \circ \mathrm {Tr}$
is a tracial linear functional on
![]() $\mathcal {L}(E)$
.
$\mathcal {L}(E)$
.
Now, let
![]() $\mathbb {R}\ni t \mapsto \sigma _{t}$
be a one-parameter automorphism group of A and
$\mathbb {R}\ni t \mapsto \sigma _{t}$
be a one-parameter automorphism group of A and
![]() $\mathbb {R} \ni t \mapsto U_{t}$
be a one-parameter group of isometries on E such that
$\mathbb {R} \ni t \mapsto U_{t}$
be a one-parameter group of isometries on E such that
![]() $U_{t}(\phi (a)\xi )=\phi (\sigma _{t}(a))U_{t}(\xi )$
and
$U_{t}(\phi (a)\xi )=\phi (\sigma _{t}(a))U_{t}(\xi )$
and
![]() $\langle U_{t}(\xi ),U_{t}(\eta )\rangle =\sigma _{t}\langle \xi ,\eta \rangle $
; we assume further that
$\langle U_{t}(\xi ),U_{t}(\eta )\rangle =\sigma _{t}\langle \xi ,\eta \rangle $
; we assume further that
![]() $\sigma $
and U are strongly continuous. Then, by the universal property, there is, for each
$\sigma $
and U are strongly continuous. Then, by the universal property, there is, for each
![]() $t \in \mathbb {R}$
, a unique automorphism
$t \in \mathbb {R}$
, a unique automorphism
![]() $\delta _{t}:{\mathcal O}_{E} \rightarrow {\mathcal O}_{E}$
such that
$\delta _{t}:{\mathcal O}_{E} \rightarrow {\mathcal O}_{E}$
such that
![]() $\delta _t(k_A(a))=k_A(\sigma _t(a))$
and
$\delta _t(k_A(a))=k_A(\sigma _t(a))$
and
![]() $\delta _t(k_E(\xi ))=k_E(U_t(\xi ))$
,
$\delta _t(k_E(\xi ))=k_E(U_t(\xi ))$
,
![]() $a \in A$
,
$a \in A$
,
![]() $\xi \in E$
. The resulting one-parameter group
$\xi \in E$
. The resulting one-parameter group
![]() $t \mapsto \delta _{t}$
is strongly continuous and is called the quasi-free dynamics on
$t \mapsto \delta _{t}$
is strongly continuous and is called the quasi-free dynamics on
![]() $\mathcal {O}_E$
associated with the module dynamics U.
$\mathcal {O}_E$
associated with the module dynamics U.
Remark 4.6 We would only be interested when
![]() $\sigma $
is the trivial dynamics on A. In that case, a module dynamics U is then a one-parameter group of isometries
$\sigma $
is the trivial dynamics on A. In that case, a module dynamics U is then a one-parameter group of isometries
![]() $t \mapsto U_t$
on E such that
$t \mapsto U_t$
on E such that
![]() $U_t(\phi (a)\xi )=\phi (a)U_t(\xi )$
and
$U_t(\phi (a)\xi )=\phi (a)U_t(\xi )$
and
![]() $\langle U_t(\xi ),U_t(\eta ) \rangle =\langle \xi ,\eta \rangle $
.
$\langle U_t(\xi ),U_t(\eta ) \rangle =\langle \xi ,\eta \rangle $
.
With these in hand, we have the following theorem about the KMS states on the Pimsner algebra.
Theorem 4.7 [Reference LanceLN04, Theorem 2.5] Let
![]() $\mathbb {R} \ni t \mapsto U_{t}$
be a one parameter group of isometries on E satisfying the following conditions.
$\mathbb {R} \ni t \mapsto U_{t}$
be a one parameter group of isometries on E satisfying the following conditions.
-
•
 $U_t(\phi (a)\xi )=\phi (a)U_t(\xi )$
and
$U_t(\phi (a)\xi )=\phi (a)U_t(\xi )$
and
 $\langle U_t(\xi ),U_t(\eta ) \rangle =\langle \xi ,\eta \rangle $
, for
$\langle U_t(\xi ),U_t(\eta ) \rangle =\langle \xi ,\eta \rangle $
, for
 $t \in \mathbb {R}$
,
$t \in \mathbb {R}$
,
 $\xi ,\eta \in E$
;
$\xi ,\eta \in E$
; -
• the vectors
 $\xi \in E$
such that
$\xi \in E$
such that
 $\mathrm {Sp}_{U}(\xi ) \subset (0,\infty )$
form a dense subspace of E, where
$\mathrm {Sp}_{U}(\xi ) \subset (0,\infty )$
form a dense subspace of E, where
 $\mathrm {Sp}_{U}(\xi )$
is the Arveson spectrum of
$\mathrm {Sp}_{U}(\xi )$
is the Arveson spectrum of
 $\xi $
with respect to U.
$\xi $
with respect to U.
Let
![]() $\delta $
be the corresponding quasi-free dynamics on
$\delta $
be the corresponding quasi-free dynamics on
![]() ${\mathcal O}_{E}$
such that:
${\mathcal O}_{E}$
such that:
-
•
 $\delta _{t}(k_E(\xi ))=k_E(U_{t}(\xi ))$
for
$\delta _{t}(k_E(\xi ))=k_E(U_{t}(\xi ))$
for
 $\xi \in E$
and
$\xi \in E$
and -
•
 $\delta _{t}(k_A(a))=k_A(a)$
for all
$\delta _{t}(k_A(a))=k_A(a)$
for all
 $a \in A$
,
$a \in A$
,
and suppose
![]() $\beta \in (0,\infty )$
.
$\beta \in (0,\infty )$
.
-
• If
 $\varphi $
is a
$\varphi $
is a
 $(\delta ,\beta )$
-KMS state on
$(\delta ,\beta )$
-KMS state on
 ${\mathcal O}_{E},$
then
${\mathcal O}_{E},$
then
 $\tau =\varphi \circ k_A$
is a tracial state on A, and
$\tau =\varphi \circ k_A$
is a tracial state on A, and $$\begin{align*}\mathrm{Tr}_{\tau}(\phi(a)e^{-\beta D}) \leq \tau(a), \text{ for } a \in A_+,\end{align*}$$
Here, D is the generator of U, i.e.,
$$\begin{align*}\mathrm{Tr}_{\tau}(\phi(a)e^{-\beta D}) \leq \tau(a), \text{ for } a \in A_+,\end{align*}$$
Here, D is the generator of U, i.e., $$\begin{align*}\mathrm{Tr}_{\tau}(\phi(a)e^{-\beta D})=\tau(a) \text{ for } a \in (\ker \phi)^{\perp}.\end{align*}$$
$$\begin{align*}\mathrm{Tr}_{\tau}(\phi(a)e^{-\beta D})=\tau(a) \text{ for } a \in (\ker \phi)^{\perp}.\end{align*}$$
 $U_{t}=e^{itD}$
and
$U_{t}=e^{itD}$
and
 $\mathrm {Tr}_{\tau }(\phi (a)e^{-\infty D})=0$
, by convention.
$\mathrm {Tr}_{\tau }(\phi (a)e^{-\infty D})=0$
, by convention.
-
• Conversely, if
 $\tau $
is a tracial state on A such that and
$\tau $
is a tracial state on A such that and $$\begin{align*}\mathrm{Tr}_{\tau}(\phi(a)e^{-\beta D}) \leq \tau(a), \text{ for } a \in A_+,\end{align*}$$
then there exists a unique
$$\begin{align*}\mathrm{Tr}_{\tau}(\phi(a)e^{-\beta D}) \leq \tau(a), \text{ for } a \in A_+,\end{align*}$$
then there exists a unique $$\begin{align*}\mathrm{Tr}_{\tau}(\phi(a)e^{-\beta D})=\tau(a) \text{ for } a \in (\ker \phi)^{\perp},\end{align*}$$
$$\begin{align*}\mathrm{Tr}_{\tau}(\phi(a)e^{-\beta D})=\tau(a) \text{ for } a \in (\ker \phi)^{\perp},\end{align*}$$
 $(\delta ,\beta )$
-KMS state
$(\delta ,\beta )$
-KMS state
 $\varphi $
on
$\varphi $
on
 ${\mathcal O}_{E}$
such that
${\mathcal O}_{E}$
such that
 $\varphi \circ k_A=\tau $
. Moreover,
$\varphi \circ k_A=\tau $
. Moreover,
 $\varphi $
is determined by
$\varphi $
is determined by
 $\tau $
through (4.1)
$\tau $
through (4.1) $$ \begin{align} \begin{aligned} {}&\varphi(k_E(\xi_{1})\dots k_E(\xi_{m})k_E(\eta_{n})^*\dots k_E(\eta_{1})^*)\\ ={}&\tau(\langle \eta_{1} \otimes \dots \otimes \eta_{n},e^{-\beta D}\xi_{1} \otimes \dots \otimes e^{-\beta D}\xi_{n} \rangle), \text{ if } m=n,\\ ={}&0, \text{ otherwise. } \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {}&\varphi(k_E(\xi_{1})\dots k_E(\xi_{m})k_E(\eta_{n})^*\dots k_E(\eta_{1})^*)\\ ={}&\tau(\langle \eta_{1} \otimes \dots \otimes \eta_{n},e^{-\beta D}\xi_{1} \otimes \dots \otimes e^{-\beta D}\xi_{n} \rangle), \text{ if } m=n,\\ ={}&0, \text{ otherwise. } \end{aligned} \end{align} $$
Remark 4.8 We would be interested not in the existence of a KMS state on the Pimsner algebra
![]() $\mathcal {O}_E$
but the fact that when it indeed does exist, it is of the form given above by equation (4.1) in Theorem 4.7.
$\mathcal {O}_E$
but the fact that when it indeed does exist, it is of the form given above by equation (4.1) in Theorem 4.7.
Remark 4.9 We remark that Arveson spectrum is defined, for example, in [Reference Pask and RenniePed18, 8.1.6, p. 385].
Theorem 4.10 Let G be a compact quantum group of Kac type, let
![]() $(A,\alpha )$
be a G-
$(A,\alpha )$
be a G-
![]() $\mathrm {C}^*$
-algebra, let
$\mathrm {C}^*$
-algebra, let
![]() $(E,\phi ,\lambda )$
be a G-equivariant
$(E,\phi ,\lambda )$
be a G-equivariant
![]() $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(A,\alpha )$
and let
$(A,\alpha )$
and let
![]() $\omega $
be the G-action on
$\omega $
be the G-action on
![]() $\mathcal {O}_E$
, as obtained in Theorem 3.9. Let
$\mathcal {O}_E$
, as obtained in Theorem 3.9. Let
![]() $\delta $
be the quasi-free dynamics induced by the module dynamics U satisfying the conditions as in Theorem 4.7. Let U be G-equivariant, i.e., for all
$\delta $
be the quasi-free dynamics induced by the module dynamics U satisfying the conditions as in Theorem 4.7. Let U be G-equivariant, i.e., for all
![]() $t \in \mathbb {R}$
,
$t \in \mathbb {R}$
,
Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $(\delta ,\beta )$
-KMS state on
$(\delta ,\beta )$
-KMS state on
![]() $\mathcal {O}_E$
, and let
$\mathcal {O}_E$
, and let
![]() $\tau =\varphi \circ k_A$
be the tracial state on A as in Theorem 4.7. Then
$\tau =\varphi \circ k_A$
be the tracial state on A as in Theorem 4.7. Then
![]() $\varphi $
is G-equivariant if and only if
$\varphi $
is G-equivariant if and only if
![]() $\tau $
is G-equivariant.
$\tau $
is G-equivariant.
Proof We assume first that
![]() $\varphi $
is G-equivariant and show that
$\varphi $
is G-equivariant and show that
![]() $\tau =\varphi \circ k_A$
is G-equivariant too. To that end, we fix
$\tau =\varphi \circ k_A$
is G-equivariant too. To that end, we fix
![]() $a \in A$
. Then we have
$a \in A$
. Then we have
 $$ \begin{align*} \begin{aligned} (\tau \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(a)={}&(\varphi \otimes \mathrm{id}_{\mathrm{C}(G)})(k_A \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(a)\\ ={}&(\varphi \otimes \mathrm{id}_{\mathrm{C}(G)})\omega(k_A(a))\\ ={}&\varphi(k_A(a)) 1_{\mathrm{C}(G)}\\ ={}&\tau(a) 1_{\mathrm{C}(G)}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (\tau \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(a)={}&(\varphi \otimes \mathrm{id}_{\mathrm{C}(G)})(k_A \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(a)\\ ={}&(\varphi \otimes \mathrm{id}_{\mathrm{C}(G)})\omega(k_A(a))\\ ={}&\varphi(k_A(a)) 1_{\mathrm{C}(G)}\\ ={}&\tau(a) 1_{\mathrm{C}(G)}, \end{aligned} \end{align*} $$
where the first equality uses the fact that
![]() $\tau =\varphi \circ k_A$
; the second equality follows from Theorem 3.9; the third equality is from our assumption that
$\tau =\varphi \circ k_A$
; the second equality follows from Theorem 3.9; the third equality is from our assumption that
![]() $\varphi $
is G-equivariant.
$\varphi $
is G-equivariant.
We now assume that
![]() $\tau $
is G-equivariant and show that
$\tau $
is G-equivariant and show that
![]() $\varphi $
too is G-equivariant. We will show that for any
$\varphi $
too is G-equivariant. We will show that for any
![]() $x \in \mathcal {O}_E$
,
$x \in \mathcal {O}_E$
,
where h is the Haar state of the CQG G. Before proving this, let us see how we can conclude the proof from this identity. We observe first that the identity can be written, using the standard convolution notation, as
Now, for any
![]() $\psi \in \mathrm {C}(G)^*$
,
$\psi \in \mathrm {C}(G)^*$
,
where the first equality uses the identity just above the computation; the second uses associativity of convolution; the third equality uses invariance of the Haar state h. Therefore, for all
![]() $\psi \in \mathrm {C}(G)^*$
and all
$\psi \in \mathrm {C}(G)^*$
and all
![]() $x \in {\mathcal O}_{E}$
,
$x \in {\mathcal O}_{E}$
,
i.e.,
Therefore, we indeed have for all
![]() $x \in {\mathcal O}_{E}$
,
$x \in {\mathcal O}_{E}$
,
which is what we wanted. So we can now proceed to prove that for any
![]() $x \in \mathcal {O}_E$
,
$x \in \mathcal {O}_E$
,
holds. As the Hilbert A-module is assumed to be full and finitely generated, the linear span of the elements of the form
![]() $k_E(\xi _{1})\dots k_E(\xi _{m})k_E(\eta _{n})^*\dots k_E(\eta _{1})^* \in {\mathcal O}_{E}$
is dense in
$k_E(\xi _{1})\dots k_E(\xi _{m})k_E(\eta _{n})^*\dots k_E(\eta _{1})^* \in {\mathcal O}_{E}$
is dense in
![]() ${\mathcal O}_{E}$
. Therefore, by linearity and continuity of the maps involved, it suffices to prove (4.2) only for
${\mathcal O}_{E}$
. Therefore, by linearity and continuity of the maps involved, it suffices to prove (4.2) only for
![]() $k_E(\xi _{1})\dots k_E(\xi _{m})k_E(\eta _{n})^*\dots k_E(\eta _{1})^* \in {\mathcal O}_{E}$
. Moreover,
$k_E(\xi _{1})\dots k_E(\xi _{m})k_E(\eta _{n})^*\dots k_E(\eta _{1})^* \in {\mathcal O}_{E}$
. Moreover,
![]() $\xi _1,\dots ,\xi _m,\eta _1,\dots ,\eta _n$
further can be chosen from the spectral submodule
$\xi _1,\dots ,\xi _m,\eta _1,\dots ,\eta _n$
further can be chosen from the spectral submodule
![]() $\mathcal {S}(E)$
, where we have an algebraic coaction of
$\mathcal {S}(E)$
, where we have an algebraic coaction of
![]() $\mathbb {C}[G]$
, hence allowing us to leverage Sweedler notation. However, we shall refrain from saying so and use Sweedler notation freely in what follows. We also remind the reader that
$\mathbb {C}[G]$
, hence allowing us to leverage Sweedler notation. However, we shall refrain from saying so and use Sweedler notation freely in what follows. We also remind the reader that
![]() $\varphi $
is determined through
$\varphi $
is determined through
![]() $\tau $
via the formula (4.1), as in Theorem 4.7. We therefore begin by fixing
$\tau $
via the formula (4.1), as in Theorem 4.7. We therefore begin by fixing
![]() $\xi _1,\dots ,\xi _m,\eta _1,\dots ,\eta _n \in E$
and assume first that
$\xi _1,\dots ,\xi _m,\eta _1,\dots ,\eta _n \in E$
and assume first that
![]() $m \neq n$
. Then we have
$m \neq n$
. Then we have
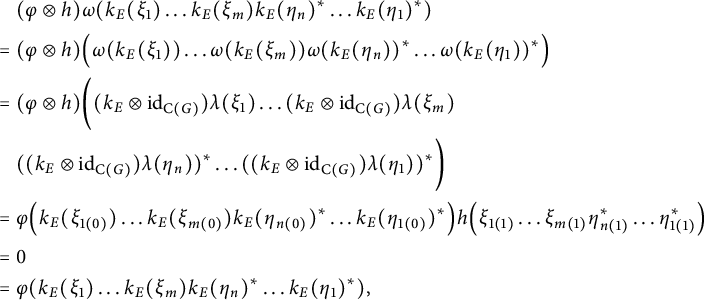 $$ \begin{align*} \begin{aligned} {}&(\varphi \otimes h)\omega(k_E(\xi_{1})\dots k_E(\xi_{m})k_E(\eta_{n})^*\dots k_E(\eta_{1})^*)\\ ={}&(\varphi \otimes h)\Big(\omega(k_E(\xi_{1}))\dots \omega(k_E(\xi_{m}))\omega(k_E(\eta_{n}))^*\dots \omega(k_E(\eta_{1}))^\ast\Big)\\ ={}&(\varphi \otimes h)\bigg((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi_1)\dots(k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi_m)\\ &{}((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\eta_n))^*\dots ((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\eta_1))^*\bigg)\\ ={}&\varphi\Big(k_E(\xi_{1(0)})\dots k_E(\xi_{m(0)})k_E(\eta_{n(0)})^*\dots k_E(\eta_{1(0)})^*\Big)h\Big(\xi_{1(1)}\dots\xi_{m(1)}\eta^*_{n(1)}\dots\eta^*_{1(1)}\Big)\\ ={}&0\\ ={}&\varphi(k_E(\xi_{1})\dots k_E(\xi_{m})k_E(\eta_{n})^*\dots k_E(\eta_{1})^*), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {}&(\varphi \otimes h)\omega(k_E(\xi_{1})\dots k_E(\xi_{m})k_E(\eta_{n})^*\dots k_E(\eta_{1})^*)\\ ={}&(\varphi \otimes h)\Big(\omega(k_E(\xi_{1}))\dots \omega(k_E(\xi_{m}))\omega(k_E(\eta_{n}))^*\dots \omega(k_E(\eta_{1}))^\ast\Big)\\ ={}&(\varphi \otimes h)\bigg((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi_1)\dots(k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi_m)\\ &{}((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\eta_n))^*\dots ((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\eta_1))^*\bigg)\\ ={}&\varphi\Big(k_E(\xi_{1(0)})\dots k_E(\xi_{m(0)})k_E(\eta_{n(0)})^*\dots k_E(\eta_{1(0)})^*\Big)h\Big(\xi_{1(1)}\dots\xi_{m(1)}\eta^*_{n(1)}\dots\eta^*_{1(1)}\Big)\\ ={}&0\\ ={}&\varphi(k_E(\xi_{1})\dots k_E(\xi_{m})k_E(\eta_{n})^*\dots k_E(\eta_{1})^*), \end{aligned} \end{align*} $$
where the second equality is by Theorem 3.9; the fourth equality is because of
![]() $m\neq n$
; the fifth equality is again because of
$m\neq n$
; the fifth equality is again because of
![]() $m\neq n$
. So (4.2) holds in this case. Now, let us consider the case where
$m\neq n$
. So (4.2) holds in this case. Now, let us consider the case where
![]() $m=n$
. We have
$m=n$
. We have
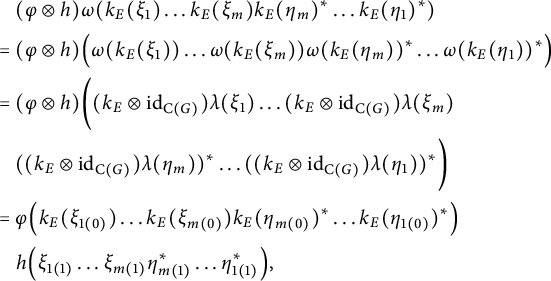 $$ \begin{align} \begin{aligned} {}&(\varphi \otimes h)\omega(k_E(\xi_{1})\dots k_E(\xi_{m})k_E(\eta_{m})^*\dots k_E(\eta_{1})^*)\\ ={}&(\varphi \otimes h)\Big(\omega(k_E(\xi_{1}))\dots \omega(k_E(\xi_{m}))\omega(k_E(\eta_{m}))^*\dots \omega(k_E(\eta_{1}))^*\Big)\\ ={}&(\varphi \otimes h)\bigg((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi_1)\dots(k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi_m)\\ &{}((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\eta_m))^*\dots ((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\eta_1))^*\bigg)\\ ={}&\varphi\Big(k_E(\xi_{1(0)})\dots k_E(\xi_{m(0)})k_E(\eta_{m(0)})^*\dots k_E(\eta_{1(0)})^*\Big)\\ &h\Big(\xi_{1(1)}\dots\xi_{m(1)}\eta^*_{m(1)}\dots\eta^*_{1(1)}\Big), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {}&(\varphi \otimes h)\omega(k_E(\xi_{1})\dots k_E(\xi_{m})k_E(\eta_{m})^*\dots k_E(\eta_{1})^*)\\ ={}&(\varphi \otimes h)\Big(\omega(k_E(\xi_{1}))\dots \omega(k_E(\xi_{m}))\omega(k_E(\eta_{m}))^*\dots \omega(k_E(\eta_{1}))^*\Big)\\ ={}&(\varphi \otimes h)\bigg((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi_1)\dots(k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\xi_m)\\ &{}((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\eta_m))^*\dots ((k_E \otimes \mathrm{id}_{\mathrm{C}(G)})\lambda(\eta_1))^*\bigg)\\ ={}&\varphi\Big(k_E(\xi_{1(0)})\dots k_E(\xi_{m(0)})k_E(\eta_{m(0)})^*\dots k_E(\eta_{1(0)})^*\Big)\\ &h\Big(\xi_{1(1)}\dots\xi_{m(1)}\eta^*_{m(1)}\dots\eta^*_{1(1)}\Big), \end{aligned} \end{align} $$
where we have used nothing but Theorem 3.9. Let us consider the expression
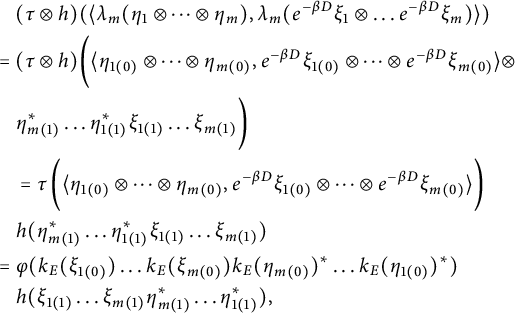 $$ \begin{align} \begin{aligned} {}&(\tau \otimes h)(\langle\lambda_m(\eta_{1}\otimes \dots \otimes \eta_{m}),\lambda_m(e^{-\beta D}\xi_{1} \otimes \dots e^{-\beta D}\xi_{m})\rangle)\\ ={}&(\tau \otimes h)\bigg(\langle\eta_{1(0)} \otimes \dots \otimes \eta_{m(0)},e^{-\beta D}\xi_{1(0)} \otimes \dots \otimes e^{-\beta D}\xi_{m(0)}\rangle \otimes\\ &\eta_{m(1)}^*\dots\eta_{1(1)}^*\xi_{1(1)}\dots\xi_{m(1)}\bigg)\\ & ={}\tau\, \bigg(\langle\eta_{1(0)} \otimes \dots \otimes \eta_{m(0)},e^{-\beta D}\xi_{1(0)} \otimes \dots \otimes e^{-\beta D}\xi_{m(0)}\rangle\bigg)\\ &h(\eta_{m(1)}^*\dots\eta_{1(1)}^*\xi_{1(1)}\dots\xi_{m(1)})\\ ={}&\varphi(k_E(\xi_{1(0)}) \dots k_E(\xi_{m(0)})k_E(\eta_{m(0)})^*\dots k_E(\eta_{1(0)})^*)\\ &h(\xi_{1(1)}\dots\xi_{m(1)}\eta_{m(1)}^*\dots\eta_{1(1)}^*), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {}&(\tau \otimes h)(\langle\lambda_m(\eta_{1}\otimes \dots \otimes \eta_{m}),\lambda_m(e^{-\beta D}\xi_{1} \otimes \dots e^{-\beta D}\xi_{m})\rangle)\\ ={}&(\tau \otimes h)\bigg(\langle\eta_{1(0)} \otimes \dots \otimes \eta_{m(0)},e^{-\beta D}\xi_{1(0)} \otimes \dots \otimes e^{-\beta D}\xi_{m(0)}\rangle \otimes\\ &\eta_{m(1)}^*\dots\eta_{1(1)}^*\xi_{1(1)}\dots\xi_{m(1)}\bigg)\\ & ={}\tau\, \bigg(\langle\eta_{1(0)} \otimes \dots \otimes \eta_{m(0)},e^{-\beta D}\xi_{1(0)} \otimes \dots \otimes e^{-\beta D}\xi_{m(0)}\rangle\bigg)\\ &h(\eta_{m(1)}^*\dots\eta_{1(1)}^*\xi_{1(1)}\dots\xi_{m(1)})\\ ={}&\varphi(k_E(\xi_{1(0)}) \dots k_E(\xi_{m(0)})k_E(\eta_{m(0)})^*\dots k_E(\eta_{1(0)})^*)\\ &h(\xi_{1(1)}\dots\xi_{m(1)}\eta_{m(1)}^*\dots\eta_{1(1)}^*), \end{aligned} \end{align} $$
where the first equality is by the expression of
![]() $\lambda _m$
as in Corollary 4.5 and the assumption that U is G-equivariant; the third equality uses the traciality of h and the expression of
$\lambda _m$
as in Corollary 4.5 and the assumption that U is G-equivariant; the third equality uses the traciality of h and the expression of
![]() $\varphi $
in formula (4.1). Now, by combining (4.3) and (4.4), we obtain
$\varphi $
in formula (4.1). Now, by combining (4.3) and (4.4), we obtain
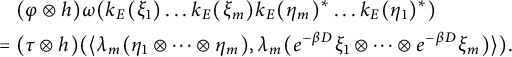 $$ \begin{align} \begin{aligned} &{}(\varphi \otimes h)\omega(k_E(\xi_{1}) \dots k_E(\xi_{m})k_E(\eta_{m})^* \dots k_E(\eta_{1})^*)\\ ={}&(\tau \otimes h)(\langle\lambda_m(\eta_{1} \otimes \dots \otimes \eta_{m}),\lambda_m(e^{-\beta D}\xi_{1} \otimes \dots \otimes e^{-\beta D}\xi_{m})\rangle). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &{}(\varphi \otimes h)\omega(k_E(\xi_{1}) \dots k_E(\xi_{m})k_E(\eta_{m})^* \dots k_E(\eta_{1})^*)\\ ={}&(\tau \otimes h)(\langle\lambda_m(\eta_{1} \otimes \dots \otimes \eta_{m}),\lambda_m(e^{-\beta D}\xi_{1} \otimes \dots \otimes e^{-\beta D}\xi_{m})\rangle). \end{aligned} \end{align} $$
But the last expression of (4.5) can be further simplified as follows:
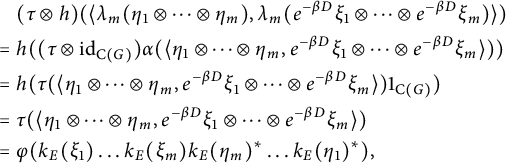 $$ \begin{align} \begin{aligned} {}&(\tau \otimes h)(\langle\lambda_m(\eta_{1} \otimes \dots \otimes \eta_{m}),\lambda_m(e^{-\beta D}\xi_{1} \otimes \dots \otimes e^{-\beta D}\xi_{m})\rangle)\\ ={}&h((\tau \otimes\mathrm{id}_{\mathrm{C}(G)})\alpha(\langle\eta_{1}\otimes \dots \otimes \eta_{m},e^{-\beta D}\xi_{1} \otimes \dots \otimes e^{-\beta D}\xi_{m}\rangle))\\ ={}&h(\tau(\langle\eta_{1} \otimes \dots \otimes\eta_{m},e^{-\beta D}\xi_{1}\otimes \dots \otimes e^{-\beta D}\xi_{m}\rangle)1_{\mathrm{C}(G)})\\ ={}&\tau(\langle\eta_{1} \otimes \dots \otimes\eta_{m},e^{-\beta D}\xi_{1}\otimes \dots \otimes e^{-\beta D}\xi_{m}\rangle)\\ ={}&\varphi(k_E(\xi_{1}) \dots k_E(\xi_{m})k_E(\eta_{m})^*\dots k_E(\eta_{1})^*), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {}&(\tau \otimes h)(\langle\lambda_m(\eta_{1} \otimes \dots \otimes \eta_{m}),\lambda_m(e^{-\beta D}\xi_{1} \otimes \dots \otimes e^{-\beta D}\xi_{m})\rangle)\\ ={}&h((\tau \otimes\mathrm{id}_{\mathrm{C}(G)})\alpha(\langle\eta_{1}\otimes \dots \otimes \eta_{m},e^{-\beta D}\xi_{1} \otimes \dots \otimes e^{-\beta D}\xi_{m}\rangle))\\ ={}&h(\tau(\langle\eta_{1} \otimes \dots \otimes\eta_{m},e^{-\beta D}\xi_{1}\otimes \dots \otimes e^{-\beta D}\xi_{m}\rangle)1_{\mathrm{C}(G)})\\ ={}&\tau(\langle\eta_{1} \otimes \dots \otimes\eta_{m},e^{-\beta D}\xi_{1}\otimes \dots \otimes e^{-\beta D}\xi_{m}\rangle)\\ ={}&\varphi(k_E(\xi_{1}) \dots k_E(\xi_{m})k_E(\eta_{m})^*\dots k_E(\eta_{1})^*), \end{aligned} \end{align} $$
where the first equality is by Corollary 4.5; the second is by our assumption that
![]() $\tau $
is G-equivariant; the third is because h is a state; and finally the fourth is by formula (4.1). Now, we combine (4.5) and (4.6), and obtain
$\tau $
is G-equivariant; the third is because h is a state; and finally the fourth is by formula (4.1). Now, we combine (4.5) and (4.6), and obtain
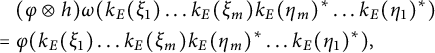 $$ \begin{align*} \begin{aligned} &{}(\varphi \otimes h)\omega(k_E(\xi_{1}) \dots k_E(\xi_{m})k_E(\eta_{m})^* \dots k_E(\eta_{1})^*)\\ ={}&\varphi(k_E(\xi_{1}) \dots k_E(\xi_{m})k_E(\eta_{m})^*\dots k_E(\eta_{1})^*), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &{}(\varphi \otimes h)\omega(k_E(\xi_{1}) \dots k_E(\xi_{m})k_E(\eta_{m})^* \dots k_E(\eta_{1})^*)\\ ={}&\varphi(k_E(\xi_{1}) \dots k_E(\xi_{m})k_E(\eta_{m})^*\dots k_E(\eta_{1})^*), \end{aligned} \end{align*} $$
which shows that (4.2) holds, settling this case as well for good. This completes the proof.
In the remaining three sections, we provide applications of the results obtained in this and the previous sections to the notion of quantum symmetries of graphs.
5 Applications to quantum symmetries of graphs I: Generalities
In this section, we specialize to the example where the
![]() $\mathrm {C}^*$
-correspondence comes from a finite graph, with some restrictions and see what the general results of the previous sections have to offer in this very concrete situation. So without further ado, we make contact via the following example.
$\mathrm {C}^*$
-correspondence comes from a finite graph, with some restrictions and see what the general results of the previous sections have to offer in this very concrete situation. So without further ado, we make contact via the following example.
Example 5.1 [Reference Muhly and SolelMS98, Example 2.9] Let
![]() ${\mathcal G}=(\mathcal {G}^{1},\mathcal {G}^{0},r,s)$
be a finite, possibly with loops and multiple edges, directed graph. Here,
${\mathcal G}=(\mathcal {G}^{1},\mathcal {G}^{0},r,s)$
be a finite, possibly with loops and multiple edges, directed graph. Here,
![]() $\mathcal {G}^{1}, \mathcal {G}^{0}$
are the sets of the edges and vertices, respectively, and
$\mathcal {G}^{1}, \mathcal {G}^{0}$
are the sets of the edges and vertices, respectively, and
![]() $r,s$
the range, source maps, respectively. Then
$r,s$
the range, source maps, respectively. Then
![]() $\mathcal {G}$
gives rise to a
$\mathcal {G}$
gives rise to a
![]() $\mathrm {C}^*$
-correspondence over the
$\mathrm {C}^*$
-correspondence over the
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}(\mathcal {G}^{0})$
as follows.
$\mathrm {C}(\mathcal {G}^{0})$
as follows.
![]() $\mathrm {C}(\mathcal {G}^{1})$
is made into a right Hilbert
$\mathrm {C}(\mathcal {G}^{1})$
is made into a right Hilbert
![]() $\mathrm {C}(\mathcal {G}^0)$
-module via
$\mathrm {C}(\mathcal {G}^0)$
-module via
where
![]() $\xi , \eta \in \mathrm {C}(\mathcal {G}^1)$
,
$\xi , \eta \in \mathrm {C}(\mathcal {G}^1)$
,
![]() $f \in \mathrm {C}(\mathcal {G}^{0})$
,
$f \in \mathrm {C}(\mathcal {G}^{0})$
,
![]() $e \in \mathcal {G}^{1}$
and
$e \in \mathcal {G}^{1}$
and
![]() $v \in \mathcal {G}^0$
. We define the unital
$v \in \mathcal {G}^0$
. We define the unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\phi : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathcal {L}(\mathrm {C}(\mathcal {G}^1))$
by
$\phi : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathcal {L}(\mathrm {C}(\mathcal {G}^1))$
by
where
![]() $\xi \in \mathrm {C}(\mathcal {G}^1)$
,
$\xi \in \mathrm {C}(\mathcal {G}^1)$
,
![]() $f \in \mathrm {C}(\mathcal {G}^0)$
,
$f \in \mathrm {C}(\mathcal {G}^0)$
,
![]() $e \in \mathcal {G}^1$
. Then since
$e \in \mathcal {G}^1$
. Then since
![]() $\mathrm {C}(\mathcal {G}^1)$
is finite dimensional, the pair
$\mathrm {C}(\mathcal {G}^1)$
is finite dimensional, the pair
![]() $(\mathrm {C}(\mathcal {G}^1),\phi )$
forms a
$(\mathrm {C}(\mathcal {G}^1),\phi )$
forms a
![]() $\mathrm {C}^*$
-correspondence over
$\mathrm {C}^*$
-correspondence over
![]() $\mathrm {C}(\mathcal {G}^0)$
. The corresponding Pimsner algebra
$\mathrm {C}(\mathcal {G}^0)$
. The corresponding Pimsner algebra
![]() $\mathcal {O}_{\mathrm {C}(\mathcal {G}^1)}$
is isomorphic to the graph
$\mathcal {O}_{\mathrm {C}(\mathcal {G}^1)}$
is isomorphic to the graph
![]() $\mathrm {C}^*$
-algebra denoted by
$\mathrm {C}^*$
-algebra denoted by
![]() $\mathrm {C}^*({\mathcal G})$
. The gauge action on the Pimsner algebra
$\mathrm {C}^*({\mathcal G})$
. The gauge action on the Pimsner algebra
![]() $\mathrm {C}^*({\mathcal G})$
coincides with the usual gauge action on the graph
$\mathrm {C}^*({\mathcal G})$
coincides with the usual gauge action on the graph
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}^*({\mathcal G})$
.
$\mathrm {C}^*({\mathcal G})$
.
Now, we shall recall a few facts about the KMS states of graph
![]() $\mathrm {C}^*$
-algebras coming from finite graphs, possibly with multiple edges but without sources, see [Reference Kajiwara and WatataniKW10] and [Reference an Huef, Laca, Raeburn and SimsaHLRS13]; by the term without sources, we shall mean that the map r is onto. To that end, let
$\mathrm {C}^*$
-algebras coming from finite graphs, possibly with multiple edges but without sources, see [Reference Kajiwara and WatataniKW10] and [Reference an Huef, Laca, Raeburn and SimsaHLRS13]; by the term without sources, we shall mean that the map r is onto. To that end, let
![]() ${\mathcal G}=(\mathcal {G}^{0},\mathcal {G}^{1},r,s)$
be a finite, directed graph, without sources and
${\mathcal G}=(\mathcal {G}^{0},\mathcal {G}^{1},r,s)$
be a finite, directed graph, without sources and
![]() $\mathrm {C}^*({\mathcal G})$
be the corresponding graph
$\mathrm {C}^*({\mathcal G})$
be the corresponding graph
![]() $\mathrm {C}^*$
-algebra; we also denote the adjacency matrix of
$\mathrm {C}^*$
-algebra; we also denote the adjacency matrix of
![]() ${\mathcal G}$
by
${\mathcal G}$
by
![]() ${\mathcal D}$
and the spectral radius of
${\mathcal D}$
and the spectral radius of
![]() ${\mathcal D}$
by
${\mathcal D}$
by
![]() $\rho ({\mathcal D})$
. Then we have the following proposition.
$\rho ({\mathcal D})$
. Then we have the following proposition.
Proposition 5.2 [Reference Joardar and MandalJM21b, Proposition 2.4] The graph
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}^*({\mathcal G})$
has a KMS-
$\mathrm {C}^*({\mathcal G})$
has a KMS-
![]() ${\ln (\rho ({\mathcal D}))}$
state if and only if
${\ln (\rho ({\mathcal D}))}$
state if and only if
![]() $\rho ({\mathcal D})$
is an eigenvalue of
$\rho ({\mathcal D})$
is an eigenvalue of
![]() ${\mathcal D}$
with eigenvectors having all its entries non-negative.
${\mathcal D}$
with eigenvectors having all its entries non-negative.
We shall call a KMS-
![]() $\ln (\rho ({\mathcal D}))$
state
$\ln (\rho ({\mathcal D}))$
state
![]() $\varphi $
distinguished if
$\varphi $
distinguished if
![]() $\varphi (p_{v_{i}})=\frac {1}{n}$
for all
$\varphi (p_{v_{i}})=\frac {1}{n}$
for all
![]() $i=1,\dots ,n$
, where
$i=1,\dots ,n$
, where
![]() $v_{1},\dots ,v_{n}$
are the vertices of the underlying graph
$v_{1},\dots ,v_{n}$
are the vertices of the underlying graph
![]() $\mathcal {G}$
. The distinguished KMS states are in abundance. For example, any regular graph admits such a distinguished KMS state on its
$\mathcal {G}$
. The distinguished KMS states are in abundance. For example, any regular graph admits such a distinguished KMS state on its
![]() $\mathrm {C}^{\ast }$
-algebra. Indeed, for a regular graph the spectral radius
$\mathrm {C}^{\ast }$
-algebra. Indeed, for a regular graph the spectral radius
![]() $\rho ({\mathcal D})$
is an eigenvalue with eigenspace spanned by the vector
$\rho ({\mathcal D})$
is an eigenvalue with eigenspace spanned by the vector
![]() $(1,\dots ,1)$
(see [Reference Joardar and MandalJM21a, Theorem 3.6] for more details).
$(1,\dots ,1)$
(see [Reference Joardar and MandalJM21a, Theorem 3.6] for more details).
Remarks 5.3
-
• Let us assume that
 $\rho ({\mathcal D})$
is an eigenvalue of
$\rho ({\mathcal D})$
is an eigenvalue of
 ${\mathcal D}$
so that
${\mathcal D}$
so that
 $\mathrm {C}^*({\mathcal G})$
admits a KMS-
$\mathrm {C}^*({\mathcal G})$
admits a KMS-
 $\ln (\rho ({\mathcal D}))$
state. If
$\ln (\rho ({\mathcal D}))$
state. If
 ${\mathcal D}$
is an
${\mathcal D}$
is an
 $n \times n$
matrix and
$n \times n$
matrix and
 $(\mu _{1},\dots ,\mu _{n})$
is a normalized eigenvector of
$(\mu _{1},\dots ,\mu _{n})$
is a normalized eigenvector of
 ${\mathcal D}$
with eigenvalue
${\mathcal D}$
with eigenvalue
 $\rho ({\mathcal D})$
(i.e.,
$\rho ({\mathcal D})$
(i.e.,
 $\sum _{i=1}^{n}\mu _{i}=1$
) then the corresponding KMS-
$\sum _{i=1}^{n}\mu _{i}=1$
) then the corresponding KMS-
 $\ln (\rho ({\mathcal D}))$
state
$\ln (\rho ({\mathcal D}))$
state
 $\varphi $
satisfies where
$\varphi $
satisfies where $$\begin{align*}\varphi(p_{v_{i}})=\mu_{i} \quad i=1,\dots,n, \end{align*}$$
$$\begin{align*}\varphi(p_{v_{i}})=\mu_{i} \quad i=1,\dots,n, \end{align*}$$
 $v_{1},\dots ,v_{n}$
are the vertices of
$v_{1},\dots ,v_{n}$
are the vertices of
 ${\mathcal G}$
. In fact, with the notation of Theorem 4.7, the tracial state
${\mathcal G}$
. In fact, with the notation of Theorem 4.7, the tracial state
 $\tau $
on
$\tau $
on
 $\mathrm {C}(\mathcal {G}^{0})$
corresponding to the KMS state
$\mathrm {C}(\mathcal {G}^{0})$
corresponding to the KMS state
 $\varphi $
is given by
$\varphi $
is given by  $$\begin{align*}\tau(\delta_{v_{i}})=\mu_{i} \quad i=1,\dots,n. \end{align*}$$
$$\begin{align*}\tau(\delta_{v_{i}})=\mu_{i} \quad i=1,\dots,n. \end{align*}$$
-
• The module dynamics in this case is nothing but the scalar dynamics, i.e.,
 $U_t=e^{it}$
,
$U_t=e^{it}$
,
 $t \in \mathbb {R}$
, for the gauge action and therefore it is G-equivariant for any compact quantum group G acting on the correspondence.
$t \in \mathbb {R}$
, for the gauge action and therefore it is G-equivariant for any compact quantum group G acting on the correspondence. -
• If for a graph
 ${\mathcal G}$
,
${\mathcal G}$
,
 $\mathrm {C}^{\ast }({\mathcal G})$
has a distinguished KMS state
$\mathrm {C}^{\ast }({\mathcal G})$
has a distinguished KMS state
 $\varphi $
, then the corresponding tracial state
$\varphi $
, then the corresponding tracial state
 $\tau $
on
$\tau $
on
 $\mathrm {C}(\mathcal {G}^{0})$
is given by So for any G-equivariant
$\mathrm {C}(\mathcal {G}^{0})$
is given by So for any G-equivariant $$\begin{align*}\tau(\delta_{v_{i}})=\frac{1}{n} \quad i=1,\dots,n. \end{align*}$$
$$\begin{align*}\tau(\delta_{v_{i}})=\frac{1}{n} \quad i=1,\dots,n. \end{align*}$$
 $\mathrm {C}^{\ast }$
-correspondence arising from a finite, directed graph
$\mathrm {C}^{\ast }$
-correspondence arising from a finite, directed graph
 ${\mathcal G}$
, possibly with multiple edges but without any source, such that
${\mathcal G}$
, possibly with multiple edges but without any source, such that
 $\mathrm {C}^{\ast }({\mathcal G})$
admits a distinguished KMS state
$\mathrm {C}^{\ast }({\mathcal G})$
admits a distinguished KMS state
 $\varphi $
, the above tracial state
$\varphi $
, the above tracial state
 $\tau $
on
$\tau $
on
 $\mathrm {C}(\mathcal {G}^{0})$
is always G-equivariant.
$\mathrm {C}(\mathcal {G}^{0})$
is always G-equivariant.
For the next proposition again,
![]() ${\mathcal D}$
is the adjacency matrix of the graph
${\mathcal D}$
is the adjacency matrix of the graph
![]() ${\mathcal G}$
and
${\mathcal G}$
and
![]() $\rho ({\mathcal D})$
is its spectral radius.
$\rho ({\mathcal D})$
is its spectral radius.
Proposition 5.4 Let
![]() ${\mathcal G}=(\mathcal {G}^{0},\mathcal {G}^{1},r,s)$
be a finite graph, possibly with multiple edges, but without any source or sink, so that the corresponding graph
${\mathcal G}=(\mathcal {G}^{0},\mathcal {G}^{1},r,s)$
be a finite graph, possibly with multiple edges, but without any source or sink, so that the corresponding graph
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}^*({\mathcal G})$
has a distinguished KMS-
$\mathrm {C}^*({\mathcal G})$
has a distinguished KMS-
![]() $\ln (\rho ({\mathcal D}))$
state
$\ln (\rho ({\mathcal D}))$
state
![]() $\varphi $
. Let G be a compact quantum group such that:
$\varphi $
. Let G be a compact quantum group such that:
-
• the
 $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
 $(\mathrm {C}(\mathcal {G}^1),\phi )$
, arising from
$(\mathrm {C}(\mathcal {G}^1),\phi )$
, arising from
 ${\mathcal G}$
is G-equivariant;
${\mathcal G}$
is G-equivariant; -
• the G-action
 $\omega $
obtained from Theorem 3.9 on
$\omega $
obtained from Theorem 3.9 on
 $\mathrm {C}^*(\mathcal {G})$
is faithful.
$\mathrm {C}^*(\mathcal {G})$
is faithful.
Then G is of Kac type if and only if the KMS state
![]() $\varphi $
is G-equivariant.
$\varphi $
is G-equivariant.
Proof Let G be compact quantum group of Kac type. Then by (2) and (3) of Remark 5.3, all the conditions of Theorem 4.10 are satisfied and the KMS state
![]() $\varphi $
on
$\varphi $
on
![]() $\mathrm {C}^*({\mathcal G})$
is G-equivariant.
$\mathrm {C}^*({\mathcal G})$
is G-equivariant.
Conversely, we assume that the KMS state
![]() $\varphi $
is G-equivariant. Then it follows from the proof of [Reference Joardar and MandalJM18, Proposition 3.8] that G is a quantum subgroup of
$\varphi $
is G-equivariant. Then it follows from the proof of [Reference Joardar and MandalJM18, Proposition 3.8] that G is a quantum subgroup of
![]() $\text {U}_{n}^{+}$
(observe that the matrix
$\text {U}_{n}^{+}$
(observe that the matrix
![]() $F^{{\mathcal G}}$
in [Reference Joardar and MandalJM18, Proposition 3.8] is the identity matrix). Hence, G is a compact quantum group of Kac type.
$F^{{\mathcal G}}$
in [Reference Joardar and MandalJM18, Proposition 3.8] is the identity matrix). Hence, G is a compact quantum group of Kac type.
Corollary 5.5 Let G be a compact matrix pseudogroup such that the fundamental corepresentation u is unitary. Then G is of Kac type if and only if
![]() $u^{t}$
is also unitary.
$u^{t}$
is also unitary.
Proof We consider the
![]() $\mathrm {C}^*$
-correspondence coming from the graph of the Cuntz algebra with n-generators. Then since the graph has only one vertex,
$\mathrm {C}^*$
-correspondence coming from the graph of the Cuntz algebra with n-generators. Then since the graph has only one vertex,
![]() $\mathrm {C}(\mathcal {G}^0)=\mathbb {C}$
and hence the Hilbert
$\mathrm {C}(\mathcal {G}^0)=\mathbb {C}$
and hence the Hilbert
![]() $\mathrm {C}^*$
-module
$\mathrm {C}^*$
-module
![]() $\mathrm {C}(\mathcal {G}^{1})$
is an n-dimensional Hilbert space. So if
$\mathrm {C}(\mathcal {G}^{1})$
is an n-dimensional Hilbert space. So if
![]() $(u_{ij})_{i,j=1,\dots ,n}$
is the unitary matrix corresponding to the fundamental unitary corepresentation u, denoting an orthonormal basis of
$(u_{ij})_{i,j=1,\dots ,n}$
is the unitary matrix corresponding to the fundamental unitary corepresentation u, denoting an orthonormal basis of
![]() $\mathrm {C}(\mathcal {G}^{1})$
by
$\mathrm {C}(\mathcal {G}^{1})$
by
![]() $e_{1},\dots ,e_{n}$
, we get a G-action on
$e_{1},\dots ,e_{n}$
, we get a G-action on
![]() $\mathrm {C}(\mathcal {G}^1)$
by
$\mathrm {C}(\mathcal {G}^1)$
by
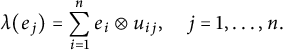 $$\begin{align*}\lambda(e_{j})=\sum_{i=1}^{n}e_{i}\otimes u_{ij}, \quad j=1,\dots,n. \end{align*}$$
$$\begin{align*}\lambda(e_{j})=\sum_{i=1}^{n}e_{i}\otimes u_{ij}, \quad j=1,\dots,n. \end{align*}$$
The G-action
![]() $\alpha $
on
$\alpha $
on
![]() $\mathrm {C}(\mathcal {G}^{0})=\mathbb {C}$
is the trivial one and it is easy to see that the above
$\mathrm {C}(\mathcal {G}^{0})=\mathbb {C}$
is the trivial one and it is easy to see that the above
![]() $\alpha $
, and
$\alpha $
, and
![]() $\lambda $
make the
$\lambda $
make the
![]() $\mathrm {C}^*$
-correspondence
$\mathrm {C}^*$
-correspondence
![]() $(\mathrm {C}(\mathcal {G}^1),\phi )$
a G-equivariant
$(\mathrm {C}(\mathcal {G}^1),\phi )$
a G-equivariant
![]() $\mathrm {C}^*$
-correspondence. Thus, there is a G-action
$\mathrm {C}^*$
-correspondence. Thus, there is a G-action
![]() $\omega $
on
$\omega $
on
![]() ${\mathcal O}_{n}$
given on the generators by
${\mathcal O}_{n}$
given on the generators by
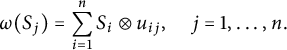 $$\begin{align*}\omega(S_{j})=\sum_{i=1}^{n}S_{i} \otimes u_{ij}, \quad j=1,\dots,n. \end{align*}$$
$$\begin{align*}\omega(S_{j})=\sum_{i=1}^{n}S_{i} \otimes u_{ij}, \quad j=1,\dots,n. \end{align*}$$
But the unique KMS state on
![]() ${\mathcal O}_{n}$
is G-equivariant if and only if
${\mathcal O}_{n}$
is G-equivariant if and only if
![]() $u^{t}=((u_{ji}))$
is unitary (see [Reference Joardar and MandalJM21a]). Now, the unique KMS state is a distinguished KMS state in the above sense. So applying Proposition 5.4, we obtain the desired conclusion.
$u^{t}=((u_{ji}))$
is unitary (see [Reference Joardar and MandalJM21a]). Now, the unique KMS state is a distinguished KMS state in the above sense. So applying Proposition 5.4, we obtain the desired conclusion.
Remark 5.6 The conclusion of the Corollary 5.5 is well-known as can be easily seen by applying
![]() $\kappa $
to
$\kappa $
to
![]() $u^*u=uu^*$
and using the fact that for a compact quantum group of Kac type,
$u^*u=uu^*$
and using the fact that for a compact quantum group of Kac type,
![]() $\kappa $
is involutive. But our proof is from the point of view of quantum symmetries.
$\kappa $
is involutive. But our proof is from the point of view of quantum symmetries.
6 Applications to quantum symmetries of graphs II: The case of simple graphs
Let A be a unital
![]() $\mathrm {C}^*$
-algebra, and let
$\mathrm {C}^*$
-algebra, and let
![]() $(E,\phi )$
be a
$(E,\phi )$
be a
![]() $\mathrm {C}^*$
-correspondence over A. We consider the category of all compact quantum groups G such that
$\mathrm {C}^*$
-correspondence over A. We consider the category of all compact quantum groups G such that
![]() $(E,\phi )$
is a G-equivariant
$(E,\phi )$
is a G-equivariant
![]() $\mathrm {C}^*$
-correspondence. Although this category is an interesting one, it has a drawback that in general it might fail to admit a universal object. For example, if one considers the
$\mathrm {C}^*$
-correspondence. Although this category is an interesting one, it has a drawback that in general it might fail to admit a universal object. For example, if one considers the
![]() $\mathrm {C}^*$
-correspondence coming from the graph of the Cuntz algebra with n-generators, any Wang algebra
$\mathrm {C}^*$
-correspondence coming from the graph of the Cuntz algebra with n-generators, any Wang algebra
![]() $A_{u}(Q)$
can be made into an object of this category and therefore it does not admit a universal object. In this section, we shall consider the
$A_{u}(Q)$
can be made into an object of this category and therefore it does not admit a universal object. In this section, we shall consider the
![]() $\mathrm {C}^*$
-correspondence coming from a finite graph, possibly with multiple edges but without any source, and make the category more restrictive so that the modified category admits a universal object. Therefore, let us begin with the following definition.
$\mathrm {C}^*$
-correspondence coming from a finite graph, possibly with multiple edges but without any source, and make the category more restrictive so that the modified category admits a universal object. Therefore, let us begin with the following definition.
Definition 6.1 Let
![]() $\mathcal {G}$
be a finite, directed graph, with n edges and m vertices (without loops or multiple edges). The compact quantum group
$\mathcal {G}$
be a finite, directed graph, with n edges and m vertices (without loops or multiple edges). The compact quantum group
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is defined to be the quotient
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is defined to be the quotient
![]() $\text {S}^+_m/(UD-DU)$
, where
$\text {S}^+_m/(UD-DU)$
, where
![]() $U=(q_{vw})_{v,w \in \mathcal {G}^{0}}$
, and D is the adjacency matrix for
$U=(q_{vw})_{v,w \in \mathcal {G}^{0}}$
, and D is the adjacency matrix for
![]() ${\mathcal G}$
. The coproduct on the generators is given by
${\mathcal G}$
. The coproduct on the generators is given by
![]() $\Delta _{\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})}(q_{vw})=\sum _{u\in \mathcal {G}^{0}}q_{vu} \otimes q_{uw}$
.
$\Delta _{\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})}(q_{vw})=\sum _{u\in \mathcal {G}^{0}}q_{vu} \otimes q_{uw}$
.
The relation
![]() $UD=DU$
, when expanded out, yields the following explicit description of the
$UD=DU$
, when expanded out, yields the following explicit description of the
![]() $\mathrm {C}^{*}$
-algebra
$\mathrm {C}^{*}$
-algebra
![]() $\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
.
$\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
.
Lemma 6.2 [Reference FultonFul06, Lemma 3.1.1] The underlying
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
of the quantum group
$\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
of the quantum group
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
for a finite, directed graph
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
for a finite, directed graph
![]() ${\mathcal G}$
with n edges and m vertices (without loops or multiple edges) is the universal
${\mathcal G}$
with n edges and m vertices (without loops or multiple edges) is the universal
![]() $\mathrm {C}^*$
-algebra generated by
$\mathrm {C}^*$
-algebra generated by
![]() $(q_{vw})_{v,w\in \mathcal {G}^{0}}$
satisfying the following relations.
$(q_{vw})_{v,w\in \mathcal {G}^{0}}$
satisfying the following relations.
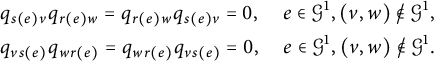 $$ \begin{align} \begin{aligned} &{}q_{s(e)v}q_{r(e)w}=q_{r(e)w}q_{s(e)v}=0, \quad e \in \mathcal{G}^{1}, (v,w) \not \in \mathcal{G}^{1},\\ &{}q_{vs(e)}q_{wr(e)}=q_{wr(e)}q_{vs(e)}=0, \quad e \in \mathcal{G}^{1}, (v,w) \not \in \mathcal{G}^{1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &{}q_{s(e)v}q_{r(e)w}=q_{r(e)w}q_{s(e)v}=0, \quad e \in \mathcal{G}^{1}, (v,w) \not \in \mathcal{G}^{1},\\ &{}q_{vs(e)}q_{wr(e)}=q_{wr(e)}q_{vs(e)}=0, \quad e \in \mathcal{G}^{1}, (v,w) \not \in \mathcal{G}^{1}. \end{aligned} \end{align} $$
The comultiplication on the generators is given by
The action on the graph is given by
Remark 6.3 Since
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is a quantum subgroup of
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is a quantum subgroup of
![]() $\text {S}_{m}^{+}$
, it is of Kac type.
$\text {S}_{m}^{+}$
, it is of Kac type.
Remark 6.4 There is another notion of quantum symmetry for directed, simple graphs due to Bichon. We refer the reader to [Reference Bédos, Kaliszewski, Quigg and RobertsonBic03] for details. The quantum automorphism group of a simple, directed graph
![]() ${\mathcal G}$
in the sense of Bichon, to be denoted by
${\mathcal G}$
in the sense of Bichon, to be denoted by
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
, is a quantum subgroup of
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
, is a quantum subgroup of
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
. The underlying
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
. The underlying
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}(\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G}))$
is again generated by
$\mathrm {C}(\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G}))$
is again generated by
![]() $q_{vw}$
,
$q_{vw}$
,
![]() $v,w\in \mathcal {G}^{0}$
and satisfy the relations in Theorem 6.2, as well as the following additional relations.
$v,w\in \mathcal {G}^{0}$
and satisfy the relations in Theorem 6.2, as well as the following additional relations.
The comultiplication on the generators is again given by
Definition 6.5 Let
![]() $\mathcal {G}=(\mathcal {G}^1,\mathcal {G}^0,r,s)$
be a finite, directed graph, without loops or multiple edges. We define the category
$\mathcal {G}=(\mathcal {G}^1,\mathcal {G}^0,r,s)$
be a finite, directed graph, without loops or multiple edges. We define the category
![]() ${\mathcal C}_{\text {Ban}}({\mathcal G})$
as follows:
${\mathcal C}_{\text {Ban}}({\mathcal G})$
as follows:
-
• An object of
 ${\mathcal C}_{\text {Ban}}({\mathcal G})$
is a triple
${\mathcal C}_{\text {Ban}}({\mathcal G})$
is a triple
 $(G,\alpha ,\lambda )$
, where G is a compact quantum group,
$(G,\alpha ,\lambda )$
, where G is a compact quantum group,
 $\alpha : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^0) \otimes \mathrm {C}(G)$
is a unital
$\alpha : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^0) \otimes \mathrm {C}(G)$
is a unital
 $*$
-homomorphism and
$*$
-homomorphism and
 $\lambda : \mathrm {C}(\mathcal {G}^1) \rightarrow \mathrm {C}(\mathcal {G}^1) \otimes \mathrm {C}(G)$
is a linear map satisfying the following conditions:
$\lambda : \mathrm {C}(\mathcal {G}^1) \rightarrow \mathrm {C}(\mathcal {G}^1) \otimes \mathrm {C}(G)$
is a linear map satisfying the following conditions:-
– The pair
 $(\mathrm {C}(\mathcal {G}^0),\alpha )$
is a G-
$(\mathrm {C}(\mathcal {G}^0),\alpha )$
is a G-
 $\mathrm {C}^*$
-algebra and the action
$\mathrm {C}^*$
-algebra and the action
 $\alpha $
is faithful;
$\alpha $
is faithful; -
– the triple
 $(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda )$
is a G-equivariant
$(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda )$
is a G-equivariant
 $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
 $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
 $(\mathrm {C}(\mathcal {G}^0),\alpha )$
;
$(\mathrm {C}(\mathcal {G}^0),\alpha )$
; -
– for all
 $f \in \mathrm {C}(\mathcal {G}^{0})$
,
$f \in \mathrm {C}(\mathcal {G}^{0})$
,
 $(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha (f)=\lambda (r_{\ast }(f))$
, where
$(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha (f)=\lambda (r_{\ast }(f))$
, where
 $r_{\ast } :\mathrm {C}(\mathcal {G}^{0}) \rightarrow \mathrm {C}(\mathcal {G}^{1})$
is the
$r_{\ast } :\mathrm {C}(\mathcal {G}^{0}) \rightarrow \mathrm {C}(\mathcal {G}^{1})$
is the
 $*$
-homomorphism given by
$*$
-homomorphism given by
 $r_{\ast }(f)(e)=f(r(e))$
for
$r_{\ast }(f)(e)=f(r(e))$
for
 $e\in \mathcal {G}^{1}$
.
$e\in \mathcal {G}^{1}$
.
-
-
• Let
 $(G_1,\alpha _1,\lambda _1)$
and
$(G_1,\alpha _1,\lambda _1)$
and
 $(G_2,\alpha _2,\lambda _2)$
be two objects of the category
$(G_2,\alpha _2,\lambda _2)$
be two objects of the category
 ${\mathcal C}_{\text {Ban}}({\mathcal G})$
. A morphism
${\mathcal C}_{\text {Ban}}({\mathcal G})$
. A morphism
 $f : (G_1,\alpha _1,\lambda _1) \rightarrow (G_2,\alpha _2,\lambda _2)$
in
$f : (G_1,\alpha _1,\lambda _1) \rightarrow (G_2,\alpha _2,\lambda _2)$
in
 ${\mathcal C}_{\text {Ban}}({\mathcal G})$
is by definition a Hopf
${\mathcal C}_{\text {Ban}}({\mathcal G})$
is by definition a Hopf
 $*$
-homomorphism
$*$
-homomorphism
 $f : \mathrm {C}(G_2) \rightarrow \mathrm {C}(G_1)$
such that:
$f : \mathrm {C}(G_2) \rightarrow \mathrm {C}(G_1)$
such that:-
–
 $(\mathrm {id}_{\mathrm {C}(\mathcal {G}^0)} \otimes f)\alpha _2=\alpha _1$
;
$(\mathrm {id}_{\mathrm {C}(\mathcal {G}^0)} \otimes f)\alpha _2=\alpha _1$
; -
–
 $(\mathrm {id}_{\mathrm {C}(\mathcal {G}^1)} \otimes f)\lambda _2=\lambda _1$
.
$(\mathrm {id}_{\mathrm {C}(\mathcal {G}^1)} \otimes f)\lambda _2=\lambda _1$
.
-
Definition 6.6 Let
![]() $\mathcal {G}=(\mathcal {G}^1,\mathcal {G}^0,r,s)$
be a finite, directed graph, without loops or multiple edges. We define the category
$\mathcal {G}=(\mathcal {G}^1,\mathcal {G}^0,r,s)$
be a finite, directed graph, without loops or multiple edges. We define the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
as follows:
${\mathcal C}_{\text {Bic}}({\mathcal G})$
as follows:
-
• An object of
 ${\mathcal C}_{\text {Bic}}({\mathcal G})$
is a triple
${\mathcal C}_{\text {Bic}}({\mathcal G})$
is a triple
 $(G,\alpha ,\lambda )$
, where G is a compact quantum group,
$(G,\alpha ,\lambda )$
, where G is a compact quantum group,
 $\alpha : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^0) \otimes \mathrm {C}(G)$
is a unital
$\alpha : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^0) \otimes \mathrm {C}(G)$
is a unital
 $*$
-homomorphism and
$*$
-homomorphism and
 $\lambda : \mathrm {C}(\mathcal {G}^1) \rightarrow \mathrm {C}(\mathcal {G}^1) \otimes \mathrm {C}(G)$
is a linear map satisfying the following conditions:
$\lambda : \mathrm {C}(\mathcal {G}^1) \rightarrow \mathrm {C}(\mathcal {G}^1) \otimes \mathrm {C}(G)$
is a linear map satisfying the following conditions:-
– The pair
 $(\mathrm {C}(\mathcal {G}^0),\alpha )$
is a G-
$(\mathrm {C}(\mathcal {G}^0),\alpha )$
is a G-
 $\mathrm {C}^*$
-algebra and the action
$\mathrm {C}^*$
-algebra and the action
 $\alpha $
is faithful;
$\alpha $
is faithful; -
– the triple
 $(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda )$
is a G-equivariant
$(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda )$
is a G-equivariant
 $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
 $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
 $(\mathrm {C}(\mathcal {G}^0),\alpha )$
;
$(\mathrm {C}(\mathcal {G}^0),\alpha )$
; -
– the pair
 $(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a G-
$(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a G-
 $\mathrm {C}^*$
-algebra.
$\mathrm {C}^*$
-algebra.
-
-
• Let
 $(G_1,\alpha _1,\lambda _1)$
and
$(G_1,\alpha _1,\lambda _1)$
and
 $(G_2,\alpha _2,\lambda _2)$
be two objects of the category
$(G_2,\alpha _2,\lambda _2)$
be two objects of the category
 ${\mathcal C}_{\text {Bic}}({\mathcal G})$
. A morphism
${\mathcal C}_{\text {Bic}}({\mathcal G})$
. A morphism
 $f : (G_1,\alpha _1,\lambda _1) \rightarrow (G_2,\alpha _2,\lambda _2)$
in
$f : (G_1,\alpha _1,\lambda _1) \rightarrow (G_2,\alpha _2,\lambda _2)$
in
 ${\mathcal C}_{\text {Bic}}({\mathcal G})$
is again by definition a Hopf
${\mathcal C}_{\text {Bic}}({\mathcal G})$
is again by definition a Hopf
 $*$
-homomorphism
$*$
-homomorphism
 $f : \mathrm {C}(G_2) \rightarrow \mathrm {C}(G_1)$
such that:
$f : \mathrm {C}(G_2) \rightarrow \mathrm {C}(G_1)$
such that:-
–
 $(\mathrm {id}_{\mathrm {C}(\mathcal {G}^0)} \otimes f)\alpha _2=\alpha _1$
;
$(\mathrm {id}_{\mathrm {C}(\mathcal {G}^0)} \otimes f)\alpha _2=\alpha _1$
; -
–
 $(\mathrm {id}_{\mathrm {C}(\mathcal {G}^1)} \otimes f)\lambda _2=\lambda _1$
.
$(\mathrm {id}_{\mathrm {C}(\mathcal {G}^1)} \otimes f)\lambda _2=\lambda _1$
.
-
The notations used for the above two categories are justified by the following theorems.
Theorem 6.7 A universal object
![]() $(G_{\text {Ban}},\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
in the category
$(G_{\text {Ban}},\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
in the category
![]() ${\mathcal C}_{\text {Ban}}({\mathcal G})$
exists. Moreover,
${\mathcal C}_{\text {Ban}}({\mathcal G})$
exists. Moreover,
![]() $G_{\text {Ban}}$
is isomorphic to
$G_{\text {Ban}}$
is isomorphic to
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
, the quantum automorphism group of
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
, the quantum automorphism group of
![]() ${\mathcal G}$
in the sense of Banica.
${\mathcal G}$
in the sense of Banica.
Theorem 6.8 A universal object
![]() $(G_{\text {Bic}},\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
in the category
$(G_{\text {Bic}},\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
in the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
exists. Moreover,
${\mathcal C}_{\text {Bic}}({\mathcal G})$
exists. Moreover,
![]() $G_{\text {Bic}}$
is isomorphic to
$G_{\text {Bic}}$
is isomorphic to
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
, the quantum automorphism group of
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
, the quantum automorphism group of
![]() ${\mathcal G}$
in the sense of Bichon.
${\mathcal G}$
in the sense of Bichon.
Proof of Theorem 6.7
We have to show first that
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
can be made into an object of the category
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
can be made into an object of the category
![]() ${\mathcal C}_{\text {Ban}}({\mathcal G})$
. We proceed to do so now. As in Theorem 6.2, we denote the generators of the underlying
${\mathcal C}_{\text {Ban}}({\mathcal G})$
. We proceed to do so now. As in Theorem 6.2, we denote the generators of the underlying
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
of
$\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
of
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
by
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
by
![]() $\{q_{wv}\}_{v,w \in \mathcal {G}^0}$
. Now, we define
$\{q_{wv}\}_{v,w \in \mathcal {G}^0}$
. Now, we define
![]() $\lambda _{\text {Ban}}$
and
$\lambda _{\text {Ban}}$
and
![]() $\alpha _{\text {Ban}}$
as
$\alpha _{\text {Ban}}$
as
The relations (6.1),(6.2), and (6.3) imply that
![]() $\alpha _{\text {Ban}}$
is a unital
$\alpha _{\text {Ban}}$
is a unital
![]() $*$
-homomorphism. The formula (6.4) for the comultiplication shows coassociativity of both
$*$
-homomorphism. The formula (6.4) for the comultiplication shows coassociativity of both
![]() $\alpha _{\text {Ban}}$
and
$\alpha _{\text {Ban}}$
and
![]() $\lambda _{\text {Ban}}$
. The Podleś conditions for
$\lambda _{\text {Ban}}$
. The Podleś conditions for
![]() $\alpha _{\text {Ban}}$
and
$\alpha _{\text {Ban}}$
and
![]() $\lambda _{\text {Ban}}$
follow from the facts that
$\lambda _{\text {Ban}}$
follow from the facts that
![]() $\mathrm {C}(\mathcal {G}^0)$
and
$\mathrm {C}(\mathcal {G}^0)$
and
![]() $\mathrm {C}(\mathcal {G}^1)$
are finite dimensional, respectively. Furthermore, the fact that
$\mathrm {C}(\mathcal {G}^1)$
are finite dimensional, respectively. Furthermore, the fact that
![]() $\{q_{vw}\}_{v,w\in \mathcal {G}^0}$
are generators of
$\{q_{vw}\}_{v,w\in \mathcal {G}^0}$
are generators of
![]() $\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
implies that
$\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
implies that
![]() $\alpha _{\text {Ban}}$
is a faithful G-action on
$\alpha _{\text {Ban}}$
is a faithful G-action on
![]() $\mathrm {C}(\mathcal {G}^0)$
. Therefore, to show that
$\mathrm {C}(\mathcal {G}^0)$
. Therefore, to show that
![]() $(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
is an object of the category
$(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
is an object of the category
![]() ${\mathcal C}_{\text {Ban}}({\mathcal G})$
, it suffices to show
${\mathcal C}_{\text {Ban}}({\mathcal G})$
, it suffices to show
We remind the reader that
![]() $\phi $
is given as in Example 5.1. Now to check identity (6.9), we note that
$\phi $
is given as in Example 5.1. Now to check identity (6.9), we note that
![]() $\phi (\delta _{v})\delta _{e}=\delta _{s(e),v}\delta _{e}$
; hence the left-hand side of (6.9) reduces to
$\phi (\delta _{v})\delta _{e}=\delta _{s(e),v}\delta _{e}$
; hence the left-hand side of (6.9) reduces to
For the right-hand side of (6.9), we have the following expression:
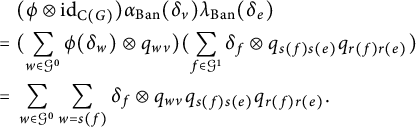 $$ \begin{align} \begin{aligned} &{}(\phi \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha_{\text{Ban}}(\delta_{v})\lambda_{\text{Ban}}(\delta_{e})\\ ={}&(\sum_{w\in \mathcal{G}^0}\phi(\delta_{w}) \otimes q_{wv})(\sum_{f\in \mathcal{G}^1}\delta_{f}\otimes q_{s(f)s(e)}q_{r(f)r(e)})\\ ={}&\sum_{w\in \mathcal{G}^0}\sum_{w=s(f)}\delta_{f}\otimes q_{wv}q_{s(f)s(e)}q_{r(f)r(e)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &{}(\phi \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha_{\text{Ban}}(\delta_{v})\lambda_{\text{Ban}}(\delta_{e})\\ ={}&(\sum_{w\in \mathcal{G}^0}\phi(\delta_{w}) \otimes q_{wv})(\sum_{f\in \mathcal{G}^1}\delta_{f}\otimes q_{s(f)s(e)}q_{r(f)r(e)})\\ ={}&\sum_{w\in \mathcal{G}^0}\sum_{w=s(f)}\delta_{f}\otimes q_{wv}q_{s(f)s(e)}q_{r(f)r(e)}. \end{aligned} \end{align} $$
But for
![]() $v \neq s(e)$
,
$v \neq s(e)$
,
![]() $q_{wv}q_{s(f)s(e)}=0$
for all
$q_{wv}q_{s(f)s(e)}=0$
for all
![]() $w=s(f)$
, from the relation (6.1); in that case, the final expression of (6.14) is zero, coinciding with (6.13) and so we have (6.9). For
$w=s(f)$
, from the relation (6.1); in that case, the final expression of (6.14) is zero, coinciding with (6.13) and so we have (6.9). For
![]() $v=s(e)$
, the final expression of (6.14) reduces to
$v=s(e)$
, the final expression of (6.14) reduces to
On the other hand, for
![]() $v=s(e)$
, we now consider (6.13).
$v=s(e)$
, we now consider (6.13).
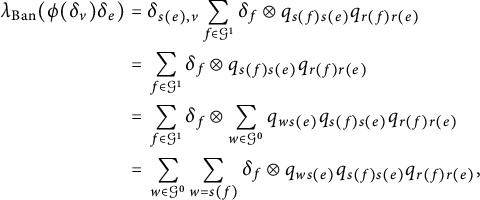 $$ \begin{align} \begin{aligned} \lambda_{\text{Ban}}(\phi(\delta_{v})\delta_{e})={}&\delta_{s(e),v}\sum_{f\in \mathcal{G}^1}\delta_{f}\otimes q_{s(f)s(e)}q_{r(f)r(e)}\\ ={}&\sum_{f \in \mathcal{G}^1}\delta_{f}\otimes q_{s(f)s(e)}q_{r(f)r(e)}\\ ={}&\sum_{f\in \mathcal{G}^1}\delta_{f}\otimes \sum_{w \in \mathcal{G}^0}q_{ws(e)}q_{s(f)s(e)}q_{r(f)r(e)}\\ ={}&\sum_{w\in \mathcal{G}^0}\sum_{w=s(f)}\delta_{f}\otimes q_{ws(e)}q_{s(f)s(e)}q_{r(f)r(e)}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \lambda_{\text{Ban}}(\phi(\delta_{v})\delta_{e})={}&\delta_{s(e),v}\sum_{f\in \mathcal{G}^1}\delta_{f}\otimes q_{s(f)s(e)}q_{r(f)r(e)}\\ ={}&\sum_{f \in \mathcal{G}^1}\delta_{f}\otimes q_{s(f)s(e)}q_{r(f)r(e)}\\ ={}&\sum_{f\in \mathcal{G}^1}\delta_{f}\otimes \sum_{w \in \mathcal{G}^0}q_{ws(e)}q_{s(f)s(e)}q_{r(f)r(e)}\\ ={}&\sum_{w\in \mathcal{G}^0}\sum_{w=s(f)}\delta_{f}\otimes q_{ws(e)}q_{s(f)s(e)}q_{r(f)r(e)}, \end{aligned} \end{align} $$
where the third equality is by (6.2); and the fourth equality is by (6.1). However, the final expression in (6.16) is nothing but (6.15). Therefore, we indeed have (6.9). We leave the checking of (6.10) to the reader, which is similar to what has just been done for (6.9). To check the identity (6.11), we note that
Then it reduces to the calculations already done in [Reference SchafhauserSW18, Section 4.1.2]. So we are left with the checking of (6.12). To that end, we note that
Therefore, the right-hand side of (6.12) becomes
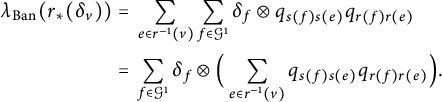 $$ \begin{align} \begin{aligned} \lambda_{\text{Ban}}(r_{\ast}(\delta_{v}))={}&\sum_{e \in r^{-1}(v)}\sum_{f \in \mathcal{G}^1}\delta_{f}\otimes q_{s(f)s(e)}q_{r(f)r(e)}\\ ={}& \sum_{f \in \mathcal{G}^1}\delta_{f}\otimes \Big(\sum_{e \in r^{-1}(v)}q_{s(f)s(e)}q_{r(f)r(e)}\Big). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \lambda_{\text{Ban}}(r_{\ast}(\delta_{v}))={}&\sum_{e \in r^{-1}(v)}\sum_{f \in \mathcal{G}^1}\delta_{f}\otimes q_{s(f)s(e)}q_{r(f)r(e)}\\ ={}& \sum_{f \in \mathcal{G}^1}\delta_{f}\otimes \Big(\sum_{e \in r^{-1}(v)}q_{s(f)s(e)}q_{r(f)r(e)}\Big). \end{aligned} \end{align} $$
On the other hand, the left-hand side of (6.12) reduces to
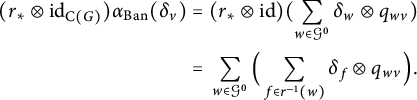 $$ \begin{align} \begin{aligned} (r_{\ast}\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha_{\text{Ban}}(\delta_{v})={}& (r_{\ast}\otimes\mathrm{id})(\sum_{w\in \mathcal{G}^0}\delta_{w}\otimes q_{wv})\\ ={}&\sum_{w\in \mathcal{G}^0}\Big(\sum_{f \in r^{-1}(w)}\delta_{f}\otimes q_{wv}\Big). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (r_{\ast}\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha_{\text{Ban}}(\delta_{v})={}& (r_{\ast}\otimes\mathrm{id})(\sum_{w\in \mathcal{G}^0}\delta_{w}\otimes q_{wv})\\ ={}&\sum_{w\in \mathcal{G}^0}\Big(\sum_{f \in r^{-1}(w)}\delta_{f}\otimes q_{wv}\Big). \end{aligned} \end{align} $$
Now, we observe that the set
![]() $\{f \in \mathcal {G}^1 \mid r(f)=w, w \in \mathcal {G}^0\}$
is the whole of
$\{f \in \mathcal {G}^1 \mid r(f)=w, w \in \mathcal {G}^0\}$
is the whole of
![]() $\mathcal {G}^1;$
and therefore, the last expression in (6.18) reduces to
$\mathcal {G}^1;$
and therefore, the last expression in (6.18) reduces to
We also have, for each
![]() $f \in \mathcal {G}^1$
,
$f \in \mathcal {G}^1$
,
moreover, since
![]() $q_{s(f)w}q_{r(f)v}=0$
whenever
$q_{s(f)w}q_{r(f)v}=0$
whenever
![]() $(v,w)$
is not an edge,
$(v,w)$
is not an edge,
Combining (6.18), (6.19), (6.20), and (6.21), we obtain
which is exactly the last expression in (6.17). Therefore (6.12) holds. This proves that indeed
![]() $(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
is an object in the category
$(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
is an object in the category
![]() ${\mathcal C}_{\text {Ban}}({\mathcal G})$
.
${\mathcal C}_{\text {Ban}}({\mathcal G})$
.
Now, we turn to the proof of the fact that
![]() $(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
is indeed the universal object in the category
$(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
is indeed the universal object in the category
![]() ${\mathcal C}_{\text {Ban}}({\mathcal G})$
. To that end, let
${\mathcal C}_{\text {Ban}}({\mathcal G})$
. To that end, let
![]() $(G,\alpha ,\lambda )$
be an object of the category
$(G,\alpha ,\lambda )$
be an object of the category
![]() ${\mathcal C}_{\text {Ban}}({\mathcal G})$
.
${\mathcal C}_{\text {Ban}}({\mathcal G})$
.
Now, as already observed, for any
![]() $v \in \mathcal {G}^0$
,
$v \in \mathcal {G}^0$
,
As the graph does not have any multiple edges or sources, for
![]() $w \in \mathcal {G}^0$
with
$w \in \mathcal {G}^0$
with
![]() $s(e)=w, r(e)=v$
,
$s(e)=w, r(e)=v$
,
Hence, we have
On the other hand, since
![]() $(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\circ \alpha =\lambda \circ r_{\ast }$
and
$(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\circ \alpha =\lambda \circ r_{\ast }$
and
![]() $\lambda (\phi (f)\xi )=(\phi \otimes \mathrm {id}_{\mathrm {C}(G)})\alpha (f)\lambda (\xi )$
for
$\lambda (\phi (f)\xi )=(\phi \otimes \mathrm {id}_{\mathrm {C}(G)})\alpha (f)\lambda (\xi )$
for
![]() $f \in \mathrm {C}(\mathcal {G}^0)$
and
$f \in \mathrm {C}(\mathcal {G}^0)$
and
![]() $\xi \in \mathrm {C}(\mathcal {G}^1)$
,
$\xi \in \mathrm {C}(\mathcal {G}^1)$
,
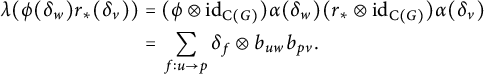 $$ \begin{align} \begin{aligned} \lambda(\phi(\delta_{w})r_{\ast}(\delta_{v}))={}&(\phi \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(\delta_{w})(r_{\ast}\otimes\mathrm{id}_{\mathrm{C}(G)})\alpha(\delta_{v})\\ ={}&\sum_{f : u \rightarrow p}\delta_{f}\otimes b_{uw}b_{pv}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \lambda(\phi(\delta_{w})r_{\ast}(\delta_{v}))={}&(\phi \otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(\delta_{w})(r_{\ast}\otimes\mathrm{id}_{\mathrm{C}(G)})\alpha(\delta_{v})\\ ={}&\sum_{f : u \rightarrow p}\delta_{f}\otimes b_{uw}b_{pv}. \end{aligned} \end{align} $$
By comparing coefficients, we get
Then the fact that
![]() $(b_{vw})_{v,w \in \mathcal {G}^0}$
satisfy the relations of
$(b_{vw})_{v,w \in \mathcal {G}^0}$
satisfy the relations of
![]() $\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
can be checked, along the lines of [Reference SchafhauserSW18, Section 4.3.3], using
$\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
can be checked, along the lines of [Reference SchafhauserSW18, Section 4.3.3], using
together with the fact that
we leave this to the reader. We therefore have shown the universality of the triple
![]() $(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
, thus completing the proof of the theorem.
$(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
, thus completing the proof of the theorem.
Remark 6.9 The compact quantum group
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is of Kac type; moreover, by Theorem 6.7
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is of Kac type; moreover, by Theorem 6.7
![]() $, (\mathrm {C}(\mathcal {G}^1),\phi ,\lambda _{\text {Ban}})$
is a
$, (\mathrm {C}(\mathcal {G}^1),\phi ,\lambda _{\text {Ban}})$
is a
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-equivariant
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-equivariant
![]() $\mathrm {C}^*$
-correspondence over the
$\mathrm {C}^*$
-correspondence over the
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(\mathrm {C}(\mathcal {G}^0),\alpha _{\text {Ban}})$
. Since the module dynamics corresponding to the gauge action is the scalar dynamics, i.e.,
$(\mathrm {C}(\mathcal {G}^0),\alpha _{\text {Ban}})$
. Since the module dynamics corresponding to the gauge action is the scalar dynamics, i.e.,
![]() $U_t=e^{it}$
,
$U_t=e^{it}$
,
![]() $t \in \mathbb {R}$
, by Theorem 4.10, the lifted
$t \in \mathbb {R}$
, by Theorem 4.10, the lifted
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-action
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-action
![]() $\omega $
of
$\omega $
of
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
on
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
on
![]() $\mathrm {C}^*({\mathcal G})$
preserves a KMS state
$\mathrm {C}^*({\mathcal G})$
preserves a KMS state
![]() $\varphi $
at the critical inverse temperature if and only if it preserves the tracial state
$\varphi $
at the critical inverse temperature if and only if it preserves the tracial state
![]() $\tau $
on
$\tau $
on
![]() $\mathrm {C}(\mathcal {G}^0)$
. This yields another proof of [Reference Joardar and MandalJM21b, Proposition 2.31].
$\mathrm {C}(\mathcal {G}^0)$
. This yields another proof of [Reference Joardar and MandalJM21b, Proposition 2.31].
It can be proved that for the universal object
![]() $(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
, we also have
$(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
, we also have
for all
![]() $f \in \mathrm {C}(\mathcal {G}^0)$
, which is the content of the next theorem.
$f \in \mathrm {C}(\mathcal {G}^0)$
, which is the content of the next theorem.
Proposition 6.10 For the universal object
![]() $(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
, we also have
$(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
, we also have
for all
![]() $f \in \mathrm {C}(\mathcal {G}^0)$
$f \in \mathrm {C}(\mathcal {G}^0)$
Proof We begin by fixing a vertex
![]() $v \in \mathcal {G}^0$
. Then, if
$v \in \mathcal {G}^0$
. Then, if
![]() $s^{-1}(v)$
is nonempty, then the arguments used in the proof of the fact
$s^{-1}(v)$
is nonempty, then the arguments used in the proof of the fact
![]() $(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha _{\text {Ban}}(f)=\lambda _{\text {Ban}}(r_{\ast }(f))$
can be repeated with obvious modifications. So we are left with the case when
$(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha _{\text {Ban}}(f)=\lambda _{\text {Ban}}(r_{\ast }(f))$
can be repeated with obvious modifications. So we are left with the case when
![]() $s^{-1}(v)$
is empty. Then
$s^{-1}(v)$
is empty. Then
![]() $s_{\ast }(\delta _{v})=0$
so that
$s_{\ast }(\delta _{v})=0$
so that
![]() $\lambda _{\text {Ban}}(s_{\ast }(\delta _{v}))=0$
. On the other hand, denoting the generators of the
$\lambda _{\text {Ban}}(s_{\ast }(\delta _{v}))=0$
. On the other hand, denoting the generators of the
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
by
$\mathrm {C}(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}))$
by
![]() $\{q_{vw}\}_{v,w\in \mathcal {G}^0}$
, as in Theorem 6.2, we obtain
$\{q_{vw}\}_{v,w\in \mathcal {G}^0}$
, as in Theorem 6.2, we obtain
But, for a fixed edge
![]() $f \in \mathcal {G}^1$
,
$f \in \mathcal {G}^1$
,
![]() $q_{s(f)v}=\sum _{w \in \mathcal {G}^0}q_{s(f)v}q_{r(f)w}$
. Since
$q_{s(f)v}=\sum _{w \in \mathcal {G}^0}q_{s(f)v}q_{r(f)w}$
. Since
![]() $s^{-1}(v)$
is empty,
$s^{-1}(v)$
is empty,
![]() $q_{s(f)v}q_{r(f)w}=0$
, which implies that
$q_{s(f)v}q_{r(f)w}=0$
, which implies that
![]() $(s_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha _{\text {Ban}}(\delta _{v})=0$
as well.
$(s_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha _{\text {Ban}}(\delta _{v})=0$
as well.
The following lemma will be useful in proving Theorem 6.8.
Lemma 6.11 Let
![]() $(G,\alpha ,\lambda )$
be an object of the category
$(G,\alpha ,\lambda )$
be an object of the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
(Definition 6.6). Then
${\mathcal C}_{\text {Bic}}({\mathcal G})$
(Definition 6.6). Then
as well as
for all
![]() $f \in \mathrm {C}(\mathcal {G}^0)$
.
$f \in \mathrm {C}(\mathcal {G}^0)$
.
Conversely, assume that one of r and s is injective. Let
![]() $(G,\alpha ,\lambda )$
be a triple, where G is a compact quantum group,
$(G,\alpha ,\lambda )$
be a triple, where G is a compact quantum group,
![]() $\alpha : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^0) \otimes \mathrm {C}(G)$
is a unital
$\alpha : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^0) \otimes \mathrm {C}(G)$
is a unital
![]() $*$
-homomorphism and
$*$
-homomorphism and
![]() $\lambda : \mathrm {C}(\mathcal {G}^1) \rightarrow \mathrm {C}(\mathcal {G}^1) \otimes \mathrm {C}(G)$
is a linear map satisfying the following conditions:
$\lambda : \mathrm {C}(\mathcal {G}^1) \rightarrow \mathrm {C}(\mathcal {G}^1) \otimes \mathrm {C}(G)$
is a linear map satisfying the following conditions:
-
• The pair
 $(\mathrm {C}(\mathcal {G}^0),\alpha )$
is a G-
$(\mathrm {C}(\mathcal {G}^0),\alpha )$
is a G-
 $\mathrm {C}^*$
-algebra;
$\mathrm {C}^*$
-algebra; -
• the triple
 $(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda )$
is a G-equivariant
$(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda )$
is a G-equivariant
 $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
 $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
 $(\mathrm {C}(\mathcal {G}^0),\alpha )$
;
$(\mathrm {C}(\mathcal {G}^0),\alpha )$
; -
• moreover,
as well as $$\begin{align*}(r_\ast\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(f)=\lambda(r_{\ast}(f)), \end{align*}$$
for all
$$\begin{align*}(r_\ast\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(f)=\lambda(r_{\ast}(f)), \end{align*}$$
for all $$\begin{align*}(s_\ast\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(f)=\lambda(s_{\ast}(f)), \end{align*}$$
$$\begin{align*}(s_\ast\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(f)=\lambda(s_{\ast}(f)), \end{align*}$$
 $f \in \mathrm {C}(\mathcal {G}^0)$
.
$f \in \mathrm {C}(\mathcal {G}^0)$
.
Then the pair
![]() $(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a G-
$(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a G-
![]() $\mathrm {C}^*$
-algebra and consequently,
$\mathrm {C}^*$
-algebra and consequently,
![]() $(G,\alpha ,\lambda )$
is an object of the category
$(G,\alpha ,\lambda )$
is an object of the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
.
${\mathcal C}_{\text {Bic}}({\mathcal G})$
.
Proof We first assume that
![]() $(G,\alpha ,\lambda )$
is an object in the category
$(G,\alpha ,\lambda )$
is an object in the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
. Let
${\mathcal C}_{\text {Bic}}({\mathcal G})$
. Let
![]() $\xi \in \mathrm {C}(\mathcal {G}^1)$
and
$\xi \in \mathrm {C}(\mathcal {G}^1)$
and
![]() $f \in \mathrm {C}(\mathcal {G}^0)$
. It is clear that
$f \in \mathrm {C}(\mathcal {G}^0)$
. It is clear that
where
![]() $\xi f$
denotes the right module action of f on
$\xi f$
denotes the right module action of f on
![]() $\xi $
and
$\xi $
and
![]() $\xi r_{\ast }(f)$
denotes the algebra multiplication in
$\xi r_{\ast }(f)$
denotes the algebra multiplication in
![]() $\mathrm {C}({\mathcal G}^{1})$
. Since
$\mathrm {C}({\mathcal G}^{1})$
. Since
![]() $\lambda $
is a G-action, we obtain
$\lambda $
is a G-action, we obtain
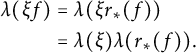 $$ \begin{align*} \begin{aligned} \lambda(\xi f)={}&\lambda(\xi r_{\ast}(f))\\ ={}&\lambda(\xi)\lambda(r_{\ast}(f)). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \lambda(\xi f)={}&\lambda(\xi r_{\ast}(f))\\ ={}&\lambda(\xi)\lambda(r_{\ast}(f)). \end{aligned} \end{align*} $$
Similarly, decoding the right module action of
![]() $\mathrm {C}(\mathcal {G}^0)\otimes \mathrm {C}(G)$
on
$\mathrm {C}(\mathcal {G}^0)\otimes \mathrm {C}(G)$
on
![]() $\mathrm {C}(\mathcal {G}^1)\otimes \mathrm {C}(G)$
, we get the following:
$\mathrm {C}(\mathcal {G}^1)\otimes \mathrm {C}(G)$
, we get the following:
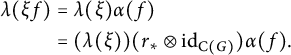 $$ \begin{align*} \begin{aligned} \lambda(\xi f)={}&\lambda(\xi)\alpha(f)\\ ={}&(\lambda(\xi))(r_{\ast}\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(f). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \lambda(\xi f)={}&\lambda(\xi)\alpha(f)\\ ={}&(\lambda(\xi))(r_{\ast}\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(f). \end{aligned} \end{align*} $$
In particular, choosing
![]() $\xi =1$
, we obtain
$\xi =1$
, we obtain
for all
![]() $f \in \mathrm {C}(\mathcal {G}^0)$
. Similarly, considering the left module action produces
$f \in \mathrm {C}(\mathcal {G}^0)$
. Similarly, considering the left module action produces
For the converse, we assume that r is injective. Then we note that it is enough to show that
![]() $\lambda $
is a
$\lambda $
is a
![]() $*$
-homomorphism. As r is injective,
$*$
-homomorphism. As r is injective,
![]() $r_{\ast } : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^1)$
is a surjective
$r_{\ast } : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^1)$
is a surjective
![]() $*$
-homomorphism. So, for
$*$
-homomorphism. So, for
![]() $\xi ,\eta \in \mathrm {C}(\mathcal {G}^1)$
,
$\xi ,\eta \in \mathrm {C}(\mathcal {G}^1)$
,
for some
![]() $f,g \in \mathrm {C}(\mathcal {G}^0)$
. Since
$f,g \in \mathrm {C}(\mathcal {G}^0)$
. Since
![]() $r_{\ast }$
and therefore
$r_{\ast }$
and therefore
![]() $(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})$
are
$(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})$
are
![]() $*$
-homomorphisms, we have
$*$
-homomorphisms, we have
which is nothing but
![]() $(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha (f)(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha (g)$
. Therefore
$(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha (f)(r_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\alpha (g)$
. Therefore
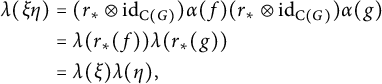 $$ \begin{align*} \begin{aligned} \lambda(\xi\eta)={}&(r_{\ast}\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(f)(r_{\ast}\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(g)\\ ={}&\lambda(r_{\ast}(f))\lambda(r_{\ast}(g))\\ ={}&\lambda(\xi)\lambda(\eta), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \lambda(\xi\eta)={}&(r_{\ast}\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(f)(r_{\ast}\otimes \mathrm{id}_{\mathrm{C}(G)})\alpha(g)\\ ={}&\lambda(r_{\ast}(f))\lambda(r_{\ast}(g))\\ ={}&\lambda(\xi)\lambda(\eta), \end{aligned} \end{align*} $$
proving that
![]() $\lambda $
is a
$\lambda $
is a
![]() $*$
-homomorphism. Similarly, if s is injective, using the identity
$*$
-homomorphism. Similarly, if s is injective, using the identity
![]() $(s_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\circ \alpha =\lambda \circ s_{\ast }$
, one can prove that
$(s_{\ast }\otimes \mathrm {id}_{\mathrm {C}(G)})\circ \alpha =\lambda \circ s_{\ast }$
, one can prove that
![]() $\lambda $
is a
$\lambda $
is a
![]() $*$
-homomorphism.
$*$
-homomorphism.
Now, we can turn to the proof of Theorem 6.8.
Proof of Theorem 6.8
First, let us prove that
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
can be made into an object of the category
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
can be made into an object of the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
. We denote the generators of
${\mathcal C}_{\text {Bic}}({\mathcal G})$
. We denote the generators of
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
by
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
by
![]() $(q_{vw})_{v,w\in \mathcal {G}^0}$
as in Remark 6.4. let us define the maps
$(q_{vw})_{v,w\in \mathcal {G}^0}$
as in Remark 6.4. let us define the maps
![]() $\lambda _{\text {Bic}}$
and
$\lambda _{\text {Bic}}$
and
![]() $\alpha _{\text {Bic}}$
by equations (6.7) and (6.8), respectively, i.e.,
$\alpha _{\text {Bic}}$
by equations (6.7) and (6.8), respectively, i.e.,
Then
![]() $\lambda _{\text {Bic}}$
is a
$\lambda _{\text {Bic}}$
is a
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
-action on
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
-action on
![]() $\mathrm {C}(\mathcal {G}^1)$
, by the definition of
$\mathrm {C}(\mathcal {G}^1)$
, by the definition of
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
. Now,
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
. Now,
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
is a quantum subgroup of
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
is a quantum subgroup of
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
. We have already proved that
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
. We have already proved that
![]() $(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda _{\text {Ban}})$
is a
$(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda _{\text {Ban}})$
is a
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-equivariant
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-equivariant
![]() $\mathrm {C}^*$
-correspondence over the
$\mathrm {C}^*$
-correspondence over the
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(\mathrm {C}(\mathcal {G}^0),\alpha _{\text {Ban}})$
. Therefore,
$(\mathrm {C}(\mathcal {G}^0),\alpha _{\text {Ban}})$
. Therefore,
![]() $(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda _{\text {Bic}})$
is a
$(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda _{\text {Bic}})$
is a
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
-equivariant
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
-equivariant
![]() $\mathrm {C}^*$
-correspondence over the
$\mathrm {C}^*$
-correspondence over the
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
-
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
-
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $(\mathrm {C}(\mathcal {G}^0),\alpha _{\text {Bic}})$
. This proves that
$(\mathrm {C}(\mathcal {G}^0),\alpha _{\text {Bic}})$
. This proves that
![]() $(\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G}),\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is an object in the category
$(\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G}),\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is an object in the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
.
${\mathcal C}_{\text {Bic}}({\mathcal G})$
.
To show that
![]() $(\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G}),\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is a universal object, we pick an object
$(\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G}),\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is a universal object, we pick an object
![]() $(G,\alpha ,\lambda )$
from the category
$(G,\alpha ,\lambda )$
from the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
. Then, by Lemma 6.11,
${\mathcal C}_{\text {Bic}}({\mathcal G})$
. Then, by Lemma 6.11,
and consequently, G becomes a quantum subgroup of
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
. Since
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
. Since
![]() $\lambda $
is an action, the relations (6.5) also hold in
$\lambda $
is an action, the relations (6.5) also hold in
![]() $\mathrm {C}(G)$
. Hence, by the universality of
$\mathrm {C}(G)$
. Hence, by the universality of
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
, G is a quantum subgroup of
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
, G is a quantum subgroup of
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
as well. This shows that
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
as well. This shows that
![]() $(\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G}),\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
indeed is a universal object in the category
$(\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G}),\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
indeed is a universal object in the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
.
${\mathcal C}_{\text {Bic}}({\mathcal G})$
.
The converse direction of Lemma 6.11 has the following corollary.
Corollary 6.12 Let
![]() ${\mathcal G}$
be a finite, simple graph without any source. If either r or s is injective, then
${\mathcal G}$
be a finite, simple graph without any source. If either r or s is injective, then
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
is isomorphic to
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
is isomorphic to
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
.
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
.
Proof We know that
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
is a quantum subgroup of
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
is a quantum subgroup of
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
. By Lemma 6.11, we conclude that the pair
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
. By Lemma 6.11, we conclude that the pair
![]() $(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a
$(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
-
![]() $\mathrm {C}^*$
-algebra and consequently,
$\mathrm {C}^*$
-algebra and consequently,
![]() $(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
is an object of the category
$(\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G}),\alpha _{\text {Ban}},\lambda _{\text {Ban}})$
is an object of the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
. But then
${\mathcal C}_{\text {Bic}}({\mathcal G})$
. But then
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is a quantum subgroup of
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is a quantum subgroup of
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
. Therefore,
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
. Therefore,
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is isomorphic to
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is isomorphic to
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
.
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
.
As an application, we shall give an example of a finite, simple graph
![]() ${\mathcal G}$
without any source such that
${\mathcal G}$
without any source such that
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is genuinely quantum and is isomorphic to
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
is genuinely quantum and is isomorphic to
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
. To that end, let us consider a graph where the map r is a bijection between the edge set and the vertex set. Note that, if we assume the graph to be connected and without multiple edges or loops, then we are not left with many choices. The graph essentially reduces to an oriented m-gon whose quantum symmetry coincides with the classical symmetry group which is
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
. To that end, let us consider a graph where the map r is a bijection between the edge set and the vertex set. Note that, if we assume the graph to be connected and without multiple edges or loops, then we are not left with many choices. The graph essentially reduces to an oriented m-gon whose quantum symmetry coincides with the classical symmetry group which is
![]() $\mathbb {Z}/m\mathbb {Z}$
[Reference Baaj and SkandalisBan05a, Theorem 4.1]. Now, if we consider disjoint union of n-number of such graphs, then the map r is still a bijection and we can apply Corollary 6.12. Combining this with [Reference Bhattacharjee, Chirvasitu and GoswamiBic04, Theorem 4.2], we obtain another proof of the following well-known result. But before stating it, let us remark that for a compact quantum group G, we denote the free wreath product of G with the quantum permutation group of n-points
$\mathbb {Z}/m\mathbb {Z}$
[Reference Baaj and SkandalisBan05a, Theorem 4.1]. Now, if we consider disjoint union of n-number of such graphs, then the map r is still a bijection and we can apply Corollary 6.12. Combining this with [Reference Bhattacharjee, Chirvasitu and GoswamiBic04, Theorem 4.2], we obtain another proof of the following well-known result. But before stating it, let us remark that for a compact quantum group G, we denote the free wreath product of G with the quantum permutation group of n-points
![]() $\text {S}^+_n$
by
$\text {S}^+_n$
by
![]() $G\wr _{\ast } \text {S}^+_n$
; we refer the reader to [Reference Bhattacharjee, Chirvasitu and GoswamiBic04] for more details on this.
$G\wr _{\ast } \text {S}^+_n$
; we refer the reader to [Reference Bhattacharjee, Chirvasitu and GoswamiBic04] for more details on this.
Theorem 6.13 [Reference Bratteli and RobinsonBV09, Theorem 3.4] Let
![]() ${\mathcal G}$
be a graph which is a disjoint union of n-number of copies of oriented m-gons. Then
${\mathcal G}$
be a graph which is a disjoint union of n-number of copies of oriented m-gons. Then
![]() $\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
and
$\mathrm {Aut}^{+}_{\text {Ban}}({\mathcal G})$
and
![]() $\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
coincide and are isomorphic to
$\mathrm {Aut}^{+}_{\text {Bic}}({\mathcal G})$
coincide and are isomorphic to
7 Applications to quantum symmetries of graphs III: The case of multigraphs
In this section, we allow the graphs to admit multiple edges. Let then
![]() ${\mathcal G}=(\mathcal {G}^0,\mathcal {G}^1,r,s)$
be a finite, directed graph, possibly with multiple edges, but without any sources. We are interested in the category
${\mathcal G}=(\mathcal {G}^0,\mathcal {G}^1,r,s)$
be a finite, directed graph, possibly with multiple edges, but without any sources. We are interested in the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
from Definition 6.6. Although for a simple graph, the above category has a smaller universal object compared to the category of Definition 6.5, for graphs with multiple edges, the category
${\mathcal C}_{\text {Bic}}({\mathcal G})$
from Definition 6.6. Although for a simple graph, the above category has a smaller universal object compared to the category of Definition 6.5, for graphs with multiple edges, the category
![]() ${\mathcal C}_{\text {Bic}}({\mathcal G})$
is more relevant. For example, in the case of the graph of Cuntz algebra, the
${\mathcal C}_{\text {Bic}}({\mathcal G})$
is more relevant. For example, in the case of the graph of Cuntz algebra, the
![]() $\text {C}^*$
-algebra
$\text {C}^*$
-algebra
![]() $\text {C}(\mathcal {G}^0)$
is
$\text {C}(\mathcal {G}^0)$
is
![]() $\mathbb {C}$
and hence has a trivial quantum symmetry and consequently, the category
$\mathbb {C}$
and hence has a trivial quantum symmetry and consequently, the category
![]() ${\mathcal C}_{\text {Ban}}({\mathcal G})$
only consists of trivial actions of compact quantum groups.
${\mathcal C}_{\text {Ban}}({\mathcal G})$
only consists of trivial actions of compact quantum groups.
Definition 7.1 Let
![]() $\mathcal {G}=(\mathcal {G}^1,\mathcal {G}^0,r,s)$
be a finite, directed graph, possibly with loops or multiple edges. We define the category
$\mathcal {G}=(\mathcal {G}^1,\mathcal {G}^0,r,s)$
be a finite, directed graph, possibly with loops or multiple edges. We define the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
as follows:
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
as follows:
-
• An object of
 ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
is a triple
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
is a triple
 $(G,\alpha ,\lambda )$
, where G is a compact quantum group,
$(G,\alpha ,\lambda )$
, where G is a compact quantum group,
 $\alpha : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^0) \otimes \mathrm {C}(G)$
is a unital
$\alpha : \mathrm {C}(\mathcal {G}^0) \rightarrow \mathrm {C}(\mathcal {G}^0) \otimes \mathrm {C}(G)$
is a unital
 $*$
-homomorphism and
$*$
-homomorphism and
 $\lambda : \mathrm {C}(\mathcal {G}^1) \rightarrow \mathrm {C}(\mathcal {G}^1) \otimes \mathrm {C}(G)$
is a linear map satisfying the following conditions:
$\lambda : \mathrm {C}(\mathcal {G}^1) \rightarrow \mathrm {C}(\mathcal {G}^1) \otimes \mathrm {C}(G)$
is a linear map satisfying the following conditions:-
– The pair
 $(\mathrm {C}(\mathcal {G}^0),\alpha )$
is a G-
$(\mathrm {C}(\mathcal {G}^0),\alpha )$
is a G-
 $\mathrm {C}^*$
-algebra.
$\mathrm {C}^*$
-algebra. -
– The triple
 $(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda )$
is a G-equivariant
$(\mathrm {C}(\mathcal {G}^1),\phi ,\lambda )$
is a G-equivariant
 $\mathrm {C}^*$
-correspondence over the G-
$\mathrm {C}^*$
-correspondence over the G-
 $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
 $(\mathrm {C}(\mathcal {G}^0),\alpha )$
.
$(\mathrm {C}(\mathcal {G}^0),\alpha )$
. -
– The pair
 $(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a G-
$(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a G-
 $\mathrm {C}^*$
-algebra and the action
$\mathrm {C}^*$
-algebra and the action
 $\lambda $
is faithful.
$\lambda $
is faithful.
-
-
• Let
 $(G_1,\alpha _1,\lambda _1)$
and
$(G_1,\alpha _1,\lambda _1)$
and
 $(G_2,\alpha _2,\lambda _2)$
be two objects of the category
$(G_2,\alpha _2,\lambda _2)$
be two objects of the category
 ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
. A morphism
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
. A morphism
 $f : (G_1,\alpha _1,\lambda _1) \rightarrow (G_2,\alpha _2,\lambda _2)$
in
$f : (G_1,\alpha _1,\lambda _1) \rightarrow (G_2,\alpha _2,\lambda _2)$
in
 ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
is again by definition a Hopf
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
is again by definition a Hopf
 $*$
-homomorphism
$*$
-homomorphism
 $f : \mathrm {C}(G_2) \rightarrow \mathrm {C}(G_1)$
such that:
$f : \mathrm {C}(G_2) \rightarrow \mathrm {C}(G_1)$
such that:-
–
 $(\mathrm {id}_{\mathrm {C}(\mathcal {G}^0)} \otimes f)\alpha _2=\alpha _1$
;
$(\mathrm {id}_{\mathrm {C}(\mathcal {G}^0)} \otimes f)\alpha _2=\alpha _1$
; -
–
 $(\mathrm {id}_{\mathrm {C}(\mathcal {G}^1)} \otimes f)\lambda _2=\lambda _1$
.
$(\mathrm {id}_{\mathrm {C}(\mathcal {G}^1)} \otimes f)\lambda _2=\lambda _1$
.
-
Theorem 7.2 For a finite, directed graph
![]() ${\mathcal G}$
which has multiple edges but has no source, the category
${\mathcal G}$
which has multiple edges but has no source, the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
admits a universal object.
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
admits a universal object.
We shall not give a proof of the above theorem as we are mainly interested in concrete examples of universal objects in the above category. In fact, we shall produce an example illustrating a general strategy to identify quantum subgroups of certain compact quantum groups. Also, we are aware that a notion of the quantum automorphism group of multigraphs is being formulated [Reference Hao and NgHG] and we believe that it will have some point of contact with the results obtained in this section. But we must wait for its final formulation to appear to say anything precise in this direction.
Remark 7.3 We remark that for any object
![]() $(G,\alpha ,\lambda )$
in the category
$(G,\alpha ,\lambda )$
in the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
, G is of Kac type. Also the G-action
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
, G is of Kac type. Also the G-action
![]() $\alpha $
preserves the restriction of the distinguished KMS state
$\alpha $
preserves the restriction of the distinguished KMS state
![]() $\varphi $
on
$\varphi $
on
![]() $\mathrm {C}(\mathcal {G}^0)$
. Therefore, the universal object in the category
$\mathrm {C}(\mathcal {G}^0)$
. Therefore, the universal object in the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
is a subobject of the universal object in the category of compact quantum groups acting faithfully on
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G})$
is a subobject of the universal object in the category of compact quantum groups acting faithfully on
![]() $\mathrm {C}^*({\mathcal G})$
, preserving the distinguished KMS state
$\mathrm {C}^*({\mathcal G})$
, preserving the distinguished KMS state
![]() $\varphi $
at the critical inverse temperature, whenever
$\varphi $
at the critical inverse temperature, whenever
![]() $\varphi $
exists.
$\varphi $
exists.
Let
![]() ${\mathcal G}$
be the graph with one vertex and n number of loops at the vertex;
${\mathcal G}$
be the graph with one vertex and n number of loops at the vertex;
![]() ${\mathcal G}^{\oplus m}$
be the disjoint union of m-copies of
${\mathcal G}^{\oplus m}$
be the disjoint union of m-copies of
![]() ${\mathcal G}$
. We note that the corresponding graph
${\mathcal G}$
. We note that the corresponding graph
![]() $\mathrm {C}^*$
-algebra is
$\mathrm {C}^*$
-algebra is
![]() $\oplus _{i=1}^{m}{\mathcal O}_{n}$
, where
$\oplus _{i=1}^{m}{\mathcal O}_{n}$
, where
![]() ${\mathcal O}_{n}$
is the Cuntz algebra generated by n number of partial isometries. So
${\mathcal O}_{n}$
is the Cuntz algebra generated by n number of partial isometries. So
![]() ${\mathcal G}^{\oplus m}$
has m-vertices with each vertex emitting and receiving n number of edges. We shall compute the universal object of the category
${\mathcal G}^{\oplus m}$
has m-vertices with each vertex emitting and receiving n number of edges. We shall compute the universal object of the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
.
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
.
Let us introduce now some notations. We denote the vertex set of
![]() ${\mathcal G}^{\oplus m}$
by
${\mathcal G}^{\oplus m}$
by
![]() $\mathcal {G}^0$
; the edge set by
$\mathcal {G}^0$
; the edge set by
![]() $\mathcal {G}^1$
, as usual. We denote the vertices by
$\mathcal {G}^1$
, as usual. We denote the vertices by
![]() $\{v_{i} \mid i=1,\dots ,m\}$
and edges by
$\{v_{i} \mid i=1,\dots ,m\}$
and edges by
![]() $\{e^{(i)}_{j} \mid i=1,\dots ,m, j=1,\dots ,n\}$
.
$\{e^{(i)}_{j} \mid i=1,\dots ,m, j=1,\dots ,n\}$
.
![]() $e^{(i)}_{j}$
denotes the jth loop in the ith copy of
$e^{(i)}_{j}$
denotes the jth loop in the ith copy of
![]() ${\mathcal G}$
. We denote by
${\mathcal G}$
. We denote by
![]() $\delta _{i}$
the function on
$\delta _{i}$
the function on
![]() $\mathcal {G}^0$
that takes the value
$\mathcal {G}^0$
that takes the value
![]() $1$
on
$1$
on
![]() $v_{i}$
and zero on the other vertices; we denote by
$v_{i}$
and zero on the other vertices; we denote by
![]() $\xi _{i}^{(k)}$
the function on
$\xi _{i}^{(k)}$
the function on
![]() $\mathcal {G}^1$
that takes the value
$\mathcal {G}^1$
that takes the value
![]() $1$
on
$1$
on
![]() $e^{(k)}_{i}$
and
$e^{(k)}_{i}$
and
![]() $0$
on the other edges. The result in the following theorem resembles the conclusion of [Reference Bhattacharjee, Chirvasitu and GoswamiBic04, Theorem 4.2].
$0$
on the other edges. The result in the following theorem resembles the conclusion of [Reference Bhattacharjee, Chirvasitu and GoswamiBic04, Theorem 4.2].
Theorem 7.4 Let us denote by
![]() $(G_{\text {univ}},\alpha _{\text {univ}},\lambda _{\text {univ}})$
the universal object of the category
$(G_{\text {univ}},\alpha _{\text {univ}},\lambda _{\text {univ}})$
the universal object of the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
. Then
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
. Then
![]() $G_{\text {univ}}$
is isomorphic to
$G_{\text {univ}}$
is isomorphic to
![]() $\text {S}_{n}^{+}\wr _{\ast } \text {S}^+_m$
.
$\text {S}_{n}^{+}\wr _{\ast } \text {S}^+_m$
.
Proof We begin by introducing some more notations. We shall denote the generators of
![]() $\text {S}^{+}_{n}$
by
$\text {S}^{+}_{n}$
by
![]() $u_{ij}$
, where
$u_{ij}$
, where
![]() $i,j=1,\dots ,n$
and the generators of
$i,j=1,\dots ,n$
and the generators of
![]() $\text {S}^{+}_{m}$
by
$\text {S}^{+}_{m}$
by
![]() $v_{kl}$
, where
$v_{kl}$
, where
![]() $k,l=1,\dots ,m$
. We also denote the embedding of the lth copy of
$k,l=1,\dots ,m$
. We also denote the embedding of the lth copy of
![]() $\text {S}^{+}_{n}$
in
$\text {S}^{+}_{n}$
in
![]() $\text {S}^{+}_{n}\underbrace {\ast \dots \ast }_{m\text {-times}}\text {S}^{+}_{n}$
by
$\text {S}^{+}_{n}\underbrace {\ast \dots \ast }_{m\text {-times}}\text {S}^{+}_{n}$
by
![]() $\nu _{l}$
. With these notations, the compact quantum group
$\nu _{l}$
. With these notations, the compact quantum group
![]() $\text {S}^{+}_{n}\wr _{\ast } \text {S}^{+}_{m}$
can be made into an object of the category
$\text {S}^{+}_{n}\wr _{\ast } \text {S}^{+}_{m}$
can be made into an object of the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
as follows. We define
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
as follows. We define
for
![]() $i=1,\dots , n$
and
$i=1,\dots , n$
and
![]() $k=1,\dots ,m$
; and
$k=1,\dots ,m$
; and
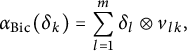 $$ \begin{align} \alpha_{\text{Bic}}(\delta_{k})=\sum_{l=1}^{m}\delta_{l}\otimes v_{lk}, \end{align} $$
$$ \begin{align} \alpha_{\text{Bic}}(\delta_{k})=\sum_{l=1}^{m}\delta_{l}\otimes v_{lk}, \end{align} $$
for
![]() $k=1,\dots ,m$
. We leave the proof of the fact that
$k=1,\dots ,m$
. We leave the proof of the fact that
![]() $(\text {S}^{+}_{n}\wr _{\ast } \text {S}^{+}_{m},\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is indeed an object of the category
$(\text {S}^{+}_{n}\wr _{\ast } \text {S}^{+}_{m},\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is indeed an object of the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
to the reader (see also [Reference Bhattacharjee, Chirvasitu and GoswamiBic04]). We only prove that the triple
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
to the reader (see also [Reference Bhattacharjee, Chirvasitu and GoswamiBic04]). We only prove that the triple
![]() $(\text {S}^{+}_{n}\wr _{\ast } \text {S}^{+}_{m},\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is the universal object in the category
$(\text {S}^{+}_{n}\wr _{\ast } \text {S}^{+}_{m},\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is the universal object in the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
.
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
.
To that end, let
![]() $(G,\alpha ,\lambda )$
be an object of the category
$(G,\alpha ,\lambda )$
be an object of the category
![]() ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
. Let, moreover,
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
. Let, moreover,
![]() $\lambda $
and
$\lambda $
and
![]() $\alpha $
be given by
$\alpha $
be given by
with the notations as in the paragraph just above the statement of the theorem. We note that since
![]() $(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a G-
$(\mathrm {C}(\mathcal {G}^1),\lambda )$
is a G-
![]() $\mathrm {C}^*$
-algebra, we have the following relations:
$\mathrm {C}^*$
-algebra, we have the following relations:
where
![]() $\kappa $
denotes the antipode of G. Also, since,
$\kappa $
denotes the antipode of G. Also, since,
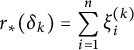 $$\begin{align*}r_{\ast}(\delta_{k})=\sum_{i=1}^{n}\xi^{(k)}_{i}\end{align*}$$
$$\begin{align*}r_{\ast}(\delta_{k})=\sum_{i=1}^{n}\xi^{(k)}_{i}\end{align*}$$
for all
![]() $k=1,\dots ,m$
and
$k=1,\dots ,m$
and
we have, for
![]() $k,l=1,\dots ,m$
,
$k,l=1,\dots ,m$
,
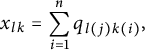 $$\begin{align*}x_{lk}=\sum_{i=1}^{n}q_{l(j)k(i)}, \end{align*}$$
$$\begin{align*}x_{lk}=\sum_{i=1}^{n}q_{l(j)k(i)}, \end{align*}$$
for all
![]() $j=1,\dots ,n$
. Clearly,
$j=1,\dots ,n$
. Clearly,
![]() $x_{lk}$
, for
$x_{lk}$
, for
![]() $k,l=1,\dots ,m$
satisfy the relations in
$k,l=1,\dots ,m$
satisfy the relations in
![]() $\text {S}_{m}^{+}$
. So in particular,
$\text {S}_{m}^{+}$
. So in particular,
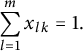 $$\begin{align*}\sum_{l=1}^{m}x_{lk}=1.\end{align*}$$
$$\begin{align*}\sum_{l=1}^{m}x_{lk}=1.\end{align*}$$
We now define
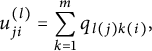 $$\begin{align*}u_{ji}^{(l)}=\sum_{k=1}^{m}q_{l(j)k(i)},\end{align*}$$
$$\begin{align*}u_{ji}^{(l)}=\sum_{k=1}^{m}q_{l(j)k(i)},\end{align*}$$
for
![]() $l=1,\dots ,m$
. Hence, by (7.6), for each
$l=1,\dots ,m$
. Hence, by (7.6), for each
![]() $l=1,\dots ,m$
,
$l=1,\dots ,m$
,
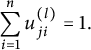 $$ \begin{align} \sum_{i=1}^{n}u^{(l)}_{ji}=1. \end{align} $$
$$ \begin{align} \sum_{i=1}^{n}u^{(l)}_{ji}=1. \end{align} $$
Now, using
we get
which after applying
![]() $\kappa $
gives us
$\kappa $
gives us
i.e., after interchanging k with l and i with j,
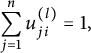 $$ \begin{align} \sum_{j=1}^{n}u^{(l)}_{ji}=1, \end{align} $$
$$ \begin{align} \sum_{j=1}^{n}u^{(l)}_{ji}=1, \end{align} $$
for all
![]() $i,l$
. An easy calculation, using
$i,l$
. An easy calculation, using
in the
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathrm {C}(\mathcal {G}^1)$
reveals that for all
$\mathrm {C}(\mathcal {G}^1)$
reveals that for all
![]() $i,j,k,l,k^{\prime },i^{\prime }$
,
$i,j,k,l,k^{\prime },i^{\prime }$
,
Hence, for all
![]() $l=1,\dots ,m$
,
$l=1,\dots ,m$
,
Now for
![]() $k \neq l$
,
$k \neq l$
,
for all
![]() $i=1,\dots ,n$
. Therefore
$i=1,\dots ,n$
. Therefore
which implies,
i.e.,
Hence, we have
For
![]() $j=r$
, as
$j=r$
, as
![]() $k \neq l$
,
$k \neq l$
,
for all
![]() $i^{\prime }$
. Therefore, for
$i^{\prime }$
. Therefore, for
![]() $j \neq r$
,
$j \neq r$
,
Using
for all
![]() $p,j,l,i^{\prime }$
, we get
$p,j,l,i^{\prime }$
, we get
whenever
![]() $k \neq l$
and
$k \neq l$
and
![]() $j \neq r$
. Now, for any
$j \neq r$
. Now, for any
![]() $l=1,\dots ,m$
and any
$l=1,\dots ,m$
and any
![]() $i,r,s=1,\dots ,n$
,
$i,r,s=1,\dots ,n$
,
which, for
![]() $r=s$
is equal to
$r=s$
is equal to
Hence, we have that
For
![]() $r \neq s$
, using (7.12), we get
$r \neq s$
, using (7.12), we get
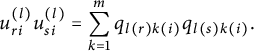 $$ \begin{align*} u^{(l)}_{ri}u^{(l)}_{si}=\sum_{k=1}^{m}q_{l(r)k(i)}q_{l(s)k(i)}. \end{align*} $$
$$ \begin{align*} u^{(l)}_{ri}u^{(l)}_{si}=\sum_{k=1}^{m}q_{l(r)k(i)}q_{l(s)k(i)}. \end{align*} $$
From (7.9), for any
![]() $l,r,k,i,s$
with
$l,r,k,i,s$
with
![]() $r \neq s$
,
$r \neq s$
,
Applying
![]() $\kappa $
to the above identity, we deduce that
$\kappa $
to the above identity, we deduce that
for all
![]() $i,k,l$
whenever
$i,k,l$
whenever
![]() $r \neq s$
. Therefore,
$r \neq s$
. Therefore,
for all
![]() $l=1,\dots ,m$
and for all
$l=1,\dots ,m$
and for all
![]() $i,r,s=1,\dots ,n$
. So for each
$i,r,s=1,\dots ,n$
. So for each
![]() $l=1,\dots ,m$
,
$l=1,\dots ,m$
,
![]() $u^{(l)}_{ji}$
,
$u^{(l)}_{ji}$
,
![]() $i,j=1,\dots ,n$
satisfy
$i,j=1,\dots ,n$
satisfy
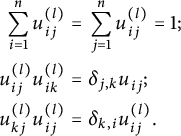 $$ \begin{align} \begin{aligned} \sum_{i=1}^{n}u^{(l)}_{ij}={}&\sum_{j=1}^{n}u^{(l)}_{ij}=1;\\ \ u^{(l)}_{ij}u_{ik}^{(l)}={}&\delta_{j,k}u^{}_{ij};\\ u^{(l)}_{kj}u^{(l)}_{ij}={}&\delta_{k,i}u_{ij}^{(l)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sum_{i=1}^{n}u^{(l)}_{ij}={}&\sum_{j=1}^{n}u^{(l)}_{ij}=1;\\ \ u^{(l)}_{ij}u_{ik}^{(l)}={}&\delta_{j,k}u^{}_{ij};\\ u^{(l)}_{kj}u^{(l)}_{ij}={}&\delta_{k,i}u_{ij}^{(l)}. \end{aligned} \end{align} $$
Also
![]() $x_{kl}$
for
$x_{kl}$
for
![]() $k,l=1,\dots ,m$
satisfy the relations of
$k,l=1,\dots ,m$
satisfy the relations of
![]() $\text {S}_{m}^{+}$
. Then, by the universal property of the free product, we get a Hopf
$\text {S}_{m}^{+}$
. Then, by the universal property of the free product, we get a Hopf
![]() $*$
-homomorphism
$*$
-homomorphism
such that
and
where, we recall that
![]() $u_{ij}$
for
$u_{ij}$
for
![]() $i,j=1,\dots ,n$
are the generators of
$i,j=1,\dots ,n$
are the generators of
![]() $\text {S}^+_n$
and
$\text {S}^+_n$
and
![]() $v_{kl}$
for
$v_{kl}$
for
![]() $k,l=1,\dots ,m$
are the generators of
$k,l=1,\dots ,m$
are the generators of
![]() $\text {S}^+_m$
. Moreover,
$\text {S}^+_m$
. Moreover,
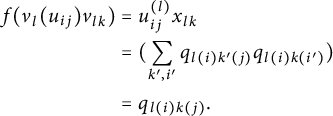 $$ \begin{align} \begin{aligned} f(\nu_{l}(u_{ij})v_{lk})={}& u^{(l)}_{ij}x_{lk}\\ ={}&(\sum_{k^{\prime},i^{\prime}}q_{l(i)k^{\prime}(j)}q_{l(i)k(i^{\prime})})\\ ={}& q_{l(i)k(j)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} f(\nu_{l}(u_{ij})v_{lk})={}& u^{(l)}_{ij}x_{lk}\\ ={}&(\sum_{k^{\prime},i^{\prime}}q_{l(i)k^{\prime}(j)}q_{l(i)k(i^{\prime})})\\ ={}& q_{l(i)k(j)}. \end{aligned} \end{align} $$
But
![]() $f(v_{lk}\nu _{l}(u_{ij}))$
is also
$f(v_{lk}\nu _{l}(u_{ij}))$
is also
![]() $q_{l(i)k(j)}$
. So by the definition of the free wreath product, f descends to a surjective Hopf
$q_{l(i)k(j)}$
. So by the definition of the free wreath product, f descends to a surjective Hopf
![]() $*$
-homomorphism
$*$
-homomorphism
intertwining the actions. Hence,
![]() $(\text {S}^+_n\wr _{\ast } \text {S}^+_m,\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is the universal object in the category
$(\text {S}^+_n\wr _{\ast } \text {S}^+_m,\alpha _{\text {Bic}},\lambda _{\text {Bic}})$
is the universal object in the category
![]() $\mathcal {C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
, and this completes the proof.
$\mathcal {C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
, and this completes the proof.
Remarks 7.5
-
• For
 $m=1$
, the graph
$m=1$
, the graph
 ${\mathcal G}^{\oplus 1}$
is the graph with one vertex and n number of loops attached with it. The universal object in the category
${\mathcal G}^{\oplus 1}$
is the graph with one vertex and n number of loops attached with it. The universal object in the category
 ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus 1})$
is
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus 1})$
is
 $\text {S}^+_n$
by Theorem 7.4. Now, the universal object in the category of compact quantum groups acting faithfully on
$\text {S}^+_n$
by Theorem 7.4. Now, the universal object in the category of compact quantum groups acting faithfully on
 ${\mathcal O}_{n}$
and preserving the KMS state, which is a distinguished one, is the free unitary quantum group
${\mathcal O}_{n}$
and preserving the KMS state, which is a distinguished one, is the free unitary quantum group
 $\text {U}_{n}^{+}$
. Hence, by Remark 7.3,
$\text {U}_{n}^{+}$
. Hence, by Remark 7.3,
 $\text {S}^+_n$
is realized as a quantum subgroup of
$\text {S}^+_n$
is realized as a quantum subgroup of
 $\text {U}^{+}_{n}$
.
$\text {U}^{+}_{n}$
. -
• Similarly, for
 $n=1$
, the graph
$n=1$
, the graph
 ${\mathcal G}^{\oplus m}$
is the disjoint union of m-loops. By [Reference Joardar and MandalJM21a, Proposition 4.2], the quantum automorphism group of the graph
${\mathcal G}^{\oplus m}$
is the disjoint union of m-loops. By [Reference Joardar and MandalJM21a, Proposition 4.2], the quantum automorphism group of the graph
 $\mathrm {C}^*$
-algebra corresponding to the graph
$\mathrm {C}^*$
-algebra corresponding to the graph
 ${\mathcal G}^{\oplus m}$
preserving the distinguished KMS state is
${\mathcal G}^{\oplus m}$
preserving the distinguished KMS state is
 $\text {H}_{m}^{\infty +}$
. Hence, again by Remark 7.3, the universal object in the category
$\text {H}_{m}^{\infty +}$
. Hence, again by Remark 7.3, the universal object in the category
 ${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
realizes
${\mathcal C}_{\text {Bic}}^{\text {mult}}({\mathcal G}^{\oplus m})$
realizes
 $\text {S}^+_m$
as a quantum subgroup of
$\text {S}^+_m$
as a quantum subgroup of
 $\text {H}^{\infty +}_{m}$
.
$\text {H}^{\infty +}_{m}$
.