Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T09:35:43.471Z Has data issue: false hasContentIssue false
  • English
  • Français

An alternative to Wiener-Hopf methods for the study of bounded processes

Published online by Cambridge University Press:  14 July 2016

J. Keilson
J. Keilson*
Affiliation:
Sylvania Electronic Systems, Waltham, Massachusetts
Get access Rights & Permissions [Opens in a new window]

Extract

Homogeneous additive processes on a finite or semi-infinite interval have been studied in many forms. Wald's identity for the first passage process on the finite interval (see for example Miller, 1961), the waiting time process of Lindley (1952), and a variety of problems in the theory of queues, dams, and inventories come to mind. These processes have been treated by and large by methods in the complex plane. Lindley's discrete parameter process on the continuum, for example, described by 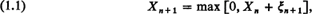where the ξn are independent identically distributed random variables, has been discussed by Wiener-Hopf methods in recent years by Lindley (1952), Smith (1953), Kemperman (1961), Keilson (1961), and many others. A review of earlier studies is given by Kemperman.

Type
Research Papers
Information
Journal of Applied Probability , Volume 1 , Issue 1 , June 1964 , pp. 85 - 120
Copyright
Copyright © Applied Probability Trust 1964 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Borovkov, A. A. (1960) Limit theorems on the distribution of maxima of sums of bounded lattice random variables, I. Theory Prob. Applications 5, No. 2, 125–155.CrossRefGoogle Scholar
[2] Daniels, H. E. (1954) Saddlepoint approximation in statistics. Ann. Math. Statist. 25, 631–650.CrossRefGoogle Scholar
[3] Feller, W. (1941) On the integral equation of renewal theory. Ann. Math. Statist. 12, 243–267.CrossRefGoogle Scholar
[4] Feller, W. and Orey, S. (1961) A renewal theorem. J. Math. and Mech. 10, 619–624.Google Scholar
[5] Keilson, J. (1961) The homogeneous random walk on the half-line and the Hilbert problem. Bull. I. S. I. 113, 33e Session, Paris.Google Scholar
[6] Keilson, J. (1962 a) The use of Green's functions in the study of bounded random walks with application to queuing theory. J. Math. and Phys. 41, 42–52.CrossRefGoogle Scholar
[7] Keilson, J. (1962 b) Non-stationary Markov walks on the lattice. J. Math. and Phys. 41, 205–211.CrossRefGoogle Scholar
[8] Keilson, J. (1962 c) The general bulk queue as a Hilbert problem. J. R. Statist. Soc. B 24, 344–358.Google Scholar
[9] Keilson, J. (1963 a) The first passage time density for homogeneous skip-free walks on the continuum. Ann. Math. Statist. 34, 1003–1011.CrossRefGoogle Scholar
[10] Keilson, J. (1963 b) On the asymptotic behaviour of queues. J. R. Statist. Soc. B 25, 464–476.Google Scholar
[11] Kemperman, J. H. B. (1961) The Passage Problem for a Stationary Markov Chain. The University of Chicago Press.CrossRefGoogle Scholar
[12] Lindley, D. V., (1952) The theory of queues with a single server. Proc. Camb.Phil. Soc, 48, 277–289.CrossRefGoogle Scholar
[13] Magnus, W. and Oberhettinger, F., (1949) Formulas and Theorems for the Special Functions of Mathematical Physics. Chelsea Publishing Company, New York.Google Scholar
[14] Mikhlin, S. G. (1957) Integral Equations. Pergamon Press, New York.CrossRefGoogle Scholar
[15] Miller, H. D. (1961) A generalization of Wald's identity with applications to random walks. Ann. Math. Statist. 32, 549–560.CrossRefGoogle Scholar
[16] Richter, W. (1957) Local limit theorems for large deviations. Theory Prob. Applications 2, No. 2, 206–220.CrossRefGoogle Scholar
[17] Saunders, L. R. (1961) Probability functions for waiting times in single-channel queues, with emphasis on simple approximations. Operat. Res. 9, 351–362.CrossRefGoogle Scholar
[18] Smith, W. L. (1953) On the distribution of queueing times. Proc. Camb. Phil. Soc. 49, 449–461.CrossRefGoogle Scholar
[19] Smith, W. L. (1958) Renewal theory and its ramifications. J. R. Statist. Soc. B 20, 243–302.Google Scholar
[20] Smith, W. L. (1962) On necessary and sufficient conditions for the convergence of the renewal density. Trans. Amer. Math. Soc. 104, 79–100.CrossRefGoogle Scholar
[21] Spitzer, F. (1961) Recurrent random walk and logarithmic potential. Fourth Berkeley Symposium on Statistics and Probability 2, 515–534.Google Scholar

A correction has been issued for this article:

Corrections