1. INTRODUCTION
The Global Positioning System (GPS) and Inertial Navigation Systems (INS) have been widely used for navigation. Since GPS satellite signals are subjected to external environmental disturbance, signal blockage is frequently experienced in urban environments, while INS errors accumulate quickly with time. To provide continuous and reliable navigation solutions, the two systems are usually employed together for their complementary characteristics. The degradation of GPS/INS navigation performance is unavoidable when GPS signals are degraded in some areas, such as forests and canyons. Special approaches should be developed to overcome this problem, such as GPS integration with additional sensors, e.g., odometers, magnetometers, broadband communication networks (cellular GSM, etc.) or receiver elevation knowledge obtained from a digital terrain model (Danezis and Gikas, Reference Danezis and Gikas2013; Farrell, Reference Farrell2008; Van Diggelen, Reference Van Diggelen2009).
Artificial intelligence and machine learning can also be used to overcome this problem by taking INS data as the input and the difference from the GPS position as the output. A multi-sensor system integration approach was introduced to fuse data from an INS and GPS hardware-utilising wavelet multi-resolution analysis and Artificial Neural Networks (ANN) (Chiang et al., Reference Chiang, Noureldin and El-Sheimy2003; Noureldin et al., Reference Noureldin, Osman and El-Sheimy2004). A multi-layer neural network was trained to map the vehicle dynamics corresponding to Kalman Filter (KF) states, which can be used to correct INS measurements when GPS measurements are unavailable (Wang et al., Reference Wang, Wang, Sinclair and Watts2006). An artificial intelligence-based segmented forward predictor was proposed to update the position and velocity architecture by utilising radial basis function neural networks for the purpose of providing metre-level positioning solutions during GPS outages (Semeniuk and Noureldin, Reference Semeniuk and Noureldin2006). An auxiliary fuzzy-based model was presented for predicting the KF positioning error states during GPS signal outages (Abdel-Hamid et al., Reference Abdel-Hamid, Noureldin and El-Sheimy2007). GPS/INS navigation solutions were calculated intelligently using the ANN based on updating the INS in a Kalman filter structure. To overcome the limitations of multi-layer feed-forward neural networks and KF-based schemes, a constructive neural network was proposed to improve positioning accuracy by 55% during GPS signal outages (El-Sheimy et al., Reference El-Sheimy, Chiang and Noureldin2008; Huang and Chiang, Reference Huang and Chiang2008). However, with neural networks it is difficult to avoid the problems of a local optimal solution, determining the topological structure and the “curse of dimensionality”.
The Support Vector Regression (SVR) algorithm is a new regression technology based on the Vapnik-Chervonenkis (VC) dimension theory of statistical learning and the structural risk minimisation principle (Vapnik, Reference Vapnik2000). The input is transformed into a high-dimension characteristic space through a nonlinear transformation, and the optimum linearity regression function is sought. The SVR avoids over-fitting by choosing a specific hyperplane among the feature spaces and overcomes the major problems faced by typical neural networks, such as local minima, over-fitting or over-training, etc. (Frangos et al., Reference Frangos, Kealy, Gikas and Hasnur2010), allowing for a much more hands-off training process that is easily deployable and scalable. Xu et al. (Reference Xu, Li, Rizos and Xu2010) established the regression model between the INS output data and the GPS position difference based on the least squares support vector machine, and the results show that the least squares support vector machine is superior to the neural network algorithm. However, the method of acquiring the optimal parameters for SVR model training was not provided.
In this paper, the pseudo-GPS position-aided GPS/INS navigation is presented during GPS outages. With the optimal parameters from genetic algorithms, the SVR algorithm is used to train a regression model between the specific force and angular rate increments of the INS measurements as input and the increments of GPS position as output. The pseudo-GPS position is calculated with the regression model. An improved adaptive filtering algorithm is then designed to estimate the covariance matrix of the pseudo-GPS position in real-time. Finally, the pseudo-position-aided navigation solution is given. The structure of this paper is as follows: Section 2 briefly introduces the theory and model of GPS position-aided INS and INS mechanisation equations, Section 3 presents the Genetic Algorithm-Support Vector Regression (GA-SVR) model and its training parameters as well as an optimisation method based on GA. The calculation of the pseudo-position and covariance estimation scheme based on improved adaptive filtering are given in Section 4. Section 5 shows testing results of the pseudo-position-aided low-cost INS scheme, and the conclusions are given in Section 6.
2. CONVENTIONAL GPS/INS INTEGRATED NAVIGATION
A Loosely Coupled (LC) Extended Kalman Filtering (EKF) (Falco et al., Reference Falco, Einicke, Malos and Dovis2012; Faruqi and Turner, Reference Faruqi and Turner2000) is applied for GPS/INS integration, with the states as follows:
where δr N, δ r E, δ r D are the position errors, δv N, δv E, δv D are the velocity errors, δφ Ro, δφ Pi, δφ Ha are the attitude errors, ∇ bx, ∇ by, ∇ bz are the accelerometer biases, ∇ fx, ∇fy, ∇fz are the accelerometer scale factor errors, ε bx, ε by, ε bz are the gyro drifts, ε fx, ε fy, ε fz are the gyro scale factor errors δl N, δlE, δlD represent the GPS antenna to INS lever arm measurement errors and δg N, δgE, δgD denote the gravity uncertainty errors.
For the GPS/INS integrated navigation system, the discrete-time form of the dynamic model is given as:
where x k and x k–1 are the state vector at epoch k and k–1, respectively, Φ k,k–1 is the state transition matrix from epoch k–1 to k, and w k is the dynamic process noise. The difference in position between GPS measurements and INS measurements in the North-East-Down (NED) frame is regarded as measurements, and the observation equation can be written as:
where zk denotes the difference between INS position and GPS position at epoch r k, Hk = [I3×3, 03×24] is the observation matrix, and r k represents the measurement noise.
We assume w k and r k satisfy the following conditions:
 $$\left\{ \matrix{E({w}_{k} ) = 0,E({w}_{k} {w}_{\,j}^T ) = {Q}_{k} \delta _{{k,j}} \cr \hskip-10ptE({r}_{k} ) = 0,E({r}_{k} {r}_{\,j}^T ) = {R}_{k} \delta _{{k,j}} \cr \hskip-75ptE({w}_{k} {r}_{\,j}^T ) = 0 } \right.$$
$$\left\{ \matrix{E({w}_{k} ) = 0,E({w}_{k} {w}_{\,j}^T ) = {Q}_{k} \delta _{{k,j}} \cr \hskip-10ptE({r}_{k} ) = 0,E({r}_{k} {r}_{\,j}^T ) = {R}_{k} \delta _{{k,j}} \cr \hskip-75ptE({w}_{k} {r}_{\,j}^T ) = 0 } \right.$$where δ k,j is the Kronecker δ-function, Q k is the variance-covariance matrices of states, and R k is the variance-covariance matrices of measurements. The discrete-time Kalman filter is then given by the following equations.
Prediction stage:
Update stage:
where ![]() ${\hat X}_{{k,k - 1}} $ is the a priori state estimate, P k,k–1 is the a priori estimate variance-covariance, K k is the Kalman matrix,
${\hat X}_{{k,k - 1}} $ is the a priori state estimate, P k,k–1 is the a priori estimate variance-covariance, K k is the Kalman matrix, ![]() ${\hat X}_{k} $ is the a posteriori state, and P k is the a posteriori estimate variance-covariance (Bar-Shalom et al., Reference Bar-Shalom, Li and Kirubarajan2001; Chiang et al., Reference Chiang, Duong, Liao, Lai, Chang, Cai and Huang2012; Gikas et al., Reference Gikas, Cross and Akuamoa1995; Parnian and Golnaraghi, Reference Parnian and Golnaraghi2010).
${\hat X}_{k} $ is the a posteriori state, and P k is the a posteriori estimate variance-covariance (Bar-Shalom et al., Reference Bar-Shalom, Li and Kirubarajan2001; Chiang et al., Reference Chiang, Duong, Liao, Lai, Chang, Cai and Huang2012; Gikas et al., Reference Gikas, Cross and Akuamoa1995; Parnian and Golnaraghi, Reference Parnian and Golnaraghi2010).
3. SVR MODEL TRAINING BASED ON GA
When the vehicle moves steadily without significantly drastic changes, there is a relatively high correlation between the increments of the GPS position and the specific force and angular rate increments of the INS measurements (Wang et al., Reference Wang, Wang, Sinclair and Watts2006; Xu et al., Reference Xu, Li, Rizos and Xu2010). The SVR model of correlation is trained based on the GA in this paper, with the specific force and angular rate increments of the INS measurements as the input X and the corresponding increments of the GPS position as the output Y of the SVR. The GA is used to search the optimal parameters of the SVR before training. A detailed block diagram of the algorithm is shown in Figure 1.

Figure 1. GA-SVR Model training.
3.1. Principle of Support Vector Regression
The SVR algorithm seeks the relationship between the input and output for a training set of data (x i, yi), i = 1,2,…,l, x iϵ Rn,yi ϵR, where x i is the ith input and y i is the corresponding output. The SVR model for nonlinear function estimation has the following representation in the feature space:
where the term ɷ is the weight vector. The nonlinear function ϕ(x) maps the input x space to a higher dimensional feature space. The term b is the bias term.
It is assumed that ε is the maximum residual between output y and the theoretical value of f(x), so
To obtain the optimum value ε min among ε
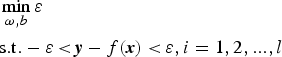 $$\eqalign{& \min _{\omega, b} \varepsilon \cr & {\rm s}{\rm. t}{\rm.}- \varepsilon \,{ \lt} \,{\bi y}-{ f}{\rm (}{\bi x}{\rm ) \lt} \,\varepsilon, i = 1,2,...,l} $$
$$\eqalign{& \min _{\omega, b} \varepsilon \cr & {\rm s}{\rm. t}{\rm.}- \varepsilon \,{ \lt} \,{\bi y}-{ f}{\rm (}{\bi x}{\rm ) \lt} \,\varepsilon, i = 1,2,...,l} $$
with slack variable ![]() $\xi ^{(*)} = (\xi _1, \xi _1^*,..., \xi _l, \xi _l^* ) \ge 0$ and penalty parameter C added to Equation (12), the calculation of ω and b can be altered to the optimisation problem as Equation (13) (Gunn, Reference Gunn1998):
$\xi ^{(*)} = (\xi _1, \xi _1^*,..., \xi _l, \xi _l^* ) \ge 0$ and penalty parameter C added to Equation (12), the calculation of ω and b can be altered to the optimisation problem as Equation (13) (Gunn, Reference Gunn1998):
 $$\mathop {\min} \limits_{{\rm \omega} \in R^n, b \in R,{\rm \xi} ^{({\rm *})} \in R^{2l}} \tau (\omega, \xi ^{(*)} ) = \displaystyle{1 \over 2}\vert\vert{\bi \omega} \vert\vert^2 + \displaystyle{C \over l}\mathop \sum \limits_{i = 1}^l \left( {\xi _i + \xi _i^*} \right)$$
$$\mathop {\min} \limits_{{\rm \omega} \in R^n, b \in R,{\rm \xi} ^{({\rm *})} \in R^{2l}} \tau (\omega, \xi ^{(*)} ) = \displaystyle{1 \over 2}\vert\vert{\bi \omega} \vert\vert^2 + \displaystyle{C \over l}\mathop \sum \limits_{i = 1}^l \left( {\xi _i + \xi _i^*} \right)$$To solve the optimisation problem above, the Lagrangian function is constructed:
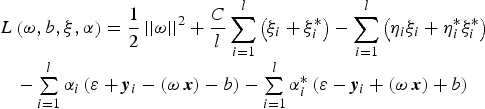 $$\matrix{ {L\left( {{\bi \omega}, b,\xi, \alpha} \right) = \displaystyle{1 \over 2}\left\vert {\left\vert {\bi \omega} \right\vert} \right\vert^2 + \displaystyle{C \over l}\mathop \sum \limits_{i = 1}^l \left( {\xi _i + \xi _i^*} \right) - \mathop \sum \limits_{i = 1}^l \left( {\eta _i \xi _i + \eta _i^* \xi _i^*} \right)} \cr { - \mathop \sum \limits_{i = 1}^l \alpha _i \left( {\varepsilon + {\bi y}_i - \left( {\omega \ {\bi x}} \right) - b} \right) - \mathop \sum \limits_{i = 1}^l \alpha _i^* \left( {\varepsilon - {\bi y}_i + \left( {\omega \ {\bi x}} \right) + b} \right)} \cr} $$
$$\matrix{ {L\left( {{\bi \omega}, b,\xi, \alpha} \right) = \displaystyle{1 \over 2}\left\vert {\left\vert {\bi \omega} \right\vert} \right\vert^2 + \displaystyle{C \over l}\mathop \sum \limits_{i = 1}^l \left( {\xi _i + \xi _i^*} \right) - \mathop \sum \limits_{i = 1}^l \left( {\eta _i \xi _i + \eta _i^* \xi _i^*} \right)} \cr { - \mathop \sum \limits_{i = 1}^l \alpha _i \left( {\varepsilon + {\bi y}_i - \left( {\omega \ {\bi x}} \right) - b} \right) - \mathop \sum \limits_{i = 1}^l \alpha _i^* \left( {\varepsilon - {\bi y}_i + \left( {\omega \ {\bi x}} \right) + b} \right)} \cr} $$
where α(*) are the Lagrange multipliers ![]() $\alpha ^{(*)} = \left( {\alpha _1, \alpha _1^*, \ldots, \alpha _l, \alpha _l^*} \right)^T \ge 0$. According to the Wolfe duality theory (Wolfe, Reference Wolfe1961), the conditions for optimality are given by:
$\alpha ^{(*)} = \left( {\alpha _1, \alpha _1^*, \ldots, \alpha _l, \alpha _l^*} \right)^T \ge 0$. According to the Wolfe duality theory (Wolfe, Reference Wolfe1961), the conditions for optimality are given by:
 $$\left\{ \matrix{\displaystyle{{\partial L} \over {\partial \omega}} = {\bi \omega} - \mathop \sum \limits_{i = 1}^l \left( {\alpha _i^* - \alpha _i} \right){\bi x}_i = 0 \cr \displaystyle{{\partial L} \over {\partial b}} = \mathop \sum \limits_{i = 1}^l \left( {\alpha _i - \alpha _i^*} \right) = 0\hfill \cr \displaystyle{{\partial L} \over {\partial \xi _i}} = \displaystyle{C \over l} - \alpha _i - \eta _i = 0\hfill \cr \displaystyle{{\partial L} \over {\partial \xi _i^*}} = \displaystyle{C \over l} - \alpha _i^* - \eta _i^* = 0\hfill} \right.$$
$$\left\{ \matrix{\displaystyle{{\partial L} \over {\partial \omega}} = {\bi \omega} - \mathop \sum \limits_{i = 1}^l \left( {\alpha _i^* - \alpha _i} \right){\bi x}_i = 0 \cr \displaystyle{{\partial L} \over {\partial b}} = \mathop \sum \limits_{i = 1}^l \left( {\alpha _i - \alpha _i^*} \right) = 0\hfill \cr \displaystyle{{\partial L} \over {\partial \xi _i}} = \displaystyle{C \over l} - \alpha _i - \eta _i = 0\hfill \cr \displaystyle{{\partial L} \over {\partial \xi _i^*}} = \displaystyle{C \over l} - \alpha _i^* - \eta _i^* = 0\hfill} \right.$$Substituting Equation (15) into Equation (14), Equation (13) can then be expressed as Equation (16):
 $$\eqalign{& \mathop {\min} \limits_{{\rm \alpha} ^{({\rm *})} \in R^{2l}} \displaystyle{1 \over 2}\mathop \sum \limits_{i,\kern2ptj \,= \,1}^l \left( {\alpha _i^* - \alpha _i} \right)\left( {\alpha _j^* - \alpha _j} \right)\varphi ^{\rm T} {\rm (}{\bi x}_i {\rm )}\varphi {\rm (}{\bi x}_j {\rm )} + \varepsilon \mathop \sum \limits_{i = 1}^l \left( {\alpha _i^* + \alpha _i} \right) - \mathop \sum \limits_{i = 1}^l y_i \left( {\alpha _i^* - \alpha _i} \right) \cr & {\rm s}.{\rm t}.\mathop \sum \limits_{i = 1}^l \left( {\alpha _i^* - \alpha _i} \right) = 0,0 \le \alpha _i^*, \alpha _i \le \displaystyle{C \over l},i = 1, 2 \ldots, l} $$
$$\eqalign{& \mathop {\min} \limits_{{\rm \alpha} ^{({\rm *})} \in R^{2l}} \displaystyle{1 \over 2}\mathop \sum \limits_{i,\kern2ptj \,= \,1}^l \left( {\alpha _i^* - \alpha _i} \right)\left( {\alpha _j^* - \alpha _j} \right)\varphi ^{\rm T} {\rm (}{\bi x}_i {\rm )}\varphi {\rm (}{\bi x}_j {\rm )} + \varepsilon \mathop \sum \limits_{i = 1}^l \left( {\alpha _i^* + \alpha _i} \right) - \mathop \sum \limits_{i = 1}^l y_i \left( {\alpha _i^* - \alpha _i} \right) \cr & {\rm s}.{\rm t}.\mathop \sum \limits_{i = 1}^l \left( {\alpha _i^* - \alpha _i} \right) = 0,0 \le \alpha _i^*, \alpha _i \le \displaystyle{C \over l},i = 1, 2 \ldots, l} $$ Equation (16) belongs to the convex quadratic programming problem, and the feasible region is empty, meaning that the optimal solution of ![]() $\bar \alpha = \left( {\bar \alpha _1, \bar \alpha _1^*, \ldots, \bar \alpha _l, \bar \alpha _l^*} \right)^{\rm T} $ in Equation (16) is solved. ω and b can be calculated as follows (Berk, Reference Berk2008; Joachims, Reference Joachims2002; Williams, Reference Williams2011):
$\bar \alpha = \left( {\bar \alpha _1, \bar \alpha _1^*, \ldots, \bar \alpha _l, \bar \alpha _l^*} \right)^{\rm T} $ in Equation (16) is solved. ω and b can be calculated as follows (Berk, Reference Berk2008; Joachims, Reference Joachims2002; Williams, Reference Williams2011):
 $$\eqalign{& {\bi \omega} = \mathop \sum \limits_{i = 1}^l \left( {\bar \alpha _i^* - \bar \alpha _i} \right)\varphi {\rm (}{\bi x}_i {\rm )} \cr & \left\{ \matrix{b = {\bi y}_i - {\bi \omega} \varphi {\rm (}{\bi x}_i {\rm )} - \varepsilon, 0 \lt \bar \alpha _i^* \lt C \cr b = {\bi y}_i - {\bi \omega} \varphi {\rm (}{\bi x}_i {\rm )} + \varepsilon, 0 \lt \bar \alpha _i \lt C } \right.} $$
$$\eqalign{& {\bi \omega} = \mathop \sum \limits_{i = 1}^l \left( {\bar \alpha _i^* - \bar \alpha _i} \right)\varphi {\rm (}{\bi x}_i {\rm )} \cr & \left\{ \matrix{b = {\bi y}_i - {\bi \omega} \varphi {\rm (}{\bi x}_i {\rm )} - \varepsilon, 0 \lt \bar \alpha _i^* \lt C \cr b = {\bi y}_i - {\bi \omega} \varphi {\rm (}{\bi x}_i {\rm )} + \varepsilon, 0 \lt \bar \alpha _i \lt C } \right.} $$As a result, the SVR model for nonlinear function estimation becomes:
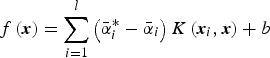 $$f\left( {\bi x} \right) = \mathop \sum \limits_{i = 1}^l \left( {\bar \alpha _i^* - \bar \alpha _i} \right)K\left( {{\bi x}_i, {\bi x}} \right) + b$$
$$f\left( {\bi x} \right) = \mathop \sum \limits_{i = 1}^l \left( {\bar \alpha _i^* - \bar \alpha _i} \right)K\left( {{\bi x}_i, {\bi x}} \right) + b$$where K(x i, x) = ϕT( x i) ϕ( x j) is a positive definite kernel matrix. Note that the Radial Basis Function (RBF) has an advantage in processing linearly inseparable data, and therefore the RBF kernel (K(x i, xj) = exp(−γ||x i − xj|| 2)) is chosen as the kernel function. The γ is the kernel width: small and kernel width may cause over-fitting, and a large kernel width may cause under-fitting (Chang et al., Reference Chang, Chen and Wang2005). A small penalty parameter (C) leads to over-fitting and a large one brings about under-fitting (Alpaydin, Reference Alpaydin2004). The performance of SVR with Gaussian RBF kernel is sensitive to the kernel width (γ) and penalty parameter (C). Several methods can be used to obtain the optimal γ and C, e.g., bootstrapping, VC bounds statistical learning theory, and inference or Bayesian learning methods (Cristianini and Ricci, Reference Cristianini and Ricci2008; Kecman, Reference Kecman2005). Genetic algorithms are developed in this paper, shown in the next section.
3.2. Parameter optimisation based on genetic algorithms
Genetic algorithms are a family of computational models inspired by evolution. These algorithms encode a potential solution to a specific problem on a simple chromosome-like data structure, and they apply recombination operators to these structures in a way that preserves critical information (Goldberg and Holland, Reference Goldberg and Holland1988). With respect to ϒ, C of SVR, the solutions of the parameter optimisation problem can be expressed as follows.
Step 1: Encoding. Note that there is only one change between two adjacent numbers and the grey code is developed in this paper. The relationship between binary code B and grey code G is:
where ⨁ represents the XOR operator.
Step 2: Initialisation. Set the range of parameters 0 ≤ ϒ ≤ 1000, 0 < C ≤ 500, 20 chromosomes of each parameter γ, C are generated randomly and the maximal genetic generation is 200.
Step 3: Fitness calculation of the individual. The fitness function is the basis of the optimisation to evaluate the quality of the individual. The Root Mean Square (RMS) of the SVR-trained residual is calculated based on K-fold cross-validation with the 20 chromosomes. Descending through the chromosomes according to the RMS, the fitness of each chromosome is then shown in Equation (20):
where sp is the assigned press difference, Pos is the position of the chromosomes and N is the population size. FitnVϵ[1, 2].
Step 4: Genetic operators.
Selection: The population of the next generation is formed by means of a probabilistic reproduction process. Individuals with a higher fitness usually have a greater chance for the next generation. The selected probability P si of the ith chromosome x i is shown in Equation (21).
where N denotes the size of the population and f i the fitness function of chromosome x i.
Crossover: Crossing over tends to enable the evolutionary process to move toward promising regions of the search space. The next generation is formed between two selected individuals, called parents, by exchanging parts of their strings. Single-point crossover is developed with the probability of 0·7 in this paper as seen in Figure 2.

Figure 2. Single-point crossover.
Mutation: Mutation is used to search for additional problem space and to avoid the local convergence of GA. For each bit in the population in this paper, ‘mutate’ changes the bit value with a low probability of 0·05.
Step 5: End the GA procedure, and output the optimal chromosome if the genetic generation reaches the maximum value, else, go to step 3.
4. PSEUDO-GPS POSITION-AIDED INS NAVIGATION
When GPS signals are available, the LC strategy, including an EKF, is adopted to combine the GPS and INS values to estimate navigation solutions. The INS errors in 24 states estimated by EKF correct the INS model in real-time. Simultaneously, the regression model is trained based on the GA-SVR, which maps the increments of the GPS position with the specific force and angular rate increments of the INS measurements. If the GPS signals are unavailable, the pseudo-GPS position can be estimated based on the trained model and the specific force and angular rate increments of the INS measurements. An improved adaptive filtering is designed to estimate the covariance matrix of the pseudo-GPS positions in real time. The INS errors estimated by improved adaptive filtering correct the INS model. The pseudo-GPS position-aided navigation solutions are then calculated as shown in Figure 3.

Figure 3. GA-SVR-Based Pseudo-Position-aided INS Navigation algorithm.
4.1. Pseudo-GPS position calculation
Assume that t i is the epoch before GPS becomes unavailable, P i is the corresponding position of the GPS. Δt is the sampling interval of the GPS measurements. At the next epoch t i + 1 (t i + 1 = t i + Δt), the GPS position increments ΔP j can be derived using the trained GA-SVR model, specific force increments ![]() $\int_{t_i} ^{t_{i + 1}} {{\bi f}_{ib}^b dt} $ and angular rate increments
$\int_{t_i} ^{t_{i + 1}} {{\bi f}_{ib}^b dt} $ and angular rate increments ![]() $\int_{t_i} ^{t_{i + 1}} {{\bi \omega} _{ib}^b dt} $ (according to Equation (18)). The pseudo-GPS position at epoch t i+1 can then be obtained as:
$\int_{t_i} ^{t_{i + 1}} {{\bi \omega} _{ib}^b dt} $ (according to Equation (18)). The pseudo-GPS position at epoch t i+1 can then be obtained as:
After n intervals, the final pseudo-GPS position at epoch t k (t k = t i + nΔt) is obtained as:
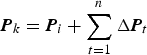 $${\bi P}_k = {\bi P}_i + \mathop \sum_{t = 1}^n \Delta {\bi P}_t $$
$${\bi P}_k = {\bi P}_i + \mathop \sum_{t = 1}^n \Delta {\bi P}_t $$4.2. Improved adaptive filtering
The EKF is disabled due to the absence of the covariance matrix of the pseudo-GPS position from the GA-SVR algorithm. In this paper, an improved adaptive filtering algorithm is proposed by combining Sage-Husa Adaptive Filtering (SHAF) with robust filtering. The SHAF can estimate the covariance matrix in real time according to the innovation to improve the estimation accuracy (Ding et al., Reference Ding, Wang, Rizos and Kinlyside2007). The predicted pseudo-GPS positions inevitably contain big errors/biases, so that a robust algorithm which can detect and solve the errors is needed, such as the equivalent weight method (Yuanxi, Reference Yuanxi1994) or Receiver Autonomous Integrity Monitoring (RAIM) (Hewitson and Wang, Reference Hewitson and Wang2007, Reference Hewitson and Wang2010).
• Sage-Husa adaptive filtering
The innovation sequence is defined as Equation (24):
The predicted error covariance matrix from the innovation sequence is:
There is clearly a relationship in Equation (25) to estimate R k. However, it requires a limited number (called ‘estimation window size’) of innovation samples to calculate E(v kvkT). Considering the number of pseudo-measurements, we use both a priori knowledge R k −1 and innovation v kvkT to estimate the covariance matrix R k as follows (Lu et al., Reference Lu, Zhao and Chen2007; Sage and Husa, Reference Sage and Husa1969):
where ![]() $d_k = \displaystyle{{1 - e} \over {1 - e^k}} \;, 0 \lt e \lt 1$, e is the forgetting factor.
$d_k = \displaystyle{{1 - e} \over {1 - e^k}} \;, 0 \lt e \lt 1$, e is the forgetting factor.
• Robust filtering
The residual sequence is defined as:
Then the mean square error factor ![]() $\hat \sigma _{_0} $ is calculated with the median method as:
$\hat \sigma _{_0} $ is calculated with the median method as:
where ε i is the ith element of the residual sequence with the weight P i. The standardised residual s i of ε i as:
Robust factors γ i based on IGGIII weight function (Yuanxi, Reference Yuanxi1994) are constructed as:
 $$\gamma _i = \left\{ \matrix{1,s_i \le k_0 \hfill\cr \displaystyle{{k_0} \over {s_i}} \times \left[ {\displaystyle{{k_1 - s_i} \over {k_1 - k_0}}} \right]^2, k_0 \lt s_i \le k_1 \cr 10^{ - 30}, s_i \gt k_1\hfill} \right.$$
$$\gamma _i = \left\{ \matrix{1,s_i \le k_0 \hfill\cr \displaystyle{{k_0} \over {s_i}} \times \left[ {\displaystyle{{k_1 - s_i} \over {k_1 - k_0}}} \right]^2, k_0 \lt s_i \le k_1 \cr 10^{ - 30}, s_i \gt k_1\hfill} \right.$$where k 0, k 1 are threshold value and k 0 = 1.0 ~ 1.5, k 1 = 2.5 ~ 8.0.
If s i ≤ k 0,we think that the ith pseudo-GPS position has no error; if k 0 < s i ≤ k 1, we think that the ith pseudo-GPS position has small error; and if s i > k 1, we think that the ith pseudo-GPS position has big error. To reduce the impact of the big errors/biases to the navigation solutions, the covariance matrix of pseudo-GPS positions is amplified with robust factors as follows:
5. TEST RESULTS
Two sets of Leica 1200 Base and Rover GPS Systems and SPAN-CPT INS units are used. Firstly initial alignment is done with the supporting software of SPAN-CPT, and then the raw IMU data from SPAN-CPT and GPS data from Leica are collected to validate the proposed algorithm in this paper. The sensor specifications of the SPAN-CPT are listed in Table 1.
Table 1. INS technical specifications.

If GPS signals are available, the loosely coupled strategy is adopted to calculate the navigation solutions of the GPS/INS integrated system based on EKF. Figure 4a shows the position errors of the GPS/INS navigation solution for the latitude, longitude and height when GPS signals are available. The lever arm between GPS antenna phase centre and IMU navigation centre directly affects the output position in a GPS/INS integrated system. According to the algorithm (Geng et al., Reference Geng, Deurloo and Bastos2011; Tang et al., Reference Tang, Wu, Wu, Wu, Hu and Shen2009), Figure 4b shows the estimated lever arm, the red line represents true values.

Figure 4. (a) Navigation solution errors (Left). (b) Lever arm estimation (Right).
The feasibility of the algorithm is verified using three tests. The data were recorded for post processing. Test 1 moved along a straight line with respect to a low-speed-stable navigation platform, Test 2 moved along a straight line with respect to a high-speed-unstable navigation platform, and Test 3 moved along a curve. Trajectories of these three tests can be seen in Figure 5.

Figure 5. Trajectories for trained and predicted data. (a) Test 1 (Left). (b) Test 2 (Middle). (c) Test 3 (Right).
Test 1: 4100 seconds of RTK-GPS (1 Hz) and IMU (100 Hz) data were collected when the vehicle moved at a speed of 20 km/h. Navigation solutions between the 1580th and 1700th seconds are provided with the proposed algorithm, assuming that the GPS signal was unavailable during that time. With a similar motion state, 101 groups of data from the 1380th to 1480th seconds were chosen as the GA-SVR training samples. The data from 1481st to 1579th seconds were not used because the vehicle was forced to stop at a crossroad.
Test 2: 2100 seconds of RTK-GPS (1 Hz) and IMU (100 Hz) data were measured at a speed of 70 km/h. Navigation solutions between the 561st and 800th seconds were solved with the algorithm, assuming that the GPS signal was unavailable during that time. With a similar motion state, 201 groups of data from the 360th to the 560th seconds were chosen as the GA-SVR training samples.
Test 3: A set of data was selected when the vehicle moved along a curve at a speed of 20 km/h. Navigation solutions between the 943rd and 1023rd seconds are provided with the proposed algorithm, assuming that the GPS signal was unavailable during that time. With a similar motion state, 81 groups of data from the 313rd to the 393rd seconds were chosen as the GA-SVR training samples.
5.1. GPS position increments based on the GA-SVR
Figure 6 shows the training data of the three tests. Note that the specific force and angular rate increments of the INS measurements are multiplied by the sample interval 0·01 s. In Test 1 and Test 2, the roll and pitch of the angular rate are no more than 0·005 radians in magnitude, and the heading is no more than 0·02 radians, which illustrates that the direction of movement of the test vehicle remains stable. The specific force increments in Test 1 appear smoother than those in Test 2, and the result for the change of the GPS position increments in Test 1 is more stable than that for Test 2. From the increments of heading, latitude and longitude, it is obvious that Test 3 passed through a curve.

Figure 6. GA-SVR training data of three tests.
Figure 7 shows the process of seeking the optimal parameters γ and C in an SVR based on genetic algorithms. The iteration-stopping criterion is defined as a difference between two adjacent fitness levels of less than 0·001. The iterations in latitude, longitude, and height are: 57, 35, and 9, respectively, in Test 1; 193, 130, and 2, respectively, in Test 2; 13, 32, and 2, respectively, in Test 3. A faster convergence rate is achieved in the height direction for tests, and the slowest convergence rate arises in the latitude in Test 2, where the changes in the GPS position increments are the largest. The optimal parameters γ and C can be seen in Table 2.

Figure 7. Genetic algorithm fitness curves. (a) Test 1 (Top). (b) Test 2 (Middle). (c) Test 3 (Bottom).
Table 2. Results of GA-SVR.

Based on SVR theory, the sample data are trained to construct regression models with the optimal parameters γ and C in the SVR determined by genetic algorithms. Figure 8 shows the results and deviations of trained and predicted GPS position increments based on the GA-SVR algorithm. With a more smooth and stable state, the trained and predicted accuracy in Test 1 and Test 3 is much better than that in Test 2. The RMS of the errors of the three tests is shown in Table 2.

Figure 8. GA-SVR training results of Latitude, Longitude, and Height. (a) Test 1 (Top). (b) Test 2 (Middle). (c) Test 3 (Bottom).
5.2. Pseudo-GPS position-aided navigation
The pseudo-GPS position is calculated by adding the predicted GPS position increments to the GPS position (recorded before the GPS outage), as shown in Section 4.1. Figure 9 shows the pseudo-GPS position and its deviations for the three tests. Note that latitude deviations are transformed to metres by multiplying the radius of the curvature in the meridian, and longitude deviations are transformed by multiplying the radius of the curvature in the prime vertical and cosine of the latitude. The RMS of the latitude, longitude, and height deviations are 1·440 m, 0·717 m, and 0·561 m, respectively in Test 1, 11·641 m, 20·148 m, and 4·350 m, respectively in Test 2, and 1·576 m, 1·874 m, and 0·077 m, respectively in Test 3. The accuracy of the pseudo-GPS position in Test 1 and Test 3 is obviously much higher than that in Test 2 due to low speeds and smooth operation.

Figure 9. Pseudo-GPS position comparison and deviations. (a) Test 1 (Left). (b) Test 2 (Middle). (c) Test 3 (Right).
INS/RTK-GPS stands for the conventional GPS/INS loosely coupled integration algorithm when GPS signals are available; INS/GA-SVR means improved adaptive filtering with the pseudo-GPS positions during the absence of GPS signals; INS-only represents the navigation system depending solely on the equipped INS. Figure 10 shows deviations in the comparisons of the INS/RTK-GPS, INS/GA-SVR, and INS-only algorithms in three dimensions. The results indicate that deviations for INS-only are drifted to 27 m in 120 seconds when the GPS is unavailable, but the RMS of the deviation with INS/GA-SVR is 1·699 m with a maximum deviation of no more than 2·734 m in Test 1. The performance is very stable. In Test 2, the deviations in the INS-only drift to 119 m in 240 seconds, while the RMS of the deviation with INS/GA-SVR is 24·026 m, with a maximum deviation of less than 36·403 m. Navigation solutions undulate frequently from 560~680 seconds and are better than INS-only after that point as the result of the accuracy of the pseudo-GPS position. In Test 3, deviations in the INS-only drift to 9 m in 81 seconds, while the RMS of the deviation with INS/GA-SVR is 2·472 m, with a maximum deviation of no more than 3·600 m.

Figure 10. Position errors comparison in three dimensions. (a) Test 1 (Top). (b) Test 2 (Middle). (c) Test 3 (Bottom).
Figure 11 shows the velocity comparison for the INS/RTK-GPS and INS/GA-SVR algorithms in the north, east, and up directions. In Test 1, the RMS of the deviation using the INS/GA-SVR algorithm are 0·051 m/s, 0·068 m/s, and 0·015 m/s, with the maximum no more than 0·146 m/s, 0·187 m/s, and 0·041 m/s in the north, east, and up directions, respectively. This is almost identical to the true velocity with INS/RTK-GPS. In Test 2, the RMS of the deviation using the INS/GA-SVR algorithm are 0·560 m/s, 0·406 m/s, and 0·075 m/s, with a maximum of no more than 1·003 m/s, 0·782 m/s, and 0·226 m/s in north, east, and up directions, respectively. In Test 3, the RMS of the deviation using the INS/GA-SVR algorithm are 0·104 m/s, 0·077 m/s, and 0·033 m/s, with a maximum deviation of less than 0·239 m/s, 0·187 m/s, and 0·040 m/s in north, east, and up directions, respectively. This result indicates that the velocity in the up direction is close to that with INS/RTK-GPS, but there are small deviations between INS/RTK-GPS and INS/GA-SVR in the north and east directions.

Figure 11. Velocity comparison. (a) Test 1 (Top). (b) Test 2 (Middle). (c) Test 3 (Bottom).
Figure 12 shows an attitude comparison of the INS/RTK-GPS and INS/GA-SVR algorithms in the roll, pitch, and heading. In Test 1, the RMS of the deviation with the INS/GA-SVR algorithm are 0·109°, 0·250°, and 0·222°, with the maximum no more than 0·161°, 0·342°, and 0·290° in the roll, pitch, and head, respectively, which are almost identical to the attitude of INS/RTK-GPS. In Test 2, the RMS of the deviation with the INS/GA-SVR algorithm are 0·039°, 0·135°, and 0·985°, with a maximum of no more than 0·088°, 0·278°, and 1·509° in the roll, pitch, and head, respectively. In Test 3, the RMS of the deviation with the INS/GA-SVR algorithm are 0·023°, 0·040°, and 0·111°, with a maximum of no more than 0·058°, 0·070°, and 0·168° in the roll, pitch, and head, respectively. These results indicate that the attitude in the roll and pitch is close to INS/RTK-GPS, but there are small differences between INS/RTK-GPS and INS/GA-SVR in the heading. The statistical results for the velocity and attitude are given in Table 3.

Figure 12. Attitude comparison. (a) Test 1 (Top). (b) Test 2 (Middle). (c) Test 3 (Bottom).
Table 3. Results of velocity and attitude comparison.

The results indicate that 1) Based on the GA-SVR algorithm, the accuracy of the pseudo-GPS position is high when the vehicle operates a low-speed-stable navigation platform along both a straight line and a curve, and low if the vehicle operates a high-speed-unstable navigation platform; 2) The velocity and attitude of navigation solutions are very close to the true value, and they benefit from the implementation of improved adaptive filtering that only adjusts the position covariance matrix rather than other states; and 3) The accuracy of navigation solutions depends largely upon the accuracy of the pseudo-GPS position when the GPS is unavailable.
6. CONCLUSIONS
To overcome the shortcomings of GPS/INS integrated navigation during GPS outages, we have proposed a pseudo-position-aided INS navigation algorithm. Based on GA-SVR, the algorithm uses the predicted pseudo-position and improved adaptive filtering to calculate reliable navigation solutions. The proposed algorithm has been tested on low-speed-stable and high-speed-unstable navigation platforms where the vehicle travels along a straight line and around a curve. Results show that the proposed new approach can provide reliable and accurate navigation solutions when the GPS is unavailable. The calculation of the optimal parameters in an SVR training model will take more time, which will affect the real-time navigation of the integrated system. Thus the optimal parameters should be trained in advance according to the INS performance and the different motion states of the vehicle. With the further development of parallel computing technology and computer performance, this issue will be resolved in the future.
ACKNOWLEDGMENTS
The work is partially sponsored by the Program for New Century Excellent Talents in University (grant number: NCET-13–1019), partially sponsored by the Fundamental Research Funds for the Central Universities (grant number: 2013RC16); and partially sponsored by A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

















