Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-25T23:20:05.274Z Has data issue: false hasContentIssue false
  • English
  • Français

The characteristics of the circular hydraulic jump and vortex structure

Published online by Cambridge University Press:  31 January 2024

Wenxi Wang Open the ORCID record for Wenxi Wang [Opens in a new window] ,
Abdelkader Baayoun Open the ORCID record for Abdelkader Baayoun [Opens in a new window]  and
Roger E. Khayat Open the ORCID record for Roger E. Khayat [Opens in a new window]
Wenxi Wang
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, ON, N6A 5B9, Canada
Abdelkader Baayoun
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, ON, N6A 5B9, Canada
Roger E. Khayat*
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, ON, N6A 5B9, Canada
*
†Email address for correspondence: rkhayat@uwo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

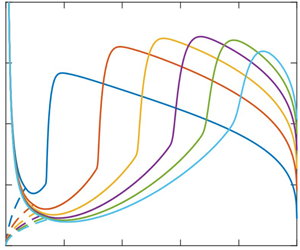
In an effort to capture the continuous hydraulic jump and flow structure for a jet impinging on a disk, we recently proposed a composite mean-field thin-film approach consisting of subdividing the flow domain into three distinct connected regions of increasing gravity strength (Wang et al., J. Fluid Mech., vol. 966, 2023, A15). In the present study, we further validate our approach, and examine the characteristics and structure of the circular jump and recirculation. The influence of the disk radius is found to be significant, especially in the subcritical region. Below a disk radius, the jump transits from type Ia to type 0 after the recirculation zone has faded. The supercritical flow and jump location are insensitive to the disk size, but the jump length and height as well as the vortex size are strongly affected, all decreasing with decreasing disk radius, exhibiting a maximum with the flow rate for a small disk. The jump is relatively steep with a strong recirculation zone for a high obstacle at the disk edge. Comparison against the Navier–Stokes solution of Askarizadeh et al. (Phys. Rev. Fluids, vol. 4, 2019, 114002; Intl J. Heat Mass Transfer, vol. 146, 2020, 118823) for the weak and intermediate surface tension suggests that the surface tension effect is unimportant for a high obstacle for a jump of type 0 or type Ia. The film thickness at the disk edge for a freely draining film is found to comprise, in addition to a static component (capillary length), a dynamic component: ${h_\infty }\sim {(Fr/{r_\infty })^{2/3}}$ that we establish by minimizing the Gibbs free energy at the disk edge, and, equivalently, is also the consequence of the flow becoming supercritical near the edge. By assuming negligible film slope and curvature at the leading edge of the jump and maximum height at the trailing edge, we show that the jump length is related to the jump radius as ${L_J}\sim Re{(F{r^2}/{r_J}^5)^{1/3}}$. The vortex length follows the same behaviour. The energy loss and conjugate depth ratio exhibit a maximum with the flow rate, which we show to originate from the descending and ascending branches of the supercritical film thickness. The presence of the jump is not necessarily commensurate with that of a recirculation; the existence of the vortex closely depends on the upstream curvature and steepness of the jump. The surface separating the regions of existence/non-existence of the recirculation is given by the universal relation $R{e^{10/3}}F{r^2} = 9r_\infty ^9/50$. The jump can be washed off the edge of the disk, particularly at low viscosity and small disk size. The flow in the supercritical region remains insensitive to the change in gravity level and disk size but is greatly affected by viscosity.

JFM classification

Boundary Layers: Boundary layer structure Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 980 , 10 February 2024 , A15
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Askarizadeh, H., Ahmadikia, H., Ehrenpreis, C., Kneer, R., Pishevar, A. & Rohlfs, W. 2019 Role of gravity and capillary waves in the origin of circular hydraulic jumps. Phys. Rev. Fluids 4, 114002.CrossRefGoogle Scholar
Askarizadeh, H., Ahmadikia, H., Ehrenpreis, C., Kneer, R., Pishevar, A. & Rohlfs, W. 2020 Heat transfer in the hydraulic jump region of circular free-surface liquid jets. Intl J. Heat Mass Transfer 146, 118823.CrossRefGoogle Scholar
Avedisian, C. & Zhao, Z. 2000 The circular hydraulic jump in low gravity. Proc. R. Soc. Lond. A 456, 2127–2151.CrossRefGoogle Scholar
Bélanger, J.B. 1841 Notes sur l'Hydraulique. Ecole Royale des Ponts et Chaussées, Paris, France, session 1842, 223.Google Scholar
Bohr, T., Dimon, P. & Putzkaradze, V. 1993 Shallow-water approach to the circular hydraulic jump. J. Fluid Mech. 254, 635–648.CrossRefGoogle Scholar
Bohr, T., Ellegaard, C., Hansen, A.E. & Haaning, A. 1996 Hydraulic jumps, flow separation and wave breaking: an experimental study. Physica B 228, 1–10.CrossRefGoogle Scholar
Bohr, T., Putkaradze, V. & Watanabe, S. 1997 Averaging theory for the structure of hydraulic jumps and separation in laminar free-surface flows. Phys. Rev. Lett. 79, 1038–1041.CrossRefGoogle Scholar
Bonn, D., Andersen, A. & Bohr, T. 2009 Hydraulic jumps in a channel. J. Fluid Mech. 618, 71–87.CrossRefGoogle Scholar
Bowles, R.I. 1995 Upstream influence and the form of standing hydraulic jumps in liquid-layer flows on favourable slopes. J. Fluid Mech. 284, 63–96.CrossRefGoogle Scholar
Bowles, R.I. & Smith, F.T. 1992 The standing hydraulic jump: theory, computations and comparisons with experiments. J. Fluid Mech. 242, 145–168.CrossRefGoogle Scholar
Bush, J.W., Aristoff, J.M. & Hosoi, A.E. 2006 An experimental investigation of the stability of the circular hydraulic jump. J. Fluid Mech. 558, 33–52.CrossRefGoogle Scholar
Bush, J.W.M. & Aristoff, J.M. 2003 The influence of surface tension on the circular hydraulic jump. J. Fluid Mech. 489, 229–238.CrossRefGoogle Scholar
Chang, H.C., Demekhin, E.A. & Takhistov, P.V. 2001 Circular hydraulic jumps triggered by boundary layer separation. J. Colloid Interface Sci. 233, 329–338.CrossRefGoogle ScholarPubMed
Chanson, H. 2012 Momentum considerations in hydraulic jumps and bores. J. Irrig. Drain. Engng 138, 382–385.CrossRefGoogle Scholar
Craik, A., Latham, R., Fawkes, M. & Gribbon, P. 1981 The circular hydraulic jump. J. Fluid Mech. 112, 347–362.CrossRefGoogle Scholar
Dhar, M., Das, G. & Das, P.K. 2020 Planar hydraulic jumps in thin film flow. J. Fluid Mech. 884, A11.CrossRefGoogle Scholar
Dressaire, E., Courbin, L., Crest, J. & Stone, H.A. 2010 Inertia dominated thin-film flows over microdecorated surfaces. Phys. Fluids 22, 073602.CrossRefGoogle Scholar
Duchesne, A. 2014 Trois problèmes autour du ressaut hydraulique circulaire. Thesis, Université Denis Diderot (Paris 7) - Sorbonne Paris Cité.Google Scholar
Duchesne, A., Lebon, L. & Limat, L. 2014 Constant Froude number in a circular hydraulic jump and its implication on the jump radius selection. Europhys. Lett. 107, 54002.CrossRefGoogle Scholar
Duchesne, A. & Limat, L. 2022 Circular hydraulic jumps: where does surface tension matter? J. Fluid Mech. 937, R2.CrossRefGoogle Scholar
Ellegaard, C., Hansen, A., Haaning, A., Hansen, K. & Bohr, T. 1996 Experimental results on flow separation and transitions in the circular hydraulic jump. Phys. Scr. T67, 105–110.CrossRefGoogle Scholar
Ellegaard, C., Hansen, A.E., Haaning, A., Hansen, K., Marcussen, A., Bohr, T., Hansen, J.L. & Watanabe, S. 1998 Creating corners in kitchen sinks. Nature 392, 767–768.CrossRefGoogle Scholar
Fernandez-Feria, R., Sanmiguel-Rojas, E. & Benilov, E.S. 2019 On the origin and structure of a stationary circular hydraulic jump. Phys. Fluids 31, 072104.CrossRefGoogle Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves, vol. 336. Springer.CrossRefGoogle Scholar
Hansen, S.H., Horluck, S., Zauner, D., Dimon, P., Ellegaard, C. & Creagh, S.C. 1997 Geometric orbits of surface waves from a circular hydraulic jump. Phys. Rev. E 55, 7048–7061.CrossRefGoogle Scholar
Higuera, F.J. 1994 The hydraulic jump in a viscous laminar flow. J. Fluid Mech. 274, 69–92.CrossRefGoogle Scholar
Ipatova, A., Smirnov, K. & Mogilevskiy, E. 2021 Steady circular hydraulic jump on a rotating disk. J. Fluid Mech. 927, A24.CrossRefGoogle Scholar
Kasimov, A.R. 2008 A stationary circular hydraulic jump, the limits of its existence and its gasdynamic analogue. J. Fluid Mech. 601, 189–198.CrossRefGoogle Scholar
Lawson, J.D. & Phillips, B.C. 1983 Circular hydraulic jump. J. Hydraul. Engng ASCE 109, 505–518.CrossRefGoogle Scholar
Lienhard, J. 2006 Heat transfer by impingement of circular free-surface liquid jets. In 18th National & 7th ISHMT-ASME Heat and Mass Transfer Conference, pp. 1–17. IIT.Google Scholar
Liu, X. & Lienhard, J. 1993 The hydraulic jump in circular jet impingement and in other thin liquid films. Exp. Fluids 15, 108–116.CrossRefGoogle Scholar
Lubarda, V. & Talke, K.A. 2011 Analysis of the equilibrium droplet shape based on an ellipsoidal droplet model. Langmuir 27, 10705–10713.CrossRefGoogle Scholar
Mohajer, B. & Li, R. 2015 Circular hydraulic jump on finite surfaces with capillary limit. Phys. Fluids 27, 117102.CrossRefGoogle Scholar
Palermo, M. & Pagliara, S. 2018 Semi-theoretical approach for energy dissipation estimation at hydraulic jumps in rough sloped channels. J. Hydraul Res. 56, 786–795.CrossRefGoogle Scholar
Passandideh-Fard, M., Teymourtash, A.R. & Khavari, M. 2011 Numerical study of circular hydraulic jump using volume-of-fluid method. J. Fluids Engng 133, 11401.CrossRefGoogle Scholar
Prince, J.F., Maynes, D. & Crockett, J. 2012 Analysis of laminar jet impingement and hydraulic jump on a horizontal surface with slip. Phys. Fluids 24, 102103.CrossRefGoogle Scholar
Prince, J.F., Maynes, D. & Crockett, J. 2014 Jet impingement and the hydraulic jump on horizontal surfaces with anisotropic slip. Phys. Fluids 26, 042104.CrossRefGoogle Scholar
Rahman, M.M., Faghri, A. & Hankey, W.L. 1992 Fluid flow and heat transfer in a radially spreading thin liquid film. Numer. Heat Transfer A: Appl. 21, 71–90.CrossRefGoogle Scholar
Rao, A. & Arakeri, J.H. 2001 Wave structure in the radial film flow with a circular hydraulic jump. Exp. Fluids 31, 542–549.CrossRefGoogle Scholar
Razis, D., Kanellopoulos, G. & Van der Weele, K. 2021 Continuous hydraulic jumps in laminar channel flow. J. Fluid Mech. 915, A8.CrossRefGoogle Scholar
Roberts, A.J. & Li, Z. 2006 An accurate and comprehensive model of thin fluid flows with inertia on curved substrates. J. Fluid Mech. 553, 33–73.CrossRefGoogle Scholar
Rojas, N.O., Argentina, M., Cerda, E. & Tirapegui, E. 2010 Inertial lubrication theory. Phys. Rev. Lett. 104, 187801.CrossRefGoogle ScholarPubMed
Rojas, N.O., Argentina, M. & Tirapegui, E. 2013 A progressive correction to the circular hydraulic jump scaling. Phys. Fluids 25, 42105.CrossRefGoogle Scholar
Scheichl, B., Bowles, R.I. & Pasias, G. 2018 Developed liquid film passing a trailing edge under the action of gravity and capillarity. J. Fluid Mech. 850, 924–953.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory, 8th edn. Springer.CrossRefGoogle Scholar
Sung, J., Choi, H.G. & Yoo, J.Y. 1999 Finite element simulation of thin liquid film flow and heat transfer including a hydraulic jump. Intl J. Numer. Methods Engng 46, 83–101.3.0.CO;2-D>CrossRefGoogle Scholar
Tani, I. 1949 Water jump in the boundary layer. J. Phys. Soc. Japan 4, 212–215.CrossRefGoogle Scholar
Wang, W., Baayoun, A. & Khayat, R.E. 2023 A coherent composite approach for the continuous circular hydraulic jump and vortex structure. J. Fluid Mech. 966, A15.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2018 Impinging jet flow and hydraulic jump on a rotating disk. J. Fluid Mech. 839, 525–560.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2019 The role of gravity in the prediction of the circular hydraulic jump radius for high-viscosity liquids. J. Fluid Mech. 862, 128–161.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2020 The influence of heating on liquid jet spreading and hydraulic jump. J. Fluid Mech. 883, A59.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2021 The effects of gravity and surface tension on the circular hydraulic jump for low- and high-viscosity liquids: a numerical investigation. Phys. Fluids 33, 012105.CrossRefGoogle Scholar
Watanabe, S., Putkaradze, V. & Bohr, T. 2003 Integral methods for shallow free-surface flows with separation. J. Fluid Mech. 480, 233–265.CrossRefGoogle Scholar
Watson, E. 1964 The spread of a liquid jet over a horizontal plane. J. Fluid Mech. 20, 481–499.CrossRefGoogle Scholar
White, F.M. 2006 Viscous Fluid Flow, 3th edn. McGraw-Hill.Google Scholar
Yang, S. & Chen, C. 1992 Laminar film condensation on a finite-size horizontal plate with suction at the wall. Appl. Math. Model. 16, 325–329.CrossRefGoogle Scholar
Yang, Y., Chen, C. & Hsu, P. 1997 Laminar film condensation on a finite-size wavy disk. Appl. Math. Model. 21, 139–144.Google Scholar
Zhou, G. & Prosperetti, A. 2022 Hydraulic jump on the surface of a cone. J. Fluid Mech. 951, A20.CrossRefGoogle Scholar