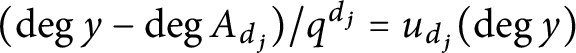1 Introduction
Rigid analytic trivializations were originally defined by Anderson [Reference Anderson1, Theorem 4] as tools for determining whether a t-module is uniformizable, i.e., that its exponential function is surjective. It was subsequently discovered by Anderson and Pellarin that specializations of rigid analytic trivializations could be used to recover the periods and quasi-periods of a Drinfeld module (see [Reference Goss16, Section 2.6], [Reference Pellarin25, Section 4]). This specialization phenomenon has led to advances in the transcendence theory of periods and quasi-periods (see, e.g., [Reference Anderson, Brownawell and Papanikolas2, Reference Chang and Papanikolas7, Reference Chang and Papanikolas8, Reference Pellarin25]). Given their centrality to the arithmetic of function fields, the focus of the present paper is to investigate new and direct ways of constructing rigid analytic trivializations for Drinfeld modules.
Our motivating example is that of the Carlitz module. Let
$\mathbb {F}_q$
be a finite field with q elements, let
be the polynomial ring in
$\theta $
over
$\mathbb {F}_q$
, and let
be its fraction field. We let
be the polynomial ring in a variable t independent from
$\theta $
. For any k-algebra R, the Carlitz module C over R is the
$\mathbf {A}$
-module structure on R determined by setting
for
$x \in R$
. If we let
be the completion of k at its infinite place, and take
$\mathbb {K}$
for the completion of an algebraic closure of
$k_\infty $
, then the Carlitz exponential
$\exp _C : \mathbb {K} \to \mathbb {K}$
is entire,
$\mathbb {F}_q$
-linear, and surjective, and it uniformizes the Carlitz module over
$\mathbb {K}$
. The kernel of
$\exp _C$
is the discrete A-submodule of
$\mathbb {K}$
of rank
$1$
generated by the Carlitz period,
$$ \begin{align} \widetilde{\pi} = -(-\theta)^{q/(q-1)} \prod_{n=1}^{\infty} \Bigl( 1- \theta^{1-q^n} \Bigr)^{-1} \in k_{\infty} \bigl( (-\theta)^{1/(q-1)} \bigr), \end{align} $$
where we have fixed a
$(q-1)$
st root of
$-\theta $
. Throughout the arithmetic of function fields,
$\widetilde {\pi }$
plays the role of
$2\pi i$
in characteristic
$0$
. This product formula for
$\widetilde {\pi }$
was essentially first derived by Carlitz [Reference Carlitz6, Theorem 5.1], and for more information on the Carlitz module and its exponential function, see [Reference Goss17, Chapter 3], [Reference Thakur31, Chapter 2].
The rigid analytic trivialization of C is the Anderson–Thakur function
where
$\mathbb {T}$
is the Tate algebra in
${\mathbb {K} [\![ t ]\!]}$
consisting of power series that converge on the closed unit disk in
$\mathbb {K}$
. In [Reference Anderson and Thakur3, Section 2.5], Anderson and Thakur showed that
$\omega _C$
satisfies a number of important properties. For
$n \in \mathbb {Z}$
, if we define the Frobenius twist
$f \mapsto f^{(n)} : {\mathbb {K} (\!( t )\!)} \to {\mathbb {K} (\!( t )\!)}$
by
$\sum c_i t^i \mapsto \sum c_i^{q^n} t^i$
, then
$$ \begin{align} \omega_C^{(1)} = (t-\theta)\omega_C. \end{align} $$
Moreover,
$\omega _C$
extends to a meromorphic function on all of
$\mathbb {K}$
, and it has a simple pole at
$t=\theta $
, where we readily verify from (1.1) that
$$ \begin{align} \operatorname{\mathrm{Res}}_{t=\theta} \omega_C = -\widetilde{\pi}. \end{align} $$
The Anderson–Thakur function further plays a central role in special values of Pellarin L-series (see, e.g., [Reference Pellarin26, Reference Perkins27]).
Letting
$\mathbb {K}[\tau ]$
be the ring of twisted polynomials in the qth power Frobenius
$\tau $
, a Drinfeld module of rank r is an
$\mathbb {F}_q$
-algebra homomorphism
$\phi : \mathbf {A} \to \mathbb {K}[\tau ]$
determined by
$$ \begin{align} \phi_t = \theta + A_1 \tau + \cdots + A_r \tau^r, \quad A_r \neq 0. \end{align} $$
Like the Carlitz module,
$\phi $
is uniformized by an exponential function
$\exp _{\phi } : \mathbb {K} \to \mathbb {K}$
, whose kernel
$\Lambda _{\phi }$
is a discrete, free A-submodule of
$\mathbb {K}$
of rank r. We call
$\Lambda _{\phi }$
the period lattice of
$\phi $
. For
$\pi \in \Lambda _{\phi }$
, we define the Anderson generating function
Initially defined by Anderson [Reference Anderson1, Section 3.2], these functions satisfy a number of useful properties which we summarize in Section 2. Most notably,
$$ \begin{align*} \theta f_{\phi}(\pi;t) + A_1 f_{\phi}(\pi;t)^{(1)} + \cdots + A_r f_{\phi}(\pi;t)^{(r)} = t f_{\phi}(\pi;t), \end{align*} $$
and
$f_{\phi }(\pi ;t)$
is a meromorphic function on
$\mathbb {K}$
with a simple pole at
$t=\theta $
(if
$\pi \neq 0$
) and
$$ \begin{align} \operatorname{\mathrm{Res}}_{t=\theta} f_{\phi}(\pi;t) = -\pi. \end{align} $$
There is an obvious parallel with (1.3) and (1.4), and in fact
$\omega _C$
is the Anderson generating function for
$\widetilde {\pi }$
on the Carlitz module (see [Reference Anderson, Brownawell and Papanikolas2, Proposition 5.1.3]).
For an A-basis
$\pi _1, \ldots , \pi _r$
of
$\Lambda _{\phi }$
, we set
for each j, and we let
Pellarin [Reference Pellarin25, Section 4.2] showed that
$\Upsilon $
is invertible in
$\operatorname {\mathrm {GL}}_r(\mathbb {T})$
; moreover, he observed that (i) by (1.6) the negatives of the residues at
$t=\theta $
of the entries of the first row yield the periods
$\pi _1, \ldots , \pi _r$
, and (ii) based on calculations of Gekeler [Reference Gekeler13, Remark 2.7], for
$1 \leqslant i \leqslant r-1$
, the value
$f_j^{(i)}(\theta )$
is a strictly reduced quasi-period for
$\phi $
associated to
$\pi _j$
. Furthermore, he proved that
$$ \begin{align} \Upsilon^{(1)} = \Theta \Upsilon, \end{align} $$
where we apply the Frobenius twist entrywise and where
The matrix
$\Theta $
arises naturally from the t-motive associated to
$\phi $
, and by definition, (1.8) makes
$\Upsilon $
into a rigid analytic trivialization for
$\phi $
(see Section 2 for details).
Remark 1.10 (1) This same specialization property that uses rigid analytic trivializations to supply periods and quasi-periods holds for other t-modules as well. For rank
$1$
objects, one can consult [Reference Anderson, Brownawell and Papanikolas2, Section 6], [Reference Brownawell and Papanikolas5, Section 4], [Reference Sinha29], for instances involving the geometric
$\Gamma $
-function, and [Reference Green and Papanikolas19, Theorem 4.6] for certain rank
$1$
Drinfeld modules over more general rings
$\mathbf {A}$
. For general t-modules, see [Reference Gazda and Maurischat12, Section 3], [Reference Green18, Section 6], [Reference Maurischat23, Section 5] for periods, and [Reference Namoijam and Papanikolas24, Section 4] for periods and quasi-periods. In all of these cases, rigid analytic trivializations are obtained through possibly higher dimensional versions of Anderson generating functions.
(2) In the present paper, we study only rigid analytic trivializations associated to the t-motive of a Drinfeld module, as opposed to the rigid analytic trivializations associated to its dual t-motive. However, as seen in [Reference Chang and Papanikolas8, Section 3.4], [Reference Hartl and Juschka20, Example 2.5.16], the two theories are related; moreover, using a theorem of Hartl and Juschka [Reference Hartl and Juschka20, Theorem 2.5.13], we can transform one to the other for general abelian and
$\mathbf {A}$
-finite t-modules [Reference Namoijam and Papanikolas24, Theorem 4.4.14].
There is one noticeable advantage of
$\omega _C(t)$
over the more general Anderson generating functions
$f_{\phi }(\pi ;t)$
: the definition of
$f_{\phi }(\pi ;t)$
ostensibly presupposes knowledge of
$\pi $
itself, whereas the product expansion in (1.2) is independent of knowing
$\widetilde {\pi }$
in advance. The coefficients of
$f_{\phi }(\pi ;t)$
form a t-division sequence of t-power torsion on
$\phi $
, but obtaining
$f_{\phi }(\pi ;t)$
exactly from these coefficients would require the precise selection of this infinite sequence. Thus, unfortunately, in order to use
$f_{\phi }(\pi ;t)$
to retrieve
$\pi $
or the quasi-periods associated to
$\pi $
, we have run into a chicken-and-egg problem.
One goal of the present paper is to construct a rigid analytic trivialization
$\Upsilon $
for
$\phi $
from a full system of Anderson generating functions
$f_1, \ldots , f_r$
, associated to an A-basis
$\pi _1, \ldots , \pi _r$
of
$\Lambda _{\phi }$
, without using
$\pi _1, \ldots , \pi _r$
as initial inputs. Much like for
$\omega _C$
, we will achieve this through an infinite product, but of matrices, which can be constructed in an effective manner, i.e., by utilizing only a finite amount of initial computation (see Theorems A and B). In this way, we can obtain
$\Upsilon $
efficiently, together with formulas for the periods and quasi-periods of our Drinfeld module, from first principles.
The outline of this construction is as follows. After establishing definitions and prior results in Section 2, we construct a matrix
$B \in \operatorname {\mathrm {Mat}}_r(\mathbb {K}[t]) \cap \operatorname {\mathrm {GL}}_r(\mathbb {T})$
in Section 3 so that
$$ \begin{align} \lVert B^{-1} \Theta^{-1} B^{(1)} - I \rVert < 1, \end{align} $$
where
$\lVert \,\cdot \, \rVert $
is the extension of the Gauss norm on
$\mathbb {T}$
to
$\operatorname {\mathrm {Mat}}_r(\mathbb {T})$
and I is the
$r\times r$
identity matrix (see Theorem 3.29). The entries of B are obtained by systematic selection of a basis of
$t^N$
-torsion points
$\xi _1, \ldots , \xi _r \in \phi [t^N]$
, where
$N \geqslant 1$
is determined by the degrees of the coefficients
$A_1, \ldots , A_r$
in (1.5) using estimates from [Reference El-Guindy and Papanikolas10] (see Remark 3.14). We choose these
$t^N$
-torsion points recursively through analysis of the Newton polygon of
$\phi _t(x) \in \mathbb {K}[x]$
(see Propositions 3.12 and 3.17); moreover,
$\phi _{t^{N-1}}(\xi _1), \ldots , \phi _{t^{N-1}}(\xi _r) \in \phi [t]$
form a strict basis of the t-torsion module
$\phi [t]$
, in that the degrees of these elements match the slopes of the Newton polygon of
$\phi _t(x)$
in a prescribed way (see Definition 3.18). By letting
the matrix
is an element of
$\operatorname {\mathrm {GL}}_r(\mathbb {T})$
(see Proposition 3.26). It further satisfies (1.11) by Theorem 3.29, which leads to the following result (stated later as Corollary 3.32), producing a rigid analytic trivialization for
$\phi $
via an infinite product of twists of matrices.
Theorem A Continuing with notation as above, the infinite product
converges with respect to the Gauss norm on
$\operatorname {\mathrm {Mat}}_r(\mathbb {T})$
and lies in
$\operatorname {\mathrm {GL}}_r(\mathbb {T})$
. Moreover,
$$ \begin{align*} \Pi^{(1)} = \Theta \Pi, \end{align*} $$
and so
$\Pi $
is a rigid analytic trivialization for
$\phi $
.
Because such a product of matrices depends on the order of the factors, we note that in Theorem A and elsewhere each successive term of the infinite product is multiplied on the right. That is, the product is
$(B^{-1} \Theta ^{-1} B^{(1)})( B^{-1} \Theta ^{-1} B^{(1)})^{(1)} ( B^{-1} \Theta ^{-1} B^{(1)})^{(2)} \cdots $
.
In the case of the Carlitz module, one checks that
$\Theta = t-\theta $
and
$B = (-\theta )^{1/(q-1)}$
in Theorem A, from which we see that
$\Pi = \omega _C$
. To what extent can we use
$\Pi $
to recover
$\Upsilon $
for general Drinfeld modules
$\phi $
? Like the Carlitz module, Drinfeld modules of rank
$1$
over more general rings possess product expansions for their rigid analytic trivializations [Reference Anglès, Ngo Dac and Tavares Ribeiro4, Section 3], [Reference Green and Papanikolas19, Section 4]. However, in general, we can in fact use
$\xi _1, \ldots , \xi _r$
to construct an A-basis
$\pi _1, \ldots , \pi _r$
of
$\Lambda _\phi $
, and then apply [Reference El-Guindy and Papanikolas10, Theorem 6.13] to show that
$\Pi $
is the same as
$\Upsilon $
in (1.7). The following is our main result in these directions (stated later with additional details in Theorem 4.4).
Theorem B Choose
$N \geqslant 1$
and
$\xi _1, \ldots , \xi _r \in \phi [t^N]$
as in Proposition 3.17. Let
$B = ( h_j^{(i-1)}) \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
be defined as in (1.12), and construct the rigid analytic trivialization
$\Pi $
for
$\phi $
as in Theorem A. Letting
, the quantities
$\pi _1, \ldots , \pi _r$
form an A-basis of
$\Lambda _{\phi }$
; moreover,
$$ \begin{align*} \Pi = \Upsilon, \end{align*} $$
where
$\Upsilon $
is defined with respect to
$\pi _1, \ldots , \pi _r$
in (1.7).
In addition to providing identities for periods and quasi-periods, Theorems A and B and their proofs lead to precise descriptions of the field generated by the period lattice over the field of definition of the Drinfeld module in Corollary 4.6. This recovers a result of Maurischat [Reference Maurischat22, Theorem 3.1] in rank
$2$
, and parts of results of Gekeler in arbitrary rank [Reference Gekeler14, Section 2]. It also wraps up a picture started in [Reference El-Guindy and Papanikolas9, Theorem 5.3].
Remark 1.13 As pointed out by one referee, the results in Theorems A and B could in principle be extended to Anderson t-modules which are abelian and rigid analytically trivial. Further investigation would be necessary to make this precise, although perhaps descriptions of rigid analytic trivializations and Anderson generating functions from [Reference Gazda and Maurischat12, Reference Green18, Reference Hartl and Juschka20, Reference Maurischat23, Reference Namoijam and Papanikolas24] would be helpful. One thing to note is that the proofs in the present paper, and especially the proof of the convergence of the product in Theorem A, rely heavily on the explicit nature of
$\Theta $
given in (1.9).
In Section 5, we investigate the case of rank
$2$
in more detail. Our findings dovetail with Maurischat’s theorem [Reference Maurischat22, Theorem 3.1], which we summarize in Theorem 5.2. Then, in Examples 5.4 and 5.5, we approximate the matrices B and
$\Pi $
for specific rank
$2$
Drinfeld modules and use these approximations to calculate periods and quasi-periods.
2 Preliminaries
The following notation will be used throughout the paper:
The absolute value
$\lvert \,\cdot \, \rvert $
on
$k_\infty $
is chosen so that
$|\theta |=q$
, its valuation satisfies
${v_{\infty }(\theta )=-1}$
, and we let
. Then
$\lvert \,\cdot \, \rvert $
,
$v_\infty $
, and
$\deg $
extend uniquely to
$\mathbb {K}$
.
2.1 Drinfeld modules
For fundamental properties of Drinfeld modules, see Goss [Reference Goss17, Chapters 3 and 4] or Thakur [Reference Thakur31, Chapter 2]. For the qth power Frobenuis map
$\tau : \mathbb {K} \to \mathbb {K}$
(
$z\mapsto z^q$
), the ring of twisted polynomials
$\mathbb {K}[\tau ]$
in
$\tau $
over
$\mathbb {K}$
satisfies
$\tau c = c^q \tau $
for all
$c \in \mathbb {K}$
. A Drinfeld module of rank r over
$\mathbb {K}$
is an
$\mathbb {F}_q$
-algebra homomorphism
$\phi :\mathbf {A} \to \mathbb {K}[\tau ]$
determined by
$$ \begin{align} \phi_t = \theta + A_1 \tau + \cdots + A_r \tau^r,\quad A_r \neq 0. \end{align} $$
As usual, we obtain an
$\mathbf {A}$
-module structure on
$\mathbb {K}$
induced by
$\phi $
by the action
for
$a\in \mathbf {A}$
,
$x\in \mathbb {K}$
. For any
$a\in \mathbf {A}$
, we take
to be the
$\mathbf {A}$
-submodule of a-torsion points on
$\phi $
. Then
$\phi [a] \cong (\mathbf {A}/(a))^r$
as
$\mathbf {A}$
-modules.
The exponential of
$\phi $
is defined to be the entire, surjective,
$\mathbb {F}_q$
-linear power series,
$$ \begin{align} \exp_\phi(z) = \sum_{n=0}^\infty \alpha_n z^{q^n}, \quad \alpha_0 =1,\ \alpha_n\in\mathbb{K}, \end{align} $$
satisfying
$\exp _\phi (a(\theta )z) = \phi _a(\exp _\phi (z))$
for every
$a\in \mathbf {A}$
. Letting
, one finds that
$\Lambda _\phi $
is a discrete, free A-module of rank r inside
$\mathbb {K}$
. We call
$\Lambda _\phi $
the period lattice of
$\phi $
, and any element of
$\Lambda _\phi $
a period of
$\phi $
. The logarithm
$\log _{\phi }(z)$
of
$\phi $
is the formal inverse of
$\exp _\phi (z)$
with respect to composition, and it has a finite radius of convergence
$P_\phi $
on
$\mathbb {K}$
. By [Reference Goss17, Proposition 4.14.2],
$$ \begin{align} P_{\phi} = \min\{ |\pi| : \pi \in \Lambda_{\phi},\, \pi \neq 0 \}. \end{align} $$
2.2 Tate algebras
The Tate algebra of power series converging on the closed unit disk of
$\mathbb {K}$
,
is a complete normed
$\mathbb {K}$
-algebra with respect to the Gauss norm
$\lVert \,\cdot \, \rVert $
, which is defined by
. We recall that
$u=\sum c_i t^i \in \mathbb {T}$
is in
$\mathbb {T}^{\times }$
if and only if (i)
$c_0 \neq 0$
and (ii) we can write
$u = c_0(1+g)$
for
$g \in \mathbb {T}$
with
$\lVert g \rVert < 1$
(see [Reference Anderson1, Lemma 2.9.1], [Reference Fresnel and van der Put11, Corollary 2.2.4]). For
$\eta \in \mathbb {K}^{\times }$
, we further define the Tate algebra
consisting of functions that converge on the closed disk of radius
$|\eta |$
. For more details on the theory of Tate algebras, see [Reference Fresnel and van der Put11, Section 2]. For a matrix
$F = (f_{ij}) \in \operatorname {\mathrm {Mat}}_{r\times s}(\mathbb {T})$
, we set
, making
$\operatorname {\mathrm {Mat}}_{r\times s}(\mathbb {T})$
into a complete normed
$\mathbb {T}$
-module.
For any
$f=\sum c_i t^i \in {\mathbb {K} (\!( t )\!)}$
and
$n\in \mathbb {Z}$
, the nth Frobenius twist of f is
. For
$F = (f_{ij}) \in \operatorname {\mathrm {Mat}}_{r\times s}({\mathbb {K} (\!( t )\!)})$
, we take
. For
$\delta> 0$
and any
$f \in \mathbb {T}_{\theta ^{\delta /q}}$
, we have
$f^{(1)} \in \mathbb {T}_{\theta ^{\delta }}$
. In particular,
$$ \begin{align} f \mapsto f^{(1)} : \mathbb{T}_{\theta^{1/q}} \to \mathbb{T}_{\theta}. \end{align} $$
For
$\Delta = b_0 + b_1\tau + \cdots + b_{\ell } \tau ^{\ell } \in \mathbb {K}[\tau ]$
and
$f \in \mathbb {T}$
, we define
thus making
$\Delta $
into an
$\mathbf {A}$
-linear endomorphism of
$\mathbb {T}$
.
2.3 Anderson generating functions
We continue with our Drinfeld module
$\phi $
in (2.1). For
$u\in \mathbb {K}$
, the Anderson generating function for
$\phi $
associated to u is defined by
Pellarin [Reference Pellarin25, Section 4.2] exhibited a partial fraction decomposition,
$$ \begin{align*} f_\phi(u;t) = \sum_{n=0}^\infty \frac{\alpha_n u^{q^n}}{\theta^{q^n}-t}, \end{align*} $$
where
$\alpha _n$
are the coefficients of
$\exp _\phi $
from (2.2). From this decomposition, we see that
$f_\phi (u;t)$
extends to a meromorphic function on
$\mathbb {K}$
with simple poles (when
$u\neq 0$
) at
$t = \theta ^{q^n}$
,
$n = 0$
,
$1, \ldots $
, with respective residues
$\operatorname {\mathrm {Res}}_{t=\theta ^{q^n}} f_\phi (u;t) = -\alpha _n u^{q^n}$
. In particular,
$$ \begin{align*} \operatorname{\mathrm{Res}}_{t=\theta} f_\phi(u;t) = -u. \end{align*} $$
It follows from (2.6) and the functional equation for
$\exp _{\phi }(z)$
that
$$ \begin{align} \phi_t(f_{\phi}(u;t)) = \theta f_{\phi}(u;t) + A_1 f_{\phi}(u;t)^{(1)} + \cdots + A_r f_{\phi}(u;t)^{(r)} = f_{\phi}(\theta u;t), \end{align} $$
and so for each
$a \in \mathbf {A}$
,
$\phi _a(f_{\phi }(u;t)) = f_{\phi }(a(\theta ) u;t)$
. Another fundamental property is that
$$ \begin{align} \phi_t(f_{\phi}(u;t)) = t f_{\phi}(u;t) + \exp_{\phi}(u). \end{align} $$
It follows that if
$\pi \in \Lambda _{\phi }$
, then for all
$a \in \mathbf {A}$
, we have
$\phi _a(f_{\phi }(\pi ;t)) = a f_{\phi }(\pi ;t)$
. The partial fraction decomposition of
$f_{\phi }(\pi ;t)$
implies that it is an element of
$\mathbb {T}_{\eta }$
for any
$\eta \in \mathbb {K}$
with
$|\eta | < |\theta |$
. Thus, by (2.4), we find that
$f_{\phi }(\pi ;t)^{(1)} \in \mathbb {T}_{\theta }$
, and, in particular,
$f_{\phi }(\pi ;t)^{(i)}$
is well defined at
$t=\theta $
for all
$i \geqslant 1$
.
2.4 Logarithm deformations
We fix a Drinfeld module
$\phi $
of rank r as in (2.1). For
$\xi \in \mathbb {K}$
, El-Guindy and the second author defined a series
$\mathcal {L}_{\phi }(\xi ;t)$
in [Reference El-Guindy and Papanikolas10], which is a deformation of
$\log _\phi (\xi )$
and is related to Anderson generating functions. This series is defined using shadowed partitions defined in [Reference El-Guindy and Papanikolas9] as follows. For n,
$r\in \mathbb {N}$
, we let
$P_r(n)$
be the set of r-tuples
$(S_1,S_2,\ldots ,S_r)$
such that (i) for each i,
$S_i \subseteq \{0,1,\ldots ,n-1\}$
, and (ii) the sets
$\{S_i + j :1\leqslant i\leqslant r, 0 \leqslant j\leqslant i-1\}$
form a partition of
$\{0,1,\ldots ,n-1\}$
. For
$n\in \mathbb {N}$
, define
Let
. For each
$n \in N(\phi )$
, let
and let
where m is the smallest index in
such that
$\mu _m \geqslant \mu _i$
for every
$i\in N(\phi )$
.
Remark 2.12 It was shown in [Reference El-Guindy and Papanikolas10, Remark 6.11 and Theorem 6.13(b)] that
$R_{\phi } \leqslant P_{\phi }$
, where
$P_{\phi }$
is the radius of convergence of
$\log _\phi (z)$
from (2.3) and that
$R_{\phi }=P_{\phi }$
if
$\mu _m> \mu _i$
for all
$i \neq m$
. We will see in Corollary 4.5 that in fact
$R_{\phi } = P_{\phi }$
in all cases.
Assuming
$|\xi | < R_{\phi }$
, we set
which converges in
$\mathbb {T}$
with respect to the Gauss norm and, as a function of t, converges on the open disk of radius
$|\theta |^q$
in
$\mathbb {K}$
[Reference El-Guindy and Papanikolas10, Proposition 6.10]. Furthermore, if
$\exp _{\phi }(u) = \xi $
and
$|u| < R_{\phi }$
, then by [Reference El-Guindy and Papanikolas10, Theorem 6.13],
$$ \begin{align*} \mathcal{L}_{\phi}(\xi; \theta) = \log_{\phi}(\xi) = u; \end{align*} $$
moreover, we recover the Anderson generating function for u, as
$$ \begin{align} \mathcal{L}_{\phi}(\xi;t) = -(t-\theta) f_{\phi}(u;t). \end{align} $$
2.5 t-motives for Drinfeld modules
Anderson originally defined t-motives in [Reference Anderson1], which we briefly review. The ring
$\mathbb {K}[t, \tau ]$
is the polynomial ring in t and
$\tau $
with coefficients in
$\mathbb {K}$
subject to the following relations:
$$ \begin{align*} tc = ct, \quad t \tau = \tau t, \quad \tau c = c^q \tau, \quad c \in \mathbb{K}. \end{align*} $$
A t-motive M is a left
$\mathbb {K}[t, \tau ]$
-module that is free and finitely generated as a left
$\mathbb {K}[\tau ]$
-module and for which there is
$\ell \in \mathbb {N}$
with
$(t - \theta )^\ell (M/\tau M) = \{0\}$
. The rank d of M as a left
$\mathbb {K}[\tau ]$
-module is the dimension of M. Diverging from Anderson’s usage somewhat, we say that M is abelian if M is also free and finitely generated as a left
$\mathbb {K}[t]$
-module. In this case, the rank of M is its rank as a
$\mathbb {K}[t]$
-module.
Given our Drinfeld module
$\phi : \mathbf {A} \to \mathbb {K}[\tau ]$
, as in (2.1), the t-motive associated to
$\phi $
, denoted
$M(\phi )$
, is defined as follows: let
and make
$M(\phi )$
into a left
$\mathbb {K}[t]$
-module by setting
, for
$m \in M(\phi )$
,
$c \in \mathbb {K}$
. The t-motive
$M(\phi )$
is abelian of rank r and dimension
$1$
.
2.6 Rigid analytic trivializations
Anderson [Reference Anderson1, Section 2.3] defined the notion of an abelian t-motive to be rigid analytically trivial, which is equivalent to the following definition. Let
$\mathbf {m} \in \operatorname {\mathrm {Mat}}_{r\times 1}(M)$
comprise a
$\mathbb {K}[t]$
-basis for M, and let
$\Theta \in \operatorname {\mathrm {Mat}}_r (\mathbb {K}[t])$
represent multiplication by
$\tau $
on M with respect to
$\mathbf {m}$
, i.e.,
$\tau \mathbf {m} = \Theta \mathbf {m}$
. It is known that
$\det \Theta = c(t-\theta )^d$
for some
$c \in \mathbb {K}^{\times }$
, where d is the dimension of M (see [Reference Anderson1, Section 3.2] or [Reference Namoijam and Papanikolas24, Proposition 3.2.5]). Then M is rigid analytically trivial if there exists
$\Upsilon \in \operatorname {\mathrm {GL}}_r (\mathbb {T})$
that satisfies
$$ \begin{align} \Upsilon^{(1)} = \Theta\Upsilon. \end{align} $$
The matrix
$\Upsilon $
is called a rigid analytic trivialization for M with respect to
$\Theta $
.
Returning to the situation of our Drinfeld module
$\phi $
from (2.1) and its associated t-motive
$M(\phi ) = \mathbb {K}[\tau ]$
, one checks that
$\{ 1, \tau , \ldots , \tau ^{r-1}\}$
forms a
$\mathbb {K}[t]$
-basis for
$M(\phi )$
(see, e.g., [Reference Anderson1, Section 4.1], [Reference Goss17, Section 5.4], [Reference Thakur31, Section 7.3]). If we let
$\mathbf {m} = (1, \tau , \cdots \tau ^{r-1})^{\mathrm {tr}}$
, then it follows (see, e.g., [Reference Namoijam and Papanikolas24, Example 4.6.7], [Reference Pellarin25, Section 4.2]) that
$\tau \mathbf {m} = \Theta \mathbf {m}$
, where
$\Theta $
is defined in (1.9).
Proposition 2.16 (Pellarin [Reference Pellarin25, Section 4.2])
Let
$\phi : \mathbf {A} \to \mathbb {K}[\tau ]$
be a Drinfeld module of rank r. Let
$\pi _1, \ldots , \pi _r$
be a basis of
$\Lambda _\phi $
, and for
$1 \leqslant j \leqslant r$
, let
. Then
is a rigid analytic trivialization for
$\phi $
with respect to
$\Theta $
in (
1.9
).
The proof of the functional equation follows from applications of (2.8). To show that
$\det \Upsilon \in \mathbb {T}^{\times }$
involves showing that it is a constant multiple of
$\omega _C$
(see, for example, [Reference Gezmiş and Papanikolas15, Section 6] or [Reference Namoijam and Papanikolas24, Proposition 4.3.10] [note that ‘
$\Upsilon $
’ in [Reference Namoijam and Papanikolas24] would be ‘
$\Upsilon ^{(1)}$
’ in the present paper]). The reader is directed to [Reference Pellarin25, Section 4] (or [Reference Chang and Papanikolas8, Section 3.4], [Reference Namoijam and Papanikolas24, Section 4.3]) for more details.
When
$r=2$
, Pellarin [Reference Pellarin26, Section 2] showed that, as we vary
$\phi $
, we can realize
$\Upsilon $
in terms of vector-valued Drinfeld modular forms, which led to special value identities for what are now called Pellarin L-series.
3 t-power torsion and matrix estimates
We fix a Drinfeld module
$\phi : \mathbf {A} \to \mathbb {K}[t]$
as in (2.1), together with the data assembled in Section 2, including
$\Theta \in \operatorname {\mathrm {Mat}}_r(\mathbb {K}[t])$
from (1.9). The main goal of this section (Theorem 3.29) is to construct a matrix
$B \in \operatorname {\mathrm {Mat}}_r(\mathbb {K}[t]) \cap \operatorname {\mathrm {GL}}_r(\mathbb {T})$
so that
$$ \begin{align} \lVert B^{-1} \Theta^{-1} B^{(1)} - I \rVert <1. \end{align} $$
We further strive for this construction to rely on only a finite amount of initial calculation of t-power torsion points of
$\phi $
. The purpose of (3.1) is the following. We first note that since
$\det \Theta = \pm (t-\theta )/A_r \in \mathbb {T}^{\times }$
, we have
$\Theta \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
. By letting
, we obtain that
$$ \begin{align*} \lVert F^{(n)}-I \rVert = \lVert F-I \rVert^{q^n} \to 0, \quad n \to \infty. \end{align*} $$
Thus, the infinite product
$\prod _{n=1}^\infty F^{(n)}$
converges in
$\operatorname {\mathrm {Mat}}_r(\mathbb {T})$
with respect to the Gauss norm, and its determinant is in
$\mathbb {T}^{\times }$
. And so, by defining
,
$$ \begin{align} \Pi^{(1)} = B^{(1)} F^{(1)} F^{(2)} \cdots = \Theta B F F^{(1)} F^{(2)}\cdots = \Theta\Pi, \end{align} $$
i.e.,
$\Pi $
is a rigid analytic trivialization for
$\phi $
with respect to
$\Theta $
(see Corollary 3.32).
To construct B, we make judicious choices of polynomials in
$\mathbb {K}[t]$
of the form
$$ \begin{align*} h = \phi_{t^{\ell-1}}(\xi) + \phi_{t^{\ell-2}}(\xi) t + \cdots + \xi t^{\ell-1}, \quad \xi \in \phi[ t^{\ell}]. \end{align*} $$
There are two things to note about such polynomials. The first is that if
$\phi _{t^{\ell -1}}(\xi ) \in \phi [t]$
is nonzero, then there is some nonzero period
$\pi \in \Lambda _\phi $
so that
$\phi _{t^{\ell -1}}(\xi ) = \exp _\phi (\pi /\theta )$
. Thus, as elements of
$\mathbb {T}$
,
$$ \begin{align} h \equiv f_{\phi}(\pi;t)\quad \pmod{t^{\ell}}, \end{align} $$
and so h is a truncation of an Anderson generating function. Though, as
$\pi $
is not uniquely determined by
$\xi $
, neither is
$f_{\phi }(\pi ;t)$
. Furthermore, taking
$\phi _t$
to be an operator on
$\mathbb {T}$
as in (2.5), one quickly checks that
$$ \begin{align} \phi_t(h) - th = -\xi t^{\ell}, \end{align} $$
which is a truncated version of (2.8). Ultimately, we will consider such polynomials for
$\xi _1, \ldots , \xi _r \in \phi [t^{\ell }]$
for which
$\phi _{t^{\ell -1}}(\xi _1), \ldots , \phi _{t^{\ell -1}}(\xi _r)$
form a strict basis of
$\phi [t]$
(see Definition 3.18). These
$\mathbb {F}_q$
-bases of
$\phi [t]$
arise in a directly similar manner to computations of Maurischat [Reference Maurischat22, Theorem 3.1] for rank
$2$
Drinfeld modules and successive minimum bases of
$\Lambda _\phi $
defined by Gekeler [Reference Gekeler14, Section 1.3].
Proposition 3.5 Let
$\ell \geqslant 1$
. For
$j=1,\ldots ,r$
, we fix
$\xi _j \in \phi [t^{\ell }]$
, and let
. Let
and assume
$\det B \neq 0$
. Then
$$ \begin{align*} B^{-1}\Theta^{-1}B^{(1)} - I = -\frac{t^{\ell}}{t-\theta} B^{-1} W, \end{align*} $$
where
$$ \begin{align} W = \begin{pmatrix} \xi_1 & \xi_2 & \cdots & \xi_r \\[6pt] 0 & 0 & \cdots & 0 \\[6pt] \vdots & \vdots & \ddots & \vdots \\[6pt] 0 & 0 & \cdots & 0 \end{pmatrix}. \end{align} $$
Proof We first observe that
$$ \begin{align} (t-\theta)\Theta^{-1} B^{(1)} &= \begin{pmatrix} A_1 & A_2 & \cdots & A_{r-1} & A_r \\[6pt] t-\theta & 0 & \cdots & 0 & 0 \\[6pt] 0 & t-\theta & \cdots & 0 & 0 \\[6pt] \vdots & \vdots & \ddots & \vdots & \vdots \\[6pt] 0 & 0 & \cdots & t-\theta & 0 \end{pmatrix} \begin{pmatrix} h_1^{(1)} & h_2^{(1)} & \ldots &h_r^{(1)} \\[6pt] h_1^{(2)} & h_2^{(2)} & \ldots &h_r^{(2)} \\[6pt] \vdots & \vdots & \ddots & \vdots \\[6pt] h_1^{(r)} & h_2^{(r)} & \ldots &h_r^{(r)} \end{pmatrix}\\[2pt] &= \begin{pmatrix} w_1 & w_2 & \cdots & w_r \\[6pt] (t-\theta) h_1^{(1)} & (t-\theta) h_2^{(1)} & \cdots & (t-\theta) h_r^{(1)} \\[6pt] \vdots & \vdots & \ddots & \vdots \\[6pt] (t-\theta) h_1^{(r-1)} & (t-\theta) h_2^{(r-1)} & \cdots & (t-\theta) h_r^{(r-1)} \\[6pt] \end{pmatrix}, \notag \end{align} $$
where
$w_j= A_1 h_j^{(1)} + \cdots + A_r h_j^{(r)} $
. For each
$j=1,\ldots ,r$
, (3.4) implies
$w_j = \phi _{t}(h_j) - \theta h_j = (t-\theta )h_j - t^{\ell }\xi _j$
. Thus,
$$ \begin{align*} (t-\theta)\Theta^{-1} B^{(1)} = -t^{\ell} W +(t-\theta)B, \end{align*} $$
and the result follows by multiplying through by
$(t-\theta )^{-1}B^{-1}$
.▪
Remark 3.9 By the above proposition, if
$B \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
so in particular
$\det (B)$
is invertible in
$\mathbb {T}$
, we have
$\lVert B^{-1}\Theta ^{-1}B^{(1)} - I \rVert = \lVert t^{\ell }/(t-\theta ) \cdot B^{-1}W \rVert $
. Since
$\lVert t^{\ell }/(t-\theta ) \rVert = 1/q$
, it follows that proving
$\lVert B^{-1}\Theta ^{-1}B^{(1)} - I \rVert < 1$
is equivalent to showing
$$ \begin{align} \lVert B^{-1}W \rVert < q. \end{align} $$
The remainder of this section is devoted to finding
$\ell \geqslant 1$
and
$\xi _1, \ldots , \xi _r \in \phi [t^{\ell }]$
so that
$B \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
and this inequality holds.
Suppose that B has been chosen as in Proposition 3.5 and that
$B \in \operatorname {\mathrm {Mat}}_r(\mathbb {K}[t]) \cap \operatorname {\mathrm {GL}}_r(\mathbb {T})$
. For each j, we note that if
$$ \begin{align*} |\xi_j| < |\phi_t(\xi_j)| < \cdots < |\phi_{t^{\ell-1}}(\xi_j)|, \end{align*} $$
then we obtain
$\lVert h_j \rVert = |\phi _{t^{\ell -1}}(\xi _j)|$
. This will facilitate estimating
$\lVert B^{-1}W \rVert $
and prompts our next investigations.
Consider the Newton polygon
$\Gamma $
(see Figure 1) of the polynomial
$$ \begin{align*} \phi_t(x) = \theta x + A_1 x^q +\cdots + A_r x^{q^r} \in \mathbb{K}[x]. \end{align*} $$
Letting
$s \geqslant 1$
be the number of edges of
$\Gamma $
, we denote its vertices by
$(q^{d_j},{-\deg A_{d_j}})$
for
$0 \leqslant j \leqslant s$
. We note that
$0 = d_0 < d_1 < \cdots < d_s = r$
and that each
$d_j$
is an element of
$N(\phi )$
as defined in Section 2. For
$0 \leqslant n < m \leqslant r$
, define
$L_{n,m}$
to be the line segment connecting vertices
$(q^n,-\deg A_n)$
and
$(q^m,-\deg A_m)$
and let
$w_{n,m}$
be its slope. For
$1 \leqslant j \leqslant s$
, let
. We observe that
$\lambda _1 < \lambda _2 < \cdots < \lambda _s$
and that the line segments
$L_{d_{0},d_1}, \ldots , L_{d_{s-1},d_s}$
form the edges of
$\Gamma $
. For more information on Newton polygons, see [Reference Goss17, Section 2] or [Reference Robert28, Section VI.1.6].
Figure 1: Newton polygon
$\Gamma $
of
$\phi _t(x).$
Lemma 3.11 Recall the definitions of
$\mu _n$
for
$n\in N(\phi )$
and
$\mu _m$
from (2.10) and (2.11). For
$1 \leqslant j \leqslant s$
, let
$a_j$
be the y-intercept of the line containing
$L_{d_{j-1},d_j}$
. The following hold.
-
(1)
$a_1 = \mu _m$
. -
(2)
$a_1> a_2 > \cdots > a_s$
. -
(3)
$-a_j \geqslant -\left ( \dfrac {\deg A_{d_j} - q^{d_j} }{q^{d_j} -1} \right )$
for every
$j=1, \ldots ,s$
.▪
Proof Recalling the definitions of
$\mu _n$
for
$n\in N(\phi )$
, we observe that
$\mu _n$
is the y-intercept of the line through the points
$(-1,1)$
and
$(q^n,-\deg A_n)$
. Due to the convexity of the Newton polygon, we have
$\mu _{d_1}\geqslant \mu _m$
. On the other hand, it follows from the definition of
$\mu _m$
that
$\mu _{d_1}\leqslant \mu _m$
. So
$\mu _{d_1} = \mu _m$
, and it is clear that
$a_1=\mu _{d_1}$
, which proves (1). For part (2), since
$\lambda _n < \lambda _{n+1}$
, we have that
$a_n> a_{n+1}$
(see Figure 2). To prove (3), we recognize that again due to the convexity of the Newton polygon, the y-intercept
$a_j$
must be at most the y-intercept
$\mu _{d_j}$
. Therefore,
$$ \begin{align*} -a_j \geqslant -\left( \frac{\deg A_{d_j} - q^{d_j} }{q^{d_j} -1} \right) \end{align*} $$
for every
$j=1, \ldots ,s$
.▪
Figure 2: Demonstrating
$a_n> a_{n+1}.$
Building on the preceding lemma, we produce an algorithm to choose a sequence of torsion points
$y_1$
,
$y_2, \ldots $
on
$\phi $
that form a t-division sequence above
$0$
(that is convergent in the sense of [Reference Hartl and Juschka20, Section 2.5.3]).
Proposition 3.12 Given nonzero
$y_1\in \phi [t]$
, there exists a recursive algorithm to choose
$y_2$
,
$y_3, \ldots \in \mathbb {K}$
such that
-
(1)
$\phi _t(y_k) = y_{k-1}$
for
$k \geqslant 2$
, -
(2)
$\deg y_1> \deg y_2 > \deg y_3 > \cdots $
, -
(3) there exists a positive integer N such that
$|y_N| < R_\phi $
, -
(4)
$\lim _{k\to \infty } \deg y_k = -\infty $
, -
(5) for
$k\geqslant N$
,
$y_k$
is uniquely determined by
$y_N$
.
Proof Since
$y_1$
is a root of
$\phi _t(x)$
, we see that
$\deg y_1 \leqslant \lambda _s$
, as
$\lambda _s$
is the slope of the final segment of the Newton polygon
$\Gamma $
. For
$k\geqslant 1$
, we perform the following recursive process. Suppose
$\deg y_k \leqslant \lambda _s$
and set
. Consider the Newton polygon of
$\phi _t(x) - y$
, which is obtained from
$\Gamma $
by adding one more point
$(0,-\deg y)$
. We observe that
$-\deg y$
must belong to one of the following intervals:
where
$a_1,\ldots ,a_s$
are defined in Lemma 3.11. To see why
$-\deg y> a_s$
, we claim that
$-\lambda _s> a_s$
, which follows from the following observation. For a line through the point
$(1,-1)$
the sum of its y-intercept and its slope is
$-1$
. If the line runs below the point
$(1,-1)$
, this sum is less than
$-1$
. We conclude that
$a_s+\lambda _s \leqslant -1$
, which makes
$a_s < -\lambda _s $
. Since
$-\deg y \geqslant -\lambda _s$
, we have
$-\deg y> a_s$
as claimed.
Now, for
$n \in N(\phi )$
, we define the rational function
.
-
(i) If
$-\deg y \in (a_1,\infty )$
, then the Newton polygon of
$\phi _t(x) - y$
is obtained from
$\Gamma $
by adding the line segment from
$(0,-\deg y)$
to
$(1,-1)$
. This new segment has slope
$\deg y -1 = u_0(\deg y)$
, so there is exactly one root of
$\phi _t(x) - y$
with degree equal to
$u_0(\deg y)$
. -
(ii) If
$-\deg y \in (a_{j+1},a_j]$
for some
$1\leqslant j \leqslant s-1$
, then the Newton polygon of
$\phi _t(x) - y$
is obtained from
$\Gamma $
by replacing line segments
$L_{d_0,d_1}$
,
$L_{d_1,d_2}, \ldots , L_{d_{j-1},d_j}$
by the line segment from
$(0,-\deg y)$
to
$(q^{d_j},-\deg A_{d_j})$
. This new segment has slope
$(\deg y - \deg A_{d_j})/q^{d_j} = u_{d_j}(\deg y)$
, and so there are
$q^{d_j}$
roots of
$\phi _t(x) - y$
with degree equal to
$u_{d_j}(\deg y)$
.
Choose
$y_{k+1}$
to be a root of
$\phi _t(x) - y$
with
$$ \begin{align*} \deg y_{k+1} = \begin{cases} u_0(\deg y), & \text{if}\ -\deg y \in (a_1,\infty), \\[3pt] u_{d_j}(\deg y), & \text{if}\ -\deg y \in (a_{j+1},a_j]. \end{cases} \end{align*} $$
First, we prove the inequality
$$ \begin{align} \deg y_{k+1} \leqslant \deg y_{k}-1. \end{align} $$
For the first case, we note simply that
$u_0(\deg y_{k}) = \deg y_{k} - 1$
. For the second case, note that
$\deg y_{k+1} = u_{d_j}(\deg y_{k})$
only if
$-\deg y_{k} \in (a_{j+1},a_j]$
for some
$1 \leqslant j \leqslant s-1$
. Lemma 3.11(3) then implies that
$\deg y_k \geqslant -a_j \geqslant (q^{d_j} - \deg A_{d_j})/(q^{d_j} -1)$
, and after some straightforward manipulations, we deduce
$\deg y_{k+1} = (\deg y_{k} - \deg A_{d_j})/q^{d_j} \leqslant \deg y_{k} -1$
. In summary, in all cases, we obtain a root
$y_{k+1}$
of
$\phi _t(x) - y_k$
, which satisfies
$\deg y_{k+1} \leqslant \deg y_k -1 < \deg y_k \leqslant \lambda _s$
. This proves (3.13), as well as sets up the next step in the recursion, proving (1) and (2). The inequality in (3.13) also readily proves (3) and (4). By (2.11) and Lemma 3.11(1), we see that once
$\deg y_k < -a_1$
, we are in case (i) above; moreover
$y_{k+1}$
is uniquely determined by
$y_k$
. Thus, taking N sufficiently large as in (3), we obtain (5).▪
Remark 3.14 To make the recursion in Proposition 3.12 effective, we further determine N explicitly from the given data. That is, we determine N so that
$\deg y_N < -a_1$
. From (2.11) and (3.13), we see that this will occur when
$$ \begin{align*} N> \deg y_1 - \log_q(R_\phi) + 1. \end{align*} $$
However, with some small effort, this can in general be improved. Continuing with the notation in the proof, we first note that
$$ \begin{align} u_n^{\circ k} (z) = \frac{z}{q^{nk}} - \left(\frac{q^{nk}-1}{q^n-1}\right) \frac{\deg A_n}{q^{nk}}, \end{align} $$
where
$u_n^{\circ k}(z)$
is the kth iterate of
$u_n$
under composition. If
$-\deg y_1 \in I_1 = (a_1,\infty )$
, then we already have
$\deg y_1 < -a_1$
and we can choose
$N=1$
. Now, assume that
$-\deg y_1 \in I_{j+1}$
for some
$1\leqslant j\leqslant s-1$
. By Lemma 3.11,
$$ \begin{align*} \lim_{k\to\infty} u_{d_j}^{\circ k} \bigl( \deg y_1 \bigr) = -\frac{\deg A_{d_j}}{q^{d_j}-1} < -a_j , \end{align*} $$
so there exists a smallest integer
$k_1$
so that
$u_{d_j}^{\circ k_1} (\deg y_1) < -a_j$
. Therefore
$-\deg y_{k_1 +1} = -u_{d_j}^{\circ k_1} (\deg y_1) \in I_1 \cup \cdots \cup I_{j}$
. Repeating the same argument, we can choose the smallest integer
$k_2\geqslant 0$
that makes
$u_{d_{j-1}}^{\circ k_2} (\deg y_{k_1 +1}) < -a_{j-1}$
, and thus
$$ \begin{align*} -\deg y_{k_2 + k_1 +1} = -u_{d_{j-1}}^{\circ k_2} (\deg y_{k_1 +1}) \in I_1 \cup \cdots \cup I_{j-1}. \end{align*} $$
Continuing inductively, we finally obtain
$k_j\geqslant 0$
with
$u_{d_1}^{\circ k_j} (\deg y_{k_{j-1} + \cdots + k_1 +1}) < -a_1$
, i.e.,
$$ \begin{align*} -\deg y_{k_j + \cdots + k_1 +1} = -u_{d_j}^{\circ k_j} (\deg y_{k_{j-1} + \cdots + k_1 +1}) \in I_1. \end{align*} $$
Letting
$$ \begin{align} N = 1+ k_1 + \cdots + k_j, \end{align} $$
we thus obtain
$-\deg y_N \in I_1$
, i.e.,
$\deg y_N < -a_1$
. Moreover, we observe that
$$ \begin{align*} \deg y_N = u_{d_1}^{\circ k_j} \circ \cdots \circ u_{d_{j-1}}^{\circ k_2} \circ u_{d_j}^{\circ k_1} (\deg y_1). \end{align*} $$
In the next proposition, we explain how the recursive process in Proposition 3.12 can be used to produce
$\xi _1,\ldots ,\xi _r$
that are suitable inputs for Proposition 3.5. Although a sequence
$\{y_k\}$
obtained from Proposition 3.12 is infinite, we construct
$\xi _1, \ldots , \xi _r$
after only finitely many applications of the recursive algorithm defining such sequences.
Proposition 3.17 Let
$x_1,\ldots ,x_r$
be an
$\mathbb {F}_q$
-basis of
$\phi [t]$
. Then there exists
$N\geqslant 1$
and
$\xi _1, \ldots , \xi _r \in \phi [t^N]$
such that for each
$j=1, \ldots , r$
,
-
(1)
$|\xi _j| < R_\phi $
, -
(2)
$\phi _{t^{N-1}}(\xi _j) = x_j$
, -
(3)
$\deg \phi _{t^{N-1}}(\xi _j)> \cdots > \deg \phi _t(\xi _j) > \deg \xi _j$
.
Proof For
$1 \leqslant j \leqslant r$
, apply Proposition 3.12 to
$x_j$
, obtaining a sequence
$x_{j,1}$
,
$x_{j,2}, \ldots $
with the designated properties (
$x_{j,1} = x_j$
). We let
$N_j$
be the positive integer from Proposition 3.12(3), e.g., from (3.16). Let
, and for
$1 \leqslant j \leqslant r$
, let
. Then, for each j, Proposition 3.12 implies
$$ \begin{align*} \phi_{t^{k}}(\xi_j) = x_{j,N-k}, \quad 0 \leqslant k \leqslant N-1. \end{align*} $$
This proves (2). Parts (1) and (3) are then consequences of Proposition 3.12(2) and (3).▪
Definition 3.18 An
$\mathbb {F}_q$
-basis
$x_1, \ldots , x_r$
of
$\phi [t]$
is strict if, for
$1\leqslant j \leqslant r$
, we have
$\deg x_j = \lambda _k$
, where
$d_{k-1}+1\leqslant j\leqslant d_k$
.
Lemma 3.19 (Cf. [Reference Gekeler14, Proposition 1.4])
There exists a strict
$\mathbb {F}_q$
-basis of
$\phi [t]$
.
Proof For
$1\leqslant k \leqslant s$
, define
We observe that
$Q_k$
is an
$\mathbb {F}_q$
-subspace of
$\phi [t]$
for each k. Since
$Q_1 = R_1\sqcup \{0\}$
and the set
$Q_1$
has
$q^{d_1}$
elements, there exist
$x_1,\ldots ,x_{d_1} \in R_1$
such that
$$ \begin{align*} Q_1 = \mathbb{F}_q x_1 \oplus \cdots \oplus \mathbb{F}_q x_{d_1}. \end{align*} $$
Now,
$Q_1 \subseteq Q_2$
and the set
$Q_2$
has
$q^{d_2}$
elements, so we can pick
$x_{d_1 + 1},\ldots ,x_{d_2}$
in
$Q_2$
such that
$$ \begin{align*} Q_2 = \mathbb{F}_q x_1 \oplus \cdots \oplus \mathbb{F}_q x_{d_1} \oplus \mathbb{F}_q x_{d_1 + 1} \oplus \cdots \oplus \mathbb{F}_q x_{d_2}. \end{align*} $$
We claim that for every
$d_1 + 1 \leqslant j \leqslant d_2$
, we have
$\deg x_j = \lambda _2$
. Indeed, fix
$d_1 + 1 \leqslant j \leqslant d_2$
and suppose that
$\deg x_j < \lambda _2$
. Since
$x_j$
is a nonzero element in
$\phi [t]$
, we have
$\deg x_j \in \{\lambda _1,\ldots ,\lambda _s\}$
, and
$\deg x_j < \lambda _2$
implies that
$\deg x_j \leqslant \lambda _1$
. But then,
$x_j\in Q_1$
, violating the
$\mathbb {F}_q$
-linear independence of
$x_1, \ldots , x_{d_2}$
. We continue inductively to produce an
$\mathbb {F}_q$
-basis
$x_1, \ldots , x_{d_s}$
of
$Q_s$
, with
$\{ x_{d_{k-1}+1}, \ldots , x_{d_{k}} \} \subseteq R_k$
for each
$1 \leqslant k \leqslant s$
. As
$d_s = r$
and
$Q_s = \phi [t]$
, we are done.▪
Definition 3.21 For the remainder of this section, we fix the following data. Pick a strict basis
$x_1, \ldots , x_r$
of
$\phi [t]$
. Choose
$N\geqslant 1$
and
$\xi _1, \ldots , \xi _r \in \phi [t^N]$
as in Proposition 3.17. For
$1\leqslant j \leqslant r$
, we set
Proposition 3.17(3) implies that
$$ \begin{align} \lVert h_j \rVert = \max_{0\leqslant m \leqslant N-1} \bigl\{ |\phi_{t^{N-1-m}} (\xi_j)| \bigr\} = |x_j|; \end{align} $$
moreover,
$|x_j|$
is the unique maximum among the norms of the coefficients of
$h_j$
. Fix B to be the
$r\times r$
matrix with
$(i,j)$
-entries defined by
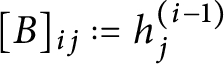
as in (3.6). For the rest of this section, our goal is to prove that B is in
$\operatorname {\mathrm {GL}}_r(\mathbb {T})$
and satisfies (3.10). Thus, by Proposition 3.5 (and Remark 3.9), B will satisfy (3.1) as desired.
Lemma 3.23 Let
$x_1,\ldots ,x_r$
be a strict basis of
$\phi [t]$
. For
$1\leqslant k \leqslant s$
and
$d_{k-1}+1\leqslant j\leqslant d_k$
,
$$ \begin{align*} \deg(c_1 x_1 + \cdots + c_{j-1} x_{j-1}+ x_j ) = \lambda_k = \deg x_j, \end{align*} $$
for every
$c_1,\ldots , c_{j-1} \in \mathbb {F}_q$
.
Proof Let
$y = c_1 x_1 + \cdots + c_{j-1} x_{j-1} + x_j$
, and let
$z = c_{d_{k-1}+1}x_{d_{k-1}+1} + \cdots + c_{j-1} x_{j-1} + x_j$
. We observe that
$\deg y \leqslant \deg x_j = \lambda _k$
. If
$\deg y \leqslant \lambda _{k-1}$
, then it must be the case that
$\deg z \leqslant \lambda _{k-1}$
, whence
$z \in Q_{k-1}$
as in (3.20). As
$x_1, \ldots , x_{d_{k-1}}$
is an
$\mathbb {F}_q$
-basis of
$Q_{k-1}$
, this would violate the
$\mathbb {F}_q$
-linear independence of
$x_1, \ldots , x_j$
.▪
Lemma 3.24 Let
$x_1 , \ldots , x_r$
be a strict basis for
$\phi [t]$
, and fix
$X \in \operatorname {\mathrm {Mat}}_r(\mathbb {K})$
so that
$[X]_{ij} = x_j^{q^{i-1}}$
. Then
$$ \begin{align*} \deg(\det X) = \sum_{j=1}^r q^{j-1}\deg x_j. \end{align*} $$
Proof As X is a Moore matrix, we obtain from [Reference Goss17, Corollary 1.3.7] that
$$ \begin{align*} \det X = \prod_{j=1}^r \prod_{c_1,\ldots, c_{j-1}\in \mathbb{F}_q} (c_1 x_1 + \cdots + c_{j-1} x_{j-1} + x_j ). \end{align*} $$
For
$1\leqslant k \leqslant s$
, let
$P_k = \{d_{k-1}+1, \ldots , d_k \}$
. Thus, by Lemma 3.23,
$$ \begin{align*} \deg(\det X) = \sum_{k=1}^s \sum_{j\in P_k} \sum_{c_1,\ldots, c_{j-1}\in \mathbb{F}_q} \deg x_j = \sum_{k=1}^s \sum_{j\in P_k} q^{j-1}\deg x_j, \end{align*} $$
which easily converts to the desired formula.▪
The following modification of the identity in Lemma 3.24 can be obtained by the same argument and will be useful in Proposition 3.26. For
$1 \leqslant j_1 < \cdots < j_{n} \leqslant r$
and
$1 \leqslant i \leqslant n$
, consider the
$n \times n$
matrix
$\widetilde {X}$
so that
$[\widetilde {X}]_{i\ell } = \bigl ( x_{j_\ell }^{q^{i-1}} \bigr )$
. Then
$$ \begin{align} \deg(\det \widetilde{X}) = \sum_{\ell=1}^n q^{\ell-1} \deg x_{j_{\ell}}. \end{align} $$
We can now compute
$\det B$
and show that
$B \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
.
Proposition 3.26 For
$1\leqslant j \leqslant r$
, write
$h_j = x_j + y_j t$
with
$y_j \in \mathbb {K}[t]$
. Let
$B = (h_j^{(i-1)})$
and let
$X = \bigl ( x_j^{q^{i-1}} \bigr )$
. Then
-
(1)
$\det B = \det X + y t$
for some
$y \in \mathbb {K}[t]$
with
$\lVert y \rVert < \lvert \det X \rvert $
, -
(2)
$B \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
.
Proof Using the calculation in (3.22) via Proposition 3.17(3), we see that
$\lVert y_j \rVert < |x_j|$
and so
$$ \begin{align*} h_j^{(i-1)} \in \mathbb{T}^{\times}, \quad 1 \leqslant i,\, j \leqslant r. \end{align*} $$
For
$1 \leqslant n \leqslant r$
, let
$\widetilde {B}$
be any
$n \times n$
minor of B, where any of the columns of B are removed and all of the final
$r-n$
rows of B are removed. Thus, we can choose
$1 \leqslant j_1 < \cdots < j_n \leqslant r$
so that
$[\widetilde {B}]_{i\ell } = (h_{j_{\ell }}^{(i-1)})$
. If
$n=r$
, then
$\widetilde {B}$
is simply B. Recalling
$\widetilde {X}$
from (3.25), we claim that for some
$\tilde {y} \in \mathbb {K}[t]$
,
$$ \begin{align*} \det \widetilde{B} = \det \widetilde{X} + \tilde{y} t, \end{align*} $$
with
$\lVert \tilde {y} \rVert < \lvert \det \widetilde {X} \rvert $
, and that
$\det \widetilde {B} \in \mathbb {T}^{\times }$
.
We proceed by induction on n. When
$n=1$
, the claim follows since
$h_j \in \mathbb {T}^{\times }$
for each j. Consider the case
$n=2$
. Then suppose
$h_{j_1} = \tilde {x}_1 + \tilde {y}_1 t$
and
$h_{j_2} = \tilde {x}_2 + \tilde {y}_2 t$
. Then
$$ \begin{align*} \det \widetilde{B} = (\tilde{x}_1 + \tilde{y}_1 t)( \tilde{x}_2^{(1)} + \tilde{y}_2^{(1)} t) - (\tilde{x}_2 + \tilde{y}_2 t)( \tilde{x}_1^{(1)} + \tilde{y}_1^{(1)} t) = \det \widetilde{X} + \tilde{y} t, \end{align*} $$
where
$\tilde {y} = \tilde {y}_1 h_{j_2}^{(1)} + \tilde {x}_1 \tilde {y}_2^{(1)} - \tilde {y}_2 h_{j_1}^{(1)} - \tilde {x}_2 \tilde {y}_1^{(1)} \in \mathbb {K}[t]$
. We quickly verify that
$$ \begin{gather*} \lVert \tilde{y}_1 h_{j_2}^{(1)} \rVert < |\tilde{x}_1| \cdot |\tilde{x}_2|^q, \quad \lVert \tilde{x}_1 \tilde{y}_2^{(1)} \rVert < |\tilde{x}_1| \cdot |\tilde{x}_2|^q, \\[3pt] \lVert \tilde{y}_1 h_{j_1}^{(1)} \rVert < |\tilde{x}_2| \cdot |\tilde{x}_1|^q, \quad \lVert \tilde{x}_2 \tilde{y}_1^{(1)} \rVert < |\tilde{x}_2| \cdot |\tilde{x}_1|^q. \end{gather*} $$
Combining these inequalities with (3.25), we have
$\lVert \tilde {y} \rVert < \lvert \det \widetilde {X} \rvert $
, and thus
$\det \widetilde {B} \in \mathbb {T}^{\times }$
.
The general argument is similar, although there is more bookkeeping. Suppose the statement is true for
$n-1<r$
, and for
$1\leqslant \ell \leqslant n$
, write
$h_{j_\ell } = \tilde {x}_{\ell } + \tilde {y}_{\ell } t$
. We can express
$$ \begin{align} \det \widetilde{B} = \sum_{\ell=1}^n (-1)^{n+\ell} h_{j_\ell}^{(n-1)} \det B_\ell, \end{align} $$
where
$B_\ell $
is the
$(n-1)\times (n-1)$
-minor matrix obtained by removing the last row and the
$\ell $
th column from
$\widetilde {B}$
. We observe that
$$ \begin{align*} B_\ell = \begin{pmatrix} h_{j_1} & \cdots & h_{j_{\ell-1}} & h_{j_{\ell+1}} & \cdots & h_{j_n} \\[6pt] \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\[6pt] h_{j_1}^{(n-2)} & \cdots & h_{j_{\ell-1}}^{(n-2)} & h_{j_{\ell+1}}^{(n-2)} & \cdots & h_{j_\ell}^{(n-2)} \end{pmatrix}. \end{align*} $$
By the induction hypothesis,
$\det B_\ell = \det X_\ell + b_\ell t$
for some
$b_\ell \in \mathbb {K}[t]$
and
$\lVert b_\ell \rVert < \lvert \det X_\ell \rvert $
(where
$X_\ell $
is the evident
$(n-1)\times (n-1)$
-minor matrix of
$\widetilde {X}$
). Starting from (3.27),
$$ \begin{align*} \det \widetilde{B} &= \sum_{\ell=1}^n (-1)^{n+\ell} \bigl(\tilde{x}_\ell^{q^{n-1}} + \tilde{y}_\ell^{(n-1)} t \bigr) (\det X_\ell + b_\ell t) \\[2pt] &= \sum_{\ell=1}^n (-1)^{n+\ell} \bigl(\tilde{x}_\ell^{q^{n-1}} \det(X_\ell) + c_\ell t \bigr), \end{align*} $$
where
, and continuing,
$$ \begin{align*} &= \det \widetilde{X} + \sum_{\ell=1}^n (-1)^{n+\ell} c_\ell t. \end{align*} $$
We claim that for each
$\ell $
,
$\lVert c_\ell \rVert < \lvert \det \widetilde {X} \rvert $
. Considering the definition of
$c_\ell $
, we estimate
$$ \begin{align*} \lVert \tilde{y}_\ell^{(n-1)} \cdot \det B_\ell \rVert < |\tilde{x}_\ell|^{q^{n-1}} \cdot \lvert \det X_\ell \rvert, \quad \lVert \tilde{x}_\ell^{q^{n-1}} \cdot b_\ell \rVert < |\tilde{x}_\ell|^{q^{n-1}} \cdot \lvert \det X_\ell \rvert. \end{align*} $$
The first inequality follows from
$\lVert \tilde {y}_\ell \rVert < |\tilde {x}_\ell |$
and
$\lVert \det B_\ell \rVert = \lvert \det X_\ell \rvert $
, and the second from
$\lVert b_\ell \rVert < \lvert \det X_\ell \rvert $
. Finally,
$|\tilde {x}_\ell |^{q^{n-1}} \cdot \lvert \det X_\ell \rvert \leqslant \lvert \det \widetilde {X} \rvert $
by (3.25). Thus, this claim and the induction are complete.▪
Remark 3.28 From the above proposition, we see that
$\lVert \det B \rVert = \lvert \det X \rvert $
, and for each minor
$\widetilde {B}$
in the proof,
$\lVert \det \widetilde {B} \rVert = \lvert \det \widetilde {X} \rvert $
.
We now prove the main theorem of this section, which verifies that the matrix B we have constructed in Proposition 3.26 satisfies (3.1).
Theorem 3.29 Let
$x_1,\ldots ,x_r$
be a strict basis of
$\phi [t]$
. Choose
$N\geqslant 1$
and
$\xi _1,\ldots ,\xi _r \in \phi [t^N]$
as in Proposition 3.17, and for
$1\leqslant j\leqslant r$
, define
Let
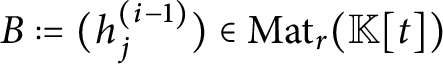
as in (3.6). Then
$B \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
and
$$ \begin{align*} \lVert B^{-1}\Theta^{-1}B^{(1)} - I \rVert < 1. \end{align*} $$
Proof That
$B \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
was proved in Proposition 3.26. By Remark 3.9, we thus see that
$\lVert B^{-1}\Theta ^{-1}B^{(1)} - I \rVert < 1$
if and only if
$\lVert B^{-1}W \rVert < q$
, where W is defined in (3.7) as
$$ \begin{align*} W = \begin{pmatrix} \xi_1 & \xi_2 & \cdots & \xi_r \\[6pt] 0 & 0 & \cdots & 0 \\[6pt] \vdots & \vdots & \ddots & \vdots \\[6pt] 0 & 0 & \cdots & 0 \end{pmatrix}. \end{align*} $$
Letting
, we find
$$ \begin{align*} B^{-1}W = \begin{pmatrix} m_{11}\xi_1 & m_{11}\xi_2 & \cdots & m_{11}\xi_r \\[6pt] m_{21}\xi_1 & m_{21}\xi_2 & \cdots & m_{21}\xi_r \\[6pt] \vdots & \vdots & \ddots & \vdots \\[6pt] m_{r1}\xi_1 & m_{r1}\xi_2 & \cdots & m_{r1}\xi_r \end{pmatrix}. \end{align*} $$
By definition,
$\lVert B^{-1}W \rVert = \max \{ \lVert m_{i1}\xi _j \rVert : 1 \leqslant i, j \leqslant r \}$
. Now, fix i and j. Expressing
$B^{-1}$
in terms of cofactors, we see that
$m_{i1} = (-1)^{i+1} (\det B^*)/(\det B)$
, where
$$ \begin{align*} B^* = \begin{pmatrix} h_1^{(1)} & \cdots & h_{i-1}^{(1)} & h_{i+1}^{(1)} & \cdots & h_r^{(1)} \\[6pt] h_1^{(2)} & \cdots & h_{i-1}^{(2)} & h_{i+1}^{(2)} & \cdots & h_r^{(2)} \\[6pt] \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\[6pt] h_1^{(r-1)} & \cdots & h_{i-1}^{(r-1)} & h_{i+1}^{(r-1)} & \cdots & h_r^{(r-1)} \end{pmatrix}. \end{align*} $$
We note that
$B^* = \widetilde {B}^{(1)}$
, where
$\widetilde {B}$
is the
$(r-1)\times (r-1)$
minor of B obtained by removing the ith column and the last row, whose properties were investigated in the proof of Proposition 3.26. In particular, if as in that proof we let
$\widetilde {X}$
be the corresponding minor of X, we see from Remark 3.28 that
$$ \begin{align*} \lVert \det B \rVert = \lvert \det X \rvert, \quad \lVert \det B^* \rVert = \lVert \widetilde{B}^{(1)} \rVert = \lvert \det \widetilde{X} \rvert^q. \end{align*} $$
We can use Lemma 3.24 to calculate
$\lvert \det X \rvert $
and (3.25) to calculate
$\lvert \det \widetilde {X} \rvert $
, and we find
$$ \begin{align} \log_q \lVert m_{i1} \xi_j \rVert &= \log_q \biggl( \frac{\lVert \det B^* \rVert\cdot |\xi_j| }{\lVert \det B \rVert} \biggr) \\[2pt] &= \sum_{\ell=1}^{i-1} q^\ell \deg x_{\ell} + \sum_{\ell=i+1}^r q^{\ell-1} \deg x_\ell + \log_q |\xi_j| - \sum_{\ell=1}^r q^{\ell-1} \deg x_\ell. \notag \end{align} $$
Using that
$\deg x_\ell \leqslant \deg x_{\ell +1}$
for all
$\ell \leqslant r-1$
, after reindexing the sum, we find
$$ \begin{align*} \sum_{\ell=1}^{i-1} q^\ell \deg x_\ell \leqslant \sum_{\ell=2}^i q^{\ell-1} \deg x_\ell. \end{align*} $$
Combining this with (3.30), we have
$$ \begin{align} \log_q \lVert m_{i1} \xi_j \rVert \leqslant -\deg x_1 + \log_q |\xi_j|. \end{align} $$
Since
$\xi _1,\ldots ,\xi _r$
are chosen so that
$|\xi _j| < R_\phi = q^{-\mu _m} $
, we have
$\log _q |\xi _j| < -\mu _m$
. Recall from Lemma 3.11(1) and its proof that
$$ \begin{align*} \mu_m = a_1 = p_{d_1} = -1-w_{0,d_1} = -1-\lambda_1 = -1 - \deg x_1. \end{align*} $$
Continuing with (3.31), we then find
$$ \begin{align*} \log_q \lVert m_{i1} \xi_j \rVert < -\deg x_1 + 1 + \deg x_1 = 1. \end{align*} $$
Thus,
$\log _q \lVert B^{-1}W \rVert = \max _{i,j} ( \log _q \lVert m_{i1} \xi _j \rVert ) < 1$
, and so
$\lVert B^{-1}W \rVert < q$
as sought.▪
Based on the discussion at the beginning of this section and in particular (3.2), the following corollary is immediate.
Corollary 3.32 Continuing with the setting of Theorem 3.29, the infinite product
converges with respect to the Gauss norm on
$\operatorname {\mathrm {Mat}}_r(\mathbb {T})$
and lies in
$\operatorname {\mathrm {GL}}_r(\mathbb {T})$
. Moreover,
$$ \begin{align*} \Pi^{(1)} = \Theta \Pi, \end{align*} $$
and so
$\Pi $
is a rigid analytic trivialization for
$\phi $
.
4 Product expansions for rigid analytic trivializations
We continue with the constructions and notations of Section 3, especially the results from Theorem 3.29 and Corollary 3.32. A natural question to ask is how the matrix
$\Pi $
from Corollary 3.32 compares to
$\Upsilon $
defined by Pellarin in Proposition 2.16. By applying results from [Reference El-Guindy and Papanikolas10], we will show in Theorem 4.4 that once we define an appropriate basis
$\pi _1, \ldots , \pi _r$
for
$\Lambda _\phi $
, using our already chosen
$\xi _1, \ldots , \xi _r \in \phi [t^N]$
, that in fact
$\Pi = \Upsilon $
(cf. [Reference Khaochim21, Section 3]).
Lemma 4.1 Set
. For
$n \geqslant 0$
, set
. Let W be the matrix defined in (3.7), and let
Then, for
$n\geqslant 0$
,
$$ \begin{align*} \Pi_n = B - t^N \sum_{m=0}^n R_m W^{(m)}. \end{align*} $$
Proof First, for
$n\geqslant 0$
, we observe that
$$ \begin{align*} \Pi_n = \Theta^{-1} \bigl( \Theta^{-1} \bigr)^{(1)} \cdots \bigl( \Theta^{-1} \bigr)^{(n)} B^{(n+1)}. \end{align*} $$
Moreover, Proposition 3.5 yields
$$ \begin{align*} \Theta^{-1}B^{(1)} = B - \frac{t^N}{t-\theta} W, \end{align*} $$
which proves the case
$n=0$
. Proceeding by induction, assume the formula holds for
$\Pi _{n-1}$
. Then, combining the previous displayed equations,
$$ \begin{align*} \Pi_n = \Theta^{-1} \bigl( \Theta^{-1} \bigr)^{(1)} \cdots \bigl( \Theta^{-1} \bigr)^{(n-1)} \biggl( B^{(n)} - \frac{t^N}{t-\theta^{q^n}} W^{(n)} \biggr) = \Pi_{n-1} - t^N R_n W^{(n)}, \end{align*} $$
and the formula for
$\Pi _n$
follows from the induction hypothesis.▪
In the previous lemma, we wrote
$\Pi _n$
as a finite sum involving the matrices B, W, and
$R_m$
,
$0\leqslant m \leqslant n$
. Next, we investigate an explicit formula for the first column of
$R_m$
. For
$n \geqslant 0$
, recall the rational function
$\mathcal {B}_n \in \mathbb {K}(t)$
from (2.9). We set
for
$n<0$
.
Lemma 4.2 For
$m \geqslant 0$
, let
$R_m$
be defined as in Lemma 4.1. Then, for
$1 \leqslant i \leqslant r$
,
$$ \begin{align*} [R_m]_{i1} = \frac{\mathcal{B}_{m-(i-1)}^{(i-1)}}{t-\theta^{q^{i-1}}}. \end{align*} $$
Proof We proceed by induction on m. As
$\mathcal {B}_0 = 1$
, the conclusion holds trivially for
$R_0$
. For general m, we observe that
$R_{m} = \Theta ^{-1}R_{m-1}^{(1)}$
, and so by combining the exact form of
$\Theta ^{-1}$
(see (3.8)), the induction hypothesis, and [Reference El-Guindy and Papanikolas10, Lemma 6.12(a)],
$$ \begin{align*} [R_m]_{11} = \sum_{k=1}^r \bigl[ \Theta^{-1} \bigr]_{1k} \bigl[ R_{m-1}^{(1)} \bigr]_{k1} = \sum_{k=1}^r\frac{A_k}{t-\theta} \frac{\mathcal{B}_{m-k}^{(k)}}{t-\theta^{q^k}} = \frac{\mathcal{B}_{m}}{t-\theta}. \end{align*} $$
The cases
$2 \leqslant i \leqslant r$
follow immediately from the induction hypothesis, as
$$ \begin{align*} [R_m]_{i1} = \sum_{k=1}^r \bigl[ \Theta^{-1} \bigr]_{ik} \bigl[ R_{m-1}^{(1)} \bigr]_{k1} = [R_{m-1}^{(1)}]_{i-1,1} = \frac{\mathcal{B}_{m-(i-1)}^{(i-1)}}{t-\theta^{q^{i-1}}}.\\[-40pt] \end{align*} $$
▪
Combining Lemmas 4.1 and 4.2, we determine the matrix
$\Pi _n$
completely.
Proposition 4.3 For
$n\geqslant 0$
and
$1\leqslant i$
,
$j \leqslant r$
,
$$ \begin{align*} [\Pi_n]_{ij} = \biggl( h_j - \frac{t^N}{t-\theta}\sum_{m=0}^{n-(i-1)} \mathcal{B}_m \xi_j^{q^m} \biggr)^{(i-1)}. \end{align*} $$
Proof Using (3.7) and Lemma 4.2, we obtain that for each m,
$$ \begin{align*} \bigl[ R_m W^{(m)} \bigr]_{ij} = [R_m]_{i1} \xi_j^{q^m} = \frac{\mathcal{B}_{m-(i-1)}^{(i-1)}}{t-\theta^{q^{i-1}}}\cdot \xi_j^{q^m}. \end{align*} $$
Substituting this into the formula for
$\Pi _n$
in Lemma 4.1, it follows that
$$ \begin{align*} [\Pi_n]_{ij} = h_j^{(i-1)} - t^N \sum_{m=0}^n \frac{\mathcal{B}_{m-(i-1)}^{(i-1)}}{t-\theta^{q^{i-1}}} \cdot \xi_j^{q^m} = \biggl( h_j - t^N \sum_{m=i-1}^{n} \frac{\mathcal{B}_{m-(i-1)}}{t-\theta} \cdot \xi_j^{q^{m-(i-1)}} \biggr)^{(i-1)}, \end{align*} $$
and the result follows by reindexing the sum.▪
The following theorem determines the entries of
$\Pi $
in terms of
$\mathcal {L}_{\phi }(\xi _j;t)$
from (2.13), starting from a strict basis
$x_1, \ldots , x_r$
of
$\phi [t]$
. As a consequence, we find that
$\Pi $
is the same as the matrix
$\Upsilon $
constructed from Anderson generating functions in Proposition 2.16.
Theorem 4.4 Let
$x_1, \ldots , x_r$
be a strict basis of
$\phi [t]$
, and choose
$N \geqslant 1$
and
$\xi _1, \ldots , \xi _r \in \phi [t^N]$
as in Proposition 3.17. Let
$B = ( h_j^{(i-1)}) \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
be defined as in Theorem 3.29, and construct the rigid analytic trivialization for
$\phi $
,
$$ \begin{align*} \Pi = B \prod_{n=0}^\infty \Bigl( B^{-1} \Theta^{-1} B^{(1)} \Bigr)^{(n)} \end{align*} $$
as in Corollary 3.32. For
$1 \leqslant i,\,j \leqslant r$
,
$$ \begin{align*} [\Pi]_{ij} = \biggl( h_j - \frac{t^N}{t-\theta} \mathcal{L}_{\phi}(\xi_j;t) \biggr)^{(i-1)}. \end{align*} $$
Moreover, letting
, the quantities
$\pi _1, \ldots , \pi _r$
form an A-basis of
$\Lambda _{\phi }$
and
$[\Pi ]_{ij} = f_{\phi }(\pi _j;t)^{(i-1)}$
. It follows that
$$ \begin{align*} \Pi = \Upsilon, \end{align*} $$
where
$\Upsilon $
is defined with respect to
$\pi _1, \ldots , \pi _r \in \Lambda _\phi $
in Proposition 2.16.
Proof Recall in Proposition 3.17 that
$\xi _1, \ldots , \xi _r$
are chosen so that
$|\xi _j|< R_{\phi }$
for each j. Thus, as in (2.13), we have
$\mathcal {L}_{\phi }(\xi _j;t) \in \mathbb {T}$
for each j by [Reference El-Guindy and Papanikolas10, Proposition 6.10]. For
$1\leqslant i,\,j \leqslant r$
fixed, it then follows from (2.13) and Proposition 4.3 that
$$ \begin{align*} [\Pi]_{ij} = \lim_{n\to \infty} \biggl( h_j - \frac{t^N}{t-\theta} \sum_{m=0}^{n-(i-1)} \mathcal{B}_m \xi_j^{q^m} \biggr)^{(i-1)} = \biggl( h_j - \frac{t^N}{t-\theta} \mathcal{L}_{\phi} (\xi_j; t) \biggr)^{(i-1)}, \end{align*} $$
thus verifying the first identity. As
$R_{\phi }$
is at most the radius of convergence of
$\log _{\phi }(z)$
(see [Reference El-Guindy and Papanikolas10, Theorem 6.13(b)], but also Corollary 4.5),
$\log _{\phi }(\xi _j)$
is well defined for each j, and so we can define
(
$\Rightarrow \xi _j = \exp _\phi (\pi _j/\theta ^N)$
). By Proposition 3.17,
$$ \begin{align*} \exp_\phi(\pi_j) = \exp_\phi \bigl( \theta^N \log_\phi(\xi_j) \bigr) = \phi_{t^N}(\xi_j)=0, \end{align*} $$
so
$\pi _1,\ldots ,\pi _r \in \Lambda _\phi $
. As in (3.3), since
$\phi _{t^{N-1}}(\xi _j)= x_j = \exp _\phi (\pi _j/\theta )$
, we have
$h_j = \sum _{m=0}^{N-1} \exp _\phi (\pi _j/\theta ^{m+1}) t^m$
. By (2.14), we find
$\mathcal {L}_{\phi }(\xi _j;t) = -(t-\theta ) f_{\phi }(\pi _j/\theta ^N;t)$
, and using the definition of Anderson generating function in (2.6), we obtain (cf. [Reference El-Guindy and Papanikolas10, Equation (7.2)])
$$ \begin{align*} h_j - \frac{t^N}{t-\theta} \mathcal{L}_{\phi}(\xi_j;t) = f_{\phi}(\pi_j;t). \end{align*} $$
Thus, for each i, j, we have
$[\Pi ]_{ij} = f_{\phi }(\pi _j;t)^{(i-1)}$
, and so
$\Pi $
has the form of
$\Upsilon $
in Proposition 2.16, but in order for that proposition to apply, it remains to verify that
$\pi _1, \ldots , \pi _r$
is an A-basis of
$\Lambda _{\phi }$
. Let
$\omega _1, \ldots , \omega _r \in \Lambda _\phi $
be any A-basis of
$\Lambda _\phi $
, and let
$U = ( f_{\phi }(\omega _j;t)^{(i-1)})$
be the corresponding matrix from (1.7). Suppose
$E \in \operatorname {\mathrm {Mat}}_r(A)$
satisfies
$$ \begin{align*} (\omega_1, \ldots, \omega_r) E = (\pi_1, \ldots, \pi_r), \end{align*} $$
and let
$\widetilde {E} \in \operatorname {\mathrm {Mat}}_r(\mathbf {A})$
be the corresponding matrix where
$\theta \mapsto t$
. From (2.7), it follows that
$U\widetilde {E}=\Pi $
, whence
$\det U\cdot \det \widetilde {E} = \det \Pi $
. Since
$\Pi $
,
$U \in \operatorname {\mathrm {GL}}_r(\mathbb {T})$
(by Proposition 2.16 and Corollary 3.32), it must be that
$\det \widetilde {E} \in \mathbb {T}^{\times }$
. However,
$\mathbb {T}^{\times } \cap \mathbf {A} = \mathbb {F}_q^{\times }$
, and so
$\det E = \det \widetilde {E} \in \mathbb {F}_q^{\times }$
. Therefore,
$\pi _1, \ldots , \pi _r$
form an A-basis of
$\Lambda _\phi $
.▪
Corollary 4.5 The radius of convergence of
$\log _{\phi }(z)$
is exactly
$R_{\phi }$
.
Proof As in (2.3), the radius of convergence
$P_{\phi }$
of
$\log _{\phi }(z)$
is the minimum norm among nonzero periods in
$\Lambda _\phi $
by [Reference Goss17, Proposition 4.14.2]. Furthermore,
$R_\phi \leqslant P_\phi $
, as explained in Remark 2.12. From our strict basis for
$\phi [t]$
, it follows that
$\deg x_1 = \lambda _1$
, and Lemma 3.11 implies
$\lambda _1 = -1 - \mu _m$
. Therefore,
$|x_1| = R_{\phi }/|\theta | < R_{\phi }$
, and it follows from the proof of Theorem 4.4 that
$\pi _1 = \theta \log (x_1)$
. Furthermore, by [Reference Goss17, Proposition 4.14.2],
$\log _{\phi }(z)$
is an isometry on the open disk of radius
$P_{\phi }$
centered at
$0$
, and so
$|\pi _1| = |\theta |\cdot |x_1| = R_{\phi }$
. Thus,
$R_{\phi } \geqslant P_{\phi }$
.▪
These results also shed light on the field generated by the period lattice. Let
$L/k_\infty $
be a finite extension, containing the coefficients
$A_1, \ldots , A_r$
. When
$r=2$
, Maurischat [Reference Maurischat22, Theorem 3.1], proved that
$L(\Lambda _{\phi }) = L(\phi [t^N])$
, using Newton polygons in a similar fashion to Propositions 3.12 and 3.17 (see Theorem 5.2). For higher ranks, Gekeler [Reference Gekeler14, Section 2] used the spectrum of successive minimum bases for
$\Lambda _{\phi }$
to extend Maurischat’s result. Although not providing the degree of detail as Gekeler’s result, we obtain the following for all ranks, whose proof has been designed in a similar manner to Maurischat’s rank
$2$
result.
Corollary 4.6 Suppose that
$\phi $
is defined over a finite extension
$L/k_{\infty }$
. Choose
$N \geqslant 1$
as in Remark 3.14 and Proposition 3.17. Then
$L(\Lambda _{\phi }) = L(\phi [t^N])$
.
Proof As finite extensions of
$k_\infty $
, L and
$L(\phi [t^N])$
are complete. By [Reference Maurischat22, Proposition 2.1], we have that
$L(\phi [t^N]) \subseteq L(\Lambda _{\phi })$
. By definition of the A-basis
$\pi _1, \ldots , \pi _r$
of
$\Lambda _{\phi }$
from Theorem 4.4,
$\pi _j = \theta ^N \log _\phi (\xi _j)$
. Since
$\log _\phi (z)$
has coefficients in L, we have
$\log _\phi (\xi _j) \in L(\phi [t^N])$
for each j.▪
Remark 4.7 It is an interesting question, brought up by one of the referees, about how much the preceding constructions and results depend on whether the initial
$\mathbb {F}_q$
-basis
$x_1, \ldots , x_r \in \phi [t]$
is strict or not. At first, the authors suspected that one could use the results for strict bases to, then, deduce the same results for nonstrict bases, but it appears to be fairly subtle, and certain conclusions may turn out to be false if the initial basis is not strict.
For example, we can look ahead to Example 5.5, where
$q=3$
,
$\phi $
has rank
$2$
, and
$N=2$
, and use the torsion elements
$x_1$
,
$x_2 \in \phi [t]$
and
$\xi _1$
,
$\xi _2 \in \phi [t^2]$
from (5.6) and (5.7). If we take
then
$x_1'$
,
$x_2'$
do not form a strict basis for
$\phi [t]$
, but the sequences
$x_1'$
,
$\xi _1', \ldots $
and
$x_2'$
,
$\xi _2', \ldots $
can be extended to t-division sequences as in Proposition 3.12 with terms of strictly decreasing degree. However, when we consider the corresponding polynomials,
$h_1' = x_1' + \xi _1't$
,
$h_2' = x_2' + \xi _2't$
, the matrix
$B' = \left (\begin {smallmatrix} h_1' & h_2' \\[6pt] {h_1'}^{(1)} & {h_2'}^{(2)} \end {smallmatrix} \right )$
has determinant in
${\mathbb {F}_3 (\!( \theta ^{-1/2} )\!)}[t]$
,
$$ \begin{align*} \det B' = -\theta^{1/2} - (\theta^{1/2} + \theta^{-1/2} + \theta^{-5} + \cdots) \cdot t + (\theta^{-11/2} + \theta^{-15} + \cdots)\cdot t^2. \end{align*} $$
The details of this computation follow quickly from (5.6) and (5.7). What we notice is that the coefficient of t in
$\det B'$
has the same
$\infty $
-adic norm as the constant term, implying the conclusion from Proposition 3.26(1) does not hold if we start with the nonstrict basis
$x_1'$
,
$x_2'$
.
5 Rank 2 Drinfeld modules and examples
We now specialize to the case that
$\phi $
has rank
$2$
, defined by
$$ \begin{align} \phi_t = \theta + A_1 \tau + A_2 \tau^2, \quad A_2 \neq 0. \end{align} $$
We seek to express the data from the previous sections explicitly, and we work out concrete examples. Though framed slightly differently, Theorem 5.2 was proved by Maurischat [Reference Maurischat22, Theorem 3.1] using similar methods to Propositions 3.12 and 3.17. It is interesting to extract it from these propositions, which we briefly summarize afterward. The Newton polygon for
$\phi _t(x)$
falls into two cases, depicted in Figure 3, where (1) it has a single bottom edge of slope
$\lambda _1$
, or (2) it has two bottom edges of slopes
$\lambda _1< \lambda _2$
. We note that
$\phi _t(x)$
belongs to case (1) if and only if
$\deg A_1 \leqslant (q+\deg A_2)/(q+1)$
.
Figure 3: Rank
$2$
Newton polygon cases for
$\phi _t(x).$
Theorem 5.2 (Maurischat [Reference Maurischat22, Theorem 3.1])
Let
$\phi $
be a rank
$2$
Drinfeld module defined as in (5.1), and consider the following cases.
-
(1)
$\deg A_1 \leqslant (q+\deg A_2)/(q+1)$
, -
(2)
$\deg A_1> (q+\deg A_2)/(q+1)$
.
In Case 2, let
$\ell \geqslant 1$
be the unique integer such that
$$ \begin{align*} \frac{q^{\ell} + \deg A_2}{q+1} \leqslant \deg A_1 < \frac{q^{\ell+1} + \deg A_2}{q+1}. \end{align*} $$
Then the positive integer N and the degrees of
$\xi _1$
,
$\xi _2 \in \phi [t^N]$
in Proposition 3.17 can be chosen to satisfy the values in Figure 4.
Figure 4: Degrees of
$\xi _1$
,
$\xi _2$
in rank
$2.$
We briefly recount how Remark 3.14 and Proposition 3.17 lead to these results in the case of rank
$2$
. Let
$x_1$
,
$x_2 \in \phi [t]$
be a strict basis. (i) In Case 1,
${\deg (x_1)=\deg (x_2)=\lambda _1}$
. As in the proof of Corollary 4.5,
$|x_j| < R_\phi $
for
$j=1$
,
$2$
, and so
$N=1$
. (ii) In Case 2,
$\deg (x_1) = \lambda _1$
,
$\deg (x_2) = \lambda _2$
, and
$\lambda _1 < \lambda _2$
. Again, as in Corollary 4.5,
$|x_1|< R_{\phi }$
, and so
$N_1=1$
. Now,
$-\lambda _2 \in (a_2,\infty ]$
, and we choose
$\kappa \geqslant 0$
minimal so that
$u_1^{\circ \kappa }(\lambda _2) < -a_1$
. Using (3.15), together with the definitions of
$a_1$
and
$\lambda _2$
, a short calculation yields that
$\kappa $
is minimal so that
$$ \begin{align*} \deg A_1 < \frac{q^{\kappa+2} + \deg A_2}{q+1}, \end{align*} $$
from which
$\kappa =\ell -1$
(cf. [Reference Maurischat22, Proof of Theorem 3.1]). Applying Remark 3.14, we then have
$N_2 = \kappa +1 = \ell $
, and the degrees of
$\xi _1$
,
$\xi _2$
follow.
As in Theorem 4.4, the periods
$\pi _1$
,
$\pi _2 \in \Lambda _\phi $
are defined by
$\pi _j = \theta ^N \log _{\phi }(\xi _j)$
, for
$j=1$
,
$2$
. As
$\xi _1$
,
$\xi _2$
are strictly within the radius of convergence of
$\log _\phi (z)$
,
$$ \begin{align} \deg \pi_j = N + \deg \xi_j, \quad j=1,\, 2, \end{align} $$
by [Reference Goss17, Proposition 4.14.2]. We now consider explicit examples to demonstrate how one can perform the constructions of B and
$\Pi $
in Sections 3 and 4. Although both examples below are Drinfeld modules with complex multiplication, the approximations that follow could be performed for any Drinfeld module, and it is not especially important that they have complex multiplication. On the other hand, we found it enlightening to compare the calculations of various quantities with those previously obtained by other methods.
Example 5.4 We let
$\phi : \mathbf {A} \to \mathbb {K}[\tau ]$
be defined by
$$ \begin{align*} \phi_t = \theta + \bigl(\theta^{q/2} + \theta^{1/2} \bigr)\tau + \tau^2, \end{align*} $$
which in essence is the Carlitz module for the ring
$\mathbb {F}_q[t^{1/2}] \supseteq \mathbf {A}$
. In this case,
$\deg A_1 = q/2$
and
$\deg A_2 = 0$
. From Theorem 5.2, we are in Case 2 and
$N=\ell =1$
. Let
$\boldsymbol {i}$
be a choice of
$(-1)^{1/(q-1)}$
, and let
$\mathbb {F} = \mathbb {F}_q(\boldsymbol {i})$
. Then, in the field
${\mathbb {F} (\!( \theta ^{-1/(2q-2)} )\!)}$
, we set
We verify that
and
form a strict basis of
$\phi [t]$
with
${\deg (x_1) = -(q-2)}/(2q-2)$
and
$\deg (x_2) = 1/(2q-2)$
. The matrix B from Theorem 3.29 is
$$ \begin{align*} B = \begin{pmatrix} \zeta \beta & \zeta \\[6pt] \zeta^q \beta^q & \zeta^q \end{pmatrix} = \zeta \begin{pmatrix} \beta & 1 \\[6pt] 1-\theta^{1/2}\beta & -\theta^{1/2} \end{pmatrix}. \end{align*} $$
A small calculation reveals that
$$ \begin{align*} B^{-1} \Theta^{-1} B^{(1)} = \begin{pmatrix} 1 - \dfrac{\theta^{1/2}\beta\, t}{t-\theta} & -\dfrac{\theta^{1/2}\,t}{t-\theta} \\[12pt] \dfrac{\theta^{1/2}\beta^{q+1}\, t}{t-\theta} & 1 + \dfrac{\theta^{1/2}\beta^q\, t}{t-\theta} \end{pmatrix}, \end{align*} $$
and we easily verify that
$\lVert B^{-1}\Theta ^{-1}B^{(1)}-I \rVert < 1$
as in Theorem 3.29. We omit the details, but it is instructive to compare approximations of residues and evaluations of
$\Pi $
at
$t=\theta $
to the expected periods and quasi-periods coming from the theory of the Carlitz module.
Example 5.5 Let
$q=3$
, and choose
$\nu \in \mathbb {K}$
so that
$\nu ^2 = \theta ^3 - \theta -1$
. Fix the Drinfeld module
$\phi : \mathbf {A} \to \mathbb {K}[\tau ]$
defined by
$$ \begin{align*} \phi_t = \theta + (\nu^3 + \nu) \tau + \tau^2. \end{align*} $$
This Drinfeld module has been widely studied as it has complex multiplication by the class number
$1$
ring
$\mathbb {F}_3[t,y]$
, where
$y^2=t^3-t-1$
and
$$ \begin{align*} \phi_y = \nu + (\nu^4-\nu^2)\tau + (\nu^9 + \nu^3 + \nu)\tau^2 + \tau^3. \end{align*} $$
Thakur [Reference Thakur30, Section 2.3(c)], [Reference Thakur31, Section 8.2], showed that the coefficients of
$\phi _t$
,
$\phi _y$
,
$\exp _{\phi }(z)$
, and
$\log _{\phi }(z)$
can be derived from its associated shtuka function, and this point of view was used in [Reference Green and Papanikolas19, Sections 4 and 9] to find explicit product expansions of the direct analogues of
$\omega _C$
and
$\widetilde {\pi }$
.
First, we observe that
$\deg A_1 = \tfrac {9}{2}$
and
$\deg A_2 = 0$
, so
$\lambda _1=-\tfrac {7}{4}$
and
$\lambda _2=\tfrac {3}{4}$
. Thus, in Theorem 5.2 and (5.3), we have
$N=\ell =2$
and
$$ \begin{align*} \deg \xi_1 = -\frac{11}{4}, \quad \deg \xi_2 = -\frac{5}{4}, \quad \deg \pi_1 = -\frac{3}{4}, \quad \deg \pi_2 = \frac{3}{4}. \end{align*} $$
These agree with [Reference El-Guindy and Papanikolas9, Section 7], where some of these quantities were also calculated. In what follows, all quantities are contained in
. We fix
. The sign function on
$k_{\infty }^{\times } \to \mathbb {F}_3^{\times }$
extends to
$L^{\times } \to \mathbb {F}_9^{\times }$
in the natural way, and we choose
$\nu $
to have sign
$+1$
. Using Newton’s method, we approximate the strict basis
$x_1$
,
$x_2$
for
$\phi [t]$
:
$$ \begin{align} x_1 &= \begin{aligned}[t] -\boldsymbol{i} \theta^{-7/4} - \boldsymbol{i} \theta^{-19/4} - \boldsymbol{i}\theta^{-27/4} + \boldsymbol{i} \theta^{-31/4} - \boldsymbol{i} \theta^{-35/4} &{}+ \boldsymbol{i} \theta^{-39/4} \\ &{}+ \boldsymbol{i} \theta^{-43/4} + O(\theta^{-51/4}), \end{aligned} \\ x_2 &= \begin{aligned}[t] \boldsymbol{i} \theta^{3/4} - \boldsymbol{i} \theta^{-1/4} + \boldsymbol{i} \theta^{-5/4} + \boldsymbol{i} \theta^{-9/4} &{}- \boldsymbol{i} \theta^{-13/4} - \boldsymbol{i}\theta^{-17/4} + \boldsymbol{i}\theta^{-21/4} \\ &{}+ \boldsymbol{i} \theta^{-33/4} - \boldsymbol{i} \theta^{-37/4} + \boldsymbol{i}\theta^{-41/4} + O(\theta^{-45/4}). \end{aligned} \notag \end{align} $$
If desired, we can solve for
$x_1$
,
$x_2$
algebraically and find
$$ \begin{align*} x_1^2 &= \theta^{1/2}(\theta+1) - \Bigl( -(\theta-1)\nu\theta^{1/2} - \theta(\theta+1)^2 \Bigr)^{1/2}, \\ x_2^2 &= \theta^{1/2}(\theta+1) + \Bigl( -(\theta-1)\nu\theta^{1/2} - \theta(\theta+1)^2 \Bigr)^{1/2}. \end{align*} $$
Again using Newton’s method, we approximate
$\xi _1$
,
$\xi _2 \in \phi [t^2]$
as in Proposition 3.17:
$$ \begin{align} \xi_1 &= \begin{aligned}[t] -\boldsymbol{i} \theta^{-11/4} - \boldsymbol{i} \theta^{-19/4} - \boldsymbol{i} \theta^{-23/4} + \boldsymbol{i} \theta^{-31/4} + \boldsymbol{i} \theta^{-35/4} &{}+ \boldsymbol{i} \theta^{-39/4}\\ &{}+ \boldsymbol{i} \theta^{-43/4} + O(\theta^{-51/4}), \end{aligned}\\ \xi_2 &= \begin{aligned}[t] -\boldsymbol{i} \theta^{-5/4} + \boldsymbol{i} \theta^{-9/4} &{}+ \boldsymbol{i} \theta^{-13/4} - \boldsymbol{i} \theta^{-17/4} + \boldsymbol{i} \theta^{-21/4} + \boldsymbol{i} \theta^{-25/4} \\ &{}- \boldsymbol{i} \theta^{-29/4} - \boldsymbol{i} \theta^{-33/4} - \boldsymbol{i} \theta^{-37/4} - \boldsymbol{i} \theta^{-45/4} + O(\theta^{-53/4}). \end{aligned} \notag \end{align} $$
We then have
$h_1 = x_1 + \xi _1 t$
and
$h_2 = x_2 + \xi _2 t$
, from which we form B as in Theorem 3.29. Writing
$F = B^{-1} \Theta ^{-1} B^{(1)}$
, we find
$$ \begin{align} [F]_{11} &= \begin{aligned}[t] 1 + \big( \theta^{-2} &{}+ \theta^{-4} + \theta^{-7} - \theta^{-8} - \theta^{-9} + \theta^{-10} + O(\theta^{-14}) \big) t^2 \\[2pt] &{}+ \big( -\theta^{-5} - \theta^{-7} - \theta^{-8} + \theta^{-10} + \theta^{-12} + O(\theta^{-15}) \big) t^3 + O(t^4), \end{aligned} \\[2pt] [F]_{12} &= \begin{aligned}[t] \big( \theta^{-1/2} &{}- \theta^{-3/2} - \theta^{-5/2} + \theta^{-13/2} + \theta^{-15/2} + \theta^{-17/2} + \theta^{-19/2} \\[2pt] &{}+ \theta^{-21/2} + O(\theta^{-27/2}) \big) t^2 + \big( -\theta^{-7/4} + \theta^{-9/2} + \theta^{-11/2} \\[2pt] &{}- \theta^{-13/2} + \theta^{-15/2} + \theta^{-17/2} + \theta^{-19/2} + O(\theta^{-27/2}) \big) t^3 + O(t^4), \end{aligned} \notag \\[2pt] [F]_{21} &= \big( \theta^{-19/2} + \theta^{-23/2} + O(\theta^{-25/2}) \big) t^2 + O(t^4), \notag \\[2pt] [F]_{22} &= 1 + \big( \theta^{-8} - \theta^{-9} - \theta^{-10} + \theta^{-11} - \theta^{-12} + O(\theta^{-13}) \big)t^2 + O(t^4). \notag \end{align} $$
Thus,
$B^{-1} \Theta ^{-1} B^{(1)}$
conforms to the expected inequality in Theorem 3.29. We can approximate
$\Pi $
using its product expansion in Theorem 4.4, and then we estimate the periods
$\pi _1$
,
$\pi _2$
, and corresponding quasi-periods
$\eta _1$
,
$\eta _2$
, for
$\phi $
as described in Section 1. Namely,
$\pi _j = -((t-\theta )[\Pi ]_{1j})|_{t=\theta }$
and
$\eta _j = ([\Pi ]_{2j})|_{t=\theta }$
for
$j=1$
,
$2$
. From this, we find
$$ \begin{align} \pi_1 &= \begin{aligned}[t] -\boldsymbol{i} \theta^{-3/4} - \boldsymbol{i}\theta^{-11/4} - \boldsymbol{i}\theta^{-15/4} - \boldsymbol{i}\theta^{-19/4} + \boldsymbol{i}\theta^{-23/4} &{}+ \boldsymbol{i}\theta^{-39/4} \\ &{}+ \boldsymbol{i}\theta^{-47/4} + O(\theta^{-55/4}), \end{aligned} \\ \pi_2 &= \begin{aligned}[t] -\boldsymbol{i} \theta^{3/4} + \boldsymbol{i} \theta^{-5/4} + \boldsymbol{i} \theta^{-9/4} - \boldsymbol{i} \theta^{-29/4} &{}- \boldsymbol{i} \theta^{-33/4} + \boldsymbol{i} \theta^{-37/4} \\ &{}- \boldsymbol{i}\theta^{-41/4} + \boldsymbol{i} \theta^{-45/4} + O(\theta^{-61/4}). \end{aligned} \notag \end{align} $$
We first note that these formulas approximate the identity
$\pi _2 = \nu \pi _1$
at least to the precision taken, as one would expect in this case of complex multiplication. Moreover, although we omit the details, this approximation for
$\pi _1$
agrees numerically with (i) the one due to Green and the second author [Reference Green and Papanikolas19, Theorem 4.6 and Remark 4.7], coming from shtuka functions, and (ii) the one of Gekeler and Hayes [Reference Goss17, Equation (7.10.6)], from the theory of sign-normalized Drinfeld modules. We further compute the quasi-periods,
$$ \begin{align} \eta_1 &= \boldsymbol{i} \theta^{-21/4} + \boldsymbol{i} \theta^{-29/4} + \boldsymbol{i} \theta^{-37/4} + \boldsymbol{i} \theta^{-45/4} - \boldsymbol{i} \theta^{-53/4} + \boldsymbol{i} \theta^{-57/4} + O(\theta^{-61/4}), \\ \eta_2 &= \begin{aligned}[t] -\boldsymbol{i} \theta^{9/4} + \boldsymbol{i} \theta^{-3/4} + \boldsymbol{i} \theta^{-11/4} - \boldsymbol{i}\theta^{-15/4} &{}+ \boldsymbol{i} \theta^{-19/4} -\boldsymbol{i} \theta^{-23/4} \\ &{}+ \boldsymbol{i}\theta^{-39/4} + \boldsymbol{i}\theta^{-47/4} + O(\theta^{-51/4}). \end{aligned} \notag \end{align} $$
Using (1.1), one checks that
$\pi _1\eta _2 - \pi _2\eta _1$
and
$\boldsymbol {i}\widetilde {\pi }$
agree to the given precision, which aligns with the Legendre relation [Reference Goss16, Section 2], [Reference Thakur31, Theorem 6.4.6].
Acknowledgment
The authors thank Q. Gazda and A. Maurischat for valuable comments on a previous version of this paper. They further thank the referees for a number of suggestions that improved some mathematical statements and greatly simplified exposition.
Open access
