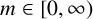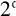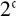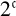1 Preliminaries
In 1844, Joseph Liouville proved the existence of transcendental numbers [Reference Angell1, Reference Baker2]. He introduced the set
![]() $\mathcal L$
of real numbers, now known as Liouville numbers, and showed that they are all transcendental. A real number x is said to be a Liouville number if for every positive integer n, there exists a pair of integers
$\mathcal L$
of real numbers, now known as Liouville numbers, and showed that they are all transcendental. A real number x is said to be a Liouville number if for every positive integer n, there exists a pair of integers
![]() $(p,q)$
with
$(p,q)$
with
![]() $q>1$
such that
$q>1$
such that
 $$ \begin{align*}0< \bigg\lvert x-\frac{p}{q}\bigg\rvert<\frac{1}{q^n}.\end{align*} $$
$$ \begin{align*}0< \bigg\lvert x-\frac{p}{q}\bigg\rvert<\frac{1}{q^n}.\end{align*} $$
In [Reference Erdős8], in 1962, Paul Erdős proved that every real number is the sum of two Liouville numbers (and also, if nonzero, is the product of two Liouville numbers). He gave two proofs. One was a constructive proof. The other proof used the fact that the set
![]() $\mathcal {L}$
of all Liouville numbers is a dense
$\mathcal {L}$
of all Liouville numbers is a dense
![]() $G_{\delta }$
-set in
$G_{\delta }$
-set in
![]() $\mathbb {R}$
and showed that every dense
$\mathbb {R}$
and showed that every dense
![]() $G_{\delta }$
-set in
$G_{\delta }$
-set in
![]() $\mathbb {R}$
has this property.
$\mathbb {R}$
has this property.
Definition 1.1. A subset W of the set
![]() $\mathbb {C}$
of all complex numbers is said to have the Erdős property [Reference Chalebgwa and Morris7] if every real number is a sum of two numbers in W. A subset V of the set
$\mathbb {C}$
of all complex numbers is said to have the Erdős property [Reference Chalebgwa and Morris7] if every real number is a sum of two numbers in W. A subset V of the set
![]() $\mathbb {C}$
of all complex numbers is said to have the multiplicative Erdős property if every positive real number is a product of two numbers in V.
$\mathbb {C}$
of all complex numbers is said to have the multiplicative Erdős property if every positive real number is a product of two numbers in V.
By the theorem proved by Erdős mentioned above, the set
![]() $\mathcal {L}$
of all Liouville numbers has the Erdős property and the multiplicative Erdős property.
$\mathcal {L}$
of all Liouville numbers has the Erdős property and the multiplicative Erdős property.
The classification of Mahler partitions the set
![]() $\mathbb {C}$
of all complex numbers into four sets denoted by A, S, T and U, characterised by the rate with which a nonzero polynomial with integer coefficients approaches zero when evaluated at a particular number. We follow the presentation in [Reference Bugeaud4, Section 3]. While the definitions and results therein are stated and proved for real numbers, they carry over to the case of complex numbers.
$\mathbb {C}$
of all complex numbers into four sets denoted by A, S, T and U, characterised by the rate with which a nonzero polynomial with integer coefficients approaches zero when evaluated at a particular number. We follow the presentation in [Reference Bugeaud4, Section 3]. While the definitions and results therein are stated and proved for real numbers, they carry over to the case of complex numbers.
Given a polynomial
![]() $P(X) \in \mathbb {C}[X]$
, recall that the height of P, denoted by
$P(X) \in \mathbb {C}[X]$
, recall that the height of P, denoted by
![]() $H(P)$
, is the maximum of the absolute values of the coefficients of P. Given a complex number
$H(P)$
, is the maximum of the absolute values of the coefficients of P. Given a complex number
![]() $\xi $
, a positive integer n, and a real number
$\xi $
, a positive integer n, and a real number
![]() $H \geq 1$
, we define the quantity
$H \geq 1$
, we define the quantity
Furthermore, we set
 $$ \begin{align*} w_n(\xi) = \limsup_{H \rightarrow \infty} \frac{- \log w_n(\xi, H)}{\log H} \end{align*} $$
$$ \begin{align*} w_n(\xi) = \limsup_{H \rightarrow \infty} \frac{- \log w_n(\xi, H)}{\log H} \end{align*} $$
and
Definition 1.2. Let
![]() $\xi $
be a complex number. Then
$\xi $
be a complex number. Then
![]() $\xi $
is said to be
$\xi $
is said to be
-
(i) an A-number if
 $w(\xi ) = 0$
;
$w(\xi ) = 0$
; -
(ii) an S-number if
 $0 < w(\xi ) < \infty $
;
$0 < w(\xi ) < \infty $
; -
(iii) a T-number if
 $w(\xi ) = \infty $
and
$w(\xi ) = \infty $
and
 $w_n(\xi ) < \infty $
for any
$w_n(\xi ) < \infty $
for any
 $n \geq 1$
;
$n \geq 1$
; -
(iv) a U-number if
 $w(\xi ) = \infty $
and
$w(\xi ) = \infty $
and
 $w_n(\xi ) = \infty $
for all
$w_n(\xi ) = \infty $
for all
 $n \geq n_0$
, for some positive integer
$n \geq n_0$
, for some positive integer
 $n_0$
.
$n_0$
.
Remark 1.3. Note the following from [Reference Baker2, Reference Bugeaud4, Reference Mahler10, Reference Mahler11].
-
(i) The A-numbers are the algebraic numbers.
-
(ii) Each Liouville number is a real U-number.
-
(iii) If the complex numbers
 $\alpha $
and
$\alpha $
and
 $\beta $
are algebraically dependent then they are in the same Mahler class; for example, the numbers
$\beta $
are algebraically dependent then they are in the same Mahler class; for example, the numbers
 $\alpha , -\alpha , n\alpha $
are all in the same Mahler set, for
$\alpha , -\alpha , n\alpha $
are all in the same Mahler set, for
 $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
. -
(iv) The two-dimensional Lebesgue measure of each of the sets A, U and T is zero; S has full two-dimensional Lebesgue measure, that is, its complement in
 $\mathbb {C}$
has zero two-dimensional Lebesgue measure.
$\mathbb {C}$
has zero two-dimensional Lebesgue measure. -
(v) The one-dimensional Lebesgue measure of each of the sets
 $A\cap \mathbb {R}$
,
$A\cap \mathbb {R}$
,
 $U\cap \mathbb {R}$
,
$U\cap \mathbb {R}$
,
 $\mathcal {L}$
and
$\mathcal {L}$
and
 $T\cap \mathbb {R}$
is zero;
$T\cap \mathbb {R}$
is zero;
 $S\cap \mathbb {R}$
has full one-dimensional Lebesgue measure, that is, its complement in
$S\cap \mathbb {R}$
has full one-dimensional Lebesgue measure, that is, its complement in
 $\mathbb {R}$
has zero one-dimensional Lebesgue measure.
$\mathbb {R}$
has zero one-dimensional Lebesgue measure. -
(vi) If a is an algebraic number with
 $a\ne 0$
, then
$a\ne 0$
, then
 $\exp (a)\in S$
.
$\exp (a)\in S$
.
André Weil (see [Reference Grosse-Erdmann9, Reference Weil16]) proved the following generalisation of the Steinhaus theorem [Reference Stromberg14].
Theorem 1.4. If G is a locally compact Hausdorff group and B is a subset of G of positive (left) Haar measure, then
![]() $BB^{-1}=\{b_1b_2^{-1}:b_1,b_2\in B\}$
contains an open neighbourhood of the identity.
$BB^{-1}=\{b_1b_2^{-1}:b_1,b_2\in B\}$
contains an open neighbourhood of the identity.
Corollary 1.5 (See [Reference Brown, Yin, Pollington and Moran3, Reference Pollington, Pollington and Moran13])
-
(i) If B is a subset of
 $\mathbb {R}$
of positive one-dimensional Lebesgue measure, then the set
$\mathbb {R}$
of positive one-dimensional Lebesgue measure, then the set
 $B-B=\{b_1-b_2:b_1,b_2\in B\}$
contains an open interval containing
$B-B=\{b_1-b_2:b_1,b_2\in B\}$
contains an open interval containing
 $0$
.
$0$
. -
(ii) If D is a subset of
 $\mathbb {C}$
of positive two-dimensional Lebesgue measure, then the set
$\mathbb {C}$
of positive two-dimensional Lebesgue measure, then the set
 $D-D=\{d_1-d_2:d_1,d_2\in D\}$
contains an open disc with centre
$D-D=\{d_1-d_2:d_1,d_2\in D\}$
contains an open disc with centre
 $0$
.
$0$
. -
(iii) If E is a subset of the multiplicative group
 $\mathbb {C}^*$
of all nonzero complex numbers, where E has positive two-dimensional Lebesgue measure, then the set
$\mathbb {C}^*$
of all nonzero complex numbers, where E has positive two-dimensional Lebesgue measure, then the set
 $EE^{-1}= \{e_1\cdot e_2^{-1}: e_1,e_2\in E\}$
contains an open disc with centre
$EE^{-1}= \{e_1\cdot e_2^{-1}: e_1,e_2\in E\}$
contains an open disc with centre
 $1$
.
$1$
. -
(iv) If F is a subset of the multiplicative group
 $\mathbb {R}^{>0}$
of all positive real numbers, then the set
$\mathbb {R}^{>0}$
of all positive real numbers, then the set
 $F F^{-1}=\{f_1\cdot f_2^{-1}: f_1,f_2\in F\}$
contains an open interval containing
$F F^{-1}=\{f_1\cdot f_2^{-1}: f_1,f_2\in F\}$
contains an open interval containing
 $1$
.
$1$
.
The following theorem was proved by Mahler [Reference Mahler10]. (See [Reference Bugeaud4, Section 3.5].)
Theorem 1.6. If a is an algebraic number with
![]() $a\ne 0$
, then
$a\ne 0$
, then
![]() $\exp (a)\in S$
.
$\exp (a)\in S$
.
Remark 1.7. It is an immediate consequence of Theorem 1.6 and Definition 1.2 that the number e and
![]() $\exp (a)$
, for a any nonzero algebraic number, are not Liouville numbers.
$\exp (a)$
, for a any nonzero algebraic number, are not Liouville numbers.
As the set of nonzero algebraic numbers is a dense subset of
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\exp $
is a continuous mapping from
$\exp $
is a continuous mapping from
![]() $\mathbb {C}$
onto
$\mathbb {C}$
onto
![]() $\mathbb {C}\setminus \{0\}$
, we obtain the following corollary.
$\mathbb {C}\setminus \{0\}$
, we obtain the following corollary.
Corollary 1.8. If
![]() $\mathbb {A'}$
is the set of all nonzero algebraic numbers, then
$\mathbb {A'}$
is the set of all nonzero algebraic numbers, then
![]() $B= \exp (\mathbb {A'})$
is a countably infinite dense subset of S (and also a countably infinite dense subset of
$B= \exp (\mathbb {A'})$
is a countably infinite dense subset of S (and also a countably infinite dense subset of
![]() $\mathbb {C}$
) and B has two-dimensional Lebesgue measure equal to zero.
$\mathbb {C}$
) and B has two-dimensional Lebesgue measure equal to zero.
Corollary 1.9. The set S is dense in the set of all transcendental numbers and in
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
2 The main results
Definition 2.1. A subset W of
![]() $\mathbb {C}$
is said to have the complex Erdős property if every complex number is a sum of two members of W. A subset V of
$\mathbb {C}$
is said to have the complex Erdős property if every complex number is a sum of two members of W. A subset V of
![]() $\mathbb {C}$
is said to have the complex multiplicative Erdős property if every nonzero complex number is a product of two members of V.
$\mathbb {C}$
is said to have the complex multiplicative Erdős property if every nonzero complex number is a product of two members of V.
Remark 2.2. Let
![]() $A\subseteq B\subseteq \mathbb {C}$
and
$A\subseteq B\subseteq \mathbb {C}$
and
![]() $C\subseteq D\subseteq \mathbb {C}$
. If A has the Erdős property, then so does B. If
$C\subseteq D\subseteq \mathbb {C}$
. If A has the Erdős property, then so does B. If
![]() $B\subseteq \mathbb {R}$
, the set of all real numbers, and A has the multiplicative Erdős property, then so does B. If C has the complex Erdős property, then so does D. If
$B\subseteq \mathbb {R}$
, the set of all real numbers, and A has the multiplicative Erdős property, then so does B. If C has the complex Erdős property, then so does D. If
![]() $C $
has the complex multiplicative Erdős property, then so does D.
$C $
has the complex multiplicative Erdős property, then so does D.
Proposition 2.3
-
(i) Let E be a subset of
 $\mathbb {C}$
of positive two-dimensional Lebesgue measure such that if
$\mathbb {C}$
of positive two-dimensional Lebesgue measure such that if
 $x\in E$
, then
$x\in E$
, then
 $-x\in E$
and
$-x\in E$
and
 $nx\in E$
, for all
$nx\in E$
, for all
 $n\in \mathbb {N}$
. Then E has the complex Erdős property.
$n\in \mathbb {N}$
. Then E has the complex Erdős property. -
(ii) Let F be a subset of
 $\mathbb {R}$
of positive one-dimensional Lebesgue measure such that if
$\mathbb {R}$
of positive one-dimensional Lebesgue measure such that if
 $x\in F$
, then
$x\in F$
, then
 $-x\in F$
and
$-x\in F$
and
 $nx\in F$
, for all
$nx\in F$
, for all
 $n\in \mathbb {N}$
. Then F has the Erdős property.
$n\in \mathbb {N}$
. Then F has the Erdős property. -
(iii) If G is a subset of
 $\mathbb {C}^*$
with positive two-dimensional Lebesgue measure such that if
$\mathbb {C}^*$
with positive two-dimensional Lebesgue measure such that if
 $x\in G$
, then
$x\in G$
, then
 $x^{-1}\in g$
and
$x^{-1}\in g$
and
 $x^n\in G$
, for all
$x^n\in G$
, for all
 $n\in \mathbb {N}$
, then G has the complex multiplicative Erdős property.
$n\in \mathbb {N}$
, then G has the complex multiplicative Erdős property. -
(iv) If H is a subset of
 $\mathbb {R}^{>0}$
with positive one-dimensional Lebesgue measure such that if
$\mathbb {R}^{>0}$
with positive one-dimensional Lebesgue measure such that if
 $x\in F$
then
$x\in F$
then
 $x^{-1}\in F$
and
$x^{-1}\in F$
and
 $x^n\in F$
, for all
$x^n\in F$
, for all
 $n\in \mathbb {N}$
, then H has the multiplicative Erdős property.
$n\in \mathbb {N}$
, then H has the multiplicative Erdős property.
Proof. By Corollary 1.5,
![]() $F-F$
contains a nonempty open interval I containing
$F-F$
contains a nonempty open interval I containing
![]() $0$
in
$0$
in
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $E-E$
contains a nonempty open disc D with centre
$E-E$
contains a nonempty open disc D with centre
![]() $0$
in
$0$
in
![]() $\mathbb {C}$
. As
$\mathbb {C}$
. As
![]() $E=-E$
and
$E=-E$
and
![]() $F=-F$
,
$F=-F$
,
So items (i) and (ii) are proved.
The proofs of items (iii) and (iv) for the multiplicative Erdős cases are analogous.
The next result follows from Proposition 2.3 and Remark 1.3(iii), (iv) and (v).
Corollary 2.4. The real Mahler set
![]() $S\cap \mathbb {R}$
has the Erdős property and the multiplicative Erdős property and the complex Mahler set S has the complex Erdős property and the complex multiplicative Erdős property.
$S\cap \mathbb {R}$
has the Erdős property and the multiplicative Erdős property and the complex Mahler set S has the complex Erdős property and the complex multiplicative Erdős property.
Remark 2.5. In contradistinction with the result of Erdős that the set
![]() $\mathcal {L}$
of zero Lebesgue measure has the Erdős property and the results in [Reference Chalebgwa and Morris7] that certain subsets of Lebesgue measure zero of the set
$\mathcal {L}$
of zero Lebesgue measure has the Erdős property and the results in [Reference Chalebgwa and Morris7] that certain subsets of Lebesgue measure zero of the set
![]() $\mathcal {L}$
have the Erdős property, we have in Corollary 2.4 and Theorem 2.6 sets of all Lebesgue measures having the Erdős property.
$\mathcal {L}$
have the Erdős property, we have in Corollary 2.4 and Theorem 2.6 sets of all Lebesgue measures having the Erdős property.
Theorem 2.6. Let
![]() $m\in [0,\infty )$
. Then there exist
$m\in [0,\infty )$
. Then there exist
![]() $2^{\mathfrak {c}}$
dense subsets W of S each of two-dimensional Lebesgue measure m such that W has the Erdős property and no two of these W are homeomorphic. There also exist
$2^{\mathfrak {c}}$
dense subsets W of S each of two-dimensional Lebesgue measure m such that W has the Erdős property and no two of these W are homeomorphic. There also exist
![]() $2^{\mathfrak {c}}$
dense subsets of S which have full two-dimensional Lebesgue measure, and no two of these are homeomorphic.
$2^{\mathfrak {c}}$
dense subsets of S which have full two-dimensional Lebesgue measure, and no two of these are homeomorphic.
Proof. First consider the case
![]() $m\in (0,\infty )$
. Let W be the set
$m\in (0,\infty )$
. Let W be the set
![]() $(S\setminus [-1,1])\cap \mathbb {R}$
. Then W is a set of positive one-dimensional Lebesgue measure and two-dimensional Lebesgue measure
$(S\setminus [-1,1])\cap \mathbb {R}$
. Then W is a set of positive one-dimensional Lebesgue measure and two-dimensional Lebesgue measure
![]() $0$
. By Proposition 2.3(ii), W has the Erdős property. By Remark 2.2, any set which contains W has the Erdős property. Let
$0$
. By Proposition 2.3(ii), W has the Erdős property. By Remark 2.2, any set which contains W has the Erdős property. Let
![]() $V_m$
be the intersection of S with any square in
$V_m$
be the intersection of S with any square in
![]() $\mathbb {C}$
of side
$\mathbb {C}$
of side
![]() $\sqrt {m}$
, X any subset of
$\sqrt {m}$
, X any subset of
![]() $[-1,1]\cap S$
and B the subset of S defined in Corollary 1.8. Then the set
$[-1,1]\cap S$
and B the subset of S defined in Corollary 1.8. Then the set
![]() $V^*_m=W\cup V_m\cup X\cup B$
is a set of two-dimensional Lebesgue measure m which has the Erdős property. As
$V^*_m=W\cup V_m\cup X\cup B$
is a set of two-dimensional Lebesgue measure m which has the Erdős property. As
![]() $S\cap [-1,1]$
has cardinality
$S\cap [-1,1]$
has cardinality
![]() $\mathfrak {c}$
, there are
$\mathfrak {c}$
, there are
![]() $2^{\mathfrak {c}}$
choices for X each resulting in a different set
$2^{\mathfrak {c}}$
choices for X each resulting in a different set
![]() $V^*_m$
. So for each
$V^*_m$
. So for each
![]() $m\in (0,\infty )$
, there are
$m\in (0,\infty )$
, there are
![]() $2^{\mathfrak {c}}$
subsets of S of two-dimensional Lebesgue measure m and having the Erdős property. Each of these sets contains the set B, and so, by Corollary 1.8, is dense in S.
$2^{\mathfrak {c}}$
subsets of S of two-dimensional Lebesgue measure m and having the Erdős property. Each of these sets contains the set B, and so, by Corollary 1.8, is dense in S.
Next, consider the case
![]() $m=0$
. We simply choose
$m=0$
. We simply choose
![]() $V_0=\emptyset $
in the above proof.
$V_0=\emptyset $
in the above proof.
Finally, consider the case of full two-dimensional Lebesgue measure. This time, we put
![]() $V_{\infty }= \mathbb {C}\setminus \mathbb {R}$
instead of
$V_{\infty }= \mathbb {C}\setminus \mathbb {R}$
instead of
![]() $V_m$
in our proof and we obtain the desired result.
$V_m$
in our proof and we obtain the desired result.
In each of the three cases above, we use the Lavrentieff theorem [Reference van Mill15, Theorem A8.5], which says that there are at most
![]() $\mathfrak {c}$
subspaces of
$\mathfrak {c}$
subspaces of
![]() $\mathbb {C}$
which are homeomorphic. Thus, there exist
$\mathbb {C}$
which are homeomorphic. Thus, there exist
![]() $2^{\mathfrak {c}}$
subsets of S of measure
$2^{\mathfrak {c}}$
subsets of S of measure
![]() $m\in [0,\infty )$
which have the Erdős property, no two of which are homeomorphic, and
$m\in [0,\infty )$
which have the Erdős property, no two of which are homeomorphic, and
![]() $2^{\mathfrak {c}}$
subsets of S of full two-dimensional Lebesgue measure which have the Erdős property, no two of which are homeomorphic.
$2^{\mathfrak {c}}$
subsets of S of full two-dimensional Lebesgue measure which have the Erdős property, no two of which are homeomorphic.
Theorem 2.7 (See [Reference Chalebgwa and Morris6, Reference Morris12])
There exist
![]() $2^{\mathfrak {c}}$
dense subsets W of S such that W has the complex Erdős property and no two of these W are homeomorphic.
$2^{\mathfrak {c}}$
dense subsets W of S such that W has the complex Erdős property and no two of these W are homeomorphic.
Proof. Let D be a closed disc in
![]() $\mathbb {C}$
of radius one with centre
$\mathbb {C}$
of radius one with centre
![]() $0$
. Put
$0$
. Put
![]() $W= S\setminus D$
. By Proposition 2.3, W has the complex Erdős property. Therefore, any set which contains W has the complex Erdős property. Let X be any subset of
$W= S\setminus D$
. By Proposition 2.3, W has the complex Erdős property. Therefore, any set which contains W has the complex Erdős property. Let X be any subset of
![]() $D\cap S$
and let B be as in Corollary 1.8. Then
$D\cap S$
and let B be as in Corollary 1.8. Then
![]() $X\cup W\cup B$
has the complex Erdős property and is dense in S. As the cardinality of
$X\cup W\cup B$
has the complex Erdős property and is dense in S. As the cardinality of
![]() $D\cap S$
is
$D\cap S$
is
![]() $\mathfrak {c}$
, there are
$\mathfrak {c}$
, there are
![]() $2^{\mathfrak {c}}$
sets
$2^{\mathfrak {c}}$
sets
![]() $X\cup W\cup B$
, each a subset of S and having the complex Erdős property. As in the proof of Theorem 2.6, the Lavrentieff theorem implies that these subsets can be chosen so that no two are homeomorphic.
$X\cup W\cup B$
, each a subset of S and having the complex Erdős property. As in the proof of Theorem 2.6, the Lavrentieff theorem implies that these subsets can be chosen so that no two are homeomorphic.
Proposition 2.8. Let
![]() $S'=\exp (S\cap \mathbb {R})\cap S$
. Then
$S'=\exp (S\cap \mathbb {R})\cap S$
. Then
![]() $S'$
has full Lebesgue measure in the set
$S'$
has full Lebesgue measure in the set
![]() $\mathbb {R}^{>0}$
of positive real numbers.
$\mathbb {R}^{>0}$
of positive real numbers.
Proof. Note that
![]() $\exp $
maps
$\exp $
maps
![]() $\mathbb {R}$
onto
$\mathbb {R}$
onto
![]() $\mathbb {R}^{>0}$
and
$\mathbb {R}^{>0}$
and
![]() $\exp $
is Lipschitz continuous on bounded sets. As
$\exp $
is Lipschitz continuous on bounded sets. As
![]() $S\cap \mathbb {R}$
has full Lebesgue measure in
$S\cap \mathbb {R}$
has full Lebesgue measure in
![]() $\mathbb {R}$
,
$\mathbb {R}$
,
![]() $\mathbb {R}\setminus S$
has Lebesgue measure zero. Therefore,
$\mathbb {R}\setminus S$
has Lebesgue measure zero. Therefore,
![]() $\exp (\mathbb {R}\setminus S)$
has Lebesgue measure zero. As the map
$\exp (\mathbb {R}\setminus S)$
has Lebesgue measure zero. As the map
![]() $\exp $
is surjective from
$\exp $
is surjective from
![]() $\mathbb {R}$
to
$\mathbb {R}$
to
![]() $\mathbb {R}^{>0}$
and
$\mathbb {R}^{>0}$
and
![]() $\exp (\mathbb {R}\setminus S)$
has zero Lebesgue measure,
$\exp (\mathbb {R}\setminus S)$
has zero Lebesgue measure,
![]() $\exp (S\cap \mathbb {R})$
has full measure in
$\exp (S\cap \mathbb {R})$
has full measure in
![]() $\mathbb {R}^{>0}$
. Noting that any subset of a set of Lebesgue measure zero has Lebesgue measure zero, we see that the set
$\mathbb {R}^{>0}$
. Noting that any subset of a set of Lebesgue measure zero has Lebesgue measure zero, we see that the set
![]() $\exp (S\cap \mathbb {R})\cap (\mathbb {R}^{>0}\setminus S)$
has Lebesgue measure zero. So
$\exp (S\cap \mathbb {R})\cap (\mathbb {R}^{>0}\setminus S)$
has Lebesgue measure zero. So
![]() $S'=\exp (S\cap \mathbb {R})\cap S$
has full Lebesgue measure in
$S'=\exp (S\cap \mathbb {R})\cap S$
has full Lebesgue measure in
![]() $\mathbb {R}^{>0}$
.
$\mathbb {R}^{>0}$
.
Proposition 2.9. The set
![]() $\exp (S\cap \mathbb {R})$
has the multiplicative Erdős property and the set
$\exp (S\cap \mathbb {R})$
has the multiplicative Erdős property and the set
![]() $\exp (S)$
has the complex multiplicative Erdős property.
$\exp (S)$
has the complex multiplicative Erdős property.
Proof. We shall apply Proposition 2.3(iv) to the set
![]() $S'=\exp (S\cap \mathbb {R})\cap S$
. First observe that
$S'=\exp (S\cap \mathbb {R})\cap S$
. First observe that
![]() $\exp $
maps
$\exp $
maps
![]() $\mathbb {R}$
onto
$\mathbb {R}$
onto
![]() $\mathbb {R}^{>0}$
. Let
$\mathbb {R}^{>0}$
. Let
![]() $x\in S'$
. Then
$x\in S'$
. Then
![]() $x\in S$
and
$x\in S$
and
![]() $x=\exp (s)$
, for some
$x=\exp (s)$
, for some
![]() $s\in S\cap \mathbb {R}$
. Now for any
$s\in S\cap \mathbb {R}$
. Now for any
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $ns\in S\cap \mathbb {R}$
and so
$ns\in S\cap \mathbb {R}$
and so
![]() $\exp (ns) \in \exp (S\cap \mathbb {R})$
. However,
$\exp (ns) \in \exp (S\cap \mathbb {R})$
. However,
![]() $\exp (ns)= (\exp (s))^n=x^n$
. As
$\exp (ns)= (\exp (s))^n=x^n$
. As
![]() $x\in S\cap \mathbb {R}$
,
$x\in S\cap \mathbb {R}$
,
![]() $x^n\in S\cap \mathbb {R}$
. Thus,
$x^n\in S\cap \mathbb {R}$
. Thus,
![]() $x^n\in S'$
. Also,
$x^n\in S'$
. Also,
![]() $x\in S$
implies
$x\in S$
implies
![]() $x^{-1}\in S$
. Further,
$x^{-1}\in S$
. Further,
![]() $x=\exp (s)$
implies
$x=\exp (s)$
implies
![]() $x^{-1}=\exp (-s)\in \exp (S)$
. So by Proposition 2.3(iv) and Proposition 2.8,
$x^{-1}=\exp (-s)\in \exp (S)$
. So by Proposition 2.3(iv) and Proposition 2.8,
![]() $\exp (S\cap \mathbb {R})\cap S$
has the multiplicative Erdős property. Thus,
$\exp (S\cap \mathbb {R})\cap S$
has the multiplicative Erdős property. Thus,
![]() $\exp (S\cap \mathbb {R})$
has the multiplicative Erdős property.
$\exp (S\cap \mathbb {R})$
has the multiplicative Erdős property.
As
![]() $\exp $
maps
$\exp $
maps
![]() $\mathbb {C}$
onto
$\mathbb {C}$
onto
![]() $\mathbb {C}\setminus \{0\}$
, an analogous argument shows that
$\mathbb {C}\setminus \{0\}$
, an analogous argument shows that
![]() $\exp (S)$
has the complex multiplicative Erdős property.
$\exp (S)$
has the complex multiplicative Erdős property.
Proposition 2.10. Let
![]() $S"=S\cap (0,\infty )$
. Then
$S"=S\cap (0,\infty )$
. Then
![]() $\log (S")\cap S$
has full Lebesgue measure in
$\log (S")\cap S$
has full Lebesgue measure in
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Proof. Clearly
![]() $(\mathbb {R}\setminus S)\cap (0,\infty )$
has zero Lebesgue measure. As
$(\mathbb {R}\setminus S)\cap (0,\infty )$
has zero Lebesgue measure. As
![]() $\log $
is Lipschitz continuous on all closed bounded subintervals of
$\log $
is Lipschitz continuous on all closed bounded subintervals of
![]() $(0,\infty )$
,
$(0,\infty )$
,
![]() $\log ((\mathbb {R}\setminus S)\cap (0,\infty ))$
has zero Lebesgue measure. Thus,
$\log ((\mathbb {R}\setminus S)\cap (0,\infty ))$
has zero Lebesgue measure. Thus,
![]() $\log S"$
has full Lebesgue measure in
$\log S"$
has full Lebesgue measure in
![]() $\mathbb {R}$
. As
$\mathbb {R}$
. As
![]() $\mathbb {R}\setminus S$
has zero Lebesgue measure,
$\mathbb {R}\setminus S$
has zero Lebesgue measure,
![]() $\log (S")\cap S$
has full Lebesgue measure in
$\log (S")\cap S$
has full Lebesgue measure in
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Proposition 2.11. The sets
![]() $\log (S")$
and
$\log (S")$
and
![]() $(\log (S"))\cap S$
have the Erdős property.
$(\log (S"))\cap S$
have the Erdős property.
Proof. Observe that if
![]() $x\in \log (S") \cap S$
, then
$x\in \log (S") \cap S$
, then
![]() $x=\log y$
,
$x=\log y$
,
![]() $y\in S"$
and
$y\in S"$
and
![]() $x\in S$
. So
$x\in S$
. So
![]() $nx=n, \log y=\log (y^n)$
and clearly
$nx=n, \log y=\log (y^n)$
and clearly
![]() $y^n\in S"$
, for any
$y^n\in S"$
, for any
![]() $n\in \mathbb {N}$
. So
$n\in \mathbb {N}$
. So
![]() $nx\in \log (S")\cap S$
. Also,
$nx\in \log (S")\cap S$
. Also,
![]() $-x =\log (1/y)$
and
$-x =\log (1/y)$
and
![]() $1/y\in S\cap (0,\infty )$
. So
$1/y\in S\cap (0,\infty )$
. So
![]() $-x\in \log (S") \cap S$
. By Propositions 2.3 and 2.10 and Remark 2.2,
$-x\in \log (S") \cap S$
. By Propositions 2.3 and 2.10 and Remark 2.2,
![]() $\log (S") $
and
$\log (S") $
and
![]() $(\log (S"))\cap S$
have the Erdős property.
$(\log (S"))\cap S$
have the Erdős property.
Remark 2.12. Let X be a subset of the set of positive real numbers and the set
![]() $Y=\{\log x: x\in X\}\cap X$
such that every positive real number is a product of two numbers in Y. If r is any positive real number strictly greater than 1, we put
$Y=\{\log x: x\in X\}\cap X$
such that every positive real number is a product of two numbers in Y. If r is any positive real number strictly greater than 1, we put
![]() $t=\log (r)$
. As t is a positive real number,
$t=\log (r)$
. As t is a positive real number,
![]() $t = y_1\cdot y_2$
, where
$t = y_1\cdot y_2$
, where
![]() $y_1,y_2\in Y$
. So
$y_1,y_2\in Y$
. So
![]() $t =y_1\cdot \log x_2= \log x_2^{y_1}$
,
$t =y_1\cdot \log x_2= \log x_2^{y_1}$
,
![]() $x_2\in X$
. So
$x_2\in X$
. So
![]() $e^t=x_2^{y_1}$
; that is,
$e^t=x_2^{y_1}$
; that is,
![]() $r=x_2^{y_1}$
. Thus,
$r=x_2^{y_1}$
. Thus,
for
![]() $b=y_1\in Y\subseteq X$
and
$b=y_1\in Y\subseteq X$
and
![]() $a=x_2\in X$
.
$a=x_2\in X$
.
This should be contrasted with the Gelfond–Schneider theorem [Reference Baker2] which says that for any algebraic numbers a and b, with
![]() $a\not =0,1$
and b not a rational number,
$a\not =0,1$
and b not a rational number,
![]() $a^b$
is a transcendental number.
$a^b$
is a transcendental number.
The authors do not know whether any interesting set X with the property stated above exists. Of course,
![]() $X=(0,\infty )$
is an example. However, we observe that Burger [Reference Burger5] proves that for any positive real number r, there exist Liouville numbers a and b such that
$X=(0,\infty )$
is an example. However, we observe that Burger [Reference Burger5] proves that for any positive real number r, there exist Liouville numbers a and b such that
![]() $r= a^b$
.
$r= a^b$
.
Acknowledgement
The authors thank the referee for helpful comments.