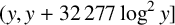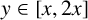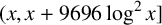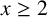1 Introduction
Selberg’s 1943 paper [Reference Selberg25] features conditional and unconditional estimates for the asymptotic behaviour of the prime number theorem (PNT) in short intervals
$(x,x+h]$
with
$h=o(x)$
. They are reached via the relationship between Chebyshev’s prime counting functions,
$\theta (x)$
and
$\psi (x)$
, and the Riemann zeta function,
$\zeta (s)$
. A notable waypoint in Selberg’s method is an estimate for
$$ \begin{align*} J(x,\delta) = \int_1^{x} \lvert\theta(y+\delta y)- \theta(y) - \delta y\rvert^2\, dy \end{align*} $$
for
$\delta \in (0,1]$
, to gauge the mean value of
$\theta (x)$
in short intervals. There has been much interest in this integral since Selberg’s paper, for its connection to the prime number theorem and prime gaps, and for estimates on the zeros of
$\zeta (s)$
and Montgomery’s pair-correlation function.
Assuming the Riemann hypothesis (RH), the best estimate for
$J(x,\delta )$
is
$$ \begin{align} J(x,\delta) \ll \delta x^2\log^2 x, \end{align} $$
for all
$\delta \in [1/x,1]$
, from Selberg [Reference Selberg25]. This estimate is given in the second display equation on page 172 of [Reference Selberg25]. Saffari and Vaughan gave a similar result in Lemma 5 of [Reference Saffari and Vaughan24], but used an averaging technique with the Riemann–von Mangoldt explicit formula. Unconditionally, one of the best results for
$J(x,\delta )$
to date is from Zaccagnini [Reference Zaccagnini30] of
$J(x,\delta ) \ll x^3\delta ^2$
for
$\delta \in [x^{-5/6-\epsilon (x)},1]$
with
$\epsilon (x)\rightarrow 0$
as
$x\rightarrow \infty $
.
Selberg’s result (1-1) is actually deduced from an estimate for a similar integral from 1 to
$\delta ^{-1}$
: see equation (13) in [Reference Selberg25]. This integral has itself been separately studied, in part because it allows a better illustration of the relationship between the size of the interval and the asymptotic behaviour of the integral. For more details on this see, for example, the introduction to [Reference Carneiro, Chandee, Chirre and Milinovich2]. Another useful reference is Zaccagnini’s review paper [Reference Zaccagnini31], which gives a survey of the literature surrounding
$J(x,\delta )$
. Also see Goldston et al. [Reference Goldston and Suriajaya9] for a version of Selberg’s proof of (1-1) for
$\psi (x)$
.
The primary goal of this paper is to prove the following explicit version of (1-1).
Theorem 1.1. Assuming the RH, for all
$x\geq 10^8$
and any
$\delta \in (0,10^{-8}]$
we have
$$ \begin{align*}\int_1^x \lvert \theta(y+\delta y)- \theta(y) - \delta y \rvert^2\, dy < 202 \delta x^2 \log^2x.\end{align*} $$
Estimates for
$J(x, \delta )$
can be used to comment on the measure of intervals that contain primes. It is usually said that an estimate holds for ‘almost all’
$y\in [x,2x]$
if the exceptional set has measure
$o(x)$
(see footnote 4 on page 161 of [Reference Selberg25] for Selberg’s definition). Under the RH, Selberg’s estimate implies that almost all intervals
$[x,x+h]$
contain a prime for any positive increasing function
$h=o(x)$
with
$h/\log ^2 x \rightarrow \infty $
(stated in [Reference Wolke29, Corollary 2]). For comparison, the best unconditional result is from Jia [Reference Jia13], of primes in almost all intervals of the form
$[x,x+x^{({1}/{20})+\epsilon }]$
, for any
$\epsilon>0$
.
With an explicit estimate for
$J(x,\delta )$
, we can explicitly determine the density of prime-containing intervals in some range. Moreover, Theorem 1.1 allows us to do so for any interval wider than
$O(\log y)$
. To demonstrate how this can be done, we prove the following corollary in Section 3.
Corollary 1.2. Assuming the RH, the set of
$y\in [x,2x]$
for which there is at least one prime in
$(y, y+ 32\,277 \log ^2 y]$
has a measure of at least
$x/2$
for all
$x\geq 2$
.
Similar statements to Corollary 1.2 can be made with other short intervals. We chose this particular interval to make a comparison with a conjecture of Cramér [Reference Cramér3], that the upper bound on gaps between consecutive primes,
$p_{n+1}-p_n$
, should be
$O(\log ^2 p_n)$
. Although the basis for this conjecture has been called into question, it is still considered likely that Cramér’s conjecture is true for powers of
$\log p_n$
above 2: see [Reference Granville12, page 23] and [Reference Pintz23]. This would predict Corollary 1.2 to be true for all
$y\in [x,2x]$
. Another comparison can be made with the result of Goldston et al. [Reference Goldston, Gonek and Montgomery10, Theorem 1], that for any fixed
$\eta>0$
there is a positive proportion of
$y\in [x,2x]$
for which
$(y,y+\eta \log y]$
contains a prime as
$x\rightarrow \infty $
.
Selberg’s result can also be used to deduce interval results for Goldbach numbers. A Goldbach number is defined as the sum of two odd primes. We have estimates for the number of Goldbach numbers in intervals, and for the smallest interval containing a Goldbach number. See Languasco [Reference Languasco16] for a survey. Linnik [Reference Linnik19] first used Hardy and Littlewood’s circle method to prove, under the RH, that there exist Goldbach numbers in
$[x,x+H]$
with
$H=O(\log ^{3+\epsilon } x)$
for any
$\epsilon>0$
. Kátai [Reference Kátai15] refined this to
$H= O(\log ^{2} x)$
using methods from [Reference Selberg25]. Montgomery and Vaughan [Reference Montgomery and Vaughan21, Theorem 2] also proved this result, but used (1-1). This result has also been proved in [Reference Goldston8] and [Reference Languasco and Perelli18, Corollary 1] using other techniques. Going a step further, Goldston [Reference Goldston8] showed that under the RH and Montgomery’s pair-correlation conjecture [Reference Montgomery20] we can take
$H=O(\log x)$
, and under the same assumptions Languasco [Reference Languasco17] proved that there is a positive proportion of Goldbach numbers in this interval. For more recent work on the average number of Goldbach numbers in intervals, see [Reference Goldston, Pintz and Yıldırım11].
We prove the following version of Montgomery and Vaughan’s result in Section 2.
Theorem 1.3. Assuming the RH, there exists a Goldbach number in the interval
$(x,x+ 9696 \log ^2 x]$
for all
$x\geq 2$
.
2 An explicit version of Selberg’s result
2.1 Preliminary lemmas
In this section we prove a number of lemmas needed to prove Theorem 1.1. Here and hereafter, let
$s=\sigma +it$
and let
$\rho =\beta +i\gamma $
denote any non-trivial zero of
$\zeta (s)$
. Selberg’s proof of (1-1) requires a mean-value estimate for the logarithmic derivative of
$\zeta (s)$
under the RH. In particular, Lemma 4 of [Reference Selberg25] states that for sufficiently large T and
$\sigma \in (1/2,3/4]$
,
$$ \begin{align} \int_0^T \bigg\lvert \frac{\zeta'}{\zeta}(\sigma+it) \bigg\rvert^2\, dt = O\bigg( \frac{T}{(\sigma-1/2)^2} \bigg). \end{align} $$
There does not appear to be an explicit version of (2-1), but Selberg’s proof is effective. See also an estimate for a similar integral from Farmer [Reference Farmer7, Lemma 2]. There are explicit estimates for
$\zeta '(s)/\zeta (s)$
in the critical strip, such as in [Reference Simonič27, Corollary 1(b)] of the order
$O((\log t)^{2(1-\sigma )} (\log \log t)^2)$
, or Lemma 2.8 of [Reference Dudek6] of
$O(\log ^2t)$
, but these would not give an estimate of the form (2-1). We make (2-1) explicit in Lemma 2.4, by way of an explicit version of [Reference Selberg25, Lemma 3] in Lemma 2.3. The latter will need Lemmas 2.1 and 2.2.
Lemma 2.1 (Karatsuba and Korolëv [Reference Karatsuba and Korolëv14, Lemma 2]).
For
$\lvert \sigma \rvert \leq 2$
and
$\lvert t\rvert \geq 10$
,
$$ \begin{align} \bigg\lvert \frac{\zeta'}{\zeta}(s) - \sum_{\rho}\frac{1}{s-\rho} \bigg\rvert \leq \frac{1}{2} \log \lvert t\rvert + 3. \end{align} $$
Lemma 2.2 (Selberg [Reference Selberg25, Lemma 2]).
For
$x>1$
, and
$\Lambda (n)$
denoting the von Mangoldt function,
$$ \begin{align*} \Lambda_x(n)= \begin{cases} \Lambda(n),&1\leq n\leq x\\ \Lambda(n)\dfrac{\log(x^2/n)}{\log x},&x\leq n\leq x^2. \end{cases} \end{align*} $$
Then, for any
$s\neq 1$
not a zero of
$\zeta (s)$
,
$$ \begin{align} -\frac{\zeta'}{\zeta}(s) &= \sum_{n<x^2}\frac{\Lambda_x(n)}{n^s} + \frac{x^{1-s}-x^{2(1-s)}}{(1-s)^2\log x} - \frac{1}{\log x}\sum_{q=1}^\infty\frac{x^{-2q-s}-x^{-2(2q+s)}}{(2q+s)^2} \\ &\qquad - \frac{1}{\log x}\sum_{\rho}\frac{x^{\rho-s}-x^{2(\rho-s)}}{(s-\rho)^2}. \nonumber \end{align} $$
Lemma 2.3. Assume the RH. For
$x\geq x_0\geq 3$
,
$\lvert t \rvert \geq 10$
,
$\tfrac 12 + ({\alpha }/{\log x}) \leq \sigma \leq 1$
, and
${\alpha \geq 0.722}$
,
$$ \begin{align*} \bigg\lvert \frac{\zeta'}{\zeta}(s) \bigg\rvert \leq A_2 \bigg\lvert \sum_{n<x^2} \frac{\Lambda_x(n)}{n^s} \bigg\rvert + \frac{A_1 A_2 ( \log \lvert t\rvert + 6 )}{2(\sigma-\frac{1}{2})\log x} + \frac{A_1 A_2 x}{t^2 \log x} + \frac{A_2 c_1 e^{-\alpha}}{t^2 x^{{5}/{2}}\log x} \end{align*} $$
where
$A_1=e^{-\alpha }+e^{-2\alpha }$
,
$A_2 = ({\alpha }/{\alpha - A_1})$
, and
$c_1 = 5/4$
for all
$x\geq 3$
.
Proof. We assume the RH throughout, so
$\rho =\tfrac 12 +i\gamma $
. Starting with Lemma 2.2, let
$Z_i$
for
$i=1, 2, 3$
denote the last three terms on the right-hand side of (2-3). For interest, we follow a similar proof to that of Lemma 2 in [Reference Simonič26]. Using (2-3), we denote
$$ \begin{align} F(s,x) = \bigg\lvert \frac{\zeta'}{\zeta}(s) + \sum_{n<x^2} \frac{\Lambda_x(n)}{n^s} \bigg\rvert \leq \lvert Z_1\rvert + \lvert Z_2\rvert + \lvert Z_3\rvert \end{align} $$
for
$x>1$
,
$1/2<\sigma \leq 1$
, and
$\lvert t\rvert>0$
. We have
$$ \begin{align*} \lvert Z_1\rvert &= \bigg\lvert \frac{x^{1-s}-x^{2(1-s)}}{(1-s)^2\log x} \bigg\rvert \leq \frac{x^{2-2\sigma} + x^{1-\sigma}}{t^2 \log x}, \end{align*} $$
and, using the sum of a geometric series,
$$ \begin{align*} \lvert Z_2\rvert &= \bigg\lvert \frac{1}{\log x} \sum_{q=1}^\infty \frac{x^{-(2q+s)}-x^{-2(2q+s)}}{(2q+s)^2} \bigg\rvert \\ &\leq \frac{1}{\log x}\bigg( \frac{x^{-(2+\sigma)} + x^{-2(2+\sigma)}}{t^2+4} + \frac{1}{t^2+16} \sum_{q=2}^\infty \bigg( x^{-(2q+\sigma)} + x^{-2(2q+\sigma)} \bigg) \bigg) \\ &\leq \frac{c_1}{(t^2+4) x^{2+\sigma} \log x}, \end{align*} $$
where
$c_1 = 1 + 2/(x_0^2-1)$
for
$x\geq x_0 \geq 3$
. For
$Z_3$
we use Lemma 2.1 and
$$ \begin{align*}\text{Re}\bigg\lbrace \frac{1}{s-\rho} \bigg\rbrace = \frac{\sigma-\frac{1}{2}}{(\sigma-\frac{1}{2})^2+(t-\gamma)^2}.\end{align*} $$
To begin,
$$ \begin{align*} \lvert Z_3\rvert &= \bigg\lvert \frac{1}{\log x}\sum_{\rho}\frac{x^{\rho-s}-x^{2(\rho-s)}}{(s-\rho)^2} \bigg\rvert \\ &\leq \frac{x^{{1}/{2}-\sigma}+x^{1-2\sigma}}{\log x} \sum_{\gamma}\frac{1}{(\sigma-\frac{1}{2})^2+(t-\gamma)^2}. \end{align*} $$
Since (2-2) implies that for
$\lvert t\rvert \geq 10$
,
$$ \begin{align*} \sum_{\rho} \text{Re}\bigg\lbrace \frac{1}{s-\rho} \bigg\rbrace \leq \text{Re}\bigg\lbrace \frac{\zeta'}{\zeta}(s) \bigg\rbrace + \frac{1}{2} \log \lvert t\rvert + 3, \end{align*} $$
and
$\text {Re}(s)\leq \lvert s\rvert $
for all s, we have
$$ \begin{align*} \lvert Z_3\rvert &\leq \frac{x^{{1}/{2}-\sigma}+x^{1-2\sigma}}{(\sigma-\frac{1}{2})\log x} \bigg( \bigg\lvert \frac{\zeta'}{\zeta}(s) \bigg\rvert + \frac{1}{2} \log \lvert t\rvert + 3 \bigg). \end{align*} $$
Substituting these bounds into (2-4), we have
$$ \begin{align*} F(s,x) \leq \frac{x^{2-2\sigma} + x^{1-\sigma}}{t^2 \log x} + \frac{c_1}{(t^2+4) x^{2+\sigma} \log x} + \frac{x^{{1}/{2}-\sigma}+x^{1-2\sigma}}{(\sigma-\frac{1}{2})\log x} \bigg( \bigg\lvert \frac{\zeta'}{\zeta}(s) \bigg\rvert + \frac{1}{2} \log \lvert t\rvert + 3 \bigg) \end{align*} $$
for
$x\geq x_0$
,
$\tfrac 12< \sigma \leq 1$
, and
$\lvert t\rvert \geq 10$
. If we further impose
$\sigma \geq \tfrac 12 + ({\alpha }/{\log x})$
with some
$\alpha>0$
, the bound simplifies to
$$ \begin{align*} F(s,x) \leq \frac{e^{-2\alpha} x + e^{-\alpha}\sqrt{x}}{t^2 \log x} + \frac{c_1 e^{-\alpha}}{(t^2+4) x^{5/2}\log x} + \frac{e^{-\alpha}+e^{-2\alpha}}{(\sigma-\frac{1}{2})\log x} \bigg( \bigg\lvert \frac{\zeta'}{\zeta}(s) \bigg\rvert + \frac{1}{2} \log \lvert t\rvert + 3 \bigg). \end{align*} $$
Let
$A_1=e^{-\alpha }+e^{-2\alpha }$
and
$A_2 = ({\alpha }/{\alpha - A_1})$
. Assuming
$\alpha> A_1$
, which is satisfied for
${\alpha \geq 0.722}$
, the above can be rearranged and simplified to
$$ \begin{align*} \bigg\lvert \frac{\zeta'}{\zeta}(s) \bigg\rvert \leq A_2 \bigg\lvert \sum_{n<x^2} \frac{\Lambda_x(n)}{n^s} \bigg\rvert + \frac{A_1 A_2 \left( \log \lvert t\rvert + 6 \right)}{2(\sigma-\frac{1}{2})\log x} + \frac{A_1 A_2 x}{t^2 \log x} + \frac{A_2c_1 e^{-\alpha}}{t^2 x^{{5}/{2}}\log x}.\\[-4pc] \end{align*} $$
Lemma 2.4. Assume the RH. For
$T\geq T_0$
,
$\tfrac 12+ ({\alpha }/{\log T}) \leq \sigma \leq \tfrac 34$
, and
$\alpha \geq 0.722$
,
$$ \begin{align} \int_0^T \bigg\lvert \frac{\zeta'}{\zeta}(\sigma+it) \bigg\rvert^2\, dt \leq \frac{A_4 T}{(\sigma-1/2)^2}, \end{align} $$
where
$A_4$
is dependent on
$\alpha $
, and given in (2-9). For
$T_0=10^3$
we can take
$A_4 = 0.576$
with
$\alpha =37$
, or for
$T_0=10^8$
we can take
$A_4 = 0.535$
with
$\alpha =26$
.
Proof. Using the Cauchy–Schwarz inequality, Lemma 2.3 implies
$$ \begin{align} \bigg\lvert \frac{\zeta'}{\zeta}(\sigma+it) \bigg\rvert^2 &\leq 2A_2^2 \bigg\lvert \sum_{n<x^2} \frac{\Lambda_x(n)}{n^s} \bigg\rvert^2 + \frac{2A_1^2 A_2^2 ( \log \lvert t\rvert + 6)^2 }{(\sigma-\frac{1}{2})^2\log^2 x} + \frac{8A_1^2 A_2^2 x^2}{t^4 \log^2 x} + \frac{8 A_2^2 c_1^2 e^{-2\alpha}}{t^4 x^5\log^2 x}, \end{align} $$
over the same range of variables and with the same constants as defined in Lemma 2.3. As (2-6) holds over
$\lvert t\rvert \geq 10$
, it can be integrated over
$t\in [10, T]$
, for some
$T>10$
. For the first term,
$$ \begin{align} \int_{10}^T \bigg\lvert \sum_{n<x^2} \frac{\Lambda_x(n)}{n^s} \bigg\rvert^2\,dt &= (T-10) \sum_{n<x^2} \frac{\Lambda_x(n)^2}{n^{2\sigma}} + \sum_{\substack{m,n<x^2 \\ m\neq n}} \frac{\Lambda_x(m)\Lambda_x(n)}{(mn)^{\sigma}} \int_{10}^T \bigg(\frac{n}{m}\bigg)^{it}\,dt\nonumber\\ &< T \sum_{n<x^2} \frac{\Lambda_x(n)^2}{n^{2\sigma}} + 2\sum_{\substack{m,n<x^2 \\ m\neq n}} \frac{\Lambda_x(m)\Lambda_x(n)}{(mn)^{\sigma} \lvert \log (m/n) \rvert}. \end{align} $$
The first sum in (2-7) can be bounded with
$$ \begin{align*} \sum_{n<x^2} \frac{\Lambda_x(n)^2}{n^{2\sigma}} &< \sum_{n=1}^\infty \frac{\Lambda(n)\log n}{n^{2\sigma}} = \frac{d}{ds} \bigg[ \frac{\zeta'}{\zeta}(s) \bigg]_{s=2\sigma}. \end{align*} $$
For non-trivial zeros
$\rho $
, and all
$s\in \mathbb {C}$
, it is known that (see, for example, (8) and (9) in [Reference Davenport4, page 80])
$$ \begin{align} \frac{d}{ds}\bigg(\frac{\zeta'(s)}{\zeta(s)} \bigg) = \frac{1}{(s-1)^2} - \sum_{n=1}^\infty \frac{1}{(s+2n)^2} - \sum_\rho \frac{1}{(s-\rho)^2}. \end{align} $$
Thus, for
$\sigma>\tfrac 12$
,
$$ \begin{align*} \sum_{n<x^2} \frac{\Lambda_x(n)^2}{n^{2\sigma}} &< \frac{1}{(2\sigma-1)^2} + \sum_{n=1}^\infty \frac{1}{(2\sigma+2n)^2} + \sum_\gamma \frac{1}{\lvert 2\sigma-1/2+i\gamma\rvert^2} \\ &\leq \frac{1}{4(\sigma-1/2)^2} + \frac{\pi^2}{8} - 1 + \sum_\gamma \frac{1}{\gamma^2}, \end{align*} $$
where
$\sum _\gamma 1/\gamma ^2 < c_0 = 0.046\,21$
, computed in [Reference Brent, Platt and Trudgian1, Corollary 1].
For the second sum in (2-7) we can use
$\log \lambda> 1 - \lambda ^{-1}$
over
$\lambda>1$
, so for
$\sigma>1/2$
,
$$ \begin{align*} \sum_{\substack{m,n<x^2 \\ m\neq n}} \frac{\Lambda_x(m)\Lambda_x(n)}{(mn)^{\sigma} \lvert \log (m/n) \rvert} < \log^2x \sum_{\substack{m,n<x^2 \\ m\neq n}} \bigg( \frac{1}{\sqrt{mn}} + \frac{1}{\lvert m-n\rvert} \bigg). \end{align*} $$
Note that the bound on
$\lvert \log (m/n)\rvert $
holds for both
$m>n$
and
$n>m$
because of the symmetry in the resulting expression. For
$x\geq 1$
, partial summation gives
$$ \begin{align*} \sum_{n<x^2} \frac{1}{\sqrt{n}} < 2x, \end{align*} $$
and the Euler–Maclaurin formula gives
$$ \begin{align*} \sum_{\substack{m,n<x^2 \\ m\neq n}} \frac{1}{\lvert m-n\rvert} = 2\sum_{m<x^2} \sum_{n<m} \frac{1}{m-n} &< 2\sum_{m<x^2} \sum_{k<x^2} \frac{1}{k} < 4x^2\log x + 2\gamma x^2 + 1, \end{align*} $$
whence we have
$$ \begin{align*} \sum_{\substack{m,n<x^2 \\ m\neq n}} \frac{\Lambda_x(m)\Lambda_x(n)}{(mn)^{\sigma} \lvert \log (m/n)\rvert} &< 4x^2\log^3 x + (4+2\gamma)x^2\log^2x + \log^2x. \end{align*} $$
Returning to (2-7), we have
$$ \begin{align*} \int_{10}^T \bigg\lvert \sum_{n<x^2} \frac{\Lambda_x(n)}{n^s} \bigg\rvert^2 \,dt &< T \bigg( \frac{1}{4(\sigma-1/2)^2} + A_3 \bigg) + 8c_2 x^2\log^3 x, \end{align*} $$
where
$A_3 = \pi ^2/8 - 1 + c_0$
and
$c_2 = 2.25$
for
$x\geq 3$
. Using this in (2-6) gives
$$ \begin{align*} &\frac{1}{A_2^2} \int_{10}^T \bigg\lvert \frac{\zeta'}{\zeta}(\sigma+it) \bigg\rvert^2 \,dt \\ &\quad \leq \frac{T}{2(\sigma-\frac{1}{2})^2} + 2 A_3 T + 16 c_2 x^2\log^3x \\ &\qquad + \frac{2A_1^2}{(\sigma-\frac{1}{2})^2\log^2 x} \int_{10}^T ( \log t + 6)^2 \,dt + 8 \bigg( \frac{A_1^2 x^2}{\log^2 x} + \frac{c_1^2 e^{-2\alpha}}{x^5\log^2 x} \bigg) \int_{10}^T \frac{1}{t^4} \,dt \\ &\quad\leq \frac{T}{2(\sigma-\frac{1}{2})^2} + 2 A_3 T + 16 c_2 x^2\log^3x + \frac{2A_1^2 c_3 T\log^2T}{(\sigma - \frac{1}{2})^2 \log^2 x} \\ &\qquad + \frac{1}{375} \bigg( \frac{A_1^2 x^2}{\log^2 x} + \frac{c_1^2 e^{-2\alpha}}{x^5\log^2 x} \bigg), \end{align*} $$
where we can take
$c_3 = 1 + \frac {10}{\log T_0} + \frac {26}{\log ^2 T_0}$
for any
$T_0> 10$
. Also note that the
$1/375$
comes from estimating the second integral over t. We now take
$x=T^{\nu }$
for any
$\nu \geq \log x_0/{\log} T_0$
, as it will be used for
$x\geq x_0$
and
$T\geq T_0$
. The previous bound becomes
$$ \begin{align*} \frac{1}{A_2^2} \int_{10}^T \bigg\lvert \frac{\zeta'}{\zeta}(\sigma+it) \bigg\rvert^2 \,dt &\leq \bigg( \frac{1}{2} + \frac{2A_1^2 c_3}{\nu^2} \bigg) \frac{T}{(\sigma-\frac{1}{2})^2} + 2 A_3 T + 16c_2 \nu^3 T^{2\nu} \log^3T \\ &\quad + \frac{A_1^2 T^{2\nu}}{375\nu^2 \log^2 T} + \frac{c_1^2 T^{1-5\nu}}{375e^{2\alpha}\nu^2 \log^2 T}. \end{align*} $$
It remains to estimate the integral over
$t\in [0,10]$
. By the maximum modulus principle,
$$ \begin{align*}\bigg\lvert \frac{\zeta'}{\zeta}(s) \bigg\rvert \leq \max_{z\in \delta S} \bigg\lvert \frac{\zeta'}{\zeta}(z) \bigg\rvert, \end{align*} $$
where
$\delta S$
is the boundary of
$S:=\{ z\in \mathbb {C}: \tfrac 12< \sigma \leq \tfrac 34, 0\leq t\leq 10 \}$
. This implies
$$ \begin{align*} \int_{0}^{10} \bigg\lvert \frac{\zeta'}{\zeta}(\sigma+it) \bigg\rvert^2 \,dt &\leq 10 \cdot 4.7^2 < 215. \end{align*} $$
Therefore, for all
$T\geq T_0$
and
$1/2<\sigma \leq 3/4$
we have
$$ \begin{align*} \int_0^T \bigg\lvert \frac{\zeta'}{\zeta}(\sigma+it) \bigg\rvert^2 \,dt \leq \frac{A_4 T}{(\sigma-\tfrac{1}{2})^2}, \end{align*} $$
where
$$ \begin{align} A_4 = A_2^2\bigg( \frac{1}{2} + \frac{2A_1^2 c_3}{\nu^2}\! + \! \frac{A_3}{8} \! +\! \bigg( c_2 \nu^3 \log^3T_0 + \frac{A_1^2/6000}{\nu^2 \log^2 T_0} \bigg) \frac{1}{T_0^{1-2\nu}} \! +\! \frac{c_1^2 e^{-2\alpha} /6000 }{\nu^2 T_0^{5\nu}\log^2 T_0} \bigg) + \frac{215}{16T_0} , \end{align} $$
for any
$\nu \in [ \log x_0/\log T_0, 1/2)$
and
$T_0\geq \exp ({3}/({1-2\nu }))$
. The latter condition is needed to ensure the
$T^{2\nu -1}\log ^3T$
term is decreasing for all
$T\geq T_0$
. Optimising
$\nu $
and
$\alpha $
with
$x_0=3$
and
$T_0=10^3$
, we can take
$A_4 = 0.576$
with
$\nu = 0.1591$
and
$\alpha =37$
. This constant
$A_4$
approaches its limit relatively quickly as
$T_0$
increases, so for
$T_0=10^8$
we can take
$A_4 = 0.535$
with
$\nu = 0.0597$
and
$\alpha =26$
.
For any choice of
$T_0\geq 10^8$
,
$A_4$
is within
$10^{-6}$
of its limit. Larger
$x_0$
also do not reduce
$A_4$
. In fact, we see the opposite. Smaller
$x_0$
allow smaller admissible
$\nu $
, which reduces the terms containing a factor of
$T^{\nu }$
. As a result, the optimal value of
$\nu $
in both cases is its lower limit. One of the most direct ways to reduce
$A_4$
would be the use of a smaller upper bound on
$\sigma $
.
2.2 Proof of Theorem 1.1
To begin, let
$$ \begin{align*}\theta_0(x) = \tfrac{1}{2} \lim_{\varepsilon\rightarrow 0}(\theta(x+\varepsilon)+\theta(x-\varepsilon) ), \end{align*} $$
so
$\theta _0(x) = \theta (x)$
except when x is prime, and let
$G(y,\delta ) = \theta (y+\delta y)- \theta (y) - \delta y$
for any
$\delta \in (0,1]$
. By Perron’s formula, we can write, for
$x>1$
,
$s=\sigma +it$
, and prime p,
$$ \begin{align} \theta_0(x) = \frac{1}{2\pi i} \int_{2-i\infty}^{2+i\infty} \frac{x^s}{s} \left( \sum_p \frac{\log p}{p^s} \right) ds. \end{align} $$
As the integral is over
$\sigma \geq 2$
, the sum can be rewritten as
$$ \begin{align*} \sum_p \frac{\log p}{p^s} = \sum_{n=2}^\infty \frac{\Lambda(n)}{n^s} - \sum_{r=2}^\infty \sum_p \frac{\log p}{p^{rs}} = -\frac{\zeta'(s)}{\zeta(s)} - g(s). \end{align*} $$
As
$g(s)$
is convergent for
$\sigma>1/2$
, it can be bounded over this region with
$$ \begin{align*} \lvert g(s)\rvert &= \bigg\lvert \sum_p \frac{\log p}{p^s(p^s-1)} \bigg\rvert \leq \sum_p \frac{\log p}{p^\sigma(p^\sigma-1)} \\ &\leq c_4 \sum_{p\geq 19} \frac{\log p}{p^{2\sigma}} + \sum_{2\leq p< 19} \frac{\log p}{p^\sigma(p^\sigma-1)} \\ &\leq c_4\sum_{n=2}^\infty \frac{\Lambda(n)}{n^{2\sigma}} + \sum_{2\leq p<19} \bigg( \frac{\log p}{p^\sigma(p^\sigma-1)} - \frac{c_4 \log p}{p^{2\sigma}} \bigg) \end{align*} $$
where
$c_4\,{=} \sqrt{19}/(\!\sqrt{19}-1) \approx 1.2978$
. This simplifies to
$$ \begin{align*} \lvert g(s)\rvert < - c_4\frac{\zeta'(2\sigma)}{\zeta(2\sigma)} + 1.4255. \end{align*} $$
By Delange’s theorem [Reference Delange5], and the second display equation on page 334 of [Reference Delange5], we have
$$ \begin{align*} - \frac{\zeta'(\sigma)}{\zeta(\sigma)} < \frac{1}{\sigma - 1} \end{align*} $$
for all
$\sigma>1$
. Hence, for
$\sigma \in (1/2, 3/4]$
and
$c_5 = 1.0053$
we can use
$$ \begin{align*} \lvert g(s)\rvert < \frac{c_4}{2\sigma-1} + 1.4255 < \frac{c_5}{\sigma - \tfrac{1}{2}}. \end{align*} $$
Returning to (2-10), we move the line of integration to some
$\sigma \in (1/2,3/4]$
. Part of this process involves evaluating a closed contour integral of the integrand in (2-10) over at most
$1/2 < \text {Re}(s) \leq 2$
and all t. The only pole of the integrand in this region is at
$s=1$
. Therefore, by Cauchy’s residue theorem,
$$ \begin{align} \theta_0(x) - x = - \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{x^{s}}{s} \bigg\{ \frac{\zeta'(s)}{\zeta(s)} + g(s) \bigg\} \,dt. \end{align} $$
We use (2-11) to set up an expression for the error term of
$\theta (x)$
in intervals. Let
$\kappa $
be defined such that
$e^\kappa = 1+\delta $
, meaning
$0< \kappa \leq \log 2$
. For
$\tau>0$
, (2-11) implies
$$ \begin{align*} \frac{\theta_0(e^{\kappa+\tau})-\theta_0(e^\tau)-\delta e^\tau}{e^{\sigma\tau}} = - \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{e^{\kappa s}-1}{s} e^{it\tau} \bigg( \frac{\zeta'}{\zeta}(s) + g(s) \bigg) \,dt. \end{align*} $$
By Plancherel’s theorem (see, for example, [Reference Wiener28, Theorem 2, page 69]),
$$ \begin{align} \int_{-\infty}^\infty \bigg\lvert \frac{\theta_0(e^{\kappa+\tau})-\theta_0(e^\tau)-\delta e^\tau}{e^{\sigma\tau}} \bigg\rvert^2 d\tau = \frac{1}{2\pi} \int_{-\infty}^\infty \bigg\lvert \frac{e^{\kappa s}-1}{s} \bigg\rvert^2 \bigg\lvert \frac{\zeta'}{\zeta}(s) + g(s) \bigg\rvert^2 \,dt. \end{align} $$
Since
$\theta _0(x) = \theta (x)$
almost everywhere, this statement is equally true for
$\theta (x)$
. As
${\lvert z\rvert ^2= z \overline {z}}$
for any complex z, the integrals in (2-12) are symmetric around 0, which implies
$$ \begin{align} \int_0^\infty \bigg\lvert \frac{G(e^{\tau}, \delta)}{e^{\sigma\tau}} \bigg\rvert^2 d\tau &< \frac{1}{\pi} \int_{0}^\infty \bigg\lvert \frac{e^{\kappa s}-1}{s} \bigg\rvert^2 \bigg( \bigg\lvert \frac{\zeta'(s)}{\zeta(s)} \bigg\rvert^2 + \lvert g(s)\rvert^2 \bigg)\, dt \nonumber \\ &= \frac{1}{\pi} \sum_{k=0}^\infty \int_{(2^k-1)/\delta}^{(2^{k+1}-1)/\delta} \bigg\lvert \frac{e^{\kappa s}-1}{s} \bigg\rvert^2 \bigg( \bigg\lvert \frac{\zeta'(s)}{\zeta(s)} \bigg\rvert^2 + \lvert g(s)\rvert^2 \bigg)\, dt. \end{align} $$
The first factor in the integrand can be bounded in two different ways. The first uses the Taylor series for
$e^x$
, and is valid for all
$\sigma \leq 3/4$
:
$$ \begin{align} \bigg\lvert \frac{e^{\kappa s}-1}{s} \bigg\rvert = \bigg\lvert \frac{1}{s} \sum_{n=1}^\infty \frac{(\kappa s)^n}{n!} \bigg\rvert = \bigg\lvert \sum_{n=0}^\infty \frac{\kappa^{n+1}s^n}{(n+1)!} \bigg\rvert \leq \kappa \bigg\lvert \sum_{n=0}^\infty \frac{(\kappa s)^n}{n!} \bigg\rvert \leq e^{{3}/{4}\kappa}\kappa. \end{align} $$
The second is more direct, and valid for all
$\sigma \in (1/2,3/4]$
:
$$ \begin{align} \bigg\lvert \frac{e^{\kappa s}-1}{s} \bigg\rvert \leq \frac{e^{\kappa \sigma} + 1}{\lvert s\rvert} \leq \frac{e^{{3}/{4}\kappa} + 1}{t}. \end{align} $$
We use (2-14) for the
$k=0$
term in (2-13), and (2-15) for the other terms, so as to have a convergent sum. Incorporating Lemma 2.4, we have
$$ \begin{align} &\int_0^\infty \bigg\lvert \frac{G(e^{\tau}, \delta)}{e^{\sigma\tau}} \bigg\rvert^2 d\tau < \frac{(A_4+c_5^2)e^{{3}/{2}\kappa}\kappa^2}{\pi\delta(\sigma-\frac{1}{2})^2} + \frac{(e^{{3}/{4}\kappa}+1)^2\delta}{\pi (\sigma-\frac{1}{2})^2} \sum_{k=1}^\infty \frac{A_4(2^{k+1}-1) + c_5^2\cdot 2^k}{(2^k-1)^2} \nonumber\\ &\quad\leq \bigg( (1+10^{-3}) (A_4+c_5^2) + (4+10^{-2})(A_4 A_5 + c_5^2 A_6) \bigg) \frac{\delta}{\pi (\sigma-\frac{1}{2})^2} \end{align} $$
for
$\delta \leq T_0^{-1}\leq 10^{-3}$
, where
$A_5 = 4.35\ldots $
and
$A_6 = 2.74\ldots $
are the two convergent sums in (2-16). In using Lemma 2.4 we assumed
$(2^{k+1}-1)/\delta \geq T_0$
, which is true over
$k\geq 0$
with
$\delta \leq T_0^{-1}$
.
We can now choose
$\sigma $
to minimise the final bound. By the upper bound on
$\sigma $
in Lemma 2.4, we can take
$\sigma = \tfrac 12 + ({\alpha }/{\log (1/\delta )})$
for
$\delta \leq \min (e^{-4\alpha },T_0^{-1})$
and
$\alpha $
defined as in Lemma 2.4. Also, to simplify the integral of interest, let
$y=e^\tau $
, so for
$y>1$
we have
$$ \begin{align*} \int_0^\infty \bigg\lvert \frac{G(e^{\tau}, \delta)}{e^{\sigma\tau}} \bigg\rvert^2 d\tau = \int_1^\infty \bigg\lvert \frac{G(y, \delta)}{y^{\sigma+\frac{1}{2}}} \bigg\rvert^2 dy = \int_1^\infty \bigg\lvert \frac{G(y, \delta)}{y^{1+\frac{\alpha}{\log(1/\delta)}}} \bigg\rvert^2 dy. \end{align*} $$
We can now use the bound in (2-16) for a version of the above integral over a finite range of y. For applications, it is useful if the range of integration is a function of
$\delta $
. The parameter
$\delta $
is important because
$G(y,\delta )$
is the error in the PNT over an interval defined by
$\delta $
. Let b be a positive parameter to write
$$ \begin{align*} \int_1^\infty \bigg\lvert \frac{G(y, \delta)}{y^{1+\frac{\alpha}{\log(1/\delta)}}} \bigg\rvert^2 dy &> \int_1^{\delta^{-b}} y^{{2\alpha}/{\log \delta}} \bigg\lvert \frac{G(y, \delta)}{y} \bigg\rvert^2 dy \\ &> \delta^{{-2\alpha b}/{\log \delta}} \int_1^{\delta^{-b}} \bigg\lvert \frac{G(y, \delta)}{y} \bigg\rvert^2 dy = \frac{1}{e^{2\alpha b}} \int_1^{\delta^{-b}} \bigg\lvert \frac{G(y, \delta)}{y} \bigg\rvert^2 dy. \end{align*} $$
Hence, by (2-16) we can conclude
$$ \begin{align} \int_1^{\delta^{-b}} \bigg\lvert \frac{G(y, \delta)}{y} \bigg\rvert^2 dy < e^{2\alpha(b-1)} A_7 \delta\log^2(1/\delta) \end{align} $$
for
$$ \begin{align*} A_7 = \frac{e^{2\alpha}}{\alpha^2 \pi} ( (1+10^{-3}) (A_4+c_5^2) + (4+10^{-2})(A_4 A_5 + c_5^2 A_6) ). \end{align*} $$
This is an explicit form of (13) in [Reference Selberg25]. This result is more precise than Theorem 1.1 for fixed
$\delta $
, but it is not as simple to use. Theorem 1.1 comes from a slightly different choice of
$\sigma $
: we instead take
$\sigma = \tfrac 12 + ({\alpha }/{\log x})$
in (2-16) for
$x\geq \max \{ e^{4\alpha }, T_0\}$
(by the bounds on
$\sigma $
from Lemma 2.4). By the same steps as above, we reach
$$ \begin{align*} \int_0^\infty \bigg\lvert \frac{G(e^{\tau}, \delta)}{e^{\sigma\tau}} \bigg\rvert^2 d\tau = \int_1^\infty \bigg\lvert \frac{G(y, \delta)}{y^{1+\frac{\alpha}{\log x}}} \bigg\rvert^2 dy> \frac{1}{e^{2\alpha}x^2} \int_1^{x} \lvert G(y, \delta)\rvert^2 dy, \end{align*} $$
and hence
$$ \begin{align} \int_1^{x} \lvert G(y, \delta) \rvert^2 dy < A_7 \delta x^2 \log^2 x \end{align} $$
for
$\delta \leq T_0^{-1}$
. Using
$T_0=10^8$
in (2-9), and optimising over
$\alpha $
and
$\nu $
, we can take
${A_7 = 202}$
with
$\alpha =2.08$
and
$\nu = 0.285$
, such that (2-18) holds for all
$x\geq 10^8$
.
3 Primes in some short intervals
Theorem 1.1 can be used to find an explicit estimate for the exceptional set of primes in short intervals of length h where
$h/\log y \rightarrow \infty $
. This is demonstrated in Corollary 1.2.
Corollary 1.2. Assuming the RH, the set of
$y\in [x,2x]$
for which there is at least one prime in
$(y, y+ 32\,277 \log ^2 y]$
has a measure of at least
$x/2$
for all
$x\geq 2$
.
Proof. As before, let
$G(y,\delta ) = \theta (y+\delta y)- \theta (y) - \delta y$
for
$\delta \in (0,1]$
. Also let
${\delta _1 = ({\lambda \log ^2(2x)}/{2x})}$
for
$x>1$
and
$\lambda \geq 1$
. We use the alternative version of Theorem 1.1 from the previous section, stated in (2-17), which is under the RH. Taking
$\delta = \delta _1$
in (2-17) gives
$$ \begin{align*} \int_1^{\delta_1^{-b}} \bigg\lvert \frac{G(y, \delta)}{y} \bigg\rvert^2 dy < e^{2\alpha(b-1)} A_7 \frac{\lambda\log^2(2x)}{2x} \log^2\bigg(\frac{2x}{\lambda\log^2(2x)}\bigg) \end{align*} $$
for any
$b>0$
and all x for which
$\delta _1\leq \min \{e^{-4\alpha },T_0^{-1}\}$
. The constants
$T_0$
and
$\alpha $
are determined by Lemma 2.4, and correspond to the
$A_4$
in the definition of
$A_7$
. Choosing
$b>1$
will make
$\delta _1 < (2x)^{-{1}/{b}}$
for sufficiently large x, and allows us to write
$$ \begin{align*} \int_1^{\delta_1^{-b}} \bigg\lvert \frac{G(y, \delta)}{y} \bigg\rvert^2 dy> \int_{x}^{2x} \bigg\lvert \frac{G(y, \delta)}{y} \bigg\rvert^2 dy. \end{align*} $$
Imposing this restriction on b thus implies
$$ \begin{align*} \int_{x}^{2x} \lvert G(y, \delta)\rvert^2 dy &< 2 e^{2\alpha(b-1)} A_7 \lambda x \log^2(2x) \log^2x < 2 e^{2\alpha(b-1)} A_7 \lambda x \log^4x \end{align*} $$
for
$\delta _1<\min \{e^{-4\alpha }, T_0^{-1}, (2x)^{-{1}/{b}} \}$
and
$x\geq 3$
.
We can use this bound to prove that for a subset of
$y\in [x, 2x]$
of measure greater than or equal to
$(1-g)x$
, with
$g\in (0,1)$
and sufficiently large x, we have
$$ \begin{align*} \lvert G(y, \delta) \rvert^2 < B \log^4 y \end{align*} $$
for some
$B>0$
. To justify this, suppose for a contradiction that there exists a subset I of
$y\in [x, 2x]$
of measure greater than or equal to
$gx$
for which
$$ \begin{align*} \lvert G(y, \delta)\rvert^2 \geq B \log^4 y. \end{align*} $$
This would imply
$$ \begin{align*} \int_{x}^{2x} \lvert G(y, \delta) \rvert^2 dy &\geq B \log^4x \int_I dy = Bg x \log^4x. \end{align*} $$
This will be a contradiction for
$B\geq 2 e^{2\alpha (b-1)} A_7 \lambda /g$
. Therefore, choosing the smallest possible B, we have for
$x \leq y\leq 2x$
,
$$ \begin{align*} \theta(y+\lambda\log^2 y)-\theta(y) &\geq \theta\bigg( y + \frac{\lambda\log^2(2x)}{2x}y \bigg) - \theta(y) - \frac{\lambda\log^2(2x)}{2x}y + \frac{\lambda\log^2(2x)}{2x}y \\ &>\bigg(-\sqrt{B} + \frac{\lambda}{2} \bigg)\log^2 y, \end{align*} $$
which implies that there will be at least one prime in the interval
$(y, y+\lambda \log ^2 y]$
for
$$ \begin{align*} -\sqrt{\frac{2 e^{2\alpha(b-1)} A_7 \lambda}{g}} + \frac{\lambda}{2}> 0. \end{align*} $$
We can conclude that, under the assumption of the RH, the set of
$y \in [x,2x]$
for which there are primes in
$(y, y+ \lambda \log ^2 y]$
has measure greater than or equal to
$(1-g)x$
for
$$ \begin{align*} \lambda> \frac{8 e^{2\alpha(b-1)} A_7}{g}. \end{align*} $$
To prove Corollary 1.2, we take
$g=1/2$
and optimise the lower bound on
$\lambda $
over b. We aim to find the smallest
$\lambda $
for which the condition on
$\delta _1$
holds over
$x\geq 4\cdot 10^{18}$
, as the computations of Oliveira e Silva et al. [Reference Oliveira e Silva, Herzog and Pardi22] can be used to verify Corollary 1.2 for
$x<4\cdot 10^{18}$
. We can also reoptimise
$\alpha $
, and use a higher
$T_0$
in Lemma 2.4 than used to reach Theorem 1.1, as it just needs to satisfy the condition on
$\delta _1$
.
For
$T_0 = 1.3\cdot 10^{11}$
we find that we can take
$A_7 = 236.72$
with
$\alpha = 1.5295$
, and with
$b=1.700\,423$
we have
$\lambda = 32\,277$
. This was achieved using a partially manual optimisation process, in that the lower bound on
$\lambda $
was first minimised over
$\alpha $
using an in-built optimising function and some guess for b. The guess for b was then adjusted until it satisfied
$\delta _1<\min \{e^{-4\alpha }, T_0^{-1}, (2x)^{-{1}/{b}} \}$
, which required a guess of an upper bound for
$\lambda $
. After a valid solution set was found, it was refined computationally in Python.
The computations in Section 2.2 of [Reference Oliveira e Silva, Herzog and Pardi22] confirm that
$(y, y+ 32\,277\log ^2 y]$
contains a prime for all
$2\leq y\leq 4\cdot 10^{18}$
. More specifically, the calculations in Section 2.2.1 of [Reference Oliveira e Silva, Herzog and Pardi22] show that there is a prime in
$(y,y+2.09\log ^2y]$
for all
$2\leq y\leq 4\cdot 10^{18}$
.
The trade-off in this type of result is between the length of the interval, the size of the exceptional set, and the range for which the result holds. Corollary 1.2 was built first on the asymptotic length of the interval, then the desired measure of the exceptional set, and lastly the constant in the interval, which was calculated based on the smallest x for which we wanted the result to hold. An alternative would have been to first fix the constant in the interval, then calculate the measure of the exceptional set. It would also be possible to consider an asymptotically larger interval than
$O(\log ^2 y)$
. In this case, the exceptional set would be asymptotically smaller than x, and could be given explicitly using Theorem 1.1 and the working in [Reference Selberg25, page 11].
4 An explicit bound for Goldbach numbers
A Goldbach number is an even positive integer that can be written as the sum of two odd primes. With Theorem 1.1 we can prove Theorem 1.3, restated here.
Theorem 1.3. Assuming the RH, there exists a Goldbach number in the interval
$(x,x+ 9696 \log ^2 x]$
for all
$x\geq 2$
.
By Theorem 1.1 and the RH, we can state that for
$x \geq 10^8$
,
$\delta \in (0,10^{-8}]$
, and any
${a\in [10^{-8}, 1)}$
,
$$ \begin{align} \int_{ax}^{x} \lvert \theta(t+\delta t) - \theta(t) - \delta t\rvert^2 \,dt \leq 202 \delta x^2 \log^2 x. \end{align} $$
To prove Theorem 1.3 we largely follow the proof of Montgomery and Vaughan’s Theorem 2 in [Reference Montgomery and Vaughan21, Section 9], and use the above bound. We also optimise a few choices in the proof.
Suppose the interval
$(x,x+h]$
contains no sum of two primes for
$1\leq h\leq x$
. Then, for any y, at least one of the two intervals
$$ \begin{align} (y, y+\tfrac{1}{2} h ],(x-y, x-y+\tfrac{1}{2}h ] \end{align} $$
will not contain a prime number. Both of these intervals can be represented by
$$ \begin{align*} \bigg(\frac{x}{2}+\frac{kh}{2}, \frac{x}{2} + \frac{(k+1) h}{2} \bigg], \end{align*} $$
and for any choice of
$k\in K = [(2a-1) xh^{-1} + 1, (1-2a)xh^{-1} - 1]$
with
$a\in (0,1/2]$
, which defines one of the intervals in (4-2), there exists another
$k\in K$
that defines the other interval such that both intervals lie in
$(ax,x-ax]$
. Each of these pairs of intervals lies symmetrically around the midpoint of
$(ax,x-ax]$
, so it is possible to completely cover
$(ax,x-ax]$
with at most
$(1-2a)x/h$
pairs of the form (4-2). Therefore, at least
$(1-2a)x/h$
of these intervals covering
$(ax,x-ax]$
do not contain a prime.
As these intervals span
$h/2$
, we can write that for
$\delta = \delta (x)\leq h/2x$
,
$$ \begin{align*} \lvert \theta(t+\delta t) - \theta(t) - \delta t\rvert = \delta t \end{align*} $$
on a set I of
$t\in (ax,x-ax]$
of measure
$(\tfrac 12 - a)x$
. Note that the condition on
$\delta $
is a result of requiring
$\delta t\leq h/2$
for all t. Therefore, we have
$$ \begin{align*} \int_{ax}^{x} \lvert \theta(t+\delta t) - \theta(t) - \delta t\rvert^2 \,dt &> \int_I \lvert \theta(t+\delta t) - \theta(t) - \delta t\rvert^2 \,dt = \delta^2 \int_I t^2 \,dt \\ &> \delta^2\int_{ax}^{x/2} t^2 \,dt = \frac{\delta^2 x^3}{3} \bigg( \frac{1}{8} - a^3 \bigg). \end{align*} $$
Taking
$\delta = h/2x$
with
$h=C\log ^2 x$
, this bound contradicts (4-1) for
$$ \begin{align*} C\geq \frac{6\cdot 202}{\frac{1}{8}-a^3} \end{align*} $$
and all x satisfying
$$ \begin{align*} \frac{\log^2 x}{x} \leq \frac{2}{10^{8}C}. \end{align*} $$
The lower bound on C is minimised at the smallest
$a=10^{-8}$
, meaning we can take
${C=9696}$
. Therefore, there must exist at least one Goldbach number in the interval
$(x,x+ 9696\log ^2 x]$
for all
$x\geq 6\cdot 10^{14}$
. The computation in [Reference Oliveira e Silva, Herzog and Pardi22] confirms the Goldbach conjecture up to
$4\cdot 10^{18}$
, so this interval must also contain a Goldbach number for all
$ x\geq 2$
.
Acknowledgements
Many thanks to Tim Trudgian, Aleks Simonič, and Daniel Johnston for their advice and suggestions. Thanks also to Nicol Leong for fixing the code.
