Introduction

Efficient subglacial drainage networks consisting of arborescent systems of channels, akin to those beneath alpine glaciers, have been postulated to develop under Greenland outlet glaciers during the summer melt season (Reference Shepherd, Hubbard, Nienow, McMillan and JoughinShepherd and others, 2009; Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010, Reference Bartholomew, Nienow, Sole, Mair, Cowton and King2012; Reference CowtonCowton and others, 2013; Reference SoleSole and others, 2013). These Röthlisberger channels (R-channels), which are formed by melting of the overlying ice by turbulent water flow (Reference RöthlisbergerRöthlisberger, 1972), are argued to reduce summer ice velocity below the winter average by drawing water from the surrounding distributed drainage system, resulting in less basal lubrication (Reference Nienow, Sharp and WillisNienow and others, 1998; Bartholomew and others, 2011; Reference ShannonShannon and others, 2013; Reference SoleSole and others, 2013).

Rapid supraglacial lake drainage events have been suggested as a cause of significant subglacial channel growth under the Greenland ice sheet (GrIS) (Reference DasDas and others, 2008; Reference Hoffman, Catania, Neumann, Andrews and RumrillHoffman and others, 2011; Reference Pimentel and FlowersPimentel and Flowers, 2011; Reference CowtonCowton and others, 2013). These rapid drainage events evacuate millions of cubic meters of water from the ice surface to the bed in a matter of hours (Reference DasDas and others, 2008; Reference DoyleDoyle and others, 2013). GPS receivers in the vicinity of lake drainage events have recorded ice surface uplift in the initial stages of drainage, followed by subsidence within 24 hours (Reference DasDas and others, 2008; Reference Hoffman, Catania, Neumann, Andrews and RumrillHoffman and others, 2011; Reference DoyleDoyle and others, 2013; Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013). This subsidence has been attributed to the presence of subglacial channels that efficiently remove the large volumes of lake water from the region (Reference DasDas and others, 2008; Reference Hoffman, Catania, Neumann, Andrews and RumrillHoffman and others, 2011; Reference Pimentel and FlowersPimentel and Flowers, 2011).

Surface meltwater also reaches the ice-sheet bed through moulins, either directly (Reference Catania, Neumann and PriceCatania and others, 2008) or via the overtopping of surface lakes (Reference Banwell, Willis and ArnoldBanwell and others, 2013). Such moulin drainage is argued to have a greater dynamic impact over the summer melt season when compared with rapid lake drainage events (Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013). Moulins in Greenland appear to be active over multiple years and are therefore argued to be likely to establish efficient drainage systems (Reference Catania and NeumannCatania and Neumann, 2010).

We are interested in determining whether efficient channels can form in interior regions of the GrIS as a result of either rapid lake or moulin drainage. Our definition of 'interior' is based on a combination of shallow ice surface slopes, thick ice and a sufficient distance from the margin that drainage systems are unlikely to be connected to low-pressure outlets. One way to determine whether channels are a primary mechanism for large-scale subglacial drainage in the interior of the GrIS is to estimate the rates of growth and closure of these channels under various pressure-forcing scenarios. If channels are to be active in rapid lake drainage or summer melt drainage through moulins, they must be capable either of sufficiently rapid growth at the inception of drainage, or of being maintained over the winter. However, shallower surface slopes and thicker ice in the interior of the GrIS may restrict basal channel growth by preventing strong hydraulic potential gradients and enhancing creep closure, making these requirements difficult to fulfill (Reference ChandlerChandler and others, 2013; Reference Meierbachtol, Harper and HumphreyMeierbachtol and others, 2013).

We apply an R-channel model to a region of thick, shallow surface-gradient ice to estimate a best-case scenario for channel growth during both lake drainage events and moulin drainage for the interior of the GrIS. We do not complicate our model by including linked-cavity drainage or turbulent sheets, which are likely to contribute to subglacial drainage (e.g. Reference Flowers and ClarkeFlowers and Clarke, 2002; Reference HewittHewitt, 2011; Reference Pimentel and FlowersPimentel and Flowers, 2011; Schoof and others, 2012; Reference Kingslake and NgKingslake and Ng, 2013), but instead focus on the physics of channel growth alone and examine whether efficient channels can form when all drainage water is focused through this type of system. Our results are therefore an upper estimate of the channel growth that might be occurring in reality.

Fig. 1. Schematic of the R-channel model applied to a lake drainage overpressure scenario.

The equations to define R-channel growth were developed by Reference RöthlisbergerRöthlisberger (1972) for a steady-state system and adapted by Reference NyeNye (1976) to apply to spatially and temporally varying hydrological networks. We apply the Reference NyeNye (1976) equations to a region with kilometer-thick interior ice to test: (1) whether subglacial channels can form during the short-lived but substantial water inputs associated with supraglacial lake drainage events; (2) how much basal channel development occurs from longer-term surface drainage into moulins; and (3) whether channels can persist with pressures below ice overburden.

R-Channel Model

Reference NyeNye (1976) developed a system of equations to describe R-channel growth based on the competition between ice melting from turbulent dissipation of heat within the channel and closure of the channel due to the weight of the overlying ice, while conserving mass and momentum. These equations have been adapted for application to the GrIS by Reference SchoofSchoof (2010), who used expressions for channel development alongside linked-cavity growth to examine hydrological development within 10 km of the ice-sheet margin. Reference ChandlerChandler and others (2013) utilized the Reference SchoofSchoof (2010) equations but omitted the cavity formation term and therefore focused only on channel growth. They examined channel growth up to 57 km from the ice margin, where ice thicknesses reach 1180 m, to estimate the impact of constant water pressures on channel growth. Our approach is to examine instead the impact of variable water pressure on basal channel growth, including the effects of water pressures greater than the ice overburden pressure, for regions of interior Greenland ice. Our model produces upper bounds on channel growth by (1) assuming sufficient water supply is available to produce the water pressures that we impose on the upper domain of our channel and (2) forcing water through the channel rather than in linked cavities or in a turbulent sheet. This maximizes the potential for subglacial channel growth; consequently, if sufficient channel growth is not seen in the model, it is unlikely to be possible in reality.

Following Reference FowlerFowler (1999) we model the development of semicircular R-channels by restating the Reference NyeNye (1976) equations in terms of the channel cross-sectional area, S (m²), and the effective pressure, N = P _i – P _w, where P _w is the water pressure and P _i = ρ _i g(h _a – h _b) is the ice overburden pressure with g = 9:81 m s⁻² the acceleration due to gravity, ρ _i = 917 kg m⁻³ the density of ice, and h _a and h _b the elevations of the ice surface and ice bed, respectively. The temporal evolution of the channel cross-sectional area S is

where m _i (m s⁻¹) is the melt rate of the channel walls. The second term on the right-hand side is related to the creep closure of ice, where parameters A = 1.6×10⁻²⁴ s⁻¹ Pa⁻³ and n = 3 from Glen’s flow law control the ice softness. The melting condition through turbulent heat generation is given by

where L = 3.35×10⁵ J kg⁻¹ is the latent heat of fusion, Q (m³ s⁻¹) is the flux of water through the channel and s (m) is the along-flow coordinate. Following Reference ShreveShreve (1972), ψ = ρ _w gh _b + P _w is the hydraulic potential with ρ _w = 1000 kg m⁻³ the density of water. The along-flow gradient of hydraulic potential is given by

The terms in the square brackets represent the geometric portion of the hydraulic potential gradient and are hereafter denoted as ϕ. The effects of geothermal heating and water produced by frictional heating from sliding are ignored because they are likely insignificant compared with the turbulent dissipation of heat generated from the potential gradient (Reference Alley, Lawson, Evenson and LarsonAlley and others, 2003). Using the Gauckler–Manning–Strickler formula for flow, v (m s⁻¹), the cross-sectional mean velocity along the channel, is

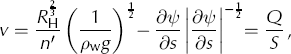
where R _H is the hydraulic radius of a semicircular channel and n’ = 0.05 s m is the Manning roughness coefficient representing a channel wall with medium roughness (Reference Cuffey and PatersonCuffey and Paterson, 2010). Q is therefore given by

Substituting Eqns (2) and (5) into Eqn (1) yields an equation for the time evolution of S:

Model Set-Up

A schematic of the model domain is shown in Figure 1. The geometry of the model domain is chosen to approximate the ice thickness and surface slope at a site ~70 km from the GrIS ice margin in the catchment of Russell Glacier, West Greenland. The site was the location of a rapid supraglacial lake drainage in June 2010 (Reference DoyleDoyle and others, 2013). The domain comprises a segment of channel with length l, with surface water input to the bed at the upstream channel boundary. This channel segment is assumed to be full at all times. The model is driven by changes in effective pressure at the water inlet, used as a proxy for the flux of water input into the surface-to-bed connection. During our lake drainage experiments the water pressure in the connecting moulin (and the upper channel boundary) is constrained by the lake level. For our diurnal moulin drainage experiments, we instead assume sufficient water is available to maintain the variable effective pressure in the moulin that we impose as a model upper boundary condition. The domain length, l, represents the region of the bed we assume is affected by the over- or under-pressure fluxes driven by the pressure in the water inlet; as this quantity is unknown, we test various channel segment lengths to assess the impact on channel growth. For all model runs, the basal and surface topographies are assumed to be planar, with bed (β) and surface (α) angles of 0.20° and 0.35°, respectively. The ice thickness, H, is 1200 m at the upstream end of the domain. The values for β, α and H are averaged from surface and basal digital elevation models (DEMs) of the case study lake site (Reference LindbäckLindbäck and others, 2014). Using these values, the geometric component of the hydraulic potential gradient, ϕ, can be defined as ϕ = ρ _w gβ + ρ _i g(α – β). We assume a constant drop in effective pressure over the channel length segment and as a result ∂N/∂s can be approximated as (N _out – N _in)/l. These approximations can be used to simplify Eqn (6) to a time-dependent ordinary differential equation:

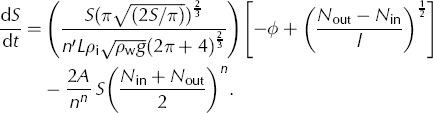
By driving channel growth with effective pressure at the inlet rather than an estimate of surface water volume input, we produce a maximum channel size; in reality, temporally variable water volume flowing through the channel will result in lower water pressures than assumed here and cause channel shrinkage. In addition, by assuming a planar topography we provide the best-case scenario for channel growth in this region; if we instead incorporated basal reverse slopes it would hinder channel growth.

In each experiment, we evolve S using Eqn (7) with an initial condition of S = 0.01 m² to represent an inefficient drainage system. The boundary condition at the domain outlet (Fig. 1) is assumed to be zero effective pressure (N _out = 0) for all experiments. This therefore represents a scenario where the outlet P _w is equal to the ice overburden pressure, a reasonable assumption under thick ice. It is this quality along with the shallow surface slope and thick ice that differentiates our study site from those nearer the margin (e.g. Reference DasDas and others, 2008; Reference Banwell, Willis and ArnoldBanwell and others, 2013; Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013). Closer to the drainage outlet it is likely that channel pressures would drop below overburden, creating a stronger hydraulic potential gradient and allowing greater channel growth. However, to estimate the distance from the margin at which this transition would occur requires a more sophisticated model. For our model approach, configured for interior ice, we vary the upper boundary condition, N _in, close to overburden pressure depending on the model test, as detailed below. All tests are run with a forward Euler method using a time step of 2 min, which allows for model convergence, so that the transient behavior of R-channel growth can be estimated.

Model Limitations

The model discussed in this paper is simplified and its purpose is not to estimate all the basal hydrological conditions of interior GrIS drainage systems. For example, lateral flow into and out of a channel from the surrounding region is not represented in the model. With pressures above overburden, hydraulic jacking will occur and water will be able to flow out into a sheet. However, as we attempt to constrain the upper bounds of channel growth it is interesting to determine the extent of channel development in extreme situations when water pressures are above overburden. This is particularly relevant for our application of this model, since the growth of channels during highly pressured lake drainage events has been suggested to allow evacuation of much of the water at the bed within a matter of hours (Reference DasDas and others, 2008; Reference Hoffman, Catania, Neumann, Andrews and RumrillHoffman and others, 2011; Reference Pimentel and FlowersPimentel and Flowers, 2011).

The presence of a pressurized distributed system adjacent to the channelized system could provide water to the channels when pressures drop below overburden. However, as we drive the model with scenarios when channel pressures are at or very near overburden, we incorporate the possible flux of water from a distributed system into the channels by assuming that sufficient water is available to maintain the imposed pressure gradient. In order to better assess the role of channels versus a distributed system in hydrological development during lake drainage, a more complex coupled model is necessary (e.g. Reference Flowers and ClarkeFlowers and Clarke, 2002; Reference HewittHewitt, 2011; Reference Pimentel and FlowersPimentel and Flowers, 2011; Reference Kingslake and NgKingslake and Ng, 2013). These models also incorporate variable channel growth along the domain, driven by changes in channel discharge. Our model lacks this variability and instead assumes uniform growth over the domain. Applying a more sophisticated model with coupled distributed and channelized drainage along with spatial variability to lake drainage events is an interesting area for future research.

As the channel pressure in our model is coupled directly with the depth of water in a moulin or supraglacial lake, the discharge required to cause that change of pressure in the inlet is not necessarily represented by the flux through the channel. This gives us the ability to put an upper bound on channel formation without having to link to a more complicated system coupled with the surface and/or a basal distributed system. For our purposes, driving channel growth with pressure alone is therefore sufficient.

The limitations in our approach likely lead to an overestimation in the channel growth in interior regions. As a result, it will be valuable for future work with more sophisticated coupled models to investigate the spatial and temporal variations in subglacial hydrology as a result of lake and moulin drainage.

Supraglacial Lake Drainage Experiments

We first apply the R-channel model to examine conduit growth during rapid lake drainage events in regions of kilometer-thick ice. Model input data are supplied from measurements of lake surface lowering during a rapid drainage event at the location in the catchment of Russell Glacier described above. The measured lake elevation is shown by the black curve in Figure 2a and determines the level of overpressure in the model (i.e. N _in < 0). R-channel growth is estimated for the recorded lake drainage event and for three scenarios in which the lake drainage is extended to two, five and ten times its original duration (Fig. 2a) to determine whether longer lake drainage events have a greater impact on subglacial R-channel growth.

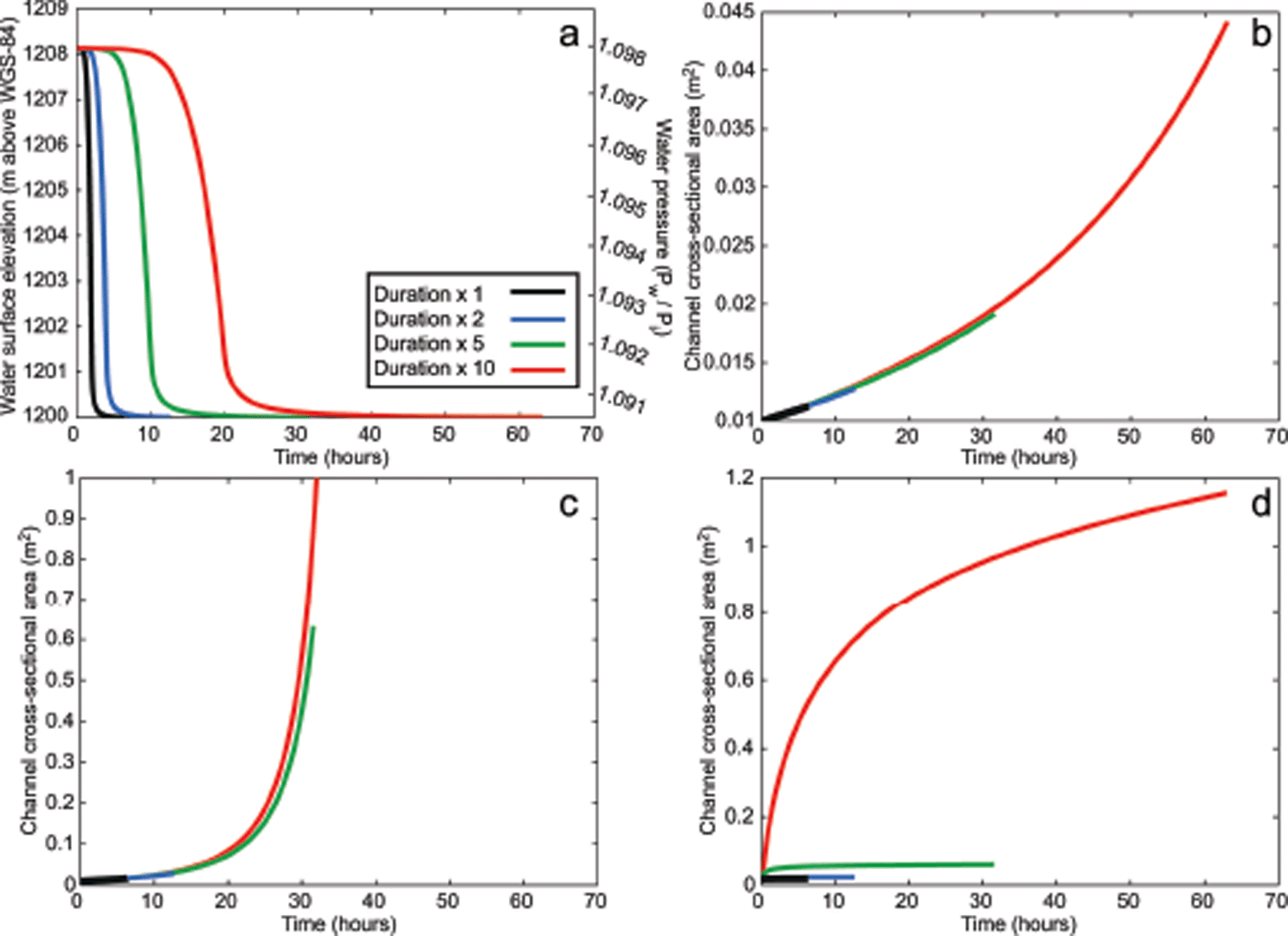
Fig. 2. R-channel model outputs testing the sensitivity of channel development to varying overpressure duration and segment length. (a) Lake surface elevation and water pressure in the surface-to-bed connection. (b) Channel cross-sectional area development over a static overpressurized segment length of 500 m, for the lake drainage durations shown in (a). (c) Channel cross-sectional area development over a static overpressurized segment length of 200 m. (d) Channel cross-sectional area development for a linearly increasing overpressurized segment length between 5 and 5000 m. Note that axes in (b–d) have different scales.

Figure 2b–d show the outputs from the overpressure duration experiment with different domain lengths l; in these experiments, l represents the downstream extent of sub-glacial overpressure during a lake drainage event. Figure 2b shows R-channel growth with l = 500 m. As the overpressure duration is increased, there is little additional channel growth. Even with an overpressure duration ten times that of the case study drainage event (>60 hours), the channel cross-sectional area grows to just ~0.04 m². This channel growth is limited by the relatively large value of l, which prevents a strong hydraulic potential gradient from forming. Figure 2c shows channel growth with a shorter overpressurized segment of l = 200 m. The shorter length over which the water pressure drops has a substantial effect on the growth of R-channels due to the higher pressure gradient driving greater water flux through the channel. Despite this, during the case study lake drainage of 2 hours’ duration, channel cross-sectional area grew to only ~0.02 m². However, if the basal system with l = 200 m is overpressurized for >30 hours, the channels can become large (>10 m²), and at 37 hours the model becomes numerically unstable. In this latter situation, the Reference NyeNye (1976) equations can no longer be used for determining channel growth.

However, it is unlikely that a section of channel would remain overpressurized over longer time periods; water would spread into a distributed system to stabilize the excess pressure (Reference Hewitt, Schoof and WerderHewitt and others, 2012). In the absence of such a process in our model, the length of the over-pressurized segment l will nevertheless also not be static during the lake drainage event due to the downstream flux of water as the drainage proceeds. To account for this, the model is run with a value of l that changes over time. Figure 2d shows R-channel growth when l is increased linearly from 5 to 5000 m over the period of drainage. The rate of increase of l is based on the expansion rate of an overpressurized water blister calculated by Reference Tsai and RiceTsai and Rice (2010) for the Reference DasDas and others (2008) lake drainage event. With this expanding region of overpressure, there is negligible R-channel growth if the duration of lake drainage is extended by five times the recorded drainage time, with the channel cross-sectional area growing to only ~0.06 m². However, for the long (~60 hour) drainage duration, there is greater channel growth, resulting in a channel cross-sectional area of 1.16 m².

These experiments indicate that, due to the limited area available for melting and the smaller fluxes (see Eqns (2) and (4)), small channels grow slowly over a timescale of hours, even with a strong pressure gradient. As a result, we conduct an experiment for assessing the growth of channels of varied initial dimensions with fixed values of l. We use this to investigate the time it would take to entirely drain the case study lake (7.1 × 10⁶ m³), using the Gauckler–Manning–Strickler channel flow criteria detailed in Eqn (4). The upper boundary (N _in; Fig. 1) pressure condition is prescribed from the measured surface lowering rate of the study lake. Following drainage of the lake, the water lowering rate is not known; therefore, in order to estimate upper bounds on channel growth, we apply a linear decrease in pressure towards overburden over a timescale of 3 hours (this simulates water-level lowering within the connecting moulin). After this period, water pressure at the inlet is set at overburden, and R-channel growth is driven only by the geometric hydraulic potential gradient. Figure 3 shows that for an overpressurized segment of 1000 m a large initial channel (>20 m²) is necessary to drain the lake water in <1 day. For a shorter overpressurized segment of 500 m, an initial channel of >7.3 m² is necessary to drain the lake water in <1 day. With a static overpressurized segment of 200 m, an initial channel size of >0.7 m² is required to drain the lake water in <1 day. For channels with initial cross-sectional areas of <1 m² and an overpressurized segment of >500 m, it would take >70 days to drain all the water from the supraglacial lake. For an overpressurized segment of 200 m, a channel of <0.25 m² initial cross-sectional area takes >70 days to drain all the lake water. Our results therefore suggest that a large pre-existing channel is necessary to drain the lake water within 1 day; however, as illustrated earlier, it is unlikely that conditions under kilometer-thick ice would allow growth of a channel of this size either prior to or during lake drainage.

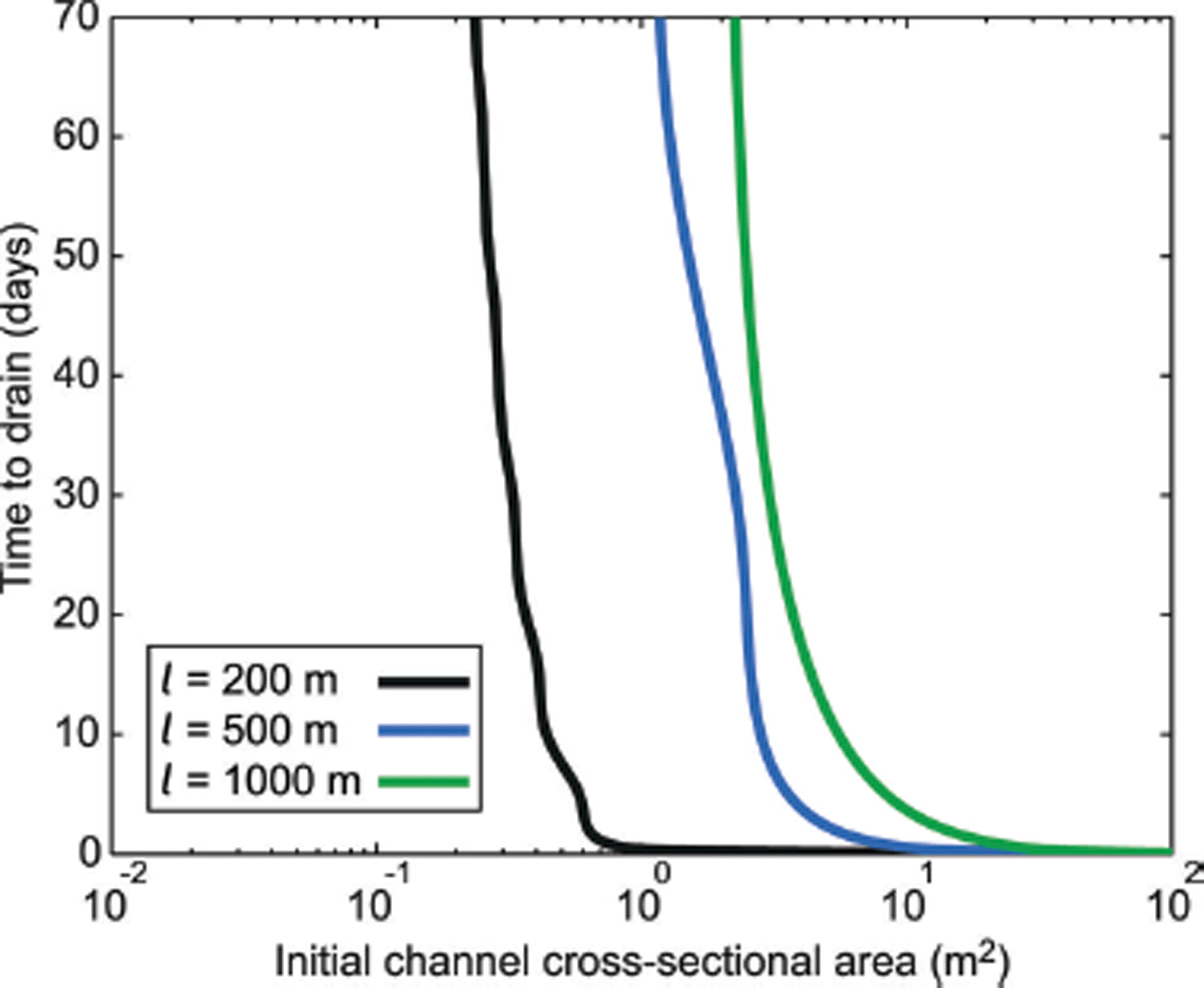
Fig. 3. Time to drain the case study lake determined by channel growth from different initial cross-sectional areas. Outputs are given for static overpressurized segment lengths of 200, 500 and 1000 m.

Moulin Experiments

A large proportion of the water that reaches the bed of the GrIS does so through surface drainage and overtopping of supraglacial lakes that feed into moulins (Reference Selmes, Murray and JamesSelmes and others, 2011; Reference Arnold, Banwell and WillisArnold and others, 2013; Reference FitzpatrickFitzpatrick and others, 2014). Furthermore, rapid lake drainage events form moulins that tap subsequent surface meltwater flux (e.g. Reference DoyleDoyle and others, 2013; Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013). We therefore examine the growth of R-channels as a result of time-varying water input into a moulin, expressed in our model as changes in moulin effective pressure, in an interior region with kilometer-thick ice. We test four pressure scenarios representing water flux over 30 days into hydro-logical systems at various stages of growth (Fig. 4a), with initial channel sizes of 0.01, 0.1, 1 and 10 m² (Fig. 4b–e). Our results indicate that even if water pressures are above overburden for up to 12 hours of the day, pressures below 95% overburden during the remainder of the day prevent channel opening and act to reduce the size of the channel (Fig. 4d–e). Only in the scenario where pressures are continually near or above overburden do the channels become more efficient (Fig. 4b–c).

Fig. 4. Channel development driven by simulated moulin water pressure. (a) Diurnally varying water pressure (as a fraction of overburden). (b–e) Channel cross-sectional area development over 30 days for different initial channel cross-sectional areas between 0.01 and 10 m². Solid curves indicate changes over a static channel segment length of 500 m; dashed curves show changes for a channel segment length of 200 m. Note that axes in (b–e) have different scales. The colors in (b–e) relate to the water pressure driving the model runs, as shown in (a).

Channel Persistence Experiments

Reference SoleSole and others (2013) suggested that the persistence of efficient low-pressure channels following cessation of surface meltwater input is responsible for enhanced slowdown in winters following warmer higher-velocity summers. Determining under what conditions and how long channels can persist is therefore of interest for understanding the dynamic response of the ice sheet to a warming climate (Reference ShannonShannon and others, 2013). We examine channel closure rates under kilometer-thick ice by prescribing the upstream pressure in our model as overburden (N _in = 0) and the downstream pressure less than overburden (N _out > 0). Our approach extends the work of Reference ChandlerChandler and others (2013) who examined closure rates of empty channels under various ice thickness conditions. We instead test closure rates for pressurized channels with cross-sectional areas between 0.1 and 100 m² with model outlet pressures between 50% and 99% of overburden. Owing to the geometric hydraulic potential gradient, the channel will never fully close if filled with water, so instead the critical closure time is determined, defined as the time when the channel cross-sectional area becomes <1 cm².

Our results show that as pressures approach overburden (e.g. 99%), it takes 169 days to close the smallest tested channel and 284 days for a channel of 10 m² (Fig. 5a). At 95% of overburden, channels close more rapidly, although it still takes >10 days to close a channel of 0.1 m² (Fig. 5a). Once pressure at the outlet drops to 90% of overburden, channels can close within 3.5–6.0 days, and at 50% of overburden, channels close within 7–12 hours (Fig. 5b). As a result, high continual pressures are required to prevent rapid channel closure under kilometer-thick ice. The presence of low-pressure channels, on the other hand, is likely precluded by rapid closure times on the scale of hours to days.

Fig. 5. Time for channels of varying cross-sectional area to close, given a drop in pressure from overburden to below overburden. All calculations are applied to a channel segment length of 500 m.

Discussion

Our R-channel model is used to assess the best-case scenario for channel growth and persistence in interior regions of the GrIS. To date, research on Greenland supraglacial lake drainage has assumed that a large channel, either pre-existing (Reference DasDas and others, 2008; Reference Hoffman, Catania, Neumann, Andrews and RumrillHoffman and others, 2011; Reference Pimentel and FlowersPimentel and Flowers, 2011) or developing during the lake drainage event (Sole and others, 2011; Reference CowtonCowton and others, 2013), is necessary to evacuate the substantial volumes of water that drain from supraglacial lakes to the bed. Our model results indicate that, for the measured lake level in the rapid lake drainage case study, significant channel growth does not occur (Fig. 2). Even when the duration of overpressurization is artificially extended, if there is no established drainage system at the bed (e.g. an initial condition of S = 0:01 m²), little channel growth occurs during lake drainage. Our results therefore suggest that the time frame of lake drainage events (often <3 hours of overpressure; Reference DasDas and others, 2008; Reference DoyleDoyle and others, 2013; Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013) is too short to allow substantial channel growth. Several studies (Reference DasDas and others, 2008; Reference Hoffman, Catania, Neumann, Andrews and RumrillHoffman and others, 2011; Reference Pimentel and FlowersPimentel and Flowers, 2011) suggested that a pre-existing channel is necessary to evacuate lake drainage water. In our experiments, if a channel is the only mechanism by which to remove lake drainage water, a pre-existing channel of >20 m² cross-sectional area would be required to evacuate lake drainage water within the period of 1 day (Fig. 3). However, as indicated by both our lake drainage (Fig. 2) and moulin drainage (Fig. 4) experiments, the small pressure gradients at our case study site prevent channel growth to such a size.

It has been shown that lakes tend to drain in bands of increasing elevation, with those downstream draining prior to those upstream (e.g. Reference LiangLiang and others, 2012; Reference FitzpatrickFitzpatrick and others, 2014). This, combined with our model outputs showing limited channel development in regions with shallow surface slopes and small pressure gradients, suggests a large pre-existing channel in the vicinity of interior lake drainage events is unlikely. It is more plausible that water is evacuated from the lake drainage event by a turbulent sheet or linked cavity network instead of a channel alone. Expansion of a turbulent sheet is also suggested by meter-scale ice surface uplift observed in the vicinity of the water input point during rapid supraglacial lake drainage (e.g. Reference DasDas and others, 2008; Reference DoyleDoyle and others, 2013). This uplift can be attributed to hydraulic ice-bed separation and suggests that the capacity of the basal drainage system is not sufficient to rapidly remove the large volume of water from lake drainage events. Instead, the drainage system at the bed becomes highly pressurized, with water spreading into a distributed system or turbulent sheet (e.g. Reference Sugiyama, Bauder, Huss, Riesen and FunkSugiyama and others, 2008). These observations of transient surface uplift support the results of our tests, which suggest that with the short-term but high-volume input associated with interior lake drainage events, efficient channels are unlikely to form.

Longer-term drainage into moulins in high-elevation regions has been argued to have a greater impact on seasonal ice dynamics than rapid lake drainage events (Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013). Our moulin experiments indicate that, under kilometer-thick ice, even if water pressure in the moulin is greater than overburden for up to 12 hours during the daily melt cycle, channel growth is limited if pressures are below 95% overburden during the remainder of the day, and therefore efficient channels cannot persist during the melt season (Fig. 4). Thus, both growing and sustaining channels in interior regions, where shallow surface slopes prevent strong hydraulic potential gradients, require continual high water pressures. Difficulty in maintaining efficient channels in regions of thick ice may explain why drainage into moulins is correlated with increases in local ice velocity, as shown by Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others (2013). Physical evidence to support the assertion that efficient channels do not form in interior regions comes from tracer experiments at a moulin located 57 km from the ice-sheet margin on Russell Glacier (Reference ChandlerChandler and others, 2013). Tracers injected at this location took ~4 days to appear at the glacier front, indicating the presence of a distributed rather than efficient drainage system. These data support our model results which suggest that, even with longer-term sustained water inputs into a moulin system, efficient channels are not likely to occur or be sustained in interior regions of the GrIS.

Efficient channel systems near the ice margin have been argued to impact ice velocity following the end of the melt season by remaining at low pressure and drawing water from the surrounding high-pressure distributed drainage network (Reference Burgess, Larsen and ForsterBurgess and others, 2013; Reference SoleSole and others, 2013; Reference TedstoneTedstone and others, 2013). For kilometer-thick ice, our tests show that a channel of >1 m² cross-sectional area can persist for >250 days if pressures remain at 99% of overburden. The hypothesis that efficient channels mediate winter ice velocities requires lower channel pressures to draw water from nearby distributed systems in order to impact ice dynamics. However, with lower pressures at <90% of overburden, our model results indicate that the channels shut within several days (Fig. 5). The combination of difficulty in growing efficient channels along with rapid closure of low-pressure channels under thick ice suggests that, in interior regions, reduced winter velocities, as seen by Reference SoleSole and others (2013) and Reference TedstoneTedstone and others (2013), are likely due to a lack of water input to the basal system as opposed to the presence of low-pressure efficient channels. For example, cessation of surface water input at the end of the melt season would cause a local paucity of water along the drainage pathways that would be recharged slowly by the more distant distributed system. If, as our model results suggest, the subglacial hydrological systems in interior regions remain distributed and inefficient throughout the year, water input during the summer melt season could cause sustained flow acceleration. Evidence of net year-on-year ice acceleration at two sites 140 km from the margin (Reference DoyleDoyle and others, 2014) supports this assertion.

Our results suggest that channel growth during lake drainage is not an important aspect of basal hydrological development for interior regions of the GrIS, and seasonal drainage allows growth of significantly smaller channels in interior regions than reported for sites nearer the ice-sheet margin. As a result, we suggest that alternative drainage mechanisms (e.g. turbulent sheets in situations of overpressure and linked-cavity systems) should be taken into account when analyzing rapid lake drainage events and interior GrIS hydrological development, as opposed to assuming substantial subglacial channel development, which has been the tendency to date (e.g. Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010, Reference Bartholomew, Nienow, Sole, Mair, Cowton and King2012; Reference CowtonCowton and others, 2013; Reference SoleSole and others, 2013).

Conclusions

Our model results give upper bounds on channel growth in interior regions of the GrIS, where ice is thick and surface slopes are low, producing small pressure gradients. These results suggest that R-channels are unlikely to form during the limited duration of overpressure associated with high-elevation supraglacial lake drainage events. Continued drainage into moulins may form channels, but only if pressures are maintained above overburden. However, closure rates of channels at pressures below 99% of overburden suggest that any interior channels are unlikely to become or remain efficient during the melt season, or to significantly draw water from a surrounding distributed system either during or following the melt season. Our results therefore suggest that analogs from thin alpine and Arctic glaciers (Reference Nienow, Sharp and WillisNienow and others, 1998; Reference Burgess, Larsen and ForsterBurgess and others, 2013; Reference SoleSole and others, 2013) and from nearer the GrIS margin (Reference Bartholomew, Nienow, Mair, Hubbard, King and SoleBartholomew and others, 2010; Reference CowtonCowton and others, 2013) are not directly transferable to interior regions of the ice sheet.