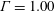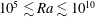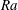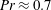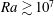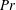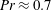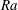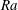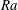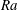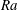1 Introduction
Rayleigh–Bénard convection, i.e. the convection of a horizontal fluid layer heated from below and cooled from above, is an excellent model system to study heat transfer and thermally induced turbulence. For reviews we refer the reader to, for example, Bodenschatz, Pesch & Ahlers (Reference Bodenschatz, Pesch and Ahlers2000), Ahlers (Reference Ahlers2009), Ahlers, Grossmann & Lohse (Reference Ahlers, Grossmann and Lohse2009), Lohse & Xia (Reference Lohse and Xia2010), Chillà & Schumacher (Reference Chillà and Schumacher2012) and Xia (Reference Xia2013). Thermally driven convection is relevant for atmospheric and oceanic flows as well as in numerous industrial processes. One of the important questions is how the heat transfer, which in dimensionless form is expressed as the Nusselt number
![]() $Nu=QL/(\unicode[STIX]{x1D706}\unicode[STIX]{x1D6E5})$
, depends on the Rayleigh number
$Nu=QL/(\unicode[STIX]{x1D706}\unicode[STIX]{x1D6E5})$
, depends on the Rayleigh number
![]() $Ra\equiv \unicode[STIX]{x1D6FD}g\unicode[STIX]{x0394}L^{3}/(\unicode[STIX]{x1D705}\unicode[STIX]{x1D708})$
, the Prandtl number
$Ra\equiv \unicode[STIX]{x1D6FD}g\unicode[STIX]{x0394}L^{3}/(\unicode[STIX]{x1D705}\unicode[STIX]{x1D708})$
, the Prandtl number
![]() $Pr\equiv \unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
and the cell aspect ratio
$Pr\equiv \unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
and the cell aspect ratio
![]() $\unicode[STIX]{x1D6E4}\equiv D/L$
. Here
$\unicode[STIX]{x1D6E4}\equiv D/L$
. Here
![]() $D$
and
$D$
and
![]() $L$
are the diameter and height of the convection cell, respectively,
$L$
are the diameter and height of the convection cell, respectively,
![]() $g$
is the gravitational acceleration,
$g$
is the gravitational acceleration,
![]() $\unicode[STIX]{x1D6FD}$
is the isobaric thermal expansion coefficient,
$\unicode[STIX]{x1D6FD}$
is the isobaric thermal expansion coefficient,
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity,
![]() $\unicode[STIX]{x1D705}$
is the thermal diffusivity and
$\unicode[STIX]{x1D705}$
is the thermal diffusivity and
![]() $\unicode[STIX]{x1D706}$
the thermal conductivity. The temperature difference between the plates is given by
$\unicode[STIX]{x1D706}$
the thermal conductivity. The temperature difference between the plates is given by
![]() $\unicode[STIX]{x1D6E5}\equiv T_{h}-T_{c}$
, where
$\unicode[STIX]{x1D6E5}\equiv T_{h}-T_{c}$
, where
![]() $T_{h}$
and
$T_{h}$
and
![]() $T_{c}$
are the temperature of the bottom and top plate, respectively;
$T_{c}$
are the temperature of the bottom and top plate, respectively;
![]() $Q$
is the heat flux per unit area crossing the fluid layer. Next to the heat transfer, also the time averaged temperature distribution and flow structure in this turbulent system are of great importance. Here we use new experimental measurements, which were performed using several compressed gases with
$Q$
is the heat flux per unit area crossing the fluid layer. Next to the heat transfer, also the time averaged temperature distribution and flow structure in this turbulent system are of great importance. Here we use new experimental measurements, which were performed using several compressed gases with
![]() $Pr\simeq 0.7$
, and direct numerical simulations (DNS) for
$Pr\simeq 0.7$
, and direct numerical simulations (DNS) for
![]() $Pr=0.7$
in cylindrical samples with
$Pr=0.7$
in cylindrical samples with
![]() $\unicode[STIX]{x1D6E4}=1.00$
to address both these issues.
$\unicode[STIX]{x1D6E4}=1.00$
to address both these issues.
For a fluid with a positive thermal expansion coefficient, the applied temperature difference in Rayleigh–Bénard convection is destabilizing in the Earth’s gravitational field. Therefore, convection occurs when the temperature difference is large enough. It is well known that in high
![]() $Ra$
number flow two thin thermal boundary layers, one below the top plate and one above the bottom plate, sustain most of the temperature difference (Ahlers et al.
Reference Ahlers, Grossmann and Lohse2009). The sample interior, or bulk, is then at a nearly uniform temperature close to
$Ra$
number flow two thin thermal boundary layers, one below the top plate and one above the bottom plate, sustain most of the temperature difference (Ahlers et al.
Reference Ahlers, Grossmann and Lohse2009). The sample interior, or bulk, is then at a nearly uniform temperature close to
![]() $T_{M}\equiv (T_{h}+T_{c})/2$
. Naively, one would expect that the temperature gradient in the bulk is destabilizing. Thus, it came as a surprise when measurements for
$T_{M}\equiv (T_{h}+T_{c})/2$
. Naively, one would expect that the temperature gradient in the bulk is destabilizing. Thus, it came as a surprise when measurements for
![]() $Ra$
near
$Ra$
near
![]() $10^{9}$
(Tilgner, Belmonte & Libchaber Reference Tilgner, Belmonte and Libchaber1993; Brown & Ahlers Reference Brown and Ahlers2007) and DNS for
$10^{9}$
(Tilgner, Belmonte & Libchaber Reference Tilgner, Belmonte and Libchaber1993; Brown & Ahlers Reference Brown and Ahlers2007) and DNS for
![]() $Ra=10^{6}$
(Schmalzl, Breuer & Hansen Reference Schmalzl, Breuer and Hansen2002; Breuer et al.
Reference Breuer, Wessling, Schmalzl and Hansen2004) showed that the temperature gradient in the bulk is stabilizing. The measurements of time averaged local temperatures were for
$Ra=10^{6}$
(Schmalzl, Breuer & Hansen Reference Schmalzl, Breuer and Hansen2002; Breuer et al.
Reference Breuer, Wessling, Schmalzl and Hansen2004) showed that the temperature gradient in the bulk is stabilizing. The measurements of time averaged local temperatures were for
![]() $Pr\simeq 5$
in the turbulent state. The DNS clearly showed a stabilizing vertical gradient of the horizontally averaged temperature for
$Pr\simeq 5$
in the turbulent state. The DNS clearly showed a stabilizing vertical gradient of the horizontally averaged temperature for
![]() $Pr=100$
; but at that
$Pr=100$
; but at that
![]() $Pr$
and
$Pr$
and
![]() $Ra=10^{6}$
the system, although probably time dependent, most likely was not turbulent (Krishnamurti Reference Krishnamurti1970). For these high
$Ra=10^{6}$
the system, although probably time dependent, most likely was not turbulent (Krishnamurti Reference Krishnamurti1970). For these high
![]() $Pr$
number cases the thermal diffusivity
$Pr$
number cases the thermal diffusivity
![]() $\unicode[STIX]{x1D705}$
is smaller than the kinematic viscosity
$\unicode[STIX]{x1D705}$
is smaller than the kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
. Therefore, one could argue that plumes emitted from the boundary layers have relatively long lifetimes and can travel along the sidewall to the opposite plate and then drift back to the sample centreline, which creates a stabilizing gradient in the sample interior. For lower
$\unicode[STIX]{x1D708}$
. Therefore, one could argue that plumes emitted from the boundary layers have relatively long lifetimes and can travel along the sidewall to the opposite plate and then drift back to the sample centreline, which creates a stabilizing gradient in the sample interior. For lower
![]() $Pr$
the plume lifetimes are expected to be shorter, and therefore one expects that it is more difficult for plumes to drift back to the sample centreline. However, surprisingly, we find that for
$Pr$
the plume lifetimes are expected to be shorter, and therefore one expects that it is more difficult for plumes to drift back to the sample centreline. However, surprisingly, we find that for
![]() $Ra\gtrsim 10^{7}$
and
$Ra\gtrsim 10^{7}$
and
![]() $Pr<1$
, when
$Pr<1$
, when
![]() $\unicode[STIX]{x1D705}$
is larger than
$\unicode[STIX]{x1D705}$
is larger than
![]() $\unicode[STIX]{x1D708}$
, the gradient at the sample centre remained stabilizing and of approximately the same size as found experimentally for
$\unicode[STIX]{x1D708}$
, the gradient at the sample centre remained stabilizing and of approximately the same size as found experimentally for
![]() $Pr\simeq 5$
. However, in § 4.2 we show that the large scale circulation (LSC) velocity increases with decreasing
$Pr\simeq 5$
. However, in § 4.2 we show that the large scale circulation (LSC) velocity increases with decreasing
![]() $Pr$
due to which plumes that are carried by the LSC can still cause a stabilizing temperature gradient at the cell centre for low
$Pr$
due to which plumes that are carried by the LSC can still cause a stabilizing temperature gradient at the cell centre for low
![]() $Pr$
number fluids.
$Pr$
number fluids.
The influence of the sidewall on heat-transport measurements has been considered by several experimentalists, see, e.g. Ahlers (Reference Ahlers2000), Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001), Niemela & Sreenivasan (Reference Niemela and Sreenivasan2003) and Ahlers et al. (Reference Ahlers, Grossmann and Lohse2009). Rayleigh–Bénard containers are more complex (see, e.g. Niemela et al. (Reference Niemela, Skrbek, Sreenivasan and Donnelly2000) and Zhong & Ahlers (Reference Zhong and Ahlers2010)) than the idealized system with an adiabatic sidewall and isothermal top and bottom plates, which is usually considered in simulations. Experimental cells are limited by the physical properties of the available materials and working fluids. Thus effects like the finite conductivity of the sidewall and the configuration of the insulation and thermal shields might influence the heat transfer and flow structures. Often these effects are accounted for simply by subtracting the corresponding heat current transferred by an empty convection cell. The phenomenological models of Ahlers (Reference Ahlers2000) and Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001) already showed that the thermal coupling between fluid and sidewall makes this procedure in principle inadequate to account for the sidewall effect. The reason is that the vertical temperature profile in the sidewall differs from that in the convecting fluid and therefore there is a lateral heat exchange between sidewall and fluid, which can influence the flow dynamics. To further explore these issues, Verzicco (Reference Verzicco2002) performed DNS of Rayleigh–Bénard convection in a cylindrical container with
![]() $\unicode[STIX]{x1D6E4}=1/2$
in which the effect of the finite conductivity of the sidewall was assessed. He found that for
$\unicode[STIX]{x1D6E4}=1/2$
in which the effect of the finite conductivity of the sidewall was assessed. He found that for
![]() $Ra<10^{9}$
the sidewall effect can change the exponent
$Ra<10^{9}$
the sidewall effect can change the exponent
![]() $\unicode[STIX]{x1D6FC}$
of the power law
$\unicode[STIX]{x1D6FC}$
of the power law
![]() $Nu\sim Ra^{\unicode[STIX]{x1D6FC}}$
by up to 10 %. Later simulations for the same geometry found that changes in the sidewall configurations can trigger different flow organizations (Stevens, Lohse & Verzicco Reference Stevens, Lohse and Verzicco2014). To explore whether sidewall effects may be responsible for the stabilizing gradients seen in experiments, we performed experiments with various fluids and simulations with different sidewall configurations.
$Nu\sim Ra^{\unicode[STIX]{x1D6FC}}$
by up to 10 %. Later simulations for the same geometry found that changes in the sidewall configurations can trigger different flow organizations (Stevens, Lohse & Verzicco Reference Stevens, Lohse and Verzicco2014). To explore whether sidewall effects may be responsible for the stabilizing gradients seen in experiments, we performed experiments with various fluids and simulations with different sidewall configurations.
It is well known that the sidewall can have a strong influence on the critical Rayleigh number
![]() $Ra_{c}$
for the onset of convection (Buell & Catton Reference Buell and Catton1983; Hébert et al.
Reference Hébert, Hufschmid, Scheel and Ahlers2010). In that case,
$Ra_{c}$
for the onset of convection (Buell & Catton Reference Buell and Catton1983; Hébert et al.
Reference Hébert, Hufschmid, Scheel and Ahlers2010). In that case,
![]() $Ra$
and thus also
$Ra$
and thus also
![]() $Ra_{c}$
for a given geometry are determined by the sidewall admittance, which measures how easily the heat transfers from the fluid to the wall,
$Ra_{c}$
for a given geometry are determined by the sidewall admittance, which measures how easily the heat transfers from the fluid to the wall,
Here
![]() $\unicode[STIX]{x1D706}$
is the thermal conductivity of the employed gas, and
$\unicode[STIX]{x1D706}$
is the thermal conductivity of the employed gas, and
![]() $d$
and
$d$
and
![]() $\unicode[STIX]{x1D706}_{w}$
are the sidewall thickness and its thermal conductivity, respectively. For the ideal adiabatic case,
$\unicode[STIX]{x1D706}_{w}$
are the sidewall thickness and its thermal conductivity, respectively. For the ideal adiabatic case,
![]() $C=\infty$
. Although it is not known whether
$C=\infty$
. Although it is not known whether
![]() $C$
is the only important factor at high
$C$
is the only important factor at high
![]() $Ra$
, we were particularly motivated by its influence near the onset. We investigate this by performing experimental measurements for
$Ra$
, we were particularly motivated by its influence near the onset. We investigate this by performing experimental measurements for
![]() $1\lesssim C\lesssim 12$
by using different gases with nearly the same
$1\lesssim C\lesssim 12$
by using different gases with nearly the same
![]() $Pr\simeq 0.7$
, but different conductivities, to vary
$Pr\simeq 0.7$
, but different conductivities, to vary
![]() $C$
. In addition to
$C$
. In addition to
![]() $Nu$
, we determined the temperature gradients near the horizontal mid-plane both on the cylinder axis and close to the sidewall. While these gradients were stabilizing and (within our resolution) independent of the used fluid when
$Nu$
, we determined the temperature gradients near the horizontal mid-plane both on the cylinder axis and close to the sidewall. While these gradients were stabilizing and (within our resolution) independent of the used fluid when
![]() $Ra$
was high, they did depend on the chosen gas (and thus on
$Ra$
was high, they did depend on the chosen gas (and thus on
![]() $C$
) for
$C$
) for
![]() $Ra\lesssim 10^{7}$
. For comparison, we performed simulations using the physical properties of neon with adiabatic boundary conditions at the side as well as with a wall domain with wall properties equal to those of the experiment included. While the adiabatic boundary condition corresponds to
$Ra\lesssim 10^{7}$
. For comparison, we performed simulations using the physical properties of neon with adiabatic boundary conditions at the side as well as with a wall domain with wall properties equal to those of the experiment included. While the adiabatic boundary condition corresponds to
![]() $C\rightarrow \infty$
, see (1.1), the wall–neon combination has the same
$C\rightarrow \infty$
, see (1.1), the wall–neon combination has the same
![]() $C=3.9$
as the experimental system. We also consider simulations with helium as working gas in a cell with a Plexiglas sidewall, which corresponds to
$C=3.9$
as the experimental system. We also consider simulations with helium as working gas in a cell with a Plexiglas sidewall, which corresponds to
![]() $C=12$
, and additional insulation layers and sidewall shields.
$C=12$
, and additional insulation layers and sidewall shields.
The presented simulations are complementary to the experiments as the simulations allow us to study the flow structures in more detail. We also use the simulations to test various sidewall configurations to assess the influence of different sample designs. To achieve this we employ, in contrast to most DNS, a more realistic model based on the Navier–Stokes–Brinkman equation in combination with the immersed boundary method to simulate the effect of the sidewall and insulation layers as a conjugate heat transfer problem. A similar modelling approach was followed by Stevens et al. (Reference Stevens, Lohse and Verzicco2014). However, in contrast to the previous study, we now present a direct comparison between experiments and simulations. In addition, Stevens et al. (Reference Stevens, Lohse and Verzicco2014) mainly focused on the effect of the sidewall on the
![]() $Nu$
number. However, now we also assess the effect of the thermal sidewall properties on the LSC. We will show that the sidewall can influence the LSC in such a way that a destabilizing temperature gradient at the cylinder axis is created for lower
$Nu$
number. However, now we also assess the effect of the thermal sidewall properties on the LSC. We will show that the sidewall can influence the LSC in such a way that a destabilizing temperature gradient at the cylinder axis is created for lower
![]() $Ra$
. Clearly, this continuous effort to accurately model the interaction between the sidewall and flow dynamics using DNS is necessary to get a better understanding of the effect this interplay may have on the heat transfer and flow structures in Rayleigh–Bénard convection. However, we emphasize that due to the complicated interactions between fluid and sidewall, and the difficulty in identifying all relevant design parameters, it remains impossible to reproduce all experimental details.
$Ra$
. Clearly, this continuous effort to accurately model the interaction between the sidewall and flow dynamics using DNS is necessary to get a better understanding of the effect this interplay may have on the heat transfer and flow structures in Rayleigh–Bénard convection. However, we emphasize that due to the complicated interactions between fluid and sidewall, and the difficulty in identifying all relevant design parameters, it remains impossible to reproduce all experimental details.
The paper has the following structure: in §§ 2 and 3 we describe the experimental and numerical procedures. In § 4, we present the experimental measurements in comparison with the simulation results obtained with an ideal adiabatic sidewall. In an attempt to explain the differences between experiments and idealized simulations, we discuss the effect of the sidewall on the heat transport and flow dynamics in § 5. We conclude with a summary and conclusion in § 6.
2 The apparatus
The overall features of the apparatus were described in detail before by Zhong & Ahlers (Reference Zhong and Ahlers2010). We used a sample with thick copper top and bottom plates and a Plexiglas (poly(methyl methacrylate)) sidewall of thickness
![]() $d_{w}=6.4$
mm. The inside dimensions were
$d_{w}=6.4$
mm. The inside dimensions were
![]() $L=D=190.5$
mm, yielding an aspect ratio
$L=D=190.5$
mm, yielding an aspect ratio
![]() $\unicode[STIX]{x1D6E4}=1.00$
.
$\unicode[STIX]{x1D6E4}=1.00$
.
A groove in the top and bottom plates directly below or above the sidewall contained an ‘O’-ring that sealed the sidewall to the plates. Two aluminium brackets, one above the top and the other below the bottom plate, pressed the plates against the ‘O’-rings and the sidewall. This compression was achieved by six steel tension rods connecting the brackets and located at a diameter larger than that of the sidewall. A thin Teflon capillary penetrated the sidewall at mid-height and was used to fill the sample. Externally the capillary was connected to the fill line coming from the gas supply cylinder, as well as to a pressure gage (Paroscientific Model 745) and another volume known as the ‘hot volume’ (HV) (Mueller, Ahlers & Pobell Reference Mueller, Ahlers and Pobell1976). The HV had a size similar to that of the sample, and its temperature could be adjusted in a feedback loop with the pressure gage to keep the sample pressure constant. Over several days the HV temperature typically increased because of the gradual diffusion of the sample gases through the Plexiglas sidewall of the sample. The diffusion rate is higher for the lighter gases. At a pressure of 4 bars, the HV heating rate was approximately
![]() $2\times 10^{-4}~\text{K}~\text{s}^{-1}$
when the sample was filled with helium and approximately
$2\times 10^{-4}~\text{K}~\text{s}^{-1}$
when the sample was filled with helium and approximately
![]() $5\times 10^{-5}~\text{K}~\text{s}^{-1}$
when
$5\times 10^{-5}~\text{K}~\text{s}^{-1}$
when
![]() $\text{SF}_{6}$
was used. The acceptable temperature range for the HV was from
$\text{SF}_{6}$
was used. The acceptable temperature range for the HV was from
![]() $20\,^{\circ }\text{C}$
to
$20\,^{\circ }\text{C}$
to
![]() $60\,^{\circ }\text{C}$
and this allowed operation for several days without adding more sample gas. We used sample pressures from 4 bars to somewhat below 1 bar.
$60\,^{\circ }\text{C}$
and this allowed operation for several days without adding more sample gas. We used sample pressures from 4 bars to somewhat below 1 bar.
The plate temperatures and the heat flux applied to a bottom-plate heater were used to determine the
![]() $Nu$
number
$Nu$
number
![]() $Nu=\unicode[STIX]{x1D706}_{eff}/\unicode[STIX]{x1D706}$
, where
$Nu=\unicode[STIX]{x1D706}_{eff}/\unicode[STIX]{x1D706}$
, where
![]() $\unicode[STIX]{x1D706}_{eff}=LQ/\unicode[STIX]{x1D6E5}$
, and
$\unicode[STIX]{x1D706}_{eff}=LQ/\unicode[STIX]{x1D6E5}$
, and
![]() $Q$
is the heat current. It is obtained as
$Q$
is the heat current. It is obtained as
![]() $Q=Q_{t}-Q_{p}$
, where
$Q=Q_{t}-Q_{p}$
, where
![]() $Q_{t}$
is the total current and
$Q_{t}$
is the total current and
![]() $Q_{p}$
the parasitic current, mainly through the sidewall. The total power
$Q_{p}$
the parasitic current, mainly through the sidewall. The total power
![]() $Q_{t}$
dissipated in the bottom-plate heater was determined from the heater current and voltage. The parasitic current
$Q_{t}$
dissipated in the bottom-plate heater was determined from the heater current and voltage. The parasitic current
![]() $Q_{p}$
was based on measurement with a nearly empty cell where no convection took place. That measurement had to be corrected for the conductive heat current due to the remaining quiescent gas to yield
$Q_{p}$
was based on measurement with a nearly empty cell where no convection took place. That measurement had to be corrected for the conductive heat current due to the remaining quiescent gas to yield
![]() $Q_{p}$
. There were contributions to
$Q_{p}$
. There were contributions to
![]() $Q_{p}$
from several sources. Some of the currents passed through the foam insulation to an isothermal shield maintained at
$Q_{p}$
from several sources. Some of the currents passed through the foam insulation to an isothermal shield maintained at
![]() $T_{M}$
. Another part was conducted by the tension rods to the water reservoir above the top plate. The sidewall conducted the remaining part. The current
$T_{M}$
. Another part was conducted by the tension rods to the water reservoir above the top plate. The sidewall conducted the remaining part. The current
![]() $Q=Q_{t}-Q_{p}$
was used to obtain a preliminary estimate
$Q=Q_{t}-Q_{p}$
was used to obtain a preliminary estimate
![]() $Nu_{0}$
of
$Nu_{0}$
of
![]() $Nu$
. An estimate of the current
$Nu$
. An estimate of the current
![]() $Q_{w}$
passing through the sidewall based on the sidewall geometry and conductivity was then used to correct
$Q_{w}$
passing through the sidewall based on the sidewall geometry and conductivity was then used to correct
![]() $Nu_{0}$
for the nonlinear sidewall effect, as discussed by Ahlers (Reference Ahlers2000) and Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001), to yield our final estimate of
$Nu_{0}$
for the nonlinear sidewall effect, as discussed by Ahlers (Reference Ahlers2000) and Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001), to yield our final estimate of
![]() $Nu$
.
$Nu$
.
While the above corrections to
![]() $Q_{t}$
and
$Q_{t}$
and
![]() $Nu_{0}$
typically are only of modest size when fluids such as water with relatively high conductivity are used, they become more critical for gases where the conductivities can be much smaller. For example, at
$Nu_{0}$
typically are only of modest size when fluids such as water with relatively high conductivity are used, they become more critical for gases where the conductivities can be much smaller. For example, at
![]() $25\,^{\circ }\text{C}$
the conductivities of water and
$25\,^{\circ }\text{C}$
the conductivities of water and
![]() $\text{SF}_{6}$
differ by a factor of approximately 50. For helium, the difference is approximately a factor 4. As we shall see below, there is good agreement between the
$\text{SF}_{6}$
differ by a factor of approximately 50. For helium, the difference is approximately a factor 4. As we shall see below, there is good agreement between the
![]() $Nu$
values obtained using all different working gases even though their conductivities vary significantly, see table 2, and the corrections to
$Nu$
values obtained using all different working gases even though their conductivities vary significantly, see table 2, and the corrections to
![]() $Q_{t}$
and
$Q_{t}$
and
![]() $Nu_{0}$
differ widely.
$Nu_{0}$
differ widely.
There were six Honeywell type 111-104HAK-H01 thermistors inside the sample. Of these we used four in the present work. Their locations are given in table 1. Two each were mounted near the end of a ceramic rod (Omega ceramic thermocouple insulators of type FRA-005132) with an outside diameter of 0.90 mm as described elsewhere (Ahlers, Bodenschatz & He Reference Ahlers, Bodenschatz and He2014; Wei & Ahlers Reference Wei and Ahlers2014; He et al.
Reference He, van Gils, Bodenschatz and Ahlers2015). Each thermistor lead passed through a 0.13 mm diameter hole in the rod and parallel to the rod axis. The rods were inserted through holes, also of nominally 0.90 mm diameter, in the 6.4 mm thick sidewall. The rods terminated near the outside of the sidewall, and there they as well as the uninsulated leads were sealed to the sidewall with epoxy. Four thermistors (held by two rods) were located on the sample axis. The remaining two were located near the sidewall at
![]() $\unicode[STIX]{x1D709}\equiv (D/2-r)/(D/2)=0.13$
, where
$\unicode[STIX]{x1D709}\equiv (D/2-r)/(D/2)=0.13$
, where
![]() $r$
is the horizontal distance from the cylinder axis. This means that
$r$
is the horizontal distance from the cylinder axis. This means that
![]() $\unicode[STIX]{x1D709}=1$
at the centre axis (
$\unicode[STIX]{x1D709}=1$
at the centre axis (
![]() $r=0$
) and
$r=0$
) and
![]() $\unicode[STIX]{x1D709}=0$
at the sidewall (
$\unicode[STIX]{x1D709}=0$
at the sidewall (
![]() $r=D/2$
).
$r=D/2$
).
Table 1. The identifiers, ID, and the radial and vertical locations of the internal thermistors. The sample height was
![]() $L=190.5$
mm and the radius was
$L=190.5$
mm and the radius was
![]() $R=95.2$
mm. The angle
$R=95.2$
mm. The angle
![]() $\unicode[STIX]{x1D703}_{int}$
(in rad) is the azimuthal location (relative to an arbitrary origin) for each thermometer, measured in a counter-clockwise direction when viewed from above.
$\unicode[STIX]{x1D703}_{int}$
(in rad) is the azimuthal location (relative to an arbitrary origin) for each thermometer, measured in a counter-clockwise direction when viewed from above.

While the vertical hole locations in the sidewall were known with high accuracy, there were two possible contributions to the uncertainties of the vertical thermistor locations. One came from any tilt of the rods relative to a line orthogonal to the cylinder axis. We believe this to be very small, probably no more than 0.2 mm on the sample axis and much less near the sidewall. Another possible contribution came from the suspension of the thermistors by their 0.10 mm diameter platinum leads (see e.g. figure 2 of He et al. (Reference He, van Gils, Bodenschatz and Ahlers2015)). Because of the fragile nature of these leads, there is an uncertainty of approximately 0.3 mm in the vertical position of the thermistor centre. Thus the total uncertainty is close to 0.5 mm. Similarly, we estimate that the uncertainty of the distance
![]() $\unicode[STIX]{x1D6FF}z$
between the two thermistors used to measure the temperature gradient is approximately 0.7 mm.
$\unicode[STIX]{x1D6FF}z$
between the two thermistors used to measure the temperature gradient is approximately 0.7 mm.
We used the thermistor pairs (V0-1, V0-4) on the centreline (
![]() $\unicode[STIX]{x1D709}=1.00$
) and (V1-1, V1-2) near the sidewall (
$\unicode[STIX]{x1D709}=1.00$
) and (V1-1, V1-2) near the sidewall (
![]() $\unicode[STIX]{x1D709}=0.13$
) for the temperature-gradient measurements, see table 1 for details. Thus for
$\unicode[STIX]{x1D709}=0.13$
) for the temperature-gradient measurements, see table 1 for details. Thus for
![]() $\unicode[STIX]{x1D709}=1.00$
the separation between the two sensors was
$\unicode[STIX]{x1D709}=1.00$
the separation between the two sensors was
![]() $\unicode[STIX]{x1D6FF}z=21.6\pm 0.7$
mm, while for
$\unicode[STIX]{x1D6FF}z=21.6\pm 0.7$
mm, while for
![]() $\unicode[STIX]{x1D709}=0.13$
it was only
$\unicode[STIX]{x1D709}=0.13$
it was only
![]() $\unicode[STIX]{x1D6FF}z=4.0\pm 0.7$
mm. The corresponding uncertainties of the gradients, due to the uncertainties of the measurement geometry, were
$\unicode[STIX]{x1D6FF}z=4.0\pm 0.7$
mm. The corresponding uncertainties of the gradients, due to the uncertainties of the measurement geometry, were
![]() $\pm 3\,\%$
for
$\pm 3\,\%$
for
![]() $\unicode[STIX]{x1D709}=1.00$
and
$\unicode[STIX]{x1D709}=1.00$
and
![]() $\pm 17\,\%$
for
$\pm 17\,\%$
for
![]() $\unicode[STIX]{x1D709}=0.13$
.
$\unicode[STIX]{x1D709}=0.13$
.
Table 2. Properties of the employed fluids at
![]() $25\,^{\circ }\text{C}$
and
$25\,^{\circ }\text{C}$
and
![]() $P=1$
bar. The Plexiglas sidewall conductivity was taken to be
$P=1$
bar. The Plexiglas sidewall conductivity was taken to be
![]() $0.0019~\text{W}~\text{cm}^{-1}~\text{K}^{-1}$
. The properties
$0.0019~\text{W}~\text{cm}^{-1}~\text{K}^{-1}$
. The properties
![]() $Pr$
,
$Pr$
,
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $C$
are nearly independent of the pressure
$C$
are nearly independent of the pressure
![]() $P$
while
$P$
while
![]() $\unicode[STIX]{x1D6FD}/(\unicode[STIX]{x1D705}\unicode[STIX]{x1D708})$
is approximately proportional to
$\unicode[STIX]{x1D6FD}/(\unicode[STIX]{x1D705}\unicode[STIX]{x1D708})$
is approximately proportional to
![]() $P^{2}$
.
$P^{2}$
.

We used the gases listed in table 2. Nearly all of the measurements were made with
![]() $T_{M}$
close to
$T_{M}$
close to
![]() $25\,^{\circ }\text{C}$
. Some of the sample properties at
$25\,^{\circ }\text{C}$
. Some of the sample properties at
![]() $25\,^{\circ }\text{C}$
and a pressure
$25\,^{\circ }\text{C}$
and a pressure
![]() $P=1$
bar are also given in the table. Each gas could be employed up to 4 bars. This allowed measurements over a little more than a decade of
$P=1$
bar are also given in the table. Each gas could be employed up to 4 bars. This allowed measurements over a little more than a decade of
![]() $Ra$
for a given gas since
$Ra$
for a given gas since
![]() $Ra$
for gases is approximately proportional to
$Ra$
for gases is approximately proportional to
![]() $P^{2}$
. The
$P^{2}$
. The
![]() $Ra$
-range covered was different for each gas because the parameter combination
$Ra$
-range covered was different for each gas because the parameter combination
![]() $\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D705}\unicode[STIX]{x1D708}$
is different, see table 2.
$\unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D705}\unicode[STIX]{x1D708}$
is different, see table 2.
In this work, we neglected the influence of the adiabatic temperature gradient, which can play a significant role in convection experiments using compressed gases (Landau & Lifshitz Reference Landau and Lifshitz1987; Chavanne et al. Reference Chavanne, Chillà, Chabaud, Castaing, Chaussy and Hébral1996; Ashkenazi & Steinberg Reference Ashkenazi and Steinberg1999), especially near their critical points. This gradient is given by
where
![]() $T_{M}$
is the absolute mean temperature and
$T_{M}$
is the absolute mean temperature and
![]() $C_{p}$
is the heat capacity per unit mass. This gradient is largest for the heaviest gas; in our case for
$C_{p}$
is the heat capacity per unit mass. This gradient is largest for the heaviest gas; in our case for
![]() $\text{SF}_{6}$
. However, even for
$\text{SF}_{6}$
. However, even for
![]() $\text{SF}_{6}$
, the adiabatic temperature gradient was well below
$\text{SF}_{6}$
, the adiabatic temperature gradient was well below
![]() $10^{-3}$
. Thus we did not make any corrections for this effect.
$10^{-3}$
. Thus we did not make any corrections for this effect.
For our experiments, the shift
![]() $(T_{0}-T_{M})/\unicode[STIX]{x1D6E5}$
of the centre temperature
$(T_{0}-T_{M})/\unicode[STIX]{x1D6E5}$
of the centre temperature
![]() $T_{0}$
relative to the mean temperature of
$T_{0}$
relative to the mean temperature of
![]() $T_{M}$
spanned the range from 0.008 to 0.018. While this corresponds to samples that are usually regarded as being well represented by the Boussinesq approximation, these values are comparable to those that we report for the temperature gradients. However, in our view, the two are unrelated. While non-Oberbeck–Boussinesq (NOB) effects create unequal temperature drops across the two horizontal boundary layers, they leave the temperature variation (and thus the variations of any fluid properties) in the bulk quite small. Thus we think the modest NOB effects do not affect the results on the temperature gradient in the bulk.
$T_{M}$
spanned the range from 0.008 to 0.018. While this corresponds to samples that are usually regarded as being well represented by the Boussinesq approximation, these values are comparable to those that we report for the temperature gradients. However, in our view, the two are unrelated. While non-Oberbeck–Boussinesq (NOB) effects create unequal temperature drops across the two horizontal boundary layers, they leave the temperature variation (and thus the variations of any fluid properties) in the bulk quite small. Thus we think the modest NOB effects do not affect the results on the temperature gradient in the bulk.
For most of the explored
![]() $Ra$
number range in this work the LSC consists of a single convection roll. In a perfect sample, where the only perturbation of the azimuthally invariant geometry is the Coriolis force due to Earth’s rotation, one expects the LSC orientation to have a broad distribution with a maximum slightly north of west (see, e.g. Brown & Ahlers (Reference Brown and Ahlers2006, Reference Brown and Ahlers2008b
) and references therein). In a real sample, the azimuthal invariance often is also broken by unintended inhomogeneities, and the LSC circulation plane assumes a preferred orientation (Brown & Ahlers Reference Brown and Ahlers2008a
). In our case, the insertion of the ceramic rods carrying the thermistors breaks this invariance. Separate measurements using thermometers located in the sidewall at the horizontal mid-plane of the sample and at eight azimuthal positions (Brown, Nikolaenko & Ahlers Reference Brown, Nikolaenko and Ahlers2005) showed that the downflow of the LSC had a preferred orientation near
$Ra$
number range in this work the LSC consists of a single convection roll. In a perfect sample, where the only perturbation of the azimuthally invariant geometry is the Coriolis force due to Earth’s rotation, one expects the LSC orientation to have a broad distribution with a maximum slightly north of west (see, e.g. Brown & Ahlers (Reference Brown and Ahlers2006, Reference Brown and Ahlers2008b
) and references therein). In a real sample, the azimuthal invariance often is also broken by unintended inhomogeneities, and the LSC circulation plane assumes a preferred orientation (Brown & Ahlers Reference Brown and Ahlers2008a
). In our case, the insertion of the ceramic rods carrying the thermistors breaks this invariance. Separate measurements using thermometers located in the sidewall at the horizontal mid-plane of the sample and at eight azimuthal positions (Brown, Nikolaenko & Ahlers Reference Brown, Nikolaenko and Ahlers2005) showed that the downflow of the LSC had a preferred orientation near
![]() $\unicode[STIX]{x1D703}_{d}=0.3$
, i.e. very close to the location of the sensor position at
$\unicode[STIX]{x1D703}_{d}=0.3$
, i.e. very close to the location of the sensor position at
![]() $\unicode[STIX]{x1D703}_{int}=\unicode[STIX]{x03C0}/8$
, see table 1. We would expect the downflow to be relatively cold, leading to a reduced mean temperature. It is not clear whether the downflow influenced the temperature gradient. As we only have one azimuthal measurement location, it is not possible to determine any statistical (or systematic) uncertainties in the measured mean temperature gradient. We expect that the preferred LSC orientation does not influence the temperature-gradient measurements at the sample centre.
$\unicode[STIX]{x1D703}_{int}=\unicode[STIX]{x03C0}/8$
, see table 1. We would expect the downflow to be relatively cold, leading to a reduced mean temperature. It is not clear whether the downflow influenced the temperature gradient. As we only have one azimuthal measurement location, it is not possible to determine any statistical (or systematic) uncertainties in the measured mean temperature gradient. We expect that the preferred LSC orientation does not influence the temperature-gradient measurements at the sample centre.
3 Numerical procedures
In the simulations, we solve the non-dimensional Navier–Stokes equations within the Boussinesq approximation (Verzicco Reference Verzicco2002; Stevens et al. Reference Stevens, Lohse and Verzicco2014) in combination with an immersed boundary method (Fadlun et al. Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000) to account for the heat transfer in the sidewall and insulation layer. The corresponding equations read,
where
![]() $\boldsymbol{f}$
and
$\boldsymbol{f}$
and
![]() $h$
are forcing terms whose values depend on the particular locations in the computational domain:
$h$
are forcing terms whose values depend on the particular locations in the computational domain:
(i)
 $\boldsymbol{f}=0$
and
$\boldsymbol{f}=0$
and
 $h=0$
in the fluid domain. The (3.1)–(3.2) reduce to the Navier–Stokes and convection–diffusion temperature equations.
$h=0$
in the fluid domain. The (3.1)–(3.2) reduce to the Navier–Stokes and convection–diffusion temperature equations.(ii)
 $\boldsymbol{f}$
is determined according to Fadlun et al. (Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000) to ensure that
$\boldsymbol{f}$
is determined according to Fadlun et al. (Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000) to ensure that
 $\boldsymbol{u}=0$
within the solid parts, i.e. sidewall and thermal shields, see figure 1. Similarly,
$\boldsymbol{u}=0$
within the solid parts, i.e. sidewall and thermal shields, see figure 1. Similarly,
 $h$
is computed to impose the desired temperature within the thermal shields while it is set to zero within those solid regions where temperature is to be determined as part of the solution.
$h$
is computed to impose the desired temperature within the thermal shields while it is set to zero within those solid regions where temperature is to be determined as part of the solution.(iii)
 $\boldsymbol{f}=-\boldsymbol{u}/K$
in the insulation layer, where
$\boldsymbol{f}=-\boldsymbol{u}/K$
in the insulation layer, where
 $K$
is the porosity. Equation (3.1) is then referred to as the Navier–Stokes–Brinkman equation. Here we use the same value as Stevens et al. (Reference Stevens, Lohse and Verzicco2014), i.e.
$K$
is the porosity. Equation (3.1) is then referred to as the Navier–Stokes–Brinkman equation. Here we use the same value as Stevens et al. (Reference Stevens, Lohse and Verzicco2014), i.e.
 $K=10$
, to ensure that the velocities in the insulation layer are an order of magnitude smaller than in the fluid. Within the insulation layer we set
$K=10$
, to ensure that the velocities in the insulation layer are an order of magnitude smaller than in the fluid. Within the insulation layer we set
 $h=0$
since no conditions on the temperature are imposed.
$h=0$
since no conditions on the temperature are imposed.

Figure 1. Sketch of numerical set-up with sidewall, insulation layer and thermal side shields. The aspect ratio of the fluid domain
![]() $\unicode[STIX]{x1D6E4}=2R_{f}/L=1$
. The Plexiglas sidewall has a thickness
$\unicode[STIX]{x1D6E4}=2R_{f}/L=1$
. The Plexiglas sidewall has a thickness
![]() $e=R_{w}-R_{f}=L/30$
such that
$e=R_{w}-R_{f}=L/30$
such that
![]() $R_{w}=0.53333L$
. The insulation layer has a thickness
$R_{w}=0.53333L$
. The insulation layer has a thickness
![]() $L_{F}=0.2L$
. For the inner thermal side shields
$L_{F}=0.2L$
. For the inner thermal side shields
![]() $L_{sc}=0.015L$
with square cross-section. The outer thermal shield has a thickness of
$L_{sc}=0.015L$
with square cross-section. The outer thermal shield has a thickness of
![]() $0.02L$
and a height
$0.02L$
and a height
![]() $L_{s}=0.96L$
, and its inner edge is located at
$L_{s}=0.96L$
, and its inner edge is located at
![]() $0.6L$
from the cylinder axis. The outer surface of insulation layer is assumed to be isothermal at
$0.6L$
from the cylinder axis. The outer surface of insulation layer is assumed to be isothermal at
![]() $\unicode[STIX]{x1D703}=(T_{c}+T_{h})/2=T_{M}$
. The temperatures of the entire bottom and top plates are fixed at
$\unicode[STIX]{x1D703}=(T_{c}+T_{h})/2=T_{M}$
. The temperatures of the entire bottom and top plates are fixed at
![]() $T_{h}$
and
$T_{h}$
and
![]() $T_{c}$
, respectively. The thermal probes are placed at
$T_{c}$
, respectively. The thermal probes are placed at
![]() $z=0.4L$
and
$z=0.4L$
and
![]() $z=0.51L$
for
$z=0.51L$
for
![]() $\unicode[STIX]{x1D709}=1.0$
(
$\unicode[STIX]{x1D709}=1.0$
(
![]() $r=0$
), while they are placed at
$r=0$
), while they are placed at
![]() $z=0.49L$
and
$z=0.49L$
and
![]() $z=0.51L$
for
$z=0.51L$
for
![]() $\unicode[STIX]{x1D709}=0.13$
(
$\unicode[STIX]{x1D709}=0.13$
(
![]() $r=0.435L$
).
$r=0.435L$
).
In the above equations,
![]() $\unicode[STIX]{x1D703}$
is the non-dimensional temperature,
$\unicode[STIX]{x1D703}$
is the non-dimensional temperature,
![]() $\boldsymbol{u}$
the velocity,
$\boldsymbol{u}$
the velocity,
![]() $p$
the pressure,
$p$
the pressure,
![]() $\hat{z}$
the unit vector pointing in the opposite direction to gravity. No-slip boundary conditions are employed at all solid surfaces and a constant temperature of
$\hat{z}$
the unit vector pointing in the opposite direction to gravity. No-slip boundary conditions are employed at all solid surfaces and a constant temperature of
![]() $T_{h}$
and
$T_{h}$
and
![]() $T_{c}$
is used at the bottom and top plate, respectively. The equations are non-dimensionalized by the fluid sample height
$T_{c}$
is used at the bottom and top plate, respectively. The equations are non-dimensionalized by the fluid sample height
![]() $L$
, the temperature difference
$L$
, the temperature difference
![]() $\unicode[STIX]{x1D6E5}=T_{h}-T_{c}$
between the plates, and the free-fall velocity
$\unicode[STIX]{x1D6E5}=T_{h}-T_{c}$
between the plates, and the free-fall velocity
![]() $U=\sqrt{\unicode[STIX]{x1D6FD}g\unicode[STIX]{x0394}L}$
.
$U=\sqrt{\unicode[STIX]{x1D6FD}g\unicode[STIX]{x0394}L}$
.
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $C^{p}$
and
$C^{p}$
and
![]() $\unicode[STIX]{x1D706}$
are, respectively, the density, the constant pressure specific heat and the thermal conductivity. The subscript
$\unicode[STIX]{x1D706}$
are, respectively, the density, the constant pressure specific heat and the thermal conductivity. The subscript
![]() $f$
refers to the properties of the fluid, while the same quantities have different values in the sidewall or the insulation layer;
$f$
refers to the properties of the fluid, while the same quantities have different values in the sidewall or the insulation layer;
![]() $R_{f}$
is the radius of the fluid domain and
$R_{f}$
is the radius of the fluid domain and
![]() $R_{w}$
the radius, including the sidewall thickness. The radial dimension of the computational domain is
$R_{w}$
the radius, including the sidewall thickness. The radial dimension of the computational domain is
![]() $R_{w}+L_{f}$
, which also includes the insulating foam layer and the thermal shields when present. This allows the entire domain to be considered in a unified computational framework. Details about the implementation of the above scheme can be found in appendix A.
$R_{w}+L_{f}$
, which also includes the insulating foam layer and the thermal shields when present. This allows the entire domain to be considered in a unified computational framework. Details about the implementation of the above scheme can be found in appendix A.
In § 4, we compare the experimental measurements with simulations in which we use an ideal adiabatic sidewall. Subsequently, in § 5, we consider the conjugate heat transfer problem of a finite-thickness sidewall with physical properties. Initially, we only include the Plexiglas sidewall, assuming that the temperature boundary condition on the ‘dry’ side (
![]() $r=R_{w}$
) is isothermal at
$r=R_{w}$
) is isothermal at
![]() $T_{M}=(T_{c}+T_{h})/2$
to mimic the nearly constant environmental temperature provided by the insulation layer in the experimental apparatus (Zhong & Ahlers Reference Zhong and Ahlers2010). We note that no temperature boundary condition is required at the fluid–sidewall interface (
$T_{M}=(T_{c}+T_{h})/2$
to mimic the nearly constant environmental temperature provided by the insulation layer in the experimental apparatus (Zhong & Ahlers Reference Zhong and Ahlers2010). We note that no temperature boundary condition is required at the fluid–sidewall interface (
![]() $r=R_{f}$
) since the temperature is solved within the entire computational domain. The bottom and top plates are assumed to extend until the edge of the sidewall, although it should be noted that this condition is strongly dependent on the method that is used to assemble the horizontal plates and the sidewall.
$r=R_{f}$
) since the temperature is solved within the entire computational domain. The bottom and top plates are assumed to extend until the edge of the sidewall, although it should be noted that this condition is strongly dependent on the method that is used to assemble the horizontal plates and the sidewall.
Finally, we simulate the whole set-up sketched in figure 1, in which we also include the insulation layer and the thermal side shields. The outer surface of the insulation layer is assumed to be isothermal at
![]() $\unicode[STIX]{x1D703}=(T_{c}+T_{h})/2=T_{M}$
. The temperatures of the entire bottom and top plates are fixed at
$\unicode[STIX]{x1D703}=(T_{c}+T_{h})/2=T_{M}$
. The temperatures of the entire bottom and top plates are fixed at
![]() $T_{h}$
and
$T_{h}$
and
![]() $T_{c}$
, respectively. This set-up resembles the configuration considered by Stevens et al. (Reference Stevens, Lohse and Verzicco2014), but the geometrical parameters and physical properties are different and taken from the reference experiment described in the previous section. The specific geometrical parameters are given in figure 1, and the material properties are listed in table 2. When compared to the case with just the Plexiglas sidewall, this situation is much closer to the experimental apparatus, although we emphasize that the actual set-up is still more complex than presented in these simulations.
$T_{c}$
, respectively. This set-up resembles the configuration considered by Stevens et al. (Reference Stevens, Lohse and Verzicco2014), but the geometrical parameters and physical properties are different and taken from the reference experiment described in the previous section. The specific geometrical parameters are given in figure 1, and the material properties are listed in table 2. When compared to the case with just the Plexiglas sidewall, this situation is much closer to the experimental apparatus, although we emphasize that the actual set-up is still more complex than presented in these simulations.
Details about the simulations, the documented
![]() $Nu$
number data and the used resolution can be found in appendices B and C. In short, we consider three different configurations, (i) a standard Rayleigh–Bénard cell with an adiabatic sidewall, (ii) a Rayleigh–Bénard cell using neon (
$Nu$
number data and the used resolution can be found in appendices B and C. In short, we consider three different configurations, (i) a standard Rayleigh–Bénard cell with an adiabatic sidewall, (ii) a Rayleigh–Bénard cell using neon (
![]() $Pr=0.7$
) as working fluid and just a Plexiglas sidewall and (iii) a cell with a Plexiglas sidewall, additional insulation layer and thermal side shields as indicated in figure 1 filled with neon and helium, respectively. All simulations are performed for
$Pr=0.7$
) as working fluid and just a Plexiglas sidewall and (iii) a cell with a Plexiglas sidewall, additional insulation layer and thermal side shields as indicated in figure 1 filled with neon and helium, respectively. All simulations are performed for
![]() $\unicode[STIX]{x1D6E4}=1.00$
.
$\unicode[STIX]{x1D6E4}=1.00$
.
The code has been used before by Stevens et al. (Reference Stevens, Lohse and Verzicco2014), where validations against different simulation (Shishkina & Thess Reference Shishkina and Thess2009; Hébert et al.
Reference Hébert, Hufschmid, Scheel and Ahlers2010; Scheel, Kim & White Reference Scheel, Kim and White2012) and experimental results were provided. For all the simulations, the
![]() $Nu$
number is computed by determining the heat flux crossing the fluid through the plates
$Nu$
number is computed by determining the heat flux crossing the fluid through the plates
![]() $Q_{f}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{R_{f}}\unicode[STIX]{x1D706}_{f}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\,|_{z=0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S/(\unicode[STIX]{x03C0}R_{f}^{2})$
. This is slightly different from what is done in the experiments where the total heat flux that enters through the hot plate is measured (
$Q_{f}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{R_{f}}\unicode[STIX]{x1D706}_{f}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\,|_{z=0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S/(\unicode[STIX]{x03C0}R_{f}^{2})$
. This is slightly different from what is done in the experiments where the total heat flux that enters through the hot plate is measured (
![]() $Q_{T}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{R_{T}}\unicode[STIX]{x1D706}_{f}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\,|_{z=0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S/(\unicode[STIX]{x03C0}R_{T}^{2})$
), which only afterwards is corrected for the parasitic heat current flowing through the sidewall. It is worth noticing that the latter is determined by empirical models. Therefore the uncertainty in this correction might be responsible for some of the later encountered discrepancies between the
$Q_{T}=\int _{0}^{2\unicode[STIX]{x03C0}}\int _{0}^{R_{T}}\unicode[STIX]{x1D706}_{f}\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}\,|_{z=0}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S/(\unicode[STIX]{x03C0}R_{T}^{2})$
), which only afterwards is corrected for the parasitic heat current flowing through the sidewall. It is worth noticing that the latter is determined by empirical models. Therefore the uncertainty in this correction might be responsible for some of the later encountered discrepancies between the
![]() $Nu$
numbers obtained from experiments and simulations. At the end of § 5, we discuss other potential reasons for discrepancies.
$Nu$
numbers obtained from experiments and simulations. At the end of § 5, we discuss other potential reasons for discrepancies.
In the simulations, we calculate the temperature gradients using flow data obtained from the probe locations used in the experiments, see table 1. Even though we performed the simulations for a very long time, up to 10 000 free-fall time units for lower
![]() $Ra$
and for approximately 300 time units for the highest
$Ra$
and for approximately 300 time units for the highest
![]() $Ra$
, the statistical convergence of the simulation data is still not as good as for the experimental data. To improve the convergence of the simulation data, we calculate the azimuthally averaged temperature gradient close to the sidewall (
$Ra$
, the statistical convergence of the simulation data is still not as good as for the experimental data. To improve the convergence of the simulation data, we calculate the azimuthally averaged temperature gradient close to the sidewall (
![]() $\unicode[STIX]{x1D709}=0.13$
). At the cylinder axis (
$\unicode[STIX]{x1D709}=0.13$
). At the cylinder axis (
![]() $\unicode[STIX]{x1D709}=1.00$
) we use the top–down symmetry in the simulations and report the average temperature gradient obtained from two measurements, i.e. ones between
$\unicode[STIX]{x1D709}=1.00$
) we use the top–down symmetry in the simulations and report the average temperature gradient obtained from two measurements, i.e. ones between
![]() $z/L=0.40$
and
$z/L=0.40$
and
![]() $z/L=0.51$
and ones between
$z/L=0.51$
and ones between
![]() $z/L=0.49$
and
$z/L=0.49$
and
![]() $z/L=0.60$
. Because, we cannot perform an azimuthal average at the cylinder axis the statistical uncertainty for the temperature gradient is higher at the cylinder axis than close to the sidewall, especially for
$z/L=0.60$
. Because, we cannot perform an azimuthal average at the cylinder axis the statistical uncertainty for the temperature gradient is higher at the cylinder axis than close to the sidewall, especially for
![]() $Ra\geqslant 6\times 10^{8}$
when the simulation length is more limited.
$Ra\geqslant 6\times 10^{8}$
when the simulation length is more limited.

Figure 2. Value of
![]() $Nu/Ra^{1/3}$
as a function of
$Nu/Ra^{1/3}$
as a function of
![]() $Ra$
for
$Ra$
for
![]() $\unicode[STIX]{x1D6E4}=1.00$
and
$\unicode[STIX]{x1D6E4}=1.00$
and
![]() $Pr\simeq 0.7$
. Solid line: prediction of the unifying theory (Grossmann & Lohse Reference Grossmann and Lohse2000; Stevens et al.
Reference Stevens, van der Poel, Grossmann and Lohse2013) for
$Pr\simeq 0.7$
. Solid line: prediction of the unifying theory (Grossmann & Lohse Reference Grossmann and Lohse2000; Stevens et al.
Reference Stevens, van der Poel, Grossmann and Lohse2013) for
![]() $Pr=0.7$
. Open circles: DNS with an adiabatic sidewall for
$Pr=0.7$
. Open circles: DNS with an adiabatic sidewall for
![]() $Pr=0.7$
. Solid symbols: experimental data of Niemela & Sreenivasan (Reference Niemela and Sreenivasan2003) using helium at temperatures near 5.3 K with
$Pr=0.7$
. Solid symbols: experimental data of Niemela & Sreenivasan (Reference Niemela and Sreenivasan2003) using helium at temperatures near 5.3 K with
![]() $Pr$
in the range from 0.68 to 0.71 (black square), new experimental results using helium (
$Pr$
in the range from 0.68 to 0.71 (black square), new experimental results using helium (
![]() $Pr=0.68$
, red down-pointing triangles), neon (
$Pr=0.68$
, red down-pointing triangles), neon (
![]() $Pr=0.66$
, green diamonds) and
$Pr=0.66$
, green diamonds) and
![]() $\text{SF}_{6}$
(
$\text{SF}_{6}$
(
![]() $Pr=0.79$
, blue up-pointing triangles).
$Pr=0.79$
, blue up-pointing triangles).
4 Measurements compared to simulations with adiabatic sidewall
4.1 Results for the
 $Nu$
number
$Nu$
number
Figure 2 shows a comparison of the compensated
![]() $Nu$
versus
$Nu$
versus
![]() $Ra$
data obtained from our new measurements, and the simulations in which an adiabatic sidewall is used. The simulation results agree excellently with the predictions from the unifying theory for
$Ra$
data obtained from our new measurements, and the simulations in which an adiabatic sidewall is used. The simulation results agree excellently with the predictions from the unifying theory for
![]() $Ra\gtrsim 2\times 10^{6}$
. However, for
$Ra\gtrsim 2\times 10^{6}$
. However, for
![]() $Ra\lesssim 2\times 10^{6}$
, the simulations give a lower heat transfer than the unifying theory, because the flow is no longer turbulent, and the unifying theory does not apply to this regime. For comparison, figure 2 also shows, as solid black squares, the experimental
$Ra\lesssim 2\times 10^{6}$
, the simulations give a lower heat transfer than the unifying theory, because the flow is no longer turbulent, and the unifying theory does not apply to this regime. For comparison, figure 2 also shows, as solid black squares, the experimental
![]() $Nu$
results of Niemela & Sreenivasan (Reference Niemela and Sreenivasan2003). While these data agree with the DNS for
$Nu$
results of Niemela & Sreenivasan (Reference Niemela and Sreenivasan2003). While these data agree with the DNS for
![]() $Ra\gtrsim 10^{10}$
, they are larger than the simulation results for lower
$Ra\gtrsim 10^{10}$
, they are larger than the simulation results for lower
![]() $Ra$
, with the difference reaching 16 % below
$Ra$
, with the difference reaching 16 % below
![]() $Ra\simeq 10^{9}$
. The experimental measurements presented here agree very well with the DNS for
$Ra\simeq 10^{9}$
. The experimental measurements presented here agree very well with the DNS for
![]() $Ra\gtrsim 10^{9}$
. As
$Ra\gtrsim 10^{9}$
. As
![]() $Ra$
decreases below
$Ra$
decreases below
![]() $10^{9}$
, they gradually rise above the simulation results, although the difference never exceeds 6 %. Interestingly, the measurement data also agree very well with the simulation results for
$10^{9}$
, they gradually rise above the simulation results, although the difference never exceeds 6 %. Interestingly, the measurement data also agree very well with the simulation results for
![]() $Ra\lesssim 2\times 10^{6}$
and show the same maximum of the compensated
$Ra\lesssim 2\times 10^{6}$
and show the same maximum of the compensated
![]() $Nu$
number near
$Nu$
number near
![]() $Ra=10^{6}$
. It thus seems that the influence of the sidewall on the measured
$Ra=10^{6}$
. It thus seems that the influence of the sidewall on the measured
![]() $Nu$
number is limited when appropriate corrections are applied to the measurements.
$Nu$
number is limited when appropriate corrections are applied to the measurements.
4.2 Results for the temperature gradients
In figure 3 we report results for the dimensionless vertical temperature gradient
where
![]() $z_{1}$
and
$z_{1}$
and
![]() $z_{2}$
,
$z_{2}$
,
![]() $z_{2}>z_{1}$
, are positions along a vertical (
$z_{2}>z_{1}$
, are positions along a vertical (
![]() $z$
) axis pointing in a direction opposite to gravity. Here
$z$
) axis pointing in a direction opposite to gravity. Here
![]() $\langle \cdots \rangle$
indicates the time average. Note that in absence of convection (when the temperature gradient is independent of
$\langle \cdots \rangle$
indicates the time average. Note that in absence of convection (when the temperature gradient is independent of
![]() $z$
)
$z$
)
![]() $\langle \unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{z}\rangle =-1$
. A positive value indicates a temperature profile that is stabilizing in the presence of gravity.
$\langle \unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{z}\rangle =-1$
. A positive value indicates a temperature profile that is stabilizing in the presence of gravity.

Figure 3. The mean vertical temperature gradient (a) on the cylinder axis (
![]() $\unicode[STIX]{x1D709}=1.00$
) and (b) close to the sidewall (
$\unicode[STIX]{x1D709}=1.00$
) and (b) close to the sidewall (
![]() $\unicode[STIX]{x1D709}=0.13$
). Please note the different scales of the two vertical axes. Open circles: DNS results using an adiabatic sidewall. Solid symbols: new experimental results using helium (red down-pointing triangles), neon (green diamonds), nitrogen (red circles) and
$\unicode[STIX]{x1D709}=0.13$
). Please note the different scales of the two vertical axes. Open circles: DNS results using an adiabatic sidewall. Solid symbols: new experimental results using helium (red down-pointing triangles), neon (green diamonds), nitrogen (red circles) and
![]() $\text{SF}_{6}$
(blue up-pointing triangles). Solid orange squares and pink left-pointing triangles: experimental results from Brown & Ahlers (Reference Brown and Ahlers2007) for
$\text{SF}_{6}$
(blue up-pointing triangles). Solid orange squares and pink left-pointing triangles: experimental results from Brown & Ahlers (Reference Brown and Ahlers2007) for
![]() $Pr=4.4$
and
$Pr=4.4$
and
![]() $Pr=5.5$
, respectively. Solid black right-pointing triangles: result of Tilgner et al. (Reference Tilgner, Belmonte and Libchaber1993) for
$Pr=5.5$
, respectively. Solid black right-pointing triangles: result of Tilgner et al. (Reference Tilgner, Belmonte and Libchaber1993) for
![]() $Pr=6.6$
.
$Pr=6.6$
.
Figure 3(a) shows results for
![]() $\unicode[STIX]{x1D709}=1.00$
, i.e. along the sample axis. One sees that the experimental results using
$\unicode[STIX]{x1D709}=1.00$
, i.e. along the sample axis. One sees that the experimental results using
![]() $\text{SF}_{6}$
(solid blue up-pointing triangles,
$\text{SF}_{6}$
(solid blue up-pointing triangles,
![]() $Pr=0.786$
) correspond approximately to
$Pr=0.786$
) correspond approximately to
![]() $\langle \unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{z}\rangle =+0.01$
, a small but definitely stabilizing gradient. This result is only somewhat smaller than the earlier measurement by Tilgner et al. (Reference Tilgner, Belmonte and Libchaber1993) for
$\langle \unicode[STIX]{x0394}\unicode[STIX]{x1D6E9}_{z}\rangle =+0.01$
, a small but definitely stabilizing gradient. This result is only somewhat smaller than the earlier measurement by Tilgner et al. (Reference Tilgner, Belmonte and Libchaber1993) for
![]() $Pr=6.6$
(solid black right-pointing triangle) and of about the same size as the data by Brown & Ahlers (Reference Brown and Ahlers2007) for
$Pr=6.6$
(solid black right-pointing triangle) and of about the same size as the data by Brown & Ahlers (Reference Brown and Ahlers2007) for
![]() $Pr=4.4$
and
$Pr=4.4$
and
![]() $Pr=5.5$
(solid orange squares and pink left-pointing triangles). Our DNS results for
$Pr=5.5$
(solid orange squares and pink left-pointing triangles). Our DNS results for
![]() $Pr=0.7$
are shown as black open circles; they also reveal a small stabilizing gradient and some wiggling in the high
$Pr=0.7$
are shown as black open circles; they also reveal a small stabilizing gradient and some wiggling in the high
![]() $Ra$
regime. The latter is presumably due to the uncertainty in the temperature gradient measured at the cylinder axis in the simulations, for a more detailed discussion see the end of § 3; clearly, the wiggling does not seem to be statistically relevant.
$Ra$
regime. The latter is presumably due to the uncertainty in the temperature gradient measured at the cylinder axis in the simulations, for a more detailed discussion see the end of § 3; clearly, the wiggling does not seem to be statistically relevant.
For higher
![]() $Pr$
it was argued that the stabilizing temperature gradient emerges due to the relatively long lifetime of the plumes which allows them to travel along the sidewall to the opposite plate and then drift back to the sample centreline, which creates a stabilizing gradient in the sample interior (Tilgner et al.
Reference Tilgner, Belmonte and Libchaber1993; Brown & Ahlers Reference Brown and Ahlers2007). To get a better understanding of this phenomenon, we estimate the plume lifetime
$Pr$
it was argued that the stabilizing temperature gradient emerges due to the relatively long lifetime of the plumes which allows them to travel along the sidewall to the opposite plate and then drift back to the sample centreline, which creates a stabilizing gradient in the sample interior (Tilgner et al.
Reference Tilgner, Belmonte and Libchaber1993; Brown & Ahlers Reference Brown and Ahlers2007). To get a better understanding of this phenomenon, we estimate the plume lifetime
![]() $\unicode[STIX]{x1D70F}_{p}=\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}^{2}/\unicode[STIX]{x1D705}$
, where
$\unicode[STIX]{x1D70F}_{p}=\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}^{2}/\unicode[STIX]{x1D705}$
, where
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$
is the thermal boundary layer thickness, and the LSC travel time from the bottom to top conducting plates
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$
is the thermal boundary layer thickness, and the LSC travel time from the bottom to top conducting plates
![]() $\unicode[STIX]{x1D70F}_{LSC}=L/U$
, with
$\unicode[STIX]{x1D70F}_{LSC}=L/U$
, with
![]() $U$
the velocity of the LSC, from which we obtain that
$U$
the velocity of the LSC, from which we obtain that
where
![]() $Re=UL/\unicode[STIX]{x1D708}$
is the Reynolds number of the LSC. Our experiments and simulations are in regime
$Re=UL/\unicode[STIX]{x1D708}$
is the Reynolds number of the LSC. Our experiments and simulations are in regime
![]() $IV_{u}$
of the unifying theory (Grossmann & Lohse Reference Grossmann and Lohse2001). To estimate the scaling of
$IV_{u}$
of the unifying theory (Grossmann & Lohse Reference Grossmann and Lohse2001). To estimate the scaling of
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{LSC}$
with
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{LSC}$
with
![]() $Ra$
and
$Ra$
and
![]() $Pr$
we use, for simplicity, that
$Pr$
we use, for simplicity, that
![]() $Nu\sim Ra^{1/3}$
and the result from the unifying theory that
$Nu\sim Ra^{1/3}$
and the result from the unifying theory that
![]() $Re\sim Pr^{-2/3}Ra^{4/9}$
in regime
$Re\sim Pr^{-2/3}Ra^{4/9}$
in regime
![]() $IV_{u}$
. This implies that
$IV_{u}$
. This implies that
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{LSC}\sim Ra^{-2/9}Pr^{1/3}$
, which means that the
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{LSC}\sim Ra^{-2/9}Pr^{1/3}$
, which means that the
![]() $Pr$
dependence of
$Pr$
dependence of
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{LSC}$
is much weaker than one would naively expect. This shows that with decreasing
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{LSC}$
is much weaker than one would naively expect. This shows that with decreasing
![]() $Pr$
, the increased LSC speed allows the transported plumes to still create a stabilizing temperature gradient at the cell centre with a similar magnitude as in high
$Pr$
, the increased LSC speed allows the transported plumes to still create a stabilizing temperature gradient at the cell centre with a similar magnitude as in high
![]() $Pr$
number fluids. We also note that the decrease of
$Pr$
number fluids. We also note that the decrease of
![]() $\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{LSC}$
with increasing
$\unicode[STIX]{x1D70F}_{p}/\unicode[STIX]{x1D70F}_{LSC}$
with increasing
![]() $Ra$
is in agreement with the observed reduction and eventual disappearance of the stabilizing mean temperature gradient at the cell centre.
$Ra$
is in agreement with the observed reduction and eventual disappearance of the stabilizing mean temperature gradient at the cell centre.
As
![]() $Ra$
is decreased, there are experimental data taken with nitrogen (solid red circles), neon (solid green diamonds) and helium (solid red down-pointing triangles) as working fluid. Each fluid covers a different range of
$Ra$
is decreased, there are experimental data taken with nitrogen (solid red circles), neon (solid green diamonds) and helium (solid red down-pointing triangles) as working fluid. Each fluid covers a different range of
![]() $Ra$
, always showing a stabilizing gradient at the higher
$Ra$
, always showing a stabilizing gradient at the higher
![]() $Ra$
of the scanned range. As
$Ra$
of the scanned range. As
![]() $Ra$
decreases, the temperature gradient becomes more destabilizing. Surprisingly, the
$Ra$
decreases, the temperature gradient becomes more destabilizing. Surprisingly, the
![]() $Ra$
value of the zero crossings depends on the fluid. Since all fluids have about the same
$Ra$
value of the zero crossings depends on the fluid. Since all fluids have about the same
![]() $Pr$
, the quantitative difference must be related to a different relationship between the thermal properties of the fluid and the sidewall. To a large extent, this can be captured by the value of the sidewall admittance
$Pr$
, the quantitative difference must be related to a different relationship between the thermal properties of the fluid and the sidewall. To a large extent, this can be captured by the value of the sidewall admittance
![]() $C$
, see (1.1). While
$C$
, see (1.1). While
![]() $C$
is the only relevant parameter that determines the critical Rayleigh number
$C$
is the only relevant parameter that determines the critical Rayleigh number
![]() $Ra_{c}$
, it is not clear that
$Ra_{c}$
, it is not clear that
![]() $C$
alone determines the system behaviour in the turbulent state. However, we note that the zero crossing of the gradient decreases monotonically with increasing
$C$
alone determines the system behaviour in the turbulent state. However, we note that the zero crossing of the gradient decreases monotonically with increasing
![]() $C$
, see table 2 for values of
$C$
, see table 2 for values of
![]() $C$
. This suggests that for the adiabatic case (
$C$
. This suggests that for the adiabatic case (
![]() $C\rightarrow \infty$
) the decrease in
$C\rightarrow \infty$
) the decrease in
![]() $\langle \unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}\rangle$
with decreasing
$\langle \unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{z}\rangle$
with decreasing
![]() $Ra$
vanishes, just as in the adiabatic DNS.
$Ra$
vanishes, just as in the adiabatic DNS.
As
![]() $Ra$
is reduced even further, the helium data indicate a sharp transition at
$Ra$
is reduced even further, the helium data indicate a sharp transition at
![]() $Ra\simeq 4\times 10^{5}$
. For the other gases, the data do not extend to sufficiently small
$Ra\simeq 4\times 10^{5}$
. For the other gases, the data do not extend to sufficiently small
![]() $Ra$
to pass through a transition. We note that the
$Ra$
to pass through a transition. We note that the
![]() $Ra$
value of the transition is consistent with the onset of turbulence as reported by Heslot, Castaing & Libchaber (Reference Heslot, Castaing and Libchaber1987).
$Ra$
value of the transition is consistent with the onset of turbulence as reported by Heslot, Castaing & Libchaber (Reference Heslot, Castaing and Libchaber1987).
Returning to the DNS data for the system with adiabatic walls (open circles in figure 3
a), we see that they behave quite differently as
![]() $Ra$
decreases. They remain stabilizing down to the smallest
$Ra$
decreases. They remain stabilizing down to the smallest
![]() $Ra$
investigated (
$Ra$
investigated (
![]() $Ra\simeq 3\times 10^{5}$
), with the magnitude of the gradient increasing as
$Ra\simeq 3\times 10^{5}$
), with the magnitude of the gradient increasing as
![]() $Ra$
decreases. Again, this is not inconsistent with the experimental data when we consider that an adiabatic sidewall may be considered as the limit
$Ra$
decreases. Again, this is not inconsistent with the experimental data when we consider that an adiabatic sidewall may be considered as the limit
![]() $C\rightarrow \infty$
. As
$C\rightarrow \infty$
. As
![]() $Ra$
is further reduced, the temperature gradient in the simulations becomes negative (unstable stratification) for
$Ra$
is further reduced, the temperature gradient in the simulations becomes negative (unstable stratification) for
![]() $Ra\approx 10^{4}$
, while it becomes
$Ra\approx 10^{4}$
, while it becomes
![]() $-1$
at the onset, just as expected.
$-1$
at the onset, just as expected.

Figure 4. Comparison of the heat transport obtained in simulations using an adiabatic sidewall (open black circles), using a Plexiglas sidewall with neon as working fluid (open pink up-pointing triangles), using the Plexiglas sidewall with working fluid neon with additional insulation layer and thermal side shields (open blue down-pointing triangles) and using the Plexiglas sidewall with working fluid helium with additional insulation layer and thermal side shields (open orange left-pointing triangles). New experimental results using helium (
![]() $Pr=0.68$
, solid red down-pointing triangles) and neon (
$Pr=0.68$
, solid red down-pointing triangles) and neon (
![]() $Pr=0.66$
, solid green diamonds).
$Pr=0.66$
, solid green diamonds).
Figure 3(b) shows the gradient near the sidewall for
![]() $\unicode[STIX]{x1D709}=0.13$
. Here the gradient is destabilizing also for
$\unicode[STIX]{x1D709}=0.13$
. Here the gradient is destabilizing also for
![]() $Ra\gtrsim 10^{8}$
but of quite a small magnitude. In this range, the experimental data agree well with the adiabatic DNS results. The magnitude of the gradient increases, i.e. the gradient decreases, quite rapidly when
$Ra\gtrsim 10^{8}$
but of quite a small magnitude. In this range, the experimental data agree well with the adiabatic DNS results. The magnitude of the gradient increases, i.e. the gradient decreases, quite rapidly when
![]() $Ra$
decreases. Again the
$Ra$
decreases. Again the
![]() $Ra$
value where this rapid decrease begins depends on the used gas. Also here we see a sharp transition as
$Ra$
value where this rapid decrease begins depends on the used gas. Also here we see a sharp transition as
![]() $Ra$
is decreased further, for helium at
$Ra$
is decreased further, for helium at
![]() $Ra\simeq 3\times 10^{5}$
and for neon at
$Ra\simeq 3\times 10^{5}$
and for neon at
![]() $Ra\simeq 2\times 10^{6}$
. While all gases yield qualitatively similar behaviour, the quantitative difference again is presumably due to the difference in the sidewall admittance, see table 2.
$Ra\simeq 2\times 10^{6}$
. While all gases yield qualitatively similar behaviour, the quantitative difference again is presumably due to the difference in the sidewall admittance, see table 2.
We observe that the Navier–Stokes equations with the Boussinesq approximation, once made non-dimensional, depend only on
![]() $Ra$
,
$Ra$
,
![]() $Pr$
, and through the boundary conditions on
$Pr$
, and through the boundary conditions on
![]() $\unicode[STIX]{x1D6E4}$
. The dependence of the temperature gradients on the specific fluid properties suggests that other physical effects play a role. The main effect is the conjugate heat transfer between the fluid and the sidewall system. As discussed above, it is not clear whether the sidewall admittance
$\unicode[STIX]{x1D6E4}$
. The dependence of the temperature gradients on the specific fluid properties suggests that other physical effects play a role. The main effect is the conjugate heat transfer between the fluid and the sidewall system. As discussed above, it is not clear whether the sidewall admittance
![]() $C$
can entirely characterize this phenomenon. To better understand this influence, we will discuss the effect of the sidewall and its influence on heat transport and flow structures as observed in simulations in the next section.
$C$
can entirely characterize this phenomenon. To better understand this influence, we will discuss the effect of the sidewall and its influence on heat transport and flow structures as observed in simulations in the next section.
5 Effect of the sidewall
Figure 4 compares the heat transport obtained in simulations using the properties of neon and helium as working fluid and those of Plexiglas for the sidewall, with and without the additional insulation layer and thermal side shields as sketched in figure 1. The reference results for an adiabatic sidewall are also reported. Figure 4 shows that for
![]() $Ra\gtrsim 8\times 10^{5}$
the heat transport is slightly smaller than the reference case when the Plexiglas sidewall is considered and at
$Ra\gtrsim 8\times 10^{5}$
the heat transport is slightly smaller than the reference case when the Plexiglas sidewall is considered and at
![]() $Ra=10^{7}$
the difference is approximately 4 %. However, for
$Ra=10^{7}$
the difference is approximately 4 %. However, for
![]() $Ra\lesssim 5\times 10^{5}$
the heat transport in the cell with the Plexiglas sidewall is higher than in the reference cell and at
$Ra\lesssim 5\times 10^{5}$
the heat transport in the cell with the Plexiglas sidewall is higher than in the reference cell and at
![]() $Ra=2\times 10^{5}$
this difference grows to approximately 15 %. When the insulation layer and thermal shields are added, their effects become significant only for
$Ra=2\times 10^{5}$
this difference grows to approximately 15 %. When the insulation layer and thermal shields are added, their effects become significant only for
![]() $Ra\leqslant 2\times 10^{6}$
with lower heat transport.
$Ra\leqslant 2\times 10^{6}$
with lower heat transport.
To explain this influence, we analyse the heat flux through the sidewall (Verzicco Reference Verzicco2002). Figure 5 shows the lateral local
![]() $Nu$
number
$Nu$
number
![]() $Nu_{l}(z)=\langle -\unicode[STIX]{x2202}_{r}\unicode[STIX]{x1D703}\rangle _{t,\unicode[STIX]{x1D719}}(z)$
where
$Nu_{l}(z)=\langle -\unicode[STIX]{x2202}_{r}\unicode[STIX]{x1D703}\rangle _{t,\unicode[STIX]{x1D719}}(z)$
where
![]() $\unicode[STIX]{x2202}_{r}$
denotes the partial derivative with respect to
$\unicode[STIX]{x2202}_{r}$
denotes the partial derivative with respect to
![]() $r$
, at the interface of the fluid (neon) and the Plexiglas sidewall, and
$r$
, at the interface of the fluid (neon) and the Plexiglas sidewall, and
![]() $\unicode[STIX]{x1D719}$
is the corresponding azimuthal angle over which we average. This gradient is determined by extrapolating the results from the fluid and sidewall domain separately while taking into account the conductivity ratio and then match them at the exact location (
$\unicode[STIX]{x1D719}$
is the corresponding azimuthal angle over which we average. This gradient is determined by extrapolating the results from the fluid and sidewall domain separately while taking into account the conductivity ratio and then match them at the exact location (
![]() $r=R_{f}$
) of the sidewall,
$r=R_{f}$
) of the sidewall,
where
![]() $R_{f}^{-}$
and
$R_{f}^{-}$
and
![]() $R_{f}^{+}$
indicate that the temperature gradient at the sidewall is determined from the fluid and sidewall side, respectively. The largest heat flux through the sidewall is measured near the junction between the sidewall and horizontal plates. The profile reveals that the sidewall acts as an extra heat conductor, which absorbs part of the heat from the fluid near the bottom plate and releases it into the fluid near the top plate, thus acting as a short circuit. The relative importance of the short circuit is higher for lower
$R_{f}^{+}$
indicate that the temperature gradient at the sidewall is determined from the fluid and sidewall side, respectively. The largest heat flux through the sidewall is measured near the junction between the sidewall and horizontal plates. The profile reveals that the sidewall acts as an extra heat conductor, which absorbs part of the heat from the fluid near the bottom plate and releases it into the fluid near the top plate, thus acting as a short circuit. The relative importance of the short circuit is higher for lower
![]() $Ra$
. For all cases, the vertically integrated heat flux through the entire sidewall is zero. Figure 5 shows that the lateral heat flux is skew–symmetric about the mid-plane. This means that the effect of the sidewall on the
$Ra$
. For all cases, the vertically integrated heat flux through the entire sidewall is zero. Figure 5 shows that the lateral heat flux is skew–symmetric about the mid-plane. This means that the effect of the sidewall on the
![]() $Nu$
number is not due to the main parasitic heat flux. Instead, the interaction between the sidewall and fluid causes a change in the flow structure, which changes the heat transfer that is supported by the flow. Figure 5 also reveals that for increasing
$Nu$
number is not due to the main parasitic heat flux. Instead, the interaction between the sidewall and fluid causes a change in the flow structure, which changes the heat transfer that is supported by the flow. Figure 5 also reveals that for increasing
![]() $Ra$
the heat flux through the sidewall near the plate can be higher when the additional insulation layer and thermal shields are added. The reason for this is the convection in the insulation layer, which we discuss below.
$Ra$
the heat flux through the sidewall near the plate can be higher when the additional insulation layer and thermal shields are added. The reason for this is the convection in the insulation layer, which we discuss below.

Figure 5. Time and azimuthally averaged heat transfer through the sidewall for (a) the simulations with neon with just the Plexiglas sidewall and (b) the simulations with the Plexiglas sidewall, the additional insulation layer and thermal side shields.

Figure 6. Time and azimuthally averaged local
![]() $Nu_{lb}$
number at the plate as function of radial position for different
$Nu_{lb}$
number at the plate as function of radial position for different
![]() $Ra$
and different sidewall configurations with the working fluid neon.
$Ra$
and different sidewall configurations with the working fluid neon.
Figure 6 shows the local heat transfer, i.e.
![]() $Nu_{lb}(r)=\langle -\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}\rangle _{t,\unicode[STIX]{x1D719}}(r)$
, as a function of the radial position at the bottom plate for the different sidewall configurations using neon as working gas. The simulations with the adiabatic sidewall show a pronounced imprint of the LSC, due to which the local heat transport is highest at
$Nu_{lb}(r)=\langle -\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}\rangle _{t,\unicode[STIX]{x1D719}}(r)$
, as a function of the radial position at the bottom plate for the different sidewall configurations using neon as working gas. The simulations with the adiabatic sidewall show a pronounced imprint of the LSC, due to which the local heat transport is highest at
![]() $r/L\sim 0.3{-}0.4$
. When approaching the sidewall, the temperature gradient at the plate, and therefore the local heat transport, decrease. The pronounced imprint of the LSC decreases with increasing
$r/L\sim 0.3{-}0.4$
. When approaching the sidewall, the temperature gradient at the plate, and therefore the local heat transport, decrease. The pronounced imprint of the LSC decreases with increasing
![]() $Ra$
, while the position of the maximum local heat transport shifts towards the sidewall. When the Plexiglas sidewall is added, the local heat transport is significantly increased close to the sidewall, especially at low
$Ra$
, while the position of the maximum local heat transport shifts towards the sidewall. When the Plexiglas sidewall is added, the local heat transport is significantly increased close to the sidewall, especially at low
![]() $Ra$
, due to the heat exchange between the sidewall and the fluid in the junction region. The local enhancement of the heat transport close to the sidewall, which is driven by the heat flux that passes through the sidewall, explains the higher overall
$Ra$
, due to the heat exchange between the sidewall and the fluid in the junction region. The local enhancement of the heat transport close to the sidewall, which is driven by the heat flux that passes through the sidewall, explains the higher overall
![]() $Nu$
at low
$Nu$
at low
![]() $Ra$
when compared to the adiabatic case. Figure 6 clearly shows that for increasing
$Ra$
when compared to the adiabatic case. Figure 6 clearly shows that for increasing
![]() $Ra$
the heat transfer through the liquid overcomes all the secondary effects and the local heat-transport distribution converges for the different sidewall configurations as confirmed by the agreement of the heat transport in the high end of
$Ra$
the heat transfer through the liquid overcomes all the secondary effects and the local heat-transport distribution converges for the different sidewall configurations as confirmed by the agreement of the heat transport in the high end of
![]() $Ra$
observed in figure 4.
$Ra$
observed in figure 4.
Figure 7 shows the time and azimuthally averaged root mean square (r.m.s.) temperature fluctuations, i.e.
![]() $\sqrt{\langle \unicode[STIX]{x1D703}^{\prime }\rangle _{\unicode[STIX]{x1D719},t}}$
, for
$\sqrt{\langle \unicode[STIX]{x1D703}^{\prime }\rangle _{\unicode[STIX]{x1D719},t}}$
, for
![]() $Ra=3\times 10^{5}$
,
$Ra=3\times 10^{5}$
,
![]() $10^{6}$
and
$10^{6}$
and
![]() $10^{7}$
for the three different model set-ups. When only an adiabatic sidewall is considered, the temperature fluctuations near the sidewall are the highest since the sidewall does not directly affect the temperature. The fluctuations are instead strongly damped when the Plexiglas sidewall is added; the reduction of the temperature fluctuations is caused by the relatively high heat capacity and steady temperature of the sidewall, induced by the isothermal condition imposed on the ‘dry’ side. This damping effect is absent with an ideal adiabatic sidewall, which is why the sidewall temperature is allowed to fluctuate freely. For the set-up with the additional insulation and thermal shield, we observe that there is almost no convection within the insulation layer at
$10^{7}$
for the three different model set-ups. When only an adiabatic sidewall is considered, the temperature fluctuations near the sidewall are the highest since the sidewall does not directly affect the temperature. The fluctuations are instead strongly damped when the Plexiglas sidewall is added; the reduction of the temperature fluctuations is caused by the relatively high heat capacity and steady temperature of the sidewall, induced by the isothermal condition imposed on the ‘dry’ side. This damping effect is absent with an ideal adiabatic sidewall, which is why the sidewall temperature is allowed to fluctuate freely. For the set-up with the additional insulation and thermal shield, we observe that there is almost no convection within the insulation layer at
![]() $Ra=3\times 10^{5}$
and
$Ra=3\times 10^{5}$
and
![]() $10^{6}$
. However, at
$10^{6}$
. However, at
![]() $Ra=10^{7}$
the thermal forcing strengthens and the convection in the porous material intensifies. This enhances the relative heat flux through the sidewall at
$Ra=10^{7}$
the thermal forcing strengthens and the convection in the porous material intensifies. This enhances the relative heat flux through the sidewall at
![]() $Ra=10^{7}$
, as shown in figure 5.
$Ra=10^{7}$
, as shown in figure 5.

Figure 7. Azimuthally and time averaged r.m.s. temperature fluctuations for (a)
![]() $Ra=3\times 10^{5}$
, (b)
$Ra=3\times 10^{5}$
, (b)
![]() $Ra=10^{6}$
and (c)
$Ra=10^{6}$
and (c)
![]() $Ra=10^{7}$
using neon as working fluid. The left, middle and right panels indicate the results for the adiabatic sidewall, Plexiglas sidewall and Plexiglas sidewall with additional insulation layer and thermal shields.
$Ra=10^{7}$
using neon as working fluid. The left, middle and right panels indicate the results for the adiabatic sidewall, Plexiglas sidewall and Plexiglas sidewall with additional insulation layer and thermal shields.
If we use the traditional definition of
![]() $Ra$
number, and neglect the influence of the porosity, the
$Ra$
number, and neglect the influence of the porosity, the
![]() $Ra$
number inside the foam can be estimated. When neon (
$Ra$
number inside the foam can be estimated. When neon (
![]() $\unicode[STIX]{x1D6FD}/k\unicode[STIX]{x1D708}=0.0144$
(
$\unicode[STIX]{x1D6FD}/k\unicode[STIX]{x1D708}=0.0144$
(
![]() $\text{s}^{2}~\text{K}^{-1}~\text{cm}^{-4}$
)) is used as working fluid, and we assume that the working fluid in the foam is air (
$\text{s}^{2}~\text{K}^{-1}~\text{cm}^{-4}$
)) is used as working fluid, and we assume that the working fluid in the foam is air (
![]() $\unicode[STIX]{x1D6FD}/k\unicode[STIX]{x1D708}=0.1034$
(
$\unicode[STIX]{x1D6FD}/k\unicode[STIX]{x1D708}=0.1034$
(
![]() $\text{s}^{2}~\text{K}^{-1}~\text{cm}^{-4}$
)) and that the height and the temperature difference in the foam are identical to the fluid inside the cavity, this gives that for
$\text{s}^{2}~\text{K}^{-1}~\text{cm}^{-4}$
)) and that the height and the temperature difference in the foam are identical to the fluid inside the cavity, this gives that for
![]() $Ra=10^{7}$
the
$Ra=10^{7}$
the
![]() $Ra$
number in the insulation layer is approximately
$Ra$
number in the insulation layer is approximately
![]() $Ra\approx 7.2\times 10^{7}$
. However, we should emphasize that the complete set-up of the calculation is very complex and to define an appropriate
$Ra\approx 7.2\times 10^{7}$
. However, we should emphasize that the complete set-up of the calculation is very complex and to define an appropriate
![]() $Ra$
in the insulation layer is complicated.
$Ra$
in the insulation layer is complicated.
Figure 8(a) shows that, in agreement with the experimental results, the temperature gradient at the cylinder axis (
![]() $\unicode[STIX]{x1D709}=1.0$
) becomes destabilizing in the low
$\unicode[STIX]{x1D709}=1.0$
) becomes destabilizing in the low
![]() $Ra$
number regime when the Plexiglas sidewall is added. In the centre of the cell the effect of adding the additional insulation layer and thermal side shields is hardly visible. In addition, the results are also nearly identical for the two different working fluids, namely helium and neon, we consider in the simulations. This means that the simulations do not capture the trend of the temperature gradient with
$Ra$
number regime when the Plexiglas sidewall is added. In the centre of the cell the effect of adding the additional insulation layer and thermal side shields is hardly visible. In addition, the results are also nearly identical for the two different working fluids, namely helium and neon, we consider in the simulations. This means that the simulations do not capture the trend of the temperature gradient with
![]() $C$
that is observed in the simulations. However, we emphasize that a real laboratory set-up has much elements than just a physical sidewall, an isolation layer of foam, and thermal side shields. It is evident that the temperature gradient at the cylinder axis depends on modelling choices such as the properties of the Plexiglas sidewall and the use of isothermal condition at the outer edge of the domain, which may not represent the experimental conditions accurately enough.
$C$
that is observed in the simulations. However, we emphasize that a real laboratory set-up has much elements than just a physical sidewall, an isolation layer of foam, and thermal side shields. It is evident that the temperature gradient at the cylinder axis depends on modelling choices such as the properties of the Plexiglas sidewall and the use of isothermal condition at the outer edge of the domain, which may not represent the experimental conditions accurately enough.

Figure 8. The mean temperature gradient (a) at the cylinder axis (
![]() $\unicode[STIX]{x1D709}=1.00$
) and (b) close to the sidewall (
$\unicode[STIX]{x1D709}=1.00$
) and (b) close to the sidewall (
![]() $\unicode[STIX]{x1D709}=0.13$
). Solid symbols: new experimental results using helium (red down-pointing triangles), neon (green diamonds), nitrogen (red circles) and
$\unicode[STIX]{x1D709}=0.13$
). Solid symbols: new experimental results using helium (red down-pointing triangles), neon (green diamonds), nitrogen (red circles) and
![]() $\text{SF}_{6}$
(blue up-pointing triangles). Open symbols: simulation results using an adiabatic sidewall (open circles), using a Plexiglas sidewall with neon as working fluid (pink open up-pointing triangles) and considering the Plexiglas sidewall with an additional insulation layer and thermal side shields (blue open down-pointing triangles), the Plexiglas sidewall with helium as working fluid with an additional insulation layer and thermal side shields (orange open left-pointing triangles).
$\text{SF}_{6}$
(blue up-pointing triangles). Open symbols: simulation results using an adiabatic sidewall (open circles), using a Plexiglas sidewall with neon as working fluid (pink open up-pointing triangles) and considering the Plexiglas sidewall with an additional insulation layer and thermal side shields (blue open down-pointing triangles), the Plexiglas sidewall with helium as working fluid with an additional insulation layer and thermal side shields (orange open left-pointing triangles).
Close to the sidewall, for
![]() $\unicode[STIX]{x1D709}=0.13$
, we see that the addition of the insulation layer and thermal side shields affect the temperature gradient in the simulations. Again the simulations with helium and neon do not capture the trend with
$\unicode[STIX]{x1D709}=0.13$
, we see that the addition of the insulation layer and thermal side shields affect the temperature gradient in the simulations. Again the simulations with helium and neon do not capture the trend with
![]() $C$
that is found in the experiments. We do not yet fully understand the origin of the differences with the experimental observations. The reason is that there are many parameters, such as porosity, the temperature boundary conditions at the outer surface of the insulation and the thermal properties of the materials, which influence the specific results. All these properties are not precisely known from the experiments, which makes it impossible to match experiments and simulations exactly. We also note that the simulations are perfectly azimuthally homogeneous, and the presented simulation data are averaged in the azimuthal direction. The experimental measurements, in contrast, are performed at one azimuthal location, which might not be fully representative of the azimuthal average.
$C$
that is found in the experiments. We do not yet fully understand the origin of the differences with the experimental observations. The reason is that there are many parameters, such as porosity, the temperature boundary conditions at the outer surface of the insulation and the thermal properties of the materials, which influence the specific results. All these properties are not precisely known from the experiments, which makes it impossible to match experiments and simulations exactly. We also note that the simulations are perfectly azimuthally homogeneous, and the presented simulation data are averaged in the azimuthal direction. The experimental measurements, in contrast, are performed at one azimuthal location, which might not be fully representative of the azimuthal average.

Figure 9. The time and azimuthally averaged vertical and radial velocities and temperature for (a–c)
![]() $Ra=3\times 10^{5}$
and (d–f)
$Ra=3\times 10^{5}$
and (d–f)
![]() $Ra=1\times 10^{7}$
with neon as working fluid. (a,d) Adiabatic sidewall; (b,e) Plexiglas sidewall; (c,f) Plexiglas sidewall, additional insulation layer and thermal shields. Left panel:
$Ra=1\times 10^{7}$
with neon as working fluid. (a,d) Adiabatic sidewall; (b,e) Plexiglas sidewall; (c,f) Plexiglas sidewall, additional insulation layer and thermal shields. Left panel:
![]() $\langle u_{z}\rangle _{t,\unicode[STIX]{x1D719}}$
, middle panel:
$\langle u_{z}\rangle _{t,\unicode[STIX]{x1D719}}$
, middle panel:
![]() $\langle u_{r}\rangle _{t,\unicode[STIX]{x1D719}}$
, right panel:
$\langle u_{r}\rangle _{t,\unicode[STIX]{x1D719}}$
, right panel:
![]() $\langle \unicode[STIX]{x1D703}\rangle _{t,\unicode[STIX]{x1D719}}$
.
$\langle \unicode[STIX]{x1D703}\rangle _{t,\unicode[STIX]{x1D719}}$
.
Finally, in figure 9 we show the azimuthally averaged mean velocity for the three model configurations for
![]() $Ra=3\times 10^{5}$
and
$Ra=3\times 10^{5}$
and
![]() $Ra=10^{7}$
. As explained in Kunnen et al. (Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011), the structure shown in these azimuthally averaged radial and axial velocity maps are a result of a titled LSC as sketched in figure 10. It is immediately clear from figure 9 that the addition of the Plexiglas sidewall results in a noticeable change in the LSC. For the simulations with the adiabatic sidewall the temperature gradient at the cylinder axis is stabilizing. In contrast, when the sidewall is added the adjusted LSC, which is created due to the coupling between the fluid and sidewall dynamics, supports a small destabilizing temperature gradient at the cylinder axis.
$Ra=10^{7}$
. As explained in Kunnen et al. (Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011), the structure shown in these azimuthally averaged radial and axial velocity maps are a result of a titled LSC as sketched in figure 10. It is immediately clear from figure 9 that the addition of the Plexiglas sidewall results in a noticeable change in the LSC. For the simulations with the adiabatic sidewall the temperature gradient at the cylinder axis is stabilizing. In contrast, when the sidewall is added the adjusted LSC, which is created due to the coupling between the fluid and sidewall dynamics, supports a small destabilizing temperature gradient at the cylinder axis.

Figure 10. Schematic side view of the tilted LSC in the cylinder. The dash-dotted line is the axis of the cylinder.
6 Summary and conclusions
We performed experiments and DNSs for a
![]() $\unicode[STIX]{x1D6E4}=1.00$
cylindrical Rayleigh–Bénard convection cell, focusing on the effect of the sidewall. We measured the heat transport and the vertical temperature gradient in the horizontal mid-plane both on the cylinder axis and close to the sidewall for
$\unicode[STIX]{x1D6E4}=1.00$
cylindrical Rayleigh–Bénard convection cell, focusing on the effect of the sidewall. We measured the heat transport and the vertical temperature gradient in the horizontal mid-plane both on the cylinder axis and close to the sidewall for
![]() $2\times 10^{5}\leqslant Ra\leqslant 4\times 10^{10}$
. We find agreement between
$2\times 10^{5}\leqslant Ra\leqslant 4\times 10^{10}$
. We find agreement between
![]() $Nu$
obtained from experiments and simulations with an adiabatic sidewall for
$Nu$
obtained from experiments and simulations with an adiabatic sidewall for
![]() $Ra\lesssim 10^{7}$
and
$Ra\lesssim 10^{7}$
and
![]() $Ra\gtrsim 10^{9}$
. For
$Ra\gtrsim 10^{9}$
. For
![]() $Ra\gtrsim 10^{8}$
we also find an agreement for the temperature gradients at the cylinder axis measured in experiments and simulations, even when we use an idealized adiabatic sidewall in the simulations. Both experiments and simulations showed a stabilizing (positive) temperature gradient, see (4.1), at the sample centre, which had not been observed before for
$Ra\gtrsim 10^{8}$
we also find an agreement for the temperature gradients at the cylinder axis measured in experiments and simulations, even when we use an idealized adiabatic sidewall in the simulations. Both experiments and simulations showed a stabilizing (positive) temperature gradient, see (4.1), at the sample centre, which had not been observed before for
![]() $Pr\simeq 0.7$
(Tilgner et al.
Reference Tilgner, Belmonte and Libchaber1993; Brown & Ahlers Reference Brown and Ahlers2007). Near the sidewall, both simulations and experiments show a small destabilizing temperature gradient for
$Pr\simeq 0.7$
(Tilgner et al.
Reference Tilgner, Belmonte and Libchaber1993; Brown & Ahlers Reference Brown and Ahlers2007). Near the sidewall, both simulations and experiments show a small destabilizing temperature gradient for
![]() $Ra\gtrsim 10^{8}$
.
$Ra\gtrsim 10^{8}$
.
However, for
![]() $Ra\lesssim 10^{8}$
significant differences between experiments and simulations with an adiabatic sidewall are observed. In the simulations, the temperature gradient at the cylinder axis remained positive and increased with decreasing
$Ra\lesssim 10^{8}$
significant differences between experiments and simulations with an adiabatic sidewall are observed. In the simulations, the temperature gradient at the cylinder axis remained positive and increased with decreasing
![]() $Ra$
, while the experimental values decrease and become negative. A relatively rapid decrease occurred both at the sample centre and near the sidewall. The
$Ra$
, while the experimental values decrease and become negative. A relatively rapid decrease occurred both at the sample centre and near the sidewall. The
![]() $Ra$
range over which this decrease occurred depended on the employed gas. The decrease appeared at a higher
$Ra$
range over which this decrease occurred depended on the employed gas. The decrease appeared at a higher
![]() $Ra$
for a sample with a smaller sidewall admittance
$Ra$
for a sample with a smaller sidewall admittance
![]() $C$
. As
$C$
. As
![]() $Ra$
decreased past
$Ra$
decreased past
![]() $Ra\simeq 10^{6}$
, the experimental data indicated a sharp transition, presumably from the onset of the turbulent state as reported by Heslot et al. (Reference Heslot, Castaing and Libchaber1987). The
$Ra\simeq 10^{6}$
, the experimental data indicated a sharp transition, presumably from the onset of the turbulent state as reported by Heslot et al. (Reference Heslot, Castaing and Libchaber1987). The
![]() $C$
-dependence of these features may explain why they were not seen in the DNS since the adiabatic sidewall corresponds to
$C$
-dependence of these features may explain why they were not seen in the DNS since the adiabatic sidewall corresponds to
![]() $C\rightarrow \infty$
and the rapid decrease of the gradients occurs at significantly lower
$C\rightarrow \infty$
and the rapid decrease of the gradients occurs at significantly lower
![]() $Ra$
. Indeed, simulations show that the internal temperature gradient becomes negative for
$Ra$
. Indeed, simulations show that the internal temperature gradient becomes negative for
![]() $Ra\approx 10^{4}$
and is
$Ra\approx 10^{4}$
and is
![]() $-1$
at the onset as it should be.
$-1$
at the onset as it should be.
Since the magnitude of the measured temperature gradient depends on the specific working fluid, it seems that the influence of the sidewall on the flow structure is crucial to explain local measurements of the vertical temperature gradient. Therefore, we have simulated the effects of a physical sidewall on the heat transfer and flow dynamics. Based on the experimental results, we used the properties of neon and helium as a working fluid in the simulations. We find that for low
![]() $Ra$
, the sidewall indeed has pronounced effects, but these tend to decrease with increasing
$Ra$
, the sidewall indeed has pronounced effects, but these tend to decrease with increasing
![]() $Ra$
. One of the essential findings is that the thermodynamic coupling between the sidewall and fluid can lead to significant reorganization of the flow. Thus the effect of the sidewall is not necessarily caused by a parasitic heat flux through the sidewall only, but mainly manifests itself due to changed characteristics of the flow. Specifically, it seems that the sidewall stabilizes the large scale flow when compared to the case when just an adiabatic sidewall is considered. As this constitutes an actual change in the heat transfer, experimental measurements cannot be corrected for this.
$Ra$
. One of the essential findings is that the thermodynamic coupling between the sidewall and fluid can lead to significant reorganization of the flow. Thus the effect of the sidewall is not necessarily caused by a parasitic heat flux through the sidewall only, but mainly manifests itself due to changed characteristics of the flow. Specifically, it seems that the sidewall stabilizes the large scale flow when compared to the case when just an adiabatic sidewall is considered. As this constitutes an actual change in the heat transfer, experimental measurements cannot be corrected for this.
The pronounced effect of the sidewall configuration on the flow properties is beautifully shown by local measurements of the vertical temperature gradient discussed above. For low
![]() $Ra$
, simulations with an adiabatic sidewall do not even capture the destabilizing temperature gradient at the cell centre, while this feature is reproduced when the sidewall is taken into account. In an attempt to mimic the experimental apparatus as closely as possible, also the insulation layer on the dry surface of the sidewall and the thermal shields have been included in the simulations. From these simulations, it becomes clear that it is extremely complicated to capture all interactions between fluid and sidewall, due to which it remains impossible to reproduce all experimental details. The difficulties arise from the challenge of identifying all relevant design parameters as well as the uncertainty of various model parameters in the full three-dimensional DNS. An important finding is that the simulations reveal that the heat exchange between the sidewall and fluid mainly occurs in the region where the plates and sidewall are connection. This heat flux is, in part, driven by the thermal side shields. Interestingly, this heat flux significantly intensifies when convection in the foam starts. This means that in the design of experiments special attention should be spent on reducing heat currents in this region.
$Ra$
, simulations with an adiabatic sidewall do not even capture the destabilizing temperature gradient at the cell centre, while this feature is reproduced when the sidewall is taken into account. In an attempt to mimic the experimental apparatus as closely as possible, also the insulation layer on the dry surface of the sidewall and the thermal shields have been included in the simulations. From these simulations, it becomes clear that it is extremely complicated to capture all interactions between fluid and sidewall, due to which it remains impossible to reproduce all experimental details. The difficulties arise from the challenge of identifying all relevant design parameters as well as the uncertainty of various model parameters in the full three-dimensional DNS. An important finding is that the simulations reveal that the heat exchange between the sidewall and fluid mainly occurs in the region where the plates and sidewall are connection. This heat flux is, in part, driven by the thermal side shields. Interestingly, this heat flux significantly intensifies when convection in the foam starts. This means that in the design of experiments special attention should be spent on reducing heat currents in this region.
An important conclusion is also that small details matter. While the simulations in which the sidewall, insulation and thermal side shields are represented allow us to reproduce various experimental observations quantitatively, they fail to capture other observations. A notable example is that the simulations do not capture the variation of the temperature gradient at the cylinder axis and close to the sidewall with the sidewall admittance
![]() $C$
. The reason for this must be that a real laboratory set-up is much more involved and subtle than what we can consider in our simulations. It is evident that even our simulations in which we consider the sidewall properties, insulation layer and the thermal side shield with additional idealized boundary conditions do not allow us to reproduce all experimental observations. The reason for this is that tiny details matter, which should be considered as a warning for experimentalists and people performing simulations.
$C$
. The reason for this must be that a real laboratory set-up is much more involved and subtle than what we can consider in our simulations. It is evident that even our simulations in which we consider the sidewall properties, insulation layer and the thermal side shield with additional idealized boundary conditions do not allow us to reproduce all experimental observations. The reason for this is that tiny details matter, which should be considered as a warning for experimentalists and people performing simulations.
The simulations reveal that the sidewall can act as an extra heat conductor, which absorbs part of the heat from the fluid near the bottom plate and releases it into the fluid near the top plate. This means that the sidewall can act as a short circuit and the relative importance of this heat transfer circuit is more important at lower
![]() $Ra$
. This concept is the basic assumption in the models by Ahlers (Reference Ahlers2000) and Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001). Both models consider excess heat entering (leaving) the sidewall at the bottom (top) which then goes sideways into (out of) the fluid in the lower (upper) half of the cell. The advantage of the Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001) model is that they devised a one-dimensional model for this process in analytic form which makes computations of the size of the effect easier than using the method by Ahlers (Reference Ahlers2000) who did everything numerically by solving a two-dimensional heat-flow problem. However, the downside of the Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001) model is that it contains an unknown parameter which is supposed to be of order one. But changing this parameter from 0.8 to 1.2 for instance has a significant effect on the sidewall correction. Thus a direct comparison of the simulations with the models is very difficult as the models are based on various assumptions, while the situation is considerably more complicated in the simulations as we have an isothermal temperature boundary condition (
$Ra$
. This concept is the basic assumption in the models by Ahlers (Reference Ahlers2000) and Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001). Both models consider excess heat entering (leaving) the sidewall at the bottom (top) which then goes sideways into (out of) the fluid in the lower (upper) half of the cell. The advantage of the Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001) model is that they devised a one-dimensional model for this process in analytic form which makes computations of the size of the effect easier than using the method by Ahlers (Reference Ahlers2000) who did everything numerically by solving a two-dimensional heat-flow problem. However, the downside of the Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001) model is that it contains an unknown parameter which is supposed to be of order one. But changing this parameter from 0.8 to 1.2 for instance has a significant effect on the sidewall correction. Thus a direct comparison of the simulations with the models is very difficult as the models are based on various assumptions, while the situation is considerably more complicated in the simulations as we have an isothermal temperature boundary condition (
![]() $T=0.5$
) on the ‘dry’ side of the Plexiglas sidewall, a three-dimensional temperature distribution in the sidewall and a set of thermal side shields at various locations in the foam, while these aspects are not represented in the models. All these aspects make a comparison to the model very complicated, which goes outside the scope of the present study. As mentioned above an important result of the present simulations is that the coupling of the flow with a physical sidewall influences the actual heat transfer in Rayleigh–Bénard convection by changing the flow structure and the models by Ahlers (Reference Ahlers2000) and Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001) cannot correct for this effect. Further research is required to determine what designs can minimize these effects.
$T=0.5$
) on the ‘dry’ side of the Plexiglas sidewall, a three-dimensional temperature distribution in the sidewall and a set of thermal side shields at various locations in the foam, while these aspects are not represented in the models. All these aspects make a comparison to the model very complicated, which goes outside the scope of the present study. As mentioned above an important result of the present simulations is that the coupling of the flow with a physical sidewall influences the actual heat transfer in Rayleigh–Bénard convection by changing the flow structure and the models by Ahlers (Reference Ahlers2000) and Roche et al. (Reference Roche, Castaing, Chabaud, Hébral and Sommeria2001) cannot correct for this effect. Further research is required to determine what designs can minimize these effects.
Acknowledgements
Z.W. gratefully acknowledges financial support from the National Natural Science Foundation of China (grant nos 11572314, 11621202, and 11772323) and China Scholarship Council (CSC). P.W. gratefully acknowledges financial support from the National Natural Science Foundation of China (grant no. 11702196) and from the Fundamental Research Funds for the Central Universities. R.S. acknowledges financial support from the European Research Council through starting grant no. 804283 UltimateRB. This work is also supported by FOM and MCEC, both funded by NWO. The authors gratefully acknowledge the Gauss Center for Supercomputing (GCS) for providing computing time for a GCS Large-Scale Project on the GCS share of the supercomputer SuperMUC at Leibniz Supercomputing center (LRZ) under grant 10628/11695/13140. GCS is the alliance of the three national supercomputing centers HLRS (Universität Stuttgart), JSC (Forschungszentrum Jülich) and LRZ (Bayerische Akademie der Wissenschaften), funded by the German Federal Ministry of Education and Research (BMBF) and the German State Ministries for Research of Baden-Württemberg (MWK), Bayern (StMWFK) and Nordrhein-Westfalen (MIWF). Part of the work was carried out on the national e-infrastructure of SURFsara, a subsidiary of SURF cooperation, the collaborative ICT organization for Dutch education and research.
Appendix A. Time discretization
In this appendix we discuss the implementation of the time discretization of the heat equation (3.2), which reads
Let us assume that a temperature
![]() $\unicode[STIX]{x1D703}_{w}$
must be imposed at the
$\unicode[STIX]{x1D703}_{w}$
must be imposed at the
![]() $i$
th spatial node using the forcing term
$i$
th spatial node using the forcing term
![]() $h$
. If we write the time-discrete version of the above equation we have
$h$
. If we write the time-discrete version of the above equation we have
which we can recast as
with
Following what Fadlun et al. (Reference Fadlun, Verzicco, Orlandi and Mohd-Yusof2000) did for the velocity
![]() $\boldsymbol{u}$
, if we want
$\boldsymbol{u}$
, if we want
![]() $\unicode[STIX]{x1D703}_{i}^{n+1}\equiv \unicode[STIX]{x1D703}_{w}$
we have to plug this equivalence into (A 3) and solve for
$\unicode[STIX]{x1D703}_{i}^{n+1}\equiv \unicode[STIX]{x1D703}_{w}$
we have to plug this equivalence into (A 3) and solve for
![]() $h_{i}$
, which yields
$h_{i}$
, which yields
which is equivalent to enforcing directly the temperature
![]() $\unicode[STIX]{x1D703}_{w}$
at the desired node.
$\unicode[STIX]{x1D703}_{w}$
at the desired node.
Appendix B. Details of simulations with adiabatic sidewall
Table 3. Simulations for
![]() $Pr=0.7$
and
$Pr=0.7$
and
![]() $\unicode[STIX]{x1D6E4}=1.00$
with an adiabatic sidewall. The columns from left to right indicate the
$\unicode[STIX]{x1D6E4}=1.00$
with an adiabatic sidewall. The columns from left to right indicate the
![]() $Ra$
number, the used resolution in the azimuthal, radial and axial directions (
$Ra$
number, the used resolution in the azimuthal, radial and axial directions (
![]() $N_{\unicode[STIX]{x1D703}}\times N_{r}\times N_{z}$
), the number of grid points in the boundary layers close to the plates and the
$N_{\unicode[STIX]{x1D703}}\times N_{r}\times N_{z}$
), the number of grid points in the boundary layers close to the plates and the
![]() $Nu$
number over the full (
$Nu$
number over the full (
![]() $Nu_{f}$
) and last half (
$Nu_{f}$
) and last half (
![]() $Nu_{h}$
) of the considered simulation interval, and the volume integral of heat flux
$Nu_{h}$
) of the considered simulation interval, and the volume integral of heat flux
![]() $Nu_{V}=1+\sqrt{RaPr}\langle u_{z}T\rangle _{V,t}$
over the whole simulation interval.
$Nu_{V}=1+\sqrt{RaPr}\langle u_{z}T\rangle _{V,t}$
over the whole simulation interval.

As is indicated in tables 3 and 4 we ensured that an adequate resolution in the bulk (Stevens, Verzicco & Lohse Reference Stevens, Verzicco and Lohse2010) and boundary layers (Shishkina et al.
Reference Shishkina, Stevens, Grossmann and Lohse2010) has been used for all simulations. For example, for
![]() $Ra=2\times 10^{10}$
,
$Ra=2\times 10^{10}$
,
![]() $Pr=0.7$
and
$Pr=0.7$
and
![]() $\unicode[STIX]{x1D6E4}=1.00$
we use a grid resolution of
$\unicode[STIX]{x1D6E4}=1.00$
we use a grid resolution of
![]() $3072\times 512\times 1024$
in the azimuthal, radial and axial, direction, respectively. This means that this simulation is considerably better resolved than similar simulations considered before. For example, in Stevens et al. (Reference Stevens, Verzicco and Lohse2010) we found that for
$3072\times 512\times 1024$
in the azimuthal, radial and axial, direction, respectively. This means that this simulation is considerably better resolved than similar simulations considered before. For example, in Stevens et al. (Reference Stevens, Verzicco and Lohse2010) we found that for
![]() $Ra=2\times 10^{10}$
,
$Ra=2\times 10^{10}$
,
![]() $Pr=0.7$
and
$Pr=0.7$
and
![]() $\unicode[STIX]{x1D6E4}=0.5$
reasonably accurate results are obtained on a
$\unicode[STIX]{x1D6E4}=0.5$
reasonably accurate results are obtained on a
![]() $512\times 128\times 512$
grid. Later, in Stevens, Lohse & Verzicco (Reference Stevens, Lohse and Verzicco2011) we concluded that a grid of
$512\times 128\times 512$
grid. Later, in Stevens, Lohse & Verzicco (Reference Stevens, Lohse and Verzicco2011) we concluded that a grid of
![]() $768\times 192\times 768$
leads to better converged flow statistics for this case. However, this still implies that a resolution of
$768\times 192\times 768$
leads to better converged flow statistics for this case. However, this still implies that a resolution of
![]() $1536\times 384\times 768$
would already have been sufficient for the simulation at
$1536\times 384\times 768$
would already have been sufficient for the simulation at
![]() $Ra=2\times 10^{10}$
,
$Ra=2\times 10^{10}$
,
![]() $Pr=0.7$
and
$Pr=0.7$
and
![]() $\unicode[STIX]{x1D6E4}=1.00$
. Similarly, according to the estimates by Shishkina et al. (Reference Shishkina, Stevens, Grossmann and Lohse2010) there should be 12 points inside the boundary layers for a simulation at
$\unicode[STIX]{x1D6E4}=1.00$
. Similarly, according to the estimates by Shishkina et al. (Reference Shishkina, Stevens, Grossmann and Lohse2010) there should be 12 points inside the boundary layers for a simulation at
![]() $Ra=2\times 10^{10}$
. In this study we used 23 in the boundary layer. Therefore, based on the experience from previous studies, in which we tested the required resolution, we are confident that the simulations in this study are very well resolved. The simulations in which the sidewall and foam layers are added follow the same strict resolution criteria.
$Ra=2\times 10^{10}$
. In this study we used 23 in the boundary layer. Therefore, based on the experience from previous studies, in which we tested the required resolution, we are confident that the simulations in this study are very well resolved. The simulations in which the sidewall and foam layers are added follow the same strict resolution criteria.
Appendix C. Data simulations with physical sidewall
Table 4. Summary of the simulations using neon and helium as working fluid for
![]() $2\times 10^{5}\leqslant Ra\leqslant 10^{7}$
. We performed simulations with just the Plexiglas sidewall and using the Plexiglas sidewall with the additional insulation layer and thermal shields as indicated in figure 1. For
$2\times 10^{5}\leqslant Ra\leqslant 10^{7}$
. We performed simulations with just the Plexiglas sidewall and using the Plexiglas sidewall with the additional insulation layer and thermal shields as indicated in figure 1. For
![]() $Ra=10^{7}$
there are 16 grid points in the Plexiglas sidewall and 48 grid points in the insulation layer;
$Ra=10^{7}$
there are 16 grid points in the Plexiglas sidewall and 48 grid points in the insulation layer;
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $C^{p}$
and
$C^{p}$
and
![]() $\unicode[STIX]{x1D706}$
are, respectively, the density, constant pressure specific heat and thermal conductivity. The subscripts
$\unicode[STIX]{x1D706}$
are, respectively, the density, constant pressure specific heat and thermal conductivity. The subscripts
![]() $f$
,
$f$
,
![]() $s$
and
$s$
and
![]() $i$
refer to the fluid, sidewall and insulation, respectively. The
$i$
refer to the fluid, sidewall and insulation, respectively. The
![]() $Nu$
data are given in tables 5–7 as indicated.
$Nu$
data are given in tables 5–7 as indicated.

Table 5. The
![]() $Nu$
number data for the simulations with neon and a Plexiglas sidewall, see table 4.
$Nu$
number data for the simulations with neon and a Plexiglas sidewall, see table 4.

Table 6. The
![]() $Nu$
number data for the simulations with neon and a Plexiglas sidewall with additional insulation layer and thermal side shields, see table 4.
$Nu$
number data for the simulations with neon and a Plexiglas sidewall with additional insulation layer and thermal side shields, see table 4.

Table 7. The
![]() $Nu$
number data for the simulations with helium and a Plexiglas sidewall with additional insulation layer and thermal side shields, see table 4.
$Nu$
number data for the simulations with helium and a Plexiglas sidewall with additional insulation layer and thermal side shields, see table 4.