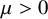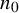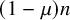1 Introduction
A key question in extremal graph theory is to find (almost-)spanning subgraphs H in a host graph G chosen from a certain class of graphs. Perhaps the simplest case along these lines may be to find (almost-)perfect matchings or (almost-)spanning trees, but even these cases have led us to a profound and intricate theory.
When the host graph G is dense, there have been extensive studies relating the existence of such (almost-)spanning subgraphs and the minimum degree of G. One of the earliest examples may be Dirac’s theorem, which states that the minimum degree condition
![]() $\delta (G)\geq n/2$
implies the existence of Hamiltonian cycles and paths. Another well-known example is that every n-vertex graph with the minimum degree
$\delta (G)\geq n/2$
implies the existence of Hamiltonian cycles and paths. Another well-known example is that every n-vertex graph with the minimum degree
![]() $\delta (G)$
contains a matching with at least
$\delta (G)$
contains a matching with at least
![]() $\min \{\delta (G),\lfloor n/2 \rfloor \}$
edges. In particular,
$\min \{\delta (G),\lfloor n/2 \rfloor \}$
edges. In particular,
![]() $\delta (G)\geq n/2$
implies that there exists a perfect matching in a graph, provided that n is even. This fact was subsequently generalized by Brandt [Reference Brandt9], who proved that a graph G contains every forest F with at most
$\delta (G)\geq n/2$
implies that there exists a perfect matching in a graph, provided that n is even. This fact was subsequently generalized by Brandt [Reference Brandt9], who proved that a graph G contains every forest F with at most
![]() $\delta (G)$
edges and at most n vertices. Note that this also includes another well-known fact that every graph G contains all trees with at most
$\delta (G)$
edges and at most n vertices. Note that this also includes another well-known fact that every graph G contains all trees with at most
![]() $\delta (G)$
edges. There have been more results along these lines (e.g., a theorem by Komlós, Sárközy and Szemerédi [Reference Komlós, Sárközy and Szemerédi20] which shows the existence of spanning trees under certain degree conditions or the bandwidth theorem by Böttcher, Schacht and Taraz [Reference Böttcher, Schacht and Taraz8]).
$\delta (G)$
edges. There have been more results along these lines (e.g., a theorem by Komlós, Sárközy and Szemerédi [Reference Komlós, Sárközy and Szemerédi20] which shows the existence of spanning trees under certain degree conditions or the bandwidth theorem by Böttcher, Schacht and Taraz [Reference Böttcher, Schacht and Taraz8]).
In contrast, finding (almost)-spanning structures in a sparse host graph G often turns out to be impossible in general, which forces one to consider more restricted classes of graphs. For example, a classical theorem of Pósa [Reference Pósa29], also obtained by Komlós and Szemerédi [Reference Komlós and Szemerédi21], states that ‘typical’ graphs with at least
![]() $(1+o(1))n\log n$
edges contain a Hamilton cycle. Recently, Montgomery [Reference Montgomery25] proved that typical graphs with
$(1+o(1))n\log n$
edges contain a Hamilton cycle. Recently, Montgomery [Reference Montgomery25] proved that typical graphs with
![]() $\Omega (n\log n)$
edges contain all spanning trees with bounded maximum degree. Other classes of graphs have also been considered (e.g., a ‘resilience’ version of these results [Reference Balogh, Csaba and Samotij5, Reference Lee and Sudakov24] or variants for randomly perturbed graphs [Reference Bohman, Frieze and Martin6, Reference Böttcher, Han, Kohayakawa, Montgomery, Parczyk and Person7, Reference Joos and Kim17, Reference Krivelevich, Kwan and Sudakov22]).
$\Omega (n\log n)$
edges contain all spanning trees with bounded maximum degree. Other classes of graphs have also been considered (e.g., a ‘resilience’ version of these results [Reference Balogh, Csaba and Samotij5, Reference Lee and Sudakov24] or variants for randomly perturbed graphs [Reference Bohman, Frieze and Martin6, Reference Böttcher, Han, Kohayakawa, Montgomery, Parczyk and Person7, Reference Joos and Kim17, Reference Krivelevich, Kwan and Sudakov22]).
Although it is known that some large minimum codegree conditions on hypergraphs ensure existence of perfect matchings, spanning trees or cycles [Reference Kühn, Mycroft and Osthus23, Reference Pavez-Signé, Sanhueza-Matamala and Stein27, Reference Rödl, Ruciński and Szemerédi30, Reference Rödl, Ruciński and Szemerédi31, Reference Rödl, Ruciński and Szemerédi32], the problem of finding spanning (or almost spanning) subhypergraphs in hypergraphs is fundamentally different from graphs. Our main goal is to explore this relatively less discovered area by proving the existence of an almost-spanning ‘hypertree’ in a well-known class of ‘sparse’ 3-uniform hypergraphs, the so-called Steiner triple systems. To further discuss our result, we first clarify what hypertrees are.
In what follows, we restrict our attention only to
![]() $3$
-uniform hypergraphs (or
$3$
-uniform hypergraphs (or
![]() $3$
-graphs briefly). A
$3$
-graphs briefly). A
![]() $3$
-graph is linear if every pair of distinct edges has at most one vertex in common. A hypertree is a connected, linear
$3$
-graph is linear if every pair of distinct edges has at most one vertex in common. A hypertree is a connected, linear
![]() $3$
-graph in which any two vertices are connected by a unique path (see Figure 1). Equivalently, a hypertree can be obtained by recursively adding edges such that each new edge intersects the current set of vertices in exactly one vertex. A matching in a
$3$
-graph in which any two vertices are connected by a unique path (see Figure 1). Equivalently, a hypertree can be obtained by recursively adding edges such that each new edge intersects the current set of vertices in exactly one vertex. A matching in a
![]() $3$
-graph H is a collection of pairwise disjoint edges of H, and a perfect matching is a matching that covers all the vertices in H.
$3$
-graph H is a collection of pairwise disjoint edges of H, and a perfect matching is a matching that covers all the vertices in H.
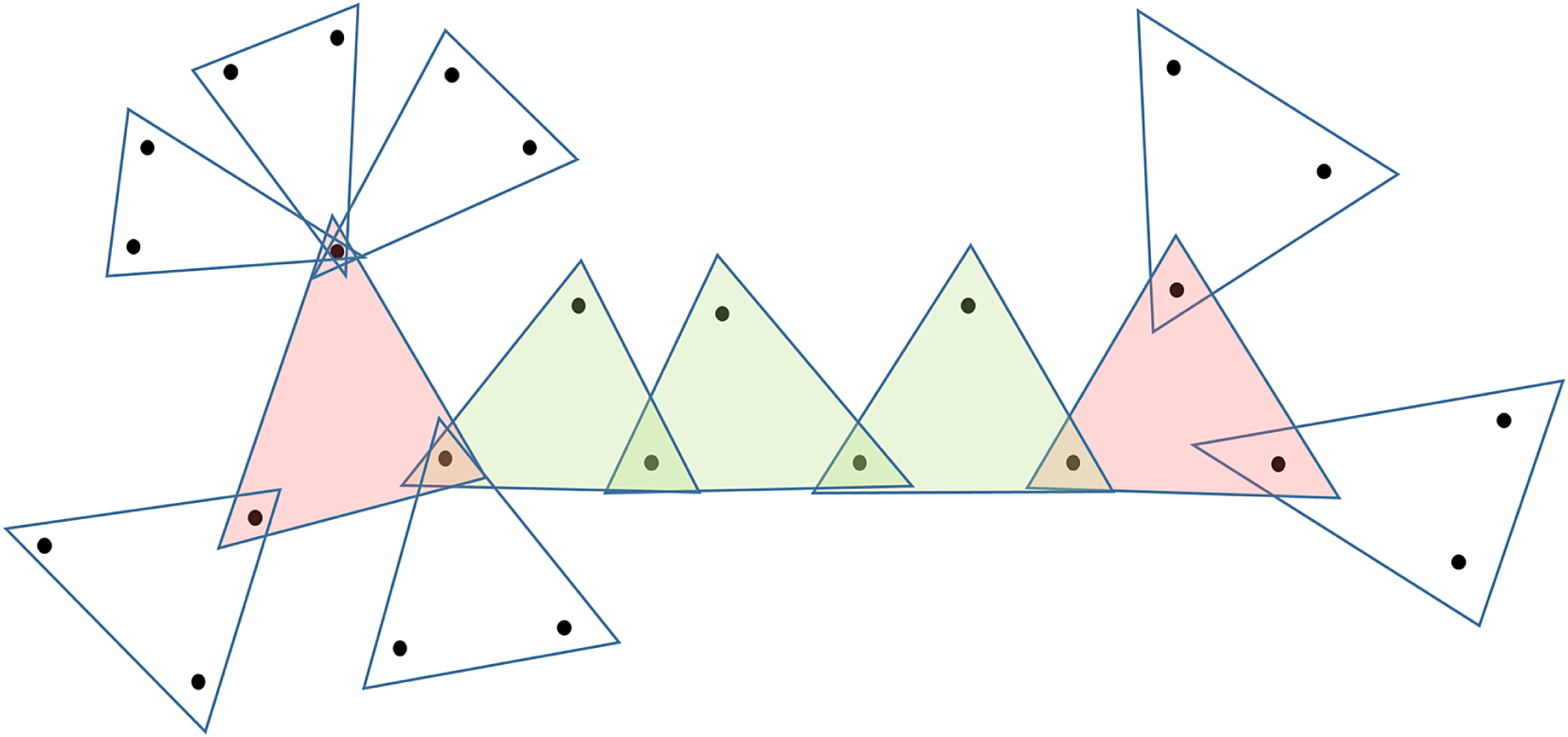
Figure 1 An example of a hypertree.
As mentioned before, (spanning) hypertrees in hypergraphs behave in a fundamentally different way from the graph case. For example, any connected graph contains at least one spanning tree; however, for
![]() $3$
-graphs, this may not be the case. First, a
$3$
-graphs, this may not be the case. First, a
![]() $3$
-graph with an even number of vertices has no spanning tree at all, as a hypertree always has an odd number of vertices. Even if we assume that the number of vertices is odd to set aside the parity issue, connectivity alone is still not sufficient to find a large hypertree. For example, a hypergraph with
$3$
-graph with an even number of vertices has no spanning tree at all, as a hypertree always has an odd number of vertices. Even if we assume that the number of vertices is odd to set aside the parity issue, connectivity alone is still not sufficient to find a large hypertree. For example, a hypergraph with
![]() $2k+1$
edges sharing the same two vertices forms a simplest
$2k+1$
edges sharing the same two vertices forms a simplest
![]() $3$
-graph with no hypertree having more than one edge. For another example illustrating the difference, a simple greedy algorithm finds all trees with
$3$
-graph with no hypertree having more than one edge. For another example illustrating the difference, a simple greedy algorithm finds all trees with
![]() $\delta (G)$
edges in a graph G with the minimum degree
$\delta (G)$
edges in a graph G with the minimum degree
![]() $\delta (G)$
, but the same algorithm for
$\delta (G)$
, but the same algorithm for
![]() $3$
-graphs only yields all hypertrees with at most
$3$
-graphs only yields all hypertrees with at most
![]() $\frac {1}{2}(\delta (G)+1)$
edges.
$\frac {1}{2}(\delta (G)+1)$
edges.
However, Goodall and de Mier [Reference Goodall and de Mier15] proved that every
![]() $3$
-graph with an odd number of vertices where every pair belongs to at least one edge contains at least one spanning hypertree. The extremal cases in their theorem are the
$3$
-graph with an odd number of vertices where every pair belongs to at least one edge contains at least one spanning hypertree. The extremal cases in their theorem are the
![]() $3$
-graphs where every pair of vertices belongs to exactly one hyperedge (i.e., Steiner triple systems).
$3$
-graphs where every pair of vertices belongs to exactly one hyperedge (i.e., Steiner triple systems).
Steiner triple systems can be seen as an analogue of complete graphs (where all possible types of spanning trees exist) for linear
![]() $3$
-graphs. However, even though the Goodall–de Mier theorem proves that every Steiner triple system contains a spanning hypertree (in fact, they proved that an n-vertex Steiner triple system contains at least
$3$
-graphs. However, even though the Goodall–de Mier theorem proves that every Steiner triple system contains a spanning hypertree (in fact, they proved that an n-vertex Steiner triple system contains at least
![]() $\Omega ((n/6)^{n/12})$
spanning hypertrees), it is far from the truth that every Steiner triple system contains all types of spanning hypertrees. For example, it is known [Reference Bryant and Horsley12] that for infinitely many odd n, there exist n-vertex Steiner triple systems with no perfect matching. Thus, any hypertree containing a perfect matching (there are super-exponentially many such hypertrees) cannot be found in those Steiner triple systems. This motivates the following natural question: what is the largest number t such that any n-vertex Steiner triple system contains all hypertrees on t vertices?
$\Omega ((n/6)^{n/12})$
spanning hypertrees), it is far from the truth that every Steiner triple system contains all types of spanning hypertrees. For example, it is known [Reference Bryant and Horsley12] that for infinitely many odd n, there exist n-vertex Steiner triple systems with no perfect matching. Thus, any hypertree containing a perfect matching (there are super-exponentially many such hypertrees) cannot be found in those Steiner triple systems. This motivates the following natural question: what is the largest number t such that any n-vertex Steiner triple system contains all hypertrees on t vertices?
This extremal question is hard even for matchings, which have a lot simpler structure than arbitrary hypertrees. A famous forty-year-old conjecture of Brouwer [Reference Brouwer10] states that every n-vertex Steiner triple system contains a matching covering
![]() $n-4$
vertices. This conjecture remains open, and the best bound known so far is the recent progress by Keevash, Pokrovskiy, Sudakov and Yepremyan [Reference Keevash, Pokrovskiy, Sudakov and Yepremyan19], proving that any n-vertex Steiner triple system contains a matching covering at least
$n-4$
vertices. This conjecture remains open, and the best bound known so far is the recent progress by Keevash, Pokrovskiy, Sudakov and Yepremyan [Reference Keevash, Pokrovskiy, Sudakov and Yepremyan19], proving that any n-vertex Steiner triple system contains a matching covering at least
![]() $n- O(\frac {\log n}{\log \log n})$
vertices. These results on matchings already allude to the fact that determining the exact value of t may be out of reach at the moment.
$n- O(\frac {\log n}{\log \log n})$
vertices. These results on matchings already allude to the fact that determining the exact value of t may be out of reach at the moment.
In 2019, Elliot and Rödl asked an ‘asymptotic’ question, which appears to be the very first step toward determining the exact value of t.
Conjecture 1.1 (Elliott and Rödl [Reference Elliott and Rödl13]).
Given
![]() $\mu \geq 0$
, there exists
$\mu \geq 0$
, there exists
![]() $n_0=n_0(\mu )$
such that if
$n_0=n_0(\mu )$
such that if
![]() $n \geq n_0$
, T is any hypertree on n vertices, and S is any Steiner triple system on
$n \geq n_0$
, T is any hypertree on n vertices, and S is any Steiner triple system on
![]() $m\geq n(1+\mu )$
vertices, then T is a subhypergraph of S.
$m\geq n(1+\mu )$
vertices, then T is a subhypergraph of S.
The conjecture implies that, although there are super-exponentially many spanning hypertrees which cannot be found in some Steiner triple systems, a completely different behavior should exist for slightly smaller hypertrees. Elliott and Rödl gave a positive evidence for the conjecture by proving it for special types of hypertrees called subdivision trees. Later, Arman, Rödl and Sales [Reference Arman, Rödl and Sales4, Reference Arman, Rödl and Sales3] proved Conjecture 1.1 for two different classes of hypertrees called d-ary hypertrees and turkeys. Our main result is to prove Conjecture 1.1 completely (i.e., for all hypertrees).
Theorem 1.2. For every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $n_0=n_0(\varepsilon )$
such that every n-vertex Steiner triple system G with
$n_0=n_0(\varepsilon )$
such that every n-vertex Steiner triple system G with
![]() $n \geq n_0$
contains every hypertree with at most
$n \geq n_0$
contains every hypertree with at most
![]() $(1-\varepsilon ) n$
vertices.
$(1-\varepsilon ) n$
vertices.
2 An outline of the proof
Our proof of Theorem 1.2 is partly motivated by the rainbow tree embedding theorem of Montgomery, Pokrovskiy and Sudakov [Reference Montgomery, Pokrovskiy and Sudakov26], which states that there exists a ‘rainbow’ copy of every tree T with at most
![]() $(1-o(1))n$
vertices in a properly edge-colored copy of
$(1-o(1))n$
vertices in a properly edge-colored copy of
![]() $K_n$
. As we consider
$K_n$
. As we consider
![]() $3$
-uniform linear hypergraphs instead of graphs, there are technical challenges to overcome, which will be discussed in due course.
$3$
-uniform linear hypergraphs instead of graphs, there are technical challenges to overcome, which will be discussed in due course.
Let T be a hypertree with
![]() $(1-o(1))n$
vertices, and let G be an n-vertex Steiner triple system. We first decompose T into
$(1-o(1))n$
vertices, and let G be an n-vertex Steiner triple system. We first decompose T into
![]() $T_0 \subseteq T_1 \subseteq \cdots \subseteq T_\ell = T$
such that
$T_0 \subseteq T_1 \subseteq \cdots \subseteq T_\ell = T$
such that
-
(1)
 $|T_0| = o(n)$
,
$|T_0| = o(n)$
, -
(2)
 $\ell =O(\text {polylog}(n))$
,
$\ell =O(\text {polylog}(n))$
, -
(3)
 $T_1$
is obtained by adding ‘large’ stars to
$T_1$
is obtained by adding ‘large’ stars to
 $T_0$
, and
$T_0$
, and -
(4) each
 $T_i$
,
$T_i$
,
 $i>1$
, is obtained by adding either
$i>1$
, is obtained by adding either
 $o(n)$
many paths of length
$o(n)$
many paths of length
 $3$
whose endpoints are in
$3$
whose endpoints are in
 $T_{i-1}$
or a matching where each edge contains exactly one vertex in
$T_{i-1}$
or a matching where each edge contains exactly one vertex in
 $T_{i-1}$
.
$T_{i-1}$
.
We will embed T into G by first embedding
![]() $T_0$
(in Step 0) and then extend
$T_0$
(in Step 0) and then extend
![]() $T_{i-1}$
to
$T_{i-1}$
to
![]() $T_{i}$
(in Step i) for each
$T_{i}$
(in Step i) for each
![]() $i \ge 1$
. We will treat the initial steps, embedding
$i \ge 1$
. We will treat the initial steps, embedding
![]() $T_0$
and extending
$T_0$
and extending
![]() $T_0$
to
$T_0$
to
![]() $T_1$
, with extra care and execute the remaining steps inductively. More precisely, we first embed
$T_1$
, with extra care and execute the remaining steps inductively. More precisely, we first embed
![]() $T_0$
by a deterministic greedy algorithm and collect a set
$T_0$
by a deterministic greedy algorithm and collect a set
![]() $\mathcal {S}$
of ‘large’ vertex-disjoint stars centered at vertices in the copy of
$\mathcal {S}$
of ‘large’ vertex-disjoint stars centered at vertices in the copy of
![]() $T_0$
(where a star centered at a vertex v is a set of edges whose pairwise intersection is
$T_0$
(where a star centered at a vertex v is a set of edges whose pairwise intersection is
![]() $\{v\}$
). Here, the stars we find are in fact almost spanning (i.e., ‘larger’ than the large stars described in (3) due to a technical reason). We then partition all the
$\{v\}$
). Here, the stars we find are in fact almost spanning (i.e., ‘larger’ than the large stars described in (3) due to a technical reason). We then partition all the
![]() $(1-o(1))n$
vertices of G that are not in the copy of
$(1-o(1))n$
vertices of G that are not in the copy of
![]() $T_0$
into
$T_0$
into
![]() $R\cup X_1\cup \cdots \cup X_\ell $
in a randomized way while also making sure that the two leaves in every edge of every star in
$R\cup X_1\cup \cdots \cup X_\ell $
in a randomized way while also making sure that the two leaves in every edge of every star in
![]() $\mathcal {S}$
lie in the same part of the partition. Given the partition, ‘most’ vertices in
$\mathcal {S}$
lie in the same part of the partition. Given the partition, ‘most’ vertices in
![]() $T_i\setminus T_{i-1}$
are embedded into
$T_i\setminus T_{i-1}$
are embedded into
![]() $X_i$
, and the remaining vertices are embedded into the ‘reservoir’ R at each step.
$X_i$
, and the remaining vertices are embedded into the ‘reservoir’ R at each step.
Let us take a closer look at each of the steps. First, let us consider Steps 0, 1. The decomposition
![]() $T_0 \subseteq T_1 \subseteq \cdots \subseteq T_\ell $
of T closely follows the ideas of [Reference Montgomery, Pokrovskiy and Sudakov26]. Finding
$T_0 \subseteq T_1 \subseteq \cdots \subseteq T_\ell $
of T closely follows the ideas of [Reference Montgomery, Pokrovskiy and Sudakov26]. Finding
![]() $\mathcal {S}$
is not hard either; it follows from adapting the switching technique in Section 8 of [Reference Montgomery, Pokrovskiy and Sudakov26], originally introduced by Woolbright [Reference Woolbright33] and Brouwer, de Vries and Wieringa [Reference Brouwer, de Vries and Wieringa11]. A technical problem occurs when we build the vertex set
$\mathcal {S}$
is not hard either; it follows from adapting the switching technique in Section 8 of [Reference Montgomery, Pokrovskiy and Sudakov26], originally introduced by Woolbright [Reference Woolbright33] and Brouwer, de Vries and Wieringa [Reference Brouwer, de Vries and Wieringa11]. A technical problem occurs when we build the vertex set
![]() $X_1$
. In [Reference Montgomery, Pokrovskiy and Sudakov26],
$X_1$
. In [Reference Montgomery, Pokrovskiy and Sudakov26],
![]() $X_1$
was simply taken by choosing each vertex independently at random, but in our
$X_1$
was simply taken by choosing each vertex independently at random, but in our
![]() $3$
-graph setting, a straightforward application of this approach no longer captures the structures of stars that we need, as the ‘leaves’ of a star in a
$3$
-graph setting, a straightforward application of this approach no longer captures the structures of stars that we need, as the ‘leaves’ of a star in a
![]() $3$
-graph are pairs of vertices rather than singletons; for instance, too few edges of a star will be selected if
$3$
-graph are pairs of vertices rather than singletons; for instance, too few edges of a star will be selected if
![]() $X_1$
is taken by choosing vertices uniformly at random. To resolve this issue, we pair the leaf vertices of each star, and we either select both vertices in each pair or we select neither of them while choosing the random subset
$X_1$
is taken by choosing vertices uniformly at random. To resolve this issue, we pair the leaf vertices of each star, and we either select both vertices in each pair or we select neither of them while choosing the random subset
![]() $X_1$
.
$X_1$
.
Now let us consider Step i for
![]() $i>1$
. Let
$i>1$
. Let
![]() $\{X_{i, 1}, X_{i, 2}\}$
be a random partition of
$\{X_{i, 1}, X_{i, 2}\}$
be a random partition of
![]() $X_i$
. For each
$X_i$
. For each
![]() $i>1$
, Step i uses the following properties of the partition
$i>1$
, Step i uses the following properties of the partition
![]() $R\cup (X_{1,1}\cup X_{1,2})\cup (X_{2,1}\cup X_{2,2})\cup \cdots \cup (X_{\ell ,1}\cup X_{\ell ,2})$
, which can be obtained by using standard concentration inequalities. For each
$R\cup (X_{1,1}\cup X_{1,2})\cup (X_{2,1}\cup X_{2,2})\cup \cdots \cup (X_{\ell ,1}\cup X_{\ell ,2})$
, which can be obtained by using standard concentration inequalities. For each
![]() $i>1$
and
$i>1$
and
![]() $j\in [2]$
,
$j\in [2]$
,
-
(i) every vertex has ‘many’ neighbors in
 $X_{i,j}$
as well as in R, and
$X_{i,j}$
as well as in R, and -
(ii) for every pair of large enough disjoint sets
 $A, B \subseteq V(G) \setminus X_{i,j}$
, the number of edges of the form
$A, B \subseteq V(G) \setminus X_{i,j}$
, the number of edges of the form
 $\{a,b,c\}$
with
$\{a,b,c\}$
with
 $a \in A$
,
$a \in A$
,
 $b \in B$
and
$b \in B$
and
 $c \in X_{i,j}$
is close to their expectation.
$c \in X_{i,j}$
is close to their expectation.
To perform (4), one should find
![]() $o(n)$
paths of length three or a matching to extend
$o(n)$
paths of length three or a matching to extend
![]() $T_{i-1}$
to
$T_{i-1}$
to
![]() $T_{i}$
. In the former case, it is not hard to find
$T_{i}$
. In the former case, it is not hard to find
![]() $o(n)$
paths of length three by using (i) and (ii) above, and this follows the ideas of [Reference Montgomery, Pokrovskiy and Sudakov26] closely. However, we use a completely different approach for finding a matching to extend
$o(n)$
paths of length three by using (i) and (ii) above, and this follows the ideas of [Reference Montgomery, Pokrovskiy and Sudakov26] closely. However, we use a completely different approach for finding a matching to extend
![]() $T_{i-1}$
to
$T_{i-1}$
to
![]() $T_i$
. Using (ii) and Pippenger’s hypergraph matching theorem, we embed most of the edges of the matching using vertices in
$T_i$
. Using (ii) and Pippenger’s hypergraph matching theorem, we embed most of the edges of the matching using vertices in
![]() $X_i = X_{i, 1} \cup X_{i,2}$
. Then we embed the remaining edges of the matching using vertices in R by making use of (i).
$X_i = X_{i, 1} \cup X_{i,2}$
. Then we embed the remaining edges of the matching using vertices in R by making use of (i).
Organization. We introduce preliminary results in Section 3. We show (i) and (ii) are true for our random process and use it to embed matchings and bare paths in Section 4. In Section 5, we show that we can embed large vertex-disjoint stars into a Steiner triple system with prescribed centers. Finally, we put everything together to iteratively find an embedding of T in Section 6. The proof of hypertree splitting lemma is illustrated in Appendix A.
3 Preliminaries and notation
As outlined in the previous section, we need to decompose a hypertree T into
![]() $T_0\subseteq T_1\subseteq \cdots \subseteq T_\ell =T$
, following the approach taken in [Reference Montgomery, Pokrovskiy and Sudakov26]. To this end, we introduce some auxiliary definitions.
$T_0\subseteq T_1\subseteq \cdots \subseteq T_\ell =T$
, following the approach taken in [Reference Montgomery, Pokrovskiy and Sudakov26]. To this end, we introduce some auxiliary definitions.
First of all, let us clarify our definition of paths. A (Berge-)path of length
![]() $\ell $
in a hypergraph is a sequence
$\ell $
in a hypergraph is a sequence
![]() $v_1,e_1,v_2,\dots ,e_\ell ,v_{\ell +1}$
of distinct vertices and edges such that
$v_1,e_1,v_2,\dots ,e_\ell ,v_{\ell +1}$
of distinct vertices and edges such that
![]() $v_i,v_{i+1}\in e_i$
for all
$v_i,v_{i+1}\in e_i$
for all
![]() $i\in [\ell ]$
. In particular, a path in a linear
$i\in [\ell ]$
. In particular, a path in a linear
![]() $3$
-graph G is a subgraph of G on
$3$
-graph G is a subgraph of G on
![]() $2\ell +1$
vertices
$2\ell +1$
vertices
![]() $\{v_0,v_1,\cdots ,v_\ell \}\cup \{u_1,\cdots ,u_{\ell }\}$
such that each
$\{v_0,v_1,\cdots ,v_\ell \}\cup \{u_1,\cdots ,u_{\ell }\}$
such that each
![]() $\{v_i,u_{i+1},v_{i+1}\}$
is an edge for
$\{v_i,u_{i+1},v_{i+1}\}$
is an edge for
![]() $i=0,1,\cdots ,\ell -1$
. Each of the two pairs
$i=0,1,\cdots ,\ell -1$
. Each of the two pairs
![]() $\{v_0,u_1\}$
and
$\{v_0,u_1\}$
and
![]() $\{u_\ell ,v_\ell \}$
in the first and the last edges of P is called an end pair of P.
$\{u_\ell ,v_\ell \}$
in the first and the last edges of P is called an end pair of P.
A hypergraph T is a hypertree if and only if there is a unique path between any pair of distinct vertices. It is straightforward to see that a hypertree is a linear hypergraph. A u–v path P (or a path P between u and v) means a path P paired with the specified end vertices u and v, each of which is chosen from each end pair, respectively. The vertices other than u and v in a u–v path P are called the internal vertices of P.
In a hypertree T, a bare path P is a subhypergraph of T such that it is a u–v path of length
![]() $\ell \geq 2$
where no edges in
$\ell \geq 2$
where no edges in
![]() $T\setminus E(P)$
are incident to the internal vertices of P. For example, the green edges in Figure 1 form a bare path, but green edges plus one of the red edges does not.
$T\setminus E(P)$
are incident to the internal vertices of P. For example, the green edges in Figure 1 form a bare path, but green edges plus one of the red edges does not.
A leaf of a hypertree T is a vertex
![]() $v\in V(T)$
of degree one such that the edge e containing v has another vertex u of degree one. That is, removing u and v from T produces a subhypertree of T. The edges that contain a leaf are called leaf edges of T. In particular, the number of leaves of T is always even unless T is a single edge.
$v\in V(T)$
of degree one such that the edge e containing v has another vertex u of degree one. That is, removing u and v from T produces a subhypertree of T. The edges that contain a leaf are called leaf edges of T. In particular, the number of leaves of T is always even unless T is a single edge.
A star of size D is a 3-graph S on
![]() $2D+1$
vertices
$2D+1$
vertices
![]() $\{v\}\cup \{u_1,\cdots ,u_D\}\cup \{w_1,\cdots ,w_D\}$
such that each triple
$\{v\}\cup \{u_1,\cdots ,u_D\}\cup \{w_1,\cdots ,w_D\}$
such that each triple
![]() $\{v,u_i,w_i\}$
is an edge for
$\{v,u_i,w_i\}$
is an edge for
![]() $i \in [D]$
. The vertex v of degree D is called the center of S. A matching M is a collection of pairwise disjoint edges. If a matching M consists of leaf edges of a hypertree T, the set of leaves of T in M is called the leaf set of M. We simply say that a vertex subset X of T is a matching leaf set of T if X is the leaf set of a matching M in T.
$i \in [D]$
. The vertex v of degree D is called the center of S. A matching M is a collection of pairwise disjoint edges. If a matching M consists of leaf edges of a hypertree T, the set of leaves of T in M is called the leaf set of M. We simply say that a vertex subset X of T is a matching leaf set of T if X is the leaf set of a matching M in T.
Using these terminologies, the following lemma formalizes (1)–(4) in the previous section by adapting the tree splitting lemma in Section 4 of [Reference Montgomery, Pokrovskiy and Sudakov26] to our linear 3-graph setting.
Lemma 3.1. Let
![]() $D, n \geq 2$
be integers, and let
$D, n \geq 2$
be integers, and let
![]() $0<\mu <1$
. For any hypertree T with at most n edges and
$0<\mu <1$
. For any hypertree T with at most n edges and
![]() $2n+1$
vertices, there exist integers
$2n+1$
vertices, there exist integers
![]() $\ell \leq 10^5 D \mu ^{-2}$
and
$\ell \leq 10^5 D \mu ^{-2}$
and
![]() $s \in [\ell ]$
and a sequence of subgraphs
$s \in [\ell ]$
and a sequence of subgraphs
![]() $T_0 \subseteq T_1 \subseteq \cdots T_\ell = T$
such that the following holds:
$T_0 \subseteq T_1 \subseteq \cdots T_\ell = T$
such that the following holds:
-
(i)
 $T_0$
has at most
$T_0$
has at most
 $\mu n$
edges and at most
$\mu n$
edges and at most
 $3\mu n$
vertices.
$3\mu n$
vertices. -
(ii)
 $T_1$
is obtained by adding stars of size at least D to
$T_1$
is obtained by adding stars of size at least D to
 $T_0$
; that is, take pairwise vertex-disjoint stars of size at least D and identify their centers with vertices in
$T_0$
; that is, take pairwise vertex-disjoint stars of size at least D and identify their centers with vertices in
 $T_0$
.
$T_0$
. -
(iii) For
 $i \notin \{ 0, s\}$
,
$i \notin \{ 0, s\}$
,
 $T_{i+1}$
is obtained by adding a matching to
$T_{i+1}$
is obtained by adding a matching to
 $T_i$
such that
$T_i$
such that
 $V(T_{i+1})\setminus V(T_i)$
is a matching leaf set of
$V(T_{i+1})\setminus V(T_i)$
is a matching leaf set of
 $T_{i+1}$
.
$T_{i+1}$
. -
(iv)
 $T_{s+1}$
is obtained by adding at most
$T_{s+1}$
is obtained by adding at most
 $\mu n$
vertex-disjoint bare paths of length
$\mu n$
vertex-disjoint bare paths of length
 $3$
to
$3$
to
 $T_s$
such that every bare path we add is a u–v path P where
$T_s$
such that every bare path we add is a u–v path P where
 $u,v\in V(T_s)$
, and
$u,v\in V(T_s)$
, and
 $V(P) \setminus \{u,v\}$
is disjoint from
$V(P) \setminus \{u,v\}$
is disjoint from
 $V(T_s)$
.
$V(T_s)$
.
Although this lemma does not seem to follow directly from [Reference Montgomery, Pokrovskiy and Sudakov26], the proof closely resembles theirs. Thus, we will give a brief proof in Appendix A.
We will frequently use standard concentration inequalities, which can be found, for example, in [Reference Alon and Spencer2].
Lemma 3.2 (One-sided Chernoff Bound).
Let
![]() $X_1, \cdots , X_n$
be mutually independent Bernoulli random variables, and let
$X_1, \cdots , X_n$
be mutually independent Bernoulli random variables, and let
![]() $X = \sum _{i=1}^n X_i$
. Then,
$X = \sum _{i=1}^n X_i$
. Then,
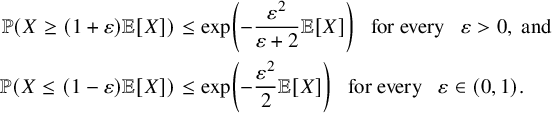 $$ \begin{align*} \mathbb{P}(X \geq (1+\varepsilon)\mathbb{E}[X]) & \leq \exp\left(-\frac{\varepsilon^2}{\varepsilon+2}\mathbb{E}[X]\right) \enspace \text{ for every } \enspace \varepsilon>0, \text{ and }\\ \mathbb{P}(X \leq (1-\varepsilon)\mathbb{E}[X]) & \leq \exp\left(-\frac{\varepsilon^2}{2}\mathbb{E}[X]\right) \enspace \text{ for every } \enspace \varepsilon \in (0, 1). \end{align*} $$
$$ \begin{align*} \mathbb{P}(X \geq (1+\varepsilon)\mathbb{E}[X]) & \leq \exp\left(-\frac{\varepsilon^2}{\varepsilon+2}\mathbb{E}[X]\right) \enspace \text{ for every } \enspace \varepsilon>0, \text{ and }\\ \mathbb{P}(X \leq (1-\varepsilon)\mathbb{E}[X]) & \leq \exp\left(-\frac{\varepsilon^2}{2}\mathbb{E}[X]\right) \enspace \text{ for every } \enspace \varepsilon \in (0, 1). \end{align*} $$
The following corollary will be enough in most of the applications.
Corollary 3.3 (The Chernoff Bound).
Let
![]() $X_1, X_2, \cdots , X_n$
be i.i.d. Bernoulli random variables, and let
$X_1, X_2, \cdots , X_n$
be i.i.d. Bernoulli random variables, and let
![]() $X= \sum _{i=1}^n X_i$
. Then for
$X= \sum _{i=1}^n X_i$
. Then for
![]() $\varepsilon \in (0, 1)$
,
$\varepsilon \in (0, 1)$
,
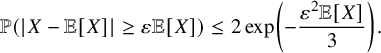 $$ \begin{align*}\mathbb{P}(|X-\mathbb{E}[X]| \geq \varepsilon \mathbb{E}[X] ) \leq 2\exp\left(-\frac{\varepsilon^2 \mathbb{E}[X]}{3}\right).\end{align*} $$
$$ \begin{align*}\mathbb{P}(|X-\mathbb{E}[X]| \geq \varepsilon \mathbb{E}[X] ) \leq 2\exp\left(-\frac{\varepsilon^2 \mathbb{E}[X]}{3}\right).\end{align*} $$
Given a probability space
![]() $\Omega = \prod _{i=1}^n \Omega _i$
and a random variable
$\Omega = \prod _{i=1}^n \Omega _i$
and a random variable
![]() $X: \Omega \rightarrow \mathbb {R}$
, X is k-Lipschitz if
$X: \Omega \rightarrow \mathbb {R}$
, X is k-Lipschitz if
![]() $|X(\omega )-X(\omega ')| \leq k$
whenever
$|X(\omega )-X(\omega ')| \leq k$
whenever
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
differ in at most one coordinate.
$\omega '$
differ in at most one coordinate.
Lemma 3.4 (Azuma’s inequality).
If
![]() $X: \prod _{i=1}^n \Omega _i \rightarrow \mathbb {R}$
is k-Lipschitz, then
$X: \prod _{i=1}^n \Omega _i \rightarrow \mathbb {R}$
is k-Lipschitz, then
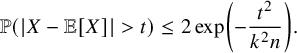 $$ \begin{align*}\mathbb{P}(|X-\mathbb{E}[X]|> t) \leq 2\exp\left(-\frac{t^2}{k^2 n}\right).\end{align*} $$
$$ \begin{align*}\mathbb{P}(|X-\mathbb{E}[X]|> t) \leq 2\exp\left(-\frac{t^2}{k^2 n}\right).\end{align*} $$
We use the notation
![]() $\ll $
for the hierarchy between constants. For instance, if we claim that a statement holds under the condition
$\ll $
for the hierarchy between constants. For instance, if we claim that a statement holds under the condition
![]() $0<a \ll b, c \ll d$
, then it means that there exist non-decreasing functions
$0<a \ll b, c \ll d$
, then it means that there exist non-decreasing functions
![]() $f_1, f_2:(0, 1] \rightarrow (0, 1]$
and
$f_1, f_2:(0, 1] \rightarrow (0, 1]$
and
![]() $g:(0, 1]^2 \rightarrow (0, 1]$
such that the statement holds if
$g:(0, 1]^2 \rightarrow (0, 1]$
such that the statement holds if
![]() $0<b \leq f_1(d)$
,
$0<b \leq f_1(d)$
,
![]() $0<c \leq f_2(d)$
, and
$0<c \leq f_2(d)$
, and
![]() $0<a \leq g(b, c)$
. We do not attempt to describe all these functions explicitly. We also write
$0<a \leq g(b, c)$
. We do not attempt to describe all these functions explicitly. We also write
![]() $a=(b \pm c)d$
if
$a=(b \pm c)d$
if
![]() $(b-c)d \leq a \leq (b+c)d$
.
$(b-c)d \leq a \leq (b+c)d$
.
For a given
![]() $3$
-graph G and
$3$
-graph G and
![]() $v \in V(G)$
,
$v \in V(G)$
,
![]() $\deg (v)$
denotes the number of edges containing v, and a vertex
$\deg (v)$
denotes the number of edges containing v, and a vertex
![]() $u \in V(G)$
is a neighbor of another vertex
$u \in V(G)$
is a neighbor of another vertex
![]() $v \in V(G)$
if there exists an edge of G containing both u and v. Let
$v \in V(G)$
if there exists an edge of G containing both u and v. Let
![]() $\delta (G)=\min _{v\in V(G)} \deg (v)$
be the minimum degree of G. In particular, the number of neighbors of v in a linear 3-graph G is exactly
$\delta (G)=\min _{v\in V(G)} \deg (v)$
be the minimum degree of G. In particular, the number of neighbors of v in a linear 3-graph G is exactly
![]() $2 \deg (v)$
. Let
$2 \deg (v)$
. Let
![]() $G[A_1, A_2, A_3]$
denote the subhypergraph of G with the vertex set
$G[A_1, A_2, A_3]$
denote the subhypergraph of G with the vertex set
![]() $A_1 \cup A_2 \cup A_3$
and the edge set
$A_1 \cup A_2 \cup A_3$
and the edge set
![]() $\{\{x,y,z\} \in E(G) : x \in A_1$
,
$\{\{x,y,z\} \in E(G) : x \in A_1$
,
![]() $y \in A_2, z \in A_3 \}$
. We allow nonempty intersection of
$y \in A_2, z \in A_3 \}$
. We allow nonempty intersection of
![]() $A_1, A_2, A_3$
so an edge in
$A_1, A_2, A_3$
so an edge in
![]() $G[A_1, A_2, A_3]$
may have more than one vertex contained in
$G[A_1, A_2, A_3]$
may have more than one vertex contained in
![]() $A_i$
for some
$A_i$
for some
![]() $i \in [3]$
. Let
$i \in [3]$
. Let
![]() $e_G(A_1,A_2,A_3)$
(or simply
$e_G(A_1,A_2,A_3)$
(or simply
![]() $e(A_1,A_2,A_3)$
) be the number of edges of
$e(A_1,A_2,A_3)$
) be the number of edges of
![]() $G[A_1, A_2, A_3]$
.
$G[A_1, A_2, A_3]$
.
With these terminologies, Pippenger’s theorem [Reference Pippenger and Spencer28], which strengthens a theorem in [Reference Frankl and Rödl14] (which also appears in [Reference Alon and Spencer2] as a standard application of Rödl’s nibble), can be stated as follows.
Lemma 3.5 (Pippenger’s theorem).
Let
![]() $\varepsilon , \delta>0$
, and let
$\varepsilon , \delta>0$
, and let
![]() $D, k$
be integers such that
$D, k$
be integers such that
![]() $0<\frac {1}{D}, \delta \ll \frac {1}{k}, \varepsilon $
. If an n-vertex k-uniform hypergraph H satisfies that
$0<\frac {1}{D}, \delta \ll \frac {1}{k}, \varepsilon $
. If an n-vertex k-uniform hypergraph H satisfies that
-
(i) the degree of v,
 $\deg (v) = (1 \pm \delta ) D$
for all
$\deg (v) = (1 \pm \delta ) D$
for all
 $v \in V(H)$
and
$v \in V(H)$
and -
(ii) for any two distinct vertices
 $u, v \in V(H)$
, the number of edges in H containing
$u, v \in V(H)$
, the number of edges in H containing
 $\{u, v\}$
is less than
$\{u, v\}$
is less than
 $\delta D$
,
$\delta D$
,
then H contains a matching of size at least
![]() $(1-\varepsilon )\frac {n}{k}$
.
$(1-\varepsilon )\frac {n}{k}$
.
4 Matchings and bare paths
Our goal in this section is to collect lemmas for extending a given hypertree
![]() $T_i$
to
$T_i$
to
![]() $T_{i+1}$
when
$T_{i+1}$
when
![]() $T_{i+1}$
is obtained by adding a matching or bare paths to
$T_{i+1}$
is obtained by adding a matching or bare paths to
![]() $T_i$
. The key tool to handle the former case is Pippenger’s theorem, and the latter case follows from standard concentration results for random edge subsets.
$T_i$
. The key tool to handle the former case is Pippenger’s theorem, and the latter case follows from standard concentration results for random edge subsets.
Let G be an n-vertex Steiner triple system. A singleton-pair partition
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $V(G)$
is a partition
$V(G)$
is a partition
![]() $\{U_1, U_2, \cdots , U_m\}$
of
$\{U_1, U_2, \cdots , U_m\}$
of
![]() $V(G)$
such that
$V(G)$
such that
![]() $|U_i|\leq 2$
for each
$|U_i|\leq 2$
for each
![]() $i\in [m]$
. Throughout this section, G always denotes an n-vertex Steiner triple system with a given singleton-pair partition
$i\in [m]$
. Throughout this section, G always denotes an n-vertex Steiner triple system with a given singleton-pair partition
![]() $\mathcal {U}$
. For such a fixed singleton-pair partition
$\mathcal {U}$
. For such a fixed singleton-pair partition
![]() $\mathcal {U}$
, the random subset
$\mathcal {U}$
, the random subset
![]() $\mathcal {U}_p$
of
$\mathcal {U}_p$
of
![]() $\mathcal {U}$
is then obtained by choosing each
$\mathcal {U}$
is then obtained by choosing each
![]() $U_i$
independently at random with probability p. Let
$U_i$
independently at random with probability p. Let
![]() $X=\bigcup _{U\in \mathcal {U}_p} U$
, which we denote by
$X=\bigcup _{U\in \mathcal {U}_p} U$
, which we denote by
![]() $X\sim \mathcal {U}_p$
.
$X\sim \mathcal {U}_p$
.
To find a large matching using Pippenger’s theorem (Lemma 3.5), we need to prove that a randomly chosen vertex set
![]() $X\sim \mathcal {U}_p$
together with certain sets
$X\sim \mathcal {U}_p$
together with certain sets
![]() $A, B$
of already-embedded vertices induces an almost-regular hypergraph (see Lemma 4.2). As we cannot specify these sets of already-embedded vertices at the beginning, we want to show that
$A, B$
of already-embedded vertices induces an almost-regular hypergraph (see Lemma 4.2). As we cannot specify these sets of already-embedded vertices at the beginning, we want to show that
![]() $X\sim \mathcal {U}_p$
together with any pair of disjoint vertex sets
$X\sim \mathcal {U}_p$
together with any pair of disjoint vertex sets
![]() $A, B$
of size at least
$A, B$
of size at least
![]() $\Omega (n)$
induces an almost-regular hypergraph. However, as there are too many choices of such vertex sets A and B, naive applications of concentration results do not yield a strong enough result to use the union bound. Hence, we first prove Lemma 4.1 which shows that
$\Omega (n)$
induces an almost-regular hypergraph. However, as there are too many choices of such vertex sets A and B, naive applications of concentration results do not yield a strong enough result to use the union bound. Hence, we first prove Lemma 4.1 which shows that
![]() $X\sim \mathcal {U}_p$
together with any pair of much smaller sets induces an almost-regular hypergraph, and we use these much smaller sets as building blocks for A and B to prove Lemma 4.2.
$X\sim \mathcal {U}_p$
together with any pair of much smaller sets induces an almost-regular hypergraph, and we use these much smaller sets as building blocks for A and B to prove Lemma 4.2.
Lemma 4.1. Let
![]() $X\sim \mathcal {U}_p$
for
$X\sim \mathcal {U}_p$
for
![]() $p \geq 1/(\log n)^{100}$
, and let
$p \geq 1/(\log n)^{100}$
, and let
![]() $\varepsilon \geq 1/{(\log n)^{100}}$
. Then the following holds with probability at least
$\varepsilon \geq 1/{(\log n)^{100}}$
. Then the following holds with probability at least
![]() $1-o(1/n)$
: For every pair of disjoint sets
$1-o(1/n)$
: For every pair of disjoint sets
![]() $A, B \subseteq V(G)$
satisfying
$A, B \subseteq V(G)$
satisfying
-
(a)
 $n^{2/5} \leq |A|, |B| \leq n^{1/2}$
,
$n^{2/5} \leq |A|, |B| \leq n^{1/2}$
, -
(b)
 $e(A,B,\{v\})\leq (\log n)^{10}$
for every
$e(A,B,\{v\})\leq (\log n)^{10}$
for every
 $v \in V(G)$
, and
$v \in V(G)$
, and -
(c) X is disjoint from
 $A\cup B$
,
$A\cup B$
,
we have
![]() $e(A,B,X)=(1\pm \varepsilon )p|A||B|$
.
$e(A,B,X)=(1\pm \varepsilon )p|A||B|$
.
Proof. Let
![]() $G_X[A, B]$
be the auxiliary bipartite graph on the bipartition
$G_X[A, B]$
be the auxiliary bipartite graph on the bipartition
![]() $A\cup B$
, where
$A\cup B$
, where
![]() $(a,b)\in A\times B$
is an edge if there exists
$(a,b)\in A\times B$
is an edge if there exists
![]() $x\in X$
such that
$x\in X$
such that
![]() $abx\in E(G)$
. As G is a Steiner triple system, every pair
$abx\in E(G)$
. As G is a Steiner triple system, every pair
![]() $(a,b)\in A\times B$
extends to a unique edge together with a vertex x, which belongs to X with probability p. Thus, the expected size of
$(a,b)\in A\times B$
extends to a unique edge together with a vertex x, which belongs to X with probability p. Thus, the expected size of
![]() $E(G_X[A, B])$
is
$E(G_X[A, B])$
is
![]() $p|A||B|$
.
$p|A||B|$
.
One may then apply Azuma’s inequality to prove concentration results for
![]() $|E(G_X[A, B])|$
. Indeed, for a fixed pair of disjoint
$|E(G_X[A, B])|$
. Indeed, for a fixed pair of disjoint
![]() $A, B \subseteq V(G)$
such that
$A, B \subseteq V(G)$
such that
![]() $e(A,B,\{v\})\leq k$
for every
$e(A,B,\{v\})\leq k$
for every
![]() $v\in V(G)$
, each event
$v\in V(G)$
, each event
![]() $U\in \mathcal {U}_p$
changes
$U\in \mathcal {U}_p$
changes
![]() $|E(G_X[A, B])|$
by at most
$|E(G_X[A, B])|$
by at most
![]() $2k$
. Therefore, by Azuma’s inequality (Lemma 3.4), the probability that
$2k$
. Therefore, by Azuma’s inequality (Lemma 3.4), the probability that
![]() $|E(G_X[A, B])|$
deviates from its expectation by more than
$|E(G_X[A, B])|$
deviates from its expectation by more than
![]() $\varepsilon p|A||B|$
is at most
$\varepsilon p|A||B|$
is at most
![]() $2 \exp (-\varepsilon ^2 p^2 |A|^2 |B|^2 / 4n k^2)$
.
$2 \exp (-\varepsilon ^2 p^2 |A|^2 |B|^2 / 4n k^2)$
.
The number of pairs
![]() $(A,B)$
such that
$(A,B)$
such that
![]() $n^{2/5} \leq |A|, |B| \leq n^{1/2}$
is at most
$n^{2/5} \leq |A|, |B| \leq n^{1/2}$
is at most
 $$ \begin{align*} \left(n^{1/2}\binom{n} {n^{1/2}}\right)^2 \leq n \left(\frac{en}{n^{1/2}}\right)^{2n^{1/2}}\leq (en^{1/2})^{2n^{1/2}+2}. \end{align*} $$
$$ \begin{align*} \left(n^{1/2}\binom{n} {n^{1/2}}\right)^2 \leq n \left(\frac{en}{n^{1/2}}\right)^{2n^{1/2}}\leq (en^{1/2})^{2n^{1/2}+2}. \end{align*} $$
Among these choices, we call a pair
![]() $(A,B)$
bad if
$(A,B)$
bad if
![]() $\big ||E(G_X[A, B])|-p|A||B|\big | \geq \varepsilon p|A||B|$
. Then the probability that there exists a bad pair
$\big ||E(G_X[A, B])|-p|A||B|\big | \geq \varepsilon p|A||B|$
. Then the probability that there exists a bad pair
![]() $(A, B)$
is at most
$(A, B)$
is at most
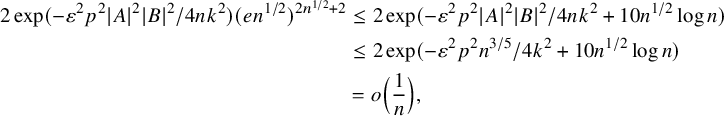 $$ \begin{align*} 2 \exp(-\varepsilon^2 p^2 |A|^2 |B|^2 / 4nk^2)(en^{1/2})^{2n^{1/2}+2} & \leq 2\exp(-\varepsilon^2 p^2 |A|^2 |B|^2 / 4 n k^2 + 10n^{1/2}\log n)\\ & \leq 2\exp(-\varepsilon^2 p^2n^{3/5}/4 k^2 + 10n^{1/2}\log n) \\ & = o\Big(\frac{1}{n}\Big), \end{align*} $$
$$ \begin{align*} 2 \exp(-\varepsilon^2 p^2 |A|^2 |B|^2 / 4nk^2)(en^{1/2})^{2n^{1/2}+2} & \leq 2\exp(-\varepsilon^2 p^2 |A|^2 |B|^2 / 4 n k^2 + 10n^{1/2}\log n)\\ & \leq 2\exp(-\varepsilon^2 p^2n^{3/5}/4 k^2 + 10n^{1/2}\log n) \\ & = o\Big(\frac{1}{n}\Big), \end{align*} $$
provided
![]() $k=(\log n)^{10}$
and
$k=(\log n)^{10}$
and
![]() $\varepsilon ,p\geq (\log n)^{-100}$
. If
$\varepsilon ,p\geq (\log n)^{-100}$
. If
![]() $X, A, B$
are pairwise disjoint, then
$X, A, B$
are pairwise disjoint, then
![]() $e(X, A, B)=|E(G_X[A, B])|$
, which completes the proof.
$e(X, A, B)=|E(G_X[A, B])|$
, which completes the proof.
By using the above lemma, we prove a concentration result for larger sets A and B of size
![]() $o(n)$
.
$o(n)$
.
Lemma 4.2. Let
![]() $X\sim \mathcal {U}_p$
for
$X\sim \mathcal {U}_p$
for
![]() $p \geq 1/(\log n)^{100}$
, and let
$p \geq 1/(\log n)^{100}$
, and let
![]() $\eta \geq 1/(\log n)^{100}$
. Then with probability
$\eta \geq 1/(\log n)^{100}$
. Then with probability
![]() $1-o(1/n)$
, every pair of disjoint subsets
$1-o(1/n)$
, every pair of disjoint subsets
![]() $A, B \subseteq V(G) \setminus X$
of size at least
$A, B \subseteq V(G) \setminus X$
of size at least
![]() $\eta n$
satisfies
$\eta n$
satisfies
![]() $e(A, B, X) = (1 \pm \eta )p|A||B|$
.
$e(A, B, X) = (1 \pm \eta )p|A||B|$
.
Proof. Let us fix disjoint subsets
![]() $A, B \subseteq V(G) \setminus X$
of size at least
$A, B \subseteq V(G) \setminus X$
of size at least
![]() $\eta n$
. We will partition A and B into ‘manageable’ subsets to which Lemma 4.1 can apply. To that end, let
$\eta n$
. We will partition A and B into ‘manageable’ subsets to which Lemma 4.1 can apply. To that end, let
![]() $s:=\lceil \frac {|A|}{3n^{2/5}} \rceil $
and
$s:=\lceil \frac {|A|}{3n^{2/5}} \rceil $
and
![]() $t:=\lceil \frac {|B|}{3n^{2/5}} \rceil $
. Partition A into s subsets
$t:=\lceil \frac {|B|}{3n^{2/5}} \rceil $
. Partition A into s subsets
![]() $A_1, A_2, \ldots , A_s$
by choosing
$A_1, A_2, \ldots , A_s$
by choosing
![]() $i_a \in [s]$
uniformly and independently at random for each
$i_a \in [s]$
uniformly and independently at random for each
![]() $a \in A$
and putting a in
$a \in A$
and putting a in
![]() $A_{i_a}$
. We also partition B in the same way but using t subsets
$A_{i_a}$
. We also partition B in the same way but using t subsets
![]() $B_1, B_2,\ldots , B_t$
. For each
$B_1, B_2,\ldots , B_t$
. For each
![]() $i\in [s]$
and
$i\in [s]$
and
![]() $j\in [t]$
, the expected sizes of each
$j\in [t]$
, the expected sizes of each
![]() $A_i$
and
$A_i$
and
![]() $B_j$
are
$B_j$
are
![]() $|A|/s$
and
$|A|/s$
and
![]() $|B|/t$
, respectively, each of which are of size
$|B|/t$
, respectively, each of which are of size
![]() $(3+o(1))n^{2/5}$
. The Chernoff bound (Lemma 3.3) then implies that all
$(3+o(1))n^{2/5}$
. The Chernoff bound (Lemma 3.3) then implies that all
![]() $A_i$
and
$A_i$
and
![]() $B_j$
are of size between
$B_j$
are of size between
![]() $n^{2/5}$
and
$n^{2/5}$
and
![]() $n^{1/2}$
with probability at least
$n^{1/2}$
with probability at least
![]() $1-2(s+t)\exp (-n^{2/5}/12) = 1-o(1/n)$
.
$1-2(s+t)\exp (-n^{2/5}/12) = 1-o(1/n)$
.
For fixed
![]() $v \in V(G)$
,
$v \in V(G)$
,
![]() $i \in [s]$
, and
$i \in [s]$
, and
![]() $j \in [t]$
, let
$j \in [t]$
, let
![]() $\mathcal {E}_e$
be the event that an edge
$\mathcal {E}_e$
be the event that an edge
![]() $e \in E(G)$
containing v is in
$e \in E(G)$
containing v is in
![]() $G[\{v\}, A_i, B_j]$
. Then
$G[\{v\}, A_i, B_j]$
. Then
![]() $\mathcal {E}_e$
occurs with probability at most
$\mathcal {E}_e$
occurs with probability at most
![]() $1/(st) = o(1/n)$
for any
$1/(st) = o(1/n)$
for any
![]() $e \in E(G)$
containing v. Furthermore, linearity of G ensures that the events
$e \in E(G)$
containing v. Furthermore, linearity of G ensures that the events
![]() $\{\mathcal {E}_e\}_{e\in E(G), e \ni v}$
are mutually independent. Thus, by the one-sided Chernoff bound (Lemma 3.2),
$\{\mathcal {E}_e\}_{e\in E(G), e \ni v}$
are mutually independent. Thus, by the one-sided Chernoff bound (Lemma 3.2),
![]() $e(A_i, B_j, \{v\}) \leq (\log n)^{10}$
with probability at least
$e(A_i, B_j, \{v\}) \leq (\log n)^{10}$
with probability at least
![]() $1-\exp (-(\log n)^8)$
. Together with the union bound, this is enough to conclude that
$1-\exp (-(\log n)^8)$
. Together with the union bound, this is enough to conclude that
![]() $e(A_i, B_j, \{v\}) \leq (\log n)^{10} $
holds for all vertices
$e(A_i, B_j, \{v\}) \leq (\log n)^{10} $
holds for all vertices
![]() $v \in V(G)$
and indices
$v \in V(G)$
and indices
![]() $i \in [s]$
,
$i \in [s]$
,
![]() $j \in [t]$
with positive probability. Therefore, there exist partitions
$j \in [t]$
with positive probability. Therefore, there exist partitions
![]() $A_1, A_2, \ldots , A_s$
of A and
$A_1, A_2, \ldots , A_s$
of A and
![]() $B_1, B_2, \ldots , B_t$
of B such that
$B_1, B_2, \ldots , B_t$
of B such that
![]() $A_i$
and
$A_i$
and
![]() $B_j$
satisfy the conditions (a) and (b) of Lemma 4.1 for every i and j.
$B_j$
satisfy the conditions (a) and (b) of Lemma 4.1 for every i and j.
Thus, Lemma 4.1 implies that, with probability at least
![]() $1-o(1/n)$
, we have
$1-o(1/n)$
, we have
![]() $e(A_i, B_j, X) = (1 \pm \eta ) p |A_i||B_j|$
for every
$e(A_i, B_j, X) = (1 \pm \eta ) p |A_i||B_j|$
for every
![]() $i \in [s], j \in [t]$
(for all choices of
$i \in [s], j \in [t]$
(for all choices of
![]() $A, B\subseteq V(G) \setminus X$
). Now, taking the sum over all
$A, B\subseteq V(G) \setminus X$
). Now, taking the sum over all
![]() $i \in [s]$
and
$i \in [s]$
and
![]() $j \in [t]$
completes the proof of the lemma.
$j \in [t]$
completes the proof of the lemma.
Finally, using Lemma 4.2, we find a matching M that covers almost all the vertices of any prescribed set A which is small enough and disjoint from the random set X.
Lemma 4.3. Let
![]() $\varepsilon>0$
be a constant and suppose
$\varepsilon>0$
be a constant and suppose
![]() $0< 1/n \ll \varepsilon $
. Let
$0< 1/n \ll \varepsilon $
. Let
![]() $X\sim \mathcal {U}_p$
for
$X\sim \mathcal {U}_p$
for
![]() $p \geq {1}/{(\log n)^{20}}$
. Then the following holds with probability
$p \geq {1}/{(\log n)^{20}}$
. Then the following holds with probability
![]() $1-o(1/n)$
. For all vertex sets
$1-o(1/n)$
. For all vertex sets
![]() $A \subseteq V(G) \setminus X$
of size at most
$A \subseteq V(G) \setminus X$
of size at most
![]() $pn/2$
, there exists a matching M of size at least
$pn/2$
, there exists a matching M of size at least
![]() $|A|-\varepsilon p n$
such that each edge
$|A|-\varepsilon p n$
such that each edge
![]() $e \in M$
satisfies
$e \in M$
satisfies
![]() $|e \cap X|=2$
and
$|e \cap X|=2$
and
![]() $|e \cap A|=1$
.
$|e \cap A|=1$
.
Proof. Choose
![]() $\tau>0$
such that
$\tau>0$
such that
![]() $0<1/n \ll \tau \ll \varepsilon $
, and let
$0<1/n \ll \tau \ll \varepsilon $
, and let
![]() $\eta = \tau p^2$
. In particular, we choose
$\eta = \tau p^2$
. In particular, we choose
![]() $\tau $
so that
$\tau $
so that
![]() $\eta =\tau p^2 \geq 1/(\log n)^{100}$
.
$\eta =\tau p^2 \geq 1/(\log n)^{100}$
.
Let
![]() $\{X_1, X_2\}$
be a random partition of X obtained by assigning each
$\{X_1, X_2\}$
be a random partition of X obtained by assigning each
![]() $U_i \in \mathcal {U}_p$
to exactly one of
$U_i \in \mathcal {U}_p$
to exactly one of
![]() $X_1, X_2$
independently at random. Then each
$X_1, X_2$
independently at random. Then each
![]() $X_i$
is a (possibly dependent) copy of
$X_i$
is a (possibly dependent) copy of
![]() $\mathcal {U}_{p/2}$
(i.e.,
$\mathcal {U}_{p/2}$
(i.e.,
![]() $X_i\sim \mathcal {U}_{p/2}$
).
$X_i\sim \mathcal {U}_{p/2}$
).
By Lemma 4.2, with probability
![]() $1-o(1/n)$
, every pair of disjoint subsets
$1-o(1/n)$
, every pair of disjoint subsets
![]() $A', B' \subseteq V(G) \setminus X_2$
of size at least
$A', B' \subseteq V(G) \setminus X_2$
of size at least
![]() $\eta n$
satisfies
$\eta n$
satisfies
![]() $e(A', B', X_2) = (1\pm \eta ) p|A'||B'|/2$
. Similarly, with probability
$e(A', B', X_2) = (1\pm \eta ) p|A'||B'|/2$
. Similarly, with probability
![]() $1-o(1/n)$
, every pair of disjoint subsets
$1-o(1/n)$
, every pair of disjoint subsets
![]() $A', B' \subseteq V(G) \setminus X_1$
of size at least
$A', B' \subseteq V(G) \setminus X_1$
of size at least
![]() $\eta n$
satisfies
$\eta n$
satisfies
![]() $e(A', X_1, B') = (1\pm \eta ) p|A'||B'|/2$
. Conditioning on these two events, say
$e(A', X_1, B') = (1\pm \eta ) p|A'||B'|/2$
. Conditioning on these two events, say
![]() $\mathcal E_1$
and
$\mathcal E_1$
and
![]() $\mathcal E_2$
, the following holds for any
$\mathcal E_2$
, the following holds for any
![]() $A^* \subseteq V(G) \setminus X$
with
$A^* \subseteq V(G) \setminus X$
with
![]() $|A^*| = pn/2$
:
$|A^*| = pn/2$
:
-
(i) For every
 $A' \subseteq A^*$
and
$A' \subseteq A^*$
and
 $X' \subseteq X_1$
of size at least
$X' \subseteq X_1$
of size at least
 $\eta n$
, we have
$\eta n$
, we have
 $e(A', X', X_2)=(1 \pm \eta ) p|A'||X'|/2$
;
$e(A', X', X_2)=(1 \pm \eta ) p|A'||X'|/2$
; -
(ii) For every
 $A' \subseteq A^*$
and
$A' \subseteq A^*$
and
 $X' \subseteq X_2$
of size at least
$X' \subseteq X_2$
of size at least
 $\eta n$
, we have
$\eta n$
, we have
 $e(A', X_1, X')=(1 \pm \eta ) p|A'||X'|/2$
.
$e(A', X_1, X')=(1 \pm \eta ) p|A'||X'|/2$
.
This implies that
![]() $e(A^*, \{v\}, X_2) = (1 \pm \eta ) p|A^*|/2$
for all but at most
$e(A^*, \{v\}, X_2) = (1 \pm \eta ) p|A^*|/2$
for all but at most
![]() $2\eta n$
vertices v in
$2\eta n$
vertices v in
![]() $X_1$
. Indeed, if not, we can collect
$X_1$
. Indeed, if not, we can collect
![]() $\eta n$
vertices to obtain a subset
$\eta n$
vertices to obtain a subset
![]() $X' \subseteq X_1$
with
$X' \subseteq X_1$
with
![]() $|X'| \geq \eta n$
and either
$|X'| \geq \eta n$
and either
![]() $e(A^*, X', X_2)> (1 +\eta ) p|A^*||X'|/2$
or
$e(A^*, X', X_2)> (1 +\eta ) p|A^*||X'|/2$
or
![]() $e(A^*, X', X_2) < (1 -\eta ) p|A^*||X'|/2$
, which contradicts the conditioned events
$e(A^*, X', X_2) < (1 -\eta ) p|A^*||X'|/2$
, which contradicts the conditioned events
![]() $\mathcal E_1$
and
$\mathcal E_1$
and
![]() $\mathcal E_2$
. Moreover, by swapping the roles of
$\mathcal E_2$
. Moreover, by swapping the roles of
![]() $X_1$
and
$X_1$
and
![]() $X_2$
, one can prove that, for all but at most
$X_2$
, one can prove that, for all but at most
![]() $2\eta n$
vertices
$2\eta n$
vertices
![]() $v\in X_2$
,
$v\in X_2$
,
![]() $e(A^*, X_1, \{v\}) = (1 \pm \eta ) p|A^*|/2$
holds. Analogously, for all but at most
$e(A^*, X_1, \{v\}) = (1 \pm \eta ) p|A^*|/2$
holds. Analogously, for all but at most
![]() $2\eta n$
vertices
$2\eta n$
vertices
![]() $v\in A^*$
,
$v\in A^*$
,
![]() $e(\{v\}, X_1, X_2) = (1 \pm \eta ) p|X_1|/2$
holds.
$e(\{v\}, X_1, X_2) = (1 \pm \eta ) p|X_1|/2$
holds.
One can also control the sizes of
![]() $X _1$
and
$X _1$
and
![]() $X_2$
. Namely, since
$X_2$
. Namely, since
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are 2-Lipschitz, Azuma’s inequality (Lemma 3.4) gives that
$X_2$
are 2-Lipschitz, Azuma’s inequality (Lemma 3.4) gives that
![]() $|X_1|, |X_2|=(1\pm \eta ) p n/2$
with probability at least
$|X_1|, |X_2|=(1\pm \eta ) p n/2$
with probability at least
In particular, for each
![]() $i \in [2]$
, we have
$i \in [2]$
, we have
![]() $(1 \pm \eta ) p|X_i|/2 = (1 \pm 3\eta )p^2 n/4$
.
$(1 \pm \eta ) p|X_i|/2 = (1 \pm 3\eta )p^2 n/4$
.
Assuming all these four high probability events occur, namely
![]() $\mathcal E_1, \mathcal E_2$
, and that
$\mathcal E_1, \mathcal E_2$
, and that
![]() $|X_1|, |X_2|=(1\pm \eta ) p n/2$
, let
$|X_1|, |X_2|=(1\pm \eta ) p n/2$
, let
![]() $A \subseteq V(G) \setminus X$
be a vertex set of size at most
$A \subseteq V(G) \setminus X$
be a vertex set of size at most
![]() $pn/2$
. By adding arbitrary vertices to A, we obtain a set
$pn/2$
. By adding arbitrary vertices to A, we obtain a set
![]() $A^*$
with
$A^*$
with
![]() $|A^*|=pn/2$
. Let H be the
$|A^*|=pn/2$
. Let H be the
![]() $3$
-graph obtained by removing all the exceptional vertices from
$3$
-graph obtained by removing all the exceptional vertices from
![]() $G[A^*, X_1, X_2]$
(i.e., those vertices whose degrees in
$G[A^*, X_1, X_2]$
(i.e., those vertices whose degrees in
![]() $G[A^*, X_1, X_2]$
are not in the range
$G[A^*, X_1, X_2]$
are not in the range
![]() $(1 \pm 3 \eta )p^2 n/4$
). By the discussion above concerning the number of such exceptional vertices, we remove at most
$(1 \pm 3 \eta )p^2 n/4$
). By the discussion above concerning the number of such exceptional vertices, we remove at most
![]() $2 \eta n$
vertices from each part. Thus, as G is linear, each remaining vertex has degree
$2 \eta n$
vertices from each part. Thus, as G is linear, each remaining vertex has degree
As H is linear, each pair of vertices has codegree at most
![]() $1$
. Therefore, by Pippenger’s theorem (Lemma 3.5), as
$1$
. Therefore, by Pippenger’s theorem (Lemma 3.5), as
![]() $(3\eta +16\eta /p^2) \ll \varepsilon /2$
, H contains a matching
$(3\eta +16\eta /p^2) \ll \varepsilon /2$
, H contains a matching
![]() $M^*$
of size at least
$M^*$
of size at least
By removing the edges containing a vertex of
![]() $A^*\setminus A$
from
$A^*\setminus A$
from
![]() $M^*$
, we obtain the desired matching M of size at least
$M^*$
, we obtain the desired matching M of size at least
![]() $|A|-\varepsilon pn.$
$|A|-\varepsilon pn.$
Lemma 4.3 allows us to extend
![]() $T_{i-1}$
to
$T_{i-1}$
to
![]() $T_i$
whenever
$T_i$
whenever
![]() $T_i$
is obtained by adding a matching, each of whose edges contains exactly one vertex in
$T_i$
is obtained by adding a matching, each of whose edges contains exactly one vertex in
![]() $T_{i-1}$
. We now proceed to the other case where we add
$T_{i-1}$
. We now proceed to the other case where we add
![]() $o(n)$
bare paths of length 3. A pair of u–v paths
$o(n)$
bare paths of length 3. A pair of u–v paths
![]() $P_1$
and
$P_1$
and
![]() $P_2$
are said to be internally vertex-disjoint if their vertex sets are disjoint except the two vertices u and v (i.e.,
$P_2$
are said to be internally vertex-disjoint if their vertex sets are disjoint except the two vertices u and v (i.e.,
![]() $(V(P_1) \setminus \{u, v\}) \cap (V(P_2) \setminus \{u, v\}) = \emptyset $
). The next lemma proves that there are ‘many’ internally vertex-disjoint paths of length
$(V(P_1) \setminus \{u, v\}) \cap (V(P_2) \setminus \{u, v\}) = \emptyset $
). The next lemma proves that there are ‘many’ internally vertex-disjoint paths of length
![]() $3$
between pairs of vertices u and v.
$3$
between pairs of vertices u and v.
Lemma 4.4. Let
![]() $0<1/n \ll \mu \ll p$
, and let
$0<1/n \ll \mu \ll p$
, and let
![]() $X\sim \mathcal {U}_p$
. Then with probability
$X\sim \mathcal {U}_p$
. Then with probability
![]() $1-o(1/n)$
, the following holds: For every pair of distinct vertices
$1-o(1/n)$
, the following holds: For every pair of distinct vertices
![]() $u, v \in V(G)$
, there exist at least
$u, v \in V(G)$
, there exist at least
![]() $\mu n$
internally vertex-disjoint u–v paths of length
$\mu n$
internally vertex-disjoint u–v paths of length
![]() $3$
such that all of their internal vertices are contained in X.
$3$
such that all of their internal vertices are contained in X.
To prove this, we need the following consequence of concentration inequalities.
Lemma 4.5. Let
![]() $0<1/n \ll p$
, and let
$0<1/n \ll p$
, and let
![]() $X\sim \mathcal {U}_p$
. Then with probability
$X\sim \mathcal {U}_p$
. Then with probability
![]() $1-o(1/n)$
, every vertex
$1-o(1/n)$
, every vertex
![]() $u \in V(G)$
satisfies
$u \in V(G)$
satisfies
![]() $e(\{u\},X,X)\geq p^2n/3$
.
$e(\{u\},X,X)\geq p^2n/3$
.
Proof. For a fixed vertex
![]() $u \in V(G)$
, let
$u \in V(G)$
, let
![]() $Y_u := e(\{u\}, X, X)$
. An edge e containing u contributes to
$Y_u := e(\{u\}, X, X)$
. An edge e containing u contributes to
![]() $Y_u$
if and only if
$Y_u$
if and only if
![]() $e\setminus \{u\} \in \mathcal {U}_p$
or the two vertices in
$e\setminus \{u\} \in \mathcal {U}_p$
or the two vertices in
![]() $e\setminus \{u\}$
are in two disjoint sets in
$e\setminus \{u\}$
are in two disjoint sets in
![]() $\mathcal {U}_p$
. Thus, e is an edge in
$\mathcal {U}_p$
. Thus, e is an edge in
![]() $G[\{u\},X,X]$
with probability either p or
$G[\{u\},X,X]$
with probability either p or
![]() $p^2$
, which implies that
$p^2$
, which implies that
![]() $p^2(n-1)/2 \leq \mathbb {E}[Y_u] \leq p(n-1)/2$
. As each event
$p^2(n-1)/2 \leq \mathbb {E}[Y_u] \leq p(n-1)/2$
. As each event
![]() $U_i \in \mathcal {U}_p$
affects at most two edges containing u,
$U_i \in \mathcal {U}_p$
affects at most two edges containing u,
![]() $Y_u$
is
$Y_u$
is
![]() $2$
-Lipshitz. This enables us to apply Azuma’s inequality (Lemma 3.4) to obtain
$2$
-Lipshitz. This enables us to apply Azuma’s inequality (Lemma 3.4) to obtain
 $$ \begin{align*} \mathbb{P}\left(Y_u < \frac{p^2n}{3}\right) \leq 2\exp \Big(-\frac{p^4 n^2}{10^3 n}\Big) \leq \frac{1}{n^3}. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(Y_u < \frac{p^2n}{3}\right) \leq 2\exp \Big(-\frac{p^4 n^2}{10^3 n}\Big) \leq \frac{1}{n^3}. \end{align*} $$
Thus, the probability that
![]() $Y_u\geq p^2n/3$
holds for every
$Y_u\geq p^2n/3$
holds for every
![]() $u\in V(G)$
is at least
$u\in V(G)$
is at least
![]() $1-1/n^2=1-o(1/n)$
.
$1-1/n^2=1-o(1/n)$
.
Proof of Lemma 4.4.
Let
![]() $\{X_1, X_2, X_3\}$
be a random partition of X obtained by assigning each
$\{X_1, X_2, X_3\}$
be a random partition of X obtained by assigning each
![]() $U_i \in \mathcal {U}_p$
to exactly one of
$U_i \in \mathcal {U}_p$
to exactly one of
![]() $X_i$
independently at random. Then each
$X_i$
independently at random. Then each
![]() $X_i$
is a (possibly dependent) copy of
$X_i$
is a (possibly dependent) copy of
![]() $\mathcal {U}_{p/3}$
.
$\mathcal {U}_{p/3}$
.
By Lemma 4.5, with probability
![]() $1-o(1/n)$
, all vertices
$1-o(1/n)$
, all vertices
![]() $u, v \in V(G)$
satisfy
$u, v \in V(G)$
satisfy
![]() $e(\{u\}, X_1, X_1) \geq p^2n/27$
and
$e(\{u\}, X_1, X_1) \geq p^2n/27$
and
![]() $e(\{v\}, X_3, X_3) \geq p^2 n/27$
. By Lemma 4.2, with probability
$e(\{v\}, X_3, X_3) \geq p^2 n/27$
. By Lemma 4.2, with probability
![]() $1-o(1/n)$
, for every pair of disjoint subsets
$1-o(1/n)$
, for every pair of disjoint subsets
![]() $A,B\subseteq V(G) \setminus X_2$
with
$A,B\subseteq V(G) \setminus X_2$
with
![]() $|A|,|B|\geq p^2n/100$
, we have
$|A|,|B|\geq p^2n/100$
, we have
![]() $e(A,X_2,B) \ge p|A||B|/6$
. As both of these two events hold simultaneously with probability
$e(A,X_2,B) \ge p|A||B|/6$
. As both of these two events hold simultaneously with probability
![]() $1-o(1/n)$
, it suffices to show that these two events imply the existence of the desired paths for all pairs of distinct vertices
$1-o(1/n)$
, it suffices to show that these two events imply the existence of the desired paths for all pairs of distinct vertices
![]() $u,v \in V(G)$
.
$u,v \in V(G)$
.
Suppose for a contradiction that there exists a pair
![]() $u,v$
of distinct vertices such that there are less than
$u,v$
of distinct vertices such that there are less than
![]() $\mu n$
internally vertex-disjoint u–v paths of length three (with their internal vertices contained in X). Choose a maximal collection
$\mu n$
internally vertex-disjoint u–v paths of length three (with their internal vertices contained in X). Choose a maximal collection
![]() $P_1, P_2, \cdots , P_k$
of internally vertex-disjoint u–v paths of length three such that their internal vertices are contained in X; then
$P_1, P_2, \cdots , P_k$
of internally vertex-disjoint u–v paths of length three such that their internal vertices are contained in X; then
![]() $k< \mu n$
. Let
$k< \mu n$
. Let
![]() $Y_i$
be the set of the internal vertices of
$Y_i$
be the set of the internal vertices of
![]() $P_i$
for
$P_i$
for
![]() $1 \le i \le k$
(so the sets
$1 \le i \le k$
(so the sets
![]() $Y_i$
are pairwise disjoint). Let
$Y_i$
are pairwise disjoint). Let
![]() $Y:=\bigcup _{i=1}^k Y_i$
, and let
$Y:=\bigcup _{i=1}^k Y_i$
, and let
![]() $E_1 := E(G[\{u\}, X_1, X_1]) - E(G[\{u\}, Y, X_1])$
and let
$E_1 := E(G[\{u\}, X_1, X_1]) - E(G[\{u\}, Y, X_1])$
and let
![]() $E_3 := E(G[\{v\}, X_3, X_3]) -E(G[\{v\}, Y, X_3])$
. As
$E_3 := E(G[\{v\}, X_3, X_3]) -E(G[\{v\}, Y, X_3])$
. As
![]() $e(\{u\}, Y, X_1) \le |Y|$
and
$e(\{u\}, Y, X_1) \le |Y|$
and
![]() $e(\{v\}, Y, X_3) \le |Y|$
(since G is linear) and
$e(\{v\}, Y, X_3) \le |Y|$
(since G is linear) and
![]() $|Y|\leq 5k \le 5\mu n$
, by the conditioned events, we have
$|Y|\leq 5k \le 5\mu n$
, by the conditioned events, we have
![]() $|E_1|, |E_3| \ge p^2n/27 - 5\mu n \geq p^2n/30$
.
$|E_1|, |E_3| \ge p^2n/27 - 5\mu n \geq p^2n/30$
.
Let
![]() $Z_1$
and
$Z_1$
and
![]() $Z_3$
be the set of vertices in the edges of
$Z_3$
be the set of vertices in the edges of
![]() $E_1$
and
$E_1$
and
![]() $E_3$
except u and v, respectively. Then
$E_3$
except u and v, respectively. Then
![]() $|Z_1|, |Z_3| \geq p^2 n/15$
. By the conditioned events, we have
$|Z_1|, |Z_3| \geq p^2 n/15$
. By the conditioned events, we have
![]() $e(Z_1, X_2, Z_3) \ge p|Z_1||Z_3|/6 \geq p^5 n^2 /2000$
. As there are at most
$e(Z_1, X_2, Z_3) \ge p|Z_1||Z_3|/6 \geq p^5 n^2 /2000$
. As there are at most
![]() $5\mu n^2$
edges incident to a vertex in Y,
$5\mu n^2$
edges incident to a vertex in Y,
![]() $e(Z_1, X_2\setminus Y, Z_3) \geq p^5 n^2 /2000 - 5 \mu n^2$
. In particular, there is an edge e in
$e(Z_1, X_2\setminus Y, Z_3) \geq p^5 n^2 /2000 - 5 \mu n^2$
. In particular, there is an edge e in
![]() $G[Z_1, X_2\setminus Y, Z_3]$
. Hence, there exists a u–v path
$G[Z_1, X_2\setminus Y, Z_3]$
. Hence, there exists a u–v path
![]() $P'$
of length three containing e such that
$P'$
of length three containing e such that
![]() $V(P')$
is disjoint from Y (i.e.,
$V(P')$
is disjoint from Y (i.e.,
![]() $P'$
is internally vertex-disjoint from the collection
$P'$
is internally vertex-disjoint from the collection
![]() $P_1, \cdots , P_k$
). Moreover, the internal vertices of
$P_1, \cdots , P_k$
). Moreover, the internal vertices of
![]() $P'$
are contained in X. This contradicts the maximality of the collection
$P'$
are contained in X. This contradicts the maximality of the collection
![]() $P_1, \cdots , P_k$
. Hence, the conditioned events, which hold with probability
$P_1, \cdots , P_k$
. Hence, the conditioned events, which hold with probability
![]() $1-o(1/n)$
, imply the existence of the desired collection of paths for all pairs
$1-o(1/n)$
, imply the existence of the desired collection of paths for all pairs
![]() $u,v \in V(G)$
of distinct vertices.
$u,v \in V(G)$
of distinct vertices.
5 Stars
In this section, we will prove that if the minimum degree of a linear hypergraph G is large enough, then we can find vertex-disjoint stars of desired size.
Lemma 5.1. Let
![]() $0<1/n\ll \varepsilon < \frac {1}{100}$
. Let G be an n-vertex linear
$0<1/n\ll \varepsilon < \frac {1}{100}$
. Let G be an n-vertex linear
![]() $3$
-uniform hypergraph with
$3$
-uniform hypergraph with
![]() $\delta (G) \geq (1-\varepsilon )n/2$
, and let
$\delta (G) \geq (1-\varepsilon )n/2$
, and let
![]() $X=\{v_1, v_2, \ldots , v_\ell \}$
be an independent set in G of size
$X=\{v_1, v_2, \ldots , v_\ell \}$
be an independent set in G of size
![]() $\ell \leq \varepsilon ^2 n/10$
. Then for any given positive integers
$\ell \leq \varepsilon ^2 n/10$
. Then for any given positive integers
![]() $n_1, n_2, \ldots , n_{\ell }$
such that
$n_1, n_2, \ldots , n_{\ell }$
such that
![]() $\sum _{i=1}^\ell n_i \leq (1-5 \varepsilon )n/2$
, G contains vertex-disjoint stars
$\sum _{i=1}^\ell n_i \leq (1-5 \varepsilon )n/2$
, G contains vertex-disjoint stars
![]() $S_1, S_2, \ldots , S_\ell $
such that each
$S_1, S_2, \ldots , S_\ell $
such that each
![]() $S_i$
has size
$S_i$
has size
![]() $n_i$
and is centered at
$n_i$
and is centered at
![]() $v_i$
.
$v_i$
.
Proof. Let
![]() $m=\lceil \varepsilon ^{-1} \rceil +1$
. As G is a linear
$m=\lceil \varepsilon ^{-1} \rceil +1$
. As G is a linear
![]() $3$
-graph with
$3$
-graph with
![]() $\delta (G)\geq (1-\varepsilon )n/2$
, there exists a vertex set W of size at most
$\delta (G)\geq (1-\varepsilon )n/2$
, there exists a vertex set W of size at most
![]() $\varepsilon n$
such that for all vertices
$\varepsilon n$
such that for all vertices
![]() $w\in V(G)\setminus (W\cup \{v_1\})$
, there exists an edge
$w\in V(G)\setminus (W\cup \{v_1\})$
, there exists an edge
![]() $v_1ww'$
in G for some
$v_1ww'$
in G for some
![]() $w'\in V(G)\setminus (W\cup \{v_1\})$
.
$w'\in V(G)\setminus (W\cup \{v_1\})$
.
We then choose vertex-disjoint stars
![]() $S_1, \cdots , S_\ell $
in G which satisfy the following:
$S_1, \cdots , S_\ell $
in G which satisfy the following:
-
(i) each
 $S_i$
is centered at
$S_i$
is centered at
 $v_i$
and has size
$v_i$
and has size
 $t_i \leq n_i + m$
. and
$t_i \leq n_i + m$
. and -
(ii) among all
 $S_1,S_2,\cdots ,S_\ell $
that satisfy (i), choose one that maximizes
$S_1,S_2,\cdots ,S_\ell $
that satisfy (i), choose one that maximizes
 $\sum _{i=1}^\ell t_i$
.
$\sum _{i=1}^\ell t_i$
.
By allowing empty
![]() $S_i$
’s, such a choice is always possible. We claim that
$S_i$
’s, such a choice is always possible. We claim that
![]() $t_i \geq n_i$
for all
$t_i \geq n_i$
for all
![]() $i \in [\ell ]$
, which concludes the proof. Suppose to the contrary that
$i \in [\ell ]$
, which concludes the proof. Suppose to the contrary that
![]() $t_1<n_1$
, by reindexing if necessary.
$t_1<n_1$
, by reindexing if necessary.
For two vertex sets
![]() $U,U'$
, denote by
$U,U'$
, denote by
![]() $N(U,U')$
the set of vertices v such that there is an edge
$N(U,U')$
the set of vertices v such that there is an edge
![]() $uu'v$
of G with
$uu'v$
of G with
![]() $u\in U$
and
$u\in U$
and
![]() $u'\in U'$
. Let M be the graph matching on
$u'\in U'$
. Let M be the graph matching on
![]() $V(G)$
where
$V(G)$
where
![]() $E(M) = \bigcup _{i\in [\ell ]}\{xy : xyv_i \in E(S_i)\}.$
Let
$E(M) = \bigcup _{i\in [\ell ]}\{xy : xyv_i \in E(S_i)\}.$
Let
![]() $N_M(U)= \bigcup _{u\in U}\{x: xu\in M\}$
for a vertex set U. These definitions are convenient for us to describe how one can replace the stars
$N_M(U)= \bigcup _{u\in U}\{x: xu\in M\}$
for a vertex set U. These definitions are convenient for us to describe how one can replace the stars
![]() $S_1,\dots , S_\ell $
with other stars contradicting the maximality in (ii). Let
$S_1,\dots , S_\ell $
with other stars contradicting the maximality in (ii). Let
![]() $A_1:=V(G)\setminus \bigcup _{i=1}^\ell V(S_i)$
. We then define
$A_1:=V(G)\setminus \bigcup _{i=1}^\ell V(S_i)$
. We then define
![]() $A_2, \cdots , A_m, B_1, \cdots , B_m \subseteq V(G)$
recursively as
$A_2, \cdots , A_m, B_1, \cdots , B_m \subseteq V(G)$
recursively as
As
![]() $|A_1| \geq n-2\sum _{i=1}^\ell (n_i + m) \geq 2\varepsilon n$
and
$|A_1| \geq n-2\sum _{i=1}^\ell (n_i + m) \geq 2\varepsilon n$
and
![]() $v_1$
has at least
$v_1$
has at least
![]() $(1-\varepsilon )n$
neighbors,
$(1-\varepsilon )n$
neighbors,
![]() $v_1$
has at least
$v_1$
has at least
![]() $\varepsilon n$
neighbors in
$\varepsilon n$
neighbors in
![]() $A_1$
. Thus,
$A_1$
. Thus,
![]() $|B_1| \geq \varepsilon n$
.
$|B_1| \geq \varepsilon n$
.
From the definition of
![]() $B_i$
and the fact that G is linear, for each
$B_i$
and the fact that G is linear, for each
![]() $y\in B_i$
, we have unique
$y\in B_i$
, we have unique
![]() $x\in A_i$
with
$x\in A_i$
with
![]() $xyv_1\in E(G)$
. Again, for each
$xyv_1\in E(G)$
. Again, for each
![]() $x \in A_i$
with
$x \in A_i$
with
![]() $i>1$
, there exists unique
$i>1$
, there exists unique
![]() $y'\in B_{i-1}$
such that
$y'\in B_{i-1}$
such that
![]() $y'x \in M$
. Hence, for each vertex
$y'x \in M$
. Hence, for each vertex
![]() $v\in \bigcup _{i\in [\ell ]}B_i$
, there exists a unique sequence
$v\in \bigcup _{i\in [\ell ]}B_i$
, there exists a unique sequence
![]() $v=y_k,x_k,y_{k-1},x_{k-1},\dots , y_1,x_1$
such that
$v=y_k,x_k,y_{k-1},x_{k-1},\dots , y_1,x_1$
such that
![]() $\{x_i\}= N(\{y_i\},\{v_1\})$
and
$\{x_i\}= N(\{y_i\},\{v_1\})$
and
![]() $\{y_{i-1}\}= N_M(\{x_i\})$
for all
$\{y_{i-1}\}= N_M(\{x_i\})$
for all
![]() $i\in [\ell ]$
. As this sequence is unique, this determines the unique
$i\in [\ell ]$
. As this sequence is unique, this determines the unique
![]() $k\in [\ell ]$
that
$k\in [\ell ]$
that
![]() $v\in B_k$
. From this, we conclude that
$v\in B_k$
. From this, we conclude that
Furthermore, for such a sequence for every vertex
![]() $v\in \bigcup _{i\in [\ell ]}B_i$
, the vertices
$v\in \bigcup _{i\in [\ell ]}B_i$
, the vertices
![]() $y_k,x_k,\dots , y_1,x_1$
are all distinct. As all
$y_k,x_k,\dots , y_1,x_1$
are all distinct. As all
![]() $A_i$
s are pairwise disjoint and all
$A_i$
s are pairwise disjoint and all
![]() $B_i$
s are pairwise disjoint, we only have to show that
$B_i$
s are pairwise disjoint, we only have to show that
![]() $x_i\neq y_j$
for all
$x_i\neq y_j$
for all
![]() $i\neq j\in [k]$
. If not, choose i and j with the minimum
$i\neq j\in [k]$
. If not, choose i and j with the minimum
![]() $|i-j|>0$
such that
$|i-j|>0$
such that
![]() $x_i=y_j$
. Then the definition ensures that
$x_i=y_j$
. Then the definition ensures that
![]() $\{x_j\}=\{y_i\} = N(\{x_i\},\{v_1\})$
, so
$\{x_j\}=\{y_i\} = N(\{x_i\},\{v_1\})$
, so
![]() $x_i=y_j$
and
$x_i=y_j$
and
![]() $x_j=y_i$
. By symmetry, assuming
$x_j=y_i$
. By symmetry, assuming
![]() $i>j$
, we know that
$i>j$
, we know that
![]() $i>j+1$
. If not, then
$i>j+1$
. If not, then
![]() $i=j+1$
, but
$i=j+1$
, but
![]() $y_j= x_i=x_{j+1}=N_M(y_j)$
, a contradiction that M forms a matching. Moreover, as we have
$y_j= x_i=x_{j+1}=N_M(y_j)$
, a contradiction that M forms a matching. Moreover, as we have
![]() $y_{i-1}=x_{j+1}= N_M(x_i)$
and
$y_{i-1}=x_{j+1}= N_M(x_i)$
and
![]() $i>j+1$
, a contradiction to the the minimality of
$i>j+1$
, a contradiction to the the minimality of
![]() $|i-j|$
.
$|i-j|$
.
For each
![]() $i\in [\ell ]$
, let
$i\in [\ell ]$
, let
![]() $L_i$
be the set of all leaf vertices of
$L_i$
be the set of all leaf vertices of
![]() $S_i$
, and let
$S_i$
, and let
![]() $L = \bigcup _{i\in [\ell ]} L_i$
. We claim that, for
$L = \bigcup _{i\in [\ell ]} L_i$
. We claim that, for
![]() $k\in [m]$
, the vertex set
$k\in [m]$
, the vertex set
![]() $B_k$
is contained in L.
$B_k$
is contained in L.
Suppose that
![]() $B_k \nsubseteq L$
while
$B_k \nsubseteq L$
while
![]() $B_{j}\subseteq L$
for all
$B_{j}\subseteq L$
for all
![]() $j<k$
. Choose
$j<k$
. Choose
![]() $y_k\in B_k \setminus L$
, and consider the unique sequence
$y_k\in B_k \setminus L$
, and consider the unique sequence
![]() $y_k,x_k, \dots , y_1,x_1$
as above. As all vertices in the sequence are distinct, we use this sequence to contradict the maximality assumption of
$y_k,x_k, \dots , y_1,x_1$
as above. As all vertices in the sequence are distinct, we use this sequence to contradict the maximality assumption of
![]() $\sum _{j=1}^{\ell } t_j$
in (ii). Delete all the edges of the form of
$\sum _{j=1}^{\ell } t_j$
in (ii). Delete all the edges of the form of
![]() $y_ix_{i+1}v_{i'}$
from
$y_ix_{i+1}v_{i'}$
from
![]() $S_{i'}$
for
$S_{i'}$
for
![]() $1 \leq i \leq k-1$
and add all edges of the form of
$1 \leq i \leq k-1$
and add all edges of the form of
![]() $x_iy_iv_1$
for
$x_iy_iv_1$
for
![]() $1 \leq i \leq k$
to
$1 \leq i \leq k$
to
![]() $S_1$
. Note that the choice of
$S_1$
. Note that the choice of
![]() $i'$
is uniquely determined for each i. As
$i'$
is uniquely determined for each i. As
![]() $x_1, y_k$
are not contained in
$x_1, y_k$
are not contained in
![]() $\bigcup _{j=1}^\ell V(S_j)$
and all
$\bigcup _{j=1}^\ell V(S_j)$
and all
![]() $x_i, y_i$
are distinct,
$x_i, y_i$
are distinct,
![]() $S_1, \cdots , S_\ell $
are still vertex disjoint stars. Moreover,
$S_1, \cdots , S_\ell $
are still vertex disjoint stars. Moreover,
![]() $S_1$
has at most
$S_1$
has at most
![]() $n_1 + k \leq n_1 + m$
edges. Thus, our new
$n_1 + k \leq n_1 + m$
edges. Thus, our new
![]() $S_1, \cdots , S_\ell $
satisfies the condition (i) and increases
$S_1, \cdots , S_\ell $
satisfies the condition (i) and increases
![]() $\sum _{j=1}^\ell t_j$
by
$\sum _{j=1}^\ell t_j$
by
![]() $1$
. Therefore,
$1$
. Therefore,
![]() $B_k \subseteq \bigcup _{j=1}^\ell V(S_j)$
.
$B_k \subseteq \bigcup _{j=1}^\ell V(S_j)$
.
As M is a perfect matching on L, we have
![]() $|A_{i+1}|=|B_i|$
for all
$|A_{i+1}|=|B_i|$
for all
![]() $i\in [m]$
. However, by the definition of
$i\in [m]$
. However, by the definition of
![]() $B_i$
, we have
$B_i$
, we have
![]() $|B_i| = |A_i \setminus W|$
for all
$|B_i| = |A_i \setminus W|$
for all
![]() $i\in [m]$
. As we have
$i\in [m]$
. As we have
![]() $|A_1| \geq n-2\sum _{i=1}^\ell (n_i + m) \geq 2\varepsilon n$
and all
$|A_1| \geq n-2\sum _{i=1}^\ell (n_i + m) \geq 2\varepsilon n$
and all
![]() $A_i$
are pairwise disjoint, we conclude that for each k,
$A_i$
are pairwise disjoint, we conclude that for each k,
This yields that
 $$ \begin{align*}\Big\vert\bigcup_{i\in [m]} B_i \Big\vert= \sum_{i\in [k]} |B_i| \geq m \varepsilon n> n,\end{align*} $$
$$ \begin{align*}\Big\vert\bigcup_{i\in [m]} B_i \Big\vert= \sum_{i\in [k]} |B_i| \geq m \varepsilon n> n,\end{align*} $$
which concludes the proof by contradiction.
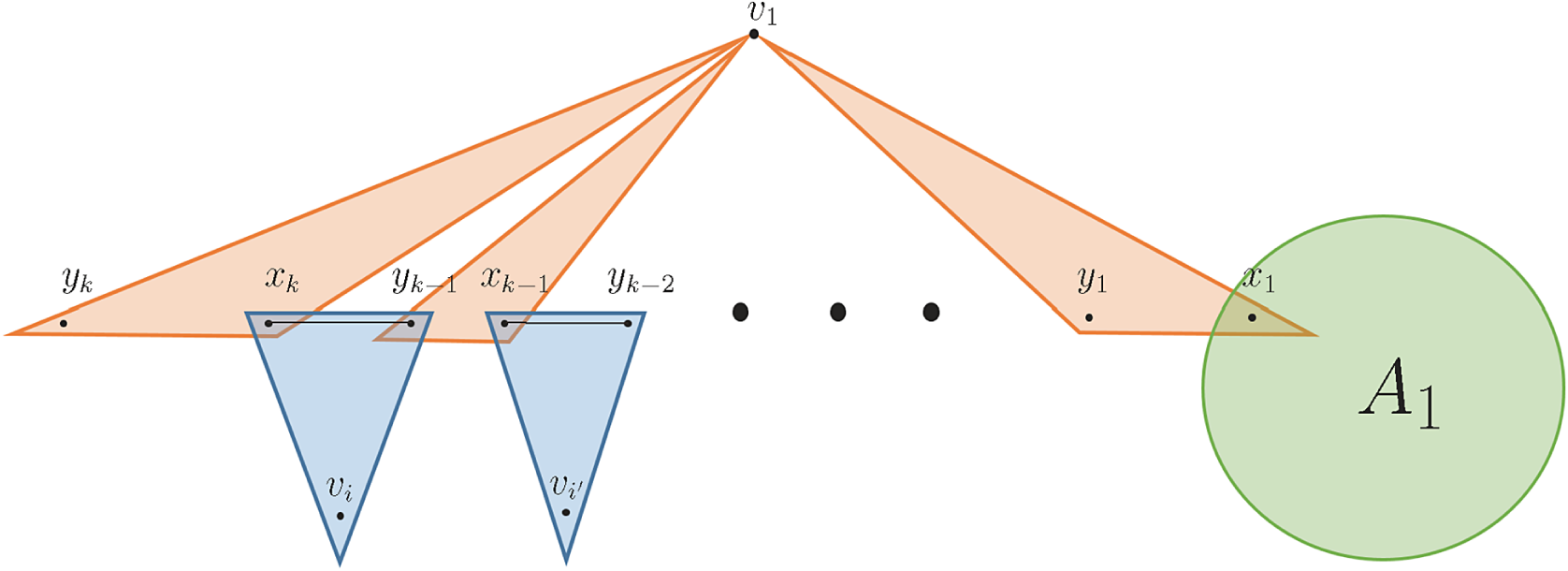
Figure 2 Choice of
![]() $x_1, y_1, \ldots , y_k=v$
.
$x_1, y_1, \ldots , y_k=v$
.
6 Proof of Theorem 1.2
We begin by stating a variant of the well-known fact which easily follows from a simple greedy algorithm. We omit the proof.
Lemma 6.1. Let G be a linear hypergraph with minimum degree
![]() $\delta $
. Then G contains every tree T with less than
$\delta $
. Then G contains every tree T with less than
![]() $\delta /2$
vertices.
$\delta /2$
vertices.
We may assume that
![]() $\varepsilon $
is small enough. Choose
$\varepsilon $
is small enough. Choose
![]() $\mu $
and n so that we have
$\mu $
and n so that we have
![]() $0<1/n \ll \mu \ll \varepsilon \ll 1$
. Let T be a hypertree with at most
$0<1/n \ll \mu \ll \varepsilon \ll 1$
. Let T be a hypertree with at most
![]() $(1-\varepsilon )n$
vertices. Applying Lemma 3.1 with
$(1-\varepsilon )n$
vertices. Applying Lemma 3.1 with
![]() $D= \lceil \log ^{10} n \rceil $
and the chosen
$D= \lceil \log ^{10} n \rceil $
and the chosen
![]() $\mu $
, we obtain a chain of sub-hypergraphs
$\mu $
, we obtain a chain of sub-hypergraphs
![]() $T_0 \subseteq T_1 \subseteq \cdots \subseteq T_\ell = T$
with
$T_0 \subseteq T_1 \subseteq \cdots \subseteq T_\ell = T$
with
![]() $\ell \leq 10^5 D \mu ^{-2}$
,
$\ell \leq 10^5 D \mu ^{-2}$
,
![]() $s \in [\ell ]$
satisfying the assertions (i)–(iv) of Lemma 3.1.
$s \in [\ell ]$
satisfying the assertions (i)–(iv) of Lemma 3.1.
By (i),
![]() $|V(T_0)| \leq 3\mu n$
, so there exists an injective homomorphism
$|V(T_0)| \leq 3\mu n$
, so there exists an injective homomorphism
![]() $\varphi :V(T_0) \rightarrow V(G)$
that embeds
$\varphi :V(T_0) \rightarrow V(G)$
that embeds
![]() $T_0$
into G by Lemma 6.1. In what follows, we shall identify
$T_0$
into G by Lemma 6.1. In what follows, we shall identify
![]() $T_0$
as its image under
$T_0$
as its image under
![]() $\varphi $
(i.e., we assume that
$\varphi $
(i.e., we assume that
![]() $T_0$
is embedded as a subgraph of G). Let
$T_0$
is embedded as a subgraph of G). Let
![]() $\{v_1, \cdots , v_k\} \subseteq V(G)$
be the set of vertices of
$\{v_1, \cdots , v_k\} \subseteq V(G)$
be the set of vertices of
![]() $T_0$
with
$T_0$
with
![]() $e_{T_1}(v_i, V(T_1 \setminus T_0), V(T_1 \setminus T_0)) \geq D$
, and let
$e_{T_1}(v_i, V(T_1 \setminus T_0), V(T_1 \setminus T_0)) \geq D$
, and let
![]() $d_i:=e_T(v_i, V(T_1 \setminus T_0), V(T_1 \setminus T_0))$
for each
$d_i:=e_T(v_i, V(T_1 \setminus T_0), V(T_1 \setminus T_0))$
for each
![]() $i \in [k]$
. Note that k is at most
$i \in [k]$
. Note that k is at most
![]() $ O(n (\log n)^{-10}) \leq \mu n \leq \varepsilon ^2 n/10$
.
$ O(n (\log n)^{-10}) \leq \mu n \leq \varepsilon ^2 n/10$
.
First, we remove all vertices in
![]() $V(T_0) \setminus \{v_1, \cdots , v_k\}$
from G. This removes at most
$V(T_0) \setminus \{v_1, \cdots , v_k\}$
from G. This removes at most
![]() $3\mu n$
edges incident to a fixed remaining vertex
$3\mu n$
edges incident to a fixed remaining vertex
![]() $x\in (V(G) \setminus V(T_0)) \cup \{v_1, \cdots , v_k\}$
. Furthermore, we remove all the edges containing at least two of
$x\in (V(G) \setminus V(T_0)) \cup \{v_1, \cdots , v_k\}$
. Furthermore, we remove all the edges containing at least two of
![]() $v_1, \cdots , v_k$
from G. This removes at most
$v_1, \cdots , v_k$
from G. This removes at most
![]() $k/2$
edges incident to any vertex
$k/2$
edges incident to any vertex
![]() $x \in V(G)$
. Thus, after removing all these edges from G, the minimum degree of the resulting hypergraph H is still at least
$x \in V(G)$
. Thus, after removing all these edges from G, the minimum degree of the resulting hypergraph H is still at least
![]() $(1-10 \mu )n/2 \geq (1-10 \mu )|V(H)|/2$
. Let
$(1-10 \mu )n/2 \geq (1-10 \mu )|V(H)|/2$
. Let
![]() $d:=\sum _{i=1}^k d_i$
, and let
$d:=\sum _{i=1}^k d_i$
, and let
![]() $n_i := \lceil \frac {d_i}{2d} n (1-\varepsilon /8)\rceil $
. Then
$n_i := \lceil \frac {d_i}{2d} n (1-\varepsilon /8)\rceil $
. Then
![]() $\sum _{i=1}^{k} n_i \leq k+\sum _{i=1}^{k}\frac {d_i}{2d} n (1-\varepsilon /8) \leq (1-\frac {\varepsilon }{10}) \frac {|V(H)|}{2}$
as
$\sum _{i=1}^{k} n_i \leq k+\sum _{i=1}^{k}\frac {d_i}{2d} n (1-\varepsilon /8) \leq (1-\frac {\varepsilon }{10}) \frac {|V(H)|}{2}$
as
![]() $|V(H)| \geq n-3\mu n$
. By applying Lemma 5.1 to H, we get vertex-disjoint stars
$|V(H)| \geq n-3\mu n$
. By applying Lemma 5.1 to H, we get vertex-disjoint stars
![]() $S_1, \cdots , S_k$
in G where each
$S_1, \cdots , S_k$
in G where each
![]() $S_i$
is centered at
$S_i$
is centered at
![]() $v_i$
of size
$v_i$
of size
![]() $d_i$
and does not contain any vertices of
$d_i$
and does not contain any vertices of
![]() $T_0$
other than
$T_0$
other than
![]() $v_i$
.
$v_i$
.
We then define a singleton-pair partition
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $V(G)$
as follows. For every
$V(G)$
as follows. For every
![]() $1 \le i \le k$
and for every edge
$1 \le i \le k$
and for every edge
![]() $xyv_i \in E(S_i)$
, let
$xyv_i \in E(S_i)$
, let
![]() $\{x, y\}$
be a part of
$\{x, y\}$
be a part of
![]() $\mathcal {U}$
. Moreover, let each of the remaining vertices of
$\mathcal {U}$
. Moreover, let each of the remaining vertices of
![]() $V(G)$
be a part of
$V(G)$
be a part of
![]() $\mathcal {U}$
of size one.
$\mathcal {U}$
of size one.
Let
![]() $p_{0} :=\varepsilon /200$
. Let
$p_{0} :=\varepsilon /200$
. Let
![]() $m_i := |V(T_i) \setminus V(T_{i-1})|$
, and let
$m_i := |V(T_i) \setminus V(T_{i-1})|$
, and let
![]() $p_i := (1+\frac {\varepsilon }{4})\frac {m_i}{n} + \frac {\varepsilon }{4\ell }$
for
$p_i := (1+\frac {\varepsilon }{4})\frac {m_i}{n} + \frac {\varepsilon }{4\ell }$
for
![]() $i \in [\ell ]$
. Recall that
$i \in [\ell ]$
. Recall that
![]() $\ell \leq 10^5 D\mu ^{-2}= O((\log n)^{10}) $
. As
$\ell \leq 10^5 D\mu ^{-2}= O((\log n)^{10}) $
. As
![]() $\varepsilon>0$
is a constant,
$\varepsilon>0$
is a constant,
![]() $p_i \geq \frac {1}{(\log n)^{20}}$
for all
$p_i \geq \frac {1}{(\log n)^{20}}$
for all
![]() $i \in [\ell ]$
.
$i \in [\ell ]$
.
Now sample
![]() $X_1 \subseteq V(G)$
by choosing each
$X_1 \subseteq V(G)$
by choosing each
![]() $U\in \mathcal {U}$
with probability
$U\in \mathcal {U}$
with probability
![]() $p_1$
independently at random and taking their union (i.e.,
$p_1$
independently at random and taking their union (i.e.,
![]() $X_1\sim \mathcal {U}_{p_1}$
).
$X_1\sim \mathcal {U}_{p_1}$
).
Provided that
![]() $X_1, X_2, \cdots , X_{i-1}$
are chosen, select each
$X_1, X_2, \cdots , X_{i-1}$
are chosen, select each
![]() $U\in \mathcal {U}$
that is not included in
$U\in \mathcal {U}$
that is not included in
![]() $X_1\cup \cdots \cup X_{i-1}$
with probability
$X_1\cup \cdots \cup X_{i-1}$
with probability
![]() $p_i/(1-p_1-p_2-\cdots - p_{i-1})$
independently at random and add it to
$p_i/(1-p_1-p_2-\cdots - p_{i-1})$
independently at random and add it to
![]() $X_i$
. After choosing
$X_i$
. After choosing
![]() $X_\ell $
, we choose the ‘reservoir’ R by selecting each
$X_\ell $
, we choose the ‘reservoir’ R by selecting each
![]() $U\in \mathcal {U}$
that is not in
$U\in \mathcal {U}$
that is not in
![]() $X_1 \cup \cdots \cup X_{\ell }$
with probability
$X_1 \cup \cdots \cup X_{\ell }$
with probability
![]() $p_0/(1-p_1-p_2-\cdots - p_{\ell })$
independently at random and adding it to R. Note that
$p_0/(1-p_1-p_2-\cdots - p_{\ell })$
independently at random and adding it to R. Note that
![]() $\sum _{i=0}^\ell p_i \leq (1+\varepsilon /4)|T|/n + \varepsilon /4 + \varepsilon /200 \leq 1$
. Then
$\sum _{i=0}^\ell p_i \leq (1+\varepsilon /4)|T|/n + \varepsilon /4 + \varepsilon /200 \leq 1$
. Then
![]() $X_i \sim \mathcal {U}_{p_i}$
for each
$X_i \sim \mathcal {U}_{p_i}$
for each
![]() $i \in [\ell ]$
and
$i \in [\ell ]$
and
![]() $R \sim \mathcal {U}_{p_0}$
.
$R \sim \mathcal {U}_{p_0}$
.
Let
![]() $\mathcal {F}, \mathcal {E}_0, \mathcal {E}_1, \mathcal {E}_M$
be the following events.
$\mathcal {F}, \mathcal {E}_0, \mathcal {E}_1, \mathcal {E}_M$
be the following events.
-
ℱ:
 $|V(T_0) \cap X_i| \leq 10p_i \mu n$
for each
$|V(T_0) \cap X_i| \leq 10p_i \mu n$
for each
 $i \in [\ell ]$
and
$i \in [\ell ]$
and
 $|V(T_0) \cap R| \leq 10p_0 \mu n$
.
$|V(T_0) \cap R| \leq 10p_0 \mu n$
. -
ℰ0: Every vertex v is incident to at least
 $10^4 \mu n$
edges e such that
$10^4 \mu n$
edges e such that
 $e \setminus \{v\} \subseteq R$
, and between every pair
$e \setminus \{v\} \subseteq R$
, and between every pair
 $u, v \in V(G)$
of distinct vertices, there are at least
$u, v \in V(G)$
of distinct vertices, there are at least
 $100 \mu n$
internally vertex-disjoint u–v paths of length 3 and all of their internal vertices are in R.
$100 \mu n$
internally vertex-disjoint u–v paths of length 3 and all of their internal vertices are in R. -
ℰ1: For each
 $i \in [k]$
,
$i \in [k]$
,
 $e(\{v_i\}, X_1, X_1) \geq d_i$
.
$e(\{v_i\}, X_1, X_1) \geq d_i$
. -
ℰ M : For each
 $2\leq i\leq \ell $
and for all sets
$2\leq i\leq \ell $
and for all sets
 $A \subseteq V(G) \setminus X_i$
of size
$A \subseteq V(G) \setminus X_i$
of size
 $|A| \leq p_i n/2$
, there exists a matching M of G of size at least
$|A| \leq p_i n/2$
, there exists a matching M of G of size at least
 $|A|-\mu p_i n$
such that each edge
$|A|-\mu p_i n$
such that each edge
 $e \in M$
satisfies
$e \in M$
satisfies
 $|e \cap X_i|=2$
and
$|e \cap X_i|=2$
and
 $|e \cap A|=1$
.
$|e \cap A|=1$
.
We first show that all of the events
![]() $\mathcal {F}, \mathcal {E}_0, \mathcal {E}_1, \mathcal {E}_M$
hold with high probability, and then conditioning on these events, we show that one can embed T into G.
$\mathcal {F}, \mathcal {E}_0, \mathcal {E}_1, \mathcal {E}_M$
hold with high probability, and then conditioning on these events, we show that one can embed T into G.
Claim 6.2.
![]() $\mathbb {P}(\mathcal {E}_0), \mathbb {P}(\mathcal {E}_1), \mathbb {P}(\mathcal {F}) = 1-o(1)$
, and
$\mathbb {P}(\mathcal {E}_0), \mathbb {P}(\mathcal {E}_1), \mathbb {P}(\mathcal {F}) = 1-o(1)$
, and
![]() $\mathbb {P}(\mathcal {E}_M) = 1-o(1)$
.
$\mathbb {P}(\mathcal {E}_M) = 1-o(1)$
.
Proof. First, Lemma 4.4 and 4.5 imply that
![]() $\mathbb {P}(\mathcal {E}_0) = 1-o(1/n)$
. Second, by Azuma’s inequality (Lemma 3.4), we have
$\mathbb {P}(\mathcal {E}_0) = 1-o(1/n)$
. Second, by Azuma’s inequality (Lemma 3.4), we have
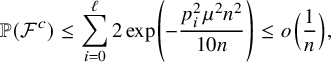 $$ \begin{align*}\mathbb{P}(\mathcal{F}^c) \leq \sum_{i=0}^\ell 2\exp\left(-\frac{p_i^2 \mu^2 n^2}{10n}\right) \leq o\Big(\frac{1}{n}\Big),\end{align*} $$
$$ \begin{align*}\mathbb{P}(\mathcal{F}^c) \leq \sum_{i=0}^\ell 2\exp\left(-\frac{p_i^2 \mu^2 n^2}{10n}\right) \leq o\Big(\frac{1}{n}\Big),\end{align*} $$
where the last inequality follows from the fact that
![]() $p_i\geq \frac {\varepsilon }{4\ell } \geq \frac {1}{(\log n)^{20}}$
for each i. Now we show
$p_i\geq \frac {\varepsilon }{4\ell } \geq \frac {1}{(\log n)^{20}}$
for each i. Now we show
![]() $\mathbb {P}(\mathcal {E}_1) = 1-o(1)$
. As
$\mathbb {P}(\mathcal {E}_1) = 1-o(1)$
. As
![]() $T_1\setminus T_0$
consists of the stars
$T_1\setminus T_0$
consists of the stars
![]() $S_1,\cdots ,S_k$
that have
$S_1,\cdots ,S_k$
that have
![]() $2d$
leaves in total,
$2d$
leaves in total,
![]() $m_1=|V(T_1)\setminus V(T_0)|=2d$
. Hence, the expected value of
$m_1=|V(T_1)\setminus V(T_0)|=2d$
. Hence, the expected value of
![]() $e(\{v_i\}, X_1, X_1)$
is
$e(\{v_i\}, X_1, X_1)$
is
Indeed, for any edge in
![]() $S_i$
, the probability that its two leaves are included in
$S_i$
, the probability that its two leaves are included in
![]() $X_1 \sim \mathcal U_{p_1}$
is equal to
$X_1 \sim \mathcal U_{p_1}$
is equal to
![]() $p_1$
, as they form a part (of size two) in the singleton-pair partition
$p_1$
, as they form a part (of size two) in the singleton-pair partition
![]() $\mathcal U$
. Moreover, these events for all edges in
$\mathcal U$
. Moreover, these events for all edges in
![]() $S_i$
are mutually independent. This enables us to use the Chernoff bound (Lemma 3.3) to prove that
$S_i$
are mutually independent. This enables us to use the Chernoff bound (Lemma 3.3) to prove that
![]() $e(\{v_i\}, X_1, X_1)$
is less than
$e(\{v_i\}, X_1, X_1)$
is less than
![]() $2d_i$
with probability at most
$2d_i$
with probability at most
 $$ \begin{align*}2\exp\Big(-\frac{\varepsilon^2 d_i}{10^3}\Big) \leq \exp\Big(-\frac{\varepsilon^2 \log^{10} n}{10^3}\Big) = o\Big(\frac{1}{n}\Big),\end{align*} $$
$$ \begin{align*}2\exp\Big(-\frac{\varepsilon^2 d_i}{10^3}\Big) \leq \exp\Big(-\frac{\varepsilon^2 \log^{10} n}{10^3}\Big) = o\Big(\frac{1}{n}\Big),\end{align*} $$
where the inequality follows from
![]() $d_i\geq D\geq \log ^{10}n$
which is guaranteed by (ii) of Lemma 3.1. Therefore,
$d_i\geq D\geq \log ^{10}n$
which is guaranteed by (ii) of Lemma 3.1. Therefore,
![]() $\mathbb {P}(\mathcal {E}_1) = 1-o(1)$
. Finally, Lemma 4.3 together with a union bound ensures that
$\mathbb {P}(\mathcal {E}_1) = 1-o(1)$
. Finally, Lemma 4.3 together with a union bound ensures that
![]() $\mathbb {P}(\mathcal {E}_M) = 1-o(\frac {\ell }{n}) = 1-o(1)$
.
$\mathbb {P}(\mathcal {E}_M) = 1-o(\frac {\ell }{n}) = 1-o(1)$
.
By Claim 6.2, the events
![]() $\mathcal {F}, \mathcal {E}_0, \mathcal {E}_1$
and
$\mathcal {F}, \mathcal {E}_0, \mathcal {E}_1$
and
![]() $\mathcal {E}_M$
occur with probability
$\mathcal {E}_M$
occur with probability
![]() $1-o(1)$
. Now we show that there exists a sequence
$1-o(1)$
. Now we show that there exists a sequence
![]() $T_0\subseteq T_1\subseteq \dots \subseteq T_\ell = T$
of subgraphs of G satisfying the following properties for all
$T_0\subseteq T_1\subseteq \dots \subseteq T_\ell = T$
of subgraphs of G satisfying the following properties for all
![]() $i \in [\ell ]$
(conditioning on the events
$i \in [\ell ]$
(conditioning on the events
![]() $\mathcal {F}, \mathcal {E}_0, \mathcal {E}_1$
and
$\mathcal {F}, \mathcal {E}_0, \mathcal {E}_1$
and
![]() $\mathcal {E}_M$
).
$\mathcal {E}_M$
).
-
(a) If
 $i\neq s+1$
, then
$i\neq s+1$
, then
 $T_i$
extends
$T_i$
extends
 $T_{i-1}$
and it satisfies
$T_{i-1}$
and it satisfies
 $V(T_i)\setminus V(T_{i-1}) \subseteq X_i \cup R$
and
$V(T_i)\setminus V(T_{i-1}) \subseteq X_i \cup R$
and
 $|(V(T_i)\setminus V(T_{i-1})) \cap R| \leq 30 p_i \mu n$
.
$|(V(T_i)\setminus V(T_{i-1})) \cap R| \leq 30 p_i \mu n$
. -
(b) If
 $i=s+1$
, then
$i=s+1$
, then
 $T_{s+1}$
extends
$T_{s+1}$
extends
 $T_{s}$
and it satisfies
$T_{s}$
and it satisfies
 $V(T_{s+1})\setminus V(T_{s}) \subseteq R$
and
$V(T_{s+1})\setminus V(T_{s}) \subseteq R$
and
 $|V(T_{s+1})\setminus V(T_{s})|\leq 7\mu n$
.
$|V(T_{s+1})\setminus V(T_{s})|\leq 7\mu n$
.
As
![]() $T_0$
vacuously satisfies the above two properties, assume that we have
$T_0$
vacuously satisfies the above two properties, assume that we have
![]() $T_0\subseteq \dots \subseteq T_{i-1}$
satisfying the above properties with the maximum i, and assume
$T_0\subseteq \dots \subseteq T_{i-1}$
satisfying the above properties with the maximum i, and assume
![]() $i\leq \ell $
. Since
$i\leq \ell $
. Since
![]() $T_0\subseteq \dots \subseteq T_{i-1}$
satisfy (a) and (b), we have
$T_0\subseteq \dots \subseteq T_{i-1}$
satisfy (a) and (b), we have
If
![]() $i=1$
, by using vertices in
$i=1$
, by using vertices in
![]() $X_1 \cap S_j$
for each
$X_1 \cap S_j$
for each
![]() $j \in [k]$
, one can extend
$j \in [k]$
, one can extend
![]() $T_0$
to
$T_0$
to
![]() $T_1$
by
$T_1$
by
![]() $\mathcal {E}_1$
. It is straightforward to check
$\mathcal {E}_1$
. It is straightforward to check
![]() $V(T_1)\setminus V(T_{0}) \subseteq X_1 \cup R$
and
$V(T_1)\setminus V(T_{0}) \subseteq X_1 \cup R$
and
![]() $|(V(T_1)\setminus V(T_{0})) \cap R|=0 $
, as we only used vertices in
$|(V(T_1)\setminus V(T_{0})) \cap R|=0 $
, as we only used vertices in
![]() $X_1$
to extend
$X_1$
to extend
![]() $T_0$
to
$T_0$
to
![]() $T_1$
. Hence, (a) is satisfied, a contradiction to the maximality of i. Hence, we have
$T_1$
. Hence, (a) is satisfied, a contradiction to the maximality of i. Hence, we have
![]() $i>1$
.
$i>1$
.
Suppose
![]() $2 \leq i \le \ell $
and
$2 \leq i \le \ell $
and
![]() $i\neq s+1$
. By (iii) of Lemma 3.1, in this case,
$i\neq s+1$
. By (iii) of Lemma 3.1, in this case,
![]() $T_i$
can be obtained by adding a matching to
$T_i$
can be obtained by adding a matching to
![]() $T_{i-1}$
such that
$T_{i-1}$
such that
![]() $V(T_i) \setminus V(T_{i-1})$
is a matching leaf set of
$V(T_i) \setminus V(T_{i-1})$
is a matching leaf set of
![]() $T_i$
. Let
$T_i$
. Let
![]() $A_i$
be the set of vertices of
$A_i$
be the set of vertices of
![]() $T_{i-1}$
that are contained in the edges of the matching
$T_{i-1}$
that are contained in the edges of the matching
![]() $E(T_i)\setminus E(T_{i-1})$
. Then
$E(T_i)\setminus E(T_{i-1})$
. Then
![]() $|A_i| = m_i/2$
. By
$|A_i| = m_i/2$
. By
![]() $\mathcal {E}_M$
, there exists a matching M in G of size at least
$\mathcal {E}_M$
, there exists a matching M in G of size at least
![]() $|A_i|-\mu p_i n$
such that each edge e satisfies
$|A_i|-\mu p_i n$
such that each edge e satisfies
![]() $|e \cap A_i| = 1$
and
$|e \cap A_i| = 1$
and
![]() $|e \cap X_i| = 2$
. Now remove all the edges that are incident to a vertex in
$|e \cap X_i| = 2$
. Now remove all the edges that are incident to a vertex in
![]() $T_0$
from M to produce a matching
$T_0$
from M to produce a matching
![]() $M'$
. By
$M'$
. By
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $|M| - |M'| \le 10 p_i \mu n$
. Adding the edges of
$|M| - |M'| \le 10 p_i \mu n$
. Adding the edges of
![]() $M'$
to
$M'$
to
![]() $T_{i-1}$
then yields a partial embedding of
$T_{i-1}$
then yields a partial embedding of
![]() $T_i$
, where at most
$T_i$
, where at most
![]() $11 p_i \mu n$
edges of
$11 p_i \mu n$
edges of
![]() $T_i$
are not embedded yet. We now show that one can use vertices of R to embed these edges (which would then show that the first part of (a) is satisfied).
$T_i$
are not embedded yet. We now show that one can use vertices of R to embed these edges (which would then show that the first part of (a) is satisfied).
As every vertex v in
![]() $A_i$
is incident to at least
$A_i$
is incident to at least
![]() $10^4 \mu n $
edges e such that
$10^4 \mu n $
edges e such that
![]() $e \setminus \{v\} \subseteq R$
by
$e \setminus \{v\} \subseteq R$
by
![]() $\mathcal E_{0}$
, (I) ensures that one can greedily choose edges to complete the embedding of
$\mathcal E_{0}$
, (I) ensures that one can greedily choose edges to complete the embedding of
![]() $T_i$
by using at most
$T_i$
by using at most
![]() $2(11 p_i \mu n) \leq 30 p_i \mu n$
vertices in R (i.e.,
$2(11 p_i \mu n) \leq 30 p_i \mu n$
vertices in R (i.e.,
![]() $|(V(T_i)\setminus V(T_{i-1})) \cap R| \leq 30 p_i \mu n$
) so (a) is satisfied, a contradiction to the maximality of i.
$|(V(T_i)\setminus V(T_{i-1})) \cap R| \leq 30 p_i \mu n$
) so (a) is satisfied, a contradiction to the maximality of i.
Suppose
![]() $i=s+1$
. By (iv) of Lemma 3.1, in this case,
$i=s+1$
. By (iv) of Lemma 3.1, in this case,
![]() $T_{s+1}$
is obtained by adding at most
$T_{s+1}$
is obtained by adding at most
![]() $\mu n$
vertex-disjoint bare paths of length 3 to
$\mu n$
vertex-disjoint bare paths of length 3 to
![]() $T_{s}$
. Conditioning on
$T_{s}$
. Conditioning on
![]() $\mathcal {E}_0$
, for every pair of vertices
$\mathcal {E}_0$
, for every pair of vertices
![]() $u, v \in V(G)$
, there are at least
$u, v \in V(G)$
, there are at least
![]() $100\mu n $
internally vertex-disjoint u–v paths (of length 3) such that all of their internal vertices are in R. By (I), the embedding of
$100\mu n $
internally vertex-disjoint u–v paths (of length 3) such that all of their internal vertices are in R. By (I), the embedding of
![]() $T_{i-1}$
already used at most
$T_{i-1}$
already used at most
![]() $40 \mu n$
vertices from R, so for any pair of vertices
$40 \mu n$
vertices from R, so for any pair of vertices
![]() $u, v \in V(G)$
, there are at least
$u, v \in V(G)$
, there are at least
![]() $60 \mu n$
internally vertex-disjoint u–v paths (of length 3) remaining. As each path of length 3 uses at most 7 vertices in R, one can greedily find at most
$60 \mu n$
internally vertex-disjoint u–v paths (of length 3) remaining. As each path of length 3 uses at most 7 vertices in R, one can greedily find at most
![]() $\mu n$
vertex-disjoint paths (of length 3) that are required for embedding
$\mu n$
vertex-disjoint paths (of length 3) that are required for embedding
![]() $T_{s+1}$
in G. As we have used at most
$T_{s+1}$
in G. As we have used at most
![]() $7 \mu n$
vertices of R, (b) is satisfied, a contradiction to the maximality of i.
$7 \mu n$
vertices of R, (b) is satisfied, a contradiction to the maximality of i.
Hence, we have
![]() $i-1 = \ell $
, and this completes the proof of Theorem 1.2.
$i-1 = \ell $
, and this completes the proof of Theorem 1.2.
Concluding remarks. As noted before, a complete graph on n vertices contains all possible trees on at most n vertices. This simple fact motivated the tree packing conjecture of Gyárfás and Lehel [Reference Gyárfás and Lehel16], which states that for
![]() $n \in \mathbb {N}$
, any given set of trees
$n \in \mathbb {N}$
, any given set of trees
![]() $T_1, T_2, \ldots , T_n$
with
$T_1, T_2, \ldots , T_n$
with
![]() $|V(T_i)|=i$
can be packed into the complete graph
$|V(T_i)|=i$
can be packed into the complete graph
![]() $K_n$
. This notorious conjecture since 1976 has driven a lot of research and it still remains open (see, for example, [Reference Allen, Böttcher, Clemens, Hladkỳ, Piguet and Taraz1, Reference Joos, Kim, Kühn and Osthus18] for results toward this conjecture).
$K_n$
. This notorious conjecture since 1976 has driven a lot of research and it still remains open (see, for example, [Reference Allen, Böttcher, Clemens, Hladkỳ, Piguet and Taraz1, Reference Joos, Kim, Kühn and Osthus18] for results toward this conjecture).
As our theorem guarantees that an n-vertex Steiner triple system contains all possible hypertrees with at most
![]() $(1-o(1))n$
vertices, it is natural to ask if a corresponding ‘packing’ statement for Steiner triple systems also holds. This question was in fact already asked by Frankl, as recorded in [Reference Elliott and Rödl13], in the following form: what is the largest integer s such that any s hypertrees
$(1-o(1))n$
vertices, it is natural to ask if a corresponding ‘packing’ statement for Steiner triple systems also holds. This question was in fact already asked by Frankl, as recorded in [Reference Elliott and Rödl13], in the following form: what is the largest integer s such that any s hypertrees
![]() $T_3, T_5, T_7, \ldots , T_{2s+1}$
with
$T_3, T_5, T_7, \ldots , T_{2s+1}$
with
![]() $|V(T_i)|=i$
can be packed into every n-vertex Steiner triple system? Indeed, this question is a natural analogue of the tree packing conjecture, since every hypertree contains an odd number of vertices. Frankl showed that any given set of hypertrees
$|V(T_i)|=i$
can be packed into every n-vertex Steiner triple system? Indeed, this question is a natural analogue of the tree packing conjecture, since every hypertree contains an odd number of vertices. Frankl showed that any given set of hypertrees
![]() $T_3, T_5, T_7, \ldots , T_{(n+3)/2}$
can be packed into every n-vertex Steiner triple system but it is not known if a larger set of hypertrees can be embedded.
$T_3, T_5, T_7, \ldots , T_{(n+3)/2}$
can be packed into every n-vertex Steiner triple system but it is not known if a larger set of hypertrees can be embedded.
By analyzing our proof more carefully with some modifications, one may prove a minimum-degree version of our theorem. That is, there exists some
![]() $\delta>0$
such that the following holds: If
$\delta>0$
such that the following holds: If
![]() $\varepsilon = \Omega (n^{-\delta })$
and n is sufficiently large, then every n-vertex linear
$\varepsilon = \Omega (n^{-\delta })$
and n is sufficiently large, then every n-vertex linear
![]() $3$
-graph G with the minimum degree at least
$3$
-graph G with the minimum degree at least
![]() $n(\frac {1}{2} - (\frac {\varepsilon }{\log n})^{100})$
contains any hypertree T with at most
$n(\frac {1}{2} - (\frac {\varepsilon }{\log n})^{100})$
contains any hypertree T with at most
![]() $(1- \varepsilon )n$
vertices. By repeatedly applying this to a Steiner triple system and deleting low degree vertices, one can also show that any given set of hypertrees
$(1- \varepsilon )n$
vertices. By repeatedly applying this to a Steiner triple system and deleting low degree vertices, one can also show that any given set of hypertrees
![]() $T_{n - j-t\log ^{100} n}$
,
$T_{n - j-t\log ^{100} n}$
,
![]() $j=0,2,4,\cdots ,2t$
, with
$j=0,2,4,\cdots ,2t$
, with
![]() $|V(T_{i})|=i$
pack into every n-vertex Steiner triple system for an appropriate choice of
$|V(T_{i})|=i$
pack into every n-vertex Steiner triple system for an appropriate choice of
![]() $t = \Theta ( \frac {n}{\mathrm {polylog}(n)})$
.
$t = \Theta ( \frac {n}{\mathrm {polylog}(n)})$
.
Appendix A Hypertree splitting
The very first step toward our proof of Theorem 1.2 is Lemma 3.1, which splits the given hypertree T into ‘manageable’ pieces. Our proofs in this section will closely follow that of [Reference Montgomery, Pokrovskiy and Sudakov26], whose first step is the following lemma for
![]() $2$
-graphs. For a (graph) tree T, a path P in T is a bare path if all the internal vertices of P have degree two.
$2$
-graphs. For a (graph) tree T, a path P in T is a bare path if all the internal vertices of P have degree two.
Lemma A.1 [Reference Montgomery, Pokrovskiy and Sudakov26].
Let
![]() $\ell , m \geq 2$
be integers, and let T be a tree with at most
$\ell , m \geq 2$
be integers, and let T be a tree with at most
![]() $\ell $
leaves. Then there exist vertex-disjoint bare paths
$\ell $
leaves. Then there exist vertex-disjoint bare paths
![]() $P_1, P_2, \cdots , P_s$
of length m such that
$P_1, P_2, \cdots , P_s$
of length m such that
where
![]() $T-P$
denotes the graph obtained by removing all of internal vertices of P from T.
$T-P$
denotes the graph obtained by removing all of internal vertices of P from T.
By considering the breadth-first search (BFS) tree of the line graph of a hypertree, this lemma can be adapted for hypertrees. To that end, we need to specify the corresponding definitions for 3-uniform hypergraphs. A semi-bare path P in a hypertree T is a path such that edges in
![]() $T\setminus E(P)$
are only incident to the vertices in its end pairs. This is a weaker notion than a bare path (in hypertrees); in Figure 1, green edges plus the right red edge form a semi-bare path but not a bare path. For a semi-bare path P, denote by
$T\setminus E(P)$
are only incident to the vertices in its end pairs. This is a weaker notion than a bare path (in hypertrees); in Figure 1, green edges plus the right red edge form a semi-bare path but not a bare path. For a semi-bare path P, denote by
![]() $T-P$
the hypergraph obtained from T by removing all vertices of P except the vertices in the edges that contains one of the end pairs of P.
$T-P$
the hypergraph obtained from T by removing all vertices of P except the vertices in the edges that contains one of the end pairs of P.
Lemma A.2. Let
![]() $\ell , m \geq 2$
be integers. Let T be a hypertree with at most
$\ell , m \geq 2$
be integers. Let T be a hypertree with at most
![]() $\ell $
leaf edges. Then there exist edge-disjoint semi-bare paths
$\ell $
leaf edges. Then there exist edge-disjoint semi-bare paths
![]() $P_1, P_2, \cdots , P_s$
of length
$P_1, P_2, \cdots , P_s$
of length
![]() $m+1$
such that
$m+1$
such that
Proof. If all the edges of T are leaf edges, then
![]() $e(T)=\ell $
, so the conclusion trivially holds. We may thus assume that there is a non-leaf edge
$e(T)=\ell $
, so the conclusion trivially holds. We may thus assume that there is a non-leaf edge
![]() $e^* \in E(T)$
. Let
$e^* \in E(T)$
. Let
![]() $\mathcal {G}$
be the auxiliary (2-)graph on the edge set
$\mathcal {G}$
be the auxiliary (2-)graph on the edge set
![]() $E(T)$
where
$E(T)$
where
![]() $e_1$
and
$e_1$
and
![]() $e_2$
are adjacent if they intersect.
$e_2$
are adjacent if they intersect.
Let
![]() $T_{\mathcal {G}}$
be the BFS tree of
$T_{\mathcal {G}}$
be the BFS tree of
![]() $\mathcal G$
rooted at
$\mathcal G$
rooted at
![]() $e^*$
. Then a leaf of
$e^*$
. Then a leaf of
![]() $T_{\mathcal {G}}$
corresponds to a leaf edge of T. Indeed, an edge e of T is a leaf edge if and only if it has only one vertex incident to other edges. Thus, if there exists a parent
$T_{\mathcal {G}}$
corresponds to a leaf edge of T. Indeed, an edge e of T is a leaf edge if and only if it has only one vertex incident to other edges. Thus, if there exists a parent
![]() $e'$
of e in the rooted tree
$e'$
of e in the rooted tree
![]() $T_{\mathcal {G}}$
, then the other edges that intersect with e also intersect with
$T_{\mathcal {G}}$
, then the other edges that intersect with e also intersect with
![]() $e'$
and the BFS puts them in the same depth as e. This makes e a leaf vertex in
$e'$
and the BFS puts them in the same depth as e. This makes e a leaf vertex in
![]() $T_{\mathcal {G}}$
. Conversely, if e is not a leaf edge in T, then deleting e disconnects the hypertree, which also disconnets the BFS tree
$T_{\mathcal {G}}$
. Conversely, if e is not a leaf edge in T, then deleting e disconnects the hypertree, which also disconnets the BFS tree
![]() $T_{\mathcal {G}}$
. In particular, e is not a leaf vertex in
$T_{\mathcal {G}}$
. In particular, e is not a leaf vertex in
![]() $T_{\mathcal {G}}$
. Since the root
$T_{\mathcal {G}}$
. Since the root
![]() $e^*$
of
$e^*$
of
![]() $T_{\mathcal {G}}$
is not a leaf edge in T, an edge
$T_{\mathcal {G}}$
is not a leaf edge in T, an edge
![]() $e\in E(T)$
is a leaf edge if and only if it is a leaf (vertex) in
$e\in E(T)$
is a leaf edge if and only if it is a leaf (vertex) in
![]() $T_{\mathcal {G}}$
. Therefore,
$T_{\mathcal {G}}$
. Therefore,
![]() $T_{\mathcal {G}}$
has at most
$T_{\mathcal {G}}$
has at most
![]() $\ell $
leaves.
$\ell $
leaves.
Moreover, a bare path of length m in
![]() $T_{\mathcal {G}}$
corresponds to a semi-bare path of length
$T_{\mathcal {G}}$
corresponds to a semi-bare path of length
![]() $m+1$
in T. Indeed, the
$m+1$
in T. Indeed, the
![]() $m-1$
internal vertices of a bare path of length m in
$m-1$
internal vertices of a bare path of length m in
![]() $T_{\mathcal {G}}$
form edges of a bare path of T because of the BFS, which uniquely extends to a semi-bare path of length
$T_{\mathcal {G}}$
form edges of a bare path of T because of the BFS, which uniquely extends to a semi-bare path of length
![]() $m+1$
. Conversely, the hyperedges of a semi-bare path in T becomes the vertex set of a bare path. Therefore, applying Lemma A.1 to
$m+1$
. Conversely, the hyperedges of a semi-bare path in T becomes the vertex set of a bare path. Therefore, applying Lemma A.1 to
![]() $T_{\mathcal {G}}$
yields the desired result.
$T_{\mathcal {G}}$
yields the desired result.
We are now ready to prove Lemma 3.1.
Proof of Lemma 3.1.
We construct a decreasing sequence
![]() $T=T^{\prime }_0 \supseteq T_1'\supseteq \cdots \supseteq T_\ell '$
, which will yield the desired increasing sequence
$T=T^{\prime }_0 \supseteq T_1'\supseteq \cdots \supseteq T_\ell '$
, which will yield the desired increasing sequence
![]() $T_k = T_{\ell -k}'$
. Let
$T_k = T_{\ell -k}'$
. Let
![]() $m:=\lceil 10^3/\mu \rceil $
. Starting from T, we iteratively remove a matching leaf set of size at least
$m:=\lceil 10^3/\mu \rceil $
. Starting from T, we iteratively remove a matching leaf set of size at least
![]() $\mu n / (50 m D)$
as many times as possible. There are at most
$\mu n / (50 m D)$
as many times as possible. There are at most
![]() $50mD/\mu $
such iterations, so starting from
$50mD/\mu $
such iterations, so starting from
![]() $T_0'=T$
gives the resulting tree
$T_0'=T$
gives the resulting tree
![]() $T_{k}'$
,
$T_{k}'$
,
![]() $k\leq 50mD/\mu $
.
$k\leq 50mD/\mu $
.
We say that a non-leaf vertex v in a leaf edge is the parent of the edge or simply a parent if it is a parent of a leaf edge. By the choice of
![]() $T_{k}'$
, there are at most
$T_{k}'$
, there are at most
![]() $\mu n / (50 m D)$
parent vertices. For every vertex v which is a parent of at least D leaf edges, remove all the leaf edges incident to v to obtain a smaller hypertree S. Then S contains at most
$\mu n / (50 m D)$
parent vertices. For every vertex v which is a parent of at least D leaf edges, remove all the leaf edges incident to v to obtain a smaller hypertree S. Then S contains at most
![]() $\mu n /50 m$
leaf edges, since each leaf edge in S is either a leaf edge in
$\mu n /50 m$
leaf edges, since each leaf edge in S is either a leaf edge in
![]() $T_k'$
which shares its parent with at most D leaf edges or it contains a parent in
$T_k'$
which shares its parent with at most D leaf edges or it contains a parent in
![]() $T_k'$
.
$T_k'$
.
Then by Lemma A.2, S contains edge-disjoint semi-bare paths
![]() $P_1, \cdots , P_r$
of length
$P_1, \cdots , P_r$
of length
![]() $m+1$
such that
$m+1$
such that
![]() $e(S-P_1-\cdots -P_r) \leq 3\mu n /25 + 2e(S)/(m+1) \leq \mu n/2$
since S has at most
$e(S-P_1-\cdots -P_r) \leq 3\mu n /25 + 2e(S)/(m+1) \leq \mu n/2$
since S has at most
![]() $\mu n /50 m$
leaf edges. As there are at most
$\mu n /50 m$
leaf edges. As there are at most
![]() $\mu n /(50mD)$
vertices in S whose degrees differ from theirs in
$\mu n /(50mD)$
vertices in S whose degrees differ from theirs in
![]() $T_k'$
, at least
$T_k'$
, at least
![]() $\max \{0, r-\mu n / (50 m D)\}$
of the semi-bare paths
$\max \{0, r-\mu n / (50 m D)\}$
of the semi-bare paths
![]() $P_1,P_2,\cdots ,P_r$
are still semi-bare paths of
$P_1,P_2,\cdots ,P_r$
are still semi-bare paths of
![]() $T_{k}'$
. Let
$T_{k}'$
. Let
![]() $Q_1, \ldots , Q_{r'}$
be such semi-bare paths with
$Q_1, \ldots , Q_{r'}$
be such semi-bare paths with
![]() $r'\geq \max \{0, r-\mu n/(50mD)\}$
. As each of the
$r'\geq \max \{0, r-\mu n/(50mD)\}$
. As each of the
![]() $Q_i$
’s contains a bare path of length three in the middle, we can remove the vertices in these bare paths to obtain
$Q_i$
’s contains a bare path of length three in the middle, we can remove the vertices in these bare paths to obtain
![]() $T_{k+1}'$
. Indeed, as
$T_{k+1}'$
. Indeed, as
![]() $Q_i$
’s are semi-bare paths that are edge-disjoint, they are vertex-disjoint except the vertices in their end pairs; thus, the removed bare paths are vertex-disjoint.
$Q_i$
’s are semi-bare paths that are edge-disjoint, they are vertex-disjoint except the vertices in their end pairs; thus, the removed bare paths are vertex-disjoint.
Starting from
![]() $T_{k+1}'$
, at each step, we delete one leaf edge from the remaining edges in each
$T_{k+1}'$
, at each step, we delete one leaf edge from the remaining edges in each
![]() $Q_i$
except the edges at the end of
$Q_i$
except the edges at the end of
![]() $Q_i$
. This yields
$Q_i$
. This yields
![]() $T_{k+2}',T_{k+3}',\cdots ,T_{k+m-3}'$
, where each
$T_{k+2}',T_{k+3}',\cdots ,T_{k+m-3}'$
, where each
![]() $T_{k+t+1}'$
is obtained by deleting vertex-disjoint leaf edges from
$T_{k+t+1}'$
is obtained by deleting vertex-disjoint leaf edges from
![]() $T_{k+t}'$
.
$T_{k+t}'$
.
The final step from
![]() $T_{k+m-3}'$
to
$T_{k+m-3}'$
to
![]() $T_{k+m-2}'$
essentially repeats what we did to obtain S. For every vertex that is a parent of at least D leaf edges in
$T_{k+m-2}'$
essentially repeats what we did to obtain S. For every vertex that is a parent of at least D leaf edges in
![]() $T^{\prime }_{k+m-3}$
, remove all the leaf edges incident to v to obtain
$T^{\prime }_{k+m-3}$
, remove all the leaf edges incident to v to obtain
![]() $T_{k+m-2}'$
and take
$T_{k+m-2}'$
and take
![]() $\ell =k+m-2$
. Then
$\ell =k+m-2$
. Then
![]() $\ell \leq m + 50 m D / \mu \leq 10^5 D \mu ^{-2}$
.
$\ell \leq m + 50 m D / \mu \leq 10^5 D \mu ^{-2}$
.
It remains to prove that
![]() $e(T_{k+m-2}') \leq \mu n$
. First, recall that
$e(T_{k+m-2}') \leq \mu n$
. First, recall that
![]() $e(S-P_1-\cdots -P_r) \leq \mu n/{2}$
. Also, if a vertex is a common parent of D leaf edges in
$e(S-P_1-\cdots -P_r) \leq \mu n/{2}$
. Also, if a vertex is a common parent of D leaf edges in
![]() $T_{k}'$
, then it is so in
$T_{k}'$
, then it is so in
![]() $T_{k+m-3}'$
as well. Thus, if an edge in
$T_{k+m-3}'$
as well. Thus, if an edge in
![]() $T_{k+m-3}'$
is not removed when obtaining
$T_{k+m-3}'$
is not removed when obtaining
![]() $T_{k+m-2}'$
, then it must have remained when obtaining S from
$T_{k+m-2}'$
, then it must have remained when obtaining S from
![]() $T_{k}'$
(i.e.,
$T_{k}'$
(i.e.,
![]() $E(T_{k+m-2}') \subseteq E(S)$
). Thus,
$E(T_{k+m-2}') \subseteq E(S)$
). Thus,
![]() $T_{k+m-2}'$
is contained in both S and
$T_{k+m-2}'$
is contained in both S and
![]() $T_{k+m-3}'=T_{k}'-Q_1-Q_2-\cdots -Q_{r'}$
, which implies that
$T_{k+m-3}'=T_{k}'-Q_1-Q_2-\cdots -Q_{r'}$
, which implies that
This completes the proof of the lemma.
Acknowledgements
We thank the anonymous referee for carefully reading our paper. SI and JK are supported by the POSCO Science Fellowship of POSCO TJ Park Foundation and by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) No. RS-2023-00210430. SI and JL are supported by National Research Foundation of Korea (NRF) grant funded by the Korea government MSIT NRF-2022R1C1C1010300 and by the Institute for Basic Science (IBS-R029-C4). JL is also supported by Samsung STF Grant SSTF-BA2201-02. AM is supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 786198), by the EPSRC, grant no. EP/S00100X/1 (A. Methuku), and by the SNSF grant 200021_196965.
Competing interest
The authors have no competing interest to declare.