1. Introduction
This paper — the second in a sequence of the study of the behaviour of the motion of a finite mass of granular mass subject to Coulomb and Voellmy-type resistive drag — is thought to be a further contribution to the understanding of the dynamics of flow avalanches, which have a negligible air-borne powder-snow contribution. It is intended to extend the work of Hutter and Savage and co-workers and, in particular, that of Reference Hutter and NohguchiHutter and Nohguchi (1990) and aims at an improved description of the classical Reference VoellmyVoellmy (1955), Reference SalmSalm (1968) and Reference Perla, Cheng and McClungPerla and others (1980) models.
Recent years have witnessed an increased impetus in the study of landslides, rockfalls and snow and ice avalanches, viz. Reference AleanAlean (1984, Reference Alean1985), Reference Beghin, Hopfinger and BritterBeghin and others (1981), Reference Hermann and HutterHermann and Hutter (1991), Reference Beghin, Hopfinger and BritterGreve and Hutter (1993), Reference GublerGubler (1987, Reference Gubler1989, Reference Gublerunpublished), Reference Gubler and HillerGubler and Hiller (1984), Reference HopfingerHopfinger (1983), Reference Hopfinger and BeghinHopfingcr and Beghin (1980), Reference HsüHsü (1975, Reference Hsü and Hutter1978), Reference Hutter and KochHutter (1992), Reference Hutter and KochHutter and Koch (1991), Reference Hutter, Savage and BonnardHutter and Savage (1988a, Reference Hutter and Savageb), Reference Hutter, Koch, Plüss and SavageHutter and others (in press), Reference Lang, Leo and HutterLang and others (1989), Reference Lang and MartinelliLang and Martinelli (1979), Reference Norem, Kristensen and TronstadNorem and others (1987, 1988), Reference Perla and MartinelliPerla and Martinelli (1978), Reference Perla, Cheng and McClungPerla and others (1980), Reference SalmSalm (1966, Reference Salm1968), Reference Savage and HutterSavage and Hutter (1989, Reference Savage and Hutter1991), Reference Savage and NohguchiSavage and Nohguchi (1988), Reference ScheiwillerScheiwiller (1986), Reference Scheiwiller and HutterScheiwiller and Hutter (1982), Reference Scheiwiller, Hutter and HermannScheiwiller and others (1987), Reference Tochon-DanguyTochon-Danguy (1977), Reference Tochon-Danguy and HopfingerTochon-Danguy and Hopfingcr (1975), Reference VilaVila (1987), Reference VoellmyVoellmy (1955), and others. All these works deal in one way or another with the mathematical formulation of the model equations of such catastrophic motions, their integration and, if possible, their verification against laboratory and field observations.
It is obvious that the direct observation of the dynamics of rockfalls or avalanches is extremely difficult and is probably only possible by remote-sensing techniques. Reference GublerGubler (1987, Reference Gublerunpublished) measured velocities and depths of flow avalanches that were artificially released in central Switzerland using radar-Doppler techniques, while Reference Norem, Kristensen and TronstadNorem and others (1986, 1988) and Reference Norem and KristensenNorem and Kristensen (1988) measured avalanche speeds and forces in the Ryggfonn Project of the Norwegian Geotechnical Institute when real avalanches were traced in three consecutive winters. The existing field data, against which theoretical models can be tested, are still very limited but it is known that the classical theoretical formulations (Reference VoellmyVoellmy, 1955; Reference SalmSalm, 1966, Reference Salm1968; Reference Perla and MartinelliPerla and Martinelli, 1978) were known to be oversimplified. Run-out distances and deposition areas cannot be sufficiently accurately predicted by these models. Reasons for these inadequacies must probably be sought in (i) the difficulties of parameter identification and in (ii) an insufficient resolution of the physics (rheological properties, sliding conditions), and of the geometry of the moving avalanche.
In this paper, our aim is not so much in a demonstration that our model will do better than the classical ones when compared with observations. For chute flows this has been demonstrated by Reference Hutter and KochHutter and Koch (1991), Greve and Hutter (1993) and Reference Hutter, Koch, Plüss and SavageHutter and others (in press). Here we take our new model, which is the first to our knowledge that describes the two-dimensional motion of the moving surface, and construct particular solutions in semi-analytical form. These solutions have diagnostic value insofar as they permit parameter studies and thereby inform us about the performance of the model; this provides physical insight.
We use the governing equations of Reference Hutter, Koch, Plüss and SavageHutter and others (in press). These were derived from the three-dimensional balance laws of mass and momentum of an incompressible continuum obeying a Coulomb-friction law. The equations emerged from depth-averaging of three-dimensional equations and incorporate a bed-friction law that is composed of a Coulomb-type and a Voellmy-type viscous contribution. We assume the angle of internal friction is constant but allows the bed-friction angle to vary with position. It is at this point where our model provides the necessary flexibility sought by the avalanche practitioners.
Conceptually, it may be of advantage if the equations governing the motion of the moving mass are decomposed into those governing the motion of the centre of mass and those describing the deformation. For the equations of Reference Hutter, Siegel, Savage and NohguchiHutter and others (in press b), this decomposition is not possible in general, but when the effect of the Voellmy drag on the deformation of the moving pile is ignored, then this decomposition describes the complete motion very accurately. The decomposition is the basis for the construction of similarity solutions. Such solutions have previously been constructed for the one-dimensional chute-flow situation (Reference Savage and NohguchiSavage and Nohguchi, 1988; Reference Nohguchi, Hutter and SavageNohguchi and others, 1989; Reference Savage and HutterSavage and Hutter, 1989; Reference Hutter and NohguchiHutter and Nohguchi, 1990); they have the property of permanent shape. In the spatially two-dimensional situation of unconfined flow, a similarity solution means that the (mathematical) structure of the shape is preserved but its aspect ratio may still change.
We show that a finite mass of gravel that starts from rest in the form of a circular or elliptical parabola will maintain its elliptical-paraboloidal shape. We derive the governing equations for the position and velocity of its centre of mass and the evolution of the semi-axis of the ellipse. These are non-linear ordinary differential equations which must be solved numerically.
In general, the motion of the centre of mass and the evolution of the deformation of the pile are coupled and separate only in special cases. We construct numerical solutions with the Runge–Kutta technique and analyze the performance of the model when the inclination angle of the plane, the initial depth to length ratio, the bed-friction angle and the Voellmy drag coefficient are varied. Solutions are discussed in detail.
2. Governing Equations
Consider free surface flow of a granular material down a slowly varying topography. Identify the mean plane surface of this topography with a plane that is parallel to the xy-plane of a three-dimensional Cartesian coordinate system. Let the x-coordinate follow the direction of steepest descent, the y-coordinate the horizontal lines and let the z-coordinate be perpendicular to these (see Fig. 1). Thus, the z-axis will be inclined with respect to the vertical by the angle ζ. The bottom and free surface of the moving mass will be defined by z = b(x,y) and z = ƒ(x,y,t), respectively; the margin curve is therefore given by the condition ƒ - b = 0. The space within 0 ≤ z – b ≤ ƒ – b = h is filled with a granular material, which is assumed to be treatable as a fluid-like continuum. This supposes that the thickness, h = ƒ – b, of the sliding and deforming body extends over several particle diameters. We accept the fact that this condition cannot be satisfied close to the margin.
Fig. 1. Definition of configuration and coordinate system (physical coordinates).
The granular continuum is regarded as incompressible, an assumption one may debate about, but this condition is sufficiently satisfied in the entire space filled by the granular material except in a very thin fluidized layer close to the bottom. This layer will be absorbed into a sliding condition.
Balance laws of mass and momentum are
in which u, ρ,p,g are the velocity vector, constant density, pressure tensor and gravity vector. In the coordinates of Figure 1 we have
Boundary conditions have to be formulated at the free surface and the base, and comprise kinematic and dynamic statements. At the free surface, F S = ƒ(x, y, t) – Z ≡ 0, we have
where n is the unit-normal vector. At the base the tangency condition for the velocity must be fulfilled. With F B = b – z ≡ 0 this reads
We regard the material as a cohesionless granular body obeying a Mohr-Coulomb yield criterion with a constant internal friction angle. This states that yielding will occur on a plane element when
where S and N are, respectively, the shear and normal stress acting on the element. By contrast, at the basal surface, the friction law is assumed to consist of two components
The first is a Coulomb-type dry-friction law, where S and N are now related by
in which δ is the bed-friction angle (which is generally smaller than ø). The second is a viscous drag, very much like the classical Voellmy drag in the early avalanche models and has the form
in which q is the dimensionless drag coefficient that may depend on the modulus of the velocity vector and the stress-normal to the basal surface. For a q independent of ∥u∥, Equation (2.8) corresponds to a quadratic dependence of S v on the velocity, but, clearly, any other dependence is also possible. Furthermore, avalanche dynamicists who are used to working with the Voellmy model usually define S v in the form
where ξ is a “viscosity” having the dimension of acceleration and
Reference Hutter, Siegel, Savage and NohguchiHutter and others (in press b) have motivated a reduction of the initial boundary-value problem outlined above. It is not our goal here to repeat this derivation; in short, the intention is not to determine the three-dimensional distribution of the velocity field, but only depth averages of this vector field. As a result, the spatially three-dimensional problem is reduced by one spatial dimension and therefore becomes much simpler.
In the derivation of the simplified equations Reference Hutter, Siegel, Savage and NohguchiHutter and others (in press b) introduced the Cartesian coordinates of Figure 1 and wrote the previous equations in dimensionless form by introducing the following scales:
Quantities in brackets are typical scales for the physical quantities under consideration, the only exceptions being the shear stresses, for which λ1 and λ2 account for their smallness. Variables carrying an asterisk are dimensionless. Reference Hutter, Siegel, Savage and NohguchiHutter and others (in press b) further supposed that the following order relations hold:
In other words, the ratio of the velocity scales equals the corresponding length scale ratio and, the time-scale equals any of the length scales divided by the corresponding velocity scale. Moreover, wc have set the characteristic longitudinal velocity square proportional to the product of the gravity constant with the longitudinal characteristic length. The ratios ∈x,∈y,∈xy
are simply definitions but the last three of Equations (2.12) suppose that the moving masses are long, wide and also shallow. Different ordering symbols are used to indicate that the moving piles may possess a large range of aspect ratios, but always such that ∈xy
< 1. (A convenient choice would be 
0.5 ≤ α ≤ 1, so that 
if α = 1 then ∈x
= ∈y
and ∈xy
= 1, a very common case we shall adopt here.) Furthermore, in presenting the reduced equations below we shall suppose that ∈x
, ∈y
are sufficiently small so that terms of order 
and 
can be ignored.
The dimensionless equations that emerge from this procedure involve the longitudinal and transverse (side-wise) pressure 
which through the Mohr-Coulomb yield criterion are expressed in terms of the overburden pressure 
. We shall distinguish between active and passive stress states by writing
In view of the dominant downward motion, we expect one principal axis of strain rate to be very nearly the xz-plane. The stress 
can then easily be related to 
with the aid of the Mohr-Coulomb yield circle (see Fig. 2), so that
It is common to assume that, if the material is at the point of yielding, the stress in the other direction 
corresponds either to the major or minor principal stress σ1 or σ2. Again, with reference to Figure 2, we may thus deduce
Relations (2.13)-(2.15) are reasonable at the bed and again at the free surface, where pzz = 0 implies pxx = pyy = 0. So, by way of continuity, the postulates (2.13)-(2.15) are logical assumptions. They are common in the soil literature. For motions along the plane-inclined surface, we have b = 0 and the depth-averaged field equations take the form
(see Reference Hutter, Siegel, Savage and NohguchiHutter and others, in press b, Equations (3.1) and (3.2)). Here we have kept 
in the expression for ||u||, because this term is not negligible at the initial stage of the motion from a state at rest. At later times – in reality immediately after the motion has set in – this higher-order term may be dropped. We shall omit this term at all times and accept the inconsistency in the procedure at early times. In Equations (2.16) and (2.17)
h is the depth,
u
and
ν
are the depth-averaged dimensionless velocity components
and all quantities are dimensionless (asterisks have been dropped for simplicity). Equation (2.16) 1 is the mass balance in depth-integrated form, and Equations (2.16) 2,3 represent the in-plane longitudinal and transverse momentum balances. Equations (2.16) are solved subject to the boundary conditions
and prescribed initial conditions, usually
Equation (2.18) describes the margin and Equation (2.19) 1 the initial mass distribution. Integration of Equations (2.16)– (2.19) is likely only numerically possible.
Fig. 2. Mohr’s circle representation of the active and passive stress states.
3. Equations Governing the Centre of Mass Motion and the Deformation
3.1. Symbolic Form of the Field Equations
Equation (2.16) are now separated into two sets of equations, one governing the motion of the centre of mass, the other describing the deformation or the deviation from the rigid-body motion. To this end, we write them as
Here, the vector and tensor quantities and the corresponding operators are two-dimensional. In particular,
and v = ( u , ν ) while e is the unit vector
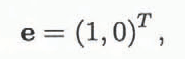
in which T denotes transposition.
3.2. Equations Describing the Centre of Mass Motion
Let A(t) be the domain in the (x, y) space that is, at time t, covered by the avalanching mass; let, further, ∂A(t) be its boundary (margin). Then integrate Equation (3.1) 1 over A, so that
By using Gauss’s theorem in the second term and Reynolds’ transport theorem in the first,
where n is the exterior unit vector normal to ∂A, Equation (3.4) becomes
In other words, the total volume of the avalanche is conserved. Because of incompressibility, this is tantamount to the conservation of mass. In much the same way, the momentum Equation (3.1) 2 may be transformed. The computations are straight-forward and the results are
In the derivation of Equation (3.7), the divergence theorem has been employed at various places, and the boundary condition that h vanishes along ∂A has been invoked. Furthermore, Reynolds’ transport theorem has been employed. Equation (3.7) is the expression of global momentum balance.
We now define averaged field quantities as follows
h is the depth averaged over the pile volume, v c the velocity of the centre of mass. The averages of the other quantities are formal means which will further be reduced below. Note, however, that owing to definition (3.2)2, B is a vector with the components
where B and D are defined in Equation (2.17). With the definitions (3.8), Equation (3.7) takes the form
We next assume geometric and dynamic symmetry of the avalanche with respect to the x-axis of Figure 1 that is in the direction of steepest descent,
Then Equation (3.8) 2 implies ν c ≡ 0 for all times, and the second component of Equation (3.10) is satisfied if, for instance
In view of Equation (3.9), the last of these requires D to be symmetric,
Going back to the original definitions (2.17) of the coefficients C, D and Ξ, it is seen that the requirements (3.12) presuppose the friction angles ø δ and the Voellmy coefficient Ξ to be symmetrically distributed. This is what we shall assume. In the above Equation (3.10), v c is the centre of mass velocity whose position, x c, is given by
It can be determined by integrating the equation of motion
It is not difficult to show that Equation (3.14) is in conformity with Equation (3.8) 2. Indeed,
in the second to last step use has been made of Equation (3.4). Clearly, because of the symmetry assumptions Equations (3.11) and (3.12), only one component of Equation (3.14) is non-trivial, namely
while d y c/dt = 0, since ν ≡ 0.
3.3. Deformation Equations
Having defined the centre of mass motion through Equations (3.10) and (3.14), we now proceed to the derivation of the deformation equation. To this end, it is convenient to define the new independent variables
from which one obtains
Introducing the difference velocity
or
and the transformation rules (3.16) and (3.17) into the governing Equations (3.1), we may, on account of Equations (3.10), derive the following deformation equations
The derivation of these equations is somewhat long but not difficult. We have also indicated that the differentiations in the operators are with respect to the coordinates ξ and η On an inclined plane with constant internal and bed-friction angles A, B, C and D are constant, implying A –
A
= 0,
B
= 0. Furthermore, if it is assumed that the difference velocities it, 
are small in comparison to
u
c, so that quadratic and higher-order terms can be ignored, then
In expressions (3.20)3,4 we have also replaced h by h , the mean depth, to avoid formation of singularities at the margin. In compensation, Ξ has been replaced by Ξ a suitable average over the avalanche. While the above relations correspond to additional ad hoc assumptions, they are needed if the separation into field variables describing the centre of mass motion and those describing the deformation is meaningful at all. On the other hand, the expressions (3.20) are also physically reasonable because, with the exception of the onset of the motion, the dispersive velocity is small in comparison to the centre of mass velocity. Moreover, singularities at the margins of the Voellmy resistive force are physically very unlikely and variations of the drag coefficient Ξ within the avalanche are difficult to determine.
With expressions (3.20), Equations (3.10), (3.15) and (3.19) reduce to the form
The first two equations correspond to the classical Voellmy model in which the resistive force on a moving mass of snow is composed of a dry Coulomb drag and a viscous drag that is proportional to the squared velocity. These two equations are equivalent to Equations (3.10) and (3.14) and thus give the Voellmy model (and its equivalents due to Salm, McClung and others) a clear interpretation. However, Equations (3.21) go beyond this simple model. The remaining Equations (3.21) describe for a restricted class of pile geometry also the deformation of the avalanche. The two sets of the equations are coupled; consequendy they cannot, in general, be integrated independently.
Several effects influence the spreading of the avalanche pile. In the downhill direction B(∂h/∂x) contributes to a dilatation as ∂h/∂x > 0 (< 0) in front of (behind) the centre of gravity. The drag forces, on the other hand, contribute to a contraction; interestingly, only the viscous drag, but not the Coulomb friction force contributes to this contraction. Sidewise spreading is enhanced by the term D(∂h/∂η) and is reduced by the friction forces; here both viscous and Coulomb-type friction contribute.
4. Similarity Solutions
4.1. Theoretical Considerations
We follow a procedure much the same as in Reference Hutter, Siegel, Savage and NohguchiHutter and others (in press b) and will now establish the governing equations for the longitudinal and sidewise spreading rates. More explicitly, we will derive similarity solutions for a granular pile with elliptical shape in plan view and parabolic distribution of the height. Strictly speaking, such similarity solutions do not exist for the model considered here; however, the reduced Equations (3.21) with the particular assumptions that were invoked to obtain them do permit existence of such similarity solutions.
Similarity solutions were previously constructed, for chute flows along a plane bed by Reference Savage and HutterSavage and Hutter (1989) and for chute flows along curved beds by Reference Savage and NohguchiSavage and Nohguchi (1988). The effect of variable friction and of a Voellmy resistive drag were then analyzed by Reference Nohguchi, Hutter and SavageNohguchi and others (1989) and Reference Hutter and NohguchiHutter and Nohguchi (1990). The first analysis of an unconfined flow along an inclined bed by Reference Hutter, Siegel, Savage and NohguchiHutter and others (in press b) contained a study of similarity solutions in which the Coulomb friction angles ø and δ were both kept constant and the Voellmy term was ignored. Here we generalize their solution.
We anticipate a solution in which the shape and difference velocity distributions are preserved, and the profiles are merely stretched or compressed in the streamwise and lateral directions. In view of this, we choose new similarity variables that are normalized by the half length of the pile (see Fig. 3), viz.
from which we may deduce
Primes denote univariate differentation. Substituting the expressions (4.2) into the last three of Equations (3.21) and seeking a solution for the difference velocity in the form
shows that expressions (4.2) will reduce to the following equation set
or after replacement of 
and 
by Equations (4.3)
Notice that both equations appear in separable form: their righthand sides are each a product of a function of v (and μ, respectively) and a function of time, t. To solve these equations, assume that the granular mass starts initially from a circular paraboloidal shape that in the course of motion deforms into an ellipsoid with parabolic distribution of its height. More specifically, g and ƒ are interpreted as the principal semi-axes of the ellipse so that the transformation of the ellipsoidal hump into the (ν, μ) plane by the transformation (4.1) maps the elliptical domain into the interior of a fixed circle with unit radius (see Fig. 3). Assuming, therefore,
yields
If H0 (t) were to be known, then these equations would form two second-order ordinary differential equations for g(t) and f(t), respectively. From the conservation of mass or volume, we can obtain this missing piece of information. Indeed, the total volume V is preserved:
With the initial volume V being prescribed, we thus have
The temporal evolution of the height is thus known, once ƒ and g are determined. The differential equations for these follow from Equations (4.8) and (4.9), when H 0, as determined from Equations (4.10) and h are employed:
There remains the corroboration that with the representations (4.3) the local mass balance in Equation (4.4) 1 is identically satisfied. This demonstration is routine and will be left to the reader. In summary, we must solve Equations (3.21) 1,2 for the motion of the centre of mass together with Equations (4.12) for the longitudinal and transverse spreading rates. The integration of these equations must be performed with initial conditions
corresponding to a granular mass with initial length 2g 0[Lx ] and initial width 2f 0[Ly ].
Fig. 3. Top view of the granular pile in the transformed dimensionless coordinates shown in its initial position (a), in a general position (b), and after a fixed-domain transformation (c), explaining the similarity solution and the related coordinate systems.
4.2. Numerical Integration
To complete the solution, the above initial value problem must be solved numerically. To this end, we transform the system of Equations (3.21) 1,2 and (4.12) to standard form and use t instead of τ:
In writing down these equations, we have also used the relation V = hπfg. Furthermore, the coefficients B, C and D are defined in Equations (2.17). We note the following properties of the system (4.14):
-
(i) Without the viscous sliding term ( Ξ → ∞), the motion of the centre of mass of the pile decouples from that of the deformation.
-
(ii) There can never be a rigid-body motion (for which g and f are constant) even for finite Ξ . This follows from Equations (4.14) 4,6. A rigid-body motion would require g′ = f′ = dg′/dt = df′/dt = 0, but the statements df′/dt = 0 and dg′/dt = 0 are not possible with f′ = 0 since the righthand sides of Equations (4.14) 4,6 are positive when f′ = 0, g′ = 0.
-
(iii) The centre of mass motion is never steady unless Ξ → ∞.
-
(iv) When the bed-friction angle, δ, varies linearly between the avalanche front and trailing edge, then Equation (4.14) 4 has on its righthand side an additional term −ΔC/2. Without a similar term also arising in Equation (4.14) 6, rigid-body and steady motions still cannot exist.
We thus have proved that within the context of similarity solutions, our model equations that incorporate Coulomb-type and Voellmy-type resistive drag cannot exhibit rigid-body motion. Likewise, the centre of mass cannot reach a finite steady speed. Alternatively, when the Voellmy drag is ignored, rigid-body motions are still not possible, but a steady, finite velocity can be reached in this case. These results contrast with earlier results of Reference Hutter and NohguchiHutter and Nohguchi (1990), who demon-strated for chute flows existence of rigid-body motions and finite steady speeds. The reason for the difference in behaviour is the influence of the sidewise spreading. Equations (4.14) contain the coefficients B, C and D, which depend on the Earth pressure coefficients 
that are given by
Therefore, depending upon whether the flow is extending or compressing, these coefficients take different values. Equations (4.14) must be solved subject to the initial conditions (4.13). A straight-forward integration, however, is not possible when 
because the system is singular at such early times. For those early times, a power-series solution must be sought when 
. This solution reads
in which
Notice that this early time solution starts with a centre of mass velocity at rest and with f′(t = 0) = f′0 = 0. This latter condition is necessary for consistency; usual initial conditions require f′0 = 0 and g 0′ = 0. Notice also that the short-time solution in Equations (4.16) breaks down when Ξ → ∞. This case is physically unrealistic anyhow and will not be considered.
5. Results
In the construction of similarity solutions, it was assumed that u ≥ 0 everywhere within the moving pile. At early times, in a motion starting from rest ( u c = 0: no centre of mass velocity, f′0 = 0 and g 0′ = 0: neither sidewise nor longitudinal initial spreading), this condition could be violated unless g′ μ u c. In view of Equations (4.16) and (4.17), this condition reads
or when invoking Equations (2.17) and (4.10)
H
0 und g
0 are the initial values of the dimensionless depth and longitudinal semi-span, both of which are usually chosen as 1. In a motion along a plane-inclined surface, the flow cannot be compressing; so only 
applies. Values for 
that depend on δ and ø are between 0.3 and 2.0 for 0 ≤ δ ≤ 35 ° and 0 ≤ ø ≤ 35 °. Generally, 
decreases with increasing ø. More generally, the right-hand side of inequality (5.2) grows with increasing ø and ζ.
Values of ∈x that do conform with inequality (5.2) are conservative because they imply that the condition u >0 is nowhere violated. One may relax this condition a bit and tolerate, at very early times and close to the upper margin, a violation. For ζ > 40 ° and δ < 30 °, condition (5.2) is almost always satisfied when ∈x < 0.5. We shall present results only for values of ∈x for which inequality (5.2) is obeyed.
Usual pile geometries have [Ly ] ≤ [Lx ]. We express this by the following orderings:
with 0 ≤ α ≤ 1; α = 1 means that [Ly ] = [Lx ] and α > 0.5 is requested for the approximation to be valid. Most ensuing computations will be performed for α = 1. Physically, it is not important what values are chosen for the parameters once the approximations have been carried through. However, if these parameters are chosen at will, then it is only meaningful to compare quantities with physical dimensions, for the non-dimensionalized quantities do then not stay in the proportions the physical quantities will. We shall make clear which choices are taken.
In the graphical representation of the results, two types of figures are presented. The first type is a kind of phase diagram in which g is plotted against g′ and f against f′ for various values of the parameters. In the second type of figure, the spreads g or f or the velocity u c and position x c of the centre of mass are plotted as functions of dimensionless time, again for various values of the parameters involved.
In all following computations, the angle of internal friction was ø = 35 °. Figure 4 shows phase-plane trajectories for g and f, respectively, for a slope angle ζ = 40 °, ∈xy = 1 (left panels) and ∈xy = 0.5 (right panels), a Voellmy coefficient Ξ = 10 and bed-friction angles δfront = 35 °, δrear = 25 °, and the aspect ratio ∈x as indicated. All phase-space trajectories start at g 0 = f 0 = 1 and g 0′ = f 0′ = 0. Figure 5 shows the same for a slope angle ζ = 60 °.
Fig. 4. Phase diagrams g versus g′ or f versus f′ plotted for an angle of internal friction ø= 35 ° and the physical parameters as shown in the insets and for the indicated values of the aspect ratios ∈x ∈x,y. The left panels show g(g′) (top) and f(f′) (bottom) for ∈xy =l and hence ∈y = ∈x the panels on the right show the same for ∈xy = 0.5. The inclination angle is ζ = 40 °.
Fig. 5. Same as Figure 4 but now for an inclination angle ζ= 60 °.
It can be seen that both the longitudinal and the sidewise spreading depend strongly upon the variation of the geometry parameters ∈x (and ∈xy ). The general tendency is the same as was observed when Ξ = 0 and Δδ = δfront – δrear = 0 (see Reference Hutter, Siegel, Savage and NohguchiHutter and others (in press b) for comparison); longitudinal spreadings are bigger than sidewise spreadings and their rates are larger when ∈ x is increased. Only for = 0.5 and steep slopes ζ = 60 °; Figure 5, right panels) sidewise spreading is bigger than longitudinal spreading. Thus, even though the condition ∈ xy = 0(1) must be fulfilled in order that the model equations are valid, the values of the initial aspect ratios are important for the geometry of the evolving masses. Granular masses which develop from relatively compact geometries spread faster than shallow masses do, and this spreading is generally larger in the longitudinal than in the transverse direction (exception again ζ = 60 °, xy = 0.5). Figure 6, which shows temporal evolutions of g(t) and f(t) for ζ = 60 ° (left panels) and ζ = 40 ° (right panels) indicates this very clearly. Depending on the value of the slope angle ζ and the aspect ratios ∈ x , ∈ xy , a granular pile developing from a circular shape will develop into an ellipse whose major semi-axis is either in the longitudinal (regular case) or transverse (ζ = 60 °, ∈xy = 0.5) direction.
Fig. 6. Temporal evolutions (dimensionless) of the semi-spreads g(t) (solid) and f{t) (dashed) calculated for ø = 35 ° and the physical parameters as shown in the insets. Panels on the left are for ζ = 60 °, those on the right for ζ = 40 °; lop panels are for ∈xy = 1, those on the bottom for ∈xy = 0.5.
One distinctive feature of the phase diagrams not exhibited when Δδ = 0 and Ξ = 0 is the fact that the trajectories g(g′) and f(f′) “bend towards the ordinate”. Thus, g′ and f′ reach an absolute maximum whose value depends on ∈x and ∈xy . Figures 4 and 5 indicate that the g-and /-trajectories bend and approach the ordinate and do this faster, the smaller ∈x is. If both trajectories reach the ordinate simultaneously, then the motion is of rigid-body type: the granular avalanche would then move like a rigid body. Figures 4, 5 and 6 show that such a rigid-body motion is approached but not reached. Deformations are, however, smaller the smaller ∈x is. Thus, flat and shallow piles deform less than do compact piles. Interesting to observe, and physically obvious, is the fact that sidewise spreading is significant only when ∈y = ∈x /∈xy is relatively large. For ∈y = 1 (∈x = 0.5, ∈xy = 0.5), the spreading is primarily in the transverse direction and actual ratios quickly reach small values. So, whereas in these instances the prerequisites of the model equations are not satisfied initially, the evolution is such that they are more and more fulfilled in the course of motion.
Similar qualitative behaviour is also seen in Figures 7 and 8 where phase diagrams g(g′) and f(f′) are shown for ∈x = 1 (left panels) and = 0.5 (right panels) and two different values of ∈x (∈x = 0.2, Fig. 7; ∈x = 0.5, Fig. 8) parameterized for slope angles ζ = 40 °, 50 ° and 60 °. According to the figures, the steeper the slope is the smaller (larger) will the longitudinal (transverse) spreading become. Moreover, the aspect ratios have again a significant influence on the spreading rates. When ∈xy > = 1, longitudinal spreading is clearly larger than sidewise spreading; when ∈xy = 0.5, this is not necessarily so as can be clearly inferred from the lower two panels in Figure 9. Not surprising is also the fact that the spreading generally decreases with increasing slope angle.
Fig. 7. Same as Figure 4, for ø = 35 ° and the physical parameters shown in the insets; however, now the aspect ratios ∈x, ∈xy are held fixed and the slope angle ζ is varied as indicated. The left panels show the result for ∈xy =1, those on the right for ∈xy = 0.5. ∈x = 0.2.
Fig. 8. Same as Figure 7 but now for ∈x = 0.5.
Fig. 9. Same as Figure 6, but now the inclination angle ζ is varied. Parameters as shown in the insets. Left panels are for ∈x = 0.2, those on the right for ∈x = 0.5.
Of particular interest is the quantitative analysis of the similarity solution to the granular-avalanche problem when, first the bed-friction angle is varied from the front to the rear end of the moving pile or, secondly, the Voellmy drag coefficient is changed. Figures 10 and 11 collect results in this regard. In the left panels of Figure 10 the g and f trajectories are shown where the Voellmy coefficient Ξ is held constant (Ξ = 10), but Δδ = δfront – δrear is varied between 0 ° and 20 °. It is seen that both longitudinal and sidewise spreadings are somewhat affected, but that the qualitative behaviour is unchanged. The trajectories bend over towards the ordinate axis. Generally, the smaller Δδ is the less will the longitudinal spreading be inhibited. The sidewise behaviour is opposite but less pronounced.
Fig. 10. Phase diagrams g versus g′ and f versus f′ plotted for an internal friction angle ø = 35 ° and the physical parameters as shown in the insets. In the left panels Δδ = δfront – δrear is varied, while Ξ = 10 is held fixed. In right panels Δδ = 10 ° while Ξ is varied. Calculations are for ∈x = ∈y = 0.5.
Quite contrary to this behaviour of the moving and deforming granular pile is its response to variations in the Voellmy parameter Ξ (right panels in Figure 10). Both, the longitudinal and the transverse spreadings are affected by the amount of viscous-type friction; however, the influence to the sidewise spreading is less dramatic. The computations for the graphs in Figure 10 have been done for ∈x = 0.5 and ∈xy = 1. For smaller values of ∈x (but ∈xy = 1), these effects are less pronounced, but for larger values they are enhanced. Similarly, a decrease of ∈xy enhances these effects. This can be seen, in parts in Figure 11, which shows the temporal evolutions of the semi-spreads for several values of Δδ (left panels) and Ξ (right panels) and value (∈x ,∈xy ) = (0.5,1) (top) and (∈x , ∈xy ) = (0.5,0.5) (bottom). An increase in Δδ, which corresponds to a more efficient ploughing, hinders a spreading though not dramatically.
Fig. 11. Temporal evolutions of the semi-spreads g(t) (solid) and f(t) (dashed), calculated for ø =35 ° and the physical parameters shown in the insets. In the left panels Δδ = δfront - δrear is varied while Ξ is held fixed, in the right panels it is the reverse, (∈x, ∈xy) = (0.5, 1) (top) and (∈x, ∈xy) = (0.5, 0.5) (bottom).
A variation of Ξ (by several powers) affects the spreading, both longitudinally and transversely, in a considerable manner. This behaviour is understandable, if one considers the governing differential Equations (4.14). The Voellmy term affects the spreadings in Equations (4.14) 2,4,6 and its influence becomes vanish-ingly small when Ξ → ∞. In Figure 11 (right panels) the role played by the Voellmy drag on the evolution of the spreadings g(t) and f(t) is very clearly seen.
As can be surmized from the dependence of the equations of motion on Ξ there must also be a strong dependence of the centre of mass motion on the Voellmy coefficient. Figure 12 provides evidence for this. In the top two panels, the centre of mass position, x c in the lower panels the centre of mass velocity, u c, (both dimension-less) are plotted against dimensionless time, t, for various values of the parameter Ξ For very large Ξ values Ξ > 1000), the centre of mass velocity is essentially linear in time and its position grows quadratically. These results are an important corroboration of our earlier calculations which were performed without the Voellmy term. With growing viscosity (decreasing Ξ values), the growth of the centre of mass velocity is more and more reduced. The velocity can even go through an absolute maximum and decrease afterwards, so that a decelerating motion of the centre of mass is possible, in principle. The fact that the graphs for ∈xy – 1 and ∈xy – = 0.5 hardly differ is an indication that the centre of mass motion is only little affected by the amount of spreading. On the other hand, that the amount of spreading crucially depends on both the dry and viscous drag behaviours, demonstrates the superiority of the present model over the classical avalanche models due to Voellmy, Salm and others.
Fig. 12. Temporal evolution of the centre of mass position, x c and its velocity, u c (both dimensionless) calculated for ø =35 ° and the physical parameters shown in the insets, when the Voellmy coefficient is varied. Computations have been done for (∈x, ∈xy) = (0.5, 0.5) (left) and (∈x, ∈xy) = (0.5, 1.0) (right).
6. Closing Remarks
In this paper, we have been concerned with the motion of a finite mass of a granular material down an inclined plane that is released from rest and may freely spread in the longitudinal and transverse directions as it moves down its track. The granular mass was treated as a cohesionless Coulomb-like continuum with a basal friction law in which the shear traction is additively composed of a Coulomb-like drag and a viscous drag proportional to the squared velocity. We believe that such a model is a valid one for the study of the dynamics of flow avalanches for the following reasons: the common mass point or hydraulic models that are used incorporate physically essentially the same complexity as this one, except that this one allows for the variation of the frictional drag within the avalanche. Mathematically or geometrically, this model has greater flexibility, as it permits a longitudinal and a sidewise spreading, both of which are not present in the Voellmy, Salm, Perla, etc. models. Thus, this model is more general than the former, yet incorporates essentially the same physics.
We used the depth-averaged equations of Reference Hutter, Siegel, Savage and NohguchiHutter and others (in press b). These equations are scaled, and dimensionless spatially two-dimensional evolution equations are derived for the distribution of the avalanche depth and depth averages of the velocity field of which analytical solutions are not likely to be found. In an approximate treatment, however, at least semi-analytical solutions were determined. To find these solutions, the motion was split into the motion of the centre of gravity of the pile plus a deformation from it. Such a decomposition cannot be achieved without additional ad hoc assumptions. The semi-analytical solutions are the so-called similarity solutions, and they enjoy the property of preserving the shape. For their existence, the granular avalanche must start from an initial shape in the form of an elliptical or circular paraboloid, and this shape will be preserved during the motion, and only its aspect ratio will change. For the existence of such similarity solutions, however, additional mild assumptions are needed: the earth-pressure coefficient must be assumed to be constant and the sidewise variation of the bed-friction angle must be ignored. Moreover, the construction of the similarity solutions is based on the formal separation of the evolution equations into one set governing the motion of the centre of mass and another governing the deformation. In general, this separation is not possible; however, with the approximations incorporated, two equation sets are obtained which are integrable. We explicitly Usted the restrictions to make the reader aware about the limitations of these solutions.
The physical parameters that govern the model are the slope angle ζ the initial depth to length ratio of the pile, ∈x, the ratio of the width to the length, ∈xy necessarily of order unity, the internal angle of friction ø, the basal-friction angle δ and the drag coefficient of the viscous sliding law Ξ called the Voellmy parameter. The effect of these parameters on the spreading rate of the granular pile that develops from a circular paraboloid led to results which may be summarized as follows:
-
(i) For the two-dimensional spreading, there exists no rigid-body motion, i.e. the length and width of the elliptical pile will always vary in time, no matter what the values of the bed-friction angle and the coefficient of viscous drag are.
-
(ii) As an immediate consequence of the above statement, there can be no steady motion of the centre of mass of the granular pile. However, for values of the dimensionless viscous-drag coefficient Ξ < 103 the centre of mass motion is greatly affected by the value of Ξ The motion can be accelerating or decelerating, or oscillate between the two.
-
(iii) The geometry of the pile depends on both the variation of the bed-friction angle with position (linear variations of tan δ in the long direction were studied) as well as on the value of the viscous-drag coefficient. However, the aspect ratio of the moving pile is influenced more by the latter than by the former.
In which way are these solutions useful to the avalanche dynamicist? First, they are capable of providing physical insight into the behaviour of a deforming finite mass of snow, in a way previous models did not. For small aspect ratios ∈x and ∈y , the model indicates small deformation. Under such conditions, a rigid-body assumption for the motion of a finite mass of snow does not seem to be too drastic a simplification. On the other hand, viscous sliding affects the deformation (spreading) considerably while ploughing does less. These inferences are qualitative and provide physical insight.
Secondly, this model could be used in actual computations along curved avalanche paths to predict deposition and its areal extent. While such a procedure will certainly be useful, we do not believe it to be accurate. In fact, laboratory experiments on the motion of a finite mass of a cohesionless granular material down an inclined plane show that similarity solutions are not reproduced. Flan views of moving granular avalanches that develop from a circular geometry rather develop into tear-drop shapes and along curved beds the shapes are even more complicated. One may therefore think that our solutions are of little use. We do not think so, as our solutions provide physical insight into the basic mechanisms of the motion and spreading of a granular pile; the model does have diagnostic value. For a prognostic use of the governing equations, however, integration from more general initial configurations are needed. Such studies are under way.
The accuracy of references in the text and in this list is the responsibility of the authors, to whom queries should be addressed.
