1. Introduction

A key problem in avalanche science is to mathematically describe streamwise variations in bulk flow density. This problem is particularly important in snow engineering applications as avalanche flow height, speed and density define the destructive power of the avalanche (Reference Bozhinskiy and LosevBozhinskiy and Losev, 1998). Avalanche flow density is strongly linked to the avalanche flow regime and therefore runout behavior (Reference Issler and GauerIssler and Gauer, 2008). For example, mixed flowing-powder avalanches exhibit not only smaller bulk flow densities in comparison to their dense (often wet) counterparts, but also larger streamwise variations in flow density (Reference Bozhinskiy and LosevBozhinskiy and Losev, 1998). There is often a transition from a disperse, fluidized-type flow structure of low density at the avalanche front to a dense, frictional-type flow at the avalanche tail (Reference SalmSalm, 1993; Reference Sovilla, Schaer, Kern and BarteltSovilla and others, 2007; Reference Gauer, Issler, Lied, Kristensen, Sandersen, Campbell, Conger and HaegeliGauer and others, 2008). Avalanche measurements in Russia (Reference Grigoryan, Urubayev and NekrasovGrigoryan and others, 1982; Reference SukhanovSukhanov, 1982; Reference Sukhanov and KholobayevSukhanov and Kholobayev, 1982), Norway (Reference GauerGauer and others, 2007a, b) and Switzerland (Reference GublerGubler, 1987; Reference Sovilla, Schaer, Kern and BarteltSovilla and others, 2007; Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009) all reveal the complex and highly dynamic streamwise flow structure of snow avalanches.

Predicting avalanche flow regime is a problem for existing avalanche dynamics models (e.g. Reference Savage and HutterSavage and Hutter, 1989; Reference Naaim, Naaim-Bouvet and FaugNaaim and others, 2003; Reference Christen, Kowalski and BarteltChristen and others, 2010). Existing models assume constant bulk flow densities in the avalanche core. This restricts the usage of these models to specific avalanche types, such as dry or wet, where calibrated flow parameters are available. Avalanche dynamics models rely on empirical parameters that are fitted to model avalanche runout from event to event. Without some physical description of how avalanche flow density changes as a function of snow quality and terrain roughness, it will be difficult to understand experimental observations, let alone propose a general avalanche dynamics model that is based on measured material properties and flow constants.

In this paper we describe how particle interactions within the flow lead to variations in avalanche flow density. The principal idea behind the model is to first distinguish between the mean, slope-parallel movements of the avalanche and the production of velocity fluctuations associated with random particle movements (Reference Bartelt, Buser and PlatzerBartelt and others, 2006). With the introduction of the random movement of the snow particles, we are able to describe friction as a dynamic process, the friction coefficients depending only on static material properties such as temperature (Reference Bartelt, Bühler, Buser, Christen and MeierBartelt and others, 2012). However, there are further consequences. With this random movement the avalanche flow height must rise to accommodate particle trajectories that are inhibited by the hard basal boundary (Reference Buser and BarteltBuser and Bartelt, 2011). The increase in height implies an increase in volume, a decrease in flow density, as well as an acceleration of the center of mass, inducing a reactive pressure on the bottom, the dispersive pressure. This pressure is accessible to measurements (Reference Platzer, Bartelt and KernPlatzer and others, 2007). Note that the source of the energy for the expansion as well as for lifting the center of mass is slope-perpendicular particle movements. These are created by the shearing within the avalanche core and at the basal boundary.

To model this behavior we derive a set of differential equations for the movement of the avalanche core perpendicular to the slope. As such, we develop time-dependent differential equations describing the slope-perpendicular momentum considering a time-dependent energy input. Because the rate of energy input is not an analytical function, we cannot expect closed-form analytical solutions. This result indicates that boundary conditions cannot be imposed a posteriori in an ad hoc manner. The mechanical feedback at the basal boundary controls the internal energy of the avalanche core. We use depth-integrated methods, commonly known as the shallow water approach. That is, we lose all details in the direction perpendicular to the flow direction (Reference WeiyanWeiyan, 1992).

We first define the flow density of the avalanche. This is necessary as a snow avalanche consists of mass in particulate form, where the particles can change their location within the volume and therefore change the flow configuration of the avalanche. We then consider the total energy within a single volume, showing how random particle movements produce accelerations that must be accounted for in the momentum balance in the slope-perpendicular direction (Reference Luca, Fang and HutterLuca and others, 2004). The equations are then introduced into an avalanche dynamics model. We demonstrate that this approach is energy-conserving. The general system of differential equations is then used to simulate a real avalanche event captured at the Vallée de la Sionne test site, Switzerland. We calculate the magnitude of streamwise density variations in both dense and mixed flowing-powder type avalanches.

2. Flow Density

The first problem we must address is to define the bulk flow density. This requires defining a representative avalanche volume V _Φ and the flowing snow mass M _Φ per unit area (kg m⁻²) in the avalanche core Φ (Fig. 1). An avalanche contains snow mass in various forms, consisting of snow-cover fragments and compacted snow granules that are shaped by particle interactions, especially during the churning motion of the avalanche (Reference Bozhinskiy and LosevBozhinskiy and Losev, 1998). The size and shape of the fragments and granules varies from a few millimeters to >10 cm (Reference Jomelli and BertranJomelli and Bertran, 2001; Reference Bartelt and McArdellBartelt and McArdell, 2009). The density of the granules forming the avalanche core varies. For example, high-density fragments from refrozen snow layers can be found in avalanche deposits. If the snow is cold and dry, the particle interactions will likewise lead to the production of ice dust. The mean particle diameters within the ice grains in the ice-dust mixture are small, typically only 0.1 mm (Reference Nishimura, Maeno, Kawad and IzumiNishimura and others, 1993; Reference Rastello, Rastello, Bello, Ousset, Dufour and MeierRastello and others, 2011).

Fig. 1. Possible streamwise density variations in the avalanche core Φ. (a) Mixed flowing avalanche containing dilute, disperse and dense flow volumes V _Φ (see Fig. 2). The volume V _Φ is defined by the flow height h _Φ and the basal area A, V _Φ = h _Φ A. (b) Dense flowing avalanche containing disperse and dense volumes. The powder cloud component is designated Π, the snow cover Σ. The height of the co-volume V ₀ is h ₀. The mass per unit area is denoted M _Φ. For a dense flowing avalanche Π = 0. For the numerical treatment the volumes are at fixed positions, i.e. not moving with the avalanche. The avalanche is flowing through the volumes.

We divide the avalanche into the core Φ, containing the larger particulate mass M _Φ, and the suspension cloud Π, containing the ice-dust mass M _Π (Fig. 1). In this paper we do not consider the suspension cloud Π. At any time, the mass in the core M _Φ is distributed within a representative volume V _Φ (Fig. 1). The height of the volume h _Φ is defined by the location of the uppermost particle (Fig. 2). This defines the height of the avalanche core. We make no assumptions regarding particle size: the particles can be large (say 10 cm) or small (say 1 cm). The distribution of mass can be disperse (Fig. 2a) or dense (Fig. 2b). When the avalanche is at rest, the volume compacts to volume V ₀, which we define as the avalanche co-volume, in analogy to the Van der Waals equation of a non-ideal gas (Reference RowlinsonRowlinson, 2002). The co-volume is then the deposition volume of the avalanche. The height of the co-volume is h ₀ (Fig. 2c), and the density of the co-volume is ρ ₀. The bulk flow density of the core is given by

Fig. 2. Different avalanche volumes in the flowing avalanche core Φ. The volume is given by V _Φ = h _Φ A, where A is the basal area. The volumes can be dense (h _Φ = h ₀), disperse (h _Φ > h ₀) or dilute (h _Φ ≫ h ₀). We use the terminology introduced by Reference Gauer, Issler, Lied, Kristensen, Sandersen, Campbell, Conger and HaegeliGauer and others (2008), except we use the term ‘dilute’ instead of ‘suspended’ as the particles descend under the action of gravity. The location of the center of mass is given by k _Φ; the co-volume center of mass is located at k ₀.

The ratio of co-volume to volume height ν,

defines the volumetric particle content of the avalanche. Thus, we define the bulk flow density with respect to the avalanche flow height.

3. Energy Components in Volume V _Φ

A representative element volume V _Φ in the avalanche core Φ contains four energies: (1) the kinetic energy K associated with the mean avalanche velocity, (2) the kinetic energy R _K associated with the random movements of the particles (granular temperature), (3) the potential energy R _V associated with particle positions within the volume (configurational energy) and (4) the internal heat energy E (thermal temperature). R _K is calculated from the difference between the individual particle velocities and the mean slope-parallel speed of the avalanche. R _V is calculated from the position of the individual particles with respect to the co-volume height as the reference. It completely describes the flow configuration of the volume. Both R _K and R _V are connected with the random position of the particles. These mechanical energies are depicted in Figure 3. The sum of R _K and R _V is denoted R:

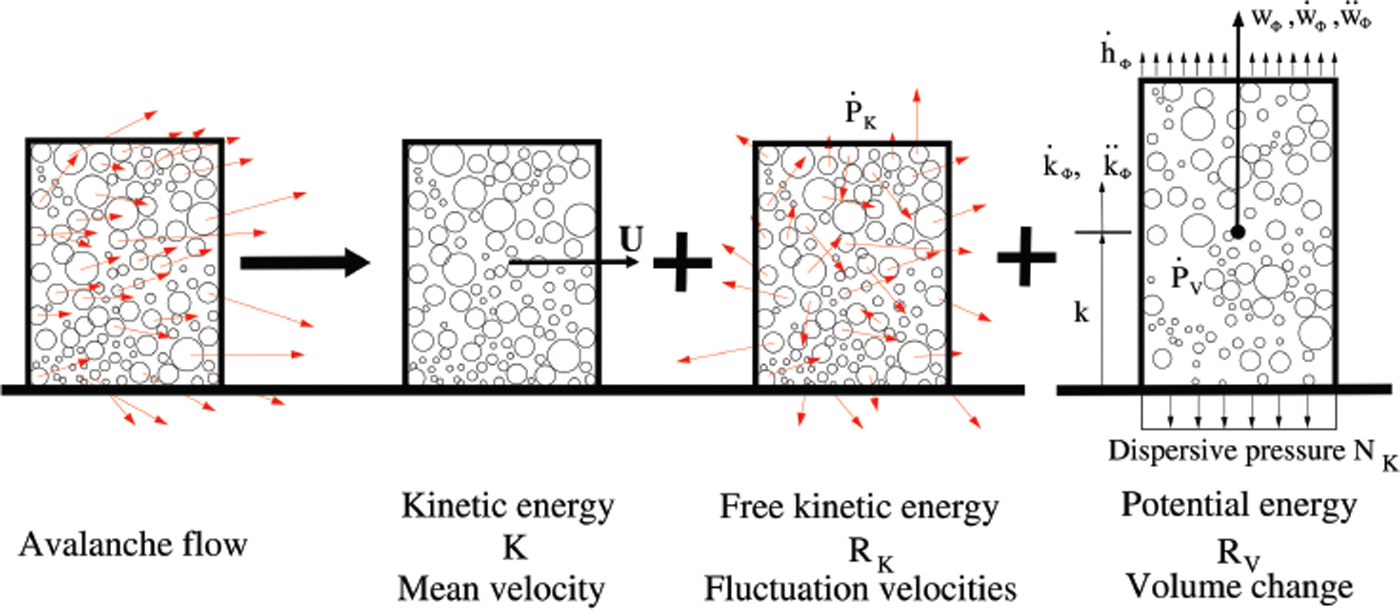
Fig. 3. Energies in a representative volume element V _Φ in the flowing avalanche core Φ. The translational kinetic energy K is associated with the mean, slope-parallel velocity of the avalanche u _Φ. The difference between the mean velocity and the velocity of the individual particles yields the random kinetic energy R _K. Free mechanical energy R is produced by shearing at the rate . The production induces an increase of volume, lifting the center of mass of the representative volume, because of the hard bottom boundary, leading to an increase of potential (configurational) energy R _V. Associated with the volume change is the dispersive pressure N _K, the reaction at the hard boundary due to the change in slope-perpendicular acceleration. An analogous argument can be used for the reverse process when the volume decreases by a reduction of R _K (e.g. by dissipation, producing heat).

Because the energy R consists of both kinetic and potential energy it is free mechanical energy within the ensemble of particles. However, the energies R _K and R _V are not independent. They are interrelated: the presence of R _K implies the existence of slope-perpendicular granular movements within the flow volume. Because particle movements in the z-direction are inhibited by the basal boundary (see Fig. 3), a fraction of R is transformed into R _V. It is perhaps a trivial observation, but changing the z-position of particles (and therefore the flow configuration and potential energy of the volume) requires particle movements in the z-direction. Particles at the top surface are especially vulnerable as they are free and can be ejected to significant heights. The position of these particles also contributes to R _V. We choose as the upper boundary of the volume V _Φ the location of the highest particle. Because the energies R _K and R _V represent the sum of all the individual particle contributions in the volume, R _V is given by the position of the center of mass (denoted k _Φ; Fig. 2).

Both R and E are energy densities defined per unit volume (J m⁻³) whereas K is defined per unit area (J m⁻²). By multiplying the energy densities by the height h we have the total internal energy (Eh _Φ) and total free energy (Rh _Φ) defined per unit area. One simplification we make is to use only depth-averaged energies defined per unit area in the avalanche core. We consider depth-averaged homogeneous values for R and E. With this assumption we lose information on the distribution of energy over the flow height, but we reduce the computational demands of the model and, perhaps more importantly, the number of free model parameters. However, the total energy balance in the streamwise flow direction is maintained. More significant is the fact that considering the total energy within avalanche volumes V _Φ confined between the basal boundary and the free upper surface allows us to derive differential equations for the slope-perpendicular movement of the center of mass, k _Φ.

The next problem we must address is how avalanche velocity in the slope-parallel direction induces slope-perpendicular processes that produce random free mechanical energy R. The mean translational velocities associated with K in the (x, y, z) directions of the representative volume are denoted (u, v, w) (Fig. 4). The velocities are divided into the slope-parallel direction (x, y) of the avalanche core u _Φ = (u, v)^T and the slope-perpendicular z-direction w. Subsequently,

Fig. 4. Differential element volume V _Φ used to derive momentum and energy balances. The velocities in the x, y, z directions are denoted u, v, w, respectively. The velocity is associated with the volume change. To calculate the slope-perpendicular movement of the center of mass k _Φ, we must find , the slope-perpendicular acceleration. Gravitational acceleration is decomposed into the (x, y, z) directions (g_x , g_y , g_z ).

where the superscript xy denotes the slope-parallel direction and superscript z the slope-perpendicular direction. As we shall show, the slope-parallel and slope-perpendicular components of K are determined by momentum balances in the (x, y, z) directions. Similar to the kinetic energy K, the gravitational work W _g and frictional work W _f can be decomposed into the slope-parallel and slope-perpendicular directions:

Both W _g and W _f are defined per unit area. The gravitational work rate has the important distinction of being the only supply of mechanical energy available to the avalanche. Because g_x and g_y are defined in the same direction as u and v, the gravitational work is positive in the downslope direction. is negative because g_z is negative in the positive z-direction, by definition. If other accelerations (centripetal, jerks) are present, g_z is replaced by the resultant acceleration. The gravitational work rate creates kinetic energy that is eventually dissipated to heat by the frictional work rate, . The frictional work rate contains the sum of all the work done by shearing, both within the volume and by boundary tractions, especially at the basal surface. The frictional work rate in the slope-parallel direction is therefore

where S _Φ = (S _Φx , S _Φy )^T is the vector of shear stresses in the slope-parallel directions. The frictional work rate is irreversible and therefore, by definition, always positive. Shearing in the slope-parallel direction, and therefore the frictional work rate, is the process that controls the dissipation of mechanical energy to heat (denoted ) and the production of R (denoted (Reference Bartelt, Buser and PlatzerBartelt and others, 2006; Reference Buser and BarteltBuser and Bartelt, 2009)). Therefore,

Congruent to the definition of the mechanical free energy R, the dissipation and production are defined per unit volume (W m⁻³). Equation (7) is a general but open statement, with little practical use. It requires a constitutive postulate to determine how much frictional work is being used to produce R and how much frictional work is being dissipated to internal heat energy E. The and are production terms inside the test volume. However, we have a flow through the volume (Fig. 1) for which convection terms are required. We therefore write

and

This splitting satisfies Eqn (7). Here we use the standard notation D()/Dt to define the material derivative, containing both the local derivative, source and convection terms. For example, for the conservation of the internal heat energy we have

The advantage of treating R and E separately is that R is a place holder for all mechanical energy that is created from shearing (like heat), but not yet heat. This energy is also responsible for changes in avalanche flow density and modifying the flow friction.

Note that the evolution of the temperature (internal energy Eh _Φ) requires consideration of additional sources of heat supply (e.g. when the avalanche entrains warm snow during its descent). These sources are not considered in this paper; the heat rise is only due to the dissipation of mechanical energy, both dissipation of kinetic energy K and dissipation of random kinetic energy R _K. The parameter α is the splitting parameter of the constitutive formulation (Reference Buser and BarteltBuser and Bartelt, 2009), which essentially defines how much shear work in the slope-parallel direction is transformed to random energy and how much is dissipated immediately to heat . The second parameter is the decay parameter β _K, which governs the dissipation of random kinetic energy R _K in the core Φ.

4. Mechanical Free Energy R _K and R _V and Their Production and

The advantage of using the kinetic and potential energies R _K and R _V is that the total free energy of the avalanche core volume V _Φ can be calculated even for complicated flow configurations and boundary conditions. We do not consider individual particle trajectories and interactions that would defy solution. This approach is similar to the virial theorem of mechanics which provides a relation between the total kinetic energy and total potential of a particle ensemble (Reference ClausiusClausius, 1870). In the avalanche problem, however, the interaction between R _K and R _V is not defined by potential forces between particles, but particle collisions and finally the hard basal boundary, which reflects particle trajectories back into the flow.

When the total free energy is produced (, Eqn (7)), a fraction of the energy is true kinetic energy R _K, while the remaining fraction R _V describes the changed location of the particles. The sum of (change in random kinetic) and (change in configuration) therefore defines the production of total free energy in the volume V _Φ (cf. Eqn (3)):

We postulate that the fraction of mechanical energy with respect to the total production of free energy is the dimensionless coefficient γ:

The parameter γ clearly depends on the properties of the snow particles, including hardness and shape. It is, however, a bulk coefficient of the ensemble of particles. The coefficient γ resembles the coefficient of thermal expansion since it describes the tendency of a material to change its volume in response to a temperature change, in this case the granular temperature. For example, when γ = 1, the entire free energy production from shearing is converted to potential energy. As R _K consists of velocity fluctuations in all three coordinate directions, it is reasonable to suppose that

implying that only the fluctuations in the z-direction can be used to create R _V. This assumes an equal distribution of random kinetic energy in all three coordinate directions. In the example calculation we take γ = 0.15.

To describe the energy fluxes within the avalanche core, we introduce three parameters: α, the splitting of the frictional work rate in the slope-parallel direction into heat and random kinetic energies; β _K, the rubbing and collisional dissipation of random energy; and γ, the partitioning of the production of the free mechanical energy into random kinetic and potential parts . We can now derive the relationship between the change in configurational energy R _V and the change in avalanche volume V _Φ.

5. Volume Changes in the Avalanche Core Φ

To model the change in volume, we first define the acceleration associated with a change of the center of mass of the element volume. We explicitly postulate that avalanche flow is located between a hard boundary, the ground, and an open boundary, the top surface of the avalanche. This implies that with basal area A

i.e. the change in volume is directly related to the change in flow height. We have no diffusion of heat or free energy through the volume walls. Defining the location of the center of mass to be located at a distance k _Φ from the bottom, then the upward, positive acceleration of the center of mass is

where the location k _Φ is related to the avalanche flow height h _Φ by the constant c. Similarly, k ₀ defines the location of the co-volume center of mass, k ₀ = ch ₀. The integral over the height h _Φ of the density distribution defines the location of the center of mass k _Φ. We see that c is a constant as long as the density distribution does not change. In the following we assume a homogeneous density distribution which yields the value c = 1/2 for all times. This assumption is made for simplicity as we have no reliable information concerning the density distributions in height. This defines the (positive) reaction at the ground, the dispersive pressure N _K,

as well as the time rate of change of the dispersive pressure ,

We can consider states far from equilibrium by writing the normal pressure in terms of the total perpendicular acceleration g′ of the center of mass of the flow volume:

The quantity N _g is the pressure from the self-weight, N _g = M _Φ g_z . The centripetal acceleration f_z defines the pressure N _f = M _Φ f_z . The magnitude and direction of N _f depend on the curvature of the track (Reference Pudasaini and HutterPudasaini and Hutter, 2007). The centripetal acceleration f_z is determined from the track curvature Γ using the vector relationship (Reference Fischer, Kowalski and PudasainiFischer and others, 2012),

The pressures (reactions) N _g and N _f are always the same, independent of the position of k _Φ, and depend only on the total mass in the volume. That is, the pressures N _g and N _f induce no movement, but determine the total reaction N. Thus, the model reduces to the standard Coulomb–Voellmy model when N _K = 0. The time rate of change of N is

Moreover, no jerk is associated with the normal pressure or centripetal pressures . In our representative volume, the mass does not change during the jerk, . The total work done per unit time by the normal pressure at the bottom of the avalanche N (which includes the normal pressure N _g, centripetal pressure N _f and the dispersive pressure N _K) must be in balance with the total working of the particle interactions per unit volume. We have termed this change in potential energy as the configurational energy production . Therefore, the total change in the volume is

and with ,

This equation states that the volume expansion by particle interactions with the ground is not a quasi-static process and therefore must include the accelerations and changes in acceleration of the avalanche flow mass. We note that the ratio physically represents the upward expansion of the avalanche in the z-direction, expressed as a strain rate :

In a first approximation the configurational strain ∊ in the z-direction is linearly distributed from the bottom to upper surface of the avalanche. We find that with the substitution for N (Eqn (18))

The change in pressure at the base of the avalanche is equal to the rate of working of (the free energy used to expand the volume). However, this energy must work against the self-weight of the avalanche. The sign of the centripetal pressure N _f will depend on the curvature and thus will either work against or exacerbate the configurational changes. Because the sum (N _g + N _f + N _K) is multiplied by the strain rate , the pressures serve as a type of material strength resisting the dispersive pressure and the expansion or contraction of the avalanche body. Interestingly, Eqn (22) can be written as a third-order differential equation in k _Φ using Eqn (20),

or, directly, in terms of the avalanche flow height h _Φ and the constant c,

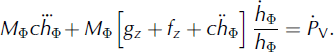
The practical significance of the triple dot – the rate of change of the acceleration or jerk – is that we no longer assume that the avalanche is near equilibrium, . This indicates that the dispersive pressure N _K cannot be empirically defined using closed-form functions because it arises from the shear work in the avalanche core α(S _Φ · u _Φ) (see Eqn (6)). The shear rate, and therefore the dispersive pressure, is not an algebraic time function. Because the production is always changing we must integrate the path-dependent motion of the avalanche core to find the dispersive pressure. For the numerical solution we must first decompose Eqn (25) into a series of three first-order equations in terms of the center-of-mass height k _Φ, velocity w _Φ and dispersive pressure N _K:

Note that the quantity k _Φ−k ₀ is a positive definite function: the volume can never collapse below the co-volume height h ₀. The production can be both positive and negative, corresponding to an increase or decrease in volume, and is the only process to change the potential energy of the avalanche core. The core will collapse when the decay of free energy overcomes the production. Settlement of detached particles will be modeled as an additional loss of potential energy R _V in Section 9. Equations (27–29) cannot be used in numerical solutions because they are attached to a volume moving with the avalanche. In numerical solutions we consider control volumes that are fixed in space and therefore must account for the convective transport of k _Φ, w _Φ and N _K. Similar to the mechanical free energy Rh _Φ or the internal heat energy Eh _Φ, the quantities k _Φ, w _Φ and N _K are transported with the avalanche. We neglect diffusive processes as we consider them to be too slow in comparison to the convective transport. There is also a jerk and a volume expansion arising from the convective transport of mass within the avalanche. In order to consider these convective terms it is necessary to change the local time derivative of Eqns (27–29) to material derivatives including the convective terms. The equations for fixed volumes are stated in the next section.

6. Model Equations with Streamwise Density Variations

The problem now is to introduce Eqn (25) (the volume change of the avalanche) into a general system of depth-averaged differential equations that describe avalanche flow in general terrain. We exploit the fact that Eqn (25) can be decomposed into three first-order differential equations: Eqns (27) (volume conservation), (28) (momentum conservation in the z-direction) and (29) (rate of change of dispersive pressure). These equations are already in depth-averaged form as we considered the total volume of an element between the basal boundary (z = 0) and the top surface of the avalanche (z = h _Φ). The equations represent the analytical solution to the problem of how the boundary conditions influence the movement of the center of mass in the z-direction. We do not discretize the equations in the z-direction as they are already in closed form; however, in the avalanche flow direction we must modify the existing depth-averaged equations to account for change in acceleration in the slope-perpendicular direction.

All quantities describing the movement of the center of mass must be convected in the flow direction. For simplicity we take k _Φ =1/2h _Φ, c = 1/2. Thus, we always have a homogeneous distribution of mass M _Φ in the volume V _Φ corresponding to a constant density. By formulating the equations within a depth-averaged framework, we facilitate the introduction into existing avalanche dynamics models. However, we must demonstrate not only that the depth-averaged equations satisfy mass and momentum balances (in all directions) but also that the total energy of the movement is conserved.

We begin by considering an avalanche volume in the x-y plane (Fig. 4). Depth-averaged mass, momentum and energy balances can be constructed for this volume element (Reference WeiyanWeiyan, 1992). These equations can be written in many forms; we chose the general form

with the four unknown state variables

The vector U _Φ includes the mass M _Φ and the avalanche momentum in the directions tangential to the slope, M _Φ u _Φ and M _Φ v _Φ. The velocities u _Φ and v _Φ are defined in the x and y directions, parallel to the avalanche slope (Fig. 4). Reference Christen, Kowalski and BarteltChristen and others (2010) describe the terrain coordinate system. The flux components (Φ _x , Φ _y ) are

The vector G _Φ contains the source terms:

The flowing avalanche is driven by the gravitational acceleration in the tangential directions G= (G_x , G_y )= (M _Φ g_x , M _Φ g_y ). The initial avalanche mass is defined by the release slab. The snow cover, however, supplies the avalanche with additional mass. Here we simulate entrainment using the method proposed by Russian authors (Reference Bozhinskiy and LosevBozhinskiy and Losev, 1998). This method assumes (1) a stationary snow cover that is entrained into the avalanche at the rate is always positive and (3) the entrained mass is accelerated immediately to the speed of the avalanche. There are no gradients in avalanche velocity in the z-direction. Removal of mass from the avalanche is not considered, .

Frictional resistance is given by the Voellmy-type shear stress S _Φ = (S _Φx , S _Φy ), with

that is, the shear stress is a function of the avalanche velocity u _Φ, configurational energy R _V and the total normal pressure N (Coulomb friction). Fluctuation energy is produced from the rate of working of the total shear work α(S _Φ · u _Φ) (Reference Bartelt, Buser and PlatzerBartelt and others, 2006); the model parameter α describes the production rate 0 ≤ α ≤ 0.2 (Reference Buser and BarteltBuser and Bartelt, 2009; Reference Bartelt, Bühler, Buser, Christen and MeierBartelt and others, 2012). Because the snow particles are inelastic, their interactions cause the fluctuation energy to decay at the rate β _K (Reference Buser and BarteltBuser and Bartelt, 2009). Useful, but empirical, relationships for the functional dependency of (μ, ξ) on R _V are

and

With this frictional ansatz, μ ₀ and ξ ₀ are the static friction coefficients associated with non-fluidized flowing snow, R _V =0. The model parameter R ₀ defines the activation energy required to fluidize the core (Reference Bartelt, Bühler, Buser, Christen and MeierBartelt and others, 2012). The friction does not depend on the granular temperature R _K, but on the configurational energy R _V, which determines the flow density of the avalanche. The acceleration is calculated by extending the depth-averaged equations (four state variables) to include the unknowns h _Φ (flow volume), M _Φ w _Φ (momentum in the z-direction) and N _K (dispersive pressure):

The extended flux components (Φ _x , Φ _y ) and driving term G_Φ are:

and

Thus, instead of four equations, we now have seven equations that must be solved numerically. In the numerical calculations, it might happen that k _Φ − k ₀ becomes negative. We treat this problem by reflecting w _Φ at the boundary k _Φ = k ₀. We apply second-order HLLE (Harten, Lax, Van Leer and Einfeldt) schemes to solve the equations on general quadrilateral grids (Reference Christen, Kowalski and BarteltChristen and others, 2010).

7. Total Energy Conservation

Momentum balances in the slope-parallel and slope-perpendicular directions place two additional constraints on the total change in avalanche kinetic energy (Reference Luca, Fang and HutterLuca and others, 2004). In the slope-parallel xy direction we have

and in the z direction,

These energy relations are automatically satisfied when solving momentum balance equations with any constitutive model for shear (e.g. Anderson, 1995). The summation of these two equations, with the substitution of Eqns (7–9) for the total frictional work rate, leads to

This is the total energy conservation for the avalanche. The equation states that the total change of kinetic energy, thermal energy and free mechanical energy is equal to the change in potential energy. The potential energy change is with respect to the center of mass. The quantity is the gravitational work rate given by the terrain, and the R _V term arises from the internal configurational changes.

8. Damping of R _V and Settlement to Co-Volume

At present we treat the movement of the avalanche in the z-direction as a reversible process. There is no friction and therefore no dissipation of R _V during the volume expansion or compression. The frictional work rate in the slope-perpendicular direction is at present undefined, although it is included in the total energy balance, Eqn (41). Friction in the z-direction can be added to the model formulation. However, of great importance is the fact that we are not free to select this friction independent of the frictional processes that we assume to act on R _K. The frictional work in the z-direction undergoes the same dissipative process as the random kinetic energy R _K, which is governed by the decay parameter β _K. This places constraints on the constitutive formulation of . The dissipation of R _K is governed by β _K R _K. Therefore,

However, R _V and R _K are both related to the total R by γ. Therefore,

and

Since is the rate of working of the particle collisions at the boundary, raising the center of mass k _Φ, we have that R _V is the total potential energy with respect to the co-volume height h ₀:

Thus,

A salient feature of this energy relation is that it ensures that all volumes of the avalanche settle to the co-volume height h ₀, which then becomes the deposition height of the avalanche. No additional model parameters are required to describe the dissipation of energy in the z-direction. In the absence of any production of free mechanical energy R, the volume will decay according to the gravitational acceleration g_z , which always opposes the volume expansion. The settlement of particles is stronger on flatter slopes. However, the volume cannot be compressed to dimensions smaller than the co-volume height h ₀. As a volume cannot sustain its height without mechanical energy R, any volume with h _Φ > h ₀ contains potential energy R _V that must be removed during the settlement process (negative ). By formulating the loss of potential energy according to Eqn (47), we enforce the settlement condition that all volumes go to the co-volume height h _Φ → h ₀ when the free energy R → 0. No additional model parameters are needed.

9. Example Calculation

In the example calculation we will demonstrate how α controls the streamwise variation in avalanche flow density ρ _Φ. For this purpose we will use Vallée de la Sionne avalanche No. 628, released on 19 January 2004. This avalanche has a well-documented starting zone allowing an estimation of the release volume (V _r = 20 000 m³, ρ _r = 250 kg m⁻³). The starting mass was calculated at 4800–5300 t. The avalanche entrained a modest amount of snow (on average, h _e = 0.25 m, ρ _e =250 kg m⁻³). The numerical treatment of entrainment is described by Reference Christen, Kowalski and BarteltChristen and others (2010). The flowing core was obscured by the suspension cloud; however, frequency-modulated continuous-wave (FMCW) radars recorded the passage of the avalanche, allowing us to make direct comparisons between measured and calculated flow heights (and therefore streamwise variations in flow density). The avalanche did not strike the measurement pylon directly, but several pressure sensors were struck, providing us with some indication of the avalanche flow height.

We simulated the avalanche using a 5m grid resolution. The starting and entrainment conditions were selected according to the measurements. We varied the parameter α from α = 0.025 (dense flow regime) to α = 0.100 (disperse–dilute flow regime). When α = 0, the simulation reduces to the standard Voellmy model (Reference Christen, Kowalski and BarteltChristen and others, 2010). In the model calculations we take γ to be a constant γ = 0.15, being aware, however, that the partitioning of R into a kinetic part R _K and volume change part R _V can depend on local terrain features, snow granularization and, most likely, entrainment processes at the avalanche front. At present it would be highly speculative to introduce the influence of these processes on γ without better experimental data. Here we wish to demonstrate the range of α that allows us to predict the streamwise density variation of dense flowing avalanches as well as mixed-flowing avalanches. We will not investigate the role of other model parameters (β _K =0.80, R ₀ =2.0 kJ m⁻², μ ₀ =0.55, ξ ₀ =1800 ms⁻²) which have been reported at length elsewhere (e.g. Reference Buser and BarteltBuser and Bartelt, 2009; Reference Christen, Kowalski and BarteltChristen and others, 2010). The selected parameters are the same as from other numerical investigations of other avalanches recorded at Vallée de la Sionne (Reference Bartelt, Bühler, Buser, Christen and MeierBartelt and others, 2012).

The calculated avalanche velocities are reported in Figure 5. These varied between 30 m s⁻¹ (α = 0.025; Fig. 5a) and 50 m s⁻¹ (α = 0.100; Fig. 5d). The calculated avalanche runout varied accordingly. For small α values, the avalanche stopped 250 m above the measurement pylon; for higher values the avalanche ran to the counterslope. The best match to the measured avalanche runout and velocity is obtained with α = 0.100, suggesting a highly fluidized mixed-flowing avalanche, in agreement with the observations. The model results reflect the strong influence of the flow regime (density variations) on the simulation results. The maximum measured avalanche velocity was slightly more than 50 m s⁻¹; the avalanche core ran up the counterslope and covered the observation bunker with granular debris (Fig. 5).

Fig. 5. Calculated maximum flow velocities of avalanche No. 628 with four different fluidization parameters α. Starting conditions, entrainment conditions and remaining flow parameters are all the same. (a) α = 0.025. (b) α = 0.050. (c) α = 0.075. (d) α = 0.100. The best match to the measured velocities and runout distance is (d). The measured maximum velocity was slightly more than 50 m s⁻¹; the avalanche ascended the counterslope and covered the observation bunker.

The avalanche flow density varies in space and time. Spatial variations are depicted in Figure 6; variations in time at the location of the FMCW radar are presented in Figure 7. The parameter α controls the flow regime: with α = 0.025, the avalanche does not fluidize, but remains in a disperse–dense flow regime. Flow densities at the avalanche front are approximately ρ _Φ = 300 kg m⁻³ (Fig. 7a). The core heights are too small, h _Φ = 1.5 m, far from the observed heights measured with the FMCW radar of 7.5 m. Flow densities behind the front are ρ _Φ > 300 kg m⁻³. That is, the avalanche tail densifies quickly. Runout distances are short and avalanche velocity reaches only 30 m s⁻¹. For increasing values of α, the calculated core height h increases and flow density decreases. For α = 0.100, the avalanche core fluidizes completely, ρ _Φ < 300 kg m⁻³. Flow densities at the avalanche front are low, ρ _Φ ≤ 200 kg m⁻³. Not only are the calculated core heights in good agreement with the FMCW radar observations, but also the time duration of the avalanche passage (a total of 35 s) is correctly represented (Fig. 8). The total avalanche mass flux at this particular location appears to be correctly modeled. However, the model predicts that the entire core, from the front to the tail, should be fluidized. The flow densities at the tail of the avalanche are 300 kg m⁻³ for α = 0.075 and <200 kg m⁻³ for α = 0.100. Even with experimental data it is difficult to state which value of α correctly models the tail motion, especially the densification after the passage of the front. It is important to note that we use only constant values of α for the entire avalanche and therefore do not take into account such effects as the smoothing of the running surface or the increase in avalanche temperature which will affect the static properties of the flowing snow.

Fig. 6. Calculated streamwise density variation of avalanche No. 628 with four different fluidization parameters α. Starting conditions, entrainment conditions and remaining flow parameters are all the same. (a) α = 0.025. (b) α = 0.050. (c) α = 0.075. (d) α = 0.100. For α ≤ 0.050, the avalanche remains in a disperse–dense flow regime. Flow densities at the avalanche front are approximately ρ _Φ= 300 kg m⁻³. Flow densities behind the front are ρ _Φ > 300 kg m⁻³. Runout distances are short, and avalanche velocities reach only 30 m s⁻¹. For α > 0.050, the avalanche core fluidizes, ρ _Φ < 300 kg m³. Flow densities at the avalanche front are low, ρ _Φ ≤ 200 kg m⁻³.

Fig. 7. Calculated core height h _Φ and density ρ _Φ at FMCW radar position B. (a) α = 0.025. (b) α = 0.050. (c) α = 0.075. (d) α = 0.100. The measured core heights were between 7.0 and 8.0 m.

Fig. 8. Comparison between measured and calculated flow height h _Φ at the FMCW radar position B, α = 0.100. Both the magnitude and the duration of the signal are in good agreement. However, the second peak behind the front is not represented in the simulations.

For completeness we also present the calculated avalanche velocity w _Φ in the slope-perpendicular direction for the four different values of α (Fig. 9). We find that for low values of α = 0.025, the velocities are small. In this case the velocities are negative, indicating that the flow, especially at the tail, is densifying. For larger values of α > 0.025, oscillations in w are clearly visible. These occur primarily at the front of the avalanche. However, for larger values α = 0.100, the oscillations persist in the tail, leading to low-density flows behind the front. In this case the peak velocities can be w _Φ >3ms⁻¹ in both the upward and downward directions.

Fig. 9. Calculated time variation in slope-perpendicular velocities w _Φ at the FMCW radar position B. (a) α = 0.025. (b) α = 0.050. (c) α = 0.075. (d) α = 0.100. For the dense flow case α = 0.025, the velocities are small and always negative, implying densification. For values α > 0.025, the velocity oscillates, particularly at the avalanche front. Only for the case α = 0.100 do the oscillations persist in the avalanche tail. For the dilute–disperse flow regime (d), the slope-perpendicular velocities of the avalanche center of mass are large, w _Φ ≈ 3.0 m s⁻¹.

As expected, the calculated dispersive pressures increase with increasing α (Fig. 10). They are small for α = 0.025 and large for α = 0.100. The largest variations in dispersive pressure are encountered at the avalanche front. For large α, the calculated dispersive pressures are a significant fraction of the pressure N _g. For example, for a 1 m flow on flat ground N _g = 4.5 kPa; the calculated values in Figure 10d vary between N _K = −1.0 kPa and N _K = 2 kPa at the location of radar B. This will not only increase (and decrease) the frictional shearing stress (which is a function of N _g + N _K), but also suggests that the self-weight can easily be overcome to fluidize the avalanche core. Figure 10 also exemplifies the fact that the shape of the signals will vary from position to position, depending on the streamwise variation in flow mass. At the front of the avalanche the increase in core height is associated with a decrease in flow density. This indicates that sufficient configurational energy has been produced to fluidize the core. An increase in flow height accompanied by an increase in density is an indication not only that the core is collapsing, but also that the frictional shear stress is increasing, producing strong gradients in flow height (pile-ups, levees). The calculated dispersive pressures appear to have many features similar to measured seismic signals (Reference Vilajosana, Surinach, Khazardadze and GauerVilajosana and others, 2007a,b). The measurement pylon was not hit directly by the avalanche core. The peak pressure measured at the mast reached 150 kPa at 2.5 m above ground. The signal lasted ∼10 s. Measured velocities using optical velocity sensors (Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009) revealed considerable noise, with velocities fluctuating between 20 and 30 m s⁻¹. The simulated velocities are in this range; the simulated flow density at the front varied between 200 and 300 kg m⁻³. Towards the middle of the flow, the velocities increase and densities decrease.

Fig. 10. Calculated time variation in dispersive pressure N _K at the FMCW radar position B. (a) α = 0.025. (b) α = 0.050. (c) α = 0.075. (d) α = 0.100.

10. Conclusions

The purpose of avalanche dynamics models is to predict impact pressures and runout distances. These are a function of the avalanche flow regime and therefore the density of the avalanche core. We present a method to calculate how avalanche flow density changes in the streamwise flow direction. We first distinguish between the avalanche core Φ and suspension layer Π. In the core Φ we will find mass in the form of hard snow particles. The particles can be densely packed (frictional flow regime) or somewhat dispersed (disperse flow regime). In extreme cases, such as at the front of mixed-flowing avalanches, we encounter dilute flow densities in which the particle interactions are completely collisional. In all cases, it is possible to define a center of mass of the flowing ensemble to study the energy fluxes associated with the random particle movements. Particle movements, and therefore random energy R, are constrained at the basal boundary of the avalanche, giving rise to energy, momentum and mass fluxes in the slope-perpendicular direction. Because of the free top surface of the avalanche, the volume of the core can increase or decrease depending on the energy input. We define the dispersive pressure as the change in slope-perpendicular acceleration induced by the particle interactions giving rise to the configurational changes in the avalanche core.

As we consider the volume change of an ensemble of free particles, the starting point of our investigations cannot be the depth-averaging of the Navier–Stokes equations. These equations do not consider the change in slope-perpendicular acceleration caused by the interaction of particles with the basal boundary. Moreover, we cannot depth-integrate a full-three-dimensional system of fluid equations and then add ad hoc boundary conditions to account for the dilatative effects of granular movements. Only when we introduce changes in accelerations can we separate the effects of the dispersive pressure and gravity in theory and experiments. It is the change in pressure that we measure in chute experiments with snow (Reference Platzer, Bartelt and KernPlatzer and others, 2007). An important feature of the model equations is that when we consider the transfer of energy from the slope-parallel mean flow to the slope-perpendicular direction, we equally account for momentum conservation in the z-direction. Therefore, the proposed method satisfies conservation of mass and volume as well as momentum conservation in the slope-parallel and slope-perpendicular directions.

At present we do not consider variations of density in the z-direction. We do not account for changes in the α, β _K and γ due to the mechanical working of the snow, which will greatly change the calculated density in the slope-parallel xy-direction. These parameters depend on temperature and on snow quality (Reference Naaim, Durand, Eckert and ChambonNaaim and others, 2013). This leads to results that can be explained within the closed template of the model, but are perhaps not quite correct for snow avalanches. For example, in our calculations with α > 0.5 we find that the tail of the avalanche fluidizes. This is a result of a continual input of R-energy. As the height of the avalanche decreases at the tail, the density will decrease, leading to fluidized motion at the tail. The overburden pressure is simply not enough to damp the energy input. This behavior has been observed in granular chute experiments (Reference Bartelt, Buser and PlatzerBartelt and others, 2007; Reference Bugnion, Schaefer and BarteltBugnion and others, 2013); whether it is valid for the movement of mixed snow avalanches requires more detailed experimental observations. We hope in the near future to propose relationships for α, β _K and γ that account for snow temperature, the smoothing of the flow surface during the passage of the avalanche and the granularization of snow.

The model equations for streamwise density variation presently assume a rigid basal boundary. For simplicity, snow-cover entrainment is considered as a simple mass flux across this stationary boundary. However, in future, more advanced entrainment models can be considered that couple the volume expansion in the core with a moveable basal boundary. The production of fluctuation energy and intake and expulsion of air can be included as the avalanche consumes the snow cover.

Finally, another point is remarkable. We do not use any explicit distribution, neither the size nor velocity of the particles, in the z-direction. We only state that there is a distribution, such that the energy attributed to the random velocity exists.