No CrossRef data available.
Article contents
On some convexity questions of Handelman
Published online by Cambridge University Press: 16 May 2024
Abstract
We resolve some questions posed by Handelman in 1996 concerning log convex 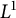 $L^1$ functions. In particular, we give a negative answer to a question he posed concerning the integrability of
$L^1$ functions. In particular, we give a negative answer to a question he posed concerning the integrability of 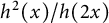 $h^2(x)/h(2x)$ when h is
$h^2(x)/h(2x)$ when h is 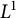 $L^1$ and log convex and
$L^1$ and log convex and 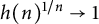 $h(n)^{1/n}\rightarrow 1$.
$h(n)^{1/n}\rightarrow 1$.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society



