Nomenclature

Introduction
Perched blocks are isolated rocks or boulders which are supported above the glacier surface on pedestals of ice. It is easily observed that rocks on a glacier either sink into the ice or grow pedestals underneath them. This is due to the difference in ablation between the exposed glacier surface and the ice beneath the rock. The pedestal may be further shaped by the action of melt water around it. This behaviour has been studied as a result of a problem encountered during the 1978 Sheffield University North-East Greenland Expedition. J.P. Allen (personal communication in 1981) observed during a survey of Roslin Gletscher that rocks used as markers by previous expeditions were moving relative to the glacier surface. This was caused by pedestals growing underneath them and the rock then falling off the pedestal.
A structure erected on a glacier or ice cap might also be expected to behave in a similar manner to isolated rocks, which may have more serious consequences than the movement of survey markers. To the author’s knowledge no previous work has been done on this subject. This study has aimed to produce a reliable method of predicting whether a rock will sink or perch and to compare it with experimental data from Bersaerkerbrae (lat. 72° 10' N., long. 24° 40' W.) in north-east Greenland.
A Mathematical Model for the Formation of Perched Blocks
The effect of pressure melting due to the weight of the rock can be neglected because the rocks are in general too small to produce a significant pressure on the ice. If the rock reduces the nett energy flux to the ice beneath it as compared to the exposed glacier then the rock will perch, because the ice under the rock will melt more slowly than the exposed ice. To quantify this process the energy exchanges at the glacier surface have to be accounted for. Heat is supplied by
-
1. Solar radiation and long-wave radiation.
-
2. Eddy conduction if the temperature gradient above the ice surface is positive and the air is turbulent.
-
3. Eddy convection i.e. the latent heat of condensation of water vapour and of freezing of rain.
Heat will be lost due to out-going long-wave radiation and due to eddy conduction if the temperature gradient is reversed. Reference Lister and TaylorLister and Taylor (1961) have shown that for Britannia Gletscher (lat.77° 14' N, long.23° 49' W.) in north-east Greenland the relative importance to ablation of the energy fluxes was

It therefore seems necessary at this similar site to consider the effects of radiation and convection on ablation. To compare the exposed and the rock-shielded ice, diurnal fluctuations in the energy balances can be eliminated by integrating over a 24h period.
Energy balance for the glacier surface
The radiative flux is divided into two parts, the short-wave radiation incident on a plane is given by Reference RobinsonRobinson (1966) as

where n is the fraction of the sky obscured by cloud, α is the surface albedo (approximately 0.4 for ice) β is the angle of tilt of the plane, ϕ is the latitude, δ is the solar declination, t is the local hour angle measured from noon and equal to π/12 radians per hour; and A is the azimuth of the normal to the plane. For a horizontal plane

The net long-wave radiation at a plane is (Reference OutcaltOutcalt, 1972)
where ε is the surface infrared emissivity and α is the Stefan-Boltzmann constant (5.67 × 10−8 W m−2k−4). Tsky is the temperature at a height at which diurnal fluctuations are negligible, and T0 is the surface temperature. The effect of cloud cover on long-wave radiation is dependent on the cloud height and percentage of the sky covered. This effect can be allowed for by multiplying Equation (3) by an additional term (Reference Halstead, Halstead, Richman, Covery and MerrymanHalstead and others, 1957) so that
where c is a non-dimensional function of the height of the cloud base, see Figure 1.

Fig. 1. Dependence of long-wave filter coefficient c on the height of cloud base, hc, after Reference PhilippsPhilipps (1940).
The net radiation flux to the ice surface in 24 h is produced by integrating the sum of the short- and long-wave radiations

Simplifying

The convective heat transfer to the glacier cannot be calculated using standard convective heat-transfer formulae because the glacier has to be considered as an infinite surface with special boundary conditions. A practical assumption is that wind speed and temperature increase logarithmically with height above a natural surface. The gradients very close to a glacier surface are so steep that this is rarely true, however as a generalization over 24 h it is adopted here in a simplified model. The coefficient for momentum transfer at height z is taken as

and the coefficient for heat transfer can be written similarly. By definition u = 0 at height z = z0. For use with variables u2 and (T2 – T0), Reference MyrupMyrup (1969) has shown that the adiabatic estimate of the turbulent transfer coefficient is adequate for model building

The convective heat transfer at the ice surface is thus
where C is the specific heat capacity of air (1.004 × 103 J kg−1K) and Tz is the temperature at height z. A mean value of z0 = 0.005 m is representative of that of many workers on glacier surface winds. It is convenient to take z = 2 m and experimental data (Fig. 2) indicate that the temperature T2 can be approximated by

where 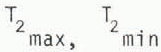 and T
2 are the maximum, minimum, and mean daily temperatures at a height of 2 m.
and T
2 are the maximum, minimum, and mean daily temperatures at a height of 2 m.

Fig. 2. Temperature distribution predicted by Equation (9) compared to air temperatures at a height of 2 m on 16 July 1982.
The total convective flux to the ice in 24 h is found by integrating Equations (7) and (8) with respect to time,

simplifying
The total energy flux to the exposed ice surface in 24 h is
Energy balance for rook-shielded ice surface
Applying the principle of conservation of energy in terms of heat and work transfer to the rock as a system of constant mass implies that as there is no work transfer, the sum of the heat transfers across the rock surfaces must be zero assuming that the internal energy of the rock at the start of the 24 h period is the same as at the end of the period. There are three types of heat transfer to consider, conduction, convection, and radiation. The conductive heat transfer across the rock-ice surface will be equal to the radiative and conductive heat transfers across the rock-atmosphere boundary.
The most convenient shape of the rock to consider is a cylinder standing on end of height h and diameter d. The wind direction and Sun’s bearing then have little influence on the geometry of the problem.
The radiation incident on the top surface of the rock, is, from Equations (2) and (3) for a horizontal plane,

The short -wave radiative flux for a vertical surface from Equation (1), the general equation for a plane, is

for the cylindrical surface of the rock presented to the sun, the azimuth of the normal of the surface is a function of time measured from local noon and equivalent to π/12 radians per hour. Hence the radiation exchange at the rock-atmosphere surface in 24 h is given by

assuming that ![]() is constant and approximately equal to
is constant and approximately equal to ![]() where
where ![]() is the mean temperature.
is the mean temperature.
From classical heat-transfer theory the forced convective heat transfer is given by (cited by Reference EdeEde, 1967, p. 76–115)
where (Pr) is the Prandtl number (0.71) and (Re) is the Reynolds number based on l, the length of the surface parallel to the flow, which for a circle is taken as the mean arc length (0.785 d), i.e.

where ρ and η are the air density and viscosity respectively (n = 1.75×10−5 kg m−1s−1). The velocity profile above the glacier surface is as before expressed using the logarithmic law, i.e.

Finally in Equation (16), a is the width of the surface normal to the flow and K is the thermal conductivity of air (2.47×l0−2 W m−1 K). The convective heat transfer at the rock surface in 24 h is thus found by applying Equation (16) to the top and vertical sides of the rock and integrating with respect to time and height above the glacier to give

assuming the rock surface temperature is a similar function of time to the air temperature, see Equation (9).
As already stated, the conductive heat transfer from the rock to the ice is equivalent to the radiative and convective heat flux to the rock from the atmosphere, i.e

If a rock is to perch, the energy flux to the ice beneath it must be less than the energy flux to the exposed glacier surface, hence the criterion for pedestal formation can be given as

Application of Model to Rocks on Bersaerkerbrae, Greenland
The above mathematical model has been applied to twelve large rocks on Bersaerkerbrae which were observed during July and August 1982. During this period meteorological data were collected on this glacier and the rocks were inspected weekly to determine whether they were perching or sinking, to aid this inspection a photographic record of the rocks was kept. To apply the model to a particular rock the dimensions of the equivalent cylinder are required; these were obtained by finding the diameters of the maximum inscribed and minimum circumscribed circles that would fit the rock’s projected upper face, the equivalent diameter was then taken as the mean of these two diameters. This method avoids misleading values which large protuberances or incisions might produce. The equivalent height was taken as the mean thickness of the rock. The remaining physical values that were used are given in Table I. With the exception of the mean rock surface temperature, the meteorological data are based directly on observations on Bersaerkerbrae. The mean rock surface temperature is based on experimental values of dry-sand temperatures (Fig. 3) obtained by burying thermistors just below the surface of a pile of sand.

Fig. 3. Surface temperature of dry sand on 16 July 1982.
Table I. Physical Values Substituted into the Model When applying it to Rocks on Bersaerkerbrae in July and August 1982

It is assumed that T0 is 0° C at height z0. This is a gross assumption (Reference Lister and TaylorLister and Taylor, 1961) but is used as a first approximation here.
The resulting value Pc, the perch criterion, the rock dimensions, and an indication of whether a rock perched or sank are given in Table II. The model has a 92% success rate in predicting whether a particular rock will perch or sink, for the one case where the model failed the rock was shaded from the sun by a moraine for part of the day which seriously affected the energy balances in a way of which the model takes no account.
Table II. Data for Naturally Positioned Rocks on Bersaerkerbrae

On two of these rocks rotation meters were attached to measure the rate of rotation as the rock perched. The rotation sensors consisted of a potentiometer with a spindle capable of rotation through 300°. The body of the potentiometer was attached to the rock and a small weighted rod was suspended from the spindle. The rotation sensors were connected to a solar-powered data-logger, the system had a sensitivity of 0.12°/digit and gives no output when there is no movement provided it is shaded from direct sunlight, otherwise uneven heating of the resistance track causes diurnal fluctuations in the readings (Reference Allen and AndrewsAllen, 1983). The results show rotations for rocks number 11 and 12 of 0.98 and 0.79° respectively. If the magnitudes of these results are used as an indication of the rate of perching, the model’s results of 26.9 kW m−2d−1 and 20.3 kW m−2d−1 for the same rocks give the same ranking, and the percentage differences between the rocks for the experimental data and the model are 21% and 27% respectively. However this is not a good criterion for assessing perching, as rotation may also depend on other factors including melt-water erosion of the perch.
During late July and August 1982 a selection of a further twenty rocks were manhandled on to a flat piece of glacier which had been cleared of debris. The rocks were positioned far enough apart to avoid mutual interference and then left for five weeks to see which sank and which would grow pedestals or perches. However because the test period was too short and too late in the melt season the rocks showed little attempt to either perch or sink. The model has also been applied to these rocks (Table III) and for those that exhibited movement has a 53% success rate, but this should be balanced against the inaccuracy of the experimental data. The lower success rate is probably due to the thicknesses of the rocks being of similar magnitude to the range of relief of the glacier surface, which will severely limit the vertical surface of the rock available for heat transfer to or from the atmosphere.
Table III. Data for Artificially Positioned Rocks on Bersaerkerbrae

Conclusions
The mathematical model is presented relating the effect of differential ablation to the formation of perched blocks on glaciers. This model gives acceptable results for rocks on Bersaerkerbrae, however further experimental data from other glaciers are needed to confirm the validity of the model. An accurate method of assessing the rate of perching of a rock is required so that the accuracy of the model in predicting this quantity can be tested.
Acknowledgements
The experimental work presented in this paper was performed during the course of the 1982 Sheffield University North-East Greenland Expedition which was supported by the Gilchrist Education Trust, the Mount Everest Foundation, the Royal Geographical Society, the Scott Polar Research Institute, and the University of Sheffield. Support was received in kind from numerous British and Icelandic companies, and the author was sponsored by the Royal Navy. Thanks are due to Dr H.A. Lister for his advice and guidance during the preparation of this paper and R.M. Andrews for his assistance during the experimental work.








