1. INTRODUCTION
The promising vista of indoor navigation applications have made this area popular with researchers worldwide. One of the challenges indoor navigation confronts is the absence of GPS signals in the indoor environment (Misra and Enge, Reference Misra and Enge2001; Noureldin et al., Reference Noureldin, Karamat and Georgy2012). To handle this issue, alternative techniques are introduced to obtain a satisfactory performance. These techniques can be roughly categorised into two groups depending on the availability of infrastructure and pre-installed sensor networks. Generally, techniques that are independent of the external operational environment are preferred for the consideration of efficiency and cost. To this end, self-contained systems like Inertial Navigation Systems (INS) (Titterton and Weston, Reference Titterton and Weston2005) and odometry are widely used in indoor navigation. Particularly, the emergence of the Micro-Electro-Mechanical System (MEMS)-based INS which is lightweight, and lower in cost and power consumption makes it ideal for personal, mobile robot and aerial vehicle applications (Aggarwal et al., Reference Aggarwal, Syed, Aboelmagd and Naser2010). However, the INS or odometry standalone systems fail to sustain a high accuracy in the long run due to their inherent error characteristics. This issue can be solved by providing periodic updates to prevent the error accumulation over time. Light Detection and Ranging (LiDAR) (Harrap and Lato, Reference Harrap and Lato2010) and vision (DeSouza and Kak, Reference DeSouza and Kak2002) are two common techniques integrated with INS and odometry in indoor navigation systems. Compared with vision, LiDAR is more accurate and efficient in computation load and processing speed. Furthermore, LiDAR is not limited by lighting conditions. Therefore, in this paper, we introduce a low-cost lightweight multi-sensor integrated navigation system that integrates INS/odometry with 2D LiDAR in a tightly coupled scheme to provide a reliable indoor navigation system for Unmanned Ground Vehicles (UGVs). The main contributions introduced in this system are summarised as follows:
• INS/odometry is used in a reduced set where only a single vertical gyroscope is used with the vehicle wheel encoder. This reduces the system complexity and overall cost.
• An error model of relative displacement/orientation changes is derived for the proposed reduced INS/Odometry system.
• A computationally efficient LiDAR-based line features detection and tracking algorithm for indoor environments is proposed. The proposed algorithm is more efficient than traditional curve-fitting-based algorithms.
• A tightly coupled Extended Kalman Filter (EKF) design is proposed for the system.
• Both simulation and real experiment with MEMS-grade sensors and a 2D laser scanner from the SICK company are carried out to analyse the performance of the proposed work. Extensive analyses of results are given.
• The work introduced in the paper can be used as an in-motion gyroscope calibration procedure.
• The proposed algorithms can be easily integrated in a more complex multi-sensor navigation system that utilises a variety of other sensors.
2. PREVIOUS WORK
LiDAR has been widely used in ground vehicles for the purpose of localisation (Lingemann et al., Reference Lingemann, Nüchter, Hertzberg and Surmann2005; Xia et al., Reference Xia, Chun-Xia and Min2010), mapping (Barber et al., Reference Barber, Mills and Smith-Voysey2008; Puente et al., Reference Puente, González-Jorge, Arias and Armesto2011) and Simultaneous Localisation and Mapping (SLAM) (Diosi and Kleeman, Reference Diosi and Kleeman2005; Grisetti et al., Reference Grisetti, Stachniss and Burgard2007). However, in most of the earlier works using LiDAR alone, they have the drawbacks that LiDAR depends on distinguishable features in the environment and the error in vehicle position derived by LiDAR will accumulate. Therefore, the integration of LiDAR and INS is essential to obtain a robust and accurate indoor navigation system. The integration of LiDAR and INS can be found in both indoor environments and urban areas (Haag et al., Reference Haag, Venable and Smearcheck2007), where LiDAR replaces GPS to correct INS periodically. Generally, LiDAR and INS are fused by Extended Kalman Filter (EKF) (Kim et al., Reference Kim, Baeg, Yang, Cho and Park2012; Ma and McKitterick, Reference Ma and McKitterick2012) or Particle Filter (PF) (Hornung et al., Reference Hornung, Wurm and Bennewitz2010; Bry et al., Reference Bry, Bachrach and Roy2012) in two different schemes. One integration scheme is to feed position and orientation derived from LiDAR being fed back to the filter to correct navigation solutions from INS (Kohlbrecher et al., Reference Kohlbrecher, Stryk, Meyer and Klingauf2011). This kind of integration is called “loosely coupled”. The problem with this kind of integration is that if the position (and/or) orientation calculated from LiDAR is missing or significantly jeopardised, overall accuracy is reduced. In contrast, another method of integration is defined as “tightly coupled” between LiDAR and INS (Soloviev et al., Reference Soloviev, Bates and van Graas2007; Soloviev, Reference Soloviev2008). In this tightly coupled integration scheme, the relative position and orientation changes estimated by LiDAR are compared with position and orientation changes predicted by INS/Odometry and the differences are fed to a filtering module (KF or PF) to estimate both errors in position and orientation changes and sensors biases. This tightly coupled integration scheme is commonly preferred over loosely coupled integration schemes due to the utilisation of the raw LiDAR measurements and also due to the dependence of relative position and orientation changes which are immune to absolute errors in position and orientation.
However, the previous works use full Inertial Measurement Units (IMU) with complicated mechanisation and error model equations that lead to quicker drifts if not periodically corrected. In addition, the earlier works commonly utilise a traditional curve-fitting-based features detection method that is computationally expensive. As an improvement to the aforementioned approaches, this paper introduces a reduced sensor set that utilises only a single vertical gyroscope, the vehicle wheel encoder and a 2D LiDAR. An error model is derived and a computationally efficient parallel line features detection and tracking algorithm that efficiently estimates 2D relative position and orientation changes is introduced. The reduced sensor set and the efficient line feature extraction and tracking algorithm make the proposed system suitable for typical 2D indoor navigation for UGVs.
3. INS/ODOMETRY–BASED NAVIGATION SYSTEM
The proposed 2D INS/Odometry-based navigation system consists of one single-axis gyroscope with its sensitive axis aligned with the vertical axis of the body (Iqbal et al., Reference Iqbal, Karamat, Okou and Noureldin2009; Iqbal et al., Reference Iqbal, Georgy, Korenberg and Noureldin2010; Atia et al., Reference Atia, Georgy, Korenberg and Noureldin2010). The system details are given as follows.
3.1. System motion model
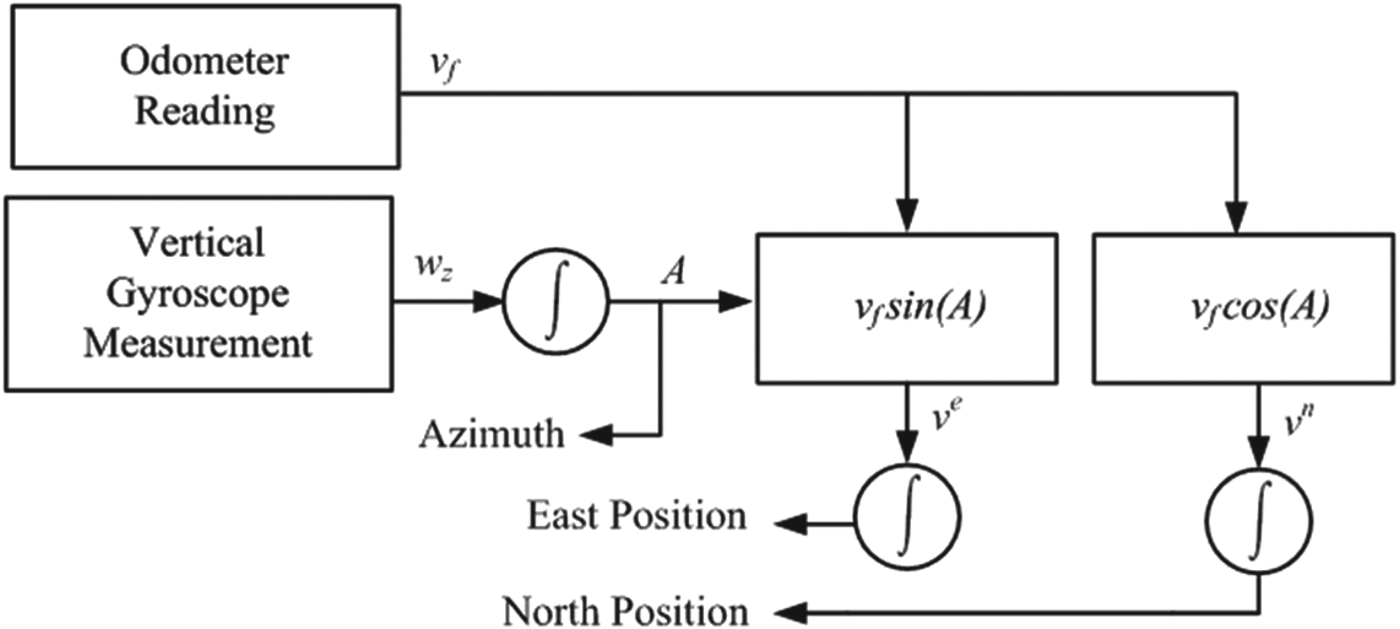
We assume the vehicle is mostly travelling in the horizontal plane (Iqbal et al., Reference Iqbal, Okou and Noureldin2008). Therefore, the forward velocity estimated from the vehicle odometry measurements combined with the azimuth obtained from integrating gyroscope rotation rate measurements yields velocity, as well as displacements, along east and north directions. However, the earth rotation along its spin axis as well as the change of local level frame (east-north-up) orientation with respect to the earth will generate a rotation rate component which will also be measured by the gyroscope. Thus, these components must be compensated and the rate of change of azimuth A can be given as follows:
where φ is latitude, wesin(φ) is earth rotation rate component along the vertical direction, ve is velocity along the east direction, R n is the earth normal radius of curvature, h is altitude, ![]() ${\textstyle{{v^e \tan (\varphi )} \over {R_n + h}}}$ is rotation rate component caused by local level frame orientation change and b z is the estimated gyroscope bias using stationary data.
${\textstyle{{v^e \tan (\varphi )} \over {R_n + h}}}$ is rotation rate component caused by local level frame orientation change and b z is the estimated gyroscope bias using stationary data.
The east and north velocities can be derived from the forward velocity v f and azimuth A given the assumption that the vehicle is mostly travelling in the horizontal plane. Velocities along the east and north directions can be written respectively as:
After deriving velocities, 2D position change can be represented as below:
where R m is the earth meridian radius of curvature and λ is longitude. A block diagram describing the 2D INS/Odometry system is shown in Figure 1.

Figure 1. 2D INS/odometry system.
3.2. Limitations of INS/Odometry-based navigation system
As self-contained systems, both INS and odometry can provide navigation independent of their environments. However, the limitations for an INS/Odometry-based navigation system are obvious. The inertial sensor errors and odometry scale factor error cause drifts that grow with time without bound, thus navigation solutions from INS/Odometry-based navigation systems deteriorate quickly. This gives rise to the requirement of periodic correction for the INS/Odometry-based navigation system. In open-sky areas, GPS is the common correction and aiding source. However, indoors, other aiding sources are needed.
4. THE PROPOSED SYSTEM
The 2D LiDAR (Adams, Reference Adams2000; Diosi and Kleeman, Reference Diosi and Kleeman2003) uses time-of-flight of a laser beam to measure distances from the scanner to the reflecting surrounding objects in a certain angular range with known angular resolution. Figure 2 shows an example of 2D LiDAR measurements in an indoor corridor where reflections of the two parallel walls are highlighted by solid dark lines.

Figure 2. 2D LiDAR scan in a hallway.
In most indoor environments, there exists a common feature that is parallel straight lines in hallways and corridors. As shown in Figure 2, the walls reflecting LiDAR beams form a parallel lines feature. If the LiDAR scans points which are represented in polar coordinate with distance and bearing are transformed into local LiDAR frame, where the origin is the position of the laser scanner while x and y axes are the transverse and forward direction respectively, LiDAR measurements will constitute the parallel lines feature shown in Figure 3.

Figure 3. Parallel lines in local LiDAR coordinate frame.
The proposed system uses the definition of normal point (Soloviev et al., Reference Soloviev, Bates and van Graas2007) and (Soloviev, Reference Soloviev2008). It is defined as the perpendicular intersection of the extracted line and a line originating from LiDAR. A normal point is characterised by its polar parameters: range ρ and angle α in the LiDAR frame as shown in Figure 4.

Figure 4. Normal point: intersection between LiDAR perpendicular beam and walls in indoor environments.
Two consecutive normal point measurements from a 2D LiDAR in a corridor are illustrated in Figure 5. In epoch (i), the LiDAR scan shows a pair of parallel lines is detected. The range and angle of the normal point on any of the lines are defined as ρ i and α i respectively. In the next epoch scan(i+1), the range and angle of the normal point on the same line are defined as ρ i+1 and α i+1 respectively.

Figure 5. Two consecutive LiDAR normal point measurements.
Having represented the normal point by its range and angle in the LiDAR frame, the range and angle changes between two consecutive scans are used in the system filter as updates from LiDAR and they can be calculated respectively as follows:
where Δx and Δy represent the displacements of the vehicle between two consecutive epochs (i, i+1). It is important to note that Δx and Δy are the relative position changes of the vehicle in the body frame, and ΔA LiDAR is the relative heading change of the vehicle.
4.1. INS/Odometry-based position/orientation changes prediction
The relative orientation change and horizontal position change in the vehicle body frame from epoch (i) to epoch (i+1) can be predicted using INS/Odometry measurements as follows:
where ΔA INS is the heading change, w z is the gyroscope measurements, b z is the gyroscope bias, and T is the sampling period. By projecting velocity in the body frame at epoch (i), velocity components along x i and y i axis v x and v y can be calculated by:
where v f is the vehicle odometry measurement. Together with these velocity components, the predicted displacements of the vehicle from epoch (i) to epoch (i+1) Δx INS and Δy INS are estimated by:
Substituting Equations (9) to (12) into Equation (6), the range change from INS can be obtained as follows:
4.2. INS/Odometry/LiDAR dynamic error model
In order to use EKF for the proposed system, a linear dynamic system error model that can be written in the following form has to be obtained:
where δx is the error state vector, F is the transition matrix, G is noise parameter matrix and w is the zero mean Gaussian noise vector whose covariance matrix Q is defined as the system noise matrix given by:
In the proposed system, the error state vector is defined as:
where δΔx is displacement error along x axis of the body frame, δΔy is displacement error along y axis of the body frame, δv f is odometry measurements error, δv x is velocity error along x axis, δv y is velocity error along y axis, δΔA is azimuth change error, δa od is error in acceleration derived from odometry measurements and δb z is error in gyroscope bias. By applying a Taylor expansion to the INS/Odometry-based dynamic system given in Equations (8) to (12) and considering only the first order term, the linearized dynamic system error model is given as:
 $$\eqalign{ \delta \dot v_x = &\sin ({\rm \Delta} A)\delta a_{od} + \cos ({\rm \Delta} A)(w_z - b_z )\delta v_f \cr &+ \left[ {a_{od} \cos ({\rm \Delta} A) - v_f \sin ({\rm \Delta} A)(w_z - b_z )} \right] \cr & \times\delta {\rm \Delta} A - v_f \cos ({\rm \Delta} A)\delta b_z} $$
$$\eqalign{ \delta \dot v_x = &\sin ({\rm \Delta} A)\delta a_{od} + \cos ({\rm \Delta} A)(w_z - b_z )\delta v_f \cr &+ \left[ {a_{od} \cos ({\rm \Delta} A) - v_f \sin ({\rm \Delta} A)(w_z - b_z )} \right] \cr & \times\delta {\rm \Delta} A - v_f \cos ({\rm \Delta} A)\delta b_z} $$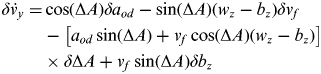 $$\eqalign{\delta \dot v_y = & \cos ({\rm \Delta} A)\delta a_{od} - \sin ({\rm \Delta} A)(w_z - b_z )\delta v_f \cr & - \left[ {a_{od} \sin ({\rm \Delta} A) + v_f \cos ({\rm \Delta} A)(w_z - b_z )} \right] \cr & \times \delta {\rm \Delta} A + v_f \sin ({\rm \Delta} A)\delta b_z} $$
$$\eqalign{\delta \dot v_y = & \cos ({\rm \Delta} A)\delta a_{od} - \sin ({\rm \Delta} A)(w_z - b_z )\delta v_f \cr & - \left[ {a_{od} \sin ({\rm \Delta} A) + v_f \cos ({\rm \Delta} A)(w_z - b_z )} \right] \cr & \times \delta {\rm \Delta} A + v_f \sin ({\rm \Delta} A)\delta b_z} $$Here, both random errors in acceleration derived from odometry and gyroscope measurements are modelled as first order Gauss-Markov processes. γ od and β z are the reciprocal of the correlation time constants of the random process associated with odometry and gyroscope measurements respectively while σ od and σ z are standard deviation of this random process (Iqbal et al., Reference Iqbal, Okou and Noureldin2008).
4.3. INS/Odometry/LiDAR measurement model
The measurement z is modelled as the following form:
Where the observation vector z is defined by:
H is the design matrix of the filter and can be given as:
v is the vector of observation random noise, which is assumed to be a zero mean Gaussian noise vector whose covariance matrix R is defined as the system noise matrix given by:
From system error model Equations (16) to (23), F and G matrices can be easily derived. Based on this, the discrete state transition matrix can be given as:
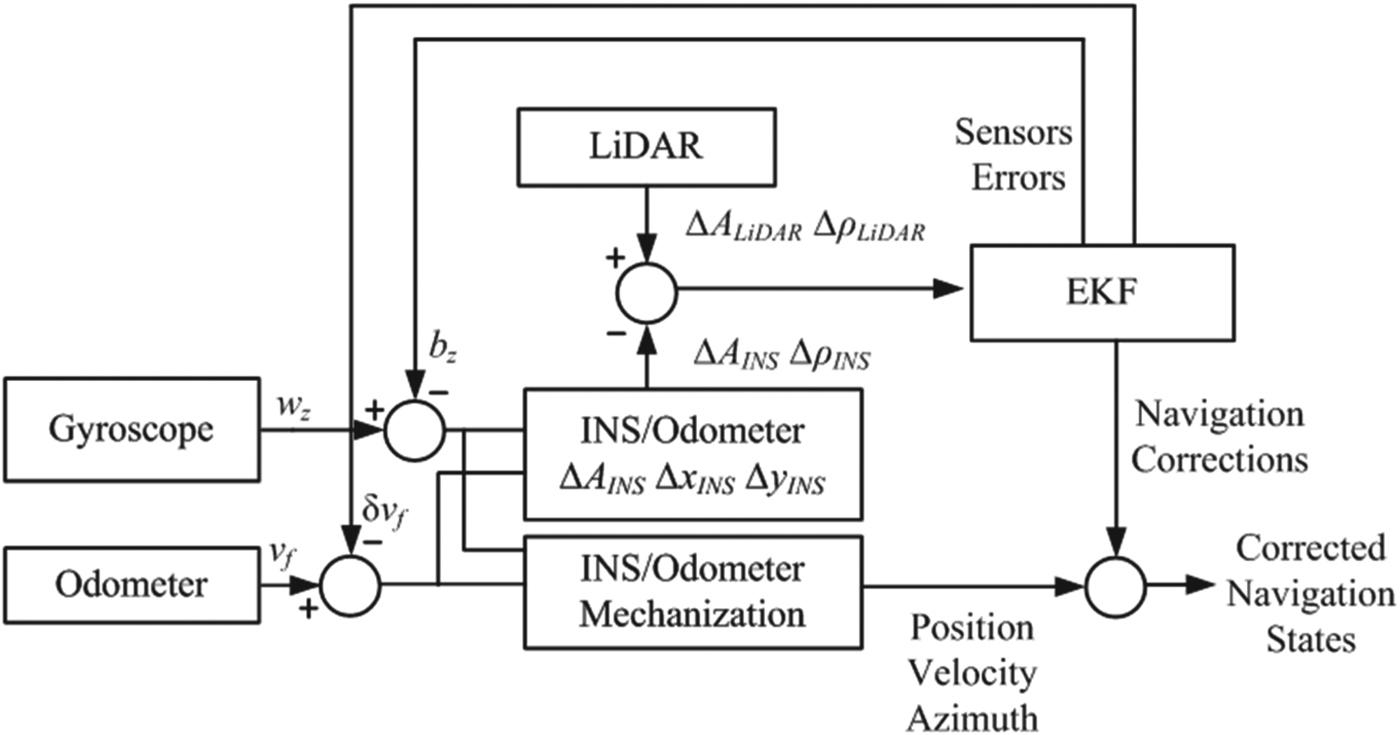
where T is the sampling period and I is the identity matrix. Then EKF equations can be applied to predict the error state vector and update it when measurements from LiDAR are available. The prediction and correction are performed in the body frame and then transformed into the navigation frame to provide corrected navigation output. A block diagram describing the system is shown in Figure 6.

Figure 6. INS/Odometry/LiDAR system.
5. LINES DETECTION/TRACKING ALGORITHM
Commonly, to detect lines in the environment using LiDAR, a curve-fitting algorithm is used in a moving window that runs over LiDAR scans (Nguyen et al., Reference Nguyen, Martinelli, Tomatis and Siegwart2005). Performing this operation is a computational bottleneck. To overcome this limitation, we propose a more efficient detection and tracking mechanism that does not need curve fitting and does not involve matrix inversions. Since we target parallel lines in indoor environments, we make use of the fact that we have prior knowledge about the targeted line features. The algorithm consists of two main steps: acquisition and tracking which is similar to the approach used in GPS receivers to acquire satellite signals (Misra and Enge, Reference Misra and Enge2001). These two steps are described as follows:
• Acquisition Mode: The algorithm performs a search in the space of possible lateral distances (distance between vehicle position and “Normal Point”) and possible vehicle headings (could be centred on azimuth calculated by INS/Odometry motion model). This search is conducted as follows:
○ Based on the lateral distance, heading, and the assumption that a parallel line feature exists, artificial LiDAR range/angle points are generated. We call these points the “replica”.
○ Whenever a LiDAR measurement is available, the replica is correlated with the real measurements. If the correlation is strong, the acquisition is declared to be true and “Normal Points” parameters are calculated.
• Tracking Mode: Once the acquisition mode detects a parallel line feature, the algorithm will switch to tracking mode. In the tracking mode, the new epoch's LiDAR measurements are predicted and consequently, the search window is greatly reduced and the search process becomes quite efficient and more accurate.
• Re-acquisition: In the tracking mode, if the correlation starts to be weak, the tracking mode is halted and the algorithm switches to the acquisition mode.
• INS/Odometry Aiding: To enhance the performance, the INS/Odometry prediction of relative displacement/orientation changes is used to enhance the consistency and further improve the accuracy and the performance.
• Singularity Issue: Since the parallel lines feature is usually found in corridors where the slopes are close to 90o, we transform all the data by an arbitrary angle to avoid singularities. After performing estimation of lines, we transform the results back to the original LiDAR frame.
A flowchart is shown in Figure 7 that describes the steps of the algorithm.

Figure 7. Flowchart of lines detection and tracking algorithm.
6. SIMULATION RESULTS AND ANALYSIS
6.1. Simulation Environment
In simulation, two motion patterns are designed, namely motion pattern #1 and motion pattern #2. In motion pattern #1, the vehicle moves in straight lines most of the time while motion pattern #2 shows more flexible movement of the vehicle in a curved trajectory. To analyse and verify the proposed system, a flexible simulation environment has been developed. In this simulation environment, corridors with known dimensions are simulated. The simulation area is an indoor environment with three corridor sections and two corners. In corner areas, parallel lines may not be detected and LiDAR measurements are unavailable. Similar to GPS signal blockage in INS/GPS systems, we define corner areas as LiDAR outage. The reference trajectories of motion pattern #1 and motion pattern #2 are illustrated in Figure 8.

Figure 8. (a) Simulation area and reference trajectory for motion pattern #1. (b) Simulation area and reference trajectory for motion pattern #2.
Reference speed and heading in different simulated motion patterns are planned in advance to analyse the filter behaviour and the system performance in different motion patterns. Noisy gyroscope measurements were obtained by applying a deterministic bias component, a deterministic bias drift rate and a Gauss-Markov-based random noise part. The random noise component was obtained from a Crossbow IMU300CC MEMS-based IMU datasheet. A scale factor error was applied to speed measurements as well. The true LiDAR range measurements were obtained based on the knowledge about the reference trajectory (position/heading) and line equations of the corridor walls. A random noise part with standard deviation obtained from a SICK LMS-200 datasheet (SICK, 2006) was added to the simulated LiDAR measurements. The specifications for Crossbow IMU300CC (Crossbow, 2007) and SICK LMS-200 are shown in Tables 1 and 2 respectively.
Table 1. Crossbow IMU300CC Specifications.

Table 2. SICK LMS-200 Specifications.

The range and azimuth changes from LiDAR for motion pattern #2 are illustrated in Figure 9. This figure indicates the noise level in range and azimuth measurements from LiDAR.

Figure 9. (a) Noise level of range change from LiDAR measurements. (b) Noise level of azimuth change from LiDAR measurements.
6.2. Navigation Modes
When moving through corridors, the vehicle is working in integrated navigation mode where LiDAR measurements are processed and applied in EKF to estimate sensors errors and position/velocity/orientation errors. In this mode, errors in gyroscope bias δb z and velocity error δv f can be estimated by EKF and used to correct vertical rotation rate measurements and velocity. When the vehicle reaches the corners where LiDAR outage occurs, the vehicle switches to prediction mode. In prediction mode, the system applies the latest gyroscope bias b z and velocity error δv f estimated by EKF in INS/Odometry motion equations to achieve 2D navigation solutions.
6.3. Simulation Results
The simulation results for motion patterns #1 and motion pattern #2 are shown in Figures 10 and 11 respectively. As can be seen, the deviation between reference trajectory and noisy trajectory generated by the INS/Odometry standalone system grows with time. This is mainly because the gyroscope bias errors are corrupted by random noise that accumulates over time. However, the LiDAR-aided system can keep close track of the reference movement during the whole process. During LiDAR outages, the latest estimations of gyroscope bias and odometry velocity error from EKF are accurate enough to maintain a reliable performance.

Figure 10. LiDAR-aided solutions for motion pattern #1.

Figure 11. LiDAR-aided solutions for motion pattern #2.
Owing to measurement updates from LiDAR in EKF, the noises in both gyroscope and odometry are estimated and compensated, thus leading to long-term sustainable centimetre-level accuracy. The true gyroscope bias and the estimated gyroscope bias from EKF in motion pattern #1 and #2 are shown in Figures 12 and 13 respectively. As can be seen from the figures, EKF can accurately estimate the gyroscope bias and drifts regardless of the motion patterns designed in the simulation experiment. During LiDAR outages, the system operates only in prediction mode and gyroscope keeps constant until LiDAR measurements become available again.

Figure 12. Gyroscope bias estimation results for motion pattern #1.

Figure 13. Gyroscope bias estimation results for motion pattern #2.
The root mean square error in position for motion pattern #1 and #2 in three corridor sections and two outages are depicted in Tables 3 and 4 respectively. From these tables, it is worth noting that the performance of motion pattern #2 is better than that of motion pattern #1. The reason for this is that in motion pattern #1 the vehicle moves in straight lines most of the time and, consequently, the angle of normal point at any scan epoch is either 0° or 180°. Substituting this angle value into design matrix H given in Equation (26) makes the observability of H for the second element in the error state vector zero. This leads to poor estimation of the error states. In contrast, when the vehicle moves in a curved trajectory, the angle of the normal point at any scan epoch keeps changing. The observability of H for the second element in the error state vector is strong enough to estimate errors. Thus, EKF can achieve better estimation results for the error states.
Table 3. Position Error for Motion Pattern #1.
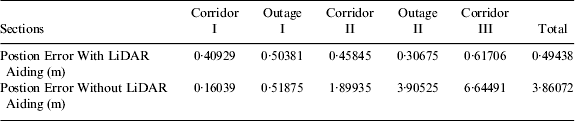
Table 4. Position Error for Motion Pattern #2.
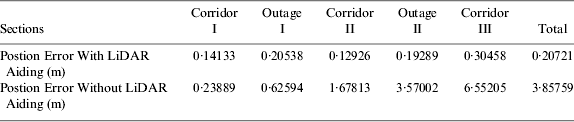
Table 5. SICK LMS111 Specifications.

7. REAL EXPERIMENT RESULTS AND ANALYSIS
Real experiments were conducted in a 70 m by 40 m indoor office environment in the Royal Military College of Canada with UGV “Husky A200” from Clearpath Robotics Inc. (Canada-based). The complete loop in the testing trajectory is around 220 m and it took around seven minutes to travel using the Husky A200 UGV. The UGV is equipped with SICK laser scanner LMS111, MEMS level inertial sensor set CHR-UM6 and a quadrature encoder. For the datasheet of CHR-UM6, one can refer to CHRobotics (2013). The specification of SICK LMS111 is shown as below. The sampling frequency for gyroscope, wheel encoder and laser scanner are 20 Hz, 10 Hz and 50 Hz respectively.
In a real scenario, navigation performance is influenced by various factors, such as the reflectivity of different objects in the environments, opening doors and people walking by etc. Due to these aspects the parallel lines feature mentioned above not do not exist in every timestamp. Figure 14 shows some laser scans at certain scenes of the environment. The scans are transformed into the LiDAR frame where the origin (0, 0) represents the position of the UGV. The pictures on the right are taken during the experiment showing the scenes of the environment corresponding to the scans on the left.

Figure 14. Laser scans and pictures in different scenes of the environment: (1·1) The red circles show two opening doors. (2·1) In a corner. (3·1) The red square demonstrates the garbage bins. (4·1) The red square indicates a small part of the wall made of glass that the beams can get through.
7.1. Performance of lines detection and tracking algorithm
We used the Husky A200 UGV to collect data as described above. Then we ran our algorithms in post-processing mode where data is loaded by MATLAB and the algorithm is applied to estimate relative displacement/orientation changes between LiDAR epochs. Some detection results are shown in Figure 15. Detected lines are identified by green lines and the portion of generated points that achieved highest correlation is identified by solid thick green points. Original LiDAR data is shown in magenta and the transformed LiDAR data is shown in blue.

Figure 15. Two detection results snapshots of the proposed lines detection and tracking algorithm.
To compare the computational performance of the proposed algorithm, we run a traditional curve-fitting-based algorithm that is based on a moving 25-points length window of LiDAR data points and performed curve-fitting and draw a histogram to estimate line parameters. The two algorithms were tested over 26,200 LiDAR scans. Results showed that on a SONY VAIO Core i5 processor, MATLAB code took an average of 0·5 seconds to process a LiDAR scan of 541 points with the traditional curve-fitting-based algorithm while it took an average of 0·2623 seconds to process a scan with the proposed algorithm. Figure 16 (a) and (b) show iteration times over a portion of 200 epochs of LiDAR scans. The epochs were selected to show examples of smooth portion where tracking was always successful (see Figure 16(a)) while Figure 16(b) shows the time changes when tracking is lost and acquisition is repeated.

Figure 16. Comparison between traditional LS-based algorithm the proposed lines detection and tracking algorithm. (a) The time taken to process LiDAR scan over 200 epochs. (b) The time during different phases (acquisition and tracking). (c) The angle estimated during the 200 LiDAR epochs processed.
In terms of accuracy, Figure 16(c) shows a comparison between line angle estimated by traditional least-square curve fitting and the proposed algorithm. We verified the accuracy by applying the estimated relative displacement/orientation changes to the EKF in the integrated navigation system and we found that the positioning accuracy is around the same. Although the proposed algorithm, in some situations, might be more sensitive to noise (which can be seen in the first portion of Figure 16(c), experimental results of the integrated navigation solution showed that the proposed algorithm performs similarly to curve-fitting-based methods in terms of accuracy but with almost 50% faster processing time.
7.2. Positioning performance of the proposed LiDAR-aided integrated navigation system
It is important to note that LiDAR updates are propagated to EKF at the frequency of 5 Hz for two reasons: firstly to guarantee that measurable relative displacement/orientation changes have been obtained and secondly to increase confidence in these relative displacement/orientation changes measurements by increasing Signal-to-Noise Ratio (SNR) in LiDAR corrections. During the whole trajectory, LiDAR updates were available only 20% of the time while during the rest of the time, the system operates in INS/Odometry prediction mode. Figure 17 illustrates the time epoch when LiDAR updates are available in red markers on the reference trajectory. As can be seen, LiDAR outages occur in places filled with unorganised objects and corners.

Figure 17. LiDAR updates availability during the whole trajectory.
The results for real experimental data are shown in Figure 18. The dark green trajectory is used as a reference trajectory derived by manual calibration of the gyroscope when the vehicle is stationary. The blue trajectory is generated using pure un-aided INS/Odometry without any LiDAR updates. The red trajectory is the performance of the proposed algorithm. Although the dark green trajectory here cannot really represent the true reference trajectory, it still can be used to evaluate the performance of the proposed algorithm. The root mean square error for LiDAR-aided trajectory was found to be 0·56 m while the root mean square error for INS/Odometry standalone system is 5·25 m which means almost 90% error reduction is obtained. Given the fact that the real measurements and real environment are much more complicated than the simulation conditions, this result can be considered consistent with the simulation results where a 94% error reduction is obtained. Figure 19 demonstrates the estimation of gyroscope bias error during a portion of the experiment. Comparing this figure with Figures 12 and 13, the gyroscope bias estimation results from real experiment match the estimation results from simulations.

Figure 18. Real experiment results.

Figure 19. Gyroscope bias estimation results for real experiment.
8. CONCLUSION
In this paper, a 2D INS/Odometry/LiDAR integrated navigation system that is suitable for UGVs in indoor environments was introduced. The INS/Odometry system was used with a reduced inertial sensor set where only a vertically aligned gyroscope is used with the vehicle wheel encoders. In addition, a line features detection and tracking algorithm was proposed that is more efficient than traditional curve-fitting-based algorithms. The LiDAR measurements were used to estimate position and orientation changes which are fused by EKF with a dynamic error model of the INS/Odometry system. Navigation states were corrected by EKF-estimated errors while gyroscope measurements were compensated by EKF-estimated bias. Both simulation and real experimental results in an indoor area showed that the sensors errors are accurately estimated by the proposed EKF scheme. Furthermore, the results showed improvement in navigation performance and robustness in real world application, thus leading to navigation performance of sub-metre accuracy.