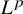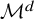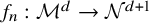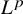1 Introduction
Background: rigidity in codimension 0
In 1850, Liouville proved that isometries in
![]() ${\mathbb R}^d$
are rigid [Reference LiouvilleLio50]: if
${\mathbb R}^d$
are rigid [Reference LiouvilleLio50]: if
![]() $\Omega \subset {\mathbb R}^d$
is open and connected and
$\Omega \subset {\mathbb R}^d$
is open and connected and
![]() $f\in C^1(\Omega; {\mathbb R}^d)$
, and if for every
$f\in C^1(\Omega; {\mathbb R}^d)$
, and if for every
![]() $x\in \Omega $
,
$x\in \Omega $
,
![]() $df(x)\in \operatorname {SO}(d)$
, then, in fact, f is a rigid motion,
$df(x)\in \operatorname {SO}(d)$
, then, in fact, f is a rigid motion,
![]() $f(x) = Qx+b$
for some
$f(x) = Qx+b$
for some
![]() $Q\in \operatorname {SO}(d)$
and
$Q\in \operatorname {SO}(d)$
and
![]() $b\in {\mathbb R}^d$
. This theorem has been generalized over the years in a number of ways:
$b\in {\mathbb R}^d$
. This theorem has been generalized over the years in a number of ways:
-
• Regularity: Reshetnyak showed that the theorem holds for Lipschitz maps [Reference ReshetnyakRes67a]. This is essentially a regularity result, as the proof proceeds by showing that such Lipschitz maps are harmonic, and hence smooth. (Reshetnyak’s theorem can be reformulated as follows: if a Lipschitz map is a.e. orientation-preserving and pulls back a smooth metric, then it is smooth.)
-
• Asymptotic stability: Reshetnyak also showed that this rigidity is stable: if
 $\operatorname {dist}(df_n, \operatorname {SO}(d)) \to 0$
in
$\operatorname {dist}(df_n, \operatorname {SO}(d)) \to 0$
in
 $L^p$
for some
$L^p$
for some
 $p\in [1,\infty )$
, then, modulo a subsequence and translations,
$p\in [1,\infty )$
, then, modulo a subsequence and translations,
 $f_n\to Qx+b$
in
$f_n\to Qx+b$
in
 $W^{1,p}(\Omega ;{\mathbb R}^d)$
[Reference ReshetnyakRes67b].
$W^{1,p}(\Omega ;{\mathbb R}^d)$
[Reference ReshetnyakRes67b]. -
• Quantitative stability: Friesecke, James and Müller (FJM) ([Reference Friesecke, James and MüllerFJM02] – see also [Reference Conti and SchweizerCS06, Section 2.4]) – proved a quantitative version of this theorem: for
 $p\in (1,\infty )$
, there exists
$p\in (1,\infty )$
, there exists
 $C=C(\Omega ,p)$
such that there exists for every
$C=C(\Omega ,p)$
such that there exists for every
 $f\in W^{1,p}(\Omega ;{\mathbb R}^d)$
a rigid map
$f\in W^{1,p}(\Omega ;{\mathbb R}^d)$
a rigid map
 $\bar {f}(x) = Qx+b$
, such that
$\bar {f}(x) = Qx+b$
, such that  $$\begin{align*}\|f-\bar{f}\|_{W^{1,p}(\Omega;{\mathbb R}^d)} \le C \|\operatorname{dist}(df, \operatorname{SO}(d))\|_{L^p(\Omega)}. \end{align*}$$
$$\begin{align*}\|f-\bar{f}\|_{W^{1,p}(\Omega;{\mathbb R}^d)} \le C \|\operatorname{dist}(df, \operatorname{SO}(d))\|_{L^p(\Omega)}. \end{align*}$$
There are many generalizations in other directions (e.g., for conformal maps, multiple energy wells, incompatible fields), which are beyond the scope of this short discussion. In the context of Riemannian geometry, Liouville’s and Reshetnyak’s theorems generalize to maps between two compact oriented Riemannian manifolds
![]() $({\mathcal M},\mathfrak {g})$
and
$({\mathcal M},\mathfrak {g})$
and
![]() $({\mathcal N},\mathfrak {h})$
of the same dimension. In this context, we denote by
$({\mathcal N},\mathfrak {h})$
of the same dimension. In this context, we denote by
![]() $\operatorname {SO}(\mathfrak {g}_q,\mathfrak {h}_{q'})$
the space of orientation-preserving isometries
$\operatorname {SO}(\mathfrak {g}_q,\mathfrak {h}_{q'})$
the space of orientation-preserving isometries
![]() $T_q{\mathcal M}\to T_{q'}{\mathcal N}$
(or simply by
$T_q{\mathcal M}\to T_{q'}{\mathcal N}$
(or simply by
![]() $\operatorname {SO}(\mathfrak {g},\mathfrak {h})$
, when no confusion may arise).
$\operatorname {SO}(\mathfrak {g},\mathfrak {h})$
, when no confusion may arise).
-
• Rigidity: The following well-known fact can be thought of as a generalization of Liouville’s theorem: if
 $f\in C^2({\mathcal M};{\mathcal N})$
satisfies
$f\in C^2({\mathcal M};{\mathcal N})$
satisfies
 $df_q \in \operatorname {SO}(\mathfrak {g}_q,\mathfrak {h}_{f(q)})$
for every
$df_q \in \operatorname {SO}(\mathfrak {g}_q,\mathfrak {h}_{f(q)})$
for every
 $q\in {\mathcal M}$
, then f is rigid, in the sense that it is determined by its value and the value of its differential at a single point. Every
$q\in {\mathcal M}$
, then f is rigid, in the sense that it is determined by its value and the value of its differential at a single point. Every
 $q\in {\mathcal M}$
has an open neighborhood
$q\in {\mathcal M}$
has an open neighborhood
 $U\ni q$
, such that where
$U\ni q$
, such that where $$\begin{align*}f|_U = \exp^{\mathfrak{h}}_{f(q)} \circ df_q \circ (\exp^{\mathfrak{g}}_q)^{-1}, \end{align*}$$
$$\begin{align*}f|_U = \exp^{\mathfrak{h}}_{f(q)} \circ df_q \circ (\exp^{\mathfrak{g}}_q)^{-1}, \end{align*}$$
 $\exp ^{\mathfrak {g}}$
and
$\exp ^{\mathfrak {g}}$
and
 $\exp ^{\mathfrak {h}}$
are the exponential maps in
$\exp ^{\mathfrak {h}}$
are the exponential maps in
 ${\mathcal M}$
and
${\mathcal M}$
and
 ${\mathcal N}$
.
${\mathcal N}$
.
-
• Regularity: If
 $f:{\mathcal M}\to {\mathcal N}$
is Lipschitz and satisfies
$f:{\mathcal M}\to {\mathcal N}$
is Lipschitz and satisfies
 $df \in \operatorname {SO}(\mathfrak {g},\mathfrak {h})$
almost everywhere, then f is a smooth isometric immersion, and the previous statement applies. This result (or variants of it) has been proved several times, using various techniques [Reference ReshetnyakRes78, Reference ReshetnyakRes94, Reference Lewicka and PakzadLP11, Reference Liimatainen and SaloLS14, Reference Kupferman, Maor and ShacharKMS19].
$df \in \operatorname {SO}(\mathfrak {g},\mathfrak {h})$
almost everywhere, then f is a smooth isometric immersion, and the previous statement applies. This result (or variants of it) has been proved several times, using various techniques [Reference ReshetnyakRes78, Reference ReshetnyakRes94, Reference Lewicka and PakzadLP11, Reference Liimatainen and SaloLS14, Reference Kupferman, Maor and ShacharKMS19]. -
• Asymptotic stability: It was shown in [Reference Kupferman, Maor and ShacharKMS19] that if
 $f_n\in W^{1,p}({\mathcal M};{\mathcal N})$
satisfy
$f_n\in W^{1,p}({\mathcal M};{\mathcal N})$
satisfy
 $\operatorname {dist}(df_n,\operatorname {SO}(\mathfrak {g},\mathfrak {h}))\to 0$
in
$\operatorname {dist}(df_n,\operatorname {SO}(\mathfrak {g},\mathfrak {h}))\to 0$
in
 $L^p({\mathcal M})$
, then (modulo a subsequence)
$L^p({\mathcal M})$
, then (modulo a subsequence)
 $f_n$
converges strongly in
$f_n$
converges strongly in
 $W^{1,p}$
to a smooth isometric immersion
$W^{1,p}$
to a smooth isometric immersion
 $f:{\mathcal M}\to {\mathcal N}$
(in particular, such an isometric immersion exists).
$f:{\mathcal M}\to {\mathcal N}$
(in particular, such an isometric immersion exists).
A generalization of the FJM quantitative stability result to a Riemannian setting is yet missing, and even its formulation as a conjecture is not obvious. A particular case concerning mappings between round spheres appears in [Reference Chen, Li and SlemrodCLS22, Theorem 3.2]; a stronger version of that result can, in fact, be deduced from the Euclidean result and will be proved in a forthcoming paper [Reference Kupferman and MaorKM24].
The above results have direct relevance to elasticity theory: In the Euclidean settings,
![]() $\|\operatorname {dist}(df, \operatorname {SO}(d))\|_{L^p}^p$
is a prototypical model for the elastic energy of a strained elastic solid; hence, these theorems relate the smallness of the elastic energy to being close to a zero energy state. Essentially, any rigorous derivation of a low-energy limit in elasticity uses these results. The Riemannian case arises in non-Euclidean elasticity, which is an elastic theory for pre-stressed bodies (see, for example, [Reference Klein, Efrati and SharonKES07, Reference Efrati, Sharon and KupfermanESK09, Reference Efrati, Sharon and KupfermanESK13, Reference Lewicka and MahadevanLM22]). The asymptotic stability result in [Reference Kupferman, Maor and ShacharKMS19], for example, implies that (as expected by physicists) if
$\|\operatorname {dist}(df, \operatorname {SO}(d))\|_{L^p}^p$
is a prototypical model for the elastic energy of a strained elastic solid; hence, these theorems relate the smallness of the elastic energy to being close to a zero energy state. Essentially, any rigorous derivation of a low-energy limit in elasticity uses these results. The Riemannian case arises in non-Euclidean elasticity, which is an elastic theory for pre-stressed bodies (see, for example, [Reference Klein, Efrati and SharonKES07, Reference Efrati, Sharon and KupfermanESK09, Reference Efrati, Sharon and KupfermanESK13, Reference Lewicka and MahadevanLM22]). The asymptotic stability result in [Reference Kupferman, Maor and ShacharKMS19], for example, implies that (as expected by physicists) if
![]() ${\mathcal M}$
cannot be immersed isometrically in
${\mathcal M}$
cannot be immersed isometrically in
![]() ${\mathcal N}$
, then the infimal elastic energy is positive, and the elastic body cannot release all of it stresses by, say, forming microstructures.
${\mathcal N}$
, then the infimal elastic energy is positive, and the elastic body cannot release all of it stresses by, say, forming microstructures.
Main result: asymptotic stability of isometric immersions in codimension-1
In this paper, we are concerned with codimension-1 versions of the above results. The classical theorem in this context (for a Euclidean target) is the fundamental theorem of surface theory (see, for example, [Reference TenenblatTen71]):
Let
![]() $({\mathcal M},\mathfrak {g})$
be an oriented, connected, simply connected, compact d-dimensional Riemannian manifold with Lipschitz boundary. Let S by a smooth symmetric
$({\mathcal M},\mathfrak {g})$
be an oriented, connected, simply connected, compact d-dimensional Riemannian manifold with Lipschitz boundary. Let S by a smooth symmetric
![]() $(1,1)$
tensor field on
$(1,1)$
tensor field on
![]() ${\mathcal M}$
. If
${\mathcal M}$
. If
![]() $\mathfrak {g}$
and S satisfy the Gauss-Codazzi compatibility conditions, then there exists a smooth isometric immersion
$\mathfrak {g}$
and S satisfy the Gauss-Codazzi compatibility conditions, then there exists a smooth isometric immersion
![]() $f:{\mathcal M}\to {\mathbb R}^{d+1}$
having shape operator S. This immersion is unique modulo a composition with a Euclidean rigid map.
$f:{\mathcal M}\to {\mathbb R}^{d+1}$
having shape operator S. This immersion is unique modulo a composition with a Euclidean rigid map.
We recall that for an immersion
![]() $f:{\mathcal M}\to {\mathbb R}^{d+1}$
, we can define the Gauss map
$f:{\mathcal M}\to {\mathbb R}^{d+1}$
, we can define the Gauss map
![]() $\mathfrak {n}_f:{\mathcal M} \to T{\mathbb R}^{d+1}\simeq {\mathbb R}^{d+1}$
, where
$\mathfrak {n}_f:{\mathcal M} \to T{\mathbb R}^{d+1}\simeq {\mathbb R}^{d+1}$
, where
![]() $\mathfrak {n}_f(q)$
is the unique unit vector such that
$\mathfrak {n}_f(q)$
is the unique unit vector such that
![]() $(df_q(u_1),\ldots ,df_q(u_d),\mathfrak {n}_f(q))$
is an oriented basis of
$(df_q(u_1),\ldots ,df_q(u_d),\mathfrak {n}_f(q))$
is an oriented basis of
![]() ${\mathbb R}^{d+1}$
for any oriented basis
${\mathbb R}^{d+1}$
for any oriented basis
![]() $(u_1,\ldots ,u_d)$
of
$(u_1,\ldots ,u_d)$
of
![]() $T_q({\mathcal M})$
. The second fundamental form of an immersion is a
$T_q({\mathcal M})$
. The second fundamental form of an immersion is a
![]() $(2,0)$
tensor which is given by
$(2,0)$
tensor which is given by
![]() $\operatorname {II}_f = -df^{T}\nabla \mathfrak {n}_f : T{\mathcal M}\times T{\mathcal M} \to {\mathbb R}$
; it contains the same information as the shape operator
$\operatorname {II}_f = -df^{T}\nabla \mathfrak {n}_f : T{\mathcal M}\times T{\mathcal M} \to {\mathbb R}$
; it contains the same information as the shape operator
![]() $S_f:T{\mathcal M}\to T{\mathcal M}$
, a (1,1) tensor implicitly defined via
$S_f:T{\mathcal M}\to T{\mathcal M}$
, a (1,1) tensor implicitly defined via
![]() $\nabla \mathfrak {n}_f = -df \circ S_f$
(which is well defined since the image of
$\nabla \mathfrak {n}_f = -df \circ S_f$
(which is well defined since the image of
![]() $\nabla \mathfrak {n}_f$
is normal to
$\nabla \mathfrak {n}_f$
is normal to
![]() $\mathfrak {n}_f$
, and thus in the image of
$\mathfrak {n}_f$
, and thus in the image of
![]() $df$
). Thus, given a metric
$df$
). Thus, given a metric
![]() $\mathfrak {g}$
and a (1,1) tensor S,
$\mathfrak {g}$
and a (1,1) tensor S,
![]() $f:{\mathcal M}\to {\mathbb R}^{d+1}$
is an isometric immersion having a shape operator S if
$f:{\mathcal M}\to {\mathbb R}^{d+1}$
is an isometric immersion having a shape operator S if
where
![]() $\mathfrak {e}$
is the Euclidean metric, and
$\mathfrak {e}$
is the Euclidean metric, and
![]() $\operatorname {O}(\mathfrak {g}_q,\mathfrak {e})$
is the set of isometric linear maps
$\operatorname {O}(\mathfrak {g}_q,\mathfrak {e})$
is the set of isometric linear maps
![]() $T_q{\mathcal M} \to {\mathbb R}^{d+1}$
.
$T_q{\mathcal M} \to {\mathbb R}^{d+1}$
.
The last clause of the fundamental theorem of surface theory is, again, a rigidity statement: An immersion
![]() $f:{\mathcal M}\to {\mathbb R}^{d+1}$
satisfying (1.1) is determined by the values of
$f:{\mathcal M}\to {\mathbb R}^{d+1}$
satisfying (1.1) is determined by the values of
![]() $f(q)$
and
$f(q)$
and
![]() $df_q$
at any
$df_q$
at any
![]() $q\in {\mathcal M}$
. This rigidity statement generalizes to any target
$q\in {\mathcal M}$
. This rigidity statement generalizes to any target
![]() $(d+1)$
-dimensional manifold
$(d+1)$
-dimensional manifold
![]() $({\mathcal N},\mathfrak {h})$
, by replacing in (1.1)
$({\mathcal N},\mathfrak {h})$
, by replacing in (1.1)
![]() $\mathfrak {e}$
with
$\mathfrak {e}$
with
![]() $\mathfrak {h}$
and
$\mathfrak {h}$
and
![]() $\nabla $
with
$\nabla $
with
![]() $\nabla ^{f^*T{\mathcal N}}$
, the pullback connection of the Levi-Civita connection of
$\nabla ^{f^*T{\mathcal N}}$
, the pullback connection of the Levi-Civita connection of
![]() $({\mathcal N},\mathfrak {h})$
, which is the natural derivative of vector fields in
$({\mathcal N},\mathfrak {h})$
, which is the natural derivative of vector fields in
![]() ${\mathcal N}$
along f – that is, maps that take
${\mathcal N}$
along f – that is, maps that take
![]() $p\in {\mathcal M}$
to a vector in
$p\in {\mathcal M}$
to a vector in
![]() $T_{f(p)}{\mathcal N}$
.Footnote
1
$T_{f(p)}{\mathcal N}$
.Footnote
1
The main focus of this article is the asymptotic stability of isometric immersions. The codimension-0 property of being
![]() $L^p$
-close to an orientation-preserving isometry is replaced by being
$L^p$
-close to an orientation-preserving isometry is replaced by being
![]() $L^p$
-close to first and second fundamental forms. For
$L^p$
-close to first and second fundamental forms. For
![]() $f:{\mathcal M}\to {\mathcal N}$
, we define
$f:{\mathcal M}\to {\mathcal N}$
, we define
The first term, denoted
![]() ${\mathcal E}_p^S(f)$
, is called a stretching energy, and the second term, denoted
${\mathcal E}_p^S(f)$
, is called a stretching energy, and the second term, denoted
![]() ${\mathcal E}_p^B(f)$
, is called a bending energy. As these names suggest, this energy is motivated by the elastic theory of thin bodies. There, one often compares the second fundamental forms (
${\mathcal E}_p^B(f)$
, is called a bending energy. As these names suggest, this energy is motivated by the elastic theory of thin bodies. There, one often compares the second fundamental forms (
![]() $(2,0)$
tensors) rather than the shape operators (
$(2,0)$
tensors) rather than the shape operators (
![]() $(1,1)$
tensors); from a physical point of view, these energies are equivalent, and using the shape operator is more convenient from a calculus of variations point of view. See [Reference Alpern, Kupferman and MaorAKM22] for further details and implications to elasticity theory.
$(1,1)$
tensors); from a physical point of view, these energies are equivalent, and using the shape operator is more convenient from a calculus of variations point of view. See [Reference Alpern, Kupferman and MaorAKM22] for further details and implications to elasticity theory.
The natural space on which the energy (1.2) is defined and finite is the space of p -Sobolev immersions,
where
![]() $\mathfrak {n}_f$
is the unit normal vector field in
$\mathfrak {n}_f$
is the unit normal vector field in
![]() ${\mathcal N}$
along f, which is defined a.e. Note that for such non-smooth maps, the pullback bundle
${\mathcal N}$
along f, which is defined a.e. Note that for such non-smooth maps, the pullback bundle
![]() $f^*T{\mathcal N}$
is a non-smooth bundle; we therefore define
$f^*T{\mathcal N}$
is a non-smooth bundle; we therefore define
![]() $\nabla ^{f^*T{\mathcal N}} \mathfrak {n}_f$
using a connector operator, as explained in the next section.
$\nabla ^{f^*T{\mathcal N}} \mathfrak {n}_f$
using a connector operator, as explained in the next section.
Our main result is the following:
Theorem 1.1. Suppose that there exists a sequence of p-immersions
![]() $f_n \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
,
$f_n \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
,
![]() $p\ge 1$
, satisfying
$p\ge 1$
, satisfying
Then there exists a subsequence of
![]() $f_n$
converging in
$f_n$
converging in
![]() $W^{1,p}({\mathcal M};{\mathcal N})$
to a smooth isometric immersion
$W^{1,p}({\mathcal M};{\mathcal N})$
to a smooth isometric immersion
![]() $f:({\mathcal M},\mathfrak {g}) \to ({\mathcal N},\mathfrak {h})$
. Furthermore,
$f:({\mathcal M},\mathfrak {g}) \to ({\mathcal N},\mathfrak {h})$
. Furthermore,
![]() $\mathfrak {n}_{f_n} \to \mathfrak {n}_f$
in
$\mathfrak {n}_{f_n} \to \mathfrak {n}_f$
in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
, and the shape operator of the limit equals the reference shape operator,
$W^{1,p}({\mathcal M};T{\mathcal N})$
, and the shape operator of the limit equals the reference shape operator,
![]() $\nabla ^{f^*T{\mathcal N}}\mathfrak {n}_f = - df\circ S$
.
$\nabla ^{f^*T{\mathcal N}}\mathfrak {n}_f = - df\circ S$
.
This result was obtained in [Reference Alpern, Kupferman and MaorAKM22] for the case where
![]() $({\mathcal N},\mathfrak {h})$
has constant sectional curvature. The proof there was essentially based on reducing the problem to the codimension-0 problem, by ‘thickening’
$({\mathcal N},\mathfrak {h})$
has constant sectional curvature. The proof there was essentially based on reducing the problem to the codimension-0 problem, by ‘thickening’
![]() $({\mathcal M},\mathfrak {g})$
into a
$({\mathcal M},\mathfrak {g})$
into a
![]() $(d+1)$
-dimensional manifold,
$(d+1)$
-dimensional manifold,
![]() $({\mathcal M}\times [-h,h],G)$
for some
$({\mathcal M}\times [-h,h],G)$
for some
![]() $h>0$
, extending f into a map
$h>0$
, extending f into a map
![]() $F: {\mathcal M}\times [-h,h]\to {\mathcal N}$
, and using the non-Euclidean version [Reference Kupferman, Maor and ShacharKMS19] of Reshetnyak’s stability theorem in codimension-0. This approach has difficulties generalizing beyond constant sectional curvature, since we exploited in constant curvature the fact that the metric G is uniquely determined by
$F: {\mathcal M}\times [-h,h]\to {\mathcal N}$
, and using the non-Euclidean version [Reference Kupferman, Maor and ShacharKMS19] of Reshetnyak’s stability theorem in codimension-0. This approach has difficulties generalizing beyond constant sectional curvature, since we exploited in constant curvature the fact that the metric G is uniquely determined by
![]() $\mathfrak {g}$
and S, independently of the maps
$\mathfrak {g}$
and S, independently of the maps
![]() $f_n$
.
$f_n$
.
We overcome this by using a different approach. As a first step, we need the following regularity theorem:
Theorem 1.2. Let
![]() $f\in \operatorname {Imm}_\infty ({\mathcal M};{\mathcal N})$
such that the first fundamental form
$f\in \operatorname {Imm}_\infty ({\mathcal M};{\mathcal N})$
such that the first fundamental form
![]() $f^*\mathfrak {h}$
and the shape operator
$f^*\mathfrak {h}$
and the shape operator
![]() $S_f$
, implicitly defined byFootnote
2
$S_f$
, implicitly defined byFootnote
2
are smooth. Then, f is smooth.
Note that if f was in
![]() $W^{2,p}$
, this result would follow by bootstrapping the expressions for the second derivatives in terms of the frame induced by
$W^{2,p}$
, this result would follow by bootstrapping the expressions for the second derivatives in terms of the frame induced by
![]() $df$
and
$df$
and
![]() $\mathfrak {n}_f$
. However, we only know that
$\mathfrak {n}_f$
. However, we only know that
![]() $f\in W^{1,\infty }$
and that
$f\in W^{1,\infty }$
and that
![]() $\mathfrak {n}_f\in W^{1,\infty }$
. The improved regularity is then deduced from compactness of low energy configurations of thin bodies of arbitrary dimension and codimension [Reference Kupferman and SolomonKS14], which, in turn, uses the FJM Euclidean rigidity estimate. It is interesting whether one can deduce Theorem 1.2 directly from elliptic regularity, as done in codimension-0, using an adaptation of the Piola identity to codimension-1 (see [Reference Kupferman, Maor and ShacharKMS19]).
$\mathfrak {n}_f\in W^{1,\infty }$
. The improved regularity is then deduced from compactness of low energy configurations of thin bodies of arbitrary dimension and codimension [Reference Kupferman and SolomonKS14], which, in turn, uses the FJM Euclidean rigidity estimate. It is interesting whether one can deduce Theorem 1.2 directly from elliptic regularity, as done in codimension-0, using an adaptation of the Piola identity to codimension-1 (see [Reference Kupferman, Maor and ShacharKMS19]).
Given this regularity result, it is sufficient, in order to prove Theorem 1.1, to prove that if
![]() ${\mathcal E}_p(f_n) \to 0$
, then
${\mathcal E}_p(f_n) \to 0$
, then
![]() $f_n$
converges in
$f_n$
converges in
![]() $W^{1.p}$
to a zero energy map. To this end, we deploy an approach using Young measures, first suggested for the proof of Reshetnyak’s asymptotic stability theorem in [Reference James, Kinderlehrer, Rascle, Serre and SlemrodJK89], and then developed in [Reference Kupferman, Maor and ShacharKMS19] for proving the non-Euclidean equivalent result. Since in our case, as in [Reference Kupferman, Maor and ShacharKMS19], the target space of
$W^{1.p}$
to a zero energy map. To this end, we deploy an approach using Young measures, first suggested for the proof of Reshetnyak’s asymptotic stability theorem in [Reference James, Kinderlehrer, Rascle, Serre and SlemrodJK89], and then developed in [Reference Kupferman, Maor and ShacharKMS19] for proving the non-Euclidean equivalent result. Since in our case, as in [Reference Kupferman, Maor and ShacharKMS19], the target space of
![]() $f_n$
is not a vector space, one needs to work in local coordinates in order to use the Young measure limit.
$f_n$
is not a vector space, one needs to work in local coordinates in order to use the Young measure limit.
As such, this approach works for
![]() $p>d$
, since only then, maps in
$p>d$
, since only then, maps in
![]() $W^{1,p}({\mathcal M};{\mathcal N})$
are guaranteed to be localizable. In [Reference Kupferman, Maor and ShacharKMS19], the lower integrability regime
$W^{1,p}({\mathcal M};{\mathcal N})$
are guaranteed to be localizable. In [Reference Kupferman, Maor and ShacharKMS19], the lower integrability regime
![]() $p\le d$
(which includes the most important case from the elasticity point of view,
$p\le d$
(which includes the most important case from the elasticity point of view,
![]() $p=2$
), is obtained by first approximating
$p=2$
), is obtained by first approximating
![]() $f_n$
by uniformly Lipschitz maps
$f_n$
by uniformly Lipschitz maps
![]() $\tilde {f}_n$
. A similar use of Lipschitz truncation for overcoming the localization problem of Sobolev maps between manifolds was done also in [Reference Krömer and MüllerKM21].
$\tilde {f}_n$
. A similar use of Lipschitz truncation for overcoming the localization problem of Sobolev maps between manifolds was done also in [Reference Krömer and MüllerKM21].
This approach, however, does not work directly on the energy
![]() ${\mathcal E}_p$
, since it is not clear how to approximate immersions in
${\mathcal E}_p$
, since it is not clear how to approximate immersions in
![]() $\operatorname {Imm}_p({\mathcal M};{\mathcal N})$
by Lipschitz immersions (the immersion property is lost in the truncation process). To overcome this difficulty, we first relax the energy
$\operatorname {Imm}_p({\mathcal M};{\mathcal N})$
by Lipschitz immersions (the immersion property is lost in the truncation process). To overcome this difficulty, we first relax the energy
![]() ${\mathcal E}_p$
into an energy
${\mathcal E}_p$
into an energy
![]() $\tilde {{\mathcal E}}_p: W^{1,p}({\mathcal M};T{\mathcal N}) \to [0,\infty )$
(see Definition 3.1), which is defined and finite over all vector fields in
$\tilde {{\mathcal E}}_p: W^{1,p}({\mathcal M};T{\mathcal N}) \to [0,\infty )$
(see Definition 3.1), which is defined and finite over all vector fields in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
, and not only for vector fields that are perpendicular to their projection on
$W^{1,p}({\mathcal M};T{\mathcal N})$
, and not only for vector fields that are perpendicular to their projection on
![]() ${\mathcal N}$
, as in
${\mathcal N}$
, as in
![]() $\operatorname {Imm}_p({\mathcal M};{\mathcal N})$
. From an elasticity point of view, the energy
$\operatorname {Imm}_p({\mathcal M};{\mathcal N})$
. From an elasticity point of view, the energy
![]() $\tilde {{\mathcal E}}_p$
is essentially an energy for director fields, rather than configurations of the elastic body. Thus, we prove a stronger version of Theorem 1.1 for the energy
$\tilde {{\mathcal E}}_p$
is essentially an energy for director fields, rather than configurations of the elastic body. Thus, we prove a stronger version of Theorem 1.1 for the energy
![]() $\tilde {{\mathcal E}}_p$
(Theorem 3.4) by applying Young measures for the case
$\tilde {{\mathcal E}}_p$
(Theorem 3.4) by applying Young measures for the case
![]() $p>d$
, and precede this analysis with a Lipschitz truncation for
$p>d$
, and precede this analysis with a Lipschitz truncation for
![]() $p\le d$
, to get to the localizable regime.
$p\le d$
, to get to the localizable regime.
Additional quantitative stability result
In the appendix, we include a short quantitative stability result, in the spirit of the FJM estimate.
We show in Theorem A.1 that if
![]() ${\mathcal N} = {\mathbb R}^{d+1}$
,
${\mathcal N} = {\mathbb R}^{d+1}$
,
![]() $p\in (1,\infty )$
, and if the metric
$p\in (1,\infty )$
, and if the metric
![]() $\mathfrak {g}$
of
$\mathfrak {g}$
of
![]() ${\mathcal M}$
and shape operator S are compatible (i.e., if there exists an isometric immersion
${\mathcal M}$
and shape operator S are compatible (i.e., if there exists an isometric immersion
![]() ${\mathcal M}\to {\mathbb R}^{d+1}$
with shape operator S), then for any
${\mathcal M}\to {\mathbb R}^{d+1}$
with shape operator S), then for any
![]() $f\in \operatorname {Imm}_p({\mathcal M};{\mathbb R}^{d+1})$
, there exists an isometric immersion
$f\in \operatorname {Imm}_p({\mathcal M};{\mathbb R}^{d+1})$
, there exists an isometric immersion
![]() $f_0:{\mathcal M}\to {\mathbb R}^{d+1}$
with shape operator S such that
$f_0:{\mathcal M}\to {\mathbb R}^{d+1}$
with shape operator S such that
where
![]() $C>0$
is a constant independent of f. In particular, this implies Theorem 1.1 for a Euclidean target space, under the assumption of compatibility. Similar results, comparing the left-hand side of two immersions with an energy that measures stretching (discrepancy of the first fundamental forms) and bending (discrepancy of the second fundamental form), appear in [Reference Ciarlet, Malin and MardareCMM19] (in particular, Theorem 4.3). These results, however, require f to be in
$C>0$
is a constant independent of f. In particular, this implies Theorem 1.1 for a Euclidean target space, under the assumption of compatibility. Similar results, comparing the left-hand side of two immersions with an energy that measures stretching (discrepancy of the first fundamental forms) and bending (discrepancy of the second fundamental form), appear in [Reference Ciarlet, Malin and MardareCMM19] (in particular, Theorem 4.3). These results, however, require f to be in
![]() $\operatorname {Imm}_q({\mathcal M};{\mathbb R}^{d+1})$
for
$\operatorname {Imm}_q({\mathcal M};{\mathbb R}^{d+1})$
for
![]() $q\ge \min \{p,2\}$
, and, more importantly, require a priori uniform bounds on the first and second fundamental forms; Theorem A.1 does not require such a priori bounds, and also admits a simpler proof. Additionally, Theorem A.1 can be generalized to director fields, using the relaxed energy
$q\ge \min \{p,2\}$
, and, more importantly, require a priori uniform bounds on the first and second fundamental forms; Theorem A.1 does not require such a priori bounds, and also admits a simpler proof. Additionally, Theorem A.1 can be generalized to director fields, using the relaxed energy
![]() $\tilde {{\mathcal E}}_p$
(Definition 3.1), whereas the result of [Reference Ciarlet, Malin and MardareCMM19] cannot. The difference is mainly because of the different structures of the stretching and bending energy (in [Reference Ciarlet, Malin and MardareCMM19], the bending energy measures a discrepancy in the second fundamental forms rather than in the shape operators). This can be seen as additional evidence that the energy
$\tilde {{\mathcal E}}_p$
(Definition 3.1), whereas the result of [Reference Ciarlet, Malin and MardareCMM19] cannot. The difference is mainly because of the different structures of the stretching and bending energy (in [Reference Ciarlet, Malin and MardareCMM19], the bending energy measures a discrepancy in the second fundamental forms rather than in the shape operators). This can be seen as additional evidence that the energy
![]() ${\mathcal E}_p$
is the natural ‘stretching plus bending’ energy from a calculus of variations point of view.
${\mathcal E}_p$
is the natural ‘stretching plus bending’ energy from a calculus of variations point of view.
Structure of the paper
In Section 2, we review the definitions of Sobolev spaces between manifolds and prove some basic properties – in particular, for Sobolev vector fields. We also introduce coordinate representations of the energy and the main fields in Section 2.1. In Section 3, we define the relaxed energy (Section 3.1) and prove Theorem 1.1, modulo the smoothness result (Theorem 1.2), which we proof in Section 4. Finally, we prove in Appendix A the codimension-1 Euclidean stability result. Figure 1 displays a table in which our results are put in context with the existing literature.

Figure 1 A summary of the results presented in the introduction. This list is not comprehensive: there are many other results on regularity of isometries (e.g., [Reference HartmanHar58, Reference Calabi and HartmanCH70, Reference TaylorTay06]), of isometric immersions without assumptions on the second fundamental form (e.g., [Reference PakzadPak04, Reference Müller and PakzadMP05, Reference HornungHor11, Reference Liu and PakzadLP13, Reference Jerrard and PakzadJP17, Reference Hornung and VelčićHV18]), and of stability of immersions in Euclidean setting in various topologies, stronger than the
![]() $L^p$
stability discussed here [Reference CiarletCia03, Reference Ciarlet and MardareCM16, Reference Ciarlet and MardareCM19, Reference Ciarlet, Malin and MardareCMM20].
$L^p$
stability discussed here [Reference CiarletCia03, Reference Ciarlet and MardareCM16, Reference Ciarlet and MardareCM19, Reference Ciarlet, Malin and MardareCMM20].
Notations
Let
![]() $(V,\mathfrak {g})$
and
$(V,\mathfrak {g})$
and
![]() $(W,\mathfrak {h})$
be oriented inner-product spaces. We denote the inner-products by
$(W,\mathfrak {h})$
be oriented inner-product spaces. We denote the inner-products by
![]() $\langle \cdot ,\cdot \rangle _{\mathfrak {g}}$
and
$\langle \cdot ,\cdot \rangle _{\mathfrak {g}}$
and
![]() $\langle \cdot ,\cdot \rangle _{\mathfrak {h}}$
. We denote the corresponding norms by
$\langle \cdot ,\cdot \rangle _{\mathfrak {h}}$
. We denote the corresponding norms by
![]() $|\cdot |$
, unless the notations
$|\cdot |$
, unless the notations
![]() $|\cdot |_{\mathfrak {g}}$
and
$|\cdot |_{\mathfrak {g}}$
and
![]() $|\cdot |_{\mathfrak {h}}$
help readability. We denote by
$|\cdot |_{\mathfrak {h}}$
help readability. We denote by
![]() $\operatorname {Hom}(V,W)$
the space of linear maps from V to W; we denote by
$\operatorname {Hom}(V,W)$
the space of linear maps from V to W; we denote by
![]() $\operatorname {O}(\mathfrak {g},\mathfrak {h})\subset \operatorname {Hom}(V,W)$
the subset of orthogonal maps. If V and W have equal dimensions, we denote by
$\operatorname {O}(\mathfrak {g},\mathfrak {h})\subset \operatorname {Hom}(V,W)$
the subset of orthogonal maps. If V and W have equal dimensions, we denote by
![]() $\operatorname {SO}(\mathfrak {g},\mathfrak {h})\subset \operatorname {O}(\mathfrak {g},\mathfrak {h})$
the set of orientation-preserving orthogonal maps. We denote the norm on
$\operatorname {SO}(\mathfrak {g},\mathfrak {h})\subset \operatorname {O}(\mathfrak {g},\mathfrak {h})$
the set of orientation-preserving orthogonal maps. We denote the norm on
![]() $\operatorname {Hom}(V,W)$
induced by
$\operatorname {Hom}(V,W)$
induced by
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {h}$
by
$\mathfrak {h}$
by
![]() $|\cdot |$
, rather than by the more cumbersome notation
$|\cdot |$
, rather than by the more cumbersome notation
![]() $|\cdot |_{\mathfrak {g},\mathfrak {h}}$
. For a set
$|\cdot |_{\mathfrak {g},\mathfrak {h}}$
. For a set
![]() $K\subset \operatorname {Hom}(V,W)$
and
$K\subset \operatorname {Hom}(V,W)$
and
![]() $A\in \operatorname {Hom}(V,W)$
, we denote by
$A\in \operatorname {Hom}(V,W)$
, we denote by
![]() $\operatorname {dist}(A,K)$
the distance (with respect to the norm
$\operatorname {dist}(A,K)$
the distance (with respect to the norm
![]() $|\cdot |$
) between the element A and the set K. These notations carry on naturally if V and W are replaced by vector bundles over a manifold (in particular, to the tangent bundle endowed with a Riemannian metric).
$|\cdot |$
) between the element A and the set K. These notations carry on naturally if V and W are replaced by vector bundles over a manifold (in particular, to the tangent bundle endowed with a Riemannian metric).
For a manifold
![]() ${\mathcal M}$
, we denote by
${\mathcal M}$
, we denote by
![]() $\Omega ^k({\mathcal M})$
the space of k-forms on
$\Omega ^k({\mathcal M})$
the space of k-forms on
![]() ${\mathcal M}$
. For a vector bundle
${\mathcal M}$
. For a vector bundle
![]() $E\to {\mathcal M}$
, we denote by
$E\to {\mathcal M}$
, we denote by
![]() $\Gamma (E)$
the space of sections of E, and by
$\Gamma (E)$
the space of sections of E, and by
![]() $\Omega ^k({\mathcal M};E)$
the space of E-valued k-forms on
$\Omega ^k({\mathcal M};E)$
the space of E-valued k-forms on
![]() ${\mathcal M}$
. Likewise, we denote by
${\mathcal M}$
. Likewise, we denote by
![]() $L^p\Gamma (E)$
,
$L^p\Gamma (E)$
,
![]() $L^p\Omega ^k({\mathcal M};E)$
,
$L^p\Omega ^k({\mathcal M};E)$
,
![]() $W^{1,p}\Gamma (E)$
and
$W^{1,p}\Gamma (E)$
and
![]() $W^{1,p}\Omega ^k({\mathcal M};E)$
the corresponding spaces having
$W^{1,p}\Omega ^k({\mathcal M};E)$
the corresponding spaces having
![]() $L^p$
- and
$L^p$
- and
![]() $W^{1,p}$
-regularity; the corresponding norms are induced by norms on
$W^{1,p}$
-regularity; the corresponding norms are induced by norms on
![]() $T{\mathcal M}$
and E. Finally, for a Riemannian manifold
$T{\mathcal M}$
and E. Finally, for a Riemannian manifold
![]() $({\mathcal M},\mathfrak {g})$
,
$({\mathcal M},\mathfrak {g})$
,
![]() $\text {d}\text {Vol}_{\mathfrak {g}}$
denotes the Riemannian volume form. More notations are introduced in the next section in the context of mappings between manifolds.
$\text {d}\text {Vol}_{\mathfrak {g}}$
denotes the Riemannian volume form. More notations are introduced in the next section in the context of mappings between manifolds.
2 Sobolev maps between manifolds
This work is concerned with Sobolev maps between Riemannian manifolds. Let
![]() $({\mathcal M},\mathfrak {g})$
and
$({\mathcal M},\mathfrak {g})$
and
![]() $(\mathfrak {X},\mathfrak {x})$
be Riemannian manifolds of arbitrary dimensions, with
$(\mathfrak {X},\mathfrak {x})$
be Riemannian manifolds of arbitrary dimensions, with
![]() ${\mathcal M}$
compact, possibly with boundary, and
${\mathcal M}$
compact, possibly with boundary, and
![]() $\mathfrak {X}$
without boundary (in the sequel,
$\mathfrak {X}$
without boundary (in the sequel,
![]() $(\mathfrak {X},\mathfrak {x})$
is either a compact Riemannian manifold
$(\mathfrak {X},\mathfrak {x})$
is either a compact Riemannian manifold
![]() $({\mathcal N},\mathfrak {h})$
, or its non-compact tangent space
$({\mathcal N},\mathfrak {h})$
, or its non-compact tangent space
![]() $(T{\mathcal N},S^{\mathfrak {h}})$
, where the metric
$(T{\mathcal N},S^{\mathfrak {h}})$
, where the metric
![]() $S^{\mathfrak {h}}$
is described below). For smooth
$S^{\mathfrak {h}}$
is described below). For smooth
![]() $f:{\mathcal M}\to \mathfrak {X}$
, we denote by
$f:{\mathcal M}\to \mathfrak {X}$
, we denote by
![]() $Df:T{\mathcal M}\to T\mathfrak {X}$
the tangent map, acting as
$Df:T{\mathcal M}\to T\mathfrak {X}$
the tangent map, acting as
which is a linear bundle morphism covering f (e.g., [Reference SaundersSau89, Chap. 2]). The map
![]() $Df$
should be distinguished from the differential
$Df$
should be distinguished from the differential
![]() $df\in \Gamma (T^*{\mathcal M}\otimes f^*T\mathfrak {X})$
, acting as
$df\in \Gamma (T^*{\mathcal M}\otimes f^*T\mathfrak {X})$
, acting as
which is a linear bundle map;
![]() $df$
is the pullback of
$df$
is the pullback of
![]() $Df$
, where as common,
$Df$
, where as common,
![]() $f^*T\mathfrak {X}$
denotes a vector bundle over
$f^*T\mathfrak {X}$
denotes a vector bundle over
![]() ${\mathcal M}$
, with the canonical identification
${\mathcal M}$
, with the canonical identification
![]() $(f^*T\mathfrak {X})_q \simeq T_{f(q)}\mathfrak {X}$
.
$(f^*T\mathfrak {X})_q \simeq T_{f(q)}\mathfrak {X}$
.
For
![]() $p\ge 1$
, the space of Sobolev maps
$p\ge 1$
, the space of Sobolev maps
![]() $W^{1,p}({\mathcal M};\mathfrak {X})$
can be defined intrinsically, along with a notion of a weak derivative (see Convent and van Schaftingen [Reference Convent and Van SchaftingenCS16] for a recent account). An equivalent extrinsic (and more common) definition is given by using Nash’s embedding theorem, introducing an isometric embedding
$W^{1,p}({\mathcal M};\mathfrak {X})$
can be defined intrinsically, along with a notion of a weak derivative (see Convent and van Schaftingen [Reference Convent and Van SchaftingenCS16] for a recent account). An equivalent extrinsic (and more common) definition is given by using Nash’s embedding theorem, introducing an isometric embedding
![]() $\iota :(\mathfrak {X},\mathfrak {x})\to ({\mathbb R}^D,\mathfrak {e})$
, for some D large enough. Then,
$\iota :(\mathfrak {X},\mathfrak {x})\to ({\mathbb R}^D,\mathfrak {e})$
, for some D large enough. Then,
This space inherits the strong and weak topologies of
![]() $W^{1,p}({\mathcal M};{\mathbb R}^D)$
, and it is independent of the embedding
$W^{1,p}({\mathcal M};{\mathbb R}^D)$
, and it is independent of the embedding
![]() $\iota $
. Moreover,
$\iota $
. Moreover,
![]() $\iota \circ W^{1,p}({\mathcal M};\mathfrak {X})$
is a weakly closed subset of
$\iota \circ W^{1,p}({\mathcal M};\mathfrak {X})$
is a weakly closed subset of
![]() $W^{1,p}({\mathcal M};{\mathbb R}^D)$
, and in particular, bounded sequences have weakly convergent subsequences for
$W^{1,p}({\mathcal M};{\mathbb R}^D)$
, and in particular, bounded sequences have weakly convergent subsequences for
![]() $p\in (1,\infty )$
. That is, if
$p\in (1,\infty )$
. That is, if
![]() $f_n \in W^{1,p}({\mathcal M};\mathfrak {X})$
satisfies that
$f_n \in W^{1,p}({\mathcal M};\mathfrak {X})$
satisfies that
![]() $\iota \circ f_n$
is bounded in
$\iota \circ f_n$
is bounded in
![]() $W^{1,p}({\mathcal M};{\mathbb R}^D)$
, then there exists a subsequence and an
$W^{1,p}({\mathcal M};{\mathbb R}^D)$
, then there exists a subsequence and an
![]() $f \in W^{1,p}({\mathcal M};\mathfrak {X})$
such that
$f \in W^{1,p}({\mathcal M};\mathfrak {X})$
such that
![]() $f_n\rightharpoonup f$
in
$f_n\rightharpoonup f$
in
![]() $W^{1,p}({\mathcal M};\mathfrak {X})$
, which by definition means that
$W^{1,p}({\mathcal M};\mathfrak {X})$
, which by definition means that
![]() $\iota \circ f_n \rightharpoonup \iota \circ f$
in
$\iota \circ f_n \rightharpoonup \iota \circ f$
in
![]() $W^{1,p}({\mathcal M};{\mathbb R}^D)$
. Even though
$W^{1,p}({\mathcal M};{\mathbb R}^D)$
. Even though
![]() $df$
has to be interpreted as a weak derivative, it still holds that
$df$
has to be interpreted as a weak derivative, it still holds that
![]() $df_q$
is a linear map from
$df_q$
is a linear map from
![]() $T_q{\mathcal M}$
to
$T_q{\mathcal M}$
to
![]() $T_{f(q)}\mathfrak {X}$
for almost every
$T_{f(q)}\mathfrak {X}$
for almost every
![]() $q\in {\mathcal M}$
. Furthermore, the chain rule holds a.e.,
$q\in {\mathcal M}$
. Furthermore, the chain rule holds a.e.,
![]() $D(\iota \circ f) = D\iota \circ Df$
[Reference Convent and Van SchaftingenCS16, Prop. 1.8].
$D(\iota \circ f) = D\iota \circ Df$
[Reference Convent and Van SchaftingenCS16, Prop. 1.8].
Our choice of working with the tangent map
![]() $Df$
rather than the differential
$Df$
rather than the differential
![]() $df$
is due to the following. When f is a Sobolev map, the pullback bundle
$df$
is due to the following. When f is a Sobolev map, the pullback bundle
![]() $f^*T\mathfrak {X}$
is a not a smooth vector bundle, and consequently,
$f^*T\mathfrak {X}$
is a not a smooth vector bundle, and consequently,
![]() $df$
is a bundle map into a non-smooth vector bundle; this is in contrast with the tangent map
$df$
is a bundle map into a non-smooth vector bundle; this is in contrast with the tangent map
![]() $Df$
, which is a map between two smooth vector bundles,
$Df$
, which is a map between two smooth vector bundles,
![]() $T{\mathcal M}$
and
$T{\mathcal M}$
and
![]() $T\mathfrak {X}$
. The price to pay is that
$T\mathfrak {X}$
. The price to pay is that
![]() $Df$
is not a linear vector bundle map, but rather a linear bundle morphism.
$Df$
is not a linear vector bundle map, but rather a linear bundle morphism.
Note that if
![]() $\iota :(\mathfrak {X},\mathfrak {x})\to ({\mathbb R}^D,\mathfrak {e})$
is an isometric embedding, then by our convention,
$\iota :(\mathfrak {X},\mathfrak {x})\to ({\mathbb R}^D,\mathfrak {e})$
is an isometric embedding, then by our convention,
which is an embedding of
![]() $T\mathfrak {X}$
into Euclidean space (though not necessarily isometric), whereas
$T\mathfrak {X}$
into Euclidean space (though not necessarily isometric), whereas
is not an embedding. For
![]() $f\in W^{1,p}({\mathcal M},\mathfrak {X})$
,
$f\in W^{1,p}({\mathcal M},\mathfrak {X})$
,
is an immersion if f is an immersion, whereas
is not. In this context,
![]() $T^*{\mathcal M}\otimes T\mathfrak {X}$
is a vector bundle over
$T^*{\mathcal M}\otimes T\mathfrak {X}$
is a vector bundle over
![]() ${\mathcal M}\times \mathfrak {X}$
, and the latter can be viewed as a fiber bundle over
${\mathcal M}\times \mathfrak {X}$
, and the latter can be viewed as a fiber bundle over
![]() ${\mathcal M}$
. A section of
${\mathcal M}$
. A section of
![]() $T^*{\mathcal M}\otimes T\mathfrak {X}\to {\mathcal M}$
is a map
$T^*{\mathcal M}\otimes T\mathfrak {X}\to {\mathcal M}$
is a map
![]() $\zeta :{\mathcal M}\to T^*{\mathcal M}\otimes T\mathfrak {X}$
, such that for
$\zeta :{\mathcal M}\to T^*{\mathcal M}\otimes T\mathfrak {X}$
, such that for
![]() $q\in {\mathcal M}$
,
$q\in {\mathcal M}$
,
![]() $\zeta (q)$
is a linear map from
$\zeta (q)$
is a linear map from
![]() $T_q{\mathcal M}$
to
$T_q{\mathcal M}$
to
![]() $T_{\pi (\zeta (q))}\mathfrak {X}$
. Moreover, we interpret
$T_{\pi (\zeta (q))}\mathfrak {X}$
. Moreover, we interpret
![]() $D\iota \circ \zeta : {\mathcal M}\to {\mathbb R}^D\times (T^*{\mathcal M}\otimes {\mathbb R}^D)$
– that is,
$D\iota \circ \zeta : {\mathcal M}\to {\mathbb R}^D\times (T^*{\mathcal M}\otimes {\mathbb R}^D)$
– that is,
![]() $D\iota $
only acts here on the
$D\iota $
only acts here on the
![]() $T\mathfrak {X}$
component. We define
$T\mathfrak {X}$
component. We define
Finally, for
![]() $\xi :{\mathcal M}\to T\mathfrak {X}$
, we denote
$\xi :{\mathcal M}\to T\mathfrak {X}$
, we denote
(that is, for
![]() $q\in {\mathcal M}$
, the norm only captures the linear part of the mapping
$q\in {\mathcal M}$
, the norm only captures the linear part of the mapping
![]() $\xi (q)\in T_{\pi (\xi (q))}\mathfrak {X}$
).
$\xi (q)\in T_{\pi (\xi (q))}\mathfrak {X}$
).
When
![]() $p>\dim {\mathcal M}$
, one can equivalently define
$p>\dim {\mathcal M}$
, one can equivalently define
![]() $W^{1,p}({\mathcal M};\mathfrak {X})$
as the set of continuous functions, which upon composition with charts in
$W^{1,p}({\mathcal M};\mathfrak {X})$
as the set of continuous functions, which upon composition with charts in
![]() ${\mathcal M}$
and
${\mathcal M}$
and
![]() $\mathfrak {X}$
are in
$\mathfrak {X}$
are in
![]() $W^{1,p}({\mathbb R}^{\dim {\mathcal M}};{\mathbb R}^{\dim \mathfrak {X}})$
; strong convergence in
$W^{1,p}({\mathbb R}^{\dim {\mathcal M}};{\mathbb R}^{\dim \mathfrak {X}})$
; strong convergence in
![]() $W^{1,p}({\mathcal M};\mathfrak {X})$
is equivalent to strong convergence in every coordinate chart [Reference WehrheimWeh04, Lemmata B.5, B.7].
$W^{1,p}({\mathcal M};\mathfrak {X})$
is equivalent to strong convergence in every coordinate chart [Reference WehrheimWeh04, Lemmata B.5, B.7].
Sobolev vector fields
Given two compact Riemannian manifolds
![]() $({\mathcal M},\mathfrak {g})$
and
$({\mathcal M},\mathfrak {g})$
and
![]() $({\mathcal N},\mathfrak {h})$
, we apply the above construction to Sobolev maps from
$({\mathcal N},\mathfrak {h})$
, we apply the above construction to Sobolev maps from
![]() ${\mathcal M}$
into vector fields in
${\mathcal M}$
into vector fields in
![]() ${\mathcal N}$
(i.e., to maps
${\mathcal N}$
(i.e., to maps
![]() $\xi : {\mathcal M}\to T{\mathcal N}$
). To this end, we need to introduce a Riemannian metric on
$\xi : {\mathcal M}\to T{\mathcal N}$
). To this end, we need to introduce a Riemannian metric on
![]() $T{\mathcal N}$
.
$T{\mathcal N}$
.
The Riemannian metric
![]() $\mathfrak {h}$
on
$\mathfrak {h}$
on
![]() $T{\mathcal N}$
induces in a canonical way a Riemannian metric on
$T{\mathcal N}$
induces in a canonical way a Riemannian metric on
![]() $T{\mathcal N}$
. Specifically, there exists a one-to-one correspondence between an affine connection
$T{\mathcal N}$
. Specifically, there exists a one-to-one correspondence between an affine connection
![]() $\nabla $
on
$\nabla $
on
![]() $T{\mathcal N}$
and a connector operator,
$T{\mathcal N}$
and a connector operator,
![]() $K: TT{\mathcal N}\to T{\mathcal N}$
, such that for
$K: TT{\mathcal N}\to T{\mathcal N}$
, such that for
![]() $q\in {\mathcal N}$
and
$q\in {\mathcal N}$
and
![]() $s\in T_q{\mathcal N}$
,
$s\in T_q{\mathcal N}$
,
The connector induces the covariant derivative via
Denote by
![]() $x\in {\mathbb R}^{\dim {\mathcal N}}$
coordinates on
$x\in {\mathbb R}^{\dim {\mathcal N}}$
coordinates on
![]() ${\mathcal N}$
; by choosing a local frame field in this coordinate patch, we obtain local coordinates
${\mathcal N}$
; by choosing a local frame field in this coordinate patch, we obtain local coordinates
![]() $(x,v)\in {\mathbb R}^{2\dim {\mathcal N}}$
of
$(x,v)\in {\mathbb R}^{2\dim {\mathcal N}}$
of
![]() $T{\mathcal N}$
. We denote the associated coordinates on
$T{\mathcal N}$
. We denote the associated coordinates on
![]() $TT{\mathcal N}$
by
$TT{\mathcal N}$
by
![]() $(x,v,w,s)\in {\mathbb R}^{4\dim {\mathcal N}}$
. In these coordinates, the projection
$(x,v,w,s)\in {\mathbb R}^{4\dim {\mathcal N}}$
. In these coordinates, the projection
![]() $\pi :T{\mathcal N}\to {\mathcal N}$
is given by
$\pi :T{\mathcal N}\to {\mathcal N}$
is given by
![]() $\pi (x,v) = x$
, its derivative
$\pi (x,v) = x$
, its derivative
![]() $D\pi :TT{\mathcal N}\to T{\mathcal N}$
by
$D\pi :TT{\mathcal N}\to T{\mathcal N}$
by
![]() $D\pi (x,v,w,s) = (x,w)$
, and the connector K is given by
$D\pi (x,v,w,s) = (x,w)$
, and the connector K is given by
where
![]() $\Gamma :{\mathbb R}^{\dim {\mathcal N}}\to \operatorname {Bil}({\mathbb R}^{\dim {\mathcal N}})$
is a smooth map into the space of bilinear maps on
$\Gamma :{\mathbb R}^{\dim {\mathcal N}}\to \operatorname {Bil}({\mathbb R}^{\dim {\mathcal N}})$
is a smooth map into the space of bilinear maps on
![]() ${\mathbb R}^{\dim {\mathcal N}}$
(representing the Christoffel symbols). In the following, we will always take the Levi-Civita connection
${\mathbb R}^{\dim {\mathcal N}}$
(representing the Christoffel symbols). In the following, we will always take the Levi-Civita connection
![]() $\nabla ^{\mathfrak {h}}$
, and its corresponding connector
$\nabla ^{\mathfrak {h}}$
, and its corresponding connector
![]() $K^{\mathfrak {h}}$
.
$K^{\mathfrak {h}}$
.
The map
![]() $D\pi \times K^{\mathfrak {h}} :TT{\mathcal N}\to T{\mathcal N}\times _{\mathcal N} T{\mathcal N}$
is a linear bundle isomorphism (covering the projection
$D\pi \times K^{\mathfrak {h}} :TT{\mathcal N}\to T{\mathcal N}\times _{\mathcal N} T{\mathcal N}$
is a linear bundle isomorphism (covering the projection
![]() $\pi :T{\mathcal N}\to {\mathcal N}$
), turned into an isometry by introducing the Sasaki metric
$\pi :T{\mathcal N}\to {\mathcal N}$
), turned into an isometry by introducing the Sasaki metric
![]() $S^{\mathfrak {h}}$
on
$S^{\mathfrak {h}}$
on
![]() $TT{\mathcal N}$
[Reference SasakiSas58],
$TT{\mathcal N}$
[Reference SasakiSas58],
By choosing an isometric embedding
![]() $\iota :(T{\mathcal N},S^{\mathfrak {h}}) \to ({\mathbb R}^D,\mathfrak {e})$
, where
$\iota :(T{\mathcal N},S^{\mathfrak {h}}) \to ({\mathbb R}^D,\mathfrak {e})$
, where
![]() $\mathfrak {e}$
is the Euclidean metric, that is,
$\mathfrak {e}$
is the Euclidean metric, that is,
we can define the Sobolev space
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
as above.
$W^{1,p}({\mathcal M};T{\mathcal N})$
as above.
The zero section
![]() $\zeta \in \Gamma (T{\mathcal N})$
is an isometric embedding of
$\zeta \in \Gamma (T{\mathcal N})$
is an isometric embedding of
![]() $({\mathcal N},\mathfrak {h})$
into
$({\mathcal N},\mathfrak {h})$
into
![]() $(T{\mathcal N},S^{\mathfrak {h}})$
: indeed, for
$(T{\mathcal N},S^{\mathfrak {h}})$
: indeed, for
![]() $q\in {\mathcal N}$
and
$q\in {\mathcal N}$
and
![]() $v,w\in T_q{\mathcal N}$
,
$v,w\in T_q{\mathcal N}$
,
 $$ \begin{align*} \langle v,w \rangle_{\zeta^\#S^{\mathfrak{h}}} &= \langle D\zeta(v),D\zeta(w) \rangle_{S^{\mathfrak{h}}} \\ &= \langle D\pi\circ D\zeta(v),D\pi \circ D\zeta(v) \rangle_{\mathfrak{h}} + \langle K^{\mathfrak{h}}\circ D\zeta(v),K^{\mathfrak{h}}\circ D\zeta(v) \rangle_{\mathfrak{h}} \\ &= \langle v,w \rangle_{\mathfrak{h}}, \end{align*} $$
$$ \begin{align*} \langle v,w \rangle_{\zeta^\#S^{\mathfrak{h}}} &= \langle D\zeta(v),D\zeta(w) \rangle_{S^{\mathfrak{h}}} \\ &= \langle D\pi\circ D\zeta(v),D\pi \circ D\zeta(v) \rangle_{\mathfrak{h}} + \langle K^{\mathfrak{h}}\circ D\zeta(v),K^{\mathfrak{h}}\circ D\zeta(v) \rangle_{\mathfrak{h}} \\ &= \langle v,w \rangle_{\mathfrak{h}}, \end{align*} $$
where the first equality is the definition of the pullback metric
![]() $\zeta ^\# S^{\mathfrak {h}}$
, and in the last passage we used the fact that
$\zeta ^\# S^{\mathfrak {h}}$
, and in the last passage we used the fact that
![]() $D\pi \circ D\zeta = {\operatorname {Id}}_{T{\mathcal N}}$
and
$D\pi \circ D\zeta = {\operatorname {Id}}_{T{\mathcal N}}$
and
![]() $K^{\mathfrak {h}}\circ D\zeta =0$
. Thus,
$K^{\mathfrak {h}}\circ D\zeta =0$
. Thus,
![]() $\jmath : {\mathcal N}\to {\mathbb R}^D$
given by
$\jmath : {\mathcal N}\to {\mathbb R}^D$
given by
![]() $\jmath = \iota \circ \zeta $
is an isometric embedding of
$\jmath = \iota \circ \zeta $
is an isometric embedding of
![]() $({\mathcal N},\mathfrak {h})$
into
$({\mathcal N},\mathfrak {h})$
into
![]() $({\mathbb R}^D,\mathfrak {e})$
(although for our uses, one can choose any other isometric embedding of
$({\mathbb R}^D,\mathfrak {e})$
(although for our uses, one can choose any other isometric embedding of
![]() ${\mathcal N}$
into Euclidean space).
${\mathcal N}$
into Euclidean space).
For a map
![]() $\xi :{\mathcal M}\to T{\mathcal N}$
, we denote
$\xi :{\mathcal M}\to T{\mathcal N}$
, we denote
![]() $f_\xi = \pi \circ \xi : {\mathcal M}\to {\mathcal N}$
. Note that by the definition of the Sasaki metric,
$f_\xi = \pi \circ \xi : {\mathcal M}\to {\mathcal N}$
. Note that by the definition of the Sasaki metric,
or equivalently,
(Note that
![]() $d\jmath :T{\mathcal N}\to {\mathbb R}^D$
rather than
$d\jmath :T{\mathcal N}\to {\mathbb R}^D$
rather than
![]() $\iota :T{\mathcal N}\to {\mathbb R}^D$
is the linear isometry.) The following lemma asserts that strong and weak convergence of a sequence
$\iota :T{\mathcal N}\to {\mathbb R}^D$
is the linear isometry.) The following lemma asserts that strong and weak convergence of a sequence
![]() $\xi _n$
implies the corresponding convergence of
$\xi _n$
implies the corresponding convergence of
![]() $f_{\xi _n}$
.
$f_{\xi _n}$
.
Lemma 2.1. Let
![]() $p\in [1,\infty )$
. If
$p\in [1,\infty )$
. If
![]() $\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
, then
$\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
, then
![]() $f_\xi \in W^{1,p}({\mathcal M};{\mathcal N})$
. Furthermore, if
$f_\xi \in W^{1,p}({\mathcal M};{\mathcal N})$
. Furthermore, if
![]() $\xi _n \rightharpoonup \xi $
in
$\xi _n \rightharpoonup \xi $
in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
, then
$W^{1,p}({\mathcal M};T{\mathcal N})$
, then
![]() $f_{\xi _n} \rightharpoonup f_\xi $
in
$f_{\xi _n} \rightharpoonup f_\xi $
in
![]() $W^{1,p}({\mathcal M};{\mathcal N})$
, and similarly for strong convergence.
$W^{1,p}({\mathcal M};{\mathcal N})$
, and similarly for strong convergence.
Proof. Let
![]() $\iota :(T{\mathcal N},S^{\mathfrak {h}})\to ({\mathbb R}^D,\mathfrak {e})$
and
$\iota :(T{\mathcal N},S^{\mathfrak {h}})\to ({\mathbb R}^D,\mathfrak {e})$
and
![]() $\jmath : ({\mathcal N},\mathfrak {h})\to ({\mathbb R}^D,\mathfrak {e})$
be defined as above. Let
$\jmath : ({\mathcal N},\mathfrak {h})\to ({\mathbb R}^D,\mathfrak {e})$
be defined as above. Let
![]() $\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
. Since
$\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
. Since
![]() ${\mathcal N}$
is compact, the fact that
${\mathcal N}$
is compact, the fact that
![]() $f_\xi \in W^{1,p}({\mathcal M};{\mathcal N})$
follows from (2.2) (or equivalently, (2.3)).
$f_\xi \in W^{1,p}({\mathcal M};{\mathcal N})$
follows from (2.2) (or equivalently, (2.3)).
Let
![]() $\xi _n \rightharpoonup \xi $
in
$\xi _n \rightharpoonup \xi $
in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
(i.e.,
$W^{1,p}({\mathcal M};T{\mathcal N})$
(i.e.,
![]() $\iota \circ \xi _n \rightharpoonup \iota \circ \xi $
in
$\iota \circ \xi _n \rightharpoonup \iota \circ \xi $
in
![]() $W^{1,p}({\mathcal M};{\mathbb R}^D)$
). By (2.3) and the compactness of
$W^{1,p}({\mathcal M};{\mathbb R}^D)$
). By (2.3) and the compactness of
![]() ${\mathcal N}$
,
${\mathcal N}$
,
![]() $\jmath \circ f_{\xi _n}$
is bounded in
$\jmath \circ f_{\xi _n}$
is bounded in
![]() $W^{1,p}({\mathcal M};{\mathbb R}^D)$
(and equi-integrable if
$W^{1,p}({\mathcal M};{\mathbb R}^D)$
(and equi-integrable if
![]() $p=1$
), and thus
$p=1$
), and thus
![]() $\jmath \circ f_{\xi _n}$
weakly converges to some
$\jmath \circ f_{\xi _n}$
weakly converges to some
![]() $F\in W^{1,p}({\mathcal M};{\mathbb R}^D)$
(modulo a subsequence). We need to show that
$F\in W^{1,p}({\mathcal M};{\mathbb R}^D)$
(modulo a subsequence). We need to show that
![]() $F = \jmath \circ f_\xi $
. Since weak
$F = \jmath \circ f_\xi $
. Since weak
![]() $W^{1,p}$
-convergence implies strong
$W^{1,p}$
-convergence implies strong
![]() $L^p$
-convergence, we can move to a subsequence and obtain that
$L^p$
-convergence, we can move to a subsequence and obtain that
![]() $\iota \circ \xi _n \to \iota \circ \xi $
almost everywhere, and thus, for that same subsequence,
$\iota \circ \xi _n \to \iota \circ \xi $
almost everywhere, and thus, for that same subsequence,
![]() $\jmath \circ f_{\xi _n}\to \jmath \circ f_\xi $
almost everywhere, which by the uniqueness of the limit implies that
$\jmath \circ f_{\xi _n}\to \jmath \circ f_\xi $
almost everywhere, which by the uniqueness of the limit implies that
![]() $F=\jmath \circ f_\xi $
. As we could have started with any subsequence of
$F=\jmath \circ f_\xi $
. As we could have started with any subsequence of
![]() $\xi _n$
and obtain the result for a sub-subsequence, the claim holds for the whole sequence.
$\xi _n$
and obtain the result for a sub-subsequence, the claim holds for the whole sequence.
Next, assume that
![]() $\xi _n \to \xi $
strongly in
$\xi _n \to \xi $
strongly in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
. Since, a fortiori,
$W^{1,p}({\mathcal M};T{\mathcal N})$
. Since, a fortiori,
![]() $\xi _n \rightharpoonup \xi $
in
$\xi _n \rightharpoonup \xi $
in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
, it follows from the previous clause that
$W^{1,p}({\mathcal M};T{\mathcal N})$
, it follows from the previous clause that
![]() $f_{\xi _n} \rightharpoonup f_\xi $
in
$f_{\xi _n} \rightharpoonup f_\xi $
in
![]() $W^{1,p}({\mathcal M};{\mathcal N})$
, or equivalently, that
$W^{1,p}({\mathcal M};{\mathcal N})$
, or equivalently, that
![]() $\jmath \circ f_{\xi _n}\rightharpoonup \jmath \circ f_\xi $
in
$\jmath \circ f_{\xi _n}\rightharpoonup \jmath \circ f_\xi $
in
![]() $W^{1,p}({\mathcal M};{\mathbb R}^D)$
. We need to show that
$W^{1,p}({\mathcal M};{\mathbb R}^D)$
. We need to show that
![]() $d(\jmath \circ f_{\xi _n})\to d(\jmath \circ f_\xi )$
in
$d(\jmath \circ f_{\xi _n})\to d(\jmath \circ f_\xi )$
in
![]() $L^p({\mathcal M};T^*{\mathcal M}\otimes {\mathbb R}^D)$
. It is sufficient to prove this for a subsequence, and thus we can assume, without loss of generality, that
$L^p({\mathcal M};T^*{\mathcal M}\otimes {\mathbb R}^D)$
. It is sufficient to prove this for a subsequence, and thus we can assume, without loss of generality, that
![]() $D\iota \circ D\xi _n \to D\iota \circ D\xi $
almost everywhere. Since
$D\iota \circ D\xi _n \to D\iota \circ D\xi $
almost everywhere. Since
![]() $D\iota $
is an embedding, it follows that
$D\iota $
is an embedding, it follows that
![]() $D\xi _n \to D\xi $
almost everywhere (as maps from
$D\xi _n \to D\xi $
almost everywhere (as maps from
![]() ${\mathcal M}\to T^*{\mathcal M}\otimes TT{\mathcal N}$
). In particular,
${\mathcal M}\to T^*{\mathcal M}\otimes TT{\mathcal N}$
). In particular,
![]() $D\pi \circ D\xi _n\to D\pi \circ D\xi $
almost everywhere (as maps
$D\pi \circ D\xi _n\to D\pi \circ D\xi $
almost everywhere (as maps
![]() ${\mathcal M} \to T^*{\mathcal M}\otimes T{\mathcal N}$
), i.e.,
${\mathcal M} \to T^*{\mathcal M}\otimes T{\mathcal N}$
), i.e.,
![]() $D f_{\xi _n} \to D f_{\xi _n}$
almost everywhere, and thus also
$D f_{\xi _n} \to D f_{\xi _n}$
almost everywhere, and thus also
![]() $d(\jmath \circ f_{\xi _n})\to d(\jmath \circ f_\xi )$
. To complete the proof, it remains to show that
$d(\jmath \circ f_{\xi _n})\to d(\jmath \circ f_\xi )$
. To complete the proof, it remains to show that
Since
![]() $D f_{\xi _n} \to D f_{\xi _n}$
almost everywhere, we also have that
$D f_{\xi _n} \to D f_{\xi _n}$
almost everywhere, we also have that
![]() $|Df_{\xi _n}|^p \to |Df_\xi |^p$
almost everywhere, and since
$|Df_{\xi _n}|^p \to |Df_\xi |^p$
almost everywhere, and since
and since it follows from the strong
![]() $W^{1,p}$
-convergence of
$W^{1,p}$
-convergence of
![]() $\xi _n$
that
$\xi _n$
that
the limit (2.4) follows from a refinement of the dominated convergence theorem (e.g., [Reference Evans and GariepyEG15, Theorem 1.20]).
The following lemma, which will be needed in the sequel, addresses a situation where
![]() $\xi _n\rightharpoonup \xi $
in
$\xi _n\rightharpoonup \xi $
in
![]() $W^{1,p}$
along with
$W^{1,p}$
along with
![]() $K^{\mathfrak {h}} \circ D\xi _n$
converging strongly in
$K^{\mathfrak {h}} \circ D\xi _n$
converging strongly in
![]() $L^p$
. The fact that the limit is, as one would expect,
$L^p$
. The fact that the limit is, as one would expect,
![]() $K^{\mathfrak {h}} \circ D\xi $
is somewhat nontrivial, since the two converging sequences have to be interpreted with respect to two different maps into
$K^{\mathfrak {h}} \circ D\xi $
is somewhat nontrivial, since the two converging sequences have to be interpreted with respect to two different maps into
![]() ${\mathbb R}^D$
. Since this suffices in the application below, we assume that p is large enough.
${\mathbb R}^D$
. Since this suffices in the application below, we assume that p is large enough.
Lemma 2.2. Let
![]() $p>\dim {\mathcal M}$
, and let
$p>\dim {\mathcal M}$
, and let
![]() $\iota $
and
$\iota $
and
![]() $\jmath $
be defined as above. Assume that
$\jmath $
be defined as above. Assume that
![]() $\xi _n \rightharpoonup \xi $
in
$\xi _n \rightharpoonup \xi $
in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
. Assume further that
$W^{1,p}({\mathcal M};T{\mathcal N})$
. Assume further that
![]() $d\jmath \circ K^{\mathfrak {h}}\circ D\xi _n \to d\jmath \circ T$
in
$d\jmath \circ K^{\mathfrak {h}}\circ D\xi _n \to d\jmath \circ T$
in
![]() $L^p({\mathcal M};T^*{\mathcal M}\otimes {\mathbb R}^D)$
for some map
$L^p({\mathcal M};T^*{\mathcal M}\otimes {\mathbb R}^D)$
for some map
![]() $T:{\mathcal M} \to \operatorname {Hom}(T{\mathcal M},T{\mathcal N})$
. Then
$T:{\mathcal M} \to \operatorname {Hom}(T{\mathcal M},T{\mathcal N})$
. Then
![]() $T = K^{\mathfrak {h}} \circ D\xi $
a.e.
$T = K^{\mathfrak {h}} \circ D\xi $
a.e.
Proof. Since
![]() $p>\dim {\mathcal M}$
,
$p>\dim {\mathcal M}$
,
![]() $\xi _n \to \xi $
uniformly; hence, we can work with local coordinates. Let
$\xi _n \to \xi $
uniformly; hence, we can work with local coordinates. Let
![]() $X:\Omega \subset {\mathbb R}^{\dim {\mathcal M}} \to {\mathcal M}$
and
$X:\Omega \subset {\mathbb R}^{\dim {\mathcal M}} \to {\mathcal M}$
and
![]() $Y: \tilde \Omega \subset {\mathbb R}^{\dim {\mathcal N}} \to {\mathcal N}$
be local coordinate systems, and denote
$Y: \tilde \Omega \subset {\mathbb R}^{\dim {\mathcal N}} \to {\mathcal N}$
be local coordinate systems, and denote
![]() $(x_n , v_n) = (DY)^{-1} \circ \xi _n \circ X$
, and similarly
$(x_n , v_n) = (DY)^{-1} \circ \xi _n \circ X$
, and similarly
![]() $(x,v) = (DY)^{-1} \circ \xi \circ X$
, both maps
$(x,v) = (DY)^{-1} \circ \xi \circ X$
, both maps
![]() $\Omega \to \tilde \Omega \times {\mathbb R}^{\dim {\mathcal N}}$
. The uniform convergence
$\Omega \to \tilde \Omega \times {\mathbb R}^{\dim {\mathcal N}}$
. The uniform convergence
![]() $\xi _n\to \xi $
implies that
$\xi _n\to \xi $
implies that
![]() $(x_n,v_n) \to (x,v)$
uniformly. The boundedness of
$(x_n,v_n) \to (x,v)$
uniformly. The boundedness of
![]() $\xi _n$
in
$\xi _n$
in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
implies the boundedness of the coordinate expressions
$W^{1,p}({\mathcal M};T{\mathcal N})$
implies the boundedness of the coordinate expressions
![]() $(x_n,v_n)$
in
$(x_n,v_n)$
in
![]() $W^{1,p}(\Omega , {\mathbb R}^{2\dim {\mathcal N}})$
; hence,
$W^{1,p}(\Omega , {\mathbb R}^{2\dim {\mathcal N}})$
; hence,
![]() $(x_n,v_n) \rightharpoonup (x,v)$
in
$(x_n,v_n) \rightharpoonup (x,v)$
in
![]() $W^{1,p}(\Omega , {\mathbb R}^{2\dim {\mathcal N}})$
to
$W^{1,p}(\Omega , {\mathbb R}^{2\dim {\mathcal N}})$
to
![]() $(x,v)$
. In these coordinates,
$(x,v)$
. In these coordinates,
Hence,
Since
![]() $Dv_n \rightharpoonup Dv$
and
$Dv_n \rightharpoonup Dv$
and
![]() $Dx_n \rightharpoonup Dx$
in
$Dx_n \rightharpoonup Dx$
in
![]() $L^p$
,
$L^p$
,
![]() $\Gamma $
is smooth and
$\Gamma $
is smooth and
![]() $(x_n,v_n)\to (x,v)$
uniformly, we obtain that
$(x_n,v_n)\to (x,v)$
uniformly, we obtain that
in
![]() $L^p(\Omega ;\tilde \Omega \times \operatorname {Hom}({\mathbb R}^{\dim {\mathcal M}},{\mathbb R}^{\dim {\mathcal N}}))$
. We have thus proved that
$L^p(\Omega ;\tilde \Omega \times \operatorname {Hom}({\mathbb R}^{\dim {\mathcal M}},{\mathbb R}^{\dim {\mathcal N}}))$
. We have thus proved that
![]() $K^{\mathfrak {h}} \circ D\xi _n \rightharpoonup K^{\mathfrak {h}} \circ D\xi $
weakly in
$K^{\mathfrak {h}} \circ D\xi _n \rightharpoonup K^{\mathfrak {h}} \circ D\xi $
weakly in
![]() $L^p$
in every coordinate patch.
$L^p$
in every coordinate patch.
Add now the fact that
![]() $dj \circ K^{\mathfrak {h}}\circ D\xi _n \to dj \circ T$
strongly in
$dj \circ K^{\mathfrak {h}}\circ D\xi _n \to dj \circ T$
strongly in
![]() $L^p$
. By moving to subsequences, we can assume that
$L^p$
. By moving to subsequences, we can assume that
![]() $dj \circ K^{\mathfrak {h}}\circ D\xi _n \to dj \circ T$
a.e. Since
$dj \circ K^{\mathfrak {h}}\circ D\xi _n \to dj \circ T$
a.e. Since
![]() $Dj:{\mathcal N}\to {\mathbb R}^{2K}$
is an embedding, it follows that
$Dj:{\mathcal N}\to {\mathbb R}^{2K}$
is an embedding, it follows that
![]() $K\circ D\xi _n \to T$
a.e. Therefore, in coordinates, for almost every
$K\circ D\xi _n \to T$
a.e. Therefore, in coordinates, for almost every
![]() $p\in \Omega $
,
$p\in \Omega $
,
Thus,
![]() $T = K \circ D\xi $
a.e. in every coordinate patch; hence, a.e.
$T = K \circ D\xi $
a.e. in every coordinate patch; hence, a.e.
The following is an immediate application of [Reference Alpern, Kupferman and MaorAKM22, Prop. D.1]:
Proposition 2.3. Let
![]() $p>\dim {\mathcal M}$
. Then,
$p>\dim {\mathcal M}$
. Then,
![]() $\xi _n\to \xi $
in
$\xi _n\to \xi $
in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
if and only if
$W^{1,p}({\mathcal M};T{\mathcal N})$
if and only if
![]() $f_{\xi _n}\to f_\xi $
in
$f_{\xi _n}\to f_\xi $
in
![]() $W^{1,p}({\mathcal M};{\mathcal N})$
, and for some isometric embedding
$W^{1,p}({\mathcal M};{\mathcal N})$
, and for some isometric embedding
![]() $\jmath :{\mathcal N}\to {\mathbb R}^D$
,
$\jmath :{\mathcal N}\to {\mathbb R}^D$
,
and
Sobolev immersions
Let
![]() $\dim {\mathcal M}=d$
and
$\dim {\mathcal M}=d$
and
![]() $\dim {\mathcal N}=d+1$
, and let
$\dim {\mathcal N}=d+1$
, and let
![]() $f\in W^{1,p}({\mathcal M};{\mathcal N})$
satisfy
$f\in W^{1,p}({\mathcal M};{\mathcal N})$
satisfy
![]() $\operatorname {rank} df=d$
a.e. We may define a.e. a map
$\operatorname {rank} df=d$
a.e. We may define a.e. a map
![]() $\mathfrak {n}_f\in L^\infty ({\mathcal M};T{\mathcal N}$
) covering f, such that
$\mathfrak {n}_f\in L^\infty ({\mathcal M};T{\mathcal N}$
) covering f, such that
![]() $\mathfrak {n}_f(q)\in T_{f(q)}{\mathcal N}$
is a unit vector, normal to the image of
$\mathfrak {n}_f(q)\in T_{f(q)}{\mathcal N}$
is a unit vector, normal to the image of
![]() $Df_q$
, and for every oriented basis
$Df_q$
, and for every oriented basis
![]() $(u_1,\dots ,u_d)\subset T_q{\mathcal M}$
,
$(u_1,\dots ,u_d)\subset T_q{\mathcal M}$
,
is an oriented basis. If
![]() $\mathfrak {n}_f \in W^{1,p}({\mathcal M};T{\mathcal N})$
, we say that f belongs to the set of p
-Sobolev immersions (this is the definition in (1.3)). Since there is a one-to-one correspondence between f and
$\mathfrak {n}_f \in W^{1,p}({\mathcal M};T{\mathcal N})$
, we say that f belongs to the set of p
-Sobolev immersions (this is the definition in (1.3)). Since there is a one-to-one correspondence between f and
![]() $\mathfrak {n}_f$
,
$\mathfrak {n}_f$
,
![]() $\operatorname {Imm}_p({\mathcal M};{\mathcal N})$
can be identified with a subset of
$\operatorname {Imm}_p({\mathcal M};{\mathcal N})$
can be identified with a subset of
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
, and specifically a subset of
$W^{1,p}({\mathcal M};T{\mathcal N})$
, and specifically a subset of
![]() $W^{1,p}({\mathcal M};S{\mathcal N})$
, where
$W^{1,p}({\mathcal M};S{\mathcal N})$
, where
![]() $S{\mathcal N}\subset T{\mathcal N}$
is the sphere bundle of
$S{\mathcal N}\subset T{\mathcal N}$
is the sphere bundle of
![]() ${\mathcal N}$
. It is, however, not a closed subset, as the rank condition is not closed under
${\mathcal N}$
. It is, however, not a closed subset, as the rank condition is not closed under
![]() $W^{1,p}$
-convergence.
$W^{1,p}$
-convergence.
For
![]() $f\in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
, the total energy (1.2) is more rigorously written as
$f\in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
, the total energy (1.2) is more rigorously written as
as this notation does not rely on non-smooth pullback bundles and their corresponding pullback connections.
Trivializations
Let
![]() $\xi _n\in W^{1,p}({\mathcal M};T{\mathcal N})$
be a sequence converging to
$\xi _n\in W^{1,p}({\mathcal M};T{\mathcal N})$
be a sequence converging to
![]() $\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
uniformly (hence, in particular,
$\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
uniformly (hence, in particular,
![]() $f_{\xi _n} \to f_\xi $
uniformly). The compactness of
$f_{\xi _n} \to f_\xi $
uniformly). The compactness of
![]() ${\mathcal M}$
and
${\mathcal M}$
and
![]() ${\mathcal N}$
implies the existence of finite open covers
${\mathcal N}$
implies the existence of finite open covers
![]() ${\mathcal U} = \{U_i\}$
and
${\mathcal U} = \{U_i\}$
and
![]() ${\mathcal V} = \{V_i\}$
of
${\mathcal V} = \{V_i\}$
of
![]() ${\mathcal M}$
and
${\mathcal M}$
and
![]() ${\mathcal N}$
such that
${\mathcal N}$
such that
![]() $T{\mathcal N}|_{V_i}$
is a trivial bundle for every i, and such that
$T{\mathcal N}|_{V_i}$
is a trivial bundle for every i, and such that
![]() $f_{\xi _n}(U_i)\subset V_i$
for n large enough. For every such U and V (to simplify notations, we omit the index i), let
$f_{\xi _n}(U_i)\subset V_i$
for n large enough. For every such U and V (to simplify notations, we omit the index i), let
![]() $R:V\to \operatorname {SO}(\mathfrak {h},{\mathbb R}^{\dim {\mathcal N}})$
be a smooth orthonormal frame (which may or may not be a coordinate frame); namely, for every
$R:V\to \operatorname {SO}(\mathfrak {h},{\mathbb R}^{\dim {\mathcal N}})$
be a smooth orthonormal frame (which may or may not be a coordinate frame); namely, for every
![]() $q\in V$
and
$q\in V$
and
![]() $\eta ,\xi \in T_q{\mathcal N}$
,
$\eta ,\xi \in T_q{\mathcal N}$
,
Such a frame exists by the triviality of
![]() $T{\mathcal N}|_V$
. Then, restricting to U,
$T{\mathcal N}|_V$
. Then, restricting to U,
where R acts on the vector part
![]() $df_{\xi _n}$
of
$df_{\xi _n}$
of
![]() $Df_{\xi _n}$
. Note that
$Df_{\xi _n}$
. Note that
![]() $R\circ Df_{\xi _n} - R\circ Df_\xi \ne R\circ (Df_{\xi _n} - Df_\xi )$
; in fact, the right-hand side is not well defined, as the images of
$R\circ Df_{\xi _n} - R\circ Df_\xi \ne R\circ (Df_{\xi _n} - Df_\xi )$
; in fact, the right-hand side is not well defined, as the images of
![]() $\xi _n$
and
$\xi _n$
and
![]() $\xi $
do not belong to the same fiber of
$\xi $
do not belong to the same fiber of
![]() $T{\mathcal N}$
.
$T{\mathcal N}$
.
Proposition 2.4. Assume that
![]() $p>\dim {\mathcal M}$
. Then,
$p>\dim {\mathcal M}$
. Then,
if and only if
for every
![]() $U\in {\mathcal U}$
. Likewise, if
$U\in {\mathcal U}$
. Likewise, if
then
for every
![]() $U\in {\mathcal U}$
.
$U\in {\mathcal U}$
.
Proof. Since
![]() $R\circ Df_{\xi _n}(x) = (f_{\xi _n}(x), R_{f_{\xi _n}(x)} \circ (df_{\xi _n})_x)$
, and
$R\circ Df_{\xi _n}(x) = (f_{\xi _n}(x), R_{f_{\xi _n}(x)} \circ (df_{\xi _n})_x)$
, and
![]() $R_q$
is a linear map depending smoothly on the footpoint, and the footpoints
$R_q$
is a linear map depending smoothly on the footpoint, and the footpoints
![]() $f_{\xi _n}$
converge uniformly to
$f_{\xi _n}$
converge uniformly to
![]() $f_\xi $
by assumption, the proof follows from the same arguments as the one of Proposition 2.2.
$f_\xi $
by assumption, the proof follows from the same arguments as the one of Proposition 2.2.
2.1 Coordinate representation of the energy
In this section, we present some of the geometric constructs and the energy (1.2) in coordinates for the benefit of readers who are more used to this notation. For simplicity, assume that both
![]() ${\mathcal M}$
and
${\mathcal M}$
and
![]() ${\mathcal N}$
are covered by single coordinate charts,
${\mathcal N}$
are covered by single coordinate charts,
A map
![]() $f:{\mathcal M}\to {\mathcal N}$
is represented by a map
$f:{\mathcal M}\to {\mathcal N}$
is represented by a map
![]() ${\mathbb R}^d\supset x_{\mathcal M}({\mathcal M}) \to {\mathbb R}^{d+1}$
,
${\mathbb R}^d\supset x_{\mathcal M}({\mathcal M}) \to {\mathbb R}^{d+1}$
,
with components
![]() $f^\alpha $
, where for the sake of clarity, we use Latin indexes for the body manifold
$f^\alpha $
, where for the sake of clarity, we use Latin indexes for the body manifold
![]() ${\mathcal M}$
and Greek indexes for the space manifold
${\mathcal M}$
and Greek indexes for the space manifold
![]() ${\mathcal N}$
.
${\mathcal N}$
.
Throughout this section, we will denote the projection of a vector bundle onto its base by
![]() $\pi $
, where the type (e.g.,
$\pi $
, where the type (e.g.,
![]() $T{\mathcal M}\to {\mathcal M}$
or
$T{\mathcal M}\to {\mathcal M}$
or
![]() $TT{\mathcal N}\to T{\mathcal N}$
) should be clear from the context. The tangent bundle
$TT{\mathcal N}\to T{\mathcal N}$
) should be clear from the context. The tangent bundle
![]() $T{\mathcal M}$
has coordinates
$T{\mathcal M}$
has coordinates
![]() $(x_{{\mathcal M}},\dot {x}_{{\mathcal M}}):T{\mathcal M}\to {\mathbb R}^d\times {\mathbb R}^d$
, where, with a slight abuse of notations which will be used repeatedly,
$(x_{{\mathcal M}},\dot {x}_{{\mathcal M}}):T{\mathcal M}\to {\mathbb R}^d\times {\mathbb R}^d$
, where, with a slight abuse of notations which will be used repeatedly,
![]() $x_{{\mathcal M}} = x_{\mathcal M}\circ \pi $
and
$x_{{\mathcal M}} = x_{\mathcal M}\circ \pi $
and
![]() $\dot {x}_{{\mathcal M}} = dx_{\mathcal M}$
; the metric
$\dot {x}_{{\mathcal M}} = dx_{\mathcal M}$
; the metric
![]() $\mathfrak {g}$
is represented by a matrix-valued function
$\mathfrak {g}$
is represented by a matrix-valued function
![]() $x_{\mathcal M}({\mathcal M})\to {\mathbb R}^d\otimes {\mathbb R}^d$
, with entries
$x_{\mathcal M}({\mathcal M})\to {\mathbb R}^d\otimes {\mathbb R}^d$
, with entries
![]() $\mathfrak {g}_{ij}$
, such that for
$\mathfrak {g}_{ij}$
, such that for
![]() $V \in T{\mathcal M}$
,
$V \in T{\mathcal M}$
,
with the Einstein summation convention over repeated indexes. Similarly, the tangent bundle
![]() $T{\mathcal N}$
has coordinates
$T{\mathcal N}$
has coordinates
![]() $(x_{{\mathcal N}},\dot {x}_{{\mathcal N}}):T{\mathcal N}\to {\mathbb R}^{d+1}\times {\mathbb R}^{d+1}$
; the metric
$(x_{{\mathcal N}},\dot {x}_{{\mathcal N}}):T{\mathcal N}\to {\mathbb R}^{d+1}\times {\mathbb R}^{d+1}$
; the metric
![]() $\mathfrak {h}$
is represented by a matrix-valued function
$\mathfrak {h}$
is represented by a matrix-valued function
![]() $x_{\mathcal N}({\mathcal N})\to {\mathbb R}^{d+1}\otimes {\mathbb R}^{d+1}$
, with entries
$x_{\mathcal N}({\mathcal N})\to {\mathbb R}^{d+1}\otimes {\mathbb R}^{d+1}$
, with entries
![]() $\mathfrak {h}_{\alpha \beta }$
, so that for a vector
$\mathfrak {h}_{\alpha \beta }$
, so that for a vector
![]() $W\in T{\mathcal N}$
,
$W\in T{\mathcal N}$
,
For
![]() $f:{\mathcal M}\to {\mathcal N}$
, the fiber of the pullback bundle
$f:{\mathcal M}\to {\mathcal N}$
, the fiber of the pullback bundle
![]() $f^*T{\mathcal N}$
at a point
$f^*T{\mathcal N}$
at a point
![]() $p\in {\mathcal M}$
is canonically identified with the fiber
$p\in {\mathcal M}$
is canonically identified with the fiber
![]() $T_{f(p)}{\mathcal N}$
; its coordinates are
$T_{f(p)}{\mathcal N}$
; its coordinates are
![]() $(x_{{\mathcal M}},\dot {x}_{{\mathcal N}}):f^*T{\mathcal N}\to {\mathbb R}^d\times {\mathbb R}^{d+1}$
, where
$(x_{{\mathcal M}},\dot {x}_{{\mathcal N}}):f^*T{\mathcal N}\to {\mathbb R}^d\times {\mathbb R}^{d+1}$
, where
![]() $x_{{\mathcal M}} = x_{{\mathcal M}}\circ \pi $
and
$x_{{\mathcal M}} = x_{{\mathcal M}}\circ \pi $
and
![]() $\dot {x}_{{\mathcal N}}$
is identified with
$\dot {x}_{{\mathcal N}}$
is identified with
![]() $\dot {x}_{\mathcal N}: T{\mathcal N}\to {\mathbb R}^{d+1}$
, via the canonical identification of fibers of
$\dot {x}_{\mathcal N}: T{\mathcal N}\to {\mathbb R}^{d+1}$
, via the canonical identification of fibers of
![]() $f^*T{\mathcal N}$
with fibers of
$f^*T{\mathcal N}$
with fibers of
![]() $T{\mathcal N}$
. The coordinate representation of
$T{\mathcal N}$
. The coordinate representation of
![]() $df\in \Gamma (f^*T{\mathcal N})$
is the map
$df\in \Gamma (f^*T{\mathcal N})$
is the map
![]() $x_{\mathcal M}({\mathcal M})\to \operatorname {Hom}({\mathbb R}^d,{\mathbb R}^{d+1})$
given by
$x_{\mathcal M}({\mathcal M})\to \operatorname {Hom}({\mathbb R}^d,{\mathbb R}^{d+1})$
given by
![]() $\partial _if^\alpha $
, whereas the coordinate representation of
$\partial _if^\alpha $
, whereas the coordinate representation of
![]() $Df:T{\mathcal M}\to T{\mathcal N}$
is the map
$Df:T{\mathcal M}\to T{\mathcal N}$
is the map
![]() $x_{\mathcal M}({\mathcal M})\to {\mathbb R}^{d+1}\times \operatorname {Hom}({\mathbb R}^d,{\mathbb R}^{d+1})$
, given by
$x_{\mathcal M}({\mathcal M})\to {\mathbb R}^{d+1}\times \operatorname {Hom}({\mathbb R}^d,{\mathbb R}^{d+1})$
, given by
![]() $(f^\alpha ,\partial _if^\alpha )$
.
$(f^\alpha ,\partial _if^\alpha )$
.
We denote by
![]() $\mathfrak {g}^{1/2}: x_{\mathcal M}({\mathcal M})\to \operatorname {Hom}({\mathbb R}^d,{\mathbb R}^d)$
and
$\mathfrak {g}^{1/2}: x_{\mathcal M}({\mathcal M})\to \operatorname {Hom}({\mathbb R}^d,{\mathbb R}^d)$
and
![]() $\mathfrak {h}^{1/2}:x_{\mathcal N}({\mathcal N})\to \operatorname {Hom}({\mathbb R}^{d+1},{\mathbb R}^{d+1})$
the symmetric positive-definite square roots of the matrices
$\mathfrak {h}^{1/2}:x_{\mathcal N}({\mathcal N})\to \operatorname {Hom}({\mathbb R}^{d+1},{\mathbb R}^{d+1})$
the symmetric positive-definite square roots of the matrices
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {h}$
; that is,
$\mathfrak {h}$
; that is,
The stretching energy of
![]() $f:{\mathcal M}\to {\mathcal N}$
takes the form
$f:{\mathcal M}\to {\mathcal N}$
takes the form
 $$\begin{align*}{\mathcal E}_p^S(f) = \int_{x_{\mathcal M}({\mathcal M})} \operatorname{dist}^p(Q(x),O(d)) \det(\mathfrak{g}^{1/2}(x))\, dx, \end{align*}$$
$$\begin{align*}{\mathcal E}_p^S(f) = \int_{x_{\mathcal M}({\mathcal M})} \operatorname{dist}^p(Q(x),O(d)) \det(\mathfrak{g}^{1/2}(x))\, dx, \end{align*}$$
where
or, in matrix form,
and the distance here is with respect to the Euclidean Frobenius norm.
We proceed with the double tangent
![]() $TT{\mathcal N}$
, which has coordinates
$TT{\mathcal N}$
, which has coordinates
where
![]() $x_{{\mathcal N}} = x_{{\mathcal N}}\circ \pi $
,
$x_{{\mathcal N}} = x_{{\mathcal N}}\circ \pi $
,
![]() $\dot {x}_{{\mathcal N}} = \dot {x}_{{\mathcal N}}\circ \pi $
,
$\dot {x}_{{\mathcal N}} = \dot {x}_{{\mathcal N}}\circ \pi $
,
![]() $v_{{\mathcal N}} = \dot {x}_{{\mathcal N}}\circ D\pi $
and
$v_{{\mathcal N}} = \dot {x}_{{\mathcal N}}\circ D\pi $
and
![]() $\dot {v}_{{\mathcal N}} = d\dot {x}_{{\mathcal N}}$
. That is, a vector in
$\dot {v}_{{\mathcal N}} = d\dot {x}_{{\mathcal N}}$
. That is, a vector in
![]() $T_{(x_{\mathcal N},\dot {x}_{\mathcal N})}T{\mathcal N}$
represents a direction of change, in
$T_{(x_{\mathcal N},\dot {x}_{\mathcal N})}T{\mathcal N}$
represents a direction of change, in
![]() $T{\mathcal N}$
, from the point
$T{\mathcal N}$
, from the point
![]() $(x_{\mathcal N},\dot {x}_{\mathcal N})$
; the coordinate
$(x_{\mathcal N},\dot {x}_{\mathcal N})$
; the coordinate
![]() $v_{{\mathcal N}}$
represents the direction of change in the coordinate
$v_{{\mathcal N}}$
represents the direction of change in the coordinate
![]() $x_{\mathcal N}$
, and
$x_{\mathcal N}$
, and
![]() $\dot {v}_{{\mathcal N}}$
the direction of change in the coordinate
$\dot {v}_{{\mathcal N}}$
the direction of change in the coordinate
![]() $\dot {x}_{{\mathcal N}}$
.
$\dot {x}_{{\mathcal N}}$
.
We further denote by
![]() $\Gamma : x_{\mathcal N}({\mathcal N})\to \operatorname {Hom}({\mathbb R}^{d+1}\otimes {\mathbb R}^{d+1},{\mathbb R}^{d+1})$
the Christoffel symbols of the Levi-Civita connection, with coordinates
$\Gamma : x_{\mathcal N}({\mathcal N})\to \operatorname {Hom}({\mathbb R}^{d+1}\otimes {\mathbb R}^{d+1},{\mathbb R}^{d+1})$
the Christoffel symbols of the Levi-Civita connection, with coordinates
![]() $\Gamma ^\alpha _{\beta \gamma }$
; the connection map
$\Gamma ^\alpha _{\beta \gamma }$
; the connection map
![]() $K^{\mathfrak {h}}:TT{\mathcal N}\to T{\mathcal N}$
is defined by
$K^{\mathfrak {h}}:TT{\mathcal N}\to T{\mathcal N}$
is defined by
Let
![]() $\xi ,Y\in \mathfrak {X}({\mathcal N})$
be vector fields having coordinate representation
$\xi ,Y\in \mathfrak {X}({\mathcal N})$
be vector fields having coordinate representation
![]() $x_{\mathcal N}({\mathcal N})\to {\mathbb R}^{d+1}$
,
$x_{\mathcal N}({\mathcal N})\to {\mathbb R}^{d+1}$
,
The coordinate representation of
![]() $D\xi (Y):{\mathcal N}\to TT{\mathcal N}$
is the map
$D\xi (Y):{\mathcal N}\to TT{\mathcal N}$
is the map
![]() $x_{\mathcal N}({\mathcal N}) \to {\mathbb R}^{d+1}\times {\mathbb R}^{d+1}\times {\mathbb R}^{d+1}$
, given by
$x_{\mathcal N}({\mathcal N}) \to {\mathbb R}^{d+1}\times {\mathbb R}^{d+1}\times {\mathbb R}^{d+1}$
, given by
Thus, the coordinate representation of
![]() $K^{\mathfrak {h}}\circ D\xi (Y):{\mathcal N}\to T{\mathcal N}$
is the map
$K^{\mathfrak {h}}\circ D\xi (Y):{\mathcal N}\to T{\mathcal N}$
is the map
![]() $x_{\mathcal N}({\mathcal N})\to {\mathbb R}^{d+1}$
, given by
$x_{\mathcal N}({\mathcal N})\to {\mathbb R}^{d+1}$
, given by
thus showing that indeed
![]() $K^{\mathfrak {h}}\circ D\xi (Y) = \nabla _Y\xi $
.
$K^{\mathfrak {h}}\circ D\xi (Y) = \nabla _Y\xi $
.
We proceed to write the bending energy in explicit form. The reference shape operator S is represented by a map
![]() $x_{\mathcal M}({\mathcal M})\to \operatorname {Hom}({\mathbb R}^d,{\mathbb R}^d)$
with indexes
$x_{\mathcal M}({\mathcal M})\to \operatorname {Hom}({\mathbb R}^d,{\mathbb R}^d)$
with indexes
![]() $S_i^j$
. The unit normal
$S_i^j$
. The unit normal
![]() $\mathfrak {n}_f$
is represented by a function
$\mathfrak {n}_f$
is represented by a function
![]() $x_{\mathcal M}({\mathcal M})\to {\mathbb R}^{d+1}$
such that
$x_{\mathcal M}({\mathcal M})\to {\mathbb R}^{d+1}$
such that
is an oriented basis for
![]() ${\mathbb R}^{d+1}$
, and
${\mathbb R}^{d+1}$
, and
![]() $\mathfrak {n}_f(x)$
is a unit vector normal to range of
$\mathfrak {n}_f(x)$
is a unit vector normal to range of
![]() $\nabla f(x)$
with respect to the inner-product
$\nabla f(x)$
with respect to the inner-product
![]() $\mathfrak {h}_{\alpha \beta }(f(x))$
. With this, we have
$\mathfrak {h}_{\alpha \beta }(f(x))$
. With this, we have
 $$\begin{align*}{\mathcal E}_p^B(f) = \int_{x_{\mathcal M}({\mathcal M})} \left(\mathfrak{g}^{ij}(x) \mathfrak{h}_{\alpha\beta}(f(x)) A_i^\alpha(x) A_j^\beta(x)\right)^{p/2} \,\det(\mathfrak{g}^{1/2}(x))\, dx, \end{align*}$$
$$\begin{align*}{\mathcal E}_p^B(f) = \int_{x_{\mathcal M}({\mathcal M})} \left(\mathfrak{g}^{ij}(x) \mathfrak{h}_{\alpha\beta}(f(x)) A_i^\alpha(x) A_j^\beta(x)\right)^{p/2} \,\det(\mathfrak{g}^{1/2}(x))\, dx, \end{align*}$$
where
represents the discrepancy between the target shape operator S and the shape operator of f as defined in (1.4).
3 Proof of Theorem 1.1
3.1 The relaxed functional
Denote as above
![]() $d = \dim {\mathcal M}$
. Consider the vector bundle of rank
$d = \dim {\mathcal M}$
. Consider the vector bundle of rank
![]() $d+1$
,
$d+1$
,
![]() $T{\mathcal M}\oplus {\mathbb R}\to {\mathcal M}$
endowed with the product metric
$T{\mathcal M}\oplus {\mathbb R}\to {\mathcal M}$
endowed with the product metric
The orientation of
![]() $T{\mathcal M}\oplus {\mathbb R}$
is induced by the orientation of
$T{\mathcal M}\oplus {\mathbb R}$
is induced by the orientation of
![]() $T{\mathcal M}$
: if
$T{\mathcal M}$
: if
![]() $(u_1,\dots ,u_d)$
is an oriented basis for
$(u_1,\dots ,u_d)$
is an oriented basis for
![]() $T_q{\mathcal M}$
, then,
$T_q{\mathcal M}$
, then,
![]() $(u_1,\dots ,u_d,1)$
is an oriented basis for
$(u_1,\dots ,u_d,1)$
is an oriented basis for
![]() $T_q{\mathcal M}\oplus {\mathbb R}$
.
$T_q{\mathcal M}\oplus {\mathbb R}$
.
For
![]() $\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
, we introduce the map
$\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
, we introduce the map
which is a linear bundle morphism covering
![]() $f_\xi $
defined a.e. by
$f_\xi $
defined a.e. by
where
![]() $q\in {\mathcal M}$
,
$q\in {\mathcal M}$
,
![]() $v\in T_q{\mathcal M}$
and
$v\in T_q{\mathcal M}$
and
![]() $t\in {\mathbb R}$
. That is, on the left-hand side we identify
$t\in {\mathbb R}$
. That is, on the left-hand side we identify
![]() $\xi (q)\in T_{f_\xi (q)}{\mathcal N}$
with
$\xi (q)\in T_{f_\xi (q)}{\mathcal N}$
with
![]() $\xi (q)\in \operatorname {Hom}({\mathbb R},T_{f_\xi (q)}{\mathcal N})$
.
$\xi (q)\in \operatorname {Hom}({\mathbb R},T_{f_\xi (q)}{\mathcal N})$
.
Definition 3.1. The relaxed energy functional
![]() $\tilde {{\mathcal E}}_p : W^{1,p}({\mathcal M};T{\mathcal N})\to [0,\infty )$
is defined by
$\tilde {{\mathcal E}}_p : W^{1,p}({\mathcal M};T{\mathcal N})\to [0,\infty )$
is defined by
 $$ \begin{align*} \tilde{{\mathcal E}}_p(\xi) &= \int_{\mathcal M} \operatorname{dist}^p(Df_\xi\oplus \xi,\operatorname{SO}(G,\mathfrak{h}))\,\text{d}\text{Vol}_{\mathfrak{g}} + \int_{\mathcal M} |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi|^p\,\text{d}\text{Vol}_{\mathfrak{g}} \\ &\equiv \tilde{{\mathcal E}}_p^S(\xi) + \tilde{{\mathcal E}}_p^B(\xi). \end{align*} $$
$$ \begin{align*} \tilde{{\mathcal E}}_p(\xi) &= \int_{\mathcal M} \operatorname{dist}^p(Df_\xi\oplus \xi,\operatorname{SO}(G,\mathfrak{h}))\,\text{d}\text{Vol}_{\mathfrak{g}} + \int_{\mathcal M} |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi|^p\,\text{d}\text{Vol}_{\mathfrak{g}} \\ &\equiv \tilde{{\mathcal E}}_p^S(\xi) + \tilde{{\mathcal E}}_p^B(\xi). \end{align*} $$
Proposition 3.2. The functional
![]() $\tilde {{\mathcal E}}_p$
is a relaxation of
$\tilde {{\mathcal E}}_p$
is a relaxation of
![]() ${\mathcal E}_p$
, in the sense that
${\mathcal E}_p$
, in the sense that
Furthermore,
![]() $\tilde {{\mathcal E}}_p^S(\xi ) = 0$
if and only if
$\tilde {{\mathcal E}}_p^S(\xi ) = 0$
if and only if
![]() $f_\xi \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
,
$f_\xi \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
,
![]() $\xi = \mathfrak {n}_{f_\xi }$
and
$\xi = \mathfrak {n}_{f_\xi }$
and
![]() $Df\in \operatorname {O}(\mathfrak {g},\mathfrak {h})$
a.e.
$Df\in \operatorname {O}(\mathfrak {g},\mathfrak {h})$
a.e.
Proof. We first prove the second claim. Let
![]() $\tilde {{\mathcal E}}_p^S(\xi ) = 0$
; that is,
$\tilde {{\mathcal E}}_p^S(\xi ) = 0$
; that is,
![]() $Df_\xi \oplus \xi \in \operatorname {SO}(G,\mathfrak {h})$
a.e. Let
$Df_\xi \oplus \xi \in \operatorname {SO}(G,\mathfrak {h})$
a.e. Let
![]() $v\in T{\mathcal M}$
. Then,
$v\in T{\mathcal M}$
. Then,
thus proving that
![]() $Df_\xi \in \operatorname {O}(\mathfrak {g},\mathfrak {h})$
. In particular,
$Df_\xi \in \operatorname {O}(\mathfrak {g},\mathfrak {h})$
. In particular,
![]() $Df_\xi $
has full rank a.e. Moreover, a.e., and for every
$Df_\xi $
has full rank a.e. Moreover, a.e., and for every
![]() $v\in T{\mathcal M}$
,
$v\in T{\mathcal M}$
,
whereas
(i.e.,
![]() $\xi = \mathfrak {n}_{f_\xi }$
) and since
$\xi = \mathfrak {n}_{f_\xi }$
) and since
![]() $\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
, it follows that
$\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
, it follows that
![]() $f_\xi \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
. The other direction is immediate.
$f_\xi \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
. The other direction is immediate.
The first claim follows from the next lemma.
Lemma 3.3. For
![]() $f\in \operatorname {Imm}_p({\mathcal M},{\mathcal N})$
, the following identity holds:
$f\in \operatorname {Imm}_p({\mathcal M},{\mathcal N})$
, the following identity holds:
Proof. This is a linear-algebraic statement. Let
![]() $(V_1,\mathfrak {g}_1)$
,
$(V_1,\mathfrak {g}_1)$
,
![]() $(V_2,\mathfrak {g}_2)$
and
$(V_2,\mathfrak {g}_2)$
and
![]() $(W,\mathfrak {h})$
be oriented d-, k- and
$(W,\mathfrak {h})$
be oriented d-, k- and
![]() $(d+k)$
-dimensional inner-product spaces. Let
$(d+k)$
-dimensional inner-product spaces. Let
![]() $A\in \operatorname {Hom}(V_1,W)$
and
$A\in \operatorname {Hom}(V_1,W)$
and
![]() $B\in \operatorname {Hom}(V_2,W)$
satisfy
$B\in \operatorname {Hom}(V_2,W)$
satisfy
-
(a)
 $A\oplus B \in \operatorname {Hom}(V_1\oplus V_2,W)$
is orientation-preserving (with respect with the natural orientation of
$A\oplus B \in \operatorname {Hom}(V_1\oplus V_2,W)$
is orientation-preserving (with respect with the natural orientation of
 $V_1\oplus V_2$
).
$V_1\oplus V_2$
). -
(b)
 ${\operatorname {Image}}(A) = ({\operatorname {Image}}(B))^\perp $
.
${\operatorname {Image}}(A) = ({\operatorname {Image}}(B))^\perp $
. -
(c)
 $B\in \operatorname {O}(\mathfrak {g}_2,\mathfrak {h})$
.
$B\in \operatorname {O}(\mathfrak {g}_2,\mathfrak {h})$
.
Then,
In the present case,
![]() $k=1$
,
$k=1$
,
![]() $A = Df$
and
$A = Df$
and
![]() $B = \mathfrak {n}_f$
. Indeed, by definition,
$B = \mathfrak {n}_f$
. Indeed, by definition,
![]() $Df\oplus \mathfrak {n}_f$
is orientation-preserving,
$Df\oplus \mathfrak {n}_f$
is orientation-preserving,
![]() $\mathfrak {n}_f$
is a unit vector, and G is a product metric.
$\mathfrak {n}_f$
is a unit vector, and G is a product metric.
The fact that
![]() ${\mathcal E}_p(f) = \tilde {{\mathcal E}}_p(\mathfrak {n}_f)$
implies that Theorem 1.1 is proved if we prove the following relaxed version:
${\mathcal E}_p(f) = \tilde {{\mathcal E}}_p(\mathfrak {n}_f)$
implies that Theorem 1.1 is proved if we prove the following relaxed version:
Theorem 3.4. Suppose that there exists a sequence
![]() $\xi _n \in W^{1,p}({\mathcal M};T{\mathcal N})$
satisfying
$\xi _n \in W^{1,p}({\mathcal M};T{\mathcal N})$
satisfying
Then there exists a subsequence of
![]() $\xi _n$
converging strongly in
$\xi _n$
converging strongly in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
to a smooth limit
$W^{1,p}({\mathcal M};T{\mathcal N})$
to a smooth limit
![]() $\xi $
. Furthermore,
$\xi $
. Furthermore,
![]() $\tilde {{\mathcal E}}_p(\xi )=0$
, implying that
$\tilde {{\mathcal E}}_p(\xi )=0$
, implying that
![]() $f_\xi \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
is a smooth isometric immersion, satisfying
$f_\xi \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
is a smooth isometric immersion, satisfying
![]() $K^{\mathfrak {h}}\circ D\mathfrak {n}_{f_\xi } = - Df_\xi \circ S$
(i.e., S is the shape operator of the limit).
$K^{\mathfrak {h}}\circ D\mathfrak {n}_{f_\xi } = - Df_\xi \circ S$
(i.e., S is the shape operator of the limit).
3.2 Basic compactness considerations
Lemma 3.5. Let
![]() $p>1$
, and assume
$p>1$
, and assume
![]() $\tilde {{\mathcal E}}_p(\xi _n) \to 0$
. Then
$\tilde {{\mathcal E}}_p(\xi _n) \to 0$
. Then
![]() $\xi _n$
has a weakly converging subsequence
$\xi _n$
has a weakly converging subsequence
![]() $\xi _n \rightharpoonup \xi $
in
$\xi _n \rightharpoonup \xi $
in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
. In particular, if
$W^{1,p}({\mathcal M};T{\mathcal N})$
. In particular, if
![]() $p>d$
, then
$p>d$
, then
![]() $\xi _n\to \xi $
uniformly. The same (weak/uniform convergence) holds for
$\xi _n\to \xi $
uniformly. The same (weak/uniform convergence) holds for
![]() $f_{\xi _n}\to f_{\xi }$
.
$f_{\xi _n}\to f_{\xi }$
.
Proof. Let
![]() $\tilde {{\mathcal E}}_p(\xi _n) \to 0$
. The uniform boundedness of the stretching energy
$\tilde {{\mathcal E}}_p(\xi _n) \to 0$
. The uniform boundedness of the stretching energy
![]() $\tilde {{\mathcal E}}_p^S(\xi _n)$
and the compactness of
$\tilde {{\mathcal E}}_p^S(\xi _n)$
and the compactness of
![]() ${\mathcal N}$
imply that
${\mathcal N}$
imply that
![]() $\xi _n$
is a bounded sequence in
$\xi _n$
is a bounded sequence in
![]() $L^p({\mathcal M},T{\mathcal N})$
and that
$L^p({\mathcal M},T{\mathcal N})$
and that
![]() $Df_{\xi _n}$
is a bounded sequence in
$Df_{\xi _n}$
is a bounded sequence in
![]() $L^p({\mathcal M};T^*{\mathcal M}\otimes T{\mathcal N})$
. Indeed,
$L^p({\mathcal M};T^*{\mathcal M}\otimes T{\mathcal N})$
. Indeed,
and
since every element of
![]() $\operatorname {SO}(G,\mathfrak {h})$
is of norm
$\operatorname {SO}(G,\mathfrak {h})$
is of norm
![]() $\sqrt {d+1}$
. The boundedness of the bending energy
$\sqrt {d+1}$
. The boundedness of the bending energy
![]() $\tilde {{\mathcal E}}_p^B(\xi _n)$
implies in turn that
$\tilde {{\mathcal E}}_p^B(\xi _n)$
implies in turn that
![]() $K^{\mathfrak {h}}\circ D\xi _n$
is a bounded sequence in
$K^{\mathfrak {h}}\circ D\xi _n$
is a bounded sequence in
![]() $L^p({\mathcal M};T^*{\mathcal M}\otimes T{\mathcal N})$
. By the definition (2.1) of the Sasaki metric, this implies that
$L^p({\mathcal M};T^*{\mathcal M}\otimes T{\mathcal N})$
. By the definition (2.1) of the Sasaki metric, this implies that
![]() $D\xi _n$
is a bounded sequence in
$D\xi _n$
is a bounded sequence in
![]() $L^p({\mathcal M};T^*{\mathcal M}\otimes TT{\mathcal N})$
(i.e.,
$L^p({\mathcal M};T^*{\mathcal M}\otimes TT{\mathcal N})$
(i.e.,
![]() $\xi _n$
is bounded in
$\xi _n$
is bounded in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
). The claim on
$W^{1,p}({\mathcal M};T{\mathcal N})$
). The claim on
![]() $\xi _n$
follows immediately, and the claim on
$\xi _n$
follows immediately, and the claim on
![]() $f_{\xi _n}$
follows from Lemma 2.1.
$f_{\xi _n}$
follows from Lemma 2.1.
3.3 The case
 $p>d$
$p>d$
We first prove Theorem 3.4 for
![]() $p>d$
; this restriction is relaxed further below. The analysis for
$p>d$
; this restriction is relaxed further below. The analysis for
![]() $p>d$
can also be applied directly to the functional
$p>d$
can also be applied directly to the functional
![]() ${\mathcal E}_p:\operatorname {Imm}_p({\mathcal M};{\mathcal N})\to [0,\infty )$
; the extension to
${\mathcal E}_p:\operatorname {Imm}_p({\mathcal M};{\mathcal N})\to [0,\infty )$
; the extension to
![]() $p\le d$
in the next part, however, cannot.
$p\le d$
in the next part, however, cannot.
Analysis of the limiting map
Let
![]() ${\mathcal U}$
,
${\mathcal U}$
,
![]() ${\mathcal V}$
and R define trivializations of
${\mathcal V}$
and R define trivializations of
![]() $T{\mathcal N}$
as in Section 2, and let
$T{\mathcal N}$
as in Section 2, and let
![]() $U\in {\mathcal U}$
; note that
$U\in {\mathcal U}$
; note that
![]() $TU = T{\mathcal M}|_U$
is a vector bundle over U. Then,
$TU = T{\mathcal M}|_U$
is a vector bundle over U. Then,
which is a section of a vector bundle over U, is a trivialization of
![]() $Df_{\xi _n}\oplus \xi _n$
satisfying
$Df_{\xi _n}\oplus \xi _n$
satisfying
The fact that
![]() $\tilde {{\mathcal E}}_p(\xi _n) \to 0$
implies in particular that
$\tilde {{\mathcal E}}_p(\xi _n) \to 0$
implies in particular that
It follows from (3.1) that
![]() $\alpha _n$
is an
$\alpha _n$
is an
![]() $L^p$
-bounded sequence of sections of
$L^p$
-bounded sequence of sections of
![]() $(TU\oplus {\mathbb R})^*\otimes {\mathbb R}^{d+1}$
. By the fundamental theorem of Young measures (see [Reference Kupferman, Maor and ShacharKMS19, Section 3.1] for a version for vector bundles), there exists an
$(TU\oplus {\mathbb R})^*\otimes {\mathbb R}^{d+1}$
. By the fundamental theorem of Young measures (see [Reference Kupferman, Maor and ShacharKMS19, Section 3.1] for a version for vector bundles), there exists an
![]() $L^p$
-Young measure
$L^p$
-Young measure
![]() $\nu \in Y^p(U,(TU\oplus {\mathbb R})^*\otimes {\mathbb R}^{d+1})$
such that
$\nu \in Y^p(U,(TU\oplus {\mathbb R})^*\otimes {\mathbb R}^{d+1})$
such that
That is, for every vector bundle
![]() $E\to U$
and every (generally nonlinear) bundle map
$E\to U$
and every (generally nonlinear) bundle map
![]() $W:(TU\oplus {\mathbb R})^*\otimes {\mathbb R}^{d+1}\to E$
for which
$W:(TU\oplus {\mathbb R})^*\otimes {\mathbb R}^{d+1}\to E$
for which
![]() $W(\alpha _n):U\to E$
is
$W(\alpha _n):U\to E$
is
![]() $L^1$
-weakly precompact,
$L^1$
-weakly precompact,
 $$\begin{align*}W(\alpha_n) \rightharpoonup \left\{q \to \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} W(A) \, d\nu_q(A)\right\} \qquad { \mathrm{in}\ L^1\Gamma(E)}. \end{align*}$$
$$\begin{align*}W(\alpha_n) \rightharpoonup \left\{q \to \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} W(A) \, d\nu_q(A)\right\} \qquad { \mathrm{in}\ L^1\Gamma(E)}. \end{align*}$$
Take
![]() $W(A)=\operatorname {dist}(A,SO(G,\mathfrak {e}))$
. Since
$W(A)=\operatorname {dist}(A,SO(G,\mathfrak {e}))$
. Since
![]() $W(\alpha _n)$
is bounded in
$W(\alpha _n)$
is bounded in
![]() $L^p(U)$
for
$L^p(U)$
for
![]() $p>1$
, it is
$p>1$
, it is
![]() $L^1$
-weakly precompact, from which follows that
$L^1$
-weakly precompact, from which follows that
 $$ \begin{align*} 0 &= \lim_{n\to\infty} \int_U \operatorname{dist}(\alpha_n,\operatorname{SO}(G,\mathfrak{e}))\,\text{d}\text{Vol}_{\mathfrak{g}} \\\ &= \int_U \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} \operatorname{dist}(A,\operatorname{SO}(G,\mathfrak{e}))\, d\nu(A)\, \text{d}\text{Vol}_{\mathfrak{g}} \end{align*} $$
$$ \begin{align*} 0 &= \lim_{n\to\infty} \int_U \operatorname{dist}(\alpha_n,\operatorname{SO}(G,\mathfrak{e}))\,\text{d}\text{Vol}_{\mathfrak{g}} \\\ &= \int_U \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} \operatorname{dist}(A,\operatorname{SO}(G,\mathfrak{e}))\, d\nu(A)\, \text{d}\text{Vol}_{\mathfrak{g}} \end{align*} $$
(i.e.,
![]() $\nu _q$
is supported on
$\nu _q$
is supported on
![]() $\operatorname {SO}(G,\mathfrak {e})$
for a.e.
$\operatorname {SO}(G,\mathfrak {e})$
for a.e.
![]() $q\in U$
).
$q\in U$
).
For general oriented inner-product spaces
![]() $(V,\mathfrak {g})$
and
$(V,\mathfrak {g})$
and
![]() $(W,\mathfrak {h})$
of equal dimension s, and a linear map
$(W,\mathfrak {h})$
of equal dimension s, and a linear map
![]() $A\in \operatorname {Hom}(V,W)$
, the determinant and the cofactor of A,
$A\in \operatorname {Hom}(V,W)$
, the determinant and the cofactor of A,
![]() $\det A \in \operatorname {Hom}({\mathbb R};{\mathbb R}) \simeq {\mathbb R}$
and
$\det A \in \operatorname {Hom}({\mathbb R};{\mathbb R}) \simeq {\mathbb R}$
and
![]() $\operatorname {cof} A \in \operatorname {Hom}(V,W)$
can be defined in a basis-independent manner by
$\operatorname {cof} A \in \operatorname {Hom}(V,W)$
can be defined in a basis-independent manner by
where
![]() $\star _{\mathfrak {g}}:\Lambda ^k V\to \Lambda ^{s-k}V$
and
$\star _{\mathfrak {g}}:\Lambda ^k V\to \Lambda ^{s-k}V$
and
![]() $\star _{\mathfrak {h}}:\Lambda ^k W\to \Lambda ^{s-k}W$
are the hodge-dual isomorphisms of the respective spaces, and
$\star _{\mathfrak {h}}:\Lambda ^k W\to \Lambda ^{s-k}W$
are the hodge-dual isomorphisms of the respective spaces, and
![]() $\wedge ^k A$
is the k-minor of A, defined by
$\wedge ^k A$
is the k-minor of A, defined by
These definitions can be equivalently obtained by choosing positive orthonormal bases for V and W and evaluating the determinant and cofactor of their matrix representations in these bases. It is well known that
With that, consider next the test functions
![]() $W(A) = A$
,
$W(A) = A$
,
![]() $W(A) = \operatorname {cof} A$
and
$W(A) = \operatorname {cof} A$
and
![]() $W(A)=\det A$
. By definition, they are compositions of minors of A of ranks 1, d and
$W(A)=\det A$
. By definition, they are compositions of minors of A of ranks 1, d and
![]() $(d+1)$
, respectively, and hodge-dual isometries. Since
$(d+1)$
, respectively, and hodge-dual isometries. Since
![]() $\mathfrak {h}$
and
$\mathfrak {h}$
and
![]() $\mathfrak {h}^{-1}$
are bounded uniformly (in coordinates) and
$\mathfrak {h}^{-1}$
are bounded uniformly (in coordinates) and
![]() $Df_{\xi _n}$
is bounded in
$Df_{\xi _n}$
is bounded in
![]() $L^p$
, both the cofactor and the determinant of
$L^p$
, both the cofactor and the determinant of
![]() $\alpha _n$
are uniformly bounded in
$\alpha _n$
are uniformly bounded in
![]() $L^{p/d}$
, and therefore,
$L^{p/d}$
, and therefore,
![]() $W(\alpha _n)$
are
$W(\alpha _n)$
are
![]() $L^1$
-weakly precompact for all above choices of W. It follows from the definition of the Young measure limit that
$L^1$
-weakly precompact for all above choices of W. It follows from the definition of the Young measure limit that
 $$ \begin{align*} \alpha_n &\rightharpoonup \left\{q \to \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} A \, d\nu_q(A)\right\} &{ \mathrm{in}\ L^1\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \\ \operatorname{cof}(\alpha_n) &\rightharpoonup \left\{q \to \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} \operatorname{cof} A \, d\nu_q(A)\right\} & { \mathrm{in}\ L^1\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \\ \det(\alpha_n) &\rightharpoonup \left\{q \to \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} \det A \, d\nu_q(A)\right\} & { \mathrm{in}\ L^1(U)}. \end{align*} $$
$$ \begin{align*} \alpha_n &\rightharpoonup \left\{q \to \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} A \, d\nu_q(A)\right\} &{ \mathrm{in}\ L^1\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \\ \operatorname{cof}(\alpha_n) &\rightharpoonup \left\{q \to \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} \operatorname{cof} A \, d\nu_q(A)\right\} & { \mathrm{in}\ L^1\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \\ \det(\alpha_n) &\rightharpoonup \left\{q \to \int_{(TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1}} \det A \, d\nu_q(A)\right\} & { \mathrm{in}\ L^1(U)}. \end{align*} $$
Since
![]() $\nu _q$
is supported on
$\nu _q$
is supported on
![]() $\operatorname {SO}(G,\mathfrak {e})$
for a.e.
$\operatorname {SO}(G,\mathfrak {e})$
for a.e.
![]() $q\in U$
, and on that set
$q\in U$
, and on that set
![]() $\operatorname {cof} A=A$
and
$\operatorname {cof} A=A$
and
![]() $\det A=1$
, it follows that
$\det A=1$
, it follows that
 $$ \begin{align} \alpha_n &\rightharpoonup \left\{q \to \int_{\operatorname{SO}(G,\mathfrak{e})} A \, d\nu_q(A)\right\} & { \mathrm{in}\ L^1\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \nonumber \\ \operatorname{cof}(\alpha_n) &\rightharpoonup \left\{q \to \int_{\operatorname{SO}(G,\mathfrak{e})} A \, d\nu_q(A)\right\} & { \mathrm{in}\ L^1\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \\ \det(\alpha_n)& \rightharpoonup 1 & { \mathrm{in}\ L^1(U)}. \nonumber \end{align} $$
$$ \begin{align} \alpha_n &\rightharpoonup \left\{q \to \int_{\operatorname{SO}(G,\mathfrak{e})} A \, d\nu_q(A)\right\} & { \mathrm{in}\ L^1\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \nonumber \\ \operatorname{cof}(\alpha_n) &\rightharpoonup \left\{q \to \int_{\operatorname{SO}(G,\mathfrak{e})} A \, d\nu_q(A)\right\} & { \mathrm{in}\ L^1\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \\ \det(\alpha_n)& \rightharpoonup 1 & { \mathrm{in}\ L^1(U)}. \nonumber \end{align} $$
Recall that
![]() $\xi _n \rightharpoonup \xi $
(hence also
$\xi _n \rightharpoonup \xi $
(hence also
![]() $f_{\xi _n} \rightharpoonup f_\xi $
) in
$f_{\xi _n} \rightharpoonup f_\xi $
) in
![]() $W^{1,p}$
. It follows from the second clause of Proposition 2.4 that
$W^{1,p}$
. It follows from the second clause of Proposition 2.4 that
Lemma 3.6. The weak
![]() $L^p$
-convergence
$L^p$
-convergence
![]() $\alpha _n\rightharpoonup \alpha $
implies that
$\alpha _n\rightharpoonup \alpha $
implies that
 $$ \begin{align} \nonumber \operatorname{cof}(\alpha_n) &\rightharpoonup \operatorname{cof}(\alpha) \qquad { \mathrm{in}\ L^{p/d}\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \\ \det(\alpha_n) &\rightharpoonup \det(\alpha) \qquad { \mathrm{in}\ L^{p/d}(U)}. \end{align} $$
$$ \begin{align} \nonumber \operatorname{cof}(\alpha_n) &\rightharpoonup \operatorname{cof}(\alpha) \qquad { \mathrm{in}\ L^{p/d}\Gamma((TU\oplus{\mathbb R})^*\otimes{\mathbb R}^{d+1})} \\ \det(\alpha_n) &\rightharpoonup \det(\alpha) \qquad { \mathrm{in}\ L^{p/d}(U)}. \end{align} $$
Proof. Since the hodge-dual operator is a linear isometry and
![]() $\xi _n\to \xi $
uniformly, it suffices to show that
$\xi _n\to \xi $
uniformly, it suffices to show that
for
![]() $k=d,d+1$
. We show more generally that for every
$k=d,d+1$
. We show more generally that for every
![]() $k=1,\dots ,d+1$
,
$k=1,\dots ,d+1$
,
We start by noting that for
![]() $v_1,\ldots ,v_k \in T_qU$
and
$v_1,\ldots ,v_k \in T_qU$
and
![]() $t_1,\dots ,t_k\in {\mathbb R}$
,
$t_1,\dots ,t_k\in {\mathbb R}$
,
 $$ \begin{align*} \wedge^k\alpha_n((v_1,t_1),\dots,(v_k,t_k)) &= \wedge_{j=1}^k (R_{f_{\xi_n}(q)}\circ D_qf_{\xi_n}(v_j) + t_j R_{f_{\xi_n}(q)}\circ\xi_n(q)) \\ &= \wedge_{j=1}^k R_{f_{\xi_n}(q)}\circ D_qf_{\xi_n}(v_j) \\ &\qquad + \sum_{\ell=1}^k (-1)^\ell t_\ell \wedge_{j\ne \ell} \left(R_{f_{\xi_n}(q)}\circ D_qf_{\xi_n}(v_j)\right)\wedge (R_{f_{\xi_n}(q)}\circ \xi_n(q)). \end{align*} $$
$$ \begin{align*} \wedge^k\alpha_n((v_1,t_1),\dots,(v_k,t_k)) &= \wedge_{j=1}^k (R_{f_{\xi_n}(q)}\circ D_qf_{\xi_n}(v_j) + t_j R_{f_{\xi_n}(q)}\circ\xi_n(q)) \\ &= \wedge_{j=1}^k R_{f_{\xi_n}(q)}\circ D_qf_{\xi_n}(v_j) \\ &\qquad + \sum_{\ell=1}^k (-1)^\ell t_\ell \wedge_{j\ne \ell} \left(R_{f_{\xi_n}(q)}\circ D_qf_{\xi_n}(v_j)\right)\wedge (R_{f_{\xi_n}(q)}\circ \xi_n(q)). \end{align*} $$
That is,
Since
![]() $\xi _n\to \xi $
uniformly, and since the product of a weakly
$\xi _n\to \xi $
uniformly, and since the product of a weakly
![]() $L^p$
-convergent sequence and a uniformly convergence sequence is weakly
$L^p$
-convergent sequence and a uniformly convergence sequence is weakly
![]() $L^p$
-convergent, it suffices to show that
$L^p$
-convergent, it suffices to show that
Since
![]() ${\mathcal M}$
and
${\mathcal M}$
and
![]() ${\mathcal N}$
are compact, the orthonormal frame R can be replaced by any other smooth frame – for example,
${\mathcal N}$
are compact, the orthonormal frame R can be replaced by any other smooth frame – for example,
![]() $R = dh$
, where
$R = dh$
, where
![]() $h:V\to {\mathbb R}^{d+1}$
is a local coordinate system. The claim reduces then to the standard weak-continuity of minors, proved inductively on k (see, for example, [Reference RindlerRin18, Lemma 5.10]).
$h:V\to {\mathbb R}^{d+1}$
is a local coordinate system. The claim reduces then to the standard weak-continuity of minors, proved inductively on k (see, for example, [Reference RindlerRin18, Lemma 5.10]).
Since
![]() $\operatorname {cof}(AB) = \operatorname {cof}(A)\,\operatorname {cof}(B)$
and
$\operatorname {cof}(AB) = \operatorname {cof}(A)\,\operatorname {cof}(B)$
and
![]() $\det (AB) = \det (A)\,\det (B)$
, and since R is an orientation-preserving isometry,
$\det (AB) = \det (A)\,\det (B)$
, and since R is an orientation-preserving isometry,
 $$ \begin{align*} \operatorname{cof}(R\circ A) &= R\circ \operatorname{cof}(A)\\ \det(R\circ A) &= \det(A), \end{align*} $$
$$ \begin{align*} \operatorname{cof}(R\circ A) &= R\circ \operatorname{cof}(A)\\ \det(R\circ A) &= \det(A), \end{align*} $$
we obtain by combining (3.4) with (3.2) that
which implies that
Thus,
![]() $\tilde {{\mathcal E}}_p^S(\xi ) = 0$
. By Proposition 3.2,
$\tilde {{\mathcal E}}_p^S(\xi ) = 0$
. By Proposition 3.2,
![]() $f_\xi \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
with
$f_\xi \in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
with
![]() $Df_\xi \in \operatorname {O}(\mathfrak {g},\mathfrak {h})$
, and
$Df_\xi \in \operatorname {O}(\mathfrak {g},\mathfrak {h})$
, and
![]() $\xi = \mathfrak {n}_{f_\xi }$
.
$\xi = \mathfrak {n}_{f_\xi }$
.
Thus, we have obtained at this stage that
![]() $\xi _n \rightharpoonup \xi $
in
$\xi _n \rightharpoonup \xi $
in
![]() $W^{1,p}$
where,
$W^{1,p}$
where,
![]() $\xi = \mathfrak {n}_{f_\xi }$
. In order to complete the proof for the case
$\xi = \mathfrak {n}_{f_\xi }$
. In order to complete the proof for the case
![]() $p>d$
, we need to show that the convergence is in fact strong and that the shape operator of
$p>d$
, we need to show that the convergence is in fact strong and that the shape operator of
![]() $\mathfrak {n}_{f_\xi }$
is S, and deduce from Theorem 1.2 that the limit is smooth.
$\mathfrak {n}_{f_\xi }$
is S, and deduce from Theorem 1.2 that the limit is smooth.
Strong convergence and second fundamental form of the limit
From the uniqueness of the limit, combining (3.2) and (3.3),
The left-hand side is a convex combination of elements in
![]() $\operatorname {SO}(G_x,\mathfrak {e})$
, and the right-hand side is in
$\operatorname {SO}(G_x,\mathfrak {e})$
, and the right-hand side is in
![]() $\operatorname {SO}(G_x,\mathfrak {e})$
(
$\operatorname {SO}(G_x,\mathfrak {e})$
(
![]() $\alpha $
is the composition of an element of
$\alpha $
is the composition of an element of
![]() $\operatorname {SO}(G,\mathfrak {h})$
and an element of
$\operatorname {SO}(G,\mathfrak {h})$
and an element of
![]() $\operatorname {SO}(\mathfrak {h},\mathfrak {e})$
). Since
$\operatorname {SO}(\mathfrak {h},\mathfrak {e})$
). Since
![]() $\operatorname {SO}(G_x,\mathfrak {e})$
is strictly convex, this convex combination must be trivial; namely,
$\operatorname {SO}(G_x,\mathfrak {e})$
is strictly convex, this convex combination must be trivial; namely,
As a consequence, for every
![]() $W:(TU\otimes {\mathbb R})^*\otimes {\mathbb R}^{d+1}\to {\mathbb R}$
for which
$W:(TU\otimes {\mathbb R})^*\otimes {\mathbb R}^{d+1}\to {\mathbb R}$
for which
![]() $W(\alpha _n)$
is
$W(\alpha _n)$
is
![]() $L^1$
-weakly precompact,
$L^1$
-weakly precompact,
We now show that
![]() $f_{\xi _n}\to f_\xi $
strongly in
$f_{\xi _n}\to f_\xi $
strongly in
![]() $W^{1,p}({\mathcal M};{\mathcal N})$
(for the moment, we have only established weak convergence, and hence in particular strong
$W^{1,p}({\mathcal M};{\mathcal N})$
(for the moment, we have only established weak convergence, and hence in particular strong
![]() $L^p$
convergence). By the first clause of Proposition 2.4, it suffices to prove that
$L^p$
convergence). By the first clause of Proposition 2.4, it suffices to prove that
![]() $\alpha _n\to \alpha $
in
$\alpha _n\to \alpha $
in
![]() $L^p\Gamma ((TU\otimes {\mathbb R})^*\otimes {\mathbb R}^{d+1})$
. We would be done if we could use (3.5) for
$L^p\Gamma ((TU\otimes {\mathbb R})^*\otimes {\mathbb R}^{d+1})$
. We would be done if we could use (3.5) for
However,
![]() $W(\alpha _n)$
is only bounded in
$W(\alpha _n)$
is only bounded in
![]() $L^1(U)$
, which does not guarantee sequential weak precompactness. Instead, let
$L^1(U)$
, which does not guarantee sequential weak precompactness. Instead, let
 $$\begin{align*}W(A)=|A- \alpha|^p \,\varphi\left(\frac{|A|}{3\sqrt{d+1}}\right), \end{align*}$$
$$\begin{align*}W(A)=|A- \alpha|^p \,\varphi\left(\frac{|A|}{3\sqrt{d+1}}\right), \end{align*}$$
where
![]() $\varphi :[0,\infty )\to {\mathbb R}$
is continuous, nonnegative, compactly supported, and satisfies
$\varphi :[0,\infty )\to {\mathbb R}$
is continuous, nonnegative, compactly supported, and satisfies
![]() $\varphi (t)=1$
for
$\varphi (t)=1$
for
![]() $t\le 1$
and
$t\le 1$
and
![]() $\varphi (t)<1$
for
$\varphi (t)<1$
for
![]() $t>1$
. Clearly,
$t>1$
. Clearly,
![]() $W(\alpha _n)$
is uniformly bounded, and hence
$W(\alpha _n)$
is uniformly bounded, and hence
![]() $L^1$
-weakly precompact, which since
$L^1$
-weakly precompact, which since
![]() $W(\alpha )=0$
implies that
$W(\alpha )=0$
implies that
On the set
we have
![]() $W(\alpha _n) = |\alpha _n - \alpha |^p$
, whereas on its complement
$W(\alpha _n) = |\alpha _n - \alpha |^p$
, whereas on its complement
![]() $U\setminus B_n$
,
$U\setminus B_n$
,
where the first inequalities follow from the fact that
![]() $|\alpha | = \sqrt {d+1}$
and
$|\alpha | = \sqrt {d+1}$
and
![]() $|\alpha _n|\ge 3\sqrt {d+1}$
, and the second inequality follows from the reverse triangle inequality. Thus, in
$|\alpha _n|\ge 3\sqrt {d+1}$
, and the second inequality follows from the reverse triangle inequality. Thus, in
![]() $U\setminus B_n$
,
$U\setminus B_n$
,
Combining the two sets,
 $$ \begin{align*} \int_U |\alpha_n- \alpha|^p\,\text{d}\text{Vol}_{\mathfrak{g}} &= \int_{B_n} |\alpha_n- \alpha|^p\,\text{d}\text{Vol}_{\mathfrak{g}} + \int_{U\setminus B_n} |\alpha_n- \alpha|^p\,\text{d}\text{Vol}_{\mathfrak{g}} \\ &\le \int_U W(\alpha_n)\,\text{d}\text{Vol}_{\mathfrak{g}} + 2^p \int_{U} \operatorname{dist}^p(\alpha_n,\operatorname{SO}(G,\mathfrak{e}))\,\text{d}\text{Vol}_{\mathfrak{g}}, \end{align*} $$
$$ \begin{align*} \int_U |\alpha_n- \alpha|^p\,\text{d}\text{Vol}_{\mathfrak{g}} &= \int_{B_n} |\alpha_n- \alpha|^p\,\text{d}\text{Vol}_{\mathfrak{g}} + \int_{U\setminus B_n} |\alpha_n- \alpha|^p\,\text{d}\text{Vol}_{\mathfrak{g}} \\ &\le \int_U W(\alpha_n)\,\text{d}\text{Vol}_{\mathfrak{g}} + 2^p \int_{U} \operatorname{dist}^p(\alpha_n,\operatorname{SO}(G,\mathfrak{e}))\,\text{d}\text{Vol}_{\mathfrak{g}}, \end{align*} $$
and both terms tend to zero as
![]() $n\to \infty $
. We conclude that
$n\to \infty $
. We conclude that
![]() $Df_{\xi _n} \to Df_{\xi }$
in
$Df_{\xi _n} \to Df_{\xi }$
in
![]() $L^p$
and therefore obtain that
$L^p$
and therefore obtain that
![]() $f_{\xi _n} \to f_{\xi }$
in
$f_{\xi _n} \to f_{\xi }$
in
![]() $W^{1,p}({\mathcal M};{\mathcal N})$
. It remains to show that S is the shape operator of
$W^{1,p}({\mathcal M};{\mathcal N})$
. It remains to show that S is the shape operator of
![]() $f_\xi $
(i.e., that
$f_\xi $
(i.e., that
![]() $K^h\circ D\xi =- Df_{\xi } \circ S$
) and that
$K^h\circ D\xi =- Df_{\xi } \circ S$
) and that
![]() $\xi _n\to \xi $
strongly in
$\xi _n\to \xi $
strongly in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
. We observe that
$W^{1,p}({\mathcal M};T{\mathcal N})$
. We observe that
 $$ \begin{align*} d\jmath\circ K^{\mathfrak{h}}\circ D\xi_n &= d\jmath\circ(K^{\mathfrak{h}}\circ D\xi_n + Df_{\xi_n}\circ S) \\ &\quad + (d\jmath\circ Df_\xi - d\jmath\circ Df_{\xi_n})\circ S \\ &\quad - d\jmath\circ Df_\xi \circ S \end{align*} $$
$$ \begin{align*} d\jmath\circ K^{\mathfrak{h}}\circ D\xi_n &= d\jmath\circ(K^{\mathfrak{h}}\circ D\xi_n + Df_{\xi_n}\circ S) \\ &\quad + (d\jmath\circ Df_\xi - d\jmath\circ Df_{\xi_n})\circ S \\ &\quad - d\jmath\circ Df_\xi \circ S \end{align*} $$
(the composition with
![]() $d\jmath $
is necessary in order to be able to add and subtract the various terms). The first term on the right-hand side tends to zero in
$d\jmath $
is necessary in order to be able to add and subtract the various terms). The first term on the right-hand side tends to zero in
![]() $L^p$
since the bending energy
$L^p$
since the bending energy
![]() $\tilde {{\mathcal E}}_p^B(\xi _n)$
tends to zero; the second term tends to zero in
$\tilde {{\mathcal E}}_p^B(\xi _n)$
tends to zero; the second term tends to zero in
![]() $L^p$
since
$L^p$
since
![]() $f_{\xi _n}\to f_\xi $
strongly in
$f_{\xi _n}\to f_\xi $
strongly in
![]() $W^{1,p}$
. Thus, the left-hand side converges strongly to
$W^{1,p}$
. Thus, the left-hand side converges strongly to
![]() $- d\jmath \circ Df \circ S$
.
$- d\jmath \circ Df \circ S$
.
It follows from Lemma 2.2 that
![]() $K^{\mathfrak {h}}\circ D\xi _n \to K^{\mathfrak {h}}\circ D\xi $
in
$K^{\mathfrak {h}}\circ D\xi _n \to K^{\mathfrak {h}}\circ D\xi $
in
![]() $L^p$
and that
$L^p$
and that
![]() $K^h\circ D\xi =- Df \circ S$
, thus proving that S is the shape operator of
$K^h\circ D\xi =- Df \circ S$
, thus proving that S is the shape operator of
![]() $f_\xi $
. Since
$f_\xi $
. Since
![]() $\xi _n\rightharpoonup \xi $
in
$\xi _n\rightharpoonup \xi $
in
![]() $W^{1,p}$
,
$W^{1,p}$
,
![]() $f_{\xi _n} \to f_{\xi }$
in
$f_{\xi _n} \to f_{\xi }$
in
![]() $W^{1,p}$
and
$W^{1,p}$
and
![]() $K^{\mathfrak {h}}\circ D\xi _n \to K^{\mathfrak {h}}\circ D\xi $
in
$K^{\mathfrak {h}}\circ D\xi _n \to K^{\mathfrak {h}}\circ D\xi $
in
![]() $L^p$
, we obtain from Proposition 2.3 that
$L^p$
, we obtain from Proposition 2.3 that
![]() $\xi _n\to \xi $
strongly, as needed.
$\xi _n\to \xi $
strongly, as needed.
Lastly,
![]() $f_\xi $
satisfies the assumptions of Theorem 1.2 (which is proved in Section 4 below), and thus
$f_\xi $
satisfies the assumptions of Theorem 1.2 (which is proved in Section 4 below), and thus
![]() $f_\xi $
is smooth, and by extension so is
$f_\xi $
is smooth, and by extension so is
![]() $\xi =\mathfrak {n}_{f_\xi }$
.
$\xi =\mathfrak {n}_{f_\xi }$
.
3.4 The case
 $p\le d$
via Sobolev truncation
$p\le d$
via Sobolev truncation
If
![]() $p \le d$
, we first need to regularize
$p \le d$
, we first need to regularize
![]() $\xi _n \in W^{1,p}({\mathcal M};T{\mathcal N})$
by replacing them with
$\xi _n \in W^{1,p}({\mathcal M};T{\mathcal N})$
by replacing them with
![]() $\tilde {\xi }_n \in W^{1,\infty }({\mathcal M};T{\mathcal N})$
, which are close to
$\tilde {\xi }_n \in W^{1,\infty }({\mathcal M};T{\mathcal N})$
, which are close to
![]() $\xi _n$
in
$\xi _n$
in
![]() $W^{1,p}$
and also uniformly Lipschitz. This is where the relaxation of the energy comes into play, since even if
$W^{1,p}$
and also uniformly Lipschitz. This is where the relaxation of the energy comes into play, since even if
![]() $\xi _n = \mathfrak {n}_{f_{\xi _n}}$
project onto immersions
$\xi _n = \mathfrak {n}_{f_{\xi _n}}$
project onto immersions
![]() $f_{\xi _n}\in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
, we do not know how to approximate them with more regular functions within the space
$f_{\xi _n}\in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
, we do not know how to approximate them with more regular functions within the space
![]() $\operatorname {Imm}_p({\mathcal M};{\mathcal N})$
. This construction follows a similar path as in other manifold-valued elasticity results – namely, [Reference Kupferman, Maor and ShacharKMS19, Reference Krömer and MüllerKM21] – with some technical complications due to the structure of the energy in codimension-1 and the non-compactness of
$\operatorname {Imm}_p({\mathcal M};{\mathcal N})$
. This construction follows a similar path as in other manifold-valued elasticity results – namely, [Reference Kupferman, Maor and ShacharKMS19, Reference Krömer and MüllerKM21] – with some technical complications due to the structure of the energy in codimension-1 and the non-compactness of
![]() $T{\mathcal N}$
.
$T{\mathcal N}$
.
First, we need the following pointwise estimate:
Lemma 3.7. Let
![]() $\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
. Denote
$\xi \in W^{1,p}({\mathcal M};T{\mathcal N})$
. Denote
![]() $M = \|S\|_\infty $
, where S is the shape operator in
$M = \|S\|_\infty $
, where S is the shape operator in
![]() ${\mathcal E}_p$
. If at a point in
${\mathcal E}_p$
. If at a point in
![]() ${\mathcal M}$
,
${\mathcal M}$
,
![]() $|D\xi | \ge (3+2M)\sqrt {d+1}$
, then at that point,
$|D\xi | \ge (3+2M)\sqrt {d+1}$
, then at that point,
Proof. By the definition of the Sasaki metric,
Consider first the case where
![]() $|Df_\xi | \ge 2\sqrt {d+1}$
. Then, by the triangle inequality and the fact that all the elements in
$|Df_\xi | \ge 2\sqrt {d+1}$
. Then, by the triangle inequality and the fact that all the elements in
![]() $\operatorname {SO}(G,\mathfrak {h})$
are of norm
$\operatorname {SO}(G,\mathfrak {h})$
are of norm
![]() $\sqrt {d+1}$
,
$\sqrt {d+1}$
,
Thus,
 $$ \begin{align} \nonumber |D\xi| &\le |Df_\xi| + |K^{\mathfrak{h}}\circ D\xi| \\ \nonumber &\le |Df_\xi| + |Df_\xi\circ S| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ &\le (1+M)|Df_\xi| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ \nonumber &\le (1+M)\operatorname{dist}(Df_\xi\oplus \xi,\operatorname{SO}(G,\mathfrak{h})) + (1+M)\sqrt{d+1} + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ \nonumber &\le 2(1+M)\operatorname{dist}(Df_\xi\oplus \xi,\operatorname{SO}(G,\mathfrak{h})) + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi|, \end{align} $$
$$ \begin{align} \nonumber |D\xi| &\le |Df_\xi| + |K^{\mathfrak{h}}\circ D\xi| \\ \nonumber &\le |Df_\xi| + |Df_\xi\circ S| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ &\le (1+M)|Df_\xi| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ \nonumber &\le (1+M)\operatorname{dist}(Df_\xi\oplus \xi,\operatorname{SO}(G,\mathfrak{h})) + (1+M)\sqrt{d+1} + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ \nonumber &\le 2(1+M)\operatorname{dist}(Df_\xi\oplus \xi,\operatorname{SO}(G,\mathfrak{h})) + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi|, \end{align} $$
which implies (3.6).
Otherwise, if
![]() $|Df_\xi | < 2\sqrt {d+1}$
and
$|Df_\xi | < 2\sqrt {d+1}$
and
![]() $|D\xi | \ge (3+2M)\sqrt {d+1}$
, then
$|D\xi | \ge (3+2M)\sqrt {d+1}$
, then
 $$ \begin{align*} |D\xi| &\le |Df_\xi| + |K^{\mathfrak{h}}\circ D\xi| \\ &\le |Df_\xi| + |Df_\xi\circ S| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ &\le (1+M)|Df_\xi| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ &\le 2(1+M)\sqrt{d+1} + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ &\le \frac{2(1+M)}{3 + 2M}|D\xi| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi|, \end{align*} $$
$$ \begin{align*} |D\xi| &\le |Df_\xi| + |K^{\mathfrak{h}}\circ D\xi| \\ &\le |Df_\xi| + |Df_\xi\circ S| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ &\le (1+M)|Df_\xi| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ &\le 2(1+M)\sqrt{d+1} + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi| \\ &\le \frac{2(1+M)}{3 + 2M}|D\xi| + |Df_\xi\circ S + K^{\mathfrak{h}}\circ D\xi|, \end{align*} $$
from which follows that
which implies (3.6).
For a given
![]() $\rho>2\sqrt {d+1}$
, denote
$\rho>2\sqrt {d+1}$
, denote
![]() $T^\rho {\mathcal N} := \{v\in T{\mathcal N} ~:~ |v|\le \rho \}$
, which is a compact submanifold of
$T^\rho {\mathcal N} := \{v\in T{\mathcal N} ~:~ |v|\le \rho \}$
, which is a compact submanifold of
![]() $T{\mathcal N}$
. Denote by
$T{\mathcal N}$
. Denote by
![]() $\varphi :[0,\infty )\to [0,1]$
a continuous, nonnegative, compactly supported function satisfying
$\varphi :[0,\infty )\to [0,1]$
a continuous, nonnegative, compactly supported function satisfying
![]() $\varphi (t)=1$
for
$\varphi (t)=1$
for
![]() $t\le 2\sqrt {d+1}$
and
$t\le 2\sqrt {d+1}$
and
![]() $\varphi (t)=0$
for
$\varphi (t)=0$
for
![]() $t\ge \rho $
, and let
$t\ge \rho $
, and let
![]() $\hat {\xi }_n = \varphi (|\xi _n|)\xi _n$
. Note that
$\hat {\xi }_n = \varphi (|\xi _n|)\xi _n$
. Note that
![]() $\hat {\xi }_n: {\mathcal M} \to T^\rho {\mathcal N}$
is uniformly bounded, and
$\hat {\xi }_n: {\mathcal M} \to T^\rho {\mathcal N}$
is uniformly bounded, and
![]() $|D\hat {\xi }_n| \le C|D\xi _n|$
for some C depending only on
$|D\hat {\xi }_n| \le C|D\xi _n|$
for some C depending only on
![]() $\varphi $
. Furthermore,
$\varphi $
. Furthermore,
 $$ \begin{align*} \{x\in {\mathcal M} ~:~ \hat{\xi}_n(x) \ne \xi_n(x)\} &\subset \{|\xi_n|>2\sqrt{d+1}\} \\ &\subset \{\operatorname{dist}(Df_{\xi_n}\oplus \xi_n,\operatorname{SO}(G,\mathfrak{h})) > \sqrt{d+1}\}, \end{align*} $$
$$ \begin{align*} \{x\in {\mathcal M} ~:~ \hat{\xi}_n(x) \ne \xi_n(x)\} &\subset \{|\xi_n|>2\sqrt{d+1}\} \\ &\subset \{\operatorname{dist}(Df_{\xi_n}\oplus \xi_n,\operatorname{SO}(G,\mathfrak{h})) > \sqrt{d+1}\}, \end{align*} $$
where the last inclusion follows from the same argument as in (3.7). Since
![]() $\tilde {{\mathcal E}}_p(\xi _n)\to 0$
, it follows that
$\tilde {{\mathcal E}}_p(\xi _n)\to 0$
, it follows that
Hence, the volumes of all the sets above tend to zero. On the one hand,
 $$ \begin{align*} \int_{\mathcal M} |\xi_n - \hat{\xi}_n|^p\,\text{d}\text{Vol}_{\mathfrak{g}} &= \int_{\{\xi_n \ne \hat{\xi}_n\}} |\xi_n - \hat{\xi}_n|^p\,\text{d}\text{Vol}_{\mathfrak{g}} \\ &\lesssim \int_{\{\xi_n \ne \hat{\xi}_n\}} |\xi_n|^p\,\text{d}\text{Vol}_{\mathfrak{g}} + \int_{\{\xi_n \ne \hat{\xi}_n\}} |\hat{\xi}_n|^p\,\text{d}\text{Vol}_{\mathfrak{g}}. \end{align*} $$
$$ \begin{align*} \int_{\mathcal M} |\xi_n - \hat{\xi}_n|^p\,\text{d}\text{Vol}_{\mathfrak{g}} &= \int_{\{\xi_n \ne \hat{\xi}_n\}} |\xi_n - \hat{\xi}_n|^p\,\text{d}\text{Vol}_{\mathfrak{g}} \\ &\lesssim \int_{\{\xi_n \ne \hat{\xi}_n\}} |\xi_n|^p\,\text{d}\text{Vol}_{\mathfrak{g}} + \int_{\{\xi_n \ne \hat{\xi}_n\}} |\hat{\xi}_n|^p\,\text{d}\text{Vol}_{\mathfrak{g}}. \end{align*} $$
The first term tends to zero as
![]() $n\to \infty $
because
$n\to \infty $
because
![]() $|\xi _n|^p$
is equi-integrable (it is bounded in
$|\xi _n|^p$
is equi-integrable (it is bounded in
![]() $W^{1,p}$
); the second term tends to zero because
$W^{1,p}$
); the second term tends to zero because
![]() $|\hat {\xi }|$
is uniformly bounded. Moreover,
$|\hat {\xi }|$
is uniformly bounded. Moreover,
 $$\begin{align*}\int_{\mathcal M} |d\iota \circ D\hat{\xi}_n - d\iota \circ D\xi_n|^p\, \text{d}\text{Vol}_{\mathfrak{g}} \lesssim \int_{\{\operatorname{dist}(Df_{\xi_n}\oplus \xi_n,\operatorname{SO}(G,\mathfrak{h}))> \sqrt{d+1}\}} |D\xi_n|^p\, \text{d}\text{Vol}_{\mathfrak{g}} \lesssim \tilde{{\mathcal E}}_p(\xi_n) \to 0, \end{align*}$$
$$\begin{align*}\int_{\mathcal M} |d\iota \circ D\hat{\xi}_n - d\iota \circ D\xi_n|^p\, \text{d}\text{Vol}_{\mathfrak{g}} \lesssim \int_{\{\operatorname{dist}(Df_{\xi_n}\oplus \xi_n,\operatorname{SO}(G,\mathfrak{h}))> \sqrt{d+1}\}} |D\xi_n|^p\, \text{d}\text{Vol}_{\mathfrak{g}} \lesssim \tilde{{\mathcal E}}_p(\xi_n) \to 0, \end{align*}$$
where the last inequality follows from (3.8). Thus,
Denote
![]() $u_n = \iota \circ \hat {\xi }_n \in W^{1,p}({\mathcal M};{\mathbb R}^D)$
. By [Reference Friesecke, James and MüllerFJM02, Proposition A.1], there exists a constant
$u_n = \iota \circ \hat {\xi }_n \in W^{1,p}({\mathcal M};{\mathbb R}^D)$
. By [Reference Friesecke, James and MüllerFJM02, Proposition A.1], there exists a constant
![]() $C>0$
, depending on
$C>0$
, depending on
![]() ${\mathcal M},\mathfrak {g},p$
and
${\mathcal M},\mathfrak {g},p$
and
![]() $\|S\|_\infty $
, and there exists a sequence of Lipschitz maps
$\|S\|_\infty $
, and there exists a sequence of Lipschitz maps
![]() $\bar {u}_n \in W^{1,\infty }({\mathcal M};{\mathbb R}^D)$
having uniform Lipschitz constant C such that
$\bar {u}_n \in W^{1,\infty }({\mathcal M};{\mathbb R}^D)$
having uniform Lipschitz constant C such that
and
Using Lemma 3.7, and the fact that
![]() $|Du_n| = |D\hat {\xi }_n|$
(since
$|Du_n| = |D\hat {\xi }_n|$
(since
![]() $\iota $
is an isometric immersion), we obtain that
$\iota $
is an isometric immersion), we obtain that
and
for some
![]() $C'>0$
. Note that the image of
$C'>0$
. Note that the image of
![]() $\bar {u}_n$
is not in
$\bar {u}_n$
is not in
![]() $\iota (T{\mathcal N})$
, which means that we cannot identify
$\iota (T{\mathcal N})$
, which means that we cannot identify
![]() $\bar {u}_n:{\mathcal M}\to {\mathbb R}^D$
with a function
$\bar {u}_n:{\mathcal M}\to {\mathbb R}^D$
with a function
![]() $\bar {\xi }_n:{\mathcal M}\to T{\mathcal N}$
; to rectify this problem, we resort to a projection. Since
$\bar {\xi }_n:{\mathcal M}\to T{\mathcal N}$
; to rectify this problem, we resort to a projection. Since
![]() $\tilde {{\mathcal E}}_p(\hat {\xi }_n)\to 0$
, it follows from (3.9) that for every
$\tilde {{\mathcal E}}_p(\hat {\xi }_n)\to 0$
, it follows from (3.9) that for every
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $n\in \mathbb {N}$
large enough (depending on
$n\in \mathbb {N}$
large enough (depending on
![]() $\varepsilon $
), every ball of radius
$\varepsilon $
), every ball of radius
![]() $\varepsilon $
in
$\varepsilon $
in
![]() ${\mathcal M}$
contains a point x for which
${\mathcal M}$
contains a point x for which
![]() $\bar {u}_n(x) = u_n(x)\in \iota (T^\rho {\mathcal N})$
. Since
$\bar {u}_n(x) = u_n(x)\in \iota (T^\rho {\mathcal N})$
. Since
![]() $\bar {u}_n$
are uniformly Lipschitz, we obtain that
$\bar {u}_n$
are uniformly Lipschitz, we obtain that
Thus, for n large enough,
![]() $\bar {u}_n(x)$
lies in a tubular neighborhood of
$\bar {u}_n(x)$
lies in a tubular neighborhood of
![]() $\iota (T{\mathcal N})$
on which the orthogonal projection operator P is well defined and smooth (this is where we use the compactness of
$\iota (T{\mathcal N})$
on which the orthogonal projection operator P is well defined and smooth (this is where we use the compactness of
![]() $T^\rho {\mathcal N}$
and the reason we had to truncate
$T^\rho {\mathcal N}$
and the reason we had to truncate
![]() $\xi _n$
to
$\xi _n$
to
![]() $\hat {\xi }_n$
– we had to ensure that the image of
$\hat {\xi }_n$
– we had to ensure that the image of
![]() $\bar {u}_n$
is uniformly close to a compact subset of
$\bar {u}_n$
is uniformly close to a compact subset of
![]() $\iota (T{\mathcal N})$
). Define
$\iota (T{\mathcal N})$
). Define
![]() $\tilde {u}_n = P\circ \bar {u}_n$
, and
$\tilde {u}_n = P\circ \bar {u}_n$
, and
![]() $\tilde {\xi }_n = \iota ^{-1}\circ \tilde {u}_n$
. A direct calculation, as in [Reference Kupferman, Maor and ShacharKMS19, pp. 391–2], shows that
$\tilde {\xi }_n = \iota ^{-1}\circ \tilde {u}_n$
. A direct calculation, as in [Reference Kupferman, Maor and ShacharKMS19, pp. 391–2], shows that
![]() $\tilde {u}_n$
and
$\tilde {u}_n$
and
![]() $\tilde {\xi }_n$
are uniformly Lipschitz and satisfy (3.9) and (3.10), and furthermore, that
$\tilde {\xi }_n$
are uniformly Lipschitz and satisfy (3.9) and (3.10), and furthermore, that
![]() $\tilde {{\mathcal E}}_q(\tilde {\xi }_n)\to 0$
for any
$\tilde {{\mathcal E}}_q(\tilde {\xi }_n)\to 0$
for any
![]() $q\in (1,\infty )$
.
$q\in (1,\infty )$
.
We can now apply the previous step for
![]() $\tilde {\xi }_n$
, for some
$\tilde {\xi }_n$
, for some
![]() $q>d\ge p$
, and obtain that
$q>d\ge p$
, and obtain that
![]() $\tilde {\xi }_n\to \xi =\mathfrak {n}_f$
in
$\tilde {\xi }_n\to \xi =\mathfrak {n}_f$
in
![]() $W^{1,q}({\mathcal M};T{\mathcal N})$
for some isometric immersion
$W^{1,q}({\mathcal M};T{\mathcal N})$
for some isometric immersion
![]() $f\in \operatorname {Imm}_\infty ({\mathcal M};{\mathcal N})$
whose shape operator is S. Since
$f\in \operatorname {Imm}_\infty ({\mathcal M};{\mathcal N})$
whose shape operator is S. Since
![]() $\|\tilde {u}_n - u_n\|_{W^{1,p}}\to 0$
, it follows by definition that
$\|\tilde {u}_n - u_n\|_{W^{1,p}}\to 0$
, it follows by definition that
![]() $\operatorname {dist}_{W^{1,p}}(\tilde {\xi }_n,\hat {\xi }_n) \to 0$
, and thus also
$\operatorname {dist}_{W^{1,p}}(\tilde {\xi }_n,\hat {\xi }_n) \to 0$
, and thus also
![]() $\operatorname {dist}_{W^{1,p}}(\tilde {\xi }_n,\xi _n) \to~0$
. It therefore follows that
$\operatorname {dist}_{W^{1,p}}(\tilde {\xi }_n,\xi _n) \to~0$
. It therefore follows that
![]() $\xi _n \to \mathfrak {n}_f$
in
$\xi _n \to \mathfrak {n}_f$
in
![]() $W^{1,p}({\mathcal M};T{\mathcal N})$
.
$W^{1,p}({\mathcal M};T{\mathcal N})$
.
4 Proof of Theorem 1.2
In this section, we prove Theorem 1.2. First, we prove that
![]() $ f\in W^{2,2} $
, in the sense that any coordinate representation of f is in
$ f\in W^{2,2} $
, in the sense that any coordinate representation of f is in
![]() $W^{2,2}$
. Then, in order to prove that f is smooth, we prove an analog version of [Reference Maor and ShacharMS19, Lemma 3.1], where the range is a Riemannian manifold instead of
$W^{2,2}$
. Then, in order to prove that f is smooth, we prove an analog version of [Reference Maor and ShacharMS19, Lemma 3.1], where the range is a Riemannian manifold instead of
![]() ${\mathbb R}^n$
(for our purpose, we are only interested in codimension-1). This is achieved by the following two propositions.
${\mathbb R}^n$
(for our purpose, we are only interested in codimension-1). This is achieved by the following two propositions.
Proposition 4.1. Let
![]() $f\in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
,
$f\in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
,
![]() $p> d$
. Suppose that
$p> d$
. Suppose that
![]() $f^*\mathfrak {h}$
(which is a priori only defined almost-everywhere) is a smooth metric on
$f^*\mathfrak {h}$
(which is a priori only defined almost-everywhere) is a smooth metric on
![]() ${\mathcal M}$
. Then
${\mathcal M}$
. Then
![]() $f\in W^{2,2}({\mathcal M};{\mathcal N})$
(in coordinates).
$f\in W^{2,2}({\mathcal M};{\mathcal N})$
(in coordinates).
In fact, the smoothness of
![]() $f^*\mathfrak {h}$
is not needed here;
$f^*\mathfrak {h}$
is not needed here;
![]() $C^1$
would suffice, and possibly even Sobolev regularity.
$C^1$
would suffice, and possibly even Sobolev regularity.
Proof. Assume
![]() $d\geq 2$
; hence,
$d\geq 2$
; hence,
![]() $p>2$
. Let
$p>2$
. Let
![]() $\iota :({\mathcal N},\mathfrak {h}) \to {\mathbb R}^D$
be an isometric embedding (i.e.,
$\iota :({\mathcal N},\mathfrak {h}) \to {\mathbb R}^D$
be an isometric embedding (i.e.,
![]() $\iota ({\mathcal N})$
is a smooth submanifold of
$\iota ({\mathcal N})$
is a smooth submanifold of
![]() ${\mathbb R}^D$
of codimension
${\mathbb R}^D$
of codimension
![]() $D - d - 1$
). We thicken
$D - d - 1$
). We thicken
![]() ${\mathcal M}$
into
${\mathcal M}$
into
![]() $ \tilde {{\mathcal M}}={\mathcal M}\times (-h, h)^{D-d}$
, with h small enough, and endow it with the product metric
$ \tilde {{\mathcal M}}={\mathcal M}\times (-h, h)^{D-d}$
, with h small enough, and endow it with the product metric
 $$\begin{align*}G= \begin{pmatrix} f^*\mathfrak{h} & 0\\ 0 & I_{D-d} \end{pmatrix}. \end{align*}$$
$$\begin{align*}G= \begin{pmatrix} f^*\mathfrak{h} & 0\\ 0 & I_{D-d} \end{pmatrix}. \end{align*}$$
Let
![]() $\{\nu _i\}_{i=2}^{D-d}$
be a smooth orthonormal frame along the submanifold
$\{\nu _i\}_{i=2}^{D-d}$
be a smooth orthonormal frame along the submanifold
![]() $\iota ({\mathcal N})\subset {\mathbb R}^D$
, orthogonally complementing the image of
$\iota ({\mathcal N})\subset {\mathbb R}^D$
, orthogonally complementing the image of
![]() $d\iota $
on
$d\iota $
on
![]() $\iota ({\mathcal N})$
. We extend f into a function
$\iota ({\mathcal N})$
. We extend f into a function
![]() $F:\tilde {{\mathcal M}} \mapsto {\mathbb R}^D$
by
$F:\tilde {{\mathcal M}} \mapsto {\mathbb R}^D$
by
 $$\begin{align*}F(q,t_1,...,t_{D-d}) = \iota \circ f(q)+t_1 d\iota_{f(q)}(\mathfrak{n}_f(q)) +\sum_{i=2}^{D-d} t_i \nu_i(\iota\circ f(q)), \end{align*}$$
$$\begin{align*}F(q,t_1,...,t_{D-d}) = \iota \circ f(q)+t_1 d\iota_{f(q)}(\mathfrak{n}_f(q)) +\sum_{i=2}^{D-d} t_i \nu_i(\iota\circ f(q)), \end{align*}$$
which we may also write in the form
 $$\begin{align*}F = \iota \circ f \circ \pi +\pi_1 \cdot (d\iota\circ \mathfrak{n}_f\circ \pi) +\sum_{i=2}^{D-d} \pi_i \cdot (\nu_i\circ \iota\circ f\circ \pi), \end{align*}$$
$$\begin{align*}F = \iota \circ f \circ \pi +\pi_1 \cdot (d\iota\circ \mathfrak{n}_f\circ \pi) +\sum_{i=2}^{D-d} \pi_i \cdot (\nu_i\circ \iota\circ f\circ \pi), \end{align*}$$
where
![]() $\pi :\tilde {\mathcal M} \to {\mathcal M}$
and
$\pi :\tilde {\mathcal M} \to {\mathcal M}$
and
![]() $\pi _i :\tilde {\mathcal M}\to {\mathbb R}$
are the natural projections,
$\pi _i :\tilde {\mathcal M}\to {\mathbb R}$
are the natural projections,
![]() $\pi (q,t_1,...,t_{D-d}) = q$
and
$\pi (q,t_1,...,t_{D-d}) = q$
and
![]() $\pi _i(q,t_1,...,t_{D-d}) = t_i$
, and in the second term, we view
$\pi _i(q,t_1,...,t_{D-d}) = t_i$
, and in the second term, we view
![]() $\mathfrak {n}_f$
as a map
$\mathfrak {n}_f$
as a map
![]() ${\mathcal M}\to T{\mathcal N}$
.
${\mathcal M}\to T{\mathcal N}$
.
Differentiating,
![]() $dF:T\tilde {\mathcal M}\to {\mathbb R}^D$
is given by
$dF:T\tilde {\mathcal M}\to {\mathbb R}^D$
is given by
 $$ \begin{align*} dF &= d\iota \circ Df\circ D\pi + d\pi_1\otimes (d\iota\circ \mathfrak{n}_f\circ \pi) +\pi_1 \cdot (d^2\iota \circ D\mathfrak{n}_f\circ D\pi) \\ &\quad + \sum_{i=2}^{D-d} d\pi_i\otimes (\nu_i\circ \iota\circ f\circ \pi) + \sum_{i=2}^{D-d} \pi_i \cdot (d\nu_i \circ D\iota \circ Df \circ D\pi). \end{align*} $$
$$ \begin{align*} dF &= d\iota \circ Df\circ D\pi + d\pi_1\otimes (d\iota\circ \mathfrak{n}_f\circ \pi) +\pi_1 \cdot (d^2\iota \circ D\mathfrak{n}_f\circ D\pi) \\ &\quad + \sum_{i=2}^{D-d} d\pi_i\otimes (\nu_i\circ \iota\circ f\circ \pi) + \sum_{i=2}^{D-d} \pi_i \cdot (d\nu_i \circ D\iota \circ Df \circ D\pi). \end{align*} $$
Consider
 $$\begin{align*}A_f = d\iota \circ Df\circ D\pi + d\pi_1\otimes (d\iota\circ \mathfrak{n}_f\circ \pi) + \sum_{i=2}^{D-d} d\pi_i\otimes (\nu_i\circ \iota\circ f\circ \pi). \end{align*}$$
$$\begin{align*}A_f = d\iota \circ Df\circ D\pi + d\pi_1\otimes (d\iota\circ \mathfrak{n}_f\circ \pi) + \sum_{i=2}^{D-d} d\pi_i\otimes (\nu_i\circ \iota\circ f\circ \pi). \end{align*}$$
Since f is an isometric immersion by the definition of
![]() $f^*\mathfrak {h}$
,
$f^*\mathfrak {h}$
,
![]() $\iota $
is an isometric embedding and
$\iota $
is an isometric embedding and
![]() $\{\nu _i\}_{i=2}^{D-d}$
is an orthonormal frame along the submanifold
$\{\nu _i\}_{i=2}^{D-d}$
is an orthonormal frame along the submanifold
![]() $\iota ({\mathcal N})\subset {\mathbb R}^D$
, and
$\iota ({\mathcal N})\subset {\mathbb R}^D$
, and
![]() $D\pi , d\pi _i$
are pairwise orthogonal by the choice of G, we obtain that
$D\pi , d\pi _i$
are pairwise orthogonal by the choice of G, we obtain that
![]() $A_f \in SO(G,\mathfrak {e})$
. Therefore,
$A_f \in SO(G,\mathfrak {e})$
. Therefore,

where in the passage to the fourth line, we used the facts that
![]() $d\mathfrak {n}_f$
and
$d\mathfrak {n}_f$
and
![]() $df$
are bounded in
$df$
are bounded in
![]() $L^2({\mathcal M})$
, and that
$L^2({\mathcal M})$
, and that
![]() $d\iota $
,
$d\iota $
,
![]() $d^2\iota $
and
$d^2\iota $
and
![]() $d\nu _i$
are bounded in
$d\nu _i$
are bounded in
![]() $ L^\infty $
as smooth functions on compact domains.
$ L^\infty $
as smooth functions on compact domains.
We have thus proved that F satisfies the finite bending property defined in [Reference Kupferman and SolomonKS14, Eq. (2.3)], where F in the present work corresponds to
![]() $f_h$
in [Reference Kupferman and SolomonKS14]. It follows from [Reference Kupferman and SolomonKS14, Thm. 5.1] that f (which unfortunately corresponds to F in [Reference Kupferman and SolomonKS14]) is in
$f_h$
in [Reference Kupferman and SolomonKS14]. It follows from [Reference Kupferman and SolomonKS14, Thm. 5.1] that f (which unfortunately corresponds to F in [Reference Kupferman and SolomonKS14]) is in
![]() $W^{2,2}$
.
$W^{2,2}$
.
Proposition 4.2. Let
![]() $f\in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
,
$f\in \operatorname {Imm}_p({\mathcal M};{\mathcal N})$
,
![]() $p> d$
. Suppose that
$p> d$
. Suppose that
![]() $\mathfrak {g} = f^*\mathfrak {h}$
is a smooth metric on
$\mathfrak {g} = f^*\mathfrak {h}$
is a smooth metric on
![]() ${\mathcal M}$
and that the shape operator S of
${\mathcal M}$
and that the shape operator S of
![]() $f({\mathcal M})$
in
$f({\mathcal M})$
in
![]() ${\mathcal N}$
is smooth. Then, f is smooth.
${\mathcal N}$
is smooth. Then, f is smooth.
The proof below works, with minor adjustments, also for a smooth second fundamental form instead of a smooth shape operator.
Proof. Since f is continuous and since smoothness is a local property, we can consider the claim in coordinates; henceforth,
![]() $f:\Omega \subset {\mathbb R}^d \to {\mathbb R}^{d+1}$
and
$f:\Omega \subset {\mathbb R}^d \to {\mathbb R}^{d+1}$
and
![]() $\mathfrak {n}_f:\Omega \to {\mathbb R}^{d+1}$
, satisfying the following set of equations,
$\mathfrak {n}_f:\Omega \to {\mathbb R}^{d+1}$
, satisfying the following set of equations,
and
Here and below, we use Latin indexes for coordinates in
![]() ${\mathcal M}$
and Greek indexes for coordinates in
${\mathcal M}$
and Greek indexes for coordinates in
![]() ${\mathcal N}$
. The Einstein summation rule is assumed;
${\mathcal N}$
. The Einstein summation rule is assumed;
![]() $\Gamma ^\alpha _{\beta \gamma }$
are the Christoffel symbols of the Levi-Civita connection in
$\Gamma ^\alpha _{\beta \gamma }$
are the Christoffel symbols of the Levi-Civita connection in
![]() ${\mathcal N}$
. It is given that
${\mathcal N}$
. It is given that
![]() $\mathfrak {g}_{ij}$
and
$\mathfrak {g}_{ij}$
and
![]() $S^j_i$
are smooth.
$S^j_i$
are smooth.
It follows from the previous proposition that
![]() $f^\alpha \in W^{2,2}(\Omega )$
, which together with (4.1) implies that
$f^\alpha \in W^{2,2}(\Omega )$
, which together with (4.1) implies that
It then follows from (4.2) that
The rest of the proof follows a standard bootstrapping procedure, differentiating (4.1) and (4.3) and substituting (4.2), using the fact that
![]() $\{\partial _if(x)\}\cup \{\mathfrak {n}_f(x)\}$
forms an
$\{\partial _if(x)\}\cup \{\mathfrak {n}_f(x)\}$
forms an
![]() $f^*\mathfrak {h}$
-orthonormal basis for
$f^*\mathfrak {h}$
-orthonormal basis for
![]() ${\mathbb R}^{d+1}$
. The bootstrapping uses the following product rule for Sobolev spaces [Reference BrezisBre11, Prop. 9.4]: let
${\mathbb R}^{d+1}$
. The bootstrapping uses the following product rule for Sobolev spaces [Reference BrezisBre11, Prop. 9.4]: let
![]() $u,v \in W^{1,p}(\Omega )\cap L^{\infty }(\Omega )$
with
$u,v \in W^{1,p}(\Omega )\cap L^{\infty }(\Omega )$
with
![]() $1\leq p\leq \infty $
. Then
$1\leq p\leq \infty $
. Then
![]() $uv\in W^{1,p}(\Omega )\cap L^{\infty }(\Omega )$
and
$uv\in W^{1,p}(\Omega )\cap L^{\infty }(\Omega )$
and
The fact that the application of the Leibniz rule requires to the very least functions in
![]() $W^{1,p}(\Omega )\cap L^{\infty }(\Omega )$
is the reason we had to first establish that
$W^{1,p}(\Omega )\cap L^{\infty }(\Omega )$
is the reason we had to first establish that
![]() $\partial _if^\alpha $
and
$\partial _if^\alpha $
and
![]() $n_f^\alpha $
are in this space.
$n_f^\alpha $
are in this space.
A Quantitative stability in codimension-1
In this appendix, we prove a quantitative version of Theorem 1.1 for the case
![]() ${\mathcal N} = {\mathbb R}^{d+1}$
, under the assumption that the metric
${\mathcal N} = {\mathbb R}^{d+1}$
, under the assumption that the metric
![]() $\mathfrak {g}$
and the shape operator S are compatible with the geometry of
$\mathfrak {g}$
and the shape operator S are compatible with the geometry of
![]() ${\mathbb R}^{d+1}$
.
${\mathbb R}^{d+1}$
.
Theorem A.1. Let
![]() $({\mathcal M},\mathfrak {g})$
be an oriented, connected, simply connected, compact d-dimensional Riemannian manifold with Lipschitz boundary, and let
$({\mathcal M},\mathfrak {g})$
be an oriented, connected, simply connected, compact d-dimensional Riemannian manifold with Lipschitz boundary, and let
![]() $p\in (1,\infty )$
. Let S be a smooth symmetric
$p\in (1,\infty )$
. Let S be a smooth symmetric
![]() $(1,1)$
tensor field on
$(1,1)$
tensor field on
![]() ${\mathcal M}$
. If
${\mathcal M}$
. If
![]() $\mathfrak {g}$
and S satisfy the Gauss-Codazzi compatibility conditions, then there exists a constant C depending on
$\mathfrak {g}$
and S satisfy the Gauss-Codazzi compatibility conditions, then there exists a constant C depending on
![]() $({\mathcal M},\mathfrak {g})$
, S and p, such that there exists for every
$({\mathcal M},\mathfrak {g})$
, S and p, such that there exists for every
![]() $f\in \operatorname {Imm}_p({\mathcal M};{\mathbb R}^{d+1})$
a smooth isometric immersion
$f\in \operatorname {Imm}_p({\mathcal M};{\mathbb R}^{d+1})$
a smooth isometric immersion
![]() $f_0:{\mathcal M}\to {\mathbb R}^{d+1}$
having shape operator S, satisfying
$f_0:{\mathcal M}\to {\mathbb R}^{d+1}$
having shape operator S, satisfying
 $$ \begin{align*} & \|f - f_0\|_{W^{1,p}({\mathcal M};{\mathbb R}^{d+1})} + \|\mathfrak{n}_f - \mathfrak{n}_{f_0}\|_{W^{1,p}({\mathcal M};{\mathbb R}^{d+1})} \le \\ &\qquad C\left(\|\operatorname{dist}(df,\operatorname{O}(\mathfrak{g},\mathfrak{e}))\|_{L^p({\mathcal M})} + \|\nabla \mathfrak{n}_f + df\circ S\|_{L^p({\mathcal M})}\right), \end{align*} $$
$$ \begin{align*} & \|f - f_0\|_{W^{1,p}({\mathcal M};{\mathbb R}^{d+1})} + \|\mathfrak{n}_f - \mathfrak{n}_{f_0}\|_{W^{1,p}({\mathcal M};{\mathbb R}^{d+1})} \le \\ &\qquad C\left(\|\operatorname{dist}(df,\operatorname{O}(\mathfrak{g},\mathfrak{e}))\|_{L^p({\mathcal M})} + \|\nabla \mathfrak{n}_f + df\circ S\|_{L^p({\mathcal M})}\right), \end{align*} $$
where
![]() $\mathfrak {n}_f$
and
$\mathfrak {n}_f$
and
![]() $\mathfrak {n}_{f_0}$
are the unit normals to
$\mathfrak {n}_{f_0}$
are the unit normals to
![]() $f({\mathcal M})$
and
$f({\mathcal M})$
and
![]() $f_0({\mathcal M})$
.
$f_0({\mathcal M})$
.
Note that the right-hand side in the equality is essentially
![]() ${\mathcal E}_p^{1/p}(f)$
. If
${\mathcal E}_p^{1/p}(f)$
. If
![]() ${\mathcal M}$
is not simply connected, one can rather assume that
${\mathcal M}$
is not simply connected, one can rather assume that
![]() $\mathfrak {g}$
and S are compatible in the sense that there exists an isometric immersion
$\mathfrak {g}$
and S are compatible in the sense that there exists an isometric immersion
![]() ${\mathcal M}\to {\mathbb R}^{d+1}$
whose shape operator is S.
${\mathcal M}\to {\mathbb R}^{d+1}$
whose shape operator is S.
Proof. Since
![]() $\mathfrak {g}$
and S are compatible, there exists, modulo a rigid transformation, a unique smooth immersion
$\mathfrak {g}$
and S are compatible, there exists, modulo a rigid transformation, a unique smooth immersion
![]() $\iota :{\mathcal M}\to {\mathbb R}^{d+1}$
, such that
$\iota :{\mathcal M}\to {\mathbb R}^{d+1}$
, such that
![]() $\mathfrak {g} = \iota ^*\mathfrak {e}$
and
$\mathfrak {g} = \iota ^*\mathfrak {e}$
and
![]() $d\mathfrak {n}_\iota = -d\iota \circ S$
, where
$d\mathfrak {n}_\iota = -d\iota \circ S$
, where
![]() $\mathfrak {n}_\iota $
is the unit-normal to
$\mathfrak {n}_\iota $
is the unit-normal to
![]() $\iota ({\mathcal M})$
.
$\iota ({\mathcal M})$
.
Consider the following diagram:

where
![]() ${\mathcal M}_h = {\mathcal M}\times (-h,h)$
, with h to be specified below,
${\mathcal M}_h = {\mathcal M}\times (-h,h)$
, with h to be specified below,
![]() $\zeta (q) = (q,0)$
, and
$\zeta (q) = (q,0)$
, and
The metric G on
![]() ${\mathcal M}_h$
is defined by
${\mathcal M}_h$
is defined by
where
![]() $v,w\in T_q{\mathcal M}$
and
$v,w\in T_q{\mathcal M}$
and
![]() $s,r\in {\mathbb R}$
. For G to be a metric, h has to be restricted; the choice of
$s,r\in {\mathbb R}$
. For G to be a metric, h has to be restricted; the choice of
![]() $h = 2/\|S\|_\infty $
guarantees that h is metric. Furthermore, G is equivalent to the product metric
$h = 2/\|S\|_\infty $
guarantees that h is metric. Furthermore, G is equivalent to the product metric
![]() $\tilde {G} = \mathfrak {g} + dt\otimes dt$
; namely,
$\tilde {G} = \mathfrak {g} + dt\otimes dt$
; namely,
for some constants c and C, depending only on
![]() $\mathfrak {g}$
and S. Finally, it follows that
$\mathfrak {g}$
and S. Finally, it follows that
![]() $\iota $
,
$\iota $
,
![]() $\zeta $
and
$\zeta $
and
![]() $\Phi $
are all isometric immersions.
$\Phi $
are all isometric immersions.
Let
![]() $f\in \operatorname {Imm}_p({\mathcal M};{\mathbb R}^{d+1})$
, which we extend into a map
$f\in \operatorname {Imm}_p({\mathcal M};{\mathbb R}^{d+1})$
, which we extend into a map
![]() $F:{\mathcal M}_h\to {\mathbb R}^{d+1}$
, given by
$F:{\mathcal M}_h\to {\mathbb R}^{d+1}$
, given by
where
![]() $\mathfrak {n}_f:{\mathcal M}\to {\mathbb R}^{d+1}$
is the unit-normal to
$\mathfrak {n}_f:{\mathcal M}\to {\mathbb R}^{d+1}$
is the unit-normal to
![]() $f({\mathcal M})$
. Denote by
$f({\mathcal M})$
. Denote by
![]() $S_f$
the shape operator of
$S_f$
the shape operator of
![]() $f({\mathcal M})$
.
$f({\mathcal M})$
.
Consider the map
By the FJM inequality, there exists an isometry
![]() $Q\in \operatorname {SO}(d+1)$
such that
$Q\in \operatorname {SO}(d+1)$
such that
where C only depends on
![]() ${\mathcal M}$
, h and p. Since
${\mathcal M}$
, h and p. Since
![]() $\Phi $
is an isometric immersion, changing variables,
$\Phi $
is an isometric immersion, changing variables,
The goal is to obtain an inequality involving only f. We start with the right-hand side of (A.1). First,
Denote
where
![]() $\operatorname {O}(df)$
is the projection of
$\operatorname {O}(df)$
is the projection of
![]() $df$
on
$df$
on
![]() $O(\mathfrak {g},\mathfrak {e})$
(for immersions, the projection is unique). We show that
$O(\mathfrak {g},\mathfrak {e})$
(for immersions, the projection is unique). We show that
![]() $A\in \operatorname {SO}(G,\mathfrak {e})$
. Indeed, For
$A\in \operatorname {SO}(G,\mathfrak {e})$
. Indeed, For
![]() $(q,t)\in {\mathcal M}_h$
and
$(q,t)\in {\mathcal M}_h$
and
![]() $(v,s)\in T_{(q,t)}{\mathcal M}_h$
,
$(v,s)\in T_{(q,t)}{\mathcal M}_h$
,
Since
![]() $\operatorname {O}(df)(v) \perp \mathfrak {n}_f$
and since
$\operatorname {O}(df)(v) \perp \mathfrak {n}_f$
and since
![]() $\operatorname {O}(df)\in \operatorname {O}(\mathfrak {g},\mathfrak {e})$
,
$\operatorname {O}(df)\in \operatorname {O}(\mathfrak {g},\mathfrak {e})$
,
The condition on the orientation holds by the very definition of
![]() $\mathfrak {n}_f$
.
$\mathfrak {n}_f$
.
Thus,
 $$ \begin{align*} \operatorname{dist}(dF,\operatorname{SO}(G,\mathfrak{e})) &\le |dF - A| \\ &\le |(df - \operatorname{O}(df)) \oplus \mathfrak{n}_f - t\, ((df\circ S_f - \operatorname{O}(df)\circ S)\oplus 0)| \\ &\le |(df - \operatorname{O}(df)) \oplus \mathfrak{n}_f| + t\, |(df\circ S_f - \operatorname{O}(df)\circ S)\oplus 0|, \end{align*} $$
$$ \begin{align*} \operatorname{dist}(dF,\operatorname{SO}(G,\mathfrak{e})) &\le |dF - A| \\ &\le |(df - \operatorname{O}(df)) \oplus \mathfrak{n}_f - t\, ((df\circ S_f - \operatorname{O}(df)\circ S)\oplus 0)| \\ &\le |(df - \operatorname{O}(df)) \oplus \mathfrak{n}_f| + t\, |(df\circ S_f - \operatorname{O}(df)\circ S)\oplus 0|, \end{align*} $$
where all the norms are with respect to G and
![]() $\mathfrak {e}$
. By the equivalence between G and the product metric
$\mathfrak {e}$
. By the equivalence between G and the product metric
![]() $\tilde {G} = \mathfrak {g} + dt\otimes dt$
, the right-hand side can be bounded by
$\tilde {G} = \mathfrak {g} + dt\otimes dt$
, the right-hand side can be bounded by
where C depends only on
![]() $\mathfrak {g}$
, S and h. Using once again the equivalence of the metrics on
$\mathfrak {g}$
, S and h. Using once again the equivalence of the metrics on
![]() ${\mathcal M}_h$
,
${\mathcal M}_h$
,
for some constant C depending only on
![]() $({\mathcal M},\mathfrak {g})$
and p.
$({\mathcal M},\mathfrak {g})$
and p.
We proceed with the left-hand side of (A.1). We have
 $$ \begin{align*} Q\circ d\Phi &= Q\circ(d\iota \oplus \mathfrak{n}_\iota) - t\, Q\circ (d\iota\circ S\oplus 0) \\ &=d(Q\circ \iota) \oplus \mathfrak{n}_{Q\circ \iota} - t\, (d(Q\circ\iota)\circ S\oplus 0). \end{align*} $$
$$ \begin{align*} Q\circ d\Phi &= Q\circ(d\iota \oplus \mathfrak{n}_\iota) - t\, Q\circ (d\iota\circ S\oplus 0) \\ &=d(Q\circ \iota) \oplus \mathfrak{n}_{Q\circ \iota} - t\, (d(Q\circ\iota)\circ S\oplus 0). \end{align*} $$
Hence,
 $$ \begin{align*} dF - Q\circ d\Phi &= df \oplus \mathfrak{n}_f - df_0 \oplus \mathfrak{n}_{f_0} - t\, \left((df\circ S_f - df_0 \circ S_{f_0})\oplus 0\right)\\ &= df \oplus \mathfrak{n}_f - df_0 \oplus \mathfrak{n}_{f_0} - t\, \left((d\mathfrak{n}_f - d\mathfrak{n}_{f_0})\oplus 0\right), \end{align*} $$
$$ \begin{align*} dF - Q\circ d\Phi &= df \oplus \mathfrak{n}_f - df_0 \oplus \mathfrak{n}_{f_0} - t\, \left((df\circ S_f - df_0 \circ S_{f_0})\oplus 0\right)\\ &= df \oplus \mathfrak{n}_f - df_0 \oplus \mathfrak{n}_{f_0} - t\, \left((d\mathfrak{n}_f - d\mathfrak{n}_{f_0})\oplus 0\right), \end{align*} $$
where
![]() $f_0 = Q\circ \iota $
, which is an isometric immersion of
$f_0 = Q\circ \iota $
, which is an isometric immersion of
![]() $({\mathcal M},\mathfrak {g})$
having shape operator
$({\mathcal M},\mathfrak {g})$
having shape operator
![]() $S_{f_0} = S$
.
$S_{f_0} = S$
.
Therefore,
 $$ \begin{align*} |dF - Q\circ d\Phi|^2 &\gtrsim |df- df_0|^2 + |\mathfrak{n}_f - \mathfrak{n}_{f_0}|^2 + t^2|d\mathfrak{n}_f - d\mathfrak{n}_{f_0}|^2 \\ &\quad + 2t (df- df_0, d\mathfrak{n}_f - d\mathfrak{n}_{f_0})_{\mathfrak{g}}. \end{align*} $$
$$ \begin{align*} |dF - Q\circ d\Phi|^2 &\gtrsim |df- df_0|^2 + |\mathfrak{n}_f - \mathfrak{n}_{f_0}|^2 + t^2|d\mathfrak{n}_f - d\mathfrak{n}_{f_0}|^2 \\ &\quad + 2t (df- df_0, d\mathfrak{n}_f - d\mathfrak{n}_{f_0})_{\mathfrak{g}}. \end{align*} $$
Define the set
and let
On the set D,
and thus,
 $$ \begin{align*} \int_{{\mathcal M}_h} |dF - Q\circ d\Phi|^p \,\text{d}\text{Vol}_G &\ge \int_{D} |dF - Q\circ d\Phi|^p \,\text{d}\text{Vol}_G \\ &\gtrsim \int_D \left(|df- df_0|^p + |\mathfrak{n}_f - \mathfrak{n}_{f_0}|^p + |t|^p|d\mathfrak{n}_f - d\mathfrak{n}_{f_0}|^p\right) \,\text{d}\text{Vol}_G \\ &\gtrsim \int_D \left(|df- df_0|^p + |\mathfrak{n}_f - \mathfrak{n}_{f_0}|^p + |t|^p|d\mathfrak{n}_f - d\mathfrak{n}_{f_0}|^p\right) \,\text{d}\text{Vol}_{\tilde{G}} \\ &= \int_{\mathcal M} \left(h|df- df_0|^p + h|\mathfrak{n}_f - \mathfrak{n}_{f_0}|^p + \frac{h^{p+1}}{p+1}|d\mathfrak{n}_f - d\mathfrak{n}_{f_0}|^2\right) \,\text{d}\text{Vol}_{\mathfrak{g}}, \end{align*} $$
$$ \begin{align*} \int_{{\mathcal M}_h} |dF - Q\circ d\Phi|^p \,\text{d}\text{Vol}_G &\ge \int_{D} |dF - Q\circ d\Phi|^p \,\text{d}\text{Vol}_G \\ &\gtrsim \int_D \left(|df- df_0|^p + |\mathfrak{n}_f - \mathfrak{n}_{f_0}|^p + |t|^p|d\mathfrak{n}_f - d\mathfrak{n}_{f_0}|^p\right) \,\text{d}\text{Vol}_G \\ &\gtrsim \int_D \left(|df- df_0|^p + |\mathfrak{n}_f - \mathfrak{n}_{f_0}|^p + |t|^p|d\mathfrak{n}_f - d\mathfrak{n}_{f_0}|^p\right) \,\text{d}\text{Vol}_{\tilde{G}} \\ &= \int_{\mathcal M} \left(h|df- df_0|^p + h|\mathfrak{n}_f - \mathfrak{n}_{f_0}|^p + \frac{h^{p+1}}{p+1}|d\mathfrak{n}_f - d\mathfrak{n}_{f_0}|^2\right) \,\text{d}\text{Vol}_{\mathfrak{g}}, \end{align*} $$
where in the passage to the third line, we used the equivalence of G and the product metric
![]() $\tilde {G}$
, and in the passage to the last line, we used Fubini’s theorem. From this and the Poincaré inequality (possibly by translating
$\tilde {G}$
, and in the passage to the last line, we used Fubini’s theorem. From this and the Poincaré inequality (possibly by translating
![]() $f_0$
), we obtain
$f_0$
), we obtain
where
![]() $c>0$
depends only on
$c>0$
depends only on
![]() $({\mathcal M},\mathfrak {g})$
, p and h. Combining (A.1), (A.2) and (A.3), we obtain the desired result.
$({\mathcal M},\mathfrak {g})$
, p and h. Combining (A.1), (A.2) and (A.3), we obtain the desired result.
Competing interest
The authors have no competing interest to declare.
Financial support
RK was partially funded by ISF Grant 560/22, and CM was partially funded by ISF Grant 1269/19 and BSF Grant 2022076.