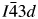I. INTRODUCTION
Synthetic anhydrous analogs of the silicate framework minerals such as leucite (KAlSi2O6) and pollucite (CsAlSi2O6) can be prepared with the general formulae A 2BSi5O12 and ACSi2O6, where A is a monovalent alkali metal cation, B is a divalent cation, and C is a trivalent cation. These structures have the same topology, with B and C cations partially substituting onto tetrahedrally coordinated sites (T-sites) in the silicate framework, and charge-balancing A cations sitting in extraframework channels. The A cations can be replaced by ion exchange, and Cs-containing silicate framework minerals are of potential technological interest as storage media for radioactive Cs from nuclear waste (Gatta et al., Reference Gatta, Rotiroti, Fisch, Kadiyski and Armbruster2008, Reference Gatta, Rinaldi, McIntyre, Nénert and Bellatreccia2009).
Many ambient temperature leucite analogs are known with different crystal structures and different A, B, and C cations (Bell, Reference Bell2024). These structures all have the same topology, CsAlSi2O6 is 
$Ia\bar{3}d$ cubic (Beger, Reference Beger1969), KBSi2O6 is 
$I\bar{4}3d$ cubic (Millini et al., Reference Millini, Montanari and Bellussi1993), and KAlSi2O6 is I41/a tetragonal (Mazzi et al., Reference Mazzi, Galli and Gottardi1976). All these high symmetry structures have disordered T-site cations. However, lower symmetry structures are also known with ordered T-site cations. Examples of these cation-ordered structures are Eu2+-doped CsZnSi2O6 (Hariyani et al., Reference Hariyani, Armijo and Brgoch2020, 
$Pa\bar{3}$ cubic), Cs2CdSi5O12 (Bell et al., Reference Bell, Redfern, Henderson and Kohn1994b, Pbca orthorhombic), and K2MgSi5O12 (Bell et al., Reference Bell, Henderson, Redfern, Cernik, Champness, Fitch and Kohn1994a, P21/c monoclinic).
However, it is also possible to synthesize analogs of leucite and pollucite in which silicon is replaced with germanium. These Ge-leucites have germanate framework structures with the same topology as the leucite structure. In these cases, A 2BGe5O12 and ACGe2O6 leucite analogs can be synthesized where B and C cations partially substitute onto tetrahedrally coordinated sites (T-sites) in the germanate framework, and charge-balancing A cations sit in extraframework channels.
Lattice parameters have been reported for A 2BGe5O12 analogs (A = Rb, Cs; B = Be, Mg, Zn, Co, Fe, Ni, Cu, Cd) (Richerson and Hummel, Reference Richerson and Hummel1972; Torres-Martinez et al., Reference Torres-Martinez, Gard and West1984; Torres-Martinez and West, Reference Torres-Martinez and West1989). Lattice parameters have also been reported for analogs ACGe2O6 (A = K, Rb, Cs, NH4; C = B, Al, Ga, Cr, Fe) (Torres-Martinez et al., Reference Torres-Martinez, Gard and West1984; Torres-Martinez and West, Reference Torres-Martinez and West1989). Additionally, lattice parameters have been reported for K0.8Rb0.2AlGe2O6 (Klaska, Reference Klaska1978).
This paper reports the Rietveld refinements (Rietveld, Reference Rietveld1969) of three Ge-leucites with stoichiometries of AAlGe2O6 (A = K, Rb, Cs). A crystal structure has been reported for CsAlGe2O6 (Tripathi and Parise, Reference Tripathi and Parise2002), but no crystal structures have yet been reported for the K and Rb analogs. Powder Diffraction File (Gates-Rector and Blanton, Reference Gates-Rector and Blanton2019) data have been reported for these three Ge-leucite analogs. The PDF numbers are 00-37-1349 (KAlGe2O6), 00-37-348 (RbAlGe2O6), 00-37-347, and 04-012-2039 (CsAlGe2O6).
II. EXPERIMENTAL
A. Sample synthesis
All three samples were prepared from appropriate stoichiometric mixtures of K2CO3, Rb2CO3, Cs2CO3.3H2O, GeO2, and Al2O3. These mixtures were loaded into Pt crucibles and heated in air in a furnace. For all three samples, the mixtures were heated for 12 h at 1073 K (to decompose carbonates). For A = K, the crucible was air quenched, but for A = Rb and Cs the crucibles were quenched by dipping the bottom of the crucible in the bucket of cold water. For A = K, the mixture was then heated for 3 days at 1373 K. The sample was then removed from the furnace, reground, and then reheated for 4 days at 1373 K. For A = Rb, the mixture was then reground before further heating for 4 days at 1373 K. For A = Cs, the mixture was then reground before further heating for 50 h at 1373 K. The sample was then ground again before heating for 1 more day at 1373 K.
B. X-ray powder diffraction data collection
After heating, the samples were removed from the Pt crucibles, ground with a mortar and pestle, and then mounted on low-background silicon wafers with a drop of acetone prior to ambient temperature X-ray powder diffraction.
For A = K, data were collected on a PANalytical X'Pert Pro MPD using Cu Kα X-rays, with a nickel β-filter and a 3.3473° 2θ wide 255 channel PIXCEL-1D area detector. Data were collected in two scans using Data Collector 5.5a (PANalytical, 2017), scan 1 lasted 1 h, and scan 2 lasted 7 h and 30 min. These data were collected over the range of 5–100° 2θ with a step width of 0.0131° 2θ and an effective counting times of 118 s per point (scan 1) and 919 s per point (scan 2). For both scans, the beam size was defined with a 20 mm mask, fixed antiscatter (¼°), and divergence (⅛°) slits. These two scans were summed together after data collection.
For A = Rb, data were also collected on a PANalytical X'Pert Pro MPD using Cu Kα X-rays, with a nickel β-filter and a 3.3473° 2θ wide 255 channel PIXCEL-1D area detector. Data were collected in a single scan over 22 h using Data Collector 5.5a (PANalytical, 2017). These data were collected over the range of 10–100° 2θ with a step width of 0.0131° 2θ and an effective counting time of 2838 s per point. The beam size was defined with a 20 mm mask, fixed antiscatter (¼°), and divergence (⅛°) slits.
For A = Cs, data were collected on a PANalytical Empyrean diffractometer using Co Kα X-rays with an iron β-filter and a 3.3473° 2θ wide 255 channel PIXCEL-3D area detector. Data were collected in a single scan over 19 h using Data Collector 5.1a (PANalytical, 2014). These data were collected over the range of 15–100° 2θ with a step width of 0.0131° 2θ and an effective counting time of 2592 s per point. The beam size was defined with a 20 mm mask, fixed divergence antiscatter (¼°) slit, and automatic divergence slit with a 20 mm long beam footprint. These diffracted intensities were converted from an automatic divergence slit mode to a fixed divergence slit mode in HighScore Plus (PANalytical, 2009) prior to data analysis.
No smoothing or α 2 stripping was done on any of these data. Both diffractometers were calibrated with an external NIST SRM640e silicon standard.
C. X-ray powder diffraction data analysis
All powder diffraction data were analyzed using HighScore Plus and the ICDD Powder Diffraction File. For A = K, analysis of the powder diffraction data showed that this sample was mostly KAlGe2O6 (PDF# 00-37-1349) with GeO2 (PDF# 00-43-1016) and KAlGeO4 (PDF# 01-78-1173) present as minor phases. For A = Rb, analysis of the powder diffraction data showed that this sample was mostly RbAlGe2O6 (PDF# 00-37-0348) with GeO2 (PDF# 04-03-0650) and Al2O3 (PDF# 01-73-5928) present as minor phases. For A = Cs, analysis of the powder diffraction data showed that this sample was single-phase CsAlGe2O6 (PDF# 00-37-0347), apart from an unassigned Bragg reflection at about 17.8° 2θ.
All Rietveld refinements (Rietveld, Reference Rietveld1969) for these data were done using GSAS-II (Toby and von Dreele, Reference Toby and Von Dreele2013). Table I shows details of the refinements, including the number of observed and calculated reflections, the number of structural parameters and profile parameters, and the R factors.
TABLE I. Details of Rietveld refinements.
For A = K, the crystal structure of KAlGe2O6 was refined using the I41/a tetragonal structure of KAlSi2O6 (Mazzi et al., Reference Mazzi, Galli and Gottardi1976) as a starting model. The lattice parameters from PDF# 00-37-1349 were used and Ge atoms were put on the Si sites. The crystal structures of GeO2 (Haines et al., Reference Haines, Cambon, Philippot, Chapon and Hull2002) and KAlGeO4 (Sun et al., Reference Sun, Li, Zheng, Pang, Jiang, Zhang and Li2019) were used for the minor phases. Rietveld refinement showed that for A = K, the sample consisted of 98.1(5) wt% KAlGe2O6, 0.32(31) wt% GeO2, and 1.57(7) wt% KAlGeO4. In this KAlGe2O6 crystal structure, all atoms were located on the I41/a 16f Wyckoff general position. There is one 16f position for K, three 16f positions for T-sites (disordered 1/3rd Al and 2/3rd Ge), and six 16f positions for O. The isotropic temperature factors of the T-site atoms Al and Ge were constrained to be the same on each T-site but were allowed to vary between different T-sites. All isotropic temperature factors for the six O sites were constrained to have the same value. The T–O interatomic distances were soft-constrained to be 1.74 ± 0.02 Å (average bond distance for tetrahedral Al–O and Ge–O). This assumption is made due to complete T-site disorder (1/3rd Al and 2/3rd Ge on each T-site) as it was not possible to refine chemically sensible T-site occupancies. This constraint distance was determined from the differences between the ionic radii for Si4+ and Ge4+ (Shannon, Reference Shannon1976) and then added the difference to the KAlSi2O6 T–O soft constraint distance of 1.68 ± 0.02 Å.
For A = Cs, the crystal structure of CsAlGe2O6 was refined using the 
$I\bar{4}3d$ cubic structure of CsAlGe2O6 (Tripathi and Parise, Reference Tripathi and Parise2002) as a starting model. Due to the presence of the unassigned Bragg reflection at about 17.8° 2θ, the data from 15 to 18° 2θ were excluded from the Rietveld refinement, which was then done assuming a single phase of CsAlGe2O6. For A = Rb, the crystal structure of CsAlGe2O6 was used as a starting model, the lattice parameters from PDF# 00-37-0348 were used, and Rb was replaced Cs in the extraframework cation site. The crystal structures of GeO2 (Haines et al., Reference Haines, Cambon, Philippot, Chapon and Hull2002) and Al2O3 (Finger and Hazen, Reference Finger and Hazen1978) were used for the minor phases. Rietveld refinement showed that for A = Rb, the sample consisted of 88.80(24) wt% RbAlGe2O6, 0.24(7) wt% GeO2, and 10.96(23) wt% Al2O3. For both A = Cs and A = Rb, the T–O interatomic distances were also soft-constrained to be 1.74 ± 0.02 Å.
VESTA (Momma and Izumi, Reference Momma and Izumi2011) was used to plot crystal structures.
III. RESULTS AND DISCUSSION
Crystal structures have been refined for AAlGe2O6 (A = K, Rb, Cs) synthetic leucite analogs from X-ray powder diffraction data. The crystal structure of KAlGe2O6 is isostructural with the I41/a tetragonal structure of KAlSi2O6. The crystal structures of RbAlGe2O6 and CsAlGe2O6 are both isostructural with the 
$I\bar{4}3d$ cubic structure of CsAlGe2O6 (Tripathi and Parise, Reference Tripathi and Parise2002). All refined structures have disordered T-site cations.
Table II shows the comparison of the refined lattice parameters for AAlGe2O6 (A = K, Rb, Cs) with the starting structures used for Rietveld refinement. Table III, Table IV, and Table V similarly show refined interatomic distances and angles. Table VI shows the tetrahedral angle variances for the T-sites (Robinson et al., Reference Robinson, Gibbs and Ribbe1971) in these germanate framework structures.
TABLE II. Refined lattice parameters compared with those for starting structures.
a Mazzi et al. (Reference Mazzi, Galli and Gottardi1976)
b This work.
c Tripathi and Parise (Reference Tripathi and Parise2002).
TABLE III. Refined interatomic A–O distances (Å) (A = K, Rb, Cs).
TABLE IV. Refined interatomic T–O distances (Å) (T = Al/Ge).
TABLE V. Refined interatomic angles (°) (T = Al/Ge).
TABLE VI. Tetrahedral angle variance [σ 2, deg2]: σ 2 = Σ(θ–109.47)2/5 (Robinson et al., Reference Robinson, Gibbs and Ribbe1971) where θ is the O–T–O tetrahedral angle.
Mean variance and standard deviation are given for the three tetrahedral sites in the A = K I4 1/a structure. Variance is given for the single tetrahedral site in the A = Rb and Cs 
$I\bar{4}3d$structures.
A. KAlGe2O6 structure
Figures 1 and 2, respectively, show the Rietveld difference and the VESTA crystal structure plots for the refined crystal structure of KAlGe2O6. Table II shows that this crystal structure has a unit cell volume that is larger than the isostructural KAlSi2O6, which was used as a starting model for Rietveld refinement, reflecting the difference between the ionic radii for Si4+ and Ge4+ (Shannon, Reference Shannon1976).
Figure 1. Rietveld difference plot for KAlGe2O6. Red circles represent observed data points, blue line represents calculated data points, and the green line represents difference curves. The upper line of black crosses represents positions of Bragg reflections for KAlGe2O6, the middle line of black crosses represents positions of Bragg reflections for GeO2, and the lower line of black crosses represents positions of Bragg reflections for KAlGeO4.
Figure 2. VESTA I41/a tetragonal structure plot for KAlGe2O6, viewed down [1–11] showing a channel for extraframework purple K+ cations. Disordered (Al/Ge)O4 tetrahedra are shown in light purple, and O2− anions are shown in red.
B. RbAlGe2O6 structure
Figures 3 and 4, respectively, show the Rietveld difference and the VESTA crystal structure plots for the refined crystal structure of RbAlGe2O6. Table II shows that the crystal structure of RbGaSi2O6 has a smaller unit cell volume than that of CsGaSi2O6, which was used as a starting model for Rietveld refinement. This also reflects the difference in the ionic radii for Rb+ and Cs+ cations (Shannon, Reference Shannon1976).
Figure 3. Rietveld difference plot for RbAlGe2O6. Red circles represent observed data points, blue line represents calculated data points, and the green line represents difference curves. The upper line of black crosses represents positions of Bragg reflections for RbAlGe2O6, the middle line of black crosses represents positions of Bragg reflections for Al2O3, and the lower line of black crosses represents positions of Bragg reflections for GeO2.
Figure 4. VESTA 
$I\bar{4}3d$ cubic structure plot for RbAlGe2O6, viewed down [111] showing a channel for extraframework pink Rb+ cations. Disordered (Al/Ge)O4 tetrahedra are shown in light purple, and O2− anions are shown in red.
C. CsAlGe2O6 structure
Figures 5 and 6, respectively, show the Rietveld difference and the VESTA crystal structure plots for the refined crystal structure of CsAlGe2O6. Table II shows that the crystal structure of CsAlGe2O6 has a slightly smaller unit cell volume than that of the CsAlGe2O6 structure (Tripathi and Parise, Reference Tripathi and Parise2002), which was used as a starting model for Rietveld refinement.
Figure 5. Rietveld difference plot for CsAlGe2O6. Red circles represent observed data points, blue line represents calculated data points, and the green line represents difference curves. The line of black crosses represents positions of Bragg reflections for CsAlGe2O6.
Figure 6. VESTA 
$I\bar{4}3d$ cubic structure plot for CsAlGe2O6, viewed down [111] showing a channel for extraframework light blue Cs+ cations. Disordered (Al/Ge)O4 tetrahedra are shown in light purple, and O2− anions are shown in red.
D. Comparisons between AAlGe2O6 structures
Figures 2, 4, and 6 show plots of the AAlGe2O6 crystal structures. Figure 2 (A = K) shows that the central channel for the I41/a tetragonal structure shows greater framework collapse (Taylor and Henderson, Reference Taylor and Henderson1968) compared to the corresponding channels for the 
$I\bar{4}3d$ cubic structures for A = Rb and Cs, reflecting the differences in the sizes of the extraframework alkali metal cations (Shannon, Reference Shannon1976).
Table III shows that the mean A–O distances are smallest for A = K and largest for A = Cs, also reflecting the differences in the sizes of the extraframework alkali metal cations (Shannon, Reference Shannon1976). Table IV shows that there are some significant differences between the mean T–O distances in these crystal structures. All refinements were done assuming stoichiometries of AAlGe2O6, with Ge and Al in a 2:1 ratio. However, the presence of impurity phases in the A = K and Rb samples could mean that the Ge and Al may not be in an exact 2:1 ratio. This could change the mean size of the T-site cation and consequently change the mean T–O distances.
Table V shows the intratetrahedral (O–T–O) and intertetrahedral (T–O–T) angles for the three crystal structures. The mean O–T–O angles are close to the ideal tetrahedral angle of 109.47°, and the mean T–O–T angles for the three structures are similar. Table VI shows that the greatest tetrahedral distortion is for the A = Cs structure.
E. Future work on the KAlGe2O6 structure
The crystal structure of KAlGe2O6 is isostructural with the I41/a tetragonal structure of KAlSi2O6 (Mazzi et al., Reference Mazzi, Galli and Gottardi1976) and KGaSi2O6 (Bell and Henderson, Reference Bell and Henderson2020). Both I41/a silicate structures undergo high temperature-phase transitions to 
$Ia\bar{3}d$ cubic structures, which was isostructural with CsAlSi2O6 (Beger, Reference Beger1969). The phase transition temperatures were 943 K (KAlSi2O6, Palmer et al., Reference Palmer, Dove, Ibberson and Powell1997) and 673–970 K (KGaSi2O6, Bell and Henderson, Reference Bell and Henderson2020). It would be interesting to see if KAlGe2O6 would undergo a similar phase transition on heating, would there be a phase transition to an 
$Ia\bar{3}d$ or 
$I\bar{4}3d$ cubic structure?
IV. CONCLUSIONS
Crystal structures have been refined for AAlGe2O6 synthetic leucite analogs (A = K, Rb, Cs). All refined structures have disordered T-site cations. KAlGe2O6 is isostructural with I41/a tetragonal KAlSi2O6 leucite. However, CsAlGe2O6 has the 
$I\bar{4}3d$ cubic space group and is isostructural with a previously published structure for CsAlGe2O6. RbAlGe2O6 also has the 
$I\bar{4}3d$ cubic space group and is isostructural with CsAlGe2O6.
V. DEPOSITED DATA
CIF files with information related to crystal structure, interatomic distances and angles, and powder diffraction data for KAlGe2O6, RbAlGe2O6, and CsAlGe2O6 synthetic leucite analogs were deposited with the ICDD. You may request these data from ICDD at [email protected].
ACKNOWLEDGEMENTS
The author wishes to acknowledge the use of the EPSRC funded National Chemical Database Service hosted by the Royal Society of Chemistry.
Open access
