INTRODUCTION
Accurate phenotypic information on quality traits is vital for successful variety selection in plant breeding programmes and for genetic research including genomic selection and the identification of quantitative trait loci. Many quality traits, such as flour yield, dough rheology and bread-baking characteristics for wheat, are obtained from multi-phase experiments in which varieties are first grown in a field trial then further processed in the laboratory. Quality testing tends to be labour intensive and expensive, so there is typically a limit to the total number of samples that can be tested. Historically, this has led to the practice of testing a single field replicate for each variety (or a single composite sample formed by combining grain from the individual replicate plots for that variety) and no randomization or replication of grain samples in the laboratory. Such an approach may preclude efficient prediction of the genetic effects of interest.
Recent work, in particular Smith et al. (Reference Smith, Lim and Cullis2006) and Brien et al. (Reference Brien, Harch, Correll and Bailey2011) have shown the importance of using sound experimental design techniques (including randomization and replication) in all phases of a multi-phase experiment. The testing of replicates from the field phase is vital since without this there is no valid estimate of error. Replication in a laboratory phase involves the splitting of the experimental units from the previous phase and testing as separate samples. Both Smith et al. (Reference Smith, Lim and Cullis2006) and Brien et al. (Reference Brien, Harch, Correll and Bailey2011) recommend laboratory replication, although the latter suggested that it is only required when ‘…uncontrolled variation in the laboratory is large relative to the first phase’ or when ‘…the relative magnitudes of field and laboratory variation are to be assessed.’ In the current authors’ experience with quality traits, one or both of these is generally the case.
The cost of quality testing and consequent restriction on number of samples was addressed in Smith et al. (Reference Smith, Lim and Cullis2006) with the use of partial replication. In this approach, and for a two-phase experiment, a sub-set of the varieties is tested using multiple field replicate samples (the remainder being tested using a single replicate only), then a sub-set of the selected field plot samples is split to produce replicate samples for the laboratory analysis. This has been found to work well in terms of minimizing both selection errors and cost, but when the field trial is a fully replicated trial it can be wasteful in the sense that field plots of some varieties are completely ignored. Smith et al. (Reference Smith, Thompson, Butler and Cullis2011) considered a similar issue but in the context of grain quality traits that are derived from a single (field) phase alone: they proposed that some varieties should be tested using individual replicate samples and others using composite samples. In this way, all field plots are used to generate data on the trait/s of interest. Smith et al. (Reference Smith, Thompson, Butler and Cullis2011) demonstrated that with such data it is possible to fit mixed models that enable the efficient prediction of genetic effects. In the present paper, the approach of Smith et al. (Reference Smith, Thompson, Butler and Cullis2011) is extended to suit the first phase in a multi-phase experiment. The concepts will be demonstrated using two motivating examples.
Motivating examples
Example 1: Wheat variety classification project
Prior to their commercial release, wheat varieties in Australia are classified according to their end-use capabilities. Classification is based on data submitted by private breeding companies to an expert advisory panel. Data on each candidate variety are obtained from a number of field trials and on a range of (multi-phase) traits including flour yield, and dough and baking characteristics. Accurate classification of varieties is crucial since growers are paid differentially on this basis. Accuracy is heavily dependent on the use of appropriate data, both in terms of the type and nature, so that protocols regarding experimental design and data requirements are fundamentally important. Currently, the data used for classification are based on fully composited data (i.e., composites of all field replicates within a trial), from several designed field trials with no experimental designs for the laboratory phases. Such data do not allow a statistical examination of protocols since potential sources of variation (including variety×trial interaction, between-plot variation in the field and between-sample variation in the laboratory) are confounded, so cannot be quantified or modelled. A recent project has been designed to enable estimation of all these sources so will ultimately allow examination of protocols for wheat variety classification. The full project spans 3 years with 24 field trials grown across Australia each year. In the present paper, the experimental design for the measurement of flour yield for one of these field trials is considered.
The field trial under study comprised 54 plots arranged in a rectangular array of six columns by nine rows. There were three replicates each of 18 varieties with replicate blocks aligned with pairs of columns. Methods for designing the milling phase of this trial will be described, noting that budgetary constraints have necessitated a restriction of 40 samples for milling.
Example 2: Genomic selection in wheat population
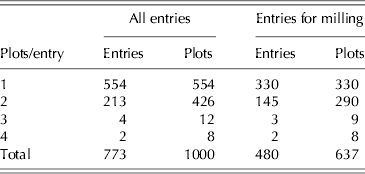
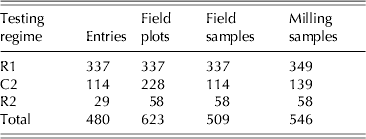
A wheat population with diverse genetic composition has been constructed in order to investigate marker-trait associations and genomic selection for a range of complex traits. The population has been genotyped using single nucleotide polymorphism (SNP) and diversity arrays technology (DArT) markers and is being phenotyped through a number of field trials. The field trial under study comprised 1000 plots arranged in a rectangular array of 50 columns×20 rows. There were 773 entries grown in the trial and these comprised 760 test lines and 13 commercial varieties. A resolvable p-replicate design (Cullis et al. Reference Cullis, Smith and Coombes2006) was used in which 554 entries were sown as single replicates and 213 as two replicates. There were six entries that had additional replication (Table 1). Replicate blocks for the replicated entries were aligned with columns with the first replicate comprising columns 1–25 and the second columns 26–50. The trait considered here is flour yield. Unlike the field trial described in the previous section, in which it was planned from the outset that all varieties would be milled, cost considerations necessitated a limit of <550 samples for milling, so it was not possible to mill all entries. It was decided to use 480 entries, chosen from the full set of 773 both on the basis of their genetic diversity as identified using the markers and the fact that they had sufficient grain for milling. The latter was important for this trial, which was unexpectedly low-yielding. A summary of the field replication status of the chosen entries is given as the final columns in Table 1.
Table 1. Example 2: summary of replication in the field for all entries and sub-sets of entries chosen for milling
DESIGN AND ANALYSIS FOR MULTI-PHASE TRIALS
Review of methods
In terms of the design of multi-phase trials, Smith et al. (Reference Smith, Lim and Cullis2006) and Brien et al. (Reference Brien, Harch, Correll and Bailey2011) demonstrate the need for the application of valid experimental design techniques (in particular, replication and randomization) in all phases. Experimental designs for field trials are well established and widely adopted. Thus in a multi-phase setting the design of the first phase is usually well constructed. The principles employed for this phase should also be applied to the second (and higher) phases. In terms of replication this means that for the two-phase milling examples there must be replication carried through from the field trial into the milling process, then replication applied in the milling process itself. The latter is achieved by taking grain samples from individual field plots and splitting into sub-samples (typically two), then milling these separately.
In the context of quality testing, fully replicated multi-phase designs are usually prohibitively expensive and not necessary from a statistical perspective. Typically, there are restrictions on the total number of samples that can be tested in the laboratory. In the context of two-phase experiments, Smith et al. (Reference Smith, Lim and Cullis2006) achieve this using ‘p/q replicate’ designs. In these designs, individual field replicates are used for a proportion, p, of varieties with the remainder tested using a single replicate only. This defines the field plots to be tested, a proportion, q of which, is then replicated in the laboratory. The approach is easily generalized for experiments requiring more than two phases.
In terms of the analysis of multi-phase trials, Smith et al. (Reference Smith, Lim and Cullis2006) use a linear mixed model approach that accommodates the block structure for each phase as well as allowing for additional sources of variation and correlation. Let k denote the number of phases in the trial and s denote the number of samples for which a measurement is obtained. The linear mixed model for the s×1 vector of data y can be written as:
 $${\bi y} = {\bi Z}_{\bi g} {\bi u}_{\bi g} + \sum\limits_{r = 1}^k {{\bi X}_r {\bi \tau} _r} + \sum\limits_{r = 1}^k {{\bi Z}_{{\bi p}_r} {\bi u}_{{\bi p}_r}} + e$$
$${\bi y} = {\bi Z}_{\bi g} {\bi u}_{\bi g} + \sum\limits_{r = 1}^k {{\bi X}_r {\bi \tau} _r} + \sum\limits_{r = 1}^k {{\bi Z}_{{\bi p}_r} {\bi u}_{{\bi p}_r}} + e$$where u g is the vector of random variety effects, τr is the vector of fixed effects associated with phase r (r=1,…,k), u pr is the vector of random non-genetic (peripheral) effects associated with phase r and e is the vector of residuals. The matrices Z g, Xr and Z pr are design matrices. Typically the vectors of random peripheral effects contain sub-vectors that will be denoted by u prt. Then the variance matrices for the random effects are given by
 $$\eqalign{{\mathop{\rm var}} ({\bi u}_{\bi g} ) =\, & {\bi G}_{\bi g} \cr {\mathop{\rm var}} ({\bi u}_{{\bi p}_{rt}} ) = \, & {\bi G}_{{\bi p}_{rt}} \Rightarrow {\mathop{\rm var}} ({\bi u}_{\bi p} ) = \oplus _{t = 1}^{q_r} {\bi G}_{{\bi p}_{rt}} \cr {\mathop{\rm var}} ({\bi e}) = \, & {\bi R}} $$
$$\eqalign{{\mathop{\rm var}} ({\bi u}_{\bi g} ) =\, & {\bi G}_{\bi g} \cr {\mathop{\rm var}} ({\bi u}_{{\bi p}_{rt}} ) = \, & {\bi G}_{{\bi p}_{rt}} \Rightarrow {\mathop{\rm var}} ({\bi u}_{\bi p} ) = \oplus _{t = 1}^{q_r} {\bi G}_{{\bi p}_{rt}} \cr {\mathop{\rm var}} ({\bi e}) = \, & {\bi R}} $$In the simplest models, all variance matrices are scaled identities with G g=σ 2gI, ![]() ${\bi G}_{{\bi p}_{rt}} = {\sigma} _{\,p_{rt}} ^2 {\bi I}$ and R = σ 2I, where identity matrices have dimensions commensurate with the length of the associated vector of effects. However, more complex forms, including separable auto-regressive processes of order 1 for the modelling of spatial correlation in the field plot effects (Smith et al. Reference Smith, Lim and Cullis2006) can be used. All analyses in the present paper were conducted using the mixed model software ASReml-R (Butler et al. Reference Butler, Cullis, Gilmour and Gogel2009) within the R statistical computing environment (R Development Core Team 2011). ASReml-R (Butler et al. Reference Butler, Cullis, Gilmour and Gogel2009) output includes residual maximum likelihood (REML) estimates of the variance parameters, empirical best linear unbiased estimates of the fixed effects and empirical best linear unbiased predictions (EBLUPs) of the random effects.
${\bi G}_{{\bi p}_{rt}} = {\sigma} _{\,p_{rt}} ^2 {\bi I}$ and R = σ 2I, where identity matrices have dimensions commensurate with the length of the associated vector of effects. However, more complex forms, including separable auto-regressive processes of order 1 for the modelling of spatial correlation in the field plot effects (Smith et al. Reference Smith, Lim and Cullis2006) can be used. All analyses in the present paper were conducted using the mixed model software ASReml-R (Butler et al. Reference Butler, Cullis, Gilmour and Gogel2009) within the R statistical computing environment (R Development Core Team 2011). ASReml-R (Butler et al. Reference Butler, Cullis, Gilmour and Gogel2009) output includes residual maximum likelihood (REML) estimates of the variance parameters, empirical best linear unbiased estimates of the fixed effects and empirical best linear unbiased predictions (EBLUPs) of the random effects.
In terms of the experimental design, first note that multi-phase experiments are typically designed sequentially rather than simultaneously with the second (and higher) phases often constructed after the field trial has been harvested. This may be necessary for several reasons including the fact that in standard selection trials only those varieties that are selected on the basis of grain yield are then tested for quality traits. Thus the varieties to be tested are only known after conclusion of the field trial. Similarly, the choice of plots to be replicated in the laboratory may be dependent on the field trial since quality testing requires a minimum amount of grain and there may be some plots with insufficient material to split into sub-samples for separate processing.
Given a valid design for the first phase, a second phase design is sought using the model-based techniques of Butler (Reference Butler2013). In this approach, one criterion that can be used is A-optimality, so that the goal is to seek designs that minimize the average pair-wise (prediction error) variance of the variety effects (or some sub-set thereof) given a pre-specified model of the form in Eqn (1). Bueno Filho & Gilmour (Reference Bueno Filho and Gilmour2007) discuss the fact that the use of this criterion minimizes the probability of making incorrect selection decisions and also provides, in the random treatment effects setting, ‘… a sensible utility function for ranking treatments and for estimating treatment effects’. All designs in the present paper were generated using the package ‘optimal design’ (od; Butler Reference Butler2013), which runs within the R statistical computing environment (R Development Core Team 2011). The syntax of od (Butler Reference Butler2013) is consistent with ASReml-R (Butler et al. Reference Butler, Cullis, Gilmour and Gogel2009). The package produces designs given a specified model (and associated variance parameter values) and starting design. To illustrate these concepts the first motivating example is considered.
Example 1: Wheat variety classification project
A fully replicated design for this experiment (assuming two laboratory replicates) would require 108 samples to be milled (i.e., 18 varieties×three field replicates×two laboratory replicates). It was noted previously that cost considerations for the project necessitated a limit of 40 samples for milling. Using the p/q replicate ideas of Smith et al. (Reference Smith, Lim and Cullis2006), one scheme that will achieve this uses values of p and q both equal to one-third. Thus six out of the 18 varieties will be milled using all three field replicates (a total of 18 plots) and the remainder using a single replicate each (a total of 12 plots). Note that for the second group, there needs to be a choice of which replicate plots to test and which to ignore. Then of the 30 field plots to be tested, ten will be replicated in the laboratory. With these values of p and q, one possible selection of varieties and plots to be replicated is shown in Fig. 1. The plots to be replicated in the milling process have been chosen to provide reasonable spatial coverage across the field. Additionally, they were chosen from plots sown with the 12 varieties that are only being milled with single field replicates. In this way, an attempt is made to balance the total number of samples for each variety (see also the following section). In the example, this results in six varieties with three samples each, ten with two and two with a single sample. Note that it may not always be possible to have the luxury of choosing the plots to be replicated (see later).

Fig. 1. Field layout for example 1 showing plots to be milled in p/q replicate design. Field trial comprises 18 varieties and 3 replicates (columns 1, 2; columns 3, 4 and columns 5, 6). Plots coloured light grey and white are to be milled as individual replicates (varieties in light grey plots have a single replicate only; varieties in white plots have all three replicates). Plots coloured dark grey will not be milled. Plots to be replicated in the milling phase are circled.
In terms of the laboratory design, first note that samples will be milled as eight samples per day for each of 5 days. There is often a break in the middle of each day, making a total of ten milling sessions (half days). Experience has shown that there are often substantial effects associated with milling sessions. This is a natural blocking factor that should be accommodated in the experimental design (Brien et al. Reference Brien, Harch, Correll and Bailey2011). Resolvability has been enforced in the sense that samples to be replicated in the laboratory are positioned with one replicate in sessions 1–5 (milling replicate 1) and the other in sessions 6–10 (milling replicate 2). This will be examined in more detail later.
In terms of the analysis the base-line mixed model for the data is as in Eqn (1) with k=2 and s=40. The only fixed effects are τ2, which is simply an overall mean (τ1 is omitted). The peripheral effects for the first phase comprise u p11 which represents the 3×1 vector of field replicate effects and up 12 which represents the 54×1 vector of field plot effects. Note that the corresponding 40×54 design matrix Z p12 will contain zero columns for those field plots that are not milled. The peripheral effects for the second phase comprise u p21 which represents the 2×1 vector of milling replicate effects and u p22 which represents the 10×1 vector of milling session effects. In the base-line mixed model all variance matrices have the simple variance component form as described previously.
The second phase design can be constructed in od (Butler Reference Butler2013) using a model that is the same as that described for the analysis except with the addition of random row and column effects for the first phase (denoted u p13 and u p14, respectively). These were added to the design model as a precautionary measure. A choice has been made not to confound field and milling replicates, so in the starting design approximately half of the samples from each field replicate have been allocated to each milling replicate (see later). This then allows estimation of both the field and milling replicate sources of variation. An example (optimized) design based on values of the variance parameters σ 2g=1·0, σ 2p11=0·1, σ 2p12=0·2, σ 2p13=0·1, σ 2p14=0·1, σ 2p21=0·3, σ 2p22=0·2 and σ 2=1·0 is shown in Fig. 2. Note that it has been assumed, without loss of generality, that the residual variance has a value of 1·0, so that all other variance values can be regarded as ratios relative to residual variance. The values were chosen on the basis of experience from analysing numerous milling trials.

Fig. 2. Milling layout for example 1 using p/q replicate design. Laboratory phase comprises 40 samples milled as four per session with two sessions per day (morning session=orders 1–4; afternoon=5–8) and for 5 days. Samples are labelled according to their variety and field replicate number. A total of 30 field samples were milled and ten of these were replicated in the milling process (samples coloured grey). Milling replicates were aligned with sessions (replicate 1=days 1 and 2 and morning of day 3; replicate 2=afternoon of day 3 and days 4 and 5).
Reduced example 1 : 8 field plots
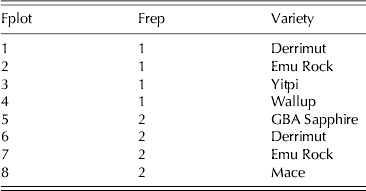
In order to more clearly illustrate the principles of resolvability and orthogonality of field and milling replicates alluded to previously, a very small sub-set of the field trial for that example is considered. The eight plots in the top left-hand corner of Fig. 1, namely rows 1 and 2 and columns 1–4, constitute a valid resolvable p replicate design (Cullis et al. Reference Cullis, Smith and Coombes2006) for six varieties. The varieties Derrimut and Emu Rock are grown in two plots each (once in each replicate) and the varieties Wallup, Yitpi, GBA Sapphire and Mace in single plots. The data for this reduced field phase are shown in Table 2. Note that due to the small size of the trial, the two-dimensional (row×column) layout has been ignored and the plots have been indexed simply as 1–8. In this example, it is assumed that all eight field plots will be milled with four of these being replicated, making a total of 12 samples to be milled (henceforth called ‘milling samples’). In terms of the choice of field plots to be replicated it is aimed to equalize the (total) number of milling samples for each variety. Thus the varieties replicated in the laboratory are those varieties that did not have field replicates (varieties Yitpi, Wallup, GBA Sapphire and Mace). This provides two observations for each variety.
Table 2. Reduced example 1: data for field trial comprising eight plots and six varieties
It is assumed that the 12 samples will be milled as three per day for each of 4 days. Days are natural blocking factors and resolvability is enforced so that the field samples to be replicated (field plots 3, 4, 5 and 8) will have one sub-sample milled in days 1 or 2 (milling replicate 1) and the other in days 3 or 4 (milling replicate 2). Finally, field and milling replicates have not been confounded, so the remaining field samples (field plots 1, 2, 6 and 7) have been allocated such that for each field replicate, the samples are balanced across both milling replicates. Therefore, a starting design that encompasses the two aspects of resolvability and orthogonality of field and milling replicates is formed. One possibility is as given in Table 3 as the first six columns. Finally, od (Butler Reference Butler2013) is used to determine an optimum design. In each iteration of the design search, two rows of the data-frame are swapped subject to the constraint that swaps may only occur within milling replicates. If the swap results in a reduction in the A-optimality value the resultant data-frame is maintained for the next iteration. The optimum design given a mixed model with random variety effects, field replicate and plot effects and milling replicate and day effects (with variance component ratios of 1, 0·1, 0·2, 0·3 and 0·2, respectively) is shown as the final columns of Table 3. Note that the A-optimality value for the starting design was 0·856, whereas for the optimum design it was 0·845.
Table 3. Reduced example 1: data-frames (starting and optimized design) for milling trial comprising 12 samples milled as 3 per day for each of 4 days

Compositing strategies
It was shown earlier how the p/q replicate ideas of Smith et al. (Reference Smith, Lim and Cullis2006) provided an approach for limiting the cost of multi-phase testing while still enabling a valid statistical analysis. However, there was substantial ‘waste’ in the sense that for the varieties to be tested, only a sub-set of the field plots was used, with many plots ignored altogether. In the first example where all varieties grown in the field were subsequently milled, only 30 out of a total of 54 plots were used in the milling process.
In the context of costly traits measured from single phase (field) trials, Smith et al. (Reference Smith, Thompson, Butler and Cullis2011) suggested the use of individual replicates for a proportion of varieties and composite samples for the remainder. For the latter a single sample is used for each variety but it represents a composite sample from all replicate plots for that variety rather than just a sample from a single replicate.
The compositing ideas of Smith et al. (Reference Smith, Thompson, Butler and Cullis2011) will now be extended for the multi-phase setting. For simplicity the focus is on two-phase experiments and compositing considered for the first phase only. The model-based approaches for design and analysis described earlier also apply here. The linear mixed model can be written as
 $$\eqalign{\hskip-3pt {\bi y} = \ & {\bi Z}_{\bi g} {\bi u}_{\bi g} + {\bi X}_1 {\bi \tau} _1 + {\bi Z}_{{\bi p}1} {\bi u}_{{\bi p}1} + {\bi X}_2 {\bi \tau} _2 + {\bi Z}_{{\bi p}2} {\bi u}_{{\bi p}2} + {\bi e} \cr =\ & {\bi Z}_{\bi g} {\bi u}_{\bi g} + {\bi C}_1 {\bi X}_1^* {\bi \tau} _1 + {\bi C}_1 {\bi Z}_{{\bi p}1}^* {\bi u}_{{\bi p}1} + {\bi X}_2 {\bi \tau} _2 + {\bi Z}_{\,p2} {\bi u}_{\,p2} + {\bi e}} $$
$$\eqalign{\hskip-3pt {\bi y} = \ & {\bi Z}_{\bi g} {\bi u}_{\bi g} + {\bi X}_1 {\bi \tau} _1 + {\bi Z}_{{\bi p}1} {\bi u}_{{\bi p}1} + {\bi X}_2 {\bi \tau} _2 + {\bi Z}_{{\bi p}2} {\bi u}_{{\bi p}2} + {\bi e} \cr =\ & {\bi Z}_{\bi g} {\bi u}_{\bi g} + {\bi C}_1 {\bi X}_1^* {\bi \tau} _1 + {\bi C}_1 {\bi Z}_{{\bi p}1}^* {\bi u}_{{\bi p}1} + {\bi X}_2 {\bi \tau} _2 + {\bi Z}_{\,p2} {\bi u}_{\,p2} + {\bi e}} $$where all terms are as previously defined for Eqn (1). The difference now is that the design matrices for the first phase are non-standard with X1=C1X*1 and ![]() ${\bi Z}_{{\bi p}1} = {\bi C}_1 {\bi Z}_{{\bi p}1}^* $, where C1 is an s×n averaging matrix that reflects the compositing of samples from the first phase (and n is the number of plots in the field trial). The concepts will be illustrated in the context of the two motivating examples.
${\bi Z}_{{\bi p}1} = {\bi C}_1 {\bi Z}_{{\bi p}1}^* $, where C1 is an s×n averaging matrix that reflects the compositing of samples from the first phase (and n is the number of plots in the field trial). The concepts will be illustrated in the context of the two motivating examples.
Example 1: Wheat variety classification project
Previously in the present paper, a milling design was constructed in which 30 field samples were tested and ten replicated in the laboratory. In that setting each field sample corresponded to a single field plot. A design will now be considered with the same number of field samples but with some of these corresponding to composites of several plots. Replication in the laboratory will remain at ten samples.
Smith et al. (Reference Smith, Thompson, Butler and Cullis2011) describe in detail compositing strategies for field trials that have two replicates and briefly allude to designs with more replicates, and suggest that in the latter there are numerous possibilities for compositing strategies. In terms of a three replicate design (as is the case in this example), Smith et al. (Reference Smith, Thompson, Butler and Cullis2011) suggest that the simplest approach would be to either test three individual plot samples for a variety or a single sample that is a composite of all three plots for the variety. In this strategy, each variety has either one or three field samples tested. In the context of the two-phase example, the required number of field samples (30) can be obtained by compositing all three replicates for each of 12 varieties and testing three individual replicates for each of six varieties. Laboratory replication is achieved by splitting ten of the individual field replicate samples for separate testing. In this strategy, henceforth called ‘A’, varieties may be classified into one of four types:
T1: the variety has three field .samples (i.e., from all individual field replicates) and none are replicated in the laboratory.
T2: as for T1 except that two of the field samples are replicated in the laboratory.
T3: as for T1 except that all three field samples are replicated in the laboratory.
T4: the variety has a single field sample (i.e., a composite of all three field replicates) and this is not replicated in the laboratory.
The number of varieties of each type for strategy A is given in the bottom section of Table 4.
Table 4. Summary of variety types (T1–T9) for example 1. An individual variety, i, has fi field samples and cij is the number of field plots in the jth sample; dij is the number of laboratory samples for the jth field sample. Values in the body of the top section of the table are the number of field/laboratory samples for a variety of a given type. These are followed by the total number of laboratory samples, ri, for a variety of a given type and the effective replication, ri−α i, for the simple mixed model described in the text with a plot variance ratio of 1/3. The lower section of the table gives the number of varieties of each type for each strategy (A–D) and the average effective replication for each strategy for the simple mixed model
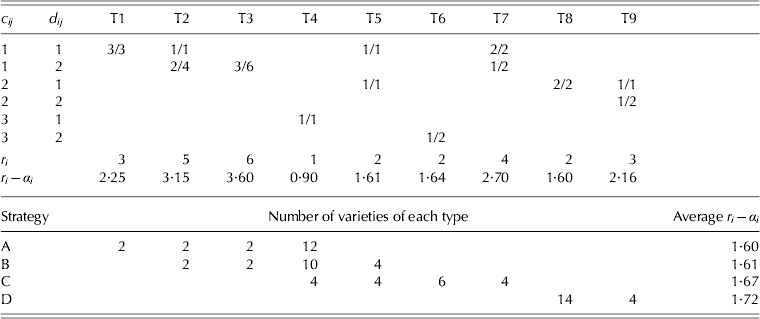
An alternative strategy involves three possible types of testing for a variety, namely one field sample (a composite of all three replicates), two field samples (a composite of two replicates and a separate sample for the remaining replicate) and three samples (individual replicate samples). With laboratory replication, this strategy (‘B’) also results in four types of variety, namely T2, T3 and T4 as previously defined, and additionally
T5: the variety has two field samples (i.e., a composite of two field replicates and a separate sample for the remaining field replicate) and neither is replicated in the laboratory.
The number of varieties of each type for strategy B is given in the bottom section of Table 4.
In strategies A and B, replication in the laboratory has been restricted to those field samples that corresponded to individual plot samples. In the second example, due to the limited amount of grain harvested for some plots, most of the field samples replicated in the laboratory phase corresponded to composite samples (see later). This possibility is therefore considered for the current example as strategy ‘C’. This has four types of variety, namely T4 and T5 as previously defined, and additionally
T6: as for T4 but the (composite) sample is replicated in the laboratory.
T7: as for T1 except that one of the field samples is replicated in the laboratory.
The number of varieties of each type for strategy C is given in the bottom section of Table 4.
Finally, a strategy suggested by a referee is considered in which all 18 varieties have two field samples, each of which is a composite of two field replicates. There are three types of composite samples, that is, corresponding to field replicates 1 and 2, field replicates 1 and 3 and field replicates 2 and 3. The allocation of varieties to composite types can be achieved as an incomplete block design with two replicates of 18 varieties and three incomplete blocks. This strategy means that 36 (rather than 30) field samples are formed so only four (rather than ten) of these can be replicated in the laboratory phase. There are therefore two types of variety for this strategy (‘D’), namely
T8: the variety has two field samples, each being a composite of two field replicates, so that one of the replicates is used twice, that is, in both composites (for example, replicates 1 and 2 in one sample and replicates 1 and 3 in the other). Neither sample is replicated in the laboratory.
T9: as for T8 but one of the field samples is replicated in the laboratory.
The number of varieties of each type for strategy D is given in the bottom section of Table 4.
The structure of all four strategies can be summarized by letting f i be the number of field samples tested for the ith variety and defining c ij (j=1,…, f i) to be the number of field plots associated with the jth field sample for variety i and d ij to be the number of laboratory samples formed from the jth field sample for variety i. Possible values of c ij for the current example are 1 (an individual field replicate sample), 2 (a composite of two field replicates) and 3 (a composite of three replicates). Possible values of d ij for the current example are 1 or 2 with the latter reflecting the fact that the field sample will be replicated in the laboratory. Table 4 gives the values of c ij and d ij for each of the types T1 through to T9, and the associated number of field and laboratory samples for an individual variety of that type.
In terms of the laboratory design, the same blocking factors as previously described were used. The base-line mixed model for analysis is as in Eqn (2) with the same fixed and random effects as for the analysis model described previously. The design matrices for the first phase involve C1 which is a 40×54 matrix that reflects the compositing strategy. For strategy A, the ith row of C1 (which corresponds to the ith sample) has elements given by:
• 1 in column j if this sample corresponds to field plot j alone;
• 1/3 in columns j, k and l if this sample corresponds to a composite of field plots j, k and l;
• 0 otherwise.
In the base-line mixed model all variance matrices have the simple variance component form as previously described.
The second phase design can be constructed using the same approach as previously described. The A-optimality values for optimized designs for the individual strategies were 0·919 (A), 0·9024 (B), 0·8147 (C) and 0·7768 (D). Thus strategy D had the lowest A-optimality value which may reflect the fact that the heterogeneity between varieties in terms of the number of samples is the smallest (most varieties have two samples, while a few have three samples: Table 4).
In order to explore the factors driving the A-optimality values for these strategies, algebraic forms for the prediction error variances (PEVs) for individual varieties are derived, as these are closely linked to the A-optimality value. This is done for a very simple linear mixed model with random effects for varieties (with variance denoted σg2) and field plots (variance σp2). As before the residual variance was fixed at σ 2=1 so that σg2 and σp2 may be interpreted as variance ratios. All fixed effects (including an overall mean) are excluded from the model. In this case, the PEV for variety i can be written as
where ![]() $r_i = \sum\nolimits_{\,j = 1}^{\,f_i} {d_{ij}} $ is the total number of samples for variety i and r i−α i may be thought of as the effective replication for variety i. The form of r i−α i for strategies A, B, C or a p/q replicate design is
$r_i = \sum\nolimits_{\,j = 1}^{\,f_i} {d_{ij}} $ is the total number of samples for variety i and r i−α i may be thought of as the effective replication for variety i. The form of r i−α i for strategies A, B, C or a p/q replicate design is ![]() $\sum\nolimits_{\,j = 1}^{\,f_i} {( {\sigma _p^2 /c_{ij} + 1/d_{ij}} )^{ - 1}} $. The forms for strategy D are more complex. For a T8 variety, r i − αi = (3σp2/8+1/2)−1 and for a T9 variety, r i − αi = (3σp2/8+3/8−1/(8(σp2+3)))−1. Note that for the full mixed model, the ratio of the sum of all field error sources of variation (i.e., field replicates, rows, columns and plots) to laboratory variation (i.e., milling replicates, sessions and the residual) was 1/3. Thus, as an example, the formulae using σp2 = 1/3 for the simple model have been applied. The resultant effective replication for a variety of any particular type is given in Table 4. Finally, simple averaging of these values across all 18 varieties for each strategy gives values of 1·6, 1·61, 1·67 and 1·72 for strategies A, B, C and D. These values are consistent with the A-optimality values of the designs optimized for the full mixed model.
$\sum\nolimits_{\,j = 1}^{\,f_i} {( {\sigma _p^2 /c_{ij} + 1/d_{ij}} )^{ - 1}} $. The forms for strategy D are more complex. For a T8 variety, r i − αi = (3σp2/8+1/2)−1 and for a T9 variety, r i − αi = (3σp2/8+3/8−1/(8(σp2+3)))−1. Note that for the full mixed model, the ratio of the sum of all field error sources of variation (i.e., field replicates, rows, columns and plots) to laboratory variation (i.e., milling replicates, sessions and the residual) was 1/3. Thus, as an example, the formulae using σp2 = 1/3 for the simple model have been applied. The resultant effective replication for a variety of any particular type is given in Table 4. Finally, simple averaging of these values across all 18 varieties for each strategy gives values of 1·6, 1·61, 1·67 and 1·72 for strategies A, B, C and D. These values are consistent with the A-optimality values of the designs optimized for the full mixed model.
It is informative to consider the effective replication for this simple model for a range of values of σp2. Figure 3 shows the average effective replication (across all varieties) for strategies A, B, C and D expressed as a percentage of the corresponding values for the p/q replicate design described earlier. The average effective replication (and thence A-optimality value) for any of the designs that employed compositing is superior to that of the p/q replicate design and this superiority increases as the field plot variance ratio increases. Among compositing strategies, strategy C is superior to all others except when the plot variance ratio is small, in which case it has slightly lower effective replication than strategy D.

Fig. 3. Effective replication for example 1 for strategies A, B, C and D as a percentage of effective replication for p/q replicate design. Computed algebraically based on the simple mixed model described in the text and for a range of values for the plot variance ratio, σp2.
A comparison of strategies using the effective replication displayed in Fig. 3 is based on the known plot and residual variances. Similarly, the superiority of strategy D over A, B and C when the full mixed model was used was measured in terms of A-optimality values from the design generation stage so that all variance parameters were assumed known. In order to confirm these findings in the context of data analysis (thence estimation of variance parameters) a simulation study was conducted. The data were generated on the basis of the designs described for strategies A, B, C and D and the p/q replicate design. The model used for data generation was the same as that used for design construction, namely with random effects for varieties (with σg2 = 1![]() $ {\cdot} 0$), field replicates (
$ {\cdot} 0$), field replicates (![]() $\sigma _{\,p11}^2 = 0 {\cdot} 1$), field plots (
$\sigma _{\,p11}^2 = 0 {\cdot} 1$), field plots (![]() $\sigma _{\,p12}^2 = 0 {\cdot} 2$), field rows (
$\sigma _{\,p12}^2 = 0 {\cdot} 2$), field rows (![]() $\sigma _{\,p13}^2 = 0 {\cdot} 1$), field columns (
$\sigma _{\,p13}^2 = 0 {\cdot} 1$), field columns (![]() $\sigma _{\,p14}^2 = 0 {\cdot} 1$), milling replicates (
$\sigma _{\,p14}^2 = 0 {\cdot} 1$), milling replicates (![]() $\sigma _{\,p21}^2 = 0 {\cdot} 3$), milling sessions (
$\sigma _{\,p21}^2 = 0 {\cdot} 3$), milling sessions (![]() $\sigma _{\,p22}^2 = 0 {\cdot} 2$) and residuals (σ 2=1·0). In each simulation only one set of effects was generated for each term in the model and used for all strategies. The model fitted to the data matched that used for design generation. The results, namely the accuracy of the variety EBLUPs and the reliability of the REML estimates of variance parameters are presented in Table 5 as means over 1000 simulations. Accuracy was defined, for each variety, as the correlation between the true and predicted effects (EBLUPs) (Mrode Reference Mrode2005). These values were then averaged across varieties to provide the accuracies shown in Table 5. Reliability for each parameter estimate was computed as a coefficient of variation (CVMSE) based on the mean-squared error, namely the square root of the mean-squared error expressed as a percentage of the true value for that parameter.
$\sigma _{\,p22}^2 = 0 {\cdot} 2$) and residuals (σ 2=1·0). In each simulation only one set of effects was generated for each term in the model and used for all strategies. The model fitted to the data matched that used for design generation. The results, namely the accuracy of the variety EBLUPs and the reliability of the REML estimates of variance parameters are presented in Table 5 as means over 1000 simulations. Accuracy was defined, for each variety, as the correlation between the true and predicted effects (EBLUPs) (Mrode Reference Mrode2005). These values were then averaged across varieties to provide the accuracies shown in Table 5. Reliability for each parameter estimate was computed as a coefficient of variation (CVMSE) based on the mean-squared error, namely the square root of the mean-squared error expressed as a percentage of the true value for that parameter.
Table 5. Example 1 simulation study: accuracy of variety EBLUPs and coefficient of variation based on mean-squared error (CV MSE) of REML estimates of variance parameters for strategy A, B, C, D and p/q replicate design (mean over 1000 simulations)
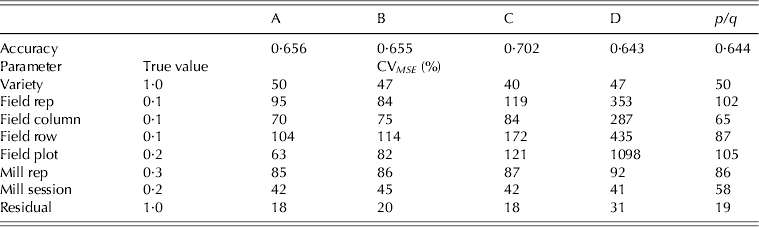
A key finding from the simulation study was that strategy D, which appeared to be the superior strategy in terms of design A-optimality values, had the poorest accuracy for variety predictions. An examination of the CVMSE of variance parameter estimates for this strategy revealed that many of the parameters, in particular the field plot error variance, were poorly estimated. This may be due to the fact that this strategy does not involve any individual field plot samples, since all are composites of two field replicates. The simulation study identified strategy C as the best in terms of the accuracy of variety predictions. Note that an identical simulation study was conducted but with larger field variance parameters, namely ![]() $\sigma _{\,p11}^2 = 0 {\cdot} 4$ for field replicates,
$\sigma _{\,p11}^2 = 0 {\cdot} 4$ for field replicates, ![]() $\sigma _{\,p13}^2 = 0 {\cdot} 2$ for field rows,
$\sigma _{\,p13}^2 = 0 {\cdot} 2$ for field rows, ![]() $\sigma _{\,p14}^2 = 0 {\cdot} 2$ for field columns and
$\sigma _{\,p14}^2 = 0 {\cdot} 2$ for field columns and ![]() $\sigma _{\,p12}^2 = 1 {\cdot} 0$ for field plots. The accuracies for this scenario were 0·576, 0·579, 0·608, 0·565 and 0·509 for strategies A, B, C, D and the p/q replicate design.
$\sigma _{\,p12}^2 = 1 {\cdot} 0$ for field plots. The accuracies for this scenario were 0·576, 0·579, 0·608, 0·565 and 0·509 for strategies A, B, C, D and the p/q replicate design.
Example 2: Genomic selection in wheat population
The 480 entries selected for milling will be tested using either individual field replicate or composite samples as follows:
• Single field sample:
C2: 114 entries with a composite sample (composite of two replicates);
R1: 337 entries with a sample from a single replicate.
• Two field samples:
R2: 29 entries with two individual replicate samples.
Thus there are a total of 509 field samples to be tested. Note that these involve 623 out of the 637 field plots sown with the 480 chosen entries (Table 1). The field sampling and compositing is summarized in Table 6.
Table 6. Example 2: distribution of field and milling samples across testing regimes for 480 entries chosen for milling. C2 entries: tested as composite of two field replicates; R1 entries: tested as single field replicate; R2 entries: tested as two field replicates
In the previous section, the varieties to be composited, as opposed to using each replicate separately, were chosen at random. In the current example, the decision was driven by the fact that there is a minimum sample size (amount of clean grain) required for milling and subsequent end-product testing. Upon harvesting of this field trial it was found that some plots had insufficient material to form a sample for quality testing. In this case, the only mechanism to facilitate quality testing of the associated entry was to use a composite sample (provided the entry was sown with more than one plot). Many of the 114 entries in the C2 group were composited for this reason.
Laboratory replication will be used for 37 of the 509 field samples making a total of 546 laboratory samples for milling. These will be milled as seven samples per day for each of 78 days. As with the choice of entries to composite, the choice of field samples to replicate in the milling process was influenced by the minimum grain requirements. In the current example, there were very few individual replicate samples with sufficient material to allow replication in the milling process. Therefore the majority (25 out of 37) of field samples replicated in the laboratory corresponded to composite samples (see Table 6).
In terms of the laboratory design similar blocking factors as described earlier are used, the only difference being the use of milling days rather than sessions (half-days). The base-line mixed model for analysis is as in Eqn (2) with the fixed effects τ2 comprising an overall mean (and τ1 omitted), the peripheral effects for the first phase comprising u p11 (the 2×1 vector of field replicate effects) and u p12 (the 623×1 vector of field plot effects) and the peripheral effects for the second phase comprising u p21 (the 2×1 vector of milling replicate effects) and u p22 (the 78×1 vector of milling day effects). The design matrices for the first phase involve C1 which is a 546×623 matrix that reflects the compositing strategy. The ith row of C1 (which corresponds to the ith sample) has elements given by:
• 1 in column j if this sample corresponds to field plot j alone;
• 1/2 in columns j and k if this sample corresponds to a composite of field plots j and k;
• 0 otherwise.
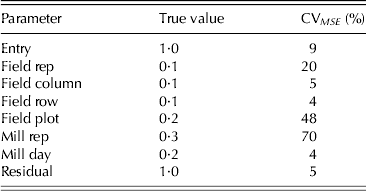
The second phase design can be constructed in od (Butler Reference Butler2013) using a model that is the same as that described for the analysis except with the addition of random row and column effects for the first phase (denoted u p13 and u p14, respectively). The starting design is constructed as resolvable so that field samples to be replicated are allocated with one sub-sample in days 1–39 (milling replicate 1) and the other in days 40–78 (milling replicate 2) and the design search is subsequently restricted to swaps within milling replicates. Once again it has been decided to not confound field and milling replicates so in the starting design it is ensured that the samples from each field replicate are allocated approximately equally across the two milling replicates. The values chosen for the variance parameters were ![]() ${\sigma _g^2 = 1 {\cdot} 0,{\kern 1pt} \;\sigma _{\,p11}^2 = 0 {\cdot} 1,\;\sigma _{\,p12}^2 = 0 {\cdot} 2,\;\sigma _{\,p13}^2 = 0 {\cdot} 1,\, \sigma _{\,p14}^2 = 0 {\cdot} 1,}$
${\sigma _g^2 = 1 {\cdot} 0,{\kern 1pt} \;\sigma _{\,p11}^2 = 0 {\cdot} 1,\;\sigma _{\,p12}^2 = 0 {\cdot} 2,\;\sigma _{\,p13}^2 = 0 {\cdot} 1,\, \sigma _{\,p14}^2 = 0 {\cdot} 1,}$![]() $\sigma _{\,p21}^2 = 0 {\cdot} 3,\;\sigma _{\,p22}^2 = 0 {\cdot} 2\;({\rm and} \ \sigma ^2 = 1.0{\rm )}{\rm.} $ As with example 1, a simulation study was conducted in order to examine the reliability of estimation. The model used for data generation was the same as that used for design construction. In each simulation the model fitted to the data matched that used for design generation. A total of 1000 simulations were conducted and the results presented as means over simulations (Table 7). The CVMSE of all parameter estimates are much lower than for the first example, due to the much larger number of samples involved. They suggest that it is possible to reliably estimate the variance parameters using the generated design.
$\sigma _{\,p21}^2 = 0 {\cdot} 3,\;\sigma _{\,p22}^2 = 0 {\cdot} 2\;({\rm and} \ \sigma ^2 = 1.0{\rm )}{\rm.} $ As with example 1, a simulation study was conducted in order to examine the reliability of estimation. The model used for data generation was the same as that used for design construction. In each simulation the model fitted to the data matched that used for design generation. A total of 1000 simulations were conducted and the results presented as means over simulations (Table 7). The CVMSE of all parameter estimates are much lower than for the first example, due to the much larger number of samples involved. They suggest that it is possible to reliably estimate the variance parameters using the generated design.
Table 7. Example 2 simulation study: coefficient of variation based on mean-squared error (CV MSE) of REML estimates of variance parameters (means over 1000 simulations)
CONCLUDING REMARKS
In the present paper, it has been shown how the use of both individual field replicate samples and composite samples can produce valid experimental designs for a multi-phase variety trial. Replication in the laboratory phase was achieved by splitting some field samples and processing separately. In contrast to the use of composite field samples alone (or a single field replicate), this approach enabled the application of an appropriate mixed model analysis to the resultant data. The use of a mixture of composite and individual plot samples was shown to be superior to the p/q replicate approach of Smith et al. (Reference Smith, Lim and Cullis2006) in terms of the accuracy of predictions of genetic effects. The gains were the greatest when (non-genetic) variation in the field was large relative to that from the laboratory phase. In the first example, in which there were three field replicates, a range of compositing strategies were possible. Four strategies were compared under simulation and it was found that in order to maximize accuracy, it was important to attempt to balance the total number of samples across varieties and to ensure that sufficient individual plot samples were tested. A key finding was that the best strategy in terms of design A-optimality value was one of the poorest in terms of accuracy (average correlation between the true and predicted variety effects) under simulation. Thus, if the aim is to maximize accuracy and thence genetic gain, this example suggests that the traditional paradigm of using A-optimality as the design criterion may not be sufficient and there may be a need to incorporate the uncertainty of variance parameter estimation. This is likely to be most critical for designs involving small numbers of samples and varieties, such as the first example. In this example, which involved 40 samples and 18 varieties, the CV of variance parameter estimates was much higher than for the second example which involved 546 samples and 480 varieties.
The approach presented in the present paper also has practical advantages compared with that of Smith et al. (Reference Smith, Lim and Cullis2006) since it offers a flexible means of dealing with the problem of minimum grain requirements. The second example was a case where, due to low plot yields, a valid design could only have been achieved with the use of the proposed approach. It was then possible to select varieties to be composited or tested as individual replicates according to the amount of grain harvested from the associated plots. Additionally, sufficient laboratory replication was achieved by splitting some of the composite samples.
In the present paper, model-based techniques have been used in order to produce designs for the second (laboratory) phase given a design for the first phase. The laboratory phases in multi-phase trials are typically unbalanced and non-orthogonal (even more so with the advent of partial compositing) and have several potential sources of non-genetic variation. An interesting design issue is the manner in which major sources of variation should be accommodated across phases. In the case of orthogonal multi-phase designs Brien et al. (Reference Brien, Harch, Correll and Bailey2011) recommended confounding ‘…big first phase unit sources … with potentially big second phase unit sources’. This has not been done in the present paper and instead, terms have been fitted in the linear mixed model to accommodate all potential sources of variation. This is particularly important in the presence of correlated random effects, for example, spatial correlation across field rows and columns, in which case the modelling of such trends, which can increase accuracy substantially, may be precluded if field rows and columns are confounded with laboratory blocking factors. Additionally, in the majority of experiments with which the authors have been involved, it would have been difficult from a practical perspective to have confounded, or even near-confounded, big first phase units with big second phase units. In the second example, the field phase comprised 50 columns and 20 rows, whereas the laboratory phase comprised 78 days and seven samples per day. Also, not all varieties grown in the field were tested in the laboratory. Thus the differential numbers and sizes of blocks in the two phases would make confounding extremely difficult. However, in the small p/q replicate example the model-based design approach resulted in confounding of this nature, with field replicate effects being confounded with milling day effects. This may have been a function of the type of model used (i.e., a simple variance component model) and the optimality criterion. In terms of the former, note that the analysis of multi-phase traits may involve more complex variance models, in particular spatial correlation structures for field plot effects. At present in od (Butler Reference Butler2013), correlated effects are only allowed at the residual level (i.e., associated with the final phase) but this will be addressed in future versions of the software. The use of more complex models for design generation may break the type of confounding observed in the small example.
We gratefully acknowledge the financial support of the Grains Research and Development Corporation of Australia and Wheat Quality Australia (WQA). We also acknowledge Marcus Newberry (CSIRO Plant Industry and Food Futures Flagship) as a lead investigator on the WQA project. We thank the referees for comments that have greatly improved the manuscript.












