Article contents
Non-Orientable Lagrangian Fillings of Legendrian Knots
Published online by Cambridge University Press: 27 September 2023
Abstract
We investigate when a Legendrian knot in the standard contact 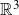 ${{\mathbb{R}}}^3$ has a non-orientable exact Lagrangian filling. We prove analogs of several results in the orientable setting, develop new combinatorial obstructions to fillability, and determine when several families of knots have such fillings. In particular, we completely determine when an alternating knot (and more generally a plus-adequate knot) is decomposably non-orientably fillable and classify the fillability of most torus and 3-strand pretzel knots. We also describe rigidity phenomena of decomposable non-orientable fillings, including finiteness of the possible normal Euler numbers of fillings and the minimisation of crosscap numbers of fillings, obtaining results which contrast in interesting ways with the smooth setting.
${{\mathbb{R}}}^3$ has a non-orientable exact Lagrangian filling. We prove analogs of several results in the orientable setting, develop new combinatorial obstructions to fillability, and determine when several families of knots have such fillings. In particular, we completely determine when an alternating knot (and more generally a plus-adequate knot) is decomposably non-orientably fillable and classify the fillability of most torus and 3-strand pretzel knots. We also describe rigidity phenomena of decomposable non-orientable fillings, including finiteness of the possible normal Euler numbers of fillings and the minimisation of crosscap numbers of fillings, obtaining results which contrast in interesting ways with the smooth setting.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 176 , Issue 1 , January 2024 , pp. 123 - 153
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
Footnotes
Partially supported by NSF grant DMS-1406093 during the preparation of this paper.
Partially supported by grants from Haverford College.
References
REFERENCES
- 1
- Cited by


