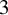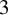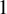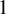1 Introduction
Hilbert schemes have been studied extensively since the pioneering work of Grothendieck [Reference Grothendieck14]. It is well known [Reference Briancon3, Reference Fogarty10, Reference Iarrobino16] that the Hilbert schemes of points, parametrizing
![]() $0$
-dimensional closed subschemes, on algebraic surfaces are smooth and irreducible. In fact, these Hilbert schemes are crepant resolutions of the symmetric products of the corresponding surfaces, via the Hilbert-Chow morphism which maps a
$0$
-dimensional closed subschemes, on algebraic surfaces are smooth and irreducible. In fact, these Hilbert schemes are crepant resolutions of the symmetric products of the corresponding surfaces, via the Hilbert-Chow morphism which maps a
![]() $0$
-dimensional closed subscheme to its support (counting with multiplicities). Their extremal Gromov-Witten invariants are defined via the moduli spaces of stable maps whose images are contracted by the Hilbert-Chow morphism and are motivated by Ruan’s Cohomological Crepant Resolution Conjecture [Reference Ruan39] which eventually evolves to the Crepant Resolution Conjecture of Bryan and Graber [Reference Bryan and Graber4], Coates, Corti, Iritani and Tseng [Reference Coates, Corti, Iritani and Tseng5], and Coates and Ruan [Reference Coates and Ruan7]. Their
$0$
-dimensional closed subscheme to its support (counting with multiplicities). Their extremal Gromov-Witten invariants are defined via the moduli spaces of stable maps whose images are contracted by the Hilbert-Chow morphism and are motivated by Ruan’s Cohomological Crepant Resolution Conjecture [Reference Ruan39] which eventually evolves to the Crepant Resolution Conjecture of Bryan and Graber [Reference Bryan and Graber4], Coates, Corti, Iritani and Tseng [Reference Coates, Corti, Iritani and Tseng5], and Coates and Ruan [Reference Coates and Ruan7]. Their
![]() $1$
-point genus-
$1$
-point genus-
![]() $0$
extremal Gromov-Witten invariants are obtained in [Reference Li and Qin27]. Okounkov and Pandharipande [Reference Okounkov and Pandharipande36] studied the genus-
$0$
extremal Gromov-Witten invariants are obtained in [Reference Li and Qin27]. Okounkov and Pandharipande [Reference Okounkov and Pandharipande36] studied the genus-
![]() $0$
equivariant extremal Gromov-Witten theory of the Hilbert schemes of points on the affine plane
$0$
equivariant extremal Gromov-Witten theory of the Hilbert schemes of points on the affine plane
![]() $ {\mathbb C} ^2$
. Using cosection localization theory [Reference Kiem and Li17], J. Li and W-P. Li [Reference Li and Li23] determined the
$ {\mathbb C} ^2$
. Using cosection localization theory [Reference Kiem and Li17], J. Li and W-P. Li [Reference Li and Li23] determined the
![]() $2$
-point genus-
$2$
-point genus-
![]() $0$
extremal Gromov-Witten invariants of the Hilbert schemes of points on surfaces. The structures of the
$0$
extremal Gromov-Witten invariants of the Hilbert schemes of points on surfaces. The structures of the
![]() $3$
-point genus-
$3$
-point genus-
![]() $0$
extremal Gromov-Witten invariants of these Hilbert schemes are analyzed in [Reference Li and Qin28] where Ruan’s Cohomological Crepant Resolution Conjecture for the Hilbert-Chow morphism is verified. Higher genus equivariant extremal Gromov-Witten theory of the Hilbert schemes of points on
$0$
extremal Gromov-Witten invariants of these Hilbert schemes are analyzed in [Reference Li and Qin28] where Ruan’s Cohomological Crepant Resolution Conjecture for the Hilbert-Chow morphism is verified. Higher genus equivariant extremal Gromov-Witten theory of the Hilbert schemes of points on
![]() $ {\mathbb C} ^2$
is investigated by Pandharipande and Tseng [Reference Pandharipande and Tseng37]. We refer to the survey book [Reference Qin38] for more details and to [Reference Maulik and Oblomkov33, Reference Oberdieck35] for related works.
$ {\mathbb C} ^2$
is investigated by Pandharipande and Tseng [Reference Pandharipande and Tseng37]. We refer to the survey book [Reference Qin38] for more details and to [Reference Maulik and Oblomkov33, Reference Oberdieck35] for related works.
In this paper, we work out explicitly all the extremal Gromov-Witten invariants of the Hilbert scheme of
![]() $3$
points on a smooth projective complex surface X. Let
$3$
points on a smooth projective complex surface X. Let
![]() $ X^{[n]}$
be the Hilbert scheme of n points on X. For
$ X^{[n]}$
be the Hilbert scheme of n points on X. For
![]() $n \ge 2$
, the extremal k-point genus-g Gromov-Witten invariants of
$n \ge 2$
, the extremal k-point genus-g Gromov-Witten invariants of
![]() $ X^{[n]}$
are of the form
$ X^{[n]}$
are of the form
where
![]() $d \ge 0$
,
$d \ge 0$
,
![]() $\gamma _1, \ldots , \gamma _k \in H^*( X^{[n]}, {\mathbb C})$
, and
$\gamma _1, \ldots , \gamma _k \in H^*( X^{[n]}, {\mathbb C})$
, and
![]() $\beta _n$
is (the homology class of the curve)
$\beta _n$
is (the homology class of the curve)
with
![]() $x_1, x_2, \ldots , x_{n-1}$
being distinct and fixed points in X. By degree reasons, if
$x_1, x_2, \ldots , x_{n-1}$
being distinct and fixed points in X. By degree reasons, if
![]() $g \ge 2$
, all genus-g extremal Gromov-Witten invariants of
$g \ge 2$
, all genus-g extremal Gromov-Witten invariants of
![]() $ X^{[n]}$
are equal to
$ X^{[n]}$
are equal to
![]() $0$
.
$0$
.
We begin with genus-
![]() $0$
extremal Gromov-Witten invariants of
$0$
extremal Gromov-Witten invariants of
![]() $ X^{[3]}$
. By the Fundamental Class Axiom and the Divisor Axiom, these invariants are reduced to the following
$ X^{[3]}$
. By the Fundamental Class Axiom and the Divisor Axiom, these invariants are reduced to the following
![]() $1$
-point,
$1$
-point,
![]() $2$
-point and
$2$
-point and
![]() $3$
-point genus-
$3$
-point genus-
![]() $0$
extremal Gromov-Witten invariants:
$0$
extremal Gromov-Witten invariants:
with
![]() $\tilde \omega _1, \tilde \omega _2 \in H^*(X^{[3]}, {\mathbb C})$
and
$\tilde \omega _1, \tilde \omega _2 \in H^*(X^{[3]}, {\mathbb C})$
and
![]() $\omega _1, \omega _2, \omega _3 \in H^4( X^{[3]}, {\mathbb C} )$
. The invariants
$\omega _1, \omega _2, \omega _3 \in H^4( X^{[3]}, {\mathbb C} )$
. The invariants
![]() $\langle \tilde \omega _1 \rangle _{0, d\beta _3}$
and
$\langle \tilde \omega _1 \rangle _{0, d\beta _3}$
and
![]() $\langle \tilde \omega _1, \tilde \omega _2 \rangle _{0, d\beta _3}$
have been computed in [Reference Li and Qin27] and [Reference Li and Li23], respectively. When
$\langle \tilde \omega _1, \tilde \omega _2 \rangle _{0, d\beta _3}$
have been computed in [Reference Li and Qin27] and [Reference Li and Li23], respectively. When
![]() $X={\mathbb P}^2$
,
$X={\mathbb P}^2$
,
![]() $\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d\beta _3}$
is partially calculated in [Reference Edidin, Li and Qin8]. The calculations in the 2003 paper [Reference Edidin, Li and Qin8] for
$\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d\beta _3}$
is partially calculated in [Reference Edidin, Li and Qin8]. The calculations in the 2003 paper [Reference Edidin, Li and Qin8] for
![]() $X={\mathbb P}^2$
are incomplete due to the lack of understanding of the invariants
$X={\mathbb P}^2$
are incomplete due to the lack of understanding of the invariants
![]() $\langle \tilde \omega _1, \tilde \omega _2 \rangle _{0, d\beta _3}$
which appear later in the 2011 paper [Reference Li and Li23]. To state our result, we fix a linear basis of
$\langle \tilde \omega _1, \tilde \omega _2 \rangle _{0, d\beta _3}$
which appear later in the 2011 paper [Reference Li and Li23]. To state our result, we fix a linear basis of
![]() $H^{4}( X^{[3]}, {\mathbb C} )$
via the Heisenberg operators of Grojnowski [Reference Grojnowski13] and Nakajima [Reference Nakajima34]:
$H^{4}( X^{[3]}, {\mathbb C} )$
via the Heisenberg operators of Grojnowski [Reference Grojnowski13] and Nakajima [Reference Nakajima34]:
 $$ \begin{align} &{\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x) |0\rangle, \quad {\mathfrak a}_{-3}(1_X)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-2}(1_X)|0\rangle, \nonumber \\ &\qquad {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(1_X)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(1_X)|0\rangle \end{align} $$
$$ \begin{align} &{\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x) |0\rangle, \quad {\mathfrak a}_{-3}(1_X)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-2}(1_X)|0\rangle, \nonumber \\ &\qquad {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(1_X)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(1_X)|0\rangle \end{align} $$
where
![]() $\{\alpha _1, \ldots , \alpha _s \}$
is a linear basis of
$\{\alpha _1, \ldots , \alpha _s \}$
is a linear basis of
![]() $H^2(X, {\mathbb C} )$
,
$H^2(X, {\mathbb C} )$
,
![]() $1 \le i, j \le s$
and
$1 \le i, j \le s$
and
![]() $1_X$
and x stand for the fundamental classes of X and a point in X, respectively. Let
$1_X$
and x stand for the fundamental classes of X and a point in X, respectively. Let
![]() $\langle \alpha , \beta \rangle = \alpha \cdot \beta $
denote the standard pairing for
$\langle \alpha , \beta \rangle = \alpha \cdot \beta $
denote the standard pairing for
![]() $\alpha , \beta \in H^*(X, {\mathbb C} )$
.
$\alpha , \beta \in H^*(X, {\mathbb C} )$
.
Theorem 1.1. Let X be a simply connected projective surface. Let
![]() ${\mathfrak B}^4$
stand for the linear basis of
${\mathfrak B}^4$
stand for the linear basis of
![]() $H^{4}( X^{[3]}, {\mathbb C} )$
from (1.1). Let
$H^{4}( X^{[3]}, {\mathbb C} )$
from (1.1). Let
![]() $d \ge 1$
and
$d \ge 1$
and
![]() $\omega _1, \omega _2, \omega _3 \in {\mathfrak B}^4$
. Then,
$\omega _1, \omega _2, \omega _3 \in {\mathfrak B}^4$
. Then,
if the unordered triple
![]() $(\omega _1, \omega _2, \omega _3)$
is not one of the following cases:
$(\omega _1, \omega _2, \omega _3)$
is not one of the following cases:
-
(i)
 $\Big ({\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle , {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _j)|0\rangle , {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _k)|0\rangle \Big )$
;
$\Big ({\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle , {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _j)|0\rangle , {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _k)|0\rangle \Big )$
; -
(ii)
 $\omega _1= \omega _2 = {\mathfrak a}_{-3}(1_X)|0\rangle $
, and
$\omega _1= \omega _2 = {\mathfrak a}_{-3}(1_X)|0\rangle $
, and
 $\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
or
$\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
or
 ${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
;
${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
; -
(iii)
 $\omega _1= \omega _2 = \omega _3 = {\mathfrak a}_{-3}(1_X)|0\rangle $
.
$\omega _1= \omega _2 = \omega _3 = {\mathfrak a}_{-3}(1_X)|0\rangle $
.
Moreover,
![]() $\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d \beta _3} = 8 \langle \alpha _i, \alpha _j \rangle \, \langle K_X, \alpha _k \rangle $
in case (i), and
$\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d \beta _3} = 8 \langle \alpha _i, \alpha _j \rangle \, \langle K_X, \alpha _k \rangle $
in case (i), and
in case (ii), where
![]() $c_{3, d}$
is the universal constant from (3.16). In case (iii),
$c_{3, d}$
is the universal constant from (3.16). In case (iii),
 $$ \begin{align*}\langle \omega_1, \omega_2, \omega_3 \rangle_{0, d \beta_3} = \bigg (-18 +5d c_{3,d} - \,\, 2 \sum_{i=1}^{d-1} i c_{3, i} + \frac{1}{3} \sum_{i=1}^{d-1} i c_{3, i} \,\, (d-i) c_{3, d-i} \bigg ) K_X^2. \end{align*} $$
$$ \begin{align*}\langle \omega_1, \omega_2, \omega_3 \rangle_{0, d \beta_3} = \bigg (-18 +5d c_{3,d} - \,\, 2 \sum_{i=1}^{d-1} i c_{3, i} + \frac{1}{3} \sum_{i=1}^{d-1} i c_{3, i} \,\, (d-i) c_{3, d-i} \bigg ) K_X^2. \end{align*} $$
The universal constants
![]() $c_{3, d}$
appearing in Theorem 1.1 come from (3.16) which governs the
$c_{3, d}$
appearing in Theorem 1.1 come from (3.16) which governs the
![]() $2$
-point genus-
$2$
-point genus-
![]() $0$
extremal Gromov-Witten invariants of
$0$
extremal Gromov-Witten invariants of
![]() $ X^{[n]}$
via (3.15). The assumption that X is simply connected is intended only to shorten the statement of Theorem 1.1. The proof of Theorem 1.1 uses geometric arguments involving applications of cosection localization theory [Reference Kiem and Li17, Reference Li and Li23] and algebraic manipulations involving the composition law of Gromov-Witten theory and the Heisenberg algebra of Grojnowski [Reference Grojnowski13] and Nakajima [Reference Nakajima34].
$ X^{[n]}$
via (3.15). The assumption that X is simply connected is intended only to shorten the statement of Theorem 1.1. The proof of Theorem 1.1 uses geometric arguments involving applications of cosection localization theory [Reference Kiem and Li17, Reference Li and Li23] and algebraic manipulations involving the composition law of Gromov-Witten theory and the Heisenberg algebra of Grojnowski [Reference Grojnowski13] and Nakajima [Reference Nakajima34].
As an application of Theorem 1.1, we obtain a direct proof of Ruan’s Cohomological Crepant Resolution Conjecture for the Hilbert-Chow morphism
![]() $\rho _3: X^{[3]} \to X^{(3)}$
(we remark that Ruan’s Cohomological Crepant Resolution Conjecture for the Hilbert-Chow morphism
$\rho _3: X^{[3]} \to X^{(3)}$
(we remark that Ruan’s Cohomological Crepant Resolution Conjecture for the Hilbert-Chow morphism
![]() $\rho _n: X^{[n]} \to X^{(n)}$
has been proved in [Reference Li and Qin28] for all
$\rho _n: X^{[n]} \to X^{(n)}$
has been proved in [Reference Li and Qin28] for all
![]() $n \ge 1$
via a representation theoretic approach).
$n \ge 1$
via a representation theoretic approach).
Corollary 1.2. Let X be a simply connected smooth projective surface. Then Ruan’s Cohomological Crepant Resolution Conjecture for the Hilbert-Chow morphism
![]() $\rho _3: X^{[3]} \to X^{(3)}$
holds (i.e., the Chen-Ruan cohomology ring of
$\rho _3: X^{[3]} \to X^{(3)}$
holds (i.e., the Chen-Ruan cohomology ring of
![]() $X^{(3)}$
is isomorphic to the quantum corrected cohomology ring of
$X^{(3)}$
is isomorphic to the quantum corrected cohomology ring of
![]() $ X^{[3]}$
).
$ X^{[3]}$
).
We refer to the proof of Corollary 4.11 (= Corollary 1.2) for the precise statement of Ruan’s Cohomological Crepant Resolution Conjecture for the Hilbert-Chow morphism
![]() $\rho _n: X^{[n]} \to X^{(n)}$
.
$\rho _n: X^{[n]} \to X^{(n)}$
.
Next, we consider the genus-
![]() $1$
extremal Gromov-Witten invariants of
$1$
extremal Gromov-Witten invariants of
![]() $ X^{[3]}$
. To put our result in perspective, note that all the genus-
$ X^{[3]}$
. To put our result in perspective, note that all the genus-
![]() $1$
extremal Gromov-Witten invariants of
$1$
extremal Gromov-Witten invariants of
![]() $ X^{[n]}$
with
$ X^{[n]}$
with
![]() $n \ge 2$
can be reduced to
$n \ge 2$
can be reduced to
![]() $\langle \rangle _{1, d \beta _n}$
. Let
$\langle \rangle _{1, d \beta _n}$
. Let
![]() $\chi (X)$
be the Euler characteristic of X. We propose the following conjecture for the invariants
$\chi (X)$
be the Euler characteristic of X. We propose the following conjecture for the invariants
![]() $\langle \rangle _{1, d \beta _n}$
.
$\langle \rangle _{1, d \beta _n}$
.
Conjecture 1.3. Let X be a smooth projective surface. Let
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $d \ge 1$
. Then there exists a universal polynomial
$d \ge 1$
. Then there exists a universal polynomial
![]() $p_{n, d}(s, t)$
, independent of X, in variables s and t such that
$p_{n, d}(s, t)$
, independent of X, in variables s and t such that
![]() $p_{n, d}(s^2, t) \cdot s^2$
has degree n in s and t, and
$p_{n, d}(s^2, t) \cdot s^2$
has degree n in s and t, and
Indeed, by [Reference Hu, Li and Qin15, Theorem 1.2], Conjecture 1.3 holds for
![]() $n=2$
:
$n=2$
:
(i.e.,
![]() $p_{2, d}(s, t)$
is the constant polynomial
$p_{2, d}(s, t)$
is the constant polynomial
![]() $1/(12d)$
). When
$1/(12d)$
). When
![]() $X = {\mathbb C}^2$
, [Reference Pandharipande and Tseng37, (0.8)] presents a formula for
$X = {\mathbb C}^2$
, [Reference Pandharipande and Tseng37, (0.8)] presents a formula for
![]() $\langle \rangle _{1, d\beta _2}$
in the equivariant setting. We prove that Conjecture 1.3 holds for
$\langle \rangle _{1, d\beta _2}$
in the equivariant setting. We prove that Conjecture 1.3 holds for
![]() $n=3$
and
$n=3$
and
![]() $d \ge 1$
as well (see Lemma 5.1):
$d \ge 1$
as well (see Lemma 5.1):
where
![]() $a_d$
and
$a_d$
and
![]() $b_d$
are universal constants depending only on d. A major part of our paper is to determine the universal constants
$b_d$
are universal constants depending only on d. A major part of our paper is to determine the universal constants
![]() $a_d$
and
$a_d$
and
![]() $b_d$
.
$b_d$
.
Theorem 1.4. Let X be a smooth projective surface. Let
![]() $d \ge 1$
, and let
$d \ge 1$
, and let
![]() $f_d$
be the constant defined in Lemma 5.10. Then,
$f_d$
be the constant defined in Lemma 5.10. Then,
![]() $\langle \rangle _{1, d\beta _3}$
is equal to
$\langle \rangle _{1, d\beta _3}$
is equal to
 $$ \begin{align*} \left(f_d - \left(\frac{-d^2+d+16}{96d} + \frac{d}{48} \sum_{d_1=1}^{d-1} \frac{1}{d_1} - \frac{1}{48} \sum_{\delta \vdash d} \frac{d^2 - d_1d_2}{d_1d_2 \cdot | \mathrm{Aut}(\delta)|} \right) + \frac{1}{12d} \cdot \chi(X) \right) \cdot K_X^2 \end{align*} $$
$$ \begin{align*} \left(f_d - \left(\frac{-d^2+d+16}{96d} + \frac{d}{48} \sum_{d_1=1}^{d-1} \frac{1}{d_1} - \frac{1}{48} \sum_{\delta \vdash d} \frac{d^2 - d_1d_2}{d_1d_2 \cdot | \mathrm{Aut}(\delta)|} \right) + \frac{1}{12d} \cdot \chi(X) \right) \cdot K_X^2 \end{align*} $$
where
![]() $\delta = (d_1, d_2) \vdash d$
denotes a length-
$\delta = (d_1, d_2) \vdash d$
denotes a length-
![]() $2$
partition of d.
$2$
partition of d.
Using the definition of
![]() $f_d$
in Lemma 5.10, one easily computes that
$f_d$
in Lemma 5.10, one easily computes that
![]() $f_1 = 7/24$
(see also Example 5.11). However, for a general
$f_1 = 7/24$
(see also Example 5.11). However, for a general
![]() $d \ge 1$
, it is unclear how to simplify the definition of
$d \ge 1$
, it is unclear how to simplify the definition of
![]() $f_d$
presented in Lemma 5.10. Note from (1.2) that to prove Theorem 1.4, it suffices to calculate
$f_d$
presented in Lemma 5.10. Note from (1.2) that to prove Theorem 1.4, it suffices to calculate
![]() $a_d$
and
$a_d$
and
![]() $b_d$
when X is a smooth projective toric surface. When X is a smooth projective toric surface, the torus
$b_d$
when X is a smooth projective toric surface. When X is a smooth projective toric surface, the torus
acts on X with finitely many fixed points
![]() $x_i, 1 \le i \le \chi (X)$
, which are the origins of the local affine charts
$x_i, 1 \le i \le \chi (X)$
, which are the origins of the local affine charts
![]() $U_i \cong {\mathbb C} ^2, 1 \le i \le \chi (X)$
. The induced
$U_i \cong {\mathbb C} ^2, 1 \le i \le \chi (X)$
. The induced
![]() ${\mathbb T}$
-action on
${\mathbb T}$
-action on
![]() $ X^{[3]}$
has finitely many fixed points and finitely many
$ X^{[3]}$
has finitely many fixed points and finitely many
![]() ${\mathbb T}$
-invariant curves contracted by the Hilbert-Chow morphism. We then utilize the virtual localization formulas of Gromov-Witten theory ([Reference Graber and Pandharipande12, Reference Kontsevich and Manin20] for the general setting and [Reference Edidin, Li and Qin8, Reference Liu and Sheshmani30] for our present setting of
${\mathbb T}$
-invariant curves contracted by the Hilbert-Chow morphism. We then utilize the virtual localization formulas of Gromov-Witten theory ([Reference Graber and Pandharipande12, Reference Kontsevich and Manin20] for the general setting and [Reference Edidin, Li and Qin8, Reference Liu and Sheshmani30] for our present setting of
![]() $ X^{[3]}$
). In the end, we reduce the computation of
$ X^{[3]}$
). In the end, we reduce the computation of
![]() $\langle \rangle _{1, d\beta _3}$
to a certain summation
$\langle \rangle _{1, d\beta _3}$
to a certain summation
![]() $\sum _{\Gamma \in {{\mathcal T}}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
over the local chart
$\sum _{\Gamma \in {{\mathcal T}}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
over the local chart
![]() $U_i$
, in terms of stable graphs
$U_i$
, in terms of stable graphs
![]() $\Gamma $
. To make our introduction here shorter, we refter to (5.13), (5.19) and (5.20) for notations and details. Next, we prove a reduction lemma (Lemma 5.4) which asserts that
$\Gamma $
. To make our introduction here shorter, we refter to (5.13), (5.19) and (5.20) for notations and details. Next, we prove a reduction lemma (Lemma 5.4) which asserts that
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
over the local chart
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
over the local chart
![]() $U_i \cong {\mathbb C} ^2$
is of the form
$U_i \cong {\mathbb C} ^2$
is of the form
 $$ \begin{align} a_d \cdot \frac{(w_i + z_i)^2}{w_i z_i} \end{align} $$
$$ \begin{align} a_d \cdot \frac{(w_i + z_i)^2}{w_i z_i} \end{align} $$
where
![]() $w_i$
and
$w_i$
and
![]() $z_i$
are the weights for the torus action on
$z_i$
are the weights for the torus action on
![]() $U_i$
, and
$U_i$
, and
![]() $a_d \in {\mathbb Q}$
is independent of i and X and depends only on d. This key reduction lemma implies that when evaluating
$a_d \in {\mathbb Q}$
is independent of i and X and depends only on d. This key reduction lemma implies that when evaluating
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
, we can ignore the stable graphs
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
, we can ignore the stable graphs
![]() $\Gamma \in {\mathcal S}_{d,i, i}$
with more than
$\Gamma \in {\mathcal S}_{d,i, i}$
with more than
![]() $2$
edges (see Lemma 5.6) and the stable graphs
$2$
edges (see Lemma 5.6) and the stable graphs
![]() $\Gamma \in {\mathcal T}_{d,i}$
with more than
$\Gamma \in {\mathcal T}_{d,i}$
with more than
![]() $5$
edges (see Lemma 5.9 for precise statements).
$5$
edges (see Lemma 5.9 for precise statements).
We remark that our reduction lemma (Lemma 5.4) may not be valid if one is only interested in calculating the analogous summation
![]() $\sum _{\Gamma \in {\mathcal T}_{d}}$
, in the equivariant setting, for the Hilbert scheme
$\sum _{\Gamma \in {\mathcal T}_{d}}$
, in the equivariant setting, for the Hilbert scheme
![]() $( {\mathbb C} ^2)^{[n]}$
. The reason is that in this new setting, the analogous summation
$( {\mathbb C} ^2)^{[n]}$
. The reason is that in this new setting, the analogous summation
![]() $\sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
does not arise, and thus
$\sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
does not arise, and thus
![]() $\sum _{\Gamma \in {\mathcal T}_{d}}$
cannot partially cancel with
$\sum _{\Gamma \in {\mathcal T}_{d}}$
cannot partially cancel with
![]() $\sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
to simplify the computations. We refer to the related discussions on [Reference Pandharipande and Tseng37, p. 8] following [Reference Pandharipande and Tseng37, Theorem 5].
$\sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
to simplify the computations. We refer to the related discussions on [Reference Pandharipande and Tseng37, p. 8] following [Reference Pandharipande and Tseng37, Theorem 5].
As for Conjecture 1.3 with
![]() $n> 3$
, there are two possible approaches. The first one is to use the standard decomposition
$n> 3$
, there are two possible approaches. The first one is to use the standard decomposition
![]() $\varphi = (\varphi _1, \ldots , \varphi _{\ell })$
from [Reference Li and Li23] (see (3.13)) associated to a genus-
$\varphi = (\varphi _1, \ldots , \varphi _{\ell })$
from [Reference Li and Li23] (see (3.13)) associated to a genus-
![]() $1$
extremal stable map
$1$
extremal stable map
![]() $\varphi : C \to X^{[n]}$
, as in the proof of Lemma 5.1 which is only for
$\varphi : C \to X^{[n]}$
, as in the proof of Lemma 5.1 which is only for
![]() $ X^{[3]}$
. Intuitively, the standard decomposition splits the Hilbert scheme
$ X^{[3]}$
. Intuitively, the standard decomposition splits the Hilbert scheme
![]() $ X^{[n]}$
and the extremal stable map
$ X^{[n]}$
and the extremal stable map
![]() $\varphi : C \to X^{[n]}$
according to the support of
$\varphi : C \to X^{[n]}$
according to the support of
![]() $\varphi (C)$
. However, complication arises when at least two of the maps
$\varphi (C)$
. However, complication arises when at least two of the maps
![]() $\varphi _1, \ldots , \varphi _{\ell }$
are not constant. The second approach to Conjecture 1.3 is to utilize the standard versus reduced method of Zinger, Vakil and Zinger, J. Li and Zinger, and Coates and Manolache (see [Reference Coates and Manolache6, Reference Li and Zinger26, Reference Vakil and Zinger40, Reference Zinger41, Reference Zinger42] and the references therein), which transfers the computation of the standard Gromov-Witten invariants
$\varphi _1, \ldots , \varphi _{\ell }$
are not constant. The second approach to Conjecture 1.3 is to utilize the standard versus reduced method of Zinger, Vakil and Zinger, J. Li and Zinger, and Coates and Manolache (see [Reference Coates and Manolache6, Reference Li and Zinger26, Reference Vakil and Zinger40, Reference Zinger41, Reference Zinger42] and the references therein), which transfers the computation of the standard Gromov-Witten invariants
![]() $\langle \rangle _{1, d\beta _n}$
to those of the reduced Gromov-Witten invariants. Roughly speaking, this approach splits the moduli space of genus-
$\langle \rangle _{1, d\beta _n}$
to those of the reduced Gromov-Witten invariants. Roughly speaking, this approach splits the moduli space of genus-
![]() $1$
extremal stable maps into the main component (which gives rise to the reduced Gromov-Witten invariants) and the ‘ghost’ components (which are related to the genus-
$1$
extremal stable maps into the main component (which gives rise to the reduced Gromov-Witten invariants) and the ‘ghost’ components (which are related to the genus-
![]() $0$
extremal Gromov-Witten invariants). A starting point might be to try the cases when both
$0$
extremal Gromov-Witten invariants). A starting point might be to try the cases when both
![]() $n> 3$
and
$n> 3$
and
![]() $d \ge 1$
are small.
$d \ge 1$
are small.
Finally, the paper is organized as follows. Section 2 contains a brief introduction to Gromov-Witten theory. Section 3 presents some background materials of the Hilbert schemes of points on surfaces, including the Heisenberg algebra of Grojnowski [Reference Grojnowski13] and Nakajima [Reference Nakajima34], Lehn’s boundary operator [Reference Lehn21], and their
![]() $1$
-point and
$1$
-point and
![]() $2$
-point genus-
$2$
-point genus-
![]() $0$
extremal Gromov-Witten invariants [Reference Li and Li23, Reference Li and Qin27]. Theorem 1.1 and Theorem 1.4 are proved in Section 4 and Section 5, respectively.
$0$
extremal Gromov-Witten invariants [Reference Li and Li23, Reference Li and Qin27]. Theorem 1.1 and Theorem 1.4 are proved in Section 4 and Section 5, respectively.
2 Stable maps and Gromov-Witten invariants
Let Y be a smooth projective variety. A k-pointed stable map to Y consists of a complete nodal curve D with k distinct ordered smooth points
![]() $p_1, \ldots , p_k$
and a morphism
$p_1, \ldots , p_k$
and a morphism
![]() $\mu : D \to Y$
such that the data
$\mu : D \to Y$
such that the data
![]() $(\mu , D, p_1, \ldots , p_k)$
has only finitely many automorphisms. In this case, the stable map is denoted by
$(\mu , D, p_1, \ldots , p_k)$
has only finitely many automorphisms. In this case, the stable map is denoted by
![]() $[\mu : (D; p_1, \ldots , p_k) \to Y]$
. For a fixed homology class
$[\mu : (D; p_1, \ldots , p_k) \to Y]$
. For a fixed homology class
![]() $\beta \in H_2(Y, \mathbb Z)$
, let
$\beta \in H_2(Y, \mathbb Z)$
, let
![]() $\overline {\mathfrak M}_{g, k}(Y, \beta )$
be the coarse moduli space parameterizing all the stable maps
$\overline {\mathfrak M}_{g, k}(Y, \beta )$
be the coarse moduli space parameterizing all the stable maps
![]() $[\mu : (D; p_1, \ldots , p_k) \to Y]$
such that
$[\mu : (D; p_1, \ldots , p_k) \to Y]$
such that
![]() $\mu _*[D] = \beta $
and the arithmetic genus of D is g. Then, we have the i-th evaluation map:
$\mu _*[D] = \beta $
and the arithmetic genus of D is g. Then, we have the i-th evaluation map:
defined by
![]() $\mathrm {ev}_i([\mu : (D; p_1, \ldots , p_k) \to Y]) = \mu (p_i) \in Y$
. It is known [Reference Behrend1, Reference Behrend and Fantechi2, Reference Fulton and Pandharipande11, Reference Li and Tian24, Reference Li and Tian25] that the coarse moduli space
$\mathrm {ev}_i([\mu : (D; p_1, \ldots , p_k) \to Y]) = \mu (p_i) \in Y$
. It is known [Reference Behrend1, Reference Behrend and Fantechi2, Reference Fulton and Pandharipande11, Reference Li and Tian24, Reference Li and Tian25] that the coarse moduli space
![]() $\overline {\mathfrak M}_{g, k}(Y, \beta )$
is projective and has a virtual fundamental class
$\overline {\mathfrak M}_{g, k}(Y, \beta )$
is projective and has a virtual fundamental class
![]() $[\overline {\mathfrak M}_{g, k}(Y, \beta )]^{\mathrm {vir}} \in A_d(\overline {\mathfrak M}_{g, k}(Y, \beta ))$
where
$[\overline {\mathfrak M}_{g, k}(Y, \beta )]^{\mathrm {vir}} \in A_d(\overline {\mathfrak M}_{g, k}(Y, \beta ))$
where
is the expected complex dimension of
![]() $\overline {\mathfrak M}_{g, k}(Y, \beta )$
, and
$\overline {\mathfrak M}_{g, k}(Y, \beta )$
, and
![]() $A_d(\overline {\mathfrak M}_{g, k}(Y, \beta ))$
is the Chow group of d-dimensional cycles in the moduli space
$A_d(\overline {\mathfrak M}_{g, k}(Y, \beta ))$
is the Chow group of d-dimensional cycles in the moduli space
![]() $\overline {\mathfrak M}_{g, k}(Y, \beta )$
.
$\overline {\mathfrak M}_{g, k}(Y, \beta )$
.
The Gromov-Witten invariants are defined by using the virtual fundamental class
![]() $[\overline {\mathfrak M}_{g, k}(Y, \beta )]^{\mathrm {vir}} $
. Recall that an element
$[\overline {\mathfrak M}_{g, k}(Y, \beta )]^{\mathrm {vir}} $
. Recall that an element
 $$ \begin{align*}\gamma \in H^*(Y, {\mathbb C}) \,\, {\buildrel\text{def}\over=} \,\, \bigoplus_{j=0}^{2 \dim_{{\mathbb C}}(Y)} H^j(Y, {\mathbb C}) \end{align*} $$
$$ \begin{align*}\gamma \in H^*(Y, {\mathbb C}) \,\, {\buildrel\text{def}\over=} \,\, \bigoplus_{j=0}^{2 \dim_{{\mathbb C}}(Y)} H^j(Y, {\mathbb C}) \end{align*} $$
is homogeneous if
![]() $\gamma \in H^j(Y, {\mathbb C})$
for some j; in this case, we take
$\gamma \in H^j(Y, {\mathbb C})$
for some j; in this case, we take
![]() $|\gamma | = j$
. Let
$|\gamma | = j$
. Let
![]() $\gamma _1, \ldots , \gamma _k \in H^*(Y, {\mathbb C})$
such that every
$\gamma _1, \ldots , \gamma _k \in H^*(Y, {\mathbb C})$
such that every
![]() $\gamma _i$
is homogeneous and
$\gamma _i$
is homogeneous and
 $$ \begin{align} \sum_{i=1}^k |\gamma_i| = 2d. \end{align} $$
$$ \begin{align} \sum_{i=1}^k |\gamma_i| = 2d. \end{align} $$
Then, we have the k-point Gromov-Witten invariant defined by:
 $$ \begin{align} \langle \gamma_1, \ldots, \gamma_k \rangle_{g, \beta} \,\, = \int_{[\overline {\mathfrak M}_{g, k}(Y, \beta)]^{\mathrm{vir}} } (\mathrm{ev}_1 \times \cdots \times \mathrm{ev}_k)^*(\gamma_1 \otimes \ldots \otimes \gamma_k). \end{align} $$
$$ \begin{align} \langle \gamma_1, \ldots, \gamma_k \rangle_{g, \beta} \,\, = \int_{[\overline {\mathfrak M}_{g, k}(Y, \beta)]^{\mathrm{vir}} } (\mathrm{ev}_1 \times \cdots \times \mathrm{ev}_k)^*(\gamma_1 \otimes \ldots \otimes \gamma_k). \end{align} $$
The Fundamental Class Axiom of the Gromov-Witten theory asserts that
if either
![]() $k+2g \ge 4$
or
$k+2g \ge 4$
or
![]() $\beta \ne 0$
and
$\beta \ne 0$
and
![]() $k \ge 1$
. The Divisor Axiom states that
$k \ge 1$
. The Divisor Axiom states that
 $$ \begin{align} \langle \gamma_1, \ldots, \gamma_{k-1}, \gamma_k \rangle_{g, \beta} \,\, = \int_{\beta} \gamma_k \cdot \langle \gamma_1, \ldots, \gamma_{k-1} \rangle_{g, \beta} \end{align} $$
$$ \begin{align} \langle \gamma_1, \ldots, \gamma_{k-1}, \gamma_k \rangle_{g, \beta} \,\, = \int_{\beta} \gamma_k \cdot \langle \gamma_1, \ldots, \gamma_{k-1} \rangle_{g, \beta} \end{align} $$
if
![]() $\gamma _k \in H^2(Y, {\mathbb C} )$
and if either
$\gamma _k \in H^2(Y, {\mathbb C} )$
and if either
![]() $k+2g \ge 4$
or
$k+2g \ge 4$
or
![]() $\beta \ne 0$
and
$\beta \ne 0$
and
![]() $k \ge 1$
. A special case of the Composition Law (see the formulas (3.3) and (3.6) in [Reference Kontsevich and Manin20]) states that
$k \ge 1$
. A special case of the Composition Law (see the formulas (3.3) and (3.6) in [Reference Kontsevich and Manin20]) states that
 $$ \begin{align} &\langle \gamma_1 \gamma_2, \gamma_3, \gamma_4 \rangle_{0, \beta} +\langle \gamma_1, \gamma_2, \gamma_3 \gamma_4 \rangle_{0, \beta} \nonumber \\ &\quad +\sum_{\beta_1 + \beta_2 = \beta, \, \beta_1, \beta_2 \ne 0} \,\, \sum_{a} \,\, \langle \gamma_1, \gamma_2, \Delta_a \rangle_{0, \beta_1} \cdot \langle \Delta^a, \gamma_3, \gamma_4 \rangle_{0, \beta_2} \nonumber \\ =&\langle \gamma_1 \gamma_3, \gamma_2, \gamma_4 \rangle_{0, \beta} +\langle \gamma_1, \gamma_3, \gamma_2 \gamma_4 \rangle_{0, \beta} \nonumber \\ &\quad +\sum_{\beta_1 + \beta_2 = \beta, \, \beta_1, \beta_2 \ne 0} \,\, \sum_{a} \,\, \langle \gamma_1, \gamma_3, \Delta_a \rangle_{0, \beta_1} \cdot \langle \Delta^a, \gamma_2, \gamma_4 \rangle_{0, \beta_2} \end{align} $$
$$ \begin{align} &\langle \gamma_1 \gamma_2, \gamma_3, \gamma_4 \rangle_{0, \beta} +\langle \gamma_1, \gamma_2, \gamma_3 \gamma_4 \rangle_{0, \beta} \nonumber \\ &\quad +\sum_{\beta_1 + \beta_2 = \beta, \, \beta_1, \beta_2 \ne 0} \,\, \sum_{a} \,\, \langle \gamma_1, \gamma_2, \Delta_a \rangle_{0, \beta_1} \cdot \langle \Delta^a, \gamma_3, \gamma_4 \rangle_{0, \beta_2} \nonumber \\ =&\langle \gamma_1 \gamma_3, \gamma_2, \gamma_4 \rangle_{0, \beta} +\langle \gamma_1, \gamma_3, \gamma_2 \gamma_4 \rangle_{0, \beta} \nonumber \\ &\quad +\sum_{\beta_1 + \beta_2 = \beta, \, \beta_1, \beta_2 \ne 0} \,\, \sum_{a} \,\, \langle \gamma_1, \gamma_3, \Delta_a \rangle_{0, \beta_1} \cdot \langle \Delta^a, \gamma_2, \gamma_4 \rangle_{0, \beta_2} \end{align} $$
where
![]() $\gamma _1, \gamma _2, \gamma _3, \gamma _4 \in H^*(Y, {\mathbb C} )$
are cohomology classes of even degrees,
$\gamma _1, \gamma _2, \gamma _3, \gamma _4 \in H^*(Y, {\mathbb C} )$
are cohomology classes of even degrees,
![]() $\{ \Delta _a \}_a$
denotes a homogeneous linear basis of
$\{ \Delta _a \}_a$
denotes a homogeneous linear basis of
![]() $H^*(Y, {\mathbb C} )$
and
$H^*(Y, {\mathbb C} )$
and
![]() $\{ \Delta ^a \}_a$
is the linear basis of
$\{ \Delta ^a \}_a$
is the linear basis of
![]() $H^*(Y, {\mathbb C} )$
dual to
$H^*(Y, {\mathbb C} )$
dual to
![]() $\{ \Delta _a \}_a$
with respect to the standard pairing on
$\{ \Delta _a \}_a$
with respect to the standard pairing on
![]() $H^*(Y, {\mathbb C} )$
(in the sense that
$H^*(Y, {\mathbb C} )$
(in the sense that
![]() $\langle \Delta _a, \Delta ^b \rangle = \delta _{a, b}$
for all a and b).
$\langle \Delta _a, \Delta ^b \rangle = \delta _{a, b}$
for all a and b).
3 Hilbert schemes of points on surfaces
In this section, we will review Hilbert schemes of points on surfaces, the Heisenberg algebra actions on the cohomology of these Hilbert schemes constructed by Grojnowski [Reference Grojnowski13] and Nakajima [Reference Nakajima34], and Lehn’s boundary operator [Reference Lehn21]. Moreover, we will recall the
![]() $1$
-point and
$1$
-point and
![]() $2$
-point genus-
$2$
-point genus-
![]() $0$
extremal Gromov-Witten invariants of these Hilbert schemes from [Reference Li and Li23, Reference Li and Qin27].
$0$
extremal Gromov-Witten invariants of these Hilbert schemes from [Reference Li and Li23, Reference Li and Qin27].
3.1 Hilbert schemes of points and Heisenberg algebra actions
Let X be a smooth projective complex surface, and let
![]() $ X^{[n]}$
be the Hilbert scheme of points in X. An element in
$ X^{[n]}$
be the Hilbert scheme of points in X. An element in
![]() $ X^{[n]}$
is represented by a length-
$ X^{[n]}$
is represented by a length-
![]() $n \ 0$
-dimensional closed subscheme
$n \ 0$
-dimensional closed subscheme
![]() $\xi $
of X. For
$\xi $
of X. For
![]() $\xi \in X^{[n]}$
, let
$\xi \in X^{[n]}$
, let
![]() $I_{\xi }$
and
$I_{\xi }$
and
![]() $\mathcal O_{\xi }$
be the corresponding sheaf of ideals and structure sheaf, respectively. It is known [Reference Fogarty10, Reference Iarrobino16] that
$\mathcal O_{\xi }$
be the corresponding sheaf of ideals and structure sheaf, respectively. It is known [Reference Fogarty10, Reference Iarrobino16] that
![]() $ X^{[n]}$
is a smooth irreducible variety of dimension
$ X^{[n]}$
is a smooth irreducible variety of dimension
![]() $2n$
. The boundary of
$2n$
. The boundary of
![]() $ X^{[n]}$
is defined to be
$ X^{[n]}$
is defined to be
For fixed distinct points
![]() $x_1, \ldots , x_{n-1} \in X$
, define the curve
$x_1, \ldots , x_{n-1} \in X$
, define the curve
We also regard
![]() $\beta _n$
as a homology class in
$\beta _n$
as a homology class in
![]() $H_2( X^{[n]}, \mathbb Z )$
. For a subset
$H_2( X^{[n]}, \mathbb Z )$
. For a subset
![]() $Y \subset X$
, define
$Y \subset X$
, define
Sending an element in
![]() $ X^{[n]}$
to its support (counting with multiplicities) in the n-th symmetric product
$ X^{[n]}$
to its support (counting with multiplicities) in the n-th symmetric product
![]() $X^{(n)}$
of X, we obtain the Hilbert-Chow morphism
$X^{(n)}$
of X, we obtain the Hilbert-Chow morphism
which is a crepant resolution of singularities. A curve in
![]() $ X^{[n]}$
is contracted by
$ X^{[n]}$
is contracted by
![]() $\rho _n$
if and only if it is homologous to
$\rho _n$
if and only if it is homologous to
![]() $d\beta _n$
for some positive integer d.
$d\beta _n$
for some positive integer d.
Grojnowski [Reference Grojnowski13] and Nakajima [Reference Nakajima34] geometrically constructed a Heisenberg algebra action on the cohomology of the Hilbert schemes
![]() $ X^{[n]}$
. Denote the Heisenberg operators by
$ X^{[n]}$
. Denote the Heisenberg operators by
![]() $ {\mathfrak a}_m(\alpha )$
where
$ {\mathfrak a}_m(\alpha )$
where
![]() $m \in \mathbb Z $
and
$m \in \mathbb Z $
and
![]() $\alpha \in H^*(X, {\mathbb C} )$
. Put
$\alpha \in H^*(X, {\mathbb C} )$
. Put
 $$ \begin{align*}{\mathbb H}_X = \bigoplus_{n=0}^{+ \infty} H^*( X^{[n]}, {\mathbb C} ). \end{align*} $$
$$ \begin{align*}{\mathbb H}_X = \bigoplus_{n=0}^{+ \infty} H^*( X^{[n]}, {\mathbb C} ). \end{align*} $$
The operators
![]() ${\mathfrak a}_m(\alpha ) \in \mathrm {End}(\mathbb H_X)$
satisfy the following commutation relation:
${\mathfrak a}_m(\alpha ) \in \mathrm {End}(\mathbb H_X)$
satisfy the following commutation relation:
where we have used
![]() $\delta _{m,-n}$
to denote
$\delta _{m,-n}$
to denote
![]() $1$
if
$1$
if
![]() $m=-n$
and
$m=-n$
and
![]() $0$
otherwise. The space
$0$
otherwise. The space
![]() ${\mathbb H}_X$
is an irreducible representation of the Heisenberg algebra generated by the operators
${\mathbb H}_X$
is an irreducible representation of the Heisenberg algebra generated by the operators
![]() $ {\mathfrak a}_m(\alpha )$
with the highest weight vector being
$ {\mathfrak a}_m(\alpha )$
with the highest weight vector being
![]() $|0\rangle = 1 \in H^*(X^{[0]}, {\mathbb C} ) = {\mathbb C} $
. In particular,
$|0\rangle = 1 \in H^*(X^{[0]}, {\mathbb C} ) = {\mathbb C} $
. In particular,
![]() $H^*( X^{[n]}, {\mathbb C} )$
is the linear span of Heisenberg monomial classes
$H^*( X^{[n]}, {\mathbb C} )$
is the linear span of Heisenberg monomial classes
where
![]() $k \ge 0, n_1, \ldots , n_k> 0$
and
$k \ge 0, n_1, \ldots , n_k> 0$
and
![]() $\alpha _1, \ldots , \alpha _k \in H^*(X, {\mathbb C} )$
.
$\alpha _1, \ldots , \alpha _k \in H^*(X, {\mathbb C} )$
.
Fix closed real cycles
![]() $X_1, \ldots , X_k$
of the surface X in general position in the sense that any subset of the
$X_1, \ldots , X_k$
of the surface X in general position in the sense that any subset of the
![]() $X_i$
’s meet transversally in the expected dimension. Define
$X_i$
’s meet transversally in the expected dimension. Define
to be the closed subset consisting of all
![]() $\xi \in X^{[n]}$
which admit filtrations
$\xi \in X^{[n]}$
which admit filtrations
with
![]() $\ell (\xi _i) = \ell (\xi _{i-1}) + n_i$
and
$\ell (\xi _i) = \ell (\xi _{i-1}) + n_i$
and
for
![]() $1 \le i \le k$
. Let
$1 \le i \le k$
. Let
![]() $ W(n_1, X_1; \ldots; n_k, X_k)^0 \subset W(n_1, X_1; \ldots; n_k, X_k)$
be the open subset consisting of all
$ W(n_1, X_1; \ldots; n_k, X_k)^0 \subset W(n_1, X_1; \ldots; n_k, X_k)$
be the open subset consisting of all
![]() $\xi \in W(n_1, X_1; \ldots; n_k, X_k)$
such that the points
$\xi \in W(n_1, X_1; \ldots; n_k, X_k)$
such that the points
![]() $x_1, \ldots , x_k$
in (3.4) are distinct.
$x_1, \ldots , x_k$
in (3.4) are distinct.
Lemma 3.1 [Reference Qin38, Proposition 3.16].
Let
![]() $\ell , k \ge 0$
,
$\ell , k \ge 0$
,
![]() $s_i \ge 0$
(
$s_i \ge 0$
(
![]() $1 \le i \le \ell $
),
$1 \le i \le \ell $
),
![]() $n_i> 0$
(
$n_i> 0$
(
![]() $1 \le i \le k$
). Let
$1 \le i \le k$
). Let
 $\alpha _1, \ldots , \alpha _k \in \displaystyle {\bigoplus _{i=1}^4 H^i(X, {\mathbb C} )}$
be represented by the cycles
$\alpha _1, \ldots , \alpha _k \in \displaystyle {\bigoplus _{i=1}^4 H^i(X, {\mathbb C} )}$
be represented by the cycles
![]() $X_1, \ldots , X_k \subset X$
, respectively, such that
$X_1, \ldots , X_k \subset X$
, respectively, such that
![]() $X_1, \ldots , X_k$
are in general position. Then,
$X_1, \ldots , X_k$
are in general position. Then,
 $$ \begin{align*} \displaystyle{\left ( \prod_{i=1}^{\ell} \frac{{\mathfrak a}_{-i}(1_X)^{s_i}}{s_i!} \right ) \left ( \prod_{i=1}^k {\mathfrak a}_{-n_i}(\alpha_i) \right ) |0\rangle} \end{align*} $$
$$ \begin{align*} \displaystyle{\left ( \prod_{i=1}^{\ell} \frac{{\mathfrak a}_{-i}(1_X)^{s_i}}{s_i!} \right ) \left ( \prod_{i=1}^k {\mathfrak a}_{-n_i}(\alpha_i) \right ) |0\rangle} \end{align*} $$
is represented by the closure of
 $$ \begin{align} W(\underbrace{1, X; \ldots; 1, X}_{s_1 \,\,\, \mathrm{times}}; \ldots; \underbrace{\ell, X; \ldots; \ell, X}_{s_{\ell} \,\,\, \mathrm{times}}; n_1, X_1; \ldots; n_k, X_k)^0. \end{align} $$
$$ \begin{align} W(\underbrace{1, X; \ldots; 1, X}_{s_1 \,\,\, \mathrm{times}}; \ldots; \underbrace{\ell, X; \ldots; \ell, X}_{s_{\ell} \,\,\, \mathrm{times}}; n_1, X_1; \ldots; n_k, X_k)^0. \end{align} $$
It follows that
![]() $1_{ X^{[n]}} = 1/n! \cdot {\mathfrak a}_{-1}(1_X)^n|0\rangle \in H^0( X^{[n]}, {\mathbb C} )$
, where
$1_{ X^{[n]}} = 1/n! \cdot {\mathfrak a}_{-1}(1_X)^n|0\rangle \in H^0( X^{[n]}, {\mathbb C} )$
, where
![]() $1_X$
denotes the fundamental cohomology class of the surface X, and
$1_X$
denotes the fundamental cohomology class of the surface X, and
where x denotes the fundamental cohomology class of a point
![]() $x \in X$
. For simplicity, we do not distinguish a homology class and its Poincaré dual.
$x \in X$
. For simplicity, we do not distinguish a homology class and its Poincaré dual.
Let
![]() $\tau _2: X \to X^2$
be the diagonal embedding and
$\tau _2: X \to X^2$
be the diagonal embedding and
![]() $\tau _{2*}: H^*(X, {\mathbb C} ) \to H^*(X^2, {\mathbb C} )$
be the induced map. For
$\tau _{2*}: H^*(X, {\mathbb C} ) \to H^*(X^2, {\mathbb C} )$
be the induced map. For
![]() $\alpha \in H^*(X, {\mathbb C} )$
and
$\alpha \in H^*(X, {\mathbb C} )$
and
![]() $m_1, m_2 \in \mathbb Z $
, define
$m_1, m_2 \in \mathbb Z $
, define
if
![]() $\tau _{2*}\alpha = \sum _i \alpha _{i,1} \otimes \alpha _{i,2}$
under the Künneth decomposition of
$\tau _{2*}\alpha = \sum _i \alpha _{i,1} \otimes \alpha _{i,2}$
under the Künneth decomposition of
![]() $H^*(X^2, {\mathbb C} )$
. For
$H^*(X^2, {\mathbb C} )$
. For
![]() $n \in \mathbb Z $
and
$n \in \mathbb Z $
and
![]() $\alpha \in H^*(X, {\mathbb C} )$
, define the linear operator
$\alpha \in H^*(X, {\mathbb C} )$
, define the linear operator
![]() $\mathfrak L_n(\alpha ) \in \mathrm {End}(\mathbb H_X)$
by
$\mathfrak L_n(\alpha ) \in \mathrm {End}(\mathbb H_X)$
by
 $$ \begin{align} &\mathfrak L_n = \left\{ {\displaystyle} \begin{array}{ll} -\dfrac{1}{2} \cdot \displaystyle{\sum_{m \in \mathbb Z }} {\mathfrak a}_m {\mathfrak a}_{n-m} \tau_{2*}, & \text{ if } n \ne 0, \\ \displaystyle{-\sum_{m> 0}} {\mathfrak a}_{-m} {\mathfrak a}_m \tau_{2*}, &\text{ if } n = 0. \end{array} \right. \end{align} $$
$$ \begin{align} &\mathfrak L_n = \left\{ {\displaystyle} \begin{array}{ll} -\dfrac{1}{2} \cdot \displaystyle{\sum_{m \in \mathbb Z }} {\mathfrak a}_m {\mathfrak a}_{n-m} \tau_{2*}, & \text{ if } n \ne 0, \\ \displaystyle{-\sum_{m> 0}} {\mathfrak a}_{-m} {\mathfrak a}_m \tau_{2*}, &\text{ if } n = 0. \end{array} \right. \end{align} $$
We have the commutation relation
Lehn [Reference Lehn21] defined the boundary operator
![]() $ \mathfrak d \in \mathrm {End}(\mathbb H_X)$
by putting
$ \mathfrak d \in \mathrm {End}(\mathbb H_X)$
by putting
for
![]() $\gamma _n \in H^*( X^{[n]}, {\mathbb C} )$
. For a linear operator
$\gamma _n \in H^*( X^{[n]}, {\mathbb C} )$
. For a linear operator
![]() $\mathfrak f \in \mathrm {End}(\mathbb H_X)$
, define its derivative
$\mathfrak f \in \mathrm {End}(\mathbb H_X)$
, define its derivative
![]() $\mathfrak f'$
by
$\mathfrak f'$
by
A fundamental result proved in [Reference Lehn21] states that
3.2
 $1$
-point and
$1$
-point and
 $2$
-point genus-
$2$
-point genus-
 $0$
extremal Gromov-Witten invariants
$0$
extremal Gromov-Witten invariants
In this subsection, let X be a simply connected smooth projective surface. We start with the
![]() $1$
-point genus-
$1$
-point genus-
![]() $0$
extremal Gromov-Witten invariants of
$0$
extremal Gromov-Witten invariants of
![]() $ X^{[n]}$
.
$ X^{[n]}$
.
Lemma 3.2 [Reference Li and Qin27, Theorem 3.5].
Let X be a simply connected smooth projective surface. Let
![]() $n \ge 2$
,
$n \ge 2$
,
![]() $d\ge 1$
and
$d\ge 1$
and
![]() $\gamma \in H^*( X^{[n]}, {\mathbb C} )$
be a Heisenberg monomial class (3.3). Then,
$\gamma \in H^*( X^{[n]}, {\mathbb C} )$
be a Heisenberg monomial class (3.3). Then,
![]() $\langle \gamma \rangle _{0, d\beta _n}=0$
unless
$\langle \gamma \rangle _{0, d\beta _n}=0$
unless
![]() $\gamma = {\mathfrak a}_{-2}(\alpha ){\mathfrak a}_{-1}(x)^{n-2}|0\rangle $
for some
$\gamma = {\mathfrak a}_{-2}(\alpha ){\mathfrak a}_{-1}(x)^{n-2}|0\rangle $
for some
![]() $\alpha \in H^2(X, {\mathbb C} )$
. Moreover, if
$\alpha \in H^2(X, {\mathbb C} )$
. Moreover, if
![]() $\gamma = {\mathfrak a}_{-2}(\alpha ){\mathfrak a}_{-1}(x)^{n-2}|0\rangle $
for some
$\gamma = {\mathfrak a}_{-2}(\alpha ){\mathfrak a}_{-1}(x)^{n-2}|0\rangle $
for some
![]() $\alpha \in H^2(X, {\mathbb C} )$
, then
$\alpha \in H^2(X, {\mathbb C} )$
, then
The
![]() $2$
-point genus-
$2$
-point genus-
![]() $0$
extremal Gromov-Witten invariants of
$0$
extremal Gromov-Witten invariants of
![]() $ X^{[n]}$
have been studied in [Reference Li and Li23] via cosection localizations [Reference Kiem and Li17]. By abusing notations, denote
$ X^{[n]}$
have been studied in [Reference Li and Li23] via cosection localizations [Reference Kiem and Li17]. By abusing notations, denote
by
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $\varphi _*[C] = d \beta _n$
, the composition
$\varphi _*[C] = d \beta _n$
, the composition
![]() $\rho _n \circ \varphi $
is a constant map. Let
$\rho _n \circ \varphi $
is a constant map. Let
be the induced map. If
![]() $\mathrm {Spt}(\varphi ) = \sum _{i=1}^{\ell } n_i x_i \in X^{(n)}$
where
$\mathrm {Spt}(\varphi ) = \sum _{i=1}^{\ell } n_i x_i \in X^{(n)}$
where
![]() $x_1, \ldots , x_{\ell }$
are distinct, then the morphism
$x_1, \ldots , x_{\ell }$
are distinct, then the morphism
![]() $\varphi $
factors through the product of punctual Hilbert schemes:
$\varphi $
factors through the product of punctual Hilbert schemes:
 $$ \begin{align} \varphi = (\varphi_1, \ldots, \varphi_{\ell}): C \to \prod_{i=1}^{\ell} M_{n_i}(x_i) \subset X^{[n]} \end{align} $$
$$ \begin{align} \varphi = (\varphi_1, \ldots, \varphi_{\ell}): C \to \prod_{i=1}^{\ell} M_{n_i}(x_i) \subset X^{[n]} \end{align} $$
where
![]() $\varphi _i$
is a morphism from C to
$\varphi _i$
is a morphism from C to
![]() $M_{n_i}(x_i)$
. The collection
$M_{n_i}(x_i)$
. The collection
is defined to be the standard decomposition of
![]() $\varphi $
, and the point
$\varphi $
, and the point
![]() $x_i$
is called the support of
$x_i$
is called the support of
![]() $\varphi _i$
. Note that the collection
$\varphi _i$
. Note that the collection
![]() $\{\varphi _1, \ldots , \varphi _{\ell } \}$
is unique up to the ordering of the
$\{\varphi _1, \ldots , \varphi _{\ell } \}$
is unique up to the ordering of the
![]() $\varphi _i$
’s. Fix a meromorphic section
$\varphi _i$
’s. Fix a meromorphic section
![]() $\theta $
of
$\theta $
of
![]() $\mathcal O_X(K_X)$
. Let
$\mathcal O_X(K_X)$
. Let
![]() $D_0$
and
$D_0$
and
![]() $D_{\infty }$
be the vanishing and pole divisors of
$D_{\infty }$
be the vanishing and pole divisors of
![]() $\theta $
, respectively.
$\theta $
, respectively.
Lemma 3.3 [Reference Li and Li23, Proposition 3.3].
Let
![]() $\Lambda _{\theta } \subset \overline {\mathfrak M}_{g, k}( X^{[n]}, d \beta _n)$
be the subset consisting of the stable maps
$\Lambda _{\theta } \subset \overline {\mathfrak M}_{g, k}( X^{[n]}, d \beta _n)$
be the subset consisting of the stable maps
![]() $\varphi = (\varphi _1, \ldots , \varphi _{\ell }) \in \overline {\mathfrak M}_{g, k}( X^{[n]}, d \beta _n)$
such that for each i, either
$\varphi = (\varphi _1, \ldots , \varphi _{\ell }) \in \overline {\mathfrak M}_{g, k}( X^{[n]}, d \beta _n)$
such that for each i, either
![]() $\varphi _i$
is a constant map or the support
$\varphi _i$
is a constant map or the support
![]() $x_i = \mathrm {Spt}(\varphi _i)$
lies in
$x_i = \mathrm {Spt}(\varphi _i)$
lies in
![]() $D_0 \cup D_{\infty }$
. Then the virtual fundamental class
$D_0 \cup D_{\infty }$
. Then the virtual fundamental class
![]() $[\overline {\mathfrak M}_{g, k}( X^{[n]}, d \beta _n)]^{\mathrm {vir}} $
is supported in
$[\overline {\mathfrak M}_{g, k}( X^{[n]}, d \beta _n)]^{\mathrm {vir}} $
is supported in
![]() $\Lambda _{\theta }$
.
$\Lambda _{\theta }$
.
Let
![]() $(\mu ^1, \mu ^2, \mu ^3)$
denote a triple of partitions with
$(\mu ^1, \mu ^2, \mu ^3)$
denote a triple of partitions with
![]() $|\mu ^1| + |\mu ^2| + |\mu ^3| = n$
. Let
$|\mu ^1| + |\mu ^2| + |\mu ^3| = n$
. Let
![]() $r = \ell (\mu ^1)$
,
$r = \ell (\mu ^1)$
,
![]() $s = \ell (\mu ^2)$
and
$s = \ell (\mu ^2)$
and
![]() $t = \ell (\mu ^3)$
be the lengths. For cohomology classes
$t = \ell (\mu ^3)$
be the lengths. For cohomology classes
![]() $\mathbf {c}_1, \ldots , \mathbf {c}_s \in H^2(X, {\mathbb C} )$
, define the class
$\mathbf {c}_1, \ldots , \mathbf {c}_s \in H^2(X, {\mathbb C} )$
, define the class
![]() $A_{\mathbf {c}}^{\mu } \in H^*( X^{[n]}, {\mathbb C} )$
by
$A_{\mathbf {c}}^{\mu } \in H^*( X^{[n]}, {\mathbb C} )$
by
 $$ \begin{align} A_{\mathbf{c}}^{\mu} = \prod_{i=1}^r {\mathfrak a}_{-\mu_i^1}(x) \cdot \prod_{j=1}^s {\mathfrak a}_{-\mu_j^2}(\mathbf{c}_j) \cdot \prod_{k=1}^t {\mathfrak a}_{-\mu_k^3}(1_X) |0\rangle. \end{align} $$
$$ \begin{align} A_{\mathbf{c}}^{\mu} = \prod_{i=1}^r {\mathfrak a}_{-\mu_i^1}(x) \cdot \prod_{j=1}^s {\mathfrak a}_{-\mu_j^2}(\mathbf{c}_j) \cdot \prod_{k=1}^t {\mathfrak a}_{-\mu_k^3}(1_X) |0\rangle. \end{align} $$
For a part
![]() $\mu _j^2$
of
$\mu _j^2$
of
![]() $\mu ^2$
, let
$\mu ^2$
, let
![]() $A_{\mathbf {c}}^{\mu - \mu _j^2}$
be the cohomology class in
$A_{\mathbf {c}}^{\mu - \mu _j^2}$
be the cohomology class in
![]() $H^*(X^{[n - \mu _j^2]}, {\mathbb C} )$
obtained from
$H^*(X^{[n - \mu _j^2]}, {\mathbb C} )$
obtained from
![]() $A_{\mathbf {c}}^{\mu }$
with the factor
$A_{\mathbf {c}}^{\mu }$
with the factor
![]() ${\mathfrak a}_{-\mu _j^2}(\mathbf {c}_j)$
deleted. We similarly define
${\mathfrak a}_{-\mu _j^2}(\mathbf {c}_j)$
deleted. We similarly define
![]() $A_{\mathbf {c}}^{\mu - \mu _i^3}$
.
$A_{\mathbf {c}}^{\mu - \mu _i^3}$
.
The following lemma summarizes some of the main results in [Reference Li and Li23] and computes the
![]() $2$
-point genus-
$2$
-point genus-
![]() $0$
extremal Gromov-Witten invariants of
$0$
extremal Gromov-Witten invariants of
![]() $ X^{[n]}$
.
$ X^{[n]}$
.
Lemma 3.4 [Reference Li and Li23].
Let
![]() $d \ge 1$
. Assume that
$d \ge 1$
. Assume that
![]() $\big \langle A_{\mathbf {e}}^{\lambda }, A_{\mathbf {c}}^{\mu } \big \rangle _{0, d \beta _n} \ne 0$
. Then,
$\big \langle A_{\mathbf {e}}^{\lambda }, A_{\mathbf {c}}^{\mu } \big \rangle _{0, d \beta _n} \ne 0$
. Then,
 $$ \begin{align*} \ell(\lambda^3) &= \ell(\mu^1) + \delta \\ \ell(\mu^3) &= \ell(\lambda^1) + (1-\delta) \end{align*} $$
$$ \begin{align*} \ell(\lambda^3) &= \ell(\mu^1) + \delta \\ \ell(\mu^3) &= \ell(\lambda^1) + (1-\delta) \end{align*} $$
where
![]() $\delta =0$
or
$\delta =0$
or
![]() $1$
. If
$1$
. If
![]() $\delta =0$
, then
$\delta =0$
, then
![]() $\lambda ^3 = \mu ^1$
, and there exists an integer
$\lambda ^3 = \mu ^1$
, and there exists an integer
![]() $\ell = \mu _i^3 = \lambda _j^2$
for some i and j such that the partition
$\ell = \mu _i^3 = \lambda _j^2$
for some i and j such that the partition
![]() $\lambda ^1$
is obtained from
$\lambda ^1$
is obtained from
![]() $\mu ^3$
with
$\mu ^3$
with
![]() $\ell $
deleted, and the partition
$\ell $
deleted, and the partition
![]() $\mu ^2$
is obtained from
$\mu ^2$
is obtained from
![]() $\lambda ^2$
with
$\lambda ^2$
with
![]() $\ell $
deleted; moreover,
$\ell $
deleted; moreover,
 $$ \begin{align} \big \langle A_{\mathbf{e}}^{\lambda}, A_{\mathbf{c}}^{\mu} \big \rangle_{0, d \beta_n} = \sum_{\ell = \mu_i^3 = \lambda_j^2} \big \langle A_{\mathbf{e}}^{\lambda - \lambda_j^2}, A_{\mathbf{c}}^{\mu - \mu_i^3} \big \rangle \cdot \langle K_X, \mathbf{e}_j \rangle \cdot c_{\ell, d} \end{align} $$
$$ \begin{align} \big \langle A_{\mathbf{e}}^{\lambda}, A_{\mathbf{c}}^{\mu} \big \rangle_{0, d \beta_n} = \sum_{\ell = \mu_i^3 = \lambda_j^2} \big \langle A_{\mathbf{e}}^{\lambda - \lambda_j^2}, A_{\mathbf{c}}^{\mu - \mu_i^3} \big \rangle \cdot \langle K_X, \mathbf{e}_j \rangle \cdot c_{\ell, d} \end{align} $$
where the universal constant
![]() $c_{\ell , d}$
is defined by the equation
$c_{\ell , d}$
is defined by the equation
 $$ \begin{align} \sum_{d \ge 1} d \, c_{\ell, d} \, q^d = (-1)^{\ell} \ell^2 \left ( \frac{\ell (-q)^{\ell}}{(-q)^{\ell}-1} - \frac{q}{1+q} \right ). \end{align} $$
$$ \begin{align} \sum_{d \ge 1} d \, c_{\ell, d} \, q^d = (-1)^{\ell} \ell^2 \left ( \frac{\ell (-q)^{\ell}}{(-q)^{\ell}-1} - \frac{q}{1+q} \right ). \end{align} $$
4 Genus-
 $0$
extremal Gromov-Witten invariants of
$0$
extremal Gromov-Witten invariants of
 $ X^{[3]}$
$ X^{[3]}$
In this section, X is a simply connected smooth projective surface. We will study the genus-
![]() $0$
extremal Gromov-Witten invariants
$0$
extremal Gromov-Witten invariants
![]() $\langle \omega _1, \ldots , \omega _k \rangle _{0, d\beta _3}$
of
$\langle \omega _1, \ldots , \omega _k \rangle _{0, d\beta _3}$
of
![]() $ X^{[3]}$
. Put
$ X^{[3]}$
. Put
for simplicity. In view of the Fundamental Class Axiom (2.5), the Divisor Axiom (2.6) and the dimension constraint (2.3), the genus-
![]() $0$
extremal Gromov-Witten invariants of
$0$
extremal Gromov-Witten invariants of
![]() $ X^{[3]}$
are reduced to the invariants
$ X^{[3]}$
are reduced to the invariants
with
![]() $\omega _1, \omega _2, \omega _3 \in H^4( X^{[3]}, {\mathbb C} )$
. The invariants
$\omega _1, \omega _2, \omega _3 \in H^4( X^{[3]}, {\mathbb C} )$
. The invariants
![]() $\langle \tilde \omega _1 \rangle _{0, d}$
and
$\langle \tilde \omega _1 \rangle _{0, d}$
and
![]() $\langle \tilde \omega _1, \tilde \omega _2 \rangle _{0, d}$
have been dealt with by Lemma 3.2 and Lemma 3.4, respectively. Therefore, it remains to calculate the
$\langle \tilde \omega _1, \tilde \omega _2 \rangle _{0, d}$
have been dealt with by Lemma 3.2 and Lemma 3.4, respectively. Therefore, it remains to calculate the
![]() $3$
-point invariants
$3$
-point invariants
![]() $\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
with
$\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
with
![]() $\omega _1, \omega _2, \omega _3 \in H^4( X^{[3]}, {\mathbb C} )$
.
$\omega _1, \omega _2, \omega _3 \in H^4( X^{[3]}, {\mathbb C} )$
.
To begin with, we fix a linear basis of
![]() $H^*( X^{[3]}, {\mathbb C} )$
which allows us to apply the composition law (2.7). Let
$H^*( X^{[3]}, {\mathbb C} )$
which allows us to apply the composition law (2.7). Let
![]() $\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
$\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
![]() $H^2(X, {\mathbb C} )$
. By (3.3), a linear basis
$H^2(X, {\mathbb C} )$
. By (3.3), a linear basis
![]() ${\mathfrak B}^2$
of
${\mathfrak B}^2$
of
![]() $H^2( X^{[3]}, {\mathbb C} )$
consists of the cohomology classes
$H^2( X^{[3]}, {\mathbb C} )$
consists of the cohomology classes
where
![]() $1 \le i \le s$
, a linear basis
$1 \le i \le s$
, a linear basis
![]() ${\mathfrak B}^{10}$
of
${\mathfrak B}^{10}$
of
![]() $H^{10}( X^{[3]}, {\mathbb C} )$
consists of
$H^{10}( X^{[3]}, {\mathbb C} )$
consists of
where
![]() $1 \le i \le s$
, and a linear basis
$1 \le i \le s$
, and a linear basis
![]() ${\mathfrak B}^8$
of
${\mathfrak B}^8$
of
![]() $H^{8}( X^{[3]}, {\mathbb C} )$
consists of the classes
$H^{8}( X^{[3]}, {\mathbb C} )$
consists of the classes
 $$ \begin{align} &{\mathfrak a}_{-1}(1_X){\mathfrak a}_{-1}(x)^2 |0\rangle, \quad {\mathfrak a}_{-3}(x)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-2}(x)|0\rangle, \nonumber \\ &\qquad {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(x)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(x)|0\rangle \end{align} $$
$$ \begin{align} &{\mathfrak a}_{-1}(1_X){\mathfrak a}_{-1}(x)^2 |0\rangle, \quad {\mathfrak a}_{-3}(x)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-2}(x)|0\rangle, \nonumber \\ &\qquad {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(x)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(x)|0\rangle \end{align} $$
where
![]() $1 \le i \le j \le s$
. A linear basis
$1 \le i \le j \le s$
. A linear basis
![]() ${\mathfrak B}^4$
of
${\mathfrak B}^4$
of
![]() $H^{4}( X^{[3]}, {\mathbb C} )$
consists of the classes
$H^{4}( X^{[3]}, {\mathbb C} )$
consists of the classes
 $$ \begin{align} &{\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x) |0\rangle, \quad {\mathfrak a}_{-3}(1_X)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-2}(1_X)|0\rangle, \nonumber \\ &\qquad {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(1_X)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(1_X)|0\rangle \end{align} $$
$$ \begin{align} &{\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x) |0\rangle, \quad {\mathfrak a}_{-3}(1_X)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-2}(1_X)|0\rangle, \nonumber \\ &\qquad {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(1_X)|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(1_X)|0\rangle \end{align} $$
where
![]() $1 \le i \le j \le s$
, and a linear basis
$1 \le i \le j \le s$
, and a linear basis
![]() ${\mathfrak B}^6$
of
${\mathfrak B}^6$
of
![]() $H^{6}( X^{[3]}, {\mathbb C} )$
consists of
$H^{6}( X^{[3]}, {\mathbb C} )$
consists of
 $$ \begin{align} &{{\mathfrak a}}_{-2}(1_X){{\mathfrak a}}_{-1}(x) |0\rangle, \quad {{\mathfrak a}}_{-1}(1_X){\mathfrak a}_{-2}(x) |0\rangle, \quad {{\mathfrak a}}_{-1}(1_X){\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(x)|0\rangle, \nonumber \\ &\qquad {\mathfrak a}_{-3}(\alpha_i)|0\rangle, \quad {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(\alpha_{j'})|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(\alpha_k)|0\rangle \end{align} $$
$$ \begin{align} &{{\mathfrak a}}_{-2}(1_X){{\mathfrak a}}_{-1}(x) |0\rangle, \quad {{\mathfrak a}}_{-1}(1_X){\mathfrak a}_{-2}(x) |0\rangle, \quad {{\mathfrak a}}_{-1}(1_X){\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(x)|0\rangle, \nonumber \\ &\qquad {\mathfrak a}_{-3}(\alpha_i)|0\rangle, \quad {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(\alpha_{j'})|0\rangle, \quad {\mathfrak a}_{-1}(\alpha_i){\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(\alpha_k)|0\rangle \end{align} $$
where
![]() $1 \le i, j' \le j \le k \le s$
. The point class in
$1 \le i, j' \le j \le k \le s$
. The point class in
![]() $H^{12}( X^{[3]}, {\mathbb C} )$
is
$H^{12}( X^{[3]}, {\mathbb C} )$
is
![]() ${\mathfrak a}_{-1}(x)^3 |0\rangle $
.
${\mathfrak a}_{-1}(x)^3 |0\rangle $
.
Definition 4.1. Let X be a simply connected smooth projective surface. Let
![]() $\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
$\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
![]() $H^2(X, {\mathbb C} )$
. Define
$H^2(X, {\mathbb C} )$
. Define
![]() $\{ \Delta _a \}$
to be the linear basis of the total cohomology
$\{ \Delta _a \}$
to be the linear basis of the total cohomology
![]() $H^*( X^{[3]}, {\mathbb C} )$
that consists of
$H^*( X^{[3]}, {\mathbb C} )$
that consists of
Let
![]() $\omega _1, \omega _2, \omega _3 \in {\mathfrak B}^4 \subset H^4( X^{[3]}, {\mathbb C} )$
. The next lemma identifies all the unordered triples
$\omega _1, \omega _2, \omega _3 \in {\mathfrak B}^4 \subset H^4( X^{[3]}, {\mathbb C} )$
. The next lemma identifies all the unordered triples
![]() $(\omega _1, \omega _2, \omega _3)$
such that
$(\omega _1, \omega _2, \omega _3)$
such that
![]() $\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
may not be
$\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
may not be
![]() $0$
. The idea is to use geometric argument involving the reduction Lemma 3.3. In order to apply Lemma 3.3, we fix a meromorphic section
$0$
. The idea is to use geometric argument involving the reduction Lemma 3.3. In order to apply Lemma 3.3, we fix a meromorphic section
![]() $\theta $
of the canonical line bundle
$\theta $
of the canonical line bundle
![]() $\mathcal O_X(K_X)$
and let
$\mathcal O_X(K_X)$
and let
![]() $D_0$
and
$D_0$
and
![]() $D_{\infty }$
be the vanishing and pole divisors of
$D_{\infty }$
be the vanishing and pole divisors of
![]() $\theta $
, respectively.
$\theta $
, respectively.
Lemma 4.2. Let
![]() $d \ge 1$
and
$d \ge 1$
and
![]() $\omega _1, \omega _2, \omega _3 \in {\mathfrak B}^4 \subset H^4( X^{[3]}, {\mathbb C} )$
. Then
$\omega _1, \omega _2, \omega _3 \in {\mathfrak B}^4 \subset H^4( X^{[3]}, {\mathbb C} )$
. Then
if the unordered triple
![]() $(\omega _1, \omega _2, \omega _3)$
is not one of the following:
$(\omega _1, \omega _2, \omega _3)$
is not one of the following:
-
(i)
 $\Big ({\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle , \, {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _j)|0\rangle , \, {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _k)|0\rangle \Big )$
;
$\Big ({\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle , \, {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _j)|0\rangle , \, {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _k)|0\rangle \Big )$
; -
(ii)
 $\omega _1= \omega _2 = {\mathfrak a}_{-3}(1_X)|0\rangle $
, and
$\omega _1= \omega _2 = {\mathfrak a}_{-3}(1_X)|0\rangle $
, and
 $\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
or
$\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
or
 ${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
;
${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
; -
(iii)
 $\omega _1= \omega _2 = \omega _3 = {\mathfrak a}_{-3}(1_X)|0\rangle $
.
$\omega _1= \omega _2 = \omega _3 = {\mathfrak a}_{-3}(1_X)|0\rangle $
.
Proof. We will only prove (4.7) when the triple
![]() $(\omega _1, \omega _2, \omega _3)$
is
$(\omega _1, \omega _2, \omega _3)$
is
since the proof of (4.7) for other triples is similar.
To show that
![]() $\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d} = 0$
, let
$\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d} = 0$
, let
![]() $C_i, C_j, C_k \subset X$
be real
$C_i, C_j, C_k \subset X$
be real
![]() $2$
-dimensional cycles representing the cohomology classes
$2$
-dimensional cycles representing the cohomology classes
![]() $\alpha _i, \alpha _j, \alpha _k \in H^2(X, {\mathbb C} )$
, respectively, such that
$\alpha _i, \alpha _j, \alpha _k \in H^2(X, {\mathbb C} )$
, respectively, such that
![]() $C_i, C_j, C_k, D_0, D_{\infty }$
are in general position. By Lemma 3.1, the classes
$C_i, C_j, C_k, D_0, D_{\infty }$
are in general position. By Lemma 3.1, the classes
are geometrically represented by the closures
![]() $W_1, W_2, W_3$
of the subsets
$W_1, W_2, W_3$
of the subsets
respectively. By Lemma 3.3, it suffices to prove that
Assume
![]() $[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \Lambda _{\theta } \cap \mathrm {ev}_1^{-1}(W_1) \cap \mathrm {ev}_2^{-1}(W_2) \cap \mathrm {ev}_3^{-1}(W_3)$
. Since
$[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \Lambda _{\theta } \cap \mathrm {ev}_1^{-1}(W_1) \cap \mathrm {ev}_2^{-1}(W_2) \cap \mathrm {ev}_3^{-1}(W_3)$
. Since
![]() $[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \mathrm {ev}_1^{-1}(W_1)$
and
$[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \mathrm {ev}_1^{-1}(W_1)$
and
![]() $\rho _3(\varphi (\Sigma ))$
is a single point in
$\rho _3(\varphi (\Sigma ))$
is a single point in
![]() $X^{(3)}$
, we see from (4.8) that
$X^{(3)}$
, we see from (4.8) that
![]() $\rho _3(\varphi (\Sigma ))$
is of the form
$\rho _3(\varphi (\Sigma ))$
is of the form
for some (possibly the same) points
![]() $x_1, x_2\in X$
such that
$x_1, x_2\in X$
such that
![]() $x_2 \in C_i$
. Since
$x_2 \in C_i$
. Since
we must have
![]() $x_1 \in C_j$
. Similarly,
$x_1 \in C_j$
. Similarly,
![]() $x_1 \in C_k$
. So
$x_1 \in C_k$
. So
![]() $x_1 \in C_j \cap C_k$
. Since
$x_1 \in C_j \cap C_k$
. Since
![]() $C_i, C_j, C_k, D_0, D_{\infty }$
are in general position,
$C_i, C_j, C_k, D_0, D_{\infty }$
are in general position,
![]() $x_1 \not \in C_i \cup D_0 \cup D_{\infty }$
and
$x_1 \not \in C_i \cup D_0 \cup D_{\infty }$
and
![]() $x_1 \ne x_2$
. Let
$x_1 \ne x_2$
. Let
![]() $\varphi = (\varphi _1, \varphi _2, \cdots )$
be the standard decomposition of
$\varphi = (\varphi _1, \varphi _2, \cdots )$
be the standard decomposition of
![]() $\varphi $
. Without loss of generality, we assume that
$\varphi $
. Without loss of generality, we assume that
![]() $\varphi _1$
is not a constant map. By Lemma 3.3,
$\varphi _1$
is not a constant map. By Lemma 3.3,
![]() $\mathrm {Spt}(\varphi _1) \in D_0 \cup D_{\infty }$
. So
$\mathrm {Spt}(\varphi _1) \in D_0 \cup D_{\infty }$
. So
![]() $x_2 = \mathrm {Spt}(\varphi _1) \in D_0 \cup D_{\infty }$
and
$x_2 = \mathrm {Spt}(\varphi _1) \in D_0 \cup D_{\infty }$
and
![]() $x_2 \in C_i \cap (D_0 \cup D_{\infty })$
. Therefore,
$x_2 \in C_i \cap (D_0 \cup D_{\infty })$
. Therefore,
![]() $\varphi _1: \Sigma \to X$
is the constant map
$\varphi _1: \Sigma \to X$
is the constant map
![]() $\varphi _1(\Sigma ) = x_2$
, contradicting the assumption that
$\varphi _1(\Sigma ) = x_2$
, contradicting the assumption that
![]() $\varphi _1$
is not constant.
$\varphi _1$
is not constant.
In the rest of this section, we will compute
![]() $\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
when the unordered triple
$\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
when the unordered triple
![]() $(\omega _1, \omega _2, \omega _3)$
is one of those listed in Lemma 4.2 (i), (ii) and (iii). Lemma 4.3 below deals with the unordered triple in Lemma 4.2 (i), and its proof uses a geometric argument similar to the proof of Lemma 4.2.
$(\omega _1, \omega _2, \omega _3)$
is one of those listed in Lemma 4.2 (i), (ii) and (iii). Lemma 4.3 below deals with the unordered triple in Lemma 4.2 (i), and its proof uses a geometric argument similar to the proof of Lemma 4.2.
Lemma 4.3. Let
![]() $\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
$\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
![]() $H^2(X, {\mathbb C} )$
. Let
$H^2(X, {\mathbb C} )$
. Let
![]() $d \ge 1$
and the unordered triple
$d \ge 1$
and the unordered triple
![]() $(\omega _1, \omega _2, \omega _3)$
be from Lemma 4.2 (i). Then,
$(\omega _1, \omega _2, \omega _3)$
be from Lemma 4.2 (i). Then,
Proof. Let
![]() $C_i, C_j, C_k \subset X$
be real
$C_i, C_j, C_k \subset X$
be real
![]() $2$
-dimensional cycles representing the cohomology classes
$2$
-dimensional cycles representing the cohomology classes
![]() $\alpha _i, \alpha _j, \alpha _k$
, respectively, such that
$\alpha _i, \alpha _j, \alpha _k$
, respectively, such that
![]() $C_i, C_j, C_k, D_0, D_{\infty }$
are in general position. By Lemma 3.1, the cohomology classes
$C_i, C_j, C_k, D_0, D_{\infty }$
are in general position. By Lemma 3.1, the cohomology classes
are geometrically represented by the closures
![]() $W_1, W_2, W_3$
of the subsets
$W_1, W_2, W_3$
of the subsets
respectively. Let
![]() $[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \Lambda _{\theta } \cap \mathrm {ev}_1^{-1}(W_1) \cap \mathrm {ev}_2^{-1}(W_2) \cap \mathrm {ev}_3^{-1}(W_3)$
. Since
$[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \Lambda _{\theta } \cap \mathrm {ev}_1^{-1}(W_1) \cap \mathrm {ev}_2^{-1}(W_2) \cap \mathrm {ev}_3^{-1}(W_3)$
. Since
![]() $[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \mathrm {ev}_3^{-1}(W_3)$
and
$[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \mathrm {ev}_3^{-1}(W_3)$
and
![]() $\rho _3(\varphi (\Sigma ))$
is a single point in
$\rho _3(\varphi (\Sigma ))$
is a single point in
![]() $X^{(3)}$
, we see from (4.12) that
$X^{(3)}$
, we see from (4.12) that
![]() $\rho _3(\varphi (\Sigma ))$
is of the form
$\rho _3(\varphi (\Sigma ))$
is of the form
for some (possibly the same) points
![]() $x_1, x_2\in X$
such that
$x_1, x_2\in X$
such that
![]() $x_2 \in C_k$
. By Lemma 3.3, since
$x_2 \in C_k$
. By Lemma 3.3, since
![]() $[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \Lambda _{\theta }$
and
$[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \Lambda _{\theta }$
and
![]() $\varphi $
is not a constant map,
$\varphi $
is not a constant map,
![]() $x_2 \in D_0 \cup D_{\infty }$
. So
$x_2 \in D_0 \cup D_{\infty }$
. So
![]() $x_2 \in C_k \cap (D_0 \cup D_{\infty })$
. Since
$x_2 \in C_k \cap (D_0 \cup D_{\infty })$
. Since
![]() $C_i, C_j, C_k, D_0$
and
$C_i, C_j, C_k, D_0$
and
![]() $D_{\infty }$
are in general position,
$D_{\infty }$
are in general position,
![]() $x_2 \not \in C_i \cup C_j$
. Since
$x_2 \not \in C_i \cup C_j$
. Since
![]() $[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \mathrm {ev}_1^{-1}(W_1) \cap \mathrm {ev}_2^{-1}(W_2)$
, we see from (4.13) that
$[\varphi : (\Sigma; \tilde p_1, \tilde p_2, \tilde p_3) \to X^{[3]}] \in \mathrm {ev}_1^{-1}(W_1) \cap \mathrm {ev}_2^{-1}(W_2)$
, we see from (4.13) that
![]() $x_1 \in C_i \cap C_j$
. It follows that
$x_1 \in C_i \cap C_j$
. It follows that
![]() $x_1 \ne x_2$
, and the standard decomposition of
$x_1 \ne x_2$
, and the standard decomposition of
![]() $\varphi $
(see (3.13)) is of the form
$\varphi $
(see (3.13)) is of the form
![]() $\varphi = (\varphi _1, \varphi _2)$
with
$\varphi = (\varphi _1, \varphi _2)$
with
![]() $\mathrm {Spt}(\varphi _1) = x_1$
and
$\mathrm {Spt}(\varphi _1) = x_1$
and
![]() $\mathrm {Spt}(\varphi _2) = 2x_2$
. In particular,
$\mathrm {Spt}(\varphi _2) = 2x_2$
. In particular,
![]() $\varphi _1: \Sigma \to X$
is the constant map sending
$\varphi _1: \Sigma \to X$
is the constant map sending
![]() $\Sigma $
to
$\Sigma $
to
![]() $x_1$
. Hence, we obtain
$x_1$
. Hence, we obtain
by splitting off the factors
![]() ${\mathfrak a}_{-1}(\alpha _i), {\mathfrak a}_{-1}(\alpha _j), {\mathfrak a}_{-1}(1_X)$
from the three classes in (4.11), respectively. It is known (see [Reference Qin38, (1.35)]) that
${\mathfrak a}_{-1}(\alpha _i), {\mathfrak a}_{-1}(\alpha _j), {\mathfrak a}_{-1}(1_X)$
from the three classes in (4.11), respectively. It is known (see [Reference Qin38, (1.35)]) that
for
![]() $n \ge 2$
. In particular,
$n \ge 2$
. In particular,
![]() $\big \langle {\mathfrak a}_{-2}(1_X)|0\rangle , \beta _2 \big \rangle = -2$
. So by the Divisor Axiom (2.6),
$\big \langle {\mathfrak a}_{-2}(1_X)|0\rangle , \beta _2 \big \rangle = -2$
. So by the Divisor Axiom (2.6),
Finally, by Lemma 3.2 with
![]() $n=2$
,
$n=2$
,
![]() $\big \langle {\mathfrak a}_{-2}(\alpha _k)|0\rangle \big \rangle _{0, d} = 2 \langle K_X, \alpha _k \rangle /d^2$
. Therefore,
$\big \langle {\mathfrak a}_{-2}(\alpha _k)|0\rangle \big \rangle _{0, d} = 2 \langle K_X, \alpha _k \rangle /d^2$
. Therefore,
To handle the unordered triples
![]() $(\omega _1, \omega _2, \omega _3)$
listed in Lemma 4.2 (ii), we will now prove three technical lemmas. For simplicity, in the rest of this section, we let
$(\omega _1, \omega _2, \omega _3)$
listed in Lemma 4.2 (ii), we will now prove three technical lemmas. For simplicity, in the rest of this section, we let
Recall from (4.14) that
![]() $\langle B_3, \beta _3 \rangle = -2$
. It follows that
$\langle B_3, \beta _3 \rangle = -2$
. It follows that
The self-intersection
![]() $c_1^2$
via Heisenberg operators is given by the lemma below.
$c_1^2$
via Heisenberg operators is given by the lemma below.
Lemma 4.4. Let
![]() $c_1 = -B_3/2$
. Then,
$c_1 = -B_3/2$
. Then,
![]() $c_1^2$
is equal to
$c_1^2$
is equal to
Proof. Recall Lehn’s boundary operator
![]() $\mathfrak d$
from (3.10). By definition,
$\mathfrak d$
from (3.10). By definition,
Moving
![]() $\mathfrak d$
all the way to the right and using
$\mathfrak d$
all the way to the right and using
![]() $\mathfrak d |0\rangle = 0$
, we get
$\mathfrak d |0\rangle = 0$
, we get
By (3.11),
![]() ${\mathfrak a}_{-2}'(1_X) = -2 \mathfrak L_{-2}(1_X) + {\mathfrak a}_{-2}(K_X)$
. So by (3.9) and (3.8),
${\mathfrak a}_{-2}'(1_X) = -2 \mathfrak L_{-2}(1_X) + {\mathfrak a}_{-2}(K_X)$
. So by (3.9) and (3.8),
 $$ \begin{align*} &{\mathfrak a}_{-2}'(1_X){\mathfrak a}_{-1}(1_X)|0\rangle \\ =&-2{\mathfrak a}_{-3}(1_X)|0\rangle - 2{\mathfrak a}_{-1}(1_X)\mathfrak L_{-2}(1_X)|0\rangle + {\mathfrak a}_{-2}(K_X){\mathfrak a}_{-1}(1_X)|0\rangle \\ =&-2{\mathfrak a}_{-3}(1_X)|0\rangle + {\mathfrak a}_{-1}(1_X) \cdot {\mathfrak a}_{-1}{\mathfrak a}_{-1}(\tau_{2*}1_X)|0\rangle + {\mathfrak a}_{-2}(K_X){\mathfrak a}_{-1}(1_X)|0\rangle. \end{align*} $$
$$ \begin{align*} &{\mathfrak a}_{-2}'(1_X){\mathfrak a}_{-1}(1_X)|0\rangle \\ =&-2{\mathfrak a}_{-3}(1_X)|0\rangle - 2{\mathfrak a}_{-1}(1_X)\mathfrak L_{-2}(1_X)|0\rangle + {\mathfrak a}_{-2}(K_X){\mathfrak a}_{-1}(1_X)|0\rangle \\ =&-2{\mathfrak a}_{-3}(1_X)|0\rangle + {\mathfrak a}_{-1}(1_X) \cdot {\mathfrak a}_{-1}{\mathfrak a}_{-1}(\tau_{2*}1_X)|0\rangle + {\mathfrak a}_{-2}(K_X){\mathfrak a}_{-1}(1_X)|0\rangle. \end{align*} $$
Similarly,
![]() ${\mathfrak a}_{-1}'(1_X)|0\rangle = -\mathfrak L_{-1}(1_X)|0\rangle = 0$
. Therefore,
${\mathfrak a}_{-1}'(1_X)|0\rangle = -\mathfrak L_{-1}(1_X)|0\rangle = 0$
. Therefore,
![]() $c_1^2$
is equal to
$c_1^2$
is equal to
Since X is simply connected, if
![]() $\{\alpha _1, \ldots , \alpha _s \}$
is a linear basis of
$\{\alpha _1, \ldots , \alpha _s \}$
is a linear basis of
![]() $H^2(X, {\mathbb C} )$
, then
$H^2(X, {\mathbb C} )$
, then
 $$ \begin{align} \tau_{2*}1_X = x \otimes 1_X + 1_X \otimes x + \sum_{1 \le j \le k \le s} b_{j,k} \, \alpha_j \otimes \alpha_k \end{align} $$
$$ \begin{align} \tau_{2*}1_X = x \otimes 1_X + 1_X \otimes x + \sum_{1 \le j \le k \le s} b_{j,k} \, \alpha_j \otimes \alpha_k \end{align} $$
for some
![]() $b_{j, k} \in {\mathbb C} $
, via the Künneth decomposition of
$b_{j, k} \in {\mathbb C} $
, via the Künneth decomposition of
![]() $H^*(X^2, {\mathbb C} )$
.
$H^*(X^2, {\mathbb C} )$
.
In the next two lemmas, we will compute certain special
![]() $1$
-point and
$1$
-point and
![]() $2$
-point genus-
$2$
-point genus-
![]() $0$
extremal Gromov-Witten invariants which will appear in our applications of the composition law (2.7) and involve the class
$0$
extremal Gromov-Witten invariants which will appear in our applications of the composition law (2.7) and involve the class
![]() $\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
.
$\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
.
Lemma 4.5. Let X be a simply connected smooth projective surface. Let
![]() $d \ge 1$
,
$d \ge 1$
,
![]() $\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
and
$\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
and
![]() $\tilde \omega = {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha )|0\rangle $
for some
$\tilde \omega = {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha )|0\rangle $
for some
![]() $\alpha \in H^2(X, {\mathbb C} )$
. Then,
$\alpha \in H^2(X, {\mathbb C} )$
. Then,
Proof. Let
![]() $\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
$\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
![]() $H^2(X, {\mathbb C} )$
. By (4.16) and (4.17),
$H^2(X, {\mathbb C} )$
. By (4.16) and (4.17),
 $$ \begin{align} \omega &= c_1^2 + \frac{1}{2} {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle + \frac{1}{2} {\mathfrak a}_{-1}(1_X) \cdot {\mathfrak a}_{-1}{\mathfrak a}_{-1}(\tau_{2*}1_X)|0\rangle \nonumber \\ & =c_1^2 + \frac{1}{2} {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle + {\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \nonumber \\ &\quad + \sum_{1 \le j \le k \le s} b_{j, k} {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(\alpha_k)|0\rangle. \end{align} $$
$$ \begin{align} \omega &= c_1^2 + \frac{1}{2} {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle + \frac{1}{2} {\mathfrak a}_{-1}(1_X) \cdot {\mathfrak a}_{-1}{\mathfrak a}_{-1}(\tau_{2*}1_X)|0\rangle \nonumber \\ & =c_1^2 + \frac{1}{2} {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle + {\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \nonumber \\ &\quad + \sum_{1 \le j \le k \le s} b_{j, k} {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(\alpha_k)|0\rangle. \end{align} $$
In view of the linear basis (4.4),
![]() ${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \cdot \tilde \omega $
is a linear combination of
${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \cdot \tilde \omega $
is a linear combination of
![]() ${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-1}(x)^{2} |0\rangle $
,
${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-1}(x)^{2} |0\rangle $
,
![]() ${\mathfrak a}_{-1}(\alpha _j){\mathfrak a}_{-1}(\alpha _k) {\mathfrak a}_{-1}(x)|0\rangle $
,
${\mathfrak a}_{-1}(\alpha _j){\mathfrak a}_{-1}(\alpha _k) {\mathfrak a}_{-1}(x)|0\rangle $
,
![]() ${\mathfrak a}_{-1}(\alpha _j){\mathfrak a}_{-2}(x)|0\rangle $
and
${\mathfrak a}_{-1}(\alpha _j){\mathfrak a}_{-2}(x)|0\rangle $
and
![]() ${\mathfrak a}_{-3}(x)|0\rangle $
. Hence,
${\mathfrak a}_{-3}(x)|0\rangle $
. Hence,
![]() $\langle {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \cdot \tilde \omega \rangle _{0, d} = 0$
by Lemma 3.2. Similarly,
$\langle {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \cdot \tilde \omega \rangle _{0, d} = 0$
by Lemma 3.2. Similarly,
whenever
![]() $1 \le j, k \le s$
. Note that
$1 \le j, k \le s$
. Note that
![]() ${\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \cdot \tilde \omega = 2{\mathfrak a}_{-1}(x){\mathfrak a}_{-2}(\alpha )|0\rangle $
. Combining with (4.19) and Lemma 3.2, we conclude that
${\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \cdot \tilde \omega = 2{\mathfrak a}_{-1}(x){\mathfrak a}_{-2}(\alpha )|0\rangle $
. Combining with (4.19) and Lemma 3.2, we conclude that
As in the proof of Lemma 4.4, using (3.11) and (3.9), we get
 $$ \begin{align*} c_1^2 \tilde \omega &=\mathfrak d \mathfrak d {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha)|0\rangle \\ &=\mathfrak d \big \{ 2 {\mathfrak a}_{-3}(\alpha) + \langle K_X, \alpha \rangle {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(x) + 2 {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-1}(\alpha){\mathfrak a}_{-1}(x) \big \}|0\rangle \\ &=-8{\mathfrak a}_{-1}(x){\mathfrak a}_{-2}(\alpha)|0\rangle + \gamma \end{align*} $$
$$ \begin{align*} c_1^2 \tilde \omega &=\mathfrak d \mathfrak d {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha)|0\rangle \\ &=\mathfrak d \big \{ 2 {\mathfrak a}_{-3}(\alpha) + \langle K_X, \alpha \rangle {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(x) + 2 {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-1}(\alpha){\mathfrak a}_{-1}(x) \big \}|0\rangle \\ &=-8{\mathfrak a}_{-1}(x){\mathfrak a}_{-2}(\alpha)|0\rangle + \gamma \end{align*} $$
where
![]() $\gamma $
is a term satisfying
$\gamma $
is a term satisfying
![]() $\langle \gamma \rangle _{0, d}=0$
. By Lemma 3.2 again,
$\langle \gamma \rangle _{0, d}=0$
. By Lemma 3.2 again,
Lemma 4.6. Let X be simply connected. Let
![]() $d \ge 1$
,
$d \ge 1$
,
![]() $c_1 = -B_3/2$
,
$c_1 = -B_3/2$
,
![]() $\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
and
$\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
and
![]() $\tilde \omega = {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha )|0\rangle $
for some
$\tilde \omega = {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha )|0\rangle $
for some
![]() $\alpha \in H^2(X, {\mathbb C} )$
. Then,
$\alpha \in H^2(X, {\mathbb C} )$
. Then,
-
(i)
 $\langle c_1 \omega , \tilde \omega \rangle _{0, d} = -12 \langle K_X, \alpha \rangle /d$
.
$\langle c_1 \omega , \tilde \omega \rangle _{0, d} = -12 \langle K_X, \alpha \rangle /d$
. -
(ii)
 $\langle \omega , c_1 \tilde \omega \rangle _{0, d} = -2 \,\, \langle K_X, \alpha \rangle \,\, c_{3, d}$
where
$\langle \omega , c_1 \tilde \omega \rangle _{0, d} = -2 \,\, \langle K_X, \alpha \rangle \,\, c_{3, d}$
where
 $c_{3, d}$
is from (3.16).
$c_{3, d}$
is from (3.16). -
(iii)
 $\langle c_1 \omega , \omega \rangle _{0, d} = 3K_X^2 \,\, c_{3, d}$
.
$\langle c_1 \omega , \omega \rangle _{0, d} = 3K_X^2 \,\, c_{3, d}$
.
Proof. (i) Since
![]() $c_1 \omega = \mathfrak d {\mathfrak a}_{-3}(1_X)|0\rangle $
, we see from (3.11) that
$c_1 \omega = \mathfrak d {\mathfrak a}_{-3}(1_X)|0\rangle $
, we see from (3.11) that
By (3.8),
![]() $\mathfrak L_{-3}(1_X)|0\rangle = - {\mathfrak a}_{-1} {\mathfrak a}_{-2}(\tau _{2*}1_X)|0\rangle $
. Thus, we have
$\mathfrak L_{-3}(1_X)|0\rangle = - {\mathfrak a}_{-1} {\mathfrak a}_{-2}(\tau _{2*}1_X)|0\rangle $
. Thus, we have
By Lemma 3.4,
![]() $\big \langle {\mathfrak a}_{-3}(K_X) |0\rangle , \tilde \omega \big \rangle _{0, d} = 0$
. Therefore,
$\big \langle {\mathfrak a}_{-3}(K_X) |0\rangle , \tilde \omega \big \rangle _{0, d} = 0$
. Therefore,
By (4.17), Lemma 3.4 and
![]() $c_{2, d} = -4/d$
, we obtain
$c_{2, d} = -4/d$
, we obtain
(ii) Similarly, by (3.11) and (3.8), we conclude that
where
![]() $\gamma $
is a term satisfying
$\gamma $
is a term satisfying
![]() $\langle \omega , \gamma \rangle _{0, d}=0$
. By Lemma 3.4,
$\langle \omega , \gamma \rangle _{0, d}=0$
. By Lemma 3.4,
(iii) We see from (4.20) that
![]() $\langle c_1 \omega , \omega \rangle _{0, d}$
is equal to
$\langle c_1 \omega , \omega \rangle _{0, d}$
is equal to
By (4.17) and Lemma 3.4, we have
![]() $\big \langle {\mathfrak a}_{-1} {\mathfrak a}_{-2}(\tau _{2*}1_X)|0\rangle , {\mathfrak a}_{-3}(1_X)|0\rangle \big \rangle _{0, d} = 0$
and
$\big \langle {\mathfrak a}_{-1} {\mathfrak a}_{-2}(\tau _{2*}1_X)|0\rangle , {\mathfrak a}_{-3}(1_X)|0\rangle \big \rangle _{0, d} = 0$
and
![]() $ \big \langle {\mathfrak a}_{-3}(K_X)|0\rangle , {\mathfrak a}_{-3}(1_X)|0\rangle \big \rangle _{0, d} = K_X^2 \,\, c_{3, d}. $
Hence,
$ \big \langle {\mathfrak a}_{-3}(K_X)|0\rangle , {\mathfrak a}_{-3}(1_X)|0\rangle \big \rangle _{0, d} = K_X^2 \,\, c_{3, d}. $
Hence,
![]() $\langle c_1 \omega , \omega \rangle _{0, d} = 3K_X^2 \,\, c_{3, d}$
.
$\langle c_1 \omega , \omega \rangle _{0, d} = 3K_X^2 \,\, c_{3, d}$
.
Our next proposition determines the invariant
![]() $\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
when the unordered triple
$\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
when the unordered triple
![]() $(\omega _1, \omega _2, \omega _3)$
is from Lemma 4.2 (ii). Its proof involves the composition law (2.7) and the linear basis
$(\omega _1, \omega _2, \omega _3)$
is from Lemma 4.2 (ii). Its proof involves the composition law (2.7) and the linear basis
![]() $\{ \Delta _a \}$
from (4.6).
$\{ \Delta _a \}$
from (4.6).
Proposition 4.7. Let
![]() $\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
$\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
![]() $H^2(X, {\mathbb C} )$
. Let
$H^2(X, {\mathbb C} )$
. Let
![]() $d \ge 1$
and
$d \ge 1$
and
![]() $\omega _1 = \omega _2 = {\mathfrak a}_{-3}(1_X)|0\rangle $
. Let
$\omega _1 = \omega _2 = {\mathfrak a}_{-3}(1_X)|0\rangle $
. Let
![]() $\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
or
$\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
or
![]() ${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
. Then,
${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
. Then,
where
![]() $c_{3, d}$
is the universal constant from (3.16).
$c_{3, d}$
is the universal constant from (3.16).
Proof. The proof of (4.21) for
![]() $\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
is similar to the proof of (4.21) for
$\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
is similar to the proof of (4.21) for
![]() $\omega _3 = {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
. So we will only prove
$\omega _3 = {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
. So we will only prove
for
![]() $\omega _3 = {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
Let
$\omega _3 = {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
Let
![]() $c_1 = -B_3/2$
. Apply the composition law (2.7) to
$c_1 = -B_3/2$
. Apply the composition law (2.7) to
We will prove (4.22) by comparing both sides of (2.7).
First of all, the left-hand side of (2.7) is equal to
 $$ \begin{align} \langle c_1^2, \omega_2, \omega_3 \rangle_{0, d} +\langle c_1, c_1, \omega_2 \omega_3 \rangle_{0, d} + \sum_{\substack{d_1 + d_2 = d\\d_1, d_2> 0}} \sum_{a} \langle c_1, c_1, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, \omega_2, \omega_3 \rangle_{0, d_2}. \end{align} $$
$$ \begin{align} \langle c_1^2, \omega_2, \omega_3 \rangle_{0, d} +\langle c_1, c_1, \omega_2 \omega_3 \rangle_{0, d} + \sum_{\substack{d_1 + d_2 = d\\d_1, d_2> 0}} \sum_{a} \langle c_1, c_1, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, \omega_2, \omega_3 \rangle_{0, d_2}. \end{align} $$
By (4.16) and Lemma 4.2,
![]() $\langle c_1^2, \omega _2, \omega _3 \rangle _{0, d} = Q$
. Since
$\langle c_1^2, \omega _2, \omega _3 \rangle _{0, d} = Q$
. Since
![]() $\langle c_1, \beta _3 \rangle = 1$
by (4.15), we get
$\langle c_1, \beta _3 \rangle = 1$
by (4.15), we get
 $$ \begin{align*} \langle c_1, c_1, \omega_2 \omega_3 \rangle_{0, d} &= d^2 \, \langle \omega_2 \omega_3 \rangle_{0, d}, \\ \langle c_1, c_1, \Delta_a \rangle_{0, d_1} &= d_1^2 \, \langle \Delta_a \rangle_{0, d_1} \end{align*} $$
$$ \begin{align*} \langle c_1, c_1, \omega_2 \omega_3 \rangle_{0, d} &= d^2 \, \langle \omega_2 \omega_3 \rangle_{0, d}, \\ \langle c_1, c_1, \Delta_a \rangle_{0, d_1} &= d_1^2 \, \langle \Delta_a \rangle_{0, d_1} \end{align*} $$
in view of (2.6). By Lemma 3.2,
![]() $\langle \Delta _a \rangle _{0, d_1} \ne 0$
only when
$\langle \Delta _a \rangle _{0, d_1} \ne 0$
only when
![]() $\Delta _a = {\mathfrak a}_{-2}(\alpha _j){\mathfrak a}_{-1}(x)|0\rangle $
for some j. If
$\Delta _a = {\mathfrak a}_{-2}(\alpha _j){\mathfrak a}_{-1}(x)|0\rangle $
for some j. If
![]() $\Delta _a = {\mathfrak a}_{-2}(\alpha _j){\mathfrak a}_{-1}(x)|0\rangle $
, then we see from (4.4) that
$\Delta _a = {\mathfrak a}_{-2}(\alpha _j){\mathfrak a}_{-1}(x)|0\rangle $
, then we see from (4.4) that
![]() $\Delta ^a$
is a linear combination of the classes
$\Delta ^a$
is a linear combination of the classes
![]() ${\mathfrak a}_{-2}(\alpha _k){\mathfrak a}_{-1}(1_X)|0\rangle $
,
${\mathfrak a}_{-2}(\alpha _k){\mathfrak a}_{-1}(1_X)|0\rangle $
,
![]() $1 \le k \le s$
. So
$1 \le k \le s$
. So
![]() $\langle \Delta ^a, \omega _2, \omega _3 \rangle _{0, d_2} = 0$
by Lemma 4.2. It follows from (4.23) that the left-hand side of (2.7) is equal to
$\langle \Delta ^a, \omega _2, \omega _3 \rangle _{0, d_2} = 0$
by Lemma 4.2. It follows from (4.23) that the left-hand side of (2.7) is equal to
![]() $ Q + d^2 \, \langle \omega _2 \omega _3 \rangle _{0, d}. $
By Lemma 4.5, we see that the left-hand side of (2.7) is equal to
$ Q + d^2 \, \langle \omega _2 \omega _3 \rangle _{0, d}. $
By Lemma 4.5, we see that the left-hand side of (2.7) is equal to
Next, the right-hand side of (2.7) is equal to
By Lemma 4.6, we have
![]() $\langle c_1 \omega _2, c_1, \omega _3 \rangle _{0, d} = d \langle c_1 \omega _2, \omega _3 \rangle _{0, d} = -12 \langle K_X, \alpha _i \rangle $
and
$\langle c_1 \omega _2, c_1, \omega _3 \rangle _{0, d} = d \langle c_1 \omega _2, \omega _3 \rangle _{0, d} = -12 \langle K_X, \alpha _i \rangle $
and
Therefore, the right-hand side of (2.7) is equal to
 $$ \begin{align} -12 \langle K_X, \alpha_i \rangle -2 \,\langle K_X, \alpha_i \rangle \,\,d c_{3, d} + \sum_{\substack{d_1 + d_2 = d\\d_1, d_2> 0}} \sum_{a} d_1d_2 \langle \omega_2, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, \omega_3 \rangle_{0, d_2}. \end{align} $$
$$ \begin{align} -12 \langle K_X, \alpha_i \rangle -2 \,\langle K_X, \alpha_i \rangle \,\,d c_{3, d} + \sum_{\substack{d_1 + d_2 = d\\d_1, d_2> 0}} \sum_{a} d_1d_2 \langle \omega_2, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, \omega_3 \rangle_{0, d_2}. \end{align} $$
By the list (4.5) of the basis
![]() ${\mathfrak B}^6$
and Lemma 3.4,
${\mathfrak B}^6$
and Lemma 3.4,
![]() $\langle \omega _2, \Delta _a \rangle _{0, d_1} \ne 0$
only if
$\langle \omega _2, \Delta _a \rangle _{0, d_1} \ne 0$
only if
![]() $\Delta _a = {\mathfrak a}_{-3}(\alpha _j)|0\rangle $
for some j with
$\Delta _a = {\mathfrak a}_{-3}(\alpha _j)|0\rangle $
for some j with
![]() $1 \le j \le s$
. If
$1 \le j \le s$
. If
![]() $\Delta _a = {\mathfrak a}_{-3}(\alpha _j)|0\rangle $
, then
$\Delta _a = {\mathfrak a}_{-3}(\alpha _j)|0\rangle $
, then
![]() $\Delta ^a$
is a linear combination of
$\Delta ^a$
is a linear combination of
![]() ${\mathfrak B}^6 - \big \{ {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(x)|0\rangle \big \}$
. So
${\mathfrak B}^6 - \big \{ {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(x)|0\rangle \big \}$
. So
![]() $\langle \Delta ^a, \omega _3 \rangle _{0, d_2} = 0$
by Lemma 3.4 again. By (4.25), the right-hand side of (2.7) is equal to
$\langle \Delta ^a, \omega _3 \rangle _{0, d_2} = 0$
by Lemma 3.4 again. By (4.25), the right-hand side of (2.7) is equal to
We are left with the computation of the invariant
![]() $\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
when the triple
$\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d}$
when the triple
![]() $(\omega _1, \omega _2, \omega _3)$
is from Lemma 4.2 (iii), that is, when
$(\omega _1, \omega _2, \omega _3)$
is from Lemma 4.2 (iii), that is, when
![]() $ \omega _1 = \omega _2 = \omega _3 = {\mathfrak a}_{-3}(1_X)|0\rangle. $
This will be done in Proposition 4.9 below. We prove a technical lemma first.
$ \omega _1 = \omega _2 = \omega _3 = {\mathfrak a}_{-3}(1_X)|0\rangle. $
This will be done in Proposition 4.9 below. We prove a technical lemma first.
Lemma 4.8. Let X be simply connected. Let
![]() $d \ge 1$
and
$d \ge 1$
and
![]() $\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
. Then,
$\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
. Then,
 $$ \begin{align} \langle \omega^2 \rangle_{0, d} = \frac{18K_X^2}{d^2} \end{align} $$
$$ \begin{align} \langle \omega^2 \rangle_{0, d} = \frac{18K_X^2}{d^2} \end{align} $$
Proof. Let
![]() $\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
$\{\alpha _1, \ldots , \alpha _s \}$
be a linear basis of
![]() $H^2(X, {\mathbb C} )$
. By (4.19),
$H^2(X, {\mathbb C} )$
. By (4.19),
 $$ \begin{align*} \omega^2 &=c_1^2 \cdot \omega + \frac{1}{2} {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \cdot \omega + {\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \cdot \omega \\ &\quad + \sum_{1 \le j \le k \le s} b_{j, k} {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(\alpha_k)|0\rangle \cdot \omega. \end{align*} $$
$$ \begin{align*} \omega^2 &=c_1^2 \cdot \omega + \frac{1}{2} {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \cdot \omega + {\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \cdot \omega \\ &\quad + \sum_{1 \le j \le k \le s} b_{j, k} {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-1}(\alpha_j){\mathfrak a}_{-1}(\alpha_k)|0\rangle \cdot \omega. \end{align*} $$
The cup products
![]() ${\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \cdot \omega $
and
${\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \cdot \omega $
and
![]() ${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-1}(\alpha _j) {\mathfrak a}_{-1}(\alpha _k)|0\rangle \cdot \omega $
are scalar multiples of
${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-1}(\alpha _j) {\mathfrak a}_{-1}(\alpha _k)|0\rangle \cdot \omega $
are scalar multiples of
![]() ${\mathfrak a}_{-3}(x)|0\rangle $
. Therefore, we conclude from Lemma 3.2 that
${\mathfrak a}_{-3}(x)|0\rangle $
. Therefore, we conclude from Lemma 3.2 that
 $$ \begin{align} \langle \omega^2 \rangle_{0, d} &= \langle c_1^2 \cdot \omega \rangle_{0, d} + \frac{1}{2} \big \langle {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \cdot \omega \big \rangle_{0, d} \nonumber \\ &= \langle \mathfrak d c_1 \omega \rangle_{0, d} + \frac{1}{2} \big \langle \omega \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle\big \rangle_{0, d}. \end{align} $$
$$ \begin{align} \langle \omega^2 \rangle_{0, d} &= \langle c_1^2 \cdot \omega \rangle_{0, d} + \frac{1}{2} \big \langle {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \cdot \omega \big \rangle_{0, d} \nonumber \\ &= \langle \mathfrak d c_1 \omega \rangle_{0, d} + \frac{1}{2} \big \langle \omega \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle\big \rangle_{0, d}. \end{align} $$
By (4.20),
![]() $c_1 \omega = 3 {\mathfrak a}_{-1} {\mathfrak a}_{-2}(\tau _{2*}1_X)|0\rangle + 3 {\mathfrak a}_{-3}(K_X)|0\rangle $
. So
$c_1 \omega = 3 {\mathfrak a}_{-1} {\mathfrak a}_{-2}(\tau _{2*}1_X)|0\rangle + 3 {\mathfrak a}_{-3}(K_X)|0\rangle $
. So
 $$ \begin{align} \langle \mathfrak d c_1 \omega \rangle_{0, d} = 3 \big \langle \mathfrak d {\mathfrak a}_{-1} {\mathfrak a}_{-2}(\tau_{2*}1_X)|0\rangle \big \rangle_{0, d} + 3 \big \langle \mathfrak d {\mathfrak a}_{-3}(K_X)|0\rangle \big \rangle_{0, d} = \frac{24K_X^2}{d^2} \end{align} $$
$$ \begin{align} \langle \mathfrak d c_1 \omega \rangle_{0, d} = 3 \big \langle \mathfrak d {\mathfrak a}_{-1} {\mathfrak a}_{-2}(\tau_{2*}1_X)|0\rangle \big \rangle_{0, d} + 3 \big \langle \mathfrak d {\mathfrak a}_{-3}(K_X)|0\rangle \big \rangle_{0, d} = \frac{24K_X^2}{d^2} \end{align} $$
by (4.17), (3.11), (3.9), (3.8) and Lemma 3.2. Similarly, by (4.19) and Lemma 3.2,
 $$ \begin{align} &\quad \big \langle \omega \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle\big \rangle_{0, d} \nonumber \\ &=\big \langle c_1^2 \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle_{0, d} + \big \langle {\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle_{0, d} \nonumber \\ &=\big \langle \mathfrak d^2 {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle_{0, d} + \frac{4K_X^2}{d^2}. \end{align} $$
$$ \begin{align} &\quad \big \langle \omega \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle\big \rangle_{0, d} \nonumber \\ &=\big \langle c_1^2 \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle_{0, d} + \big \langle {\mathfrak a}_{-1}(1_X)^2{\mathfrak a}_{-1}(x)|0\rangle \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle_{0, d} \nonumber \\ &=\big \langle \mathfrak d^2 {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle_{0, d} + \frac{4K_X^2}{d^2}. \end{align} $$
By (3.11), (3.9) and (3.8), we see that
![]() $\mathfrak d {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle $
is equal to
$\mathfrak d {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle $
is equal to
Applying (3.11), (3.9), (3.8) and Lemma 3.2 repeatedly, we get
 $$ \begin{align*} &\quad \big \langle \mathfrak d^2 {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle_{0, d} \\ &=-2 \big \langle \mathfrak d {\mathfrak a}_{-3}(K_X)|0\rangle \big \rangle_{0, d} + 2\big \langle \mathfrak d {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-1}(x) {\mathfrak a}_{-1}(K_X)|0\rangle \big \rangle_{0, d} \\ & \qquad + K_X^2 \big \langle \mathfrak d {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-2}(x)|0\rangle \big \rangle_{0, d} \\ &=-\frac{12K_X^2}{d^2} - \frac{4K_X^2}{d^2} \\ &=-\frac{16K_X^2}{d^2}. \end{align*} $$
$$ \begin{align*} &\quad \big \langle \mathfrak d^2 {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle_{0, d} \\ &=-2 \big \langle \mathfrak d {\mathfrak a}_{-3}(K_X)|0\rangle \big \rangle_{0, d} + 2\big \langle \mathfrak d {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-1}(x) {\mathfrak a}_{-1}(K_X)|0\rangle \big \rangle_{0, d} \\ & \qquad + K_X^2 \big \langle \mathfrak d {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-2}(x)|0\rangle \big \rangle_{0, d} \\ &=-\frac{12K_X^2}{d^2} - \frac{4K_X^2}{d^2} \\ &=-\frac{16K_X^2}{d^2}. \end{align*} $$
Combining with (4.30), we have
![]() $\big \langle \omega \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle _{0, d} = -{12K_X^2}/{d^2}.$
Together with (4.28) and (4.29), we obtain
$\big \langle \omega \cdot {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(K_X)|0\rangle \big \rangle _{0, d} = -{12K_X^2}/{d^2}.$
Together with (4.28) and (4.29), we obtain
![]() $\langle \omega ^2 \rangle _{0, d} = {18K_X^2}/{d^2}$
.
$\langle \omega ^2 \rangle _{0, d} = {18K_X^2}/{d^2}$
.
Proposition 4.9. Let X be a simply connected projective surface. Let
![]() $d \ge 1$
. Then,
$d \ge 1$
. Then,
![]() $\big \langle {\mathfrak a}_{-3}(1_X)|0\rangle , {\mathfrak a}_{-3}(1_X)|0\rangle , {\mathfrak a}_{-3}(1_X)|0\rangle \big \rangle _{0, d}$
is equal to
$\big \langle {\mathfrak a}_{-3}(1_X)|0\rangle , {\mathfrak a}_{-3}(1_X)|0\rangle , {\mathfrak a}_{-3}(1_X)|0\rangle \big \rangle _{0, d}$
is equal to
 $$ \begin{align} -18K_X^2 +5K_X^2 \, d c_{3,d} - \,\, 2 K_X^2\sum_{i=1}^{d-1} i c_{3, i} + \frac{1}{3} K_X^2 \, \sum_{i=1}^{d-1} i c_{3, i} \,\, (d-i) c_{3, d-i} \end{align} $$
$$ \begin{align} -18K_X^2 +5K_X^2 \, d c_{3,d} - \,\, 2 K_X^2\sum_{i=1}^{d-1} i c_{3, i} + \frac{1}{3} K_X^2 \, \sum_{i=1}^{d-1} i c_{3, i} \,\, (d-i) c_{3, d-i} \end{align} $$
where
![]() $c_{3, d}$
is the universal constant from (3.16).
$c_{3, d}$
is the universal constant from (3.16).
Proof. For simplicity, let
![]() $\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
and
$\omega = {\mathfrak a}_{-3}(1_X)|0\rangle $
and
![]() $Q' = \big \langle \omega , \omega , \omega \big \rangle _{0, d}$
. Our idea to compute
$Q' = \big \langle \omega , \omega , \omega \big \rangle _{0, d}$
. Our idea to compute
![]() $Q'$
is the same as in the proof of Proposition 4.7. Let
$Q'$
is the same as in the proof of Proposition 4.7. Let
![]() $c_1 = -B_3/2$
. We apply the composition law (2.7) to
$c_1 = -B_3/2$
. We apply the composition law (2.7) to
![]() $\gamma _1 = \gamma _2 = c_1$
and
$\gamma _1 = \gamma _2 = c_1$
and
![]() $\gamma _3 = \gamma _4 = \omega $
.
$\gamma _3 = \gamma _4 = \omega $
.
First of all, notice that the left-hand-side of (2.7) is equal to
By (4.16), Lemma 4.2 and Proposition 4.7, we have
![]() $ \langle c_1^2, \omega , \omega \rangle _{0, d} = Q' + K_X^2 \, d c_{3,d}. $
By (2.6) and Lemma 4.8, we get
$ \langle c_1^2, \omega , \omega \rangle _{0, d} = Q' + K_X^2 \, d c_{3,d}. $
By (2.6) and Lemma 4.8, we get
![]() $\langle c_1, c_1, \omega ^2 \rangle _{0, d} = d^2 \langle \omega ^2 \rangle _{0, d} = 18K_X^2$
. Next, note from (4.3) and (4.4) that if
$\langle c_1, c_1, \omega ^2 \rangle _{0, d} = d^2 \langle \omega ^2 \rangle _{0, d} = 18K_X^2$
. Next, note from (4.3) and (4.4) that if
![]() $\Delta _a = {\mathfrak a}_{-2}(\alpha _i){\mathfrak a}_{-1}(x)|0\rangle $
, then
$\Delta _a = {\mathfrak a}_{-2}(\alpha _i){\mathfrak a}_{-1}(x)|0\rangle $
, then
![]() $ \Delta ^a = -{1}/{2} \cdot {\mathfrak a}_{-2}(\alpha ^i){\mathfrak a}_{-1}(1_X)|0\rangle $
where
$ \Delta ^a = -{1}/{2} \cdot {\mathfrak a}_{-2}(\alpha ^i){\mathfrak a}_{-1}(1_X)|0\rangle $
where
![]() $\{ \alpha ^1, \ldots , \alpha ^s \} \subset H^2(X, {\mathbb C} )$
is the dual basis of
$\{ \alpha ^1, \ldots , \alpha ^s \} \subset H^2(X, {\mathbb C} )$
is the dual basis of
![]() $\{ \alpha _1, \ldots , \alpha _s \}$
with respect to the pairing of X. So by Lemma 3.2 and Proposition 4.7, we obtain
$\{ \alpha _1, \ldots , \alpha _s \}$
with respect to the pairing of X. So by Lemma 3.2 and Proposition 4.7, we obtain
 $$ \begin{align*} &\quad \sum_{a} \,\, \langle c_1, c_1, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, \omega, \omega \rangle_{0, d_2} \\ &= \sum_{i=1}^s \,\, d_1^2 \big \langle {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(x)|0\rangle \big \rangle_{0, d_1} \cdot \left (-\frac{1}{2} \right ) \big \langle {\mathfrak a}_{-2}(\alpha^i){\mathfrak a}_{-1}(1_X)|0\rangle, \omega, \omega \big \rangle_{0, d_2} \\ &=\sum_{i=1}^s \,\, 2\langle K_X, \alpha_i \rangle \cdot \langle K_X, \alpha^i \rangle \,\,d_2 c_{3, d_2}. \end{align*} $$
$$ \begin{align*} &\quad \sum_{a} \,\, \langle c_1, c_1, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, \omega, \omega \rangle_{0, d_2} \\ &= \sum_{i=1}^s \,\, d_1^2 \big \langle {\mathfrak a}_{-2}(\alpha_i){\mathfrak a}_{-1}(x)|0\rangle \big \rangle_{0, d_1} \cdot \left (-\frac{1}{2} \right ) \big \langle {\mathfrak a}_{-2}(\alpha^i){\mathfrak a}_{-1}(1_X)|0\rangle, \omega, \omega \big \rangle_{0, d_2} \\ &=\sum_{i=1}^s \,\, 2\langle K_X, \alpha_i \rangle \cdot \langle K_X, \alpha^i \rangle \,\,d_2 c_{3, d_2}. \end{align*} $$
Since
![]() $\sum _{i=1}^s \langle K_X, \alpha _i \rangle \cdot \langle K_X, \alpha ^i \rangle = K_X^2$
, we conclude that
$\sum _{i=1}^s \langle K_X, \alpha _i \rangle \cdot \langle K_X, \alpha ^i \rangle = K_X^2$
, we conclude that
In summary, we see that the left-hand side of (2.7) is equal to
Next, the right-hand side of (2.7) is equal to
 $$ \begin{align*} &\quad \langle c_1 \omega, c_1, \omega \rangle_{0, d} +\langle c_1, \omega, c_1 \omega \rangle_{0, d} + \sum_{\substack{d_1 + d_2 = d\\d_1, d_2> 0}} \,\, \sum_{a} \,\, \langle c_1, \omega, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, c_1, \omega \rangle_{0, d_2} \\ &= 6K_X^2 \, d c_{3,d} + \sum_{d_1 + d_2 = d, \, d_1, d_2 > 0} \,\, \sum_{a} \,\, d_1 \langle \omega, \Delta_a \rangle_{0, d_1} \, d_2 \langle \Delta^a, \omega \rangle_{0, d_2} \end{align*} $$
$$ \begin{align*} &\quad \langle c_1 \omega, c_1, \omega \rangle_{0, d} +\langle c_1, \omega, c_1 \omega \rangle_{0, d} + \sum_{\substack{d_1 + d_2 = d\\d_1, d_2> 0}} \,\, \sum_{a} \,\, \langle c_1, \omega, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, c_1, \omega \rangle_{0, d_2} \\ &= 6K_X^2 \, d c_{3,d} + \sum_{d_1 + d_2 = d, \, d_1, d_2 > 0} \,\, \sum_{a} \,\, d_1 \langle \omega, \Delta_a \rangle_{0, d_1} \, d_2 \langle \Delta^a, \omega \rangle_{0, d_2} \end{align*} $$
by Lemma 4.6 (iii). If
![]() $\Delta _a = {\mathfrak a}_{-3}(\alpha _i)|0\rangle $
, then
$\Delta _a = {\mathfrak a}_{-3}(\alpha _i)|0\rangle $
, then
![]() $\Delta ^a = {1}/{3} \cdot {\mathfrak a}_{-3}(\alpha ^i)|0\rangle .$
Therefore,
$\Delta ^a = {1}/{3} \cdot {\mathfrak a}_{-3}(\alpha ^i)|0\rangle .$
Therefore,
 $$ \begin{align*} & \sum_{a} \,\, \langle \omega, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, \omega \rangle_{0, d_2} \\ =&\sum_{i=1}^s \big \langle {\mathfrak a}_{-3}(1_X)|0\rangle, {\mathfrak a}_{-3}(\alpha_i)|0\rangle \big \rangle_{0, d_1} \cdot \frac{1}{3} \big \langle {\mathfrak a}_{-3}(\alpha^i)|0\rangle, {\mathfrak a}_{-3}(1_X)|0\rangle \big \rangle_{0, d_2} \\ =&\sum_{i=1}^s \langle K_X, \alpha_i \rangle c_{3, d_1} \cdot \frac{1}{3} \langle K_X, \alpha^i \rangle c_{3, d_2} \\ =&\frac{1}{3} K_X^2 \,\, c_{3, d_1} \,\, c_{3, d_2} \end{align*} $$
$$ \begin{align*} & \sum_{a} \,\, \langle \omega, \Delta_a \rangle_{0, d_1} \, \langle \Delta^a, \omega \rangle_{0, d_2} \\ =&\sum_{i=1}^s \big \langle {\mathfrak a}_{-3}(1_X)|0\rangle, {\mathfrak a}_{-3}(\alpha_i)|0\rangle \big \rangle_{0, d_1} \cdot \frac{1}{3} \big \langle {\mathfrak a}_{-3}(\alpha^i)|0\rangle, {\mathfrak a}_{-3}(1_X)|0\rangle \big \rangle_{0, d_2} \\ =&\sum_{i=1}^s \langle K_X, \alpha_i \rangle c_{3, d_1} \cdot \frac{1}{3} \langle K_X, \alpha^i \rangle c_{3, d_2} \\ =&\frac{1}{3} K_X^2 \,\, c_{3, d_1} \,\, c_{3, d_2} \end{align*} $$
by Lemma 3.4. In summary, we see that the right-hand side of (2.7) is equal to
 $$ \begin{align} 6K_X^2 \, d c_{3,d} + \frac{1}{3} K_X^2 \,\, \sum_{d_1 + d_2 = d, \, d_1, d_2> 0} \,\, d_1c_{3, d_1} \,\, d_2 c_{3, d_2}. \end{align} $$
$$ \begin{align} 6K_X^2 \, d c_{3,d} + \frac{1}{3} K_X^2 \,\, \sum_{d_1 + d_2 = d, \, d_1, d_2> 0} \,\, d_1c_{3, d_1} \,\, d_2 c_{3, d_2}. \end{align} $$
The results in this section are summarized into a theorem.
Theorem 4.10. Let X be a simply connected smooth projective surface. Assume that
![]() $\{\alpha _1, \ldots , \alpha _s \}$
is a linear basis of
$\{\alpha _1, \ldots , \alpha _s \}$
is a linear basis of
![]() $H^2(X, {\mathbb C} )$
, and let
$H^2(X, {\mathbb C} )$
, and let
![]() ${\mathfrak B}^4$
stand for the linear basis of
${\mathfrak B}^4$
stand for the linear basis of
![]() $H^{4}( X^{[3]}, {\mathbb C} )$
from (4.4). Let
$H^{4}( X^{[3]}, {\mathbb C} )$
from (4.4). Let
![]() $d \ge 1$
and
$d \ge 1$
and
![]() $\omega _1, \omega _2, \omega _3 \in {\mathfrak B}^4$
. Then,
$\omega _1, \omega _2, \omega _3 \in {\mathfrak B}^4$
. Then,
if the unordered triple
![]() $(\omega _1, \omega _2, \omega _3)$
is not one of the following four cases:
$(\omega _1, \omega _2, \omega _3)$
is not one of the following four cases:
-
(i)
 $\Big ({\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle , {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _j)|0\rangle , {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _k)|0\rangle \Big )$
;
$\Big ({\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle , {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _j)|0\rangle , {\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _k)|0\rangle \Big )$
; -
(ii)
 $\omega _1= \omega _2 = {\mathfrak a}_{-3}(1_X)|0\rangle $
, and
$\omega _1= \omega _2 = {\mathfrak a}_{-3}(1_X)|0\rangle $
, and
 $\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
or
$\omega _3 = {\mathfrak a}_{-2}(1_X){\mathfrak a}_{-1}(\alpha _i)|0\rangle $
or
 ${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
;
${\mathfrak a}_{-1}(1_X){\mathfrak a}_{-2}(\alpha _i)|0\rangle $
; -
(iii)
 $\omega _1= \omega _2 = \omega _3 = {\mathfrak a}_{-3}(1_X)|0\rangle $
.
$\omega _1= \omega _2 = \omega _3 = {\mathfrak a}_{-3}(1_X)|0\rangle $
.
Moreover,
![]() $\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d \beta _3} = 8 \langle \alpha _i, \alpha _j \rangle \, \langle K_X, \alpha _k \rangle $
in case (i), and
$\langle \omega _1, \omega _2, \omega _3 \rangle _{0, d \beta _3} = 8 \langle \alpha _i, \alpha _j \rangle \, \langle K_X, \alpha _k \rangle $
in case (i), and
in case (ii), where
![]() $c_{3, d}$
is the universal constant from (3.16). In case (iii),
$c_{3, d}$
is the universal constant from (3.16). In case (iii),
 $$ \begin{align*}\langle \omega_1, \omega_2, \omega_3 \rangle_{0, d \beta_3} = \left (-18 +5d c_{3,d} - \,\, 2 \sum_{i=1}^{d-1} i c_{3, i} + \frac{1}{3} \sum_{i=1}^{d-1} i c_{3, i} \,\, (d-i) c_{3, d-i} \right ) K_X^2. \end{align*} $$
$$ \begin{align*}\langle \omega_1, \omega_2, \omega_3 \rangle_{0, d \beta_3} = \left (-18 +5d c_{3,d} - \,\, 2 \sum_{i=1}^{d-1} i c_{3, i} + \frac{1}{3} \sum_{i=1}^{d-1} i c_{3, i} \,\, (d-i) c_{3, d-i} \right ) K_X^2. \end{align*} $$
Via a representation theoretic approach, [Reference Li and Qin28] presents a complicated proof of Ruan’s Cohomological Crepant Resolution Conjecture for the Hilbert-Chow morphism
![]() $\rho _n: X^{[n]} \to X^{(n)}$
for all
$\rho _n: X^{[n]} \to X^{(n)}$
for all
![]() $n \ge 1$
. As an application of Theorem 4.10 (together with the results in [Reference Li and Li23, Reference Li and Qin27] about the
$n \ge 1$
. As an application of Theorem 4.10 (together with the results in [Reference Li and Li23, Reference Li and Qin27] about the
![]() $1$
-point and
$1$
-point and
![]() $2$
-point genus-
$2$
-point genus-
![]() $0$
extremal Gromov-Witten invariants of
$0$
extremal Gromov-Witten invariants of
![]() $ X^{[n]}$
), we now give a direct (but tedious) proof of this conjecture when
$ X^{[n]}$
), we now give a direct (but tedious) proof of this conjecture when
![]() $n=3$
.
$n=3$
.
Corollary 4.11. Let X be a simply connected smooth projective surface. Then Ruan’s Cohomological Crepant Resolution Conjecture for the Hilbert-Chow morphism
![]() $\rho _3: X^{[3]} \to X^{(3)}$
holds (i.e., the Chen-Ruan cohomology ring of
$\rho _3: X^{[3]} \to X^{(3)}$
holds (i.e., the Chen-Ruan cohomology ring of
![]() $X^{(3)}$
is isomorphic to the quantum corrected cohomology ring of
$X^{(3)}$
is isomorphic to the quantum corrected cohomology ring of
![]() $ X^{[3]}$
).
$ X^{[3]}$
).
Proof. First of all, we briefly recall from [Reference Ruan39] and [Reference Qin38, Chapter 16] that the Cohomological Crepant Resolution Conjecture for
![]() $\rho _n: X^{[n]} \to X^{(n)}$
asserts that there exists a ring isomorphism
$\rho _n: X^{[n]} \to X^{(n)}$
asserts that there exists a ring isomorphism
where
![]() $H_{CR}^*(X^{(n)}, {\mathbb C} )$
is the Chen-Ruan cohomology of
$H_{CR}^*(X^{(n)}, {\mathbb C} )$
is the Chen-Ruan cohomology of
![]() $X^{(n)}$
, and
$X^{(n)}$
, and
![]() $H_{\rho _n}^*( X^{[n]}, {\mathbb C} )$
is the cohomology
$H_{\rho _n}^*( X^{[n]}, {\mathbb C} )$
is the cohomology
![]() $H^*( X^{[n]}, {\mathbb C} )$
together with the quantum corrected ring product
$H^*( X^{[n]}, {\mathbb C} )$
together with the quantum corrected ring product
![]() $\cdot _{\rho _n}$
. For
$\cdot _{\rho _n}$
. For
![]() $w_1, w_2 \in H^*( X^{[n]}, {\mathbb C} )$
, the product
$w_1, w_2 \in H^*( X^{[n]}, {\mathbb C} )$
, the product
![]() $w_1 \cdot _{\rho _n} w_2$
is defined by putting
$w_1 \cdot _{\rho _n} w_2$
is defined by putting
where
![]() $w_3 \in H^*( X^{[n]}, {\mathbb C} )$
,
$w_3 \in H^*( X^{[n]}, {\mathbb C} )$
,
![]() $\langle \cdot , \cdot \rangle $
on the left-hand side is the pairing on
$\langle \cdot , \cdot \rangle $
on the left-hand side is the pairing on
![]() $H^*( X^{[n]}, {\mathbb C} )$
, and
$H^*( X^{[n]}, {\mathbb C} )$
, and
with q being a variable. Put
By [Reference Qin38, Theorem 10.1], the space
![]() $\mathcal F_X$
is an irreducible representation of the Heisenberg algebra generated by the operators
$\mathcal F_X$
is an irreducible representation of the Heisenberg algebra generated by the operators
![]() $\mathfrak p_m(\alpha ) \in \mathrm {End}(\mathcal F_X), m \in \mathbb Z$
and
$\mathfrak p_m(\alpha ) \in \mathrm {End}(\mathcal F_X), m \in \mathbb Z$
and
![]() $\alpha \in H^*(X, {\mathbb C} )$
with the commutation relation
$\alpha \in H^*(X, {\mathbb C} )$
with the commutation relation
and with the vacuum vector
![]() $|0\rangle = 1 \in H^*(pt, {\mathbb C} ) \cong {\mathbb C} $
. Define
$|0\rangle = 1 \in H^*(pt, {\mathbb C} ) \cong {\mathbb C} $
. Define
![]() $\Psi _n$
by putting
$\Psi _n$
by putting
Then,
![]() $\Psi _n: H_{CR}^*(X^{(n)}, {\mathbb C} ) \to H_{\rho _n}^*( X^{[n]}, {\mathbb C} )$
is an isomorphism of vector spaces. To show
$\Psi _n: H_{CR}^*(X^{(n)}, {\mathbb C} ) \to H_{\rho _n}^*( X^{[n]}, {\mathbb C} )$
is an isomorphism of vector spaces. To show
![]() $\Psi _n$
is a ring isomorphism, we must prove that for all
$\Psi _n$
is a ring isomorphism, we must prove that for all
![]() $w_1, w_2, w_3 \in H_{\rho _n}^*( X^{[n]}, {\mathbb C} )$
,
$w_1, w_2, w_3 \in H_{\rho _n}^*( X^{[n]}, {\mathbb C} )$
,
In the rest of the proof, we assume
![]() $n =3$
. To prove (4.34), it suffices to prove it as
$n =3$
. To prove (4.34), it suffices to prove it as
![]() $w_1, w_2, w_3$
run over the linear basis (4.6) of
$w_1, w_2, w_3$
run over the linear basis (4.6) of
![]() $H_{\rho _n}^*( X^{[3]}, {\mathbb C} )$
. We will only prove (4.34) for the case
$H_{\rho _n}^*( X^{[3]}, {\mathbb C} )$
. We will only prove (4.34) for the case
with
![]() $\alpha _i \in H^2(X, {\mathbb C} )$
since the remaining cases are similar, long and tedious. By Theorem 4.10 (ii) and (3.16),
$\alpha _i \in H^2(X, {\mathbb C} )$
since the remaining cases are similar, long and tedious. By Theorem 4.10 (ii) and (3.16),
![]() $\langle w_1, w_2, w_3 \rangle _{\rho _n}(q)$
is equal to
$\langle w_1, w_2, w_3 \rangle _{\rho _n}(q)$
is equal to
 $$ \begin{align*}\langle w_1, w_2, w_3 \rangle -2 \langle K_X, \alpha_i \rangle \sum_{d \ge 1} d c_{3, d} q^d = \langle w_1, w_2, w_3 \rangle + 18 \langle K_X, \alpha_i \rangle \left ( \frac{3q^3}{q^3+1} - \frac{q}{q+1} \right ). \end{align*} $$
$$ \begin{align*}\langle w_1, w_2, w_3 \rangle -2 \langle K_X, \alpha_i \rangle \sum_{d \ge 1} d c_{3, d} q^d = \langle w_1, w_2, w_3 \rangle + 18 \langle K_X, \alpha_i \rangle \left ( \frac{3q^3}{q^3+1} - \frac{q}{q+1} \right ). \end{align*} $$
So
![]() $\langle w_1, w_2, w_3 \rangle _{\rho _n}(-1) = \langle w_1, w_2, w_3 \rangle + 18 \langle K_X, \alpha _i \rangle $
. We claim that
$\langle w_1, w_2, w_3 \rangle _{\rho _n}(-1) = \langle w_1, w_2, w_3 \rangle + 18 \langle K_X, \alpha _i \rangle $
. We claim that
Indeed, we see from the first five lines in the proof of Lemma 4.8 that
Note that
![]() $\langle c_1^2 \cdot w_1, w_3 \rangle = \langle c_1 w_1, c_1 w_3 \rangle $
. By (4.20),
$\langle c_1^2 \cdot w_1, w_3 \rangle = \langle c_1 w_1, c_1 w_3 \rangle $
. By (4.20),
![]() $\langle w_1, w_2, w_3 \rangle $
is equal to
$\langle w_1, w_2, w_3 \rangle $
is equal to
 $$ \begin{align*}3\langle {\mathfrak a}_{-1} {\mathfrak a}_{-2} &(\tau_{2*}1_X)|0\rangle, c_1 w_3 \rangle + 3\langle {\mathfrak a}_{-3}(K_X)|0\rangle, c_1 w_3 \rangle\\&+ \frac12 \langle {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-2}(K_X)|0\rangle \cdot w_1, w_3 \rangle.\end{align*} $$
$$ \begin{align*}3\langle {\mathfrak a}_{-1} {\mathfrak a}_{-2} &(\tau_{2*}1_X)|0\rangle, c_1 w_3 \rangle + 3\langle {\mathfrak a}_{-3}(K_X)|0\rangle, c_1 w_3 \rangle\\&+ \frac12 \langle {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-2}(K_X)|0\rangle \cdot w_1, w_3 \rangle.\end{align*} $$
Similar to (4.20),
![]() $c_1 w_3$
is equal to
$c_1 w_3$
is equal to
Together with
![]() $\langle {\mathfrak a}_{-3}(K_X)|0\rangle , {\mathfrak a}_{-3}(\alpha _i)|0\rangle \rangle = 3 \langle K_X, \alpha _i \rangle $
, we see that
$\langle {\mathfrak a}_{-3}(K_X)|0\rangle , {\mathfrak a}_{-3}(\alpha _i)|0\rangle \rangle = 3 \langle K_X, \alpha _i \rangle $
, we see that
By a similar calculation,
![]() $\langle {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-2}(K_X)|0\rangle \cdot w_1, w_3 \rangle = 12 \langle K_X, \alpha _i \rangle $
. So we get
$\langle {\mathfrak a}_{-1}(1_X) {\mathfrak a}_{-2}(K_X)|0\rangle \cdot w_1, w_3 \rangle = 12 \langle K_X, \alpha _i \rangle $
. So we get
![]() $ \langle w_1, w_2, w_3 \rangle = -24 \langle K_X, \alpha _i \rangle + 6 \langle K_X, \alpha _i \rangle = -18 \langle K_X, \alpha _i \rangle. $
This proves (4.36). Thus,
$ \langle w_1, w_2, w_3 \rangle = -24 \langle K_X, \alpha _i \rangle + 6 \langle K_X, \alpha _i \rangle = -18 \langle K_X, \alpha _i \rangle. $
This proves (4.36). Thus,
On the orbifold side, the calculation of
![]() $\langle \Psi _3^{-1}(w_1), \Psi _3^{-1}(w_2), \Psi _3^{-1}(w_3) \rangle _{CR}$
is similar but much simpler. Indeed, by the results in [Reference Qin38],
$\langle \Psi _3^{-1}(w_1), \Psi _3^{-1}(w_2), \Psi _3^{-1}(w_3) \rangle _{CR}$
is similar but much simpler. Indeed, by the results in [Reference Qin38],
can be read from its counterpart
![]() $\langle w_1, w_2, w_3 \rangle $
by replacing every term
$\langle w_1, w_2, w_3 \rangle $
by replacing every term
![]() $\langle K_X, \alpha _i \rangle $
by
$\langle K_X, \alpha _i \rangle $
by
![]() $0$
. Hence,
$0$
. Hence,
![]() $ \langle \Psi _3^{-1}(w_1), \Psi _3^{-1}(w_2), \Psi _3^{-1}(w_3) \rangle _{CR} = 0 $
by (4.36). Together with (4.37), we conclude that (4.34) holds for the case (4.35).
$ \langle \Psi _3^{-1}(w_1), \Psi _3^{-1}(w_2), \Psi _3^{-1}(w_3) \rangle _{CR} = 0 $
by (4.36). Together with (4.37), we conclude that (4.34) holds for the case (4.35).
5 Genus-
 $1$
extremal Gromov-Witten invariants of
$1$
extremal Gromov-Witten invariants of
 $ X^{[3]}$
$ X^{[3]}$
In this section, we determine the genus-
![]() $1$
extremal Gromov-Witten invariants of the Hilbert scheme
$1$
extremal Gromov-Witten invariants of the Hilbert scheme
![]() $ X^{[3]}$
. First of all, we show that Conjecture 1.3 holds for
$ X^{[3]}$
. First of all, we show that Conjecture 1.3 holds for
![]() $n=3$
.
$n=3$
.
Lemma 5.1. Let X be a smooth projective surface, and let
![]() $d \ge 1$
. Then,
$d \ge 1$
. Then,
where
![]() $a_d$
and
$a_d$
and
![]() $b_d$
are universal constants depending only on d.
$b_d$
are universal constants depending only on d.
Proof. Let
![]() $[\varphi : D \to X^{[3]}] \in {\overline {\mathfrak M}}_{1, 0}( X^{[3]}, d\beta _3)$
. Then,
$[\varphi : D \to X^{[3]}] \in {\overline {\mathfrak M}}_{1, 0}( X^{[3]}, d\beta _3)$
. Then,
![]() $\varphi (D)$
is contracted by the Hilbert-Chow morphism
$\varphi (D)$
is contracted by the Hilbert-Chow morphism
![]() $\rho _3: X^{[3]} \to X^{(3)}$
. So either
$\rho _3: X^{[3]} \to X^{(3)}$
. So either
![]() $\rho _3(\varphi (D)) = x_1 + 2x_2$
for some points
$\rho _3(\varphi (D)) = x_1 + 2x_2$
for some points
![]() $x_1 \ne x_2$
, or
$x_1 \ne x_2$
, or
![]() $\rho _3(\varphi (D)) = 3x$
for some point
$\rho _3(\varphi (D)) = 3x$
for some point
![]() $x \in X$
. When
$x \in X$
. When
![]() $\rho _3(\varphi (D)) = x_1 + 2x_2$
, every image
$\rho _3(\varphi (D)) = x_1 + 2x_2$
, every image
![]() $\varphi (p)$
is of the form
$\varphi (p)$
is of the form
![]() $x_1 + \xi (p)$
for some
$x_1 + \xi (p)$
for some
![]() $\xi (p) \in M_2(x_2)$
. Define
$\xi (p) \in M_2(x_2)$
. Define
by
![]() $\varphi '(p) = \xi (p)$
. Then
$\varphi '(p) = \xi (p)$
. Then
![]() $\varphi '$
is a stable map, and gives rise to an element
$\varphi '$
is a stable map, and gives rise to an element
The stable map
![]() $\varphi '$
is one of the two components in the standard decomposition of
$\varphi '$
is one of the two components in the standard decomposition of
![]() $\varphi $
(see (3.13)). The other component in the standard decomposition of
$\varphi $
(see (3.13)). The other component in the standard decomposition of
![]() $\varphi $
is the constant map
$\varphi $
is the constant map
![]() $D \to x_1 \in X$
. Conversely, given a point
$D \to x_1 \in X$
. Conversely, given a point
![]() $x_1 \in X$
and an element
$x_1 \in X$
and an element
with
![]() $\{x_1\} \ne \mathrm {Supp} \big (\rho _2(\varphi '(D)) \big )$
, we can define a unique stable map
$\{x_1\} \ne \mathrm {Supp} \big (\rho _2(\varphi '(D)) \big )$
, we can define a unique stable map
by
![]() $\varphi (p) = x_1 + \varphi '(p)$
. Using the arguments in [Reference Li and Qin28], we conclude that
$\varphi (p) = x_1 + \varphi '(p)$
. Using the arguments in [Reference Li and Qin28], we conclude that
for some universal constants
![]() $a_d$
and
$a_d$
and
![]() $b_d$
depending only on d.
$b_d$
depending only on d.
In the rest of this section, we will determine the universal constants
![]() $a_d$
and
$a_d$
and
![]() $b_d$
in Lemma 5.1. We will let X be a smooth projective toric surface and use torus actions and virtual localizations as in [Reference Edidin, Li and Qin8, Reference Graber and Pandharipande12, Reference Kontsevich and Manin20, Reference Liu and Sheshmani30] to compute
$b_d$
in Lemma 5.1. We will let X be a smooth projective toric surface and use torus actions and virtual localizations as in [Reference Edidin, Li and Qin8, Reference Graber and Pandharipande12, Reference Kontsevich and Manin20, Reference Liu and Sheshmani30] to compute
![]() $\langle \rangle _{1, d\beta _3}$
.
$\langle \rangle _{1, d\beta _3}$
.
5.1 The contracted
 $( {\mathbb C} ^*)^2$
-invariant curves in
$( {\mathbb C} ^*)^2$
-invariant curves in
 $ X^{[3]}$
for a toric surface X
$ X^{[3]}$
for a toric surface X
Let X be a smooth projective toric surface. In this subsection, we will write down all the invariant curves contracted by the Hilbert-Chow morphism
![]() $\rho _3: X^{[3]} \to X^{(3)}$
.
$\rho _3: X^{[3]} \to X^{(3)}$
.
We begin with some standard setups. The surface X is determined by a fan
![]() $\Sigma $
which is a finite collection of strongly convex rational polyhedral cones
$\Sigma $
which is a finite collection of strongly convex rational polyhedral cones
![]() $\sigma $
contained in
$\sigma $
contained in
![]() $N = \mathrm {Hom}(M, \mathbb Z)$
, where
$N = \mathrm {Hom}(M, \mathbb Z)$
, where
![]() $M \cong \mathbb Z^2$
. So X is obtained by gluing together affine toric varieties
$M \cong \mathbb Z^2$
. So X is obtained by gluing together affine toric varieties
![]() $X_{\sigma }$
and
$X_{\sigma }$
and
![]() $X_{\tau }$
along
$X_{\tau }$
along
![]() $X_{\sigma \cap \tau }$
for
$X_{\sigma \cap \tau }$
for
![]() $\sigma , \tau \in \Sigma $
. The coordinate ring of
$\sigma , \tau \in \Sigma $
. The coordinate ring of
![]() $X_{\sigma }$
is
$X_{\sigma }$
is
![]() $ {\mathbb C} [\sigma ^{\vee } \cap M]$
, which is the
$ {\mathbb C} [\sigma ^{\vee } \cap M]$
, which is the
![]() $ {\mathbb C} $
-algebra with generators
$ {\mathbb C} $
-algebra with generators
![]() $\chi ^m$
for
$\chi ^m$
for
![]() $m \in \sigma ^{\vee } \cap M$
and multiplication defined by
$m \in \sigma ^{\vee } \cap M$
and multiplication defined by
![]() $\chi ^m \cdot \chi ^{m'} = \chi ^{m+m'}$
. By definition,
$\chi ^m \cdot \chi ^{m'} = \chi ^{m+m'}$
. By definition,
![]() $\sigma ^{\vee } \cap M$
is the set of elements
$\sigma ^{\vee } \cap M$
is the set of elements
![]() $m \in M$
satisfying
$m \in M$
satisfying
![]() $v(m) \ge 0$
for all
$v(m) \ge 0$
for all
![]() $v \in \sigma $
. The torus
$v \in \sigma $
. The torus
acts on X with finitely many fixed points
![]() $x_1, \ldots , x_{\chi (X)}$
. For each i, the point
$x_1, \ldots , x_{\chi (X)}$
. For each i, the point
![]() $x_i$
lies in
$x_i$
lies in
![]() $U_i := X_{\sigma _i}$
for some
$U_i := X_{\sigma _i}$
for some
![]() $\sigma _i \in \Sigma $
. As X is smooth and
$\sigma _i \in \Sigma $
. As X is smooth and
![]() $U_i$
possesses a unique fixed point
$U_i$
possesses a unique fixed point
![]() $x_i$
,
$x_i$
,
![]() $U_i$
is isomorphic to the affine plane with
$U_i$
is isomorphic to the affine plane with
![]() $x_i$
corresponding to the origin. Let
$x_i$
corresponding to the origin. Let
![]() $u_i, v_i$
be the affine coordinates of
$u_i, v_i$
be the affine coordinates of
![]() $U_i$
. Assume that
$U_i$
. Assume that
for
![]() $(s, t) \in {\mathbb T}$
, where
$(s, t) \in {\mathbb T}$
, where
![]() $\lambda _i(s,t)$
and
$\lambda _i(s,t)$
and
![]() $\mu _i(s,t)$
are two independent characters of
$\mu _i(s,t)$
are two independent characters of
![]() $ {\mathbb T}$
. Denote the weights of
$ {\mathbb T}$
. Denote the weights of
![]() $\lambda _i(s,t)$
and
$\lambda _i(s,t)$
and
![]() $\mu _i(s,t)$
by
$\mu _i(s,t)$
by
![]() $w_i$
and
$w_i$
and
![]() $z_i$
, respectively, that is,
$z_i$
, respectively, that is,
in the equivariant Chow group
![]() $A^{ {\mathbb T}}_*(pt)$
. By the Atiyah-Bott localization formula,
$A^{ {\mathbb T}}_*(pt)$
. By the Atiyah-Bott localization formula,
 $$ \begin{align} K_X^2 = \int_X c_1(T_X)^2 = \sum_{i=1}^{\chi(X)} \frac{(w_i + z_i)^2}{w_iz_i} \end{align} $$
$$ \begin{align} K_X^2 = \int_X c_1(T_X)^2 = \sum_{i=1}^{\chi(X)} \frac{(w_i + z_i)^2}{w_iz_i} \end{align} $$
noting that
![]() $T_{x_i, X} = \big ( \lambda _i(s,t) \big )^{-1} + \big ( \mu _i(s,t) \big )^{-1}$
as representations.
$T_{x_i, X} = \big ( \lambda _i(s,t) \big )^{-1} + \big ( \mu _i(s,t) \big )^{-1}$
as representations.
The
![]() $ {\mathbb T}$
-action on the toric surface X induces a
$ {\mathbb T}$
-action on the toric surface X induces a
![]() $ {\mathbb T}$
-action on the Hilbert scheme
$ {\mathbb T}$
-action on the Hilbert scheme
![]() $ X^{[3]}$
with a finite number of fixed points. The
$ X^{[3]}$
with a finite number of fixed points. The
![]() $ {\mathbb T}$
-fixed points in
$ {\mathbb T}$
-fixed points in
![]() $ X^{[3]}$
are enumerated as follows. For each
$ X^{[3]}$
are enumerated as follows. For each
![]() $1 \le i \le \chi (X)$
, there are three
$1 \le i \le \chi (X)$
, there are three
![]() $ {\mathbb T}$
-fixed points
$ {\mathbb T}$
-fixed points
in
![]() $M_3(x_i) \subset X^{[3]}$
corresponding, respectively, to the partitions
$M_3(x_i) \subset X^{[3]}$
corresponding, respectively, to the partitions
![]() $(2,1)$
,
$(2,1)$
,
![]() $(3)$
and
$(3)$
and
![]() $(1,1,1)$
of
$(1,1,1)$
of
![]() $3$
. The corresponding ideals are
$3$
. The corresponding ideals are
![]() $(v_i^2, v_iu_i, u_i^2)$
,
$(v_i^2, v_iu_i, u_i^2)$
,
![]() $(v_i^3, u_i)$
and
$(v_i^3, u_i)$
and
![]() $(v_i, u_i^3)$
. Also for each ordered pair
$(v_i, u_i^3)$
. Also for each ordered pair
![]() $(i, j)$
with
$(i, j)$
with
![]() $i, j \in \{1, \ldots , \chi (X)\}$
and
$i, j \in \{1, \ldots , \chi (X)\}$
and
![]() $i \ne j$
, we have two fixed points
$i \ne j$
, we have two fixed points
in
![]() $ X^{[3]}$
, where
$ X^{[3]}$
, where
![]() $\xi _{i, 1}, \xi _{i, 2} \in M_2(x_i)$
correspond to the ideals
$\xi _{i, 1}, \xi _{i, 2} \in M_2(x_i)$
correspond to the ideals
![]() $(v_i^2, u_i), (v_i, u_i^2)$
, respectively. Furthermore, whenever
$(v_i^2, u_i), (v_i, u_i^2)$
, respectively. Furthermore, whenever
![]() $i, j, k \in \{1, \ldots , \chi (X)\}$
are mutually distinct,
$i, j, k \in \{1, \ldots , \chi (X)\}$
are mutually distinct,
![]() $x_i+x_j+x_k \in X^{[3]}$
is a
$x_i+x_j+x_k \in X^{[3]}$
is a
![]() $ {\mathbb T}$
-fixed point in
$ {\mathbb T}$
-fixed point in
![]() $ X^{[3]}$
. Denote the tangent space of
$ X^{[3]}$
. Denote the tangent space of
![]() $ X^{[3]}$
at
$ X^{[3]}$
at
![]() $\xi \in X^{[3]}$
by
$\xi \in X^{[3]}$
by
![]() $T_{\xi }$
. As representations of
$T_{\xi }$
. As representations of
![]() $ {\mathbb T}$
, we have the decompositions (see [Reference Ellingsrud and Strømme9]):
$ {\mathbb T}$
, we have the decompositions (see [Reference Ellingsrud and Strømme9]):
There are exactly three
![]() $ {\mathbb T}$
-invariant curves
$ {\mathbb T}$
-invariant curves
![]() $C_{0, 1}^{(i)}$
,
$C_{0, 1}^{(i)}$
,
![]() $C_{0, 2}^{(i)}$
and
$C_{0, 2}^{(i)}$
and
![]() $C_{1, 2}^{(i)}$
in
$C_{1, 2}^{(i)}$
in
![]() $M_3(x_i)$
. Namely,
$M_3(x_i)$
. Namely,
![]() $C_{0, 1}^{(i)}$
goes through
$C_{0, 1}^{(i)}$
goes through
![]() $Q_{i, 0}$
and
$Q_{i, 0}$
and
![]() $Q_{i, 1}$
, and is the fixed locus of
$Q_{i, 1}$
, and is the fixed locus of
![]() $\ker (\lambda _i \mu _i^{-2})$
;
$\ker (\lambda _i \mu _i^{-2})$
;
![]() $C_{0, 2}^{(i)}$
goes through
$C_{0, 2}^{(i)}$
goes through
![]() $Q_{i, 0}$
and
$Q_{i, 0}$
and
![]() $Q_{i, 2}$
, and is the fixed locus of
$Q_{i, 2}$
, and is the fixed locus of
![]() $\ker (\lambda _i^{-2}\mu _i)$
;
$\ker (\lambda _i^{-2}\mu _i)$
;
![]() $C_{1, 2}^{(i)}$
goes through
$C_{1, 2}^{(i)}$
goes through
![]() $Q_{i, 1}$
and
$Q_{i, 1}$
and
![]() $Q_{i, 2}$
, and is the fixed locus of
$Q_{i, 2}$
, and is the fixed locus of
![]() $\ker (\lambda _i^{-1}\mu _i)$
. The following is from [Reference Edidin, Li and Qin8].
$\ker (\lambda _i^{-1}\mu _i)$
. The following is from [Reference Edidin, Li and Qin8].
Lemma 5.2. There are exactly
![]() $\chi (X)(\chi (X)+2) \ {\mathbb T}$
-invariant curves contracted by the Hilbert-Chow morphism
$\chi (X)(\chi (X)+2) \ {\mathbb T}$
-invariant curves contracted by the Hilbert-Chow morphism
![]() $\rho _3: X^{[3]} \to X^{(3)}$
. They are described as follows:
$\rho _3: X^{[3]} \to X^{(3)}$
. They are described as follows:
-
(i) the curves
 $C_{i, j} = M_2(x_i) + x_j$
where
$C_{i, j} = M_2(x_i) + x_j$
where
 $1 \le i, j \le \chi (X)$
and
$1 \le i, j \le \chi (X)$
and
 $i \neq j$
;
$i \neq j$
; -
(ii) the curves
 $C_{k, \ell }^{(i)} \subset M_3(x_i)$
where
$C_{k, \ell }^{(i)} \subset M_3(x_i)$
where
 $1 \le i \le \chi (X)$
and
$1 \le i \le \chi (X)$
and
 $0 \leq k < \ell \le 2$
.
$0 \leq k < \ell \le 2$
.
Moreover,
![]() $C_{i, j} \sim C_{0,1}^{(i)} \sim C_{0,2}^{(i)} \sim \beta _3$
and
$C_{i, j} \sim C_{0,1}^{(i)} \sim C_{0,2}^{(i)} \sim \beta _3$
and
![]() $C_{1,2}^{(i)} \sim 3\beta _3$
for every
$C_{1,2}^{(i)} \sim 3\beta _3$
for every
![]() $1 \le i \ne j \le \chi (X)$
.
$1 \le i \ne j \le \chi (X)$
.
Next, let
![]() $f: {\mathbb P}^1 \to X^{[3]}$
be a degree-d morphism such that the image is one of the
$f: {\mathbb P}^1 \to X^{[3]}$
be a degree-d morphism such that the image is one of the
![]() $ {\mathbb T}$
-invariant curves in Lemma 5.2 and f is totally ramified at the two
$ {\mathbb T}$
-invariant curves in Lemma 5.2 and f is totally ramified at the two
![]() $ {\mathbb T}$
-fixed points in
$ {\mathbb T}$
-fixed points in
![]() $f({\mathbb P}^1)$
. The Euler characteristic
$f({\mathbb P}^1)$
. The Euler characteristic
![]() $\chi (f^*T_{ X^{[3]}})$
(as a representation) has been computed in [Reference Edidin, Li and Qin8]. When
$\chi (f^*T_{ X^{[3]}})$
(as a representation) has been computed in [Reference Edidin, Li and Qin8]. When
![]() $f({\mathbb P}^1) = C_{0,1}^{(i)}$
, we have
$f({\mathbb P}^1) = C_{0,1}^{(i)}$
, we have
 $$ \begin{align} \chi(f^*T_{ X^{[3]}}) &=(1 + \lambda_i^{-1}\mu_i^2 +\lambda_i\mu_i^{-2} + \lambda_i^{-1}\mu_i + \mu_i^{-1} + \lambda_i^{-1} + \mu_i^{-1} - \lambda_i^{-1}\mu_i^{-1}) \nonumber \\ &\quad + (\lambda_i^{-1}\mu_i^2 + 1 + \lambda_i^{-1}\mu_i - \lambda_i^{-2}\mu_i - \lambda_i^{-1}\mu_i^{-1} - \lambda_i^{-1})\Theta_{0,1}^{(i)} \end{align} $$
$$ \begin{align} \chi(f^*T_{ X^{[3]}}) &=(1 + \lambda_i^{-1}\mu_i^2 +\lambda_i\mu_i^{-2} + \lambda_i^{-1}\mu_i + \mu_i^{-1} + \lambda_i^{-1} + \mu_i^{-1} - \lambda_i^{-1}\mu_i^{-1}) \nonumber \\ &\quad + (\lambda_i^{-1}\mu_i^2 + 1 + \lambda_i^{-1}\mu_i - \lambda_i^{-2}\mu_i - \lambda_i^{-1}\mu_i^{-1} - \lambda_i^{-1})\Theta_{0,1}^{(i)} \end{align} $$
where
![]() $\Theta _{0,1}^{(i)} = \sum _{m= 1}^{d-1} (\lambda _i\mu _i^{-2})^{m/d}$
(
$\Theta _{0,1}^{(i)} = \sum _{m= 1}^{d-1} (\lambda _i\mu _i^{-2})^{m/d}$
(
![]() $\Theta _{0,1}^{(i)} = 0$
when
$\Theta _{0,1}^{(i)} = 0$
when
![]() $d=1$
). If
$d=1$
). If
![]() $f({\mathbb P}^1) = C_{0,2}^{(i)}$
, then
$f({\mathbb P}^1) = C_{0,2}^{(i)}$
, then
 $$ \begin{align} \chi(f^*T_{ X^{[3]}}) &=(1 + \mu_i^{-1}\lambda_i^2 +\mu_i\lambda_i^{-2} + \mu_i^{-1}\lambda_i + \lambda_i^{-1} + \mu_i^{-1} + \lambda_i^{-1} - \mu_i^{-1}\lambda_i^{-1}) \nonumber \\ &\quad + (\mu_i^{-1}\lambda_i^2 + 1 + \mu_i^{-1}\lambda_i - \mu_i^{-2}\lambda_i - \mu_i^{-1}\lambda_i^{-1} - \mu_i^{-1})\Theta_{0,2}^{(i)} \end{align} $$
$$ \begin{align} \chi(f^*T_{ X^{[3]}}) &=(1 + \mu_i^{-1}\lambda_i^2 +\mu_i\lambda_i^{-2} + \mu_i^{-1}\lambda_i + \lambda_i^{-1} + \mu_i^{-1} + \lambda_i^{-1} - \mu_i^{-1}\lambda_i^{-1}) \nonumber \\ &\quad + (\mu_i^{-1}\lambda_i^2 + 1 + \mu_i^{-1}\lambda_i - \mu_i^{-2}\lambda_i - \mu_i^{-1}\lambda_i^{-1} - \mu_i^{-1})\Theta_{0,2}^{(i)} \end{align} $$
where
![]() $\Theta _{0,2}^{(i)} = \sum _{m=1}^{d-1} (\mu _i\lambda _i^{-2})^{m/d}$
(
$\Theta _{0,2}^{(i)} = \sum _{m=1}^{d-1} (\mu _i\lambda _i^{-2})^{m/d}$
(
![]() $\Theta _{0,2}^{(i)} = 0$
when
$\Theta _{0,2}^{(i)} = 0$
when
![]() $d = 1$
). Let
$d = 1$
). Let
![]() $\Theta _{1,2}^{(i)} = \sum _{m= 1}^{d-1} (\lambda _i\mu _i^{-1})^{m/d}$
with
$\Theta _{1,2}^{(i)} = \sum _{m= 1}^{d-1} (\lambda _i\mu _i^{-1})^{m/d}$
with
![]() $\Theta _{1,2}^{(i)} = 0$
when
$\Theta _{1,2}^{(i)} = 0$
when
![]() $d=1$
. If
$d=1$
. If
![]() $f({\mathbb P}^1) = C_{1,2}^{(i)}$
, then
$f({\mathbb P}^1) = C_{1,2}^{(i)}$
, then
![]() $\chi (f^*T_{ X^{[3]}})$
is equal to
$\chi (f^*T_{ X^{[3]}})$
is equal to
 $$ \begin{align} &(1 + \lambda_i^{-1}\mu_i^2 + \mu_i +\lambda_i + \lambda_i^{-1}\mu_i - \lambda_i^{-2} - \lambda_i^{-1}\mu_i^{-1} - \lambda_i^{-3} - \lambda_i^{-2}\mu_i^{-1}- \lambda_i^{-1}\mu_i^{-2}) \Theta_{1,2}^{(i)} \notag\\ &\qquad\quad +\, (\lambda_i^{-1} + \mu_i^{-1}+ \lambda_i^{-1}\mu_i+1 + \lambda_i\mu_i^{-1} + \lambda_i^{-1}\mu_i^2 + \mu_i + \lambda_i + \lambda_i^2\mu_i^{-1} \notag \\ &\qquad\qquad\qquad -\, \lambda_i^{-1}\mu_i^{-1} - \lambda_i^{-2}\mu_i^{-1} -\lambda_i^{-1}\mu_i^{-2}). \end{align} $$
$$ \begin{align} &(1 + \lambda_i^{-1}\mu_i^2 + \mu_i +\lambda_i + \lambda_i^{-1}\mu_i - \lambda_i^{-2} - \lambda_i^{-1}\mu_i^{-1} - \lambda_i^{-3} - \lambda_i^{-2}\mu_i^{-1}- \lambda_i^{-1}\mu_i^{-2}) \Theta_{1,2}^{(i)} \notag\\ &\qquad\quad +\, (\lambda_i^{-1} + \mu_i^{-1}+ \lambda_i^{-1}\mu_i+1 + \lambda_i\mu_i^{-1} + \lambda_i^{-1}\mu_i^2 + \mu_i + \lambda_i + \lambda_i^2\mu_i^{-1} \notag \\ &\qquad\qquad\qquad -\, \lambda_i^{-1}\mu_i^{-1} - \lambda_i^{-2}\mu_i^{-1} -\lambda_i^{-1}\mu_i^{-2}). \end{align} $$
Finally, when
![]() $f({\mathbb P}^1) = C_{i, j}$
, then
$f({\mathbb P}^1) = C_{i, j}$
, then
![]() $\chi (f^*T_{ X^{[3]}})$
is equal to
$\chi (f^*T_{ X^{[3]}})$
is equal to
 $$ \begin{align} &(1 + \lambda_i^{-1}\mu_i +\lambda_i\mu_i^{-1} + \lambda_i^{-1} + \mu_i^{-1} + \lambda_j^{-1} + \mu_j^{-1} - \lambda_i^{-1}\mu_i^{-1}) \nonumber \\ &\qquad\quad \ + (1 + \lambda_i^{-1}\mu_i - \lambda_i^{-2} - \lambda_i^{-1}\mu_i^{-1} )\Theta_{1,2}^{(i)}. \end{align} $$
$$ \begin{align} &(1 + \lambda_i^{-1}\mu_i +\lambda_i\mu_i^{-1} + \lambda_i^{-1} + \mu_i^{-1} + \lambda_j^{-1} + \mu_j^{-1} - \lambda_i^{-1}\mu_i^{-1}) \nonumber \\ &\qquad\quad \ + (1 + \lambda_i^{-1}\mu_i - \lambda_i^{-2} - \lambda_i^{-1}\mu_i^{-1} )\Theta_{1,2}^{(i)}. \end{align} $$
5.2
 $ {\mathbb T}$
-invariant stable maps, stable graphs and localizations
$ {\mathbb T}$
-invariant stable maps, stable graphs and localizations
Let X be a smooth projective toric surface and
![]() $d \ge 1$
. For simplicity, put
$d \ge 1$
. For simplicity, put
In this subsection, using virtual localization formula, we will express the genus-
![]() $1$
extremal Gromov-Witten invariant
$1$
extremal Gromov-Witten invariant
![]() $\langle \rangle _{1, d\beta _3}$
in terms of stable graphs.
$\langle \rangle _{1, d\beta _3}$
in terms of stable graphs.
As in [Reference Graber and Pandharipande12, Reference Kontsevich19], if
![]() $[f: C \to X^{[3]}] \in {\overline {\mathfrak M}}_{1, 0, d}$
is
$[f: C \to X^{[3]}] \in {\overline {\mathfrak M}}_{1, 0, d}$
is
![]() $ {\mathbb T}$
-invariant, then all the nodes, contracted components and ramification points are mapped into the
$ {\mathbb T}$
-invariant, then all the nodes, contracted components and ramification points are mapped into the
![]() $ {\mathbb T}$
-fixed point set
$ {\mathbb T}$
-fixed point set
![]() $( X^{[3]})^{{\mathbb T}}$
. Moreover, if
$( X^{[3]})^{{\mathbb T}}$
. Moreover, if
![]() $\widetilde C \subset C$
is a noncontracted component, then
$\widetilde C \subset C$
is a noncontracted component, then
![]() $\widetilde C = {\mathbb P}^1$
,
$\widetilde C = {\mathbb P}^1$
,
![]() $f(\widetilde C)$
is one of the
$f(\widetilde C)$
is one of the
![]() $ {\mathbb T}$
-invariant curves in Lemma 5.2, and
$ {\mathbb T}$
-invariant curves in Lemma 5.2, and
![]() $f|_{\widetilde C}$
is of the form
$f|_{\widetilde C}$
is of the form
where
![]() $\tilde d = \deg (f|_{\widetilde C})$
. Therefore, to each stable map
$\tilde d = \deg (f|_{\widetilde C})$
. Therefore, to each stable map
![]() $[f: C \to X^{[3]}] \in ( {\overline {\mathfrak M}}_{1, 0, d})^{{\mathbb T}}$
, we can associate a stable graph
$[f: C \to X^{[3]}] \in ( {\overline {\mathfrak M}}_{1, 0, d})^{{\mathbb T}}$
, we can associate a stable graph
![]() $\Gamma $
as follows. The stable graph
$\Gamma $
as follows. The stable graph
![]() $\Gamma $
has one vertex for each connected component of
$\Gamma $
has one vertex for each connected component of
![]() $f^{-1}(( X^{[3]})^{{\mathbb T}})$
and one edge for every noncontracted component. The edge e is marked with the degree
$f^{-1}(( X^{[3]})^{{\mathbb T}})$
and one edge for every noncontracted component. The edge e is marked with the degree
![]() $d_e$
of f restricted to that noncontracted component
$d_e$
of f restricted to that noncontracted component
![]() $C_e = {\mathbb P}^1$
, and the connected component corresponding to a vertex v is denoted by
$C_e = {\mathbb P}^1$
, and the connected component corresponding to a vertex v is denoted by
![]() $C_v$
. Let
$C_v$
. Let
![]() $V(\Gamma )$
(respectively,
$V(\Gamma )$
(respectively,
![]() $E(\Gamma )$
) denote the set of vertices (respectively, edges) of
$E(\Gamma )$
) denote the set of vertices (respectively, edges) of
![]() $\Gamma $
. Define the labeling map
$\Gamma $
. Define the labeling map
by putting
![]() $\mathfrak L(v) = f(C_v)$
. The vertices have an additional labeling
$\mathfrak L(v) = f(C_v)$
. The vertices have an additional labeling
![]() $g(v)$
which is the arithmetic genus of
$g(v)$
which is the arithmetic genus of
![]() $C_v$
(
$C_v$
(
![]() $g(v) = 0$
if
$g(v) = 0$
if
![]() $C_v$
is a point) and satisfies the identity
$C_v$
is a point) and satisfies the identity
The valence of v, denoted by
![]() $\mathrm {val}(v)$
, is the number of edges connected to v. Define a flag F of the graph
$\mathrm {val}(v)$
, is the number of edges connected to v. Define a flag F of the graph
![]() $\Gamma $
to be an incident edge-vertex pair
$\Gamma $
to be an incident edge-vertex pair
![]() $(e, v)$
. Put
$(e, v)$
. Put
A flag
![]() $F = (e, v)$
is defined to be stable if
$F = (e, v)$
is defined to be stable if
![]() $2g(v) + \mathrm {val}(v) \ge 3$
. Since
$2g(v) + \mathrm {val}(v) \ge 3$
. Since
![]() $\mathrm {val}(v) \ge 1$
, F is not stable if
$\mathrm {val}(v) \ge 1$
, F is not stable if
![]() $g(v) = 0$
and
$g(v) = 0$
and
![]() $\mathrm {val}(v) = 1$
or
$\mathrm {val}(v) = 1$
or
![]() $2$
(in these cases, the component
$2$
(in these cases, the component
![]() $C_v$
is simply a point). Let
$C_v$
is simply a point). Let
![]() $F(\Gamma )$
(respectively,
$F(\Gamma )$
(respectively,
![]() $F(\Gamma )^{\mathrm {sta}}$
) be the set of flags (respectively, stable flags) in
$F(\Gamma )^{\mathrm {sta}}$
) be the set of flags (respectively, stable flags) in
![]() $\Gamma $
. The edge e in
$\Gamma $
. The edge e in
![]() $F = (e, v)$
is incident to one other vertex
$F = (e, v)$
is incident to one other vertex
![]() $v'$
. Define
$v'$
. Define
![]() $j(F) = \mathfrak L(v')$
. If
$j(F) = \mathfrak L(v')$
. If
![]() $\mathrm {val}(v) = 1$
, let
$\mathrm {val}(v) = 1$
, let
![]() $F(v)$
be the unique flag containing v; if
$F(v)$
be the unique flag containing v; if
![]() $\mathrm {val}(v) = 2$
, let
$\mathrm {val}(v) = 2$
, let
![]() $F_1(v)$
and
$F_1(v)$
and
![]() $F_2(v)$
denote the two flags containing v.
$F_2(v)$
denote the two flags containing v.
Now the connected components of
![]() $( {\overline {\mathfrak M}}_{1, 0, d})^{{\mathbb T}}$
are indexed by stable graphs corresponding to stable maps whose images are unions of the
$( {\overline {\mathfrak M}}_{1, 0, d})^{{\mathbb T}}$
are indexed by stable graphs corresponding to stable maps whose images are unions of the
![]() $ {\mathbb T}$
-invariant curves in Lemma 5.2 and whose contracted components and special points are mapped into
$ {\mathbb T}$
-invariant curves in Lemma 5.2 and whose contracted components and special points are mapped into
![]() $( X^{[3]})^{{\mathbb T}}$
. We use
$( X^{[3]})^{{\mathbb T}}$
. We use
![]() $\Gamma $
to denote these stable graphs. So we have
$\Gamma $
to denote these stable graphs. So we have
where
![]() ${ {\overline {\mathfrak M}}}_{\Gamma }$
denotes the connected component of
${ {\overline {\mathfrak M}}}_{\Gamma }$
denotes the connected component of
![]() $( {\overline {\mathfrak M}}_{1, 0, d})^{{\mathbb T}}$
indexed by
$( {\overline {\mathfrak M}}_{1, 0, d})^{{\mathbb T}}$
indexed by
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\overline {M}_{g, n}$
be the moduli space of n-pointed genus-g stable curves. Put
$\overline {M}_{g, n}$
be the moduli space of n-pointed genus-g stable curves. Put
(
![]() $\overline {M}_{0, 1}$
and
$\overline {M}_{0, 1}$
and
![]() $\overline {M}_{0, 2}$
are treated as points in this product). Then there is a finite map
$\overline {M}_{0, 2}$
are treated as points in this product). Then there is a finite map
![]() $\overline {M}_{\Gamma } \to {\overline {\mathfrak M}}_{\Gamma }$
such that
$\overline {M}_{\Gamma } \to {\overline {\mathfrak M}}_{\Gamma }$
such that
![]() $ {\overline {\mathfrak M}}_{\Gamma } = \overline {M}_{\Gamma }/\mathbf {A}_{\Gamma }$
where
$ {\overline {\mathfrak M}}_{\Gamma } = \overline {M}_{\Gamma }/\mathbf {A}_{\Gamma }$
where
![]() $\mathbf {A}_{\Gamma }$
fits in the exact sequence
$\mathbf {A}_{\Gamma }$
fits in the exact sequence
Since a stable curve is connected, we see from the description of the
![]() $ {\mathbb T}$
-invariant curves in Lemma 5.2 that a summation over all the stable graphs
$ {\mathbb T}$
-invariant curves in Lemma 5.2 that a summation over all the stable graphs
![]() $\Gamma $
breaks up as
$\Gamma $
breaks up as
 $$ \begin{align} \sum_{\Gamma} \,\, = \,\, \sum_{1 \leq i\neq j \leq \chi(X)} \,\, \sum_{\Gamma \in {{\mathcal S}}_{d,i,j}} \,\, +\,\, \sum_{i=1}^{\chi(X)} \,\,\sum_{\Gamma \in {\mathcal T}_{d,i}} \end{align} $$
$$ \begin{align} \sum_{\Gamma} \,\, = \,\, \sum_{1 \leq i\neq j \leq \chi(X)} \,\, \sum_{\Gamma \in {{\mathcal S}}_{d,i,j}} \,\, +\,\, \sum_{i=1}^{\chi(X)} \,\,\sum_{\Gamma \in {\mathcal T}_{d,i}} \end{align} $$
where
![]() ${{\mathcal S}}_{d,i,j}$
is the set of all stable graphs
${{\mathcal S}}_{d,i,j}$
is the set of all stable graphs
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $f(C) = C_{i,j}$
for every
$f(C) = C_{i,j}$
for every
![]() $[f: C \to X^{[3]}] \in {\overline {\mathfrak M}}_{\Gamma }$
, and
$[f: C \to X^{[3]}] \in {\overline {\mathfrak M}}_{\Gamma }$
, and
![]() ${\mathcal T}_{d,i}$
is the set of all stable graphs
${\mathcal T}_{d,i}$
is the set of all stable graphs
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $f(C) \subset C_{0,1}^{(i)} \cup C_{0,2}^{(i)} \cup C_{1,2}^{(i)}$
for every
$f(C) \subset C_{0,1}^{(i)} \cup C_{0,2}^{(i)} \cup C_{1,2}^{(i)}$
for every
![]() $[f: C \to X^{[3]}] \in {\overline {\mathfrak M}}_{\Gamma }$
.
$[f: C \to X^{[3]}] \in {\overline {\mathfrak M}}_{\Gamma }$
.
By the virtual localization formula of [Reference Graber and Pandharipande12], we have
 $$ \begin{align} \langle \rangle_{1, d\beta_3} \quad = \quad \int_{[ {\overline{\mathfrak M}}_{1, 0, d}]^{\mathrm{vir}} } 1 \quad = \quad \sum_{\Gamma} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]^{\mathrm{vir}} } \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align} $$
$$ \begin{align} \langle \rangle_{1, d\beta_3} \quad = \quad \int_{[ {\overline{\mathfrak M}}_{1, 0, d}]^{\mathrm{vir}} } 1 \quad = \quad \sum_{\Gamma} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]^{\mathrm{vir}} } \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align} $$
Here,
![]() $[\overline {M}_{\Gamma }]^{\mathrm {vir}} $
is the pullback of
$[\overline {M}_{\Gamma }]^{\mathrm {vir}} $
is the pullback of
![]() $[ {\overline {\mathfrak M}}_{\Gamma }]^{\mathrm {vir}} $
to
$[ {\overline {\mathfrak M}}_{\Gamma }]^{\mathrm {vir}} $
to
![]() $M_{\Gamma }$
via the finite map
$M_{\Gamma }$
via the finite map
![]() $\overline {M}_{\Gamma } \to {\overline {\mathfrak M}}_{\Gamma }$
, and
$\overline {M}_{\Gamma } \to {\overline {\mathfrak M}}_{\Gamma }$
, and
![]() $e(N_{\Gamma }^{\mathrm {vir}} )$
is the pullback of the Euler class of the moving part
$e(N_{\Gamma }^{\mathrm {vir}} )$
is the pullback of the Euler class of the moving part
![]() $N_{\Gamma }^{\mathrm {vir}} $
of the tangent-obstruction complex. Let
$N_{\Gamma }^{\mathrm {vir}} $
of the tangent-obstruction complex. Let
![]() ${{\mathcal T}}^1$
and
${{\mathcal T}}^1$
and
![]() ${{\mathcal T}}^2$
be the cohomology sheaves of the restriction of the tangent-obstruction complex on
${{\mathcal T}}^2$
be the cohomology sheaves of the restriction of the tangent-obstruction complex on
![]() $ {\overline {\mathfrak M}}_{1, 0, d}$
to
$ {\overline {\mathfrak M}}_{1, 0, d}$
to
![]() $ {\overline {\mathfrak M}}_{\Gamma }$
. The fibers of
$ {\overline {\mathfrak M}}_{\Gamma }$
. The fibers of
![]() ${{\mathcal T}}^1$
and
${{\mathcal T}}^1$
and
![]() ${{\mathcal T}}^2$
at a point associated to a stable map
${{\mathcal T}}^2$
at a point associated to a stable map
![]() $[f: C \to X^{[3]}] \in {\overline {\mathfrak M}}_{\Gamma }$
fit into the exact sequence
$[f: C \to X^{[3]}] \in {\overline {\mathfrak M}}_{\Gamma }$
fit into the exact sequence
 $$ \begin{align*} 0 &\to \mathrm{Ext}^0(\Omega_C,{\mathcal O}_C) \to H^0(C, f^*T_{ X^{[3]}}) \to {{\mathcal T}}^1 \\ & \to \mathrm{Ext}^1(\Omega_C,{\mathcal O}_C)\to H^1(C, f^*T_{ X^{[3]}}) \to {{\mathcal T}}^2 \to 0. \end{align*} $$
$$ \begin{align*} 0 &\to \mathrm{Ext}^0(\Omega_C,{\mathcal O}_C) \to H^0(C, f^*T_{ X^{[3]}}) \to {{\mathcal T}}^1 \\ & \to \mathrm{Ext}^1(\Omega_C,{\mathcal O}_C)\to H^1(C, f^*T_{ X^{[3]}}) \to {{\mathcal T}}^2 \to 0. \end{align*} $$
To understand
![]() $H^i(C, f^*T_{ X^{[3]}})$
, consider the normalization sequence resolving the nodes of C coming from all the intersections
$H^i(C, f^*T_{ X^{[3]}})$
, consider the normalization sequence resolving the nodes of C coming from all the intersections
![]() $x_F := C_v \cap C_e$
:
$x_F := C_v \cap C_e$
:
Tensoring by
![]() $f^*T_{ X^{[3]}}$
and taking cohomology, we obtain an exact sequence
$f^*T_{ X^{[3]}}$
and taking cohomology, we obtain an exact sequence
Note that
![]() $H^1(C_v, f^*T_{ X^{[3]}}) = H^1(C_v, \mathcal O_{C_v}) \otimes T_{\mathfrak L(v)}$
where
$H^1(C_v, f^*T_{ X^{[3]}}) = H^1(C_v, \mathcal O_{C_v}) \otimes T_{\mathfrak L(v)}$
where
![]() $H^1(C_v, \mathcal O_{C_v})$
forms the dual of the Hodge bundle
$H^1(C_v, \mathcal O_{C_v})$
forms the dual of the Hodge bundle
![]() $\mathcal H_{g(v)}$
over
$\mathcal H_{g(v)}$
over
![]() $\overline {M}_{g(v), \mathrm {val}(v)}$
. By the five formulas (5.2)-(5.6), the fixed parts of
$\overline {M}_{g(v), \mathrm {val}(v)}$
. By the five formulas (5.2)-(5.6), the fixed parts of
![]() $T_{i(F)}$
and
$T_{i(F)}$
and
![]() $H^1(C_v, f^*T_{ X^{[3]}})$
vanish. Examining the terms in the four formulas (5.7)-(5.10) which carry negative signs, we see that the fixed part of
$H^1(C_v, f^*T_{ X^{[3]}})$
vanish. Examining the terms in the four formulas (5.7)-(5.10) which carry negative signs, we see that the fixed part of
![]() $H^1(C_e, f^*T_{ X^{[3]}})$
also vanishes. By (5.15), the fixed part of
$H^1(C_e, f^*T_{ X^{[3]}})$
also vanishes. By (5.15), the fixed part of
![]() $H^1(C, f^*T_{ X^{[3]}})$
vanishes. Thus,
$H^1(C, f^*T_{ X^{[3]}})$
vanishes. Thus,
![]() ${{\mathcal T}}^{2, f} = 0$
, and the fixed stack is smooth with tangent bundle
${{\mathcal T}}^{2, f} = 0$
, and the fixed stack is smooth with tangent bundle
![]() ${{\mathcal T}}^{1, f}$
. Hence,
${{\mathcal T}}^{1, f}$
. Hence,
![]() $[ {\overline {\mathfrak M}}_{\Gamma }]^{\mathrm {vir}} = [ {\overline {\mathfrak M}}_{\Gamma }]$
and
$[ {\overline {\mathfrak M}}_{\Gamma }]^{\mathrm {vir}} = [ {\overline {\mathfrak M}}_{\Gamma }]$
and
![]() $[\overline {M}_{\Gamma }]^{\mathrm {vir}} = [\overline {M}_{\Gamma }]$
. By (5.14), we obtain
$[\overline {M}_{\Gamma }]^{\mathrm {vir}} = [\overline {M}_{\Gamma }]$
. By (5.14), we obtain
 $$ \begin{align*} \langle \rangle_{1, d\beta_3} \quad = \quad \sum_{\Gamma} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align*} $$
$$ \begin{align*} \langle \rangle_{1, d\beta_3} \quad = \quad \sum_{\Gamma} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align*} $$
In view of the splitting (5.13), the invariant
![]() $\langle \rangle _{1, d\beta _3}$
can be written as
$\langle \rangle _{1, d\beta _3}$
can be written as
 $$ \begin{align} \sum_{1 \leq i\neq j \leq \chi(X)} \,\, \sum_{\Gamma \in {{\mathcal S}}_{d,i,j}} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} \,\, + \,\, \sum_{i=1}^{\chi(X)} \,\,\sum_{\Gamma \in {\mathcal T}_{d,i}} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} \end{align} $$
$$ \begin{align} \sum_{1 \leq i\neq j \leq \chi(X)} \,\, \sum_{\Gamma \in {{\mathcal S}}_{d,i,j}} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} \,\, + \,\, \sum_{i=1}^{\chi(X)} \,\,\sum_{\Gamma \in {\mathcal T}_{d,i}} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} \end{align} $$
5.3 Reformulation of
 $ \sum _{1 \leq i \neq j \leq \chi (X)} \,\, \sum _{\Gamma \in {{ \mathcal S}}_{d,i,j}}$
$ \sum _{1 \leq i \neq j \leq \chi (X)} \,\, \sum _{\Gamma \in {{ \mathcal S}}_{d,i,j}}$
In this subsection, we will reformulate the summation
![]() $\sum _{1 \leq i\neq j \leq \chi (X)} \,\, \sum _{\Gamma \in {{\mathcal S}}_{d,i,j}}$
in (5.16) by a suitable genus-
$\sum _{1 \leq i\neq j \leq \chi (X)} \,\, \sum _{\Gamma \in {{\mathcal S}}_{d,i,j}}$
in (5.16) by a suitable genus-
![]() $1$
Gromov-Witten invariant of
$1$
Gromov-Witten invariant of
![]() $X \times {X^{[2]}}$
. It allows us to reduce the computation of
$X \times {X^{[2]}}$
. It allows us to reduce the computation of
![]() $\langle \rangle _{1, d\beta _3}$
to the local affine charts
$\langle \rangle _{1, d\beta _3}$
to the local affine charts
![]() $U_i \ni x_i$
.
$U_i \ni x_i$
.
For
![]() $1 \le i \le \chi (X)$
and
$1 \le i \le \chi (X)$
and
![]() $1 \le k \le 2$
, let
$1 \le k \le 2$
, let
![]() $R_{i,i}^{(k)} = (x_i, \xi _{i, k}) \in X \times {X^{[2]}}$
and
$R_{i,i}^{(k)} = (x_i, \xi _{i, k}) \in X \times {X^{[2]}}$
and
For
![]() $1 \le i \ne j \le \chi (X)$
, regard the curve
$1 \le i \ne j \le \chi (X)$
, regard the curve
![]() $C_{i, j} \subset X^{[3]}$
in Lemma 5.2 (i) as the curve
$C_{i, j} \subset X^{[3]}$
in Lemma 5.2 (i) as the curve
![]() $\{ x_j \} \times M_2(x_i) \subset X \times {X^{[2]}}$
. The
$\{ x_j \} \times M_2(x_i) \subset X \times {X^{[2]}}$
. The
![]() $ {\mathbb T}$
-action on X induces a
$ {\mathbb T}$
-action on X induces a
![]() $ {\mathbb T}$
-action on
$ {\mathbb T}$
-action on
![]() $X \times {X^{[2]}}$
. The
$X \times {X^{[2]}}$
. The
![]() $ {\mathbb T}$
-fixed point set
$ {\mathbb T}$
-fixed point set
![]() $(X \times {X^{[2]}})^{{\mathbb T}}$
consists of the points
$(X \times {X^{[2]}})^{{\mathbb T}}$
consists of the points
![]() $R_{i,j}^{(k)}$
with
$R_{i,j}^{(k)}$
with
![]() $1 \le i, j \le \chi (X)$
and
$1 \le i, j \le \chi (X)$
and
![]() $1 \le k \le 2$
. The
$1 \le k \le 2$
. The
![]() $ {\mathbb T}$
-invariant curves in
$ {\mathbb T}$
-invariant curves in
![]() $X \times {X^{[2]}}$
contracted by
$X \times {X^{[2]}}$
contracted by
are precisely the curves
![]() $C_{i, j}$
with
$C_{i, j}$
with
![]() $1 \le i, j \le \chi (X)$
. The decompositions of the tangent spaces of
$1 \le i, j \le \chi (X)$
. The decompositions of the tangent spaces of
![]() $X \times {X^{[2]}}$
at the points
$X \times {X^{[2]}}$
at the points
![]() $R_{i,j}^{(k)}$
are given by the right-hand sides of (5.5) and (5.6). So we keep using
$R_{i,j}^{(k)}$
are given by the right-hand sides of (5.5) and (5.6). So we keep using
![]() $T_{R_{i,j}^{(k)}}$
to denote the tangent space of
$T_{R_{i,j}^{(k)}}$
to denote the tangent space of
![]() $X \times {X^{[2]}}$
at
$X \times {X^{[2]}}$
at
![]() $R_{i,j}^{(k)}$
. Similarly, if
$R_{i,j}^{(k)}$
. Similarly, if
![]() $f: {\mathbb P}^1 \to X \times {X^{[2]}}$
is a degree-d morphism such that
$f: {\mathbb P}^1 \to X \times {X^{[2]}}$
is a degree-d morphism such that
![]() $f({\mathbb P}^1) = C_{i,j}$
and f is totally ramified at the two
$f({\mathbb P}^1) = C_{i,j}$
and f is totally ramified at the two
![]() $ {\mathbb T}$
-fixed points in
$ {\mathbb T}$
-fixed points in
![]() $f({\mathbb P}^1)$
, then the Euler characteristic
$f({\mathbb P}^1)$
, then the Euler characteristic
![]() $\chi (f^*T_{X \times {X^{[2]}}})$
is given by the right-hand side of (5.10).
$\chi (f^*T_{X \times {X^{[2]}}})$
is given by the right-hand side of (5.10).
Regard
![]() $\beta _2 \in H_2( {X^{[2]}})$
as in
$\beta _2 \in H_2( {X^{[2]}})$
as in
![]() $H_2(X \times {X^{[2]}})$
. Apply localization to the moduli space
$H_2(X \times {X^{[2]}})$
. Apply localization to the moduli space
whose expected dimension is equal to
![]() $0$
. The connected components of the
$0$
. The connected components of the
![]() $ {\mathbb T}$
-fixed point set
$ {\mathbb T}$
-fixed point set
![]() $\big ( {\overline {\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta _2) \big )^{{\mathbb T}}$
are indexed by stable graphs
$\big ( {\overline {\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta _2) \big )^{{\mathbb T}}$
are indexed by stable graphs
![]() $\Gamma $
. For
$\Gamma $
. For
![]() $1 \le i, j \le \chi (X)$
, let
$1 \le i, j \le \chi (X)$
, let
![]() ${{\mathcal S}}_{d,i,j}$
be the set of all stable graphs
${{\mathcal S}}_{d,i,j}$
be the set of all stable graphs
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $f(C) = C_{i,j}$
for every stable map
$f(C) = C_{i,j}$
for every stable map
![]() $[f: C \to X \times {X^{[2]}}]$
in the connected component
$[f: C \to X \times {X^{[2]}}]$
in the connected component
![]() $ {\overline {\mathfrak M}}_{\Gamma }$
indexed by
$ {\overline {\mathfrak M}}_{\Gamma }$
indexed by
![]() $\Gamma $
. Note that when
$\Gamma $
. Note that when
![]() $i \ne j$
,
$i \ne j$
,
![]() ${{\mathcal S}}_{d,i,j}$
can be identified with the set
${{\mathcal S}}_{d,i,j}$
can be identified with the set
![]() ${{\mathcal S}}_{d,i,j}$
introduced in (5.13). Moreover, for
${{\mathcal S}}_{d,i,j}$
introduced in (5.13). Moreover, for
![]() $\Gamma \in {{\mathcal S}}_{d,i,j}$
with
$\Gamma \in {{\mathcal S}}_{d,i,j}$
with
![]() $i \ne j$
,
$i \ne j$
,
![]() $ {\overline {\mathfrak M}}_{\Gamma }$
can be identified with the connected component
$ {\overline {\mathfrak M}}_{\Gamma }$
can be identified with the connected component
![]() $ {\overline {\mathfrak M}}_{\Gamma }$
introduced in (5.11). By the virtual localization formula,
$ {\overline {\mathfrak M}}_{\Gamma }$
introduced in (5.11). By the virtual localization formula,
 $$ \begin{align} \int_{[ {\overline{\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta_2)]^{\mathrm{vir}} } 1 \quad = \quad \sum_{1 \leq i, j \leq \chi(X)} \,\, \sum_{\Gamma \in {{\mathcal S}}_{d,i,j}} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align} $$
$$ \begin{align} \int_{[ {\overline{\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta_2)]^{\mathrm{vir}} } 1 \quad = \quad \sum_{1 \leq i, j \leq \chi(X)} \,\, \sum_{\Gamma \in {{\mathcal S}}_{d,i,j}} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align} $$
Note that for each graph
![]() $\Gamma \in {{\mathcal S}}_{d,i,j}$
with
$\Gamma \in {{\mathcal S}}_{d,i,j}$
with
![]() $i \ne j$
, the summand
$i \ne j$
, the summand
 $\displaystyle {\frac {1}{|\mathbf {A}_{\Gamma }|} \int _{[\overline {M}_{\Gamma }]} \frac {1}{e(N_{\Gamma }^{\mathrm {vir}} )}}$
in (5.17) is equal to the corresponding summand in (5.16).
$\displaystyle {\frac {1}{|\mathbf {A}_{\Gamma }|} \int _{[\overline {M}_{\Gamma }]} \frac {1}{e(N_{\Gamma }^{\mathrm {vir}} )}}$
in (5.17) is equal to the corresponding summand in (5.16).
Lemma 5.3.
 $\displaystyle {\int _{[ {\overline {\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta _2)]^{\mathrm {vir}} } 1 \,\, = \,\, \frac {1}{12d} \cdot \chi (X) \cdot K_X^2}$
.
$\displaystyle {\int _{[ {\overline {\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta _2)]^{\mathrm {vir}} } 1 \,\, = \,\, \frac {1}{12d} \cdot \chi (X) \cdot K_X^2}$
.
Proof. We have
![]() $ {\overline {\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta _2) \cong X \times {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
. By the results in [Reference Hu, Li and Qin15], the moduli space
$ {\overline {\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta _2) \cong X \times {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
. By the results in [Reference Hu, Li and Qin15], the moduli space
![]() $ {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
is smooth (as a stack) with dimension
$ {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
is smooth (as a stack) with dimension
![]() $(2d+2)$
, and the obstruction sheaf
$(2d+2)$
, and the obstruction sheaf
![]() $\mathcal Ob = R^1(f_{1,0})_*\mathrm {ev}_1^*T_{ {X^{[2]}}}$
on
$\mathcal Ob = R^1(f_{1,0})_*\mathrm {ev}_1^*T_{ {X^{[2]}}}$
on
![]() $ {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
is locally free of rank
$ {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
is locally free of rank
![]() $(2d+2)$
where
$(2d+2)$
where
![]() $f_{1,0}$
(respectively,
$f_{1,0}$
(respectively,
![]() $\mathrm {ev}_1$
) denotes the forgetful (respectively, evaluation) map on
$\mathrm {ev}_1$
) denotes the forgetful (respectively, evaluation) map on
![]() $ {\overline {\mathfrak M}}_{1, 1}( {X^{[2]}}, d\beta _2)$
. Moreover, we have
$ {\overline {\mathfrak M}}_{1, 1}( {X^{[2]}}, d\beta _2)$
. Moreover, we have
Let
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
be the two projections on
$\phi _2$
be the two projections on
![]() $X \times {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
. Let
$X \times {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
. Let
![]() $\mathcal H_1$
be the (rank-
$\mathcal H_1$
be the (rank-
![]() $1$
) Hodge bundle over the moduli space
$1$
) Hodge bundle over the moduli space
![]() $ {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
. A direct computation shows that the obstruction sheaf over
$ {\overline {\mathfrak M}}_{1, 0}( {X^{[2]}}, d\beta _2)$
. A direct computation shows that the obstruction sheaf over
![]() $ {\overline {\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta _2)$
is isomorphic to
$ {\overline {\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta _2)$
is isomorphic to
which is locally free of rank
![]() $(2d+4)$
. Therefore, we conclude that
$(2d+4)$
. Therefore, we conclude that
 $$ \begin{align*} [ {\overline{\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta_2)]^{\mathrm{vir}} &= c_{2d+4}\big ((\phi_1^*T_X \otimes \phi_2^*\mathcal H_1^{\vee}) \oplus \phi_2^*\mathcal Ob \big ) \\ &= c_2\big (\phi_1^*T_X \otimes \phi_2^*\mathcal H_1^{\vee}\big ) \cdot c_{2d+2}\big (\phi_2^*\mathcal Ob \big ). \end{align*} $$
$$ \begin{align*} [ {\overline{\mathfrak M}}_{1, 0}(X \times {X^{[2]}}, d\beta_2)]^{\mathrm{vir}} &= c_{2d+4}\big ((\phi_1^*T_X \otimes \phi_2^*\mathcal H_1^{\vee}) \oplus \phi_2^*\mathcal Ob \big ) \\ &= c_2\big (\phi_1^*T_X \otimes \phi_2^*\mathcal H_1^{\vee}\big ) \cdot c_{2d+2}\big (\phi_2^*\mathcal Ob \big ). \end{align*} $$
Combining this with (5.18), we immediately verify our lemma.
From (5.16), (5.17) and Lemma 5.3, we conclude that
 $$ \begin{align} \langle \rangle_{1, d\beta_3} = \frac{1}{12d} \cdot \chi(X) \cdot K_X^2 \,\, + \,\, \sum_{i=1}^{\chi(X)} \,\, \left (\sum_{\Gamma \in {\mathcal T}_{d,i}} - \sum_{\Gamma \in {\mathcal S}_{d,i, i}} \right ) \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align} $$
$$ \begin{align} \langle \rangle_{1, d\beta_3} = \frac{1}{12d} \cdot \chi(X) \cdot K_X^2 \,\, + \,\, \sum_{i=1}^{\chi(X)} \,\, \left (\sum_{\Gamma \in {\mathcal T}_{d,i}} - \sum_{\Gamma \in {\mathcal S}_{d,i, i}} \right ) \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align} $$
Note that
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
depends only on the local chart
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
depends only on the local chart
![]() $U_i \ni x_i$
.
$U_i \ni x_i$
.
For simplicity, whenever S is a set of stable graphs, we use
![]() $\sum _{\Gamma \in S}$
to denote
$\sum _{\Gamma \in S}$
to denote
 $$ \begin{align} \sum_{\Gamma \in S} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align} $$
$$ \begin{align} \sum_{\Gamma \in S} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )}. \end{align} $$
5.4 A reduction lemma
In this subsection, we will prove a reduction lemma which indicates that we may ignore most of the stable graphs in
![]() ${\mathcal T}_{d,i}$
and
${\mathcal T}_{d,i}$
and
![]() ${\mathcal S}_{d,i, i}$
when we evaluate the summation
${\mathcal S}_{d,i, i}$
when we evaluate the summation
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
in (5.19).
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
in (5.19).
Before we state the reduction lemma, we present the motivations. As we will see in the next two subsections,
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is of the form
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is of the form
 $$ \begin{align*}(w_i + z_i)^2 \cdot \frac{p_{1,1}(w_i, z_i)}{q_{1,1}(w_i, z_i)} + (w_i + z_i)^3 \cdot \frac{p_{1,2}(w_i, z_i)}{q_{1,2}(w_i, z_i)} \end{align*} $$
$$ \begin{align*}(w_i + z_i)^2 \cdot \frac{p_{1,1}(w_i, z_i)}{q_{1,1}(w_i, z_i)} + (w_i + z_i)^3 \cdot \frac{p_{1,2}(w_i, z_i)}{q_{1,2}(w_i, z_i)} \end{align*} $$
where
![]() $p_{1,1}(w_i, z_i), q_{1,1}(w_i, z_i), p_{1,2}(w_i, z_i), q_{1,2}(w_i, z_i) \in {\mathbb Q}[w_i, z_i]$
are symmetric homogeneous polynomials independent of i and X,
$p_{1,1}(w_i, z_i), q_{1,1}(w_i, z_i), p_{1,2}(w_i, z_i), q_{1,2}(w_i, z_i) \in {\mathbb Q}[w_i, z_i]$
are symmetric homogeneous polynomials independent of i and X,
![]() $(w_i + z_i) \nmid q_{1,1}(w_i, z_i)$
,
$(w_i + z_i) \nmid q_{1,1}(w_i, z_i)$
,
![]() $(w_i + z_i) \nmid q_{1,2}(w_i, z_i)$
,
$(w_i + z_i) \nmid q_{1,2}(w_i, z_i)$
,
![]() $\deg (q_{1,1}) = \deg (p_{1,1}) + 2$
,
$\deg (q_{1,1}) = \deg (p_{1,1}) + 2$
,
![]() $\deg (q_{1,2}) = \deg (p_{1,2}) + 3$
and all the roots of
$\deg (q_{1,2}) = \deg (p_{1,2}) + 3$
and all the roots of
![]() $q_{1,1}(w, 1)$
and
$q_{1,1}(w, 1)$
and
![]() $q_{1,2}(w, 1)$
are rational. Note that
$q_{1,2}(w, 1)$
are rational. Note that
![]() $p_{1,1}(w_i, z_i), q_{1,1}(w_i, z_i), p_{1,2}(w_i, z_i)$
and
$p_{1,1}(w_i, z_i), q_{1,1}(w_i, z_i), p_{1,2}(w_i, z_i)$
and
![]() $q_{1,2}(w_i, z_i)$
can be expressed as polynomials in
$q_{1,2}(w_i, z_i)$
can be expressed as polynomials in
![]() $w_i + z_i$
and
$w_i + z_i$
and
![]() $w_iz_i$
. So the summation
$w_iz_i$
. So the summation
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
can be rewritten as
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
can be rewritten as
 $$ \begin{align*}(w_i + z_i)^2 \cdot \frac{\tilde a \cdot (w_iz_i)^m}{q_{1,1}(w_i, z_i)} + (w_i + z_i)^3 \cdot \frac{p_{2,2}(w_i, z_i)}{q_{1,2}(w_i, z_i)} \end{align*} $$
$$ \begin{align*}(w_i + z_i)^2 \cdot \frac{\tilde a \cdot (w_iz_i)^m}{q_{1,1}(w_i, z_i)} + (w_i + z_i)^3 \cdot \frac{p_{2,2}(w_i, z_i)}{q_{1,2}(w_i, z_i)} \end{align*} $$
where
![]() $\tilde a$
and m are independent of i and X, and
$\tilde a$
and m are independent of i and X, and
![]() $p_{2,2}(w_i, z_i)$
is a symmetric homogeneous polynomial independent of i and X. Put
$p_{2,2}(w_i, z_i)$
is a symmetric homogeneous polynomial independent of i and X. Put
![]() $q_{1,1}(w_i, z_i) = \tilde a_0 (w_iz_i)^{m+1} + \tilde a_1 (w_iz_i)^{m}(w_i + z_i)^2 + \ldots + \tilde a_{m+1}(w_i + z_i)^{2(m+1)}$
. Then,
$q_{1,1}(w_i, z_i) = \tilde a_0 (w_iz_i)^{m+1} + \tilde a_1 (w_iz_i)^{m}(w_i + z_i)^2 + \ldots + \tilde a_{m+1}(w_i + z_i)^{2(m+1)}$
. Then,
 $$ \begin{align*}(w_i + z_i)^2 \cdot \frac{\tilde a \cdot (w_iz_i)^m}{q_{1,1}(w_i, z_i)} = a \cdot \frac{(w_i + z_i)^2}{w_i z_i} - (w_i + z_i)^4 \cdot \frac{p_{2,1}(w_i, z_i)}{w_iz_i \cdot q_{1,1}(w_i, z_i)} \end{align*} $$
$$ \begin{align*}(w_i + z_i)^2 \cdot \frac{\tilde a \cdot (w_iz_i)^m}{q_{1,1}(w_i, z_i)} = a \cdot \frac{(w_i + z_i)^2}{w_i z_i} - (w_i + z_i)^4 \cdot \frac{p_{2,1}(w_i, z_i)}{w_iz_i \cdot q_{1,1}(w_i, z_i)} \end{align*} $$
where
![]() $a = \tilde a/\tilde a_0$
, and
$a = \tilde a/\tilde a_0$
, and
![]() $p_{2,1}(w_i, z_i)$
is a symmetric homogeneous polynomial independent of i and X. It follows that
$p_{2,1}(w_i, z_i)$
is a symmetric homogeneous polynomial independent of i and X. It follows that
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is of the form
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is of the form
 $$ \begin{align} a_d \cdot \frac{(w_i + z_i)^2}{w_i z_i} + (w_i + z_i)^3 \cdot \frac{p_d(w_i, z_i)}{q_d(w_i, z_i)} \end{align} $$
$$ \begin{align} a_d \cdot \frac{(w_i + z_i)^2}{w_i z_i} + (w_i + z_i)^3 \cdot \frac{p_d(w_i, z_i)}{q_d(w_i, z_i)} \end{align} $$
where
![]() $a_d (= a), p_d(w_i, z_i)$
and
$a_d (= a), p_d(w_i, z_i)$
and
![]() $q_d(w_i, z_i)$
are independent of i and X and depend only on d,
$q_d(w_i, z_i)$
are independent of i and X and depend only on d,
![]() $a_d \in {\mathbb Q}$
,
$a_d \in {\mathbb Q}$
,
![]() $p_d(w_i, z_i)$
and
$p_d(w_i, z_i)$
and
![]() $q_d(w_i, z_i)$
are symmetric homogeneous polynomials in
$q_d(w_i, z_i)$
are symmetric homogeneous polynomials in
![]() ${\mathbb Q}[w_i, z_i]$
,
${\mathbb Q}[w_i, z_i]$
,
![]() $(w_i + z_i) \nmid q_d(w_i, z_i)$
and the roots of
$(w_i + z_i) \nmid q_d(w_i, z_i)$
and the roots of
![]() $q_d(w, 1)$
are rational. Our reduction lemma below asserts that
$q_d(w, 1)$
are rational. Our reduction lemma below asserts that
![]() $p_d = 0$
.
$p_d = 0$
.
Lemma 5.4. The summation
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is of the form
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is of the form
 $$ \begin{align} a_d \cdot \frac{(w_i + z_i)^2}{w_i z_i} \end{align} $$
$$ \begin{align} a_d \cdot \frac{(w_i + z_i)^2}{w_i z_i} \end{align} $$
where
![]() $a_d \in {\mathbb Q}$
is independent of i and X and depends only on d, and
$a_d \in {\mathbb Q}$
is independent of i and X and depends only on d, and
 $$ \begin{align} \langle \rangle_{1, d\beta_3} = \left ( a_d + \frac{1}{12d} \cdot \chi(X) \right ) K_X^2. \end{align} $$
$$ \begin{align} \langle \rangle_{1, d\beta_3} = \left ( a_d + \frac{1}{12d} \cdot \chi(X) \right ) K_X^2. \end{align} $$
Proof. Note that (5.23) follows from (5.19), (5.22) and (5.1). In the following, we will prove (5.22) (i.e., we will show that
![]() $p_d = 0$
in (5.21)). For convenience, we will simply write
$p_d = 0$
in (5.21)). For convenience, we will simply write
![]() $a, p, q$
instead of
$a, p, q$
instead of
![]() $a_d, p_d, q_d$
. Assume
$a_d, p_d, q_d$
. Assume
![]() $p \ne 0$
. We will draw contradictions. We may further assume that
$p \ne 0$
. We will draw contradictions. We may further assume that
![]() $p(w_i, z_i)$
and
$p(w_i, z_i)$
and
![]() $q(w_i, z_i)$
have no common factors of positive degrees and that
$q(w_i, z_i)$
have no common factors of positive degrees and that
![]() $q(w, 1)$
is monic.
$q(w, 1)$
is monic.
First of all, we conclude from (5.19), (5.21) and (5.1) that
 $$ \begin{align} \sum_{i=1}^{\chi(X)} (w_i + z_i)^3 \cdot \frac{p(w_i, z_i)}{q(w_i, z_i)} = \langle \rangle_{1, d\beta_3} - \frac{1}{12d} \cdot \chi(X) \cdot K_X^2 - aK_X^2. \end{align} $$
$$ \begin{align} \sum_{i=1}^{\chi(X)} (w_i + z_i)^3 \cdot \frac{p(w_i, z_i)}{q(w_i, z_i)} = \langle \rangle_{1, d\beta_3} - \frac{1}{12d} \cdot \chi(X) \cdot K_X^2 - aK_X^2. \end{align} $$
For simplicity, denote the right-hand side of (5.24) by
![]() $e(X, d)$
. The symmetric polynomials
$e(X, d)$
. The symmetric polynomials
![]() $p(w_i, z_i)$
and
$p(w_i, z_i)$
and
![]() $q(w_i, z_i)$
can be expressed as polynomials in
$q(w_i, z_i)$
can be expressed as polynomials in
![]() $(w_i + z_i)$
and
$(w_i + z_i)$
and
![]() $w_iz_i$
. Since
$w_iz_i$
. Since
![]() $(w_i + z_i) \nmid q(w_i, z_i)$
,
$(w_i + z_i) \nmid q(w_i, z_i)$
,
![]() $q(w_i, z_i)$
is of the form
$q(w_i, z_i)$
is of the form
 $$ \begin{align} q(w_i, z_i) = (w_iz_i)^{n_0} \cdot \tilde q(w_i, z_i) = (w_iz_i)^{n_0} \cdot \prod_{j=1}^k \big ( (w_i + z_i)^2 + a_j w_i z_i \big )^{n_j} \end{align} $$
$$ \begin{align} q(w_i, z_i) = (w_iz_i)^{n_0} \cdot \tilde q(w_i, z_i) = (w_iz_i)^{n_0} \cdot \prod_{j=1}^k \big ( (w_i + z_i)^2 + a_j w_i z_i \big )^{n_j} \end{align} $$
where
![]() $n_0 \ge 0$
,
$n_0 \ge 0$
,
![]() $k \ge 0$
,
$k \ge 0$
,
![]() $a_1, \ldots , a_k$
are distinct and
$a_1, \ldots , a_k$
are distinct and
![]() $a_j \ne 0$
and
$a_j \ne 0$
and
![]() $n_j> 0$
for every j. So
$n_j> 0$
for every j. So
![]() $\deg (q)$
is even,
$\deg (q)$
is even,
![]() $\deg (p) = \deg (q) - 3$
is odd and
$\deg (p) = \deg (q) - 3$
is odd and
![]() $(w_i + z_i)|p(w_i, z_i)$
. Put
$(w_i + z_i)|p(w_i, z_i)$
. Put
Being of even degree, the symmetric homogeneous polynomial
![]() $\tilde p(w_i, z_i)$
is a polynomial of
$\tilde p(w_i, z_i)$
is a polynomial of
![]() $(w_i + z_i)^2$
and
$(w_i + z_i)^2$
and
![]() $w_i z_i$
. By (5.24), we have
$w_i z_i$
. By (5.24), we have
 $$ \begin{align} \sum_{i=1}^{\chi(X)} (w_i + z_i)^4 \cdot \frac{\tilde p(w_i, z_i)}{q(w_i, z_i)} = e(X, d). \end{align} $$
$$ \begin{align} \sum_{i=1}^{\chi(X)} (w_i + z_i)^4 \cdot \frac{\tilde p(w_i, z_i)}{q(w_i, z_i)} = e(X, d). \end{align} $$
For
![]() $X = {\mathbb P}^2$
and
$X = {\mathbb P}^2$
and
![]() ${\mathbb P}^1 \times {\mathbb P}^1$
, the weights
${\mathbb P}^1 \times {\mathbb P}^1$
, the weights
![]() $w_i$
and
$w_i$
and
![]() $z_i$
are of the form
$z_i$
are of the form
 $$ \begin{align*} & \{(w_i, z_i)| 1 \le i \le \chi(X) \} \\ =&\begin{cases} \{(w,z), (w-z, -z), (z-w, -w) \},&\mbox{if } X = {\mathbb P}^2 \\ \{(w,z), (-w, -z), (w, -z), (-w, z) \},& \mbox{if } X = {\mathbb P}^1 \times {\mathbb P}^1. \end{cases} \end{align*} $$
$$ \begin{align*} & \{(w_i, z_i)| 1 \le i \le \chi(X) \} \\ =&\begin{cases} \{(w,z), (w-z, -z), (z-w, -w) \},&\mbox{if } X = {\mathbb P}^2 \\ \{(w,z), (-w, -z), (w, -z), (-w, z) \},& \mbox{if } X = {\mathbb P}^1 \times {\mathbb P}^1. \end{cases} \end{align*} $$
Set
![]() $z=1$
. Letting
$z=1$
. Letting
![]() $X = {\mathbb P}^2$
and
$X = {\mathbb P}^2$
and
![]() $X = {\mathbb P}^1 \times {\mathbb P}^1$
in (5.26), respectively, we obtain
$X = {\mathbb P}^1 \times {\mathbb P}^1$
in (5.26), respectively, we obtain
where
![]() $e_1=e({\mathbb P}^2, d)$
and
$e_1=e({\mathbb P}^2, d)$
and
![]() $e_2 = e({\mathbb P}^1 \times {\mathbb P}^1, d)/2$
. Since
$e_2 = e({\mathbb P}^1 \times {\mathbb P}^1, d)/2$
. Since
![]() $p(w_i, z_i)$
and
$p(w_i, z_i)$
and
![]() $q(w_i, z_i)$
have no common factor of positive degree, neither do
$q(w_i, z_i)$
have no common factor of positive degree, neither do
![]() $\tilde p(w, 1)$
and
$\tilde p(w, 1)$
and
![]() $\tilde q(w, 1)$
. If
$\tilde q(w, 1)$
. If
![]() $k \ge 1$
, then by (5.28) and (5.25),
$k \ge 1$
, then by (5.28) and (5.25),
![]() $\tilde q(w, 1)|\tilde q(-w, 1)$
. So
$\tilde q(w, 1)|\tilde q(-w, 1)$
. So
![]() $\tilde q(w, 1) = \tilde q(-w, 1)$
since they are monic and
$\tilde q(w, 1) = \tilde q(-w, 1)$
since they are monic and
![]() $\tilde q(w_i, z_i) = \tilde q(-w_i, z_i)$
. Since the roots of
$\tilde q(w_i, z_i) = \tilde q(-w_i, z_i)$
. Since the roots of
![]() $q(w, 1)$
are rational,
$q(w, 1)$
are rational,
![]() $a_j \ne -2$
and
$a_j \ne -2$
and
for j and i. Therefore,
![]() $(w_i + z_i)^2 + a_j w_i z_i$
and
$(w_i + z_i)^2 + a_j w_i z_i$
and
![]() $(w_i - z_i)^2 - a_j w_i z_i$
are distinct factors in the decomposition (5.25) of
$(w_i - z_i)^2 - a_j w_i z_i$
are distinct factors in the decomposition (5.25) of
![]() $q(w_i, z_i)$
, and
$q(w_i, z_i)$
, and
![]() $q(w_i, z_i) $
can be rewritten as
$q(w_i, z_i) $
can be rewritten as
 $$ \begin{align} & (w_iz_i)^{n_0} \cdot \prod_{j=1}^s \big ( ((w_i + z_i)^2 + a_j w_i z_i) ((w_i - z_i)^2 - a_j w_i z_i) \big )^{n_j} \end{align} $$
$$ \begin{align} & (w_iz_i)^{n_0} \cdot \prod_{j=1}^s \big ( ((w_i + z_i)^2 + a_j w_i z_i) ((w_i - z_i)^2 - a_j w_i z_i) \big )^{n_j} \end{align} $$
 $$ \begin{align} =&(w_iz_i)^{n_0} \cdot \prod_{j=1}^s \big ((w_i^2 + z_i^2)^2 - \tilde a_j (w_i z_i)^2 \big )^{n_j} \end{align} $$
$$ \begin{align} =&(w_iz_i)^{n_0} \cdot \prod_{j=1}^s \big ((w_i^2 + z_i^2)^2 - \tilde a_j (w_i z_i)^2 \big )^{n_j} \end{align} $$
where
![]() $s = k/2 \ge 0$
,
$s = k/2 \ge 0$
,
![]() $\tilde a_j = (2+a_j)^2$
and
$\tilde a_j = (2+a_j)^2$
and
![]() $\tilde a_1, \ldots , \tilde a_s$
are distinct. Since the roots of
$\tilde a_1, \ldots , \tilde a_s$
are distinct. Since the roots of
![]() $(w +1)^2 + a_j w$
are rational,
$(w +1)^2 + a_j w$
are rational,
![]() $\tilde a_j \ge 4$
. Since
$\tilde a_j \ge 4$
. Since
![]() $(w_i + z_i) \nmid q(w_i, z_i)$
,
$(w_i + z_i) \nmid q(w_i, z_i)$
,
![]() $\tilde a_j \ne 4$
. So
$\tilde a_j \ne 4$
. So
![]() $\tilde a_j> 4$
, and
$\tilde a_j> 4$
, and
![]() $a_j \ne 0, -4$
. Let
$a_j \ne 0, -4$
. Let
![]() $n = \deg (q) = 2n_0 + 4(n_1 + \ldots + n_s).$
Then
$n = \deg (q) = 2n_0 + 4(n_1 + \ldots + n_s).$
Then
![]() $\deg (\tilde p) = n-4$
.
$\deg (\tilde p) = n-4$
.
If
![]() $n_0$
is positive and even, then as a polynomial in
$n_0$
is positive and even, then as a polynomial in
![]() $(w_i + z_i)^2$
and
$(w_i + z_i)^2$
and
![]() $w_i z_i$
,
$w_i z_i$
,
![]() $\tilde p(w_i, z_i)$
contains the monomial
$\tilde p(w_i, z_i)$
contains the monomial
![]() $(w_i + z_i)^{n - 4}$
with nonzero coefficient. So
$(w_i + z_i)^{n - 4}$
with nonzero coefficient. So
![]() $(w + 1)^4 \, \tilde p(w, 1)$
is a polynomial of degree n in w. Since
$(w + 1)^4 \, \tilde p(w, 1)$
is a polynomial of degree n in w. Since
![]() $q(w, 1)$
is of degree
$q(w, 1)$
is of degree
![]() $n - n_0$
, letting
$n - n_0$
, letting
![]() $w \to \infty $
in (5.28), we get
$w \to \infty $
in (5.28), we get
![]() $\infty = e_2$
. This is impossible since
$\infty = e_2$
. This is impossible since
![]() $e_2$
is a finite number.
$e_2$
is a finite number.
If
![]() $n_0$
is odd with
$n_0$
is odd with
![]() $n_0 \ge 3$
, then write
$n_0 \ge 3$
, then write
![]() $\tilde p(w_i, z_i) = \sum _{j=0}^{n-4} h_j w_i^j z_i^{(n-4)-j}$
. Since
$\tilde p(w_i, z_i) = \sum _{j=0}^{n-4} h_j w_i^j z_i^{(n-4)-j}$
. Since
![]() $\tilde p(w_i, z_i)$
is symmetric,
$\tilde p(w_i, z_i)$
is symmetric,
![]() $h_j = h_{(n-4)-j}$
. Since
$h_j = h_{(n-4)-j}$
. Since
![]() $(w_iz_i) \nmid \tilde p(w_i, z_i)$
,
$(w_iz_i) \nmid \tilde p(w_i, z_i)$
,
![]() $h_0 \ne 0$
. Since
$h_0 \ne 0$
. Since
![]() $a_j \not \in \{0, -4\}$
, we see that
$a_j \not \in \{0, -4\}$
, we see that
![]() $w \nmid q(w-1, -1)$
and
$w \nmid q(w-1, -1)$
and
![]() $w \nmid \tilde q(1-w, -w)$
. Substitute (5.30) into (5.27) and (5.28). Expanding the left-hand sides of (5.27) and (5.28), we get
$w \nmid \tilde q(1-w, -w)$
. Substitute (5.30) into (5.27) and (5.28). Expanding the left-hand sides of (5.27) and (5.28), we get
 $$ \begin{align*} \big ( (n_0 + 8)h_0 + 2h_1 \big )w^{-(n_0-1)} + O(w^{-(n_0-2)}) &= e_1, \\ (8 h_0 + 2h_1)w^{-(n_0-1)} + O(w^{-(n_0-3)}) &= e_2 \end{align*} $$
$$ \begin{align*} \big ( (n_0 + 8)h_0 + 2h_1 \big )w^{-(n_0-1)} + O(w^{-(n_0-2)}) &= e_1, \\ (8 h_0 + 2h_1)w^{-(n_0-1)} + O(w^{-(n_0-3)}) &= e_2 \end{align*} $$
where
![]() $O(w^{-i})$
with
$O(w^{-i})$
with
![]() $i> 0$
denotes a term such that as
$i> 0$
denotes a term such that as
![]() $w \to 0$
,
$w \to 0$
,
![]() $|O(w^{-i})| \le c |w^{-i}|$
for some constant c. The two coefficients of
$|O(w^{-i})| \le c |w^{-i}|$
for some constant c. The two coefficients of
![]() $w^{-(n_0-1)}$
cannot be
$w^{-(n_0-1)}$
cannot be
![]() $0$
simultaneously. So letting
$0$
simultaneously. So letting
![]() $w \to 0$
, we have either
$w \to 0$
, we have either
![]() $\infty = e_1$
or
$\infty = e_1$
or
![]() $\infty = e_2$
. This is absurd.
$\infty = e_2$
. This is absurd.
By the previous two paragraphs,
![]() $n_0 = 0$
or
$n_0 = 0$
or
![]() $1$
. Since
$1$
. Since
![]() $\deg (q) \ge 3$
,
$\deg (q) \ge 3$
,
![]() $s \ge 1$
. The roots of
$s \ge 1$
. The roots of
![]() $(w^2 + 1)^2 - \tilde a_j w^2$
are
$(w^2 + 1)^2 - \tilde a_j w^2$
are
![]() $\alpha , \alpha ^{-1}, -\alpha , -\alpha ^{-1}$
for some rational number
$\alpha , \alpha ^{-1}, -\alpha , -\alpha ^{-1}$
for some rational number
![]() $\alpha \ne 0, 1$
, and these four roots are mutually distinct. Let
$\alpha \ne 0, 1$
, and these four roots are mutually distinct. Let
![]() $\alpha _0, \alpha _0^{-1}, -\alpha _0, -\alpha _0^{-1}$
be the roots of
$\alpha _0, \alpha _0^{-1}, -\alpha _0, -\alpha _0^{-1}$
be the roots of
![]() $(w^2 + 1)^2 - \tilde a_1 w^2$
. By symmetry, let
$(w^2 + 1)^2 - \tilde a_1 w^2$
. By symmetry, let
![]() $0 < \alpha _0 < 1$
. If
$0 < \alpha _0 < 1$
. If
![]() $(w + \alpha _0) \nmid \big (q(w-1,-1)q(1-w, -w) \big )$
, then letting
$(w + \alpha _0) \nmid \big (q(w-1,-1)q(1-w, -w) \big )$
, then letting
![]() $w \to -\alpha _0$
in (5.27), we obtain the contradiction
$w \to -\alpha _0$
in (5.27), we obtain the contradiction
![]() $\infty = e_1$
. If
$\infty = e_1$
. If
![]() $(w + \alpha _0)|q(w-1,-1)$
, then
$(w + \alpha _0)|q(w-1,-1)$
, then
![]() $(\alpha _0 + 1) \ne 0$
is a root of
$(\alpha _0 + 1) \ne 0$
is a root of
![]() $q(w, 1)$
. Therefore,
$q(w, 1)$
. Therefore,
![]() $1/(\alpha _0 + 1)$
is a root of
$1/(\alpha _0 + 1)$
is a root of
![]() $q(w, 1)$
as well. Similarly, if
$q(w, 1)$
as well. Similarly, if
![]() $(w + \alpha _0)|q(1-w, -w)$
, then
$(w + \alpha _0)|q(1-w, -w)$
, then
![]() $-(\alpha _0 + 1)/\alpha _0$
is a root of
$-(\alpha _0 + 1)/\alpha _0$
is a root of
![]() $q(w, 1)$
; in this case,
$q(w, 1)$
; in this case,
![]() $\alpha _0/(\alpha _0 + 1)$
is also a root of
$\alpha _0/(\alpha _0 + 1)$
is also a root of
![]() $q(w, 1)$
. Note that
$q(w, 1)$
. Note that
![]() $0 < 1/(\alpha _0 + 1), \alpha _0/(\alpha _0 + 1) < 1$
. Define two functions
$0 < 1/(\alpha _0 + 1), \alpha _0/(\alpha _0 + 1) < 1$
. Define two functions
So there exists
![]() $\psi _1 \in \{\phi _1, \phi _2\}$
such that
$\psi _1 \in \{\phi _1, \phi _2\}$
such that
![]() $\psi _1(\alpha _0)$
is a root of
$\psi _1(\alpha _0)$
is a root of
![]() $q(w, 1)$
. Putting
$q(w, 1)$
. Putting
![]() $\alpha _1 = \psi _1(\alpha _0)$
and repeating the above process, we see that
$\alpha _1 = \psi _1(\alpha _0)$
and repeating the above process, we see that
![]() $q(w, 1)$
has a sequence of roots
$q(w, 1)$
has a sequence of roots
where
![]() $\psi _1, \ldots , \psi _k \in \{\phi _1, \phi _2\}$
. By induction, we get
$\psi _1, \ldots , \psi _k \in \{\phi _1, \phi _2\}$
. By induction, we get
![]() $0 < \alpha _k < 1$
for every
$0 < \alpha _k < 1$
for every
![]() $k \ge 0$
.
$k \ge 0$
.
Claim.
![]() $\alpha _i \ne \alpha _k$
whenever
$\alpha _i \ne \alpha _k$
whenever
![]() $i, k \ge 0$
and
$i, k \ge 0$
and
![]() $i \ne k$
.
$i \ne k$
.
Proof. Assume
![]() $\alpha _i = \alpha _k$
with
$\alpha _i = \alpha _k$
with
![]() $0 \le i < k$
. Then,
$0 \le i < k$
. Then,
![]() $\alpha _k = \psi _k \cdots \psi _{i+1}(\alpha _i)$
. So we may assume that
$\alpha _k = \psi _k \cdots \psi _{i+1}(\alpha _i)$
. So we may assume that
![]() $i = 0$
,
$i = 0$
,
![]() $\alpha _0 = \alpha _k$
and
$\alpha _0 = \alpha _k$
and
![]() $\alpha _k = \psi _k \cdots \psi _1(\alpha _0)$
. Since
$\alpha _k = \psi _k \cdots \psi _1(\alpha _0)$
. Since
![]() $\psi _1, \ldots , \psi _k \in \{\phi _1, \phi _2\}$
, we see from induction that
$\psi _1, \ldots , \psi _k \in \{\phi _1, \phi _2\}$
, we see from induction that
![]() $\alpha _k = (a \alpha _0 + b)/(c \alpha _0 + d)$
for some integers
$\alpha _k = (a \alpha _0 + b)/(c \alpha _0 + d)$
for some integers
![]() $a \ge 0, b \ge 0, c \ge 1, d \ge 1$
satisfying
$a \ge 0, b \ge 0, c \ge 1, d \ge 1$
satisfying
![]() $ad - bc = \pm 1$
. So
$ad - bc = \pm 1$
. So
![]() $\alpha _0 = (a \alpha _0 + b)/(c \alpha _0 + d)$
, and we get
$\alpha _0 = (a \alpha _0 + b)/(c \alpha _0 + d)$
, and we get
Since
![]() $\alpha _0$
is a rational number,
$\alpha _0$
is a rational number,
![]() $(d-a)^2 + 4bc = f^2$
for some integer f. If
$(d-a)^2 + 4bc = f^2$
for some integer f. If
![]() $ad - bc = -1$
, then
$ad - bc = -1$
, then
![]() $f^2 = (d+a)^2 + 4$
, and so
$f^2 = (d+a)^2 + 4$
, and so
![]() $d + a = 0$
, which contradicts
$d + a = 0$
, which contradicts
![]() $a \ge 0$
and
$a \ge 0$
and
![]() $d \ge 1$
. If
$d \ge 1$
. If
![]() $ad - bc = 1$
, then
$ad - bc = 1$
, then
![]() $f^2 + 4 = (d+a)^2$
, and so
$f^2 + 4 = (d+a)^2$
, and so
![]() $f=0$
and
$f=0$
and
![]() $d + a = 2$
. Since
$d + a = 2$
. Since
![]() $a \ge 0, b \ge 0, c \ge 1, d \ge 1$
are integers satisfying
$a \ge 0, b \ge 0, c \ge 1, d \ge 1$
are integers satisfying
![]() $ad - bc = 1$
, we must have
$ad - bc = 1$
, we must have
![]() $a = d = 1$
,
$a = d = 1$
,
![]() $b = 0$
and
$b = 0$
and
![]() $\alpha _0 = 0$
. This contradicts
$\alpha _0 = 0$
. This contradicts
![]() $\alpha _0 \ne 0$
.
$\alpha _0 \ne 0$
.
We continue the proof of our lemma. By the above claim, the polynomial
![]() $q(w, 1)$
has infinitely many roots
$q(w, 1)$
has infinitely many roots
![]() $\alpha _k, k \ge 0$
which are mutually distinct. This is absurd.
$\alpha _k, k \ge 0$
which are mutually distinct. This is absurd.
In view of Lemma 5.4, we introduce the following notation.
Notation 5.5. We use
![]() $M((w+z)^n)$
to denote an expression of the form
$M((w+z)^n)$
to denote an expression of the form
where
![]() $p(w,z)$
and
$p(w,z)$
and
![]() $q(w,z)$
are polynomials in w and z with
$q(w,z)$
are polynomials in w and z with
![]() $(w+z) \nmid q(w,z)$
, and all the roots of the polynomial
$(w+z) \nmid q(w,z)$
, and all the roots of the polynomial
![]() $q(w, 1)$
are rational numbers.
$q(w, 1)$
are rational numbers.
By Lemma 5.4, when we evaluate the summation
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
in (5.19), we can ignore those stable graphs
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
in (5.19), we can ignore those stable graphs
![]() $\Gamma $
in
$\Gamma $
in
![]() ${\mathcal T}_{d,i}$
and
${\mathcal T}_{d,i}$
and
![]() ${\mathcal S}_{d,i, i}$
satisfying
${\mathcal S}_{d,i, i}$
satisfying
 $$ \begin{align*}\frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} = M \big ((w_i+z_i)^3 \big ). \end{align*} $$
$$ \begin{align*}\frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} = M \big ((w_i+z_i)^3 \big ). \end{align*} $$
5.5 Computation of
 $ \sum _{ \Gamma \in {\mathcal S}_{d,i, i}}$
$ \sum _{ \Gamma \in {\mathcal S}_{d,i, i}}$
For simplicity, in the rest of the paper, we put
 $$ \begin{align*} w &= w_i = c_1(\lambda_i),\\ z &= z_i = c_1(\mu_i). \end{align*} $$
$$ \begin{align*} w &= w_i = c_1(\lambda_i),\\ z &= z_i = c_1(\mu_i). \end{align*} $$
Also, define
![]() $P_1(a, b) = 1$
. For
$P_1(a, b) = 1$
. For
![]() $n \ge 2$
, we define
$n \ge 2$
, we define
Now let
![]() $\Gamma \in {{\mathcal S}}_{d,i,i}$
. Similar to the formulas (4.18) to (4.21) in [Reference Edidin, Li and Qin8] (see also [Reference Liu and Sheshmani30]), we have the decomposition
$\Gamma \in {{\mathcal S}}_{d,i,i}$
. Similar to the formulas (4.18) to (4.21) in [Reference Edidin, Li and Qin8] (see also [Reference Liu and Sheshmani30]), we have the decomposition
Here,
![]() $e_{\Gamma }^{\mathrm {E}}, e_{\Gamma }^{\mathrm {V}}, e_{\Gamma }^{\mathrm {F}}$
denote the contributions of the edges, vertices and flags with
$e_{\Gamma }^{\mathrm {E}}, e_{\Gamma }^{\mathrm {V}}, e_{\Gamma }^{\mathrm {F}}$
denote the contributions of the edges, vertices and flags with
 $$ \begin{align} e_{\Gamma}^{\mathrm{E}} &=\prod_{e \in E(\Gamma)} \frac{(-1)^{d_e -1}((d_e-1)!)^2 w^2 z^2 (w - z)^{2d_e}} {(w + z) P_{d_e}(-2d_ew, w - z) P_{d_e}(-d_e(w + z), w - z)} \end{align} $$
$$ \begin{align} e_{\Gamma}^{\mathrm{E}} &=\prod_{e \in E(\Gamma)} \frac{(-1)^{d_e -1}((d_e-1)!)^2 w^2 z^2 (w - z)^{2d_e}} {(w + z) P_{d_e}(-2d_ew, w - z) P_{d_e}(-d_e(w + z), w - z)} \end{align} $$
 $$ \begin{align} e_ {\Gamma}^{\mathrm{V}} &=\prod_{\substack{v \in V(\Gamma)\\g(v) = 0\\\mathrm{val}(v) = 2}} (\omega_{F_1(v)}+ \omega_{F_2(v)}) \cdot \prod_{\substack{v \in V(\Gamma)\\g(v) = 0\\\mathrm{val}(v) = 1}} \omega_{F(v)}^{-1} \cdot \prod_{v \in V(\Gamma)} \frac{e(T_{{\mathfrak L}(v)})} {e(\mathcal H_{g(v)}^{\vee} \otimes T_{{\mathfrak L}(v)})} \end{align} $$
$$ \begin{align} e_ {\Gamma}^{\mathrm{V}} &=\prod_{\substack{v \in V(\Gamma)\\g(v) = 0\\\mathrm{val}(v) = 2}} (\omega_{F_1(v)}+ \omega_{F_2(v)}) \cdot \prod_{\substack{v \in V(\Gamma)\\g(v) = 0\\\mathrm{val}(v) = 1}} \omega_{F(v)}^{-1} \cdot \prod_{v \in V(\Gamma)} \frac{e(T_{{\mathfrak L}(v)})} {e(\mathcal H_{g(v)}^{\vee} \otimes T_{{\mathfrak L}(v)})} \end{align} $$
 $$ \begin{align} e_{\Gamma}^{\mathrm{F}} &=\prod_{F \in F(\Gamma)^{\mathrm{sta}}}(\omega_F - \psi_F) \cdot \prod_{F \in F(\Gamma)} e(T_{i(F)})^{-1} \end{align} $$
$$ \begin{align} e_{\Gamma}^{\mathrm{F}} &=\prod_{F \in F(\Gamma)^{\mathrm{sta}}}(\omega_F - \psi_F) \cdot \prod_{F \in F(\Gamma)} e(T_{i(F)})^{-1} \end{align} $$
where (5.33) (which is the product of the equivariant Euler classes of the moving parts
![]() $\chi (((f|_{C_e})^*T_{X^{[3]}})^{\mathrm {mov}})$
,
$\chi (((f|_{C_e})^*T_{X^{[3]}})^{\mathrm {mov}})$
,
![]() $e \in E(\Gamma )$
) follows from (5.10) by reading its nonconstant terms,
$e \in E(\Gamma )$
) follows from (5.10) by reading its nonconstant terms,
![]() $\omega _F = e(T_{i(F)}C_{i,i})/d_e$
for a flag
$\omega _F = e(T_{i(F)}C_{i,i})/d_e$
for a flag
![]() $F = (v, e)$
and
$F = (v, e)$
and
![]() $\psi _F$
denotes the first Chern class of the line bundle on
$\psi _F$
denotes the first Chern class of the line bundle on
![]() $\overline M_{\Gamma }$
whose fiber is the cotangent space of the component associated to v at the point corresponding to F. Note from (5.5) and (5.6) that
$\overline M_{\Gamma }$
whose fiber is the cotangent space of the component associated to v at the point corresponding to F. Note from (5.5) and (5.6) that
![]() $T_{R_{i,i}^{(1)}}C_{i,i} = \lambda _i^{-1} \mu _i$
and
$T_{R_{i,i}^{(1)}}C_{i,i} = \lambda _i^{-1} \mu _i$
and
![]() $T_{R_{i,i}^{(2)}}C_{i,i} = \lambda _i \mu _i^{-1}$
. Thus, we obtain
$T_{R_{i,i}^{(2)}}C_{i,i} = \lambda _i \mu _i^{-1}$
. Thus, we obtain
 $$ \begin{align} \omega_F = \begin{cases} (-w + z)/d_e,&\mbox{if } i(F) = R_{i,i}^{(1)} \\ (w - z)/d_e,& \mbox{if } i(F) = R_{i,i}^{(2)}. \end{cases} \end{align} $$
$$ \begin{align} \omega_F = \begin{cases} (-w + z)/d_e,&\mbox{if } i(F) = R_{i,i}^{(1)} \\ (w - z)/d_e,& \mbox{if } i(F) = R_{i,i}^{(2)}. \end{cases} \end{align} $$
In (5.34), when
![]() $g(v) = 0$
,
$g(v) = 0$
,
![]() $e(\mathcal H_{g(v)}^{\vee } \otimes T_{{\mathfrak L}(v)})$
is treated as
$e(\mathcal H_{g(v)}^{\vee } \otimes T_{{\mathfrak L}(v)})$
is treated as
![]() $1$
; when
$1$
; when
![]() $g(v) = 1$
,
$g(v) = 1$
,
![]() $\mathcal H_{g(v)}$
is the rank-
$\mathcal H_{g(v)}$
is the rank-
![]() $1$
Hodge bundle over
$1$
Hodge bundle over
![]() $\overline {M}_{g(v), \mathrm {val}(v)}$
. Let
$\overline {M}_{g(v), \mathrm {val}(v)}$
. Let
![]() $\lambda = c_1(\mathcal H_1)$
. It is known that
$\lambda = c_1(\mathcal H_1)$
. It is known that
 $$ \begin{align} \lambda^2 = 0, \qquad \int_{\overline{M}_{1,1}} \lambda = \frac{1}{24}. \end{align} $$
$$ \begin{align} \lambda^2 = 0, \qquad \int_{\overline{M}_{1,1}} \lambda = \frac{1}{24}. \end{align} $$
For
![]() $1 \le j \le n$
, let
$1 \le j \le n$
, let
![]() $\psi _j$
be the first Chern class of the line bundle on
$\psi _j$
be the first Chern class of the line bundle on
![]() $\overline M_{1, n}$
whose fiber at an n-pointed stable curve is the cotangent space of the curve at the j-th marked point. Then it is known (e.g., see [Reference Kock18]) that
$\overline M_{1, n}$
whose fiber at an n-pointed stable curve is the cotangent space of the curve at the j-th marked point. Then it is known (e.g., see [Reference Kock18]) that
![]() $\psi _1 = \lambda $
on
$\psi _1 = \lambda $
on
![]() $\overline M_{1, 1}$
and
$\overline M_{1, 1}$
and
 $$ \begin{align} \int_{\overline{M}_{1,2}} \psi_1^2 = \int_{\overline{M}_{1,2}} \psi_2^2 = \int_{\overline{M}_{1,2}} \psi_1 \psi_2 = \frac{1}{24}. \end{align} $$
$$ \begin{align} \int_{\overline{M}_{1,2}} \psi_1^2 = \int_{\overline{M}_{1,2}} \psi_2^2 = \int_{\overline{M}_{1,2}} \psi_1 \psi_2 = \frac{1}{24}. \end{align} $$
Lemma 5.6. Let
![]() $d \ge 1$
, and let
$d \ge 1$
, and let
![]() $\Gamma \in {{\mathcal S}}_{d,i,i}$
. Then, we have
$\Gamma \in {{\mathcal S}}_{d,i,i}$
. Then, we have
 $$ \begin{align} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} = M \big ( (w+z)^{|E(\Gamma)|} \big ). \end{align} $$
$$ \begin{align} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} = M \big ( (w+z)^{|E(\Gamma)|} \big ). \end{align} $$
Proof. We see from (5.33) that
![]() $(w+z)^{|E(\Gamma )|}$
divides the denominator of
$(w+z)^{|E(\Gamma )|}$
divides the denominator of
![]() $e_{\Gamma }^{\mathrm {E}}$
. Moreover,
$e_{\Gamma }^{\mathrm {E}}$
. Moreover,
![]() $(w+z)$
does not divide the numerators in (5.33). So we have
$(w+z)$
does not divide the numerators in (5.33). So we have
 $$ \begin{align} \frac{1}{e_{\Gamma}^{\mathrm{E}}} = (w+z)^{|E(\Gamma)|} \cdot \frac{p_{\Gamma, 1}(w,z)}{q_{\Gamma, 1}(w,z)} \end{align} $$
$$ \begin{align} \frac{1}{e_{\Gamma}^{\mathrm{E}}} = (w+z)^{|E(\Gamma)|} \cdot \frac{p_{\Gamma, 1}(w,z)}{q_{\Gamma, 1}(w,z)} \end{align} $$
where
![]() $p_{\Gamma , 1}(w,z)$
and
$p_{\Gamma , 1}(w,z)$
and
![]() $q_{\Gamma , 1}(w,z)$
are polynomials in w and z with
$q_{\Gamma , 1}(w,z)$
are polynomials in w and z with
![]() $(w+z) \nmid q_{\Gamma , 1}(w,z)$
, and all the roots of
$(w+z) \nmid q_{\Gamma , 1}(w,z)$
, and all the roots of
![]() $q_{\Gamma , 1}(w, 1)$
are rational. By (5.34), (5.35), (5.36), (5.5) and (5.6),
$q_{\Gamma , 1}(w, 1)$
are rational. By (5.34), (5.35), (5.36), (5.5) and (5.6),
 $$ \begin{align*}\frac{1}{e_{\Gamma}^{\mathrm{V}} \cdot e_{\Gamma}^{\mathrm{F}}} = \frac{p_{\Gamma, 2}(w,z)}{q_{\Gamma, 2}(w,z)} \end{align*} $$
$$ \begin{align*}\frac{1}{e_{\Gamma}^{\mathrm{V}} \cdot e_{\Gamma}^{\mathrm{F}}} = \frac{p_{\Gamma, 2}(w,z)}{q_{\Gamma, 2}(w,z)} \end{align*} $$
where
![]() $p_{\Gamma , 2}(w,z)$
and
$p_{\Gamma , 2}(w,z)$
and
![]() $q_{\Gamma , 2}(w,z)$
are polynomials in w and z with
$q_{\Gamma , 2}(w,z)$
are polynomials in w and z with
![]() $(w+z) \nmid q_{\Gamma , 2}(w,z)$
, and all the roots of
$(w+z) \nmid q_{\Gamma , 2}(w,z)$
, and all the roots of
![]() $q_{\Gamma , 2}(w, 1)$
are rational. By (5.32) and (5.40), we get (5.39).
$q_{\Gamma , 2}(w, 1)$
are rational. By (5.32) and (5.40), we get (5.39).
Lemma 5.7. Let
![]() $d \ge 1$
. Then, the summation
$d \ge 1$
. Then, the summation
![]() $\sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is equal to
$\sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is equal to
 $$ \begin{align*}\left (\frac{-d^2+d+16}{96d} + \frac{d}{48} \sum_{d_1=1}^{d-1} \frac{1}{d_1} - \frac{1}{48} \sum_{\delta \vdash d} \frac{d^2 - d_1d_2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \right ) \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ) \end{align*} $$
$$ \begin{align*}\left (\frac{-d^2+d+16}{96d} + \frac{d}{48} \sum_{d_1=1}^{d-1} \frac{1}{d_1} - \frac{1}{48} \sum_{\delta \vdash d} \frac{d^2 - d_1d_2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \right ) \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ) \end{align*} $$
where
![]() $\delta = (d_1, d_2) \vdash d$
denotes a length-
$\delta = (d_1, d_2) \vdash d$
denotes a length-
![]() $2$
partition of d,
$2$
partition of d,
![]() $|\mathrm {Aut}(\delta )| = 1$
if
$|\mathrm {Aut}(\delta )| = 1$
if
![]() $d_1 \ne d_2$
and
$d_1 \ne d_2$
and
![]() $|\mathrm {Aut}(\delta )| = 2$
if
$|\mathrm {Aut}(\delta )| = 2$
if
![]() $d_1 = d_2$
.
$d_1 = d_2$
.
Proof. By Lemma 5.6, we need only to consider those stable graphs
![]() $\Gamma \in {\mathcal S}_{d,i, i}$
with
$\Gamma \in {\mathcal S}_{d,i, i}$
with
![]() $|E(\Gamma )| = 1$
or
$|E(\Gamma )| = 1$
or
![]() $2$
. We begin with the case
$2$
. We begin with the case
![]() $|E(\Gamma )| = 1$
(i.e.,
$|E(\Gamma )| = 1$
(i.e.,
![]() $\Gamma \in {\mathcal S}_{d,i, i}$
has exactly one edge). There are exactly two such stable graphs:
$\Gamma \in {\mathcal S}_{d,i, i}$
has exactly one edge). There are exactly two such stable graphs:
where
![]() $V(\Gamma ) = \{v_1, v_2\}$
,
$V(\Gamma ) = \{v_1, v_2\}$
,
![]() $\mathfrak L(v_1) = R_{i, i}^{(1)}$
,
$\mathfrak L(v_1) = R_{i, i}^{(1)}$
,
![]() $\mathfrak L(v_2) = R_{i, i}^{(2)}$
,
$\mathfrak L(v_2) = R_{i, i}^{(2)}$
,
![]() $g(v_1) \in \{1, 0\}$
and
$g(v_1) \in \{1, 0\}$
and
![]() $g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. In both cases,
$g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. In both cases,
![]() $|\mathbf {A}_{\Gamma }| = d \cdot |{\mathrm {Aut}} (\Gamma )| = d$
by (5.12). Using (5.32)-(5.37) and noticing that (5.33) is unchanged when w and z are switched, we get
$|\mathbf {A}_{\Gamma }| = d \cdot |{\mathrm {Aut}} (\Gamma )| = d$
by (5.12). Using (5.32)-(5.37) and noticing that (5.33) is unchanged when w and z are switched, we get
 $$ \begin{align} \sum_{\substack{\Gamma \in {\mathcal S}_{d,i, i}, \, |E(\Gamma)| = 1}} = \frac{9-d}{48d}\cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align} $$
$$ \begin{align} \sum_{\substack{\Gamma \in {\mathcal S}_{d,i, i}, \, |E(\Gamma)| = 1}} = \frac{9-d}{48d}\cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align} $$
Next, we consider the stable graphs
![]() $\Gamma \in {\mathcal S}_{d,i, i}$
with
$\Gamma \in {\mathcal S}_{d,i, i}$
with
![]() $|E(\Gamma )| = 2$
. So
$|E(\Gamma )| = 2$
. So
![]() $\Gamma \in {\mathcal S}_{d,i, i}$
has exactly two edges. Denoting the distributions of the degree d on the two edges by
$\Gamma \in {\mathcal S}_{d,i, i}$
has exactly two edges. Denoting the distributions of the degree d on the two edges by
![]() $d_1$
and
$d_1$
and
![]() $d_2$
, we see that these stable graphs are of the form:
$d_2$
, we see that these stable graphs are of the form:
-
(i)
where
 $\mathfrak L(v_1) \in \big \{R_{i, i}^{(1)}, R_{i, i}^{(2)} \big \}$
,
$\mathfrak L(v_1) \in \big \{R_{i, i}^{(1)}, R_{i, i}^{(2)} \big \}$
,
 $\mathfrak L(v_2) = \mathfrak L(v_3) \in \big \{R_{i, i}^{(1)}, R_{i, i}^{(2)} \big \} - \big \{\mathfrak L(v_1) \big \}$
,
$\mathfrak L(v_2) = \mathfrak L(v_3) \in \big \{R_{i, i}^{(1)}, R_{i, i}^{(2)} \big \} - \big \{\mathfrak L(v_1) \big \}$
,
 $g(v_1) \in \{1, 0\}$
,
$g(v_1) \in \{1, 0\}$
,
 $g(v_2) \in \{1,0\} - \{g(v_1)\}$
,
$g(v_2) \in \{1,0\} - \{g(v_1)\}$
,
 $g(v_3) = 0$
and
$g(v_3) = 0$
and
 $\delta = (d_1, d_2) \vdash d$
is a partition of d. There are exactly
$\delta = (d_1, d_2) \vdash d$
is a partition of d. There are exactly
 $4$
types of such graphs if we ignore the edge weights. By (5.12),
$4$
types of such graphs if we ignore the edge weights. By (5.12),
 $|\mathbf {A}_{\Gamma }| = d_1 d_2$
if
$|\mathbf {A}_{\Gamma }| = d_1 d_2$
if
 $g(v_1) = 0$
, while
$g(v_1) = 0$
, while
 $|\mathbf {A}_{\Gamma }| = d_1 d_2 \cdot |{\mathrm {Aut}} (\delta )|$
if
$|\mathbf {A}_{\Gamma }| = d_1 d_2 \cdot |{\mathrm {Aut}} (\delta )|$
if
 $g(v_1) = 1$
.
$g(v_1) = 1$
.
-
(ii)
where
 $\mathfrak L(v_1) = R_{i, i}^{(1)}$
,
$\mathfrak L(v_1) = R_{i, i}^{(1)}$
,
 $\mathfrak L(v_2) = R_{i, i}^{(2)}$
,
$\mathfrak L(v_2) = R_{i, i}^{(2)}$
,
 $g(v_1) = g(v_2) = 0$
and
$g(v_1) = g(v_2) = 0$
and
 $\delta = (d_1, d_2) \vdash d$
is a partition of d. We have
$\delta = (d_1, d_2) \vdash d$
is a partition of d. We have
 $|\mathbf {A}_{\Gamma }| = d_1 d_2 \cdot |{\mathrm {Aut}} (\delta )|$
.
$|\mathbf {A}_{\Gamma }| = d_1 d_2 \cdot |{\mathrm {Aut}} (\delta )|$
.
A lengthy computation via (5.32)-(5.38) shows that
![]() $\sum _{\Gamma \in {\mathcal S}_{d,i, i}, \, |E(\Gamma )| = 2}$
is equal to
$\sum _{\Gamma \in {\mathcal S}_{d,i, i}, \, |E(\Gamma )| = 2}$
is equal to
 $$ \begin{align*}\left (\frac{-d^2+3d-2}{96d} + \frac{d}{48} \sum_{d_1=1}^{d-1} \frac{1}{d_1} - \frac{1}{48} \sum_{\delta \vdash d} \frac{d^2 - d_1d_2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \right ) \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
$$ \begin{align*}\left (\frac{-d^2+3d-2}{96d} + \frac{d}{48} \sum_{d_1=1}^{d-1} \frac{1}{d_1} - \frac{1}{48} \sum_{\delta \vdash d} \frac{d^2 - d_1d_2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \right ) \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
Summing this with (5.41), we complete the proof of our lemma.
5.6 Computation of
 $ \sum _{ \Gamma \in { \mathcal T}_{d, i}}$
$ \sum _{ \Gamma \in { \mathcal T}_{d, i}}$
Let
![]() $\Gamma \in {\mathcal T}_{d,i}$
. For an edge
$\Gamma \in {\mathcal T}_{d,i}$
. For an edge
![]() $e \in E(\Gamma )$
and for
$e \in E(\Gamma )$
and for
![]() $0\le j < k \le 2$
, define
$0\le j < k \le 2$
, define
![]() $e \in E_{j, k}(\Gamma )$
if the component
$e \in E_{j, k}(\Gamma )$
if the component
![]() $C_e$
is mapped to
$C_e$
is mapped to
![]() $C_{j, k}^{(i)}$
. By Lemma 5.2, the curves
$C_{j, k}^{(i)}$
. By Lemma 5.2, the curves
![]() $C_{0,1}^{(i)}$
,
$C_{0,1}^{(i)}$
,
![]() $C_{0,2}^{(i)}$
and
$C_{0,2}^{(i)}$
and
![]() $C_{1,2}^{(i)}$
are homologous to
$C_{1,2}^{(i)}$
are homologous to
![]() $\beta _3$
,
$\beta _3$
,
![]() $\beta _3$
and
$\beta _3$
and
![]() $3\beta _3$
, respectively. Therefore,
$3\beta _3$
, respectively. Therefore,
 $$ \begin{align} \sum_{e \in E_{0, 1}(\Gamma)} d_e +\sum_{e \in E_{0, 2}(\Gamma)} d_e + \sum_{e \in E_{1, 2}(\Gamma)}3d_e = d. \end{align} $$
$$ \begin{align} \sum_{e \in E_{0, 1}(\Gamma)} d_e +\sum_{e \in E_{0, 2}(\Gamma)} d_e + \sum_{e \in E_{1, 2}(\Gamma)}3d_e = d. \end{align} $$
Now formulas (5.32), (5.34) and (5.35) still hold with the understanding that
 $$ \begin{align} \omega_F = \begin{cases} (w - 2z)/d_e,&\mbox{if } e \in E_{0, 1}(\Gamma) \mbox{ and } i(F) = Q_{i,0} \\ (-w + 2z)/d_e,& \mbox{if } e \in E_{0, 1}(\Gamma) \mbox{ and } i(F) = Q_{i,1} \\ (-2w + z)/d_e,&\mbox{if } e \in E_{0, 2}(\Gamma) \mbox{ and } i(F) = Q_{i,0} \\ (2w - z)/d_e,& \mbox{if } e \in E_{0, 2}(\Gamma) \mbox{ and } i(F) = Q_{i,2} \\ (-w + z)/d_e,&\mbox{if } e \in E_{1, 2}(\Gamma) \mbox{ and } i(F) = Q_{i,1} \\ (w - z)/d_e,& \mbox{if } e \in E_{1, 2}(\Gamma) \mbox{ and } i(F) = Q_{i,2} \end{cases} \end{align} $$
$$ \begin{align} \omega_F = \begin{cases} (w - 2z)/d_e,&\mbox{if } e \in E_{0, 1}(\Gamma) \mbox{ and } i(F) = Q_{i,0} \\ (-w + 2z)/d_e,& \mbox{if } e \in E_{0, 1}(\Gamma) \mbox{ and } i(F) = Q_{i,1} \\ (-2w + z)/d_e,&\mbox{if } e \in E_{0, 2}(\Gamma) \mbox{ and } i(F) = Q_{i,0} \\ (2w - z)/d_e,& \mbox{if } e \in E_{0, 2}(\Gamma) \mbox{ and } i(F) = Q_{i,2} \\ (-w + z)/d_e,&\mbox{if } e \in E_{1, 2}(\Gamma) \mbox{ and } i(F) = Q_{i,1} \\ (w - z)/d_e,& \mbox{if } e \in E_{1, 2}(\Gamma) \mbox{ and } i(F) = Q_{i,2} \end{cases} \end{align} $$
since
![]() $T_{Q_{i,0}}C_{0,1}^{(i)} = \lambda _i \mu _i^{-2}$
,
$T_{Q_{i,0}}C_{0,1}^{(i)} = \lambda _i \mu _i^{-2}$
,
![]() $T_{Q_{i,1}}C_{0,1}^{(i)} = \lambda _i^{-1} \mu _i^{2}$
,
$T_{Q_{i,1}}C_{0,1}^{(i)} = \lambda _i^{-1} \mu _i^{2}$
,
![]() $T_{Q_{i,0}}C_{0,2}^{(i)} = \lambda _i^{-2} \mu _i$
,
$T_{Q_{i,0}}C_{0,2}^{(i)} = \lambda _i^{-2} \mu _i$
,
![]() $T_{Q_{i,2}}C_{0,2}^{(i)} = \lambda _i^{2} \mu _i^{-1}$
,
$T_{Q_{i,2}}C_{0,2}^{(i)} = \lambda _i^{2} \mu _i^{-1}$
,
![]() $T_{Q_{i,1}}C_{1,2}^{(i)} = \lambda _i^{-1} \mu _i$
and
$T_{Q_{i,1}}C_{1,2}^{(i)} = \lambda _i^{-1} \mu _i$
and
![]() $T_{Q_{i,2}}C_{1,2}^{(i)} = \lambda _i \mu _i^{-1}$
in view of (5.2), (5.3) and (5.4). Moreover, we see from (5.7), (5.8) and (5.9) that the factor
$T_{Q_{i,2}}C_{1,2}^{(i)} = \lambda _i \mu _i^{-1}$
in view of (5.2), (5.3) and (5.4). Moreover, we see from (5.7), (5.8) and (5.9) that the factor
![]() $e_{\Gamma }^{\mathrm {E}}$
in (5.32) is given by
$e_{\Gamma }^{\mathrm {E}}$
in (5.32) is given by
 $$ \begin{align*}\prod_{e \in E_{0,1}(\Gamma)} \left ( \frac{(-1)^{d_e -1}((d_e-1)!)^2(w - 2z)^{2d_e} (w-z)w z^2} {(w + z) P_{d_e}(-d_e (2w-z), w - 2z)} \right. \end{align*} $$
$$ \begin{align*}\prod_{e \in E_{0,1}(\Gamma)} \left ( \frac{(-1)^{d_e -1}((d_e-1)!)^2(w - 2z)^{2d_e} (w-z)w z^2} {(w + z) P_{d_e}(-d_e (2w-z), w - 2z)} \right. \end{align*} $$
 $$ \begin{align*}\cdot \left. \frac{P_{d_e}(-d_e(w - z), w - 2z)} {P_{d_e}(-d_e(w + z), w - 2z) P_{d_e}(-d_e w, w - 2z)} \right ) \end{align*} $$
$$ \begin{align*}\cdot \left. \frac{P_{d_e}(-d_e(w - z), w - 2z)} {P_{d_e}(-d_e(w + z), w - 2z) P_{d_e}(-d_e w, w - 2z)} \right ) \end{align*} $$
 $$ \begin{align*}\cdot \prod_{e \in E_{0,2}(\Gamma)} \left ( \frac{(-1)^{d_e -1}((d_e-1)!)^2(z - 2w)^{2d_e} (z-w)z w^2} {(z + w) P_{d_e}(-d_e (2z-w), z - 2w)} \right. \end{align*} $$
$$ \begin{align*}\cdot \prod_{e \in E_{0,2}(\Gamma)} \left ( \frac{(-1)^{d_e -1}((d_e-1)!)^2(z - 2w)^{2d_e} (z-w)z w^2} {(z + w) P_{d_e}(-d_e (2z-w), z - 2w)} \right. \end{align*} $$
 $$ \begin{align*}\cdot \left. \frac{P_{d_e}(-d_e(z - w), z - 2w)} {P_{d_e}(-d_e(z + w), z - 2w) P_{d_e}(-d_e z, z - 2w)} \right ) \end{align*} $$
$$ \begin{align*}\cdot \left. \frac{P_{d_e}(-d_e(z - w), z - 2w)} {P_{d_e}(-d_e(z + w), z - 2w) P_{d_e}(-d_e z, z - 2w)} \right ) \end{align*} $$
 $$ \begin{align*}\cdot \prod_{e \in E_{1,2}(\Gamma)} \left ( \frac{(-1)^{d_e}((d_e-1)!)^2(2w-z)(w-2z) (w-z)^{2d_e} w^2 z^2} {(w+z)(2w+z)(w+2z) P_{d_e}(-2d_e w, w - z) P_{d_e}(-d_e (w+z), w - z)} \right. \end{align*} $$
$$ \begin{align*}\cdot \prod_{e \in E_{1,2}(\Gamma)} \left ( \frac{(-1)^{d_e}((d_e-1)!)^2(2w-z)(w-2z) (w-z)^{2d_e} w^2 z^2} {(w+z)(2w+z)(w+2z) P_{d_e}(-2d_e w, w - z) P_{d_e}(-d_e (w+z), w - z)} \right. \end{align*} $$
 $$ \begin{align} \left. \quad \cdot \frac{P_{d_e}(-d_e (w-2z), w - z) P_{d_e}(d_e z, w - z) P_{d_e}(d_e w, w - z)} {P_{d_e}(-3d_e w, w - z) P_{d_e}(-d_e (2w+z), w - z) P_{d_e}(-d_e (w+2z), w - z)} \right ). \end{align} $$
$$ \begin{align} \left. \quad \cdot \frac{P_{d_e}(-d_e (w-2z), w - z) P_{d_e}(d_e z, w - z) P_{d_e}(d_e w, w - z)} {P_{d_e}(-3d_e w, w - z) P_{d_e}(-d_e (2w+z), w - z) P_{d_e}(-d_e (w+2z), w - z)} \right ). \end{align} $$
Notation 5.8. Let
![]() $d \ge 1$
, and let
$d \ge 1$
, and let
![]() $\Gamma \in {{\mathcal T}}_{d,i}$
. We use
$\Gamma \in {{\mathcal T}}_{d,i}$
. We use
![]() $V_0(\Gamma )$
to denote the subset of
$V_0(\Gamma )$
to denote the subset of
![]() $V(\Gamma )$
consisting of all the vertices v of
$V(\Gamma )$
consisting of all the vertices v of
![]() $\Gamma $
such that
$\Gamma $
such that
for the two edges
![]() $e_1(v)$
and
$e_1(v)$
and
![]() $e_2(v)$
attaching to v, and
$e_2(v)$
attaching to v, and
![]() $e_j(v) \in E_{0,j}(\Gamma )$
for
$e_j(v) \in E_{0,j}(\Gamma )$
for
![]() $j = 1, 2$
.
$j = 1, 2$
.
If
![]() $v_1, v_2 \in V_0(\Gamma )$
are distinct, then
$v_1, v_2 \in V_0(\Gamma )$
are distinct, then
![]() $\mathfrak L(v_1) = Q_{i,0} = \mathfrak L(v_2)$
. So none of the two edges attaching to
$\mathfrak L(v_1) = Q_{i,0} = \mathfrak L(v_2)$
. So none of the two edges attaching to
![]() $v_1$
coincide with any of the two edges attaching to
$v_1$
coincide with any of the two edges attaching to
![]() $v_2$
, and
$v_2$
, and
Lemma 5.9. Let
![]() $d \ge 1$
and
$d \ge 1$
and
![]() $\Gamma \in {{\mathcal T}}_{d,i}$
. Then,
$\Gamma \in {{\mathcal T}}_{d,i}$
. Then,
 $$ \begin{align*}\displaystyle{\frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} = M \big ( (w+z)^3 \big ) } \end{align*} $$
$$ \begin{align*}\displaystyle{\frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} = M \big ( (w+z)^3 \big ) } \end{align*} $$
unless one of the following cases happens:
-
(i)
 $|V_0(\Gamma )| = 2$
and
$|V_0(\Gamma )| = 2$
and
 $|E(\Gamma )| = 4$
;
$|E(\Gamma )| = 4$
; -
(ii)
 $|V_0(\Gamma )| = 1$
and
$|V_0(\Gamma )| = 1$
and
 $|E(\Gamma )| = 2$
;
$|E(\Gamma )| = 2$
; -
(iii)
 $|V_0(\Gamma )| = 1$
and
$|V_0(\Gamma )| = 1$
and
 $|E(\Gamma )| = 3$
;
$|E(\Gamma )| = 3$
; -
(iv)
 $|V_0(\Gamma )| = 0$
and
$|V_0(\Gamma )| = 0$
and
 $|E(\Gamma )| = 1$
;
$|E(\Gamma )| = 1$
; -
(v)
 $|V_0(\Gamma )| = 0$
and
$|V_0(\Gamma )| = 0$
and
 $|E(\Gamma )| = 2$
.
$|E(\Gamma )| = 2$
.
Proof. First of all, let us examine the factor
![]() $e_{\Gamma }^{\mathrm {E}}$
. If
$e_{\Gamma }^{\mathrm {E}}$
. If
![]() $e \in E_{0,1}(\Gamma )$
, then we see from (5.31) that
$e \in E_{0,1}(\Gamma )$
, then we see from (5.31) that
![]() $(w+z)| P_{d_e}(-d_e(w - z), w - 2z)$
if and only if
$(w+z)| P_{d_e}(-d_e(w - z), w - 2z)$
if and only if
![]() $3|d_e$
; moreover, if
$3|d_e$
; moreover, if
![]() $3|d_e$
, then
$3|d_e$
, then
![]() $(w+z)^2 \nmid P_{d_e}(-d_e(w - z), w - 2z)$
and
$(w+z)^2 \nmid P_{d_e}(-d_e(w - z), w - 2z)$
and
![]() $(w+z)|P_{d_e}(-d_e w, w - 2z)$
. Applying a similar argument to
$(w+z)|P_{d_e}(-d_e w, w - 2z)$
. Applying a similar argument to
![]() $e \in E_{0,2}(\Gamma )$
and
$e \in E_{0,2}(\Gamma )$
and
![]() $e \in E_{1, 2}(\Gamma )$
, we conclude that
$e \in E_{1, 2}(\Gamma )$
, we conclude that
 $$ \begin{align} \frac{1}{e_{\Gamma}^{\mathrm{E}}} = M \big ( (w+z)^{|E(\Gamma)|} \big ). \end{align} $$
$$ \begin{align} \frac{1}{e_{\Gamma}^{\mathrm{E}}} = M \big ( (w+z)^{|E(\Gamma)|} \big ). \end{align} $$
Next, by (5.34), (5.35), (5.2), (5.3) and (5.4), the only possible factors in
![]() $1/(e_{\Gamma }^{\mathrm {V}} \cdot e_{\Gamma }^{\mathrm {F}})$
divisible by
$1/(e_{\Gamma }^{\mathrm {V}} \cdot e_{\Gamma }^{\mathrm {F}})$
divisible by
![]() $(w+z)$
come from
$(w+z)$
come from
![]() $(\omega _{F_1(v)}+ \omega _{F_2(v)})$
with
$(\omega _{F_1(v)}+ \omega _{F_2(v)})$
with
![]() $g(v) = 0$
and
$g(v) = 0$
and
![]() $ \mathrm {val} (v) = 2$
. If such a factor
$ \mathrm {val} (v) = 2$
. If such a factor
![]() $(\omega _{F_1(v)}+ \omega _{F_2(v)})$
is divisible by
$(\omega _{F_1(v)}+ \omega _{F_2(v)})$
is divisible by
![]() $(w+z)$
, then we see from (5.43) that
$(w+z)$
, then we see from (5.43) that
![]() $\mathfrak L(v) = Q_{i,0}$
,
$\mathfrak L(v) = Q_{i,0}$
,
![]() $d_{e_1(v)} = d_{e_2(v)}$
for the two edges
$d_{e_1(v)} = d_{e_2(v)}$
for the two edges
![]() $e_1(v)$
and
$e_1(v)$
and
![]() $e_2(v)$
attaching to v,
$e_2(v)$
attaching to v,
 $$ \begin{align*}(\omega_{F_1(v)}+ \omega_{F_2(v)}) = -\frac{1}{d_{e_j(v)}} \cdot (w+z), \end{align*} $$
$$ \begin{align*}(\omega_{F_1(v)}+ \omega_{F_2(v)}) = -\frac{1}{d_{e_j(v)}} \cdot (w+z), \end{align*} $$
and
![]() $e_j(v) \in E_{0,j}(\Gamma )$
for
$e_j(v) \in E_{0,j}(\Gamma )$
for
![]() $j = 1, 2$
. Hence,
$j = 1, 2$
. Hence,
![]() $v \in V_0(\Gamma )$
. It follows that
$v \in V_0(\Gamma )$
. It follows that
 $$ \begin{align*}\frac{1}{e_{\Gamma}^{\mathrm{V}} \cdot e_{\Gamma}^{\mathrm{F}}} = M \big ( (w+z)^{-|V_0(\Gamma)|} \big ). \end{align*} $$
$$ \begin{align*}\frac{1}{e_{\Gamma}^{\mathrm{V}} \cdot e_{\Gamma}^{\mathrm{F}}} = M \big ( (w+z)^{-|V_0(\Gamma)|} \big ). \end{align*} $$
Combining this with (5.32) and (5.46), we conclude that
 $$ \begin{align*}\frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} = M \big ( (w+z)^{|E(\Gamma)| - |V_0(\Gamma)|} \big ). \end{align*} $$
$$ \begin{align*}\frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} = M \big ( (w+z)^{|E(\Gamma)| - |V_0(\Gamma)|} \big ). \end{align*} $$
By (5.45), we have
![]() $|E(\Gamma )| - |V_0(\Gamma )| \ge |V_0(\Gamma )|$
. Now our lemma follows.
$|E(\Gamma )| - |V_0(\Gamma )| \ge |V_0(\Gamma )|$
. Now our lemma follows.
Lemma 5.10. Let
![]() $d \ge 1$
. Then, the summation
$d \ge 1$
. Then, the summation
![]() $\sum _{\Gamma \in {\mathcal T}_{d, i}}$
is equal to
$\sum _{\Gamma \in {\mathcal T}_{d, i}}$
is equal to
where
![]() $f_d$
is a universal constant depending only on d and is given by
$f_d$
is a universal constant depending only on d and is given by
 $$ \begin{align*}\frac{4}{9d^2} \sum_{\delta \vdash d/2} \frac{d_1d_2}{|\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 +\frac{1}{54d} \sum_{\delta \vdash d/2} \frac{d_1^2}{d_2} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 -\frac{1}{108} \sum_{\delta \vdash d/2} \frac{d_1^2 + d_1d_2 + d_2^2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 \end{align*} $$
$$ \begin{align*}\frac{4}{9d^2} \sum_{\delta \vdash d/2} \frac{d_1d_2}{|\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 +\frac{1}{54d} \sum_{\delta \vdash d/2} \frac{d_1^2}{d_2} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 -\frac{1}{108} \sum_{\delta \vdash d/2} \frac{d_1^2 + d_1d_2 + d_2^2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 \end{align*} $$
 $$ \begin{align*}+ \frac{4d-49}{216d} \cdot \gamma_{d/2}^2 + \sum_{2d_1+3d_2=d} \left ( \frac{d_1d_2}{d^2} - \frac{d^2}{432d_1d_2} + \frac{1}{72} + \frac{d}{16d_1^3} + \frac{d_1^2}{54d d_2} \right ) \cdot \gamma_{d_1}^2 {\widetilde \gamma}_{d_2} \end{align*} $$
$$ \begin{align*}+ \frac{4d-49}{216d} \cdot \gamma_{d/2}^2 + \sum_{2d_1+3d_2=d} \left ( \frac{d_1d_2}{d^2} - \frac{d^2}{432d_1d_2} + \frac{1}{72} + \frac{d}{16d_1^3} + \frac{d_1^2}{54d d_2} \right ) \cdot \gamma_{d_1}^2 {\widetilde \gamma}_{d_2} \end{align*} $$
 $$ \begin{align*}+ \sum_{2d_1+d_2=d} \frac{(-1)^{d}(2d^2+d_2^2)}{216d_1(d_1+d_2)} \cdot \gamma_{d_1}^2 \gamma_{d_2} + \frac{(-1)^d}{24} \left ( \frac{5}{9} - \sum_{1 \le m \le d-1, m \ne d/3} \frac{d}{d-3m} \right ) \cdot \gamma_{d} \end{align*} $$
$$ \begin{align*}+ \sum_{2d_1+d_2=d} \frac{(-1)^{d}(2d^2+d_2^2)}{216d_1(d_1+d_2)} \cdot \gamma_{d_1}^2 \gamma_{d_2} + \frac{(-1)^d}{24} \left ( \frac{5}{9} - \sum_{1 \le m \le d-1, m \ne d/3} \frac{d}{d-3m} \right ) \cdot \gamma_{d} \end{align*} $$
 $$ \begin{align*}+ \sum_{\delta \vdash d} \frac{(-1)^{d}(-69d^4+77d^3d_1+307d^2d_1^2-704dd_1^3+384d_1^4)} {1728d^2 d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1} \gamma_{d_2} \end{align*} $$
$$ \begin{align*}+ \sum_{\delta \vdash d} \frac{(-1)^{d}(-69d^4+77d^3d_1+307d^2d_1^2-704dd_1^3+384d_1^4)} {1728d^2 d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1} \gamma_{d_2} \end{align*} $$
 $$ \begin{align*}+ \frac{(-1)^{d}}{108} \sum_{d_1+d_2 = d, d_1 \ne d_2} \frac{d_1^2}{(d_1-d_2)d_2} \cdot \gamma_{d_1} \gamma_{d_2} + \sum_{d_1+3d_2 = d} \frac{(-1)^{d_1}(2d^2+d_1^2)}{36(d^2-d_1^2)} \cdot {\gamma}_{d_1} {\widetilde \gamma}_{d_2} \end{align*} $$
$$ \begin{align*}+ \frac{(-1)^{d}}{108} \sum_{d_1+d_2 = d, d_1 \ne d_2} \frac{d_1^2}{(d_1-d_2)d_2} \cdot \gamma_{d_1} \gamma_{d_2} + \sum_{d_1+3d_2 = d} \frac{(-1)^{d_1}(2d^2+d_1^2)}{36(d^2-d_1^2)} \cdot {\gamma}_{d_1} {\widetilde \gamma}_{d_2} \end{align*} $$
 $$ \begin{align*}+ \sum_{\delta \vdash d/3} \frac{3(d_1^4-d_1^3d_2+8d_1^2d_2^2-3d_1d_2^3-d_2^4)} {16d^2d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \cdot {\widetilde \gamma}_{d_1} {\widetilde \gamma}_{d_2}. \end{align*} $$
$$ \begin{align*}+ \sum_{\delta \vdash d/3} \frac{3(d_1^4-d_1^3d_2+8d_1^2d_2^2-3d_1d_2^3-d_2^4)} {16d^2d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \cdot {\widetilde \gamma}_{d_1} {\widetilde \gamma}_{d_2}. \end{align*} $$
In the above,
![]() $d_1>0$
,
$d_1>0$
,
![]() $d_2>0$
,
$d_2>0$
,
![]() $\delta = (d_1, d_2)$
is a length-
$\delta = (d_1, d_2)$
is a length-
![]() $2$
partition,
$2$
partition,
![]() $\gamma _{d_1} = -2$
if
$\gamma _{d_1} = -2$
if
![]() $3|d_1$
and
$3|d_1$
and
![]() $\gamma _{d_1} = 1$
if
$\gamma _{d_1} = 1$
if
![]() $3 \nmid d_1$
,
$3 \nmid d_1$
,
![]() ${\widetilde \gamma }_{d_2} = 3$
if
${\widetilde \gamma }_{d_2} = 3$
if
![]() $2|d_2$
and
$2|d_2$
and
![]() ${\widetilde \gamma }_{d_2} = 1$
if
${\widetilde \gamma }_{d_2} = 1$
if
![]() $2 \nmid d_2$
, and a summand containing
$2 \nmid d_2$
, and a summand containing
![]() $\sum _{\delta \vdash d/2}$
or
$\sum _{\delta \vdash d/2}$
or
![]() $\gamma _{d/2}$
(respectively,
$\gamma _{d/2}$
(respectively,
![]() $\sum _{\delta \vdash d/3}$
) does not appear if
$\sum _{\delta \vdash d/3}$
) does not appear if
![]() $2 \nmid d$
(respectively, if
$2 \nmid d$
(respectively, if
![]() $3 \nmid d$
).
$3 \nmid d$
).
Proof. By Lemma 5.9, the computation of
![]() $\sum _{\Gamma \in {\mathcal T}_{d, i}}$
is reduced to those stable graphs
$\sum _{\Gamma \in {\mathcal T}_{d, i}}$
is reduced to those stable graphs
![]() $\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (i), (ii), (iii), (iv) or (v).
$\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (i), (ii), (iii), (iv) or (v).
To begin, the stable graphs
![]() $\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (i) are:
$\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (i) are:
-
(i-1)
where
 $\{v_1, v_4\} = V_0(\Gamma )$
(so that
$\{v_1, v_4\} = V_0(\Gamma )$
(so that
 $\mathfrak L(v_1) = Q_{i,0} = \mathfrak L(v_4)$
),
$\mathfrak L(v_1) = Q_{i,0} = \mathfrak L(v_4)$
),
 $\mathfrak L(v_2) = Q_{i,1}$
,
$\mathfrak L(v_2) = Q_{i,1}$
,
 $\mathfrak L(v_3) = Q_{i,2}$
,
$\mathfrak L(v_3) = Q_{i,2}$
,
 $g(v_j) = 0$
for every j,
$g(v_j) = 0$
for every j,
 $2|d$
and
$2|d$
and
 $\delta = (d_1, d_2) \vdash d/2$
denotes a length-
$\delta = (d_1, d_2) \vdash d/2$
denotes a length-
 $2$
partition of
$2$
partition of
 $d/2$
. By (5.12),
$d/2$
. By (5.12),
 $ |\mathbf {A}_{\Gamma }| = d_1^2 d_2^2 \cdot |{\mathrm {Aut}} (\Gamma )| = d_1^2 d_2^2 \cdot |{\mathrm {Aut}} (\delta )|. $
By (5.32), (5.44), (5.34), (5.35) and (5.43), we have
$ |\mathbf {A}_{\Gamma }| = d_1^2 d_2^2 \cdot |{\mathrm {Aut}} (\Gamma )| = d_1^2 d_2^2 \cdot |{\mathrm {Aut}} (\delta )|. $
By (5.32), (5.44), (5.34), (5.35) and (5.43), we have  $$ \begin{align*}\sum_{\substack{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (i-1)}}} = \frac{4}{9d^2} \sum_{\delta \vdash d/2} \frac{d_1d_2}{|\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ) \end{align*} $$
$$ \begin{align*}\sum_{\substack{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (i-1)}}} = \frac{4}{9d^2} \sum_{\delta \vdash d/2} \frac{d_1d_2}{|\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ) \end{align*} $$
where
 $\gamma _{d_1} = -2$
if
$\gamma _{d_1} = -2$
if
 $3|d_1$
and
$3|d_1$
and
 $\gamma _{d_1} = 1$
if
$\gamma _{d_1} = 1$
if
 $3 \nmid d_1$
.
$3 \nmid d_1$
. -
(i-2)
where
 $\{v_2, v_4\} = V_0(\Gamma )$
,
$\{v_2, v_4\} = V_0(\Gamma )$
,
 $\mathfrak L(v_3) \in \big \{Q_{i,1}, Q_{i,2}\big \}$
,
$\mathfrak L(v_3) \in \big \{Q_{i,1}, Q_{i,2}\big \}$
,
 $\mathfrak L(v_1) = \mathfrak L(v_5) \in \big \{Q_{i,1}, Q_{i,2}\big \} - \big \{\mathfrak L(v_3)\big \}$
,
$\mathfrak L(v_1) = \mathfrak L(v_5) \in \big \{Q_{i,1}, Q_{i,2}\big \} - \big \{\mathfrak L(v_3)\big \}$
,
 $g(v_1) = 1$
,
$g(v_1) = 1$
,
 $g(v_j) = 0$
for every
$g(v_j) = 0$
for every
 $j \ne 1$
,
$j \ne 1$
,
 $2|d$
and
$2|d$
and
 $\delta = (d_1, d_2) \vdash d/2$
denotes a length-
$\delta = (d_1, d_2) \vdash d/2$
denotes a length-
 $2$
partition of
$2$
partition of
 $d/2$
. There are exactly
$d/2$
. There are exactly
 $2$
types of such graphs if we ignore the edge weights. By (5.12),
$2$
types of such graphs if we ignore the edge weights. By (5.12),
 $|\mathbf {A}_{\Gamma }| = d_1^2 d_2^2$
. By (5.32), (5.44), (5.34), (5.35) and (5.43) together with (5.37), we get
$|\mathbf {A}_{\Gamma }| = d_1^2 d_2^2$
. By (5.32), (5.44), (5.34), (5.35) and (5.43) together with (5.37), we get  $$ \begin{align*}\sum_{\substack{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (i-2)}}} = \frac{1}{54d} \sum_{\delta \vdash d/2} \frac{d_1^2}{d_2} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
$$ \begin{align*}\sum_{\substack{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (i-2)}}} = \frac{1}{54d} \sum_{\delta \vdash d/2} \frac{d_1^2}{d_2} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
-
(i-3)
 $\Gamma $
has the same shape as Figure (i-2) with
$\Gamma $
has the same shape as Figure (i-2) with
 $\{v_2, v_4\} = V_0(\Gamma )$
,
$\{v_2, v_4\} = V_0(\Gamma )$
,
 $\mathfrak L(v_3) \in \big \{Q_{i,1}, Q_{i,2}\big \}$
,
$\mathfrak L(v_3) \in \big \{Q_{i,1}, Q_{i,2}\big \}$
,
 $\mathfrak L(v_1) = \mathfrak L(v_5) \in \big \{Q_{i,1}, Q_{i,2}\big \} - \big \{\mathfrak L(v_3)\big \}$
,
$\mathfrak L(v_1) = \mathfrak L(v_5) \in \big \{Q_{i,1}, Q_{i,2}\big \} - \big \{\mathfrak L(v_3)\big \}$
,
 $g(v_3) = 1$
,
$g(v_3) = 1$
,
 $g(v_j) = 0$
for every
$g(v_j) = 0$
for every
 $j \ne 3$
, and
$j \ne 3$
, and
 $2|d$
. There are exactly
$2|d$
. There are exactly
 $2$
types of such graphs if we ignore the edge weights. By (5.12),
$2$
types of such graphs if we ignore the edge weights. By (5.12),
 $|\mathbf {A}_{\Gamma }| = d_1^2 d_2^2 \cdot |{\mathrm {Aut}} (\delta )|$
. By (5.32), (5.44), (5.34), (5.35) and (5.43), together with (5.37) and (5.38), we obtain
$|\mathbf {A}_{\Gamma }| = d_1^2 d_2^2 \cdot |{\mathrm {Aut}} (\delta )|$
. By (5.32), (5.44), (5.34), (5.35) and (5.43), together with (5.37) and (5.38), we obtain  $$ \begin{align*}\sum_{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (i-3)}} = -\frac{1}{108} \sum_{\delta \vdash d/2} \frac{d_1^2 + d_1d_2 + d_2^2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
$$ \begin{align*}\sum_{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (i-3)}} = -\frac{1}{108} \sum_{\delta \vdash d/2} \frac{d_1^2 + d_1d_2 + d_2^2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \cdot \gamma_{d_1}^2 \gamma_{d_2}^2 \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
Next, the stable graphs
![]() $\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (ii) are:
$\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (ii) are:
-
(ii)
where
 $2|d$
,
$2|d$
,
 $\{v_1\} = V_0(\Gamma )$
,
$\{v_1\} = V_0(\Gamma )$
,
 $\mathfrak L(v_2) = Q_{i,1}$
,
$\mathfrak L(v_2) = Q_{i,1}$
,
 $\mathfrak L(v_3) = Q_{i,2}$
,
$\mathfrak L(v_3) = Q_{i,2}$
,
 $g(v_j) = 1$
for some
$g(v_j) = 1$
for some
 $j \in \{2, 3\}$
and
$j \in \{2, 3\}$
and
 $g(v_k) = 0$
if
$g(v_k) = 0$
if
 $k \ne j$
. There are
$k \ne j$
. There are
 $2$
types of such graphs, and
$2$
types of such graphs, and  $$ \begin{align*}\sum_{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (ii)}} = \frac{4d-49}{216d} \cdot \gamma_{d/2}^2 \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
$$ \begin{align*}\sum_{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (ii)}} = \frac{4d-49}{216d} \cdot \gamma_{d/2}^2 \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
The stable graphs
![]() $\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (iii) are:
$\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (iii) are:
-
(iii-1)
where
 $\{v_1\} = V_0(\Gamma )$
(so that
$\{v_1\} = V_0(\Gamma )$
(so that
 $\mathfrak L(v_1) = Q_{i,0}$
),
$\mathfrak L(v_1) = Q_{i,0}$
),
 $\mathfrak L(v_2) = Q_{i,1}$
,
$\mathfrak L(v_2) = Q_{i,1}$
,
 $\mathfrak L(v_3) = Q_{i,2}$
,
$\mathfrak L(v_3) = Q_{i,2}$
,
 $g(v_j) = 0$
for every j and
$g(v_j) = 0$
for every j and
 $2d_1 + 3d_2 = d$
. We have
$2d_1 + 3d_2 = d$
. We have  $$ \begin{align*} \sum_{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (iii-1)}} = \sum_{2d_1+3d_2=d} \frac{d_1d_2}{d^2} \cdot \gamma_{d_1}^2 {\widetilde \gamma}_{d_2} \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ) \end{align*} $$
$$ \begin{align*} \sum_{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (iii-1)}} = \sum_{2d_1+3d_2=d} \frac{d_1d_2}{d^2} \cdot \gamma_{d_1}^2 {\widetilde \gamma}_{d_2} \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ) \end{align*} $$
where
 ${\widetilde \gamma }_{d_2} = 3$
if
${\widetilde \gamma }_{d_2} = 3$
if
 $2|d_2$
and
$2|d_2$
and
 ${\widetilde \gamma }_{d_2} = 1$
if
${\widetilde \gamma }_{d_2} = 1$
if
 $2 \nmid d_2$
.
$2 \nmid d_2$
. -
(iii-2)
where
 $\{v_1\} = V_0(\Gamma )$
,
$\{v_1\} = V_0(\Gamma )$
,
 $\mathfrak L(v_2) = Q_{i,1}$
,
$\mathfrak L(v_2) = Q_{i,1}$
,
 $\mathfrak L(v_3) = Q_{i,2}$
,
$\mathfrak L(v_3) = Q_{i,2}$
,
 $\mathfrak L(v_4) = Q_{i,0}$
(respectively,
$\mathfrak L(v_4) = Q_{i,0}$
(respectively,
 $Q_{i,2}$
),
$Q_{i,2}$
),
 $2d_1 + d_2 = d$
(respectively,
$2d_1 + d_2 = d$
(respectively,
 $2d_1 + 3d_2 = d$
),
$2d_1 + 3d_2 = d$
),
 $g(v_j) = 1$
for some
$g(v_j) = 1$
for some
 $j \in \{2,3,4\}$
and
$j \in \{2,3,4\}$
and
 $g(v_k) = 0$
if
$g(v_k) = 0$
if
 $k \ne j$
. There are exactly
$k \ne j$
. There are exactly
 $6$
types of such graphs if we ignore the edge weights.
$6$
types of such graphs if we ignore the edge weights.
-
(iii-3)
 $\Gamma $
has the same shape as Figure (iii-2) with
$\Gamma $
has the same shape as Figure (iii-2) with
 $\{v_1\} = V_0(\Gamma )$
,
$\{v_1\} = V_0(\Gamma )$
,
 $\mathfrak L(v_2) = Q_{i,2}$
,
$\mathfrak L(v_2) = Q_{i,2}$
,
 $\mathfrak L(v_3) = Q_{i,1}$
,
$\mathfrak L(v_3) = Q_{i,1}$
,
 $\mathfrak L(v_4) = Q_{i,0}$
(respectively,
$\mathfrak L(v_4) = Q_{i,0}$
(respectively,
 $Q_{i,1}$
),
$Q_{i,1}$
),
 $2d_1 + d_2 = d$
(respectively,
$2d_1 + d_2 = d$
(respectively,
 $2d_1 + 3d_2 = d$
),
$2d_1 + 3d_2 = d$
),
 $g(v_j) = 1$
for some
$g(v_j) = 1$
for some
 $j \in \{2,3,4\}$
and
$j \in \{2,3,4\}$
and
 $g(v_k) = 0$
if
$g(v_k) = 0$
if
 $k \ne j$
. There are exactly
$k \ne j$
. There are exactly
 $6$
types of such graphs if we ignore the edge weights. We see that
$6$
types of such graphs if we ignore the edge weights. We see that
 $\sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (iii-2)}} + \sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (iii-3)}}$
is equal to
$\sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (iii-2)}} + \sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (iii-3)}}$
is equal to  $$ \begin{align*}\bigg (\sum_{2d_1+3d_2=d} \left (-\frac{d^2}{432d_1d_2} + \frac{1}{72} + \frac{d}{16d_1^3} + \frac{d_1^2}{54d d_2} \right ) \cdot \gamma_{d_1}^2 {\widetilde \gamma}_{d_2} \end{align*} $$
$$ \begin{align*}\bigg (\sum_{2d_1+3d_2=d} \left (-\frac{d^2}{432d_1d_2} + \frac{1}{72} + \frac{d}{16d_1^3} + \frac{d_1^2}{54d d_2} \right ) \cdot \gamma_{d_1}^2 {\widetilde \gamma}_{d_2} \end{align*} $$
 $$ \begin{align*}+ \sum_{2d_1+d_2=d} \frac{(-1)^{d}(2d^2+d_2^2)}{216d_1(d_1+d_2)} \cdot \gamma_{d_1}^2 \gamma_{d_2} \bigg ) \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
$$ \begin{align*}+ \sum_{2d_1+d_2=d} \frac{(-1)^{d}(2d^2+d_2^2)}{216d_1(d_1+d_2)} \cdot \gamma_{d_1}^2 \gamma_{d_2} \bigg ) \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
The stable graphs
![]() $\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (iv) are:
$\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (iv) are:
-
(iv-1)
where
 $\mathfrak L(v_1) = Q_{i,0}$
,
$\mathfrak L(v_1) = Q_{i,0}$
,
 $\mathfrak L(v_2) \in \big \{Q_{i,1}, Q_{i,2} \big \}$
,
$\mathfrak L(v_2) \in \big \{Q_{i,1}, Q_{i,2} \big \}$
,
 $g(v_1) \in \{1, 0\}$
and
$g(v_1) \in \{1, 0\}$
and
 $g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. There are exactly
$g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. There are exactly
 $4$
types of such graphs. We see that the summation
$4$
types of such graphs. We see that the summation
 $\sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (iv-1)}} $
is equal to
$\sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (iv-1)}} $
is equal to  $$ \begin{align*}\left (\frac{(-1)^d}{24} \left ( \frac{5}{9} - \sum_{1 \le m \le d-1, m \ne d/3} \frac{d}{d-3m} \right ) - \frac{17 (-1)^d}{54d} \right ) \gamma_{d} \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
$$ \begin{align*}\left (\frac{(-1)^d}{24} \left ( \frac{5}{9} - \sum_{1 \le m \le d-1, m \ne d/3} \frac{d}{d-3m} \right ) - \frac{17 (-1)^d}{54d} \right ) \gamma_{d} \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
-
(iv-2)
where
 $3|d$
,
$3|d$
,
 $\mathfrak L(v_1) = Q_{i,1}$
,
$\mathfrak L(v_1) = Q_{i,1}$
,
 $\mathfrak L(v_2) = Q_{i,2}$
,
$\mathfrak L(v_2) = Q_{i,2}$
,
 $g(v_1) \in \{1, 0\}$
and
$g(v_1) \in \{1, 0\}$
and
 $g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. There are exactly
$g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. There are exactly
 $2$
types of such graphs. We obtain
$2$
types of such graphs. We obtain  $$ \begin{align*}\sum_{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (iv-2)}} = \frac{49-7d}{144d} \cdot {\widetilde \gamma}_{d/3} \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
$$ \begin{align*}\sum_{\Gamma \in {\mathcal T}_{d, i}, \, \text{Case (iv-2)}} = \frac{49-7d}{144d} \cdot {\widetilde \gamma}_{d/3} \cdot \frac{(w+z)^2}{wz} + M \big ((w+z)^3 \big ). \end{align*} $$
Finally, the stable graphs
![]() $\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (v) are:
$\Gamma \in {\mathcal T}_{d, i}$
satisfying Lemma 5.9 (v) are:
-
(v-1)
where
 $\mathfrak L(v_1) = Q_{i,j_1}$
and
$\mathfrak L(v_1) = Q_{i,j_1}$
and
 $\mathfrak L(v_2) = Q_{i,j_2}$
for some
$\mathfrak L(v_2) = Q_{i,j_2}$
for some
 $j_1, j_2 \in \{0, 1, 2\}$
with
$j_1, j_2 \in \{0, 1, 2\}$
with
 $j_1 < j_2$
and
$j_1 < j_2$
and
 $g(v_1) = g(v_2) = 0$
. There are exactly
$g(v_1) = g(v_2) = 0$
. There are exactly
 $3$
types of such graphs if we ignore the edge weights.
$3$
types of such graphs if we ignore the edge weights.
-
(v-2)
where
 $\mathfrak L(v_1) = Q_{i,j_1}$
for some
$\mathfrak L(v_1) = Q_{i,j_1}$
for some
 $j_1 \in \{0, 1, 2\}$
,
$j_1 \in \{0, 1, 2\}$
,
 $\mathfrak L(v_2) = Q_{i,j_2}$
and
$\mathfrak L(v_2) = Q_{i,j_2}$
and
 $\mathfrak L(v_3) = Q_{i,j_3}$
for some
$\mathfrak L(v_3) = Q_{i,j_3}$
for some
 $j_2, j_3 \in \{0, 1, 2\} - \{j_1\}$
with
$j_2, j_3 \in \{0, 1, 2\} - \{j_1\}$
with
 $j_2 \le j_3$
,
$j_2 \le j_3$
,
 $g(v_1) = 1$
and
$g(v_1) = 1$
and
 $g(v_2) = g(v_3) = 0$
. There are
$g(v_2) = g(v_3) = 0$
. There are
 $9$
types of such graphs if we ignore the edge weights.
$9$
types of such graphs if we ignore the edge weights.
-
(v-3)
 $\Gamma $
has the same shape as Figure (v-2) with
$\Gamma $
has the same shape as Figure (v-2) with
 $\mathfrak L(v_1) = Q_{i,j_1}$
for some
$\mathfrak L(v_1) = Q_{i,j_1}$
for some
 $j_1 \in \{0, 1, 2\}$
,
$j_1 \in \{0, 1, 2\}$
,
 $\mathfrak L(v_2) = Q_{i,j_2}$
and
$\mathfrak L(v_2) = Q_{i,j_2}$
and
 $\mathfrak L(v_3) = Q_{i,j_3}$
for some
$\mathfrak L(v_3) = Q_{i,j_3}$
for some
 $j_2, j_3 \in \{0, 1, 2\} - \{j_1\}$
,
$j_2, j_3 \in \{0, 1, 2\} - \{j_1\}$
,
 $g(v_2) = 1$
,
$g(v_2) = 1$
,
 $g(v_1) = g(v_3) = 0$
and
$g(v_1) = g(v_3) = 0$
and
 $d_1 \ne d_2$
if
$d_1 \ne d_2$
if
 $j_1 = 0$
and
$j_1 = 0$
and
 $j_2 \ne j_3$
. There are exactly
$j_2 \ne j_3$
. There are exactly
 $12$
types of such graphs if we ignore the edge weights.
$12$
types of such graphs if we ignore the edge weights.
We see that the summation
![]() $\sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (v-1)}} + \sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (v-2)}} + \sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (v-3)}}$
is equal to the last three lines in the formula of
$\sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (v-1)}} + \sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (v-2)}} + \sum _{\Gamma \in {\mathcal T}_{d, i}, \, \text {Case (v-3)}}$
is equal to the last three lines in the formula of
![]() $f_d$
in our lemma.
$f_d$
in our lemma.
Example 5.11. Let
![]() $d = 1$
. Then, we have
$d = 1$
. Then, we have
![]() $|E(\Gamma )| = 1$
and
$|E(\Gamma )| = 1$
and
![]() $|V(\Gamma )| = 2$
for every stable graph
$|V(\Gamma )| = 2$
for every stable graph
![]() $\Gamma \in {\mathcal S}_{d,i, i} \cup {\mathcal T}_{d,i}$
. If
$\Gamma \in {\mathcal S}_{d,i, i} \cup {\mathcal T}_{d,i}$
. If
![]() $\Gamma \in {\mathcal S}_{d,i, i}$
, then
$\Gamma \in {\mathcal S}_{d,i, i}$
, then
![]() $\Gamma $
is one of the two stable graphs stated in the first paragraph in the proof of Lemma 5.7:
$\Gamma $
is one of the two stable graphs stated in the first paragraph in the proof of Lemma 5.7:
where
![]() $\mathfrak L(v_1) = R_{i, i}^{(1)}$
,
$\mathfrak L(v_1) = R_{i, i}^{(1)}$
,
![]() $\mathfrak L(v_2) = R_{i, i}^{(2)}$
,
$\mathfrak L(v_2) = R_{i, i}^{(2)}$
,
![]() $g(v_1) \in \{1, 0\}$
and
$g(v_1) \in \{1, 0\}$
and
![]() $g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. An easy computation shows that
$g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. An easy computation shows that
![]() $\sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is equal to
$\sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is equal to
 $$ \begin{align} 4 \int_{\overline{M}_{1,1}} \lambda \cdot \frac{(w+z)^2}{wz} = \frac16 \cdot \frac{(w+z)^2}{wz} \end{align} $$
$$ \begin{align} 4 \int_{\overline{M}_{1,1}} \lambda \cdot \frac{(w+z)^2}{wz} = \frac16 \cdot \frac{(w+z)^2}{wz} \end{align} $$
where w and z denote
![]() $w_i$
and
$w_i$
and
![]() $z_i$
, respectively. Similarly, if
$z_i$
, respectively. Similarly, if
![]() $\Gamma \in {\mathcal T}_{d,i}$
, then
$\Gamma \in {\mathcal T}_{d,i}$
, then
![]() $\Gamma $
is one of the four stable graphs stated in Case (iv-1) in the proof of Lemma 5.10:
$\Gamma $
is one of the four stable graphs stated in Case (iv-1) in the proof of Lemma 5.10:
where
![]() $\mathfrak L(v_1) = Q_{i,0}$
,
$\mathfrak L(v_1) = Q_{i,0}$
,
![]() $\mathfrak L(v_2) \in \big \{Q_{i,1}, Q_{i,2} \big \}$
,
$\mathfrak L(v_2) \in \big \{Q_{i,1}, Q_{i,2} \big \}$
,
![]() $g(v_1) \in \{1, 0\}$
and
$g(v_1) \in \{1, 0\}$
and
![]() $g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. A straightforward but lengthy computation shows that
$g(v_2) \in \{1, 0\} - \{g(v_1)\}$
. A straightforward but lengthy computation shows that
 $$ \begin{align*} \sum_{\Gamma \in {\mathcal T}_{d,i}, \,\, g(v_1) = 0} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} &=\frac1{24} \cdot \frac{(w+z)^2}{wz} \cdot \frac{8w^2 + 8z^2}{(w-2z)(2w-z)}, \\ \sum_{\Gamma \in {\mathcal T}_{d,i}, \,\, g(v_1) = 1} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} &=\frac1{24} \cdot \frac{(w+z)^2}{wz} \cdot \frac{6w^2 -35wz + 6z^2}{(w-2z)(2w-z)}. \end{align*} $$
$$ \begin{align*} \sum_{\Gamma \in {\mathcal T}_{d,i}, \,\, g(v_1) = 0} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} &=\frac1{24} \cdot \frac{(w+z)^2}{wz} \cdot \frac{8w^2 + 8z^2}{(w-2z)(2w-z)}, \\ \sum_{\Gamma \in {\mathcal T}_{d,i}, \,\, g(v_1) = 1} \frac{1}{|\mathbf{A}_{\Gamma}|} \int_{[\overline{M}_{\Gamma}]} \frac{1}{e(N_{\Gamma}^{\mathrm{vir}} )} &=\frac1{24} \cdot \frac{(w+z)^2}{wz} \cdot \frac{6w^2 -35wz + 6z^2}{(w-2z)(2w-z)}. \end{align*} $$
It follows that
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} = \sum _{\Gamma \in {\mathcal T}_{d,i}, \,\, g(v_1) = 0} + \sum _{\Gamma \in {\mathcal T}_{d,i}, \,\, g(v_1) = 1}$
is equal to
$\sum _{\Gamma \in {\mathcal T}_{d,i}} = \sum _{\Gamma \in {\mathcal T}_{d,i}, \,\, g(v_1) = 0} + \sum _{\Gamma \in {\mathcal T}_{d,i}, \,\, g(v_1) = 1}$
is equal to
In particular, the constant
![]() $f_1$
in (5.47) is equal to
$f_1$
in (5.47) is equal to
![]() $7/24$
, as asserted by Lemma 5.10. Combining with (5.48), we conclude that
$7/24$
, as asserted by Lemma 5.10. Combining with (5.48), we conclude that
![]() $\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is equal to
$\sum _{\Gamma \in {\mathcal T}_{d,i}} - \sum _{\Gamma \in {\mathcal S}_{d,i, i}}$
is equal to
Hence, we see from (5.19) that for a smooth projective toric surface X,
 $$ \begin{align} \langle \rangle_{1, \beta_3} = \frac{1}{12} \cdot \chi(X) \cdot K_X^2 + \frac18 \cdot K_X^2 = \left (\frac18 + \frac{1}{12} \cdot \chi(X)\right ) \cdot K_X^2. \end{align} $$
$$ \begin{align} \langle \rangle_{1, \beta_3} = \frac{1}{12} \cdot \chi(X) \cdot K_X^2 + \frac18 \cdot K_X^2 = \left (\frac18 + \frac{1}{12} \cdot \chi(X)\right ) \cdot K_X^2. \end{align} $$
By Lemma 5.1, formula (5.49) holds for every smooth projective surface X.
It is unclear how to simplify the constant
![]() $f_d$
in Lemma 5.10 for a general
$f_d$
in Lemma 5.10 for a general
![]() $d \ge 1$
. Finally, we are able to determine the genus-
$d \ge 1$
. Finally, we are able to determine the genus-
![]() $1$
extremal invariant
$1$
extremal invariant
![]() $\langle \rangle _{1, d\beta _3}$
.
$\langle \rangle _{1, d\beta _3}$
.
Theorem 5.12. Let X be a smooth projective surface. Let
![]() $d \ge 1$
, and let
$d \ge 1$
, and let
![]() $f_d$
be the constant defined in Lemma 5.10. Then,
$f_d$
be the constant defined in Lemma 5.10. Then,
![]() $\langle \rangle _{1, d\beta _3}$
is equal to
$\langle \rangle _{1, d\beta _3}$
is equal to
 $$ \begin{align*}\left (f_d - \left (\frac{-d^2+d+16}{96d} + \frac{d}{48} \sum_{d_1=1}^{d-1} \frac{1}{d_1} - \frac{1}{48} \sum_{\delta \vdash d} \frac{d^2 - d_1d_2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \right ) + \frac{1}{12d} \cdot \chi(X) \right ) \cdot K_X^2 \end{align*} $$
$$ \begin{align*}\left (f_d - \left (\frac{-d^2+d+16}{96d} + \frac{d}{48} \sum_{d_1=1}^{d-1} \frac{1}{d_1} - \frac{1}{48} \sum_{\delta \vdash d} \frac{d^2 - d_1d_2}{d_1d_2 \cdot |\mathrm{Aut}(\delta)|} \right ) + \frac{1}{12d} \cdot \chi(X) \right ) \cdot K_X^2 \end{align*} $$
where
![]() $\delta = (d_1, d_2) \vdash d$
denotes a length-
$\delta = (d_1, d_2) \vdash d$
denotes a length-
![]() $2$
partition of d.
$2$
partition of d.
Proof. By Lemma 5.1,
![]() $\langle \rangle _{1, d\beta _3} = (a_d + b_d \cdot \chi (X)) \cdot K_X^2$
where
$\langle \rangle _{1, d\beta _3} = (a_d + b_d \cdot \chi (X)) \cdot K_X^2$
where
![]() $a_d$
and
$a_d$
and
![]() $b_d$
are universal constants depending only on d. By (5.19), Lemma 5.4, Lemma 5.7 and Lemma 5.10, our theorem holds when X is a smooth projective toric surface. Therefore, the theorem holds for every smooth projective surface X.
$b_d$
are universal constants depending only on d. By (5.19), Lemma 5.4, Lemma 5.7 and Lemma 5.10, our theorem holds when X is a smooth projective toric surface. Therefore, the theorem holds for every smooth projective surface X.
Acknowledgements
The authors would like to thank Professors Hua-Zhong Ke and Wei-Ping Li for valuable discussions and assistance. The authors also would like to thank the referees for carefully reading the paper and providing valuable comments which have greatly improved the exposition of the paper.
Conflict of Interest
The authors have no conflict of interest to declare.
Funding statement
The research of the first author was partially supported by NSFC Grants [11831017, 11890662].