1. Introduction
Over the last few decades, since the development of molecular markers, linkage analysis has become an important tool in plant and animal science. The linkage analysis of experiments based on inbred line crosses is less complicated than of other crosses. Most plant model species and many important crop species being autogamous, this enhanced the linkage analysis for inbreeding species. In outbreeding species where the number of progeny per mother is limited, i.e. many animal species, the linkage analysis has to make use of large pedigrees of several generations, which makes the methods extra complicated. The reason for this is that the information about the transmission of alleles, the linkage phases and thus recombination is less than with inbred line crosses. There are, however, also many economically important plant and animal outbreeding species, for which it is possible to generate large-enough full-sib families suitable for linkage analysis. Examples of such species are fruit tree species such as apple, citrus and grape, forest tree species such as fir, pine and eucalyptus, fish species such as trout, salmon and cod, and other species such as prawn and oyster. The linkage analysis of an allogamous full-sib family is more powerful than that of above-mentioned multi-generation pedigrees because more linkage information is available. However, it still is more complicated than with inbred line crosses and as a result is less advanced. Therefore, any method enhancing the accuracy will be welcomed by the research community for outbreeding species.
A major distinction between linkage analysis of a regular experimental population derived from a cross between two inbred lines and that of a full-sib family from a cross between two individuals of an outbreeding species is the number of alleles per locus that can segregate in the offspring. This is limited to two with the inbred lines, whereas it ranges from two to four in the full-sib family of an outbreeding species, and importantly, it may vary from locus to locus within the same family. The original approach to linkage analysis of a full-sib family of an outbreeding species is to split the genetic marker observations into two sets of observations representing the two parental meioses. This enables the application of the less complicated linkage analysis of the inbred lines backcross for each set of observations separately. Grattapaglia & Sederoff (Reference Grattapaglia and Sederoff1994) called this approach the two-way pseudo-testcross (PT) strategy. It results in two maps, a maternal map and a paternal map. To obtain the relation between the two, the maps must be integrated. This can usually be done if sufficient markers segregate in both parental meioses; such markers are called anchor markers. Single-nucleotide polymorphism (SNP) markers are used more and more, also in outbreeding species; they normally have just two alleles. If both parents are heterozygous for these, then they can be used as anchor markers. However, in the PT analysis the heterozygous observations of such markers cannot be used, because the parental origin of the two alleles cannot be decided upon. This results in the loss of on average half the observations and therefore the two-way PT strategy loses much information. A more advanced approach with which no marker information is lost is feasible if a likelihood model accounting for both meioses is used.
In order to improve the genetic mapping in a full-sib family of outbreeding species, several methods have been developed. Ritter & Salamini (Reference Ritter and Salamini1996) present an overview of nearly all possible allelic configurations of two loci in the allogamous full-sib family, the applicable two-point estimators of the recombination frequency (RF) and a method for the construction of a linkage map. The map construction method was given as an improvement over earlier work by Ritter et al. (Reference Ritter, Gebhardt and Salamini1990). Ridout et al. (Reference Ridout, Tong, Vowden and Tobutt1998) proposed to improve on this method by using the more accurate three-point maximum likelihood linkage analysis rather than two-point. Wu et al. (Reference Wu, Ma, Painter and Zeng2002a) continue with the three-point likelihood analysis and present equations for solving all possible configurations with the expectation–maximization (EM) algorithm.
Usually the recombination probability has been modelled to be the same in both parental meioses; however, Wu et al. (Reference Wu, Ma, Wu and Zeng2002b) argued that it would be better to allow different levels of recombination. In symmetrical crosses with inbred lines (e.g. F2, recombinant inbred line family) male and female recombination cannot be distinguished, but in the full-sib family of an outbreeding species it often can. A priori there is no reason why recombination probabilities should be equal in male and female meiosis as they are distinct processes. Apart from any systematic differences in recombination between the sexes, there will also be random differences. A mapping population can be considered to be a combination of two independent finite samples of recombination events, one sample from the mother and the other from the father. As the samples are finite, differences in realized RFs between the two parents will occur simply due to random variation. The first step in linkage analysis is estimating the number of recombination events. This is done best using a model closest to reality; thus, it makes sense to allow differences in recombination between the parents.
All mentioned methods have the disadvantage that they are computationally slow, making them less suitable for current increasingly dense maps. Jansen (Reference Jansen2005) introduced a fast mapping method for outbreeding species based on simulated annealing. The method, however, produces minimum numbers of recombination events rather than map distances. Therefore, it should be considered to be an ordering algorithm.
The estimation of the RF depends on the linkage phase configuration at the loci in the parents, which often is not known and has to be inferred. All proposed methods try to estimate the linkage phases simultaneously with the RFs, which rather complicates the procedure. This may be avoided because current practical experience shows that linkage phases are estimated without problem using the approach of Maliepaard et al. (Reference Maliepaard, Jansen and Van Ooijen1997) based on the estimates of two-point RFs, if not directly then usually indirectly through other pairs of loci.
Jansen et al. (Reference Jansen, De Jong and Van Ooijen2001) introduced a fast Monte Carlo multipoint maximum likelihood algorithm for crosses between inbred lines. The present paper shows how this algorithm was extended for a full-sib family of an outbreeding species. The new approach benefits from the speed of the algorithm, allows different levels of recombination in the two parents and at the end estimates an integrated map.
2. Extension of the multipoint maximum likelihood mapping algorithm for a full-sib family of an outbreeding species
(i) Short description of the algorithm of Jansen et al. (Reference Jansen, De Jong and Van Ooijen2001)
The multipoint maximum likelihood algorithm of Jansen et al. (Reference Jansen, De Jong and Van Ooijen2001) consists of two distinct parts: map order optimization and multipoint maximum likelihood estimation of the RFs. The map order optimization uses the general Monte Carlo optimization method called simulated annealing to minimize the sum of RFs in adjacent segments, which is a function of the map order (Kirkpatrick et al., Reference Kirkpatrick, Gelatt and Vecchi1983). Minimizing this sum is approximately equivalent to finding the order with the highest likelihood (Jansen et al., Reference Jansen, De Jong and Van Ooijen2001). Using the sum of RFs rather than the likelihood enormously reduces the computations, so that high speeds may be attained.
If markers provide all genetic information, then two-point estimates of the RF are identical to multipoint estimates. However, practical datasets of molecular markers usually have some information missing: markers could not be observed for some of the individuals or some markers had dominant alleles. Such marker observations are called incomplete. In these cases, the more accurate multipoint estimates are to be preferred. The multipoint estimation of RFs is based on missing data imputation using Gibbs sampling. Gibbs sampling is a general method using a Monte Carlo EM algorithm to obtain maximum likelihood estimates (Dempster et al., Reference Dempster, Laird and Rubin1977). It is applied here as follows. First, all incomplete observations are assigned random complete genotypes. Next, in a random order all originally incomplete observations are sampled to form complete genotypes, each time replacing the current complete genotypes. The sampling is done conditional on the observation, on the complete genotypes of its flanking markers on the map and on the map distances to the flanking markers. Performing this procedure many times generates a long sequence of complete genotype datasets. At regular intervals from this sequence the current values of two-point RFs are sampled for all marker pairs. This is done only after an initial burn-in period to remove the effects of the random start condition. By averaging over sets of sampled two-point RFs new map distances are determined. These new map distances are then used in a new cycle of missing data imputation. In practice, three or four of such cycles are sufficient to achieve the state in which the likelihood is not improved any further. The algorithm obtains the same multipoint estimates as with the EM maximum likelihood method of Lander & Green (Reference Lander and Green1987), but for dense maps with a much better speed.
The map order optimization has to start the first time with two-point estimates because the multipoint estimates become available only after applying Gibbs sampling. Gibbs sampling can be done only if a map order is available. Therefore, the map order optimization and the multipoint RF estimation are applied several times after each other. In practice, three to four rounds of alternated map order optimization and multipoint RF estimation are adequate to reach a state at which no further progress is obtained. In order to extend this mapping algorithm for a full-sib family of an outbreeding species, both the map order optimization and the multipoint RF estimation were adapted.
(ii) Map order optimization
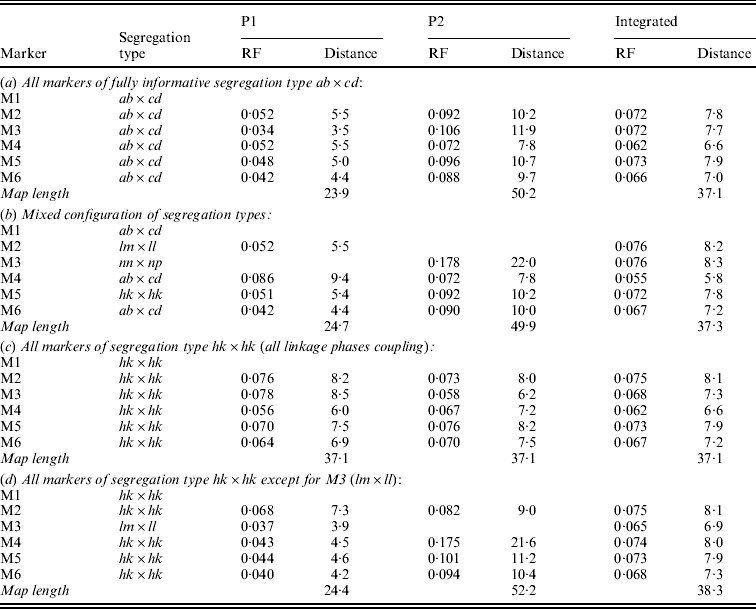
In symmetrical inbred line crosses, such as the F2 and the recombinant inbred line family, it is not possible to distinguish between male and female meiosis because the same genotype is used both as mother and as father. In an allogamous full-sib family, the two parents are different from each other. Therefore, it is possible with informative markers to observe recombination events in the parents separately. Obviously, of markers segregating from just one parent the recombinations can be observed for that parent only. Having determined the RFs for the two parents separately will allow the estimation of both the male and the female map. Under normal circumstances, it makes sense to assume that the order of markers in both maps is the same. Markers segregating from just one parent will appear on the corresponding map only. To apply the map order optimization part of the algorithm of Jansen et al. (Reference Jansen, De Jong and Van Ooijen2001) to a full-sib family of an allogamous species, the procedure must be extended to minimize the sum of RFs in adjacent segments for the two maps simultaneously, but under the restriction of identical orders in both maps. Because the two meioses are independent, this means the sum of RFs in adjacent segments in the two maps must be minimized. For instance, for the two examples of Fig. 1 the sum would be r1+r2+r3+r4. For the presentation of the final result, RFs are translated to map distances using Haldane's mapping function.
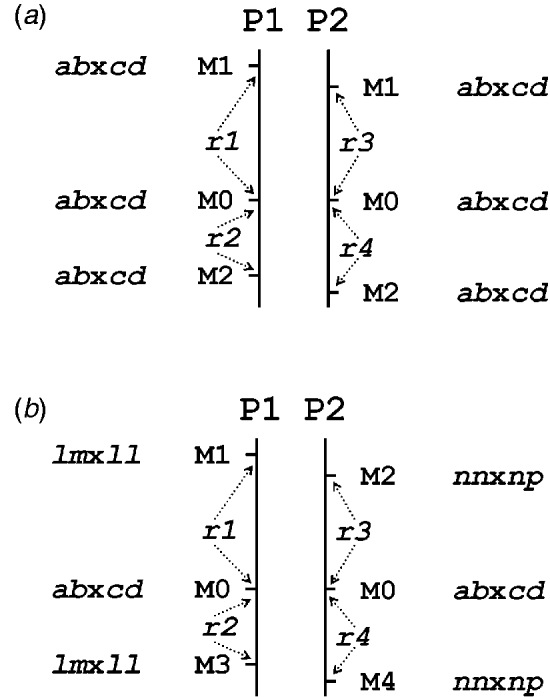
Fig. 1. Two situations with the two parental maps (P1 and P2) illustrating different configurations of markers (M1 to M4, with corresponding segregation type) around the marker to be sampled (M0), with four recombination frequencies for the segments (r1 to r4): (a) all markers segregate in both parents; (b) mixed segregation configuration.
(iii) Multipoint recombination estimation
Before discussing the way to extend the algorithm for an allogamous full-sib family it is more convenient to first address the concept of the segregation type as presented by Maliepaard et al. (Reference Maliepaard, Jansen and Van Ooijen1997) . The segregation type defines the allelic configuration at a locus in the two parents of a cross with two characters left of a×symbol and two right, representing the alleles of the first and the second parent, respectively; distinct characters stand for distinct alleles. The most common segregation types are ab×cd, ef×eg, hk×hk, lm×ll and nn×np. In this paper, different characters are used for the alleles in the mentioned segregation types, so that any offspring genotype implicitly defines its corresponding segregation type. For instance, when addressing genotype hk, the corresponding segregation type is hk×hk. Further, it is good to realize that there are several genetically equivalent segregation types because they provide identical segregation information in the same parents: ef×eg is equivalent to ab×cd, ab×cc to lm×ll and aa×bc to nn×np. Finally, knowing the genotypes of the parents is essential in determining the segregation types.
For the multipoint estimation of the RF, it is important to know which markers, respectively, provide complete and incomplete genotypic information. The Gibbs sampling procedure must then be adjusted to obtain a corresponding missing data imputation system. In the following, markers are assumed to be in coupling phase in both parents. This implies that the grandparental origin of an allele is defined by the position of the allele in the segregation type. Subsequently, linkage phases are ignored to improve readability; it is straightforward to adjust for other linkage phase configurations.
Markers with segregation type ab×cd provide complete information, so that the estimation of RFs between pairs of these is simply a matter of counting. For the adjusted Gibbs sampling procedure, the four genotypes ac, ad, bc and bd are considered to be the complete genotypes in an allogamous full-sib family. A missing marker observation must be sampled from these four (conditional on the observation, on the complete flanking marker genotypes and their map distances).
The hh and kk genotypes provide complete information, as they correspond to the ac and bd genotypes, respectively. But for the hk genotype it is unknown whether the h-allele was obtained from the mother and the k-allele from the father, or the other way around. Thus, the hk genotype is partly informative, as it corresponds to the ad and bc genotypes. The Gibbs sampler must then sample from these two permissible complete genotypes. Obviously there are three permissible complete genotypes for observations where the h- or the k-allele is dominant over the other.
Markers with segregation types lm×ll and nn×np provide complete information of one of the parents, but no information of the other. Each of their genotype observations will thus correspond to two permissible complete genotypes, e.g. lm corresponds to bc and bd, i.e. the first-parent allele is b, the second-parent allele is unresolved. As these markers will appear in just one of the maps, their RFs are to be estimated only in the relevant map. Therefore, despite there being two optional complete genotypes for such observations, there is no need for any sampling because that information will be ignored anyway.
In the Gibbs sampling procedure, an incomplete observation is sampled to a permissible complete genotype using the normal Mendelian recombination probabilities with its flanking markers, conditional on the male and the female map, on the genotypes of these flanking markers and on the observed phenotype of the marker itself. Now that the genotypes that provide incomplete information in the allogamous full-sib family are known, as well as their permissible complete genotypes, it is straightforward to adjust the Gibbs sampling procedure accordingly. There is one final aspect that deserves attention: although the two parental meioses are independent, the Gibbs sampling for the two meioses should not be performed independently. The reason for this is that, when dealing with hk observations, the result of sampling an allele for one of the parents would completely determine the allele to be taken, rather than sampled, from the other parent. For instance, given that ad and bc are the permissible genotypes for hk, then sampling the a-allele for the first parent using the flanking genotypes and the map of the first parent only would automatically determine that the other parent should have transmitted the d-allele. However, assigning this d-allele without taking the flanking genotypes and the map of the second parent into account would be inconsistent with the probabilities for the two alternatives (ad, bc), because these depend on flanking marker genotypes and map distances of both parents. Therefore, the sampling must be done for both parents simultaneously.
In the present approach, Gibbs sampling conditional on the two parental maps means not only that RFs with the flanking markers may differ between the maps (Fig. 1(a)) but also that the flanking markers may be different ones in the two maps since lm×ll and nn×np type markers appear in just one of the maps (Fig. 1(b)).
(iv) Map integration
The map order optimization is done under the restriction of identical orders in both parental maps, and so for producing a single map containing all markers a straightforward strategy can be employed. First, map distances between anchor markers are computed as the averages over the two parental distances. Next, markers segregating in only one of the parents and positioned between anchor markers are placed on the integrated map by interpolation according to the relative position between the flanking anchor markers on the relevant parental map. Finally, markers segregating in only one of the parents and positioned distal to the outermost anchor markers are placed on the integrated map by extrapolation, i.e. they maintain the distances to the anchor markers they had in the parental maps.
3. Demonstration using simulated data
(i) Methods
To illustrate some basic aspects of the extended mapping algorithm, a segregating full-sib family of an outbreeding species was simulated according to regular Mendelian rules. A set of six markers with segregation type ab×cd in coupling phases was created, with 5 cM distance between markers on the map of the first parent and 10 cM on the second. To prevent random variation obscuring the results, a big population size of 500 individuals was used. From the fully informative (FI) genotypes any phenotype of a less informative segregation type can be produced. Thus, an ab×cd-type marker can be turned into a marker of any other segregation type and also the data can be split up into two separate parental sets. In this way, a few basic example configurations were created based on the same FI dataset. Each configuration was mapped with the new mapping algorithm, which resulted in two parental maps and an integrated map.
To illustrate the algorithm for a more realistic situation a full-sib family of 100 individuals was simulated with ab×cd markers every 5 cM on a 100 cM map. From this FI dataset a derived set was created as could occur with SNPs: the markers on positions 0, 25, 50, 75 and 100 cM were changed into hk×hk markers, the other markers alternately into lm×ll and nn×np markers, while in addition a random 10% of all observations was made missing. This ‘SNP-like’ dataset was mapped with the new algorithm (NA) and also with the two-way PT method. The results were compared with those of the FI dataset.
(ii) Results for the basic example configurations
Table 1 presents the results of applying the mapping algorithm on the basic example configurations. In all these cases, the algorithm resulted in the correct order. In the first case with all markers having the FI segregation type the algorithm correctly counts the recombinations per parent separately (Table 1(a)). The numbers are identical to the results when the data were split up into the separate parental sets, which could be analysed as a testcross with the original mapping algorithm for inbred lines (results not shown). The estimated map lengths are close to the simulated lengths of 25 and 50 cM, respectively, for the two parental maps. The RF estimates of the integrated map are slightly different from the averages of the parental RFs; this is due to the fact that for the map integration the parental map distances are used and the integrated map RFs are computed from these integrated map distances using the inverse of Haldane's map function.
Table 1. The estimated RFs of markers (M1 to M6) with the preceding informative marker in the two parental maps (P1, P2) and in the integrated map under four different configurations (a to d) with respect to segregation types. Distances (cM) in P1 and P2 are computed from the RFs using Haldane's mapping function. The RFs of the integrated map are computed from the distances using the inverse of Haldane's mapping function
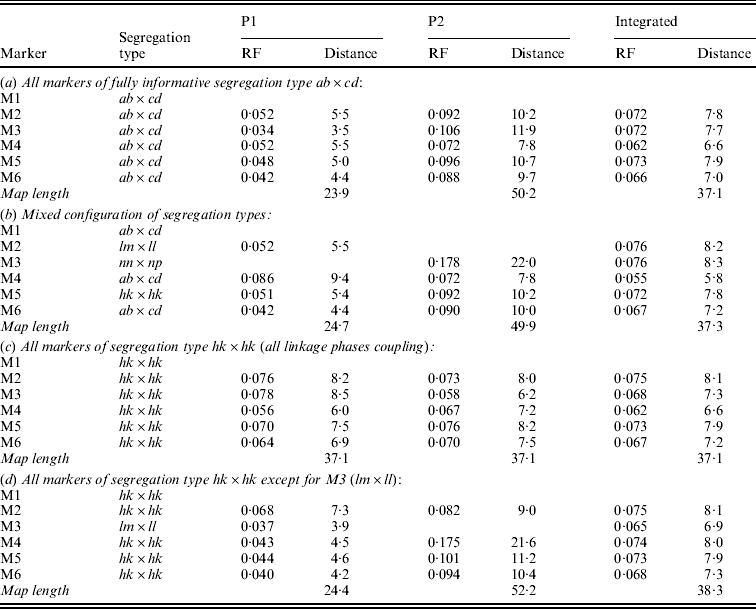
In the mixed configuration the RFs for the lm×ll and nn×np markers are properly counted in the separate parental maps (Table 1(b), P1, P2). In P1 the RF for the segment M1–M2 is 0·052 in both the mixed and the FI configuration, and the RF for the segment M2–M4 is 0·086 which corresponds exactly with the sum of 0·034 and 0·052 in the FI configuration. In P2 the segment M3–M4 has an RF of 0·072 in both configurations, but the RF for the segment M1–M3 is 0·178 which is different from the sum of 0·092 and 0·106 in the FI configuration. Inspection of the complete marker data revealed that there were five individuals with a double recombination in the segments M1–M2–M3, which explains this difference exactly. More interestingly, the RF estimates obtained with hk×hk marker M5 closely correspond to those of the FI situation.
In the configuration with all markers in segregation type hk×hk (and all linkage phases were coupling), the algorithm has no power to distinguish between the two parental meioses. The minor differences are just reflecting the Monte Carlo nature of the algorithm (Table 1(c)). This lack of power is due to the complete symmetry. The configuration is identical to a normal F2. As soon as the configuration contains one asymmetric segregation type, however, then the algorithm does have the power to discriminate between the two meioses: the results are close to the FI situation (Table 1(d)).
(iii) Results for the SNP-like dataset
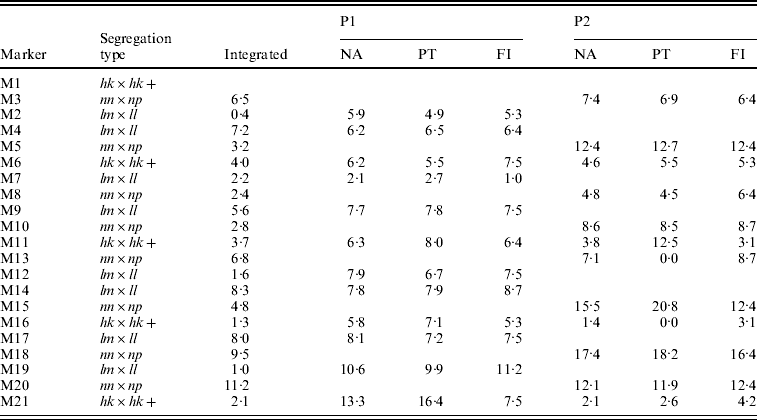
The integrated map obtained with the NA had the correct order except for two anchored segments in which the lm×ll and nn×np markers were not correctly placed with respect to each other (Table 2, M2–M3, M12–M13). The separate parental maps were ordered correctly with the NA (Table 2, NA). Their distances compared better to the parental maps as determined with the FI dataset than those of the PT analysis: for P1 the correlation coefficients with FI were 0·76 vs. 0·55 for NA and PT, respectively, and for P2 0·97 vs. 0·71, respectively. In P2, the PT analysis even resulted in two zero multipoint distance estimates (Table 2, P2, PT, M11–M13, M15–M16), whereas in the NA results these distances correspond better to the FI dataset. Obviously, the lower accuracy of the PT results is caused by the loss of information of the hk×hk markers which in turn is due to the inability to utilize the heterozygous hk genotypes.
Table 2. The estimated map distances (in cM) to the preceding marker of a simulated SNP-like dataset under various situations: after map integration (Integrated) of the separate parental maps (P1, P2) as obtained with the NA, in the two-way PT analysis, in the FI dataset. Anchor markers are indicated with a+symbol
4. Discussion
The presented extension of the mapping algorithm of Jansen et al. (Reference Jansen, De Jong and Van Ooijen2001) for a full-sib family of an outbreeding species advances the linkage analysis of outbreeding species to multipoint maximum likelihood. The many possibilities of segregation in an allogamous full-sib family have different kinds of incomplete genotypes. The use of the Gibbs sampler on the incomplete genotypes to obtain the multipoint estimates of the RFs avoids the need to derive and use the many mathematical formulas that would be necessary for an EM method to maximize the multipoint likelihood. Examples of such formulas for ‘just’ the three-point analysis can be found in the papers of Wu et al. (Reference Wu, Ma, Painter and Zeng2002a, Reference Wu, Ma, Wu and Zengb). A multipoint method is able to obtain more information through the neighbouring loci, thereby increasing the accuracy. A simple example is the following. Suppose, on three loci in the order L1–L2–L3 the genotype ac–hk–ad was observed for an individual (all phases coupling). Between L1 and L2 this implies there was one recombination event, either in the first- or in the second-parent meiosis. Between L2 and L3 the observation implies there was either no recombination event or there were two, the latter being much less likely, of course. As a consequence the recombination event between L1 and L2 is much more likely to have occurred in the second-parent meiosis than in the first-parent meiosis, which is important to know if separate parental maps are being estimated.
The analyses of the simulated data illustrate that the NA is able to properly estimate distances where there are differences between the parental meioses. This is also true if the symmetrical segregation type hk×hk is involved, unless all markers in the linkage group are of this type and in the same linkage phases. The ability to fully utilize the hk×hk markers is important, because more and more use is being made of SNP markers which usually have just two alleles. In the two-way PT approach, the heterozygote hk cannot be used and therefore recombination events can go undetected. This leads to a lower accuracy than with the NA, as was illustrated with the simulated SNP-like dataset.
An integrated map is necessary to determine the positions of markers segregating in only one parent relative to each other. It is also necessary for the QTL analysis if the QTL analysis software is not able to use separate parental maps with an allogamous full-sib family. On the integrated map of the simulated SNP-like dataset a few lm×ll and nn×np markers were ordered incorrectly. Ordering of lm×ll markers with respect to nn×np markers is done indirectly through anchor markers. The correct ordering depends on where recombination events are realized within the anchored segments in the independent parental meioses. Therefore, nearby lm×ll and nn×np markers will always be prone to incorrect ordering in any map integration algorithm. Only using larger population sizes will be able to increase the ordering power.
The NA will be built into the next version of the software JoinMap (Van Ooijen, Reference Van Ooijen2006).
Hans Jansen of Biometris and Chris Maliepaard of Wageningen University are thanked for their comments on earlier versions of the manuscript. The work for this paper was financed by Kyazma B.V.