The earliest extant Chinese mathematical writings include two components of particular relevance to the history of manuals and handbooks. On the one hand, they present knowledge in relation to mathematical problems that often evoke tasks carried out by officials working in the imperial bureaucracy. On the other hand, they contain mathematical ‘procedures’ (術), or ‘algorithms’ in today's parlance, solving these problems. This description fits most of the mathematical documents produced in China until the seventh century. However, in this article, for reasons of method that are explained below, I will leave aside manuscripts from early imperial China, recently discovered in tombs, and concentrate on writings that were handed down through the written tradition. This is the case of The Nine Chapters on Mathematical Procedures (九章算術, hereafter The Nine Chapters), which, in my view, was completed in the first century CE (Figure 1).Footnote 1 This book, which was later considered a ‘canon’ (經), was used as a textbook, notably, from the seventh century onwards, in the ‘School of Mathematics’ which was part of the Imperial University, and most probably earlier.Footnote 2 My argument in this essay will rely on one of its chapters.

Figure 1. The Nine Chapters on Mathematical Procedures 九章算術, first century CE, in the 1261 subcommentary by Yang Hui, entitled Mathematical Methods Explaining in Detail The Nine Chapters, 1842 edn, pp. 1a–b. Online at https://archive.org/details/02094041.cn. From right to left, the boxes with decreasing shades of grey show (1) the title of Chapter 7, ‘Excess and deficit’, which is also the name of the first operation executed by the algorithms given at the beginning of the chapter; (2) the older layers of commentary; (3) the first ‘procedure’ for ‘excess and deficit’; (4) the second ‘procedure’; (5) the later layers of commentary.
When dealing with a book like The Nine Chapters, two meanings of the term ‘instructional’ apply. This writing was instructional in the sense that its procedures gave readers instructions to do things. In other words, readers derived from the texts of its procedures lists of operations enabling them to achieve a goal. Moreover, the book was instructional in the sense that, together with other writings, it was used to teach mathematics. Here, I will focus on The Nine Chapters as instructional in the first sense.
In relation to this feature of the book and similar writings, since the nineteenth century, historians have regularly argued that these documents were how-to manuals for officials, or more broadly for practitioners learning mathematics with the sole intention of applying it. For these modern scholars, the ‘procedures’ (or ‘rules’) that books like The Nine Chapters contained were only means to ends. Their implicit assumption was that the mathematical problems considered actually corresponded to concrete tasks that officials had to fulfil. According to the logic of this interpretation, officials must have used these books in pieces, extracting procedures as necessary for specific purposes. The texts of ‘procedures’ thus extracted were meant to be followed, or even ‘obeyed’, but not understood. Following the rules required no high-level knowledge, certainly no substantial mathematical knowledge as such. These historiographical assumptions, in turn, have often informed how historians have read these ancient algorithms. In line with such interpretations, mathematical sources were considered to be evidence of a divide between ‘East’ and ‘West’.Footnote 3
In my view, the trouble with these assumptions is that they derive from reading ancient documents like their modern counterparts. This way of interpreting the sources thus surreptitiously brings in observers’ categories. My aim here is to set observers’ representations of instructions aside, and to concentrate rather on actors’ conceptions and practices. From this perspective, I intend in particular to shed light on various forms of knowledge that producers and users of procedural texts, active in specific contexts, had to possess to work with instructions as well as with collections of instructional texts. If we accept the view that these Chinese mathematical writings provided means to do things in the form of ‘procedures’, then what can they tell us about the knowledge required, in a given context, to produce a text of procedure and to compose a collection of such ‘procedures’, as well as about the knowledge needed to use them? In order to work from a concrete example, I consider a few procedures from The Nine Chapters, which shed light on these issues. But the first question to address is this: why The Nine Chapters?
The sources
Three main reasons motivate the choice to focus on this book. First, in relation to the fact that The Nine Chapters was handed down over centuries, commentaries have been composed on the book. These commentaries are crucial, since they give us evidence of how ancient readers interpreted the text of the canon. We can thus rely on them to approach the engagement with instructions in a historical fashion. In fact, The Nine Chapters is the only ancient Chinese mathematical book composed of problems and procedures for which we can document different readings.
Some of these commentaries were selected by the written tradition to be handed down with the canon, to the extent that all extant ancient editions of The Nine Chapters include them. These are (1) the commentary completed by Liu Hui 劉徽 in 263 CE and (2) the subcommentary on The Nine Chapters and Liu Hui's commentary that Li Chunfeng 李淳風 presented to the throne in 656 CE. In my view, the boundary between these two layers of commentary has sometimes become blurred during the process of textual transmission, and in places I consider it difficult to distinguish them from one another.Footnote 4 This is typically the case for the chapter titled ‘Excess and deficit’ (the seventh chapter), on which I focus here.Footnote 5 Accordingly, for the sake of simplicity, I will designate these two layers of commentary together as ‘the ancient layers of commentary’. To give a sense of the experience of reading a canon with its commentaries, let us observe, in Figure 1, the first page of the chapter ‘Excess and deficit’, in an ancient edition of The Nine Chapters to which I return below. In this edition, in this chapter the text of the canon begins with two procedures to execute the eponymous operation, whereas in the other extant editions the first four problems are placed before the text of these procedures. We will discuss this editorial issue in the section entitled ‘The reading of the general procedure evidenced by the ancient layers of commentary’.
Reading from right to left, after the title of the chapter, composed in large characters (darker shade of grey), the edition features the ancient layers of commentary on the first procedure in smaller characters, arranged in double columns per column of text (slightly lighter shade of grey in Figure 1). Immediately afterwards, the reader reaches the text of two procedures of The Nine Chapters itself, for the operation ‘excess and deficit’ (next-lighter shade of grey in Figure 1). The edition also features them in large characters, like the text of The Nine Chapters in general. To be more accurate, the reader first finds a general procedure, which, together with two other related procedures placed later in the chapter, could solve all problems in Chapter 7.Footnote 6 These procedures justify the cohesion of the chapter as a textual unit. The reader then finds a second procedure, which, together with the related procedures also occurring later, specifically (and only) solves the first eight of the twenty problems that the chapter contains. The distinction between the types of problem in this chapter is a key feature of my argument.
In the eleventh and thirteenth centuries, scholars resumed commenting on The Nine Chapters and its two ancient layers of commentary. Two witnesses for this are Jia Xian's 賈憲 eleventh-century and Yang Hui's 楊輝 thirteenth-century subcommentaries, which were handed down only partially. In 1261 Yang Hui completed his subcommentary, entitled Mathematical Methods Explaining in Detail The Nine Chapters (詳解九章算法, hereafter Mathematical Methods), which included all the layers of canon and commentary described above, as well the eleventh-century subcommentary on them ascribed to Jia Xian.Footnote 7 This is the edition reproduced in Figure 1. As had been the case for the ancient layers of commentary, which, in the extant ancient editions, seem to have been mixed with each other, this edition bespeaks the fact that, through the textual transmission, Jia Xian's and Yang Hui's subcommentaries became combined in a way that is not yet clear.Footnote 8 I designate them conjointly as ‘the later layers of commentary’. These more recent layers feature in Figure 1, in the box with the lightest shade of grey. In sum, thirteenth-century readers of Mathematical Methods could consult, on the same page, the general and specific procedures, together with both the ancient and the later layers of commentary. For us, the essential point is this: the ancient and later layers of commentary attest to how readers of different periods interpreted, and handled, ancient instructional texts from The Nine Chapters. Interestingly, they testify to different types of approach to the text of the same procedure, allowing us to problematize and historicize what it meant, in these contexts, to practice and write up mathematics in the form of problems and procedures.
My second reason for concentrating on The Nine Chapters is that, as the title makes clear, the book has chapters. In fact, these chapters have a mathematical meaning. They embody a classification of procedures that reflects how instructional texts were formulated in The Nine Chapters. The title of Yang Hui's subcommentary refers to its ambition of ‘explaining’ these procedures ‘in detail’. In relation to this project, the later layers of commentary offer a rewriting of these procedures in the form of ‘methods’ (which, in my interpretation of the title, thus ‘explain’ the procedures), and accordingly reclassify methods and problems in an additional chapter of Mathematical Methods (‘Compiling categories’ 纂類).Footnote 9 These documents thus yield evidence on the activity of classifying procedures, and the meaning it has from an actor's viewpoint.
Finally, the choice of concentrating on The Nine Chapters derives from a remark: this canon evidences complex operations brought into play to produce instructional texts, which in turn require complex operations on the part of the reader to operationalize these texts. This point can be illustrated precisely by the procedure for the operation ‘excess and deficit’, as well as by the procedures given for multiplying quantities with integers and fractions and for dividing a quantity of this kind by another like quantity.Footnote 10 In The Nine Chapters, the related procedural texts show that mathematical knowledge was needed not only to determine which arithmetical operations one should use to solve any possible case, but also to write up a single text of ‘procedure’ that covered all possible cases. The textual means by which these instructional writings covered all the possible cases – which embodies a form of generality – are striking. They reveal that actors prized the epistemological value of generality. They further highlight competences that readers had to acquire in order to use these instructional texts. Elsewhere, I have argued that, to turn the texts into action, readers had to understand the ‘meaning’ of the operations prescribed. This paper examines the part played by mathematical problems in enabling readers to grasp this ‘meaning’.Footnote 11 This exposes the problem that historians create when they try to differentiate following a rule and understanding it. Let us now focus on the general procedure for the operation ‘excess and deficit’, to illustrate these assertions.
Evidence on the work carried out to produce and use the text of a procedure
From a computational viewpoint, to determine the unknown(s) sought in the context of any mathematical problem in Chapter 7 of The Nine Chapters, the general procedure ‘excess and deficit’ relies on four numbers: two suppositions made on a given magnitude, and the excess and deficit these suppositions respectively cause with respect to another given quantity. Apparently, the text of this procedure caused its readers problems, because the ancient editions of The Nine Chapters and of the ancient layers of commentary present arguably more variations here than anywhere else. The editorial interventions of modern editors are also the most significant.Footnote 12 In my view, this is due to the fact that later readers did not understand how earlier readers were expected to process the text when the procedure was written. This failure is evidenced at the latest in the thirteenth century.
To explain this point, in Figure 2 I have reproduced the text of the procedure on the right-hand side (its translation is given in the section entitled ‘The reading of the general procedure evidenced by the later layers of commentary’). Although the text is continuous and does not bear marks indicating parts, I have distinguished five sections in it (sections I to V), which I represent as a column of boxes coloured in decreasing shades of grey. With one exception (section IV; see below), this division into sections yields the textual units for which the ancient layers of commentary formulate a meaning. We see that, after two lists of operations placed one after the other in the procedure (sections I and II), the text has a first condition, followed by an operation (section III), and then a second condition (section IV), also followed by a list of operations (section V).Footnote 13
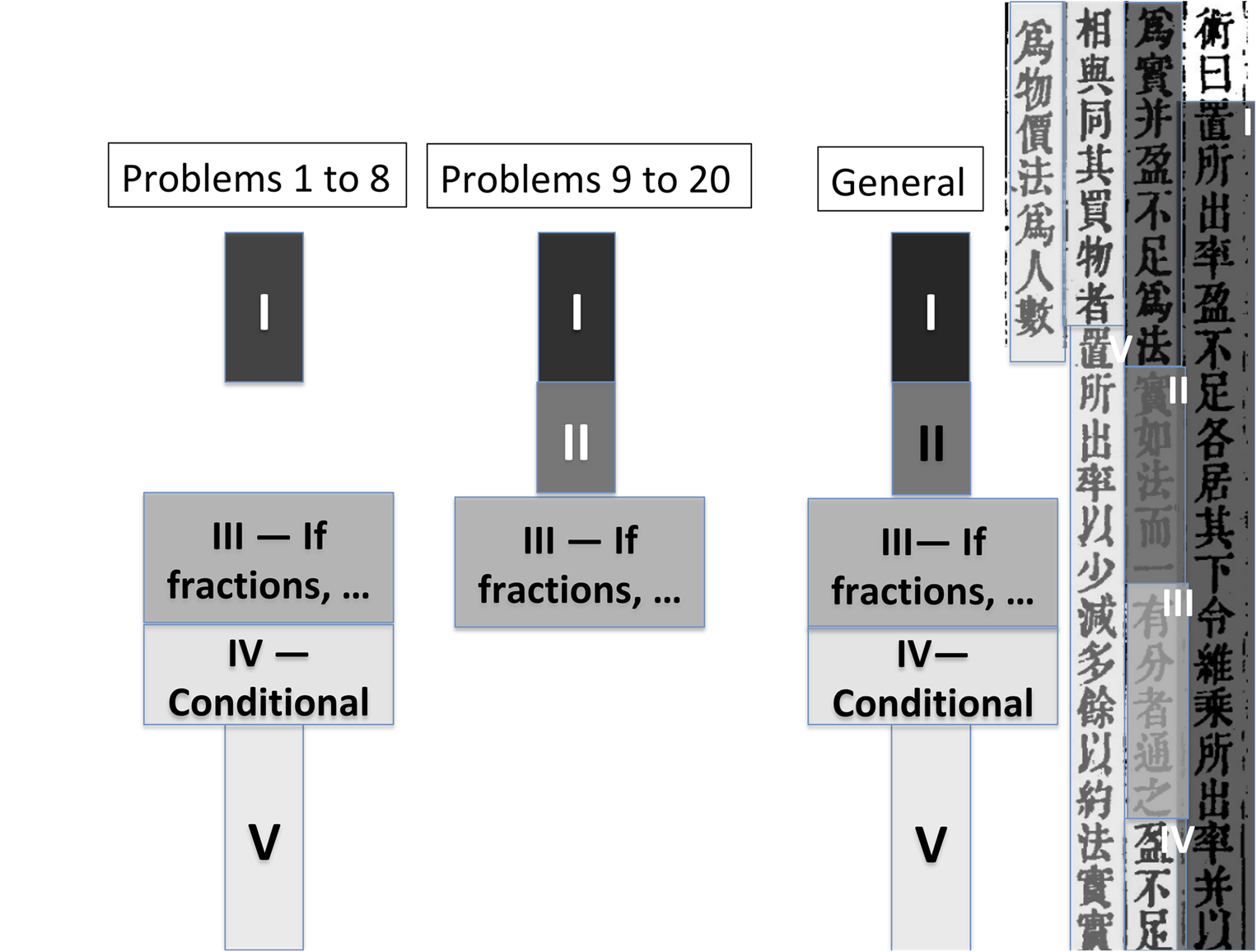
Figure 2. The handling of a text of procedure, and the meaning of a chapter.
To understand the meaning of the first and general procedure for ‘excess and deficit’, we need to observe how the various problems gathered in the chapter are solved by the procedure. In fact, the chapter contains two categories of problems, each solved by only some sections of the general procedure, and characterized by the sections solving it. The first problem of Chapter 7 reads as follows:
Suppose a purchase is entered into (by several persons) together. If everybody pays 8 (a), there is a surplus of 3 (b). If everybody pays 7 (a′), there is a deficit of 4 (b′). What are, respectively, the number of people involved and the price of the thing purchased?
Answer: 7 persons; the price of the thing is 53.Footnote 14
Interestingly, this problem does not seem to reflect a task that officials had to carry out. Note that in this problem, the two suppositions (a and a′) which are made on what every individual pays, together with the excess and deficit (b and b′) that these individual contributions respectively generate with respect to the price to be paid, form the data given by the problem. The general procedure under consideration then relies on these four numerical values to determine the two unknowns; that is, the number of people involved and the price of the thing. The key observation is this: determining these unknowns does not put in play the whole sequence of operations of the general procedure, but only the operations of section I, followed by the operations of section V. Moreover, in this case, the amount paid by every individual to gather an amount equal to the exact price does not feature among the unknowns: the mathematical problem uses the ‘suppositions’, the ‘excess’ and the ‘deficit’ to express a relationship between the unknowns. The first eight problems of the chapter share these essential features, in contrast to all subsequent problems. These problems fall within what I call ‘the first category’.
Problems 9 to 20 in the chapter ‘Excess and deficit’ are solved by another list of operations extracted from the general procedure, which shows that they entertain a completely different relationship with the general procedure. Moreover, in contrast with the first eight problems, each of these problems is followed by a specific procedure, which makes explicit part of the operations needed to solve the problem using the general procedure.Footnote 15 To explain this point, let us take the example of the first problem of the chapter exemplifying this phenomenon; that is, problem 9. This problem and the related specific procedure (in small capitals), along with the older layer of commentary (in lower case), read as follows:Footnote 16
Suppose that there is an unknown quantity of husked grain in a 10 dou bucket. The bucket is filled to the brim by adding unhusked grain, which is then husked. We then obtain 7 dou of husked grain. One asks how much husked grain there was in the bucket to begin with.
Answer: 2 dou 5 sheng
Procedure: One looks for this using the procedure of excess and deficit. If one assumes that the original [amount of] husked grain was 2 dou, there would be a deficit of 2 sheng. If one assumes that the original [amount of] husked grain was 3 dou, there would be 2 sheng left. Relying on the fact that the bucket contains one hu, when one supposed that the original [amount of] husked grain was 2 dou, one had to add 8 dou to fill it. 8 dou yields 4 dou 8 sheng of coarsely husked grain. Compared to 7 dou, that makes a deficit of 2 sheng; when one supposed that the original [amount of] husked grain was 3 dou, one had to add 7 dou to fill it. 7 dou yields 4 dou 2 sheng of coarsely husked grain. Compared to 7 dou, that makes a surplus of 2 sheng …
The specific procedure that The Nine Chapters formulates after problem 9 states explicitly that the problem is solved using ‘the procedure of excess and deficit’; that is, the general procedure under consideration. It further makes explicit the ‘suppositions’, and the ‘excess’ and ‘deficit’, to which this general procedure should be applied. These four values are thus no longer given in the statement of the problem. The opening section of the ancient layers of commentary, which I also translated, yields an explanation for how the values of the ‘excess’ and the ‘deficit’ stated in the specific procedure of the canon were obtained on the basis of the numerical values of the ‘suppositions’ put forward also in the procedure.
The explanation suggests that the numerical values of the ‘suppositions’ were, respectively, entered into a list of computations deriving from the statement of the problem. The reasoning goes as follows: assuming that the original amount of husked grain in the bucket (that is, the unknown) was two dou (resp. three dou), the commentator explains, subtracting this from ten dou – that is, the global capacity of the bucket (the first datum given in the problem) – yields what corresponds to the amount of unhusked grain added to fill up the bucket. Usually, in The Nine Chapters, generic grain references are to ‘unhusked millet’ and ‘coarsely husked millet’. This assumption fits with the equivalence that the commentator uses in this case: unhusked and coarsely husked millet are in the ratio of five to three. A rule of three thus yields the amount of husked grain corresponding to what was added. Adding this amount to the one supposed to have originally been present in the bucket yields a numerical value, which is then compared with the other datum given in the problem; that is, the amount of husked grain that one has at the end of the operation: seven dou. This comparison generates the ‘excess’ or the ‘deficit’ stated in the specific procedure, thereby accounting for it. We thus see how the commentator understands that the statement of the problem was transformed into a list of mathematical operations, which links the value of a supposition and that of an excess or a deficit. This list of operations is interpreted step by step by reference to the situation described by the problem.
The general procedure for ‘excess and deficit’ is subsequently applied to these four values. As above, the general procedure thus relies on two ‘suppositions’, an ‘excess’, and a ‘deficit’. However, the meaning of these terms now differs from what it was above. Here, the term ‘suppositions’ no longer designates values that allow the practitioner to express a relationship between the unknowns, but instead hypotheses that she makes on the sought unknown. Similarly, the terms ‘excess’ and ‘deficit’ no longer refer to values that are likewise given, but they now derive from these ‘suppositions’. This feature characterizes the problems falling under ‘the second category’.
In addition, in this case, as in the previous case, the way in which the general procedure under analysis brings these four values into play to yield the solution to the problem (and similar problems) is also unexpected. Here too, despite the fact that the specific procedure given after problem 9 calls for the general ‘procedure of excess and deficit’, it is not the whole list of operations of this general procedure that is used. In addition, the sequence of operations taken from the ‘procedure of excess and deficit’ differs from the list used to solve the first eight problems in the chapter. As the commentator explains subsequently, one only needs to use the operations in section I, and then section II of the general procedure, to solve problems such as problem 9. This is the second key observation, which holds true for the second category of problems.
To recapitulate, what held Chapter 7 together was a general procedure, which required a specific handling depending on the problem dealt with. If we momentarily ignore section III, the two representations placed on the left-hand side of Figure 2 show that, depending on whether the practitioner dealt with problems 1 to 8 (‘first category’) or problems 9 to 20 (‘second category’), she had to navigate through the text of the general procedure in a specific way to draw from it, in each case, the correct list of operations. The text of the procedure does not conform to the simplistic expectation that one should follow it step by step to solve a problem. How and why was such a text of procedure composed, and how was the user supposed to handle it correctly?
For the problems of the first category, The Nine Chapters also gave specific procedures, simpler than the general procedure in that they required fewer and simpler operations. For problem 1, for instance, this is the second procedure that, as we described above, is placed immediately after the general procedure (see Figure 1, fourth shade of grey in decreasing order). One finds a similar specific procedure after the cognate general procedure for the operation ‘two excesses, or two deficits’. The expression introducing these specific procedures, ‘Another procedure’ (其一術), insists on the fact that, for problems of the first category, the general procedure and the specific procedure are alternative to one another. This remark suggests that, in addition to a simpler and specific procedure solving each problem or set of similar problems, the authors had a particular interest in formulating a general procedure, from which the solution of all the problems in the chapter could be derived, provided it was used correctly. Another way of perceiving the importance given to this general procedure is to note that it is precisely this procedure that expresses the mathematical cohesion of Chapter 7. The interest in procedures of this kind bespeaks the fact that actors prized the epistemological value of generality. They did so in a specific way, which this kind of procedure embodies. Indeed, it shows how one can formulate ways of solving all the problems of the chapter that share a common initial section (section I). This feature of the text highlights the mathematical work actors carried out to satisfy their interest in generality.
This interest can be seen from how the text of the procedure was composed, with section II following section I, in relation to the solution of problems of the second category. This is the reading of sections I and II of the general procedure to which the ancient layers of commentary attest. The authors then placed section V after sections I and II (we still leave aside section III for the moment), for the solutions of problems of the first category – a conclusion likewise supported by the ancient layers of commentary. However, before section V, the authors inserted the condition that constitutes my section IV. Since at least the thirteenth century, the meaning of this condition has puzzled commentators. What we have shown about the composition of the general procedure strongly suggests that section IV formulated a condition referring to the first category of problems and marking the beginning of the second part of the list of operations solving them, once section I has been executed. We can interpret its formulation along these lines.Footnote 17
The reader confronted with such a text thus had to determine where the initial part (section I) ended. In other words, she had to decide from which operation in the list of operations before the statement of the condition she should either go on with section II (for problems of the second category), or jump to section V (to continue with the list of operations needed to solve problems of the first category). How practitioners did so illustrates part of the knowledge that they had to possess and also part of the work they carried out to use such texts of procedures.
One possibility is that practitioners had to rely on the specific syntactic properties of the list of operations to navigate correctly through the text, and so treat the conditional occurring in section IV in a correct way. I have discussed elsewhere the write-up of conditionals in texts of procedures in The Nine Chapters.Footnote 18 They all occur in texts of procedures like this one, whose ambition is to give, with a single text, the different lists of operations required for the different cases of a general problem, provided that one adequately navigates through this text. Among these texts, we might mention the procedures allowing practitioners to execute division and multiplication, whatever the nature of the operands might be. I have shown that conditionals of this kind systematically occur in the final sections of texts of procedures, and that the reader begins reading the text of the procedure from these conditionals. Interestingly, in this case, this would mean beginning precisely with the part of the text (sections IV and V) specifically dealing with the case represented by the first four problems, in relation to which the text of the general procedure was given. Section V, then, calls for a dividend and a divisor, whose computation is precisely the point of section I. This remark suggests that the reader would first determine that she agrees to condition IV and begin the computations with section V, until the moment when she meets with the mention of a dividend and a divisor, for which she would backtrack to section I. Alternatively, in cases when the condition formulated in section IV did not apply, she would simply begin the procedure from section I, ending with section II.
This is one way of representing the knowledge required to derive from the text of the general procedure the two lists of operations appropriate for each category of problems. Another possibility would be that practitioners relied on the meaning of the computations, as made explicit by the ancient layers of commentary, to determine what to do. There, two options are possible. One would be that the readers knew that they had to seek the meaning of the operations, in a sense to be discussed in the next section, to be able to use the text correctly. Another option would be that the readers relied on the formulation of the meaning as provided in the ancient layers of commentary to understand how to navigate through the text. This would explain why the text of The Nine Chapters was handed down with commentaries. Whatever the case might be, the same conclusion follows: the text of the general procedure, like many other procedures in The Nine Chapters and other writings, required that its user understand the meaning of the operations to put the text into play.Footnote 19 This is another way of representing the knowledge that readers had to possess to employ texts of procedures.
The two types of knowledge that I have distinguished in fact mesh with each other. Without being explicit about their navigation within the text of the general procedure, the authors of the ancient layers of commentary formulated the ‘meaning’ 意 of the various sections that I have identified in relation to the relevant type of problems, taken in an appropriate order, thereby tacitly stating how the various sections of the text should be used. In fact, the way in which, according to the ancient layers of commentary, the conditional that we have not yet considered (section III) should be handled also suggests that readers needed both types of knowledge to use the text correctly.
Indeed, if we follow the way the ancient layers of commentary interpreted it, section III introduced an operation needed to adapt the general procedure in the case when the ‘suppositions’ were not merely integers but had fractions. Two remarks are essential here. First, depending on whether the ancient layers of commentary interpreted this operation in the context of problems of the first or the second category, they translated it into different actions that had to be taken.Footnote 20 This shows that the syntactic properties of the text of the procedure did not suffice to determine what should be done. Second, as above, the ancient layers of commentary understood that the actions corresponding to the operation prescribed in section III should be taken before the operations prescribed in section I (but after the positioning of the numerical values on the calculating surface; we return to this point below). Before the operations of section I, the actions deriving from section III were the same for the two types of problem. However, these actions also had an impact on the way in which the operations of section II and section V respectively were to be carried out. This impact was likewise different, in a way that evokes the general procedure given in The Nine Chapters to carry out division in all cases.Footnote 21
How do the ancient layers of commentary illustrate more precisely the types of knowledge that the reader had to possess to use the procedure? This is the issue that we will now examine, focusing only on sections I, II, IV and V of the general procedure, and ignoring computations with fractions.
The reading of the general procedure evidenced by the ancient layers of commentary
The key feature of the ancient layers of commentary on the general procedure under consideration is that they use the first problem of Chapter 7 to project both categories of problems onto it and thereby interpret all sections of the text.Footnote 22 To understand why this is possible, let us further examine the example of problem 9, which we gave above to illustrate the second category of problems. We have seen that the procedure specific to this problem put forward two ‘suppositions’ on the unknown, and stated the ‘excess’ and ‘deficit’ respectively corresponding to them. Moreover, the older layers of commentary explained how ‘excess’ and ‘deficit’ derived from the ‘suppositions’ using a list of computations linked step by step to the statement of the problem. On the basis of these four values, the general procedure for the operation ‘excess and deficit’ determined the unknown. This pattern shows that the situation described in the mathematical problem actually played the part of establishing a relationship between ‘suppositions’, ‘excess’, and ‘deficit’, and nothing else. Whatever the problem might have been, it suffices that the relationship between these four values that it establishes be the same for the unknown to have the same value.Footnote 23 This remark underscores that the general procedure ignores the specifics of a problem and treats the problem as if it were merely a way of establishing a relationship in an undetermined way.
From this perspective, we can now read the first problem in a new way. If we view it as it was originally formulated, its unknowns are the number of people and the price of a thing bought conjointly. The ‘suppositions’, the ‘excess’ and the ‘deficit’ are the values expressing a relationship between these unknowns that will allow the problem to be solved. However, we can alternatively consider that the number of people buying conjointly and the price of the thing are indeterminates (as opposed to unknowns), and that the problem merely states the relationship that these indeterminates establish between two ‘suppositions’ and the excess (respectively ‘deficit’), without specifying the nature of this relationship. If, in contrast with the actual problem, we consider that the unknown is the exact amount of money paid by everybody to buy the thing, the problem then falls within the second category, and it suffices precisely to know the relationship between the four required numerical values to use the general procedure for this category of problems and conclude. This is how the ancient layers of commentary proceeded, using the first problem to interpret successively the lists of operations, I, II and then V.
Before explaining this key point in greater detail, let me insist on how far this practice with mathematical problems is from the assumption that problems would be the statement of practical tasks. In fact, we will see here how problems like problem 1 play a key part in the formulation of the meaning of the operations, and, more specifically in this case, that they fulfil this function in a very flexible way. We had underscored that problem 1 did not look like a practical task. The ancient layers of commentary invite the assumption that problem 1 was shaped to serve very specific theoretical ends, related to the shaping of the general procedure.
A remark on the structure of the first pages of Chapter 7 supports this latter claim. Indeed, two procedures are given in relation to the first problem of this chapter (or, to be more precise, in relation to problems 1 to 4): a general one and a specific one. Giving similarly two procedures for each problem is a more global feature of The Nine Chapters.Footnote 24 However, in Chapter 7, this feature is realized in a particular way. Instead of promoting a general procedure as the opening section, and placing, immediately after it, a sequence of problems with their specific procedures, the general and specific procedures are given together in relation to the first four problems. The meaning of the operations of the specific procedure is interpreted with respect to the situation common to the first four problems, taken as being of the first category.Footnote 25 The meaning of the operations of the general procedure will likewise use the first problem, but in a different way. The specific arrangement of the first pages of Chapter 7 might have been a reflection of this dual role played by the first problem.
To explain the ancient commentators’ use of this problem, I will now introduce in turn the computations prescribed by the general procedure and their interpretation as formulated by the ancient layers of commentary, by reference to problem 1 quoted above. The first operations under focus are the multiplication of the ‘suppositions’, respectively, by the ‘excess’ or ‘the deficit’ that do not correspond to them.
Problem 1 begins with the following statement: ‘If everybody pays 8 (a), there is a surplus of 3 (b)’. The multiplication of the supposition 8 (a) prescribed by the procedure is interpreted by reference to the transformed statement: ‘If everybody pays 4 (b′) times 8 (a), there is a surplus of 4 (b′) times 3 (b)’; that is, a surplus of 12 (bb′), granted that 4 (b′) things are purchased instead of 1. Similarly, the symmetric multiplication is interpreted as follows: ‘If everybody pays 3 (b) times 7 (a′), there is a deficit of 3 (b) times 4 (b′)’; that is, now a deficit of 12 (bb′), provided that 3 (b) things are purchased instead of 1. By reference to these transformations, the ancient layers of commentary assert that the excess and deficit were ‘equalized’ (tong 同), and what every person paid was accordingly ‘homogenized’ (qi 齊). We will explain below what is at stake in the use of these terms. For the moment, suffice it to note that the transformation of what everybody paid is stated to derive from, and be correlated with, the aim of making excess and deficit equal and modifying the ‘suppositions’ accordingly.Footnote 26 From the equality of the new ‘excess’ and ‘deficit’, the ancient layers of commentary derive a crucial fact: if we add the new ‘suppositions’ (that is, 32 (b′a) and 21 (ba′)), they form yet another new ‘supposition’ that would leave neither any ‘excess’ nor any ‘deficit’, provided that we take into account that 7 (b + b′) things are bought instead of 1. Adding 32 (b′a) and 21 (ba′), and then 3 and 4 (b + b′), are precisely the two operations concluding section I.
At this point of the ancient layers of commentary, a new relationship between ‘suppositions’, ‘excess’ and ‘deficit’ has thus been proved correct: if everybody pays 32 + 21 (b′a + ba′), the people buy conjointly an amount of things corresponding to the sum of the ‘excess’ and the ‘deficit’ (7; that is, b + b′), leaving neither excess nor deficit. This statement can be read in two ways. One might consider it either from the viewpoint of the new ‘supposition’ on the unknown that would be what everybody pays (the problem is thus read with an unknown different from the one asked for in problem 1, and hence as falling under the second category), or from the viewpoint that a new relationship between the two unknowns has actually been found (thus reading problem 1 as being of the first category). The two readings shed light on the difference of meaning of the four operands (‘suppositions’, ‘excess’ and ‘deficit’) depending on the category of problem in relation to which they are considered. The ancient layers of commentary refer to the value first computed in section I, 32 + 21 (b′a + ba′), as ‘the exact number without excess or deficit’, whereas the second value computed will change interpretation, depending on the category of problems considered. The Nine Chapters refers to these values, respectively, as ‘dividend’ and ‘divisor’.
To the fact that section I is used for the solution of both categories of problems, there corresponds an interpretation in the ancient layers of commentary that has two facets. The operations are the same (one carries out the same multiplication and the same sum), but their interpretation differs in a subtle way, which will prove important for establishing the correctness of all the particular procedures deriving from the general procedure. This remark underscores the formal dimension of the act of considering a list of operations as the same, although the meaning of the operations differs. This dimension, which characterizes a facet of the knowledge at play in dealing with procedures in this way, is important from the perspective of a history of algebra. It also highlights the mathematical work involved in working with instructions in this way. In fact, another remark will illustrate how much this case study is remarkable in this respect. The ancient layers of commentary shed light on another formal dimension of the operations here. To understand this point, let us return to the operations of ‘equalization’ and ‘homogenization’ that this commentary introduced. Interestingly, the operation of ‘equalization’ was used only to establish the meaning of the operations prescribed at the beginning of the general procedure as ‘homogenization’. However, actually solving a problem does not require that the related deficit and excess equal to one another be computed. The ‘equalization’ is only used for making sense of the first list of operations of section I and thereby proving the correctness of the procedure. However, underlining this pattern is a way in which the ancient layers of commentary indicate that this general procedure proceeds formally in a way identical to the strategies followed to produce other procedures.Footnote 27 This remark confirms that actors had an interest in the form of computations, and not merely in computations as means to an end. Interestingly, the facet of the knowledge under discussion is particularly conspicuous with regard to section I, which yields a basis for formulating a single general procedure for all problems in the chapter.
From the establishment of the new statement onward, the computations given afterwards, as well as the interpretation, will diverge, depending on the type of problem dealt with. If we consider problem 1 with the amount paid by everybody to buy the thing as the unknown, to the value first computed in section I – that is, 32 + 21 (b′a + ba′), which the ancient layers of commentary designate as ‘the exact number without excess or deficit’ – there corresponds the second value computed – that is, 4 + 3 (b + b′), which is interpreted as the number of times suppositions were made.Footnote 28 From the new statement obtained – that is, if everybody pays 32 + 21 (b′a + ba′), the people buy conjointly an amount of things corresponding to the sum of the ‘excess’ and the ‘deficit’ without excess or deficit – the unknown follows immediately: one should divide the amount paid collectively (b′a + ba′, called ‘dividend’ in The Nine Chapters) by the number of things bought (b′ + b, called ‘divisor’), to get the value that, multiplied by the number of people, will yield the price of the thing, even if both latter values remain indeterminates. This division constitutes precisely the operation prescribed in section II of the general procedure, and this is the argument given in the ancient layers of commentary to account for its correctness. By this interpretation, the commentary thereby marks section II as a stand-alone part of the text of the procedure, in the same way as it had marked section I as a coherent part above.Footnote 29
Suppose, now, that we consider problem 1 as it was stated. The same new statement implies that (b′a + ba′) times the number of people is equal to (b′ + b) times the price of the thing. This is how we interpret this statement as yielding a new relationship between the actual unknowns of problem 1. The two values computed at the end of section I thus mean that (b′a + ba′) is to the price of the thing as (b′ + b) is to the number of people. At this juncture, the ancient layers of commentary return to the original statement of the problem, which asserted, ‘If everybody pays 8 (a), there is a surplus of 3 (b)’ and ‘If everybody pays 7 (a′), there is a deficit of 4 (b′).’ From these two relationships, the commentary derives this: if, subtracting one statement from the other, one considered that everybody paid 8–7 (a – a′), the amount of money gathered would be a known amount: 4 + 3 (b + b′). The commentary refers to the former value as a ‘reduced supposition’ and to the latter as a ‘determined dividend’; that is, a value in the meaning of which no unknown enters. The former (a – a′) is the result of the first operation prescribed by section V of the general procedure. Designating the result a ‘reduced supposition’ is a way of stating that it enters into the formulation of a new relationship between the unknowns. On the other hand, the latter value (b + b′), designated a ‘determined dividend’, was already computed in section I. However, now, in relation to the fact that it enters into the solution of problems of the first category, its value is interpreted in a new way, in the context of the new relationship established. The ancient layers of commentary formulate its meaning as the amount of money gathered by all the people if everybody paid an amount equal to the difference between the two suppositions (8–7, or a – a′).Footnote 30 This new relationship formulated by the commentary implies that dividing 4 + 3 (b + b′) – what The Nine Chapters referred to as ‘divisor’ at the end of section I – by 8–7 (a – a′) yields the number of people. Accordingly, on the basis of the new relationship established earlier, this shows that dividing 32 + 21 (b′a + ba′ [called ‘dividend’ in The Nine Chapters]) by 8–7 (a – a′) yields the price of the thing. These are precisely the two divisions that conclude section V. The ancient layers of commentary have thus established their correctness, while at the same time showing that the set of computations that constitutes section V has a unity of meaning. In conclusion, we see that the ‘dividend’ and ‘divisor’ computed at the end of section I enter in different lists of computations, depending on which category of problem they will be used for.
Clearly, seen from the viewpoint of the ancient layers of commentary, the mathematical problem that opens Chapter 7 is far more than a question whose answer is sought, and which could be solved by the specific ‘other’ procedure. It provides multiple possibilities of interpretation, which the ancient layers of commentary exploit to establish the correctness of all the procedures that are derived from the text of the general procedure. It thus seems that this might have motivated the authors of The Nine Chapters to place this problem and the similar ones at the beginning of Chapter 7, in relation to both the general procedure and the specific procedure.Footnote 31 This remark makes us surreptitiously glide from the problem as read by the ancient commentators to the problem as used in The Nine Chapters. Another remark seems to confirm that this might have been the function of the problem in the eyes of the authors of the canon: there is an adequacy between the way in which the general procedure is composed and the nature of the first problems, notably problem 1. This is where we might return to an issue about the critical edition of the canon, which we have raised above. We have seen that in the ancient edition reproduced in Figure 1, both the general and the specific procedures were placed before the related problems like problem 1. However, in the line of ancient editions on which Dai Zhen relied to prepare his critical editions at the end of the eighteenth century and which are no longer extant (see note 13 above), the first four problems, all similar to problem 1 just examined, appeared before both procedures. The discussion above leads us to favour the hypothesis that the order of problems and procedure might have originally conformed to the latter order.
To conclude, this analysis illustrates how the ancient layers of commentary shed light on actors’ conceptions of and practices with instructions. What we have seen about the composition of the text of the general procedure shows the complex operations carried out in producing the instructional text. Producing this text involved a specific mathematical work of an algebraic kind with operations, also meaningful from the viewpoint of a history of algorithms. It further shows that actors did not use procedures as independent textual pieces, but inquired into connections between them. This harmonizes with a way of valuing generality in this context, for which we have more evidence. This also allows us to connect the specificities of the general procedures and the mathematical work engaged in gathering problems and procedures into a chapter: the general procedure (and the similar procedures of, respectively, two excesses, two deficits, etc.) was what lent the chapter coherence.
From the perspective of the knowledge required to use such texts of procedures, what we have seen shows that readers could not blindly ‘obey’ prescriptions step by step. The instructional text that we have analysed required that they be active and understand the meaning of the operations, to be able to take decisions about how to use the text of the general procedure in different contexts. Knowing how to use the instructional text thus meant knowing how to navigate between its parts (that is, between sections I and V), and in particular which operations the text meant (think of section III) and how to interpret their ‘meaning’, in addition to knowing how to execute them. Note that the older layers of commentary do not discuss the goals of these different applications of the general procedures as practical, but as requiring different types of mathematical knowledge. Readers thus seem to look for procedures that can be applied to different mathematical cases, not different concrete cases.
The reading of the general procedure evidenced by the later layers of commentary
So far, we have relied on the ancient layers of commentary to approach the knowledge required to produce and use these texts of procedures. The later layers of commentary that we introduced in the section entitled ‘The sources’ also shed light on the latter issue, but in another way, which we will now examine.
In these later layers, both contained in Mathematical Methods, to begin with, the commentary takes the form of reformulating the ‘procedure’ of the canon as what actors called a ‘method’ (fa 法). From an observer's viewpoint, ‘procedure’ and ‘method’ look alike. How could ‘methods’ that were a mere reformulation of ‘procedures’ be perceived as explanations? We will address this issue by focusing on how the reformulation is carried out in the method analysed.
Interestingly, the reformulation, presented in large characters in the box shown on Figure 1 with the lightest shade of grey, as well as the annotations, added in smaller characters between the steps of the ‘method’, cast light on different facets of the knowledge required to read and handle the text. The reason is that the commentary now feels the need to provide explanations of a different kind on how to turn the text into action.
To better understand the nature of the reformulation and the annotations, we will first translate the text of the general procedure analysed above, as it is formulated in The Nine Chapters. It read as follows:Footnote 32
Procedure:
I. One puts (on the calculating surface) the lüs of what is paid. The excess and the deficit occupy, respectively, (the positions) under them. One makes the cross-multiplication of the lüs of what is paid, one sums, and takes (the result) as dividend. Summing excess and deficit makes the divisor.
II. One divides the dividend by the divisor.
III. If there are parts, one makes them communicate.
IV. If the excess and the deficit are linked with one another in a case where the (numbers of people) who buy the thing are equal,
V. One puts (on the calculating surface) the lüs of what is paid and one subtracts the smaller from the larger. With the remainder, one simplifies divisor and dividend.
The dividend makes the price of the thing,
and the divisor makes the number of people.
The general procedure is thus formulated with respect to problems like the first four problems of Chapter 7. It sketches a positioning of their four data on the calculating surface on which computations were carried out with numbers represented with rods. However, here, like elsewhere, the canon provides no illustration of these configurations of numbers. This is typical of the ancient texts until at least the tenth century.Footnote 33 Once the positioning has been sketched, the text of the procedure prescribes computations by reference to it.
How does the reformulation of the ‘procedure’ given in Mathematical Methods into a ‘method’ with annotations not only ‘explain’ the ‘procedure’, but also highlight the knowledge readers had to possess to use its text? In fact, the latter layers of commentary add various elements to the ancient text. These additions materialize bits of knowledge that these commentators considered tacit in the ancient text and yet required for their intended readers to deal with instructions from The Nine Chapters. I will thus examine each of these additions in turn.
The first transformation of the ancient text of the procedure is the addition of an annotation after the opening sentence of the procedure, as follows:Footnote 34
Method:
I. One puts (on the calculating surface) the lüs of what is paid. The excess and the deficit occupy, respectively, (the positions) under them.
lü of what is paid lü of what is paid
excess deficit
The annotation thus uses the space of the double column, in which usually annotations are inscribed with smaller characters, to offer a representation of the layout of the four numerical values on the calculating surface. Illustrations of this kind were added more generally to the purely discursive texts of procedures (in particular, the ancient ones) in all the extant writings published after the eleventh century. This addition makes explicit knowledge about features of the practice of the calculating surface that the reader was perceived to need to make sense of the instruction. Note that neither the canon nor the ancient layers of commentary dwelled on this. How this knowledge was conveyed to the reader at the time remains unclear. This is the first notable aspect of the transformation of the ancient text of ‘procedure’ into the corresponding ‘method’ in Mathematical Methods.
The next additions bear on the subsequent operation prescribed in the text of The Nine Chapters. They consist in the addition of a clause in large characters, which I represent as underlined, and three annotations, as follows:
Method (continued):
‘With excess and deficit,
excess corresponds to too much, deficit to deficient
one makes the cross-multiplication
the four are multiplied crosswise
of the lüs of what is paid,
the (products) respectively enter the lüs paid.’
The key operation that The Nine Chapters prescribed on the basis of the layout of the four values was a ‘cross-multiplication’. An annotation on this technical term makes its meaning explicit, bringing the term in relation with how the operation materially relies on the configuration of numbers on the calculating surface. The addition in large characters apparently also intends to specify how this operation was carried out, but from another perspective. It reveals that in the eyes of the later commentators, the text of The Nine Chapters mentioned explicitly only two out of the four operands needed by the cross-multiplication (the two ‘lüs of what is paid’). The addition in large characters specifies the other two operands (‘excess’ and ‘deficit’), and it is complemented by an annotation explaining to which lü each of these was, respectively, linked. This addition might reveal a change in the mathematical language with which the procedures were written up, or, alternatively, a change in the readers’ knowledge of how to handle instructions of this kind. In the context of The Nine Chapters, operands that were kept tacit systematically referred to the last values computed. From the perspective of the later commentators, this mode of reference was not clearly enough specified, since they felt the need to make all the operands explicit. This illustrates a second aspect of the rewriting of the ancient text of ‘procedure’ into the corresponding ‘method’.
The latter additions examined share the property of highlighting knowledge required to interpret the text and derive from it the operations meant. By contrast, the last annotation translated above makes explicit knowledge needed to turn the text into actual computation on the calculating surface. The addition of this explanation indicates that in the later commentators’ eyes, once the cross-multiplication had been carried out, the user had to know where to place the results on the instrument. By contrast, the older layers of commentary bespeak no need to explain this facet of the knowledge essential to actually use the text. The products obtained through the cross-multiplication, the annotation specifies, are put on the surface in place of the values of ‘the lü paid’. This practice of positioning and substituting numbers for others on the calculating surface is essential for the procedures of The Nine Chapters to work. However, nowhere is it made explicit, either in the canon or in the older layers of commentary. In the thirteenth century, we see that this kind of knowledge could no longer be taken for granted, the annotations thereby shedding light on what the intended user of Mathematical Methods further needed to know to use texts like that for the general procedure. Gradually, it thus becomes clear how the later layers of commentary reveal the competences that the ancient reader was expected to possess to use the instructional texts of The Nine Chapters. The later layers of commentary in Mathematical Methods go on as follows:
Method (continued):
I. … “one sums, and takes (the result) as dividend.
one sums the lü of what was paid already multiplied.
In the same way as indicated above, the subsequent operation in the text of The Nine Chapters (‘one sums’) leaves the operands to which it is applied unspecified. The ancient reader was clearly expected to understand that these were the results of the previous operation; that is, the two products yielded by the cross-multiplication and put in place of the ‘lüs of what was paid’. As above, the later layers of commentary add an annotation making the operands explicit. However, here, the explanation has two facets. Indeed, it likewise refers to the meaning of the operands (the results of the cross-products). Moreover, it further insists that the numbers to be added are not the ‘lüs of what was paid’ – that is, the values mentioned in the sentence of the instructional text occurring immediately before this instruction – but the numerical values placed in their positions, instead of them, on the calculating surface, after the previous operation was executed. The formulation of the previous sentence read, ‘one makes the cross-multiplication of the lüs of what is paid’. To interpret these instructions correctly, the reader had to understand that the results of these multiplications replaced the operands made explicit on the calculating surface. As a result, the next operation would be applied to the new numerical values put in these positions. In other words, the ancient texts of procedures referred to, and put in play terms referring to, positions on the calculating surface, under the assumption that the values placed in these positions constantly changed throughout the procedures. Each time the instructional text referred to these positions, what it meant was the values these positions contained at the moment when the reference occurred in the text. What the later layers of commentary in Mathematical Methods make explicit here is that the user picks up the content of the positions ‘lü of what was paid’, which, however, had already been transformed by the previous computation. This interpretation is coherent with features of the text that we discuss below. Mathematical Methods thereby highlights skills expected from ancient readers to be able to use the text. It further implies that this convention required an explanation for the more recent readers of the ancient instructional texts, whom the later commentators had in mind. This explanation is made explicit through the rewriting of the ‘procedure’ into a ‘method’.
The analysis developed so far clearly illustrates the striking contrast between the readings as well as the types of knowledge, to which the ancient and the later layers of commentary attest. The subsequent annotation might further bespeak a major difference between the two. It reads,
Method (continued):
I. … ‘Summing excess and deficit makes the divisor.
summing to one another hence makes the number of people.’
Like the ancient layers of commentary, the later layers read the general procedure by reference to the first problem of the chapter. This problem asked for the determination of the number of people involved in a joint purchase. We have seen that the general procedure determined this unknown through dividing the ‘divisor’ by the difference between the two ‘suppositions’. Why does, hence, the annotation claim here that the ‘divisor’ yields ‘the number of people’? If the statement is interpreted in this way, the assertion can only be understood if we recall that in the first problem, the difference between the two suppositions was 1. Dividing by 1 would not change the value of the ‘divisor’, which is thus equal to the unknown sought. This interpretation would mean that some annotations in the later layers of commentary might be valid only for problem 1, whereas in the ancient layers, the problem was used as paradigm; that is, as able to embody the general case. However, things are perhaps not so simple. Indeed, maybe we should interpret the verb ‘makes’ (為), which connects the sum computed and the number of people, in another way; that is, as a technical term pointing out that the former value will eventually generate the value of the unknown (hence one would rather translate as ‘summing will hence make …’). This seems to be the way in which the same verb is used in the subsequent annotation on the next operation prescribed by the text of the ‘method’ in Mathematical Methods:
Method (continued):
II. ‘… One divides the dividend by the divisor.
The lüs of what was paid make the dividend; excess and deficit make the divisor.’
Interestingly, here too the expressions ‘lüs of what was paid’, ‘excess’ and ‘deficit’ appear to refer to the positions in which these values were first placed. A previous annotation made clear that in these positions, the original ‘lüs of what was paid’ had been replaced by other values: these are precisely the values generating the dividend. The annotation actually points out how the upper positions will generate the dividend, and the lower ones the divisor. In other words, the later layers of commentary focus on explaining the interpretation of the text and the related management of the positions on the calculating surface. In contrast with the ancient layers of commentary, here the ‘meaning’ of the result of the division is not addressed. In particular, there is no mention of the fact that the operation relates to problems of the second category, and not to those like problem 1. This corresponds to the fact that the conditional in section IV is interpreted in a completely different way. We return below to this point.
The last annotation to the text of the ‘method’ in Mathematical Methods that we will examine makes explicit another facet of the knowledge required to use the ancient text of the general procedure: the handling of conditionals. Indeed, next, the text of the ‘method’ also repeats verbatim the subsequent sentence of the ancient ‘procedure’, which contains a conditional. The annotation explains its management as follows:
Method (continued):
III. ‘… If there are fractions, one makes them communicate.
If there are fractions, one makes communicate. If there are none, one does not use the previous text, which means that this is an indication that one only goes through.’
Again, the ancient layers of commentary never address this kind of background knowledge about the handling of conditionals, which is nevertheless essential to use the text of the procedure. Mathematical Methods goes on providing explanations on the text of the general procedure, which, except for the additions in large characters discussed above, the ‘method’ further repeats verbatim. I will not continue analysing closely the annotations, since the previous annotations give us an overview of the nature of the later layers of commentary.Footnote 35
I will rather conclude this examination of the later layers of commentary by making do with some global remarks that will allow me to analyse the relationship between procedures and the classification of problems in Mathematical Methods. If we rely on the testimony of the extant ancient editions of the canon, for the opening section of Chapter 7, the older layers of commentary occur, as usual, between the sentences of the general procedure, and not in the text of the first four problems, in relation to which it is given. By contrast, Mathematical Methods shapes a close relation between its later layers of commentary on the first four problems and the interpretation of the general procedure to which they attest.
To reach my conclusion, I need to sketch the structure of its opening section, after the general ‘method’. Immediately after, an ‘other method’ repeats the ‘other procedure’ of the canon, alternative to the general procedure, with slight changes in the formulation. Interestingly, in relation to the fact that the text of this ‘other method’ can be used step by step, there are only two annotations. One of them makes explicit the reference of an anaphora (之, ‘this’), while the other underlines the ‘direct’ character of the computation, in comparison with the process followed by the ‘general procedure’. Next, Mathematical Methods places an ‘Explanation of the problem’ (解題), which adds specifications about the management of the numbers on the calculating surface in relation to the nature of the prescriptions in the general procedure. The four problems are then used to explain further how the general procedure is turned into action. This is done in particular through adding ‘details of the procedure’ (草), in which the prescriptions are explained by the concrete illustrations to which they correspond.
The key point for my argument is this: the ‘explanation of the problem’ in problems 3 and 4 respectively asserts that the former corresponds to section III of the general procedure – that is, the conditional on fractions – and the latter to section IV. For problem 3, the explanations provided in the ‘details of the procedure’ show that Mathematical Methods interprets the prescription on fractions in ways that differ from the ancient layers of commentary. But this is not my focus here. What matters is that the ‘explanation of the problem’ makes clear that for the later layers of commentary, section IV, like section III, referred to a specific type of problem in the first category that we have distinguished above (the one illustrated by problem 4). Moreover, in the thirteenth century, the general procedure appeared to be interpreted as given primarily for problems of the first category.
As a result, the later layers of commentary for Chapter 7 show that Yang Hui did not grasp how to handle the text of the general procedure. He did not understand that the text yields lists of operations I and II for some problems, but lists I and V for others. Consequently, he considered the whole procedure (lists of operations I, II, to V, one after the other; see Figure 2) was to be followed step by step from beginning to end and that all these steps were needed to solve problems of the first type. In fact, the reformulations and annotations added in Mathematical Methods are what later books claiming to rely on The Nine Chapters take for the ancient canon. This is the case, for instance, with Wu Jing's 吳敬 All-Encompassing Compendium of the Detailed Annotations on The Nine Chapters and Analogical (Problems) 九章詳註比類大全 (hereafter All-Encompassing Compendium), completed in 1450.Footnote 36 This insight yields essential information for extracting evidence from the All-Encompassing Compendium that can shed light on parts of the later long-since lost layers of commentary. If we rely on evidence of this type about the later layers of commentary, my conclusion about how Yang Hui dealt with similar instructional texts seems to be confirmed by the rewriting of other texts of general procedure that required similar handling, like the general procedures for multiplying and dividing with all types of numbers.
If we return to Chapter 7, this failure to read the ancient procedure as referring to the solution of the two types of problem has a consequence for how the later layers of commentary deal with problems of the second category. Indeed, they systematically provide alternative methods for these problems.Footnote 37 Accordingly, in the chapter ‘Compiling categories’, in which Yang Hui compiles the ‘methods’ of the later layers of commentary to reclassify the problems of The Nine Chapters, he offers a reorganization of the ancient Chapter 7. Only problems of the first type are kept (with three additional problems that present specificities). All the other problems of the second category are now reclassified in relation to the alternative methods that the later layers of commentary offered.Footnote 38
This effort reveals the key relationship between formulating procedures and classifying problems, and how a change in the interpretation of the former led to a mutation in the latter. It also shows the knowledge involved in such formulation and classification. Finally, this sheds light on the limits of views that took ancient mathematical texts of procedures as offering readers only means to do things.
Conclusion
In this essay, we have concentrated on the old canon from the first century CE The Nine Chapters, which is instructional in the sense that its procedures gave readers instructions for doing things. Our purpose was to highlight that, in order to derive, from the text of a procedure, knowledge about how to do something, readers needed to possess various types of knowledge about how to engage with the text. I have argued that this, in turn, reflected the knowledge required to write up the type of instruction that this ancient canon bespeaks.
Our strategy to address these issues has been to analyse the way in which the thirteenth-century work entitled Mathematical Methods allowed its intended readers to read and use The Nine Chapters and its procedures. Indeed, Mathematical Methods included older and later layers of commentary on The Nine Chapters, and we have shown that each of these different commentaries focused on different facets of the knowledge needed to use the texts of instructions. As a result, these different layers of commentary allowed us to grasp the various dimensions of the knowledge involved in the production and the processing of instructions.
The ancient layers of commentary dealt with the interpretation of the intentions of the operations (their ‘meaning’ (意)). To do so, they relied on the first problem in a specific way. Moreover, this search for the meaning enabled ancient commentators to shed light on the subtle structure of the general procedure. The structure, and the specific navigation that it required for the procedure to be truly general, allowed the authors to give a single procedure for types of problem that were structurally different. We have underlined the mathematical knowledge at play in the shaping of this structure. Accordingly, the ancient layers of commentary reveal the work involved in the production of the instructions as well as the textual environment shaped to carry out this work. They also shed light on the fact that actors had developed specific engagements with the various textual elements that made up this environment.
By contrast, the later layers of commentary on these instructional texts focused on another type of knowledge needed to produce and use the texts of procedure, which the older commentators left unattended. They made explicit the knowledge required to handle the instructions concretely, which prominently included interpreting the operands of the operations and managing the computations on the calculating surface. In doing so, these later layers of commentary show a different use of problems. For them, problems illustrated different cases and different segments of the text of the procedure. Their detailed solution added explanation with respect to how to use the general procedure concretely.
One might say that the two bodies of commentary that we have analysed illustrate two ways of making sense of, and engaging with, the same instructional text. However, they also bespeak different readers’ assumptions with respect to how the text of the procedure should be handled, and hence how it conveyed meaning. This clearly illustrates why our observers’ assumptions are too poor to account for the variety of actors’ conceptions and practices of instructions.
Acknowledgements
This article was written in the context of the Learning by the Book project, led by Angela Creager, Elaine Leong and Mathias Grote. It is a great pleasure to thank them and the participants of the two meetings, during which we prepared this collection of articles. I would also like to pay tribute to the two referees for their critical and yet benevolent reading. These various feedbacks on my text helped me to improve my ideas and presentation significantly. I am quite grateful to the editorial team of the BJHS Themes, in particular Trish Hatton and Simon Werrett, for their support in the final processing of this article. I take full responsibility for the remaining shortcomings.





