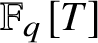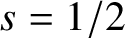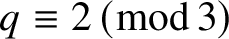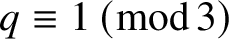1 Introduction
An extension of a famous conjecture of Chowla predicts that  ${\textstyle L(\frac {1}{2}, \chi)} \neq 0$ for Dirichlet L-functions attached to primitive characters
${\textstyle L(\frac {1}{2}, \chi)} \neq 0$ for Dirichlet L-functions attached to primitive characters ![]() $\chi $. Chowla’s original conjecture [Reference Chowla6, Chapter 8] is restricted to
$\chi $. Chowla’s original conjecture [Reference Chowla6, Chapter 8] is restricted to ![]() $\chi $ a quadratic character, which is the most studied case. For quadratic Dirichlet L-functions, Özlük and Snyder [Reference Özlük and Snyder30] showed, under the generalised Riemann hypothesis (GRH), that at least
$\chi $ a quadratic character, which is the most studied case. For quadratic Dirichlet L-functions, Özlük and Snyder [Reference Özlük and Snyder30] showed, under the generalised Riemann hypothesis (GRH), that at least ![]() $15/16$ of the L-functions
$15/16$ of the L-functions  ${\textstyle L(\frac {1}{2}, \chi )} $ attached to quadratic characters
${\textstyle L(\frac {1}{2}, \chi )} $ attached to quadratic characters ![]() $\chi $ do not vanish, by computing the one-level density for the low-lying zeroes in the family. The conjectures of Katz and Sarnak [Reference Katz and Sarnak25] on the zeroes of L-functions imply that
$\chi $ do not vanish, by computing the one-level density for the low-lying zeroes in the family. The conjectures of Katz and Sarnak [Reference Katz and Sarnak25] on the zeroes of L-functions imply that  ${\textstyle L(\frac {1}{2}, \chi )} \neq 0$ for almost all quadratic Dirichlet L-functions. Without assuming the GRH, Soundararajan [Reference Soundararajan35] proved that at least
${\textstyle L(\frac {1}{2}, \chi )} \neq 0$ for almost all quadratic Dirichlet L-functions. Without assuming the GRH, Soundararajan [Reference Soundararajan35] proved that at least ![]() $87.5 \%$ of the quadratic Dirichlet L-functions do not vanish at
$87.5 \%$ of the quadratic Dirichlet L-functions do not vanish at ![]() $s=1/2$, by computing the first two mollified moments. It is well known that using the first two (nonmollified) moments does not lead to a positive proportion of nonvanishing, as they grow too fast (see [Reference Cho and Park12] and the work of Jutila [Reference Jutila24].) Soundararajan [Reference Soundararajan35] also computed asymptotics for the first three moments, and Shen [Reference Shen34] obtained an asymptotic formula with the leading order term for the fourth moment (conditionally on the GRH), building on work of Soundararajan and Young [Reference Soundararajan and Young37]. A different approach was used by Diaconu, Goldfeld and Hoffstein [Reference David, Lalín and Nam16] to compute the third moment. Over function fields, asymptotics for the first four moments were obtained by Florea [Reference Florea18, Reference Florea19, Reference Florea20]. We refer the reader to those papers for more details. Moreover, in the function-field case, Bui and Florea [Reference Bary-Soroker and Meisner3] obtained a proportion of nonvanishing of at least
$s=1/2$, by computing the first two mollified moments. It is well known that using the first two (nonmollified) moments does not lead to a positive proportion of nonvanishing, as they grow too fast (see [Reference Cho and Park12] and the work of Jutila [Reference Jutila24].) Soundararajan [Reference Soundararajan35] also computed asymptotics for the first three moments, and Shen [Reference Shen34] obtained an asymptotic formula with the leading order term for the fourth moment (conditionally on the GRH), building on work of Soundararajan and Young [Reference Soundararajan and Young37]. A different approach was used by Diaconu, Goldfeld and Hoffstein [Reference David, Lalín and Nam16] to compute the third moment. Over function fields, asymptotics for the first four moments were obtained by Florea [Reference Florea18, Reference Florea19, Reference Florea20]. We refer the reader to those papers for more details. Moreover, in the function-field case, Bui and Florea [Reference Bary-Soroker and Meisner3] obtained a proportion of nonvanishing of at least ![]() $94 \%$ for quadratic Dirichlet L-functions, by computing the one-level density (those results are unconditional, as the GRH is true over function fields).
$94 \%$ for quadratic Dirichlet L-functions, by computing the one-level density (those results are unconditional, as the GRH is true over function fields).
In this paper, we consider the case of cubic Dirichlet L-functions. There are few articles in the literature about cubic Dirichlet L-functions, compared to the abundance of papers on quadratic Dirichlet L-functions, as this family is more difficult, in part because of the presence of cubic Gauss sums. The first moment of  ${\textstyle L(\frac {1}{2}, \chi )} $, where
${\textstyle L(\frac {1}{2}, \chi )} $, where ![]() $\chi $ is a primitive cubic character, was computed by Baier and Young over
$\chi $ is a primitive cubic character, was computed by Baier and Young over ![]() $\mathbb Q$ [Reference Bui and Florea1] (the non-Kummer case), by Luo for a thin subfamily over
$\mathbb Q$ [Reference Bui and Florea1] (the non-Kummer case), by Luo for a thin subfamily over ![]() $\mathbb Q(\sqrt {-3})$ [Reference Luo28] (the Kummer case) and by David, Florea and Lalin [Reference David, Florea and Lalin13] over function fields, in both the Kummer and the non-Kummer case, and for the full families.
$\mathbb Q(\sqrt {-3})$ [Reference Luo28] (the Kummer case) and by David, Florea and Lalin [Reference David, Florea and Lalin13] over function fields, in both the Kummer and the non-Kummer case, and for the full families.
In these three papers, the authors obtained lower bounds for the number of nonvanishing cubic twists, but not positive proportions, by using upper bounds on higher moments. Ellenberg, Li and Shusterman [Reference Ellenberg, Li and Shusterman17] use algebraic-geometry techniques to extend the results of [Reference David, Florea and Lalin13] to ![]() $\ell $-twists over function fields and improve upon the lower bound for the number of nonvanishing cubic twists (but the proportion is still nonpositive). Obtaining an asymptotic for the second moment for cubic Dirichlet L-functions is still an open question, over functions fields or number fields. Moreover, for the case of cubic Dirichlet L-functions, computing the one-level density can only be done for limited support of the Fourier transform of the test function, and that is not enough to lead to a positive proportion of nonvanishing for the full family, even under the GRH [Reference Conrey, Farmer, Keating, Rubinstein and Snaith5, Reference Meisner29]. Recently David and Güloğlu [Reference David and Güloğlu14] obtained a positive proportion of nonvanishing for Luo’s thin family [Reference Luo28] by computing the one-level density.
$\ell $-twists over function fields and improve upon the lower bound for the number of nonvanishing cubic twists (but the proportion is still nonpositive). Obtaining an asymptotic for the second moment for cubic Dirichlet L-functions is still an open question, over functions fields or number fields. Moreover, for the case of cubic Dirichlet L-functions, computing the one-level density can only be done for limited support of the Fourier transform of the test function, and that is not enough to lead to a positive proportion of nonvanishing for the full family, even under the GRH [Reference Conrey, Farmer, Keating, Rubinstein and Snaith5, Reference Meisner29]. Recently David and Güloğlu [Reference David and Güloğlu14] obtained a positive proportion of nonvanishing for Luo’s thin family [Reference Luo28] by computing the one-level density.
We prove in this paper that there is a positive proportion of nonvanishing for cubic Dirichlet L-functions at ![]() $s=1/2$ over function fields, in the non-Kummer case.
$s=1/2$ over function fields, in the non-Kummer case.
Theorem 1.1. Let ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$. Let
$q \equiv 2 \,(\mathrm {mod}\,3)$. Let ![]() $\mathcal {C}(g)$ be the set of primitive cubic Dirichlet characters of genus g over
$\mathcal {C}(g)$ be the set of primitive cubic Dirichlet characters of genus g over ![]() $\mathbb F_q[T]$. Then, as
$\mathbb F_q[T]$. Then, as ![]() $g \rightarrow \infty $,
$g \rightarrow \infty $,
 $$ \begin{align*} \# \left\{ \chi \in \mathcal{C}(g) : {\textstyle L\left(\frac{1}{2}, \chi\right)} \neq 0 \right\} \gg_k \# \mathcal{C}(g). \end{align*} $$
$$ \begin{align*} \# \left\{ \chi \in \mathcal{C}(g) : {\textstyle L\left(\frac{1}{2}, \chi\right)} \neq 0 \right\} \gg_k \# \mathcal{C}(g). \end{align*} $$ This theorem is obtained by using the breakthrough work on sharp upper bounds for moments of ![]() $\lvert \zeta (1/2+it)\rvert $ by Soundararajan [Reference Soundararajan36] and Harper [Reference Harper21], under the GRH. Their techniques, together with ideas appearing in the work of Radziwiłł and Soundararajan [Reference Rosen32] on distributions of central L-values of quadratic twists of elliptic curves, were further developed by Lester and Radziwiłł in [Reference Lester and Radziwiłł27], where they obtained sharp upper bounds for mollified moments of quadratic twists of modular forms. Our work owes a lot to these papers and circles of ideas.
$\lvert \zeta (1/2+it)\rvert $ by Soundararajan [Reference Soundararajan36] and Harper [Reference Harper21], under the GRH. Their techniques, together with ideas appearing in the work of Radziwiłł and Soundararajan [Reference Rosen32] on distributions of central L-values of quadratic twists of elliptic curves, were further developed by Lester and Radziwiłł in [Reference Lester and Radziwiłł27], where they obtained sharp upper bounds for mollified moments of quadratic twists of modular forms. Our work owes a lot to these papers and circles of ideas.
To obtain Theorem 1.1, we need to compute the first mollified moment, generalising our previous work [Reference David, Florea and Lalin13] (Theorem 1.3) and obtain a sharp upper bound for the second mollified moment (Theorem 1.6). In fact, we obtain upper bounds for all mollified moments, not only the second moment and integral moments. Using Theorems 1.3 and 1.6, the positive proportion of Theorem 1.1 follows from a simple application of the Cauchy–Schwarz inequality.
As noted by Harper in the case of the Riemann zeta function, the sharp upper bound for the kth moment is obtained at the cost of an enormous constant of the order ![]() $e^{e^{c k}}$, for some absolute constant
$e^{e^{c k}}$, for some absolute constant ![]() $c> 0$. Hence our positive proportion of nonvanishing is extremely small, but explicit nonetheless.
$c> 0$. Hence our positive proportion of nonvanishing is extremely small, but explicit nonetheless.
We first state the standard conjecture for moments of the family of cubic Dirichlet L-functions. We refer the reader to Section 2 for more information about the family of cubic Dirichlet L-functions over function fields in the non-Kummer case (i.e., ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$).
$q \equiv 2 \,(\mathrm {mod}\,3)$).
Conjecture 1.2. Let ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$. Let
$q \equiv 2 \,(\mathrm {mod}\,3)$. Let ![]() $\mathcal {C}(g)$ be the set of primitive cubic Dirichlet characters of genus g over
$\mathcal {C}(g)$ be the set of primitive cubic Dirichlet characters of genus g over ![]() $\mathbb F_q[T]$. Then as
$\mathbb F_q[T]$. Then as ![]() $g \rightarrow \infty $,
$g \rightarrow \infty $,
 $$ \begin{align*} \frac{1}{\# \mathcal{C}(g)} \sum_{\chi \in {\mathcal{C}}(g)} {\textstyle\left\lvert L\left(\frac{1}{2},\chi\right) \right\rvert^{2k}} \sim \frac{{a_k \mathfrak{g}_k}}{\left(k^2\right)!} P_k(g), \end{align*} $$
$$ \begin{align*} \frac{1}{\# \mathcal{C}(g)} \sum_{\chi \in {\mathcal{C}}(g)} {\textstyle\left\lvert L\left(\frac{1}{2},\chi\right) \right\rvert^{2k}} \sim \frac{{a_k \mathfrak{g}_k}}{\left(k^2\right)!} P_k(g), \end{align*} $$where ![]() $P_k(g)$ is a monic polynomial of degree
$P_k(g)$ is a monic polynomial of degree ![]() $k^2$,
$k^2$, ![]() $a_k$ is an arithmetic factor depending on the family and
$a_k$ is an arithmetic factor depending on the family and
 $$ \begin{align*} \mathfrak{g}_k= (k^2)! \prod_{j=0}^{k-1}\frac{j!}{(j+k)!}. \end{align*} $$
$$ \begin{align*} \mathfrak{g}_k= (k^2)! \prod_{j=0}^{k-1}\frac{j!}{(j+k)!}. \end{align*} $$ A testament to the fact that moments of L-functions are hard to compute is the fact that simply conjecturing an asymptotic is very difficult. The constants ![]() $\mathfrak {g}_k$ were obtained by Keating and Snaith based on considerations from random matrix theory [Reference Keating and Snaith26]. Number-theoretic heuristic arguments were used in the work of Conrey, Farmer, Keating, Rubinstein and Snaith [Reference Cho and Park12] to generalise Conjecture 1.2 to include lower-order terms, and more recently by Conrey and Keating [Reference Conrey and Keating7, Reference Conrey and Keating8, Reference Conrey and Keating9, Reference Conrey and Keating10, Reference Conrey and Keating11]. The order of magnitude
$\mathfrak {g}_k$ were obtained by Keating and Snaith based on considerations from random matrix theory [Reference Keating and Snaith26]. Number-theoretic heuristic arguments were used in the work of Conrey, Farmer, Keating, Rubinstein and Snaith [Reference Cho and Park12] to generalise Conjecture 1.2 to include lower-order terms, and more recently by Conrey and Keating [Reference Conrey and Keating7, Reference Conrey and Keating8, Reference Conrey and Keating9, Reference Conrey and Keating10, Reference Conrey and Keating11]. The order of magnitude  $g^{k^2}$ is easy to conjecture, as it comes from the size of the contribution of the diagonal terms. In the case of cubic characters, this will come from the fact that cubic characters are trivial on cubes. For the first moment, only diagonal terms contribute to the asymptotic of the previously cited work [Reference Bui and Florea1, Reference David, Florea and Lalin13, Reference Luo28]. For the second (and higher) moments, there will be a contribution from the off-diagonal terms. The contribution of off-diagonal terms can be estimated in the case of quadratic characters, but it is open for the family of cubic characters, where only the first moment without absolute value – the sum of
$g^{k^2}$ is easy to conjecture, as it comes from the size of the contribution of the diagonal terms. In the case of cubic characters, this will come from the fact that cubic characters are trivial on cubes. For the first moment, only diagonal terms contribute to the asymptotic of the previously cited work [Reference Bui and Florea1, Reference David, Florea and Lalin13, Reference Luo28]. For the second (and higher) moments, there will be a contribution from the off-diagonal terms. The contribution of off-diagonal terms can be estimated in the case of quadratic characters, but it is open for the family of cubic characters, where only the first moment without absolute value – the sum of  ${\textstyle L(\frac {1}{2},\chi )}$ – is known. The work of Soundararajan and Harper provides an upper bound of the exact order of magnitude for all moments of
${\textstyle L(\frac {1}{2},\chi )}$ – is known. The work of Soundararajan and Harper provides an upper bound of the exact order of magnitude for all moments of ![]() $\zeta (s)$. This follows from a key result of Soundararajan, who proved that one can upper bound
$\zeta (s)$. This follows from a key result of Soundararajan, who proved that one can upper bound  $\log \lvert L(\frac {1}{2},\chi ) \rvert $ by a short sum over primes. In our setting, we use Lemma 3.1, which is the analogue of Soundararajan’s key inequality. These arguments lead to a constant for the upper bound which is much larger than
$\log \lvert L(\frac {1}{2},\chi ) \rvert $ by a short sum over primes. In our setting, we use Lemma 3.1, which is the analogue of Soundararajan’s key inequality. These arguments lead to a constant for the upper bound which is much larger than ![]() $\mathfrak {g}_k$. In particular, shortening the Dirichlet polynomial produces a large contribution from the
$\mathfrak {g}_k$. In particular, shortening the Dirichlet polynomial produces a large contribution from the ![]() $(g+2)/N$ term. The techniques used to get the upper bound generate a constant of size
$(g+2)/N$ term. The techniques used to get the upper bound generate a constant of size ![]() $e^{e^{ck}}$, as noted by Harper [Reference Harper21].
$e^{e^{ck}}$, as noted by Harper [Reference Harper21].
1.1 Statement of the results
We state our two results about the mollified moments. Set ![]() $\kappa>0$. The mollifier we use,
$\kappa>0$. The mollifier we use,  $M(\chi; \frac {1}{\kappa })$, is defined in Section 3.2 and depends on the parameter
$M(\chi; \frac {1}{\kappa })$, is defined in Section 3.2 and depends on the parameter ![]() $\kappa $. We will later choose
$\kappa $. We will later choose ![]() $\kappa =1$ in the application to Theorem 1.3.
$\kappa =1$ in the application to Theorem 1.3.
Theorem 1.3. Let ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$. Let
$q \equiv 2 \,(\mathrm {mod}\,3)$. Let ![]() $\mathcal {C}(g)$ be the set of primitive cubic Dirichlet characters of genus g over
$\mathcal {C}(g)$ be the set of primitive cubic Dirichlet characters of genus g over ![]() $\mathbb F_q[T]$. Then as
$\mathbb F_q[T]$. Then as ![]() $g \rightarrow \infty $,
$g \rightarrow \infty $,
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} {\textstyle L\left(\frac{1}{2},\chi\right) }{\textstyle M(\chi;1)} = A q^{g+2}+ O \left(q^{\delta g} \right), \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} {\textstyle L\left(\frac{1}{2},\chi\right) }{\textstyle M(\chi;1)} = A q^{g+2}+ O \left(q^{\delta g} \right), \end{align*} $$for some ![]() $0<\delta <1$ (see formula (8.30) for more details on
$0<\delta <1$ (see formula (8.30) for more details on ![]() $\delta $) and where the constant A is given in formula (8.25).
$\delta $) and where the constant A is given in formula (8.25).
Corollary 1.4. With the same notation as before, we have
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} {\textstyle L\left(\frac{1}{2},\chi\right) }{\textstyle M(\chi;1)} \geq 0.6143 q^{g+2}. \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} {\textstyle L\left(\frac{1}{2},\chi\right) }{\textstyle M(\chi;1)} \geq 0.6143 q^{g+2}. \end{align*} $$Remark 1.5. It is easy to estimate that ![]() $\# \mathcal {C}(g) \sim c_3 q^{g+2}$ for some explicit constant
$\# \mathcal {C}(g) \sim c_3 q^{g+2}$ for some explicit constant ![]() $c_3$ [Reference David, Florea and Lalin13]. Dividing by the size of the family, we then prove that the first mollified moment of
$c_3$ [Reference David, Florea and Lalin13]. Dividing by the size of the family, we then prove that the first mollified moment of  $L(\frac {1}{2}, \chi )$ is asymptotic to a constant, which is the conjectural asymptotic. This is also the asymptotic for the nonmollified moment (with a different constant), as proven in [Reference David, Florea and Lalin13]. This asymptotic is not included in Conjecture 1.2, which is concerned with the moments of the absolute value of the L-functions. The moments of
$L(\frac {1}{2}, \chi )$ is asymptotic to a constant, which is the conjectural asymptotic. This is also the asymptotic for the nonmollified moment (with a different constant), as proven in [Reference David, Florea and Lalin13]. This asymptotic is not included in Conjecture 1.2, which is concerned with the moments of the absolute value of the L-functions. The moments of  $L(\frac {1}{2}, \chi )^{k_1} {\overline {L(\frac {1}{2}, \chi )^{k_2}}}$, for general positive
$L(\frac {1}{2}, \chi )^{k_1} {\overline {L(\frac {1}{2}, \chi )^{k_2}}}$, for general positive ![]() $k_1, k_2$, are conjectured to grow as a polynomial of degree
$k_1, k_2$, are conjectured to grow as a polynomial of degree ![]() $k_1 k_2$ in g (see [Reference Diaconu, Goldfeld and Hoffstein15]). Note that the conjectures in [Reference Diaconu, Goldfeld and Hoffstein15] hold for cubic twists of elliptic curves, but both families have the same symmetry, so the main terms will have a similar shape. Theorem 1.3 corresponds to the case
$k_1 k_2$ in g (see [Reference Diaconu, Goldfeld and Hoffstein15]). Note that the conjectures in [Reference Diaconu, Goldfeld and Hoffstein15] hold for cubic twists of elliptic curves, but both families have the same symmetry, so the main terms will have a similar shape. Theorem 1.3 corresponds to the case ![]() $k_1=1, k_2=0$, and Conjecture 1.2 to the case
$k_1=1, k_2=0$, and Conjecture 1.2 to the case ![]() $k_1=k_2=k$.
$k_1=k_2=k$.
The following upper bound for the moment is the analogue of [Reference Lester and Radziwiłł27, Proposition 4.1]:
Theorem 1.6. Set ![]() $k, \kappa> 0$ such that
$k, \kappa> 0$ such that ![]() $k \kappa $ is an even integer and
$k \kappa $ is an even integer and ![]() $k \kappa \leq C$ for some absolute constant C. Let
$k \kappa \leq C$ for some absolute constant C. Let ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$. Let
$q \equiv 2 \,(\mathrm {mod}\,3)$. Let ![]() $\mathcal {C}(g)$ be the set of primitive cubic Dirichlet characters of genus g over
$\mathcal {C}(g)$ be the set of primitive cubic Dirichlet characters of genus g over ![]() $\mathbb F_q[T]$. Then as
$\mathbb F_q[T]$. Then as ![]() $g \rightarrow \infty $,
$g \rightarrow \infty $,
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} {\textstyle\left\lvert L\left(\frac{1}{2},\chi\right) \right\rvert^{ k} \left\lvert M\left(\chi;\frac{1}{\kappa}\right)\right\rvert^{ k \kappa }} \ll_k q^g. \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} {\textstyle\left\lvert L\left(\frac{1}{2},\chi\right) \right\rvert^{ k} \left\lvert M\left(\chi;\frac{1}{\kappa}\right)\right\rvert^{ k \kappa }} \ll_k q^g. \end{align*} $$Remark 1.7. Because of the presence of the mollifier, dividing by ![]() $\# \mathcal {C}(g)$, all moments are bounded by a constant, and they do not grow. Using the first and second moment then leads to a positive proportion of nonvanishing.
$\# \mathcal {C}(g)$, all moments are bounded by a constant, and they do not grow. Using the first and second moment then leads to a positive proportion of nonvanishing.
1.2 Proof of Theorem 1.1
The proof of Theorem 1.1 follows from a simple application of Cauchy–Schwarz and Theorems 1.3 and 1.6 for ![]() $\kappa =1$. Indeed,
$\kappa =1$. Indeed,
 $$ \begin{align*} \sum_{\substack{ \chi \in \mathcal{C}(g) \\L\left(\frac{1}{2}, \chi\right) \neq 0}} 1 \geq \frac{ \left\lvert \sum_{\chi \in \mathcal{C}(g)} \displaystyle {\textstyle L\left(\frac{1}{2},\chi\right) }{\textstyle M(\chi;1)}\right\rvert ^2}{ \displaystyle \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right) }{\textstyle M(\chi;1)}\right\rvert^2} \gg q^{g}. \hfill \end{align*} $$
$$ \begin{align*} \sum_{\substack{ \chi \in \mathcal{C}(g) \\L\left(\frac{1}{2}, \chi\right) \neq 0}} 1 \geq \frac{ \left\lvert \sum_{\chi \in \mathcal{C}(g)} \displaystyle {\textstyle L\left(\frac{1}{2},\chi\right) }{\textstyle M(\chi;1)}\right\rvert ^2}{ \displaystyle \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right) }{\textstyle M(\chi;1)}\right\rvert^2} \gg q^{g}. \hfill \end{align*} $$Remark 1.8. Combining Corollary 1.4 and formula (7.11), we get the explicit proportion
 $$ \begin{align} \#\left\{ \chi \in \mathcal{C}(g) \mid {\textstyle L\left(\frac{1}{2}, \chi\right)} \neq 0\right\} \geq 0.3773 e^{-e^{182}} q^{g+2}, \end{align} $$
$$ \begin{align} \#\left\{ \chi \in \mathcal{C}(g) \mid {\textstyle L\left(\frac{1}{2}, \chi\right)} \neq 0\right\} \geq 0.3773 e^{-e^{182}} q^{g+2}, \end{align} $$and using formula (2.6),
 $$ \begin{align*} \frac{\#\left\{\chi \in \mathcal{C}(g) \mid L\left(\frac{1}{2}, \chi\right) \neq 0\right\}}{\#\mathcal{C}(g)}\geq \left(1-e^{-e^{84}}\right)^2\frac{e^{-e^{182}}}{\zeta_q(2)^3\zeta_q(3)^2}\geq 0.4718e^{-e^{182}}. \end{align*} $$
$$ \begin{align*} \frac{\#\left\{\chi \in \mathcal{C}(g) \mid L\left(\frac{1}{2}, \chi\right) \neq 0\right\}}{\#\mathcal{C}(g)}\geq \left(1-e^{-e^{84}}\right)^2\frac{e^{-e^{182}}}{\zeta_q(2)^3\zeta_q(3)^2}\geq 0.4718e^{-e^{182}}. \end{align*} $$1.3 Overview of the paper
This paper contains two main results, which are proven with different techniques.
We first prove the upper bound for the mollified moments, adapting the setting and notation of [Reference Lester and Radziwiłł27] to the case of cubic characters (and to the function-field case). The combinatorics to give an upper bound to the contribution of the diagonal terms are significantly more complicated, in part because the special values of the cubic L-functions are not real numbers, and they have to be considered in absolute value, and in part because we are identifying cubes and not squares. This also applies to the proof of the almost-sharp upper bound for the L-functions we consider, which is needed as a starting point to prove the sharp upper bound. Because we are dealing with cubic characters, we also have to bound the contribution of the squares of the primes, unlike the case of quadratic characters, where the squares of the primes contribute to the main term. In the language of random matrix theory, the family of cubic characters is a unitary family, and the family of quadratic characters is a symplectic family (for Dirichlet twists) or an orthogonal family (for twists of a modular form). In [Reference Harper21], the author also bounds the contribution of the squares of the primes to get sharp upper bounds on the moments of  ${\textstyle \lvert \zeta (\frac 12 + it)\rvert }$, which is a unitary family. In our case, because of the presence of the mollifier, mixing the square of the primes with the primes is very cumbersome, and we treat them separately with an additional use of the Cauchy–Schwarz inequality. The contribution from the squares of the primes morally behaves like
${\textstyle \lvert \zeta (\frac 12 + it)\rvert }$, which is a unitary family. In our case, because of the presence of the mollifier, mixing the square of the primes with the primes is very cumbersome, and we treat them separately with an additional use of the Cauchy–Schwarz inequality. The contribution from the squares of the primes morally behaves like ![]() $L(1,\overline {\chi })$. Bounding this contribution is similar to getting an upper bound for the average of
$L(1,\overline {\chi })$. Bounding this contribution is similar to getting an upper bound for the average of ![]() $L(1,\chi )$, which is much simpler than the original problem of bounding the average of
$L(1,\chi )$, which is much simpler than the original problem of bounding the average of  $L(\frac 12, \chi).$
$L(\frac 12, \chi).$
We then proceed to evaluating the first mollified moment. Because the mollifier is a finite Dirichlet polynomial, this amounts to the computation of a ‘twisted first moment’ (see Proposition 8.1). Evaluating this twisted first moment is similar to evaluating the first moment for the non-Kummer family in [Reference David, Florea and Lalin13], relying on the approximate functional equation and powerful results on the distribution of cubic Gauss sums.
The structure of the paper is as follows. Section 2 contains the standard properties of cubic characters over function fields that are used throughout the paper. Section 3 contains the proof of Theorem 1.6 modulo three important results proven in three subsequent sections: a technical lemma proven in Section 3.5, an upper bound for the contribution of the square of the primes in Section 5 and the proof of a proposition giving an almost-sharp upper bound for the unmollified moments of  ${\textstyle L(\frac {1}{2},\chi )}$ in Section 6. In Section 7 we give some estimates on the (extremely small) positive proportion of Theorem 1.1. Finally, Section 8 contains the asymptotic for the first mollified moment, following the lines of [Reference David, Florea and Lalin13] where the first moment is computed.
${\textstyle L(\frac {1}{2},\chi )}$ in Section 6. In Section 7 we give some estimates on the (extremely small) positive proportion of Theorem 1.1. Finally, Section 8 contains the asymptotic for the first mollified moment, following the lines of [Reference David, Florea and Lalin13] where the first moment is computed.
2 Background
Let q be an odd prime power. We denote by ![]() $\mathcal {M}_q$ the set of monic polynomials of
$\mathcal {M}_q$ the set of monic polynomials of ![]() $\mathbb F_q[T]$, by
$\mathbb F_q[T]$, by ![]() $\mathcal {M}_{q,\leq d}$ the subset of degree less than or equal to d and by
$\mathcal {M}_{q,\leq d}$ the subset of degree less than or equal to d and by ![]() $\mathcal {M}_{q,d}$ the subset of degree exactly d. Similarly,
$\mathcal {M}_{q,d}$ the subset of degree exactly d. Similarly, ![]() $\mathcal {H}_q$,
$\mathcal {H}_q$, ![]() $\mathcal {H}_{q, \leq d}$ and
$\mathcal {H}_{q, \leq d}$ and ![]() $\mathcal {H}_{q,d}$ denote the analogous sets of monic square-free polynomials. In general, all sums over polynomials in
$\mathcal {H}_{q,d}$ denote the analogous sets of monic square-free polynomials. In general, all sums over polynomials in ![]() $\mathbb F_q[T]$ are always taken over monic polynomials. The norm of a polynomial
$\mathbb F_q[T]$ are always taken over monic polynomials. The norm of a polynomial ![]() $f(T)\in \mathbb F_q[T]$ is given by
$f(T)\in \mathbb F_q[T]$ is given by
 $$ \begin{align*} \lvert f\rvert_q=q^{\deg\left(f\right)}. \end{align*} $$
$$ \begin{align*} \lvert f\rvert_q=q^{\deg\left(f\right)}. \end{align*} $$In particular, if ![]() $f(T)\in \mathbb F_{q^n}[T]$, we have
$f(T)\in \mathbb F_{q^n}[T]$, we have  $\lvert f\rvert _{q^n}=q^{n\deg \left (f\right )}$ for any positive n. We will write
$\lvert f\rvert _{q^n}=q^{n\deg \left (f\right )}$ for any positive n. We will write ![]() $\lvert f\rvert $ instead of
$\lvert f\rvert $ instead of ![]() $\lvert f\rvert _q$ when there is no ambiguity.
$\lvert f\rvert _q$ when there is no ambiguity.
The following notation will be used often. We will write ![]() $A \leq _\varepsilon B$ to mean
$A \leq _\varepsilon B$ to mean ![]() $A \leq (1 + \varepsilon )B$ for any
$A \leq (1 + \varepsilon )B$ for any ![]() $\varepsilon>0$ as
$\varepsilon>0$ as ![]() $g \rightarrow \infty $.
$g \rightarrow \infty $.
The primes of ![]() $\mathbb F_q[T]$ are the monic irreducible polynomials. Let
$\mathbb F_q[T]$ are the monic irreducible polynomials. Let ![]() $\pi (n)$ be the number of primes of
$\pi (n)$ be the number of primes of ![]() $\mathbb F_q[T]$ of degree n. By considering all the roots of these polynomials, we see that
$\mathbb F_q[T]$ of degree n. By considering all the roots of these polynomials, we see that ![]() $n\pi (n)$ counts the number of elements in
$n\pi (n)$ counts the number of elements in ![]() $\mathbb F_{q^n}$ of degree exactly n over the base field
$\mathbb F_{q^n}$ of degree exactly n over the base field ![]() $\mathbb F_q$, which is less than or equal to the total number of elements in
$\mathbb F_q$, which is less than or equal to the total number of elements in ![]() $\mathbb F_{q^n}$. Therefore,
$\mathbb F_{q^n}$. Therefore,
 $$ \begin{align} \pi(n)\leq \frac{q^n}{n}. \end{align} $$
$$ \begin{align} \pi(n)\leq \frac{q^n}{n}. \end{align} $$More precisely, the Prime Polynomial Theorem [Reference Radziwiłł and Soundararajan33, Theorem 2.2] states that the number ![]() $\pi (n)$ of primes of
$\pi (n)$ of primes of ![]() $\mathbb F_q[T]$ of degree n satisfies
$\mathbb F_q[T]$ of degree n satisfies
 $$ \begin{align} \pi(n)=\frac{q^n}{n}+O\left(\frac{q^{n/2}}{n}\right). \end{align} $$
$$ \begin{align} \pi(n)=\frac{q^n}{n}+O\left(\frac{q^{n/2}}{n}\right). \end{align} $$The von Mangoldt function is defined as
 $$ \begin{align*} \Lambda(f) = \begin{cases} \deg(P) & \text{if } f=cP^k, c \in \mathbb F_q^{*}, P \text{ is prime}, \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \Lambda(f) = \begin{cases} \deg(P) & \text{if } f=cP^k, c \in \mathbb F_q^{*}, P \text{ is prime}, \\ 0 & \text{otherwise}. \end{cases} \end{align*} $$Recall that for ![]() $f\in \mathbb F_q[T]$ the Möbius function
$f\in \mathbb F_q[T]$ the Möbius function ![]() $\mu (f)$ is
$\mu (f)$ is ![]() $0$ if f is not square-free and
$0$ if f is not square-free and ![]() $(-1)^t$ if f is a constant times a product of t different primes. The Euler
$(-1)^t$ if f is a constant times a product of t different primes. The Euler ![]() $\phi _q$ function is defined as
$\phi _q$ function is defined as ![]() $\# \left (\mathbb F_q[T]/\left ( f \mathbb F_q[T]\right )\right )^{*}$. It satisfies
$\# \left (\mathbb F_q[T]/\left ( f \mathbb F_q[T]\right )\right )^{*}$. It satisfies
 $$ \begin{align*} \phi_q(f)=\lvert f\rvert_q\prod_{P\mid f}\left(1-\lvert P\rvert_q^{-1}\right), \end{align*} $$
$$ \begin{align*} \phi_q(f)=\lvert f\rvert_q\prod_{P\mid f}\left(1-\lvert P\rvert_q^{-1}\right), \end{align*} $$and
 $$ \begin{align*} \sum_{\substack{d\in \mathcal{M}_q\\d\mid f}}\frac{\mu(d)}{\lvert d\rvert_q}=\frac{\phi_q(f)}{\lvert f\rvert_q}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{d\in \mathcal{M}_q\\d\mid f}}\frac{\mu(d)}{\lvert d\rvert_q}=\frac{\phi_q(f)}{\lvert f\rvert_q}. \end{align*} $$When ![]() $f(T) \in \mathbb F_{q^n}[T]$, we may consider
$f(T) \in \mathbb F_{q^n}[T]$, we may consider ![]() $\phi _{q^n}$ defined similarly.
$\phi _{q^n}$ defined similarly.
In this paper we consider the non-Kummer case of cubic Dirichlet character over ![]() $\mathbb F_q[T]$, where
$\mathbb F_q[T]$, where ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$. For more details, we refer the reader to [Reference Bui, Florea, Keating and Roditty-Gershon2, Reference David, Florea and Lalin13] for the function-field case and [Reference Bui and Florea1] for the number-field case. In the function-field case, when
$q \equiv 2 \,(\mathrm {mod}\,3)$. For more details, we refer the reader to [Reference Bui, Florea, Keating and Roditty-Gershon2, Reference David, Florea and Lalin13] for the function-field case and [Reference Bui and Florea1] for the number-field case. In the function-field case, when ![]() $q\equiv 2\,(\mathrm {mod}\,3)$ these characters are best described as a subset of the cubic characters over
$q\equiv 2\,(\mathrm {mod}\,3)$ these characters are best described as a subset of the cubic characters over ![]() $\mathbb F_{q^2}[T]$. Notice that
$\mathbb F_{q^2}[T]$. Notice that ![]() $q^2 \equiv 1 \,(\mathrm {mod}\,3)$. Therefore, we will first discuss the case
$q^2 \equiv 1 \,(\mathrm {mod}\,3)$. Therefore, we will first discuss the case ![]() $q\equiv 1 \,(\mathrm {mod}\,3)$, which we will later apply to
$q\equiv 1 \,(\mathrm {mod}\,3)$, which we will later apply to ![]() $q^2$. We proceed to construct cubic Dirichlet characters over
$q^2$. We proceed to construct cubic Dirichlet characters over ![]() $\mathbb F_{q}[T]$ as follows. We fix an isomorphism
$\mathbb F_{q}[T]$ as follows. We fix an isomorphism ![]() $\Omega $ between the third roots of unity
$\Omega $ between the third roots of unity ![]() $\mu _3\subset \mathbb C^*$ and the cubic roots of 1 in
$\mu _3\subset \mathbb C^*$ and the cubic roots of 1 in ![]() $\mathbb F_{q}^*$. Let P be a prime polynomial in
$\mathbb F_{q}^*$. Let P be a prime polynomial in ![]() $\mathbb F_{q}[T]$, and let
$\mathbb F_{q}[T]$, and let ![]() $f \in \mathbb F_{q}[T]$ be such that
$f \in \mathbb F_{q}[T]$ be such that ![]() $P\nmid f$. Then there is a unique
$P\nmid f$. Then there is a unique ![]() $\alpha \in \mu _3$ such that
$\alpha \in \mu _3$ such that
 $$ \begin{align*} f^{\frac{q^{\deg(P)}-1}{3}}\equiv \Omega(\alpha) \,(\mathrm{mod}\,P). \end{align*} $$
$$ \begin{align*} f^{\frac{q^{\deg(P)}-1}{3}}\equiv \Omega(\alpha) \,(\mathrm{mod}\,P). \end{align*} $$Note that this equation is solvable because ![]() $q \equiv 1 \,(\mathrm {mod}\,3)$. Then we set
$q \equiv 1 \,(\mathrm {mod}\,3)$. Then we set
We remark that there are two such characters, ![]() $\chi _P$ and
$\chi _P$ and  $\overline {\chi _P}=\chi _P^2$, depending on the choice of
$\overline {\chi _P}=\chi _P^2$, depending on the choice of ![]() $\Omega $.
$\Omega $.
This construction is extended by multiplicativity to any monic polynomial ![]() $F\in \mathbb F_q[T]$. In other words, if
$F\in \mathbb F_q[T]$. In other words, if ![]() $F=P_1^{e_1}\dotsm P_s^{e_s}$, where the
$F=P_1^{e_1}\dotsm P_s^{e_s}$, where the ![]() $P_i$ are distinct primes, then
$P_i$ are distinct primes, then
 $$ \begin{align*} \chi_F=\chi_{P_1}^{e_1}\dotsm \chi_{P_s}^{e_s}. \end{align*} $$
$$ \begin{align*} \chi_F=\chi_{P_1}^{e_1}\dotsm \chi_{P_s}^{e_s}. \end{align*} $$We have that ![]() $\chi _F$ is a cubic character modulo
$\chi _F$ is a cubic character modulo ![]() $P_1\dotsm P_s$. It is primitive if and only if
$P_1\dotsm P_s$. It is primitive if and only if ![]() $e_i=1$ or
$e_i=1$ or ![]() $e_i=2$ for all i.
$e_i=2$ for all i.
If ![]() $q \equiv 1 \,(\mathrm {mod}\,6)$, then we have perfect cubic reciprocity. Namely, let
$q \equiv 1 \,(\mathrm {mod}\,6)$, then we have perfect cubic reciprocity. Namely, let ![]() $a, b \in \mathbb F_q[T]$ be relatively prime monic polynomials, and let
$a, b \in \mathbb F_q[T]$ be relatively prime monic polynomials, and let ![]() $\chi _a$ and
$\chi _a$ and ![]() $\chi _b$ be the cubic residue symbols already defined. If
$\chi _b$ be the cubic residue symbols already defined. If ![]() $q \equiv 1 \,(\mathrm {mod}\,6)$, then
$q \equiv 1 \,(\mathrm {mod}\,6)$, then
Throughout the paper, we will fix ![]() $q\equiv 2\,(\mathrm {mod}\,3)$ (and then
$q\equiv 2\,(\mathrm {mod}\,3)$ (and then ![]() $q^2\equiv 1\,(\mathrm {mod}\,3)$, as we already mentioned). When
$q^2\equiv 1\,(\mathrm {mod}\,3)$, as we already mentioned). When ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$, the foregoing construction of
$q \equiv 2 \,(\mathrm {mod}\,3)$, the foregoing construction of ![]() $\chi _P$ will also give a cubic character as long as P has even degree, and the character can be extended by multiplicativity. In the non-Kummer case, a better way to describe cubic characters is to see them as restriction characters defined over
$\chi _P$ will also give a cubic character as long as P has even degree, and the character can be extended by multiplicativity. In the non-Kummer case, a better way to describe cubic characters is to see them as restriction characters defined over ![]() $\mathbb F_{q^2}[T]$. This description was formulated by Bary-Soroker and Meisner [Reference Bui, Florea, Keating and Roditty-Gershon2], who generalised the work of Baier and Young [Reference Bui and Florea1] from number fields to function fields. We summarise their work here. Let
$\mathbb F_{q^2}[T]$. This description was formulated by Bary-Soroker and Meisner [Reference Bui, Florea, Keating and Roditty-Gershon2], who generalised the work of Baier and Young [Reference Bui and Florea1] from number fields to function fields. We summarise their work here. Let ![]() $\pi $ be a prime in
$\pi $ be a prime in ![]() $\mathbb F_{q^2}[T]$ lying over a prime
$\mathbb F_{q^2}[T]$ lying over a prime ![]() $P\in \mathbb F_q[T]$ of even degree. Then P splits and we can write
$P\in \mathbb F_q[T]$ of even degree. Then P splits and we can write ![]() $P=\pi \tilde {\pi }$, where
$P=\pi \tilde {\pi }$, where ![]() $\tilde {\pi }$ denotes the Galois conjugate of
$\tilde {\pi }$ denotes the Galois conjugate of ![]() $\pi $. Remark that
$\pi $. Remark that ![]() $P \in \mathbb F_q[T]$ splits if and only if
$P \in \mathbb F_q[T]$ splits if and only if ![]() $\deg (P)$ is even. Then the restrictions of
$\deg (P)$ is even. Then the restrictions of ![]() $\chi _\pi $ and
$\chi _\pi $ and ![]() $\chi _{\tilde {\pi }}$ to
$\chi _{\tilde {\pi }}$ to ![]() $\mathbb F_q[T]$ are
$\mathbb F_q[T]$ are ![]() $\chi _P$ and
$\chi _P$ and ![]() $\overline {\chi _P}$ (possibly exchanging the order of characters). Using multiplicativity, it follows that the cubic characters over
$\overline {\chi _P}$ (possibly exchanging the order of characters). Using multiplicativity, it follows that the cubic characters over ![]() $\mathbb F_q[T]$ are given by the characters
$\mathbb F_q[T]$ are given by the characters ![]() $\chi _F$ where
$\chi _F$ where ![]() $F \in \mathbb F_{q^2}[T]$ is square-free and not divisible by any prime
$F \in \mathbb F_{q^2}[T]$ is square-free and not divisible by any prime ![]() $P(T) \in \mathbb F_q[T]$.
$P(T) \in \mathbb F_q[T]$.
Given a primitive cubic Dirichlet character ![]() $\chi $ of conductor
$\chi $ of conductor ![]() $F=P_1\dotsm P_s$, the L-function is defined by
$F=P_1\dotsm P_s$, the L-function is defined by
 $$ \begin{align*} L(s,\chi):=\sum_{f \in \mathcal{M}_q}\frac{\chi(f)}{\lvert f\rvert_q^s}= \sum_{d<\deg(F)} q^{-ds} \sum_{f \in \mathcal{M}_{q,d}} \chi(f), \end{align*} $$
$$ \begin{align*} L(s,\chi):=\sum_{f \in \mathcal{M}_q}\frac{\chi(f)}{\lvert f\rvert_q^s}= \sum_{d<\deg(F)} q^{-ds} \sum_{f \in \mathcal{M}_{q,d}} \chi(f), \end{align*} $$where the second equality follows from the orthogonality relations for ![]() $\chi $. This L-function can be written as a polynomial by making the change of variables
$\chi $. This L-function can be written as a polynomial by making the change of variables ![]() $u=q^{-s}$, namely,
$u=q^{-s}$, namely,
 $$ \begin{align*} \mathcal{L}(u,\chi)= \sum_{d<\deg(F)} u^d \sum_{f \in \mathcal{M}_{q,d}} \chi(f). \end{align*} $$
$$ \begin{align*} \mathcal{L}(u,\chi)= \sum_{d<\deg(F)} u^d \sum_{f \in \mathcal{M}_{q,d}} \chi(f). \end{align*} $$Let C be a curve of genus g over ![]() $\mathbb F_q(T)$ whose function field is a cyclic cubic extension of
$\mathbb F_q(T)$ whose function field is a cyclic cubic extension of ![]() $\mathbb F_q(T)$. From the Weil conjectures, the zeta function of the curve is given by
$\mathbb F_q(T)$. From the Weil conjectures, the zeta function of the curve is given by
 $$ \begin{align*} \mathcal{Z}_C(u)=\frac{\mathcal{P}_C(u)}{(1-u)(1-qu)}. \end{align*} $$
$$ \begin{align*} \mathcal{Z}_C(u)=\frac{\mathcal{P}_C(u)}{(1-u)(1-qu)}. \end{align*} $$In the case under consideration (that is, ![]() $q\equiv 2 \,(\mathrm {mod}\,3)$), we have
$q\equiv 2 \,(\mathrm {mod}\,3)$), we have
 $$ \begin{align} \mathcal{P}_C(u)=\frac{\mathcal{L}(u,\chi)\mathcal{L}\left(u,\overline{\chi}\right)}{(1-u)^2},\end{align} $$
$$ \begin{align} \mathcal{P}_C(u)=\frac{\mathcal{L}(u,\chi)\mathcal{L}\left(u,\overline{\chi}\right)}{(1-u)^2},\end{align} $$where ![]() $\chi $ and
$\chi $ and ![]() $\overline {\chi }$ are the two cubic Dirichlet characters corresponding to the function field of C. Because of the additional factors of
$\overline {\chi }$ are the two cubic Dirichlet characters corresponding to the function field of C. Because of the additional factors of ![]() $(1-u)$ in the denominator of equation (2.4), there are extra sums in the approximate functional equation for
$(1-u)$ in the denominator of equation (2.4), there are extra sums in the approximate functional equation for ![]() $\mathcal {L}(u,\chi )$ in this case (see Proposition 2.1). Furthermore, the Riemann–Hurwitz formula implies that the conductor F of
$\mathcal {L}(u,\chi )$ in this case (see Proposition 2.1). Furthermore, the Riemann–Hurwitz formula implies that the conductor F of ![]() $\chi $ and
$\chi $ and ![]() $\overline {\chi }$ satisfies
$\overline {\chi }$ satisfies ![]() $\deg (F)=g+2.$
$\deg (F)=g+2.$
As in the introduction, let ![]() $\mathcal {C}(g)$ denote the set of primitive cubic Dirichlet characters of genus g over
$\mathcal {C}(g)$ denote the set of primitive cubic Dirichlet characters of genus g over ![]() $\mathbb F_q[T]$. From the foregoing discussion, we have
$\mathbb F_q[T]$. From the foregoing discussion, we have
 $$ \begin{align} \mathcal{C}(g) = \left\{ \chi_F \in {\mathcal{H}}_{q^2, g/2+1} : P \mid F \Rightarrow P \not\in \mathbb F_q[T] \right\}, \end{align} $$
$$ \begin{align} \mathcal{C}(g) = \left\{ \chi_F \in {\mathcal{H}}_{q^2, g/2+1} : P \mid F \Rightarrow P \not\in \mathbb F_q[T] \right\}, \end{align} $$and in particular g is even. In that case, from [Reference David, Florea and Lalin13, Lemma 2.10] we have
 $$ \begin{align*} \# \mathcal{C}(g) =c_3q^{g+2}+O\left(q^{\frac{g}{2}(1+\varepsilon)}\right), \end{align*} $$
$$ \begin{align*} \# \mathcal{C}(g) =c_3q^{g+2}+O\left(q^{\frac{g}{2}(1+\varepsilon)}\right), \end{align*} $$where
 $$ \begin{align*} c_3=\prod_{\substack{R \in \mathbb F_q[T]\\\deg(R) \text{ odd}} }\left(1-\frac{1}{\lvert R\rvert^2}\right)\prod_{\substack{R \in \mathbb F_q[T]\\\deg(R) \text{ even}} }\left(1-\frac{3}{\lvert R\rvert^2}+\frac{2}{\lvert R\rvert^3}\right). \end{align*} $$
$$ \begin{align*} c_3=\prod_{\substack{R \in \mathbb F_q[T]\\\deg(R) \text{ odd}} }\left(1-\frac{1}{\lvert R\rvert^2}\right)\prod_{\substack{R \in \mathbb F_q[T]\\\deg(R) \text{ even}} }\left(1-\frac{3}{\lvert R\rvert^2}+\frac{2}{\lvert R\rvert^3}\right). \end{align*} $$We remark that
 $$ \begin{align} c_3\leq \prod_{\substack{R \in \mathbb F_q[T]} }\left(1-\frac{1}{\lvert R\rvert^2}\right)=\zeta_q(2)^{-1}. \end{align} $$
$$ \begin{align} c_3\leq \prod_{\substack{R \in \mathbb F_q[T]} }\left(1-\frac{1}{\lvert R\rvert^2}\right)=\zeta_q(2)^{-1}. \end{align} $$The following statement [Reference David, Florea and Lalin13, Proposition 2.5] provides the approximate functional equation of the L-function:
Proposition 2.1 Approximate functional equation, [Reference David, Florea and Lalin13, Proposition 2.5]
Let ![]() $q\equiv 2 \,(\mathrm {mod}\,3)$ and let
$q\equiv 2 \,(\mathrm {mod}\,3)$ and let ![]() $\chi $ be a primitive cubic character of modulus F. Let
$\chi $ be a primitive cubic character of modulus F. Let ![]() $X \leq g$. Then
$X \leq g$. Then
 $$ \begin{align*} {\textstyle\mathcal{L}\left( \frac{1}{\sqrt{q}} ,\chi \right)} &=\sum_{f \in \mathcal{M}_{q, \leq X}} \frac{ \chi(f)}{ q^{\deg(f)/2}} + \omega (\chi) \sum_{f \in \mathcal{M}_{q, \leq g-X-1}} \frac{ \overline{\chi}(f)}{q^{\deg(f)/2}} \\ & \quad + \frac{1}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q, X+1}} \frac{ \chi(f)}{q^{\deg(f)/2}} + \frac{\omega(\chi)}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q,g-X}} \frac{ \overline{\chi}(f)}{q^{\deg(f)/2}}, \end{align*} $$
$$ \begin{align*} {\textstyle\mathcal{L}\left( \frac{1}{\sqrt{q}} ,\chi \right)} &=\sum_{f \in \mathcal{M}_{q, \leq X}} \frac{ \chi(f)}{ q^{\deg(f)/2}} + \omega (\chi) \sum_{f \in \mathcal{M}_{q, \leq g-X-1}} \frac{ \overline{\chi}(f)}{q^{\deg(f)/2}} \\ & \quad + \frac{1}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q, X+1}} \frac{ \chi(f)}{q^{\deg(f)/2}} + \frac{\omega(\chi)}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q,g-X}} \frac{ \overline{\chi}(f)}{q^{\deg(f)/2}}, \end{align*} $$where
 $$ \begin{align}\omega(\chi) = -q^{-(\deg(F)-2)/2} \sum_{f \in \mathcal{M}_{\deg(F)-1}} \chi(f) \end{align} $$
$$ \begin{align}\omega(\chi) = -q^{-(\deg(F)-2)/2} \sum_{f \in \mathcal{M}_{\deg(F)-1}} \chi(f) \end{align} $$is the root number and ![]() $g=\deg (F)-2$.
$g=\deg (F)-2$.
Now let ![]() $\chi $ be a primitive cubic character of conductor F defined over
$\chi $ be a primitive cubic character of conductor F defined over ![]() $\mathbb F_q[T]$. Then for
$\mathbb F_q[T]$. Then for ![]() $\operatorname {\mathrm {Re}}(s) \geq 1/2$ and for all
$\operatorname {\mathrm {Re}}(s) \geq 1/2$ and for all ![]() $\varepsilon> 0$, we have the following upper bound:
$\varepsilon> 0$, we have the following upper bound:
For ![]() $\operatorname {\mathrm {Re}}(s) \geq 1$ and for all
$\operatorname {\mathrm {Re}}(s) \geq 1$ and for all ![]() $\varepsilon> 0$, we also have the lower bound
$\varepsilon> 0$, we also have the lower bound
(See [Reference David, Florea and Lalin13, Lemmas 2.6 and 2.7].)
We recall Perron’s formula over ![]() $\mathbb F_q[T]$, which will be used several times in Section 8:
$\mathbb F_q[T]$, which will be used several times in Section 8:
Lemma 2.2 Perron’s formula
If the generating series  $\mathcal {A}(u) =\sum _{f \in \mathcal {M}_q} a(f) u^{\deg (f)}$ is absolutely convergent in
$\mathcal {A}(u) =\sum _{f \in \mathcal {M}_q} a(f) u^{\deg (f)}$ is absolutely convergent in ![]() $\lvert u\rvert \leq r<1$, then
$\lvert u\rvert \leq r<1$, then
 $$ \begin{align*} \sum_{{f} \in \mathcal{M}_{q,n}} a(f)=\frac{1}{2\pi i}\oint_{\lvert u\rvert=r} \frac{\mathcal{A}(u)}{u^n} \frac{du}{u} \end{align*} $$
$$ \begin{align*} \sum_{{f} \in \mathcal{M}_{q,n}} a(f)=\frac{1}{2\pi i}\oint_{\lvert u\rvert=r} \frac{\mathcal{A}(u)}{u^n} \frac{du}{u} \end{align*} $$and
 $$ \begin{align*} \sum_{{f} \in \mathcal{M}_{q,\leq n}} a(f)=\frac{1}{2\pi i}\oint_{\lvert u\rvert=r} \frac{\mathcal{A}(u)}{u^{n}(1-u)} \frac{du}{u}, \end{align*} $$
$$ \begin{align*} \sum_{{f} \in \mathcal{M}_{q,\leq n}} a(f)=\frac{1}{2\pi i}\oint_{\lvert u\rvert=r} \frac{\mathcal{A}(u)}{u^{n}(1-u)} \frac{du}{u}, \end{align*} $$where, in the usual notation, we take ![]() $\oint $ to signify the integral over the circle around the origin oriented counterclockwise.
$\oint $ to signify the integral over the circle around the origin oriented counterclockwise.
Finally, we recall the Weil bound for sums over primes. Let ![]() $\chi $ be a character modulo B, where B is not a cube. Then
$\chi $ be a character modulo B, where B is not a cube. Then
 $$ \begin{align} \left\lvert\sum_{P \in \mathcal{P}_n} \chi(P) \right\rvert \ll q^{n/2} \frac{\deg(B)}{n}, \end{align} $$
$$ \begin{align} \left\lvert\sum_{P \in \mathcal{P}_n} \chi(P) \right\rvert \ll q^{n/2} \frac{\deg(B)}{n}, \end{align} $$where the sum is over monic, irreducible polynomials of degree n.
2.1 Cubic Gauss sums
Let ![]() $q \equiv 1 \,(\mathrm {mod}\,3)$. We now define cubic Gauss sums, and we state the result for the distribution of cubic Gauss sums that we are using in Section 8. Since we will work with
$q \equiv 1 \,(\mathrm {mod}\,3)$. We now define cubic Gauss sums, and we state the result for the distribution of cubic Gauss sums that we are using in Section 8. Since we will work with ![]() $q\equiv 2\,(\mathrm {mod}\,3)$, the general theory presented here will be applied to
$q\equiv 2\,(\mathrm {mod}\,3)$, the general theory presented here will be applied to ![]() $q^2$.
$q^2$.
Let ![]() $\chi $ be a (not necessarily primitive) cubic character of modulus F. The generalised cubic Gauss sum is defined by
$\chi $ be a (not necessarily primitive) cubic character of modulus F. The generalised cubic Gauss sum is defined by
 $$ \begin{align} G_q(V,F) = \sum_{u \,(\mathrm{mod}\,F)} \chi_F(u) e_q\left( \frac{uV}{F} \right ), \end{align} $$
$$ \begin{align} G_q(V,F) = \sum_{u \,(\mathrm{mod}\,F)} \chi_F(u) e_q\left( \frac{uV}{F} \right ), \end{align} $$where
 $$ \begin{align*} e_q(a) = e^{\frac{2 \pi i \operatorname{\mathrm{tr}}_{\mathbb F_q/\mathbb F_p}\left(a_1\right) }{p}} \end{align*} $$
$$ \begin{align*} e_q(a) = e^{\frac{2 \pi i \operatorname{\mathrm{tr}}_{\mathbb F_q/\mathbb F_p}\left(a_1\right) }{p}} \end{align*} $$is the exponential defined by Hayes [Reference Hayes22], for any ![]() $a \in \mathbb {F}_q((1/T))$.
$a \in \mathbb {F}_q((1/T))$.
When ![]() $(A, F)=1$, it is easy to see that
$(A, F)=1$, it is easy to see that
Furthermore, the shifted Gauss sum is almost multiplicative as a function of F. Namely, if ![]() $q \equiv 1 \,(\mathrm {mod}\,6)$, and if
$q \equiv 1 \,(\mathrm {mod}\,6)$, and if ![]() $(F_1 ,F_2)=1$, then
$(F_1 ,F_2)=1$, then
 $$ \begin{align*} G_q(V,F_1 F_2) = \chi_{F_1}(F_2)^2 G_q(V, F_1 )G_q(V, F_2). \end{align*} $$
$$ \begin{align*} G_q(V,F_1 F_2) = \chi_{F_1}(F_2)^2 G_q(V, F_1 )G_q(V, F_2). \end{align*} $$The generating series of the Gauss sums are given by
 $$ \begin{align*} \Psi_q(f,u)= \sum_{F \in \mathcal{M}_q} G_q(f,F)u^{\deg(F)} \end{align*} $$
$$ \begin{align*} \Psi_q(f,u)= \sum_{F \in \mathcal{M}_q} G_q(f,F)u^{\deg(F)} \end{align*} $$and
 $$ \begin{align} \tilde{\Psi}_q(f,u) = \sum_{\substack{F \in \mathcal{M}_q \\ \left(F,f\right)=1}} G_q(f,F) u^{\deg(F)}. \end{align} $$
$$ \begin{align} \tilde{\Psi}_q(f,u) = \sum_{\substack{F \in \mathcal{M}_q \\ \left(F,f\right)=1}} G_q(f,F) u^{\deg(F)}. \end{align} $$The function ![]() $\Psi _q(f,u)$ was studied by Hoffstein [Reference Hoffstein23] and Patterson [Reference Patterson31]. In [Reference David, Florea and Lalin13] we worked with
$\Psi _q(f,u)$ was studied by Hoffstein [Reference Hoffstein23] and Patterson [Reference Patterson31]. In [Reference David, Florea and Lalin13] we worked with  $\tilde {\Psi }_q(f,u)$ and proved the following results:
$\tilde {\Psi }_q(f,u)$ and proved the following results:
Proposition 2.3 [Reference David, Florea and Lalin13, Proposition 3.1 and Lemmas 3.9 and 3.11]
Let  $f=f_1 f_2^2 f_3^3$, where
$f=f_1 f_2^2 f_3^3$, where ![]() $f_1$ and
$f_1$ and ![]() $f_2$ are square-free and coprime, and let
$f_2$ are square-free and coprime, and let ![]() $f_3^*$ be the product of the primes dividing
$f_3^*$ be the product of the primes dividing ![]() $f_3$ but not dividing
$f_3$ but not dividing ![]() $f_1f_2$. Then
$f_1f_2$. Then
 $$ \begin{align*} \sum_{\substack{F \in \mathcal{M}_{q,d}\\ \left(F,f\right)=1}} G_q(f,F) & = \delta_{f_2=1} \frac{ q^{\frac{4d}{3} - \frac{4}{3} \left[d+ \deg\left(f_1\right)\right]_3} }{ \zeta_q(2)\lvert f_1\rvert_q^{2/3}} \overline{G_q(1,f_1)} \rho(1, [d+ \deg(f_1)]_3)\prod_{P\mid f_1 f_3^*} \left ( 1+\frac{1}{\lvert P\rvert_q}\right )^{-1} \\ \nonumber & \quad + O \left ( \delta_{f_2=1} \frac{q^{\frac{d}{3}+\varepsilon d}} {\lvert f_1\rvert_q^{\frac{1}{6}}}\right ) + \frac{1}{2\pi i} \oint_{\lvert u\rvert=q^{-\sigma}} \frac{\tilde{\Psi}_q(f,u)}{u^d}\frac{du}{u}, \end{align*} $$
$$ \begin{align*} \sum_{\substack{F \in \mathcal{M}_{q,d}\\ \left(F,f\right)=1}} G_q(f,F) & = \delta_{f_2=1} \frac{ q^{\frac{4d}{3} - \frac{4}{3} \left[d+ \deg\left(f_1\right)\right]_3} }{ \zeta_q(2)\lvert f_1\rvert_q^{2/3}} \overline{G_q(1,f_1)} \rho(1, [d+ \deg(f_1)]_3)\prod_{P\mid f_1 f_3^*} \left ( 1+\frac{1}{\lvert P\rvert_q}\right )^{-1} \\ \nonumber & \quad + O \left ( \delta_{f_2=1} \frac{q^{\frac{d}{3}+\varepsilon d}} {\lvert f_1\rvert_q^{\frac{1}{6}}}\right ) + \frac{1}{2\pi i} \oint_{\lvert u\rvert=q^{-\sigma}} \frac{\tilde{\Psi}_q(f,u)}{u^d}\frac{du}{u}, \end{align*} $$with ![]() $2/3<\sigma < 4/3$ and where
$2/3<\sigma < 4/3$ and where  $\tilde {\Psi }_q(f,u)$ is given by equation (2.13),
$\tilde {\Psi }_q(f,u)$ is given by equation (2.13), ![]() $[x]_3$ denotes an integer
$[x]_3$ denotes an integer ![]() $a\in \{0,1,2\}$ such that
$a\in \{0,1,2\}$ such that ![]() $x\equiv a\,(\mathrm {mod}\,3)$,
$x\equiv a\,(\mathrm {mod}\,3)$,
 $$ \begin{align*} \rho(1, a)= \begin{cases}1, & a=0,\\ \tau(\chi_3) q, &a=1,\\ 0, &a=2, \end{cases} \end{align*} $$
$$ \begin{align*} \rho(1, a)= \begin{cases}1, & a=0,\\ \tau(\chi_3) q, &a=1,\\ 0, &a=2, \end{cases} \end{align*} $$and
 $$ \begin{align*} \tau(\chi_3) =\sum_{a\in \mathbb F_q^*} \chi_3(a)e^{2\pi i \operatorname{\mathrm{tr}}_{\mathbb F_q/\mathbb F_p}(a)/p}, \qquad \chi_3(a)=\Omega^{-1}\left (a^{\frac{q-1}{3}} \right). \end{align*} $$
$$ \begin{align*} \tau(\chi_3) =\sum_{a\in \mathbb F_q^*} \chi_3(a)e^{2\pi i \operatorname{\mathrm{tr}}_{\mathbb F_q/\mathbb F_p}(a)/p}, \qquad \chi_3(a)=\Omega^{-1}\left (a^{\frac{q-1}{3}} \right). \end{align*} $$Moreover, we have
 $$ \begin{align*}\frac{1}{2\pi i} \oint_{\lvert u\rvert=q^{-\sigma}} \frac{\tilde{\Psi}_q(f,u)}{u^d}\frac{du}{u} \ll q^{\sigma d} \lvert f\rvert_q^{\frac{1}{2} \left( \frac{3}{2} - \sigma\right)} \quad \text{and} \quad \tilde{\Psi}_q(f,u) \ll \lvert f\rvert_q^{{\frac{1}{2}}\left(\frac{3}{2}-\sigma\right)+\varepsilon}.\end{align*} $$
$$ \begin{align*}\frac{1}{2\pi i} \oint_{\lvert u\rvert=q^{-\sigma}} \frac{\tilde{\Psi}_q(f,u)}{u^d}\frac{du}{u} \ll q^{\sigma d} \lvert f\rvert_q^{\frac{1}{2} \left( \frac{3}{2} - \sigma\right)} \quad \text{and} \quad \tilde{\Psi}_q(f,u) \ll \lvert f\rvert_q^{{\frac{1}{2}}\left(\frac{3}{2}-\sigma\right)+\varepsilon}.\end{align*} $$ When ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$, the root number in equation (2.7) can be expressed in terms of cubic Gauss sums over
$q \equiv 2 \,(\mathrm {mod}\,3)$, the root number in equation (2.7) can be expressed in terms of cubic Gauss sums over ![]() $\mathbb F_{q^2}[T]$, as proven in [Reference David, Florea and Lalin13, Section 4.4]. Let
$\mathbb F_{q^2}[T]$, as proven in [Reference David, Florea and Lalin13, Section 4.4]. Let ![]() $\chi $ be a primitive character of conductor
$\chi $ be a primitive character of conductor ![]() $F \in \mathbb F_q[T]$. Then F is square-free and divisible only by primes
$F \in \mathbb F_q[T]$. Then F is square-free and divisible only by primes ![]() $P(T)$ of even degree and
$P(T)$ of even degree and
 $$ \begin{align} \omega(\chi)=q^{-\frac{g}{2}-1}G_{q^2}(1,F), \end{align} $$
$$ \begin{align} \omega(\chi)=q^{-\frac{g}{2}-1}G_{q^2}(1,F), \end{align} $$where
 $$ \begin{align} G_{q^2}(1,F)=q^{\deg(F)} \end{align} $$
$$ \begin{align} G_{q^2}(1,F)=q^{\deg(F)} \end{align} $$for ![]() $F\in \mathbb F_q[T]$ square-free (see [Reference David, Florea and Lalin13, Lemma 4.4]).
$F\in \mathbb F_q[T]$ square-free (see [Reference David, Florea and Lalin13, Lemma 4.4]).
3 Setting and proof of Theorem 1.6
3.1 Setting
Following the work of Soundararajan on upper bounds for the Riemann zeta function [Reference Soundararajan36], we first show that we can bound  $\log \left \lvert {\textstyle L\left (\frac {1}{2},\chi \right ) }\right \rvert $ by a short Dirichlet polynomial. The following statement is analogous to [Reference Baier and Young4, Proposition 4.3]:
$\log \left \lvert {\textstyle L\left (\frac {1}{2},\chi \right ) }\right \rvert $ by a short Dirichlet polynomial. The following statement is analogous to [Reference Baier and Young4, Proposition 4.3]:
Lemma 3.1. Let ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$ and let
$q \equiv 2 \,(\mathrm {mod}\,3)$ and let ![]() $\chi $ be a cubic Dirichlet character of genus g over
$\chi $ be a cubic Dirichlet character of genus g over ![]() $\mathbb F_q[T]$. Then for
$\mathbb F_q[T]$. Then for ![]() $N\leq g+2$ we have
$N\leq g+2$ we have
 $$ \begin{align*} \log \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert & \leq \Re \left( \sum_{\deg(f) \leq N} \frac{ \Lambda(f) \chi(f)(N-\deg(f))}{N \lvert f\rvert^{\frac{1}{2}+\frac{1}{N\log q}} \deg(f)} \right)+ \frac{g+2}{N} \nonumber \\ &= \sum_{\deg(f) \leq N} \frac{ \Lambda(f) \left( \chi(f)+ \overline{\chi(f)}\right)(N-\deg(f))}{2 N \lvert f\rvert^{\frac{1}{2}+\frac{1}{N\log q}} \deg(f)} + \frac{g+2}{N}. \end{align*} $$
$$ \begin{align*} \log \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert & \leq \Re \left( \sum_{\deg(f) \leq N} \frac{ \Lambda(f) \chi(f)(N-\deg(f))}{N \lvert f\rvert^{\frac{1}{2}+\frac{1}{N\log q}} \deg(f)} \right)+ \frac{g+2}{N} \nonumber \\ &= \sum_{\deg(f) \leq N} \frac{ \Lambda(f) \left( \chi(f)+ \overline{\chi(f)}\right)(N-\deg(f))}{2 N \lvert f\rvert^{\frac{1}{2}+\frac{1}{N\log q}} \deg(f)} + \frac{g+2}{N}. \end{align*} $$Proof. The proof follows that of [Reference Baier and Young4, Proposition 4.3], by setting ![]() $z=0$,
$z=0$, ![]() $N=h$ and using the fact that
$N=h$ and using the fact that ![]() $m=g+2$.
$m=g+2$.
Since ![]() $\Lambda (f)=0$ unless f is a prime power and
$\Lambda (f)=0$ unless f is a prime power and ![]() $\Lambda \left (P^j\right )=\deg (P)$, we have
$\Lambda \left (P^j\right )=\deg (P)$, we have
 $$ \begin{align*} \log \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert &\leq \frac{1}{2} \sum_{\deg(P) \leq N} \frac{\left( \chi(P) + \overline{\chi}(P)\right)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2}+\frac{1}{N \log q}}} + \frac{g+2}{N}\\ & \quad + \frac{1}{4} \sum_{\deg(P) \leq N/2} \frac{\left( \chi(P) + \overline{\chi}(P)\right)(N-2\deg(P))}{N\lvert P\rvert ^{1+\frac{2}{N \log q}}}\\ & \quad +\sum_{l \geq 3} \frac{1}{2l}\sum_{\deg(P) \leq N/l} \frac{ \left(\chi(P)^l + \overline{\chi}(P)^l\right)(N-l \deg(P))}{N\lvert P\rvert^{\frac{l}{2}+\frac{l}{N \log q}}}. \end{align*} $$
$$ \begin{align*} \log \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert &\leq \frac{1}{2} \sum_{\deg(P) \leq N} \frac{\left( \chi(P) + \overline{\chi}(P)\right)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2}+\frac{1}{N \log q}}} + \frac{g+2}{N}\\ & \quad + \frac{1}{4} \sum_{\deg(P) \leq N/2} \frac{\left( \chi(P) + \overline{\chi}(P)\right)(N-2\deg(P))}{N\lvert P\rvert ^{1+\frac{2}{N \log q}}}\\ & \quad +\sum_{l \geq 3} \frac{1}{2l}\sum_{\deg(P) \leq N/l} \frac{ \left(\chi(P)^l + \overline{\chi}(P)^l\right)(N-l \deg(P))}{N\lvert P\rvert^{\frac{l}{2}+\frac{l}{N \log q}}}. \end{align*} $$It is easy to see that the powers of primes with ![]() $l \geq 3$ contribute
$l \geq 3$ contribute ![]() $O(1)$ to this expression. More precisely, using the Prime Polynomial Theorem (2.1), we have
$O(1)$ to this expression. More precisely, using the Prime Polynomial Theorem (2.1), we have
 $$ \begin{align*} & \sum_{l \geq 3} \sum_{\deg(P) \leq N/l} \frac{ \left(\chi(P)^l + \overline{\chi}(P)^l\right)(N-l \deg(P))}{2lN\lvert P\rvert^{\frac{l}{2}+\frac{l}{N \log q}}} \leq \sum_{l=3}^N \sum_{j \leq N/l} \frac{q^j(N-lj)}{lj Nq^{lj\left(\frac{1}{2}+\frac{1}{N\log q}\right)}}\\ & \quad \leq \frac{1}{N} \sum_{h=3}^N \frac{N-h}{hq^{h\left(\frac{1}{2}+\frac{1}{N\log q}\right)}} \sum_{\substack{j\mid h \\ j \leq h/3}} q^j \leq \frac{1}{N} \sum_{h=3}^{N} \frac{N-h}{hq^{h\left(\frac{1}{2}+\frac{1}{N \log q}\right)}} q^{h/3} \tau(h) \leq 2 \sum_{h=3}^{N} \frac{1}{q^{h\left(\frac{1}{6}+\frac{1}{N\log q}\right)} \sqrt{h}} \\ & \quad \leq 2 \sum_{h=3}^{\infty} \frac{1}{5^{\frac{h}{6}} \sqrt{h}}=:\eta=1.676972\dotsc. \end{align*} $$
$$ \begin{align*} & \sum_{l \geq 3} \sum_{\deg(P) \leq N/l} \frac{ \left(\chi(P)^l + \overline{\chi}(P)^l\right)(N-l \deg(P))}{2lN\lvert P\rvert^{\frac{l}{2}+\frac{l}{N \log q}}} \leq \sum_{l=3}^N \sum_{j \leq N/l} \frac{q^j(N-lj)}{lj Nq^{lj\left(\frac{1}{2}+\frac{1}{N\log q}\right)}}\\ & \quad \leq \frac{1}{N} \sum_{h=3}^N \frac{N-h}{hq^{h\left(\frac{1}{2}+\frac{1}{N\log q}\right)}} \sum_{\substack{j\mid h \\ j \leq h/3}} q^j \leq \frac{1}{N} \sum_{h=3}^{N} \frac{N-h}{hq^{h\left(\frac{1}{2}+\frac{1}{N \log q}\right)}} q^{h/3} \tau(h) \leq 2 \sum_{h=3}^{N} \frac{1}{q^{h\left(\frac{1}{6}+\frac{1}{N\log q}\right)} \sqrt{h}} \\ & \quad \leq 2 \sum_{h=3}^{\infty} \frac{1}{5^{\frac{h}{6}} \sqrt{h}}=:\eta=1.676972\dotsc. \end{align*} $$ Then, for any ![]() $k> 0$,
$k> 0$,
 $$ \begin{align} \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert^k &\leq \exp \left\{ k \Re \left( \sum_{\deg(P) \leq N} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2}+\frac{1}{N \log q}}} \right) + \frac{k (g+2)}{N}+ k \eta \right. \nonumber\\ & \quad + \left. k \Re \left( \sum_{\deg(P) \leq N/2} \frac{\chi(P) (N-2\deg(P))}{2N\lvert P\rvert^{1+\frac{2}{N \log q }}} \right) \right\}. \end{align} $$
$$ \begin{align} \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert^k &\leq \exp \left\{ k \Re \left( \sum_{\deg(P) \leq N} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2}+\frac{1}{N \log q}}} \right) + \frac{k (g+2)}{N}+ k \eta \right. \nonumber\\ & \quad + \left. k \Re \left( \sum_{\deg(P) \leq N/2} \frac{\chi(P) (N-2\deg(P))}{2N\lvert P\rvert^{1+\frac{2}{N \log q }}} \right) \right\}. \end{align} $$ Similarly as in [Reference Lester and Radziwiłł27], we separate the sum over primes in ![]() $J+1$ sums over the intervals
$J+1$ sums over the intervals
where for ![]() $0 \leq j \leq J$, we define
$0 \leq j \leq J$, we define
 $$ \begin{align*} \theta_j = \frac{e^j}{(\log g)^{1000}}, \qquad \ell_j = 2\left[ \theta_j^{-b}\right], \end{align*} $$
$$ \begin{align*} \theta_j = \frac{e^j}{(\log g)^{1000}}, \qquad \ell_j = 2\left[ \theta_j^{-b}\right], \end{align*} $$for some ![]() $0<b<1$. In view of equation (2.5), it is natural to use
$0<b<1$. In view of equation (2.5), it is natural to use ![]() $g+2$ instead of g in the definition of the intervals
$g+2$ instead of g in the definition of the intervals ![]() $I_j$.
$I_j$.
We will choose J such that ![]() $\theta _J$ is a small positive constant. We discuss in Section 7 explicit upper bounds and how to choose
$\theta _J$ is a small positive constant. We discuss in Section 7 explicit upper bounds and how to choose ![]() $\theta _J$. We remark that for a given choice of
$\theta _J$. We remark that for a given choice of ![]() $\theta _J$, we have
$\theta _J$, we have  $J = \left [ \log (\log g)^{{1000}} + \log {\theta _J}\right ]$. The power of 1000, together with the parameters chosen in Section 7, guarantees that J is positive for any
$J = \left [ \log (\log g)^{{1000}} + \log {\theta _J}\right ]$. The power of 1000, together with the parameters chosen in Section 7, guarantees that J is positive for any ![]() $g\geq 3$.
$g\geq 3$.
For each interval ![]() $I_j$, we define
$I_j$, we define
 $$ \begin{align*} P_{I_j} (\chi;u) = \sum_{P \in I_j} \frac{ a(P;u) \chi(P)}{\sqrt{\lvert P\rvert}}, \end{align*} $$
$$ \begin{align*} P_{I_j} (\chi;u) = \sum_{P \in I_j} \frac{ a(P;u) \chi(P)}{\sqrt{\lvert P\rvert}}, \end{align*} $$where
 $$ \begin{align*} a(P; u) = \frac{1}{\lvert P\rvert^{\frac{1}{(g+2) \theta_u \log q}}} \left( 1 - \frac{\deg{P}}{(g+2) \theta_u} \right), \end{align*} $$
$$ \begin{align*} a(P; u) = \frac{1}{\lvert P\rvert^{\frac{1}{(g+2) \theta_u \log q}}} \left( 1 - \frac{\deg{P}}{(g+2) \theta_u} \right), \end{align*} $$for ![]() $0\leq u\leq J$, and we extend this to a completely multiplicative function in the first variable. By
$0\leq u\leq J$, and we extend this to a completely multiplicative function in the first variable. By ![]() $P \in I_j$, we always mean that
$P \in I_j$, we always mean that ![]() $\deg {P} \in I_j$.
$\deg {P} \in I_j$.
In order to use Lemma 3.1 we need bounds for  $\exp \left ( \Re P_{I_j}(\chi; u) \right )$ on each interval
$\exp \left ( \Re P_{I_j}(\chi; u) \right )$ on each interval ![]() $I_j$. Set
$I_j$. Set ![]() $t \in \mathbb R$ and let
$t \in \mathbb R$ and let ![]() $\ell $ be a positive even integer. Let
$\ell $ be a positive even integer. Let
 $$ \begin{align} E_{\ell}(t) = \sum_{s \leq \ell} \frac{t^s}{s!}. \end{align} $$
$$ \begin{align} E_{\ell}(t) = \sum_{s \leq \ell} \frac{t^s}{s!}. \end{align} $$Note that ![]() $E_\ell (t) \geq 1$ if
$E_\ell (t) \geq 1$ if ![]() $t \geq 0$ and that
$t \geq 0$ and that ![]() $E_\ell (t)> 0$, since
$E_\ell (t)> 0$, since ![]() $\ell $ is even. We also have that for
$\ell $ is even. We also have that for ![]() $t \leq \ell /e^2$,
$t \leq \ell /e^2$,
 $$ \begin{align} e^t \leq \left(1+e^{-\ell/2}\right) E_{\ell}(t). \end{align} $$
$$ \begin{align} e^t \leq \left(1+e^{-\ell/2}\right) E_{\ell}(t). \end{align} $$ Let ![]() $\nu (f)$ be the multiplicative function defined by
$\nu (f)$ be the multiplicative function defined by  $\nu (P^a) = \frac {1}{a!},$ and let
$\nu (P^a) = \frac {1}{a!},$ and let ![]() $\nu _j(f)= ( \nu * \dotsb * \nu )(f)$ be the j-fold convolution of
$\nu _j(f)= ( \nu * \dotsb * \nu )(f)$ be the j-fold convolution of ![]() $\nu $. We then have
$\nu $. We then have  $\nu _j(P^a) = \frac {j^a}{a!}$.
$\nu _j(P^a) = \frac {j^a}{a!}$.
The following lemma gives a formula for the powers  $\left ( \Re P_{I_j}(\chi; u) \right )^s$, and will be used frequently in the paper:
$\left ( \Re P_{I_j}(\chi; u) \right )^s$, and will be used frequently in the paper:
Lemma 3.2. Let ![]() $a(f)$ be a completely multiplicative function from
$a(f)$ be a completely multiplicative function from ![]() $\mathbb F_q[T]$ to
$\mathbb F_q[T]$ to ![]() $\mathbb C$, and let I be some interval. Define
$\mathbb C$, and let I be some interval. Define ![]() $P_I := \sum _{P \in I} a(P)$. Then for any integer s, we have
$P_I := \sum _{P \in I} a(P)$. Then for any integer s, we have
 $$ \begin{align*} P_I^s &= s! \sum_{\substack{P\mid f \Rightarrow P \in I \\ \Omega(f)=s}} a(f) \nu(f) ,\\ \left( \Re P_I \right)^s &= \frac{ s!}{2^s} \sum_{\substack{P\mid f h \Rightarrow P \in I \\ \Omega(f h )=s}} a(f) \overline{a(h)} \nu(f) \nu(h). \end{align*} $$
$$ \begin{align*} P_I^s &= s! \sum_{\substack{P\mid f \Rightarrow P \in I \\ \Omega(f)=s}} a(f) \nu(f) ,\\ \left( \Re P_I \right)^s &= \frac{ s!}{2^s} \sum_{\substack{P\mid f h \Rightarrow P \in I \\ \Omega(f h )=s}} a(f) \overline{a(h)} \nu(f) \nu(h). \end{align*} $$Proof. We have
 $$ \begin{align*} P_I^s=\sum_{\substack{P\mid f \Rightarrow P \in I\\ \Omega(f)=s}} a(f) \sum_{P_1 \dotsm P_s = f}1. \end{align*} $$
$$ \begin{align*} P_I^s=\sum_{\substack{P\mid f \Rightarrow P \in I\\ \Omega(f)=s}} a(f) \sum_{P_1 \dotsm P_s = f}1. \end{align*} $$Note that if ![]() $f= Q_1^{\alpha _1} \dotsm Q_r^{\alpha _r}$, then
$f= Q_1^{\alpha _1} \dotsm Q_r^{\alpha _r}$, then ![]() $s= \alpha _1+\dotsb +\alpha _r$, and
$s= \alpha _1+\dotsb +\alpha _r$, and
 $$ \begin{align*} \sum_{P_1 \dotsm P_s = f}1 = {s\choose \alpha_1} {s-\alpha_1 \choose \alpha_2} \dotsm {s-\alpha_1-\dotsb-\alpha_{r-1} \choose \alpha_r}= \frac{s!}{\alpha_1! \dotsm \alpha_r!} = s! \nu(f), \end{align*} $$
$$ \begin{align*} \sum_{P_1 \dotsm P_s = f}1 = {s\choose \alpha_1} {s-\alpha_1 \choose \alpha_2} \dotsm {s-\alpha_1-\dotsb-\alpha_{r-1} \choose \alpha_r}= \frac{s!}{\alpha_1! \dotsm \alpha_r!} = s! \nu(f), \end{align*} $$so
 $$ \begin{align*} P_I^s = s! \sum_{\substack{P\mid f \Rightarrow P \in I \\ \Omega(f)=s}} a(f) \nu(f). \end{align*} $$
$$ \begin{align*} P_I^s = s! \sum_{\substack{P\mid f \Rightarrow P \in I \\ \Omega(f)=s}} a(f) \nu(f). \end{align*} $$We also have
 $$ \begin{align*} \left( \Re P_{I}\right)^s &= \frac{1}{2^s} \sum_{r=0}^s {s \choose r} \sum_{\substack{P\mid f h \Rightarrow P \in I_j \\ \Omega(f)=r \\ \Omega(h)=s-r}} a(f) \overline{a(h)} \sum_{f = P_1 \dotsm P_r} 1 \sum_{h= P_1 \dotsm P_{s-r}} 1 \nonumber \\ &= \frac{1}{2^s} \sum_{r=0}^s {s \choose r} \sum_{\substack{P\mid f h \Rightarrow P \in I_j \\ \Omega(f)=r \\ \Omega(h)=s-r}} a(f) \overline{a(h)} r! \nu(f) (s-r)! \nu(h) \nonumber \\ &= \frac{ s!}{2^s} \sum_{\substack{P\mid f h \Rightarrow P \in I_j \\ \Omega(f h )=s}} a(f) \overline{a(h)} \nu(f) \nu(h).\\[-58pt] \end{align*} $$
$$ \begin{align*} \left( \Re P_{I}\right)^s &= \frac{1}{2^s} \sum_{r=0}^s {s \choose r} \sum_{\substack{P\mid f h \Rightarrow P \in I_j \\ \Omega(f)=r \\ \Omega(h)=s-r}} a(f) \overline{a(h)} \sum_{f = P_1 \dotsm P_r} 1 \sum_{h= P_1 \dotsm P_{s-r}} 1 \nonumber \\ &= \frac{1}{2^s} \sum_{r=0}^s {s \choose r} \sum_{\substack{P\mid f h \Rightarrow P \in I_j \\ \Omega(f)=r \\ \Omega(h)=s-r}} a(f) \overline{a(h)} r! \nu(f) (s-r)! \nu(h) \nonumber \\ &= \frac{ s!}{2^s} \sum_{\substack{P\mid f h \Rightarrow P \in I_j \\ \Omega(f h )=s}} a(f) \overline{a(h)} \nu(f) \nu(h).\\[-58pt] \end{align*} $$ For ![]() $j \leq J$, and for any real number
$j \leq J$, and for any real number ![]() $k \neq 0$, let
$k \neq 0$, let
 $$ \begin{align} D_{j, k} (\chi) = \prod_{r=0}^j \left(1+e^{-\ell_r/2}\right)E_{\ell_r}\left( k \Re P_{I_r}(\chi;j)\right). \end{align} $$
$$ \begin{align} D_{j, k} (\chi) = \prod_{r=0}^j \left(1+e^{-\ell_r/2}\right)E_{\ell_r}\left( k \Re P_{I_r}(\chi;j)\right). \end{align} $$We remark that the weights are ![]() $a(\cdot; j)$ for all intervals
$a(\cdot; j)$ for all intervals ![]() $I_0, \dotsc , I_j$ in the formula for
$I_0, \dotsc , I_j$ in the formula for ![]() $D_{j, k} (\chi )$. Note that we have
$D_{j, k} (\chi )$. Note that we have
 $$ \begin{align} E_{\ell_r}\left( k \Re P_{I_r}(\chi;j)\right)&= \sum_{s \leq \ell_r} \frac{ \left(k \Re P_{I_r}(\chi;j)\right)^s}{s!}\nonumber \\ &= \sum_{\substack{P\mid fh \Rightarrow P \in I_r \\ \Omega(f h)\leq \ell_r}} \frac{(k/2)^{\Omega(f h)} a(f; j)a(h;j) \chi(f) \overline{\chi}(h) \nu(f) \nu(h)}{\sqrt{\lvert f h \rvert}}, \end{align} $$
$$ \begin{align} E_{\ell_r}\left( k \Re P_{I_r}(\chi;j)\right)&= \sum_{s \leq \ell_r} \frac{ \left(k \Re P_{I_r}(\chi;j)\right)^s}{s!}\nonumber \\ &= \sum_{\substack{P\mid fh \Rightarrow P \in I_r \\ \Omega(f h)\leq \ell_r}} \frac{(k/2)^{\Omega(f h)} a(f; j)a(h;j) \chi(f) \overline{\chi}(h) \nu(f) \nu(h)}{\sqrt{\lvert f h \rvert}}, \end{align} $$where we have used Lemma 3.2.
We also define the following term, which corresponds to the sum over the square of primes in formula (3.1):
 $$ \begin{align} S_{j,k}(\chi)=\exp \left(k \Re\left( \sum_{\deg(P) \leq (g+2) \theta_j/2} \frac{ \chi(P)b(P;j)}{\lvert P\rvert}\right)\right), \end{align} $$
$$ \begin{align} S_{j,k}(\chi)=\exp \left(k \Re\left( \sum_{\deg(P) \leq (g+2) \theta_j/2} \frac{ \chi(P)b(P;j)}{\lvert P\rvert}\right)\right), \end{align} $$where
 $$ \begin{align} b(P;j)=\frac{1}{2\lvert P\rvert^{\frac{2}{(g+2)\theta_j\log q}}}\left(1-\frac{2\deg P}{(g+2) \theta_j}\right). \end{align} $$
$$ \begin{align} b(P;j)=\frac{1}{2\lvert P\rvert^{\frac{2}{(g+2)\theta_j\log q}}}\left(1-\frac{2\deg P}{(g+2) \theta_j}\right). \end{align} $$Proposition 3.3. Let k be positive. For each ![]() $\chi $ a primitive cubic character of genus g, we have either
$\chi $ a primitive cubic character of genus g, we have either
 $$ \begin{align*} \max_{0\leq u \leq J} \left\lvert\Re P_{I_0}(\chi;u)\right\rvert> \frac{\ell_0}{k e^2} \end{align*} $$
$$ \begin{align*} \max_{0\leq u \leq J} \left\lvert\Re P_{I_0}(\chi;u)\right\rvert> \frac{\ell_0}{k e^2} \end{align*} $$or
 $$ \begin{align*} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^k & \leq \exp(k(1/\theta_J+\eta)) D_{J,k}(\chi) S_{J,k}(\chi)\\ & \quad +\sum_{\substack{0\leq j \leq J-1 \\ j<u\leq J}} \exp\left(k \left(1/\theta_j+\eta\right)\right) D_{j,k}(\chi) S_{j,k}(\chi)\left(\frac{e^2 k \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}}, \end{align*} $$
$$ \begin{align*} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^k & \leq \exp(k(1/\theta_J+\eta)) D_{J,k}(\chi) S_{J,k}(\chi)\\ & \quad +\sum_{\substack{0\leq j \leq J-1 \\ j<u\leq J}} \exp\left(k \left(1/\theta_j+\eta\right)\right) D_{j,k}(\chi) S_{j,k}(\chi)\left(\frac{e^2 k \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}}, \end{align*} $$for any ![]() $s_j$ even integers and
$s_j$ even integers and ![]() $\eta =1.676972\dotsc $.
$\eta =1.676972\dotsc $.
Proof. For ![]() $r = 0, 1, \ldots , J$, let
$r = 0, 1, \ldots , J$, let
 $$ \begin{align} \mathcal{T}_r = \left\{ \chi \text{ primitive cubic, genus}(\chi)=g : \max_{r \leq u \leq J} \left\lvert \Re P_{I_r}(\chi;u)\right\rvert \leq \frac{\ell_r}{k e^2} \right\}. \end{align} $$
$$ \begin{align} \mathcal{T}_r = \left\{ \chi \text{ primitive cubic, genus}(\chi)=g : \max_{r \leq u \leq J} \left\lvert \Re P_{I_r}(\chi;u)\right\rvert \leq \frac{\ell_r}{k e^2} \right\}. \end{align} $$ For each ![]() $\chi $ we have one of the following:
$\chi $ we have one of the following:
1.
 $ \chi \notin \mathcal {T}_0$.
$ \chi \notin \mathcal {T}_0$.2.
 $\chi \in \mathcal {T}_r$ for each
$\chi \in \mathcal {T}_r$ for each  $r \leq J$.
$r \leq J$.3. There exists a
 $j <J$ such that
$j <J$ such that  $\chi \in \mathcal {T}_r$ for
$\chi \in \mathcal {T}_r$ for  $r \leq j$ and
$r \leq j$ and  $\chi \notin \mathcal {T}_{j+1}$.
$\chi \notin \mathcal {T}_{j+1}$.
If the first condition is satisfied, then we are done. If not, assume that condition (2) is satisfied. Then in formula (3.1) we take ![]() $N= (g+2) \theta _J$, and we get
$N= (g+2) \theta _J$, and we get
 $$ \begin{align*} \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} & \leq \exp(k(1/\theta_J+\eta)) \prod_{j=0}^J \exp \left( k \Re P_{I_j}(\chi;J)\right) S_{J,k}(\chi)\\ & \leq \exp(k(1/\theta_J+\eta)) D_{J,k}(\chi) S_{J,k}(\chi). \end{align*} $$
$$ \begin{align*} \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} & \leq \exp(k(1/\theta_J+\eta)) \prod_{j=0}^J \exp \left( k \Re P_{I_j}(\chi;J)\right) S_{J,k}(\chi)\\ & \leq \exp(k(1/\theta_J+\eta)) D_{J,k}(\chi) S_{J,k}(\chi). \end{align*} $$ Now assume that condition (3) holds. Then there exist ![]() $j = j(\chi )$ and
$j = j(\chi )$ and ![]() $u=u(\chi )> j=j(\chi )$ such that
$u=u(\chi )> j=j(\chi )$ such that  $\left \lvert \Re P_{I_{j+1}} (\chi ;u)\right \rvert> \ell _{j+1}/\left (k e^2\right )$. We then have
$\left \lvert \Re P_{I_{j+1}} (\chi ;u)\right \rvert> \ell _{j+1}/\left (k e^2\right )$. We then have
 $$ \begin{align*} 1 \leq \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}}\right)^{s_{j+1}}, \end{align*} $$
$$ \begin{align*} 1 \leq \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}}\right)^{s_{j+1}}, \end{align*} $$for any even integer ![]() $s_{j+1}$, and taking
$s_{j+1}$, and taking ![]() $N= (g+2) \theta _j$ in formula (3.1) we get
$N= (g+2) \theta _j$ in formula (3.1) we get
 $$ \begin{align*} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} &\leq \exp\left(k \left(1/\theta_j+\eta\right)\right) D_{j,k}(\chi) S_{j,k}(\chi) \left(\frac{e^2 k \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}}. \end{align*} $$
$$ \begin{align*} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} &\leq \exp\left(k \left(1/\theta_j+\eta\right)\right) D_{j,k}(\chi) S_{j,k}(\chi) \left(\frac{e^2 k \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}}. \end{align*} $$Then, if (3) holds, we have
 $$ \begin{align} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^k \leq \sum_{\substack{0\leq j \leq J-1 \\ j<u\leq J}} \exp\left(k\left(1/\theta_j+\eta\right)\right) D_{j,k}(\chi) S_{j,k}(\chi)\left(\frac{e^2 k \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}}, \end{align} $$
$$ \begin{align} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^k \leq \sum_{\substack{0\leq j \leq J-1 \\ j<u\leq J}} \exp\left(k\left(1/\theta_j+\eta\right)\right) D_{j,k}(\chi) S_{j,k}(\chi)\left(\frac{e^2 k \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}}, \end{align} $$where in the bound of the right-hand side, j and u are independent of ![]() $\chi $.
$\chi $.
Remark 3.4. In this proof, we could have written  $\max _{\substack {0\leq j \leq J-1 \\ j<u\leq J}}$ instead of
$\max _{\substack {0\leq j \leq J-1 \\ j<u\leq J}}$ instead of  $\sum _{\substack {0\leq j \leq J-1 \\ j<u\leq J}}$ in the bound (3.10). However, this maximum depends on
$\sum _{\substack {0\leq j \leq J-1 \\ j<u\leq J}}$ in the bound (3.10). However, this maximum depends on ![]() $\chi $, and in future applications of Proposition 3.3 we will need the right-hand side to be independent of
$\chi $, and in future applications of Proposition 3.3 we will need the right-hand side to be independent of ![]() $\chi $ so that we can exchange the bound with a sum over all the possible
$\chi $ so that we can exchange the bound with a sum over all the possible ![]() $\chi $.
$\chi $.
3.2 The mollifier
Let ![]() $\kappa $ be a positive real number, and define
$\kappa $ be a positive real number, and define
 $$ \begin{align*} {\textstyle M_j\left(\chi;\frac{1}{\kappa}\right) }:={\textstyle E_{\ell_j}\left(-\frac{1}{\kappa}P_{I_j}(\chi;J)\right)}= \sum_{\substack{P \mid f \Rightarrow P \in I_j \\ \Omega(f) \leq \ell_j}} \frac{a(f;J) \chi(f) \lambda(f)\nu(f)}{\kappa^{\Omega(f)}\sqrt{\lvert f\rvert}}, \end{align*} $$
$$ \begin{align*} {\textstyle M_j\left(\chi;\frac{1}{\kappa}\right) }:={\textstyle E_{\ell_j}\left(-\frac{1}{\kappa}P_{I_j}(\chi;J)\right)}= \sum_{\substack{P \mid f \Rightarrow P \in I_j \\ \Omega(f) \leq \ell_j}} \frac{a(f;J) \chi(f) \lambda(f)\nu(f)}{\kappa^{\Omega(f)}\sqrt{\lvert f\rvert}}, \end{align*} $$where ![]() $\lambda (f)$ is the Liouville function. We also define
$\lambda (f)$ is the Liouville function. We also define
 $$ \begin{align*} {\textstyle M\left(\chi;\frac{1}{\kappa}\right)} = \prod_{j=0}^J {\textstyle M_j\left(\chi;\frac{1}{\kappa}\right) }. \end{align*} $$
$$ \begin{align*} {\textstyle M\left(\chi;\frac{1}{\kappa}\right)} = \prod_{j=0}^J {\textstyle M_j\left(\chi;\frac{1}{\kappa}\right) }. \end{align*} $$We have, for any positive integer n,
 $$ \begin{align*} {\textstyle M_j\left(\chi;\frac{1}{\kappa}\right) }^{n} = \sum_{\substack{P \mid f \Rightarrow P \in I_j \\ \Omega(f) \leq n \ell_j}} \frac{a(f;J) \chi(f) \lambda(f)}{\kappa^{\Omega(f)}\sqrt{\lvert f\rvert}} \nu_{n}\left(f;\ell_j\right), \end{align*} $$
$$ \begin{align*} {\textstyle M_j\left(\chi;\frac{1}{\kappa}\right) }^{n} = \sum_{\substack{P \mid f \Rightarrow P \in I_j \\ \Omega(f) \leq n \ell_j}} \frac{a(f;J) \chi(f) \lambda(f)}{\kappa^{\Omega(f)}\sqrt{\lvert f\rvert}} \nu_{n}\left(f;\ell_j\right), \end{align*} $$where
 $$ \begin{align*} \nu_{n}\left(f;\ell_j\right) = \sum_{\substack{f= f_1 \cdot \dotsm \cdot f_{n} \\ \Omega(f_1) \leq \ell_j,\dotsc, \Omega(f_{n}) \leq \ell_j}} \nu(f_1) \dotsm \nu(f_{n}). \end{align*} $$
$$ \begin{align*} \nu_{n}\left(f;\ell_j\right) = \sum_{\substack{f= f_1 \cdot \dotsm \cdot f_{n} \\ \Omega(f_1) \leq \ell_j,\dotsc, \Omega(f_{n}) \leq \ell_j}} \nu(f_1) \dotsm \nu(f_{n}). \end{align*} $$Then, taking ![]() $\kappa $ such that
$\kappa $ such that ![]() $k \kappa $ is an even integer,
$k \kappa $ is an even integer,
 $$ \begin{align} & {\textstyle \left\lvert M_j\left(\chi;\frac{1}{\kappa}\right)\right\rvert }^{k \kappa} \nonumber \\ &\quad = \sum_{\substack{P \mid f_j h_j \Rightarrow P \in I_j \\ \Omega\left(f_j\right) \leq \frac{k \kappa}{2} \ell_j, \Omega\left(h_j\right) \leq \frac{k \kappa }{2} \ell_j}} \frac{ a\left(f_j;J\right) a\left(h_j;J\right) \chi\left(f_j\right) \overline{\chi}\left(h_j\right) \lambda\left(f_j\right) \lambda\left(h_j\right)}{{\kappa^{\Omega\left(f_j h_j\right)} }\sqrt{\left\lvert f_jh_j\right\rvert}} \nu_{k \kappa /2}\left(f_j; \ell_j\right) \nu_{k \kappa /2}\left(h_j;\ell_j\right). \end{align} $$
$$ \begin{align} & {\textstyle \left\lvert M_j\left(\chi;\frac{1}{\kappa}\right)\right\rvert }^{k \kappa} \nonumber \\ &\quad = \sum_{\substack{P \mid f_j h_j \Rightarrow P \in I_j \\ \Omega\left(f_j\right) \leq \frac{k \kappa}{2} \ell_j, \Omega\left(h_j\right) \leq \frac{k \kappa }{2} \ell_j}} \frac{ a\left(f_j;J\right) a\left(h_j;J\right) \chi\left(f_j\right) \overline{\chi}\left(h_j\right) \lambda\left(f_j\right) \lambda\left(h_j\right)}{{\kappa^{\Omega\left(f_j h_j\right)} }\sqrt{\left\lvert f_jh_j\right\rvert}} \nu_{k \kappa /2}\left(f_j; \ell_j\right) \nu_{k \kappa /2}\left(h_j;\ell_j\right). \end{align} $$We remark that the mollifier should be a Dirichlet polynomial approximating  $\lvert \textstyle {L(\frac {1}{2}, \chi )}\rvert ^{-1}$. Indeed, taking
$\lvert \textstyle {L(\frac {1}{2}, \chi )}\rvert ^{-1}$. Indeed, taking ![]() $\kappa =1$ and k an even integer in the foregoing definition, we see that
$\kappa =1$ and k an even integer in the foregoing definition, we see that ![]() $\lvert M_j (\chi; 1)\rvert ^k$ is a Dirichlet polynomial on the interval
$\lvert M_j (\chi; 1)\rvert ^k$ is a Dirichlet polynomial on the interval ![]() $I_j$ in view of formula (3.1), approximating the exponential with the finite sum
$I_j$ in view of formula (3.1), approximating the exponential with the finite sum ![]() $E_{\ell _j}$ on each interval (we do not claim that the finite sum is an upper bound, but it is close enough to work on average) – that is, it is very close to equation (3.6), with the added Liouville function taking care of the cancellation. Taking
$E_{\ell _j}$ on each interval (we do not claim that the finite sum is an upper bound, but it is close enough to work on average) – that is, it is very close to equation (3.6), with the added Liouville function taking care of the cancellation. Taking ![]() $\kappa \neq 1$ allows us to mollify all moments, not just in the case when k is an even integer, by taking the mollifier to be
$\kappa \neq 1$ allows us to mollify all moments, not just in the case when k is an even integer, by taking the mollifier to be  ${\textstyle \lvert M_j(\chi ;\frac {1}{\kappa })\rvert }^{k \kappa }$ on each interval
${\textstyle \lvert M_j(\chi ;\frac {1}{\kappa })\rvert }^{k \kappa }$ on each interval ![]() $I_j$ as already defined. We remark that for any
$I_j$ as already defined. We remark that for any ![]() $\kappa $, the term with
$\kappa $, the term with ![]() $f_j h_j = P$ in the Dirichlet series (3.11) is
$f_j h_j = P$ in the Dirichlet series (3.11) is
 $$ \begin{align*} - \frac{k}{2} \frac{a(P, J) \left( \chi(P) + \overline{\chi}(P) \right)}{\lvert P\rvert^{1/2}}, \end{align*} $$
$$ \begin{align*} - \frac{k}{2} \frac{a(P, J) \left( \chi(P) + \overline{\chi}(P) \right)}{\lvert P\rvert^{1/2}}, \end{align*} $$which is independent of ![]() $\kappa $, and of the correct size to approximate
$\kappa $, and of the correct size to approximate  $\left \lvert {\textstyle L\left (\frac {1}{2}, \chi \right )} \right \rvert ^{-k}$.
$\left \lvert {\textstyle L\left (\frac {1}{2}, \chi \right )} \right \rvert ^{-k}$.
Now we will introduce the main technical lemma that will be required to prove Theorem 1.6. We postpone its proof until Section 4.
Lemma 3.5. Let ![]() $j=0,\dotsc ,J -1$,
$j=0,\dotsc ,J -1$, ![]() $0 \leq u \leq J $ for (i) and
$0 \leq u \leq J $ for (i) and ![]() $j < u \leq J $ for (iii). Let
$j < u \leq J $ for (iii). Let ![]() $s_j$ be an integer with
$s_j$ be an integer with  $a k \kappa \ell _j \leq s_j \leq \frac {1}{d \theta _j},$ where a and d are such that
$a k \kappa \ell _j \leq s_j \leq \frac {1}{d \theta _j},$ where a and d are such that ![]() $a>2$,
$a>2$, ![]() $d>8$, and
$d>8$, and  $4ad \theta _J ^{1-b} \leq 1$, with
$4ad \theta _J ^{1-b} \leq 1$, with ![]() $0<b<1$.
$0<b<1$.
Then we have
 $$ \begin{align*} \text{(i)} \sum_{\chi \in \mathcal{C}(g)}& \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2 k \kappa} \left( \Re P_{I_0}(\chi;u)\right)^{2s_0} \leq_{\varepsilon} 2 q^{g+2} e^{k^2J } H(0) \left( \sum_{P \in I_0} \frac{1}{\lvert P\rvert} \right)^{s_0} \frac{\left(\frac{5}{3}\right)^{\left(2-4/a\right)s_0/3}(2s_{0})!}{ 4^{s_{0}} \left\lfloor\frac{\left(2-4/a\right)s_{0}}{3}\right\rfloor!}, \\ \text{(ii)} \sum_{\chi \in \mathcal{C}(g)} & D_{J ,k}(\chi)^2\left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2 k \kappa} \leq_{\varepsilon} q^{g+2} \mathcal{D}_k C(k), \\ \text{(iii)}\sum_{\chi \in \mathcal{C}(g)} & D_{j, k}(\chi)^2 \left( \Re P_{I_{j+1}}(\chi;u) \right)^{2s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2 k \kappa} \leq_{\varepsilon} 2 q^{g+2} \mathcal{D}_kC(k)\exp\left(k^2 +2k\right) \\ & \times e^{k^2\left(J -j-1\right)} \left( \sum_{P \in I_{j+1}} \frac{1}{\lvert P\rvert} \right)^{s_{j+1}} \frac{\left(\frac{5}{3}\right)^{\left(2-4/a\right)s_{j+1}/3}\left(2s_{j+1}\right)!}{ 4^{s_{j+1}} \left\lfloor\frac{\left(2-4/a\right)s_{j+1}}{3}\right\rfloor!} , \end{align*} $$
$$ \begin{align*} \text{(i)} \sum_{\chi \in \mathcal{C}(g)}& \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2 k \kappa} \left( \Re P_{I_0}(\chi;u)\right)^{2s_0} \leq_{\varepsilon} 2 q^{g+2} e^{k^2J } H(0) \left( \sum_{P \in I_0} \frac{1}{\lvert P\rvert} \right)^{s_0} \frac{\left(\frac{5}{3}\right)^{\left(2-4/a\right)s_0/3}(2s_{0})!}{ 4^{s_{0}} \left\lfloor\frac{\left(2-4/a\right)s_{0}}{3}\right\rfloor!}, \\ \text{(ii)} \sum_{\chi \in \mathcal{C}(g)} & D_{J ,k}(\chi)^2\left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2 k \kappa} \leq_{\varepsilon} q^{g+2} \mathcal{D}_k C(k), \\ \text{(iii)}\sum_{\chi \in \mathcal{C}(g)} & D_{j, k}(\chi)^2 \left( \Re P_{I_{j+1}}(\chi;u) \right)^{2s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2 k \kappa} \leq_{\varepsilon} 2 q^{g+2} \mathcal{D}_kC(k)\exp\left(k^2 +2k\right) \\ & \times e^{k^2\left(J -j-1\right)} \left( \sum_{P \in I_{j+1}} \frac{1}{\lvert P\rvert} \right)^{s_{j+1}} \frac{\left(\frac{5}{3}\right)^{\left(2-4/a\right)s_{j+1}/3}\left(2s_{j+1}\right)!}{ 4^{s_{j+1}} \left\lfloor\frac{\left(2-4/a\right)s_{j+1}}{3}\right\rfloor!} , \end{align*} $$where ![]() $\mathcal {D}_k$ is given in equation (4.15),
$\mathcal {D}_k$ is given in equation (4.15), ![]() $H(0)$ is bounded by formula (4.21) and
$H(0)$ is bounded by formula (4.21) and ![]() $C(k)$ is a constant satisfying
$C(k)$ is a constant satisfying  $C(2)=e^{e^{15}}$.
$C(2)=e^{e^{15}}$.
3.3 Averages over the family
Lemma 3.6. Let ![]() $I_0,I_1,\dotsc , I_J$ be intervals such that
$I_0,I_1,\dotsc , I_J$ be intervals such that ![]() $I_0=(0,(g+2) \theta _0], I_1=((g+2) \theta _0,(g+2)\theta _1],\dotsc , I_J=((g+2) \theta _{J-1},(g+2) \theta _J]$. Let
$I_0=(0,(g+2) \theta _0], I_1=((g+2) \theta _0,(g+2)\theta _1],\dotsc , I_J=((g+2) \theta _{J-1},(g+2) \theta _J]$. Let ![]() $B, C, b$ and c be any functions supported on
$B, C, b$ and c be any functions supported on ![]() $\mathbb {F}_q[T]$. Suppose
$\mathbb {F}_q[T]$. Suppose ![]() $s_j$ and
$s_j$ and ![]() $\ell _{j}$ are nonnegative integers for
$\ell _{j}$ are nonnegative integers for ![]() $j=0,\dotsc ,J$ such that
$j=0,\dotsc ,J$ such that
 $$ \begin{align} 2 \sum_{j=0}^J \theta_j s_{j}+ 3 \sum_{j=0}^J \theta_j \ell_{j} \leq 1/2. \end{align} $$
$$ \begin{align} 2 \sum_{j=0}^J \theta_j s_{j}+ 3 \sum_{j=0}^J \theta_j \ell_{j} \leq 1/2. \end{align} $$Then we have

Remark 3.7. We will also use this lemma in slightly different cases. We will allow the following variations:
• The condition
 $\Omega \left (F_jH_j\right ) \leq s_j $ is replaced by
$\Omega \left (F_jH_j\right ) \leq s_j $ is replaced by  $\Omega \left (F_jH_j\right ) = s_j$.
$\Omega \left (F_jH_j\right ) = s_j$.• The condition
 $ P\mid F_jH_j \Rightarrow P\in I_j$ is replaced by
$ P\mid F_jH_j \Rightarrow P\in I_j$ is replaced by  $P\mid F_jH_j \Rightarrow \deg (P)=m_j$, where
$P\mid F_jH_j \Rightarrow \deg (P)=m_j$, where  $m_j$ is a fixed element in
$m_j$ is a fixed element in  $I_j$.
$I_j$.
These variations will happen for some values of j and may happen both at the same time. In all cases, the results are analogous.
Proof. Expanding the left-hand side of the equation obtained and exchanging the order of summation, we need to evaluate sums of the form
 $$ \begin{align*} \sum_{R \in \mathcal{M}_{q^2,g/2+1}} \chi_R\left(\prod_{j=0}^J F_jH_j^2f_jh_j^2\right) = \sum_{R \in \mathcal{M}_{q^2,g/2+1}} \chi_{\prod_{j=0}^J F_jH_j^2f_jh_j^2}(R), \end{align*} $$
$$ \begin{align*} \sum_{R \in \mathcal{M}_{q^2,g/2+1}} \chi_R\left(\prod_{j=0}^J F_jH_j^2f_jh_j^2\right) = \sum_{R \in \mathcal{M}_{q^2,g/2+1}} \chi_{\prod_{j=0}^J F_jH_j^2f_jh_j^2}(R), \end{align*} $$since ![]() $q^2 \equiv 1 \,(\mathrm {mod}\,6)$, and we have cubic reciprocity over
$q^2 \equiv 1 \,(\mathrm {mod}\,6)$, and we have cubic reciprocity over ![]() $\mathbb F_{q^2}[T]$. If
$\mathbb F_{q^2}[T]$. If , then
, then
 $$ \begin{align*} \sum_{j=0}^J\deg\left(F_jH_j^2f_jh_j^2\right)\leq (g+2)\left( 2\sum_{j=0}^J\theta_j s_j+3\sum_{j=0}^J \theta_j \ell_j\right)\leq (g+2)/2 = \deg(R), \end{align*} $$
$$ \begin{align*} \sum_{j=0}^J\deg\left(F_jH_j^2f_jh_j^2\right)\leq (g+2)\left( 2\sum_{j=0}^J\theta_j s_j+3\sum_{j=0}^J \theta_j \ell_j\right)\leq (g+2)/2 = \deg(R), \end{align*} $$and the character sum vanishes. We are then left with the contribution of those terms with  . Since
. Since 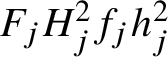 $F_jH_j^2f_jh_j^2$ is only divisible by primes in
$F_jH_j^2f_jh_j^2$ is only divisible by primes in ![]() $I_j$ and the intervals
$I_j$ and the intervals ![]() $I_j$ are disjoint, it follows that we must have
$I_j$ are disjoint, it follows that we must have  for each
for each ![]() $j\leq J $. For any
$j\leq J $. For any ![]() $c \in \mathbb F_{q^2}[T]$,
$c \in \mathbb F_{q^2}[T]$, ![]() and
and ![]() $\deg {c} \leq g/2 + 1$, we have
$\deg {c} \leq g/2 + 1$, we have
 $$ \begin{align*} \sum_{R \in \mathcal{M}_{q^2,g/2+1}} \chi_R( c) = \sum_{\substack{d \in \mathcal{M}_{q^2} \\ d \mid c}} \mu(d) \sum_{\substack {R \in \mathcal{M}_{q^2,g/2+1}\\ d \mid R}} 1 = q^{g + 2} \sum_{\substack{d \in \mathcal{M}_{q^2} \\ d \mid c}} \mu(d) q^{-2 \deg{d}} = q^{g+2} \frac{\phi_{q^2}(c)}{\lvert c\rvert_{q^2}}, \end{align*} $$
$$ \begin{align*} \sum_{R \in \mathcal{M}_{q^2,g/2+1}} \chi_R( c) = \sum_{\substack{d \in \mathcal{M}_{q^2} \\ d \mid c}} \mu(d) \sum_{\substack {R \in \mathcal{M}_{q^2,g/2+1}\\ d \mid R}} 1 = q^{g + 2} \sum_{\substack{d \in \mathcal{M}_{q^2} \\ d \mid c}} \mu(d) q^{-2 \deg{d}} = q^{g+2} \frac{\phi_{q^2}(c)}{\lvert c\rvert_{q^2}}, \end{align*} $$and using  $c = \prod _{j=0}^J F_jH_j^2f_jh_j^2$, the conclusion follows.
$c = \prod _{j=0}^J F_jH_j^2f_jh_j^2$, the conclusion follows.
3.4 Proof of Theorem 1.6
Proof. We write
 $$ \begin{align} \sum_{\chi\in \mathcal{C}(g) } \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} & = \sum_{\chi\in \mathcal{C}(g)\cap \mathcal{T}_0} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} + \sum_{\chi \in \mathcal{C}(g)\setminus \mathcal{T}_0} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa}, \end{align} $$
$$ \begin{align} \sum_{\chi\in \mathcal{C}(g) } \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} & = \sum_{\chi\in \mathcal{C}(g)\cap \mathcal{T}_0} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} + \sum_{\chi \in \mathcal{C}(g)\setminus \mathcal{T}_0} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa}, \end{align} $$where ![]() $\mathcal {T}_r$ is defined in equation (3.9). We first focus on the second term. Since
$\mathcal {T}_r$ is defined in equation (3.9). We first focus on the second term. Since ![]() $\chi \not \in \mathcal {T}_0$, there exists
$\chi \not \in \mathcal {T}_0$, there exists ![]() $u=u(\chi )$ such that
$u=u(\chi )$ such that ![]() $0 \leq u \leq J $ and
$0 \leq u \leq J $ and
 $$ \begin{align*} \left\lvert\Re P_{I_0}(\chi;u)\right\rvert> \frac{\ell_0}{k e^2}. \end{align*} $$
$$ \begin{align*} \left\lvert\Re P_{I_0}(\chi;u)\right\rvert> \frac{\ell_0}{k e^2}. \end{align*} $$Choosing ![]() $s_0$ even and multiplying by
$s_0$ even and multiplying by  $ (\frac {ke^2 \Re P_{I_0}(\chi ;u)}{\ell _0})^{s_0}>1$, completing the sum for all
$ (\frac {ke^2 \Re P_{I_0}(\chi ;u)}{\ell _0})^{s_0}>1$, completing the sum for all ![]() $\chi \in \mathcal {C}(g)$ (since all the involved terms are positive) and applying Cauchy–Schwarz, we obtain
$\chi \in \mathcal {C}(g)$ (since all the involved terms are positive) and applying Cauchy–Schwarz, we obtain
 $$ \begin{align} \nonumber &\sum_{u=0}^J \sum_{\substack{\chi \in \mathcal{C}(g)\setminus \mathcal{T}_0\\ u(\chi)=u}} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{ k \kappa} \leq \sum_{u=0}^J \sum_{\chi\in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \left( \frac{k e^2 \Re P_{I_0}(\chi;u)}{\ell_0} \right)^{s_0} \notag \\ &\quad \leq J ^{1/2} \left( \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{2 k} \right)^{1/2} \left( \sum_{u=0}^J \sum_{\chi \in \mathcal{C}(g)} \left( \frac{ k e^2}{\ell_0} \right)^{2s_0} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa } \left( \Re P_{I_0}(\chi;u)\right)^{2s_0} \right)^{1/2}, \end{align} $$
$$ \begin{align} \nonumber &\sum_{u=0}^J \sum_{\substack{\chi \in \mathcal{C}(g)\setminus \mathcal{T}_0\\ u(\chi)=u}} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{ k \kappa} \leq \sum_{u=0}^J \sum_{\chi\in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \left( \frac{k e^2 \Re P_{I_0}(\chi;u)}{\ell_0} \right)^{s_0} \notag \\ &\quad \leq J ^{1/2} \left( \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{2 k} \right)^{1/2} \left( \sum_{u=0}^J \sum_{\chi \in \mathcal{C}(g)} \left( \frac{ k e^2}{\ell_0} \right)^{2s_0} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa } \left( \Re P_{I_0}(\chi;u)\right)^{2s_0} \right)^{1/2}, \end{align} $$where we choose ![]() $s_0$ to be an even integer such that
$s_0$ to be an even integer such that
 $$ \begin{align*}a k \kappa \ell_0 \leq s_0 \leq \frac{1}{d \theta_0},\end{align*} $$
$$ \begin{align*}a k \kappa \ell_0 \leq s_0 \leq \frac{1}{d \theta_0},\end{align*} $$with a and d as in Lemma 3.5.
For the first sum in formula (3.14), we have an upper bound of size ![]() $q^{g/2} g^{O(1)}$ using Lemma 6.1. We aim to obtain some saving from the second sum. Using Lemma 3.5(i) and Stirling’s formula, we get, for
$q^{g/2} g^{O(1)}$ using Lemma 6.1. We aim to obtain some saving from the second sum. Using Lemma 3.5(i) and Stirling’s formula, we get, for ![]() $c = 2-4/a$,
$c = 2-4/a$,
 $$ \begin{align*} &\left( \sum_{u=0}^J \sum_{\chi\in \mathcal{C}(g)} \left( \frac{ k e^2}{\ell_0} \right)^{2s_0} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa } \left( \Re P_{I_0}(\chi;u)\right)^{2s_0} \right)^{1/2} \\ &\qquad \ll q^{g/2} g^{O(1)} \left( \frac{k e^{1+c/6} \theta_0^{b} s_0^{1-c/6} 5^{c/6} }{2c^{c/6}} \right)^{ s_0} (\log g)^{s_0/2}\\ &\qquad \ll \frac{q^{g/2}}{q^{\left(\log g\right)^\delta}} \ll \frac{q^{g/2}}{g^A} \end{align*} $$
$$ \begin{align*} &\left( \sum_{u=0}^J \sum_{\chi\in \mathcal{C}(g)} \left( \frac{ k e^2}{\ell_0} \right)^{2s_0} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa } \left( \Re P_{I_0}(\chi;u)\right)^{2s_0} \right)^{1/2} \\ &\qquad \ll q^{g/2} g^{O(1)} \left( \frac{k e^{1+c/6} \theta_0^{b} s_0^{1-c/6} 5^{c/6} }{2c^{c/6}} \right)^{ s_0} (\log g)^{s_0/2}\\ &\qquad \ll \frac{q^{g/2}}{q^{\left(\log g\right)^\delta}} \ll \frac{q^{g/2}}{g^A} \end{align*} $$for ![]() $\delta> 1$ and all
$\delta> 1$ and all ![]() $A \geq 1$, where the last line is obtained by setting
$A \geq 1$, where the last line is obtained by setting ![]() $s_0 = 2[a k \kappa \ell _0/2]+2$. We also used the bound (4) for
$s_0 = 2[a k \kappa \ell _0/2]+2$. We also used the bound (4) for ![]() $H(0)$ from Lemma 3.5(i) in the second line. Replacing the two estimates in formula (3.14), we get
$H(0)$ from Lemma 3.5(i) in the second line. Replacing the two estimates in formula (3.14), we get
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)\setminus \mathcal{T}_0} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} = o ( q^{g}), \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)\setminus \mathcal{T}_0} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} = o ( q^{g}), \end{align*} $$and the sum over the characters ![]() $\chi \not \in \mathcal {T}_0$ does not contribute to the sharp upper bound.
$\chi \not \in \mathcal {T}_0$ does not contribute to the sharp upper bound.
For the first sum of equation (3.13) over the characters ![]() $\chi \in \mathcal {T}_0$, we use Proposition 3.3. As before, we first bound the sum by the completed sum over all
$\chi \in \mathcal {T}_0$, we use Proposition 3.3. As before, we first bound the sum by the completed sum over all ![]() $\chi \in \mathcal {C}(g)$, since all the extra terms are positive. We have
$\chi \in \mathcal {C}(g)$, since all the extra terms are positive. We have
 $$ \begin{align} &\sum_{\chi \in \mathcal{C}(g)\cap \mathcal{T}_0} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \leq \exp ( k (1/\theta_J + \eta ) ) \sum_{\chi\in \mathcal{C}(g)} D_{J , k}(\chi)S_{J , k}(\chi)\left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa}\notag \\ &\quad +\sum_{\substack{{0\leq j \leq J -1}\\ j<u \leq J }} \exp \left( k \left(1/\theta_j + \eta \right) \right) \sum_{\chi\in \mathcal{C}(g)} D_{j, k}(\chi) S_{j, k}(\chi) \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{ k \kappa }, \end{align} $$
$$ \begin{align} &\sum_{\chi \in \mathcal{C}(g)\cap \mathcal{T}_0} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \leq \exp ( k (1/\theta_J + \eta ) ) \sum_{\chi\in \mathcal{C}(g)} D_{J , k}(\chi)S_{J , k}(\chi)\left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa}\notag \\ &\quad +\sum_{\substack{{0\leq j \leq J -1}\\ j<u \leq J }} \exp \left( k \left(1/\theta_j + \eta \right) \right) \sum_{\chi\in \mathcal{C}(g)} D_{j, k}(\chi) S_{j, k}(\chi) \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{ k \kappa }, \end{align} $$where ![]() $s_{j+1}$ is even.
$s_{j+1}$ is even.
Using Cauchy–Schwarz, we write
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} D_{J , k}(\chi)S_{J , k}(\chi)\left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \leq \left( \sum_{\chi \in \mathcal{C}(g)} D_{J , k}(\chi)^2 \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa} \right)^{1/2} \left( \sum_{\chi \in \mathcal{C}(g)}S_{J , k}(\chi)^2 \right)^{1/2} , \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} D_{J , k}(\chi)S_{J , k}(\chi)\left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \leq \left( \sum_{\chi \in \mathcal{C}(g)} D_{J , k}(\chi)^2 \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa} \right)^{1/2} \left( \sum_{\chi \in \mathcal{C}(g)}S_{J , k}(\chi)^2 \right)^{1/2} , \end{align} $$and similarly,
 $$ \begin{align} &\sum_{\chi \in \mathcal{C}(g)}D_{j,k}(\chi)S_{j,k}(\chi) \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \notag\\ &\quad \leq \left( \sum_{\chi \in \mathcal{C}(g)} D_{j,k}(\chi)^2 \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{2s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa} \right)^{1/2} \left( \sum_{\chi \in \mathcal{C}(g)}S_{j,k}(\chi)^2 \right)^{1/2}. \end{align} $$
$$ \begin{align} &\sum_{\chi \in \mathcal{C}(g)}D_{j,k}(\chi)S_{j,k}(\chi) \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \notag\\ &\quad \leq \left( \sum_{\chi \in \mathcal{C}(g)} D_{j,k}(\chi)^2 \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{2s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa} \right)^{1/2} \left( \sum_{\chi \in \mathcal{C}(g)}S_{j,k}(\chi)^2 \right)^{1/2}. \end{align} $$To bound formula (3.16), we use Lemmas 3.5(ii) and 5.1, which give
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)}D_{J , k}(\chi)S_{J , k}(\chi)\left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \leq q^{g+2} \mathcal{D}_k^{1/2}C(k)^{1/2} \mathcal{S}_k^{1/2}. \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)}D_{J , k}(\chi)S_{J , k}(\chi)\left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \leq q^{g+2} \mathcal{D}_k^{1/2}C(k)^{1/2} \mathcal{S}_k^{1/2}. \end{align} $$ Similarly, to bound formula (3.17) we use Lemmas 3.5(iii) and 5.1. When we bound the first term in formula (3.17) with Lemma 3.5(iii), we use Stirling’s formula and note that the sum over primes is bounded by ![]() $\log \left ( \theta _{j+1}/\theta _j\right )=1$. Now we pick
$\log \left ( \theta _{j+1}/\theta _j\right )=1$. Now we pick  $s_{j+1} = 2 \left [1/\left (2d\theta _{j+1}\right )\right ]$, and then when
$s_{j+1} = 2 \left [1/\left (2d\theta _{j+1}\right )\right ]$, and then when ![]() $g \to \infty $, we have
$g \to \infty $, we have
 $$ \begin{align} & \sum_{\chi \in \mathcal{C}(g)}D_{j,k}(\chi)^2 \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{2s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa} \nonumber \\ & \qquad \leq_\varepsilon \frac{2\sqrt{6}}{\sqrt{c}} q^{g+2} \mathcal{D}_k C(k)\exp \left(k^2+2k \right) e^{k^2\left(J-j-1\right)} \left( \frac{k^2 e^{2+c/3} \theta_{j+1}^{2b} s_{j+1}^{2-c/3} 5^{c/3}} {4 c^{c/3} } \right)^{s_{j+1}} \nonumber \\ & \qquad =\frac{2 \sqrt{6}}{\sqrt{c}} q^{g+2} \mathcal{D}_k C(k)\exp \left(k^2+2k \right) \exp \left(k^2\left(J -j-1\right)+ \frac{ \alpha \log \theta_{j+1}}{ d \theta_{j+1}}+ \frac{\log F}{d \theta_{j+1}} \right), \end{align} $$
$$ \begin{align} & \sum_{\chi \in \mathcal{C}(g)}D_{j,k}(\chi)^2 \left( \frac{ k e^2 \Re P_{I_{j+1}}(\chi;u)}{\ell_{j+1}} \right)^{2s_{j+1}} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{2k \kappa} \nonumber \\ & \qquad \leq_\varepsilon \frac{2\sqrt{6}}{\sqrt{c}} q^{g+2} \mathcal{D}_k C(k)\exp \left(k^2+2k \right) e^{k^2\left(J-j-1\right)} \left( \frac{k^2 e^{2+c/3} \theta_{j+1}^{2b} s_{j+1}^{2-c/3} 5^{c/3}} {4 c^{c/3} } \right)^{s_{j+1}} \nonumber \\ & \qquad =\frac{2 \sqrt{6}}{\sqrt{c}} q^{g+2} \mathcal{D}_k C(k)\exp \left(k^2+2k \right) \exp \left(k^2\left(J -j-1\right)+ \frac{ \alpha \log \theta_{j+1}}{ d \theta_{j+1}}+ \frac{\log F}{d \theta_{j+1}} \right), \end{align} $$where
 $$ \begin{align*} \alpha=2b-2+\frac{c}{3}, \qquad F= \frac{k^2e^{2+c/3}5^{c/3}}{4d^{2-c/3}c^{c/3}}, \end{align*} $$
$$ \begin{align*} \alpha=2b-2+\frac{c}{3}, \qquad F= \frac{k^2e^{2+c/3}5^{c/3}}{4d^{2-c/3}c^{c/3}}, \end{align*} $$with ![]() $c=2-4/a$ and a and d as in Lemma 3.5. We now replace in formula (3.17), and using Lemma 5.1, the sum over
$c=2-4/a$ and a and d as in Lemma 3.5. We now replace in formula (3.17), and using Lemma 5.1, the sum over ![]() $j,u,\chi $ in formula (3.15) is bounded by
$j,u,\chi $ in formula (3.15) is bounded by
 $$ \begin{align*} \exp(k \eta) \left( \frac{2 \sqrt{6}}{\sqrt{c}} \mathcal{D}_k C(k)\exp \left(k^2+2k \right) \mathcal{S}_k \right)^{1/2} C_J q^{g+2}, \end{align*} $$
$$ \begin{align*} \exp(k \eta) \left( \frac{2 \sqrt{6}}{\sqrt{c}} \mathcal{D}_k C(k)\exp \left(k^2+2k \right) \mathcal{S}_k \right)^{1/2} C_J q^{g+2}, \end{align*} $$where
 $$ \begin{align} C_J := \sum_{\substack{0 \leq j \leq J -1 \\ j<u \leq J }} & \exp \left(\frac{k}{\theta_j} +\frac{k^2(J -j-1)}{2}+\frac{\alpha \log \theta_{j+1}}{ 2d \theta_{j+1}}+ \frac{\log F}{2d \theta_{j+1}} \right) \nonumber \\[6pt] &= \sum_{0 \leq j\leq J -1} (J -j) \exp \left(\frac{k}{\theta_j} +\frac{k^2(J -j-1)}{2}+\frac{ \alpha \log \theta_{j+1}}{ 2d \theta_{j+1}}+ \frac{\log F}{2d \theta_{j+1}} \right) \nonumber \\[6pt] &= \sum_{0 \leq u \leq J -1} (u+1) \exp \left( \frac{k e^{u+1}}{\theta_J }+\frac{k^2u}{2} - \frac{\alpha ue^u}{2d\theta_J }+\frac{ \alpha e^u \log \theta_J }{2d \theta_J }+\frac{e^u \log F}{2d \theta_J } \right) \nonumber \\[6pt] &= O(1). \end{align} $$
$$ \begin{align} C_J := \sum_{\substack{0 \leq j \leq J -1 \\ j<u \leq J }} & \exp \left(\frac{k}{\theta_j} +\frac{k^2(J -j-1)}{2}+\frac{\alpha \log \theta_{j+1}}{ 2d \theta_{j+1}}+ \frac{\log F}{2d \theta_{j+1}} \right) \nonumber \\[6pt] &= \sum_{0 \leq j\leq J -1} (J -j) \exp \left(\frac{k}{\theta_j} +\frac{k^2(J -j-1)}{2}+\frac{ \alpha \log \theta_{j+1}}{ 2d \theta_{j+1}}+ \frac{\log F}{2d \theta_{j+1}} \right) \nonumber \\[6pt] &= \sum_{0 \leq u \leq J -1} (u+1) \exp \left( \frac{k e^{u+1}}{\theta_J }+\frac{k^2u}{2} - \frac{\alpha ue^u}{2d\theta_J }+\frac{ \alpha e^u \log \theta_J }{2d \theta_J }+\frac{e^u \log F}{2d \theta_J } \right) \nonumber \\[6pt] &= O(1). \end{align} $$Now using also formula (3.18) and the fact that the characters in ![]() $\mathcal {T}_0$ do not contribute to the upper bound, we finally have
$\mathcal {T}_0$ do not contribute to the upper bound, we finally have
 $$ \begin{align} \sum_{\substack{ \chi \in \mathcal{C}(g) }} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} & \leq_\varepsilon \mathcal{D}_k^{1/2} C(k)^{1/2}\mathcal{S}_k^{1/2} \exp{\left( \frac{k^2}{2} + (1+\eta) k \right)} \end{align} $$
$$ \begin{align} \sum_{\substack{ \chi \in \mathcal{C}(g) }} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} & \leq_\varepsilon \mathcal{D}_k^{1/2} C(k)^{1/2}\mathcal{S}_k^{1/2} \exp{\left( \frac{k^2}{2} + (1+\eta) k \right)} \end{align} $$ $$ \begin{align} & \quad \times \left( \exp(k/\theta_J) + \sqrt[4]{\frac{24}{c}} \;C_J \right) \;q^{g+2}. \end{align} $$
$$ \begin{align} & \quad \times \left( \exp(k/\theta_J) + \sqrt[4]{\frac{24}{c}} \;C_J \right) \;q^{g+2}. \end{align} $$This completes the proof of Theorem 1.6. In Section 7 we find an explicit numerical value for the constant in the upper bound (3.21) when ![]() $k=2$, which depends on the bound for
$k=2$, which depends on the bound for ![]() $C_J$.
$C_J$.
4 Proof of Lemma 3.5
Proof. Following [Reference Bui, Florea, Keating and Roditty-Gershon2, Reference David, Florea and Lalin13], the sum over ![]() $\chi \in \mathcal {C}(g)$ can be rewritten as the sum over the cubic residue symbols
$\chi \in \mathcal {C}(g)$ can be rewritten as the sum over the cubic residue symbols ![]() $\chi _R$, for monic square-free polynomials
$\chi _R$, for monic square-free polynomials ![]() $R \in \mathbb F_{q^2}[T]$ of degree
$R \in \mathbb F_{q^2}[T]$ of degree ![]() ${g/2+1}$, with the property that if
${g/2+1}$, with the property that if ![]() $P\mid R$, then
$P\mid R$, then ![]() $P \notin \mathbb {F}_q[T]$. Since all the summands in the foregoing expressions are positive, we first bound the sums over
$P \notin \mathbb {F}_q[T]$. Since all the summands in the foregoing expressions are positive, we first bound the sums over ![]() $\chi \in \mathcal {C}(g)$ by the sum over all
$\chi \in \mathcal {C}(g)$ by the sum over all ![]() $R \in \mathcal {M}_{q^2,g/2+1}$.
$R \in \mathcal {M}_{q^2,g/2+1}$.
We prove the last upper bound; the first two are just simpler cases of that one. We note that ![]() $D_{j, k}(\chi )^2$ contributes primes from the intervals
$D_{j, k}(\chi )^2$ contributes primes from the intervals ![]() $I_0, \dotsc , I_j$,
$I_0, \dotsc , I_j$, ![]() $\Re P_{I_{j+1}}(\chi ;u)$ contributes primes from
$\Re P_{I_{j+1}}(\chi ;u)$ contributes primes from ![]() $I_{j+1}$ and the mollifier contributes primes from all the intervals
$I_{j+1}$ and the mollifier contributes primes from all the intervals ![]() $I_0, \dotsc , I_J $. To prove (iii), we have to bound
$I_0, \dotsc , I_J $. To prove (iii), we have to bound
 $$ \begin{align} \sum_{R \in \mathcal{M}_{q^2,g/2+1}} \prod_{r=0}^j \left(1+e^{-\ell_r/2}\right)^2 \mathcal{E}_R(r) \times \mathcal{E}_R(j+1)\times \prod_{r=j+2}^J \mathcal{E}_R(r),\end{align} $$
$$ \begin{align} \sum_{R \in \mathcal{M}_{q^2,g/2+1}} \prod_{r=0}^j \left(1+e^{-\ell_r/2}\right)^2 \mathcal{E}_R(r) \times \mathcal{E}_R(j+1)\times \prod_{r=j+2}^J \mathcal{E}_R(r),\end{align} $$where the ![]() $\mathcal {E}_R(r)$ are defined as follows. For
$\mathcal {E}_R(r)$ are defined as follows. For ![]() $r=0,\dotsc , j$,
$r=0,\dotsc , j$,
 $$ \begin{align*} \mathcal{E}_R(r)&= \sum_{\substack{P\mid f_r h_r F_{r1}F_{r2} H_{r1} H_{r2} \Rightarrow P \in I_r \\ \Omega(F_{r1} H_{r1}) \leq \ell_r \\\Omega(F_{r2} H_{r2}) \leq \ell_r \\ \Omega(f_r) \leq (k \cdot \kappa)\ell_r \\ \Omega(h_r) \leq (k \cdot \kappa) \ell_r }} \frac{(k/2)^{\Omega\left(F_{r1} F_{r2} H_{r1} H_{r2}\right)} a(F_{r1} F_{r2} H_{r1} H_{r2}; j) \nu(F_{r1}) \nu(F_{r2}) \nu(H_{r1}) \nu(H_{r2}) }{ \kappa^{\Omega\left(f_r h_r\right)} \sqrt{ \lvert f_r h_r F_{r1}F_{r2} H_{r1} H_{r2}\rvert}} \\ & \quad \times a (f_r h_r; J ) \lambda(f_r h_r) \nu_{k \kappa} (f_r;\ell_r) \nu_{k \kappa}(h_r;\ell_r)\chi_R\left(f_rh_r^2F_{r1} F_{r2}H_{r1}^2H_{r2}^2\right). \end{align*} $$
$$ \begin{align*} \mathcal{E}_R(r)&= \sum_{\substack{P\mid f_r h_r F_{r1}F_{r2} H_{r1} H_{r2} \Rightarrow P \in I_r \\ \Omega(F_{r1} H_{r1}) \leq \ell_r \\\Omega(F_{r2} H_{r2}) \leq \ell_r \\ \Omega(f_r) \leq (k \cdot \kappa)\ell_r \\ \Omega(h_r) \leq (k \cdot \kappa) \ell_r }} \frac{(k/2)^{\Omega\left(F_{r1} F_{r2} H_{r1} H_{r2}\right)} a(F_{r1} F_{r2} H_{r1} H_{r2}; j) \nu(F_{r1}) \nu(F_{r2}) \nu(H_{r1}) \nu(H_{r2}) }{ \kappa^{\Omega\left(f_r h_r\right)} \sqrt{ \lvert f_r h_r F_{r1}F_{r2} H_{r1} H_{r2}\rvert}} \\ & \quad \times a (f_r h_r; J ) \lambda(f_r h_r) \nu_{k \kappa} (f_r;\ell_r) \nu_{k \kappa}(h_r;\ell_r)\chi_R\left(f_rh_r^2F_{r1} F_{r2}H_{r1}^2H_{r2}^2\right). \end{align*} $$ For ![]() $r=j+1$,
$r=j+1$,
 $$ \begin{align*} & \mathcal{E}_R(r) = \frac{(2s_r)!}{4^{s_r}} \\ &\enspace \times\sum_{\substack{P\mid f_r h_r F_r H_r\Rightarrow P \in I_r \\ \Omega(F_r H_r) = 2s_r \\ \Omega(f_r) \leq (k \cdot \kappa)\ell_r \\ \Omega(h_r) \leq ( k \cdot \kappa) \ell_r }} \frac{a(F_r H_r; u) \nu(F_r) \nu(H_r) a (f_r h_r; J ) \lambda(f_r h_r) \nu_{k \kappa} (f_r;\ell_r) \nu_{k \kappa }(h_r;\ell_r) \chi_R\left(f_rh_r^2F_rH_r^2\right)}{ \kappa^{\Omega\left(f_r h_r\right)} \sqrt{ \lvert f_r F_r h_r H_r\rvert}}. \end{align*} $$
$$ \begin{align*} & \mathcal{E}_R(r) = \frac{(2s_r)!}{4^{s_r}} \\ &\enspace \times\sum_{\substack{P\mid f_r h_r F_r H_r\Rightarrow P \in I_r \\ \Omega(F_r H_r) = 2s_r \\ \Omega(f_r) \leq (k \cdot \kappa)\ell_r \\ \Omega(h_r) \leq ( k \cdot \kappa) \ell_r }} \frac{a(F_r H_r; u) \nu(F_r) \nu(H_r) a (f_r h_r; J ) \lambda(f_r h_r) \nu_{k \kappa} (f_r;\ell_r) \nu_{k \kappa }(h_r;\ell_r) \chi_R\left(f_rh_r^2F_rH_r^2\right)}{ \kappa^{\Omega\left(f_r h_r\right)} \sqrt{ \lvert f_r F_r h_r H_r\rvert}}. \end{align*} $$ For ![]() $r=j+2,\dotsc , J $,
$r=j+2,\dotsc , J $,
 $$ \begin{align*} \mathcal{E}_R(r)= \sum_{\substack{P\mid f_r h_r \Rightarrow P \in I_r \\ \Omega(f_r) \leq (k \cdot \kappa)\ell_r \\ \Omega(h_r) \leq ( k \cdot \kappa) \ell_r }} \frac{ a (f_r h_r; J ) \lambda(f_r h_r) \nu_{k \kappa} (f_r;\ell_r) \nu_{k \kappa}(h_r;\ell_r) \chi_R\left(f_rh_r^2\right)}{ \kappa^{\Omega\left(f_r h_r\right)} \sqrt{ \lvert f_r h_r\rvert}}. \end{align*} $$
$$ \begin{align*} \mathcal{E}_R(r)= \sum_{\substack{P\mid f_r h_r \Rightarrow P \in I_r \\ \Omega(f_r) \leq (k \cdot \kappa)\ell_r \\ \Omega(h_r) \leq ( k \cdot \kappa) \ell_r }} \frac{ a (f_r h_r; J ) \lambda(f_r h_r) \nu_{k \kappa} (f_r;\ell_r) \nu_{k \kappa}(h_r;\ell_r) \chi_R\left(f_rh_r^2\right)}{ \kappa^{\Omega\left(f_r h_r\right)} \sqrt{ \lvert f_r h_r\rvert}}. \end{align*} $$ For ![]() $\theta _J $ small enough (depending on
$\theta _J $ small enough (depending on ![]() $d, k, \kappa $), note that we can apply Lemma 3.6 to evaluate formula (4.1), because from our choice of parameters, we have, for any
$d, k, \kappa $), note that we can apply Lemma 3.6 to evaluate formula (4.1), because from our choice of parameters, we have, for any ![]() $j \leq J -1$,
$j \leq J -1$,
 $$ \begin{align} 4\sum_{r \leq j} \theta_r\ell_r + 4\theta_{j+1} s_{j+1} + 3 \sum_{r=0}^J \theta_r k \kappa \ell_r \leq 1/2. \end{align} $$
$$ \begin{align} 4\sum_{r \leq j} \theta_r\ell_r + 4\theta_{j+1} s_{j+1} + 3 \sum_{r=0}^J \theta_r k \kappa \ell_r \leq 1/2. \end{align} $$We then obtain that formula (4.1) is bounded by
 $$ \begin{align} q^{g+2} \left( \prod_{r=0}^j \left(1 + e^{-\ell_r/2} \right)^2 E(r) \times E({j+1}) \times \prod_{r=j+2}^J E(r) \right), \end{align} $$
$$ \begin{align} q^{g+2} \left( \prod_{r=0}^j \left(1 + e^{-\ell_r/2} \right)^2 E(r) \times E({j+1}) \times \prod_{r=j+2}^J E(r) \right), \end{align} $$where the ![]() $E(r)$ are the factors obtained after doing the average over R from Lemma 3.6. We proceed to address the three cases, depending on the value of r.
$E(r)$ are the factors obtained after doing the average over R from Lemma 3.6. We proceed to address the three cases, depending on the value of r.
For ![]() $r=0, \dotsc , j$, we have
$r=0, \dotsc , j$, we have

Notice that if ![]() $\max \{\Omega (f_r),\Omega (h_r),\Omega (F_{r1}H_{r1}), \Omega (F_{r2} H_{r2})\}\geq \ell _r$, we have
$\max \{\Omega (f_r),\Omega (h_r),\Omega (F_{r1}H_{r1}), \Omega (F_{r2} H_{r2})\}\geq \ell _r$, we have ![]() $2^{\Omega \left (f_rh_rF_{r1}H_{r1} F_{r2} H_{r2}\right )}\geq 2^{\ell _r}$. We write
$2^{\Omega \left (f_rh_rF_{r1}H_{r1} F_{r2} H_{r2}\right )}\geq 2^{\ell _r}$. We write ![]() $F_r=F_{r1} F_{r2}$,
$F_r=F_{r1} F_{r2}$, ![]() $H_r=H_{r1}H_{r2}$, and we recall that
$H_r=H_{r1}H_{r2}$, and we recall that ![]() $\nu _2(F_r) = (\nu * \nu )(F_r)$. We have
$\nu _2(F_r) = (\nu * \nu )(F_r)$. We have

where we have used the bounds  $\phi _{q^2}\left (f_r h_r^2 F_r H_r^2\right )/\left \lvert f_r h_r^2 F_r H_r^2\right \rvert _{q^2}, \lambda (f_r h_r), \nu (F_r), \nu (H_r) \leq 1$,
$\phi _{q^2}\left (f_r h_r^2 F_r H_r^2\right )/\left \lvert f_r h_r^2 F_r H_r^2\right \rvert _{q^2}, \lambda (f_r h_r), \nu (F_r), \nu (H_r) \leq 1$, ![]() $ a(F_rH_r;j), a(f_r h_r; J ) \leq 1$ in the second term. Now using the facts that
$ a(F_rH_r;j), a(f_r h_r; J ) \leq 1$ in the second term. Now using the facts that ![]() $\nu _{k \kappa }(f_r) \leq (k \kappa )^{\Omega \left (f_r\right )}$ and
$\nu _{k \kappa }(f_r) \leq (k \kappa )^{\Omega \left (f_r\right )}$ and ![]() $\nu _2(F_r) \leq 2^{\Omega \left (F_r\right )}$, we get that the second term in formula (4.4) is
$\nu _2(F_r) \leq 2^{\Omega \left (F_r\right )}$, we get that the second term in formula (4.4) is

Now write ![]() $(f_r,h_r)=X$ and
$(f_r,h_r)=X$ and ![]() $(F_r,H_r)=Y$ and let
$(F_r,H_r)=Y$ and let ![]() $f_r=f_{r,0}X$,
$f_r=f_{r,0}X$, ![]() $h_r=h_{r,0}X$,
$h_r=h_{r,0}X$, ![]() $F_r=F_{r,0}Y$ and
$F_r=F_{r,0}Y$ and ![]() $H_r=H_{r,0}Y$. Then
$H_r=H_{r,0}Y$. Then  . Write
. Write ![]() $\left (f_{r,0},H_{r,0}\right )=S$ and
$\left (f_{r,0},H_{r,0}\right )=S$ and ![]() $\left (h_{r,0},F_{r,0}\right )=T$, and write
$\left (h_{r,0},F_{r,0}\right )=T$, and write ![]() $f_{r,0}=f_{r,1}S$,
$f_{r,0}=f_{r,1}S$, ![]() $h_{r,0}=h_{r,1}T$,
$h_{r,0}=h_{r,1}T$, ![]() $F_{r,0}=F_{r,1}T$ and
$F_{r,0}=F_{r,1}T$ and ![]() $H_{r,0}=H_{r,1}S$. Then
$H_{r,0}=H_{r,1}S$. Then  with
with ![]() $\left (f_{r,1}F_{r,1}, h_{r,1}H_{r,1}\right )=1$, and it follows that
$\left (f_{r,1}F_{r,1}, h_{r,1}H_{r,1}\right )=1$, and it follows that ![]() ,
, ![]() . Let
. Let ![]() $\left (f_{r,1},F_{r,1}\right )=M$,
$\left (f_{r,1},F_{r,1}\right )=M$, ![]() $f_{r,1}=f_{r,2}M$,
$f_{r,1}=f_{r,2}M$, ![]() $F_{r,1}=F_{r,2}M$. Then
$F_{r,1}=F_{r,2}M$. Then ![]() . Write
. Write ![]() with
with ![]() $(C,D)=1$ and
$(C,D)=1$ and ![]() $C, D$ square-free. Then
$C, D$ square-free. Then ![]() and it follows that
and it follows that  ,
,  , where
, where ![]() $C_1C_2=C$ and
$C_1C_2=C$ and ![]() $D_1D_2=D$. Then we replace
$D_1D_2=D$. Then we replace
 $$ \begin{align*} f_r\rightarrow X SCD^2C_1D_1^2f_r^3, \qquad F_r\rightarrow YTCD^2C_2D_2^2F_r^3, \end{align*} $$
$$ \begin{align*} f_r\rightarrow X SCD^2C_1D_1^2f_r^3, \qquad F_r\rightarrow YTCD^2C_2D_2^2F_r^3, \end{align*} $$and similarly
 $$ \begin{align*} h_r\rightarrow X TAB^2A_1B_1^2h_r^3, \qquad H_r\rightarrow YSAB^2A_2B_2^2H_r^3, \end{align*} $$
$$ \begin{align*} h_r\rightarrow X TAB^2A_1B_1^2h_r^3, \qquad H_r\rightarrow YSAB^2A_2B_2^2H_r^3, \end{align*} $$with ![]() $A_1A_2=A$ and
$A_1A_2=A$ and ![]() $B_1B_2=B$. We ignore the coprimality conditions when bounding the second term of formula (4.4), and for the first term we keep the condition
$B_1B_2=B$. We ignore the coprimality conditions when bounding the second term of formula (4.4), and for the first term we keep the condition ![]() $(S,T)=1$, which we need to get the cancellation between the mollifier and the short Dirichlet polynomial of the L-function.
$(S,T)=1$, which we need to get the cancellation between the mollifier and the short Dirichlet polynomial of the L-function.
Replacing in formula (4.5), we get that the second term in formula (4.4) is bounded by
 $$ \begin{align*} &\leq \frac{1}{2^{\ell_r}}\sum_{\substack{P\mid XYSTABCDf_r h_r F_r H_r\Rightarrow P \in I_r}} \frac{ (2k) ^{\Omega\left(X^2Y^2S^2T^2A^3B^6C^3D^6f_r^3h_r^3F_r^3H_r^3\right)}}{\left\lvert XYSTB^3D^3\right\rvert \lvert ACf_rh_rF_rH_r\rvert^{3/2} } \nonumber\\ & \quad = \frac{1}{2^{\ell_r}} \prod_{P \in I_r} \left(1-\frac{ (2k)^2}{\lvert P\rvert} \right)^{-4} \left(1- \frac{ (2k)^3}{\lvert P\rvert^{3/2}} \right)^{-6} \left(1- \frac{(2k)^6}{\lvert P\rvert^3} \right)^{-2}\nonumber. \end{align*} $$
$$ \begin{align*} &\leq \frac{1}{2^{\ell_r}}\sum_{\substack{P\mid XYSTABCDf_r h_r F_r H_r\Rightarrow P \in I_r}} \frac{ (2k) ^{\Omega\left(X^2Y^2S^2T^2A^3B^6C^3D^6f_r^3h_r^3F_r^3H_r^3\right)}}{\left\lvert XYSTB^3D^3\right\rvert \lvert ACf_rh_rF_rH_r\rvert^{3/2} } \nonumber\\ & \quad = \frac{1}{2^{\ell_r}} \prod_{P \in I_r} \left(1-\frac{ (2k)^2}{\lvert P\rvert} \right)^{-4} \left(1- \frac{ (2k)^3}{\lvert P\rvert^{3/2}} \right)^{-6} \left(1- \frac{(2k)^6}{\lvert P\rvert^3} \right)^{-2}\nonumber. \end{align*} $$Let ![]() $F(r)$ denote this expression. Using the inequality form of the Prime Polynomial Theorem (2.1), note that for
$F(r)$ denote this expression. Using the inequality form of the Prime Polynomial Theorem (2.1), note that for ![]() $r \neq 0$, we have
$r \neq 0$, we have
 $$ \begin{align*} F(r) \leq_{\varepsilon} \frac{1}{2^{\ell_r}}\exp \left(4(2k)^2+ 6(2k)^3 \sum_{(g+2)\theta_{r-1}<n\leq (g+2) \theta_r} \frac{1}{nq^{n/2}}+2(2k)^6 \sum_{(g+2)\theta_{r-1}<n\leq (g+2) \theta_r} \frac{1}{nq^{2n}} \right), \end{align*} $$
$$ \begin{align*} F(r) \leq_{\varepsilon} \frac{1}{2^{\ell_r}}\exp \left(4(2k)^2+ 6(2k)^3 \sum_{(g+2)\theta_{r-1}<n\leq (g+2) \theta_r} \frac{1}{nq^{n/2}}+2(2k)^6 \sum_{(g+2)\theta_{r-1}<n\leq (g+2) \theta_r} \frac{1}{nq^{2n}} \right), \end{align*} $$and hence
 $$ \begin{align} F(r)\leq_\varepsilon \frac{1}{2^{\ell_r}} \exp\left(16 k^2\right). \end{align} $$
$$ \begin{align} F(r)\leq_\varepsilon \frac{1}{2^{\ell_r}} \exp\left(16 k^2\right). \end{align} $$For ![]() $r=0$, we have
$r=0$, we have
 $$ \begin{align*} F(r) \leq_{\varepsilon} \frac{1}{2^{\ell_0}} ((g+2) \theta_0)^{O(1)}, \end{align*} $$
$$ \begin{align*} F(r) \leq_{\varepsilon} \frac{1}{2^{\ell_0}} ((g+2) \theta_0)^{O(1)}, \end{align*} $$and we remark that
 $$ \begin{align*} \lim_{g \rightarrow \infty} F(0)= 0. \end{align*} $$
$$ \begin{align*} \lim_{g \rightarrow \infty} F(0)= 0. \end{align*} $$For the first term in formula (4.4), using the change of variable from before, we get
 $$ \begin{align*} &\sum_{\substack{P\mid ABCDf_r h_r F_r H_r\Rightarrow P \in I_r \\ C_1C_2=C, D_1D_2=D\\ A_1A_2=A, B_1B_2=B}}\frac{ (k/2)^{\Omega\left(CD^2C_2D_2^2AB^2A_2B_2^2F_r^3H_r^3\right)} \lambda(CC_1AA_1f_rh_r)}{\kappa^{\Omega\left(CD^2C_1D_1^2AB^2A_1B_1^2f_r^3 h_r^3\right)} \sqrt{ \left\lvert C^3D^6 A^3B^6f_r^3 h_r^3F_r^3 H_r^3\right\rvert}}\\[6pt] &\qquad \times a\left(f_r^3h_r^3;J \right)a\left(AB^2A_1 B_1^2CD^2C_1D_1^2;J \right) a\left(F_r^3H_r^3;j\right) a\left(AB^2A_2B_2^2CD^2C_2D_2^2;j\right) \\[6pt] & \qquad \times \sum_{\substack{P\mid STXY\Rightarrow P \in I_r\\ \left(S, T\right)=1}} \frac{ (k/2)^{\Omega\left(Y^2ST\right)} a(S;J ) a(S; j) a(T;J ) a(T;j) a(X; J )^2 a(Y; j)^2 \lambda(ST) }{\kappa^{\Omega\left(X^2 ST\right)} \lvert YX ST\rvert } \\[6pt] & \qquad \times \nu_2\left( YTCD^2C_2D_2^2F_r^3\right) \nu_2\left(YSAB^2A_2B_2^2H_r^3\right) \\[6pt] & \qquad \times \nu_{k \kappa} \left(X SCD^2C_1D_1^2f_r^3\right) \nu_{k \kappa}\left(X TAB^2A_1B_1^2h_r^3\right) \\[6pt] & \qquad \times \frac{\phi_{q^2}\left(X^3 S^3T^3Y^3C^3D^6 A^6B^{12}f_r^3h_r^6F_r^3H_r^6\right)}{ \left\lvert X^3 S^3T^3Y^3C^3D^6 A^6B^{12}f_r^3h_r^6F_r^3H_r^6\right\rvert_{q^2}}. \end{align*} $$
$$ \begin{align*} &\sum_{\substack{P\mid ABCDf_r h_r F_r H_r\Rightarrow P \in I_r \\ C_1C_2=C, D_1D_2=D\\ A_1A_2=A, B_1B_2=B}}\frac{ (k/2)^{\Omega\left(CD^2C_2D_2^2AB^2A_2B_2^2F_r^3H_r^3\right)} \lambda(CC_1AA_1f_rh_r)}{\kappa^{\Omega\left(CD^2C_1D_1^2AB^2A_1B_1^2f_r^3 h_r^3\right)} \sqrt{ \left\lvert C^3D^6 A^3B^6f_r^3 h_r^3F_r^3 H_r^3\right\rvert}}\\[6pt] &\qquad \times a\left(f_r^3h_r^3;J \right)a\left(AB^2A_1 B_1^2CD^2C_1D_1^2;J \right) a\left(F_r^3H_r^3;j\right) a\left(AB^2A_2B_2^2CD^2C_2D_2^2;j\right) \\[6pt] & \qquad \times \sum_{\substack{P\mid STXY\Rightarrow P \in I_r\\ \left(S, T\right)=1}} \frac{ (k/2)^{\Omega\left(Y^2ST\right)} a(S;J ) a(S; j) a(T;J ) a(T;j) a(X; J )^2 a(Y; j)^2 \lambda(ST) }{\kappa^{\Omega\left(X^2 ST\right)} \lvert YX ST\rvert } \\[6pt] & \qquad \times \nu_2\left( YTCD^2C_2D_2^2F_r^3\right) \nu_2\left(YSAB^2A_2B_2^2H_r^3\right) \\[6pt] & \qquad \times \nu_{k \kappa} \left(X SCD^2C_1D_1^2f_r^3\right) \nu_{k \kappa}\left(X TAB^2A_1B_1^2h_r^3\right) \\[6pt] & \qquad \times \frac{\phi_{q^2}\left(X^3 S^3T^3Y^3C^3D^6 A^6B^{12}f_r^3h_r^6F_r^3H_r^6\right)}{ \left\lvert X^3 S^3T^3Y^3C^3D^6 A^6B^{12}f_r^3h_r^6F_r^3H_r^6\right\rvert_{q^2}}. \end{align*} $$ For every fixed value of ![]() $A, B, C, D, f_r, h_r, F_r, H_r, A_1, A_2, B_1, B_2, C_1, C_2, D_1, D_2$, let
$A, B, C, D, f_r, h_r, F_r, H_r, A_1, A_2, B_1, B_2, C_1, C_2, D_1, D_2$, let
 $$ \begin{align*} &\mathcal{F} (A, B, C, D, f_r, h_r, F_r, H_r, A_1, A_2, B_1, B_2, C_1, C_2, D_1, D_2) \\ &:=\prod_{\substack{P \in I_r \\P^a \parallel A, P^b \parallel B, \dotsc, P^{d_1} \parallel D_1, P^{d_2} \parallel D_2, P^f\parallel f_r, P^h\parallel h_r, P^F\parallel F_r, P^H\parallel H_r}} \hspace{-40pt}\sigma(P; a,b,c,d,f,h,F,H, a_1, a_2, b_1, b_2, c_1, c_2, d_1, d_2), \end{align*} $$
$$ \begin{align*} &\mathcal{F} (A, B, C, D, f_r, h_r, F_r, H_r, A_1, A_2, B_1, B_2, C_1, C_2, D_1, D_2) \\ &:=\prod_{\substack{P \in I_r \\P^a \parallel A, P^b \parallel B, \dotsc, P^{d_1} \parallel D_1, P^{d_2} \parallel D_2, P^f\parallel f_r, P^h\parallel h_r, P^F\parallel F_r, P^H\parallel H_r}} \hspace{-40pt}\sigma(P; a,b,c,d,f,h,F,H, a_1, a_2, b_1, b_2, c_1, c_2, d_1, d_2), \end{align*} $$where
 $$ \begin{align*} & \sigma(P; a,b,c,d,f,h,F,H, a_1, a_2, b_1, b_2, c_1, c_2, d_1, d_2)\\ & \quad := \sum_{s, t, x, y \geq 0, st =0} \Bigg( (k/2)^{s+t+2y} (1/\kappa)^{s+t+2x} a(P; j)^{s+t+2y} a(P; J )^{s+t+2x} (-1)^{s + t} \\ & \qquad \phantom{\Bigg(} \times \nu_2\left(P^{t + y+c+2d+c_2+2 d_2 +3F}\right) \nu_2\left(P^{s + y+a+2b+a_2+2b_2+3H}\right) \\ & \qquad \phantom{\Bigg(} \times \nu_{k \kappa}\left(P^{s + x+c+2d+c_1+2d_1+3f}\right) \nu_{k \kappa}\left(P^{t+ x+a+2b+a_1+2b_1+3h}\right)\\ & \qquad \times \frac{\phi_{q^2}\left(P^{3s + 3t + 3x + 3y+3c+6d+6a+12b+3f+6h+3F+6H}\right)}{\left\lvert P^{3s + 3t + 3x + 3y+3c+6d+6a+12b+3f+6h+3F+6H}\right\rvert_{q^2}} \frac{1}{\lvert P\rvert^{s+t+x+y}} \Bigg). \end{align*} $$
$$ \begin{align*} & \sigma(P; a,b,c,d,f,h,F,H, a_1, a_2, b_1, b_2, c_1, c_2, d_1, d_2)\\ & \quad := \sum_{s, t, x, y \geq 0, st =0} \Bigg( (k/2)^{s+t+2y} (1/\kappa)^{s+t+2x} a(P; j)^{s+t+2y} a(P; J )^{s+t+2x} (-1)^{s + t} \\ & \qquad \phantom{\Bigg(} \times \nu_2\left(P^{t + y+c+2d+c_2+2 d_2 +3F}\right) \nu_2\left(P^{s + y+a+2b+a_2+2b_2+3H}\right) \\ & \qquad \phantom{\Bigg(} \times \nu_{k \kappa}\left(P^{s + x+c+2d+c_1+2d_1+3f}\right) \nu_{k \kappa}\left(P^{t+ x+a+2b+a_1+2b_1+3h}\right)\\ & \qquad \times \frac{\phi_{q^2}\left(P^{3s + 3t + 3x + 3y+3c+6d+6a+12b+3f+6h+3F+6H}\right)}{\left\lvert P^{3s + 3t + 3x + 3y+3c+6d+6a+12b+3f+6h+3F+6H}\right\rvert_{q^2}} \frac{1}{\lvert P\rvert^{s+t+x+y}} \Bigg). \end{align*} $$We can rewrite the first term in formula (4.4) as
 $$ \begin{align} A(r) & := \prod_{P \in I_r} \sum_{\substack{P\mid ABCDf_r h_r F_r H_r\Rightarrow P \in I_r \\ C_1C_2=C, D_1D_2=D\\ A_1A_2=A, B_1B_2=B}}\frac{ (k/2)^{\Omega\left(CD^2C_2D_2^2AB^2A_2B_2^2F_r^3H_r^3\right)} \lambda(CC_1AA_1f_rh_r)}{\kappa^{\Omega\left(CD^2C_1D_1^2AB^2A_1B_1^2f_r^3 h_r^3\right)} \sqrt{ \left\lvert C^3D^6 A^3B^6f_r^3 h_r^3F_r^3 H_r^3\right\rvert}} \nonumber\\ & \quad \times a\left(f_r^3h_r^3;J \right)a\left(AB^2CD^2C_1D_1^2A_1 B_1^2;J \right) a\left(F_r^3H_r^3;j\right) a\left(AB^2CD^2A_2B_2^2C_2D_2^2;j\right) \nonumber \\ & \quad \times \mathcal{F} (A, B, C, D, f_r, h_r, F_r, H_r, A_1, A_2, B_1, B_2, C_1, C_2, D_1, D_2), \end{align} $$
$$ \begin{align} A(r) & := \prod_{P \in I_r} \sum_{\substack{P\mid ABCDf_r h_r F_r H_r\Rightarrow P \in I_r \\ C_1C_2=C, D_1D_2=D\\ A_1A_2=A, B_1B_2=B}}\frac{ (k/2)^{\Omega\left(CD^2C_2D_2^2AB^2A_2B_2^2F_r^3H_r^3\right)} \lambda(CC_1AA_1f_rh_r)}{\kappa^{\Omega\left(CD^2C_1D_1^2AB^2A_1B_1^2f_r^3 h_r^3\right)} \sqrt{ \left\lvert C^3D^6 A^3B^6f_r^3 h_r^3F_r^3 H_r^3\right\rvert}} \nonumber\\ & \quad \times a\left(f_r^3h_r^3;J \right)a\left(AB^2CD^2C_1D_1^2A_1 B_1^2;J \right) a\left(F_r^3H_r^3;j\right) a\left(AB^2CD^2A_2B_2^2C_2D_2^2;j\right) \nonumber \\ & \quad \times \mathcal{F} (A, B, C, D, f_r, h_r, F_r, H_r, A_1, A_2, B_1, B_2, C_1, C_2, D_1, D_2), \end{align} $$and we will show that
 $$ \begin{align} \prod_{r=0}^j A(r) \leq C(k) \end{align} $$
$$ \begin{align} \prod_{r=0}^j A(r) \leq C(k) \end{align} $$for some constant ![]() $C(k)$.
$C(k)$.
Since we need an explicit constant, in the case ![]() $k=2$ we will prove that that we can take
$k=2$ we will prove that that we can take  $C(2)=e^{e^{15}}$. We can write
$C(2)=e^{e^{15}}$. We can write ![]() $A(r)$ as an Euler product, and we look at the coefficients of
$A(r)$ as an Euler product, and we look at the coefficients of ![]() $1/\lvert P\rvert $,
$1/\lvert P\rvert $, ![]() $1/\lvert P\rvert ^{3/2}$,
$1/\lvert P\rvert ^{3/2}$, ![]() $1/\lvert P\rvert ^2$ and
$1/\lvert P\rvert ^2$ and ![]() $1/\lvert P\rvert ^{5/2}$. Recall that
$1/\lvert P\rvert ^{5/2}$. Recall that  $\nu _\ell (P^a)=\frac {\ell ^a}{a!}$. For the coefficient of
$\nu _\ell (P^a)=\frac {\ell ^a}{a!}$. For the coefficient of ![]() $1/\lvert P\rvert $, we need to consider
$1/\lvert P\rvert $, we need to consider ![]() $A=B=C=D=f_r=h_r=F_r=H_r=1$ and
$A=B=C=D=f_r=h_r=F_r=H_r=1$ and ![]() $s,t,x$ or
$s,t,x$ or ![]() $y=1$. This gives
$y=1$. This gives
 $$ \begin{align*} \alpha_{j,1}(P):=k^2(a(P;J)-a(P,j))^2\frac{\phi_{q^2}\left(P^3\right)}{\left\lvert P^3\right\rvert_{q^2}} \end{align*} $$
$$ \begin{align*} \alpha_{j,1}(P):=k^2(a(P;J)-a(P,j))^2\frac{\phi_{q^2}\left(P^3\right)}{\left\lvert P^3\right\rvert_{q^2}} \end{align*} $$for the coefficient of ![]() $1/\lvert P\rvert $. Since
$1/\lvert P\rvert $. Since ![]() $0< a(P;j)<a(P;J)<1$, we remark that
$0< a(P;j)<a(P;J)<1$, we remark that ![]() $0<\alpha _{j,1}(P)<k^2$.
$0<\alpha _{j,1}(P)<k^2$.
For the coefficient of ![]() $1/\lvert P\rvert ^{3/2}$ we consider
$1/\lvert P\rvert ^{3/2}$ we consider ![]() $f_r=P$,
$f_r=P$, ![]() $h_r=P, F_r=P, H_r=P$ and
$h_r=P, F_r=P, H_r=P$ and ![]() $A=P, A_1=1$ and
$A=P, A_1=1$ and ![]() $A=P, A_1=P$,
$A=P, A_1=P$, ![]() $C=P, C_1=1$ and
$C=P, C_1=1$ and ![]() $C=P, C_1=P$, while
$C=P, C_1=P$, while ![]() $s=t=x=y=0$. When
$s=t=x=y=0$. When ![]() $f_r=P$ (and everything else is
$f_r=P$ (and everything else is ![]() $1$) we get a factor of
$1$) we get a factor of
 $$ \begin{align*} -\frac{1}{\kappa^3}a(P;J )^3 \nu_{k \kappa} \left(P^3\right) \frac{\phi_{q^2}\left(P^3\right)}{\lvert P\rvert^{3/2}\lvert P\rvert_{q^2}^3}= -\frac{k^3 a(P;J )^3 \phi_{q^2}\left(P^3\right)}{6\lvert P\rvert^{3/2} \left\lvert P^3\right\rvert_{q^2}}. \end{align*} $$
$$ \begin{align*} -\frac{1}{\kappa^3}a(P;J )^3 \nu_{k \kappa} \left(P^3\right) \frac{\phi_{q^2}\left(P^3\right)}{\lvert P\rvert^{3/2}\lvert P\rvert_{q^2}^3}= -\frac{k^3 a(P;J )^3 \phi_{q^2}\left(P^3\right)}{6\lvert P\rvert^{3/2} \left\lvert P^3\right\rvert_{q^2}}. \end{align*} $$We get the same term when ![]() $h_r=P$. If
$h_r=P$. If ![]() $F_r=P$, we get
$F_r=P$, we get
 $$ \begin{align*} \frac{k^3 a(P;j)^3\phi_{q^2}\left(P^3\right)}{6\lvert P\rvert^{3/2}\left\lvert P^3\right\rvert_{q^2}}, \end{align*} $$
$$ \begin{align*} \frac{k^3 a(P;j)^3\phi_{q^2}\left(P^3\right)}{6\lvert P\rvert^{3/2}\left\lvert P^3\right\rvert_{q^2}}, \end{align*} $$and when ![]() $H_r=P$ we get the same factor. If
$H_r=P$ we get the same factor. If ![]() $A=P, A_1=1$, we get the term
$A=P, A_1=1$, we get the term
 $$ \begin{align*} - \frac{k^2a(P;J ) a(P;j)^2}{\kappa} \frac{k \kappa \phi_{q^2}\left(P^6\right)}{2\lvert P\rvert^{3/2}\left\lvert P^6\right\rvert_{q^2}}= -\frac{k^3 a(P;J ) a(P;j)^2 \phi_{q^2}\left(P^6\right)}{2 \lvert P\rvert^{3/2} \left\lvert P^6\right\rvert_{q^2}}. \end{align*} $$
$$ \begin{align*} - \frac{k^2a(P;J ) a(P;j)^2}{\kappa} \frac{k \kappa \phi_{q^2}\left(P^6\right)}{2\lvert P\rvert^{3/2}\left\lvert P^6\right\rvert_{q^2}}= -\frac{k^3 a(P;J ) a(P;j)^2 \phi_{q^2}\left(P^6\right)}{2 \lvert P\rvert^{3/2} \left\lvert P^6\right\rvert_{q^2}}. \end{align*} $$Similarly, when ![]() $A=P, A_1=P$, we get
$A=P, A_1=P$, we get
 $$ \begin{align*} \frac{k^3 a(P;J )^2 a(P;j) \phi_{q^2}\left(P^6\right)}{2 \lvert P\rvert^{3/2} \left\lvert P^6\right\rvert_{q^2}}. \end{align*} $$
$$ \begin{align*} \frac{k^3 a(P;J )^2 a(P;j) \phi_{q^2}\left(P^6\right)}{2 \lvert P\rvert^{3/2} \left\lvert P^6\right\rvert_{q^2}}. \end{align*} $$Putting all of this together, we get
 $$ \begin{align*} \alpha_{j,3/2}(P):=-k^3(a(P;J)-a(P;j))^3 \frac{\phi_{q^2} \left(P^3\right)}{3\left\lvert P^3\right\rvert_{q^2}} \end{align*} $$
$$ \begin{align*} \alpha_{j,3/2}(P):=-k^3(a(P;J)-a(P;j))^3 \frac{\phi_{q^2} \left(P^3\right)}{3\left\lvert P^3\right\rvert_{q^2}} \end{align*} $$for the coefficient of ![]() $1/\lvert P\rvert ^{3/2}$. We remark that
$1/\lvert P\rvert ^{3/2}$. We remark that  $-\frac {k^3}{3}<\alpha _{j,3/2}(P)<0$, since
$-\frac {k^3}{3}<\alpha _{j,3/2}(P)<0$, since ![]() $a(P;j)<a(P;J)$.
$a(P;j)<a(P;J)$.
For the coefficient of ![]() $1/\lvert P\rvert ^{2}$, we must take
$1/\lvert P\rvert ^{2}$, we must take ![]() $A=B=C=D=f_r=h_r=F_r=H_r=1$ and
$A=B=C=D=f_r=h_r=F_r=H_r=1$ and ![]() $s+t+x+y=2$, and we proceed as before to obtain
$s+t+x+y=2$, and we proceed as before to obtain
 $$ \begin{align*} \alpha_{j,2}(P):=k^4(a(P;J)-a(P;j))^4 \frac{\phi_{q^2} \left(P^6\right)}{4\left\lvert P^6\right\rvert_{q^2}}, \end{align*} $$
$$ \begin{align*} \alpha_{j,2}(P):=k^4(a(P;J)-a(P;j))^4 \frac{\phi_{q^2} \left(P^6\right)}{4\left\lvert P^6\right\rvert_{q^2}}, \end{align*} $$and we have that  $0<\alpha _{j,2}(P)<\frac {k^4}{4}$.
$0<\alpha _{j,2}(P)<\frac {k^4}{4}$.
For the coefficient of ![]() $1/\lvert P\rvert ^{5/2}$, we obtain the product of the coefficients of
$1/\lvert P\rvert ^{5/2}$, we obtain the product of the coefficients of ![]() $1/\lvert P\rvert $ and
$1/\lvert P\rvert $ and ![]() $1/\lvert P\rvert ^{3/2}$, resulting in
$1/\lvert P\rvert ^{3/2}$, resulting in
 $$ \begin{align*} \alpha_{j,5/2}(P):=-k^5(a(P;J)-a(P,j))^5\frac{\phi_{q^2}\left(P^3\right)^2}{3\left\lvert P^6\right\rvert_{q^2}}, \end{align*} $$
$$ \begin{align*} \alpha_{j,5/2}(P):=-k^5(a(P;J)-a(P,j))^5\frac{\phi_{q^2}\left(P^3\right)^2}{3\left\lvert P^6\right\rvert_{q^2}}, \end{align*} $$which satisfies  $-\frac {k^5}{3}<\alpha _{j,5/2}(P)<0$.
$-\frac {k^5}{3}<\alpha _{j,5/2}(P)<0$.
Overall, for the sum over ![]() $A,B,C,D, A_1, C_1, B_1, D_1,F_r,h_r,F_r,H_r$ we get
$A,B,C,D, A_1, C_1, B_1, D_1,F_r,h_r,F_r,H_r$ we get
 $$ \begin{align} A(r) = \prod_{P \in I_r} \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}+\frac{\alpha_{j,3/2}(P)}{\lvert P\rvert^{3/2}}+\frac{\alpha_{j,2}(P)}{\lvert P\rvert^2} +\frac{\alpha_{j,5/2}(P)}{\lvert P\rvert^{5/2}}+ O \left( \frac{1}{\lvert P\rvert^{3}} \right) \right). \end{align} $$
$$ \begin{align} A(r) = \prod_{P \in I_r} \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}+\frac{\alpha_{j,3/2}(P)}{\lvert P\rvert^{3/2}}+\frac{\alpha_{j,2}(P)}{\lvert P\rvert^2} +\frac{\alpha_{j,5/2}(P)}{\lvert P\rvert^{5/2}}+ O \left( \frac{1}{\lvert P\rvert^{3}} \right) \right). \end{align} $$ Since we want to obtain an explicit constant for the case ![]() $k=2$, we proceed to bound the term corresponding to
$k=2$, we proceed to bound the term corresponding to  $O \left ( \frac {1}{\lvert P\rvert ^{3}} \right ) $. To do this we bound the terms of the form
$O \left ( \frac {1}{\lvert P\rvert ^{3}} \right ) $. To do this we bound the terms of the form ![]() $1/\lvert P\rvert ^{n/2}$ for
$1/\lvert P\rvert ^{n/2}$ for ![]() $n>5$ in the Euler product corresponding to the sum of formula (4.7). We bound trivially the signs and the terms involving
$n>5$ in the Euler product corresponding to the sum of formula (4.7). We bound trivially the signs and the terms involving ![]() $a(\cdot , j)$ and
$a(\cdot , j)$ and ![]() $a(\cdot , J)$, and we recall that
$a(\cdot , J)$, and we recall that  $\nu _\ell (P^a)=\frac {\ell ^a}{a!}$. Thus, the terms contributing to
$\nu _\ell (P^a)=\frac {\ell ^a}{a!}$. Thus, the terms contributing to ![]() $1/\lvert P\rvert ^{n/2}$ can be bounded by
$1/\lvert P\rvert ^{n/2}$ can be bounded by
 $$ \begin{align*} &\sum_{2s+2t+2x+2y+3a+6b+3c+6d+3f+3h+3F+3H=n} \left(\frac{k}{\lvert P\rvert^{1/2}}\right)^{2s+2t+2x+2y+3a+6b+3c+6d+3f+3h+3F+3H}\\& \qquad \times \frac{1}{(s+x+c+2d+c_1+2d_1+3f)!(t+x+a+2b+a_1+2b_1+3h)!}\\ & \qquad \times\frac{1}{ (t+y+c+2d+c_2+2d_2+3F)! (s+y+a+2b+a_2+2b_2+3H)!}. \end{align*} $$
$$ \begin{align*} &\sum_{2s+2t+2x+2y+3a+6b+3c+6d+3f+3h+3F+3H=n} \left(\frac{k}{\lvert P\rvert^{1/2}}\right)^{2s+2t+2x+2y+3a+6b+3c+6d+3f+3h+3F+3H}\\& \qquad \times \frac{1}{(s+x+c+2d+c_1+2d_1+3f)!(t+x+a+2b+a_1+2b_1+3h)!}\\ & \qquad \times\frac{1}{ (t+y+c+2d+c_2+2d_2+3F)! (s+y+a+2b+a_2+2b_2+3H)!}. \end{align*} $$ The number of terms in this sum is bounded by the number of ways of choosing values for the indices ![]() $a_1,a_2,\dotsc ,d_2,s,t,x,y,f,h,F,H$ subject to the condition that
$a_1,a_2,\dotsc ,d_2,s,t,x,y,f,h,F,H$ subject to the condition that ![]() $2s+2t+2x+2y+3a_1+3a_2+6b_1+6b_2+3c_1+3c_2+6d_1+6d_2+3f+3h+3F+3H=n$. Since there are 16 indices, this number is bounded by
$2s+2t+2x+2y+3a_1+3a_2+6b_1+6b_2+3c_1+3c_2+6d_1+6d_2+3f+3h+3F+3H=n$. Since there are 16 indices, this number is bounded by  $\binom {n+15}{15}$. In addition, note that the numbers in the four factorials sum up to n. Thus, the fraction involving the four factorials can be bounded by
$\binom {n+15}{15}$. In addition, note that the numbers in the four factorials sum up to n. Thus, the fraction involving the four factorials can be bounded by ![]() $\frac {4^n}{n!}$. Putting all of this together and summing over the powers of
$\frac {4^n}{n!}$. Putting all of this together and summing over the powers of ![]() $1/\lvert P\rvert ^{1/2}$ starting from
$1/\lvert P\rvert ^{1/2}$ starting from ![]() $1/\lvert P\rvert ^{3}$, we get that the contribution of the higher powers of
$1/\lvert P\rvert ^{3}$, we get that the contribution of the higher powers of ![]() $1/\lvert P\rvert ^{1/2}$ is bounded by
$1/\lvert P\rvert ^{1/2}$ is bounded by
 $$ \begin{align*} \sum_{\ell=6}^\infty \frac{\binom{\ell+15}{15}}{\ell!}\left(\frac{4k}{\lvert P\rvert^{1/2}}\right)^\ell. \end{align*} $$
$$ \begin{align*} \sum_{\ell=6}^\infty \frac{\binom{\ell+15}{15}}{\ell!}\left(\frac{4k}{\lvert P\rvert^{1/2}}\right)^\ell. \end{align*} $$Notice that  $\frac {\binom {\ell +15}{15}}{\ell !}$ is decreasing in
$\frac {\binom {\ell +15}{15}}{\ell !}$ is decreasing in ![]() $6\leq \ell $, with a maximum at
$6\leq \ell $, with a maximum at ![]() $\ell =6$. We thus get
$\ell =6$. We thus get
 $$ \begin{align*} \leq \frac{2261}{30} \sum_{\ell=6}^\infty \left(\frac{4k}{\lvert P\rvert^{1/2}}\right)^\ell \leq \frac{1}{\lvert P\rvert^3} \frac{2261 \cdot 2^{11} k^6}{15\left(1-\frac{4k}{\lvert P\rvert^{1/2}}\right)} \end{align*} $$
$$ \begin{align*} \leq \frac{2261}{30} \sum_{\ell=6}^\infty \left(\frac{4k}{\lvert P\rvert^{1/2}}\right)^\ell \leq \frac{1}{\lvert P\rvert^3} \frac{2261 \cdot 2^{11} k^6}{15\left(1-\frac{4k}{\lvert P\rvert^{1/2}}\right)} \end{align*} $$whenever ![]() $\lvert P\rvert ^{1/2}>4k$.
$\lvert P\rvert ^{1/2}>4k$.
We now suppose that ![]() $k=2$. Considering the worst case,
$k=2$. Considering the worst case, ![]() $q=5$, we can apply the foregoing, provided that
$q=5$, we can apply the foregoing, provided that ![]() $\deg (P)\geq 3$. Writing
$\deg (P)\geq 3$. Writing ![]() $\prod _r A(r)$ as a product over primes with
$\prod _r A(r)$ as a product over primes with ![]() $\deg (P) \leq (g+2) \theta _j$, and restricting to those primes with
$\deg (P) \leq (g+2) \theta _j$, and restricting to those primes with ![]() $\deg (P) \geq 3$, we get that this contribution is bounded by
$\deg (P) \geq 3$, we get that this contribution is bounded by
 $$ \begin{align*} &\prod_{3\leq \deg(P) \leq (g+2) \theta_j} \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}+\frac{\alpha_{j,3/2}(P)}{\lvert P\rvert^{3/2}}+\frac{\alpha_{j,2}(P)}{\lvert P\rvert^2} +\frac{\alpha_{j,5/2}(P)}{\lvert P\rvert^{5/2}}+ \frac{1}{\lvert P\rvert^3} \frac{2261 \cdot 2^{17} }{15\left(1-\frac{8}{5^{3/2}}\right)} \right)\\ &\quad \leq \prod_{3\leq \deg(P) \leq (g+2) \theta_j } \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}\right) \left(1+ \frac{\alpha_{j,2}(P)}{\left\lvert P^2\right\rvert}\right) \left(1+ \frac{1}{\lvert P\rvert^3} \frac{2261 \cdot 2^{17} }{15\left(1-\frac{8}{5^{3/2}}\right)}\right). \end{align*} $$
$$ \begin{align*} &\prod_{3\leq \deg(P) \leq (g+2) \theta_j} \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}+\frac{\alpha_{j,3/2}(P)}{\lvert P\rvert^{3/2}}+\frac{\alpha_{j,2}(P)}{\lvert P\rvert^2} +\frac{\alpha_{j,5/2}(P)}{\lvert P\rvert^{5/2}}+ \frac{1}{\lvert P\rvert^3} \frac{2261 \cdot 2^{17} }{15\left(1-\frac{8}{5^{3/2}}\right)} \right)\\ &\quad \leq \prod_{3\leq \deg(P) \leq (g+2) \theta_j } \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}\right) \left(1+ \frac{\alpha_{j,2}(P)}{\left\lvert P^2\right\rvert}\right) \left(1+ \frac{1}{\lvert P\rvert^3} \frac{2261 \cdot 2^{17} }{15\left(1-\frac{8}{5^{3/2}}\right)}\right). \end{align*} $$Noticing that
 $$ \begin{align*} a(P;J )-a(P;j) &= \frac{1}{\lvert P\rvert^{\frac{1}{(g+2) \theta_J \log q}}} - \frac{1}{\lvert P\rvert^{\frac{1}{(g+2) \theta_j \log q}}}+ \frac{\deg(P)}{(g+2) \theta_j \lvert P\rvert^{\frac{1}{(g+2) \theta_j \log q}}} -\frac{\deg(P)}{(g+2) \theta_J \lvert P\rvert^{\frac{1}{(g+2) \theta_J \log q}}} \\ & \leq 1- \left(1- \frac{\deg(P) }{(g+2) \theta_j}\right)+ \frac{\deg(P)}{(g+2) \theta_j} \leq \frac{2 \deg(P) }{(g+2) \theta_j}, \end{align*} $$
$$ \begin{align*} a(P;J )-a(P;j) &= \frac{1}{\lvert P\rvert^{\frac{1}{(g+2) \theta_J \log q}}} - \frac{1}{\lvert P\rvert^{\frac{1}{(g+2) \theta_j \log q}}}+ \frac{\deg(P)}{(g+2) \theta_j \lvert P\rvert^{\frac{1}{(g+2) \theta_j \log q}}} -\frac{\deg(P)}{(g+2) \theta_J \lvert P\rvert^{\frac{1}{(g+2) \theta_J \log q}}} \\ & \leq 1- \left(1- \frac{\deg(P) }{(g+2) \theta_j}\right)+ \frac{\deg(P)}{(g+2) \theta_j} \leq \frac{2 \deg(P) }{(g+2) \theta_j}, \end{align*} $$we obtain
 $$ \begin{align} \prod_{3\leq \deg{P} \leq (g+2) \theta_j} \left( 1 + \frac{\alpha_{j,1}(P)}{\lvert P\rvert} \right) & \leq \exp \left(\sum_{\deg{P} \leq (g+2) \theta_j} \frac{\alpha_{j,1}(P)}{\lvert P\rvert} \right) \nonumber \\ & \leq \exp \left(\frac{16 }{(g+2)\theta_j}\sum_{\deg{P} \leq (g+2) \theta_j} \frac{\deg(P)}{\lvert P\rvert} \right) \leq \exp(16). \end{align} $$
$$ \begin{align} \prod_{3\leq \deg{P} \leq (g+2) \theta_j} \left( 1 + \frac{\alpha_{j,1}(P)}{\lvert P\rvert} \right) & \leq \exp \left(\sum_{\deg{P} \leq (g+2) \theta_j} \frac{\alpha_{j,1}(P)}{\lvert P\rvert} \right) \nonumber \\ & \leq \exp \left(\frac{16 }{(g+2)\theta_j}\sum_{\deg{P} \leq (g+2) \theta_j} \frac{\deg(P)}{\lvert P\rvert} \right) \leq \exp(16). \end{align} $$We also have
 $$ \begin{align} \prod_{3\leq \deg{P} \leq (g+2) \theta_j} \left(1+ \frac{\alpha_{j,2}(P)}{\left\lvert P^2\right\rvert}\right)\leq \prod_P \left(1+ \frac{4}{\left\lvert P^2\right\rvert}\right)\leq \left(\frac{\zeta_q(2)}{\zeta_q(4)}\right)^{4}<3 \end{align} $$
$$ \begin{align} \prod_{3\leq \deg{P} \leq (g+2) \theta_j} \left(1+ \frac{\alpha_{j,2}(P)}{\left\lvert P^2\right\rvert}\right)\leq \prod_P \left(1+ \frac{4}{\left\lvert P^2\right\rvert}\right)\leq \left(\frac{\zeta_q(2)}{\zeta_q(4)}\right)^{4}<3 \end{align} $$and
 $$ \begin{align} \prod_{3\leq \deg{P} \leq (g+2) \theta_j} \left(1+ \frac{1}{\lvert P\rvert^3} \frac{2261 \cdot 2^{17} }{15\left(1-\frac{8}{5^{3/2}}\right)}\right)\leq \left(\frac{\zeta_q(3)}{\zeta_q(6)}\right)^{e^{18.1}}\leq e^{e^{14.9}}. \end{align} $$
$$ \begin{align} \prod_{3\leq \deg{P} \leq (g+2) \theta_j} \left(1+ \frac{1}{\lvert P\rvert^3} \frac{2261 \cdot 2^{17} }{15\left(1-\frac{8}{5^{3/2}}\right)}\right)\leq \left(\frac{\zeta_q(3)}{\zeta_q(6)}\right)^{e^{18.1}}\leq e^{e^{14.9}}. \end{align} $$When ![]() $\deg (P)\leq 2$ and
$\deg (P)\leq 2$ and ![]() $k=2$, we can bound
$k=2$, we can bound
 $$ \begin{align*}\sum_{\ell=6}^\infty \frac{\binom{\ell+15}{15}}{\ell!}\left(\frac{8}{\lvert P\rvert^{1/2}}\right)^\ell & \leq 2^{15}\sum_{\ell=6}^\infty \frac{1}{\ell!}\left(\frac{16}{\lvert P\rvert^{1/2}}\right)^\ell\\ & \leq \frac{2^{10}}{45}\left(\frac{16}{\lvert P\rvert^{1/2}}\right)^6 \exp \left( \frac{16}{\lvert P\rvert^{1/2}}\right). \end{align*} $$
$$ \begin{align*}\sum_{\ell=6}^\infty \frac{\binom{\ell+15}{15}}{\ell!}\left(\frac{8}{\lvert P\rvert^{1/2}}\right)^\ell & \leq 2^{15}\sum_{\ell=6}^\infty \frac{1}{\ell!}\left(\frac{16}{\lvert P\rvert^{1/2}}\right)^\ell\\ & \leq \frac{2^{10}}{45}\left(\frac{16}{\lvert P\rvert^{1/2}}\right)^6 \exp \left( \frac{16}{\lvert P\rvert^{1/2}}\right). \end{align*} $$Applying the Prime Polynomial Theorem, this gives
 $$ \begin{align} \prod_{\deg (P)\leq 2 } & \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}+\frac{\alpha_{j,3/2}(P)}{\lvert P\rvert^{3/2}}+\frac{\alpha_{j,2}(P)}{\lvert P\rvert^2} +\frac{\alpha_{j,5/2}(P)}{\lvert P\rvert^{5/2}}+ \frac{1}{\lvert P\rvert^3} \frac{2^{34}}{45} \exp \left( \frac{16}{\lvert P\rvert^{1/2}}\right) \right) \nonumber \\ & \leq \prod_{\deg (P)\leq 2 } \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}+\frac{\alpha_{j,2}(P)}{\lvert P\rvert^2} + \frac{1}{\lvert P\rvert^3} \frac{2^{34}}{45} \exp \left( \frac{16}{\lvert P\rvert^{1/2}}\right) \right) \nonumber \\ & \leq e^{36} \left(1+ \frac{4}{q}+\frac{20}{q^2}+ \frac{1}{q^3} \frac{2^{34}}{45} \exp \left( \frac{16}{q^{1/2}}\right) \right)^q\left(1+ \frac{4}{q^2}+\frac{20}{q^4}+ \frac{1}{q^6} \frac{2^{34}}{45} \exp \left( \frac{16}{q}\right) \right)^{q^2/2} \nonumber \\ & \leq e^{36+1084+38}\leq e^{e^{8}}. \end{align} $$
$$ \begin{align} \prod_{\deg (P)\leq 2 } & \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}+\frac{\alpha_{j,3/2}(P)}{\lvert P\rvert^{3/2}}+\frac{\alpha_{j,2}(P)}{\lvert P\rvert^2} +\frac{\alpha_{j,5/2}(P)}{\lvert P\rvert^{5/2}}+ \frac{1}{\lvert P\rvert^3} \frac{2^{34}}{45} \exp \left( \frac{16}{\lvert P\rvert^{1/2}}\right) \right) \nonumber \\ & \leq \prod_{\deg (P)\leq 2 } \left(1+ \frac{\alpha_{j,1}(P)}{\lvert P\rvert}+\frac{\alpha_{j,2}(P)}{\lvert P\rvert^2} + \frac{1}{\lvert P\rvert^3} \frac{2^{34}}{45} \exp \left( \frac{16}{\lvert P\rvert^{1/2}}\right) \right) \nonumber \\ & \leq e^{36} \left(1+ \frac{4}{q}+\frac{20}{q^2}+ \frac{1}{q^3} \frac{2^{34}}{45} \exp \left( \frac{16}{q^{1/2}}\right) \right)^q\left(1+ \frac{4}{q^2}+\frac{20}{q^4}+ \frac{1}{q^6} \frac{2^{34}}{45} \exp \left( \frac{16}{q}\right) \right)^{q^2/2} \nonumber \\ & \leq e^{36+1084+38}\leq e^{e^{8}}. \end{align} $$Combining formulas (4.10), (4.11), (4.12) and (4.13), it follows that we can take
 $$ \begin{align*} C(2)=e^{e^{15}}. \end{align*} $$
$$ \begin{align*} C(2)=e^{e^{15}}. \end{align*} $$We remark that we expect the value of ![]() $C(2)$ to be much smaller, which could potentially be proven by exploiting the cancellation in the Liouville function in formula (4.7). We have decided not to to do that here, since it does not change the final value of the constant in formula (1.1), as the worst contribution to this constant comes from the upper bound for
$C(2)$ to be much smaller, which could potentially be proven by exploiting the cancellation in the Liouville function in formula (4.7). We have decided not to to do that here, since it does not change the final value of the constant in formula (1.1), as the worst contribution to this constant comes from the upper bound for ![]() $C_J$ computed in Section 7.
$C_J$ computed in Section 7.
Now we go back to expressing bounds for general k. Combining formula (4.6) and (4.8), and incorporating everything in formula (4.4), we get that the contributions from the intervals ![]() $I_0, \dotsc , I_j$ are bounded by
$I_0, \dotsc , I_j$ are bounded by
 $$ \begin{align} \prod_{r=0}^j \left(1 + e^{-\ell_r / 2}\right)^2 E(r) & \leq \prod_{r=0}^j \left( \prod_{P \in I_r} ( A(r)+F(r) ) \right) \left(1+e^{-\ell_r/2}\right)^2 \nonumber \\ & \leq_\varepsilon \mathcal{D}_k C(k), \end{align} $$
$$ \begin{align} \prod_{r=0}^j \left(1 + e^{-\ell_r / 2}\right)^2 E(r) & \leq \prod_{r=0}^j \left( \prod_{P \in I_r} ( A(r)+F(r) ) \right) \left(1+e^{-\ell_r/2}\right)^2 \nonumber \\ & \leq_\varepsilon \mathcal{D}_k C(k), \end{align} $$where
 $$ \begin{align} \mathcal{D}_k= \left(1+e^{-\ell_0/2}\right)^2 \prod_{r=1}^J \left(1+e^{-\ell_r/2}\right)^2\left(1+\frac{e^{16k^2}}{2^{\ell_r}} \right). \end{align} $$
$$ \begin{align} \mathcal{D}_k= \left(1+e^{-\ell_0/2}\right)^2 \prod_{r=1}^J \left(1+e^{-\ell_r/2}\right)^2\left(1+\frac{e^{16k^2}}{2^{\ell_r}} \right). \end{align} $$ We now look at the term ![]() $r= j+1$ from formula (4.3), which involves the mollifier and
$r= j+1$ from formula (4.3), which involves the mollifier and  $\left (\Re P_{I_{r}}(\chi )\right )^{2s_r}$. We first write
$\left (\Re P_{I_{r}}(\chi )\right )^{2s_r}$. We first write

where we have bounded  $\lambda (f_r h_r), a(f_r h_r; J ) a(F_r H_r; u), \phi _{q^2} \left (f_r h_r^2 F_r H_r^2\right )/ \left \lvert \left (f_r h_r^2 F_r H_r^2\right )\right \rvert _{q^2} \leq 1$,
$\lambda (f_r h_r), a(f_r h_r; J ) a(F_r H_r; u), \phi _{q^2} \left (f_r h_r^2 F_r H_r^2\right )/ \left \lvert \left (f_r h_r^2 F_r H_r^2\right )\right \rvert _{q^2} \leq 1$, ![]() $\nu _{k \kappa }(f_r; \ell _r) \leq \nu _{k \kappa }(f_r)$.
$\nu _{k \kappa }(f_r; \ell _r) \leq \nu _{k \kappa }(f_r)$.
Using the change of variable as before, we can rewrite the sum of formula (4.16) as
 $$ \begin{align} &\sum_{\substack{X, S, T, C, D, A, B, f_r, h_r \\ C_1 C_2 = C, D_1 D_2 = D \\ A_1 A_2 = A, B_1 B_2 = B \\ P\mid XST f_r h_r ABCD \Rightarrow P \in I_r \\ \Omega\left(XSCD^2C_1D_1^2f_r^3\right) \leq k \kappa \ell_r \\ \Omega\left(XTAB^2A_1B_1^2h_r^3\right) \leq k \kappa \ell_r}} \frac{ \nu_{k \kappa} \left(XSCD^2C_1D_1^2f_r^3\right) \nu_{k \kappa}\left(XTAB^2 A_1 B_1^2 h_r^3\right) }{ \kappa^{\Omega\left(X^2SCD^2C_1D_1^2f_r^3 TAB^2 A_1 B_1^2 h_r^3\right)} \sqrt{ \left\lvert X^2 S^2 T^2 C^3 A^3 B^6 D^6 f_r^3 h_r^3\right\rvert}} \notag\\ &\quad \times \sum_{\substack{Y, F_r, H_r \\ P\mid Y F_r H_r \Rightarrow P \in I_r\\\Omega\left(Y^2 F_r^3 H_r^3\right) = 2s_r - \Omega\left(TCD^2 C_2 D_2^2 S A B^2 A_2 B_2^2 \right)}} \frac{ \nu(Y)^2 \nu(F_r) \nu(H_r)}{\lvert Y\rvert \lvert F_r H_r\rvert^{3/2} 3^{\Omega\left(F_r\right)} 3^{\Omega\left(H_r\right)}}, \end{align} $$
$$ \begin{align} &\sum_{\substack{X, S, T, C, D, A, B, f_r, h_r \\ C_1 C_2 = C, D_1 D_2 = D \\ A_1 A_2 = A, B_1 B_2 = B \\ P\mid XST f_r h_r ABCD \Rightarrow P \in I_r \\ \Omega\left(XSCD^2C_1D_1^2f_r^3\right) \leq k \kappa \ell_r \\ \Omega\left(XTAB^2A_1B_1^2h_r^3\right) \leq k \kappa \ell_r}} \frac{ \nu_{k \kappa} \left(XSCD^2C_1D_1^2f_r^3\right) \nu_{k \kappa}\left(XTAB^2 A_1 B_1^2 h_r^3\right) }{ \kappa^{\Omega\left(X^2SCD^2C_1D_1^2f_r^3 TAB^2 A_1 B_1^2 h_r^3\right)} \sqrt{ \left\lvert X^2 S^2 T^2 C^3 A^3 B^6 D^6 f_r^3 h_r^3\right\rvert}} \notag\\ &\quad \times \sum_{\substack{Y, F_r, H_r \\ P\mid Y F_r H_r \Rightarrow P \in I_r\\\Omega\left(Y^2 F_r^3 H_r^3\right) = 2s_r - \Omega\left(TCD^2 C_2 D_2^2 S A B^2 A_2 B_2^2 \right)}} \frac{ \nu(Y)^2 \nu(F_r) \nu(H_r)}{\lvert Y\rvert \lvert F_r H_r\rvert^{3/2} 3^{\Omega\left(F_r\right)} 3^{\Omega\left(H_r\right)}}, \end{align} $$where we have used the fact that  $\nu \left (Z^3\right ) \leq \nu (Z)/3^{\Omega (Z)}$ and
$\nu \left (Z^3\right ) \leq \nu (Z)/3^{\Omega (Z)}$ and ![]() $\nu (\cdot ) \leq 1$.
$\nu (\cdot ) \leq 1$.
Now note that  $ \Omega \left (TCD^2 C_2 D_2^2 S A B^2 A_2 B_2^2\right ) \leq \Omega \left ((ST) \left (CD^2\right )^2\left (AB^2\right )^2\right ) \leq 4 k \kappa \ell _r$ and by hypothesis
$ \Omega \left (TCD^2 C_2 D_2^2 S A B^2 A_2 B_2^2\right ) \leq \Omega \left ((ST) \left (CD^2\right )^2\left (AB^2\right )^2\right ) \leq 4 k \kappa \ell _r$ and by hypothesis  $ 4 k \kappa \ell _r \leq \frac {4}{a} s_r$, so
$ 4 k \kappa \ell _r \leq \frac {4}{a} s_r$, so  $\Omega \left (Y^2 F_r^3 H_r^3\right ) \geq \left (2-\frac {4}{a}\right )s_r:=c s_r$.
$\Omega \left (Y^2 F_r^3 H_r^3\right ) \geq \left (2-\frac {4}{a}\right )s_r:=c s_r$.
Let  $\alpha =2s_r - \Omega \left (TCD^2 C_2 D_2^2 S A B^2 A_2 B_2^2\right ) $. Using the fact that
$\alpha =2s_r - \Omega \left (TCD^2 C_2 D_2^2 S A B^2 A_2 B_2^2\right ) $. Using the fact that ![]() $\nu (Y)^2 \leq \nu (Y)$, since
$\nu (Y)^2 \leq \nu (Y)$, since ![]() $\nu (Y) \leq 1$, the sum over
$\nu (Y) \leq 1$, the sum over ![]() $Y, F_r, H_r$ is bounded by
$Y, F_r, H_r$ is bounded by
 $$ \begin{align} \sum_{2i+3j+3k=\alpha} \sum_{\substack{P\mid Y \Rightarrow P \in I_r \\ \Omega(Y) = i}} \frac{\nu(Y)}{\lvert Y\rvert} \sum_{\substack{P\mid F_r \Rightarrow P \in I_r \\ \Omega\left(F_r\right)=j}} \frac{\nu(F_r)}{3^{\Omega\left(F_r\right)} \lvert F_r\rvert^{3/2}} \sum_{\substack{P\mid H_r \Rightarrow P \in I_r \\ \Omega\left(H_r\right)=k}} \frac{\nu(H_r)}{3^{\Omega\left(H_r\right)} \lvert H_r\rvert^{3/2}}. \end{align} $$
$$ \begin{align} \sum_{2i+3j+3k=\alpha} \sum_{\substack{P\mid Y \Rightarrow P \in I_r \\ \Omega(Y) = i}} \frac{\nu(Y)}{\lvert Y\rvert} \sum_{\substack{P\mid F_r \Rightarrow P \in I_r \\ \Omega\left(F_r\right)=j}} \frac{\nu(F_r)}{3^{\Omega\left(F_r\right)} \lvert F_r\rvert^{3/2}} \sum_{\substack{P\mid H_r \Rightarrow P \in I_r \\ \Omega\left(H_r\right)=k}} \frac{\nu(H_r)}{3^{\Omega\left(H_r\right)} \lvert H_r\rvert^{3/2}}. \end{align} $$Now
 $$ \begin{align*} \sum_{\substack{P\mid F_r \Rightarrow P \in I_r \\ \Omega\left(F_r\right)=j}} \frac{\nu(F_r)}{3^{\Omega\left(F_r\right)} \lvert F_r\rvert^{3/2}} = \frac{1}{j!} \left( \sum_{P \in I_r} \frac{1}{3\lvert P\rvert^{3/2}} \right)^j, \end{align*} $$
$$ \begin{align*} \sum_{\substack{P\mid F_r \Rightarrow P \in I_r \\ \Omega\left(F_r\right)=j}} \frac{\nu(F_r)}{3^{\Omega\left(F_r\right)} \lvert F_r\rvert^{3/2}} = \frac{1}{j!} \left( \sum_{P \in I_r} \frac{1}{3\lvert P\rvert^{3/2}} \right)^j, \end{align*} $$a similar expression holds for the sum over ![]() $H_r$ and
$H_r$ and
 $$ \begin{align*} \sum_{\substack{P\mid Y \Rightarrow P \in I_r \\ \Omega(Y) = i}} \frac{\nu(Y)}{\lvert Y\rvert} = \frac{1}{i!} \left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^i. \end{align*} $$
$$ \begin{align*} \sum_{\substack{P\mid Y \Rightarrow P \in I_r \\ \Omega(Y) = i}} \frac{\nu(Y)}{\lvert Y\rvert} = \frac{1}{i!} \left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^i. \end{align*} $$Using the inequalities from before, it follows that
 $$ \begin{align} (4.18) & \leq \left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{\alpha/2} \sum_{2i+3j+3k=\alpha} \frac{1}{i!j!k!3^{j+k}} = \left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{\alpha/2} \sum_{\substack{i \leq \alpha/2\\3\mid (\alpha-2i)}} \left( \frac{2}{3} \right)^{\frac{\alpha-2i}{3}} \frac{1}{ i! \left( \frac{\alpha-2i}{3}\right) !} \nonumber \\ & \leq \left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{\alpha/2}\left( \frac{2}{3} \right)^{\alpha/3} \left( \sum_{i \leq \alpha/3} \frac{\left( \frac{2}{3} \right)^{\frac{-2i}{3}}}{i! \left\lfloor \frac{\alpha}{3}-i \right\rfloor!}+ \sum_{\substack{\alpha/3<i\leq \alpha/2\\3 \mid (\alpha-2i)}} \frac{\left( \frac{2}{3} \right)^{\frac{-2i}{3}}}{\left\lfloor \frac{2i}{3}\right\rfloor! \left( \frac{\alpha-2i}{3}\right)!} \right) \nonumber\\ &\leq 2\left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{\alpha/2}\left( \frac{2}{3} \right)^{\alpha/3} \frac{\left(\frac{5}{2}\right)^{\alpha/3}}{\lfloor \alpha/3\rfloor!}\leq 2\left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{s_r}\frac{\left(\frac{5}{3}\right)^{c s_r/3}}{\lfloor cs_r/3\rfloor !}. \end{align} $$
$$ \begin{align} (4.18) & \leq \left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{\alpha/2} \sum_{2i+3j+3k=\alpha} \frac{1}{i!j!k!3^{j+k}} = \left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{\alpha/2} \sum_{\substack{i \leq \alpha/2\\3\mid (\alpha-2i)}} \left( \frac{2}{3} \right)^{\frac{\alpha-2i}{3}} \frac{1}{ i! \left( \frac{\alpha-2i}{3}\right) !} \nonumber \\ & \leq \left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{\alpha/2}\left( \frac{2}{3} \right)^{\alpha/3} \left( \sum_{i \leq \alpha/3} \frac{\left( \frac{2}{3} \right)^{\frac{-2i}{3}}}{i! \left\lfloor \frac{\alpha}{3}-i \right\rfloor!}+ \sum_{\substack{\alpha/3<i\leq \alpha/2\\3 \mid (\alpha-2i)}} \frac{\left( \frac{2}{3} \right)^{\frac{-2i}{3}}}{\left\lfloor \frac{2i}{3}\right\rfloor! \left( \frac{\alpha-2i}{3}\right)!} \right) \nonumber\\ &\leq 2\left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{\alpha/2}\left( \frac{2}{3} \right)^{\alpha/3} \frac{\left(\frac{5}{2}\right)^{\alpha/3}}{\lfloor \alpha/3\rfloor!}\leq 2\left( \sum_{P \in I_r} \frac{1}{\lvert P\rvert} \right)^{s_r}\frac{\left(\frac{5}{3}\right)^{c s_r/3}}{\lfloor cs_r/3\rfloor !}. \end{align} $$ We now consider the exterior sum in formula (4.17). For the sum over ![]() $A_1$ (recall that A is square-free), we have
$A_1$ (recall that A is square-free), we have
 $$ \begin{align*} \sum_{A_1\mid A} \frac{\nu_{k \kappa}(A_1)}{\kappa^{\Omega\left(A_1\right)}} = \prod_{P\mid A}(1+k). \end{align*} $$
$$ \begin{align*} \sum_{A_1\mid A} \frac{\nu_{k \kappa}(A_1)}{\kappa^{\Omega\left(A_1\right)}} = \prod_{P\mid A}(1+k). \end{align*} $$Then overall we get
 $$ \begin{align*} \sum_{P\mid A \Rightarrow P \in I_r} \frac{\nu_{k \kappa}(A)}{\kappa^{\Omega(A)}} (k+1)^{\omega(A)} \frac{1}{\lvert A\rvert^{3/2}} = \prod_{P \in I_r} \left( 1+ \frac{k(k+1)}{\lvert P\rvert^{3/2}} \right). \end{align*} $$
$$ \begin{align*} \sum_{P\mid A \Rightarrow P \in I_r} \frac{\nu_{k \kappa}(A)}{\kappa^{\Omega(A)}} (k+1)^{\omega(A)} \frac{1}{\lvert A\rvert^{3/2}} = \prod_{P \in I_r} \left( 1+ \frac{k(k+1)}{\lvert P\rvert^{3/2}} \right). \end{align*} $$Similar expressions hold for the sums over ![]() $C, B, D$, and overall for the sum over
$C, B, D$, and overall for the sum over ![]() $X,S,T,A,B,C,D, f_r, h_r$ we get that it is
$X,S,T,A,B,C,D, f_r, h_r$ we get that it is
 $$ \begin{align*} \leq \prod_{P \in I_r} \left( 1+ \frac{k(k+1)}{\lvert P\rvert^{3/2}} \right)^2 \left(1+ \frac{k^2\left(k^2/2+1\right)}{2\lvert P\rvert^3} \right)^2 \left(1+ \frac{k^3}{6\lvert P\rvert^{3/2}} \right)^2 \left( 1+\frac{k^2}{\lvert P\rvert}\right)\left( 1+ \frac{k}{\lvert P\rvert}\right)^2 := H(r). \end{align*} $$
$$ \begin{align*} \leq \prod_{P \in I_r} \left( 1+ \frac{k(k+1)}{\lvert P\rvert^{3/2}} \right)^2 \left(1+ \frac{k^2\left(k^2/2+1\right)}{2\lvert P\rvert^3} \right)^2 \left(1+ \frac{k^3}{6\lvert P\rvert^{3/2}} \right)^2 \left( 1+\frac{k^2}{\lvert P\rvert}\right)\left( 1+ \frac{k}{\lvert P\rvert}\right)^2 := H(r). \end{align*} $$Using the Prime Polynomial Theorem (2.1), we get
 $$ \begin{align*} H(r) \leq_\varepsilon \exp \left( k^2+2k+ \frac{2k(k+1)}{q^{(g+2) \theta_{r-1}/2}} + \frac{ k^3}{3q^{(g+2) \theta_{r-1}/2}} + \frac{k^2 \left(\frac{k^2}{2}+1\right)}{q^{2(g+2) \theta_{r-1}}}\right) \end{align*} $$
$$ \begin{align*} H(r) \leq_\varepsilon \exp \left( k^2+2k+ \frac{2k(k+1)}{q^{(g+2) \theta_{r-1}/2}} + \frac{ k^3}{3q^{(g+2) \theta_{r-1}/2}} + \frac{k^2 \left(\frac{k^2}{2}+1\right)}{q^{2(g+2) \theta_{r-1}}}\right) \end{align*} $$for ![]() $r \neq 0$, and then
$r \neq 0$, and then
 $$ \begin{align} H(r) \leq _{\varepsilon} \exp\left(k^2+2k\right),\end{align} $$
$$ \begin{align} H(r) \leq _{\varepsilon} \exp\left(k^2+2k\right),\end{align} $$which is what we need to prove (iii). For ![]() $r=0$, we have
$r=0$, we have
In (i), the bound will depend on ![]() $H(0)$. Replacing formulas (4.19) and (4.20) in formulas (4.17) and finally (4.16), it follows that
$H(0)$. Replacing formulas (4.19) and (4.20) in formulas (4.17) and finally (4.16), it follows that
 $$ \begin{align} E(j+1) \leq_{\varepsilon} 2 \exp\left(k^2+2k\right) \left( \sum_{P \in I_{j+1}} \frac{1}{\lvert P\rvert} \right)^{s_{j+1}} \frac{\left(\frac{5}{3}\right)^{cs_{j+1}/3}\left(2s_{j+1}\right)!}{ 4^{s_{j+1}} \left\lfloor\frac{cs_{j+1}}{3}\right\rfloor!}. \end{align} $$
$$ \begin{align} E(j+1) \leq_{\varepsilon} 2 \exp\left(k^2+2k\right) \left( \sum_{P \in I_{j+1}} \frac{1}{\lvert P\rvert} \right)^{s_{j+1}} \frac{\left(\frac{5}{3}\right)^{cs_{j+1}/3}\left(2s_{j+1}\right)!}{ 4^{s_{j+1}} \left\lfloor\frac{cs_{j+1}}{3}\right\rfloor!}. \end{align} $$ Finally, we consider the case where ![]() $r \geq j+2$. In this case, only the mollifier contributes primes in this interval in the factors of formula (4.3). It is easy to see that
$r \geq j+2$. In this case, only the mollifier contributes primes in this interval in the factors of formula (4.3). It is easy to see that

where we used the same bound as before on the functions appearing in the mollifier, and we also used the fact that ![]() $\nu _{k \kappa }(g_r) \leq (k \kappa )^{\Omega \left (g_r\right )}$. Note that
$\nu _{k \kappa }(g_r) \leq (k \kappa )^{\Omega \left (g_r\right )}$. Note that
is equivalent to ![]() $f_r = g_r S_r^3$ and
$f_r = g_r S_r^3$ and ![]() $h_r = g_r T_r^3$ for
$h_r = g_r T_r^3$ for ![]() $(S_r, T_r)=1$. Then the term corresponding to a fixed r in this product is bounded by
$(S_r, T_r)=1$. Then the term corresponding to a fixed r in this product is bounded by
 $$ \begin{align*} \leq \sum_{\substack{P \mid g_r \Rightarrow P \in I_r}} \frac{k^{2 \Omega\left(g_r\right)}}{\lvert g_r\rvert} \sum_{\substack{P \mid S_r \Rightarrow P \in I_r}} \frac{k^{\Omega\left(S_r^3\right)}}{\lvert S_r\rvert^{3/2}} \sum_{\substack{P \mid T_r \Rightarrow P \in I_r}} \frac{k^{\Omega\left(T_r^3\right)}}{\lvert T_r\rvert^{3/2} } =\prod_{P \in I_r} \left( 1-\frac{k^2}{\lvert P\rvert}\right)^{-1} \left(1- \frac{k^3}{\lvert P\rvert^{3/2}} \right)^{-2}. \end{align*} $$
$$ \begin{align*} \leq \sum_{\substack{P \mid g_r \Rightarrow P \in I_r}} \frac{k^{2 \Omega\left(g_r\right)}}{\lvert g_r\rvert} \sum_{\substack{P \mid S_r \Rightarrow P \in I_r}} \frac{k^{\Omega\left(S_r^3\right)}}{\lvert S_r\rvert^{3/2}} \sum_{\substack{P \mid T_r \Rightarrow P \in I_r}} \frac{k^{\Omega\left(T_r^3\right)}}{\lvert T_r\rvert^{3/2} } =\prod_{P \in I_r} \left( 1-\frac{k^2}{\lvert P\rvert}\right)^{-1} \left(1- \frac{k^3}{\lvert P\rvert^{3/2}} \right)^{-2}. \end{align*} $$ Using the fact that ![]() $-\log (1-x) < \frac {x}{1-x}$, we get
$-\log (1-x) < \frac {x}{1-x}$, we get
 $$ \begin{align*} \prod_{P \in I_r} \left(1- \frac{k^2}{\lvert P\rvert} \right)^{-1} & \leq \exp \left( \sum_{P \in I_r} \frac{k^2}{\lvert P\rvert-k^2} \right) \leq \exp \left(k^2 \left( \sum_{n=(g+2) \theta_{r-1}}^{(g+2) \theta_r} \frac{1}{n} + \sum_{n=(g+2) \theta_{r-1}}^{(g+2) \theta_r} \frac{k^2}{n\left(q^n-k^2\right)} \right) \right) \\ & \leq_{\epsilon} \exp \left( k^2+\frac{k^4}{q^{\left(g+2\right) \theta_{r-1}}-k^2} \right). \end{align*} $$
$$ \begin{align*} \prod_{P \in I_r} \left(1- \frac{k^2}{\lvert P\rvert} \right)^{-1} & \leq \exp \left( \sum_{P \in I_r} \frac{k^2}{\lvert P\rvert-k^2} \right) \leq \exp \left(k^2 \left( \sum_{n=(g+2) \theta_{r-1}}^{(g+2) \theta_r} \frac{1}{n} + \sum_{n=(g+2) \theta_{r-1}}^{(g+2) \theta_r} \frac{k^2}{n\left(q^n-k^2\right)} \right) \right) \\ & \leq_{\epsilon} \exp \left( k^2+\frac{k^4}{q^{\left(g+2\right) \theta_{r-1}}-k^2} \right). \end{align*} $$Similarly,
 $$ \begin{align*} \prod_{P \in I_r} \left( 1-\frac{k^3}{\lvert P\rvert^{3/2}} \right)^{-2} & \leq \exp \left(2 \sum_{P \in I_r} \frac{k^3}{\lvert P\rvert^{3/2}-k^3} \right) \leq \exp \left(2k^3 \sum_{n=(g+2) \theta_{r-1}}^{(g+2) \theta_r} \left( \frac{1}{nq^{n/2}}+O \left(\frac{1}{nq^{2n}} \right) \right) \right) \\ & \leq_{\epsilon} \exp \left( \frac{2k^3}{q^{(g+2) \theta_{r-1}/2}}+O \left(\frac{1}{q^{2(g+2) \theta_{r-1}}} \right) \right). \end{align*} $$
$$ \begin{align*} \prod_{P \in I_r} \left( 1-\frac{k^3}{\lvert P\rvert^{3/2}} \right)^{-2} & \leq \exp \left(2 \sum_{P \in I_r} \frac{k^3}{\lvert P\rvert^{3/2}-k^3} \right) \leq \exp \left(2k^3 \sum_{n=(g+2) \theta_{r-1}}^{(g+2) \theta_r} \left( \frac{1}{nq^{n/2}}+O \left(\frac{1}{nq^{2n}} \right) \right) \right) \\ & \leq_{\epsilon} \exp \left( \frac{2k^3}{q^{(g+2) \theta_{r-1}/2}}+O \left(\frac{1}{q^{2(g+2) \theta_{r-1}}} \right) \right). \end{align*} $$ Then the contribution from ![]() $r \geq j+2$ will be bounded by
$r \geq j+2$ will be bounded by
 $$ \begin{align} &\leq_{\epsilon} e^{k^2\left(J -j-1\right)} \prod_{r=j+2}^J \exp \left( \frac{k^4}{q^{(g+2) \theta_{r-1}}-k^2}+ \frac{2k^3}{q^{(g+2) \theta_{r-1}/2}}+ O \left( \frac{1}{q^{2(g+2) \theta_{r-1}}} \right) \right) \nonumber \\ & \leq_\varepsilon e^{k^2\left(J -j-1\right)}. \end{align} $$
$$ \begin{align} &\leq_{\epsilon} e^{k^2\left(J -j-1\right)} \prod_{r=j+2}^J \exp \left( \frac{k^4}{q^{(g+2) \theta_{r-1}}-k^2}+ \frac{2k^3}{q^{(g+2) \theta_{r-1}/2}}+ O \left( \frac{1}{q^{2(g+2) \theta_{r-1}}} \right) \right) \nonumber \\ & \leq_\varepsilon e^{k^2\left(J -j-1\right)}. \end{align} $$ Combining the contribution of the intervals ![]() $I_r$ with
$I_r$ with ![]() $r \leq j$ from formula (4.14), the contribution of the interval
$r \leq j$ from formula (4.14), the contribution of the interval ![]() $I_{ j+1}$ from formula (4.22) and the contribution of the intervals
$I_{ j+1}$ from formula (4.22) and the contribution of the intervals ![]() $I_r$ with
$I_r$ with ![]() $j+2\leq r \leq J $ from formula (4.23), we get the bound of the last inequality.
$j+2\leq r \leq J $ from formula (4.23), we get the bound of the last inequality.
We prove the first inequality corresponding to “![]() $j=-1$” in the same way, except that the bound for
$j=-1$” in the same way, except that the bound for ![]() $H(r)$ in formula (4.20) is not valid for
$H(r)$ in formula (4.20) is not valid for ![]() $r=0$, so we just keep
$r=0$, so we just keep ![]() $H(0)$ on the right-hand side. The second inequality corresponds to
$H(0)$ on the right-hand side. The second inequality corresponds to ![]() $j=J$.
$j=J$.
5 Squares of the primes
In this section we prove an upper bound for the average over the square of the primes appearing in the kth moment. Our proof is similar to [Reference Harper21], but it is simpler because we separate the primes and the square of the primes from the start by using Cauchy–Schwarz in order to deal with the mollifier.
We recall that
 $$ \begin{align} S_{j,k}(\chi)=\exp \left(k \Re\left( \sum_{\deg(P) \leq (g+2) \theta_j/2} \frac{ \chi(P)b(P;j)}{\lvert P\rvert}\right)\right), \end{align} $$
$$ \begin{align} S_{j,k}(\chi)=\exp \left(k \Re\left( \sum_{\deg(P) \leq (g+2) \theta_j/2} \frac{ \chi(P)b(P;j)}{\lvert P\rvert}\right)\right), \end{align} $$where the positive weights ![]() $b(P;j)$ are defined by equation (3.8). Then
$b(P;j)$ are defined by equation (3.8). Then  $b(P;j) \leq \frac 12$, which is the only property that we use in this section.
$b(P;j) \leq \frac 12$, which is the only property that we use in this section.
Lemma 5.1. Let ![]() $S_{j,k}$ be the sum defined by equation (3.7) and set
$S_{j,k}$ be the sum defined by equation (3.7) and set ![]() $\beta>1$. For
$\beta>1$. For ![]() $j=0,\dotsc ,J $ we have
$j=0,\dotsc ,J $ we have
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)}S_{j,k}(\chi)^2 \leq q^{g+2} \left( \exp\left(k+\frac{2k}{\beta-1} \right)+ \frac{3 e^{k \left(\gamma+1\right)} }{4} \sum_{m=1}^{\infty} \exp \left(k \log m+ \frac{2k}{\beta^{m}(\beta-1)} \right) \frac{ \beta^{4m}}{ q^{2m}} \right). \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)}S_{j,k}(\chi)^2 \leq q^{g+2} \left( \exp\left(k+\frac{2k}{\beta-1} \right)+ \frac{3 e^{k \left(\gamma+1\right)} }{4} \sum_{m=1}^{\infty} \exp \left(k \log m+ \frac{2k}{\beta^{m}(\beta-1)} \right) \frac{ \beta^{4m}}{ q^{2m}} \right). \end{align*} $$In particular, choosing ![]() $\beta =2$ and using the fact that
$\beta =2$ and using the fact that ![]() $q\geq 5$, we have
$q\geq 5$, we have
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)}S_{j,k}(\chi)^2 \leq q^{g+2} \mathcal{S}_k, \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)}S_{j,k}(\chi)^2 \leq q^{g+2} \mathcal{S}_k, \end{align} $$where
 $$ \begin{align*} \mathcal{S}_k:=e^{3k}+ \frac{4 k!e^{k \left(\gamma+2\right)} }{3} \left(\frac{25}{9}\right)^{k}, \end{align*} $$
$$ \begin{align*} \mathcal{S}_k:=e^{3k}+ \frac{4 k!e^{k \left(\gamma+2\right)} }{3} \left(\frac{25}{9}\right)^{k}, \end{align*} $$and in particular
Proof. Let
 $$ \begin{align*} F_m(\chi;j) = \sum_{P \in \mathcal{P}_m} \frac{\chi(P) b(P;j)}{\lvert P\rvert}, \end{align*} $$
$$ \begin{align*} F_m(\chi;j) = \sum_{P \in \mathcal{P}_m} \frac{\chi(P) b(P;j)}{\lvert P\rvert}, \end{align*} $$where the sum is over the monic irreducible polynomials of degree m. For ease of notation, we will simply denote this sum by ![]() $F_m(\chi )$. Let
$F_m(\chi )$. Let
 $$ \begin{align*} \mathcal{F}(m) = \left\{ \chi \in \mathcal{C}(g) : \lvert \Re F_m(\chi) \rvert> \frac{1}{\beta^m}, \text{but } \lvert \Re F_n(\chi) \rvert \leq \frac{1}{\beta^n}, \ \forall m+1 \leq n \leq (g+2) \theta_j/2 \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{F}(m) = \left\{ \chi \in \mathcal{C}(g) : \lvert \Re F_m(\chi) \rvert> \frac{1}{\beta^m}, \text{but } \lvert \Re F_n(\chi) \rvert \leq \frac{1}{\beta^n}, \ \forall m+1 \leq n \leq (g+2) \theta_j/2 \right\}. \end{align*} $$Note that  $F_0(\chi )=\frac {1}{2}$, so the set
$F_0(\chi )=\frac {1}{2}$, so the set ![]() $\mathcal {F}(0)$ is empty. Since the sets
$\mathcal {F}(0)$ is empty. Since the sets ![]() $\mathcal {F}(m)$ are disjoint, note that we have
$\mathcal {F}(m)$ are disjoint, note that we have
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)}S_{j,k}(\chi)^2 \leq \sum_{m=1}^{(g+2) \theta_j/2} \sum_{\chi \in \mathcal{F}(m)} S_{j,k}(\chi)^2 + \sum_{\chi \notin \mathcal{F}(m), \forall m} S_{j,k}(\chi)^2. \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)}S_{j,k}(\chi)^2 \leq \sum_{m=1}^{(g+2) \theta_j/2} \sum_{\chi \in \mathcal{F}(m)} S_{j,k}(\chi)^2 + \sum_{\chi \notin \mathcal{F}(m), \forall m} S_{j,k}(\chi)^2. \end{align} $$If ![]() $\chi $ does not belong to any of the sets
$\chi $ does not belong to any of the sets ![]() $\mathcal {F}(m)$, then
$\mathcal {F}(m)$, then
 $$ \begin{align*} \lvert \Re F_n(\chi)\rvert \leq \frac{1}{\beta^n} \end{align*} $$
$$ \begin{align*} \lvert \Re F_n(\chi)\rvert \leq \frac{1}{\beta^n} \end{align*} $$for all ![]() $1 \leq n \leq (g+2) \theta _j/2$, so in this case we have
$1 \leq n \leq (g+2) \theta _j/2$, so in this case we have
 $$ \begin{align*} S_{j,k}(\chi)^2 \leq \exp\left(k+\frac{2k}{\beta-1} \right). \end{align*} $$
$$ \begin{align*} S_{j,k}(\chi)^2 \leq \exp\left(k+\frac{2k}{\beta-1} \right). \end{align*} $$Now assume that ![]() $\chi \in \mathcal {F}(m)$ for some
$\chi \in \mathcal {F}(m)$ for some ![]() $1 \leq m \leq (g+2) \theta _j/2$. Then we have
$1 \leq m \leq (g+2) \theta _j/2$. Then we have
 $$ \begin{align*} \sum_{l=1}^{(g+2) \theta_j/2} \Re F_l(\chi) \leq \sum_{l=1}^m \frac{1}{2l} + \sum_{l=m+1}^{(g+2) \theta_j/2} \frac{1}{\beta^l} \leq \frac{1}{2} ( \log m+\gamma +1 )+\frac{1}{\beta^{m+1}\left(1-\frac{1}{\beta}\right)}, \end{align*} $$
$$ \begin{align*} \sum_{l=1}^{(g+2) \theta_j/2} \Re F_l(\chi) \leq \sum_{l=1}^m \frac{1}{2l} + \sum_{l=m+1}^{(g+2) \theta_j/2} \frac{1}{\beta^l} \leq \frac{1}{2} ( \log m+\gamma +1 )+\frac{1}{\beta^{m+1}\left(1-\frac{1}{\beta}\right)}, \end{align*} $$where ![]() $\gamma $ is the Euler–Mascheroni constant. Therefore, in this case we have
$\gamma $ is the Euler–Mascheroni constant. Therefore, in this case we have
 $$ \begin{align*} S_{j,k}(\chi)^2 \leq \exp \left(k (\log m+\gamma+1)+ \frac{2k}{\beta^{m+1}\left(1-\frac{1}{\beta}\right)} \right). \end{align*} $$
$$ \begin{align*} S_{j,k}(\chi)^2 \leq \exp \left(k (\log m+\gamma+1)+ \frac{2k}{\beta^{m+1}\left(1-\frac{1}{\beta}\right)} \right). \end{align*} $$If ![]() $\chi \in \mathcal {F}(m)$, also note that
$\chi \in \mathcal {F}(m)$, also note that ![]() $(\beta ^m \Re F_m(\chi ))^4>1$, so combining with this inequality, we get
$(\beta ^m \Re F_m(\chi ))^4>1$, so combining with this inequality, we get
 $$ \begin{align} \sum_{\chi \in \mathcal{F}(m)} S_{j,k}(\chi)^2 \leq \exp \left(k (\log m+\gamma+1)+ \frac{2k}{\beta^{m+1}\left(1-\frac{1}{\beta}\right)} \right) \sum_{\chi \in \mathcal{C}(g)} (\beta^m \Re F_m(\chi))^4. \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{F}(m)} S_{j,k}(\chi)^2 \leq \exp \left(k (\log m+\gamma+1)+ \frac{2k}{\beta^{m+1}\left(1-\frac{1}{\beta}\right)} \right) \sum_{\chi \in \mathcal{C}(g)} (\beta^m \Re F_m(\chi))^4. \end{align} $$Note that by Lemma 3.2,
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} (\beta^m \Re F_m(\chi))^4= \frac{4! \beta^{4m}}{2^4} \sum_{\chi \in \mathcal{C}(g)}\sum_{\substack{ P \mid fh \Rightarrow P \in \mathcal{P}_m \\ \Omega(fh)=4}} \frac{b(f;j)b(f;J ) \chi(f) \overline{\chi}(h) \nu(f) \nu(h)}{\lvert fh\rvert}. \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} (\beta^m \Re F_m(\chi))^4= \frac{4! \beta^{4m}}{2^4} \sum_{\chi \in \mathcal{C}(g)}\sum_{\substack{ P \mid fh \Rightarrow P \in \mathcal{P}_m \\ \Omega(fh)=4}} \frac{b(f;j)b(f;J ) \chi(f) \overline{\chi}(h) \nu(f) \nu(h)}{\lvert fh\rvert}. \end{align*} $$Using Lemma 3.6 (note that ![]() $8m \leq (g+2)/2$, since
$8m \leq (g+2)/2$, since ![]() $\theta _J $ is small enough), we get
$\theta _J $ is small enough), we get

When
, we can write  $f=b f_1^3, h=b h_1^3$ with
$f=b f_1^3, h=b h_1^3$ with ![]() $(f_1,h_1)=1$. Since
$(f_1,h_1)=1$. Since  $\Omega \left (b^2f_1^3h_1^3\right )=4$, it follows that
$\Omega \left (b^2f_1^3h_1^3\right )=4$, it follows that ![]() $f_1=h_1=1$ and
$f_1=h_1=1$ and ![]() $\Omega (b)=2$. Then using the fact that
$\Omega (b)=2$. Then using the fact that ![]() $\nu (b)^2 \leq \nu (b)$, we get
$\nu (b)^2 \leq \nu (b)$, we get

where for the last inequality we used the Prime Polynomial Theorem (2.1). Combining this and formulas (5.4) and (5.5), we get
 $$ \begin{align} \sum_{m=1}^{(g+2) \theta_j/2} \sum_{\chi \in \mathcal{F}(m)} S_{j,k}(\chi)^2 \leq q^{g+2} \sum_{m=1}^{(g+2)\theta_j/2} \exp \left(k (\log m+\gamma+1)+ \frac{2k}{\beta^{m+1}\left(1-\frac{1}{\beta}\right)} \right) \frac{4! \beta^{4m}}{2^5 q^{2m}}. \end{align} $$
$$ \begin{align} \sum_{m=1}^{(g+2) \theta_j/2} \sum_{\chi \in \mathcal{F}(m)} S_{j,k}(\chi)^2 \leq q^{g+2} \sum_{m=1}^{(g+2)\theta_j/2} \exp \left(k (\log m+\gamma+1)+ \frac{2k}{\beta^{m+1}\left(1-\frac{1}{\beta}\right)} \right) \frac{4! \beta^{4m}}{2^5 q^{2m}}. \end{align} $$Note that for any ![]() $1<\beta <\sqrt {q}$, this expression will be
$1<\beta <\sqrt {q}$, this expression will be ![]() $\ll q^{g+2}$.
$\ll q^{g+2}$.
Now we take ![]() $\beta =2$. We use the fact that
$\beta =2$. We use the fact that ![]() $\exp ( 2k/(\beta ^m(\beta -1))) \leq e^k$, and the fact that
$\exp ( 2k/(\beta ^m(\beta -1))) \leq e^k$, and the fact that
 $$ \begin{align*} \sum_{m=1}^{\infty} m^k x^m \leq \frac{xk!}{(1-x)^{k+1}} \end{align*} $$
$$ \begin{align*} \sum_{m=1}^{\infty} m^k x^m \leq \frac{xk!}{(1-x)^{k+1}} \end{align*} $$for ![]() $x<1$. Since
$x<1$. Since ![]() $q \geq 5$, using this inequality and formula (5.6), inequality (5.2) follows.
$q \geq 5$, using this inequality and formula (5.6), inequality (5.2) follows.
6 Upper bounds for moments of L-functions
Here, we will prove the following upper bound:
Proposition 6.1. For any positive real number k and any ![]() $\varepsilon>0$, we have
$\varepsilon>0$, we have
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{2k} \ll q^{g+2} g^{k^2+\varepsilon}. \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{2k} \ll q^{g+2} g^{k^2+\varepsilon}. \end{align*} $$We first prove the following result:
Lemma 6.2. Let l and y be integers such that ![]() $3 l y \leq g/2+1$. For any complex numbers
$3 l y \leq g/2+1$. For any complex numbers ![]() $a(P)$ with
$a(P)$ with ![]() $\lvert a(P)\rvert \ll 1$, we have
$\lvert a(P)\rvert \ll 1$, we have
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \ll q^g \frac{ (l!)^2 5^{2l/3} }{\lfloor 2l/3 \rfloor ! 9^{l/3}} \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l. \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \ll q^g \frac{ (l!)^2 5^{2l/3} }{\lfloor 2l/3 \rfloor ! 9^{l/3}} \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l. \end{align} $$If we also assume that  $l \leq \displaystyle \left (\sum _{\deg (P) \leq y} \frac {\lvert a(P)\rvert ^2}{\lvert P\rvert }\right )^{3-\varepsilon }$, then we have
$l \leq \displaystyle \left (\sum _{\deg (P) \leq y} \frac {\lvert a(P)\rvert ^2}{\lvert P\rvert }\right )^{3-\varepsilon }$, then we have
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \ll q^g l! \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l. \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \ll q^g l! \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l. \end{align} $$Proof. We extend ![]() $a(P)$ to a completely multiplicative function. We have
$a(P)$ to a completely multiplicative function. We have
 $$ \begin{align} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} = (l!)^2 \sum_{\substack{P\mid fh \Rightarrow \deg(P) \leq y \\ \Omega(f)=l \\ \Omega(h)=l}} \frac{a(f) \overline{a(h)} \nu(f) \nu(h) \chi\left(fh^2\right)}{\sqrt{\lvert fh\rvert}}. \end{align} $$
$$ \begin{align} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} = (l!)^2 \sum_{\substack{P\mid fh \Rightarrow \deg(P) \leq y \\ \Omega(f)=l \\ \Omega(h)=l}} \frac{a(f) \overline{a(h)} \nu(f) \nu(h) \chi\left(fh^2\right)}{\sqrt{\lvert fh\rvert}}. \end{align} $$Note that
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \leq \sum_{F \in \mathcal{M}_{q^2,g/2+1}} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi_F(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l}. \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \leq \sum_{F \in \mathcal{M}_{q^2,g/2+1}} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi_F(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l}. \end{align*} $$Using this and equation (6.3), note that if ![]() $fh^2$ is not a cube, then the character sum over
$fh^2$ is not a cube, then the character sum over ![]() $F \in \mathcal {M}_{q^2,g/2+1}$ vanishes, since
$F \in \mathcal {M}_{q^2,g/2+1}$ vanishes, since ![]() $\deg {(fh^2}) \leq 3 l y \leq g/2+1$ by hypothesis. Then
$\deg {(fh^2}) \leq 3 l y \leq g/2+1$ by hypothesis. Then

The condition
can be rewritten as  $f=bf_1^3$ and
$f=bf_1^3$ and  $h=bh_1^3$ with
$h=bh_1^3$ with ![]() $(f_1,h_1)=1$. Then we get
$(f_1,h_1)=1$. Then we get
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} & \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \leq q^{g+2} (l!)^2 \sum_{\substack{P\mid b \Rightarrow \deg(P) \leq y \\ \Omega(b) \leq l \\ \Omega(b) \equiv l \,(\mathrm{mod}\,3)}} \frac{ \lvert a(b)\rvert^2 \nu(b)}{\lvert b\rvert} \left( \sum_{\substack{ P\mid f \Rightarrow \deg(P) \leq y \\ \Omega(f) = (l- \Omega(b))/3 }} \frac{ \lvert a(f)\rvert^3 \nu(f)}{\lvert f\rvert^{3/2} 3^{\Omega(f)}} \right)^2 \nonumber \\ &= q^{g+2} (l!)^2 \sum_{\substack{P\mid b \Rightarrow \deg(P) \leq y \\ \Omega(b) \leq l \\ \Omega(b) \equiv l \,(\mathrm{mod}\,3)}} \frac{ \lvert a(b)\rvert^2 \nu(b) }{\lvert b\rvert} \frac{1}{(( (l-\Omega(b))/3)!)^2} \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^3}{3\lvert P\rvert^{3/2}} \right)^{2(l-\Omega(b))/3}, \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} & \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \leq q^{g+2} (l!)^2 \sum_{\substack{P\mid b \Rightarrow \deg(P) \leq y \\ \Omega(b) \leq l \\ \Omega(b) \equiv l \,(\mathrm{mod}\,3)}} \frac{ \lvert a(b)\rvert^2 \nu(b)}{\lvert b\rvert} \left( \sum_{\substack{ P\mid f \Rightarrow \deg(P) \leq y \\ \Omega(f) = (l- \Omega(b))/3 }} \frac{ \lvert a(f)\rvert^3 \nu(f)}{\lvert f\rvert^{3/2} 3^{\Omega(f)}} \right)^2 \nonumber \\ &= q^{g+2} (l!)^2 \sum_{\substack{P\mid b \Rightarrow \deg(P) \leq y \\ \Omega(b) \leq l \\ \Omega(b) \equiv l \,(\mathrm{mod}\,3)}} \frac{ \lvert a(b)\rvert^2 \nu(b) }{\lvert b\rvert} \frac{1}{(( (l-\Omega(b))/3)!)^2} \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^3}{3\lvert P\rvert^{3/2}} \right)^{2(l-\Omega(b))/3}, \end{align} $$where we used the fact that ![]() $\nu (ab) \leq \nu (a) \nu (b)$,
$\nu (ab) \leq \nu (a) \nu (b)$,  $\nu \left (f^3\right ) \leq \nu (f)/3^{\Omega (f)}$ and
$\nu \left (f^3\right ) \leq \nu (f)/3^{\Omega (f)}$ and ![]() $\nu (b)^2 \leq \nu (b)$, and we ignored the condition that
$\nu (b)^2 \leq \nu (b)$, and we ignored the condition that ![]() $(f_1,h_1)=1$.
$(f_1,h_1)=1$.
We further get that this is
 $$ \begin{align} &\ll q^{g} (l!)^2 \sum_{\substack{i=0 \\ i \equiv l \,(\mathrm{mod}\,3)}}^l \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^i \frac{1}{ i! ( ((l-i)/3)!)^23^{2(l-i)/3}} \end{align} $$
$$ \begin{align} &\ll q^{g} (l!)^2 \sum_{\substack{i=0 \\ i \equiv l \,(\mathrm{mod}\,3)}}^l \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^i \frac{1}{ i! ( ((l-i)/3)!)^23^{2(l-i)/3}} \end{align} $$ $$ \begin{align} & \ll q^{g} \frac{ (l!)^2}{9^{l/3}} \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l \sum_{j=0}^{\lfloor l/3\rfloor} \frac{9^j}{(3j)! \left( \frac{l}{3}-j\right)!^2},\end{align} $$
$$ \begin{align} & \ll q^{g} \frac{ (l!)^2}{9^{l/3}} \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l \sum_{j=0}^{\lfloor l/3\rfloor} \frac{9^j}{(3j)! \left( \frac{l}{3}-j\right)!^2},\end{align} $$where we get the first line by using the facts that ![]() $\lvert a(P)\rvert \ll 1$ and
$\lvert a(P)\rvert \ll 1$ and  $\sum _{n=1}^{\infty } \frac {1}{nq^{n/2}}<1$ and that the sum over primes in formula (6.4) is bounded. Using the trinomial expansion formula, we get
$\sum _{n=1}^{\infty } \frac {1}{nq^{n/2}}<1$ and that the sum over primes in formula (6.4) is bounded. Using the trinomial expansion formula, we get
 $$ \begin{align*} \sum_{j=0}^{\lfloor l/3\rfloor} \frac{9^j}{(3j)! \left( \frac{l}{3}-j\right)!^2}\leq \sum_{j=0}^{\lfloor l/3\rfloor} \frac{3^{2j}}{(2j)! \left( \frac{l}{3}-j\right)!^2}\leq \sum_{a+b+c=\lfloor 2l/3\rfloor } \frac{3^a}{a!b!c!}\leq \frac{5^{2l/3}}{\lfloor 2l/3 \rfloor !}. \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{\lfloor l/3\rfloor} \frac{9^j}{(3j)! \left( \frac{l}{3}-j\right)!^2}\leq \sum_{j=0}^{\lfloor l/3\rfloor} \frac{3^{2j}}{(2j)! \left( \frac{l}{3}-j\right)!^2}\leq \sum_{a+b+c=\lfloor 2l/3\rfloor } \frac{3^a}{a!b!c!}\leq \frac{5^{2l/3}}{\lfloor 2l/3 \rfloor !}. \end{align*} $$Replacing in formulas (6.6) and then (6.4), we get
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \ll q^g \frac{ (l!)^2 5^{2l/3} }{\lfloor 2l/3 \rfloor ! 9^{l/3}} \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l. \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \left\lvert \sum_{\deg(P) \leq y} \frac{ \chi(P) a(P)}{\sqrt{\lvert P\rvert}} \right\rvert^{2l} \ll q^g \frac{ (l!)^2 5^{2l/3} }{\lfloor 2l/3 \rfloor ! 9^{l/3}} \left( \sum_{\deg(P) \leq y} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l. \end{align*} $$Now let
 $$ \begin{align*} x = \sum_{\deg(P) \leq y} \frac{ \lvert a(P)\rvert^2}{\lvert P\rvert}, \end{align*} $$
$$ \begin{align*} x = \sum_{\deg(P) \leq y} \frac{ \lvert a(P)\rvert^2}{\lvert P\rvert}, \end{align*} $$and we assume that ![]() $l \leq x^{3-\varepsilon }$. We claim that for
$l \leq x^{3-\varepsilon }$. We claim that for ![]() $i \leq l$ with
$i \leq l$ with ![]() $i \equiv l \,(\mathrm {mod}\,3)$, we have
$i \equiv l \,(\mathrm {mod}\,3)$, we have
 $$ \begin{align} \frac{x^i 3^{2i/3}}{i! ( (l-i)/3)!^2} \ll \frac{x^l}{l!}. \end{align} $$
$$ \begin{align} \frac{x^i 3^{2i/3}}{i! ( (l-i)/3)!^2} \ll \frac{x^l}{l!}. \end{align} $$Using Stirling’s formula, we need to show that for ![]() $l \leq x^{3-\varepsilon }$, we have
$l \leq x^{3-\varepsilon }$, we have
 $$ \begin{align*} \frac{2i}{3} \log 3+ l \log l - l -i \log i +i - \frac{2(l-i)}{3} \log \left( \frac{l-i}{3} \right)+\frac{2(l-i)}{3} \leq (l-i) \log x+\log C, \end{align*} $$
$$ \begin{align*} \frac{2i}{3} \log 3+ l \log l - l -i \log i +i - \frac{2(l-i)}{3} \log \left( \frac{l-i}{3} \right)+\frac{2(l-i)}{3} \leq (l-i) \log x+\log C, \end{align*} $$for some constant C. Now let
 $$ \begin{align*} f(i)= i \log x+\frac{2i}{3} \log 3+ l \log l - l -i \log i +i - \frac{2(l-i)}{3} \log \left( \frac{l-i}{3} \right)+\frac{2(l-i)}{3}. \end{align*} $$
$$ \begin{align*} f(i)= i \log x+\frac{2i}{3} \log 3+ l \log l - l -i \log i +i - \frac{2(l-i)}{3} \log \left( \frac{l-i}{3} \right)+\frac{2(l-i)}{3}. \end{align*} $$Then
 $$ \begin{align*} f'(i) = \log\left(3^{2/3}x\right) - \log i+ \frac{2}{3} \log \left(\frac{l-i}{3} \right), \end{align*} $$
$$ \begin{align*} f'(i) = \log\left(3^{2/3}x\right) - \log i+ \frac{2}{3} \log \left(\frac{l-i}{3} \right), \end{align*} $$and f attains its maximum on ![]() $[0,l]$ at i with
$[0,l]$ at i with ![]() $i^3=x^3(l-i)^2$. Since
$i^3=x^3(l-i)^2$. Since ![]() $l \leq x^{3-\varepsilon }$, it follows that f attains its maximum at some
$l \leq x^{3-\varepsilon }$, it follows that f attains its maximum at some ![]() $i_0$ with
$i_0$ with ![]() $i_0>l/2$. Indeed, if we suppose that
$i_0>l/2$. Indeed, if we suppose that ![]() $i_0 \leq l/2$, then
$i_0 \leq l/2$, then ![]() $l-i_0 \geq l/2$, and since
$l-i_0 \geq l/2$, and since ![]() $x^3>l$ it follows that
$x^3>l$ it follows that  $i_0^3> l^3/4$ – which is a contradiction, since we assumed that
$i_0^3> l^3/4$ – which is a contradiction, since we assumed that  $i_0^3 \leq l^3/8$. Let
$i_0^3 \leq l^3/8$. Let ![]() $i_1=i_0/l$. We have
$i_1=i_0/l$. We have ![]() $1/2<i_1<1$. Then
$1/2<i_1<1$. Then
 $$ \begin{align*} f(i_0)= l i_1 \log x+ \frac{l(1-i_1)}{3} \log l+ \frac{2i_0}{3} \log 3-l-l i_1 \log i_1+i_0-\frac{2l(1-i_1)}{3} \log \left(\frac{1-i_1}{3} \right)+\frac{2l(1-i_1)}{3}. \end{align*} $$
$$ \begin{align*} f(i_0)= l i_1 \log x+ \frac{l(1-i_1)}{3} \log l+ \frac{2i_0}{3} \log 3-l-l i_1 \log i_1+i_0-\frac{2l(1-i_1)}{3} \log \left(\frac{1-i_1}{3} \right)+\frac{2l(1-i_1)}{3}. \end{align*} $$Since ![]() $1/2<i_1<1$, it follows that
$1/2<i_1<1$, it follows that
which establishes formula (6.7). Combining formulas (6.5) and (6.7), and since ![]() $l /3^{2l/3}<1$, the conclusion follows.
$l /3^{2l/3}<1$, the conclusion follows.
Proof of Proposition 6.1. The proof is similar to the proof of [Reference Soundararajan36, Corollary A]. Let
 $$ \begin{align*} N(V) = \left \lvert\left \{ \chi \text{ primitive cubic, genus}(\chi)=g : \log \left\lvert{\textstyle L\left(\frac{1}{2}, \chi\right)} \right\rvert \geq V \right \} \right\rvert. \end{align*} $$
$$ \begin{align*} N(V) = \left \lvert\left \{ \chi \text{ primitive cubic, genus}(\chi)=g : \log \left\lvert{\textstyle L\left(\frac{1}{2}, \chi\right)} \right\rvert \geq V \right \} \right\rvert. \end{align*} $$Then
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)} \right\rvert^{2k} =2k \int_{-\infty}^{\infty} \exp (2kV) N(V) dV. \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)} \right\rvert^{2k} =2k \int_{-\infty}^{\infty} \exp (2kV) N(V) dV. \end{align} $$In formula (3.1) with ![]() $k=1$, note that we can bound the contribution from primes square by
$k=1$, note that we can bound the contribution from primes square by ![]() $O(\log \log g)$. Indeed, we split the sum over P with
$O(\log \log g)$. Indeed, we split the sum over P with ![]() $\deg (P) \leq N/2$ into primes P with
$\deg (P) \leq N/2$ into primes P with ![]() $\deg (P) \leq 4 \log _q g$ and primes P with
$\deg (P) \leq 4 \log _q g$ and primes P with ![]() $4 \log _q g<\deg (P) \leq N/2$. For the first term, we use the trivial bound, which gives the bound
$4 \log _q g<\deg (P) \leq N/2$. For the first term, we use the trivial bound, which gives the bound ![]() $O(\log \log g)$. For the second term, we use the Weil bound (2.10), yielding an upper bound of size
$O(\log \log g)$. For the second term, we use the Weil bound (2.10), yielding an upper bound of size ![]() $o(1)$. So we have
$o(1)$. So we have
 $$ \begin{align} \log \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert \leq \Re \left( \sum_{\deg(P) \leq N} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2} +\frac{1}{N \log q}}} \right) + \frac{g+2}{N}+O(\log \log g). \end{align} $$
$$ \begin{align} \log \left\lvert {\textstyle L\left(\frac{1}{2},\chi\right) }\right\rvert \leq \Re \left( \sum_{\deg(P) \leq N} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2} +\frac{1}{N \log q}}} \right) + \frac{g+2}{N}+O(\log \log g). \end{align} $$Let
 $$ \begin{align*} \frac{g+2}{N} = \frac{V}{A} \end{align*} $$
$$ \begin{align*} \frac{g+2}{N} = \frac{V}{A} \end{align*} $$and ![]() $N_0=N/\log g$, where
$N_0=N/\log g$, where
 $$ \begin{align} A = \begin{cases} \frac{\log \log g}{2} & \mbox{ if } V \leq \log g,\\ \frac{\log g}{2V} \log \log g & \mbox{ if } \log g< V \leq \frac{1}{12} \log g \log \log g, \\ 6 & \mbox{ if } \frac{1}{12} \log g \log \log g <V. \end{cases} \end{align} $$
$$ \begin{align} A = \begin{cases} \frac{\log \log g}{2} & \mbox{ if } V \leq \log g,\\ \frac{\log g}{2V} \log \log g & \mbox{ if } \log g< V \leq \frac{1}{12} \log g \log \log g, \\ 6 & \mbox{ if } \frac{1}{12} \log g \log \log g <V. \end{cases} \end{align} $$We only need to consider  $\sqrt {\log g}<V$. Indeed, note that the contribution from
$\sqrt {\log g}<V$. Indeed, note that the contribution from  $V \leq \sqrt {\log g}$ in the integral on the right-hand side of equation (6.8) is
$V \leq \sqrt {\log g}$ in the integral on the right-hand side of equation (6.8) is  $o\left (q^gg^{k^2}\right )$, by trivially bounding
$o\left (q^gg^{k^2}\right )$, by trivially bounding ![]() $N(V) \ll q^g$. If
$N(V) \ll q^g$. If ![]() $\chi $ is such that
$\chi $ is such that  $\log \left \lvert {\textstyle L\left (\frac {1}{2}, \chi \right )} \right \rvert \geq V$, then
$\log \left \lvert {\textstyle L\left (\frac {1}{2}, \chi \right )} \right \rvert \geq V$, then
 $$ \begin{align*} \Re \left( \sum_{\deg(P) \leq N} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2} +\frac{1}{N \log q}}} \right) \geq V - \frac{V}{A} + O \left( \log{\log{g}} \right) \geq V \left(1-\frac{2}{A} \right) \end{align*} $$
$$ \begin{align*} \Re \left( \sum_{\deg(P) \leq N} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2} +\frac{1}{N \log q}}} \right) \geq V - \frac{V}{A} + O \left( \log{\log{g}} \right) \geq V \left(1-\frac{2}{A} \right) \end{align*} $$for g large enough, since  $\sqrt {\log g}<V$.
$\sqrt {\log g}<V$.
Let
 $$ \begin{align*} S_1(\chi)= \left\lvert \sum_{\deg(P) \leq N_0} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2} +\frac{1}{N \log q}}} \right\rvert, \qquad S_2(\chi)= \left\lvert \sum_{N_0 < \deg(P) \leq N} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2} +\frac{1}{N \log q}}}\right\rvert. \end{align*} $$
$$ \begin{align*} S_1(\chi)= \left\lvert \sum_{\deg(P) \leq N_0} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2} +\frac{1}{N \log q}}} \right\rvert, \qquad S_2(\chi)= \left\lvert \sum_{N_0 < \deg(P) \leq N} \frac{ \chi(P)(N-\deg(P))}{N\lvert P\rvert^{\frac{1}{2} +\frac{1}{N \log q}}}\right\rvert. \end{align*} $$Then if  $\log \left \lvert {\textstyle L\left (\frac {1}{2}, \chi \right )} \right \rvert \geq V$, either
$\log \left \lvert {\textstyle L\left (\frac {1}{2}, \chi \right )} \right \rvert \geq V$, either
Let
 $$ \begin{align*} \mathcal{F}_1 &= \{\, \chi \text{ primitive cubic, genus}(\chi)=g : S_1(\chi) \geq V_1 \}\\ \mathcal{F}_2 &= \{\, \chi \text{ primitive cubic, genus}(\chi)=g : S_2(\chi) \geq V/A \}. \end{align*} $$
$$ \begin{align*} \mathcal{F}_1 &= \{\, \chi \text{ primitive cubic, genus}(\chi)=g : S_1(\chi) \geq V_1 \}\\ \mathcal{F}_2 &= \{\, \chi \text{ primitive cubic, genus}(\chi)=g : S_2(\chi) \geq V/A \}. \end{align*} $$Using formula (6.1) of Lemma 6.2, we get
 $$ \begin{align*} \lvert \mathcal{F}_2\rvert \leq \sum_{\chi \in \mathcal{C}(g)} \left( \frac{S_2(\chi)}{V/A} \right)^{2l} \ll q^g \left(\frac{A}{V} \right)^{2l} \frac{(l!)^2 (25/9)^{l/3} }{\lfloor2l/3\rfloor !} \left( \sum_{N_0 < \deg(P) \leq N} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l, \end{align*} $$
$$ \begin{align*} \lvert \mathcal{F}_2\rvert \leq \sum_{\chi \in \mathcal{C}(g)} \left( \frac{S_2(\chi)}{V/A} \right)^{2l} \ll q^g \left(\frac{A}{V} \right)^{2l} \frac{(l!)^2 (25/9)^{l/3} }{\lfloor2l/3\rfloor !} \left( \sum_{N_0 < \deg(P) \leq N} \frac{\lvert a(P)\rvert^2}{\lvert P\rvert} \right)^l, \end{align*} $$for any l such that ![]() $3l N \leq g/2+1 \iff l \leq V/(6A)$ and where
$3l N \leq g/2+1 \iff l \leq V/(6A)$ and where  $a(P) = (N-\deg (P))/\left (N\lvert P\rvert ^{1/N\log q}\right )$. Picking
$a(P) = (N-\deg (P))/\left (N\lvert P\rvert ^{1/N\log q}\right )$. Picking ![]() $l =6\lfloor V/(36A)\rfloor $, this gives
$l =6\lfloor V/(36A)\rfloor $, this gives
 $$ \begin{align} \lvert\mathcal{F}_2\rvert \ll q^g \left(\frac{A}{V} \right)^{2l} \left(\frac{l}{e} \right)^{4l/3} (5/2)^{2l/3} (\log \log g)^l \ll q^g \exp \left( - \frac{V}{10 A} \log V \right). \end{align} $$
$$ \begin{align} \lvert\mathcal{F}_2\rvert \ll q^g \left(\frac{A}{V} \right)^{2l} \left(\frac{l}{e} \right)^{4l/3} (5/2)^{2l/3} (\log \log g)^l \ll q^g \exp \left( - \frac{V}{10 A} \log V \right). \end{align} $$ If ![]() $\chi \in \mathcal {F}_1$ and
$\chi \in \mathcal {F}_1$ and ![]() $V \leq (\log g)^{2-\varepsilon }$, then we pick
$V \leq (\log g)^{2-\varepsilon }$, then we pick  $l=\left \lfloor V_1^2/\log g \right \rfloor $. Note that since
$l=\left \lfloor V_1^2/\log g \right \rfloor $. Note that since  $a(P)=(N-\deg (P))/\left (N \lvert P\rvert ^{1/N \log g}\right )$, we have
$a(P)=(N-\deg (P))/\left (N \lvert P\rvert ^{1/N \log g}\right )$, we have  $\sum _{\deg (P ) \leq N_0} \lvert a(P)\rvert ^2/\lvert P\rvert = \log g + o(\log g)$, and then
$\sum _{\deg (P ) \leq N_0} \lvert a(P)\rvert ^2/\lvert P\rvert = \log g + o(\log g)$, and then  $l \leq \left (\sum _{\deg (P) \leq N_0} \lvert a(P)\rvert ^2/\lvert P\rvert \right )^{3-\varepsilon }$. We can then apply formula (6.2) of Lemma 6.2, and we get
$l \leq \left (\sum _{\deg (P) \leq N_0} \lvert a(P)\rvert ^2/\lvert P\rvert \right )^{3-\varepsilon }$. We can then apply formula (6.2) of Lemma 6.2, and we get
 $$ \begin{align*} \lvert \mathcal{F}_1\rvert \leq \sum_{\chi \in \mathcal{C}(g)} \left( \frac{S_1(\chi)}{V_1} \right)^{2l} \ll q^g \sqrt{l} \exp \left(l \log \left( \frac{l \log g}{eV_1^2} \right) \right) \ll q^g \frac{V}{\sqrt{\log g}} \exp \left(- \frac{V_1^2}{\log g} \right). \end{align*} $$
$$ \begin{align*} \lvert \mathcal{F}_1\rvert \leq \sum_{\chi \in \mathcal{C}(g)} \left( \frac{S_1(\chi)}{V_1} \right)^{2l} \ll q^g \sqrt{l} \exp \left(l \log \left( \frac{l \log g}{eV_1^2} \right) \right) \ll q^g \frac{V}{\sqrt{\log g}} \exp \left(- \frac{V_1^2}{\log g} \right). \end{align*} $$If ![]() $V>(\log g)^{2-\varepsilon }$, then we pick
$V>(\log g)^{2-\varepsilon }$, then we pick ![]() $l=18V$ and apply formula (6.1) to get
$l=18V$ and apply formula (6.1) to get
 $$ \begin{align*} \lvert \mathcal{F}_1\rvert \ll q^g \left(\frac{l^{4/3} 25^{1/3} \log g}{e^{4/3} 4^{1/3} V_1^2 } \right)^l \ll q^g \exp(-2V \log V). \end{align*} $$
$$ \begin{align*} \lvert \mathcal{F}_1\rvert \ll q^g \left(\frac{l^{4/3} 25^{1/3} \log g}{e^{4/3} 4^{1/3} V_1^2 } \right)^l \ll q^g \exp(-2V \log V). \end{align*} $$Using this and the values for A of equation (6.10), we prove the following:
If  $\sqrt {\log g} \leq V \leq \log g$, then
$\sqrt {\log g} \leq V \leq \log g$, then
 $$ \begin{align} N(V) \ll q^g \exp \left(- \frac{V^2}{\log g} \left(1-\frac{6}{ \log \log g} \right)^2 \right). \end{align} $$
$$ \begin{align} N(V) \ll q^g \exp \left(- \frac{V^2}{\log g} \left(1-\frac{6}{ \log \log g} \right)^2 \right). \end{align} $$ If  $\log g < V \leq \frac {1}{12} \log g \log \log g$, then
$\log g < V \leq \frac {1}{12} \log g \log \log g$, then
 $$ \begin{align} N(V) \ll q^g \exp \left(-\frac{V^2}{ \log g} \left(1- \frac{6V}{ \log g \log \log g} \right)^2 \right). \end{align} $$
$$ \begin{align} N(V) \ll q^g \exp \left(-\frac{V^2}{ \log g} \left(1- \frac{6V}{ \log g \log \log g} \right)^2 \right). \end{align} $$ If  $V> \frac {1}{12} \log g \log \log g$, then
$V> \frac {1}{12} \log g \log \log g$, then
 $$ \begin{align} N(V) \ll q^g \exp \left(- \frac{V \log V}{60} \right). \end{align} $$
$$ \begin{align} N(V) \ll q^g \exp \left(- \frac{V \log V}{60} \right). \end{align} $$Now we use the bounds (6.12), (6.13) and (6.14) in the form  $N(V) \ll q^g g^{o(1)} \exp \left (-V^2/\log g\right )$ if
$N(V) \ll q^g g^{o(1)} \exp \left (-V^2/\log g\right )$ if ![]() $V \leq 4 k \log g$ and
$V \leq 4 k \log g$ and ![]() $N(V) \ll q^g g^{o(1)} \exp (-4kV)$ if
$N(V) \ll q^g g^{o(1)} \exp (-4kV)$ if ![]() $V>4k \log g$ in equation (6.8) to prove Proposition 6.1. Indeed, we have
$V>4k \log g$ in equation (6.8) to prove Proposition 6.1. Indeed, we have
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)} \right\rvert^{2k} &\ll_k q^g g^{o(1)} \int_{\sqrt{\log{g}}}^{4k \log{g}} \exp \left(2kV - V^2/\log{g}\right) dV + q^g g^{o(1)} \int_{4 k \log{g}}^{\infty} \exp (-2kV) dV \\ &\ll_k q^g g^{o(1)} \exp{\left(k^2 \log{g}\right)}, \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)} \right\rvert^{2k} &\ll_k q^g g^{o(1)} \int_{\sqrt{\log{g}}}^{4k \log{g}} \exp \left(2kV - V^2/\log{g}\right) dV + q^g g^{o(1)} \int_{4 k \log{g}}^{\infty} \exp (-2kV) dV \\ &\ll_k q^g g^{o(1)} \exp{\left(k^2 \log{g}\right)}, \end{align*} $$and the desired upper bound follows. As mentioned in [Reference Soundararajan36], it is interesting to remark that the proof suggests that the dominant contribution for the ![]() $2k$th moment comes from the characters
$2k$th moment comes from the characters ![]() $\chi $ such that
$\chi $ such that  $\left \lvert {\textstyle L\left (\frac {1}{2}, \chi \right )} \right \rvert $ has size
$\left \lvert {\textstyle L\left (\frac {1}{2}, \chi \right )} \right \rvert $ has size ![]() $g^k$, and the measure of this set is about
$g^k$, and the measure of this set is about  $q^g g^{-k^2}$.
$q^g g^{-k^2}$.
7 Explicit upper bound for mollified moments
Here we will obtain an explicit upper bound for expression (3.21), which means that we want to find an upper bound for ![]() $C_J$ from equation (3.20) by choosing
$C_J$ from equation (3.20) by choosing ![]() $\theta _J , a,b$ and d subject to the constraints in Lemma 3.5 and subject to formula (4.2).
$\theta _J , a,b$ and d subject to the constraints in Lemma 3.5 and subject to formula (4.2).
Let
 $$ \begin{align*} f(u)=R_1 e^u-R_2 ue^u+\frac{k^2u \theta_J }{2}, \end{align*} $$
$$ \begin{align*} f(u)=R_1 e^u-R_2 ue^u+\frac{k^2u \theta_J }{2}, \end{align*} $$with
 $$ \begin{align} R_1 =k e+\frac{\alpha}{2d} \log \theta_J + \frac{\log F}{2d}, \qquad R_2 = \frac{\alpha}{2d} , \end{align} $$
$$ \begin{align} R_1 =k e+\frac{\alpha}{2d} \log \theta_J + \frac{\log F}{2d}, \qquad R_2 = \frac{\alpha}{2d} , \end{align} $$where we recall that
 $$ \begin{align*} \alpha= 2 b-2+\frac{c}{3} , \qquad F= \frac{k^2 e^{2+c/3} 5^{c/3}}{4d^{2-c/3}c^{c/3}}, \qquad c=2-4/a, \end{align*} $$
$$ \begin{align*} \alpha= 2 b-2+\frac{c}{3} , \qquad F= \frac{k^2 e^{2+c/3} 5^{c/3}}{4d^{2-c/3}c^{c/3}}, \qquad c=2-4/a, \end{align*} $$and a and d are as in Lemma 3.5. We will pick ![]() $\theta _J $ subject to the condition (4.2) and such that
$\theta _J $ subject to the condition (4.2) and such that ![]() $R_1>0$.
$R_1>0$.
We have
 $$ \begin{align*} f'(u) = e^u(R_1 -R_2 -R_2 u)+ \frac{k^2 \theta_J }{2}, \end{align*} $$
$$ \begin{align*} f'(u) = e^u(R_1 -R_2 -R_2 u)+ \frac{k^2 \theta_J }{2}, \end{align*} $$and notice that for ![]() $u \leq (R_1 -R_2 )/R_2 $ we have
$u \leq (R_1 -R_2 )/R_2 $ we have ![]() $f'(u)>0$, so f is increasing on
$f'(u)>0$, so f is increasing on ![]() $[0,(R_1 -R_2 )/R_2 ]$ – that is, f is increasing on
$[0,(R_1 -R_2 )/R_2 ]$ – that is, f is increasing on  $\left [0, \frac {2dk e}{\alpha }+\log \theta _J +\frac {\log F}{\alpha }-1\right ]$. Also note that
$\left [0, \frac {2dk e}{\alpha }+\log \theta _J +\frac {\log F}{\alpha }-1\right ]$. Also note that
 $$ \begin{align*} f'(R_1 /R_2 )= -R_2 e^{R_1 /R_2 }+ \frac{k^2 \theta_J }{2}<0, \end{align*} $$
$$ \begin{align*} f'(R_1 /R_2 )= -R_2 e^{R_1 /R_2 }+ \frac{k^2 \theta_J }{2}<0, \end{align*} $$so the maximum of f occurs at some ![]() $m \in (R_1 /R_2 -1,R_1 /R_2 )$. With this notation, we write
$m \in (R_1 /R_2 -1,R_1 /R_2 )$. With this notation, we write
 $$ \begin{align*} C_J \leq 2\int_0^{J } (u+1) \exp \left( \frac{1}{\theta_J } \left(R_1 e^u-R_2 u e^u + \frac{k^2 u \theta_J }{2} \right) \right) du. \end{align*} $$
$$ \begin{align*} C_J \leq 2\int_0^{J } (u+1) \exp \left( \frac{1}{\theta_J } \left(R_1 e^u-R_2 u e^u + \frac{k^2 u \theta_J }{2} \right) \right) du. \end{align*} $$For ![]() $u \geq 4R_1 /R_2 $ we have
$u \geq 4R_1 /R_2 $ we have ![]() $R_1 e^u+ k^2 u \theta _J /2<R_2 ue^u/2$, so
$R_1 e^u+ k^2 u \theta _J /2<R_2 ue^u/2$, so
 $$ \begin{align} \int_{4A/B}^{J } (u+1) \exp \left( \frac{1}{\theta_J } \left(R_1 e^u-R_2 u e^u + \frac{k^2 u \theta_J }{2} \right) \right) du \leq \int_{4R_1 /R_2 }^{\infty} e^{-u} du = e^{-4R_1 /R_2 }. \end{align} $$
$$ \begin{align} \int_{4A/B}^{J } (u+1) \exp \left( \frac{1}{\theta_J } \left(R_1 e^u-R_2 u e^u + \frac{k^2 u \theta_J }{2} \right) \right) du \leq \int_{4R_1 /R_2 }^{\infty} e^{-u} du = e^{-4R_1 /R_2 }. \end{align} $$Now
 $$ \begin{align} \int_0^{4R_1 /R_2 } & (u+1) \exp \left( \frac{1}{\theta_J } \left(R_1 e^u-R_2 u e^u + \frac{k^2 u \theta_J }{2} \right) \right) du \nonumber\\ &\leq \frac{4R_1 }{R_2 } \left(\frac{4R_1 }{R_2 }+1 \right) \exp \left( \frac{1}{\theta_J } \left(R_1 e^m-R_2 m e^m + \frac{k^2 m \theta_J }{2} \right) \right)\nonumber \\ & \leq \frac{4R_1 }{R_2 }\left(\frac{4R_1 }{R_2 }+1 \right) \exp \left(\frac{k^2R_1 }{2R_2 } \right) \exp \left(\frac{R_2 e^{\frac{R_1 }{R_2 }-1}}{\theta_J } \right), \end{align} $$
$$ \begin{align} \int_0^{4R_1 /R_2 } & (u+1) \exp \left( \frac{1}{\theta_J } \left(R_1 e^u-R_2 u e^u + \frac{k^2 u \theta_J }{2} \right) \right) du \nonumber\\ &\leq \frac{4R_1 }{R_2 } \left(\frac{4R_1 }{R_2 }+1 \right) \exp \left( \frac{1}{\theta_J } \left(R_1 e^m-R_2 m e^m + \frac{k^2 m \theta_J }{2} \right) \right)\nonumber \\ & \leq \frac{4R_1 }{R_2 }\left(\frac{4R_1 }{R_2 }+1 \right) \exp \left(\frac{k^2R_1 }{2R_2 } \right) \exp \left(\frac{R_2 e^{\frac{R_1 }{R_2 }-1}}{\theta_J } \right), \end{align} $$where in the third line we used the fact that ![]() $m \in (R_1 /R_2 -1,R_1 /R_2 )$. Combining formulas (7.2) and (7.3), we get
$m \in (R_1 /R_2 -1,R_1 /R_2 )$. Combining formulas (7.2) and (7.3), we get
 $$ \begin{align*} C_J \leq 2 \left(e^{-4R_1 /R_2 }+\frac{4R_1 }{R_2 } \left( \frac{4R_1 }{R_2 }+1 \right) \exp \left(\frac{k^2R_1 }{2R_2 } \right) \exp \left(\frac{R_2 e^{\frac{R_1 }{R_2 }-1}}{\theta_J } \right)\right). \end{align*} $$
$$ \begin{align*} C_J \leq 2 \left(e^{-4R_1 /R_2 }+\frac{4R_1 }{R_2 } \left( \frac{4R_1 }{R_2 }+1 \right) \exp \left(\frac{k^2R_1 }{2R_2 } \right) \exp \left(\frac{R_2 e^{\frac{R_1 }{R_2 }-1}}{\theta_J } \right)\right). \end{align*} $$Now using this inequality back in formula (3.21), we get
 $$ \begin{align} &\sum_{\substack{ \chi \in \mathcal{C}(g) }} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \leq_\varepsilon q^{g+2}\mathcal{D}_k^{1/2}C(k)^{1/2}\mathcal{S}_k^{1/2} \exp{\left(\frac{k^2}{2} + (1+\eta) k \right)}\notag \\ &\quad \times \left( \exp(k/\theta_J) + 2 \sqrt[4]{\frac{24}{c}} \left[e^{-4R_1 /R_2 }+\frac{4R_1 }{R_2 } \left( \frac{4R_1 }{B}+1 \right) \exp \left(\frac{k^2R_1 }{2R_2 } \right) \exp \left(\frac{R_2 e^{\frac{R_1 }{R_2}-1}}{\theta_J } \right) \right] \right), \end{align} $$
$$ \begin{align} &\sum_{\substack{ \chi \in \mathcal{C}(g) }} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{k} \left\lvert{\textstyle M\left(\chi;\frac{1}{\kappa}\right)}\right\rvert^{k \kappa} \leq_\varepsilon q^{g+2}\mathcal{D}_k^{1/2}C(k)^{1/2}\mathcal{S}_k^{1/2} \exp{\left(\frac{k^2}{2} + (1+\eta) k \right)}\notag \\ &\quad \times \left( \exp(k/\theta_J) + 2 \sqrt[4]{\frac{24}{c}} \left[e^{-4R_1 /R_2 }+\frac{4R_1 }{R_2 } \left( \frac{4R_1 }{B}+1 \right) \exp \left(\frac{k^2R_1 }{2R_2 } \right) \exp \left(\frac{R_2 e^{\frac{R_1 }{R_2}-1}}{\theta_J } \right) \right] \right), \end{align} $$where we recall that ![]() $R_1 $ and
$R_1 $ and ![]() $R_2 $ are given in equation (7.1) and
$R_2 $ are given in equation (7.1) and ![]() $\mathcal {S}_k$ is defined in Lemma 5.1.
$\mathcal {S}_k$ is defined in Lemma 5.1.
From the explicit upper bound obtained, we remark that because of the term  $\exp \left (R_2 e^{R_1 /R_2 -1}/\theta _J \right )$, the upper bound we obtain is of the form
$\exp \left (R_2 e^{R_1 /R_2 -1}/\theta _J \right )$, the upper bound we obtain is of the form ![]() $e^{e^{O(k)}}$.
$e^{e^{O(k)}}$.
Now we take ![]() $\kappa =1, k=2$. Condition (4.2) becomes
$\kappa =1, k=2$. Condition (4.2) becomes
 $$ \begin{align*} 10 \sum_{r=0}^J \theta_r \ell_r + \frac{4}{d} \leq \frac{1}{2}. \end{align*} $$
$$ \begin{align*} 10 \sum_{r=0}^J \theta_r \ell_r + \frac{4}{d} \leq \frac{1}{2}. \end{align*} $$Note that any ![]() $\theta _J $ with
$\theta _J $ with
 $$ \begin{align*} \theta_J ^{1-b} \frac{e^{1-b}}{e^{1-b}-1} \leq \frac{d-8}{40d} \end{align*} $$
$$ \begin{align*} \theta_J ^{1-b} \frac{e^{1-b}}{e^{1-b}-1} \leq \frac{d-8}{40d} \end{align*} $$satisfies this condition. We will pick ![]() $\theta _J $ such that
$\theta _J $ such that
 $$ \begin{align} \theta_J = \left(\frac{d-8}{40d} \left(1-\frac{1}{e} \right)\right)^{\frac{1}{1-b}}. \end{align} $$
$$ \begin{align} \theta_J = \left(\frac{d-8}{40d} \left(1-\frac{1}{e} \right)\right)^{\frac{1}{1-b}}. \end{align} $$Now, in formula (7.4), in order to obtain an optimal constant, we set
 $$ \begin{align*} \frac{1}{\theta_J }= e^{R_1 /R_2 }, \end{align*} $$
$$ \begin{align*} \frac{1}{\theta_J }= e^{R_1 /R_2 }, \end{align*} $$and the term ![]() $\log F/(2d)$ in the expression for
$\log F/(2d)$ in the expression for ![]() $R_1 $ is small compared to the rest, so in order to optimise the constant, we set
$R_1 $ is small compared to the rest, so in order to optimise the constant, we set
 $$ \begin{align} \log \frac{1}{\theta_J } = \frac{2de}{2b-2+\frac{c}{3}}. \end{align} $$
$$ \begin{align} \log \frac{1}{\theta_J } = \frac{2de}{2b-2+\frac{c}{3}}. \end{align} $$Now from Lemma 3.5 we need
 $$ \begin{align*} 4ad \theta_J ^{1-b} \leq 1, \end{align*} $$
$$ \begin{align*} 4ad \theta_J ^{1-b} \leq 1, \end{align*} $$so combining this with equation (7.5) it follows that
 $$ \begin{align*} c \leq 2-\frac{2(d-8)(e-1)}{5e}. \end{align*} $$
$$ \begin{align*} c \leq 2-\frac{2(d-8)(e-1)}{5e}. \end{align*} $$Now, to minimise equation (7.6) we need c to be maximal, so we will pick
 $$ \begin{align} c= 2-\frac{2(d-8)(e-1)}{5e}. \end{align} $$
$$ \begin{align} c= 2-\frac{2(d-8)(e-1)}{5e}. \end{align} $$From equations (7.5), (7.6) and (7.7), it follows that
 $$ \begin{align} b= 1- \frac{cx}{6(de+x)}, \end{align} $$
$$ \begin{align} b= 1- \frac{cx}{6(de+x)}, \end{align} $$where ![]() $x= \log (40 de/((d-8)(e-1)))$. With choices (7.8) and (7.7) for b and c, we want to minimise equation (7.6), and this translates into minimising the function of d given by
$x= \log (40 de/((d-8)(e-1)))$. With choices (7.8) and (7.7) for b and c, we want to minimise equation (7.6), and this translates into minimising the function of d given by
 $$ \begin{align*} \frac{de+x}{1-\frac{(d-8)(e-1)}{5e}} \end{align*} $$
$$ \begin{align*} \frac{de+x}{1-\frac{(d-8)(e-1)}{5e}} \end{align*} $$for ![]() $d>8$.
$d>8$.
The minimum of this function is achieved for
and in that case,
 $$ \begin{align*} \log \frac{1}{\theta_J } = \frac{2de}{2b-2+\frac{c}{3}} \approx 92.65. \end{align*} $$
$$ \begin{align*} \log \frac{1}{\theta_J } = \frac{2de}{2b-2+\frac{c}{3}} \approx 92.65. \end{align*} $$With this choice for d, we get
Choosing ![]() $b,c,d$ as in formulas (7.9) and (7.10), we obtain the upper bound
$b,c,d$ as in formulas (7.9) and (7.10), we obtain the upper bound
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{ 2} \left\lvert M(\chi;1)\right\rvert^2 \leq_{\varepsilon} e^{e^{182}} q^{g+2}. \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} \left\lvert{\textstyle L\left(\frac{1}{2},\chi\right)}\right\rvert^{ 2} \left\lvert M(\chi;1)\right\rvert^2 \leq_{\varepsilon} e^{e^{182}} q^{g+2}. \end{align} $$8 The mollified first moment
Here we will prove Theorem 1.3. We consider the mollified first moment with ![]() $\kappa =1$. We have
$\kappa =1$. We have
 $$ \begin{align} M(\chi):=M(\chi,1) = \sum_{\substack{h_0 \cdot \dotsb \cdot h_J =h\\ P\mid h_j \Rightarrow P \in I_j\\ \Omega\left(h_j\right) \leq \ell_j}} \frac{a(h; J ) \chi(h) \lambda(h) \nu(h_0) \cdot \dotsb \cdot \nu(h_J )}{\sqrt{\lvert h\rvert}}, \end{align} $$
$$ \begin{align} M(\chi):=M(\chi,1) = \sum_{\substack{h_0 \cdot \dotsb \cdot h_J =h\\ P\mid h_j \Rightarrow P \in I_j\\ \Omega\left(h_j\right) \leq \ell_j}} \frac{a(h; J ) \chi(h) \lambda(h) \nu(h_0) \cdot \dotsb \cdot \nu(h_J )}{\sqrt{\lvert h\rvert}}, \end{align} $$and then
 $$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} {\textstyle L\left(\frac{1}{2}, \chi\right)} M(\chi) = \sum_{\substack{h_0 \cdot \dotsb \cdot h_J =h\\ P\mid h_j \Rightarrow P \in I_j\\ \Omega\left(h_j\right) \leq \ell_j}} \frac{a(h; J ) \lambda(h) \nu(h_0) \cdot \dotsb \cdot \nu(h_J )}{ \sqrt{\lvert h\rvert}} \sum_{\chi \in \mathcal{C}(g)} \chi(h) {\textstyle L\left(\frac{1}{2}, \chi\right)}. \end{align} $$
$$ \begin{align} \sum_{\chi \in \mathcal{C}(g)} {\textstyle L\left(\frac{1}{2}, \chi\right)} M(\chi) = \sum_{\substack{h_0 \cdot \dotsb \cdot h_J =h\\ P\mid h_j \Rightarrow P \in I_j\\ \Omega\left(h_j\right) \leq \ell_j}} \frac{a(h; J ) \lambda(h) \nu(h_0) \cdot \dotsb \cdot \nu(h_J )}{ \sqrt{\lvert h\rvert}} \sum_{\chi \in \mathcal{C}(g)} \chi(h) {\textstyle L\left(\frac{1}{2}, \chi\right)}. \end{align} $$We will evaluate the twisted first moment in the following proposition:
Proposition 8.1. Let ![]() $q \equiv 2 \,(\mathrm {mod}\,3)$, and let h be a polynomial in
$q \equiv 2 \,(\mathrm {mod}\,3)$, and let h be a polynomial in ![]() $\mathbb {F}_q[T]$ with
$\mathbb {F}_q[T]$ with  $\deg (h) < g \left ( \frac {1}{10}-\varepsilon \right )$. Let
$\deg (h) < g \left ( \frac {1}{10}-\varepsilon \right )$. Let ![]() $h=CS^2E^3$, where C and S are square-free and coprime. Then we have
$h=CS^2E^3$, where C and S are square-free and coprime. Then we have
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \chi(h) {\textstyle L\left(\frac{1}{2}, \chi\right)} & = \frac{ q^{g+2} \zeta_q(3/2)}{\zeta_q(3)\lvert C\rvert \sqrt{\lvert S\rvert}} \mathcal{A}_{\mathrm{nK}} \left( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} M_R \left( \frac{1}{q^2},\frac{1}{q^{3/2}} \right) \\ & \quad + O \left(q^{\frac{7g}{8}+ \frac{\deg(h)}{4}+\varepsilon g} \right), \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \chi(h) {\textstyle L\left(\frac{1}{2}, \chi\right)} & = \frac{ q^{g+2} \zeta_q(3/2)}{\zeta_q(3)\lvert C\rvert \sqrt{\lvert S\rvert}} \mathcal{A}_{\mathrm{nK}} \left( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} M_R \left( \frac{1}{q^2},\frac{1}{q^{3/2}} \right) \\ & \quad + O \left(q^{\frac{7g}{8}+ \frac{\deg(h)}{4}+\varepsilon g} \right), \end{align*} $$where  $\mathcal {A}_{\mathrm {nK}} \left ( \frac {1}{q^2}, \frac {1}{q^{3/2}} \right )$ and
$\mathcal {A}_{\mathrm {nK}} \left ( \frac {1}{q^2}, \frac {1}{q^{3/2}} \right )$ and  $M_R \left ( \frac {1}{q^2},\frac {1}{q^{3/2}} \right ) $ are given in equations (8.14) and (8.15).
$M_R \left ( \frac {1}{q^2},\frac {1}{q^{3/2}} \right ) $ are given in equations (8.14) and (8.15).
Proof. The proof is similar to the proof of [Reference David, Florea and Lalin13, Theorem 1.1]. Using the explicit description of the characters ![]() $\chi \in \mathcal {C}(g)$ given by equation (2.5), along with Proposition 2.1, we write
$\chi \in \mathcal {C}(g)$ given by equation (2.5), along with Proposition 2.1, we write
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \chi(h) {\textstyle L\left(\frac{1}{2}, \chi\right)} = S_{1, \text{principal}} + S_{1, \text{dual}}, \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \chi(h) {\textstyle L\left(\frac{1}{2}, \chi\right)} = S_{1, \text{principal}} + S_{1, \text{dual}}, \end{align*} $$where
 $$ \begin{align} S_{1, \text{principal}} & = \sum_{f \in \mathcal{M}_{q, \leq X}}\frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2, g/2+1} \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} \chi_F(fh) \nonumber \\ &\quad + \frac{1}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q, X+1}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2, g/2+1} \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} \chi_F(fh) \end{align} $$
$$ \begin{align} S_{1, \text{principal}} & = \sum_{f \in \mathcal{M}_{q, \leq X}}\frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2, g/2+1} \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} \chi_F(fh) \nonumber \\ &\quad + \frac{1}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q, X+1}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2, g/2+1} \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} \chi_F(fh) \end{align} $$and
 $$ \begin{align} S_{1, \text{dual}} & = \sum_{f \in \mathcal{M}_{q, \leq g-X-1}}\frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2, g/2+1} \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} \omega(\chi_F) \overline{\chi_F}\left(fh^2\right) \end{align} $$
$$ \begin{align} S_{1, \text{dual}} & = \sum_{f \in \mathcal{M}_{q, \leq g-X-1}}\frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2, g/2+1} \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} \omega(\chi_F) \overline{\chi_F}\left(fh^2\right) \end{align} $$ $$ \begin{align} & \qquad\qquad\qquad +\frac{1}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q, g-X}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2, g/2+1} \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} \omega(\chi_F) \overline{\chi_F}\left(fh^2\right). \end{align} $$
$$ \begin{align} & \qquad\qquad\qquad +\frac{1}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q, g-X}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2, g/2+1} \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} \omega(\chi_F) \overline{\chi_F}\left(fh^2\right). \end{align} $$We will choose ![]() $X \equiv 2 \deg (h) \,(\mathrm {mod}\,3)$. For the principal term, we will compute the contribution from polynomials f such that
$X \equiv 2 \deg (h) \,(\mathrm {mod}\,3)$. For the principal term, we will compute the contribution from polynomials f such that ![]() $fh$ is a cube and bound the contribution from
$fh$ is a cube and bound the contribution from ![]() $fh$ noncube. We write
$fh$ noncube. We write

where

corresponds to the sum with ![]() $fh$ a cube in equation (8.3) and
$fh$ a cube in equation (8.3) and

corresponds to the sum with ![]() $fh$ not a cube – namely,
$fh$ not a cube – namely,

and

Since ![]() $X \equiv 2 \deg (h) \,(\mathrm {mod}\,3)$, note that the second term in equation (8.3) does not contribute to equation (8.6).
$X \equiv 2 \deg (h) \,(\mathrm {mod}\,3)$, note that the second term in equation (8.3) does not contribute to equation (8.6).
8.1 The main term
Now we focus on . Since
. Since ![]() $h= CS^2E^3$, where
$h= CS^2E^3$, where ![]() $C, S$ are square-free and
$C, S$ are square-free and ![]() $(C,S)=1$ and
$(C,S)=1$ and![]() , it follows that we can write
, it follows that we can write ![]() $f= C^2 S K^3$. Then
$f= C^2 S K^3$. Then

We first look at the generating series of the sum over F. We use the fact that
 $$ \begin{align} \sum_{\substack{D \in \mathbb F_q[T]\\D \mid F}} \mu(D) = \begin{cases} 1 & \text{if } F \text{ has no prime divisor in } \mathbb F_q[T], \\ 0 & \text{otherwise}, \end{cases} \end{align} $$
$$ \begin{align} \sum_{\substack{D \in \mathbb F_q[T]\\D \mid F}} \mu(D) = \begin{cases} 1 & \text{if } F \text{ has no prime divisor in } \mathbb F_q[T], \\ 0 & \text{otherwise}, \end{cases} \end{align} $$where ![]() $\mu $ is the Möbius function over
$\mu $ is the Möbius function over ![]() $\mathbb F_q[T]$. The generating series corresponding to the inner sum in equation (8.8) is
$\mathbb F_q[T]$. The generating series corresponding to the inner sum in equation (8.8) is
 $$ \begin{align} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right) =1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} x^{\deg(F)} = \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right)=1}} x^{\deg(F)} \sum_{\substack{D \in \mathbb{F}_q[T] \\ D\mid F}} \mu(D) = \sum_{\substack{D \in \mathbb{F}_q[T] \\ \left(D,Kh\right)=1}} \mu(D) x^{\deg(D)} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,DKh\right)=1}} x^{\deg(F)}. \end{align} $$
$$ \begin{align} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right) =1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} x^{\deg(F)} = \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right)=1}} x^{\deg(F)} \sum_{\substack{D \in \mathbb{F}_q[T] \\ D\mid F}} \mu(D) = \sum_{\substack{D \in \mathbb{F}_q[T] \\ \left(D,Kh\right)=1}} \mu(D) x^{\deg(D)} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,DKh\right)=1}} x^{\deg(F)}. \end{align} $$We evaluate the sum over F and have
 $$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,KDh\right)=1}} x^{\deg(F)} = \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \nmid DKh}} \left(1+x^{\deg(P)}\right) = \frac{ \mathcal{Z}_{q^2}(x)}{\mathcal{Z}_{q^2}\left(x^2\right)\displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \mid DKh}} \left(1+x^{\deg(P)}\right)}, \end{align*} $$
$$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,KDh\right)=1}} x^{\deg(F)} = \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \nmid DKh}} \left(1+x^{\deg(P)}\right) = \frac{ \mathcal{Z}_{q^2}(x)}{\mathcal{Z}_{q^2}\left(x^2\right)\displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \mid DKh}} \left(1+x^{\deg(P)}\right)}, \end{align*} $$and combining this with equation (8.10), it follows that
 $$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right) =1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} x^{\deg(F)} = \frac{ \mathcal{Z}_{q^2}(x)}{\mathcal{Z}_{q^2}\left(x^2\right) \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid Kh}} \left(1+x^{\deg(P)}\right)} \sum_{\substack{D \in \mathbb{F}_q[T] \\ \left(D,Kh\right)=1}} \frac{ \mu(D)x^{\deg(D)}}{ \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid D}} \left(1+x^{\deg(P)}\right)}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right) =1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} x^{\deg(F)} = \frac{ \mathcal{Z}_{q^2}(x)}{\mathcal{Z}_{q^2}\left(x^2\right) \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid Kh}} \left(1+x^{\deg(P)}\right)} \sum_{\substack{D \in \mathbb{F}_q[T] \\ \left(D,Kh\right)=1}} \frac{ \mu(D)x^{\deg(D)}}{ \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid D}} \left(1+x^{\deg(P)}\right)}. \end{align*} $$Now we write down an Euler product for the sum over D, and we have
 $$ \begin{align} \sum_{\substack{D \in \mathbb{F}_q[T] \\ \left(D,Kh\right)=1}} \frac{ \mu(D)x^{\deg(D)}}{ \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid D}} \left(1+x^{\deg(P)}\right)} = \prod_{\substack{R \in \mathbb{F}_q[T] \\ \left(R,Kh\right)=1 \\ \deg(R) \text{ odd}}} \left ( 1- \frac{x^{\deg(R)}}{1+x^{\deg(R)}} \right )\prod_{\substack{R \in \mathbb{F}_q[T] \\ \left(R,Kh\right)=1 \\ \deg(R) \text{ even}}} \left ( 1- \frac{x^{\deg(R)}}{\left(1+x^{\frac{\deg(R)}{2}}\right)^2} \right), \end{align} $$
$$ \begin{align} \sum_{\substack{D \in \mathbb{F}_q[T] \\ \left(D,Kh\right)=1}} \frac{ \mu(D)x^{\deg(D)}}{ \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid D}} \left(1+x^{\deg(P)}\right)} = \prod_{\substack{R \in \mathbb{F}_q[T] \\ \left(R,Kh\right)=1 \\ \deg(R) \text{ odd}}} \left ( 1- \frac{x^{\deg(R)}}{1+x^{\deg(R)}} \right )\prod_{\substack{R \in \mathbb{F}_q[T] \\ \left(R,Kh\right)=1 \\ \deg(R) \text{ even}}} \left ( 1- \frac{x^{\deg(R)}}{\left(1+x^{\frac{\deg(R)}{2}}\right)^2} \right), \end{align} $$where the product over R is over monic, irreducible polynomials. Let ![]() $A_R(x)$ denote the first Euler factor and
$A_R(x)$ denote the first Euler factor and ![]() $B_R(x)$ the second. Using equation (8.11) and putting everything together, it follows that
$B_R(x)$ the second. Using equation (8.11) and putting everything together, it follows that
 $$ \begin{align} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right) =1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} x^{\deg(F)} = \frac{ \mathcal{Z}_{q^2}(x) \displaystyle \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd}}} A_R(x) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}} B_R(x) }{\mathcal{Z}_{q^2}\left(x^2\right) \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid Kh}} \left(1+x^{\deg(P)}\right) \displaystyle \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid Kh \\ \deg(R) \text{ odd}}} A_R(x) \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid Kh \\ \deg(R) \text{ even}}} B_R(x) }. \end{align} $$
$$ \begin{align} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right) =1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} x^{\deg(F)} = \frac{ \mathcal{Z}_{q^2}(x) \displaystyle \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd}}} A_R(x) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}} B_R(x) }{\mathcal{Z}_{q^2}\left(x^2\right) \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid Kh}} \left(1+x^{\deg(P)}\right) \displaystyle \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid Kh \\ \deg(R) \text{ odd}}} A_R(x) \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid Kh \\ \deg(R) \text{ even}}} B_R(x) }. \end{align} $$We now introduce the sum over K, and we get
 $$ \begin{align*} &\sum_{K \in \mathcal{M}_q} \frac{ u^{\deg(K)} }{ \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid K, P \nmid h}} \left(1+x^{\deg(P)}\right) \displaystyle \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid K, R \nmid h \\ \deg(R) \text{ odd}}} A_R(x) \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid K, R \nmid h \\ \deg(R) \text{ even}}} B_R(x) } \\ &=\prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \nmid h}} \left[ 1+ \frac{u^{\deg(R)}}{\left(1+x^{\deg(R)}\right) A_R(x) \left(1-u^{\deg(R)}\right)}\right] \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R \nmid h}} \left[1+ \frac{u^{\deg(R)}}{\left(1+x^{\frac{\deg(R)}{2}}\right)^2 B_R(x) \left(1-u^{\deg(R)}\right)} \right] \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{1}{1-u^{\deg(R)}}, \end{align*} $$
$$ \begin{align*} &\sum_{K \in \mathcal{M}_q} \frac{ u^{\deg(K)} }{ \displaystyle \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid K, P \nmid h}} \left(1+x^{\deg(P)}\right) \displaystyle \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid K, R \nmid h \\ \deg(R) \text{ odd}}} A_R(x) \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid K, R \nmid h \\ \deg(R) \text{ even}}} B_R(x) } \\ &=\prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \nmid h}} \left[ 1+ \frac{u^{\deg(R)}}{\left(1+x^{\deg(R)}\right) A_R(x) \left(1-u^{\deg(R)}\right)}\right] \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R \nmid h}} \left[1+ \frac{u^{\deg(R)}}{\left(1+x^{\frac{\deg(R)}{2}}\right)^2 B_R(x) \left(1-u^{\deg(R)}\right)} \right] \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{1}{1-u^{\deg(R)}}, \end{align*} $$where R denotes a monic irreducible polynomial in ![]() $\mathbb {F}_q[T]$. Combining this equation and equation (8.12), we get the generating series
$\mathbb {F}_q[T]$. Combining this equation and equation (8.12), we get the generating series
 $$ \begin{align} &\sum_{K \in \mathcal{M}_q} u^{\deg(K)}\sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right) =1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} x^{\deg(F)} =\frac{ \mathcal{Z}_{q^2}(x)}{\mathcal{Z}_{q^2}\left(x^2\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \nmid h}} \frac{1}{\left(1+x^{\deg(R)}\right)\left(1-u^{\deg(R)}\right)} \nonumber \\ &\qquad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R \nmid h}} \frac{1}{\left(1+x^{\frac{\deg(R)}{2}}\right)^2} \left ( 1+2x^{\frac{\deg(R)}{2}} + \frac{u^{\deg(R)}}{1-u^{\deg(R)}}\right ) \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid h}} \frac{1}{1+x^{\deg(P)}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{1}{1-u^{\deg(R)}} \nonumber \\ &\quad = \mathcal{Z}_q (u) \frac{ \mathcal{Z}_{q^2}(x)}{\mathcal{Z}_{q^2}\left(x^2\right)} \mathcal{A}_{\mathrm{nK}}(x,u) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} M_R(x,u), \end{align} $$
$$ \begin{align} &\sum_{K \in \mathcal{M}_q} u^{\deg(K)}\sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,Kh\right) =1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} x^{\deg(F)} =\frac{ \mathcal{Z}_{q^2}(x)}{\mathcal{Z}_{q^2}\left(x^2\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \nmid h}} \frac{1}{\left(1+x^{\deg(R)}\right)\left(1-u^{\deg(R)}\right)} \nonumber \\ &\qquad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R \nmid h}} \frac{1}{\left(1+x^{\frac{\deg(R)}{2}}\right)^2} \left ( 1+2x^{\frac{\deg(R)}{2}} + \frac{u^{\deg(R)}}{1-u^{\deg(R)}}\right ) \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid h}} \frac{1}{1+x^{\deg(P)}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{1}{1-u^{\deg(R)}} \nonumber \\ &\quad = \mathcal{Z}_q (u) \frac{ \mathcal{Z}_{q^2}(x)}{\mathcal{Z}_{q^2}\left(x^2\right)} \mathcal{A}_{\mathrm{nK}}(x,u) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} M_R(x,u), \end{align} $$where
 $$ \begin{align} \mathcal{A}_{\mathrm{nK}}(x,u) &= \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd}}} \frac{1}{1+x^{\deg(R)}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}}\frac{1}{\left(1+x^{\frac{\deg(R)}{2}}\right)^2} \left ( 1+2x^{\frac{\deg(R)}{2}} \left(1-u^{\deg(R)}\right) \right ), \end{align} $$
$$ \begin{align} \mathcal{A}_{\mathrm{nK}}(x,u) &= \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd}}} \frac{1}{1+x^{\deg(R)}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}}\frac{1}{\left(1+x^{\frac{\deg(R)}{2}}\right)^2} \left ( 1+2x^{\frac{\deg(R)}{2}} \left(1-u^{\deg(R)}\right) \right ), \end{align} $$ $$ \begin{align} M_R(x,u) &= \frac{1}{1+2x^{\deg(R)/2}\left(1-u^{\deg(R)}\right)}. \end{align} $$
$$ \begin{align} M_R(x,u) &= \frac{1}{1+2x^{\deg(R)/2}\left(1-u^{\deg(R)}\right)}. \end{align} $$ We remark that if ![]() $h=1$, this generating series is the same as in [Reference David, Florea and Lalin13, Section 4.3], and we compute the asymptotic for
$h=1$, this generating series is the same as in [Reference David, Florea and Lalin13, Section 4.3], and we compute the asymptotic for

in the exact same way, keeping the dependence on h. Using Perron’s formula (Lemma 2.2) twice in equation (8.8) and the generating series just obtained, we get that

where we are integrating along circles of radii  $\lvert u\rvert <1/q^{\frac {3}{2}}$ and
$\lvert u\rvert <1/q^{\frac {3}{2}}$ and ![]() $\lvert x\rvert <1/{q^2}$. As in [Reference David, Florea and Lalin13], we have that
$\lvert x\rvert <1/{q^2}$. As in [Reference David, Florea and Lalin13], we have that ![]() $\mathcal {A}_{\mathrm {nK}}(x,u)$ is analytic for
$\mathcal {A}_{\mathrm {nK}}(x,u)$ is analytic for  $\lvert x\rvert <1/q, \lvert xu\rvert <1/q, \left \lvert xu^2\right \rvert <1/q^2$. We initially pick
$\lvert x\rvert <1/q, \lvert xu\rvert <1/q, \left \lvert xu^2\right \rvert <1/q^2$. We initially pick  $\lvert u\rvert =1/q^{\frac {3}{2}+\varepsilon }$ and
$\lvert u\rvert =1/q^{\frac {3}{2}+\varepsilon }$ and ![]() $\lvert x\rvert =1/q^{2+\varepsilon }$. We shift the contour over x to
$\lvert x\rvert =1/q^{2+\varepsilon }$. We shift the contour over x to ![]() $\lvert x\rvert =1/q^{1+\varepsilon }$ and we encounter a pole at
$\lvert x\rvert =1/q^{1+\varepsilon }$ and we encounter a pole at ![]() $x=1/q^2$. Note that the new double integral will be bounded by
$x=1/q^2$. Note that the new double integral will be bounded by  $O\left (q^{\frac {g}{2}+\varepsilon g}\right )$. Then
$O\left (q^{\frac {g}{2}+\varepsilon g}\right )$. Then

We shift the contour of integration to ![]() $\lvert u\rvert =q^{-\varepsilon }$ and we encounter two simple poles: one at
$\lvert u\rvert =q^{-\varepsilon }$ and we encounter two simple poles: one at  $u=1/q^{\frac {3}{2}}$ and one at
$u=1/q^{\frac {3}{2}}$ and one at ![]() $u=1/q$. Evaluating the residues, we get
$u=1/q$. Evaluating the residues, we get

8.2 The contribution from noncubes
Let ![]() $S_{11}$ be the first term in equation (8.7) and
$S_{11}$ be the first term in equation (8.7) and ![]() $S_{12}$ the second. Note that it is enough to bound
$S_{12}$ the second. Note that it is enough to bound ![]() $S_{11}$, since bounding
$S_{11}$, since bounding ![]() $S_{12}$ will follow in a similar way. We use equation (8.9) again for the sum over F, and we have
$S_{12}$ will follow in a similar way. We use equation (8.9) again for the sum over F, and we have

Remark that we used ![]() $\chi _D(fh)=1$, because
$\chi _D(fh)=1$, because ![]() $D,f,h \in \mathbb {F}_q[T]$. Looking at the generating series of the sum over F, we have
$D,f,h \in \mathbb {F}_q[T]$. Looking at the generating series of the sum over F, we have
 $$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,D\right)=1}} \chi_F(fh) u^{\deg(F)} &= \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \nmid Dfh}} \left ( 1+\chi_P (fh) u^{\deg(P)} \right ) \nonumber \\ & = \frac{ \mathcal{L}_{q^2} \left(u, \chi_{fh}\right) }{\mathcal{L}_{q^2}\left(u^2, \overline{\chi_{fh}}\right)} \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \nmid fh \\ P\mid D}} \frac{ 1- \chi_P(fh) u^{\deg(P)} }{ 1- \overline{\chi_P}(fh) u^{2 \deg(P)}}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2} \\ \left(F,D\right)=1}} \chi_F(fh) u^{\deg(F)} &= \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \nmid Dfh}} \left ( 1+\chi_P (fh) u^{\deg(P)} \right ) \nonumber \\ & = \frac{ \mathcal{L}_{q^2} \left(u, \chi_{fh}\right) }{\mathcal{L}_{q^2}\left(u^2, \overline{\chi_{fh}}\right)} \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \nmid fh \\ P\mid D}} \frac{ 1- \chi_P(fh) u^{\deg(P)} }{ 1- \overline{\chi_P}(fh) u^{2 \deg(P)}}. \end{align*} $$Using Perron’s formula (Lemma 2.2) and the generating series obtained, we have
 $$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2,\frac{g}{2}+1-\deg(D)} \\ \left(F,D\right)=1}} \chi_F(fh) = \frac{1}{2 \pi i} \oint \frac{ \mathcal{L}_{q^2} \left(u,\chi_{fh}\right) }{\mathcal{L}_{q^2}\left(u^2, \overline{\chi_{fh}}\right) u^{\frac{g}{2}+1-\deg(D)}} \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \nmid fh \\ P\mid D}} \frac{ 1- \chi_P(fh) u^{\deg(P)} }{ 1- \overline{\chi_P}(fh) u^{2 \deg(P)} } \frac{du}{u}, \end{align*} $$
$$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2,\frac{g}{2}+1-\deg(D)} \\ \left(F,D\right)=1}} \chi_F(fh) = \frac{1}{2 \pi i} \oint \frac{ \mathcal{L}_{q^2} \left(u,\chi_{fh}\right) }{\mathcal{L}_{q^2}\left(u^2, \overline{\chi_{fh}}\right) u^{\frac{g}{2}+1-\deg(D)}} \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P \nmid fh \\ P\mid D}} \frac{ 1- \chi_P(fh) u^{\deg(P)} }{ 1- \overline{\chi_P}(fh) u^{2 \deg(P)} } \frac{du}{u}, \end{align*} $$where the integral takes place along a circle of radius ![]() $\lvert u\rvert = 1/q$ around the origin. Now we use the Lindelöf bound for the L-function in the numerator and a lower bound for the L-function in the denominator (formulas (2.8) and (2.9)), and we obtain
$\lvert u\rvert = 1/q$ around the origin. Now we use the Lindelöf bound for the L-function in the numerator and a lower bound for the L-function in the denominator (formulas (2.8) and (2.9)), and we obtain
 $$ \begin{align*} \left\lvert \mathcal{L}_{q^2} \left(u,\chi_{fh}\right) \right\rvert \ll q^{2 \varepsilon \deg\left(fh\right)}, \qquad \left\lvert \mathcal{L}_{q^2} \left(u^2, \overline{\chi_{fh}}\right) \right\rvert \gg q^{-2 \varepsilon\deg\left(fh\right)}. \end{align*} $$
$$ \begin{align*} \left\lvert \mathcal{L}_{q^2} \left(u,\chi_{fh}\right) \right\rvert \ll q^{2 \varepsilon \deg\left(fh\right)}, \qquad \left\lvert \mathcal{L}_{q^2} \left(u^2, \overline{\chi_{fh}}\right) \right\rvert \gg q^{-2 \varepsilon\deg\left(fh\right)}. \end{align*} $$Therefore,
 $$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2,\frac{g}{2}+1-\deg(D)} \\ \left(F,D\right)=1}} \chi_F(fh) \ll q^{\frac{g}{2}-\deg(D)} q^{4 \varepsilon \deg\left(fh\right)+2 \varepsilon \deg(D)}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{F \in \mathcal{H}_{q^2,\frac{g}{2}+1-\deg(D)} \\ \left(F,D\right)=1}} \chi_F(fh) \ll q^{\frac{g}{2}-\deg(D)} q^{4 \varepsilon \deg\left(fh\right)+2 \varepsilon \deg(D)}. \end{align*} $$Trivially bounding the sums over D and f in equation (8.17) gives a total upper bound of
 $$ \begin{align*} S_{11}\ll q^{\frac{X+g}{2}+\varepsilon g}, \end{align*} $$
$$ \begin{align*} S_{11}\ll q^{\frac{X+g}{2}+\varepsilon g}, \end{align*} $$and similarly for ![]() $S_{12}$.
$S_{12}$.
8.3 The dual term
Now we focus on ![]() $S_{1 , \text {dual}}$. From equation (8.5), using equations (2.14) and (2.12), we have
$S_{1 , \text {dual}}$. From equation (8.5), using equations (2.14) and (2.12), we have
 $$ \begin{align} S_{1, \text{dual}} &= q^{-\frac{g}{2}-1}\sum_{f \in \mathcal{M}_{q, \leq g-X-1}}\frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2,\frac{g}{2}+1} \\ \left(F,fh\right)=1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T] }}G_{q^2}\left(fh^2,F\right) \end{align} $$
$$ \begin{align} S_{1, \text{dual}} &= q^{-\frac{g}{2}-1}\sum_{f \in \mathcal{M}_{q, \leq g-X-1}}\frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2,\frac{g}{2}+1} \\ \left(F,fh\right)=1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T] }}G_{q^2}\left(fh^2,F\right) \end{align} $$ $$ \begin{align} & \qquad +\frac{q^{-\frac{g}{2}-1}}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q, g-X}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2,\frac{g}{2}+1} \\ \left(F,fh\right)=1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T] }}G_{q^2}\left(fh^2,F\right). \end{align} $$
$$ \begin{align} & \qquad +\frac{q^{-\frac{g}{2}-1}}{1-\sqrt{q}} \sum_{f \in \mathcal{M}_{q, g-X}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{F \in \mathcal{H}_{q^2,\frac{g}{2}+1} \\ \left(F,fh\right)=1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T] }}G_{q^2}\left(fh^2,F\right). \end{align} $$We write ![]() $S_{1,\text {dual}}= S_{11,\text {dual}}+S_{12,\text {dual}}$ for terms (8.18) and (8.19), respectively, on the right-hand side of this equation.
$S_{1,\text {dual}}= S_{11,\text {dual}}+S_{12,\text {dual}}$ for terms (8.18) and (8.19), respectively, on the right-hand side of this equation.
We have
 $$ \begin{align} \sum_{\substack{F \in \mathcal{H}_{q^2, \frac{g}{2}+1} \\ \left(F,fh\right)=1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} G_{q^2}\left(fh^2, F\right) &= \sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) \sum_{\substack{F \in \mathcal{M}_{ q^2,\frac{g}{2}+1-\deg(N)}\\ \left(F, fh\right)=1}} G_{q^2}\left(fh^2, NF\right) \nonumber \\ &= \sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2, N\right) \sum_{\substack{F \in \mathcal{M}_{ q^2,\frac{g}{2}+1-\deg(N)}\\ \left(F, Nfh\right)=1}} G_{q^2}\left(fh^2N, F\right). \end{align} $$
$$ \begin{align} \sum_{\substack{F \in \mathcal{H}_{q^2, \frac{g}{2}+1} \\ \left(F,fh\right)=1 \\ P \mid F \Rightarrow P \not\in \mathbb F_q[T]}} G_{q^2}\left(fh^2, F\right) &= \sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) \sum_{\substack{F \in \mathcal{M}_{ q^2,\frac{g}{2}+1-\deg(N)}\\ \left(F, fh\right)=1}} G_{q^2}\left(fh^2, NF\right) \nonumber \\ &= \sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2, N\right) \sum_{\substack{F \in \mathcal{M}_{ q^2,\frac{g}{2}+1-\deg(N)}\\ \left(F, Nfh\right)=1}} G_{q^2}\left(fh^2N, F\right). \end{align} $$Now let ![]() $(f,h)=B$ and write
$(f,h)=B$ and write ![]() $f= B \tilde {f}$ and
$f= B \tilde {f}$ and ![]() $h = B \tilde {h}$, where
$h = B \tilde {h}$, where  $\tilde {f}= f_1 f_2^2 f_3^3$ and
$\tilde {f}= f_1 f_2^2 f_3^3$ and  $\tilde {h} = h_1 h_2^2 h_3^3$ with
$\tilde {h} = h_1 h_2^2 h_3^3$ with ![]() $(f_1,f_2)=1$,
$(f_1,f_2)=1$, ![]() $(h_1,h_2)=1$ and
$(h_1,h_2)=1$ and ![]() $f_1,f_2,h_1,h_2$ square-free. Using Proposition 2.3, we get
$f_1,f_2,h_1,h_2$ square-free. Using Proposition 2.3, we get
 $$ \begin{align*} &\sum_{\substack{F \in \mathcal{M}_{ q^2,\frac{g}{2}+1-\deg(N)}\\ \left(F, fhN\right)=1}} G_{q^2}\left(fh^2N, F\right) = \delta_{f_2h_1=1} \frac{q^{\frac{4g}{3}+\frac{8}{3}-4 \deg(N)-\frac{4}{3} \deg(f_1)-\frac{4}{3} \deg(h_2)-\frac{8}{3} \left[\frac{g}{2}+1+\deg(f_1h_2)\right]_3 }}{\zeta_{q^2}(2)} \\ & \quad \times \overline{G_{q^2}(1,f_1h_2N)} \rho(1, [g/2+1+\deg(f_1h_2)]_3) \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid fhN}} \left(1+ \frac{1}{\lvert P\rvert_{q^2}} \right)^{-1} \\ & \quad + O \left( \delta_{f_2h_1=1} q^{\frac{g}{3}+\varepsilon g - \deg(N) - \frac{\deg\left(f_1\right)}{3}-\frac{\deg\left(h_2\right)}{3}} \right) + \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \frac{ \tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{\frac{g}{2}+1-\deg(D)}} \frac{du}{u}, \end{align*} $$
$$ \begin{align*} &\sum_{\substack{F \in \mathcal{M}_{ q^2,\frac{g}{2}+1-\deg(N)}\\ \left(F, fhN\right)=1}} G_{q^2}\left(fh^2N, F\right) = \delta_{f_2h_1=1} \frac{q^{\frac{4g}{3}+\frac{8}{3}-4 \deg(N)-\frac{4}{3} \deg(f_1)-\frac{4}{3} \deg(h_2)-\frac{8}{3} \left[\frac{g}{2}+1+\deg(f_1h_2)\right]_3 }}{\zeta_{q^2}(2)} \\ & \quad \times \overline{G_{q^2}(1,f_1h_2N)} \rho(1, [g/2+1+\deg(f_1h_2)]_3) \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid fhN}} \left(1+ \frac{1}{\lvert P\rvert_{q^2}} \right)^{-1} \\ & \quad + O \left( \delta_{f_2h_1=1} q^{\frac{g}{3}+\varepsilon g - \deg(N) - \frac{\deg\left(f_1\right)}{3}-\frac{\deg\left(h_2\right)}{3}} \right) + \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \frac{ \tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{\frac{g}{2}+1-\deg(D)}} \frac{du}{u}, \end{align*} $$with ![]() $2/3<\sigma <4/3$. Combining formulas (8.18) and (8.20), we write
$2/3<\sigma <4/3$. Combining formulas (8.18) and (8.20), we write ![]() $S_{11,\text {dual}}=M_1+E_1$, where
$S_{11,\text {dual}}=M_1+E_1$, where ![]() $M_1$ corresponds to the first term in this equation. Using equation (2.15) and following similar steps as in [Reference David, Florea and Lalin13], we get
$M_1$ corresponds to the first term in this equation. Using equation (2.15) and following similar steps as in [Reference David, Florea and Lalin13], we get
 $$ \begin{align*} M_1 &= \frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}} \frac{1}{q^{\deg(B)/2}} \sum_{\substack{\deg\left(\tilde{f}\right) \leq g-X-1-\deg(B)\\\left(\tilde{f},\tilde{h}\right)=1}} \frac{ \delta_{f_2h_1=1} q^{-\frac{8}{3} \left[\frac{g}{2}+1+\deg(f_1h_2)\right]_3}}{q^{\deg\left(\tilde{f}\right)/2+\deg(f_1h_2)/3}} \\ & \quad \times \sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) q^{-2 \deg(N)} \left\lvert G_{q^2}(1,N)\right\rvert^2\\ & \quad \times \rho(1, [g/2+1+\deg(f_1h_2)]_3) \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid \tilde{f}hN}} \left(1+ \frac{1}{\lvert P\rvert_{q^2}} \right)^{-1} \\ & = \frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}} \frac{1}{q^{\deg(B)/2}} \sum_{\substack{\deg\left(\tilde{f}\right) \leq g-X-1-\deg(B)\\\left(\tilde{f},\tilde{h}\right)=1}} \frac{ \delta_{f_2h_1=1} q^{-\frac{8}{3} \left[\frac{g}{2}+1+\deg(f_1h_2)\right]_3}}{q^{\deg\left(\tilde{f}\right)/2+\deg(f_1h_2)/3}} \\ & \quad \times \rho(1, [g/2+1+\deg(f_1h_2)]_3) \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid\tilde{f}h}} \left(1+ \frac{1}{\lvert P\rvert_{q^2}} \right)^{-1} \\ & \quad \times \sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) q^{-2 \deg(N)} \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid N}} \left(1+ \frac{1}{\lvert P\rvert_{q^2}} \right)^{-1}, \end{align*} $$
$$ \begin{align*} M_1 &= \frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}} \frac{1}{q^{\deg(B)/2}} \sum_{\substack{\deg\left(\tilde{f}\right) \leq g-X-1-\deg(B)\\\left(\tilde{f},\tilde{h}\right)=1}} \frac{ \delta_{f_2h_1=1} q^{-\frac{8}{3} \left[\frac{g}{2}+1+\deg(f_1h_2)\right]_3}}{q^{\deg\left(\tilde{f}\right)/2+\deg(f_1h_2)/3}} \\ & \quad \times \sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) q^{-2 \deg(N)} \left\lvert G_{q^2}(1,N)\right\rvert^2\\ & \quad \times \rho(1, [g/2+1+\deg(f_1h_2)]_3) \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid \tilde{f}hN}} \left(1+ \frac{1}{\lvert P\rvert_{q^2}} \right)^{-1} \\ & = \frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}} \frac{1}{q^{\deg(B)/2}} \sum_{\substack{\deg\left(\tilde{f}\right) \leq g-X-1-\deg(B)\\\left(\tilde{f},\tilde{h}\right)=1}} \frac{ \delta_{f_2h_1=1} q^{-\frac{8}{3} \left[\frac{g}{2}+1+\deg(f_1h_2)\right]_3}}{q^{\deg\left(\tilde{f}\right)/2+\deg(f_1h_2)/3}} \\ & \quad \times \rho(1, [g/2+1+\deg(f_1h_2)]_3) \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid\tilde{f}h}} \left(1+ \frac{1}{\lvert P\rvert_{q^2}} \right)^{-1} \\ & \quad \times \sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) q^{-2 \deg(N)} \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid N}} \left(1+ \frac{1}{\lvert P\rvert_{q^2}} \right)^{-1}, \end{align*} $$where we have used  $G_{q^2}\left (fh^2,N\right )=\chi _N\left (fh^2\right )G_{q^2}(1,N)$ and the fact that the first sum is zero unless
$G_{q^2}\left (fh^2,N\right )=\chi _N\left (fh^2\right )G_{q^2}(1,N)$ and the fact that the first sum is zero unless ![]() $h_1=f_2=1$.
$h_1=f_2=1$.
Similarly as in [Reference David, Florea and Lalin13], we use Perron’s formula and the generating series to rewrite the sum over N. Again, the only difference is the presence of h in these formulas. We have
 $$ \begin{align*} &\sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) q^{-2\deg(N)} \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid N}} \left (1+ \frac{1}{\lvert P\rvert_{q^2}} \right )^{-1} \\ &\quad\quad\quad \quad = \frac{1}{2 \pi i} \oint \frac{\mathcal{J}_{\mathrm{nK}}(w)}{w^{g/2+1}(1-w)} \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \mid fh}} A_{\text{dual},R}(w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid fh}} B_{\text{dual},R}(w)^{-1} \frac{dw}{w}, \end{align*} $$
$$ \begin{align*} &\sum_{\substack{N \in \mathbb F_q[T]\\ \deg(N) \leq \frac{g}{2} + 1\\\left(N,fh\right)=1}} \mu(N) q^{-2\deg(N)} \prod_{\substack{P \in \mathbb{F}_{q^2}[T] \\ P\mid N}} \left (1+ \frac{1}{\lvert P\rvert_{q^2}} \right )^{-1} \\ &\quad\quad\quad \quad = \frac{1}{2 \pi i} \oint \frac{\mathcal{J}_{\mathrm{nK}}(w)}{w^{g/2+1}(1-w)} \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \mid fh}} A_{\text{dual},R}(w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid fh}} B_{\text{dual},R}(w)^{-1} \frac{dw}{w}, \end{align*} $$where
 $$ \begin{align*} \mathcal{J}_{\mathrm{nK}}(w) = \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd}}} A_{\text{dual},R}(w) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}} B_{\text{dual},R}(w) \end{align*} $$
$$ \begin{align*} \mathcal{J}_{\mathrm{nK}}(w) = \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd}}} A_{\text{dual},R}(w) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}} B_{\text{dual},R}(w) \end{align*} $$and
 $$ \begin{align*} A_{\text{dual},R}(w)=1-\frac{w^{\deg(R)}}{q^{2\deg(R)}\left(1+\frac{1}{q^{2\deg(R)}}\right)}\qquad \text{and}\qquad B_{\text{dual},R}(w)=1-\frac{w^{\deg(R)}}{q^{2\deg(R)}\left(1+\frac{1}{q^{\deg(R)}}\right)^2}. \end{align*} $$
$$ \begin{align*} A_{\text{dual},R}(w)=1-\frac{w^{\deg(R)}}{q^{2\deg(R)}\left(1+\frac{1}{q^{2\deg(R)}}\right)}\qquad \text{and}\qquad B_{\text{dual},R}(w)=1-\frac{w^{\deg(R)}}{q^{2\deg(R)}\left(1+\frac{1}{q^{\deg(R)}}\right)^2}. \end{align*} $$Introducing the sums over B and ![]() $\tilde {f}$, we have
$\tilde {f}$, we have
 $$ \begin{align} \nonumber M_1&=\frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}} \frac{1}{q^{\deg(B)/2}} \sum_{\substack{\deg\left(\tilde{f}\right) \leq g-X-1-\deg(B) \\ \left(\tilde{f},\tilde{h}\right)=1}} \frac{ \delta_{f_2h_1=1} q^{-\frac{8}{3} \left[\frac{g}{2}+1+\deg(f_1h_2)\right]_3}}{q^{\deg\left(\tilde{f}\right)/2+\deg(f_1h_2)/3}} \\ & \quad \times \rho(1, [g/2+1+\deg(f_1h_2)]_3) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \mid fh}} \left(1+\frac{1}{q^{2\deg(R)}}\right)^{-1} \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R \mid fh}} \left(1+\frac{1}{q^{\deg(R)}}\right)^{-2} \\ \nonumber & \quad \times \frac{1}{2 \pi i} \oint \frac{\mathcal{J}_{\mathrm{nK}}(w)}{w^{g/2+1}(1-w)}\prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \mid fh}} A_{\text{dual},R}(w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid fh}} B_{\text{dual},R}(w)^{-1} \frac{dw}{w}. \end{align} $$
$$ \begin{align} \nonumber M_1&=\frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}} \frac{1}{q^{\deg(B)/2}} \sum_{\substack{\deg\left(\tilde{f}\right) \leq g-X-1-\deg(B) \\ \left(\tilde{f},\tilde{h}\right)=1}} \frac{ \delta_{f_2h_1=1} q^{-\frac{8}{3} \left[\frac{g}{2}+1+\deg(f_1h_2)\right]_3}}{q^{\deg\left(\tilde{f}\right)/2+\deg(f_1h_2)/3}} \\ & \quad \times \rho(1, [g/2+1+\deg(f_1h_2)]_3) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \mid fh}} \left(1+\frac{1}{q^{2\deg(R)}}\right)^{-1} \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R \mid fh}} \left(1+\frac{1}{q^{\deg(R)}}\right)^{-2} \\ \nonumber & \quad \times \frac{1}{2 \pi i} \oint \frac{\mathcal{J}_{\mathrm{nK}}(w)}{w^{g/2+1}(1-w)}\prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \mid fh}} A_{\text{dual},R}(w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid fh}} B_{\text{dual},R}(w)^{-1} \frac{dw}{w}. \end{align} $$We let
 $$ \begin{align*} \mathcal{H}_{\mathrm{nK}}(h;u,w)= \sum_{\left(\tilde{f}, \tilde{h}\right)=1} \frac{\delta_{f_2=1}}{q^{\deg\left(\tilde{f}\right)/2+\deg(f_1)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \mid \tilde{f} \\ R \nmid h}} C_R(w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid \tilde{f} \\ R \nmid h}} D_R(w)^{-1} u^{\deg(f)}, \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\mathrm{nK}}(h;u,w)= \sum_{\left(\tilde{f}, \tilde{h}\right)=1} \frac{\delta_{f_2=1}}{q^{\deg\left(\tilde{f}\right)/2+\deg(f_1)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \mid \tilde{f} \\ R \nmid h}} C_R(w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid \tilde{f} \\ R \nmid h}} D_R(w)^{-1} u^{\deg(f)}, \end{align*} $$where
 $$ \begin{align*} C_R(w) & = A_{\text{dual},R}(w) \left(1+\frac{1}{q^{2\deg(R)}}\right) = 1+\frac{1}{q^{2\deg(R)}}-\frac{w^{\deg(R)}}{q^{2\deg(R)}} \\ D_R(w) &=B_{\text{dual},R}(w)\left(1+\frac{1}{q^{\deg(R)}}\right)^2=\left(1+\frac{1}{q^{\deg(R)}}\right)^2-\frac{w^{\deg(R)}}{q^{2\deg(R)}}. \end{align*} $$
$$ \begin{align*} C_R(w) & = A_{\text{dual},R}(w) \left(1+\frac{1}{q^{2\deg(R)}}\right) = 1+\frac{1}{q^{2\deg(R)}}-\frac{w^{\deg(R)}}{q^{2\deg(R)}} \\ D_R(w) &=B_{\text{dual},R}(w)\left(1+\frac{1}{q^{\deg(R)}}\right)^2=\left(1+\frac{1}{q^{\deg(R)}}\right)^2-\frac{w^{\deg(R)}}{q^{2\deg(R)}}. \end{align*} $$ Then we can write down an Euler product for ![]() $\mathcal {H}_{\mathrm {nK}}(h;u,w)$, and we have
$\mathcal {H}_{\mathrm {nK}}(h;u,w)$, and we have
 $$ \begin{align*} \mathcal{H}_{\mathrm{nK}}(h;u,w) &= \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \nmid h}} \left[1+C_R(w)^{-1} \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right] \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R \nmid h}} \left[1+D_R(w)^{-1} \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right] \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B\\ R \nmid \tilde{h} }} \left[1+ \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right]. \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\mathrm{nK}}(h;u,w) &= \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R \nmid h}} \left[1+C_R(w)^{-1} \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right] \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R \nmid h}} \left[1+D_R(w)^{-1} \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right] \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B\\ R \nmid \tilde{h} }} \left[1+ \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right]. \end{align*} $$Following [Reference David, Florea and Lalin13], let
 $$ \begin{align*} \mathcal{H}_{\mathrm{nK}}(u,w) & = \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} }} \left[1+C_R(w)^{-1} \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right] \\ & \qquad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}} \left[1+D_R(w)^{-1} \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right]\\ & = \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd}}} \left[1+C_R(w)^{-1} \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right )\right]\\ & \qquad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}} \left[1+D_R(w)^{-1} \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right ) \right]\\ & = \mathcal{Z} \left ( \frac{u}{q^{5/6}}\right ) \mathcal{B}_{\mathrm{nK}}(u,w), \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\mathrm{nK}}(u,w) & = \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} }} \left[1+C_R(w)^{-1} \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right] \\ & \qquad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}} \left[1+D_R(w)^{-1} \left ( \frac{1}{q^{\deg(R)/3}} \sum_{j=0}^{\infty} \frac{ u^{\left(3j+1\right) \deg(R)}}{q^{\left(3j+1\right) \deg(R)/2}} + \sum_{j=1}^{\infty} \frac{ u^{3j \deg(R)}}{q^{3j\deg(R)/2}}\right ) \right]\\ & = \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd}}} \left[1+C_R(w)^{-1} \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right )\right]\\ & \qquad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even}}} \left[1+D_R(w)^{-1} \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right ) \right]\\ & = \mathcal{Z} \left ( \frac{u}{q^{5/6}}\right ) \mathcal{B}_{\mathrm{nK}}(u,w), \end{align*} $$with ![]() $\mathcal {B}_{\mathrm {nK}}(u,w)$ analytic in a wider region – for example,
$\mathcal {B}_{\mathrm {nK}}(u,w)$ analytic in a wider region – for example, ![]() $\mathcal {B}_{\mathrm {nK}}(u,w)$ is absolutely convergent for
$\mathcal {B}_{\mathrm {nK}}(u,w)$ is absolutely convergent for  $\lvert u\rvert <q^{\frac {11}{6}}$ and
$\lvert u\rvert <q^{\frac {11}{6}}$ and  $\lvert uw\rvert < q^{\frac {11}{6}}$.
$\lvert uw\rvert < q^{\frac {11}{6}}$.
After simplifying and making similar computations to the ones in [Reference David, Florea and Lalin13], we have
 $$ \begin{align} \mathcal{H}_{\mathrm{nK}} (h;u,w) & = \mathcal{H}_{\mathrm{nK}}(u,w) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} \left[1+C_R(w)^{-1} \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right )\right]^{-1} \nonumber \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} \left[1+D_R(w)^{-1} \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right ) \right]^{-1} \nonumber \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} \left[1+ \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right )\right] \nonumber \\ & = \mathcal{Z} \left ( \frac{u}{q^{5/6}}\right ) \mathcal{B}_{\mathrm{nK}}(u,w) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R(u,w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R(u,w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R(u). \end{align} $$
$$ \begin{align} \mathcal{H}_{\mathrm{nK}} (h;u,w) & = \mathcal{H}_{\mathrm{nK}}(u,w) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} \left[1+C_R(w)^{-1} \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right )\right]^{-1} \nonumber \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} \left[1+D_R(w)^{-1} \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right ) \right]^{-1} \nonumber \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} \left[1+ \left ( \frac{u^{\deg(R)}}{\lvert R\rvert_q^{5/6} \left(1- \frac{u^{3 \deg(R)}}{\lvert R\rvert_q^{3/2}}\right)} + \frac{ u^{3 \deg(R)}}{ \lvert R\rvert_q^{3/2}-u^{3 \deg(R)}}\right )\right] \nonumber \\ & = \mathcal{Z} \left ( \frac{u}{q^{5/6}}\right ) \mathcal{B}_{\mathrm{nK}}(u,w) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R(u,w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R(u,w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R(u). \end{align} $$ We now rewrite ![]() $M_1$ using the generating series we have obtained and Perron’s formula for the sum over
$M_1$ using the generating series we have obtained and Perron’s formula for the sum over ![]() $\tilde {f}$. We need to deal with the terms involving
$\tilde {f}$. We need to deal with the terms involving ![]() $[g/2+1+\deg (f_1h_2)]_3$ that appear in equation (8.21). We notice that if
$[g/2+1+\deg (f_1h_2)]_3$ that appear in equation (8.21). We notice that if ![]() $g/2+1+\deg (f_1h_2) \equiv 0 \,(\mathrm {mod}\,3)$, then
$g/2+1+\deg (f_1h_2) \equiv 0 \,(\mathrm {mod}\,3)$, then ![]() $\deg (f_1) \equiv g - \deg (h_2)-1 \,(\mathrm {mod}\,3)$, and in that case,
$\deg (f_1) \equiv g - \deg (h_2)-1 \,(\mathrm {mod}\,3)$, and in that case, ![]() $\rho (1,[g/2+1+\deg (f_1h_2)]_3)=1$. If
$\rho (1,[g/2+1+\deg (f_1h_2)]_3)=1$. If ![]() $g/2+1+\deg (f_1h_2) \equiv 1 \,(\mathrm {mod}\,3)$, then
$g/2+1+\deg (f_1h_2) \equiv 1 \,(\mathrm {mod}\,3)$, then ![]() $\deg (f_1) \equiv g - \deg (h_2) \,(\mathrm {mod}\,3)$. In this case we also have
$\deg (f_1) \equiv g - \deg (h_2) \,(\mathrm {mod}\,3)$. In this case we also have ![]() $\tau (\chi _3)=q$ by Proposition 2.3, and
$\tau (\chi _3)=q$ by Proposition 2.3, and ![]() $\rho (1, [g/2+1+\deg (f_1h_2)]_3)=q^3$, since we are working over
$\rho (1, [g/2+1+\deg (f_1h_2)]_3)=q^3$, since we are working over ![]() $\mathbb F_{q^2}$. Using Perron’s formula (Lemma 2.2) twice and keeping in mind that
$\mathbb F_{q^2}$. Using Perron’s formula (Lemma 2.2) twice and keeping in mind that ![]() $X \equiv 2 \deg (h) \,(\mathrm {mod}\,3)$, we get
$X \equiv 2 \deg (h) \,(\mathrm {mod}\,3)$, we get
 $$ \begin{align*} &M_1 =\frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B\mid h \\ \deg(B) \leq g-X-1}} \frac{\delta_{h_1=1}}{q^{\deg(B)/2+\deg(h_2)/3}} \frac{1}{(2 \pi i)^2} \oint \oint \frac{\mathcal{H}_{\mathrm{nK}}(h;u,w) \mathcal{J}_{\mathrm{nK}}(w)}{w^{g/2+1}(1-w)} \\ & \enspace\times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} C_R(w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} D_R(w)^{-1} \left[ \frac{1}{u^{g-X-1-\deg(B)} \left(1-u^3\right)} + \frac{ q^{1/3}}{u^{g-X-3-\deg(B)}\left(1-u^3\right)} \right] \frac{dw}{w} \frac{du}{u}. \end{align*} $$
$$ \begin{align*} &M_1 =\frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B\mid h \\ \deg(B) \leq g-X-1}} \frac{\delta_{h_1=1}}{q^{\deg(B)/2+\deg(h_2)/3}} \frac{1}{(2 \pi i)^2} \oint \oint \frac{\mathcal{H}_{\mathrm{nK}}(h;u,w) \mathcal{J}_{\mathrm{nK}}(w)}{w^{g/2+1}(1-w)} \\ & \enspace\times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} C_R(w)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} D_R(w)^{-1} \left[ \frac{1}{u^{g-X-1-\deg(B)} \left(1-u^3\right)} + \frac{ q^{1/3}}{u^{g-X-3-\deg(B)}\left(1-u^3\right)} \right] \frac{dw}{w} \frac{du}{u}. \end{align*} $$We proceed as in [Reference David, Florea and Lalin13], shifting the contour of integration over w to ![]() $\lvert w\rvert =q^{1-\varepsilon }$ and computing the residue at
$\lvert w\rvert =q^{1-\varepsilon }$ and computing the residue at ![]() $w=1$. Writing
$w=1$. Writing
we get
 $$ \begin{align*} M_1 & = \frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}}\frac{\delta_{h_1=1}}{q^{\deg(B)/2+\deg(h_2)/3}} \frac{1}{2 \pi i} \oint \frac{ \mathcal{K}_{\mathrm{nK}}(u)}{\left(1-uq^{1/6}\right)\left(1-u^3\right) u^{g-X-1}} \left(1+ q^{1/3}u^2\right) \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R(u,1)^{-1} C_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R(u,1)^{-1} D_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R(u) \frac{du}{u} \\ & \quad +O\left(q^{\frac{g}{2}-\frac{X}{6}+\varepsilon g}\right). \end{align*} $$
$$ \begin{align*} M_1 & = \frac{q^{5g/6+5/3}}{\zeta_{q^2}(2)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}}\frac{\delta_{h_1=1}}{q^{\deg(B)/2+\deg(h_2)/3}} \frac{1}{2 \pi i} \oint \frac{ \mathcal{K}_{\mathrm{nK}}(u)}{\left(1-uq^{1/6}\right)\left(1-u^3\right) u^{g-X-1}} \left(1+ q^{1/3}u^2\right) \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R(u,1)^{-1} C_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R(u,1)^{-1} D_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R(u) \frac{du}{u} \\ & \quad +O\left(q^{\frac{g}{2}-\frac{X}{6}+\varepsilon g}\right). \end{align*} $$ Shifting the contour of integration to ![]() $\lvert u\rvert =q^{-\varepsilon }$ and computing the residue at
$\lvert u\rvert =q^{-\varepsilon }$ and computing the residue at  $u=q^{-\frac {1}{6}}$,
$u=q^{-\frac {1}{6}}$,
 $$ \begin{align*} M_1 & = 2 q^{g-\frac{X}{6}+2} \frac{ \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\zeta_{q^2}(2) \left(\sqrt{q}-1\right)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}}\frac{\delta_{h_1=1}}{q^{2\deg(B)/3+\deg(h_2)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R|h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R\left(q^{-1/6}\right) + O \left(q^{\frac{5g}{6}+\varepsilon g} \right). \end{align*} $$
$$ \begin{align*} M_1 & = 2 q^{g-\frac{X}{6}+2} \frac{ \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\zeta_{q^2}(2) \left(\sqrt{q}-1\right)} \sum_{\substack{B \mid h \\ \deg(B) \leq g-X-1}}\frac{\delta_{h_1=1}}{q^{2\deg(B)/3+\deg(h_2)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R|h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R\left(q^{-1/6}\right) + O \left(q^{\frac{5g}{6}+\varepsilon g} \right). \end{align*} $$Now note that we can extend the sum over B to include all ![]() $B\mid h$ at the expense of an error term of size
$B\mid h$ at the expense of an error term of size  $O\left (\tau (h) / q^{\frac {2}{3}(g-X)}\right )$, giving a total error term of size
$O\left (\tau (h) / q^{\frac {2}{3}(g-X)}\right )$, giving a total error term of size  $O\left (q^{\frac {g}{3}+\frac {X}{2}+\varepsilon g}\right )$. Then
$O\left (q^{\frac {g}{3}+\frac {X}{2}+\varepsilon g}\right )$. Then
 $$ \begin{align} M_1 & = 2 q^{g-\frac{X}{6}+2} \frac{ \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\zeta_{q^2}(2) \left(\sqrt{q}-1\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \nonumber \\ & \quad \times \sum_{B \mid h} \frac{\delta_{h_1=1}}{q^{2\deg(B)/3+\deg(h_2)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R\left(q^{-1/6}\right) + O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right). \end{align} $$
$$ \begin{align} M_1 & = 2 q^{g-\frac{X}{6}+2} \frac{ \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\zeta_{q^2}(2) \left(\sqrt{q}-1\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \nonumber \\ & \quad \times \sum_{B \mid h} \frac{\delta_{h_1=1}}{q^{2\deg(B)/3+\deg(h_2)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R\left(q^{-1/6}\right) + O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right). \end{align} $$Recall that ![]() $h=CS^2 E^3$ with
$h=CS^2 E^3$ with ![]() $C,S$ square-free and coprime. Then for the sum over B we can write an Euler product as follows:
$C,S$ square-free and coprime. Then for the sum over B we can write an Euler product as follows:
 $$ \begin{align*} \sum_{B \mid h} & \frac{\delta_{h_1=1}}{q^{2\deg(B)/3+\deg(h_2)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R\left(q^{-1/6}\right) \\ & \quad = \prod_{\substack{ R \in \mathbb{F}_q[T] \\ R\mid C}} \left(\sum_{\substack{j=1 \\ j \equiv 1 \,(\mathrm{mod}\,3)}}^{\operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{2j/3}} +\sum_{\substack{j=2 \\ j \equiv 2 \,(\mathrm{mod}\,3)}}^{ \operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{\frac{1}{3}+\frac{2j}{3}}}+ \frac{F_R\left(q^{-1/6}\right)}{\lvert R\rvert_q^{ \frac{2 \operatorname{\mathrm{ord}}_R(h)}{3}}} \right) \\ & \qquad \times \prod_{\substack{ R \in \mathbb{F}_q[T] \\ R\mid S}} \left(\sum_{\substack{j=2 \\ j \equiv 2 \,(\mathrm{mod}\,3)}}^{\operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{2j/3}} +\sum_{\substack{j=0 \\ j \equiv 0 \,(\mathrm{mod}\,3)}}^{ \operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{\frac{1}{3}+\frac{2j}{3}}}+ \frac{F_R\left(q^{-1/6}\right)}{\lvert R\rvert_q^{ \frac{2 \operatorname{\mathrm{ord}}_R(h)}{3}}} \right) \\ & \qquad \times \prod_{\substack{ R \in \mathbb{F}_q[T] \\ R\mid E \\ R \nmid CS}} \left(\sum_{\substack{j=0 \\ j \equiv 0 \,(\mathrm{mod}\,3)}}^{\operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{2j/3}} +\sum_{\substack{j=1 \\ j \equiv 1 \,(\mathrm{mod}\,3)}}^{ \operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{\frac{1}{3}+\frac{2j}{3}}}+ \frac{F_R\left(q^{-1/6}\right)}{\lvert R\rvert_q^{ \frac{2 \operatorname{\mathrm{ord}}_R(h)}{3}}} \right). \end{align*} $$
$$ \begin{align*} \sum_{B \mid h} & \frac{\delta_{h_1=1}}{q^{2\deg(B)/3+\deg(h_2)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R\left(q^{-1/6}\right) \\ & \quad = \prod_{\substack{ R \in \mathbb{F}_q[T] \\ R\mid C}} \left(\sum_{\substack{j=1 \\ j \equiv 1 \,(\mathrm{mod}\,3)}}^{\operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{2j/3}} +\sum_{\substack{j=2 \\ j \equiv 2 \,(\mathrm{mod}\,3)}}^{ \operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{\frac{1}{3}+\frac{2j}{3}}}+ \frac{F_R\left(q^{-1/6}\right)}{\lvert R\rvert_q^{ \frac{2 \operatorname{\mathrm{ord}}_R(h)}{3}}} \right) \\ & \qquad \times \prod_{\substack{ R \in \mathbb{F}_q[T] \\ R\mid S}} \left(\sum_{\substack{j=2 \\ j \equiv 2 \,(\mathrm{mod}\,3)}}^{\operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{2j/3}} +\sum_{\substack{j=0 \\ j \equiv 0 \,(\mathrm{mod}\,3)}}^{ \operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{\frac{1}{3}+\frac{2j}{3}}}+ \frac{F_R\left(q^{-1/6}\right)}{\lvert R\rvert_q^{ \frac{2 \operatorname{\mathrm{ord}}_R(h)}{3}}} \right) \\ & \qquad \times \prod_{\substack{ R \in \mathbb{F}_q[T] \\ R\mid E \\ R \nmid CS}} \left(\sum_{\substack{j=0 \\ j \equiv 0 \,(\mathrm{mod}\,3)}}^{\operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{2j/3}} +\sum_{\substack{j=1 \\ j \equiv 1 \,(\mathrm{mod}\,3)}}^{ \operatorname{\mathrm{ord}}_R(h)-1} \frac{1}{\lvert R\rvert_q^{\frac{1}{3}+\frac{2j}{3}}}+ \frac{F_R\left(q^{-1/6}\right)}{\lvert R\rvert_q^{ \frac{2 \operatorname{\mathrm{ord}}_R(h)}{3}}} \right). \end{align*} $$Simplifying and using the fact that  $F_R\left (q^{-1/6}\right ) = \frac {\lvert R\rvert _q}{\lvert R\rvert _q-1},$ we get
$F_R\left (q^{-1/6}\right ) = \frac {\lvert R\rvert _q}{\lvert R\rvert _q-1},$ we get
 $$ \begin{align*} \sum_{B \mid h} \frac{\delta_{h_1=1}}{q^{2\deg(B)/3+\deg(h_2)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R\left(q^{-1/6}\right) = \frac{1}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1}. \end{align*} $$
$$ \begin{align*} \sum_{B \mid h} \frac{\delta_{h_1=1}}{q^{2\deg(B)/3+\deg(h_2)/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid B \\ R \nmid \tilde{h}}} F_R\left(q^{-1/6}\right) = \frac{1}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3}} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1}. \end{align*} $$Using this and equation (8.23), it follows that
 $$ \begin{align*} M_1 & = 2 q^{g-\frac{X}{6}+2} \frac{ \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3} \zeta_{q^2}(2) \left(\sqrt{q}-1\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R|h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1}+O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right). \end{align*} $$
$$ \begin{align*} M_1 & = 2 q^{g-\frac{X}{6}+2} \frac{ \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3} \zeta_{q^2}(2) \left(\sqrt{q}-1\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \\ & \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R|h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1}+O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right). \end{align*} $$Putting everything together, we get
 $$ \begin{align*} &S_{11,\text{dual}}\\[4pt] & = \frac{ 2q^{g-\frac{X}{6}+2} \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3} \zeta_{q^2}(2) \left(\sqrt{q}-1\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \\[4pt]& \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} +O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right) \\[4pt]& \quad +q^{-\frac{g}{2}-1} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q,\leq g-X-1}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u}. \end{align*} $$
$$ \begin{align*} &S_{11,\text{dual}}\\[4pt] & = \frac{ 2q^{g-\frac{X}{6}+2} \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3} \zeta_{q^2}(2) \left(\sqrt{q}-1\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \\[4pt]& \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} +O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right) \\[4pt]& \quad +q^{-\frac{g}{2}-1} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q,\leq g-X-1}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u}. \end{align*} $$We treat ![]() $S_{12,\text {dual}}$ similarly, and since
$S_{12,\text {dual}}$ similarly, and since ![]() $\deg (f) = g-X$ we have
$\deg (f) = g-X$ we have ![]() $[g/2+1+ \deg (f_1h_2)]_3 = 1$. Then, as before,
$[g/2+1+ \deg (f_1h_2)]_3 = 1$. Then, as before, ![]() $\rho (1,1)=\tau (\chi _3) = q^3$, and we get
$\rho (1,1)=\tau (\chi _3) = q^3$, and we get
 $$ \begin{align*} &S_{12,\text{dual}} \\[4pt] & = \frac{q^{g-\frac{X}{6}+2} \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3} \zeta_{q^2}(2) \left(1-\sqrt{q}\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \\[4pt]& \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} +O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right) \\[4pt]& \quad + \frac{ q^{-\frac{g}{2}-1}}{1-\sqrt{q}} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q, g-X}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u}. \end{align*} $$
$$ \begin{align*} &S_{12,\text{dual}} \\[4pt] & = \frac{q^{g-\frac{X}{6}+2} \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3} \zeta_{q^2}(2) \left(1-\sqrt{q}\right)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \\[4pt]& \quad \times \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} +O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right) \\[4pt]& \quad + \frac{ q^{-\frac{g}{2}-1}}{1-\sqrt{q}} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q, g-X}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u}. \end{align*} $$Combining the two previous equations, we get
 $$ \begin{align} S_{1,\text{dual}} & = - \frac{q^{g-\frac{X}{6}+2} \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)\zeta_q(1/2)}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3} \zeta_{q^2}(2)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \nonumber\\[4pt]&\quad\prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} +O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right) \\[-6pt] \nonumber \\ & + q^{-g/2-1} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q,\leq g-X-1}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u} \nonumber \\ & + \frac{ q^{-\frac{g}{2}-1}}{1-\sqrt{q}} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q, g-X}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u}. \nonumber \end{align} $$
$$ \begin{align} S_{1,\text{dual}} & = - \frac{q^{g-\frac{X}{6}+2} \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)\zeta_q(1/2)}{\lvert C\rvert_q^{2/3} \lvert S\rvert_q^{1/3} \zeta_{q^2}(2)} \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ odd} \\ R\mid h}} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \nonumber\\[4pt]&\quad\prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} G_R\left(q^{-1/6},1\right)^{-1} D_R(1)^{-1} \prod_{\substack{R \in \mathbb{F}_q[T] \\ R\mid h}} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} +O \left(q^{\frac{5g}{6}+\varepsilon g}+q^{\frac{g}{3}+\frac{X}{2}+\varepsilon g} \right) \\[-6pt] \nonumber \\ & + q^{-g/2-1} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q,\leq g-X-1}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u} \nonumber \\ & + \frac{ q^{-\frac{g}{2}-1}}{1-\sqrt{q}} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q, g-X}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u}. \nonumber \end{align} $$Now using the work from [Reference David, Florea and Lalin13], we have
 $$ \begin{align*} \frac{ \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{ \zeta_{q^2}(2)} = \frac{ \mathcal{A}_{\mathrm{nK}}\left(1/q^2,1/q\right) }{\zeta_q(3)}. \end{align*} $$
$$ \begin{align*} \frac{ \mathcal{K}_{\mathrm{nK}}\left(q^{-1/6}\right)}{ \zeta_{q^2}(2)} = \frac{ \mathcal{A}_{\mathrm{nK}}\left(1/q^2,1/q\right) }{\zeta_q(3)}. \end{align*} $$When ![]() $\deg (R)$ is odd, note that we have
$\deg (R)$ is odd, note that we have
 $$ \begin{align*} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} =1, \end{align*} $$
$$ \begin{align*} E_R\left(q^{-1/6},1\right)^{-1} C_R(1)^{-1} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} =1, \end{align*} $$and when ![]() $\deg (R)$ is even, we have
$\deg (R)$ is even, we have
 $$ \begin{align*} G_R\left(q^{-1/6},1\right)^{-1}D_R^{-1} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} =\frac{\lvert R\rvert_q^2}{\lvert R\rvert_q^2+2\lvert R\rvert_q-2} = M_R \left( \frac{1}{q^2},\frac{1}{q} \right). \end{align*} $$
$$ \begin{align*} G_R\left(q^{-1/6},1\right)^{-1}D_R^{-1} \frac{\lvert R\rvert_q}{\lvert R\rvert_q-1} =\frac{\lvert R\rvert_q^2}{\lvert R\rvert_q^2+2\lvert R\rvert_q-2} = M_R \left( \frac{1}{q^2},\frac{1}{q} \right). \end{align*} $$Hence combining equations (8.24) and (8.16), we get

Using Proposition 2.3 and following similar steps as in the proof at [Reference David, Florea and Lalin13, page 48], we get
 $$ \begin{align*} &q^{-\frac{g}{2}-1} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q,\leq g-X-1}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u} \\ &\quad\quad\quad\quad\quad \ll g q^{\frac{3g}{2}-(2-\sigma)X + 2\deg(h) \left( \tfrac{3}{2}-\sigma\right)}, \end{align*} $$
$$ \begin{align*} &q^{-\frac{g}{2}-1} \frac{1}{2 \pi i} \oint_{\lvert u\rvert=q^{-2\sigma}} \sum_{f \in \mathcal{M}_{q,\leq g-X-1}} \frac{1}{q^{\deg(f)/2}} \sum_{\substack{N \in \mathbb{F}_q[T] \\ \deg(N) \leq \frac{g}{2}+1 \\ \left(N,fh\right)=1}} \mu(N) G_{q^2}\left(fh^2,N\right) \frac{\tilde{\Psi}_{q^2}\left(fh^2N,u\right)}{u^{g/2+1-\deg(N)}} \frac{du}{u} \\ &\quad\quad\quad\quad\quad \ll g q^{\frac{3g}{2}-(2-\sigma)X + 2\deg(h) \left( \tfrac{3}{2}-\sigma\right)}, \end{align*} $$as long as ![]() $\sigma \geq 7/6$. The second integral involving the sum over
$\sigma \geq 7/6$. The second integral involving the sum over ![]() $f \in \mathcal {M}_{q, g-X}$ is similarly bounded.
$f \in \mathcal {M}_{q, g-X}$ is similarly bounded.
Collecting the estimate for with the proper error terms and the estimate for
with the proper error terms and the estimate for from Section 8.2, we get
from Section 8.2, we get
 $$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \chi(h) {\textstyle L\left(\frac{1}{2}, \chi\right)} & = \frac{ q^{g+2} \zeta_q(3/2)}{\zeta_q(3)\lvert C\rvert_q \sqrt{\lvert S\rvert_q}} \mathcal{A}_{\mathrm{nK}} \left ( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right ) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} M_R \left( \frac{1}{q^2},\frac{1}{q^{3/2}} \right) \\ & \quad +O \left(q^{\frac{X+g}{2}+\varepsilon g} + q^{\frac{3g}{2} - (2-\sigma) X + 2 \deg(h)\left( \frac{3}{2}-\sigma\right)} +q^{\frac{5g}{6}+\varepsilon g}+q^{g-\frac{X}{2}+\varepsilon g}\right), \end{align*} $$
$$ \begin{align*} \sum_{\chi \in \mathcal{C}(g)} \chi(h) {\textstyle L\left(\frac{1}{2}, \chi\right)} & = \frac{ q^{g+2} \zeta_q(3/2)}{\zeta_q(3)\lvert C\rvert_q \sqrt{\lvert S\rvert_q}} \mathcal{A}_{\mathrm{nK}} \left ( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right ) \prod_{\substack{R \in \mathbb{F}_q[T] \\ \deg(R) \text{ even} \\ R\mid h}} M_R \left( \frac{1}{q^2},\frac{1}{q^{3/2}} \right) \\ & \quad +O \left(q^{\frac{X+g}{2}+\varepsilon g} + q^{\frac{3g}{2} - (2-\sigma) X + 2 \deg(h)\left( \frac{3}{2}-\sigma\right)} +q^{\frac{5g}{6}+\varepsilon g}+q^{g-\frac{X}{2}+\varepsilon g}\right), \end{align*} $$where ![]() $7/6 \leq \sigma <4/3$. We pick
$7/6 \leq \sigma <4/3$. We pick ![]() $\sigma =7/6$ and
$\sigma =7/6$ and  $X= \frac {3g}{4} + \frac {\deg (h)}{2}$. Then the error term becomes
$X= \frac {3g}{4} + \frac {\deg (h)}{2}$. Then the error term becomes  $O \left (q^{\frac {7g}{8}+\frac {\deg (h)}{4} +\varepsilon g} \right )$. Since
$O \left (q^{\frac {7g}{8}+\frac {\deg (h)}{4} +\varepsilon g} \right )$. Since ![]() $\deg (h) < \frac {g}{10}-\varepsilon g$, the main term dominates the error term, and we have a genuine asymptotic formula.
$\deg (h) < \frac {g}{10}-\varepsilon g$, the main term dominates the error term, and we have a genuine asymptotic formula.
8.4 Proof of Theorem 1.3
Proof. Here we will finish the proof of Theorem 1.3. From equation (8.2) and Proposition 8.1, it follows that the main term in the mollified first moment is equal to
 $$ \begin{align} \frac{q^{g+2} \zeta_q(3/2)}{\zeta_q(3)} \mathcal{A}_{\mathrm{nK}}\left(\frac{1}{q^{2}},\frac{1}{ q^{3/2}}\right) \prod_{r = 0}^J T(r), \end{align} $$
$$ \begin{align} \frac{q^{g+2} \zeta_q(3/2)}{\zeta_q(3)} \mathcal{A}_{\mathrm{nK}}\left(\frac{1}{q^{2}},\frac{1}{ q^{3/2}}\right) \prod_{r = 0}^J T(r), \end{align} $$where
 $$ \begin{align*} T(r) &= \sum_{\substack{ P\mid h_r \Rightarrow P \in I_r\\ \Omega\left(h_r\right) \leq \ell_r\\ h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free}}} \frac{a(h_r; J ) \lambda(h_r) \nu(h_r)}{ \lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}} \prod_{\substack{R \in \mathbb F_q[T] \\ \deg{R} \text{ even} \\ R \mid h_r}} M_R\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}} \right)\\ &\geq \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free}}} \frac{a(h_r; J ) \lambda(h_r) \nu(h_r)}{ {\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}} \prod_{\substack{R \in \mathbb F_q[T] \\ \deg{R} \text{ even} \\ R \mid h_r}} M_R\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right) \\ & \quad - \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free} }} \frac{2^{\Omega\left(h_r\right)}}{ 2^{\ell_r}{\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}}, \end{align*} $$
$$ \begin{align*} T(r) &= \sum_{\substack{ P\mid h_r \Rightarrow P \in I_r\\ \Omega\left(h_r\right) \leq \ell_r\\ h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free}}} \frac{a(h_r; J ) \lambda(h_r) \nu(h_r)}{ \lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}} \prod_{\substack{R \in \mathbb F_q[T] \\ \deg{R} \text{ even} \\ R \mid h_r}} M_R\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}} \right)\\ &\geq \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free}}} \frac{a(h_r; J ) \lambda(h_r) \nu(h_r)}{ {\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}} \prod_{\substack{R \in \mathbb F_q[T] \\ \deg{R} \text{ even} \\ R \mid h_r}} M_R\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right) \\ & \quad - \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free} }} \frac{2^{\Omega\left(h_r\right)}}{ 2^{\ell_r}{\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}}, \end{align*} $$where in the second line we have added the ![]() $h_r$ with
$h_r$ with ![]() $\Omega (h_r) \geq \ell _r$ to the main sum, and we have also used the facts that
$\Omega (h_r) \geq \ell _r$ to the main sum, and we have also used the facts that ![]() $2^{\ell _r}\leq 2^{\Omega (h_r)}$ and the bound
$2^{\ell _r}\leq 2^{\Omega (h_r)}$ and the bound ![]() $\nu (h_r)\leq 1$. Now we have
$\nu (h_r)\leq 1$. Now we have
 $$ \begin{align*} \frac{1}{2^{\ell_r}} & \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free} }} \frac{2^{\Omega\left(h_r\right)}}{ {\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}} \\ & \leq \frac{1}{2^{\ell_r}} \sum_{P\mid C_r \Rightarrow P \in I_r} \frac{2^{\Omega\left(C_r\right)}}{\lvert C_r\rvert_q^{3/2}} \sum_{P\mid S_r \Rightarrow P \in I_r} \frac{4^{\Omega\left(S_r\right)}}{\lvert S_r\rvert_q^{3/2}} \\ & \quad \times \sum_{P\mid E_r \Rightarrow P \in I_r} \frac{8^{\Omega\left(E_r\right)}}{\lvert E_r\rvert_q^{3/2}} = \frac{1}{2^{\ell_r}} \prod_{P \in I_r} \left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)^{-1}\left(1- \frac{4}{\lvert P\rvert_q^{3/2}} \right)^{-1} \left(1- \frac{8}{\lvert P\rvert_q^{3/2}} \right)^{-1}, \end{align*} $$
$$ \begin{align*} \frac{1}{2^{\ell_r}} & \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free} }} \frac{2^{\Omega\left(h_r\right)}}{ {\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}} \\ & \leq \frac{1}{2^{\ell_r}} \sum_{P\mid C_r \Rightarrow P \in I_r} \frac{2^{\Omega\left(C_r\right)}}{\lvert C_r\rvert_q^{3/2}} \sum_{P\mid S_r \Rightarrow P \in I_r} \frac{4^{\Omega\left(S_r\right)}}{\lvert S_r\rvert_q^{3/2}} \\ & \quad \times \sum_{P\mid E_r \Rightarrow P \in I_r} \frac{8^{\Omega\left(E_r\right)}}{\lvert E_r\rvert_q^{3/2}} = \frac{1}{2^{\ell_r}} \prod_{P \in I_r} \left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)^{-1}\left(1- \frac{4}{\lvert P\rvert_q^{3/2}} \right)^{-1} \left(1- \frac{8}{\lvert P\rvert_q^{3/2}} \right)^{-1}, \end{align*} $$so combining the two previous equations, we get
 $$ \begin{align*} T(r) & \geq \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free}}} \frac{a(h_r; J ) \lambda(h_r) \nu(h_r)}{ {\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}} \prod_{\substack{R \in \mathbb F_q[T] \\ \deg{R} \text{ even} \\ R \mid h_r}} M_R\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right) \\ & \quad - \frac{1}{2^{\ell_r}} \prod_{P \in I_r} \left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)^{-1}\left(1- \frac{4}{\lvert P\rvert_q^{3/2}} \right)^{-1} \left(1- \frac{8}{\lvert P\rvert_q^{3/2}} \right)^{-1}. \end{align*} $$
$$ \begin{align*} T(r) & \geq \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free}}} \frac{a(h_r; J ) \lambda(h_r) \nu(h_r)}{ {\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}} \prod_{\substack{R \in \mathbb F_q[T] \\ \deg{R} \text{ even} \\ R \mid h_r}} M_R\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right) \\ & \quad - \frac{1}{2^{\ell_r}} \prod_{P \in I_r} \left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)^{-1}\left(1- \frac{4}{\lvert P\rvert_q^{3/2}} \right)^{-1} \left(1- \frac{8}{\lvert P\rvert_q^{3/2}} \right)^{-1}. \end{align*} $$ Let ![]() $U(r)$ denote the first term. Then
$U(r)$ denote the first term. Then
 $$ \begin{align} \prod_{r =0}^{J} T(r) \geq \prod_{r=0}^{J} U(r) \prod_{r=0}^{J} \left(1- \frac{1}{2^{\ell_r} U(r) \prod_{P \in I_r} \left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)\left(1- \frac{4}{\lvert P\rvert_q^{3/2}} \right) \left(1- \frac{8}{\lvert P\rvert_q^{3/2}} \right) }\right). \end{align} $$
$$ \begin{align} \prod_{r =0}^{J} T(r) \geq \prod_{r=0}^{J} U(r) \prod_{r=0}^{J} \left(1- \frac{1}{2^{\ell_r} U(r) \prod_{P \in I_r} \left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)\left(1- \frac{4}{\lvert P\rvert_q^{3/2}} \right) \left(1- \frac{8}{\lvert P\rvert_q^{3/2}} \right) }\right). \end{align} $$We first focus on
 $$ \begin{align} \mathcal{U}:=\prod_{r=0}^{J} U(r) & = \prod_{r=0}^J \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free}}} \frac{a(h_r; J ) \lambda(h_r) \nu(h_r)}{ {\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}} \prod_{\substack{R \in \mathbb F_q[T] \\ \deg{R} \text{ even} \\ R \mid h_r}} M_R\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right) \nonumber \\ & = \prod_{r=0}^J \prod_{P\in I_r} \left[1+\sum_{e=0}^\infty \frac{a(P;J )^{3e+1}(-1)^{3e+1}}{\lvert P\rvert_q^{3(e+1)/2}(3e+3)!}\right.\\ \nonumber & \quad \left. \vphantom{\sum_{e=0}^\infty \frac{a(P;J )^{3e+1}(-1)^{3e+1}}{\lvert P\rvert_q^{3(e+1)/2}(3e+3)!}} \times \left(a(P;J )^2+3(e+1)(-a(P;J )+3e+2)\right)N_P\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right)\right], \end{align} $$
$$ \begin{align} \mathcal{U}:=\prod_{r=0}^{J} U(r) & = \prod_{r=0}^J \sum_{\substack{P \mid h_r \Rightarrow P \in I_r\\h_r = C_r S_r^2 E_r^3\\ \left(C_r, S_r\right) =1, C_r, S_r \text{ square-free}}} \frac{a(h_r; J ) \lambda(h_r) \nu(h_r)}{ {\lvert C_r\rvert_q^{3/2} \lvert S_r\rvert_q^{3/2} \lvert E_r\rvert_q^{3/2}}} \prod_{\substack{R \in \mathbb F_q[T] \\ \deg{R} \text{ even} \\ R \mid h_r}} M_R\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right) \nonumber \\ & = \prod_{r=0}^J \prod_{P\in I_r} \left[1+\sum_{e=0}^\infty \frac{a(P;J )^{3e+1}(-1)^{3e+1}}{\lvert P\rvert_q^{3(e+1)/2}(3e+3)!}\right.\\ \nonumber & \quad \left. \vphantom{\sum_{e=0}^\infty \frac{a(P;J )^{3e+1}(-1)^{3e+1}}{\lvert P\rvert_q^{3(e+1)/2}(3e+3)!}} \times \left(a(P;J )^2+3(e+1)(-a(P;J )+3e+2)\right)N_P\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right)\right], \end{align} $$where  $N_P\left (\frac {1}{q^{2}}, \frac {1}{q^{3/2}}\right )=M_P\left (\frac {1}{q^{2}}, \frac {1}{q^{3/2}}\right )$ or 1 according to whether
$N_P\left (\frac {1}{q^{2}}, \frac {1}{q^{3/2}}\right )=M_P\left (\frac {1}{q^{2}}, \frac {1}{q^{3/2}}\right )$ or 1 according to whether ![]() $\deg (P)$ is even or odd. Thus
$\deg (P)$ is even or odd. Thus
 $$ \begin{align} \mathcal{U} &= \prod_{\deg(P) \leq (g+2) \theta_{J}} \left[1+\left[\frac{1}{3}\left(1+\frac{1}{\lvert P\rvert_q^{1/2}}+\frac{1}{\lvert P\rvert_q}\right)\exp\left( -\frac{a(P;J )}{\lvert P\rvert_q^{1/2}}\right)\right.\right. \nonumber \\ & \quad \left.+\frac{1}{3}\left(1+\frac{\xi_3}{\lvert P\rvert_q^{1/2}}+\frac{\xi_3^2}{\lvert P\rvert_q}\right) \exp\left( -\frac{\xi_3a(P;J )}{\lvert P\rvert_q^{1/2}}\right)+\frac{1}{3}\left(1+\frac{\xi_3^2}{\lvert P\rvert_q^{1/2}}+\frac{\xi_3}{\lvert P\rvert_q}\right) \exp\left( -\frac{\xi_3^2a(P;J )}{\lvert P\rvert_q^{1/2}}\right)-1\right] \nonumber \\ & \quad \times \left. \vphantom{\frac{\xi_3^2}{\lvert P\rvert_q^{1/2}}} N_P\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right)\right]. \end{align} $$
$$ \begin{align} \mathcal{U} &= \prod_{\deg(P) \leq (g+2) \theta_{J}} \left[1+\left[\frac{1}{3}\left(1+\frac{1}{\lvert P\rvert_q^{1/2}}+\frac{1}{\lvert P\rvert_q}\right)\exp\left( -\frac{a(P;J )}{\lvert P\rvert_q^{1/2}}\right)\right.\right. \nonumber \\ & \quad \left.+\frac{1}{3}\left(1+\frac{\xi_3}{\lvert P\rvert_q^{1/2}}+\frac{\xi_3^2}{\lvert P\rvert_q}\right) \exp\left( -\frac{\xi_3a(P;J )}{\lvert P\rvert_q^{1/2}}\right)+\frac{1}{3}\left(1+\frac{\xi_3^2}{\lvert P\rvert_q^{1/2}}+\frac{\xi_3}{\lvert P\rvert_q}\right) \exp\left( -\frac{\xi_3^2a(P;J )}{\lvert P\rvert_q^{1/2}}\right)-1\right] \nonumber \\ & \quad \times \left. \vphantom{\frac{\xi_3^2}{\lvert P\rvert_q^{1/2}}} N_P\left(\frac{1}{q^{2}}, \frac{1}{q^{3/2}}\right)\right]. \end{align} $$For the second product of formula (8.26), we have
 $$ \begin{align*} \prod_{r=0}^{J} \left( \vphantom{\left(\frac{1}{\left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)}\right)} 1- \right. & \left. \frac{1}{2^{\ell_r} U(r) \prod_{P \in I_r} \left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)\left(1- \frac{4}{\lvert P\rvert_q^{3/2}} \right) \left(1- \frac{8}{\lvert P\rvert_q^{3/2}} \right) }\right)\\ & \geq \left(1- \frac{1}{2^{\ell_0}} \exp \left( \sum_{n=1}^{\infty} \frac{q^n}{n} \left(\frac{1}{q^{3n/2}-1}+\frac{2}{q^{3n/2}-2}+\frac{4}{q^{3n/2}-4}+\frac{8}{q^{3n/2}-8} \right) \right) \right) \\ & \quad \times \prod_{r=1}^{J} \left( 1- \frac{1}{2^{\ell_r} } \exp\left( \sum_{n=(g+2) \theta_{r-1}}^{(g+2) \theta_r} \frac{15}{nq^{n/2}} +O\left(\frac{1}{q^{2g \theta_{r-1}}} \right) \right)\right) \\ & \geq \left(1-\frac{1}{2^{\ell_0}} K \right)\prod_{r=1}^{J} \left(1-\frac{1}{2^{\ell_r}} +O \left(\frac{1}{2^{\ell_r} q^{g \theta_{r-1}/2}} \right) \right) \\ & \geq 1-\frac{1}{e^{e^{84}}}, \end{align*} $$
$$ \begin{align*} \prod_{r=0}^{J} \left( \vphantom{\left(\frac{1}{\left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)}\right)} 1- \right. & \left. \frac{1}{2^{\ell_r} U(r) \prod_{P \in I_r} \left(1- \frac{2}{\lvert P\rvert_q^{3/2}} \right)\left(1- \frac{4}{\lvert P\rvert_q^{3/2}} \right) \left(1- \frac{8}{\lvert P\rvert_q^{3/2}} \right) }\right)\\ & \geq \left(1- \frac{1}{2^{\ell_0}} \exp \left( \sum_{n=1}^{\infty} \frac{q^n}{n} \left(\frac{1}{q^{3n/2}-1}+\frac{2}{q^{3n/2}-2}+\frac{4}{q^{3n/2}-4}+\frac{8}{q^{3n/2}-8} \right) \right) \right) \\ & \quad \times \prod_{r=1}^{J} \left( 1- \frac{1}{2^{\ell_r} } \exp\left( \sum_{n=(g+2) \theta_{r-1}}^{(g+2) \theta_r} \frac{15}{nq^{n/2}} +O\left(\frac{1}{q^{2g \theta_{r-1}}} \right) \right)\right) \\ & \geq \left(1-\frac{1}{2^{\ell_0}} K \right)\prod_{r=1}^{J} \left(1-\frac{1}{2^{\ell_r}} +O \left(\frac{1}{2^{\ell_r} q^{g \theta_{r-1}/2}} \right) \right) \\ & \geq 1-\frac{1}{e^{e^{84}}}, \end{align*} $$where in the second line we used the inequality form of the Prime Polynomial Theorem (2.1),  $K = \exp \left ( \sum _{n=1}^{\infty } \frac {q^n}{n} \left (\frac {1}{q^{3n/2}-1}+\frac {2}{q^{3n/2}-2}+\frac {4}{q^{3n/2}-4}+\frac {8}{q^{3n/2}-8} \right ) \right ),$ and the estimate in the last line is taken with the constants chosen in Section 7.
$K = \exp \left ( \sum _{n=1}^{\infty } \frac {q^n}{n} \left (\frac {1}{q^{3n/2}-1}+\frac {2}{q^{3n/2}-2}+\frac {4}{q^{3n/2}-4}+\frac {8}{q^{3n/2}-8} \right ) \right ),$ and the estimate in the last line is taken with the constants chosen in Section 7.
Putting together all this information, we obtain
 $$ \begin{align} \frac{q^{g+2} \zeta_q(3/2)}{\zeta_q(3)} \mathcal{A}_{\mathrm{nK}}\left(\frac{1}{q^{2}},\frac{1}{ q^{3/2}}\right) \prod_{r = 0}^J T(r) \geq \left(1-\frac{1}{e^{e^{84}}}\right) \frac{ q^{g+2} \zeta_q(3/2)}{\zeta_q(3)} \mathcal{A}_{\mathrm{nK}} \left ( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right ) \mathcal{U}. \end{align} $$
$$ \begin{align} \frac{q^{g+2} \zeta_q(3/2)}{\zeta_q(3)} \mathcal{A}_{\mathrm{nK}}\left(\frac{1}{q^{2}},\frac{1}{ q^{3/2}}\right) \prod_{r = 0}^J T(r) \geq \left(1-\frac{1}{e^{e^{84}}}\right) \frac{ q^{g+2} \zeta_q(3/2)}{\zeta_q(3)} \mathcal{A}_{\mathrm{nK}} \left ( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right ) \mathcal{U}. \end{align} $$Finally, summing the error term coming from Proposition 8.1 gives
 $$ \begin{align} q^{\frac{7g}{8}+\varepsilon g}\sum_{\deg(h) \leq w(g+2)} \frac{\lvert h\rvert^{1/4}}{\lvert h\rvert^{1/2}}\sim q^{\frac{7g}{8}+\varepsilon g + \frac{3w(g+2)}{4}} , \end{align} $$
$$ \begin{align} q^{\frac{7g}{8}+\varepsilon g}\sum_{\deg(h) \leq w(g+2)} \frac{\lvert h\rvert^{1/4}}{\lvert h\rvert^{1/2}}\sim q^{\frac{7g}{8}+\varepsilon g + \frac{3w(g+2)}{4}} , \end{align} $$where  $w=\sum _{j=0}^J \theta _j \ell _j$. Note that because of formula (4.2), we have
$w=\sum _{j=0}^J \theta _j \ell _j$. Note that because of formula (4.2), we have
 $$ \begin{align*} \sum_{j=0}^{J} \theta_j \ell_j \leq \frac{1}{20}, \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{J} \theta_j \ell_j \leq \frac{1}{20}, \end{align*} $$so formula (8.30) constitutes an error term. This finishes the proof of Theorem 1.3.
Proof of Corollary 1.4. Note that from expression (8.27), we can write
 $$ \begin{align*} \mathcal{U} &\geq \prod_{\deg(P) \leq (g+2) \theta_{J}} \left( 1- \frac{a(P;J)}{6\lvert P\rvert^{3/2}} ( a(P;J)^2-3a(P;J)+6) \right) \\ &\geq \prod_{\deg(P) \leq (g+2) \theta_{J}}\left( 1- \frac{1}{\lvert P\rvert^{3/2}}\right)\\ &\geq \zeta_q(3/2)^{-1}. \end{align*} $$
$$ \begin{align*} \mathcal{U} &\geq \prod_{\deg(P) \leq (g+2) \theta_{J}} \left( 1- \frac{a(P;J)}{6\lvert P\rvert^{3/2}} ( a(P;J)^2-3a(P;J)+6) \right) \\ &\geq \prod_{\deg(P) \leq (g+2) \theta_{J}}\left( 1- \frac{1}{\lvert P\rvert^{3/2}}\right)\\ &\geq \zeta_q(3/2)^{-1}. \end{align*} $$We also have
 $$ \begin{align*} \mathcal{A}_{\mathrm{nK}} \left ( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right )= \prod_{\substack{R \in \mathbb F_q[T]\\\deg(R) \text{ odd}}}\frac{1}{1+\frac{1}{\lvert R\rvert^2}}\prod_{\substack{R \in \mathbb F_q[T]\\\deg(R) \text{even}}}\frac{1+\frac{2}{\lvert R\rvert}\left(1-\frac{1}{\lvert R\rvert^{3/2}}\right)}{\left(1+\frac{1}{\lvert R\rvert}\right)^2}. \end{align*} $$
$$ \begin{align*} \mathcal{A}_{\mathrm{nK}} \left ( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right )= \prod_{\substack{R \in \mathbb F_q[T]\\\deg(R) \text{ odd}}}\frac{1}{1+\frac{1}{\lvert R\rvert^2}}\prod_{\substack{R \in \mathbb F_q[T]\\\deg(R) \text{even}}}\frac{1+\frac{2}{\lvert R\rvert}\left(1-\frac{1}{\lvert R\rvert^{3/2}}\right)}{\left(1+\frac{1}{\lvert R\rvert}\right)^2}. \end{align*} $$For the factors involving R of even degree, we have
 $$ \begin{align*} 1-\frac{1}{(\lvert R\rvert+1)^2}- \frac{2}{\lvert R\rvert^{1/2}(\lvert R\rvert+1)^2}>\left(1-\frac{1}{\lvert R\rvert^2} \right)^2, \end{align*} $$
$$ \begin{align*} 1-\frac{1}{(\lvert R\rvert+1)^2}- \frac{2}{\lvert R\rvert^{1/2}(\lvert R\rvert+1)^2}>\left(1-\frac{1}{\lvert R\rvert^2} \right)^2, \end{align*} $$and this leads to
 $$ \begin{align*} \mathcal{A}_{\mathrm{nK}} \left ( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right ) \geq \zeta_q(2)^{-2}. \end{align*} $$
$$ \begin{align*} \mathcal{A}_{\mathrm{nK}} \left ( \frac{1}{q^2}, \frac{1}{q^{3/2}} \right ) \geq \zeta_q(2)^{-2}. \end{align*} $$Combining everything, the main term of the mollified moment in formula (8.29) satisfies
 $$ \begin{align*} \geq \left(1-\frac{1}{e^{e^{84}}}\right) \frac{q^{g+2}}{\zeta_q(2)^2\zeta_q(3)}\geq0.6143 q^{g+2}, \end{align*} $$
$$ \begin{align*} \geq \left(1-\frac{1}{e^{e^{84}}}\right) \frac{q^{g+2}}{\zeta_q(2)^2\zeta_q(3)}\geq0.6143 q^{g+2}, \end{align*} $$where we have bounded by the worst case ![]() $q = 5$.
$q = 5$.
9 Conclusion
The method we used for the family of cubic L-functions would be expected to work in general for families where one can compute the first moment with a power-saving error term, and it is useful in families where the second moment is not known. The method allows us to get a sharp upper bound for the second mollified moment, which is enough to obtain a positive proportion of nonvanishing (under the GRH). For the family of cubic twists, we expect that the Kummer case would be similar, and the results would hold in that setting as well. Our results should also transfer over to number fields, but it would be conditional on the GRH.
Acknowledgments
The authors would like to thank Maksym Radziwiłł for drawing our attention to his work with Lester and for very helpful discussions, and Stephen Lester for interesting insights and comments. The authors would also like to thank the referee for a careful reading of the paper and for the many useful comments and suggestions.
Funding statement
The research of the first and third authors is supported by the National Science and Engineering Research Council of Canada (NSERC Discovery Grant 155635-2019 to CD, 335412-2013 to ML) and the Fonds de recherche du Québec – Nature et technologies (FRQNT Projet de recherche en équipe 256442 and 300951 to CD and ML). The second author was supported by the National Science Foundation (NSF DMS-2101769, NSF - Postdoctoral Fellowship DMS-1703695) during part of the research which led to this paper, and she wishes to thank the initiative “A Room of One’s Own” for focused time.
Conflicts of interest
None.