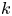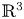1. Introduction
The aim of this work is to study $k$![]() -folding map-germs on complex surfaces in $\mathbb {C}^3$
-folding map-germs on complex surfaces in $\mathbb {C}^3$![]() and relate them to the extrinsic differential geometry of smooth surfaces in $\mathbb {R}^3$
and relate them to the extrinsic differential geometry of smooth surfaces in $\mathbb {R}^3$![]() .
.
The standard Whitney fold of order $k$![]() with respect to the plane $\pi _0:y=0$
with respect to the plane $\pi _0:y=0$![]() in $\mathbb {C}^3$
in $\mathbb {C}^3$![]() is the map $\omega _k\colon \mathbb {C}^3\to \mathbb {C}^3,$
is the map $\omega _k\colon \mathbb {C}^3\to \mathbb {C}^3,$![]() given by $\omega _k(x,y,z)=(x,y^k,z).$
given by $\omega _k(x,y,z)=(x,y^k,z).$![]() The map $\omega _k$
The map $\omega _k$![]() ‘folds’ the space $\mathbb {C}^3$
‘folds’ the space $\mathbb {C}^3$![]() along the plane $\pi _0$
along the plane $\pi _0$![]() , gluing the points $(x,y,z),$
, gluing the points $(x,y,z),$![]() $(x,\xi y,z),\dots,(x,\xi ^{k-1}y,z),$
$(x,\xi y,z),\dots,(x,\xi ^{k-1}y,z),$![]() where $\xi ={\rm {e}}^{2\pi {{\rm i}}/k}$
where $\xi ={\rm {e}}^{2\pi {{\rm i}}/k}$![]() is a primitive $k{\rm {th}}$
is a primitive $k{\rm {th}}$![]() -root of unity. The Whitney fold of order $k$
-root of unity. The Whitney fold of order $k$![]() with respect to any plane $\pi$
with respect to any plane $\pi$![]() , denoted by $\omega _k^{\pi }$
, denoted by $\omega _k^{\pi }$![]() , is defined similarly in § 2.
, is defined similarly in § 2.
Let $M$![]() be a complex surface in $\mathbb {C}^3$
be a complex surface in $\mathbb {C}^3$![]() . We call the restriction of $\omega _k^{\pi }$
. We call the restriction of $\omega _k^{\pi }$![]() to $M$
to $M$![]() the $k$
the $k$![]() -folding map on $M$
-folding map on $M$![]() with respect to $\pi$
with respect to $\pi$![]() . As our study is local, given a point $p$
. As our study is local, given a point $p$![]() on $M$
on $M$![]() and a plane $\pi$
and a plane $\pi$![]() in $\mathbb {C}^3$
in $\mathbb {C}^3$![]() through $p$
through $p$![]() , we choose a coordinate system so that $M$
, we choose a coordinate system so that $M$![]() is locally the graph of a function $z=f(x,y)$
is locally the graph of a function $z=f(x,y)$![]() and $\pi =\pi _0:y=0$
and $\pi =\pi _0:y=0$![]() (see remark 2.3(4)). Then the germ at $p_0$
(see remark 2.3(4)). Then the germ at $p_0$![]() of the $k$
of the $k$![]() -folding map is represented in standard form by the map-germ $F_k: (\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$
-folding map is represented in standard form by the map-germ $F_k: (\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$![]() , given by
, given by
For an analytic (resp. smooth) surface $M\subset \mathbb {R}^3$![]() , the $k$
, the $k$![]() -folding map at a point $p$
-folding map at a point $p$![]() on $M$
on $M$![]() is constructed by complexifying $M$
is constructed by complexifying $M$![]() (resp. a certain jet of a parametrization of $M$
(resp. a certain jet of a parametrization of $M$![]() ) at $p$
) at $p$![]() . The singularities of a $k$
. The singularities of a $k$![]() -folding map-germ encode the local symmetries of $M$
-folding map-germ encode the local symmetries of $M$![]() with respect to the (complex) reflection group of order $k$
with respect to the (complex) reflection group of order $k$![]() whose hyperplane arrangement consists of the single plane $\pi$
whose hyperplane arrangement consists of the single plane $\pi$![]() .
.
The study of $2$![]() -folding map-germs on surfaces in $\mathbb {R}^3$
-folding map-germs on surfaces in $\mathbb {R}^3$![]() was carried out by Bruce and Wilkinson [Reference Bruce5, Reference Bruce and Wilkinson8, Reference Wilkinson32] (see [Reference Bruce, Giblin and Tari6, Reference Giblin and Tari12–Reference Izumiya, Takahashi and Tari15, Reference Wilkinson32] for more work on the subject), without resorting to complexification. The real map-germs in [Reference Bruce5, Reference Bruce and Wilkinson8, Reference Wilkinson32] are called folding map-germs and our $2$
was carried out by Bruce and Wilkinson [Reference Bruce5, Reference Bruce and Wilkinson8, Reference Wilkinson32] (see [Reference Bruce, Giblin and Tari6, Reference Giblin and Tari12–Reference Izumiya, Takahashi and Tari15, Reference Wilkinson32] for more work on the subject), without resorting to complexification. The real map-germs in [Reference Bruce5, Reference Bruce and Wilkinson8, Reference Wilkinson32] are called folding map-germs and our $2$![]() -folding map-germs are their complexifications. Complexifying does not give extra information when $k=2$
-folding map-germs are their complexifications. Complexifying does not give extra information when $k=2$![]() . For $k\geq 3$
. For $k\geq 3$![]() , per contra, $k$
, per contra, $k$![]() -folding maps reveal a great deal of new geometric information. The local symmetries captured by these map-germs cannot be seen in the real case, which is why we call them hidden symmetries of $M\subset \mathbb {R}^3$
-folding maps reveal a great deal of new geometric information. The local symmetries captured by these map-germs cannot be seen in the real case, which is why we call them hidden symmetries of $M\subset \mathbb {R}^3$![]() . The loci of their singularities are visible on $M$
. The loci of their singularities are visible on $M$![]() and capture extrinsic geometric information of the surface.
and capture extrinsic geometric information of the surface.
Bruce and Wilkinson showed that folding maps capture the sub-parabolic and ridge curves, as well as umbilic points and other special points on these curves: these are robust features of the surface (i.e. they are special geometric features that can be traced on an evolving surface; see § 6.2 for details). Passing to the complex setting, we show that the singularities of $k$![]() -folding maps, $k\ge 2$
-folding maps, $k\ge 2$![]() , capture in a unified way, known robust features obtained by considering the contact of the surface with lines, planes or spheres (parabolic, sub-parabolic, ridge and flecnodal curves, umbilic points, $B_3$
, capture in a unified way, known robust features obtained by considering the contact of the surface with lines, planes or spheres (parabolic, sub-parabolic, ridge and flecnodal curves, umbilic points, $B_3$![]() , $C_3$
, $C_3$![]() and $S_3$
and $S_3$![]() -points, $A^*_2$
-points, $A^*_2$![]() -points, cusps of Gauss (gulls-points) and butterfly-points). Our approach also reveals a new robust feature on surfaces: when $k$
-points, cusps of Gauss (gulls-points) and butterfly-points). Our approach also reveals a new robust feature on surfaces: when $k$![]() is divisible by $3$
is divisible by $3$![]() , we obtain a new curve, which we call the $H_3$
, we obtain a new curve, which we call the $H_3$![]() -curve. We also obtain new special points on previously known curves as well as on the $H_3$
-curve. We also obtain new special points on previously known curves as well as on the $H_3$![]() -curve. This motivates the following question: can the $H_3$
-curve. This motivates the following question: can the $H_3$![]() -curve be obtained via the contact of the surface with some special geometric object? Further work is also required for understanding the link between local (hidden) symmetries of a surface and its contact with lines and planes.
-curve be obtained via the contact of the surface with some special geometric object? Further work is also required for understanding the link between local (hidden) symmetries of a surface and its contact with lines and planes.
The paper is organized as follows. In § 2, we set notation and give some preliminaries. In § 3, we obtain formulae for the invariants $C,$![]() $T,$
$T,$![]() $\mu ({\mathcal {D}})$
$\mu ({\mathcal {D}})$![]() and $r({\mathcal {D}})$
and $r({\mathcal {D}})$![]() of $k$
of $k$![]() -folding map-germs. These are respectively, the number of cross-caps, the number of triple points, the Milnor number and the number of branches of the double-point curve. These invariants determine the finite $\mathcal {A}$
-folding map-germs. These are respectively, the number of cross-caps, the number of triple points, the Milnor number and the number of branches of the double-point curve. These invariants determine the finite $\mathcal {A}$![]() -determinacy and the topological class of a $k$
-determinacy and the topological class of a $k$![]() -folding map-germ.
-folding map-germ.
We show that there are no $\mathcal {A}$![]() -simple $k$
-simple $k$![]() -folding map-germs for $k\ge 5$
-folding map-germs for $k\ge 5$![]() ; also the modality of the map-germs is large for $k$
; also the modality of the map-germs is large for $k$![]() large. This is why producing normal forms of finitely $\mathcal {A}$
large. This is why producing normal forms of finitely $\mathcal {A}$![]() -determined germs, as is usually done in singularity theory, is not of great use here. Our classification is of strata in the jet space which are manifolds formed by unions of finitely $\mathcal {A}$
-determined germs, as is usually done in singularity theory, is not of great use here. Our classification is of strata in the jet space which are manifolds formed by unions of finitely $\mathcal {A}$![]() -determined germs with the property that all germs in a given stratum are topologically equivalent.
-determined germs with the property that all germs in a given stratum are topologically equivalent.
We produce in § 4 a stratification of the $l$![]() -jet space of $k$
-jet space of $k$![]() -folding map-germs in standard form which is identified with the $l$
-folding map-germs in standard form which is identified with the $l$![]() -jet space of germs of functions $J^{l}(2,1)$
-jet space of germs of functions $J^{l}(2,1)$![]() . The stratification results are summarized as follows.
. The stratification results are summarized as follows.
Theorem 1.1 For any integer $k\ge 2$![]() , there is a stratification $\mathcal {S}_k$
, there is a stratification $\mathcal {S}_k$![]() of $J^{11}(2,1)$
of $J^{11}(2,1)$![]() such that, for any stratum $S$
such that, for any stratum $S$![]() in $\mathcal {S}_k$
in $\mathcal {S}_k$![]() of codimension $\le \! 4$
of codimension $\le \! 4$![]() , all $k$
, all $k$![]() -folding map-germs in standard form with $11$
-folding map-germs in standard form with $11$![]() -jets in $S$
-jets in $S$![]() are finitely $\mathcal {A}$
are finitely $\mathcal {A}$![]() -determined and are pairwise topologically equivalent.
-determined and are pairwise topologically equivalent.
We relate in § 6 the stratification of the jet space to the extrinsic differential geometry of surfaces in $\mathbb {R}^3$![]() . After clarifying what it means for a surface to be generic, we deduce the following result about the topological classes of $k$
. After clarifying what it means for a surface to be generic, we deduce the following result about the topological classes of $k$![]() -folding map-germs.
-folding map-germs.
Theorem 1.2 Let $k\geq 3$![]() be an integer and let $M$
be an integer and let $M$![]() be a generic smooth surface in $\mathbb {R}^3$
be a generic smooth surface in $\mathbb {R}^3$![]() (or a complex surface in $\mathbb {C}^3$
(or a complex surface in $\mathbb {C}^3$![]() ). Then, at any point $p$
). Then, at any point $p$![]() on $M$
on $M$![]() and for any plane $\pi$
and for any plane $\pi$![]() through $p$
through $p$![]() , the $k$
, the $k$![]() -folding map-germ at $p$
-folding map-germ at $p$![]() with respect to $\pi$
with respect to $\pi$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to one of the following map-germs:
-determined and is topologically equivalent to one of the following map-germs:

$({\dagger} )$![]() The constants $a_{j,j'},b_{j,j'}$
The constants $a_{j,j'},b_{j,j'}$![]() (resp. $c_{j}$
(resp. $c_{j}$![]() ) are as in proposition 4.23 (resp. 4.25) and the conditions on the indices are as in table 6.
) are as in proposition 4.23 (resp. 4.25) and the conditions on the indices are as in table 6.
It is worth noting that $3$![]() -folding map-germs can have $\mathcal {A}$
-folding map-germs can have $\mathcal {A}$![]() -simple singularities and their corresponding strata in $\mathcal {S}_3$
-simple singularities and their corresponding strata in $\mathcal {S}_3$![]() are $\mathcal {A}$
are $\mathcal {A}$![]() -constant. For $k\ge 4$
-constant. For $k\ge 4$![]() , none of the $k$
, none of the $k$![]() -folding map-germs are $\mathcal {A}$
-folding map-germs are $\mathcal {A}$![]() -simple, except for immersions and for $M^4_1$
-simple, except for immersions and for $M^4_1$![]() , which is the $C_3$
, which is the $C_3$![]() -singularity. The strata of $\mathcal {S}_k$
-singularity. The strata of $\mathcal {S}_k$![]() give rise to moduli of finitely determined map-germs with constant invariants $C,T,\mu (\mathcal {D})$
give rise to moduli of finitely determined map-germs with constant invariants $C,T,\mu (\mathcal {D})$![]() and $r(\mathcal {D})$
and $r(\mathcal {D})$![]() .
.
The representatives ${\bf M}^k_0$![]() and ${\bf M}^k_1$
and ${\bf M}^k_1$![]() are quasi-homogeneous, and ${\bf M}^k_l$
are quasi-homogeneous, and ${\bf M}^k_l$![]() , with $2\nmid k$
, with $2\nmid k$![]() , ${\bf Q}^k_3$
, ${\bf Q}^k_3$![]() , with $12\nmid k$
, with $12\nmid k$![]() , ${\bf R}^k_4$
, ${\bf R}^k_4$![]() , with $20\nmid k$
, with $20\nmid k$![]() and ${\bf U}^k_4$
and ${\bf U}^k_4$![]() , with $3\nmid k$
, with $3\nmid k$![]() , can be replaced by quasi-homogeneous representatives of the same topological class (see remarks 4.10). For these cases, the invariants can be calculated in terms of the weights and degrees [Reference Mond24] and the topological triviality of the strata in the jet space follows from equisingularity results in [Reference Damon9].
, can be replaced by quasi-homogeneous representatives of the same topological class (see remarks 4.10). For these cases, the invariants can be calculated in terms of the weights and degrees [Reference Mond24] and the topological triviality of the strata in the jet space follows from equisingularity results in [Reference Damon9].
The robust features captured by $k$![]() -folding map-germs on a generic surface are sketched in figure 1. An interesting finding is that, having studied symmetries of infinitely many orders (for any $k\ge 2$
-folding map-germs on a generic surface are sketched in figure 1. An interesting finding is that, having studied symmetries of infinitely many orders (for any $k\ge 2$![]() ), we obtain a finite collection of robust features that occur along curves and a finite collection of special points on these curves if we discard the ${\bf V}^{k,j,j'}$
), we obtain a finite collection of robust features that occur along curves and a finite collection of special points on these curves if we discard the ${\bf V}^{k,j,j'}$![]() and ${\bf W}^{k,j}$
and ${\bf W}^{k,j}$![]() -points.
-points.
2. Preliminaries
We introduce here $k$![]() -folding map-germs and notation from singularity theory that are needed in the paper. We start with the singularity theory notation, see for example [Reference Mond and Nuño-Ballesteros25, Reference Wall31] for more details.
-folding map-germs and notation from singularity theory that are needed in the paper. We start with the singularity theory notation, see for example [Reference Mond and Nuño-Ballesteros25, Reference Wall31] for more details.
2.1 Singularities of map-germs
We deal with germs $F\colon (M,p)\to (N,F(p))$![]() of holomorphic maps between complex manifolds. Taking coordinate charts, this is the same as dealing with map-germs $(\mathbb {C}^n,0)\to (\mathbb {C}^p,0)$
of holomorphic maps between complex manifolds. Taking coordinate charts, this is the same as dealing with map-germs $(\mathbb {C}^n,0)\to (\mathbb {C}^p,0)$![]() .
.
Let ${\mathcal {O}}_n$![]() be the local ring of germs of holomorphic functions $(\mathbb {C}^n,0 ) \to \mathbb {C}$
be the local ring of germs of holomorphic functions $(\mathbb {C}^n,0 ) \to \mathbb {C}$![]() and ${\mathfrak m}_n$
and ${\mathfrak m}_n$![]() its maximal ideal (which is the subset of germs that vanish at the origin). Denote by $\mathcal {O}(n,p)$
its maximal ideal (which is the subset of germs that vanish at the origin). Denote by $\mathcal {O}(n,p)$![]() the $\mathcal {O}_n$
the $\mathcal {O}_n$![]() -module of holomorphic map-germs $(\mathbb {C}^n,0)\to \mathbb {C}^p$
-module of holomorphic map-germs $(\mathbb {C}^n,0)\to \mathbb {C}^p$![]() , so $\mathcal {O}(n,p)=\bigoplus _p\mathcal {O}_n$
, so $\mathcal {O}(n,p)=\bigoplus _p\mathcal {O}_n$![]() .
.
Let ${\mathcal {R}}$![]() (resp. ${\mathcal {L}}$
(resp. ${\mathcal {L}}$![]() ) be the group of bi-holomorphic germs $(\mathbb {C}^n,0)\to (\mathbb {C}^n,0)$
) be the group of bi-holomorphic germs $(\mathbb {C}^n,0)\to (\mathbb {C}^n,0)$![]() (resp. $(\mathbb {C}^p,0)\to (\mathbb {C}^p,0)$
(resp. $(\mathbb {C}^p,0)\to (\mathbb {C}^p,0)$![]() ). The group ${\mathcal {A}}={\mathcal {R}}\times {\mathcal {L}}$
). The group ${\mathcal {A}}={\mathcal {R}}\times {\mathcal {L}}$![]() of right-left equivalence acts on ${\mathfrak {m}}_n\cdot {\mathcal {O}}(n,p)$
of right-left equivalence acts on ${\mathfrak {m}}_n\cdot {\mathcal {O}}(n,p)$![]() by $(h_1,h_2)\cdot G=h_2\circ G\circ h_1^{-1}$
by $(h_1,h_2)\cdot G=h_2\circ G\circ h_1^{-1}$![]() . Two germs $H,G$
. Two germs $H,G$![]() are said to be $\mathcal {A}$
are said to be $\mathcal {A}$![]() -equivalent, and write $H\sim _{\mathcal {A}} G$
-equivalent, and write $H\sim _{\mathcal {A}} G$![]() , if $H=(h_1,h_2)\cdot G$
, if $H=(h_1,h_2)\cdot G$![]() for some $(h_1,h_2)\in \mathcal {A}$
for some $(h_1,h_2)\in \mathcal {A}$![]() .
.
The $l$![]() -jet space of map-germs in $\mathfrak {m}_n\cdot \mathcal {O}(n,p)$
-jet space of map-germs in $\mathfrak {m}_n\cdot \mathcal {O}(n,p)$![]() is by definition
is by definition
Given a germ $G\in \mathfrak {m}_n\cdot {\mathcal {O}}(n,p)$![]() , we identified its $l$
, we identified its $l$![]() -jet $j^lG$
-jet $j^lG$![]() with its Taylor polynomial of degree $l$
with its Taylor polynomial of degree $l$![]() at the origin. Let $\mathcal {A}_{l}$
at the origin. Let $\mathcal {A}_{l}$![]() be the subgroup of $\mathcal {A}$
be the subgroup of $\mathcal {A}$![]() whose elements have $l$
whose elements have $l$![]() -jets the germ of the identity. The group $\mathcal {A}_l$
-jets the germ of the identity. The group $\mathcal {A}_l$![]() is a normal subgroup of $\mathcal {A}$
is a normal subgroup of $\mathcal {A}$![]() . Define $\mathcal {A}^{(l)}=\mathcal {A}/\mathcal {A}_l$
. Define $\mathcal {A}^{(l)}=\mathcal {A}/\mathcal {A}_l$![]() . The elements of $\mathcal {A}^{(l)}$
. The elements of $\mathcal {A}^{(l)}$![]() are the $l$
are the $l$![]() -jets of the elements of $\mathcal {A}$
-jets of the elements of $\mathcal {A}$![]() . The action of $\mathcal {A}$
. The action of $\mathcal {A}$![]() on ${\mathfrak {m}}_n\cdot {\mathcal {O}}(n,p)$
on ${\mathfrak {m}}_n\cdot {\mathcal {O}}(n,p)$![]() induces an action of the jet group $\mathcal {A}^{(l)}$
induces an action of the jet group $\mathcal {A}^{(l)}$![]() on $J^l(n,p)$
on $J^l(n,p)$![]() as follows. For $j^lG\in J^l(n,p)$
as follows. For $j^lG\in J^l(n,p)$![]() and $j^l(h_1,h_2)\in \mathcal {A}^{(l)}$
and $j^l(h_1,h_2)\in \mathcal {A}^{(l)}$![]() , $j^l(h_1,h_2)\cdot j^rG=j^l((h_1,h_2)\cdot G).$
, $j^l(h_1,h_2)\cdot j^rG=j^l((h_1,h_2)\cdot G).$![]()
A germ $G$![]() is said to be finitely $\mathcal {A}$
is said to be finitely $\mathcal {A}$![]() -determined if there exist an integer $l$
-determined if there exist an integer $l$![]() such that $G\sim _{\mathcal {A}}H$
such that $G\sim _{\mathcal {A}}H$![]() for any $H$
for any $H$![]() with $j^lH=j^lG$
with $j^lH=j^lG$![]() ; $j^lG$
; $j^lG$![]() is then said to be a sufficient jet of $G$
is then said to be a sufficient jet of $G$![]() . The germ $G$
. The germ $G$![]() is then said to be $l$
is then said to be $l$![]() -$\mathcal {A}$
-$\mathcal {A}$![]() -determined. The least $l$
-determined. The least $l$![]() satisfying this property is called the degree of determinacy of $G$
satisfying this property is called the degree of determinacy of $G$![]() .
.
There are classifications of finitely determined map-germs for various pairs $(n,p)$![]() . When $p=1$
. When $p=1$![]() , there is Arnold's extensive list of the $\mathcal {R}$
, there is Arnold's extensive list of the $\mathcal {R}$![]() -classification of germs of functions [Reference Arnold, Guseĭn-Zade and Varchenko1]. For $(n,p)=(2,2)$
-classification of germs of functions [Reference Arnold, Guseĭn-Zade and Varchenko1]. For $(n,p)=(2,2)$![]() , classifications were carried out by several authors, the most extensive ones are given in [Reference Goryunov16, Reference Rieger29]. Here we need only the singularities of $\mathcal {A}_e$
, classifications were carried out by several authors, the most extensive ones are given in [Reference Goryunov16, Reference Rieger29]. Here we need only the singularities of $\mathcal {A}_e$![]() -codimension $\le \! 2$
-codimension $\le \! 2$![]() , which we reproduce in table 9. For $(n,p)=(2,3)$
, which we reproduce in table 9. For $(n,p)=(2,3)$![]() , Mond [Reference Mond22] produced an extensive list of finitely $\mathcal {A}$
, Mond [Reference Mond22] produced an extensive list of finitely $\mathcal {A}$![]() -determined map-germs. We use in this paper the following singularities from [Reference Mond22]:
-determined map-germs. We use in this paper the following singularities from [Reference Mond22]:

The notion of a simple germ is defined in [Reference Arnold, Guseĭn-Zade and Varchenko1] as follows. Let $X$![]() be a manifold and $\mathcal {G}$
be a manifold and $\mathcal {G}$![]() a Lie group acting on $X$
a Lie group acting on $X$![]() . The modality of a point $g\in X$
. The modality of a point $g\in X$![]() under the action of $\mathcal {G}$
under the action of $\mathcal {G}$![]() on $X$
on $X$![]() is the least number $m$
is the least number $m$![]() such that a sufficiently small neighbourhood of $g$
such that a sufficiently small neighbourhood of $g$![]() may be covered by a finite number of $m$
may be covered by a finite number of $m$![]() -parameter families of orbits. The point $g$
-parameter families of orbits. The point $g$![]() is said to be simple if its modality is $0$
is said to be simple if its modality is $0$![]() , that is, a sufficiently small neighbourhood intersects only a finite number of orbits. The modality of a finitely $\mathcal {A}$
, that is, a sufficiently small neighbourhood intersects only a finite number of orbits. The modality of a finitely $\mathcal {A}$![]() -determined map-germ is the modality of a sufficient jet in the jet-space under the action of the jet-group.
-determined map-germ is the modality of a sufficient jet in the jet-space under the action of the jet-group.
We also need the notion of topological equivalence. We say that two germs $H, G\in {\mathfrak {m}}_n\cdot {\mathcal {O}(n,p)}$![]() are topologically equivalent if $H=h_2\circ G\circ h_1^{-1}$
are topologically equivalent if $H=h_2\circ G\circ h_1^{-1}$![]() for some germs of homeomorphisms $h_1$
for some germs of homeomorphisms $h_1$![]() and $h_2$
and $h_2$![]() of, respectively, the source and target.
of, respectively, the source and target.
2.2 Reflections and $k$ -folding maps
-folding maps
In all this paper, we fix the inner product $\langle a,b\rangle =\sum _ia_i\overline {b_i}$![]() in $\mathbb {C}^3$
in $\mathbb {C}^3$![]() .
.
Let $\pi$![]() be an element of the affine Grassmannian ${\rm {Graff}}(2,3)$
be an element of the affine Grassmannian ${\rm {Graff}}(2,3)$![]() of planes in $\mathbb {C}^3$
of planes in $\mathbb {C}^3$![]() . A plane $\pi$
. A plane $\pi$![]() has equation $\left \langle q,v\right \rangle =d$
has equation $\left \langle q,v\right \rangle =d$![]() , where $v$
, where $v$![]() is a fixed non-zero vector orthogonal to $\pi$
is a fixed non-zero vector orthogonal to $\pi$![]() and $d$
and $d$![]() is a fixed scalar. However, any non-zero scalar multiple of $(d,v)$
is a fixed scalar. However, any non-zero scalar multiple of $(d,v)$![]() gives an equation of $\pi$
gives an equation of $\pi$![]() , so $\pi$
, so $\pi$![]() is identified with the class $\overline {(d,v)}\in \mathbb {C} P^3$
is identified with the class $\overline {(d,v)}\in \mathbb {C} P^3$![]() of $(d,v)\in \mathbb {C}^4$
of $(d,v)\in \mathbb {C}^4$![]() .
.
Let $\pi :\left \langle q,v\right \rangle =d$![]() be a plane in $\mathbb {C}^3$
be a plane in $\mathbb {C}^3$![]() . The orthogonal projection of a point $p\in \mathbb {C}^3$
. The orthogonal projection of a point $p\in \mathbb {C}^3$![]() to $\pi$
to $\pi$![]() along the vector $v$
along the vector $v$![]() is the point $q= p+\lambda v\in \pi$
is the point $q= p+\lambda v\in \pi$![]() with $\lambda =(d-\left \langle p,v\right \rangle )/\left \langle v,v\right \rangle$
with $\lambda =(d-\left \langle p,v\right \rangle )/\left \langle v,v\right \rangle$![]() .
.
Consider the map $\omega _k^{\pi }\colon \mathbb {C}^3\to \mathbb {C}^3$![]() given by
given by
If we take $(d',v')=(\alpha d,\alpha v)$![]() , $\alpha \in \mathbb {C}\setminus 0$
, $\alpha \in \mathbb {C}\setminus 0$![]() , as another representative of $\pi =\overline {(d,v)}$
, as another representative of $\pi =\overline {(d,v)}$![]() , then
, then

Clearly, the map $\omega _k^{\pi }$![]() depends on the points on the line $(\alpha d, \alpha v)\in \mathbb {C}^4$
depends on the points on the line $(\alpha d, \alpha v)\in \mathbb {C}^4$![]() and not merely on the class of the line $\overline {(d,v)}\in \mathbb {C}P^3$
and not merely on the class of the line $\overline {(d,v)}\in \mathbb {C}P^3$![]() . However, all these maps are $\mathcal {L}$
. However, all these maps are $\mathcal {L}$![]() -equivalent: the bi-holomorphic map $q-\lambda v\mapsto q-\lambda \alpha ^{\frac {1-k}{k}}v$
-equivalent: the bi-holomorphic map $q-\lambda v\mapsto q-\lambda \alpha ^{\frac {1-k}{k}}v$![]() composed (on the left) with the map $\omega _k^{\pi }$
composed (on the left) with the map $\omega _k^{\pi }$![]() with $\pi$
with $\pi$![]() represented by $(d,v)$
represented by $(d,v)$![]() gives the map $\omega _k^{\pi }$
gives the map $\omega _k^{\pi }$![]() with $\pi$
with $\pi$![]() represented by $(\alpha d, \alpha v)$
represented by $(\alpha d, \alpha v)$![]() . Therefore, the $\mathcal {L}$
. Therefore, the $\mathcal {L}$![]() -class of $\omega _k^{\pi }$
-class of $\omega _k^{\pi }$![]() depends only on $\pi$
depends only on $\pi$![]() .
.
Definition 2.1 The Whitney fold of order $k$![]() ( $k$
( $k$![]() -fold for short) with respect to a plane $\pi \in {\rm {Graff}}(2,3)$
-fold for short) with respect to a plane $\pi \in {\rm {Graff}}(2,3)$![]() is the $\mathcal {L}$
is the $\mathcal {L}$![]() -class of the map $\omega ^k_{\pi }$
-class of the map $\omega ^k_{\pi }$![]() . We still denote by $\omega _k^{\pi }$
. We still denote by $\omega _k^{\pi }$![]() any representative of $\omega _k^{\pi }$
any representative of $\omega _k^{\pi }$![]() obtained by choosing a representative $(p,v)$
obtained by choosing a representative $(p,v)$![]() of $\pi =\overline {(d,v)}\in \mathbb {C}P^3$
of $\pi =\overline {(d,v)}\in \mathbb {C}P^3$![]() .
.
A $k$![]() -fold may be viewed as generalization of the Whitney fold $(x,y^2,z)\mapsto (x,y^2,z)$
-fold may be viewed as generalization of the Whitney fold $(x,y^2,z)\mapsto (x,y^2,z)$![]() . While the Whitney fold folds the space along the plane $\{y=0\}$
. While the Whitney fold folds the space along the plane $\{y=0\}$![]() and identifies the points $(x,y,z)$
and identifies the points $(x,y,z)$![]() and $(x,-y,z)$
and $(x,-y,z)$![]() , the Whitney fold of order $k$
, the Whitney fold of order $k$![]() with respect to a plane $\pi$
with respect to a plane $\pi$![]() represented by $(d,v)$
represented by $(d,v)$![]() is a generically a $k$
is a generically a $k$![]() -to-1 branched cover, ramified along $\pi$
-to-1 branched cover, ramified along $\pi$![]() , and identifies $k$
, and identifies $k$![]() -tuples of points $q-\lambda v, q-\xi \lambda v, \dots, q-\xi ^{k-1}\lambda v,$
-tuples of points $q-\lambda v, q-\xi \lambda v, \dots, q-\xi ^{k-1}\lambda v,$![]() where $\xi ={\rm {e}}^{2\pi {{\rm i}}/k}$
where $\xi ={\rm {e}}^{2\pi {{\rm i}}/k}$![]() is a primitive $k{\rm {th}}$
is a primitive $k{\rm {th}}$![]() -root of unity and $q\in \pi$
-root of unity and $q\in \pi$![]() .
.
The map $\omega _k^{\pi }$![]() can also be viewed as the quotient map associated to the action of the cyclic group $\mathbb {Z}/k\mathbb {Z}$
can also be viewed as the quotient map associated to the action of the cyclic group $\mathbb {Z}/k\mathbb {Z}$![]() , regarded as a complex reflection group whose hyperplane arrangement consist of the single plane $\pi$
, regarded as a complex reflection group whose hyperplane arrangement consist of the single plane $\pi$![]() . We regard $\mathbb {Z}/k\mathbb {Z}$
. We regard $\mathbb {Z}/k\mathbb {Z}$![]() as the group generated by the order $k$
as the group generated by the order $k$![]() complex reflection $q-\lambda v\mapsto q-\xi \lambda v$
complex reflection $q-\lambda v\mapsto q-\xi \lambda v$![]() . Observe that, even though the plane $\pi$
. Observe that, even though the plane $\pi$![]() does not determine $\omega _k^{\pi }$
does not determine $\omega _k^{\pi }$![]() uniquely (it depends on the choice of a representative of $\pi =\overline {(d,v)}\in \mathbb {C}P^3$
uniquely (it depends on the choice of a representative of $\pi =\overline {(d,v)}\in \mathbb {C}P^3$![]() ), the action of $\mathbb {Z}/k\mathbb {Z}$
), the action of $\mathbb {Z}/k\mathbb {Z}$![]() on $\mathbb {C}^3$
on $\mathbb {C}^3$![]() is determined uniquely by $\pi$
is determined uniquely by $\pi$![]() .
.
Given any subset $X\subseteq \mathbb {C}^3$![]() , $\omega _k^{\pi }(X)$
, $\omega _k^{\pi }(X)$![]() encodes the order $k$
encodes the order $k$![]() reflectional symmetries of $X$
reflectional symmetries of $X$![]() with respect to $\pi$
with respect to $\pi$![]() . See [Reference Peñafort Sanchis17] for a recent work on singular maps related to reflection groups.
. See [Reference Peñafort Sanchis17] for a recent work on singular maps related to reflection groups.
Definition 2.2 Let $M\subset \mathbb {C}^3$![]() be a complex surface, $p$
be a complex surface, $p$![]() a point on $M$
a point on $M$![]() and $k\geq 2$
and $k\geq 2$![]() an integer. Given $\pi \in {\rm {Graff}}(2,3)$
an integer. Given $\pi \in {\rm {Graff}}(2,3)$![]() , the $k$
, the $k$![]() -folding map-germ on $M$
-folding map-germ on $M$![]() at $p$
at $p$![]() with respect to $\pi$
with respect to $\pi$![]() is the $\mathcal {A}$
is the $\mathcal {A}$![]() -class of the restriction of $\omega _k^{\pi }$
-class of the restriction of $\omega _k^{\pi }$![]() to $M$
to $M$![]() at $p$
at $p$![]() . We denote any representative of the class by $F_k^{\pi }\colon (M,p)\to ( \mathbb {C}^3,\omega _k^{\pi }(p)).$
. We denote any representative of the class by $F_k^{\pi }\colon (M,p)\to ( \mathbb {C}^3,\omega _k^{\pi }(p)).$![]()
Remarks 2.3 1. All the map-germs $F_k^{\pi }$![]() with $\pi$
with $\pi$![]() represented by $(\alpha d, \alpha v)$
represented by $(\alpha d, \alpha v)$![]() , $\alpha \in \mathbb {C}$
, $\alpha \in \mathbb {C}$![]() , are $\mathcal {A}$
, are $\mathcal {A}$![]() -equivalent as the maps $\omega _k^{\pi }$
-equivalent as the maps $\omega _k^{\pi }$![]() are $\mathcal {L}$
are $\mathcal {L}$![]() -equivalent. Thus, the $\mathcal {A}$
-equivalent. Thus, the $\mathcal {A}$![]() -class of $F_k^{\pi }$
-class of $F_k^{\pi }$![]() depends only on $\pi$
depends only on $\pi$![]() and not on the choice of a representative $(p,v)$
and not on the choice of a representative $(p,v)$![]() of $\pi =\overline {(d,v)} \in \mathbb {C}P^3$
of $\pi =\overline {(d,v)} \in \mathbb {C}P^3$![]() . In all the paper, we work with a representative of the $\mathcal {A}$
. In all the paper, we work with a representative of the $\mathcal {A}$![]() -class of $F_k^{\pi }$
-class of $F_k^{\pi }$![]() .
.
2. If $p\notin \pi$![]() , then $F_k^{\pi }$
, then $F_k^{\pi }$![]() is the germ of an immersion. Thus, to obtain any meaningful local geometric information about the surface $M$
is the germ of an immersion. Thus, to obtain any meaningful local geometric information about the surface $M$![]() we should take the plane $\pi$
we should take the plane $\pi$![]() passing through the point $p\in M$
passing through the point $p\in M$![]() .
.
3. The image of $F_k^{\pi }$![]() is the image by $\omega _k^{\pi }$
is the image by $\omega _k^{\pi }$![]() of the germ $(M,p)$
of the germ $(M,p)$![]() , so for $p\in \pi \cap M$
, so for $p\in \pi \cap M$![]() , $F_k^{\pi }$
, $F_k^{\pi }$![]() captures order $k$
captures order $k$![]() local symmetries of $M$
local symmetries of $M$![]() with respect to $\pi$
with respect to $\pi$![]() . The aim of this paper is to understand how these local symmetries are captured by the $\mathcal {A}$
. The aim of this paper is to understand how these local symmetries are captured by the $\mathcal {A}$![]() -singularities of $F_k^{\pi }$
-singularities of $F_k^{\pi }$![]() .
.
4. Let $p_0\in \pi \cap M$![]() and $(d,v)$
and $(d,v)$![]() a representative of $\pi$
a representative of $\pi$![]() . If $v\notin T_{p_0}M$
. If $v\notin T_{p_0}M$![]() , then $F^{\pi }_k$
, then $F^{\pi }_k$![]() is a germ of an immersion and is $\mathcal {A}$
is a germ of an immersion and is $\mathcal {A}$![]() -equivalent to $(x,y)\mapsto (x,y^k,y)$
-equivalent to $(x,y)\mapsto (x,y^k,y)$![]() . Suppose that $v\in T_{p_0}M$
. Suppose that $v\in T_{p_0}M$![]() . We choose a coordinates system in $\mathbb {C}^3$
. We choose a coordinates system in $\mathbb {C}^3$![]() so that $p_0$
so that $p_0$![]() is the origin, the $z$
is the origin, the $z$![]() -axis is along a normal vector to $M$
-axis is along a normal vector to $M$![]() at $p_0$
at $p_0$![]() , the $y$
, the $y$![]() -axis along $v$
-axis along $v$![]() and the $x$
and the $x$![]() -axis orthogonal to the previous two axes. Then we can take $M$
-axis orthogonal to the previous two axes. Then we can take $M$![]() locally at $p_0$
locally at $p_0$![]() as the graph $z=f(x,y)$
as the graph $z=f(x,y)$![]() of some holomorphic map $f$
of some holomorphic map $f$![]() in a neighbourhood $U$
in a neighbourhood $U$![]() of the origin. In this coordinate system, we have $\pi =\pi _0:y=0$
of the origin. In this coordinate system, we have $\pi =\pi _0:y=0$![]() . Consequently, the $k$
. Consequently, the $k$![]() -folding map-germ on $M$
-folding map-germ on $M$![]() at $p_0$
at $p_0$![]() is the germ $F_k=F_k^{\pi _0}:(\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$
is the germ $F_k=F_k^{\pi _0}:(\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$![]() , given in standard form $F_k(x,y)=(x,y^k,f(x,y))$
, given in standard form $F_k(x,y)=(x,y^k,f(x,y))$![]() . In view of this, we shall always take a given $k$
. In view of this, we shall always take a given $k$![]() -folding map-germ in standard form (1.1).
-folding map-germ in standard form (1.1).
5. Definition 2.2 is adapted as follows for the real case. When $M$![]() is an analytic surface in $\mathbb {R}^3$
is an analytic surface in $\mathbb {R}^3$![]() , denote by $M_{\mathbb {C},p}$
, denote by $M_{\mathbb {C},p}$![]() its local complexification at $p$
its local complexification at $p$![]() and by $\pi _{\mathbb {C}}$
and by $\pi _{\mathbb {C}}$![]() the complexification of $\pi$
the complexification of $\pi$![]() . The $k$
. The $k$![]() -folding map-germ on $M$
-folding map-germ on $M$![]() at $p$
at $p$![]() with respect to $\pi$
with respect to $\pi$![]() is then defined as the $\mathcal {A}$
is then defined as the $\mathcal {A}$![]() -class of the restriction of $\omega _k^{\pi _{\mathbb {C}}}$
-class of the restriction of $\omega _k^{\pi _{\mathbb {C}}}$![]() to $M_{\mathbb {C},p}$
to $M_{\mathbb {C},p}$![]() at $p$
at $p$![]() . When $M$
. When $M$![]() is a smooth surface, we consider the $k$
is a smooth surface, we consider the $k$![]() -folding map-germ of a given jet of (a parametrization of) $M$
-folding map-germ of a given jet of (a parametrization of) $M$![]() at $p$
at $p$![]() .
.
3. Topological invariants
We recall the definitions of some key $\mathcal {A}$![]() -invariants of map-germs $(\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$
-invariants of map-germs $(\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$![]() . These are the Milnor number of the double-point curve $\mu (\mathcal {D})$
. These are the Milnor number of the double-point curve $\mu (\mathcal {D})$![]() , the number of cross-caps $C$
, the number of cross-caps $C$![]() and the number of triple points $T$
and the number of triple points $T$![]() . We give formulae for computing these invariants for $k$
. We give formulae for computing these invariants for $k$![]() -folding map-germs, and use the invariants to study the finite $\mathcal {A}$
-folding map-germs, and use the invariants to study the finite $\mathcal {A}$![]() -determinacy and topological equivalence of these germs.
-determinacy and topological equivalence of these germs.
3.1 The double-point curve
We start by recalling the definition of the double- and triple-point spaces of a corank one map-germ $F\colon (\mathbb {C}^n,0)\to (\mathbb {C}^{n+1},0)$![]() from [Reference Marar and Mond19]. Any such germ can be written in a suitable coordinate system in the form $F(x,y)=(x,f_{n}(x,y),f_{n+1}(x,y)),$
from [Reference Marar and Mond19]. Any such germ can be written in a suitable coordinate system in the form $F(x,y)=(x,f_{n}(x,y),f_{n+1}(x,y)),$![]() with $x=(x_1,\dots,x_{n-1})\in (\mathbb {C}^{n-1},0)$
with $x=(x_1,\dots,x_{n-1})\in (\mathbb {C}^{n-1},0)$![]() and $y\in (\mathbb {C},0)$
and $y\in (\mathbb {C},0)$![]() .
.
Given $h\in \mathcal {O}_n$![]() , the iterated divided differences of $h$
, the iterated divided differences of $h$![]() are defined as
are defined as

The multiple point ideals of a map-germ $F$![]() as above are defined as
as above are defined as

The double- and triple-point spaces of $F$![]() are, respectively,
are, respectively,

By counting variables and generators, it follows that ${\mathcal {D}}^2(F)$![]() (resp. ${\mathcal {D}}^3(F)$
(resp. ${\mathcal {D}}^3(F)$![]() ) is a complete intersection whenever it has dimension $n-1$
) is a complete intersection whenever it has dimension $n-1$![]() (resp. $n-2$
(resp. $n-2$![]() ).
).
The double-point space ${\mathcal {D}}^2(F)$![]() , as a subset of $(\mathbb {C}^{n-1}\times \mathbb {C}\times \mathbb {C},0)$
, as a subset of $(\mathbb {C}^{n-1}\times \mathbb {C}\times \mathbb {C},0)$![]() , consists of points $(x,y,y')$
, consists of points $(x,y,y')$![]() such that either $y\neq y'$
such that either $y\neq y'$![]() and $F(x,y)=F(x,y')$
and $F(x,y)=F(x,y')$![]() or $y'=y$
or $y'=y$![]() and $F$
and $F$![]() is singular at $(x,y)$
is singular at $(x,y)$![]() .
.
To define the source double-point space, we assume that $F$![]() is finite. Then, the projection $\pi \colon {\mathcal {D}}^2(F)\to \mathbb {C}^{n-1}\times \mathbb {C}$
is finite. Then, the projection $\pi \colon {\mathcal {D}}^2(F)\to \mathbb {C}^{n-1}\times \mathbb {C}$![]() given by $(x,y,y')\mapsto (x,y)$
given by $(x,y,y')\mapsto (x,y)$![]() is also finite. As a consequence, the image of $\pi$
is also finite. As a consequence, the image of $\pi$![]() can be given a complex structure as the $0$
can be given a complex structure as the $0$![]() -th Fitting ideal $\mathcal {F}_0(\pi _*\mathcal {O}_{{\mathcal {D}}^2(F)})$
-th Fitting ideal $\mathcal {F}_0(\pi _*\mathcal {O}_{{\mathcal {D}}^2(F)})$![]() of the push forward module $\pi _*\mathcal {O}_{{\mathcal {D}}^2(F)}$
of the push forward module $\pi _*\mathcal {O}_{{\mathcal {D}}^2(F)}$![]() (see [Reference Mond and Pellikaan26] for details). The source double-point space ${\mathcal {D}}(F)$
(see [Reference Mond and Pellikaan26] for details). The source double-point space ${\mathcal {D}}(F)$![]() is defined as the projection $\pi ({\mathcal {D}}^2(F))$
is defined as the projection $\pi ({\mathcal {D}}^2(F))$![]() endowed with this complex space structure, that is,
endowed with this complex space structure, that is,
To compute the source double-point space of a $k$![]() -folding map-germ, we need the following result.
-folding map-germ, we need the following result.
Lemma 3.1 Let $Z$![]() be a germ of an $n$
be a germ of an $n$![]() -dimensional Cohen–Macaulay space and let $h_1,\dots,h_r$
-dimensional Cohen–Macaulay space and let $h_1,\dots,h_r$![]() in $\mathcal {O}_Z$
in $\mathcal {O}_Z$![]() be regular elements. Write $X_j=V(h_j)$
be regular elements. Write $X_j=V(h_j)$![]() and $X=V(h_1\dots h_r)$
and $X=V(h_1\dots h_r)$![]() . Let $\phi \colon Z\to (\mathbb {C}^n,0)$
. Let $\phi \colon Z\to (\mathbb {C}^n,0)$![]() be a germ of a morphism of complex spaces such that the restrictions $\phi \vert _{X_j}\colon X_j\to (\mathbb {C}^n,0)$
be a germ of a morphism of complex spaces such that the restrictions $\phi \vert _{X_j}\colon X_j\to (\mathbb {C}^n,0)$![]() are finite. Then $\mathcal {F}_0((\phi \vert _{X})_*\mathcal {O}_{X})=\prod _{j=1}^r\mathcal {F}_0((\phi \vert _{X_j})_*\mathcal {O}_{X_j}).$
are finite. Then $\mathcal {F}_0((\phi \vert _{X})_*\mathcal {O}_{X})=\prod _{j=1}^r\mathcal {F}_0((\phi \vert _{X_j})_*\mathcal {O}_{X_j}).$![]()
Proof. It is enough to prove the statement for the case $r=2$![]() . We can assume that $X_1$
. We can assume that $X_1$![]() and $X_2$
and $X_2$![]() have no common irreducible component as topological spaces. Indeed, consider the two subspaces $\mathcal {X}_1=V(h_1-t)$
have no common irreducible component as topological spaces. Indeed, consider the two subspaces $\mathcal {X}_1=V(h_1-t)$![]() and $\mathcal {X}_2=V(h_2)$
and $\mathcal {X}_2=V(h_2)$![]() of $Z\times (\mathbb {C},0)$
of $Z\times (\mathbb {C},0)$![]() and the map $\phi \times \operatorname {Id}\colon Z\times (\mathbb {C},0)\to (\mathbb {C}^{n+1},0)$
and the map $\phi \times \operatorname {Id}\colon Z\times (\mathbb {C},0)\to (\mathbb {C}^{n+1},0)$![]() . The spaces $\mathcal {X}_1$
. The spaces $\mathcal {X}_1$![]() and $\mathcal {X}_2$
and $\mathcal {X}_2$![]() have no common irreducible component. Moreover, if the statement holds for $\phi \times \operatorname {Id}$
have no common irreducible component. Moreover, if the statement holds for $\phi \times \operatorname {Id}$![]() , then it holds for $\phi$
, then it holds for $\phi$![]() . This is a consequence of the fact that Fitting ideals commute with base change (see lemma 1.2 in [Reference Mond and Pellikaan26]). Now consider the disjoint union $X_1\sqcup X_2\subseteq Z\sqcup Z$
. This is a consequence of the fact that Fitting ideals commute with base change (see lemma 1.2 in [Reference Mond and Pellikaan26]). Now consider the disjoint union $X_1\sqcup X_2\subseteq Z\sqcup Z$![]() and the commutative diagram
and the commutative diagram

The map $\alpha$![]() is generically a local isomorphism (i.e. a local isomorphism on a Zariski open and dense subset) because $X_1$
is generically a local isomorphism (i.e. a local isomorphism on a Zariski open and dense subset) because $X_1$![]() and $X_2$
and $X_2$![]() are assumed to have no common component. Moreover, both $X$
are assumed to have no common component. Moreover, both $X$![]() and $X_1\sqcup X_2$
and $X_1\sqcup X_2$![]() are Cohen–Macaulay spaces, which implies that the ideals $\mathcal {F}_0(\psi _*\mathcal {O}_{X_1\sqcup X_2})$
are Cohen–Macaulay spaces, which implies that the ideals $\mathcal {F}_0(\psi _*\mathcal {O}_{X_1\sqcup X_2})$![]() and $\mathcal {F}_0((\phi \vert _{X})_*\mathcal {O}_{X})$
and $\mathcal {F}_0((\phi \vert _{X})_*\mathcal {O}_{X})$![]() are principal. Since $\alpha$
are principal. Since $\alpha$![]() is generically a local isomorphism, they are necessarily equal. The statement then follows from the equalities
is generically a local isomorphism, they are necessarily equal. The statement then follows from the equalities
Theorem 3.2 For a $k$![]() -folding map-germ $F_k(x,y)=(x,y^k,f(x,y))$
-folding map-germ $F_k(x,y)=(x,y^k,f(x,y))$![]() , the double-point space ${\mathcal {D}}$
, the double-point space ${\mathcal {D}}$![]() is the zero locus $V(\lambda )$
is the zero locus $V(\lambda )$![]() , where $\lambda =\prod _{j=1}^{k-1}\lambda _j$
, where $\lambda =\prod _{j=1}^{k-1}\lambda _j$![]() and
and
for $1\le j\le k-1.$![]() We have thus a decomposition ${\mathcal {D}}=\bigcup _{j=1}^{k-1}{\mathcal {D}}_j$
We have thus a decomposition ${\mathcal {D}}=\bigcup _{j=1}^{k-1}{\mathcal {D}}_j$![]() , with ${\mathcal {D}}_j=V(\lambda _j)$
, with ${\mathcal {D}}_j=V(\lambda _j)$![]() .
.
Proof. The double-point space ${\mathcal {D}}^2(F_k)$![]() is the intersection of the zero loci of the divided differences
is the intersection of the zero loci of the divided differences
Since $((y')^k-y^k)/{(y'-y)}=\prod _{j=1}^{k-1}(y'-\xi ^j y)$![]() , we conclude that, as a set, the space ${\mathcal {D}}^2(F_k)$
, we conclude that, as a set, the space ${\mathcal {D}}^2(F_k)$![]() is the union of the spaces
is the union of the spaces
for $j=1,\ldots, k-1$![]() . Each of the sets ${\mathcal {D}}^2_j$
. Each of the sets ${\mathcal {D}}^2_j$![]() projects to $V(\lambda _j)$
projects to $V(\lambda _j)$![]() , which shows that ${\mathcal {D}}(F_k)=V(\lambda )$
, which shows that ${\mathcal {D}}(F_k)=V(\lambda )$![]() as sets.
as sets.
To show the equality as complex spaces, observe that the possible dimension of ${\mathcal {D}}^2(F_k)$![]() is one or two. If ${\mathcal {D}}^2(F_k)$
is one or two. If ${\mathcal {D}}^2(F_k)$![]() has dimension two, then some branch ${\mathcal {D}}^2_j$
has dimension two, then some branch ${\mathcal {D}}^2_j$![]() has dimension two. Therefore, the corresponding function $\lambda _j$
has dimension two. Therefore, the corresponding function $\lambda _j$![]() is identically zero, which in turn implies $\lambda =0$
is identically zero, which in turn implies $\lambda =0$![]() . Since $F_k$
. Since $F_k$![]() is finite by construction, the projection ${\mathcal {D}}^2(F_k)$
is finite by construction, the projection ${\mathcal {D}}^2(F_k)$![]() is finite, hence the image of ${\mathcal {D}}^2_j$
is finite, hence the image of ${\mathcal {D}}^2_j$![]() is a germ of a 2-dimensional analytic closed subset of $(\mathbb {C}^2,0)$
is a germ of a 2-dimensional analytic closed subset of $(\mathbb {C}^2,0)$![]() , so is equal to $(\mathbb {C}^2,0)$
, so is equal to $(\mathbb {C}^2,0)$![]() . This implies that ${\mathcal {D}}(F_k)= (\mathbb {C}^2,0)=V(0)$
. This implies that ${\mathcal {D}}(F_k)= (\mathbb {C}^2,0)=V(0)$![]() .
.
Suppose now that ${\mathcal {D}}^2(F_k)$![]() has dimension one. This implies that the functions $\prod _{j=1}^{k-1}(y'-\xi ^j y)$
has dimension one. This implies that the functions $\prod _{j=1}^{k-1}(y'-\xi ^j y)$![]() and $f[x,y,y']$
and $f[x,y,y']$![]() form a regular sequence. Applying lemma 3.1 with $Z=V(f[x,y,y'])$
form a regular sequence. Applying lemma 3.1 with $Z=V(f[x,y,y'])$![]() gives ${\mathcal {D}}(F_k)=V(\prod _{j=1}^{k-1}\mathcal {F}_0((\pi \vert _{{\mathcal {D}}^2_j})_*\mathcal {O}_{{\mathcal {D}}^2_j})))$
gives ${\mathcal {D}}(F_k)=V(\prod _{j=1}^{k-1}\mathcal {F}_0((\pi \vert _{{\mathcal {D}}^2_j})_*\mathcal {O}_{{\mathcal {D}}^2_j})))$![]() , where the ${\mathcal {D}}^2_j$
, where the ${\mathcal {D}}^2_j$![]() , $j=1,\ldots, k-1$
, $j=1,\ldots, k-1$![]() , are given the natural complex space structure. Each of the morphisms $\pi \vert _{{\mathcal {D}}^2_j}\colon {\mathcal {D}}^2_j\to \mathbb {C}^2$
, are given the natural complex space structure. Each of the morphisms $\pi \vert _{{\mathcal {D}}^2_j}\colon {\mathcal {D}}^2_j\to \mathbb {C}^2$![]() consists of forgetting the third coordinate of the tuple $(x,y,\xi ^j y)$
consists of forgetting the third coordinate of the tuple $(x,y,\xi ^j y)$![]() , and this implies $\mathcal {F}_0((\pi \vert _{{\mathcal {D}}^2_j})_*\mathcal {O}_{{\mathcal {D}}^2_j}))=\langle \lambda _j\rangle$
, and this implies $\mathcal {F}_0((\pi \vert _{{\mathcal {D}}^2_j})_*\mathcal {O}_{{\mathcal {D}}^2_j}))=\langle \lambda _j\rangle$![]() .
.
Now we introduce some results we use to check finite $\mathcal {A}$![]() -determinacy of a $k$
-determinacy of a $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() and topological triviality in families of such germs. The first of these results was proven in [Reference Marar and Mond19] for corank one map-germs, then extended to arbitrary corank in [Reference Marar, Nuño-Ballesteros and Peñafort-Sanchis20].
and topological triviality in families of such germs. The first of these results was proven in [Reference Marar and Mond19] for corank one map-germs, then extended to arbitrary corank in [Reference Marar, Nuño-Ballesteros and Peñafort-Sanchis20].
Theorem 3.3 A finite map-germ $F \colon (\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined if and only if its double-point curve ${\mathcal {D}}$
-determined if and only if its double-point curve ${\mathcal {D}}$![]() is reduced.
is reduced.
The decomposition ${\mathcal {D}}=\bigcup _{j=1}^{k-1}{\mathcal {D}}_j$![]() in theorem 3.2 can be used to compute $\mu ({\mathcal {D}})$
in theorem 3.2 can be used to compute $\mu ({\mathcal {D}})$![]() , making it easier to apply theorem 3.3 (and theorem 3.10 below). We denote by ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$
, making it easier to apply theorem 3.3 (and theorem 3.10 below). We denote by ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$![]() the intersection multiplicity of two distinct branches of the double-point curve. Clearly, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}={\mathcal {D}}_{j'}\cdot {\mathcal {D}}_{j}$
the intersection multiplicity of two distinct branches of the double-point curve. Clearly, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}={\mathcal {D}}_{j'}\cdot {\mathcal {D}}_{j}$![]() , and
, and
Proposition 3.4 A $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined if and only if the Milnor numbers $\mu ({\mathcal {D}}_j)$
-determined if and only if the Milnor numbers $\mu ({\mathcal {D}}_j)$![]() , $j=1,\ldots,k-1$
, $j=1,\ldots,k-1$![]() , and the intersection multiplicities ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$
, and the intersection multiplicities ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$![]() of all pairs ${\mathcal {D}}_j$
of all pairs ${\mathcal {D}}_j$![]() and ${\mathcal {D}}_j'$
and ${\mathcal {D}}_j'$![]() , with $j'\neq j$
, with $j'\neq j$![]() , are finite. In that case,
, are finite. In that case,

Proof. By theorem 3.3, $F_k$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined if and only if $\mu ({\mathcal {D}}(F_k))$
-determined if and only if $\mu ({\mathcal {D}}(F_k))$![]() is finite, equivalently, ${\mathcal {D}}(F_k)$
is finite, equivalently, ${\mathcal {D}}(F_k)$![]() has an isolated singularity. This occurs if and only if every branch ${\mathcal {D}}_j$
has an isolated singularity. This occurs if and only if every branch ${\mathcal {D}}_j$![]() has an isolated singularity and no pair of branches ${\mathcal {D}}_j$
has an isolated singularity and no pair of branches ${\mathcal {D}}_j$![]() and ${\mathcal {D}}_{j'}$
and ${\mathcal {D}}_{j'}$![]() , with $j\ne j'$
, with $j\ne j'$![]() , have a common component. Using the formula $\mu =2\delta -r+1$
, have a common component. Using the formula $\mu =2\delta -r+1$![]() for plane curves (see [Reference Milnor21]) and the property $\delta (X\cup Y)=\delta (X)+\delta (Y)+X\cdot Y$
for plane curves (see [Reference Milnor21]) and the property $\delta (X\cup Y)=\delta (X)+\delta (Y)+X\cdot Y$![]() , we get
, we get

Remarks 3.5 1. Suppose that ${\mathcal {D}}_j$![]() is a germ of a regular curve parametrized by a regular map-germ $\alpha \colon (\mathbb {C},0)\to (\mathbb {C}^2,0)$
is a germ of a regular curve parametrized by a regular map-germ $\alpha \colon (\mathbb {C},0)\to (\mathbb {C}^2,0)$![]() . Then, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=\mathrm {ord}(h_{j'}\circ \alpha ),$
. Then, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=\mathrm {ord}(h_{j'}\circ \alpha ),$![]() which is the degree of the first non-zero term in the Taylor expansion of $\lambda _{j'}(\alpha (t))$
which is the degree of the first non-zero term in the Taylor expansion of $\lambda _{j'}(\alpha (t))$![]() .
.
2. If both ${\mathcal {D}}_j$![]() and ${\mathcal {D}}_{j'}$
and ${\mathcal {D}}_{j'}$![]() are regular curves, we refer to ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$
are regular curves, we refer to ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$![]() as the order of contact between ${\mathcal {D}}_j$
as the order of contact between ${\mathcal {D}}_j$![]() and ${\mathcal {D}}_{j'}$
and ${\mathcal {D}}_{j'}$![]() . We have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=1$
. We have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=1$![]() if and only if the two curves intersect transversally. Suppose they are tangential and parametrized, respectively, by $t\mapsto (t,\gamma _j(t))$
if and only if the two curves intersect transversally. Suppose they are tangential and parametrized, respectively, by $t\mapsto (t,\gamma _j(t))$![]() and $t\mapsto (t,\gamma _{j'}(t))$
and $t\mapsto (t,\gamma _{j'}(t))$![]() . Then ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=\mathrm {ord}(\gamma _j-\gamma _{j'}).$
. Then ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=\mathrm {ord}(\gamma _j-\gamma _{j'}).$![]()
3. Let $F_k$![]() be a finitely $\mathcal {A}$
be a finitely $\mathcal {A}$![]() -determined $k$
-determined $k$![]() -folding map-germ. Then any pair of branches ${\mathcal {D}}_j$
-folding map-germ. Then any pair of branches ${\mathcal {D}}_j$![]() and ${\mathcal {D}}_j'$
and ${\mathcal {D}}_j'$![]() , with $j\ne j'$
, with $j\ne j'$![]() , cannot have any common irreducible component, otherwise ${\mathcal {D}}(F_k)$
, cannot have any common irreducible component, otherwise ${\mathcal {D}}(F_k)$![]() would fail to be reduced. Hence, we have $r({\mathcal {D}})=\sum _{j=1}^{k-1}r({\mathcal {D}}_j).$
would fail to be reduced. Hence, we have $r({\mathcal {D}})=\sum _{j=1}^{k-1}r({\mathcal {D}}_j).$![]()
The defining functions $\lambda _j$![]() of the branches ${\mathcal {D}}_j$
of the branches ${\mathcal {D}}_j$![]() of the double-point curve play a major role in our study of finite $\mathcal {A}$
of the double-point curve play a major role in our study of finite $\mathcal {A}$![]() -determinacy and topological equivalence of $k$
-determinacy and topological equivalence of $k$![]() -folding map-germs. We take $F_k(x,y)=(x,y^k,f(x,y))$
-folding map-germs. We take $F_k(x,y)=(x,y^k,f(x,y))$![]() and write, for any given integer $p\ge 1$
and write, for any given integer $p\ge 1$![]() ,
,

Then,

with
The constants $\vartheta _{sj}$![]() play a significant role in determining the singularity type of the germs $\lambda _j$
play a significant role in determining the singularity type of the germs $\lambda _j$![]() and in computing ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$
and in computing ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$![]() . The following properties are needed in § 4.
. The following properties are needed in § 4.
Lemma 3.6 The numbers $\vartheta _{sj}$![]() satisfy the following properties:
satisfy the following properties:
(1) $\vartheta _{sj}=0$
 if and only if $k\mid sj$
if and only if $k\mid sj$ .
.(2) $\vartheta _{sj}=1$
 if and only if $k\mid (s-1)j$
if and only if $k\mid (s-1)j$ .
.(3) If $\vartheta _{sj}=\vartheta _{sj'}$
 , then $\vartheta _{sj}$
, then $\vartheta _{sj}$ is either $0$
is either $0$ or $1$
or $1$ .
.
Proof. We observe that $\vartheta _{0j}=0$![]() , $\vartheta _{1j}=1$
, $\vartheta _{1j}=1$![]() and, for any integers $m,n$
and, for any integers $m,n$![]() , we have $\vartheta _{mj}=\vartheta _{(m+n)j}$
, we have $\vartheta _{mj}=\vartheta _{(m+n)j}$![]() if and only if $k\mid nj$
if and only if $k\mid nj$![]() . For (1) we take $m=0$
. For (1) we take $m=0$![]() and $n=s$
and $n=s$![]() , and for (2) we take $m=1$
, and for (2) we take $m=1$![]() and $n=s-1$
and $n=s-1$![]() .
.
For (3), we observe that the constants $\vartheta _{sj}$![]() lie in the images of the curves $\gamma _n: S^1\subset \mathbb {C}\to \mathbb {C}$
lie in the images of the curves $\gamma _n: S^1\subset \mathbb {C}\to \mathbb {C}$![]() given by $\gamma _n(z)={(1-z^{n+1})}/{(1-z)}=1+z+\cdots +z^n.$
given by $\gamma _n(z)={(1-z^{n+1})}/{(1-z)}=1+z+\cdots +z^n.$![]() We show that the self intersection points of the curves $\gamma _n$
We show that the self intersection points of the curves $\gamma _n$![]() are $0$
are $0$![]() and $1$
and $1$![]() (for $n\ge 3$
(for $n\ge 3$![]() ).
).
Write $z={\rm e}^{{\rm i}\theta }$![]() , with $\theta \in [0,2\pi )$
, with $\theta \in [0,2\pi )$![]() . Then $\gamma _n(\theta )=x+{\rm i}y$
. Then $\gamma _n(\theta )=x+{\rm i}y$![]() , with $(x,y)\in \mathbb {R}^2$
, with $(x,y)\in \mathbb {R}^2$![]() , gives $1-{\rm e}^{{\rm i}(n+1)\theta }=(x+{\rm i}y)(1-{\rm e}^{{\rm i}\theta }).$
, gives $1-{\rm e}^{{\rm i}(n+1)\theta }=(x+{\rm i}y)(1-{\rm e}^{{\rm i}\theta }).$![]() Therefore,
Therefore,
Now the identity $\cos ((n+1)\theta )^2+\sin ((n+1)\theta )^2=1$![]() gives
gives
Suppose that $y=0$![]() . Then equation (3.3) becomes $(1-\cos (\theta ))x(x-1)=0$
. Then equation (3.3) becomes $(1-\cos (\theta ))x(x-1)=0$![]() , so $x=0$
, so $x=0$![]() or $1$
or $1$![]() or $\theta =0$
or $\theta =0$![]() .
.
When $x=0$![]() , we have $1-{\rm {e}}^{{{\rm i}}\theta }\ne 0$
, we have $1-{\rm {e}}^{{{\rm i}}\theta }\ne 0$![]() , so $1-{\rm {e}}^{{{\rm i}}(n+1)\theta }=0$
, so $1-{\rm {e}}^{{{\rm i}}(n+1)\theta }=0$![]() . That gives $\theta = {2\pi j}/{(n+1)}, j=1,\ldots, n$
. That gives $\theta = {2\pi j}/{(n+1)}, j=1,\ldots, n$![]() . Therefore, $\gamma _n$
. Therefore, $\gamma _n$![]() passes $n$
passes $n$![]() -times through the origin.
-times through the origin.
When $x=1$![]() , we get ${\rm e}^{{\rm i}n\theta }=1$
, we get ${\rm e}^{{\rm i}n\theta }=1$![]() , so $\theta ={2\pi j}/{n}, j=1,\ldots, n-1$
, so $\theta ={2\pi j}/{n}, j=1,\ldots, n-1$![]() . Therefore, $\gamma _n$
. Therefore, $\gamma _n$![]() passes $(n-1)$
passes $(n-1)$![]() -times through the point $1$
-times through the point $1$![]() .
.
When $\theta =0$![]() , we have $\gamma _n(0)=n+1$
, we have $\gamma _n(0)=n+1$![]() and the curve has no self-intersections at that point. See figure 2 for the cases $n=5,6,7.$
and the curve has no self-intersections at that point. See figure 2 for the cases $n=5,6,7.$![]()

FIGURE 2. Maple plots of the curves $\gamma _n$![]() for $n=5,6,7$
for $n=5,6,7$![]() (from left to right).
(from left to right).
Suppose now that $y\ne 0$![]() . Then equation (3.3) can be written as $\cot ({\theta }/{2})={(x^2+y^2-x)}/{y}.$
. Then equation (3.3) can be written as $\cot ({\theta }/{2})={(x^2+y^2-x)}/{y}.$![]() This shows that, for any $(x,y)\in \mathbb {R}^2$
This shows that, for any $(x,y)\in \mathbb {R}^2$![]() with $y\ne 0$
with $y\ne 0$![]() , there is at most one $\theta \in [0,2\pi )$
, there is at most one $\theta \in [0,2\pi )$![]() satisfying $\gamma _n(\theta )=x+{\rm i}y$
satisfying $\gamma _n(\theta )=x+{\rm i}y$![]() . Therefore, the only self-intersection points of $\gamma _n$
. Therefore, the only self-intersection points of $\gamma _n$![]() are $0$
are $0$![]() and $1$
and $1$![]() .
.
3.2 Cross-caps and triple points
The number of cross-caps and triple points are invariants of finitely $\mathcal {A}$![]() -determined map-germs $F\colon (\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$
-determined map-germs $F\colon (\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$![]() that can be described using stable deformations. A stable mapping $U\to (\mathbb {C}^3,0)$
that can be described using stable deformations. A stable mapping $U\to (\mathbb {C}^3,0)$![]() with $U$
with $U$![]() an open neighbourhood of the origin in $\mathbb {C}^2$
an open neighbourhood of the origin in $\mathbb {C}^2$![]() exhibits only regular points, transverse double points along curves, cross-caps and isolated transverse triple points. Every stable deformation $F_t$
exhibits only regular points, transverse double points along curves, cross-caps and isolated transverse triple points. Every stable deformation $F_t$![]() of $F$
of $F$![]() exhibits the same number $C$
exhibits the same number $C$![]() of cross-caps and $T$
of cross-caps and $T$![]() of triple points [Reference Mond23]. For a corank one map-germ, these are given by the formulae
of triple points [Reference Mond23]. For a corank one map-germ, these are given by the formulae
where $JF$![]() is the ideal generated by the $2\times 2$
is the ideal generated by the $2\times 2$![]() minors of the differential matrix of $F$
minors of the differential matrix of $F$![]() [Reference Mond23] (the formula for $C$
[Reference Mond23] (the formula for $C$![]() holds without the corank one assumption).
holds without the corank one assumption).
For $j,j'\in \{1,\dots,k-1\}$![]() , with $j\neq j'$
, with $j\neq j'$![]() , we set
, we set
and define
Observe that $T_{j,j'}=T_{j',j}$![]() for all $j\neq j'$
for all $j\neq j'$![]() .
.
Proposition 3.8 The number of cross-caps and of triple points of a finitely $\mathcal {A}$![]() -determined $k$
-determined $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() are given by
are given by

Proof. The formula for $C$![]() is trivial. For $T$
is trivial. For $T$![]() , we claim that
, we claim that

is a radical ideal of $\mathcal {O}_{4}$![]() whose zero locus is
whose zero locus is
Clearly, $Z$![]() is contained in the zero locus $V(J)$
is contained in the zero locus $V(J)$![]() . The converse inclusion follows by considering the degree of the generators of $J$
. The converse inclusion follows by considering the degree of the generators of $J$![]() and by the fact that $V(J)$
and by the fact that $V(J)$![]() is generically reduced. Since $V(J)$
is generically reduced. Since $V(J)$![]() is also a complete intersection, it is reduced. Thus $J$
is also a complete intersection, it is reduced. Thus $J$![]() is a radical ideal.
is a radical ideal.
The irreducible decomposition of $Z$![]() consists of the branches
consists of the branches
Thus, we may decompose ${\mathcal {D}}^3(F_k)$![]() , as a set, as the union of the (not necessarily irreducible) branches
, as a set, as the union of the (not necessarily irreducible) branches
Eliminating $y'$![]() and $y''$
and $y''$![]() , gives ${\mathcal {D}}^3_{j,j'}(F_k)=\langle \lambda _j,\lambda _{j,j'}\rangle$
, gives ${\mathcal {D}}^3_{j,j'}(F_k)=\langle \lambda _j,\lambda _{j,j'}\rangle$![]() . Therefore, we only need to show that $\operatorname {dim}_\mathbb {C} ({\mathcal {O}_4}/{I^3(F_k)})=\sum _{j\neq j'}\operatorname {dim}_\mathbb {C} ({\mathcal {O}_2}/({\langle \lambda _{j},\lambda _{j,j'}\rangle })$
. Therefore, we only need to show that $\operatorname {dim}_\mathbb {C} ({\mathcal {O}_4}/{I^3(F_k)})=\sum _{j\neq j'}\operatorname {dim}_\mathbb {C} ({\mathcal {O}_2}/({\langle \lambda _{j},\lambda _{j,j'}\rangle })$![]() . It is clear that the same decomposition of ${\mathcal {D}}^3(F_k)$
. It is clear that the same decomposition of ${\mathcal {D}}^3(F_k)$![]() applies to an unfolding $\tilde {F}_k(x,y,t)=(x,y^k,f_t(x,y),t)$
applies to an unfolding $\tilde {F}_k(x,y,t)=(x,y^k,f_t(x,y),t)$![]() of $F_k$
of $F_k$![]() , and fixing a representative and a nonzero parameter $\delta$
, and fixing a representative and a nonzero parameter $\delta$![]() , the same holds for $(\tilde {F}_k)_{\delta }$
, the same holds for $(\tilde {F}_k)_{\delta }$![]() . This gives a decomposition of ${\mathcal {D}}^3(({\tilde {F}_k})_{\delta })$
. This gives a decomposition of ${\mathcal {D}}^3(({\tilde {F}_k})_{\delta })$![]() into the branches ${\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })$
into the branches ${\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })$![]() .
.
It is possible to choose an unfolding where the branches ${\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })$![]() are pairwise disjoint. Indeed, it follows from their defining equations that two spaces ${\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })$
are pairwise disjoint. Indeed, it follows from their defining equations that two spaces ${\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })$![]() and ${\mathcal {D}}^3_{s,s'}(({\tilde {F}_k})_{\delta })$
and ${\mathcal {D}}^3_{s,s'}(({\tilde {F}_k})_{\delta })$![]() can only intersect on $\{y=0\}$
can only intersect on $\{y=0\}$![]() , so it is enough to find an unfolding where ${\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })\cap \{y=0\}$
, so it is enough to find an unfolding where ${\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })\cap \{y=0\}$![]() is empty. Again, it follows from the defining equations that a point $(x,0,0,0)\in {\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })$
is empty. Again, it follows from the defining equations that a point $(x,0,0,0)\in {\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })$![]() if $({\partial f_{\delta }}/{\partial x})(x,0)=({\partial f^2_{\delta }}/{\partial x^2})(x,0)=0$
if $({\partial f_{\delta }}/{\partial x})(x,0)=({\partial f^2_{\delta }}/{\partial x^2})(x,0)=0$![]() , a condition that can be avoided by choosing a suitable deformation $f_t$
, a condition that can be avoided by choosing a suitable deformation $f_t$![]() of $f$
of $f$![]() .
.
We take now an unfolding as above. Since $Z$![]() is reduced, ${\mathcal {D}}^3(({\tilde {F}_k})_{\delta })$
is reduced, ${\mathcal {D}}^3(({\tilde {F}_k})_{\delta })$![]() is isomorphic to the union of the ${\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })$
is isomorphic to the union of the ${\mathcal {D}}^3_{j,j'}(({\tilde {F}_k})_{\delta })$![]() as complex spaces. The equality we need to show follows now from the constancy of the numbers involved under continuous deformations. Defining $\lambda _{j}^{\delta }$
as complex spaces. The equality we need to show follows now from the constancy of the numbers involved under continuous deformations. Defining $\lambda _{j}^{\delta }$![]() and $\lambda _{j,j'}^{\delta }$
and $\lambda _{j,j'}^{\delta }$![]() in the obvious way, we obtain
in the obvious way, we obtain

Since $T_{j,j'}=T_{j',j}$![]() , we add only the numbers $T_{j,j'}$
, we add only the numbers $T_{j,j'}$![]() , with $j< j'$
, with $j< j'$![]() , and replace $1/6$
, and replace $1/6$![]() by $1/3$
by $1/3$![]() .
.
3.3 Topological triviality
We say that two subspaces $S$![]() and $S'$
and $S'$![]() of a topological space $X$
of a topological space $X$![]() have the same topological type if there is a homeomorphism $X\to X$
have the same topological type if there is a homeomorphism $X\to X$![]() restricting to an homeomorphism $S\to S'$
restricting to an homeomorphism $S\to S'$![]() . Milnor showed that two isolated hypersurface singularities with same topological type have the same Milnor number. In the case of our invariants, a similar result can be obtained using the results in [Reference Nemethi and Pinter28, Reference Siersma30] (see [Reference Bobadilla, Peñafort and Sampaio4] for details).
. Milnor showed that two isolated hypersurface singularities with same topological type have the same Milnor number. In the case of our invariants, a similar result can be obtained using the results in [Reference Nemethi and Pinter28, Reference Siersma30] (see [Reference Bobadilla, Peñafort and Sampaio4] for details).
Proposition 3.9 Let $F,G:(\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$![]() be finitely $\mathcal {A}$
be finitely $\mathcal {A}$![]() -determined map-germs. If $F$
-determined map-germs. If $F$![]() and $G$
and $G$![]() are topologically equivalent, then $\mu ({\mathcal {D}}(F))=\mu ({\mathcal {D}}(G))$
are topologically equivalent, then $\mu ({\mathcal {D}}(F))=\mu ({\mathcal {D}}(G))$![]() , $r({\mathcal {D}}(F))=r({\mathcal {D}}(G))$
, $r({\mathcal {D}}(F))=r({\mathcal {D}}(G))$![]() , $C(F)=C(G)$
, $C(F)=C(G)$![]() and $T(F)=T(G)$
and $T(F)=T(G)$![]() .
.
The Milnor number of the double-point curve is enough to determine the topological triviality of families of finitely $\mathcal {A}$![]() -determined map-germs.
-determined map-germs.
Proposition 3.10 (Corollary 40 [Reference Bobadilla and Pe Pereira3])
A family of finitely $\mathcal {A}$![]() -determined map-germs $G_t\colon (\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$
-determined map-germs $G_t\colon (\mathbb {C}^2,0)\to (\mathbb {C}^3,0)$![]() is topologically trivial if and only if $\mu ({\mathcal {D}}(G_t))$
is topologically trivial if and only if $\mu ({\mathcal {D}}(G_t))$![]() is constant along the parameter $t$
is constant along the parameter $t$![]() .
.
Using the upper semi-continuity of the numbers involved, proposition 3.10 can be combined with proposition 3.4 to yield the following result.
Corollary 3.11 Let $F_k^t=(x,y^k,f_t(x,y))$![]() be a family of finitely $\mathcal {A}$
be a family of finitely $\mathcal {A}$![]() -determined $k$
-determined $k$![]() -folding map-germs. The following statements are equivalent:
-folding map-germs. The following statements are equivalent:
(1) The family $F_k^t$
 is topologically trivial.
is topologically trivial.(2) The numbers $\mu ({\mathcal {D}}_j)$
 and ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$
and ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$ are constant along the family $F_k^t$
are constant along the family $F_k^t$ .
.(3) The numbers $C, \mu ({\mathcal {D}}_j), {\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}$
 and $T_{j,j'}$
and $T_{j,j'}$ are constant along the family $F_k^t$
are constant along the family $F_k^t$ .
.
4. The jet space stratification
In this section, we study the singularities of $k$![]() -folding map-germs which we take in standard form $F_k(x,y)=(x,y^k,f(x,y))$
-folding map-germs which we take in standard form $F_k(x,y)=(x,y^k,f(x,y))$![]() (see remark 2.3(4)). We identify the set of such germs with the set $\mathcal {O}_2$
(see remark 2.3(4)). We identify the set of such germs with the set $\mathcal {O}_2$![]() of germs, at the origin, of holomorphic functions $f$
of germs, at the origin, of holomorphic functions $f$![]() . For each $k$
. For each $k$![]() , we obtain a stratification $\mathcal {S}_k$
, we obtain a stratification $\mathcal {S}_k$![]() of $J^{11}(2,1)$
of $J^{11}(2,1)$![]() (and hence of $J^{l}(2,1)$
(and hence of $J^{l}(2,1)$![]() for $l\ge 11$
for $l\ge 11$![]() ). The stratification consists of the strata of codimension $\leq \! 4$
). The stratification consists of the strata of codimension $\leq \! 4$![]() stated in theorem 1.1 together with the complement of their union (i.e. the union of strata of codimension $\ge \! 5$
stated in theorem 1.1 together with the complement of their union (i.e. the union of strata of codimension $\ge \! 5$![]() ). Every stratum of codimension $\leq \! 4$
). Every stratum of codimension $\leq \! 4$![]() of $\mathcal {S}_k$
of $\mathcal {S}_k$![]() consists of finitely $\mathcal {A}$
consists of finitely $\mathcal {A}$![]() -determined and pairwise topologically equivalent $k$
-determined and pairwise topologically equivalent $k$![]() -folding map-germs. The jet level $l=11$
-folding map-germs. The jet level $l=11$![]() is determined by the conditions defining the strata of $\mathcal {S}_k$
is determined by the conditions defining the strata of $\mathcal {S}_k$![]() which involve the coefficients of $f$
which involve the coefficients of $f$![]() in (3.1) up to degree $11$
in (3.1) up to degree $11$![]() (see tables 1, 2, 4, 6).
(see tables 1, 2, 4, 6).
TABLE 1. Strata of $\mathcal {S}_3$![]() of codimension $\le \! 4$
of codimension $\le \! 4$![]()

 $\begin{align*}CndH_2 & = a_{32}a_{44}-a_{55}a_{21} \\ CndH_3 & = a_{88}a_{21}^3-(a_{77}a_{32}+a_{44}a_{65})a_{21}^2+a_{44}(a_{42}a_{44}+ a_{32}a_{54})a_{21}-a_{31}a_{44}^2a_{32}. \\ CndH_4 & = a_{11,11}a_{21}^5 -(a_{44}a_{98}+a_{10,10}a_{32}+a_{77}a_{65})a_{21}^4\\ & \quad +(a_{44}a_{87}a_{32}+a_{32}a_{54}a_{77}+a_{44}a_{54}a_{65}+2a_{44}a_{77}a_{42}+a_{44}^2a_{75})a_{21}^3\\ & \quad -(a_{52}a_{44}^2+a_{44}a_{31}a_{65}+2a_{42}a_{44}a_{54}+a_{44}a_{64}a_{32}\\ & \quad +2a_{77}a_{32}a_{31}+a_{54}^2a_{32})a_{44}a_{21}^2\\ &\quad +(2a_{44}a_{31}a_{42}+a_{44}a_{41}a_{32}+3a_{32}a_{54}a_{31})a_{44}^2a_{21}-2a_{31}^2a_{32}a_{44}^3 \\ CndUm_8 & = a_{55}(a_{31}a_{55}-a_{54}a_{32})+a_{77}a_{32}^2 \, \, \mbox {(see table 6)}\end{align*}$
$\begin{align*}CndH_2 & = a_{32}a_{44}-a_{55}a_{21} \\ CndH_3 & = a_{88}a_{21}^3-(a_{77}a_{32}+a_{44}a_{65})a_{21}^2+a_{44}(a_{42}a_{44}+ a_{32}a_{54})a_{21}-a_{31}a_{44}^2a_{32}. \\ CndH_4 & = a_{11,11}a_{21}^5 -(a_{44}a_{98}+a_{10,10}a_{32}+a_{77}a_{65})a_{21}^4\\ & \quad +(a_{44}a_{87}a_{32}+a_{32}a_{54}a_{77}+a_{44}a_{54}a_{65}+2a_{44}a_{77}a_{42}+a_{44}^2a_{75})a_{21}^3\\ & \quad -(a_{52}a_{44}^2+a_{44}a_{31}a_{65}+2a_{42}a_{44}a_{54}+a_{44}a_{64}a_{32}\\ & \quad +2a_{77}a_{32}a_{31}+a_{54}^2a_{32})a_{44}a_{21}^2\\ &\quad +(2a_{44}a_{31}a_{42}+a_{44}a_{41}a_{32}+3a_{32}a_{54}a_{31})a_{44}^2a_{21}-2a_{31}^2a_{32}a_{44}^3 \\ CndUm_8 & = a_{55}(a_{31}a_{55}-a_{54}a_{32})+a_{77}a_{32}^2 \, \, \mbox {(see table 6)}\end{align*}$
TABLE 2. Strata of codimension $\le \! 4$![]() in branch 2
in branch 2

$\begin {array}{l} {CndNA}_3=a_{43}^2-4a_{31}a_{55}\\ {CndNA}_5=8a_{31}^3a_{77}-4a_{65}a_{43}a_{31}^2+ 2a_{53}a_{43}^2a_{31}- a_{41}^2a_{43}^3 \end {array}$![]()
TABLE 3. Topological invariants of germs in the strata in table 2

TABLE 4. Strata of codimension $\le \! 4$![]() in branch 3
in branch 3

$\begin {array}{rcl} CndQm_5 & = & a_{32}a_{55} - a_{21}a_{66}\\ CndQm_6 & = & a_{43} a_{55}-a_{21} a_{77}\\ CndRm_5 & = & a_{32}a_{66}-a_{21}a_{77} \end {array}$
TABLE 5. Topological invariants of germs in the strata in table 4

TABLE 6. Strata of codimension $\leq \! 4$![]() in branch 4
in branch 4

$\begin {array}{rcl} \Delta _j^k & = & (a_{32}^2-4a_{31}a_{33})\xi ^{2j}+2(a_{32}^2-2a_{31}a_{33})\xi ^j+a_{32}^2-4a_{31}a_{33}\\ \Omega _{j,j'}^k & = & a_{31}a_{33}(1+\xi ^j+\xi ^{j'})^2-a_{32}^2(\xi ^j+\xi ^{j'}+\xi ^{j+j'})\\ CndUm_8 & = & a_{55}(a_{31}a_{55}-a_{54}a_{32})+a_{77}a_{32}^2\\ {CndVm_5}_{j,j'} & = & a_{32}^2a_{44}\beta _{j,j'} +a_{32}a_{33}(2a_{33}a_{42}-a_{32}a_{43})\alpha _{j,j'}+a_{41}a_{33}^3,\, \mbox {with}\\ & & \alpha _{j,j'} =\frac {\xi ^j+\xi ^{j'}+\xi ^{j+j'}}{(1+\xi ^j+\xi ^{j'})^2},\\ & & \beta _{j,j'}=\frac {\xi ^{j+3j'}+\xi ^{3j+j'}+\xi ^{3j'}+2\xi ^{2j+j'}+2\xi ^{j+2j'}+\xi ^{3j}+2\xi ^{j+j'}+\xi ^{j}+\xi ^{j'} }{(1+\xi ^{j}+\xi ^{j'})^4}. \\ CndWA_2 & = & (a_{41}a_{33}+a_{31}a_{43})a_{32}^3-2a_{31}(a_{42}a_{33}+2a_{31}a_{44})a_{32}^2+8a_{31}^3a_{33}a_{44}\\ {Cnd\widetilde {W}m}_8 & = & a_{31}a_{55}-a_{42}a_{44}\\ {CndYA}_3 & = & a_{43}^2-4a_{31}a_{55}\\ {CndYm_6}_j & = & (a_{31}a_{44}^2+a_{55}a_{32}^2-a_{43}a_{44}a_{32})\xi ^{4j}\\& & \quad + a_{44}(2a_{31}a_{44}-a_{32}a_{43})\xi ^{2j}+a_{31}a_{44}^2\\ (*) & & j< j'; (j,j')\ne (p,2p) when k=3p\\ (**) & & \mbox {If} 2\mid k then j\ne k/2\\ (***) & & \mbox {If} k=3p, then j\ne p,2p \end {array}$
As pointed out in the Introduction, the case $k=2$![]() was studied in [Reference Bruce5, Reference Bruce and Wilkinson8, Reference Wilkinson32]. The stratification $\mathcal {S}_2$
was studied in [Reference Bruce5, Reference Bruce and Wilkinson8, Reference Wilkinson32]. The stratification $\mathcal {S}_2$![]() can be recovered from the results in this paper. The different $\mathcal {A}$
can be recovered from the results in this paper. The different $\mathcal {A}$![]() -classes obtained in [Reference Bruce5] correspond to different topological classes. This follows by analysing the invariants $C,T,\mu (\mathcal {D})$
-classes obtained in [Reference Bruce5] correspond to different topological classes. This follows by analysing the invariants $C,T,\mu (\mathcal {D})$![]() and $r(\mathcal {D})$
and $r(\mathcal {D})$![]() . We shall suppose here that $k\ge 3$
. We shall suppose here that $k\ge 3$![]() and write the jets of $f$
and write the jets of $f$![]() as in (3.1).
as in (3.1).
It is clear that $F_k$![]() is an immersion if and only if $a_{11}\neq 0$
is an immersion if and only if $a_{11}\neq 0$![]() . All immersions are $\mathcal {A}$
. All immersions are $\mathcal {A}$![]() -finitely determined and pairwise topologically equivalent. Moreover, only immersions have $\mathcal {D}=\emptyset$
-finitely determined and pairwise topologically equivalent. Moreover, only immersions have $\mathcal {D}=\emptyset$![]() , hence $r(\mathcal {D})=0$
, hence $r(\mathcal {D})=0$![]() . We define $a_{11}\neq 0$
. We define $a_{11}\neq 0$![]() as the open stratum of $\mathcal {S}_k$
as the open stratum of $\mathcal {S}_k$![]() (corresponding to the jets of all immersions) and choose
(corresponding to the jets of all immersions) and choose
as a normal form for topological equivalence of germs in this stratum. The strata corresponding to singular germs are organized into four branches according to the following result.
Lemma 4.1 For $k\ge 3$![]() , every singular $k$
, every singular $k$![]() -folding map-germ is $\mathcal {A}$
-folding map-germ is $\mathcal {A}$![]() -equivalent to a $k$
-equivalent to a $k$![]() -folding map-germ whose $2$
-folding map-germ whose $2$![]() -jet is equal to $(x,0,xy+y^2), (x,0,y^2), (x,0,xy)$
-jet is equal to $(x,0,xy+y^2), (x,0,y^2), (x,0,xy)$![]() or $(x,0,0).$
or $(x,0,0).$![]()
Proof. As we are assuming $F_k$![]() to be singular at the origin, we have $a_{11}=0$
to be singular at the origin, we have $a_{11}=0$![]() . Then $F_k$
. Then $F_k$![]() is $\mathcal {A}$
is $\mathcal {A}$![]() -equivalent to a germ whose $2$
-equivalent to a germ whose $2$![]() -jet is $(x,0,a_{21}xy+a_{22}y^2)$
-jet is $(x,0,a_{21}xy+a_{22}y^2)$![]() . Depending on the coefficients $a_{21}$
. Depending on the coefficients $a_{21}$![]() and $a_{22}$
and $a_{22}$![]() , the $2$
, the $2$![]() -jet can be taken to one of the following forms:
-jet can be taken to one of the following forms:

We have the following about $\mathcal {A}$![]() -simplicity of germs of $k$
-simplicity of germs of $k$![]() -folding maps.
-folding maps.
Proposition 4.2 There are no $\mathcal {A}$![]() -simple $k$
-simple $k$![]() -folding map-germs for $k\ge 5$
-folding map-germs for $k\ge 5$![]() .
.
Proof. It is enough to show that the orbit of a map-germ $F_k$![]() with a 2-jet $(x,0, xy+y^2)$
with a 2-jet $(x,0, xy+y^2)$![]() is not simple as the orbits of germs in the remaining branches in lemma 4.1 are adjacent to it. For such a germ, we have $j^kF_k\sim _{\mathcal {A}^{(k)}}(x,(y-({1}/{2})x)^k,y^2)$
is not simple as the orbits of germs in the remaining branches in lemma 4.1 are adjacent to it. For such a germ, we have $j^kF_k\sim _{\mathcal {A}^{(k)}}(x,(y-({1}/{2})x)^k,y^2)$![]() . The result follows by theorem 1:1 in [Reference Mond22] as there are no $\mathcal {A}$
. The result follows by theorem 1:1 in [Reference Mond22] as there are no $\mathcal {A}$![]() -simple germs of the form $(x,y^2,f(x,y))$
-simple germs of the form $(x,y^2,f(x,y))$![]() with $j^4f\equiv 0$
with $j^4f\equiv 0$![]() .
.
When $k=4$![]() and for $F_4$
and for $F_4$![]() in branch 1, we have $j^4F_4\sim _{\mathcal {A}^{(4)}}(x,xy^3+x^3y,y^2)$
in branch 1, we have $j^4F_4\sim _{\mathcal {A}^{(4)}}(x,xy^3+x^3y,y^2)$![]() . This is a $C_3$
. This is a $C_3$![]() -singularity and is $\mathcal {A}$
-singularity and is $\mathcal {A}$![]() -simple [Reference Mond22]. For $F_4$
-simple [Reference Mond22]. For $F_4$![]() in branch 2, we have $j^4F_4\sim _{\mathcal {A}^{(4)}}(x,0,y^2)$
in branch 2, we have $j^4F_4\sim _{\mathcal {A}^{(4)}}(x,0,y^2)$![]() so it leads to non $\mathcal {A}$
so it leads to non $\mathcal {A}$![]() -simple germs. By adjacency, the germs in branches 3 and 4 also lead to non-$\mathcal {A}$
-simple germs. By adjacency, the germs in branches 3 and 4 also lead to non-$\mathcal {A}$![]() -simple germs. Therefore, the $C_3$
-simple germs. Therefore, the $C_3$![]() -singularity is the only $\mathcal {A}$
-singularity is the only $\mathcal {A}$![]() -simple singularity of $4$
-simple singularity of $4$![]() -folding map-germs.
-folding map-germs.
The case $k=3$![]() is treated in § 4.1 where there are several $\mathcal {A}$
is treated in § 4.1 where there are several $\mathcal {A}$![]() -simple singularities of $3$
-simple singularities of $3$![]() -folding map-germs.
-folding map-germs.
Remarks 4.3 1. The degree of $\mathcal {A}$![]() -determinacy of a singular germ $F_k$
-determinacy of a singular germ $F_k$![]() is greater or equal to $k$
is greater or equal to $k$![]() (the germ $(x,y)\mapsto (x,0,f(x,y))$
(the germ $(x,y)\mapsto (x,0,f(x,y))$![]() is not finitely $\mathcal {A}$
is not finitely $\mathcal {A}$![]() -determined for any $f$
-determined for any $f$![]() ).
).
2. For germs in branch 1 or branch 2, we have $F_k\sim _{\mathcal {A}} (x,yp(x,y^2),y^2)$![]() for some germ $p$
for some germ $p$![]() . One can study the germ $p$
. One can study the germ $p$![]() , as was done in [Reference Mond22], instead of $F_k$
, as was done in [Reference Mond22], instead of $F_k$![]() , but this blurs the order of the original $k$
, but this blurs the order of the original $k$![]() -folding map-germ. Also, the approach in [Reference Mond22] of reducing the action of $\mathcal {A}$
-folding map-germ. Also, the approach in [Reference Mond22] of reducing the action of $\mathcal {A}$![]() on the set of $2$
on the set of $2$![]() -folding map-germs to the action of a subgroup of $\mathcal {K}$
-folding map-germs to the action of a subgroup of $\mathcal {K}$![]() on $\mathfrak {m}_2$
on $\mathfrak {m}_2$![]() does not extend to germs of $k$
does not extend to germs of $k$![]() -folding maps for $k\ge 3$
-folding maps for $k\ge 3$![]() .
.
4.1 The case $k= 3$
When $k=3$![]() we get several $\mathcal {A}$
we get several $\mathcal {A}$![]() -simple map-germs. For this reason, we treat this case separately.
-simple map-germs. For this reason, we treat this case separately.
Theorem 4.4 The only $\mathcal {A}$![]() -simple singularities a $3$
-simple singularities a $3$![]() -folding map-germ $F_3$
-folding map-germ $F_3$![]() can have are those of type $S_{2l-1}$
can have are those of type $S_{2l-1}$![]() , $l\ge 2$
, $l\ge 2$![]() , or $H_s$
, or $H_s$![]() , $s\ge 3$
, $s\ge 3$![]() . In the real case, the $S_{2l-1}$
. In the real case, the $S_{2l-1}$![]() -singularities are of type $S_{2l-1}^-$
-singularities are of type $S_{2l-1}^-$![]() . The strata of $\mathcal {S}_3$
. The strata of $\mathcal {S}_3$![]() of codimension $\le \! 4$
of codimension $\le \! 4$![]() are given in table 1.
are given in table 1.
Proof. We can write $f(x,y)=f_0(x,y^3)+yf_1(x,y^3)+y^2f_2(x,y^3)$![]() , for some germs of holomorphic functions $f_i$
, for some germs of holomorphic functions $f_i$![]() , $i=0,1,2$
, $i=0,1,2$![]() . Then $F_3\sim _{\mathcal {A}} (x,y^3,yf_1(x,y^3)+y^2f_2(x,y^3)).$
. Then $F_3\sim _{\mathcal {A}} (x,y^3,yf_1(x,y^3)+y^2f_2(x,y^3)).$![]()
Suppose that $a_{10}=0$![]() ($F_3$
($F_3$![]() is singular) and $a_{22}\ne 0$
is singular) and $a_{22}\ne 0$![]() . Then
. Then
for some germs of holomorphic functions $g\in \mathfrak {m}_1$![]() , $h\in \mathcal {O}_2$
, $h\in \mathcal {O}_2$![]() and $k\in \mathfrak {m}_2$
and $k\in \mathfrak {m}_2$![]() . We can make successive changes of coordinates in the target so that $j^pF_3\sim _{\mathcal {A}^{(p)}}(x,y^3,yL(x)+a_{22}y^2)$
. We can make successive changes of coordinates in the target so that $j^pF_3\sim _{\mathcal {A}^{(p)}}(x,y^3,yL(x)+a_{22}y^2)$![]() for any $p\ge 3$
for any $p\ge 3$![]() . It is not difficult to show that $F_3$
. It is not difficult to show that $F_3$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined if and only if $ord(L)=ord(g)=ord( f_y (x,0))$
-determined if and only if $ord(L)=ord(g)=ord( f_y (x,0))$![]() is finite. Suppose that this is the case and denote by $l$
is finite. Suppose that this is the case and denote by $l$![]() that order. Then $j^lL(x)=a_{l1}x^l$
that order. Then $j^lL(x)=a_{l1}x^l$![]() , $a_{l1}\ne 0$
, $a_{l1}\ne 0$![]() , and the change of coordinates $y\mapsto y-(a_{l1}/2a_{22})x^l$
, and the change of coordinates $y\mapsto y-(a_{l1}/2a_{22})x^l$![]() in the source yields $j^{2l+1}F_3\sim _{\mathcal {A}^{(2l+1)}}(x,y^3-3(a_{l1}/2a_{22})^2yx^{2l},a_{22}y^2)$
in the source yields $j^{2l+1}F_3\sim _{\mathcal {A}^{(2l+1)}}(x,y^3-3(a_{l1}/2a_{22})^2yx^{2l},a_{22}y^2)$![]() . This is an $S_{2l-1}$
. This is an $S_{2l-1}$![]() -singularity, and since it is $(2l+1)$
-singularity, and since it is $(2l+1)$![]() -$\mathcal {A}$
-$\mathcal {A}$![]() -determined, we have $F_3\sim _{\mathcal {A}} (x,y^3-yx^{2l},y^2)$
-determined, we have $F_3\sim _{\mathcal {A}} (x,y^3-yx^{2l},y^2)$![]() . In the real case, this is an $S_{2l-1}^{-}$
. In the real case, this is an $S_{2l-1}^{-}$![]() -singularity.
-singularity.
The above calculations show, in particular, that we do not get the simple singularities $B_l^{\pm }$![]() , $C_l^{\pm }$
, $C_l^{\pm }$![]() and $F_4$
and $F_4$![]() whose 2-jets are $\mathcal {A}^{(2)}$
whose 2-jets are $\mathcal {A}^{(2)}$![]() -equivalent to $(x,0,y^2)$
-equivalent to $(x,0,y^2)$![]() .
.
Similar calculations show that when $a_{11}=a_{22}=0$![]() and $a_{21}\ne 0$
and $a_{21}\ne 0$![]() , we get an $H_l$
, we get an $H_l$![]() -singularity when the singularity of $F_3$
-singularity when the singularity of $F_3$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined.
-determined.
The remaining cases are studied in the same way as in the case $k\ge 4$![]() (table 6). We get three strata with topological normal forms ${\bf U}_4^{3}, {\bf X}_4^{3}$
(table 6). We get three strata with topological normal forms ${\bf U}_4^{3}, {\bf X}_4^{3}$![]() and ${\bf W}_4^{3,1}$
and ${\bf W}_4^{3,1}$![]() (the germs in these strata are not $\mathcal {A}$
(the germs in these strata are not $\mathcal {A}$![]() -simple) together with the stratum represented by the topological normal form ${\bf U}^3_3$
-simple) together with the stratum represented by the topological normal form ${\bf U}^3_3$![]() , which is topologically equivalent to Mond's singularity $X_4$
, which is topologically equivalent to Mond's singularity $X_4$![]() (see § 2 and [Reference Mond22]).
(see § 2 and [Reference Mond22]).
Remark 4.5 The invariants associated to the simple singularities can be found in [Reference Mond23]; those associated to ${\bf U}_4^{3}, {\bf X}_4^{3}, {\bf W}_4^{3,1}$![]() are given in table 7.
are given in table 7.
TABLE 7. Topological invariants of germs in strata in table 6

4.2 The case $k\ge 4$
We consider here the case when $k\ge 4$![]() , which we divide into the four branches according to the $\mathcal {A}^{(2)}$
, which we divide into the four branches according to the $\mathcal {A}^{(2)}$![]() -orbits in lemma 4.1. In all that follows, $j\in \{1,\ldots,k-1\}$
-orbits in lemma 4.1. In all that follows, $j\in \{1,\ldots,k-1\}$![]() , and subindices of singularities indicate the codimension of the stratum.
, and subindices of singularities indicate the codimension of the stratum.
4.2.1 Branch 1: $a_{11}=0$ , $a_{21}a_{22}\neq 0$
, $a_{21}a_{22}\neq 0$
Theorem 4.6 Any germ $F_k$![]() of a $k$
of a $k$![]() -folding map satisfying $a_{11}=0$
-folding map satisfying $a_{11}=0$![]() and $a_{21}a_{22}\neq 0$
and $a_{21}a_{22}\neq 0$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to
-determined and is topologically equivalent to
The invariants take the values $\mu ({\mathcal {D}})=(k-2)^2$![]() , $C=k-1$
, $C=k-1$![]() , $T=0$
, $T=0$![]() and $r({\mathcal {D}})=k-1$
and $r({\mathcal {D}})=k-1$![]() and the double-point curve of $F_k$
and the double-point curve of $F_k$![]() is the union of $k-1$
is the union of $k-1$![]() regular curves intersecting transversally.
regular curves intersecting transversally.
Proof. The functions defining the branches ${\mathcal {D}}_j$![]() of the double-point curve (see theorem 3.2) are given by $\lambda _j=a_{21}x+(1+\xi ^j)a_{22}y+O(2),$
of the double-point curve (see theorem 3.2) are given by $\lambda _j=a_{21}x+(1+\xi ^j)a_{22}y+O(2),$![]() where $O(l)$
where $O(l)$![]() denotes a remainder of order $l$
denotes a remainder of order $l$![]() . Clearly, all of the branches ${\mathcal {D}}_j$
. Clearly, all of the branches ${\mathcal {D}}_j$![]() are regular curves. As the scalars $1+\xi ^j$
are regular curves. As the scalars $1+\xi ^j$![]() are pairwise distinct, the space ${\mathcal {D}}={\mathcal {D}}(F_k)=\bigcup _j{\mathcal {D}}_j$
are pairwise distinct, the space ${\mathcal {D}}={\mathcal {D}}(F_k)=\bigcup _j{\mathcal {D}}_j$![]() consists of $k-1$
consists of $k-1$![]() regular curves intersecting transversally at the origin.
regular curves intersecting transversally at the origin.
We have $\mu ({\mathcal {D}}_j)=0$![]() and ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=1$
and ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=1$![]() , and from proposition 3.4 we obtain $\mu ({\mathcal {D}})=(k-2)^2$
, and from proposition 3.4 we obtain $\mu ({\mathcal {D}})=(k-2)^2$![]() . By theorem 3.3, any germ $F_k$
. By theorem 3.3, any germ $F_k$![]() satisfying the conditions in the statement of the theorem is finitely $\mathcal {A}$
satisfying the conditions in the statement of the theorem is finitely $\mathcal {A}$![]() -determined. These germs form a stratum of codimension 1 defined by $\{a_{11}=0,a_{21}a_{22}\neq 0\}$
-determined. These germs form a stratum of codimension 1 defined by $\{a_{11}=0,a_{21}a_{22}\neq 0\}$![]() . Since this stratum is path connected, we conclude by theorem 3.10 that it consists of topologically equivalent germs. We choose for a topological model the germ ${\bf M}^k_1$
. Since this stratum is path connected, we conclude by theorem 3.10 that it consists of topologically equivalent germs. We choose for a topological model the germ ${\bf M}^k_1$![]() given in the statement of the theorem.
given in the statement of the theorem.
By proposition 3.11, it is enough to compute $C$![]() and $T_{j,j'}$
and $T_{j,j'}$![]() for ${\bf M}^k_1$
for ${\bf M}^k_1$![]() as these invariants are constant along the stratum. We have $C=\operatorname {dim}_\mathbb {C} {\mathcal {O}_2}/{\langle y^{k-1},x+2y\rangle }=k-1$
as these invariants are constant along the stratum. We have $C=\operatorname {dim}_\mathbb {C} {\mathcal {O}_2}/{\langle y^{k-1},x+2y\rangle }=k-1$![]() and $T_{j,j'}=\operatorname {dim}_\mathbb {C} {\mathcal {O}_2}/{\langle x+(1+\xi ^j)y,1\rangle }=0.$
and $T_{j,j'}=\operatorname {dim}_\mathbb {C} {\mathcal {O}_2}/{\langle x+(1+\xi ^j)y,1\rangle }=0.$![]()
Remark 4.7 The singularity ${\bf M}^4_1$![]() is the $\mathcal {A}$
is the $\mathcal {A}$![]() -simple singularity $C_3$
-simple singularity $C_3$![]() (see the proof of proposition 4.2).
(see the proof of proposition 4.2).
The proofs for the cases in the remaining branches follow by similar arguments used in the proof of theorem 4.6 (except for the calculations of $T$![]() ). To avoid repetition, we highlight only key differences in each case. The notation for the conditions that define the strata are those indicated in the tables.
). To avoid repetition, we highlight only key differences in each case. The notation for the conditions that define the strata are those indicated in the tables.
4.2.2 Branch 2: $a_{11}=a_{21}=0$ , $a_{22}\ne 0$
, $a_{22}\ne 0$
Theorem 4.8 The strata of codimension $\le \! 4$![]() of finitely $\mathcal {A}$
of finitely $\mathcal {A}$![]() -determined $k$
-determined $k$![]() -folding map-germs in the branch $a_{11}=a_{21}=0$
-folding map-germs in the branch $a_{11}=a_{21}=0$![]() , $a_{22}\ne 0$
, $a_{22}\ne 0$![]() are those given in table 2. The invariants associated to the germs in each stratum are given in table 3.
are those given in table 2. The invariants associated to the germs in each stratum are given in table 3.
For germs in this branch, the map-germ $(x,y)\mapsto (x,f(x,y))$![]() is finite and generically two-to-one. Therefore, $T=0$
is finite and generically two-to-one. Therefore, $T=0$![]() for any finitely $\mathcal {A}$
for any finitely $\mathcal {A}$![]() -determined map-germ in this branch.
-determined map-germ in this branch.
The germs of the functions defining the double-point branch ${\mathcal {D}}_j$![]() is given by
is given by
The branch ${\mathcal {D}}_j$![]() is thus regular if and only if $\vartheta _{2j}\ne 0$
is thus regular if and only if $\vartheta _{2j}\ne 0$![]() . By lemma 3.6, $\vartheta _{2j}=0$
. By lemma 3.6, $\vartheta _{2j}=0$![]() when $k$
when $k$![]() is even and $j=k/2$
is even and $j=k/2$![]() .
.
Proposition 4.9 Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() satisfying $a_{11}=a_{21}=\cdots = a_{l1}=0$
satisfying $a_{11}=a_{21}=\cdots = a_{l1}=0$![]() , $a_{22}a_{(l+1)1}\neq 0$
, $a_{22}a_{(l+1)1}\neq 0$![]() , for some $l\ge 2$
, for some $l\ge 2$![]() , and $a_{33}\ne 0$
, and $a_{33}\ne 0$![]() when $k=2p$
when $k=2p$![]() , is finitely $\mathcal {A}$
, is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to
-determined and is topologically equivalent to
The invariants $C$![]() , $T$
, $T$![]() , $\mu (\mathcal {D})$
, $\mu (\mathcal {D})$![]() and $r(\mathcal {D})$
and $r(\mathcal {D})$![]() are as in table 2. All the double-point branches are regular curves except for the branch $\mathcal {D}_p$
are as in table 2. All the double-point branches are regular curves except for the branch $\mathcal {D}_p$![]() , when $k=2p$
, when $k=2p$![]() , which has an $A_{l-1}$
, which has an $A_{l-1}$![]() -singularity. We have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=l$
-singularity. We have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=l$![]() , for all $j\ne j'$
, for all $j\ne j'$![]() .
.
Proof. Fix an index $j$![]() and assume that $2\nmid k$
and assume that $2\nmid k$![]() or that $k=2p$
or that $k=2p$![]() but $j\neq p$
but $j\neq p$![]() . Then ${\mathcal {D}}_j$
. Then ${\mathcal {D}}_j$![]() is a regular curve and can be parametrized by $t\mapsto (t,\gamma _j(t))$
is a regular curve and can be parametrized by $t\mapsto (t,\gamma _j(t))$![]() , with $\gamma _j(t)=-({a_{l+1,1}}/{((1+\xi ^j)a_{22})})t^{l}+O(l+1).$
, with $\gamma _j(t)=-({a_{l+1,1}}/{((1+\xi ^j)a_{22})})t^{l}+O(l+1).$![]() Clearly, any two distinct branches have order of contact equal to $l$
Clearly, any two distinct branches have order of contact equal to $l$![]() .
.
Suppose now that $k=2p$![]() . As $\vartheta ^2_{p}=0$
. As $\vartheta ^2_{p}=0$![]() , the coefficients of $x^sy$
, the coefficients of $x^sy$![]() in $\lambda _p$
in $\lambda _p$![]() vanish for all $s\ge 1$
vanish for all $s\ge 1$![]() . Moreover, since $\vartheta ^3_{p}=1$
. Moreover, since $\vartheta ^3_{p}=1$![]() , the function $\lambda _p$
, the function $\lambda _p$![]() is of the form $\lambda _p=a_{l+1,1}x^l+a_{33}y^2+y^3h(y).$
is of the form $\lambda _p=a_{l+1,1}x^l+a_{33}y^2+y^3h(y).$![]() This implies that $\lambda _p$
This implies that $\lambda _p$![]() is $\mathcal {R}$
is $\mathcal {R}$![]() -equivalent to $y^2+x^{l}$
-equivalent to $y^2+x^{l}$![]() if and only if $a_{33}\neq 0$
if and only if $a_{33}\neq 0$![]() , in which case it has an $A_{l-1}$
, in which case it has an $A_{l-1}$![]() -singularity. As for the contact between branches, $ord(\lambda _p(t,({-a_{l+1,1}}/{((1+\xi ^j)a_{22})})t^{l}+O(l+1))=l,$
-singularity. As for the contact between branches, $ord(\lambda _p(t,({-a_{l+1,1}}/{((1+\xi ^j)a_{22})})t^{l}+O(l+1))=l,$![]() hence ${\mathcal {D}}_j\cdot {\mathcal {D}}_{p}=l$
hence ${\mathcal {D}}_j\cdot {\mathcal {D}}_{p}=l$![]() . This determines $\mu (\mathcal {D})$
. This determines $\mu (\mathcal {D})$![]() , and hence the topological triviality and the constancy of the invariants along the stratum.
, and hence the topological triviality and the constancy of the invariants along the stratum.
Remarks 4.10 1. Branch 1 can be considered as a particular case of the strata ${\bf M}^k_l$![]() in proposition 4.9 (the condition $a_{33}\ne 0$
in proposition 4.9 (the condition $a_{33}\ne 0$![]() is not needed when $l=1$
is not needed when $l=1$![]() ).
).
2. When $2\nmid k$![]() , the term $y^3$
, the term $y^3$![]() in ${\bf M}^k_l$
in ${\bf M}^k_l$![]() is irrelevant for topological equivalence. We include it to represent both $k$
is irrelevant for topological equivalence. We include it to represent both $k$![]() even and $k$
even and $k$![]() odd by the same map-germ. We do this for all subsequent topological normal forms.
odd by the same map-germ. We do this for all subsequent topological normal forms.
Proposition 4.11 Suppose that $k=2p$![]() . Any $k$
. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() satisfying $a_{11}=a_{21}=a_{33}=0$
satisfying $a_{11}=a_{21}=a_{33}=0$![]() , $a_{22}a_{31}\ne 0$
, $a_{22}a_{31}\ne 0$![]() and the additional conditions in ${\rm {(a)}}$
and the additional conditions in ${\rm {(a)}}$![]() or ${\rm {(b)}}$
or ${\rm {(b)}}$![]() below is finitely $\mathcal {A}$
below is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to one of the germs
-determined and is topologically equivalent to one of the germs
The invariants $\mu ({\mathcal {D}(F_k)}), C,T, r({\mathcal {D}}(F_k))$![]() are as in table 3. The branches ${\mathcal {D}}_j$
are as in table 3. The branches ${\mathcal {D}}_j$![]() are regular curves for all $j\ne p$
are regular curves for all $j\ne p$![]() and ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$
and ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$![]() for all $j\neq j'$
for all $j\neq j'$![]() .
.
${\rm {(a)}}$![]() If ${CndNA}_3\ne 0$
If ${CndNA}_3\ne 0$![]() , then the branch ${\mathcal {D}}_p$
, then the branch ${\mathcal {D}}_p$![]() has an $A_{3}$
has an $A_{3}$![]() -singularity and the map-germ is topologically equivalent to ${\bf N}^k_3$
-singularity and the map-germ is topologically equivalent to ${\bf N}^k_3$![]() .
.
${\rm {(b)}}$![]() If ${CndNA}_3=0$
If ${CndNA}_3=0$![]() and ${CndNA}_5\ne 0$
and ${CndNA}_5\ne 0$![]() , then ${\mathcal {D}}_p$
, then ${\mathcal {D}}_p$![]() has an $A_{5}$
has an $A_{5}$![]() -singularity and the map-germ is topologically equivalent to ${\bf N}^k_4$
-singularity and the map-germ is topologically equivalent to ${\bf N}^k_4$![]() .
.
Proof. We have $\lambda _{p}= a_{31}x^2+a_{41}x^3+a_{43}xy^2+a_{51}x^4+ a_{53}x^2y^2+a_{55}y^4 +O(5).$![]() It has an $A_3$
It has an $A_3$![]() -singularity if and only if ${CndNA}_3\ne 0$
-singularity if and only if ${CndNA}_3\ne 0$![]() . When ${CndNA}_3=0$
. When ${CndNA}_3=0$![]() , we need to consider the $7$
, we need to consider the $7$![]() -jet of $\lambda _p$
-jet of $\lambda _p$![]() . A calculation shows that $\lambda _p$
. A calculation shows that $\lambda _p$![]() has an $A_5$
has an $A_5$![]() -singularity if and only if ${CndNA}_5\ne 0$
-singularity if and only if ${CndNA}_5\ne 0$![]() . In both cases, we have $ord(\lambda _p(t,-{a_{31}}/{((1+\xi ^j)a_{22})}t^{2}+O(3)))=2$
. In both cases, we have $ord(\lambda _p(t,-{a_{31}}/{((1+\xi ^j)a_{22})}t^{2}+O(3)))=2$![]() for all $j\ne p$
for all $j\ne p$![]() .
.
Proposition 4.12 Suppose that $k=2p$![]() . Any $k$
. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() satisfying $a_{11}=a_{21}=a_{31}=a_{33}=0$
satisfying $a_{11}=a_{21}=a_{31}=a_{33}=0$![]() and $a_{22}a_{41}a_{43}\ne 0$
and $a_{22}a_{41}a_{43}\ne 0$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to
-determined and is topologically equivalent to
The codimension of the stratum is $4$![]() and the invariants $\mu ({\mathcal {D}}(F_k)), C,T,$
and the invariants $\mu ({\mathcal {D}}(F_k)), C,T,$![]() $r({\mathcal {D}}(F_k))$
$r({\mathcal {D}}(F_k))$![]() are as in table 3. The branches ${\mathcal {D}}_j,$
are as in table 3. The branches ${\mathcal {D}}_j,$![]() $j\ne p$
$j\ne p$![]() , are regular curves and ${\mathcal {D}}_p$
, are regular curves and ${\mathcal {D}}_p$![]() has a $D_{4}$
has a $D_{4}$![]() -singularity. We have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$
-singularity. We have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$![]() for the distinct regular branches and ${\mathcal {D}}_j\cdot {\mathcal {D}}_{p}=3$
for the distinct regular branches and ${\mathcal {D}}_j\cdot {\mathcal {D}}_{p}=3$![]() , for $j\ne p$
, for $j\ne p$![]() .
.
Proof. The result follows from the fact that $\lambda _{p}=a_{41}x^3+a_{43}xy^2+O(4).$![]()
4.2.3 Branch 3: $a_{11}=a_{22}=0$ , $a_{21}\ne 0$
, $a_{21}\ne 0$
Theorem 4.13 The strata of codimension $\le \! 4$![]() of finitely $\mathcal {A}$
of finitely $\mathcal {A}$![]() -determined $k$
-determined $k$![]() -folding map-germs in the branch $a_{11}=a_{22}=0$
-folding map-germs in the branch $a_{11}=a_{22}=0$![]() , $a_{21}\ne 0$
, $a_{21}\ne 0$![]() are those given in table 4. The invariants of the germs in each stratum are given in table 5.
are those given in table 4. The invariants of the germs in each stratum are given in table 5.
For any finitely $\mathcal {A}$![]() -determined $k$
-determined $k$![]() -folding map-germ in this branch, we have $C=\operatorname {dim}_\mathbb {C} {\mathcal {O}_2}/{\langle y^{k-1},a_{21}x+O(2)\rangle }=k-1.$
-folding map-germ in this branch, we have $C=\operatorname {dim}_\mathbb {C} {\mathcal {O}_2}/{\langle y^{k-1},a_{21}x+O(2)\rangle }=k-1.$![]()
The double-point branches are regular curves that can be parametrized by $t\mapsto (\gamma _j(t),t)$![]() , with
, with

The strata are determined by the contact between the branches of the double-point curve which depend on $\vartheta _{sj}$![]() as well as on the coefficients $a_{pq}$
as well as on the coefficients $a_{pq}$![]() . We start with the case $a_{33}\ne 0$
. We start with the case $a_{33}\ne 0$![]() , where the strata depend on the divisibility of $k$
, where the strata depend on the divisibility of $k$![]() by $3$
by $3$![]() .
.
Proposition 4.14 Suppose that $a_{11}=a_{22}=0$![]() and $a_{21}a_{33}\neq 0$
and $a_{21}a_{33}\neq 0$![]() . Any $k$
. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() in case ${\rm {(a)}}$
in case ${\rm {(a)}}$![]() or satisfying the additional conditions in ${\rm {(b)}}$
or satisfying the additional conditions in ${\rm {(b)}}$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to one of the map-germs
-determined and is topologically equivalent to one of the map-germs
The invariants $\mu ({\mathcal {D}}), C,T, r(\mathcal {D})$![]() are as in table 5. We have contact ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$
are as in table 5. We have contact ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$![]() , except for ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}$
, except for ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}$![]() when $k=3p$
when $k=3p$![]() which is given in ${\rm {(b)}}$
which is given in ${\rm {(b)}}$![]() .
.
(a) If $3\nmid k$
 , then $F_k$
, then $F_k$ is topologically equivalent to ${\bf P}^k_2$
is topologically equivalent to ${\bf P}^k_2$ .
.(b) If $k=3p$
 , then the strata are as follows:
, then the strata are as follows:
If $CndH_2\ne 0$
 , then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=4$
, then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=4$ and $F_k$
and $F_k$ is topologically equivalent to ${\bf P}^k_2$
is topologically equivalent to ${\bf P}^k_2$ .
.If $CndH_2=0$
 and $CndH_3\ne 0$
and $CndH_3\ne 0$ , then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=7$
, then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=7$ and $F_k$
and $F_k$ is topologically equivalent to ${\bf P}^k_3$
is topologically equivalent to ${\bf P}^k_3$ .
.If $CndH_2=CndH_3=0$
 and $CndH_4\ne 0$
and $CndH_4\ne 0$ , then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=10$
, then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=10$ and $F_k$
and $F_k$ is topologically equivalent to ${\bf P}^k_4$
is topologically equivalent to ${\bf P}^k_4$ .
.
Proof. If $3\nmid k$![]() , then by lemma 3.6 we have $\vartheta _{3j}\ne 0$
, then by lemma 3.6 we have $\vartheta _{3j}\ne 0$![]() and $\vartheta _{3j}\ne \vartheta _{3j'}$
and $\vartheta _{3j}\ne \vartheta _{3j'}$![]() for all $j\neq j'$
for all $j\neq j'$![]() . This implies ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$
. This implies ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$![]() for all $j\neq j'$
for all $j\neq j'$![]() .
.
If $k=3p$![]() , then by lemma 3.6 the equality $\vartheta _{3j}=\vartheta _{3j'}$
, then by lemma 3.6 the equality $\vartheta _{3j}=\vartheta _{3j'}$![]() holds only when $\{j,j'\}=\{p,2p\}$
holds only when $\{j,j'\}=\{p,2p\}$![]() . Again, we obtain ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$
. Again, we obtain ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=2$![]() for all $j\neq j'$
for all $j\neq j'$![]() with $\{j,j'\}\neq \{p,2p\}$
with $\{j,j'\}\neq \{p,2p\}$![]() .
.
We have $\vartheta _{3p}=\vartheta _{3(2p)}=0$![]() , $\vartheta _{4p}=\vartheta _{4(2p)}=1$
, $\vartheta _{4p}=\vartheta _{4(2p)}=1$![]() and $\vartheta _{5p}=\vartheta _{2(2p)}$
and $\vartheta _{5p}=\vartheta _{2(2p)}$![]() (lemma 3.6). Using the parametrizations of ${\mathcal {D}}_p$
(lemma 3.6). Using the parametrizations of ${\mathcal {D}}_p$![]() and ${\mathcal {D}}_{2p}$
and ${\mathcal {D}}_{2p}$![]() , we get ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=4$
, we get ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=4$![]() if and only if $a_{32}a_{44}-a_{21}a_{55}\ne 0$
if and only if $a_{32}a_{44}-a_{21}a_{55}\ne 0$![]() , equivalently, $CndH_2\ne 0$
, equivalently, $CndH_2\ne 0$![]() .
.
When $CndH_2=0$![]() , the exceptional branches ${\mathcal {D}}_p$
, the exceptional branches ${\mathcal {D}}_p$![]() and ${\mathcal {D}}_{2p}$
and ${\mathcal {D}}_{2p}$![]() are parametrized by $x=-({a_{44}}/{a_{21}})y^3+\beta _sy^7+O(9)$
are parametrized by $x=-({a_{44}}/{a_{21}})y^3+\beta _sy^7+O(9)$![]() , $s=1,2$
, $s=1,2$![]() , with $\beta _1-\beta _2\ne 0$
, with $\beta _1-\beta _2\ne 0$![]() if and only if $CndH_3\ne 0$
if and only if $CndH_3\ne 0$![]() . Then, ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=7$
. Then, ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=7$![]() .
.
When $CndH_2=CndH_3=0$![]() , the exceptional branches are parametrized by $x=-({a_{44}}/{a_{21}})y^3+\beta _sy^{10}+O(11)$
, the exceptional branches are parametrized by $x=-({a_{44}}/{a_{21}})y^3+\beta _sy^{10}+O(11)$![]() , $s=1,2$
, $s=1,2$![]() , with $\beta _1-\beta _2\ne 0$
, with $\beta _1-\beta _2\ne 0$![]() if and only if $CndH_4\ne 0$
if and only if $CndH_4\ne 0$![]() . Then, ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=10$
. Then, ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=10$![]() .
.
The values of $T$![]() can be computed using the models ${\bf P}^k_l$
can be computed using the models ${\bf P}^k_l$![]() . We have $\lambda _j=x+\vartheta _{3j}y^2+\vartheta _{(3l-1)j}y^{3l-2}$
. We have $\lambda _j=x+\vartheta _{3j}y^2+\vartheta _{(3l-1)j}y^{3l-2}$![]() and $\lambda _{j,j'}=(\vartheta _{3j}-\vartheta _{3j'})y+(\vartheta _{3l-1,j}-\vartheta _{3l-1,j'})y^{3l-3}.$
and $\lambda _{j,j'}=(\vartheta _{3j}-\vartheta _{3j'})y+(\vartheta _{3l-1,j}-\vartheta _{3l-1,j'})y^{3l-3}.$![]() By lemma 3.6, $T_{j,j'}=\operatorname {dim}_\mathbb {C} ({\mathcal {O}_2}/{\langle x,y\rangle })=1$
By lemma 3.6, $T_{j,j'}=\operatorname {dim}_\mathbb {C} ({\mathcal {O}_2}/{\langle x,y\rangle })=1$![]() when $3\nmid k$
when $3\nmid k$![]() or when $k=3p$
or when $k=3p$![]() but $\{j,j'\}\neq \{p,2p\}$
but $\{j,j'\}\neq \{p,2p\}$![]() . For $k=3p$
. For $k=3p$![]() , we show that $\vartheta _{3l-1,p}\neq \vartheta _{3l-1,2p}$
, we show that $\vartheta _{3l-1,p}\neq \vartheta _{3l-1,2p}$![]() so $T_{p,2p}=3l-3$
so $T_{p,2p}=3l-3$![]() .
.
Remark 4.15 The singularity ${\bf P}^4_2\colon (x,y)\mapsto (x,y^4,xy+y^3+y^5)$![]() is topologically equivalent to the singularity $T_4\colon (x,y)\mapsto (x,y^4,xy+y^3)$
is topologically equivalent to the singularity $T_4\colon (x,y)\mapsto (x,y^4,xy+y^3)$![]() in [Reference Mond22]. Observe that according to proposition 4.14, if $k$
in [Reference Mond22]. Observe that according to proposition 4.14, if $k$![]() is not divisible by $3$
is not divisible by $3$![]() , then the $y^{3l-1}$
, then the $y^{3l-1}$![]() term can be removed from the expression of ${\bf P}^k_l$
term can be removed from the expression of ${\bf P}^k_l$![]() , without changing the topological class of the germ.
, without changing the topological class of the germ.
Proposition 4.16 Suppose that $a_{11}=a_{22}=a_{33}=0$![]() and $a_{21}a_{44}\neq 0$
and $a_{21}a_{44}\neq 0$![]() . Any $k$
. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() in case ${\rm {(a)}}$
in case ${\rm {(a)}}$![]() or satisfying the additional conditions in ${\rm {(b)}}$
or satisfying the additional conditions in ${\rm {(b)}}$![]() , ${\rm {(c)}}$
, ${\rm {(c)}}$![]() or ${\rm {(d)}}$
or ${\rm {(d)}}$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to one of the following map-germs:
-determined and is topologically equivalent to one of the following map-germs:
The invariants are as in table 5. We have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=3$![]() except when $j$
except when $j$![]() and $j'$
and $j'$![]() are in the sets $J$
are in the sets $J$![]() or $J'$
or $J'$![]() below.
below.
(a) If $3\nmid k$
 and $4\nmid k$
and $4\nmid k$ , then there are no exceptional branches and the germs in this stratum are topologically equivalent to ${\bf Q}_3^k$
, then there are no exceptional branches and the germs in this stratum are topologically equivalent to ${\bf Q}_3^k$ .
.(b) If $k=3p$
 and $4\nmid k$
and $4\nmid k$ , then $J=\{p,2p\}$
, then $J=\{p,2p\}$ .
.
(b1) If $CndH_2\ne 0$
 , then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=4$
, then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=4$ and $F_k$
and $F_k$ is topologically equivalent to ${\bf Q}_3^k$
is topologically equivalent to ${\bf Q}_3^k$ .
.(b2) If $CndH_2=0$
 and $CndH_3\ne 0$
and $CndH_3\ne 0$ , then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=7$
, then ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=7$ and $F_k$
and $F_k$ is topologically equivalent to ${\bf Q}_4^k$
is topologically equivalent to ${\bf Q}_4^k$ .
.
(c) If $k=4p$
 , $3\nmid k$
, $3\nmid k$ , then $J=\{p,2p,3p\}$
, then $J=\{p,2p,3p\}$ .
.
(c1) If $CndQm_5\ne 0$
 , then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=5$
, then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=5$ , for all $j,j'\in J, j\ne j'$
, for all $j,j'\in J, j\ne j'$ , and $F_k$
, and $F_k$ is topologically equivalent to ${\bf Q}_3^k$
is topologically equivalent to ${\bf Q}_3^k$ .
.(c2) If $CndQm_5=0$
 and $CndQm_6\ne 0$
and $CndQm_6\ne 0$ , then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=6$
, then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=6$ , for all $j,j'\in J, j\ne j'$
, for all $j,j'\in J, j\ne j'$ , and $F_k$
, and $F_k$ is topologically equivalent to $\widetilde {\bf Q}_4^k$
is topologically equivalent to $\widetilde {\bf Q}_4^k$ .
.
(d) If $k=12p$
 , the exceptional contact between double-point branches occurs when the indices are in $J=\{4p,8p\}$
, the exceptional contact between double-point branches occurs when the indices are in $J=\{4p,8p\}$ or $J'=\{3p,6p,9p\}$
or $J'=\{3p,6p,9p\}$ . There are three strata:
. There are three strata:
(d1) If $CndH_2\ne 0$
 and $CndQm_5\ne 0$
and $CndQm_5\ne 0$ , then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=4$
, then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=4$ (resp. ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=5$
(resp. ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=5$ ) for all distinct pairs with $j,j'$
) for all distinct pairs with $j,j'$ in $J$
in $J$ (resp. $J'$
(resp. $J'$ ), and $F_k$
), and $F_k$ is topologically equivalent to ${\bf Q}_3^k$
is topologically equivalent to ${\bf Q}_3^k$ .
.(d2) If $CndH_2=0, CndH_3\ne 0$
 and $CndQm_5\ne 0$
and $CndQm_5\ne 0$ , then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=7$
, then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=7$ (resp. ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=5$
(resp. ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=5$ ) for all distinct pairs with $j,j'$
) for all distinct pairs with $j,j'$ in $J$
in $J$ (resp. $J'$
(resp. $J'$ ), and $F_k$
), and $F_k$ is topologically equivalent to ${\bf Q}_4^k$
is topologically equivalent to ${\bf Q}_4^k$ .
.(d3) If $CndQm_5=0, CndQm_6\ne 0,$
 and $CndH_2\ne 0$
and $CndH_2\ne 0$ , then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=4$
, then ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=4$ (resp. ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=6$
(resp. ${\mathcal {D}}_{j}\cdot {\mathcal {D}}_{j'}=6$ ) for all distinct pairs with $j,j'$
) for all distinct pairs with $j,j'$ in $J$
in $J$ (resp. $J'$
(resp. $J'$ ), and $F_k$
), and $F_k$ is topologically equivalent to $\widetilde {\bf Q}_4^k$
is topologically equivalent to $\widetilde {\bf Q}_4^k$ .
.
Proof. The branches $\mathcal {D}_j$![]() can be parametrized by $t\mapsto (\gamma _j(t),t)$
can be parametrized by $t\mapsto (\gamma _j(t),t)$![]() with
with

(a) If $3\nmid k$![]() , $4\nmid k$
, $4\nmid k$![]() , then $\vartheta _{4j}\ne \vartheta _{4j'}$
, then $\vartheta _{4j}\ne \vartheta _{4j'}$![]() for all $j,j'$
for all $j,j'$![]() with $j\ne j'$
with $j\ne j'$![]() (lemma 3.6). Therefore, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=3$
(lemma 3.6). Therefore, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=3$![]() for all distinct pairs.
for all distinct pairs.
(b) If $k=3p$![]() and $4\nmid p$
and $4\nmid p$![]() , then $\vartheta _{4j}\ne \vartheta _{4j'}$
, then $\vartheta _{4j}\ne \vartheta _{4j'}$![]() for all distinct pairs with $j$
for all distinct pairs with $j$![]() or $j'$
or $j'$![]() not in $J=\{p,2p\}$
not in $J=\{p,2p\}$![]() . For such pairs, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=3$
. For such pairs, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=3$![]() .
.
Using the fact that $\vartheta _{6p}=\vartheta _{6(2p)}=\vartheta _{3p}=\vartheta _{3(2p)}=0$![]() , $\vartheta _{4p}=\vartheta _{4(2p)}=1$
, $\vartheta _{4p}=\vartheta _{4(2p)}=1$![]() and $\vartheta _{5p}=\vartheta _{2p}\neq \vartheta _{5(2p)}=\vartheta _{2(2p)}$
and $\vartheta _{5p}=\vartheta _{2p}\neq \vartheta _{5(2p)}=\vartheta _{2(2p)}$![]() , the parametrization of the exceptional branch $\mathcal {D}_p$
, the parametrization of the exceptional branch $\mathcal {D}_p$![]() becomes
becomes
A parametrization of $\mathcal {D}_{2p}$![]() is obtained by replacing $\vartheta _{2p}$
is obtained by replacing $\vartheta _{2p}$![]() by $\vartheta _{2(2p)}$
by $\vartheta _{2(2p)}$![]() in the expression of $\gamma _p$
in the expression of $\gamma _p$![]() . Therefore, ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=4$
. Therefore, ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=4$![]() if and only if $a_{32}a_{44}-a_{21}a_{55}\ne 0$
if and only if $a_{32}a_{44}-a_{21}a_{55}\ne 0$![]() , i.e. $CndH_2\ne 0$
, i.e. $CndH_2\ne 0$![]() .
.
When $CndH_2= 0$![]() , we have
, we have
For $\gamma _{2p}$![]() , we replace $\vartheta ^2_{p}$
, we replace $\vartheta ^2_{p}$![]() by $\vartheta ^2_{2p}$
by $\vartheta ^2_{2p}$![]() in $\gamma _{p}$
in $\gamma _{p}$![]() . It follows that ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=7$
. It follows that ${\mathcal {D}}_p\cdot {\mathcal {D}}_{2p}=7$![]() if and only if $CndH_3\ne 0$
if and only if $CndH_3\ne 0$![]() .
.
(c) If $k=4p$![]() and $3\nmid p$
and $3\nmid p$![]() , we have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=3$
, we have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=3$![]() for $j$
for $j$![]() or $j'$
or $j'$![]() not in $\{p,2p,3p\}$
not in $\{p,2p,3p\}$![]() .
.
The parametrization of $\mathcal {D}_p$![]() becomes $\gamma _{p}(t)={a_{55}}/{a_{21}}t^4+ {\vartheta ^2_{p}(a_{32}a_{55} - a_{21}a_{66})}/{a_{21}^2} t^5+O(6),$
becomes $\gamma _{p}(t)={a_{55}}/{a_{21}}t^4+ {\vartheta ^2_{p}(a_{32}a_{55} - a_{21}a_{66})}/{a_{21}^2} t^5+O(6),$![]() and similarly for $\gamma _{2p}$
and similarly for $\gamma _{2p}$![]() and $\gamma _{3p}$
and $\gamma _{3p}$![]() replacing $p$
replacing $p$![]() by $2p$
by $2p$![]() and $3p$
and $3p$![]() respectively. Consequently, the branches $\mathcal {D}_p$
respectively. Consequently, the branches $\mathcal {D}_p$![]() , $\mathcal {D}_{2p}$
, $\mathcal {D}_{2p}$![]() , $\mathcal {D}_{3p}$
, $\mathcal {D}_{3p}$![]() have pairwise order of contact $5$
have pairwise order of contact $5$![]() if and only if $a_{32}a_{55} - a_{21}a_{66}\ne 0$
if and only if $a_{32}a_{55} - a_{21}a_{66}\ne 0$![]() , i.e. $CndQm_5\ne 0.$
, i.e. $CndQm_5\ne 0.$![]()
When $CndQm_5=0$![]() , $\gamma _{p}=-{a_{55}}/{a_{21}}t^4- \vartheta _{2p}\vartheta _{3p}({a_{21} a_{77} - a_{43} a_{55}})/ {a_{21}^2}t^6+O(7)$
, $\gamma _{p}=-{a_{55}}/{a_{21}}t^4- \vartheta _{2p}\vartheta _{3p}({a_{21} a_{77} - a_{43} a_{55}})/ {a_{21}^2}t^6+O(7)$![]() , with similar adjustments as above for $\gamma _{2p}$
, with similar adjustments as above for $\gamma _{2p}$![]() and $\gamma _{3p}$
and $\gamma _{3p}$![]() . Therefore, the three exceptional branches have pairwise order of contact $6$
. Therefore, the three exceptional branches have pairwise order of contact $6$![]() if and only if $a_{21} a_{77}-a_{43} a_{55}\ne 0$
if and only if $a_{21} a_{77}-a_{43} a_{55}\ne 0$![]() , i.e. $CndQm_6\ne 0$
, i.e. $CndQm_6\ne 0$![]() .
.
(d) This follows by lemma 3.6 and (b) and (c) above.
The contact between the branches determines $\mu (\mathcal {D})$![]() , the topological types and their associated strata. It remains to compute $T$
, the topological types and their associated strata. It remains to compute $T$![]() for each normal form.
for each normal form.
For ${\bf Q}^k_3$![]() we have $\lambda _j=x+\vartheta _{4j}y^3+\vartheta _{5j}y^{5}+\vartheta _{6j}y^5,$
we have $\lambda _j=x+\vartheta _{4j}y^3+\vartheta _{5j}y^{5}+\vartheta _{6j}y^5,$![]() and $\lambda _{j,j'}=(\vartheta _{4j}-\vartheta _{4j'})y^2+(\vartheta _{5j}-\vartheta _{5j'})y^3+(\vartheta _{6j}-\vartheta _{6j'})y^4.$
and $\lambda _{j,j'}=(\vartheta _{4j}-\vartheta _{4j'})y^2+(\vartheta _{5j}-\vartheta _{5j'})y^3+(\vartheta _{6j}-\vartheta _{6j'})y^4.$![]() Using the properties of $\vartheta _{sj}$
Using the properties of $\vartheta _{sj}$![]() in lemma 3.6, we have $T_{j,j'}=2$
in lemma 3.6, we have $T_{j,j'}=2$![]() unless $k=3p$
unless $k=3p$![]() and $j,j'\in \{p,2p\}$
and $j,j'\in \{p,2p\}$![]() , or $k=4p$
, or $k=4p$![]() and $j,j'\in \{p,2p,3p\}$
and $j,j'\in \{p,2p,3p\}$![]() . In the first case we get $T_{j,j'}=3$
. In the first case we get $T_{j,j'}=3$![]() and in the second $T_{j,j'}=4$
and in the second $T_{j,j'}=4$![]() . The invariant for the germ ${\bf Q}^k_4$
. The invariant for the germ ${\bf Q}^k_4$![]() differs from ${\bf Q}^k_3$
differs from ${\bf Q}^k_3$![]() only when $k$
only when $k$![]() is divisible by $3$
is divisible by $3$![]() . For $k=3p$
. For $k=3p$![]() , we have $T_{p,2p}=6$
, we have $T_{p,2p}=6$![]() and $T_{j,j'}=4$
and $T_{j,j'}=4$![]() if $k=4q$
if $k=4q$![]() and $j,j'\in \{q,2q,3q\}$
and $j,j'\in \{q,2q,3q\}$![]() . All other indices $j$
. All other indices $j$![]() and $j'$
and $j'$![]() give $T_{j,j'}=2$
give $T_{j,j'}=2$![]() . Similarly, for the germ $\widetilde {\bf Q}^k_4$
. Similarly, for the germ $\widetilde {\bf Q}^k_4$![]() and for $k=4p$
and for $k=4p$![]() , we get $T_{j,j'}=5$
, we get $T_{j,j'}=5$![]() if $j,j'\in \{p,2p,3p\}$
if $j,j'\in \{p,2p,3p\}$![]() . If $k=3q$
. If $k=3q$![]() , then $T_{q,2q}=3$
, then $T_{q,2q}=3$![]() . All other indices $j$
. All other indices $j$![]() and $j'$
and $j'$![]() give $T_{j,j'}=2$
give $T_{j,j'}=2$![]() .
.
Remark 4.17 When $k$![]() is divisible by $12$
is divisible by $12$![]() , the germs ${\bf Q}^k_4$
, the germs ${\bf Q}^k_4$![]() and $\widetilde {\bf Q}^k_4$
and $\widetilde {\bf Q}^k_4$![]() have the same invariants $C,T,\mu (D)$
have the same invariants $C,T,\mu (D)$![]() and $r(D)$
and $r(D)$![]() but they are not topologically equivalent as their associated sets of contacts between double-points branches are distinct (see [Reference Zariski33]).
but they are not topologically equivalent as their associated sets of contacts between double-points branches are distinct (see [Reference Zariski33]).
Proposition 4.18 Suppose that $a_{11}=a_{22}=a_{33}=a_{44}=0$![]() and $a_{21}a_{55}\neq 0$
and $a_{21}a_{55}\neq 0$![]() . Any $k$
. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() in case ${\rm {(a)}}$
in case ${\rm {(a)}}$![]() or satisfying the additional conditions in ${\rm {(b)}}$
or satisfying the additional conditions in ${\rm {(b)}}$![]() or ${\rm {(c)}}$
or ${\rm {(c)}}$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to
-determined and is topologically equivalent to
The invariants associated to the germs in the stratum are as in table 5. We have ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=4$![]() except for the exceptional pairs of branches below.
except for the exceptional pairs of branches below.
(a) If $4\nmid k$
 and $5\nmid k$
and $5\nmid k$ , there are no additional conditions and no exceptional branches.
, there are no additional conditions and no exceptional branches.(b) If $k=4p$
 , $5\nmid k$
, $5\nmid k$ and $CndQm_5\ne 0$
and $CndQm_5\ne 0$ , then ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=5$
, then ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=5$ for all distinct pairs with $j,j'$
for all distinct pairs with $j,j'$ in $J=\{p,2p,3p\}$
in $J=\{p,2p,3p\}$ .
.(c) If $k=5p$
 , $4\nmid k$
, $4\nmid k$ and $CndRm_5\ne 0$
and $CndRm_5\ne 0$ , ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=5$
, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=5$ for all distinct pairs with $j,j'$
for all distinct pairs with $j,j'$ in $J=\{p,2p,3p,4p\}$
in $J=\{p,2p,3p,4p\}$ .
.(d) If $k=20p$
 , $CndQm_5\ne 0$
, $CndQm_5\ne 0$ and $CndRm_5\ne 0$
and $CndRm_5\ne 0$ , then ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=5$
, then ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=5$ for all distinct pairs with $j,j'$
for all distinct pairs with $j,j'$ in $J=\{5p,10p,15p\}$
in $J=\{5p,10p,15p\}$ or in $J'=\{4p,8p,12p,16p\}$
or in $J'=\{4p,8p,12p,16p\}$ .
.
Proof. The branches $\mathcal {D}_j$![]() can be parametrized by $t\mapsto (\gamma _j(t),t)$
can be parametrized by $t\mapsto (\gamma _j(t),t)$![]() with
with

(a) If $4\nmid k$![]() and $5\nmid k$
and $5\nmid k$![]() , then $\vartheta _{5j}\ne \vartheta _{5j'}$
, then $\vartheta _{5j}\ne \vartheta _{5j'}$![]() for all $j,j'$
for all $j,j'$![]() with $j\ne j'$
with $j\ne j'$![]() (by lemma 3.6). Therefore, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=4$
(by lemma 3.6). Therefore, ${\mathcal {D}}_j\cdot {\mathcal {D}}_{j'}=4$![]() for all distinct pairs.
for all distinct pairs.
(b) If $k=4p$![]() and $5\nmid k$
and $5\nmid k$![]() , then $\vartheta _{5p}=1$
, then $\vartheta _{5p}=1$![]() , $\vartheta _{6p}=\vartheta _{2p}$
, $\vartheta _{6p}=\vartheta _{2p}$![]() , and we can write $\gamma _p(t)=-a_{55}/a_{21}t^4+\vartheta _{2p}CndQm_5/a_{21}^2t^5+O(6)$
, and we can write $\gamma _p(t)=-a_{55}/a_{21}t^4+\vartheta _{2p}CndQm_5/a_{21}^2t^5+O(6)$![]() . We get similarly $\gamma _{2p}(t)$
. We get similarly $\gamma _{2p}(t)$![]() and $\gamma _{3p}(t)$
and $\gamma _{3p}(t)$![]() by substituting $\vartheta _{2p}$
by substituting $\vartheta _{2p}$![]() by, respectively, $\vartheta _{2(2p)}$
by, respectively, $\vartheta _{2(2p)}$![]() and $\vartheta _{2(3p)}$
and $\vartheta _{2(3p)}$![]() in $\gamma _p$
in $\gamma _p$![]() . The result follows as $\vartheta _{2s}\ne \vartheta _{2s'}$
. The result follows as $\vartheta _{2s}\ne \vartheta _{2s'}$![]() for $s,s'\in \{p,2p,3p\}$
for $s,s'\in \{p,2p,3p\}$![]() , $s\ne s'$
, $s\ne s'$![]() .
.
(c) If $k=5p$![]() and $4\nmid k$
and $4\nmid k$![]() , then $\vartheta _{5p}=0$
, then $\vartheta _{5p}=0$![]() , $\vartheta _{6p}=1$
, $\vartheta _{6p}=1$![]() , $\vartheta _{7p}=\vartheta _{2p}$
, $\vartheta _{7p}=\vartheta _{2p}$![]() , so $\gamma _p(t)=-a_{66}/a_{21}t^5+\vartheta _{2p}CndRm_5/a_{21}^2t^6+O(7)$
, so $\gamma _p(t)=-a_{66}/a_{21}t^5+\vartheta _{2p}CndRm_5/a_{21}^2t^6+O(7)$![]() . The expressions $\gamma _{sp}$
. The expressions $\gamma _{sp}$![]() , $s=2,3,4,$
, $s=2,3,4,$![]() are obtaining by substituting $\vartheta _{2p}$
are obtaining by substituting $\vartheta _{2p}$![]() by $\vartheta _{2(sp)}$
by $\vartheta _{2(sp)}$![]() in $\gamma _p$
in $\gamma _p$![]() .
.
(d) The case $k=20p$![]() follows in a similarly way to that of proposition 4.16(d).
follows in a similarly way to that of proposition 4.16(d).
The calculations for $T$![]() are similar to those in the proof of proposition 4.16. We obtain $T_{j,j'}=4$
are similar to those in the proof of proposition 4.16. We obtain $T_{j,j'}=4$![]() if $k=4p$
if $k=4p$![]() and $j,j'\in \{p,2p,3p\}$
and $j,j'\in \{p,2p,3p\}$![]() , and $T_{j,j'}=5$
, and $T_{j,j'}=5$![]() if $k=5q$
if $k=5q$![]() and $j,j'\in \{q,2q,3q,4q\}$
and $j,j'\in \{q,2q,3q,4q\}$![]() . All remaining indices $j$
. All remaining indices $j$![]() and $j'$
and $j'$![]() give $T_{j,j'}=3$
give $T_{j,j'}=3$![]() .
.
Remark 4.19 The singularities ${\bf Q}^4_3$![]() and ${\bf R}^4_4$
and ${\bf R}^4_4$![]() have the same invariants, but the contact of their double-point branches shows that they are not topologically equivalent.
have the same invariants, but the contact of their double-point branches shows that they are not topologically equivalent.
4.2.4 Branch 4: $a_{11}=a_{21}=a_{22}=0$
Theorem 4.20 The strata of codimension $\le \! 4$![]() of finitely $\mathcal {A}$
of finitely $\mathcal {A}$![]() -determined $k$
-determined $k$![]() -folding map-germs in the branch $a_{11}=a_{22}=a_{21}=0$
-folding map-germs in the branch $a_{11}=a_{22}=a_{21}=0$![]() are those given in table 6. The invariants of the germs in each stratum are given in table 7.
are those given in table 6. The invariants of the germs in each stratum are given in table 7.
The functions defining the double-point branches $\mathcal {D}_j$![]() have the following initial terms:
have the following initial terms:
Consequently, the branches $\mathcal {D}_j$![]() are singular. A branch $\mathcal {D}_j$
are singular. A branch $\mathcal {D}_j$![]() has an $A_1$
has an $A_1$![]() -singularity unless the discriminant $\Delta _j^k$
-singularity unless the discriminant $\Delta _j^k$![]() of the quadratic part of $\lambda _j$
of the quadratic part of $\lambda _j$![]() vanishes. We have
vanishes. We have
An $A_1$![]() -singularity is a transverse intersection of two regular curves. Two branches $\mathcal {D}_j$
-singularity is a transverse intersection of two regular curves. Two branches $\mathcal {D}_j$![]() and $\mathcal {D}_{j'}$
and $\mathcal {D}_{j'}$![]() with an $A_1$
with an $A_1$![]() -singularity may have one or both of their components being tangential (i.e. the tangent cones of the two branches have a non-trivial intersection). Taking the resultant of $j^2\lambda _j$
-singularity may have one or both of their components being tangential (i.e. the tangent cones of the two branches have a non-trivial intersection). Taking the resultant of $j^2\lambda _j$![]() and $j^2\lambda _{j'}$
and $j^2\lambda _{j'}$![]() with respect to one of the variables, we find that this happens if and only if $a_{31}a_{33}=0$
with respect to one of the variables, we find that this happens if and only if $a_{31}a_{33}=0$![]() or
or
We have $1+\xi ^j+\xi ^{j'}=0$![]() or $\xi ^j+\xi ^{j'}+\xi ^{j+j'}=0$
or $\xi ^j+\xi ^{j'}+\xi ^{j+j'}=0$![]() if and only if $k=3p$
if and only if $k=3p$![]() and $j,j'\in \{p,2p\}$
and $j,j'\in \{p,2p\}$![]() . Therefore, if $3\nmid k$
. Therefore, if $3\nmid k$![]() or if $k=3p$
or if $k=3p$![]() and $j,j'\notin \{p,2p\}$
and $j,j'\notin \{p,2p\}$![]() , $V(\Omega ^k_{j,j'})$
, $V(\Omega ^k_{j,j'})$![]() is a codimension 1 algebraic variety in $J^l(2,1)$
is a codimension 1 algebraic variety in $J^l(2,1)$![]() , for $l\ge 3$
, for $l\ge 3$![]() . For such pairs, we set
. For such pairs, we set
We have the following properties of $\Delta _j^k$![]() and $\Omega _{j,j'}^k$
and $\Omega _{j,j'}^k$![]() when $a_{31}a_{33}\ne 0$
when $a_{31}a_{33}\ne 0$![]() ; the case $a_{31}a_{33}=0$
; the case $a_{31}a_{33}=0$![]() is dealt with in propositions 4.26 and 4.27.
is dealt with in propositions 4.26 and 4.27.
Proposition 4.21 Suppose that $a_{31}a_{33}\ne 0$![]() and that $3\nmid k$
and that $3\nmid k$![]() or $k=3p$
or $k=3p$![]() and $j,j'\notin \{p,2p\}$
and $j,j'\notin \{p,2p\}$![]() . Then:
. Then:
${\rm {(1)}}$![]() $\Delta _{j}^k=\xi ^{2j}\Delta _{k-j}^k$
$\Delta _{j}^k=\xi ^{2j}\Delta _{k-j}^k$![]() , and if $\Delta _{j}^k=0$
, and if $\Delta _{j}^k=0$![]() then $\Delta _{s}^k\ne 0$
then $\Delta _{s}^k\ne 0$![]() for $s\notin \{j,k-j\}$
for $s\notin \{j,k-j\}$![]() , so the solutions of $\Delta _{j}^k=0$
, so the solutions of $\Delta _{j}^k=0$![]() in the $k{\rm th}$
in the $k{\rm th}$![]() -roots of unity come in pairs.
-roots of unity come in pairs.
${\rm {(2)}}$![]() For $\Delta _{j}^k$
For $\Delta _{j}^k$![]() to vanish requires $\alpha$
to vanish requires $\alpha$![]() in (4.3) to belong to the real semi-line $(-\infty, 3)$
in (4.3) to belong to the real semi-line $(-\infty, 3)$![]() .
.
${\rm {(3)}}$![]() $\alpha _{j,j'}=\alpha _{j',j}$
$\alpha _{j,j'}=\alpha _{j',j}$![]() for all pairs $(j,j')$
for all pairs $(j,j')$![]() . We have $\alpha _{j,j'}=\alpha _{k-j,j'-j}=\alpha _{k-j',j-j'}$
. We have $\alpha _{j,j'}=\alpha _{k-j,j'-j}=\alpha _{k-j',j-j'}$![]() and the pairs $(j,j'), (k-j,j'-j), (k-j',j-j')$
and the pairs $(j,j'), (k-j,j'-j), (k-j',j-j')$![]() are pairwise distinct. Furthermore, $\alpha ^k_{l,q}=\alpha ^k_{j,j'}$
are pairwise distinct. Furthermore, $\alpha ^k_{l,q}=\alpha ^k_{j,j'}$![]() if and only if $(l,q)$
if and only if $(l,q)$![]() or $(q,l)$
or $(q,l)$![]() is one of those $3$
is one of those $3$![]() pairs.
pairs.
${\rm {(4)}}$![]() $\alpha _{j,j'}$
$\alpha _{j,j'}$![]() is real if and only if $j'=k-j$
is real if and only if $j'=k-j$![]() or $j'=2j$
or $j'=2j$![]() . In that case, by ${\rm {(3)}}$
. In that case, by ${\rm {(3)}}$![]() , $\alpha _{k-j,2j}$
, $\alpha _{k-j,2j}$![]() is also real. Then, $\alpha _{j,k-j}=\alpha _{j,2j}=\alpha _{k-j,2j}=(1+\xi ^j+\xi ^{k-j})^{-1}$
is also real. Then, $\alpha _{j,k-j}=\alpha _{j,2j}=\alpha _{k-j,2j}=(1+\xi ^j+\xi ^{k-j})^{-1}$![]() .
.
${\rm {(5)}}$![]() If $\alpha$
If $\alpha$![]() is real then $\Omega ^k_{j,j'}=0$
is real then $\Omega ^k_{j,j'}=0$![]() if and only if $j'=k-j$
if and only if $j'=k-j$![]() or $j'=2j$
or $j'=2j$![]() . Then by ${\rm {(3)}}$
. Then by ${\rm {(3)}}$![]() , we also have $\Omega ^k_{k-j,2j}=0$
, we also have $\Omega ^k_{k-j,2j}=0$![]() .
.
${\rm {(6)}}$![]() If $\alpha$
If $\alpha$![]() is real, then $\Omega ^k_{j_0,k-j_0}=0$
is real, then $\Omega ^k_{j_0,k-j_0}=0$![]() implies $\Delta _j^k\ne 0$
implies $\Delta _j^k\ne 0$![]() for all $j$
for all $j$![]() . Conversely, if $\Delta _{j_0}^k=0$
. Conversely, if $\Delta _{j_0}^k=0$![]() , then $\Omega ^k_{j,k-j}\ne 0$
, then $\Omega ^k_{j,k-j}\ne 0$![]() for all $j$
for all $j$![]() .
.
${\rm {(7)}}$![]() If $\Delta _j^k\Delta _{j'}^k\ne 0$
If $\Delta _j^k\Delta _{j'}^k\ne 0$![]() and $\Omega ^k_{j,j'}\ne 0$
and $\Omega ^k_{j,j'}\ne 0$![]() for all $j,j'$
for all $j,j'$![]() with $j'\ne j$
with $j'\ne j$![]() , then $\mathcal {D}_j\cdot \mathcal {D}_{j'}=4$
, then $\mathcal {D}_j\cdot \mathcal {D}_{j'}=4$![]() .
.
Proof. (1) As $\xi ^{-j}=\xi ^{k-j}$![]() , factoring out $\xi ^{2j}$
, factoring out $\xi ^{2j}$![]() in (4.1) gives $\Delta _{j}^k=\xi ^{2j}\Delta _{k-j}^k$
in (4.1) gives $\Delta _{j}^k=\xi ^{2j}\Delta _{k-j}^k$![]() .
.
If $a_{32}^2-4a_{31}a_{33}=0$![]() , then for $\Delta _j^k$
, then for $\Delta _j^k$![]() to vanish requires $a_{32}^2-2a_{31}a_{33}=0$
to vanish requires $a_{32}^2-2a_{31}a_{33}=0$![]() . This would imply $a_{31}a_{33}=0$
. This would imply $a_{31}a_{33}=0$![]() . Therefore, under the hypothesis of the proposition, we can assume that $a_{32}^2-4a_{31}a_{33}\ne 0$
. Therefore, under the hypothesis of the proposition, we can assume that $a_{32}^2-4a_{31}a_{33}\ne 0$![]() . Then
. Then
with $\alpha$![]() as in (4.3). If $\xi ^j$
as in (4.3). If $\xi ^j$![]() is a solution of the above quadratic equation, then so is $\xi ^{k-j}=\xi ^{-j}$
is a solution of the above quadratic equation, then so is $\xi ^{k-j}=\xi ^{-j}$![]() . Therefore, for $\alpha$
. Therefore, for $\alpha$![]() fixed, if $\Delta _j^k=0$
fixed, if $\Delta _j^k=0$![]() , then $\Delta _s^k\ne 0$
, then $\Delta _s^k\ne 0$![]() for $s\notin \{ j,k-j \}$
for $s\notin \{ j,k-j \}$![]() .
.
(2) When $a_{31}a_{33}\ne 0$![]() , we can write $\Delta _j^k=a_{31}a_{33}((1+\xi ^j)^2\alpha -4(1+\xi ^j+\xi ^{2j})).$
, we can write $\Delta _j^k=a_{31}a_{33}((1+\xi ^j)^2\alpha -4(1+\xi ^j+\xi ^{2j})).$![]() Clearly, $\Delta _j^k\ne 0$
Clearly, $\Delta _j^k\ne 0$![]() when $\xi ^j=-1$
when $\xi ^j=-1$![]() . Thus, $\Delta _j^k=0$
. Thus, $\Delta _j^k=0$![]() if and only if $\alpha =4(1+\xi ^j+\xi ^{2j})/(1+\xi ^j)^2$
if and only if $\alpha =4(1+\xi ^j+\xi ^{2j})/(1+\xi ^j)^2$![]() , which shows that if $\Delta _j^k=0$
, which shows that if $\Delta _j^k=0$![]() then $\alpha$
then $\alpha$![]() must be real. The discriminant of the quadratic equation $(\xi ^j+1)^2\alpha -4(\xi ^{2j}+\xi ^j+1)=0$
must be real. The discriminant of the quadratic equation $(\xi ^j+1)^2\alpha -4(\xi ^{2j}+\xi ^j+1)=0$![]() in $\xi ^j$
in $\xi ^j$![]() is $4(\alpha -3)$
is $4(\alpha -3)$![]() , so $\alpha <3$
, so $\alpha <3$![]() as the solutions $\xi ^j$
as the solutions $\xi ^j$![]() are not real.
are not real.
(3) Clearly as $\alpha _{j,j'}=({\xi ^j+\xi ^{j'}+\xi ^{j+j'}})/({(1+\xi ^j+\xi ^{j'})^2})$![]() , we have $\alpha _{j,j'}=\alpha _{j',j}$
, we have $\alpha _{j,j'}=\alpha _{j',j}$![]() . Factoring our $\xi ^{2j}$
. Factoring our $\xi ^{2j}$![]() (resp. $\xi ^{2j'}$
(resp. $\xi ^{2j'}$![]() ) from the numerator and denominator gives $\alpha _{k-j,j'-j}=\alpha _{k-j,j'-j}=\alpha _{k-j',j-j'}$
) from the numerator and denominator gives $\alpha _{k-j,j'-j}=\alpha _{k-j,j'-j}=\alpha _{k-j',j-j'}$![]() .
.
We now seek pairs $(l,q)$![]() for which $\alpha _{l,q}=\alpha _{j,j'}$
for which $\alpha _{l,q}=\alpha _{j,j'}$![]() . We know from the above that we have at least three such pairs. To show that these are the only ones, we write $\alpha _{j,j'}=c+id$
. We know from the above that we have at least three such pairs. To show that these are the only ones, we write $\alpha _{j,j'}=c+id$![]() (so $(c,d)\ne (0,0)$
(so $(c,d)\ne (0,0)$![]() ) and represent points on the unit circle, with $-1$
) and represent points on the unit circle, with $-1$![]() removed, in the form $z={(1-t^2)}/{(1+t^2)}+{\rm i}({2t}/{(1+t^2)})$
removed, in the form $z={(1-t^2)}/{(1+t^2)}+{\rm i}({2t}/{(1+t^2)})$![]() and $w={(1-s^2)}/{(1+s^2)}+{\rm i}({2s}/{(1+s^2)})$
and $w={(1-s^2)}/{(1+s^2)}+{\rm i}({2s}/{(1+s^2)})$![]() , with $t,s\in \mathbb {R}$
, with $t,s\in \mathbb {R}$![]() . We set
. We set
The real and imaginary parts of $\alpha _{z,w}-(c+{\rm i}d)$![]() vanish if and only if $P_{(c,d)}(s,t)=Q_{(c,d)}(s,t)=0$
vanish if and only if $P_{(c,d)}(s,t)=Q_{(c,d)}(s,t)=0$![]() , where
, where


Observe that $P_{(c,d)}$![]() and $Q_{(c,d)}$
and $Q_{(c,d)}$![]() are symmetric polynomials. Their resultant with respect to $t$
are symmetric polynomials. Their resultant with respect to $t$![]() vanishes if and only if $s^2=3$
vanishes if and only if $s^2=3$![]() or $R_{(c,d)}(s)=0$
or $R_{(c,d)}(s)=0$![]() , with
, with

We have $s^2=3$![]() if and only if $k=3p$
if and only if $k=3p$![]() and $w=\xi ^p$
and $w=\xi ^p$![]() or $w=\xi ^{2p}$
or $w=\xi ^{2p}$![]() , and this is excluded from the hypotheses. The component $R_{(c,d)}$
, and this is excluded from the hypotheses. The component $R_{(c,d)}$![]() of the resultant is a cubic polynomial in $s^2$
of the resultant is a cubic polynomial in $s^2$![]() provided $c^2+d^2-1\ne 0$
provided $c^2+d^2-1\ne 0$![]() , i.e.$|\alpha _{j,j'}|\ne 1$
, i.e.$|\alpha _{j,j'}|\ne 1$![]() . Suppose that $|\alpha _{j,j'}|\ne 1$
. Suppose that $|\alpha _{j,j'}|\ne 1$![]() . Then the discriminant of $R_{(c,d)}$
. Then the discriminant of $R_{(c,d)}$![]() vanishes if and only if $d=0$
vanishes if and only if $d=0$![]() (i.e.$\alpha _{j,j'}$
(i.e.$\alpha _{j,j'}$![]() is real and this is treated in (4) below) or
is real and this is treated in (4) below) or
For $(c,d)$![]() in the interior region bounded by the curve $\delta _R=0$
in the interior region bounded by the curve $\delta _R=0$![]() (see figure 3), $R_{(c,d)}$
(see figure 3), $R_{(c,d)}$![]() has a unique solution in $s^2$
has a unique solution in $s^2$![]() . As we know that there are at least three distinct solution pairs to the problem, it follows that $(c,d)$
. As we know that there are at least three distinct solution pairs to the problem, it follows that $(c,d)$![]() must be in the exterior region $(R^+)$
must be in the exterior region $(R^+)$![]() bounded by the curve $\delta _R=0$
bounded by the curve $\delta _R=0$![]() .
.

FIGURE 3. Red curve is the discriminant of $R_{(c,d)}$![]() , the blue curve is the unit circle and the green lines are the values of $\alpha _{p,w}$
, the blue curve is the unit circle and the green lines are the values of $\alpha _{p,w}$![]() and $\alpha _{2p,w}$
and $\alpha _{2p,w}$![]() when $k=3p$
when $k=3p$![]() .
.
Observe that $s=0$![]() is a root of $R_{(c,d)}$
is a root of $R_{(c,d)}$![]() if and only if $\delta _R=0$
if and only if $\delta _R=0$![]() . Therefore, the roots of $R_{(c,d)}$
. Therefore, the roots of $R_{(c,d)}$![]() in $s^2$
in $s^2$![]() do not change sign in $(R^+)$
do not change sign in $(R^+)$![]() . Choosing any point in that region, we find that they are all positive. It follows that $R_{(c,d)}$
. Choosing any point in that region, we find that they are all positive. It follows that $R_{(c,d)}$![]() has six roots $\pm s_1,\pm s_2,\pm s_3$
has six roots $\pm s_1,\pm s_2,\pm s_3$![]() . These correspond to six points on the unit circle $w_1,w_2,w_3$
. These correspond to six points on the unit circle $w_1,w_2,w_3$![]() and $\overline {w}_1,\overline {w}_2,\overline {w}_3.$
and $\overline {w}_1,\overline {w}_2,\overline {w}_3.$![]()
For each root of $R_{(c,d)}$![]() we show, by considering the subresultant (see e.g. [Reference El Kahoui18]) of $P_{(c,d)}$
we show, by considering the subresultant (see e.g. [Reference El Kahoui18]) of $P_{(c,d)}$![]() and $Q_{(c,d)}$
and $Q_{(c,d)}$![]() that $P_{(c,d)}(\pm s_i,t)$
that $P_{(c,d)}(\pm s_i,t)$![]() and $Q_{(c,d)}(\pm s_i,t)$
and $Q_{(c,d)}(\pm s_i,t)$![]() have only one common root. As $P_{(c,d)}$
have only one common root. As $P_{(c,d)}$![]() and $Q_{(c,d)}$
and $Q_{(c,d)}$![]() are symmetric polynomials, that common root is a root of $R_{(c,d)}$
are symmetric polynomials, that common root is a root of $R_{(c,d)}$![]() . Interchanging $w_i$
. Interchanging $w_i$![]() with $\overline {w}_i$
with $\overline {w}_i$![]() if necessary, we can set $w_1=\xi ^j$
if necessary, we can set $w_1=\xi ^j$![]() , $w_1=\xi ^{k-j}$
, $w_1=\xi ^{k-j}$![]() , $w_1=\xi ^{k-j'}$
, $w_1=\xi ^{k-j'}$![]() , Then the solutions of $\alpha _{z,w}-c-id=0$
, Then the solutions of $\alpha _{z,w}-c-id=0$![]() are exactly, up to permutation of $z$
are exactly, up to permutation of $z$![]() and $w$
and $w$![]() , $(\xi ^j,\xi ^{j'})$
, $(\xi ^j,\xi ^{j'})$![]() , $(\xi ^{k-j},\xi ^{j'-j})$
, $(\xi ^{k-j},\xi ^{j'-j})$![]() , $(\xi ^{k-j'},\xi ^{j-j'})$
, $(\xi ^{k-j'},\xi ^{j-j'})$![]() .
.
We turn now to the case when $|\alpha _{j,j'}|=1$![]() , i.e. $c^2+d^2-1=0$
, i.e. $c^2+d^2-1=0$![]() . This occurs if and only if $2\mid k$
. This occurs if and only if $2\mid k$![]() and $j'=j+{k}/{2}$
and $j'=j+{k}/{2}$![]() or $j'={k}/{2}$
or $j'={k}/{2}$![]() . Suppose that $2\mid k$
. Suppose that $2\mid k$![]() and $j'=j+{k}/{2}$
and $j'=j+{k}/{2}$![]() . Then $\alpha _{j,j+{k}/{2}}=-\xi ^{2j}$
. Then $\alpha _{j,j+{k}/{2}}=-\xi ^{2j}$![]() , and $\alpha _{l,l+{k}/{2}}= \alpha _{j,j+{k}/{2}}$
, and $\alpha _{l,l+{k}/{2}}= \alpha _{j,j+{k}/{2}}$![]() if, and only if, $l=j$
if, and only if, $l=j$![]() or $l=j+{k}/{2}$
or $l=j+{k}/{2}$![]() . In both cases, we get only the pair $(j,j+{k}/{2})$
. In both cases, we get only the pair $(j,j+{k}/{2})$![]() . Now $\alpha _{{k}/{2},l}=-\xi ^{-2l}$
. Now $\alpha _{{k}/{2},l}=-\xi ^{-2l}$![]() , so $\alpha _{{k}/{2},l}=\alpha _{j,j+{k}/{2}}$
, so $\alpha _{{k}/{2},l}=\alpha _{j,j+{k}/{2}}$![]() if and only if $l=k-j$
if and only if $l=k-j$![]() or $l= {k}/{2}-j$
or $l= {k}/{2}-j$![]() . This shows that $\alpha _{j,j+{k}/{2}}=\alpha _{k-j,{k}/{2}}=\alpha _{{k}/{2}-j,{k}/{2}}$
. This shows that $\alpha _{j,j+{k}/{2}}=\alpha _{k-j,{k}/{2}}=\alpha _{{k}/{2}-j,{k}/{2}}$![]() and the equality $\alpha _{j,j+{k}/{2}}= \alpha _{l,q}$
and the equality $\alpha _{j,j+{k}/{2}}= \alpha _{l,q}$![]() holds only for these three pairs.
holds only for these three pairs.
(4) We can write $\alpha _{j,j'}$![]() in the form
in the form
Therefore, $\alpha _{j,j'}$![]() is real if and only if $\zeta =\xi ^{j-2j'}+\xi ^{j+j'} + \xi ^{j'-2j}$
is real if and only if $\zeta =\xi ^{j-2j'}+\xi ^{j+j'} + \xi ^{j'-2j}$![]() is real. Setting $\theta =j-2j'$
is real. Setting $\theta =j-2j'$![]() and $\phi =j'-2j$
and $\phi =j'-2j$![]() , we get $\Im (\zeta )=\sin ({2\pi \theta }/{k})+\sin ({2\pi \phi }/{k})-\sin ({(2\pi (\theta +\phi ))}/{k})$
, we get $\Im (\zeta )=\sin ({2\pi \theta }/{k})+\sin ({2\pi \phi }/{k})-\sin ({(2\pi (\theta +\phi ))}/{k})$![]() . Then
. Then

Now, $\sin ({(\pi (\theta +\phi ))}/{k})=0$![]() when $j'=k-j$
when $j'=k-j$![]() and $\cos ({(\pi (\theta -\phi ))}/{k})=\cos ({(\pi (\theta \!+\!\phi ))} /{k})$
and $\cos ({(\pi (\theta -\phi ))}/{k})=\cos ({(\pi (\theta \!+\!\phi ))} /{k})$![]() when $j'=2j$
when $j'=2j$![]() or $j=2j'$
or $j=2j'$![]() . Clearly, $\alpha _{j,k-j}=1/(1+\xi ^j+\xi ^{k-j})=\alpha _{j,2j}.$
. Clearly, $\alpha _{j,k-j}=1/(1+\xi ^j+\xi ^{k-j})=\alpha _{j,2j}.$![]()
(5) As $a_{31}a_{33}\ne 0$![]() , we can write $\Omega _{j,j'}^k=a_{31}a_{33}(1-\alpha _{j,j'}\alpha )$
, we can write $\Omega _{j,j'}^k=a_{31}a_{33}(1-\alpha _{j,j'}\alpha )$![]() , so $\Omega _{j,j'}^k=0$
, so $\Omega _{j,j'}^k=0$![]() if and only if $\alpha _{j,j'}=1/\alpha$
if and only if $\alpha _{j,j'}=1/\alpha$![]() and the statement follows by (4).
and the statement follows by (4).
(6) When $\alpha$![]() is real, by (4), we have $\Omega _{j_0,k-j_0}=0$
is real, by (4), we have $\Omega _{j_0,k-j_0}=0$![]() when $\xi ^j_0+\xi ^{k-j_0}+1=\alpha$
when $\xi ^j_0+\xi ^{k-j_0}+1=\alpha$![]() . It follows that $\xi ^j_0=\eta _1$
. It follows that $\xi ^j_0=\eta _1$![]() with $\eta _1={(\alpha -1)}/{2}\pm {\rm i}\sqrt {1-({(\alpha -1)}/{2})^2}.$
with $\eta _1={(\alpha -1)}/{2}\pm {\rm i}\sqrt {1-({(\alpha -1)}/{2})^2}.$![]() Suppose that there exist a $j$
Suppose that there exist a $j$![]() for which $\Delta _{j}^k=0$
for which $\Delta _{j}^k=0$![]() , equivalently, $\xi ^{2j}+({2(\alpha -2)}/{(\alpha -4)})\xi ^j+1=0$
, equivalently, $\xi ^{2j}+({2(\alpha -2)}/{(\alpha -4)})\xi ^j+1=0$![]() . Then $\xi ^j+\xi ^{k-j}=-({(2\alpha -2)}/{(\alpha -4)})$
. Then $\xi ^j+\xi ^{k-j}=-({(2\alpha -2)}/{(\alpha -4)})$![]() which gives $\xi _j=\eta _2$
which gives $\xi _j=\eta _2$![]() with $\eta _2=-({(\alpha -2)}/{(\alpha -4)})\pm {\rm i}\sqrt {1-({(\alpha -2)}/{(\alpha -4)})^2}.$
with $\eta _2=-({(\alpha -2)}/{(\alpha -4)})\pm {\rm i}\sqrt {1-({(\alpha -2)}/{(\alpha -4)})^2}.$![]() We have $\eta _1=\eta _2$
We have $\eta _1=\eta _2$![]() if and only if $\alpha =0$
if and only if $\alpha =0$![]() or $3$
or $3$![]() . Then $k=3p$
. Then $k=3p$![]() and $j_0=p$
and $j_0=p$![]() or $2p$
or $2p$![]() , which is excluded from our hypotheses, so $\eta _1\ne \eta _2$
, which is excluded from our hypotheses, so $\eta _1\ne \eta _2$![]() .
.
The complex number $\eta _1$![]() (resp. $\eta _2$
(resp. $\eta _2$![]() ) is a $k{\rm {th}}$
) is a $k{\rm {th}}$![]() -root of unity if and only if $\alpha$
-root of unity if and only if $\alpha$![]() is a root of the polynomial $P_1(\alpha )$
is a root of the polynomial $P_1(\alpha )$![]() (resp. $P_2(\alpha )$
(resp. $P_2(\alpha )$![]() ) of degree $k$
) of degree $k$![]() obtained by taking the numerator of $\Re ({\eta _1}^k)-1$
obtained by taking the numerator of $\Re ({\eta _1}^k)-1$![]() (resp. $\Re ({\eta _2}^k)-1$
(resp. $\Re ({\eta _2}^k)-1$![]() ). But if $P_1$
). But if $P_1$![]() and $P_2$
and $P_2$![]() have one common root, all the other roots must also be common. (This follows from the fact that the map $\cos \theta =-(\alpha -2)/(\alpha -4)$
have one common root, all the other roots must also be common. (This follows from the fact that the map $\cos \theta =-(\alpha -2)/(\alpha -4)$![]() is a bijection for $\alpha \in (-\infty,3]$
is a bijection for $\alpha \in (-\infty,3]$![]() and $\cos \theta =(\alpha -1)/2$
and $\cos \theta =(\alpha -1)/2$![]() is also a bijection for $\alpha \in (-1,3]$
is also a bijection for $\alpha \in (-1,3]$![]() .) As $P_1$
.) As $P_1$![]() and $P_2$
and $P_2$![]() are distinct polynomials, it follows that they have no common roots. Consequently, $\Delta _{j}^k\ne 0$
are distinct polynomials, it follows that they have no common roots. Consequently, $\Delta _{j}^k\ne 0$![]() for all $j$
for all $j$![]() .
.
The argument for showing that $\Omega ^k_{j,k-j}\ne 0$![]() when $\Delta _{j_0}^k=0$
when $\Delta _{j_0}^k=0$![]() is the same as above.
is the same as above.
(7) We have, with the hypothesis, $\mathcal {D}_j\cdot \mathcal {D}_{j'}=\operatorname {dim}_{\mathbb {C}}\mathcal {O}_2/\left \langle xy,x^2+y^2\right \rangle =4$![]() .
.
In view of proposition 4.21(7), we give in the rest of this section $\mathcal {D}_j\cdot \mathcal {D}_{j'}$![]() for the exceptional branches only, i.e. when one or both branches have a singularity more degenerate than $A_1$
for the exceptional branches only, i.e. when one or both branches have a singularity more degenerate than $A_1$![]() or one or both of their components are tangential (which is equivalent to $\mathcal {D}_j\cdot \mathcal {D}_{j'}>4$
or one or both of their components are tangential (which is equivalent to $\mathcal {D}_j\cdot \mathcal {D}_{j'}>4$![]() ). We start with the case when all the branches have an $A_1$
). We start with the case when all the branches have an $A_1$![]() -singularity.
-singularity.
Proposition 4.22 Suppose that $a_{11}=a_{21}=a_{22}=0$![]() , $a_{31}a_{33}\ne 0$
, $a_{31}a_{33}\ne 0$![]() and $\Delta _j^k\ne 0$
and $\Delta _j^k\ne 0$![]() for all $j$
for all $j$![]() . Any $k$
. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() satisfying the additional conditions in ${\rm {(a)}}$
satisfying the additional conditions in ${\rm {(a)}}$![]() or ${\rm {(b)}}$
or ${\rm {(b)}}$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to one of the following germs:
-determined and is topologically equivalent to one of the following germs:
Every branch of the double-point curve has an $A_1$![]() -singularity and the invariants associated to the germs in these strata are as in table 7.
-singularity and the invariants associated to the germs in these strata are as in table 7.
(a) If $3\nmid k$
 and $\Omega ^k_{j,j'}\ne 0$
and $\Omega ^k_{j,j'}\ne 0$ for all distinct pairs, then $F_k$
for all distinct pairs, then $F_k$ is topologically equivalent to ${\bf U}^k_{3}$
is topologically equivalent to ${\bf U}^k_{3}$ .
.(b) Suppose that $k=3p$
 and $\Omega ^k_{j,j'}\ne 0$
and $\Omega ^k_{j,j'}\ne 0$ for all distinct pairs with $j,j'\ne \{p,2p\}$
for all distinct pairs with $j,j'\ne \{p,2p\}$ .
.
If $a_{44}\ne 0$
 , then ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=5$
, then ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=5$ and $F_k$
and $F_k$ is topologically equivalent to ${\bf U}^k_{3}$
is topologically equivalent to ${\bf U}^k_{3}$ .
.If $a_{44}=0$
 and $CndUm_8\ne 0$
and $CndUm_8\ne 0$ , then ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=8$
, then ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=8$ and $F_k$
and $F_k$ is topologically equivalent to ${\bf U}^k_{4}$
is topologically equivalent to ${\bf U}^k_{4}$ .
.
Proof. Each branch of the double-point curve consists of a transverse intersection of two regular curves. In (a) all of these curves are pairwise transverse.
In (b), $j^2\lambda _s(x,y)=x(a_{31}x+a_{32}\vartheta _{2s}y)$![]() for $s=p,2p$
for $s=p,2p$![]() . Observe that $a_{32}\ne 0$
. Observe that $a_{32}\ne 0$![]() as we supposed $\Delta ^k_s\ne 0$
as we supposed $\Delta ^k_s\ne 0$![]() , so the branches $\mathcal {D}_p$
, so the branches $\mathcal {D}_p$![]() and $\mathcal {D}_{2p}$
and $\mathcal {D}_{2p}$![]() have one common line $x=0$
have one common line $x=0$![]() in their tangent cone and their associated curves tangent to this line are parametrized by $t\mapsto (\gamma _s(t),t)$
in their tangent cone and their associated curves tangent to this line are parametrized by $t\mapsto (\gamma _s(t),t)$![]() with $\gamma _s(t)=-(a_{44}/({\vartheta _{2s} a_{32}}))t^2+O(3)$
with $\gamma _s(t)=-(a_{44}/({\vartheta _{2s} a_{32}}))t^2+O(3)$![]() , so they have order of contact 2 when $a_{44}\ne 0$
, so they have order of contact 2 when $a_{44}\ne 0$![]() . Then $\mathcal {D}_p\cdot \mathcal {D}_{2p}=\operatorname {dim}_{\mathbb {C}}\mathcal {O}_2/\left \langle xy,x^2+y^3\right \rangle =5$
. Then $\mathcal {D}_p\cdot \mathcal {D}_{2p}=\operatorname {dim}_{\mathbb {C}}\mathcal {O}_2/\left \langle xy,x^2+y^3\right \rangle =5$![]() .
.
When $a_{44}=0$![]() , the two curves are parametrized by $t\mapsto (\gamma _s(t),t)$
, the two curves are parametrized by $t\mapsto (\gamma _s(t),t)$![]() with
with
and have contact order 5 when $(a_{55}(a_{31}a_{55}-a_{54}a_{32})+a_{77}a_{32}^2\ne 0$![]() , i.e.$CndUm_8\ne 0$
, i.e.$CndUm_8\ne 0$![]() . Then $\mathcal {D}_p\cdot \mathcal {D}_{2p}=\operatorname {dim}_{\mathbb {C}}\mathcal {O}_2/\left \langle xy,x^2+y^6\right \rangle =8.$
. Then $\mathcal {D}_p\cdot \mathcal {D}_{2p}=\operatorname {dim}_{\mathbb {C}}\mathcal {O}_2/\left \langle xy,x^2+y^6\right \rangle =8.$![]()
For the topological normal forms, we choose $a_{31},a_{32},a_{33}$![]() real with $\alpha > 3$
real with $\alpha > 3$![]() . By proposition 4.21(2), all $\Delta _j^k$
. By proposition 4.21(2), all $\Delta _j^k$![]() are non-zero. Also, by proposition 4.21(4) and (5) $\Omega _{j,k-j}=0$
are non-zero. Also, by proposition 4.21(4) and (5) $\Omega _{j,k-j}=0$![]() when $\xi ^j+\xi ^{k-j}+1=\alpha$
when $\xi ^j+\xi ^{k-j}+1=\alpha$![]() , which cannot happen when $\alpha >3$
, which cannot happen when $\alpha >3$![]() , so the $\Omega _{j,j'}^k$
, so the $\Omega _{j,j'}^k$![]() in (a) and (b) are non-zero. As the strata are connected sets, we can choose $a_{31}=a_{32}=1,a_{32}=2$
in (a) and (b) are non-zero. As the strata are connected sets, we can choose $a_{31}=a_{32}=1,a_{32}=2$![]() so that the conditions on $\Delta _j^k$
so that the conditions on $\Delta _j^k$![]() and $\Omega _{j,j'}^k$
and $\Omega _{j,j'}^k$![]() are satisfied.
are satisfied.
The number of triple points is calculated as in proposition 4.16. If $k=3p$![]() , the germ ${\bf U}^k_{3}$
, the germ ${\bf U}^k_{3}$![]() (resp. ${\bf U}^k_{4}$
(resp. ${\bf U}^k_{4}$![]() ) has $T_{p,2p}=3$
) has $T_{p,2p}=3$![]() (resp. $T_{p,2p}=6$
(resp. $T_{p,2p}=6$![]() ), while all other indices $j$
), while all other indices $j$![]() and $j'$
and $j'$![]() give $T_{j,j'}=2$
give $T_{j,j'}=2$![]() .
.
Proposition 4.23 Suppose that $a_{11}=a_{21}=a_{22}=0$![]() , $a_{31}a_{33}\ne 0$
, $a_{31}a_{33}\ne 0$![]() , $a_{32}\ne 0$
, $a_{32}\ne 0$![]() and $\Omega ^k_{j_0,j_0'}=0$
and $\Omega ^k_{j_0,j_0'}=0$![]() for some pair $(j_0,j'_0)$
for some pair $(j_0,j'_0)$![]() , with $j_0,j'_0\notin \{p,2p\}$
, with $j_0,j'_0\notin \{p,2p\}$![]() when $k=3p$
when $k=3p$![]() . Then ${\mathcal {D}}_{s}\cdot \mathcal {D}_{q}=5$
. Then ${\mathcal {D}}_{s}\cdot \mathcal {D}_{q}=5$![]() for $(s,q)\in \{(j_0,j'_0), (k-j_0,j'_0-j_0), (k-j'_0,j_0-j'_0)\}$
for $(s,q)\in \{(j_0,j'_0), (k-j_0,j'_0-j_0), (k-j'_0,j_0-j'_0)\}$![]() if and only if ${CndVm_5}_{j_0,j_0'}\ne 0$
if and only if ${CndVm_5}_{j_0,j_0'}\ne 0$![]() . For $k=3p$
. For $k=3p$![]() , we have ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=5$
, we have ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=5$![]() if and only if $a_{44}\ne 0$
if and only if $a_{44}\ne 0$![]() . Any $k$
. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() satisfying the above conditions is finitely $\mathcal {A}$
satisfying the above conditions is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to
-determined and is topologically equivalent to

The invariants associated to germs in these strata are as in table 7.
Proof. When $a_{32}=0$![]() and $k=3p$
and $k=3p$![]() , we have $\Delta _p^k=\Delta _{2p}^k=0$
, we have $\Delta _p^k=\Delta _{2p}^k=0$![]() . This case is dealt with in proposition 4.25. With the hypothesis and proposition 4.21(5), we have $\Omega _{j_0,j'_0}=\Omega _{k-j_0,j'_0-j_0}=\Omega _{k-j'_0,j_0-j'_0}=0.$
. This case is dealt with in proposition 4.25. With the hypothesis and proposition 4.21(5), we have $\Omega _{j_0,j'_0}=\Omega _{k-j_0,j'_0-j_0}=\Omega _{k-j'_0,j_0-j'_0}=0.$![]()
We need to consider the order of contact between the two tangential components of the pairs $(\mathcal {D}_{s},\mathcal {D}_{q})$![]() with $(s,q)\in \{(j_0,j'_0), (k-j_0,j'_0-j_0), (k-j'_0,j_0-j'_0)\}$
with $(s,q)\in \{(j_0,j'_0), (k-j_0,j'_0-j_0), (k-j'_0,j_0-j'_0)\}$![]() . Using the fact that if two quadratic equations $x^2+a_ix+b_i=0$
. Using the fact that if two quadratic equations $x^2+a_ix+b_i=0$![]() , $i=1,2$
, $i=1,2$![]() , have one root in common, then the root is given by $x=-(b_1-b_2)/(a_1-a_2)$
, have one root in common, then the root is given by $x=-(b_1-b_2)/(a_1-a_2)$![]() , we can get the initial terms of parametrizations of the tangential components of the above pairs. These are given by $t\mapsto (t,\gamma _l(t))$
, we can get the initial terms of parametrizations of the tangential components of the above pairs. These are given by $t\mapsto (t,\gamma _l(t))$![]() , $l=s,q$
, $l=s,q$![]() , with $\gamma _l(t)= -{a_{33}}/{a_{32}}(1+\xi ^{s}+\xi ^{q})t+\lambda _lt^2+O(3), l=s,q.$
, with $\gamma _l(t)= -{a_{33}}/{a_{32}}(1+\xi ^{s}+\xi ^{q})t+\lambda _lt^2+O(3), l=s,q.$![]() A calculation shows that $\lambda _s-\lambda _q=0$
A calculation shows that $\lambda _s-\lambda _q=0$![]() if and only if
if and only if
with
Observe that $\beta _{j,j'}=\beta _{k-j,j'-j}=\beta _{k-j',j-j'}$![]() , so ${CndVm_5}_{s,q}$
, so ${CndVm_5}_{s,q}$![]() has the same value for $(s,q)\in \{ (j_0,j'_0), (k-j_0,j'_0-j_0), (k-j'_0,j_0-j'_0)\}.$
has the same value for $(s,q)\in \{ (j_0,j'_0), (k-j_0,j'_0-j_0), (k-j'_0,j_0-j'_0)\}.$![]() It follows that ${\mathcal {D}}_{s}\cdot \mathcal {D}_{q}=\operatorname {dim}_{\mathbb {C}}\mathcal {O}_2/\left < xy,x^2+y^3\right >=5$
It follows that ${\mathcal {D}}_{s}\cdot \mathcal {D}_{q}=\operatorname {dim}_{\mathbb {C}}\mathcal {O}_2/\left < xy,x^2+y^3\right >=5$![]() if and only if ${CndVm_5}_{j_0,j_0'}\ne 0$
if and only if ${CndVm_5}_{j_0,j_0'}\ne 0$![]() .
.
For the topological model, we take $a_{31}=a_{32}=1$![]() and $a_{33}=\alpha _{j_0,j'_0}$
and $a_{33}=\alpha _{j_0,j'_0}$![]() so $\Omega _{j_0,j'_0}=0$
so $\Omega _{j_0,j'_0}=0$![]() . We also set $a_{44}=1$
. We also set $a_{44}=1$![]() , $a_{42}=a_{43}=0$
, $a_{42}=a_{43}=0$![]() , then ${CndVm_5}_{j_0,j'_0}=\beta _{j_0,j'_0} +a_{41}\alpha _{j_0,j'_0}^3$
, then ${CndVm_5}_{j_0,j'_0}=\beta _{j_0,j'_0} +a_{41}\alpha _{j_0,j'_0}^3$![]() . We set $a_{41}=1-\beta _{j_0,j'_0}/\alpha _{j_0,j'_0}^3$
. We set $a_{41}=1-\beta _{j_0,j'_0}/\alpha _{j_0,j'_0}^3$![]() , so that ${CndVm_5}_{j_0,j'_0}\ne 0$
, so that ${CndVm_5}_{j_0,j'_0}\ne 0$![]() . For calculating the triple points, we find that $T_{j,j'}=3$
. For calculating the triple points, we find that $T_{j,j'}=3$![]() for all $j$
for all $j$![]() and $j'$
and $j'$![]() with $j\ne j'$
with $j\ne j'$![]() .
.
We deal now with the case when one pair of branches of the double-point curve has a singularity more degenerate than $A_1$![]() (see proposition 4.21(1)).
(see proposition 4.21(1)).
Remark 4.24 For $k=3p$![]() , the singularities ${\bf U}^k_4$
, the singularities ${\bf U}^k_4$![]() and ${\bf V}^{k,j,j'}_4$
and ${\bf V}^{k,j,j'}_4$![]() have the same invariants, but the intersection numbers between their double-point branches shows that they are not topologically equivalent.
have the same invariants, but the intersection numbers between their double-point branches shows that they are not topologically equivalent.
Proposition 4.25 Suppose that $a_{11}=a_{21}=a_{22}=0$![]() , $a_{31}a_{33}\ne 0$
, $a_{31}a_{33}\ne 0$![]() . The strata below are of codimension $4$
. The strata below are of codimension $4$![]() , and the invariants associated to germs in the strata are as in table 7.
, and the invariants associated to germs in the strata are as in table 7.
${\rm {(1)}}$![]() Suppose that $\Delta _{j_0}^k=\Delta _{k-j_0}^k=0$
Suppose that $\Delta _{j_0}^k=\Delta _{k-j_0}^k=0$![]() , with $j_0\notin \{ p,2p\}$
, with $j_0\notin \{ p,2p\}$![]() when $k=3p$
when $k=3p$![]() (so $a_{32}\ne 0{)}$
(so $a_{32}\ne 0{)}$![]() . The branches $\mathcal {D}_{j_0}$
. The branches $\mathcal {D}_{j_0}$![]() and $\mathcal {D}_{k-j_0}$
and $\mathcal {D}_{k-j_0}$![]() have an $A_2$
have an $A_2$![]() -singularity if and only if $CndWA_2\ne 0$
-singularity if and only if $CndWA_2\ne 0$![]() . We have ${\mathcal {D}}_{j_0}\cdot \mathcal {D}_{j}={\mathcal {D}}_{k-j_0}\cdot \mathcal {D}_{j}=4$
. We have ${\mathcal {D}}_{j_0}\cdot \mathcal {D}_{j}={\mathcal {D}}_{k-j_0}\cdot \mathcal {D}_{j}=4$![]() for all distinct pairs. When $k=3p$
for all distinct pairs. When $k=3p$![]() and $a_{44}\ne 0$
and $a_{44}\ne 0$![]() , we have ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=5$
, we have ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=5$![]() . Any $k$
. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() satisfying the above conditions is $\mathcal {A}$
satisfying the above conditions is $\mathcal {A}$![]() -finitely determined and is topologically equivalent to
-finitely determined and is topologically equivalent to
${\rm {(2)}}$![]() If $k=3p$
If $k=3p$![]() and $j_0=p$
and $j_0=p$![]() , then ${\mathcal {D}}_p$
, then ${\mathcal {D}}_p$![]() and $\mathcal {D}_{2p}$
and $\mathcal {D}_{2p}$![]() have an $A_2$
have an $A_2$![]() -singularity if and only if $a_{44}\ne 0$
-singularity if and only if $a_{44}\ne 0$![]() . We have ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=8$
. We have ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=8$![]() if and only if ${Cnd\widetilde {W}m}_8\ne 0$
if and only if ${Cnd\widetilde {W}m}_8\ne 0$![]() , and ${\mathcal {D}}_s\cdot \mathcal {D}_j=5$
, and ${\mathcal {D}}_s\cdot \mathcal {D}_j=5$![]() for $s=p,2p$
for $s=p,2p$![]() and $j\ne s$
and $j\ne s$![]() . Any $k$
. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() satisfying the above conditions is $\mathcal {A}$
satisfying the above conditions is $\mathcal {A}$![]() -finitely determined and is topologically equivalent to
-finitely determined and is topologically equivalent to
Proof. The condition for an $A_2$![]() -singularity of $\mathcal {D}_{j_0}$
-singularity of $\mathcal {D}_{j_0}$![]() and $\mathcal {D}_{k-j_0}$
and $\mathcal {D}_{k-j_0}$![]() follows by analysing the 3-jets of, respectively, $\lambda _{j_0}$
follows by analysing the 3-jets of, respectively, $\lambda _{j_0}$![]() and $\lambda _{k-j_0}$
and $\lambda _{k-j_0}$![]() . Observe that when $2\mid k$
. Observe that when $2\mid k$![]() , $\xi ^{j_0}=-1$
, $\xi ^{j_0}=-1$![]() is a solution of $\Delta _{j_0}^k=\Delta _{k-j_0}^k=0$
is a solution of $\Delta _{j_0}^k=\Delta _{k-j_0}^k=0$![]() if and only if $a_{31}a_{33}=0$
if and only if $a_{31}a_{33}=0$![]() . As we are assuming $a_{31}a_{33}\ne 0$
. As we are assuming $a_{31}a_{33}\ne 0$![]() , we have $j_0\ne k/2$
, we have $j_0\ne k/2$![]() in (1) when $2\mid k$
in (1) when $2\mid k$![]() .
.
With the hypothesis in (1), ${\mathcal {D}}_{j_0}\cdot \mathcal {D}_{j}={\mathcal {D}}_{k-j_0}\cdot \mathcal {D}_{j}=\operatorname {dim}_{\mathbb {C}}\mathcal {O}_2/\left \langle x^2+y^3,x^2-y^2\right \rangle =4$![]() for any distinct pairs.
for any distinct pairs.
For (2), we have ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=\operatorname {dim}_{\mathbb {C}}\mathcal {O}_2/\left \langle x^2+y^3,y^4\right \rangle =8$![]() when ${Cnd\widetilde {W}m}_8\ne 0$
when ${Cnd\widetilde {W}m}_8\ne 0$![]() .
.
For the topological normal forms, we use the fact that $\Delta _{j_0}^k=0$![]() if and only if $\alpha ={a_{32}^2}/({a_{31}a_{33}})=4(\xi ^{2j_0}+\xi ^{j_0}+1)/{(\xi ^{j_0}+1)^2}$
if and only if $\alpha ={a_{32}^2}/({a_{31}a_{33}})=4(\xi ^{2j_0}+\xi ^{j_0}+1)/{(\xi ^{j_0}+1)^2}$![]() (see the proof of proposition 4.21) and set $a_{31}=a_{32}=1$
(see the proof of proposition 4.21) and set $a_{31}=a_{32}=1$![]() , so $a_{33}={(\xi ^{j_0}+1)^2}/{4(\xi ^{2j_0}+\xi ^{j_0}+1)}$
, so $a_{33}={(\xi ^{j_0}+1)^2}/{4(\xi ^{2j_0}+\xi ^{j_0}+1)}$![]() . We have $T_{j,j'}=2$
. We have $T_{j,j'}=2$![]() for all $j$
for all $j$![]() and $j'$
and $j'$![]() with $j\ne j'$
with $j\ne j'$![]() .
.
Proposition 4.26 Suppose that $a_{11}=a_{21}=a_{22}=0$![]() , $a_{31}=0$
, $a_{31}=0$![]() , $a_{33}a_{32}\ne 0$
, $a_{33}a_{32}\ne 0$![]() . All the branches of the double-point curve share only one line in their tangent cones except when $k=3p$
. All the branches of the double-point curve share only one line in their tangent cones except when $k=3p$![]() where the branches $\mathcal {D}_p$
where the branches $\mathcal {D}_p$![]() and $\mathcal {D}_{2p}$
and $\mathcal {D}_{2p}$![]() have the same tangent cone. Any $k$
have the same tangent cone. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() satisfying the additional conditions in ${\rm {(a)}}$
satisfying the additional conditions in ${\rm {(a)}}$![]() , ${\rm {(b)}}$
, ${\rm {(b)}}$![]() , ${\rm {(c)}}$
, ${\rm {(c)}}$![]() or ${\rm {(d)}}$
or ${\rm {(d)}}$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to
-determined and is topologically equivalent to
The stratum is of codimension $4$![]() , and the invariants associated to the germs in the strata above are as in table 7.
, and the invariants associated to the germs in the strata above are as in table 7.
(a) If $2\nmid k$
 , $3\nmid k$
, $3\nmid k$ , all of the branches $\mathcal {D}_{j}$
, all of the branches $\mathcal {D}_{j}$ of the double-point curve have an $A_1$
of the double-point curve have an $A_1$ -singularity and ${\mathcal {D}}_j\cdot \mathcal {D}_{j'}=5$
-singularity and ${\mathcal {D}}_j\cdot \mathcal {D}_{j'}=5$ , $j\ne j'$
, $j\ne j'$ , when $a_{41}\ne 0$
, when $a_{41}\ne 0$ .
.(b) If $k=2p$
 , $3\nmid k$
, $3\nmid k$ , the branches $\mathcal {D}_{j}$
, the branches $\mathcal {D}_{j}$ , $j\ne p$
, $j\ne p$ , behave as in ${\rm {(a)}}$
, behave as in ${\rm {(a)}}$ . The branch $\mathcal {D}_p$
. The branch $\mathcal {D}_p$ has an $A_2$
has an $A_2$ -singularity if and only if $a_{41}\ne 0$
-singularity if and only if $a_{41}\ne 0$ . We also have ${\mathcal {D}}_j\cdot \mathcal {D}_{p}=5$
. We also have ${\mathcal {D}}_j\cdot \mathcal {D}_{p}=5$ , $j\ne p$
, $j\ne p$ .
.(c) If $k=3p$
 , $2\nmid k$
, $2\nmid k$ , the branches $\mathcal {D}_{j}$
, the branches $\mathcal {D}_{j}$ behave as in ${\rm {(a)}}$
behave as in ${\rm {(a)}}$ except for $\mathcal {D}_{p}$
except for $\mathcal {D}_{p}$ and $\mathcal {D}_{2p}$
and $\mathcal {D}_{2p}$ where ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=6$
where ${\mathcal {D}}_p\cdot \mathcal {D}_{2p}=6$ when $a_{41}a_{44}\ne 0$
when $a_{41}a_{44}\ne 0$ .
.(d) If $k=6p$
 , when $a_{41}a_{44}\ne 0$
, when $a_{41}a_{44}\ne 0$ , the exceptional branches of the double-point curve behave as in ${\rm {(b)}}$
, the exceptional branches of the double-point curve behave as in ${\rm {(b)}}$ and ${\rm {(c)}}$
and ${\rm {(c)}}$ , the remaining branches behave as in ${\rm {(a)}}$
, the remaining branches behave as in ${\rm {(a)}}$ .
.
Proof. We have $j^2\lambda _j(x,y)= y(\vartheta _{2j}a_{32}x+\vartheta _{3j}a_{33}y)$![]() . For (a), ${\vartheta _{2j}}\ne 0$
. For (a), ${\vartheta _{2j}}\ne 0$![]() for all $j$
for all $j$![]() and ${\vartheta _{2j}}/{\vartheta _{2j}}\ne {\vartheta _{3j'}}/{\vartheta _{2j'}}$
and ${\vartheta _{2j}}/{\vartheta _{2j}}\ne {\vartheta _{3j'}}/{\vartheta _{2j'}}$![]() for $j\ne j'$
for $j\ne j'$![]() , so all of the branches of the double-point curve have an $A_1$
, so all of the branches of the double-point curve have an $A_1$![]() -singularity and one common line $y=0$
-singularity and one common line $y=0$![]() in their tangent cone. The component of ${\mathcal {D}}_j$
in their tangent cone. The component of ${\mathcal {D}}_j$![]() with tangent $y=0$
with tangent $y=0$![]() can be parametrized by $t\mapsto (t,\gamma _j(t))$
can be parametrized by $t\mapsto (t,\gamma _j(t))$![]() with by $\gamma _j(t)=-{a_{41}}/({(1+\xi ^j)a_{32}})t^2+O(3)$
with by $\gamma _j(t)=-{a_{41}}/({(1+\xi ^j)a_{32}})t^2+O(3)$![]() . Therefore, when $a_{41}\ne 0$
. Therefore, when $a_{41}\ne 0$![]() , we have ${\mathcal {D}}_j\cdot \mathcal {D}_{j'}=\operatorname {dim}_{\mathbb {C}} \mathcal {O}_2/\left \langle xy,y^2+x^3\right \rangle =5$
, we have ${\mathcal {D}}_j\cdot \mathcal {D}_{j'}=\operatorname {dim}_{\mathbb {C}} \mathcal {O}_2/\left \langle xy,y^2+x^3\right \rangle =5$![]() .
.
The remaining parts of the proof follow similarly and are omitted.
Proposition 4.27 Suppose that $a_{11}=a_{21}=a_{22}=0$![]() , $a_{33}=0$
, $a_{33}=0$![]() , $a_{31}a_{32}\ne 0$
, $a_{31}a_{32}\ne 0$![]() . All the branches of the double-point curve share only one line in their tangent cones. Any $k$
. All the branches of the double-point curve share only one line in their tangent cones. Any $k$![]() -folding map-germ $F_k$
-folding map-germ $F_k$![]() satisfying the additional conditions in ${\rm {(a)}}$
satisfying the additional conditions in ${\rm {(a)}}$![]() or ${\rm {(b)}}$
or ${\rm {(b)}}$![]() is finitely $\mathcal {A}$
is finitely $\mathcal {A}$![]() -determined and is topologically equivalent to
-determined and is topologically equivalent to
The stratum is of codimension $4$![]() , and the invariants associated to germs in the stratum are as in table 7.
, and the invariants associated to germs in the stratum are as in table 7.
(a) If $2\nmid k$
 , all of the branches of the double-point curve have an $A_1$
, all of the branches of the double-point curve have an $A_1$ -singularity and ${\mathcal {D}}_j\cdot \mathcal {D}_{j'}=5$
-singularity and ${\mathcal {D}}_j\cdot \mathcal {D}_{j'}=5$ , $j\ne j'$
, $j\ne j'$ , when $a_{44}\ne 0$
, when $a_{44}\ne 0$ .
.(b) If $k=2p$
 , the branch ${\mathcal {D}}_p$
, the branch ${\mathcal {D}}_p$ has an $A_3$
has an $A_3$ -singularity if and only if ${CndYA}_3\ne 0$
-singularity if and only if ${CndYA}_3\ne 0$ . Then ${\mathcal {D}}_p\cdot \mathcal {D}_{j}=6$
. Then ${\mathcal {D}}_p\cdot \mathcal {D}_{j}=6$ , $j\ne p$
, $j\ne p$ , and ${\mathcal {D}}_j\cdot \mathcal {D}_{p+j}=6$
, and ${\mathcal {D}}_j\cdot \mathcal {D}_{p+j}=6$ , $1\le j< p$
, $1\le j< p$ , if and only if ${CndYm_6}_j\ne 0$
, if and only if ${CndYm_6}_j\ne 0$ . The other pairs of branches behave as in ${\rm {(a)}}$
. The other pairs of branches behave as in ${\rm {(a)}}$ .
.
Proof. We have $j^2\lambda _j(x,y)=x(a_{31}x+a_{32}\vartheta _{2j} y)$![]() so when $2\nmid k$
so when $2\nmid k$![]() , all of the branches of the double-point curve have an $A_1$
, all of the branches of the double-point curve have an $A_1$![]() -singularity as $\vartheta _{2j}\ne 0$
-singularity as $\vartheta _{2j}\ne 0$![]() for all $j$
for all $j$![]() . All the branches have only $x=0$
. All the branches have only $x=0$![]() as a common line in their tangent cone. The components of the branches which are tangent to $x=0$
as a common line in their tangent cone. The components of the branches which are tangent to $x=0$![]() are parametrized by $t\mapsto (\gamma _j(t),t)$
are parametrized by $t\mapsto (\gamma _j(t),t)$![]() , with $\gamma _j(t)=-{a_{44}(1+\xi ^{2j})}/{a_{32}}t^2+O(3)$
, with $\gamma _j(t)=-{a_{44}(1+\xi ^{2j})}/{a_{32}}t^2+O(3)$![]() . When $a_{44}\ne 0$
. When $a_{44}\ne 0$![]() , ${\mathcal {D}}_j\cdot \mathcal {D}_{j'}=\operatorname {dim}_{\mathbb {C}} \mathcal {O}_2/\left \langle xy,x^2+y^3\right \rangle =5$
, ${\mathcal {D}}_j\cdot \mathcal {D}_{j'}=\operatorname {dim}_{\mathbb {C}} \mathcal {O}_2/\left \langle xy,x^2+y^3\right \rangle =5$![]() .
.
When $k=2p$![]() , we have $\vartheta _{2p}=\vartheta _{4p}=0$
, we have $\vartheta _{2p}=\vartheta _{4p}=0$![]() , so considering the 4-jet of $\lambda _p$
, so considering the 4-jet of $\lambda _p$![]() , we find that the branch $\mathcal {D}_p$
, we find that the branch $\mathcal {D}_p$![]() has an $A_3$
has an $A_3$![]() -singularity if and only if ${CndYA}_3\ne 0$
-singularity if and only if ${CndYA}_3\ne 0$![]() . When this is the case, ${\mathcal {D}}_p\cdot \mathcal {D}_{j}=\operatorname {dim}_{\mathbb {C}} \mathcal {O}_2/\left \langle xy,x^2+y^4\right \rangle =6$
. When this is the case, ${\mathcal {D}}_p\cdot \mathcal {D}_{j}=\operatorname {dim}_{\mathbb {C}} \mathcal {O}_2/\left \langle xy,x^2+y^4\right \rangle =6$![]() , for $j\ne p$
, for $j\ne p$![]() .
.
All pairs of branches $\mathcal {D}_j$![]() , $\mathcal {D}_{p+j}$
, $\mathcal {D}_{p+j}$![]() , $1\le j< p$
, $1\le j< p$![]() have tangential component parametrized by $t\mapsto (\gamma _s(t),t)$
have tangential component parametrized by $t\mapsto (\gamma _s(t),t)$![]() , with $\gamma _s(t)=-{a_{44}(1+\xi ^2_{j})}/{a_{32}}t^2+\alpha _{s}t^3+O(4)$
, with $\gamma _s(t)=-{a_{44}(1+\xi ^2_{j})}/{a_{32}}t^2+\alpha _{s}t^3+O(4)$![]() , $s=j,p+j$
, $s=j,p+j$![]() , with $\alpha _1-\alpha _2\ne 0$
, with $\alpha _1-\alpha _2\ne 0$![]() if and only if ${CndYm_6}_j\ne 0$
if and only if ${CndYm_6}_j\ne 0$![]() . When this is the case, ${\mathcal {D}}_j\cdot \mathcal {D}_{p+j}=\operatorname {dim}_{\mathbb {C}} \mathcal {O}_2/\left \langle xy,x^2+y^4\right \rangle =6$
. When this is the case, ${\mathcal {D}}_j\cdot \mathcal {D}_{p+j}=\operatorname {dim}_{\mathbb {C}} \mathcal {O}_2/\left \langle xy,x^2+y^4\right \rangle =6$![]() , for $1\le j< p$
, for $1\le j< p$![]() . The other pairs of branches behave as when $2\nmid k$
. The other pairs of branches behave as when $2\nmid k$![]() .
.
Remark 4.28 The stratification $\mathcal {S}_k$![]() is determined, for each $k\geq 4$
is determined, for each $k\geq 4$![]() , by the conditions in tables 2, 4 and 6 ($\mathcal {S}_2$
, by the conditions in tables 2, 4 and 6 ($\mathcal {S}_2$![]() follows from the results in [Reference Bruce and Wilkinson8] and $\mathcal {S}_3$
follows from the results in [Reference Bruce and Wilkinson8] and $\mathcal {S}_3$![]() is indicated in table 1). One can easily check that the strata are smooth manifolds (they are also algebraic sets so in particular, $\mathcal {S}_k$
is indicated in table 1). One can easily check that the strata are smooth manifolds (they are also algebraic sets so in particular, $\mathcal {S}_k$![]() admits a sub-stratification which is Whitney (a) and (b) regular).
admits a sub-stratification which is Whitney (a) and (b) regular).
Germs in the following strata have pairwise the same Milnor number of their double-point curves:
Table 5: ${\bf Q}^{k}_{4}$![]() and $\tilde {\bf {Q}}^{k}_{4}$
and $\tilde {\bf {Q}}^{k}_{4}$![]() for $12\mid k$
for $12\mid k$![]() ,
,
Table 7: ${\bf U}^{k}_{4}$![]() and ${\bf {V}}^{k,j,j'}_{3}$
and ${\bf {V}}^{k,j,j'}_{3}$![]() for $3\mid k$
for $3\mid k$![]() ,
,
Table 7: ${\bf X}^{k}_{4}$![]() and ${\bf Y}^{k}_{4}$
and ${\bf Y}^{k}_{4}$![]() for $2\nmid k$
for $2\nmid k$![]() and $3\nmid k$
and $3\nmid k$![]() .
.
A simple calculation shows that all the Milnor numbers of the double-point curves in tables 3, 5 and 7, except those of the above pairs, are pairwise distinct. Therefore, removing the exceptional pairs, each stratum is precisely the connected component of the jets for which the Milnor number of the double-point curve is constant.
5. Generic singularities of $k$ -folding map-germs
-folding map-germs
We define, by varying the plane $\pi \in {\rm {Graff}}(2,3)$![]() , the family of Whitney $k$
, the family of Whitney $k$![]() -folds $\Omega ^k:\mathbb {C}^3\times {\rm {Graff}}(2,3)\to {\mathbb {C}}^3$
-folds $\Omega ^k:\mathbb {C}^3\times {\rm {Graff}}(2,3)\to {\mathbb {C}}^3$![]() , given by $\Omega ^k(p,\pi )=\omega ^k_{\pi }(p)$
, given by $\Omega ^k(p,\pi )=\omega ^k_{\pi }(p)$![]() , with $\omega ^k_{\pi }$
, with $\omega ^k_{\pi }$![]() as in definition 2.2.
as in definition 2.2.
Given a complex surface $M$![]() in $\mathbb {C}^3$
in $\mathbb {C}^3$![]() , we call the restriction of $\Omega ^k$
, we call the restriction of $\Omega ^k$![]() to $M$
to $M$![]() the family of $k$
the family of $k$![]() -folding maps on $M$
-folding maps on $M$![]() and denote it by ${\mathcal {F}}_k$
and denote it by ${\mathcal {F}}_k$![]() . We have ${\mathcal {F}}_k(p,\pi )=F^{\pi }_k(p)=\omega ^k_{\pi }(p)$
. We have ${\mathcal {F}}_k(p,\pi )=F^{\pi }_k(p)=\omega ^k_{\pi }(p)$![]() for all $p\in M$
for all $p\in M$![]() and $\pi \in {\rm {Graff}}(2,3)$
and $\pi \in {\rm {Graff}}(2,3)$![]() .
.
Recall that a property of surfaces is said to be generic if it is satisfied in a residual set of embeddings of the surfaces to $\mathbb {C}^3$![]() . The image of a surface $M$
. The image of a surface $M$![]() by an embedding in the residual set is then called generic, or simply that $M$
by an embedding in the residual set is then called generic, or simply that $M$![]() is generic. When $k$
is generic. When $k$![]() is large, the $\mathcal {A}$
is large, the $\mathcal {A}$![]() -singularities of $F^{\pi }_k$
-singularities of $F^{\pi }_k$![]() may have high $\mathcal {A}_e$
may have high $\mathcal {A}_e$![]() -codimensions (for the cases in this paper, this means high modality). However, they do occur on generic surfaces. To make sense of this, we follow a similar approach to that in [Reference Bruce5] and proceed as follows.
-codimensions (for the cases in this paper, this means high modality). However, they do occur on generic surfaces. To make sense of this, we follow a similar approach to that in [Reference Bruce5] and proceed as follows.
As we are interested here in the local singularities of $k$![]() -folding maps, we consider the setting in remark 2.3(4) at a point $p_0\in M$
-folding maps, we consider the setting in remark 2.3(4) at a point $p_0\in M$![]() and choose a suitable system of coordinates so that $\pi _0:y=0$
and choose a suitable system of coordinates so that $\pi _0:y=0$![]() and $F_k=F^{\pi _0}_k(x,y)=(x,y^k, f(x,y))$
and $F_k=F^{\pi _0}_k(x,y)=(x,y^k, f(x,y))$![]() for $(x,y)$
for $(x,y)$![]() in a small enough neighbourhood $U$
in a small enough neighbourhood $U$![]() of the origin. A plane $\pi =\overline {(d,v)}$
of the origin. A plane $\pi =\overline {(d,v)}$![]() near $\pi _0$
near $\pi _0$![]() is obtained by applying a translation $T_{\pi }$
is obtained by applying a translation $T_{\pi }$![]() followed by an orthogonal transformation $R_{\pi }\in U(3)$
followed by an orthogonal transformation $R_{\pi }\in U(3)$![]() to $\pi _0$
to $\pi _0$![]() . We choose $T_{\pi }$
. We choose $T_{\pi }$![]() and $R_{\pi }$
and $R_{\pi }$![]() as follows. The translation $T_{\pi }$
as follows. The translation $T_{\pi }$![]() takes the origin to the point of intersection of $\pi$
takes the origin to the point of intersection of $\pi$![]() with the $y$
with the $y$![]() -axis (the point exists because $\pi _0$
-axis (the point exists because $\pi _0$![]() is orthogonal to the $y$
is orthogonal to the $y$![]() -axis and $\pi$
-axis and $\pi$![]() is close to $\pi _0$
is close to $\pi _0$![]() ). The transformation $R_{\pi }$
). The transformation $R_{\pi }$![]() near the identity (and is taken to be the identity if $v$
near the identity (and is taken to be the identity if $v$![]() is parallel to $v_0$
is parallel to $v_0$![]() ) takes $v/||v||$
) takes $v/||v||$![]() to $v_0=(0,1,0)$
to $v_0=(0,1,0)$![]() and fixes the line through the origin orthogonal to $v_0$
and fixes the line through the origin orthogonal to $v_0$![]() and $v$
and $v$![]() . By varying the planes $\pi$
. By varying the planes $\pi$![]() in a neighbourhood $V$
in a neighbourhood $V$![]() of $\pi _0$
of $\pi _0$![]() in ${\rm {Graff}}(2,3)$
in ${\rm {Graff}}(2,3)$![]() , we get the family of $k$
, we get the family of $k$![]() -folding maps given by ${\mathcal {F}}_k:U\times V\to \mathbb {C}^3$
-folding maps given by ${\mathcal {F}}_k:U\times V\to \mathbb {C}^3$![]() , with
, with
with $\phi (x,y)=(x,y,f(x,y))$![]() . (We choose $R_{\pi }$
. (We choose $R_{\pi }$![]() and $T_{\pi }$
and $T_{\pi }$![]() to depend analytically on $\pi$
to depend analytically on $\pi$![]() .) The $\mathcal {A}$
.) The $\mathcal {A}$![]() -type of the singularity of $F^{\pi }_k$
-type of the singularity of $F^{\pi }_k$![]() at a given point in $U$
at a given point in $U$![]() is the same as that of the germ of
is the same as that of the germ of
at that point. At any point $p=(x,y)\in U$![]() , there exist a bi-holomorphic map-germ $K:(\mathbb {C}^2,0)\to (\mathbb {C}^2,(x,y))$
, there exist a bi-holomorphic map-germ $K:(\mathbb {C}^2,0)\to (\mathbb {C}^2,(x,y))$![]() such that
such that
for some germ of a holomorphic function $g_{p}$![]() , where $(\bar {x},\bar {y},\bar {z})=(R_{\pi }\circ T_{\pi })^{-1}(\phi (x,y)).$
, where $(\bar {x},\bar {y},\bar {z})=(R_{\pi }\circ T_{\pi })^{-1}(\phi (x,y)).$![]() Composing $\tilde {F}_{\pi }^k$
Composing $\tilde {F}_{\pi }^k$![]() with $K$
with $K$![]() gives the germ $(\tilde {F}_{\pi }^k)_p$
gives the germ $(\tilde {F}_{\pi }^k)_p$![]() of $\tilde {F}_{\pi }^k$
of $\tilde {F}_{\pi }^k$![]() at $p$
at $p$![]()

Observe that $g_{p}$![]() depends on the choice of $R_{\pi }$
depends on the choice of $R_{\pi }$![]() , $T_{\pi }$
, $T_{\pi }$![]() and of the coordinates system, but the $\mathcal {A}$
and of the coordinates system, but the $\mathcal {A}$![]() -class of the resulting germs $(\tilde {F}_{\pi }^k)_p$
-class of the resulting germs $(\tilde {F}_{\pi }^k)_p$![]() is independent of these choices.
is independent of these choices.
Clearly, a necessary condition for $(\tilde {F}^{\pi }_k)_p$![]() to be singular at the origin is $\bar {y}=0$
to be singular at the origin is $\bar {y}=0$![]() , equivalently, $p\in \pi$
, equivalently, $p\in \pi$![]() . We define the family of maps $\Phi :U\times V\to \mathbb {C}\times J^l(2,1)$
. We define the family of maps $\Phi :U\times V\to \mathbb {C}\times J^l(2,1)$![]() given by
given by
The map $\Phi$![]() plays a similar role in the Monge–Taylor map in [Reference Bruce5]. Here we include the first component to capture the planes through a given point $p\in M$
plays a similar role in the Monge–Taylor map in [Reference Bruce5]. Here we include the first component to capture the planes through a given point $p\in M$![]() which can give rise to singular $k$
which can give rise to singular $k$![]() -folding map-germs at $p$
-folding map-germs at $p$![]() .
.
We stratify $\mathbb {C}\times J^l(2,1)$![]() by $0\times \mathcal {S}_k$
by $0\times \mathcal {S}_k$![]() , together with $\mathbb {C}\times J^l(2,1)\setminus 0\times J^l(2,1)$
, together with $\mathbb {C}\times J^l(2,1)\setminus 0\times J^l(2,1)$![]() . Following standard transversality arguments (see e.g. [Reference Bruce5]), one can show that for a residual set of local embeddings of $M$
. Following standard transversality arguments (see e.g. [Reference Bruce5]), one can show that for a residual set of local embeddings of $M$![]() in $\mathbb {C}^3$
in $\mathbb {C}^3$![]() , the map $\Phi$
, the map $\Phi$![]() is transverse to the strata in $\mathbb {C}\times J^l(2,1)$
is transverse to the strata in $\mathbb {C}\times J^l(2,1)$![]() . As the domain of the family $\Phi$
. As the domain of the family $\Phi$![]() is of dimension 5, for a generic local embedding of $M$
is of dimension 5, for a generic local embedding of $M$![]() in $\mathbb {C}^3$
in $\mathbb {C}^3$![]() , $\Phi$
, $\Phi$![]() intersects a stratum $0\times X$
intersects a stratum $0\times X$![]() only when $X$
only when $X$![]() has codimension $\le \! 4$
has codimension $\le \! 4$![]() in $J^l(2,1)$
in $J^l(2,1)$![]() . This means that the only singularities of $k$
. This means that the only singularities of $k$![]() -folding maps that can occur on a generic surface are those belonging to the strata listed in tables 1, 2, 4 and 6. Furthermore, $\Phi$
-folding maps that can occur on a generic surface are those belonging to the strata listed in tables 1, 2, 4 and 6. Furthermore, $\Phi$![]() is transverse to these strata. Therefore, the locus of points where the $l$
is transverse to these strata. Therefore, the locus of points where the $l$![]() -jets of the $k$
-jets of the $k$![]() -folding map-germs belong to a stratum $X$
-folding map-germs belong to a stratum $X$![]() of codimension $3$
of codimension $3$![]() (resp. $4$
(resp. $4$![]() ) is a regular curve on $M$
) is a regular curve on $M$![]() (resp. isolated points on this curve). The above discussion also clarifies why the singularities of $F^{\pi }_k$
(resp. isolated points on this curve). The above discussion also clarifies why the singularities of $F^{\pi }_k$![]() occur generically even though they may have high $\mathcal {A}_e$
occur generically even though they may have high $\mathcal {A}_e$![]() -codimensions: they belong to strata of low codimension. (The strata can be viewed as a gluing of non $\mathcal {A}$
-codimensions: they belong to strata of low codimension. (The strata can be viewed as a gluing of non $\mathcal {A}$![]() -equivalent orbits which depends on a finite set of moduli.)
-equivalent orbits which depends on a finite set of moduli.)
It is worth observing that the above discussion is valid for smooth surfaces in $\mathbb {R}^3$![]() .
.
6. ${k}$ -Folding map-germs on surfaces in $\mathbb {R}^3$
-Folding map-germs on surfaces in $\mathbb {R}^3$
We consider in this section the geometry of $k$![]() -folding maps-germs on smooth (i.e. regular and of class $C^{\infty }$
-folding maps-germs on smooth (i.e. regular and of class $C^{\infty }$![]() ) surfaces in $\mathbb {R}^3$
) surfaces in $\mathbb {R}^3$![]() .
.
6.1 Robust features on surfaces
Robust features on a surface in $\mathbb {R}^3$![]() is a terminology introduced by Ian Porteous to indicate special characteristic features that can be traced when the surface evolves. What is sought after in applications are robust features which are represented by curves or points on the surface as these form a ‘skeletal structure’ of the surface (open regions bounded by robust curves are also robust features). They play an important role in computer vision and shape recognition (see e.g. [Reference Musuvathy27]) as they can be used to distinguish two shapes (surfaces) from each other and, in some cases, reconstruct the surface.
is a terminology introduced by Ian Porteous to indicate special characteristic features that can be traced when the surface evolves. What is sought after in applications are robust features which are represented by curves or points on the surface as these form a ‘skeletal structure’ of the surface (open regions bounded by robust curves are also robust features). They play an important role in computer vision and shape recognition (see e.g. [Reference Musuvathy27]) as they can be used to distinguish two shapes (surfaces) from each other and, in some cases, reconstruct the surface.
We consider here the parabolic, ridge, sub-parabolic and flecnodal curves on a smooth surface $M$![]() in $\mathbb {R}^3$
in $\mathbb {R}^3$![]() and special points on these curves (see [Reference Izumiya, Romero-Fuster, Ruas and Tari14] for references on work on these curves from a singularity theory point of view). These are robust features on $M$
and special points on these curves (see [Reference Izumiya, Romero-Fuster, Ruas and Tari14] for references on work on these curves from a singularity theory point of view). These are robust features on $M$![]() . We recall briefly what they are.
. We recall briefly what they are.
The parabolic curve is the locus of points where the Gaussian curvature vanishes. It is captured by the contact of the surface $M$![]() with planes: it is the locus of points where the height function along a normal direction to $M$
with planes: it is the locus of points where the height function along a normal direction to $M$![]() has an $A_{\ge 2}$
has an $A_{\ge 2}$![]() -singularity. The parabolic curve is regular on a generic surface, and the height function has an $A_2$
-singularity. The parabolic curve is regular on a generic surface, and the height function has an $A_2$![]() -singularity at its points except at isolated ones, called Cusps of Gauss, where it has an $A_3$
-singularity at its points except at isolated ones, called Cusps of Gauss, where it has an $A_3$![]() -singularity.
-singularity.
The ridge is the locus of points on $M$![]() where a principal curvature is extremal along its associated lines of principal curvature. It is also the locus of points on $M$
where a principal curvature is extremal along its associated lines of principal curvature. It is also the locus of points on $M$![]() which correspond to singular points on its focal set. The ridge is captured by the contact of $M$
which correspond to singular points on its focal set. The ridge is captured by the contact of $M$![]() with spheres: it is the locus of points on $M$
with spheres: it is the locus of points on $M$![]() where the distance squared function from a given point in $\mathbb {R}^3$
where the distance squared function from a given point in $\mathbb {R}^3$![]() (the point belong to the focal set) has an $A_{\ge 3}$
(the point belong to the focal set) has an $A_{\ge 3}$![]() -singularity. Away from umbilic points (i.e. points where the principal curvatures coincide), the ridge is a regular curve on a generic surface and the distance squared function has an $A_3$
-singularity. Away from umbilic points (i.e. points where the principal curvatures coincide), the ridge is a regular curve on a generic surface and the distance squared function has an $A_3$![]() -singularity at its points except at isolated points where it has an $A_4$
-singularity at its points except at isolated points where it has an $A_4$![]() -singularity. At umbilics, the ridge consist of one regular curve or a transverse intersection of three regular curves. (Umbilics and $A_4$
-singularity. At umbilics, the ridge consist of one regular curve or a transverse intersection of three regular curves. (Umbilics and $A_4$![]() -points are used as seed points for drawing ridges on a given shape, see [Reference Musuvathy27].)
-points are used as seed points for drawing ridges on a given shape, see [Reference Musuvathy27].)
The sub-parabolic curve is the locus of points on $M$![]() corresponding to parabolic points of its focal set. It is the locus of geodesic inflections of the lines of principal curvature; it is also the locus of points along which a principal curvature is extremal along the other lines of curvature. It is captured by the singularities of the 2-folding map on $M$
corresponding to parabolic points of its focal set. It is the locus of geodesic inflections of the lines of principal curvature; it is also the locus of points along which a principal curvature is extremal along the other lines of curvature. It is captured by the singularities of the 2-folding map on $M$![]() : it is the locus of points where some map $F_2^{\pi }$
: it is the locus of points where some map $F_2^{\pi }$![]() has an $S_{\ge 2}$
has an $S_{\ge 2}$![]() -singularity (or one which is adjacent to an $S_2$
-singularity (or one which is adjacent to an $S_2$![]() -singularity). The singularities of $F_2$
-singularity). The singularities of $F_2$![]() and their geometric characterization on a generic surface parametrized in Monge form $z=f(x,y)$
and their geometric characterization on a generic surface parametrized in Monge form $z=f(x,y)$![]() at a given non-umbilic point, with $f$
at a given non-umbilic point, with $f$![]() as in (3.1), are as in table 8. At umbilics, the sub-parabolic curve consist of one regular curve or a transverse intersection of three regular curves. Observe that the ridge is also captured by the singularities of $F_2^{\pi }$
as in (3.1), are as in table 8. At umbilics, the sub-parabolic curve consist of one regular curve or a transverse intersection of three regular curves. Observe that the ridge is also captured by the singularities of $F_2^{\pi }$![]() (see table 8).
(see table 8).
TABLE 8. Geometric characterization of the singularities of the folding-map $F_{2}$![]()

The flecnodal curve is the locus of geodesic inflections of the asymptotic curves. It is captured by the contact of the surface $M$![]() with lines: it is the locus of points where the orthogonal projection of the surface has a singularity of type swallowtail or worse. We recall briefly some results on these projections as they are needed for interpreting the singularities of $k$
with lines: it is the locus of points where the orthogonal projection of the surface has a singularity of type swallowtail or worse. We recall briefly some results on these projections as they are needed for interpreting the singularities of $k$![]() -folding maps. The orthogonal projection $P_v$
-folding maps. The orthogonal projection $P_v$![]() of $M$
of $M$![]() along the direction $v\in S^2$
along the direction $v\in S^2$![]() to the plane $T_vS^2$
to the plane $T_vS^2$![]() is given by $P_v(p)=p-(p\cdot v)v$
is given by $P_v(p)=p-(p\cdot v)v$![]() , with $p\in M$
, with $p\in M$![]() . This can be represented locally by a map-germ from the plane to the plane. Varying $v$
. This can be represented locally by a map-germ from the plane to the plane. Varying $v$![]() yields the family of orthogonal projections $P:M\times S^2\to TS^2$
yields the family of orthogonal projections $P:M\times S^2\to TS^2$![]() given by $P(p,v)=(v,P_v(p))$
given by $P(p,v)=(v,P_v(p))$![]() .
.
A transversality theorem asserts that for an open and dense (i.e.generic) set of embeddings $\phi :U\to \mathbb {R}^3$![]() , the surface $M=\phi (U)$
, the surface $M=\phi (U)$![]() has the following property: for any $v\in S^2$
has the following property: for any $v\in S^2$![]() the map-germ $P_v$
the map-germ $P_v$![]() has only local singularities $\mathcal {A}$
has only local singularities $\mathcal {A}$![]() -equivalent to one in table 9 at any point on $M$
-equivalent to one in table 9 at any point on $M$![]() . By translating $p_0\in M$
. By translating $p_0\in M$![]() to the origin and taking $M$
to the origin and taking $M$![]() locally at $p_0$
locally at $p_0$![]() in Monge form, an open subset of $M$
in Monge form, an open subset of $M$![]() is parametrized by $\phi (x,y)=(x,y,f(x,y))$
is parametrized by $\phi (x,y)=(x,y,f(x,y))$![]() , with $f$
, with $f$![]() having no constant nor linear terms. Projecting along the direction $v=(0,1,0)$
having no constant nor linear terms. Projecting along the direction $v=(0,1,0)$![]() gives $P_v(x,y)=(x,f(x,y))$
gives $P_v(x,y)=(x,f(x,y))$![]() , which is singular at the origin. Table 9 shows the conditions on the coefficients of $f$
, which is singular at the origin. Table 9 shows the conditions on the coefficients of $f$![]() for the map-germ $P_v$
for the map-germ $P_v$![]() to have a singularity at the origin of $\mathcal {A}_e$
to have a singularity at the origin of $\mathcal {A}_e$![]() -codimension $\le \! 2$
-codimension $\le \! 2$![]() , where $d_e(G,\mathcal {A})$
, where $d_e(G,\mathcal {A})$![]() denotes the $\mathcal {A}_e$
denotes the $\mathcal {A}_e$![]() -codimension of $G$
-codimension of $G$![]() (see e.g. [Reference Izumiya, Romero-Fuster, Ruas and Tari14]).
(see e.g. [Reference Izumiya, Romero-Fuster, Ruas and Tari14]).
TABLE 9. $\mathcal {A}_e$![]() -Codimension $\le \! 2$
-Codimension $\le \! 2$![]() singularities of map-germs $G:(\mathbb {R}^2,0)\to (\mathbb {R}^2,0)$
singularities of map-germs $G:(\mathbb {R}^2,0)\to (\mathbb {R}^2,0)$![]()

The projection $P_v$![]() has a fold singularity at $p$
has a fold singularity at $p$![]() if, and only if, $v$
if, and only if, $v$![]() is a non-asymptotic tangent direction to $M$
is a non-asymptotic tangent direction to $M$![]() at $p$
at $p$![]() . The singularity at $p$
. The singularity at $p$![]() is of type cusp or worse if, and only if, $v$
is of type cusp or worse if, and only if, $v$![]() is an asymptotic direction at $p$
is an asymptotic direction at $p$![]() . For a generic surface $M$
. For a generic surface $M$![]() , the closure of the set of points where $P_v$
, the closure of the set of points where $P_v$![]() has a swallowtail (resp. lips/beaks) singularity is a precisely the flecnodal (resp. parabolic) curve. The flecnodal curve meets tangentially the parabolic curve at the cusps of the Gauss map, which are the gulls singularities of $P_v$
has a swallowtail (resp. lips/beaks) singularity is a precisely the flecnodal (resp. parabolic) curve. The flecnodal curve meets tangentially the parabolic curve at the cusps of the Gauss map, which are the gulls singularities of $P_v$![]() [Reference Banchoff, Gaffney and McCrory2]. We call a point where this happens a gulls-point of $M$
[Reference Banchoff, Gaffney and McCrory2]. We call a point where this happens a gulls-point of $M$![]() .
.
The goose (resp. butterfly) singularities of $P_v$![]() appear at special points on the parabolic (resp. flecnodal) curve. We call a point on $M$
appear at special points on the parabolic (resp. flecnodal) curve. We call a point on $M$![]() where these singularities occur a goose-point (resp. butterfly-point) on $M$
where these singularities occur a goose-point (resp. butterfly-point) on $M$![]() .
.
The above robust features are defined in terms of the principal curvatures $\kappa _1$![]() and $\kappa _2$
and $\kappa _2$![]() . We can suppose $\kappa _1<\kappa _2$
. We can suppose $\kappa _1<\kappa _2$![]() (away from umbilic curves) and give different colours to the robust features associated to each principal curvature. For instance, we can have a blue ridge (associated to $\kappa _1$
(away from umbilic curves) and give different colours to the robust features associated to each principal curvature. For instance, we can have a blue ridge (associated to $\kappa _1$![]() ) and a red ridge (associated to $\kappa _2$
) and a red ridge (associated to $\kappa _2$![]() ).
).
6.2 The geometry of $k$ -folding map-germs
-folding map-germs
We obtain here the robust features determined by the singularities of $k$![]() -folding map-germs, for $k\geq 3$
-folding map-germs, for $k\geq 3$![]() . We start with the case where $p$
. We start with the case where $p$![]() is not an umbilic point and treat the $k=3$
is not an umbilic point and treat the $k=3$![]() case separately.
case separately.
Theorem 6.1 Let $M$![]() be a generic surface in $\mathbb {R}^3$
be a generic surface in $\mathbb {R}^3$![]() , $p$
, $p$![]() a non-umbilical point on $M$
a non-umbilical point on $M$![]() and $\pi$
and $\pi$![]() a plane through $p$
a plane through $p$![]() and orthogonal to $v$
and orthogonal to $v$![]() . The map-germ $F_3^{\pi }$
. The map-germ $F_3^{\pi }$![]() at $p$
at $p$![]() is an immersion if and only if $v$
is an immersion if and only if $v$![]() is not tangent to $M$
is not tangent to $M$![]() at $p$
at $p$![]() . It has an $S_1$
. It has an $S_1$![]() -singularity if and only if $v\in T_pM$
-singularity if and only if $v\in T_pM$![]() but is neither a principal nor an asymptotic direction. We have the following when $v$
but is neither a principal nor an asymptotic direction. We have the following when $v$![]() is a principal or an asymptotic direction at $p$
is a principal or an asymptotic direction at $p$![]() .
.
(1) If $v$
 is a principal direction at $p$
is a principal direction at $p$ , then the possible singularities of $F_3^{\pi }$
, then the possible singularities of $F_3^{\pi }$ at $p$
at $p$ and their geometric characterizations are as follows:
and their geometric characterizations are as follows:$S_3$
 : $p$
: $p$ is not on the sub-parabolic curve associated to $v$
is not on the sub-parabolic curve associated to $v$ .
.$S_5$
 : $p$
: $p$ is a generic point on the sub-parabolic curve associated to $v$
is a generic point on the sub-parabolic curve associated to $v$ .
.$S_7$
 : $p$
: $p$ is an $S_3$
is an $S_3$ -point on the sub-parabolic curve associated to $v$
-point on the sub-parabolic curve associated to $v$ .
.(2) Suppose that $v$
 is an asymptotic and that $p$
is an asymptotic and that $p$ is a hyperbolic point. Then $F_3^{\pi }$
is a hyperbolic point. Then $F_3^{\pi }$ has a singularity at $p$
has a singularity at $p$ of type $H_{k},k=2,3,4$
of type $H_{k},k=2,3,4$ . The $H_{3}$
. The $H_{3}$ -singularities occur on a regular curve on $M$
-singularities occur on a regular curve on $M$ . We call its closure the $H_3$
. We call its closure the $H_3$ -curve. The $H_4$
-curve. The $H_4$ -singularities occur at isolated points on this curve.
-singularities occur at isolated points on this curve.(3) If $p$
 is a parabolic point and $v$
is a parabolic point and $v$ is the unique asymptotic direction at $p$
is the unique asymptotic direction at $p$ which is also a principal direction, then the possible topological classes of $F_3^{\pi }$
which is also a principal direction, then the possible topological classes of $F_3^{\pi }$ at $p$
at $p$ and their geometric characterizations are as follows:
and their geometric characterizations are as follows:$X_4$
 : $p$
: $p$ is a generic point on the parabolic curve.
is a generic point on the parabolic curve.${\bf U}^3_4$
 : $p$
: $p$ is an $A_2^*$
is an $A_2^*$ -point (see [Reference Giblin and Janeczko10, Reference Giblin, Warder and Zakalyukin11] ); it is on the closure of the $H_3$
-point (see [Reference Giblin and Janeczko10, Reference Giblin, Warder and Zakalyukin11] ); it is on the closure of the $H_3$ -curve.
-curve.${\bf X}^3_4$
 : $p$
: $p$ is on the sub-parabolic curve associated to $v$
is on the sub-parabolic curve associated to $v$ ; the principal map with value $v$
; the principal map with value $v$ at $p$
at $p$ has a beaks singularity at $p$
has a beaks singularity at $p$ [Reference Bruce and Tari7].
[Reference Bruce and Tari7].${\bf W}^{3,1}_4$
 : $p$
: $p$ is on the sub-parabolic curve associated to the other principal direction $v^{\perp }$
is on the sub-parabolic curve associated to the other principal direction $v^{\perp }$ ; it is on the closure of the $H_3$
; it is on the closure of the $H_3$ -curve; the frame map has a cross-cap singularity at $p$
-curve; the frame map has a cross-cap singularity at $p$ [Reference Bruce and Tari7].
[Reference Bruce and Tari7].
Proof. The proof follows by considering the defining equations and the open conditions of the strata of $3$![]() -folding map-germs in theorem 4.4 and the geometric interpretation of the algebraic conditions in table 1 given in tables 8 and 9.
-folding map-germs in theorem 4.4 and the geometric interpretation of the algebraic conditions in table 1 given in tables 8 and 9.
Proposition 6.2 The $H_3$![]() -curve of a generic surface is a regular curve and meets the parabolic curve tangentially at $A_2^*$
-curve of a generic surface is a regular curve and meets the parabolic curve tangentially at $A_2^*$![]() and ${\bf W}^{3,1}_4$
and ${\bf W}^{3,1}_4$![]() -points.
-points.
Proof. The regularity of the $H_3$![]() -curve follows by a transversality argument. We compute the 1-jets of the parabolic and $H_3$
-curve follows by a transversality argument. We compute the 1-jets of the parabolic and $H_3$![]() -curves and find that they are tangential at their points of intersection. This is expected as the $H_3$
-curves and find that they are tangential at their points of intersection. This is expected as the $H_3$![]() -singularities of $F_3^{\pi }$
-singularities of $F_3^{\pi }$![]() occur when $v$
occur when $v$![]() is an asymptotic direction, so the $H_3$
is an asymptotic direction, so the $H_3$![]() -curve lies in the closure of the hyperbolic region of the surface.
-curve lies in the closure of the hyperbolic region of the surface.
We turn now to the case $k\ge 4$![]() , still assuming $p$
, still assuming $p$![]() not to be an umbilical point. We recall that some topological classes in tables 2, 4 and 6 come with divisibility conditions on $k$
not to be an umbilical point. We recall that some topological classes in tables 2, 4 and 6 come with divisibility conditions on $k$![]() . For example, the ${\bf N}^k_3$
. For example, the ${\bf N}^k_3$![]() class requires $2\mid k$
class requires $2\mid k$![]() (see remarks 6.4).
(see remarks 6.4).
Theorem 6.3 Let $k\geq 4$![]() and let $M$
and let $M$![]() be a generic surface in $\mathbb {R}^3$
be a generic surface in $\mathbb {R}^3$![]() , $p$
, $p$![]() a non-umbilical point on $M$
a non-umbilical point on $M$![]() and $\pi$
and $\pi$![]() a plane through $p$
a plane through $p$![]() and orthogonal to $v$
and orthogonal to $v$![]() . The map-germ $F_k^{\pi }$
. The map-germ $F_k^{\pi }$![]() at $p$
at $p$![]() is an immersion if and only if $v$
is an immersion if and only if $v$![]() is not tangent to $M$
is not tangent to $M$![]() at $p$
at $p$![]() . It has a singularity which is topologically equivalent to $M^k_1$
. It has a singularity which is topologically equivalent to $M^k_1$![]() if and only if $v\in T_pM$
if and only if $v\in T_pM$![]() but is neither a principal nor an asymptotic direction at $p$
but is neither a principal nor an asymptotic direction at $p$![]() . We have the following when $v$
. We have the following when $v$![]() is a principal or an asymptotic direction at $p$
is a principal or an asymptotic direction at $p$![]() .
.
(1) If $v$
 is a principal direction at $p$
is a principal direction at $p$ , then $F_k^{\pi }$
, then $F_k^{\pi }$ belongs to a stratum in table 2. The possible topological classes of $F_k^{\pi }$
belongs to a stratum in table 2. The possible topological classes of $F_k^{\pi }$ and their geometric interpretations are as follows:
and their geometric interpretations are as follows:${\bf M}^k_2$
 : $p$
: $p$ is not on the sub-parabolic curve associated to $v$
is not on the sub-parabolic curve associated to $v$ .
.${\bf M}^k_3$
 : $p$
: $p$ is a generic point on the sub-parabolic curve associated to $v$
is a generic point on the sub-parabolic curve associated to $v$ .
.${\bf M}^k_4$
 : $p$
: $p$ is an $S_3$
is an $S_3$ -point on the sub-parabolic curve associated to $v$
-point on the sub-parabolic curve associated to $v$ .
.${\bf N}^k_3$
 : $p$
: $p$ is a generic point on the ridge curve associated to $v$
is a generic point on the ridge curve associated to $v$ .
.${\bf N}^k_4$
 : $p$
: $p$ is a $B_3$
is a $B_3$ -point on the ridge curve associated to $v$
-point on the ridge curve associated to $v$ .
.${\bf O}^k_4$
 : $p$
: $p$ is a $C_3$
is a $C_3$ -point (intersection point of the ridge and sub-parabolic curves associated to $v$
-point (intersection point of the ridge and sub-parabolic curves associated to $v$ ).
).(2) If $p$
 is a hyperbolic point and $v$
is a hyperbolic point and $v$ is an asymptotic direction at $p$
is an asymptotic direction at $p$ , then $F_k^{\pi }$
, then $F_k^{\pi }$ belongs to a stratum in table 4. The possible topological classes of $F_k^{\pi }$
belongs to a stratum in table 4. The possible topological classes of $F_k^{\pi }$ and their geometric interpretations are as follows:
and their geometric interpretations are as follows:${\bf P}^k_2$
 : $p$
: $p$ is not on the flecnodal curve associated to $v$
is not on the flecnodal curve associated to $v$ , and is not on the $H_3$
, and is not on the $H_3$ -curve associated to $v$
-curve associated to $v$ when $3\mid k$
when $3\mid k$ .
.${\bf P}^k_3$
 : $p$
: $p$ is a generic point on the $H_3$
is a generic point on the $H_3$ -curve associated to $v$
-curve associated to $v$ .
.${\bf P}^k_4$
 : $p$
: $p$ is an $H_4$
is an $H_4$ -point on the $H_3$
-point on the $H_3$ -curve associated to $v$
-curve associated to $v$ .
.${\bf Q}^k_3$
 : $p$
: $p$ is a generic point on the flecnodal curve associated to $v$
is a generic point on the flecnodal curve associated to $v$ .
.${\bf Q}^k_4$
 : $p$
: $p$ is a point of intersection of the flecnodal and $H_3$
is a point of intersection of the flecnodal and $H_3$ -curves associated to $v$
-curves associated to $v$ .
.$\widetilde {\bf Q}^k_4$
 : $p$
: $p$ is a special point on the flecnodal curve associated to $v$
is a special point on the flecnodal curve associated to $v$ .
.${\bf R}^k_4$
 : $p$
: $p$ is a butterfly-point on the flecnodal curve associated to $v$
is a butterfly-point on the flecnodal curve associated to $v$ .
.(3) If $p$
 is a parabolic point and $v$
is a parabolic point and $v$ is an asymptotic (and a principal) direction at $p$
is an asymptotic (and a principal) direction at $p$ , then $F_k^{\pi }$
, then $F_k^{\pi }$ belongs to a stratum in table 6. The possible topological classes of $F_k^{\pi }$
belongs to a stratum in table 6. The possible topological classes of $F_k^{\pi }$ and their geometric interpretations are as follows:
and their geometric interpretations are as follows:${\bf U}^k_3$
 : $p$
: $p$ is a generic point on the parabolic curve.
is a generic point on the parabolic curve.${\bf U}^k_4$
 : $p$
: $p$ is an $A^*_2$
is an $A^*_2$ -point.
-point.${\bf V}^{k,j,j'}_4\!\!$
 : $p$
: $p$ is a special point on the parabolic curve.
is a special point on the parabolic curve.${\bf W}^{k,j}_4$
 : $p$
: $p$ is a special point on the parabolic curve.
is a special point on the parabolic curve.${\bf W}^{3q,q}_4$
 : $p$
: $p$ is on the sub-parabolic curve associated to $v^{\perp }$
is on the sub-parabolic curve associated to $v^{\perp }$ ; it is on the closure of the $H_3$
; it is on the closure of the $H_3$ -curve associated to $v$
-curve associated to $v$ ; the frame map has a cross-cap singularity at $p$
; the frame map has a cross-cap singularity at $p$ [Reference Bruce and Tari7].
[Reference Bruce and Tari7].${\bf X}^k_4$
 : $p$
: $p$ is on the intersection of the parabolic and sub-parabolic curves associated to $v$
is on the intersection of the parabolic and sub-parabolic curves associated to $v$ ; the principal map with value $v$
; the principal map with value $v$ at $p$
at $p$ has a beaks singularity at $p$
has a beaks singularity at $p$ [Reference Bruce and Tari7].
[Reference Bruce and Tari7].${\bf Y}^k_4$
 : $p$
: $p$ is a cusp of Gauss point and a gulls-point.
is a cusp of Gauss point and a gulls-point.
Proof. With the setting as in the proof of theorem 6.1, the results follow by interpreting the conditions in tables 2, 4 and 6 using tables 8 and 9.
Remarks 6.4 1. The singularities in branches 1 and 2 are associated to principal directions, those in branch 3 to asymptotic directions at hyperbolic points and those in branch 4 to asymptotic directions at parabolic points.
2. Theorems 6.1 and 6.3 show clearly that $k$![]() -folding maps capture the robust features obtained by $2$
-folding maps capture the robust features obtained by $2$![]() -folding maps and by the contact of the surface with lines, planes and spheres, giving thus new geometric characterizations of these features and a unified approach to study them. We also obtain a new 1-dimensional robust feature (the $H_3$
-folding maps and by the contact of the surface with lines, planes and spheres, giving thus new geometric characterizations of these features and a unified approach to study them. We also obtain a new 1-dimensional robust feature (the $H_3$![]() -curve) and several $0$
-curve) and several $0$![]() -dimensional ones: the $H_4$
-dimensional ones: the $H_4$![]() , ${\bf Q}^k_4$
, ${\bf Q}^k_4$![]() , $\widetilde {\bf Q}^k_4$
, $\widetilde {\bf Q}^k_4$![]() , ${\bf V}^{k,j,j'}_4$
, ${\bf V}^{k,j,j'}_4$![]() and ${\bf W}^{k,j}_4$
and ${\bf W}^{k,j}_4$![]() points.
points.
3. The $H_3$![]() -curve is captured by $k$
-curve is captured by $k$![]() -folding maps when $k$
-folding maps when $k$![]() is divisible by $3$
is divisible by $3$![]() . The sub-parabolic and flecnodal curves are captured by $k$
. The sub-parabolic and flecnodal curves are captured by $k$![]() -folding maps for any $k$
-folding maps for any $k$![]() while the ridge curve is captured by $k$
while the ridge curve is captured by $k$![]() -folding maps when $k$
-folding maps when $k$![]() is even. Regarding the ridge, it is the locus of points where the surface has more infinitesimal symmetry with respect to planes [Reference Bruce and Wilkinson8]. The map-germs $(x,y)\mapsto (x,y^{2p},f(x,y))$
is even. Regarding the ridge, it is the locus of points where the surface has more infinitesimal symmetry with respect to planes [Reference Bruce and Wilkinson8]. The map-germs $(x,y)\mapsto (x,y^{2p},f(x,y))$![]() identify the pair of points $(x,y)$
identify the pair of points $(x,y)$![]() and $(x,-y),$
and $(x,-y),$![]() which explains why all the $F_{2p}$
which explains why all the $F_{2p}$![]() folding maps capture the ridge curve.
folding maps capture the ridge curve.
4. The condition $\Delta _j^k=0$![]() can be satisfied for any $k,j$
can be satisfied for any $k,j$![]() when the coefficients $a_{sl}$
when the coefficients $a_{sl}$![]() are real, so ${\bf W}^{k,j}_4$
are real, so ${\bf W}^{k,j}_4$![]() -points can occur on surfaces in $\mathbb {R}^3$
-points can occur on surfaces in $\mathbb {R}^3$![]() for all $k,j$
for all $k,j$![]() . For the ${\bf V}^{k,j,j'}_4$
. For the ${\bf V}^{k,j,j'}_4$![]() topological class, it follows from proposition 4.21 that only ${\bf V}^{k,j,k-j}_4$
topological class, it follows from proposition 4.21 that only ${\bf V}^{k,j,k-j}_4$![]() , ${\bf V}^{k,j,2j}_4$
, ${\bf V}^{k,j,2j}_4$![]() and ${\bf V}^{k,k-j,2j}_4$
and ${\bf V}^{k,k-j,2j}_4$![]() -points can occur on surfaces in $\mathbb {R}^3$
-points can occur on surfaces in $\mathbb {R}^3$![]() .
.
5. Theorem 6.1 gives a new geometric interpretation for the $A^*_2$![]() -points in [Reference Giblin and Janeczko10, Reference Giblin, Warder and Zakalyukin11].
-points in [Reference Giblin and Janeczko10, Reference Giblin, Warder and Zakalyukin11].
6. Observe that the open conditions (those involving expressions $\ne 0$![]() ) for the singularities of the $k$
) for the singularities of the $k$![]() -folding map in tables 1, 2, 4 and 6 and their associated ones in tables 8 and 9 are not always identical. For the $0$
-folding map in tables 1, 2, 4 and 6 and their associated ones in tables 8 and 9 are not always identical. For the $0$![]() -dimensional robust features, the open conditions in both tables are satisfied on a generic surface. For the $1$
-dimensional robust features, the open conditions in both tables are satisfied on a generic surface. For the $1$![]() -dimensional robust features, this means that some special points in one setting are not special in the other. For example, the $3$
-dimensional robust features, this means that some special points in one setting are not special in the other. For example, the $3$![]() -folding map does not distinguish between a $C_3$
-folding map does not distinguish between a $C_3$![]() -point and a generic point on the sub-parabolic curve.
-point and a generic point on the sub-parabolic curve.
We consider now the situation at umbilic points. For a generic surface $M$![]() , these occur at isolated points in its elliptic region, and every direction in the tangent plane of $M$
, these occur at isolated points in its elliptic region, and every direction in the tangent plane of $M$![]() at such points can be considered a principal direction. We take $M$
at such points can be considered a principal direction. We take $M$![]() locally in Monge form $z=f(x,y)$
locally in Monge form $z=f(x,y)$![]() , consider the origin to be an umbilic point and write $f(x,y)={\kappa }/{2}(x^2+y^2)+C(x,y)+ O_4(x,y)$
, consider the origin to be an umbilic point and write $f(x,y)={\kappa }/{2}(x^2+y^2)+C(x,y)+ O_4(x,y)$![]() where $C$
where $C$![]() is a homogeneous cubic form in $x,y$
is a homogeneous cubic form in $x,y$![]() . We can take $C(x,y)$
. We can take $C(x,y)$![]() to be the real part of $z^2+\beta z^2\overline {z}$
to be the real part of $z^2+\beta z^2\overline {z}$![]() , with $z=x+{\rm i}y$
, with $z=x+{\rm i}y$![]() and $\beta =s+{\rm i}t$
and $\beta =s+{\rm i}t$![]() (see e.g. [Reference Bruce and Wilkinson8]). Then, $C=(1+s)x^3-tx^2y+(s-3)xy^2-ty^3.$
(see e.g. [Reference Bruce and Wilkinson8]). Then, $C=(1+s)x^3-tx^2y+(s-3)xy^2-ty^3.$![]()
Theorem 6.5 Let $k\ge 3$![]() and let $M$
and let $M$![]() be a generic smooth surface in $\mathbb {R}^3$
be a generic smooth surface in $\mathbb {R}^3$![]() , $p$
, $p$![]() an umbilic point on $M$
an umbilic point on $M$![]() and $\pi$
and $\pi$![]() a plane through $p$
a plane through $p$![]() and orthogonal to $v\in T_{p}M$
and orthogonal to $v\in T_{p}M$![]() .
.
1. If $2\nmid k$
 , then for almost all directions $v$
, then for almost all directions $v$ in $T_{p}M$
in $T_{p}M$ the singularity of $F_k^{\pi }$
the singularity of $F_k^{\pi }$ at $p$
at $p$ is of type $S_3$
is of type $S_3$ when $k=3$
when $k=3$ and of type ${\bf M}^k_2$
and of type ${\bf M}^k_2$ when $k\ge 4$
when $k\ge 4$ . There are three directions (resp. one direction) where the singularity is of type $S_5$
. There are three directions (resp. one direction) where the singularity is of type $S_5$ when $k=3$
when $k=3$ and of type ${\bf M}^k_3$
and of type ${\bf M}^k_3$ when $k\ge 4$
when $k\ge 4$ if $\beta$
if $\beta$ is inside (resp. outside) the outer hypocycloid $\beta =-3(2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta })$
is inside (resp. outside) the outer hypocycloid $\beta =-3(2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta })$ in figure 4.
in figure 4.2. If $2\mid k$
 , then for almost all directions $v$
, then for almost all directions $v$ in $T_{p}M$
in $T_{p}M$ the singularity of $F_k^{\pi }$
the singularity of $F_k^{\pi }$ at $p$
at $p$ is of type ${\bf M}^k_2$
is of type ${\bf M}^k_2$ . There are three directions (resp. one direction) where the singularity is of type ${\bf M}^k_3$
. There are three directions (resp. one direction) where the singularity is of type ${\bf M}^k_3$ if $\beta$
if $\beta$ is inside (resp. outside) the hypocycloid $\beta =-3(2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta })$
is inside (resp. outside) the hypocycloid $\beta =-3(2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta })$ . There are also three directions (resp. one direction) where the singularity is of type ${\bf N}^k_3$
. There are also three directions (resp. one direction) where the singularity is of type ${\bf N}^k_3$ when $\beta$
when $\beta$ is inside (resp. outside) the inner hypocycloid $\beta =2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta }$
is inside (resp. outside) the inner hypocycloid $\beta =2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta }$ in figure 4.
in figure 4.

FIGURE 4. Partition of the space of cubic forms.
Proof. We take $v=(\cos (\theta ),\sin (\theta ),0)$![]() , $\theta \in [0,2\pi ]$
, $\theta \in [0,2\pi ]$![]() and consider the rotation
and consider the rotation

which takes the direction $(0,1,0)$![]() to $v$
to $v$![]() . Then,
. Then,
Changes of coordinates in the source give
We denote by $\bar {a}_{lj}$![]() the coefficient of $X^{l-j}Y^j$
the coefficient of $X^{l-j}Y^j$![]() in the Taylor expansion of $f(X\sin (\theta )+Y\cos (\theta ),-X\cos (\theta )+Y\sin (\theta ))$
in the Taylor expansion of $f(X\sin (\theta )+Y\cos (\theta ),-X\cos (\theta )+Y\sin (\theta ))$![]() . The proof follows then considering the conditions for the singularities of $F_k^{\pi }$
. The proof follows then considering the conditions for the singularities of $F_k^{\pi }$![]() in tables 1 and 2.
in tables 1 and 2.
(1) We have
When $2\nmid k$![]() and $\bar {a}_{31}\ne 0$
and $\bar {a}_{31}\ne 0$![]() , the singularity of $F_k^{\pi }$
, the singularity of $F_k^{\pi }$![]() at the origin is of type $S_3$
at the origin is of type $S_3$![]() when $k=3$
when $k=3$![]() or of type $M^k_2$
or of type $M^k_2$![]() when $k\ge 4$
when $k\ge 4$![]() .
.
The coefficient $\bar {a}_{31}$![]() is a cubic form in $\cos (\theta )$
is a cubic form in $\cos (\theta )$![]() and $\sin (\theta )$
and $\sin (\theta )$![]() . Its discriminant is the hypocycloid $\beta =-3(2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta })$
. Its discriminant is the hypocycloid $\beta =-3(2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta })$![]() . The cubic has three roots for $\beta$
. The cubic has three roots for $\beta$![]() inside the hypocycloid and one root when it is outside. For $v$
inside the hypocycloid and one root when it is outside. For $v$![]() corresponding to one of these roots, the singularity of $F_k^{\pi }$
corresponding to one of these roots, the singularity of $F_k^{\pi }$![]() is of type $S_5$
is of type $S_5$![]() when $k=3$
when $k=3$![]() and of type ${\bf M}^k_3$
and of type ${\bf M}^k_3$![]() when $k\ge 4$
when $k\ge 4$![]() , provided $\bar {a}_{41}\ne 0$
, provided $\bar {a}_{41}\ne 0$![]() . The condition $\bar {a}_{41}\ne 0$
. The condition $\bar {a}_{41}\ne 0$![]() is satisfied at umbilic points on generic surfaces.
is satisfied at umbilic points on generic surfaces.
(2) We have
When $2\mid k$![]() (so $k\ge 4$
(so $k\ge 4$![]() ) and $\bar {a}_{33}\ne 0$
) and $\bar {a}_{33}\ne 0$![]() , the singularity of $F_k^{\pi }$
, the singularity of $F_k^{\pi }$![]() at the origin is of type ${\bf M}^k_2$
at the origin is of type ${\bf M}^k_2$![]() . We also get the ${\bf M}^k_3$
. We also get the ${\bf M}^k_3$![]() singularities as in (1) when $\bar {a}_{31}=0$
singularities as in (1) when $\bar {a}_{31}=0$![]() .
.
The coefficient $\bar {a}_{33}$![]() is also a cubic form in $\cos (\theta )$
is also a cubic form in $\cos (\theta )$![]() and $\sin (\theta )$
and $\sin (\theta )$![]() . Its discriminant is the hypocycloid $\beta =2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta }$
. Its discriminant is the hypocycloid $\beta =2{\rm e}^{2{\rm i}\theta }+{\rm e}^{-4{\rm i}\theta }$![]() . The cubic has three roots for $\beta$
. The cubic has three roots for $\beta$![]() inside the hypocycloid and one root when it is outside. For $v$
inside the hypocycloid and one root when it is outside. For $v$![]() corresponding to one of these roots, the singularity of $F_k^{\pi }$
corresponding to one of these roots, the singularity of $F_k^{\pi }$![]() is of type ${\bf N}^k_3$
is of type ${\bf N}^k_3$![]() if $\bar {a}_{31}\ne 0$
if $\bar {a}_{31}\ne 0$![]() .
.
We have $\bar {a}_{33}=\bar {a}_{31}=0$![]() if and only if $\beta$
if and only if $\beta$![]() is on one of the tangent lines $t(3s^2-t^2)=0$
is on one of the tangent lines $t(3s^2-t^2)=0$![]() to the hypocycloids at their cusp points, see figure 4. (On these lines, the singularity is of type ${\bf O}^k_4$
to the hypocycloids at their cusp points, see figure 4. (On these lines, the singularity is of type ${\bf O}^k_4$![]() or more degenerate. This singularity does not occur at umbilic points on a generic surface.)
or more degenerate. This singularity does not occur at umbilic points on a generic surface.)
Remark 6.6 1. Theorem 6.5 is merely another interpretation of the results in [Reference Bruce and Wilkinson8, Reference Wilkinson32] when using the geometric characterizations of the singularities of $k$![]() -folding maps in theorems 6.1 and 6.3. We know from [Reference Bruce5, Reference Bruce and Wilkinson8, Reference Wilkinson32] that there are one or three ridge curves and one or three sub-parabolic curves at umbilic points on a generic surface. These curves meet transversally and change colour at the umbilic point.
-folding maps in theorems 6.1 and 6.3. We know from [Reference Bruce5, Reference Bruce and Wilkinson8, Reference Wilkinson32] that there are one or three ridge curves and one or three sub-parabolic curves at umbilic points on a generic surface. These curves meet transversally and change colour at the umbilic point.
2. Figure 4 is first obtained in [Reference Bruce and Wilkinson8] when considering 2-folding maps. In that case both hypocycloids are present, whereas when $k\ge 3$![]() only one of them is present when $k$
only one of them is present when $k$![]() is odd (both are present when $k$
is odd (both are present when $k$![]() is even). Also in [Reference Bruce and Wilkinson8] is considered the circle $|\beta |=3$
is even). Also in [Reference Bruce and Wilkinson8] is considered the circle $|\beta |=3$![]() which corresponds to the Monge–Taylor map failing to be transverse to the umbilics stratum. The circle $|\beta |=1$
which corresponds to the Monge–Taylor map failing to be transverse to the umbilics stratum. The circle $|\beta |=1$![]() is also exceptional and corresponds to two ridges through the umbilic being tangential, see [Reference Bruce, Giblin and Tari6]. As these conditions are geometric, the circles $|\beta |=1$
is also exceptional and corresponds to two ridges through the umbilic being tangential, see [Reference Bruce, Giblin and Tari6]. As these conditions are geometric, the circles $|\beta |=1$![]() and $|\beta |=3$
and $|\beta |=3$![]() can also be considered exceptional for $k$
can also be considered exceptional for $k$![]() -folding maps and are added to figure 4.
-folding maps and are added to figure 4.
3. Umbilic points on a generic surface occur at elliptic points, that is why we do not get flecnodal curves or $H_3$![]() -curves through such points.
-curves through such points.
Acknowledgements
The authors would like to thank the referee for useful and pertinent comments. GPS was partially supported by the Basque Government through the BERC 2018–2021 programme and Gobierno Vasco Grant IT1094-16, by the Spanish Ministry of Science, Innovation and Universities: BCAM Severo Ochoa accreditation SEV-2017-0718, by the ERCEA Consolidator Grant 615655 NMST, and by Programa de Becas Posdoctorales en la UNAM, DGAPA, Instituto de Matemáticas, UNAM. FT was partially supported by the FAPESP Thematic project grant 2019/07316-0 and the CNPq research grant 303772/2018-2.