3.1. Experimental conditions

The experiment consisted in a $3$ m high and $D=0.4$ m internal diameter bubble column functioning with air and water. The gas injector was a 10 mm thick Plexiglas plate perforated by 352 orifices of 1 mm internal diameter. These orifices were uniformly distributed over the column cross-section. The column was filled with tap water at an initial height $H_0=2.02$ m. The surface tension of the tap water used was $67\ {\rm mN} {\rm m}^{-1}$ at $25\,^\circ {\rm C}$, its pH evolved in the interval $[7.7, 7.9]$ and its conductivity varied within the range $330\unicode{x2013}450\ \mathrm {\mu }{\rm S}\ {\rm cm}^{-1}$, indicating the presence of a significant solid content. All the data presented here were gathered at $H=1.45$ m above injection, that is at $H/D=3.625$, a position well within the quasi-fully developed region. Besides, and owing to the large ratio $H_0/D=5.05$, the information collected in this zone is not sensitive to the static liquid height $H_0$. Experiments were performed for superficial gas velocities $V_{sg}$ ranging from $0.6\ {\rm cm}\ {\rm s}^{-1}$ to $26\ {\rm cm}\ {\rm s}^{-1}$; the maximum global volume fraction was approximately 35 %.

Information relative to bubbles was acquired with the Doppler probe. For each bubble detected, the probe gives access to the gas residence time $t_G$, that is the time spent by the probe tip inside the bubble. The void fraction is given by the sum of residence times divided by the measuring duration. For the present flow conditions in terms of fluids, bubble size, absolute velocity of bubbles and probe dimension, the uncertainty on void fraction measurements is less than 1 % according to the study of Vejražka et al. (Reference Vejražka, Večeř, Orvalho, Sechet, Ruzicka and Cartellier2010) in air–water systems. Besides, a Doppler signal is recorded from the rear interface (that is at the gas to liquid transition) for some bubble signatures, and its analysis provides the bubble velocity $V_b$ projected along the fibre axis. When both the gas residence time $t_{Gi}$ and the bubble velocity $V_{bi}$ are available for the $i$th bubble, one can infer the gas chord $C_i = V_{bi} t_{Gi}$ cut by the probe through that bubble. The typical reproducibility on chord length measurements is of order 3 % on the mean value, and less than 20 % on the standard deviation (Lefebvre et al. Reference Lefebvre, Mezui, Obligado, Gluck and Cartellier2022).

For the liquid phase, velocity statistics were measured with a Pavlov device made of two parallel tubes (external diameter 6 mm, internal diameter 5 mm), each drilled with a 0.5 mm in diameter hole. These two orifices faced opposite directions: they were aligned along a vertical, and the vertical distance between them was 12 mm. The pressure transducer was a Rosemount 2051 CD2 with a dynamics of ${\pm }15\,000$ Pa, a resolution of ${\pm }9.75$ Pa and a response time of $130$ ms. The differential pressure was transformed into the local liquid velocity using $v_L^2(t) = \pm 2 \vert p(t) \vert / \rho _L$ (no correction dependent on void fraction was considered) with the appropriate sign. Hence, the range in velocity was ${\pm }5.48\ {\rm m}\ {\rm s}^{-1}$ and the resolution $\pm 0.14\ {\rm m}\ {\rm s}^{-1}$.

Liquid and gas velocity probability density functions (p.d.f.s) measured with these sensors in the centre of the column are illustrated figure 2. By construction, the Pavlov tube detects both positive (upward directed, i.e. against gravity) and negative (downward directed, i.e. along gravity) velocities. For bubbles, as the Doppler probe detects only inclusions approaching it head on, the p.d.f.s were built by cumulating the information gathered over the same measuring duration and at the same position with an upward directed probe and with a downward directed probe. More details and discussion concerning these measurements are presented in Lefebvre et al. (Reference Lefebvre, Mezui, Obligado, Gluck and Cartellier2022). The reproducibility on mean bubble velocity and on its standard deviation is better than ${\pm }5\,\%$.

Figure 2. Velocity p.d.f.s for the liquid (blue lines) and for the bubbles (red lines) measured on the column axis at $H/D=3.625$ for $v_{sg}=13\ {\rm cm}\ {\rm s}^{-1}$ (a), $v_{sg}=16.25\ {\rm cm}\ {\rm s}^{-1}$ (b) and $v_{sg}=22.75\ {\rm cm}\ {\rm s}^{-1}$ (c).

Concerning the bubble size, the analysis of the axial evolution of chords distributions along the column indicates that coalescence was absent (or at least extremely weak) in our experimental conditions (Lefebvre et al. Reference Lefebvre, Mezui, Obligado, Gluck and Cartellier2022), most probably because of the partial contamination of the tap water used. Over the investigated range of superficial velocities, the Sauter mean vertical diameter of bubbles remained in the interval $[6.2\ {\rm mm}; 6.7\ {\rm mm}]$ while their Sauter mean horizontal diameter measured with the correlation technique (Raimundo et al. Reference Raimundo, Cartellier, Beneventi, Forret and Augier2016) increased with $V_{sg}$ from 6.6 to 7.8 mm. Overall, the mean equivalent bubble diameter remained in the interval $[6.62\ {\rm mm}; 7.35\ {\rm mm}]$: that corresponds to a terminal velocity from $21\ {\rm cm}\ {\rm s}^{-1}$ to $23\ {\rm cm}\ {\rm s}^{-1}$ (Maxworthy et al. Reference Maxworthy, Gnann, Kürten and Durst1996) and to particle Reynolds numbers in the range 1450–1550.

The local void fraction measured on the column axis $\varepsilon _{axis}$ is plotted vs the gas superficial velocity in figure 3(a). The homogeneous regime ends for $V_{sg}$ between ${\sim }4\ {\rm cm}\ {\rm s}^{-1}$ and ${\sim }5\ {\rm cm}\ {\rm s}^{-1}$, while the ‘pure’ heterogeneous regime starts at $V_{sg} \sim 6.5\ {\rm cm}\ {\rm s}^{-1}$. Following Krishna et al. (Reference Krishna, Wilkinson and Van Dierendonck1991), these data are plotted as $V_{sg}/\varepsilon _{axis}$ vs $V_{sg}$ in figure 3(b): they exhibit a constant rise velocity, close to the bubble terminal velocity $U_T$, up to $V_{sg} \sim 4\ {\rm cm}\ {\rm s}^{-1}$, that is within the homogeneous regime. Beyond that, the apparent rise velocity (called ‘rise velocity of swarm’ by Krishna et al. Reference Krishna, Wilkinson and Van Dierendonck1991), monotonically increases with the gas superficial velocity. It reaches a magnitude of approximately 3 times $U_T$ at the largest $V_{sg}$ investigated here (namely $24.7\ {\rm cm}\ {\rm s}^{-1}$). That increase is the signature of the heterogeneous regime. Note also that the latter correspond to a void fraction on the axis that exceeds 20 %. In the following, the transition will be represented by a vertical dash line at $V_{sg}=5\ {\rm cm}\ {\rm s}^{-1}$ in figures as a guide to the eye.

Figure 3. (a) Evolution of the local void fraction $\varepsilon _{axis}$ on the column axis with the gas superficial velocity $V_{sg}$. (b) Plot of the apparent rise velocity estimated as $V_{sg}/\varepsilon _{axis}$ vs $V_{sg}$. Measurements with a downward directed Doppler probe at a height $H/D=3.625$ above injection.

3.2. Local gas and liquid velocity on the column axis vs $V_{sg}$

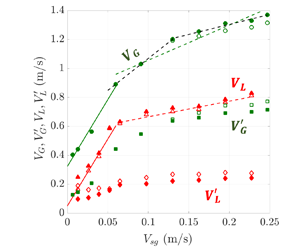
Figure 4 provides the mean vertical velocities of bubbles $V_G$ and of the liquid $V_L$ on the column axis as well as the standard deviations $V_G'$ for the gas phase and $V_L'$ for the liquid phase. Two datasets are presented for the mean velocities.

Figure 4. Evolution of the mean vertical velocities of the bubbles $V_G$ and of the liquid $V_L$, and of their standard deviation ($V_G'$ for the gas, $V_L'$ for the liquid), with the gas superficial velocity $V_{sg}$. Measurements performed in a $D=0.4$ m column, at $H/D=3.625$ and on the column axis. The bubble velocities were measured with a Doppler probe and the liquid velocities with a Pavlov tube. The straight lines in the homogeneous (continuous lines) and in the heterogeneous (dashed lines) regimes are linear fits of the data. Note that in the heterogeneous regime, two plausible trends (green and black dashed lines) are proposed for the mean bubble velocity. The difference between ‘up flow’ and ‘up and down flow’ sets is explained in the text.

For bubbles, a set named ‘up flow’ corresponds to measurements achieved with a Doppler probe pointing downwards that collects only upward directed (i.e. positive) vertical velocities. A second dataset named ‘up and down flow’ was obtained by gathering direct (i.e. without interpolation) velocity measurements from a probe pointing downward, with direct (i.e. without interpolation) velocity measurements from the same probe pointing upward. In this process, the measuring duration was the same for the two probe orientations. In the flow conditions considered here, the mean velocities from these two sets are close, with a difference of at most 4 % (Lefebvre et al. Reference Lefebvre, Mezui, Obligado, Gluck and Cartellier2022). Similarly, the difference on bubble velocity standard deviations from these two sets is at most 8 %.

For the liquid velocities, two datasets are also presented: one corresponds to moments evaluated over the entire distribution (named ‘up and down flow’) while the other concerns positive velocities only (named ‘up flow’). In the heterogeneous regime, the difference between the two sets is at most 3.6 % for the mean value and 18 % for the standard deviation. Oddly, larger liquid velocity deviations between ‘up flow’ and ‘up and down flow’ statistics appear in the homogeneous regime. The difference is especially pronounced for $V_{sg}$ below $3\ {\rm cm}\ {\rm s}^{-1}$. These deviations are related with the unexpected apparition of a significant negative tail in the liquid velocity p.d.f.s when $V_{sg}$ becomes small, a defect that may possibly be due to the flow perturbation induced by the rather large probe holder used in our experimental set-up.

Except for these low $V_{sg}$ cases, the differences between the ‘up flow’ and the ‘up and down flow’ datasets remain weak. These small differences partly come from the fact that these data are all collected on the column axis, where the probability of occurrence of absolute negative velocities in the laboratory frame remains small. Indeed, in our experiments, the probability to observe a downward directed liquid velocity on the axis was less than 3 % for any $V_{sg}$ in the heterogeneous regime. Similarly, Xue et al. (Reference Xue, Al-Dahhan, Dudukovic and Mudde2008) found a probability for observing negative bubble velocities on the column axis between 4 % and 4.5 % at $V_{sg}=14\ {\rm cm}\ {\rm s}^{-1}$ and approximately 6 % at $V_{sg}=60\ {\rm cm}\ {\rm s}^{-1}$. For the gas phase, and because of the positive (upward directed) relative velocity, these probabilities should be lower than the above figures. Hence, considering either ‘up flow’ or ‘up and down flow’ datasets does not change the conclusions proposed hereafter. Yet, the distinction between the two series is worth to be kept in mind in the perspective of analysing other radial positions where the probability of occurrence of downward flow increases.

From the data presented figure 4, a series of comments and conclusions emerge:

1. (i) The local relative velocity $V_G-V_L$ remains nearly constant in the homogeneous regime. It is approximately $27\ {\rm cm}\ {\rm s}^{-1}$, a magnitude comparable to the ‘mean’ terminal velocity $U_T$ of the bubbles generated in the column.

2. (ii) In the heterogeneous regime, the relative velocity becomes larger than $U_T$. Furthermore, it seems to monotonically increase with $V_{sg}$ (see the trend indicated by the green and red dashed lines in figure 4). At approximately $V_{sg}=19.5\ {\rm m}\ {\rm s}^{-1}$, the measured relative velocity amounts to $54.6\ {\rm cm}\ {\rm s}^{-1}$ that is 2.5 times the terminal velocity $U_T$. Thus, these direct velocity measurements are consistent with the behaviour of the ‘rise velocity of swarm’ $V_{sg}/\varepsilon _{axis}$ shown in figure 3(b). They also confirm the conclusion we previously obtained (see Raimundo et al. Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019) by analysing the flow in the core region of the bubble column: the apparent relative velocity was indeed found to range between 2 and 8 times $U_T$ using a conservative evaluation of the gas liquid flow rate in the core region of the bubble column.

3. (iii) The relative fluctuations in velocity $V'/V$ are nearly constant in the heterogeneous regime (as shown figure 5). For the liquid phase, the average of $V_L'/V_L$ over the data collected in the heterogeneous regime equals 36.5 %, in agreement with previous findings (see the discussion in Raimundo et al. Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019). For the gas phase, the average of $V_G'/V_G$ is even higher; it equals 52 %–53 % when considering positive velocities only, and it rises up to 56 %–57 % when combining positive and negative velocities measurements (Lefebvre et al. Reference Lefebvre, Mezui, Obligado, Gluck and Cartellier2022). These strong figures confirm that intense turbulent motions take place in heterogeneous conditions.

4. (iv) From a closer examination of figures 4 and 5, two different behaviours could possibly be distinguished in the heterogeneous regime. From the homogeneous/heterogeneous transition up to $V_{sg}$ approximately $13\unicode{x2013}15\ {\rm cm}\ {\rm s}^{-1}$, the relative velocity $V_G-V_L$ and also to some extent the fluctuation $V_G'/V_G$ exhibit a clear monotonic increase with the gas superficial velocity. Above $V_{sg} \sim 13\unicode{x2013}15\ {\rm cm}\ {\rm s}^{-1}$, these two quantities seem to become constant. In particular, the increase in the bubble velocity illustrated by the black dashed line in figure 4 becomes nearly parallel to that of the mean liquid velocity (dashed red line in figure 4): accordingly, the relative velocity seems to stabilize at a value approximately $2.3\unicode{x2013}2.4 U_T$ at large $V_{sg}$. With regard to flow dynamics and scaling laws, it would be worthwhile to clarify whether the relative velocity reaches an asymptote, or if it continues to grow with $V_{sg}$: more experimental data covering an enlarged range of gas superficial velocities are required for that.

Figure 5. Vertical velocity fluctuations $V'/V$ of liquid and gas phases vs the gas superficial velocity $V_{sg}$. Measurements performed in a $D=0.4$ m column, on the column axis at $H/D=3.625$.

To test the scaling proposed in (2.2) on these experimental data, we used local void fraction and velocities measured on the axis and at the same height $H/D$ above the injector. Since the two sets ‘up flow’ and ‘up and down flow’ are close, let us consider only ‘up and down flow’ velocity statistics for the analysis. The mean velocities as well as the standard deviations scaled by $(gD\varepsilon )^{1/2}$ are represented for both phases in figure 6. Clearly, all these quantities remain nearly constant for all flow conditions pertaining to the heterogeneous regime. For the mean bubble velocity on the column axis, one gets

(3.1)\begin{equation} V_G/(gD\varepsilon)^{1/2} \sim 1.09\pm0.02, \end{equation}

while for the mean liquid velocity on the column axis

(3.2)\begin{equation} V_L/(gD\varepsilon)^{1/2} \sim 0.68\pm0.01. \end{equation}

Figure 6. Evolution of phasic velocities (‘up and down flow’ velocity statistics) scaled by $(gD\varepsilon )^{1/2}$ vs the superficial velocity $V_{sg}$. The mean ($V$) and fluctuating ($V'$) components of the bubble and the liquid vertical velocities as well as the void fraction $\varepsilon$ are local quantities measured in a $D=0.4$ m column, on the column axis at $H/D=3.625$.

According to these results, the relative velocity on the column axis scales as $U_R \sim 0.41 (gD\varepsilon )^{1/2}$, i.e. it monotonically increases with the void fraction $\varepsilon$. Such an increase of the relative velocity with the void fraction has been identified in bubble columns using indirect arguments (see for e.g. Raimundo et al. Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019). It has also been observed in other gas–liquid systems. Such a behaviour is sometimes represented by a swarm coefficient that quantifies the decrease of the drag force acting on a bubble with the void fraction (Ishii & Zuber Reference Ishii and Zuber1979; Simonnet et al. Reference Simonnet, Gentric, Olmos and Midoux2007). Nowadays, ad hoc swarm coefficients are routinely introduced in numerical simulations based on two-fluid models (e.g. McClure et al. Reference McClure, Kavanagh, Fletcher and Barton2017; Gemello et al. Reference Gemello, Cappello, Augier, Marchisio and Plais2018). We bring here direct experimental evidence of the increase of the relative velocity with the void fraction in a bubble column operated in the heterogeneous regime.

Concerning the standard deviation of velocities, the standard deviation being proportional to the mean (see figure 4), they also follow the same scaling with $V_G'/(gD\varepsilon )^{1/2} \sim 0.6\pm 0.02$ and $V_L'/(gD\varepsilon )^{1/2} \sim 0.22 \pm 0.02$. Hence, all the above results obtained on the mean and on the fluctuating components of bubbles and liquid velocities confirm the soundness of the scaling proposed in (2.2) with respect to void fraction.

The scaling resulting from an inertia–buoyancy equilibrium proposed above also includes an increase of velocities with the square root of the bubble column diameter. As the experiments presented in this section concern only one bubble column diameter, the dependency with the column diameter cannot be tested. New experimental data gathered in bubble columns of variable diameters are needed to test the validity of the proposed scale. In that perspective, available experiments from the literature and relative to bubble columns of variable diameter will be analysed in the next section.

Nevertheless, we already have accumulated strong experimental evidence of the relevance of the square root of the bubble column diameter as a scaling factor for the mean liquid velocity (Raimundo et al. Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019). Indeed, the neat upward liquid flow rate $Q_{Lup}$ in the column, where $Q_{Lup}$ is obtained by integrating the liquid flux $(1-\varepsilon ) V_L$ over the core region (i.e. from the axis up to $0.7\unicode{x2013}0.71 R$), happens not to depend on $V_{sg}$ in the heterogeneous regime. In the present experiments, we also found that $Q_{Lup}$ is independent on $V_{sg}$ in the heterogeneous regime. That conclusion was confirmed from data collected at three heights above injection, namely $H/D=2.625$, $H/D=3.625$ and $H/D=4.875$. The result is $Q_{Lup}=0.0122\ {\rm m}^3\ {\rm s}^{-1}$, with variations between $+0.001\ {\rm m}^3\ {\rm s}^{-1}$ and $0.0007\ {\rm m}^3\ {\rm s}^{-1}$ depending on the set of data considered to evaluate the mean.

Moreover, we have previously shown (Raimundo et al. Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019) that $Q_{Lup}$ is proportional to $D^2 (gD)^{1/2}$ over a significant range of column diameters (from $D=0.15$ m to 3 m) and of gas superficial velocities (from $V_{sg}=9$ to $25\ {\rm cm}\ {\rm s}^{-1}$). As shown figure 7(a), the present experiments confirm that finding in a $D=0.4$ m column, for $V_{sg}$ between $6.5\ {\rm cm}\ {\rm s}^{-1}$ and $22.7\ {\rm cm}\ {\rm s}^{-1}$ and for $2.625 \leqslant H/D \leqslant 4.875$. The dependency of $Q_{Lup}$ with $D$ is further illustrated in figure 7(b) where we have reported the present data, the data collected by Raimundo et al. (Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019), as well as one data produced by Guan et al. (Reference Guan, Gao, Tian, Wang, Cheng and Li2015) in the following flow condition: $V_{sg}=47\ {\rm cm}\ {\rm s}^{-1}$ in a $D=0.8$ m column and for $2.75 \leqslant H/D \leqslant 4.625$. All these data fall onto the same curve. Overall, the observed liquid flow rate – column diameter relationship writes

(3.3)\begin{equation} Q_{Lup}=0.0386\pm0.002 D^2 (gD)^{1/2}. \end{equation}

Figure 7. (a) Upward directed liquid flux $Q_{Lup} / [D^2 (gD)^{1/2}]$ vs $V_{sg}$ measured at different heights above injection in $D=0.4$ m columns. (b) Evolution of $Q_{Lup}$ with the bubble column diameter from Raimundo et al. (Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019), from Guan et al. (Reference Guan, Gao, Tian, Wang, Cheng and Li2015) and from present data.

This result can also be expressed as a Froude number based on the average liquid velocity $Q_{Lup}/S_{core}$ in the core region. Here, the cross-section $S_{core}$ of the ascending flow zone is evaluated as ${\rm \pi} D^2/8$ (the mean liquid becomes zero at a radial position between $0.7R$ and $0.71R$: that limit is well approximated as $2^{1/2}/2 R= 0.707 R$). Hence, $Fr_L = (Q_{Lup}/S_{core}) / (gD)^{1/2} = 0.098$. (There is a typo error in (13) of Raimundo et al. (Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019): the coefficient 0.024 should be replaced by 0.098.) All the above mentioned experiments bring clear evidence that the velocity of the mean liquid circulation in a bubble column operated in the heterogeneous regime scales as $(gD)^{1/2}$ with the column diameter.

4.1. Mean liquid velocity on the column axis

We start this section by briefly detailing the datasets from the literature that will be discussed. Tables 1 and 2 lists the experiments that obey the above constraints and that provide the liquid velocity and the local void fraction on the bubble column axis. Some choices were made to exploit the data. For Hills (Reference Hills1974), we considered only the data acquired with the ‘plate B’ that corresponds to a uniform gas injection over the column cross-section. In Forret et al. (Reference Forret, Schweitzer, Gauthier, Krishna and Schweich2006), the only quantitative data on gas hold-up are global void fractions deduced from static and dynamic liquid heights. We transformed the global void fraction into a local void fraction on the axis by multiplying it by 1.5 as done by the authors (see their (4)), but this factor could be inappropriate. The local void fractions for the data of Vial et al. (Reference Vial, Laine, Poncin, Midoux and Wild2001) were collected in Camarasa et al. (Reference Camarasa, Vial, Poncin, Wild, Midoux and Bouillard1999). For Yao et al. (Reference Yao, Zheng, Gasche and Hofmann1991), we present the data they collected at various heights with $H/D$ from 2.6 up to 12, and we use an extrapolation to evaluate the void fraction at $V_{sg}=10\ {\rm cm}\ {\rm s}^{-1}$. Note also that these authors imposed a forced liquid motion but the mean velocity of $1\ {\rm cm}\ {\rm s}^{-1}$ is negligible compared with the measured liquid and gas velocities on the column axis: these data are therefore believed to be representative of a bubble column operated in a batch mode and they have been kept in the analysis. Finally, all the measurements mentioned in tables 1 and 2 considered positive and negative velocity realizations, although some (hard to evaluate) bias may be present notably with Pavlov tubes, as evoked by Hills (Reference Hills1974). To be consistent, we compared with our data series named ‘up and down flow’ (see § 3).

Figure 8 provides the quantity $V_L/(gD\varepsilon )^{1/2}$ vs the superficial gas velocity with $V_L$ and $\varepsilon$ measured on the axis. The figure includes all the contributions listed in tables 1 and 2, and that have been collected in the homogeneous regime as well as in the heterogeneous regime. The data concern column diameters from 0.1 to 3 m and superficial velocities varying from 1.2 to $62\ {\rm cm}\ {\rm s}^{-1}$. In the limit of small superficial gas velocities, $V_L/(gD\varepsilon )^{1/2}$evolves between 0.01 and 1.02. As $V_{sg}$ increases, the range of variation of $V_L/(gD\varepsilon )^{1/2}$ smoothly diminishes. Above $V_{sg} \sim 15\ {\rm cm}\ {\rm s}^{-1}$, $V_L/(gD\varepsilon )^{1/2}$ evolves within the interval $[0.48 ; 0.77]$. Note that this interval corresponds to bubble column diameters ranging from 0.1 m to 3 m. Above $V_{sg} \sim 20\ {\rm cm}\ {\rm s}^{-1}$, that interval further narrows and the quantity $V_L/(gD\varepsilon )^{1/2}$ tends to be constant in the pure heterogeneous regime: that feature supports the scaling argument presented in § 2. Although experimental data are lacking at very large $V_{sg}$ to precisely define the asymptotic behaviour, the latter is estimated as

(4.1)\begin{equation} V_L\sim0.58(gD\varepsilon)^{1/2}, \end{equation}

as shown by the inset in figure 8 that provides $V_L$ vs $(gD\varepsilon )^{1/2}$ for all available data at $V_{sg}$ above $8\ {\rm cm}\ {\rm s}^{-1}$. The proportionality factor equals 0.5774 (and the correlation coefficient is 0.867). Note that the same plot using all data available at $V_{sg}$ above $6\ {\rm cm}\ {\rm s}^{-1}$ also provides a linear behaviour with a proportionality factor equals to 0.5786 (and a correlation coefficient of 0.87). Alternately, when the quantity $V_L/(gD)$ is plotted vs the local void fraction for all the data shown in figure 8, $V_L/(gD)$ is found to evolve as $\varepsilon ^{0.50\pm 0.01}$: this is fully consistent with the $\varepsilon ^{1/2}$ dependency predicted.

Figure 8. Evolution of $V_L/(gD\varepsilon )^{1/2}$ where $V_L$ and $\varepsilon$ are measured on the column axis vs the superficial gas velocity from the contributions quoted in tables 1 and 2. The inset plots $V_L$ vs $(gD\varepsilon )^{1/2}$ for all data collected on the column axis in the heterogeneous regime for $V_{sg} \geqslant 8\ {\rm cm}\ {\rm s}^{-1}$ and for $0.1\ {\rm m} \leqslant D \leqslant 3\ {\rm m}$: the dashed line in the inset corresponds to the fit $V_L= 0.577 (gD\varepsilon )^{1/2}$.

It is worth discussing the uncertainty on these figures as the data presented in figure 8 come from different operators and from various measuring techniques. The typical dispersion in the measurements can be appreciated by comparing the data collected in identical bubble columns. For example, in the $D=0.15$ m column and at $V_{sg} \sim 20\ {\rm cm}\ {\rm s}^{-1}$, there is a 0.2 difference in $V_L/(gD\varepsilon )^{1/2}$ between the data from Forret et al. (Reference Forret, Schweitzer, Gauthier, Krishna and Schweich2006) and those from Raimundo et al. (Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019). Similarly, in the $D=0.4$ m column and at $V_{sg}\sim 20\ {\rm cm}\ {\rm s}^{-1}$, the values of $V_L/(gD\varepsilon )^{1/2}$ deduced from the data of Forret et al. (Reference Forret, Schweitzer, Gauthier, Krishna and Schweich2006), from those of Raimundo et al. (Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019) and from the present work all fall within a 0.1 band. These are quite reasonable dispersions especially when considering that the water quality was not always the same, so that the coalescence efficiency varied. Finally, as far as we can judge from the available information given in articles, all the experimental conditions in figure 8 correspond to no or weak coalescence. The monotonic allure of the evolution of the local void fraction on the axis with $V_{sg}$ shown in figure 9 also supports that statement.

Figure 9. Evolution of the local void fraction on the column axis vs the superficial gas velocity for all the contributions quoted in tables 1 and 2 and exploited in figure 8. For Forret et al. (Reference Forret, Schweitzer, Gauthier, Krishna and Schweich2006), the local void fraction has been estimated as the global void fraction divided by 1.5.

4.2. Mean gas velocity on the column axis

Experiments providing statistics on the bubble velocity are not common. This is due to the lack of reliable measuring techniques giving access to bubble velocity in the difficult conditions encountered in the heterogeneous regime, in particular with respect to high void fractions, flow unsteadiness and ‘chaotic’ 3-D trajectories of bubbles. Each bubble velocity technique has its own limitations, and their respective uncertainty and resolution in such flow conditions are not well known. For example, for phase detection techniques based on immersed probes either single, double or multiple, it is well known that erroneous velocity data are collected in heterogeneous conditions because of the unsteady 3-D motions of these two-phase flows. Yet, average quantities relative to velocity or size seem to be meaningful (Chaumat et al. Reference Chaumat, Billet-Duquenne, Augier, Mathieu and Delmas2007; Raimundo et al. Reference Raimundo, Cartellier, Beneventi, Forret and Augier2016). Moreover, while some bias may alter the statistics and when the latter occurs, it is usually hard to quantify. For all these reasons, we will not discuss further the respective merits of each measuring technique: instead, we report all available raw data as given in the original papers, keeping in mind that some issues on resolution, accuracy or bias remain as an open question.

Tables 3 and 4 summarize the set of experiments used to analyse the gas velocity that corresponds here to the velocity of bubbles. The corresponding data on the mean bubble velocity scaled by $(gD\varepsilon )^{1/2}$, where both the velocity and the void fraction were measured on the column axis, are reported vs $V_{sg}$ in figure 10 irrespective of the flow regime.

Figure 10. Evolution of $V_G/(gD\varepsilon )^{1/2}$ where $V_L$ and $\varepsilon$ are measured on the column axis vs the superficial gas velocity $V_{sg}$ for all gas or bubble velocity measurements from the articles quoted in tables 3 and 4.

We will now provide some information on how the data were exploited for the datasets used in this section. First, when different injectors were tested, we always selected the data acquired with multiple-orifice injectors distributed over the entire column cross-section. Second, original data were sometimes interpolated to estimate missing local void fraction data: that process was used only when the interpolation process was safe. If some extrapolation was required, the corresponding data were discarded unless otherwise specifically stated in the text in the legend. It is worth to notice that almost all data correspond to tap water and air (under ambient pressure and temperature conditions), with two exceptions: Yao et al. (Reference Yao, Zheng, Gasche and Hofmann1991) used deionized water, and one set of data from Camarasa et al. (Reference Camarasa, Vial, Poncin, Wild, Midoux and Bouillard1999) was gathered in an aqueous solution of alcohol (water and pentanol at a concentration $4 \times 10^{-4}\ {\rm mol}\ {\rm l}^{-1}$).

We also mention some specific choices we made when extracting the data. For Yao et al. (Reference Yao, Zheng, Gasche and Hofmann1991), only the bubble velocity detected by the ultrasound technique is plotted because these authors found comparable results with their five-point conductivity probe. In Camarasa et al. (Reference Camarasa, Vial, Poncin, Wild, Midoux and Bouillard1999), the bubble velocity was measured by an ultrasonic Doppler technique for single orifice and porous plate gas injection but not for the multiple orifice nozzle that provides the injection conditions we are looking for here. For that sparger, the bubble velocity was measured by a DGD (dynamic gas disengagement) technique: Camarasa et al. (Reference Camarasa, Vial, Poncin, Wild, Midoux and Bouillard1999) report the velocity of ‘large’ bubbles and of ‘small bubbles’ but they do not explicitly specify how ‘large’ bubbles are distinguished from ‘small’ ones. It happens that, for a given flow condition, the mean velocity of ‘small bubbles’ measured by Camarasa et al. (Reference Camarasa, Vial, Poncin, Wild, Midoux and Bouillard1999) is 2 to 4 times (in water) and 2 to 2.5 times (in aqueous solution of alcohol) lower than the mean velocity measured for ‘large bubbles’. Presumably, ‘small’ bubbles correspond to the 1–2 mm bubbles at the lower end of the bubble size distributions they provide, while ‘large’ bubble can be as large as 8–10 mm in water (see their figure 10) and 6–8 mm in water plus pentanol (see their figure 20). According to these comments, only the data for ‘large’ bubbles are reported in figure 10.

Let us finally mention that, for the data of Camarasa et al. (Reference Camarasa, Vial, Poncin, Wild, Midoux and Bouillard1999) gathered in the aqueous solution of pentanol, no data are given on the local void fraction and we used the global void fraction instead. Accordingly, the values of $V_G/(gD\varepsilon )^{1/2}$ are overestimated for that series. Chen et al. (Reference Chen, Tsutsumi, Otawara and Shigaki2003) performed measurements in a $D=0.4$ m bubble column at $H/D=2.6$, and in a $D=0.8$ m bubble column at $H/D=1.3$: the latter case, for which they observed non-symmetrical flows, was discarded because the data were not collected in the quasi-fully developed region.

Concerning the experiments by Xue et al. (Reference Xue, Al-Dahhan, Dudukovic and Mudde2008), all the data they collected in the heterogeneous regime at $H/D=5.1$ correspond to strongly asymmetrical flows. Indeed, the velocity difference between the upward motion on one side of the column and the downward motion on the opposite side ranges between $20\ {\rm cm}\ {\rm s}^{-1}$ and $40\ {\rm cm}\ {\rm s}^{-1}$: these figures are therefore quite significant compared with the mean bubble motion on the column axis that evolved between $40$ and $90\ {\rm cm}\ {\rm s}^{-1}$. That asymmetry was further confirmed by void fraction and bubble detection frequency profiles. The only symmetrical bubble velocity profile reported by Xue et al. (Reference Xue, Al-Dahhan, Dudukovic and Mudde2008) was collected at a larger distance from injection (namely $H/D=8.5$) and at $V_{sg}=30\ {\rm cm}\ {\rm s}^{-1}$. Unfortunately, they do not provide the void fraction for these conditions. Despite these shortcomings, all the data of Xue et al. (Reference Xue, Al-Dahhan, Dudukovic and Mudde2008) collected at $H/D=5.1$ have been integrated in our analysis. Let us also underline that these authors are among the very few who have explored large gas superficial velocities.

Among the contributions listed in tables 3 and 4, almost all gathered (at least in principle) positive and negative bubble velocities, except for Raimundo (Reference Raimundo2015) and Raimundo et al. (Reference Raimundo, Cartellier, Beneventi, Forret and Augier2016) who collected positive velocities only since they exploited the dewetting of a single fibre tip. Yet, as the sources of bias are usually not analysed for bubble velocity measurement techniques, it is difficult to ascertain that the information collected was indeed the faithful assembly of positive and negative realizations. An indication of these difficulties is that the standard deviation of bubble size distributions are never provided, nor discussed, except by Yao et al. (Reference Yao, Zheng, Gasche and Hofmann1991) who measured bubble velocity fluctuations with an ultrasound technique. As for the liquid phase, and to be consistent, we thus consider our data series from § 3 named ‘up and down flow’ for the comparison.

The data presented figure 10 concern column diameters from 0.1 to 1 m and gas superficial velocities varying over two decades from 0.6 to $60\ {\rm cm}\ {\rm s}^{-1}$. At low gas superficial velocities, say below a few ${\rm cm}\ {\rm s}^{-1}$, that is within the homogeneous regime, the quantity $V_G/(gD\varepsilon )^{1/2}$ evolves from 0.2 up to 1.8. That ratio significantly varies from one experiment to the other. For a given data series, the ratio $V_G/(gD\varepsilon )^{1/2}$ tends to become somewhat constant when moving towards large superficial velocities. For $V_{sg}$ above approximately $10\ {\rm cm}\ {\rm s}^{-1}$, that is well within the heterogeneous regime, the dispersion of the data significantly diminishes and $V_G/(gD\varepsilon )^{1/2}$ evolves inside a narrower band between 0.6 and 1.4. Note that these last figures encompass bubble column diameters ranging from 0.15 to 1 m. The trends are therefore the same as those detected when analysing the liquid velocity. Yet, the fluctuations observed from one series to another are larger than those observed for the liquid velocity. This is probably because of the stronger uncertainties of gas velocity measuring techniques. Also, and compared with the mean liquid velocity presented figure 8, it is more difficult to estimate the asymptotic value of $V_G/(gD\varepsilon )^{1/2}$. According to Xue et al. (Reference Xue, Al-Dahhan, Dudukovic and Mudde2008) and to some runs of Raimundo et al. (Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019), that limit is near 0.8 while from the present data, as well as from those of Yao et al. (Reference Yao, Zheng, Gasche and Hofmann1991), the limit is possibly closer to 1. Again, experimental data at very large $V_{sg}$ are required to more accurately determine the asymptotic behaviour of $V_G/(gD\varepsilon )^{1/2}$. Despite the limitations on available data, the trends observed on $V_G/(gD\varepsilon )^{1/2}$ for column diameters between 0.1 and 1 m are consistent with the scaling argument proposed in § 2.

Figure 11 provides the evolution of the void fraction on the axis with $V_{sg}$ for all the experiments quoted in tables 3 and 4. As in figure 9, all these evolutions are monotonic, so that they presumably all correspond to no or weak coalescence. Yet, in terms of local void fraction, one data series happens to be neatly above all others: this is the one from Xue et al. (Reference Xue, Al-Dahhan, Dudukovic and Mudde2008). Contrary to all other experiments presented in figure 10 (see also tables 3 and 4), the coalescence was probably significant in their experiments. Indeed, they observe an increase of the mean bubble chord length on the axis from 2–3 mm in the homogeneous regime up to 6 mm in the heterogeneous regime while the standard deviation of the size distribution growths from approximately 1 mm up to 10 mm. Also, their bubble chord distributions indicate that bubbles up to 15 mm are detected, and bubbles on the axis are significantly larger than near walls where their mean chord is less than 3 mm. Let us also underline that the local void fractions measured by Xue et al. (Reference Xue, Al-Dahhan, Dudukovic and Mudde2008) in the heterogeneous regime are among the largest of all data series presented figures 9 and 11. Xue et al. (Reference Xue, Al-Dahhan, Dudukovic and Mudde2008) used injectors made of orifices 0.5 mm in diameter, and small orifices are known to produce smaller bubbles and thus to increase the maximum void fraction reached in the homogeneous regime (Joshi et al. Reference Joshi, Parasu, Prasad, Phanikumar, Deshpande and Thorat1998).

Figure 11. Evolution of the local void fraction on the column axis vs the superficial gas velocity for contributions quoted in tables 3 and 4 and exploited in figure 10.

Chaumat, Billet & Delmas (Reference Chaumat, Billet and Delmas2006) obtained similar large values of the local hold-up when using the same small orifices: yet, the values of $V_G/(gD\varepsilon )^{1/2}$ deduced from their measurements remain comparable to other contributions for $V_{sg}$ below $0.13\ {\rm m}\ {\rm s}^{-1}$ (figure 10). These comments indicate that a characterization of flow conditions with respect to coalescence is not easy. In addition, experimental data on bubble velocity are missing to evaluate how much the magnitude of $V_G/(gD\varepsilon )^{1/2}$ may vary with the coalescence efficiency.

So far, the scaling of the liquid velocity has been discussed based on data collected on the axis. For the liquid, it is known that, in the heterogeneous regime, both the transverse liquid velocity and the local void fraction profiles assume self-similar shapes when scaled by their respective value on the axis (Forret et al. Reference Forret, Schweitzer, Gauthier, Krishna and Schweich2006). Hence, all the above findings are expected to remain valid at any radial position in the column provided one remains in the quasi-fully developed region. For the gas phase, we have shown in Lefebvre et al. (Reference Lefebvre, Mezui, Obligado, Gluck and Cartellier2022) that the bubble velocity profiles collected in the quasi-fully developed region when in heterogeneous conditions also happen to be self-similar when scaled by the bubble velocity on the column axis. Hence, the proposed scaling is also expected to remain valid at any radial position for the gas phase.

4.3. Liquid and gas velocity fluctuations

Experimental data on velocity fluctuations collected in bubble columns are scarce, and this is particularly true in the heterogeneous regime. For the liquid phase, Menzel et al. (Reference Menzel, In der Weide, Staudacher, Wein and Onken1990) provide two profiles of the axial liquid velocity fluctuations (quantified here by the standard deviation $V'$ of the velocity distribution). Nevertheless, these datasets were gathered in a 80 wt% glycerol/water mixture and, unfortunately, the authors do not indicate the corresponding mean velocities and void fractions for that fluid. Otherwise, data for the liquid phase are available in Yao et al. (Reference Yao, Zheng, Gasche and Hofmann1991), Vial et al. (Reference Vial, Laine, Poncin, Midoux and Wild2001), Forret (Reference Forret2003), Raimundo et al. (Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019) and from the present contribution. All these data concern deionized or tap water.

For the gas phase, single tip or multiple tips probes that exploit a transit time technique for velocity measurements are common, but, with these techniques, the measured velocity distributions are strongly biased by the detection of erroneous, large velocities (see e.g. Chaumat et al. Reference Chaumat, Billet-Duquenne, Augier, Mathieu and Delmas2007; Raimundo et al. Reference Raimundo, Cartellier, Beneventi, Forret and Augier2016). It happens that the mean velocity is significant, but the standard deviation is not reliable. Also, some authors (such as Chen et al. Reference Chen, Tsutsumi, Otawara and Shigaki2003; Xue et al. Reference Xue, Al-Dahhan, Dudukovic and Mudde2008; Guan & Yang Reference Guan and Yang2017) provide velocity distributions but the standard deviations are not quantified. For these reasons, one is left only with the data from Yao et al. (Reference Yao, Zheng, Gasche and Hofmann1991) acquired from an ultrasound technique in a $D=0.29$ m column with deionized water/air as fluids, and the data we collected with the Doppler probe in a $D=0.4$ m column with tap water/air as fluids (see Lefebvre et al. Reference Lefebvre, Mezui, Obligado, Gluck and Cartellier2022).

The experiments of Menzel et al. (Reference Menzel, In der Weide, Staudacher, Wein and Onken1990) indicate that, in the heterogeneous regime, the radial profiles of liquid velocity fluctuations remain self-similar when normalized by their maximum. One can also use the velocity fluctuations evaluated on the axis of the bubble column for that normalization. Hence, in the following, we focus our discussion on velocity fluctuations measured on the axis. The relative fluctuation $V_L'/V_L$ in the liquid phase (respectively $V_G'/V_G$ for the gas phase) measured on the column axis is presented figure 12 (respectively figure 13) vs the superficial gas velocity. All these measurements have been done in the quasi-fully developed region. Despite the limited number of independent data, each of the quantities $V_L'/V_L$ and $V_G'/V_G$ tends towards a constant value when moving inside the heterogeneous regime. That feature is well established for the liquid phase since the data come from different operators and from different sensors. Remarkably, the asymptotic behaviour is the same whatever the column diameter ranging from 0.15 to 3 m. The only series exhibiting a different trend are those from Yao et al. (Reference Yao, Zheng, Gasche and Hofmann1991) for the liquid phase. These data were obtained from hot-film probes, a technique that could be delicate to exploit in bubbly flows. The difficulties are expected to be even stronger in the conditions encountered in bubble columns at high gas superficial velocities. Unfortunately, Yao et al. (Reference Yao, Zheng, Gasche and Hofmann1991) do not comment on the signals they collected, nor on the signal processing they develop: it is therefore difficult to evaluate the reliability of their measurements.

Figure 12. Evolution of the relative fluctuation in the liquid phase velocity $V_L'/V_L$ measured on the column axis vs the superficial gas velocity.

Figure 13. Evolution of the relative fluctuation $V_G'/V_G$ of the velocity of bubbles measured on the column axis vs the superficial gas velocity.

Figures 12 and 13 show that, in the heterogeneous regime, the velocity fluctuations in the liquid as well as in the gas remain proportional to the mean velocity. Hence, all the findings on the scaling of mean velocities in the core region of the bubble column also apply to velocity fluctuations. One may be puzzled by such result, but physical arguments similar to those evoked in § 2 can explain that feature. The idea is that, in the heterogeneous regime, the contributions to velocity fluctuations in the liquid phase by the relative motion at the bubble scale, i.e. the so-called bubble-induced turbulence, which is at the origin of large ratio $V_L'/V_L$ observed figure 12 in the homogeneous regime (see Risso Reference Risso2018), is not the leading mechanism. Instead, in the heterogeneous regime, the agitation in the liquid is due to the presence of meso-scale structures. The later have been put in evidence and quantified with a 1-D Voronoï analysis performed on the phase indicator function delivered by optical probes. With such Voronoï tessellations, we have shown that in the heterogeneous regime these flows as organized in clusters (high void fraction regions) and voids (low void fraction regions) (Raimundo et al. Reference Raimundo, Cloupet, Cartellier, Beneventi and Augier2019). The variations in void fraction from one meso-scale structure to the other induce buoyancy forces that spatially fluctuate, and hence a velocity field that changes from one structure to the other. These meso-scale structures are transported by the mean flow and they could also form and disappear. Hence, at a fixed point in space, the passage of successive structures induces the velocity fluctuations that are precisely those detected by an Eulerian measuring technique, i.e. they are the quantities $V_L'$ and $V_G'$ measured with local probes.