We study Hele–Shaw flows with a moving boundary and multipole singularities. We find that such flows can be defined only on a finite time interval. Using a complex variable approach, we construct a family of explicit solutions for a single multipole. These solutions turn out to have the maximal possible lifetime in a certain class of solutions.

We also discuss the generalized Hele-Shaw model in which surface tension at the moving boundary is considered, and develop a method of finding steady shapes. This method yields new one-parameter families of stationary solutions. In the Appendix we discuss a connection between these solutions and a variational problem of potential theory.

This paper deals with the mathematical characterization of microstructure in elastic solids. We formulate our ideas in terms of rank-one convexity and identify the set of probability measures for which Jensen's inequality for this type of functions holds. This is the set of laminates. We also introduce generalized convex hulls of sets of matrices and investigate their structure.

The existence, uniqueness and regularity of the solution to a one-dimensional linear thermoelastic problem with unilateral contact of the Signorini type are established. A finite element approximation is described, and an error bound is derived. It is shown that if the time step is O(h2), then the error in L2 in the temperature and in L∞ in the displacement is O(h). Some numerical experiments are presented.

Plane, quasi-steady, free-boundary flows of an incompressible viscous fluid with surface tension in a container are considered. The mathematical problem is decomposed into an auxiliary elliptic problem for the Stokes system in a fixed flow domain, whose solution leads to the Cauchy problem for the free boundary with the so-called ‘normal velocity’ operator. By introducing the complex stress-stream function and applying time-dependent conformal mapping, the auxiliary problem is reduced to a boundary integral equation via consideration of two Hilbert problems for analytic functions in a unit disc. As an application, plane capillary flow with moving contact points is investigated asymptotically for small capillary numbers. We prove that in the case when a dynamic contact angle is equal to π, this problem is well-posed for a filling regime, and ill-posed for a drying one.

Linear Fredholm operators (J, k) of the form u(x, t) = (J, k) v (x, t) ≡ J(t) v (x, t)+ 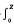k(t, s) v (x, s)ds can be found which map solutions v of the linear matrix system of n partial differential equations ∂u/∂t = DLv + Bv, into solutions u of the like system ∂u/∂t = DLu + Au, when the diagonal matrix D with positive elements and the matrices A and B commute with the linear, scalar operator L. For solution sets in appropriate function spaces, this mapping (J, k) is unique, independent of L, and 1–1 onto if it preserves initial values so that u(x, 0) = v(x, 0). When the set of solutions is restricted to those with zero initial values, this uniqueness aspect of (j, k) breaks down, and there are many linear maps of this Fredholm form which preserve the zero initial conditions and map all such solutions of the first equation in the appropriate function space into solutions of the second. When L is an unbounded operator like the Laplacian ∇2, the initial value problems have many solutions depending on the values of u and u on the boundaries of the region of the solutions, as well as their values in the region at time t = 0. Danckwerts introduced the concept of a ‘constant preserving’ map of Volterra form mapping solutions of the scalar diffusion equation ∂u/∂t = D∇2u, which are initially zero, onto solutions of a scalar diffusion equation ∂u/∂t = D∇2u + Au, with a linear, homogeneous, constant coefficient source term. This concept of a ‘constant preserving’ map extends to the nth order matrix Fredholm maps described. A map (J, k∗) is said to be constant preserving if for all constant n x n matrices C, (J, k∗)C = C, and hence J(t) + 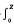k∗(t, s)ds = I, where I is the unit matrix. In the restricted solution spaces where u(x, 0) and v(x, 0) are zero, there is a unique 1–1 onto Danckwerts map of this type transforming solutions of the v equation into solutions of the u equation. In the cases where the coupling matrix A is constant and B is zero, the kernel k∗ of the Danckwerts map can be expressed in terms of the kernel k for the more general Fredholm map associated with the same equations, but mapping the larger solution sets containing elements which need not vanish at time zero. The Danckwerts mapping is used to establish a generalized Ussing flux-ratio theorem for some coupled diffusion problems involving several chemically interacting components.

We describe the slow evolution of the wave speed and reaction temperature in a model of filtration combustion. In the counterflow configuration of the process, a porous solid matrix is converted to a porous solid product by injecting an oxidizing gas at high pressure into one end of a fresh sample of the solid while igniting it at the other end. The solid and gas react exothermically at high activation energy and, under favourable conditions, a self-sustaining combustion wave travels along the sample, converting reactants to product. Since the reaction rate depends on the gas pressure p in the pores, small gradients in p cause variations in the conditions of combustion, which, in turn, cause inhomogeneities in the physical properties of the product. We determine the slow evolution of the wave speed, the reaction temperature, and the mass flux of the gas downstream of the reaction zone. In the absence of a pressure gradient, there is a branch of steadily propagating solutions which has a fold. For planar disturbances on the slow time scale, we show that the middle part of the branch is unstable, with the change of stability occurring at the turning points of the branch. When the pressure gradient is nonzero, there are no steadily propagating solutions and the wave continually evolves. Conditions on the state of the gas at the inlet are described such that the variation in the wave speed and reaction temperature throughout the process can be minimized.