1 Introduction

To understand how ablation on a glacier may change if climate changes, one needs to know the components of the surface-energy balance. It is generally accepted that, at least on mid-latitude valley glaciers, the most important processes delivering melt energy in summer are absorption of solar radiation and turbulent exchange of sensible heat. On most glaciers, solar radiation typically provides 75%) of the melt energy, although on the lower parts of maritime glaciers this may be closer to 50%.

In recent years, glacier mass-balance models have been developed that are based on a calculation of all energy transfers between atmosphere and glacier surface (e.g. Reference Greuell, van den Broeke, Knap, Reijmer, Smeets and StruijkGreuell and Oerlemans, 1986; Reference OerlemansOerlemans, 1993; Reference Oerlemans and FortuinOerlemans and Fortuin, 1992). Radiative and turbulent energy fluxes are calculated from climalological data by schemes used widely in boundary-layer meteorology. In the course of time, the usefulness of such schemes has been tested with Held experiments on glaciers in which the components of the energy balance were measured (e.g. Reference AmbachAmbach, 1979: Reference KuhnKuhn, 1981; Reference MunroMunro, 1989). Such studies were usually performed over a short period during the melt season and at a single location. In more recent years, detailed information about altitudinal gradients has been obtained as a result of experiments carried out simultaneously at a number of meteorological stations (e.g. Reference Oerlemans and VugtsOerlemans and Vugts, 1993; Reference Van den Broeke, Duynkerke and HennekenVan den Broeke and others, 1994; Reference Greuell and OerlemansGreuell and others, 1995). However, these experiments were also restricted to the summer.

In spite of the energy-balance work done so far and the significant increase in our knowledge this has brought about, there is still a need for meteorological data on glaciers collected over longer periods. In particular, the parameterization used for albedo in mass-balance models needs further testing with data that cover both the transition from snow to firn and to glacier ice, as well as the transition from a bare-ice surface to snow cover in the fall.

It is, however, not easy to obtain such data. Ablation zones are difficult to work in throughout the year, because of melt water, high melt rates causing continuous changes in die surface relief and difficult access in early winter (danger of avalanches and crevasses). Furthermore, for budgetary and logistic reasons, it is not feasible to have a permanently manned station on a glacier tongue.

Nevertheless, there are a few places where some of these difficulties can be overcome; one such place is Morteratschgletscher, Switzerland (see Fig. 1). This glacier flows in a northerly direction, is about 7 km long and has an area of 16.4 km^J. Altitude ranges from 4049 (Piz Bernina) to about 2100m (glacier front}. Access to the tongue is possible in almost all conditions. A meteorological station was installed here in September 1995 and has been functioning ever since.

In this paper, we present an analysis of the solar radiation measurements for the period 1 October 1995-30 September 1996. We first present a brief description of the instrumental set-up and then discuss certain features of the data. Next, a simple model for calculating the daily albedo is introduced. As input, it uses snow depth and dates of snowfall events. The model is fitted to the albedo data by optimizing five control parameters, namely, albedo of fresh snow, albedo of Inn, albedo of tee, e-folding constant for effect of ageing on snow albedo, e-folding constant for effect of snow depth on albedo.

2 The Instruments

The automatic weather station (AWS) is located on the tongue of Morteratschgletscher, about 500 m from the glacier snout at an elevation of 2104 m (as obtained from GPS measurements on 29 September 1995). It is placed on an homogeneous part of the glacier which slopes gradually (about 5°).

Fig. 1. A view over Morteratschglelscher, Switzerland. The location of the automatic weather station is indicated by an arrow. (Photograph by W. Haeberli, September 1989.)

The AWS stands freely on the ire and sinks with the melting surface. The distance between sensors and surface, being 3.5 m, thus remains approximately constant when snow cover is absent. In winter, the height of the sensors is 15 m minus the snow depth at the AWS site. For the year considered here, the maximum snow depth was only 62 cm, which is only half of the long-term average ’according to information from local mountain guides). Consequently, the height of the sensors varied between 2.9 and 15 m.

The AWS is equipped with sensors for temperature (aspirated), air pressure, wind speed and wind direction, and with upward and downward looking pyranometers. In addition, snow temperatures are measured. Data are sampled every 2 min and then converted into half-hourly mean values and stored on a Campbell CR10 data logger. Power is supplied by a solar panel combined with lithium batteries. The relative surface height is obtained from an acoustic sensor attached to a separate construction drilled into the ice. This allows monitoring of melt and snow accumulation. Stake readings were also carried out during regular visits to the station.

The Aanderaa pyranometer is not the most accurate instrument on the market but it is nevertheless suitable in view of errors inherent in measuring using an AWS. The potentially important error sources are snow, condensation and riming on the instruments, and tilting of the mast. The field of view of the downward-facing pyranometer is relatively large, because the instrument is between 3 and 3.5 m above the surface.

It is possible to determine global radiation by using the upward-looking sensor by partitioning the incoming radiation into direct and diffuse components, and assuming that the two-stream approximation is valid. However, the partitioning is the problem, since no observations of cloud cover and reflectivity of surrounding slopes are available. We have chosen to correct the data directly by comparing them with the data horn carefully calibrated Kipp and Zonen pyranometers operated for 4 weeks in spring very close to the AWS site. The procedure is described in the Appendix.

The station has been operational since 29 September 1995 and was visited and observed on 16-17 December (immediately after a 30 cm snowfall), 19 February (during light snow), 19 March, 18-19 April, 12-13 May, 16 June-1 July, 31 July-1 August, 6-12 September. So, in spite of the fact that the station was not manned, many observations on its performance and on the surface conditions are available.

During these visits, riming or condensation was hardly ever observed. According to mountain guides working in the region, foggy conditions on the lower part of the glacier do not occur frequently, so possibly the error resulting from condensation is not too large, especially if daily means are considered.

The till of the mast was measured on all the visits mentioned above. In September 1995, the station was placed horizontally. On 16 December, the tilt appeared to be 6° to the north. This must have been due to the considerable amount of melt (about 0.4m) in October 1995. During the winter, spring and summer the tilt did not change more than a few degrees. In October 1996, the tilt was again measured accurately, still giving a value of 6° in a northerly direction.

With regard to the albedo measurements, it is fortunate that the shading angle of the surrounding mountains, typically 30°, is significantly larger than the till of the mast. Consequently, direct radiation can never enter the downward-looking pyranometer. This means that the potentially largest error source is absent. In this paper, we define the albedo with respect to a horizontal surface. Therefore, all calculations have been done using data reduced to the horizontal plane as described in the Appendix.

3 Global Radiation

For a proper interpretation of the measurements presented here, some basic concepts on solar radiation need to be clarified. The solar constant S is defined as the energy flux of radiation originating from the Sun. perpendicular to the solar beam, for the annual mean Earth Sun distance (e.g. Liou, 1992:, The currently accepted value is 1368 ± 3 W m⁻². For reference, it is useful to define the extra-terrestrial irradiance Q_ex as

(1)

Here, λ is solar elevation. Q_ex thus represents the flux of energy through a surface of unit area perpendicular to the Earth surface at the “top" of the atmosphere. An effective transmissivity T_eff can now be introduced by relating the global radiation G to Q_ex :

(2)

It should be stressed that here global radiation refers to the flux impinging on an imaginary horizontal surface through a point on the sloping glacier surface.

The result of a number of processes is absorbed in T_eff. First of all, atmospheric processes, that is, scattering and absorption of solar radiation by air, aerosol and clouds, make r_c.ff significantly smaller than unity. Reflection from the surrounding slopes, on the other hand, normally leads to an increase in global radiation, i.e. an increase in T_eff. In principle, T_eff can therefore be larger than unity but this rarely happens.

Global radiation can be partitioned into direct radiation (solar beam impinging on the surface) and diffuse radiation (coming from all other directions). The proportion of diffuse radiation increases with cloudiness and reflectivity of the surrounding slopes. A full treatment of what happens with solar radiation in a glacierized valley of given geometry therefore becomes a complicated mailer, so complicated that only computer time-consuming Monte Carlo methods can deal with all aspects. This is not feasible for the study of the energy balance of a glacier surface, in which other processes such as turbulent fluxes introduce significant uncertainties.

A frequently made assumption in radiative-transfer calculations is that the diffusive solar radiation, including radiation reflected by the glacier surface, is isotropic. This implies that the amount of reflected radiation measured with a down-facing pyranometer should not depend on the till of the instrument, unless it is tilled so much that direct radiation can enter the dome when the Sun is very low (Maimstein, 1985).

We now turn lo the measurements. As an example, Figure 2 shows the record of global and reflected radiation for the first 8 days of April 1996. A few centimetres of snow it fell on 2 April. The extra-terrestrial irradiance for 1 day is also shown for reference. The large cut-off in global radiation, because of shading by the surrounding mountains, is clearly seen. This, of course, is typical for a north-facing glacier in the Northern Hemisphere. 8 April apparently had variable light clouds and at some instant a peak global radiation very close to the extra-terrestrial irradiance. This must have been due to reflections between cloud, glacier surface and surrounding slopes.

Daily mean values of G for the entire year of measurements are plotted in Figure 3, together with the extra-terrestrial irradiance. Air temperatures (also daily means) are shown for reference. The most striking feature in the radiation record is the large day-to-day variability in the summer half-year compared to the winter half-year. We believe that this is associated with the presence of snow on the valley slopes. The effect of multiple reflections on global radiation is far more important when the slopes are covered with snow than when they are not. Therefore, in eases where the slopes are covered with snow, multiple reflections decrease the contrast between sunny and cloudy days. It is possible that another process, associated with different cloud characteristics, contributed to the difference between summer and winter. In winter, clouds are probably optically thinner.

As noted earlier, interception of solar radiation by surrounding mountains strongly reduces the incoming radiation, notably from easterly (early morning) and westerly (late afternoon) directions. Consequently, there is a large difference between daily mean global radiation and extraterrestrial irradiance.

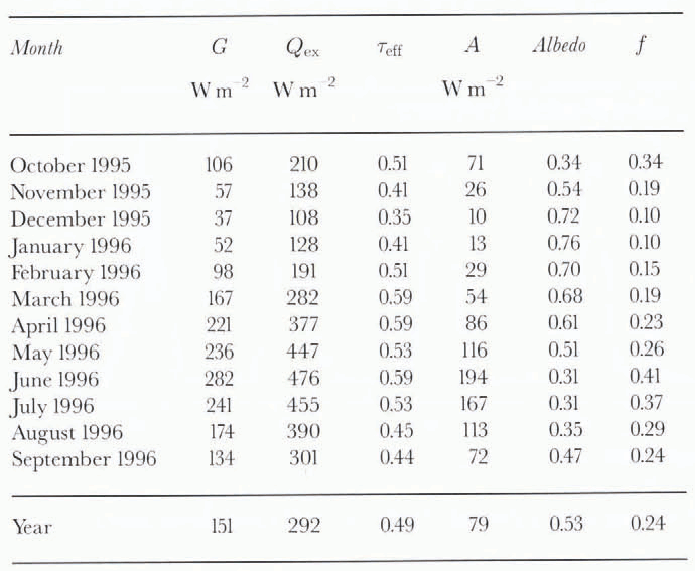
Table 1 lists monthly mean values of G, Q_ex and T_eff, (the last three columns are discussed later). In summer, about half of the potential solar energy reaches the glacier surface. In winter, the fraction is even lower.

4 Albedo

Figure 4 shows all the measurements of incoming and reflectcd radiation. Each dot represents a half-hourly mean value (total number of data points: 17568). There is a clear grouping in the diagram. Apparently, characteristic albedos for snow/firn and ice are emerging.

Fig. 2. Example of measured global radiation (solid) and reflected solar radiation (dashed). Shown are half-hourly mean values. Extra-terrestrial irradiance is shown for reference.

Fig. 3. Daily mean values of air temperature (upper panel, smoothed curve also shown) and global radiation flower panel).

Occasionally, albedo values larger than one occur. Closer inspection of the data in relation to the snow-depth record (discussed in more detail later) shows that ibis happens during snowfall and must be due to snowflakes adbering to the upward-looking sensor, whereas the downward-looking sensor remains free of snow. The AWS was visited once in light snow but then the sensors were clean. During a visit after a heavy snowfall (35 cm, 18 October 1996), the effect could be clearly observed (upward-looking sensor covered by a few centimetres of snow, downward-looking sensor free of snow). In any case, such measuring errors have only a small effect on the overall pattern.

Table 1. Solar-radiation characteristics in monthly mean values. G is global radiation, Q_ex is extra-terrestrial irradiance, T_effis transmissivity, A is absorbed solar radiation, f is absorbed solar radiation scaled by extra-terrestrial irradiance. In this table, albedo is the ratio of monthly mean reflected to global radiation

On most days, albedo shows some variation during the day. We hesitate to give a full analysis of this, because several factors that may cause this variation (varying till of sensors, riming, snowdrift, etc.) could not be observed because the station is unmanned. From now on, the discussion will be restricted to daily albedos. First, daily albedo is defined as the ratio of daily amount of reflected solar radiation to the daily global radiation. Note that this differs from the daily mean albedo, which is the mean of all instantaneously determined albedo values during daylight. However, when the Sun is very low, this quantity may be influenced greatly by measuring errors. In view of this, daily mean albedo is not a very useful quantity in analysing measurements and instead the daily albedos should be studied.

Fig. 4. All half-hourly means of global and reflected radiation in a scatter plot. Two clusters emerge, associated with snow and ice.

Figure 5 shows daily albedos for the entire year. For reasons explained above, 1 day appeared to have an albedo exceeding 0.9. For this day, its value was set at 0.9. Also shown in Figure 5 is snow depth derived from the acoustic sensor. As expected, there is a clear relation between albedo and snowfall events (seen in the record of the acoustic sensor as an almost stepwise increase in snow depth).

In general, snow albedo is lower in spring than in winter, except when large amounts of snow fall (as on 21-22 June. when a few centimetres of snow bring the albedo up to over 0.8). It also appears that ice albedo increases slowly in August and September. There are three snowfall events in late summer (27 August, 12 and 24 September). In all cases, snow melted away within a few days but the albedo remained relatively high, Consequently, the monthly albedo for September 1996 was significantly higher than for October 1995. However, October 1995 was exceptionally sunny and warm (see also the temperature curve in Figure 3). All the monthly albedos are given in Table 1.

The last two columns in Table 1 show absorbed solar radiation A and the efficiency of absorbing solar radiation (f) defined as

(3)

So, f indicates how much of the insolation at the top of the atmosphere is actually absorbed at the glacier surface. In the annual mean, only one-quarter of the extra-terrestrial irradiance would be absorbed by a horizontal surface on the glacier at the AWS site! The amount will be even less for the actual glacier surface, which has at the AWS site a slope of about 6 in a northerly direction.

5 Modelling Albedo

In mass-balance models based on a calculation of the energy balance, albedo should be a prognostic variable determined by the nature and history of the melt process. In earlier studies, simple formulations for albedo have been used in which one or more of the following parameters plays a role: snow depth, accumulated melt, age of snow, snow density, distance to equilibrium line, etc. Because of the lack of data, such formulations have never been checked thoroughly. Although the present dataset is far from ideal and concerns only a single point on a glacier, it provides an opportunity to test some of tile ideas behind the albedo schemes.

Here, we will fit an albedo scheme, described briefly, to the 366 daily albedo values. Although one could argue that one loses information by not looking at half-hourly values, the additional information, notably on snowfall events, would not be accurate enough for a study with a high resolution in time. In the calculation, values of five parameters are determined in such a way that the rms difference (σ) between observed and simulated daily albedos is minimized.

Fig. 5. Daily albedo (upper panel) and snow depth (lower panel), derived from the acoustic sensor (except the peak marked *, for which snow depth was arbitrarily described).

First of all, we anticipate that the albedo of the snow-covered glacier site at day (i) will depend on the age of the snow at the surface, so

(4)

Note that this expression introduces three parameters: a characteristic albedo for firn α_firn, for fresh snow(α_frsnow and a time-scale t* determining how fast the snow albedo approaches the fini albedo after a snowfall. In this equation, s is the number of the day on which the last snowfall occurred. Because of the daily resolution used here, the albedo of fresh snow should be interpreted as the characteristic albedo for snow that is not more than 1 day old. So, it may (and does) differ from the albedo of a snow surface during or immediately after a snowfall.

Next, we require a smooth transition to the characteristic ice albedo α_ice when snow depth (d) is small. This can be achieved by writing for the final albedo

(5)

Here, d* is a characteristic scale for snow depth. When snow depth is if, the snow cover contributes 1/e to the albedo, the underlying surface (l-1/e). If snow depth equals 3d*, the underlying surface still contributes about 5% to the albedo. Therefore, there are now five control parameters α_frsnow, α_firn, α_ice t* and d*.Before optimal values for these can be calculated, the snowfall events have to be defined. First of all, daily mean values of the snow-depth measurements from the acoustic sensor (sampling every 3 hours) were calculated to remove noise. It was assumed that there was a snowfall on day (i) if

(6)

Here, d(i) is the daily mean snow depth. The value of 0.02m was chosen, because it is twice the estimated snow-depth error for daily mean values. The resulting snowfall events are shown in Figure 6. Very probably, a few of the snowfalls derived from the application of Equation (6) to the snow-depth data are not real and a few may be missing. This is the price one has to pay when using data from an automatic station.

It is not difficult to calculate the optimal values for the control parameters. We found that the mutual dependence of optimal control parameters is small and that a unique solution could be obtained by minimizing σ. The results are given in Table 2 (full model). Although the correlation coefficient is significant (0.93), σ is still fairly large (0.067). Judging from Figure 6, in which observed and calculated albedos are compared, there are at least two reasons. Around days 135 and 160, the effect of ageing is apparently overestimated in the model. A possible reason is that in these periods light snowfalls were not revealed by the analysis of the snow events. A second factor concerns the tendency of the observed ice albedo to increase- from the beginning of June to the end of September.

Table 2. Summary of model results. For each model, the best values for the control parameters are listed, as well as the rms difference (σ) between simulated and observed albedo and corresponding correlation coefficient (r)

Fig. 6. Upper panel: snowfall events derived from the acoustic snow-depth measurements. Lower panel: a comparison of observed and simulated albedo.

Fig. 7. rms difference between simulated and observed albedo (σ) for varying control parameters. Control parameters were varied one by one. The minimum in each curve corresponds to the best fit with the full model given in Table 2.

To investigate the stability of the albedo model, the control parameters were varied around the optimal values. Figure 7 shows the result in terms of the rms difference between observed and simulated albedo (σ). Ice and snow albedos appear to be better defined than the firn albedo. The curve for the ageing time-scale t* is rather flat: it would not make much difference if t* were to be increased or decreased by a few days. The snow-depth scale d* is more sharply determined. The implication is that, for a snow depth of 10 cm, 95% of the albedo is determined by the snow cover and only 5% by the underlying ice surface. This is in good agreement with the theoretical results of Wiscoimbe and Warren (1980).

One may well wonder whether simpler albedo models would give a simulation of comparable quality. In Table 2 the results of a calculation using simpler models are summarized. First, we consider a model without ageing effect of the snow. So, a single value for snow albedo is used. The best result is obtained with a snow albedo of 0.70, the resulting value of σ being 0.076. One may therefore conclude that the simulation without an ageing effect is significantly, although not dramatically, worse.

Another simplification would be to omit the snow depth (i.e. put d* to zero). This leads to an optimal simulation with σ =0.084, clearly demonstrating that it makes sense to take snow depth into account explicitly, Finally, a run was done in which only two albedo values were used: one For snow and one for ice, no account being taken of effects of snow depth or ageing. Now, the best simulation that can be achieved has σ =0.087, which is 30% larger than the result for the full model.

We made several further attempts to improve the simulation by taking into account air temperature and solar elevation. This was not successful and the results of these additional calculations are therefore not shown.

6. Concluding Remarks

Although a 1 year record does not constitute a climatology, we may conclude that, on an annual basis, the tongue of Morteratschgletscher absorbs less than 25% of the solar radiation available at the top of the atmosphere. For the 4 month period June-September, when most of the melting takes place, the percentage is higher, namely about 32% (because shading by the surrounding mountains is less effective then).The order-of-magnitude is probably typical for larger north-facing glaciers in the Alps.

Albedo was found to vary strongly in time, notably in late spring and fall when snow falls every now and then on bare ice. An albedo scheme with five control parameters is able to reproduce the observations reasonably well if snowfall events and snow depth are used as input. From comparative tests with simpler versions of this scheme, we conclude that the albedo model formulated here is suitable for simulating the albedo. Its degree of complexity is in balance with the type and quality of the measurements.

Fig. 8. A comparison of data from the Aanderaa pyranometers, mounted on the AWS, and the Kipp pyranometers, placed perfectly horizontal. Each dot represents a half-hourly mean value. The top panel shows global radiation and the bottom panel shows reflected solar radiation. Period: 18 April 1530 h until 15 May 0930 h UT 1996.

The albedo scheme proposed here can be incorporated in glacier mass-balance models, if basic information is available on snow depth and frequency of snowfall events. We hope that it will be possible to use this scheme for other points on a glacier by adjusting only the ice albedo. For many glaciers, the variation in the characteristic ice albedo can be estimated from high-resolution satellite images (e.g. optical channels of Landsat TM) acquired on a suitable day in the second half of the ablation season (see e.g. Reference Knap, Brock, Oerlemans and WillisKnap and others, in press).