Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-16T19:06:06.397Z Has data issue: false hasContentIssue false
  • English
  • Français

John’s walk

Part of: Markov processes

Published online by Cambridge University Press:  10 November 2022

Adam Gustafson  and
Hariharan Narayanan Open the ORCID record for Hariharan Narayanan [Opens in a new window]
Adam Gustafson*
Affiliation:
Microsoft Corporation
Hariharan Narayanan*
Affiliation:
TIFR Mumbai
*
*Email address: [email protected]
**Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

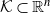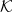We present an affine-invariant random walk for drawing uniform random samples from a convex body $\mathcal{K} \subset \mathbb{R}^n$ that uses maximum-volume inscribed ellipsoids, known as John’s ellipsoids, for the proposal distribution. Our algorithm makes steps using uniform sampling from the John’s ellipsoid of the symmetrization of $\mathcal{K}$ at the current point. 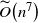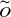We show that from a warm start, the random walk mixes in ${\widetilde{O}}\!\left(n^7\right)$ steps, where the log factors hidden in the ${\widetilde{O}}$ depend only on constants associated with the warm start and desired total variation distance to uniformity. We also prove polynomial mixing bounds starting from any fixed point x such that for any chord pq of 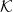$\mathcal{K}$ containing x, 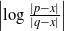$\left|\log \frac{|p-x|}{|q-x|}\right|$ is bounded above by a polynomial in n.

Keywords

Random walkconvex bodyJohn’s ellipsoid

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces
Type
Original Article
Information
Advances in Applied Probability , Volume 55 , Issue 2 , June 2023 , pp. 473 - 491
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, K. (1992). Ellipsoids of maximal volume in convex bodies. Geom. Dedicata 41, 241–250.CrossRefGoogle Scholar
Chen, Y., Dwivedi, R., Wainwright, M. J. and Yu, B. (2017). Fast MCMC sampling algorithms on polytopes. Preprint. Available at https://arxiv.org/abs/1710.08165.Google Scholar
Gruber, P. M. (1988). Minimal ellipsoids and their duals. Rend. Circ. Mat. Palermo 37, 35–64.CrossRefGoogle Scholar
John, F. (1948). Extremum problems with inequalities as subsidiary conditions. In Studies and Essays: Courant Anniversary Volume, eds K. O. Friedrichs, O. E. Neugebauer and J. J. Stoker, Wiley-Interscience, New York, pp. 187–204.Google Scholar
Kannan, R., Lovász, L. and Simonovits, M. (1997). Random walks and an ${O}^*\big(n^5\big)$ volume algorithm for convex bodies. Random Structures Algorithms 11, 1–50.3.0.CO;2-X>CrossRefGoogle Scholar
Kannan, R. and Narayanan, H. (2012). Random walks on polytopes and an affine interior point method for linear programming. Math. Operat. Res. 37, 1–20.CrossRefGoogle Scholar
Laddha, A., Lee, Y. T. and Vempala, S. S. (2020). Strong self-concordance and sampling. In Proc. 52nd Annual ACM SIGACT Symposium on Theory of Computing (STOC 2020), eds K. Makarychev, Y. Makarychev, M. Tulsiani, G. Kamath and J. Chuzhoy, Association for Computing Machinery, New York, pp. 1212–1222.CrossRefGoogle Scholar
Lee, Y. T. and Sidford, A. (2013). Path finding I: solving linear programs with $\widetilde{O}(\sqrt{rank})$ linear system solves. Preprint. Available at https://arxiv.org/abs/1312.6677.Google Scholar
Lovász, L. (1999). Hit-and-run mixes fast. Math. Program. 86, 443–461.Google Scholar
Lovász, L. and Simonovits, M. (1993). Random walks in a convex body and an improved volume algorithm. Random Structures Algorithms 4, 359–412.CrossRefGoogle Scholar
Lovász, L. and Vempala, S. (2006). Hit-and-run from a corner. SIAM J. Computing 35, 985–1005.CrossRefGoogle Scholar
Lovász, L. and Vempala, S. (2007). The geometry of logconcave functions and sampling algorithms. Random Structures Algorithms 30, 307–358.CrossRefGoogle Scholar
Narayanan, H. (2016). Randomized interior point methods for sampling and optimization. Ann. Appl. Prob. 26, 597–641.CrossRefGoogle Scholar