No CrossRef data available.
Article contents
Nonlinear evolution of vortical disturbances entrained in the entrance region of a circular pipe
Published online by Cambridge University Press: 29 October 2024
Abstract
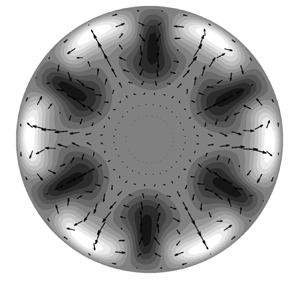
The nonlinear evolution of free-stream vortical disturbances entrained in the entrance region of a circular pipe is investigated using asymptotic and numerical methods. Attention is focused on the low-frequency disturbances that induce streamwise elongated structures. A pair of vortical modes with opposite azimuthal wavenumbers is used to model the free-stream disturbances. Their amplitude is assumed to be intense enough for nonlinear interactions to occur inside the pipe. The formation and evolution of the perturbation flow are described by the nonlinear unsteady boundary-region equations in the cylindrical coordinate system, derived and solved herein for the first time. Matched asymptotic expansions are employed to construct appropriate initial conditions and the initial–boundary value problem is solved numerically by a marching procedure in the streamwise direction. Numerical results show the stabilising effect of nonlinearity on the intense algebraic growth of the disturbances and an increase of the wall-shear stress due to the nonlinear interactions. A parametric study is carried out to evince the effect of the Reynolds number, the streamwise and azimuthal wavelengths, and the radial length scale of the inlet disturbance on the nonlinear flow evolution. Elongated pipe-entrance nonlinear structures (EPENS) occupying the whole pipe cross-section are discovered. EPENS with  $h$-fold rotational symmetry comprise
$h$-fold rotational symmetry comprise  $h$ high-speed streaks positioned near the wall, and
$h$ high-speed streaks positioned near the wall, and  $h$ low-speed streaks centred around the pipe core. These distinct structures display a striking resemblance to nonlinear travelling waves found numerically and observed experimentally in fully developed pipe flow. Good agreement of our mean-flow and root mean square data with experimental measurements is obtained.
$h$ low-speed streaks centred around the pipe core. These distinct structures display a striking resemblance to nonlinear travelling waves found numerically and observed experimentally in fully developed pipe flow. Good agreement of our mean-flow and root mean square data with experimental measurements is obtained.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press



