Introduction

During the past two decades there have been rapid decreases in Arctic sea-ice extent (e.g. Reference ComisoComiso, 2012), thickness (e.g. Reference Haas, Pfaffling, Hendricks, Rabenstein and RigorHaas and others, 2008; Reference KwokKwok and Rothrock, 2009; Reference HansenHansen and others, 2013; Reference RennerRenner and others, 2014) and, as a result, volume (e.g. Reference Schweiger, Lindsay, Zhang, Steele, Stern and KwokSchweiger and others, 2011; Reference LaxonLaxon and others, 2013). Passive microwave sensors and data from drifting buoys show that the Arctic sea-ice regime is becoming increasingly seasonal in nature, i.e. multi-year sea ice (MYI) is disappearing and being replaced with first-year sea ice (FYI; Reference RigorRigor and Wallace, 2004; Reference Maslanik, Stroeve, Fowler and EmeryMaslanik and others, 2011). This regime shift has implications for the transfer of momentum and energy between the sea ice, the ocean and the atmosphere. Sea-ice properties such as ice-drift speed (e.g. Reference Spreen, Kwok and MenemenlisSpreen and others, 2011; Reference Kwok, Spreen and PangKwok and others, 2013) and deformation rate (e.g. Reference Rampal, Weiss and MarsanRampal and others, 2009) are changing as the ice thins and weakens. Enhanced deformation implies increased formation of open-water leads between floes and enhanced ridge formation, ice rafting and potentially rougher ice surfaces. Roughness both influences and is influenced by the formation and development of melt ponds (e.g. Reference Eicken, Grenfell, Perovich and SFreyEicken and others, 2004). Enhanced roughness has important implications for maritime operations, remote sensing (e.g. Reference Peterson and PrinsenbergPeterson and others, 2008), and modeling and measuring the interactions between sea ice, the atmosphere and the ocean, such as drag, drift and the vertical transport of water (e.g. Reference RabeRabe and others, 2011). The combination of increased drift speed and deformation could be an important mechanism contributing to the observed decline in sea-ice extent. Enhanced surface roughness could result in an ice pack with a greater wind drag or water drag leading to increased ice-drift speeds and decreased sea-ice extent. By monitoring the temporal changes in surface roughness of sea ice in different regions and ice regimes, our understanding and quantification of these changes, and predictions of ice drift, volume and area changes can be improved.

Fram Strait and the Nansen Basin region north of Svalbard are two important and dramatically different regions for the study of sea ice in the context of changing ice regimes. Fram Strait is the largest and deepest outflow region of the Arctic Ocean (Reference KwokKwok and others, 2004; Reference SerrezeSerreze and others, 2006; Reference KwokKwok, 2009). Ice drifting through Fram Strait integrates changes in the Arctic Ocean over a large area and over several years. The ice in Fram Strait is a mixture of FYI and MYI (e.g. Reference Renner, Hendricks, Gerland, Beckers, Haas and KrumpenRenner and others, 2013). In addition, Fram Strait often contains fast ice near the coast of Greenland, the Norske Øer Ice Barrier (Fig. 1; Reference Hughes, Wilkinson and WadhamsHughes and others, 2011). The Norske Øer Ice Barrier is composed of icebergs and fast ice and extends out into the path of the Fram Strait drift ice. The mean and modal ice thickness and the fraction of ice >5m thick have all decreased in Fram Strait over the past two decades (Reference HansenHansen and others, 2013; Reference RennerRenner and others, 2014). Furthermore, changes in the drift speeds and deformation rates in Fram Strait have implications for ice export and volume loss for the entire Arctic basin. In contrast, the ice in the Nansen Basin north of Svalbard is a seasonal ice regime at the margins of the Arctic ice pack (Reference Renner, Dumont, Beckers, Gerland and HaasRenner and others, 2013b); however, we have limited knowledge of the changes in the sea-ice thickness and roughness that are occurring in this region. The changes in ice properties occurring in these areas provide an important glimpse into potential future sea-ice conditions over other regions of the Arctic basin.

Fig. 1. Map of study region overlain on ASCAT C-band scatterometer backscatter data from 6 September 2010. Backscatter variations over sea ice correspond to different ice concentration, ice type distribution and ice roughness. Over open water backscatter varies with wind speed and direction.

The spatial distributions of sea-ice ridges, roughness and floe size have traditionally been estimated from airborne laser altimeter measurements (e.g. Reference HiblerHibler, 1972; Reference HiblerHibler and others, 1972; Reference DierkingDierking, 1995; Reference Von Saldern, Haas and Dierkingvon Saldern and others, 2006), aircraft-mounted laser scanners (e.g. Reference Kurtz, Markus, Cavalieri, Krabill and MillerKurtz and others, 2008; Reference Doble, Skouroup and WadhamsDoble and others, 2011) or upward-looking sonar sensors (e.g. Reference WadhamsWadhams and Doble, 2008). In contrast to laser sensors, upward-looking sonar sensors measure the roughness of the underside of the ice. Single-beam laser altimeters have been included in airborne electromagnetic induction (AEM) sensors since 1999 and are used for processing AEM data (Reference Haas, Lobach, Hendricks, Rabenstein and PfafflingHaas and others, 2009) and investigating surface roughness and ridging properties (e.g. Reference Von Saldern, Haas and Dierkingvon Saldern and others, 2006; Reference Tan, Li, Lu, Haas and NicolausTan and others, 2012). While sampling only in the direction of flight, one can use laser altimeter data in a similar fashion to laser scanner data, assuming that the distribution and orientation of leads, ridges, floe dimensions, rafted ice, hummocks and open water is random. However, this assumption is not valid for all sea-ice regions (e.g. where there are persistent ocean or atmospheric currents at the surface). Laser altimeters are used in AEM data processing to retrieve the distance between the sensor and the top of the ice surface while the AEM system measures the distance to the water below the sea ice. The sea-ice thickness retrieved for a three-dimensional (3-D) AEM sensor footprint is thus the difference between the laser altimeter measurement and the AEM system (Reference Haas, Lobach, Hendricks, Rabenstein and PfafflingHaas and others, 2009).

Airborne laser scanners provide two-dimensional (2-D) swaths of surface elevation measurements and related surface properties along extensive transects with the same high spatial resolution and accuracy as a one-dimensional (1-D) single-beam altimeter. To do so, accurate knowledge of the scanner viewing geometry is required; therefore, airborne laser scanners are normally operated in conjunction with an inertial navigation system (INS) or inertial measurement unit (IMU), and a differential, dual-frequency GPS system (DGPS). The processing and correction of the scanner attitude data using the INS/IMU and DGPS systems is non-trivial as each sensor has its own fixed orientation, timing offset, uncertainty, and drift relative to the other sensors. Laser scanner processing typically requires a survey over known, well-defined targets (e.g. buildings) to estimate sensor biases and uncertainties (e.g. possible laser squint angle).

From 20 to 29 August and 4 to 13 September 2010, AEM surveys were performed by helicopter in Fram Strait and over the Nansen Basin (Fig. 1; Reference Renner, Hendricks, Gerland, Beckers, Haas and KrumpenRenner and others, 2013a,Reference Renner, Dumont, Beckers, Gerland and Haasb). During these surveys, a laser scanner system was installed in the AEM sensor for the first time; however, the system did not include an INS/IMU.

Here we present a method of retrieving a relative surface elevation and the sea-ice surface roughness from the laser scanner without INS/IMU and DGPS sensors. The method does not require surveys over well-known targets but it only provides relative measurements of surface elevation with the level-ice surface as the reference datum. Using the standard deviation of the relative surface elevation as a proxy for roughness, we present a comparison of surface roughness estimates from the traditionally used single-beam laser altimeter and the laser scanner data in order to improve our understanding of the properties of the ice in these two regions. We contrast the results of the single-beam laser altimeter to the new laser scanner over various scales to examine their representativeness. Finally, we compare and contrast the two regions using the AEM ice thickness measurements and the new surface roughness estimates.

Measurements and Methods

A Riegl Laser Measurement Systems (Riegl LMS) Q120 laser scanner was mounted in the nose of the AEM sensor. Table 1 provides the important characteristics of the scanner and scanner settings adapted from Riegl LMS (2010). The scanner rotates a laser beam by a set angle across the 80° field of view, resulting in a laser range measurement for each across-track angle. A scan line is all of the scanner measurements taken during one complete rotation across the field of view. The dataset collected in 2010 includes the laser scanner range (Fig. 2d) and signal strength (Fig. 2b), GPS position data and the AEM measurements of the total snow plus ice thickness, referred to hereafter as total thickness (Reference Renner, Dumont, Beckers, Gerland and HaasRenner and others, 2013b). Using the GPS timestamps and measurement ID numbers, the data streams from the different sensors were merged, and coincident measurements were extracted. The system was flown 15 ± 5 m above the ice, at a speed of 4 0 ± 5 m s ¹ . Data acquired when the AEM sensor was >30m above the ice were removed from the analysis, and all data were resampled to 50 Hz using linear interpolation.

Table 1. Riegl LMS Q120 laser scanner characteristics. Data adapted from scanner settings used during study and the scanner specifications (Riegl LMS, 2010)

Fig. 2. Laser-scanner results from example section of sea ice north of Svalbard. (a) Example curve-fit procedure for scanner line 1255; (b) laser return strength; (c) nadir photograph taken from helicopter; (d) raw laser scanner range measurements; (e) estimated flat surface; (f) relative elevation of measurements (d) to flat surface in (e).

An example of the laser scanner measurements (Fig. 2b and d) and the processing methodology (Fig. 2a and d-f) for a 40 m section of sea ice in the Nansen Basin is shown (Fig. 2), omitting the true spacing of 0.7 m between successive line scans. The across-track spacing is much smaller, 0.1-0.2 m for standard survey heights of 10-15 m, respectively. The return strength of the laser scanner (Fig. 2b) is sensitive to changes in the small-scale roughness properties, as illustrated by the lower return strength from the refrozen melt pond in the upper left corner of Figure 2b and c. Smooth surfaces reflect the laser light away from the sensor in a specular manner while rough surfaces widen the angular distribution of scatterers reflecting the light in a diffuse manner, thereby increasing the power returned to the sensor. It may be possible to retrieve open-water and melt-pond information from the scanner return strength. In our data, many of the melt ponds are refrozen, or are drained and thus do not appear different from other ice surfaces. Figure 2d presents the range, the distance between the sensor and the surface, measured by the laser scanner. The main ridge visible in Figure 2c is also visible in Figure 2d as a shift in the range. Figure 2d is not corrected for sensor roll. Roll changes the reported range value by increasing the incidence angle of a scanner beam from its nominal value if the sensor had a roll angle of 0°, i.e. a roll angle of +2° means that the incidence angle for the 0° beam is changed from 0° to +2°. Roll also changes the surface location that is sampled. The roll angle and range to the surface for the true nadir scanner beam are retrieved using

(1)

where y is the across-track range of an individual scanner beam, A is the range to the nadir scanner beam, 6 is the across-track angle of the scanner beam and B is the roll of the scanner. Variables A and B are obtained by iterative curve-fitting using nonlinear least-squares optimization (WaveMetrics, 2014). Equation (1) is applied to the range data of each scan line (Fig. 2a). After the curve fitting is performed, points where the range is less than the fitted curve are discarded and the curve-fitting process is run again. This process is repeated once more (Fig. 2a). By removing points with a range less than the fitted curve, the curve fit is adjusted to fit the points with a greater range, the lower level-ice surfaces (Fig. 2a and e). The curve fitting was performed three times to strike a balance between the adjustment to the level ice, and processing times. Sensor roll was nominally less than ±10°, but occasionally more than ±20° when the helicopter was turning. After calculating the roll and distance to the true nadir location, the laser range is removed from the fitted range, resulting in a relative surface elevation for each laser scanner beam that is relative to the fitted surface representing the local level-ice surface (Fig. 2f). As the fit is performed for each individual scan line, significant changes in the line-to-line surface elevation, or the absence of level ice, can lead to incorrect relative surface elevation retrievals. These problems are observable as across-track stripes in the relative surface elevation data (e.g. at scan line 1265 in Fig. 2e). In the absence of a level-ice surface, the relative surface elevation will be overestimated because while the fit will trend towards the minimum surface (maximum range), this range will not be the level-ice surface. By adjusting the fit twice, we attempt to minimize the error for scan lines with low amounts of or no level ice. For one flight we extracted the roll-corrected nadir beam of the scanner and processed the data as a single-beam laser altimeter following the Reference HiblerHibler (1972) processing scheme, referred to hereafter as H72. This processing method is commonly used when examining relative surface elevation and surface roughness measurements from single-beam laser altimeters when INS and DGPS data are not available (e.g. Reference Von Saldern, Haas and Dierkingvon Saldern and others, 2006; Reference Tan, Li, Lu, Haas and NicolausTan and others, 2012). However the results did not show a conclusive improvement over the method presented above, so the H72 method was not applied.

When comparing laser scanner results to laser altimeter results, the roll-corrected nadir beam is extracted from the laser scanner line. Hereafter, when the term altimeter or single-beam altimeter is used, it refers to the roll-corrected nadir beam of the scanner. Although the method corrects for sensor roll, changes in the yaw and pitch angles of the sensor are not corrected for.

Sources of Uncertainty

The major sources of uncertainty are the result of not correcting for the yaw and pitch angles, or the slant-range distortion. It was not possible to correct the sensor yaw, the rotation of the sensor around the vertical axis, from the available dataset. The AEM sensor was suspended from the helicopter by a 20 m long towline, so the AEM sensor experiences pendular motion. The yaw angle of the AEM sensor changes rapidly due to small changes in speed, direction of travel, and from the pendular motion. The GPS direction-of-travel information is provided at 1 Hz and thus can only be used to estimate low-frequency changes in yaw angle that result from the pendular motion of the sensor. IMU measurements from an AEM survey conducted in 2011 showed variations in yaw angle around the direction of travel of about ±2° (two standard deviations) (Haas and others, unpublished data) with both a low- and high-frequency component. At the maximum scan angle of +40° and assuming a range of 15 m and no roll or pitch, a yaw angle away from the direction of travel of ±2° results in sampling with a lateral offset of ∼0.4m ahead of the nadir beam, or nearly the distance between successive scan lines. Yaw does not cause a geometric distortion, only a change in the surface sampling location by changing the orientation of the scan line over the surface.

IMU measurements from an AEM survey conducted in the Lincoln Sea, Arctic Ocean, in 2011 showed variations in pitch angle of about ±2.4° (two standard deviations) (Haas and others, unpublished data). When unaccounted for, the ±2° pitch angle also leads to an overestimation of the range to the surface of 0.01 m and a lateral offset of 0.53 m. The large circular drag-tail of the AEM sensor stabilizes the bird against yaw and pitch angle changes but because it is circular it does not reduce high-frequency roll. The drag skirt is able to reduce the low-frequency roll caused by the aforementioned pendular motion of the bird below the helicopter.

Relief distortion, or slant-range distortion, i.e. the error caused by not measuring the height of a ridge normal to the surface but the distance along the scanner beam to the surface, also remains uncorrected. Relief distortion is greater for greater scan angles than for those close to nadir. While yaw and pitch errors were shown to be relatively small and affect the entire swath, the slant-range distortions may partially explain some of the differences observed between the scanner and the altimeter. Furthermore, the slant-range distortion is greater for points further away from nadir and causes an increase in the apparent height of the surface since the measurement of height is made along the scanner laser beam.

Results

Firstly we explore the relative surface elevation, and surface roughness for two small sections (37m x 20m; 38m x 20 m) of flight FS20100906f1 (Fig. 3). Here the surface roughness for the laser scanner is the standard deviation of the relative surface elevation estimates for each scan line, and the standard deviation of a five-data-point moving window for the altimeter. The scanner standard deviation provides clear evidence of the off-nadir surface features (e.g. rafted blocks or ridges); these features are all missed by the laser altimeter (compare dashed (altimeter) to solid (scanner) line). At the scale of an individual floe, the laser altimeter may over- or underestimate the roughness of the floe based on the random location of the surface roughness features with respect to the direction and location of the survey. The scanner is able to resolve small features such as a crack in a rafted piece of ice, narrow melt channels, small melt ponds and small brash-ice features (Fig. 3). The minimum size of detectable features is limited by the orientation of the feature and the along- and across-track measurement spacing. Furthermore, the laser scanner provides more measurements over smooth open water where specular reflections result in missing data in the altimeter data record (e.g. right part of lower figure where dashed line is missing).

Fig. 3. Comparison of standard deviation of relative surface elevation from the laser scanner and laser altimeter for two short sections of sea ice in Fram Strait from flight FS20100906f1. Adjacent photographs were taken from the helicopter and show the AEM sensor. The scanner standard deviation is the standard deviation of relative surface elevation of all beams in a single scan line. The laser altimeter standard deviation is computed using a running five-point along-track window.

The scanner data have many potential uses including the examination of surface roughness and improving the sensor range measurement for an AEM footprint. The change in the distribution of surface roughness from the laser scanner is shown for different moving-window sizes with which surface roughness was calculated for three flight sections: in the Nansen Basin, in Fram Strait, and the fast ice in Fram Strait (Fig. 4a–c). Also shown is the change in the fractional proportion of ice with a relative surface elevation >0.8m (the high-elevation fraction (HEF)), taken to be ridged or rafted ice, with increasing profile length as represented by the number of scan lines, for both the scanner and the altimeter (Fig. 4d–f). Both the scanner and altimeter respond similarly for all flights. North of Svalbard, the two datasets converge while in Fram Strait the data diverge after a significant portion of the profile. In Fram Strait, it does not appear that a steady value is reached, but both datasets exhibit the same changes over the length of the profile. Over the fast ice, the two datasets appear to reach a constant value.

Fig. 4. (a–c) Change in the distribution of surface roughness for different window sizes (box-car filter length (m)) used to calculate the surface roughness. PDF: probability density function. The profiles presented are 38 km, 40 km and 45 km long flight sections for the ice north of Svalbard, in Fram Strait and over the fast ice in Fram Strait, respectively. (d–f) High-elevation fraction (HEF) is the the number of points higher than 0.8 m divided by the total number of points in an increasing length of a profile, represented by the number of scan lines, for the altimeter and scanner for all measurements in each region.

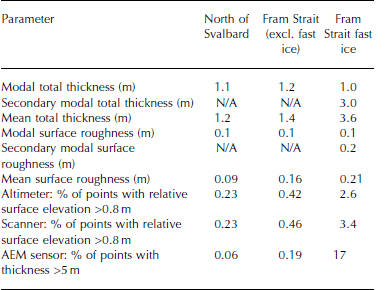
Table 2 presents measurements of the ice properties including mean and modal thickness from the AEM sensor, mean and modal surface roughness, and the HEF for the ice north of Svalbard and in Fram Strait, and the fast ice in Fram Strait. The mean total thickness for the Fram Strait drift ice is greater than for the ice north of Svalbard, although the modal thickness only differs by 0.1 m. The mean and modal thickness of the fast ice in Fram Strait was greater than that observed for the measurements over the drift ice flowing through Fram Strait. The fast ice in Fram Strait has the greatest HEF, followed by the drift ice in Fram Strait, and finally the ice north of Svalbard.

Table 2. Total thickness and roughness data measured over the sea ice north of Svalbard, the drift ice in Fram Strait, and the fast ice in Fram Strait. AEM statistics calculated using data coincident with laser scanner observations

Next, statistical distributions of total thickness, relative surface elevation, and surface roughness for the three ice regimes are investigated (Fig. 5). The surface roughness is the standard deviation of the relative surface elevations within a 60 m along-track window, roughly corresponding to the footprint of the AEM sensor at typical flying heights. The ice north of Svalbard exhibits the narrowest distributions in all properties, followed by the Fram Strait drift ice and the Fram Strait fast ice. In shape, the statistical distributions of surface roughness (Fig. 5a–c) match those of the AEM thickness observations (Fig. 5f); the surface roughness and thickness distributions for Fram Strait are broader than for the ice north of Svalbard. Over the Fram Strait fast ice, the surface roughness and thickness histograms show a multimodal distribution. We examined the data for differences in surface roughness due to prevailing ice-drift conditions or orientation of surface roughness features, using histograms of data collected within a 90° window around each of the four cardinal directions, north, south, east and west (e.g. for north, GPS headings of 315–360° and 0–45° were used). In Fram Strait, the surface roughness for east to west (E–W) flight sections was slightly greater than observed for the north to south (N–S) flight sections (Fig. 5e); no directional differences in roughness were observed for the ice north of Svalbard (Fig. 5e). The survey over the Norske Øer fast ice was predominantly E–W; thus, not enough data were collected N–S to do a comparison for this region. An increase in surface roughness with increasing thickness is observed over the fast ice in Fram Strait (Fig. 5i) but not for the drift ice in Fram Strait (Fig. 5h) or the ice north of Svalbard (Fig. 5g). Note that in Figure 5g–i, each data point is the average of a 1 km long section of the airborne survey

Fig. 5. (a–c) Statistical distributions of surface roughness for all data collected over the three observed ice regimes, seasonal ice north of Svalbard, FYI/MYI mixture in Fram Strait, and fast ice in Fram Strait. (d, e) Distribution of surface roughness for data collected while flying in different cardinal directions (north, south, east and west). (f) Statistical distribution of total thickness measured by the AEM sensor for the three study regions. (g–i) Comparison of surface roughness and total thickness (snow plus ice thickness) for the three observed ice regimes using average values from successive 1 km sections of flight.

Discussion

Conclusions

We have presented a method to retrieve relative surface elevation to estimate sea-ice surface roughness from an airborne laser scanner using the scanner data to correct for sensor roll. The method does not rely on data from an INS/ IMU or DGPS unit. The retrieved relative surface elevation is the difference between the data and a theoretical flat surface representing the local level-ice component of each scan line. The method is suitable when absolute measurements of surface elevation are not required, such as when examining surface roughness, relative ridge heights, widths, and spatial distributions. The identification of the level-ice surface on a scan-line by scan-line basis usually provided reasonable relative surface elevation results. However, some flight sections exhibited striping and variability where a level-ice surface was not present or present in low fractions, such as where ridges run mainly across-track. A potential solution for the line-to-line variability in these situations is to use the method described here to retrieve sensor roll and estimate the local ice surface, then adjust the ice surface elevation of the nadir beam using the H72 processing method. As the H72 method utilizes data over greater distances, the results can provide elevations that are relative to an approximated local water or local level ice; however, the result is still relative surface elevation. The relative surface elevation retrieved by the H72 method is calculated over a longer distance and thus should provide better estimates of relative surface height where level ice is not present or present in low fractions, reducing line-to-line biases in the determination of the local level ice. The combination of the two methods would also allow for estimation of the line-to-line bias in the estimation of the level ice surface.

As a laser scanner is generally more expensive than a laser altimeter, the improved usefulness of a scanner compared to an altimeter is dependent on the measurement platform, the survey objectives, and the surface being sampled. We present a comparison of the scanner swath data to a traditionally used single-beam altimeter for measurements collected in 2010 in Fram Strait and north of Svalbard. Furthermore, surface roughness is a highly scale-dependent variable and can be defined for scales ranging from those of a specific surface feature, over a sea-ice floe or for a region, i.e. from centimetres to kilometres.

Over distances more than ∼5 km the laser altimeter provided representative measurements of relative surface elevation compared to the scanner for the more homogeneous ice found north of Svalbard. Longer sections of at least 15 km of altimeter data were needed to reproduce the statistical distribution of the scanner data in Fram Strait. In Fram Strait, ice roughness was higher for east-west profiles, perpendicular to the main ice drift, than for north-south profiles showing the ice anisotropy in this region with a predominant ridge direction. No such anisotropy was observed north of Svalbard. The sea ice in Fram Strait showed greater thickness and roughness values and wider distributions in both parameters than the ice north of Svalbard. The HEF for drift ice in Fram Strait was twice as high as for the ice north of Svalbard. Furthermore, the HEF converged with increasing flight length for the ice north of Svalbard but did not converge for the ice in Fram Strait. This indicates that an altimeter may not always provide a representative estimate of surface roughness or proper estimates of ridge density, etc., compared to a laser scanner. The fast ice of the Norske Øer Ice Barrier had a much greater fraction of ridged ice than the drift ice in Fram Strait and north of Svalbard. This fast ice exhibited a strong linear relationship between roughness and thickness that we believe is related to the seasonal changes experienced by the fast ice over multiple years.

Laser scanner measurements offer the potential for new insights into 2-D anisotropy of physical properties of the sea-ice surface, improved AEM measurements, improved upscaling of in situ to satellite data, and better observations and understanding of the changes in surface roughness that may occur as the Arctic sea-ice cover switches to a more seasonal regime. In future work, the method presented here will be refined by the application of the H72 method to the scanner data and by providing more robust information for ridge and melt-pond detection, and spatial measurements of their dimensions and orientation.