Introduction
Within ice masses, crystal size, debris concentration, and temperature are all variables. However, the combined effect of these parameters on the flow of ice has never been investigated.
Recent studies have demonstrated that, at constant temperature and stress, the creep of polycrystalline ice with a random orientation of c-axes is quite sensitive to variations in ice-crystal size.Reference BakerBaker (1978) found that there is apparently an inversion between dislocation-controlled creep and diffusion-controlled creep at an average crystal size of about 1 mm and that this is an optimum grain-size for creep resistance. Increasing or decreasing the average crystal size from this critical value results in an increase in secondary creep-rate.
The first study of the influence of temperature on creep-rate was conducted by Reference GlenGlen (1955), who tested blocks of polycrystalline ice in uniaxial compression and showed that his data fit Arrhenius law with the secondary creep-rate obeying the following equation:
Here, A’ is a temperature-dependent constant, n≈3, σ is the applied stress, Q is the activation energy for creep, R is the gas constant, and T is the absolute temperature. Probably the most detailed study to date using inclusion-free ice, was conducted by Reference Mellor and TestaMellor and Testa (1969) who found a linear variation of log ϵ̇ with 1/T over a temperature range of —10 to —60°C. For this range of temperatures Q ≈ 67 kJ mol −1 (16 kcal mol−1). At temperatures above —10°C, Reference GlenGlen (1955) and Reference Mellor and TestaMellor and Testa (1969) showed that the variation of log ϵ̇ with 1/T is non-linear and the Arrhenius relation (Equations (1)) for temperature dependence is invalid.
Prior to the present study, no detailed investigation of the effect of dispersed-solid inclusions on the creep of ice over a wide range of temperatures had been conducted. For a narrow range of temperatures near the melting point (above —10°C), Reference NayarNayar (unpublished) found a non-linear variation of log ϵ̇ with 1/T for ice containing a 1% dispersion of fine silica particles.
Constant-temperature tests on inclusion-bearing ice have been conducted by Reference Nayar, Nayar, Lenel and AnsellNayar and others (1971) and Reference Hooke, Hooke, Dahlin and KauperHooke and others (1972). Both of these studies showed that creep-rate decreases exponentially with increasing volume fraction of dispersed particles. In addition, both studies showed scatter in the measured creep-rates at low inclusion concentrations. Variations in creep at low debris concentrations have also been reported by Butkovitch and Reference Butkovitch and LandauerLandauer (1958) and Reference SwinzowSwinzow (1962) who found, in the TUTO ice tunnel in Greenland, that tunnel closure rates were higher in slightly dirty ice than in clean ice.Reference BakerBaker (1978) showed that during freezing the presence of inclusions in low concentrations inhibits crystal growth so that an increase in the volume-fraction of inclusions results in a reduction in average ice-crystal size. Thus the variation in creep-rates observed in the earlier studies could be the result of grain-size differences among the samples due to variable inclusion concentrations.
Experimental procedure
Polycrystalline ice samples containing dispersed-solid inclusions were prepared by packing a porous mixture of well-sorted (having passed a 125 µm seive but retained on a 106 µm seive) Ottawa sand and powdered ice, made from deionized distilled water, into cylindrical moulds 19.5 mm in diameter and 100 mm long. The moulds were de-aerated and the void spaces filled by admitting air-free distilled water at 0°C. A 30 mm section was cut from the portion of the sample having the most uniform sand distribution, and the ends of this sample were carefully faced perpendicular to the long axis. Sample length and diameter, measured at twelve points, were determined using a micrometer which could be read to ±1 µm. After completion of the compression test, samples were halved and inclusion concentrations in the two halves determined by melting the ice and weighing the sand residue. By assuming a density of 0.9 Mg m−3 (0.9 g cm−3) for ice and 2.7 Mg m−3 (2.7 g cm−3) for sand, concentrations were reduced to volume per cent sand. Inclusion concentrations in the two halves of the same sample generally varied by less than 5% of the amount present.
A constant uniaxial load was applied parallel to the long axis of each sample. Tests were run in a cold laboratory, generally kept at about —10°C, using the ice-compression apparatus used by Reference BakerBaker (1978) in earlier deformation experiments. To prevent sublimation and control temperature, ice samples were immersed in a bath of kerosene. The bath was stirred with a miniature gear pump and temperature was controlled with a Lauda–Brinkman K-4/R circulator. Bath temperature generally fluctuated less than 0.5 deg during a run.
Deformation measurements were made using a Hewlett Packard 7 DCDT-500 displacement transducer connected to a strip-chart recorder. Details of the deformation-measuring procedure were described by Reference BakerBaker (1978). Because stress differences between runs ranged from 0.53 to 0.57 MN m−2 (5.3 to 5.7 bars), creep-rates were normalized to a stress of 0.56 MN m−2 (5.6 bars) using the following relationship which is based on Glen’s flow law:
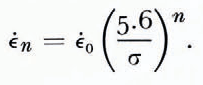
Here, ϵ̇ n is the normalized secondary creep-rate, ϵ̇0 is the experimental secondary creep-rate, and the other terms are as defined earlier.
To study the effect of temperature on creep-rate, samples were subjected to a constant load and secondary creep was established; then the temperature was systematically varied without relaxation of the applied load. This procedure was adopted instead of testing a number of samples at different temperatures over the same range of total strain because of the difficulties involved in making samples with identical macroscopic textures. A possible problem with this method is that it assumes that creep-rate is independent of dislocation distribution and density. However, since the density of dislocations during steady-state creep depends only on the applied stress Reference Bird, Bird, Mukherjee, Dorn, Brandon and Rosen(Bird and others, 1969), and since stress was held constant throughout each test, this procedure appears to be justified.
At each temperature setting, a minimum of 12 h was allowed for thermal equilibrium to become established before the strain-rate was measured. For most tests, the first and second temperature settings were — 5°C and — 40°C, respectively. The next four settings were alternated between these two extremes in a random order.
During the variable-temperature tests, which generally exceeded 400 h in duration, the sample diameter increased due to strain. This increase often resulted in a decrease in applied stress of as much as 0.02 MN m−2 (0.2 bars). In an attempt to correct for this, the approximate sample diameter at the beginning of each temperature setting was calculated using the total strain versus time data and the fact that ice is incompressible. These values were then used to calculate the stress and strain-rate at each setting. As a check, the calculated final diameter was compared to the measured final diameter. In all cases the calculated value was slightly larger than the measured value—generally less than 1% larger. It is believed that this discrepancy is primarily due to sublimation during the tests.
Thin sections were cut from samples both before and after testing. These sections were photographed and average crystal size was determined from enlarged photographs using the maximum chord-intercept method of Reference KrumbeinKrumbein (1935). This technique was recently shown to be highly efficient in approximating the true seive-diameter distribution from thin sections Reference Kellerhals, Kellerhals, Shaw and Arora(Kellerhals and others, 1975). Since crystal sizes and shapes appeared to be uniform, it is assumed that this method provides an accurate measure of the average grain size. From a given thin-section photograph, the measured average crystal size was reproducible to within ±0.05 mm. The average crystal size from thin sections cut from both ends of samples generally varied by less than 0.1±0.05 mm; a grain-size difference of less than 10%. For a more detailed description of the experimental procedure, the reader is referred to Reference BakerBaker (unpublished).
Results
Results of the investigations into the effect of temperature on creep of both inclusion-free and inclusion-bearing ice are presented in Table I. Data from this table were used to make the diagrams of log ϵ̇ versus inverse temperature shown inFigure 1. From Figure 1., it can be seen that in some cases there is considerable scatter of points from a straight line through the data. This non-linearity is most pronounced, however, at temperatures above —10°C.
Table I. Effect of temperature on secondary creep-rate


Fig. 1. Effect of temperature on creep-rate of samples with varying volume fraction of inclusions. f is the volume fraction of inclusions present in the sample. Numbers next to data points show order in which tests on a given sample were made. On all points, error bars representing 99% confidence limits on the slope of the secondary creep curve Reference Krumbein and Graybill(Krumbein and Graybill, 1965, p. 230) are smaller than dot. All creep data are plotted as uniaxial compressive strain-rates.
As mentioned previously, non-linear variation of log ϵ̇ with 1/T has been observed in other studies on polycrystalline ice (Reference GlenGlen, 1955; Reference NayarNayar, unpublished; Reference Mellor and TestaMellor and Testa, 1969) Reference Mellor and TestaMellor and Testa (1969) argue that this variation is due to an increase in grain-boundary slip at higher temperatures. Reference Weertman, Whalley, Whauey, Jones and GoldWeertman (1973), however, suggests that recrystallization and grain growth during creep tests could account for the non-linearity.
In the present study, recrystallization and grain growth were observed in all five of the samples tested (Fig. 2). From Table II and Figure 3, it can be seen that the amount of change in average crystal size due to recrystallization decreased with increasing volume-fraction inclusions.

Fig. 2. Thin sections of sample tested in uniaxial compression showing evidence for recrystallization and grain growth. Sample diameters are approximately 1.9 cm. (a) Thin section of sample before recrystallization. (b) Thin section of the same sample after recrystallization.
Table II. Summary of grain growth due to recrystallization


Fig. 3. The effect of dispersed inclusions on recrystallization of polycrystalline ice.
The role of inclusions in primary recrystallization of two-phase metal alloys has been treated in detail by Reference Cahn and CahnCahn (1965). He discussed how it is possible for a dispersed second phase to exert two opposed influences on a deformed alloy:
-
(i) Nucleation of new grains may be accelerated if the second phase particles are large compared to the average crystal size. If they are small, nucleation is retarded or prevented altogether.
-
(ii) Growth of grains is always impeded, because of the drag exerted on a migrating grain boundary by dispersed particles, especially if they are small and numerous.
In the present study, the inclusion size (0.1 mm) was approximately an order of magnitude smaller than the average ice-crystal size in all of the ice samples tested and Figure 3 suggests that the inclusions inhibited, rather than enhanced, crystal growth during recrystallization. According to Reference Cahn and CahnCahn (1965), the average crystal size produced by recrystallization is an inverse function of the concentration of dispersed inclusions. The trends observed for ice in Figure 3 are therefore compatible with recrystallization experiments from metals.
Reference BakerBaker (1978) conducted creep tests on inclusion-free ice at temperatures of about —9°C and detected virtually no grain growth. A. J. Gow (personal communication in 1974) has demonstrated that recrystallization of unstressed ice occurs rapidly, however, at temperatures approaching the melting point and when the recrystallization occurs under stress (dynamic recrystallization), this process is hastened considerably. Thus in the present variable-temperature tests, it seems reasonable to assume that most, if not all, recrystallization occurred during those temperature settings which were about —8°C or above.
The highest temperatures were generally employed at the last or next-to-last temperature setting. By measuring the amount of grain growth that occurred at this setting and knowing what effect this magnitude of grain-size variation should have on creep, it was possible to adjust these data to eliminate the effect of recrystallization (Fig. 4). The normalization procedure is as follows:
-
(1) For each sample, the initial and final crystal sizes were used in conjunction with figure 2 of Reference BakerBaker (1978) to determine the approximate change (increase or decrease) in creep-rate due to recrystallization and grain growth.
-
(2) This creep-rate increment, ∆ϵ̇, was then adjusted, using the normalization equation described by Reference BakerBaker (1978), in order to determine its value at the temperature settings in question (the settings above —8°C, where all grain growth is assumed to have occurred, and all subsequent settings).
-
(3) These normalized creep-rate increments were then added to or subtracted from the measured creep-rate at each of the points in question.

Fig. 4. The effect of temperature on creep. f is the volume fraction of inclusions present in the sample, d is the average crystal diameter, and Q is the effective activation energy for creep in kJ mol−1 (kcal mol−1). Numbers next to data points show order in which tests on a given sample were made. Starred numbers are data points normalized to account for grain growth. (The unadjusted data are plotted in Figure 1.) Lines were fitted to the data gathered below —10°C using least-squares methods, with effective activation energies determined from the least-squares calculations. Error bars are smaller than the plotted dots
For example, the initial and final crystal sizes for sample A in Figure 1 were 1.22 mm and 2.14 mm, respectively. From figure 2 of the previous study Reference Baker(Baker, 1978) a change in grain size from 1.22 mm to 2.14 mm should result in an increase in creep rate ∆ϵ̇ of about 7.61×10−8 S−1(2.4 year−1) at —9.1°C. The temperature setting for data point 5 in sample A was —8.77°C. At this temperature the adjusted value of ∆ϵ̇ is (7.99×10−8 S−1(2.52 year−1). Thus, because of recrystallization, the creep-rate measured for point 5 is 7.99×10−8 S−1 too high. Consequently, the adjusted value of ∆ϵ̇ (7.99×10−8 S−1) is subtracted from the measured creep rate (1.28×10−7 S−1) and the difference is plotted in Figure 4 as data point 5⋆.
Discussion
Creep Enhancement Near the Melting Point
On the average, recrystallization and grain growth resulted in an 80% creep-rate enhancement near the melting point. By comparing Figure 4 with Figure 1, it can be seen that eliminating this effect makes the variation of log ϵ̇ with 1/T much more linear. Notice, however, that in all cases the highest temperature data (those above —8°C) are still displaced above a straight line drawn through the lower temperature points (Fig. 4). Thus, grain growth alone cannot totally account for the non-linearity of log ϵ̇ versus 1/T observed at temperatures above —8°C.
In a comprehensive discussion of high-temperature creep of ice, Reference Barnes, Barnes, Tabor and WalkerBarnes and others (1971) indicate that while grain-boundary sliding in ice may occur at lower temperatures, it is most important above —8°C where intergranular water occurs at the junctions of three or more crystals. They cite the works of Reference CliffordClifford (1967), Reference SteinemannSteinemann (1958), Nye and Reference Nye and FrankFrank (1973), Reference Bell, Bell, Myatt and RichardsBell and others (1971), and Reference ShreveShreve (1972) for theoretical explanations as well as direct evidence of intergranular water in ice at temperatures down to —8°C. Reference Mellor and TestaMellor and Testa (1969, p. 141) also give evidence for intergranular water in their samples above temperatures of about —8°C based on electrical conductivity measurements. This is supported by the work of Reference Jones and BrunetJones and Brunet (1978) who found that for single crystals of ice above —8°C the variation of creep-rate with inverse temperature is linear. According to Reference Barnes, Barnes, Tabor and WalkerBarnes and others (1971), grain-boundary sliding normally relieves stresses developing within a sample, but it will also generate high stresses near triple junctions of grain boundaries. If liquid is present at the triple points, these high stresses are partly eliminated. Thus grain-boundary sliding and the liquid at triple points may play reinforcing roles in ice and result in creep-rate enhancement at temperatures above —8°C.
Following the ideas of Reference Barnes, Barnes, Tabor and WalkerBarnes and others (1971), if the non-linearity of log ϵ̇ versus 1/T at temperatures above —8°C in Figure 4 is due to the presence of liquid at triple junctions and grain-boundary sliding, then the average creep-rate enhancement due to these effects is approximately 25% (Fig. 4). This is certainly compatible with observations made on pure metals near their melting points where as much as 30% of the total strain may arise from grain-boundary shear Reference Hayden, Hayden, Moffatt and Wulff(Hayden and others, 1965).
Thus, it appears that the non-linearity of log ϵ̇ with inverse temperatures near the melting point is due to the combined effects of crystal growth and grain-boundary sliding which play reinforcing roles affecting creep. The combination of these factors results in a creep-rate enhancement of about a factor of two.
Effect of Crystal Size and Inclusions on Diffusion at High Temperatures
It can be seen in Figure 4 that at a constant temperature of about —10°C, in general, creep-rate increases with increasing volume fraction of inclusions and, contrariwise, decreases with increasing inclusion concentration at temperatures of about — 40°C. Thus, in general, apparent activation energies for creep increase with increasing volume fraction of inclusions (decreasing average crystal size).
Reference Raj and AshbyRaj and Ashby (1971) discuss how, at elevated temperatures, it is possible for grain-boundary sliding to be controlled by diffusional processes. They show how stresses developed along non-planar crystal boundaries can set up a diffusive flux of matter from portions of the boundary under compression to those under tension. If diffusion is the primary mechanism accommodating the incompatibilities caused by grain-boundary sliding, diffusional flow, and sliding are not independent. They are coupled and according to Reference Raj and AshbyRaj and Ashby (1971, p. 1121) the resulting deformation is correctly described as “diffusional creep”, or as “grain-boundary sliding with diffusional accommodation”.
Recent investigations have shown that the creep-rate of fine-grained polycrystalline ice (d < 1 mm) is apparently controlled by diffusional processes Reference Baker(Baker, 1978). In the present study, all of the samples tested, with the exception of Sample A, had average crystal sizes of less than 1 mm. Thus, in order to discuss the increase in creep-rates with increasing volume fraction of inclusions at temperatures of about —10°C seen in Figure 4, it is necessary to derive an equation for diffusion-controlled creep which incorporates the influence of both grain size and solid inclusions.
The dual roles of bulk diffusion and grain-boundary diffusion in high-temperature creep have been discussed by Reference Raj and AshbyRaj and Ashby (1971) and Reference GittusGittus (1975) who modified the Nabarro-Herring creep equation to the following:

where δ is the width of a grain boundary, Ω is the atomic volume, k is Boltzmann’s constant, d is the average grain diameter, DB and DV are the coefficients for grain-boundary and bulk diffusion respectively, and the other terms are as defined earlier. From this equation it may be noted that at constant stress and temperature, if πδD B /dD V is much less than 1, the creep-rate is proportional to 1/d 2. For ice at —10°C, D V ≈ 1×10−9mm2s−1 (Reference GlenGlen, 1974, p. 44), D B ≈ 1×10−5 mm2 s−1 Reference Glen(Glen, 1974, p. 44), and δ = 9×10−8 cm Reference Goodman, Goodman, Frost and Ashby(Goodman and others, (1977). Using d=1.22 mm (Sample A, Fig. 4) it follows that πδD B/dD V ≈ 0.023⪡ 1.Thus, from Equations (3), for inclusion-free ice (Sample A)

We will now proceed to derive an equation similar to Equations (3) but incorporating the influence of solid inclusions. If it can be assumed that grain-boundary sliding is the rate-determining process for high-temperature creep of fine-grained ice, the effect of inclusions on grain boundaries can be examined by using the analysis of Reference Raj and AshbyRaj and Ashby (1971). This model gives creep-rate as a function of the rate of grain-boundary sliding u̇ where inclusions lie along the boundaries. That is,

where γ̇ is the shear strain-rate, τ is the shear stress, λ is the spacing between particles, a is the particle diameter and the other terms are the same as in Equations (3).
Although Equations (5) was derived from continuum considerations, Raj and Ashby discuss whether there should not be some microscopic influence of the particles which may provide a threshold stress below which no diffusional creep would take place. Reference Vickers and GreenfieldVickers and Greenfield (1968) have considered the effect of inclusions along grain boundaries and discuss how inclusions oppose diffusional creep because they exert internal stresses σi which oppose the applied stress. Thus the stresses causing flow are lower, and the applied stress should be reduced to an effective stress
Taking this into account and using the Lévy–Mises equivalent (ϵ̇/σ = γ̇/3τ) for comparison with compressional strain-rates, Equations (5) becomes

In order to use this equation for analysis of the data presented in Figure 4, it is necessary to express the particle spacing λ in terms of particle size a and volume fraction of inclusions f. Reference BakerBaker (1978) has derived such an expression, finding that particle spacing depends upon inclusion size and concentration according to the relationship

From Equations (7) and (8), assuming all inclusions are on crystal boundaries (a reasonable assumption since Reference BakerBaker (1978) found 87% of the included sand particles in similar samples were located on grain boundaries), it is found that

It can be seen from this equation that at constant temperature, stress, and volume fraction of inclusions, creep-rate is again proportional to the inverse square of the grain-size.
The diameter of inclusions used in the present study was 0.1 mm. Thus, at a temperature of —10°C, the term 5δD B/aD v ≈ 0.45. Using this value as well as the grain-size and volume-fraction inclusion data from Figure 4, relative creep-rates can be calculated using Equations (9) and compared to the result obtained from Equations (3) for inclusion-free ice. These results are given in Table III.
Table III. Effects of average crystal size and volume-fraction inclusions on relative creep-rate

If the results in Table III are now compared with the data at —10°C in Figure 4, several important trends can be observed. First, in Figure 4 it is found that creep-rates increase with increasing volume fraction of inclusions; a result predicted in Table III although the high creep-rates predicted at 0.013 and 0.022 volume-fraction inclusions were not found experimentally. Secondly, at volume-fraction inclusions higher than 0.04, the predictions in Table III show the creep-rate to be approximately constant. This agrees well with the measured creep-rates at —10°C presented in Figure 4 (Samples D and E). Normally, variations in inclusion concentration and average crystal size have competing effects on creep-rate, which decreases with increasing volume-fraction inclusions and increases with decreasing grain size (Equations (9)). Thus, the constant creep-rate at higher volume-fraction inclusions may indicate that the competing effects of increasing inclusion concentration and decreasing crystal size are cancelling one another (d 2f ≈ constant).
Equations (3) and (9) predict similar trends to those indicated in Table III throughout the entire range of temperatures in Figure 4. However, if the data at about — 40°C (Fig. 4) are examined, it can be seen that, in general, creep-rates decrease with increasing volume-fraction inclusions. This trend is inconsistent with that predicted in Table III if one considers the inclusion-free versus the inclusion-bearing samples. Furthermore, Equations (3) and (9) predict an opposite trend in apparent activation energies than that observed in Figure 4. Thus, a simple model for grain-boundary diffusion over the full range of temperatures is by itself insufficient to explain the results in Figure 4.
Effect of Inclusions on Activation Energy
Since the previous model does not fit the experimental data over the full range of temperatures, it appears that another rate-limiting step or steps may be controlling creep at low temperatures. Thus, a simple thermal-activation approach to creep will be adopted in order to test the effect of rigid inclusions on activation energy.
Reference Kocks, Kocks, Argon and AshbyKocks and others (1975) show that by beginning with a creep equation such as that of Dieter ([C1976], p. 470)

where A is a constant, Q is the true activation energy for creep, v is the activation volume, and the other terms are as defined previously, the effect of internal stresses due to inclusions can be incorporated so that Equations (10) becomes

From this equation, it can be seen that the internal stress σi combines with the true activation energy Q indicating that the apparent activation energy Q0 is a measure of both thermal activation and internal stress (Q0=Q+νσi). Thus, inclusion-bearing samples should have higher apparent activation energies than inclusion-free samples and since σi increases with increasing volume-fraction inclusions, so should apparent activation energies. As an example, Reference Vickers and GreenfieldVickers and Greenfield (1968) found for pure magnesium at about 0.8T m, the true activation energy was 134 kJ mol−1 (32 kcal mol−1) while for magnesium containing a 1% dispersion of fine magnesium oxide, the apparent activation energy was 419 kJ mol−1 (100 kcal mol−1). Thus the increase in apparent activation energy with increasing volume fraction of inclusions observed in Figure 4 appears to be the result of a thermally activated process which is modified by the internal stresses created by the included sand particles.
Alternatively, the thermal-activation equation of Reference Kocks, Kocks, Argon and AshbyKocks and others (1975, p. 108) could be adopted.

Here However, over the range of temperatures employed, this yields essentially the same result as Equations (11).
The magnitude of the internal stress term was estimated in two unique ways. First, one may associate the ν value in Equations (11) with the shear activation volume V⋆ of the deformation process. If the activation volume were relatively constant, then a plot of apparent activation energy versus volume fraction of inclusions would give the strength of the internal stress term. Estimating V⋆ as b 2l, with the burgers vector b equal to 4.52 Å and l ≈ λ from Equations (8), one determines V ⋆ to range from about 4.0 to 6.1×10–19 cm3. If these values are now used to estimate the strength of the internal stress term, very realistic estimates of 0.036 to 0.141 MN m−2 (0.36 to 1.41 bars) result; values which are approximately 6 to 25% of the applied creep stress. Furthermore, the internal stresses increase with increasing volume fraction of inclusions as might be expected. A second method of estimating the internal stresses would be to assume they are Orowan stresses Reference Orowan(Orowan, 1948) using λ and b as above with an elastic modulus of 9.5×103 MN m−2 Reference Hobbs(Hobbs, 1974). This gives values of 0.028 to 0.044 MN m−2 (0.28 to 0.44 bars) which increase with inclusion concentration. In either case, these are significant internal stresses which could account for the apparent increase in activation energy measured experimentally.
The only previous study which made measurements of the effect of temperature on creep of inclusion-bearing ice Reference Nayar, Nayar, Lenel and Ansell(Nayar and others, 1971), did so in the temperature range of —2°C to —13°C—temperatures where grain-boundary sliding can be enhanced by the presence of intergranular water. Their results showed that the apparent activation energy for creep of ice containing a 1.0% dispersion of ultra-fine amorphous silica (average particle diameter 1.5×10−5 mm) was 406 kJ mol−1 (97 kcal mol−1) ; approximately three times the activation energy for creep of clean ice measured over the same temperature range (Reference GlenGlen, 1955; Reference Mellor and TestaMellor and Testa, 1969; Reference Barnes, Barnes, Tabor and WalkerBarnes and others, 1971). This is in qualitative agreement with the apparent activation energies measured over a lower range of temperatures in the present study.
Because average crystal size decreased with increasing volume-fraction inclusions, the possibility remains that the activation energy for creep is influenced by variations in ice-crystal size. In the present study, no tests were conducted on the variation of log ϵ̇ with 1/T for inclusion-free ice with different grain-sizes. However, a number of previous studies of the effect of temperature on creep of polycrystalline ice have made at least approximate measurements of average crystal size. These are summarized in Table IV. Although in most cases the grain-size measurements were not precise, no systematic relationship between activation energy and crystal size is apparent. On this basis, it appears that variations in ice-crystal Size have little or no effect on activation energy for creep and that the differences in Q observed in Table IV may have been due to other factors such as creep-rate enhancement at high-temperature settings due to the presence of intergranular water; possible recrystallization and grain growth at the high-temperature settings; and possible variations in the orientation of c-axes among the samples tested. This matter, however, clearly warrants further detailed study.
Table IV. Values of activation energy for creep and grain-size from steady-state creep tests on polycrystalline ice

Conclusions
-
(1) Dynamic recrystallization and grain growth is inhibited by the presence of dispersed-solid inclusions. The average crystal size produced by recrystallization is an inverse function of the concentration of dispersed inclusions.
-
(2) At temperatures above — 8°C, both recrystallization with accompanying grain growth and grain-boundary sliding appear to play reinforcing roles affecting creep and combine to result in creep-rate enhancement by about a factor of two.
-
(3) (a) The apparent activation energy for creep over the temperature range —10°C to — 4 °C increases with increasing volume fraction of inclusions (decreasing average crystal size). This appears to be the result of a thermally activated process which is modified by the internal stresses created by the included sand particles. (b) Estimates of the magnitude of these internal stresses range from 0.036 to 0.141 MN m−2 or approximately 6 to 25% of the applied creep stress.
Acknowledgements
This study was supported by National Science Foundation Grants GA-19310, GA-42728, EAR-7712981, and EAR-7901761, and the Glaciology Division, Department of the Environment, Canada. The authors are particularly grateful to R. L. Hooke for many perceptive discussions on the rheology of ice and for the use of a computer program which formed the basis for the creep-rate calculations. We are also indebted to R. Plunkett and P. J. Hudleston for suggestions they offered during various phases of this study, and to an anonymous reviewer whose comments resulted in considerable improvements in the paper.
Discussion
W. F. Budd: The growth of crystals you showed suggests tertiary creep was occurring which usually sets in after several per-cent strain. Did you find any development of anisotropy in your deformed samples?
R. W. Baker: Ice-fabric measurements made on samples both before and after testing detected only very slight fabric development. In general, the change in percentage of points in 1% of the area of the fabric diagrams was 2 to 4% and in all cases the fabrics were still quite random after testing—having less than 14% of the axes in 1% of the area.
T. J. Hughes: Congratulations on a first-rate creep study that has been needed in glaciology for a long time. As you know, primary creep lasts longer at low temperatures and tertiary creep begins sooner at high temperatures. So if you ran a creep test at one temperature until steady-state creep dominated, and then you either lowered or raised temperature, what precautions did you take to insure against reversion to primary or tertiary creep?
Baker: Thank you. When temperature settings were changed, creep measuring continued in order to monitor the response of samples. In many instances this resulted in observable decelerating creep-rates. Therefore, secondary creep-rate was not computed until the curve of total strain versus time returned to linearity. In all cases, after changing the test temperature a minimum of 12 h had elapsed prior to the start of the creep-rate measurement. To test if some primary creep might be included in the measured strain-rate, Andrade’s law was fitted to the curve of total strain versus time. In general, the secondary creep-rate determined by this method differed from the slope of a least-squares straight line through the data by less than 0.01 year–1.
S. J. Jones: Have you done enough tests to be sure your results are statistically significant? In Figure 4, diagrams B, C, and D showed a systematic increase in inclusions but an activation energy which jumped from 17.7 to 19.0 and then back to 17.6 kcal/mol. How do you explain this?
Baker: As a check, two “control” samples were tested. One specimen had no inclusions and the other contained about the same concentration of inclusions as Sample E. Activation energies for these samples were about 14 and 22 kcal/mol respectively. Therefore, we feel that the general increase in apparent activation energy with increasing inclusion concentration is real. The lack of agreement of Sample D with our model and the trends established by the other samples, we believe can be explained by the normal scatter which is to be expected in any mechanical test of this type.
N. W. Young : Considering you used the one sample for measurements over a considerable range of temperatures and it suffered substantial strain over the series, did you return to any previous temperature to repeat the measurements and note any change in the values obtained?
Baker: Whenever a test temperature was duplicated, virtually identical creep-rates were measured as long as none of the previous temperature settings had been above about —8°C. If, however, a temperature was repeated after the sample had been tested above —8°C, the creep-rates always differed. This I attributed to the effect of grain-size changes on creep.
D. R. Homer (written contribution): You cite the work of Reference Nayar, Nayar, Lenel and AnsellNayar and others (1971) as supporting evidence for your results. It is, however, worth remembering that Nayar’s specimens were substantially different from yours. His were probably of columnar-grained ice, yours are randomly oriented polycrystals. Such a difference will affect the value of the apparent creep activation energy.
Baker: As I recall, Reference Nayar, Nayar, Lenel and AnsellNayar and others (1971) indicated that their samples had random fabrics. However, even if they used columnar-grained ice, I still feel their results support the data I have presented here. For instance, Reference MugurumaMuguruma (1969), Reference RamseierRamseier (unpublished), and Reference Gold, Whalley, Whalley, Jones and GoldGold (1973) all tested columnar ice with no inclusions and found activation energies for creep, measured at temperatures below —10°C, which are quite close to the value I determined for sample A. Based on this agreement, I believe that the high apparent activation energy measured by Reference Nayar, Nayar, Lenel and AnsellNayar and others (1971), when compared with the lower values determined for inclusion-free ice over a similar range of temperatures, supports our results.
J. G. Paren(written contribution): Do you believe it to be a coincidence that the secondary creep rate at around —30°C is virtually independent of crystal size and volume fraction of impurities?
Baker: Our model for thermally activated creep predicts that there should be an apparent increase in activation energy with increasing concentration of inclusions. Thus one should expect that if two curves of log ϵ̇ versus 1/T, measured for samples with different inclusion concentrations, are plotted on the same graph, they should intersect at some temperature. If this is done for our data, the curves all intersect at temperatures of about —25°C. Normally, grain-size and inclusion variations play competing roles affecting diffusional creep. Creep-rate generally increases with decreasing grain size and decreases with increasing inclusion concentration. The intersection of the curves may indicate that grain-boundary effects dominate above —25°C, that inclusions control creep rate below —25°C, and that at about —25°C these competing effects cancel one another resulting in a creep-rate which is approximately constant.










