Introduction
Thermal conditions at the beds of polar glaciers and ice sheets are important not only because they have a fundamental bearing on ice dynamics through basal sliding and sediment deformation but also because they exert a critical control on glacier erosion, sediment entrainment, transport and deposition (Reference Sugden and JohnSugden and John, 1976). Furthermore, investigations of large, long-lived subglacial lakes underlying the East Antarctic ice sheet (EAIS) highlight the role that ice-sheet thermomechanics plays in their extent, volume and continued longevity. Herein, we present field and modelling data that indicate the existence of a warm, wet-based zone under the tongue of Taylor Glacier, an outlet glacier of the EAIS terminating within the Dry Valleys. Reference RobinsonRobinson (1984) suggested on the basis of theoretical evidence that Taylor Glacier has extensive areas of temperate basal ice. The ice-penetrating radar and modelling evidence presented extends this interpretation and has implications for the genesis of debris-laden ice which, at Taylor Glacier, is most likely adfrozen to the sole of the glacier from an overdeepening, 5 km up-glacier of the terminus, to which it is subsequently advected and becomes exposed.
Debris-laden ice (DLI) has been observed at the base of a number of glaciers and ice caps in Arctic and Antarctic regions where the prevailing climatic regime yields a predominantly frozen (or cold) ice–bed interface (Reference MercerMercer, 1971; Reference Gemmell, Sharp and SugdenGemmell and others, 1986; Reference FitzsimonsFitzsimons, 1996; Reference GowGow and others, 1997). The presence of DLI is important because it is less viscous than pure glacier ice at the same temperature and thus, where present, exerts an influence on ice dynamics. Reference Holdsworth and BullHoldsworth and Bull (1970) observed that the ‘opaque basal ice’ of Meserve Glacier, Dry Valleys, was significantly softer than debris-free ice at the same temperature (–18˚C), yielding a flow-law exponent of 4.5 compared to 1.9 for the overlying glacier ice. Reference Holdsworth and BullHoldsworth and Bull (1970) tentatively associated this observed contrast in rheology with the impurities present in the basal layer at Meserve Glacier. Investigations into the genesis of such layers have generally concluded that the necessary entrainment occurs whilst the bed of the glacier is at the pressure-melting point, yielding conditions advantageous to melting and refreezing, abrasion, plucking and entrainment (e.g. Reference Knight, Sugden and MintyKnight and others, 1994).
However, Reference CuffeyCuffey and others (2000), in their detailed analysis of the gas and isotopic composition of Meserve Glacier, propose that the basal DLI layers observed at that site result from entrainment occurring at subfreezing temperatures. These authors invoke the presence of a supercooled interfacial water film at –17˚C to refine a mechanism first proposed by Reference ShreveShreve (1984) by which cold-based ice slides over microscale roughness elements through regelation. Thus even under frozen bed conditions this mechanism will give rise to the processes of abrasion and striation, and the generation of erosive fines. Such an important conclusion, they note, provides a significant challenge to the widely held view that cold-based glaciers are protective of their substrates and only wet-based glaciers are capable of accomplishing any significant geomorphic work on the landscape.
The field and modelling evidence presented here that indicates temperate subglacial conditions, and possibly water ponding, across the bed of Taylor Glacier tongue is important because this glacier also has a well-developed and extensive basal DLI layer, similar to that observed at Meserve Glacier. Although this correspondence of wet-bed conditions and DLI does not discount the above hypothesis for cold-based entrainment of debris, it does indicate that the thermal character of the bed of Taylor Glacier, and possibly other glaciers in the Dry Valleys, may be more complex than Reference CuffeyCuffey and others (2000) recognized.
Field Area and Methods
Taylor Glacier (77˚43' S, 162˚15' E) is a 100 km long outlet of Taylor Dome, part of the EAIS, which breaches the Transantarctic Mountains and terminates at the head of one of the major valley systems of the Dry Valleys, south Victoria Land. Our study is concerned with the lower 10 km tongue of this glacier, which is 1–3km wide and is bounded by ice cliffs, up to 35 m high, which extend some 6km up-glacier from the terminus. With a mean annual surface temperature of –17˚C at its terminus (Reference RobinsonRobinson, 1984), it is generally believed that sublimation accounts for up to 80% of the ablation over glaciers in the Dry Valleys. However, active dry-calving of the glacier’s margins is also occurring, and observations in 2001/02 indicate that in exceptional summers, when ambient air temperatures exceed 0˚C for extended periods, substantial amounts of supraglacial melt-water are generated which activate ephemeral fluvial channels (personal communication from T. Nylen, 2002). Debris-poor and relatively homogeneous glacier ice is underlain by a layer of DLI that is 0.5–3m thick across the terminus of the glacier and ∼3 km up both margins. This DLI merges indistinctly into the underlying frozen sediments.
Ice-penetrating radar
The ice-penetrating radar used is based on the Reference Narod and CNarod and Clarke (1994) impulse transmitter in conjunction with an airwave-triggered Tektronix 100MHz digital oscilloscope, a system which has been extensively used to determine basal topography, hydrological conditions and englacial structure at both temperate and polythermal glaciers (e.g. Reference SharpSharp and others, 1993; Reference Welch, Pfeffer, Harper and HumphreyWelch and others, 1998; Reference PattynPattyn and others, 2003). Inline orientated (E-plane) resistivity loaded dipoles were used for the transmitter and receiver and sized for a centre frequency of 10MHz. The scope traces were recorded digitally, along with position, using a Trimble 4700 differential global positioning system (GPS) and two base stations, which yielded a precision of < 1m in most instances. Traces and positions were recorded on foot at ∼900 locations on six transects to 2 km beyond Church Rock, located ∼6 km up-glacier from the terminus. The margins and terminus were also surveyed optically along with the approximate cliff angle, height and any notable glacier or basal ice facies at ∼70m intervals.
Ice depth
Ice depth at each location was determined by manually picking the two-way travel time from each digital trace assuming a wave propagation velocity through ice of 0.17m ns–1. Since the digital oscilloscope was airwave-triggered, a static correction for the separation of the transmitter and receiver of 15m was made assuming an airwave velocity of 0.3 mns–1. Despite generally low background scatter due to the absence of internal reflectors, yielding good bed signals in over 800 traces, 225 of the traces yielded a confused basal reflection, probably due to complex topography or basal layering. Such traces were ignored and the remaining ice-thickness measurements were estimated to be accurate to ∼16%, up to 68 m in the deepest regions. In conjunction with the measured surface and margin GPS positions, these ice depths were used to produce glacier surface and bed DEMs (Fig. 1a and b) on 50m horizontal grids using a kriging interpolation which honoured the input elevations. The resulting surface and bed DEMs have an estimated error of up to 15 and 75 m respectively. These data are used to provide topographic boundary conditions for thermomechanical modelling and to calculate the subglacial hydraulic potential (Φ) surface using Reference ShreveShreve’s (1972) relation:
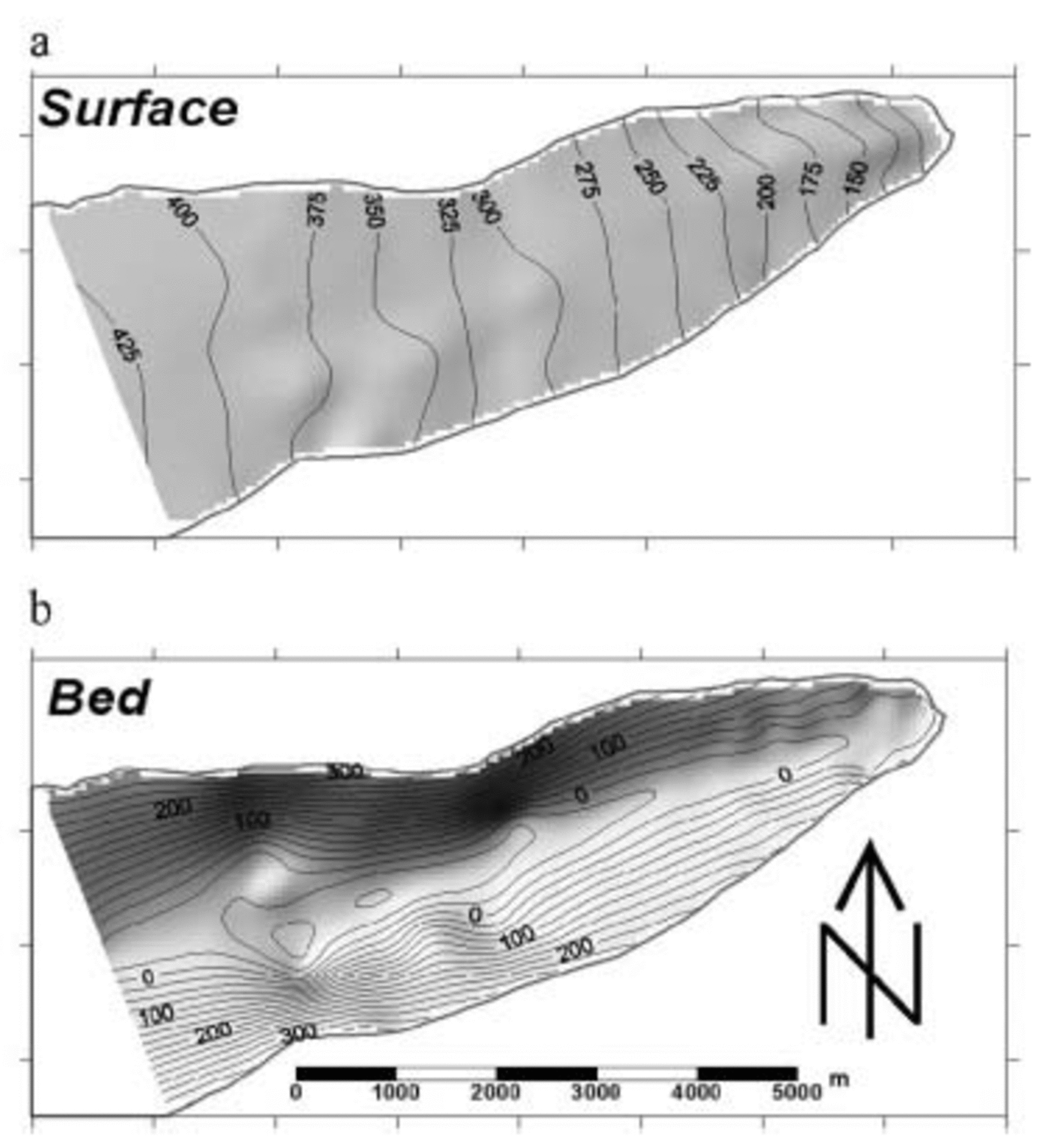
Fig. 1. The surface (a) and subglacial bed (b) topography of Taylor Glacier tongue interpolated onto 50m grids from GPS, radar and ice-margin surveys. Units in m and contoured at 25 m intervals.
where ρ w and ρ i are the densities of water and ice respectively, g is gravity, S is the glacier surface elevation, B the bed elevation and f is a factor between 0 and 1 which indicates the connectivity between the bed and atmosphere, which determines the subglacial water pressure as a fraction of the overburden pressure (Fig. 2a and b).
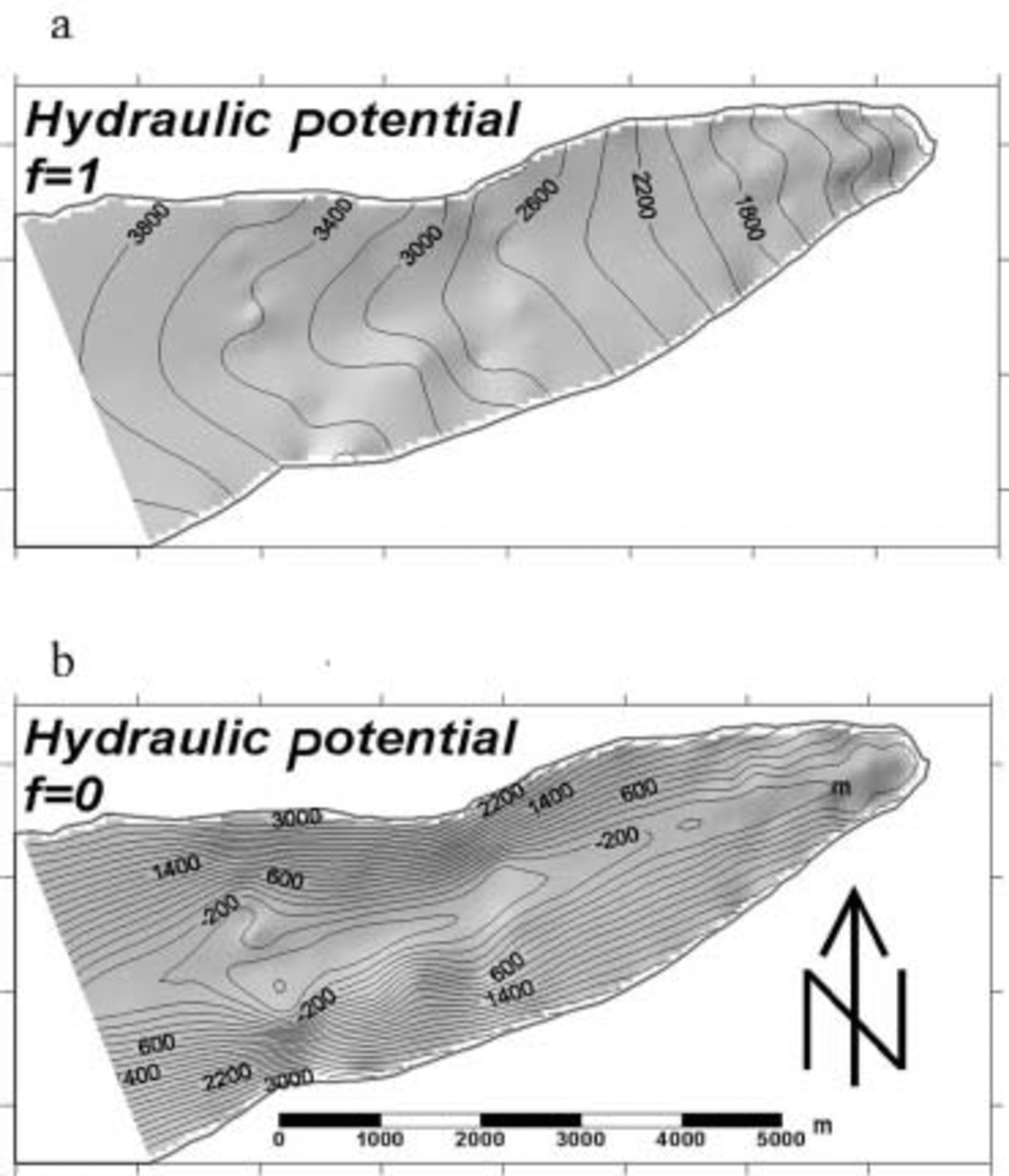
Fig. 2. Calculated subglacial hydraulic potential surfaces for (a) f = 1 where the basal hydrological system is fully isolated from the atmosphere, and (b) f = 0, where the basal hydrological system is completely connected to the atmosphere. Units in kPa and contoured at 200 kPa intervals.
Internal and bed reflection power
Following the method specified by Reference Gades, Raymond, Conway and JacobelGades and others (2000) and further refined by Reference Copland and SharpCopland and Sharp (2001) for a high-Arctic glacier, the scope traces were analyzed for relative internal reflection power (IRP) and bed reflection power (BRP) to provide insight into conditions at the ice–bed interface of the glacier. This procedure was carried out simultaneously with the picking routine described above, and involved the integration of the return traces from three manually specified points along the time axis: (1) 600 ns after the surface-wave peak, (2) 200 ns before the bed-signal peak, and (3) 600 ns after the bed-signal peak. Such variable ‘time windows’ following the procedure of Reference Copland and SharpCopland and Sharp (2001) were necessary in order to capture total BRP.
Since BRP is highly dependent on the path length of the returned signal through geometric spreading, dielectric absorption and scatter from internal features, it is necessary to isolate these effects before it can be used to infer basal conditions. Following Reference Copland and SharpCopland and Sharp (2001), all traces that yielded large values of IRP (>2mV2 ns–1), corresponding to internal structures which could potentially absorb much of the transmitted signal, were excluded from the analysis. This left 408 traces with a high BRP/IRP ratio with which to establish an empirical relation between BRP and ice thickness to isolate the effects of geometric spreading and dielectric absorption. An exponential function with an R 2 of 0.80 yielded the least-squares best-fit relation between BRP and ice depth (Fig. 3). From this relation, the residual, or depth-corrected, BRPR was calculated following Reference Gades, Raymond, Conway and JacobelGades and others (2000) by dividing the measured BRP by the predicted BRP. The resulting BRPR ratio, now corrected for depth attenuation effects, has high values in traces recording a strong basal signal, and low values in traces recording a low bed reflectivity. The technique thereby provides a means by which the distribution of BRPR may be used to infer basal conditions.

Fig. 3. The relationship between ice depth and bed reflection power (BRP) for the radar traces where the ratio of BRP to internal return power was suitably high. The best-fit exponential function is overlain and represents the predicted attenuation of BRP with ice depth.
Thermomechanical modelling
To calculate thermal conditions across the bed of Taylor Glacier tongue, a thermal model was applied based on the heat supplied to the bed by geothermal flux and friction from ice deformation, and the temperature gradient required to conduct that heat away. Frictional heating supplied to the bed (H) is calculated by:
where ▽(S) is the ice surface slope, and Q i is the ice discharge. Under the assumption that the majority of motion, and thus heating, takes place in the lowest layers of the glacier (i.e. within the DLI), then frictional heating (H) and the geothermal heat flux (G) can be combined to yield the steady-state temperature gradient required to maintain thermal equilibrium:
where k is the thermal conductivity of ice and ∂T/∂z is the vertical temperature gradient. Vertical integration of this relation yields an expression for the internal and basal temperature of the glacier under an assumed surface temperature boundary condition. A value of 88.0 Mwm–2 was taken for the geothermal heat flux (G) on the basis of Reference Decker and BucherDecker and Bucher’s (1977) measurements at the base of boreholes nearby at the geologically similar Lake Vanda, during the Dry Valleys Drilling Project. The surface temperature field was determined from Reference RobinsonRobinson’s (1984) temperature measurements at the base of a series of short ice-core holes into the surface of Taylor Glacier which yield a mean annual surface temperature of –17˚C at the terminus and a lapse rate of 0.004 Cm–1.
The above thermal scheme was implicitly coupled with Reference BlatterBlatter’s (1995) first-order approximation and applied in three dimensions bounded by the surface and bed DEMs at 150m resolution. The model was modified to provide a dual-layer rheological domain so as to account for the softer DLI layer in accordance with Reference Hubbard, Hubbard, Lawson and AndresonHubbard and others (in press). By optimizing modelled flow against measured surface velocities and displacements in a vertical cliff section, Reference Hubbard, Hubbard, Lawson and AndresonHubbard and others (in press) were able to determine values for a flow enhancement factor (A E) and exponent (n) of 2.3 and 1 for glacier ice, and 58.0 and 4 for DLI, in Glen’s generalized flow law (Reference NyeNye, 1953). These values for glacier ice and DLI yield a close fit with the observed measurements and are also in accordance with the results of Reference Holdsworth and BullHoldsworth and Bull (1970) for Meserve Glacier (above).
Results and Discussion
Topography and hydraulic potential
The main feature of the lower tongue of Taylor Glacier is the substantial overdeepening to 80 m below sea level which lies 3–6km up-glacier from the terminus (Fig. 1b). This over-deepening corresponds to a maximum ice depth of 470m but does not appear to influence the glacier surface markedly. Apart from a bed-induced bulge on its southern margin, this surface rises with a uniform gradient from 80m at the terminus to 420 m ∼8 km up-glacier (Fig. 1a).
The subglacial hydraulic potential surfaces with total isolation of the hydrological system from the atmosphere (f = 1; Fig. 2a) and complete connectivity of the hydrological system with the atmosphere (f = 0; Fig. 2b); both indicate strong convergence of subglacial water pathways into the overdeepening (Fig. 1b). Noting that any water present at the bed is likely to be routed from areas of high to low hydraulic potential, and normal to the equipotential contours, then the strongest convergence of basal water flow corresponds to an area ∼5 km up-glacier where the bed gradient is steepest. Across the lower glacier tongue, the subglacial hydraulic equipotential indicates strong divergent routing of any basal waters away from the glacier centre line and towards the margins. The subglacial drainage reconstruction under the assumption that the hydrological system is fully connected to the atmosphere (f = 0; Fig. 2b) does not substantially alter the hydraulic potential surface across the upper tongue, but does indicate that under these hydraulic conditions extensive subglacial water ponding may occur within the overdeepening. In both cases, it is possible to conclude that there is a strong topographic control of subglacial water routing, if such water were present, at Taylor Glacier.
Residual bed reflection power
The calculated distribution of BRPR across Taylor Glacier tongue displays marked spatial contrasts: predominantly low values (< 2) are recorded at the margins and along the lower tongue, and higher values of 5–8 within the central region of the upper tongue (Fig. 4a–d). The two upper cross-profiles (Fig. 4b and c) located 4 and 5.5 km up-glacier from the terminus yield maximum BRPR values of 6 and 7 respectively. These correspond closely to the lowest point of the bed topography. Subsequent values of BRPR appear to fall off rapidly towards the margins. The lowest cross-profile, located 2 km up-glacier from the terminus (Fig. 4a), has generally low BRPR but does exhibit peaks of 2 and 1.5 which occur ∼400m either side of the topographic low-point located at the middle of the transect. Although the long-profile BRPR distribution (Fig. 4d) also exhibits much heterogeneity, a more consistent trend of BRPR is observed with values increasing from generally less than 2 for some 3.5 km up-glacier, to values of consistently over 4 and up to 8 from 4.5 to 7km up-glacier from the terminus.

Fig. 4. The distribution in BRPR (dotted line) overlain on the glacier surface and bed geometry (solid lines) for three cross-profiles (a–c) and the long profile up the glacier centre line (d).
Since water has a considerably higher dielectric constant than ice and rock, and the power of a reflected signal is strongly related to the dielectric contrast between the interfacing materials, it follows that a high BRPR most likely indicates wet or temperate conditions at the bed, while a low BRPR is interpreted in terms of frozen or cold basal conditions. With this assumption in mind, a strong correspondence can be noted between both the basal overdeepening (Fig. 1b) and associated convergence of subglacial water pathways directed by the hydraulic equipotential surface (Fig. 2a and b) and the distribution of high BRPR observed across the upper tongue. Furthermore, beneath the lower glacier tongue, the BRPR maxima (Fig. 4a) displaced towards the margins correlate well with the two main subglacial pathways predicted by the subglacial hydraulic equipotential surface (Fig. 3a and b) which anticipates divergent flow away from the glacier centre line towards the margins in this region. Based on the correspondence between high BRPR and subglacial drainage indicated by the hydraulic equipotential surface, it does seem very likely that there is a real relationship between high BRPR and the presence of temperate ice, water or saturated sediments at the base of Taylor Glacier. However, despite this high level of correspondence, the association between high BRPR and the presence of water cannot be made with certainty. It is possible, for example, that the measured variations in BRPR are indicative of disparities in the basal character at Taylor Glacier, but that they denote the extent or thickness of basal DLI rather than the distribution of thermal conditions per se. Although this possibility cannot be discounted entirely, there are two arguments against it. First, the very high values (< 15) of BRPR observed require a substantial difference in dielectric constant (d.e.) across the interface generating them. Such a dielectric contrast is only likely to be realistically obtained within a glacier between ice (d.e.∼4) and water at 0˚C (d.e.∼88) (Reference Copland and SharpCopland and Sharp, 2001). Second, low BRPR values are measured even where distinct basal DLI layers up to 3 m thick are exposed at the margins of Taylor Glacier. In reality, it is likely that the observed variation in BRPR denotes the distribution of a combination of both thermal conditions and the extent of DLI at the bed of Taylor Glacier. That 225 radar traces returned exhibited strong, but confused, bed signals, despite little internal background noise, indicates that both the thermal conditions and structure at the bed of Taylor Glacier may be complex.
Basal thermal conditions
The distribution of modelled basal temperature under Taylor Glacier tongue shows large variations: from –18˚C at the uppermost margins to –7.8˚C at the centre of the over-deepening (Fig. 5). That the highest temperature modelled at the bed coincides with the overdeepening is not unexpected since it is here that the overlying ice is at its thickest, yielding maximum insulation and frictional heating arising from glacier motion. However, nowhere across the glacier tongue do modelled temperatures approach the pressure-melting point (PMP). Sensitivity analysis of the thermally coupled first-order flow model reveals that this modelling result is robust. This is largely because Taylor Glacier tongue is currently too thin to sufficiently insulate the bed, while ice velocities (< 7 ma–1 across the glacier tongue) provide little frictional heating. It is also pertinent to note that the modelled temperature distribution presented here is a liberal one, since not all the frictional heating component is likely to be delivered exclusively to the glacier bed, as is implicitly assumed in the thermally coupled flow model.
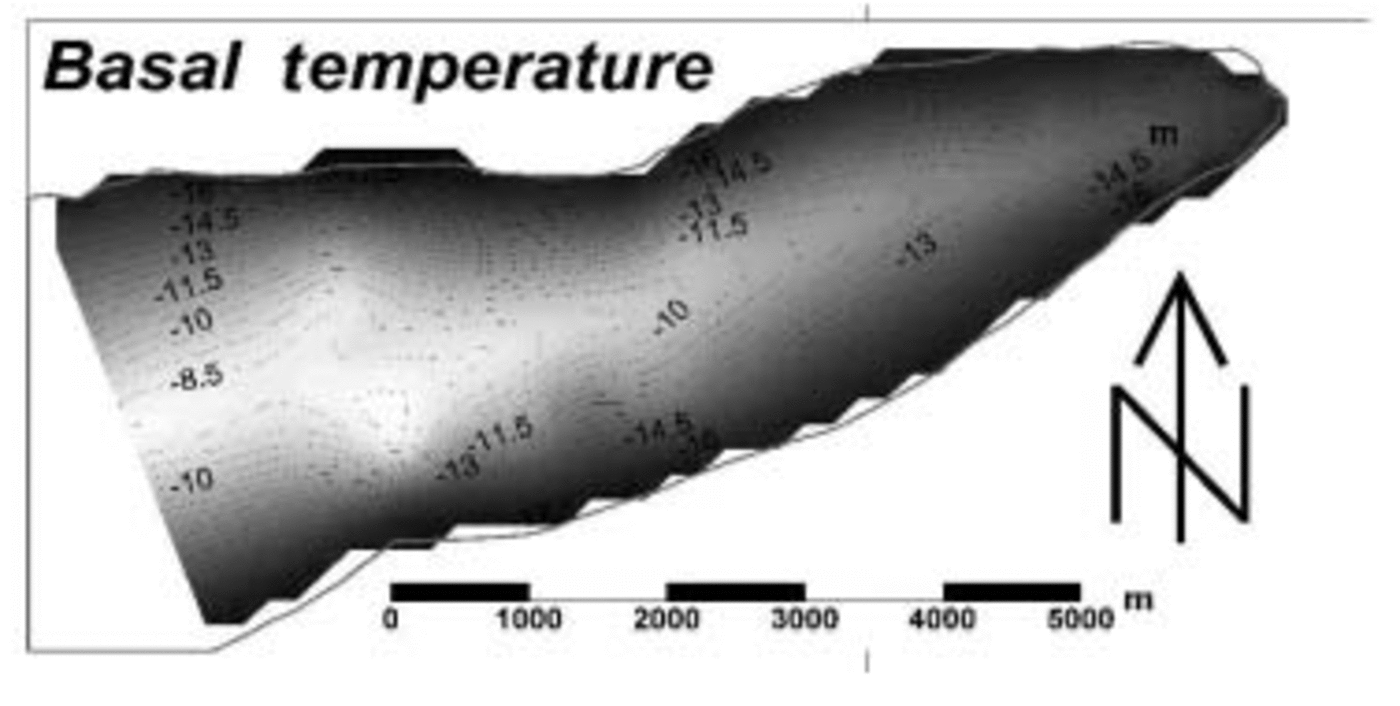
Fig. 5. The modelled subglacial temperature distribution under Taylor Glacier tongue. Values in ˚C and contoured at 0.5˚C intervals.
Reference RobinsonRobinson (1984) concluded that up to 50% of the bed of Taylor Glacier may be at the PMP, but this study focused on an area up-glacier of the present study where the ice was thicker. Thus, significantly less than 50% of the lower tongue of the glacier would be expected to be at the PMP on the basis of Robinson’s analyses. This inference is consistent with the thermal modelling presented above. Hence, Robinson’s and our results indicate that the base of the lower tongue of Taylor Glacier is well below the PMP. This interpretation is at odds with our BRPR analysis, though, which suggests that an extensive zone of water is present in some form at the glacier bed. A possible reconciliation of these apparently contradictory results may be provided by Reference Doran, Fritsen, McKay, Priscu and AdamsDoran and others (2003), who reported the presence of hypersaline brine at the base of nearby Lake Vida. Until recently, Lake Vida was presumed to be solid and frozen to its bed, but a 16m core revealed that the permanent ice cover is underlain by water with salinity up to seven times that of sea water, allowing it to remain liquid below –10˚C (Reference Doran, Fritsen, McKay, Priscu and AdamsDoran and others, 2003). The chemistry of Blood Falls, a deep-orange-coloured ice feature emerging from the terminus of Taylor Glacier, which contains high concentrations of both iron oxide and salt thought to have a marine origin (personal communication from H. Keys, 1999), lends support to the hypothesis that the glacier bed could indeed be hypersaline.
Conclusions
The high correlation between the pattern of high BRPR and the predicted locations of subglacial water pathways indicates that there is water present under Taylor Glacier tongue. The relationship between BRPR and the presence of wet conditions is most likely since the dielectric constant of water is significantly higher than that of any other naturally occurring subglacial material whose presence could reasonably be expected. However, the actual hydraulic conditions present are undefined and could take any form, from a thin distributed water film to extensive water ponding or even a thick layer of saturated sediments. It can be noted, though, that 225 of the radar traces exhibited a correspondence of wet-bed conditions with a complex basal structure as would be anticipated from the presence of an extensive layer of DLI. The presence of liquid water at the bed of Taylor Glacier can only be reconciled with thermal modelling, which indicates basal temperatures of lower than –8˚C, if that water is hypersaline. Such an interpretation is consistent with the presence of salt-rich ice at the glacier. The interpretation may also have bearing on investigations of sediment entrainment and transport of DLI that have hitherto reasonably assumed the presence of a frozen basal interface at sub-zero temperatures.
Acknowledgements
We are indebted to Antarctica New Zealand and the University of Canterbury for logistical support, and to R. Hindmarsh for assistance with the fieldwork. A.H. gratefully acknowledges support from the Royal Society of Edinburgh, the Royal Society of London and the Royal Geographical Society.







