Introduction
Within the Ross Sea there are a number of ice tongues which flow out for considerable distances beyond the coastline. Frequently, the length/breadth ratio exceeds 5, where lengths are of order 10–20 km. One of the most spectacular of these ice tongues is Erebus Glacier tongue (Fig. 1) which now extends more than 12 km into McMurdo Sound. This tongue is believed to be floating for its entire length for the following reasons:
(1) Surface structural features such as marginal teeth, surface rolls (Reference DebenhamDebenham, 1965) and cracks are consistent with a floating tongue.
(2) Gravimeter measurements by the author in 1966 showed that a considerable part of the central tongue and the north-central edge oscillates with the swell (tongue oscillation period about 16 s).
(3) Water-depth soundings around the outer end and south middle side of the tongue show that the water is deep enough there for the ice (of known thickness) to be free floating.
A slight curvature, concave to the north, of the tongue might be explained by differential exit speeds of the ice at either side of the hinge line (line of flotation). The possibility exists that the north edge may be grazing the bottom near the coastward end causing retardation of the north edge. However, these possible effects are apparently of minor consequence because the stress/strain-rate relation derived for the glacier is shown later to be essentially consistent with a floating tongue.

Fig. 1. Aerial oblique photograph of Erebus Glacier tongue (U.S. Navy 2/18/65).
Past and Present Records of the Ice Tongue
The tongue was first completely mapped in 1911 (Reference DebenhamDebenham, 1923), although a position for the end of the tongue was also given for 1902. These early surveys are known to contain some inaccuracies (U.S.G.S. map, Ross Island ST 57-60/6). A calving of great significance was recorded in March 1911 (Reference TaylorTaylor, 1922), when a section measuring 4–5 km by 1.2 km broke off the end during a gale.
The next documentation of the glacier is provided by the 1947 U.S. Navy (Highjump) photography. Subsequent air photography covering the tongue has been obtained for 1956, 1959, 1965, 1967 and 1970. The tongue has been mapped for these years using radial-line plots for vertical photographs and a Wilson Photo-alidade for oblique photographs. Figure 2 shows the 1970 position and the outlines of the end of the tongue at previous dates. A mean net forward rate of advance of about 158 m a−1 for the end of the ice tongue since 1947 is plotted as line DE in Figure 3. Point A represents the end of the tongue in January 1911 and point B indicates the position of the tongue in March 1911 after the calving. Suppose that subsequently the end of the tongue advanced at a rate comparable to the value given by the slope of DE (note that as the tongue length increases, the flow rate from n to E should increase by an amount equal to the strain-rate × distance increase; the same applies to BC); and suppose that a calving took place shortly before 1947. Representing this event is the line CD drawn horizontally so that C is vertically above A and D is vertically above B. The line CD is a first approximation only and, although it is shown corresponding to 1942, it might have been as late as 1946, putting C further into the zone 1 km wide set by the uncertainty in the earlier surveys as well as by the variability in the geometry of different calvings. The trajectory ABCDE traces out what appears to be a cycle of period about 30 years.

Fig. 2. Map of Erebus Glacier tongue. The full outline applies to 31 January 1970). Apparent swing of tongue may be due to orientation errors in the mapping.

Fig. 3. Erebus Glacier time–position diagram for end of glacier, based on data from Scott expedition reports and maps and U.S. Navy air photography.
This cycle is considered to be idealized; large departures from it are possible. To fully understand this cycle would lead to an understanding of the mechanism of calving. If the concept of a “critical length” is introduced, then one is prompted to predict that in the region EF (Fig. 3), representing the time interval 1972–77, the tongue will again be susceptible to calving, with the probability of calving increasing with time.

Fig. 4. (A) Longitudinal section through the center line of the tongue based on 1967 and 1970 U.S. Navy air photography and a radio-echo sounding traverse carried out by the Scott Polar Research Institute in December 1967. (B) The longitudinal mean density
Figure 4 shows the long section of the tongue in 1967. At the end of the supposed “stable length” of about 7–8 km, the central ice thickness is about 180 m. Beyond this point the progressively thinning tongue approaches a “critical length” with respect to a certain set of oceanographic boundary conditions.
Glacier-Tongue Regime
To examine the regime of the tongue, the mass equation (Reference BuddBudd, 1966, Equations (31)) is used. If H is the thickness of the ice at a distance x(m) from the hinge, and t is time, the assumption of steady state gives:


where
Using values of
Calving Behaviour
It was reported that the calving of the end of the tongue in 1911 was associated with a gale during open-water conditions and possibly a back surge of water in McMurdo Sound was an important factor in the calving process (Reference DebenhamDebenham, 1965). To consider this idea further, the possibility exists that due to a combination of wind stresses and stresses induced by swell and the back surge, the bending stress reached a maximum at the section between about 7.o and 8.o km from the hinge (fig. 4A), where, if differential oscillation occurred between the thicker landward section and the thinner seaward section, a phenomenon resembling whiplash might have occurred. On the basis of the preceding discussion, it is contended that the section of the tongue beyond about 7 km from the hinge is reaching a critical length where the combined effects of extreme weather and oceanographic conditions could induce a calving of the same magnitude as the one that occurred in 1911.
Another type of calving (Reference ReehReeh, 1968) involves a downward curling of the ice edge due to the imbalance there of ice and water pressures. As a result, icebergs are produced of length approximately equal to the ice thickness at the edge. For the period 1947–70, a comparison of the mean flow rate of the end of the tongue (~158 m a−1) to the flow rate of the last tooth (165 m a−1) indicates that the end could have suffered this type of calving once in the last 23 years—which is in accordance with the predictions of Reeh for this thickness and temperature of ice. Along the edges, occasional teeth are missing but others have persisted for more than 23 years with little significant change in form. Here, the ice is up to 40% thinner than the center-line ice, thus the expected frequency of calving is decreased (Reference ReehReeh, 1968, p. 227).
Structural Features
A significant surface feature, the “rolls” (Reference DebenhamDebenham, 1965), is evidently related to the teeth, the initial spacing of both being of order 500 m, which is about four times the distance the ice moves per year. The troughs of the rolls probably result from a process of plastic necking as the ice becomes afloat. The profile of the base of the ice near the hinge line is not known with sufficient accuracy to check for possible basal necking. Such a feature appears to occur in the seismic profiles of Reference RobinRobin (1958) for the Maudheim Ice Shelf and in the radio-echo sounding profiles of Reference Robin, Robin, Swithinbank and SmithRobin and others (1970) for the Ross Ice Shelf.
At the edges of the tongue a gash is formed by rupture of the ice as it is suddenly forced to acquire the speed of flow of the central ice. The periodic formation of these gashes is thought to control the local rate of stretch of the ice at the hinge line and thus to control the periodic formation of the troughs of the rolls. The marginal gashes open to become the notches between a series of teeth. On the south side of the tongue a series of 15 teeth had developed by January 1970, while to teeth existed in 1947. By mapping the positions of the points of these teeth, which are easily identifiable in photographs taken in seven different years, mean flow rates in the x direction have been determined by regression analysis. Although the time-distance plots are slightly curved, considering the errors involved, a linear regression analysis is sufficient for practical purposes. The assumption is made that the longitudinal strain-rate shown by the teeth is a close reflection of the longitudinal strain-rate along the center of the tongue. Figure 5 shows the longitudinal flow rate, u (m a−1), plotted against distance x, from which the longitudinal strain-rate

Fig. 5. Plot of horizontal flow rate u against distance x from the hinge, based on mean flow rate of 15 teeth on the south edge
Flow Law
In order to study the stress-strain-rate relation for the tongue, some simplifying assumptions are made. Since the tongue is free to expand laterally as well as longitudinally, we assume
so that the approximating condition of incompressibility gives:
the z direction being vertical. The effective shear strain-rate,

On the assumption of equal creep in two mutually perpendicular directions, the effective shear stress (τ) is found from the Weertman solution (Reference WeertmanWeertman, 1957) to be:

where g is the acceleration of gravity, ρ w is the density of sea-water and h is the height of the ice above water level. The ice-density function ρ(z) is assumed to be of a similar form to that derived by Reference SchyttSchytt (1958) for the Maudheim Ice Shelf. In particular:

where z is measured from the base upwards and where the constants β and a are determined for each profile along the tongue so that

equals the value of average tongue density calculated from known values of H and h and by extrapolation of a mean value fit (fig. 4B). Ice-thickness values for H < 190 m have been calculated using known values of h (determined photogrammetrically) and the extrapolated value
To solve Equations (5), an iterative process is used where the value of β is selected on the basis of an estimated surface tongue density (based on some measurements in 1966, together with data from Reference Stuart and BullStuart and Bull (1963) and Paige (unpublished data)); a value of a is then found which satisfies Equations (5).
The double integral in Equations (3) which reduces to:

is evaluated by numerical integration. The value of τ(x) along the tongue is shown in figure 4C.
On the assumption of a flow law:
where n is an exponent to be determined, and B is a factor dependent on the ice temperature, composition and structure, the plot of log
If in Figure 6 a least-squares analysis is performed on the present data, a line of slope n = 2.5 results with a correlation coefficient of 0.98, but until more data are available a value of n ≈ 3 is considered acceptable for the range of stresses 0.10 MN m−2 > τ > 0.03 MN m−2. This still leaves unanswered what value of n is appropriate for τ < 0.03 MN m−2 (Reference ThomasThomas, 1971, p. 86).
Unfortunately strain-rate and ice-thickness data available (Reference HeineHeine, 1967, Reference Heine1970) for parts of the much thinner McMurdo Ice Shelf apply to an area of strong compression and it is not possible to use the information directly to obtain points in the low stress range (τ < 0.03 MN m−2) which would be suitable for plotting in Figure 6. Only if a large part of the ice shelf became detached would it be possible to obtain useful measurements.
A value of B ≈ 1 × 108 N m−2

Fig. 6. Log
Conclusions
In comparing Thomas’s data with the present results it is seen that, within the experimental error, the conclusions about the flow law are similar. In Figure 6 the apparent shift of the Erebus Glacier tongue line may be slightly reduced if account is taken of the transverse thinning of the ice tongue, in which case
If the mean temperature of the Erebus Glacier tongue is actually warmer than that estimated (–15° C), this would help explain the shift of the Erebus Glacier tongue data to the left of Thomas’s line. Because the major part of the ice is flowing off the side of an active volcano (Mount Erebus), this possibility must be considered.
In addition, for the case of an exposed ice tongue subject to tidal (and swell) flexure, a part of the total longitudinal strain-rate which was measured may be due to the effects of bending stresses (Reference HoldsworthHoldsworth, 1969). Finally, if stress concentrations exist in the notches between teeth, higher marginal strain-rates than expected may be produced. Thus the values of
It is apparently difficult to obtain reliable data in the low stress range. One possibility is to use the Arctic ice islands (T3, WH4) but here the mean ice temperature is close to –10° C and the mean densities are at least 0.90 Mg m−3.
Acknowledgements
I thank the U.S. Navy for supplying the air photographs and the U.S. Antarctic Research Programs for enabling me to visit the glacier in 1966 and for arranging a special photographic mission in 1970. The Scott Polar Research Institute (Cambridge) supplied the 1967 ice-thickness data. R. A. Paige supplied information on ice densities and accumulation rates, and J. Clarkson helped me with photogrammetric and plotting work. I should specially like to thank R. H. Thomas (British Antarctic Survey) for substantial help with data interpretation and the computations, and members of the Inland Waters Branch who made suggestions to improve the manuscript.


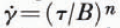 where
where 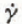 is the effective shear strain-rate, values of the exponent
is the effective shear strain-rate, values of the exponent  are determined. These are in fair agreement with published values.
are determined. These are in fair agreement with published values.





