Introduction
Many recent studies have concentrated on the surface mass balance (SMB) (Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others, 1999; Reference Arthern, Winebrenner and VaughanArthern and others, 2006; Reference MonaghanMonaghan and others, 2006; Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others, 2006) and mass changes (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; Reference ZwallyZwally and others, 2005) of the Antarctic ice sheet in order to assess Antarctica’s contribution to changes in global sea level. New techniques such as radar altimetry have made it possible to study continent-wide elevation changes with high accuracy. These changes are often related to changes in precipitation on the East Antarctic plateau (EAP) (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; Reference ZwallyZwally and others, 2005). However, these techniques only cover short time periods; it is important to obtain ground truth over longer time periods to understand how observed changes relate to the past.
To date, there have been very few in situ measurements of SMB available from the interior of the EAP. The present SMB estimates are mainly based on remote sensing (e.g. Reference Arthern, Winebrenner and VaughanArthern and others, 2006) or numerical modelling (e.g. Reference MonaghanMonaghan and others, 2006; Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others, 2006) calibrated by very sparse in situ measurements for the interior of the continent. There are also indications that there are a non-negligible number of zero accumulation sites (so-called glazed areas) in the interior of the EAP that are often not taken into account by mass-balance estimates, and can change their value significantly (Reference Frezzotti, Gandolfi, La Marca and UrbiniFrezzotti and others, 2002; Reference Scambos, Haran, Frezzotti, Jezek, Long and FarnessScambos and others, 2008). It is clear that more accumulation data are required to study the spatial and temporal variability of SMB and to improve the spatial resolution and accuracy of large-scale accumulation studies.
The SMB is the aggregate of many processes such as precipitation from clouds and clear skies, the formation of hoar frost at the surface and within the snowpack, sublimation, melting and runoff, wind scouring and drift deposition (Reference EisenEisen and others, 2008). Snow accumulation can be derived using various methods (e.g. Reference EisenEisen and others, 2008). Snow-pit, firn- and ice-core studies provide valuableincrease in SMB observed by several studies is information about mean SMB for a certain point location (Reference Takahashi, Ageta, Fujii and WatanabeTakahashi and others, 1994; Reference Isaksson, Karlén, Gundestrup, Mayewski, Whitlow and TwicklerIsaksson and others, 1996; Anschütz and others, in press). These point measurements can be spatially extended by ground-penetrating radar (GPR). SMB is proportional to the reflector depth within the firn pack, as variations in vertical strain rates can be neglected in the top tens of metres of the ice sheet (Reference NyeNye, 1963). GPR has previously been successfully used to follow isochronous firn layers providing detailed information about the SMB variability across Antarctica (Reference FujitaFujita and others, 1999; Reference Richardson-NäslundRichardson-Näslund, 2004; Reference Rotschky, Eisen, Wilhelms, Nixdorf and OerterRotschky and others, 2004; Reference Spikes, Hamilton, Arcone, Kaspari and MayewskiSpikes and others, 2004; Reference Arcone, Spikes and HamiltonArcone and others, 2005a), although large regions of the EAP still remain uncovered.
We show SMB derived by GPR data collected during the first leg of the Norwegian–US Scientific Traverse of East Antarctica (http://traverse.npolar.no/) during the 2007/08 austral summer (NUS07). This joint project is part of the larger Trans-Antarctic Scientific Traverses Expeditions – Ice Divide of East Antarctica (TASTE-IDEA), and the International Partnerships in Ice Coring Sciences (IPICS) (Reference GoldmanGoldman, 2008).
Study Site
Our 860 km long profile traverses one of the least-known parts of East Antarctica (Fig. 1). The profile follows one of the main ice divides on the inland side, 100–200 m below its crest passing five firn cores at sites NUS07-2, –3, –4, –5 and –6 drilled during the traverse (Fig. 1). The study area extends from 76.1˚ to 81.4˚ S and 22.5˚ to 49.4˚ E, with increasing elevation from 3580 to 3680 m along the profile (Fig. 2a). The annual mean temperature is about –50˚C (Reference ComisoComiso, 2000), and the annual mean wind speed usually remains below 6 ms−1 (Reference Van Lipzig, Turner, Colwell and van den BroekeVan Lipzig and others, 2004) in the study area.

Fig. 1. Map of the study area. GPR sections 1–9 are shown as alternating light and dark-grey lines. Firn-core sites used as GPR tie points are represented as black triangles (DEP) and black squares (chemistry). Topography is shown as 100 m contour lines taken from the RADARSAT Antarctic Mapping Project (RAMP) digital elevation model (Jezek and others, 2002).

Fig. 2. (a) Elevations above World Geodetic System 1984 (WGS84) ellipsoid for the snow surface along the GPR profile (black curve) and the large-scale topography smoothed over 100 km (grey curve). (b) Slope in degrees for 10 km (black curve) and 100 km (grey curve) intervals of the surface elevation. (c) The depth to the Tambora deposition expressed as two-way travel time (TWT) of the GPR signal. (d) SMB since the Tambora eruption (SMBtam) calculated from Equation (3), and location and SMB estimates (crosses) of tie points.
Previous measurements of SMB have been made as point measurements from snow pits and firn cores in the vicinity of the ice divide and the near-plateau region (Reference Picciotto, Crozaz, De Breuck and CraryPicciotto and others, 1971; Reference Endo and FujiwaraEndo and Fujiwara, 1973; Reference Takahashi, Ageta, Fujii and WatanabeTakahashi and others, 1994). The Japanese Antarctic Research Expedition (JARE) South Pole traverse during 1968/69 crossed our profile at Plateau Station, and measured a SMB of 30 kg m–2 a−1 from a snow pit there (Reference Endo and FujiwaraEndo and Fujiwara, 1973). Reference Picciotto, Crozaz, De Breuck and CraryPicciotto and others (1971) measured a SMB of 27 kg m–2 a−1 at Plateau Station and 31 kgm–2 a−1 for the Pole of Inaccessibility for the period 1955–65. Reference Takahashi, Ageta, Fujii and WatanabeTakahashi and others (1994) measured SMB by gross β activity of 35 and 33 kg m–2 a−1 at two sites on the eastern flank of the ice divide at elevations of 3648 and 3761 m, respectively. Analysis of NUS07-3, –4 and –6 yields SMB values of <22 kg m–2 a−1 over the last 200 years in the study area (Anschütz and others, in press).
Methods
Ground-penetrating radar
We used a frequency-modulated continuous-wave (FM-CW) radar, which is an updated version of the radar described by Reference Hamran, Langley, Daniels and ChenHamran and Langley (2006). The system has a centre frequency of 5.3 GHz and sweeps over a bandwidth of 1 GHz. The unambiguous range in air is 67.4 m with 451 samples in the frequency domain. Its two quad-ridged horn antennae were separated by 10 cm and are treated as monostatic. They were suspended 65 cm above the snow surface extending from the side of a Berco TL6 tracked vehicle. Traces were collected every 0.2 s, which corresponds to a trace interval of approximately 0.4 m at an average driving speed of 2 m s–1 .
Data are recorded in the frequency domain and transferred to the time domain by fast Fourier transform (FFT) after Hamming window filtering. Each trace contains 1024 samples with a time increment of 0.219 ns. The effective time window (measured from the snow surface reflection) is 177 ns, corresponding to a penetration depth of about 20 m in dry polar firn (Fig. 3). The nominal vertical resolution in air is 15 cm and 11 cm in a firn pack with relative permittivity of 1.8, corresponding to a density of 400 kg m−3 (Reference Kovacs, Gow and MoreyKovacs and others, 1995). Signal-to-noise ratio was improved by stacking traces over 10 m intervals determined by the GPS coordinates, which, on average, corresponds to a 25-fold trace stack at a driving speed of 2ms–1 . We converted amplitude values to weighted backscatter in decibels (dB), as described by Reference LangleyLangley and others (2007), to compensate for spreading losses and increase display quality.

Fig. 3. GPR section 4 (left) with the conductivity–depth distribution from firn core NUS07-4 (right) drilled at the end of section 4. The conductivity curve shows a clear double peak at the depth of Tambora, and was used as a tie for the GPR data. The selected Tambora layer is indicated as a white dashed line. The depth axis to the right is calculated for a velocity of 0.23 m n s−1 . The distance axis is relative to the total profile length as in Figure 2.
Global positioning system
Global positioning system (GPS) elevation data were recorded together with the GPR data. A Garmin 60CSx hand-held unit with external antenna was directly connected to the GPR system, and recorded the latitude, longitude and GPS time every 2 s. In addition, a Trimble geodetic GPS collected positioning data including elevation every second. The Trimble raw data format was processed using Terratec’s TerraPos software, which allows high precision for kinematic GPS measurements. Decimetre precision in x and y and sub-metre precision in elevation is achieved by employing precise satellite orbits and satellite clock corrections coupled with state-of-the-art error modelling without the need for a reference station (Reference Zumberge, Heflin, Jefferson, Watkins and WebbZumberge and others, 1997). GPS elevations from the Trimble data were aligned with the hand-held units using the GPS time stamps. The offset between the external Garmin and Trimble antenna was 0.5 m.
The elevations above the World Geodetic System 1984 (WGS84) ellipsoid for the snow surface are shown as a black curve in Figure 2a. The elevation data were smoothed over 100 km to represent the large-scale topography. Slopes over 10 and 100 km were calculated to represent changes in the small- and large-scale topography, respectively (Fig. 2b).
Firn cores
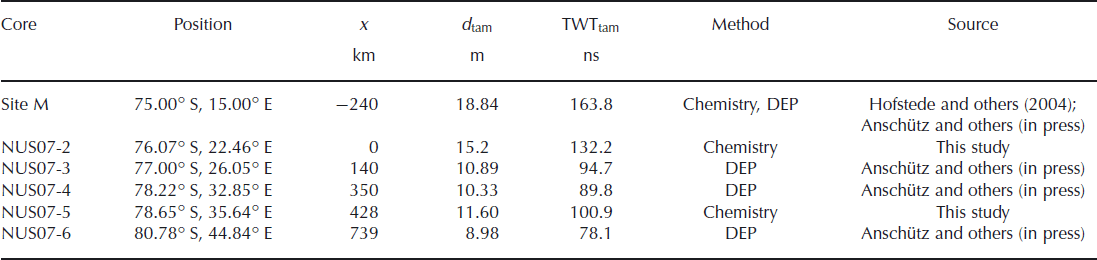
Five firn cores labelled NUS07-2 to –6 along the GPR profile served as calibration points for the GPR data (Fig. 1; Table 1). A broad range of chemical species and elements including total sulphur were measured in firn cores NUS07-2 and –5 using a continuous melter system coupled to two high-resolution inductively coupled plasma mass spectrometers (HR-ICP-MS) (Reference McConnell, Lamorey, Lambert and TaylorMcConnell and others, 2002; Reference McConnell and EdwardsMcConnell and Edwards, 2008). While the distinctive double peaks associated with fallout from the Tambora 1815/unknown 1809 depositions were readily identified in each core, we confirmed the dating using comparisons to similar measurements in cores from high-snow-accumulation regions. Tambora refers to a historically known eruption of the Tambora (Indonesia) volcano in 1815, which is assumed to have deposited in Antarctica in 1816 (Reference Traufetter, Oerter, Fischer, Weller and MillerTraufetter and others, 2004). In addition, cores NUS07-3, –4 and –6 were previously dated by dielectric profiling (DEP) (Anschütz and others, in press). The Tambora deposition was identified as a characteristic double peak in the normalized conductivity.
Table 1 Firn cores used in this study. The distance x represents the distance along the GPR profile. Negative values give the shortest distance to NUS07-2, the start of the profile. The depth and two-way travel time to the Tambora deposition are denoted d tam and TWTtam, respectively
Surface mass balance
Mean SMB along the GPR profile was derived by following widely used processing steps summarized by Reference EisenEisen and others (2008):
-
1. track isochrones;
-
2. make a time-depth conversion;
-
3. make an age estimation from available cores; and
-
4. calculate SMB from cumulative mass.
We began by making a depth-time conversion for the Tambora layer identified in the firn cores along the profile in order to tie in the GPR profile (Table 1). The DEP-derived permittivity values were converted to interval velocities which were then averaged to the known depth of Tambora for each of the DEP sites individually. The mean velocities to the depth of Tambora were 0.23 m ns–1 (NUS07-3), 0.24 m ns–1 (NUS07-4) and 0.23 mns–1 (NUS07-6). These velocities were used to calculate the two-way travel time (TWT) to Tambora at DEP core sites (Table 1). A microwave velocity of 0.23 m ns–1 was assumed when calculating the TWT to Tambora at core sites NUS07-2 and –5 and for the general depth-time conversion of the GPR data. Depth d of the selected layer in the GPR data could therefore be calculated as d = (TWT/2) × 0.23 m ns–1.
Figure 3 shows GPR section 4 as an example and the tie to Tambora identified in core NUS07-4. A reflector or a pattern of reflectors was followed in the GPR data, beginning from the calculated depth at the core site.
We need to estimate the mass accumulated over time in order to convert the selected depth to SMB. Measured bulk densities of the firn-core pieces (ρi) from all five cores were converted to mean bulk densities ![]() over depth using
over depth using

where i denotes the depth interval and l
int,
i is the length of the core piece at that interval. The density distribution with depth for all cores is similar (see Fig. 4), with a standard deviation of 30.4 kg m−3
![]() for all cores. We therefore assume from mean a laterally homogeneous firn pack represented by a second-order polynomial (Equation (2)) fitted to these densities in the depth range 0–26 m (Fig. 4):
for all cores. We therefore assume from mean a laterally homogeneous firn pack represented by a second-order polynomial (Equation (2)) fitted to these densities in the depth range 0–26 m (Fig. 4):
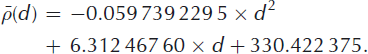
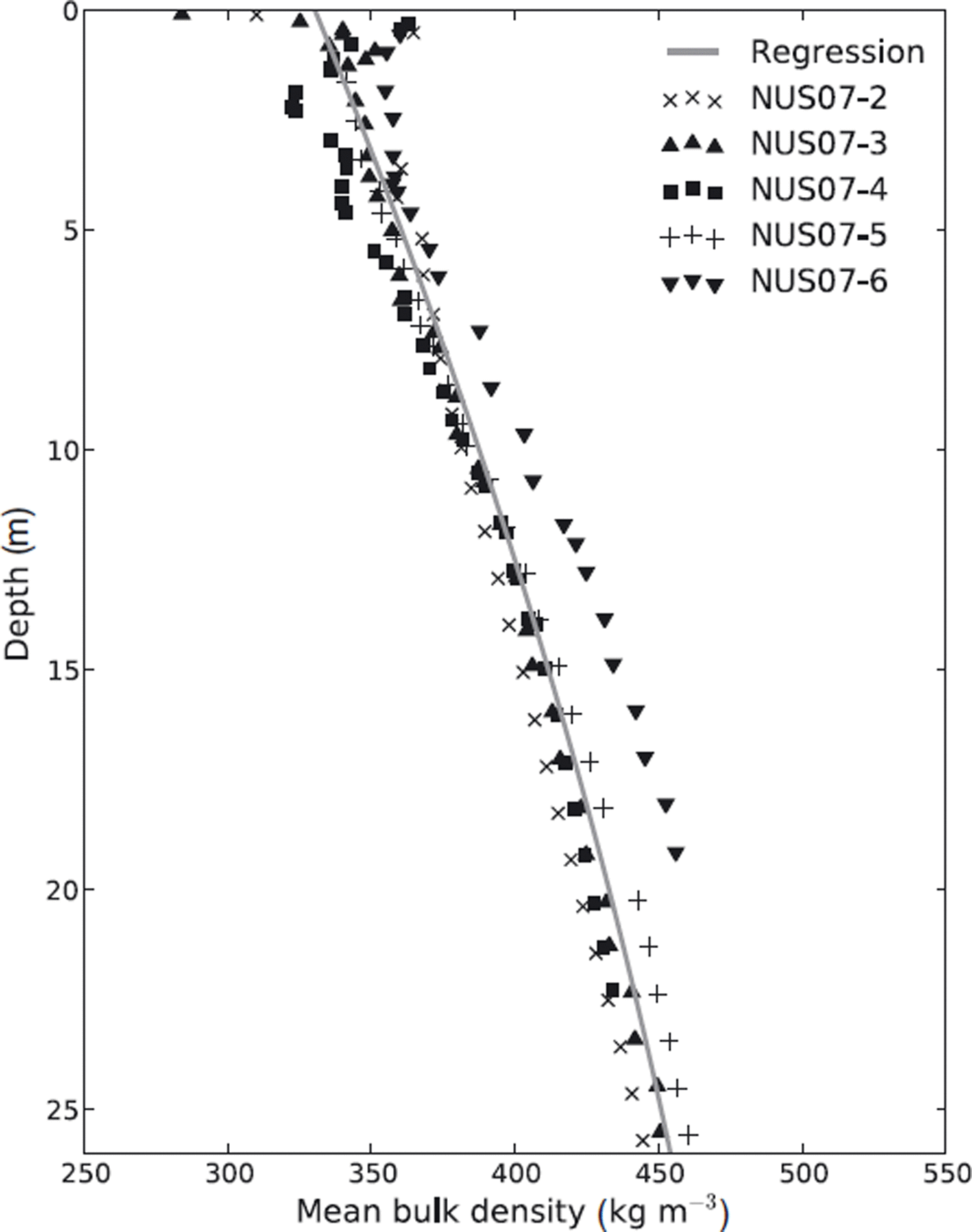
Fig. 4. Mean measured bulk density to depth values from firn cores NUS07–2, –3, –4, –5 and –6. The density–depth relation for the SMB calculation is a second-order polynomial (Equation (2)) fit to these values over the shown depth range (grey curve).
Correlation coefficients between measured and calculated densities are higher than 0.95. We calculate a mean SMB along the GPR transect over the last 200 years using Equation (3):
where SMBtam is the mean SMB since the Tambora eruption (kg m–2 2 a−1), d is the depth to the reflecting horizon calculated from the GPR TWT and a is the 191 year period between the Tambora deposition in 1816 and the collection of the firn cores and GPR data in 2007/08.
The GPR profile was divided into nine sections relative to data gaps. The sections were numbered (from north to south) from 1 to 9 as indicated in Figure 1 . Gaps in the GPR profile result from very poor data quality due to temperature sensitivity of the system, or glazed areas previously identified using satellite imagery (Reference Frezzotti, Gandolfi, La Marca and UrbiniFrezzotti and others, 2002; Reference Scambos, Haran, Frezzotti, Jezek, Long and FarnessScambos and others, 2008) around 123 and 270 km. It was not possible to follow the reflector over these discontinuities. However, five firn cores allowed us to tie in most GPR sections directly, and the gaps to GPR sections where no tie points were available were overcome by layer pattern comparison (as the example in Fig. 5 shows). All gaps along the GPR profile account for a total length of 133 km, with the longest gap (61 km) between sections 3 and 4.

Fig. 5. The last 10 km of GPR section 1 (left) and the first 10 km of section 2 (right), showing how it was possible to track Tambora over a gap in GPR data. Arrows indicate patterns of layers which are identified on both sides of the gap. The selected Tambora layer is indicated by a white dashed line. The distance axis is relative to the total profile length as in Figure 2.
The total length of the accumulation profile derived from the GPR data was limited by two factors. Firstly, the depth to the Tambora layer is almost 19 m at Site M (Reference HofstedeHofstede and others, 2004) north of the start of the profile (Fig. 1), which is close to the maximum penetration depth of our GPR. The signal-to-noise ratio no longer allows a clear identification of a single reflector at that depth. Secondly, the data quality decreases due to temperature sensitivity of the system at the end of section 9 south of NUS07–6, which prevented the Tambora layer being traced further south.
Results and Discussion
The Tambora layer identified in firn cores NUS07–2 to –6 was followed over the 860 km long GPR profile shown in Figure 1. Its depth, derived from the GPR TWT (Fig. 2c), varies between 4.8 and 17.1 m and decreases southwards. Applying Equation (3) gives SMBtam values between 9.1 and 37.7 kg m–2 a−1 along the profile, with a mean of 23.7 kg m–2 a–1 and a standard deviation of 4.7 kg m–2 a−1 over the period 1816–2007/08 (Fig. 2d). The profile shows that five firn cores used to calibrate the GPR data represent minima in SMB along the profile. The trend along our profile shows a decrease in SMBtam by 1.3 kg m–2 a−1 (100 km)−1 from north to south, correlating with increasing elevation and continentality as previously observed on the EAP (Reference Takahashi, Ageta, Fujii and WatanabeTakahashi and others, 1994; Anschütz and others, in press).
The characteristic of SMBtam variability changes along the profile. On the first 410 km and the last part from 660 km onwards, SMBtam has higher variability compared to the part in between. SMBtam varies between 38 and 16 kg m–2 a−1 over the first 410 km of the profile, where changes of up to 17 kg m–2 a−1 over a distance of 4 km occur. Elevation increases gently over this part of the profile, but small surface undulations of a few metres on a 10–20 km scale characterize the topography. Slopes over 10 km vary between 0.04˚ and –0.04˚ (Fig. 2b).
Reference King, Anderson, Vaughan, Mann, Mobbs and VosperKing and others (2004) demonstrated that very small topographic variations, particularly on small spatial scales, can have a disproportionately large impact on snow accumulation. Since precipitation will not vary on such a local scale, we conclude that changes in wind vectors due to these undulations are the reason for the high variability. The flat large-scale topography (grey curve in Fig. 2a and b) does not allow high katabatic wind speeds. Snow will therefore not travel far, but only be redistributed locally. Over the last 200 km of the profile, topographical features are similar to those on the first 410 km, and the variability in SMBtam is the same as for the first 410 km. The mean SMBtam of 20 kg m–2 a−1 is slightly lower due to the increased elevation and continentality.
Between 410 and 660 km, the elevation rises by 70 m, showing the steepest large-scale topographical change along the profile. Here SMBtam is fairly constant around 21 kg m–2 a−1, varying only by ±3 kg m–2 a−1 (14%). Changes in SMBtam over 5 km are at a maximum of 4 kg m–2 a−1 . The steeper large-scale slope allows higher wind speeds that move mass downslope. Local redistribution on the 10–20 km scale is therefore smaller and the SMBtam downslope will be higher, as can be observed in our profile (Fig. 2d).
No overall correlation between small-scale surface topography and SMBtam was found, although higher accumulation corresponds in some parts to troughs and gentle slopes (e.g. 395 km), and lower accumulation to bumps and steeper slope (e.g. 185 km), as also observed by Reference Takahashi, Ageta, Fujii and WatanabeTakahashi and others (1994) on the scale of 10–30 km on the EAP.
The arbitrary orientation of the profile relative to the largest slopes and/or largest wind vector may explain why no relationship between SMB and slope was found as for the West Antarctic ice sheet (Reference Arcone, Spikes and HamiltonArcone and others, 2005b). It should be noted, however, that the glazed areas at 123 and 270 km correspond to the largest small-scale slopes along the profile (Fig. 2b). Our data do not allow us to determine if the SMB in these areas is very small, zero or even negative.
Generally, our SMB values are lower than found in this region earlier. However, the previous direct SMB measurements cover more recent and much shorter time periods after 1950, from a few years up to a few decades, and their spatial representativeness remains unknown.
Our results show that the 200 year mean SMB along our profile is up to 70% lower than estimated in the continent-wide SMB studies for the last 50 years by Reference Arthern, Winebrenner and VaughanArthern and others (2006), Reference MonaghanMonaghan and others (2006) and Reference Van de Berg, van den Broeke, Reijmer and van MeijgaardVan de Berg and others (2006). The regional trend shows a decrease from the start of the profile to about 450 km, however, followed by a fairly constant SMB in all studies. Part of the discrepancy can be explained by an accumulation and density minimum in the vicinity of the crest of the ice divide where our profile is located (Reference Endo and FujiwaraEndo and Fujiwara, 1973). The grid resolution of the continent-wide compilations is equal to or larger than 55 km. The map values will therefore represent the average over 3 × 103 to 10 × 103 km2. As there are no in situ SMB data perpendicular to our profile, it is impossible to estimate how well our GPR line represents the areal average. On the other hand, the large-scale maps are guided by previously very sparse in situ measurements in this area, and the spatial density of these measurements will affect their accuracy.
It is more likely, however, that a recent increase of SMB observed on the EAP (e.g. Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; Reference ZwallyZwally and others, 2005) can explain the differences between previous SMB estimates and our data averaged over the last 200 years. The increase is also indicated by firn- and ice-core studies at both ends of our GPR profile (Reference Mosley-Thompson, Paskievitch, Gow and ThompsonMosley-Thompson and others, 1999; Reference HofstedeHofstede and others, 2004) and in several other places on the EAP during the last 50 years (Reference Oerter, Graf, Wilhelms, Minikin and MillerOerter and others, 1999; Reference StenniStenni and others, 2002; Reference FrezzottiFrezzotti and others, 2005). For example, Reference Mosley-Thompson, Paskievitch, Gow and ThompsonMosley-Thompson and others (1999) report an SMB increase of 30% at the South Pole since the 1960s. The large-scale studies have calibrated their SMB maps using these data, which may also partly explain the large differences between our 200 year mean SMB and their SMB values for the last 50 years.
Error estimates
Uncertainties in the GPR-derived layer depth and conversion to SMBtam originate from four main sources:
-
1. unknown density distribution between firn cores;
-
2. layer picking;
-
3. digitization; and
-
4. uncertainty in dating.
Error estimates in SMBtam relate to the time period 1816–2007/08. The errors increase with depth due to the compaction of the firn pack. The following maximum errors are therefore always given for the deepest layer found at 17.1 m.
-
1. The largest error is assumed to result from firn density variations over depth and between the core sites. Maximum deviation from the mean density of all cores at a certain depth interval is 30.4 kg m–3 . This was assumed to be the standard error in density since only one measurement was taken at each location. The largest error in SMBtam due to the maximum standard error in density (δρ) is calculated by differentiating Equation (3) with respect to ρ and multiplying by 30.4 kg m–3, yielding 2.7 kg m–2 a–1.
-
2. The high frequency of the GPR means that interfaces of different dielectric properties appear rough, which leads to increased diffuse scattering, rather than specular reflections from interfaces of different dielectric properties. Horizons in the GPR profile therefore appear very broad, and selecting a single layer is difficult. We estimate the uncertainty to be ±2 ns. This corresponds to an uncertainty in depth of 0.46 m, assuming a microwave velocity of 0.23 m ns–1 . The maximum error in SMBtam due to the uncertainty in layer selection (δ p) is calculated by differentiating Equation (3) with respect to d (taking into account that ρ is also a function of d) and multiplying it by 0.46 m, yielding 1.2 kg m–2 a–1 .
-
3. Inaccurate isochrone depths also result from the digitization of the recorded radar signal. The sampling interval in time is 0.219 ns, which corresponds to an uncertainty in depth of about 0.025 m. Calculating the error in SMBtam from digitization (δ d ) as in (2) gives a negligible value of 0.065 kgm–2a–1.
-
4. GPR reflections do not represent annual firn layers since the annual-layer thickness is less than what the GPR could resolve. For example, at site NUS07–3, the Tambora deposition was identified at 10.9 m depth. That would mean an average annual-layer thickness of 0.06 m, where compression will lead to tighter layers with depth. Having a nominal resolution of 0.11 m in a firn pack of 400 kg m–3 density, our GPR detects an integrated signal over two annual firn layers at best. Broadening introduced by the Hamming window filter and diffuse scattering from interfaces will result in even lower resolution in practice. The absolute errors for SMBtam in cores NUS07–3, –4 and –6 lie in the range 0.3–0.5 kg m–2 a–1. Anschutz and others (in press) give an error of 2.3% in dating the firn cores for the period 1816–2007/08. We therefore assume a dating error of 4.3 years. Equation (3) is differentiated with respect to a and multiplied by 4.3 years, giving a maximum error in SMBtam with regard to age (δ a) of 1.1 kgm–2 a–1.
The combined maximum error from sources (1)-(4) is calculated as follows:
The estimated maximum cumulative error found for the deepest layers at 17.1 m is 3.1 kgm–2a–1 ; the error decreases for shallower parts. It should also be noted that very low- or zero-accumulation sites (glazed areas) were excluded from the study since it was not possible to trace layers over them. The mean SMBtam along the profile may therefore be slightly lowerthan the value of 23.7 kg m–2 a–1.
Conclusions
We show a continuous SMB profile in an area of the EAP not previously covered, where sparse in situ measurements were available. We used a high-frequency FMCW GPR to interpolate SMB measured by DEP and sulphur concentration from firn cores. The mean SMB over the last 200 years along our 860 km long profile is 23.7 kgm–2 a–1, with an assumed maximum error of 3.1 kgm–2a–1 . Increasing elevation and continentality lead to a decrease in SMB by about 1.3 kgm–2a–1 (100km)–1 southwards along the profile. SMB ranges from 9.1 to 37.7 kgm–2a–1 along the whole profile.
The 200 year SMB along our profile is significantly lower than most of the SMB estimates over shorter time periods in this region. It can be partly explained by a SMB minimum in the vicinity of the ice divide. However, it is more likely that a recent increase in SMB observed in several studies (Reference Mosley-Thompson, Paskievitch, Gow and ThompsonMosley-Thompson and others, 1999; Reference Oerter, Graf, Wilhelms, Minikin and MillerOerter and others, 1999; Reference StenniStenni and others, 2002; Reference HofstedeHofstede and others, 2004; Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005; Reference FrezzottiFrezzotti and others, 2005; Reference ZwallyZwally and others, 2005) is largely responsible for the observed discrepancy.
This is the first time that small-scale variability of SMB has been defined for this region. SMB has a standard deviation of 4.7 kgm–2a–1, corresponding to an average variation around the mean of about 20%. The variations are connected to the surface topography with undulations of 1–20 km wavelength over the flat parts. Variation can be as high as 17kgm–2a–1 over 4km, but is generally lower than 10 kg m–2 a−1 over that distance. On the slope from 410 to 660 km, the variability decreases. This is assumed to be due to a large-scale slope allowing higher wind speeds that are capable of moving snow to distant areas, instead of redistributing it locally.
The results show that the SMB point measurements by Anschütz and others (in press) used as tie points for our GPR data were located on the low-accumulation sites along the profile, giving a smaller SMB than the profile mean by up to 33%.
Acknowledgements
The paper is a contribution to the Norwegian–US Antarctic International Polar Year traverse with funding from the Norwegian Research Council, Norwegian Polar Institute (NPI) and National Science Foundation. We thank G. Melland and S. Trondstad from NPI for processing the GPS data. Special thanks go to the members of the traverse team for making this work possible. We thank K. Matsuoka and two anonymous reviewers for their valuable input and comments, and also B. Kulessa for his efforts as scientific editor.








