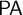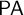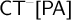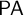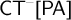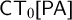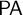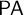1 Introduction
Intuitively speaking, a binary relation S on a model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
(Peano arithmetic) is said to be a satisfaction class if S ‘behaves like’ the usual Tarskian satisfaction relation Sat
$\mathsf {PA}$
(Peano arithmetic) is said to be a satisfaction class if S ‘behaves like’ the usual Tarskian satisfaction relation Sat
![]() $_{\mathcal {M}}$
on
$_{\mathcal {M}}$
on
![]() $\mathcal {M}$
, but in sharp contrast to the usual Tarskian satisfaction relation on
$\mathcal {M}$
, but in sharp contrast to the usual Tarskian satisfaction relation on
![]() $\mathcal {M}$
, if
$\mathcal {M}$
, if
![]() $\mathcal {M}$
is nonstandard, then S is required to decide the ‘truth’ of at least some nonstandard ‘formulae’ of
$\mathcal {M}$
is nonstandard, then S is required to decide the ‘truth’ of at least some nonstandard ‘formulae’ of
![]() $\mathcal {M}$
. This notion was brought to prominence in the 1970s and 1980s, thanks to the fine efforts of a number of logicians, including (in alphabetical order) Barwise, Kotlarski, Krajewski, Lachlan, Murawski, Ratajczyk, Kossak, Schlipf, Schmerl, Smith, and Wilmers. A notable precursor is Robinson whose landmark 1963 paper [Reference Robinson28] probed the subtle obstacles in the development of a coherent Tarski-style semantic framework for nonstandard formulae.
$\mathcal {M}$
. This notion was brought to prominence in the 1970s and 1980s, thanks to the fine efforts of a number of logicians, including (in alphabetical order) Barwise, Kotlarski, Krajewski, Lachlan, Murawski, Ratajczyk, Kossak, Schlipf, Schmerl, Smith, and Wilmers. A notable precursor is Robinson whose landmark 1963 paper [Reference Robinson28] probed the subtle obstacles in the development of a coherent Tarski-style semantic framework for nonstandard formulae.
The flurry of activity in the 1970s and 1980s revealed two distinct ‘flavors’ of satisfaction classes: full satisfaction classes and inductive satisfaction classes. A full satisfaction class on a model
![]() $\mathcal {M}$
of arithmetic is required to decide the ‘truth’ of every arithmetic ‘formula’ in
$\mathcal {M}$
of arithmetic is required to decide the ‘truth’ of every arithmetic ‘formula’ in
![]() $\mathcal {M}$
(including the nonstandard ones, if
$\mathcal {M}$
(including the nonstandard ones, if
![]() $\mathcal {M}$
is nonstandard) while obeying the usual Tarskian recursive clauses that relate the truth of a formula to the truth of its components. In contrast, an inductive satisfaction class S on a model
$\mathcal {M}$
is nonstandard) while obeying the usual Tarskian recursive clauses that relate the truth of a formula to the truth of its components. In contrast, an inductive satisfaction class S on a model
![]() $\mathcal {M}$
is required to satisfy the following two properties: (1) S obeys Tarski’s recursive clauses for (at least) all standard arithmetical formulae; and (2) the expansion
$\mathcal {M}$
is required to satisfy the following two properties: (1) S obeys Tarski’s recursive clauses for (at least) all standard arithmetical formulae; and (2) the expansion
![]() $(\mathcal {M},S)$
of
$(\mathcal {M},S)$
of
![]() $\mathcal {M}$
satisfies the scheme of induction in the language obtained by augmenting the arithmetical language with a new predicate symbol representing S. Kaye’s textbook [Reference Kaye18] covers the basics of both types of satisfaction classes. It is known that if
$\mathcal {M}$
satisfies the scheme of induction in the language obtained by augmenting the arithmetical language with a new predicate symbol representing S. Kaye’s textbook [Reference Kaye18] covers the basics of both types of satisfaction classes. It is known that if
![]() $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
![]() $\mathsf {PA}$
that carries a satisfaction class that is either full or inductive, then
$\mathsf {PA}$
that carries a satisfaction class that is either full or inductive, then
![]() $\mathcal {M}$
is recursively saturated. For countable models, the converse also holds, i.e., every countable recursively saturated model
$\mathcal {M}$
is recursively saturated. For countable models, the converse also holds, i.e., every countable recursively saturated model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
carries a full satisfaction class
$\mathsf {PA}$
carries a full satisfaction class
![]() $S_{1} $
, as well as an inductive satisfaction class
$S_{1} $
, as well as an inductive satisfaction class
![]() $S_{2}$
; but the existence of a satisfaction class on
$S_{2}$
; but the existence of a satisfaction class on
![]() $\mathcal {M}$
that is both full and inductive implies that the formal consistency of
$\mathcal {M}$
that is both full and inductive implies that the formal consistency of
![]() $\mathsf {PA}$
holds in
$\mathsf {PA}$
holds in
![]() $\mathcal {M}$
(and much more) and thus by Gödel’s second incompleteness theorem not every countable recursively saturated model of
$\mathcal {M}$
(and much more) and thus by Gödel’s second incompleteness theorem not every countable recursively saturated model of
![]() $\mathsf {PA}$
carries a satisfaction class that is both full and inductive. The monograph [Reference Kossak and Schmerl20] by Kossak and Schmerl includes a more advanced treatment of inductive satisfaction classes, but it does not contain material on full satisfaction classes. This can be explained by the fact that inductive satisfaction classes have proved to be indispensable in the model theory of arithmetic, but full satisfaction classes have not played a comparable role. To the best of the author’s knowledge, the only known prominent application of full satisfaction classes over nonstandard models to the model theory of
$\mathsf {PA}$
carries a satisfaction class that is both full and inductive. The monograph [Reference Kossak and Schmerl20] by Kossak and Schmerl includes a more advanced treatment of inductive satisfaction classes, but it does not contain material on full satisfaction classes. This can be explained by the fact that inductive satisfaction classes have proved to be indispensable in the model theory of arithmetic, but full satisfaction classes have not played a comparable role. To the best of the author’s knowledge, the only known prominent application of full satisfaction classes over nonstandard models to the model theory of
![]() $\mathsf {PA}$
is due to Smith [Reference Smith29], who employed them to calibrate the logical complexity of the notions of recursive saturation and resplendence in the context of models of
$\mathsf {PA}$
is due to Smith [Reference Smith29], who employed them to calibrate the logical complexity of the notions of recursive saturation and resplendence in the context of models of
![]() $\mathsf {PA}$
(as respectively
$\mathsf {PA}$
(as respectively
![]() $\Sigma _{1}^{1}$
and
$\Sigma _{1}^{1}$
and
![]() $\Delta _{2}^{1})$
.
$\Delta _{2}^{1})$
.
However, full satisfaction classes have captured the imagination of philosophical logicians since they are intimately linked with the grand topic of axiomatic theories of truth, and in particular they shed light on the vibrant debate concerning the deflationist conception of truth, especially in connection with the so-called conservativeness argument. This philosophical interest has galvanized the subject of satisfaction classes and has led to a new wave of technical advances and questions over the past decade. The monographs by Halbach [Reference Halbach16] and Cieśliński [Reference Cieśliński4] provide an overview of the philosophical motivations as well as minutiae of the technical preliminaries.
There is also a notable methodological asymmetry between inductive satisfaction classes and full satisfaction classes: given an arbitrary model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
it is routine to construct an elementary extension of
$\mathsf {PA}$
it is routine to construct an elementary extension of
![]() $\mathcal {M}$
that carries an inductive satisfaction class with the help of the standard tools of the trade (the ingredients are definable partial satisfaction classes, and compactness). However, an air of mystery has surrounded full satisfaction classes ever since the original tour de force Kotlarski–Krajewski–Lachlan construction [Reference Kotlarski, Krajewski and Lachlan23] that was based on the ad hoc technology of
$\mathcal {M}$
that carries an inductive satisfaction class with the help of the standard tools of the trade (the ingredients are definable partial satisfaction classes, and compactness). However, an air of mystery has surrounded full satisfaction classes ever since the original tour de force Kotlarski–Krajewski–Lachlan construction [Reference Kotlarski, Krajewski and Lachlan23] that was based on the ad hoc technology of
![]() $\mathcal {M}$
-logic (an infinitary logical system based on a nonstandard model
$\mathcal {M}$
-logic (an infinitary logical system based on a nonstandard model
![]() $\mathcal {M}$
). The Kotlarski–Krajewski–Lachlan construction implies that the axiomatic theory of truth commonly known as
$\mathcal {M}$
). The Kotlarski–Krajewski–Lachlan construction implies that the axiomatic theory of truth commonly known as
![]() $\mathsf {CT}^{-}[\mathsf {PA}]= \mathsf {CT}^{-}+\mathsf {PA}$
is conservative over
$\mathsf {CT}^{-}[\mathsf {PA}]= \mathsf {CT}^{-}+\mathsf {PA}$
is conservative over
![]() $\mathsf {PA}$
, i.e., if an arithmetical sentence
$\mathsf {PA}$
, i.e., if an arithmetical sentence
![]() $\varphi $
is provable in
$\varphi $
is provable in
![]() $\mathsf {CT}^{-}[\mathsf {PA}] $
, then
$\mathsf {CT}^{-}[\mathsf {PA}] $
, then
![]() $\varphi $
is already provable in
$\varphi $
is already provable in
![]() $\mathsf {PA}$
. Here
$\mathsf {PA}$
. Here
![]() $\mathsf {CT}^{-}$
is a finitely axiomatized theory formulated in the language of arithmetic augmented with a truth predicate
$\mathsf {CT}^{-}$
is a finitely axiomatized theory formulated in the language of arithmetic augmented with a truth predicate
![]() $\mathsf {T}$
(the minus superscript indicates that no instances of the induction scheme mentioning
$\mathsf {T}$
(the minus superscript indicates that no instances of the induction scheme mentioning
![]() $\mathsf {T}$
have been added to the theory). Decades later, a new versatile model-theoretic method of constructing full satisfaction classes was presented by Visser and the author [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12]; this new method has been refined in various directions, e.g., as in Cieśliński’s monograph [Reference Cieśliński4], and in the joint work of Łełyk and Wcisło with the author [Reference Enayat, Łełyk and Wcisło9]. The conservativity of
$\mathsf {T}$
have been added to the theory). Decades later, a new versatile model-theoretic method of constructing full satisfaction classes was presented by Visser and the author [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12]; this new method has been refined in various directions, e.g., as in Cieśliński’s monograph [Reference Cieśliński4], and in the joint work of Łełyk and Wcisło with the author [Reference Enayat, Łełyk and Wcisło9]. The conservativity of
![]() $\mathsf {CT}^{-}[\mathsf {PA}]$
over
$\mathsf {CT}^{-}[\mathsf {PA}]$
over
![]() $\mathsf {PA}$
has also been established by proof theoretic methods by Leigh [Reference Leigh25], and more recently by Cieśliński [Reference Cieśliński5].
$\mathsf {PA}$
has also been established by proof theoretic methods by Leigh [Reference Leigh25], and more recently by Cieśliński [Reference Cieśliński5].
The conservativity of
![]() $\mathsf {CT}^{-}[\mathsf {PA}]$
over
$\mathsf {CT}^{-}[\mathsf {PA}]$
over
![]() $\mathsf {PA}$
together with Gödel’s second incompleteness theorem implies that the sentence
$\mathsf {PA}$
together with Gödel’s second incompleteness theorem implies that the sentence
![]() $\mathrm {Con(}\mathsf {PA}\mathrm {)}$
expressing the consistency of
$\mathrm {Con(}\mathsf {PA}\mathrm {)}$
expressing the consistency of
![]() $\mathsf {PA}$
is not provable in
$\mathsf {PA}$
is not provable in
![]() $\mathsf {CT}^{-}[\mathsf {PA}]\mathsf {.}$
However, it is well-known that the formal consistency of
$\mathsf {CT}^{-}[\mathsf {PA}]\mathsf {.}$
However, it is well-known that the formal consistency of
![]() $\mathsf {PA}$
(and much more) is readily provable in the stronger theory
$\mathsf {PA}$
(and much more) is readily provable in the stronger theory
![]() $\mathsf {CT}[\mathsf {PA}]$
, which is the result of strengthening
$\mathsf {CT}[\mathsf {PA}]$
, which is the result of strengthening
![]() $\mathsf {CT}^{-}[\mathsf {PA}]$
with the scheme of induction over natural numbers for all formulae in extended language (i.e., the language obtained by extending the language of
$\mathsf {CT}^{-}[\mathsf {PA}]$
with the scheme of induction over natural numbers for all formulae in extended language (i.e., the language obtained by extending the language of
![]() $\mathsf {PA}$
with a truth predicate). Indeed, it is straightforward to demonstrate the consistency of
$\mathsf {PA}$
with a truth predicate). Indeed, it is straightforward to demonstrate the consistency of
![]() $\mathsf {PA}$
within the subsystem
$\mathsf {PA}$
within the subsystem
![]() $\mathsf {CT}_{1}[\mathsf {PA}]$
of
$\mathsf {CT}_{1}[\mathsf {PA}]$
of
![]() $\mathsf {CT}[\mathsf {PA}]$
, where
$\mathsf {CT}[\mathsf {PA}]$
, where
![]() $\mathsf {CT}_{n}[\mathsf {PA}]$
is the subtheory of
$\mathsf {CT}_{n}[\mathsf {PA}]$
is the subtheory of
![]() $\mathsf {CT}\mathrm {[}\mathsf {PA}\mathrm {]} $
with the scheme of induction over natural numbers limited to formulae in the extended language that are at most of complexity
$\mathsf {CT}\mathrm {[}\mathsf {PA}\mathrm {]} $
with the scheme of induction over natural numbers limited to formulae in the extended language that are at most of complexity
![]() $\Sigma _{n}$
[Reference Wcisło and Łełyk32, theorem 2.8]. However, the case of
$\Sigma _{n}$
[Reference Wcisło and Łełyk32, theorem 2.8]. However, the case of
![]() $\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
has taken considerable effort to analyze. Kotlarski [Reference Kotlarski22] established that
$\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
has taken considerable effort to analyze. Kotlarski [Reference Kotlarski22] established that
![]() $\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
is a subtheory of
$\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
is a subtheory of
![]() $\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {Ref(PA)}$
, where
$\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {Ref(PA)}$
, where
![]() $+\mathsf {Ref(PA)}$
is the sentence in the extended language stating that “every first-order consequence of
$+\mathsf {Ref(PA)}$
is the sentence in the extended language stating that “every first-order consequence of
![]() $\mathsf {PA}$
is true”. Łełyk [Reference Łełyk26] demonstrated that the converse also holds, which immediately implies that
$\mathsf {PA}$
is true”. Łełyk [Reference Łełyk26] demonstrated that the converse also holds, which immediately implies that
![]() $\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
is not conservative over
$\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
is not conservative over
![]() $\mathsf {PA}$
since the formal consistency of
$\mathsf {PA}$
since the formal consistency of
![]() $\mathsf {PA}$
is readily provable in
$\mathsf {PA}$
is readily provable in
![]() $\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {Ref}\mathrm {(}\mathsf {PA}\mathrm {)}\mathsf {.}$
Footnote
1
Kotlarski’s aforementioned theorem was refined by Cieśliński [Reference Cieśliński3] who proved that
$\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {Ref}\mathrm {(}\mathsf {PA}\mathrm {)}\mathsf {.}$
Footnote
1
Kotlarski’s aforementioned theorem was refined by Cieśliński [Reference Cieśliński3] who proved that
![]() $\mathsf {CT}^{-}[\mathsf {PA}]\mathsf {+}$
“
$\mathsf {CT}^{-}[\mathsf {PA}]\mathsf {+}$
“
![]() $\mathsf {T}$
is closed under propositional proofs” and
$\mathsf {T}$
is closed under propositional proofs” and
![]() $\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {Ref(PA)}$
axiomatize the same theory. Later Cieśliński’s result was refined by Pakhomov and the author [Reference Enayat and Pakhomov10] by demonstrating that
$\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {Ref(PA)}$
axiomatize the same theory. Later Cieśliński’s result was refined by Pakhomov and the author [Reference Enayat and Pakhomov10] by demonstrating that
![]() $\mathsf {CT}^{-}\mathrm {[\mathrm {I}\mathsf {\Delta }_{0}}+\mathsf {Exp}\mathrm {]}+\mathsf {DC}$
and
$\mathsf {CT}^{-}\mathrm {[\mathrm {I}\mathsf {\Delta }_{0}}+\mathsf {Exp}\mathrm {]}+\mathsf {DC}$
and
![]() $\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
axiomatize the same first-order theory, where
$\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
axiomatize the same first-order theory, where
![]() $\mathsf {DC}$
(disjunctive correctness) is the axiom that states that a disjunction is true iff one of its disjuncts is true. This result in particular shows that
$\mathsf {DC}$
(disjunctive correctness) is the axiom that states that a disjunction is true iff one of its disjuncts is true. This result in particular shows that
![]() $\mathsf {CT}^{-}\mathrm {[I}\mathsf {\Delta }_{0}+\mathsf {Exp}\mathrm {]}+\mathsf {DC}$
and
$\mathsf {CT}^{-}\mathrm {[I}\mathsf {\Delta }_{0}+\mathsf {Exp}\mathrm {]}+\mathsf {DC}$
and
![]() $\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {DC}$
axiomatize the same theory.
$\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {DC}$
axiomatize the same theory.
The recent work of Cieśliński, Łełyk, and Wcisło [Reference Cieśliński, Łełyk and Wcisło7] refined the aforementioned work of Pakhomov and the author by showing that
![]() $\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {DC}_{\mathrm {out}}$
is an axiomatization of
$\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {DC}_{\mathrm {out}}$
is an axiomatization of
![]() $\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
, where
$\mathsf {CT}_{0}\mathrm {[}\mathsf {PA}\mathrm {]}$
, where
![]() $\mathsf {DC}_{\mathrm {out}}$
is the ‘half’ of
$\mathsf {DC}_{\mathrm {out}}$
is the ‘half’ of
![]() $\mathrm {DC}$
that says every true disjunction has a true disjunct. In summary, the arithmetical strength of
$\mathrm {DC}$
that says every true disjunction has a true disjunct. In summary, the arithmetical strength of
![]() $\mathsf {CT}^{-}[\mathsf {PA}]$
augmented with seemingly innocuous axioms such as “truth is closed propositional proofs” or even “If a disjunction is true, then it has a true disjunct” goes beyond
$\mathsf {CT}^{-}[\mathsf {PA}]$
augmented with seemingly innocuous axioms such as “truth is closed propositional proofs” or even “If a disjunction is true, then it has a true disjunct” goes beyond
![]() $\mathsf {PA} $
.Footnote
2
The philosophical ramifications of the nonconservativity of
$\mathsf {PA} $
.Footnote
2
The philosophical ramifications of the nonconservativity of
![]() $\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {DC}$
has been explored by Fujimoto [Reference Fujimoto14], whose work shows that the nonconservativity of
$\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {DC}$
has been explored by Fujimoto [Reference Fujimoto14], whose work shows that the nonconservativity of
![]() $\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {DC} $
over
$\mathsf {CT}^{-}[\mathsf {PA}]+\mathsf {DC} $
over
![]() $\mathsf {PA}$
introduces a new twist to the conservativity argument in relation to the deflationist conception of truth.
$\mathsf {PA}$
introduces a new twist to the conservativity argument in relation to the deflationist conception of truth.
In this paper we present two new constructions of extensional satisfaction classes over models of
![]() $\mathsf {PA}$
, such satisfaction classes are inter-definable with their less famous siblings known as ‘truth classes’ (see Proposition 2.14). The specific features of the truth classes constructed in this paper can be summarized as follows.
$\mathsf {PA}$
, such satisfaction classes are inter-definable with their less famous siblings known as ‘truth classes’ (see Proposition 2.14). The specific features of the truth classes constructed in this paper can be summarized as follows.
The first construction (at work in the proofs of Theorem 3.3 and 3.4) employs basic results in the model theory of
![]() $\mathsf {PA}$
to show that given a countable recursively saturated model
$\mathsf {PA}$
to show that given a countable recursively saturated model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
, there are arbitrarily large cuts I in
$\mathsf {PA}$
, there are arbitrarily large cuts I in
![]() $\mathcal {M}$
with the property that there is a truth class T on
$\mathcal {M}$
with the property that there is a truth class T on
![]() $\mathcal {M}$
that is compositional for the collection of sentences that have at most i occurrences of closed terms for some i in I, and it satisfies disjunctive correctness for such sentences. Note that the truth classes constructed in Theorem 3.3 and 3.4 are not full, and as indicated in Question 3.7 it is not clear whether they can be extended to full satisfaction classes.
$\mathcal {M}$
that is compositional for the collection of sentences that have at most i occurrences of closed terms for some i in I, and it satisfies disjunctive correctness for such sentences. Note that the truth classes constructed in Theorem 3.3 and 3.4 are not full, and as indicated in Question 3.7 it is not clear whether they can be extended to full satisfaction classes.
The second construction (at work in the proof of Theorem 4.5) is far more involved than the first one since it uses a vast array of technical results to elaborate the construction of full truth classes in the joint paper [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12] of Visser and the author to show that given a countable recursively saturated model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
, there are arbitrarily large cuts I in
$\mathsf {PA}$
, there are arbitrarily large cuts I in
![]() $\mathcal {M}$
such that there is a full truth class T on
$\mathcal {M}$
such that there is a full truth class T on
![]() $\mathcal {M}$
that is disjunctively correct for disjunctions whose number of disjuncts is in
$\mathcal {M}$
that is disjunctively correct for disjunctions whose number of disjuncts is in
![]() $I.$
This shows that in the aforementioned result of Pakhomov and the author the assumption of disjunctive correctness cannot be replaced with any of its approximations. As indicated in Remark 4.7, Theorem 4.5 implies the conservativity of an axiomatic theory of truth over
$I.$
This shows that in the aforementioned result of Pakhomov and the author the assumption of disjunctive correctness cannot be replaced with any of its approximations. As indicated in Remark 4.7, Theorem 4.5 implies the conservativity of an axiomatic theory of truth over
![]() $\mathsf {PA}$
that uses a parameterized family of truth predicate
$\mathsf {PA}$
that uses a parameterized family of truth predicate
![]() $\mathsf {T}_{x}$
(where x varies over the domain of discourse) such that
$\mathsf {T}_{x}$
(where x varies over the domain of discourse) such that
![]() $\mathsf {T}_{x}$
satisfies
$\mathsf {T}_{x}$
satisfies
![]() $\mathsf {CT}^{-}$
and
$\mathsf {CT}^{-}$
and
![]() $\mathsf {T}_{x}$
is disjunctively correct for disjunctions whose number of disjuncts is at most x.
$\mathsf {T}_{x}$
is disjunctively correct for disjunctions whose number of disjuncts is at most x.
We should draw attention to the recent joint work [Reference Abdul-Quader and Łełyk1] of Athar Abdul-Quader and Mateusz Łełyk who also explore approximations of disjunctive correctness, but their results are complementary to those obtained in this paper since their focus is on a different set of problems (see also Remark 4.6).
The main idea of the first construction was discovered by the author in 2009; the same idea was earlier hit upon in 1980 by Smoryński in a letter to Jim Schmerl; for more detail see Section 6 of [Reference Enayat8] (which is a preliminary version of the present paper). The protoform of the second construction appeared in a privately circulated manuscript [Reference Enayat and Visser11] written in collaboration with Albert Visser, and is included here with his kind permission.
2 Preliminaries
In this section we present the relevant notations, conventions, definitions, and results that are needed in the subsequent sections.
2.1 Models of arithmetic
Definition 2.1. The language of Peano Arithmetic,
![]() $\mathcal {L}_{\mathsf {PA}}$
, is
$\mathcal {L}_{\mathsf {PA}}$
, is
![]() $\{+,\cdot ,\mathrm {S},0\}.$
We use the convention of writing M,
$\{+,\cdot ,\mathrm {S},0\}.$
We use the convention of writing M,
![]() $M_{0}, N$
, etc. to (respectively) denote the universes of discourse of structures
$M_{0}, N$
, etc. to (respectively) denote the universes of discourse of structures
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {M}_{0}, \mathcal {N},$
etc. In what follows
$\mathcal {M}_{0}, \mathcal {N},$
etc. In what follows
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are models of
$\mathcal {N}$
are models of
![]() $\mathsf {PA}$
.
$\mathsf {PA}$
.
-
(a)
 $\mathsf {PA}$
(Peano arithmetic) is the result of adding the scheme of induction for all
$\mathsf {PA}$
(Peano arithmetic) is the result of adding the scheme of induction for all
 $\mathcal {L}_{\mathsf {PA}}$
-formulae to the finitely axiomatizable theory known as (Robinson’s)
$\mathcal {L}_{\mathsf {PA}}$
-formulae to the finitely axiomatizable theory known as (Robinson’s)
 $\mathrm {Q}$
.
$\mathrm {Q}$
. -
(b)
 $\Sigma _{0}=\Pi _{0}=\Delta _{0}$
= the collection of
$\Sigma _{0}=\Pi _{0}=\Delta _{0}$
= the collection of
 $\mathcal {L}_{\mathsf {PA}}$
-formulae all of whose quantifiers are bounded by
$\mathcal {L}_{\mathsf {PA}}$
-formulae all of whose quantifiers are bounded by
 $\mathcal {L}$
-terms (i.e., they are of the form
$\mathcal {L}$
-terms (i.e., they are of the form
 $\exists x\leq t,$
or of the form
$\exists x\leq t,$
or of the form
 $\forall x\leq t,$
where t is an
$\forall x\leq t,$
where t is an
 $\mathcal {L}_{\mathsf {PA}}$
-term not involving x). More generally,
$\mathcal {L}_{\mathsf {PA}}$
-term not involving x). More generally,
 $\Sigma _{n+1}$
consists of formulae of the form
$\Sigma _{n+1}$
consists of formulae of the form
 $\exists x_{0}\dots \exists x_{k-1}\ \varphi $
, where
$\exists x_{0}\dots \exists x_{k-1}\ \varphi $
, where
 $\varphi \in \Pi _{n};$
and
$\varphi \in \Pi _{n};$
and
 $\Pi _{n+1}$
consists of formulae of the form
$\Pi _{n+1}$
consists of formulae of the form
 $\forall x_{0}\dots \forall x_{k-1}\ \varphi $
, where
$\forall x_{0}\dots \forall x_{k-1}\ \varphi $
, where
 $\varphi \in \Sigma _{n}$
(with the convention that
$\varphi \in \Sigma _{n}$
(with the convention that
 $k=0$
corresponds to an empty block of quantifiers).
$k=0$
corresponds to an empty block of quantifiers). -
(c) If
 $p\in M$
and
$p\in M$
and
 $\varphi (\overline {x}.y)$
is an
$\varphi (\overline {x}.y)$
is an
 $\mathcal {L}_{\mathsf {PA}}$
-formula, where
$\mathcal {L}_{\mathsf {PA}}$
-formula, where
 $\overline {x}$
is an n-tuple of variables
$\overline {x}$
is an n-tuple of variables
 $, \varphi (\overline {x},p)^{\mathcal {M}}:=\{\overline {m}\in M^{n}:\mathcal {M}\models \varphi (\overline {m},p\}$
. For
$, \varphi (\overline {x},p)^{\mathcal {M}}:=\{\overline {m}\in M^{n}:\mathcal {M}\models \varphi (\overline {m},p\}$
. For
 $X\subseteq M^{n} $
, X is
$X\subseteq M^{n} $
, X is
 $\mathcal {M}$
-definable if
$\mathcal {M}$
-definable if
 $X=\ \varphi (\overline {x},p)^{\mathcal {M}}$
for some
$X=\ \varphi (\overline {x},p)^{\mathcal {M}}$
for some
 $\mathcal {L}_{\mathsf {PA}}$
-formula
$\mathcal {L}_{\mathsf {PA}}$
-formula
 $\varphi (\overline {x}.y)$
and for some parameter p in M.
$\varphi (\overline {x}.y)$
and for some parameter p in M. -
(d) A subset X of M is
 $\mathcal {M}$
-finite (or
$\mathcal {M}$
-finite (or
 $\mathcal {M}$
-coded) if
$\mathcal {M}$
-coded) if
 $X=c_{E}$
for some
$X=c_{E}$
for some
 $c\in M$
, where
$c\in M$
, where
 $c_{E}=\{m\in M:\mathcal {M}\models m\in _{\mathrm {Ack}}c\},$
and
$c_{E}=\{m\in M:\mathcal {M}\models m\in _{\mathrm {Ack}}c\},$
and
 $m\in _{\mathrm {Ack}}c$
is shorthand for the
$m\in _{\mathrm {Ack}}c$
is shorthand for the
 $\mathcal {L}_{\mathsf {PA}}$
-formula expressing “the mth bit of the binary expansion of c is 1”.
$\mathcal {L}_{\mathsf {PA}}$
-formula expressing “the mth bit of the binary expansion of c is 1”. -
(e) We identify the longest well-founded initial segment of models of PA with the ordinal
 $\omega $
. In this context, when
$\omega $
. In this context, when
 $\mathcal {M}$
is nonstandard, we refer to members of
$\mathcal {M}$
is nonstandard, we refer to members of
 $\omega $
as standard elements, and we refer to
$\omega $
as standard elements, and we refer to
 $\omega $
as the standard cut of
$\omega $
as the standard cut of
 $\mathcal {M}$
.
$\mathcal {M}$
. -
(f) A subset I of M is a cut of
 $\mathcal {M}$
if I is an initial segment of
$\mathcal {M}$
if I is an initial segment of
 $\mathcal {M}$
with no last element.
$\mathcal {M}$
with no last element.
Both constructions presented in this paper employ known isomorphism results about countable recursively saturated models of arithmetic. The following classical result can be found in Kaye’s monograph [Reference Kaye18].
Theorem 2.2. Suppose
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are countable recursively saturated models of
$\mathcal {N}$
are countable recursively saturated models of
![]() $\mathsf {PA.}\ \mathcal {M}$
and
$\mathsf {PA.}\ \mathcal {M}$
and
![]() $\mathcal {N}$
are isomorphic iff
$\mathcal {N}$
are isomorphic iff
![]() $\mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N})$
and
$\mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N})$
and
![]() $\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N})$
.
$\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N})$
.
In order to state the next isomorphism theorem we need to recall the following definitions:
Definition 2.3. Suppose I is a proper cut of
![]() $\mathcal {M}\mathfrak {.}\ I$
is
$\mathcal {M}\mathfrak {.}\ I$
is
![]() $\omega $
-coded from below (above) in
$\omega $
-coded from below (above) in
![]() $\mathcal {M}$
iff for some
$\mathcal {M}$
iff for some
![]() $c\in M, \{(c)_{n}:n\in \omega \}$
is cofinal in I (downward cofinal in
$c\in M, \{(c)_{n}:n\in \omega \}$
is cofinal in I (downward cofinal in
![]() $M\backslash I)$
; here
$M\backslash I)$
; here
![]() $(c)_{n}$
is the exponent of the nth prime in the prime factorization of c within
$(c)_{n}$
is the exponent of the nth prime in the prime factorization of c within
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Definition 2.4. Suppose I is a cut of a model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
.
$\mathsf {PA}$
.
![]() $\mathrm {SSy}_{I}(\mathcal {M})$
is the collection of subsets of I that are coded in
$\mathrm {SSy}_{I}(\mathcal {M})$
is the collection of subsets of I that are coded in
![]() $\mathcal {M}$
. More precisely,
$\mathcal {M}$
. More precisely,
![]() $\mathrm {SSy}_{I}(\mathcal {M})$
consists of sets of the form
$\mathrm {SSy}_{I}(\mathcal {M})$
consists of sets of the form
![]() $c_{E}\cap I,$
as c ranges in
$c_{E}\cap I,$
as c ranges in
![]() $\mathcal {M}$
, where
$\mathcal {M}$
, where
![]() $c_{E}=\{x\in M:\mathcal {M}\models x\in _{\mathrm {Ack}}c\}$
and
$c_{E}=\{x\in M:\mathcal {M}\models x\in _{\mathrm {Ack}}c\}$
and
![]() $\in _{\mathrm {Ack}}$
is the Ackermann membership defined by:
$\in _{\mathrm {Ack}}$
is the Ackermann membership defined by:
![]() $x\in _{\mathrm {Ack}}c$
iff the xth digit of the binary expansion of c is
$x\in _{\mathrm {Ack}}c$
iff the xth digit of the binary expansion of c is
![]() $1$
.
$1$
.
Theorem 2.5 (Kossak–Kotlarski [Reference Kossak and Kotlarski19, theorem 2.1, corollary 2.3]).
Suppose
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are countable recursively saturated models of
$\mathcal {N}$
are countable recursively saturated models of
![]() $\mathsf {PA}$
with
$\mathsf {PA}$
with
![]() $\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N}) $
, and furthermore suppose that I is a cut shared by
$\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N}) $
, and furthermore suppose that I is a cut shared by
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $\mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathcal {N})$
and I is not
$\mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathcal {N})$
and I is not
![]() $\omega $
-coded from above in
$\omega $
-coded from above in
![]() $\mathcal {M}$
or in
$\mathcal {M}$
or in
![]() $\mathcal {N}$
. Then
$\mathcal {N}$
. Then
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are isomorphic over I, i.e., there is an isomorphism
$\mathcal {N}$
are isomorphic over I, i.e., there is an isomorphism
![]() $f$
between
$f$
between
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $f(i)=i$
for each
$f(i)=i$
for each
![]() $i\in I.$
$i\in I.$
Remark 2.6. Suppose
![]() $\mathcal {M}$
is a nonstandard model of
$\mathcal {M}$
is a nonstandard model of
![]() $\mathsf {PA}$
.
$\mathsf {PA}$
.
-
(a) Thanks to overspill, a cut I of
 $\mathcal {M}$
cannot be both
$\mathcal {M}$
cannot be both
 $\omega $
-coded from above and
$\omega $
-coded from above and
 $\omega $
-coded from below in
$\omega $
-coded from below in
 $\mathcal {M}$
. In particular, if c is a nonstandard element of
$\mathcal {M}$
. In particular, if c is a nonstandard element of
 $\mathcal {M}$
, then the cut determined by finite powers of c is not
$\mathcal {M}$
, then the cut determined by finite powers of c is not
 $\omega $
-coded from above in
$\omega $
-coded from above in
 $\mathcal {M}$
. Thus there are arbitrarily large cuts in
$\mathcal {M}$
. Thus there are arbitrarily large cuts in
 $\mathcal {M}$
that are not
$\mathcal {M}$
that are not
 $\omega $
-coded from above in
$\omega $
-coded from above in
 $\mathcal {M}$
.
$\mathcal {M}$
. -
(b) It is easy to see that if I is a strong cut of
 $\mathcal {M}$
, then I is not
$\mathcal {M}$
, then I is not
 $\omega $
-coded from above.
$\omega $
-coded from above. -
(c) Suppose
 $\mathcal {M}$
is countable and recursively saturated. There are arbitrarily large strong cuts J of
$\mathcal {M}$
is countable and recursively saturated. There are arbitrarily large strong cuts J of
 $\mathcal {M}$
such that
$\mathcal {M}$
such that
 $J\prec \mathcal {M}$
and
$J\prec \mathcal {M}$
and
 $J\cong \mathcal {M}$
. One way of seeing this is as follows: by the resplendence property of
$J\cong \mathcal {M}$
. One way of seeing this is as follows: by the resplendence property of
 $\mathcal {M}$
,
$\mathcal {M}$
,
 $\mathcal {M}$
carries an inductive satisfaction class S. Next, use the Phillips–Gaifman refinement of the MacDowell–Specker theorem to build a countable conservative elementary end extension
$\mathcal {M}$
carries an inductive satisfaction class S. Next, use the Phillips–Gaifman refinement of the MacDowell–Specker theorem to build a countable conservative elementary end extension
 $(\mathcal {M}^{\ast },S^{\ast })$
of
$(\mathcal {M}^{\ast },S^{\ast })$
of
 $\left ( \mathcal {M},S\right ) $
. Note that
$\left ( \mathcal {M},S\right ) $
. Note that
 $\mathrm {ACA}_{0}$
holds in
$\mathrm {ACA}_{0}$
holds in
 $\left ( \mathcal {M},\mathrm {SSy}_{M}(\mathcal {M}^{\ast })\right ) $
since
$\left ( \mathcal {M},\mathrm {SSy}_{M}(\mathcal {M}^{\ast })\right ) $
since
 $\mathcal {M}^{\ast }$
is a conservative extension of
$\mathcal {M}^{\ast }$
is a conservative extension of
 $\mathcal {M}$
and therefore by [Reference Kossak and Schmerl20, theorem 7.3.2]
$\mathcal {M}$
and therefore by [Reference Kossak and Schmerl20, theorem 7.3.2]
 $\mathcal {M}$
is strong in
$\mathcal {M}$
is strong in
 $\mathcal {M}^{\ast }.$
Also observe that
$\mathcal {M}^{\ast }.$
Also observe that
 $\mathcal {M}^{\ast }$
is recursively saturated since
$\mathcal {M}^{\ast }$
is recursively saturated since
 $\mathcal {M}^{\ast }$
carries an inductive satisfaction class. By part (a), given any c in
$\mathcal {M}^{\ast }$
carries an inductive satisfaction class. By part (a), given any c in
 $\mathcal {M}$
there is a cut I of
$\mathcal {M}$
there is a cut I of
 $\mathcal {M}$
that includes c such that I is not
$\mathcal {M}$
that includes c such that I is not
 $\omega $
-coded from above in
$\omega $
-coded from above in
 $\mathcal {M}$
. Since
$\mathcal {M}$
. Since
 $\mathcal {M}^{\ast }$
is an end extension of
$\mathcal {M}^{\ast }$
is an end extension of
 $\mathcal {M}$
, I is not
$\mathcal {M}$
, I is not
 $\omega $
-coded from above in
$\omega $
-coded from above in
 $\mathcal {M}^{\ast }$
and
$\mathcal {M}^{\ast }$
and
 $\mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathcal {M}^{\ast }).$
Therefore by Theorem 2.5 there is an isomorphism
$\mathrm {SSy}_{I}(\mathcal {M})=\mathrm {SSy}_{I}(\mathcal {M}^{\ast }).$
Therefore by Theorem 2.5 there is an isomorphism
 $f:\mathcal {M}^{\ast }\rightarrow \mathcal {M}$
that is the identity on
$f:\mathcal {M}^{\ast }\rightarrow \mathcal {M}$
that is the identity on
 $I.$
So if we let
$I.$
So if we let
 $J=f(M)$
, it is evident that J is a strong cut of
$J=f(M)$
, it is evident that J is a strong cut of
 $\mathcal {M}$
that includes c,
$\mathcal {M}$
that includes c,
 $J\prec \mathcal {M},$
and
$J\prec \mathcal {M},$
and
 $J\cong \mathcal {M}$
.
$J\cong \mathcal {M}$
.
2.2 Satisfaction and truth classes
Truth and satisfaction are often used interchangeably in mathematical logic, and this conflation is also at work when it comes to the terms ‘truth class’ and ‘satisfaction class’. In this subsection we provide the precise definitions of each. As we shall see in Proposition 2.14, a truth class is essentially an extensional satisfaction class.Footnote 3
Definition 2.7. We will use the following abbreviations relating to the arithmetization of syntax; note that all the formulae in the list below are
![]() $\mathcal {L}_{\mathsf {PA}}$
-formulae.
$\mathcal {L}_{\mathsf {PA}}$
-formulae.
-
(a)
 $\mathsf {Form}(x)$
is the formula expressing “x is (the code of) an
$\mathsf {Form}(x)$
is the formula expressing “x is (the code of) an
 $\mathcal {L}_{\mathsf {PA}}$
-formula”.
$\mathcal {L}_{\mathsf {PA}}$
-formula”. -
(b)
 $\mathsf {Sent}(x)$
is the conjunction of
$\mathsf {Sent}(x)$
is the conjunction of
 $\mathsf {Form}(x)$
and the formula expressing “x has no free variables”.
$\mathsf {Form}(x)$
and the formula expressing “x has no free variables”. -
(c)
 $\mathsf {Var}(x)$
is the formula expressing “x is (the code of) a variable”.
$\mathsf {Var}(x)$
is the formula expressing “x is (the code of) a variable”. -
(d)
 $\mathsf {Asn}(\alpha )$
is the formula expressing “
$\mathsf {Asn}(\alpha )$
is the formula expressing “
 $\alpha $
is the code of an assignment”, where an assignment here simply refers to a function whose domain consists of a (finite) set of variables.
$\alpha $
is the code of an assignment”, where an assignment here simply refers to a function whose domain consists of a (finite) set of variables. -
(e)
 $y\in \mathsf {FV}(x)$
is the formula expressing “
$y\in \mathsf {FV}(x)$
is the formula expressing “
 $\mathsf {Form}(x)$
and y is a free variable of x”.
$\mathsf {Form}(x)$
and y is a free variable of x”. -
(f)
 $y\in \mathsf {Dom}(\alpha )$
is the formula expressing “the domain of
$y\in \mathsf {Dom}(\alpha )$
is the formula expressing “the domain of
 $\alpha $
includes y”.
$\alpha $
includes y”. -
(g)
 $\mathsf {Asn}(\alpha ,x)$
is the following formula expressing “
$\mathsf {Asn}(\alpha ,x)$
is the following formula expressing “
 $\alpha $
is an assignment for x”:
$\alpha $
is an assignment for x”: $$ \begin{align*} \mathsf{Form}(x)\wedge \mathsf{Asn}(\alpha )\wedge \forall y\left( y\in \mathsf{Dom}(\alpha )\leftrightarrow y\in \mathsf{FV}(x)\right). \end{align*} $$
$$ \begin{align*} \mathsf{Form}(x)\wedge \mathsf{Asn}(\alpha )\wedge \forall y\left( y\in \mathsf{Dom}(\alpha )\leftrightarrow y\in \mathsf{FV}(x)\right). \end{align*} $$
-
(h) For assignments
 $\alpha $
and
$\alpha $
and
 $\alpha ^{\prime }$
,
$\alpha ^{\prime }$
,
 $\alpha ^{\prime }\supseteq \alpha $
expresses “the domain of
$\alpha ^{\prime }\supseteq \alpha $
expresses “the domain of
 $\alpha ^{\prime }$
extends the domain of
$\alpha ^{\prime }$
extends the domain of
 $\alpha $
and
$\alpha $
and
 $\alpha (v)=\alpha ^{\prime }(v)$
for all v in the domain of
$\alpha (v)=\alpha ^{\prime }(v)$
for all v in the domain of
 $\alpha $
”.
$\alpha $
”. -
(i)
 $x\vartriangleleft y$
is the formula expressing “x is the code of an immediate subformula of the
$x\vartriangleleft y$
is the formula expressing “x is the code of an immediate subformula of the
 $\mathcal {L}_{\mathsf {PA}}$
-formula coded by y”, i.e.,
$\mathcal {L}_{\mathsf {PA}}$
-formula coded by y”, i.e.,
 $x\vartriangleleft y$
abbreviates the conjunction of
$x\vartriangleleft y$
abbreviates the conjunction of
 $y\in \mathsf {Form}$
and the following disjunction:
$y\in \mathsf {Form}$
and the following disjunction: $$ \begin{align*} \left( y=\lnot x\right) \vee \exists z\left( \left( y=x\vee z\right) \vee \left( y=z\vee x\right) \right) \vee \exists v\in \mathsf{Var}\left( y=\exists v\ x\right). \end{align*} $$
$$ \begin{align*} \left( y=\lnot x\right) \vee \exists z\left( \left( y=x\vee z\right) \vee \left( y=z\vee x\right) \right) \vee \exists v\in \mathsf{Var}\left( y=\exists v\ x\right). \end{align*} $$
-
(j) Given an
 $\mathcal {L}_{\mathsf {PA}}$
-term s and an assignment
$\mathcal {L}_{\mathsf {PA}}$
-term s and an assignment
 $\alpha $
whose domain includes the free variables of s,
$\alpha $
whose domain includes the free variables of s,
 $\mathsf {val}(s,\alpha )$
is the
$\mathsf {val}(s,\alpha )$
is the
 $\mathsf {PA}$
-definable function that outputs the value of s when its free variables are replaced by the values specified by
$\mathsf {PA}$
-definable function that outputs the value of s when its free variables are replaced by the values specified by
 $\alpha .$
$\alpha .$
Definition 2.8. The theory
![]() $\mathsf {CS}^{-}\left ( \mathsf {F}\right ) $
defined below is formulated in an expansion of
$\mathsf {CS}^{-}\left ( \mathsf {F}\right ) $
defined below is formulated in an expansion of
![]() $\mathcal {L}_{\mathsf {PA}}$
by adding a fresh binary predicate
$\mathcal {L}_{\mathsf {PA}}$
by adding a fresh binary predicate
![]() $\mathsf {S}(x,y)$
(denoting satisfaction) and a fresh unary predicate
$\mathsf {S}(x,y)$
(denoting satisfaction) and a fresh unary predicate
![]() $\mathsf {F}$
(denoting a specified collection of formulae). The binary/unary distinction is of course not an essential one since
$\mathsf {F}$
(denoting a specified collection of formulae). The binary/unary distinction is of course not an essential one since
![]() $\mathsf {PA}$
has access to a definable pairing function. However, the binary/unary distinction at the conceptual level marks the key difference between the concepts of satisfaction and truth.
$\mathsf {PA}$
has access to a definable pairing function. However, the binary/unary distinction at the conceptual level marks the key difference between the concepts of satisfaction and truth.
-
(a)
 $\mathsf {CS}^{-}\left ( \mathsf {F}\right ) $
is the conjunction of the universal generalizations of the formulae
$\mathsf {CS}^{-}\left ( \mathsf {F}\right ) $
is the conjunction of the universal generalizations of the formulae
 $\mathsf {tarski}_{0}(\mathsf {S},\mathsf {F})$
through
$\mathsf {tarski}_{0}(\mathsf {S},\mathsf {F})$
through
 $\mathsf {tarski}_{4}(\mathsf {S},\mathsf {F})$
described below with the proviso that in what follows
$\mathsf {tarski}_{4}(\mathsf {S},\mathsf {F})$
described below with the proviso that in what follows
 $\alpha $
and
$\alpha $
and
 $\alpha ^{\prime }$
range over assignments, and s and t range over
$\alpha ^{\prime }$
range over assignments, and s and t range over
 $\mathcal {L}_{\mathsf {PA}}$
-terms (that might have free variables). It is helpful to bear in mind that the axioms of
$\mathcal {L}_{\mathsf {PA}}$
-terms (that might have free variables). It is helpful to bear in mind that the axioms of
 $\mathsf {CS}^{-}(\mathsf {F})$
collectively express “
$\mathsf {CS}^{-}(\mathsf {F})$
collectively express “
 $\mathsf {F}$
is a subset of arithmetical formulae that is closed under immediate subformulae; each member of
$\mathsf {F}$
is a subset of arithmetical formulae that is closed under immediate subformulae; each member of
 $\mathsf {S}$
is an ordered pair of the form
$\mathsf {S}$
is an ordered pair of the form
 $(x,\alpha )$
, where
$(x,\alpha )$
, where
 $x $
is in
$x $
is in
 $\mathsf {F}$
and
$\mathsf {F}$
and
 $\alpha $
is an assignment for
$\alpha $
is an assignment for
 $x;$
and
$x;$
and
 $\mathsf {S}$
satisfies Tarski’s compositional clauses for a satisfaction predicate”.
$\mathsf {S}$
satisfies Tarski’s compositional clauses for a satisfaction predicate”.
-
•
 $\mathsf {tarski}_{0}(\mathsf {S},\mathsf {F}):=\left [ \mathsf {F}(x)\rightarrow \mathsf {Form}(x)\right ] \wedge \left [ y\vartriangleleft x\wedge \mathsf {F}(x)\rightarrow \mathsf {F}(y)\right ] \wedge \left [ \mathsf {S}(x,\alpha )\rightarrow \left ( \mathsf {F}(x)\wedge \alpha \in \mathsf {Asn}(x)\right ) \right ]. $
$\mathsf {tarski}_{0}(\mathsf {S},\mathsf {F}):=\left [ \mathsf {F}(x)\rightarrow \mathsf {Form}(x)\right ] \wedge \left [ y\vartriangleleft x\wedge \mathsf {F}(x)\rightarrow \mathsf {F}(y)\right ] \wedge \left [ \mathsf {S}(x,\alpha )\rightarrow \left ( \mathsf {F}(x)\wedge \alpha \in \mathsf {Asn}(x)\right ) \right ]. $
-
•
 $\mathsf {tarski}_{1}(\mathsf {S,F}):=\left [ \mathsf {F}(x)\wedge x=\ulcorner s=t\urcorner \wedge \alpha \in \mathsf {Asn}(x)\right ] \rightarrow \left [ \mathsf {S}(x,\alpha )\leftrightarrow \mathsf {val}(s,\alpha )=\mathsf {val}(t,\alpha )\right ] .$
$\mathsf {tarski}_{1}(\mathsf {S,F}):=\left [ \mathsf {F}(x)\wedge x=\ulcorner s=t\urcorner \wedge \alpha \in \mathsf {Asn}(x)\right ] \rightarrow \left [ \mathsf {S}(x,\alpha )\leftrightarrow \mathsf {val}(s,\alpha )=\mathsf {val}(t,\alpha )\right ] .$
-
•
 $\mathsf {tarski}_{2}(\mathsf {S},\mathsf {F}):=\left [ \mathsf {F}(x)\wedge (x=\lnot y)\wedge \alpha \in \mathsf {Asn}(x)\right ] \rightarrow \left [ \mathsf {S}(x,\alpha )\leftrightarrow \lnot \mathsf {S}(y,\alpha )\right ] .$
$\mathsf {tarski}_{2}(\mathsf {S},\mathsf {F}):=\left [ \mathsf {F}(x)\wedge (x=\lnot y)\wedge \alpha \in \mathsf {Asn}(x)\right ] \rightarrow \left [ \mathsf {S}(x,\alpha )\leftrightarrow \lnot \mathsf {S}(y,\alpha )\right ] .$
-
•
 $\mathsf {tarski}_{3}(\mathsf {S},\mathsf {F}):=\left [ \mathsf {F}(x)\wedge \left ( x=y_{1}\vee y_{2}\right ) \wedge \alpha \in \mathsf {Asn}(x)\right ] \rightarrow $
$\mathsf {tarski}_{3}(\mathsf {S},\mathsf {F}):=\left [ \mathsf {F}(x)\wedge \left ( x=y_{1}\vee y_{2}\right ) \wedge \alpha \in \mathsf {Asn}(x)\right ] \rightarrow $
 $$ \begin{align*} \left[ \mathsf{S}(x,\alpha )\leftrightarrow \left( \mathsf{S}\left( y_{1},\alpha \upharpoonright \mathsf{FV}(y_{1})\right) \vee \mathsf{S}\left( y_{2},\alpha \upharpoonright \mathsf{FV}(y_{2})\right) \right) \right] .\end{align*} $$
$$ \begin{align*} \left[ \mathsf{S}(x,\alpha )\leftrightarrow \left( \mathsf{S}\left( y_{1},\alpha \upharpoonright \mathsf{FV}(y_{1})\right) \vee \mathsf{S}\left( y_{2},\alpha \upharpoonright \mathsf{FV}(y_{2})\right) \right) \right] .\end{align*} $$
-
•
 $\mathsf {tarski}_{4}(\mathsf {S},\mathsf {F}):=\left [ \mathsf {F}(x)\wedge (x=\exists v\ y)\wedge \alpha \in \mathsf {Asn}(x))\right ] \rightarrow \left [ \mathsf {S}(x,\alpha )\leftrightarrow \exists \alpha ^{\prime }\supseteq\alpha \ \mathsf {S}(y,\alpha ^{\prime })\right ] .$
$\mathsf {tarski}_{4}(\mathsf {S},\mathsf {F}):=\left [ \mathsf {F}(x)\wedge (x=\exists v\ y)\wedge \alpha \in \mathsf {Asn}(x))\right ] \rightarrow \left [ \mathsf {S}(x,\alpha )\leftrightarrow \exists \alpha ^{\prime }\supseteq\alpha \ \mathsf {S}(y,\alpha ^{\prime })\right ] .$
-
(b)
 $\mathsf {CS}^{-}$
is the theory whose axioms are obtained by substituting the predicate
$\mathsf {CS}^{-}$
is the theory whose axioms are obtained by substituting the predicate
 $\mathsf {F}(x)$
by the
$\mathsf {F}(x)$
by the
 $\mathcal {L}_{\mathsf {PA}}$
-formula
$\mathcal {L}_{\mathsf {PA}}$
-formula
 $\mathsf {Form}(x)$
in the axioms of
$\mathsf {Form}(x)$
in the axioms of
 $\mathsf {CS}^{-}(\mathsf {F})$
. Thus the axioms on
$\mathsf {CS}^{-}(\mathsf {F})$
. Thus the axioms on
 $\mathsf {CS}^{-}$
are formulated in the language obtained by adding
$\mathsf {CS}^{-}$
are formulated in the language obtained by adding
 $\mathsf {S}$
to
$\mathsf {S}$
to
 $\mathcal {L}_{\mathsf {PA}}$
(with no mention of
$\mathcal {L}_{\mathsf {PA}}$
(with no mention of
 $\mathsf {F}$
).
$\mathsf {F}$
).
Definition 2.9. Let
![]() $\mathcal {M}\models \mathsf {PA}$
, and suppose
$\mathcal {M}\models \mathsf {PA}$
, and suppose
![]() $F\subseteq \mathsf {Form}^{\mathcal {M}}=\left \{ m\in M:\mathcal {M}\models \mathsf {Form}(m)\right \} $
.
$F\subseteq \mathsf {Form}^{\mathcal {M}}=\left \{ m\in M:\mathcal {M}\models \mathsf {Form}(m)\right \} $
.
-
(a) A subset S of
 $M^{2}$
is said to be an F-satisfaction class on
$M^{2}$
is said to be an F-satisfaction class on
 $\mathcal {M}$
if
$\mathcal {M}$
if
 $(\mathcal {M},F,S)\models \mathsf {CS}^{-}(\mathsf {F})$
, here the interpretation of
$(\mathcal {M},F,S)\models \mathsf {CS}^{-}(\mathsf {F})$
, here the interpretation of
 $\mathsf {F}$
is F and the interpretation of
$\mathsf {F}$
is F and the interpretation of
 $\mathsf {S}$
is
$\mathsf {S}$
is
 $S.\ S$
is a satisfaction class on
$S.\ S$
is a satisfaction class on
 $\mathcal {M}$
if S is an F-satisfaction class for some F.
$\mathcal {M}$
if S is an F-satisfaction class for some F. -
(b) An F-satisfaction class S is extensional if for all
 $\varphi _{0}$
and
$\varphi _{0}$
and
 $\varphi _{1}$
in F,
$\varphi _{1}$
in F,
 $\mathcal {M}{\kern-1pt}\models{\kern-1pt} (\varphi _{0},\alpha _{0})\thicksim (\varphi _{1},\alpha _{1})$
implies
$\mathcal {M}{\kern-1pt}\models{\kern-1pt} (\varphi _{0},\alpha _{0})\thicksim (\varphi _{1},\alpha _{1})$
implies
 $(\varphi _{0},\alpha _{0})\in S$
iff
$(\varphi _{0},\alpha _{0})\in S$
iff
 $(\varphi _{1},\alpha _{1})\in S$
, where
$(\varphi _{1},\alpha _{1})\in S$
, where
 $(\varphi _{0},\alpha _{0})\thicksim (\varphi _{1},\alpha _{1})$
means that after substituting numerals in
$(\varphi _{0},\alpha _{0})\thicksim (\varphi _{1},\alpha _{1})$
means that after substituting numerals in
 $\varphi _{0}$
in accordance with
$\varphi _{0}$
in accordance with
 $\alpha _{0}$
we obtain precisely the same formula obtained by substituting numerals in
$\alpha _{0}$
we obtain precisely the same formula obtained by substituting numerals in
 $\varphi _{1}$
in accordance with
$\varphi _{1}$
in accordance with
 $\alpha _{1}.$
$\alpha _{1}.$
-
(c) A subset T of M is said to be a full satisfaction class on
 $\mathcal {M}$
if
$\mathcal {M}$
if
 $(\mathcal {M},S)\models \mathsf {CS}^{-}$
(equivalently: if
$(\mathcal {M},S)\models \mathsf {CS}^{-}$
(equivalently: if
 $(\mathcal {M},F,S)\models \mathsf {CT}^{-}(\mathsf {F}))$
for
$(\mathcal {M},F,S)\models \mathsf {CT}^{-}(\mathsf {F}))$
for
 $F=\mathsf {Form}^{\mathcal {M}}$
.
$F=\mathsf {Form}^{\mathcal {M}}$
.
Definition 2.10. The theory
![]() $\mathsf {CT}^{-}\left ( \mathsf {F}\right ) $
defined below is formulated in an expansion of
$\mathsf {CT}^{-}\left ( \mathsf {F}\right ) $
defined below is formulated in an expansion of
![]() $\mathcal {L}_{\mathsf {PA}}$
by adding a fresh unary predicate
$\mathcal {L}_{\mathsf {PA}}$
by adding a fresh unary predicate
![]() $\mathsf {T}(x)$
(denoting satisfaction) and a fresh unary predicate
$\mathsf {T}(x)$
(denoting satisfaction) and a fresh unary predicate
![]() $\mathsf {F}$
(denoting a specified collection of formulae).
$\mathsf {F}$
(denoting a specified collection of formulae).
-
(a)
 $\mathsf {CT}^{-}\left ( \mathsf {F}\right ) $
is the conjunction of the universal generalizations of the formulae
$\mathsf {CT}^{-}\left ( \mathsf {F}\right ) $
is the conjunction of the universal generalizations of the formulae
 $\mathsf {tarski}_{0}(\mathsf {S},\mathsf {F})$
through
$\mathsf {tarski}_{0}(\mathsf {S},\mathsf {F})$
through
 $\mathsf {tarski}_{4}(\mathsf {S},\mathsf {F}).$
In what follows we use following conventions:
$\mathsf {tarski}_{4}(\mathsf {S},\mathsf {F}).$
In what follows we use following conventions:
 $\mathsf {FSent}(x)$
expresses “x is an
$\mathsf {FSent}(x)$
expresses “x is an
 $\mathcal {L}_{\mathsf {PA}}$
-sentence obtained by substituting closed terms of
$\mathcal {L}_{\mathsf {PA}}$
-sentence obtained by substituting closed terms of
 $\mathcal {L}_{\mathsf {PA}}$
for every free variable of a formula in
$\mathcal {L}_{\mathsf {PA}}$
for every free variable of a formula in
 $\mathsf {F}$
”;
$\mathsf {F}$
”;
 $y\vartriangleleft x$
expresses “y is an immediate subformula of x” as in Definition 2.7(i); s and t range over closed terms of
$y\vartriangleleft x$
expresses “y is an immediate subformula of x” as in Definition 2.7(i); s and t range over closed terms of
 $\mathcal {L}_{\mathsf {PA}}$
;
$\mathcal {L}_{\mathsf {PA}}$
;
 $s^{\circ }$
denotes the value of the closed term s, i.e.,
$s^{\circ }$
denotes the value of the closed term s, i.e.,
 ${s}^{\circ }=\mathsf {val}(\alpha ,\varnothing )$
(where
${s}^{\circ }=\mathsf {val}(\alpha ,\varnothing )$
(where
 $\mathsf {val}$
is as in Definition 2.7(j) and
$\mathsf {val}$
is as in Definition 2.7(j) and
 $\varnothing $
is the empty assignment);
$\varnothing $
is the empty assignment);
 $\sigma $
and its variants (
$\sigma $
and its variants (
 $\sigma ^{\prime }, \sigma _{1}$
,
$\sigma ^{\prime }, \sigma _{1}$
,
 $\sigma _{2}$
) range over elements of
$\sigma _{2}$
) range over elements of
 $\mathsf {FSent}$
;
$\mathsf {FSent}$
;
 $\varphi (v)$
ranges over
$\varphi (v)$
ranges over
 $\mathcal {L}_{\mathsf {PA}}$
-formulae;
$\mathcal {L}_{\mathsf {PA}}$
-formulae;
 ${{\mathsf {F}}}_{\leq 1}(\varphi (v))$
expresses “
${{\mathsf {F}}}_{\leq 1}(\varphi (v))$
expresses “
 $\mathsf {F}(\varphi )$
and
$\mathsf {F}(\varphi )$
and
 $\varphi $
has at most one free variable v”; and
$\varphi $
has at most one free variable v”; and
 $\varphi \lbrack \underline {x}/v]$
is (the code of) the formula obtained by substituting all occurrences of the variable v in
$\varphi \lbrack \underline {x}/v]$
is (the code of) the formula obtained by substituting all occurrences of the variable v in
 $\varphi $
with the numeral representing
$\varphi $
with the numeral representing
 $x.$
$x.$
-
•
 $\mathsf {tarski}_{0}(\mathsf {T,F}):=\left [ \mathsf {T}(x)\rightarrow \mathsf {FSent}(x)\right ] \wedge \left [ y\vartriangleleft x\wedge \mathsf {F}(x)\rightarrow \mathsf {F}(y)\right ] .$
$\mathsf {tarski}_{0}(\mathsf {T,F}):=\left [ \mathsf {T}(x)\rightarrow \mathsf {FSent}(x)\right ] \wedge \left [ y\vartriangleleft x\wedge \mathsf {F}(x)\rightarrow \mathsf {F}(y)\right ] .$
-
•
 $\mathsf {tarski}_{1}(\mathsf {T,F}):=\mathsf {T}(s=t)\leftrightarrow {s}^{\circ }={t}^{\circ }.$
$\mathsf {tarski}_{1}(\mathsf {T,F}):=\mathsf {T}(s=t)\leftrightarrow {s}^{\circ }={t}^{\circ }.$
-
•
 $\mathsf {tarski}_{2}(\mathsf {T,F}):=\left [ \mathsf {FSent}(\sigma )\wedge \left ( \sigma =\lnot \sigma ^{\prime }\right ) \right ] \rightarrow \left ( \mathsf {T}(\sigma )\leftrightarrow \lnot \mathsf {T}(\sigma ^{\prime })\right ) .$
$\mathsf {tarski}_{2}(\mathsf {T,F}):=\left [ \mathsf {FSent}(\sigma )\wedge \left ( \sigma =\lnot \sigma ^{\prime }\right ) \right ] \rightarrow \left ( \mathsf {T}(\sigma )\leftrightarrow \lnot \mathsf {T}(\sigma ^{\prime })\right ) .$
-
•
 $\mathsf {tarski}_{3}(\mathsf {T,F}):=\left [ \mathsf {FSent}(\sigma )\wedge \sigma =\sigma _{1}\vee \sigma _{2}\right ] \rightarrow \left [ \mathsf {T}(\sigma )\leftrightarrow \left ( \mathsf {T}(\sigma _{1})\vee \mathsf {T}(\sigma _{2})\right ) \right ] .$
$\mathsf {tarski}_{3}(\mathsf {T,F}):=\left [ \mathsf {FSent}(\sigma )\wedge \sigma =\sigma _{1}\vee \sigma _{2}\right ] \rightarrow \left [ \mathsf {T}(\sigma )\leftrightarrow \left ( \mathsf {T}(\sigma _{1})\vee \mathsf {T}(\sigma _{2})\right ) \right ] .$
-
•
 $\mathsf {tarski}_{4}(\mathsf {T,F}):={{\mathsf {F}}}_{\leq 1}(\varphi (v))\rightarrow \left [ \mathsf {T}(\exists v\ \varphi )\leftrightarrow \exists x~\mathsf {T}(\varphi \lbrack \underline {x}/v])\right ] .$
$\mathsf {tarski}_{4}(\mathsf {T,F}):={{\mathsf {F}}}_{\leq 1}(\varphi (v))\rightarrow \left [ \mathsf {T}(\exists v\ \varphi )\leftrightarrow \exists x~\mathsf {T}(\varphi \lbrack \underline {x}/v])\right ] .$
-
(b)
 $\mathsf {CT}^{-}$
is the theory whose axioms are obtained by substituting the predicate
$\mathsf {CT}^{-}$
is the theory whose axioms are obtained by substituting the predicate
 $\mathsf {F}(x)$
by the
$\mathsf {F}(x)$
by the
 $\mathcal {L}_{\mathsf {PA}}$
-formula
$\mathcal {L}_{\mathsf {PA}}$
-formula
 $\mathsf {Form}(x)$
in the axioms of
$\mathsf {Form}(x)$
in the axioms of
 $\mathsf {CT}^{-}(\mathsf {F})$
. Thus the axioms on
$\mathsf {CT}^{-}(\mathsf {F})$
. Thus the axioms on
 $\mathsf {CT}^{-}$
are formulated in the language obtained by adding
$\mathsf {CT}^{-}$
are formulated in the language obtained by adding
 $\mathsf {T}$
to
$\mathsf {T}$
to
 $\mathcal {L}_{\mathsf {PA}}$
(with no mention of
$\mathcal {L}_{\mathsf {PA}}$
(with no mention of
 $\mathsf {F}$
).
$\mathsf {F}$
).
Definition 2.11. Let
![]() $\mathcal {M}\models \mathsf {PA}$
, and suppose
$\mathcal {M}\models \mathsf {PA}$
, and suppose
![]() $F\subseteq \mathsf {Form}^{\mathcal {M}}$
, and F is closed under direct subformulae of
$F\subseteq \mathsf {Form}^{\mathcal {M}}$
, and F is closed under direct subformulae of
![]() $\mathcal {M}$
. Recall that
$\mathcal {M}$
. Recall that
![]() $\mathsf {FSent}^{(\mathcal {M},F)}$
consists of
$\mathsf {FSent}^{(\mathcal {M},F)}$
consists of
![]() $m\in M$
such that
$m\in M$
such that
![]() $(\mathcal {M},F)$
satisfies “m is an
$(\mathcal {M},F)$
satisfies “m is an
![]() $\mathcal {L}_{\mathsf {PA}}$
-sentence obtained by substituting closed terms of
$\mathcal {L}_{\mathsf {PA}}$
-sentence obtained by substituting closed terms of
![]() $\mathcal {L}_{\mathsf {PA}}$
for the free variables of a formula in
$\mathcal {L}_{\mathsf {PA}}$
for the free variables of a formula in
![]() $\mathsf {F}$
”.
$\mathsf {F}$
”.
-
(a) A subset T of M is an F-truth class on
 $\mathcal {M}$
if
$\mathcal {M}$
if
 $(\mathcal {M},F,T)\models \mathsf {CT}^{-}(\mathsf {F})$
, here the interpretation of
$(\mathcal {M},F,T)\models \mathsf {CT}^{-}(\mathsf {F})$
, here the interpretation of
 $\mathsf {F}$
is F and the interpretation of
$\mathsf {F}$
is F and the interpretation of
 $\mathsf {T}$
is
$\mathsf {T}$
is
 $T.\ T$
is a truth class on
$T.\ T$
is a truth class on
 $\mathcal {M}$
if T is an F-truth class for some F.
$\mathcal {M}$
if T is an F-truth class for some F. -
(b) A subset T of M is a full truth class on
 $\mathcal {M}$
if
$\mathcal {M}$
if
 $(\mathcal {M},T)\models \mathsf {CT}^{-}$
; equivalently: if
$(\mathcal {M},T)\models \mathsf {CT}^{-}$
; equivalently: if
 $(\mathcal {M},F,T)\models \mathsf {CT}^{-}(\mathsf {F})$
for
$(\mathcal {M},F,T)\models \mathsf {CT}^{-}(\mathsf {F})$
for
 $F=\mathsf {Form}^{\mathcal {M}}$
.
$F=\mathsf {Form}^{\mathcal {M}}$
. -
(c) An F-truth class T on
 $\mathcal {M}$
is F-disjunctively correct, if whenever
$\mathcal {M}$
is F-disjunctively correct, if whenever
 $\delta \in \mathsf {FSent}^{\mathcal {M}}$
and
$\delta \in \mathsf {FSent}^{\mathcal {M}}$
and
 $\left \{ \varphi _{i}:i<m\right \} $
is an
$\left \{ \varphi _{i}:i<m\right \} $
is an
 $\mathcal {M}$
-coded subset of
$\mathcal {M}$
-coded subset of
 $\mathsf {Sent}^{\mathcal {M}}$
(for some possibly nonstandard
$\mathsf {Sent}^{\mathcal {M}}$
(for some possibly nonstandard
 $m\in M$
), the following holds:(▽)where any grouping of
$m\in M$
), the following holds:(▽)where any grouping of $$ \begin{align} \left( \mathcal{M}\models \delta =\bigvee\limits_{i<m}\varphi _{i}\right) \Longrightarrow \left( \delta \in T\Leftrightarrow \exists i<m\ \varphi _{i}\in T\right),\end{align} $$
$$ \begin{align} \left( \mathcal{M}\models \delta =\bigvee\limits_{i<m}\varphi _{i}\right) \Longrightarrow \left( \delta \in T\Leftrightarrow \exists i<m\ \varphi _{i}\in T\right),\end{align} $$
 $\left \{ \varphi _{i}:i<m\right \} $
can be used in
$\left \{ \varphi _{i}:i<m\right \} $
can be used in
 $\mathcal {M}$
for forming the disjunction
$\mathcal {M}$
for forming the disjunction
 $\delta .$
$\delta .$
-
(d) Given a cut I of
 $\mathcal {M}$
, an F-truth class T on
$\mathcal {M}$
, an F-truth class T on
 $\mathcal {M}$
is I-disjunctively correct if T is disjunctively correct for disjunctions whose number of disjuncts is a member of I; more precisely, if (▽) holds whenever
$\mathcal {M}$
is I-disjunctively correct if T is disjunctively correct for disjunctions whose number of disjuncts is a member of I; more precisely, if (▽) holds whenever
 $\delta \in \mathsf {FSent}^{\mathcal {M}}$
and
$\delta \in \mathsf {FSent}^{\mathcal {M}}$
and
 $m\in I$
.
$m\in I$
. -
(e) Let
 $\mathsf {Val}^{\mathcal {M}}$
be the set of theorems of first-order logic as computed in
$\mathsf {Val}^{\mathcal {M}}$
be the set of theorems of first-order logic as computed in
 $\mathcal {M}$
. Given an F-truth class T on
$\mathcal {M}$
. Given an F-truth class T on
 $\mathcal {M}$
, T is F-deductively correct if whenever
$\mathcal {M}$
, T is F-deductively correct if whenever
 $\sigma \in T$
,
$\sigma \in T$
,
 $\sigma ^{\prime }\in \mathsf {FSent}^{\mathcal {M}}$
, and
$\sigma ^{\prime }\in \mathsf {FSent}^{\mathcal {M}}$
, and
 $\left ( \sigma \rightarrow \sigma ^{\prime }\right ) \in \mathsf {Val}^{\mathcal {M}}$
, then
$\left ( \sigma \rightarrow \sigma ^{\prime }\right ) \in \mathsf {Val}^{\mathcal {M}}$
, then
 $\sigma ^{\prime }\in T.$
$\sigma ^{\prime }\in T.$
-
(f) Given a cut I of
 $\mathcal {M}$
and a truth class T on
$\mathcal {M}$
and a truth class T on
 $\mathcal {M}$
, T is I-deductively correct if T is F-deductively correct for
$\mathcal {M}$
, T is I-deductively correct if T is F-deductively correct for
 $F=\mathsf {Form}^{\mathcal {M}}\cap I.$
$F=\mathsf {Form}^{\mathcal {M}}\cap I.$
Remark 2.12. Let
![]() $\mathcal {M}$
be a nonstandard model of PA, and
$\mathcal {M}$
be a nonstandard model of PA, and
![]() $\mathrm {Sat}_{\mathcal {M}}$
be the usual Tarskian truth predicate on
$\mathrm {Sat}_{\mathcal {M}}$
be the usual Tarskian truth predicate on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
![]() $\mathrm {Sat}_{\mathcal {M}}$
induces an
$\mathrm {Sat}_{\mathcal {M}}$
induces an
![]() $\omega $
-truth class
$\omega $
-truth class
![]() $\mathrm {True}_{\mathcal {M}}$
on
$\mathrm {True}_{\mathcal {M}}$
on
![]() $\mathcal {M}$
, where
$\mathcal {M}$
, where
![]() $\omega $
is the standard cut of
$\omega $
is the standard cut of
![]() $\mathcal {M}$
. More specifically, suppose
$\mathcal {M}$
. More specifically, suppose
![]() $\varphi (x_{1},\dots ,x_{k})$
is a standard
$\varphi (x_{1},\dots ,x_{k})$
is a standard
![]() $k$
-ary formula, and
$k$
-ary formula, and
![]() $t_{1},\dots ,t_{k}$
are (codes of) closed
$t_{1},\dots ,t_{k}$
are (codes of) closed
![]() $\mathcal {L}_{\mathsf {PA}}$
-terms in the sense of
$\mathcal {L}_{\mathsf {PA}}$
-terms in the sense of
![]() $\mathcal {M}$
(thus
$\mathcal {M}$
(thus
![]() $t_{1},\dots ,t_{k}$
need not be standard). Since
$t_{1},\dots ,t_{k}$
need not be standard). Since
![]() $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
![]() $\mathsf {PA}$
, the closed-term-evaluation function
$\mathsf {PA}$
, the closed-term-evaluation function
![]() $t\mapsto t^{\circ }$
is
$t\mapsto t^{\circ }$
is
![]() $\mathcal {M}$
-definable, and therefore there are elements
$\mathcal {M}$
-definable, and therefore there are elements
![]() $m_{1},\dots ,m_{k}$
in M such that
$m_{1},\dots ,m_{k}$
in M such that
![]() $\mathcal {M}\models t_{i}^{\circ }=m_{i}$
for
$\mathcal {M}\models t_{i}^{\circ }=m_{i}$
for
![]() $1\leq i\leq k.$
Thus
$1\leq i\leq k.$
Thus
![]() $\mathrm {True}_{\mathcal {M}}$
can be defined as follows:
$\mathrm {True}_{\mathcal {M}}$
can be defined as follows:
![]() $\varphi (t_{1}/x_{1},\dots ,t_{k}/x_{k})\in \mathrm {True}_{\mathcal {M}}$
iff
$\varphi (t_{1}/x_{1},\dots ,t_{k}/x_{k})\in \mathrm {True}_{\mathcal {M}}$
iff
![]() $\left ( \varphi ,\alpha \right ) \in \mathrm {Sat}_{\mathcal {M}}$
, where
$\left ( \varphi ,\alpha \right ) \in \mathrm {Sat}_{\mathcal {M}}$
, where
![]() $\alpha $
is the assignment given by
$\alpha $
is the assignment given by
![]() $x_{i}\mapsto m_{i}.$
It is evident that
$x_{i}\mapsto m_{i}.$
It is evident that
![]() $\mathrm {True}_{\mathcal {M}}$
is
$\mathrm {True}_{\mathcal {M}}$
is
![]() $\omega $
-disjunctively and
$\omega $
-disjunctively and
![]() $\omega $
-deductively correct.
$\omega $
-deductively correct.
Remark 2.13. It is well-known [Reference Hájek and Pudlák15, sec. V.5] that for each nonzero
![]() $n\in \omega $
there is a unary
$n\in \omega $
there is a unary
![]() $\Sigma _{n}$
-formula
$\Sigma _{n}$
-formula
![]() $\mathrm {True}_{\Sigma _{n}}$
that serves as a universal
$\mathrm {True}_{\Sigma _{n}}$
that serves as a universal
![]() $\Sigma _{n}$
-predicate within
$\Sigma _{n}$
-predicate within
![]() $\mathsf {PA}$
(indeed
$\mathsf {PA}$
(indeed
![]() $\mathrm {I\Delta }_{0}+\mathrm {Exp}$
suffices for this purpose). Thus, if
$\mathrm {I\Delta }_{0}+\mathrm {Exp}$
suffices for this purpose). Thus, if
![]() $\mathcal {M}\models \mathsf {PA}$
, and
$\mathcal {M}\models \mathsf {PA}$
, and
![]() $F_{n}$
= the set of
$F_{n}$
= the set of
![]() $\Sigma _{n}$
-formulae as computed in
$\Sigma _{n}$
-formulae as computed in
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $\mathrm {True}_{\Sigma _{n}}^{\mathcal {M}}$
is an
$\mathrm {True}_{\Sigma _{n}}^{\mathcal {M}}$
is an
![]() $F_{n}$
-truth class that is
$F_{n}$
-truth class that is
![]() $F_{n}$
-disjunctively and
$F_{n}$
-disjunctively and
![]() $F_{n}$
-deductively correct. Note that if
$F_{n}$
-deductively correct. Note that if
![]() $\mathcal {M}$
is nonstandard,
$\mathcal {M}$
is nonstandard,
![]() $F_{n}$
includes nonstandard formulae.
$F_{n}$
includes nonstandard formulae.
The following proposition codifies the inter-definability of truth classes and extensional satisfaction classes. The close relationship between extensional satisfaction classes and truth classes was first made explicit in [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12]; for further elaborations see [Reference Cieśliński4, Chapter 7] and [Reference Wcisło31]. In what follows
![]() $\mathsf {num}$
is the
$\mathsf {num}$
is the
![]() $\mathsf {PA}$
-definable function
$\mathsf {PA}$
-definable function
![]() $m\mapsto _{\mathsf {num}}\underline {m}$
,where
$m\mapsto _{\mathsf {num}}\underline {m}$
,where
![]() $\underline {m}$
is the numeral for
$\underline {m}$
is the numeral for
![]() $m\in M,$
and
$m\in M,$
and
![]() $\varphi (\mathsf {num}\circ \alpha )$
is the
$\varphi (\mathsf {num}\circ \alpha )$
is the
![]() $\mathcal {L}_{\mathsf {PA}}$
-sentence obtained by replacing each occurrence of a free variable x of
$\mathcal {L}_{\mathsf {PA}}$
-sentence obtained by replacing each occurrence of a free variable x of
![]() $\varphi $
with
$\varphi $
with
![]() $\underline {m}$
, where
$\underline {m}$
, where
![]() $\alpha (x)=m.$
$\alpha (x)=m.$
Proposition 2.14. Suppose
![]() $\mathcal {M}\models \mathsf {PA}$
, T is an
$\mathcal {M}\models \mathsf {PA}$
, T is an
![]() $F$
-truth class on
$F$
-truth class on
![]() $\mathcal {M}$
, and S is an extensional F-satisfaction class on
$\mathcal {M}$
, and S is an extensional F-satisfaction class on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
-
(a)
 $\mathcal {S}(T)$
is an extensional F-satisfaction class on
$\mathcal {S}(T)$
is an extensional F-satisfaction class on
 $\mathcal {M}$
, where
$\mathcal {M}$
, where
 $\mathcal {S}(T)$
is defined as the collection of ordered pairs
$\mathcal {S}(T)$
is defined as the collection of ordered pairs
 $(\varphi ,\alpha )$
such that
$(\varphi ,\alpha )$
such that
 $\varphi (\mathsf {num}\circ \alpha )\in T.$
$\varphi (\mathsf {num}\circ \alpha )\in T.$
-
(b)
 $\mathcal {T}(S)$
is an F-truth class on
$\mathcal {T}(S)$
is an F-truth class on
 $\mathcal {M}$
, where
$\mathcal {M}$
, where
 $\mathcal {T}(S)$
is defined as the collection of
$\mathcal {T}(S)$
is defined as the collection of
 $\varphi $
such that
$\varphi $
such that
 $\left ( \varphi ,\varnothing \right ) \in S$
(where
$\left ( \varphi ,\varnothing \right ) \in S$
(where
 $\varnothing $
is the empty assignment).
$\varnothing $
is the empty assignment). -
(c)
 $\mathcal {S}(\mathcal {T}(S))=S$
, and
$\mathcal {S}(\mathcal {T}(S))=S$
, and
 $\mathcal {T}(\mathcal {S(}T))=T.$
$\mathcal {T}(\mathcal {S(}T))=T.$
The following result plays a key role in this paper; for a modern exposition see [Reference Hájek and Pudlák15, theorem I.4.33].
Mostowski’s Reflection Theorem 2.15.
For each
![]() $n\in \omega $
, the consistency of the set of sentences in
$n\in \omega $
, the consistency of the set of sentences in
![]() $\mathrm{True}_{\Sigma _{n}}$
is provable in
$\mathrm{True}_{\Sigma _{n}}$
is provable in
![]() $\mathsf {PA}$
. In particular,
$\mathsf {PA}$
. In particular,
![]() $\mathsf {PA}$
proves the consistency of each of its finitely axiomatizable subtheories.
$\mathsf {PA}$
proves the consistency of each of its finitely axiomatizable subtheories.
Remark 2.16. Mostowski’s Reflection Theorem, together with the Arithmetized Completeness Theorem allow us to start with any model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
and build an end extension
$\mathsf {PA}$
and build an end extension
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathcal {M}$
that satisfies
$\mathcal {M}$
that satisfies
![]() $\mathsf {PA}$
, and moreover
$\mathsf {PA}$
, and moreover
![]() $\mathcal {N}$
is strongly interpretable in
$\mathcal {N}$
is strongly interpretable in
![]() $\mathcal {M}$
in the sense that
$\mathcal {M}$
in the sense that
![]() $\mathcal {N}$
is interpretable in
$\mathcal {N}$
is interpretable in
![]() $\mathcal {M}$
and there is an
$\mathcal {M}$
and there is an
![]() $\mathcal {M}$
-definable F-truth class
$\mathcal {M}$
-definable F-truth class
![]() $T_{\mathcal {N}}$
on
$T_{\mathcal {N}}$
on
![]() $\mathcal {N}$
for
$\mathcal {N}$
for
![]() $F=\mathsf {Form}^{\mathcal {M}}.$
To see this, consider the arithmetical formula
$F=\mathsf {Form}^{\mathcal {M}}.$
To see this, consider the arithmetical formula
![]() $\theta (i):=\mathrm {Con}\left ( \mathsf {PA}_{i}\right ) $
, where
$\theta (i):=\mathrm {Con}\left ( \mathsf {PA}_{i}\right ) $
, where
![]() $\mathsf {PA}_{i}$
is the set of axioms of
$\mathsf {PA}_{i}$
is the set of axioms of
![]() $\mathsf {PA}$
whose code is at most i. Mostowski’s Reflection Theorem implies that
$\mathsf {PA}$
whose code is at most i. Mostowski’s Reflection Theorem implies that
![]() $\mathcal {M}\models \theta (n)$
for each standard
$\mathcal {M}\models \theta (n)$
for each standard
![]() $n.$
Hence by overspill
$n.$
Hence by overspill
![]() $\mathcal {M}\models \theta (e)$
for some nonstandard element e of
$\mathcal {M}\models \theta (e)$
for some nonstandard element e of
![]() $\mathcal {M}$
. By invoking the Arithmetized Completeness Theorem (as in [Reference Kaye18, theorem 13.13]) within
$\mathcal {M}$
. By invoking the Arithmetized Completeness Theorem (as in [Reference Kaye18, theorem 13.13]) within
![]() $\mathcal {M}$
we can conclude that there is a model
$\mathcal {M}$
we can conclude that there is a model
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathsf {PA}$
whose elementary diagram is
$\mathsf {PA}$
whose elementary diagram is
![]() $\mathcal {M}$
-definable; and moreover, by a straightforward internal recursion within
$\mathcal {M}$
-definable; and moreover, by a straightforward internal recursion within
![]() $\mathcal {M}$
there is an
$\mathcal {M}$
there is an
![]() $\mathcal {M}$
-definable embedding j of
$\mathcal {M}$
-definable embedding j of
![]() $\mathcal {M}$
onto an initial segment of
$\mathcal {M}$
onto an initial segment of
![]() $\mathcal {N}$
. Thus by identifying
$\mathcal {N}$
. Thus by identifying
![]() $\mathcal {M}$
with its image under j, we can assume without loss of generality that
$\mathcal {M}$
with its image under j, we can assume without loss of generality that
![]() $\mathcal {N}$
is an end extension of
$\mathcal {N}$
is an end extension of
![]() $\mathcal {M}$
. Note that the Arithmetized Completeness Theorem applied within
$\mathcal {M}$
. Note that the Arithmetized Completeness Theorem applied within
![]() $\mathcal {M}$
yields an
$\mathcal {M}$
yields an
![]() $\mathcal {M}$
-definable predicate
$\mathcal {M}$
-definable predicate
![]() $T_{0}$
such that
$T_{0}$
such that
![]() $(\mathcal {N},T_{0})$
satisfies the slightly weaker form of
$(\mathcal {N},T_{0})$
satisfies the slightly weaker form of
![]() $\mathsf {CT}^{-}(\mathsf {F})$
for
$\mathsf {CT}^{-}(\mathsf {F})$
for
![]() $F=\mathsf {Form}^{\mathcal {M}}$
in which the closed terms are limited to those in
$F=\mathsf {Form}^{\mathcal {M}}$
in which the closed terms are limited to those in
![]() $\mathcal {M}$
. However, thanks to the availability of the closed-term-evaluation function in
$\mathcal {M}$
. However, thanks to the availability of the closed-term-evaluation function in
![]() $\mathcal {N}$
, the simple ‘trick’ used in Remark 2.12 can be used to obtain an
$\mathcal {N}$
, the simple ‘trick’ used in Remark 2.12 can be used to obtain an
![]() $\mathcal {M}$
-definable predicate T such that
$\mathcal {M}$
-definable predicate T such that
![]() $(\mathcal {N},F,T)$
satisfies
$(\mathcal {N},F,T)$
satisfies
![]() $\mathsf {CT}^{-}(\mathsf {F}).$
Note that since
$\mathsf {CT}^{-}(\mathsf {F}).$
Note that since
![]() $\mathcal {N}$
is an end extension of
$\mathcal {N}$
is an end extension of
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathrm {True}_{\Sigma _{1}}^{\mathcal {M}}\subseteq \mathrm {True}_{\Sigma _{1}}^{\mathcal {M}}$
, and therefore if s is a closed arithmetical term in the sense of
$\mathrm {True}_{\Sigma _{1}}^{\mathcal {M}}\subseteq \mathrm {True}_{\Sigma _{1}}^{\mathcal {M}}$
, and therefore if s is a closed arithmetical term in the sense of
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $\mathrm {val}^{\mathcal {M}}(s)=\mathrm {val}^{\mathcal {N}}(s)$
. Since
$\mathrm {val}^{\mathcal {M}}(s)=\mathrm {val}^{\mathcal {N}}(s)$
. Since
![]() $T_{0}$
is the Tarskian satisfaction class of the structure
$T_{0}$
is the Tarskian satisfaction class of the structure
![]() $\mathcal {N}$
as computed in the model
$\mathcal {N}$
as computed in the model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
,
$\mathsf {PA}$
,
![]() $T_{0}$
as well as T have many regularity properties of Tarskian satisfaction classes; in particular T is both M-deductively and M-deductively closed. As shown in (Stage 1 of) the proof of Theorem 3.3, if
$T_{0}$
as well as T have many regularity properties of Tarskian satisfaction classes; in particular T is both M-deductively and M-deductively closed. As shown in (Stage 1 of) the proof of Theorem 3.3, if
![]() $\mathcal {M}$
is a countable recursively saturated model of
$\mathcal {M}$
is a countable recursively saturated model of
![]() $\mathsf {PA}$
, we can additionally require that there is an isomorphism
$\mathsf {PA}$
, we can additionally require that there is an isomorphism
![]() $f:\mathcal {N}\rightarrow \mathcal {M}$
. Therefore by defining the cut I of
$f:\mathcal {N}\rightarrow \mathcal {M}$
. Therefore by defining the cut I of
![]() $\mathcal {M}$
as
$\mathcal {M}$
as
![]() $f(M)$
, the image
$f(M)$
, the image
![]() $f(T)$
of T is under f is an
$f(T)$
of T is under f is an
![]() $F\cap I$
-satisfaction class on
$F\cap I$
-satisfaction class on
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $f(T)$
is both I-disjunctively and I-deductively correct.
$f(T)$
is both I-disjunctively and I-deductively correct.
3 The first construction
Suppose I is a cut of a countable recursively saturated model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
. In Definition 3.1 we define a subset
$\mathsf {PA}$
. In Definition 3.1 we define a subset
![]() $\mathsf {Frug}_{I}^{\mathcal {M}}$
of
$\mathsf {Frug}_{I}^{\mathcal {M}}$
of
![]() $\mathsf {Form}^{\mathcal {M}}$
, and then in Theorem 3.3 we build an F-truth class T on
$\mathsf {Form}^{\mathcal {M}}$
, and then in Theorem 3.3 we build an F-truth class T on
![]() $\mathcal {M}$
for
$\mathcal {M}$
for
![]() $F=\mathsf {Frug}_{\omega }^{\mathcal {M}}$
(i.e., for
$F=\mathsf {Frug}_{\omega }^{\mathcal {M}}$
(i.e., for
![]() $I=\omega ,$
where
$I=\omega ,$
where
![]() $\omega $
is the standard cut of
$\omega $
is the standard cut of
![]() $\mathcal {M}$
) such that T is F-disjunctively correct (in the sense of Definition 2.11(c)). In Theorem 3.4 we extend this result to arbitrarily large cuts I of
$\mathcal {M}$
) such that T is F-disjunctively correct (in the sense of Definition 2.11(c)). In Theorem 3.4 we extend this result to arbitrarily large cuts I of
![]() $\mathcal {M}$
. Theorem 3.3 and 3.4 could have been packaged as a single result, but in the interest of offering the reader a clear intuition of the mechanism of the first construction we opted for the current format; as a result we provide the full details of the proof of Theorem 3.3 and only offer a proof outline for Theorem 3.4.
$\mathcal {M}$
. Theorem 3.3 and 3.4 could have been packaged as a single result, but in the interest of offering the reader a clear intuition of the mechanism of the first construction we opted for the current format; as a result we provide the full details of the proof of Theorem 3.3 and only offer a proof outline for Theorem 3.4.
Definition 3.1. A formula
![]() $\varphi $
is frugal if
$\varphi $
is frugal if
![]() $\varphi $
has no occurrence of a closed term. We use
$\varphi $
has no occurrence of a closed term. We use
![]() $\mathsf {Frug}(\mathcal {\varphi })$
for the
$\mathsf {Frug}(\mathcal {\varphi })$
for the
![]() $\mathcal {L}_{\mathsf {PA}}$
-formula that expresses “
$\mathcal {L}_{\mathsf {PA}}$
-formula that expresses “
![]() $\varphi $
is a frugal
$\varphi $
is a frugal
![]() $\mathcal {L}_{\mathsf {PA}} $
-formula”. Given
$\mathcal {L}_{\mathsf {PA}} $
-formula”. Given
![]() $\mathcal {M}\models \mathsf {PA}$
, and
$\mathcal {M}\models \mathsf {PA}$
, and
![]() $m\in M$
, we define:
$m\in M$
, we define:
For a cut I of
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathsf {Frug}_{I}^{\mathcal {M}}:=\bigcup \limits _{i\in I}\mathsf {Frug}_{\leq i}^{\mathcal {M}}$
.
$\mathsf {Frug}_{I}^{\mathcal {M}}:=\bigcup \limits _{i\in I}\mathsf {Frug}_{\leq i}^{\mathcal {M}}$
.
Remark 3.2. The above definitions make it evident that for any cut I of
![]() $\mathcal {M}$
that is closed under addition,
$\mathcal {M}$
that is closed under addition,
![]() $\mathsf {Frug}_{I}^{\mathcal {M}}$
is closed under Boolean connectives, existential quantification, and immediate subformulae (here we are assuming the coding of formulae is done in a standard way that ensures that the code of every immediate subformulae of a given formula
$\mathsf {Frug}_{I}^{\mathcal {M}}$
is closed under Boolean connectives, existential quantification, and immediate subformulae (here we are assuming the coding of formulae is done in a standard way that ensures that the code of every immediate subformulae of a given formula
![]() $\varphi $
is less than the code of
$\varphi $
is less than the code of
![]() $\varphi $
). In particular, if T is an F-truth class on
$\varphi $
). In particular, if T is an F-truth class on
![]() $\mathcal {M}$
for
$\mathcal {M}$
for
![]() $F=\mathsf {Frug}_{I}^{\mathcal {M}}$
and
$F=\mathsf {Frug}_{I}^{\mathcal {M}}$
and
![]() $\sigma $
is a sentence in
$\sigma $
is a sentence in
![]() $\mathcal {M}$
that is obtained from replacing all of the free variables of a formula in F with closed terms, i.e.,
$\mathcal {M}$
that is obtained from replacing all of the free variables of a formula in F with closed terms, i.e.,
![]() $\sigma \in \mathsf {FSent}^{(\mathcal {M},F)}$
, then by
$\sigma \in \mathsf {FSent}^{(\mathcal {M},F)}$
, then by
![]() $\mathsf {tarski}_{2}(\mathsf {T,F})$
either
$\mathsf {tarski}_{2}(\mathsf {T,F})$
either
![]() $\sigma \in T$
or
$\sigma \in T$
or
![]() $\lnot \sigma \in T$
(but not both). Also note that in this context the sentences
$\lnot \sigma \in T$
(but not both). Also note that in this context the sentences
![]() $\sigma \in \mathsf {FSent}^{(\mathcal {M},F)}$
are precisely those sentences
$\sigma \in \mathsf {FSent}^{(\mathcal {M},F)}$
are precisely those sentences
![]() $\sigma \in \mathsf {Sent}^{\mathcal {M}}$
such that for some
$\sigma \in \mathsf {Sent}^{\mathcal {M}}$
such that for some
![]() $i\in I$
the number of distinct closed terms that occur in
$i\in I$
the number of distinct closed terms that occur in
![]() $\sigma $
is i (as computed in
$\sigma $
is i (as computed in
![]() $\mathcal {M}$
).
$\mathcal {M}$
).
Theorem 3.3. Suppose
![]() $\mathcal {M}$
is a countable recursively saturated model of
$\mathcal {M}$
is a countable recursively saturated model of
![]() $\mathsf {PA}$
, and let
$\mathsf {PA}$
, and let
![]() $F=\mathsf {Frug}_{\omega }^{\mathcal {M}}$
. There is an F-truth class T on
$F=\mathsf {Frug}_{\omega }^{\mathcal {M}}$
. There is an F-truth class T on
![]() $\mathcal {M}$
that is F-disjunctively correct.
$\mathcal {M}$
that is F-disjunctively correct.
Proof. The proof has two stages.
STAGE 1. In this stage, starting with a countable recursively saturated model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
, we use a variant of the construction outlined in Remark 2.16 to build an appropriate end extension
$\mathsf {PA}$
, we use a variant of the construction outlined in Remark 2.16 to build an appropriate end extension
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathcal {M}$
with two key properties:
$\mathcal {M}$
with two key properties:
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are isomorphic, and yet there is an F-truth class
$\mathcal {N}$
are isomorphic, and yet there is an F-truth class
![]() $T_{\mathcal {N}}$
on
$T_{\mathcal {N}}$
on
![]() $\mathcal {N}$
that is definable in
$\mathcal {N}$
that is definable in
![]() $\mathcal {M}$
, where
$\mathcal {M}$
, where
![]() $F=\mathsf {Form}^{\mathcal {M}}$
. To build such an
$F=\mathsf {Form}^{\mathcal {M}}$
. To build such an
![]() $\mathcal {N}$
, we first observe that by recursive saturation we can find an element c in
$\mathcal {N}$
, we first observe that by recursive saturation we can find an element c in
![]() $\mathcal {M}$
that codes
$\mathcal {M}$
that codes
![]() $\mathrm {Th}(\mathcal {M})$
by realizing the recursive type
$\mathrm {Th}(\mathcal {M})$
by realizing the recursive type
![]() $\Sigma (v)$
, where
$\Sigma (v)$
, where
where
![]() $\ulcorner \varphi \urcorner $
is the Gödel number for
$\ulcorner \varphi \urcorner $
is the Gödel number for
![]() $\varphi $
,
$\varphi $
,
![]() $\in _{\mathsf {Ack}}$
is “Ackermann’s
$\in _{\mathsf {Ack}}$
is “Ackermann’s
![]() $\in $
”, as in Definition 2.1(d). Next, let
$\in $
”, as in Definition 2.1(d). Next, let
![]() $\left \langle \varphi _{n}:n\in \omega \right \rangle $
be a recursive enumeration of
$\left \langle \varphi _{n}:n\in \omega \right \rangle $
be a recursive enumeration of
![]() $\mathcal {L}_{\mathsf {PA}}$
-sentences, and consider the arithmetical formula
$\mathcal {L}_{\mathsf {PA}}$
-sentences, and consider the arithmetical formula
![]() $\gamma (i)$
defined below:
$\gamma (i)$
defined below:
where
![]() $\mathrm {Con}(X)$
expresses the formal consistency of X. It is easy to see, using Mostowski’s Reflection Theorem and our choice of c that
$\mathrm {Con}(X)$
expresses the formal consistency of X. It is easy to see, using Mostowski’s Reflection Theorem and our choice of c that
![]() $\mathcal {M}\models \gamma (n)$
for each standard
$\mathcal {M}\models \gamma (n)$
for each standard
![]() $n.$
Hence by overspill
$n.$
Hence by overspill
![]() $\mathcal {M}\models \gamma (d)$
for some nonstandard element d of
$\mathcal {M}\models \gamma (d)$
for some nonstandard element d of
![]() $\mathcal {M}$
. By invoking the Arithmetized Completeness Theorem [Reference Kaye18, theorem 13.13] within
$\mathcal {M}$
. By invoking the Arithmetized Completeness Theorem [Reference Kaye18, theorem 13.13] within
![]() $\mathcal {M}$
, with a reasoning similar to that in Remark 2.16 we can conclude that there is a model
$\mathcal {M}$
, with a reasoning similar to that in Remark 2.16 we can conclude that there is a model
![]() $\mathcal {N}$
of T with the following properties:
$\mathcal {N}$
of T with the following properties:
-
(1)
 $\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N}).$
$\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N}).$
-
(2) There is an
 $\mathcal {M}$
-definable
$\mathcal {M}$
-definable
 $T_{\mathcal {N}}$
such that
$T_{\mathcal {N}}$
such that
 $(\mathcal {N},\mathsf {Form}^{\mathcal {M}},T)\models \mathsf {CT}^{-}(\mathsf {F})$
.
$(\mathcal {N},\mathsf {Form}^{\mathcal {M}},T)\models \mathsf {CT}^{-}(\mathsf {F})$
. -
(3)
 $\mathcal {N}$
is recursively saturated.
$\mathcal {N}$
is recursively saturated. -
(4) There is an
 $\mathcal {M}$
-definable embedding j of
$\mathcal {M}$
-definable embedding j of
 $\mathcal {M}$
as an initial segment of
$\mathcal {M}$
as an initial segment of
 $\mathcal {N}$
.
$\mathcal {N}$
. -
(5)
 $\mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N}).$
$\mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N}).$
-
(6) There is an isomorphism
 $f:\mathcal {M}\rightarrow \mathcal {N}.$
$f:\mathcal {M}\rightarrow \mathcal {N}.$
Note that (3) is a consequence of (2) and a routine overspill argument, as in Proposition 15.4 of [Reference Kaye18]; (5) is consequence of (4) since standard systems are preserved by end extension; and (6) follows from (1) and (5) by Theorem 2.2.
STAGE 2. In this stage we construct the desired F-truth class
![]() $T $
on
$T $
on
![]() $\mathcal {M}$
for
$\mathcal {M}$
for
![]() ${F=\mathsf {Frug}_{\omega }^{\mathcal {M}}}$
. Suppose
${F=\mathsf {Frug}_{\omega }^{\mathcal {M}}}$
. Suppose
![]() $\varphi (x_{1},x_{2},\dots ,x_{k})\in F$
, where
$\varphi (x_{1},x_{2},\dots ,x_{k})\in F$
, where
![]() $k\in \omega ,$
and let
$k\in \omega ,$
and let
![]() $t_{1},t_{2},\dots ,t_{k}$
be elements of
$t_{1},t_{2},\dots ,t_{k}$
be elements of
![]() $\mathsf {ClTerm}^{\mathcal {M}}$
(closed terms in the sense of
$\mathsf {ClTerm}^{\mathcal {M}}$
(closed terms in the sense of
![]() $\mathcal {M}$
). Note that
$\mathcal {M}$
). Note that
![]() $\varphi $
as well as
$\varphi $
as well as
![]() $t_{1},t_{2},\dots ,t_{k}$
are allowed to be nonstandard. Using the truth class
$t_{1},t_{2},\dots ,t_{k}$
are allowed to be nonstandard. Using the truth class
![]() $T_{\mathcal {N}}$
as in (2) of Stage 1, together with the isomorphism f as (6) of Stage 1, we define T to consist of
$T_{\mathcal {N}}$
as in (2) of Stage 1, together with the isomorphism f as (6) of Stage 1, we define T to consist of
![]() $\varphi (t_{1},t_{2},\dots ,t_{k})\in \mathsf {FSent}^{\left ( \mathcal {M},F\right ) }$
such that
$\varphi (t_{1},t_{2},\dots ,t_{k})\in \mathsf {FSent}^{\left ( \mathcal {M},F\right ) }$
such that
where
![]() $m_{1},m_{2},\dots ,m_{k}$
are elements of M such that
$m_{1},m_{2},\dots ,m_{k}$
are elements of M such that
![]() $\mathcal {M}\models m_{i}=t_{i}^{\circ }$
for
$\mathcal {M}\models m_{i}=t_{i}^{\circ }$
for
![]() $1\leq i\leq k.$
In other words,
$1\leq i\leq k.$
In other words,
In the above we simply write
![]() $t^{\circ }$
for the element of
$t^{\circ }$
for the element of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathcal {M}\models m=t^{\circ }$
. As noted in the last sentence of Remark 2.16, since
$\mathcal {M}\models m=t^{\circ }$
. As noted in the last sentence of Remark 2.16, since
![]() $t\in M, t^{\circ }$
as-computed-in-
$t\in M, t^{\circ }$
as-computed-in-
![]() $\mathcal {M}$
coincides with
$\mathcal {M}$
coincides with
![]() $t^{\circ }$
as-computed-in
$t^{\circ }$
as-computed-in
![]() $\mathcal {N}.$
$\mathcal {N}.$
We first verify that T is an F-truth class on
![]() $\mathcal {M}$
. By the definition of T, the axiom
$\mathcal {M}$
. By the definition of T, the axiom
![]() $\mathrm {tarski}_{0}(\mathsf {F})=\forall x\ \ \left [ \mathsf {T}(x)\rightarrow x\in \mathsf {FSent}\right ] $
clearly holds in
$\mathrm {tarski}_{0}(\mathsf {F})=\forall x\ \ \left [ \mathsf {T}(x)\rightarrow x\in \mathsf {FSent}\right ] $
clearly holds in
![]() $(\mathcal {M},F,T)$
. Recall that
$(\mathcal {M},F,T)$
. Recall that
![]() $\mathrm {tarski}_{1}(\mathsf {F,T})$
asserts the equivalence of
$\mathrm {tarski}_{1}(\mathsf {F,T})$
asserts the equivalence of
![]() $\mathsf {T}(s=t)$
and
$\mathsf {T}(s=t)$
and
![]() ${s}^{\circ }={t}^{\circ }$
for all closed terms s and t. To see that
${s}^{\circ }={t}^{\circ }$
for all closed terms s and t. To see that
![]() $(\mathcal {M},F,T)\models \mathrm {tarski}_{1}(\mathsf {F})$
we argue as follows:
$(\mathcal {M},F,T)\models \mathrm {tarski}_{1}(\mathsf {F})$
we argue as follows:
 $$ \begin{align*} (s=t)&\in T\text{ iff }\left( \underline{f(s^{\circ })}=\underline{f(t^{\circ })}\right) \in T_{\mathcal{N}},\\ &\ [\text{by the definition of }T]\\ \Big( \underline{f(s^{\circ })}&=\underline{f(t^{\circ })}\Big) \in T_{\mathcal{N}}\text{ iff }f(s^{\circ })=f(t^{\circ }),\\ [\text{since }\left( \underline{x}\right) ^{\circ }&=x\text{ and }(\mathcal{N},F,T_{\mathcal{N}})\models \mathrm{tarski}_{0}(\mathsf{F})]\\ &f(s^{\circ })=f(t^{\circ })\text{ iff }s^{\circ }=t^{\circ }.\\ &\ \ [\text{since }f\text{ is injective}].\end{align*} $$
$$ \begin{align*} (s=t)&\in T\text{ iff }\left( \underline{f(s^{\circ })}=\underline{f(t^{\circ })}\right) \in T_{\mathcal{N}},\\ &\ [\text{by the definition of }T]\\ \Big( \underline{f(s^{\circ })}&=\underline{f(t^{\circ })}\Big) \in T_{\mathcal{N}}\text{ iff }f(s^{\circ })=f(t^{\circ }),\\ [\text{since }\left( \underline{x}\right) ^{\circ }&=x\text{ and }(\mathcal{N},F,T_{\mathcal{N}})\models \mathrm{tarski}_{0}(\mathsf{F})]\\ &f(s^{\circ })=f(t^{\circ })\text{ iff }s^{\circ }=t^{\circ }.\\ &\ \ [\text{since }f\text{ is injective}].\end{align*} $$
Next we verify that
![]() $(\mathcal {M},F,T)$
satisfies
$(\mathcal {M},F,T)$
satisfies
![]() $\mathrm {tarski}_{2}(\mathsf {F,T})$
, which stipulates that
$\mathrm {tarski}_{2}(\mathsf {F,T})$
, which stipulates that
![]() $\mathsf {T}$
commutes with negation. Suppose
$\mathsf {T}$
commutes with negation. Suppose
![]() $\varphi (t_{1},t_{2},\dots ,t_{k})=\lnot \psi (t_{1},t_{2},\dots ,t_{k})\in \mathsf {FSent}^{(\mathcal {M},F)}.$
Then we have:
$\varphi (t_{1},t_{2},\dots ,t_{k})=\lnot \psi (t_{1},t_{2},\dots ,t_{k})\in \mathsf {FSent}^{(\mathcal {M},F)}.$
Then we have:
 $$ \begin{align*} \lnot \psi (t_{1},t_{2},&\dots,t_{k})\in T\text{ iff }\lnot \psi (\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}},\\&\quad\qquad[\text{by the definition of }T]\\\lnot \psi (\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},&\dots, \underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}}\text{ iff }\psi (\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\notin T_{\mathcal{N}},\\\qquad&[\text{since }(\mathcal{N},F,T_{\mathcal{N}})\models \mathrm{tarski}_{2}(\mathsf{F}) ]\\\psi (\underline{f(t_{1}^{\circ })},&\underline{f(t_{2}^{\circ })},\dots, \underline{f(t_{k}^{\circ })})\notin T_{\mathcal{N}}\text{ iff }\psi (t_{1},t_{2},\dots,t_{k})\notin T.\\&\qquad[\text{by the definition of }T] \end{align*} $$
$$ \begin{align*} \lnot \psi (t_{1},t_{2},&\dots,t_{k})\in T\text{ iff }\lnot \psi (\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}},\\&\quad\qquad[\text{by the definition of }T]\\\lnot \psi (\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},&\dots, \underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}}\text{ iff }\psi (\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\notin T_{\mathcal{N}},\\\qquad&[\text{since }(\mathcal{N},F,T_{\mathcal{N}})\models \mathrm{tarski}_{2}(\mathsf{F}) ]\\\psi (\underline{f(t_{1}^{\circ })},&\underline{f(t_{2}^{\circ })},\dots, \underline{f(t_{k}^{\circ })})\notin T_{\mathcal{N}}\text{ iff }\psi (t_{1},t_{2},\dots,t_{k})\notin T.\\&\qquad[\text{by the definition of }T] \end{align*} $$
An argument similar to the above shows that
![]() $\mathsf {T}$
commutes with disjunction, thus
$\mathsf {T}$
commutes with disjunction, thus
![]() $\mathrm {tarski}_{3}(\mathsf {F,T})$
holds in
$\mathrm {tarski}_{3}(\mathsf {F,T})$
holds in
![]() $(\mathcal {M},F,T)$
; we leave the proof for the reader.
$(\mathcal {M},F,T)$
; we leave the proof for the reader.
The axiom
![]() $\mathrm {tarski}_{4}(\mathsf {F})$
stipulates that
$\mathrm {tarski}_{4}(\mathsf {F})$
stipulates that
![]() $\mathsf {T}$
commutes with existential quantification. For this purpose suppose
$\mathsf {T}$
commutes with existential quantification. For this purpose suppose
![]() $\varphi (t_{1},t_{2},\dots ,t_{k})=\exists v\ \psi (x,t_{1},\dots ,t_{k})\in \mathsf {FSent}^{(\mathcal {M},F)}.$
Then we have:
$\varphi (t_{1},t_{2},\dots ,t_{k})=\exists v\ \psi (x,t_{1},\dots ,t_{k})\in \mathsf {FSent}^{(\mathcal {M},F)}.$
Then we have:
 $$ \begin{align*} \exists v\ \psi (x,t_{1},\dots,t_{k})\in T\text{ iff }\exists v\ \psi (v, \underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}},\qquad\qquad\qquad\\ [\text{by the definition of }T]\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\ \exists v\ \psi (v,\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ})},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}}\text{ iff }\exists b\in N \psi (\underline{b},\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}},\\ [\text{since }(\mathcal{N},F_{0},T_{\mathcal{N}})\models \mathrm{tarski}_{4}(\mathsf{F})]\qquad\qquad\qquad\qquad\qquad\qquad\\ \exists b\in N \psi (\underline{b},\underline{f(t_{1}^{\circ })}, \underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}}\text{ iff }\exists c\in M\ f(c)=b, \psi (\underline{c}, t_{1},\dots,t_{k})\in T.\\ \quad[\text{by the definition of }T,\text{ together with surjectivity of }f]\qquad\qquad\qquad \end{align*} $$
$$ \begin{align*} \exists v\ \psi (x,t_{1},\dots,t_{k})\in T\text{ iff }\exists v\ \psi (v, \underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}},\qquad\qquad\qquad\\ [\text{by the definition of }T]\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\ \exists v\ \psi (v,\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ})},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}}\text{ iff }\exists b\in N \psi (\underline{b},\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}},\\ [\text{since }(\mathcal{N},F_{0},T_{\mathcal{N}})\models \mathrm{tarski}_{4}(\mathsf{F})]\qquad\qquad\qquad\qquad\qquad\qquad\\ \exists b\in N \psi (\underline{b},\underline{f(t_{1}^{\circ })}, \underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}}\text{ iff }\exists c\in M\ f(c)=b, \psi (\underline{c}, t_{1},\dots,t_{k})\in T.\\ \quad[\text{by the definition of }T,\text{ together with surjectivity of }f]\qquad\qquad\qquad \end{align*} $$
This concludes our verification that T is an F-satisfaction class on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
To see that T is F-disjunctively correct suppose
![]() $\delta =\bigvee \limits _{i<m}\varphi _{i}\in \mathsf {FSent}^{\left ( \mathcal {M}, F\right ) }=\mathsf {Sent}_{\omega }^{\mathcal {M}}$
(where m is a possibly nonstandard element of
$\delta =\bigvee \limits _{i<m}\varphi _{i}\in \mathsf {FSent}^{\left ( \mathcal {M}, F\right ) }=\mathsf {Sent}_{\omega }^{\mathcal {M}}$
(where m is a possibly nonstandard element of
![]() $\mathcal {M}$
). Note that each
$\mathcal {M}$
). Note that each
![]() $\varphi _{i}$
can be written as
$\varphi _{i}$
can be written as
![]() $\varphi _{i}(t_{1},\dots ,t_{k})$
for some
$\varphi _{i}(t_{1},\dots ,t_{k})$
for some
![]() $k\in \omega $
with the understanding that the closed terms occurring in
$k\in \omega $
with the understanding that the closed terms occurring in
![]() $\varphi _{i}$
are among
$\varphi _{i}$
are among
![]() $t_{1},\dots ,t_{k}.$
Then we have:
$t_{1},\dots ,t_{k}.$
Then we have:
 $$ \begin{align*} \Bigg( \bigvee\limits_{i<m}\varphi _{i}(t_{1},&\dots,t_{k})\Bigg) \in T\text{ iff } \left( \bigvee\limits_{i<m}\varphi _{i}(\underline{f(t_{1}^{\circ })}, \underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ})})\right) \in T_{\mathcal{N}},\\ &\qquad\qquad[\text{by the definition of }T]\\[-2.6pc]\end{align*} $$
$$ \begin{align*} \Bigg( \bigvee\limits_{i<m}\varphi _{i}(t_{1},&\dots,t_{k})\Bigg) \in T\text{ iff } \left( \bigvee\limits_{i<m}\varphi _{i}(\underline{f(t_{1}^{\circ })}, \underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ})})\right) \in T_{\mathcal{N}},\\ &\qquad\qquad[\text{by the definition of }T]\\[-2.6pc]\end{align*} $$
 $$ \begin{align*} \Bigg( \bigvee\limits_{i<m}\varphi _{i}&(\underline{f(t_{1}^{\circ })}, \underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\Bigg) \in T_{\mathcal{N}}\text{ iff }\exists i<m \varphi_{i}(\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}},\\ &\qquad[\text{since }T_{\mathcal{N}}\text{ is }F\text{-disjunctively correct and }\delta \in \mathsf{FSent}^{\left( \mathcal{M},F\right) }],\\[-2.4pc]\end{align*} $$
$$ \begin{align*} \Bigg( \bigvee\limits_{i<m}\varphi _{i}&(\underline{f(t_{1}^{\circ })}, \underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\Bigg) \in T_{\mathcal{N}}\text{ iff }\exists i<m \varphi_{i}(\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}},\\ &\qquad[\text{since }T_{\mathcal{N}}\text{ is }F\text{-disjunctively correct and }\delta \in \mathsf{FSent}^{\left( \mathcal{M},F\right) }],\\[-2.4pc]\end{align*} $$
 $$ \begin{align*} \exists i<m \varphi _{i}(\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},&\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}}\text{ iff }\exists i<m \bigvee\limits_{i<m}\varphi _{i}(t_{1},\dots,t_{k})\in T.\\ &\quad[\text{by the definition of }T]\\[-35pt] \end{align*} $$
$$ \begin{align*} \exists i<m \varphi _{i}(\underline{f(t_{1}^{\circ })},\underline{f(t_{2}^{\circ })},&\dots,\underline{f(t_{k}^{\circ })})\in T_{\mathcal{N}}\text{ iff }\exists i<m \bigvee\limits_{i<m}\varphi _{i}(t_{1},\dots,t_{k})\in T.\\ &\quad[\text{by the definition of }T]\\[-35pt] \end{align*} $$
Theorem 3.4. Suppose
![]() $\mathcal {M}$
is a countable recursively saturated model of
$\mathcal {M}$
is a countable recursively saturated model of
![]() $\mathsf {PA}$
. There are arbitrarily large cuts
$\mathsf {PA}$
. There are arbitrarily large cuts
![]() $I\prec \mathcal {M}$
such that
$I\prec \mathcal {M}$
such that
![]() $I\cong \mathcal {M}$
with the property that there is an F-truth class T on
$I\cong \mathcal {M}$
with the property that there is an F-truth class T on
![]() $\mathcal {M}$
for
$\mathcal {M}$
for
![]() $F=\mathsf {Frug}_{I}^{\mathcal {M}}$
such that T is F-disjunctively correct.
$F=\mathsf {Frug}_{I}^{\mathcal {M}}$
such that T is F-disjunctively correct.
Proof outline.
Proceed as in Stage 1 of the proof of Theorem 3.3 to get hold of the model
![]() $\mathcal {N}$
, but in Stage 2 invoke Remark 2.6(c) and use Theorem 2.5 instead of Theorem 2.2 to get hold of an isomorphism f between
$\mathcal {N}$
, but in Stage 2 invoke Remark 2.6(c) and use Theorem 2.5 instead of Theorem 2.2 to get hold of an isomorphism f between
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
that pointwise fixes a prescribed cut of
$\mathcal {N}$
that pointwise fixes a prescribed cut of
![]() $\mathcal {M}$
. Note that by Remark 2.6(c) there are arbitrarily large strong cuts I in
$\mathcal {M}$
. Note that by Remark 2.6(c) there are arbitrarily large strong cuts I in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $I\prec \mathcal {M}$
and
$I\prec \mathcal {M}$
and
![]() $I\cong \mathcal {M}$
, and by Remark 2.6(b) such cuts are not
$I\cong \mathcal {M}$
, and by Remark 2.6(b) such cuts are not
![]() $\omega $
-coded from above in
$\omega $
-coded from above in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Remark 3.5. The proofs of Theorem 3.3 and 3.4 show that these two results can be strengthened by requiring the truth predicate T to satisfy further desirable properties such as alphabetic correctness, which stipulates that T is invariant under the renaming of bound variables, and generalized term-extensionality, which stipulates that T is invariant under replacing of terms with the same value. As shown by Łełyk and Wcisło [Reference Łełyk and Wcisło27, theorem 23] the theory obtained by the addition of axioms stipulating alphabetic correctness and generalized term extensionality to
![]() $\mathsf {CT}^{-}[\mathsf {PA}]$
remains conservative over
$\mathsf {CT}^{-}[\mathsf {PA}]$
remains conservative over
![]() $\mathsf {PA}$
.
$\mathsf {PA}$
.
Remark 3.6. In answer to a question of the author, Lawrence Wong noted that Wciłso’s proof of Lachlan’s theorem (as presented in [Reference Kossak and Wcisło21]) shows that if
![]() $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
![]() $\mathsf {PA}$
that has an expansion to a
$\mathsf {PA}$
that has an expansion to a
![]() $\mathsf {Form}_{\omega }^{\mathcal {M}}$
-truth class, then
$\mathsf {Form}_{\omega }^{\mathcal {M}}$
-truth class, then
![]() $\mathcal {M}$
is recursively saturated.
$\mathcal {M}$
is recursively saturated.
Question 3.7. Does every countable recursively saturated model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
carry a full truth class T that is
$\mathsf {PA}$
carry a full truth class T that is
![]() $\mathsf {Form}_{\omega }^{\mathcal {M}}$
-disjunctively correct? More specifically, are the truth classes constructed in Theorem 3.3 and 3.4 extendable to full truth classes?
$\mathsf {Form}_{\omega }^{\mathcal {M}}$
-disjunctively correct? More specifically, are the truth classes constructed in Theorem 3.3 and 3.4 extendable to full truth classes?
4 The second construction
The second construction in this paper employs an arithmetized form of the main construction in [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12] as in Theorem 4.1. Our method of proof of Theorem 4.1 is through an arithmetization of the construction of a truth class satisfying of
![]() $\mathsf {CT}^{-}[$
$\mathsf {CT}^{-}[$
![]() $\mathsf {PA}$
$\mathsf {PA}$
![]() $],$
presented both in [Reference Enayat, Łełyk and Wcisło9, Reference Kossak and Wcisło21], which refine the model-theoretic construction given in [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12] for
$],$
presented both in [Reference Enayat, Łełyk and Wcisło9, Reference Kossak and Wcisło21], which refine the model-theoretic construction given in [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12] for
![]() $\mathsf {PA}$
formulated in a relational language. As we shall see, the compactness and elementary chain argument used in the model-theoretic conservativity proof of
$\mathsf {PA}$
formulated in a relational language. As we shall see, the compactness and elementary chain argument used in the model-theoretic conservativity proof of
![]() $\mathsf {CT}^{-}[\mathsf {PA}]$
over
$\mathsf {CT}^{-}[\mathsf {PA}]$
over
![]() $\mathsf {PA}$
can be proved in the fragment
$\mathsf {PA}$
can be proved in the fragment
![]() $\mathrm {I}\Sigma _{2}$
of
$\mathrm {I}\Sigma _{2}$
of
![]() $\mathsf {PA}$
with the help of the so-called Low Basis Theorem of Recursion Theory.Footnote
4
Note that the results of this section that appear before Theorem 4.5 can be also established by the arithmetization method presented in [Reference Enayat, Łełyk and Wcisło9], or by taking advantage of the main proof-theoretic result of [Reference Leigh25].
$\mathsf {PA}$
with the help of the so-called Low Basis Theorem of Recursion Theory.Footnote
4
Note that the results of this section that appear before Theorem 4.5 can be also established by the arithmetization method presented in [Reference Enayat, Łełyk and Wcisło9], or by taking advantage of the main proof-theoretic result of [Reference Leigh25].
Theorem 4.1 (Joint with Albert Visser).
Suppose
![]() $\mathsf {PA}\vdash \mathrm {Con}(\mathsf {B}),$
where
$\mathsf {PA}\vdash \mathrm {Con}(\mathsf {B}),$
where
![]() $\mathsf {B}$
is some recursively axiomatizable theory extending
$\mathsf {B}$
is some recursively axiomatizable theory extending
![]() $\mathrm {I}\Delta _{0}+\ \mathsf {Exp}$
. Then
$\mathrm {I}\Delta _{0}+\ \mathsf {Exp}$
. Then
![]() $\mathsf {PA}$
strongly interprets
$\mathsf {PA}$
strongly interprets
![]() $\mathsf {CT}^{-}[\mathsf {B}]$
, i.e., there are definitions
$\mathsf {CT}^{-}[\mathsf {B}]$
, i.e., there are definitions
![]() $\delta _{1}$
and
$\delta _{1}$
and
![]() $\delta _{2}$
within
$\delta _{2}$
within
![]() $\mathsf {PA}$
such that for every model
$\mathsf {PA}$
such that for every model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {PA}$
,
$\mathsf {PA}$
,
![]() $\delta _{1}^{\mathcal {M}}=\left ( \mathcal {M}^{\ast },T\right ) \models \mathsf {CT}^{-}[\mathsf {B}]$
and
$\delta _{1}^{\mathcal {M}}=\left ( \mathcal {M}^{\ast },T\right ) \models \mathsf {CT}^{-}[\mathsf {B}]$
and
![]() $\delta _{2}^{\mathcal {M}}$
is the elementary diagram of
$\delta _{2}^{\mathcal {M}}$
is the elementary diagram of
![]() $\left ( \mathcal {M}^{\ast },T\right )$
as viewed from
$\left ( \mathcal {M}^{\ast },T\right )$
as viewed from
![]() $\mathcal {M}.$
$\mathcal {M}.$
Proof. Before starting the proof, we need to review some key definitions and ideas from Recursion Theory. In what follows X and Y are subsets of
![]() $\omega .$
$\omega .$
-
• X is low-
 $\Delta _{2}$
, if X is
$\Delta _{2}$
, if X is
 $\Delta _{2}$
, and
$\Delta _{2}$
, and
 $X^{\prime }\leq _{T}0^{\prime }$
(where
$X^{\prime }\leq _{T}0^{\prime }$
(where
 $\leq _{T}$
denotes Turing reducibility, and
$\leq _{T}$
denotes Turing reducibility, and
 $Z^{\prime }$
is the Turing-jump of Z).
$Z^{\prime }$
is the Turing-jump of Z). -
• More generally, Y is low-
 $\Delta _{2}$
in the oracle X, if Y is
$\Delta _{2}$
in the oracle X, if Y is
 $\Delta _{2}$
in the oracle X, and
$\Delta _{2}$
in the oracle X, and
 $Y^{\prime }\leq _{T}X^{\prime }$
.
$Y^{\prime }\leq _{T}X^{\prime }$
.
By classical recursion theory, we have:
-
(1)
 $X\leq _{T}Y^{\prime }$
iff X is
$X\leq _{T}Y^{\prime }$
iff X is
 $\Delta _{2}$
in the oracle Y. Next, observe that if
$\Delta _{2}$
in the oracle Y. Next, observe that if
 $X^{\prime }\leq _{T}0^{\prime }$
and
$X^{\prime }\leq _{T}0^{\prime }$
and
 $Y^{\prime }\leq _{T}X^{\prime }$
, then
$Y^{\prime }\leq _{T}X^{\prime }$
, then
 $Y^{\prime }\leq _{T}0^{\prime }$
, hence Y is low-
$Y^{\prime }\leq _{T}0^{\prime }$
, hence Y is low-
 $\Delta _{2}$
by (1). Therefore:
$\Delta _{2}$
by (1). Therefore: -
(2) If X is low-
 $\Delta _{2}$
, and Y is low-
$\Delta _{2}$
, and Y is low-
 $\Delta _{2}$
in the oracle X, then Y is low-
$\Delta _{2}$
in the oracle X, then Y is low-
 $\Delta _{2}.$
$\Delta _{2}.$
The classical ‘Low Basis Theorem’ of Jockusch and Soare [Reference Jockusch and Soare17] asserts that every infinite finitely branching recursive tree has an infinite branch B such that B is low-
![]() $\Delta _{2}$
. Moreover, it is known that the Low Basis Theorem is provable in
$\Delta _{2}$
. Moreover, it is known that the Low Basis Theorem is provable in
![]() $\mathrm {I}\Delta _{0}+\mathrm {B}\Sigma _{2}$
(this is due to Clote, whose argument is presented in [Reference Hájek and Pudlák15, chap. I, sec. 3(c)]). In particular,
$\mathrm {I}\Delta _{0}+\mathrm {B}\Sigma _{2}$
(this is due to Clote, whose argument is presented in [Reference Hájek and Pudlák15, chap. I, sec. 3(c)]). In particular,
![]() $\mathrm {I}\Delta _{0}+\mathrm {B}\Sigma _{2}$
can prove that every countable consistent
$\mathrm {I}\Delta _{0}+\mathrm {B}\Sigma _{2}$
can prove that every countable consistent
![]() $\Delta _{1}$
-set of first-order sentences has a low-
$\Delta _{1}$
-set of first-order sentences has a low-
![]() $\Delta _{2}$
completion. Since the Henkin construction of a model of a prescribed complete theory can already be performed in
$\Delta _{2}$
completion. Since the Henkin construction of a model of a prescribed complete theory can already be performed in
![]() $\mathrm {I}\Sigma _{1} $
, this shows that
$\mathrm {I}\Sigma _{1} $
, this shows that
-
(3)
 $\mathrm {I}\Delta _{0}+\mathrm {B}\Sigma _{2}$
proves that every consistent
$\mathrm {I}\Delta _{0}+\mathrm {B}\Sigma _{2}$
proves that every consistent
 $\Delta _{1}$
set of first-order sentences has a model
$\Delta _{1}$
set of first-order sentences has a model
 $\mathcal {M}$
such that the satisfaction predicate
$\mathcal {M}$
such that the satisfaction predicate
 $\mathsf {Sat}_{\mathcal {M}} $
of
$\mathsf {Sat}_{\mathcal {M}} $
of
 $\mathcal {M}$
is low-
$\mathcal {M}$
is low-
 $\Delta _{2}.$
$\Delta _{2}.$
We are now ready to establish Theorem 4.1. We argue model-theoretically for ease of exposition, and we will work with satisfaction classes instead of truth classes.
-
• From this point on, we assume the reader is familiar with [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12] and follow the notation therein.
Let
![]() $\mathcal {M}\models \mathsf {PA}$
, and
$\mathcal {M}\models \mathsf {PA}$
, and
![]() $\mathsf {B}$
be as in the assumption of the theorem. By (3) there is a model
$\mathsf {B}$
be as in the assumption of the theorem. By (3) there is a model
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathsf {B}$
that is strongly interpretable in
$\mathsf {B}$
that is strongly interpretable in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathsf {Sat}_{\mathcal {N}}$
is low-
$\mathsf {Sat}_{\mathcal {N}}$
is low-
![]() $\Delta _{2}$
. Using a truth-predicate for
$\Delta _{2}$
. Using a truth-predicate for
![]() $\Delta _{2}$
-predicates we can execute the construction of Lemma 3.1 of [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12] (the same idea can be applied to the counterpart of Lemma 3.1 in the proof of the conservativity of [Reference Enayat, Łełyk and Wcisło9, Reference Kossak and Wcisło21]); the key idea is that if
$\Delta _{2}$
-predicates we can execute the construction of Lemma 3.1 of [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12] (the same idea can be applied to the counterpart of Lemma 3.1 in the proof of the conservativity of [Reference Enayat, Łełyk and Wcisło9, Reference Kossak and Wcisło21]); the key idea is that if
![]() $\mathsf {Sat}_{\left ( \mathcal {N},S\right ) }$
is low-
$\mathsf {Sat}_{\left ( \mathcal {N},S\right ) }$
is low-
![]() $\Delta _{2}$
, then so is
$\Delta _{2}$
, then so is
![]() $\mathsf {Th}^{+}(\mathcal {N})$
, where
$\mathsf {Th}^{+}(\mathcal {N})$
, where
![]() $\mathsf {Th}^{+}(\mathcal {N})$
is the theory defined as in [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12, Lemma 3.1] involving extra predicates added to the language of arithmetic whose consistency is established by building a partial satisfaction predicate ‘by hand’ by examining an arbitrarily chosen finite configuration of
$\mathsf {Th}^{+}(\mathcal {N})$
is the theory defined as in [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12, Lemma 3.1] involving extra predicates added to the language of arithmetic whose consistency is established by building a partial satisfaction predicate ‘by hand’ by examining an arbitrarily chosen finite configuration of
![]() $\mathcal {N}$
-formulae. Therefore there is some elementary extension
$\mathcal {N}$
-formulae. Therefore there is some elementary extension
![]() $\mathcal {N}_{1}$
of
$\mathcal {N}_{1}$
of
![]() $\mathcal {N}$
, and some
$\mathcal {N}$
, and some
![]() $\mathsf {Form}^{\mathcal {N}}$
-satisfaction class
$\mathsf {Form}^{\mathcal {N}}$
-satisfaction class
![]() $S_{1}\supseteq S$
such that
$S_{1}\supseteq S$
such that
![]() $\mathsf {Sat}_{\left ( \mathcal {N}_{1},S_{1}\right ) }$
is also low-
$\mathsf {Sat}_{\left ( \mathcal {N}_{1},S_{1}\right ) }$
is also low-
![]() $\Delta _{2}$
, thanks to (2) and the Low Basis Theorem. This shows that the construction
$\Delta _{2}$
, thanks to (2) and the Low Basis Theorem. This shows that the construction
can be uniformly described in
![]() $\mathrm {I}\Sigma _{2}+\mathrm {Con}(\mathsf {B})$
. This allows one to obtain an
$\mathrm {I}\Sigma _{2}+\mathrm {Con}(\mathsf {B})$
. This allows one to obtain an
![]() $\mathcal {M}$
-definable increasing sequence of structures
$\mathcal {M}$
-definable increasing sequence of structures
![]() $\left \langle \left ( \mathcal {M}_{i},S_{i}\right ) :i\in M\right \rangle $
(as in the proof of Theorem 3.3 of [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12]) with the additional feature that each
$\left \langle \left ( \mathcal {M}_{i},S_{i}\right ) :i\in M\right \rangle $
(as in the proof of Theorem 3.3 of [Reference Enayat, Visser, Achourioti, Galinon, Fujimoto and Martínez-Fernández12]) with the additional feature that each
![]() $\left ( \mathcal {M}_{i},S_{i}\right ) $
is strongly interpretable in
$\left ( \mathcal {M}_{i},S_{i}\right ) $
is strongly interpretable in
![]() $\mathcal {M}$
. Consider the limit model:
$\mathcal {M}$
. Consider the limit model:
![]() $\left ( \mathcal {N},S\right ) $
is clearly interpretable in
$\left ( \mathcal {N},S\right ) $
is clearly interpretable in
![]() $\mathcal {M}$
, and additionally (thanks to the elementary chains theorem applied within
$\mathcal {M}$
, and additionally (thanks to the elementary chains theorem applied within
![]() $\mathcal {M}$
) the reduct
$\mathcal {M}$
) the reduct
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\left ( \mathcal {N},S\right ) $
is strongly interpretable in
$\left ( \mathcal {N},S\right ) $
is strongly interpretable in
![]() $\mathcal {M}$
, thus
$\mathcal {M}$
, thus
![]() $\mathcal {M}$
“knows” that
$\mathcal {M}$
“knows” that
![]() $\mathcal {N}$
is a model of
$\mathcal {N}$
is a model of
![]() $\mathsf {B}$
.
$\mathsf {B}$
.
However, there is no reason to expect that the expansion
![]() $\left ( \mathcal {N},S\right ) $
is strongly interpretable in
$\left ( \mathcal {N},S\right ) $
is strongly interpretable in
![]() $\mathcal {M}$
. To circumvent this problem, we appeal to a trick found by Łełyk (first introduced in [Reference Enayat, Łełyk and Wcisło9]) to take advantage of
$\mathcal {M}$
. To circumvent this problem, we appeal to a trick found by Łełyk (first introduced in [Reference Enayat, Łełyk and Wcisło9]) to take advantage of
![]() $\left ( \mathcal {N},S\right ) $
in order to show that
$\left ( \mathcal {N},S\right ) $
in order to show that
![]() $\mathcal {M}$
satisfies
$\mathcal {M}$
satisfies
![]() $\mathrm {Con}(\mathsf {CT}^{-}[\mathsf {B}])$
, thereby concluding the existence of a model of
$\mathrm {Con}(\mathsf {CT}^{-}[\mathsf {B}])$
, thereby concluding the existence of a model of
![]() $\mathsf {CT}^{-}[\mathsf {B}]$
that is strongly interpretable in
$\mathsf {CT}^{-}[\mathsf {B}]$
that is strongly interpretable in
![]() $\mathcal {M}$
. The key idea is to resort to (1) the classical fact of proof theory that any deduction in first order logic can be replaced by another deduction with same conclusion but which has the subformula property,Footnote
5
(2) the fact that
$\mathcal {M}$
. The key idea is to resort to (1) the classical fact of proof theory that any deduction in first order logic can be replaced by another deduction with same conclusion but which has the subformula property,Footnote
5
(2) the fact that
![]() $\mathsf {CT}^{-}[\mathsf {B}]$
is the result of augmenting
$\mathsf {CT}^{-}[\mathsf {B}]$
is the result of augmenting
![]() $\mathsf {B}$
with only finitely many truth axioms, and (3) the fact that
$\mathsf {B}$
with only finitely many truth axioms, and (3) the fact that
![]() $\mathcal {M}$
has full access to the elementary diagram of
$\mathcal {M}$
has full access to the elementary diagram of
![]() $\mathcal {N}.$
The veracity of
$\mathcal {N}.$
The veracity of
![]() $\mathrm {Con}(\mathsf {CT}^{-}[\mathsf {B}])$
within
$\mathrm {Con}(\mathsf {CT}^{-}[\mathsf {B}])$
within
![]() $\mathcal {M}$
then allows us to invoke the completeness theorem of first-order logic within
$\mathcal {M}$
then allows us to invoke the completeness theorem of first-order logic within
![]() $\mathcal {M}$
to get hold of a model of
$\mathcal {M}$
to get hold of a model of
![]() $\mathsf {CT}^{-}[\mathsf {B}]$
that is strongly interpretable in
$\mathsf {CT}^{-}[\mathsf {B}]$
that is strongly interpretable in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Corollary 4.2.
![]() $\mathsf {PA}$
strongly interprets
$\mathsf {PA}$
strongly interprets
![]() $\mathsf {CT}^{-}[\mathsf {PA}]$
.
$\mathsf {CT}^{-}[\mathsf {PA}]$
.
Proof. Let
![]() $\mathcal {M}$
be an arbitrary model of
$\mathcal {M}$
be an arbitrary model of
![]() $\mathsf {PA}$
. Within
$\mathsf {PA}$
. Within
![]() $\mathcal {M}$
, if
$\mathcal {M}$
, if
![]() $\mathsf {PA}$
is inconsistent let
$\mathsf {PA}$
is inconsistent let
![]() $\mathsf {B}$
be
$\mathsf {B}$
be
![]() $\mathrm {I}\Sigma _{k}$
, where k is the first n such that
$\mathrm {I}\Sigma _{k}$
, where k is the first n such that
![]() $\mathrm {I}\Sigma _{n+1}$
is inconsistent, otherwise let
$\mathrm {I}\Sigma _{n+1}$
is inconsistent, otherwise let
![]() $\mathsf {B}=\mathsf {PA}$
. Thus
$\mathsf {B}=\mathsf {PA}$
. Thus
![]() $\mathrm {Con}(\mathsf {B})$
holds in
$\mathrm {Con}(\mathsf {B})$
holds in
![]() $\mathcal {M}$
. By Mostowski’s Reflection Theorem,
$\mathcal {M}$
. By Mostowski’s Reflection Theorem,
![]() $\mathsf {B}$
extends
$\mathsf {B}$
extends
![]() $\mathrm {I}\Sigma _{n}$
for each
$\mathrm {I}\Sigma _{n}$
for each
![]() $n\in \omega $
, and therefore
$n\in \omega $
, and therefore
![]() $\mathsf {B}$
extends
$\mathsf {B}$
extends
![]() $\mathsf {PA}$
(from an external point of view). Thus Theorem 4.1 applies.
$\mathsf {PA}$
(from an external point of view). Thus Theorem 4.1 applies.
Corollary 4.3.
![]() $\mathsf {PA}\vdash \mathrm {Con}(\mathsf {CT}^{-}[\mathsf {B}])$
for every finitely axiomatized subtheory
$\mathsf {PA}\vdash \mathrm {Con}(\mathsf {CT}^{-}[\mathsf {B}])$
for every finitely axiomatized subtheory
![]() $\mathsf {B}$
of
$\mathsf {B}$
of
![]() $\mathsf {PA}$
that extends
$\mathsf {PA}$
that extends
![]() $\mathrm {I} \Delta _{0}+\mathsf {Exp}$
.
$\mathrm {I} \Delta _{0}+\mathsf {Exp}$
.
Proof. Let
![]() $\mathsf {B}$
be a finitely axiomatizable subtheory of
$\mathsf {B}$
be a finitely axiomatizable subtheory of
![]() $\mathsf {PA}$
. The formal consistency of
$\mathsf {PA}$
. The formal consistency of
![]() $\mathsf {B}_{0}$
is verifiable in
$\mathsf {B}_{0}$
is verifiable in
![]() $\mathsf {PA}$
by Mostowski’s Reflection Theorem. Therefore by Theorem 4.1
$\mathsf {PA}$
by Mostowski’s Reflection Theorem. Therefore by Theorem 4.1
![]() $\mathsf {PA}$
can produce an internal model of
$\mathsf {PA}$
can produce an internal model of
![]() $\mathsf {CT}^{-}[\mathsf {B}]$
for which it has a satisfaction predicate; which in turn immediately implies that
$\mathsf {CT}^{-}[\mathsf {B}]$
for which it has a satisfaction predicate; which in turn immediately implies that
![]() $\mathrm {Con}(\mathsf {CT}^{-}[\mathsf {B}])$
is provable in
$\mathrm {Con}(\mathsf {CT}^{-}[\mathsf {B}])$
is provable in
![]() $\mathsf {PA}$
.
$\mathsf {PA}$
.
Corollary 4.4.
![]() $\mathsf {CT}^{-}[\mathsf {PA}]$
is not finitely axiomatizable.
$\mathsf {CT}^{-}[\mathsf {PA}]$
is not finitely axiomatizable.
Proof. Put Corollary 4.3 together with Gödel’s second incompleteness theorem.
We are now ready to present the main result of this section. Recall that the notions of I-disjunctive correctness and I-deductive correctness were defined in Definition 2.11(d,f).
Theorem 4.5 (Joint with Albert Visser).
Let
![]() $\mathcal {M}$
be a countable recursively saturated model of
$\mathcal {M}$
be a countable recursively saturated model of
![]() $\mathsf {PA.}$
There are arbitrarily large cuts I of
$\mathsf {PA.}$
There are arbitrarily large cuts I of
![]() $\mathcal {M}$
for which
$\mathcal {M}$
for which
![]() $I\prec \mathcal {M}$
and
$I\prec \mathcal {M}$
and
![]() $I\cong \mathcal {M}$
, and for each such cut I there is a full truth class T on
$I\cong \mathcal {M}$
, and for each such cut I there is a full truth class T on
![]() $\mathcal {M}$
that is I-disjunctively and I-deductively correct.
$\mathcal {M}$
that is I-disjunctively and I-deductively correct.
Proof. Let
![]() $\mathcal {M}$
be a countable recursively saturated model of
$\mathcal {M}$
be a countable recursively saturated model of
![]() $\mathsf {PA}$
. Let
$\mathsf {PA}$
. Let
![]() $\mathcal {N}$
be as in the proof of Stage 1 of the proof of Theorem 3.4, thus
$\mathcal {N}$
be as in the proof of Stage 1 of the proof of Theorem 3.4, thus
![]() $\mathcal {N}$
is an elementary extension of
$\mathcal {N}$
is an elementary extension of
![]() $\mathcal {M}$
that is strongly interpreted in
$\mathcal {M}$
that is strongly interpreted in
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N}).$
Thanks to Corollary 4.3 there is an elementary extension
$\mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N}).$
Thanks to Corollary 4.3 there is an elementary extension
![]() $\mathcal {N}^{\ast }$
of
$\mathcal {N}^{\ast }$
of
![]() $\mathcal {N}$
that carries a truth class
$\mathcal {N}$
that carries a truth class
![]() $T_{\mathcal {N}^{\ast }}$
such that
$T_{\mathcal {N}^{\ast }}$
such that
![]() $(\mathcal {N}^{\ast },T_{\mathcal {N}^{\ast }})\models \mathsf {CT}^{-}[\mathsf {PA}],$
and
$(\mathcal {N}^{\ast },T_{\mathcal {N}^{\ast }})\models \mathsf {CT}^{-}[\mathsf {PA}],$
and
![]() $(\mathcal {N}^{\ast },T_{\mathcal {N}^{\ast }})$
is strongly interpretable in
$(\mathcal {N}^{\ast },T_{\mathcal {N}^{\ast }})$
is strongly interpretable in
![]() $\mathcal {M}$
, which in turn will allow us to conclude that
$\mathcal {M}$
, which in turn will allow us to conclude that
![]() $(\mathcal {N}^{\ast },T_{\mathcal {N}^{\ast }})$
satisfies the following four properties:
$(\mathcal {N}^{\ast },T_{\mathcal {N}^{\ast }})$
satisfies the following four properties:
-
(1)
 $T_{\mathcal {N}^{\ast }}$
is M-disjunctively and M-deductively correct. This is handled the by usual argument by induction that shows that the classical Tarskian truth predicate respects arbitrary disjunctions and is closed under deductions, as noted in Remark 2.12.
$T_{\mathcal {N}^{\ast }}$
is M-disjunctively and M-deductively correct. This is handled the by usual argument by induction that shows that the classical Tarskian truth predicate respects arbitrary disjunctions and is closed under deductions, as noted in Remark 2.12. -
(2) There is an
 $\mathcal {M}$
-definable embedding of
$\mathcal {M}$
-definable embedding of
 $\mathcal {M} $
as an initial segment of
$\mathcal {M} $
as an initial segment of
 $\mathcal {N}^{\ast }.$
$\mathcal {N}^{\ast }.$
-
(3)
 $\mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N}^{\ast }). $
$\mathrm {SSy}(\mathcal {M})=\mathrm {SSy}(\mathcal {N}^{\ast }). $
-
(4)
 $\mathcal {N}^{\ast }$
is recursively saturated.
$\mathcal {N}^{\ast }$
is recursively saturated.
Note that
![]() $\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N}^{\ast })$
since
$\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N}^{\ast })$
since
![]() $\mathcal {N}^{\ast }$
elementarily extends
$\mathcal {N}^{\ast }$
elementarily extends
![]() $\mathcal {N}$
, and
$\mathcal {N}$
, and
![]() $\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N})$
. Together with (3), (4) and Theorem 2.2, this allows us to conclude that
$\mathrm {Th}(\mathcal {M})=\mathrm {Th}(\mathcal {N})$
. Together with (3), (4) and Theorem 2.2, this allows us to conclude that
![]() $\mathcal {M}\cong \mathcal {N}^{\ast }$
, which implies that we ‘copy over’
$\mathcal {M}\cong \mathcal {N}^{\ast }$
, which implies that we ‘copy over’
![]() $T_{\mathcal {N}^{\ast }}$
on
$T_{\mathcal {N}^{\ast }}$
on
![]() $\mathcal {M}$
, thus
$\mathcal {M}$
, thus
![]() $\mathcal {M}$
carries a full truth T class that is I-disjunctively and I-deductively correct for some cut I of
$\mathcal {M}$
carries a full truth T class that is I-disjunctively and I-deductively correct for some cut I of
![]() $\mathcal {M}$
. By using Theorem 2.5 and Remark 2.6 we can conclude that such cuts I can be arranged to be arbitrarily large in
$\mathcal {M}$
. By using Theorem 2.5 and Remark 2.6 we can conclude that such cuts I can be arranged to be arbitrarily large in
![]() $\mathcal {M}$
. More specifically, by Remark 2.6(c) there are arbitrarily large strong cuts I in
$\mathcal {M}$
. More specifically, by Remark 2.6(c) there are arbitrarily large strong cuts I in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $I\prec \mathcal {M}$
and
$I\prec \mathcal {M}$
and
![]() $I\cong \mathcal {M}$
, and by Remark 2.6(b) such cuts are not
$I\cong \mathcal {M}$
, and by Remark 2.6(b) such cuts are not
![]() $\omega $
-coded from above in
$\omega $
-coded from above in
![]() $\mathcal {M}$
. Therefore by Theorem 2.5 for such a given cut I there is an isomorphism
$\mathcal {M}$
. Therefore by Theorem 2.5 for such a given cut I there is an isomorphism
![]() $f:\mathcal {N}^{\ast }\rightarrow \mathcal {M}$
with
$f:\mathcal {N}^{\ast }\rightarrow \mathcal {M}$
with
![]() $f(i)=i$
for all
$f(i)=i$
for all
![]() $i\in I$
. This makes it clear that
$i\in I$
. This makes it clear that
![]() $T:=f(T_{\mathcal {N}^{\ast }})$
is the desired full truth class on
$T:=f(T_{\mathcal {N}^{\ast }})$
is the desired full truth class on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Remark 4.6. Suppose
![]() $\mathcal {M}\models \mathsf {PA}+\mathsf {\lnot }\mathrm {Con}\mathsf {(PA)}$
and
$\mathcal {M}\models \mathsf {PA}+\mathsf {\lnot }\mathrm {Con}\mathsf {(PA)}$
and
![]() $\mathcal {M}$
is countable and recursively saturated. Then
$\mathcal {M}$
is countable and recursively saturated. Then
![]() $\mathcal {M}$
carries an inductive satisfaction class S [Reference Kaye18, corollary 15.12]. For such an S, there is a topped nonstandard initial segment I of
$\mathcal {M}$
carries an inductive satisfaction class S [Reference Kaye18, corollary 15.12]. For such an S, there is a topped nonstandard initial segment I of
![]() $\mathcal {M}$
such that S satisfies the Tarski conditions for all formulas in I. If
$\mathcal {M}$
such that S satisfies the Tarski conditions for all formulas in I. If
![]() $\mathcal {M}$
, and
$\mathcal {M}$
, and
![]() $\pi \in M$
codes up a proof of inconsistency of
$\pi \in M$
codes up a proof of inconsistency of
![]() $\mathsf {PA}$
in
$\mathsf {PA}$
in
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $\pi \notin I$
. As shown by Abdul-Quader and Łełyk [Reference Abdul-Quader and Łełyk1, proposition 43], the methodology employed in [Reference Cieśliński, Łełyk and Wcisło7] can be used to show that we cannot expect to build a full satisfaction class S that is disjunctively correct on a cut I that contains
$\pi \notin I$
. As shown by Abdul-Quader and Łełyk [Reference Abdul-Quader and Łełyk1, proposition 43], the methodology employed in [Reference Cieśliński, Łełyk and Wcisło7] can be used to show that we cannot expect to build a full satisfaction class S that is disjunctively correct on a cut I that contains
![]() $\pi $
if S satisfies both the regularity axiom (also known as generalized term extensionality, as in Remark 3.5) and also internal induction. This is in contrast to Theorem 4.5 that shows that a full satisfaction class that is I-disjunctively correct can always be arranged for arbitrarily high cuts I in
$\pi $
if S satisfies both the regularity axiom (also known as generalized term extensionality, as in Remark 3.5) and also internal induction. This is in contrast to Theorem 4.5 that shows that a full satisfaction class that is I-disjunctively correct can always be arranged for arbitrarily high cuts I in
![]() $\mathcal {M}$
. Thus, even though the full satisfaction classes constructed in Theorem 4.5 can be arranged to satisfy the regularity axiom, in general they do not satisfy the internal induction axiom.
$\mathcal {M}$
. Thus, even though the full satisfaction classes constructed in Theorem 4.5 can be arranged to satisfy the regularity axiom, in general they do not satisfy the internal induction axiom.
Remark 4.7. Suppose
![]() $\mathsf {T}(x,y)$
is a binary predicate; we will write it as
$\mathsf {T}(x,y)$
is a binary predicate; we will write it as
![]() $\mathsf {T}_{x}(y)$
to indicate that for a fixed x,
$\mathsf {T}_{x}(y)$
to indicate that for a fixed x,
![]() $\mathsf {T}_{x}$
is a truth predicate. Let
$\mathsf {T}_{x}$
is a truth predicate. Let
![]() $\mathsf {CT}^{\ast }$
be the sentence in the language of
$\mathsf {CT}^{\ast }$
be the sentence in the language of
![]() $\mathsf {PA}$
augmented with
$\mathsf {PA}$
augmented with
![]() $\mathsf {T}_{x}(y)$
that says that for all x the axioms of
$\mathsf {T}_{x}(y)$
that says that for all x the axioms of
![]() $\mathsf {CT}^{-}$
hold for
$\mathsf {CT}^{-}$
hold for
![]() $\mathsf {T}_{x}.$
Then by putting Theorem 4.5 together with the completeness theorem of first-order logic, and the fact that every countable model of
$\mathsf {T}_{x}.$
Then by putting Theorem 4.5 together with the completeness theorem of first-order logic, and the fact that every countable model of
![]() $\mathsf {PA}$
has a countable elementary extension that is recursively saturated we can conclude that the theory
$\mathsf {PA}$
has a countable elementary extension that is recursively saturated we can conclude that the theory
![]() $\mathsf {PA}+ \mathsf {CT}^{\ast }$
+ “
$\mathsf {PA}+ \mathsf {CT}^{\ast }$
+ “
![]() $\forall x \mathsf {T}_{x}$
is disjunctively correct for disjunctions whose number of disjuncts is at most x” is conservative over
$\forall x \mathsf {T}_{x}$
is disjunctively correct for disjunctions whose number of disjuncts is at most x” is conservative over
![]() $\mathsf {PA}$
.
$\mathsf {PA}$
.
Remark 4.8. As pointed by the referee, one can give a “soft” proof of Theorem 4.5 for the special case when
![]() $\mathcal {M}$
is a model of True Arithmetic (the theory of the standard model of
$\mathcal {M}$
is a model of True Arithmetic (the theory of the standard model of
![]() $\mathsf {PA}$
). The argument goes as follows. It is known that if I is a cut of a countable recursively saturated model of
$\mathsf {PA}$
). The argument goes as follows. It is known that if I is a cut of a countable recursively saturated model of
![]() $\mathsf {PA}$
that properly contains the Skolem closure of 0 in
$\mathsf {PA}$
that properly contains the Skolem closure of 0 in
![]() $\mathcal {M}$
, then for every
$\mathcal {M}$
, then for every
![]() $a\in I$
and every
$a\in I$
and every
![]() $c\in M$
, there is a
$c\in M$
, there is a
![]() $b\in M$
such that
$b\in M$
such that
![]() $c<b$
and the type of a in
$c<b$
and the type of a in
![]() $\mathcal {M}$
coincides with the type of b in
$\mathcal {M}$
coincides with the type of b in
![]() $\mathcal {M}$
. This observation allows one to build an automorphism f of
$\mathcal {M}$
. This observation allows one to build an automorphism f of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $f(a)=b$
, which in turn shows that
$f(a)=b$
, which in turn shows that
![]() $(\mathcal {M},I)\cong (\mathcal {M},J)$
for
$(\mathcal {M},I)\cong (\mathcal {M},J)$
for
![]() $J=f(I)$
. It follows that if
$J=f(I)$
. It follows that if
![]() $\mathcal {M}$
has a full satisfaction class that is I-disjunctively correct, then
$\mathcal {M}$
has a full satisfaction class that is I-disjunctively correct, then
![]() $\mathcal {M}$
also has a satisfaction class that is J-disjunctively correct (and the same for deductive correctness). Since the theory
$\mathcal {M}$
also has a satisfaction class that is J-disjunctively correct (and the same for deductive correctness). Since the theory
![]() $T(I,S)$
that says that I is a cut and S is an I-disjunctively correct full satisfaction class is consistent with
$T(I,S)$
that says that I is a cut and S is an I-disjunctively correct full satisfaction class is consistent with
![]() $\mathrm {Th}(\mathcal {M)}$
, by chronic resplendence
$\mathrm {Th}(\mathcal {M)}$
, by chronic resplendence
![]() $\mathcal {M}$
has a cut I and a full satisfaction class S such that
$\mathcal {M}$
has a cut I and a full satisfaction class S such that
![]() $(\mathcal {M},I,S)$
is a resplendent model of
$(\mathcal {M},I,S)$
is a resplendent model of
![]() $T(I,S)$
. In particular I is above the Skolem closure of
$T(I,S)$
. In particular I is above the Skolem closure of
![]() $0$
and thus the aforementioned observation applies.
$0$
and thus the aforementioned observation applies.
Acknowledgments
I have benefitted from priceless feedback concerning the work reported here from Lawrence Wong, Bartosz Wcisło, Albert Visser, Jim Schmerl, Mateusz Łełyk, Roman Kossak, Cezary Cieśliński, and Athar Abdul-Quader (in reverse alphabetical order). Also many thanks to the anonymous referee whose detailed comments were instrumental in reshaping the preliminary draft of this paper into its current format.
Funding
The research presented in this paper was supported by the National Science Centre, Poland (NCN), grant number 2019/34/A/HS1/00399.