Introduction
Polar glaciers often show long stripes that seem to follow the ice flow. They are reminiscent of medial moraines but there may be no rock debris. Physically, the flow stripes may be longitudinal streets or contrasts in surface texture, in density or style of crevasses, or they can be longitudinal ridges and troughs. Both types occur on Ice Stream B (Reference Vornberger and WhillansVornberger and Whillans, 1986) and in Byrd Glacier (Reference Casassa and BrecherCasassa and Brecher, 1993). On Byrd Glacier, the textural flow stripes are erased by snow accumulation as they are advected on to the Ross Ice Shelf, so only the topographic stripes occur on the ice shelf (Reference Casassa and BrecherCasassa and Brecher, 1993).
Variously called flow stripes, streamlines, flowlines and flow traces, they have been shown in many cases to be parallel to ice-motion vectors (e.g. Reference Crabtree and DoakeCrabtree and Doake, 1980; Reference Dowdeswell and McIntyreDowdeswell and McIntyre, 1987; Reference Swithinbank, Brunk and SieversSwithinbank and others, 1988; Reference Casassa and TurnerCasassa and Turner, 1991; Reference Merry and WhillansMerry and Whillans, 1993), although there can be exceptions (Reference Casassa, Jezek, Turner and WhillansCasassa and others, 1991).
The formation mechanism and long persistence of flow stripes is not understood. They can originate in shear margins in grounded ice (Reference Merry and WhillansMerry and Whillans, 1993). They can be traced on satellite imagery for hundreds of kilometers on ice streams and ice shelves.
The decay of flow stripes can be measured on satellite imagery. The peak-to-peak near-infrared brightness contrast across a flow stripe, as measured by the Advanced Very High Resolution Radiometer (AVHRR), decays with distance along flow stripes. Considering that the wavelength of flow stripes is approximately constant as the undulations decay, this brightness contrast is proportional to surface slope if flow stripes are only topographic in nature. Close to the grounding line of Byrd Glacier (where flow stripes have both a topographic and a textural character, the brightness contrast is 6–7 brightness values (digital numbers). This contrast decreases approximately exponentially until close to the calving ice front (where the stripes are topographic in nature) it is 1. The 1/e folding distance is 310 km, which translates to a decay time of 500 years. Considering a wavelength of 2800 m and a viscosity value of l08 Pa a, simple theory of creep relaxation in an infinite half-space indicates that surface perturbations on ice would decay in about one-tenth of the decay time observed on satellite imagery. Such a large discrepancy needs explanation.
This contribution describes a model for the decay of flow stripes on the Ross Ice Shelf (Fig. 1). The objective is to understand their persistence and determine whether ordinary processes can account for them, or whether special features such as ice-structural contrasts are required.

Fig. 1. Western sector of the Ross Ice Shelf. The lines represent flow stripes that appear on AVHRR imagery. The coordinate system is that used by Reference Thomas, Mac Ayeal, Eilers and GaylordThomas and others (1984), in which 1° is equal to 110 km
Theory
The steady-state, linear viscous flow model of Reference Whillans and JohnsenWhillans and Johnsen (1983) is extended to incorporate time-dependency. Flow is separated into an average flow that describes the deformation pattern in an ice shelf without flow stripes and flow variations due to the flow stripes. The variations from the average flow are of interest here. Reference Van, Veen and WhillansVan der Veen and Whillans (1989) compared the use of a linear flow law with a more realistic power-law relation and found that the schemes yielded similar results. The model has been described in detail by Reference CasassaCasassa (in press).
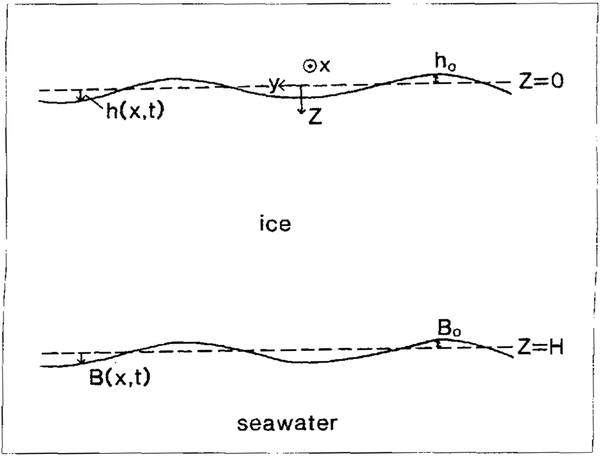
Flow deviations in a transverse vertical section are considered. The coordinate system is defined as shown in Figure 2 with y transverse and z vertically downward. Because the flow stripes are parallel to ice flow, only flow distortions in the y – z plane need to be considered.

Fig. 2. Transverse section through the ice shelf with surface and bed undulations. Coordinate axes are shown
The solution method follows common procedure for linear viscous flow (e.g. Reference BuddBudd, 1970; Reference Hutter, Legerer and SpringHutter and others, 1981). The notation and definitions of Reference Whillans and JohnsenWhillans and Johnsen (1983) are used here. Force balance is ensured through the definition of a stress function,ϕ. The stress function is related to stress variations as follows:

The stress function is used to obtain the biharmonic equation. Solutions to that equation are sought that are periodic in y and that show time (t) change. That is
in which ![]() and ω determines the transverse periodicity. The parameter k is the decay rate. The following result is obtained through the solution of a fourth-order ordinary differential equation:
and ω determines the transverse periodicity. The parameter k is the decay rate. The following result is obtained through the solution of a fourth-order ordinary differential equation:
The ai are constants that are determined from considerations of boundary conditions.
The top surface of the ice shelf has a known spatial periodicity, ω, and initial amplitude, h 0. Therefore, the top surface may be defined by
Time is measured from when the surface amplitude is h 0. Close to the grounding line of Byrd Glacier h 0 is 15 m and the wavelength of flow stripes is 2800 m (Reference Casassa and BrecherCasassa and Brecher, 1993).
Since there is no reason to suspect asymmetry, and to simplify the interpretation, the basal surface is taken to be in phase or anti-phase with the top surface:
B 0 is to be determined by the solution. Because the model is linear, the decay rate of the bed may be taken to be the same as that of the top surface. This is done here.
As the solution is taken as symmetric, four of the parameters (a 5, a 6,a 7, and a 8) are found to be zero. That leaves six unknowns (four a i ,k and B 0). The boundary conditions are zero shear stress (1) at the top and (2) at the base, (3) zero normal stress perpendicular to the top surface (which leads to gravitational loading at z = 0), (4) hvdrostatic water pressure at the base (which accounts for buoyancy), and vertical velocity set to the rate of relief decay at (5) the top and (6) the basal surfaces (the possibility of differential accumulation and ablation is neglected). The first of these boundary conditions includes the value of average horizontal deviatoric stress near the top surface. This is omitted from the second boundary condition, because average deviatoric stresses near the base are very small on account of the large ice temperature at depth. Similar boundary conditions have been employed by Reference Hutter, Legerer and SpringHutter and others (1981),Reference Morland and ShoemakerMorland and Shoemaker (1982), Reference Whillans and JohnsenWhillans and Johnsen (1983), Reference Whillans and JezekWhillans and Jezek (1987) and Reference CasassaCasassa(in press).
The solution leads to a quadratic equation with two roots, which for reasons that are developed below, we term the buckle and pinch-and-swell solutions. Both solutions indicate decay with time (positive k).
The solutions are not overly sensitive to the range of values appropriate to an ice shelf. The sensitivity has been discussed in more detail by Reference CasassaCasassa (in press). Here, the results for typical values for an ice shelf are described. These values are: zero average horizontal deviatoric stress, ice thickness of 600 m (Reference Bentley, Clough, Jezek and ShabtaieBentley and others, 1979), flow-stripe transverse wavelength of 2800 m and surface amplitude of flow stripes of 15 m at their start (t = 0). A viscosity of ice of 108 Pa a, as found appropriate for ice of similar temperature along the Bynd Station Strain Network (Reference Whillans and JohnsenWhillans and Johnsen, 1983). is adopted.
Results
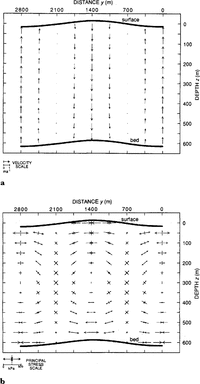
The pattern of motion is shown with velocity vectors in Figures 3a and 4a. In both cases, material is being redistributed so as to eliminate the variations. Velocities are five times smaller in the pinch-and-swell case than in the buckle case. Unlike the study of Reference Whillans and JohnsenWhillans and Johnsen (1983), where such flow variations are superimposed on a large average flow, in this case there is very little average flow along the transverse (y) direction, and these diagrams represent almost the full velocity pattern in the y – z plane in an ice shelf
The features have decay times of about 700 years (pinch-and-swell) and 13 years (buckle). These values are approximately proportional to the ice viscosity, thickness and wavelength, and are independent of amplitude h 0.
Pinch-and-swell solution
The roots are amplified mirror images of the surface undulations in the pinch-and-swell solution (Fig. 3). The amplification factor is −8.3. The tendency to decay is largely compensated by the buoyancy of the root below. For perfect isostasy, the amplification would be 7.7, so the solution shows that upward surface perturbations are more than isostatically balanced by roots. In other rocks such shapes are called boudins, if caused by tension, and mullions, if caused by compression (Reference SmithSmith, 1975). In our case, their genesis is not known, so we use the morphologic term “pinch-and-swell”.

Fig. 3. The pinch-and-swell solution. The heavy way lines represent the specified surface undulations and calculated bed shape: (a) velocities; (b) principal stresses.
Stresses are rather small. Full stresses depart no more than 140kPa from stresses in a plane ice shelf (Fig. 3b). There is lateral tension on the surface ridges and compression in the troughs, as expected for progressive decay. Vertical shear stresses are almost zero, as has been commonly estimated for ice shelves (e.g. Reference Sanderson and DoakeSanderson and Doake, 1979).
Buckle solution
The second solution is a fold in which the perturbations at the bed mimic those at the surface but with smaller amplitude (Fig. 4). In this case, the ice shelf is far from being in isostatic balance and the relief is entirely supported by dynamic stresses. The model predicts a basal amplitude, B 0, of 14 m, slightly smaller than the surface amplitude (15 m).

Fig. 4. The buckle solution: (a) velocities; (b) principal stresses. Velocity and stress scales differ from those in Figure 3.
The stress pattern corresponds to that of a bending slab, in which one surface is under tension and the other under compression. Vertical shear stresses are very important and reach 164 kPa at the half-depth and half-way between the ridges and troughs. In this case, the estimate that such stresses are negligible does not hold. However, these features decay rapidly.
Discussion
Flow stripes may start as a combination of buckles and pinch-and-swell structures. The model predicts that the buckle aspect decays in only about 13 years, leaving pineh-and-swell structures dominant. The transit time of ice from Byrd Glacier across the ice shelf is about 600 years.
The decay time of the pinch-and-swell structures predicted by the model is 700 years. This is in close agreement with the decay time of 500 years inferred from brightness measured on AVHRR satellite imagery, which may include the combined rapid decay of textural stripes with the slower decay of topographic stripes.
The confirmation that vertical shear stresses are small after about 13 years of transit on the ice shelf (the decay time of buckles) is important. It means that the simple ice-shelf models can continue to be applied with some confidence.
The model predicts reasonable flow stripes without considering the possibility of horizontal variations in ice strength. There is little constraint on what those variations might be at the 5 km scale. The predictions of the model could be altered in any sense depending on what strength variations arc proposed. However, because the model predictions agree quite well with observation, strength variations are not called for.
A similar model would provide somewhat different predictions for grounded ice. The biggest difference is that for grounded ice the bed is not determined by ice flow but is determined externally. Therefore, there may be no deep root and decay would proceed much more rapidly than in the pinch-and-swell solution. The rather small transverse stresses that operate on ice shelves play a small role in preserving the stripes (Reference CasassaCasassa, in press). However, on grounded ice, lateral compression may be important to the preservation of flow stripes, as has been suggested by Reference Merry and WhillansMerry and Whillans (1993).
The preservation of flow stripes is accounted for without needing to invoke horizontal strength variations. The stripes persist because of strong basal relief. This prediction can be tested with field measurements of surface elevation and ice thickness. Surface topographic variations without roots, as predicted here, could mark strength anomalies.
In fact, we suspect that there are also strength gradients. For example, a large fracture developed in the Filchner Ice Shelf along a flow stripe (figure 1 in Reference Swithinbank, Brunk and SieversSwithinbank and others, 1988). This may be evidence of a stripe associated with weaker ice. Such strength variation may be critical to future calving events and ice-shelf stability.
Acknowledgements
Dr J. Bolzan and Dr C.J. van der Veen provided advice. This work was done while one of the authors (G. C.) was supported by NASA’s Global Change Fellowship Program. U.S. National Science Foundation grant No. DPP-9020760 also supported the work. J. Nagy and S. Kim drafted the figures. This is Byrd Polar Research Center contribution No. 883.