Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-21T02:51:41.572Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE CODEGREES OF STRONGLY MONOLITHIC CHARACTERS OF FINITE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  07 November 2024

TEMHA ERKOÇ Open the ORCID record for TEMHA ERKOÇ [Opens in a new window]  and
UTKU YIlMAZTÜRK Open the ORCID record for UTKU YIlMAZTÜRK [Opens in a new window]
TEMHA ERKOÇ
Affiliation:
Department of Mathematics, Faculty of Science, Istanbul University, 34134 Istanbul, Turkey e-mail: [email protected]
UTKU YIlMAZTÜRK*
Affiliation:
Department of Mathematics, Faculty of Science, Istanbul University, 34134 Istanbul, Turkey
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite group and let 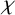$\chi $ be an irreducible character of G. The number 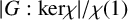$|G:\mathrm {ker}\chi |/\chi (1)$ is called the codegree of the character 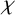$\chi $. We provide several relations between the structure of G and the codegrees of the characters in a given subset of 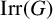$\mathrm {Irr}(G)$, where 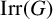$\mathrm {Irr}(G)$ is the set of all complex irreducible characters of G. For example, we show that if the codegrees of all strongly monolithic characters of G are odd, then G is solvable, analogous to the well-known fact that if all irreducible character degrees of a finite group are odd, then that group is solvable.

Keywords

finite groupsstrongly monolithic characterscodegreesfitting length

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 2 , April 2025 , pp. 283 - 289
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The work of the authors was supported by the Scientific and Technological Research Council of Turkey (TÜBİTAK), project number 123F260.

References

Chillag, D., Mann, A. and Manz, O., ‘The co-degrees of irreducible characters’, Israel J. Math. 73 (1991), 207–223.CrossRefGoogle Scholar
Erkoç, T., Güngör, S. B. and Özkan, J. M., ‘Strongly monolithic characters of finite groups’, J. Algebra Appl. 108 (2023), 120–124.Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Lu, J. and Meng, H., ‘The square-free hypothesis on co-degrees of irreducible characters’, Mediterr. J. Math. 21(1) (2024), Article no. 32.CrossRefGoogle Scholar
Özkan, J. M. and Erkoç, T., ‘On the relations between the structures of finite groups and their strongly monolithic characters’, Comm. Algebra 51(2) (2023), 657–662.CrossRefGoogle Scholar
Qian, G., Wang, Y. and Wei, H., ‘Co-degrees of irreducible characters in finite groups’, J. Algebra 312(2) (2007), 946–955.CrossRefGoogle Scholar
Xiaoyou, C. and Lewis, M. L., ‘Solvable groups whose monomial, monolithic characters have prime power codegrees’, Int. J. Group Theory 12(4) (2023), 223–226.Google Scholar