1 Introduction

Ice Stream C, West Antarctica, one of the Ross ice steams, has slowed to speeds of between 1 and 13 m a^-1 (Reference Whillans, Bolzan and ShabtaieWhillans and others, 1987) within the last two centuries (Reference RoseRose, 1979; Reference Shabtaie, Whillans and BentleyShabtaie and Bentley, 1987; Reference RetzlafT and BentleyRetzlaff and Bentley, 1993). Neighboring Ice Stream B flows rapidly (400- 800 m a¹) even though it is grossly similar to Ice Stream C in physical dimensions, accumulation and temperature (Reference Shabtaic and BentleyShabtaie and others, 1987). The likely candidates for the restraining stress are the sides and the bed of the ice stream. In this paper we concentrate on the bed.

The sources of restraining stress at the bed are some unknown combination of the rheological properties of the till and the so-called “sticky spots” at the glacial/ subglacial interface (Reference Bindschadler and ScambosBindschadler and Scambos, 1991; Reference AlleyAlley, 1993; Reference Whillans and van der VeenWhillans and Van der Veen, 1993). The sticky spots are regions of the bed where shear stress is concentrated and that, in sum, balance some or all of the driving stress. The deforming till beneath Ice Stream B (Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1987; Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others, 1990) permits last flow but may provide little restraint to the driving stress of Ice Stream B (Reference Alley and WhillansAlley and Wihillam, 1991). Thus, the sticky spots may be important in basal drag.

We assume that conditions beneath Ice Stream C, when it flowed rapidly ( > 130 a ago). were similar to those currently beneath fast-flowing Ice Stream B. Thus, by extension, differences between lee Streams Band C today are analogous to differences between Ice Stream C today and its condition two centuries ago. Identifying the critical parameter(s) that differentiate Ice Streams Band C could aid in developing theories for the shut-down of Ice Stream C. One of the most striking differences between the two ice streams is the rate, distribution and size of basal microearthquake activity.

The basal events are two orders-of-magnitude more numerous, 1^-2 orders-of-magnitude larger moment, and more widely spatially distributed beneath Ice Stream C as compared to Ice Stream B (Reference Anandakrishnan and BentleyAnandakrishnan and Bentley, 1993). The events beneath both ice streams share the same depth-zone (the base of the ice) and the same focal mechanism (low-angle thrust faults in the direction of local driving stress), suggesting that the principal directions of stress at the bed are similar in both cases. We do not insist on this interpretation because slip on pre-existing faults is not necessarily determined by the stress directions, Nonetheless, we suggest that the difference in microearthquake rate and size is due to a difference in material properties (most notably friction) and the difference in spatial density is due to a difference in either friction or till rheology.

Reference Alley, Anandakrishnan, Bentley and LordAlley and others (1994) proposed that an important parameter in controlling the velocity of ice streams is the state of lubrication of sticky Spots. They hypothesized that basal water has been diverted away from Ice Stream C, resulting in a disruption of a Weertman-type water film. This water film (in their hypothesis) existed when Ice Stream C flowed fast but is currently either non-existent or discontinuous. In either case, the lubrication of sticky spots is reduced and Ice Stream C shuts down.

As we now demonstrate, the till rheology (as determined by porosity) is unlikely to have been much affected by the disruption of the water film. Thus, the sticky spots are as important to the dynamics of Ice Stream C flow as they are for Ice Stream B.

We now demonstrate that dewatering the till (changing the porosity from 40 to 30%) by conduction through the till requires O (10⁶a). The volumetric flow rate u through a permeable medium is given by Darcy’s law as u = -KdH/dx, where K is the hydraulic conductivity (K = 10^-6 m s^-1) and the hydrologic potential gradient dH/dx = 10^-3.The flow rate per unit width is q = u × h, where h is the thickness of the permeable till. For a 10 m thickness of till, q = 10^-8 m² s^-1, and to move 10% of the water to the grounding line (10⁵ m) would require t = (10⁵m × 10 m × 0.1)/q = 10⁶a.

If, on the other hand, channels were to form at the base of the ice stream, the till would dewater upwards and that water would be quickly removed. However, after the top few centimeters of till had dewatered, the hydraulic conductivity of that zone would decrease by many orders to magnitude (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987) and slow the dewatering process for the deeper till. The cap over the till would tend to maintain the porosity of the till on time-scales on the order of centuries. We argue that an unconsolidated till at the bed of Ice Stream C that permitted fast ice flow 130 a ago would likely still exist. Supporting these theoretical considerations is the discovery of a 20 km wide band of presumed dilatant till beneath Ice Stream C flanked by till of indeterminate dilatancy (Reference Atre and BentleyAtre and Bentley, 1993). These results arc from an analysis of the phase-reversals of reflections from the bed during an explosive-source seismic profile on Ice Stream C.

2 Analysis

During the austral summer of 1987-88, a seismic array recorded 161 thrust-faulting events from the base of Ice Stream C (Reference Anandakrishnan and BentleyAnandakrishnan and Bentley, 1993). All the events shared the same fault-plane solution of slip at an angle of 30° to the long axis of the ice stream at a dip of a few degrees. All the events were therefore subject to the same stress field that is due almost exclusively to the surface and basal slopes of the ice stream.

The events were within 10m of the bed of the ice stream, and Reference Anandakrishnan and BentleyAnandakrishnan and Bentley (1993) argued that they are most probably either in the subglacial region or at the interface, rather than within the ice. They argued that under the low strain rates present at the base of Ice Stream C, and the high temperature (close to or slightly below freezing), it is unlikely that ice would fracture (Reference HobbsHobbs, 1974). Rather, the basal shear stress is transmitted to the bed. Events on the interface between the ice and sediment would have moments determined by the average source parameters of the two media. We consider this situation most likely and use a moment determination that is intermediate between one calculated for ice and one calculated for the sediment.

The threshold-detection algorithm for the Ice Stream C events was used in two modes: single-station trigger and dual-station trigger. The single-station trigger would initiate recording of all seismograms in the array when the trigger station detected an event. To discriminate against small events, we occasionally used dual-station triggering where two widely separated stations must both detect an event before recording was initiated. The single-station- trigger events were on average smaller (lower seismic moment) than the dual-station-trigger events, but still had excellent signal-to-noise ratios (SNR > 18 dB).

2.1 Time-series analysis

We extract from this data set a list of event-occurrence times t_i , inter-event times τ_i = t_i - t_i-1 , and the associated successive-event horizontal separation d_i = |r_i-r_i-1| where r_i is the horizontal position of event i and || denotes the magnitude of the enclosed vector. We include event i if events t_i and t_i-1 were not separated by any down-time of the recording system. This reduced the set to 53 events.

The counting statistic n(T) is defined as the number of events in a time window of length T (Reference Madariaga and KanamoriPapoulis, 1984). The probability distribution function P(n; T) is a Poisson distribution if all the events are independent. The horizontal separation d_i we defined for each pair of events t_i, t_i-1 is now used to test whether the events are described by a Poisson process at all scales. That is, we now examine whether there is some critical event separation D such that the sub-set described by d_i ≤ D is not distributed as a Poisson, but events described by d_i > D are Poisson. Certainly D < 蜴 must exist because events at some (possibly great) distance must be independent. If D = 0, then the microearthquake events are independcnt one from another at all distances. We call the distance D the "radius-of-influence" (ROI) of a microearthquake.

We test whether a distribution is Poisson by a X² test and reject the hypothesis of Poisson if the goodness-of-tit parameter q is small. The goodness-of-fit parameter q = Q(x²||v) is the probability that the observed chi-square will exceed the value X² by chance even though the model is correct; the function Q is the X² distribution function (Walpole and Myers, 1975). Because of the small sample size, we reject the Poisson hypothesis if q is O (10^-10) but accept the hypothesis for q that is O (10⁵). This is not entirely arbitrary; examination of Figure 1 demonstrates that q tends to fall into two regions: q≥10^-5 and q≪10^-10

The counting distribution n(T) depends on the counting length T. For T short compared to mean inter-event time τ̄, any distribution will be well described by a Poisson (Reference Madariaga and KanamoriPapoulis, 1984). Thus, we test for Poisson distributions by varying T from T ≪τ to T ≫ τ̄ If we cannot reject the Poisson hypothesis at all T, then we must accept it.

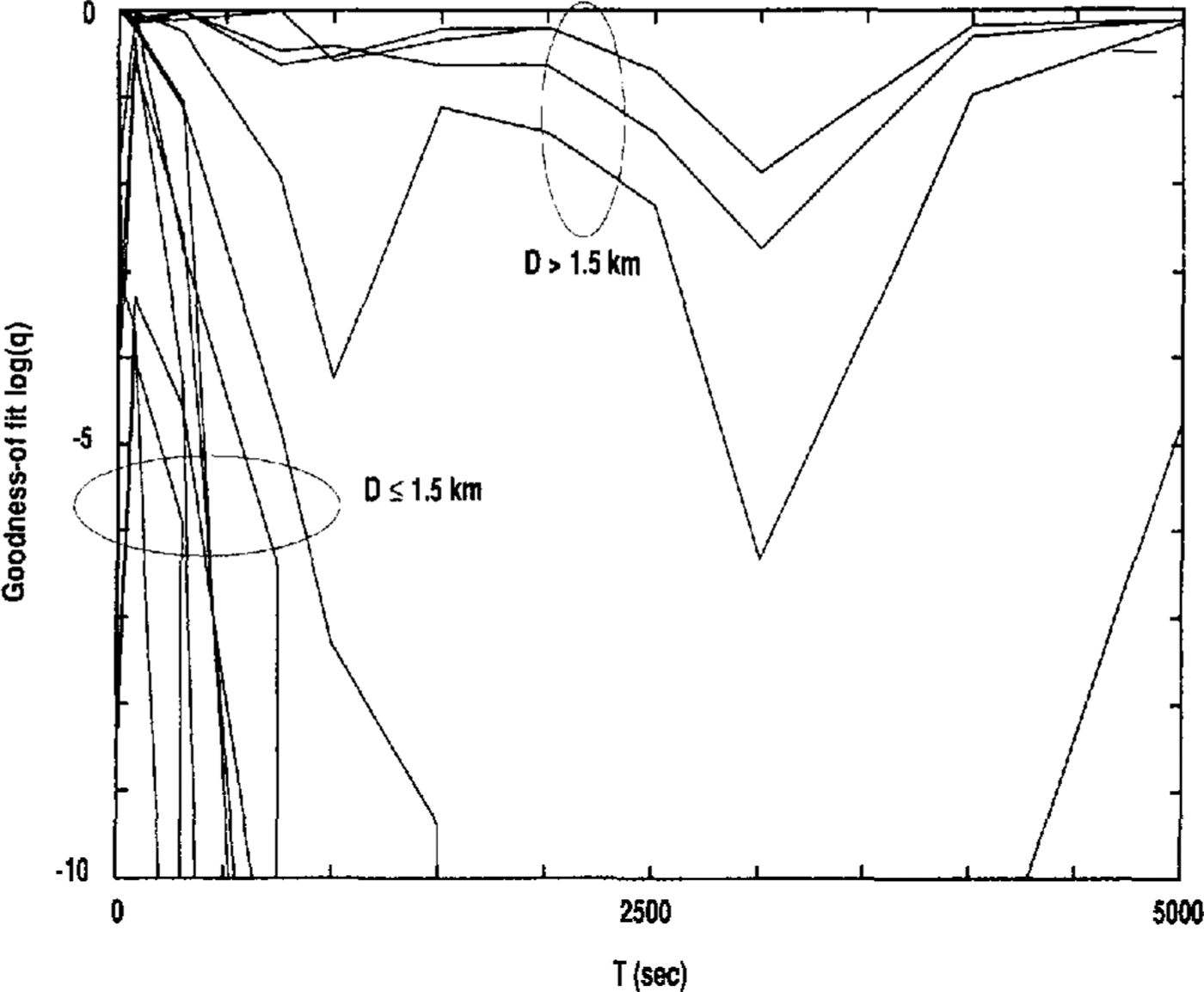
Fig. 1. Plot showing log of the X² goodness-of-fit parameter q versus the counting time T. The different curves are for different values of D, the critical distance between successive events.

Figure 1 is a plot of q vs counting time T. The range of T is from 1 s to 5000 s with τ̄ ≈ 800 s . The different lines are for the sub-set d_i < D, with D ranging-from 100m to 2500m. For D≤1500 m, we reject the hypothesis of Poisson distribution because q≪ 10^-5 at some T (generally at T ≳τ̄, q drops sharply from O (10⁵) to O (10^-20) or less). Note that, in accordance with theory, q = 1, indicating a good fit with the Poisson distribution at T = 1 s (a time much shorter than the mean inter-event time τ̄ ). For D > 1500 m, the hypothesis of Poisson distribution cannot be rejected. The threshold level of q = 10^-5 is somewhat arbitrary, but it is clear that for the three curves marked D > 1500, the hypothesis of Poisson is more plausible than for the other curves, which are marked D≤1500 m. Though the number of data points for the large-separation curves (D> 1500 m) is small (n = 15), the goodness-of-fit parameter q is large (≥10²) at most T and never drops to 10^-20 as do the curves marked D ≤ 1500 m.

2.2 Spectral characteristics

Using the spectrum of the compressional-wave arrival, Reference Anandakrishnan and BentleyAnandakrishnan and Bentley (1993) calculated the seismic moment of the events using the methods of Reference Aki and RichardsAki and Richards (1980) and Reference BruneBrune (1970). The seismic moment calculation is a function of source density and shear-wave velocity. Assuming source parameters intermediate between ice and sediment, we calculate that the seismic moments M ₀ for the 161 events beneath Ice Stream C averaged M̄₀ = 10⁷ N m.

Frequency analysis of the seismic wave forms using the method of Reference BruneBrune (1970) and Reference Madariaga and KanamoriMadariaga (1983) can be used to calculate the source radius. In one generally used method Reference Aki and Richards(Aki and Richards, 1980), the spectrum of the displacement wave form is fitted to a function of the form u ₀/(1 + (ω₀/ω)²)where u _o is related to the moment (and is a robust measure thereof) and ω ₀ is related to the fault-plane area S. The angular frequencies ω and ω ₀ are defined as ω≡ 2π/f and ω ₀≡ 2π/f ₀, where f and f₀ are spectral frequencies in Hz. Calculations of fault-plane area are highly model-dependent and therefore fault area S is not as well constrained as moment M₀, but is good to an order-of-magnitude. We estimate the fault area as S∼10²m²

Finally, using the moment and fault-plane area, we calculate the stress drop associated with the events by Δσ≈M0/aL³≈10⁵ Pa where L ∼√S is the characteristic dimension (radius or length) of the fault and a = 0.1 is a fudge factor for fault shape and could go to 0.3 (Reference Kostrov and DasKostrov and Das, 1989), Again, because of the uncertainty in L, the stress-drop Δσ is an order of-magnitude approximation.

Using simple Darcy’s law arguments, we demonstrated that the till is likely to retain a high porosity regardless of the state of the basal water system. The results from the microearthquake time-series analysis suggest the same conclusion. The ROI for events at the bed of Ice Stream C is 1.5 km. A qualitative interpretation of this result is that the intervening material has low strength. Work in progress is aimed at quantifying a relation between ROI and sediment rigidity.

We now estimate whether the driving stress of the ice streams is balanced entirely by the stress drops of the microearthquakes. We assume that the bed alone supports the driving stress of the ice stream and ignore the role of the sides of the ice stream.

The shear stress at the base of the ice is given by σ_i = ρghα ≈ 0.01 MPa (Paterson, 1981) where ρ = 10³kgm ³ is the density of ice, g = 10ms^-2 is the acceleration due to gravity, h = 10³m is the ice thickness and α = 10^-3 is the surface slope. The mean separation of events is approximately 400 m. If we assume that the inter-sticky-spot material is weak, then the stress of a (400m) ² area is concentrated on one sticky spot (on average). The force on each such sticky spot is F = (400 m) ² × 0.01 M Pa = 1.6 × 109 N. The area of each of the sticky spots is S∼10² m and thus the shear stress on each sticky spot is σ = F / S ∼10 M Pa. The seismically measured stress drop is 0.1 M Pa.

Theories of partial stress drop hypothesize that an earthquake only releases a fraction of the total applied stress on the fault. Estimates of the fraction vary from 1 to 10% (Reference BruneBrune, 1970). Thus, if partial stress drop is 1%, then the driving force of the ice stream is entirely balanced by the sticky spots; if it is 10% then only 10% of the driving force is balanced by sticky spots.

3 Conclusion

Microearthquakes at the bed of Ice Stream C occur at discrete zones of high friction that are separated by low-strength till. These sticky spots balance most, if not all, of the driving stress of the ice stream and are strong candidates for the mechanism for restraining ice flow. We have demonstrated that, even though the fault radius of an individual microearthquake event is O (10 m), the events can modify the stress at locations up to 1.5 km away. This argues for a weak intervening material.

For sticky spots with a mean separation of 400 m, a mean radius of 10 m and with a weak intervening till, the sticky spots support 10-100% of driving stress for ice flow. Thus, we suggest a model of the base of the ice streams that consists of a weak, unconsolidated till interspersed with discrete zones of higher strength that are on the order of 10² m² in area. These zones have a spatial density, on the order of 10 km^-2. The frictional character of these sticky spots is a possible candidate for the controlling parameter for ice-stream flow speed.

The suggested diversion of Ice Stream C basal water (Reference Alley, Anandakrishnan, Bentley and LordAlley and others, 1994) and the consequent slowing of Ice Stream C is likely to have preserved the porosity of the till and the size and density of the sticky spots. The friction on the sticky spots is the only parameter likely to have changed. We suggest that sticky spots exist beneath Ice Stream B but only rarely do they manifest themselves seismically. The microearthquakes emanating from the base of Ice Stream C are the first direct evidence of the difference in frictional character of sticky spots between the fast and slow ice streams.

Acknowledgements

We thank M. C. Teich and B. E. A. Saleh for helpful discussions about triggered-event statistics. One of us (S.A.) is supported by the Lucille and David Packard Fellowship Fund. We thank the National Science Foundation Office of Polar Programs for additional support.