1. Introduction
Marine ice streams are characterized by relatively high velocities caused by the small traction at their beds. Generally motion of a marine ice stream is affected by the side walls, surrounding stagnant ice sheet and flow-band geometry, etc. (Reference Van der Veen and WhillansVan der Veen and Whillans, 1996). Understanding of the simple two-dimensional (2–D) steady isothermal flow of marine ice streams is still not comprehensive. This concerns mainly the ice-stream-ice-shelf interaction as well as the stream-shelf transition-zone characteristics. Therefore, development of a 2–D mathematical model of marine-ice-stream flow is necessary for studying ice streams, whose flow is close to 2–D, and could help in studying three-dimensional flow of ice streams, because the model shows some non-trivial features of the ice flow, especially near the grounding line.
When the flow is 2–D, then the conventional view (Reference Muszynski and BirchfieldMuszynski and Birchfield, 1987; Reference MacAyealMacAyeal, 1989) is that the shear stress in the ice stream is much less than the longitudinal deviatoric stress and the ice-stream dynamics are similar to those of the ice shelf. In this case, it has reasonably been assumed (Reference Thomas and BentleyThomas and Bentley, 1978; Reference Muszynski and BirchfieldMuszynski and Birchfield, 1987; Reference Hindmarsh and PeltierHindmarsh, 1993) that in the stream-shelf transition zone the shear stress is also much less than the longitudinal deviatoric stress, so the stream-shelf transition zone has not been considered as singular and its analysis has not yet been carried out.
The problem of modelling marine-ice-stream dynamics is described by relations among independent and dependent fields and their gradients (e.g. upper surface slope), which will be determined in solving the problem. Evidently, scales of the dependent parameters are functions of the scales of the independent ones. We will call a scaling consistent when the scales of dependent parameters are determined in scaling analysis of governing equations, based on our understanding of the physical processes under consideration. In the present study, we apply consistent scaling to consider ice streams with different relations between the shear and longitudinal deviatoric stresses. We also present a theoretical analysis of the ice-stream-ice-shelf transition zone.
The scaling analysis of the ice-stream and ice-shelf flows is based on two main assumptions: first, that the force driving the ice flow is the longitudinal pressure drop caused by the negative slope of the ice upper surface (which is balanced by the gradient of the shear or longitudinal stress deviator); second, that the aspect ratios of the ice stream and the ice shelf are comparable with the typical slopes of the upper and the lower ice surfaces respectively. The first assumption is physically reasonable. The second one can be ascertained by survey data. The cases when the second assumption is not valid are not investigated closely in this paper, but will also be discussed; revealing that the singularity of the transition zone is not based on the second assumption and is applied to the general case of 2–D flow.
Whereas the "shallow-ice approximation" is generally used to describe the boundary-layer approximation of the shearing flow of ice (Reference HutterHutter, 1983), let us for brevity use it to describe any reduced model of the ice flow obtained with the use of the smallness of the aspect ratio.
Notations
Letter subscripts denote derivatives. Scales are denoted by brackets.
2. Governing Equations
Let us put the origin of a rectangular righthand coordinate system at the begining of the ice stream (Fig. 1). In particular, the point of the begining can be an ice divide.
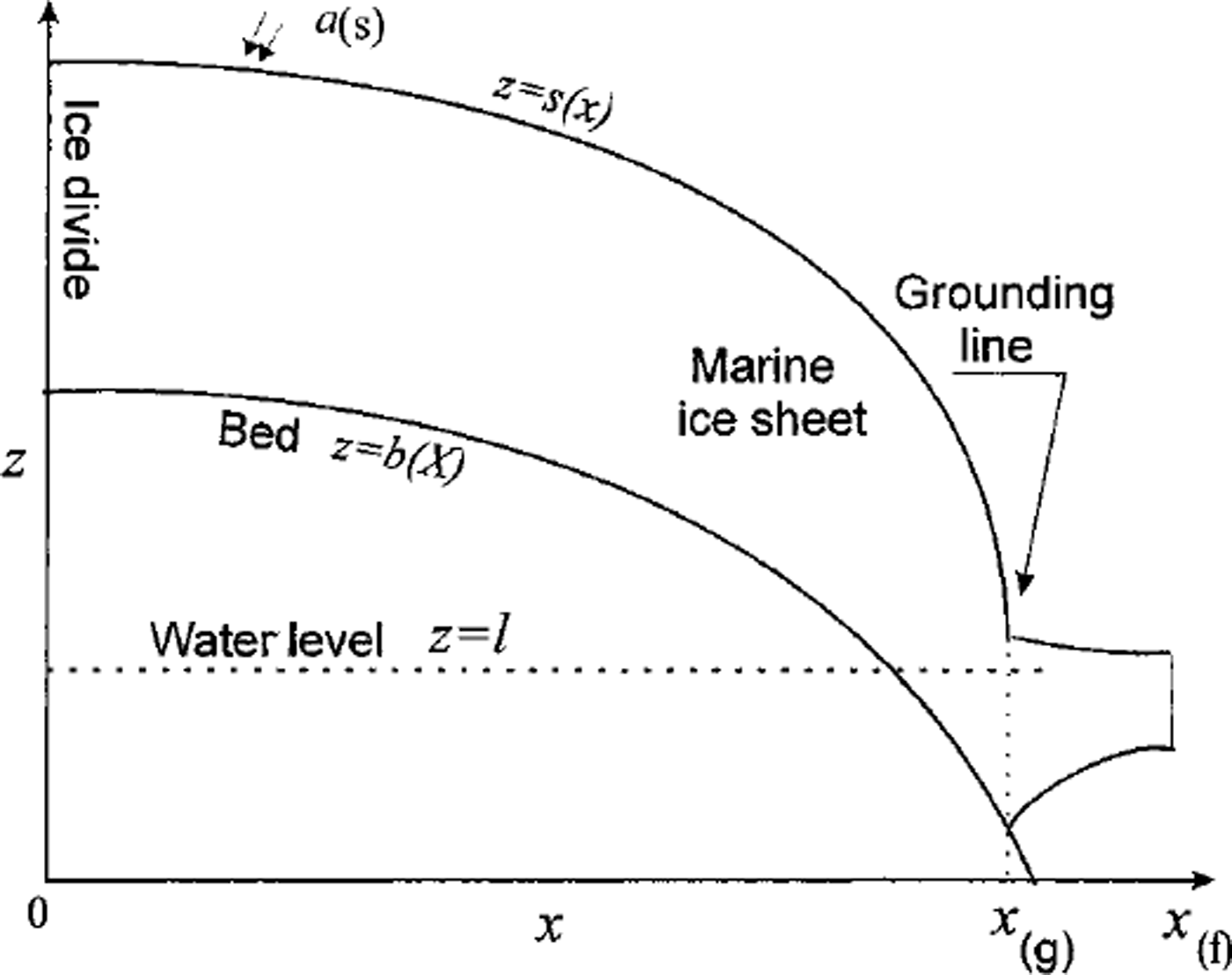
Fig. 1. Marine ice stream.
Two-dimensional steady isothermal ice motion is described by the following conservation and constitutive equations:
Boundary conditions are common (e.g. Reference Muszynski and BirchfieldMuszynski and Birchfield, 1987). In particular, at the begining of the ice stream, the ice thickness, h,d), and horizontal mass flux, q<d), are assumed to be known. If the begining of the ice stream is an ice divide then q,d) = 0, which determines the ice thickness. At the ice front it is sufficient to impose a value of the normal stress (Reference WeertmanWeertman, 1957).
At the bedrock we use the exponential sliding law (Reference FowlerFowler, 1987)
where k is the sliding coefficient assumed to be known as a function of x. Generally, behaviour of the function k depends on subglacial cavity volumes, water pressure, etc. (Reference LliboutryLiboutry, 1979; Reference FowlerFowler, 1987). Here we consider the situation when the sliding coefficient has a value of the same order along all the ice-stream length. We also assume that u > 0 and sx≤0 in the ice stream and the ice shelf. The latter assumption, s× ≤ 0, may break down near the grounding line.
Evidently, we can find the continuous velocities, stresses and surface profiles (solution of Equations (1)–(10)) only for certain grounding-line positions and their ice thicknesses, which determine the solution of the marine-ice-stream problem. Because Equations (1)-(6) for determining the velocities, stresses and upper surface profile, written for 0 ≤ × ≤ xf are assumed to be valid in the whole zone of the ice flow (which means that smooth solutions are sought), we impose the condition of continuity of the lower surface profile at the grounding line, b(–0) = 6(+0), to determine the grounding-line position.
We also will use the following integral equations
Equations (11), (12) and (13) are derived first by integration of (1) and (2), respectively, with respect to z from b to s. Then equation (11) is derived by integration with respect to × from × ≤ x(g) to x(g) and Equation (12) is derived by integration with respect to × from X > X(g) to x{{). Therefore, Equations (11) and (12) describe the force balance in the ice volumes bounded by the planes × = const, × = x(g) and × = const, × = x(f), respectively. Equation (13) describes force balance in the section × = const. Using these equations, instead of one of the boundary conditions at the upper surface, is convenient in analysis, because the shear stress is much less than its typical value at the upper surface (Reference HutterHutter, 1983; Reference Johnson and McMeekingJohnson and McMeeking, 1984).
3. Ice Stream
3.1. Scaling analysis
If the sliding velocity has order not much higher than the component velocity due to shearing deformation, then scales of fields describing shearing flow in glaciers (subscript o) are well-known (Reference Salamatin and MazoSalamatin and Mazo, 1984):
Here [x] and [a] can be determined from observations. Physically, this relation, between ε0, [a] and the other parameters, is determined by equality of the scales of the pressure longitudinal drop and the vertical gradient of the shear stress. From observations it is known that ε≤ ε0 ∼ 10"2 - 10−3.
The case when the shear stress has an order not less than the longitudinal deviatoric stress in ice streams ([T1]>[τ2]) was considered by Reference FowlerFowler (1982) and that of slow varying traction was considered by Reference Hindmarsh and PeltierHindmarsh (1993). Here we consider all the situations when the shear stress can be much less or much higher than the longitudinal deviatoric stress.
Here we assume [x] to be prescribed and known from observations. Along the ice stream, the ice thickness is assumed to decrease by a value comparable with the thickness itself, therefore [Ux] = [u]/[x]. Evidently [u] = [q]/[z] and w = eu from mass conservation. Because the ice stream can have a large catchment area, we generally do not assume [q] = [a][x]. Scale for the pressure is [z]p(i)g. It should be noted that if the upper surface slope is much less than the ice-stream aspect ratio, then [px] ≪ p(i)ge. Again, if the ice-thickness gradient is much less than the aspect ratio, then ux ] ≪ [u]/[x]. These cases require more subtle scaling analysis which is not considered here. However, when the ice-thickness gradient is comparable with the upper surface slope and both are less than the aspect ratio, then in scaling analysis we can assume the typical ice thickness [z] (instead of [x]) to be prescribed and find the typical slope of the upper surface from scaling analysis, which will determine [x] much higher than the ice-stream length.
To find [Uz] we decompose u = U(sl) + vu(sh), where U(sl) is the sliding velocity and Vu(sh) is the shearing component velocity. The dimensionless parameter v is to be chosen so that [U(sh)] = [u] and is a typical ratio of the shearing component of velocity to the velocity u. Hence [Uz] = v[u]/[z] and from Equations (4) and (5) we have [τ2]/[τ1] ∼ ejv if ε2 < v determining uz. On the other hand, from the boundary conditions at the upper surface we have 
hence at the upper surface T ∼ er2, therefore in the ice stream. This means that */>£2 always.
For the stresses we have
where 
when (the typical shear stress is not less then the typical longitudinal deviatoric stress) and when 
(the typical longitudinial stress is not less then the typical shear stress). From the sliding law in Equations (10) we derive
Determination of v using the sliding law is correct only if the shear stress has an order at the bed not less than at the upper surface (shearing is determined mainly by the traction at the bed and τ1(x,b)∼[τ1]), when the order of the sliding velocity is not less than the order of the shearing component velocity. This is because this determination corresponds to finding the scale of the shear stress [n] from the sliding law. If then this determination is not valid. On the other hand, if we derive v » 1, then it means that sliding is negligible and we must put v = 1 in further analysis.
When the shear stress is maximal at the upper surface, then, as it was shown above, v ∼ ε2. Therefore, in order for Equations (16) and (17) to be correct, it is sufficient that ε2 ≪ v, which is, as will be seen later (Equation (18)), equivalent to the confirmation that a value of the second term of (1) is negligible in comparison with the other terms.
3.2. Governing equation in dimensionless form
Denoting dimensionless variables by capital letters, for the ice stream we obtain
where
and
Boundary conditions:
3.3. Determination of dependent scales
From Equation (18) we infer that A must be of order 1. Letting A = 1, we can find the typical ice thickness or the ice-stream aspect ratio
When v derived from Equations (16) and (17) is not higher than 1, we can write these formulas as one via [k]:
This equation does not include information about rheology Comparing aspect ratios of glaciers of the same typical length with sliding ε and without it ε0, we can write
From Equations (27)–(30) we have
We can find typical value [k] (τ) k](r) of the sliding coefficient determining equality of the scales of the shear and longitudinal deviatoric stresses. Equating ε = v yields
Putting v = 1, we can find typical value [k](v) of the sliding coefficient determining equality of the scales of the sliding velocity and the shearing component velocity:
3.4. Shelf-like dynamics of ice streams
The parameter ε2/v in (18) determines the importance of the longitudinal stress deviator in the momentum conservation equations. If ε2 /v ∼ 1, then we expect an analogy with shelf dynamics. Reference Hindmarsh and PeltierHindmarsh (1993) calls such streams "shelfy streams". In this case U = U(sl) + O(e2) and the equation for the ice thickness will be (Reference Muszynski and BirchfieldMuszynski and Birchfield, 1987)
with the boundary condition determining the ice thickness at the grounding line to be found.
3.5. Plug and shearing flow
Let us consider the situation when ε2/v ≪ 1. In this case to order O(e2 /v) + O(ε2) from Equations (18)–(26) we derive
Mass balance:
Boundary conditions which have not yet been taken into account:
If v ≪ 1, then Q = KH(-SxH)m + O(y). If v ∼ 1, then Q = KH(-SxH)m + |Sx|nHn+ 2/(n+2). In the first case (plug flow) we have an equation for the ice thickness (Reference FowlerFowler, 1982)
In the second case we derive (e.g. Reference Salamatin and MazoSalamatin and Mazo, 1984)
Equations (42) and (43) require boundary conditions at the grounding line to be found. One can note that (42) and (43), contrary to (34), do not require the value of the ice thickness at the begining of the ice stream to be imposed.
For ice streams we expect v ≪ 1, while for glaciers with no-slip condition: v ∼ 1. Therefore it is necessary to estimate value ε2/ v to determine what model to apply: Equation (34) or (42) and (43). Evidently, if ε ≤ v (order of the shear stress is not less than the order of the longitudinal deviatoric stress), then and (42) and (43) are to be applied. If v<e, then from Equations (30) we find 
. For Ice Stream E we have [x] = 300 km, [z]0
= 2.4 km, [z] = 1.1km (e.g. Reference LingleLingle, 1984), therefore for n = 3 we obtain ε2/*/ ∼ 0.005 and we do not expect "shelf-like" dynamics of this ice stream. For ice streams of Vilcheck Land (Franz-Josef Land) ε = 0.01, ε0 =0.02, therefore ε2/v ∼ 0.01 for n = 3 and we arrive at the same conclusion. On the other hand, putting v = ε2, we find and typical ice thickness is of the order of only several metres, which is not observed.
4. Ice Shelf
Ice-shelf dynamics have been studied by many authors (e.g. Reference WeertmanWeertman, 1957; Reference ThomasThomas, 1973; Reference SandersonSanderson, 1979; Reference Van der VeenVan der Veen, 1983; Reference Muszynski and BirchfieldMuszynski and Birchfield, 1987). We show only the main points of analysis of 2–D isothermal flow of an ice shelf. Evidently, because the ice shelf is afloat, the upper surface slope is about ten times (1/ δ) less than the lower surface slope. We expect that shearing is determined mainly by the ice-thickness gradient and reaches its maximum at the lower surface; the steepest one in the flow direction. We introduce the spatial scales and assume Boundary conditions at the lower surface yield [τ1] = ε(s) [τ2], which is equivalent to where determines the importance of the component velocity due to the shearing deformation in relation to the component velocity due to the longitudinal deformation (analogous to U(sl)). It is necessary to point out that in the ice shelf the driving force (longitudinal pressure drop) is estimated as [px] = ε(s)P(i)gS (about ten times less than it would be in the ice stream with the same aspect ratio). Scale for the velocity is as usual [u] = [q]/[z](s) As with the ice stream, we find that parameter λ(s) = λ/δ is of order 1. However, in studying ice-shelf dynamics it is sometimes convenient not to equate λ(s) = 1 at this step. Neglecting terms of order 
we derive new variables pointed by tildes:
Equating the factor at the right side to 1, we obtain
Finally, solution of (44) can be found as (Reference Van der VeenVan der Veen, 1983)
where
Here constant V determining the ice thickness at the grounding line is to be determined from matching the solutions found for different zones.
5. Ice-Stream-Ice-Shelf Transition Zone
5.1. Revealing singularity near the grounding line
Differential equations (34), (42) and (43) determining the ice-stream thickness require the boundary condition at the grounding line. Solution (46), determining the ice-shelf thickness, has one free parameter determining the ice-shelf thickness at the grounding line. Evidently, if the shear stress in the ice stream is much larger than the longitudinal stress deviator, then all the stresses in the transition zone are of the same order and the transition zone is singular (e.g. Reference Chugunov and WilchinskyChugunov and Wilchinsky, 1996). Let us then consider the situation when the value of the parameter v, describing the importance of the shearing component velocity, is small near the grounding line and presume that the (shallow-ice-approximation) solution for the ice shelf found (46) is valid up to the grounding line. In this case the solution of the problem of marine-ice-stream dynamics determines the ice thickness at hydrostatic equilibrium and continuous stresses at the grounding line. This means that strain rate is also continuous at the grounding line. On the other hand, due to the small value of v, to order of O(y) we have Hence, because Q and H are continuous at the grounding line, we obtain continuity of the ice-thickness gradient at the grounding line.
First, we consider the situation when the upper surface slope in the ice stream has order not less than the ice-thickness gradient S× > Hx. At the same time H× ∼ Sx/6 in the ice shelf, due to the condition of hydrostatic equilibrium. This yields in other words, such a solution determines a ten-time break of the upper surface slope and Sxx much higher near the grounding line, than it is in the ice stream or in the ice shelf. However, from physical considerations we expect the smooth upper surface profile.
Second, we consider the situation when the upper surface slope in the ice stream is much less than the ice-thickness gradient. Evidently, such a situation can occur only if B× > 0 when X ≤ Xg. In this case we start from investigation of the solution for the ice shelf (46). In deriving this solution we assumed that S× ≤ 0, which is physically consistent. Therefore, this determines Hx(X(g)+) ≤ 0 and Bx(X(g)+) ≥ 0 at the grounding line. Evidently, if Bx(X{g)-) ≠ Bx(X{g)+) then matching the strain rate also determines a break of the upper surface. Although investigation of Equation (34), written for the ice stream and for the ice shelf, does not allow us to conclude that if Bx(X(g)-) = Bx(X(g)+) then the strain-rate is continuous at the grounding line, one could assume it. However, in this case the condition Bx(X{g)-) =Bx(X{g)+) implies that H(w)(X(g)) = (1–δ)H(X(g)+) and H(w)× (X(g))=(1–δ)Hx(X(g)+), where H(w) is the water depth. Therefore, due to (44) the water depth H M at the grounding line must satisfy the equation
which is assumed to be a very strong restriction on the bed profile determining the existing of the solution of the marine-ice-stream dynamics.
Eventually, we conclude that in any case, even if we consider "shelf-like" dynamics of the ice stream, the reduced models found adequate in the ice stream or in the ice shelf are not adequate near the grounding line and the transition zone is singular. This can be caused not only by the change of flow style in the transition zone, but also by the change of boundary condition at the base from the absence of the Archimedes force to the presence of it.
5.2. Scaling analysis
Let us determine the scales of the transition zone. For this purpose we consider Equation (1).
First, in the transition zone we expect that all the stresses important in both the ice stream and the ice shelf are important in the transition zone. Therefore, all terms in (1), describing the influence of the stresses, must have the same order (as in the ice shelf), because all these terms determine the change in flow style in the xz plane.Footnote *
Second, if the longitudinal deviatoric stress in the ice stream is much larger than the shear stress and this holds in the transition zone, then the boundary condition at the lower surface yields [τ1]/[τ2] ∼ ε(s) ≪ 1 and the shallow-ice approximation is valid in the transition zone, which contradicts the conclusion made above. Hence, in any case in the transition zone all the stresses are of the same order.
On the other hand, both statements are possible only when [τ1] = [τ2], [a;] = [z] = [h] (generally [u] + [w]). This means that the full system of Stokes equations must be solved in the ice-stream-ice-shelf transition zone.
Denoting h (g) h(x(g)) the ice thickness at the grounding line, we introduce new variables, pointed by bars with the same (yet unknown) scale [τ] for the stresses and the excess pressure; and the scale h(g) for the coordinates and the ice thickness. We also move the origin of the coordinate system to the bed at the grounding line.
Integral equations (12) and (13) for X > 0 (in the ice shelf) take the forms
where
Eliminating 
from Equations (47) and (48), we derive
where
From this equation it can be seen that 0 ∼ 1, otherwise either the first term on the righthand side (which describes the driving force in the ice shelf) is not balanced 
or is not important 
which contradicts the transitional behaviour of the flow. Hence, Equation (47) means that to order O(S) the ice thickness can be found from the condition of hydrostatic equilibrium and the upper surface slope is of order O(S). However, for high sliding velocities the latter estimate can be improved in the ice stream near the transition zone, where the shallow-ice approximation is still valid.
First, for determining [τ] we use Equation (11) taking into account (48):
Here we assumed that B× ∼ ε when X ≤ 0. This equation is written at X ∼ 1, where the shallow-ice approximation is valid (near the transition zone, but not in it). Due to the above estimate on the upper surface slope, we have 
. The scales of the shear stress and longitudinal stress deviator at so chosen X (near the transition zone, but where the shallow-ice approximation is valid) are denoted by [τ1]0, [τ2]0 and are generally different from those in the ice stream. Evidently, the scale of the shear stress, τ1 b in the zone of integration is the maximum of the typical shear stresses near the transition zone [τ1]0 and in it [r].
Equating the typical values of lefthand-side and right-hand-side terms yields the physically reasonable relation
The scales [τ1]0, [τ2]0 can be found from Equation (15) using (16), (17) and (29) to determine the typical ice-surface slope of the ice stream particularly near the grounding line as a function of h(g) (in this case) when the shallow-ice approximation is valid (one should not forget that these formulas were derived with the assumption s× ∼ hx). On the other hand, from (49) we derive [r] = h(g)P&gS. Elimination of h(g) yields
These estimates are valid when the value, v(t), of the parameter v near (not in) the transition zone is no higher than 1 (v(t) is not equal to the value of v in the ice stream because the scales of the flow near the the transition zone and in the ice stream are generally different). Equating v(t) = 1 in (16) and using (15) and (55) we derive [τ] and the corresponding value [k](v,t) of the sliding coefficient making v(t) ∼ 1:
For the typical ice-stream surface slope near (not in) the transition zone ε(t) from (29) we obtain
Although these relations determine the typical upper surface slope near the transition zone, because they were derived using estimates for the shallow-ice approximation, we expect that these estimates are also valid in the transition zone. Otherwise, if the surface slope in the transition zone is much higher, this could lead to much higher longitudinal deviatoric stress, which contradicts (52).
IF V(t) ∼ 1 (sliding is negligible), then substituting Equation (55) in (45) for [z]s and using (56) we find that in this case the typical slope of the ice shelf surface near the transition zone is 2−2n–1.
In the derivation of Equations (53)–(59) we used formulas (16) and (17), valid when the shear stress in the ice stream near (but not in) the transition zone reaches its maximum at the lower surface. It is true particularly when the gradient of the longitudinal deviatoric stress in (1) is much less than the other terms. Evidently, if in the ice stream the shear stress is much larger than the longitudinal deviatoric stress then this is true. If the situation is the contrary and we assume that all the terms in (1) have the same order, then equating [px] = P(i)g[h(g)]/[x] = [T2x} = [τ]/[x] we find [T]=P(i)g[h(g)], which contradicts (55). Hence our scaling is adequate.
For the use of formulas (53)–(59) we can find the typical value [k](t) of the sliding coefficient, which determines [τ1]0 ∼ [τ2]0. Equating [τ1]0 = [τ2]0 yields
Evidently [τ1]c τ2 when [k] (t) [k] and vice versa.
To compare the typical values of the sliding coefficient determining different flow styles, we find the following ratios:
Using these formulas we derive for m == n and 6 == 0.1:
It can be seen that the value of the sliding coefficient determining the equality of the typical sliding velocity and the shearing component velocity in the ice stream [k]M also determines the equality of the typical longitudinal deviatoric stress and the shear stress near the grounding line, where the shallow-ice approximation is still valid. This value is much less than that determining the equality of the typical longitudinal deviatoric stress and the shear stress in the ice stream [k] (τ) This is caused by the higher surface slope near the grounding line than that in the ice stream.
5.3. Problem for the transition zone
In order to find the boundary condition at the grounding line relating the ice thickness and horizontal mass flux at it, we scale values in the transition zone by the scales of flow without sliding (shearing flow):
Here q(g) is the (yet unknown as well as h(g)) horizontal mass flux at the grounding line. In the transition zone the full system of Stokes equations (considered as the inner problem) must be solved (new variables are pointed by hats):
where
Boundary conditions:
where
For determination of the suface profiles, instead of the boundary conditions at the free surfaces, we use the integral equations:
where
The initial condition is β, In these variables ff (w is unknown.
The parameter (3, as it will be seen later, plays an important role and is proportional to the ratio of the longitudinal stress deviator found with the shallow-shelf approximation to the shear stress found for the Pouiselle flow at the grounding line.
Solution of the problem (65)-(78) and matching the solutions found for the ice stream, ice shelf and transition zone is beyond the scope of this work. However, it should be noted that values in (65)-(78) are not of order 1. If expansion on 6 is used, then, proper scaling must first be performed. For example, near the grounding line we cannot neglect the upper surface slope (as it was done in the case of the no-slip condition at the bed; see Reference Chugunov and WilchinskyChugunov and Wilchinsky, 1996), because the longitudinal deviatoric stress, which plays a significant role in the transition zone, is determined by it. We can assume that the upper surface is plane and horizontal (to order O(δ)\ but the value of 
must enter the kinematic boundary condition at the upper surface (70), which in case of no-slip condition at the base yields 
and does not include information about the surface slope.
5.4. Boundary condition at the grounding line
It is physically consistent to presume that when the bed profile and horizontal mass flux are monotone functions of x, then a unique solution of the complete problem describing the ice flow in the ice stream, transition zone and ice shelf exists. In this case, because the (outer) solutions found for the ice stream and ice shelf have free parameters (their thicknesses at the grounding line) to be determined from matching with the solution of the (inner) problem (65)(78), problem (65)-(78) has a unique solution not including free parameters. On the other hand, problem (65)-(78) includes only five dimensionless parameters n, m, β, γ, δ which determine similar flows in the transition zone. Influence of the outer flow is "hidden" in /3 and γ, where the parameter /3 includes the unknown ice thickness at the grounding line h(g), and parameter 7 is a known function of x(g). Presumption of uniqeness of the solution leads to the relation /3 = β(n, m, S, 7 ). That is for certain choices of n, m,γ,δ, only the one value of /3 determines continuous fields at the grounding line. If sliding is negligible, then /3 depends only n and 6. As can be seen from (49) and (78), the typical value of β is [τ]/[r](t)
Finally, the boundary condition at the grounding line (78) relating the ice thickness and horizontal mass flux can be written as
which, when dependence β(n, m, 6, 7 γ and Hw(n, m, 6, 7 γ is known, lets us determine x(g) and h(g), because h(g) = h(w) (x)/H{w)(n, m, S, 7 ) , and the lefthand as well as righthand parts of (79) are known functions of x(g) It should be noted, that the form of (79) generally implies that several solutions x(g) can exist if b(x) or q(x) are not monotone.
In variables scaled by the scales of flow without sliding we derive
where Q(g) = Q(X(g)) and £ is the aspect ratio of the glacier without sliding (14).
6. Discussion
Because this work retrieves many results mainly concerning ice-stream dynamics, differences in the conclusions must be pointed out.
First we compare the results with those of Reference Muszynski and BirchfieldMuszynski and Birchfield (1987). For convenience we will use the definition A = 1/(27?). According to the cited work for n = 3 the longitudinal stress deviator is much larger than the shear stress if [τ2]/[τ1] = ([u]/( A[x])1/3)/(e[p]) » 1. The typical values for ice streams were taken as follows [u] = 200 ma–1, [x] = 100 km, A = 1 × 10–17 a–1 Pa–3, [p] = 2.5 × 106 Pa. For ε = 0.01 this yields [τ2] / [τ1] ∼ 2 and for ε= 0.005 this yields [τ2]/[τ1] ∼ 5. Therefore, we generally do not expect the shear stress to be negligible in the ice streams characterized by such typical values. The difference is that in the cited work ( [τ2]/[τ1])3 was estimated and this value evidently can be much higher than 1.
The other difference concerns the determination of the scale of the strain rate Ux. Here we assume that the typical strain rate in the ice stream does not depend on the typical strain rate in the ice shelf. And the equality of the strain rates determines the characteristics of the transition zone. In the cited work, the strain rates in the ice stream and the ice shelf are equal and this determines the typical velocity in the ice stream [u] = A[x](δ[p])3 For the typical values pointed out above, we derive [u] ∼ l0kma−1. However, the last overestimate may be caused by using the same spatial scales for the ice stream and the ice shelf.
On the other hand, one can consider the following situation. For low traction at the bed, the typical ice thickness of the ice stream (found with the assumption that the surface slope and the ice-thickness gradient are of the same order) is much less than the typical thickness of the ice shelf. This is because the continuity of the longitudinal stress deviators at the grounding line (Hx(X{g)-) = Hx(X{g)+)) implies that the upper surface slope of the ice shelf is 1/6 times less than that of the ice stream, which causes the decrease in the driving force, the longitudinal pressure drop associated with the upper surface slope. In this case, we expect that the ice-stream aspect ratio is determined by the ice thickness at the grounding line. Therefore, in scaling analysis one should consider the ice thickness at the grounding line as a prescribed quantity rather than the ice-stream length, as was performed in this work. Moreover, we expect that the upper surface slope of the ice stream will be much less than its aspect ratio. Such a conclusion corresponds to the characteristics of surface slopes of Ice Stream B (e.g. see simulation by Reference MacAyealMacAyeal (1989)) and to the qualitative analysis by Reference Hindmarsh and PeltierHindmarsh (1993). If such a situation occurs, then we cannot assert that "shelf-like dynamics" are not expected for ice streams.
Let us turn to the results derived by Reference Hindmarsh and PeltierHindmarsh (1993) on modelling ice flow with slowly varying traction at the bed. Different flow styles are described with the parameter λ = [τ1]/[T2] = v/ε. Different typical values of A correspond to different flow styles: shearing (ice sheet, v ∼ 1, λ= ε-1/n), plug (called"meso-traction stream" by the author, v ∼ e, λ = 1) and shelf-like dynamics of ice streams {v ∼ e\ λ = 1/ε). Generally the derived results correspond to each other, except for the estimate for the longitudinal stress deviator in the ice sheet. We determine the scale in the region where the shearing mostly occurs and in which the flow mostly determines the ice-sheet dynamics. Therefore we derive the conventional result λ = 1/e. In the cited work the scale is chosen as the typical longitudinal stress deviator at the upper surface, whereas it is really larger for Glen’s flow law. However, the upper layer is not believed to influence the ice-sheet flow strongly (Reference Johnson and McMeekingJohnson and McMeeking, 1984), therefore this discrepancy is not significant.
Here, as in the work by Reference Hindmarsh and PeltierHindmarsh (1993), it is assumed that the typical upper surface slope depends on the sliding conditions (traction) at the bed. Again, in the present work the ratio of the typical longitudinal stress deviator to the pressure is also assumed, depending on the sliding condition, whereas Reference Hindmarsh and PeltierHindmarsh (1993) assumes this ratio (denoted δ in the cited work) constant and equal to e(n+1)/n for any traction at the bed. Therefore we consider the presented scaling approach as a generalization, which could help take into account as many affects as possible.
7. Conclusions
The analysis of two-dimensional isothermal flow of a marine ice stream shows that in the ice-stream-ice-shelf transition zone the shallow-ice approximation is inadequate and the full system of Stokes equations must be solved. The shear and longitudinal deviatoric stresses have values of the same order in the transition zone. The horizontal gradient of the longitudinal stress deviator is negligible in the momentum-conservation equation along the longitudinal coordinate written for ice streams, which are characterized by the same order of the upper surface slope and the ice-thickness gradient. An assumption of "shelf-like" dynamics for ice streams leads to an estimate of the typical ice thickness of only several metres for such ice streams. However, "shelf-like" dynamics can be expected for ice streams, which are characterized by an upper surface slope smaller than the ice-thickness gradient.
The boundary condition at the grounding line, relating the ice thickness and horizontal mass flux, can be presented in the form of Equation (80) (cf. Reference Chugunov and WilchinskyChugunov and Wilchinsky, 1996) including the parameter (5 (proportional to the ratio of the longitudinal stress deviator found with the shallow-shelf approximation to the shear stress found for the Pouiselle flow at the grounding line) determined from solution of the problem in the transition zone (Equations (61–72)) or from glaciological data. When sliding is negligible, then (5 depends only on the flow-law exponent and the normalized difference between the water and ice densities.
The style of the ice flow with sliding on the bed is characterized not only by the relation among the stresses, but also by that among their derivatives, surface slope and ice-thickness gradient, etc. Therefore asymptotic expansions on several small parameters must be used with great care and after correct scaling, otherwise real values of neglected terms will be underestimated.
Acknowledgements
Publication of this work would not have been possible without financial assistence from the Institut fur Mechanik, Technische Universität Darmstadt and the EISMINT program of the European Science Foundation.
