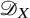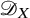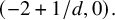1. Introduction
Throughout
![]() $f=f_{1} \cdots f_{d} \in R = \mathbb {C}[x_{1}, \dots , x_{n}]$
is a defining equation, factored into linears, of a
$f=f_{1} \cdots f_{d} \in R = \mathbb {C}[x_{1}, \dots , x_{n}]$
is a defining equation, factored into linears, of a
![]() $\deg (f) = d$
reduced hyperplane arrangement
$\deg (f) = d$
reduced hyperplane arrangement
![]() $\mathscr {A}$
in
$\mathscr {A}$
in
![]() $X = \mathbb {C}^{n}$
and with complement
$X = \mathbb {C}^{n}$
and with complement
![]() $U = X \setminus \mathscr {A}$
. By default, we regard X as a Stein manifold with analytic structure sheaf
$U = X \setminus \mathscr {A}$
. By default, we regard X as a Stein manifold with analytic structure sheaf
![]() $\mathscr {O}_{X}$
. Along with the de Rham complex
$\mathscr {O}_{X}$
. Along with the de Rham complex
![]() $(\Omega _{X}^{\bullet }, d)$
, there is the meromorphic de Rham complex
$(\Omega _{X}^{\bullet }, d)$
, there is the meromorphic de Rham complex
where d is the exterior derivative and
![]() $(\star \mathscr {A})$
means we allow poles of arbitrary order along
$(\star \mathscr {A})$
means we allow poles of arbitrary order along
![]() $\mathscr {A}$
. K. Saito [Reference Saito28] introduced the logarithmic de Rham complex
$\mathscr {A}$
. K. Saito [Reference Saito28] introduced the logarithmic de Rham complex
![]() $(\Omega _{X}^{\bullet }(\log \mathscr {A}), d)$
as the subcomplex of the meromorphic de Rham complex characterized by
$(\Omega _{X}^{\bullet }(\log \mathscr {A}), d)$
as the subcomplex of the meromorphic de Rham complex characterized by
That is, both
![]() $\eta $
and
$\eta $
and
![]() $d(\eta )$
have poles of order at most one along
$d(\eta )$
have poles of order at most one along
![]() $\mathscr {A}$
. Note that these are complexes of sheaves of
$\mathscr {A}$
. Note that these are complexes of sheaves of
![]() $\mathscr {O}_{X}$
-modules, neither of which depends on the choice of defining equation f of
$\mathscr {O}_{X}$
-modules, neither of which depends on the choice of defining equation f of
![]() $\mathscr {A}$
. There are algebraic analogues: the algebraic logarithmic de Rham complex
$\mathscr {A}$
. There are algebraic analogues: the algebraic logarithmic de Rham complex
![]() $\Omega _{R}^{\bullet }(\log \mathscr {A})$
; the algebraic rational de Rham complex
$\Omega _{R}^{\bullet }(\log \mathscr {A})$
; the algebraic rational de Rham complex
![]() $\Omega _{R}^{\bullet }(\star \mathscr {A})$
. These complexes of R-modules have similar definitions to the analytic ones.
$\Omega _{R}^{\bullet }(\star \mathscr {A})$
. These complexes of R-modules have similar definitions to the analytic ones.
Our original motivation was to answer a well-studied conjecture (Conjecture 3.1 of [Reference Terao33]) of Terao from 1977:
Conjecture 1.1 (Terao’s LCT conjecture).
The algebraic Logarithmic Comparison Theorem holds for reduced hyperplane arrangements. That is, the natural inclusion of the algebraic logarithmic de Rham complex into the algebraic rational de Rham complex is a quasi-isomorphism:
Here,
![]() $\mathbb {C}_{U}$
is the the rank one
$\mathbb {C}_{U}$
is the the rank one
![]() $\mathbb {C}$
-valued constant sheaf on U.
$\mathbb {C}$
-valued constant sheaf on U.
That
![]() $H^{\bullet }(\Omega _{R}^{\bullet }(\star \mathscr {A}), d) \simeq H^{\bullet }(U, \mathbb {C}_{U})$
is a consequence of Grothendieck’s Comparison Theorem [Reference Grothendieck17]. So Conjecture 1.1 promises that logarithmic data of
$H^{\bullet }(\Omega _{R}^{\bullet }(\star \mathscr {A}), d) \simeq H^{\bullet }(U, \mathbb {C}_{U})$
is a consequence of Grothendieck’s Comparison Theorem [Reference Grothendieck17]. So Conjecture 1.1 promises that logarithmic data of
![]() $\mathscr {A}$
determine the cohomology of the complement via the conjectured quasi-isomorphism.
$\mathscr {A}$
determine the cohomology of the complement via the conjectured quasi-isomorphism.
We prove Conjecture 1.1 as a corollary to more general result: the Twisted Logarithmic Comparison Theorem. This promises that twisting the differential of the logarithmic de Rham complex by a certain logarithmic form computes the cohomology of the complement U in the corresponding rank one local system.
To explain this, let
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
be weights, one for each hyperplane
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
be weights, one for each hyperplane
![]() $\operatorname {\mathrm {V}}(f_{k})$
of
$\operatorname {\mathrm {V}}(f_{k})$
of
![]() $\mathscr {A}$
, and let the weights define a logarithmic one form
$\mathscr {A}$
, and let the weights define a logarithmic one form
 $$\begin{align*}\omega = \sum_{k} \lambda_{k} \frac{df_{k}}{f_{k}} = \sum_{k} \lambda_{k} d \log f_{k}. \end{align*}$$
$$\begin{align*}\omega = \sum_{k} \lambda_{k} \frac{df_{k}}{f_{k}} = \sum_{k} \lambda_{k} d \log f_{k}. \end{align*}$$
Using
![]() $\omega $
, we twist the exterior derivative for both the logarithmic and meromorphic de Rham complex (along with the algebraic analogues): We replace the differential
$\omega $
, we twist the exterior derivative for both the logarithmic and meromorphic de Rham complex (along with the algebraic analogues): We replace the differential
![]() $d(-)$
with the twisted differential
$d(-)$
with the twisted differential
![]() $\nabla _{\omega }(-) = d(-)+ \omega \wedge (-).$
$\nabla _{\omega }(-) = d(-)+ \omega \wedge (-).$
On the local system side, it is well known that all rank one local systems on the complement
![]() $U = X \setminus \mathscr {A}$
are parameterized by torus points
$U = X \setminus \mathscr {A}$
are parameterized by torus points
![]() $\boldsymbol {\beta } \in (\mathbb {C}^{\star })^{d}$
. Essentially, each
$\boldsymbol {\beta } \in (\mathbb {C}^{\star })^{d}$
. Essentially, each
![]() $\beta _{k}$
encodes the monodromy around the hyperplane
$\beta _{k}$
encodes the monodromy around the hyperplane
![]() $\operatorname {\mathrm {V}}(f_{k})$
. Denote
$\operatorname {\mathrm {V}}(f_{k})$
. Denote
![]() $\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
the local system corresponding to
$\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
the local system corresponding to
![]() $\boldsymbol {\beta }$
. By Deligne and Grothendieck’s algebraic de Rham theorems (see the summary of the arrangement case in [Reference Orlik25]), the algebraic twisted de Rham complex computes the cohomology on U with one of these local systems:
$\boldsymbol {\beta }$
. By Deligne and Grothendieck’s algebraic de Rham theorems (see the summary of the arrangement case in [Reference Orlik25]), the algebraic twisted de Rham complex computes the cohomology on U with one of these local systems:
![]() $\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}$
corresponds to the torus point obtained by replacing each component
$\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}$
corresponds to the torus point obtained by replacing each component
![]() $\lambda _{k}$
of the weights
$\lambda _{k}$
of the weights
![]() $\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d})$
with
$\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d})$
with
![]() $e^{2 \pi i \lambda _{k}}$
.
$e^{2 \pi i \lambda _{k}}$
.
Our two main results are: the analytic Twisted Logarithmic Comparison Theorem; the algebraic Twisted Logarithmic Comparison Theorem. In both cases, we have very mild combinatorial arithmetic restrictions on the weights defining the twist. Recall
![]() $\mathscr {L}(A)$
is the intersection lattice of
$\mathscr {L}(A)$
is the intersection lattice of
![]() $\mathscr {A}$
; its constituents are called edges. The majority of work is in proving our analytic Theorem 1.2:
$\mathscr {A}$
; its constituents are called edges. The majority of work is in proving our analytic Theorem 1.2:
Theorem 1.2 (Analytic Twisted Logarithmic Comparison Theorem).
Let
![]() $f = f_{1} \cdots f_{d} \in R$
cut out a reduced hyperplane arrangement
$f = f_{1} \cdots f_{d} \in R$
cut out a reduced hyperplane arrangement
![]() $\mathscr {A}$
. Suppose that
$\mathscr {A}$
. Suppose that
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
are weights such that, for each edge
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
are weights such that, for each edge
![]() $E \in \mathscr {L}(\mathscr {A})$
,
$E \in \mathscr {L}(\mathscr {A})$
,
 $$ \begin{align} \sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align} $$
$$ \begin{align} \sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align} $$
Let
![]() $\omega = \sum _{k} \lambda _{k} \frac {df_{k}}{f_{k}}$
be the logarithmic one form determined by the
$\omega = \sum _{k} \lambda _{k} \frac {df_{k}}{f_{k}}$
be the logarithmic one form determined by the
![]() $\{\lambda _{k}\}$
. Then the analytic Twisted Logarithmic Comparison Theorem with respect to
$\{\lambda _{k}\}$
. Then the analytic Twisted Logarithmic Comparison Theorem with respect to
![]() $\{\lambda _{k}\}$
holds:
$\{\lambda _{k}\}$
holds:
The statement
![]() $`(= \mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})\text{'}$
means there is equality in the derived category (of perverse sheaves), where
$`(= \mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})\text{'}$
means there is equality in the derived category (of perverse sheaves), where ![]() is the inclusion.
is the inclusion.
From this, we deduce the algebraic Theorem 3.8, though here impose centrality:
Theorem 1.3 (Algebraic Twisted Logarithmic Comparison Theorem).
Let
![]() $f = f_{1} \cdots f_{d}$
cut out a central, reduced hyperplane arrangement
$f = f_{1} \cdots f_{d}$
cut out a central, reduced hyperplane arrangement
![]() $\mathscr {A}$
, and let
$\mathscr {A}$
, and let
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
be weights such that, for each edge E,
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
be weights such that, for each edge E,
 $$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*}$$
$$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*}$$
Furthermore, let
![]() $\omega = \sum _{k} \lambda _{k} df_{k} / f_{k}$
. Then the algebraic Twisted Logarithmic Comparison Theorem holds along with an additional quasi-isomorphism:
$\omega = \sum _{k} \lambda _{k} df_{k} / f_{k}$
. Then the algebraic Twisted Logarithmic Comparison Theorem holds along with an additional quasi-isomorphism:
Here,
![]() $(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}))$
means there are isomorphisms on the level of cohomology and
$(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}))$
means there are isomorphisms on the level of cohomology and
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A})_{-\iota _{E}(\omega )}, \nabla _{\omega })$
is the homogeneous subcomplex of degree
$(\Omega _{R}^{\bullet }(\log \mathscr {A})_{-\iota _{E}(\omega )}, \nabla _{\omega })$
is the homogeneous subcomplex of degree
![]() $- \iota _{E}(\omega ) = -( \lambda _{1} + \cdots + \lambda _{d})$
, which is a complex of finite dimensional
$- \iota _{E}(\omega ) = -( \lambda _{1} + \cdots + \lambda _{d})$
, which is a complex of finite dimensional
![]() $\mathbb {C}$
-vector spaces.
$\mathbb {C}$
-vector spaces.
The combinatorial arithmetic conditions (1.1) on the intersection lattice are relatively benign. (And are closely related to data about Bernstein–Sato ideals, cf. Theorem 1.9, Section 4.) We justify this assessment in Proposition 3.12:
Proposition 1.4. For an arbitrary rank one local system
![]() $\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
on U, there exists a
$\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
on U, there exists a
![]() $\boldsymbol {\lambda } \in \operatorname {\mathrm {Exp}}^{-1}(\boldsymbol {\beta })$
such that all the aforementioned Twisted Logarithmic Comparison Theorems hold with respect to the weights
$\boldsymbol {\lambda } \in \operatorname {\mathrm {Exp}}^{-1}(\boldsymbol {\beta })$
such that all the aforementioned Twisted Logarithmic Comparison Theorems hold with respect to the weights
![]() $\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}).$
$\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}).$
These Twisted Logarithmic Comparison Theorems can be considered as an extension of the results in [Reference Esnault, Schechtman and Viehweg16]. Therein projective hyperplane arrangements are considered, but using a Leray spectral sequence there is a precise cohomological relationship between local systems on the complement of a central affine arrangement and the corresponding local system on the complement of the associated projective arrangement, cf. Theorem 5.2 of [Reference Dimca15]. In [Reference Esnault, Schechtman and Viehweg16], the authors prove that the twisted Orlik–Solomon algebra, that is, the twisted Brieskorn algebra, with differential wedging
![]() $\omega = \sum \lambda _{k} df_{k}/f_{k}$
, computes the cohomology of the associated rank one local system on the projective complement provided that: (1) the sum
$\omega = \sum \lambda _{k} df_{k}/f_{k}$
, computes the cohomology of the associated rank one local system on the projective complement provided that: (1) the sum
![]() $\lambda _{1} + \cdots + \lambda _{k} = 0$
; (2) a similar condition to Equation (1.1) holds on the residues of
$\lambda _{1} + \cdots + \lambda _{k} = 0$
; (2) a similar condition to Equation (1.1) holds on the residues of
![]() $\omega $
at dense edges. The first requirement means these twisted Orlik–Solomon algebra can only detect local systems belong to nontorsion translated components of the characteristic variety, that is, resonance varieties, cf. Example 4.1 of [Reference Suciu31] or Section 3 of [Reference Cohen11]. This is a feature of twisted Orlik–Solomon algebras: They are blind to the local systems populating the torsion translated components by [Reference Cohen and Suciu12].
$\omega $
at dense edges. The first requirement means these twisted Orlik–Solomon algebra can only detect local systems belong to nontorsion translated components of the characteristic variety, that is, resonance varieties, cf. Example 4.1 of [Reference Suciu31] or Section 3 of [Reference Cohen11]. This is a feature of twisted Orlik–Solomon algebras: They are blind to the local systems populating the torsion translated components by [Reference Cohen and Suciu12].
In contrast, any local system on the complement of an arrangement can be detected via these Twisted Logarithmic Comparison Theorems, after an appropriate twist, essentially because there is no stricture like
![]() $\lambda _{1} + \cdots + \lambda _{d} = 0$
. So Theorem 1.2 and Theorem 1.3 extend the results of [Reference Esnault, Schechtman and Viehweg16] to all rank one local systems, at the cost of replacing the Orlik–Solomon algebra with the logarithmic de Rham complex. To demonstrate this, in Example 3.14 we use our results to compute the Betti numbers of
$\lambda _{1} + \cdots + \lambda _{d} = 0$
. So Theorem 1.2 and Theorem 1.3 extend the results of [Reference Esnault, Schechtman and Viehweg16] to all rank one local systems, at the cost of replacing the Orlik–Solomon algebra with the logarithmic de Rham complex. To demonstrate this, in Example 3.14 we use our results to compute the Betti numbers of
![]() $H^{\bullet }(U, \operatorname {\mathrm {L}}_{\boldsymbol {\beta }})$
for a special local system on the complement of the deleted
$H^{\bullet }(U, \operatorname {\mathrm {L}}_{\boldsymbol {\beta }})$
for a special local system on the complement of the deleted
![]() $B_{3}$
arrangement. This system
$B_{3}$
arrangement. This system
![]() $\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
is invisible to Orlik–Solomon methods.
$\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
is invisible to Orlik–Solomon methods.
From Theorem 1.2 we quickly conclude the (untwisted) analytic Logarithmic Comparison Theorem holds in Corollary 3.6:
Corollary 1.5 (Analytic Logarithmic Comparison Theorem).
For a reduced hyperplane arrangement
![]() $\mathscr {A}$
, the analytic Logarithmic Comparison Theorem holds:
$\mathscr {A}$
, the analytic Logarithmic Comparison Theorem holds:
We also prove the algebraic (untwisted) Logarithmic Comparison Theorem in Corollary 3.10, positively resolving Terao’s Conjecture 1.1. Here, there is no centrality assumption and
![]() $A^{\bullet }(\mathscr {A})$
is the Orlik–Solomon algebra.
$A^{\bullet }(\mathscr {A})$
is the Orlik–Solomon algebra.
Corollary 1.6 (Algebraic Logarithmic Comparison Theorem).
Let
![]() $\mathscr {A}$
be a reduced hyperplane arrangement. Then the algebraic Logarithmic Comparison Theorem holds giving a sequence of quasi-isomorphisms
$\mathscr {A}$
be a reduced hyperplane arrangement. Then the algebraic Logarithmic Comparison Theorem holds giving a sequence of quasi-isomorphisms
Moreover,
![]() $A^{j}(\mathscr {A}) = H^{j}(\Omega _{R}^{\bullet }(\log \mathscr {A}), d)$
.
$A^{j}(\mathscr {A}) = H^{j}(\Omega _{R}^{\bullet }(\log \mathscr {A}), d)$
.
Previously, Conjecture 1.1 has been confirmed in special cases of arrangements and other divisors: necessary and sufficient conditions for quasi-homogeneous divisors with isolated singularities [Reference Holland and Mond19]; strongly quasi-homogeneous free divisors [Reference Castro-Jiménez, Narváez-Macarro and Mond9] (in this setting, see also [Reference Calderón Moreno and Narváez Macarro8] for a less explicit twisted version than what we find and [Reference Narváez Macarro23] for the current state of the art); tame arrangements and arrangements of rank at most 4 [Reference Wiens and Yuzvinsky36]. Both free and tame impose homological restrictions on the logarithmic forms: Free means
![]() $\Omega _{R}^{1}(\log \mathscr {A})$
is a free R-module; tame means the projective dimension of
$\Omega _{R}^{1}(\log \mathscr {A})$
is a free R-module; tame means the projective dimension of
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
is at most j.
$\Omega _{R}^{j}(\log \mathscr {A})$
is at most j.
Our approach to the analytic Twisted Logarithmic Comparison Theorem (Theorem 1.2) inhabits the architecture of Castro Jiménez, Mond and Narváez Macarro’s inductive proof of the analytic (untwisted) Logarithmic Comparison Theorem for strongly quasi-homogeneous free divisors [Reference Castro-Jiménez, Narváez-Macarro and Mond9], with the induction happening on the rank of edges
![]() $E \in \mathscr {L}(\mathscr {A})$
(or equivalently on the dimension of logarithmic strata as in loc. cit. see [Reference Saito28]). Within this inductive scheme, the obstacle is understanding a spectral sequence with first page
$E \in \mathscr {L}(\mathscr {A})$
(or equivalently on the dimension of logarithmic strata as in loc. cit. see [Reference Saito28]). Within this inductive scheme, the obstacle is understanding a spectral sequence with first page
where
![]() $V \ni 0$
is a small Stein open,
$V \ni 0$
is a small Stein open,
![]() $\mathscr {A}$
is central, and this page’s vertical differential is induced by
$\mathscr {A}$
is central, and this page’s vertical differential is induced by
![]() $\nabla _{\omega }$
. The goal is to show only certain entries survive on the second page. Homological restrictions on the logarithmic j-forms limit the complexity of this first page: In [Reference Castro-Jiménez, Narváez-Macarro and Mond9], under freeness, only two columns may not vanish; in [Reference Wiens and Yuzvinsky36], under tameness, the problematic entries are confined to two diagonal lines. With these simplifications, both [Reference Castro-Jiménez, Narváez-Macarro and Mond9] and [Reference Wiens and Yuzvinsky36] can then use graded data to show the required entries on the second page vanish (though [Reference Wiens and Yuzvinsky36] crucially invokes Brieskorn’s Theorem at this step).
$\nabla _{\omega }$
. The goal is to show only certain entries survive on the second page. Homological restrictions on the logarithmic j-forms limit the complexity of this first page: In [Reference Castro-Jiménez, Narváez-Macarro and Mond9], under freeness, only two columns may not vanish; in [Reference Wiens and Yuzvinsky36], under tameness, the problematic entries are confined to two diagonal lines. With these simplifications, both [Reference Castro-Jiménez, Narváez-Macarro and Mond9] and [Reference Wiens and Yuzvinsky36] can then use graded data to show the required entries on the second page vanish (though [Reference Wiens and Yuzvinsky36] crucially invokes Brieskorn’s Theorem at this step).
Without any homological assumptions the first page (1.2) is arbitrarily daedal. However, the first page’s data are governed by the complexes of modules of analytic Čech cohomology
attached to the open cover
![]() $\{D(x_{i})\}$
of
$\{D(x_{i})\}$
of
![]() $X \setminus 0$
. In subsection 2.3, we show the cohomology of Equation (1.3) is determined by a ‘homogeneous’ subcomplex in the sense of Laurent expansions. Thus, to show the necessary entries of our spectral sequence’s second page vanish, it suffices to show that this ‘homogeneous’ subcomplex is the zero complex. Corollary 2.31 uses a GAGA argument to relate this vanishing to the vanishing of certain graded components of the algebraic local cohomology: in notation, to
$X \setminus 0$
. In subsection 2.3, we show the cohomology of Equation (1.3) is determined by a ‘homogeneous’ subcomplex in the sense of Laurent expansions. Thus, to show the necessary entries of our spectral sequence’s second page vanish, it suffices to show that this ‘homogeneous’ subcomplex is the zero complex. Corollary 2.31 uses a GAGA argument to relate this vanishing to the vanishing of certain graded components of the algebraic local cohomology: in notation, to
![]() $H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A}))_{\ell }$
. We show the appropriate components are zero in Theorem 2.29, where we bound the Castelnuovo–Mumford regularity of
$H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A}))_{\ell }$
. We show the appropriate components are zero in Theorem 2.29, where we bound the Castelnuovo–Mumford regularity of
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
:
$\Omega _{R}^{j}(\log \mathscr {A})$
:
Theorem 1.7. For
![]() $\mathscr {A}$
a central, essential, reduced hyperplane arrangement, the Castelnuovo–Mumford regularity of
$\mathscr {A}$
a central, essential, reduced hyperplane arrangement, the Castelnuovo–Mumford regularity of
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
is bounded by
$\Omega _{R}^{j}(\log \mathscr {A})$
is bounded by
When
![]() $j = 0$
or
$j = 0$
or
![]() $j=\operatorname {\mathrm {rank}}(\mathscr {A})$
, the module of logarithmic zero or
$j=\operatorname {\mathrm {rank}}(\mathscr {A})$
, the module of logarithmic zero or
![]() $\operatorname {\mathrm {rank}}(\mathscr {A})$
-forms are free R-modules and so only
$\operatorname {\mathrm {rank}}(\mathscr {A})$
-forms are free R-modules and so only
![]() $H_{\mathfrak {m}}^{\operatorname {\mathrm {rank}}{\mathscr {A}}}(-) \neq 0$
. In these cases,
$H_{\mathfrak {m}}^{\operatorname {\mathrm {rank}}{\mathscr {A}}}(-) \neq 0$
. In these cases,
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{0}(\log \mathscr {A})) = 0$
and
$\operatorname {\mathrm {reg}}(\Omega _{R}^{0}(\log \mathscr {A})) = 0$
and
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}(\log \mathscr {A})) = \operatorname {\mathrm {rank}}(\mathscr {A}) - \deg (\mathscr {A})$
.
$\operatorname {\mathrm {reg}}(\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}(\log \mathscr {A})) = \operatorname {\mathrm {rank}}(\mathscr {A}) - \deg (\mathscr {A})$
.
We obtain this using linear approximation methods due to Derksen and Sidman [Reference Derksen and Sidman14]. Therein they bound the regularity of the logarithmic derivations of an arrangement (and M. Saito improved this in [Reference Saito30]), but there is nontrivial difficulty in applying their techniques to the case of logarithmic differential forms.
We conclude with some applications to classical questions for
![]() $\mathscr {D}_{X}$
-modules. This helps demystify the combinatorial arithmetic conditions (1.1). Here,
$\mathscr {D}_{X}$
-modules. This helps demystify the combinatorial arithmetic conditions (1.1). Here,
![]() $\mathscr {D}_{X}$
is the sheaf of
$\mathscr {D}_{X}$
is the sheaf of
![]() $\mathbb {C}$
-linear analytic differential operators. One expects the analytic Logarithmic Comparison Theorem to inform certain
$\mathbb {C}$
-linear analytic differential operators. One expects the analytic Logarithmic Comparison Theorem to inform certain
![]() $\mathscr {D}_{X}$
-constructions, especially Bernstein–Sato polynomials. See the surveys [Reference Torrelli34], [Reference Narváez Macarro22]. For some free divisors, there is an intrinsic
$\mathscr {D}_{X}$
-constructions, especially Bernstein–Sato polynomials. See the surveys [Reference Torrelli34], [Reference Narváez Macarro22]. For some free divisors, there is an intrinsic
![]() $\mathscr {D}_{X}$
-theoretic formulation of the Logarithmic Comparison Theorem as developed in [Reference Calderón Moreno and Narváez Macarro8]; see also [Reference Narváez Macarro23] for current developments.
$\mathscr {D}_{X}$
-theoretic formulation of the Logarithmic Comparison Theorem as developed in [Reference Calderón Moreno and Narváez Macarro8]; see also [Reference Narváez Macarro23] for current developments.
The existing literature primarily focuses on the untwisted, univariate case, and thus questions like: Does the cyclic
![]() $\mathscr {D}_{X}$
-module generated by
$\mathscr {D}_{X}$
-module generated by
![]() $f^{-1}$
equal (as a submodule) the
$f^{-1}$
equal (as a submodule) the
![]() $\mathscr {D}_{X}$
-module
$\mathscr {D}_{X}$
-module
![]() $\mathscr {O}_{X}(\star \mathscr {A})$
(the module with poles of arbitrary order along
$\mathscr {O}_{X}(\star \mathscr {A})$
(the module with poles of arbitrary order along
![]() $\mathscr {A})$
? This corresponds to
$\mathscr {A})$
? This corresponds to
![]() $-1$
being the smallest
$-1$
being the smallest
![]() $\mathbb {Z}$
-root of the Bernstein–Sato polynomial of f, which was proved for arrangements by Leykin in [Reference Walther35].
$\mathbb {Z}$
-root of the Bernstein–Sato polynomial of f, which was proved for arrangements by Leykin in [Reference Walther35].
We ask a more subtle question: For a fixed
![]() $\boldsymbol {\lambda } \in \mathbb {C}^{d}$
, does the cyclic
$\boldsymbol {\lambda } \in \mathbb {C}^{d}$
, does the cyclic
![]() $\mathscr {D}_{X}$
-module generated by
$\mathscr {D}_{X}$
-module generated by
![]() $f^{\boldsymbol {\lambda }} = f_{1}^{\lambda _{1}} \cdots f_{d}^{\lambda _{d}}$
equal (as a submodule) the
$f^{\boldsymbol {\lambda }} = f_{1}^{\lambda _{1}} \cdots f_{d}^{\lambda _{d}}$
equal (as a submodule) the
![]() $\mathscr {D}_{X}$
-module
$\mathscr {D}_{X}$
-module
![]() $\mathscr {O}_{X}(\star f^{\lambda }) = \cup _{\textbf {p} \in \mathbb {N}^{d}} \mathscr {D}_{X} f^{\boldsymbol {\lambda } - \textbf {p}}$
? Using ideas of Torelli [Reference Torrelli34], in Theorem 4.4 we give an answer, contingent on our familiar combinatorial arithmetic properties on
$\mathscr {O}_{X}(\star f^{\lambda }) = \cup _{\textbf {p} \in \mathbb {N}^{d}} \mathscr {D}_{X} f^{\boldsymbol {\lambda } - \textbf {p}}$
? Using ideas of Torelli [Reference Torrelli34], in Theorem 4.4 we give an answer, contingent on our familiar combinatorial arithmetic properties on
![]() $\boldsymbol {\lambda }$
:
$\boldsymbol {\lambda }$
:
Theorem 1.8. Let
![]() $f = f_{1} \cdots f_{d}$
cut out a central, reduced hyperplane arrangement and let
$f = f_{1} \cdots f_{d}$
cut out a central, reduced hyperplane arrangement and let
![]() $\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}) \in \mathbb {C}^{d}$
be weights such that for each edge E
$\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}) \in \mathbb {C}^{d}$
be weights such that for each edge E
 $$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*}$$
$$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*}$$
Then
As in the case of
![]() $f^{-1}$
, one hopes there is an equivalent interpretation in terms of Bernstein–Sato ideals. However, unlike the univariate case (
$f^{-1}$
, one hopes there is an equivalent interpretation in terms of Bernstein–Sato ideals. However, unlike the univariate case (
![]() $f^{-1}$
, Bernstein–Sato polynomials), the multivariate case (
$f^{-1}$
, Bernstein–Sato polynomials), the multivariate case (
![]() $f^{\boldsymbol {\lambda }}$
, Bernstein–Sato ideals) and the associated
$f^{\boldsymbol {\lambda }}$
, Bernstein–Sato ideals) and the associated
![]() $\mathscr {D}_{X}[s_{1}, \dots , s_{d}]$
-modules are more nuanced and the precise connection remains unclear. These issues are central to the approach of [Reference Maisonobe21] and [Reference Budur, van der Veer, Wu and Zhou6], where methods and theory were developed for the multivariate setting.
$\mathscr {D}_{X}[s_{1}, \dots , s_{d}]$
-modules are more nuanced and the precise connection remains unclear. These issues are central to the approach of [Reference Maisonobe21] and [Reference Budur, van der Veer, Wu and Zhou6], where methods and theory were developed for the multivariate setting.
Using the generically Cohen–Macaulay strategy developed in [Reference Budur, van der Veer, Wu and Zhou6] as well as other intricate techniques, in Theorem 4.7 we are able to give a very good bound (i.e., sharp, see the formula for a generic arrangement in Theorem 3.23 of [Reference Bath1]) for the codimension one components of the zero locus of the Bernstein–Sato ideal. Here, we consider arbitrary factorizations
![]() $F = (f_{1}, \dots , f_{r})$
of f.
$F = (f_{1}, \dots , f_{r})$
of f.
Theorem 1.9. For
![]() $F = (f_{1}, \dots , f_{r})$
an arbitrary factorization of a reduced, central arrangement f, the codimension one components of the Bernstein–Sato ideal attached to F has the following restriction:
$F = (f_{1}, \dots , f_{r})$
an arbitrary factorization of a reduced, central arrangement f, the codimension one components of the Bernstein–Sato ideal attached to F has the following restriction:
 $$\begin{align*}Z_{r-1}(B_{F,0}) \subseteq \bigcup_{\substack{E \in \mathscr{L}(\mathscr{A}) \\ E \text{ dense}}} \bigcup_{v=0}^{Q_{E}} \left\{ \sum\limits_{\{1 \leq k \leq r \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} d_{E,k} s_{k} + \operatorname{\mathrm{rank}}(E) + v = 0 \right\} \end{align*}$$
$$\begin{align*}Z_{r-1}(B_{F,0}) \subseteq \bigcup_{\substack{E \in \mathscr{L}(\mathscr{A}) \\ E \text{ dense}}} \bigcup_{v=0}^{Q_{E}} \left\{ \sum\limits_{\{1 \leq k \leq r \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} d_{E,k} s_{k} + \operatorname{\mathrm{rank}}(E) + v = 0 \right\} \end{align*}$$
where
![]() $d_{E,k}$
is as in Definition 4.6 and
$d_{E,k}$
is as in Definition 4.6 and
 $$\begin{align*}Q_{E} = \begin{cases} 2 d_{E} - \operatorname{\mathrm{rank}}(E) - \min\{2, \operatorname{\mathrm{rank}}(E)\} \text{ for } F \text{ a factorization into linears}; \\ 2 d_{E} - \operatorname{\mathrm{rank}}(E) - \min\{2, \operatorname{\mathrm{rank}}(E)\} \text{ for } F \text{ any factorization } \& \text{ } E = \{0\}; \\ 2 d_{E} - \operatorname{\mathrm{rank}}(E) - 1 \text{ for } F \text{ not a factorization into linears }\& \text{ } E \neq \{0\}. \end{cases} \end{align*}$$
$$\begin{align*}Q_{E} = \begin{cases} 2 d_{E} - \operatorname{\mathrm{rank}}(E) - \min\{2, \operatorname{\mathrm{rank}}(E)\} \text{ for } F \text{ a factorization into linears}; \\ 2 d_{E} - \operatorname{\mathrm{rank}}(E) - \min\{2, \operatorname{\mathrm{rank}}(E)\} \text{ for } F \text{ any factorization } \& \text{ } E = \{0\}; \\ 2 d_{E} - \operatorname{\mathrm{rank}}(E) - 1 \text{ for } F \text{ not a factorization into linears }\& \text{ } E \neq \{0\}. \end{cases} \end{align*}$$
In particular, when
![]() $F = (f)$
is the trivial factorization and f is not smooth, the roots of the Bernstein–Sato polynomial are contained in
$F = (f)$
is the trivial factorization and f is not smooth, the roots of the Bernstein–Sato polynomial are contained in
![]() $(-2 + 1/d, 0).$
$(-2 + 1/d, 0).$
To clarify notation:
![]() $Z_{r-1}(B_{F,0})$
denotes the codimension one components of the Bernstein–Sato ideal attached to F at the origin,
$Z_{r-1}(B_{F,0})$
denotes the codimension one components of the Bernstein–Sato ideal attached to F at the origin,
![]() $d_{E}$
equals the number of hyperplanes containing the edge E, and
$d_{E}$
equals the number of hyperplanes containing the edge E, and
![]() $d_{E,k}$
equals the number of hyperplanes containing the edge E that themselves are contained in
$d_{E,k}$
equals the number of hyperplanes containing the edge E that themselves are contained in
![]() $\operatorname {\mathrm {V}}(f_{k})$
, cf. Definition 4.6.
$\operatorname {\mathrm {V}}(f_{k})$
, cf. Definition 4.6.
In the simpler case of Bernstein–Sato polynomials, Theorem 1.9 gives an entirely new proof of M. Saito’s result [Reference Saito29] that the roots of the Bernstein–Sato polynomial of a non-smooth central arrangement lie in
![]() $(-2+1/d, 0)$
.
$(-2+1/d, 0)$
.
Here is the paper’s structure. Section 2 introduces paper-wide notation, develops tools for studying complexes of algebraic local cohomology of logarithmic forms (subsection 2.2, subsection 2.5), studying the analytic analogue of complexes of Čech cohomology of logarithmic forms (subsection 2.3), converting algebraic results to analytic ones (subsection 2.6) and bounding the Castelnuovo–Mumford regularity (subsection 2.4). Section 3 uses these results to prove our four (un)Twisted Logarithmic Comparison Theorems (two analytic, two algebraic), prove that the theorems apply to all rank one local systems (Proposition 3.12) and compute Example 3.14. Section 4 gives
![]() $\mathscr {D}_{X}$
-module applications, including a bound on the codimension one components of the Bernstein–Sato ideal of an arbitrary factorization of our arrangement.
$\mathscr {D}_{X}$
-module applications, including a bound on the codimension one components of the Bernstein–Sato ideal of an arbitrary factorization of our arrangement.
2. Logarithmic forms and local cohomology
In the first subsection, we set up necessary notation and background knowledge used throughout the paper. The rest of the section is devoted to studying the local cohomology of logarithmic forms in the algebraic setting as well as a sort of analytic analogue: the Čech cohomology of the logarithmic forms with respect to the cover
![]() $\{D(x_{i})\}$
of
$\{D(x_{i})\}$
of
![]() $X \setminus 0$
. While we require knowledge of both contexts, the analytic analogue is vital. On the other hand, the techniques in the algebraic setting inspire those for the analytic one.
$X \setminus 0$
. While we require knowledge of both contexts, the analytic analogue is vital. On the other hand, the techniques in the algebraic setting inspire those for the analytic one.
In subsection 2.2, we build up tools for studying complexes of such algebraic local cohomology modules with twisted differentials, focusing on establishing useful contracting homotopies; in subsection 2.3, we morally repeat the strategy in the analytic Čech case, again obtaining a useful contracting homotopy; in subsection 2.4, we bound the Castelnuovo–Mumford regularity of logarithmic forms in the algebraic case; in subsection 2.5, we use this bound to obtain an acyclicity criterion in the algebraic case; in subsection 2.6, we use a GAGA argument to get a similar acyclicity criterion in the analytic setting. The last result powers our proof of the analytic (un)Twisted Logarithmic Comparison Theorem.
2.1. Terminology and background
We will use
![]() $f=f_{1} \cdots f_{d} \in R = \mathbb {C}[x_{1}, \dots , x_{n}]$
to denote a defining equation of a reduced hyperplane arrangement
$f=f_{1} \cdots f_{d} \in R = \mathbb {C}[x_{1}, \dots , x_{n}]$
to denote a defining equation of a reduced hyperplane arrangement
![]() $\mathscr {A}$
of degree d (i.e.,
$\mathscr {A}$
of degree d (i.e.,
![]() $\deg (f) = d)$
. We use X to denote
$\deg (f) = d)$
. We use X to denote
![]() $\mathbb {C}^{n}$
and will, unless otherwise stated, consider X as a Stein manifold with analytic structure sheaf
$\mathbb {C}^{n}$
and will, unless otherwise stated, consider X as a Stein manifold with analytic structure sheaf
![]() $\mathscr {O}_{X}$
. The complement
$\mathscr {O}_{X}$
. The complement
![]() $U = X \setminus \mathscr {A}$
of our arrangement includes into X via
$U = X \setminus \mathscr {A}$
of our arrangement includes into X via ![]() . As is standard, we denote the constant
. As is standard, we denote the constant
![]() $\mathbb {C}$
-valued rank one system on U by
$\mathbb {C}$
-valued rank one system on U by
![]() $\mathbb {C}_{U}$
.
$\mathbb {C}_{U}$
.
Let
![]() $\mathscr {L}(\mathscr {A})$
be the intersection lattice of the hyperplane arrangement
$\mathscr {L}(\mathscr {A})$
be the intersection lattice of the hyperplane arrangement
![]() $\mathscr {A}$
; its members are called edges (sometimes flats in the literature). We say the rank of
$\mathscr {A}$
; its members are called edges (sometimes flats in the literature). We say the rank of
![]() $\mathscr {A}$
, denoted
$\mathscr {A}$
, denoted
![]() $\operatorname {\mathrm {rank}}(\mathscr {A})$
, is the rank of the lattice
$\operatorname {\mathrm {rank}}(\mathscr {A})$
, is the rank of the lattice
![]() $\mathscr {L}(\mathscr {A})$
;
$\mathscr {L}(\mathscr {A})$
;
![]() $\mathscr {A}$
is reduced when f is reduced;
$\mathscr {A}$
is reduced when f is reduced;
![]() $\mathscr {A}$
is central when
$\mathscr {A}$
is central when
![]() $\{0\} \subseteq \cap _{E \in \mathscr {L}(\mathscr {A})} E$
, that is, f is homogeneous;
$\{0\} \subseteq \cap _{E \in \mathscr {L}(\mathscr {A})} E$
, that is, f is homogeneous;
![]() $\mathscr {A}$
is essential when
$\mathscr {A}$
is essential when
![]() $\{0\} = \cap _{E \in \mathscr {L}(\mathscr {A})} E$
;
$\{0\} = \cap _{E \in \mathscr {L}(\mathscr {A})} E$
;
![]() $\mathscr {A}$
is decomposable when, after a possible coordinate change, there are polynomials g and h in disjoint, nonempty variable sets such that
$\mathscr {A}$
is decomposable when, after a possible coordinate change, there are polynomials g and h in disjoint, nonempty variable sets such that
![]() $f = gh$
; an edge
$f = gh$
; an edge
![]() $E \in \mathscr {L}(\mathscr {A})$
is dense when the subarrangement of all hyperplanes containing E is indecomposable; the rank of
$E \in \mathscr {L}(\mathscr {A})$
is dense when the subarrangement of all hyperplanes containing E is indecomposable; the rank of
![]() $E \in \mathscr {L}(\mathscr {A})$
is the rank of the subarrangement of hyperplanes containing E. Alternatively, the rank of A or E is the codimension of the corresponding subspace in X.
$E \in \mathscr {L}(\mathscr {A})$
is the rank of the subarrangement of hyperplanes containing E. Alternatively, the rank of A or E is the codimension of the corresponding subspace in X.
We recall the types of de Rham complexes appearing in the Introduction.
Definition 2.1. Let
![]() $(\Omega _{X}^{\bullet }, d)$
be the canonical de Rham complex. The meromorphic de Rham complex is
$(\Omega _{X}^{\bullet }, d)$
be the canonical de Rham complex. The meromorphic de Rham complex is
where d is the exterior derivative and
![]() $\Omega _{X}^{j}(\star \mathscr {A})$
is the localization of
$\Omega _{X}^{j}(\star \mathscr {A})$
is the localization of
![]() $\Omega _{X}^{j}$
along f, that is,
$\Omega _{X}^{j}$
along f, that is,
![]() $(\star \mathscr {A})$
means we have poles of arbitrary order along
$(\star \mathscr {A})$
means we have poles of arbitrary order along
![]() $\mathscr {A}$
. The logarithmic de Rham complex
$\mathscr {A}$
. The logarithmic de Rham complex
![]() $(\Omega _{X}^{\bullet }(\log \mathscr {A}), d)$
is the subcomplex of the meromorphic de Rham complex characterized by
$(\Omega _{X}^{\bullet }(\log \mathscr {A}), d)$
is the subcomplex of the meromorphic de Rham complex characterized by
that is, its the largest subcomplex where both
![]() $\eta $
and
$\eta $
and
![]() $d(\eta )$
have poles of order at most one along
$d(\eta )$
have poles of order at most one along
![]() $\mathscr {A}$
. Both are complexes of
$\mathscr {A}$
. Both are complexes of
![]() $\mathscr {O}_{X}$
-modules with
$\mathscr {O}_{X}$
-modules with
![]() $\mathbb {C}$
-linear differentials.
$\mathbb {C}$
-linear differentials.
There are global algebraic analogues: the algebraic rational de Rham complex
![]() $\Omega _{R}^{\bullet }(\star \mathscr {A})$
; the algebraic logarithmic de Rham complex
$\Omega _{R}^{\bullet }(\star \mathscr {A})$
; the algebraic logarithmic de Rham complex
![]() $\Omega _{R}^{\bullet }(\log \mathscr {A})$
. These are complexes of R-modules with
$\Omega _{R}^{\bullet }(\log \mathscr {A})$
. These are complexes of R-modules with
![]() $\mathbb {C}$
-linear differentials and have entirely similar definitions:
$\mathbb {C}$
-linear differentials and have entirely similar definitions:
![]() $\Omega _{R}^{j}(\star \mathscr {A}) = \Omega _{R}^{j}[f^{-1}]$
;
$\Omega _{R}^{j}(\star \mathscr {A}) = \Omega _{R}^{j}[f^{-1}]$
;
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
satisfies its version of Equation (2.1).
$\Omega _{R}^{j}(\log \mathscr {A})$
satisfies its version of Equation (2.1).
There are natural inclusion of complexes:

We say
![]() $\mathscr {A}$
satisfies the analytic Logarithmic Comparison Theorem when first inclusion (2.2) is a quasi-isomorphism; it satisfies the algebraic Logarithmic Comparison Theorem when the second is a quasi-isomorphism. We often abbreviate ‘Logarithmic Comparison Theorem’ to ‘LCT.’
$\mathscr {A}$
satisfies the analytic Logarithmic Comparison Theorem when first inclusion (2.2) is a quasi-isomorphism; it satisfies the algebraic Logarithmic Comparison Theorem when the second is a quasi-isomorphism. We often abbreviate ‘Logarithmic Comparison Theorem’ to ‘LCT.’
A dual object to
![]() $\Omega _{R}^{1}(\log \mathscr {A})$
are the logarithmic derivations
$\Omega _{R}^{1}(\log \mathscr {A})$
are the logarithmic derivations
These can be defined analytically as well. We sometimes replace ‘
![]() $\log \mathscr {A}$
’ with ‘
$\log \mathscr {A}$
’ with ‘
![]() $\log f$
’ when working with a defining equation f of
$\log f$
’ when working with a defining equation f of
![]() $\mathscr {A}$
. Note that none of these constructions depend on the choice of f (nor coordinate systems).
$\mathscr {A}$
. Note that none of these constructions depend on the choice of f (nor coordinate systems).
Remark 2.2. Suppose
![]() $\mathscr {A}$
is a product (i.e., decomposable):
$\mathscr {A}$
is a product (i.e., decomposable):
![]() $\mathscr {A} = \mathscr {B} \oplus \mathscr {C}$
. This means the defining equation may be written as
$\mathscr {A} = \mathscr {B} \oplus \mathscr {C}$
. This means the defining equation may be written as
![]() $f = g h$
, where
$f = g h$
, where
![]() $g \in B = \mathbb {C}[x_{1}, \dots , x_{i}]$
cuts out
$g \in B = \mathbb {C}[x_{1}, \dots , x_{i}]$
cuts out
![]() $\mathscr {B}$
and
$\mathscr {B}$
and
![]() $h \in C=\mathbb {C}[x_{i+1}, \dots , x_{n}]$
cuts out
$h \in C=\mathbb {C}[x_{i+1}, \dots , x_{n}]$
cuts out
![]() $\mathscr {C}$
(changing coordinates as necessary). Then the logarithmic differential forms satisfy a Kunneth formula; see, for example, Lemma 3.10 of [Reference Cohen, Denham, Falk and Varchenko10]:
$\mathscr {C}$
(changing coordinates as necessary). Then the logarithmic differential forms satisfy a Kunneth formula; see, for example, Lemma 3.10 of [Reference Cohen, Denham, Falk and Varchenko10]:
 $$\begin{align*}\Omega_{R}^{k}(\log \mathscr{A}) \simeq \bigoplus_{i+j = k} \Omega_{B}^{i}(\log \mathscr{B}) \otimes_{\mathbb{C}} \Omega_{C}^{j}(\log \mathscr{C}). \end{align*}$$
$$\begin{align*}\Omega_{R}^{k}(\log \mathscr{A}) \simeq \bigoplus_{i+j = k} \Omega_{B}^{i}(\log \mathscr{B}) \otimes_{\mathbb{C}} \Omega_{C}^{j}(\log \mathscr{C}). \end{align*}$$
The same type of Kunneth formula holds on the sheaf level and for
![]() $\operatorname {\mathrm {Der}}_{R}(-\log \mathscr {A})$
, cf. Lemma 1.2 of [Reference Saito30].
$\operatorname {\mathrm {Der}}_{R}(-\log \mathscr {A})$
, cf. Lemma 1.2 of [Reference Saito30].
Recall that the Orlik–Solomon algebra
![]() $A^{\bullet }(\mathscr {A})$
can be identified by the
$A^{\bullet }(\mathscr {A})$
can be identified by the
![]() $\mathbb {C}$
-algebra generated by the differential forms
$\mathbb {C}$
-algebra generated by the differential forms
![]() $\{d f_{k} / f_{k}\}$
, one for each hyperplane
$\{d f_{k} / f_{k}\}$
, one for each hyperplane
![]() $f_{k}$
. Under this characterization, it is called the Brieskorn algebra. Brieskorn’s Theorem [Reference Brieskorn4] combined with Grothendieck’s Comparison Theorem [Reference Grothendieck17] gives a quasi-isomorphism
$f_{k}$
. Under this characterization, it is called the Brieskorn algebra. Brieskorn’s Theorem [Reference Brieskorn4] combined with Grothendieck’s Comparison Theorem [Reference Grothendieck17] gives a quasi-isomorphism
where ‘
![]() $(\simeq H^{\bullet }(U, \mathbb {C}_{U}))$
’ means the cohomology objects are isomorphic, cf. Section 5.4 [Reference Orlik and Terao26].
$(\simeq H^{\bullet }(U, \mathbb {C}_{U}))$
’ means the cohomology objects are isomorphic, cf. Section 5.4 [Reference Orlik and Terao26].
We turn to twisted de Rham complexes and nontrivial rank one local systems.
Definition 2.3. For
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
, consider the logarithmic one form
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
, consider the logarithmic one form
 $$\begin{align*}\omega = \sum_{k} \lambda_{k} \frac{d f_{k}}{f_{k}} = \sum_{k} \lambda_{k} d \log f_{k}. \end{align*}$$
$$\begin{align*}\omega = \sum_{k} \lambda_{k} \frac{d f_{k}}{f_{k}} = \sum_{k} \lambda_{k} d \log f_{k}. \end{align*}$$
This induces a twisted meromorphic de Rham complex
where, for a meromorphic j-form
![]() $\eta $
,
$\eta $
,
Since the logarithmic de Rham complex is closed under exterior products,
![]() $\nabla _{\omega }$
also induces the analytic twisted logarithmic de Rham complex
$\nabla _{\omega }$
also induces the analytic twisted logarithmic de Rham complex
Because
![]() $\omega \in \Omega _{R}^{1}(\log \mathscr {A})$
, we have global algebraic analogues: the twisted rational de Rham complex
$\omega \in \Omega _{R}^{1}(\log \mathscr {A})$
, we have global algebraic analogues: the twisted rational de Rham complex
![]() $(\Omega _{R}^{\bullet }(\star \mathscr {A}), \nabla _{\omega })$
; the algebraic twisted logarithmic de Rham complex
$(\Omega _{R}^{\bullet }(\star \mathscr {A}), \nabla _{\omega })$
; the algebraic twisted logarithmic de Rham complex
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega }).$
We sometimes drop ‘analytic’ or ‘algebraic’ when the context is clear.
$(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega }).$
We sometimes drop ‘analytic’ or ‘algebraic’ when the context is clear.
Analogizing the untwisted case, we say
![]() $\mathscr {A}$
satisfies the analytic Twisted Logarithmic Comparison Theorem when the natural inclusion of complexes is a quasi-isomorphism, that is when:
$\mathscr {A}$
satisfies the analytic Twisted Logarithmic Comparison Theorem when the natural inclusion of complexes is a quasi-isomorphism, that is when:
![]() $\mathscr {A}$
satisfies the algebraic Twisted Logarithmic Comparison Theorem when the corresponding inclusion of algebraic complexes is a quasi-isomorphism. We often abbreviate ‘Twisted Logarithmic Comparison Theorem’ to ‘TLCT’.
$\mathscr {A}$
satisfies the algebraic Twisted Logarithmic Comparison Theorem when the corresponding inclusion of algebraic complexes is a quasi-isomorphism. We often abbreviate ‘Twisted Logarithmic Comparison Theorem’ to ‘TLCT’.
As the meromorphic de Rham complex relates to cohomology with constant coefficients, the twisted meromorphic de Rham complex relates to cohomology with a nontrivial rank one local system.
Definition 2.4. Recall
![]() $U = X \setminus \mathscr {A}$
and
$U = X \setminus \mathscr {A}$
and ![]() is the inclusion. It is well known that the
is the inclusion. It is well known that the
![]() $\mathbb {C}$
-valued rank one local systems on U are in one to one correspondence with the torus points
$\mathbb {C}$
-valued rank one local systems on U are in one to one correspondence with the torus points
For a point
![]() $\boldsymbol {\beta }$
in the torus
$\boldsymbol {\beta }$
in the torus
![]() $(\mathbb {C}^{\star })^{r}$
, we define
$(\mathbb {C}^{\star })^{r}$
, we define
![]() $\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
to be the corresponding rank one local system on U. We recall
$\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
to be the corresponding rank one local system on U. We recall
is an object in the derived category of bounded
![]() $\mathbb {C}_{X}$
-complexes. In fact, it is a perverse sheaf.
$\mathbb {C}_{X}$
-complexes. In fact, it is a perverse sheaf.
Now, let
![]() $\operatorname {\mathrm {Exp}} : \mathbb {C}^{d} \to (\mathbb {C}^{\star })^{d}$
be the exponential map:
$\operatorname {\mathrm {Exp}} : \mathbb {C}^{d} \to (\mathbb {C}^{\star })^{d}$
be the exponential map:
Then every point
![]() $\boldsymbol {\lambda } \in \mathbb {C}^{d}$
, along with its integer translates, corresponds to the rank one local system on U we’ve called
$\boldsymbol {\lambda } \in \mathbb {C}^{d}$
, along with its integer translates, corresponds to the rank one local system on U we’ve called
![]() $\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}.$
$\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}.$
Similar to the untwisted case, by a combination of Deligne’s and Grothendieck’s algebraic de Rham theorems we have isomorphisms in cohomology:
See [Reference Orlik25] for a discussion of this in the arrangement case. In the analytic setting, we have a well-known identification in the derived category:
We give details on this in Proposition 4.3. So the analytic twisted meromorphic de Rham complex has all the data of the derived direct image of the local system in question. An analytic/algebraic Twisted Logarithmic Comparison Theorem guarantees these data are determined by only logarithmic content.
Convention 2.5. Unless otherwise stated,
![]() $R = \mathbb {C}[x_{1}, \dots , x_{n}]$
and is canonically graded with
$R = \mathbb {C}[x_{1}, \dots , x_{n}]$
and is canonically graded with
![]() $x_{i}$
given weight one. Denote the irrelevant ideal
$x_{i}$
given weight one. Denote the irrelevant ideal
![]() $R \cdot (x_{1}, \dots , x_{n})$
of R by
$R \cdot (x_{1}, \dots , x_{n})$
of R by
![]() $\mathfrak {m}$
. In general, we allow R-modules to be
$\mathfrak {m}$
. In general, we allow R-modules to be
![]() $\mathbb {Z}$
-graded. We grade
$\mathbb {Z}$
-graded. We grade
![]() $\Omega _{R}^{j}$
by giving
$\Omega _{R}^{j}$
by giving
![]() $dx_{i}$
weight one, and we grade
$dx_{i}$
weight one, and we grade
![]() $R[x_{I}^{-1}]$
(the localization of R at each
$R[x_{I}^{-1}]$
(the localization of R at each
![]() $x_{i}$
for
$x_{i}$
for
![]() $i \in I \subseteq [n]$
) by giving
$i \in I \subseteq [n]$
) by giving
![]() $x_{i}^{-1}$
weight one; for a graded R-module M, we grade
$x_{i}^{-1}$
weight one; for a graded R-module M, we grade
![]() $M[x_{I}^{-1}]$
similarly. We also grade
$M[x_{I}^{-1}]$
similarly. We also grade
![]() $\Omega _{R}^{j}(\star \mathscr {A})$
and
$\Omega _{R}^{j}(\star \mathscr {A})$
and
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
by giving
$\Omega _{R}^{j}(\log \mathscr {A})$
by giving
![]() $dx_{i}$
weight one and
$dx_{i}$
weight one and
![]() $\frac {1}{f}$
weight
$\frac {1}{f}$
weight
![]() $- \deg (f)$
; we grade
$- \deg (f)$
; we grade
![]() $\operatorname {\mathrm {Der}}_{R}(-\log f)$
by giving
$\operatorname {\mathrm {Der}}_{R}(-\log f)$
by giving
![]() $\partial _{i}$
weight
$\partial _{i}$
weight
![]() $-1$
.
$-1$
.
2.2. Complexes of local cohomology modules of logarithmic forms
In this section, we work algebraically, developing some technical tools for studying both twisted logarithmic de Rham complexes and twisted complexes of local cohomology of logarithmic forms. By the latter, we mean a complex of local cohomology modules induced by the twisted logarithmic de Rham complex. Much of the time is spent showing this latter complex is well-defined and the correct notion of a twisted Lie derivative obeys a nice formula. The primary objective is Proposition 2.15, which reduces computing cohomology of these complexes to computing the cohomology of a particular subcomplex of finite-dimensional
![]() $\mathbb {C}$
-vector spaces.
$\mathbb {C}$
-vector spaces.
In subsection 2.3, we recycle these ideas in an analytic setting.
Convention 2.6. In this subsection,
![]() $\mathscr {A}$
is always assumed to be central with a homogeneous defining equation f.
$\mathscr {A}$
is always assumed to be central with a homogeneous defining equation f.
First, let us recall basic facts about local cohomology modules:
Definition 2.7. Let M be a finite R-module,
![]() $Q \subseteq R$
an ideal. Consider the functor
$Q \subseteq R$
an ideal. Consider the functor
Then
![]() $H_{Q}^{t}(M)$
, the
$H_{Q}^{t}(M)$
, the
![]() $t^{\text {th}}$
local cohomology module of M with respect to Q, is the
$t^{\text {th}}$
local cohomology module of M with respect to Q, is the
![]() $t^{\text {th}}$
derived functor of
$t^{\text {th}}$
derived functor of
![]() $\Gamma _{Q}(M)$
.
$\Gamma _{Q}(M)$
.
Remark 2.8.
-
(a) We usually work with R canonically graded, M a
 $\mathbb {Z}$
or
$\mathbb {Z}$
or
 $\mathbb {N}$
-graded module,
$\mathbb {N}$
-graded module,
 $\mathfrak {m} = R \cdot (x_{1} , \dots , x_{n})$
and the local cohomology modules
$\mathfrak {m} = R \cdot (x_{1} , \dots , x_{n})$
and the local cohomology modules
 $H_{\mathfrak {m}}^{t}(M)$
. In this graded setting, there are well-known (non)vanishing theorems:
$H_{\mathfrak {m}}^{t}(M)$
. In this graded setting, there are well-known (non)vanishing theorems:-
(1)
 $H_{\mathfrak {m}}^{t}(M) = 0 \text { for } t < \operatorname {\mathrm {depth}}(M) \text { or } t> \dim M$
;
$H_{\mathfrak {m}}^{t}(M) = 0 \text { for } t < \operatorname {\mathrm {depth}}(M) \text { or } t> \dim M$
; -
(2)
 $\text {If } t = \operatorname {\mathrm {depth}}(M) \text { or } t = \dim M \text {, then } H_{\mathfrak {m}}^{t}(M) \neq 0$
.
$\text {If } t = \operatorname {\mathrm {depth}}(M) \text { or } t = \dim M \text {, then } H_{\mathfrak {m}}^{t}(M) \neq 0$
.
Consequently,
 $H_{\mathfrak {m}}^{t}(R)$
is nonzero only when
$H_{\mathfrak {m}}^{t}(R)$
is nonzero only when
 $t = n$
.
$t = n$
. -
-
(b) There is a practical way to compute local cohomology using the algebraic Čech complex. Let
 $q_{1}, \dots , q_{p}$
generate the ideal
$q_{1}, \dots , q_{p}$
generate the ideal
 $Q \subseteq R$
. The algebraic Čech complex is where the differential
$Q \subseteq R$
. The algebraic Čech complex is where the differential $$\begin{align*}C(q_{1}, \dots, q_{p}; M) = 0 \to M \to \cdots \to \bigoplus_{\substack{I \subseteq [p] \\ \mid I \mid = t}} M[q_{I}^{-1}] \to \cdots \to M[q_{[p]}^{-1}] \to 0, \end{align*}$$
$$\begin{align*}C(q_{1}, \dots, q_{p}; M) = 0 \to M \to \cdots \to \bigoplus_{\substack{I \subseteq [p] \\ \mid I \mid = t}} M[q_{I}^{-1}] \to \cdots \to M[q_{[p]}^{-1}] \to 0, \end{align*}$$
 $\epsilon : \oplus _{\substack {I \subseteq [p] \\ \mid I \mid = t}} M[q_{I}^{-1}] \to \oplus _{\substack {I \subseteq [p] \\ \mid I \mid = t+1}} M[q_{I}^{-1}]$
takes By
$\epsilon : \oplus _{\substack {I \subseteq [p] \\ \mid I \mid = t}} M[q_{I}^{-1}] \to \oplus _{\substack {I \subseteq [p] \\ \mid I \mid = t+1}} M[q_{I}^{-1}]$
takes By $$\begin{align*}M[q_{I}^{-1}] \ni m_{I} \mapsto \sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} m_{I \cup \{\ell\}} \in \sum_{\ell \not in I} M[q_{I \cup \{\ell\}}^{-1}]. \end{align*}$$
$$\begin{align*}M[q_{I}^{-1}] \ni m_{I} \mapsto \sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} m_{I \cup \{\ell\}} \in \sum_{\ell \not in I} M[q_{I \cup \{\ell\}}^{-1}]. \end{align*}$$
 $m_{I \cup \{\ell \}}$
, we mean the image of
$m_{I \cup \{\ell \}}$
, we mean the image of
 $m_{I}$
in the localization
$m_{I}$
in the localization
 $M[q_{I}^{-1}] \to M[q_{I \cup \{\ell \}}^{-1}]$
; by
$M[q_{I}^{-1}] \to M[q_{I \cup \{\ell \}}^{-1}]$
; by
 $\sigma _{I}(\ell )$
, we mean the number of elements in I less than
$\sigma _{I}(\ell )$
, we mean the number of elements in I less than
 $\ell $
. There is natural identification
$\ell $
. There is natural identification  $$\begin{align*}H_{Q}^{t}(M) = H^{t}(C(q_{1}, \dots, q_{p}; M)). \end{align*}$$
$$\begin{align*}H_{Q}^{t}(M) = H^{t}(C(q_{1}, \dots, q_{p}; M)). \end{align*}$$
-
(c) If Q is homogeneous, M is
 $\mathbb {Z}$
-graded, and we grade
$\mathbb {Z}$
-graded, and we grade
 $M[x_{I}^{-1}]$
naturally by granting
$M[x_{I}^{-1}]$
naturally by granting
 $x_{i}^{-1}$
weight one, then
$x_{i}^{-1}$
weight one, then
 $H_{Q}^{t}(M)$
is naturally
$H_{Q}^{t}(M)$
is naturally
 $\mathbb {Z}$
-graded by the above.
$\mathbb {Z}$
-graded by the above.
We want to construct a very large commutative diagram of horizontal and vertical complexes, visualized in
![]() $\mathbb {Z}^{2}$
, that we eventually name
$\mathbb {Z}^{2}$
, that we eventually name
![]() $N^{\bullet , \bullet }$
. This diagram will let us understand the interplay between local cohomology modules of logarithmic differential forms and the twisted differential
$N^{\bullet , \bullet }$
. This diagram will let us understand the interplay between local cohomology modules of logarithmic differential forms and the twisted differential
![]() $\nabla _{\omega }$
.
$\nabla _{\omega }$
.
Picture
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
as a column with differentials pointed upwards. In fact, put
$(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
as a column with differentials pointed upwards. In fact, put
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
on the y-axis. For each
$(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
on the y-axis. For each
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
, consider the Čech complex
$\Omega _{R}^{j}(\log \mathscr {A})$
, consider the Čech complex
![]() $C(x_{1}, \dots , x_{n}; \Omega _{R}^{j}(\log \mathscr {A}))$
that computes the local cohomology modules
$C(x_{1}, \dots , x_{n}; \Omega _{R}^{j}(\log \mathscr {A}))$
that computes the local cohomology modules
![]() $H_{\mathfrak {m}}^{\bullet }(\Omega _{R}^{j}(\log \mathscr {A}))$
. Position each
$H_{\mathfrak {m}}^{\bullet }(\Omega _{R}^{j}(\log \mathscr {A}))$
. Position each
![]() $C(x_{1}, \dots , x_{n}; \Omega _{R}^{j}(\log \mathscr {A}))$
as a horizontal complex, with differentials oriented rightwards, located on the line
$C(x_{1}, \dots , x_{n}; \Omega _{R}^{j}(\log \mathscr {A}))$
as a horizontal complex, with differentials oriented rightwards, located on the line
![]() $y = j$
. Shift the Čech complex so that its
$y = j$
. Shift the Čech complex so that its
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
term overlaps with the corresponding object of
$\Omega _{R}^{j}(\log \mathscr {A})$
term overlaps with the corresponding object of
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
.
$(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
.
The map
![]() $\nabla _{\omega }$
naturally lifts to a map between the objects of the Čech complex. We want to verify this induces a chain map of Čech complexes, that is, we must confirm the squares
$\nabla _{\omega }$
naturally lifts to a map between the objects of the Čech complex. We want to verify this induces a chain map of Čech complexes, that is, we must confirm the squares

commute. Here, for
![]() $\eta _{I} \in \Omega _{R}^{j}(\log \mathscr {A})$
and
$\eta _{I} \in \Omega _{R}^{j}(\log \mathscr {A})$
and
![]() $Q_{I} \in R[x_{I}^{-1}]$
, the horiziontal map is defined by
$Q_{I} \in R[x_{I}^{-1}]$
, the horiziontal map is defined by
where
![]() $Q_{I \cup \{\ell \}}\eta _{I}$
denotes the image of
$Q_{I \cup \{\ell \}}\eta _{I}$
denotes the image of
![]() $Q_{I}\eta _{I} \in \Omega _{R}^{j}(\log \mathscr {A})[x_{I}^{-1}]$
in the subsequent localization
$Q_{I}\eta _{I} \in \Omega _{R}^{j}(\log \mathscr {A})[x_{I}^{-1}]$
in the subsequent localization
![]() $\Omega _{R}^{j}(\log \mathscr {A})[x_{I \cup \{\ell \}}^{-1}]$
and
$\Omega _{R}^{j}(\log \mathscr {A})[x_{I \cup \{\ell \}}^{-1}]$
and
![]() $\sigma _{I}(\ell )$
is the number of elements in I less than
$\sigma _{I}(\ell )$
is the number of elements in I less than
![]() $\ell $
. To suppress potential confusion, the vertical
$\ell $
. To suppress potential confusion, the vertical
![]() $\nabla _{\omega }$
are defined by
$\nabla _{\omega }$
are defined by
Note that
![]() $d(Q_{I}) \wedge \eta _{I} \in \Omega _{R}^{j+1}(\log \mathscr {A})[x_{I}^{-1}]$
since
$d(Q_{I}) \wedge \eta _{I} \in \Omega _{R}^{j+1}(\log \mathscr {A})[x_{I}^{-1}]$
since
![]() $d(Q_{I}) \in \Omega _{R}^{1}[x_{I}^{-1}]$
and
$d(Q_{I}) \in \Omega _{R}^{1}[x_{I}^{-1}]$
and
![]() $\Omega _{R}^{1} \wedge \Omega _{R}^{j}(\log \mathscr {A}) \subseteq \Omega _{R}^{j+1}(\log \mathscr {A})$
, which together entail that
$\Omega _{R}^{1} \wedge \Omega _{R}^{j}(\log \mathscr {A}) \subseteq \Omega _{R}^{j+1}(\log \mathscr {A})$
, which together entail that
![]() $d(Q_{I}) \wedge \eta _{I} \in \Omega _{R}^{1}[x_{I}^{-1}] \wedge \Omega _{R}^{j}(\log \mathscr {A}) \subseteq \Omega _{R}^{j+1}(\log \mathscr {A})[x_{I}^{-1}]$
.
$d(Q_{I}) \wedge \eta _{I} \in \Omega _{R}^{1}[x_{I}^{-1}] \wedge \Omega _{R}^{j}(\log \mathscr {A}) \subseteq \Omega _{R}^{j+1}(\log \mathscr {A})[x_{I}^{-1}]$
.
That Equation (2.3) commutes follows from the definitions:
 $$ \begin{align*} \nabla_{\omega}(\epsilon(Q_{I} \eta_{I}) &= \nabla_{\omega}(\sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} Q_{I \cup \{\ell\}} \eta_{I}) \\ &= \sum_{\ell \notin I}(-1)^{\sigma_{I}(\ell)}( (d(Q_{I \cup \{\ell\}}) \wedge \eta_{I} + Q_{I\cup \{\ell\}} \wedge d(\eta_{I}) + Q_{I \cup \{\ell\}} \omega \wedge \eta_{I}); \\ \epsilon(\nabla_{\omega}(Q_{I} \eta_{I}) &= \epsilon( d(Q_{I}) \wedge \eta_{I} + Q_{I} \wedge d(\eta_{I}) + Q_{I} \omega \wedge \eta_{I}) \\ &= \epsilon(d(Q_{I}) \wedge \eta_{I}) + \sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} (Q_{I \cup \{\ell\}} \wedge d(\eta_{I}) + Q_{I \cup \{\ell\}} \omega \wedge \eta_{I}). \end{align*} $$
$$ \begin{align*} \nabla_{\omega}(\epsilon(Q_{I} \eta_{I}) &= \nabla_{\omega}(\sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} Q_{I \cup \{\ell\}} \eta_{I}) \\ &= \sum_{\ell \notin I}(-1)^{\sigma_{I}(\ell)}( (d(Q_{I \cup \{\ell\}}) \wedge \eta_{I} + Q_{I\cup \{\ell\}} \wedge d(\eta_{I}) + Q_{I \cup \{\ell\}} \omega \wedge \eta_{I}); \\ \epsilon(\nabla_{\omega}(Q_{I} \eta_{I}) &= \epsilon( d(Q_{I}) \wedge \eta_{I} + Q_{I} \wedge d(\eta_{I}) + Q_{I} \omega \wedge \eta_{I}) \\ &= \epsilon(d(Q_{I}) \wedge \eta_{I}) + \sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} (Q_{I \cup \{\ell\}} \wedge d(\eta_{I}) + Q_{I \cup \{\ell\}} \omega \wedge \eta_{I}). \end{align*} $$
We are done once we confirm
![]() $\sum _{\ell \notin I} (-1)^{\sigma _{I}(\ell )} d(Q_{I \cup \{\ell \}}) \wedge \eta _{I} = \epsilon (d(Q_{I}) \wedge \eta _{I})$
. Let
$\sum _{\ell \notin I} (-1)^{\sigma _{I}(\ell )} d(Q_{I \cup \{\ell \}}) \wedge \eta _{I} = \epsilon (d(Q_{I}) \wedge \eta _{I})$
. Let
![]() $Q_{I} = \frac {a}{x_{I}^{p}}$
. Then
$Q_{I} = \frac {a}{x_{I}^{p}}$
. Then
 $$ \begin{align*} \epsilon(d(Q_{I}) \wedge \eta_{I}) &= \epsilon( (\sum_{1 \leq i \leq n} \frac{(\partial_{i} \bullet a) dx_{i}}{x_{I}^{p}} - \frac{(\partial_{i} \bullet x_{I}^{p}) a dx_{i}}{x_{I}^{2p}}) \wedge \eta_{I}) \\ & = \epsilon( \sum_{1 \leq i \leq n} (\frac{(\partial_{i} \bullet a)} {x_{I}^{p}} - \frac{(\partial_{i} \bullet x_{I}^{p}) a} {x_{I}^{2p}}) dx_{i} \wedge \eta_{I} \\ &= \sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} d(Q_{I \cup \{\ell\}}) \wedge \eta_{I} \end{align*} $$
$$ \begin{align*} \epsilon(d(Q_{I}) \wedge \eta_{I}) &= \epsilon( (\sum_{1 \leq i \leq n} \frac{(\partial_{i} \bullet a) dx_{i}}{x_{I}^{p}} - \frac{(\partial_{i} \bullet x_{I}^{p}) a dx_{i}}{x_{I}^{2p}}) \wedge \eta_{I}) \\ & = \epsilon( \sum_{1 \leq i \leq n} (\frac{(\partial_{i} \bullet a)} {x_{I}^{p}} - \frac{(\partial_{i} \bullet x_{I}^{p}) a} {x_{I}^{2p}}) dx_{i} \wedge \eta_{I} \\ &= \sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} d(Q_{I \cup \{\ell\}}) \wedge \eta_{I} \end{align*} $$
since the image of
![]() $\partial _{i} \bullet Q_{I}$
in
$\partial _{i} \bullet Q_{I}$
in
![]() $R[x_{I \cup \{\ell \}}^{-1}]$
agrees with
$R[x_{I \cup \{\ell \}}^{-1}]$
agrees with
![]() $\partial _{i}$
applied to
$\partial _{i}$
applied to
![]() $Q_{I\cup \{\ell \}} \in R[x_{I \cup \{\ell \}}^{-1}]$
.
$Q_{I\cup \{\ell \}} \in R[x_{I \cup \{\ell \}}^{-1}]$
.
We summarize our construction of
![]() $N^{\bullet , \bullet }$
:
$N^{\bullet , \bullet }$
:
Proposition 2.9. There is a commutative diagram
![]() $N^{\bullet , \bullet }$
, positioned in
$N^{\bullet , \bullet }$
, positioned in
![]() $\mathbb {Z}^{2}$
, where each row and column is a chain complex, and each square looks like:
$\mathbb {Z}^{2}$
, where each row and column is a chain complex, and each square looks like:

The horizontal maps are the natural R-linear maps induced by the Čech complex
![]() $C(x_{1}, \dots , x_{n}; \Omega _{R}^{j}(\log \mathscr {A}))$
(see Equation (2.4)), the vertical maps are the natural
$C(x_{1}, \dots , x_{n}; \Omega _{R}^{j}(\log \mathscr {A}))$
(see Equation (2.4)), the vertical maps are the natural
![]() $\mathbb {C}$
-linear maps induced by
$\mathbb {C}$
-linear maps induced by
![]() $(\Omega _{R}^{\bullet }, \nabla _{\omega })$
(see Equation (2.5)), and each square commutes (see the computations following Equation (2.3)).
$(\Omega _{R}^{\bullet }, \nabla _{\omega })$
(see Equation (2.5)), and each square commutes (see the computations following Equation (2.3)).
We now construct a well-behaved map
![]() $N^{j+1, t} \to N^{j,t}$
that is R-linear.
$N^{j+1, t} \to N^{j,t}$
that is R-linear.
Definition 2.10. Let
![]() $E = \sum _{i} x_{i} \partial _{i} \in \operatorname {\mathrm {Der}}_{X}(-\log \mathscr {A})$
be the Euler operator and recall the classical contraction
$E = \sum _{i} x_{i} \partial _{i} \in \operatorname {\mathrm {Der}}_{X}(-\log \mathscr {A})$
be the Euler operator and recall the classical contraction
![]() $\iota _{E}: \Omega _{R}^{j+1} \to \Omega _{R}^{j}$
along E. Since E is logarithmic, this induces a contraction on the logarithmic differential forms (cf. 1.6 [Reference Saito28])
$\iota _{E}: \Omega _{R}^{j+1} \to \Omega _{R}^{j}$
along E. Since E is logarithmic, this induces a contraction on the logarithmic differential forms (cf. 1.6 [Reference Saito28])
as well as a contraction on the meromorphic differential forms
It also induces a contraction map
given by, for
![]() $\eta _{I} \in \Omega _{R}^{j+1}(\log \mathscr {A})$
,
$\eta _{I} \in \Omega _{R}^{j+1}(\log \mathscr {A})$
,
Proposition 2.11. Let E be the Euler operator, and let
![]() $N^{\bullet , \bullet }$
as in Proposition 2.9. Then the diagram
$N^{\bullet , \bullet }$
as in Proposition 2.9. Then the diagram

commutes.
Proof. Let
![]() $Q_{I} \in R[x_{I}^{-1}]$
and
$Q_{I} \in R[x_{I}^{-1}]$
and
![]() $\eta _{I} \in \Omega _{R}^{j+1}(\log \mathscr {A})$
so that
$\eta _{I} \in \Omega _{R}^{j+1}(\log \mathscr {A})$
so that
![]() $Q_{I} \eta _{I} \in \Omega _{R}^{j+1}(\log \mathscr {A})[x_{I}^{-1}]$
. Then
$Q_{I} \eta _{I} \in \Omega _{R}^{j+1}(\log \mathscr {A})[x_{I}^{-1}]$
. Then
 $$ \begin{align*} \epsilon(\iota_{E}(Q_{I} \eta_{I})) = \epsilon(Q_{I}( \iota_{E}(\eta_{I}))) &= \sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} Q_{I \cup \{\ell\}} \iota_{E}(\eta_{I}) \\ &= \iota_{E}(\sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} Q_{I \cup \{\ell\}} \eta_{I}) = \iota_{E}(\epsilon (Q_{I}\eta_{I})).\\[-47pt] \end{align*} $$
$$ \begin{align*} \epsilon(\iota_{E}(Q_{I} \eta_{I})) = \epsilon(Q_{I}( \iota_{E}(\eta_{I}))) &= \sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} Q_{I \cup \{\ell\}} \iota_{E}(\eta_{I}) \\ &= \iota_{E}(\sum_{\ell \notin I} (-1)^{\sigma_{I}(\ell)} Q_{I \cup \{\ell\}} \eta_{I}) = \iota_{E}(\epsilon (Q_{I}\eta_{I})).\\[-47pt] \end{align*} $$
We now begin to reap some fruits of our mostly formal labors. From our first set of commutative diagrams, we have constructed a complex of
![]() $\mathbb {C}$
-modules; from our second set, a complex of R-modules:
$\mathbb {C}$
-modules; from our second set, a complex of R-modules:
Proposition 2.12. The complex
 $$ \begin{align} (H_{\mathfrak{m}}^{t}(\Omega_{R}^{\bullet}(\log \mathscr{A})), \nabla_{\omega}) = 0 \to H_{\mathfrak{m}}^{t}(\Omega_{R}^{0}(\log \mathscr{A})) &\xrightarrow[]{\nabla_{\omega}} H_{\mathfrak{m}}^{t}(\Omega_{R}^{1}(\log \mathscr{A})) \xrightarrow[]{\nabla_{\omega}} \cdots \\ &\xrightarrow[]{\nabla_{\omega}} H_{\mathfrak{m}}^{t}(\Omega_{R}^{n}(\log \mathscr{A}) \to 0 \nonumber \end{align} $$
$$ \begin{align} (H_{\mathfrak{m}}^{t}(\Omega_{R}^{\bullet}(\log \mathscr{A})), \nabla_{\omega}) = 0 \to H_{\mathfrak{m}}^{t}(\Omega_{R}^{0}(\log \mathscr{A})) &\xrightarrow[]{\nabla_{\omega}} H_{\mathfrak{m}}^{t}(\Omega_{R}^{1}(\log \mathscr{A})) \xrightarrow[]{\nabla_{\omega}} \cdots \\ &\xrightarrow[]{\nabla_{\omega}} H_{\mathfrak{m}}^{t}(\Omega_{R}^{n}(\log \mathscr{A}) \to 0 \nonumber \end{align} $$
with
![]() $\mathbb {C}$
-linear differential
$\mathbb {C}$
-linear differential
![]() $\nabla _{\omega }$
, as described in Equation (2.5), is well-defined. Additionally, for E the Euler operator, the complex
$\nabla _{\omega }$
, as described in Equation (2.5), is well-defined. Additionally, for E the Euler operator, the complex
 $$ \begin{align} (H_{\mathfrak{m}}^{t}(\Omega_{R}^{\bullet}(\log \mathscr{A})), \iota_{E}) = 0 \to H_{\mathfrak{m}}^{t}(\Omega_{R}^{n}(\log \mathscr{A})) &\xrightarrow[]{\iota_{E}} H_{\mathfrak{m}}^{t}(\Omega_{R}^{n-1}(\log \mathscr{A})) \xrightarrow[]{\iota_{E}} \cdots \\ &\xrightarrow[]{\iota_{E}} H_{\mathfrak{m}}^{t}(\Omega_{R}^{0}(\log \mathscr{A}) \to 0 \nonumber \end{align} $$
$$ \begin{align} (H_{\mathfrak{m}}^{t}(\Omega_{R}^{\bullet}(\log \mathscr{A})), \iota_{E}) = 0 \to H_{\mathfrak{m}}^{t}(\Omega_{R}^{n}(\log \mathscr{A})) &\xrightarrow[]{\iota_{E}} H_{\mathfrak{m}}^{t}(\Omega_{R}^{n-1}(\log \mathscr{A})) \xrightarrow[]{\iota_{E}} \cdots \\ &\xrightarrow[]{\iota_{E}} H_{\mathfrak{m}}^{t}(\Omega_{R}^{0}(\log \mathscr{A}) \to 0 \nonumber \end{align} $$
with R-linear differential induced by
![]() $\iota _{E}$
, as in Definition 2.10, is well-defined.
$\iota _{E}$
, as in Definition 2.10, is well-defined.
Proof. That the squares (2.6) from Proposition 2.9 commute amounts to saying
![]() $\nabla _{\omega }$
gives a chain map from
$\nabla _{\omega }$
gives a chain map from
![]() $N^{j, \bullet } \to N^{j+1, \bullet }$
for all j. So the induced maps on cohomology
$N^{j, \bullet } \to N^{j+1, \bullet }$
for all j. So the induced maps on cohomology
are well-defined. Since
![]() $\nabla _{\omega }^{2} = 0$
, certainly
$\nabla _{\omega }^{2} = 0$
, certainly
![]() $(H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
is a complex.
$(H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
is a complex.
The case of
![]() $(H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A})), \iota _{E})$
is similar, now using Proposition 2.11.
$(H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A})), \iota _{E})$
is similar, now using Proposition 2.11.
Thus, we can discuss the cohomology of the twisted differential
![]() $\nabla _{\omega }$
on local cohomology modules of logarithmic forms. Grade R and
$\nabla _{\omega }$
on local cohomology modules of logarithmic forms. Grade R and
![]() $\Omega _{R}^{\bullet }(\log \mathscr {A})$
by the edict of the the Euler derivation
$\Omega _{R}^{\bullet }(\log \mathscr {A})$
by the edict of the the Euler derivation
![]() $\sum x_{i} \partial _{i}$
; that is, give x and
$\sum x_{i} \partial _{i}$
; that is, give x and
![]() $dx_{i}$
weight one,
$dx_{i}$
weight one,
![]() $\frac {1}{f}$
weight
$\frac {1}{f}$
weight
![]() $- \deg (f)$
. Local cohomology
$- \deg (f)$
. Local cohomology
![]() $H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
inherits a natural
$H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
inherits a natural
![]() $\mathbb {Z}$
-grading by making
$\mathbb {Z}$
-grading by making
![]() $x^{-1}$
have weight
$x^{-1}$
have weight
![]() $-1$
. Exterior differentiation preserves degree as does the exterior product with
$-1$
. Exterior differentiation preserves degree as does the exterior product with
![]() $\omega $
(since
$\omega $
(since
![]() $df_{k}/f_{k}$
has weight zero). Therefore, our complexes decompose into their homogeneous subcomplexes:
$df_{k}/f_{k}$
has weight zero). Therefore, our complexes decompose into their homogeneous subcomplexes:
Clearly, cohomology is well behaved with respect to this direct sum decomposition.
Following Lemma 2.1 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9], we can extend a nice formula involving Lie derivative and homogeneous elements to the twisted and local cohomological cases:
Lemma 2.13. Suppose that E is the Euler operator and that R,
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
, and
$\Omega _{R}^{j}(\log \mathscr {A})$
, and
![]() $H_{\mathfrak {m}}^{t}(\log \mathscr {A})$
are graded accordingly, that is, with
$H_{\mathfrak {m}}^{t}(\log \mathscr {A})$
are graded accordingly, that is, with
![]() $x_{i}$
and
$x_{i}$
and
![]() $dx_{i}$
given weight one. The twisted Lie derivative with respect to E on
$dx_{i}$
given weight one. The twisted Lie derivative with respect to E on
![]() $\Omega _{R}^{\bullet }(\log \mathscr {A})$
$\Omega _{R}^{\bullet }(\log \mathscr {A})$
satisfies, for
![]() $\eta $
a homogeneous logarithmic j-form,
$\eta $
a homogeneous logarithmic j-form,
where
![]() $\omega = \sum \lambda _{k} d \log f_{k}.$
The induced twisted Lie derivative on a homogeneous class
$\omega = \sum \lambda _{k} d \log f_{k}.$
The induced twisted Lie derivative on a homogeneous class
![]() $[\zeta ] \in H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
satisfies
$[\zeta ] \in H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
satisfies
Proof. We first do the case of logarithmic forms. The untwisted statement is due to Naruki according to Lemma 2.1 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9] and is a straightforward computation. Since contraction and exterior differentiation are additive, we need only to confirm that
 $$ \begin{align*} \omega \wedge \iota_{E}(\eta) + \iota_{E}(\omega \wedge \eta) &= \omega \wedge \iota_{E}(\eta) + \iota_{E}(\omega) \wedge \eta - \omega \wedge \iota_{E}(\eta) \\ &= \iota_{E}(\omega) \eta = (\sum \lambda_{k} \iota_{E}(d \log f_{k}) )\eta = (\sum \lambda_{k}) \eta. \end{align*} $$
$$ \begin{align*} \omega \wedge \iota_{E}(\eta) + \iota_{E}(\omega \wedge \eta) &= \omega \wedge \iota_{E}(\eta) + \iota_{E}(\omega) \wedge \eta - \omega \wedge \iota_{E}(\eta) \\ &= \iota_{E}(\omega) \eta = (\sum \lambda_{k} \iota_{E}(d \log f_{k}) )\eta = (\sum \lambda_{k}) \eta. \end{align*} $$
This gives Equation (2.10). As for Equation (2.11), first note that we have confirmed
![]() $\iota _{E}$
and
$\iota _{E}$
and
![]() $\nabla _{\omega }$
are well-defined maps on local cohomology and are defined by taking representatives. So the second formula follows from the first because: Naruki’s computation for the untwisted case extends to
$\nabla _{\omega }$
are well-defined maps on local cohomology and are defined by taking representatives. So the second formula follows from the first because: Naruki’s computation for the untwisted case extends to
![]() $\Omega _{R}^{j}(\log \mathscr {A})[x_{I}^{-1}]$
; we can compute the twisted Lie derivative on a homogeneous representative of our homogeneous class of
$\Omega _{R}^{j}(\log \mathscr {A})[x_{I}^{-1}]$
; we can compute the twisted Lie derivative on a homogeneous representative of our homogeneous class of
![]() $H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
.
$H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
.
Convention 2.14. A quick computation verifies
![]() $\iota _{E}(\omega ) = \lambda _{1} + \cdots + \lambda _{d}$
. We use
$\iota _{E}(\omega ) = \lambda _{1} + \cdots + \lambda _{d}$
. We use
![]() $\iota _{E}(\omega )$
throughout the paper instead of writing this sum.
$\iota _{E}(\omega )$
throughout the paper instead of writing this sum.
Here is the workman’s result of this subsection: It reduces computing cohomology of these twisted complexes to a finite-dimensional linear algebra problem. Indeed, only a particular homogeneous subcomplex needs to be considered. Because R is
![]() $\mathbb {N}$
-graded, this homogeneous subcomplex is a finite-dimensional
$\mathbb {N}$
-graded, this homogeneous subcomplex is a finite-dimensional
![]() $\mathbb {C}$
-module. Again, this lemma tracks with ideas from [Reference Castro-Jiménez, Narváez-Macarro and Mond9], but we have extended the result to the both the twisted case and to the case of local cohomology.
$\mathbb {C}$
-module. Again, this lemma tracks with ideas from [Reference Castro-Jiménez, Narváez-Macarro and Mond9], but we have extended the result to the both the twisted case and to the case of local cohomology.
Proposition 2.15. Suppose that E is the Euler operator and that R,
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
,
$\Omega _{R}^{j}(\log \mathscr {A})$
,
![]() $H^{i}_{\mathfrak {m}}(\Omega _{R}^{j}(\log \mathscr {A}))$
are graded accordingly, that is, with
$H^{i}_{\mathfrak {m}}(\Omega _{R}^{j}(\log \mathscr {A}))$
are graded accordingly, that is, with
![]() $x_{i}$
and
$x_{i}$
and
![]() $dx_{i}$
given weight one. Then
$dx_{i}$
given weight one. Then
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
and
$(\Omega _{R}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
and
![]() $(H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
have homogeneous differentials and decompose as direct sum of their homogeneous subcomplexes. Moreover, the following homogeneous subcomplex inclusions are quasi-isomorphisms:
$(H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
have homogeneous differentials and decompose as direct sum of their homogeneous subcomplexes. Moreover, the following homogeneous subcomplex inclusions are quasi-isomorphisms:
(Here,
![]() $(-)_{-\iota _{E}(\omega )}$
denotes the
$(-)_{-\iota _{E}(\omega )}$
denotes the
![]() $-\iota _{E}(\omega )$
-homogeneous subspace of
$-\iota _{E}(\omega )$
-homogeneous subspace of
![]() $(-)$
.)
$(-)$
.)
Proof. Clearly, d is degree preserving map. Since
![]() $\omega = \sum \lambda _{k} \frac {df_{k}}{f_{k}}$
is homogeneous of grade zero,
$\omega = \sum \lambda _{k} \frac {df_{k}}{f_{k}}$
is homogeneous of grade zero,
![]() $\nabla _{\omega }$
is also a degree-preserving map. That all these complexes decompose into direct sums of their homogeneous parts follows.
$\nabla _{\omega }$
is also a degree-preserving map. That all these complexes decompose into direct sums of their homogeneous parts follows.
As for the quasi-isomorphisms, we first do the case of the logarithmic de Rham complex. Thanks to the direct sum decomposition (which certainly extends to cohomology), it is enough to prove that, for
![]() $q \neq - \iota _{E}(\omega )$
, the degree q subcomplex
$q \neq - \iota _{E}(\omega )$
, the degree q subcomplex
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A})_{q}, \nabla _{\omega })$
is acyclic. Thanks to Equation (2.10) from Lemma 2.13, and the fact
$(\Omega _{R}^{\bullet }(\log \mathscr {A})_{q}, \nabla _{\omega })$
is acyclic. Thanks to Equation (2.10) from Lemma 2.13, and the fact
![]() $\iota _{E}$
is itself degree preserving,
$\iota _{E}$
is itself degree preserving,
![]() $\iota _{E}$
defines a chain homotopy between
$\iota _{E}$
defines a chain homotopy between
and the zero map
Since
![]() $q + \iota _{E}(\omega ) \neq 0$
, the first map is a quasi-isomorphism and so
$q + \iota _{E}(\omega ) \neq 0$
, the first map is a quasi-isomorphism and so
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A})_{q}, \nabla _{\omega })$
is acyclic. The result for the logarithmic de Rham complex follows.
$(\Omega _{R}^{\bullet }(\log \mathscr {A})_{q}, \nabla _{\omega })$
is acyclic. The result for the logarithmic de Rham complex follows.
As for the local cohomology complexes, the same argument works:
![]() $\iota _{E}$
defines a chain homotopy between similar maps, now using Equation (2.11) from Lemma 2.13.
$\iota _{E}$
defines a chain homotopy between similar maps, now using Equation (2.11) from Lemma 2.13.
2.3. Complexes of analytic Čech cohomology of logarithmic forms
The purpose of this subsection is to repeat the constructions of the previous subsection in the appropriate analytic setting. Specifically, we want an analytic version of Proposition 2.15. This involves working with the coherent sheaves
![]() $\Omega _{X}^{j}(\log \mathscr {A})$
of
$\Omega _{X}^{j}(\log \mathscr {A})$
of
![]() $\mathscr {O}_{X}$
-modules. Often, we will replace
$\mathscr {O}_{X}$
-modules. Often, we will replace
![]() $`\log \mathscr {A}'$
with
$`\log \mathscr {A}'$
with
![]() $`\log f'$
. In this subsection, we will always assume
$`\log f'$
. In this subsection, we will always assume
![]() $\mathscr {A}$
is central and so f is homogeneous.
$\mathscr {A}$
is central and so f is homogeneous.
Instead of working with the algebraic Čech complex attached to the maximal ideal
![]() $\mathfrak {m}$
(the irrelevant ideal of R), we will work with the sheaf-theoretic analytic Čech complex attached to the open cover
$\mathfrak {m}$
(the irrelevant ideal of R), we will work with the sheaf-theoretic analytic Čech complex attached to the open cover
![]() $\{D(x_{i})\} = \{ \{x_{i} \neq 0 \}\}_{1 \leq i \leq n}$
of
$\{D(x_{i})\} = \{ \{x_{i} \neq 0 \}\}_{1 \leq i \leq n}$
of
![]() $X \setminus 0$
. For an index set
$X \setminus 0$
. For an index set
![]() $I \subseteq [n]$
, let
$I \subseteq [n]$
, let
![]() $x_{I}$
, denote
$x_{I}$
, denote
![]() $\prod _{i \in I} x_{i}$
and let
$\prod _{i \in I} x_{i}$
and let
![]() $D(x_{I}) = \{x_{I} \neq 0\}$
the open set in
$D(x_{I}) = \{x_{I} \neq 0\}$
the open set in
![]() $X = \mathbb {C}^{n}$
. Since
$X = \mathbb {C}^{n}$
. Since
![]() $D(x_{I})$
is a Rienhardt (i.e., multicircular) domain, every analytic function on
$D(x_{I})$
is a Rienhardt (i.e., multicircular) domain, every analytic function on
![]() $D(x_{I})$
has a unique Laurent expansion at
$D(x_{I})$
has a unique Laurent expansion at
![]() $0$
that converges absolutely on
$0$
that converges absolutely on
![]() $D(x_{I})$
and uniformly on compact sets. This Laurent expansion is a formal power series in
$D(x_{I})$
and uniformly on compact sets. This Laurent expansion is a formal power series in
![]() $\mathbb {C}[[x_{1}^{\pm 1}, \dots , x_{n}^{\pm 1}]]$
, but using absolute convergence one can check that every monomial
$\mathbb {C}[[x_{1}^{\pm 1}, \dots , x_{n}^{\pm 1}]]$
, but using absolute convergence one can check that every monomial
![]() $c_{\boldsymbol {\alpha }}x^{\boldsymbol {\alpha }}$
with some
$c_{\boldsymbol {\alpha }}x^{\boldsymbol {\alpha }}$
with some
![]() $\alpha _{k} < 0$
for
$\alpha _{k} < 0$
for
![]() $k \notin I$
has
$k \notin I$
has
![]() $c_{\boldsymbol {\alpha }} = 0$
. When considering an analytic function on
$c_{\boldsymbol {\alpha }} = 0$
. When considering an analytic function on
![]() $D(x_{I})$
, we will identify it with this Laurent expansion and so its associated element of the formal power series ring
$D(x_{I})$
, we will identify it with this Laurent expansion and so its associated element of the formal power series ring
![]() $\mathbb {C}[[x_{1}, \dots , x_{n}, x_{i_{1}}^{-1}, \dots , x_{i_{t}}^{-1}]]$
, where
$\mathbb {C}[[x_{1}, \dots , x_{n}, x_{i_{1}}^{-1}, \dots , x_{i_{t}}^{-1}]]$
, where
![]() $I = \{i_{1}, \dots , i_{t}\}$
.
$I = \{i_{1}, \dots , i_{t}\}$
.
In particular, an element
![]() $\eta _{I} \in \Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
is of the form
$\eta _{I} \in \Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
is of the form
 $$ \begin{align} \eta_{I} = \sum_{\substack{J \subseteq [n] \\ |J| =j}} \frac{ g_{I,J} dx_{J}}{f}, \end{align} $$
$$ \begin{align} \eta_{I} = \sum_{\substack{J \subseteq [n] \\ |J| =j}} \frac{ g_{I,J} dx_{J}}{f}, \end{align} $$
where
![]() $g_{I,J} \in \mathbb {C}[[x_{1}, \dots , x_{n}, x_{i_{1}}^{-1}, \dots , x_{i_{t}}^{-1}]]$
is the convergent Laurent expansion (at
$g_{I,J} \in \mathbb {C}[[x_{1}, \dots , x_{n}, x_{i_{1}}^{-1}, \dots , x_{i_{t}}^{-1}]]$
is the convergent Laurent expansion (at
![]() $0$
) on
$0$
) on
![]() $D(x_{I})$
and
$D(x_{I})$
and
![]() $dx_{J} = \prod _{j \in J} dx_{j}$
. (We order the
$dx_{J} = \prod _{j \in J} dx_{j}$
. (We order the
![]() $j \in J$
in increasing order as is the norm.) Since each
$j \in J$
in increasing order as is the norm.) Since each
![]() $g_{I,J}$
is canonically identified with its Laurent expansion, and because this series converges absolutely, we may write
$g_{I,J}$
is canonically identified with its Laurent expansion, and because this series converges absolutely, we may write
where
 $$\begin{align*}g_{I,J,p} = \sum_{\substack{\textbf{p} \in \mathbb{Z}^{n} \\ |\textbf{p}| = p}} c_{\textbf{p}} x^{\textbf{p}} = \sum_{\substack{\textbf{p} \in \mathbb{Z}^{n} \\ |\textbf{p}| = p}} c_{\textbf{p}} x_{1}^{p_{1}} \cdots x_{n}^{p_{n}} \end{align*}$$
$$\begin{align*}g_{I,J,p} = \sum_{\substack{\textbf{p} \in \mathbb{Z}^{n} \\ |\textbf{p}| = p}} c_{\textbf{p}} x^{\textbf{p}} = \sum_{\substack{\textbf{p} \in \mathbb{Z}^{n} \\ |\textbf{p}| = p}} c_{\textbf{p}} x_{1}^{p_{1}} \cdots x_{n}^{p_{n}} \end{align*}$$
and it is understood that
![]() $\textbf {p}$
is restricted to integral vectors whose potential negative components correspond to entries from I. This decomposition of
$\textbf {p}$
is restricted to integral vectors whose potential negative components correspond to entries from I. This decomposition of
![]() $g_{I,J}$
into the infinite sum
$g_{I,J}$
into the infinite sum
![]() $\sum _{p \in \mathbb {Z}} g_{I,J,p}$
is a decomposition of an analytic function into homogeneous parts under the standard weighting giving
$\sum _{p \in \mathbb {Z}} g_{I,J,p}$
is a decomposition of an analytic function into homogeneous parts under the standard weighting giving
![]() $x_{i}$
weight
$x_{i}$
weight
![]() $1$
and
$1$
and
![]() $x_{i}^{-1}$
weight
$x_{i}^{-1}$
weight
![]() $-1$
. We extend this weighting to
$-1$
. We extend this weighting to
![]() $\Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
by, as before, weighting
$\Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
by, as before, weighting
![]() $\deg (1/f) = -\deg (f)$
and
$\deg (1/f) = -\deg (f)$
and
![]() $\deg (dx_{J}) = |J|$
. Then every element
$\deg (dx_{J}) = |J|$
. Then every element
![]() $\eta _{I} \in \Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
has a (infinite) decomposition into homogeneous parts
$\eta _{I} \in \Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
has a (infinite) decomposition into homogeneous parts
 $$ \begin{align} \eta_{I} = \sum_{p \in \mathbb{Z}} \eta_{I,p} \quad \text{ where } \quad \eta_{I,p} = \sum_{\substack{J \subseteq [n] \\ |J| =j}} \frac{ g_{I,J,p+\deg(f)-|J|} dx_{J}}{f} \end{align} $$
$$ \begin{align} \eta_{I} = \sum_{p \in \mathbb{Z}} \eta_{I,p} \quad \text{ where } \quad \eta_{I,p} = \sum_{\substack{J \subseteq [n] \\ |J| =j}} \frac{ g_{I,J,p+\deg(f)-|J|} dx_{J}}{f} \end{align} $$
is a homogeneous (infinite sum) of weight p.
Remark 2.16.
-
(a) If
 $g_{I} = \sum _{p \in \mathbb {Z}} g_{I,p}$
is the homogeneous decomposition of a Laurent expansion (at
$g_{I} = \sum _{p \in \mathbb {Z}} g_{I,p}$
is the homogeneous decomposition of a Laurent expansion (at
 $0$
) of a holomorphic function on
$0$
) of a holomorphic function on
 $D(x_{I})$
, then each
$D(x_{I})$
, then each
 $g_{I,p}$
is also the Laurent expansion (at
$g_{I,p}$
is also the Laurent expansion (at
 $0$
) of a holomorphic function on
$0$
) of a holomorphic function on
 $D(x_{I})$
. This follows from the fact
$D(x_{I})$
. This follows from the fact
 $g_{I}$
is absolutely convergent and so not only can the series terms be rearranged, but subseries
$g_{I}$
is absolutely convergent and so not only can the series terms be rearranged, but subseries
 $g_{I,p}$
is also absolutely convergent on all of
$g_{I,p}$
is also absolutely convergent on all of
 $D(x_{I})$
. Also note that, by comparing homogeneous terms, the (partial) derivatives of
$D(x_{I})$
. Also note that, by comparing homogeneous terms, the (partial) derivatives of
 $g_{I,p}$
are recovered from the (partial) derivatives of
$g_{I,p}$
are recovered from the (partial) derivatives of
 $g_{I}$
.
$g_{I}$
. -
(b) If
 $\eta _{I} = \sum _{p \in \mathbb {Z}} \eta _{I,p}$
is the homogeneous decomposition of a logarithmic j-form from
$\eta _{I} = \sum _{p \in \mathbb {Z}} \eta _{I,p}$
is the homogeneous decomposition of a logarithmic j-form from
 $\Gamma (D(x_{I}), \Omega _{X}^{j}(\log \mathscr {A}))$
then so is each
$\Gamma (D(x_{I}), \Omega _{X}^{j}(\log \mathscr {A}))$
then so is each
 $\eta _{p}$
. The previous item shows
$\eta _{p}$
. The previous item shows
 $\eta _{p} \in \frac {1}{f} \Gamma (D(x_{I}), \Omega _{X}^{j}(\log \mathscr {A}))$
. So we need only verify
$\eta _{p} \in \frac {1}{f} \Gamma (D(x_{I}), \Omega _{X}^{j}(\log \mathscr {A}))$
. So we need only verify
 $d(\eta _{p})$
also has a pole of order at most one along f. We know
$d(\eta _{p})$
also has a pole of order at most one along f. We know
 $d(\eta )$
has a pole of order at most one along f, which equates to
$d(\eta )$
has a pole of order at most one along f, which equates to
 $d(f) \wedge \sum _{p \in \mathbb {Z}} \sum _{\substack {J \subseteq [n] \\ |J| =j}} g_{I,J,p+\deg (f)-|J|} dx_{J}$
belonging to
$d(f) \wedge \sum _{p \in \mathbb {Z}} \sum _{\substack {J \subseteq [n] \\ |J| =j}} g_{I,J,p+\deg (f)-|J|} dx_{J}$
belonging to
 $f \cdot \Gamma (D(x_{I}), \Omega _{X}^{j+1})$
. Because
$f \cdot \Gamma (D(x_{I}), \Omega _{X}^{j+1})$
. Because
 $\eta _{I}$
is absolutely convergent, we may compute this wedge product term-by-term; because
$\eta _{I}$
is absolutely convergent, we may compute this wedge product term-by-term; because
 $d(f)$
is homogeneous of degree
$d(f)$
is homogeneous of degree
 $\deg (f)$
, wedging with
$\deg (f)$
, wedging with
 $d(f)$
sends a homogeneous series of degree k to a homogeneous series of degree
$d(f)$
sends a homogeneous series of degree k to a homogeneous series of degree
 $k+\deg (f)$
. By comparing the homogeneous decomposition of the result of wedging with
$k+\deg (f)$
. By comparing the homogeneous decomposition of the result of wedging with
 $d(f)$
(and using the fact the function
$d(f)$
(and using the fact the function
 $0$
has a unique Laurent expansion (at
$0$
has a unique Laurent expansion (at
 $0$
) on
$0$
) on
 $D(x_{I})$
), we conclude
$D(x_{I})$
), we conclude
 $d(f) \wedge \sum _{\substack {J \subseteq [n] \\ |J| =j}} g_{I,J,p+\deg (f)-|J|} dx_{J}$
also belongs to
$d(f) \wedge \sum _{\substack {J \subseteq [n] \\ |J| =j}} g_{I,J,p+\deg (f)-|J|} dx_{J}$
also belongs to
 $f \cdot \Gamma (D(x_{I}), \Omega _{X}^{j+1})$
.
$f \cdot \Gamma (D(x_{I}), \Omega _{X}^{j+1})$
.
We explicitly study the sheaf-theoretic Čech complex of
![]() $\Omega _{X}^{j}(\log \mathscr {A})$
attached to the open cover
$\Omega _{X}^{j}(\log \mathscr {A})$
attached to the open cover
![]() $\{D(x_{i})\}$
of
$\{D(x_{i})\}$
of
![]() $X \setminus 0$
. We name this
$X \setminus 0$
. We name this
where
![]() $\epsilon $
is the standard Čech differential (and defined similarly to the algebraic Čech differential). We almost always omit the
$\epsilon $
is the standard Čech differential (and defined similarly to the algebraic Čech differential). We almost always omit the
![]() $\epsilon $
for aesthetic reasons. When working with a particular element from the Čech complex, we use the notation
$\epsilon $
for aesthetic reasons. When working with a particular element from the Čech complex, we use the notation
 $$\begin{align*}\eta = \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}} \eta_{I} = \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}}\sum_{p \in \mathbb{Z}} \eta_{I,p} \in \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}} \Gamma(D(x_{I}), \Omega_{X}^{j}(\log f)), \end{align*}$$
$$\begin{align*}\eta = \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}} \eta_{I} = \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}}\sum_{p \in \mathbb{Z}} \eta_{I,p} \in \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}} \Gamma(D(x_{I}), \Omega_{X}^{j}(\log f)), \end{align*}$$
where
![]() $\eta _{I}$
is as in Equation (2.12) and
$\eta _{I}$
is as in Equation (2.12) and
![]() $\eta _{I,p}$
is as in Equation (2.13).
$\eta _{I,p}$
is as in Equation (2.13).
Similar arguments as in the previous subsection show that the differentials
![]() $\nabla _{\omega }$
and
$\nabla _{\omega }$
and
![]() $\iota _{E}$
commute with the Čech differentials, yielding commutative diagrams similar to those of Proposition 2.9 and Proposition 2.11. Therefore, as in Proposition 2.12 these induce well-defined complexes on Čech cohomology. We give notation for this:
$\iota _{E}$
commute with the Čech differentials, yielding commutative diagrams similar to those of Proposition 2.9 and Proposition 2.11. Therefore, as in Proposition 2.12 these induce well-defined complexes on Čech cohomology. We give notation for this:
Definition 2.17. For the open cover
![]() $\{D(x_{i})\}$
of
$\{D(x_{i})\}$
of
![]() $X \setminus 0$
, denote the
$X \setminus 0$
, denote the
![]() $t^{\text {th}}$
Čech cohomology of
$t^{\text {th}}$
Čech cohomology of
![]() $\Omega _{X}^{j}(\log \mathscr {A})$
with respect to this cover by
$\Omega _{X}^{j}(\log \mathscr {A})$
with respect to this cover by
The resultant complex on Čech cohomology induced by
![]() $\nabla _{\omega }$
is named
$\nabla _{\omega }$
is named
and the resultant complex on Čech cohomolgy induced by
![]() $\iota _{E}$
is named
$\iota _{E}$
is named
It is clear that the Čech differential sends homogeneous elements of weight k in
![]() $C^{t}(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})$
to homogeneous elements of weight k in
$C^{t}(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})$
to homogeneous elements of weight k in
![]() $C^{t+1}(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})$
. Here, by homogeneous, we mean an element
$C^{t+1}(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})$
. Here, by homogeneous, we mean an element
![]() $\eta = \bigoplus _{I} \eta _{I} \in \bigoplus _{I} \Gamma (D(x_{I}), \Omega _{X}^{j}(\log \mathscr {A}))$
whose homogeneous decomposition (cf. Equation (2.13)) satisfies
$\eta = \bigoplus _{I} \eta _{I} \in \bigoplus _{I} \Gamma (D(x_{I}), \Omega _{X}^{j}(\log \mathscr {A}))$
whose homogeneous decomposition (cf. Equation (2.13)) satisfies
![]() $\bigoplus _{I} \eta _{I} = \bigoplus _{I} \sum _{p \in \mathbb {Z}} \eta _{I,p} = \bigoplus _{I} \eta _{I,k}$
, that is,
$\bigoplus _{I} \eta _{I} = \bigoplus _{I} \sum _{p \in \mathbb {Z}} \eta _{I,p} = \bigoplus _{I} \eta _{I,k}$
, that is,
![]() $\eta $
is homogeneous of weight k when, for each I,
$\eta $
is homogeneous of weight k when, for each I,
![]() $\eta _{I,m} = 0$
for all
$\eta _{I,m} = 0$
for all
![]() $m \neq k$
. And since
$m \neq k$
. And since
![]() $\iota _{E}$
and
$\iota _{E}$
and
![]() $\nabla _{\omega }$
also preserve the weight of homogeneous elements, we are authorized to make the following definition:
$\nabla _{\omega }$
also preserve the weight of homogeneous elements, we are authorized to make the following definition:
Definition 2.18. We denote by
the subcomplex of the Čech complex
![]() $(C^{\bullet }(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})), \epsilon )$
comprised solely of homogeneous terms of weight m, where by homogeneous we mean in the Laurent series sense as described above. We denote this subcomplex’s cohomology by
$(C^{\bullet }(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})), \epsilon )$
comprised solely of homogeneous terms of weight m, where by homogeneous we mean in the Laurent series sense as described above. We denote this subcomplex’s cohomology by
We also have a map of complexes
which is induced by including
![]() $C^{\bullet }(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})_{m})$
into the whole Čech complex and is well-defined because
$C^{\bullet }(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})_{m})$
into the whole Čech complex and is well-defined because
![]() $\nabla _{\omega }$
commutes with the Čech differential
$\nabla _{\omega }$
commutes with the Čech differential
![]() $\epsilon $
and both preserve weights.
$\epsilon $
and both preserve weights.
With this setup, we can now state our intended generalization of Proposition 2.15: We intend to show that with
![]() $m = - \iota _{E}(\omega )$
, the map (2.14) of complexes induces a surjection on the level of cohomology. While we still use twisted Lie derivative formulas as in Lemma 2.13, unlike the algebraic case their application is not immediate. We track a similar procedure as in [Reference Castro-Jiménez, Narváez-Macarro and Mond9], but whereas they work directly with analytic logarithmic de Rham complexes, we work a level deeper with their Čech cohomology, making our version more technically involved. The key tool is the following map:
$m = - \iota _{E}(\omega )$
, the map (2.14) of complexes induces a surjection on the level of cohomology. While we still use twisted Lie derivative formulas as in Lemma 2.13, unlike the algebraic case their application is not immediate. We track a similar procedure as in [Reference Castro-Jiménez, Narváez-Macarro and Mond9], but whereas they work directly with analytic logarithmic de Rham complexes, we work a level deeper with their Čech cohomology, making our version more technically involved. The key tool is the following map:
Definition 2.19. Define a map
 $$\begin{align*}\phi: \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}} \Gamma(D(x_{I}), \Omega_{X}^{j}(\log f)) \to \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}} \Gamma(D(x_{I}), \Omega_{X}^{j}(\log f)) \end{align*}$$
$$\begin{align*}\phi: \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}} \Gamma(D(x_{I}), \Omega_{X}^{j}(\log f)) \to \bigoplus_{\substack{I \subseteq [n] \\ |I| = t}} \Gamma(D(x_{I}), \Omega_{X}^{j}(\log f)) \end{align*}$$
by sending each I-component
![]() $\eta _{I}$
of
$\eta _{I}$
of
![]() $\eta $
to
$\eta $
to
 $$\begin{align*}\phi(\eta_{I}) = \phi(\sum_{p} \eta_{I,p}) = \sum_{ p \neq - \iota_{E}(w) } \frac{\eta_{I, p}}{p + \iota_{E}(\omega)}. \end{align*}$$
$$\begin{align*}\phi(\eta_{I}) = \phi(\sum_{p} \eta_{I,p}) = \sum_{ p \neq - \iota_{E}(w) } \frac{\eta_{I, p}}{p + \iota_{E}(\omega)}. \end{align*}$$
Proposition 2.20. The assignment
![]() $\phi : \Gamma (D(x_{I}),\Omega _{X}^{j}(\log f)) \to \Gamma (D(x_{I}),\Omega _{X}^{j}(\log f))$
is well-defined.
$\phi : \Gamma (D(x_{I}),\Omega _{X}^{j}(\log f)) \to \Gamma (D(x_{I}),\Omega _{X}^{j}(\log f))$
is well-defined.
Proof. It is enough to verify the claim for
![]() $\phi (\eta _{I})$
. We first show that
$\phi (\eta _{I})$
. We first show that
![]() $\phi (\eta _{I}) \in \frac {1}{f}\Gamma (D(x_{I}), \Omega _{X}^{j})$
, which is essentially a statement about the appropriate Laurent series converging absolutely. By Remark 2.16 and the absolute convergence of Laurent expansions, the
$\phi (\eta _{I}) \in \frac {1}{f}\Gamma (D(x_{I}), \Omega _{X}^{j})$
, which is essentially a statement about the appropriate Laurent series converging absolutely. By Remark 2.16 and the absolute convergence of Laurent expansions, the
![]() $-\iota _{E}(\omega )$
-homogeneous piece
$-\iota _{E}(\omega )$
-homogeneous piece
![]() $\eta _{I, -\iota _{E}(\omega )}$
is itself in
$\eta _{I, -\iota _{E}(\omega )}$
is itself in
![]() $\frac {1}{f}\Gamma (D(x_{I}), \Omega _{X}^{j})$
. And
$\frac {1}{f}\Gamma (D(x_{I}), \Omega _{X}^{j})$
. And
![]() $\phi (\eta _{I}) = \phi (\eta _{I} - \eta _{I,-\iota _{E}(\omega )})$
. To test absolute convergence, we apply the modulus to an evaluation of the formal Laurent series
$\phi (\eta _{I}) = \phi (\eta _{I} - \eta _{I,-\iota _{E}(\omega )})$
. To test absolute convergence, we apply the modulus to an evaluation of the formal Laurent series
![]() $\phi (\eta _{I} - \eta _{I,-\iota _{E}(\omega )})$
at some point. Under
$\phi (\eta _{I} - \eta _{I,-\iota _{E}(\omega )})$
at some point. Under
![]() $\phi $
, every (nonzero) homogeneous
$\phi $
, every (nonzero) homogeneous
![]() $\eta _{I, p}$
of
$\eta _{I, p}$
of
![]() $\eta _{I} - \eta _{I, -\iota _{E}(\omega )}$
gets sent to
$\eta _{I} - \eta _{I, -\iota _{E}(\omega )}$
gets sent to
![]() $(1/p+\iota _{E}(\omega )) \eta _{I,p}$
. After applying the modulus, and using the fact that
$(1/p+\iota _{E}(\omega )) \eta _{I,p}$
. After applying the modulus, and using the fact that
![]() $|1/(p+\iota _{E}(\omega )| \to 0$
as
$|1/(p+\iota _{E}(\omega )| \to 0$
as
![]() $|p| \to \infty $
, we see that each
$|p| \to \infty $
, we see that each
![]() $\mid (1/p+\iota _{E}(\omega )) \eta _{I,p}\mid $
is smaller than
$\mid (1/p+\iota _{E}(\omega )) \eta _{I,p}\mid $
is smaller than
![]() $\mid \eta _{I,p}\mid $
, provided p is sufficiently far from
$\mid \eta _{I,p}\mid $
, provided p is sufficiently far from
![]() $0$
. Since finite sums of convergent series converge,
$0$
. Since finite sums of convergent series converge,
![]() $\phi (\eta _{I})$
does live in
$\phi (\eta _{I})$
does live in
![]() $\frac {1}{f}\Gamma (D(x_{I}), \Omega _{X}^{j})$
.
$\frac {1}{f}\Gamma (D(x_{I}), \Omega _{X}^{j})$
.
Now, we confirm that
![]() $\phi (\eta _{I}) \in \Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
by showing
$\phi (\eta _{I}) \in \Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
by showing
![]() $df/f \wedge \phi (\eta _{I}) \in \frac {1}{f} \Gamma (D(x_{I}), \Omega _{X}^{j+1}).$
Using Remark 2.16 again,
$df/f \wedge \phi (\eta _{I}) \in \frac {1}{f} \Gamma (D(x_{I}), \Omega _{X}^{j+1}).$
Using Remark 2.16 again,
![]() $\eta _{I, -\iota _{E}(\omega )}$
is logarithmic, and so
$\eta _{I, -\iota _{E}(\omega )}$
is logarithmic, and so
![]() $\eta _{I} - \eta _{I, -\iota _{E}(\omega )}$
is also logarithmic. Consequently,
$\eta _{I} - \eta _{I, -\iota _{E}(\omega )}$
is also logarithmic. Consequently,
![]() $df/f \wedge (\eta _{I} - \eta _{I, -\iota _{E}(\omega )}) \in \frac {1}{f} \Gamma (D(x_{I}, \Omega _{X}^{j+1}).$
But because
$df/f \wedge (\eta _{I} - \eta _{I, -\iota _{E}(\omega )}) \in \frac {1}{f} \Gamma (D(x_{I}, \Omega _{X}^{j+1}).$
But because
![]() $df/f$
is homogeneous of weight zero, as formal Laurent series we have the equalities
$df/f$
is homogeneous of weight zero, as formal Laurent series we have the equalities
And so the same argument about absolute convergence from the first paragraph, now applied to
![]() $\phi (df/f \wedge (\eta _{I} - \eta _{I, -\iota _{E}(\omega )}))$
, shows
$\phi (df/f \wedge (\eta _{I} - \eta _{I, -\iota _{E}(\omega )}))$
, shows
![]() $df/f \wedge \phi (\eta _{I}) \in \frac {1}{f} \Gamma (D(x_{I}), \Omega _{X}^{j+1})$
as required.
$df/f \wedge \phi (\eta _{I}) \in \frac {1}{f} \Gamma (D(x_{I}), \Omega _{X}^{j+1})$
as required.
Proposition 2.21. The assignment
![]() $\phi $
preserves cycles and boundaries of the Čech complex
$\phi $
preserves cycles and boundaries of the Čech complex
![]() $C^{\bullet }(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})).$
$C^{\bullet }(\{D(x_{i})\}, \Omega _{X}^{j}(\log \mathscr {A})).$
Proof. Suppose
![]() $\eta = \bigoplus _{I} \eta _{I} \in \bigoplus _{I} \Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
is a t-cycle (so
$\eta = \bigoplus _{I} \eta _{I} \in \bigoplus _{I} \Gamma (D(x_{I}), \Omega _{X}^{j}(\log f))$
is a t-cycle (so
![]() $|I| = t)$
. This means that for each
$|I| = t)$
. This means that for each
![]() $M \subseteq [n]$
of cardinality
$M \subseteq [n]$
of cardinality
![]() $t+1$
we have, in
$t+1$
we have, in
![]() $\Gamma (D(x_{M}), \Omega _{X}^{j}(\log f))$
, the equalities
$\Gamma (D(x_{M}), \Omega _{X}^{j}(\log f))$
, the equalities
 $$ \begin{align*} \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \eta_{M \setminus \{m\}} &= \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \sum_{p} \eta_{M \setminus \{m\}, p} \\ & = \sum_{p} \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \eta_{M \setminus \{m\}, p} \\ & = 0. \end{align*} $$
$$ \begin{align*} \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \eta_{M \setminus \{m\}} &= \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \sum_{p} \eta_{M \setminus \{m\}, p} \\ & = \sum_{p} \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \eta_{M \setminus \{m\}, p} \\ & = 0. \end{align*} $$
(Here,
![]() $\eta _{M \setminus \{m\}}$
is naturally regarded in
$\eta _{M \setminus \{m\}}$
is naturally regarded in
![]() $\Gamma (D(x_{M}),\Omega _{X}^{j}(\log f))$
by restriction.) We see that, for each individual p,
$\Gamma (D(x_{M}),\Omega _{X}^{j}(\log f))$
by restriction.) We see that, for each individual p,
Moreover, the M-component of
![]() $\epsilon (\phi (\eta ))$
is
$\epsilon (\phi (\eta ))$
is
 $$ \begin{align*} \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \phi(\eta_{M \setminus \{m\}}) &= \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \sum_{ p \neq - \iota_{E}(\omega)}\frac{\eta_{M \setminus \{m\}}}{p + \iota_{E}(\omega)} \\ &= \sum_{p \neq - \iota_{E}(\omega)} \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \frac{\eta_{M \setminus \{m\}, p}}{p + \iota_{E}(\omega)}. \end{align*} $$
$$ \begin{align*} \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \phi(\eta_{M \setminus \{m\}}) &= \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \sum_{ p \neq - \iota_{E}(\omega)}\frac{\eta_{M \setminus \{m\}}}{p + \iota_{E}(\omega)} \\ &= \sum_{p \neq - \iota_{E}(\omega)} \sum_{m \in M} (-1)^{\sigma_{M \setminus \{m\}}(m)} \frac{\eta_{M \setminus \{m\}, p}}{p + \iota_{E}(\omega)}. \end{align*} $$
By Equation (2.15), we conclude the above equation equals zero and
![]() $\epsilon (\phi (\eta )) = 0$
as well.
$\epsilon (\phi (\eta )) = 0$
as well.
The case of boundaries is similar. If
![]() $\eta $
is a t-boundary, that means there is a
$\eta $
is a t-boundary, that means there is a
![]() $\zeta $
such that
$\zeta $
such that
![]() $\epsilon (\zeta ) = \eta $
. Arguing as above, the I-component of
$\epsilon (\zeta ) = \eta $
. Arguing as above, the I-component of
![]() $\epsilon (\zeta )$
and
$\epsilon (\zeta )$
and
![]() $\eta $
agree at each homogeneous piece:
$\eta $
agree at each homogeneous piece:
![]() $\epsilon (\zeta )_{I, p} = \eta _{I,p}$
for all I of cardinality t and all
$\epsilon (\zeta )_{I, p} = \eta _{I,p}$
for all I of cardinality t and all
![]() $p \in \mathbb {Z}$
. As
$p \in \mathbb {Z}$
. As
![]() $\phi (\zeta )$
and
$\phi (\zeta )$
and
![]() $\phi (\eta )$
both scale each homogeneous term in a fixed way,
$\phi (\eta )$
both scale each homogeneous term in a fixed way,
![]() $\epsilon (\phi (\zeta )) = \phi (\eta )$
.
$\epsilon (\phi (\zeta )) = \phi (\eta )$
.
Lemma 2.22. When
![]() $\mathscr {A}$
is central, the map of complexes (2.14) with
$\mathscr {A}$
is central, the map of complexes (2.14) with
![]() $m = -\iota _{E}(\omega )$
, that is,
$m = -\iota _{E}(\omega )$
, that is,
induces surjections on the level of cohomology for all
![]() $0 \leq j \leq n$
:
$0 \leq j \leq n$
:
Proof. Consider
We apply
![]() $L_{\omega } = \nabla _{\omega }(\iota _{E}) + \iota _{E}(\nabla _{\omega })$
, the twisted Lie derivative, to
$L_{\omega } = \nabla _{\omega }(\iota _{E}) + \iota _{E}(\nabla _{\omega })$
, the twisted Lie derivative, to
![]() $[\bigoplus _{I} \eta _{I}] = [\bigoplus _{I} \sum _{p} \eta _{I,p}]$
. Since this is done by applying
$[\bigoplus _{I} \eta _{I}] = [\bigoplus _{I} \sum _{p} \eta _{I,p}]$
. Since this is done by applying
![]() $L_{\omega }$
to a representative and since we may do so term-by-term thanks to absolute convergence, we may use Lemma 2.13 to compute
$L_{\omega }$
to a representative and since we may do so term-by-term thanks to absolute convergence, we may use Lemma 2.13 to compute
That is,
![]() $\bigoplus _{I} \sum _{p \in \mathbb {Z}} (p + \iota _{E}(\omega ))\eta _{I,p} - \nabla _{\omega }(\bigoplus _{I} \iota _{E}(\eta _{I}))$
is a Čech t-boundary. By Proposition 2.21, if we apply
$\bigoplus _{I} \sum _{p \in \mathbb {Z}} (p + \iota _{E}(\omega ))\eta _{I,p} - \nabla _{\omega }(\bigoplus _{I} \iota _{E}(\eta _{I}))$
is a Čech t-boundary. By Proposition 2.21, if we apply
![]() $\phi $
to this Čech t-boundary we get another Čech t-boundary. Since
$\phi $
to this Čech t-boundary we get another Čech t-boundary. Since
![]() $\nabla _{\omega }$
preserves weights,
$\nabla _{\omega }$
preserves weights,
![]() $\phi $
and
$\phi $
and
![]() $\nabla _{\omega }$
commute. So applying
$\nabla _{\omega }$
commute. So applying
![]() $\phi $
to our Čech t-boundary gives the Čech t-boundary
$\phi $
to our Čech t-boundary gives the Čech t-boundary
With some mild rearranging, we have an equality of Čech cohomology classes
(Here, we use the fact that
![]() $\bigoplus _{I} \sum _{p \in \mathbb {Z}} \eta _{I,p}$
was assumed to be a Čech t-cycle, and so, because the Čech complex preserves weight, each of its homogeneous parts is also a Čech t-cycle.)
$\bigoplus _{I} \sum _{p \in \mathbb {Z}} \eta _{I,p}$
was assumed to be a Čech t-cycle, and so, because the Čech complex preserves weight, each of its homogeneous parts is also a Čech t-cycle.)
This means that we have the following equality of cohomology classes in
![]() $H^{j}(H_{\operatorname {\mathrm {\check {C}ech}}}^{t} (\Omega _{X}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
:
$H^{j}(H_{\operatorname {\mathrm {\check {C}ech}}}^{t} (\Omega _{X}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
:
Since the map (2.14) explicitly obeys
we have, thanks to Equation (2.16), the induced identification
 $$ \begin{align*} H^{j}(H_{\operatorname{\mathrm{\check{C}ech}}}^{t}(\Omega_{X}^{\bullet}(\log \mathscr{A})_{-\iota_{E}(\omega)}), \nabla_{\omega}) & \ni [[\bigoplus_{I} \eta_{I,-\iota_{E}(\omega)}]] \\ &\mapsto [[\bigoplus_{I} \eta_{I}]] \in H^{j}(H_{\operatorname{\mathrm{\check{C}ech}}}^{t}(\Omega_{X}^{\bullet}(\log \mathscr{A})), \nabla_{\omega}). \end{align*} $$
$$ \begin{align*} H^{j}(H_{\operatorname{\mathrm{\check{C}ech}}}^{t}(\Omega_{X}^{\bullet}(\log \mathscr{A})_{-\iota_{E}(\omega)}), \nabla_{\omega}) & \ni [[\bigoplus_{I} \eta_{I,-\iota_{E}(\omega)}]] \\ &\mapsto [[\bigoplus_{I} \eta_{I}]] \in H^{j}(H_{\operatorname{\mathrm{\check{C}ech}}}^{t}(\Omega_{X}^{\bullet}(\log \mathscr{A})), \nabla_{\omega}). \end{align*} $$
The proves the desired cohomological surjections.
As a final comment, we note that a similar strategy applies to the cohomology analytic twisted logarithmic de Rham complex directly. That is, the stalk at the origin of the twisted analytic logarithmic (resp. analytic) de Rham complex is quasi-isomorphic to a particular homogeneous subcomplex. Again, we mean homogeneous in the sense of the Laurent series expansion (at
![]() $0$
). As this does not involve Čech complexes, this is essentially the same procedure as [Reference Castro-Jiménez, Narváez-Macarro and Mond9].
$0$
). As this does not involve Čech complexes, this is essentially the same procedure as [Reference Castro-Jiménez, Narváez-Macarro and Mond9].
Lemma 2.23. When
![]() $\mathscr {A}$
is central, the following inclusions are quasi-isomorphisms:
$\mathscr {A}$
is central, the following inclusions are quasi-isomorphisms:

Proof. We just do part involving the twisted logarithmic de Rham complexes, as the meromorphic case is similar. Here, we consider
![]() $\phi $
as a map from
$\phi $
as a map from
![]() $\Omega _{X,0}^{j}(\log \mathscr {A}) \xrightarrow[]{} \Omega _{X,0}^{j}(\log \mathscr {A})$
with an entirely similar definition as before. Let
$\Omega _{X,0}^{j}(\log \mathscr {A}) \xrightarrow[]{} \Omega _{X,0}^{j}(\log \mathscr {A})$
with an entirely similar definition as before. Let
![]() $\eta $
be a logarithmic j-form that is a
$\eta $
be a logarithmic j-form that is a
![]() $\nabla _{\omega }$
-cycle. One one hand,
$\nabla _{\omega }$
-cycle. One one hand,
![]() $L_{\omega }(\eta ) = \nabla _{\omega }(\sum _{p} \eta _{p}) = \sum _{p} (p + \iota _{E}(\omega )) \eta _{p}$
; on the other hand,
$L_{\omega }(\eta ) = \nabla _{\omega }(\sum _{p} \eta _{p}) = \sum _{p} (p + \iota _{E}(\omega )) \eta _{p}$
; on the other hand,
![]() $L_{\omega }(\eta ) = \nabla _{\omega }(\iota _{E}(\eta ))$
. Then
$L_{\omega }(\eta ) = \nabla _{\omega }(\iota _{E}(\eta ))$
. Then
![]() $\nabla _{\omega }(\phi (\iota _{E}(\eta ))) = \eta - \eta _{-\iota _{E}(\omega )}$
. So the class
$\nabla _{\omega }(\phi (\iota _{E}(\eta ))) = \eta - \eta _{-\iota _{E}(\omega )}$
. So the class
![]() $[\eta ]$
equals the class
$[\eta ]$
equals the class
![]() $[\eta _{-\iota _{E}(\omega )}]$
.
$[\eta _{-\iota _{E}(\omega )}]$
.
2.4. Castelnuovo–Mumford regularity of logarithmic forms
We return to the algebraic setting. In light of Proposition 2.15, it is useful to understand which graded components of
![]() $H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
are zero and which are not. For, if particular graded components vanish, Proposition 2.15 lets us conclude the twisted de Rham complex on local cohomology modules is acyclic. Instead of trying to answer this question for each pair
$H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
are zero and which are not. For, if particular graded components vanish, Proposition 2.15 lets us conclude the twisted de Rham complex on local cohomology modules is acyclic. Instead of trying to answer this question for each pair
![]() $(t, j) \in [n]^{2}$
, it is much easier to fix j and let t vary. Even still, it is easier to package the data for
$(t, j) \in [n]^{2}$
, it is much easier to fix j and let t vary. Even still, it is easier to package the data for
![]() $\{(0,j), (1,j), \dots , (n, j)\}$
together as in the following classical definition:
$\{(0,j), (1,j), \dots , (n, j)\}$
together as in the following classical definition:
Definition 2.24. Let
![]() $R = \mathbb {C}[x_{1}, \dots , x_{n}]$
be graded canonically (so
$R = \mathbb {C}[x_{1}, \dots , x_{n}]$
be graded canonically (so
![]() $\deg (x_{i}) = 1)$
,
$\deg (x_{i}) = 1)$
,
![]() $\mathfrak {m}$
the irrelevant ideal, and M a graded module. We allow M to be
$\mathfrak {m}$
the irrelevant ideal, and M a graded module. We allow M to be
![]() $\mathbb {Z}$
-graded. The Castelnuovo–Mumford regularity
$\mathbb {Z}$
-graded. The Castelnuovo–Mumford regularity
![]() $\operatorname {\mathrm {reg}}(M)$
is
$\operatorname {\mathrm {reg}}(M)$
is
where
![]() $\max \deg H_{\mathfrak {m}}^{t}(M)$
is the largest
$\max \deg H_{\mathfrak {m}}^{t}(M)$
is the largest
![]() $u \in \mathbb {Z}$
such that
$u \in \mathbb {Z}$
such that
![]() $H_{\mathfrak {m}}^{t}(M)_{u} \neq 0$
, is
$H_{\mathfrak {m}}^{t}(M)_{u} \neq 0$
, is
![]() $\infty $
if no such maximum exists, and is
$\infty $
if no such maximum exists, and is
![]() $-\infty $
if
$-\infty $
if
![]() $H_{\mathfrak {m}}^{t}(M) = 0$
. In particular, the Castelnuovo–Mumford regularity of the zero module is
$H_{\mathfrak {m}}^{t}(M) = 0$
. In particular, the Castelnuovo–Mumford regularity of the zero module is
![]() $-\infty $
.
$-\infty $
.
The purpose of this subsection is to find a good upper bound on the Castelnuovo–Mumford regularity of
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
, with the eventual aim of showing
$\Omega _{R}^{j}(\log \mathscr {A})$
, with the eventual aim of showing
![]() $(H_{\mathfrak {m}}^{t}( \Omega _{R}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
(and later its analytic counterpart
$(H_{\mathfrak {m}}^{t}( \Omega _{R}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
(and later its analytic counterpart
![]() $(H_{\operatorname {\mathrm {\check {C}ech}}}^{t}(\Omega _{X}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
) is acyclic via Proposition 2.15 (subject to relatively benign conditions on
$(H_{\operatorname {\mathrm {\check {C}ech}}}^{t}(\Omega _{X}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
) is acyclic via Proposition 2.15 (subject to relatively benign conditions on
![]() $\omega $
).
$\omega $
).
Convention 2.25. We use the suffix
![]() $-(m)$
, with
$-(m)$
, with
![]() $m \in \mathbb {Z}$
, to denote a twist in the grading. Explicitly, the u-homogeneous part of
$m \in \mathbb {Z}$
, to denote a twist in the grading. Explicitly, the u-homogeneous part of
![]() $R(m)$
is:
$R(m)$
is:
![]() $R(m)_{u} = R_{u + m}$
. If an isomorphism is written as
$R(m)_{u} = R_{u + m}$
. If an isomorphism is written as
![]() $M \simeq R(m)$
, then the isomorphism honors the grading. Another convention: we use just
$M \simeq R(m)$
, then the isomorphism honors the grading. Another convention: we use just
![]() $\operatorname {\mathrm {reg}}(M)$
without specifying the ring in question, hoping context rectifies any confusion.
$\operatorname {\mathrm {reg}}(M)$
without specifying the ring in question, hoping context rectifies any confusion.
Remark 2.26.
-
(a) Since R is free,
 $H_{\mathfrak {m}}^{t}(R) = 0$
for all
$H_{\mathfrak {m}}^{t}(R) = 0$
for all
 $t \neq n$
. Using the Čech complex to compute local cohomology, and so
$t \neq n$
. Using the Čech complex to compute local cohomology, and so $$\begin{align*}H_{\mathfrak{m}}^{n}(R) \simeq \frac{R[x_{1}^{-1}, \dots, x_{n}^{-1}]}{\sum_{1 \leq i \leq n} R[x_{1}^{-1}, \dots, x_{i-1}^{-1}, x_{i+1}^{-1}, \dots, x_{n}^{-1}]} \end{align*}$$
$$\begin{align*}H_{\mathfrak{m}}^{n}(R) \simeq \frac{R[x_{1}^{-1}, \dots, x_{n}^{-1}]}{\sum_{1 \leq i \leq n} R[x_{1}^{-1}, \dots, x_{i-1}^{-1}, x_{i+1}^{-1}, \dots, x_{n}^{-1}]} \end{align*}$$
 $H_{\mathfrak {m}}^{n}(R)_{-n} = \mathbb {C} \cdot x_{1}^{-1} \cdots x_{n}^{-1}$
and higher homogeneous subspaces vanish. So
$H_{\mathfrak {m}}^{n}(R)_{-n} = \mathbb {C} \cdot x_{1}^{-1} \cdots x_{n}^{-1}$
and higher homogeneous subspaces vanish. So
 $\operatorname {\mathrm {reg}}(R) = 0$
.
$\operatorname {\mathrm {reg}}(R) = 0$
.
-
(b) If M and N are graded R-modules such that
 $M(\ell ) = N$
, then
$M(\ell ) = N$
, then
 $H_{\mathfrak {m}}^{t}(M)(\ell ) = H_{\mathfrak {m}}^{t}(N)$
and
$H_{\mathfrak {m}}^{t}(M)(\ell ) = H_{\mathfrak {m}}^{t}(N)$
and
 $\operatorname {\mathrm {reg}}(N) + \ell = \operatorname {\mathrm {reg}}(M).$
$\operatorname {\mathrm {reg}}(N) + \ell = \operatorname {\mathrm {reg}}(M).$
-
(c) Because the Čech complex definition of local cohomology implies direct sums commutes with local cohomology, we have:
 $$ \begin{align*} \operatorname{\mathrm{reg}}(M \oplus N) &= \max\limits_{t} \{ \max\{ \max \deg (H_{\mathfrak{m}}^{t}(M))), \max \deg (H_{\mathfrak{m}}^{t}(N))\}+ t \} \\ &= \max\{ \operatorname{\mathrm{reg}}(M), \operatorname{\mathrm{reg}}(N)\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{reg}}(M \oplus N) &= \max\limits_{t} \{ \max\{ \max \deg (H_{\mathfrak{m}}^{t}(M))), \max \deg (H_{\mathfrak{m}}^{t}(N))\}+ t \} \\ &= \max\{ \operatorname{\mathrm{reg}}(M), \operatorname{\mathrm{reg}}(N)\}. \end{align*} $$
-
(d) Suppose A and B are polynomial k-algebras that are
 $\mathbb {N}$
-graded. Let N (resp. M) be a graded A (resp. B) module. If
$\mathbb {N}$
-graded. Let N (resp. M) be a graded A (resp. B) module. If
 $A_{0}$
and
$A_{0}$
and
 $B_{0}$
are finitely generated over k and the irrelevant ideal of A (resp. B) is
$B_{0}$
are finitely generated over k and the irrelevant ideal of A (resp. B) is
 $A_{> 0}$
(resp.
$A_{> 0}$
(resp.
 $B_{>0}$
), one can define graded local cohomology and regularity similarly to Definition 2.24. Then the Kunneth formula for local cohomology modules leads to a Kunneth formula for regularity: where
$B_{>0}$
), one can define graded local cohomology and regularity similarly to Definition 2.24. Then the Kunneth formula for local cohomology modules leads to a Kunneth formula for regularity: where $$\begin{align*}\operatorname{\mathrm{reg}}(N \otimes_{k} M) = \operatorname{\mathrm{reg}}(N) + \operatorname{\mathrm{reg}}(M), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{reg}}(N \otimes_{k} M) = \operatorname{\mathrm{reg}}(N) + \operatorname{\mathrm{reg}}(M), \end{align*}$$
 $\operatorname {\mathrm {reg}}(N \otimes _{k} M)$
considers
$\operatorname {\mathrm {reg}}(N \otimes _{k} M)$
considers
 $N \otimes _{k} M$
as a
$N \otimes _{k} M$
as a
 $A \otimes _{k} B$
-module,
$A \otimes _{k} B$
-module,
 $\operatorname {\mathrm {reg}}(N)$
considers N as a A-module and
$\operatorname {\mathrm {reg}}(N)$
considers N as a A-module and
 $\operatorname {\mathrm {reg}}(M)$
considers M as a B-module. See Lemma 1.5(5) of [Reference Symonds32] for details; Proposition 2.4 of [Reference Benson3] for a different proof.
$\operatorname {\mathrm {reg}}(M)$
considers M as a B-module. See Lemma 1.5(5) of [Reference Symonds32] for details; Proposition 2.4 of [Reference Benson3] for a different proof.
In [Reference Derksen and Sidman14], Derksen and Sidman gave a method to approximate Castelnuovo–Mumford regularity which is particularly potent for objects attached to hyperplane arrangements thanks to their amenability to addition/subtraction techniques. It is:
Corollary 2.27 (Corollary 3.7 of [Reference Derksen and Sidman14]).
Let
![]() $F = \oplus R(0)$
be a finite, free R-module generated in degree zero. Suppose that
$F = \oplus R(0)$
be a finite, free R-module generated in degree zero. Suppose that
![]() $M \subseteq F$
is a graded R-module and that we have modules
$M \subseteq F$
is a graded R-module and that we have modules
![]() $M_{1}, \dots , M_{\ell } \subseteq F$
and ideals
$M_{1}, \dots , M_{\ell } \subseteq F$
and ideals
![]() $I_{1}, \dots , I_{\ell } \subseteq R$
such that
$I_{1}, \dots , I_{\ell } \subseteq R$
such that
If
![]() $I_{1} + \cdots + I_{\ell } = \mathfrak {m}$
and
$I_{1} + \cdots + I_{\ell } = \mathfrak {m}$
and
![]() $\operatorname {\mathrm {reg}}(M_{i}) \leq r - 1$
for some
$\operatorname {\mathrm {reg}}(M_{i}) \leq r - 1$
for some
![]() $r \geq 2$
and all i, then
$r \geq 2$
and all i, then
![]() $\operatorname {\mathrm {reg}}(M) \leq r$
.
$\operatorname {\mathrm {reg}}(M) \leq r$
.
We have emphasized F is generated in degree zero to be in the situation of loc. cit.
Derksen and Sidman use this result to get an upper bound on the regularity of
![]() $\operatorname {\mathrm {Der}}_{R}(-\log \mathscr {A})$
. In Proposition 1.3 of [Reference Saito30], M. Saito showed their argument essentially proved (i.e., with only a minor adjustment) a stronger bound: for a central, essential arrangement A,
$\operatorname {\mathrm {Der}}_{R}(-\log \mathscr {A})$
. In Proposition 1.3 of [Reference Saito30], M. Saito showed their argument essentially proved (i.e., with only a minor adjustment) a stronger bound: for a central, essential arrangement A,
(We use the convention
![]() $\deg (\partial _{i}) = -1$
.) Taking M. Saito’s improvement as a model, we estimate the regularity of the logarithmic j-forms
$\deg (\partial _{i}) = -1$
.) Taking M. Saito’s improvement as a model, we estimate the regularity of the logarithmic j-forms
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
along
$\Omega _{R}^{j}(\log \mathscr {A})$
along
![]() $\mathscr {A}$
. Our situation is more involved because: (1) One cannot apply Corollary 3.7 of [Reference Derksen and Sidman14] to
$\mathscr {A}$
. Our situation is more involved because: (1) One cannot apply Corollary 3.7 of [Reference Derksen and Sidman14] to
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
itself; (2) the inductive scheme mandates relating
$\Omega _{R}^{j}(\log \mathscr {A})$
itself; (2) the inductive scheme mandates relating
![]() $(j-1)$
-logarithmic forms to j-logarithmic forms; (3) the case of
$(j-1)$
-logarithmic forms to j-logarithmic forms; (3) the case of
![]() $\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A}) - 1}(\log \mathscr {A})$
is bespoke.
$\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A}) - 1}(\log \mathscr {A})$
is bespoke.
Example 2.28. Consider
![]() $\mathscr {A}$
cut out by
$\mathscr {A}$
cut out by
![]() $f = x_{1} \cdots x_{n} \in R$
, that is, a simple normal crossing divisor. It is easy to check that
$f = x_{1} \cdots x_{n} \in R$
, that is, a simple normal crossing divisor. It is easy to check that
![]() $\Omega _{R}^{0}(\log \mathscr {A}) = R$
and
$\Omega _{R}^{0}(\log \mathscr {A}) = R$
and
![]() $\Omega _{R}^{1}(\log \mathscr {A}) = R \cdot \frac {dx_{1}}{x_{1}} \oplus \cdots \oplus R \cdot \frac {dx_{n}}{x_{n}} \simeq R \oplus \cdots \oplus R$
(for example, use K. Saito’s freeness criterion for logarithmic
$\Omega _{R}^{1}(\log \mathscr {A}) = R \cdot \frac {dx_{1}}{x_{1}} \oplus \cdots \oplus R \cdot \frac {dx_{n}}{x_{n}} \simeq R \oplus \cdots \oplus R$
(for example, use K. Saito’s freeness criterion for logarithmic
![]() $1$
-forms), where the last isomorphism is graded. Since f is free,
$1$
-forms), where the last isomorphism is graded. Since f is free,
![]() $\Omega _{R}^{j}(\log \mathscr {A}) = \wedge ^{j} \Omega _{R}^{1}(\log \mathscr {A}) \simeq \oplus ^{\binom {n}{j}} R$
, with the last isomorphism graded. So for simple normal crossing divisors in
$\Omega _{R}^{j}(\log \mathscr {A}) = \wedge ^{j} \Omega _{R}^{1}(\log \mathscr {A}) \simeq \oplus ^{\binom {n}{j}} R$
, with the last isomorphism graded. So for simple normal crossing divisors in
![]() $\mathbb {C}[x_{1}, \dots , x_{n}]$
,
$\mathbb {C}[x_{1}, \dots , x_{n}]$
,
With this example in hand, here is our theorem bounding Castelnuovo–Mumford regularity of logarithmic j-forms:
Theorem 2.29. For
![]() $\mathscr {A}$
a central, essential, reduced hyperplane arrangement, the Castelnuovo–Mumford regularity of
$\mathscr {A}$
a central, essential, reduced hyperplane arrangement, the Castelnuovo–Mumford regularity of
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
is bounded by:
$\Omega _{R}^{j}(\log \mathscr {A})$
is bounded by:
When
![]() $j = 0$
or
$j = 0$
or
![]() $j=\operatorname {\mathrm {rank}}(\mathscr {A})$
, the module of logarithmic zero or
$j=\operatorname {\mathrm {rank}}(\mathscr {A})$
, the module of logarithmic zero or
![]() $\operatorname {\mathrm {rank}}(\mathscr {A})$
-forms are free R-modules and so only
$\operatorname {\mathrm {rank}}(\mathscr {A})$
-forms are free R-modules and so only
![]() $H_{\mathfrak {m}}^{\operatorname {\mathrm {rank}}{\mathscr {A}}}(-) \neq 0$
. In these cases,
$H_{\mathfrak {m}}^{\operatorname {\mathrm {rank}}{\mathscr {A}}}(-) \neq 0$
. In these cases,
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{0}(\log \mathscr {A})) = 0$
and
$\operatorname {\mathrm {reg}}(\Omega _{R}^{0}(\log \mathscr {A})) = 0$
and
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}(\log \mathscr {A})) = \operatorname {\mathrm {rank}}(\mathscr {A}) - \deg (\mathscr {A})$
.
$\operatorname {\mathrm {reg}}(\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}(\log \mathscr {A})) = \operatorname {\mathrm {rank}}(\mathscr {A}) - \deg (\mathscr {A})$
.
Proof. Throughout, let
![]() $f = f_{1} \cdots f_{d}$
be a defining equation for
$f = f_{1} \cdots f_{d}$
be a defining equation for
![]() $\mathscr {A}$
and, if not explicitly changed,
$\mathscr {A}$
and, if not explicitly changed,
![]() $n = \operatorname {\mathrm {rank}}(\mathscr {A})$
,
$n = \operatorname {\mathrm {rank}}(\mathscr {A})$
,
![]() $d = \deg (\mathscr {A})$
.
$d = \deg (\mathscr {A})$
.
Step 0: We handle the straightforward cases
![]() $j=0$
or
$j=0$
or
![]() $j=\operatorname {\mathrm {rank}}(\mathscr {A})$
. All we must show is freeness and then compute regularity. It is well known (and easy to verify using Equation (2.17) below) that
$j=\operatorname {\mathrm {rank}}(\mathscr {A})$
. All we must show is freeness and then compute regularity. It is well known (and easy to verify using Equation (2.17) below) that
![]() $\Omega _{R}^{0}(\log \mathscr {A}) = R$
. Consequently,
$\Omega _{R}^{0}(\log \mathscr {A}) = R$
. Consequently,
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{0}(\log \mathscr {A})) = 0.$
Now, consider
$\operatorname {\mathrm {reg}}(\Omega _{R}^{0}(\log \mathscr {A})) = 0.$
Now, consider
![]() $j=\operatorname {\mathrm {rank}}(\mathscr {A})$
. If
$j=\operatorname {\mathrm {rank}}(\mathscr {A})$
. If
![]() $\eta \in \frac {1}{f} \Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}$
, then
$\eta \in \frac {1}{f} \Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}$
, then
![]() $d(\eta ) = 0 \in \frac {1}{f}\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})+1} = 0$
. So
$d(\eta ) = 0 \in \frac {1}{f}\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})+1} = 0$
. So
![]() $\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}(\log \mathscr {A}) = \frac {1}{f} \Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})} = R(\deg (\mathscr {A}) - \operatorname {\mathrm {rank}}(\mathscr {A}))$
;
$\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}(\log \mathscr {A}) = \frac {1}{f} \Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})} = R(\deg (\mathscr {A}) - \operatorname {\mathrm {rank}}(\mathscr {A}))$
;
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}(\log \mathscr {A})) = \operatorname {\mathrm {rank}}(\mathscr {A}) - \deg (\mathscr {A})$
.
$\operatorname {\mathrm {reg}}(\Omega _{R}^{\operatorname {\mathrm {rank}}(\mathscr {A})}(\log \mathscr {A})) = \operatorname {\mathrm {rank}}(\mathscr {A}) - \deg (\mathscr {A})$
.
Step 1: To deal with
![]() $1 \leq j \leq \operatorname {\mathrm {rank}}(\mathscr {A}) - 1$
, we change our target in order to apply Corollary 3.7 of [Reference Derksen and Sidman14] (transcribed as Corollary 2.27). Observe: The logarithmic j-forms can be characterized by
$1 \leq j \leq \operatorname {\mathrm {rank}}(\mathscr {A}) - 1$
, we change our target in order to apply Corollary 3.7 of [Reference Derksen and Sidman14] (transcribed as Corollary 2.27). Observe: The logarithmic j-forms can be characterized by
![]() $\sum _{\mid I \mid = j} \frac {a_{I}}{f} dx_{I} \in \Omega _{R}^{j}(\log \mathscr {A})$
if and only if
$\sum _{\mid I \mid = j} \frac {a_{I}}{f} dx_{I} \in \Omega _{R}^{j}(\log \mathscr {A})$
if and only if
![]() $d(\sum _{\mid I \mid = j} \frac {a_{I}}{f} dx_{I}) \in \frac {1}{f} \Omega _{R}^{j+1}$
if and only if
$d(\sum _{\mid I \mid = j} \frac {a_{I}}{f} dx_{I}) \in \frac {1}{f} \Omega _{R}^{j+1}$
if and only if
![]() $\sum _{\mid I \mid = j} \frac {a_{I}}{f^{2}} d(f) \wedge dx_{I} \in \frac {1}{f} \cdot \Omega _{R}^{j+1}$
if and only if
$\sum _{\mid I \mid = j} \frac {a_{I}}{f^{2}} d(f) \wedge dx_{I} \in \frac {1}{f} \cdot \Omega _{R}^{j+1}$
if and only if
![]() $\sum _{\mid I \mid = j} \frac {a_{I}}{f} d(f) \wedge dx_{I} \in \Omega _{R}^{j+1}$
if and only if
$\sum _{\mid I \mid = j} \frac {a_{I}}{f} d(f) \wedge dx_{I} \in \Omega _{R}^{j+1}$
if and only if
![]() $\sum _{\mid I \mid = j} a_{I} d(f) \wedge dx_{I} \in f \cdot \Omega _{R}^{j+1}$
. Since R is a UFD and
$\sum _{\mid I \mid = j} a_{I} d(f) \wedge dx_{I} \in f \cdot \Omega _{R}^{j+1}$
. Since R is a UFD and
![]() $f = f_{1} \cdots f_{d}$
is a factorization into irreducibles, we conclude:
$f = f_{1} \cdots f_{d}$
is a factorization into irreducibles, we conclude:
 $$ \begin{align} \sum_{\mid I \mid = j} \frac{a_{I}}{f} dx_{I} \in \Omega_{R}^{j}(\log \mathscr{A}) \iff \sum_{\mid I \mid = j} a_{I} d(f_{k}) \wedge dx_{I} \in f_{k} \cdot \Omega_{R}^{j+1} \text{ for all } f_{k}. \end{align} $$
$$ \begin{align} \sum_{\mid I \mid = j} \frac{a_{I}}{f} dx_{I} \in \Omega_{R}^{j}(\log \mathscr{A}) \iff \sum_{\mid I \mid = j} a_{I} d(f_{k}) \wedge dx_{I} \in f_{k} \cdot \Omega_{R}^{j+1} \text{ for all } f_{k}. \end{align} $$
Define
and note that
The equivalence (2.17) tells us the map
![]() $\sum _{\mid I \mid = j} \frac {a_{I}}{f} dx_{I} \mapsto \sum _{\mid I \mid = j} a_{I} dx_{I}$
gives an isomorphism
$\sum _{\mid I \mid = j} \frac {a_{I}}{f} dx_{I} \mapsto \sum _{\mid I \mid = j} a_{I} dx_{I}$
gives an isomorphism
![]() $\Omega _{R}^{j}(\log \mathscr {A}) \xrightarrow[]{\simeq } L^{j}(\mathscr {A})$
that sends homogeneous elements of degree u to homogeneous elements of degree
$\Omega _{R}^{j}(\log \mathscr {A}) \xrightarrow[]{\simeq } L^{j}(\mathscr {A})$
that sends homogeneous elements of degree u to homogeneous elements of degree
![]() $u + \deg (\mathscr {A})$
. Therefore,
$u + \deg (\mathscr {A})$
. Therefore,
Consequently,
![]() $H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))(-\deg (\mathscr {A})) \simeq H_{\mathfrak {m}}^{t}(L^{j}(\mathscr {A}))$
and
$H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))(-\deg (\mathscr {A})) \simeq H_{\mathfrak {m}}^{t}(L^{j}(\mathscr {A}))$
and
Therefore, our theorem is equivalent to
![]() $\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A})) \leq \deg (\mathscr {A})$
, making the following our new objective:
$\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A})) \leq \deg (\mathscr {A})$
, making the following our new objective:
Step 2: We first prove The Claim for
![]() $L^{1}(\mathscr {A})$
by induction on the rank and the degree of our arrangement. If
$L^{1}(\mathscr {A})$
by induction on the rank and the degree of our arrangement. If
![]() $\operatorname {\mathrm {rank}}(\mathscr {A}) = 2$
with
$\operatorname {\mathrm {rank}}(\mathscr {A}) = 2$
with
![]() $d = \deg (\mathscr {A})$
, then the arrangement is automatically free and by standard considerations,
$d = \deg (\mathscr {A})$
, then the arrangement is automatically free and by standard considerations,
![]() $\Omega _{R}^{1}(\log \mathscr {A}) \simeq R \delta _{1} \oplus R \delta _{2}$
, where
$\Omega _{R}^{1}(\log \mathscr {A}) \simeq R \delta _{1} \oplus R \delta _{2}$
, where
![]() $\delta _{1}$
has degree
$\delta _{1}$
has degree
![]() $2-d$
and
$2-d$
and
![]() $\delta _{2}$
has degree
$\delta _{2}$
has degree
![]() $0$
. (Note that the determinant of the Saito matrix corresponding to
$0$
. (Note that the determinant of the Saito matrix corresponding to
![]() $\delta _{1}, \delta _{2}$
equals, up to unit,
$\delta _{1}, \delta _{2}$
equals, up to unit,
![]() $\frac {1}{f}dx_{1}dx_{2}$
, and one logarithmic form,
$\frac {1}{f}dx_{1}dx_{2}$
, and one logarithmic form,
![]() $\delta _{1}$
, corresponds to the Euler operator, whereas the other,
$\delta _{1}$
, corresponds to the Euler operator, whereas the other,
![]() $\delta _{2}$
, corresponds to
$\delta _{2}$
, corresponds to
![]() $(\partial _{1} \bullet f)\partial _{2} - (\partial _{2} \bullet f)\partial _{1}$
.) So
$(\partial _{1} \bullet f)\partial _{2} - (\partial _{2} \bullet f)\partial _{1}$
.) So
![]() $\Omega _{R}^{1}(\log \mathscr {A}) \simeq R(d-2) \oplus R$
and
$\Omega _{R}^{1}(\log \mathscr {A}) \simeq R(d-2) \oplus R$
and
![]() $\operatorname {\mathrm {reg}}( \Omega _{R}^{1}(\log \mathscr {A})) = \max \{ 2-d, 0 \} = 0$
since, by essentiality,
$\operatorname {\mathrm {reg}}( \Omega _{R}^{1}(\log \mathscr {A})) = \max \{ 2-d, 0 \} = 0$
since, by essentiality,
![]() $d \geq 2$
. So
$d \geq 2$
. So
![]() $\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A})) = d$
.
$\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A})) = d$
.
Assume the rank of
![]() $\mathscr {A}$
is at least
$\mathscr {A}$
is at least
![]() $3$
, the degree of
$3$
, the degree of
![]() $\mathscr {A}$
is
$\mathscr {A}$
is
![]() $d+1$
and the claim holds for all essential, central arrangements of smaller degree or rank. (The base case of a simple normal crossing divisor with rank(
$d+1$
and the claim holds for all essential, central arrangements of smaller degree or rank. (The base case of a simple normal crossing divisor with rank(
![]() $\mathscr {A}$
) hyperplanes is handled in Example 2.28.) By essentiality, we may find n hyperplanes from
$\mathscr {A}$
) hyperplanes is handled in Example 2.28.) By essentiality, we may find n hyperplanes from
![]() $\mathscr {A}$
cutting out the origin.
$\mathscr {A}$
cutting out the origin.
Case 2.1: There exists n hyperplanes
![]() $f_{1}, \dots , f_{n}$
(relabelling as necessary) from
$f_{1}, \dots , f_{n}$
(relabelling as necessary) from
![]() $\mathscr {A}$
such that: (1)
$\mathscr {A}$
such that: (1)
![]() $\mathfrak {m} = (f_{1}, \dots , f_{n})$
; (2) deleting any
$\mathfrak {m} = (f_{1}, \dots , f_{n})$
; (2) deleting any
![]() $\operatorname {\mathrm {V}}(f_{i})$
from
$\operatorname {\mathrm {V}}(f_{i})$
from
![]() $\mathscr {A}$
produces an essential arrangement. Let
$\mathscr {A}$
produces an essential arrangement. Let
![]() $\mathscr {A}_{i} = \mathscr {A} \setminus \operatorname {\mathrm {V}}(f_{i})$
be the result post deletion. By Equation (2.18),
$\mathscr {A}_{i} = \mathscr {A} \setminus \operatorname {\mathrm {V}}(f_{i})$
be the result post deletion. By Equation (2.18),
![]() $L^{1}(\mathscr {A}) \subseteq L^{1}(\mathscr {A}_{i}).$
And using Equations (2.17) and (2.18), we confirm that
$L^{1}(\mathscr {A}) \subseteq L^{1}(\mathscr {A}_{i}).$
And using Equations (2.17) and (2.18), we confirm that
![]() $f_{i} \cdot L^{1}(\mathscr {A}_{i}) \subseteq L^{1}(\mathscr {A})$
. So we use the inductive hypothesis to get
$f_{i} \cdot L^{1}(\mathscr {A}_{i}) \subseteq L^{1}(\mathscr {A})$
. So we use the inductive hypothesis to get
![]() $\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A}_{i})) \leq d$
and
$\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A}_{i})) \leq d$
and
![]() $\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A}_{i})(1)) \leq d -1.$
As
$\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A}_{i})(1)) \leq d -1.$
As
![]() $L^{1}(\mathscr {A}) \subseteq R dx_{1} \oplus \cdots \oplus R dx_{n} = R(-1) \oplus \cdots \oplus R(-1)$
, if we shift degrees and consider
$L^{1}(\mathscr {A}) \subseteq R dx_{1} \oplus \cdots \oplus R dx_{n} = R(-1) \oplus \cdots \oplus R(-1)$
, if we shift degrees and consider
![]() $L^{1}(\mathscr {A})(1)$
,
$L^{1}(\mathscr {A})(1)$
,
![]() $L^{1}(\mathscr {A}_{i})(1) \subseteq R(0) \oplus \cdots \oplus R(0)$
we may invoke Corollary 3.7 of [Reference Derksen and Sidman14] (see Corollary 2.27) to get
$L^{1}(\mathscr {A}_{i})(1) \subseteq R(0) \oplus \cdots \oplus R(0)$
we may invoke Corollary 3.7 of [Reference Derksen and Sidman14] (see Corollary 2.27) to get
![]() $\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A})(1)) \leq d$
or equivalently
$\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A})(1)) \leq d$
or equivalently
![]() $\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A})) \leq d + 1$
, finishing the case.
$\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A})) \leq d + 1$
, finishing the case.
Case 2.2: There exists a hyperplane
![]() $f_{i}$
such that the deleted arrangement
$f_{i}$
such that the deleted arrangement
![]() $\mathscr {A} \setminus \operatorname {\mathrm {V}}(f_{i})$
is nonessential. Then, after possibly changing coordinates,
$\mathscr {A} \setminus \operatorname {\mathrm {V}}(f_{i})$
is nonessential. Then, after possibly changing coordinates,
![]() $\mathscr {A}$
has a defining equation
$\mathscr {A}$
has a defining equation
![]() $x_{n} g$
, where
$x_{n} g$
, where
![]() $\operatorname {\mathrm {V}}(g) = \mathscr {A}_{i}$
,
$\operatorname {\mathrm {V}}(g) = \mathscr {A}_{i}$
,
![]() $g \in S = \mathbb {C}[x_{1}, \dots , x_{n-1}]$
and
$g \in S = \mathbb {C}[x_{1}, \dots , x_{n-1}]$
and
![]() $x_{n}$
corresponds to the deleted hyperplane
$x_{n}$
corresponds to the deleted hyperplane
![]() $f_{i}$
. By the Kunneth formula for products, see Remark 2.2,
$f_{i}$
. By the Kunneth formula for products, see Remark 2.2,
and by the Kunneth formula for local cohomology and regularity; see Remark 2.26,
Because
![]() $\Omega _{\mathbb {C}[x_{n}]}^{1}(\operatorname {\mathrm {V}}(x_{n})) = \mathbb {C}[x_{n}]\frac {dx_{n}}{x_{n}} \simeq \mathbb {C}[x_{n}]$
(a graded isomorphism), the only regularity term of the four summands that is potentially nonzero is
$\Omega _{\mathbb {C}[x_{n}]}^{1}(\operatorname {\mathrm {V}}(x_{n})) = \mathbb {C}[x_{n}]\frac {dx_{n}}{x_{n}} \simeq \mathbb {C}[x_{n}]$
(a graded isomorphism), the only regularity term of the four summands that is potentially nonzero is
![]() $\operatorname {\mathrm {reg}}(\Omega _{S}^{1}(\operatorname {\mathrm {V}}(g)))$
. So
$\operatorname {\mathrm {reg}}(\Omega _{S}^{1}(\operatorname {\mathrm {V}}(g)))$
. So
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{1}(\log \mathscr {A})) \leq \max \{\operatorname {\mathrm {reg}}(\Omega _{S}^{1}(\operatorname {\mathrm {V}}(g))), 0\}$
. Since
$\operatorname {\mathrm {reg}}(\Omega _{R}^{1}(\log \mathscr {A})) \leq \max \{\operatorname {\mathrm {reg}}(\Omega _{S}^{1}(\operatorname {\mathrm {V}}(g))), 0\}$
. Since
![]() $\mathscr {A}$
is essential of rank at least three,
$\mathscr {A}$
is essential of rank at least three,
![]() $\operatorname {\mathrm {V}}(g)$
must be essential of rank at least two (and of one less degree), and so we can use the induction hypothesis:
$\operatorname {\mathrm {V}}(g)$
must be essential of rank at least two (and of one less degree), and so we can use the induction hypothesis:
![]() $\operatorname {\mathrm {reg}}(L^{1}(\operatorname {\mathrm {V}}(g)) \leq d$
and, by Equation (2.19),
$\operatorname {\mathrm {reg}}(L^{1}(\operatorname {\mathrm {V}}(g)) \leq d$
and, by Equation (2.19),
![]() $\operatorname {\mathrm {reg}}(\Omega _{S}^{1}(\operatorname {\mathrm {V}}(g))) \leq 0$
. Thus,
$\operatorname {\mathrm {reg}}(\Omega _{S}^{1}(\operatorname {\mathrm {V}}(g))) \leq 0$
. Thus,
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{1}(\operatorname {\mathrm {V}}(f)) \leq 0$
and
$\operatorname {\mathrm {reg}}(\Omega _{R}^{1}(\operatorname {\mathrm {V}}(f)) \leq 0$
and
![]() $\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A})) = d+1$
, completing this case and terminating the inductive step.
$\operatorname {\mathrm {reg}}(L^{1}(\mathscr {A})) = d+1$
, completing this case and terminating the inductive step.
Step 3: Now, we prove The Claim holds for
![]() $L^{j}(\mathscr {A})$
, for any
$L^{j}(\mathscr {A})$
, for any
![]() $1 \leq j \leq \operatorname {\mathrm {rank}}(\mathscr {A}) - 1$
, by induction on
$1 \leq j \leq \operatorname {\mathrm {rank}}(\mathscr {A}) - 1$
, by induction on
![]() $\deg (\mathscr {A})$
and
$\deg (\mathscr {A})$
and
![]() $\operatorname {\mathrm {rank}}(\mathscr {A})$
, utilizing Step 2. In particular, we may assume
$\operatorname {\mathrm {rank}}(\mathscr {A})$
, utilizing Step 2. In particular, we may assume
![]() $\operatorname {\mathrm {rank}} (\mathscr {A}) \geq 3$
and
$\operatorname {\mathrm {rank}} (\mathscr {A}) \geq 3$
and
![]() $j \geq 2$
. The minimal value
$j \geq 2$
. The minimal value
![]() $\deg \mathscr {A}$
can obtain while remaining essential is
$\deg \mathscr {A}$
can obtain while remaining essential is
![]() $\operatorname {\mathrm {rank}}(\mathscr {A})$
in which case Example 2.28 applies. So assume that the claim holds for any central, essential
$\operatorname {\mathrm {rank}}(\mathscr {A})$
in which case Example 2.28 applies. So assume that the claim holds for any central, essential
![]() $\mathscr {B}$
whose degree is less than
$\mathscr {B}$
whose degree is less than
![]() $\deg (\mathscr {A})$
or whose rank is smaller than
$\deg (\mathscr {A})$
or whose rank is smaller than
![]() $\operatorname {\mathrm {rank}}(\mathscr {A})$
. Now, we do three cases, the first two similar to those from Step 2.
$\operatorname {\mathrm {rank}}(\mathscr {A})$
. Now, we do three cases, the first two similar to those from Step 2.
Case 3.1: There exist n hyperplanes
![]() $f_{1}, \dots , f_{n}$
(relabelling as necessary) from
$f_{1}, \dots , f_{n}$
(relabelling as necessary) from
![]() $\mathscr {A}$
such that: (1) these n hyperplanes generate
$\mathscr {A}$
such that: (1) these n hyperplanes generate
![]() $\mathfrak {m}$
; (2) the arrangement
$\mathfrak {m}$
; (2) the arrangement
![]() $\mathscr {A}_{i} = \mathscr {A} \setminus \operatorname {\mathrm {V}}(f_{i})$
is essential. Since each
$\mathscr {A}_{i} = \mathscr {A} \setminus \operatorname {\mathrm {V}}(f_{i})$
is essential. Since each
![]() $\mathscr {A}_{i}$
is promised to be essential,
$\mathscr {A}_{i}$
is promised to be essential,
![]() $\operatorname {\mathrm {rank}}(\mathscr {A}_{i}) = \operatorname {\mathrm {rank}}(\mathscr {A})$
and so the
$\operatorname {\mathrm {rank}}(\mathscr {A}_{i}) = \operatorname {\mathrm {rank}}(\mathscr {A})$
and so the
![]() $\mathscr {A}_{i}$
fall into our inductive scheme:
$\mathscr {A}_{i}$
fall into our inductive scheme:
![]() $\deg (\mathscr {A}_{i}) = \deg (\mathscr {A}) - 1$
and
$\deg (\mathscr {A}_{i}) = \deg (\mathscr {A}) - 1$
and
![]() $j \leq \operatorname {\mathrm {rank}}(\mathscr {A}) - 1 = \operatorname {\mathrm {rank}}(\mathscr {A}_{i}) - 1$
. So we know that
$j \leq \operatorname {\mathrm {rank}}(\mathscr {A}) - 1 = \operatorname {\mathrm {rank}}(\mathscr {A}_{i}) - 1$
. So we know that
![]() $\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A}_{i})) \leq \deg (\mathscr {A}_{i}) = \deg (\mathscr {A}) - 1$
. Or, as we will prefer,
$\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A}_{i})) \leq \deg (\mathscr {A}_{i}) = \deg (\mathscr {A}) - 1$
. Or, as we will prefer,
![]() $\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A}_{i})(j)) \leq \deg (\mathscr {A}) - 1 - j.$
Using Equations (2.17) and (2.18), we again have
$\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A}_{i})(j)) \leq \deg (\mathscr {A}) - 1 - j.$
Using Equations (2.17) and (2.18), we again have
Now,
![]() $L^{j}(\mathscr {A}) \subseteq \oplus _{\mid I \mid = j} R dx_{I} = \oplus _{\mid I \mid = j} R(-j).$
Shift degrees as in Case 2.1 so that
$L^{j}(\mathscr {A}) \subseteq \oplus _{\mid I \mid = j} R dx_{I} = \oplus _{\mid I \mid = j} R(-j).$
Shift degrees as in Case 2.1 so that
![]() $L^{j}(\mathscr {A})(j)$
,
$L^{j}(\mathscr {A})(j)$
,
![]() $L^{j}(\mathscr {A}_{i})(j) \subseteq \oplus _{\mid I \mid = j} R$
. Now, we can appeal to Corollary 3.7 of [Reference Derksen and Sidman14] (see Corollary 2.27) to find that
$L^{j}(\mathscr {A}_{i})(j) \subseteq \oplus _{\mid I \mid = j} R$
. Now, we can appeal to Corollary 3.7 of [Reference Derksen and Sidman14] (see Corollary 2.27) to find that
![]() $\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A})(j)) \leq \deg (\mathscr {A}) - j$
, that is
$\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A})(j)) \leq \deg (\mathscr {A}) - j$
, that is
![]() $\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A})) \leq \deg (\mathscr {A})$
, as required.
$\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A})) \leq \deg (\mathscr {A})$
, as required.
Case 3.2: Both: (1) there is a hyperplane
![]() $f_{i}$
, where
$f_{i}$
, where
![]() $\operatorname {\mathrm {rank}}(\mathscr {A} \setminus \operatorname {\mathrm {V}}(f_{i})) < \operatorname {\mathrm {rank}}(\mathscr {A})$
; (2)
$\operatorname {\mathrm {rank}}(\mathscr {A} \setminus \operatorname {\mathrm {V}}(f_{i})) < \operatorname {\mathrm {rank}}(\mathscr {A})$
; (2)
![]() $j < \operatorname {\mathrm {rank}}(\mathscr {A}) - 1 = n-1$
. Here, we may, changing coordinates as needed, assume
$j < \operatorname {\mathrm {rank}}(\mathscr {A}) - 1 = n-1$
. Here, we may, changing coordinates as needed, assume
![]() $f = x_{n}g$
where
$f = x_{n}g$
where
![]() $g \in S = \mathbb {C}[x_{1}, \dots , x_{n-1}]$
. Since
$g \in S = \mathbb {C}[x_{1}, \dots , x_{n-1}]$
. Since
![]() $\mathscr {A}$
is essential,
$\mathscr {A}$
is essential,
![]() $\operatorname {\mathrm {V}}(g)$
is itself an essential arrangement whose rank is
$\operatorname {\mathrm {V}}(g)$
is itself an essential arrangement whose rank is
![]() $\operatorname {\mathrm {rank}}(\mathscr {A}) - 1$
. And
$\operatorname {\mathrm {rank}}(\mathscr {A}) - 1$
. And
![]() $2 \leq j \leq \operatorname {\mathrm {rank}}(\mathscr {A}) - 2 = \operatorname {\mathrm {rank}}(\operatorname {\mathrm {V}}(g)) - 1$
. So
$2 \leq j \leq \operatorname {\mathrm {rank}}(\mathscr {A}) - 2 = \operatorname {\mathrm {rank}}(\operatorname {\mathrm {V}}(g)) - 1$
. So
![]() $\operatorname {\mathrm {V}}(g)$
falls into the inductive setup and
$\operatorname {\mathrm {V}}(g)$
falls into the inductive setup and
![]() $\operatorname {\mathrm {reg}}(L^{q}(\operatorname {\mathrm {V}}(g))) \leq \deg (\operatorname {\mathrm {V}}(g)) = \deg (\mathscr {A}) - 1$
for all
$\operatorname {\mathrm {reg}}(L^{q}(\operatorname {\mathrm {V}}(g))) \leq \deg (\operatorname {\mathrm {V}}(g)) = \deg (\mathscr {A}) - 1$
for all
![]() $1 \leq q \leq j$
. We may use the Kunneth formula for products (Remark 2.2) to find
$1 \leq q \leq j$
. We may use the Kunneth formula for products (Remark 2.2) to find
and, using the fact
![]() $\Omega _{\mathbb {C}[x_{n}]}^{1}(\operatorname {\mathrm {V}}(x_{n})) \simeq \mathbb {C}[x_{n}]$
(graded), the induced Kunneth formula on regularity (Remark 2.26) gives
$\Omega _{\mathbb {C}[x_{n}]}^{1}(\operatorname {\mathrm {V}}(x_{n})) \simeq \mathbb {C}[x_{n}]$
(graded), the induced Kunneth formula on regularity (Remark 2.26) gives
By the inductive setup,
![]() $\operatorname {\mathrm {reg}}(\Omega _{S}^{j}(\operatorname {\mathrm {V}}(g))) \leq 0$
and
$\operatorname {\mathrm {reg}}(\Omega _{S}^{j}(\operatorname {\mathrm {V}}(g))) \leq 0$
and
![]() $\operatorname {\mathrm {reg}}(\Omega _{S}^{j-1}(\operatorname {\mathrm {V}}(g))) \leq 0$
. So
$\operatorname {\mathrm {reg}}(\Omega _{S}^{j-1}(\operatorname {\mathrm {V}}(g))) \leq 0$
. So
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{j}(\log \mathscr {A})) \leq 0$
and
$\operatorname {\mathrm {reg}}(\Omega _{R}^{j}(\log \mathscr {A})) \leq 0$
and
![]() $\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A})) \leq \deg (\mathscr {A})$
.
$\operatorname {\mathrm {reg}}(L^{j}(\mathscr {A})) \leq \deg (\mathscr {A})$
.
Case 3.3: j =
![]() $\operatorname {\mathrm {rank}}(\mathscr {A}) -1 = n-1.$
Write
$\operatorname {\mathrm {rank}}(\mathscr {A}) -1 = n-1.$
Write
![]() $d = \deg (\mathscr {A})$
. Here, with
$d = \deg (\mathscr {A})$
. Here, with
![]() $\widehat {dx_{i}} = dx_{1} \wedge \cdots \wedge dx_{i-1} \wedge dx_{i+1} \wedge dx_{n}$
and
$\widehat {dx_{i}} = dx_{1} \wedge \cdots \wedge dx_{i-1} \wedge dx_{i+1} \wedge dx_{n}$
and
![]() $dx = dx_{1} \wedge \cdots \wedge dx_{n}$
, the equivalence (2.17) is enriched:
$dx = dx_{1} \wedge \cdots \wedge dx_{n}$
, the equivalence (2.17) is enriched:
 $$ \begin{align*} \sum_{i} \frac{a_{i}}{f} \widehat{dx_{i}} \in \Omega_{R}^{n-1}(\log \mathscr{A}) &\iff \sum_{i} a_{i} d(f) \widehat{dx_{i}} = (\sum_{i} (-1)^{i-1} a_{i} \partial_{i} \bullet f)) dx \in R \cdot f dx \\ & \iff (\sum_{i} (-1)^{i-1} a_{i} \partial_{i}) \bullet f \in R \cdot f \\ & \iff (\sum_{i} (-1)^{i-1} a_{i} \partial_{i}) \in \operatorname{\mathrm{Der}}_{R}(-\log \mathscr{A}). \end{align*} $$
$$ \begin{align*} \sum_{i} \frac{a_{i}}{f} \widehat{dx_{i}} \in \Omega_{R}^{n-1}(\log \mathscr{A}) &\iff \sum_{i} a_{i} d(f) \widehat{dx_{i}} = (\sum_{i} (-1)^{i-1} a_{i} \partial_{i} \bullet f)) dx \in R \cdot f dx \\ & \iff (\sum_{i} (-1)^{i-1} a_{i} \partial_{i}) \bullet f \in R \cdot f \\ & \iff (\sum_{i} (-1)^{i-1} a_{i} \partial_{i}) \in \operatorname{\mathrm{Der}}_{R}(-\log \mathscr{A}). \end{align*} $$
In other words,
![]() $\Omega _{R}^{n-1}(\log \mathscr {A}) \ni \sum _{i} a_{i} \widehat {dx_{i}} \mapsto (\sum _{i} (-1)^{i-1} a_{i} \partial _{i}) \in \operatorname {\mathrm {Der}}_{R}(-\log \mathscr {A})$
is an isomorphism sending homogeneous elements of degree u to homogeneous elements of degree
$\Omega _{R}^{n-1}(\log \mathscr {A}) \ni \sum _{i} a_{i} \widehat {dx_{i}} \mapsto (\sum _{i} (-1)^{i-1} a_{i} \partial _{i}) \in \operatorname {\mathrm {Der}}_{R}(-\log \mathscr {A})$
is an isomorphism sending homogeneous elements of degree u to homogeneous elements of degree
![]() $u + d - n$
. (We use the convention that
$u + d - n$
. (We use the convention that
![]() $\partial _{i}$
has degree
$\partial _{i}$
has degree
![]() $-1$
as in [Reference Saito30].) Therefore,
$-1$
as in [Reference Saito30].) Therefore,
and
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{n-1}(\log \mathscr {A})) = \operatorname {\mathrm {reg}}(\operatorname {\mathrm {Der}}_{R}(\log \mathscr {A})) + n - d$
. By Proposition 1.3 of [Reference Saito30],
$\operatorname {\mathrm {reg}}(\Omega _{R}^{n-1}(\log \mathscr {A})) = \operatorname {\mathrm {reg}}(\operatorname {\mathrm {Der}}_{R}(\log \mathscr {A})) + n - d$
. By Proposition 1.3 of [Reference Saito30],
![]() $\operatorname {\mathrm {reg}}(\operatorname {\mathrm {Der}}_{R}(\log \mathscr {A})) \leq d - n$
and so
$\operatorname {\mathrm {reg}}(\operatorname {\mathrm {Der}}_{R}(\log \mathscr {A})) \leq d - n$
and so
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{n-1}(\log \mathscr {A})) \leq 0$
. Therefore,
$\operatorname {\mathrm {reg}}(\Omega _{R}^{n-1}(\log \mathscr {A})) \leq 0$
. Therefore,
![]() $\operatorname {\mathrm {reg}}(L^{n-1}(\mathscr {A})) \leq \deg (\mathscr {A})$
completing this case, the induction and the proof.
$\operatorname {\mathrm {reg}}(L^{n-1}(\mathscr {A})) \leq \deg (\mathscr {A})$
completing this case, the induction and the proof.
2.5. Acyclic complexes of local cohomology modules
We are now in position to utilize our work on Castelnuovo–Mumford regularity and prove that, when
![]() $\omega = \sum \lambda _{k} df_{k} / f_{k}$
and
$\omega = \sum \lambda _{k} df_{k} / f_{k}$
and
![]() $\{\lambda _{k}\}$
satisfy some combinatorial numerical restrictions, the complexes of local cohomology modules of logarithmic de Rham modules, with differential induced by
$\{\lambda _{k}\}$
satisfy some combinatorial numerical restrictions, the complexes of local cohomology modules of logarithmic de Rham modules, with differential induced by
![]() $\nabla _{\omega }$
, is acyclic.
$\nabla _{\omega }$
, is acyclic.
Corollary 2.30. Let
![]() $f = f_{1} \cdots f_{d} \in R = \mathbb {C}[x_{1}, \dots , x_{n}]$
be a central, essential and reduced hyperplane arrangement,
$f = f_{1} \cdots f_{d} \in R = \mathbb {C}[x_{1}, \dots , x_{n}]$
be a central, essential and reduced hyperplane arrangement,
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
weights and
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
weights and
![]() $\omega = \sum \lambda _{k} df_{k}/f_{k} = \sum \lambda _{k} d \log f_{k}$
the associated logarithmic one form. If
$\omega = \sum \lambda _{k} df_{k}/f_{k} = \sum \lambda _{k} d \log f_{k}$
the associated logarithmic one form. If
then for each
![]() $0 \leq t \leq n$
the following complex is acyclic:
$0 \leq t \leq n$
the following complex is acyclic:
Proof.
Case 1:
![]() $\operatorname {\mathrm {rank}}(\mathscr {A}) \geq 2$
.
$\operatorname {\mathrm {rank}}(\mathscr {A}) \geq 2$
.
By Proposition 2.15, we know that the inclusion of
![]() $-\iota _{E}(\omega )$
-homogeneous subcomplex of
$-\iota _{E}(\omega )$
-homogeneous subcomplex of
![]() $(H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
is a quasi-isomorphism:
$(H_{\mathfrak {m}}^{t}(\Omega _{R}^{\bullet }(\log \mathscr {A})), \nabla _{\omega })$
is a quasi-isomorphism:
Since
![]() $\iota _{E}(\omega ) = \sum \lambda _{k}$
, it is enough to show that for each t and each j the subspace of
$\iota _{E}(\omega ) = \sum \lambda _{k}$
, it is enough to show that for each t and each j the subspace of
![]() $H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
degree
$H_{\mathfrak {m}}^{t}(\Omega _{R}^{j}(\log \mathscr {A}))$
degree
![]() $-\sum \lambda _{k}$
elements is zero. For then the left-hand side of Equation (2.21) is a complex of zero modules. In an equation, it suffices to show
$-\sum \lambda _{k}$
elements is zero. For then the left-hand side of Equation (2.21) is a complex of zero modules. In an equation, it suffices to show
First of all, if
![]() $\sum \lambda _{k} \notin \mathbb {Z}$
, the criterion (2.22) trivially holds. So we may assume
$\sum \lambda _{k} \notin \mathbb {Z}$
, the criterion (2.22) trivially holds. So we may assume
![]() $\sum \lambda _{k} \in \mathbb {Z}$
. And, because the j-logarithmic forms are reflexive (cf. subsection 2.2 of [Reference Denham and Schulze13]), they have depth at least two. By standard facts about local cohomology,
$\sum \lambda _{k} \in \mathbb {Z}$
. And, because the j-logarithmic forms are reflexive (cf. subsection 2.2 of [Reference Denham and Schulze13]), they have depth at least two. By standard facts about local cohomology,
![]() $H_{\mathfrak {m}}^{0}(\Omega _{R}^{j}(\log \mathscr {A}))$
and
$H_{\mathfrak {m}}^{0}(\Omega _{R}^{j}(\log \mathscr {A}))$
and
![]() $H_{\mathfrak {m}}^{1}(\Omega _{R}^{j}(\log \mathscr {A}))$
then vanish. Certainly, Equation (2.22) then holds for
$H_{\mathfrak {m}}^{1}(\Omega _{R}^{j}(\log \mathscr {A}))$
then vanish. Certainly, Equation (2.22) then holds for
![]() $t=0,1$
.
$t=0,1$
.
We must deal with
![]() $t \geq 2$
, where we use the regularity estimate of Theorem 2.29:
$t \geq 2$
, where we use the regularity estimate of Theorem 2.29:
![]() $\operatorname {\mathrm {reg}}(\Omega _{R}^{j}(\log \mathscr {A})) \leq 0.$
Combining this with the definition of regularity in terms of local cohomology modules yields
$\operatorname {\mathrm {reg}}(\Omega _{R}^{j}(\log \mathscr {A})) \leq 0.$
Combining this with the definition of regularity in terms of local cohomology modules yields
Therefore, for all
![]() $t \geq 2$
and for all j,
$t \geq 2$
and for all j,
Then our hypothesis (2.20) ensures Equation (2.22) holds for
![]() $t \geq 2$
, completing Case 1.
$t \geq 2$
, completing Case 1.
Case 2:
![]() $\operatorname {\mathrm {rank}}(\mathscr {A}) = 1$
.
$\operatorname {\mathrm {rank}}(\mathscr {A}) = 1$
.
We argue in the same way, except noting that because
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
is automatically free and R has depth one, that
$\Omega _{R}^{j}(\log \mathscr {A})$
is automatically free and R has depth one, that
![]() $H_{\mathfrak {m}}^{0}(\Omega _{R}^{j}(\mathscr {A}))$
vanishes. Thus, we need to show that
$H_{\mathfrak {m}}^{0}(\Omega _{R}^{j}(\mathscr {A}))$
vanishes. Thus, we need to show that
for
![]() $j = 0$
and
$j = 0$
and
![]() $j = 1$
. Now, use Example 2.28.
$j = 1$
. Now, use Example 2.28.
2.6. Acyclic complexes of analytic Čech cohomology
Now, we can prove an analytic version of Corollary 2.30, using the setup and notation of subsection 2.3. This will be the crucial result powering the proof of Theorem 3.4 (analytic Twisted Logarithmic Comparison Theorem).
Instead of twisted complexes of local cohomology modules, we have twisted complexes of Čech cohomology, cf. Definition 2.17, and the role of the homogeneous subcomplex in the proof of Corollary 2.30 is played by the subcomplex of homogeneous forms in the Laurent series sense of subsection 2.3, cf. Definition 2.18. The argument uses GAGA machinery to enrich the arguments of the previous subsection; consequently, it still utilizes the bound on Castelnuovo–Mumford regularity provided in Theorem 2.29 to employ Lemma 2.22. Within the proof, we use
![]() $(-)^{\operatorname {\mathrm {an}}}$
(resp.
$(-)^{\operatorname {\mathrm {an}}}$
(resp.
![]() $(-)_{\operatorname {\mathrm {alg}}}$
) to denote the analytic (resp. algebraic) interpretation of
$(-)_{\operatorname {\mathrm {alg}}}$
) to denote the analytic (resp. algebraic) interpretation of
![]() $(-)$
.
$(-)$
.
Corollary 2.31. Let
![]() $f = f_{1} \cdots f_{d} \in R = \mathbb {C}[x_{1}, \dots , x_{n}]$
be a central, essential and reduced hyperplane arrangement,
$f = f_{1} \cdots f_{d} \in R = \mathbb {C}[x_{1}, \dots , x_{n}]$
be a central, essential and reduced hyperplane arrangement,
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
weights and
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
weights and
![]() $\omega = \sum \lambda _{k} df_{k}/f_{k} = \sum \lambda _{k} d \log f_{k}$
the associated logarithmic one form. If
$\omega = \sum \lambda _{k} df_{k}/f_{k} = \sum \lambda _{k} d \log f_{k}$
the associated logarithmic one form. If
and if
![]() $n \geq 2$
, then for each
$n \geq 2$
, then for each
![]() $1 \leq t \leq n$
the following complex is acyclic:
$1 \leq t \leq n$
the following complex is acyclic:
Proof. By Lemma 2.22, it suffices to show that for
![]() $0 \leq j \leq n$
, the Čech cohomology
$0 \leq j \leq n$
, the Čech cohomology
![]() $H_{\operatorname {\mathrm {\check {C}ech}}}^{t}(\Omega _{X^{\operatorname {\mathrm {an}}}}^{j}(\log \mathscr {A})_{-\iota _{E}(\omega )})$
vanishes whenever
$H_{\operatorname {\mathrm {\check {C}ech}}}^{t}(\Omega _{X^{\operatorname {\mathrm {an}}}}^{j}(\log \mathscr {A})_{-\iota _{E}(\omega )})$
vanishes whenever
![]() $ 1 \leq t \leq n$
. If
$ 1 \leq t \leq n$
. If
![]() $-\iota _{E}(\omega ) \notin \mathbb {Z}$
, the claim is immediate: There are no homogeneous (in the Laurent series sense) elements of nonintegral weight. So we may assume
$-\iota _{E}(\omega ) \notin \mathbb {Z}$
, the claim is immediate: There are no homogeneous (in the Laurent series sense) elements of nonintegral weight. So we may assume
![]() $-\iota _{E}(\omega ) \in \mathbb {Z}$
and will proceed by a GAGA argument.
$-\iota _{E}(\omega ) \in \mathbb {Z}$
and will proceed by a GAGA argument.
Consider the graded R-module
![]() $\Omega _{R}^{j}(\log \mathscr {A})(-\iota _{E}(\omega ))$
. The sheafification
$\Omega _{R}^{j}(\log \mathscr {A})(-\iota _{E}(\omega ))$
. The sheafification
![]() $\widetilde {\Omega _{R}^{j}(\log \mathscr {A})(-\iota _{E}(\omega )})$
of this graded module gives a coherent algebraic sheaf of
$\widetilde {\Omega _{R}^{j}(\log \mathscr {A})(-\iota _{E}(\omega )})$
of this graded module gives a coherent algebraic sheaf of
![]() $\mathscr {O}_{\mathbb {P}_{\operatorname {\mathrm {alg}}}^{n-1}}$
-modules on
$\mathscr {O}_{\mathbb {P}_{\operatorname {\mathrm {alg}}}^{n-1}}$
-modules on
![]() $\mathbb {P}_{\operatorname {\mathrm {alg}}}^{n-1}$
. It is well known that for all
$\mathbb {P}_{\operatorname {\mathrm {alg}}}^{n-1}$
. It is well known that for all
![]() $t \geq 1$
we have the following identification of sheaf cohomology with local cohomology:
$t \geq 1$
we have the following identification of sheaf cohomology with local cohomology:
On one hand, the condition (2.23) on the residue of
![]() $\omega $
implies that the left-hand size of Equation (2.24) vanishes. Indeed, this follows from Castelnuovo–Mumford regularity estimate of Theorem 2.29 as in Corollary 2.30. On the other hand, let
$\omega $
implies that the left-hand size of Equation (2.24) vanishes. Indeed, this follows from Castelnuovo–Mumford regularity estimate of Theorem 2.29 as in Corollary 2.30. On the other hand, let
![]() $K^{j, \operatorname {\mathrm {an}}}$
be the analytification of
$K^{j, \operatorname {\mathrm {an}}}$
be the analytification of
![]() $\widetilde {\Omega _{R}^{j}(\log \mathscr {A})(-\iota _{E}(\omega )})$
. By GAGA,
$\widetilde {\Omega _{R}^{j}(\log \mathscr {A})(-\iota _{E}(\omega )})$
. By GAGA,
![]() $K^{j, \operatorname {\mathrm {an}}}$
is a coherent analytic sheaf of
$K^{j, \operatorname {\mathrm {an}}}$
is a coherent analytic sheaf of
![]() $\mathscr {O}_{\mathbb {P}^{n-1, \operatorname {\mathrm {an}}}}$
-modules on
$\mathscr {O}_{\mathbb {P}^{n-1, \operatorname {\mathrm {an}}}}$
-modules on
![]() $\mathbb {P}^{n-1, \operatorname {\mathrm {an}}}$
. Again by GAGA, the sheaf cohomology of
$\mathbb {P}^{n-1, \operatorname {\mathrm {an}}}$
. Again by GAGA, the sheaf cohomology of
![]() $K^{j,\operatorname {\mathrm {an}}}$
equals the right-hand side of Equation (2.24). Altogether this gives
$K^{j,\operatorname {\mathrm {an}}}$
equals the right-hand side of Equation (2.24). Altogether this gives
![]() $0 = H^{t}(K^{j, \operatorname {\mathrm {an}}})$
for all
$0 = H^{t}(K^{j, \operatorname {\mathrm {an}}})$
for all
![]() $t \geq 1$
.
$t \geq 1$
.
Now, consider the Čech complex
![]() $C^{\bullet }(\{D^{+}(x_{i})\}, K^{j, \operatorname {\mathrm {an}}})$
attached to the open cover
$C^{\bullet }(\{D^{+}(x_{i})\}, K^{j, \operatorname {\mathrm {an}}})$
attached to the open cover
![]() $\{D^{+}(x_{i})\}_{1 \leq i \leq n}$
of
$\{D^{+}(x_{i})\}_{1 \leq i \leq n}$
of
![]() $\mathbb {P}^{n-1, \operatorname {\mathrm {an}}}$
. Since
$\mathbb {P}^{n-1, \operatorname {\mathrm {an}}}$
. Since
![]() $D^{+}(x_{i})$
and any intersection of the
$D^{+}(x_{i})$
and any intersection of the
![]() $\{D^{+}(x_{i})\}$
is Stein, and since higher sheaf cohomology (of coherent sheaves) vanishes on Steins, this Čech complex computes the sheaf cohomology
$\{D^{+}(x_{i})\}$
is Stein, and since higher sheaf cohomology (of coherent sheaves) vanishes on Steins, this Čech complex computes the sheaf cohomology
![]() $K^{j, \operatorname {\mathrm {an}}}$
. So for all
$K^{j, \operatorname {\mathrm {an}}}$
. So for all
![]() $t \geq 1$
we have
$t \geq 1$
we have
Recall
![]() $K^{j, \operatorname {\mathrm {an}}}$
is the analytification of
$K^{j, \operatorname {\mathrm {an}}}$
is the analytification of
![]() $\widetilde {\Omega _{R}^{j}(\log \mathscr {A})(-\iota _{E}(\omega )})$
. Because membership in
$\widetilde {\Omega _{R}^{j}(\log \mathscr {A})(-\iota _{E}(\omega )})$
. Because membership in
![]() $\Omega _{R}^{j}(\log \mathscr {A})[x_{I}^{-1}]$
is determined by the kernel of a map defined wholly in terms of
$\Omega _{R}^{j}(\log \mathscr {A})[x_{I}^{-1}]$
is determined by the kernel of a map defined wholly in terms of
![]() $\partial _{1} \bullet f, \dots , \partial _{n} \bullet f, f$
, all of which are algebraic polynomials, and because analytification is exact, the analytification of
$\partial _{1} \bullet f, \dots , \partial _{n} \bullet f, f$
, all of which are algebraic polynomials, and because analytification is exact, the analytification of
![]() $\Gamma (D(x_{I}), \widetilde {\Omega _{R}^{j}(\log \mathscr {A})})$
is
$\Gamma (D(x_{I}), \widetilde {\Omega _{R}^{j}(\log \mathscr {A})})$
is
![]() $\Gamma (D(x_{I}), \Omega _{X^{\operatorname {\mathrm {an}}}}(\log \mathscr {A}))$
. (This is an affine statement:
$\Gamma (D(x_{I}), \Omega _{X^{\operatorname {\mathrm {an}}}}(\log \mathscr {A}))$
. (This is an affine statement:
![]() $D(x_{I}) \subseteq \mathbb {C}^{n}$
.) Because
$D(x_{I}) \subseteq \mathbb {C}^{n}$
.) Because
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
is generated by homogeneous terms (as
$\Omega _{R}^{j}(\log \mathscr {A})$
is generated by homogeneous terms (as
![]() $\mathscr {A}$
is central), we deduce
$\mathscr {A}$
is central), we deduce
where by
![]() $(-)_{-\iota _{E}(\omega )}$
we mean the homogeneous elements in the sense of Laurent series. This means
$(-)_{-\iota _{E}(\omega )}$
we mean the homogeneous elements in the sense of Laurent series. This means
 $$ \begin{align*} H^{t}(C^{\bullet}(\{D^{+}(x_{i})\}, K^{j, \operatorname{\mathrm{an}}})) &= H^{t}(C^{\bullet}(\{D(x_{i})\}, \Omega_{X^{\operatorname{\mathrm{an}}}}^{j}(\log \mathscr{A}))_{-\iota_{E}(\omega)}) \\ &= H_{\operatorname{\mathrm{\check{C}ech}}}^{t}(\Omega_{X^{\operatorname{\mathrm{an}}}}^{j}(\log \mathscr{A}))_{-\iota_{E}(\omega)}. \end{align*} $$
$$ \begin{align*} H^{t}(C^{\bullet}(\{D^{+}(x_{i})\}, K^{j, \operatorname{\mathrm{an}}})) &= H^{t}(C^{\bullet}(\{D(x_{i})\}, \Omega_{X^{\operatorname{\mathrm{an}}}}^{j}(\log \mathscr{A}))_{-\iota_{E}(\omega)}) \\ &= H_{\operatorname{\mathrm{\check{C}ech}}}^{t}(\Omega_{X^{\operatorname{\mathrm{an}}}}^{j}(\log \mathscr{A}))_{-\iota_{E}(\omega)}. \end{align*} $$
By Equation (2.25), we conclude
![]() $0 = H_{\operatorname {\mathrm {\check {C}ech}}}^{t}(\Omega _{X^{\operatorname {\mathrm {an}}}}^{j}(\log \mathscr {A}))_{-\iota _{E}(\omega )}$
, as required.
$0 = H_{\operatorname {\mathrm {\check {C}ech}}}^{t}(\Omega _{X^{\operatorname {\mathrm {an}}}}^{j}(\log \mathscr {A}))_{-\iota _{E}(\omega )}$
, as required.
3. The (un)Twisted Logarithmic Comparison Theorem
This section is devoted to proving the Twisted Logarithmic Comparison Theorem for reduced hyperplane arrangements, subject to a relatively mild restriction on the weights in both the analytic (Theorem 3.4) and algebraic (Theorem 3.8) cases. The latter requires centrality, the former does not. Consequences are (all not necessarily central): the global analytic Twisted Logarithmic Comparison Theorem (Corollary 3.7); the analytic (untwisted) Logarithmic Comparison Theorem (Corollary 3.6); the algebraic (untwisted) Logarithmic Comparison Theorem (Corollary 3.6). The last result positively answers Terao’s conjecture (Conjecture 1.1). In sum, these result show that the cohomology of the complement in an arbitrary rank one local system can be completely understood by an appropriately twisted logarithmic de Rham complex.
The analytic Twisted Logarithmic Comparison Theorem is the main result insofar as the others follow with significantly less difficulty. The argument synthesizes analytic and algebraic techniques. We utilize the analytic paradigm of Theorem 1.1 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9]: We repeat their inductive setup (either using the rank of
![]() $\mathscr {A}$
as we do here or using Saito-holonomic induction as in loc. cit.) and exploit the relationships between the four consequent spectral sequences, some of which incorporate the inductive hypothesis. The argument hinges on showing that on the second page of one of these spectral sequences all but one column vanishes. In loc. cit. (or similarly in [Reference Wiens and Yuzvinsky36]) homological criterion on the logarithmic differential forms greatly simplifies the first page. With no homological assumptions, we have no control over the first page’s complexity. It is here that we utilize algebraic techniques and our bound on the Castelnuovo–Mumford regularity of logarithmic forms: Using Corollary 2.31 and subsection 2.3, we can translate these data into our analytic situation, furnishing adequate control over vanishing on the second page.
$\mathscr {A}$
as we do here or using Saito-holonomic induction as in loc. cit.) and exploit the relationships between the four consequent spectral sequences, some of which incorporate the inductive hypothesis. The argument hinges on showing that on the second page of one of these spectral sequences all but one column vanishes. In loc. cit. (or similarly in [Reference Wiens and Yuzvinsky36]) homological criterion on the logarithmic differential forms greatly simplifies the first page. With no homological assumptions, we have no control over the first page’s complexity. It is here that we utilize algebraic techniques and our bound on the Castelnuovo–Mumford regularity of logarithmic forms: Using Corollary 2.31 and subsection 2.3, we can translate these data into our analytic situation, furnishing adequate control over vanishing on the second page.
Before embarking, note that in Proposition 3.12, we show that all rank one local systems on
![]() $U = X \setminus \mathscr {A}$
can be computed via these Twisted Logarithmic Comparison Theorems. This is not the case for the twisted Orlik–Solomon algebra, cf. [Reference Cohen and Suciu12], [Reference Suciu31], [Reference Cohen11]. When
$U = X \setminus \mathscr {A}$
can be computed via these Twisted Logarithmic Comparison Theorems. This is not the case for the twisted Orlik–Solomon algebra, cf. [Reference Cohen and Suciu12], [Reference Suciu31], [Reference Cohen11]. When
![]() $\mathscr {A}$
is central, Theorem 3.8 and Remark 3.11 imply these computations are explicit, finite-dimensional linear algebra. Example 3.14 exemplifies this: We compute the Betti numbers of
$\mathscr {A}$
is central, Theorem 3.8 and Remark 3.11 imply these computations are explicit, finite-dimensional linear algebra. Example 3.14 exemplifies this: We compute the Betti numbers of
![]() $H^{\bullet }(U, \operatorname {\mathrm {L}}_{\boldsymbol {\beta }})$
for a
$H^{\bullet }(U, \operatorname {\mathrm {L}}_{\boldsymbol {\beta }})$
for a
![]() $\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
belonging to a translated component of the characteristic variety – precisely the components undetectable by Orlik–Solomon methods.
$\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
belonging to a translated component of the characteristic variety – precisely the components undetectable by Orlik–Solomon methods.
3.1. The analytic case
Before we can prove Theorem 3.4, we require a significant amount of lemmas. First, the analytic twisted logarithmic comparison can be checked stalkwise. Using this, the following lemma says it is enough to check the analytic Twisted Logarithmic Comparison Theorem on sufficiently small Stein opens
![]() $V \subseteq X$
. The proof is exactly the same as in Lemma 2.5 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9] and is tantamount to the following: Because higher sheaf cohomology of coherent modules over Stein opens vanishes, taking hypercohomology amounts to taking global sections.
$V \subseteq X$
. The proof is exactly the same as in Lemma 2.5 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9] and is tantamount to the following: Because higher sheaf cohomology of coherent modules over Stein opens vanishes, taking hypercohomology amounts to taking global sections.
Lemma 3.1 (Lemma 2.5 [Reference Castro-Jiménez, Narváez-Macarro and Mond9]).
Let
![]() $f = f_{1} \cdots f_{d}$
cut out a hyperplane arrangement
$f = f_{1} \cdots f_{d}$
cut out a hyperplane arrangement
![]() $\mathscr {A}$
, and consider the weights
$\mathscr {A}$
, and consider the weights
![]() $\lambda _{1}, \dots , \lambda _{d}$
with their associated one-form
$\lambda _{1}, \dots , \lambda _{d}$
with their associated one-form
![]() $\omega = \sum _{k} \lambda _{k} df_{k} / f_{k}.$
Then the following are equivalent:
$\omega = \sum _{k} \lambda _{k} df_{k} / f_{k}.$
Then the following are equivalent:
-
(a)
 ;
; -
(b) For each (sufficiently small) Stein open
 $V \subseteq X$
and each
$V \subseteq X$
and each
 $p \geq 0$
, the map induced by inclusion is an isomorphism.
$p \geq 0$
, the map induced by inclusion is an isomorphism. $$\begin{align*}H^{p}(\Gamma(V, \Omega_{X}^{\bullet}(\log \mathscr{A})), \nabla_{\omega}) \xrightarrow[]{} H^{p}(\Gamma(V \setminus \mathscr{A}, \Omega_{X}^{\bullet}(\star \mathscr{A})), \nabla_{\omega}) \end{align*}$$
$$\begin{align*}H^{p}(\Gamma(V, \Omega_{X}^{\bullet}(\log \mathscr{A})), \nabla_{\omega}) \xrightarrow[]{} H^{p}(\Gamma(V \setminus \mathscr{A}, \Omega_{X}^{\bullet}(\star \mathscr{A})), \nabla_{\omega}) \end{align*}$$
Proof. Exactly as in Lemma 2.5 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9].
The majority of preliminary work is to recreate the inductive setup from [Reference Castro-Jiménez, Narváez-Macarro and Mond9] in the twisted case. This will let information about smaller rank arrangements percolate to edges of a larger rank arrangement. Since we have
![]() $\omega \neq 0$
, unlike loc. cit., there are several technical details that must be checked.
$\omega \neq 0$
, unlike loc. cit., there are several technical details that must be checked.
First, we want to be able to study the twisted logarithmic comparison at a point
![]() $\mathfrak {x}$
that only lies in a subset of the hyperplanes of
$\mathfrak {x}$
that only lies in a subset of the hyperplanes of
![]() $\mathscr {A}$
. The next lemma says that such a point, we can throw out the summands
$\mathscr {A}$
. The next lemma says that such a point, we can throw out the summands
![]() $\lambda _{k} d \log f_{k}$
of
$\lambda _{k} d \log f_{k}$
of
![]() $\omega $
corresponding to hyperplanes
$\omega $
corresponding to hyperplanes
![]() $\operatorname {\mathrm {V}}(f_{k})$
that do not pass through
$\operatorname {\mathrm {V}}(f_{k})$
that do not pass through
![]() $\mathfrak {x}$
. The argument uses an idea from Lemma 2.1 of [Reference Kawahara20].
$\mathfrak {x}$
. The argument uses an idea from Lemma 2.1 of [Reference Kawahara20].
Lemma 3.2. Suppose that
![]() $f = f_{1} \cdots f_{d}$
cuts out a reduced hyperplane arrangement
$f = f_{1} \cdots f_{d}$
cuts out a reduced hyperplane arrangement
![]() $\mathscr {A}$
. For weights
$\mathscr {A}$
. For weights
![]() $\lambda _{1}, \dots , \lambda _{r} \in \mathbb {C}$
, we have the associated one form
$\lambda _{1}, \dots , \lambda _{r} \in \mathbb {C}$
, we have the associated one form
 $$\begin{align*}\omega = \sum_{k} \lambda_{k} \frac{df_{k}}{f_{k}}. \end{align*}$$
$$\begin{align*}\omega = \sum_{k} \lambda_{k} \frac{df_{k}}{f_{k}}. \end{align*}$$
For
![]() $\mathfrak {x} \in X$
, let
$\mathfrak {x} \in X$
, let
![]() $f^{\prime } = \prod _{\{1 \leq k \leq d \mid \mathfrak {x} \in \operatorname {\mathrm {V}}(f_{k})\}} f_{k}$
and let
$f^{\prime } = \prod _{\{1 \leq k \leq d \mid \mathfrak {x} \in \operatorname {\mathrm {V}}(f_{k})\}} f_{k}$
and let
 $$\begin{align*}\omega^{\prime} = \sum_{\{1 \leq k \leq d \mid \mathfrak{x} \in \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \frac{df_{k}}{f_{k}}. \end{align*}$$
$$\begin{align*}\omega^{\prime} = \sum_{\{1 \leq k \leq d \mid \mathfrak{x} \in \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \frac{df_{k}}{f_{k}}. \end{align*}$$
Then for small enough Stein opens
![]() $V \ni \mathfrak {x}$
, we have isomorphisms
$V \ni \mathfrak {x}$
, we have isomorphisms
-
(a)
 $(\Omega _{V}^{\bullet }(\log f), \nabla _{\omega }) \xrightarrow[]{\simeq } (\Omega _{V}^{\bullet }(\log f^{\prime }), \nabla _{\omega ^{\prime }})$
;
$(\Omega _{V}^{\bullet }(\log f), \nabla _{\omega }) \xrightarrow[]{\simeq } (\Omega _{V}^{\bullet }(\log f^{\prime }), \nabla _{\omega ^{\prime }})$
; -
(b)
 $(\Omega _{V}^{\bullet }(\star f), \nabla _{\omega }) \xrightarrow[]{\simeq } (\Omega _{V}^{\bullet }(\star f^{\prime }), \nabla _{\omega ^{\prime }})$
.
$(\Omega _{V}^{\bullet }(\star f), \nabla _{\omega }) \xrightarrow[]{\simeq } (\Omega _{V}^{\bullet }(\star f^{\prime }), \nabla _{\omega ^{\prime }})$
.
These isomorphisms are compatible with ![]()
Proof. It is enough to prove the assertion for V the complement of all the hyperplanes
![]() $\operatorname {\mathrm {V}}(f_{j})$
that do not contain the point
$\operatorname {\mathrm {V}}(f_{j})$
that do not contain the point
![]() $\mathfrak {x}$
. Observe:
$\mathfrak {x}$
. Observe:
 $$\begin{align*}\omega^{\prime} = \omega - \sum_{\{1 \leq k \leq d \mid \mathfrak{x} \notin \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{j} \frac{df_{k}}{f_{k}} = \omega - \sum_{\{1 \leq k \leq d \mid \mathfrak{x} \notin \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} (d \log f_{k}). \end{align*}$$
$$\begin{align*}\omega^{\prime} = \omega - \sum_{\{1 \leq k \leq d \mid \mathfrak{x} \notin \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{j} \frac{df_{k}}{f_{k}} = \omega - \sum_{\{1 \leq k \leq d \mid \mathfrak{x} \notin \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} (d \log f_{k}). \end{align*}$$
Rename every such
![]() $f_{j}$
not vanishing at
$f_{j}$
not vanishing at
![]() $\mathfrak {x}$
as
$\mathfrak {x}$
as
![]() $u_{j}$
. We construct isomorphisms
$u_{j}$
. We construct isomorphisms
We construct the first map of Equation (3.1). We may assume
![]() $\lambda _{1} \neq 0$
. Consider the diagram
$\lambda _{1} \neq 0$
. Consider the diagram

Since
![]() $u_{1}$
is a unit,
$u_{1}$
is a unit,
![]() $u_{1}^{-\lambda _{1}}$
is a unit as well, making the horizontal maps isomorphisms. A quick computation verifies the diagram commutes. Therefore, multiplication by
$u_{1}^{-\lambda _{1}}$
is a unit as well, making the horizontal maps isomorphisms. A quick computation verifies the diagram commutes. Therefore, multiplication by
![]() $u_{1}^{-\lambda _{1}}$
is an invertible chain map, and we have constructed the first isomorphism of Equation (3.1). Iterating the procedure demonstrates (a).
$u_{1}^{-\lambda _{1}}$
is an invertible chain map, and we have constructed the first isomorphism of Equation (3.1). Iterating the procedure demonstrates (a).
The same construction works for the twisted meromorphic de Rham complex, giving (b). And multiplication by
![]() $u_{1}^{\lambda }$
is compatible with including the twisted logarithmic de Rham complex into the meromorphic one.
$u_{1}^{\lambda }$
is compatible with including the twisted logarithmic de Rham complex into the meromorphic one.
Second, when working at a point
![]() $\mathfrak {x}$
whose corresponding edge and subarrangement is of nonmaximal rank, we want to be able to reduce the ambient dimension. This corresponds to, and is proved similarly to, Lemma 2.2 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9].
$\mathfrak {x}$
whose corresponding edge and subarrangement is of nonmaximal rank, we want to be able to reduce the ambient dimension. This corresponds to, and is proved similarly to, Lemma 2.2 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9].
Lemma 3.3. Suppose
![]() $f = f_{1} \cdots f_{d}$
cuts out a hyperplane arrangement
$f = f_{1} \cdots f_{d}$
cuts out a hyperplane arrangement
![]() $\mathscr {A}$
. For weights
$\mathscr {A}$
. For weights
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
, we have the associated one form
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
, we have the associated one form
 $$\begin{align*}\omega = \sum_{k} \lambda_{k} \frac{df_{k}}{f_{k}}. \end{align*}$$
$$\begin{align*}\omega = \sum_{k} \lambda_{k} \frac{df_{k}}{f_{k}}. \end{align*}$$
Assume that on some Stein manifold
![]() $V \subseteq X$
, the divisor
$V \subseteq X$
, the divisor
![]() $\operatorname {\mathrm {Div}}(f)$
is locally a product
$\operatorname {\mathrm {Div}}(f)$
is locally a product
![]() $(V, \operatorname {\mathrm {Div}}(f)) = (\mathbb {C} \times V^{\prime }, \mathbb {C} \times \operatorname {\mathrm {Div}}(f^{\prime }))$
for
$(V, \operatorname {\mathrm {Div}}(f)) = (\mathbb {C} \times V^{\prime }, \mathbb {C} \times \operatorname {\mathrm {Div}}(f^{\prime }))$
for
![]() $V^{\prime }$
a Stein manifold of smaller dimension. Let
$V^{\prime }$
a Stein manifold of smaller dimension. Let
![]() $\pi : V \to V^{\prime }$
be the projection, let
$\pi : V \to V^{\prime }$
be the projection, let
![]() $f^{\prime }$
and
$f^{\prime }$
and
![]() $f_{k}^{\prime }$
$f_{k}^{\prime }$
![]() $\in \mathscr {O}_{V^{\prime }}$
satisfy
$\in \mathscr {O}_{V^{\prime }}$
satisfy
![]() $\operatorname {\mathrm {Div}}(f) = \mathbb {C} \times \operatorname {\mathrm {Div}}(f^{\prime })$
and
$\operatorname {\mathrm {Div}}(f) = \mathbb {C} \times \operatorname {\mathrm {Div}}(f^{\prime })$
and
![]() $\mathbb {C} \times \operatorname {\mathrm {Div}}(f_{k}^{\prime }) = \operatorname {\mathrm {Div}}(f_{k}))$
and let
$\mathbb {C} \times \operatorname {\mathrm {Div}}(f_{k}^{\prime }) = \operatorname {\mathrm {Div}}(f_{k}))$
and let
 $$\begin{align*}\omega^{\prime} = \sum_{k} \lambda_{k} \frac{df^{\prime}_{k}}{f^{\prime}_{k}}. \end{align*}$$
$$\begin{align*}\omega^{\prime} = \sum_{k} \lambda_{k} \frac{df^{\prime}_{k}}{f^{\prime}_{k}}. \end{align*}$$
Then
-
(a)
 $\pi ^{-1}(\Omega _{V^{\prime }}^{\bullet }(\log f^{\prime }), \nabla _{\omega ^{\prime }}) \to (\Omega _{V}^{\bullet }(\log f), \nabla _{\omega })$
is a quasi-isomorphism;
$\pi ^{-1}(\Omega _{V^{\prime }}^{\bullet }(\log f^{\prime }), \nabla _{\omega ^{\prime }}) \to (\Omega _{V}^{\bullet }(\log f), \nabla _{\omega })$
is a quasi-isomorphism; -
(b)
 $\pi ^{-1}(\Omega _{V^{\prime }}^{\bullet }(\star f^{\prime }), \nabla _{\omega ^{\prime }}) \to (\Omega _{V}^{\bullet }(\star f), \nabla _{\omega })$
is a quasi-isomorphism.
$\pi ^{-1}(\Omega _{V^{\prime }}^{\bullet }(\star f^{\prime }), \nabla _{\omega ^{\prime }}) \to (\Omega _{V}^{\bullet }(\star f), \nabla _{\omega })$
is a quasi-isomorphism.
Proof. Pick local coordinates
![]() $(t, x^{\prime })$
for
$(t, x^{\prime })$
for
![]() $V = \mathbb {C} \times V^{\prime }$
. And note that
$V = \mathbb {C} \times V^{\prime }$
. And note that
![]() $f_{k} = u_{k} f_{k}^{\prime }$
, where
$f_{k} = u_{k} f_{k}^{\prime }$
, where
![]() $u_{k}$
is a unit. Arguing as in Lemma 3.2,
$u_{k}$
is a unit. Arguing as in Lemma 3.2,
![]() $(\Omega _{V}^{\bullet }(\log f^{\prime }), \nabla _{\omega ^{\prime }}) \xrightarrow[]{\simeq } (\Omega _{V}^{\bullet }(\log f), \nabla _{\omega })$
, where here
$(\Omega _{V}^{\bullet }(\log f^{\prime }), \nabla _{\omega ^{\prime }}) \xrightarrow[]{\simeq } (\Omega _{V}^{\bullet }(\log f), \nabla _{\omega })$
, where here
![]() $f^{\prime }$
and
$f^{\prime }$
and
![]() $\omega ^{\prime }$
are viewed as functions and forms over V. (Note that we are removing the summands
$\omega ^{\prime }$
are viewed as functions and forms over V. (Note that we are removing the summands
![]() $\lambda _{k} d \log u_{k}$
from
$\lambda _{k} d \log u_{k}$
from
![]() $\omega $
). Now, weight the local coordinates
$\omega $
). Now, weight the local coordinates
![]() $(t, x^{\prime })$
by giving t weight one, each
$(t, x^{\prime })$
by giving t weight one, each
![]() $x_{i}^{\prime }$
weight zero,
$x_{i}^{\prime }$
weight zero,
![]() $dx_{i}^{\prime }$
weight zero and
$dx_{i}^{\prime }$
weight zero and
![]() $dt$
weight one. Let
$dt$
weight one. Let
![]() $\chi = t \partial _{t}$
be a logarithmic derivation on
$\chi = t \partial _{t}$
be a logarithmic derivation on
![]() $f^{\prime }$
. Then we can argue as in Lemma 2.23: The twisted Lie derivative
$f^{\prime }$
. Then we can argue as in Lemma 2.23: The twisted Lie derivative
![]() $\nabla _{\omega ^{\prime }}(\iota _{\chi }) + \iota _{\chi }(\nabla _{\omega ^{\prime }})$
induces a quasi-isomorphism
$\nabla _{\omega ^{\prime }}(\iota _{\chi }) + \iota _{\chi }(\nabla _{\omega ^{\prime }})$
induces a quasi-isomorphism ![]() , where the weight zero subcomplex is defined by the aforementioned weighting. (Note that
, where the weight zero subcomplex is defined by the aforementioned weighting. (Note that
![]() $\iota _{\chi }(\omega ) = 0$
and the previous claim can be checked stalkwise.) This weight zero subcomplex is
$\iota _{\chi }(\omega ) = 0$
and the previous claim can be checked stalkwise.) This weight zero subcomplex is
![]() $\pi ^{-1}(\Omega _{V^{\prime }}^{\bullet }(\log f^{\prime }), \nabla _{\omega ^{\prime }})$
, giving (a). The proof of (b) is similar.
$\pi ^{-1}(\Omega _{V^{\prime }}^{\bullet }(\log f^{\prime }), \nabla _{\omega ^{\prime }})$
, giving (a). The proof of (b) is similar.
With the preparations complete, we can prove the main theorem. The infrastructure is that of Theorem 1.1 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9], but we have to be careful manipulating the form
![]() $\omega $
; the Čech cohomology/local cohomology argument (Step 3) is much more subtle. To sketch the recipe for the latter, we use subsection 2.3 to reduce to a ‘homogeneous’ subcomplex of a twisted complex of analytic Čech cohomology modules; use the GAGA considerations of Corollary 2.31 to show the vanishing of this subcomplex on the nose is dictated by algebraic Castelnuovo–Mumford regularity bounds; use Theorem 2.29 to bound the regularity.
$\omega $
; the Čech cohomology/local cohomology argument (Step 3) is much more subtle. To sketch the recipe for the latter, we use subsection 2.3 to reduce to a ‘homogeneous’ subcomplex of a twisted complex of analytic Čech cohomology modules; use the GAGA considerations of Corollary 2.31 to show the vanishing of this subcomplex on the nose is dictated by algebraic Castelnuovo–Mumford regularity bounds; use Theorem 2.29 to bound the regularity.
Theorem 3.4 (Analytic Twisted Logarithmic Comparison Theorem).
Let
![]() $f = f_{1} \cdots f_{d} \in R$
cut out a reduced hyperplane arrangement
$f = f_{1} \cdots f_{d} \in R$
cut out a reduced hyperplane arrangement
![]() $\mathscr {A}$
. Suppose that
$\mathscr {A}$
. Suppose that
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
are weights such that, for each edge
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
are weights such that, for each edge
![]() $E \in \mathscr {L}(\mathscr {A})$
,
$E \in \mathscr {L}(\mathscr {A})$
,
 $$ \begin{align} \sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align} $$
$$ \begin{align} \sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align} $$
Let
![]() $\omega = \sum _{k} \lambda _{k} \frac {df_{k}}{f_{k}}$
be the logarithmic one form determined by the
$\omega = \sum _{k} \lambda _{k} \frac {df_{k}}{f_{k}}$
be the logarithmic one form determined by the
![]() $\{\lambda _{k}\}$
. Then the analytic Twisted Logarithmic Comparison Theorem with respect to
$\{\lambda _{k}\}$
. Then the analytic Twisted Logarithmic Comparison Theorem with respect to
![]() $\{\lambda _{k}\}$
holds:
$\{\lambda _{k}\}$
holds:
Proof. While the result is well known, we defer giving details on the derived category identification ‘
![]() $(= \mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})$
’ until Proposition 4.3.
$(= \mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})$
’ until Proposition 4.3.
Step 0: Reductions and the inductive scheme.
We proceed stalkwise and induce on
![]() $\dim X$
. When
$\dim X$
. When
![]() $\dim X = 1$
the result is well known and easy to check. So assume
$\dim X = 1$
the result is well known and easy to check. So assume
![]() $\dim X = n$
and the claim holds for all reduced arrangements in
$\dim X = n$
and the claim holds for all reduced arrangements in
![]() $\mathbb {C}^{p}$
for
$\mathbb {C}^{p}$
for
![]() $p < n$
. Let
$p < n$
. Let
![]() $\mathfrak {x} \in X$
and E the smallest edge containing
$\mathfrak {x} \in X$
and E the smallest edge containing
![]() $\mathfrak {x}$
. If the subarrangement
$\mathfrak {x}$
. If the subarrangement
![]() $f^{\prime }$
consisting of all hyperplanes containing
$f^{\prime }$
consisting of all hyperplanes containing
![]() $\mathfrak {x}$
is of rank less than
$\mathfrak {x}$
is of rank less than
![]() $\dim X$
, then the induction hypothesis applies. For if V is a small Stein containing
$\dim X$
, then the induction hypothesis applies. For if V is a small Stein containing
![]() $\mathfrak {x}$
and
$\mathfrak {x}$
and
 $$\begin{align*}\omega^{\prime} = \sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \frac{df_{k}}{f_{k}}, \end{align*}$$
$$\begin{align*}\omega^{\prime} = \sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \frac{df_{k}}{f_{k}}, \end{align*}$$
then Lemma 3.2 says Equation (3.3) holds at
![]() $\mathfrak {x}$
is if and only if
$\mathfrak {x}$
is if and only if ![]() holds at
holds at
![]() $\mathfrak {x}$
. Since
$\mathfrak {x}$
. Since
![]() $f^{\prime }$
is of rank less than
$f^{\prime }$
is of rank less than
![]() $\dim X$
at
$\dim X$
at
![]() $\mathfrak {x}$
it is a product, and we use Lemma 3.3 to invoke the inductive hypothesis. Note that
$\mathfrak {x}$
it is a product, and we use Lemma 3.3 to invoke the inductive hypothesis. Note that
![]() $\omega ^{\prime }$
satisfies its version of Equation (3.2) since
$\omega ^{\prime }$
satisfies its version of Equation (3.2) since
![]() $\omega $
satisfies Equation (3.2) itself.
$\omega $
satisfies Equation (3.2) itself.
If the subarrangement
![]() $f^{\prime }$
at
$f^{\prime }$
at
![]() $\mathfrak {x}$
has rank n, we may change coordinates and assume that
$\mathfrak {x}$
has rank n, we may change coordinates and assume that
![]() $\mathfrak {x} = 0$
and
$\mathfrak {x} = 0$
and
![]() $f^{\prime }$
is central and essential. By Lemma 3.2, the quasi-isomorphism (3.3) holds at
$f^{\prime }$
is central and essential. By Lemma 3.2, the quasi-isomorphism (3.3) holds at
![]() $\mathfrak {x}$
exactly when the corresponding Twisted Logarithmic Comparison Theorem holds for
$\mathfrak {x}$
exactly when the corresponding Twisted Logarithmic Comparison Theorem holds for
![]() $f^{\prime }$
and
$f^{\prime }$
and
![]() $\omega ^{\prime }$
at
$\omega ^{\prime }$
at
![]() $0$
(in these new coordinates).
$0$
(in these new coordinates).
Therefore, it suffices to prove the following: If
![]() $\mathscr {A}$
is a central, essential, reduced hyperplane arrangement such that the Equation (3.3) holds at all points outside of
$\mathscr {A}$
is a central, essential, reduced hyperplane arrangement such that the Equation (3.3) holds at all points outside of
![]() $0$
, then Equation (3.3) holds at
$0$
, then Equation (3.3) holds at
![]() $0$
. By Lemma 3.1, we may verify this (equivalently) by checking Equation (3.3) holds at a small open Stein
$0$
. By Lemma 3.1, we may verify this (equivalently) by checking Equation (3.3) holds at a small open Stein
![]() $V \ni 0$
.
$V \ni 0$
.
Step 1: Setting up the spectral sequences.
For the rest of the proof, we inhabit the spectral sequence infrastructure from the proof of Theorem 1.1 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9] but refine it using the results of our previous sections. Let V be small Stein open about
![]() $0$
. Define the Stein opens
$0$
. Define the Stein opens
![]() $V_{i} = V \setminus \{x_{i} = 0\}$
and
$V_{i} = V \setminus \{x_{i} = 0\}$
and
![]() $V_{i}^{\prime } = V_{i} \setminus (V \cap \mathscr {A})$
. We have Stein open covers
$V_{i}^{\prime } = V_{i} \setminus (V \cap \mathscr {A})$
. We have Stein open covers
![]() $\{V_{i}\}$
and
$\{V_{i}\}$
and
![]() $\{V_{i}^{\prime }\}$
of
$\{V_{i}^{\prime }\}$
of
![]() $V \setminus 0$
and
$V \setminus 0$
and
![]() $V \setminus (V \cap \mathscr {A})$
respectively. Consider the following two double complexes with objects:
$V \setminus (V \cap \mathscr {A})$
respectively. Consider the following two double complexes with objects:
 $$ \begin{align*} K^{p, q} &= \bigoplus_{1 \leq i_{1} \leq \cdots \leq i_{q} \leq n} \Gamma(\bigcap_{i=0}^{q} V_{i_{j}}, \Omega_{X}^{p}(\log \mathscr{A})); \\ \widetilde{K}^{p, q} &= \bigoplus_{1 \leq i_{1} \leq \cdots \leq i_{q} \leq n} \Gamma(\bigcap_{i=0}^{q} V_{i_{j}}^{\prime}, \Omega_{X}^{p}(\star \mathscr{A})). \end{align*} $$
$$ \begin{align*} K^{p, q} &= \bigoplus_{1 \leq i_{1} \leq \cdots \leq i_{q} \leq n} \Gamma(\bigcap_{i=0}^{q} V_{i_{j}}, \Omega_{X}^{p}(\log \mathscr{A})); \\ \widetilde{K}^{p, q} &= \bigoplus_{1 \leq i_{1} \leq \cdots \leq i_{q} \leq n} \Gamma(\bigcap_{i=0}^{q} V_{i_{j}}^{\prime}, \Omega_{X}^{p}(\star \mathscr{A})). \end{align*} $$
Each complex is positioned in the lattice
![]() $\mathbb {Z}^{2}$
so that, for example,
$\mathbb {Z}^{2}$
so that, for example,
![]() $K^{p,q}$
, occurs in row p and column q.
$K^{p,q}$
, occurs in row p and column q.
![]() $K^{\bullet , \bullet }$
has horizontal differential the Čech differential and vertical differential
$K^{\bullet , \bullet }$
has horizontal differential the Čech differential and vertical differential
![]() $\nabla _{\omega }$
;
$\nabla _{\omega }$
;
![]() $\widetilde {K}^{\bullet , \bullet }$
has the same. And restriction commutes with the differentials, giving a map
$\widetilde {K}^{\bullet , \bullet }$
has the same. And restriction commutes with the differentials, giving a map
![]() $\rho _{0}^{\bullet , \bullet }: K^{\bullet , \bullet } \to \widetilde {K}^{\bullet , \bullet }$
.
$\rho _{0}^{\bullet , \bullet }: K^{\bullet , \bullet } \to \widetilde {K}^{\bullet , \bullet }$
.
We will consider the resulting four spectral sequences arising from these double complexes using similar notation as in [Reference Castro-Jiménez, Narváez-Macarro and Mond9]. As shorthand,
![]() $^{\prime }(-)$
denotes the spectral sequence first taking cohomology vertically and
$^{\prime }(-)$
denotes the spectral sequence first taking cohomology vertically and
![]() $^{\prime \prime }(-)$
first taking cohomology horizontally. To be precise:
$^{\prime \prime }(-)$
first taking cohomology horizontally. To be precise:
 $$ \begin{align*} ^{\prime}E_{1}^{p,q} &= \bigoplus_{1 \leq i_{0} \leq \cdots \leq i_{q} \leq n} H^{p} (\Gamma(\bigcap_{j=0}^{q} V_{i_{j}}, (\Omega_{X}^{\bullet}(\log \mathscr{A}), \nabla_{\omega}))); \\^{\prime \prime}E_{1}^{p,q} &= H^{q}(V \setminus 0, \Omega_{X}^{p}(\log \mathscr{A})); \\^{\prime}\widetilde{E}_{1}^{p,q} &= \bigoplus_{1 \leq i_{0} \leq \cdots \leq i_{q} \leq n} H^{p} (\Gamma(\bigcap_{j=0}^{q} V_{i_{j}}^{\prime} , (\Omega_{X}^{\bullet}(\star \mathscr{A}), \nabla_{\omega}))); \\^{\prime \prime}\widetilde{E}_{1}^{p,q} &= H^{q}(V \setminus (V \cap \mathscr{A}), \Omega_{X}^{p}(\star \mathscr{A})). \end{align*} $$
$$ \begin{align*} ^{\prime}E_{1}^{p,q} &= \bigoplus_{1 \leq i_{0} \leq \cdots \leq i_{q} \leq n} H^{p} (\Gamma(\bigcap_{j=0}^{q} V_{i_{j}}, (\Omega_{X}^{\bullet}(\log \mathscr{A}), \nabla_{\omega}))); \\^{\prime \prime}E_{1}^{p,q} &= H^{q}(V \setminus 0, \Omega_{X}^{p}(\log \mathscr{A})); \\^{\prime}\widetilde{E}_{1}^{p,q} &= \bigoplus_{1 \leq i_{0} \leq \cdots \leq i_{q} \leq n} H^{p} (\Gamma(\bigcap_{j=0}^{q} V_{i_{j}}^{\prime} , (\Omega_{X}^{\bullet}(\star \mathscr{A}), \nabla_{\omega}))); \\^{\prime \prime}\widetilde{E}_{1}^{p,q} &= H^{q}(V \setminus (V \cap \mathscr{A}), \Omega_{X}^{p}(\star \mathscr{A})). \end{align*} $$
Step 2: The
![]() $^{\prime }(-)$
spectral sequences.
$^{\prime }(-)$
spectral sequences.
By the inductive setup, Equation (3.3) holds at all points outside the origin. This means that the aformentioned natural map
is an isomorphism. As
![]() $\rho _{0}^{\bullet , \bullet }$
commutes with the differentials, this isomorphism continues on further pages. Since the spectral sequences converge, we have
$\rho _{0}^{\bullet , \bullet }$
commutes with the differentials, this isomorphism continues on further pages. Since the spectral sequences converge, we have
Step 3: The
![]() $^{\prime \prime }(-)$
spectral sequences.
$^{\prime \prime }(-)$
spectral sequences.
We first consider
![]() $^{\prime \prime }\widetilde {E}^{\bullet , \bullet }$
. Because
$^{\prime \prime }\widetilde {E}^{\bullet , \bullet }$
. Because
![]() $V \setminus (V \cap \mathscr {A})$
is Stein and
$V \setminus (V \cap \mathscr {A})$
is Stein and
![]() $\Omega _{X}^{p}(\star f) |_{U}$
is coherent, the higher sheaf cohomology
$\Omega _{X}^{p}(\star f) |_{U}$
is coherent, the higher sheaf cohomology
![]() $^{\prime \prime }\widetilde {E}_{1}^{p,q}$
vanishes for
$^{\prime \prime }\widetilde {E}_{1}^{p,q}$
vanishes for
![]() $q> 0$
. So this page’s nonzero terms lie on the y-axis, the spectral sequence converges on the second page where the nonzero terms still lie on the y-axis, and
$q> 0$
. So this page’s nonzero terms lie on the y-axis, the spectral sequence converges on the second page where the nonzero terms still lie on the y-axis, and
We claim
![]() $^{\prime \prime }E^{\bullet , \bullet }$
has the same vanishing behavior. Combine the long exact sequence of cohomology supported on
$^{\prime \prime }E^{\bullet , \bullet }$
has the same vanishing behavior. Combine the long exact sequence of cohomology supported on
![]() $\{0\}$
$\{0\}$
with the higher cohomological vanishing of
![]() $H^{q}(V, \Omega _{X}^{p}(\log \mathscr {A}))$
for
$H^{q}(V, \Omega _{X}^{p}(\log \mathscr {A}))$
for
![]() $q \geq 1$
, to get a natural isomorphism
$q \geq 1$
, to get a natural isomorphism
for all
![]() $q \geq 1$
. By excision,
$q \geq 1$
. By excision,
Again, use the long exact sequence of cohomology supported on
![]() $\{0\}$
to get
$\{0\}$
to get
for all
![]() $q \geq 1$
. Since
$q \geq 1$
. Since
![]() $\{D(x_{i})\}_{1 \leq i \leq n}$
is an open cover of
$\{D(x_{i})\}_{1 \leq i \leq n}$
is an open cover of
![]() $X \setminus 0$
and since every
$X \setminus 0$
and since every
![]() $D(x_{i})$
along with every intersection of elements of the
$D(x_{i})$
along with every intersection of elements of the
![]() $\{D(x_{i})\}$
is a Stein manifold, the Čech complex
$\{D(x_{i})\}$
is a Stein manifold, the Čech complex
![]() $C^{\bullet }(\{D(x_{i})\}, \Omega _{X}^{p}(\log \mathscr {A}))$
computes the sheaf cohomology
$C^{\bullet }(\{D(x_{i})\}, \Omega _{X}^{p}(\log \mathscr {A}))$
computes the sheaf cohomology
![]() $H^{\bullet }(X \setminus 0, \Omega _{X}^{p}(\log \mathscr {A}))$
.
$H^{\bullet }(X \setminus 0, \Omega _{X}^{p}(\log \mathscr {A}))$
.
Combining these equivalences and using the notation of subsection 2.3 yields
for all
![]() $q \geq 1$
. The second page
$q \geq 1$
. The second page
![]() $^{\prime \prime }E_{2}^{\bullet , \bullet }$
arises from the first by taking cohomology vertically with respect to the differential
$^{\prime \prime }E_{2}^{\bullet , \bullet }$
arises from the first by taking cohomology vertically with respect to the differential
![]() $\nabla _{\omega }$
. So
$\nabla _{\omega }$
. So
for all
![]() $q \geq 1.$
Now, our condition on the weights (3.2) considered at the origin become
$q \geq 1.$
Now, our condition on the weights (3.2) considered at the origin become
![]() $\sum \lambda _{k} \notin \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(\mathscr {A})\}}$
. So we may apply Corollary 2.31 to Equation (3.6), deducing
$\sum \lambda _{k} \notin \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(\mathscr {A})\}}$
. So we may apply Corollary 2.31 to Equation (3.6), deducing
![]() $^{\prime \prime }E_{2}^{p,q}$
vanishes for
$^{\prime \prime }E_{2}^{p,q}$
vanishes for
![]() $q \geq 1$
. Therefore, the nonzero terms of the second page
$q \geq 1$
. Therefore, the nonzero terms of the second page
![]() $^{\prime \prime }E_{2}^{\bullet , \bullet }$
all lie on the y-axis, the spectral sequence converges on this second page, and
$^{\prime \prime }E_{2}^{\bullet , \bullet }$
all lie on the y-axis, the spectral sequence converges on this second page, and
Since
![]() $X = \mathbb {C}^{n}$
with
$X = \mathbb {C}^{n}$
with
![]() $n \geq 2$
by assumption, the reflexivity of
$n \geq 2$
by assumption, the reflexivity of
![]() $\Omega _{X}^{j}(\log \mathscr {A})$
(see, for example, Proposition 1.5 [Reference Holland and Mond19]) implies that the global sections of
$\Omega _{X}^{j}(\log \mathscr {A})$
(see, for example, Proposition 1.5 [Reference Holland and Mond19]) implies that the global sections of
![]() $V \setminus 0$
are the global sections of V, meaning the only nonzero terms of the second page
$V \setminus 0$
are the global sections of V, meaning the only nonzero terms of the second page
![]() $^{\prime \prime }E_{2}^{\bullet , \bullet }$
are
$^{\prime \prime }E_{2}^{\bullet , \bullet }$
are
Step 4: The end.
Because
![]() $^{\prime \prime }E_{2}^{\bullet ,\bullet }$
consists of only one column on the y-axis, convergence to
$^{\prime \prime }E_{2}^{\bullet ,\bullet }$
consists of only one column on the y-axis, convergence to
![]() $H^{\bullet }\text {Tot}(K^{\bullet ,\bullet })$
happens on the second page. And because there is only one column, the induced filtration on
$H^{\bullet }\text {Tot}(K^{\bullet ,\bullet })$
happens on the second page. And because there is only one column, the induced filtration on
![]() $H^{\bullet }\text {Tot}(K^{\bullet ,\bullet })$
is trivial. Using Equation (3.7), we have
$H^{\bullet }\text {Tot}(K^{\bullet ,\bullet })$
is trivial. Using Equation (3.7), we have
Similarly,
![]() $^{\prime \prime }\widetilde {E}_{2}^{\bullet ,\bullet }$
has only one column on the y-axis, so convergence to
$^{\prime \prime }\widetilde {E}_{2}^{\bullet ,\bullet }$
has only one column on the y-axis, so convergence to
![]() $H^{\bullet } \text {Tot}(\widetilde {K}^{\bullet , \bullet })$
happens on the second page and the isomorphism has no graded data. Using Equation (3.5), we have
$H^{\bullet } \text {Tot}(\widetilde {K}^{\bullet , \bullet })$
happens on the second page and the isomorphism has no graded data. Using Equation (3.5), we have
On the other hand, the isomorphism
![]() $\enspace ^{\prime }E_{\infty }^{\bullet , \bullet } \xrightarrow[]{\simeq } \enspace ^{\prime }\widetilde {E}_{\infty }^{\bullet , \bullet }$
from Equation (3.4) gives (ignoring the extra graded data) the natural isomorphism
$\enspace ^{\prime }E_{\infty }^{\bullet , \bullet } \xrightarrow[]{\simeq } \enspace ^{\prime }\widetilde {E}_{\infty }^{\bullet , \bullet }$
from Equation (3.4) gives (ignoring the extra graded data) the natural isomorphism
Putting the three displayed equations of this step together produces
which is what we required.
Remark 3.5. The base case of the induction,
![]() $\mathscr {A} = \operatorname {\mathrm {V}}(x)$
, requires
$\mathscr {A} = \operatorname {\mathrm {V}}(x)$
, requires
![]() $\mathbb {Z}_{\geq 1}$
in Equation (3.2); the base case fails if
$\mathbb {Z}_{\geq 1}$
in Equation (3.2); the base case fails if
![]() $\mathbb {Z}_{\geq 2}$
is used in Equation (3.2) instead.
$\mathbb {Z}_{\geq 2}$
is used in Equation (3.2) instead.
Let us record two immediate corollaries. As it is of independent interest, we state the untwisted version:
Corollary 3.6 (Analytic Logarithmic Comparison Theorem).
For a reduced hyperplane arrangement
![]() $\mathscr {A}$
, the analytic Logarithmic Comparison Theorem holds:
$\mathscr {A}$
, the analytic Logarithmic Comparison Theorem holds:
Proof. Use Theorem 3.4, and set all the weights
![]() $\{\lambda _{k}\}$
to zero.
$\{\lambda _{k}\}$
to zero.
We also obtain a global version as in Corollary 1.4 of [Reference Castro-Jiménez, Narváez-Macarro and Mond9]. We continue to not require centrality.
Corollary 3.7. Let
![]() $f = f_{1} \cdots f_{d} \in R$
be a reduced hyperplane arrangement
$f = f_{1} \cdots f_{d} \in R$
be a reduced hyperplane arrangement
![]() $\mathscr {A}$
equipped with a factorization into linear forms. Suppose that
$\mathscr {A}$
equipped with a factorization into linear forms. Suppose that
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
are weights such that, for each edge
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
are weights such that, for each edge
![]() $E \in \mathscr {L}(\mathscr {A})$
,
$E \in \mathscr {L}(\mathscr {A})$
,
 $$ \begin{align*} \sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*} $$
$$ \begin{align*} \sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*} $$
Let
![]() $\omega = \sum _{k} \lambda _{k} \frac {df_{k}}{f_{k}}$
be the logarithmic one form determined by the
$\omega = \sum _{k} \lambda _{k} \frac {df_{k}}{f_{k}}$
be the logarithmic one form determined by the
![]() $\{\lambda _{k}\}$
. Then the global analytic Twisted Logarithmic Comparison Theorem holds:
$\{\lambda _{k}\}$
. Then the global analytic Twisted Logarithmic Comparison Theorem holds:
where ‘
![]() $(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\exp (\boldsymbol {\lambda })}))$
’ means there are cohomological isomorphisms.
$(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\exp (\boldsymbol {\lambda })}))$
’ means there are cohomological isomorphisms.
Proof. The quasi-isomorphism induced by inclusion in Theorem 3.4 gives isomorphisms in hypercohomology:
Since X and
![]() $U = X \setminus \mathscr {A}$
are Stein and
$U = X \setminus \mathscr {A}$
are Stein and
![]() $\Omega _{X}^{j}(\log \mathscr {A})$
and
$\Omega _{X}^{j}(\log \mathscr {A})$
and
![]() $\Omega _{U}^{j}$
are coherent, their higher sheaf cohomology vanishes. So the hypercohomology in Equation (3.8) amounts to taking global sections and then taking cohomology. This gives the promised quasi-isomorphism. As for the claim involving ‘
$\Omega _{U}^{j}$
are coherent, their higher sheaf cohomology vanishes. So the hypercohomology in Equation (3.8) amounts to taking global sections and then taking cohomology. This gives the promised quasi-isomorphism. As for the claim involving ‘
![]() $(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\exp (\boldsymbol {\lambda })}))$
’, it is well known that
$(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\exp (\boldsymbol {\lambda })}))$
’, it is well known that
![]() $\textbf {H}^{t} (\mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}) = H^{t}(U, \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})$
.
$\textbf {H}^{t} (\mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}) = H^{t}(U, \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})$
.
3.2. The algebraic case
Now, we turn to the problem of the algebraic Twisted Logarithmic Comparison Theorem. We cannot always repeat the proof of Theorem 3.4 because of Lemma 3.2: This construction requires multiplying by
![]() $f_{k}^{\lambda _{k}}$
at places where
$f_{k}^{\lambda _{k}}$
at places where
![]() $f_{k}$
is a unit. Because
$f_{k}$
is a unit. Because
![]() $\lambda _{k}$
may not be integral, in the algebraic category this may be nonsensical.
$\lambda _{k}$
may not be integral, in the algebraic category this may be nonsensical.
Nevertheless, when
![]() $\mathscr {A}$
is central we can deduce the algebraic Twisted Logarithmic Comparison Theorem from the analytic one. We highlight that the cohomology of the complement U in the attached local system is computed by a particular homogeneous subcomplex of the twisted logarithmic de Rham complex. So computing the complement’s cohomology is a finite-dimensional linear algebra problem.
$\mathscr {A}$
is central we can deduce the algebraic Twisted Logarithmic Comparison Theorem from the analytic one. We highlight that the cohomology of the complement U in the attached local system is computed by a particular homogeneous subcomplex of the twisted logarithmic de Rham complex. So computing the complement’s cohomology is a finite-dimensional linear algebra problem.
Theorem 3.8 (Algebraic Twisted Logarithmic Comparison Theorem).
Let
![]() $f = f_{1} \cdots f_{d}$
cut out a central, reduced hyperplane arrangement
$f = f_{1} \cdots f_{d}$
cut out a central, reduced hyperplane arrangement
![]() $\mathscr {A}$
and let
$\mathscr {A}$
and let
![]() $\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
be weights such that, for each edge E,
$\lambda _{1}, \dots , \lambda _{d} \in \mathbb {C}$
be weights such that, for each edge E,
 $$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*}$$
$$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*}$$
Furthermore, let
![]() $\omega = \sum _{k} \lambda _{k} df_{k} / f_{k}$
. Then the algebraic Twisted Logarithmic Comparison Theorem holds along with an additional quasi-isomorphism:
$\omega = \sum _{k} \lambda _{k} df_{k} / f_{k}$
. Then the algebraic Twisted Logarithmic Comparison Theorem holds along with an additional quasi-isomorphism:
Here,
![]() $(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}))$
means there are isomorphisms on the level of cohomology and
$(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}))$
means there are isomorphisms on the level of cohomology and
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A})_{-\iota _{E}(\omega )}, \nabla _{\omega })$
is the homogeneous subcomplex of degree
$(\Omega _{R}^{\bullet }(\log \mathscr {A})_{-\iota _{E}(\omega )}, \nabla _{\omega })$
is the homogeneous subcomplex of degree
![]() $- \iota _{E}(\omega ) = -( \lambda _{1} + \cdots + \lambda _{d})$
, which is a complex of finite-dimensional
$- \iota _{E}(\omega ) = -( \lambda _{1} + \cdots + \lambda _{d})$
, which is a complex of finite-dimensional
![]() $\mathbb {C}$
-vector spaces.
$\mathbb {C}$
-vector spaces.
Proof. The claim involving
![]() $(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\exp (\boldsymbol {\lambda })}))$
follows from the algebraic de Rham theorems of Deligne and Grothendieck, cf. [Reference Orlik25]. That, when
$(\simeq H^{\bullet }(U, \operatorname {\mathrm {L}}_{\exp (\boldsymbol {\lambda })}))$
follows from the algebraic de Rham theorems of Deligne and Grothendieck, cf. [Reference Orlik25]. That, when
![]() $\mathscr {A}$
is central, the map
$\mathscr {A}$
is central, the map ![]() is a quasi-isomorphism is the first part of Proposition 2.15. As for the finite-dimensional claim: Since R and
is a quasi-isomorphism is the first part of Proposition 2.15. As for the finite-dimensional claim: Since R and
![]() $\Omega _{R}^{j}(\log \mathscr {A})$
do not have elements of arbitrary large negative degree, the
$\Omega _{R}^{j}(\log \mathscr {A})$
do not have elements of arbitrary large negative degree, the
![]() $-\iota _{E}(\omega )$
-homogeneous subspace
$-\iota _{E}(\omega )$
-homogeneous subspace
![]() $\Omega _{R}^{j}(\log \mathscr {A})_{-\iota _{E}(\omega )}$
is finite dimensional.
$\Omega _{R}^{j}(\log \mathscr {A})_{-\iota _{E}(\omega )}$
is finite dimensional.
It remains to validate the purported quasi-isomorphism ![]() . Consider the following commutative diagram:
. Consider the following commutative diagram:

The displayed quasi-isomorphisms are justified by Lemma 2.23 and Proposition 2.15. As for displayed equalities, let
![]() $\eta = \sum _{p} \eta _{p} \in \Omega _{X,0}^{j}(\log \mathscr {A})$
be the homogeneous decomposition of
$\eta = \sum _{p} \eta _{p} \in \Omega _{X,0}^{j}(\log \mathscr {A})$
be the homogeneous decomposition of
![]() $\eta $
as in subsection 2.3, though here this arises from, up to a pole along f, convergent formal power series in
$\eta $
as in subsection 2.3, though here this arises from, up to a pole along f, convergent formal power series in
![]() $\mathbb {C}[[x_{1}, \dots , x_{n}]]$
as opposed to a Laurent series. If
$\mathbb {C}[[x_{1}, \dots , x_{n}]]$
as opposed to a Laurent series. If
![]() $\eta $
is homogeneous of weight
$\eta $
is homogeneous of weight
![]() $-\iota _{E}(\omega )$
, then
$-\iota _{E}(\omega )$
, then
![]() $\eta = \eta _{-\iota _{E}(\omega )}$
, the latter of which is, up to its pole along
$\eta = \eta _{-\iota _{E}(\omega )}$
, the latter of which is, up to its pole along
![]() $\mathscr {A}$
, an algebraic j-form. So
$\mathscr {A}$
, an algebraic j-form. So
![]() $\eta _{-\iota _{E}(\omega )} \in \Omega _{R}^{j}(\log \mathscr {A})_{-\iota _{E}(\omega )}$
. The same story applies for the nonlogarithmic displayed equality. This diagram concludes the proof: Theorem 3.4 implies the topmost horizontal map is a quasi-isomorphism, whence the bottom-most horizontal map is a quasi-isomorphism.
$\eta _{-\iota _{E}(\omega )} \in \Omega _{R}^{j}(\log \mathscr {A})_{-\iota _{E}(\omega )}$
. The same story applies for the nonlogarithmic displayed equality. This diagram concludes the proof: Theorem 3.4 implies the topmost horizontal map is a quasi-isomorphism, whence the bottom-most horizontal map is a quasi-isomorphism.
Remark 3.9. The proof of the Theorem 3.8 nontrivially exploits the centrality assumption. Without centrality
![]() $\Omega _R^j(\log \mathscr {A})$
may not have a decomposition into a direct sum of homogeneous components, as the homogeneous terms of a logarithmic j-form may not be logarithmic. Consequently,
$\Omega _R^j(\log \mathscr {A})$
may not have a decomposition into a direct sum of homogeneous components, as the homogeneous terms of a logarithmic j-form may not be logarithmic. Consequently,
![]() $(\Omega _{R}^{\bullet }(\log \mathscr {A})_{-\iota _{E}(\omega )}, \nabla _{\omega })$
may be relatively vacuous, preventing any form of Equation (3.9) holding and in turn obstructing our method of deducing Theorem 3.8 from Theorem 3.4. For similar reasons, one should not expect the quasi-isomorphism
$(\Omega _{R}^{\bullet }(\log \mathscr {A})_{-\iota _{E}(\omega )}, \nabla _{\omega })$
may be relatively vacuous, preventing any form of Equation (3.9) holding and in turn obstructing our method of deducing Theorem 3.8 from Theorem 3.4. For similar reasons, one should not expect the quasi-isomorphism ![]() of Theorem 3.8 to hold (or be sensible) without a centrality assumption. On the other hand, the quasi-isomorphism
of Theorem 3.8 to hold (or be sensible) without a centrality assumption. On the other hand, the quasi-isomorphism ![]() of Theorem 3.8 may hold without centrality. One could try to check this at each maximal ideal, where
of Theorem 3.8 may hold without centrality. One could try to check this at each maximal ideal, where
![]() $\mathscr {A}$
can be assumed to be central, but outside the analytic category technical issues related to
$\mathscr {A}$
can be assumed to be central, but outside the analytic category technical issues related to
![]() $\nabla _\omega $
appear (see the proof of Lemma 3.2).
$\nabla _\omega $
appear (see the proof of Lemma 3.2).
This paper’s original objective was to solve Terao’s Conjecture 1.1, that is, to prove the algebraic (untwisted) Logarithmic Comparison Theorem. (This evolved out of Conjecture 3.1 of [Reference Terao33].) We can now do this quite easily, and, for aesthetic reasons, we include Brieskorn’s Theorem in its statement. Note that we do not require centrality, which forces us to do more work.
Corollary 3.10 (Algebraic Logarithmic Comparison Theorem).
Let
![]() $\mathscr {A}$
be a reduced hyperplane arrangement. Then the algebraic Logarithmic Comparison Theorem holds giving a sequence of quasi-isomorphisms
$\mathscr {A}$
be a reduced hyperplane arrangement. Then the algebraic Logarithmic Comparison Theorem holds giving a sequence of quasi-isomorphisms
Moreover,
![]() $A^{j}(\mathscr {A}) = H^{j}(\Omega _{R}^{\bullet }(\log \mathscr {A}), d)$
.
$A^{j}(\mathscr {A}) = H^{j}(\Omega _{R}^{\bullet }(\log \mathscr {A}), d)$
.
Proof. Brieskorn’s Theorem says the composition of maps in Equation (3.10) is a quasi-isomorphism, so if we show the algebraic Logarithmic Comparison Theorem is true we can conclude the first map in Equation (3.10) is a quasi-isomorphism. From this, the claim
![]() $A^{j}(\mathscr {A}) = H^{j}(\Omega _{R}^{\bullet }(\log \mathscr {A}), d)$
is easy: The implicit differential of exterior differentiation on
$A^{j}(\mathscr {A}) = H^{j}(\Omega _{R}^{\bullet }(\log \mathscr {A}), d)$
is easy: The implicit differential of exterior differentiation on
![]() $A^{\bullet }(\mathscr {A})$
is trivial.
$A^{\bullet }(\mathscr {A})$
is trivial.
It remains to prove the algebraic Logarithmic Comparison Theorem. When
![]() $\mathscr {A}$
is central this follows from Theorem 3.8 by setting the weights to zero.
$\mathscr {A}$
is central this follows from Theorem 3.8 by setting the weights to zero.
For noncentral
![]() $\mathscr {A}$
, first note that we can define a sheaf-theoretic version of the algebraic twisted logarithmic and rational de Rham complexes:
$\mathscr {A}$
, first note that we can define a sheaf-theoretic version of the algebraic twisted logarithmic and rational de Rham complexes:
![]() $(\Omega _{X_{\operatorname {\mathrm {alg}}}}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
and
$(\Omega _{X_{\operatorname {\mathrm {alg}}}}^{\bullet }(\log \mathscr {A}), \nabla _{\omega })$
and
![]() $(\Omega _{X_{\operatorname {\mathrm {alg}}}}^{\bullet }(\star \mathscr {A}), \nabla _{\omega })$
, respectively. These are complexes of
$(\Omega _{X_{\operatorname {\mathrm {alg}}}}^{\bullet }(\star \mathscr {A}), \nabla _{\omega })$
, respectively. These are complexes of
![]() $\mathscr {O}_{X_{\operatorname {\mathrm {alg}}}}$
-modules. If we prove
$\mathscr {O}_{X_{\operatorname {\mathrm {alg}}}}$
-modules. If we prove
then we can deduce that taking global sections preserves the quasi-isomorphism by arguing as in Corollary 3.7. The proof of Theorem 3.4 gives a proof of Equation (3.11) once you replace every occurrence of ‘Stein’ with ‘affine’. Indeed, note that: Lemma 3.1 holds after replacing ‘Stein’ with ‘affine’; Lemma 3.2 is never invoked since
![]() $\omega = 0$
in our case; we may still use Lemma 3.3 since the change of coordinates is linear, and hence algebraic; in Step 3 of the proof,
$\omega = 0$
in our case; we may still use Lemma 3.3 since the change of coordinates is linear, and hence algebraic; in Step 3 of the proof,
![]() $E_{1}^{p,q} \simeq H_{0}^{q+1}(V, \Omega _{X}^{p}(\log \mathscr {A}))$
which is isomorphic to
$E_{1}^{p,q} \simeq H_{0}^{q+1}(V, \Omega _{X}^{p}(\log \mathscr {A}))$
which is isomorphic to
![]() $H_{\mathfrak {m}}^{q+1}(\Omega _{R}^{p}(\log \mathscr {A}))$
by Exercise III.2.3, III.3.3 [Reference Hartshorne18], and so Corollary 2.30 can be applied to
$H_{\mathfrak {m}}^{q+1}(\Omega _{R}^{p}(\log \mathscr {A}))$
by Exercise III.2.3, III.3.3 [Reference Hartshorne18], and so Corollary 2.30 can be applied to
![]() $E_{2}^{p,q}$
directly (i.e., without subsection 2.3 and subsection 2.6).
$E_{2}^{p,q}$
directly (i.e., without subsection 2.3 and subsection 2.6).
Remark 3.11. If
![]() $\mathscr {A}$
is central and the combinatorial conditions are satisfied, Equation (3.9) also shows that
$\mathscr {A}$
is central and the combinatorial conditions are satisfied, Equation (3.9) also shows that
3.3. Feasibility
In this minisicule section, we ask which rank one local systems can be studied by our assorted (un)Twisted Logarithmic Comparison Theorems. Recall that when
![]() $\mathscr {A}$
is central, this means computing
$\mathscr {A}$
is central, this means computing
![]() $(\mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\beta })})_{0}$
or
$(\mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\beta })})_{0}$
or
![]() $H^{\bullet }(U, \operatorname {\mathrm {L}}_{\boldsymbol {\beta }})$
is a finite-dimensional linear algebra problem (Theorem 3.8; Remark 3.11). The answer is: All such local systems are computable this way.
$H^{\bullet }(U, \operatorname {\mathrm {L}}_{\boldsymbol {\beta }})$
is a finite-dimensional linear algebra problem (Theorem 3.8; Remark 3.11). The answer is: All such local systems are computable this way.
Proposition 3.12. For an arbitrary rank one local system
![]() $\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
on U, there exists a
$\operatorname {\mathrm {L}}_{\boldsymbol {\beta }}$
on U, there exists a
![]() $\boldsymbol {\lambda } \in \operatorname {\mathrm {Exp}}^{-1}(\boldsymbol {\beta })$
such that all the aforementioned Twisted Logarithmic Comparison Theorems hold with respect to the weights
$\boldsymbol {\lambda } \in \operatorname {\mathrm {Exp}}^{-1}(\boldsymbol {\beta })$
such that all the aforementioned Twisted Logarithmic Comparison Theorems hold with respect to the weights
![]() $\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}).$
$\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}).$
Proof. We must produce
![]() $\boldsymbol {\lambda } \in \operatorname {\mathrm {Exp}}^{-1}(\boldsymbol {\beta })$
such that the combinatorial arithmetical restrictions
$\boldsymbol {\lambda } \in \operatorname {\mathrm {Exp}}^{-1}(\boldsymbol {\beta })$
such that the combinatorial arithmetical restrictions
 $$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}} \end{align*}$$
$$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}} \end{align*}$$
are satisfied at each edge E of the intersection lattice. To do this, pick an arbitrary
![]() $\boldsymbol {\lambda } \in \operatorname {\mathrm {Exp}}^{-1}(\boldsymbol {\beta })$
and replace
$\boldsymbol {\lambda } \in \operatorname {\mathrm {Exp}}^{-1}(\boldsymbol {\beta })$
and replace
![]() $\boldsymbol {\lambda }$
with
$\boldsymbol {\lambda }$
with
![]() $\boldsymbol {\lambda } - \textbf {z}$
, where
$\boldsymbol {\lambda } - \textbf {z}$
, where
![]() $\textbf {z} = (z, \dots , z) \in \mathbb {Z}^{d}$
and
$\textbf {z} = (z, \dots , z) \in \mathbb {Z}^{d}$
and
![]() $z \gg 0$
.
$z \gg 0$
.
Remark 3.13.
-
(a) If we require
 $\mathscr {A}$
to be central and let
$\mathscr {A}$
to be central and let
 $P(\mathscr {A})$
be the associated projective arrangement, then the Leray spectral sequence of the fibration
$P(\mathscr {A})$
be the associated projective arrangement, then the Leray spectral sequence of the fibration
 $\mathbb {C}^{\star } \to \mathbb {C}^{n} \setminus \mathscr {A} \to \mathbb {P}^{n-1} \setminus P(\mathscr {A})$
gives a dictionary between cohomology of the affine complement with a rank one local system and the cohomology of the projective complement with the corresponding local system, cf. Theorem 5.2 [Reference Dimca15]. In the projective case, if we require the weights
$\mathbb {C}^{\star } \to \mathbb {C}^{n} \setminus \mathscr {A} \to \mathbb {P}^{n-1} \setminus P(\mathscr {A})$
gives a dictionary between cohomology of the affine complement with a rank one local system and the cohomology of the projective complement with the corresponding local system, cf. Theorem 5.2 [Reference Dimca15]. In the projective case, if we require the weights
 $\{\lambda _{k}\}$
to satisfy
$\{\lambda _{k}\}$
to satisfy
 $\lambda _{1} + \cdots + \lambda _{d} = 0$
, then it is proved in [Reference Esnault, Schechtman and Viehweg16] that there are similar combinatorial arithmetic conditions on the dense edges of the intersection lattice of
$\lambda _{1} + \cdots + \lambda _{d} = 0$
, then it is proved in [Reference Esnault, Schechtman and Viehweg16] that there are similar combinatorial arithmetic conditions on the dense edges of the intersection lattice of
 $\mathscr {A}$
that, when satisfied, ensure Here,
$\mathscr {A}$
that, when satisfied, ensure Here, $$\begin{align*}H^{\bullet}((A^{\bullet}(\mathscr{A}), \nabla_{\omega})) \simeq H^{\bullet}(U, \operatorname{\mathrm{L}}_{\operatorname{\mathrm{Exp}}(\boldsymbol{\lambda})}). \end{align*}$$
$$\begin{align*}H^{\bullet}((A^{\bullet}(\mathscr{A}), \nabla_{\omega})) \simeq H^{\bullet}(U, \operatorname{\mathrm{L}}_{\operatorname{\mathrm{Exp}}(\boldsymbol{\lambda})}). \end{align*}$$
 $(A^{\bullet }(\mathscr {A}), \nabla _{\omega })$
is the Orlik–Solomon algebra equipped with the differential
$(A^{\bullet }(\mathscr {A}), \nabla _{\omega })$
is the Orlik–Solomon algebra equipped with the differential
 $\omega \wedge $
, a twisted Orlik–Solomon algebra. Alternatively,
$\omega \wedge $
, a twisted Orlik–Solomon algebra. Alternatively,
 $A^{\bullet }(\mathscr {A})$
is canonically identified with the Brieskorn algebra: the algebra generated by wedge products of the one-forms
$A^{\bullet }(\mathscr {A})$
is canonically identified with the Brieskorn algebra: the algebra generated by wedge products of the one-forms
 $\{ df_{k} / f_{k} \}$
.
$\{ df_{k} / f_{k} \}$
.
-
(b) It is well known that not all rank one local systems can be computed by the machinery of the previous item since, in particular,
 $\lambda _{1} + \cdots + \lambda _{d} = 0$
may not be satisfied, cf. Example 3.14. The undetectable systems correspond to torsion translated subtori of the characteristic variety, cf. [Reference Cohen and Suciu12]. This is not a defect of [Reference Esnault, Schechtman and Viehweg16]: The invisibility of the torsion translated subtori is intrinsic to Orlik–Solomon methods.
$\lambda _{1} + \cdots + \lambda _{d} = 0$
may not be satisfied, cf. Example 3.14. The undetectable systems correspond to torsion translated subtori of the characteristic variety, cf. [Reference Cohen and Suciu12]. This is not a defect of [Reference Esnault, Schechtman and Viehweg16]: The invisibility of the torsion translated subtori is intrinsic to Orlik–Solomon methods. -
(c) In [Reference Saito29] (subsection 2.2), M. Saito removes the requirement
 $\lambda _{1} + \cdots + \lambda _{d} = 0$
at the cost of taking a resolution of singularities
$\lambda _{1} + \cdots + \lambda _{d} = 0$
at the cost of taking a resolution of singularities
 $(\widetilde {X}, \widetilde {\mathscr {A}}) \to (X, \mathscr {A})$
and doing the computations upstairs in
$(\widetilde {X}, \widetilde {\mathscr {A}}) \to (X, \mathscr {A})$
and doing the computations upstairs in
 $\widetilde {X}$
. This is difficult to use since, even for arrangements, resolutions of singularities are unwieldy.
$\widetilde {X}$
. This is difficult to use since, even for arrangements, resolutions of singularities are unwieldy.
Example 3.14 (Deleted
 $B_{3}$
arrangement).
$B_{3}$
arrangement).
Let
![]() $f = yz(x+y)(x-y)(x+z)(x-z)(y+z)(y-z)$
, let
$f = yz(x+y)(x-y)(x+z)(x-z)(y+z)(y-z)$
, let
![]() $\boldsymbol {\lambda } = (1/2,1/2, -1/2, -1/2, 1/4, 1/4, 1/4, 1/4)$
be a collection of weights, ordered by the factors listed and let
$\boldsymbol {\lambda } = (1/2,1/2, -1/2, -1/2, 1/4, 1/4, 1/4, 1/4)$
be a collection of weights, ordered by the factors listed and let
![]() $\omega $
be the associated one-form. This is a free arrangement with exponents
$\omega $
be the associated one-form. This is a free arrangement with exponents
![]() $\{1, 3, 4\}$
. The local system
$\{1, 3, 4\}$
. The local system
![]() $\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}$
on
$\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}$
on
![]() $U = \mathbb {C}^{3} \setminus \operatorname {\mathrm {V}}(f)$
belongs to a translated component of the rank one local systems on U, cf. Example 4.1 of [Reference Suciu31] or Section 3 of [Reference Cohen11]. So it is undetectable by any twisted Orlik–Solomon algebra:
$U = \mathbb {C}^{3} \setminus \operatorname {\mathrm {V}}(f)$
belongs to a translated component of the rank one local systems on U, cf. Example 4.1 of [Reference Suciu31] or Section 3 of [Reference Cohen11]. So it is undetectable by any twisted Orlik–Solomon algebra:
![]() $H^{k}(A^{\bullet }(\mathscr {A}), \nabla _{\omega }) = 0$
for
$H^{k}(A^{\bullet }(\mathscr {A}), \nabla _{\omega }) = 0$
for
![]() $0 \leq k \leq 3$
. In loc. cit. Suciu computes
$0 \leq k \leq 3$
. In loc. cit. Suciu computes
![]() $\dim _{\mathbb {C}}(H^{1}(U, \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})) = 1$
. The weights
$\dim _{\mathbb {C}}(H^{1}(U, \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})) = 1$
. The weights
![]() $\boldsymbol {\lambda }$
satisfy the conditions of our Twisted Logarithmic Comparison Theorems. Macaulay2 claims:
$\boldsymbol {\lambda }$
satisfy the conditions of our Twisted Logarithmic Comparison Theorems. Macaulay2 claims:
 $$ \begin{align*} \dim_{\mathbb{C}} (\text{im} [ \Omega_{R}^{1}(\log \mathscr{A})_{-1} \xrightarrow[]{\nabla_{\omega}} \Omega_{R}^{2}(\log \mathscr{A})_{-1}]) = 8;\\ \dim_{\mathbb{C}} (\text{im} [ \Omega_{R}^{2}(\log \mathscr{A})_{-1} \xrightarrow[]{\nabla_{\omega}} \Omega_{R}^{3}(\log \mathscr{A})_{-1}]) = 8. \end{align*} $$
$$ \begin{align*} \dim_{\mathbb{C}} (\text{im} [ \Omega_{R}^{1}(\log \mathscr{A})_{-1} \xrightarrow[]{\nabla_{\omega}} \Omega_{R}^{2}(\log \mathscr{A})_{-1}]) = 8;\\ \dim_{\mathbb{C}} (\text{im} [ \Omega_{R}^{2}(\log \mathscr{A})_{-1} \xrightarrow[]{\nabla_{\omega}} \Omega_{R}^{3}(\log \mathscr{A})_{-1}]) = 8. \end{align*} $$
Using Theorem 3.8, we compute the dimensions of the nonzero
![]() $H^{k}(U,\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})$
:
$H^{k}(U,\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })})$
:
 $$ \begin{align*} \dim_{\mathbb{C}}(H^{1}(U, \operatorname{\mathrm{L}}_{\operatorname{\mathrm{Exp}}(\boldsymbol{\lambda})})) = \dim_{\mathbb{C}} (H^{1}(\Omega_{R}^{\bullet}(\log f)_{-1}, \nabla_{\omega})) = 1; \\ \dim_{\mathbb{C}}(H^{2}(U, \operatorname{\mathrm{L}}_{\operatorname{\mathrm{Exp}}(\boldsymbol{\lambda})})) = \dim_{\mathbb{C}} (H^{2}(\Omega_{R}^{\bullet}(\log f)_{-1}, \nabla_{\omega})) = 8; \\ \dim_{\mathbb{C}}(H^{3}(U, \operatorname{\mathrm{L}}_{\operatorname{\mathrm{Exp}}(\boldsymbol{\lambda})})) = \dim_{\mathbb{C}} (H^{3}(\Omega_{R}^{\bullet}(\log f)_{-1}, \nabla_{\omega})) = 7. \end{align*} $$
$$ \begin{align*} \dim_{\mathbb{C}}(H^{1}(U, \operatorname{\mathrm{L}}_{\operatorname{\mathrm{Exp}}(\boldsymbol{\lambda})})) = \dim_{\mathbb{C}} (H^{1}(\Omega_{R}^{\bullet}(\log f)_{-1}, \nabla_{\omega})) = 1; \\ \dim_{\mathbb{C}}(H^{2}(U, \operatorname{\mathrm{L}}_{\operatorname{\mathrm{Exp}}(\boldsymbol{\lambda})})) = \dim_{\mathbb{C}} (H^{2}(\Omega_{R}^{\bullet}(\log f)_{-1}, \nabla_{\omega})) = 8; \\ \dim_{\mathbb{C}}(H^{3}(U, \operatorname{\mathrm{L}}_{\operatorname{\mathrm{Exp}}(\boldsymbol{\lambda})})) = \dim_{\mathbb{C}} (H^{3}(\Omega_{R}^{\bullet}(\log f)_{-1}, \nabla_{\omega})) = 7. \end{align*} $$
4. Applications to
 $\mathscr {D}_{X}$
-modules and Bernstein–Sato ideals
$\mathscr {D}_{X}$
-modules and Bernstein–Sato ideals
Hereafter, we will require
![]() $\mathscr {A}$
to be central. Let
$\mathscr {A}$
to be central. Let
![]() $\mathscr {D}_{X}$
be the analytic sheaf of
$\mathscr {D}_{X}$
be the analytic sheaf of
![]() $\mathbb {C}$
-linear differential operators. We will mostly focus on the analytic setting but will track statements that also work for the algebraic one.
$\mathbb {C}$
-linear differential operators. We will mostly focus on the analytic setting but will track statements that also work for the algebraic one.
Because the Logarithmic Comparison Theorem (twisted or otherwise) offers a quasi-isomorphism between the logarithmic de Rham complex and the meromorphic de Rham complex and because the meromorphic de Rham complex is obtained by applying the de Rham functor to a certain
![]() $\mathscr {D}_{X}$
-module, it is natural to hope for a intrinsic complex of
$\mathscr {D}_{X}$
-module, it is natural to hope for a intrinsic complex of
![]() $\mathscr {D}_{X}$
-modules whose image under the de Rham functor is the logarithmic de Rham complex. There is a good candidate for free divisors and the result is known for certain such free divisors; see [Reference Calderón Moreno and Narváez Macarro8] as well as the survey [Reference Narváez Macarro22]. Consequently, there is a package of
$\mathscr {D}_{X}$
-modules whose image under the de Rham functor is the logarithmic de Rham complex. There is a good candidate for free divisors and the result is known for certain such free divisors; see [Reference Calderón Moreno and Narváez Macarro8] as well as the survey [Reference Narváez Macarro22]. Consequently, there is a package of
![]() $\mathscr {D}_{X}$
-theoretic results divisors satisfying Logarithmic Comparison Theorems ‘ought’ to possess. For certain free divisors, the most thorough treatment is [Reference Narváez Macarro23], especially Theorem 4.7 and Corollary 4.2/4.3 from which most of the ‘expected’ properties discussed in [Reference Torrelli34] can be deduced in this case; see also loc. cit. and [Reference Narváez Macarro22] for more discussion. Despite having (un)Twisted Logarithmic Comparison Theorems for reduced hyperplane arrangements we do not have a good candidate for the ‘pre’-de Rham complex of
$\mathscr {D}_{X}$
-theoretic results divisors satisfying Logarithmic Comparison Theorems ‘ought’ to possess. For certain free divisors, the most thorough treatment is [Reference Narváez Macarro23], especially Theorem 4.7 and Corollary 4.2/4.3 from which most of the ‘expected’ properties discussed in [Reference Torrelli34] can be deduced in this case; see also loc. cit. and [Reference Narváez Macarro22] for more discussion. Despite having (un)Twisted Logarithmic Comparison Theorems for reduced hyperplane arrangements we do not have a good candidate for the ‘pre’-de Rham complex of
![]() $\mathscr {D}_{X}$
-modules corresponding to the logarithmic de Rham complex.
$\mathscr {D}_{X}$
-modules corresponding to the logarithmic de Rham complex.
Nevertheless, we are able to obtain many of the desired
![]() $\mathscr {D}_{X}$
-related results for reduced hyperplane arrangements f. In the first subsection, we study
$\mathscr {D}_{X}$
-related results for reduced hyperplane arrangements f. In the first subsection, we study
![]() $\mathscr {O}_{X}(\star f^{\boldsymbol {\lambda }})$
for a set of weights
$\mathscr {O}_{X}(\star f^{\boldsymbol {\lambda }})$
for a set of weights
![]() $\boldsymbol {\lambda } \in \mathbb {C}^{d}$
, showing that (Theorem 4.4) under familiar hypotheses on the weights,
$\boldsymbol {\lambda } \in \mathbb {C}^{d}$
, showing that (Theorem 4.4) under familiar hypotheses on the weights,
![]() $f^{-\textbf {1} + \boldsymbol {\lambda }}$
generates this
$f^{-\textbf {1} + \boldsymbol {\lambda }}$
generates this
![]() $\mathscr {D}_{X}$
-module. This should be thought of as a multivariate generalization of fact
$\mathscr {D}_{X}$
-module. This should be thought of as a multivariate generalization of fact
![]() $f^{-1}$
generates
$f^{-1}$
generates
![]() $\mathscr {O}_{X}(\star f)$
; the theorem recovers this univariate statement. We also justify our previous claim
$\mathscr {O}_{X}(\star f)$
; the theorem recovers this univariate statement. We also justify our previous claim
![]() $(\Omega _{X}^{\bullet }(\star \mathscr {A}), \nabla _{\omega }) = \mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}$
in the derived category (Proposition 4.3). In the second subsection, we give a sharp bound on the candidates of the codimension one components of the zero locus of the Bernstein–Sato ideal of f (for any factorization). This is Theorem 4.7 and should be thought of as a sort of generalization of M. Saito’s result [Reference Saito29] that the roots of the Bernstein–Sato polynomial of f live in
$(\Omega _{X}^{\bullet }(\star \mathscr {A}), \nabla _{\omega }) = \mathbf {R} j_{\star } \operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })}$
in the derived category (Proposition 4.3). In the second subsection, we give a sharp bound on the candidates of the codimension one components of the zero locus of the Bernstein–Sato ideal of f (for any factorization). This is Theorem 4.7 and should be thought of as a sort of generalization of M. Saito’s result [Reference Saito29] that the roots of the Bernstein–Sato polynomial of f live in
![]() $(-2 + 1/\deg (f), 0)$
– in fact, the univariate version of Theorem 4.7 gives a new proof of this fact.
$(-2 + 1/\deg (f), 0)$
– in fact, the univariate version of Theorem 4.7 gives a new proof of this fact.
4.1. Generators of twisted meromorphic powers
First, recall that
![]() $\mathscr {O}_{X}(\star \mathscr {A})$
is naturally a
$\mathscr {O}_{X}(\star \mathscr {A})$
is naturally a
![]() $\mathscr {D}_{X}$
-module: The action of a derivation on
$\mathscr {D}_{X}$
-module: The action of a derivation on
![]() $f^{-p} $
, for
$f^{-p} $
, for
![]() $p \in \mathbb {N}$
and with f defining
$p \in \mathbb {N}$
and with f defining
![]() $\mathscr {A}$
, is given by the chain rule. Nothing depends on the choice of defining equation for
$\mathscr {A}$
, is given by the chain rule. Nothing depends on the choice of defining equation for
![]() $\mathscr {A}$
and we note that the cyclic
$\mathscr {A}$
and we note that the cyclic
![]() $\mathscr {D}_{X}$
-module generated by
$\mathscr {D}_{X}$
-module generated by
![]() $f^{-p}$
sits inside
$f^{-p}$
sits inside
![]() $\mathscr {O}_{X}(\star \mathscr {A})$
. In particular, as
$\mathscr {O}_{X}(\star \mathscr {A})$
. In particular, as
![]() $\mathscr {D}_{X}$
-modules,
$\mathscr {D}_{X}$
-modules,
Now, let
![]() $f = f_{1} \cdots f_{d}$
be a factorization into irreducibles and take
$f = f_{1} \cdots f_{d}$
be a factorization into irreducibles and take
![]() $\textbf {p} \in \mathbb {Z}^{d}$
. Denote
$\textbf {p} \in \mathbb {Z}^{d}$
. Denote
![]() $f_{1}^{p_{1}} \cdots f_{d}^{p_{d}}$
by
$f_{1}^{p_{1}} \cdots f_{d}^{p_{d}}$
by
![]() $f^{\textbf {p}}$
. Then, as
$f^{\textbf {p}}$
. Then, as
![]() $\mathscr {D}_{X}$
-modules,
$\mathscr {D}_{X}$
-modules,
 $$\begin{align*}\bigcup_{\textbf{p} \in \mathbb{N}^{d}} \mathscr{D}_{X} f^{ -\textbf{p}} = \mathscr{O}_{X}(\star \mathscr{A}) = \mathscr{O}_{X}(\star f). \end{align*}$$
$$\begin{align*}\bigcup_{\textbf{p} \in \mathbb{N}^{d}} \mathscr{D}_{X} f^{ -\textbf{p}} = \mathscr{O}_{X}(\star \mathscr{A}) = \mathscr{O}_{X}(\star f). \end{align*}$$
We can tell the same story for nonstandard powers of the
![]() $f_{k}$
. To this end, let
$f_{k}$
. To this end, let
![]() $\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}) \in \mathbb {C}^{d}$
be weights as before, define the
$\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}) \in \mathbb {C}^{d}$
be weights as before, define the
![]() $\mathscr {D}_{X}$
-action on
$\mathscr {D}_{X}$
-action on
![]() $f^{ \boldsymbol {\lambda }}$
via the chain and product rule and make the
$f^{ \boldsymbol {\lambda }}$
via the chain and product rule and make the
![]() $\mathscr {D}_{X}$
-module identification/definition
$\mathscr {D}_{X}$
-module identification/definition
 $$\begin{align*}\bigcup_{p \in \mathbb{N}^{d}} \mathscr{D}_{X} f^{ \boldsymbol{\lambda} - \textbf{p}} = \mathscr{O}_{X}(\star f^{ \boldsymbol{\lambda}}). \end{align*}$$
$$\begin{align*}\bigcup_{p \in \mathbb{N}^{d}} \mathscr{D}_{X} f^{ \boldsymbol{\lambda} - \textbf{p}} = \mathscr{O}_{X}(\star f^{ \boldsymbol{\lambda}}). \end{align*}$$
Repeating the construction algebraically produces a
![]() $D_{X_{\operatorname {\mathrm {alg}}}}$
-module
$D_{X_{\operatorname {\mathrm {alg}}}}$
-module
![]() $\mathscr {O}_{X_{\operatorname {\mathrm {alg}}}}(\star f^{\boldsymbol {\lambda }}).$
$\mathscr {O}_{X_{\operatorname {\mathrm {alg}}}}(\star f^{\boldsymbol {\lambda }}).$
For technical reasons, we will work with the following equivalent object:
Proposition 4.1. Consider
![]() $\mathscr {O}_{X}(\star f)$
as an
$\mathscr {O}_{X}(\star f)$
as an
![]() $\mathscr {D}_{X}$
-module. Let
$\mathscr {D}_{X}$
-module. Let
![]() $\textbf {p} \in \mathbb {N}^{d}$
. We let
$\textbf {p} \in \mathbb {N}^{d}$
. We let
![]() $\delta \in \operatorname {\mathrm {Der}}_{X}$
act on
$\delta \in \operatorname {\mathrm {Der}}_{X}$
act on
![]() $g f^{-\textbf {p}}$
by
$g f^{-\textbf {p}}$
by
This defines a connection
![]() $\nabla ^{\boldsymbol {\lambda }}$
on
$\nabla ^{\boldsymbol {\lambda }}$
on
![]() $\mathscr {O}_{X}(\star f)$
satisfying the commutative diagram of
$\mathscr {O}_{X}(\star f)$
satisfying the commutative diagram of
![]() $\mathscr {D}_{X}$
-maps
$\mathscr {D}_{X}$
-maps

where
![]() $(\mathscr {D}_{X} f^{-\textbf {p}}, \nabla ^{\boldsymbol {\lambda }})$
denotes the module generated by
$(\mathscr {D}_{X} f^{-\textbf {p}}, \nabla ^{\boldsymbol {\lambda }})$
denotes the module generated by
![]() $f^{-\textbf {p}}$
under this new connection
$f^{-\textbf {p}}$
under this new connection
![]() $\nabla ^{\boldsymbol {\lambda }}$
and the vertical isomorphisms are determined by
$\nabla ^{\boldsymbol {\lambda }}$
and the vertical isomorphisms are determined by
![]() $g f^{-\textbf {p}} \mapsto g f^{-\textbf {p} + \boldsymbol {\lambda }}$
.
$g f^{-\textbf {p}} \mapsto g f^{-\textbf {p} + \boldsymbol {\lambda }}$
.
Proof. The vertical maps in the diagram are certainly
![]() $\mathscr {O}_{X}$
-isomorphisms, and it is easy to check that action of a derivation
$\mathscr {O}_{X}$
-isomorphisms, and it is easy to check that action of a derivation
![]() $\delta $
commutes with the vertical maps:
$\delta $
commutes with the vertical maps:
![]() $\psi (\nabla _{\delta }^{\boldsymbol {\lambda }} (-)) = \delta (\psi (-)).$
This fact simplifies the straightforward calculations mandatory in checking
$\psi (\nabla _{\delta }^{\boldsymbol {\lambda }} (-)) = \delta (\psi (-)).$
This fact simplifies the straightforward calculations mandatory in checking
![]() $\nabla ^{\boldsymbol {\lambda }}$
is a well-defined connection (and then certifies the vertical maps are
$\nabla ^{\boldsymbol {\lambda }}$
is a well-defined connection (and then certifies the vertical maps are
![]() $\mathscr {D}_{X}$
-isomorphisms).
$\mathscr {D}_{X}$
-isomorphisms).
Remark 4.2.
-
(a) Note that
 $\nabla _{\delta }^{\boldsymbol {\lambda }}(1) = \nabla _{\delta }^{\boldsymbol {\lambda }}(f^{\boldsymbol {0}}) = \sum _{k} \delta (f_{k}) f^{-\boldsymbol {e_{k}}}$
, where
$\nabla _{\delta }^{\boldsymbol {\lambda }}(1) = \nabla _{\delta }^{\boldsymbol {\lambda }}(f^{\boldsymbol {0}}) = \sum _{k} \delta (f_{k}) f^{-\boldsymbol {e_{k}}}$
, where
 $\boldsymbol {e_{k}}$
are the standard unit vectors.
$\boldsymbol {e_{k}}$
are the standard unit vectors. -
(b) Proposition 4.1 also holds in the algebraic setting.
Before proceeding, let us complete our proofs of the analytic (un)Twisted Logarithmic Comparison Theorems by justifying the relationship between the analytic twisted meromorphic de Rham complex and the derived direct image of a rank one local system on the the complement
![]() $U = X \setminus \mathscr {A}$
. This is known to experts and follows from the explicit Riemann–Hilbert correspondence.
$U = X \setminus \mathscr {A}$
. This is known to experts and follows from the explicit Riemann–Hilbert correspondence.
Proposition 4.3. Let
![]() $f = f_{1} \cdots f_{d} \in R$
be a reduced hyperplane arrangement
$f = f_{1} \cdots f_{d} \in R$
be a reduced hyperplane arrangement
![]() $\mathscr {A}$
equipped with a factorization into linear forms. Suppose that
$\mathscr {A}$
equipped with a factorization into linear forms. Suppose that
![]() $\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}) \in \mathbb {C}^{d}$
, and let
$\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}) \in \mathbb {C}^{d}$
, and let
![]() $\omega = \sum _{k} \lambda _{k} df_{k} / f_{k}$
the one-form determined by
$\omega = \sum _{k} \lambda _{k} df_{k} / f_{k}$
the one-form determined by
![]() $\boldsymbol {\lambda }$
. And let
$\boldsymbol {\lambda }$
. And let
![]() $\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\lambda }$
be the rank one local system on
$\operatorname {\mathrm {L}}_{\operatorname {\mathrm {Exp}}(\lambda }$
be the rank one local system on
![]() $X \setminus \mathscr {A}$
corresponding to the torus point
$X \setminus \mathscr {A}$
corresponding to the torus point
![]() $\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })$
; let
$\operatorname {\mathrm {Exp}}(\boldsymbol {\lambda })$
; let ![]() be the inclusion. Then we have the following equality in the category of perverse sheaves:
be the inclusion. Then we have the following equality in the category of perverse sheaves:
Proof. We justify the following:
Note that the equalities occur in the derived category. Indeed,
![]() $\stackrel {(1)}{=}$
is nothing more than a straightforward computation; since
$\stackrel {(1)}{=}$
is nothing more than a straightforward computation; since
![]() $\mathscr {O}_{X}(\star f^{\boldsymbol {\lambda }})$
is regular holonomic (cf. Theorem 5.2 [Reference Budur5]) and since
$\mathscr {O}_{X}(\star f^{\boldsymbol {\lambda }})$
is regular holonomic (cf. Theorem 5.2 [Reference Budur5]) and since
![]() $\operatorname {\mathrm {DR}}(-)$
gives an equivalence of categories between regular holonomic
$\operatorname {\mathrm {DR}}(-)$
gives an equivalence of categories between regular holonomic
![]() $\mathscr {D}_{X}$
-modules and perverse sheaves, by Proposition 4.1 we have
$\mathscr {D}_{X}$
-modules and perverse sheaves, by Proposition 4.1 we have
![]() $\stackrel {(2)}{=}$
in the category of perverse sheaves; the explicit Riemann–Hilbert correspondence gives
$\stackrel {(2)}{=}$
in the category of perverse sheaves; the explicit Riemann–Hilbert correspondence gives
![]() $\stackrel {(3)}{=}$
(cf. Theorem 5.2 [Reference Budur5]).
$\stackrel {(3)}{=}$
(cf. Theorem 5.2 [Reference Budur5]).
Using the identification within Proposition 4.1, we can use the Twisted Logarithmic Comparison Theorem to locate choices of
![]() $\boldsymbol {\lambda }$
such that
$\boldsymbol {\lambda }$
such that
![]() $\mathscr {D}_{X} f^{-\textbf {1} + \boldsymbol {\lambda }} = \mathscr {O}_{X}(\star f^{\boldsymbol {\lambda }})$
. The following is based off an observation of Torelli in the univariate, untwisted case (cf. Proposition 3.1 [Reference Torrelli34]).
$\mathscr {D}_{X} f^{-\textbf {1} + \boldsymbol {\lambda }} = \mathscr {O}_{X}(\star f^{\boldsymbol {\lambda }})$
. The following is based off an observation of Torelli in the univariate, untwisted case (cf. Proposition 3.1 [Reference Torrelli34]).
Theorem 4.4. Let
![]() $f = f_{1} \cdots f_{d}$
cut out a central, reduced hyperplane arrangement, and let
$f = f_{1} \cdots f_{d}$
cut out a central, reduced hyperplane arrangement, and let
![]() $\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}) \in \mathbb {C}^{d}$
be weights such that for each edge E
$\boldsymbol {\lambda } = (\lambda _{1}, \dots , \lambda _{d}) \in \mathbb {C}^{d}$
be weights such that for each edge E
 $$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*}$$
$$\begin{align*}\sum_{\{1 \leq k \leq d \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} \lambda_{k} \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}}. \end{align*}$$
Then
Proof. Doing this stalk-by-stalk, with the standard reduction to a smaller rank arrangement at points not the origin, and using the Proposition 4.1, it suffices to prove that the inclusion
![]() $(\mathscr {D}_{X,0}f^{-\textbf {1}}, \nabla ^{\boldsymbol {\lambda }}) \subseteq (\mathscr {O}_{X,0}(\star f), \nabla ^{\boldsymbol {\lambda }})$
is an equality.
$(\mathscr {D}_{X,0}f^{-\textbf {1}}, \nabla ^{\boldsymbol {\lambda }}) \subseteq (\mathscr {O}_{X,0}(\star f), \nabla ^{\boldsymbol {\lambda }})$
is an equality.
Define the
![]() $\mathscr {D}_{X,0}$
-module Q to be the cokernel of this inclusion:
$\mathscr {D}_{X,0}$
-module Q to be the cokernel of this inclusion:
Apply the de Rham functor
![]() $\operatorname {\mathrm {DR}}(-)$
to this short exact sequence. By the inductive hypothesis, Q is supported at the origin; by Kashiwara’s equivalence, it is isomorphic to a direct sum of copies of
$\operatorname {\mathrm {DR}}(-)$
to this short exact sequence. By the inductive hypothesis, Q is supported at the origin; by Kashiwara’s equivalence, it is isomorphic to a direct sum of copies of
![]() $\mathscr {D}_{X,0}/\mathscr {D}_{X,0} \cdot \mathfrak {m}_{0} \simeq \mathbb {C}[\partial _{1}, \dots , \partial _{n}]$
. The de Rham complex attached to this
$\mathscr {D}_{X,0}/\mathscr {D}_{X,0} \cdot \mathfrak {m}_{0} \simeq \mathbb {C}[\partial _{1}, \dots , \partial _{n}]$
. The de Rham complex attached to this
![]() $\mathscr {D}_{X,0}$
-module is essentially the Koszul complex of the regular sequence
$\mathscr {D}_{X,0}$
-module is essentially the Koszul complex of the regular sequence
![]() $\partial _{1}, \dots , \partial _{n}$
on
$\partial _{1}, \dots , \partial _{n}$
on
![]() $\mathbb {C}[\partial _{1}, \dots , \partial _{n}]$
. Thus,
$\mathbb {C}[\partial _{1}, \dots , \partial _{n}]$
. Thus,
![]() $H^{j}(\operatorname {\mathrm {DR}}(Q)) = 0 $
for all
$H^{j}(\operatorname {\mathrm {DR}}(Q)) = 0 $
for all
![]() $j \neq n$
. This means the long exact sequence arising from applying the de Rham functor to Equation (4.1) is a collection of isomorphisms and one short exact sequence:
$j \neq n$
. This means the long exact sequence arising from applying the de Rham functor to Equation (4.1) is a collection of isomorphisms and one short exact sequence:
Note that the first nontrivial map is induced by
![]() $\operatorname {\mathrm {DR}}(-)$
applied to a submodule inclusion.
$\operatorname {\mathrm {DR}}(-)$
applied to a submodule inclusion.
On the other hand, by the definition of the de Rham functor one can easily check that we have an inclusion of complexes
where the last complex equals
![]() $(\Omega _{X,0}^{\bullet }(\star f), \nabla _{\omega })$
. By Theorem 3.4, the composition of maps in Equation (4.3) is a quasi-isomorphism. So the second map in Equation (4.3) is a surjection on the level of cohomology. Specifically, for
$(\Omega _{X,0}^{\bullet }(\star f), \nabla _{\omega })$
. By Theorem 3.4, the composition of maps in Equation (4.3) is a quasi-isomorphism. So the second map in Equation (4.3) is a surjection on the level of cohomology. Specifically, for
![]() $H^{n}(-)$
, this surjection is the same map as the first nontrivial map in Equation (4.2) since both are induced by submodule inclusion. We deduce
$H^{n}(-)$
, this surjection is the same map as the first nontrivial map in Equation (4.2) since both are induced by submodule inclusion. We deduce
![]() $H^{n}(\operatorname {\mathrm {DR}}(Q)) = 0$
and
$H^{n}(\operatorname {\mathrm {DR}}(Q)) = 0$
and
![]() $\operatorname {\mathrm {DR}}(Q)$
is acyclic.
$\operatorname {\mathrm {DR}}(Q)$
is acyclic.
Since
![]() $(\mathscr {O}_{X,0}(\star f), \nabla ^{\boldsymbol {\lambda }}) \simeq \mathscr {O}_{X,0}(\star f^{\boldsymbol {\lambda }})$
is regular holonomic (Theorem 5.2 [Reference Budur5]) and these properties are preserved under subquotients, Q is regular holonomic. By the Riemann–Hilbert correspondence, there is an equivalence of categories between regular holonomic
$(\mathscr {O}_{X,0}(\star f), \nabla ^{\boldsymbol {\lambda }}) \simeq \mathscr {O}_{X,0}(\star f^{\boldsymbol {\lambda }})$
is regular holonomic (Theorem 5.2 [Reference Budur5]) and these properties are preserved under subquotients, Q is regular holonomic. By the Riemann–Hilbert correspondence, there is an equivalence of categories between regular holonomic
![]() $\mathscr {D}_{X,0}$
-modules and perverse sheaves. As have shown
$\mathscr {D}_{X,0}$
-modules and perverse sheaves. As have shown
![]() $\operatorname {\mathrm {DR}}(Q)$
corresponds to the zero perverse sheaf, we deduce
$\operatorname {\mathrm {DR}}(Q)$
corresponds to the zero perverse sheaf, we deduce
![]() $Q = 0$
, completing the proof.
$Q = 0$
, completing the proof.
4.2. Codimension one components of Bernstein–Sato ideals
We conclude with a sharp estimate of the codimension one components of the Bernstein–Sato ideal attached to an arbitrary factorization of a central, reduced hyperplane arrangement. We first give a quick tour of some of the necessary concepts, with some other tools deferred to the proof.
Let f cut out a central, reduced hyperplane arrangement, and let
![]() $f = f_{1} \cdots f_{r}$
be an arbitrary factorization of f, not necessarily into linear forms. We encode this factorization by
$f = f_{1} \cdots f_{r}$
be an arbitrary factorization of f, not necessarily into linear forms. We encode this factorization by
![]() $F = (f_{1}, \dots , f_{r}).$
Formally invert f, add r dummy variables
$F = (f_{1}, \dots , f_{r}).$
Formally invert f, add r dummy variables
![]() $s_{1}, \dots , s_{r}$
and consider the
$s_{1}, \dots , s_{r}$
and consider the
![]() $\mathscr {O}_{X,0}[\frac {1}{f}, S] = \mathscr {O}_{X,0}[\frac {1}{f}, s_{1}, \dots , s_{r}]$
-module generated by
$\mathscr {O}_{X,0}[\frac {1}{f}, S] = \mathscr {O}_{X,0}[\frac {1}{f}, s_{1}, \dots , s_{r}]$
-module generated by
![]() $f_{1}^{s_{1}} \cdots f_{r}^{s_{r}}$
; call this
$f_{1}^{s_{1}} \cdots f_{r}^{s_{r}}$
; call this
![]() $\mathscr {O}_{X,0}[\frac {1}{f}, S] F^{S}$
. This is a
$\mathscr {O}_{X,0}[\frac {1}{f}, S] F^{S}$
. This is a
![]() $\mathscr {D}_{X,0}[S] = \mathscr {D}_{X,0}[s_{1}, \dots , s_{r}]$
-module where the action of derivation on
$\mathscr {D}_{X,0}[S] = \mathscr {D}_{X,0}[s_{1}, \dots , s_{r}]$
-module where the action of derivation on
![]() $F^{S} = f_{1}^{s_{r}} \cdots f_{r}^{s_{r}}$
is given by formally applying the chain and product rule. The cyclic
$F^{S} = f_{1}^{s_{r}} \cdots f_{r}^{s_{r}}$
is given by formally applying the chain and product rule. The cyclic
![]() $\mathscr {D}_{X,0}[S]$
-submodule generated by
$\mathscr {D}_{X,0}[S]$
-submodule generated by
![]() $F^{S}$
(resp.
$F^{S}$
(resp.
![]() $F^{S+1} = f_{1}^{s_{1}+1} \cdots f_{r}^{s_{r}+1}$
) is denoted by
$F^{S+1} = f_{1}^{s_{1}+1} \cdots f_{r}^{s_{r}+1}$
) is denoted by
![]() $\mathscr {D}_{X,0}[S] F^{S}$
(resp.
$\mathscr {D}_{X,0}[S] F^{S}$
(resp.
![]() $\mathscr {D}_{X,0}[S] F^{S+1}$
).
$\mathscr {D}_{X,0}[S] F^{S+1}$
).
Definition 4.5. Consider the
![]() $\mathscr {D}_{X}[S]$
-module
$\mathscr {D}_{X}[S]$
-module
 $$\begin{align*}M = \frac{\mathscr{D}_{X,0}[S] F^{S}}{\mathscr{D}_{X,0}[S] F^{S+1}}. \end{align*}$$
$$\begin{align*}M = \frac{\mathscr{D}_{X,0}[S] F^{S}}{\mathscr{D}_{X,0}[S] F^{S+1}}. \end{align*}$$
The
![]() $\mathbb {C}[S] = \mathbb {C}[s_{1}, \dots , s_{r}]$
-module annihilator of this module is the Bernstein–Sato ideal. It is denoted by
$\mathbb {C}[S] = \mathbb {C}[s_{1}, \dots , s_{r}]$
-module annihilator of this module is the Bernstein–Sato ideal. It is denoted by
We call the zero locus of the Bernstein–Sato ideal
![]() $Z(B_{F,0}) \subseteq \mathbb {C}^{r}$
, and we single out its codimension one components with
$Z(B_{F,0}) \subseteq \mathbb {C}^{r}$
, and we single out its codimension one components with
When working with a factorization
![]() $F = (f_{1}, \dots , f_{r})$
into more than one term (i.e.,
$F = (f_{1}, \dots , f_{r})$
into more than one term (i.e.,
![]() $r \geq 2$
) we call this the multivariate situation; when the factorization
$r \geq 2$
) we call this the multivariate situation; when the factorization
![]() $F = (f)$
is trivial (i.e.,
$F = (f)$
is trivial (i.e.,
![]() $r = 1$
), we call this the univariate situation. In the univariate situation, the Bernstein–Sato polynomial is the monic generator of the (necessarily principal) Bernstein–Sato ideal.
$r = 1$
), we call this the univariate situation. In the univariate situation, the Bernstein–Sato polynomial is the monic generator of the (necessarily principal) Bernstein–Sato ideal.
It is well known that the Bernstein–Sato ideal (both the univariate and multivariate versions) is nonzero. We recommend the modern treatments [Reference Maisonobe21, Reference Budur, van der Veer, Wu and Zhou6, Reference Budur, van der Veer, Wu and Zhou7] which focus on the multivariate situation, especially since we utilize many of the ideas therein. In [Reference Maisonobe21], Maisonobe realized studying the
![]() $\operatorname {\mathrm {Ext}}$
-modules
$\operatorname {\mathrm {Ext}}$
-modules
is crucial to understanding Bernstein–Sato ideals. In particular, he proved the first nonvanishing
![]() $\operatorname {\mathrm {Ext}}$
-module sits in slot
$\operatorname {\mathrm {Ext}}$
-module sits in slot
![]() $n+1$
(recall
$n+1$
(recall
![]() $n = \dim X$
). In [Reference Budur, van der Veer, Wu and Zhou6], the authors: (1) developed the theory of localized
$n = \dim X$
). In [Reference Budur, van der Veer, Wu and Zhou6], the authors: (1) developed the theory of localized
![]() $\mathscr {D}_{X,0}[S]$
-modules, for example, replacing the
$\mathscr {D}_{X,0}[S]$
-modules, for example, replacing the
![]() $\mathscr {D}_{X,0}[S]$
-module M with the
$\mathscr {D}_{X,0}[S]$
-module M with the
![]() $\mathscr {D}_{X,0} \otimes _{\mathbb {C}} T^{-1}\mathbb {C}[S]$
-module
$\mathscr {D}_{X,0} \otimes _{\mathbb {C}} T^{-1}\mathbb {C}[S]$
-module
![]() $M \otimes _{\mathbb {C}} T^{-1} \mathbb {C}[S]$
for a multiplicatively closed subset
$M \otimes _{\mathbb {C}} T^{-1} \mathbb {C}[S]$
for a multiplicatively closed subset
![]() $T \subseteq \mathbb {C}[S]$
; (2) showed that when M is
$T \subseteq \mathbb {C}[S]$
; (2) showed that when M is
![]() $(n+1)$
-Cohen–Macaulay, that is, when amongst all the
$(n+1)$
-Cohen–Macaulay, that is, when amongst all the
![]() $\operatorname {\mathrm {Ext}}$
-modules of Equation (4.4) only the
$\operatorname {\mathrm {Ext}}$
-modules of Equation (4.4) only the
![]() $\operatorname {\mathrm {Ext}}$
-module sitting in slot
$\operatorname {\mathrm {Ext}}$
-module sitting in slot
![]() $n+1$
is nonzero, M has very nice properties.
$n+1$
is nonzero, M has very nice properties.
We will make use of the approach of [Reference Budur, van der Veer, Wu and Zhou6] where they show M is generically
![]() $(n+1)$
-Cohen–Macaulay (generic with respect to points of
$(n+1)$
-Cohen–Macaulay (generic with respect to points of
![]() $\mathbb {C}^{r}$
). We will also make use of the result of the previous subsection. For
$\mathbb {C}^{r}$
). We will also make use of the result of the previous subsection. For
![]() $\textbf {a} = (a_{1}, \dots , a_{r}) \in \mathbb {C}^{r}$
, let
$\textbf {a} = (a_{1}, \dots , a_{r}) \in \mathbb {C}^{r}$
, let
![]() $\mathbb {C}_{\textbf {a}}$
be the associated residue field. There is a natural surjective specialization map of
$\mathbb {C}_{\textbf {a}}$
be the associated residue field. There is a natural surjective specialization map of
![]() $\mathscr {D}_{X,0}$
-modules
$\mathscr {D}_{X,0}$
-modules
obtained by replacing all
![]() $s_{k}$
with
$s_{k}$
with
![]() $a_{k}$
. (See [Reference Oaku and Takayama24] and Section 5 of [Reference Budur5] for details.) Theorem 4.4 will, with suitable caution, let us use some of the results from [Reference Oaku and Takayama24] regarding this specialization.
$a_{k}$
. (See [Reference Oaku and Takayama24] and Section 5 of [Reference Budur5] for details.) Theorem 4.4 will, with suitable caution, let us use some of the results from [Reference Oaku and Takayama24] regarding this specialization.
Because we care about arbitrary factorizations F of f, we require some technical notation exclusive to hyperplane arrangements.
Definition 4.6. Let
![]() $f = \ell _{1} \cdots \ell _{d}$
be a factorization of a central, reduced arrangement f into linear terms. For an edge E in the intersection lattice
$f = \ell _{1} \cdots \ell _{d}$
be a factorization of a central, reduced arrangement f into linear terms. For an edge E in the intersection lattice
![]() $\mathscr {L}(\mathscr {A})$
, let
$\mathscr {L}(\mathscr {A})$
, let
![]() $J(E) = \{ j \in [d] \mid E \subseteq \operatorname {\mathrm {V}}(\ell _{j})\}$
so that
$J(E) = \{ j \in [d] \mid E \subseteq \operatorname {\mathrm {V}}(\ell _{j})\}$
so that
![]() $f_{E} = \prod _{j \in J(X)} \ell _{j}$
is the arrangement consisting of all hyperplanes containing E. The factorization
$f_{E} = \prod _{j \in J(X)} \ell _{j}$
is the arrangement consisting of all hyperplanes containing E. The factorization
![]() $F = (f_{1}, \cdots , f_{r})$
amounts to a disjoint partition of
$F = (f_{1}, \cdots , f_{r})$
amounts to a disjoint partition of
![]() $[d]$
into r subsets; let
$[d]$
into r subsets; let
![]() $S_{k} = \{ j \in [d] \mid \operatorname {\mathrm {V}}(\ell _{j}) \subseteq \operatorname {\mathrm {V}}(f_{k})\}$
. Thus
$S_{k} = \{ j \in [d] \mid \operatorname {\mathrm {V}}(\ell _{j}) \subseteq \operatorname {\mathrm {V}}(f_{k})\}$
. Thus
![]() $f_{k} = \prod _{j \in S_{k}} \ell _{j}$
. The factorization F of f induces a factorization
$f_{k} = \prod _{j \in S_{k}} \ell _{j}$
. The factorization F of f induces a factorization
![]() $f_{E} = f_{E, 1} \cdots f_{E, r}$
, where
$f_{E} = f_{E, 1} \cdots f_{E, r}$
, where
 $$\begin{align*}f_{E,k} = \prod_{j \in S_{k} \cap J(E)} \ell_{j}. \end{align*}$$
$$\begin{align*}f_{E,k} = \prod_{j \in S_{k} \cap J(E)} \ell_{j}. \end{align*}$$
Finally, let
![]() $d = \deg (f)$
,
$d = \deg (f)$
,
![]() $d_{E} = \deg (f_{E}) = \mid J(E) \mid $
and
$d_{E} = \deg (f_{E}) = \mid J(E) \mid $
and
![]() $d_{E,k} = \deg (f_{E,k}) = \mid J(E) \cap S_{k} \mid .$
Note that
$d_{E,k} = \deg (f_{E,k}) = \mid J(E) \cap S_{k} \mid .$
Note that
![]() $\deg (f_{E,k})$
can equal zero.
$\deg (f_{E,k})$
can equal zero.
Now, we can state and prove the subsection’s main result. What is new below is the upper bound
![]() $Q_{E}$
on the size of v; that all the codimension one components of
$Q_{E}$
on the size of v; that all the codimension one components of
![]() $Z(B_{F,0})$
are of this form (without any restriction other than the nonnegativity of v) was proved in Theorem 4.18 of [Reference Bath2]. We highlight that, in the univariate case, this independently recovers (by a very different argument) M. Saito’s result [Reference Saito29] that the roots of the Bernstein–Sato polynomial of a smooth, central, reduced arrangement lie in
$Z(B_{F,0})$
are of this form (without any restriction other than the nonnegativity of v) was proved in Theorem 4.18 of [Reference Bath2]. We highlight that, in the univariate case, this independently recovers (by a very different argument) M. Saito’s result [Reference Saito29] that the roots of the Bernstein–Sato polynomial of a smooth, central, reduced arrangement lie in
![]() $(-2 + \frac {1}{d}, 0)$
.
$(-2 + \frac {1}{d}, 0)$
.
Theorem 4.7. For
![]() $F = (f_{1}, \dots , f_{r})$
an arbitrary factorization of a reduced, central arrangement f, the codimension one components of the Bernstein–Sato ideal attached to F has the following restriction:
$F = (f_{1}, \dots , f_{r})$
an arbitrary factorization of a reduced, central arrangement f, the codimension one components of the Bernstein–Sato ideal attached to F has the following restriction:
 $$\begin{align*}Z_{r-1}(B_{F,0}) \subseteq \bigcup_{\substack{E \in \mathscr{L}(\mathscr{A}) \\ E \text{ dense}}} \bigcup_{v=0}^{Q_{E}} \left\{ \sum\limits_{\{1 \leq k \leq r \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} d_{E,k} s_{k} + \operatorname{\mathrm{rank}}(E) + v = 0 \right\}, \end{align*}$$
$$\begin{align*}Z_{r-1}(B_{F,0}) \subseteq \bigcup_{\substack{E \in \mathscr{L}(\mathscr{A}) \\ E \text{ dense}}} \bigcup_{v=0}^{Q_{E}} \left\{ \sum\limits_{\{1 \leq k \leq r \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} d_{E,k} s_{k} + \operatorname{\mathrm{rank}}(E) + v = 0 \right\}, \end{align*}$$
where
![]() $d_{E,k}$
is as in Definition 4.6 and
$d_{E,k}$
is as in Definition 4.6 and
 $$\begin{align*}Q_{E} = \begin{cases} 2 d_{E} - \operatorname{\mathrm{rank}}(E) - \min\{2, \operatorname{\mathrm{rank}}(E)\} \text{ for } F \text{ a factorization into linears}; \\ 2 d_{E} - \operatorname{\mathrm{rank}}(E) - \min\{2, \operatorname{\mathrm{rank}}(E)\} \text{ for} F \text{ any factorization } \& \text{ } E = \{0\}; \\ 2 d_{E} - \operatorname{\mathrm{rank}}(E) - 1 \text{ for } F \text{ not a factorization into linears }\& \text{ } E \neq \{0\}. \end{cases} \end{align*}$$
$$\begin{align*}Q_{E} = \begin{cases} 2 d_{E} - \operatorname{\mathrm{rank}}(E) - \min\{2, \operatorname{\mathrm{rank}}(E)\} \text{ for } F \text{ a factorization into linears}; \\ 2 d_{E} - \operatorname{\mathrm{rank}}(E) - \min\{2, \operatorname{\mathrm{rank}}(E)\} \text{ for} F \text{ any factorization } \& \text{ } E = \{0\}; \\ 2 d_{E} - \operatorname{\mathrm{rank}}(E) - 1 \text{ for } F \text{ not a factorization into linears }\& \text{ } E \neq \{0\}. \end{cases} \end{align*}$$
In particular, when
![]() $F = (f)$
is the trivial factorization and f is not smooth, the roots of the Bernstein–Sato polynomial are contained in
$F = (f)$
is the trivial factorization and f is not smooth, the roots of the Bernstein–Sato polynomial are contained in
![]() $(-2 + 1/d, 0).$
$(-2 + 1/d, 0).$
Proof.
Case 1: We first assume
![]() $r = d$
(i.e., F is a factorization into linear terms) and establish notation and a plan that will be used by the other cases.
$r = d$
(i.e., F is a factorization into linear terms) and establish notation and a plan that will be used by the other cases.
General notation: Fix an arbitrary dense edge E, and then fix an integer
![]() $\ell \in [0, d_{E})$
. Choose the integer
$\ell \in [0, d_{E})$
. Choose the integer
![]() $m \in \mathbb {Z}$
by the mandate
$m \in \mathbb {Z}$
by the mandate
 $$ \begin{align} m &= \min\{ p \in \{ \operatorname{\mathrm{rank}}(E) + \ell + z \cdot d_{E} \mid z \in \mathbb{Z} \} \mid -p \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}} \} \\ &\in [-\min\{2, \operatorname{\mathrm{rank}}(E)\} + 1, - \min\{2, \operatorname{\mathrm{rank}}(E)\} + d_{E}], \nonumber \end{align} $$
$$ \begin{align} m &= \min\{ p \in \{ \operatorname{\mathrm{rank}}(E) + \ell + z \cdot d_{E} \mid z \in \mathbb{Z} \} \mid -p \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}} \} \\ &\in [-\min\{2, \operatorname{\mathrm{rank}}(E)\} + 1, - \min\{2, \operatorname{\mathrm{rank}}(E)\} + d_{E}], \nonumber \end{align} $$
and consider the prime ideal in
![]() $\mathbb {C}[S] = \mathbb {C}[s_{1}, \dots , s_{r}]$
$\mathbb {C}[S] = \mathbb {C}[s_{1}, \dots , s_{r}]$
 $$ \begin{align} \mathfrak{q} = \mathbb{C}[S] \cdot \sum_{\{1 \leq k \leq r \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} d_{E,k} s_{k} + m. \end{align} $$
$$ \begin{align} \mathfrak{q} = \mathbb{C}[S] \cdot \sum_{\{1 \leq k \leq r \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} d_{E,k} s_{k} + m. \end{align} $$
Furthermore, let
![]() $\tau : \mathbb {C}[S] \to \mathbb {C}[S]$
be the ring isomorphism defined by
$\tau : \mathbb {C}[S] \to \mathbb {C}[S]$
be the ring isomorphism defined by
![]() $s_{k} \mapsto s_{k}+1$
for all k. This induces a map
$s_{k} \mapsto s_{k}+1$
for all k. This induces a map ![]() sending
sending ![]() In particular,
In particular,
![]() $(\tau ^{\sharp })^{j} : \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})) \to \operatorname {\mathrm {V}}(\mathfrak {q})$
is a homeomorphism in the Zariski topology. To make this plain, if
$(\tau ^{\sharp })^{j} : \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})) \to \operatorname {\mathrm {V}}(\mathfrak {q})$
is a homeomorphism in the Zariski topology. To make this plain, if
![]() $j \in \mathbb {Z}$
, then
$j \in \mathbb {Z}$
, then
General Plan: We know from Theorem 4.18 of [Reference Bath2] that every codimension one component of
![]() $Z(B_{F,0})$
is of the form
$Z(B_{F,0})$
is of the form
![]() $\operatorname {\mathrm {V}}(\sum _{\{1 \leq k \leq r \mid E \subseteq \operatorname {\mathrm {V}}(f_{k})\}} d_{E,k} s_{k} + \operatorname {\mathrm {rank}}(E) + u)$
for some dense edge
$\operatorname {\mathrm {V}}(\sum _{\{1 \leq k \leq r \mid E \subseteq \operatorname {\mathrm {V}}(f_{k})\}} d_{E,k} s_{k} + \operatorname {\mathrm {rank}}(E) + u)$
for some dense edge
![]() $E \in \mathscr {L}(\mathscr {A})$
and some nonnegative integer u. Therefore, showing the following claim proves the theorem:
$E \in \mathscr {L}(\mathscr {A})$
and some nonnegative integer u. Therefore, showing the following claim proves the theorem:
Indeed, in Equation (4.5) we selected
![]() $ - \min \{2, \operatorname {\mathrm {rank}}(E)\} + 1 \leq m \leq - \min \{2, \operatorname {\mathrm {rank}}(E)\} + d_{E}$
. So if we prove The Claim (4.7) we have proved every codimension one component of
$ - \min \{2, \operatorname {\mathrm {rank}}(E)\} + 1 \leq m \leq - \min \{2, \operatorname {\mathrm {rank}}(E)\} + d_{E}$
. So if we prove The Claim (4.7) we have proved every codimension one component of
![]() $Z(B_{F,0})$
associated to the dense edge E is of of the form
$Z(B_{F,0})$
associated to the dense edge E is of of the form
![]() $\operatorname {\mathrm {V}}(\sum _{\{1 \leq k \leq r \mid E \subseteq \operatorname {\mathrm {V}}(f_{k}) \}} d_{k} s_{k} + v)$
where
$\operatorname {\mathrm {V}}(\sum _{\{1 \leq k \leq r \mid E \subseteq \operatorname {\mathrm {V}}(f_{k}) \}} d_{k} s_{k} + v)$
where
![]() $- \min \{2, \operatorname {\mathrm {rank}}(E)\} + 1 \leq v \leq - \min \{2, \operatorname {\mathrm {rank}}(E)\} + 2 d_{E}$
. Combining this with the first sentence of the General Plan means the codimension one components of
$- \min \{2, \operatorname {\mathrm {rank}}(E)\} + 1 \leq v \leq - \min \{2, \operatorname {\mathrm {rank}}(E)\} + 2 d_{E}$
. Combining this with the first sentence of the General Plan means the codimension one components of
![]() $Z(B_{F,0})$
associated to the dense edge E are of the form
$Z(B_{F,0})$
associated to the dense edge E are of the form
 $$\begin{align*}\operatorname{\mathrm{V}}(\sum_{\{1 \leq k \leq r \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} d_{E,k} s_{k} + \operatorname{\mathrm{rank}}(E) + w), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{V}}(\sum_{\{1 \leq k \leq r \mid E \subseteq \operatorname{\mathrm{V}}(f_{k})\}} d_{E,k} s_{k} + \operatorname{\mathrm{rank}}(E) + w), \end{align*}$$
where
To prove The Claim, we find a nonempty dense set
![]() $\Gamma \subseteq \operatorname {\mathrm {V}}(\mathfrak {q})$
such that for all
$\Gamma \subseteq \operatorname {\mathrm {V}}(\mathfrak {q})$
such that for all
![]() $j \in \{2, 3, \dots , \}$
the translate
$j \in \{2, 3, \dots , \}$
the translate
![]() $(\tau ^{\sharp })^{-j}(\Gamma )$
and the zero locus
$(\tau ^{\sharp })^{-j}(\Gamma )$
and the zero locus
![]() $Z(B_{F,0})$
are disjoint. Since
$Z(B_{F,0})$
are disjoint. Since
![]() $(\tau ^{\sharp })^{-j}(\Gamma ) \subseteq (\tau ^{\sharp })^{-j}(\mathfrak {q}) = \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})$
, this shows
$(\tau ^{\sharp })^{-j}(\Gamma ) \subseteq (\tau ^{\sharp })^{-j}(\mathfrak {q}) = \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})$
, this shows
![]() $\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})$
is not a codimension one component of
$\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})$
is not a codimension one component of
![]() $Z(B_{F,0})$
certifying The Claim. The set
$Z(B_{F,0})$
certifying The Claim. The set
![]() $\Gamma $
is constructed by intersecting the elements of two countable collections of Zariski open sets: In Step 1, we identify a countable collection of Zariski opens so that for points in their intersection M satisfies the
$\Gamma $
is constructed by intersecting the elements of two countable collections of Zariski open sets: In Step 1, we identify a countable collection of Zariski opens so that for points in their intersection M satisfies the
![]() $(n+1)$
-Cohen–Macaulay property a la the approach of [Reference Budur, van der Veer, Wu and Zhou6]; in Step 2, we identify a different countable collection of opens so that points in all these opens satisfy the setup of Theorem 4.4. In Step 3, we intersect all these opens, call it
$(n+1)$
-Cohen–Macaulay property a la the approach of [Reference Budur, van der Veer, Wu and Zhou6]; in Step 2, we identify a different countable collection of opens so that points in all these opens satisfy the setup of Theorem 4.4. In Step 3, we intersect all these opens, call it
![]() $\Gamma $
, and use the generic properties of Step 1 and Step 2 to study points in
$\Gamma $
, and use the generic properties of Step 1 and Step 2 to study points in
![]() $(\tau ^{\sharp })^{-j}(\Gamma ) \cap Z(B_{F,0})$
; in Step 4, we show
$(\tau ^{\sharp })^{-j}(\Gamma ) \cap Z(B_{F,0})$
; in Step 4, we show
![]() $\Gamma $
is nonempty and dense using the Baire Category Theorem.
$\Gamma $
is nonempty and dense using the Baire Category Theorem.
Step 1: generic Cohen–Macaulay translates.
We begin by utilizing the main technique of [Reference Budur, van der Veer, Wu and Zhou6] (see Lemma 3.5.2). For j some integer, consider the localization of M at the multiplicatively closed set
![]() $T_{j} = \mathbb {C}[S]\setminus \cup _{\mathfrak {m} \in \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))} \mathfrak {m}$
. Then
$T_{j} = \mathbb {C}[S]\setminus \cup _{\mathfrak {m} \in \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))} \mathfrak {m}$
. Then
![]() $M \otimes _{\mathbb {C}[S]} T_{j}^{-1}\mathbb {C}[S]$
is relative holonomic (Definition 3.2.3 of [Reference Budur, van der Veer, Wu and Zhou6]) and has a Bernstein–Sato ideal (since M satisfies both before localization); moreover, the zero locus of this Bernstein–Sato ideal sits inside
$M \otimes _{\mathbb {C}[S]} T_{j}^{-1}\mathbb {C}[S]$
is relative holonomic (Definition 3.2.3 of [Reference Budur, van der Veer, Wu and Zhou6]) and has a Bernstein–Sato ideal (since M satisfies both before localization); moreover, the zero locus of this Bernstein–Sato ideal sits inside
![]() $\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
. Following Lemma 3.5.2 of [Reference Budur, van der Veer, Wu and Zhou6] (or just using the result), we can consider the zero locus
$\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
. Following Lemma 3.5.2 of [Reference Budur, van der Veer, Wu and Zhou6] (or just using the result), we can consider the zero locus
![]() $Z_{p,j} \subseteq \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
of the Bernstein–Sato ideal of
$Z_{p,j} \subseteq \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
of the Bernstein–Sato ideal of
Provided
![]() $p \geq n+2$
, each
$p \geq n+2$
, each
![]() $Z_{p,j} \subseteq \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
is Zariski closed and of codimension (with respect to this containment) of at least one. Consider the nonempty Zariski open set
$Z_{p,j} \subseteq \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
is Zariski closed and of codimension (with respect to this containment) of at least one. Consider the nonempty Zariski open set
 $$\begin{align*}C_{j} = \operatorname{\mathrm{V}}(\tau^{j}(\mathfrak{q})) \setminus \left( \bigcup_{p = n+2}^{p = n+r} Z_{p,j} \right) \subseteq \operatorname{\mathrm{V}}(\tau^{j}(\mathfrak{q})), \end{align*}$$
$$\begin{align*}C_{j} = \operatorname{\mathrm{V}}(\tau^{j}(\mathfrak{q})) \setminus \left( \bigcup_{p = n+2}^{p = n+r} Z_{p,j} \right) \subseteq \operatorname{\mathrm{V}}(\tau^{j}(\mathfrak{q})), \end{align*}$$
and let
![]() $D_{j} \subseteq T_{j}^{-1}\mathbb {C}[S]$
the corresponding multiplicatively closed set. Then
$D_{j} \subseteq T_{j}^{-1}\mathbb {C}[S]$
the corresponding multiplicatively closed set. Then
![]() $M \otimes _{\mathbb {C}[S]} T_{j}^{-1} \mathbb {C}[S] \otimes _{\mathbb {C}[S]} D_{j}^{-1} \mathbb {C}[S]$
is
$M \otimes _{\mathbb {C}[S]} T_{j}^{-1} \mathbb {C}[S] \otimes _{\mathbb {C}[S]} D_{j}^{-1} \mathbb {C}[S]$
is
![]() $(n+1)$
-Cohen–Macaulay (over points in
$(n+1)$
-Cohen–Macaulay (over points in
![]() $C_{j})$
. (See Lemma 3.5.2 of [Reference Budur, van der Veer, Wu and Zhou6] for more details.)
$C_{j})$
. (See Lemma 3.5.2 of [Reference Budur, van der Veer, Wu and Zhou6] for more details.)
Let
![]() $\mathbb {C}_{\textbf {a}}$
be the residue field corresponding to the point
$\mathbb {C}_{\textbf {a}}$
be the residue field corresponding to the point
![]() $\textbf {a} \in \mathbb {C}^{r}$
. Suppose that
$\textbf {a} \in \mathbb {C}^{r}$
. Suppose that
![]() $\textbf {a} \in C_{j}$
. Since Bernstein–Sato ideals of relative holonomic modules localize (Lemma 3.4.1 and Remark 3.2.1 of [Reference Budur, van der Veer, Wu and Zhou6]), our point
$\textbf {a} \in C_{j}$
. Since Bernstein–Sato ideals of relative holonomic modules localize (Lemma 3.4.1 and Remark 3.2.1 of [Reference Budur, van der Veer, Wu and Zhou6]), our point
![]() $\textbf {a}$
is in the zero locus of the Bernstein–Sato ideal of M if and only if
$\textbf {a}$
is in the zero locus of the Bernstein–Sato ideal of M if and only if
![]() $\textbf {a}$
is in the zero locus of the Bernstein–Sato ideal of
$\textbf {a}$
is in the zero locus of the Bernstein–Sato ideal of
![]() $M \otimes _{\mathbb {C}[S]} T_{j}^{-1} \mathbb {C}[S] \otimes _{\mathbb {C}[S]} D_{j}^{-1} \mathbb {C}[S]$
, the latter of which is
$M \otimes _{\mathbb {C}[S]} T_{j}^{-1} \mathbb {C}[S] \otimes _{\mathbb {C}[S]} D_{j}^{-1} \mathbb {C}[S]$
, the latter of which is
![]() $(n+1)$
-Cohen–Macaulay by construction. By Proposition 3.4.3 of of [Reference Budur, van der Veer, Wu and Zhou6] and the Cohen–Macaulay-ness,
$(n+1)$
-Cohen–Macaulay by construction. By Proposition 3.4.3 of of [Reference Budur, van der Veer, Wu and Zhou6] and the Cohen–Macaulay-ness,
![]() $\textbf {a} \in Z(B_{F,0})$
if and only if
$\textbf {a} \in Z(B_{F,0})$
if and only if
![]() $M \otimes _{\mathbb {C}[S]} \mathbb {C}_{\textbf {a}} \neq 0.$
$M \otimes _{\mathbb {C}[S]} \mathbb {C}_{\textbf {a}} \neq 0.$
Recall that
![]() $(\tau ^{\sharp })^{j}: \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})) \to \operatorname {\mathrm {V}}(\mathfrak {q})$
is a homeomorphism. Consider the collection of nonempty Zariski opens
$(\tau ^{\sharp })^{j}: \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})) \to \operatorname {\mathrm {V}}(\mathfrak {q})$
is a homeomorphism. Consider the collection of nonempty Zariski opens
and note that all elements of
![]() $\mathscr {C}$
not only lie in
$\mathscr {C}$
not only lie in
![]() $\operatorname {\mathrm {V}}(\mathfrak {q})$
but are dense therein. Moreover, if
$\operatorname {\mathrm {V}}(\mathfrak {q})$
but are dense therein. Moreover, if
![]() $\textbf {a} \in \bigcap _{U \in \mathscr {C}} U$
, then for all
$\textbf {a} \in \bigcap _{U \in \mathscr {C}} U$
, then for all
![]() $j \in \mathbb {Z}_{\geq 0}$
we have that
$j \in \mathbb {Z}_{\geq 0}$
we have that
![]() $\textbf {a} \in (\tau ^{\sharp })^{j}(C_{j})$
. Alternatively,
$\textbf {a} \in (\tau ^{\sharp })^{j}(C_{j})$
. Alternatively,
![]() $(\tau ^{\sharp })^{-j}(\textbf {a}) \in C_{j}$
. This puts
$(\tau ^{\sharp })^{-j}(\textbf {a}) \in C_{j}$
. This puts
![]() $(\tau ^{\sharp })^{-j}(\textbf {a})$
within the
$(\tau ^{\sharp })^{-j}(\textbf {a})$
within the
![]() $(n+1)$
-Cohen–Macaulay locus of
$(n+1)$
-Cohen–Macaulay locus of
![]() $\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
and hence
$\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
and hence
![]() $(\tau ^{\sharp })^{-j}(\textbf {a}) \in Z(B_{F,0})$
if and only if
$(\tau ^{\sharp })^{-j}(\textbf {a}) \in Z(B_{F,0})$
if and only if
![]() $M \otimes _{\mathbb {C}[S]} \mathbb {C}_{(\tau ^{\sharp })^{-j}(\textbf {a})} \neq 0.$
This gives us a criterion for verifying that none of the translates
$M \otimes _{\mathbb {C}[S]} \mathbb {C}_{(\tau ^{\sharp })^{-j}(\textbf {a})} \neq 0.$
This gives us a criterion for verifying that none of the translates
![]() $\{ (\tau ^{\sharp })^{-j}(\textbf {a})\}$
of
$\{ (\tau ^{\sharp })^{-j}(\textbf {a})\}$
of
![]() $\textbf {a} \in \bigcap _{U \in \mathscr {C}} U$
lie in the zero locus of the Bernstein–Sato ideal of M: No translate lies in this zero locus provided
$\textbf {a} \in \bigcap _{U \in \mathscr {C}} U$
lie in the zero locus of the Bernstein–Sato ideal of M: No translate lies in this zero locus provided
![]() $M \otimes _{\mathbb {C}[S]} \mathbb {C}_{(\tau ^{\sharp })^{-j}(\textbf {a})} = 0$
for all
$M \otimes _{\mathbb {C}[S]} \mathbb {C}_{(\tau ^{\sharp })^{-j}(\textbf {a})} = 0$
for all
![]() $j \in \mathbb {Z}_{\geq 0}$
.
$j \in \mathbb {Z}_{\geq 0}$
.
Step 2: generically generating
![]() $\mathscr {O}_{X}(\star f^{\lambda })$
.
$\mathscr {O}_{X}(\star f^{\lambda })$
.
For each edge
![]() $E^{\prime } \in \mathscr {L}(\mathscr {A})$
and each
$E^{\prime } \in \mathscr {L}(\mathscr {A})$
and each
![]() $p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E)\}}$
, consider the nonempty distinguished Zariski open set
$p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E)\}}$
, consider the nonempty distinguished Zariski open set
 $$\begin{align*}G_{E^{\prime}, p} = \{ \boldsymbol{\lambda} \in \mathbb{C}^{d} \mid \sum_{\{1 \leq j \leq d \mid E^{\prime} \subseteq \operatorname{\mathrm{V}}(f_{j}) \}} \lambda_{j} \neq p) \} \subseteq \mathbb{C}^{d}. \end{align*}$$
$$\begin{align*}G_{E^{\prime}, p} = \{ \boldsymbol{\lambda} \in \mathbb{C}^{d} \mid \sum_{\{1 \leq j \leq d \mid E^{\prime} \subseteq \operatorname{\mathrm{V}}(f_{j}) \}} \lambda_{j} \neq p) \} \subseteq \mathbb{C}^{d}. \end{align*}$$
Consider the countable collection of these opens, parameterized both by p and by
![]() $E^{\prime }$
:
$E^{\prime }$
:
By Theorem 4.4, if
![]() $\boldsymbol {\lambda }$
lies in the intersection of all these
$\boldsymbol {\lambda }$
lies in the intersection of all these
![]() $G_{E^{\prime },p}$
, then
$G_{E^{\prime },p}$
, then
Let
![]() $\gamma $
be the ring map of localization at
$\gamma $
be the ring map of localization at
![]() $T_{j} = \mathbb {C}[S]\setminus \cup _{\mathfrak {m} \in \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))} \mathfrak {m}$
:
$T_{j} = \mathbb {C}[S]\setminus \cup _{\mathfrak {m} \in \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))} \mathfrak {m}$
:
And let
![]() $\gamma ^{\sharp }: \operatorname {\mathrm {V}}(\mathfrak {q}) \to \operatorname {\mathrm {Spec}} \mathbb {C}[s_{1}, \dots , s_{d}]$
be the induced map on spectra. By definition
$\gamma ^{\sharp }: \operatorname {\mathrm {V}}(\mathfrak {q}) \to \operatorname {\mathrm {Spec}} \mathbb {C}[s_{1}, \dots , s_{d}]$
be the induced map on spectra. By definition
![]() $\textbf {a} \in \operatorname {\mathrm {V}}(\mathfrak {q})$
equates to
$\textbf {a} \in \operatorname {\mathrm {V}}(\mathfrak {q})$
equates to
 $$ \begin{align} \sum_{\{1 \leq j \leq d \mid E \subseteq \operatorname{\mathrm{V}}(\ell_{j})\}} (\gamma^{\sharp}(\textbf{a}))_{j} = -m \leq -( - \min\{2, \operatorname{\mathrm{rank}}(E)\} + 1), \end{align} $$
$$ \begin{align} \sum_{\{1 \leq j \leq d \mid E \subseteq \operatorname{\mathrm{V}}(\ell_{j})\}} (\gamma^{\sharp}(\textbf{a}))_{j} = -m \leq -( - \min\{2, \operatorname{\mathrm{rank}}(E)\} + 1), \end{align} $$
where E and m are as determined in the General Plan (see Equation (4.5)). Therefore,
![]() $(\gamma ^{\sharp })^{-1}(G_{E, p})$
is nonempty for all
$(\gamma ^{\sharp })^{-1}(G_{E, p})$
is nonempty for all
![]() $p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E)\}}$
.
$p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E)\}}$
.
Additionally, for edges
![]() $E^{\prime } \neq E$
and for all
$E^{\prime } \neq E$
and for all
![]() $p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E)\}}$
we claim our Zariski open
$p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E)\}}$
we claim our Zariski open
![]() $(\gamma ^{\sharp })^{-1}(G_{E^{\prime }, p})$
is nonempty. If there exists a k such that
$(\gamma ^{\sharp })^{-1}(G_{E^{\prime }, p})$
is nonempty. If there exists a k such that
![]() $\operatorname {\mathrm {V}}(f_{k}) \subseteq E$
and
$\operatorname {\mathrm {V}}(f_{k}) \subseteq E$
and
![]() $\operatorname {\mathrm {V}}(f_{k}) \nsubseteq E^{\prime }$
, then for a point
$\operatorname {\mathrm {V}}(f_{k}) \nsubseteq E^{\prime }$
, then for a point
![]() $\boldsymbol {\beta } \in G_{E^{\prime }, p}$
there is no restriction on the entry
$\boldsymbol {\beta } \in G_{E^{\prime }, p}$
there is no restriction on the entry
![]() $(\boldsymbol {\beta })_{k}$
. So changing this value moves
$(\boldsymbol {\beta })_{k}$
. So changing this value moves
![]() $\boldsymbol {\beta }$
within
$\boldsymbol {\beta }$
within
![]() $G_{E^{\prime }, p}$
, and thus, we can change this value such that Equation (4.9) is satisfied. Conversely, if there exists a k such that
$G_{E^{\prime }, p}$
, and thus, we can change this value such that Equation (4.9) is satisfied. Conversely, if there exists a k such that
![]() $\operatorname {\mathrm {V}}(f_{k}) \subseteq E^{\prime }$
but
$\operatorname {\mathrm {V}}(f_{k}) \subseteq E^{\prime }$
but
![]() $\operatorname {\mathrm {V}}(f_{k}) \nsubseteq E$
, then we can take a point
$\operatorname {\mathrm {V}}(f_{k}) \nsubseteq E$
, then we can take a point
![]() $\textbf {a} \in \operatorname {\mathrm {V}}(\mathfrak {q})$
, and change the entry
$\textbf {a} \in \operatorname {\mathrm {V}}(\mathfrak {q})$
, and change the entry
![]() $(\boldsymbol {\gamma }^{\sharp }(\textbf {a}))_{k}$
so that the point moves into
$(\boldsymbol {\gamma }^{\sharp }(\textbf {a}))_{k}$
so that the point moves into
![]() $G_{E^{\prime }, p}$
, but Equation (4.9) is not affected.
$G_{E^{\prime }, p}$
, but Equation (4.9) is not affected.
Therefore,
is a countable collection of nonempty sets lying in
![]() $\operatorname {\mathrm {V}}(\mathfrak {q})$
, all of which are Zariski open in
$\operatorname {\mathrm {V}}(\mathfrak {q})$
, all of which are Zariski open in
![]() $\operatorname {\mathrm {V}}(\mathfrak {q})$
. And if
$\operatorname {\mathrm {V}}(\mathfrak {q})$
. And if
![]() $\textbf {a} \in \bigcap _{U \in \mathscr {G}} U$
, we have that
$\textbf {a} \in \bigcap _{U \in \mathscr {G}} U$
, we have that
Step 3: combining generic properties.
Define
![]() $\Gamma \subseteq \operatorname {\mathrm {V}}(\mathfrak {q})$
by
$\Gamma \subseteq \operatorname {\mathrm {V}}(\mathfrak {q})$
by
and let
![]() $\textbf {a} \in \Gamma $
. We will show that if
$\textbf {a} \in \Gamma $
. We will show that if
![]() $j \in \{2, 3, \dots , \}$
then
$j \in \{2, 3, \dots , \}$
then
![]() $(\tau ^{\sharp })^{-j}(\Gamma )$
is disjoint from the
$(\tau ^{\sharp })^{-j}(\Gamma )$
is disjoint from the
![]() $Z(B_{F,0})$
, zero locus of the Bernstein–Sato ideal of M. This verifies The Claim.
$Z(B_{F,0})$
, zero locus of the Bernstein–Sato ideal of M. This verifies The Claim.
By [Reference Sabbah27] (see also Proposition 3.2 of [Reference Oaku and Takayama24]), only finitely many of
![]() $\{(\tau ^{\sharp })^{-j})(\textbf {a}) \mid j \in \{2, 3, \dots \} \}$
intersect
$\{(\tau ^{\sharp })^{-j})(\textbf {a}) \mid j \in \{2, 3, \dots \} \}$
intersect
![]() $Z(B_{F,0})$
. Assume, towards contradiction, that the intersection is nonempty, and fix
$Z(B_{F,0})$
. Assume, towards contradiction, that the intersection is nonempty, and fix
![]() $j \in \{2, 3, \dots \}$
to be the largest choice such that
$j \in \{2, 3, \dots \}$
to be the largest choice such that
![]() $(\tau ^{\sharp })^{-j}(\textbf {a}) \in Z(B_{F,0})$
. For notational ease, let
$(\tau ^{\sharp })^{-j}(\textbf {a}) \in Z(B_{F,0})$
. For notational ease, let
![]() $\textbf {j} = (j, \dots , j) \in \mathbb {C}^{d}$
and recall that
$\textbf {j} = (j, \dots , j) \in \mathbb {C}^{d}$
and recall that
![]() $\gamma ^{\sharp }((\tau ^{\sharp })^{-j}(\textbf {a})) = - \textbf {j} + \gamma ^{\sharp }(\textbf {a}).$
Now, consider the following commutative diagram of
$\gamma ^{\sharp }((\tau ^{\sharp })^{-j}(\textbf {a})) = - \textbf {j} + \gamma ^{\sharp }(\textbf {a}).$
Now, consider the following commutative diagram of
![]() $\mathscr {D}_{X, 0}$
-maps:
$\mathscr {D}_{X, 0}$
-maps:

(Recall that
![]() $\mathbb {C}_{\boldsymbol {\beta }}$
is the residue field of the point
$\mathbb {C}_{\boldsymbol {\beta }}$
is the residue field of the point
![]() $\boldsymbol {\beta } \in \operatorname {\mathrm {Spec}} \mathbb {C}[S]$
.) Here, the horizontal specialization maps are always surjections, the rightmost vertical map is submodule inclusion, and the leftmost vertical map
$\boldsymbol {\beta } \in \operatorname {\mathrm {Spec}} \mathbb {C}[S]$
.) Here, the horizontal specialization maps are always surjections, the rightmost vertical map is submodule inclusion, and the leftmost vertical map
![]() $\nabla _{(\tau ^{\sharp })^{-j + 1}(\textbf {a})}$
is induced by sending
$\nabla _{(\tau ^{\sharp })^{-j + 1}(\textbf {a})}$
is induced by sending
![]() $s_{k} \mapsto s_{k} + 1$
for all k, cf. Definition 3.7 of [Reference Bath1] and/or the commutative square of subsection 5.10 of [Reference Budur5], where
$s_{k} \mapsto s_{k} + 1$
for all k, cf. Definition 3.7 of [Reference Bath1] and/or the commutative square of subsection 5.10 of [Reference Budur5], where
![]() $\nabla _{(\tau ^{\sharp })^{-j + 1}(\textbf {a})}$
goes by
$\nabla _{(\tau ^{\sharp })^{-j + 1}(\textbf {a})}$
goes by
![]() $\rho _{(\tau ^{\sharp })^{-j + 1}(\textbf {a})}$
. Because j is the largest possible value such that
$\rho _{(\tau ^{\sharp })^{-j + 1}(\textbf {a})}$
. Because j is the largest possible value such that
![]() $(\tau ^{\sharp })^{-j}(\textbf {a}) \in Z(B_{F,0})$
, Proposition 3.6 of [Reference Oaku and Takayama24] says the bottom horizontal map is an isomorphism. And because
$(\tau ^{\sharp })^{-j}(\textbf {a}) \in Z(B_{F,0})$
, Proposition 3.6 of [Reference Oaku and Takayama24] says the bottom horizontal map is an isomorphism. And because
![]() $-j + 1 \leq -1$
and
$-j + 1 \leq -1$
and
![]() $\textbf {a} \in \Gamma $
, the rightmost vertical map is actually an equality (see Equations (4.10), (4.11)).
$\textbf {a} \in \Gamma $
, the rightmost vertical map is actually an equality (see Equations (4.10), (4.11)).
Therefore,
![]() $\nabla _{(\tau ^{\sharp })^{-j + 1}(\textbf {a})}$
is surjective. This means its cokernel vanishes:
$\nabla _{(\tau ^{\sharp })^{-j + 1}(\textbf {a})}$
is surjective. This means its cokernel vanishes:
Since
![]() $\textbf {a} \in \Gamma $
, the definition (4.8) of
$\textbf {a} \in \Gamma $
, the definition (4.8) of
![]() $\mathscr {C}$
and the subsequent remarks imply that the vanishing of this cokernel equates to
$\mathscr {C}$
and the subsequent remarks imply that the vanishing of this cokernel equates to
But this contradicts our choice that
![]() $j \in \{2, 3, \dots , \}$
was the largest possible value such that
$j \in \{2, 3, \dots , \}$
was the largest possible value such that
![]() $(\tau ^{\sharp })^{-j}(\textbf {a}) \in Z(B_{F,0}).$
We conclude that
$(\tau ^{\sharp })^{-j}(\textbf {a}) \in Z(B_{F,0}).$
We conclude that
Step 4: Baire Category Theorem.
The points
![]() $\Gamma \subseteq \operatorname {\mathrm {V}}(\mathfrak {q})$
from Step 3 are obtained by taking a countable intersection of nonempty Zariski open sets. By the Baire Category Theorem
$\Gamma \subseteq \operatorname {\mathrm {V}}(\mathfrak {q})$
from Step 3 are obtained by taking a countable intersection of nonempty Zariski open sets. By the Baire Category Theorem
![]() $\Gamma $
is nonempty and dense in
$\Gamma $
is nonempty and dense in
![]() $\operatorname {\mathrm {V}}(\mathfrak {q})$
. Moreover,
$\operatorname {\mathrm {V}}(\mathfrak {q})$
. Moreover,
![]() $(\tau ^{\sharp })^{-j}(\Gamma ) \subseteq (\tau ^{\sharp })^{-j}(\operatorname {\mathrm {V}}(\mathfrak {q})) = \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
is also dense in
$(\tau ^{\sharp })^{-j}(\Gamma ) \subseteq (\tau ^{\sharp })^{-j}(\operatorname {\mathrm {V}}(\mathfrak {q})) = \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
is also dense in
![]() $\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
since
$\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
since
![]() $\tau ^{\sharp }$
is a homeomorphism. By Step 3 and Equation (4.14), for all
$\tau ^{\sharp }$
is a homeomorphism. By Step 3 and Equation (4.14), for all
![]() $j \in \{2, 3, \dots , \}$
, the codimension one component
$j \in \{2, 3, \dots , \}$
, the codimension one component
![]() $\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})) \nsubseteq Z(B_{F,0})$
lest
$\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q})) \nsubseteq Z(B_{F,0})$
lest
![]() $\emptyset \neq (\tau ^{\sharp })^{-j}(\Gamma ) \subseteq Z(B_{F,0})$
. This proves The Claim and by the discussion in the General Plan completes the proof for Case 1.
$\emptyset \neq (\tau ^{\sharp })^{-j}(\Gamma ) \subseteq Z(B_{F,0})$
. This proves The Claim and by the discussion in the General Plan completes the proof for Case 1.
Case 2: We assume
![]() $d> r > 1$
, that is, F is neither the trivial factorization
$d> r > 1$
, that is, F is neither the trivial factorization
![]() $F = (f)$
nor a factorization into linear forms.
$F = (f)$
nor a factorization into linear forms.
The strategy is entirely similar to Case 1 but with some mild alterations involving Step 2. First, if
![]() $E \neq \{0\}$
change Equation (4.5) and the consequent definition of
$E \neq \{0\}$
change Equation (4.5) and the consequent definition of
![]() $\mathfrak {q} \in \operatorname {\mathrm {Spec}} \mathbb {C}[S]$
so that
$\mathfrak {q} \in \operatorname {\mathrm {Spec}} \mathbb {C}[S]$
so that
 $$ \begin{align} m &= \min\{ p \in \{ \operatorname{\mathrm{rank}}(E) + \ell + z \cdot d_{E} \mid z \in \mathbb{Z} \} \mid -p \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}} \} \\ &\in [0, d_{E} - 1]. \nonumber \end{align} $$
$$ \begin{align} m &= \min\{ p \in \{ \operatorname{\mathrm{rank}}(E) + \ell + z \cdot d_{E} \mid z \in \mathbb{Z} \} \mid -p \notin \mathbb{Z}_{\geq \min\{2, \operatorname{\mathrm{rank}}(E)\}} \} \\ &\in [0, d_{E} - 1]. \nonumber \end{align} $$
If
![]() $E = \{0\}$
, make no such changes.
$E = \{0\}$
, make no such changes.
The construction of
![]() $\mathscr {C}$
(see Equation (4.8)) from Step 1 does not change. As for the construction of
$\mathscr {C}$
(see Equation (4.8)) from Step 1 does not change. As for the construction of
![]() $\mathscr {G}$
from Step 2, let
$\mathscr {G}$
from Step 2, let
![]() $\beta : \mathbb {C}[s_{1}, \dots , s_{d}] \to \mathbb {C}[s_{1}, \dots , s_{r}]$
be the ring homomorphism induced by the factorization F of f (see Definition 4.6):
$\beta : \mathbb {C}[s_{1}, \dots , s_{d}] \to \mathbb {C}[s_{1}, \dots , s_{r}]$
be the ring homomorphism induced by the factorization F of f (see Definition 4.6):
 $$\begin{align*}\beta: \mathbb{C}[s_{1}, \dots, s_{d}] \to \frac{\mathbb{C}[s_{1}, \dots, s_{d}]}{(\{ s_{t} - s_{j} \mid t, j \in S_{k}, 1 \leq k \leq r\})} = \mathbb{C}[s_{1}, \dots, s_{r}]. \end{align*}$$
$$\begin{align*}\beta: \mathbb{C}[s_{1}, \dots, s_{d}] \to \frac{\mathbb{C}[s_{1}, \dots, s_{d}]}{(\{ s_{t} - s_{j} \mid t, j \in S_{k}, 1 \leq k \leq r\})} = \mathbb{C}[s_{1}, \dots, s_{r}]. \end{align*}$$
And change
![]() $\gamma $
from Step 2 so that
$\gamma $
from Step 2 so that
![]() $\gamma $
is the composition of
$\gamma $
is the composition of
![]() $\beta $
with the localization at
$\beta $
with the localization at
![]() $T_{j} = \mathbb {C}[S]\setminus \cup _{\mathfrak {m} \in \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))} \mathfrak {m}$
:
$T_{j} = \mathbb {C}[S]\setminus \cup _{\mathfrak {m} \in \operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))} \mathfrak {m}$
:
And
![]() $\gamma ^{\sharp }: \operatorname {\mathrm {V}}(\mathfrak {q}) \to \operatorname {\mathrm {Spec}} \mathbb {C}[s_{1}, \dots , s_{d}]$
is the induced map on spectra. As before, define
$\gamma ^{\sharp }: \operatorname {\mathrm {V}}(\mathfrak {q}) \to \operatorname {\mathrm {Spec}} \mathbb {C}[s_{1}, \dots , s_{d}]$
is the induced map on spectra. As before, define
and, as before, we must show each element of
![]() $\mathscr {G}$
is nonempty.
$\mathscr {G}$
is nonempty.
Under these modifications,
![]() $\textbf {a} \in \operatorname {\mathrm {V}}(\mathfrak {q})$
equates to
$\textbf {a} \in \operatorname {\mathrm {V}}(\mathfrak {q})$
equates to
 $$\begin{align*}\sum_{\{1 \leq j \leq d \mid E \subseteq \operatorname{\mathrm{V}}(\ell_{j})\}} (\gamma^{\sharp}(\textbf{a}))_{j} = -m \leq \begin{cases} 0 \text{ if } E \neq \{0\}; \\ -1 \text{ if } E = \{0\}. \end{cases} \end{align*}$$
$$\begin{align*}\sum_{\{1 \leq j \leq d \mid E \subseteq \operatorname{\mathrm{V}}(\ell_{j})\}} (\gamma^{\sharp}(\textbf{a}))_{j} = -m \leq \begin{cases} 0 \text{ if } E \neq \{0\}; \\ -1 \text{ if } E = \{0\}. \end{cases} \end{align*}$$
There are two cases. If
![]() $-m \leq 0$
, then
$-m \leq 0$
, then
![]() $\mathbb {Q}_{\leq 0}^{r}$
intersects
$\mathbb {Q}_{\leq 0}^{r}$
intersects
![]() $\operatorname {\mathrm {V}}(\mathfrak {q})$
nontrivially. Certainly,
$\operatorname {\mathrm {V}}(\mathfrak {q})$
nontrivially. Certainly,
![]() $\mathbb {Q}_{\leq 0}^{d} \subseteq G_{E^{\prime }, p}$
for arbitrary
$\mathbb {Q}_{\leq 0}^{d} \subseteq G_{E^{\prime }, p}$
for arbitrary
![]() $E^{\prime } \in \mathscr {L}(\mathscr {A})$
and
$E^{\prime } \in \mathscr {L}(\mathscr {A})$
and
![]() $p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E^{\prime })\}}.$
So for all such
$p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E^{\prime })\}}.$
So for all such
![]() $E^{\prime }$
and p, we know
$E^{\prime }$
and p, we know
![]() $\emptyset \neq \gamma ^{\sharp }(\mathbb {Q}_{\leq 0}^{r} \cap \operatorname {\mathrm {V}}(\mathfrak {q})) \subseteq \mathbb {Q}_{\leq 0}^{d} \subseteq G_{E^{\prime }, p}$
for arbitrary
$\emptyset \neq \gamma ^{\sharp }(\mathbb {Q}_{\leq 0}^{r} \cap \operatorname {\mathrm {V}}(\mathfrak {q})) \subseteq \mathbb {Q}_{\leq 0}^{d} \subseteq G_{E^{\prime }, p}$
for arbitrary
![]() $E^{\prime } \in \mathscr {L}(\mathscr {A})$
and
$E^{\prime } \in \mathscr {L}(\mathscr {A})$
and
![]() $p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E^{\prime })\}}.$
Thus, when
$p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E^{\prime })\}}.$
Thus, when
![]() $-m \leq 0$
every member of
$-m \leq 0$
every member of
![]() $\mathscr {G}$
is nonempty and Zariski open in
$\mathscr {G}$
is nonempty and Zariski open in
![]() $\operatorname {\mathrm {V}}(\mathfrak {q})$
. If
$\operatorname {\mathrm {V}}(\mathfrak {q})$
. If
![]() $-m> 0$
, then by Equations (4.5) and (4.15) we conclude
$-m> 0$
, then by Equations (4.5) and (4.15) we conclude
![]() $-m = 1$
and
$-m = 1$
and
![]() $E = \{0\}$
. Let
$E = \{0\}$
. Let
![]() $\textbf {1/d} = (1/d, \dots , 1/d) \in \mathbb {C}^{d}$
, and note that
$\textbf {1/d} = (1/d, \dots , 1/d) \in \mathbb {C}^{d}$
, and note that
![]() $\textbf {1/d} \in G_{E^{\prime }, p}$
for all
$\textbf {1/d} \in G_{E^{\prime }, p}$
for all
![]() $E^{\prime } \neq \{0\}$
and
$E^{\prime } \neq \{0\}$
and
![]() $p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E^{\prime })\}}$
(this amounts to
$p \in \mathbb {Z}_{\geq \min \{2, \operatorname {\mathrm {rank}}(E^{\prime })\}}$
(this amounts to
![]() $d_{E^{\prime }} < d$
). Certainly,
$d_{E^{\prime }} < d$
). Certainly,
![]() $(\beta ^{\sharp })^{-1}(\textbf {1/d}) \in \operatorname {\mathrm {V}}(\mathfrak {q})$
, so in this case each relevant
$(\beta ^{\sharp })^{-1}(\textbf {1/d}) \in \operatorname {\mathrm {V}}(\mathfrak {q})$
, so in this case each relevant
![]() $(\beta ^{\sharp })^{-1}(G_{E^{\prime }, p}) \neq \emptyset $
.
$(\beta ^{\sharp })^{-1}(G_{E^{\prime }, p}) \neq \emptyset $
.
With these alterations and arguments, the construction of
![]() $\mathscr {G}$
from Step 2 has the same properties as before. So the argument in Case 1 applies to Case 2. Note that the change in
$\mathscr {G}$
from Step 2 has the same properties as before. So the argument in Case 1 applies to Case 2. Note that the change in
![]() $Q_{E}$
for edges not
$Q_{E}$
for edges not
![]() $\{0\}$
matches the change in the lower bound for m.
$\{0\}$
matches the change in the lower bound for m.
Case 3: We assume
![]() $r=1$
, that is, F is the trivial factorization
$r=1$
, that is, F is the trivial factorization
![]() $F = (f)$
.
$F = (f)$
.
We argue similarly to Case 2. First, note that the changes to
![]() $\mathscr {G}$
therein apply here as well which, because
$\mathscr {G}$
therein apply here as well which, because
![]() $\operatorname {\mathrm {Spec}} \mathbb {C}[S] = \mathbb {C}$
, means
$\operatorname {\mathrm {Spec}} \mathbb {C}[S] = \mathbb {C}$
, means
![]() $\mathscr {G}$
consists of copies of
$\mathscr {G}$
consists of copies of
![]() $\operatorname {\mathrm {V}}(\mathfrak {q})$
. And because
$\operatorname {\mathrm {V}}(\mathfrak {q})$
. And because
![]() $r=1$
, it is easy to check M is automatically
$r=1$
, it is easy to check M is automatically
![]() $(n+1)$
-Cohen–Macaulay (e.g., Lemma 3.3.3 of [Reference Budur, van der Veer, Wu and Zhou6]). So
$(n+1)$
-Cohen–Macaulay (e.g., Lemma 3.3.3 of [Reference Budur, van der Veer, Wu and Zhou6]). So
![]() $\mathscr {C}$
from Step 1 is simply copies of
$\mathscr {C}$
from Step 1 is simply copies of
![]() $\operatorname {\mathrm {V}}(\mathfrak {q})$
. This means
$\operatorname {\mathrm {V}}(\mathfrak {q})$
. This means
![]() $\Gamma = \operatorname {\mathrm {V}}(\mathfrak {q})$
and the rest of the argument (i.e., Step 3) holds. (There is no need to appeal to the Baire Category Theorem nor dense subset arguments since Step 3 applies to all of
$\Gamma = \operatorname {\mathrm {V}}(\mathfrak {q})$
and the rest of the argument (i.e., Step 3) holds. (There is no need to appeal to the Baire Category Theorem nor dense subset arguments since Step 3 applies to all of
![]() $\Gamma = \operatorname {\mathrm {V}}(\mathfrak {q})$
.) Finally, the containment of the roots of the Bernstein–Sato polynomial in
$\Gamma = \operatorname {\mathrm {V}}(\mathfrak {q})$
.) Finally, the containment of the roots of the Bernstein–Sato polynomial in
![]() $(-2 + 1/d, 0)$
is immediate from the bound of codimension one components (i.e., roots) provided.
$(-2 + 1/d, 0)$
is immediate from the bound of codimension one components (i.e., roots) provided.
Remark 4.8.
-
(a) The bound in Theorem 4.7 is sharp: The formula Theorem 3.23 of [Reference Bath1] for the Bernstein–Sato ideal of a generic arrangement exhibits this.
-
(b) Theorem 4.7 is a significant improvement to the bound of Corollary 3.21 of [Reference Bath1] as there tameness was required in order to lift M. Saito’s univariate’s bound (cf. [Reference Saito29]) to the multivariate setting.
-
(c) Because the proof of Theorem 4.7 depends on generic properties it yields no concrete evidence that
 $\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
is disjoint from
$\operatorname {\mathrm {V}}(\tau ^{j}(\mathfrak {q}))$
is disjoint from
 $Z(B_{F,0})$
for
$Z(B_{F,0})$
for
 $j \in \{2, 3, \dots \}$
: All we show is that the complement of their intersection is dense. In the tame case, the intersection is disjoint because
$j \in \{2, 3, \dots \}$
: All we show is that the complement of their intersection is dense. In the tame case, the intersection is disjoint because
 $Z(B_{F,0})$
is purely codimension one; see Corollary 3.5 [Reference Bath1].
$Z(B_{F,0})$
is purely codimension one; see Corollary 3.5 [Reference Bath1].
Acknowledgements
We thank Guillem Blanco, Nero Budur, Francisco Castro Jiménez, Luis Narváez Macarro and Robin van der Veer for combinations of helpful conversations, comments and inspiring our interest in the subject. We also thank the referee for their helpful comments. We are very grateful to Avi Steiner for detailed comments, including identifying a gap of justification in a previous version. And we sincerely appreciate Uli Walther’s general support as well as his generosity in fielding an untold number of technical questions.
Financial support
The author is supported by FWO grant #G097819N and FWO grant #12E9623N.
Competing interests
The authors have no competing interest to declare.