Introduction
Recent true triaxial compression experiments on both granular and columnar-grained freshwater ice (Reference Golding, Schulson and RenshawGolding and others, 2010, Reference Golding, Schulson and Renshaw2012) have established that, when confined and loaded rapidly under compression, the material exhibits two distinct modes of brittle or brittle-like failure. Under lower levels of confinement, where confinement is defined as the ratio of the lowest to the highest principal stress, brittle failure is characterized by the development of a macroscopic shear fault composed of gouge material and a wide zone of coalesced microcracks, orientated following the dictates of the Mohr–Coulomb relationship. The mechanism governing this mode of failure, termed frictional or Coulombic (C) faulting, has been discussed in terms of crack mechanics, where frictional sliding on primary inclined cracks drives out-of-plane initiation, growth and interaction of secondary cracks via the comb-crack mechanism (Reference Renshaw and SchulsonRenshaw and Schulson, 2001). An underlying requirement for C-faulting is that the applied rate of deformation must exceed a critical level, as set by the competition between crack growth and crack blunting. Mechanically, C-faulting is associated with confinement-dependent failure strength, an increase in relative volume at failure, localized heat production from frictional sliding and a low degree of post-failure cohesion (Reference Golding, Schulson and RenshawGolding and others, 2010, Reference Golding, Schulson and Renshaw2011).
Under higher levels of confinement, the hydrostatic component of the stress state becomes sufficiently large to suppress frictional sliding along microcracks. As a result, C-faulting is suppressed. Under these higher confinements, brittle-like failure is instead characterized by the development of a narrow shear band composed of recrystallized grains oriented along the direction of maximum shear. The mechanism governing this mode of failure, referred to here as plastic (P) faulting, has been discussed for terrestrial ice (T ≥ –40° C) in terms of dislocation mechanics (Reference Rist and MurrellRist and Murrell, 1994; Reference Sammonds, Murrell and RistSammonds and others, 1998; Reference SchulsonSchulson, 2002) and the localization of plastic deformation through adiabatic heating (Reference Golding, Schulson and RenshawGolding and others, 2012). (The term plastic is used here in the crystallographic sense to refer to volume-conserving inelastic deformation.) A critical applied rate of deformation must also be achieved for P-faulting, as set by a critical plastic strain and, among other factors, by the rate at which the heat of plastic work is conducted away from its origin (Reference Golding, Schulson and RenshawGolding and others, 2012). Mechanically, P-faulting is associated with confinement-independent strength, volume-conserving deformation, localized heat production from dislocation motion and a high degree of post-failure cohesion (Reference Golding, Schulson and RenshawGolding and others, 2010, Reference Golding, Schulson and Renshaw2011).
A question arising from all this is: what about saltwater ice, as in the ice cover on the Arctic Ocean, for instance? Although composed predominantly of ‘pure’ ice of volume fraction typically >0.95, at temperatures of about T = –10°C, saltwater ice may be viewed as a multiphase composite material composed not only of pure ice but also of brine and undissolved air, which are entrapped within sub-millimetersized pores distributed both inter- and intra-granularly. The microstructure is made more complicated by the precipitation over a range of temperatures from T = –3°C to T = –40°C of a host of solid salts and, on the scale of a sheet of first-year ice, by centimeter-sized brine-drainage channels (Reference WeeksWeeks, 2010). The question is whether these other features affect the story told by freshwater ice.
We knew from earlier work that in a number of respects the inelastic behavior of first-year sea ice mirrors that of freshwater ice, at least in the laboratory: when compressed rapidly under moderate confinement it fails via C-faulting (Reference Schulson, Fortt, Iliescu and RenshawSchulson and others, 2006); its brittle compressive failure envelope is essentially indistinguishable from that of freshwater ice, at least at T = –10°C (Reference Schulson, Fortt, Iliescu and RenshawSchulson and others, 2006); and its frictional behavior is largely indistinguishable, at least when sliding slowly over itself (Reference Fortt and SchulsonFortt and Schulson, 2011; Reference Lishman, Sammonds and FelthamLishman and others, 2011). Also, the strain rate that marks its ductile-to-brittle transition obeys the model first developed for freshwater ice and then applied to other materials (Reference Renshaw and SchulsonRenshaw and Schulson, 2001). What we did not know is whether saltwater ice exhibits P-faulting.
It was with that question in mind that the following experiments were performed. This work was designed not to repeat what had gone before, nor to be exhaustive, but to answer that one question. The work is not only of scientific interest but is also of practical interest, particularly in relation to ice–structure interactions where indentation pressure is governed by the modes by which ice fails (Reference Kim, Golding, Schulson, Løset and RenshawKim and others, 2012). Based upon the observations described below, P-faulting is determined to be a mode of failure in saltwater ice. This process, however, is made more complicated by what appears to be a mechanism of pore collapse, a mode of failure not previously reported for saltwater ice.
Experimental Procedure
The ice
Both columnar-grained freshwater ice and saltwater ice were produced in the laboratory though unidirectional solidification in an 800 L polycarbonate tank. Freshwater columnar S2 ice was grown as described by Reference Golding, Schulson and RenshawGolding and others (2010). Saltwater columnar S2 ice was produced as follows: 2.06 wt% of ‘Instant Ocean’ brand salt mixture was added to filtered (<1 μm) tap water. The salinity of the well-mixed solution was measured using a YSI Model 32 conductance meter probe, immersed 150 mm below the surface of the solution, and calculated based on the Practical Salinity Scale (PSS-78) from the measured conductivity and temperature. Owing to uncertainty in the initial moisture content of the salt mixture, the saltwater ratio was adjusted iteratively to reach a salinity of 17.5% by mass. The solution was then chilled to T = 4 ± 0.5°C to maximize density and ensure that no turbulent mass flow developed during freezing. To maintain a uniform column diameter, the top of the solution was seeded with ice crystals passed through a 4 mm sieve. Growth was allowed to continue for 5–7 days using a top-loaded cold plate maintained at T = –20 ± 0.1°C. A pressure-relief valve was attached to the tank to allow for expansion during the freezing process and thus minimize stresses in the ice.
Cube-shaped specimens 100 mm on edge were prepared for triaxial loading using a horizontal mill. (Changes in specimen size and geometry had no effect on sample strength, fault orientation or fault microstructure, implying that a reasonably uniform stress distribution was applied within the bulk of the material under the present loading conditions. In addition, tests that were stopped at incremental levels of strain prior to failure revealed that shear fault initiation occurred, at least in some cases, within the bulk of the material, i.e. fault initiation is seen to develop independently of specimen boundaries. These results are presented by Reference Golding, Schulson and RenshawGolding and others (2012).) Freshwater columnar specimens were fully transparent and had a density of ρ = 914.1 ± 1.6 kg m–3 at T = –1°C. Column diameter, as measured in a plane normal to the direction of growth using the linear intercept method, varied between 2 and 4 mm at one end of the cube and between 4 and 7 mm at the other. Saltwater columnar specimens were cloudy in appearance and contained distinct brine drainage channels of 2–5 mm diameter. Column diameter varied between 5 and 7 mm at one end of the cube and between 7 and 10 mm at the other. Specimen density ranged from ρ = 878.3 to 914.4 kg m–3 at T = –10°C and meltwater salinity was 4.2 ± 0.4%.
Loading procedure
The ice was loaded triaxially in compression using a servo-hydraulic true multiaxial loading system (MALS) as described by Reference Golding, Schulson and RenshawGolding and others (2010). In short, the MALS applies a load in three orthogonal directions using six independently controlled actuators. During loading, one pair of actuators acts as the master: it compresses the ice at a fixed displacement rate to a preset level of displacement, at which point the ice is unloaded. The remaining two pairs of actuators are slaved to the master and apply an independently set proportional load. The loading path is defined by the ratio of the applied stresses, where11 is the master and most compressive stress as applied across the columns along direction X 1, σ 22 is the major slaved stress as applied across the columns along direction X 2 and σ 33 is the minor slaved stress as applied along the columns along direction X 3 (see Fig. 1 of Reference Golding, Schulson and RenshawGolding and others (2010) for micrographs of the ice structure and the defined Xi coordinate system). The loading path is expressed as (1.0: R 21: R 31), where R 21 = σ 22/σ 11 and R 31 = σ 33/σ 11. To avoid specimen edge blowout during loading (Reference Weiss and SchulsonWeiss and Schulson, 1995), thin (0.2 mm) brass edge-brackets were attached to the ice.

Fig. 1. Photographs of a P-fault in thin sections of (a) columnar freshwater ice and (b) columnar saltwater ice as viewed under polarized illumination. Faulting generated under (1.0: R
21: R
31) = (1.0: 0.5: 0.2) at T = –20°C at ![]() Minimum feature size on scale is 1 mm.
Minimum feature size on scale is 1 mm.
All tests were performed under a high level of confinement, (1.0: R
21: R
31) = (1.0: 0.5: 0.2) at T = –20 ± 0.2°C, to an inelastic strain along the direction of maximum compression of ![]() . The applied strain rate is defined here as the displacement rate of the hydraulic actuators along the most compressive direction divided by the initial length of the specimen, and was varied from
. The applied strain rate is defined here as the displacement rate of the hydraulic actuators along the most compressive direction divided by the initial length of the specimen, and was varied from ![]() . Inelastic, i.e. non-recoverable, strain imparted to the ice was determined from actuator displacement after subtracting the effects of machine compliance and the elastic strain component from the ice. Stress was determined in each of the loading directions by dividing actuator load by the initial cross-sectional area of the ice. An effective stress,
. Inelastic, i.e. non-recoverable, strain imparted to the ice was determined from actuator displacement after subtracting the effects of machine compliance and the elastic strain component from the ice. Stress was determined in each of the loading directions by dividing actuator load by the initial cross-sectional area of the ice. An effective stress, ![]() is defined using Hill’s criterion (Reference HillHill, 1950) for anisotropic materials (Reference Golding, Schulson and RenshawGolding and others, 2010).
is defined using Hill’s criterion (Reference HillHill, 1950) for anisotropic materials (Reference Golding, Schulson and RenshawGolding and others, 2010).
Observations
Fault features
Figure 1 shows developed P-faults in thin sections of freshwater ice and saltwater ice loaded at T = –20°C. The microstructure of the P-fault is extremely similar in both kinds of ice. In each case the fault is inclined by ∽45° from the direction of the maximum principal stress, i.e. parallel to the direction of maximum shear stress. Similarly, in each case the fault is composed of a narrow band (less than one column diameter in width) of recrystallized grains ranging in diameter from 50 to 500 mm. Cracking in the ice is evenly distributed, i.e. crack interaction or coalescence is not observed, and cracks do not extend beyond the grain boundary under the high levels of confinement examined. In the saltwater ice (Fig. 1b), pockets of recrystallization are also evident in specific columns of the ice matrix.
Strength and critical strain rate
Figure 2 shows triaxial compressive strength versus applied strain rate for columnar freshwater ice and columnar saltwater ice at T = –20°C. Strength is defined here as the difference between the maximum and minimum compressive principal stresses taken at peak load, i.e. the peak differential stress (σ
d = σ
1 – σ
3) observed during loading. The results indicate two distinct regions of behavior. Under lower strain rates both materials exhibit strain-rate hardening, and corresponding stress–strain curves are indicative of global ductile flow. The stress sensitivity exponent n in the power-law relationship ![]() is the same for both materials (n = 3.1 with a correlation coefficient of r
2 = 0.99 for freshwater ice, and n = 3.2 with r
2 = 0.99 for saltwater ice) and the creep parameter B is over an order of magnitude larger for saltwater ice (B = 9.8 × 10–7 MPa–n
s–1) than for freshwater ice (B = 3.5 10–8 MPa–n
s–1).
is the same for both materials (n = 3.1 with a correlation coefficient of r
2 = 0.99 for freshwater ice, and n = 3.2 with r
2 = 0.99 for saltwater ice) and the creep parameter B is over an order of magnitude larger for saltwater ice (B = 9.8 × 10–7 MPa–n
s–1) than for freshwater ice (B = 3.5 10–8 MPa–n
s–1).

Fig. 2. Log–log plot of material strength versus applied strain rate for columnar freshwater ice and columnar saltwater ice deformed under (1.0: R 21: R 31) = (1.0: 0.5: 0.2) at T = –20°C. Fault character is determined from thin-section examination. Specimens labeled ‘Trans.’ refer to material that does not exhibit globally distributed deformation characterized by power-law creep or sudden brittle-like failure characterized by P-faulting. Solid and dashed lines represent best-fit linear regression.
Under higher strain rates both materials exhibit a slight strain-rate weakening, and corresponding stress–strain curves are indicative of sudden brittle-like failure (see below). Correspondingly, the microstructure reveals the development of distinct P-faults. The critical applied strain rate required to generate P-faulting in freshwater ice ![]() is about an order of magnitude lower than in saltwater ice
is about an order of magnitude lower than in saltwater ice ![]() There does not, however, appear to be a significant difference in the strength measured during P-faulting in freshwater and saltwater ice, possibly because the fault in both cases is composed of equiaxed grains of about the same size.
There does not, however, appear to be a significant difference in the strength measured during P-faulting in freshwater and saltwater ice, possibly because the fault in both cases is composed of equiaxed grains of about the same size.
Pore collapse
In addition to P-faulting, saltwater ice loaded rapidly under a high degree of confinement may also exhibit a different mode of failure. Figure 3 shows stress- and strain-time plots typical of P-faulting in freshwater ice, P-faulting in saltwater ice, and failure in saltwater ice via a different mode. Several differences are evident in the mechanical response of material exhibiting P-faulting (either freshwater or saltwater ice) and saltwater ice that does not exhibit P-faulting. First, the terminal stress, or failure strength, of the saltwater ice that does not exhibit P-faulting is not reached under the maximum level of deformation ![]() applied in the present study. In contrast to the sudden brittle-like loss of strength observed during P-faulting (Fig. 3a and c), the stress supported by the ice continues to increase with increased deformation when P-faulting is not observed (Fig. 3e). That being said, the maximum stress reached during P-faulting is significantly higher than (roughly double) the maximum stress reached by saltwater ice that does not exhibit P-faulting, under the same levels of deformation (compare Fig. 3a and c with e).
applied in the present study. In contrast to the sudden brittle-like loss of strength observed during P-faulting (Fig. 3a and c), the stress supported by the ice continues to increase with increased deformation when P-faulting is not observed (Fig. 3e). That being said, the maximum stress reached during P-faulting is significantly higher than (roughly double) the maximum stress reached by saltwater ice that does not exhibit P-faulting, under the same levels of deformation (compare Fig. 3a and c with e).

Fig. 3. Typical plots of stress versus time and inelastic strain versus time for (a, b) freshwater columnar ice where failure occurs by P-faulting, (c, d) saltwater columnar ice where failure occurs by P-faulting and (e, f) saltwater columnar ice where failure occurs by pore collapse. Specimens loaded under (1.0: R
21: R
31) = (1.0: 0.5: 0.2) at T = –20°C at ![]() .
.
Second, and perhaps more important, a significant decrease in material volume is evident in saltwater ice that does not exhibit P-faulting. For example, in Figure 3f the change in relative volume can be seen to decrease near-linearly during loading, with a magnitude over half the measured inelastic deformation along the direction of maximum compression. (The relative volume change is defined here as ![]() , where compressive strains are taken as positive values, such that a negative relative volume change corresponds to a decrease in material volume.) In contrast, specimens that exhibit P-faulting show a smaller change in relative volume (Fig. 3b and d) and this change remains constant with continued deformation after failure. (As discussed by Reference Golding, Schulson and RenshawGolding and others (2012), a small apparent decrease in material volume is expected from the present experimental technique and may be accounted for by extrusion of material between the brass edge-brackets under the high pressures examined.) Table 1 lists the average maximum change in relative volume recorded for material that exhibits P-faulting and for material that does not exhibit P-faulting.
, where compressive strains are taken as positive values, such that a negative relative volume change corresponds to a decrease in material volume.) In contrast, specimens that exhibit P-faulting show a smaller change in relative volume (Fig. 3b and d) and this change remains constant with continued deformation after failure. (As discussed by Reference Golding, Schulson and RenshawGolding and others (2012), a small apparent decrease in material volume is expected from the present experimental technique and may be accounted for by extrusion of material between the brass edge-brackets under the high pressures examined.) Table 1 lists the average maximum change in relative volume recorded for material that exhibits P-faulting and for material that does not exhibit P-faulting.
Table 1 Average density, porosity and salinity of all 27 specimens tested. Results are separated by material and observed mode of failure. Porosity is determined from specimen density and a theoretical density of ρ = 918.9 kg m–3 at T = –10°C (Reference Petrenko and WhitworthPetrenko and Whitworth, 1999). The average maximum change in relative volume recorded during loading is also reported

The governing mode of failure in saltwater ice was found to depend on material density, or conversely the level of porosity. Table 1 lists the average specimen density and porosity recorded from all tests. As shown in Table 1, material with a higher density (which implies a lower porosity) failed by P-faulting, while material with a lower density (or higher porosity) failed by what appears to be a process of pore collapse. That the failure of ice containing a high porosity is driven by pore collapse is supported by the measured decrease in material volume during loading (Fig. 3; Table 1). Note that the salinity, as measured from meltwater, was the same for material that failed by P-faulting and for material that failed by pore collapse.
Comparison with Previous Results
As it has not previously been discussed, it is relevant to note that observations of faulting in ice made under true triaxial loading at constant confinement (i.e. proportional loading) are consistent with observations of faulting in ice made under conventional triaxial loading. Under conventional triaxial loading, i.e. where an axial deviatoric stress is applied under a constant hydrostatic confining pressure, shear faulting that exhibits both pressure-dependent strength (C-faulting) and pressure-independent strength (P-faulting) has been observed in freshwater ice (Reference Kirby, Durham, Beeman, Heard and DaleyKirby and others, 1987; Reference Rist and MurrellRist and Murrell, 1994) and saltwater ice (Reference Sammonds, Murrell and RistSammonds and others, 1998). In addition, the critical level of confinement that defines the C-fault to P-fault transition is comparable for loading under constant confining pressure and under constant confinement. For example, Reference Rist and MurrellRist and Murrell (1994) report that fault strength in freshwater ice loaded under constant confining pressure at T = –40°C is pressure-dependent below confining pressures of P = 10 MPa and pressure-independent at higher confining pressures. This corresponds to a transition confinement between C-faulting and P-faulting (our words) of R = σ 3/σ 1 = p /(σ d + p) = 0.16, where P = 10 MPa is the confining pressure at the transition and σ d = 52 MPa is the fault strength at the transition. This compares well with Reference Golding, Schulson and RenshawGolding and others (2011), who report that the C-fault to P-fault transition in freshwater ice loaded under constant confinement at T = –40°C begins at a confinement of R = 0.15 and C-faulting is fully suppressed by R = 0.20.
Similarly, the critical strain rate required to generate P-faulting is comparable for loading under constant confining pressure and under constant confinement. Reference Rist and MurrellRist and Murrell (1994) report that freshwater granular ice loaded under a high level of confining pressure at T = –40°C fails by shear faulting at applied strain rates of ![]() and by global ductile flow at applied strain rates of
and by global ductile flow at applied strain rates of ![]() At higher temperatures (T = –20°C), they report that failure under high levels of confining pressure followed global ductile flow under the range of strain rates examined
At higher temperatures (T = –20°C), they report that failure under high levels of confining pressure followed global ductile flow under the range of strain rates examined ![]() , i.e. the critical strain rate required for P-faulting was
, i.e. the critical strain rate required for P-faulting was ![]() This is consistent with Reference Golding, Schulson and RenshawGolding and others (2012) who report that the critical strain rate required for P-faulting in freshwater granular ice loaded under constant confinement is
This is consistent with Reference Golding, Schulson and RenshawGolding and others (2012) who report that the critical strain rate required for P-faulting in freshwater granular ice loaded under constant confinement is ![]() at T = –10°C and that it decreases with decreasing temperature (based on results from freshwater columnar ice, it decreases by a factor of about 7 at T = –40°C). In addition, Reference Meglis, Melanson and JordaanMeglis and others (1999) report from creep tests on freshwater granular ice loaded under constant confining pressure that shear faulting under high levels of confining pressure occurred only at the highest applied differential loads examined (corresponding to strain rates on the order of
at T = –10°C and that it decreases with decreasing temperature (based on results from freshwater columnar ice, it decreases by a factor of about 7 at T = –40°C). In addition, Reference Meglis, Melanson and JordaanMeglis and others (1999) report from creep tests on freshwater granular ice loaded under constant confining pressure that shear faulting under high levels of confining pressure occurred only at the highest applied differential loads examined (corresponding to strain rates on the order of ![]() ) and that specimens were often characterized by both lateral strain and a shear fault. The development of both lateral strain and P-faulting is similarly observed near the ductile to P-fault transition strain rate under constant confinement loading in freshwater ice (Reference Golding, Schulson and RenshawGolding and others, 2012), with higher rates of deformation leading to shear faulting with almost no lateral strain. It is important to note, however, that faulting is not a failure process unique to high rates of deformation. For example, at extremely low temperatures (T = –196°C), Reference Durham, Heard and KirbyDurham and others (1983) and Reference Kirby, Durham, Beeman, Heard and DaleyKirby and others (1987) observe both C-faulting and P-faulting in freshwater ice (again, our words) at strain rates as low as
) and that specimens were often characterized by both lateral strain and a shear fault. The development of both lateral strain and P-faulting is similarly observed near the ductile to P-fault transition strain rate under constant confinement loading in freshwater ice (Reference Golding, Schulson and RenshawGolding and others, 2012), with higher rates of deformation leading to shear faulting with almost no lateral strain. It is important to note, however, that faulting is not a failure process unique to high rates of deformation. For example, at extremely low temperatures (T = –196°C), Reference Durham, Heard and KirbyDurham and others (1983) and Reference Kirby, Durham, Beeman, Heard and DaleyKirby and others (1987) observe both C-faulting and P-faulting in freshwater ice (again, our words) at strain rates as low as ![]()
Having noted the similarities in faulting under true triaxial loading at constant confinement and faulting under conventional triaxial loading at constant confining pressure, the present observation of P-faulting in laboratory-grown salt-water ice is consistent with previous observations from natural saltwater ice loaded triaxially. Specifically, Sammonds and others (1998) report shear faulting with pressure-independent strength in multi-year sea ice loaded under constant confining pressure at T = –20°C. The average strength observed there (σ d,Ave = 25.5 MPa for confining pressures R > 0.14 at failure) compares well with the average P-fault strength observed in the present work (σ d,Ave = 26.3 Ave = 26.3 MPa from Fig. 3).
Concluding Remarks
In summary, the results of this study indicate that P-faulting is a mode of failure that occurs in both freshwater and saltwater ice. Furthermore, the microstructure and mechanical behavior of P-faulting in these two materials is found to be very similar. The results also show that porous saltwater ice loaded rapidly under a high degree of confinement fails through what appears to be a mechanism of pore collapse. Although not previously reported in saltwater ice, pore collapse is a mode of failure well documented in geologically comparable materials, such as rocks and minerals (Reference Curran and CarrollCurran and Carroll, 1979; Reference Zhu, Baud and WongZhu and others, 2010), and its potential for operation in porous ice is not surprising. However, the exact level of porosity that governs the transition from failure by P-faulting to failure by pore collapse in either freshwater or saltwater ice loaded under high confinement has yet to be determined. Similarly, a systematic examination of the mechanical and microstructural response of ice undergoing pore collapse has yet to be conducted. Specifically, one might wonder what happens to porous ice at still higher levels of strain, after compaction of the pore space has occurred.
Acknowledgements
We acknowledge the helpful comments of two anonymous reviewers. This research was supported by US National Science Foundation (NSF) grants EAR-0911071 and EAR-081019.


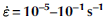 demonstrate that plastic (P) faulting is a mode of failure in saltwater ice when rapidly loaded under a high degree of confinement. In terms of microstructure, mechanical behavior and strength, saltwater ice that fails via P-faulting is almost indistinguishable from columnar S2 freshwater ice that fails via P-faulting loaded under the same conditions. The results also demonstrate that saltwater ice loaded rapidly may exhibit yet another mode of failure, in addition to P-faulting, through what appears to be a mechanism of pore collapse.
demonstrate that plastic (P) faulting is a mode of failure in saltwater ice when rapidly loaded under a high degree of confinement. In terms of microstructure, mechanical behavior and strength, saltwater ice that fails via P-faulting is almost indistinguishable from columnar S2 freshwater ice that fails via P-faulting loaded under the same conditions. The results also demonstrate that saltwater ice loaded rapidly may exhibit yet another mode of failure, in addition to P-faulting, through what appears to be a mechanism of pore collapse.



