1. Introduction
Manipulating colloidal particles suspended in viscous media is a challenging task and is of paramount importance in various fields of engineering and natural sciences. Frequently, taking into account the fluid-mediated hydrodynamic interactions between particles moving through a liquid is essential to predict the behaviour of colloidal suspensions and polymer solutions (Probstein Reference Probstein2005; Mewis & Wagner Reference Mewis and Wagner2012). Recent advances in micro- and nanofluidic technologies have permitted the fabrication and manufacturing of channels with well-defined geometries and characteristic dimensions ranging from the micro- to the nanoscale. A deep understanding of the nature of the mutual interactions between particles and their confining interfaces is of crucial importance in guiding the design of devices and tools for an optimal nanoscale control of biological macromolecules. Notable examples include single-molecule manipulation (Turner et al. Reference Turner, Perez, Lopez and Craighead1998; Campbell et al. Reference Campbell, Wilkinson, Manz, Camilleri and Humphreys2004), DNA mapping for genomic applications (Reisner et al. Reference Reisner, Morton, Riehn, Wang, Yu, Rosen, Sturm, Chou, Frey and Austin2005; Riehn et al. Reference Riehn, Lu, Wang, Lim, Cox and Austin2005; Persson & Tegenfeldt Reference Persson and Tegenfeldt2010), DNA separation and sorting (Doyle et al. Reference Doyle, Bibette, Bancaud and Viovy2002; Cross, Strychalski & Craighead Reference Cross, Strychalski and Craighead2007; Xia, Yan & Hou Reference Xia, Yan and Hou2012), and rheological probing of complex structures using atomic force microscopy cantilevers (François et al. Reference François, Lasne, Amarouchene, Lounis and Kellay2008, Reference François, Amarouchene, Lounis and Kellay2009; Dufour et al. Reference Dufour, Maali, Amarouchene, Ayela, Caillard, Darwiche, Guirardel, Kellay, Lemaire and Mathieu2012; Darwiche et al. Reference Darwiche, Ingremeau, Amarouchene, Maali, Dufour and Kellay2013).
At these small scales, fluid flows are governed by low-Reynolds-number hydrodynamics, where viscous effects dominate over inertial effects (Kim & Karrila Reference Kim and Karrila2013). Solutions for fluid flows due to point forces, or stokeslets, acting close to confining boundaries have been tabulated for various types of geometries, as summarised in the classic textbook by Happel & Brenner (Reference Happel and Brenner1983). The study of the fluid-mediated hydrodynamic interactions in a channel confinement has received significant attention from many researchers over the past couple of years. In the following, we provide a survey of the current state of the art and summarise the relevant literature on this subject.
The first attempt to address the motion of a spherical particle confined between two infinitely extended no-slip walls dates back to Faxén (Reference Faxén1921), who calculated in his PhD dissertation the hydrodynamic mobility parallel to the walls. These calculations were performed when the particle is located in the quarter-plane or mid-plane between the two confining walls (Happel & Brenner Reference Happel and Brenner1983). Later, Oseen (Reference Oseen1928) suggested that the hydrodynamic mobility between two walls could approximately be obtained by superposition of the contributions resulting from each single wall. A modified coherent superposition approximation was further suggested by Benesch, Yiacoumi & Tsouris (Reference Benesch, Yiacoumi and Tsouris2003), providing the diffusion coefficients of a Brownian sphere in confining channels. These predictions were found to match more accurately the existing experimental data reported in the literature.
Exact solutions for a point-force singularity acting at an arbitrary position between two walls were first obtained using the image technique in a seminal article by Liron & Mochon (Reference Liron and Mochon1976). It was noted that the effect of the second wall becomes important when the distance separating the particle from the closest wall is larger than approximately one-tenth of the channel width (Brenner Reference Brenner1999). Using this solution, Liron (Reference Liron1978) further investigated the fluid transport problem of cilia between two parallel plates. A joint analytical–numerical approach (Ganatos, Pfeffer & Weinbaum Reference Ganatos, Pfeffer and Weinbaum1980a; Ganatos, Weinbaum & Pfeffer Reference Ganatos, Weinbaum and Pfeffer1980b) as well as a multipole expansion technique (Swan & Brady Reference Swan and Brady2010) were presented to address the motion of an extended particle confined between two hard walls. Bhattacharya & Bławzdziewicz (Reference Bhattacharya and Bławzdziewicz2002) constructed the image system for the flow field produced by a force multipole in a space bounded by two parallel walls using the image representation for Stokes flow. In addition, compressibility effects were examined by Felderhof (Reference Felderhof2006, Reference Felderhof2010a,Reference Felderhofb). In this context, Hackborn (Reference Hackborn1990) investigated the asymmetric Stokes flow between two parallel planes due to a rotlet singularity, the axis of which is parallel to the boundary planes. Further, Ozarkar & Sangani (Reference Ozarkar and Sangani2008) prescribed an analytical approach using the image-system technique for determining the Stokes flow around particles in a thin film bounded by a wall and a gas–liquid interface. More recently, Daddi-Moussa-Ider, Guckenberger & Gekle (Reference Daddi-Moussa-Ider, Guckenberger and Gekle2016) provided the frequency-dependent hydrodynamic mobility functions between two planar elastic interfaces endowed with resistance towards shear and bending deformation modes.
Experimentally, Dufresne, Altman & Grier (Reference Dufresne, Altman and Grier2001) reported direct imaging measurements of a colloidal particle diffusing between two parallel surfaces, finding a good agreement with the superposition approximation suggested by Oseen. In addition, video microscopy (Faucheux & Libchaber Reference Faucheux and Libchaber1994) combined with optical tweezers (Lin, Yu & Rice Reference Lin, Yu and Rice2000; Tränkle, Ruh & Rohrbach Reference Tränkle, Ruh and Rohrbach2016) as well as dynamic light scattering (Lobry & Ostrowsky Reference Lobry and Ostrowsky1996) have also allowed for good agreement with available theoretical predictions. Further experimental investigations have focused on DNA conformation and diffusion in slit-like confinements (Balducci et al. Reference Balducci, Mao, Han and Doyle2006; Stein et al. Reference Stein, van der Heyden, Koopmans and Dekker2006; Strychalski, Levy & Craighead Reference Strychalski, Levy and Craighead2008; Tang et al. Reference Tang, Levy, Trahan, Jones, Craighead and Doyle2010; Graham Reference Graham2011; Dai et al. Reference Dai, Tree, van der Maarel, Dorfman and Doyle2013; Jones, van der Maarel & Doyle Reference Jones, van der Maarel and Doyle2013).
Concerning collective properties, the behaviour of suspensions in a channel bounded by two planar walls has received a lot of attention. For instance, Bhattacharya, Bławzdziewicz & Wajnryb (Reference Bhattacharya, Bławzdziewicz and Wajnryb2005) examined the fluid-mediated hydrodynamic interactions in a suspension of spherical particles confined between two parallel planar walls under creeping-flow conditions. In addition, Bhattacharya (Reference Bhattacharya2008) considered the collective motion of a two-dimensional periodic array of colloidal particles in a slit pore. Using a novel accelerated Stokesian-dynamics algorithm, Baron, Bławzdziewicz & Wajnryb (Reference Baron, Bławzdziewicz and Wajnryb2008) performed fully resolved computer simulations to investigate the collective motion of linear trains and regular square arrays of particles suspended in a viscous fluid bounded by two parallel plates. Further, Bławzdziewicz & Wajnryb (Reference Bławzdziewicz and Wajnryb2008) analysed the far-field response to external forcing of a suspension of particles in a channel. Swan & Brady (Reference Swan and Brady2011) presented a numerical method for computing the hydrodynamic forces exerted on particles in a suspension confined between two parallel walls. Furthermore, Saintillan, Shaqfeh & Darve (Reference Saintillan, Shaqfeh and Darve2006) employed Brownian dynamics simulations to investigate the effect of chain flexibility on the cross-streamline migration of short polymers in a pressure-driven flow between two flat plates. The latter numerical study confirmed the existence of a shear-induced migration towards the channel centreline away from the confining solid boundaries.
The hydrodynamic problem of particles freely moving between plane-parallel walls in the presence of an incident flow has been further considered in still more details. Under an external flow, Uspal, Eral & Doyle (Reference Uspal, Eral and Doyle2013) showed how shape and geometric confinement of rigid microparticles can conveniently be tailored for self-steering. Jones (Reference Jones2004) made use of a two-dimensional Fourier-transform technique to obtain an analytic expression of the Green tensor for the Stokes equations with an incident Poiseuille flow. In addition, he provided the elements of the resistance and mobility tensors in this slit-like geometry. Bhattacharya, Bławzdziewicz & Wajnryb (Reference Bhattacharya, Bławzdziewicz and Wajnryb2006) introduced a novel numerical algorithm based on transformations between Cartesian and spherical representations of Stokes flow to account for an incident Poiseuille flow. Staben, Zinchenko & Davis (Reference Staben, Zinchenko and Davis2003) presented a novel boundary-integral algorithm for the motion of a particle between two parallel planar walls in Poiseuille flow. The boundary-integral method formulated in their work allowed the effects of the confining walls to be directly incorporated into the stress tensor, without requiring discretisation of the two walls. In this context, Griggs, Zinchenko & Davis (Reference Griggs, Zinchenko and Davis2007) and Janssen & Anderson (Reference Janssen and Anderson2007, Reference Janssen and Anderson2008) employed boundary-integral methods to examine the motion of a deformable drop between two parallel walls in Poiseuille flow, where lateral migration towards the channel centre is observed.
Geometric confinement significantly alters the behaviour of swimming micro-organisms and can affect the motility of self-propelling active particles in a pronounced way (Lauga & Powers Reference Lauga and Powers2009; Menzel Reference Menzel2013, Reference Menzel2015; Bechinger et al. Reference Bechinger, Di Leonardo, Löwen, Reichhardt, Volpe and Volpe2016; Lauga Reference Lauga2016; Zöttl & Stark Reference Zöttl and Stark2016; Ostapenko et al. Reference Ostapenko, Schwarzendahl, Böddeker, Kreis, Cammann, Mazza and Bäumchen2018; Gompper et al. Reference Gompper, Winkler, Speck, Solon, Nardini, Peruani, Löwen, Golestanian, Kaupp and Alvarez2020; Shaebani et al. Reference Shaebani, Wysocki, Winkler, Gompper and Rieger2020). Surface-related effects on microswimmers can lead to crucial implications for biofilm formation and microbial activity. In a channel bounded by two walls, Bilbao et al. (Reference Bilbao, Wajnryb, Vanapalli and Bławzdziewicz2013) studied the locomotion of a model nematode, finding that the swimming organism tends to swim faster and navigate more effectively under confinement. Furthermore, Wu et al. (Reference Wu, Thiébaud, Hu, Farutin, Rafai, Lai, Peyla and Misbah2015, Reference Wu, Farutin, Hu, Thiébaud, Rafaï, Peyla, Lai and Misbah2016) investigated the effect of confinement on the swimming behaviour of a model eukaryotic cell undergoing amoeboid motion. There, the swimmer has been modelled as an inextensible membrane deploying local active force. It has been found that confinement can strongly alter the swimming gait. In addition, Brotto et al. (Reference Brotto, Caussin, Lauga and Bartolo2013) described theoretically the dynamics of self-propelling active particles in rigidly confined thin liquid films. They demonstrated that, due to hydrodynamic friction with the nearby rigid walls, confined microswimmers not only reorient themselves in response to flow gradients but also can show reorientation in uniform flows. In this context, Mathijssen et al. (Reference Mathijssen, Doostmohammadi, Yeomans and Shendruk2016) investigated theoretically the hydrodynamics of self-propelling microswimmers in a thin film. Daddi-Moussa-Ider et al. (Reference Daddi-Moussa-Ider, Lisicki, Mathijssen, Hoell, Goh, Bławzdziewicz, Menzel and Löwen2018) examined the behaviour of a three-sphere microswimmer in a channel bounded by two walls, where different swimming states have been observed. More recently, amoeboid swimming in a compliant channel was numerically investigated (Dalal, Farutin & Misbah Reference Dalal, Farutin and Misbah2020).
In all of the above-mentioned studies, the confining channel was assumed to be of infinite extent or periodically replicated along the lateral directions. Instead, here we consider the hydrodynamic problem for a point force acting near two coaxially positioned disks of finite radius. In many biologically and industrially relevant applications, finite-size effects become crucial for an accurate and reliable description of transport processes ranging from the microscale to the nanoscale. Prime examples include the ionic transport and electrokinetics in small-scale capacitors (Marini Bettolo Marconi & Melchionna Reference Marini Bettolo Marconi and Melchionna2012; Thakore & Hickman Reference Thakore and Hickman2015; Babel, Eikerling & Löwen Reference Babel, Eikerling and Löwen2018; Asta et al. Reference Asta, Palaia, Trizac, Levesque and Rotenberg2019), electrochemomechanical energy conversion in microfluidic channels (Daiguji et al. Reference Daiguji, Yang, Szeri and Majumdar2004), and the rheology of droplets, capsules or cells in constricted/structured microchannels (Park & Dimitrakopoulos Reference Park and Dimitrakopoulos2013; Le Goff et al. Reference Le Goff, Kaoui, Kurzawa, Haszon and Salsac2017; Trégouët et al. Reference Trégouët, Salez, Monteux and Reyssat2018, Reference Trégouët, Salez, Monteux and Reyssat2019), where boundary effects may play a pivotal role.
In this paper, we take a step towards addressing this context by presenting an analytical theory for the viscous flow resulting from a stokeslet singularity acting along the centre axis of two coaxially positioned disks of no-slip surfaces. We formulate the hydrodynamic problem as a mixed boundary-value problem, which we then transform into a system of dual integral equations. Along this path, we show that the solution of the flow field in the fluid region bounded by the two disks exhibits viscous toroidal eddies. In addition to that, we derive expressions for the hydrodynamics mobility functions and discuss the applicability and limitations of the superposition approximation. Moreover, we support our semi-analytical results by numerical simulations using a finite-element method (FEM), which leads to a good agreement.
The remainder of this paper is organised as follows. In § 2, we formulate the problem mathematically and derive the corresponding system of dual integral equations, from which the solution for the hydrodynamic flow fields can be obtained. We then make use of this solution in § 3 to yield an integral expression of the mobility function of a point-like particle slowly translating along the axis of the disks. Concluding remarks and outlooks are contained in § 4. In appendix A, we detail the analytical derivation of the kernel functions arising in the resulting integral equations.
2. Mathematical formulation
We examine the axisymmetric flow induced by a stokeslet singularity acting on the axis of symmetry of two coaxially positioned circular disks of equal radius 
$R$. Moreover, we suppose that the disks are located within the planes 
$z=-H/2$ and 
$z=H/2$, with 
$H$ denoting the separation distance between the disks. Their centres are positioned on the 
$z$ axis. In addition, we assume that the surrounding viscous fluid is Newtonian, of constant dynamic viscosity 
$\eta$, and that the flow is incompressible.
2.1. Governing equations
In low-Reynolds-number hydrodynamics, the fluid dynamics is governed by the Stokes equations (Happel & Brenner Reference Happel and Brenner1983)
\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{v} = 0 , \end{gather}
\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{\sigma} + F \delta(\boldsymbol{r}-\boldsymbol{r}_0) \, \hat{\boldsymbol{e}}_z = \boldsymbol{0} , \end{gather}
where 
$\boldsymbol {v}$ and 
$\boldsymbol {\sigma }$ denote, respectively, the fluid velocity field and the hydrodynamic stress tensor. For a Newtonian fluid, the latter is given by 
$\boldsymbol {\sigma } = -p {\boldsymbol{\mathsf{I}}} + 2\eta {\boldsymbol{\mathsf{E}}}$, where 
$p$ is the pressure field and 
${\boldsymbol{\mathsf{E}}} = (\boldsymbol {\nabla } \boldsymbol {v} + (\boldsymbol {\nabla } \boldsymbol {v})^{\mathrm {T}})/2$ is the rate-of-strain tensor, with the superscript T denoting a transpose. In addition, 
$\delta$ stands for the Dirac delta function, and 
$F$ is the amplitude of a stationary point force acting on the fluid at position 
$\boldsymbol {r}_0 = h \hat {\boldsymbol {e}}_z$, where 
$-H/2 < h < H/2$, with 
$\hat {\boldsymbol {e}}_z$ denoting the unit vector along the 
$z$ direction. See figure 1 for an illustration of the system set-up. In the remainder of this paper, we scale all the lengths involved in the problem by the separation 
$H$ of the two disks.
Figure 1. Schematic of the system. The surrounding viscous Newtonian fluid is set into motion through the action of a point-force singularity located on the symmetry axis of two coaxially positioned disks.
We designate by the subscript 1 the variables and parameters in the fluid region underneath the plane containing the lower disk, for which 
$z \le -1/2$, by the subscript 2 the fluid domain bounded by the planes 
$z=-1/2$ and 
$z=1/2$, and by the subscript 3 the region above the plane containing the upper disk, for which 
$z \ge 1/2$. Since the system is axisymmetric, all field variables are thus functions of the radial and axial coordinates only. Accordingly, the Stokes equations (2.1) can be projected onto the cylindrical coordinate system as
\begin{gather} \frac{v_r}{r} + \frac{\partial v_r}{\partial r} + \frac{\partial v_z}{\partial z} = 0 , \end{gather}
\begin{gather} -\frac{\partial p}{\partial r} + \eta \left( \Delta v_r - \frac{v_r}{r^2} \right) = 0 , \end{gather}
\begin{gather} -\frac{\partial p}{\partial z} + \eta \Delta v_z + F \delta(\boldsymbol{r} - \boldsymbol{r}_0) = 0 , \end{gather}
wherein 
$v_r$ and 
$v_z$ denote the radial and axial fluid velocities, respectively, and 
$\Delta$ is the Laplace operator given by
\begin{equation} \Delta := \frac{\partial^2}{\partial r^2} + \frac{1}{r} \frac{\partial}{\partial r} + \frac{\partial^2}{\partial z^2} . \end{equation}
We note that the three-dimensional Dirac delta function is expressed in axisymmetric cylindrical coordinates as 
$\delta (\boldsymbol {r} - \boldsymbol {r}_0) = ({\rm \pi} r)^{-1} \delta (r)\delta (z-h)$ (Bracewell Reference Bracewell1999).
In an unbounded viscous fluid, i.e. in the absence of the disks, the solution of equations (2.2) is given by the Oseen tensor, commonly denominated as the free-space Green function (Kim & Karrila Reference Kim and Karrila2013)
\begin{equation} v_r^{S} = \frac{F}{8{\rm \pi}\eta} \frac{r \left(z-h\right)}{\rho^3}, \quad v_z^{S} = \frac{F}{8{\rm \pi}\eta} \left( \frac{2}{\rho} - \frac{r^2}{\rho^3} \right) , \end{equation}
with the distance from the position of the point force 
$\rho = (r^2 + (z-h)^2)^{{1}/{2}}$. The corresponding pressure field reads
\begin{equation} p^{S} = \frac{F}{4{\rm \pi}} \frac{z-h}{\rho^3}. \end{equation}In the presence of the confining disks, the solution of the flow problem can be expressed as a superposition of the solution in an unbounded fluid, given above by (2.4a,b) and (2.5), and a complementary solution, the sum of the two solutions being required to satisfy the underlying regularity and boundary conditions. Then
\begin{equation} \boldsymbol{v} = \boldsymbol{v}^{S} + \boldsymbol{v}^*, \quad p = p^{S} + p^*, \end{equation}
wherein 
$\boldsymbol {v}^*$ and 
$p^*$ stand for the complementary solutions (also referred to as the image solution (Blake Reference Blake1971)) for the velocity and pressure fields, respectively.
For an axisymmetric Stokes flow, the general solution can be expressed in terms of two harmonic functions 
$\phi$ and 
$\psi$ as (Imai Reference Imai1973; Kim Reference Kim1983)
\begin{equation} v_r^* = z \frac{\partial \phi}{\partial r} + \frac{\partial \psi}{\partial r}, \quad v_z^* = z \frac{\partial \phi}{\partial z} - \phi + \frac{\partial \psi}{\partial z}, \quad p^* = 2\eta \frac{\partial \phi}{\partial z}, \end{equation}with
\begin{equation} \Delta \phi = 0 , \quad \Delta \psi = 0. \end{equation}In each of the three fluid domains introduced above, the solution of Laplace's equations (2.8a,b) can be expressed in terms of Fourier–Bessel integrals as
\begin{gather} \phi_i = \frac{F}{8{\rm \pi}\eta} \int_0^{\infty} \left( A_i^+(\lambda) \textrm{e}^{\lambda z} + A_i^-(\lambda) \textrm{e}^{-\lambda z} \right) J_0 (\lambda r) \, \mathrm{d} \lambda, \end{gather}
\begin{gather} \psi_i = \frac{F}{8{\rm \pi}\eta} \int_0^{\infty} \left( B_i^+(\lambda) \textrm{e}^{\lambda z} + B_i^-(\lambda) \textrm{e}^{-\lambda z} \right) J_0 (\lambda r) \,\mathrm{d} \lambda , \end{gather}
for 
$i \in \{1,2,3\}$, with 
$\lambda$ denoting the wavenumber and 
$J_k$ the 
$k$th-order Bessel function of the first kind (Abramowitz & Stegun Reference Abramowitz and Stegun1972). In addition, 
$A_i^{\pm }$ and 
$B_i^{\pm }$ are wavenumber-dependent unknown coefficients, to be determined from the regularity and boundary conditions. Then, the components of the image velocity and pressure fields are given by
\begin{gather} {v_r^*}_i = - \frac{F}{8{\rm \pi}\eta} \int_0^{\infty} \lambda \left( ( z A_i^+ + B_i^+ ) \textrm{e}^{\lambda z} + ( z A_i^- + B_i^- ) \textrm{e}^{-\lambda z} \right) J_1(\lambda r) \, \mathrm{d} \lambda , \end{gather}
\begin{gather} {v_z^*}_i = - \frac{F}{8{\rm \pi}\eta} \int_0^{\infty} \left( E_i^+\textrm{e}^{\lambda z} + E_i^- \textrm{e}^{-\lambda z} \right) J_0(\lambda r) \, \mathrm{d} \lambda, \end{gather}
\begin{gather} p^*_i = \frac{F}{4{\rm \pi}} \int_0^{\infty} \lambda \left( A_i^+ \textrm{e}^{\lambda z} - A_i^- \textrm{e}^{-\lambda z} \right) J_0(\lambda r) \, \mathrm{d} \lambda, \end{gather}
for 
$i \in \{1,2,3\}$, where we have defined the abbreviations 
$E_i^{\pm } = ( 1 \mp \lambda z ) A_i^{\pm } \mp \lambda B_i^{\pm }$.
2.2. Boundary conditions and dual integral equations
As regularity conditions, for the image field we require the velocity and pressure far away from the singularity location to vanish as 
$\rho \to \infty$. This implies that 
$A_1^- = B_1^- = A_3^+ = B_3^+ = 0$. In what follows, to simplify notation, we drop the plus sign in the fluid domain underneath the lower disk to denote 
$A_1 = A_1^+$ and 
$B_1 = B_1^+$, and we drop the minus sign in the fluid domain above the upper disk to denote 
$A_3 = A_3^-$ and 
$B_3 = B_3^-$.
The boundary conditions consist of requiring 
$(a)$ the natural continuity of the total fluid velocity field at the interfaces between the fluid domains, 
$(b)$ vanishing total velocities at the surfaces of the disks (the no-slip and no-permeability boundary condition Lauga, Brenner & Stone Reference Lauga, Brenner, Stone, Tropea, Yarin and Foss2007), and 
$(c)$ continuity of the total viscous-stress vectors at the interfaces between the fluid domains outside the regions occupied by the disks. Mathematically, these conditions can be expressed as
\begin{gather} (\boldsymbol{v}_1 - \boldsymbol{v}_2) \rvert_{z=-{1}/{2}}= (\boldsymbol{v}_2 - \boldsymbol{v}_3) \rvert_{z={1}/{2}} = \boldsymbol{0} \quad (r > 0) , \end{gather}
\begin{gather} \boldsymbol{v}_1 \rvert_{z = -{1}/{2}} = \boldsymbol{v}_2 \rvert_{z = {\pm}{1}/{2}} = \boldsymbol{v}_3 \rvert_{z = {1}/{2}} = \boldsymbol{0} \quad (r < R), \end{gather}
\begin{gather} \left( \boldsymbol{\sigma}_2 - \boldsymbol{\sigma}_1 \right) \boldsymbol{\cdot} \hat{\boldsymbol{e}}_z \rvert_{z=-{1}/{2}} = \left( \boldsymbol{\sigma}_3 - \boldsymbol{\sigma}_2 \right) \boldsymbol{\cdot} \hat{\boldsymbol{e}}_z \rvert_{z={1}/{2}} = \boldsymbol{0} \quad (r>R) , \end{gather}where the components of the stress vector are expressed in cylindrical coordinates for an axisymmetric flow field by
\begin{equation} \boldsymbol{\sigma}_i \boldsymbol{\cdot} \hat{\boldsymbol{e}}_z = \eta \left( \frac{\partial {v_r}_i}{\partial z} + \frac{\partial {v_z}_i}{\partial r} \right) \hat{\boldsymbol{e}}_r + \left( -p_i + 2\eta \, \frac{\partial {v_z}_i}{\partial z} \right) \hat{\boldsymbol{e}}_z, \quad i \in \{1,2,3\} . \end{equation} Applying the continuity of the radial components of the fluid velocity at the surfaces occupied by the two disks yields the expressions of the wavenumber-dependent coefficients associated with the intermediate fluid domain bounded by the two disks as functions of those in the lower and upper fluid domains. Defining 
$\boldsymbol {X}_2 = ( A_2^-, B_2^-, A_2^+, B_2^+ )^{\mathrm {T}}$ and 
$\boldsymbol {X}_{13} = ( A_1, B_1, A_3, B_3 )^{\mathrm {T}}$, we obtain
\begin{equation} \boldsymbol{X}_2 = {\boldsymbol{\mathsf{Q}}} \boldsymbol{\cdot} \boldsymbol{X}_{13} , \end{equation}
where the matrix 
${\boldsymbol{\mathsf{Q}}}$ is given by
\begin{equation} {\boldsymbol{\mathsf{Q}}} = \left( s^2-\lambda^2 \right)^{-1} \begin{pmatrix} \frac{1}{2} \left(s+\lambda c\right) & - \lambda s & - \frac{1}{2} \, \phi^+ & - \lambda^2\\ \frac{1}{4} \lambda s & \frac{1}{2} \left(s-\lambda c\right) & -\frac{1}{4} \lambda^2 & - \frac{1}{2} \, \phi^-\\ - \frac{1}{2} \, \phi^+ & \lambda^2 & \frac{1}{2} \left(s+\lambda c\right) & \lambda s\\ \frac{1}{4} \lambda^2 & - \frac{1}{2} \, \phi^- & -\frac{1}{4} \lambda s & \frac{1}{2} \left( s-\lambda c \right) \end{pmatrix}. \end{equation}
Here, we have defined for convenience the abbreviations 
$s = \sinh (\lambda )$ and 
$c = \cosh (\lambda )$. In addition, 
$\phi ^{\pm } = \lambda (\lambda \pm 1) + s\textrm {e}^{-\lambda }$.
On the one hand, by addressing the no-slip velocity boundary conditions at the surfaces of the disks prescribed by (2.11b) and projecting the resulting equations onto the radial and tangential directions, four integral equations on the inner domain are obtained:
\begin{gather} \int_0^{\infty} \lambda \left( \tfrac{1}{2} A_1 - B_1 \right) \textrm{e}^{-({\lambda}/{2})} J_1(\lambda r) \, \mathrm{d} \lambda = \psi_1^+ (r) \quad (r < R), \end{gather}
\begin{gather} \int_0^{\infty} \lambda \left(\tfrac{1}{2} A_3 + B_3 \right) \textrm{e}^{-({\lambda}/{2})} J_1(\lambda r) \, \mathrm{d} \lambda = \psi_1^- (r) \quad (r < R), \end{gather}
\begin{gather} \int_0^{\infty} \left( A_1 + \lambda\left(\tfrac{1}{2}A_1-B_1\right) \right) \textrm{e}^{-({\lambda}/{2})} J_0(\lambda r) \, \mathrm{d} \lambda = \psi_2^+ (r) \quad (r < R), \end{gather}
\begin{gather} \int_0^{\infty} \left( A_3 + \lambda\left(\tfrac{1}{2}A_3+B_3\right) \right) \textrm{e}^{-({\lambda}/{2})} J_0(\lambda r) \, \mathrm{d} \lambda = \psi_2^- (r) \quad (r < R) . \end{gather}Here the terms appearing on the right-hand sides in these equations are radial functions resulting from the evaluation of the terms associated with the flow velocity field induced by the free-space stokeslet at the surfaces of the coaxially positioned disks. They are explicitly given by
\begin{equation} \psi_1^{\pm} (r) = \frac{\pm r \left( h \pm \tfrac{1}{2} \right)}{\left(r^2+\left(h \pm\tfrac{1}{2}\right)^2\right)^{{3}/{2}}} , \quad \psi_2^{\pm} (r) = \frac{ r^2 + 2 \left(h\pm \tfrac{1}{2}\right)^2}{\left(r^2+\left(h\pm \tfrac{1}{2}\right)^2\right)^{{3}/{2}}} . \end{equation} On the other hand, four integral equations on the outer domain are obtained by addressing the continuity of the hydrodynamic stress vector at 
$z=\pm 1/2$ prescribed by (2.11c). They can be cast in the form
\begin{gather} \int_0^{\infty} g_i(\lambda) J_1(\lambda r) \, \mathrm{d} \lambda = 0 \quad (r>R), \quad i \in \{1,3\}, \end{gather}
\begin{gather} \int_0^{\infty} g_i(\lambda) J_0(\lambda r) \, \mathrm{d} \lambda = 0 \quad (r>R) , \quad i \in \{2,4\}, \end{gather}where we have defined the wavenumber-dependent quantities
\begin{gather} g_1(\lambda) = \lambda^2 \left( \left( \tfrac{1}{2} A_2^--B_2^- \right) \textrm{e}^{{\lambda}/{2}} + \left( \tfrac{1}{2} \left( A_1 - A_2^+ \right) + B_2^+ - B_1 \right) \textrm{e}^{-({\lambda}/{2})} \right) , \end{gather}
\begin{gather} g_3(\lambda) = \lambda^2 \left( \left( \tfrac{1}{2} A_2^+ + B_2^+ \right) \textrm{e}^{{\lambda}/{2}} + \left( \tfrac{1}{2} \left( A_3 - A_2^- \right) + B_3-B_2^- \right) \textrm{e}^{-({\lambda}/{2})} \right) , \end{gather}
\begin{gather} g_2(\lambda) = C^- \textrm{e}^{{\lambda}/{2}} + \lambda \left( \left(1+\tfrac{1}{2}\lambda\right) \left( A_1-A_2^+ \right) + \lambda \left( B_2^+ - B_1 \right) \right) \textrm{e}^{-({\lambda}/{2})} , \end{gather}
\begin{gather} g_4(\lambda) = C^+ \textrm{e}^{{\lambda}/{2}} + \lambda \left( \left(1+\tfrac{1}{2}\lambda\right) \left(A_3-A_2^-\right) + \lambda \left(B_3 - B_2^-\right) \right) \textrm{e}^{-({\lambda}/{2})} , \end{gather}
wherein 
$C^{\pm } = \lambda ( (1-\lambda /2) A_2^{\pm } \mp \lambda B_2^{\pm })$.
Inserting (2.13) and (2.14), equations (2.15)–(2.18) form a system of four dual integral equations (Tricomi Reference Tricomi1985) for the unknown wavenumber-dependent coefficients regrouped in 
$\boldsymbol {X}_{13}$. A solution of such types of dual integral equations with Bessel kernels can be obtained by the methods prescribed by Sneddon (Reference Sneddon1960, Reference Sneddon1966) and Copson (Reference Copson1961). A similar procedure has recently been employed by some of us to address the axisymmetric flow induced by a stokeslet near a circular elastic membrane (Daddi-Moussa-Ider, Kaoui & Löwen Reference Daddi-Moussa-Ider, Kaoui and Löwen2019), and the asymmetric flow field near a finite-sized rigid disk (Daddi-Moussa-Ider et al. Reference Daddi-Moussa-Ider, Lisicki, Löwen and Menzel2020). Once 
$\boldsymbol {X}_{13}$ is determined from solving the dual integral equations derived above, the remaining wavenumber-dependent coefficients expressed by 
$\boldsymbol {X}_{2}$ follow forthwith from (2.13) and (2.14).
The core idea of our solution approach consists of expressing the solution of (2.17) as definite integrals of the forms
\begin{equation} g_i(\lambda) = 2\lambda^{{1}/{2}} \int_0^R f_i(t) J_{{3}/{2}} (\lambda t) \, \mathrm{d} t , \quad i \in \{1,3\} , \end{equation}and
\begin{equation} g_i(\lambda) = 2\lambda^{{1}/{2}} \int_0^R f_i(t) J_{{1}/{2}} (\lambda t) \, \mathrm{d} t , \quad i \in \{2,4\} , \end{equation}
where 
$f_i: [0,R] \to \mathbb {R}$, for 
$i \in \{1,2,3,4\}$, are unknown functions to be determined. Accordingly, the integral equations in the outer domain boundaries are automatically satisfied upon making use of the following identity, which holds for any positive integer 
$p$ (Abramowitz & Stegun Reference Abramowitz and Stegun1972),
\begin{equation} \int_0^{\infty} \lambda^{{1}/{2}} J_p(\lambda r) J_{p+{1}/{2}} (\lambda t) \, \mathrm{d} \lambda = 0 \quad (0 < t < r) . \end{equation} By solving (2.18) for the coefficients 
$A_1$, 
$B_1$, 
$A_3$ and 
$B_3$ upon making use of (2.13) and (2.14), equation (2.15) can be rewritten as
\begin{gather} \int_{0}^{\infty} \left(2\lambda\right)^{-1} \left( g_{1}(\lambda) + \left( \lambda - 1 \right) \textrm{e}^{-\lambda} g_{3}(\lambda) + \lambda \textrm{e}^{-\lambda} g_{4}(\lambda) \right) J_{1}(\lambda r) \, \mathrm{d} \lambda = \psi_{1}^{+}(r) , \end{gather}
\begin{gather} \int_{0}^{\infty} \left(2\lambda\right)^{-1} \left( \left( \lambda - 1 \right) \textrm{e}^{-\lambda} g_{1}(\lambda) + \lambda \textrm{e}^{-\lambda} g_{2}(\lambda) + g_{3}(\lambda) \right) J_{1}(\lambda r) \, \mathrm{d} \lambda = \psi_{1}^{-}(r) , \end{gather}
\begin{gather} \int_{0}^{\infty} \left(2\lambda\right)^{-1} \left( g_{2}(\lambda) + \lambda \textrm{e}^{-\lambda} g_{3}(\lambda) + \left( \lambda + 1 \right) \textrm{e}^{-\lambda} g_{4}(\lambda) \right) J_{0}(\lambda r) \, \mathrm{d} \lambda = \psi_{2}^{+}(r) , \end{gather}
\begin{gather} \int_{0}^{\infty} \left(2\lambda\right)^{-1} \left( \lambda \textrm{e}^{-\lambda} g_{1}(\lambda) + \left( \lambda + 1 \right) \textrm{e}^{-\lambda} g_{2}(\lambda) + g_{4}(\lambda) \right) J_{0}(\lambda r) \, \mathrm{d} \lambda = \psi_{2}^{-}(r) . \end{gather} Next, by substituting (2.19) into (2.21) and interchanging the order of the integrations with respect to the variables 
$t$ and 
$\lambda$, the equations associated with the inner problem can be expressed in the following final forms:
\begin{equation} \int_0^R \left( L_5(r,t) f_1(t) + L_4(r,t) f_3(t) + L_1(r,t) f_4(t) \right) \,\mathrm{d} t = \psi_1^+(r), \end{equation}
\begin{equation} \int_0^R \left( L_4(r,t) f_1(t) + L_1(r,t) f_2(t) + L_5(r,t) f_3(t) \right) \,\mathrm{d} t = \psi_1^-(r), \end{equation}
\begin{equation} \int_0^R \left( L_6(r,t) f_2(t) + L_3(r,t) f_3(t) + L_2(r,t) f_4(t) \right) \,\mathrm{d} t = \psi_2^+(r), \end{equation}
\begin{equation} \int_0^R \left( L_3(r,t) f_1(t) + L_2(r,t) f_2(t) + L_6(r,t) f_4(t) \right) \,\mathrm{d} t = \psi_2^-(r), \end{equation}
where the kernels 
$L_i: [0,R]^2 \to \mathbb {R}$, for 
$i \in \{1,2,3,4\}$, are complex mathematical functions that are defined and provided in appendix A.
Equations (2.22) form a system of four Fredholm integral equations of the first kind (Smithies Reference Smithies1958; Polyanin & Manzhirov Reference Polyanin and Manzhirov1998) for the unknown functions 
$f_i(t)$, 
$i \in \{1,2,3,4\}$. Owing to the complicated nature of the kernel functions, we make recourse to numerical solutions.
2.3. Numerical solution of the integral equations and comparison with FEM simulations
We now summarise the main steps involved in the numerical computations of the flow field. First, the integration over the intervals 
$[0,R]$ in (2.22) are partitioned into 
$N$ subintervals and each integral is approximated by the standard middle Riemann sum (Davis & Rabinowitz Reference Davis and Rabinowitz2007). The four resulting equations are evaluated at 
$N$ values of 
$t_j$ that are uniformly distributed over the interval 
$[0,R]$ such that 
$t_j = (j-1/2)(R/N)$, with 
$j = 1, \ldots , N$. Secondly, the discrete values of 
$f_i (t_j)$, with 
$i \in \{1,2,3,4\}$, are obtained by solving the resulting linear system of 
$4N$ equations. Thirdly, the four integrals in (2.19) are converted into well-behaved definite integrals over 
$[0,{\rm \pi} /2]$ by using the change of variable 
$\lambda = \tan u$ and thus 
$\mathrm {d} \lambda = \mathrm {d} u / {\cos ^2 u}$. Thereupon, the resulting integrals are also approximated by the middle Riemann sum, and the wavenumber-dependent functions 
$g_i(\lambda _k = \tan u_k)$, 
$k = 1, \ldots , M$, are evaluated at discrete values of 
$u_k$ such that 
$u_k = (k-1/2)({\rm \pi} / 2 )/M$. Fourthly, the values of 
$\boldsymbol {X}_2$ at each discrete point 
$\lambda _k$ are readily obtained by inverting the linear system of four equations given by (2.18). In addition, it follows from (2.13) that 
$\boldsymbol {X}_{13} = {\boldsymbol{\mathsf{Q}}}^{-1} \boldsymbol {\cdot } \boldsymbol {X}_2$. Finally, the image flow fields are obtained from (2.10) by approximating, again, the integrals by the middle Riemann sum.
Even though the approach employed here may seem cumbersome at first glance, it has the advantage of being amenable to straightforward implementation. Unlike many direct numerical simulation techniques, which generally require discretisation of the entire three-dimensional fluid domain, or of at least an effectively two-dimensional domain when the axial symmetry is exploited, the integral formulation presented in this work reduces the solution of the flow problem to a set of one-dimensional integrals. Besides, the present semi-analytical approach might serve as a motivation for various theoretical investigations of related problems that could possibly pave the way towards real engineering applications.
In figure 2, we present a log–log plot of the variations of the discretisation error (Roy Reference Roy2010) associated with the numerical computation of the amplitude of the image velocity field versus the number of discrete points used in the numerical integration of (2.22) while keeping 
$M=10N$ in the discretisation of (2.19) and (2.10). The error is estimated relative to the numerical solution on a finer gird size for 
$N=15\,000$ and 
$M=150\,000$ at three different points of the fluid domain. We observe that the error decays approximately algebraically as 
$N^{-3/2}$ over the whole range of considered values of 
$N$ and lies well below 
$10^{-3}\,\%$ for 
$N \ge 5000$. We have checked that a similar behaviour is also found when varying the position of the stokeslet or the evaluation point within the fluid domain.
Figure 2. Log–log plot of the relative discretisation error occurring in the computation of the amplitude of the image velocity field versus the number of discretisation points, evaluated at various positions within the fluid domain. Here, we set 
$R=H$, 
$h/H=0.3$ and 
$M = 10N$. The errors are estimated relative to the corresponding values computed using a finer grid spacing with 
$N=15\,000$ and 
$M=150\,000$.
To validate our semi-analytical solution, we perform direct numerical simulations for the same geometry as well. We use a piecewise-quadratic finite-element discretisation of the Stokes problem stated by (2.2) in cylindrical coordinates. Since such an equal-order discretisation does not satisfy the inf-sup condition, we add stabilisation terms of local projection type (Becker & Braack Reference Becker and Braack2001). The numerical domain is artificially limited to 
$(0,R)\times (-Z,Z)$ with 
$R,Z\in \mathbb {R}$ being sufficiently large numbers so as to avoid spurious feedback to the region of interest close to the plates. In addition, the Dirac delta function forcing the flow is represented exactly in the variational formulation by means of
\begin{equation} \int_0^R\int_{-Z}^Z r \delta (\boldsymbol{r}-\boldsymbol{r}_0)\phi_z(\boldsymbol{r})\,\mathrm{d} r\,\mathrm{d} z = \phi_z(\boldsymbol{r}_0), \end{equation}
where 
$\phi _z$ is the test function corresponding to the vertical direction. Numerically, the singularity calls for very fine mesh resolution close to 
$\boldsymbol {r}_0$ and in proximity to the coaxially positioned plates, which we accomplish by local mesh adaptivity (Braack & Richter Reference Braack and Richter2006). Further details on the discretisation method and the solution of the resulting linear systems of equations can be found in Richter (Reference Richter2017).
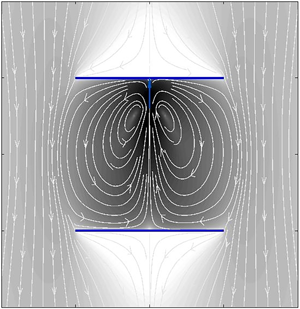
In figure 3, we represent the graphs of the resulting streamlines as well as contour plots of the total velocity field resulting from a stokeslet singularity axisymmetrically acting at various positions along the axis of two coaxially disposed disks of unit radius. Here, we set the numbers of discrete points to 
$N=15\,000$ and 
$M=150\,000$ in our numerical evaluation of the analytical description. The magnitude of the scaled velocity field is shown on a logarithmic scale in order to better appreciate the difference in magnitude between the different fluid regions. In each panel, we depict on the left-hand side the results obtained via our semi-analytical approach derived in the present work. On the right-hand side in each panel, we include the corresponding flow fields determined via the FEM simulations. Good agreement between the two solution procedures is obtained over the whole fluid domain, demonstrating the robustness and applicability of our semi-analytical approach. Most noticeably, we observe the existence of adjacent counter-rotating eddies, the axis of rotation of which is directed along the azimuthal direction. Accordingly, the resulting flow field in the inner region consists of toroidal eddies on account of the axisymmetric nature of the flow (Moffatt Reference Moffatt1964). In contrast to that, descending streamlines are obtained in the outer region. For infinitely large disks, analogous toroidal structures have previously been identified and proven to decay exponentially with distance from the singularity position (Liron & Blake Reference Liron and Blake1981). Moreover, we remark that the overall magnitude of the flow field becomes less important as the point force gets closer to a confining plate. This behaviour is accompanied by a notable increase of the asymmetry of the counter-rotating eddies.
Figure 3. Streamlines and contour plots of the flow field induced by a point-force singularity acting inside two coaxially positioned disks of no-slip surfaces and of rescaled unit radius for various values of the vertical distance 
$h/H$. In each panel, the flow velocity field obtained using the present semi-analytical approach is displayed in the left domain corresponding to 
$x \le 0$, while the solution obtained using FEM simulations is presented in the right domain corresponding to 
$x \ge 0$ for the same set of parameters. Here, we have defined the scaled flow velocity as 
$\boldsymbol {V} = \boldsymbol {v} / (F/(8{\rm \pi} \eta ))$. (a) 
$h/H = 0$, (b) 
$h/H = 0.1$, (c) 
$h/H = 0.2$, (d) 
$h/H = 0.25$, (e) 
$h/H = 0.3$, (f) 
$h/H = 0.4$.
Having derived the solution of the flow problem due to an axisymmetric stokeslet acting near two finite-sized coaxially positioned disks, we next employ our formalism to recover the solution earlier obtained by Liron & Mochon (Reference Liron and Mochon1976) for a stokeslet acting between two parallel planar walls of infinite extent along the transverse direction.
2.4. Solution for 
$R\to \infty$
For infinitely large disks, the integral equations (2.21) in the inner domain become defined for the whole axis of positive real numbers. Accordingly, the solution for the unknown functions 
$g_i(\lambda )$, for 
$i \in \{1,2,3,4\}$, can be obtained using inverse Hankel transforms. By making use of the orthogonality property of Bessel functions (Abramowitz & Stegun Reference Abramowitz and Stegun1972)
\begin{equation} \int_{0}^{\infty} r J_{\nu}(\lambda r) J_{\nu}(\lambda' r) \, \mathrm{d} r = \lambda^{-1} \delta(\lambda - \lambda') , \end{equation}we readily obtain
\begin{equation} {\boldsymbol{\mathsf{H}}} \boldsymbol{\cdot} \boldsymbol{g} = \hat{\boldsymbol{\psi}} , \end{equation}
where we have defined the unknown vector 
$\boldsymbol {g} = (g_1, g_2, g_3, g_4)^{\mathrm {T}}$, the wavenumber-dependent matrix
\begin{equation} {\boldsymbol{\mathsf{H}}} = \begin{pmatrix} \textrm{e}^{\lambda} & 0 & \lambda -1 & \lambda \\ \lambda -1 & \lambda & \textrm{e}^{\lambda} & 0 \\ 0 & \textrm{e}^{\lambda} & \lambda & \lambda + 1 \\ \lambda & \lambda + 1 & 0 & \textrm{e}^{\lambda} \end{pmatrix}, \end{equation}
and where 
$\hat {\boldsymbol {\psi }} = (\hat {\psi }_{1}^{+}, \hat {\psi }_{1}^{-}, \hat {\psi }_{2}^{+}, \hat {\psi }_{2}^{-})^{\mathrm {T}}$ gathers the inverse Hankel transforms of the previously introduced auxiliary functions defined by (2.16a,b). Specifically, we have
\begin{gather} \hat{\psi}_{1}^{\pm}(\lambda) = \int_{0}^{\infty} r \psi_{1}^{\pm}(r) J_{1}(\lambda r) \, \mathrm{d} r = ( \tfrac{1}{2} \pm h) \exp ({-\lambda (\tfrac{1}{2} \pm h )}) , \end{gather}
\begin{gather} \hat{\psi}_{2}^{\pm}(\lambda) = \int_{0}^{\infty} r \psi_{2}^{\pm}(r) J_{0}(\lambda r) \, \mathrm{d} r = \left( \frac{1}{\lambda} + \frac{1}{2} \pm h \right) \exp\left({- \lambda \left(\frac{1}{2} \pm h \right)}\right), \end{gather}
for 
$|h| < 1/2$. Solving the linear system of equations given by (2.25) and (2.26) for the unknown vector function 
$\boldsymbol {g}$ upon making use of (2.13), (2.14) and (2.18) leads to
\begin{equation} \boldsymbol{X}_{13} = ( \textrm{e}^{-\lambda h}, -h \textrm{e}^{-\lambda h}, \textrm{e}^{\lambda h}, -h \textrm{e}^{\lambda h} )^{\mathrm{T}}. \end{equation} Accordingly, the total velocity and pressure fields in the lower and upper regions vanish in the limit 
$R\to \infty$. The corresponding solution in the intermediate fluid domain can readily be obtained by invoking (2.13) and (2.14).
3. Hydrodynamic mobility
Our calculation of the flow field presented in the previous section can be employed in order to probe the effect of the two hard disks on the hydrodynamic drag acting on an enclosed point-like particle axially moving along the coaxially positioned axis. This effect is commonly quantified by the hydrodynamic mobility function, which relates the velocity of a particle to the net force exerted on its surface (Leal Reference Leal1980; Swan & Brady Reference Swan and Brady2007; Daddi-Moussa-Ider & Gekle Reference Daddi-Moussa-Ider and Gekle2016, Reference Daddi-Moussa-Ider and Gekle2017, Reference Daddi-Moussa-Ider and Gekle2018; Driscoll & Delmotte Reference Driscoll and Delmotte2019). In a bulk Newtonian fluid of constant dynamic viscosity 
$\eta$, the mobility function 
$\mu$ of a spherical particle of radius 
$a$ is given by the familiar Stokes law (Stokes Reference Stokes1851), which states that in this case the mobility is 
$\mu _0 = 1/(6{\rm \pi} \eta a)$. In the presence of the confining disks, the leading-order correction to the particle mobility for an axisymmetric motion along the axis is obtained by evaluating the image flow field at the particle position as
\begin{equation} \Delta\mu = F^{-1}\lim_{(r,z) \to (0, h)} {v_z^*}_2 (r,z). \end{equation}Evaluating the limit in the latter equation and scaling by the bulk mobility, the scaled correction to the particle mobility is obtained as
\begin{equation} \frac{\Delta\mu}{\mu_0} = -k a, \end{equation}where
\begin{equation} k = \tfrac{3}{4} \int_0^{\infty} \left( \left( \left(1-\lambda h\right)A_2^+ - \lambda B_2^+ \right) \textrm{e}^{\lambda h} + \left( \left(1+\lambda h\right)A_2^- + \lambda B_2^- \right) \textrm{e}^{-\lambda h} \right)\,\mathrm{d} \lambda \end{equation}is a positive dimensionless number commonly denominated as the correction factor of the Stokes steady mobility (Happel & Brenner Reference Happel and Brenner1983). Unfortunately, an analytical evaluation of this infinite integral is not auspicious. Therefore, we make recourse to a numerical evaluation.
For infinitely large disks, i.e. as 
$R\to \infty$, the correction factor 
$k$ in (3.2) can conveniently be cast into the simple integral form
\begin{equation} k_{\infty} = \tfrac{3}{8} \int_0^{\infty} W(\lambda) \left( \sinh^2\lambda - \lambda^2 \right)^{-1} \, \mathrm{d} \lambda , \end{equation}where we have defined the wavenumber-dependent function
\begin{equation} W(\lambda) = \varGamma_+ + \varGamma_- + \gamma_+ + \gamma_- + \textrm{e}^{-2\lambda} - \beta_+\beta_- \lambda^3 - 2\lambda^2 - 2\lambda - 1 , \end{equation}with
\begin{equation} \beta_{\pm} = 1 \pm 2h , \quad \varGamma_{\pm} = ( 1 + \tfrac{1}{2} \, \lambda^2 \beta_{\pm}^2 ) \sinh ( \lambda \beta_{\mp} ) , \quad \gamma_{\pm} = \lambda \beta_{\pm} \cosh ( \lambda \beta_{\mp} ) . \end{equation}This result is found to be in full agreement with the expression obtained by Swan & Brady (Reference Swan and Brady2010), who used a two-dimensional Fourier transform technique.
In figure 4, we present a linear–logarithmic plot of the correction factor of the mobility function versus the radius of the disks for various values of the singularity position. Results are obtained by integrating (3.3) numerically. We observe that the curves follow a sigmoid-logistic-like phenomenology, implying that the correction factor increases significantly in the range of small radii before it reaches a saturation value. The latter corresponds to the correction factor predicted near two infinitely large disks given by (3.4).
Figure 4. Variations of the correction factor of the hydrodynamic mobility as defined by (3.3) versus 
$R/H$ for various values of 
$h/H$. Horizontal dashed lines correspond to the correction factor near two infinitely large disks as given by (3.4). Inset: Evolution of 
$R_{99}/H$ versus 
$h/H$, where 
$R_{99}$ is defined such that 
$k (R_{99}/H) = 0.99k_{\infty }$, for which the correction factor near infinitely large disks is almost recovered.
Next, in order to quantify the effect of finite disk size on the correction to the hydrodynamic mobility, we customarily define the radius 
$R_{99}$ for which the mobility near infinitely large disks is essentially reached, such that 
$k(R_{99}) = 0.99 k_{\infty }$. In the inset of figure 4, we display the variations of 
$R_{99}$ versus 
$h$ based on the data presented in the main plot. We observe that 
$R_{99}$ reaches a maximum value of approximately 0.62 at the mid-plane of the channel before it monotonically decreases with 
$h$. This observation suggests that, to a good approximation, the mobility near two infinitely large disks can adequately be used to estimate the mobility at an arbitrary position along the axis provided that the ratio of radius to channel height is above 0.62. Hence, accounting for the finite-size effect here becomes crucial only for values below this threshold.
Finally, we comment on the applicability of the often-used approximation originally suggested by Oseen (Reference Oseen1928) to predict the particle mobility between two boundaries by superimposing separately the leading-order effects of each boundary. Accordingly,
\begin{equation} \frac{\Delta\mu_{Sup}}{\mu_0} = -k_{Sup} a, \quad k_{Sup} = -a^{-1} \left( \left. \frac{\Delta\mu_{Disk}}{\mu_0} \right|_{b={1}/{2}-h} + \left. \frac{\Delta\mu_{Disk}}{\mu_0} \right|_{b={1}/{2}+h} \right) , \end{equation}where the leading-order correction to the mobility function for axisymmetric motion normal to one rigid circular disk has previously been obtained by Kim (Reference Kim1983) and is expressed by
\begin{equation} \frac{\Delta\mu_{Disk}}{\mu_0} = -\frac{3}{4{\rm \pi}} \left( \frac{3+5\xi^2}{(1+\xi^2)^2} + \frac{3}{\xi} \arctan \left( \frac{1}{\xi} \right) \right) \frac{a}{R} , \end{equation}
wherein 
$\xi = b/R$ is a dimensionless parameter with 
$b$ denoting the distance between the particle and the centre of the disk. This solution was obtained by formulating the flow problem in terms of a mixed boundary-value problem and solving the resulting dual integral equations using an approach analogous to that employed in the present work. Notably, for 
$\xi \to 0$ we recover the familiar correction to the hydrodynamic mobility near an infinitely extended plane solid wall of no-slip boundary condition at its surface, namely 
$\Delta \mu _{Disk}/\mu _0 = -9a/(8b)$, as originally obtained by Lorentz using the reciprocal theorem more than a century ago (Lorentz Reference Lorentz1907; Lee, Chadwick & Leal Reference Lee, Chadwick and Leal1979).
We now assess the accuracy of the superposition approximation stated by (3.7a,b) by direct comparison with the exact prediction given by (3.3). In figure 5, we plot the variations of the percentage relative error between the correction factors 
$k_{Sup}$ and 
$k$ versus the radius of the disks 
$R$ for various values of the particle position 
$h$. In the range of small values of 
$R$, the relative error amounts to small values, typically smaller than 10 % for 
$R < 0.1$. Upon increasing 
$R$, the relative error gradually increases in a logistic-like manner, before it saturates on a plateau value as 
$R$ gets larger. The maximum error is obtained for the particle located on the mid-plane between the two disks for 
$h=0$ and is found to be approximately 55 % in the limit of infinite disk radius. Therefore, the superposition approximation cannot be applied properly in this case. Nonetheless, as the particle position gets closer to either disk, the maximum error notably decreases to amount to only approximately 12 % for 
$h = 0.4$. Consequently, the superposition approximation can frequently be utilised in this range of values to predict the hydrodynamic mobility for axisymmetric motion along the axis of the disks.
4. Conclusions
To summarise, we have examined the axisymmetric Stokes flow resulting from a stokeslet singularity acting on the axis of two coaxially positioned circular disks of equal radius. We have formulated the solution for the viscous incompressible flow field as a mixed boundary-value problem, which we have then reduced to a system of dual integral equations for four unknown wavenumber-dependent functions. Most importantly, we have shown the existence of viscous toroidal eddies in the fluid region bounded by the two plates. In the limit of infinitely large disks, we have successfully recovered the classic solution by Liron & Mochon (Reference Liron and Mochon1976) for a stokeslet acting normal to two parallel planar walls.
Additionally, we have provided an integral expression of the hydrodynamic mobility function quantifying the effect of the confining plates on the motion of a point-like particle moving along the axis of the coaxially positioned disks. Furthermore, we have demonstrated that accounting for the finite-size effect of the disks becomes essential only below a threshold value of the ratio of radius to channel height. Beyond this value, the mobility near two infinitely large disks can appropriately be employed. Finally, we have tested the validity and robustness of Oseen's approximation that postulates that the particle mobility between two boundaries could approximately be predicted by superimposing the contributions from each boundary independently. We have found that this simplistic approximation works quite well as the particle gets closer to either boundary but severely breaks down when the particle is located in the mid-plane between the two disks.
The analytical approach in the present paper is based on the assumption of flow axisymmetry. The Stokes flow induced by a stokeslet directed along an arbitrary direction in the presence of two coaxially positioned disks would be worth investigating in a future study. We conjecture that this solution might be obtained by making use of the Green and Neumann functions supplemented by the edge function, following the approach by Miyazaki (Reference Miyazaki1984). This solution can then be employed to evaluate the translational and rotational mobility functions of particles located at arbitrary positions between the two disks. Alternatively, the problem can possibly be approached differently by means of multipole expansion methods involving the expression of the relevant hydrodynamic fields using oblate spheroidal coordinates (Lee & Leal Reference Lee and Leal1980). This approach has been widely employed in the context of micromechanics of heterogeneous composite materials and fracture analysis (Kushch & Sangani Reference Kushch and Sangani2000; Kushch Reference Kushch2013). In principle, our calculations can be extended to account for higher-order correction factors in the aspect ratio between the radius of the disks and the distance between the particle and the bounding plates (Swan & Brady Reference Swan and Brady2010), but this would require a very challenging effort.
For applications requiring the precise manipulation of single molecules at the nanoscale level, the no-slip boundary condition may need to be lifted. In this context, the effect of partial slip at the surfaces of the disks is commonly characterised by assuming that the velocity components of the fluid tangent to the surfaces of the disks is proportional to the rate of strain at the surfaces (Lauga & Squires Reference Lauga and Squires2005; Lasne et al. Reference Lasne, Maali, Amarouchene, Cognet, Lounis and Kellay2008). This is an interesting aspect that could be included in our formalism and represents a worthwhile extension of the problem for future studies. We hope that our study will prove useful to researchers as well as practitioners working on particulate flow problems involving finitely sized boundaries, and pave the way towards better design and control of various processes in micro- and nanofluidic systems.
Acknowledgements
A.D.M.I., H.L. and A.M.M. gratefully acknowledge support from the DFG (Deutsche Forschungsgemeinschaft) through the projects DA 2107/1-1, LO 418/16-3 and ME 3571/2-2.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Analytical expressions for the kernel functions
In this appendix, we provide technical details regarding the analytical derivation of the kernel functions appearing in the system of Fredholm integral equations of the first kind given by (2.22) of the main body of the paper.
The kernel functions can be expressed as infinite integrals over the wavenumber 
$\lambda$ as
\begin{gather} L_1 (r,t) = \int_0^{\infty} \lambda^{{1}/{2}} \textrm{e}^{-\lambda} J_1 (\lambda r) J_{{1}/{2}} (\lambda t) \, \mathrm{d}\lambda, \end{gather}
\begin{gather} L_2 (r,t) = \int_0^{\infty} \left( \lambda^{{1}/{2}}+\lambda^{-{1}/{2}} \right) \textrm{e}^{-\lambda} J_0 (\lambda r) J_{{1}/{2}} (\lambda t) \, \mathrm{d}\lambda, \end{gather}
\begin{gather} L_3 (r,t) = \int_0^{\infty} \lambda^{{1}/{2}} \textrm{e}^{-\lambda} J_0 (\lambda r) J_{{3}/{2}} (\lambda t) \, \mathrm{d} \lambda , \end{gather}
\begin{gather} L_4 (r,t) = \int_0^{\infty} \left( \lambda^{{1}/{2}}-\lambda^{-{1}/{2}} \right) \textrm{e}^{-\lambda} J_1 (\lambda r) J_{{3}/{2}} (\lambda t) \, \mathrm{d}\lambda , \end{gather}
\begin{gather} L_5(r,t) = \int_0^{\infty} \lambda^{-{1}/{2}} J_1(\lambda r) J_{{3}/{2}} (\lambda t) \, \mathrm{d} \lambda, \end{gather}
\begin{gather} L_6(r,t) = \int_0^{\infty} \lambda^{-{1}/{2}} J_0(\lambda r) J_{{1}/{2}} (\lambda t) \, \mathrm{d} \lambda, \end{gather}
where 
$(r,t) \in [0,R]^2$. It can be shown that the first four integrals can conveniently be expressed in closed mathematical forms as
\begin{gather} L_1(r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} \frac{1}{r} \operatorname{Im} ( \xi_+ \delta_+ ) , \end{gather}
\begin{gather} L_2(r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} \left( \operatorname{Re} (\varLambda ) + \operatorname{Im} (\delta_-) \right) , \end{gather}
\begin{gather} L_3(r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} \operatorname{Re} ( \varLambda t^{-1} - \delta_- ) , \end{gather}
\begin{gather} L_4(r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} \left(\operatorname{Re} ( \chi_1 ) + \operatorname{Im} ( \chi_2 ) \right) , \end{gather}where we have defined the abbreviations
\begin{gather} \xi_{\pm} = 1 \pm \textrm{i}t , \quad \delta_{\pm} = \left( r^2 + \xi_{\pm}^2 \right)^{-{1}/{2}} , \quad \varLambda = \arcsin \left( \frac{t+\textrm{i}}{r} \right), \quad \sigma = \frac{r}{\xi_- + \delta_-^{-1}} , \end{gather}
\begin{gather} \alpha = \frac{t}{r} , \quad \chi_1 = \delta_- \left( \frac{r}{2} \left(1+\sigma^2\right) + \frac{\xi_-}{r} \right) - \frac{\varLambda}{2\alpha}, \quad \chi_2 = \frac{1}{rt\delta_-} + \frac{\delta_-}{8\alpha} \left( \xi_- - r\sigma^3 \right) . \end{gather} In addition, the integrals 
$L_5$ and 
$L_6$ have analytical forms and can be calculated directly from standard integration tables or software algebra systems such as Mathematica (Wolfram Reference Wolfram1999) as
\begin{gather} L_5(r,t) = \frac{1}{2} \left( \frac{\rm \pi}{2t} \right)^{{1}/{2}} \alpha^{-1} H(t-r) + \left( \frac{1}{2{\rm \pi} t} \right)^{{1}/{2}} \left( \alpha^{-1} \arcsin (\alpha) - ( 1-\alpha^2 )^{{1}/{2}} \right) H (r-t), \end{gather}
\begin{gather} L_6(r,t) = \left( \frac{\rm \pi}{2t} \right)^{{1}/{2}} H(t-r) + \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} \arcsin (\alpha) H(r-t), \end{gather}
where 
$H(\cdot )$ denotes the Heaviside step function.
In the following, we will show how the integrals given by (A 1) can be evaluated analytically. The core idea of our approach consists of expressing these integrals in the form of Laplace transforms of Bessel functions of the first kind (Spiegel Reference Spiegel1965; Widder Reference Widder2015),
\begin{equation} \mathcal{L}\left\{ J_k(z)\right\} (p) = (1+p^2 )^{-{1}/{2}} \left( p + (1+p^2 )^{{1}/{2}} \right)^{-k} , \end{equation}and using the recurrence relation (Abramowitz & Stegun Reference Abramowitz and Stegun1972)
\begin{equation} \frac{2k}{z} J_k(z) = J_{k-1}(z) + J_{k+1} (z) . \end{equation}In addition, we will employ the following identities providing closed-form expressions for the Bessel functions of the first kind of half-integer order in terms of the standard trigonometric functions,
\begin{gather} J_{{1}/{2}}(z) = \left(\frac{2}{{\rm \pi} z}\right)^{{1}/{2}} \sin(z), \end{gather}
\begin{gather} J_{-{1}/{2}}(z) = \left(\frac{2}{{\rm \pi} z}\right)^{{1}/{2}} \cos(z) . \end{gather}A.1. Evaluation of the integral $L_1$
By making use of the identity given by (A 7a), the integral 
$L_1$ stated by (A 1a) can be expressed as
\begin{equation} L_1 (r,t) = \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} \int_0^{\infty} \textrm{e}^{-\lambda} J_1 (\lambda r)\sin(\lambda t) \, \mathrm{d}\lambda. \end{equation}
Using the change of variable 
$x=\lambda r$ and Euler's representation of the sine function, the latter integral can be expressed as
\begin{equation} L_1(r,t) = \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} \frac{1}{r} \operatorname{Im} \left(\int_0^{\infty} \exp\left({-\frac{x}{r}\left( 1-\textrm{i}t \right)}\right) J_1 (x) \, \mathrm{d}x \right). \end{equation}
This leads to (A 2a) after making use of the Laplace transform given by (A 5) for 
$k=1$ and 
$p=(1-\textrm {i}t)/r$. We note that 
$\operatorname {Im}(z) = -\operatorname {Im}(\bar {z})$ for 
$z \in \mathbb {C}$, where 
$\bar {z}$ denotes the complex conjugate of 
$z$.
A.2. Evaluation of the integral $L_2$
We next consider the integral defined by (A 1b), which can conveniently be decomposed into two parts as
\begin{equation} L_2(r,t) = L_{2,1} (r,t) + L_{2,2} (r,t) , \end{equation}where
\begin{gather} L_{2,1} (r,t) = \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} \int_0^{\infty} \textrm{e}^{-\lambda} J_0 (\lambda r)\sin(\lambda t) \, \mathrm{d}\lambda , \end{gather}
\begin{gather} L_{2,2} (r,t) = \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} \int_0^t\,\mathrm{d} u \int_0^{\infty} \textrm{e}^{-\lambda} J_0 (\lambda r)\cos(\lambda u) \, \mathrm{d}\lambda . \end{gather}Here, we have made use of (A 7a) together with the integral representation
\begin{equation} \sin(\lambda t) = \lambda \int_0^t \cos(\lambda u) \, \mathrm{d} u. \end{equation} Using Euler's relation together with (A 5) for 
$k=0$, (A 11) can be evaluated as
\begin{gather} L_{2,1} (r,t) = \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} \operatorname{Im}\left( \left(r^2+(1-\textrm{i}t)^2\right)^{-{1}/{2}} \right) , \end{gather}
\begin{gather} L_{2,2} (r,t) = \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} \operatorname{Re} \left( \int_0^t \left(r^2+(1-\textrm{i}u)^2\right)^{-{1}/{2}} \, \mathrm{d}u \right). \end{gather}The definite integral in (A 13b) can be evaluated as
\begin{equation} L_{2,2} (r,t) = \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} \operatorname{Re} \left( \arcsin \left( \frac{t+\textrm{i}}{r} \right) \right). \end{equation}Equation (A 2b) follows forthwith after collecting terms.
It is worth mentioning that, for a given complex number 
$z=x+\textrm {i}y$, the arcsine function is defined when 
${\pm }x \notin (1,\infty )$ as (Abramowitz & Stegun Reference Abramowitz and Stegun1972)
\begin{equation} \arcsin (z) = \arcsin (\alpha_-) + \textrm{i}\operatorname{sign}(y) \ln \left( \alpha_+ + \left( \alpha_+^2 - 1 \right)^{{1}/{2}} \right) , \end{equation}where
\begin{equation} \alpha_{\pm} = \tfrac{1}{2} ((x+1)^2+y^2)^{{1}/{2}} \pm \tfrac{1}{2} ((x-1)^2+y^2)^{{1}/{2}} . \end{equation}A.3. Evaluation of the integral $L_3$
Analogously, the integral 
$L_3$ defined by (A 1c) can be decomposed into two parts as
\begin{equation} L_3(r,t) = L_{3,1}(r,t) - L_{3,2}(r,t) , \end{equation}
upon using the recurrence relation stated by (A 6) and setting 
$k=1/2$ together with the identities given by (A 7). Here, we have defined 
$L_{3,1}(r,t) = t^{-1} L_{2,2} (r,t)$ and
\begin{equation} L_{3,2}(r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} \int_0^{\infty} \textrm{e}^{-\lambda} J_0(\lambda r) \cos(\lambda t) \, \mathrm{d} \lambda , \end{equation}which can readily be evaluated as (A 11a) but this time by taking the real part. This leads to (A 2c) upon collecting terms.
A.4. Evaluation of the integral $L_4$
Finally, upon using (A 6) for 
$k=1/2$ and the identities given by (A 7), the integral 
$L_4$ can be decomposed into four parts:
\begin{equation} L_4 (r,t) = L_{4,1} + L_{4,2} - ( L_{4,3} + L_{4,4} ) , \end{equation}where we have defined
\begin{gather} L_{4,1} (r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} t^{-1} \int_0^{\infty} \lambda^{-1} \textrm{e}^{-\lambda} J_1 (\lambda r)\sin(\lambda t) \, \mathrm{d}\lambda, \end{gather}
\begin{gather} L_{4,2} (r,t) = \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} \int_0^{\infty} \lambda^{-1} \textrm{e}^{-\lambda} J_1 (\lambda r)\cos(\lambda t) \, \mathrm{d}\lambda , \end{gather}
\begin{gather} L_{4,3} (r,t) = \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} \int_0^{\infty} \textrm{e}^{-\lambda} J_1 (\lambda r)\cos(\lambda t) \, \mathrm{d}\lambda, \end{gather}
\begin{gather} L_{4,4} (r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} t^{-1} \int_0^{\infty} \lambda^{-2} \textrm{e}^{-\lambda} J_1 (\lambda r)\sin(\lambda t) \, \mathrm{d}\lambda. \end{gather}In the following, we will make use when appropriate of the shorthand notation defined in (A 3a). By using the integral representation of the sine function given by (A 12), the first integral can be expressed as
\begin{equation} L_{4,1} (r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} t^{-1} \int_0^t\,\mathrm{d} u\int_0^{\infty} \textrm{e}^{-\lambda} J_1 (\lambda r)\cos(\lambda u) \, \mathrm{d}\lambda. \end{equation}
Similarly, the evaluation of the indefinite integral over 
$\lambda$ can be performed using the Laplace transform of the Bessel function given by (A 5) to obtain
\begin{equation} L_{4,1} (r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} (tr)^{-1} \operatorname{Re} \left( \int_0^t \left(1 - (1-\textrm{i}u) \left(r^2+(1-\textrm{i}u)^2\right)^{-{1}/{2}} \right)\,\mathrm{d} u \right) . \end{equation}The definite integral in the latter equation can then be evaluated and cast in the final simplified form
\begin{equation} L_{4,1} (r,t) = \left( \frac{2}{{\rm \pi} t} \right)^{{1}/{2}} r^{-1} \left(1 + t^{-1} \operatorname{Im} ( \delta_-^{-1} ) \right) . \end{equation} Next, the evaluation of the second integral is straightforward after expressing the first-order Bessel function as a function of the zeroth- and second-order Bessel functions using the recurrence relation given by (A 6) for 
$k=1$ to obtain
\begin{equation} L_{4,2} (r,t) = r (2{\rm \pi} t )^{-{1}/{2}} \int_0^{\infty} \textrm{e}^{-\lambda} \left( J_0(\lambda r) + J_2(\lambda r) \right) \cos(\lambda t) \, \mathrm{d}\lambda , \end{equation}which can readily be evaluated as
\begin{equation} L_{4,2} (r,t) = r (2{\rm \pi} t )^{-{1}/{2}} \operatorname{Re}\left( \delta_- \left( 1 + \sigma^2 \right) \right) . \end{equation} The third integral can be deduced from the calculation of 
$L_1 (r,t)$ given by (A 9), this time by taking the real part to obtain
\begin{equation} L_{4,3}= \left(\frac{2}{{\rm \pi} t}\right)^{{1}/{2}} r^{-1} \operatorname{Re} (1 - \xi_- \delta_- ). \end{equation}Lastly, the fourth integral can be decomposed into two parts as
\begin{equation} L_{4,4} (r,t) = L_{4,4,1} (r,t) + L_{4,4,2} (r,t) , \end{equation}
where 
$L_{4,4,1} (r,t) = (2\alpha )^{-1} L_{2,2} (r,t)$ and
\begin{equation} L_{4,4,2} (r,t) = (2{\rm \pi} t)^{-{1}/{2}} \frac{r}{t} \int_0^{\infty} \lambda^{-1} \textrm{e}^{-\lambda} J_2 (\lambda r)\sin(\lambda t) \, \mathrm{d}\lambda . \end{equation}This integral can be handled using the recurrence formula given by (A 6) to obtain
\begin{equation} L_{4,4,2} (r,t)= (2{\rm \pi} t)^{-{1}/{2}} \frac{r^2}{4t}\int_0^{\infty} \textrm{e}^{-\lambda} \left(J_1 (\lambda r) + J_3(\lambda r) \right)\sin(\lambda t) \, \mathrm{d}\lambda . \end{equation}The latter integral can be calculated and cast in the final simplified form
\begin{equation} L_{4,4,2} (r,t) = (2{\rm \pi} t)^{-{1}/{2}} (4\alpha )^{-1} \left( r\operatorname{Im} (\delta_- \sigma^3 ) -\operatorname{Im} (\xi_- \delta_- ) \right) . \end{equation}By collecting terms, (A 2d) is readily obtained.
Open access
