No CrossRef data available.
Article contents
Arbitrary-order sensitivities of the incompressible base flow and its eigenproblem
Published online by Cambridge University Press: 23 April 2024
Abstract
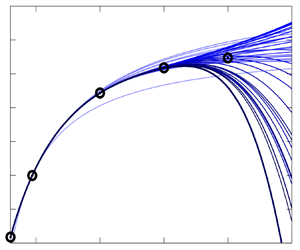
First-order sensitivities and adjoint analysis are used widely to control the linear stability of unstable flows. Second-order sensitivities have recently helped to increase accuracy. In this paper, a method is presented to calculate arbitrary high-order sensitivities based on Taylor expansions of the incompressible base flow and its eigenproblem around a scalar parameter. For the incompressible Navier–Stokes equations, general expressions for the sensitivities are derived, into which parameter-specific information can be inserted. The computational costs are low since, for all orders, a linear equation system has to be solved, of which the left-hand-side matrix stays constant and thus its preconditioning can be exploited. Two flow scenarios are examined. First, the cylinder flow equations are expanded around the inverse of the Reynolds number, enabling the prediction of the two-dimensional cylinder base flow and its leading eigenvalue as a function of the Reynolds number. This approach computes accurately the base flow and eigenvalue even in the unstable regime, providing, when executed subsequently, a mean to calculate unstable base flows. This case gives a clear introduction into the method and allows us to discuss its constraints regarding convergence behaviour. Second, a small control cylinder is introduced into the domain of the cylinder flow for stabilization. Higher-order sensitivity maps are calculated by modelling the small cylinder with a steady forcing. These maps help to identify stabilizing areas of the flow field for Reynolds numbers within the laminar vortex shedding regime, with the required number of orders increasing as the Reynolds number rises. The results obtained through the proposed method align well with numerically calculated eigenvalues that incorporate the cylinder directly into the grid.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press



