1. Introduction
When an area of floating ice shelf is halted by grounding, accumulation over the pinned area may lead to the formation of a dome-shaped ice rise. The flow in such a system is approximately radial and largely independent of the surrounding ice shelf. Under constant climatic conditions an equilibrium should be reached between gains due to accumulation and losses due to outward flow. The surface profile of the ice rise in equilibrium is a consequence of the flow properties of ice and the geometry of the bed on which it rests. Many ice rises rest on nearly horizontal beds, either because the ice shelf has grounded on a shoal or because any irregularities have been eroded by the ice shelf. Many are of a convenient size for experiment, and conditions of mean annual temperature, mean density, and accumulation are expected to vary little over their extent. Ice rises are therefore particularly well suited to the study of ice deformation under quite simple conditions. Here we describe measurements carried out on four ice rises located on Larsen Ice Shelf, which stretches along the east coast of the Antarctic Peninsula.
Other studies have been made on similar features in the Antarctic. Surface and bedrock profiles have been measured for Drygalski Island (Reference KapitsaKapitsa, 1958; Reference Savel’yevSavel’yev, 1961), an isolated island some 18 km long and 415 m thick, and an extensive survey has been made of Roosevelt Island (Reference Bentley and GiovinettoBentley and Giovinetto, 1962; Reference ClappClapp, 1965), a very large ice rise on the Ross Ice Shelf, of size 120 × 70 km2 and thickness some 750 m. Reference BuddBudd (1969) has studied the rheology of ice using data from Law Dome, a large dome-shaped promontory attached to the Antarctic ice sheet, but the present study is the first to investigate the flow of ice in small Antarctic ice rises.
2. Basic description
The ice rises studied are shown in Figure 1: Gipps Ice Rise (68° 45’ S., 60° 05’ W.), Ewing Island (69° 58’ S., 61° 25’ W.), Dolleman Island (70° 35’ S., 60° 50’ W.), and Butler Island (72° 13’ S., 60° 50’ W.). They are roughly elliptical in plan, with diameters between 5 and 20 km and ratios of major to minor axis of about 1.5. They are between 280 and 460 m thick. Table I summarizes data on their dimensions.

Fig. 1. Map showing location of ice rises on the Antarctic Peninsula. The inset shows their position relative to Antarctica as a whole. The hatclied lines represent approximate ice-shelf edges.
Table I. Ice-rise data

These sites, situated on the east coast of the Antarctic Peninsula, have a continental climate (Reference Martin and PeelMartin and Peel, 1978), with 10 m temperatures of about – 17.7°C (personal communication from D. A. Peel). Accumulation has been measured on the summit of three of the ice rises by means of annual oxygen-isotope variations in snow cores (personal communication from D. A. Peel). It lies in the region 0.2–0.4 m a−1 of ice. The ice rises have been depth-sounded in previous years using airborne radio echo-equipment. These flights, made along the long axis of each island, show the bedrock to be smooth to within the resolution of the equipment (some 10 m). Bedrock under Dolleman Island rises by about 100 m towards the summit, but under the remaining three ice rises the bedrock is horizontal to within some 20 m. The bed shows no evidence of isostatic depression towards the centre. Ice thicknesses at the summit have an expected error of about 15 m. Table I shows 10 m temperature, accumulation, and summit thickness for each ice rise. For Ewing Island, the temperature and accumulation rates are conjectural.
The ice rises were visited during the 1976–77 field season in order to make accurate measurements of surface profiles. Optical levelling equipment was used, so that relative height are accurate to within a few centimetres. The measured profiles are shown by the solid lines in Figure 2; dashed and dotted lines refer to models constructed later in this paper. In addition, velocity measurements were made on the western axis of Butler Island using a line of stakes at 300 m intervals which was re-measured after two months by oversnow taping.

Fig. 2. Measured profiles of minor axes of four Antarctic ice rises (solid lines). Dashed lines show the best fit of Equation (11) to the profiles; dotted lines show the expected profile if the ice rises were perfectly symmetrical. Vertical scale is exaggerated by a factor of ten.
3. Temperature and density profiles
Knowing surface snow temperatures and annual accumulation we can use estimated values for the geothermal heat flux to calculate an expected temperature profile through an ice rise (Reference RobinRobin, 1955). This should indicate whether the glacier is frozen to its bed or is sliding over it.
Robin’s solution for temperature T(z) at height z above bedrock is:

with

where h is the total ice thickness, a is the annual accumulation, k is the thermal diffusivity of ice, and (∂T/∂z) b is the basal temperature gradient due to geothermal heat flux.
Taking

and
we find that the temperature at the base is – 12.8°C and the average temperature is –15.7°C. This calculation is valid strictly only near to the centre of the ice rise where horizontal advection terms are negligible, but it serves to show that the ice rise must be frozen to its bed.
Reference SchyttSchytt (1958) shows that density ρ(z) can be modelled by
where ρ i = 917 kg m−3, the density of pure ice, b = 0.0258 m−1, the value used by Schytt for his observations at Maudheim, and d is related to surface snow density. Measurements of density on Dolleman Island showed the density at 10 m depth to be 580±20 kg m−3 (personal communication from D. A. Peel), which yields d = 436 kg m−3. The average density ρ through 300 m thickness of ice is then 860 kg m−3. This is the value we shall use.
4. Velocity measurements
(a) Flow law
We define strain-rates ε̇ ij , stresses σ ij (i, j = x, y, z), and stress deviators
and
Then we postulate the flow law (Reference PatersonPaterson, 1969, p. 85)
where ε̇ and τ are defined through the second invariants of the strain-rate and stress-deviator tensors, and

B and n are parameters which depend on the properties of glacier ice; n reflects the mechanism of deformation, and B is a factor which is dependent on temperature and density; B is expected to vary with depth.
We introduce the requirement that at any point strain-rates are parallel and proportional to the corresponding stress deviators and find, using Equation (2), the flow-law formula,
By analysing velocity and profile data we can determine whether Equation (4) is suitable and what are the appropriate values for B and n.
(b) Velocity formula
Since the ice rise is frozen to its bed, any surface velocity is the result of shear within the ice mass. Consider a velocity u in the x direction, where x is measured radially from the centre and z is measured vertically upwards from the glacier bed (Fig. 3). We then have:
where it has been assumed that the ice deforms by simple shear. Therefore, by Equation (4),


Fig. 3. Symbols used in discussion of ice rises
The term τ n–1 is a function of both shear and longitudinal stresses (Equation (3)). We can show that over most of the ice rise longitudinal stress deviators can be neglected. Consider the relative magnitudes of longitudinal strain-rate and shear strain-rate averaged over the thickness of the ice rise. From Equation (5) we can represent average shear strain-rate by approximately
Direct measurements of surface velocities, and hence strain-rates were made along the western axis of Butler Island. Thickness values are available from surface-profile measurements combined with radio echo-sounding at the summit. The quantities ε̇ xx and
Table II. Comparison of longitudinal and shear quantities


it is also true that shear stresses generally dominate longitudinal stress deviators. Now, the full expression for τ(n-1) is, for n = 3,
Stress terms appear here squared; longitudinal stress deviator terms are therefore typically an order of magnitude smaller than shear-stress terms (Table II). We shall neglect them.
Now, the stresses σ xy and σ xz should vanish by geometrical considerations, so that we can write
and hence by Equation (6)

Neglecting longitudinal stress gradients (Reference CollinsCollins, 1968) we have
Inserting this into Equation (7) and integrating, the surface velocity is found to be (Reference BuddBudd, 1969, p. 118):

where B’ is a weighted average over depth of the variable B. It is

B’ is heavily weighted towards the base of the glacier and it is effectively determined by the bottom 10–20% of the ice.
(c) Comparison with measurements
Velocities on Butler Island were found to be in the range 0 to 8 m a−1, increasing steadily away from the summit, which was assumed to be stationary.
Now from Equation (9) we have
where

In Figure 4 the data are plotted logarithmically. The slope of the graph yields a value for n and the scatter of points yields the expected error. We find that
with a linear correlation coefficient of 0.986. The good correlation indicates that Equation (2) is an appropriate flow law and that Equation (9) is a reliable formula for velocity.

Fig. 4. Logarithmic plot of u/h against hα (Butler Island western axis). The graph gives n = 3.13±0.52. It also shows the range of basal stress covered.
There are theoretical grounds for believing that n should equal three for creep processes involving dislocation motion (Reference Weertman, Whalley, Whalley, Jones and GoldWeertman, 1973[a]; Reference Weertman, Li and MukherjeeWeertman, [1975]), although the theories available for dislocation velocity are unable to account for observed rates (Reference WhitworthWhitworth and others, 1976; Reference FrostFrost and others, 1976). We shall therefore assume that n is exactly three. The flow parameter B’ is then determined as
These observations refer to the stress range 0.5–1.3 bar and a temperature of about –13.5°C. The grain-size is unknown. Ice density in the lower 20% of the ice rise is, by Equadon (1), about 916 kg m−3, practically that of pure ice.
5. Equilibrium profiles
(i) Theory
Analytic expressions for the equilibrium profile of ice caps have been provided by Reference NyeNye (1959) and Reference HaefeliHaefeli (1961). Reference NagataNagata (1977) has claimed that neither of these analyses satisfies the equation of mass continuity, since a moving column of ice always has a component of velocity outwards through a sloping surface, and therefore ice must be “taken off into the outer atmosphere by the ablation effect”. We do not agree with Nagata, because a particle near the surface in an accumulation area moves downwards rather than horizontally. The ice caps considered by Nye and by Haefeli are all defined in terms of positive accumulation over their entire surface.
The condition for steady state is that the total accumulation over the catchment zone for a position x should be exactly balanced by the outflow at position x. For a two-dimensional ice rise we have
where ū is the average velocity of a column at x, and a is the accumulation rate. For an ice rise of circular plan we have
or
In general the ice rises being studied are elliptical in plan and are intermediate between these two cases. Profiles were surveyed on their minor axes, since flow lines on the major axes are more likely to be disturbed or widely divergent. Since flow lines were also unknown on the minor axis we write:
where ξ is a factor which corrects for the geometry and is in the range 1.3–1.5.
Now, from Equations (7) and (8), it can be shown that the average velocity of a vertical column is

where B” is again a weighted average of B. The full expression is involved, but B” is typically less than B’ by approximately four per cent. It is again heavily weighted towards the bottom of the ice rise. Inserting this into Equation (10) and writing α= dh/dx gives a simple differential equation in h and x having the solution

where H is the thickness of the ice rise at its summit x = 0, and L is the radius of the ice rise at bedrock level z = 0.L is given by:

(ii) Fitting of profiles
It is apparent from Figure 2 that Butler Island, Gipps Ice Rise, and Ewing Island show a pronounced asymmetry. Only one arm of Dolleman Island was surveyed. In each case the axis leading towards the junction with ice shelf is of longer radius than the axis leading to open water; a similar asymmetry was present on the major axis of Butler Island, the only other profile surveyed. The asymmetry amounts to between 5 and 15%. Further, on fitting model profiles according to Equation (12) with n = 3, it is found that in general a satisfactory fit is obtained for the axes leading to open water, while the axes leading to ice shelf show marked deviations. In Figure 2 the dashed line shows the model profile deemed to be the best fit to each axis and the dotted line shows the profile expected for the axes towards ice shelf if the ice rises were perfectly symmetrical.
Because the axes towards open water agree well with the model profiles we shall use them for calculation of the flow parameter and in the next section provide some explanation of the asymmetry of the other axes.
From Equation (13) we find, with n = 3,

Applying this equation to the profile data, and taking ξ = 1.5, we find the value of the flow parameter B” to be

where the values of the radius L used are the intersections of the best-fit models with the x axis (Fig. 2). Data from Dolleman Island have not been used since the only axis surveyed was the one leading towards a junction with the ice shelf, which shows marked deviation from any expected profile. Combining these B” values with the value of (1.01 ±0.11) × 108 N m−2 s
referring to a stress range of 0.5–1.3 bar and a temperature of about –13.5°C. This value sits nicely on the curve published by Thomas (1973[b], fig. 2) of flow parameter B plotted against temperature. The values of B’ and B” determined by the eastern profile of Butler Island and by the velocities on the western profile of Butler Island differ by 30%. This may be due to differences between conditions on the two axes or to non-steady-state behaviour, but the discrepancy is not very significant. It has been pointed out (Reference ThomasThomas and others, 1980) that the discrepancy can also be explained by allowing a decrease in B’ of some 25% between the summit and the edge, due possibly to effects of recrystallization and fabric softening.
6. Asymmetry of profile
Reference Weertman, Whalley, Whalley, Jones and GoldWeertman (1973[b]) treats three mechanisms which should lead to a shift of the ice divide away from the geometrical centre of an ice cap: non-uniform accumulation, non-uniform bedrock, and non-uniform sliding. We shall ignore the last of these since sliding does not occur. Weertman’s analysis of the other factors also assumes a sliding law, so we have made the calculations afresh using Equation (13); the results are substantially the same.
Accumulation rate must vary greatly over an ice cap in order to result in any significant asymmetry. If the two axes of an ice rise are subject to two uniform but differing accumulation-rates, then Equation (13) shows that these rates must differ by a factor of between two and three in order to account for the observed asymmetry. The accumulation rate must be greater on the shorter axis. It seems improbable that such a large variation could occur in the long term over a topographical feature some 10 km in extent and 300 m in height. None the less, Reference SwithinbankSwithinbank (1957, p. 133) reports that on Hill “B” of Maudheim Is-Shelf (a feature of similar, though slightly greater dimensions) measurements over one year showed that accumulation varied by a factor of three across the hill, being on average greater by a factor of 1.6 on the eastern side. Accumulation-rates may therefore be responsible for the asymmetry; they would, however, also have to show gross non-uniformities over the inland arms of the ice rises to account for the marked deviation of these axes from any theoretical profile.
Secondly, Weertman proposes that there are different bedrock heights for the two axes of an ice cap. Again using Equation (13) we find that height differences of 30−50 m are required to account for the asymmetry. Radio echo-studies show no evidence of such differences along the major axes which were sounded, but it remains possible that such variations may occur on the minor axes.
A further explanation could be provided by variations in flow parameter B, but there is no reason to suppose that B should vary over such a small area of study.
We shall develop here an alternative explanation involving the influence of the ice shelf on the boundary conditions at its junction with the ice rise. This accounts for the fact that the asymmetry invariably lies with the longer arm towards the ice-shelf junction.
We consider the shape of ice rise which should form on a base which has a horizontal central area but a gentle slope downwards at its edges (Fig. 5). It is unlikely that the bedrock beneath an ice rise falls off sharply at the edges, so this is a realistic assumption for the form of the bedrock. The bedrock slope is assumed to be θ = 0.10 rad, or 5.7°. It will be shown that the pressure of an ice shelf flowing against the boundary of an ice rise can cause extensive vertical strain-rates which allow the junction of the ice rise to migrate down the sloping bedrock. At the boundary with open water the ice rise terminates with the onset of the slope.

Fig. 5. Migration of grounding line down sloping bedrock, under compressive stress from an ice shelf. Vertical scale is exaggerated by a factor of ten.
Reference Thomas and BentleyThomas and Bentley (1978) have analysed the process of advance and retreat of ice-shelf grounding lines under the influence of varying constraints. At the grounding line itself, the rate of thickening of ice shelf with time is given by the mass continuity equation

This equation expresses the rate of thickening of ice shelf at a point fixed in space as a function of accumulation-rate a, melt-rate m, horizontal advection at velocity ū for surface slope α and bedrock slope θ, and rate of thickening of a column moving in the ice shelf and having vertical strain-rate ε̇ zz. α and θ are negative for surfaces sloping downwards in the direction of movement. Clearly if ∂h/∂t is positive, the ice shelf is thickening and the grounding line advances; if ∂h/∂t is negative the ice shelf is thinning and the grounding line retreats. The ice shelf must advance or retreat until it finds an equilibrium point where ∂h/∂t = 0. There it will remain.
In the region near the grounding line we should, strictly, include both longitudinal and shear stresses when calculating the effective stress term τ in the flow law Reference Weertman(Weertman, 1974). To simplify matters we shall calculate ice-shelf strain-rates neglecting shear stresses. In that case the vertical strain-rate in an ice shelf may be written Reference Thomas(Thomas, 1973[b])

where B is the average of B over depth, ρw is the density of sea-water and σ R is the total external stress acting on the ice shelf in an up-stream direction, not including water-pressure effects. For a density function of the form given in Equation (1), this can be written Reference Sanderson(Sanderson, 1979):

Knowing the values of a, m, u, θ, α, and h at the grounding line then enables us to calculate the stress σ R needed to be applied to the ice shelf in order to make the grounding line stable. This is done simply by setting ∂h/∂t = 0 in Equation (14) and then inserting Equation (15).
For the purposes of illustration we consider an ice rise of 300 m maximum thickness resting on a bed having a horizontal portion 6700 m long. Beyond that the bedrock dips at 5.7°. Sea-level is at 25 m above central bedrock. We assume an accumulation rate of 0.23 m a–1 and that the steady-state ideal radius is 3700 m. The inland axis of the ice rise therefore has a sloping bed from the 3000 m mark onwards. In stipulating this we are introducing an asymmetry, but our purpose is to calculate the stresses necessary to sustain the asymmetry and to show that they are reasonable. By a numerical iteration process we calculate what the form of the inland arm of the ice rise is after the downward slope begins; in effect we are solving numerically the differential equation which led to Equation (12). This form is shown in Figure 5. It is seen that surface slope α is reduced when bedrock slope is introduced. This is because h is increased and so a given velocity u can be achieved by a smaller surface slope (Equation (11)). At a distance of 4300 m from the ice divide, the ice is of the right depth to begin to float and so it becomes ice shelf.
Consider now the conditions at the grounding line. At x = 4300 m the ice thickness is 185 m, the surface slope is α = –0.0956 and the velocity is 5.8 m a–1. We assume the bottom melt-rate to be 1.0 m a–1. Through Equation (14) this means that the ice must be subject to vertical strain-rate ε̇ zz = 1.45 × 10–10 s–1 in extension in order for the grounding line to remain stationary. Equation (15) then shows that a compressive stress σ R = 1.25 bar is required at the grounding line. This stress can easily be provided by the compressive regime as an ice shelf flows up against a stationary ice rise; stresses at the McDonald Ice Rumples were found to reach 17 bar Reference Thomas(Thomas, 1973[a]).
On the other hand, the junction on the seaward side has no such restraining force available. At the point of flotation the ice must be some 30 m in thickness, and sloping quite sharply. Surface slopes from the theoretical model are unreliable very near the edge, since they diverge towards infinity, so we take slopes from the observed profiles in Figure 2. A realistic surface slope is α = –0.12 or 6.8° near the edge. If the ice rise were to migrate to the sloping portion of bedrock it would require a compressive stress of 1.33 bar to prevent it from immediately beginning to retreat. No such stress is present, so it cannot migrate. Whilst on the flat portion, however, Equation (14) shows that ∂h/∂t should be positive, and the grounding line tends to advance. This means that the grounding line is in a position of stable equilibrium at the change of slope, unable either to advance or retreat.
This model provides a plausible explanation of the observed asymmetry. We have not attempted an accurate simulation of a particular case, since real values for θ, m, and σ R are unknown. In addition, the model has used a simplified view of the combination of longitudinal and shear stress near the grounding line. It does, however, present the nature of the effect, which shows a similarity in form, though not in detail, to the profiles presented in Figure 2.
7. The summit region
Analyses of satellite images have indicated the presence of ridges on the summits of Antarctic ice rises (Martin, 1976). However, Reference WeertmanWeertman (1961) has proposed that the summit region of an ice cap should be flatter than predicted by a theory which considers only shear stresses, since longitudinal stresses become important. A detailed survey was made of the area surrounding the summit of Gipps Ice Rise, to discover any anomaly in behaviour. The result is shown in Figure 6 and it is compared with the theoretical profile determined for the ice rise as a whole, as in Figure 2. No significant deviation is apparent; the average error over the area covered is 30 cm, or 0.1% of the thickness. The real profile is, if anything, slightly flatter near the summit than the theoretical profile, but the difference is comparable to the height of sastrugi. We can certainly conclude that no anomalous ridge exists.

Fig. 6. Detailed summit profile of Gipps ice Rise. The dashed line shows the theoretical profile with L = 3550 m. Vertical scale is exaggerated by a factor of 40.
The question remains, why do satellite images display apparent ridges? In a sense there is a ridge in that the surface slope changes over a relatively short distance from negative to positive, but the slopes in question are minimal. The surface slopes near the summit are of the order 0.75−1.5°, and yet an image taken with a sun elevation of 20° displays a distinct apparent shadow. We can suggest that the effect may be due to different reflective properties of superficial snow, perhaps to crystal orientation, but the relationship between satellite imagery and surface topography remains a fruitful area for investigation.
Acknowledgements
We are grateful to colleagues at the British Antarctic Survey for useful discussions, and to Dr R. H. Thomas, who introduced us to his work on grounding-line dynamics.


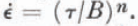 . Each ice rise is bounded on one side by ice shelf and on the other side by open sea. Towards open sea the profiles are found to agree well with steady-state theoretical profiles and they supply a value of
. Each ice rise is bounded on one side by ice shelf and on the other side by open sea. Towards open sea the profiles are found to agree well with steady-state theoretical profiles and they supply a value of 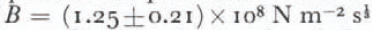 for temperature – 13.5°C and stress range 0.5–1.3 bar. Towards ice shelf the profiles are elongated and they deviate from the theoretical profile. This may be due to compressive stress in the ice shelf causing migration of the grounding line down sloping bedrock. No significantly anomalous behaviour is found in the summit region.
for temperature – 13.5°C and stress range 0.5–1.3 bar. Towards ice shelf the profiles are elongated and they deviate from the theoretical profile. This may be due to compressive stress in the ice shelf causing migration of the grounding line down sloping bedrock. No significantly anomalous behaviour is found in the summit region.







