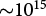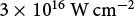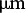Introduction
The interaction of laser radiation with solid matter at intensities above 1015 ![]() $\mathrm{W\,cm^{-2}}$ gives rise to the ionization of matter, creating plasma on the surface of the target, and leads to production of accelerated particles and X-ray photons (Refs Reference Láska, Jungwirth, Krása, Pfeifer, Rohlena, Ullschmied, Badziak, Parys, Wolowski, Gammino, Torrisi and Boody1, Reference Gitomer, Jones, Begay, Ehler, Kephart and Kristal2). In the recent years, high-energy and high-intensity laser-plasma experiments have been used to study the generation of energetic particles and high energy radiation (Ref. Reference Singh, Cui, Adak, Lad, Chatterjee, Brijesh, Sheng and Kumar3). The production of hot electron in laser–plasma interaction (LPI) has important relevance not only in the context of inertial confinement fusion (Refs Reference Zylstra, Hurricane, Callahan, Kritcher, Ralph, Robey, Ross, Young, Baker, Casey, Doppner, Divol, Hohenberger, Pape, Pak, Patel, Tommasini, Ali, Amendt, Atherton, Bachmann, Bailey, Benedetti, Hopkins, Betti, Bhandarkar, Biener, Bionta, Birge, Bond, Bradley, Braun, Briggs, Bruhn, Celliers, Chang, Chapman, Chen, Choate, Christopherson, Clark, Crippen, Dewald, Dittrich, Edwards, Farmer, Field, Fittinghoff, Frenje, Gaffney, Johnson, Glenzer, Grim, Haan, Hahn, Hall, Hammel, Harte, Hartouni, Heebner, Hernandez, Herrmann, Herrmann, Hinkel, Ho, Holder, Hsing, Huang, Humbird, Izumi, Jarrott, Jeet, Jones, Kerbel, Kerr, Khan, Kilkenny, Kim, Kleinrath, Kleinrath, Kong, Koning, Kroll, Kruse, Kustowski, Landen, Langer, Larson, Lemos, Lindl, Ma, MacDonald, MacGowan, Mackinnon, MacLaren, MacPhee, Marinak, Mariscal, Marley, Masse, Meaney, Meezan, Michel, Millot, Milovich, Moody, Moore, Morton, Murphy, Newman, Nicola, Nikroo, Nora, Patel, Pelz, Peterson, Ping, Pollock, Ratledge, Rice, Rinderknecht, Rosen, Rubery, Salmonson, Sater, Schiaffino, Schlossberg, Schneider, Schroeder, Scott, Sepke, Sequoia, Sherlock, Shin, Smalyuk, Spears, Springer, Stadermann, Stoupin, Strozzi, Suter, Thomas, Town, Tubman, Trosseille, Volegov, Weber, Widmann, Wild, Wilde, Wonterghem, Woods, Woodworth, Yamaguchi, Yang and Zimmerman4, Reference Kritcher, Young, Robey, Weber, Zylstra, Hurricane, Callahan, Ralph, Ross, Baker, Casey, Clark, Döppner, Divol, Hohenberger, Berzak Hopkins, Le Pape, Meezan, Pak, Patel, Tommasini, Ali, Amendt, Atherton, Bachmann, Bailey, Benedetti, Betti, Bhandarkar, Biener, Bionta, Birge, Bond, Bradley, Braun, Briggs, Bruhn, Celliers, Chang, Chapman, Chen, Choate, Christopherson, Crippen, Dewald, Dittrich, Edwards, Farmer, Field, Fittinghoff, Frenje, Gaffney, Gatu Johnson, Glenzer, Grim, Haan, Hahn, Hall, Hammel, Harte, Hartouni, Heebner, Hernandez, Herrmann, Herrmann, Hinkel, Ho, Holder, Hsing, Huang, Humbird, Izumi, Jarrott, Jeet, Jones, Kerbel, Kerr, Khan, Kilkenny, Kim, Geppert-Kleinrath, Geppert-Kleinrath, Kong, Koning, Kruse, Kroll, Kustowski, Landen, Langer, Larson, Lemos, Lindl, Ma, MacDonald, MacGowan, Mackinnon, MacLaren, MacPhee, Marinak, Mariscal, Marley, Masse, Meaney, Michel, Millot, Milovich, Moody, Moore, Morton, Murphy, Newman, Nicola, Nikroo, Nora, Patel, Pelz, Peterson, Ping, Pollock, Ratledge, Rice, Rinderknecht, Rosen, Rubery, Salmonson, Sater, Schiaffino, Schlossberg, Schneider, Schroeder, Scott, Sepke, Sequoia, Sherlock, Shin, Smalyuk, Spears, Springer, Stadermann, Stoupin, Strozzi, Suter, Thomas, Town, Trosseille, Tubman, Volegov, Widmann, Wild, Wilde, Wonterghem, Woods, Woodworth, Yamaguchi, Yang and Zimmerman5) but also broadens the understanding of the generation mechanism of spontaneous magnetic field (Refs Reference Pisarczyk, Renner, Dudzak, Chodukowski, Rusiniak, Domanski, Badziak, Dostal, Krupka, Singh, Klir, Ehret, Gajdos, Szydłowska, Rosinski, Tchórz, Szymanski, Krasa, Burian, Pfeifer, Cikhardt, Jelinek, Kocourkova, Batani, Batani, Santos, Vlachos, Ospina-Bohórquez, Volpe, Borodziuk, Krus and Juha6, Reference Pisarczyk, Gus’kov, Chodukowski, Dudzak, Korneev, Demchenko, Kalinowska, Dostal, Zaras-Szydlowska, Borodziuk, Juha, Cikhardt, Krasa, Klir, Cikhardtova, Kubes, Krousky, Krus, Ullschmied, Jungwirth, Hrebicek, Medrik, Golasowski, Pfeifer, Renner, Singh, Kar, Ahmed, Skala and Pisarczyk7) as well as experimental studies in high-energy density physics (Ref. Reference Antici, Albertazzi, Audebert, Buffechoux, Hannachi, d’Humières, Gobet, Grismayer, Mancic, Nakatsutsumi, Plaisir, Romagnani, Tarisien, Pépin, Sentoku and Fuchs8) and laboratory astrophysics (Ref. Reference Pisarczyk, Gus’kov, Zaras-Szydłowska, Dudzak, Renner, Chodukowski, Dostal, Rusiniak, Burian, Borisenko, Rosinski, Krupka, Parys, Klir, Cikhardt, Rezac, Krasa, Rhee, Kubes, Singh, Borodziuk, Krus, Juha, Jungwirth, Hrebicek, Medrik, Golasowski, Pfeifer, Skala, Pisarczyk and Korneev9).
$\mathrm{W\,cm^{-2}}$ gives rise to the ionization of matter, creating plasma on the surface of the target, and leads to production of accelerated particles and X-ray photons (Refs Reference Láska, Jungwirth, Krása, Pfeifer, Rohlena, Ullschmied, Badziak, Parys, Wolowski, Gammino, Torrisi and Boody1, Reference Gitomer, Jones, Begay, Ehler, Kephart and Kristal2). In the recent years, high-energy and high-intensity laser-plasma experiments have been used to study the generation of energetic particles and high energy radiation (Ref. Reference Singh, Cui, Adak, Lad, Chatterjee, Brijesh, Sheng and Kumar3). The production of hot electron in laser–plasma interaction (LPI) has important relevance not only in the context of inertial confinement fusion (Refs Reference Zylstra, Hurricane, Callahan, Kritcher, Ralph, Robey, Ross, Young, Baker, Casey, Doppner, Divol, Hohenberger, Pape, Pak, Patel, Tommasini, Ali, Amendt, Atherton, Bachmann, Bailey, Benedetti, Hopkins, Betti, Bhandarkar, Biener, Bionta, Birge, Bond, Bradley, Braun, Briggs, Bruhn, Celliers, Chang, Chapman, Chen, Choate, Christopherson, Clark, Crippen, Dewald, Dittrich, Edwards, Farmer, Field, Fittinghoff, Frenje, Gaffney, Johnson, Glenzer, Grim, Haan, Hahn, Hall, Hammel, Harte, Hartouni, Heebner, Hernandez, Herrmann, Herrmann, Hinkel, Ho, Holder, Hsing, Huang, Humbird, Izumi, Jarrott, Jeet, Jones, Kerbel, Kerr, Khan, Kilkenny, Kim, Kleinrath, Kleinrath, Kong, Koning, Kroll, Kruse, Kustowski, Landen, Langer, Larson, Lemos, Lindl, Ma, MacDonald, MacGowan, Mackinnon, MacLaren, MacPhee, Marinak, Mariscal, Marley, Masse, Meaney, Meezan, Michel, Millot, Milovich, Moody, Moore, Morton, Murphy, Newman, Nicola, Nikroo, Nora, Patel, Pelz, Peterson, Ping, Pollock, Ratledge, Rice, Rinderknecht, Rosen, Rubery, Salmonson, Sater, Schiaffino, Schlossberg, Schneider, Schroeder, Scott, Sepke, Sequoia, Sherlock, Shin, Smalyuk, Spears, Springer, Stadermann, Stoupin, Strozzi, Suter, Thomas, Town, Tubman, Trosseille, Volegov, Weber, Widmann, Wild, Wilde, Wonterghem, Woods, Woodworth, Yamaguchi, Yang and Zimmerman4, Reference Kritcher, Young, Robey, Weber, Zylstra, Hurricane, Callahan, Ralph, Ross, Baker, Casey, Clark, Döppner, Divol, Hohenberger, Berzak Hopkins, Le Pape, Meezan, Pak, Patel, Tommasini, Ali, Amendt, Atherton, Bachmann, Bailey, Benedetti, Betti, Bhandarkar, Biener, Bionta, Birge, Bond, Bradley, Braun, Briggs, Bruhn, Celliers, Chang, Chapman, Chen, Choate, Christopherson, Crippen, Dewald, Dittrich, Edwards, Farmer, Field, Fittinghoff, Frenje, Gaffney, Gatu Johnson, Glenzer, Grim, Haan, Hahn, Hall, Hammel, Harte, Hartouni, Heebner, Hernandez, Herrmann, Herrmann, Hinkel, Ho, Holder, Hsing, Huang, Humbird, Izumi, Jarrott, Jeet, Jones, Kerbel, Kerr, Khan, Kilkenny, Kim, Geppert-Kleinrath, Geppert-Kleinrath, Kong, Koning, Kruse, Kroll, Kustowski, Landen, Langer, Larson, Lemos, Lindl, Ma, MacDonald, MacGowan, Mackinnon, MacLaren, MacPhee, Marinak, Mariscal, Marley, Masse, Meaney, Michel, Millot, Milovich, Moody, Moore, Morton, Murphy, Newman, Nicola, Nikroo, Nora, Patel, Pelz, Peterson, Ping, Pollock, Ratledge, Rice, Rinderknecht, Rosen, Rubery, Salmonson, Sater, Schiaffino, Schlossberg, Schneider, Schroeder, Scott, Sepke, Sequoia, Sherlock, Shin, Smalyuk, Spears, Springer, Stadermann, Stoupin, Strozzi, Suter, Thomas, Town, Trosseille, Tubman, Volegov, Widmann, Wild, Wilde, Wonterghem, Woods, Woodworth, Yamaguchi, Yang and Zimmerman5) but also broadens the understanding of the generation mechanism of spontaneous magnetic field (Refs Reference Pisarczyk, Renner, Dudzak, Chodukowski, Rusiniak, Domanski, Badziak, Dostal, Krupka, Singh, Klir, Ehret, Gajdos, Szydłowska, Rosinski, Tchórz, Szymanski, Krasa, Burian, Pfeifer, Cikhardt, Jelinek, Kocourkova, Batani, Batani, Santos, Vlachos, Ospina-Bohórquez, Volpe, Borodziuk, Krus and Juha6, Reference Pisarczyk, Gus’kov, Chodukowski, Dudzak, Korneev, Demchenko, Kalinowska, Dostal, Zaras-Szydlowska, Borodziuk, Juha, Cikhardt, Krasa, Klir, Cikhardtova, Kubes, Krousky, Krus, Ullschmied, Jungwirth, Hrebicek, Medrik, Golasowski, Pfeifer, Renner, Singh, Kar, Ahmed, Skala and Pisarczyk7) as well as experimental studies in high-energy density physics (Ref. Reference Antici, Albertazzi, Audebert, Buffechoux, Hannachi, d’Humières, Gobet, Grismayer, Mancic, Nakatsutsumi, Plaisir, Romagnani, Tarisien, Pépin, Sentoku and Fuchs8) and laboratory astrophysics (Ref. Reference Pisarczyk, Gus’kov, Zaras-Szydłowska, Dudzak, Renner, Chodukowski, Dostal, Rusiniak, Burian, Borisenko, Rosinski, Krupka, Parys, Klir, Cikhardt, Rezac, Krasa, Rhee, Kubes, Singh, Borodziuk, Krus, Juha, Jungwirth, Hrebicek, Medrik, Golasowski, Pfeifer, Skala, Pisarczyk and Korneev9).
When a high intensity laser pulse interacts with a solid target, its prepulse having duration up to several nanoseconds and intensity level ![]() ${\sim}10\%$ of the maximum amplitude, creates a preplasma. The interaction of the main laser pulse with this preplasma produces relativistic electrons (Ref. Reference Singh, Cui, Adak, Lad, Chatterjee, Brijesh, Sheng and Kumar3) by various physical processes, such as resonance absorption (Ref. Reference Forslund, Kindel and Lee10), vacuum heating (Ref. Reference Brunel11), betatron resonance (Ref. Reference Mangles, Walton, Tzoufras, Najmudin, Clarke, Dangor, Evans, Fritzler, Gopal, Hernandez-Gomez, Mori, Rozmus, Tatarakis, Thomas, Tsung, Wei and Krushelnick12), wakefield acceleration (Refs Reference Malka, Fritzler, Lefebvre, Aleonard, Burgy, Chambaret, Chemin, Krushelnick, Malka, Mangles, Najmudin, Pittman, Rousseau, Scheurer, Walton and Dangor13, Reference Tajima and Dawson14), inverse bremsstrahlung, etc. (Refs Reference Ridgers, Brady, Duclous, Kirk, Bennett, Arber, Robinson and Bell15, Reference Ta Phuoc, Corde, Thaury, Malka, Tafzi, Goddet, Shah, Sebban and Rousse16). One of the important aspects governing these processes is laser absorption into hot electrons (Ref. Reference Singh, Armstrong, Kang, Ren, Liu, Hua, Rusby, Klimo, Versaci, Zhang, Sun, Zhu, Lei, Ouyang, Lancia, Garcia, Wagner, Cowan, Zhu, Schlegel, Weber, McKenna, Neely, Tikhonchuk and Kumar17). These electrons subsequently penetrate inside the target and produce bremsstrahlung emission (Ref. Reference Singh, Armstrong, Kang, Ren, Liu, Hua, Rusby, Klimo, Versaci, Zhang, Sun, Zhu, Lei, Ouyang, Lancia, Garcia, Wagner, Cowan, Zhu, Schlegel, Weber, McKenna, Neely, Tikhonchuk and Kumar17), which constitutes an X-ray source that may be used in various applications, such as radiography of dense plasma (Ref. Reference Glinec, Faure, Le Dain, Darbon, Hosokai, Santos, Lefebvre, Rousseau, Burgy, Mercier and Malka18), photonuclear studies (Refs Reference Cowan, Hunt, Phillips, Wilks, Perry, Brown, Fountain, Hatchett, Johnson, Key, Parnell, Pennington, Snavely and Takahashi19, Reference Singh, Versaci, Laso Garcia, Morejon, Ferrari, Molodtsova, Schwengner, Kumar and Cowan20). Moreover, the collisional effect is found to be significant when the incident laser intensity is less than
${\sim}10\%$ of the maximum amplitude, creates a preplasma. The interaction of the main laser pulse with this preplasma produces relativistic electrons (Ref. Reference Singh, Cui, Adak, Lad, Chatterjee, Brijesh, Sheng and Kumar3) by various physical processes, such as resonance absorption (Ref. Reference Forslund, Kindel and Lee10), vacuum heating (Ref. Reference Brunel11), betatron resonance (Ref. Reference Mangles, Walton, Tzoufras, Najmudin, Clarke, Dangor, Evans, Fritzler, Gopal, Hernandez-Gomez, Mori, Rozmus, Tatarakis, Thomas, Tsung, Wei and Krushelnick12), wakefield acceleration (Refs Reference Malka, Fritzler, Lefebvre, Aleonard, Burgy, Chambaret, Chemin, Krushelnick, Malka, Mangles, Najmudin, Pittman, Rousseau, Scheurer, Walton and Dangor13, Reference Tajima and Dawson14), inverse bremsstrahlung, etc. (Refs Reference Ridgers, Brady, Duclous, Kirk, Bennett, Arber, Robinson and Bell15, Reference Ta Phuoc, Corde, Thaury, Malka, Tafzi, Goddet, Shah, Sebban and Rousse16). One of the important aspects governing these processes is laser absorption into hot electrons (Ref. Reference Singh, Armstrong, Kang, Ren, Liu, Hua, Rusby, Klimo, Versaci, Zhang, Sun, Zhu, Lei, Ouyang, Lancia, Garcia, Wagner, Cowan, Zhu, Schlegel, Weber, McKenna, Neely, Tikhonchuk and Kumar17). These electrons subsequently penetrate inside the target and produce bremsstrahlung emission (Ref. Reference Singh, Armstrong, Kang, Ren, Liu, Hua, Rusby, Klimo, Versaci, Zhang, Sun, Zhu, Lei, Ouyang, Lancia, Garcia, Wagner, Cowan, Zhu, Schlegel, Weber, McKenna, Neely, Tikhonchuk and Kumar17), which constitutes an X-ray source that may be used in various applications, such as radiography of dense plasma (Ref. Reference Glinec, Faure, Le Dain, Darbon, Hosokai, Santos, Lefebvre, Rousseau, Burgy, Mercier and Malka18), photonuclear studies (Refs Reference Cowan, Hunt, Phillips, Wilks, Perry, Brown, Fountain, Hatchett, Johnson, Key, Parnell, Pennington, Snavely and Takahashi19, Reference Singh, Versaci, Laso Garcia, Morejon, Ferrari, Molodtsova, Schwengner, Kumar and Cowan20). Moreover, the collisional effect is found to be significant when the incident laser intensity is less than ![]() $10^{16}\ \mathrm{W\,cm^{-2}}$ (Ref. Reference Cui, Wang, Sheng, Li and Zhang21), which tends to enhance the resonance absorption and reduce the vacuum heating under different plasma parameters. At higher intensities, various collisionless absorption mechanisms dominate with a large number of hot electrons produced. The scaling of hot electron temperatures is found to depend upon the dominant absorption mechanisms (Ref. Reference Cui, Wang, Sheng, Li and Zhang21). The precise measurements of the energy distribution and temperature of hot electrons at different laser intensity are crucial for better understanding of these mechanisms.
$10^{16}\ \mathrm{W\,cm^{-2}}$ (Ref. Reference Cui, Wang, Sheng, Li and Zhang21), which tends to enhance the resonance absorption and reduce the vacuum heating under different plasma parameters. At higher intensities, various collisionless absorption mechanisms dominate with a large number of hot electrons produced. The scaling of hot electron temperatures is found to depend upon the dominant absorption mechanisms (Ref. Reference Cui, Wang, Sheng, Li and Zhang21). The precise measurements of the energy distribution and temperature of hot electrons at different laser intensity are crucial for better understanding of these mechanisms.
The multichannel electron spectrometers based on magnetic deflection (Ref. Reference Krupka, Singh, Pisarczyk, Dostal, Kalal, Krasa, Dudzak, Burian, Jelinek, Chodukowski, Rusiniak, Krus and Juha22) have often been used to provide an indication on the angular distribution of fast electrons escaped from the target plasma. Moreover, indirect measurements of bremsstrahlung radiation generated by such hot electrons inside the plasma provides the quantitative estimate of the fast electron energy distribution, conversion efficiency of laser energy into fast electrons and their angular distribution (Refs Reference Pisarczyk, Kalal, Gus’kov, Batani, Renner, Santos, Dudzak, Zaras-Szydłowska, Chodukowski, Rusiniak, Dostal, Krasa, Krupka, Kochetkov, Singh, Cikhardt, Burian, Krus, Pfeifer, Cristoforetti, Gizzi, Baffigi, Antonelli, Demchenko, Rosinski, Terwinska, Borodziuk, Kubes, Ehret, Juha, Skala and Korneev23, Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24). The intense emission of hot electrons in laser–solid interaction depends on achieving the highest possible conversion efficiency and electron temperature with the least amount of invested laser energy. The conversion efficiency of laser energy into electron energy and associated bremsstrahlung radiation relies on the laser energy, intensity, material, geometry and thickness of the target (Ref. Reference Galy, Maučec, Hamilton, Edwards and Magill25). In the recent experiment, Rusby et al. reported results from a high-intensity and picosecond scale laser interaction with cone targets that significantly increase the temperature and flux of the hot electrons over a traditional planar target (Ref. Reference Rusby, Cochran, Aghedo, Albert, Armstrong, Haid, Kemp, Kerr, King, Lemos, Manuel, Ma, MacPhee, Pagano, Pak, Scott, Siders, Simpson, Sinclair, Wilks, Williams and Mackinnon26). The enhancement in electron temperature and flux is caused by a substantial increase in the plasma density within the cone target geometry, which was induced by a prepulse that arrived 1.5 ns prior to the main laser intensity (![]() ${\ge}10^{19}\ \mathrm{W\,cm^{-2}}$).
${\ge}10^{19}\ \mathrm{W\,cm^{-2}}$).
Since very limited investigations have been reported on the characterization of the hot electrons produced by kJ-ns class lasers, in this experiment carried out at the Prague Asterix Laser System (PALS) (Ref. Reference Jungwirth, Cejnarova, Juha, Kralikova, Krasa, Krousky, Krupickova, Laska, Masek, Mocek, Pfeifer, Präg, Renner, Rohlena, Rus, Skala, Straka and Ullschmied27), hot electrons are characterized by interaction of sub-nanosecond laser beam with thin metal foil targets (Cu, Ta, Ti, Sn, Pb) for laser intensities between ![]() $4 \times 10^{15}$ and
$4 \times 10^{15}$ and ![]() $3 \times 10^{16}\ \mathrm{W\,cm ^{-2}}$. The thicknesses of the foil targets were varied for optimizing the emitted electron temperature and energy distribution in angular direction with laser axis. The energy distribution functions of electrons were measured by angularly resolved multichannel electron spectrometer (Ref. Reference Krupka, Singh, Pisarczyk, Dostal, Kalal, Krasa, Dudzak, Burian, Jelinek, Chodukowski, Rusiniak, Krus and Juha22). The energy distribution and electron temperature were compared with experimental and simulation results and known scaling laws at higher laser intensities. In addition, the angular characteristics of hot electrons spectra are scaled with laser energy and target thickness of different materials. Due to the nanosecond duration of the laser pulse at the
$3 \times 10^{16}\ \mathrm{W\,cm ^{-2}}$. The thicknesses of the foil targets were varied for optimizing the emitted electron temperature and energy distribution in angular direction with laser axis. The energy distribution functions of electrons were measured by angularly resolved multichannel electron spectrometer (Ref. Reference Krupka, Singh, Pisarczyk, Dostal, Kalal, Krasa, Dudzak, Burian, Jelinek, Chodukowski, Rusiniak, Krus and Juha22). The energy distribution and electron temperature were compared with experimental and simulation results and known scaling laws at higher laser intensities. In addition, the angular characteristics of hot electrons spectra are scaled with laser energy and target thickness of different materials. Due to the nanosecond duration of the laser pulse at the ![]() $10\%$ level of the laser pulse maximum, the peak of laser pulse interacts with the pre-plasma produced by front of the laser pulse also plays an important role in generation of hot electrons. Moreover, in non-relativistic regime the conversion efficiency of hot electron energy from laser energy is also discussed for different target materials. For the given experimental conditions, nonlinearity associated in the profile of conversion efficiency and relevant physics are also summarized.
$10\%$ level of the laser pulse maximum, the peak of laser pulse interacts with the pre-plasma produced by front of the laser pulse also plays an important role in generation of hot electrons. Moreover, in non-relativistic regime the conversion efficiency of hot electron energy from laser energy is also discussed for different target materials. For the given experimental conditions, nonlinearity associated in the profile of conversion efficiency and relevant physics are also summarized.
The paper is organized as follows. The experimental layout and diagnostic system are described in ‘Experimental layout and diagnostic system’ section. The description of the experimental results is discussed in ‘Experimental results’ section. The major outcome and summary of the paper are presented in next section. The conclusion is summarized in last section.
Experimental layout and diagnostic system
The experiment was carried out at the PALS facility using a single beam iodine photodissociation laser system (Ref. Reference Jungwirth, Cejnarova, Juha, Kralikova, Krasa, Krousky, Krupickova, Laska, Masek, Mocek, Pfeifer, Präg, Renner, Rohlena, Rus, Skala, Straka and Ullschmied27). The layout of the experimental set-up is shown in Figure 1. The iodine laser supplies up to ![]() $700 \ \mathrm{J}$ of energy at the fundamental wavelength
$700 \ \mathrm{J}$ of energy at the fundamental wavelength ![]() $1.315 \ \unicode{x03BC}\mathrm{m}$ with pulse duration
$1.315 \ \unicode{x03BC}\mathrm{m}$ with pulse duration ![]() $\approx350 \ \mathrm{ps}$. The laser is capable to deliver the energy up to
$\approx350 \ \mathrm{ps}$. The laser is capable to deliver the energy up to ![]() $700 \ \mathrm{J}$ onto a target. The laser beam is focused to a spot of diameter
$700 \ \mathrm{J}$ onto a target. The laser beam is focused to a spot of diameter ![]() $\approx100 \ \unicode{x03BC}\mathrm{m}$ using a
$\approx100 \ \unicode{x03BC}\mathrm{m}$ using a ![]() $f/2$ aspherical lens with focal length
$f/2$ aspherical lens with focal length ![]() $600 \ \mathrm{mm}$, reaching the power density up to
$600 \ \mathrm{mm}$, reaching the power density up to ![]() $3 \times 10^{16} \ \mathrm{W\,cm}^{-2}$. The repetition rate of the laser system is one shot per
$3 \times 10^{16} \ \mathrm{W\,cm}^{-2}$. The repetition rate of the laser system is one shot per ![]() $30 \ \mathrm{min}$ and the polarization of the output beam is linear. The focused beam was incident on targets at normal incidence in the equatorial plane. The intensity of the laser pulse was varied in the range of
$30 \ \mathrm{min}$ and the polarization of the output beam is linear. The focused beam was incident on targets at normal incidence in the equatorial plane. The intensity of the laser pulse was varied in the range of ![]() $4 \times 10^{15}$ to
$4 \times 10^{15}$ to ![]() $3 \times 10^{16}$ W cm−2. The targets were chosen from different materials (low to high Z, where Z is the atomic number of the material), such as Ti, Cu, Sn, Ta and Pb foils. The thickness of foil targets were ranges between 1 and 100
$3 \times 10^{16}$ W cm−2. The targets were chosen from different materials (low to high Z, where Z is the atomic number of the material), such as Ti, Cu, Sn, Ta and Pb foils. The thickness of foil targets were ranges between 1 and 100 ![]() $\unicode{x03BC}\mathrm{m}$. The metal foils were irradiated by laser pulse in the energy range between 100 and 600 Joules.
$\unicode{x03BC}\mathrm{m}$. The metal foils were irradiated by laser pulse in the energy range between 100 and 600 Joules.

Figure 1. The typical layout of the experimental setup along with angularly resolved multichannel electron spectrometer. In this configuration, eight electron spectrometers are placed at various angles from the direction of laser beam. The spectrometers are installed at the breadboard inside a vacuum chamber.
The angularly resolved multichannel magnetic electron spectrometers were developed for the measurements of the energy distribution of hot electrons (Ref. Reference Krupka, Singh, Pisarczyk, Dostal, Kalal, Krasa, Dudzak, Burian, Jelinek, Chodukowski, Rusiniak, Krus and Juha22). The spectrometers were installed in an angular array configuration around the foil target covering the angles on the horizontal plane as shown in Figure 1. The compact design, innovative idea of the plastic collimator and shielding mechanism were implemented in the geometry of the spectrometers to reduce the background noise from the measurements. The aperture (≈ 1 mm) of each spectrometer subtended a solid angle of about ![]() $\approx10^{-5}$ sr at the target centre. The collimated electrons are spectrally dispersed in a magnetic field and detected by an image plate (IP) of type BAS-Super Resolution (BAS-SR). The IPs were absolutely calibrated to provide absolute electron flux for respective electron energies (Ref. Reference Singh, Slavicek, Hodak, Versaci, Pridal and Kumar28). The spectrometer measures electron energies in the range from 50 keV to 2.5 MeV using ferrite magnets having magnetic field of 95 mT (Ref. Reference Krupka, Singh, Pisarczyk, Dostal, Kalal, Krasa, Dudzak, Burian, Jelinek, Chodukowski, Rusiniak, Krus and Juha22).
$\approx10^{-5}$ sr at the target centre. The collimated electrons are spectrally dispersed in a magnetic field and detected by an image plate (IP) of type BAS-Super Resolution (BAS-SR). The IPs were absolutely calibrated to provide absolute electron flux for respective electron energies (Ref. Reference Singh, Slavicek, Hodak, Versaci, Pridal and Kumar28). The spectrometer measures electron energies in the range from 50 keV to 2.5 MeV using ferrite magnets having magnetic field of 95 mT (Ref. Reference Krupka, Singh, Pisarczyk, Dostal, Kalal, Krasa, Dudzak, Burian, Jelinek, Chodukowski, Rusiniak, Krus and Juha22).
Experimental results
In this experiment, we have characterized physical quantities derived from the hot electron energy distribution functions measured by an array of electron spectrometers. By means of experimental observations, we determined hot electron temperature, total number of emitted electrons, charge, maximum electron energy and the conversion efficiency from laser energy to hot electrons.
Figure 2 shows the temperature scaling of hot electron with laser intensity for different target materials, such as Ta, Cu, Ti, Pb and Sn. For PALS laser and plasma parameters, electron temperature (T hot) varies in the range from 20 to 80 keV in the intensity range from ![]() $4 \times 10^{15}$ to
$4 \times 10^{15}$ to ![]() $3 \times 10^{16}$ W cm−2. In addition, the temperature scaling of different targets is compared with experimental and simulation results from sub-nanosecond, sub-picosecond and multi-picosecond laser systems (see Figure 2 and relevant references) (Refs Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24, Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29–Reference Chen, Link, Sentoku, Audebert, Fiuza, Hazi, Heeter, Hill, Hobbs, Kemp, Kemp, Kerr, Meyerhofer, Myatt, Nagel, Park, Tommasini and Williams35). The electron temperature T hot is considerably higher than the ‘suprathermal’ temperature, which should be less than 20 keV in our experiment (Refs Reference Gibbon and Bell37, Reference Gibbon38). The electron temperature from measured data shows that the temperature scaling is mostly consistent with the Beg scaling (Ref. Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29), i.e.
$3 \times 10^{16}$ W cm−2. In addition, the temperature scaling of different targets is compared with experimental and simulation results from sub-nanosecond, sub-picosecond and multi-picosecond laser systems (see Figure 2 and relevant references) (Refs Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24, Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29–Reference Chen, Link, Sentoku, Audebert, Fiuza, Hazi, Heeter, Hill, Hobbs, Kemp, Kemp, Kerr, Meyerhofer, Myatt, Nagel, Park, Tommasini and Williams35). The electron temperature T hot is considerably higher than the ‘suprathermal’ temperature, which should be less than 20 keV in our experiment (Refs Reference Gibbon and Bell37, Reference Gibbon38). The electron temperature from measured data shows that the temperature scaling is mostly consistent with the Beg scaling (Ref. Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29), i.e. ![]() $T_{\textrm{hot}} \approx$ (
$T_{\textrm{hot}} \approx$ (![]() $I \lambda^2)^{1/3}$, where I and λ are the laser intensity and wavelength, respectively. The Beg scaling is typically observed for picosecond laser-matter interaction which is in agreement with the experimental results by Kluge et al. (Ref. Reference Kluge, Bussmann, Schramm and Cowan39). Moreover, past experimental results by Kluge et al. (Ref. Reference Kluge, Cowan, Debus, Schramm, Zeil and Bussmann34) show that at lower laser intensities (≤1016 W cm−2), the electron temperature scaling varies in between Beg scaling and ponderomotive scaling (see Eqn. 1) (Ref. Reference Wilks, Kruer, Tabak and Langdon30) which are also in closer agreement with results shown in Figure 2:
$I \lambda^2)^{1/3}$, where I and λ are the laser intensity and wavelength, respectively. The Beg scaling is typically observed for picosecond laser-matter interaction which is in agreement with the experimental results by Kluge et al. (Ref. Reference Kluge, Bussmann, Schramm and Cowan39). Moreover, past experimental results by Kluge et al. (Ref. Reference Kluge, Cowan, Debus, Schramm, Zeil and Bussmann34) show that at lower laser intensities (≤1016 W cm−2), the electron temperature scaling varies in between Beg scaling and ponderomotive scaling (see Eqn. 1) (Ref. Reference Wilks, Kruer, Tabak and Langdon30) which are also in closer agreement with results shown in Figure 2:

Figure 2. The variation of hot electron temperature as function of laser intensity for different target materials (Ta, Cu, Ti, Pb & Sn) having similar thickness range, i.e. ![]() $\approx10\ \unicode{x03BC}$m (see square symbols). The electron temperature scaling is compared with known Beg (Ref. Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29), ponderomotive (Ref. Reference Wilks, Kruer, Tabak and Langdon30) and Pukhov (Ref. Reference Pukhov, Sheng and Meyer-ter Vehn31) scaling laws. These measurements are also scaled from the experiments of sub-nanosecond, sub-picosecond and multi-picosecond laser-matter interaction at different laser facilities. The legend symbols correspond to specific targets and references relevant with data for the temperature scaling (Refs Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24, Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29–Reference Simpson, Scott, Mariscal, Rusby, King, Grace, Aghedo, Pagano, Sinclair, Armstrong, Manuel, Haid, Flippo, Winslow, Gatu-Johnson, Frenje, Neely, Kerr, Williams, Andrews, Cauble, Charron, Costa, Fischer, Maricle, Stuart, Albert, Lemos, Mackinnon, MacPhee, Pak and Ma36).
$\approx10\ \unicode{x03BC}$m (see square symbols). The electron temperature scaling is compared with known Beg (Ref. Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29), ponderomotive (Ref. Reference Wilks, Kruer, Tabak and Langdon30) and Pukhov (Ref. Reference Pukhov, Sheng and Meyer-ter Vehn31) scaling laws. These measurements are also scaled from the experiments of sub-nanosecond, sub-picosecond and multi-picosecond laser-matter interaction at different laser facilities. The legend symbols correspond to specific targets and references relevant with data for the temperature scaling (Refs Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24, Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29–Reference Simpson, Scott, Mariscal, Rusby, King, Grace, Aghedo, Pagano, Sinclair, Armstrong, Manuel, Haid, Flippo, Winslow, Gatu-Johnson, Frenje, Neely, Kerr, Williams, Andrews, Cauble, Charron, Costa, Fischer, Maricle, Stuart, Albert, Lemos, Mackinnon, MacPhee, Pak and Ma36).
 \begin{equation}
{{T_{\textrm{hot}}} = 511 {\left( \sqrt{\mathrm 1 + {{I} \ \lambda^2 [ {\mathrm{W}\ \mathrm{cm}^{-2}}\ \mu \mathrm{m^2]} \over {1.37 \times 10^{18}} }}-1 \right) [\mathrm {keV}]}}.
\end{equation}
\begin{equation}
{{T_{\textrm{hot}}} = 511 {\left( \sqrt{\mathrm 1 + {{I} \ \lambda^2 [ {\mathrm{W}\ \mathrm{cm}^{-2}}\ \mu \mathrm{m^2]} \over {1.37 \times 10^{18}} }}-1 \right) [\mathrm {keV}]}}.
\end{equation} Furthermore in the under-dense region of the plasma, primarily produced via ablation from the laser prepulse, electron acceleration occurs due to stochastic processes. It should be noted that for relatively high laser intensity ![]() $\ge10^{18}$ W cm−2, the electron temperature is given by Pukhov scaling (Ref. Reference Pukhov, Sheng and Meyer-ter Vehn31), i.e.
$\ge10^{18}$ W cm−2, the electron temperature is given by Pukhov scaling (Ref. Reference Pukhov, Sheng and Meyer-ter Vehn31), i.e. ![]() $T_{\mathrm{hot}} \approx$
$T_{\mathrm{hot}} \approx$ ![]() $1.5 \times \sqrt($ I
$1.5 \times \sqrt($ I ![]() $\lambda^2/10^{18})$ [MeV]. In high intensity and multi-picosecond laser-plasma experiments, the measured electron temperature by Chen et al. (Ref. Reference Chen, Link, Sentoku, Audebert, Fiuza, Hazi, Heeter, Hill, Hobbs, Kemp, Kemp, Kerr, Meyerhofer, Myatt, Nagel, Park, Tommasini and Williams35) and Simpson et al. (Ref. Reference Simpson, Scott, Mariscal, Rusby, King, Grace, Aghedo, Pagano, Sinclair, Armstrong, Manuel, Haid, Flippo, Winslow, Gatu-Johnson, Frenje, Neely, Kerr, Williams, Andrews, Cauble, Charron, Costa, Fischer, Maricle, Stuart, Albert, Lemos, Mackinnon, MacPhee, Pak and Ma36) were found in close agreement with Pukhov scaling as shown in Figure 2.
$\lambda^2/10^{18})$ [MeV]. In high intensity and multi-picosecond laser-plasma experiments, the measured electron temperature by Chen et al. (Ref. Reference Chen, Link, Sentoku, Audebert, Fiuza, Hazi, Heeter, Hill, Hobbs, Kemp, Kemp, Kerr, Meyerhofer, Myatt, Nagel, Park, Tommasini and Williams35) and Simpson et al. (Ref. Reference Simpson, Scott, Mariscal, Rusby, King, Grace, Aghedo, Pagano, Sinclair, Armstrong, Manuel, Haid, Flippo, Winslow, Gatu-Johnson, Frenje, Neely, Kerr, Williams, Andrews, Cauble, Charron, Costa, Fischer, Maricle, Stuart, Albert, Lemos, Mackinnon, MacPhee, Pak and Ma36) were found in close agreement with Pukhov scaling as shown in Figure 2.
The hot electron temperature Thot is determined by the slope of the energy distribution measured using multichannel electron spectrometer. Figures 3 and 4 show the hot electron temperature as function of different atomic numbers for thin (5–8 ![]() $\unicode{x03BC}\mathrm{m}$) and relatively thick foil (10–15
$\unicode{x03BC}\mathrm{m}$) and relatively thick foil (10–15 ![]() $\unicode{x03BC}\mathrm{m}$) targets, respectively. The target thickness of individual metal foil is mentioned in Figures 3 and 4. The electron temperature varies in the range from 30 to 80 keV for respective foil targets. For thin foil targets, the electron temperature is slowly decreasing with increasing atomic numbers however, it does not depends on atomic numbers for relatively thick foil targets (see Figure 4).
$\unicode{x03BC}\mathrm{m}$) targets, respectively. The target thickness of individual metal foil is mentioned in Figures 3 and 4. The electron temperature varies in the range from 30 to 80 keV for respective foil targets. For thin foil targets, the electron temperature is slowly decreasing with increasing atomic numbers however, it does not depends on atomic numbers for relatively thick foil targets (see Figure 4).

Figure 3. Dependence of hot electron temperature with respect to target material for the very thin foil targets (thickness range: 5–8 ![]() $\unicode{x03BC}\mathrm{m}$). The errorbar associated with each data point represents shot to shot fluctuation.
$\unicode{x03BC}\mathrm{m}$). The errorbar associated with each data point represents shot to shot fluctuation.

Figure 4. Dependence of hot electron temperature with respect to target material for the moderately thin foil targets, i.e. thickness range: 10–15 ![]() $\unicode{x03BC}\mathrm{m}$.
$\unicode{x03BC}\mathrm{m}$.
The total flux of hot electrons was measured by spectrometers in the front and back directions with respect to target plane and laser axis. Figures 5 and 6 show the total number of hot electrons emitted from the foil targets having different Z in front and back direction, respectively. The results indicate that in front direction from foil targets, the total electron flux increases slightly with increasing atomic numbers (Z) however, it does not strongly depends on atomic numbers in the back directions (see Figure 6). The different characteristics of electron flux in front and backward directions could be attributed to the recirculation and scattering of electrons inside the target plasma. In addition, it is noted that the optical thickness of the target is also important in the hot electron characteristics which is described later in this section. Moreover, due to the Z-dependence of the conversion from laser energy to hot electrons, the appropriate target consist of a high Z material is recommended for the experiment to increase hot electron flux.

Figure 5. The variation in total number of hot electrons in the front side of the target with respect to laser direction for elements with increasing atomic number.

Figure 6. The profile of hot electron flux in the back side of the target for the same elements (low to high Z) as shown in Figure 5.
In the laser-target interaction experiment, the characteristics of the plasma and emitted electrons also depend on the thickness of the target material. Figure 7 shows the variation in electron temperature for the different thickness (1–100 μm) of the copper target for similar laser energy in the range of 550 and 600 J. The electron temperature varies in the range between 30 and 90 keV; however, the average electron temperature is around 50 keV. The electron temperature is relatively high (≥60 keV) for thin targets (2–5 μm) and it is comparatively lower (≤40 keV) for the thick targets (≥10 μm). In the case of thick targets, lower temperature of hot electrons can be attributed to recirculation, refluxing or scattering of electrons inside the target plasma (Ref. Reference Quinn, Yuan, Lin, Carroll, Tresca, Gray, Coury, Li, Li, Brenner, Robinson, Neely, Zielbauer, Aurand, Fils, Kuehl and McKenna40).

Figure 7. Dependence of hot electron temperature with respect to the thickness of the copper target. The result indicates that electron temperature decreases with increasing target thickness.
Figures 8 and 9 represent the variation of electron flux with target thickness for copper target in front and back directions, respectively, for the same laser energy as discussed in Figure 7. The profiles of Figs. 8 and 9 show that electron flux is higher for thin target (≤10 μm) and flux decreases as target thickness increases in both front and back direction. The deficiency in electron flux can be attributed to expected energy lost by hot electrons while traversing thick targets (Ref. Reference Berger, Coursey and Zucker41). The results conclude that for the given laser parameters, thin targets are appropriate choice for optimal generation of hot electrons.

Figure 8. Number of emitted electrons from the front side with respect to the different thickness of copper target.

Figure 9. Number of emitted electrons from the back side with respect to the different thickness of copper target.
In order to characterize the hot electron emission, measurements relevant with angular distribution of electron energy are essential. Figure 10 represents the angular characteristics of hot electron temperature and electron flux at different angles with laser axis for ![]() $10\ \unicode{x03BC}$m thick copper and tantalum targets, respectively. The results indicate that the hot electron temperature is in the range of 40–60 keV (see Figure 10(A)) and it depends on angular direction for both target materials, i.e. the electron temperature is bit higher at laser axis in comparison with other angular directions. Following the profile of electron temperature, electron flux shows similar characteristics (see Figure 10(B)). The flux is higher along the laser axis and it decreases along angular directions for both kind of targets. However, it should be noted that hot electron temperature and flux is slightly higher in case of
$10\ \unicode{x03BC}$m thick copper and tantalum targets, respectively. The results indicate that the hot electron temperature is in the range of 40–60 keV (see Figure 10(A)) and it depends on angular direction for both target materials, i.e. the electron temperature is bit higher at laser axis in comparison with other angular directions. Following the profile of electron temperature, electron flux shows similar characteristics (see Figure 10(B)). The flux is higher along the laser axis and it decreases along angular directions for both kind of targets. However, it should be noted that hot electron temperature and flux is slightly higher in case of ![]() $10\ \unicode{x03BC}$m thick tantalum target in comparison to copper target having same thickness. Comparatively higher electron flux for tantalum case is attributed to high Z material which has been used as a bremsstrahlung converter for better efficiency in high intensity laser–solid interaction experiments (Ref. Reference Galy, Maučec, Hamilton, Edwards and Magill25).
$10\ \unicode{x03BC}$m thick tantalum target in comparison to copper target having same thickness. Comparatively higher electron flux for tantalum case is attributed to high Z material which has been used as a bremsstrahlung converter for better efficiency in high intensity laser–solid interaction experiments (Ref. Reference Galy, Maučec, Hamilton, Edwards and Magill25).

Figure 10. A comparison of angular characteristics of hot electron temperature (A) and flux (B) in between copper and tantalum targets (see legend colours).
Total conversion efficiency associated with laser energy to hot electron is also determined for mentioned targets having different materials. In this case, the thickness of all targets was kept winthin a similar range, i.e. of the order of ![]() $10\ \unicode{x03BC}$m. Total number of hot electrons per shot (
$10\ \unicode{x03BC}$m. Total number of hot electrons per shot (![]() ${\sim}6 \times 10^{11}$) is estimated by integrating the measured electron spectra in angular direction to the entire 4π solid angle which corresponds to total charge of about
${\sim}6 \times 10^{11}$) is estimated by integrating the measured electron spectra in angular direction to the entire 4π solid angle which corresponds to total charge of about ![]() ${\sim}0.1\ \unicode{x03BC}$C. The total energy carried with these electrons is of the order of 6 mJ. This implies a conversion efficiency from laser energy (∼600 J) to electrons of about
${\sim}0.1\ \unicode{x03BC}$C. The total energy carried with these electrons is of the order of 6 mJ. This implies a conversion efficiency from laser energy (∼600 J) to electrons of about ![]() ${\sim}0.001\%$. In addition, the measured profile of the conversion efficiency associated with specific targets for different laser energy is shown in Figure 11. The characteristics of the profile show step-like behaviour in the laser energy above 200 J. We observed that conversion efficiency is varying nonlinearly with increasing laser energy in the range between
${\sim}0.001\%$. In addition, the measured profile of the conversion efficiency associated with specific targets for different laser energy is shown in Figure 11. The characteristics of the profile show step-like behaviour in the laser energy above 200 J. We observed that conversion efficiency is varying nonlinearly with increasing laser energy in the range between ![]() ${\sim}10^{-6}$ and
${\sim}10^{-6}$ and ![]() ${\sim}10^{-3}$ for laser energy from 100 to 600 J (Ref. Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24). The physical mechanism relevant with these nonlinearities is described in the next section.
${\sim}10^{-3}$ for laser energy from 100 to 600 J (Ref. Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24). The physical mechanism relevant with these nonlinearities is described in the next section.

Figure 11. The profile of conversion efficiency from laser energy to electron kinetic energy as a function of incident laser energy. The colour code in the legend represents different target materials having similar thickness range, i.e. ![]() $\approx10\ \unicode{x03BC}$m. The data of different target materials are compared with published result of the tantalum target (see Figure 10 of the reference by Singh et al., (Ref. Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24)).
$\approx10\ \unicode{x03BC}$m. The data of different target materials are compared with published result of the tantalum target (see Figure 10 of the reference by Singh et al., (Ref. Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24)).
Summary and discussion
The paper outlined the results of temperature scaling and characteristics of hot electrons from thin foil metal targets irradiated by terawatt class iodine laser. It has already been reported that laser-plasma instabilities and relevant nonlinear processes due to spacial inhomogenities in plasma density and electron temperature play a major role in the fluctuations of the plasma parameters (Ref. Reference Montgomery42). Laser energy deposited near plasma critical density is thermally transported to denser and cooler regions, causing more material ablation, creating inward directed ablation pressure, as well as producing X-rays (bremsstrahlung radiation) in the target. As shown in Figures 3–10, ablation depends on the characteristics of the target material, i.e. atomic number and its thickness. The largest fluctuations of the electron temperature are observed in Ti and Sn plasmas, however, fluctuations in number density of fast electrons can be found in the Ta and Cu plasmas. It should be noted that plasma produced using Sn targets show very low density fluctuations which is in contrary to relatively high temperature fluctuations for the same target parameters. On the other hand, Pb plasma shows low fluctuations in density as well as in electron temperature measurements. In physical mechanism, the ponderomotive force that drives plasma density and temperature fluctuations depends on the spatial gradient of the electric field pressure due to the beating between the laser and scattered light waves driven by parametric instabilities, such as stimulated Raman scattering (SRS) and two-plasmon decay (TPD) (Ref. Reference Cristoforetti, Antonelli, Mancelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, D’Amato, Dostal, Dudzak, Filippov, Gu, Juha, Klimo, Krus, Malko, Martynenko, Nicolai, Ospina, Pikuz, Renner, Santos, Tikhonchuk, Trela, Viciani, Volpe, Weber and Gizzi43). In the case of parametric instabilities, the convective growth of the scattered light is the thermal noise which arises from Thomson scattering of the thermal density fluctuations as well as bremsstrahlung from the hot plasma. In addition to the parametric instabilities, self-focusing of the laser light can also play a crucial role in the fluctuations, causing the laser beam to filament and increase its intensity. Self-focusing occurs due to localized intense region of the laser which creates a plasma density depression, in presence of laser driven ponderomotive pressure or localized thermal heating. The density depression acts like a positive lens, further focusing the intense region, creating an unstable situation. Since self-focusing increases the laser intensity, this can further lead to increased growth rate of parametric instabilities. A counter interplay between these processes enhances the shot-shot fluctuations in the plasma parameters. Moreover, the hydrodynamic evolution of the target also affected the levels of parametric instabilities due to density and velocity fluctuations from the plasma formation process. Furthermore, quasi-spherical nature of the ablative expansion of the plasma and associated density distribution can be related to diverse mechanisms including relevant plasma instabilities, spontaneous magnetic field pressure gradient and partially also a nonideality of the irradiation process (Ref. Reference Pisarczyk, Kalal, Gus’kov, Batani, Renner, Santos, Dudzak, Zaras-Szydłowska, Chodukowski, Rusiniak, Dostal, Krasa, Krupka, Kochetkov, Singh, Cikhardt, Burian, Krus, Pfeifer, Cristoforetti, Gizzi, Baffigi, Antonelli, Demchenko, Rosinski, Terwinska, Borodziuk, Kubes, Ehret, Juha, Skala and Korneev23). In order to avoid shot to shot fluctuations in the laser-plasma experiments, single shot can be recommended for the precise measurements and cross verification with additional supporting diagnostics however, single shot measurement is limited by the statistical uncertainty in the measured data.
As shown by Figure 2, electron temperature scaling is compared by Beg, ponderomotive and Pukhov scalings along with other experimental results obtained using sub-nanosecond, sub-picosecond and multi-picosecond lasers. In this experiment, the measured data points are consistent with the fact that at lower laser intensities (≤1016 W cm−2), the electron temperature scaling varies between Beg and ponderomotive scalings (Ref. Reference Kluge, Cowan, Debus, Schramm, Zeil and Bussmann34), however; electron temperature is in accordance with Beg scaling (Ref. Reference Kluge, Bussmann, Schramm and Cowan39) at high intensities, i.e. >1016 W cm−2 (see Figure 2). Moreover, Beg scaling is observed in long plasma scale length (![]() ${\sim}100\,\unicode{x03BC}$m); however, ponderomotive scaling is usually valid for small plasma scale lengths where laser pulse is tightly focused. In addition, the electron temperature scaling is bit different from the one that corresponds to the suprathermal one (Ref. Reference Gibbon and Bell37), however, Beg dependence is in consistent with the extended Gibbons model (Ref. Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29). For the given experimental conditions, a positive correlation is observed between the electrons following the Beg scaling (Ref. Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29) and maximum energy of accelerated ions (Ref. Reference Krasa, Klir, Rezac, Cikhardt, Krus, Velyhan, Pfeifer, Buryskova, Dostal, Burian, Dudzak, Turek, Pisarczyk, Kalinowska, Chodukowski and Kaufman44), however; identifying the physical mechanism is bit difficult due to presence of the different instabilities under mentioned intensity range of the experiment.
${\sim}100\,\unicode{x03BC}$m); however, ponderomotive scaling is usually valid for small plasma scale lengths where laser pulse is tightly focused. In addition, the electron temperature scaling is bit different from the one that corresponds to the suprathermal one (Ref. Reference Gibbon and Bell37), however, Beg dependence is in consistent with the extended Gibbons model (Ref. Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29). For the given experimental conditions, a positive correlation is observed between the electrons following the Beg scaling (Ref. Reference Beg, Bell, Dangor, Danson, Fews, Glinsky, Hammel, Lee, Norreys and Tatarakis29) and maximum energy of accelerated ions (Ref. Reference Krasa, Klir, Rezac, Cikhardt, Krus, Velyhan, Pfeifer, Buryskova, Dostal, Burian, Dudzak, Turek, Pisarczyk, Kalinowska, Chodukowski and Kaufman44), however; identifying the physical mechanism is bit difficult due to presence of the different instabilities under mentioned intensity range of the experiment.
Apart from characteristics of the electron temperature scaling and fluctuations in electron parameters, the step like behaviour in the profile of conversion efficiency from laser energy to hot electrons (see Figure 11) indicates the specific non-linearity that can be attributed to experimental conditions and plasma parameters. At laser intensity of ![]() ${\sim}10^{16}$ W cm−2, LPI is dominated by parametric instabilities (SRS, TPD) which can be responsible for non-collisional absorption and generate large fluxes of hot electrons. Cristoforetti et al. investigated the extent and time history of SRS and TPD instabilities, driven by the interaction of PALS laser at an intensity
${\sim}10^{16}$ W cm−2, LPI is dominated by parametric instabilities (SRS, TPD) which can be responsible for non-collisional absorption and generate large fluxes of hot electrons. Cristoforetti et al. investigated the extent and time history of SRS and TPD instabilities, driven by the interaction of PALS laser at an intensity ![]() ${\sim}1.2 \times 10^{16}$ W cm−2 with plasma scalelength
${\sim}1.2 \times 10^{16}$ W cm−2 with plasma scalelength ![]() ${\sim}100 \ \unicode{x03BC}$m produced from irradiation of a flat plastic target (Ref. Reference Cristoforetti, Antonelli, Mancelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, D’Amato, Dostal, Dudzak, Filippov, Gu, Juha, Klimo, Krus, Malko, Martynenko, Nicolai, Ospina, Pikuz, Renner, Santos, Tikhonchuk, Trela, Viciani, Volpe, Weber and Gizzi43). Moreover, Cristoforetti et al. measured the hot electron energy in the range of 40–50 keV which is in close agreement with the electron temperature of our measurements. In addition, the self-focusing of the laser beam in the plasma can be produced by a relativistic mechanism (Ref. Reference Sun, Ott, Lee and Guzdar45). The relativistic nonlinearity should appear immediately when the power of the incident laser exceeds the threshold required for self-focusing (Pcr = 17.4
${\sim}100 \ \unicode{x03BC}$m produced from irradiation of a flat plastic target (Ref. Reference Cristoforetti, Antonelli, Mancelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, D’Amato, Dostal, Dudzak, Filippov, Gu, Juha, Klimo, Krus, Malko, Martynenko, Nicolai, Ospina, Pikuz, Renner, Santos, Tikhonchuk, Trela, Viciani, Volpe, Weber and Gizzi43). Moreover, Cristoforetti et al. measured the hot electron energy in the range of 40–50 keV which is in close agreement with the electron temperature of our measurements. In addition, the self-focusing of the laser beam in the plasma can be produced by a relativistic mechanism (Ref. Reference Sun, Ott, Lee and Guzdar45). The relativistic nonlinearity should appear immediately when the power of the incident laser exceeds the threshold required for self-focusing (Pcr = 17.4 ![]() ${n_{cr}/n_e}$) in GW (Ref. Reference Habara, Adumi, Yabuuchi, Nakamura, Chen, Kashihara, Kodama, Kondo, Kumar, Lei, Matsuoka, Mima and Tanaka46), where ncr and ne are the critical density and measured value of plasma density, respectively.
${n_{cr}/n_e}$) in GW (Ref. Reference Habara, Adumi, Yabuuchi, Nakamura, Chen, Kashihara, Kodama, Kondo, Kumar, Lei, Matsuoka, Mima and Tanaka46), where ncr and ne are the critical density and measured value of plasma density, respectively.
Furthermore, at the lower intensity case (≤1016 W cm−2), self-focusing does not occur because the power could barely reach the critical power of relativistic self-focusing (Pcr). However, the measured data from femtosecond interferometry shows that electron plasma density ![]() $n_e \approx 3 \times 10^{19}$ W cm−2 of the scale length ≈ 100 μm, can be produced on the front surface of the irradiated target, 100 ps before the maximum laser power (Ref. Reference Pisarczyk, Kalal, Gus’kov, Batani, Renner, Santos, Dudzak, Zaras-Szydłowska, Chodukowski, Rusiniak, Dostal, Krasa, Krupka, Kochetkov, Singh, Cikhardt, Burian, Krus, Pfeifer, Cristoforetti, Gizzi, Baffigi, Antonelli, Demchenko, Rosinski, Terwinska, Borodziuk, Kubes, Ehret, Juha, Skala and Korneev23). For the laser wavelength 1.315 μm, the required
$n_e \approx 3 \times 10^{19}$ W cm−2 of the scale length ≈ 100 μm, can be produced on the front surface of the irradiated target, 100 ps before the maximum laser power (Ref. Reference Pisarczyk, Kalal, Gus’kov, Batani, Renner, Santos, Dudzak, Zaras-Szydłowska, Chodukowski, Rusiniak, Dostal, Krasa, Krupka, Kochetkov, Singh, Cikhardt, Burian, Krus, Pfeifer, Cristoforetti, Gizzi, Baffigi, Antonelli, Demchenko, Rosinski, Terwinska, Borodziuk, Kubes, Ehret, Juha, Skala and Korneev23). For the laser wavelength 1.315 μm, the required ![]() $P_{cr} \approx$ 0.45 TW is less than the 1.5 TW used in this experiment which implies that for laser energy
$P_{cr} \approx$ 0.45 TW is less than the 1.5 TW used in this experiment which implies that for laser energy ![]() $\ge250$ J and intensity
$\ge250$ J and intensity ![]() $\ge8 \times 10^{15}$ W cm−2, the possibility of self-focusing cannot be ignored along with other nonlinear effects (Ref. Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24). In the given experimental scenarios, plasma density must be sufficiently thick to allow the creation of a self-focusing channel and the threshold intensity for both the ponderomotive and relativistic filamentation which is reachable during the LPI. Moreover, the nonlinear characteristic in the profile of conversion efficiency can be seen at energy threshold ∼250 J (see Figure 11) which is in closer agreement with our analogy and hypothesis. Figure 11 clearly shows that the relativistic self-focusing is not emerging significantly for laser energies ≤250 J, however; for given laser and plasma parameters, it can occur at higher laser energies (≥250 J).
$\ge8 \times 10^{15}$ W cm−2, the possibility of self-focusing cannot be ignored along with other nonlinear effects (Ref. Reference Singh, Krupka, Istokskaia, Krasa, Giuffrida, Dudzak, Dostal, Burian, Versaci, Margarone, Pisarczyk, Krus and Juha24). In the given experimental scenarios, plasma density must be sufficiently thick to allow the creation of a self-focusing channel and the threshold intensity for both the ponderomotive and relativistic filamentation which is reachable during the LPI. Moreover, the nonlinear characteristic in the profile of conversion efficiency can be seen at energy threshold ∼250 J (see Figure 11) which is in closer agreement with our analogy and hypothesis. Figure 11 clearly shows that the relativistic self-focusing is not emerging significantly for laser energies ≤250 J, however; for given laser and plasma parameters, it can occur at higher laser energies (≥250 J).
Conclusion
This paper presents basic results of an experiment in which a sub-nanosecond pulse (∼350 ps) from an iodine laser was focused on metal foil targets having different atomic numbers (Cu, Ta, Ti, Sn, Pb) for laser intensities between ![]() ${\sim}10^{15}$ and
${\sim}10^{15}$ and ![]() ${\sim}3 \times 10^{16}\ \mathrm{W\,cm^{-2}}$. The hot electrons were characterized by measuring the energy spectrum using array of electron spectrometers for different thickness of foil targets in the range of 1–100
${\sim}3 \times 10^{16}\ \mathrm{W\,cm^{-2}}$. The hot electrons were characterized by measuring the energy spectrum using array of electron spectrometers for different thickness of foil targets in the range of 1–100 ![]() $\unicode{x03BC}\mathrm{m}$. The measured electron temperature is observed in the range between 30 and 80 keV for the given range of laser intensities. The temperature scaling of different targets is also compared with experimental and simulation results from sub-nanosecond, sub-picosecond and multi-picosecond laser systems. In this experimental condition, the electron temperature scaling varies in between Beg and ponderomotive scalings. Moreover, we also observed that conversion efficiency from laser energy to hot electrons is showing step-like behaviour and it varies nonlinearly with increasing laser energy in the range between
$\unicode{x03BC}\mathrm{m}$. The measured electron temperature is observed in the range between 30 and 80 keV for the given range of laser intensities. The temperature scaling of different targets is also compared with experimental and simulation results from sub-nanosecond, sub-picosecond and multi-picosecond laser systems. In this experimental condition, the electron temperature scaling varies in between Beg and ponderomotive scalings. Moreover, we also observed that conversion efficiency from laser energy to hot electrons is showing step-like behaviour and it varies nonlinearly with increasing laser energy in the range between ![]() ${\sim}10^{-6}$ and
${\sim}10^{-6}$ and ![]() ${\sim}10^{-3}$ for laser energy in the range between 100 and 600 J, respectively. For the given plasma parameters, the nonlinear profile of conversion efficiency which has step-like behaviour can be attributed to either or combined effects of parametric instabilities, self-focusing and relativistic filamentation. The experimental results associated with conversion efficiency and temperature scaling for different foil targets are not only important for the understanding of hot electron generation in long-pulse, high-intensity laser–solid interaction experiments, but also crucial for the experiments relevant to fast-ignition (Ref. Reference Klimo, Psikal, Tikhonchuk and Weber47), laboratory astrophysics (Ref. Reference Kumar, Singh, Ahmed, Dudžák, Dostál, Chodukowski, Giuffrida, Hadjisolomu, Hodge, Juha, Krouský, Krůs, Li, Lutoslawski, Marco, Pfeifer, Rusiniak, Skála, Ullschmeid, Pisarczyk, Borghesi and Kar48, Reference Sanyasi, Awasthi, Mattoo, Srivastava, Singh, Singh and Kaw49) and high energy density science (Ref. Reference Weber, Bechet, Borneis, Brabec, Bučka, Chacon-Golcher, Ciappina, DeMarco, Fajstavr, Falk, Garcia, Grosz, Gu, Hernandez, Holec, Janečka, Jantač, Jirka, Kadlecova, Khikhlukha, Klimo, Korn, Kramer, Kumar, Lastovička, Lutoslawski, Morejon, Olšovcová, Rajdl, Renner, Rus, Singh, Šmid, Sokol, Versaci, Vrána, Vranic, Vyskočil, Wolf and Yu50).
${\sim}10^{-3}$ for laser energy in the range between 100 and 600 J, respectively. For the given plasma parameters, the nonlinear profile of conversion efficiency which has step-like behaviour can be attributed to either or combined effects of parametric instabilities, self-focusing and relativistic filamentation. The experimental results associated with conversion efficiency and temperature scaling for different foil targets are not only important for the understanding of hot electron generation in long-pulse, high-intensity laser–solid interaction experiments, but also crucial for the experiments relevant to fast-ignition (Ref. Reference Klimo, Psikal, Tikhonchuk and Weber47), laboratory astrophysics (Ref. Reference Kumar, Singh, Ahmed, Dudžák, Dostál, Chodukowski, Giuffrida, Hadjisolomu, Hodge, Juha, Krouský, Krůs, Li, Lutoslawski, Marco, Pfeifer, Rusiniak, Skála, Ullschmeid, Pisarczyk, Borghesi and Kar48, Reference Sanyasi, Awasthi, Mattoo, Srivastava, Singh, Singh and Kaw49) and high energy density science (Ref. Reference Weber, Bechet, Borneis, Brabec, Bučka, Chacon-Golcher, Ciappina, DeMarco, Fajstavr, Falk, Garcia, Grosz, Gu, Hernandez, Holec, Janečka, Jantač, Jirka, Kadlecova, Khikhlukha, Klimo, Korn, Kramer, Kumar, Lastovička, Lutoslawski, Morejon, Olšovcová, Rajdl, Renner, Rus, Singh, Šmid, Sokol, Versaci, Vrána, Vranic, Vyskočil, Wolf and Yu50).
Data availability statement
The data generated and/or analyzed during the current study are not publicly available for legal/ethical reasons but are available from the corresponding author on reasonable request. The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgements
The research presented in this paper was supported by the Access to the PALS RI under the Laserlab-Europe V project (Grant Agreement No. 871124), by the Czech Republic’s Ministry of Education, Youth and Sports – the projects: Prague Asterix Laser System (LM2023068) and Creating and probing dense plasmas at the PALS facility (CZ.02.1.01/0.0/0.0/16013/0001552). The research leading to these results has received funding from the Czech Science Foundation (Grant No. 23-05027M and 19-24619S). The support of CTU student support project ‘Research on optical (nano) structures and laser plasma’ SGS19/192/OHK4/3T/14 is gratefully acknowledged as well as the support by the international project called ‘PMW’, co-financed by the Polish Ministry of Science and Higher Education within the framework of the scientific financial resources for 2021–2022 under the Contract No. 5084/PALS/2020/0 (Project No. PALS002628). This scientific work is also supported by the project Advanced research using high intensity laser produced photons and particles (ADONIS) CZ.02.1.01/0.0/0.0/16019/0000789 from European Regional Development Fund (ERDF) as well as supported by EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200-EUROfusion).