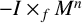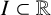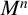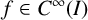1 Introduction
Given a spacelike hypersurface
![]() $\psi :\Sigma ^n\looparrowright \mathbb R_1^{n+1}$
(which means that the induced metric of
$\psi :\Sigma ^n\looparrowright \mathbb R_1^{n+1}$
(which means that the induced metric of
![]() $\Sigma ^n$
via the immersion
$\Sigma ^n$
via the immersion
![]() $\psi $
is Riemannian) in the
$\psi $
is Riemannian) in the
![]() $(n+1)$
-dimensional Minkowski space
$(n+1)$
-dimensional Minkowski space
![]() $\mathbb R_1^{n+1}$
, we recall that the spacelike mean curvature flow associated to
$\mathbb R_1^{n+1}$
, we recall that the spacelike mean curvature flow associated to
![]() $\psi $
is a family of smooth spacelike immersions
$\psi $
is a family of smooth spacelike immersions
![]() $\Psi _t=\Psi (t,\cdot ):\Sigma ^n\rightarrow \mathbb R_1^{n+1}$
with corresponding images
$\Psi _t=\Psi (t,\cdot ):\Sigma ^n\rightarrow \mathbb R_1^{n+1}$
with corresponding images
![]() $\Sigma ^n_t=\Psi _t(\Sigma ^n)$
satisfying the evolution equation,
$\Sigma ^n_t=\Psi _t(\Sigma ^n)$
satisfying the evolution equation,
 $$ \begin{align*} \begin{cases} \dfrac{\partial\Psi}{\partial t}=\vec{H},\\[4pt] \Psi(0,x)=\psi(x), \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \dfrac{\partial\Psi}{\partial t}=\vec{H},\\[4pt] \Psi(0,x)=\psi(x), \end{cases} \end{align*} $$
on some time interval, where
![]() $\vec {H}$
stands for the (nonnormalized) mean curvature vector of the spacelike submanifold
$\vec {H}$
stands for the (nonnormalized) mean curvature vector of the spacelike submanifold
![]() $\Sigma ^n_t$
in
$\Sigma ^n_t$
in
![]() $\mathbb R_1^{n+1}$
.
$\mathbb R_1^{n+1}$
.
Mean curvature flow in the Minkowski space and, more generally, in a Lorentzian manifold has been extensively studied by several authors (see, for example, [Reference Gao, Li and Wu28, Reference Lambert31, Reference Spruck and Xiao41]) and an important justification for this interest is the fact that spacelike self-shrinkers and, in a more general setting, spacelike mean curvature flow solitons (which constitute singularities of the spacelike mean curvature flow) can be regarded as a natural way of foliating spacetimes by almost null-like hypersurfaces. Particular examples may give insight into the structure of certain spacetimes at null infinity and have possible applications in general relativity. For example, they were used in the first proof of the positive mass theorem [Reference Schoen and Yau39, Reference Schoen and Yau40] and in the analysis of the Cauchy problem for asymptotically flat spacetimes [Reference Choquet-Bruhat, York and Held23, Reference Lichnerowicz33].
In [Reference Chen and Qiu22], Chen and Qiu proved that any complete m-dimensional spacelike self-shrinkers in pseudo-Euclidean spaces
![]() $\mathbb R_n^{m+n}$
of index n must be affine planes, and that there exists no complete m-dimensional spacelike translating soliton in
$\mathbb R_n^{m+n}$
of index n must be affine planes, and that there exists no complete m-dimensional spacelike translating soliton in
![]() $\mathbb R_n^{m+n}$
. Subsequently, Xu and Liu [Reference Xu and Liu44] classified m-dimensional complete spacelike translating solitons in
$\mathbb R_n^{m+n}$
. Subsequently, Xu and Liu [Reference Xu and Liu44] classified m-dimensional complete spacelike translating solitons in
![]() $\mathbb R_n^{m+n}$
by affine techniques and classical gradient estimates, and they obtained a Bernstein-type theorem when the translating vector is spacelike. In addition, Lambert and Lotay [Reference Lambert and Lotay32] proved long-time existence and convergence results for spacelike solitons to mean curvature flow in
$\mathbb R_n^{m+n}$
by affine techniques and classical gradient estimates, and they obtained a Bernstein-type theorem when the translating vector is spacelike. In addition, Lambert and Lotay [Reference Lambert and Lotay32] proved long-time existence and convergence results for spacelike solitons to mean curvature flow in
![]() $\mathbb R_n^{n+m}$
that are entire or defined on bounded domains and satisfy Neumann or Dirichlet boundary conditions.
$\mathbb R_n^{n+m}$
that are entire or defined on bounded domains and satisfy Neumann or Dirichlet boundary conditions.
Related to the Riemannian setting, Alías, de Lira and Rigoli [Reference Alías, de Lira and Rigoli9] introduced the general definition of self-similar mean curvature flow in a Riemannian manifold
![]() $\overline {M}^{n+1}$
endowed with a conformal vector field K, and they established the corresponding notion of a mean curvature flow soliton. In particular, when
$\overline {M}^{n+1}$
endowed with a conformal vector field K, and they established the corresponding notion of a mean curvature flow soliton. In particular, when
![]() $\overline {M}^{n+1}$
is a Riemannian warped product of the type
$\overline {M}^{n+1}$
is a Riemannian warped product of the type
![]() $I\times _fM^n$
and
$I\times _fM^n$
and
![]() $\mathcal K=f(t)\partial _t$
, they applied weak maximum principles to guarantee that a complete n-dimensional mean curvature flow soliton is a slice of
$\mathcal K=f(t)\partial _t$
, they applied weak maximum principles to guarantee that a complete n-dimensional mean curvature flow soliton is a slice of
![]() $\overline {M}^{n+1}$
. In [Reference Colombo, Mari and Rigoli24], Colombo et al. also studied some properties of mean curvature flow solitons in general Riemannian manifolds and in warped products, focusing on splitting and rigidity results under various geometric conditions, ranging from the stability of the soliton to the fact that the image of its Gauss map be contained in suitable regions of the sphere.
$\overline {M}^{n+1}$
. In [Reference Colombo, Mari and Rigoli24], Colombo et al. also studied some properties of mean curvature flow solitons in general Riemannian manifolds and in warped products, focusing on splitting and rigidity results under various geometric conditions, ranging from the stability of the soliton to the fact that the image of its Gauss map be contained in suitable regions of the sphere.
More recently, Alías et al. [Reference Alías, de Lira and Rigoli10] established a natural framework for the stability of mean curvature flow solitons in warped product spaces. By regarding these solitons as stationary immersions for a weighted volume functional, they were able to find geometric conditions for finiteness of the index and some characterizations of stable solitons. When the ambient space is a Lorentzian product space, the first author jointly with Batista [Reference Batista and de Lima15] established nonexistence results for complete spacelike translating solitons under suitable curvature constraints on the curvatures of the Riemannian base of the ambient space.
Here, our purpose is to investigate geometric aspects of complete spacelike mean curvature flow solitons of codimension one in a generalized Robertson–Walker (GRW) spacetime
![]() $-I\times _{f}M^n$
, with base
$-I\times _{f}M^n$
, with base
![]() $I\subset \mathbb R$
, Riemannian fiber
$I\subset \mathbb R$
, Riemannian fiber
![]() $M^n$
and warping function
$M^n$
and warping function
![]() $f\in C^\infty (I)$
. In this context and inspired by the techniques developed in [Reference Alías, de Lira and Rigoli9, Reference Batista and de Lima15, Reference Colombo, Mari and Rigoli24], in Section 3 we apply suitable maximum principles to guarantee that such a mean curvature flow soliton is a slice of the ambient space and to obtain nonexistence results concerning these solitons. For example, we apply an extension of Hopf’s theorem to prove the following rigidity result (see Theorem 3.4).
$f\in C^\infty (I)$
. In this context and inspired by the techniques developed in [Reference Alías, de Lira and Rigoli9, Reference Batista and de Lima15, Reference Colombo, Mari and Rigoli24], in Section 3 we apply suitable maximum principles to guarantee that such a mean curvature flow soliton is a slice of the ambient space and to obtain nonexistence results concerning these solitons. For example, we apply an extension of Hopf’s theorem to prove the following rigidity result (see Theorem 3.4).
Theorem 1.1. Let
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime that obeys the null convergence condition (3-20), with equality holding only in isolated points of I. Let
$\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime that obeys the null convergence condition (3-20), with equality holding only in isolated points of I. Let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a complete spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a complete spacelike mean curvature flow soliton with soliton constant
![]() $c\not =0$
lying in a timelike bounded region
$c\not =0$
lying in a timelike bounded region
![]() $\mathcal {B}_{t_1,t_2}$
. If its second soliton function
$\mathcal {B}_{t_1,t_2}$
. If its second soliton function
![]() $\tilde {\zeta }_{c}=|A|^2+cf'(h)$
is nonnegative and
$\tilde {\zeta }_{c}=|A|^2+cf'(h)$
is nonnegative and
![]() $|\nabla H|\in \mathcal L^1(\Sigma ^n)$
, then
$|\nabla H|\in \mathcal L^1(\Sigma ^n)$
, then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
In the previous statement,
![]() $\mathcal L^1(\Sigma ^n)$
stands for the space of Lebesgue integrable functions on
$\mathcal L^1(\Sigma ^n)$
stands for the space of Lebesgue integrable functions on
![]() $\Sigma ^n$
. Moreover, among other results, we apply Omori–Yau’s maximum principle to prove the following nonexistence result, which can be regarded as a sort of extension of [Reference Chen and Qiu22, Theorem 3] (see Theorem 3.20).
$\Sigma ^n$
. Moreover, among other results, we apply Omori–Yau’s maximum principle to prove the following nonexistence result, which can be regarded as a sort of extension of [Reference Chen and Qiu22, Theorem 3] (see Theorem 3.20).
Theorem 1.2. Let
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime satisfying the strong null convergence condition (3-25). There is no complete spacelike mean curvature flow soliton immersed in
$\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime satisfying the strong null convergence condition (3-25). There is no complete spacelike mean curvature flow soliton immersed in
![]() $\overline {M}^{n+1}$
with soliton constant
$\overline {M}^{n+1}$
with soliton constant
![]() $c\neq 0$
such that
$c\neq 0$
such that
![]() $cf'(h)\geq 0$
and
$cf'(h)\geq 0$
and
![]() $({(n-1)f"(h)+cf(h)f'(h)})/{f(h)}$
is bounded from below.
$({(n-1)f"(h)+cf(h)f'(h)})/{f(h)}$
is bounded from below.
In particular, in Section 3.3, we deal with entire graphs constructed over the Riemannian fiber
![]() $M^n$
that are spacelike mean curvature flow solitons. Then, in Section 4, we explore the geometry of a conformal vector field to establish topological and further rigidity results for compact (without boundary) mean curvature flow solitons in a GRW spacetime. For example, we obtain the following result (see Theorem 4.9).
$M^n$
that are spacelike mean curvature flow solitons. Then, in Section 4, we explore the geometry of a conformal vector field to establish topological and further rigidity results for compact (without boundary) mean curvature flow solitons in a GRW spacetime. For example, we obtain the following result (see Theorem 4.9).
Theorem 1.3. Let
![]() $\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
$\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
![]() $c\neq 0$
. Suppose that
$c\neq 0$
. Suppose that
![]() $\Sigma ^n$
is totally umbilical and is not contained in a slice of
$\Sigma ^n$
is totally umbilical and is not contained in a slice of
![]() $\overline {M}^{n+1}$
. If
$\overline {M}^{n+1}$
. If
![]() $\Sigma ^n$
has finite fundamental group, then
$\Sigma ^n$
has finite fundamental group, then
![]() $\Sigma ^n$
is diffeomorphic to an Euclidean sphere.
$\Sigma ^n$
is diffeomorphic to an Euclidean sphere.
Furthermore, motivated by [Reference Alías, de Lira and Rigoli10], in Section 5, we study the stability of spacelike mean curvature flow solitons with respect to an appropriate stability operator
![]() $L_{cu}$
, which is defined in (5-11). In this setting, we deduce the following result (see Theorem 5.6).
$L_{cu}$
, which is defined in (5-11). In this setting, we deduce the following result (see Theorem 5.6).
Theorem 1.4. Let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with soliton constant
![]() $c\not =0$
.
$c\not =0$
.
-
(a) If
 $\zeta ^{\prime }_c(t)\leq 0$
on
$\zeta ^{\prime }_c(t)\leq 0$
on
 $\Sigma ^n$
, then
$\Sigma ^n$
, then
 $\psi :\Sigma ^n\looparrowright -I\times _fM^n$
is
$\psi :\Sigma ^n\looparrowright -I\times _fM^n$
is
 $L_{cu}$
-stable.
$L_{cu}$
-stable. -
(b) If
 $\Sigma ^n$
is compact and
$\Sigma ^n$
is compact and
 $\zeta ^{\prime }_c(t)\geq 0$
on it, then
$\zeta ^{\prime }_c(t)\geq 0$
on it, then
 $\psi :\Sigma ^n\looparrowright -I\times _fM^n$
is
$\psi :\Sigma ^n\looparrowright -I\times _fM^n$
is
 $L_{cu}$
-stable if and only if
$L_{cu}$
-stable if and only if
 $\zeta _c(t)$
is constant on
$\zeta _c(t)$
is constant on
 $\Sigma ^n$
.
$\Sigma ^n$
. -
(c) If
 $\Sigma ^n$
is compact and
$\Sigma ^n$
is compact and
 $\zeta ^{\prime }_c(t)>0$
on it, then
$\zeta ^{\prime }_c(t)>0$
on it, then
 $\psi :\Sigma ^n\looparrowright -I\times _fM^n$
cannot be
$\psi :\Sigma ^n\looparrowright -I\times _fM^n$
cannot be
 $L_{cu}$
-stable.
$L_{cu}$
-stable.
According to the terminology introduced in [Reference Alías, de Lira and Rigoli9, Reference Colombo, Mari and Rigoli24],
![]() $\zeta _c(t)$
denotes the soliton function and it is defined in (2-7). Standard examples of spacelike mean curvature flow solitons in GRW spacetimes are given in this paper (see Section 2.3) as well as applications related to these examples.
$\zeta _c(t)$
denotes the soliton function and it is defined in (2-7). Standard examples of spacelike mean curvature flow solitons in GRW spacetimes are given in this paper (see Section 2.3) as well as applications related to these examples.
2 Background
In this section, we quote some basic concepts, facts and standard examples which will be used and addressed in the following sections.
2.1 Some preliminaries
Let
![]() $(M^n,\langle \,,\rangle _M)$
be a connected, n-dimensional, oriented Riemannian manifold, let
$(M^n,\langle \,,\rangle _M)$
be a connected, n-dimensional, oriented Riemannian manifold, let
![]() $I\subset \mathbb {R}$
be an open interval and let
$I\subset \mathbb {R}$
be an open interval and let
![]() $f:I\rightarrow \mathbb {R}$
be a positive smooth function. Also, in the product manifold
$f:I\rightarrow \mathbb {R}$
be a positive smooth function. Also, in the product manifold
![]() $\overline {M}^{n+1}=I\times M^{n}$
let
$\overline {M}^{n+1}=I\times M^{n}$
let
![]() $\pi _I$
and
$\pi _I$
and
![]() $\pi _M$
denote the canonical projections onto the factors I and
$\pi _M$
denote the canonical projections onto the factors I and
![]() $M^{n}$
, respectively.
$M^{n}$
, respectively.
The class of Lorentzian manifolds of concern here is the one obtained by furnishing
![]() $\overline {M}^{n+1}$
with the Lorentzian metric
$\overline {M}^{n+1}$
with the Lorentzian metric
![]() $\langle \,,\rangle $
given by
$\langle \,,\rangle $
given by
where
![]() $-dt^{2}$
stands for the standard metric of
$-dt^{2}$
stands for the standard metric of
![]() $I\subset \mathbb R$
. In this article, we simply write
$I\subset \mathbb R$
. In this article, we simply write
According to the nomenclature established in [Reference Alías, Romero and SÁnchez11], we say that
![]() $\overline {M}^{n+1}$
is a GRW spacetime with warping function f and Riemannian fiber
$\overline {M}^{n+1}$
is a GRW spacetime with warping function f and Riemannian fiber
![]() $M^n$
. When
$M^n$
. When
![]() $M^n$
has constant sectional curvature, (2-1) has been known in the mathematical literature as a Robertson–Walker (RW) spacetime, an allusion to the fact that, for
$M^n$
has constant sectional curvature, (2-1) has been known in the mathematical literature as a Robertson–Walker (RW) spacetime, an allusion to the fact that, for
![]() $n=3$
, it is an exact solution of Einstein’s field equations (see, for example, [Reference O’Neill35, Ch. 12]).
$n=3$
, it is an exact solution of Einstein’s field equations (see, for example, [Reference O’Neill35, Ch. 12]).
In this setting, we consider the timelike conformal closed vector field
globally defined on
![]() $\overline {M}$
, where
$\overline {M}$
, where
![]() $\partial _t={\partial }/{\partial _t}$
stands for the coordinate timelike vector field tangential to I. From the relationship between the Levi–Civita connections of
$\partial _t={\partial }/{\partial _t}$
stands for the coordinate timelike vector field tangential to I. From the relationship between the Levi–Civita connections of
![]() $\overline {M}^{n+1}$
and those of I and
$\overline {M}^{n+1}$
and those of I and
![]() $M^n$
(see [Reference O’Neill35, Proposition
$M^n$
(see [Reference O’Neill35, Proposition
![]() $7.35$
]), it follows that
$7.35$
]), it follows that
for all
![]() $V\in \mathfrak {X}(\overline {M})$
, where
$V\in \mathfrak {X}(\overline {M})$
, where
![]() $\overline {\nabla }$
is the Levi–Civita connection of
$\overline {\nabla }$
is the Levi–Civita connection of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Let
![]() $\Sigma ^n$
be an n-dimensional connected manifold. A smooth immersion
$\Sigma ^n$
be an n-dimensional connected manifold. A smooth immersion
![]() ${\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}}$
is said to be a spacelike hypersurface if
${\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}}$
is said to be a spacelike hypersurface if
![]() $\Sigma ^n$
, furnished with the metric induced from
$\Sigma ^n$
, furnished with the metric induced from
![]() $\langle \,,\rangle $
via
$\langle \,,\rangle $
via
![]() $\psi $
, is a Riemannian manifold. We denote by
$\psi $
, is a Riemannian manifold. We denote by
![]() $\nabla $
the Levi–Civita connection of
$\nabla $
the Levi–Civita connection of
![]() $\Sigma ^n$
endowed with its induced metric (which will be denoted by
$\Sigma ^n$
endowed with its induced metric (which will be denoted by
![]() $\langle \,,\rangle $
). Since
$\langle \,,\rangle $
). Since
![]() $\overline {M}$
is time-orientable, it follows from the connectedness of
$\overline {M}$
is time-orientable, it follows from the connectedness of
![]() $\Sigma ^n$
that one can uniquely choose a globally defined timelike unit vector field
$\Sigma ^n$
that one can uniquely choose a globally defined timelike unit vector field
![]() $N\in \mathfrak {X}^\perp (\Sigma )$
that has the same time-orientation as
$N\in \mathfrak {X}^\perp (\Sigma )$
that has the same time-orientation as
![]() $\partial _t$
, that is, such that
$\partial _t$
, that is, such that
![]() $\langle N,\partial _t\rangle <0$
. In this case, one says that N is the future-pointing Gauss map of
$\langle N,\partial _t\rangle <0$
. In this case, one says that N is the future-pointing Gauss map of
![]() $\Sigma ^n$
and we always assume such a timelike orientation for
$\Sigma ^n$
and we always assume such a timelike orientation for
![]() $\Sigma ^n$
. From the inverse Cauchy–Schwarz inequality (see [Reference O’Neill35, Proposition
$\Sigma ^n$
. From the inverse Cauchy–Schwarz inequality (see [Reference O’Neill35, Proposition
![]() $5.30$
]), we have that
$5.30$
]), we have that
![]() ${\langle N,\partial _t\rangle \leq -1}$
, with the equality holding at a point
${\langle N,\partial _t\rangle \leq -1}$
, with the equality holding at a point
![]() $p\in \Sigma ^n$
if and only if
$p\in \Sigma ^n$
if and only if
![]() $N=\partial _t$
at p.
$N=\partial _t$
at p.
We denote by A and
![]() $H=-\mathrm {trace}(A)$
the shape operator and the mean curvature function of the spacelike hypersurface
$H=-\mathrm {trace}(A)$
the shape operator and the mean curvature function of the spacelike hypersurface
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
with respect to its future-pointing Gauss map N. Throughout this paper, the mean curvature H, taken with respect to such a choice of orientation N, will be called the future mean curvature of
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
with respect to its future-pointing Gauss map N. Throughout this paper, the mean curvature H, taken with respect to such a choice of orientation N, will be called the future mean curvature of
![]() $\Sigma ^n$
. In particular, for a fixed
$\Sigma ^n$
. In particular, for a fixed
![]() $t_\ast \in I$
, from [Reference Alías, Brasil and Colares6, Example
$t_\ast \in I$
, from [Reference Alías, Brasil and Colares6, Example
![]() $5.6$
] we have that the slice
$5.6$
] we have that the slice
![]() $\{t_\ast \}\times M^n$
has constant future mean curvature
$\{t_\ast \}\times M^n$
has constant future mean curvature
 $$ \begin{align*}H=n\frac{f'(t_\ast)}{f(t_\ast)}\end{align*} $$
$$ \begin{align*}H=n\frac{f'(t_\ast)}{f(t_\ast)}\end{align*} $$
with respect to
![]() $N=\partial _t$
.
$N=\partial _t$
.
It follows from (2-2) that
 $$ \begin{align} \overline{\nabla}_{V}\partial_{\,t}=\overline{\nabla}_{V}\bigg(\frac{1}{f(t)}\,\mathcal{K}\bigg)=-\frac{1}{f(t)^{2}}\,\langle V,\overline{\nabla}\,\overline{f}\rangle \mathcal{K}+\frac{1}{f(t)}\,f'(t)V \end{align} $$
$$ \begin{align} \overline{\nabla}_{V}\partial_{\,t}=\overline{\nabla}_{V}\bigg(\frac{1}{f(t)}\,\mathcal{K}\bigg)=-\frac{1}{f(t)^{2}}\,\langle V,\overline{\nabla}\,\overline{f}\rangle \mathcal{K}+\frac{1}{f(t)}\,f'(t)V \end{align} $$
and a simple computation shows that
So, from (2-3),
 $$ \begin{align} \overline{\nabla}_V\partial_t=\frac{f'(\pi_I)}{f(\pi_I)}\{V+\langle V,\partial_t\rangle\partial_t\}. \end{align} $$
$$ \begin{align} \overline{\nabla}_V\partial_t=\frac{f'(\pi_I)}{f(\pi_I)}\{V+\langle V,\partial_t\rangle\partial_t\}. \end{align} $$
2.2 Spacelike mean curvature flow solitons in GRW spacetimes
We recall that the spacelike mean curvature flow
![]() $\Psi :[0,T)\times \Sigma ^n\looparrowright \overline {M}^{n+1}$
related to a spacelike hypersurface
$\Psi :[0,T)\times \Sigma ^n\looparrowright \overline {M}^{n+1}$
related to a spacelike hypersurface
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
in an
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
in an
![]() $(n+1)$
-dimensional Lorentzian manifold
$(n+1)$
-dimensional Lorentzian manifold
![]() $\overline {M}^{n+1}$
, satisfying
$\overline {M}^{n+1}$
, satisfying
![]() $\Psi (0,\cdot )=\psi (\cdot )$
, looks for solutions of the equation
$\Psi (0,\cdot )=\psi (\cdot )$
, looks for solutions of the equation
where
![]() $\vec {H}(t,\cdot )$
is the (nonnormalized) mean curvature vector of
$\vec {H}(t,\cdot )$
is the (nonnormalized) mean curvature vector of
![]() $\Sigma ^n_t=\Psi (t,\Sigma ^n)$
(see, for example, [Reference Lambert and Lotay32]). In our context, according to [Reference Alías, de Lira and Rigoli9, Definition
$\Sigma ^n_t=\Psi (t,\Sigma ^n)$
(see, for example, [Reference Lambert and Lotay32]). In our context, according to [Reference Alías, de Lira and Rigoli9, Definition
![]() $(1.1)$
] and [Reference Colombo, Mari and Rigoli24, Definition
$(1.1)$
] and [Reference Colombo, Mari and Rigoli24, Definition
![]() $(1.1)$
], a spacelike hypersurface
$(1.1)$
], a spacelike hypersurface
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
immersed in a GRW spacetime
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
immersed in a GRW spacetime
![]() ${\overline {M}^{n+1}=-I\times _fM^n}$
is called a spacelike mean curvature flow soliton with respect to
${\overline {M}^{n+1}=-I\times _fM^n}$
is called a spacelike mean curvature flow soliton with respect to
![]() ${\mathcal K=f(t)\partial _t}$
and has soliton constant
${\mathcal K=f(t)\partial _t}$
and has soliton constant
![]() $c\in \mathbb R$
when its (nonnormalized) future-pointing mean curvature vector
$c\in \mathbb R$
when its (nonnormalized) future-pointing mean curvature vector
![]() $\vec {H}=HN$
satisfies
$\vec {H}=HN$
satisfies
where
![]() $\mathcal K^\perp $
stands for the orthogonal projection of
$\mathcal K^\perp $
stands for the orthogonal projection of
![]() $\mathcal K$
in the direction of the future-pointing Gauss map N. Adopting the terminology introduced in [Reference Alías, de Lira and Rigoli9, Reference Colombo, Mari and Rigoli24], we also consider the soliton function
$\mathcal K$
in the direction of the future-pointing Gauss map N. Adopting the terminology introduced in [Reference Alías, de Lira and Rigoli9, Reference Colombo, Mari and Rigoli24], we also consider the soliton function
So, each slice
![]() $M_{t_\ast }=\{t_\ast \}\times M^n$
is a spacelike mean curvature flow soliton with respect to
$M_{t_\ast }=\{t_\ast \}\times M^n$
is a spacelike mean curvature flow soliton with respect to
![]() $\mathcal K=f(t)\partial _t$
and with soliton constant c given by
$\mathcal K=f(t)\partial _t$
and with soliton constant c given by
 $$ \begin{align} c=-n\dfrac{f'(t_\ast)}{f(t_\ast)^2}. \end{align} $$
$$ \begin{align} c=-n\dfrac{f'(t_\ast)}{f(t_\ast)^2}. \end{align} $$
Moreover,
![]() $t_\ast $
is implicitly given by the condition
$t_\ast $
is implicitly given by the condition
![]() $\zeta _c(t_\ast )=0$
.
$\zeta _c(t_\ast )=0$
.
2.3 Standard examples
In this subsection, we quote standard examples of spacelike mean curvature flow solitons in GRW spacetimes.
Example 2.1. Using a method similar to that of [Reference de Lira and Martín27], for the Lorentzian product space
![]() $-I\times M^n$
, from (2-8) we get that the slices
$-I\times M^n$
, from (2-8) we get that the slices
![]() $\{t\}\times M^n$
are spacelike mean curvature flow solitons with soliton constant
$\{t\}\times M^n$
are spacelike mean curvature flow solitons with soliton constant
![]() $c=0$
with respect to vector field
$c=0$
with respect to vector field
![]() $\mathcal {K}=\partial _{\,t}$
. Similarly to what happens in the Minkowski space
$\mathcal {K}=\partial _{\,t}$
. Similarly to what happens in the Minkowski space
![]() $\mathbb R_1^{n+1}=-\mathbb {R}\times \mathbb {R}^n$
, such solitons are called spacelike translating solitons.
$\mathbb R_1^{n+1}=-\mathbb {R}\times \mathbb {R}^n$
, such solitons are called spacelike translating solitons.
Example 2.2. As in [Reference Alías, Colares and de Lima8, Section 4], the future temporal cone
![]() $\Lambda ^{+}$
of the Minkowski space
$\Lambda ^{+}$
of the Minkowski space
![]() $\mathbb R_1^{n+1}$
is defined as the set
$\mathbb R_1^{n+1}$
is defined as the set
where
![]() $e_{1}=(1,0,\ldots ,0)$
. We observe that
$e_{1}=(1,0,\ldots ,0)$
. We observe that
![]() $\Lambda ^{+}$
can be regarded as the GRW spacetime
$\Lambda ^{+}$
can be regarded as the GRW spacetime
where
![]() $\mathbb H^n=\{x\in \mathbb R_1^{n+1}:\langle x,x\rangle =-1,\,\, x_{1}>0\}$
denotes the n-dimensional hyperbolic space. Indeed, it is not difficult to verify that the map
$\mathbb H^n=\{x\in \mathbb R_1^{n+1}:\langle x,x\rangle =-1,\,\, x_{1}>0\}$
denotes the n-dimensional hyperbolic space. Indeed, it is not difficult to verify that the map
![]() $\Phi :-\mathbb R^+\times _t\mathbb H^n\rightarrow \Lambda ^{+}$
, given by
$\Phi :-\mathbb R^+\times _t\mathbb H^n\rightarrow \Lambda ^{+}$
, given by
![]() $\Phi (t,x)=tx$
, is an isometry. In this setting, we have that the slices
$\Phi (t,x)=tx$
, is an isometry. In this setting, we have that the slices
![]() $\{\!\sqrt {-{n}/{c}}\}\times \mathbb H^n$
are spacelike mean curvature flow solitons with soliton constant
$\{\!\sqrt {-{n}/{c}}\}\times \mathbb H^n$
are spacelike mean curvature flow solitons with soliton constant
![]() $c<0$
with respect to vector field
$c<0$
with respect to vector field
![]() $\mathcal {K}=t\partial _{\,t}$
.
$\mathcal {K}=t\partial _{\,t}$
.
Example 2.3. The four-dimensional Einstein–de Sitter spacetime
![]() $-\mathbb R^+\times _{t^{2/3}}\mathbb {R}^3$
, where
$-\mathbb R^+\times _{t^{2/3}}\mathbb {R}^3$
, where
![]() $\mathbb R^3$
stands for the three-dimensional Euclidean space endowed with its canonical metric, is a classical exact solution to the Einstein field equation without a cosmological constant. It is an open Friedmann–Robertson–Walker model, which incorporates homogeneity and isotropy (the cosmological principle) and permitted expansion (for more details, see [Reference O’Neill35, Ch. 12]). Here, we consider the
$\mathbb R^3$
stands for the three-dimensional Euclidean space endowed with its canonical metric, is a classical exact solution to the Einstein field equation without a cosmological constant. It is an open Friedmann–Robertson–Walker model, which incorporates homogeneity and isotropy (the cosmological principle) and permitted expansion (for more details, see [Reference O’Neill35, Ch. 12]). Here, we consider the
![]() $(n+1)$
-dimensional Einstein–de Sitter spacetime
$(n+1)$
-dimensional Einstein–de Sitter spacetime
![]() $-\mathbb R^+\times _{t^{2/3}}\mathbb {R}^n$
. From (2-8), we conclude that the slices
$-\mathbb R^+\times _{t^{2/3}}\mathbb {R}^n$
. From (2-8), we conclude that the slices
![]() $\{(-{2n}/{3c})^{3/5}\}\times \mathbb R^n$
are spacelike mean curvature flow solitons with respect to
$\{(-{2n}/{3c})^{3/5}\}\times \mathbb R^n$
are spacelike mean curvature flow solitons with respect to
![]() $\mathcal K=t^{2/3}\partial _{t}$
and with soliton constant
$\mathcal K=t^{2/3}\partial _{t}$
and with soliton constant
![]() $c<0$
.
$c<0$
.
Example 2.4. According to the terminology introduced by Albujer and Alías [Reference Albujer and Alías2], a GRW spacetime
![]() $-\mathbb R\times _{e^t}M^n$
is called a steady-state-type spacetime. This terminology is due to the fact that the steady-state model of the universe
$-\mathbb R\times _{e^t}M^n$
is called a steady-state-type spacetime. This terminology is due to the fact that the steady-state model of the universe
![]() $\mathcal H^4$
, proposed by Bondi–Gold [Reference Bondi and Gold17] and Hoyle [Reference Hoyle30] when looking for a model of the universe that looks the same not only at all points and in all directions (that is, is spatially isotropic and homogeneous) but also at all times, is isometric to the GRW spacetime
$\mathcal H^4$
, proposed by Bondi–Gold [Reference Bondi and Gold17] and Hoyle [Reference Hoyle30] when looking for a model of the universe that looks the same not only at all points and in all directions (that is, is spatially isotropic and homogeneous) but also at all times, is isometric to the GRW spacetime
![]() $-\mathbb R\times _{e^t}\mathbb R^3$
(for more details, see [Reference Hawking and Ellis29]). From (2-8), we conclude that the slices
$-\mathbb R\times _{e^t}\mathbb R^3$
(for more details, see [Reference Hawking and Ellis29]). From (2-8), we conclude that the slices
![]() $\{\ln (-{n}/{c})\}\times M^n$
are spacelike mean curvature flow solitons with respect to
$\{\ln (-{n}/{c})\}\times M^n$
are spacelike mean curvature flow solitons with respect to
![]() $\mathcal K=e^t\partial _{t}$
and with soliton constant
$\mathcal K=e^t\partial _{t}$
and with soliton constant
![]() $c<0$
.
$c<0$
.
Example 2.5. From [Reference Montiel34, Example
![]() $4.2$
], the
$4.2$
], the
![]() $(n+1)$
-dimensional de Sitter space
$(n+1)$
-dimensional de Sitter space
![]() $\mathbb S_1^{n+1}$
is isometric to the GRW spacetime
$\mathbb S_1^{n+1}$
is isometric to the GRW spacetime
![]() $-\mathbb R\times _{\cosh t}\mathbb {S}^n$
, where
$-\mathbb R\times _{\cosh t}\mathbb {S}^n$
, where
![]() $\mathbb S^n$
denotes the n-dimensional unit Euclidean sphere endowed with its standard metric. Taking into account the terminology introduced in [Reference Aledo, Alías and Romero5], the open half-space
$\mathbb S^n$
denotes the n-dimensional unit Euclidean sphere endowed with its standard metric. Taking into account the terminology introduced in [Reference Aledo, Alías and Romero5], the open half-space
![]() $\mathbb R^+\times \mathbb {S}^n\subset \mathbb S_1^{n+1}$
(respectively,
$\mathbb R^+\times \mathbb {S}^n\subset \mathbb S_1^{n+1}$
(respectively,
![]() $\mathbb R^-\times \mathbb {S}^n\subset \mathbb S_1^{n+1}$
) is called the chronological future (respectively, past) of
$\mathbb R^-\times \mathbb {S}^n\subset \mathbb S_1^{n+1}$
) is called the chronological future (respectively, past) of
![]() $\mathbb S_1^{n+1}$
with respect to the totally geodesic equator
$\mathbb S_1^{n+1}$
with respect to the totally geodesic equator
![]() $\{0\}\times \mathbb S^n$
. From (2-8), we see that the equator is a spacelike mean curvature flow soliton with respect to
$\{0\}\times \mathbb S^n$
. From (2-8), we see that the equator is a spacelike mean curvature flow soliton with respect to
![]() $\mathcal K=\cosh t\,\partial _t$
and with soliton constant
$\mathcal K=\cosh t\,\partial _t$
and with soliton constant
![]() $c=0$
and that the slices
$c=0$
and that the slices
![]() $\{\sinh ^{-1}(({-n\pm \sqrt {n^2-4c^2}})/{2c})\}\times \mathbb S^n$
are spacelike mean curvature flow solitons with respect to
$\{\sinh ^{-1}(({-n\pm \sqrt {n^2-4c^2}})/{2c})\}\times \mathbb S^n$
are spacelike mean curvature flow solitons with respect to
![]() $\mathcal K=\cosh t\,\partial _{t}$
and with soliton constant
$\mathcal K=\cosh t\,\partial _{t}$
and with soliton constant
![]() $0<|c|\leq ({n}/{2})$
.
$0<|c|\leq ({n}/{2})$
.
Example 2.6. Taking into account once more [Reference Montiel34, Example
![]() $4.2$
], we consider the open region of
$4.2$
], we consider the open region of
![]() $\mathbb S_1^{n+1}$
that is isometric to the GRW spacetime
$\mathbb S_1^{n+1}$
that is isometric to the GRW spacetime
![]() $-\mathbb R^+\times _{\sinh t}\mathbb {H}^n$
, where
$-\mathbb R^+\times _{\sinh t}\mathbb {H}^n$
, where
![]() $\mathbb H^n$
denotes the n-dimensional hyperbolic space endowed with its standard metric. From (2-8), we have that the slices
$\mathbb H^n$
denotes the n-dimensional hyperbolic space endowed with its standard metric. From (2-8), we have that the slices
![]() $\{\cosh ^{-1}(({-n-\sqrt {n^2+4c^2}})/{2c})\}\times \mathbb H^n$
are spacelike mean curvature flow solitons with respect to
$\{\cosh ^{-1}(({-n-\sqrt {n^2+4c^2}})/{2c})\}\times \mathbb H^n$
are spacelike mean curvature flow solitons with respect to
![]() $\mathcal K=\sinh t\,\partial _{t}$
and with soliton constant
$\mathcal K=\sinh t\,\partial _{t}$
and with soliton constant
![]() $c<0$
.
$c<0$
.
Example 2.7. Motivated by [Reference Montiel34, Example
![]() $4.3$
], we consider the open subset of the
$4.3$
], we consider the open subset of the
![]() $(n+1)$
-dimensional anti-de Sitter space
$(n+1)$
-dimensional anti-de Sitter space
![]() $\mathbb H_1^{n+1}$
that is isometric to the GRW spacetime
$\mathbb H_1^{n+1}$
that is isometric to the GRW spacetime
![]() $-(-{\pi }/{2},{\pi }/{2})\times _{\cos t}\mathbb {H}^n$
. Analogous to the nomenclature of the de Sitter space, the open half-space
$-(-{\pi }/{2},{\pi }/{2})\times _{\cos t}\mathbb {H}^n$
. Analogous to the nomenclature of the de Sitter space, the open half-space
![]() $(0,{\pi }/{2})\times \mathbb {H}^n\subset \mathbb H_1^{n+1}$
(respectively,
$(0,{\pi }/{2})\times \mathbb {H}^n\subset \mathbb H_1^{n+1}$
(respectively,
![]() $(-{\pi }/{2},0)\times \mathbb {H}^n\subset \mathbb H_1^{n+1}$
) will be called the chronological future (respectively, past) of
$(-{\pi }/{2},0)\times \mathbb {H}^n\subset \mathbb H_1^{n+1}$
) will be called the chronological future (respectively, past) of
![]() $\mathbb H_1^{n+1}$
with respect to the totally geodesic equator
$\mathbb H_1^{n+1}$
with respect to the totally geodesic equator
![]() $\{0\}\times \mathbb H^n$
. From (2-8), we see that the equator is a spacelike mean curvature flow soliton with respect to
$\{0\}\times \mathbb H^n$
. From (2-8), we see that the equator is a spacelike mean curvature flow soliton with respect to
![]() $\mathcal K=\cos t\,\partial _t$
and with soliton constant
$\mathcal K=\cos t\,\partial _t$
and with soliton constant
![]() $c=0$
, and that the slices
$c=0$
, and that the slices
![]() $\{\sin ^{-1}(({-n\pm \sqrt {n^2+4c^2}})/{2c})\}\times \mathbb H^n$
are spacelike mean curvature flow solitons with respect to
$\{\sin ^{-1}(({-n\pm \sqrt {n^2+4c^2}})/{2c})\}\times \mathbb H^n$
are spacelike mean curvature flow solitons with respect to
![]() $\mathcal K=\cos t\,\partial _{t}$
and with soliton constant
$\mathcal K=\cos t\,\partial _{t}$
and with soliton constant
![]() $c\neq 0$
.
$c\neq 0$
.
3 Nonexistence and rigidity of spacelike mean curvature flow solitons
In this section, we study the nonexistence and rigidity of complete spacelike mean curvature flow solitons immersed in a GRW spacetime. For this, we need to develop some previous computations.
3.1 Some previous computations
Let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton, as described in Section 2. The height function of
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton, as described in Section 2. The height function of
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
, denoted by h, is the restriction of the projection
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
, denoted by h, is the restriction of the projection
![]() $\pi _{I}(t,y)=t$
to
$\pi _{I}(t,y)=t$
to
![]() $\Sigma ^n$
: that is,
$\Sigma ^n$
: that is,
![]() $h:\Sigma ^n\rightarrow I$
is given by
$h:\Sigma ^n\rightarrow I$
is given by
Thus, the hyperbolic angle
![]() $\Theta $
of
$\Theta $
of
![]() $\Sigma ^n$
verifies
$\Sigma ^n$
verifies
where N denotes the future-pointing Gauss map of
![]() $\Sigma ^n$
. From (2-4), we have that the gradient of
$\Sigma ^n$
. From (2-4), we have that the gradient of
![]() $\pi _{I}$
on
$\pi _{I}$
on
![]() $-I\times _{f}M^n$
is given by
$-I\times _{f}M^n$
is given by
![]() $\overline {\nabla }\pi _{I}=-\partial _{\,t}$
. Then, the gradient of h on
$\overline {\nabla }\pi _{I}=-\partial _{\,t}$
. Then, the gradient of h on
![]() $\Sigma ^n$
is given by
$\Sigma ^n$
is given by
where
![]() $\partial _{\,t}=\partial _{\,t}^{\top }+\partial _{\,t}^{\perp }$
. Here,
$\partial _{\,t}=\partial _{\,t}^{\top }+\partial _{\,t}^{\perp }$
. Here,
![]() $\partial _{\,t}^{\top }\in \mathfrak {X}(\Sigma ^n)$
and
$\partial _{\,t}^{\top }\in \mathfrak {X}(\Sigma ^n)$
and
![]() $\partial _{\,t}^{\perp }\in \mathfrak {X}^{\perp }(\Sigma ^n)$
denote, respectively, the tangential and normal components of
$\partial _{\,t}^{\perp }\in \mathfrak {X}^{\perp }(\Sigma ^n)$
denote, respectively, the tangential and normal components of
![]() $\partial _{\,t}$
.
$\partial _{\,t}$
.
Thus, (3-3) gives the relationship
where
![]() $|\,\cdot \,|$
stands for the norm of a tangential vector field on
$|\,\cdot \,|$
stands for the norm of a tangential vector field on
![]() $\Sigma ^n$
considered with its induced metric.
$\Sigma ^n$
considered with its induced metric.
Hence, from (3-3) and (2-5), we deduce that, for any
![]() $X\in \mathfrak {X}(\Sigma ^n)$
, the Hessian of h in the metric
$X\in \mathfrak {X}(\Sigma ^n)$
, the Hessian of h in the metric
![]() $\langle \,,\rangle $
is given by
$\langle \,,\rangle $
is given by
 $$ \begin{align} \nabla^2h(X,X)=&\ \langle\nabla_X\nabla h,X\rangle\nonumber\\ =&-\frac{f'(h)}{f(h)}\{|X|^2+\langle X,\nabla h\rangle^2\}+\langle AX,X\rangle\Theta. \end{align} $$
$$ \begin{align} \nabla^2h(X,X)=&\ \langle\nabla_X\nabla h,X\rangle\nonumber\\ =&-\frac{f'(h)}{f(h)}\{|X|^2+\langle X,\nabla h\rangle^2\}+\langle AX,X\rangle\Theta. \end{align} $$
In what follows, we also consider the function
where
![]() $g:I\rightarrow \mathbb {R}$
is an arbitrary primitive of f. Since
$g:I\rightarrow \mathbb {R}$
is an arbitrary primitive of f. Since
![]() $g'=f>0$
,
$g'=f>0$
,
![]() $u=g(h)$
can be thought as a reparametrization of the height function. In particular, from (3-3), we have that the gradient of u on
$u=g(h)$
can be thought as a reparametrization of the height function. In particular, from (3-3), we have that the gradient of u on
![]() $\Sigma ^n$
is given by
$\Sigma ^n$
is given by
where
![]() $\mathcal {K}^{\top }$
denotes the tangential component of the closed conformal vector field
$\mathcal {K}^{\top }$
denotes the tangential component of the closed conformal vector field
![]() $\mathcal {K}$
, defined in (2-2). Taking into account this previous digression, we obtain the following auxiliary result.
$\mathcal {K}$
, defined in (2-2). Taking into account this previous digression, we obtain the following auxiliary result.
Lemma 3.1. Let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with respect to
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with respect to
![]() $\mathcal {K}=f(t)\partial _{\,t}$
and with soliton constant
$\mathcal {K}=f(t)\partial _{\,t}$
and with soliton constant
![]() $c\not =0.$
Then,
$c\not =0.$
Then,
for all
![]() $X,Y\in \mathfrak {X}(\Sigma )$
. Furthermore,
$X,Y\in \mathfrak {X}(\Sigma )$
. Furthermore,
Proof. First, we note that
 $$ \begin{align*} \nabla^2u(X,X)=&\ \langle\nabla_X\nabla u,X\rangle\nonumber\\ =&\ \langle\nabla_X(f(h)\nabla h),X\rangle\nonumber\\ =&\ f(h)\langle\nabla_X\nabla h,X\rangle+\langle\nabla_X f(h)\nabla h,X\rangle\nonumber\\ =&\ f(h)\nabla^2h(X,X)+f'(h)\langle X,\nabla h\rangle^2. \end{align*} $$
$$ \begin{align*} \nabla^2u(X,X)=&\ \langle\nabla_X\nabla u,X\rangle\nonumber\\ =&\ \langle\nabla_X(f(h)\nabla h),X\rangle\nonumber\\ =&\ f(h)\langle\nabla_X\nabla h,X\rangle+\langle\nabla_X f(h)\nabla h,X\rangle\nonumber\\ =&\ f(h)\nabla^2h(X,X)+f'(h)\langle X,\nabla h\rangle^2. \end{align*} $$
Thus, from (3-5), we get that
 $$ \begin{align*} \nabla^2u(X,X)=&f(h)\bigg(-\frac{f'(h)}{f(h)}\{|X|^2+\langle X,\nabla h\rangle^2\}+\langle AX,X\rangle\Theta\bigg)+f'(h)\langle X,\nabla h\rangle^2\nonumber\\ =& -f'(h)|X|^2-f'(h)\langle X,\nabla h\rangle^2+f(h)\langle AX,X\rangle\Theta+f'(h)\langle X,\nabla h\rangle^2\nonumber\\ =& -f'(h)|X|^2+f(h)\langle AX,X\rangle\Theta. \end{align*} $$
$$ \begin{align*} \nabla^2u(X,X)=&f(h)\bigg(-\frac{f'(h)}{f(h)}\{|X|^2+\langle X,\nabla h\rangle^2\}+\langle AX,X\rangle\Theta\bigg)+f'(h)\langle X,\nabla h\rangle^2\nonumber\\ =& -f'(h)|X|^2-f'(h)\langle X,\nabla h\rangle^2+f(h)\langle AX,X\rangle\Theta+f'(h)\langle X,\nabla h\rangle^2\nonumber\\ =& -f'(h)|X|^2+f(h)\langle AX,X\rangle\Theta. \end{align*} $$
On the other hand,
 $$ \begin{align} \frac{1}{c}\langle \nabla H, X\rangle =&\ \langle \overline{\nabla}_X \mathcal{K},N\rangle+\langle \mathcal{K},\overline{\nabla}_{X}N\rangle\nonumber \\ =&-\langle A(X),\mathcal{K}\rangle=\langle X,A(\nabla u)\rangle, \end{align} $$
$$ \begin{align} \frac{1}{c}\langle \nabla H, X\rangle =&\ \langle \overline{\nabla}_X \mathcal{K},N\rangle+\langle \mathcal{K},\overline{\nabla}_{X}N\rangle\nonumber \\ =&-\langle A(X),\mathcal{K}\rangle=\langle X,A(\nabla u)\rangle, \end{align} $$
for every vector field
![]() $X\in \mathfrak {X}(\Sigma ^n)$
, so that, from (3-7), we conclude the desired result.
$X\in \mathfrak {X}(\Sigma ^n)$
, so that, from (3-7), we conclude the desired result.
Remark 3.2. We point out that (3-8) is close to the definition of Ricci solitons and, therefore, it is interesting to make a study of mean curvature flow solitons with this point of view.
Naturally attached to
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
, we can consider the support function
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
, we can consider the support function
 $$ \begin{align} \varphi_{\mathcal{K}}:\Sigma^n&\rightarrow\mathbb{R}\nonumber\\ q&\mapsto\varphi_{\mathcal{K}}(q)\langle \mathcal{K}(q),N(q)\rangle. \end{align} $$
$$ \begin{align} \varphi_{\mathcal{K}}:\Sigma^n&\rightarrow\mathbb{R}\nonumber\\ q&\mapsto\varphi_{\mathcal{K}}(q)\langle \mathcal{K}(q),N(q)\rangle. \end{align} $$
Hence, from (3-2),
Furthermore, from [Reference Caminha and de Lima19, Proposition
![]() $2.1$
] and (3-4),
$2.1$
] and (3-4),
where
![]() $\nabla H$
is the gradient of H in the metric of
$\nabla H$
is the gradient of H in the metric of
![]() $\Sigma ^n$
,
$\Sigma ^n$
,
![]() $\overline {\mathrm {Ric}}$
is the Ricci tensor of
$\overline {\mathrm {Ric}}$
is the Ricci tensor of
![]() $\overline {M}^{n+1}$
and
$\overline {M}^{n+1}$
and
![]() $|A|$
is the Hilbert–Schmidt norm of A.
$|A|$
is the Hilbert–Schmidt norm of A.
In addition, we get that
 $$ \begin{align} N(f')=-f"\Theta=-\frac{f"}{f}\varphi_{\mathcal{K}}. \end{align} $$
$$ \begin{align} N(f')=-f"\Theta=-\frac{f"}{f}\varphi_{\mathcal{K}}. \end{align} $$
On the other hand, since
![]() $N=N^{\ast }-\Theta \partial _{\,t}$
, where
$N=N^{\ast }-\Theta \partial _{\,t}$
, where
![]() $N^\ast =\pi _M(N)$
is the orthogonal projection of N onto
$N^\ast =\pi _M(N)$
is the orthogonal projection of N onto
![]() $M^n$
, it follows from [Reference O’Neill35, Corollary
$M^n$
, it follows from [Reference O’Neill35, Corollary
![]() $7.43$
] that
$7.43$
] that
 $$ \begin{align} \overline{\mathrm{Ric}}(N,N)=&\ \overline{\mathrm{Ric}}(N^\ast,N^\ast)+\Theta^2\overline{\mathrm{Ric}}(\partial_{\,t},\partial_{\,t})\nonumber\\ =&\ \mathrm{Ric}_M(N^\ast,N^\ast)+\langle N^\ast,N^\ast\rangle\bigg\{\dfrac{f"}{f}+(n-1)\dfrac{(f')^2}{f^2}\bigg\}-\dfrac{nf"}{f}\Theta^2\nonumber\\ =&\ \mathrm{Ric}_M(N^\ast,N^\ast)-\bigg\{\dfrac{f"}{f}+(n-1)\dfrac{(f')^2}{f^2}\bigg\}-(n-1)\bigg(\dfrac{f'}{f}\bigg)^{'}\Theta^2, \end{align} $$
$$ \begin{align} \overline{\mathrm{Ric}}(N,N)=&\ \overline{\mathrm{Ric}}(N^\ast,N^\ast)+\Theta^2\overline{\mathrm{Ric}}(\partial_{\,t},\partial_{\,t})\nonumber\\ =&\ \mathrm{Ric}_M(N^\ast,N^\ast)+\langle N^\ast,N^\ast\rangle\bigg\{\dfrac{f"}{f}+(n-1)\dfrac{(f')^2}{f^2}\bigg\}-\dfrac{nf"}{f}\Theta^2\nonumber\\ =&\ \mathrm{Ric}_M(N^\ast,N^\ast)-\bigg\{\dfrac{f"}{f}+(n-1)\dfrac{(f')^2}{f^2}\bigg\}-(n-1)\bigg(\dfrac{f'}{f}\bigg)^{'}\Theta^2, \end{align} $$
where
![]() $\mathrm {Ric}_{M}$
denotes the Ricci tensor of
$\mathrm {Ric}_{M}$
denotes the Ricci tensor of
![]() $M^n$
. We note that the relationship
$M^n$
. We note that the relationship
![]() ${\langle N^\ast ,N^\ast \rangle =\Theta ^2-1}$
is used in the last equality above.
${\langle N^\ast ,N^\ast \rangle =\Theta ^2-1}$
is used in the last equality above.
Thus, inserting (3-13) and (3-14) into (3-12), we obtain
 $$ \begin{align} \Delta(\varphi_{\mathcal{K}})=&\ \bigg\{\mathrm{Ric}_M(N^\ast,N^\ast)+|A|^2-\bigg\{\dfrac{f"}{f}+(n-1)\dfrac{(f')^2}{f^2}\bigg\}-(n-1)\bigg(\dfrac{f'}{f}\bigg)^{'}\Theta^2\bigg\}\varphi_{\mathcal{K}}\nonumber\\ &+\bigg\{n\dfrac{f"}{f}\varphi_{\mathcal{K}}+Hf'\bigg\}+\langle\mathcal{K},\nabla H\rangle\nonumber\\ =&\ \bigg\{\mathrm{Ric}_M(N^\ast,N^\ast)+|A|^2+\dfrac{f"f-(f')^2}{f^2}-(n-1)\bigg(\dfrac{f'}{f}\bigg)'\Theta^2\bigg\}\varphi_{\mathcal{K}}+Hf'+\langle\mathcal{K},\nabla H\rangle \nonumber\\ =&\ \{\mathrm{Ric}_M(N^\ast,N^\ast)+(n-1)(\ln f)"(1-\Theta^2)+|A|^2\}\varphi_{\mathcal{K}}+Hf'+\langle\mathcal{K},\nabla H\rangle \nonumber\\ =&\ \{\mathrm{Ric}_M(N^\ast,N^\ast)-(n-1)(\ln f)"|\nabla h|^2+|A|^2\}\varphi_{\mathcal{K}}+Hf'+\langle\mathcal{K},\nabla H\rangle. \end{align} $$
$$ \begin{align} \Delta(\varphi_{\mathcal{K}})=&\ \bigg\{\mathrm{Ric}_M(N^\ast,N^\ast)+|A|^2-\bigg\{\dfrac{f"}{f}+(n-1)\dfrac{(f')^2}{f^2}\bigg\}-(n-1)\bigg(\dfrac{f'}{f}\bigg)^{'}\Theta^2\bigg\}\varphi_{\mathcal{K}}\nonumber\\ &+\bigg\{n\dfrac{f"}{f}\varphi_{\mathcal{K}}+Hf'\bigg\}+\langle\mathcal{K},\nabla H\rangle\nonumber\\ =&\ \bigg\{\mathrm{Ric}_M(N^\ast,N^\ast)+|A|^2+\dfrac{f"f-(f')^2}{f^2}-(n-1)\bigg(\dfrac{f'}{f}\bigg)'\Theta^2\bigg\}\varphi_{\mathcal{K}}+Hf'+\langle\mathcal{K},\nabla H\rangle \nonumber\\ =&\ \{\mathrm{Ric}_M(N^\ast,N^\ast)+(n-1)(\ln f)"(1-\Theta^2)+|A|^2\}\varphi_{\mathcal{K}}+Hf'+\langle\mathcal{K},\nabla H\rangle \nonumber\\ =&\ \{\mathrm{Ric}_M(N^\ast,N^\ast)-(n-1)(\ln f)"|\nabla h|^2+|A|^2\}\varphi_{\mathcal{K}}+Hf'+\langle\mathcal{K},\nabla H\rangle. \end{align} $$
From Equations (2-6) and (3-10), we have that
![]() $H=c\,\varphi _{\mathcal {K}}$
, and from (3-7) we get
$H=c\,\varphi _{\mathcal {K}}$
, and from (3-7) we get
![]() $\nabla u=-\mathcal {K}^\top $
, where u is the reparametrization of the height function h given in (3-6). Consequently, we can rewrite (3-15) as
$\nabla u=-\mathcal {K}^\top $
, where u is the reparametrization of the height function h given in (3-6). Consequently, we can rewrite (3-15) as
We recall that the drift Laplacian on
![]() $\Sigma ^n$
is defined by
$\Sigma ^n$
is defined by
for all
![]() $\varphi \in C^{\infty }(\Sigma ^n)$
. So, from (3-16) and (3-17), we conclude that the drift Laplacian
$\varphi \in C^{\infty }(\Sigma ^n)$
. So, from (3-16) and (3-17), we conclude that the drift Laplacian
![]() $\Delta _{cu}$
acting on
$\Delta _{cu}$
acting on
![]() $\varphi _{\mathcal {K}}$
is given by
$\varphi _{\mathcal {K}}$
is given by
where
![]() $\tilde {\zeta }_{c}\in C^{\infty }(\Sigma ^n)$
is the function defined by
$\tilde {\zeta }_{c}\in C^{\infty }(\Sigma ^n)$
is the function defined by
for every
![]() $q\in \Sigma ^n$
, which will be called the second soliton function associated to the spacelike mean curvature flow soliton
$q\in \Sigma ^n$
, which will be called the second soliton function associated to the spacelike mean curvature flow soliton
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
. Such nomenclature for
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
. Such nomenclature for
![]() $\tilde {\zeta }_{c}$
is motivated by [Reference Alías, de Lira and Rigoli9, Equation (6.11)].
$\tilde {\zeta }_{c}$
is motivated by [Reference Alías, de Lira and Rigoli9, Equation (6.11)].
3.2 Rigidity and nonexistence results
In this subsection, beyond nonexistence results, we establish several theorems that guarantee that, under some necessary hypothesis (see Remark 3.25), a spacelike mean curvature flow soliton must coincide with a slice of the ambient GRW spacetime. We observe that these results are related to each other in the sense that they ensure the rigidity of a complete spacelike mean curvature flow soliton with nonnegative second soliton function that lies in a timelike bounded region of a GRW spacetime and obeys a suitable convergence condition.
In what follows, we assume that the GRW spacetime
![]() $-I\times _{f}M^n$
satisfies the null convergence condition (NCC)
$-I\times _{f}M^n$
satisfies the null convergence condition (NCC)
which was originally established by Montiel [Reference Montiel34], where
![]() $\mathrm {Ric}_{M}$
denotes the Ricci tensor of the Riemannian fiber
$\mathrm {Ric}_{M}$
denotes the Ricci tensor of the Riemannian fiber
![]() $M^n$
. It is not difficult to verify that all the GRW spacetimes described in Section 2.2 satisfy the NCC. For this, in the case of a steady-state-type spacetime (see Example 2.4), it is necessary to assume that its Riemannian fiber has nonnegative Ricci curvature.
$M^n$
. It is not difficult to verify that all the GRW spacetimes described in Section 2.2 satisfy the NCC. For this, in the case of a steady-state-type spacetime (see Example 2.4), it is necessary to assume that its Riemannian fiber has nonnegative Ricci curvature.
Before we prove the first rigidity result, we start by quoting an extension of Hopf’s theorem on a complete Riemannian manifold
![]() $\Sigma ^n$
due to Yau in [Reference Yau45]. For this, we adopt the notation
$\Sigma ^n$
due to Yau in [Reference Yau45]. For this, we adopt the notation
for the space of Lebesgue integrable functions on
![]() $\Sigma ^n$
, where
$\Sigma ^n$
, where
![]() $d\Sigma $
stands for the volume element induced by the metric of
$d\Sigma $
stands for the volume element induced by the metric of
![]() $\Sigma ^n$
, and we denote by
$\Sigma ^n$
, and we denote by
![]() $\mathcal L_{cu}^1(\Sigma ^n)$
the set of Lebesgue integrable functions on
$\mathcal L_{cu}^1(\Sigma ^n)$
the set of Lebesgue integrable functions on
![]() $\Sigma ^n$
with respect to the modified volume element
$\Sigma ^n$
with respect to the modified volume element
We also recall that a smooth function
![]() $\varphi $
on
$\varphi $
on
![]() $\Sigma ^n$
is said to be
$\Sigma ^n$
is said to be
![]() $(cu)$
-subharmonic (respectively,
$(cu)$
-subharmonic (respectively,
![]() $(cu)$
-superharmonic) if
$(cu)$
-superharmonic) if
![]() $\Delta _{cu}(\varphi )\geq 0$
(respectively,
$\Delta _{cu}(\varphi )\geq 0$
(respectively,
![]() $\Delta _{cu}(\varphi )\leq 0$
) on
$\Delta _{cu}(\varphi )\leq 0$
) on
![]() $\Sigma ^n$
. So, it is not difficult to verify that, from [Reference Caminha18, Proposition
$\Sigma ^n$
. So, it is not difficult to verify that, from [Reference Caminha18, Proposition
![]() $2.1$
], we obtain the following auxiliary lemma.
$2.1$
], we obtain the following auxiliary lemma.
Lemma 3.3. Let
![]() $\Sigma ^n$
be an n-dimensional complete oriented Riemannian manifold. If
$\Sigma ^n$
be an n-dimensional complete oriented Riemannian manifold. If
![]() $\varphi \in C^\infty (\Sigma ^n)$
is a
$\varphi \in C^\infty (\Sigma ^n)$
is a
![]() $(cu)$
-subharmonic function (or a
$(cu)$
-subharmonic function (or a
![]() $(cu)$
-superharmonic function) on
$(cu)$
-superharmonic function) on
![]() $\Sigma ^n$
and
$\Sigma ^n$
and
![]() $|\nabla \varphi |\in \mathcal L_{cu}^1(\Sigma ^n)$
, then
$|\nabla \varphi |\in \mathcal L_{cu}^1(\Sigma ^n)$
, then
![]() $\Delta _{cu}(\varphi )=0$
on
$\Delta _{cu}(\varphi )=0$
on
![]() $\Sigma ^n$
.
$\Sigma ^n$
.
Given a GRW spacetime
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
obeying the NCC (3-20), we require a suitable behavior of the second soliton function associated to a spacelike mean curvature flow soliton
$\overline {M}^{n+1}=-I\times _{f}M^n$
obeying the NCC (3-20), we require a suitable behavior of the second soliton function associated to a spacelike mean curvature flow soliton
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
, and of the norm of the gradient of its mean curvature function, to establish our first uniqueness result. For this, we consider a timelike bounded region of
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
, and of the norm of the gradient of its mean curvature function, to establish our first uniqueness result. For this, we consider a timelike bounded region of
![]() $\overline {M}^{n+1}$
defined by
$\overline {M}^{n+1}$
defined by
Taking into account that all spacelike mean curvature solitons that appear in this paper are considered with respect to the closed conformal vector field
![]() $\mathcal {K}=f(t)\partial _{\,t}$
, we are in position to present our first main result.
$\mathcal {K}=f(t)\partial _{\,t}$
, we are in position to present our first main result.
Theorem 3.4. Let
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime that obeys the NCC (3-20), with equality holding only in isolated points of I. Let
$\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime that obeys the NCC (3-20), with equality holding only in isolated points of I. Let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a complete spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a complete spacelike mean curvature flow soliton with soliton constant
![]() $c\not =0$
that lies in a timelike bounded region
$c\not =0$
that lies in a timelike bounded region
![]() $\mathcal {B}_{t_1,t_2}$
. If its second soliton function
$\mathcal {B}_{t_1,t_2}$
. If its second soliton function
![]() $\tilde {\zeta }_{c}=|A|^2+cf'(h)$
is nonnegative and
$\tilde {\zeta }_{c}=|A|^2+cf'(h)$
is nonnegative and
![]() $|\nabla H|\in \mathcal L^1(\Sigma ^n)$
, then
$|\nabla H|\in \mathcal L^1(\Sigma ^n)$
, then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Proof. From (3-20), we obtain that
 $$ \begin{align} &\mathrm{Ric}_M(N^*,N^*)-(n-1)(\ln f)"(h)|\nabla h|^2\nonumber\\ &\quad\geq (n-1)(f(h)f"(h)-f'(h)^2)|N^*|_M^2-(n-1)(\ln f)"(h)|\nabla h|^2 \nonumber \\ &\quad=(n-1)(f(h)f"(h)-f'(h)^2)|N+\Theta\partial_{\,t}|_M^2-(n-1)\bigg(\dfrac{f'}{f}\bigg)'(h)|\nabla h|^2 \nonumber\\ &\quad=(n-1)\bigg\{(f(h)f"(h)-f'(h)^2)\dfrac{|\nabla h|^2}{f(h)^2}-\bigg(\dfrac{f(h)f"(h)-f'(h)^2}{f(h)^2}\bigg)|\nabla h|^2\bigg\}=0. \end{align} $$
$$ \begin{align} &\mathrm{Ric}_M(N^*,N^*)-(n-1)(\ln f)"(h)|\nabla h|^2\nonumber\\ &\quad\geq (n-1)(f(h)f"(h)-f'(h)^2)|N^*|_M^2-(n-1)(\ln f)"(h)|\nabla h|^2 \nonumber \\ &\quad=(n-1)(f(h)f"(h)-f'(h)^2)|N+\Theta\partial_{\,t}|_M^2-(n-1)\bigg(\dfrac{f'}{f}\bigg)'(h)|\nabla h|^2 \nonumber\\ &\quad=(n-1)\bigg\{(f(h)f"(h)-f'(h)^2)\dfrac{|\nabla h|^2}{f(h)^2}-\bigg(\dfrac{f(h)f"(h)-f'(h)^2}{f(h)^2}\bigg)|\nabla h|^2\bigg\}=0. \end{align} $$
Thus, since
![]() $\tilde {\zeta }_{c}\geq 0$
on
$\tilde {\zeta }_{c}\geq 0$
on
![]() $\Sigma ^n$
, from (3-18) and (3-22) we get that the support function
$\Sigma ^n$
, from (3-18) and (3-22) we get that the support function
![]() $\varphi _K$
defined in (3-10) satisfies
$\varphi _K$
defined in (3-10) satisfies
On the other hand, since
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is contained in a timelike bounded region
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is contained in a timelike bounded region
![]() $\mathcal {B}_{t_1,t_2}$
of
$\mathcal {B}_{t_1,t_2}$
of
![]() $-I\times _{f}M^n$
, h is bounded on
$-I\times _{f}M^n$
, h is bounded on
![]() $\Sigma ^n$
and, consequently, the same happens with
$\Sigma ^n$
and, consequently, the same happens with
![]() $u=g(h)$
and
$u=g(h)$
and
![]() $e^{cu}$
. So, since
$e^{cu}$
. So, since
![]() $c\not =0$
, from (3-21), (2-6), (3-10) and
$c\not =0$
, from (3-21), (2-6), (3-10) and
![]() $|\nabla H|\in \mathcal L^1(\Sigma ^n)$
we get
$|\nabla H|\in \mathcal L^1(\Sigma ^n)$
we get
![]() $|\nabla (\varphi _{\mathcal {K}})|\in \mathcal L_{cu}^1(\Sigma ^n)$
. Next, from Lemma 3.3 we obtain that
$|\nabla (\varphi _{\mathcal {K}})|\in \mathcal L_{cu}^1(\Sigma ^n)$
. Next, from Lemma 3.3 we obtain that
![]() $\Delta _{cu}(\varphi _{\mathcal {K}})=0$
on
$\Delta _{cu}(\varphi _{\mathcal {K}})=0$
on
![]() $\Sigma ^n$
. Since
$\Sigma ^n$
. Since
![]() $f(h)>0$
and
$f(h)>0$
and
![]() $\Theta <0$
on
$\Theta <0$
on
![]() $\Sigma ^n$
, from (3-22) and (3-23) we must have on
$\Sigma ^n$
, from (3-22) and (3-23) we must have on
![]() $\Sigma ^n$
that
$\Sigma ^n$
that
But, taking into account that the equality in (3-20) occurs only in isolated points of I, we can conclude that
![]() $|\nabla h|=0$
on
$|\nabla h|=0$
on
![]() $\Sigma ^n$
and, consequently, h is constant on
$\Sigma ^n$
and, consequently, h is constant on
![]() $\Sigma ^n$
. Therefore,
$\Sigma ^n$
. Therefore,
![]() $\psi (\Sigma ^n)$
is a slice.
$\psi (\Sigma ^n)$
is a slice.
Remark 3.5. From (2-5), we have that the slice
![]() $M_{t}^n$
is a spacelike hypersurface whose shape operator (with respect to the orientation
$M_{t}^n$
is a spacelike hypersurface whose shape operator (with respect to the orientation
![]() $\partial _{\,t}$
)
$\partial _{\,t}$
)
![]() $A_{t}$
is given by
$A_{t}$
is given by
 $$ \begin{align} \mathcal{A}_{t_\ast}:\mathfrak{X}(M_{t_\ast}^n)&\rightarrow\mathfrak{X}(M_{t_\ast}^n)\nonumber\\ V&\mapsto\mathcal{A}_{t_\ast}(V)=-\overline{\nabla}_V(\partial_{\,t_\ast})=-\dfrac{f'(t_\ast)}{f(t_\ast)}\,V. \end{align} $$
$$ \begin{align} \mathcal{A}_{t_\ast}:\mathfrak{X}(M_{t_\ast}^n)&\rightarrow\mathfrak{X}(M_{t_\ast}^n)\nonumber\\ V&\mapsto\mathcal{A}_{t_\ast}(V)=-\overline{\nabla}_V(\partial_{\,t_\ast})=-\dfrac{f'(t_\ast)}{f(t_\ast)}\,V. \end{align} $$
Thus, from (3-24) we obtain that the principal curvatures
![]() $\kappa _i^{t_\ast }$
of the shape operator
$\kappa _i^{t_\ast }$
of the shape operator
![]() $\mathcal {A}_{t_\ast }$
of a slice
$\mathcal {A}_{t_\ast }$
of a slice
![]() $M_{t_\ast }^n=\{t_\ast \}\times M^n$
,
$M_{t_\ast }^n=\{t_\ast \}\times M^n$
,
![]() $t_\ast \in I$
, are given by
$t_\ast \in I$
, are given by
![]() $\kappa _i^{t_\ast }=-{f'(t_\ast )}/{f(t_\ast )}$
for all
$\kappa _i^{t_\ast }=-{f'(t_\ast )}/{f(t_\ast )}$
for all
![]() $i\in \{1,\ldots ,n\}$
. So, from (2-8) and (3-19),
$i\in \{1,\ldots ,n\}$
. So, from (2-8) and (3-19),
 $$ \begin{align*}\tilde{\zeta}_{c}=c\,f'(t_\ast)+|\mathcal{A}_{t_\ast}|^2=\sum_{i=1}^n(\kappa_i^{t_\ast})^2+\bigg(-\dfrac{n\,f'(t_\ast)}{f^2(t_\ast)}\bigg)f'(t_\ast)=0\end{align*} $$
$$ \begin{align*}\tilde{\zeta}_{c}=c\,f'(t_\ast)+|\mathcal{A}_{t_\ast}|^2=\sum_{i=1}^n(\kappa_i^{t_\ast})^2+\bigg(-\dfrac{n\,f'(t_\ast)}{f^2(t_\ast)}\bigg)f'(t_\ast)=0\end{align*} $$
on
![]() $M_{t_\ast }^n$
. Hence, our restriction on the values of the second soliton function
$M_{t_\ast }^n$
. Hence, our restriction on the values of the second soliton function
![]() $\tilde {\zeta }_{c}$
in Theorem 3.4 constitutes a mild hypothesis in the sense that it is natural to detect slices of
$\tilde {\zeta }_{c}$
in Theorem 3.4 constitutes a mild hypothesis in the sense that it is natural to detect slices of
![]() $-I\times _{f}M^n$
.
$-I\times _{f}M^n$
.
From Theorem 3.4, we derive the following consequence.
Corollary 3.6. Let
![]() $\psi :\Sigma ^n\looparrowright -\mathbb R^+\times _{t^{2/3}}\mathbb {R}^n$
be a complete spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright -\mathbb R^+\times _{t^{2/3}}\mathbb {R}^n$
be a complete spacelike mean curvature flow soliton with soliton constant
![]() $c<0$
lying in a timelike bounded region of the Einstein–de Sitter spacetime
$c<0$
lying in a timelike bounded region of the Einstein–de Sitter spacetime
![]() $-\mathbb R^+\times _{t^{2/3}}\mathbb {R}^n$
. If
$-\mathbb R^+\times _{t^{2/3}}\mathbb {R}^n$
. If
![]() $|A|$
does not vanish and
$|A|$
does not vanish and
![]() $h\geq -{8c^3}/{27|A|^6}$
and
$h\geq -{8c^3}/{27|A|^6}$
and
![]() $|\nabla H|\in \mathcal L^1(\Sigma ^n)$
, then
$|\nabla H|\in \mathcal L^1(\Sigma ^n)$
, then
![]() $\Sigma ^n$
is the slice
$\Sigma ^n$
is the slice
![]() $\{(-{2n}/{3c})^{3/5}\}\times \mathbb R^n$
.
$\{(-{2n}/{3c})^{3/5}\}\times \mathbb R^n$
.
When the ambient space is a steady-state-type spacetime, Theorem 3.4 gives the following rigidity result.
Corollary 3.7. Let
![]() $\overline {M}^{n+1}=-I\times _{e^t}M^n$
be a steady-state-type spacetime whose Riemannian fiber
$\overline {M}^{n+1}=-I\times _{e^t}M^n$
be a steady-state-type spacetime whose Riemannian fiber
![]() $M^n$
has positive Ricci curvature. Let
$M^n$
has positive Ricci curvature. Let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a complete spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a complete spacelike mean curvature flow soliton with soliton constant
![]() $c<0$
and lying in a timelike bounded region. If
$c<0$
and lying in a timelike bounded region. If
![]() $|A|$
does not vanish and
$|A|$
does not vanish and
![]() $h\geq \ln (-{|A|^2}/{c})$
and
$h\geq \ln (-{|A|^2}/{c})$
and
![]() $|\nabla H|\in \mathcal L^1(\Sigma ^n)$
, then
$|\nabla H|\in \mathcal L^1(\Sigma ^n)$
, then
![]() $\Sigma ^n$
is the slice
$\Sigma ^n$
is the slice
![]() $\{\ln (-{n}/{c})\}\times M^n$
.
$\{\ln (-{n}/{c})\}\times M^n$
.
From Theorem 3.4 we also get the following nonexistence results.
Corollary 3.8. There is no complete spacelike translating soliton lying in a timelike bounded region of a Lorentzian product space
![]() $-I\times M^n$
, whose Riemannian fiber
$-I\times M^n$
, whose Riemannian fiber
![]() $M^n$
has positive Ricci curvature, that has soliton constant
$M^n$
has positive Ricci curvature, that has soliton constant
![]() $c\not =0$
and is such that
$c\not =0$
and is such that
![]() $|\nabla H|\in \mathcal L^1(\Sigma ^n)$
.
$|\nabla H|\in \mathcal L^1(\Sigma ^n)$
.
Corollary 3.9. There is no complete spacelike mean curvature flow soliton lying in a timelike bounded region of a steady-state-type spacetime
![]() $-I\times _{e^t}M^n$
, whose Riemannian fiber
$-I\times _{e^t}M^n$
, whose Riemannian fiber
![]() $M^n$
has positive Ricci curvature, that has soliton constant
$M^n$
has positive Ricci curvature, that has soliton constant
![]() $c>0$
and is such that
$c>0$
and is such that
![]() $|\nabla H|\in \mathcal L^1(\Sigma ^n)$
.
$|\nabla H|\in \mathcal L^1(\Sigma ^n)$
.
According to the classical terminology in linear potential theory, a Riemannian manifold
![]() $\Sigma ^n$
is called
$\Sigma ^n$
is called
![]() $(cu)$
-parabolic if the constant functions are the only functions
$(cu)$
-parabolic if the constant functions are the only functions
![]() $\varphi \in C^2(\Sigma )$
that are bounded from below and satisfy
$\varphi \in C^2(\Sigma )$
that are bounded from below and satisfy
![]() $\Delta _{cu}(\varphi )\leq 0$
. Inspired by the ideas of Romero et al. [Reference Romero, Rubio and Salamanca37, Reference Romero, Rubio and Salamanca38], Albujer et al. established in [Reference Albujer, de Lima, Oliveira and VelÁsquez4, Theorem
$\Delta _{cu}(\varphi )\leq 0$
. Inspired by the ideas of Romero et al. [Reference Romero, Rubio and Salamanca37, Reference Romero, Rubio and Salamanca38], Albujer et al. established in [Reference Albujer, de Lima, Oliveira and VelÁsquez4, Theorem
![]() $1$
] the following parabolicity criterion, which provides conditions for a complete spacelike hypersurface immersed in GRW spacetime
$1$
] the following parabolicity criterion, which provides conditions for a complete spacelike hypersurface immersed in GRW spacetime
![]() $-I\times _{f}M^n$
to be
$-I\times _{f}M^n$
to be
![]() $(cu)$
-parabolic. For this, we consider the function
$(cu)$
-parabolic. For this, we consider the function
![]() $\tilde {u}:=g(\pi _I)\circ \tilde {\pi }$
, where
$\tilde {u}:=g(\pi _I)\circ \tilde {\pi }$
, where
![]() $\tilde {\pi }:\widetilde {M}^n\rightarrow M^n$
is the universal covering map of the Riemannian fiber
$\tilde {\pi }:\widetilde {M}^n\rightarrow M^n$
is the universal covering map of the Riemannian fiber
![]() $M^n$
.
$M^n$
.
Lemma 3.10. Let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a complete spacelike hypersurface immersed in a GRW spacetime
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a complete spacelike hypersurface immersed in a GRW spacetime
![]() $-I\times _{f}M^n$
, whose Riemannian fiber
$-I\times _{f}M^n$
, whose Riemannian fiber
![]() $M^n$
has
$M^n$
has
![]() $(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
$(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
![]() $c\neq 0$
. If the hyperbolic angle
$c\neq 0$
. If the hyperbolic angle
![]() $\Theta $
is bounded from below, and the warping function f and the height function h are such that
$\Theta $
is bounded from below, and the warping function f and the height function h are such that
![]() $\sup _{\Sigma ^n}f(h)<+\infty $
and
$\sup _{\Sigma ^n}f(h)<+\infty $
and
![]() $\inf _{\Sigma ^n}f(h)>0$
, then
$\inf _{\Sigma ^n}f(h)>0$
, then
![]() $\Sigma ^n$
is
$\Sigma ^n$
is
![]() $(cu)$
-parabolic.
$(cu)$
-parabolic.
We can state the following rigidity result for spacelike mean curvature flow solitons in GRW spacetimes.
Theorem 3.11. Let
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime obeying the NCC (3-20), with equality holding only in isolated points of I and such that the Riemannian fiber
$\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime obeying the NCC (3-20), with equality holding only in isolated points of I and such that the Riemannian fiber
![]() $M^n$
has
$M^n$
has
![]() $(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
$(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
![]() $c\neq 0$
. Let
$c\neq 0$
. Let
![]() ${\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}}$
be a complete spacelike mean curvature flow soliton with soliton constant c, lying in a timelike bounded region
${\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}}$
be a complete spacelike mean curvature flow soliton with soliton constant c, lying in a timelike bounded region
![]() $\mathcal {B}_{t_1,t_2}$
. If the hyperbolic angle
$\mathcal {B}_{t_1,t_2}$
. If the hyperbolic angle
![]() $\Theta $
is bounded from below and the second soliton function
$\Theta $
is bounded from below and the second soliton function
![]() $\tilde {\zeta }_{c}=|A|^2+cf'(h)$
is nonnegative, then
$\tilde {\zeta }_{c}=|A|^2+cf'(h)$
is nonnegative, then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Proof. From (3-23), we get that
![]() $\Delta _{cu}(\varphi _K)\leq 0$
on
$\Delta _{cu}(\varphi _K)\leq 0$
on
![]() $\Sigma ^n$
. Thus, since we are assuming that
$\Sigma ^n$
. Thus, since we are assuming that
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is contained in a timelike bounded region, Lemma 3.10 guarantees that
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is contained in a timelike bounded region, Lemma 3.10 guarantees that
![]() $\Sigma ^n$
is
$\Sigma ^n$
is
![]() $(cu)$
-parabolic and, consequently,
$(cu)$
-parabolic and, consequently,
![]() $\varphi _{\mathcal {K}}$
is constant on
$\varphi _{\mathcal {K}}$
is constant on
![]() $\Sigma ^n$
. At this point, we can reason as in the last part of the proof of Theorem 3.4 to conclude that there is
$\Sigma ^n$
. At this point, we can reason as in the last part of the proof of Theorem 3.4 to conclude that there is
![]() $t\in I$
such that
$t\in I$
such that
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
From Theorem 3.11, we obtain the following applications.
Corollary 3.12. Let
![]() $\overline {M}^{n+1}=-I\times _{e^t}M^n$
be a steady-state-type spacetime whose Riemannian fiber
$\overline {M}^{n+1}=-I\times _{e^t}M^n$
be a steady-state-type spacetime whose Riemannian fiber
![]() $M^n$
has positive Ricci curvature and
$M^n$
has positive Ricci curvature and
![]() $(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
$(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
![]() $c<0$
. Let
$c<0$
. Let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a complete spacelike mean curvature flow soliton with soliton constant c, lying in a timelike bounded region
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a complete spacelike mean curvature flow soliton with soliton constant c, lying in a timelike bounded region
![]() $\mathcal {B}_{t_1,t_2}$
. If
$\mathcal {B}_{t_1,t_2}$
. If
![]() $\Theta $
is bounded from below and
$\Theta $
is bounded from below and
![]() $h\geq \ln (-{|A|^2}/{c})$
, then
$h\geq \ln (-{|A|^2}/{c})$
, then
![]() $\Sigma ^n$
is the slice
$\Sigma ^n$
is the slice
![]() $\{\ln (-{n}/{c})\}\times M^n$
.
$\{\ln (-{n}/{c})\}\times M^n$
.
Corollary 3.13. Let
![]() $\overline {M}^{n+1}=-I\times _{e^t}M^n$
be a steady-state-type spacetime whose Riemannian fiber
$\overline {M}^{n+1}=-I\times _{e^t}M^n$
be a steady-state-type spacetime whose Riemannian fiber
![]() $M^n$
has positive Ricci curvature and
$M^n$
has positive Ricci curvature and
![]() $(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
$(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
![]() $c>0$
. There is no complete spacelike mean curvature flow soliton lying in a timelike bounded region of
$c>0$
. There is no complete spacelike mean curvature flow soliton lying in a timelike bounded region of
![]() $\overline {M}^{n+1}$
that has soliton constant c and is such that
$\overline {M}^{n+1}$
that has soliton constant c and is such that
![]() $\Theta $
is bounded from below.
$\Theta $
is bounded from below.
Corollary 3.14. Let
![]() $\overline {M}^{n+1}=-I\times M^n$
be a Lorentzian product space, whose Riemannian fiber
$\overline {M}^{n+1}=-I\times M^n$
be a Lorentzian product space, whose Riemannian fiber
![]() $M^n$
has positive Ricci curvature and
$M^n$
has positive Ricci curvature and
![]() $(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
$(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
![]() $c\neq 0$
. There is no complete spacelike translating soliton in
$c\neq 0$
. There is no complete spacelike translating soliton in
![]() $\overline {M}^{n+1}$
that has soliton constant c and is such that
$\overline {M}^{n+1}$
that has soliton constant c and is such that
![]() $\Theta $
is bounded from below.
$\Theta $
is bounded from below.
Considering the strong null convergence condition (SNCC)
which was introduced by Alías and Colares [Reference Alías and Colares7], where
![]() $K_M$
denotes the sectional curvature of the Riemannian fiber
$K_M$
denotes the sectional curvature of the Riemannian fiber
![]() $M^n$
, and adding a suitable control to the growing of the height function through the second soliton function of a spacelike mean curvature flow soliton, we get the following version of Omori–Yau’s maximum principle.
$M^n$
, and adding a suitable control to the growing of the height function through the second soliton function of a spacelike mean curvature flow soliton, we get the following version of Omori–Yau’s maximum principle.
Proposition 3.15. Let
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime obeying the SNCC (3-25), and let
$\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime obeying the SNCC (3-25), and let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a complete spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a complete spacelike mean curvature flow soliton with soliton constant
![]() $c\not =0$
. If the function
$c\not =0$
. If the function
![]() $({(n-1)f"(h)+cf(h)f'(h)})/{f(h)}$
is bounded from below on
$({(n-1)f"(h)+cf(h)f'(h)})/{f(h)}$
is bounded from below on
![]() $\Sigma ^n$
, then Omori–Yau’s maximum principle holds for the drift Laplacian
$\Sigma ^n$
, then Omori–Yau’s maximum principle holds for the drift Laplacian
![]() $\Delta _{cu}$
: that is, for
$\Delta _{cu}$
: that is, for
![]() $\varphi \in C^2(\Sigma ^n)$
with
$\varphi \in C^2(\Sigma ^n)$
with
![]() $\sup _{\Sigma }\varphi <+\infty $
, there exists a sequence of points
$\sup _{\Sigma }\varphi <+\infty $
, there exists a sequence of points
![]() $\{p_k\}_{k\geq 1}$
in
$\{p_k\}_{k\geq 1}$
in
![]() $\Sigma ^n$
such that
$\Sigma ^n$
such that
Proof. We recall that the curvature tensor R of
![]() $\Sigma ^n$
can be described in terms of its Weingarten operator A and the curvature tensor
$\Sigma ^n$
can be described in terms of its Weingarten operator A and the curvature tensor
![]() $\overline {R}$
of the ambient
$\overline {R}$
of the ambient
![]() $-I\times _{f} M^{n}$
by the so-called Gauss equation, which is given by
$-I\times _{f} M^{n}$
by the so-called Gauss equation, which is given by
for every tangential vector field
![]() $X,Y,Z\in \mathfrak X(\Sigma ^n)$
. Here, as in [Reference O’Neill35], the curvature tensor R is given by
$X,Y,Z\in \mathfrak X(\Sigma ^n)$
. Here, as in [Reference O’Neill35], the curvature tensor R is given by
where
![]() $[~,~]$
denotes the Lie bracket and
$[~,~]$
denotes the Lie bracket and
![]() $X,Y,Z\in \mathfrak X(\Sigma ^n)$
.
$X,Y,Z\in \mathfrak X(\Sigma ^n)$
.
We consider
![]() $X\in \mathfrak {X}(\Sigma ^n)$
and take a (local) orthonormal frame
$X\in \mathfrak {X}(\Sigma ^n)$
and take a (local) orthonormal frame
![]() $\{E_1,\ldots ,E_n\}$
. It follows from the Gauss equation (3-26) that the Ricci curvature
$\{E_1,\ldots ,E_n\}$
. It follows from the Gauss equation (3-26) that the Ricci curvature
![]() $\mathrm {Ric}$
of
$\mathrm {Ric}$
of
![]() $\Sigma ^n$
satisfies
$\Sigma ^n$
satisfies
Thus, from (3-8) and (3-27), we get
To estimate the first summand on the right-hand side of inequality (3-28), we consider
![]() $X^\ast =(\pi _M)_{\ast }(X)$
and
$X^\ast =(\pi _M)_{\ast }(X)$
and
![]() $E_i^\ast =(\pi _M)_{\ast }(E_i)$
. So, from [Reference O’Neill35, Proposition 7.42] and (3-3),
$E_i^\ast =(\pi _M)_{\ast }(E_i)$
. So, from [Reference O’Neill35, Proposition 7.42] and (3-3),
 $$ \begin{align} \sum_{i}\langle\overline{R}(X,E_i)X,E_i\rangle=&\sum_{i}\langle{R}_M(X^\ast,E_i^\ast)X^\ast,E_i^\ast\rangle+(n-1)((\ln f)'(h))^2|X|^2\nonumber\\ &-(n-2)(\ln f)"(h)\langle X,\nabla h\rangle^2-(\ln f)"(h)|\nabla h|^2|X|^2, \end{align} $$
$$ \begin{align} \sum_{i}\langle\overline{R}(X,E_i)X,E_i\rangle=&\sum_{i}\langle{R}_M(X^\ast,E_i^\ast)X^\ast,E_i^\ast\rangle+(n-1)((\ln f)'(h))^2|X|^2\nonumber\\ &-(n-2)(\ln f)"(h)\langle X,\nabla h\rangle^2-(\ln f)"(h)|\nabla h|^2|X|^2, \end{align} $$
where
![]() ${R}_M$
denotes the curvature tensor of the Riemannian fiber
${R}_M$
denotes the curvature tensor of the Riemannian fiber
![]() $M^n$
. By writing
$M^n$
. By writing
![]() ${X^\ast =X+\langle X,\partial _t\rangle \partial _t}$
, we can estimate the first summand on the right-hand side of (3-29) to get
${X^\ast =X+\langle X,\partial _t\rangle \partial _t}$
, we can estimate the first summand on the right-hand side of (3-29) to get
 $$ \begin{align} \sum_{i}\langle{R}_M(X^\ast,E_i^\ast)X^\ast,E_i^\ast\rangle&=f^2(h)(|X^\ast|_ M^2|E^\ast|_ M^2-\langle X^\ast,E^\ast\rangle_M^2) K_M(X^\ast,E^\ast)\nonumber\\ &\geq\dfrac{1}{f^2(h)}((n-1)|X|^2+|\nabla h^2||X|^2\nonumber\\ &\quad+(n-2)\langle X,\nabla h\rangle^2)\min_{i}K_M(X^\ast,E_i^\ast). \end{align} $$
$$ \begin{align} \sum_{i}\langle{R}_M(X^\ast,E_i^\ast)X^\ast,E_i^\ast\rangle&=f^2(h)(|X^\ast|_ M^2|E^\ast|_ M^2-\langle X^\ast,E^\ast\rangle_M^2) K_M(X^\ast,E^\ast)\nonumber\\ &\geq\dfrac{1}{f^2(h)}((n-1)|X|^2+|\nabla h^2||X|^2\nonumber\\ &\quad+(n-2)\langle X,\nabla h\rangle^2)\min_{i}K_M(X^\ast,E_i^\ast). \end{align} $$
Consequently, since our ambient space obeys (3-25), from (3-30),
 $$ \begin{align} &\sum_{i}\langle R_M(X^\ast,E_i^\ast)X^\ast,E_i^\ast\rangle\nonumber\\ &\quad \geq((n-1)|X|^2+|\nabla h|^2|X|^2+(n-2)\langle X,\nabla h\rangle^2)(\ln f)"(h). \end{align} $$
$$ \begin{align} &\sum_{i}\langle R_M(X^\ast,E_i^\ast)X^\ast,E_i^\ast\rangle\nonumber\\ &\quad \geq((n-1)|X|^2+|\nabla h|^2|X|^2+(n-2)\langle X,\nabla h\rangle^2)(\ln f)"(h). \end{align} $$
Substituting (3-31) into (3-29) gives
 $$ \begin{align} \sum_{i}\langle\overline{R}(X,E_i)X,E_i\rangle&\geq((n-1)|X|^2\!+\!|\nabla h|^2|X|^2\!+\!(n-2)\langle X,\nabla h\rangle^2)(\ln f)"(h)\!\nonumber\\[-9pt] &\quad+(n-1)((\ln f)'(h))^2|X|^2-(n-2)(\ln f)"(h)\langle X,\nabla h\rangle^2\nonumber\\ &\quad-(\ln f)"(h)|\nabla h|^2|X|^2\nonumber\\ &=(n-1)\dfrac{f"(h)}{f(h)}|X|^2. \end{align} $$
$$ \begin{align} \sum_{i}\langle\overline{R}(X,E_i)X,E_i\rangle&\geq((n-1)|X|^2\!+\!|\nabla h|^2|X|^2\!+\!(n-2)\langle X,\nabla h\rangle^2)(\ln f)"(h)\!\nonumber\\[-9pt] &\quad+(n-1)((\ln f)'(h))^2|X|^2-(n-2)(\ln f)"(h)\langle X,\nabla h\rangle^2\nonumber\\ &\quad-(\ln f)"(h)|\nabla h|^2|X|^2\nonumber\\ &=(n-1)\dfrac{f"(h)}{f(h)}|X|^2. \end{align} $$
Hence, from (3-28) and (3-32), we obtain
 $$ \begin{align*}\mathrm{Ric}-c\nabla^{2}u\geq ((n-1)\dfrac{f"(h)}{f(h)}+cf'(h))\langle\,,\rangle.\end{align*} $$
$$ \begin{align*}\mathrm{Ric}-c\nabla^{2}u\geq ((n-1)\dfrac{f"(h)}{f(h)}+cf'(h))\langle\,,\rangle.\end{align*} $$
Therefore, since the right-hand side of the above inequality is bounded from below, we conclude our proof by applying [Reference Chen and Qiu22, Theorem 1].
To proceed, we use Proposition 3.15 to establish the following result.
Theorem 3.16. Let
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime obeying the SNCC (3-25), and let
$\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime obeying the SNCC (3-25), and let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a complete spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a complete spacelike mean curvature flow soliton with soliton constant
![]() $c\not =0$
such that
$c\not =0$
such that
![]() $({(n-1)f"(h)+cf(h)f'(h)})/{f(h)}$
is bounded from below. If
$({(n-1)f"(h)+cf(h)f'(h)})/{f(h)}$
is bounded from below. If
![]() $\inf _{\Sigma }f(h)>0$
, the second soliton function
$\inf _{\Sigma }f(h)>0$
, the second soliton function
![]() $\tilde {\zeta }_{c}=|A|^2+cf'(h)$
is nonnegative and the height function h satisfies
$\tilde {\zeta }_{c}=|A|^2+cf'(h)$
is nonnegative and the height function h satisfies
then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Proof. Since
![]() $\varphi _{\mathcal {K}}<0$
on
$\varphi _{\mathcal {K}}<0$
on
![]() $\Sigma ^n$
, Proposition 3.15 ensures the existence of a sequence of points
$\Sigma ^n$
, Proposition 3.15 ensures the existence of a sequence of points
![]() $\{p_k\}_{k\in \mathbb {N}}\subset \Sigma ^n$
such that
$\{p_k\}_{k\in \mathbb {N}}\subset \Sigma ^n$
such that
Hence, from (3-23), we get
But, since we are assuming that
![]() $\inf _{\Sigma }f(h)>0$
, we have that
$\inf _{\Sigma }f(h)>0$
, we have that
![]() $\sup _{\Sigma ^n}\varphi _{\mathcal {K}}<0$
. Consequently, from (3-34) we must have
$\sup _{\Sigma ^n}\varphi _{\mathcal {K}}<0$
. Consequently, from (3-34) we must have
![]() $\lim _{j\rightarrow +\infty }\tilde {\zeta }_{c}(p_k)=0$
, and hence
$\lim _{j\rightarrow +\infty }\tilde {\zeta }_{c}(p_k)=0$
, and hence
![]() $\inf _{\Sigma ^n}\tilde {\zeta }_{c}=0$
. Therefore, the result follows from hypothesis (3-33).
$\inf _{\Sigma ^n}\tilde {\zeta }_{c}=0$
. Therefore, the result follows from hypothesis (3-33).
Remark 3.17. We note that in Theorem 3.16 the hypotheses that the expression
![]() $((n-1)f"(h) +cf(h)f'(h))/{f(h)}$
is bounded from below and
$((n-1)f"(h) +cf(h)f'(h))/{f(h)}$
is bounded from below and
![]() $\inf _{\Sigma }f(h)>0$
are automatically satisfied if we assume that the spacelike mean curvature flow soliton lies in a timelike bounded region of the ambient spacetime.
$\inf _{\Sigma }f(h)>0$
are automatically satisfied if we assume that the spacelike mean curvature flow soliton lies in a timelike bounded region of the ambient spacetime.
From Theorem 3.16, we obtain the following applications.
Corollary 3.18. Let
![]() $\psi :\Sigma ^n\looparrowright -\mathbb R^+\times _t\mathbb H^n$
be a complete spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright -\mathbb R^+\times _t\mathbb H^n$
be a complete spacelike mean curvature flow soliton with soliton constant
![]() $c<0$
. If
$c<0$
. If
![]() $\inf _{\Sigma }h>0$
, the second soliton function
$\inf _{\Sigma }h>0$
, the second soliton function
![]() ${\tilde {\zeta }_{c}=|A|^2+c}$
is nonnegative and
${\tilde {\zeta }_{c}=|A|^2+c}$
is nonnegative and
![]() $|\nabla h|\leq \inf _{\Sigma ^n}\tilde {\zeta }_{c}$
, then
$|\nabla h|\leq \inf _{\Sigma ^n}\tilde {\zeta }_{c}$
, then
![]() $\Sigma ^n$
is a slice
$\Sigma ^n$
is a slice
![]() $\{\!\sqrt {-{n}/{c}}\}\times \mathbb H^n$
.
$\{\!\sqrt {-{n}/{c}}\}\times \mathbb H^n$
.
Corollary 3.19. There is no complete spacelike mean curvature flow soliton
![]() $\psi :\Sigma ^n\looparrowright -\mathbb R^+\times _t\mathbb H^n$
with soliton constant
$\psi :\Sigma ^n\looparrowright -\mathbb R^+\times _t\mathbb H^n$
with soliton constant
![]() $c>0$
such that
$c>0$
such that
![]() $\inf _{\Sigma }h>0$
and
$\inf _{\Sigma }h>0$
and
![]() $|\nabla h|\leq \inf _{\Sigma ^n}|A|^2+c$
.
$|\nabla h|\leq \inf _{\Sigma ^n}|A|^2+c$
.
Our next result can be regarded as a sort of extension of [Reference Chen and Qiu22, Theorem 3].
Theorem 3.20. Let
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime satisfying the SNCC (3-25). There is no complete spacelike mean curvature flow soliton immersed in
$\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime satisfying the SNCC (3-25). There is no complete spacelike mean curvature flow soliton immersed in
![]() $\overline {M}^{n+1}$
with soliton constant
$\overline {M}^{n+1}$
with soliton constant
![]() $c\neq 0$
such that
$c\neq 0$
such that
![]() $cf'(h)\geq 0$
and
$cf'(h)\geq 0$
and
![]() $({(n-1)f"(h)+cf(h)f'(h)})/ {f(h)}$
is bounded from below.
$({(n-1)f"(h)+cf(h)f'(h)})/ {f(h)}$
is bounded from below.
Proof. Let us suppose, by contradiction, the existence of such a complete spacelike mean curvature flow soliton
![]() $\Sigma ^n$
immersed in
$\Sigma ^n$
immersed in
![]() $\overline {M}^{n+1}$
. Since we are supposing that
$\overline {M}^{n+1}$
. Since we are supposing that
![]() $cf'(h)\geq 0$
and that
$cf'(h)\geq 0$
and that
![]() $\overline {M}^{n+1}$
satisfies the SNCC (3-25), we conclude from (3-18) and (3-22) that
$\overline {M}^{n+1}$
satisfies the SNCC (3-25), we conclude from (3-18) and (3-22) that
From the above equation, we get
Since
![]() $\varphi _{\mathcal {K}}={H}/{c}$
,
$\varphi _{\mathcal {K}}={H}/{c}$
,
With a straightforward computation, we can verify that
 $$ \begin{align} \Delta_{cu}\bigg(\frac{-1}{\sqrt{1+H^{2}}}\bigg)=\frac{\Delta_{cu}H^{2}}{2(1+H^{2})^{3/2}}-\frac{3}{4}\frac{|\nabla H^{2}|^{2}}{(1+H^{2})^{5/2}}. \end{align} $$
$$ \begin{align} \Delta_{cu}\bigg(\frac{-1}{\sqrt{1+H^{2}}}\bigg)=\frac{\Delta_{cu}H^{2}}{2(1+H^{2})^{3/2}}-\frac{3}{4}\frac{|\nabla H^{2}|^{2}}{(1+H^{2})^{5/2}}. \end{align} $$
Hence, from (3-35) and (3-36), we obtain
 $$ \begin{align*}\Delta_{cu}\bigg(\frac{-1}{\sqrt{1+H^{2}}}\bigg)\geq \frac{H^{4}}{n(1+H^{2})^{3/2}}-\frac{3}{4}\frac{|\nabla H^{2}|^{2}}{(1+H^{2})^{5/2}}.\end{align*} $$
$$ \begin{align*}\Delta_{cu}\bigg(\frac{-1}{\sqrt{1+H^{2}}}\bigg)\geq \frac{H^{4}}{n(1+H^{2})^{3/2}}-\frac{3}{4}\frac{|\nabla H^{2}|^{2}}{(1+H^{2})^{5/2}}.\end{align*} $$
Therefore, since
![]() $({(n-1)f"(h)+cf(h)f'(h)})/{f(h)}$
is bounded from below, from Proposition 3.15 we can apply Omori–Yau’s maximum principle and reason as in the proof of [Reference Chen and Qiu22, Theorem 3] to conclude that
$({(n-1)f"(h)+cf(h)f'(h)})/{f(h)}$
is bounded from below, from Proposition 3.15 we can apply Omori–Yau’s maximum principle and reason as in the proof of [Reference Chen and Qiu22, Theorem 3] to conclude that
![]() $H\equiv 0$
, which corresponds to an absurdity.
$H\equiv 0$
, which corresponds to an absurdity.
From Theorem 3.20, we get the following nonexistence results.
Corollary 3.21. There is no complete spacelike translating soliton with soliton constant
![]() $c\not =0$
immersed in
$c\not =0$
immersed in
![]() $-I\times M^n$
whose Riemannian fiber
$-I\times M^n$
whose Riemannian fiber
![]() $M^n$
has nonnegative sectional curvature.
$M^n$
has nonnegative sectional curvature.
Corollary 3.22. There is no complete mean curvature flow soliton with soliton constant
![]() $c>0$
, lying in a timelike bounded region of the steady-state-type spacetime
$c>0$
, lying in a timelike bounded region of the steady-state-type spacetime
![]() $-\mathbb R\times _{e^t}M^n$
, whose Riemannian fiber
$-\mathbb R\times _{e^t}M^n$
, whose Riemannian fiber
![]() $M^n$
has nonnegative sectional curvature.
$M^n$
has nonnegative sectional curvature.
Corollary 3.23. There is no complete spacelike mean curvature flow soliton with soliton constant
![]() $c>0$
lying in a timelike bounded region of the Einstein–de Sitter spacetime
$c>0$
lying in a timelike bounded region of the Einstein–de Sitter spacetime
![]() $-\mathbb R^+\times _{t^{2/3}}\mathbb {R}^n$
.
$-\mathbb R^+\times _{t^{2/3}}\mathbb {R}^n$
.
Corollary 3.24. There is no complete mean curvature flow soliton with soliton constant
![]() $c\neq 0$
immersed in
$c\neq 0$
immersed in
![]() $-(-{\pi }/{2},{\pi }/{2})\times _{\cos t}\mathbb {H}^n\subset \mathbb H^{n+1}_1$
such that
$-(-{\pi }/{2},{\pi }/{2})\times _{\cos t}\mathbb {H}^n\subset \mathbb H^{n+1}_1$
such that
![]() $c\sin (h)\leq 0$
.
$c\sin (h)\leq 0$
.
Remark 3.25. Fixing a constant
![]() $c\in \mathbb R$
with
$c\in \mathbb R$
with
![]() $0<|c|<1$
, from [Reference de Lima and Lima26, Example
$0<|c|<1$
, from [Reference de Lima and Lima26, Example
![]() $4.4$
] we have that
$4.4$
] we have that
is a complete spacelike translating soliton of the mean curvature flow with respect to
![]() $\partial _t$
that has soliton constant c and constant future mean curvature
$\partial _t$
that has soliton constant c and constant future mean curvature
Moreover, we also get that
 $$ \begin{align*}|\nabla h|=\frac{|c|}{\sqrt{1-c^2}}=|A|.\end{align*} $$
$$ \begin{align*}|\nabla h|=\frac{|c|}{\sqrt{1-c^2}}=|A|.\end{align*} $$
Hence, since the static GRW spacetime
![]() $-\mathbb R\times \mathbb H^n$
obeys neither the NCC (3-20) nor the SNCC (3-25), we can verify that it works as a counterexample related to our previous theorems. Consequently, we conclude that some hypothesis is needed.
$-\mathbb R\times \mathbb H^n$
obeys neither the NCC (3-20) nor the SNCC (3-25), we can verify that it works as a counterexample related to our previous theorems. Consequently, we conclude that some hypothesis is needed.
Now, we deal with compact (without boundary) mean curvature flow solitons.
Theorem 3.26. Let
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime and let
$\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact mean curvature flow soliton with soliton constant
![]() $c\neq 0$
. If
$c\neq 0$
. If
![]() $c>0$
, then
$c>0$
, then
where
![]() $h_{*}$
and
$h_{*}$
and
![]() $h^{*}$
are the minimum and maximum of the height function on
$h^{*}$
are the minimum and maximum of the height function on
![]() $\Sigma ^n$
. Similarly, if
$\Sigma ^n$
. Similarly, if
![]() $c<0$
, then
$c<0$
, then
Proof. From (3-8),
We consider
![]() $c>0$
and let
$c>0$
and let
![]() $p_0$
be a minimum point of the height function h. Since a primitive g of f is an increasing function, we have that
$p_0$
be a minimum point of the height function h. Since a primitive g of f is an increasing function, we have that
![]() $h(p_0)=h_{*}$
is a minimum point of the function
$h(p_0)=h_{*}$
is a minimum point of the function
![]() $u=g(h)$
, and hence
$u=g(h)$
, and hence
![]() $\Delta u(p_0)\geq 0$
. Thus, from (3-37), we get that
$\Delta u(p_0)\geq 0$
. Thus, from (3-37), we get that
Analogously, taking a maximum point of h, we are able to conclude that
The proof of the case
![]() $c<0$
follows the same steps as the case
$c<0$
follows the same steps as the case
![]() $c>0$
.
$c>0$
.
From the above result, we conclude directly the following nonexistence result.
Corollary 3.27. There exists no compact spacelike translating soliton with soliton constant
![]() $c\neq 0$
immersed in
$c\neq 0$
immersed in
![]() $-I\times M^{n}$
.
$-I\times M^{n}$
.
We finish this subsection by establishing a rigidity result derived from Theorem 3.26.
Corollary 3.28. Let
![]() $\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime and let
$\overline {M}^{n+1}=-I\times _{f}M^n$
be a GRW spacetime and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact mean curvature flow soliton with soliton constant
![]() $c\neq 0$
. Assume that
$c\neq 0$
. Assume that
![]() $f"(t)\leq 0$
for
$f"(t)\leq 0$
for
![]() $h_{*}\leq t\leq h^{*}$
, where
$h_{*}\leq t\leq h^{*}$
, where
![]() $h_{*}$
and
$h_{*}$
and
![]() $h^{*}$
are the minimum and maximum on
$h^{*}$
are the minimum and maximum on
![]() $\Sigma ^n$
of its height function h, respectively. If H is constant, then
$\Sigma ^n$
of its height function h, respectively. If H is constant, then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Proof. Indeed, since
![]() $f"(t)\leq 0$
, we have that
$f"(t)\leq 0$
, we have that
![]() $f'$
is nondecreasing. In addition, since H is constant, from Theorem 3.26 we conclude that
$f'$
is nondecreasing. In addition, since H is constant, from Theorem 3.26 we conclude that
for
![]() $h_{*}\leq t\leq h^{*}$
. Thus, from the above equation jointly with (3-37), we have that
$h_{*}\leq t\leq h^{*}$
. Thus, from the above equation jointly with (3-37), we have that
![]() $\Delta u=0$
. Therefore, since
$\Delta u=0$
. Therefore, since
![]() $\Sigma ^n$
is compact, we conclude that u is constant, which means that
$\Sigma ^n$
is compact, we conclude that u is constant, which means that
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
3.3 The spacelike mean curvature flow soliton equation
Let
![]() $\Omega \subseteq M^n$
be a connected domain and let
$\Omega \subseteq M^n$
be a connected domain and let
![]() $z\in C^\infty (\Omega )$
be a smooth function such that
$z\in C^\infty (\Omega )$
be a smooth function such that
![]() $z(\Omega )\subseteq I$
. Then
$z(\Omega )\subseteq I$
. Then
![]() $\Sigma ^n(z)$
will denote the (vertical) graph over
$\Sigma ^n(z)$
will denote the (vertical) graph over
![]() $\Omega $
determined by z, that is,
$\Omega $
determined by z, that is,
The graph is said to be entire if
![]() $\Omega =M^n$
. Observe that
$\Omega =M^n$
. Observe that
![]() $h(z(p),p)=z(p),p\in \Omega $
. Hence, h and z can be identified in a natural way. The metric induced on
$h(z(p),p)=z(p),p\in \Omega $
. Hence, h and z can be identified in a natural way. The metric induced on
![]() $\Omega $
from the Lorentzian metric of the ambient GRW spacetime via
$\Omega $
from the Lorentzian metric of the ambient GRW spacetime via
![]() $\Sigma ^n(z)$
is
$\Sigma ^n(z)$
is
It follows from (3-38) that a graph
![]() $\Sigma ^n(z)$
is a spacelike hypersurface if and only if
$\Sigma ^n(z)$
is a spacelike hypersurface if and only if
![]() $|Dz|_{M}<f(z)$
, where
$|Dz|_{M}<f(z)$
, where
![]() $Dz$
stands for the gradient of z in
$Dz$
stands for the gradient of z in
![]() $M^n$
and
$M^n$
and
![]() $|Dz|_M$
denotes its norm, both with respect to the metric
$|Dz|_M$
denotes its norm, both with respect to the metric
![]() $g_M$
. On the other hand, in the case where
$g_M$
. On the other hand, in the case where
![]() $M^n$
is a simply connected manifold, from [Reference Alías, Romero and SÁnchez11, Lemma 3.1] we have that every complete spacelike hypersurface
$M^n$
is a simply connected manifold, from [Reference Alías, Romero and SÁnchez11, Lemma 3.1] we have that every complete spacelike hypersurface
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
such that the warping function f is bounded on
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
such that the warping function f is bounded on
![]() $\Sigma ^n$
is an entire spacelike graph over
$\Sigma ^n$
is an entire spacelike graph over
![]() $M^n$
. In particular, this happens for complete spacelike hypersurfaces lying in a timelike bounded region of
$M^n$
. In particular, this happens for complete spacelike hypersurfaces lying in a timelike bounded region of
![]() $-I\times _{f}M^n$
. It is also interesting to point out that, in contrast to the case of graphs in a Riemannian space, an entire spacelike graph
$-I\times _{f}M^n$
. It is also interesting to point out that, in contrast to the case of graphs in a Riemannian space, an entire spacelike graph
![]() $\Sigma ^n(z)$
in a GRW spacetime is not necessarily complete, in the sense that the induced Riemannian metric (3-38) is not necessarily complete on
$\Sigma ^n(z)$
in a GRW spacetime is not necessarily complete, in the sense that the induced Riemannian metric (3-38) is not necessarily complete on
![]() $M^n$
. For example, Albujer [Reference Albujer1, Section 3] constructed explicit examples of noncomplete entire maximal spacelike graphs (that is, whose mean curvature is identically zero) in the Lorentzian product space
$M^n$
. For example, Albujer [Reference Albujer1, Section 3] constructed explicit examples of noncomplete entire maximal spacelike graphs (that is, whose mean curvature is identically zero) in the Lorentzian product space
![]() $-\mathbb R\times \mathbb H^2$
.
$-\mathbb R\times \mathbb H^2$
.
The future-pointing Gauss map of a spacelike graph
![]() $\Sigma ^n(z)$
over
$\Sigma ^n(z)$
over
![]() $\Omega $
is given by the vector field
$\Omega $
is given by the vector field
 $$ \begin{align} N(p)=\frac{f(z(p))}{\sqrt{f^2(z(p))-|Dz(p)|_M^2}}\bigg(\partial_t|_{(z(p),p)}+\frac{Dz(p)}{f^2(z(p))}\bigg)\quad \forall p\in\Omega. \end{align} $$
$$ \begin{align} N(p)=\frac{f(z(p))}{\sqrt{f^2(z(p))-|Dz(p)|_M^2}}\bigg(\partial_t|_{(z(p),p)}+\frac{Dz(p)}{f^2(z(p))}\bigg)\quad \forall p\in\Omega. \end{align} $$
From (3-39), we have that the shape operator related to the future-pointing Gauss map (3-39) is given by
 $$ \begin{align} AX&=-\frac{1}{f(u)\sqrt{f^2(z)-|Dz|_M^2}}D_XDz-\frac{f'(z)}{\sqrt{f^2(z)-|Dz|_M^2}}X\nonumber\\ &\qquad+\bigg(\frac{-g_M(D_XDz,Dz)}{f(z)(f^2(z)-|Dz|_M^2)^{3/2}}+\frac{f'(z)g_M(Dz,X)}{(f^2(z)-|Dz|_M^2)^{3/2}}\bigg)Dz, \end{align} $$
$$ \begin{align} AX&=-\frac{1}{f(u)\sqrt{f^2(z)-|Dz|_M^2}}D_XDz-\frac{f'(z)}{\sqrt{f^2(z)-|Dz|_M^2}}X\nonumber\\ &\qquad+\bigg(\frac{-g_M(D_XDz,Dz)}{f(z)(f^2(z)-|Dz|_M^2)^{3/2}}+\frac{f'(z)g_M(Dz,X)}{(f^2(z)-|Dz|_M^2)^{3/2}}\bigg)Dz, \end{align} $$
for any vector field X tangential to
![]() $\Omega $
, where D denotes the Levi–Civita connection of
$\Omega $
, where D denotes the Levi–Civita connection of
![]() $(M^n,g_M)$
. Consequently, if
$(M^n,g_M)$
. Consequently, if
![]() $\Sigma ^n(z)$
is a spacelike graph defined over a domain
$\Sigma ^n(z)$
is a spacelike graph defined over a domain
![]() $\Omega \subseteq M^n$
, it is not difficult to verify from (3-40) that the future mean curvature function
$\Omega \subseteq M^n$
, it is not difficult to verify from (3-40) that the future mean curvature function
![]() $H(z)$
of
$H(z)$
of
![]() $\Sigma ^n(z)$
is given by
$\Sigma ^n(z)$
is given by
 $$ \begin{align} H(z)=\mathrm{div}_M\bigg(\dfrac{Dz}{nf(z)\sqrt{f^2(z)-|Dz|_M^2}}\bigg)+\dfrac{f'(z)}{n\sqrt{f^2(z)-|Dz|_M^2}}\bigg(n+\dfrac{|Dz|_M^2}{f^2(z)}\bigg), \end{align} $$
$$ \begin{align} H(z)=\mathrm{div}_M\bigg(\dfrac{Dz}{nf(z)\sqrt{f^2(z)-|Dz|_M^2}}\bigg)+\dfrac{f'(z)}{n\sqrt{f^2(z)-|Dz|_M^2}}\bigg(n+\dfrac{|Dz|_M^2}{f^2(z)}\bigg), \end{align} $$
where
![]() $\mathrm {div}_M$
stands for the divergence operator computed in the metric
$\mathrm {div}_M$
stands for the divergence operator computed in the metric
![]() $g_M$
.
$g_M$
.
Hence, from (2-6) and (3-41), we have that
![]() $\Sigma ^n(z)$
is a spacelike mean curvature flow soliton with respect to
$\Sigma ^n(z)$
is a spacelike mean curvature flow soliton with respect to
![]() $K=f(t)\partial _t$
and with soliton constant c if and only if
$K=f(t)\partial _t$
and with soliton constant c if and only if
![]() $|Dz|_{M}<f(z)$
and z is a solution of the nonlinear differential equation
$|Dz|_{M}<f(z)$
and z is a solution of the nonlinear differential equation
 $$ \begin{align} \mathrm{div}_M\bigg(\dfrac{Dz}{f(z)\sqrt{f(z)^{2}-|Dz|_M^2}}\bigg)=-\dfrac{1}{\sqrt{f(z)^{2}-|Dz|_M^2}}\bigg\{cf(z)^2+f'(z)\bigg(n+\dfrac{|Dz|_M^2}{f(z)^{2}}\bigg)\bigg\}. \end{align} $$
$$ \begin{align} \mathrm{div}_M\bigg(\dfrac{Dz}{f(z)\sqrt{f(z)^{2}-|Dz|_M^2}}\bigg)=-\dfrac{1}{\sqrt{f(z)^{2}-|Dz|_M^2}}\bigg\{cf(z)^2+f'(z)\bigg(n+\dfrac{|Dz|_M^2}{f(z)^{2}}\bigg)\bigg\}. \end{align} $$
We say that
![]() $z\in C^\infty (M)$
has finite
$z\in C^\infty (M)$
has finite
![]() $C^2$
norm when
$C^2$
norm when
In this context, we obtain the following result.
Theorem 3.29. Let
![]() $\overline {M}^{n+1}=-I\times _fM^n$
be a GRW spacetime obeying the SNCC (3-20), with equality occurring only in isolated points of I and whose Riemannian fiber
$\overline {M}^{n+1}=-I\times _fM^n$
be a GRW spacetime obeying the SNCC (3-20), with equality occurring only in isolated points of I and whose Riemannian fiber
![]() $M^n$
is complete. Let
$M^n$
is complete. Let
![]() $z\in C^{\infty }(M)$
be an entire solution of Equation (3-42) for
$z\in C^{\infty }(M)$
be an entire solution of Equation (3-42) for
![]() $c\neq 0$
, with finite
$c\neq 0$
, with finite
![]() $C^2$
norm, such that
$C^2$
norm, such that
![]() $|Dz|_M\leq \alpha f(z)$
, for some constant
$|Dz|_M\leq \alpha f(z)$
, for some constant
![]() $0<\alpha <1$
, and the second soliton function
$0<\alpha <1$
, and the second soliton function
![]() $\tilde {\zeta }_{c}(z)=|A|^2+cf'(z)$
is nonnegative. If
$\tilde {\zeta }_{c}(z)=|A|^2+cf'(z)$
is nonnegative. If
![]() $|Dz|_M\in \mathcal L^1(M)$
, then
$|Dz|_M\in \mathcal L^1(M)$
, then
![]() $z\equiv t_\ast $
for some
$z\equiv t_\ast $
for some
![]() $t_\ast \in I$
, which is implicitly given by the condition
$t_\ast \in I$
, which is implicitly given by the condition
![]() $\zeta (t_\ast )=0$
.
$\zeta (t_\ast )=0$
.
Proof. Let
![]() $z\in C^{\infty }(M)$
be such a solution of Equation (3-42). It follows from (3-40) that the shape operator A of
$z\in C^{\infty }(M)$
be such a solution of Equation (3-42). It follows from (3-40) that the shape operator A of
![]() $\Sigma ^n(z)$
is bounded provided that z has finite
$\Sigma ^n(z)$
is bounded provided that z has finite
![]() $C^2$
. We note also that the finiteness of the
$C^2$
. We note also that the finiteness of the
![]() $C^2$
norm of z implies, in particular, that z is bounded, which, in turn, guarantees that
$C^2$
norm of z implies, in particular, that z is bounded, which, in turn, guarantees that
![]() $\Sigma ^n(z)$
is contained in a bounded timelike region of
$\Sigma ^n(z)$
is contained in a bounded timelike region of
![]() $\overline {M}^{n+1}$
. Consequently, since we are also assuming that
$\overline {M}^{n+1}$
. Consequently, since we are also assuming that
![]() $|Dz|_M\leq \alpha f(z)$
, for some constant
$|Dz|_M\leq \alpha f(z)$
, for some constant
![]() $0<\alpha <1$
, we get that
$0<\alpha <1$
, we get that
for
![]() $\beta =(1-\alpha ^2)\inf _{\Sigma (z)}f^2(z)$
. Thus, we can apply [Reference Albujer, de Lima, Oliveira and VelÁsquez3, Proposition 1] to conclude that
$\beta =(1-\alpha ^2)\inf _{\Sigma (z)}f^2(z)$
. Thus, we can apply [Reference Albujer, de Lima, Oliveira and VelÁsquez3, Proposition 1] to conclude that
![]() $\Sigma ^n(z)$
is complete.
$\Sigma ^n(z)$
is complete.
We also have that
![]() $N=N^\ast -\Theta \partial _t$
, where
$N=N^\ast -\Theta \partial _t$
, where
![]() $N^\ast $
denotes the projection of N onto the fiber
$N^\ast $
denotes the projection of N onto the fiber
![]() $M^n$
. Consequently, from (3-39), we get
$M^n$
. Consequently, from (3-39), we get
Thus, from (3-39) and (3-43), we obtain
 $$ \begin{align} |\nabla z|^2=\frac{|Dz|_M^2}{f^2(z)-|Dz|_M^2}. \end{align} $$
$$ \begin{align} |\nabla z|^2=\frac{|Dz|_M^2}{f^2(z)-|Dz|_M^2}. \end{align} $$
On the other hand, it follows from (3-38) that
![]() $d\Sigma =\sqrt {|G|}dM$
, where
$d\Sigma =\sqrt {|G|}dM$
, where
![]() $dM$
and
$dM$
and
![]() $d\Sigma ^n$
stand for the Riemannian volume elements of
$d\Sigma ^n$
stand for the Riemannian volume elements of
![]() $(M^n,g_M)$
and
$(M^n,g_M)$
and
![]() $(\Sigma ^n(z),g_z)$
, respectively, and
$(\Sigma ^n(z),g_z)$
, respectively, and
![]() $G=det(g_{ij})$
with
$G=det(g_{ij})$
with
Here,
![]() $\{E_1,\ldots ,E^n\}$
denotes a local orthonormal frame with respect to the metric
$\{E_1,\ldots ,E^n\}$
denotes a local orthonormal frame with respect to the metric
![]() $g_M$
. So, it is not difficult to verify that
$g_M$
. So, it is not difficult to verify that
Consequently,
Thus, from (3-44) and (3-45), we get
Hence, since z is bounded and
![]() $|Dz|_{M}\in \mathcal {L}^1(M)$
, from Equation (3-46) we conclude that
$|Dz|_{M}\in \mathcal {L}^1(M)$
, from Equation (3-46) we conclude that
![]() $|\nabla z|\in \mathcal {L}^1(\Sigma ^n(z))$
. Consequently, from (3-9) we get that
$|\nabla z|\in \mathcal {L}^1(\Sigma ^n(z))$
. Consequently, from (3-9) we get that
![]() $|\nabla (\varphi _{\mathcal {K}})|\in \mathcal L_{cu}^1(\Sigma ^n(z))$
. Therefore, we can reason as in the last part of the proof of Theorem 3.4 to conclude the result.
$|\nabla (\varphi _{\mathcal {K}})|\in \mathcal L_{cu}^1(\Sigma ^n(z))$
. Therefore, we can reason as in the last part of the proof of Theorem 3.4 to conclude the result.
From Theorem 3.11, we obtain the following consequence.
Theorem 3.30. Let
![]() $\overline {M}^{n+1}=-I\times _fM^n$
be a GRW spacetime obeying the SNCC (3-20), with equality occurring only in isolated points of I and whose Riemannian fiber
$\overline {M}^{n+1}=-I\times _fM^n$
be a GRW spacetime obeying the SNCC (3-20), with equality occurring only in isolated points of I and whose Riemannian fiber
![]() $M^n$
is complete with a
$M^n$
is complete with a
![]() $(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
$(c\tilde {u})$
-parabolic universal Riemannian covering for some constant
![]() $c\neq 0$
. If
$c\neq 0$
. If
![]() $z\in C^{\infty }(M)$
is an entire solution of Equation (3-42) for c, with finite
$z\in C^{\infty }(M)$
is an entire solution of Equation (3-42) for c, with finite
![]() $C^1$
norm, such that
$C^1$
norm, such that
![]() $|Dz|_M\leq \alpha f(z)$
, for some constant
$|Dz|_M\leq \alpha f(z)$
, for some constant
![]() $0<\alpha <1$
, and the second soliton function
$0<\alpha <1$
, and the second soliton function
![]() $\tilde {\zeta }_{c}(z)=|A|^2+cf'(z)$
is nonnegative, then
$\tilde {\zeta }_{c}(z)=|A|^2+cf'(z)$
is nonnegative, then
![]() $z\equiv t_\ast $
for some
$z\equiv t_\ast $
for some
![]() $t_\ast \in I$
, which is implicitly given by the condition
$t_\ast \in I$
, which is implicitly given by the condition
![]() $\zeta (t_\ast )=0$
.
$\zeta (t_\ast )=0$
.
Proof. Observing that h satisfies (3-2) and (3-43), from (3-40) we obtain
 $$ \begin{align} |\nabla h|^2=\frac{|Dz|_M^2}{f(z)^2-|Dz|_M^2}. \end{align} $$
$$ \begin{align} |\nabla h|^2=\frac{|Dz|_M^2}{f(z)^2-|Dz|_M^2}. \end{align} $$
Hence, since we are assuming that z has finite
![]() $C^1$
norm and taking into account once more that
$C^1$
norm and taking into account once more that
![]() $\Theta ^2=|\nabla h|^2+1$
, with the aid of (3-47) we conclude that
$\Theta ^2=|\nabla h|^2+1$
, with the aid of (3-47) we conclude that
![]() $\Theta $
is bounded. Therefore, the result follows by applying Theorem 3.11.
$\Theta $
is bounded. Therefore, the result follows by applying Theorem 3.11.
From Theorem 3.16, we also obtain the following result.
Theorem 3.31. Let
![]() $\overline {M}^{n+1}=-I\times _fM^n$
be a GRW spacetime obeying the SNCC (3-20) whose Riemannian fiber
$\overline {M}^{n+1}=-I\times _fM^n$
be a GRW spacetime obeying the SNCC (3-20) whose Riemannian fiber
![]() $M^n$
is complete. Let
$M^n$
is complete. Let
![]() $z\in C^{\infty }(M)$
be a bounded entire solution of Equation (3-42) for some constant
$z\in C^{\infty }(M)$
be a bounded entire solution of Equation (3-42) for some constant
![]() $c\neq 0$
such that
$c\neq 0$
such that
![]() $|Dz|_M\leq \alpha f(z)$
, for some constant
$|Dz|_M\leq \alpha f(z)$
, for some constant
![]() $0<\alpha <1$
, and the second soliton function
$0<\alpha <1$
, and the second soliton function
![]() $\tilde {\zeta }_{c}(z)=|A|^2+cf'(z)$
is nonnegative. If
$\tilde {\zeta }_{c}(z)=|A|^2+cf'(z)$
is nonnegative. If
then
![]() $z\equiv t_\ast $
for some
$z\equiv t_\ast $
for some
![]() $t_\ast \in I$
, which is implicitly given by the condition
$t_\ast \in I$
, which is implicitly given by the condition
![]() $\zeta (t_\ast )=0$
.
$\zeta (t_\ast )=0$
.
Proof. From (3-47) and (3-48), we see that hypothesis (3-33) is satisfied. Therefore, the result follows by applying Theorem 3.16.
We close this subsection with the following application of Theorem 3.20
Theorem 3.32. Let
![]() $\overline {M}^{n+1}=-I\times _fM^n$
be a GRW spacetime obeying the SNCC (3-25) whose Riemannian fiber
$\overline {M}^{n+1}=-I\times _fM^n$
be a GRW spacetime obeying the SNCC (3-25) whose Riemannian fiber
![]() $M^n$
is complete. For any constant
$M^n$
is complete. For any constant
![]() $c\neq 0$
, there is no bounded entire solution
$c\neq 0$
, there is no bounded entire solution
![]() $z\in C^{\infty }(M)$
of Equation (3-42) such that
$z\in C^{\infty }(M)$
of Equation (3-42) such that
![]() $|Dz|_M\leq \alpha f(z)$
, for some constant
$|Dz|_M\leq \alpha f(z)$
, for some constant
![]() $0<\alpha <1$
, and
$0<\alpha <1$
, and
![]() $cf'(z)\geq 0$
.
$cf'(z)\geq 0$
.
4 Further rigidity and topological results
Given a smooth function
![]() $\varphi :\Sigma ^n\rightarrow \mathbb {R}$
and a
$\varphi :\Sigma ^n\rightarrow \mathbb {R}$
and a
![]() $(0,2)$
-tensor T defined on a Riemannian manifold
$(0,2)$
-tensor T defined on a Riemannian manifold
![]() $\Sigma ^n$
, we recall that the
$\Sigma ^n$
, we recall that the
![]() $\varphi $
-divergence of T is given by
$\varphi $
-divergence of T is given by
From Equation (4-1), we get the following auxiliary result.
Lemma 4.1. Given a
![]() $(0,2)$
-tensor T and smooth functions
$(0,2)$
-tensor T and smooth functions
![]() $v,\varphi :\Sigma ^n\rightarrow \mathbb {R}$
,
$v,\varphi :\Sigma ^n\rightarrow \mathbb {R}$
,
Proof. Indeed, let
![]() $\{E_i\}$
be a geodesic referential at a point
$\{E_i\}$
be a geodesic referential at a point
![]() $p\in \Sigma ^n$
. Then
$p\in \Sigma ^n$
. Then
 $$ \begin{align*} (\mathrm{div}T)(\nabla v)=&E_i(T(E_i,\nabla v))-T(E_i,\nabla_{E_i}\nabla v)\\ =&\ \mathrm{div}[T(\nabla v)]-\langle T(E_i),\nabla^{2}v(E_i)\rangle\\ =&\ \mathrm{div}[T(\nabla v)]-\langle T,\nabla^{2}v\rangle. \end{align*} $$
$$ \begin{align*} (\mathrm{div}T)(\nabla v)=&E_i(T(E_i,\nabla v))-T(E_i,\nabla_{E_i}\nabla v)\\ =&\ \mathrm{div}[T(\nabla v)]-\langle T(E_i),\nabla^{2}v(E_i)\rangle\\ =&\ \mathrm{div}[T(\nabla v)]-\langle T,\nabla^{2}v\rangle. \end{align*} $$
Hence, since
![]() $\mathrm {div}_{\varphi }(T(\nabla v))=\mathrm {div}(T(\nabla v))-T(\nabla v,\nabla \varphi )$
, we get the desired result from (4-1).
$\mathrm {div}_{\varphi }(T(\nabla v))=\mathrm {div}(T(\nabla v))-T(\nabla v,\nabla \varphi )$
, we get the desired result from (4-1).
We also need the following lemma, the proof of which can be found in [Reference Case, Shu and Wei20, Equation
![]() $(3.8)$
].
$(3.8)$
].
Lemma 4.2. Given a smooth function
![]() $v:\Sigma ^n\rightarrow \mathbb {R}$
, we have that
$v:\Sigma ^n\rightarrow \mathbb {R}$
, we have that
where
![]() $\mathrm {Ric}(.)$
stands for the linear operator metrically equivalent to the Ricci tensor of
$\mathrm {Ric}(.)$
stands for the linear operator metrically equivalent to the Ricci tensor of
![]() $\Sigma ^n$
.
$\Sigma ^n$
.
We recall that the traceless tensor associated with a tensor T is defined by
With this notation, from Equation (3-8), we can verify the equation
where
![]() $u=g(h)$
.
$u=g(h)$
.
Now, we are able to state and prove our next result.
Theorem 4.3. Let
![]() $\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
$\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
![]() $c\neq 0$
. If
$c\neq 0$
. If
![]() $H^2\geq {n^{2}f"(h)}/{2f(h)}$
and
$H^2\geq {n^{2}f"(h)}/{2f(h)}$
and
![]() $\mathrm {Ric}(\nabla h,\nabla h)\geq 0$
, then
$\mathrm {Ric}(\nabla h,\nabla h)\geq 0$
, then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Proof. We recall that, from (3-8),
Taking the trace of Equation (4-2), we get that
On the other hand, taking the divergence of (4-2) and using the relationship given in Lemma 4.2, we obtain the divergence of
![]() $HA$
as
$HA$
as
Inserting (4-3) into (4-4) gives
Since
![]() $H\stackrel {\circ }{A}=H(A-{tr A}/{n}\langle \,,\rangle )=H(A+{H}/{n}\langle \,,\rangle )$
, we reach
$H\stackrel {\circ }{A}=H(A-{tr A}/{n}\langle \,,\rangle )=H(A+{H}/{n}\langle \,,\rangle )$
, we reach
Hence, from (4-6) and (4-5), we obtain
Therefore, from (3-9) and (4-7), we deduce that
From now on, we take
![]() $\varphi =-{2(n-1)c}/{n} u$
. So, we conclude that
$\varphi =-{2(n-1)c}/{n} u$
. So, we conclude that
 $$ \begin{align} (\mathrm{div}_{\varphi}H{\stackrel{\circ}{A}})(c\nabla u)= \frac{2(n-1)c^2}{n^{2}}H^2|\nabla u|^2-c^2f"(h)f(h)|\nabla h|^2(n-1)+ c^2\mathrm{Ric}(\nabla u,\nabla u). \end{align} $$
$$ \begin{align} (\mathrm{div}_{\varphi}H{\stackrel{\circ}{A}})(c\nabla u)= \frac{2(n-1)c^2}{n^{2}}H^2|\nabla u|^2-c^2f"(h)f(h)|\nabla h|^2(n-1)+ c^2\mathrm{Ric}(\nabla u,\nabla u). \end{align} $$
But, from Lemma 4.1,
 $$ \begin{align} \mathrm{div}_{\varphi}[H{\stackrel{\circ}{A}}(c\nabla u)]=&\ \langle H{\stackrel{\circ}{A}}, c\nabla^2 u\rangle+ (\mathrm{div}_{\varphi} H{\stackrel{\circ}{A}})(c\nabla u)\nonumber\\ =&\ |H\stackrel{\circ}{A}|^2+(\mathrm{div}_{\varphi}H{\stackrel{\circ}{A}})(c\nabla u). \end{align} $$
$$ \begin{align} \mathrm{div}_{\varphi}[H{\stackrel{\circ}{A}}(c\nabla u)]=&\ \langle H{\stackrel{\circ}{A}}, c\nabla^2 u\rangle+ (\mathrm{div}_{\varphi} H{\stackrel{\circ}{A}})(c\nabla u)\nonumber\\ =&\ |H\stackrel{\circ}{A}|^2+(\mathrm{div}_{\varphi}H{\stackrel{\circ}{A}})(c\nabla u). \end{align} $$
Thus, from Equations (4-9) and (4-8), we obtain
 $$ \begin{align} \int_{\Sigma^n}\bigg((n-1)c^2|\nabla u|^2\bigg(\frac{-f"(h)}{f(h)}+\frac{2H^2}{n^{2}}\bigg)+c^2\mathrm{Ric}(\nabla u,\nabla u)\bigg)e^{-\varphi}\,d\Sigma\leq 0, \end{align} $$
$$ \begin{align} \int_{\Sigma^n}\bigg((n-1)c^2|\nabla u|^2\bigg(\frac{-f"(h)}{f(h)}+\frac{2H^2}{n^{2}}\bigg)+c^2\mathrm{Ric}(\nabla u,\nabla u)\bigg)e^{-\varphi}\,d\Sigma\leq 0, \end{align} $$
with equality holding if and only if
![]() $\Sigma ^n$
is totally umbilical. Hence, from our hypothesis we conclude that
$\Sigma ^n$
is totally umbilical. Hence, from our hypothesis we conclude that
![]() $\Sigma ^n$
is totally umbilical and that
$\Sigma ^n$
is totally umbilical and that
![]() $\mathrm {Ric}_{\Sigma }(\nabla u,\nabla u)=0$
.
$\mathrm {Ric}_{\Sigma }(\nabla u,\nabla u)=0$
.
Consequently, since
![]() $\Sigma ^n$
is totally umbilical, we conclude from (4-9) that
$\Sigma ^n$
is totally umbilical, we conclude from (4-9) that
![]() $\nabla u$
is a conformal vector field on
$\nabla u$
is a conformal vector field on
![]() $\Sigma ^n$
with
$\Sigma ^n$
with
From Lemma 4.2 and Equation (4-11),
Therefore, from (4-12) jointly with Stokes’ theorem, we deduce that
![]() $\Delta u=0$
, and hence we conclude that h is constant on
$\Delta u=0$
, and hence we conclude that h is constant on
![]() $\Sigma ^n$
.
$\Sigma ^n$
.
Proceeding, we present our next rigidity result for compact spacelike mean curvature flow solitons in a GRW spacetime.
Theorem 4.4. Let
![]() $\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime satisfying the SNCC (3-25) and let
$\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime satisfying the SNCC (3-25) and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
![]() $c\neq 0$
. If
$c\neq 0$
. If
![]() $\mathfrak {L}_{\nabla u}(H)\leq 0$
, where
$\mathfrak {L}_{\nabla u}(H)\leq 0$
, where
![]() $\mathfrak {L}_{\nabla u}$
stands for the Lie derivative on
$\mathfrak {L}_{\nabla u}$
stands for the Lie derivative on
![]() $\Sigma ^n$
with respect to
$\Sigma ^n$
with respect to
![]() $\nabla u$
, then
$\nabla u$
, then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Proof. From (3-27), (3-32) and (3-8), we conclude that
 $$ \begin{align*} \mathrm{Ric}(\nabla u,\nabla u)-(n-1)\frac{f"(h)}{f(h)}|\nabla u|^{2}\geq&\ H\langle A\nabla u,\nabla u\rangle \\ =&\ \frac{H}{c}\langle \nabla H,\nabla u\rangle. \end{align*} $$
$$ \begin{align*} \mathrm{Ric}(\nabla u,\nabla u)-(n-1)\frac{f"(h)}{f(h)}|\nabla u|^{2}\geq&\ H\langle A\nabla u,\nabla u\rangle \\ =&\ \frac{H}{c}\langle \nabla H,\nabla u\rangle. \end{align*} $$
Since
![]() ${H}/{c}$
is negative and
${H}/{c}$
is negative and
![]() $\mathfrak {L}_{\nabla u}(H)=\langle \nabla H,\nabla u\rangle \leq 0$
, we conclude, from (4-10) and the above inequality, that
$\mathfrak {L}_{\nabla u}(H)=\langle \nabla H,\nabla u\rangle \leq 0$
, we conclude, from (4-10) and the above inequality, that
![]() $\Sigma ^n$
is totally umbilical.
$\Sigma ^n$
is totally umbilical.
Since
![]() $\Sigma ^n$
is totally umbilical, from (3-9),
$\Sigma ^n$
is totally umbilical, from (3-9),
Thus,
Now, taking into account that
![]() $cH<0$
, we conclude from the above inequality that
$cH<0$
, we conclude from the above inequality that
![]() $\nabla u=0$
. Therefore,
$\nabla u=0$
. Therefore,
![]() $\Sigma ^n$
must be a slice of
$\Sigma ^n$
must be a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Motivated by [Reference Tadano43, Theorem 10], we establish the following diameter estimate.
Theorem 4.5. Let
![]() $\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
$\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
![]() $c\neq 0$
such that the mean curvature is not constant. If
$c\neq 0$
such that the mean curvature is not constant. If
![]() $f'\neq 0$
, then we have the lower estimate for the diameter of
$f'\neq 0$
, then we have the lower estimate for the diameter of
![]() $\Sigma ^n$
given by
$\Sigma ^n$
given by
 $$ \begin{align*}\mathrm{diam}(\Sigma)\geq |c|\frac{u_{\max}-u_{\min}}{\sqrt{H^{2}_{\max}-H^{2}_{\min}}},\end{align*} $$
$$ \begin{align*}\mathrm{diam}(\Sigma)\geq |c|\frac{u_{\max}-u_{\min}}{\sqrt{H^{2}_{\max}-H^{2}_{\min}}},\end{align*} $$
where
![]() $H^{2}_{\max }$
and
$H^{2}_{\max }$
and
![]() $H^{2}_{\min }$
are the maximum and minimum values of
$H^{2}_{\min }$
are the maximum and minimum values of
![]() $H^{2}$
on
$H^{2}$
on
![]() $\Sigma ^n$
, respectively.
$\Sigma ^n$
, respectively.
Proof. First, from (3-4) we get that
Let
![]() $p\in \Sigma ^n$
be a minimum point of
$p\in \Sigma ^n$
be a minimum point of
![]() $f^{2}(h)$
. Then
$f^{2}(h)$
. Then
On the other hand,
for any
![]() $x\in \Sigma ^n.$
From the above inequality and (4-14), we conclude that
$x\in \Sigma ^n.$
From the above inequality and (4-14), we conclude that
In particular, p is a minimum point of
![]() $H^{2}$
, that is,
$H^{2}$
, that is,
![]() $H^{2}=H^{2}_{\min }.$
From (4-15) we conclude that
$H^{2}=H^{2}_{\min }.$
From (4-15) we conclude that
From the above equation and the mean value theorem,
 $$ \begin{align*}u_{\max}-u_{\min}\leq \max_{\Sigma}{|\nabla u|}\mathrm{diam}(\Sigma)\leq \frac{{\sqrt{H^{2}_{\max}-H^{2}_{\min}}}}{|c|}\mathrm{diam}(\Sigma),\end{align*} $$
$$ \begin{align*}u_{\max}-u_{\min}\leq \max_{\Sigma}{|\nabla u|}\mathrm{diam}(\Sigma)\leq \frac{{\sqrt{H^{2}_{\max}-H^{2}_{\min}}}}{|c|}\mathrm{diam}(\Sigma),\end{align*} $$
and hence we have the desired estimate.
From the previous theorem, we obtain the following consequence.
Corollary 4.6. Let
![]() $\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
$\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
![]() $c\neq 0$
such that the mean curvature is constant. If
$c\neq 0$
such that the mean curvature is constant. If
![]() $f'(h)\neq 0$
, then
$f'(h)\neq 0$
, then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Our next result provides a sufficient condition to guarantee that a compact spacelike mean curvature flow soliton is totally umbilical.
Theorem 4.7. Let
![]() $\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
$\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
![]() $c\neq 0$
. If
$c\neq 0$
. If
then
![]() $\nabla u$
is a conformal vector field and, therefore,
$\nabla u$
is a conformal vector field and, therefore,
![]() $\Sigma ^n$
is totally umbilical. Moreover, if H is constant, then
$\Sigma ^n$
is totally umbilical. Moreover, if H is constant, then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Proof. From Bochner’s formula [Reference Bochner16],
But, we note that
Substituting the above equality into (4-16) and applying Stokes’ theorem gives
 $$ \begin{align*} \int_{\Sigma^n}|{\stackrel\circ {\nabla^2}}u|^2 \,d\Sigma =\frac{n-1}{n}\int_{\Sigma^n}(\Delta u)^2\,d\Sigma-\int_{\Sigma^n}\mathrm{Ric}(\nabla u,\nabla u)\,d\Sigma. \end{align*} $$
$$ \begin{align*} \int_{\Sigma^n}|{\stackrel\circ {\nabla^2}}u|^2 \,d\Sigma =\frac{n-1}{n}\int_{\Sigma^n}(\Delta u)^2\,d\Sigma-\int_{\Sigma^n}\mathrm{Ric}(\nabla u,\nabla u)\,d\Sigma. \end{align*} $$
From our hypothesis on the Ricci tensor and (4-3), we conclude that
![]() $\nabla u$
is a conformal vector field. Moreover, since
$\nabla u$
is a conformal vector field. Moreover, since
![]() $c\neq 0$
, from equality (4-13) we have that
$c\neq 0$
, from equality (4-13) we have that
![]() $H\neq 0$
. Finally, from (4-9), we conclude that
$H\neq 0$
. Finally, from (4-9), we conclude that
![]() $\Sigma ^n$
is totally umbilical.
$\Sigma ^n$
is totally umbilical.
On the other hand, since
![]() $\Sigma ^n$
is totally umbilical, from (3-9),
$\Sigma ^n$
is totally umbilical, from (3-9),
From the above equation, a straightforward calculation shows that
![]() $He^{{c}/{n}u}$
is constant. Thus, supposing that H is a constant, we conclude that
$He^{{c}/{n}u}$
is constant. Thus, supposing that H is a constant, we conclude that
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}$
.
$\overline {M}$
.
Inspired by [Reference Pan36], we also obtain the following result.
Proposition 4.8. Let
![]() $\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
$\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
![]() $c\neq 0$
. Suppose that
$c\neq 0$
. Suppose that
![]() $\Sigma ^n$
is totally umbilical and
$\Sigma ^n$
is totally umbilical and
![]() $\mathrm {Ric}$
is nonpositive. Then
$\mathrm {Ric}$
is nonpositive. Then
![]() $\Sigma ^n$
is a slice of
$\Sigma ^n$
is a slice of
![]() $\overline {M}^{n+1}$
.
$\overline {M}^{n+1}$
.
Proof. Using the same ideas as in the previous theorem, we conclude that
![]() $\nabla u$
is a conformal vector field. Thus, from (4-12),
$\nabla u$
is a conformal vector field. Thus, from (4-12),
Applying Stokes’ theorem, we conclude that
and, therefore, h is constant.
The last result of this section provides an interesting topological characterization for a compact spacelike mean curvature flow soliton.
Theorem 4.9. Let
![]() $\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
$\overline {M}^{n+1}=-I\times _f M^{n}$
be a GRW spacetime and let
![]() $\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright \overline {M}^{n+1}$
be a compact spacelike mean curvature flow soliton with soliton constant
![]() $c\neq 0$
. Suppose that
$c\neq 0$
. Suppose that
![]() $\Sigma ^n$
is totally umbilical and it is not contained in a slice of
$\Sigma ^n$
is totally umbilical and it is not contained in a slice of
![]() $\overline {M}^{n+1}$
. If
$\overline {M}^{n+1}$
. If
![]() $\Sigma ^n$
has finite fundamental group, then
$\Sigma ^n$
has finite fundamental group, then
![]() $\Sigma ^n$
is diffeomorphic to an Euclidean sphere.
$\Sigma ^n$
is diffeomorphic to an Euclidean sphere.
Proof. Since we are assuming that
![]() $\Sigma ^n$
is totally umbilical and that
$\Sigma ^n$
is totally umbilical and that
![]() $\Sigma ^n$
it is not contained in a slice, we conclude that
$\Sigma ^n$
it is not contained in a slice, we conclude that
![]() $\nabla u$
is a non-Killing conformal vector field. Therefore, since
$\nabla u$
is a non-Killing conformal vector field. Therefore, since
![]() $\Sigma ^n$
has finite fundamental group, we conclude the desired result from [Reference Suyama and Tsukamoto42, Theorem 2].
$\Sigma ^n$
has finite fundamental group, we conclude the desired result from [Reference Suyama and Tsukamoto42, Theorem 2].
5 Stability of spacelike mean curvature flow solitons in GRW spacetimes
Let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a complete spacelike mean curvature flow soliton with soliton constant c. We recall that a variation with compact support and fixed boundary of
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a complete spacelike mean curvature flow soliton with soliton constant c. We recall that a variation with compact support and fixed boundary of
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is a smooth mapping
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is a smooth mapping
such that:
-
(i) for
 $s\in (-\epsilon ,\epsilon )$
, the map
$s\in (-\epsilon ,\epsilon )$
, the map
 $F_s:\Sigma ^n\looparrowright -I\times _{f}M^n$
given by
$F_s:\Sigma ^n\looparrowright -I\times _{f}M^n$
given by
 $F_s(q)=F(s,q)$
is an spacelike immersion with
$F_s(q)=F(s,q)$
is an spacelike immersion with
 $F_0=x$
; and
$F_0=x$
; and -
(ii)
 $F_s|_{\partial \Sigma }=\psi |_{\partial \Sigma }$
for all
$F_s|_{\partial \Sigma }=\psi |_{\partial \Sigma }$
for all
 $s\in (-\epsilon ,\epsilon )$
.
$s\in (-\epsilon ,\epsilon )$
.
In all that follows, we let
![]() $dM_s$
denote the volume element of the metric induced on
$dM_s$
denote the volume element of the metric induced on
![]() $\Sigma ^n$
by
$\Sigma ^n$
by
![]() $F_s$
and let
$F_s$
and let
![]() $N_s$
denote the unit normal vector field along
$N_s$
denote the unit normal vector field along
![]() $F_s$
. Moreover, we also consider in
$F_s$
. Moreover, we also consider in
![]() $\Sigma ^n$
the weighted volume form given by
$\Sigma ^n$
the weighted volume form given by
![]() $d\mu _s=e^{-f}dM_s$
. When
$d\mu _s=e^{-f}dM_s$
. When
![]() $s=0$
, all of these objects coincide with the ones defined in
$s=0$
, all of these objects coincide with the ones defined in
![]() $\Sigma ^n$
.
$\Sigma ^n$
.
The variational field associated to the variation F is the vector field
![]() ${\partial F}/{\partial s}|_{s=0}$
. Letting
${\partial F}/{\partial s}|_{s=0}$
. Letting
we get
 $$ \begin{align*}\frac{\partial F}{\partial s}\bigg|_{s=0}=u_0N+\bigg(\frac{\partial F}{\partial s}\bigg|_{s=0}\bigg)^\top,\end{align*} $$
$$ \begin{align*}\frac{\partial F}{\partial s}\bigg|_{s=0}=u_0N+\bigg(\frac{\partial F}{\partial s}\bigg|_{s=0}\bigg)^\top,\end{align*} $$
where
![]() $(\cdot )^\top $
stands for tangential components.
$(\cdot )^\top $
stands for tangential components.
Denoting the set of all smooth functions on
![]() $\Sigma ^n$
with compact support by
$\Sigma ^n$
with compact support by
![]() $C_0^{\infty }(\Sigma ^n)$
, according to [Reference Barros, Brasil and Caminha14, Lemma
$C_0^{\infty }(\Sigma ^n)$
, according to [Reference Barros, Brasil and Caminha14, Lemma
![]() $2.1$
] and [Reference Barbosa and do Carmo13, Lemma
$2.1$
] and [Reference Barbosa and do Carmo13, Lemma
![]() $2.1$
], every function
$2.1$
], every function
![]() $\varphi \in C_0^{\infty }(\Sigma ^n)$
with
$\varphi \in C_0^{\infty }(\Sigma ^n)$
with
induces a variation of
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
of the type (5-1), with variational normal field
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
of the type (5-1), with variational normal field
![]() ${\partial F}/{\partial s}|_{s=0}=\varphi N$
and with first variation
${\partial F}/{\partial s}|_{s=0}=\varphi N$
and with first variation
![]() $\delta _\varphi \mathbb {A}$
of the area functional
$\delta _\varphi \mathbb {A}$
of the area functional
 $$ \begin{align*} \mathbb{A}:(-\epsilon,\epsilon)&\rightarrow\mathbb{R}\\ s&\mapsto\mathbb{A}(s)=\mathrm{Area}(F_s(\Sigma^n))=\int_{\Sigma^n}\,d\Sigma_s, \end{align*} $$
$$ \begin{align*} \mathbb{A}:(-\epsilon,\epsilon)&\rightarrow\mathbb{R}\\ s&\mapsto\mathbb{A}(s)=\mathrm{Area}(F_s(\Sigma^n))=\int_{\Sigma^n}\,d\Sigma_s, \end{align*} $$
given by
Here, N stands for a normal unit vector field globally defined on
![]() $\Sigma ^n$
,
$\Sigma ^n$
,
![]() $d\Sigma _s$
denotes the volume element of
$d\Sigma _s$
denotes the volume element of
![]() $\Sigma ^n$
with respect to the metric induced by
$\Sigma ^n$
with respect to the metric induced by
![]() $F_s:\Sigma ^n\looparrowright -I\times _{f}M^n$
and H is the mean curvature function of
$F_s:\Sigma ^n\looparrowright -I\times _{f}M^n$
and H is the mean curvature function of
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with respect to N.
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with respect to N.
As a consequence of (5-3), maximal compact spacelike mean curvature flow solitons of
![]() $-I\times _{f}M^n$
(that is, with mean curvature identically zero) are characterized as critical points of the area functional
$-I\times _{f}M^n$
(that is, with mean curvature identically zero) are characterized as critical points of the area functional
![]() $\mathbb {A}$
, whereas any compact spacelike mean curvature flow soliton
$\mathbb {A}$
, whereas any compact spacelike mean curvature flow soliton
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with constant mean curvature H is a critical point of
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with constant mean curvature H is a critical point of
![]() $\mathbb {A}$
restricted to functions
$\mathbb {A}$
restricted to functions
![]() $\varphi \in C^{\infty }(\Sigma ^n)$
that satisfy condition (5-2). Geometrically, this additional condition means that the variations under consideration preserve a certain volume functional (for more details, see [Reference Barbosa and do Carmo13]).
$\varphi \in C^{\infty }(\Sigma ^n)$
that satisfy condition (5-2). Geometrically, this additional condition means that the variations under consideration preserve a certain volume functional (for more details, see [Reference Barbosa and do Carmo13]).
For these critical points, [Reference Barros, Brasil and Caminha14, Proposition
![]() $2.3$
] asserts that the stability of the corresponding variational problem is given by the second variation of the area functional
$2.3$
] asserts that the stability of the corresponding variational problem is given by the second variation of the area functional
![]() $\mathbb {A}$
, which is given by
$\mathbb {A}$
, which is given by
 $$ \begin{align*} \delta^{\,2}_\varphi\,\mathbb{A}=\frac{d^{\,2}\mathbb{A}}{ds^2}(0)(\varphi)=\int_{\Sigma^n}\{\Delta(\varphi)-\{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi\}\varphi\,d\Sigma, \end{align*} $$
$$ \begin{align*} \delta^{\,2}_\varphi\,\mathbb{A}=\frac{d^{\,2}\mathbb{A}}{ds^2}(0)(\varphi)=\int_{\Sigma^n}\{\Delta(\varphi)-\{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi\}\varphi\,d\Sigma, \end{align*} $$
where
![]() $\Delta $
stands for the Laplacian operator on
$\Delta $
stands for the Laplacian operator on
![]() $\Sigma ^n$
,
$\Sigma ^n$
,
![]() $\overline {\mathrm {Ric}}$
is the Ricci tensor of the GRW spacetime
$\overline {\mathrm {Ric}}$
is the Ricci tensor of the GRW spacetime
![]() $-I\times _fM^n$
and
$-I\times _fM^n$
and
![]() $|A|$
denotes the length of the shape operator A of
$|A|$
denotes the length of the shape operator A of
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with respect to N. In this setting, we establish the following definition.
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with respect to N. In this setting, we establish the following definition.
Definition 5.1. A compact spacelike mean curvature flow soliton
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with constant mean curvature H is said to be strongly stable if
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with constant mean curvature H is said to be strongly stable if
![]() $\delta ^{\,2}_\varphi \,\mathbb {A}\leq 0$
for every
$\delta ^{\,2}_\varphi \,\mathbb {A}\leq 0$
for every
![]() $\varphi \in C^{\infty }(\Sigma ^n)$
.
$\varphi \in C^{\infty }(\Sigma ^n)$
.
In our next result, we impose a suitable behavior on the warping function f to obtain a nonexistence result for strongly stable spacelike mean curvature flow solitons immersed in
![]() $-I\times _fM^n$
.
$-I\times _fM^n$
.
Theorem 5.2. There is no strongly stable compact spacelike mean curvature flow soliton
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with soliton constant
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with soliton constant
![]() $c\not =0$
whose mean curvature H is constant and whose height function h satisfies
$c\not =0$
whose mean curvature H is constant and whose height function h satisfies
![]() $cf'(h)f(h)+nf"(h)>0$
on
$cf'(h)f(h)+nf"(h)>0$
on
![]() $\Sigma ^n$
.
$\Sigma ^n$
.
Proof. By contradiction, let us suppose the existence of such a soliton
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
. From the first equation in the proof of [Reference Caminha and de Lima19, Proposition
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
. From the first equation in the proof of [Reference Caminha and de Lima19, Proposition
![]() $2.1$
], we have
$2.1$
], we have
 $$ \begin{align} \Delta(\varphi_{\mathcal{K}})=&\ \{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}-\{nN(f'(h))-Hf'(h)\}+\langle \mathcal{K},\nabla H\rangle\nonumber\\ =&\ \{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}+c\,\varphi_{\mathcal{K}}f'(h)-nN(f'(h)), \end{align} $$
$$ \begin{align} \Delta(\varphi_{\mathcal{K}})=&\ \{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}-\{nN(f'(h))-Hf'(h)\}+\langle \mathcal{K},\nabla H\rangle\nonumber\\ =&\ \{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}+c\,\varphi_{\mathcal{K}}f'(h)-nN(f'(h)), \end{align} $$
where
![]() $\varphi _{\mathcal {K}}\in C^{\infty }(\Sigma ^n)$
is the support function defined in (3-10).
$\varphi _{\mathcal {K}}\in C^{\infty }(\Sigma ^n)$
is the support function defined in (3-10).
On the other hand, we also have
 $$ \begin{align} N(f'(h))=-\langle f"(h)\partial_{\,t},N\rangle\,=-\,\dfrac{f"(h)}{f(h)}\,\varphi_{\mathcal{K}}. \end{align} $$
$$ \begin{align} N(f'(h))=-\langle f"(h)\partial_{\,t},N\rangle\,=-\,\dfrac{f"(h)}{f(h)}\,\varphi_{\mathcal{K}}. \end{align} $$
Thus, from (5-4) and (5-5), we get
 $$ \begin{align} \Delta(\varphi_{\mathcal{K}})\,=&\ \{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}+c\,\varphi_{\mathcal{K}}f'(h)-nN(f'(h)) \nonumber \\ =&\ \{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}+\bigg\{c\,f'(h)+n\,\dfrac{f"(h)}{f(h)}\bigg\}\,\varphi_{\mathcal{K}}. \end{align} $$
$$ \begin{align} \Delta(\varphi_{\mathcal{K}})\,=&\ \{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}+c\,\varphi_{\mathcal{K}}f'(h)-nN(f'(h)) \nonumber \\ =&\ \{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}+\bigg\{c\,f'(h)+n\,\dfrac{f"(h)}{f(h)}\bigg\}\,\varphi_{\mathcal{K}}. \end{align} $$
Moreover, since
![]() $H=c\,\varphi _{\mathcal {K}}$
is constant and
$H=c\,\varphi _{\mathcal {K}}$
is constant and
![]() $c\not =0$
, we have that
$c\not =0$
, we have that
![]() $\varphi _{\mathcal {K}}$
is also constant on
$\varphi _{\mathcal {K}}$
is also constant on
![]() $\Sigma ^n$
. Hence, from (5-6), we obtain
$\Sigma ^n$
. Hence, from (5-6), we obtain
 $$ \begin{align} -\{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}=\bigg\{c\,f'(h)+n\,\dfrac{f"(h)}{f(h)}\bigg\}\,\varphi_{\mathcal{K}}. \end{align} $$
$$ \begin{align} -\{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}=\bigg\{c\,f'(h)+n\,\dfrac{f"(h)}{f(h)}\bigg\}\,\varphi_{\mathcal{K}}. \end{align} $$
Now, from our hypothesis of strong stability and taking into account Definition 5.1, we currently have
for every
![]() $\varphi \in C^{\infty }(\Sigma ^n)$
.
$\varphi \in C^{\infty }(\Sigma ^n)$
.
Thus, making
![]() $\varphi =\varphi _{\mathcal {K}}<0$
(see (3-11)), from the hypothesis that
$\varphi =\varphi _{\mathcal {K}}<0$
(see (3-11)), from the hypothesis that
![]() $cf'(h)f(h)+nf"(h)>0$
jointly with (5-7) we get
$cf'(h)f(h)+nf"(h)>0$
jointly with (5-7) we get
 $$ \begin{align*} 0<\int_{\Sigma^n}\bigg\{c\,f'(h)+n\,\dfrac{f"(h)}{f(h)}\bigg\}\,\varphi_{\mathcal{K}}^2=\int_{\Sigma^n}\{\underbrace{\Delta(\varphi_{\mathcal{K}})}_{0}-\{\overline{\mathrm{ Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}\}\varphi_{\mathcal{K}}\,d\Sigma\leq0, \end{align*} $$
$$ \begin{align*} 0<\int_{\Sigma^n}\bigg\{c\,f'(h)+n\,\dfrac{f"(h)}{f(h)}\bigg\}\,\varphi_{\mathcal{K}}^2=\int_{\Sigma^n}\{\underbrace{\Delta(\varphi_{\mathcal{K}})}_{0}-\{\overline{\mathrm{ Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}\}\varphi_{\mathcal{K}}\,d\Sigma\leq0, \end{align*} $$
and we reach an absurdity.
From Theorem 5.2, we get the following application.
Corollary 5.3. There is no strongly stable compact spacelike mean curvature flow soliton in a steady-state-type spacetime
![]() $-I\times _{e^t}M^n$
with soliton constant
$-I\times _{e^t}M^n$
with soliton constant
![]() $c>0$
and constant mean curvature.
$c>0$
and constant mean curvature.
In what follows, we consider the function
where
![]() $g:I\rightarrow \mathbb {R}$
is the primitive of the warping function f that was used to define the reparametrization
$g:I\rightarrow \mathbb {R}$
is the primitive of the warping function f that was used to define the reparametrization
![]() $u=-g(h)$
of the height function h of the spacelike mean curvature flow soliton
$u=-g(h)$
of the height function h of the spacelike mean curvature flow soliton
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
(see (3-6)). From (3-1), we observe that
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
(see (3-6)). From (3-1), we observe that
![]() $\overline {u}=u$
on
$\overline {u}=u$
on
![]() $\Sigma ^n$
, and hence
$\Sigma ^n$
, and hence
![]() $\bar {u}$
is a smooth extension of u. Following [Reference Bakry, Émery, Azéma and Yor12], we consider the Bakry–Émery–Ricci tensor
$\bar {u}$
is a smooth extension of u. Following [Reference Bakry, Émery, Azéma and Yor12], we consider the Bakry–Émery–Ricci tensor
![]() $\overline {\mathrm {Ric}}_{c\bar {u}}$
of
$\overline {\mathrm {Ric}}_{c\bar {u}}$
of
![]() $-I\times _{f}M^n$
, which is given by
$-I\times _{f}M^n$
, which is given by
where
![]() $\overline {\mathrm {Ric}}$
and
$\overline {\mathrm {Ric}}$
and
![]() $\overline {\nabla }^{2}$
are the standard Ricci tensor and the Hessian in
$\overline {\nabla }^{2}$
are the standard Ricci tensor and the Hessian in
![]() $-I\times _{f}M^n$
, respectively. We also consider the modified volume element
$-I\times _{f}M^n$
, respectively. We also consider the modified volume element
 $$ \begin{align*} d\bar{\mu}=e^{c\bar{u}}dV, \end{align*} $$
$$ \begin{align*} d\bar{\mu}=e^{c\bar{u}}dV, \end{align*} $$
where
![]() $dV$
denotes the standard volume element of
$dV$
denotes the standard volume element of
![]() $-I\times _{f}M^n$
. We note that, on
$-I\times _{f}M^n$
. We note that, on
![]() $\Sigma ^n$
,
$\Sigma ^n$
,
![]() $d\bar {\mu }$
coincides with the modified volume element
$d\bar {\mu }$
coincides with the modified volume element
![]() $d\mu $
previously defined in (3-21).
$d\mu $
previously defined in (3-21).
With all of these considerations, we have that any function
![]() $\varphi \in C_0^{\infty }(\Sigma ^n)$
with
$\varphi \in C_0^{\infty }(\Sigma ^n)$
with
induces a variation of
![]() $\psi:\Sigma^n\looparrowright -I\times_{f}M^n$
, having compact support and fixed boundary, with variational normal field
$\psi:\Sigma^n\looparrowright -I\times_{f}M^n$
, having compact support and fixed boundary, with variational normal field
![]() ${\partial F}/{\partial s}|_{s=0}=\varphi N$
and with first variation
${\partial F}/{\partial s}|_{s=0}=\varphi N$
and with first variation
![]() $\delta _\varphi (\mathbb {A}_{cu})$
of the modified area functional
$\delta _\varphi (\mathbb {A}_{cu})$
of the modified area functional
 $$ \begin{align*} \begin{aligned} \mathbb{A}_{\,cu}:(-\epsilon,\epsilon)&\rightarrow\mathbb{R}\\ s&\mapsto\mathbb{A}_{cu}(s)=\int_{\Sigma^n}d\mu \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathbb{A}_{\,cu}:(-\epsilon,\epsilon)&\rightarrow\mathbb{R}\\ s&\mapsto\mathbb{A}_{cu}(s)=\int_{\Sigma^n}d\mu \end{aligned} \end{align*} $$
given by
(see, for example, [Reference Castro and Rosales21, Lemma
![]() $3.2$
]), where
$3.2$
]), where
![]() $H_{c\bar {u}}$
is the modified mean curvature of
$H_{c\bar {u}}$
is the modified mean curvature of
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
defined by
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
defined by
But, since
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is a spacelike mean curvature flow soliton with respect to the closed conformal vector field
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is a spacelike mean curvature flow soliton with respect to the closed conformal vector field
![]() $\mathcal {K}=f(t)\partial _{\,t}$
and with soliton constant
$\mathcal {K}=f(t)\partial _{\,t}$
and with soliton constant
![]() $c\not =0$
, from (2-6) and (3-7) we get that
$c\not =0$
, from (2-6) and (3-7) we get that
 $$ \begin{align} H_{c\overline{u}}=&\ cf(h)\Theta-c\langle\overline{\nabla}(\bar{u}),N\rangle=cf(h)\Theta-c\langle(\overline{\nabla}(\bar{u})^\top+\overline{\nabla}(\bar{u})^\perp),N\rangle \nonumber \\ =&\ cf(h)\Theta-c\langle\overline{\nabla}(\bar{u})^\perp\,,N\rangle=cf(h)\Theta-c\langle(-g'(h)\overline{\nabla}\pi_I))^\perp\,,N\rangle.\nonumber \\ =&\ cf(h)\Theta-cf(h)\langle\partial_{\,t}\,,N\rangle=0. \end{align} $$
$$ \begin{align} H_{c\overline{u}}=&\ cf(h)\Theta-c\langle\overline{\nabla}(\bar{u}),N\rangle=cf(h)\Theta-c\langle(\overline{\nabla}(\bar{u})^\top+\overline{\nabla}(\bar{u})^\perp),N\rangle \nonumber \\ =&\ cf(h)\Theta-c\langle\overline{\nabla}(\bar{u})^\perp\,,N\rangle=cf(h)\Theta-c\langle(-g'(h)\overline{\nabla}\pi_I))^\perp\,,N\rangle.\nonumber \\ =&\ cf(h)\Theta-cf(h)\langle\partial_{\,t}\,,N\rangle=0. \end{align} $$
Therefore, from (5-9) and (5-10), we obtain that any spacelike mean curvature flow soliton
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with respect to the closed conformal vector field
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
with respect to the closed conformal vector field
![]() ${\mathcal {K}=f(t)\partial _{\,t}}$
and with soliton constant
${\mathcal {K}=f(t)\partial _{\,t}}$
and with soliton constant
![]() $c\not =0$
is a critical point of the modified area functional
$c\not =0$
is a critical point of the modified area functional
![]() $\mathbb {A}_{cu}$
. Furthermore, the stability operator
$\mathbb {A}_{cu}$
. Furthermore, the stability operator
![]() $L_{cu}:C_0^{\infty }(\Sigma ^n)\rightarrow C_0^{\infty }(\Sigma ^n)$
for this variational problem is given by the second variation formula
$L_{cu}:C_0^{\infty }(\Sigma ^n)\rightarrow C_0^{\infty }(\Sigma ^n)$
for this variational problem is given by the second variation formula
![]() $\delta ^2_{\varphi }(\mathbb {A}_{cu})$
of
$\delta ^2_{\varphi }(\mathbb {A}_{cu})$
of
![]() $\mathbb {A}_{cu}$
, which, in our case, is written as (see, for example, [Reference Castro and Rosales21, Proposition
$\mathbb {A}_{cu}$
, which, in our case, is written as (see, for example, [Reference Castro and Rosales21, Proposition
![]() $3.5$
] for the case
$3.5$
] for the case
![]() $H_{c\bar {u}}=0$
)
$H_{c\bar {u}}=0$
)
 $$ \begin{align*} \delta^2_{\varphi}(\mathbb{A}_{cu})=\frac{d^{\,2}\mathbb{A}_{cu}}{ds^2}(0)(\varphi)=\int_{\Sigma^n}\varphi L_{cu}(\varphi)\,d\mu, \end{align*} $$
$$ \begin{align*} \delta^2_{\varphi}(\mathbb{A}_{cu})=\frac{d^{\,2}\mathbb{A}_{cu}}{ds^2}(0)(\varphi)=\int_{\Sigma^n}\varphi L_{cu}(\varphi)\,d\mu, \end{align*} $$
with
where
![]() $\Delta _{cu}$
is the drift Laplacian operator on
$\Delta _{cu}$
is the drift Laplacian operator on
![]() $\Sigma ^n$
given in (3-17). So, using (5-8), we can rewrite the stability operator
$\Sigma ^n$
given in (3-17). So, using (5-8), we can rewrite the stability operator
![]() $L_{cu}$
as
$L_{cu}$
as
The following notion of stability concerning spacelike mean curvature flow solitons in GRW spacetime now makes sense.
Definition 5.4. Let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with soliton constant
![]() $c\not =0$
. We say that
$c\not =0$
. We say that
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is
![]() $L_{cu}$
-stable if
$L_{cu}$
-stable if
![]() $\delta ^2_{\varphi }(\mathbb {A}_{cu})\leq 0$
for all
$\delta ^2_{\varphi }(\mathbb {A}_{cu})\leq 0$
for all
![]() $\varphi \in C_0^{\infty }(\Sigma ^n)$
.
$\varphi \in C_0^{\infty }(\Sigma ^n)$
.
The next auxiliary result gives a sufficient condition to guarantee that a spacelike mean curvature flow soliton must be
![]() $L_{cu}$
-stable (for its proof, see [Reference de Lima, de Lima and dos Santos25, Lemma
$L_{cu}$
-stable (for its proof, see [Reference de Lima, de Lima and dos Santos25, Lemma
![]() $3.2$
]).
$3.2$
]).
Lemma 5.5. Let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with soliton constant
![]() $c\not =0$
. If there exists a positive smooth function
$c\not =0$
. If there exists a positive smooth function
![]() $\varphi \in C^{\infty }(\Sigma ^n)$
such that
$\varphi \in C^{\infty }(\Sigma ^n)$
such that
![]() $L_{cu}(\varphi )\leq 0$
, then
$L_{cu}(\varphi )\leq 0$
, then
![]() $\Sigma ^n$
is
$\Sigma ^n$
is
![]() $L_{cu}$
-stable.
$L_{cu}$
-stable.
Now, we analyze the behavior of the warping function f along a spacelike mean curvature flow soliton to infer its
![]() $L_{cu}$
-stability.
$L_{cu}$
-stability.
Theorem 5.6. Let
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with soliton constant
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
be a spacelike mean curvature flow soliton with soliton constant
![]() $c\not =0$
.
$c\not =0$
.
-
(a) If
 $\zeta ^{\prime }_c(t)\leq 0$
on
$\zeta ^{\prime }_c(t)\leq 0$
on
 $\Sigma ^n$
, then
$\Sigma ^n$
, then
 $\psi :\Sigma ^n\looparrowright -I\times _fM^n$
is
$\psi :\Sigma ^n\looparrowright -I\times _fM^n$
is
 $L_{cu}$
-stable.
$L_{cu}$
-stable. -
(b) If
 $\Sigma ^n$
is compact and
$\Sigma ^n$
is compact and
 $\zeta ^{\prime }_c(t)\geq 0$
on it, then
$\zeta ^{\prime }_c(t)\geq 0$
on it, then
 $\psi :\Sigma ^n\looparrowright -I\times _fM^n$
is
$\psi :\Sigma ^n\looparrowright -I\times _fM^n$
is
 $L_{cu}$
-stable if and only if
$L_{cu}$
-stable if and only if
 $\zeta _c(t)$
is constant on
$\zeta _c(t)$
is constant on
 $\Sigma ^n$
.
$\Sigma ^n$
. -
(c) If
 $\Sigma ^n$
is compact and
$\Sigma ^n$
is compact and
 $\zeta ^{\prime }_c(t)>0$
on it, then
$\zeta ^{\prime }_c(t)>0$
on it, then
 $\psi :\Sigma ^n\looparrowright -I\times _fM^n$
cannot be
$\psi :\Sigma ^n\looparrowright -I\times _fM^n$
cannot be
 $L_{cu}$
-stable.
$L_{cu}$
-stable.
Proof. From (5-6),
 $$ \begin{align*} \Delta(\varphi_{\mathcal{K}})=\{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}+\bigg\{c\,f'(h)+n\,\dfrac{f"(h)}{f(h)}\bigg\}\,\varphi_{\mathcal{K}}, \end{align*} $$
$$ \begin{align*} \Delta(\varphi_{\mathcal{K}})=\{\overline{\mathrm{Ric}}(N,N)+|A|^2\}\varphi_{\mathcal{K}}+\bigg\{c\,f'(h)+n\,\dfrac{f"(h)}{f(h)}\bigg\}\,\varphi_{\mathcal{K}}, \end{align*} $$
where
![]() $\varphi _{\mathcal {K}}\in C^{\infty }(\Sigma ^n)$
is the support function defined in (3-10). So, by applying
$\varphi _{\mathcal {K}}\in C^{\infty }(\Sigma ^n)$
is the support function defined in (3-10). So, by applying
![]() $\varphi _{\mathcal {K}}$
to the stability operator
$\varphi _{\mathcal {K}}$
to the stability operator
![]() $L_{cu}$
and using the last equation, we get
$L_{cu}$
and using the last equation, we get
 $$ \begin{align*} L_{cu}(\varphi_{\mathcal{K}})=\Delta_{cu}(\varphi_{\mathcal{K}})-\{\overline{\mathrm{Ric}}(N,N)-cf'(h)+|A|^2\}\varphi_{\mathcal{K}}=\bigg\{2cf'(h)+n\,\dfrac{f"(h)}{f(h)}\,\bigg\}\varphi_{\mathcal{K}}. \end{align*} $$
$$ \begin{align*} L_{cu}(\varphi_{\mathcal{K}})=\Delta_{cu}(\varphi_{\mathcal{K}})-\{\overline{\mathrm{Ric}}(N,N)-cf'(h)+|A|^2\}\varphi_{\mathcal{K}}=\bigg\{2cf'(h)+n\,\dfrac{f"(h)}{f(h)}\,\bigg\}\varphi_{\mathcal{K}}. \end{align*} $$
Hence,
where
![]() $-\varphi _{\mathcal {K}}$
is a positive smooth function on
$-\varphi _{\mathcal {K}}$
is a positive smooth function on
![]() $\Sigma ^n$
and, with a direct application of Lemma 5.5, the result of item (a) is obtained directly.
$\Sigma ^n$
and, with a direct application of Lemma 5.5, the result of item (a) is obtained directly.
Now, let us consider item (b). Note that, in this case,
![]() $C_0^{\infty }(\Sigma ^n)=C^{\infty }(\Sigma ^n)$
. So, if
$C_0^{\infty }(\Sigma ^n)=C^{\infty }(\Sigma ^n)$
. So, if
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is
![]() $L_{cu}$
-stable, from Definition 5.4 and Equation (5-12) we get
$L_{cu}$
-stable, from Definition 5.4 and Equation (5-12) we get
 $$ \begin{align} 0\geq&\ \delta^{\,2}_{(-\varphi_{\mathcal{K}})}(\mathbb{A}_{cu})=\int_{\Sigma^n}(-\varphi_{\mathcal{K}})L_{cu}(-\varphi_{\mathcal{K}})\,d\mu\nonumber\\ =&\int_{\Sigma^n}\{2cf'(h)f(h)+nf"(h)\}(-\varphi_{\mathcal{K}})^2\,d\mu\geq0, \end{align} $$
$$ \begin{align} 0\geq&\ \delta^{\,2}_{(-\varphi_{\mathcal{K}})}(\mathbb{A}_{cu})=\int_{\Sigma^n}(-\varphi_{\mathcal{K}})L_{cu}(-\varphi_{\mathcal{K}})\,d\mu\nonumber\\ =&\int_{\Sigma^n}\{2cf'(h)f(h)+nf"(h)\}(-\varphi_{\mathcal{K}})^2\,d\mu\geq0, \end{align} $$
which guarantees that
![]() $\zeta _c(t)$
is constant on
$\zeta _c(t)$
is constant on
![]() $\Sigma ^n$
. The converse follows from item (a).
$\Sigma ^n$
. The converse follows from item (a).
Finally, we prove item (c). Assuming the opposite, if
![]() $\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is
$\psi :\Sigma ^n\looparrowright -I\times _{f}M^n$
is
![]() $L_{cu}$
-stable, then, from the analysis of signs studied in (5-13),
$L_{cu}$
-stable, then, from the analysis of signs studied in (5-13),
which is an absurdity.
From Theorem 5.6, we obtain the following applications.
Corollary 5.7. Every spacelike translating soliton immersed in the Lorentzian product space
![]() $-I\times M^n$
with soliton constant
$-I\times M^n$
with soliton constant
![]() $c\not =0$
is
$c\not =0$
is
![]() $L_{cu}$
-stable.
$L_{cu}$
-stable.
Corollary 5.8. Every spacelike mean curvature flow soliton immersed in the future temporal cone
![]() $-\mathbb R^+\times _t\mathbb H^n$
with soliton constant
$-\mathbb R^+\times _t\mathbb H^n$
with soliton constant
![]() $c<0$
and such that
$c<0$
and such that
![]() $h\geq \sqrt {-{n}/{c}}$
is
$h\geq \sqrt {-{n}/{c}}$
is
![]() $L_{cu}$
-stable.
$L_{cu}$
-stable.
Corollary 5.9. There is no
![]() $L_{cu}$
-stable compact spacelike mean curvature flow soliton immersed in a steady-state-type spacetime
$L_{cu}$
-stable compact spacelike mean curvature flow soliton immersed in a steady-state-type spacetime
![]() $-I\times _{e^t}M^n$
with soliton constant
$-I\times _{e^t}M^n$
with soliton constant
![]() $c>0$
.
$c>0$
.
Acknowledgement
The authors would like to thank the referee for reading the manuscript in great detail and for his/her valuable suggestions and useful comments which improved the paper.