1. Introduction
Ever since its conception, Parfit’s (Reference Parfit and Bayles1976, Reference Parfit1982, Reference Parfit1984) repugnant conclusion has remained a fundamental criterion used to assess the ethical merits of population principles. Roughly speaking, the repugnant conclusion states that population size can always be used as a substitute for quality of life, even if the lives of those alive are barely worth living. Initially intended as an argument against total utilitarianism, avoidance of the repugnant conclusion has become a condition that, although not universally accepted, is widely endorsed by a substantial number of scholars in the field. Authors who suggest that the repugnant conclusion may be acceptable include Mackie (Reference Mackie, Mackie and Mackie1985), Hare (Reference Hare1988), Tännsjö (Reference Tännsjö2002), Huemer (Reference Huemer2008), Spears and Budolfson (Reference Spears and Budolfson2021) and Gustafsson (Reference Gustafsson, Arrhenius, Bykvist, Campbell and Finneron-Burns2022). Attempts to avoid the repugnant conclusion are reviewed by Arrhenius et al. (Reference Arrhenius, Ryberg, Tännsjö and Zalta2017).
A population principle is expressed by means of an ordering that ranks utility distributions, where utility is a measure of lifetime well-being and utility distributions may be associated with different populations and different population sizes. As is common in population ethics, we assume that individual utilities are normalized so that a lifetime utility level of zero corresponds to a neutral life. A life is worth living for a person if it is associated with level of lifetime utility above neutrality; if lifetime utility is below the neutrality level, it is not worth living. The observations of this paper do not depend on a specific account of a neutral life; all we need is a level of utility that corresponds to neutrality.
The repugnant conclusion is implied if, for any population size n, any arbitrarily high positive utility level
![]() ${\xi}$
, and any arbitrarily low positive utility level
${\xi}$
, and any arbitrarily low positive utility level
![]() ${\varepsilon}$
, there exists a larger population size
${\varepsilon}$
, there exists a larger population size
![]() $m \, \gt \, n$
such that a distribution in which the m people alive experience the (arbitrarily close to zero) utility level
$m \, \gt \, n$
such that a distribution in which the m people alive experience the (arbitrarily close to zero) utility level
![]() ${\varepsilon}$
is better than a distribution in which the n individuals alive are at the (arbitrarily high) utility level
${\varepsilon}$
is better than a distribution in which the n individuals alive are at the (arbitrarily high) utility level
![]() ${\xi}$
. In other words, a principle that implies the repugnant conclusion permits mass poverty to substitute for quality of life – an observation that seems very repugnant indeed.
${\xi}$
. In other words, a principle that implies the repugnant conclusion permits mass poverty to substitute for quality of life – an observation that seems very repugnant indeed.
An early response to Parfit’s repugnant conclusion is provided in a fundamental contribution by Hurka (Reference Hurka1983). He proposes the notion of a variable-value principle, the purpose of which is to capture the behaviour of a total principle (such as total utilitarianism) for small population sizes and that of an average rule for large numbers. Thus, the value assigned to an additional life varies depending on the size of the existing population. The variable-value principles are obtained by multiplying the utility of an equal distribution by a non-decreasing dampening function of population size. As Hurka (Reference Hurka1983) demonstrates, if the function is bounded, the repugnant conclusion is indeed avoided: the effect of the total-utilitarian criterion is dampened for large populations by applying this function, and this dampening procedure allows for an escape from the repugnant conclusion. A fully specified variant of these principles appears in Ng (Reference Ng1986) who proposes the number-dampened utilitarian principles. They are defined for all distributions and use the criterion that is obtained by multiplying average utility by the value of a non-decreasing dampening function. The resulting population principle avoids the repugnant conclusion if and only if the dampening function is bounded; see, for example, Blackorby et al. (Reference Blackorby, Bossert and Donaldson2005: 172).
The class of critical-level utilitarian principles introduced and analysed by Blackorby and Donaldson (Reference Blackorby and Donaldson1984) represents another method of avoiding the repugnant conclusion. A critical level of lifetime well-being is a level of utility such that if a person with that utility level is added to a utility-unaffected population, the expanded distribution is as good as the original. A critical level need not exist for some principles and for some distributions. If a critical level exists, it may depend on the distribution under consideration, and it may not be unique. Critical-level utilitarianism ranks distributions by means of the sum of the differences between individual utilities and a fixed critical level. A special case is total utilitarianism, which is obtained if the critical level is equal to zero – the level of neutrality. The repugnant conclusion is avoided if and only if the critical level is positive; see Blackorby and Donaldson (Reference Blackorby and Donaldson1984).
An alternative assessment criterion for population principles is introduced by Arrhenius (Reference Arrhenius2000). A principle implies the sadistic conclusion if there is an initial utility distribution such that adding only people with negative levels of well-being (below neutrality) to that distribution is better than adding only individuals with positive utilities (above neutrality).
It is well-known that there is a tension between the two objectives of avoiding the repugnant conclusion and avoiding the sadistic conclusion; this conflict has been analysed quite thoroughly in the earlier literature for some specific classes of population principles. In particular, Blackorby et al. (Reference Blackorby, Bossert and Donaldson2005: 164, Theorem 5.4) show that there is no principle with utilitarian fixed-number restrictions that can avoid both conclusions under a mild regularity condition. Other incompatibilities in population ethics are examined by Ng (Reference Ng1989) and by Carlson (Reference Carlson1998), for instance.
Arrhenius (Reference Arrhenius2000) shows that a subclass of the number-dampened utilitarian principles leads to the sadistic conclusion. Although he only proves this for a specific functional form of the dampening function, his observation generalizes to all members of the class that employ a bounded function. Thus, in the context of the number-dampened utilitarian principles, the incompatibility between avoidance of the repugnant conclusion and avoidance of the sadistic conclusion is well-established and well-understood. Analogously, no critical-level utilitarian principles can avoid the repugnant conclusion and the sadistic conclusion, as demonstrated by Blackorby et al. (Reference Blackorby, Bossert, Donaldson, Ryberg and Tännsjö2004); see also Bossert (Reference Bossert, Arrhenius, Bykvist, Campbell and Finneron-Burns2022). They show that a critical-level utilitarian principle avoids the sadistic conclusion if and only if the critical level is equal to zero. Combined with the above-mentioned observation that avoidance of the repugnant conclusion is satisfied if and only if the critical level is positive, the impossibility result follows immediately.
In this paper, we extend incompatibility results of this nature by demonstrating that they apply to a considerably more general class of population principles. These principles are what we refer to as the generalized variable-value principles, and they generalize Hurka’s (Reference Hurka1983) class of variable-value principles by allowing for a reference level of utility that need not be equal to the level of neutrality. In particular, the principles assess equal distributions by comparing the difference between the equal utility level and a reference level, modified by the value of a non-decreasing dampening function that depends on the population size. Hurka’s class of variable-value principles emerges as a special case if the reference level is equal to zero. In addition to the variable-value principles and the critical-level utilitarian principles, numerous others are included in our class. As a prominent example, the rank-discounted reference-level utilitarian principles of Asheim and Zuber (Reference Asheim and Zuber2014) are among them.
The generality of our observations comes at a price. Because the (generalized) variable-value principles are defined solely on the basis of equal utility distributions, an additional condition is required; without such a property, avoidance of the sadistic conclusion does not have enough bite if nothing can be said about unequal distributions. This is a feature that our approach shares with some earlier contributions to the literature. The additional condition that we use is what we label the limit property. It is a weakening of the aggregation property that is employed by Spears and Budolfson (Reference Spears and Budolfson2021), and it slightly strengthens the conjunction of the positive limit property and the negative limit property used by Blackorby et al. (Reference Blackorby, Bossert, Donaldson and Fleurbaey1998) who consider orderings that are not necessarily anonymous. The specific limit property that we use in this paper requires that, as the total population becomes large, inequities that may be present in a given distribution eventually become negligible. This means that the condition ensures that equitable assessments are approached in the limit.
We note that all of our observations remain valid if any continuous and increasing transformation that preserves the neutrality normalization is applied to all utility values. The reason why we do not work with the resulting generalized principles is ease of exposition.
Section 2 introduces our class of generalized variable-value principles, along with some examples. In section 3, we provide formal definitions of the repugnant and sadistic conclusions and our limit property. Moreover, we state and prove our main result, along with a related impossibility result obtained for Parfit’s (Reference Parfit1984) axiom of mere addition in place of the sadistic conclusion. Section 4 is devoted to a discussion, and section 5 concludes.
2. Generalized variable-value principles
We use individual utility as an indicator of lifetime well-being. Following the standard convention, utilities are normalized in a way such that a value of zero represents a neutral life. A life is neutral if it is, from the viewpoint of the person leading it, neither better nor worse than a life without any experiences.
A utility distribution is a list of individual lifetime utility levels, one level for each person in existence in the requisite distribution. Thus, for a population of
![]() $n \in \mathbb{N}$
individuals, a distribution is given by a vector
$n \in \mathbb{N}$
individuals, a distribution is given by a vector
![]() $u = ({u_1}, \ldots ,{u_n}) \in {{\mathbb{R}}^n}$
. The vector consisting of
$u = ({u_1}, \ldots ,{u_n}) \in {{\mathbb{R}}^n}$
. The vector consisting of
![]() $n \in \mathbb{N}$
ones is denoted by
$n \in \mathbb{N}$
ones is denoted by
![]() ${{\bf 1}_n}$
.
${{\bf 1}_n}$
.
A population principle is an ordering (that is, a complete and transitive binary relation) R defined on the set of possible distributions
![]() $\Omega = { \cup _{n \in \mathbb{N}}}{{\mathbb{R}}^n}$
. The statement uRv is interpreted to mean that distribution
$\Omega = { \cup _{n \in \mathbb{N}}}{{\mathbb{R}}^n}$
. The statement uRv is interpreted to mean that distribution
![]() $u \in \Omega $
is at least as good as distribution
$u \in \Omega $
is at least as good as distribution
![]() $v \in \Omega $
according to the population principle identified by R. We use P and I to denote the asymmetric and symmetric parts of R, that is, uPv indicates that u is better than v, and uIv means that u and v are equally good.
$v \in \Omega $
according to the population principle identified by R. We use P and I to denote the asymmetric and symmetric parts of R, that is, uPv indicates that u is better than v, and uIv means that u and v are equally good.
Consider a population principle R and a utility distribution
![]() $u \in \Omega $
. A utility level
$u \in \Omega $
. A utility level
![]() $c \in \mathbb{R}$
is a critical level for the principle R and the distribution u if the distribution
$c \in \mathbb{R}$
is a critical level for the principle R and the distribution u if the distribution
![]() $(u,c)$
that results from adding a person with lifetime utility c to the distribution u is as good as u. Note that, without further assumptions, a critical level need not exist for all distributions, and it need not be unique if it exists. Moreover, a critical level may depend on the utility distribution under consideration.
$(u,c)$
that results from adding a person with lifetime utility c to the distribution u is as good as u. Note that, without further assumptions, a critical level need not exist for all distributions, and it need not be unique if it exists. Moreover, a critical level may depend on the utility distribution under consideration.
The class of population principles that we focus on is given by the generalized variable-value principles defined as follows. An ordering R on Ω is a generalized variable-value principle if there exist a number
![]() $\gamma \in \mathbb{R}$
and a non-decreasing function
$\gamma \in \mathbb{R}$
and a non-decreasing function
![]() $f:\mathbb{N} \to {{\mathbb{R}}_{ + + }}$
such that, for all population sizes
$f:\mathbb{N} \to {{\mathbb{R}}_{ + + }}$
such that, for all population sizes
![]() $n,m \in \mathbb{N}$
and for all utility levels
$n,m \in \mathbb{N}$
and for all utility levels
![]() $a,b \in \mathbb{R}$
,
$a,b \in \mathbb{R}$
,
The parameter
![]() ${\gamma}$
is a reference level of utility and f is a dampening function that determines the value attached to an additional person as a function of the population size. The term variable value is motivated by the observation that this value may depend on the number of people already in existence. Thus, generalized variable-value principles assess equal distributions by comparing the difference between the equal utility level and this reference level, modified by the value of the function f that depends on the population size. This class generalizes the variable-value principles employed by Hurka (Reference Hurka1983); the parameter
${\gamma}$
is a reference level of utility and f is a dampening function that determines the value attached to an additional person as a function of the population size. The term variable value is motivated by the observation that this value may depend on the number of people already in existence. Thus, generalized variable-value principles assess equal distributions by comparing the difference between the equal utility level and this reference level, modified by the value of the function f that depends on the population size. This class generalizes the variable-value principles employed by Hurka (Reference Hurka1983); the parameter
![]() ${\gamma}$
is equal to zero in Hurka’s account.
${\gamma}$
is equal to zero in Hurka’s account.
As mentioned in the Introduction, all of our observations extend easily to the generalized variants of these principles. These generalizations are obtained by applying a continuous and increasing transformation that preserves the zero normalization for neutrality to all utilities. All that needs to be done is to replace utilities by transformed utilities in our arguments.
Generalized variable-value population principles encompass a plethora of orderings because their definition merely imposes a restriction on comparisons that involve equal utility distributions. Moreover, they generalize the traditional number-dampened principles because they allow for the reference utility
![]() ${\gamma}$
to differ from the neutrality level zero. As a consequence, they are capable of accommodating critical-level principles such as those introduced by Blackorby and Donaldson (Reference Blackorby and Donaldson1984) and discussed by Blackorby et al. (Reference Blackorby, Bossert and Donaldson2005), among others.
${\gamma}$
to differ from the neutrality level zero. As a consequence, they are capable of accommodating critical-level principles such as those introduced by Blackorby and Donaldson (Reference Blackorby and Donaldson1984) and discussed by Blackorby et al. (Reference Blackorby, Bossert and Donaldson2005), among others.
The first of the special cases we mention here is number-dampened utilitarianism; see Hurka (Reference Hurka1983) and Ng (Reference Ng1986). An ordering R on Ω is a number-dampened utilitarian principle if there exists a non-decreasing function
![]() $f:\mathbb{N} \to {\mathbb{R}}_{ + + }$
such that, for all
$f:\mathbb{N} \to {\mathbb{R}}_{ + + }$
such that, for all
![]() $n,m \in \mathbb{N}$
, for all
$n,m \in \mathbb{N}$
, for all
![]() $u \in {{\mathbb{R}}^n}$
, and for all
$u \in {{\mathbb{R}}^n}$
, and for all
![]() $v \in {\mathbb{R}}^m$
,
$v \in {\mathbb{R}}^m$
,
The reference level of utility
![]() ${\gamma}$
is equal to zero in this case. If f is equal to the identity mapping (or any increasing linear function), total utilitarianism is obtained. For a constant function f, average utilitarianism results.
${\gamma}$
is equal to zero in this case. If f is equal to the identity mapping (or any increasing linear function), total utilitarianism is obtained. For a constant function f, average utilitarianism results.
A second example is the class of Sider’s (Reference Sider1991) principles, also referred to as geometrism. To define these principles, we require more notation. For
![]() $n \in \mathbb{N}$
and
$n \in \mathbb{N}$
and
![]() $u \in {{\mathbb{R}}^n}$
, let
$u \in {{\mathbb{R}}^n}$
, let
![]() ${u_{[\;]}}$
denote a non-decreasing rearrangement of the components of u, that is,
${u_{[\;]}}$
denote a non-decreasing rearrangement of the components of u, that is,
Analogously, let
![]() ${u_{(\;)}}$
be a non-increasing rearrangement of u so that
${u_{(\;)}}$
be a non-increasing rearrangement of u so that
For a utility distribution
![]() $u \in \Omega $
, the number of non-negative components in u is denoted by
$u \in \Omega $
, the number of non-negative components in u is denoted by
![]() ${n^ + }(u)$
, and the number of negative components is
${n^ + }(u)$
, and the number of negative components is
![]() ${n^{ - - }}(u)$
. Let
${n^{ - - }}(u)$
. Let
![]() ${u^{( + )}}$
be a non-increasing rearrangement of the non-negative components of u so that
${u^{( + )}}$
be a non-increasing rearrangement of the non-negative components of u so that
and, analogously,
![]() ${u^{[ - - ]}}$
is a non-decreasing rearrangement of negative components of u, that is,
${u^{[ - - ]}}$
is a non-decreasing rearrangement of negative components of u, that is,
An ordering R on Ω is geometrist if there exists
![]() $\beta \in (0,1)$
such that, for all
$\beta \in (0,1)$
such that, for all
![]() $n,m \in \mathbb{N}$
, for all
$n,m \in \mathbb{N}$
, for all
![]() $u \in {{\mathbb{R}}^n}$
, and for all
$u \in {{\mathbb{R}}^n}$
, and for all
![]() $v \in {{\mathbb{R}}^m}$
,
$v \in {{\mathbb{R}}^m}$
,
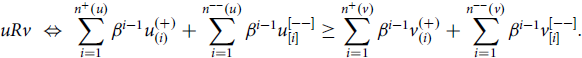 $$uRv\; \Leftrightarrow \;\sum\limits_{i = 1}^{{n^ + }(u)} {\beta ^{i - 1}}u_{(i)}^{( + )} + \sum\limits_{i = 1}^{{n^{ - - }}(u)} {\beta ^{i - 1}}u_{[i]}^{[ - - ]} \ge \sum\limits_{i = 1}^{{n^ + }(v)} {\beta ^{i - 1}}v_{(i)}^{( + )} + \sum\limits_{i = 1}^{{n^{ - - }}(v)} {\beta ^{i - 1}}v_{[i]}^{[ - - ]}.$$
$$uRv\; \Leftrightarrow \;\sum\limits_{i = 1}^{{n^ + }(u)} {\beta ^{i - 1}}u_{(i)}^{( + )} + \sum\limits_{i = 1}^{{n^{ - - }}(u)} {\beta ^{i - 1}}u_{[i]}^{[ - - ]} \ge \sum\limits_{i = 1}^{{n^ + }(v)} {\beta ^{i - 1}}v_{(i)}^{( + )} + \sum\limits_{i = 1}^{{n^{ - - }}(v)} {\beta ^{i - 1}}v_{[i]}^{[ - - ]}.$$
Sider’s geometrist principles can be considered conceptually related to rank-discounted utilitarianism. An ordering R on Ω is rank-discounted utilitarian if there exists
![]() $\beta \in (0,1)$
such that, for all
$\beta \in (0,1)$
such that, for all
![]() $n,m \in \mathbb{N}$
, for all
$n,m \in \mathbb{N}$
, for all
![]() $u \in {{\mathbb{R}}^n}$
, and for all
$u \in {{\mathbb{R}}^n}$
, and for all
![]() $v \in {{\mathbb{R}}^m}$
,
$v \in {{\mathbb{R}}^m}$
,
As is the case for number-dampened utilitarianism, the reference level of utility for geometrism and for rank-discounted utilitarianism is equal to zero – the level that represents neutrality. If
![]() ${\gamma}$
is allowed to assume values other than zero, the rank-discounted reference-level utilitarian principles of Asheim and Zuber (Reference Asheim and Zuber2014) result. An ordering R on Ω is rank-discounted reference-level utilitarian if there exist
${\gamma}$
is allowed to assume values other than zero, the rank-discounted reference-level utilitarian principles of Asheim and Zuber (Reference Asheim and Zuber2014) result. An ordering R on Ω is rank-discounted reference-level utilitarian if there exist
![]() $\beta \in (0,1)$
and
$\beta \in (0,1)$
and
![]() $\gamma \in {{\mathbb{R}}_ + }$
such that, for all
$\gamma \in {{\mathbb{R}}_ + }$
such that, for all
![]() $n,m \in \mathbb{N}$
, for all
$n,m \in \mathbb{N}$
, for all
![]() $u \in {{\mathbb{R}}^n}$
, and for all
$u \in {{\mathbb{R}}^n}$
, and for all
![]() $v \in {{\mathbb{R}}^m}$
,
$v \in {{\mathbb{R}}^m}$
,
Asheim and Zuber (Reference Asheim and Zuber2014) refer to these principles as rank-discounted critical-level utilitarian principles. We prefer to use the term reference level rather than critical level because the parameter
![]() ${\gamma}$
is not a critical level in the sense employed here. This is the case because adding a person at the utility level
${\gamma}$
is not a critical level in the sense employed here. This is the case because adding a person at the utility level
![]() ${\gamma}$
to a utility-unaffected population does not necessarily lead to a distribution that is as good as the original. See also Pivato (Reference Pivato2020) and Asheim and Zuber (Reference Asheim, Zuber, Arrhenius, Bykvist, Campbell and Finneron-Burns2022) for alternative generalized classes.
${\gamma}$
to a utility-unaffected population does not necessarily lead to a distribution that is as good as the original. See also Pivato (Reference Pivato2020) and Asheim and Zuber (Reference Asheim, Zuber, Arrhenius, Bykvist, Campbell and Finneron-Burns2022) for alternative generalized classes.
The class of critical-level utilitarian principles introduced by Blackorby and Donaldson (Reference Blackorby and Donaldson1984) and further discussed by Blackorby et al. (Reference Blackorby, Bossert and Donaldson2005) represents yet another special case. An ordering R on Ω is critical-level utilitarian if there exists
![]() $\alpha \in \mathbb{R}$
such that, for all
$\alpha \in \mathbb{R}$
such that, for all
![]() $n,m \in \mathbb{N}$
, for all
$n,m \in \mathbb{N}$
, for all
![]() $u \in {{\mathbb{R}}^n}$
, and for all
$u \in {{\mathbb{R}}^n}$
, and for all
![]() $v \in {{\mathbb{R}}^m}$
,
$v \in {{\mathbb{R}}^m}$
,
In this case, the parameter
![]() ${\gamma}$
in the definition of the generalized variable-value principles is equal to the constant critical level
${\gamma}$
in the definition of the generalized variable-value principles is equal to the constant critical level
![]() ${\alpha}$
, and the function f is any increasing linear function. In contrast to the rank-discounted principles, the parameter
${\alpha}$
, and the function f is any increasing linear function. In contrast to the rank-discounted principles, the parameter
![]() $\gamma = \alpha $
is indeed a critical level.
$\gamma = \alpha $
is indeed a critical level.
3. The repugnant and sadistic conclusions
This section presents our main result, along with a discussion of some of its features. We show that, under a mild additional restriction, the generalized variable-value principles that avoid the repugnant conclusion must entail the sadistic conclusion. The additional restriction is needed as a consequence of the general nature of the generalized variable-value principles. Because these principles are defined by exclusively referring to equal distributions, more structure is needed in order to obtain observations that allow some interpersonal variation in individual utility values.
We begin with a formal statement of Parfit’s (Reference Parfit and Bayles1976, Reference Parfit1982, Reference Parfit1984) repugnant conclusion. See, for instance, Spears and Budolfson (Reference Spears and Budolfson2021) for alternative definitions. A population principle R implies the repugnant conclusion if, for all
![]() $n \in \mathbb{N}$
, for all
$n \in \mathbb{N}$
, for all
![]() $\xi \in {\mathbb{R}}_{ + + }$
, and for all
$\xi \in {\mathbb{R}}_{ + + }$
, and for all
![]() $\varepsilon \in (0,\xi )$
, there exists
$\varepsilon \in (0,\xi )$
, there exists
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, n$
such that
$m \, \gt \, n$
such that
![]() $\varepsilon {{\bf 1}_m}P\xi {{\bf 1}_n}$
. The axiom avoidance of the repugnant conclusion is obtained by negating this statement.
$\varepsilon {{\bf 1}_m}P\xi {{\bf 1}_n}$
. The axiom avoidance of the repugnant conclusion is obtained by negating this statement.
Avoidance of the repugnant conclusion. There exist
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
![]() $\xi \in {\mathbb{R}}_{ + + }$
, and
$\xi \in {\mathbb{R}}_{ + + }$
, and
![]() $\varepsilon \in (0,\xi )$
such that, for all
$\varepsilon \in (0,\xi )$
such that, for all
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, n$
,
$m \, \gt \, n$
,
A population principle implies the sadistic conclusion (Arrhenius Reference Arrhenius2000) if adding people with negative utility levels can be better than adding people with positive utility levels to a given population. To provide a formal definition, we use the notation
![]() ${\Omega _{ + + }} = \cup _{n \in \mathbb{N}}{\mathbb{R}}_{ + + }^n$
and
${\Omega _{ + + }} = \cup _{n \in \mathbb{N}}{\mathbb{R}}_{ + + }^n$
and
![]() ${\Omega _{ - - }} = \cup _{n \in \mathbb{N}}{\mathbb{R}}_{ - - }^n$
to denote the set of all positive distributions and the set of all negative distributions. Thus, the sadistic conclusion is implied by a population principle R if there exist
${\Omega _{ - - }} = \cup _{n \in \mathbb{N}}{\mathbb{R}}_{ - - }^n$
to denote the set of all positive distributions and the set of all negative distributions. Thus, the sadistic conclusion is implied by a population principle R if there exist
![]() $u \in \Omega $
,
$u \in \Omega $
,
![]() $v \in {\Omega _{ + + }}$
, and
$v \in {\Omega _{ + + }}$
, and
![]() $w \in {\Omega _{ - - }}$
such that
$w \in {\Omega _{ - - }}$
such that
![]() $(u,w)P(u,v)$
. Negating this statement, we obtain the following axiom.
$(u,w)P(u,v)$
. Negating this statement, we obtain the following axiom.
Avoidance of the sadistic conclusion. For all
![]() $u \in \Omega $
, for all
$u \in \Omega $
, for all
![]() $v \in {\Omega _{ + + }}$
, and for all
$v \in {\Omega _{ + + }}$
, and for all
![]() $w \in {\Omega _{ - - }}$
,
$w \in {\Omega _{ - - }}$
,
![]() $(u,v)R(u,w)$
.
$(u,v)R(u,w)$
.
As alluded to earlier, we require an additional property to be able to deal with some distributions that do not involve equal utilities for everyone. We employ a variant of the aggregation axiom of Spears and Budolfson (Reference Spears and Budolfson2021).
Limit property. For all
![]() $n \in \mathbb{N}$
, for all
$n \in \mathbb{N}$
, for all
![]() $u \in {{\mathbb{R}}^n}$
, for all
$u \in {{\mathbb{R}}^n}$
, for all
![]() $\kappa \in \mathbb{R}$
, and for all
$\kappa \in \mathbb{R}$
, and for all
![]() $\delta \in {\mathbb{R}}_{ + + }$
, there exists
$\delta \in {\mathbb{R}}_{ + + }$
, there exists
![]() ${m^*} \in \mathbb{N}$
such that, for all
${m^*} \in \mathbb{N}$
such that, for all
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, {m^*}$
,
$m \, \gt \, {m^*}$
,
We note that both of the distributions
![]() $(\kappa {{\bf 1}_m},u)$
and
$(\kappa {{\bf 1}_m},u)$
and
![]() $(u,\kappa {{\bf 1}_m})$
appear in the definition of the limit property. This is necessary because we do not impose the anonymity axiom that requires any distribution to be as good as any of its permutations.
$(u,\kappa {{\bf 1}_m})$
appear in the definition of the limit property. This is necessary because we do not impose the anonymity axiom that requires any distribution to be as good as any of its permutations.
Spears and Budolfson’s (Reference Spears and Budolfson2021) axiom of aggregation is obtained by replacing the at-least-as-good relation with betterness in the consequent of the limit property regarding the utility distribution
![]() $(\kappa {{\bf 1}_m},u)$
. Thus, in the presence of the anonymity axiom, Spears and Budolfson’s aggregation axiom implies the limit property; indeed, anonymity is one of their basic axioms. Because they employ anonymity, there is no need to explicitly include the distribution
$(\kappa {{\bf 1}_m},u)$
. Thus, in the presence of the anonymity axiom, Spears and Budolfson’s aggregation axiom implies the limit property; indeed, anonymity is one of their basic axioms. Because they employ anonymity, there is no need to explicitly include the distribution
![]() $(u,\kappa {{\bf 1}_m})$
in their formulation. Moreover, we note that Spears and Budolfson’s aggregation axiom is a strengthening of the positive limit property and its negative counterpart introduced by Blackorby et al. (Reference Blackorby, Bossert, Donaldson and Fleurbaey1998). The limit property is also a strengthening of their positive and negative limit properties. The limit property is appealing because it requires that, as the total population becomes large, any inequities that may be present in an original distribution
$(u,\kappa {{\bf 1}_m})$
in their formulation. Moreover, we note that Spears and Budolfson’s aggregation axiom is a strengthening of the positive limit property and its negative counterpart introduced by Blackorby et al. (Reference Blackorby, Bossert, Donaldson and Fleurbaey1998). The limit property is also a strengthening of their positive and negative limit properties. The limit property is appealing because it requires that, as the total population becomes large, any inequities that may be present in an original distribution
![]() $u \in {{\mathbb{R}}^n}$
are trumped by the inequalities
$u \in {{\mathbb{R}}^n}$
are trumped by the inequalities
![]() $\kappa + \delta \, \gt \, \kappa \, \gt \, \kappa - \delta $
. Thus, the condition pushes towards equitable assessments in the limit.
$\kappa + \delta \, \gt \, \kappa \, \gt \, \kappa - \delta $
. Thus, the condition pushes towards equitable assessments in the limit.
Our main result establishes the fundamental incompatibility of avoidance of the repugnant conclusion and avoidance of the sadistic conclusion for the class of generalized variable-value principles.
Theorem 1. Let R be a generalized variable-value principle that satisfies the limit property. If R avoids the repugnant conclusion, then R implies the sadistic conclusion.
Arrhenius (Reference Arrhenius2000: 261) shows that avoidance of the repugnant conclusion is incompatible with avoidance of the sadistic conclusion in the presence of some other axioms, including what he refers to as the minimal non-extreme priority principle. To see that our result is independent of his, note that there exists a generalized variable-value principle that satisfies the limit property but it does not satisfy the minimal non-extreme priority principle so that it is not covered by Arrhenius’s (Reference Arrhenius2000) impossibility result; an example of such a generalized variable-value principle is given by the variable-value median principles that we present in the next section. Therefore, his impossibility result cannot be applied to either the whole class of generalized variable-value principles or its subclass consisting of those that satisfy the limit property.
We use four auxiliary results to prove this theorem. The first of these generalizes an analogous observation of Blackorby and Donaldson (Reference Blackorby and Donaldson1984) for the critical-level utilitarian principles to our class. It does not rely on the limit property.
Lemma 1.
Let R be a generalized variable-value principle. If
![]() $\gamma \, \gt \, 0$
, then R avoids the repugnant conclusion.
$\gamma \, \gt \, 0$
, then R avoids the repugnant conclusion.
Proof. Assume that
![]() $\gamma \, \gt \, 0$
. Let
$\gamma \, \gt \, 0$
. Let
![]() $\xi = \gamma $
and
$\xi = \gamma $
and
![]() $\varepsilon \in (0,\xi ) = (0,\gamma )$
. Furthermore, let
$\varepsilon \in (0,\xi ) = (0,\gamma )$
. Furthermore, let
![]() $n \in \mathbb{N}$
be arbitrary. Because f is positive-valued, it follows that
$n \in \mathbb{N}$
be arbitrary. Because f is positive-valued, it follows that
for all
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, n$
so that, by definition of the generalized variable-value principles,
$m \, \gt \, n$
so that, by definition of the generalized variable-value principles,
![]() $\xi {{\bf 1}_n}P\varepsilon {{\bf 1}_m}$
and hence
$\xi {{\bf 1}_n}P\varepsilon {{\bf 1}_m}$
and hence
![]() $\xi {{\bf 1}_n}R\varepsilon {{\bf 1}_m}$
for all
$\xi {{\bf 1}_n}R\varepsilon {{\bf 1}_m}$
for all
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, n$
. ▪
$m \, \gt \, n$
. ▪
The following lemma also has its foundation in an earlier result. As stated in Blackorby et al. (Reference Blackorby, Bossert and Donaldson2005: 172), a number-dampened utilitarian ordering avoids the repugnant conclusion if and only if the function f is bounded. This observation readily generalizes to our class of principles. Again, the limit property is not required in this result.
Lemma 2.
Let R be a generalized variable-value principle. If
![]() $\gamma \le 0$
, then R avoids the repugnant conclusion if and only if f is bounded.
$\gamma \le 0$
, then R avoids the repugnant conclusion if and only if f is bounded.
Proof. ‘If.’ Assume that
![]() $\gamma \le 0$
and f is bounded. To prove that R avoids the repugnant conclusion, we have to establish the existence of
$\gamma \le 0$
and f is bounded. To prove that R avoids the repugnant conclusion, we have to establish the existence of
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
![]() $\xi \in {\mathbb{R}}_{ + + }$
, and
$\xi \in {\mathbb{R}}_{ + + }$
, and
![]() $\varepsilon \in (0,\xi )$
such that, for all
$\varepsilon \in (0,\xi )$
such that, for all
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, n$
,
$m \, \gt \, n$
,
Let
![]() $\xi \in {\mathbb{R}}_{ + + }$
and
$\xi \in {\mathbb{R}}_{ + + }$
and
![]() $\varepsilon \in (0,\xi )$
. Since
$\varepsilon \in (0,\xi )$
. Since
![]() $\gamma \le 0$
, it follows that the differences
$\gamma \le 0$
, it follows that the differences
![]() $\xi - \gamma $
and
$\xi - \gamma $
and
![]() $\varepsilon - \gamma $
are positive and, moreover, that
$\varepsilon - \gamma $
are positive and, moreover, that
Because f is non-decreasing and bounded,
![]() $f(n)$
converges to a finite limit
$f(n)$
converges to a finite limit
![]() ${f^*}$
as n approaches infinity. Thus, there exists
${f^*}$
as n approaches infinity. Thus, there exists
![]() $n \in \mathbb{N}$
such that
$n \in \mathbb{N}$
such that
Again using the non-decreasingness of f, it follows that
![]() $f(n) \le f(m) \le {f^*}$
and hence
$f(n) \le f(m) \le {f^*}$
and hence
for all
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, n$
. Because f is positive-valued, this implies that
$m \, \gt \, n$
. Because f is positive-valued, this implies that
for all
![]() $m \in \mathbb{N}$
such that
$m \in \mathbb{N}$
such that
![]() $m \, \gt \, n$
. By definition of the generalized variable-value principles, it follows that
$m \, \gt \, n$
. By definition of the generalized variable-value principles, it follows that
![]() $\xi {{\bf 1}_n}P\varepsilon {{\bf 1}_m}$
and hence
$\xi {{\bf 1}_n}P\varepsilon {{\bf 1}_m}$
and hence
![]() $\xi {{\bf 1}_n}R\varepsilon {{\bf 1}_m}$
, as was to be shown.
$\xi {{\bf 1}_n}R\varepsilon {{\bf 1}_m}$
, as was to be shown.
‘Only if.’ Assume that f is unbounded. Let
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
![]() $\xi \in {\mathbb{R}}_{ + + }$
, and
$\xi \in {\mathbb{R}}_{ + + }$
, and
![]() $\varepsilon \in (0,\xi )$
. Since
$\varepsilon \in (0,\xi )$
. Since
![]() $\gamma \le 0$
, it follows that the differences
$\gamma \le 0$
, it follows that the differences
![]() $\varepsilon - \gamma $
and
$\varepsilon - \gamma $
and
![]() $\xi - \gamma $
are positive. Because f is unbounded and non-decreasing, there exists a population size
$\xi - \gamma $
are positive. Because f is unbounded and non-decreasing, there exists a population size
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, n$
such that
$m \, \gt \, n$
such that
By definition of the generalized variable-value principles, this inequality is equivalent to the statement
![]() $\varepsilon {{\bf 1}_m}P\xi {{\bf 1}_n}$
so that the repugnant conclusion is implied. ▪
$\varepsilon {{\bf 1}_m}P\xi {{\bf 1}_n}$
so that the repugnant conclusion is implied. ▪
The remaining two lemmas focus on the sadistic conclusion. Both of them employ the limit property. First, we consider the case of a positive parameter value
![]() ${\gamma}$
.
${\gamma}$
.
Lemma 3.
Let R be a generalized variable-value principle that satisfies the limit property. If
![]() $\gamma \, \gt \, 0$
, then R implies the sadistic conclusion.
$\gamma \, \gt \, 0$
, then R implies the sadistic conclusion.
Proof. Assume that
![]() $\gamma \, \gt \, 0$
. Let
$\gamma \, \gt \, 0$
. Let
![]() $a,b \in {\mathbb{R}}_{ + + }$
and
$a,b \in {\mathbb{R}}_{ + + }$
and
![]() $c \in {\mathbb{R}}_{ - - }$
be such that
$c \in {\mathbb{R}}_{ - - }$
be such that
![]() $a \, \gt \, \gamma \, \gt \, b \, \gt \, 0 \, \gt \, c$
. We first show that there exists
$a \, \gt \, \gamma \, \gt \, b \, \gt \, 0 \, \gt \, c$
. We first show that there exists
![]() $m \in \mathbb{N}$
such that
$m \in \mathbb{N}$
such that
Let
![]() $\delta \in {\mathbb{R}}_{ + + }$
be such that
$\delta \in {\mathbb{R}}_{ + + }$
be such that
![]() $a - \delta \, \gt \, \gamma $
. By the limit property, there exists
$a - \delta \, \gt \, \gamma $
. By the limit property, there exists
![]() ${m^*} \in \mathbb{N}$
such that, for all
${m^*} \in \mathbb{N}$
such that, for all
![]() ${m'} \in \mathbb{N}$
with
${m'} \in \mathbb{N}$
with
![]() ${m'} \, \gt \, {m^*}$
,
${m'} \, \gt \, {m^*}$
,
Let
![]() $m = {m^*} + 1$
. Then, we obtain
$m = {m^*} + 1$
. Then, we obtain
Thus, it follows that
Since (2) is satisfied for
![]() $m' = m$
, we obtain (1) by the transitivity of R.
$m' = m$
, we obtain (1) by the transitivity of R.
Now assume that
![]() $m \in \mathbb{N}$
is such that (1) is satisfied. Let
$m \in \mathbb{N}$
is such that (1) is satisfied. Let
![]() $\delta \in {\mathbb{R}}_{ + + }$
be such that
$\delta \in {\mathbb{R}}_{ + + }$
be such that
![]() $b + \delta \, \lt \, \gamma $
. The limit property implies that there exists
$b + \delta \, \lt \, \gamma $
. The limit property implies that there exists
![]() ${n^*} \in \mathbb{N}$
such that, for all
${n^*} \in \mathbb{N}$
such that, for all
![]() $n \in \mathbb{N}$
with
$n \in \mathbb{N}$
with
![]() $n \, \gt \, {n^*}$
,
$n \, \gt \, {n^*}$
,
Note that, for any
![]() $n \, \gt \, {n^*}$
, we obtain
$n \, \gt \, {n^*}$
, we obtain
because
![]() $b + \delta - \gamma \, \lt \, 0$
and thus
$b + \delta - \gamma \, \lt \, 0$
and thus
By the transitivity of R, we obtain
From (1) and transitivity, it follows that
This means that R implies the sadistic conclusion. ▪
Lemma 4.
Let R be a generalized variable-value principle that satisfies the limit property. If
![]() $\gamma \le 0$
and f is bounded, then R implies the sadistic conclusion.
$\gamma \le 0$
and f is bounded, then R implies the sadistic conclusion.
Proof. Assume that
![]() $\gamma \le 0$
and f is bounded. Let
$\gamma \le 0$
and f is bounded. Let
![]() $a,b \in {\mathbb{R}}_{ + + }$
and
$a,b \in {\mathbb{R}}_{ + + }$
and
![]() $c \in {\mathbb{R}}_{ - - }$
be such that
$c \in {\mathbb{R}}_{ - - }$
be such that
![]() $a \, \gt \, b \, \gt \, 0 \, \gt \, c$
. Since f is non-decreasing and bounded, it converges to a finite limit
$a \, \gt \, b \, \gt \, 0 \, \gt \, c$
. Since f is non-decreasing and bounded, it converges to a finite limit
![]() ${f^*}$
as n approaches infinity. Define
${f^*}$
as n approaches infinity. Define
![]() $\overline f = {f^*}/f(1)$
, and let
$\overline f = {f^*}/f(1)$
, and let
![]() $\delta \in {\mathbb{R}}_{ + + }$
be such that
$\delta \in {\mathbb{R}}_{ + + }$
be such that
The limit property implies that there exists
![]() $\overline m \in \mathbb{N}$
such that, for all
$\overline m \in \mathbb{N}$
such that, for all
![]() $m \, \gt \, \overline m $
,
$m \, \gt \, \overline m $
,
Since
![]() $a - \delta - \gamma \, \gt \, b - \gamma \, \gt \, 0$
, the definition of
$a - \delta - \gamma \, \gt \, b - \gamma \, \gt \, 0$
, the definition of
![]() $\overline f $
implies that there exists
$\overline f $
implies that there exists
![]() $\overline n \, \gt \, 0$
such that, for all
$\overline n \, \gt \, 0$
such that, for all
![]() $n \, \gt \, \overline n $
,
$n \, \gt \, \overline n $
,
Next, observe that there exists a sufficiently small
![]() $\varepsilon \in {\mathbb{R}}_{ + + }$
such that, for all
$\varepsilon \in {\mathbb{R}}_{ + + }$
such that, for all
![]() $n \, \gt \, \overline n $
,
$n \, \gt \, \overline n $
,
From the limit property, for all
![]() $m \, \gt \, \overline m $
, there exists
$m \, \gt \, \overline m $
, there exists
![]() ${n_m} \, \gt \, \overline n $
such that, for all
${n_m} \, \gt \, \overline n $
such that, for all
![]() $n \, \gt \, {n_m}$
,
$n \, \gt \, {n_m}$
,
Let
![]() ${m^*} \, \gt \max \{ \overline n ,\overline m \} $
. Since
${m^*} \, \gt \max \{ \overline n ,\overline m \} $
. Since
![]() ${m^*} \, \gt \, \overline m $
, it follows from (4) that
${m^*} \, \gt \, \overline m $
, it follows from (4) that
Now let
![]() ${n^*} = {n_{{m^*}}} + 1$
. It follows that (6) is satisfied for any n with
${n^*} = {n_{{m^*}}} + 1$
. It follows that (6) is satisfied for any n with
![]() $n \ge {n^*}$
and for
$n \ge {n^*}$
and for
![]() $m = {m^*}$
. From (6), we obtain
$m = {m^*}$
. From (6), we obtain
Note that
Since f is non-decreasing and positive-valued, we obtain
By (9), we obtain
Note that (5) is satisfied for
![]() $n = {m^*}$
because
$n = {m^*}$
because
![]() ${m^*} \, \gt \, \overline n $
. Since
${m^*} \, \gt \, \overline n $
. Since
![]() $f(1) \, \gt \, 0$
, it follows that
$f(1) \, \gt \, 0$
, it follows that
Therefore, we obtain
which implies
By the transitivity of R and combining (7), (8) and (10), it follows that
which means that R implies the sadistic conclusion. ▪
Proof of Theorem 1. By Lemmas 1 and 2, R avoids the repugnant conclusion if and only if
![]() $\gamma \, \gt \, 0$
or
$\gamma \, \gt \, 0$
or
![]() $\gamma \le 0$
and f is bounded. If
$\gamma \le 0$
and f is bounded. If
![]() $\gamma \, \gt \, 0$
, Lemma 3 implies that R entails the sadistic conclusion. If
$\gamma \, \gt \, 0$
, Lemma 3 implies that R entails the sadistic conclusion. If
![]() $\gamma \le 0$
and f is bounded, Lemma 4 implies that R entails the sadistic conclusion. ▪
$\gamma \le 0$
and f is bounded, Lemma 4 implies that R entails the sadistic conclusion. ▪
In Theorem 1, we restrict attention to generalized variable-value principles. This raises the question whether the impossibility result is valid for a more general class of population principles. Consider the principle that is defined by letting
and
for all remaining
![]() $n,m \in \mathbb{N}$
,
$n,m \in \mathbb{N}$
,
![]() $u \in {\mathbb{R}}^n$
, and
$u \in {\mathbb{R}}^n$
, and
![]() $v \in {\mathbb{R}}^m$
. According to this principle, all one-person distributions are better than all distributions with more than one individual alive, and all other comparisons are performed by means of the total-utilitarian criterion. This principle satisfies avoidance of the repugnant conclusion, avoidance of the sadistic conclusion, and the limit property. Moreover, it satisfies the fixed-population-size properties of anonymity and strong Pareto; the latter requires that uPv for all
$v \in {\mathbb{R}}^m$
. According to this principle, all one-person distributions are better than all distributions with more than one individual alive, and all other comparisons are performed by means of the total-utilitarian criterion. This principle satisfies avoidance of the repugnant conclusion, avoidance of the sadistic conclusion, and the limit property. Moreover, it satisfies the fixed-population-size properties of anonymity and strong Pareto; the latter requires that uPv for all
![]() $n \in \mathbb{N}$
and for all
$n \in \mathbb{N}$
and for all
![]() $u,v \in {\mathbb{R}}^n$
such that
$u,v \in {\mathbb{R}}^n$
such that
![]() ${u_i} \ge {v_i}$
for all
${u_i} \ge {v_i}$
for all
![]() $i \in \{ 1, \ldots ,n\} $
with at least one strict inequality. It is clear that this example is not a generalized variable-value principle because there cannot exist a dampening function f that is non-decreasing; note that the value of f at population size one would have to exceed the values of f at all other population sizes, which is not possible if the monotonicity property of f is to be respected. Thus, the result of Theorem 1 is rather tight.
$i \in \{ 1, \ldots ,n\} $
with at least one strict inequality. It is clear that this example is not a generalized variable-value principle because there cannot exist a dampening function f that is non-decreasing; note that the value of f at population size one would have to exceed the values of f at all other population sizes, which is not possible if the monotonicity property of f is to be respected. Thus, the result of Theorem 1 is rather tight.
Parfit’s (Reference Parfit1984) axiom of mere addition expresses a requirement akin to avoidance of the sadistic conclusion. It requires that adding people with positive utilities to any given initial distribution leads to a distribution that is at least as good as the original.
Mere addition. For all
![]() $u \in \Omega $
and for all
$u \in \Omega $
and for all
![]() $v \in {\Omega _{ + + }}$
,
$v \in {\Omega _{ + + }}$
,
![]() $(u,v)Ru$
.
$(u,v)Ru$
.
As is well-known, Sider’s principles satisfy mere addition. This observation raises the question whether avoidance of the sadistic conclusion can be replaced with mere addition in the statement of Theorem 1. The answer is in the affirmative, as stated in the following theorem. Because the observation is closely related to an impossibility result of Blackorby et al. (Reference Blackorby, Bossert, Donaldson and Fleurbaey1998: Theorem 2), we claim very little credit for it. We provide a proof for completeness but stress that it is, in essence, a mere reformulation of that employed by these authors.
Theorem 2. Let R be a generalized variable-value principle that satisfies the limit property. If R avoids the repugnant conclusion, then R violates mere addition.
Proof. Assume that R is a generalized variable-value principle that satisfies the limit property and avoidance of the repugnant conclusion. Avoidance of the repugnant conclusion implies that there exist
![]() $n \in \mathbb{N}$
,
$n \in \mathbb{N}$
,
![]() $\xi \in {\mathbb{R}}_{ + + }$
, and
$\xi \in {\mathbb{R}}_{ + + }$
, and
![]() $\varepsilon \in (0,\xi )$
such that, for all
$\varepsilon \in (0,\xi )$
such that, for all
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, n$
,
$m \, \gt \, n$
,
Let
![]() $\mu \in {\mathbb{R}}_{ + + }$
be such that
$\mu \in {\mathbb{R}}_{ + + }$
be such that
![]() $\mu \, \lt \, \varepsilon $
. Because R is a generalized variable-value principle, this inequality implies that, for all
$\mu \, \lt \, \varepsilon $
. Because R is a generalized variable-value principle, this inequality implies that, for all
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, n$
,
$m \, \gt \, n$
,
Let
![]() $\delta \in {\mathbb{R}}_{ + + }$
be such that
$\delta \in {\mathbb{R}}_{ + + }$
be such that
![]() $\delta \, \lt \, \mu $
. By the limit property, there exists
$\delta \, \lt \, \mu $
. By the limit property, there exists
![]() $m \, \gt \, n$
such that
$m \, \gt \, n$
such that
Because R is transitive, it follows that
![]() $\xi {{\bf 1}_n}P(\xi {{\bf 1}_n},(\mu - \delta ){{\bf 1}_{m - n}})$
, contradicting mere addition. ▪
$\xi {{\bf 1}_n}P(\xi {{\bf 1}_n},(\mu - \delta ){{\bf 1}_{m - n}})$
, contradicting mere addition. ▪
Recent work of Franz and Spears (Reference Franz and Spears2020) shows that avoidance of the sadistic conclusion and mere addition become equivalent under some additional axioms including continuity and the Pareto principle; see also Greaves (Reference Greaves2017). Theorems 1 and 2 together reassert the similarity between avoidance of the sadistic conclusion and mere addition in the context of the generalized variable-value principles that satisfy the limit property.
As mentioned earlier, one notable feature of our analysis is that we do not require population principles to be anonymous. Our choice of the domain Ω does, however, entail an equal-treatment property by imposing a specific population structure. Only the set
![]() $\{ 1, \ldots ,n\} $
can appear as a population with n individuals and, thus, alternative population compositions such as
$\{ 1, \ldots ,n\} $
can appear as a population with n individuals and, thus, alternative population compositions such as
![]() $\{ 2,4, \ldots ,2n\} $
or
$\{ 2,4, \ldots ,2n\} $
or
![]() $\{ 1, \ldots ,n - 1,n + 1\} $
are not covered. In contrast, Blackorby et al. (Reference Blackorby, Bossert, Donaldson and Fleurbaey1998) operate in a framework that is capable of accommodating any set of n individuals as a population with n members. We stress that, in spite of this apparent limitation, our results can be extended to the setting of Blackorby et al. (Reference Blackorby, Bossert, Donaldson and Fleurbaey1998). This is accomplished by replacing all of the distributions that we employ with suitably chosen generalized counterparts; details are available from the authors on request. The reason for working with a more restrictive domain is that the general setting comes at the price of added expositional complexity, and one of our objectives is to ensure that the paper is accessible to a wide audience.
$\{ 1, \ldots ,n - 1,n + 1\} $
are not covered. In contrast, Blackorby et al. (Reference Blackorby, Bossert, Donaldson and Fleurbaey1998) operate in a framework that is capable of accommodating any set of n individuals as a population with n members. We stress that, in spite of this apparent limitation, our results can be extended to the setting of Blackorby et al. (Reference Blackorby, Bossert, Donaldson and Fleurbaey1998). This is accomplished by replacing all of the distributions that we employ with suitably chosen generalized counterparts; details are available from the authors on request. The reason for working with a more restrictive domain is that the general setting comes at the price of added expositional complexity, and one of our objectives is to ensure that the paper is accessible to a wide audience.
4. Discussion
Our main result shows that the limit property is a sufficient condition for a generalized variable-value principle to be subject to the repugnant conclusion or the sadistic conclusion. As noted earlier, numerous population principles are members of the class of generalized variable-value principles that satisfy the limit property, among them number-dampened utilitarianism and critical-level utilitarianism. Therefore, these population principles necessarily face the tension between the repugnant and sadistic conclusions. With regard to the case of number-dampened utilitarianism, our result shows that Arrhenius’s (Reference Arrhenius2000) proof using the geometric case of f is valid generally without specifying the function f.
We provide another class of generalized variable-value principles that satisfy the limit property. For all
![]() $n \in \mathbb{N}$
and for all
$n \in \mathbb{N}$
and for all
![]() $u \in {\mathbb{R}}^n$
, let
$u \in {\mathbb{R}}^n$
, let
![]() ${u_{{\rm{med}}}}$
denote the median of u. Formally,
${u_{{\rm{med}}}}$
denote the median of u. Formally,
As the definition shows, we set the median of a distribution as the mean of the two middle values if the population size is even. The ordering R is a variable-value median principle if there exists a non-decreasing and bounded function
![]() $f:\mathbb{N} \to {\mathbb{R}}_{ + + }$
such that, for all
$f:\mathbb{N} \to {\mathbb{R}}_{ + + }$
such that, for all
![]() $n,m \in \mathbb{N}$
, for all
$n,m \in \mathbb{N}$
, for all
![]() $u \in {\mathbb{R}}^n$
, and for all
$u \in {\mathbb{R}}^n$
, and for all
![]() $v \in {\mathbb{R}}^m$
,
$v \in {\mathbb{R}}^m$
,
The variable-value median principles satisfy the limit property since, for all
![]() $n \in \mathbb{N}$
, for all
$n \in \mathbb{N}$
, for all
![]() $u \in {\mathbb{R}}^n$
, and for all
$u \in {\mathbb{R}}^n$
, and for all
![]() $\kappa \in {\mathbb{R}}$
, there exists
$\kappa \in {\mathbb{R}}$
, there exists
![]() ${m^*} \in \mathbb{N}$
such that, for all
${m^*} \in \mathbb{N}$
such that, for all
![]() $m \in \mathbb{N}$
with
$m \in \mathbb{N}$
with
![]() $m \, \gt \, {m^*}$
,
$m \, \gt \, {m^*}$
,
Our main result implies that the variable-value median principles cannot satisfy both avoidance of the repugnant conclusion and avoidance of the sadistic conclusion. Note that the class of variable-value median principles is distinct from number-dampened utilitarianism. For instance, for the three-person utility distributions
![]() $u = (1,2,3)$
and
$u = (1,2,3)$
and
![]() $v = (0,0,6)$
, all variable-value median principles conclude, irrespectively of the function f employed, that u is better than v, whereas u and v are declared equally good according to all number-dampened utilitarian principles. Therefore, our result applies to a large class of generalized variable-value principles including the variable-value median principles as well as number-dampened utilitarianism and critical-level utilitarianism.
$v = (0,0,6)$
, all variable-value median principles conclude, irrespectively of the function f employed, that u is better than v, whereas u and v are declared equally good according to all number-dampened utilitarian principles. Therefore, our result applies to a large class of generalized variable-value principles including the variable-value median principles as well as number-dampened utilitarianism and critical-level utilitarianism.
Clearly, there are classes of generalized variable-value principles that do not satisfy the limit property. For example, Sider’s (Reference Sider1991) principles do not satisfy the limit property. To illustrate this observation, consider the distributions
![]() $(b{{\bf 1}_n},a)$
and
$(b{{\bf 1}_n},a)$
and
![]() $(b + \delta {){\bf 1}_{n + 1}}$
, where
$(b + \delta {){\bf 1}_{n + 1}}$
, where
![]() $a,b \in {\mathbb{R}}_{ + + }$
are such that
$a,b \in {\mathbb{R}}_{ + + }$
are such that
![]() $a \, \gt \, b$
and
$a \, \gt \, b$
and
![]() $\delta \in {\mathbb{R}}_{ + + }$
. According to the definition of Sider’s principles, it follows that
$\delta \in {\mathbb{R}}_{ + + }$
. According to the definition of Sider’s principles, it follows that
The limit property requires that, for all
![]() $\delta \in {\mathbb{R}}_{ + + }$
, there exists
$\delta \in {\mathbb{R}}_{ + + }$
, there exists
![]() ${n^*} \in \mathbb{N}$
such that
${n^*} \in \mathbb{N}$
such that
for all
![]() $n \in \mathbb{N}$
such that
$n \in \mathbb{N}$
such that
![]() $n \, \gt \, {n^*}$
. This can only be true if
$n \, \gt \, {n^*}$
. This can only be true if
However, this inequality is not valid for sufficiently small values of
![]() ${\delta}$
because
${\delta}$
because
![]() $a \, \gt \, b$
. Therefore, the limit property is not satisfied.
$a \, \gt \, b$
. Therefore, the limit property is not satisfied.
Another class of generalized variable-value principles that do not satisfy the limit property consists of what we label the variable-value maximin principles. The ordering R is a variable-value maximin principle if there exists a non-decreasing and bounded function
![]() $f:\mathbb{N} \to {\mathbb{R}}_{ + + }$
such that, for all
$f:\mathbb{N} \to {\mathbb{R}}_{ + + }$
such that, for all
![]() $n,m \in \mathbb{N}$
, for all
$n,m \in \mathbb{N}$
, for all
![]() $u \in {\mathbb{R}}^n$
, and for all
$u \in {\mathbb{R}}^n$
, and for all
![]() $v \in {\mathbb{R}}^m$
,
$v \in {\mathbb{R}}^m$
,
where
![]() ${u_{\min }} = {u_{(n)}} = \min \{ {u_1}, \ldots ,{u_n}\} $
and
${u_{\min }} = {u_{(n)}} = \min \{ {u_1}, \ldots ,{u_n}\} $
and
![]() ${v_{\min }} = {v_{(m)}} = \min \{ {v_1}, \ldots ,{v_m}\} $
. Alternative maximin-based principles are examined by Bossert (Reference Bossert1990), Blackorby et al. (Reference Blackorby, Bossert and Donaldson2005), and Zuber (Reference Zuber2018). To see that the variable-value maximin principles do not satisfy the limit property, consider the distributions
${v_{\min }} = {v_{(m)}} = \min \{ {v_1}, \ldots ,{v_m}\} $
. Alternative maximin-based principles are examined by Bossert (Reference Bossert1990), Blackorby et al. (Reference Blackorby, Bossert and Donaldson2005), and Zuber (Reference Zuber2018). To see that the variable-value maximin principles do not satisfy the limit property, consider the distributions
![]() $(b{{\bf 1}_n},c)$
and
$(b{{\bf 1}_n},c)$
and
![]() $(b - \delta {){\bf 1}_{n + 1}}$
, where
$(b - \delta {){\bf 1}_{n + 1}}$
, where
![]() $b,c,\delta \in {\mathbb{R}}_{ + + }$
are such that
$b,c,\delta \in {\mathbb{R}}_{ + + }$
are such that
![]() $b \, \gt \, c$
and
$b \, \gt \, c$
and
![]() $\delta \, \lt \, b - c$
. Using the definition of variable-value maximin, it follows that
$\delta \, \lt \, b - c$
. Using the definition of variable-value maximin, it follows that
for all
![]() $n \in \mathbb{N}$
because
$n \in \mathbb{N}$
because
![]() $b - \delta \, \gt \, c$
. This is incompatible with the limit property.
$b - \delta \, \gt \, c$
. This is incompatible with the limit property.
Sider’s principles and some of the variable-value maximin principles (for example, those associated with a dampening function f satisfying
![]() $f(n) = 1$
for all
$f(n) = 1$
for all
![]() $n \ge 2$
) avoid both the repugnant and sadistic conclusions. This observation establishes that an axiom such as the limit property is indeed required for our theorem.
$n \ge 2$
) avoid both the repugnant and sadistic conclusions. This observation establishes that an axiom such as the limit property is indeed required for our theorem.
Finally, as we noted earlier, the limit property is a sufficient condition, not a necessary condition, for a generalized variable-value principle that avoids the repugnant conclusion to imply the sadistic conclusion. Therefore, there exists a class of generalized variable-value principles that do not satisfy the limit property but also cannot satisfy both avoidance of the repugnant conclusion and avoidance of the sadistic conclusion; that is, a class of generalized variable-value principles that is out of the scope of our result but is subject to the population-ethics dilemma. For instance, rank-discounted reference-level utilitarianism does not satisfy the limit property since any rank-discounted reference-level utilitarian principle concludes that
![]() $(\kappa - \delta ){{\bf{1}}_{m + n}}$
is better than
$(\kappa - \delta ){{\bf{1}}_{m + n}}$
is better than
![]() $(\kappa {{\bf{1}}_m},a{{\bf{1}}_n})$
for all
$(\kappa {{\bf{1}}_m},a{{\bf{1}}_n})$
for all
![]() $m \in \mathbb{N}$
, provided that
$m \in \mathbb{N}$
, provided that
![]() $a \, \lt \, \kappa $
, n is sufficiently large, and
$a \, \lt \, \kappa $
, n is sufficiently large, and
![]() $\delta \, \gt \, 0$
is sufficiently close to zero; we thank an anonymous referee for pointing out this observation. Asheim and Zuber (Reference Asheim and Zuber2014) show that rank-discounted reference-level utilitarianism can avoid the repugnant conclusion and what Arrhenius (Forthcoming) labels the very sadistic conclusion; see also Arrhenius (Reference Arrhenius2000) where he refers to it as the strong sadistic conclusion. According to the very sadistic conclusion, there exist a positive utility distribution u and a negative utility distribution v such that v is better than u. Although rank-discounted reference-level utilitarianism avoids the very sadistic conclusion, it implies the sadistic conclusion. This can be verified as follows. If the parameter
$\delta \, \gt \, 0$
is sufficiently close to zero; we thank an anonymous referee for pointing out this observation. Asheim and Zuber (Reference Asheim and Zuber2014) show that rank-discounted reference-level utilitarianism can avoid the repugnant conclusion and what Arrhenius (Forthcoming) labels the very sadistic conclusion; see also Arrhenius (Reference Arrhenius2000) where he refers to it as the strong sadistic conclusion. According to the very sadistic conclusion, there exist a positive utility distribution u and a negative utility distribution v such that v is better than u. Although rank-discounted reference-level utilitarianism avoids the very sadistic conclusion, it implies the sadistic conclusion. This can be verified as follows. If the parameter
![]() ${\gamma}$
of a rank-discounted reference-level utilitarian principle is positive, (1) in the proof of Lemma 3 holds by assuming that a is sufficiently large and c is sufficiently close to zero. Furthermore, the rank-discounted reference-level utilitarian principle implies (3) in the proof of Lemma 3. Thus, our argument employed in the proof of Lemma 3 applies to rank-discounted reference-level utilitarianism. Now, consider the case
${\gamma}$
of a rank-discounted reference-level utilitarian principle is positive, (1) in the proof of Lemma 3 holds by assuming that a is sufficiently large and c is sufficiently close to zero. Furthermore, the rank-discounted reference-level utilitarian principle implies (3) in the proof of Lemma 3. Thus, our argument employed in the proof of Lemma 3 applies to rank-discounted reference-level utilitarianism. Now, consider the case
![]() $\gamma = 0$
. Assuming an arbitrary rank-discount factor
$\gamma = 0$
. Assuming an arbitrary rank-discount factor
![]() $\beta \in (0,1)$
, let
$\beta \in (0,1)$
, let
![]() $m \in \mathbb{N}$
and
$m \in \mathbb{N}$
and
![]() $a,b,c \in \mathbb{R}$
be such that
$a,b,c \in \mathbb{R}$
be such that
![]() $c \, \lt \, 0 \, \lt \, b \, \lt \, a$
, and consider
$c \, \lt \, 0 \, \lt \, b \, \lt \, a$
, and consider
![]() $u \in {\mathbb{R}}^2$
and
$u \in {\mathbb{R}}^2$
and
![]() $v \in {\mathbb{R}}^3$
defined by
$v \in {\mathbb{R}}^3$
defined by
We obtain that, if m is sufficiently large,
since
This means that the sadistic conclusion is implied.
5. Concluding remarks
To the best of our knowledge, our class of generalized variable-value principles does not appear in the previous literature. It includes a plethora of existing principles as special cases and, thus, our results provide a significant generalization of previously established impossibility results. As long as the limit property is satisfied, any principle in this class faces the fundamental incompatibility between avoidance of the repugnant conclusion and avoidance of the sadistic conclusion. This complements an earlier observation by Blackorby et al. (Reference Blackorby, Bossert and Donaldson2005: 164, Theorem 5.4). Blackorby et al. consider principles that use total utility as the criterion to compare any two distributions of the same population size and impose a mild regularity condition that is weaker than the assumption that critical levels exist for all distributions. Their result establishes that these principles cannot simultaneously avoid the repugnant conclusion and the sadistic conclusion. Because all members of their class satisfy the limit property, our impossibility theorem offers a generalization of this earlier observation.
Acknowledgements
We thank Shu Ishida, Marcus Pivato, Dean Spears, and two referees for comments and suggestions. Financial support from the Japan Securities Scholarship Foundation through a grant for research in population ethics in social choice theory, from KAKENHI through grants Nos. JP20H01446 and JP20K01565, and from the Mitsubishi Foundation through grant No. ID201920011 is gratefully acknowledged.
Competing Interest
None.
Walter Bossert is Professor of Economics and CIREQ Research Fellow at the University of Montreal. His research interests include decision theory, rational choice, social choice, and population ethics. He is a coauthor (with Charles Blackorby and David Donaldson) of Population Issues in Social Choice Theory, Welfare Economics, and Ethics, published by Cambridge University Press in 2005. Together with Kotaro Suzumura, he wrote Consistency, Choice, and Rationality (Harvard University Press, 2010). He is the recipient of the 2004 John Rae Prize awarded by the Canadian Economics Association. Email: [email protected].
Susumu Cato is Associate Professor of Economics at the Institute of Social Science, University of Tokyo. His research interests include decision theory, social choice theory, political philosophy and organizational economics. Email: [email protected].
Kohei Kamaga is Professor of Economics at Sophia University. His research interests include decision theory, social choice, inequality and poverty measurement, intergenerational equity and population ethics.



