Research Article
Lower Bounds for Eigenvalues of the Stokes Operator
-
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1-18
-
- Article
- Export citation
Two-Level Stabilized Finite Volume Methods for the Stationary Navier-Stokes Equations
-
- Published online by Cambridge University Press:
- 03 June 2015, pp. 19-35
-
- Article
- Export citation
Two-Level Newton Iteration Methods for Navier-Stokes Type Variational Inequality Problem
-
- Published online by Cambridge University Press:
- 03 June 2015, pp. 36-54
-
- Article
- Export citation
Fully HOC Scheme for Mixed Convection Flow in a Lid-Driven Cavity Filled with a Nanofluid
-
- Published online by Cambridge University Press:
- 03 June 2015, pp. 55-77
-
- Article
- Export citation
Convergent Overdetermined-RBF-MLPG for Solving Second Order Elliptic PDEs
-
- Published online by Cambridge University Press:
- 03 June 2015, pp. 78-89
-
- Article
- Export citation
Free Vibration Analysis of Nanocomposite Plates Reinforced by Graded Carbon Nanotubes Based on First-Order Shear Deformation Plate Theory
-
- Published online by Cambridge University Press:
- 03 June 2015, pp. 90-112
-
- Article
- Export citation
An Error Analysis for the Finite Element Approximation to the Steady-State Poisson-Nernst-Planck Equations
-
- Published online by Cambridge University Press:
- 03 June 2015, pp. 113-130
-
- Article
- Export citation

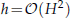 or a large general Stokes equations for the Newton two-level stabilized finite volume method on a fine mesh with mesh size
or a large general Stokes equations for the Newton two-level stabilized finite volume method on a fine mesh with mesh size 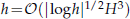 . These methods we studied provide an approximate solution
. These methods we studied provide an approximate solution 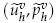 with the convergence rate of same order as the standard stabilized finite volume method, which involve solving one large nonlinear problem on a fine mesh with mesh size
with the convergence rate of same order as the standard stabilized finite volume method, which involve solving one large nonlinear problem on a fine mesh with mesh size